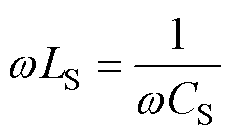（1）
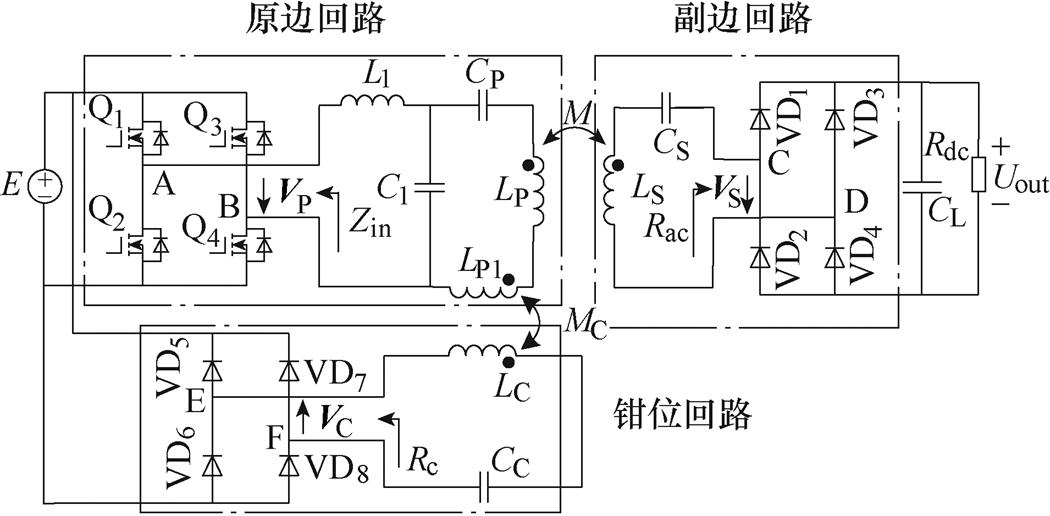
图1 带钳位电路的LCC-S补偿型IPT系统拓扑
Fig.1 The LCC-S compensated IPT system with a clamp circuit
摘要 在感应电能传输（IPT）系统中，线圈错位难以避免，造成的耦合变化会导致系统的传输功率不稳定。为了保证IPT系统的供电灵活性，系统需具有容忍线圈宽范围偏移的能力。为此，该文借鉴模态切换的思想，提出一种基于钳位电路的LCC-S补偿型IPT系统，用于增强系统抗偏移性。与传统多模态切换的IPT系统相比，该系统中的钳位电路可根据耦合变化自适应地导通或关断，以调节工作模态，从而实现近乎恒定的功率输出，该方法无需耦合识别、输出检测及反馈通信等辅助手段。该文对系统不同工作模态的功率传输特性进行了推导和分析，并结合系统设计相关约束条件，提供一套参数化设计方法。最后设计并搭建一套500 W的实验装置，验证了理论分析的正确性与可行性。实验结果表明，该方法在耦合度为0.205～0.42的情况下，输出功率稳定在470～505 W之间，效率为83.29%～90.21%。
关键词：感应电能传输（IPT） 钳位电路 耦合变化 参数化设计 恒功率输出
相较于传统有线拔插系统，感应电能传输（Inductive Power Transfer, IPT）技术通过高频电磁场近场耦合原理实现电能的非物理接触传输[1]，具有安全便捷、供电灵活等优点。目前，已在消费电子、生物医疗设备、电动汽车等[2]领域得到广泛应用。其中，如何实现相对稳定的功率传输是IPT系统充电技术需要解决的关键问题之一。原边与副边线圈的相对位置难以避免地存在错位现象，而错位现象引起的耦合变化将导致传输功率和系统效率的降低。为了保证IPT系统功率传输的平稳性，现有方法主要集中在控制方法、耦合机构设计、拓扑设计三个方面。
常见的控制策略[3-4]包括在系统发射端前级或接收端后级级联DC-DC变换器[3]，或者通过移相控制的方法调节逆变器输出等效基波电压幅值[4]等。这类方式通常需要添加原边与副边检测、通信、控制设备，且对接收端检测设备的检测精度、通信的实时性以及系统的控制裕度都有较高要求。此外，受调制深度限制，多数控制方法调节范围有限，当系统发生较大的偏移时，系统效率较低[5]。为了减缓控制压力，简化系统控制复杂度，有学者利用耦合机构及电路拓扑的自身特性提升IPT系统的偏移能力。
对于耦合机构的设计来说，其基本原理是通过磁场的叠加[6]或抵消[7]，令原边线圈产生相对均匀的磁场，从而在一定偏移范围内实现原边线圈和副边线圈之间互感的相对恒定。但耦合机构设计方法大多用于特定的一个或两个偏移方向。为此有学者提出利用IPT系统拓扑自身特性来提高抗偏移性 能[8-13]。对于拓扑的设计来说，则主要分为混合拓扑、失谐拓扑和重构拓扑。混合拓扑通过组合两种随耦合变化呈不同变化趋势的拓扑，从而平缓输出功率在偏移过程中的变化趋势。例如，文献[8]利用两组自解耦的DD线圈，组合成LCC-LCC和S-S两种拓扑结构，在x轴正向偏移距离12 cm、负向偏移距离8 cm，y轴正负向偏移距离16 cm内，将系统输出波动保持在10%以内。然而，该方法需要两种拓扑的相互配合，从而增加了系统的成本和复杂性。失谐拓扑通过对系统补偿参数进行特殊设计，使系统在偏移过程中，原边线圈电流按照所设计的变化趋势而变化，从而维持系统在允许的耦合系数变化范围内功率传输的相对稳定。常见的失谐拓扑有S-S[9]、LCC-S[10]等。例如，文献[10]在耦合系数0.18～0.32变化范围内，将系统输出功率的波动控制在20%以内。然而，该类拓扑耦合系数变化范围相对较窄且输出功率浮动较大。为了在同等功率波动条件下，进一步增大耦合偏移范围，有学者提出了重构电路系统。该方案主要通过增加有源控制元件并结合参数设计，使有源控制元件导通前后的系统输出功率曲线进行拼接，从而增大耦合偏移范围。文献[11]通过有源控制元件让原边结构改变，使系统拓扑在LCC-S和S-S之间切换，从而实现切换系统输出曲线的效果。文献[12]在一定区域内铺设多个处于不同位置的原边线圈，通过检测装置选取对应原边线圈并激活，保证了该区域内副边能量接受的相对稳定。文献[13]通过有源控制元件使副边整流器在全桥和半桥工作状态之间切换，改变等效输入电阻大小，同样实现了切换系统输出曲线的效果。然而，这种方法引入了新的控制元件和检测、反馈、通信等功能模块，造成系统复杂度的增加及可靠性的减弱。
为此，本文提出了一种带有钳位电路的LCC-S补偿型IPT系统，该系统能够在耦合机构偏移变化过程中自适应地实现工作模态的切换，以匹配耦合系数变化区间，而无需检测、反馈通信以及控制设备。首先，对所提出的带钳位电路的LCC-S补偿型IPT系统进行了建模分析并讨论了输出特性。然后，给出了该系统参数化设计流程并进行了实例设计。最后，搭建原理样机对所提出的IPT系统进行实验验证。
本文所提出的带钳位电路的LCC-S补偿型IPT系统拓扑如图1所示，拓扑结构由三个部分组成：原边回路、副边回路和钳位回路。其中，原边回路包括电感L1，线圈LP、LP1、电容C1、CP以及由4个MOSFET（Q1～Q4）组成的输出角频率为w 交流电压的全桥逆变器；副边回路包括线圈LS、电容CS、由4个二极管（VD1～VD4）组成的全桥整流器以及滤波电容CL和直流等效负载Rdc。由于副边回路失谐会导致系统效率的下降[13]，令LS与CS完全补偿，满足关系
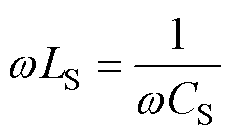（1）
图1 带钳位电路的LCC-S补偿型IPT系统拓扑
Fig.1 The LCC-S compensated IPT system with a clamp circuit
钳位回路包括线圈LC、电容CC以及4个二极管（VD5～VD8）组成的全桥整流器。根据文献[11]，直流电源输入电压E与交流输出等效基波电压有效值VP，以及整流器输入阻抗Rac与直流负载Rdc满足
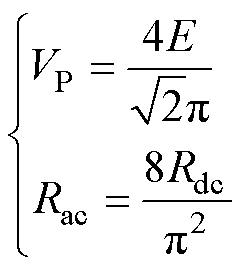（2）
M、k分别为线圈LP与线圈LS之间的互感及耦合系数，它们之间的关系可表示为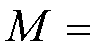
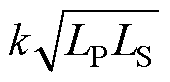。同理，MC为线圈LP1与线圈LC之间的互感。
图1系统可化简为如图2所示，图中Rac为钳位回路整流器等效输入电阻。对于钳位回路，根据线圈LC所感应电压的不同，可将由VD4～VD8组成的全桥整流器分为三种工作状态[14]：未导通状态、部分导通状态、完全导通状态。假设钳位电路线圈LC的感应电压峰值为|VC|，上述三种状态分别对应：|VC|＜E，E≤|VC|＜4E/p，4E/p≤|VC|，下面分情况进行讨论。
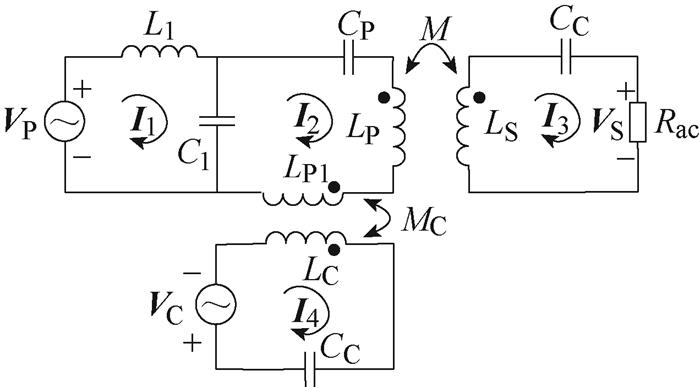
图2 简化等效电路模型
Fig.2 Simplified equivalent circuit model
当钳位电路线圈LC感应电压峰值|VC|＜E时，钳位电路线圈LC感应电压低于直流电源电压，钳位电路二极管承受负向电压，处于未导通状态，钳位回路电流IC=0。因此，图2所示系统模型如图3a所示。
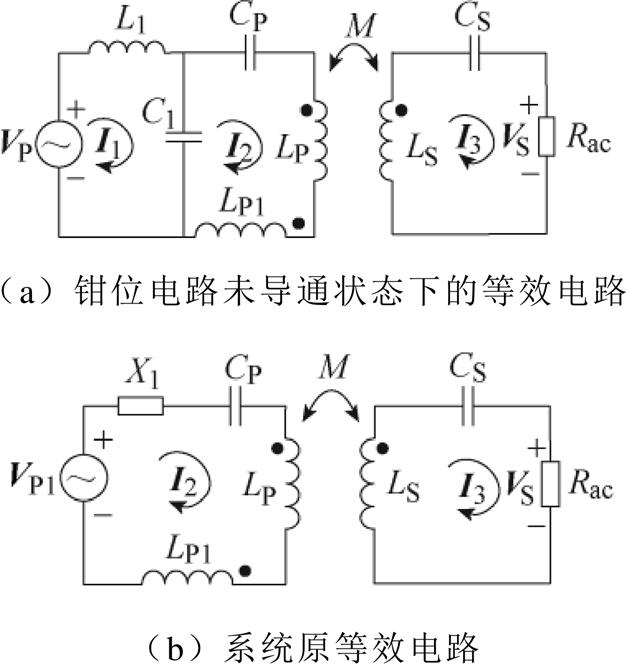
图3 等效电路模型
Fig.3 Equivalent circuit model
根据戴维南-诺顿等效定理，图3a系统可化简为图3b所示，其中VP1为变换后的等效基波输入电压，X1为变换后的等效电抗，满足
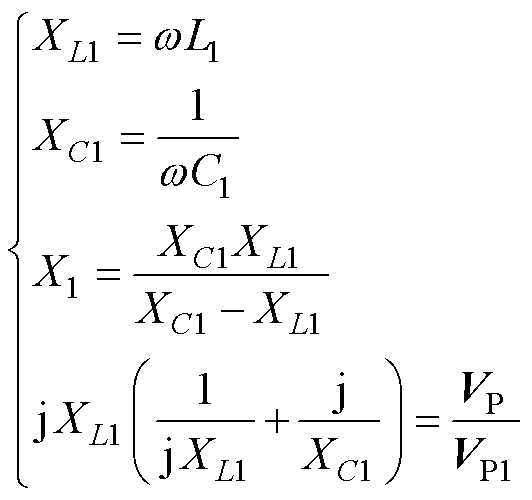（3）
为方便表示，令
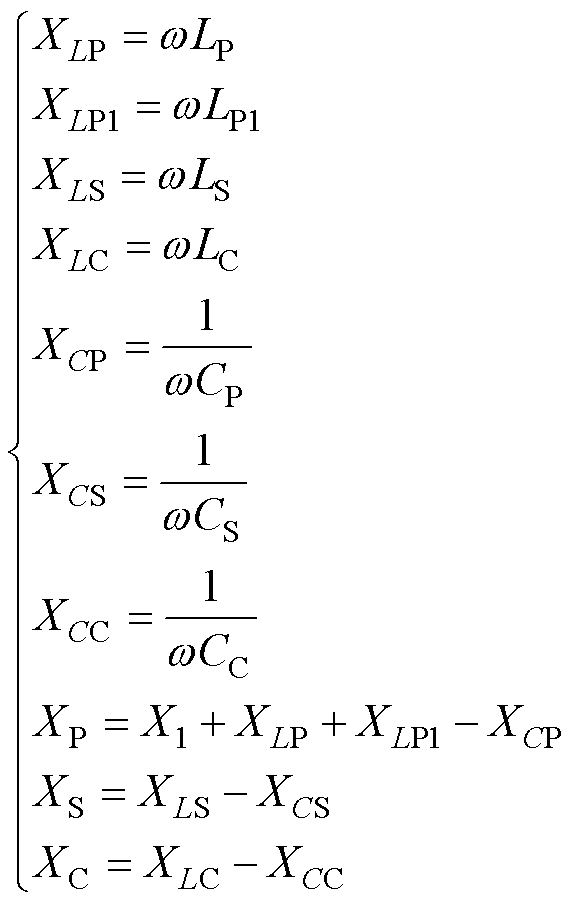（4）
式中，XP为简化后原边侧的等效回路电抗；XC为钳位回路电抗。
在钳位电路处于未导通状态如图3b所示时，根据戴维南-诺顿等效定理，其对应的系统回路方程组可列为
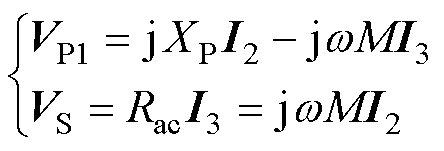（5）
各回路电流与耦合系数k的关系表达式有
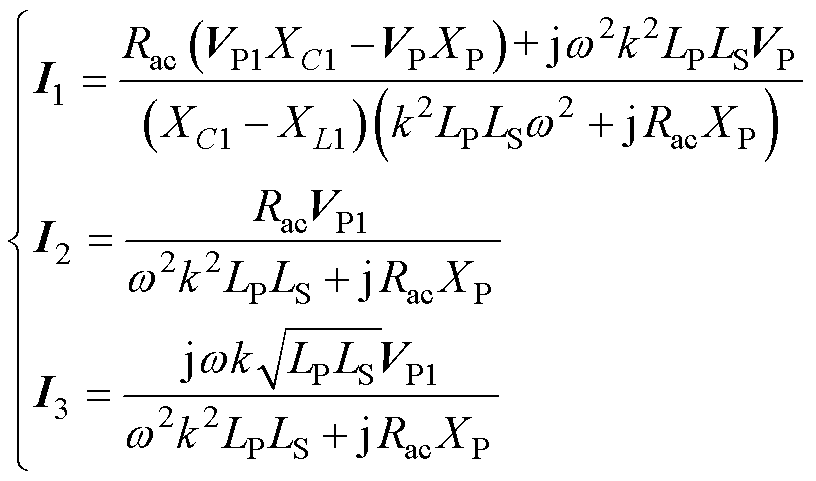（6）
根据式（6），可得钳位电路未导通状态下输出功率P1表达式为
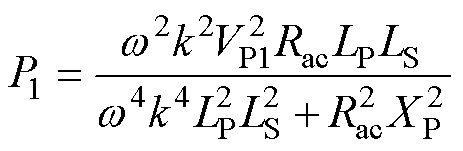（7）
根据式（7）可得系统输出功率P1与耦合系数k的关系曲线如图4所示。
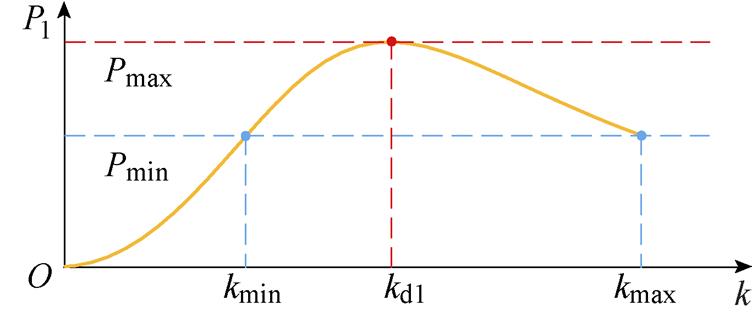
图4 输出功率P1与耦合系数k的关系曲线
Fig.4 P1-k curve of the clamped IPT system
可以看出，在一定耦合系数变化范围内（kmin, kmax），随着耦合系数k从kmax减小，系统输出功率呈先上升后下降的趋势，并在kd1达到极值。
令dP1/dk=0，可求得输出功率顶点对应的耦合系数kd1与对应的最大输出功率为
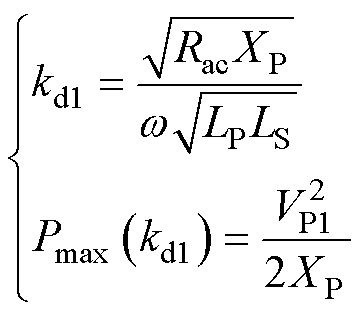（8）
根据变压器感应原理，可以得到钳位电路线圈LC的感应电压VC和感应电压峰值|VC|表达式分别为
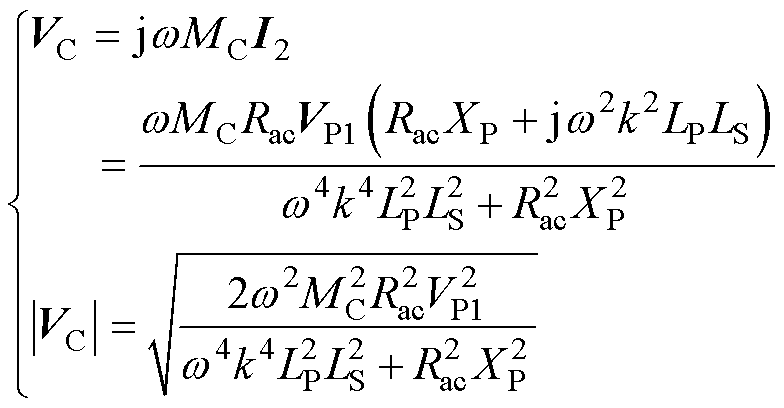（9）
由式（6）、式（9）可知，随着原边与副边偏移距离的增加，耦合系数k不断减小，原边电流I2将随之增大，钳位电路线圈LC的感应电压峰值|VC|也将随之增大，直至钳位电路线圈LC感应电压峰值|VC|=E，钳位电路进入到部分导通状态，此时对应的耦合系数k1由式（9）计算可得
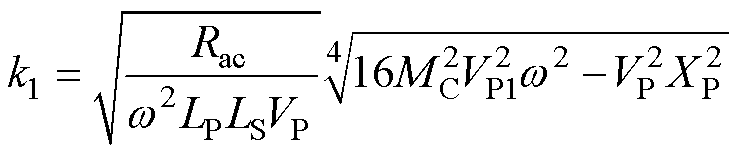（10）
当钳位电路线圈LC感应电压峰值E≤|VC|＜4E/p 时，钳位电路处于部分导通状态，钳位电路回路电流断续且幅值较小可忽略[14]。因此，这两种状态可共同视作图3b电路进行分析。
当系统耦合系数k进一步减小直至钳位电路线圈LC感应电压峰值|VC|达到4E/p 时，钳位电路进入到完全导通状态，该临界耦合系数k1由式（9）计算得
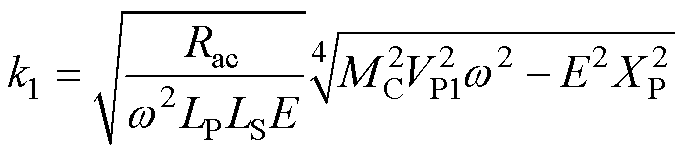（11）
在此状态下，由VD5～VD8组成的全桥整流器完全导通，钳位电路整流器输入电压为交流方波且钳位回路电流连续[15]。此时，钳位整流器输入电压有效值VC为
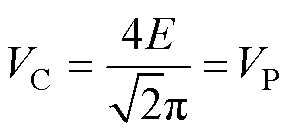（12）
同理，当钳位电路处于完全导通状态时，经过戴维南-诺顿等效变换后的等效电路模型如图5所示，其系统方程组为
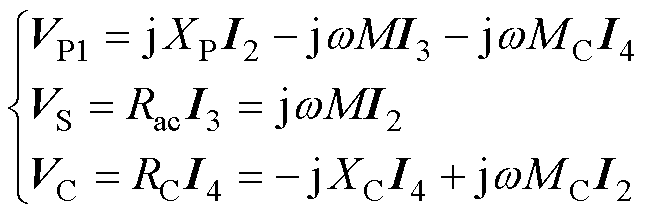（13）
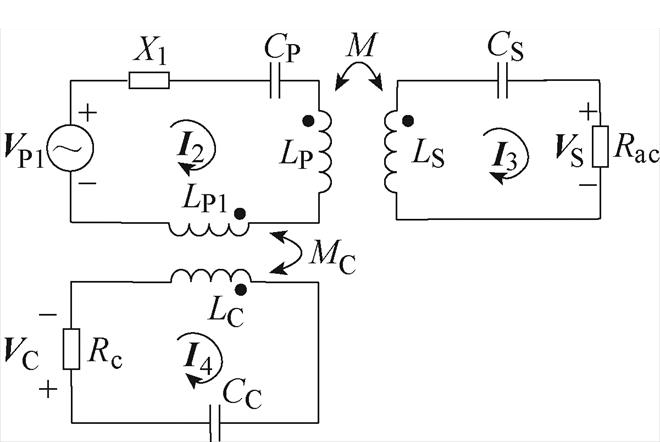
图5 钳位电路完全导通状态下的等效电路模型
Fig.5 Equivalent circuit model when the clamp circuit is fully activated
将式（12）代入到式（13）求解，各回路电流与耦合系数k的表达式有
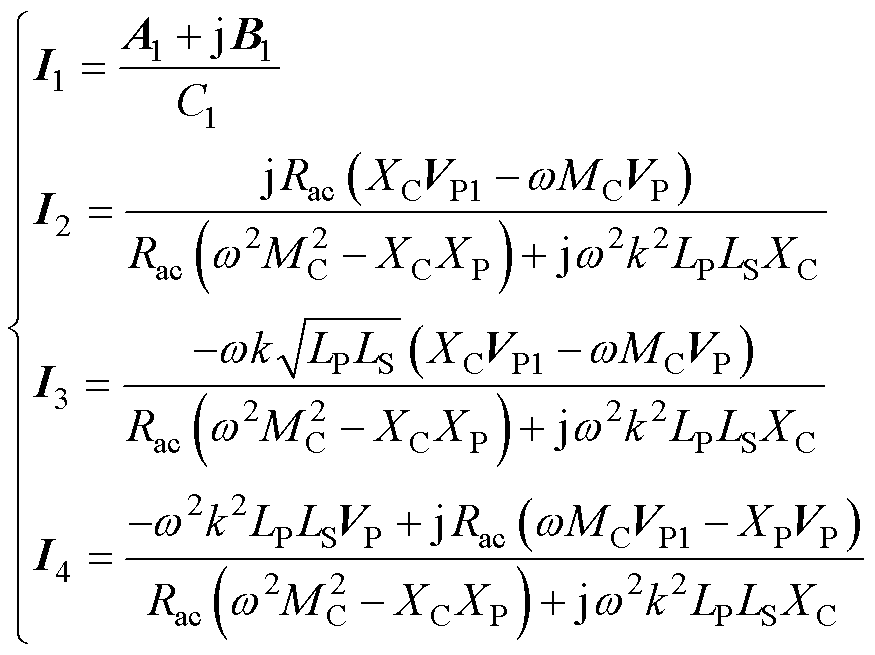（14）
其中
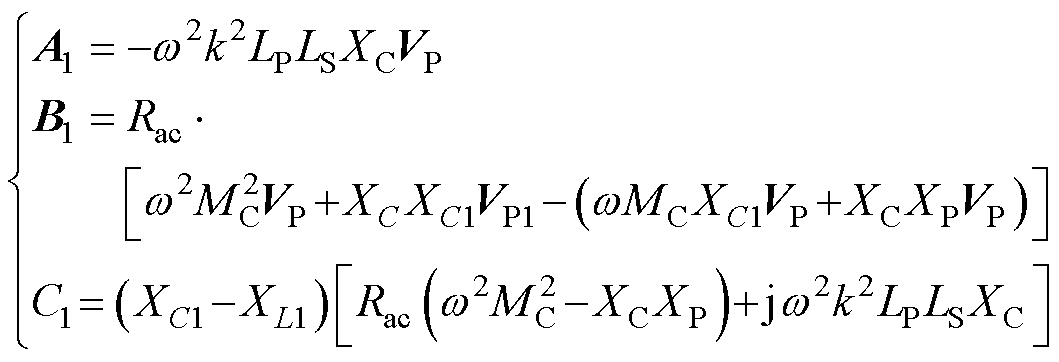
同理，可得输出功率P2相应表达式为
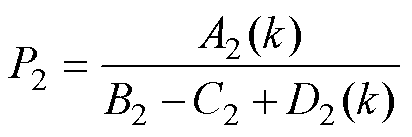（15）
其中
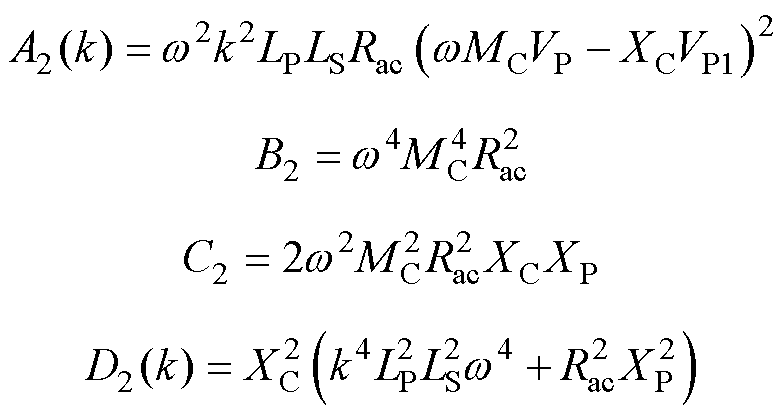
由式（15）可知，系统输出功率P2与耦合系数k的关系曲线与图4类似，同样在一定耦合系数变化范围内，随耦合系数k的减小呈先上升后下降的趋势，同样存在kd2对应输出功率极值。
令dP2/dk=0，同理可得
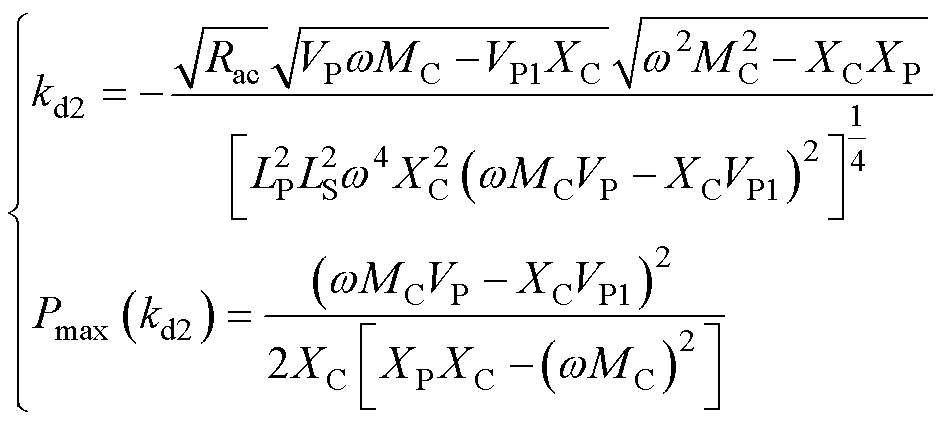（16）
由上述推导可知，系统偏移程度的增加致使耦合系数k的减小将导致钳位电路逐渐从未导通状态转变为部分导通状态，再进一步转变为完全导通状态。可以得出，经过合理的参数设计，钳位电路导通前后的系统输出功率与耦合系数k的关系曲线如图6所示，图中，耦合系数kmax对应系统无偏移状态，随着耦合系数k的减小，系统分别到达状态切换点k1和k2，系统输出功率在A点、C点、E点到达允许最低输出功率值，在B点、D点到达允许最高输出功率值，从而实现系统在较宽耦合系数变化下保持一定波动范围内的功率输出特性。
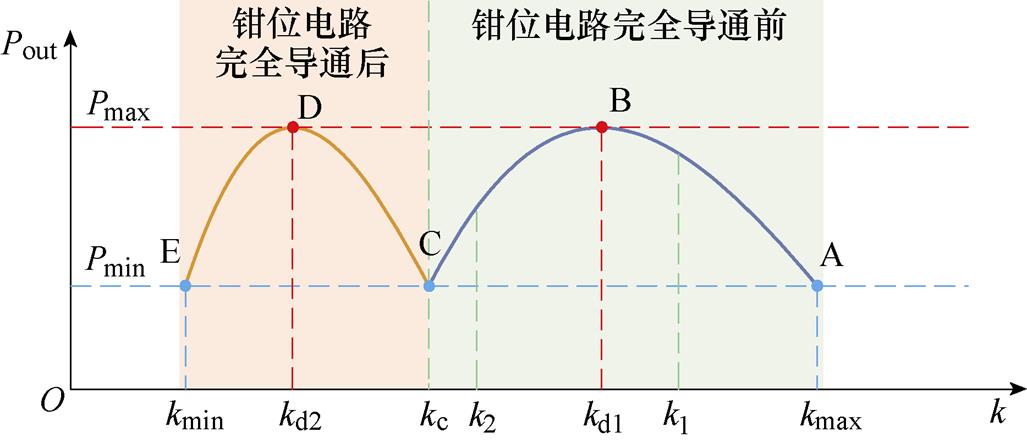
图6 系统输出功率Pout与耦合系数k的关系曲线
Fig.6 The ideal curve of output power versus coupling coefficient
根据1.2节的分析可知，k2是决定模态切换的理论临界点，为保证系统模态的平稳切换，k2应该对应系统输出功率曲线的C点。然而上文的理论推导是基于基波近似（First Harmonic Approximation, FHA）方法，在实际电路中，由于谐波成分的存在，系统耦合系数减小至k2或略小于k2时，钳位整流器仍然处于部分导通状态[15]，也就是说，实际状态临界点kc与前文分析所得理论状态临界点k2存在一定偏差。因此，求解实际切换点kc对于系统参数化设计至关重要。
为此，本文通过时域分析法对所提出系统的状态临界点kc进行计算。与文献[16]类似，本文也将系统划分为P、O、N三种状态。图7为P、O、N三种状态下的等效电路。VP为逆变器输出正向电压的幅值，VC为整流器输入电压幅值，各环路电流以箭头所指为正，其大小可表示为与时间相关的函数。
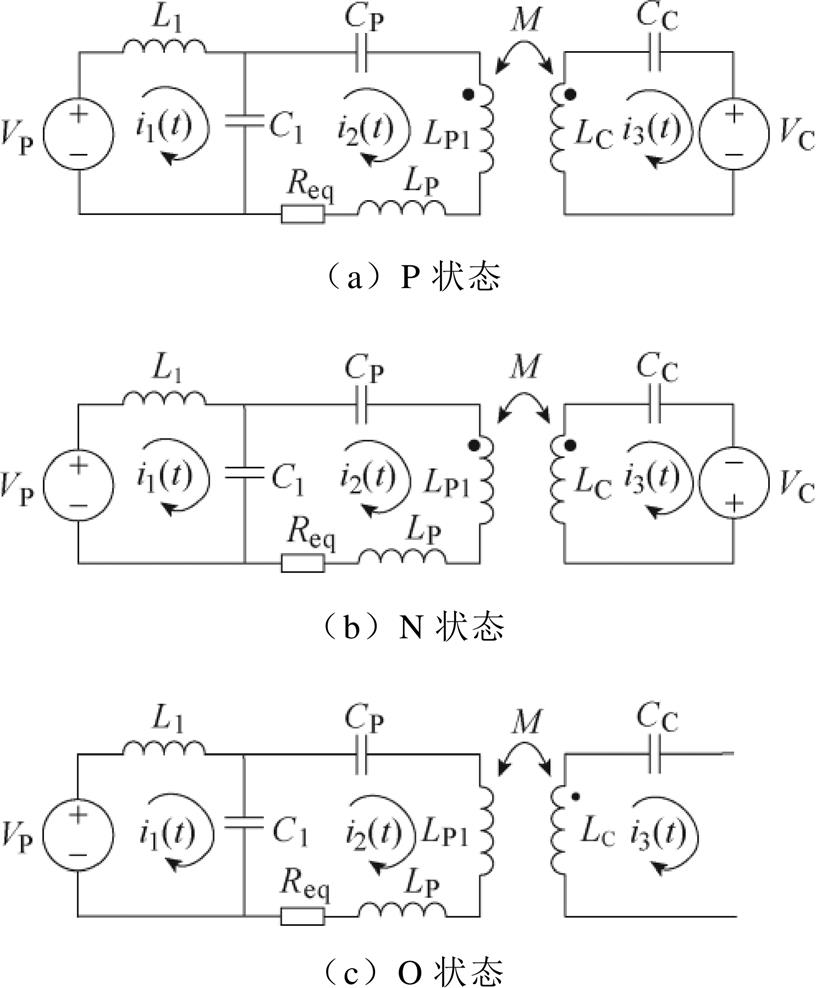
图7 钳位电路的三种工作状态
Fig.7 Three operation modes of the clamp circuit
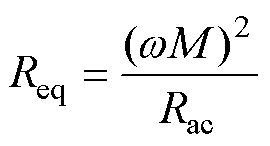（17）
式中，Req为副边反射电阻[17]。
通过对系统时域方程组的求解，得到系统电流不同状态的通解，然后以不同状态间的连续性为微分方程初值提供约束条件，即可准确地求出系统的电压、电流相关波形。然后通过钳位电路电流连续性的判断，即可确定钳位电路是否处于完全导通的工作状态。
随着耦合系数k的减小，钳位电路整流器将由未导通状态转变为部分导通状态，然后进一步改变为完全导通状态。当系统耦合系数k处于k1～kc之间时，钳位电路整流器处于部分导通状态，钳位电路电流断续，此时逆变器输出电压、钳位整流器输入电压、输入电流如图8a所示，存在P、O、N三种状态。在系统进一步偏移至耦合系数小于kc后，钳位电路整流器转换为完全导通状态，钳位电路电流进入连续状态，逆变器输出电压、钳位整流器输入电压、输入电流如图8b所示。此时，系统只存在P、N两种状态。也就是说，随着偏移范围的增大，t1时刻与t2时刻会逐渐接近直到重合。系统钳位电路在t1与t2重合时由部分导通状态切换到完全导通状态。
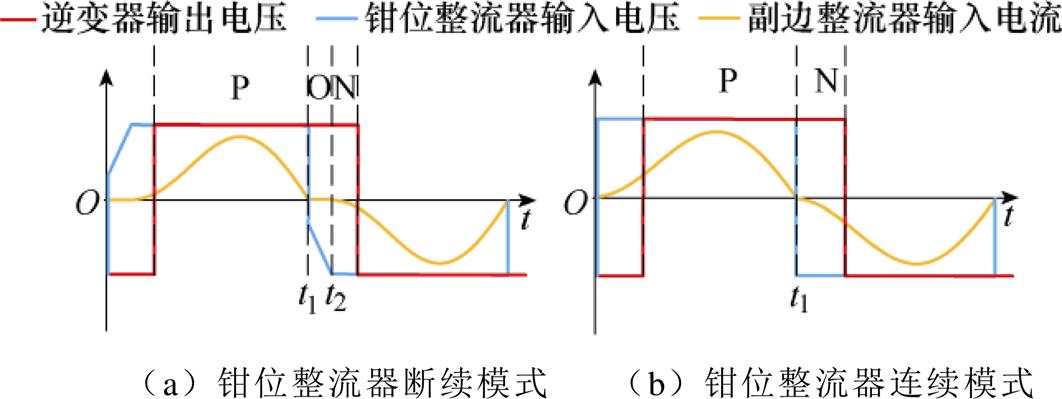
图8 钳位电路断续和连续两种工作状态
Fig.8 Discontinuous and continuous mode of the clamp circuit
由于WPT变换器稳态工作过程中正负半周期具有对称性，本文仅对正半开关周期进行分析。即令VP(t)=E，P状态下，VC(t)=E且与VP同样朝上，i3(t)＞0；O状态下，VC＜E，i3(t)=0；N状态下，VC(t)=E且与VP异向朝下，i3(t)＜0。
根据图7a、图7b，可列出P、N状态对应的时域分析方程组如下
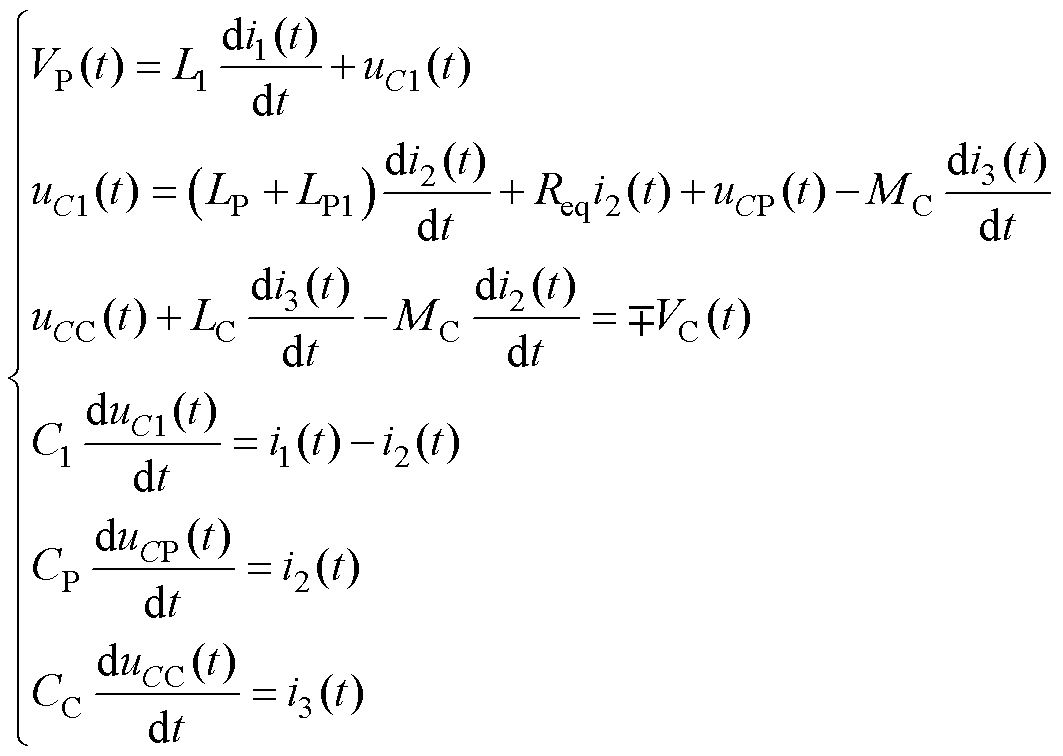（18）
式中，uC1(t)、uCP(t)、uCC(t)为电容C1、CP、CC上的电压。
式（18）第三个表达式中，VC(t)在P状态下取“-”，在N状态下取“+”。由数值求解方法，上述方程可解得三对共轭复根为
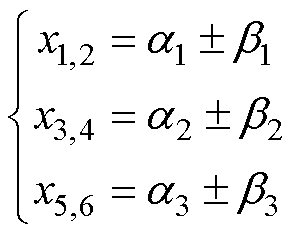（19）
根据图7c，令i3(t)=0，O状态下的时域分析方程组为
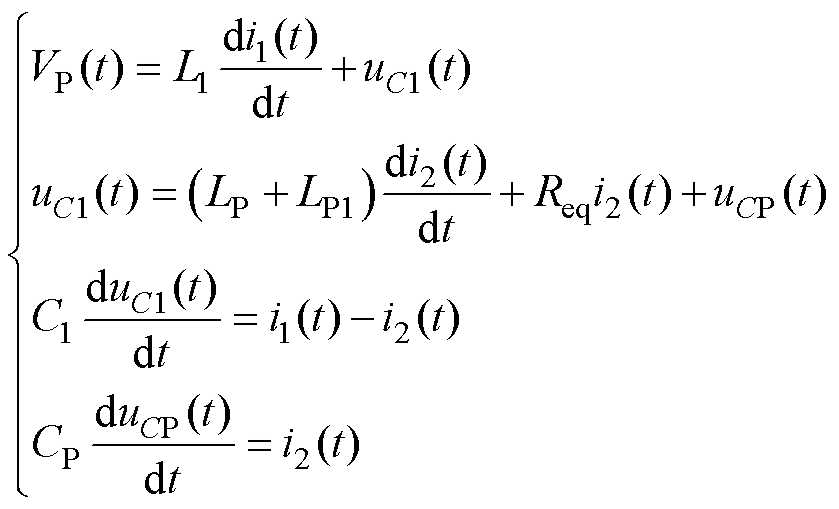（20）
同理，上述方程可解出两对共轭复根为
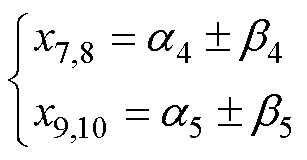（21）
以上P、O、N状态对应解应为
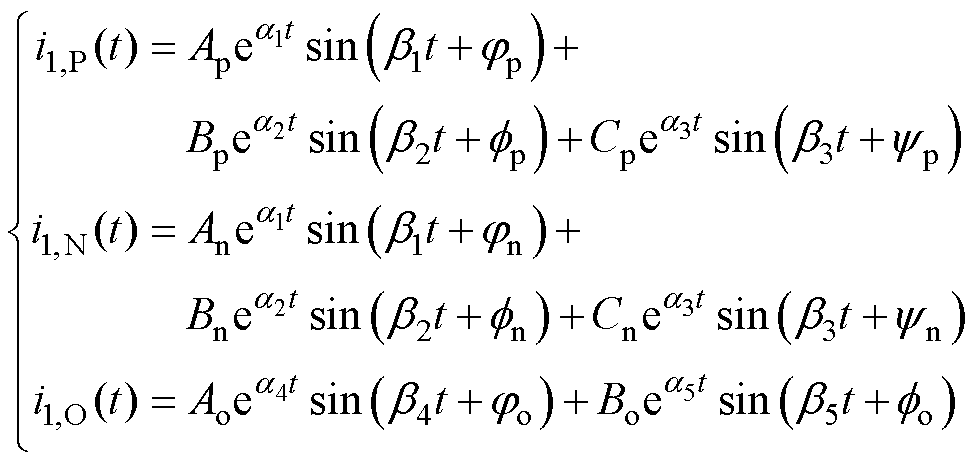（22）
将VP、VC统一由E表示，系统其余相关参数可通过i1(t)表示为
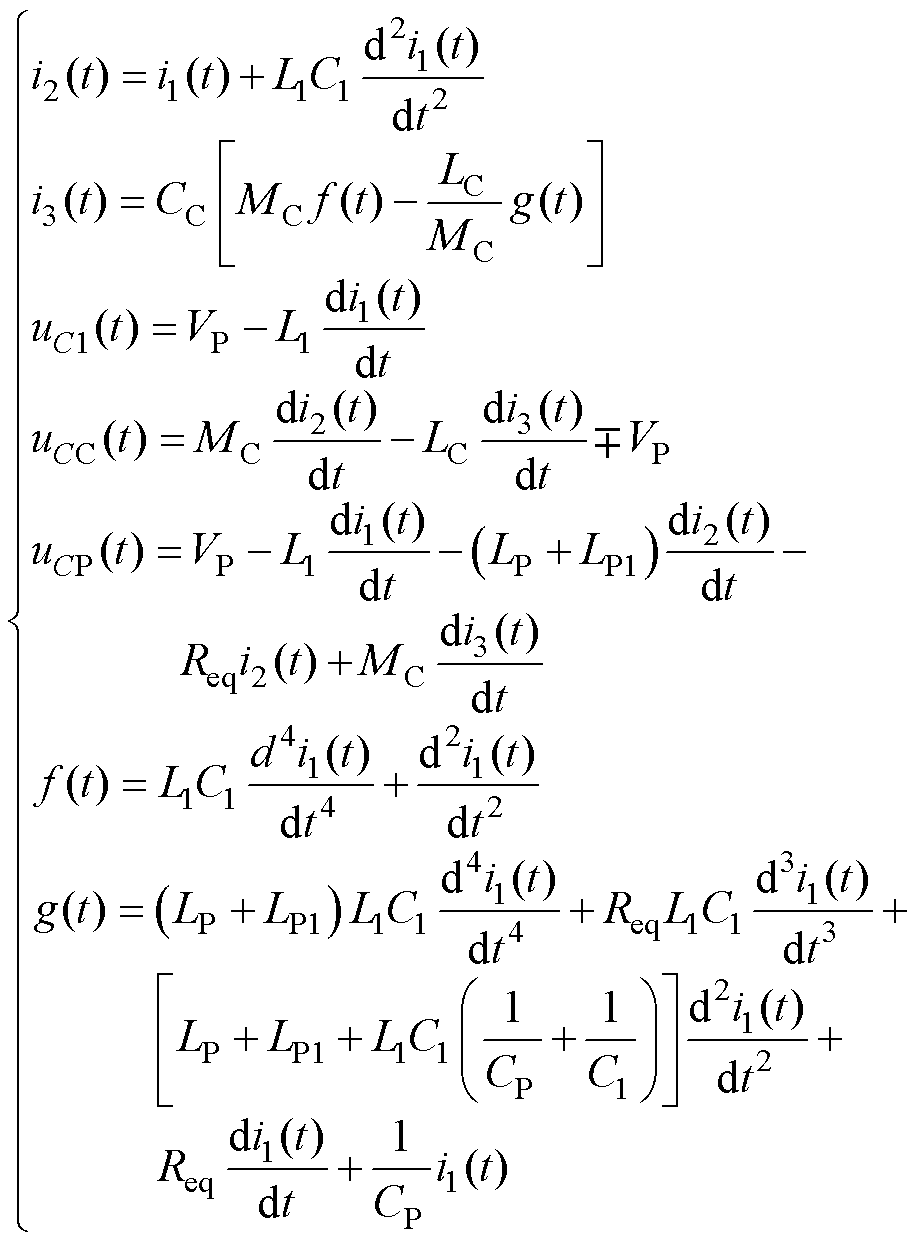（23）
经过上述推导，对于P、N状态方程组，未知参数有：Ap、Bp、CP、An、Bn、Cn、jp、fp、yp、jn、fn、yn；对于O状态方程组，未知参数有：Ao、Bo、jo、fo；另外，还有未知时间参数t1、t2，共18个未知参数。
在从P状态切换到O状态的切换点t1时刻、从O状态切换到N状态的切换点t2时刻，两个状态变量都应具有连续性，其中，在子区间（t1, t2）（O状态）内，钳位电路电流i3(t)始终为0。
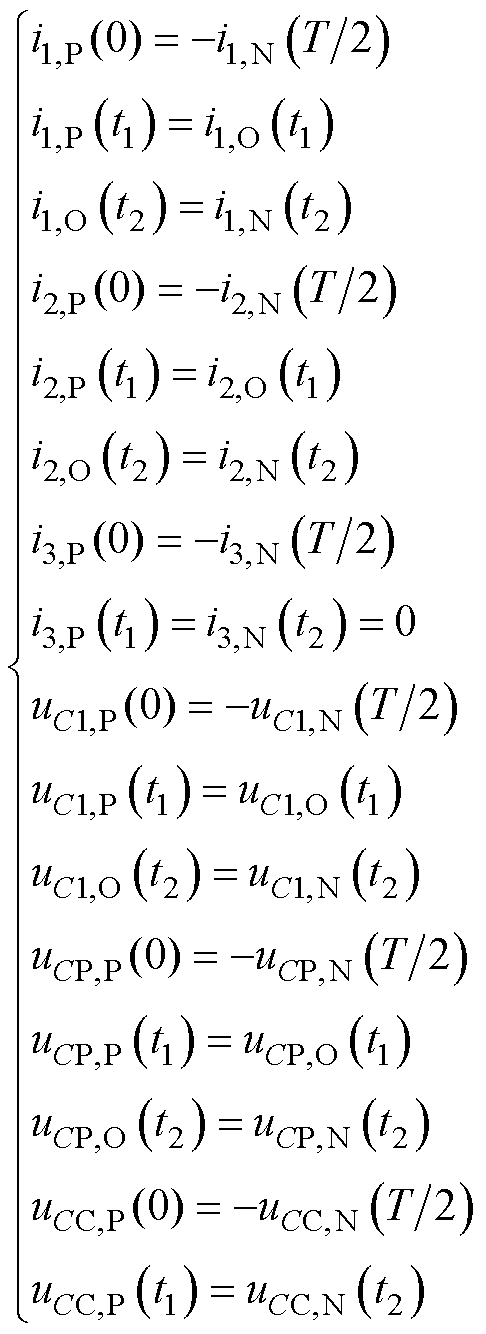（24）
在逆变器输出电压为正半周期时，由变量的连续性可以得到相关边界条件方程组如式（23）所示。
状态连续性提供了17个相互独立的超越方程组。此外，在O状态结束、N状态开始的t2时刻，di3(t)/dt=0，加上di3(t2)/dt=0这一边界条件，共18个相互独立的边界条件，具有唯一解，但难以求出其解析解。
对于这种情况，可使用Matlab软件中的fsolve函数，通过高斯-牛顿最小二乘法求解。其迭代初始值分别取jp、fp、yp、jn、fn、yn、jo、fo，取值范围是（-p, p），故将它们的迭代初始值都设置为居中的0；t1、t2的取值范围是（0, T/2），故将t1与t2分别设置为T/6与T/3。经过迭代计算，可求出各未知参数。
通过时域计算的方法可对系统的参数设计进行验证，保证钳位电路的实际状态切换点kc与理论状态切换点k2一致，实现状态的自适应切换。
定义输出功率波动系数
[11]为
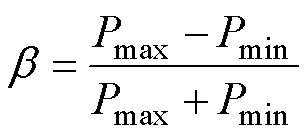（25）
根据需求设定后，结合系统目标参数Pmax和耦合机构参数LP、LS，即可求出相应元件参数包括：元件参数L1、C1、CP、CS、LP1、LC、CC和原边与钳位电路之间的互感MC。系统相关参数的设计需要结合系统的约束条件进行求解，约束条件如下。
已知副边完全谐振，因此副边电容CS满足式（1）。
根据系统输出功率波动约束条件，钳位电路处于未导通及部分导通状态下的工作曲线应满足
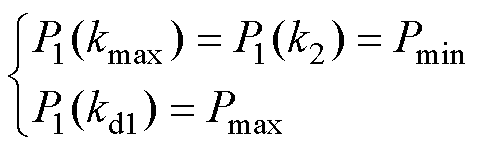（26）
kmax和式（8）分别代入式（7）并通过式（24）求解化简可得XP和理论切换点k2分别为
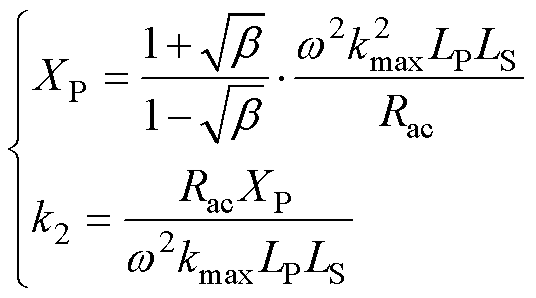（27）
同时，为满足原边等效变换后系统的最大输出功率，变换后的基波电压VP1与最大输出功率Pmax、原边等效环路电抗XP存在关系式如式（8）所示，将式（26）代入式（8）可得
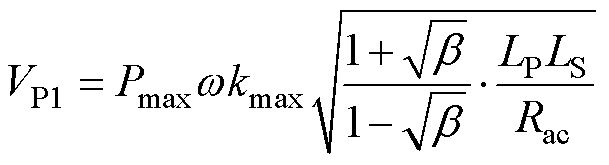（28）
同理，为满足系统输出功率波动要求，并保障功率曲线状态切换前后的连续性，钳位电路完全导通状态下工作曲线需满足
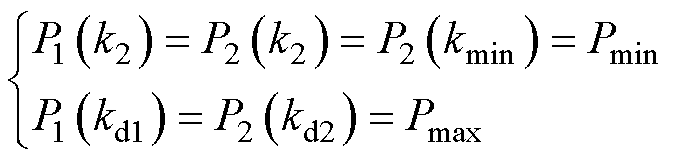（29）
将式（16）、式（26）分别代入式（15）、式（28）求解化简可得XC、MC以及最小耦合系数点kmin分别为
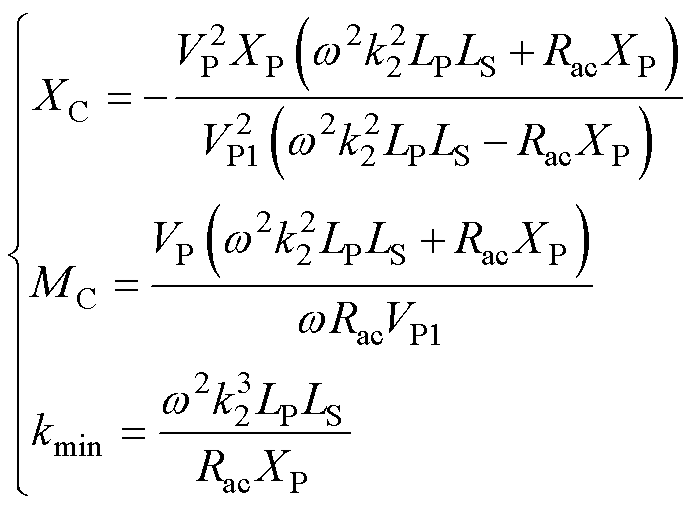（30）
在IPT系统的参数设计中，零电压软开关（Zero Voltage Switching, ZVS）通常是不可或缺的约束条件。其原因在于，当系统处于ZVS状态时，逆变器MOSFET的关断损耗大幅降低，系统效率能够得到相应提升。
为实现逆变器的ZVS状态，系统输入阻抗应呈轻微弱感性。因此，根据图2和式（6）、式（14），对于逆变器ZVS的实现，系统应存在如下约束条件。
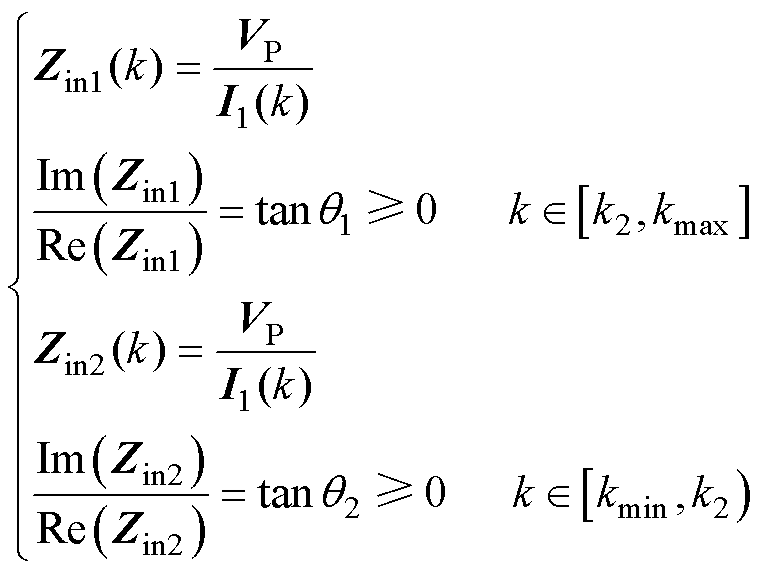（31）
式中，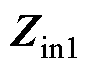
为钳位电路完全导通前的输入阻抗；
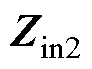为钳位电路完全导通后的输入阻抗。
通过迭代计算，可求得满足关系式（3）、式（30）的L1、C1。迭代计算的具体操作为：首先，设定L1初始值为1 mH，然后通过式（3）求得对应C1，将此组参数L1、C1代入到式（30）进行判定，若该组参数能够使输入阻抗在耦合系数变化范围（kmin, kmax）内呈弱感性，则提取参数；反之，则令L1增加一定变量DL1继续迭代。
假定钳位变压器为紧耦合变压器，耦合系数取为0.9，根据式（29），可知耦合互感MC，而LC、LP1尚未确定。如文献[18]所述，实际切换点kc与系统所有元件参数相关。为此，可通过调节钳位变压器两侧自感大小LC、LP1来保证理论切换点k2与实际切换点kc一致。在确定好磁心和线材材料及形状后，LC从最小值XC/w 开始迭代，通过电磁仿真软件Maxwell，可在已知MC的情况下求得对应的LP1，然后根据式（4）求得CP、CC，得到一套对应的系统元件参数，将其代入1.3节进行验证，最终求得满足条件的LC、LP1参数。
上述设计步骤对应流程如图9所示。
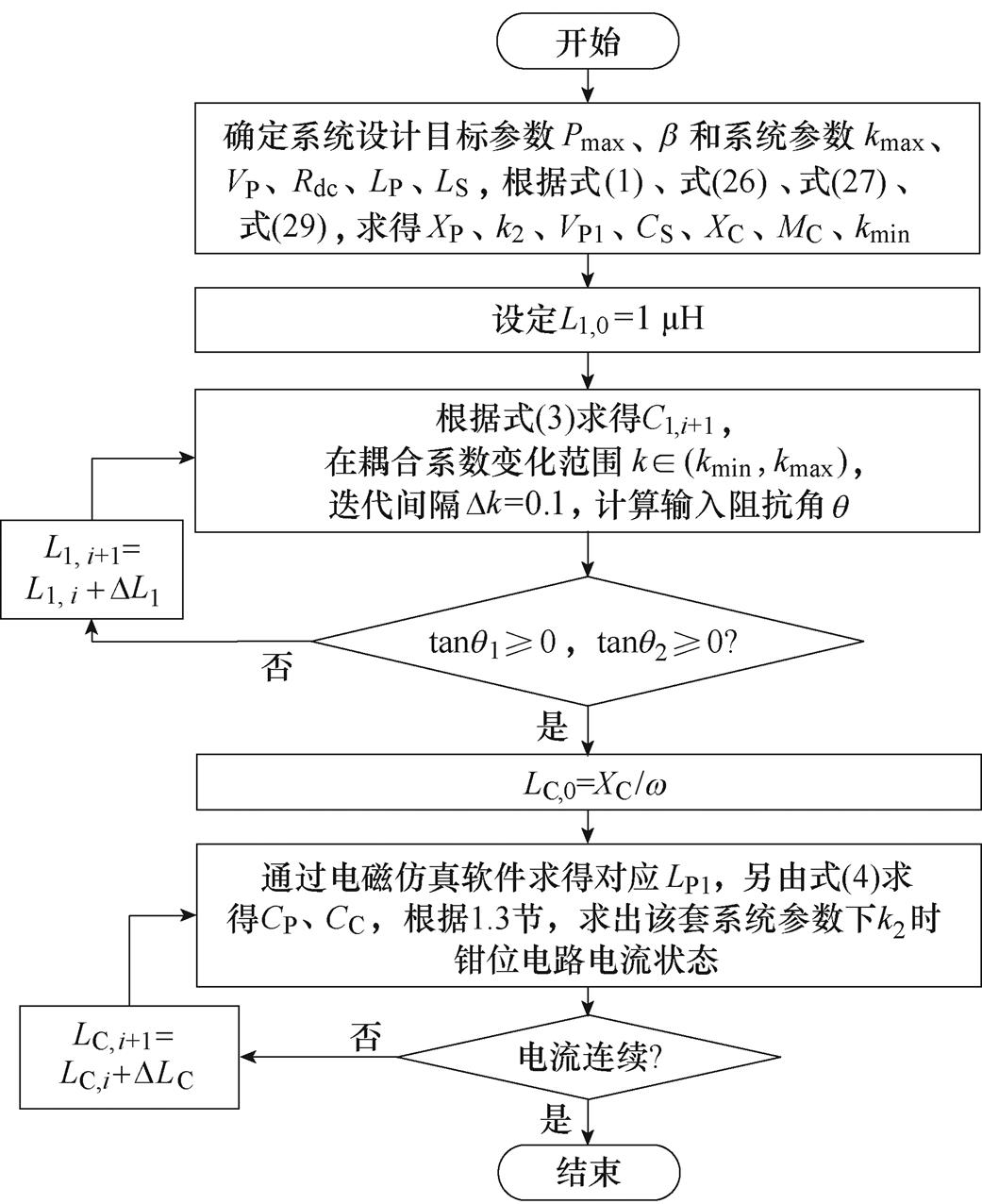
图9 参数化设计流程
Fig.9 Flow chart of parametric design
（1）确定系统设计目标参数Pmax、b 和系统参数kmax、VP、Rdc、LP、LS。
（2）根据式（1）、式（27）、式（28）、式（30），求得CS、XP、k2、VP1、XC、MC、kmin。
（3）结合式（3）和式（31），迭代求得L1、C1。
（4）由2.3节方法，LC自最小值XC/w 进行迭代计算，并根据式（4）求得对应CP、CC，最终求得满足1.3节判定条件的LP1、LC。
为验证所提出方法的正确性和可行性，本文构建了如图9所示的500 W实验样机，系统实验参数见表1。系统由直流电压源供电，逆变器输出方波电压，通过失谐LCC-S拓扑通路向副边传送能量。逆变器驱动信号由TMS320F28335型DSP提供，电子负载IT8518B设置为恒阻模式，使用Agilent DSO-X 3034A型示波器对实验波形进行录制，系统效率由HIOKI PW6001型功率分析仪测量。
图10 实验原理样机
Fig.10 The experimental prototype
表1 系统实验参数
Tab.1 Configuration of the IPT system
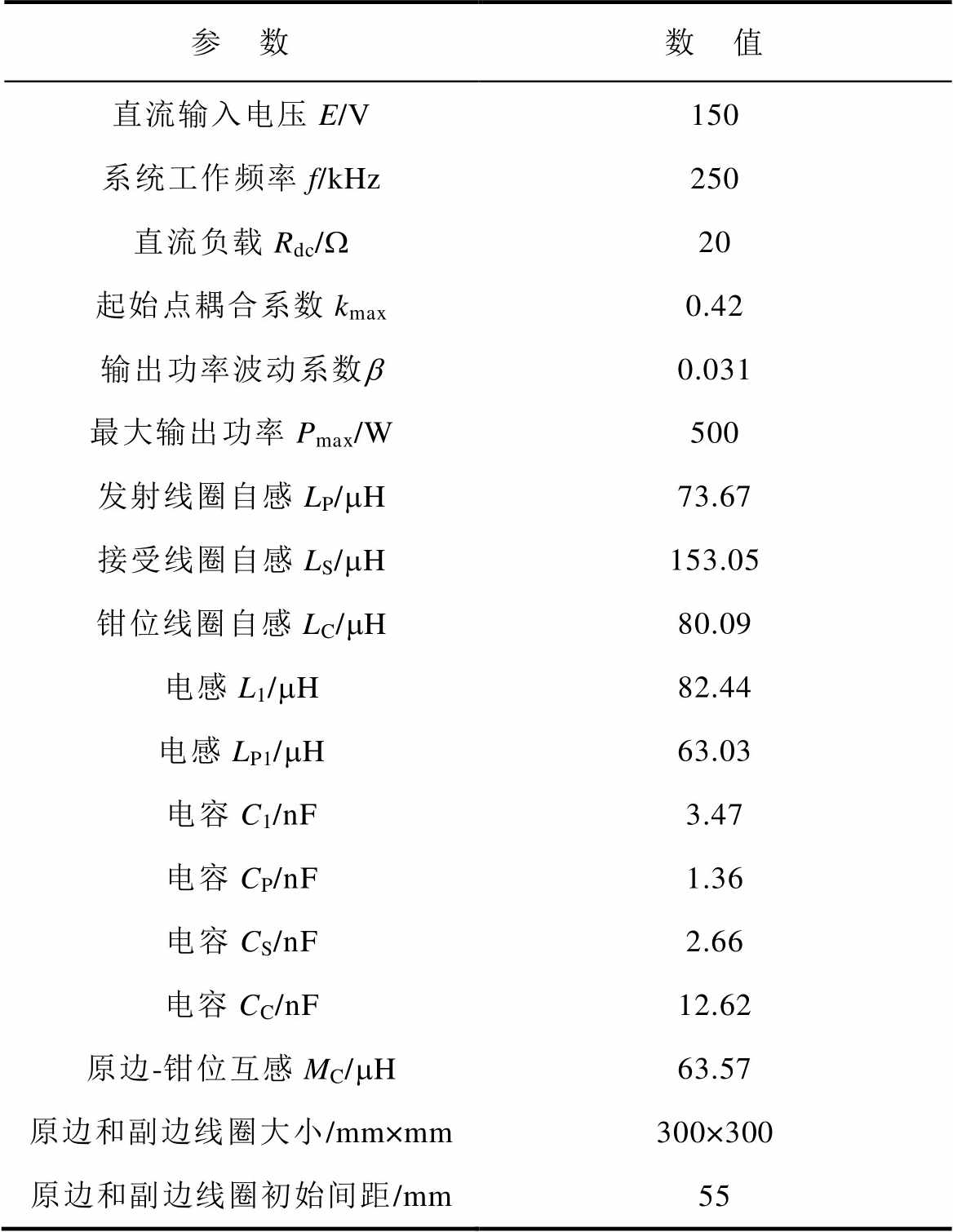
参 数数 值 直流输入电压E/V150 系统工作频率f/kHz250 直流负载Rdc/W20 起始点耦合系数kmax0.42 输出功率波动系数b0.031 最大输出功率Pmax/W500 发射线圈自感LP/mH73.67 接受线圈自感LS/mH153.05 钳位线圈自感LC/mH80.09 电感L1/mH82.44 电感LP1/mH63.03 电容C1/nF3.47 电容CP/nF1.36 电容CS/nF2.66 电容CC/nF12.62 原边-钳位互感MC/mH63.57 原边和副边线圈大小/mm×mm300×300 原边和副边线圈初始间距/mm55
逆变器实验波形如图10所示，图中，VP为逆变器输出电压、IP为输出电流、VC为钳位整流器输入电压、IC为输入电流、VS为副边整流器输入电压、IS为输入电流波形。图10a～图10c分别为系统在偏移起始点、偏移到钳位电路部分导通状态下的最大输出功率点、偏移到钳位电路完全导通状态下的最大输出功率点的原边回路-副边回路电压电流波形和原边-钳位电压电流波形。当系统偏移至kd1时，钳位电路电流极小且呈断续形式，钳位线圈感应电压相位超前于逆变电压。当系统偏移至kc时，钳位线圈感应电压呈完整方波形式，其相位略超前于逆变电压。当系统偏移至kd2时，钳位电路电流呈连续形式，钳位线圈感应电压与逆变电压几乎同相位。在整个有效偏移范围内，输出功率波动始终小于5%，系统效率最高为90.21%。
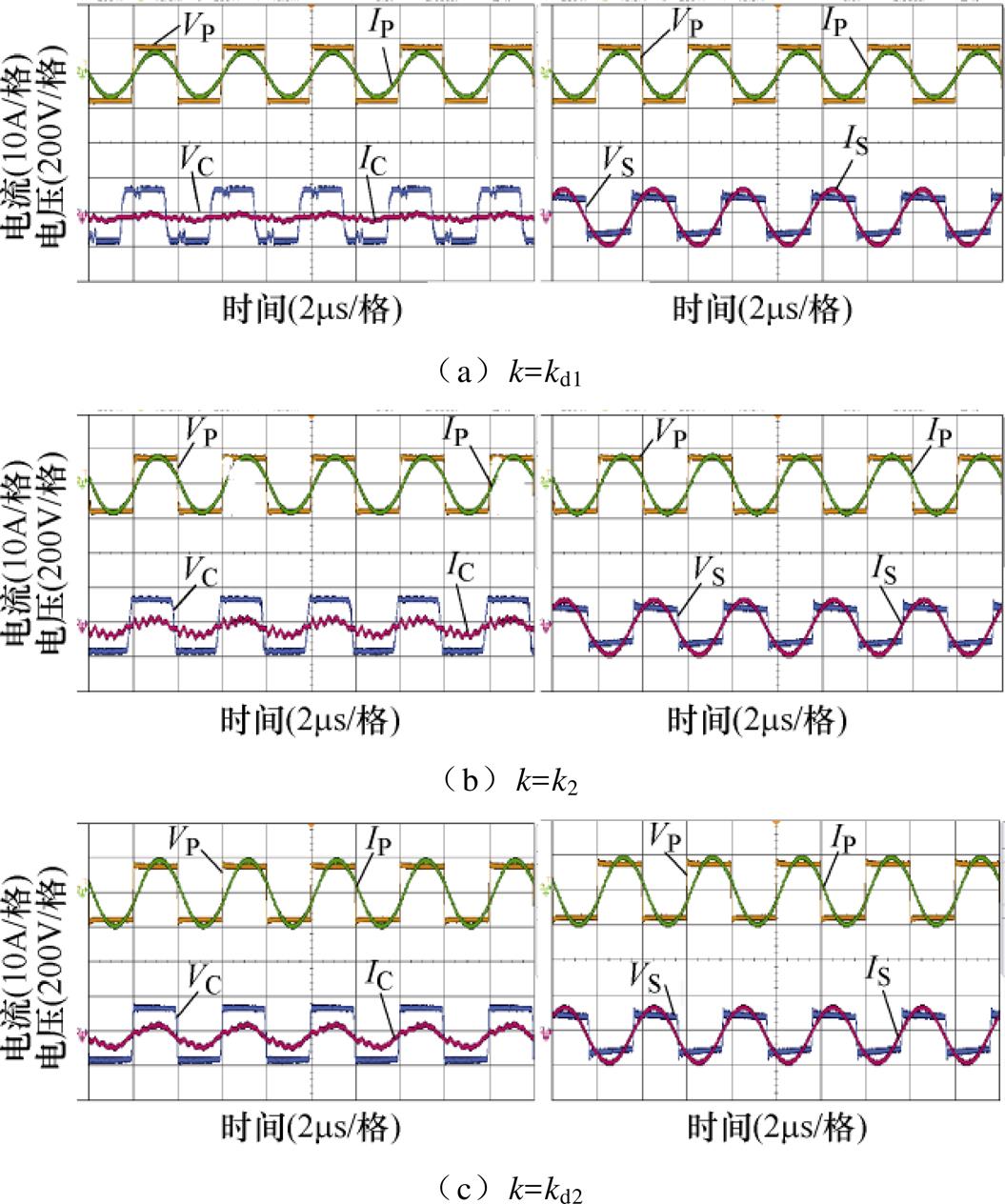
图11 逆变器实验波形
Fig.11 Experimental waveforms of the inverter
图12为系统在有效耦合变化范围的输出功率和效率。图中，耦合系数k从0.205增加到0.42，系统的输出功率变化保持在470～505 W之间，最大横向偏移距离为110 mm。由于FHA方法对系统的分析在钳位整流器处于部分导通状态时并不精 确[15]，导致实际功率输出相对理论计算存在一定偏差，但总体看来，实际功率输出曲线与理论计算所得曲线变化趋势基本一致。理论切换点与实际切换点吻合，系统效率维持在83.29%以上，最高可达90.21%，由 (Pmax-Pmin)/(Pmax+Pmin) 计算可得功率波动为3.59%。
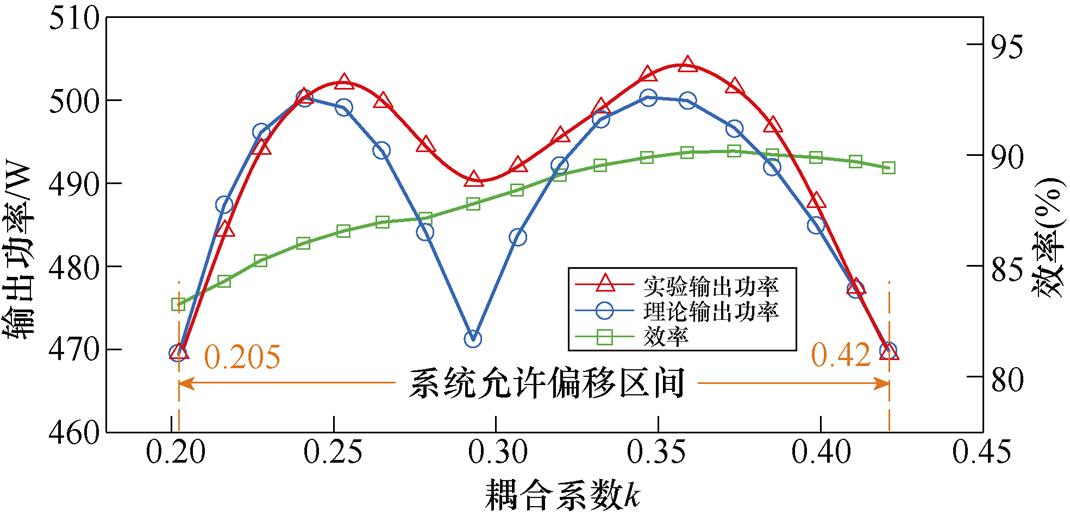
图12 耦合系数k变化实测输出功率与效率
Fig.12 Measured power output and efficiency versus coupling coefficient k
图13为失谐IPT系统接入钳位回路和断开钳位回路的系统输出功率与效率的对比，可以看出，本文所提出系统在目标工作区间内的功率波动抑制效果明显好于不采用文中方法，即断开钳位回路的系统，同时，通过副边完全补偿[13]和原边逆变器ZVS的设计，能够保有较高的效率。
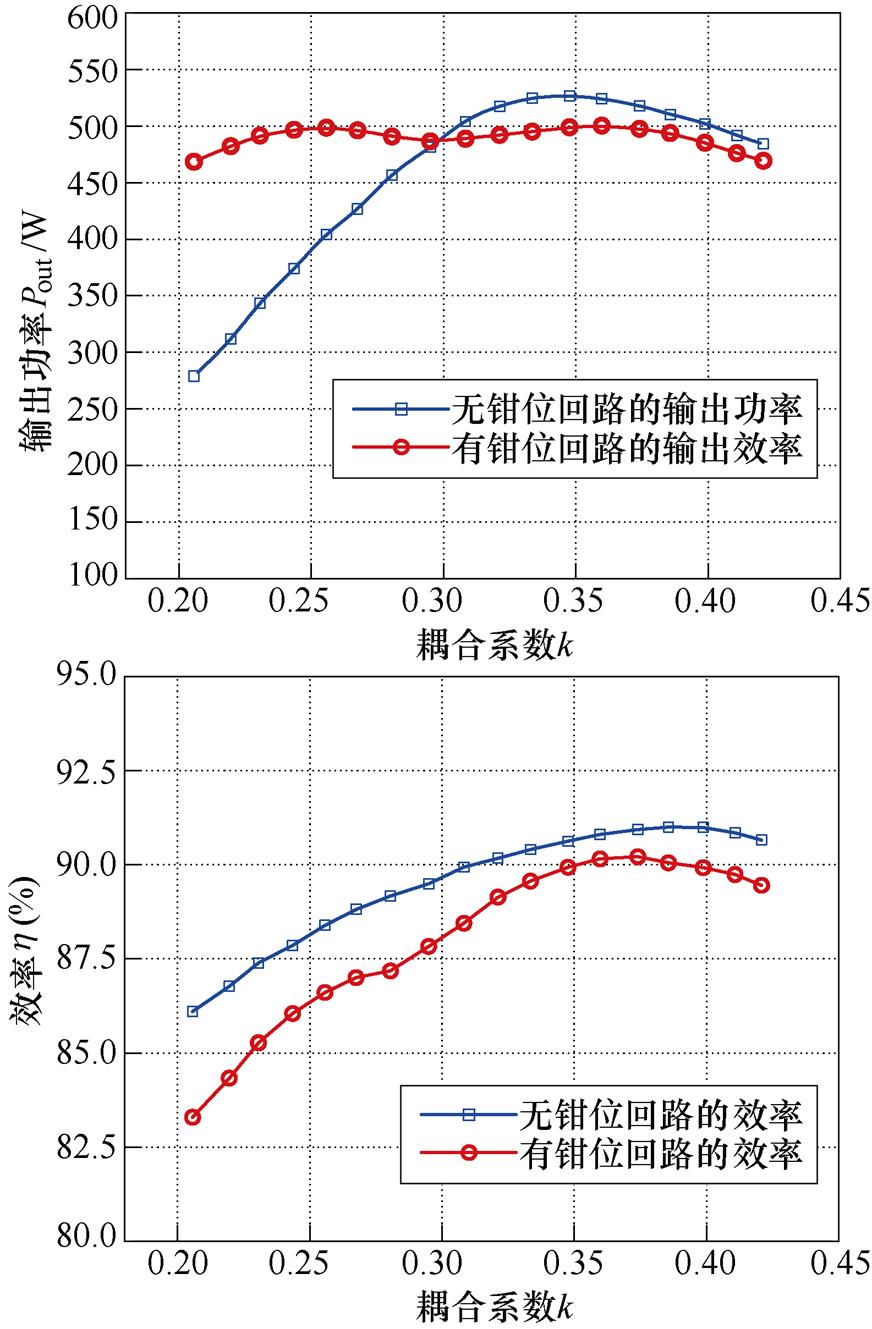
图13 输出功率、效率曲线对比
Fig.13 Comparison diagram of output power and efficiency
表2所示为本文所提出系统与已有补偿拓扑设计系统的性能对比，通过对比可说明本文所提出系统具有良好的抗偏移稳定传输效果，同时，该系统无需引入有源开关器件以及检测、反馈功能模块即可实现工作模态切换的效果，且具备应对三维偏移情况的能力。
表2 本文与已有研究方法对比结果
Tab.2 Comparison results between this paper and other methods
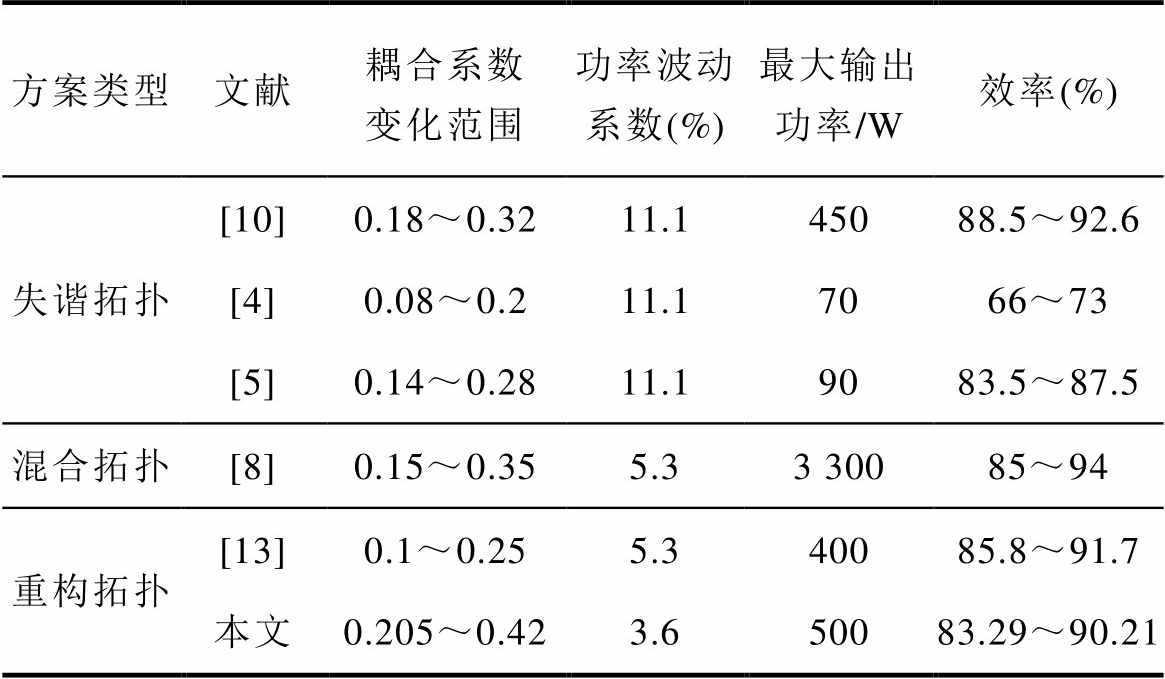
方案类型文献耦合系数变化范围功率波动系数(%)最大输出功率/W效率(%) 失谐拓扑[10]0.18～0.3211.145088.5～92.6 [4]0.08～0.211.17066～73 [5]0.14～0.2811.19083.5～87.5 混合拓扑[8]0.15～0.355.33 30085～94 重构拓扑[13]0.1～0.255.340085.8～91.7 本文0.205～0.423.650083.29～90.21
本文提出了一种通过钳位电路自适应地切换系统模态以匹配不同耦合偏移区间的IPT系统，从而为IPT系统保证可靠性同时提升输出平稳性提供了解决方法。得到以下结论：
1）分析了带钳位电路的LCC-S补偿型IPT系统的工作原理并通过系统相关约束条件提供了参数化设计方法，通过设计案例，得出了该系统具有良好的抗偏移性能。
2）说明了理论切换点与实际切换点存在偏差的原因，通过时域分析提供了实际切换点的计算方法，并根据参数化设计案例进行了理论验证。
3）在此基础上，搭建了一套500 W的原理样机，实验说明，该系统在系统耦合系数变动210%的同时能够保证输出功率波动始终保持在3.2%以内。实验结果证明了理论分析的有效性。
本文提出的方案暂未考虑负载变化情况，后续研究将关注系统负载变化情况下系统输出平稳性的提升。
参考文献
[1] 麦瑞坤, 徐丹露, 杨鸣凯, 等. 基于最小电流比值的IPT系统频率跟踪的动态调谐方法[J]. 电工技术学报, 2018, 33(6): 1276-1284.
Mai Ruikun, Xu Danlu, Yang Mingkai, et al. Dynamic tuning method of frequency tracking based on the minimum current ratio for IPT system[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(6): 1276-1284.
[2] 苑朝阳, 张献, 杨庆新, 等. 无线供电高铁列车非对称耦合机构[J]. 电工技术学报, 2017, 32(18): 18-25.
Yuan Zhaoyang, Zhang Xian, Yang Qingxin, et al. Asymmetric coupling mechanism of wireless power transmission system for high-speed train[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(18): 18-25.
[3] Li Hongchang, Li Jie, Wang Kangping, et al. A maximum efficiency point tracking control scheme for wireless power transfer systems using magnetic resonant coupling[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3998-4008.
[4] Feng Hao, Cai Tao, Duan Shanxu, et al. A dual- side-detuned series-series compensated resonant converter for wide charging region in a wireless power transfer system[J]. IEEE Transactions on Industrial Electronics, 2018, 65(3): 2177-2188.
[5] Feng Hao, Dayerizadeh A, Lukic S M. A coupling- insensitive X-type IPT system for high position tolerance[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 68(8): 6917-6926.
[6] Zaheer A, Hao Hao, Covic G A, et al. Investigation of multiple decoupled coil primary pad topologies in lumped IPT systems for interoperable electric vehicle charging[J]. IEEE Transactions on Power Electronics, 2014, 30(4): 1937-1955.
[7] Chen Yang, Mai Ruikun, Zhang Youyuan, et al. Improving misalignment tolerance for IPT system using a third-coil[J]. IEEE Transactions on Power Electronics, 2018, 34(4): 3009-3013.
[8] Zhao Lei, Thrimawithana D J, Madawala U K, et al. A misalignment-tolerant series-hybrid wireless EV charging system with integrated magnetics[J]. IEEE Transactions on Power Electronics, 2018, 34(2): 1276-1285.
[9] 胡宏晟, 蔡涛, 段善旭, 等. 用于WPT系统的一次侧失谐SS型补偿拓扑及其参数设计方法[J]. 电工技术学报, 2017, 32(18): 73-82.
Hu Hongsheng, Cai Tao, Duan Shanxu, et al. Study of the primary side detuned series-series compensated topology and parameter design for WPT system[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 73-82.
[10] 丰昊, 蔡涛, 段善旭, 等. 一种抗宽范围耦合系数波动的三元件补偿型感应式能量传输系统[J]. 电工技术学报, 2017, 32(增刊2): 10-17.
Feng Hao, Cai Tao, Duan Shanxu, et al. A three- element inductive power transfer system with high misalignment tolerance[J]. Transactions of China Electrotechnical Society, 2017, 32(S2): 10-17.
[11] Chen Yang, Yang Bin, Li Qiao, et al. Reconfigurable topology for IPT system maintaining stable trans- mission power over large coupling variation[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 4915-4924.
[12] Zhong Wenxing, Zhang Siyuan, Chen Min, et al. Reconfigurable resonant topology linking two-, three-, and four-coil modes for WPT with large coupling range and fixed frequency[J]. IEEE Transactions on Power Electronics, 2022, 37(7): 8713-8725.
[13] Chen Yang, He Shuangjiang, Yang Bin, et al. Recon- figurable rectifier-based detuned series-series com- pensated IPT system for anti-misalignment and efficiency improvement[J]. IEEE Transactions on Power Electronics, 2022, 38(2): 2720-2729.
[14] Huang Zhicong, Wang Guoyu, Yu Jidong, et al. A novel clamp coil assisted IPT battery charger with inherent CC-to-CV transition capability[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 8607-8611.
[15] Qu Xiaohui, Jing Yanyan, Lian Jing, et al. Design for continuous-current-mode operation of inductive- power-transfer converters with load-independent output[J]. IET Power Electronics, 2019, 12(10): 2458- 2465.
[16] 刘硕, 苏建徽, 张健, 等. 近距离下串联补偿无线电能传输变换器特性时域分析[J]. 电力自动化设备, 2022, 42(2): 155-162.
Liu Shuo, Su Jianhui, Zhang Jian, et al. Time domain analysis of series compensated wireless power transfer converter at short range[J]. Electric Power Automation Equipment. 2022, 42(2): 155-162.
[17] Jiang Bing, Tan Longzhao, Yu Zihao, et al. A novel distance measurement method based on reflected impedance for resonant wireless power transmission system[C]//2020 Asia Energy and Electrical Engin- eering Symposium (AEEES), Chengdu, China, 2020: 1-5.
[18] Mai Jianwei, Zeng Xianrui, Yao Yousu, et al. Impedance analysis and design of IPT system to improve system efficiency and reduce output voltage or current fluctuations[J]. IEEE Transactions on Power Electronics, 2021, 36(12): 14029-14038.
Abstract Inductive power transfer (IPT) technology delivers power through electromagnetic induction between the coupled coils without physical contact. However, the misalignment between coils is often unavoidable in applications, and the coupling variation caused by the misalignment can cause the instability of the IPT system. Therefore, ensuring output stability has become one of the main problems in the application and development of IPT technology. Topology design solutions are favored because of their simplicity and reliability. Topology design solutions include mixed topology, detuning topology, and reconfigurable topology. The reconfigurable topology solution needs to apply active switching devices, the detection module, and the communication module, causing higher costs and lower reliability. Based on the idea of mode switching, this paper proposes a novel detuning IPT system with a clamp circuit to enhance the anti-misalignment ability of the system. Compared with the traditional multi-mode IPT system, the clamp circuit in the system can be switched on or off adaptively according to the coupling variation to adjust the system mode and achieve nearly constant power output without auxiliary equipment, such as coupling identification, output detection, and feedback com- munication.
First, according to the characteristics of unidirectional conduction and discontinuous/continuous of the clamp circuit, the proposed system has multi-mode characteristics, and the corresponding system output power curves of different modes are different. The working principle and power output characteristics of the IPT system with or without the clamp circuit activation are derived and analyzed, and the expressions of the system power output curve with or without the clamp circuit activation are given. Feasible splicing methods are proposed based on the corresponding output power curves of different system modes.
Then, by analyzing the function of each topology structure of the proposed IPT system and the output power curve of the system under different working modes, reasonable constraint conditions are provided for the parametric design of the system. The feasible parametric design process method is obtained. At the same time, this paper provides a set of methods to judge the system mode according to the time domain analysis method to ensure the accuracy of the switching point, and also gives a design case. By subinterval analysis method, the output characteristics of the IPT converter under the PN and PON modes are analyzed, and the currents of the clamp circuit in different modes are calculated to verify if the clamp circuit is activated.
A 500 W experimental prototype is built, and the changes in output power and efficiency during coupling variation are measured. Experimental results show that when the coupling coefficient changes during 0.205～0.42, the output power of the proposed system fluctuates between 470～505 W, the maximum output power fluctuation is 35 W, the output power fluctuation rate is less than 3.6%, and the efficiency changes between 90.21% and 83.29%.
keywords：Inductive power transfer (IPT), clamp circuit, coupling variation, parametric design, stable power transfer
国家自然科学基金（52207226）和四川省科技计划（2023NSFSC0819, 2023JDRC0102）资助项目。
收稿日期 2023-03-03
改稿日期 2023-04-11
DOI: 10.19595/j.cnki.1000-6753.tces.230246
中图分类号：TM724
张滨山 男，1998年生，硕士研究生，研究方向为无线电能传输系统抗偏移性能提升。E-mail: zbs@my.swjtu.edu.cn
陈 阳 男，1992年生，博士，助理研究员，研究方向为无线电能传输技术。E-mail: yangchen@swjtu.edu.cn（通信作者）
（编辑 陈 诚）