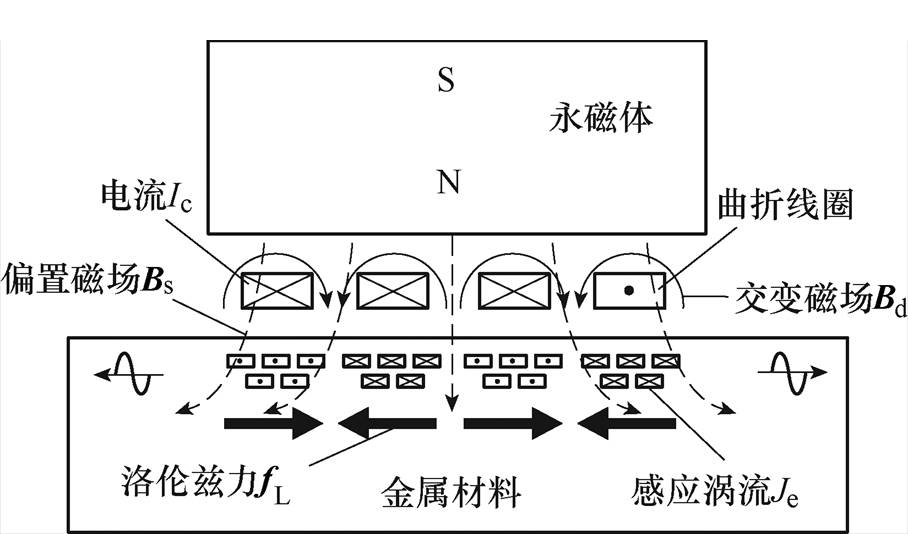
图1 单阵元Lamb波EMAT示意图
Fig.1 Schematic diagram of single element Lamb wave EMAT
摘要 为了解决传统Barker码脉冲压缩技术受脉冲功率放大器额定参数（占空比，最大脉冲宽度等）限制而导致的脉冲压缩效果下降、检测速度降低等问题，提出一种基于Barker码脉冲压缩技术的多阵元Lamb波电磁超声换能器（EMAT）。建立了基于tone-burst信号激励-Barker码脉冲压缩技术的多阵元Lamb波EMAT检测过程的有限元模型，分析了永磁体的配置形式、阵元序列长度、激励信号周期数、曲折线圈匝数等因素对脉冲压缩后的主旁瓣比和主瓣宽度的影响，并进行了实验验证。结果表明：曲折线圈匝数为4和Barker码序列长度为13位的多阵元EMAT在配置3对外置永磁体后，其信噪比（SNR）可提高9.8 dB。综合考虑检测回波的空间分辨率和SNR，多阵元Lamb波EMAT最佳参数为：曲折线圈匝数为10、激励信号周期数为11、Barker序列为13位，并配置3对外置永磁体。
关键词：电磁超声换能器 Barker码脉冲压缩 多阵元Lamb波EMAT 信噪比 空间分辨率
随着工业技术的发展，钢板在工业中扮演着越来越重要的角色，因其良好的性能被广泛应用于化工[1]、核电[2]、能源[3]等领域。在钢板的服役过程中，腐蚀[4-7]是最常见的失效形式之一，而锅炉[8]、核岛、储罐[9]等承压类设备作为大部分工业的基础设施，长期处于高温高压等恶劣环境中，极易形成钢板腐蚀且难以被检出，一旦发生事故，就会导致整个工厂紧急关闭，并且会在停机、维修等方面产生高昂的费用，甚至还会造成生命危险。因此对在役大规格钢板进行原位快速检测以保证其服役安全性，对保护公众安全、保障经济增长具有重要意义。
近几年，超声检测因具有灵敏度高、通用性强、穿透性强、指向性好、便于检测和接收、检测速度快等优点[10-12]，被广泛应用。其中电磁超声换能器（Electromagnetic Acoustic Transducer, EMAT）通常包括永磁体、线圈和待测导电或导磁金属试样三部分，通过电磁耦合原理激励和接收超声波，因其无需耦合剂、非接触等优点[13-14]，被广泛应用于金属试样的表面粗糙度的识别与预测[15]、450℃高温顺磁钢检测[16]、锅炉水冷壁管腐蚀缺陷检测[17]、铸钢板坯边钻孔相控阵检测[18]、变厚铝板塑性形变[19]等应用场合。其中电磁超声导波技术在检测大规格薄板类[20]和薄管类[21-23]构件上优势明显且应用广泛。为解决EMAT换能效率低和信噪比差等问题，国内外学者提出基于脉冲压缩技术的电磁超声检测方法。
脉冲压缩技术通过发射宽脉冲激励，经滤波网络后获得窄脉冲[20-25]，既拥有宽脉冲的强检测能力，也拥有窄脉冲的高距离分辨率，在不增加EMAT检测系统的输出功率和噪声抑制能力的条件下，可以有效地提高EMAT检测回波的SNR和空间分辨率。目前，脉冲压缩技术应用于超声检测的研究已经取得较大进展，例如，Fu Juan等[26]提出一种使用线性调频载波的新型Barker编码激励方法，与常规使用正弦载波的Barker编码激励方法相比，其轴向分辨率可以提高一倍，SNR可以提高约3 dB。H. Mitsuta等[27]开发了一种基于脉冲压缩技术的高灵敏度超声波检测系统，与传统使用尖脉冲激励的超声检测系统相比，噪声幅值降低了66%，可以检测到直径f20 mm的缺陷。S. Laureti等[28]开发了一种基于脉冲压缩技术的压电复合传感器及其检测系统，可以在混凝土覆盖深度55 mm下获得良好的钢筋检测结果。
然而，在传统脉冲压缩技术中，常常因为编码激励信号持续时间过长，容易超过脉冲功率放大器的占空比和最大脉冲宽度等参数的限制，从而导致放大器性能下降，甚至完全功能性损坏。以RPR 4000高功率脉冲发生器/接收器为例，其技术规格要求占空比不超过1%，最大脉冲宽度不超过200 ms，序列长度13位、中心频率0.2 MHz和码元周期数4对应的Barker码激励信号脉冲宽度为260 ms，已经超过放大器最大脉冲宽度的限制，将会对设备造成不可逆的损坏。另外，放大器的占空比会限制脉冲重复频率的增加，导致检测速度下降，同时过长的Barker码激励信号将造成较大的检测盲区。
传统解决方法是在减小编码激励信号持续时间和降低脉冲压缩效果的基础上，对EMAT进行优化设计或加入先进的降噪算法，以提高信噪比。EMAT优化设计一般是对线圈的尺寸结构、永磁体的形状尺寸及配置形式等方面进行优化设计。时亚等[29]通过正交试验设计对表面波EMAT进行优化，优化后的多根分裂曲折线圈EMAT的接收信号幅值可以提高50.8%。刘素贞等[30]设计出一种新型窄永磁体聚焦式表面波EMAT，在同等磁通密度下激发的表面波信号时域幅值比常规EMAT提高了55.9%，信号频域基频幅值提升69.7%。D. Gandomzadeh等[31]研究了磁致伸缩换能器磁心几何形状对EMAT性能的影响，结果表明，磁心横截面略微伸长会增加最大径向和纵向磁致伸缩力。Kang Lei等[32]建立了表面波EMAT传播过程三维有限元模型，利用正交试验表，研究了EMAT设计参数对表面波的影响。经过优化后，EMAT检测回波信号幅度增加了25.2%。Pei Cuixiang等[33]提出了一种改进的曲折线圈EMAT，与传统曲折线圈EMAT相比，磁通密度提高了1.9倍，且实验表明使用新型EMAT的SNR相比于传统EMAT提高了5.3倍。在先进降噪算法方面，Sun Mingjian等[34]使用经验模态分解（Empirical Modes Decomposition, EMD）来处理超声波信号，并通过实验验证了该算法的可行性。Nie Zhichao 等[35]应用小波和集合经验模态分解（Ensemble Empirical Mode Decomposition, EEMD）对超声波信号进行去噪，以突出真实的频域分量。Si Dan等[36]提出了一种改进的变分模态分解（Variational Mode Decomposition, VMD）链接小波方法进行EMAT去噪，与EMD-小波去噪算法和小波去噪算法相比，该方法的SNR分别提高了18%和37%。
EMAT优化设计和先进降噪算法可以显著提高电磁超声检测回波的SNR，但是相对于脉冲压缩技术，其SNR提升作用有限。本研究提出一种基于tone-burst激励的Barker码脉冲压缩技术的新型多阵元Lamb波EMAT，以解决传统脉冲压缩技术受脉冲功率放大器的占空比和最大脉冲宽度等参数限制和检测盲区过大等难题。
本研究以大型薄壁钢板为检测对象，提出一种新型基于tone-burst激励的Barker码脉冲压缩技术的多阵元Lamb波EMAT设计方法。首先，分析了基于Barker码脉冲压缩技术的多阵元EMAT设计原理；然后，建立了基于tone-burst激励的Barker码脉冲压缩技术的多阵元Lamb波新型EMAT检测过程有限元模型，通过数值计算，分析了外置永磁体、序列长度、激励信号周期数、曲折线圈匝数等参数对脉冲压缩效果的影响；最后，制作了新型多阵元Lamb波EMAT，并进行了实验验证。
图1为单阵元Lamb波EMAT示意图。多阵元EMAT与单阵元EMAT都是通过产生洛伦兹力来带动粒子振动，从而激发Lamb波，即线圈中通以高频大功率激励电流Ic，在试样表面就会产生方向相反、频率相同的感应涡流Je。相邻导线的感应涡流流向相反，在永磁体提供的静态偏置Bs和Ic产生的交变磁场Bd作用下，产生洛伦兹力fL。fL带动粒子振动，在试样内部产生超声波，并在两个自由界面发生反射、折射，耦合后形成向两侧传播的Lamb波。fL计算表达式[37]为
图1 单阵元Lamb波EMAT示意图
Fig.1 Schematic diagram of single element Lamb wave EMAT
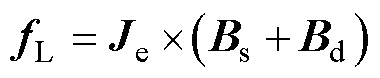（1）
超声波在试样中传播的控制方程[37]为
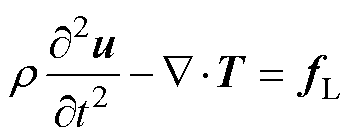（2）
式中，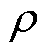
为材料密度；t为时间；u为质点位移矢量；T为弹性应力张量。
Barker码序列是一种相位编码信号，具有良好的自相关特性，目前已知的Barker码序列共有9组，序列长度最长为13位，其序列为{1, 1, 1, 1, 1, -1, -1, 1, 1, -1, 1, -1, 1}。传统Barker码脉冲压缩技术是将tone-burst信号作为Barker码序列的码元，得到的Barker码信号作为EMAT的激励电流，如图2a所示。Barker码信号和码元序列表达式[38-39]为
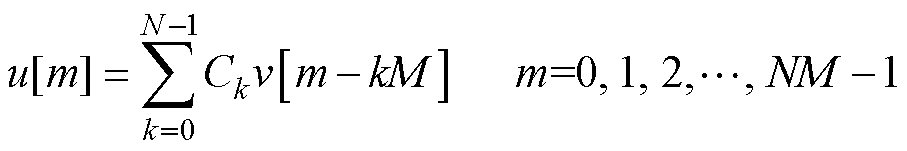（3）
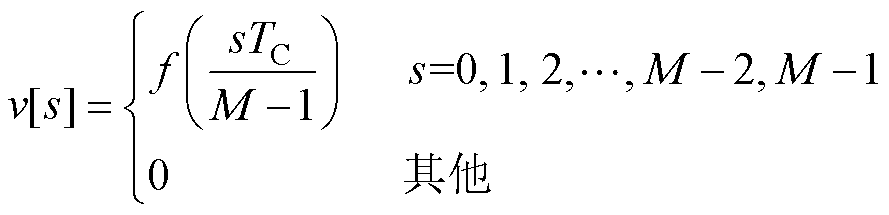（4）
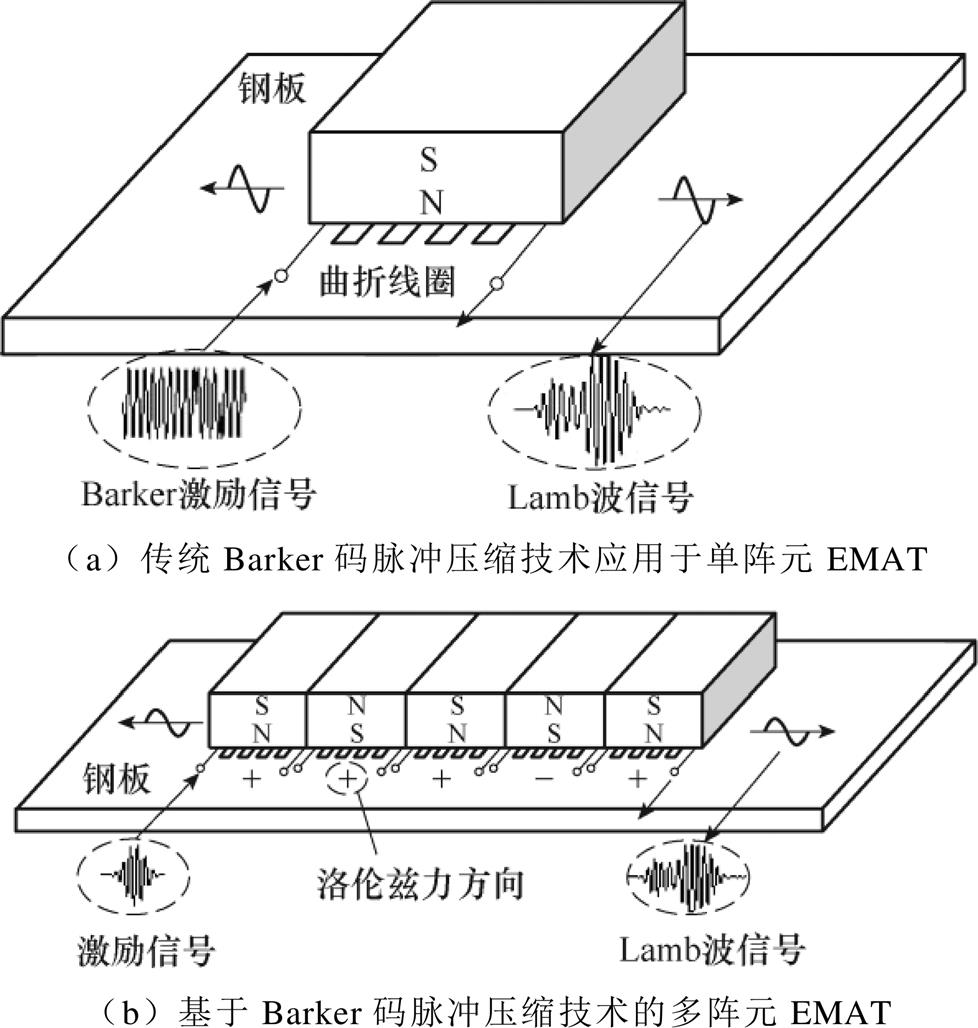
图2 基于Barker码脉冲压缩技术的EMAT示意图
Fig.2 Schematic diagram of EMAT based on Barker code pulse compression technology
式中，N为子脉冲的个数；M为码元编号；Ck为Barker码编码序列；TC为码元的持续时间。
Barker码信号u[m]加载到激励EMAT，得到的接收信号为s[m]，脉冲压缩后的信号yi[m][38-39]为
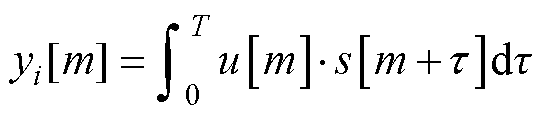（5）
式中，T为超声回波信号长度；τ为自变量。
如图2b所示，基于Barker码脉冲压缩技术的多阵元EMAT与传统Barker码脉冲压缩技术应用于单阵元EMAT的区别在于，多阵元EMAT将一个永磁体和一个曲折线圈视为一组阵元，通过控制每组阵元中永磁体的磁场方向与曲折线圈的电流方向来控制其洛伦兹力的方向，继而使其激励的Lamb波相位{0, 180°}与Barker码序列{1, -1}一致，最终激励出Barker码形式的Lamb波。
经过脉冲压缩后，主瓣两侧会分布间隔时间相同、大小相等的旁瓣。通过引入加权因子，确定单次延时时间t后，可以有效地抑制旁瓣。多阵元EMAT的延时时间t与相邻阵元的中心间距d和Lamb波波速v有关，其计算公式为
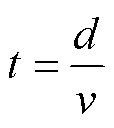（6）
基于Barker码脉冲压缩技术的多阵元Lamb波EMAT有限元建模如图3所示，建模参数见表1。
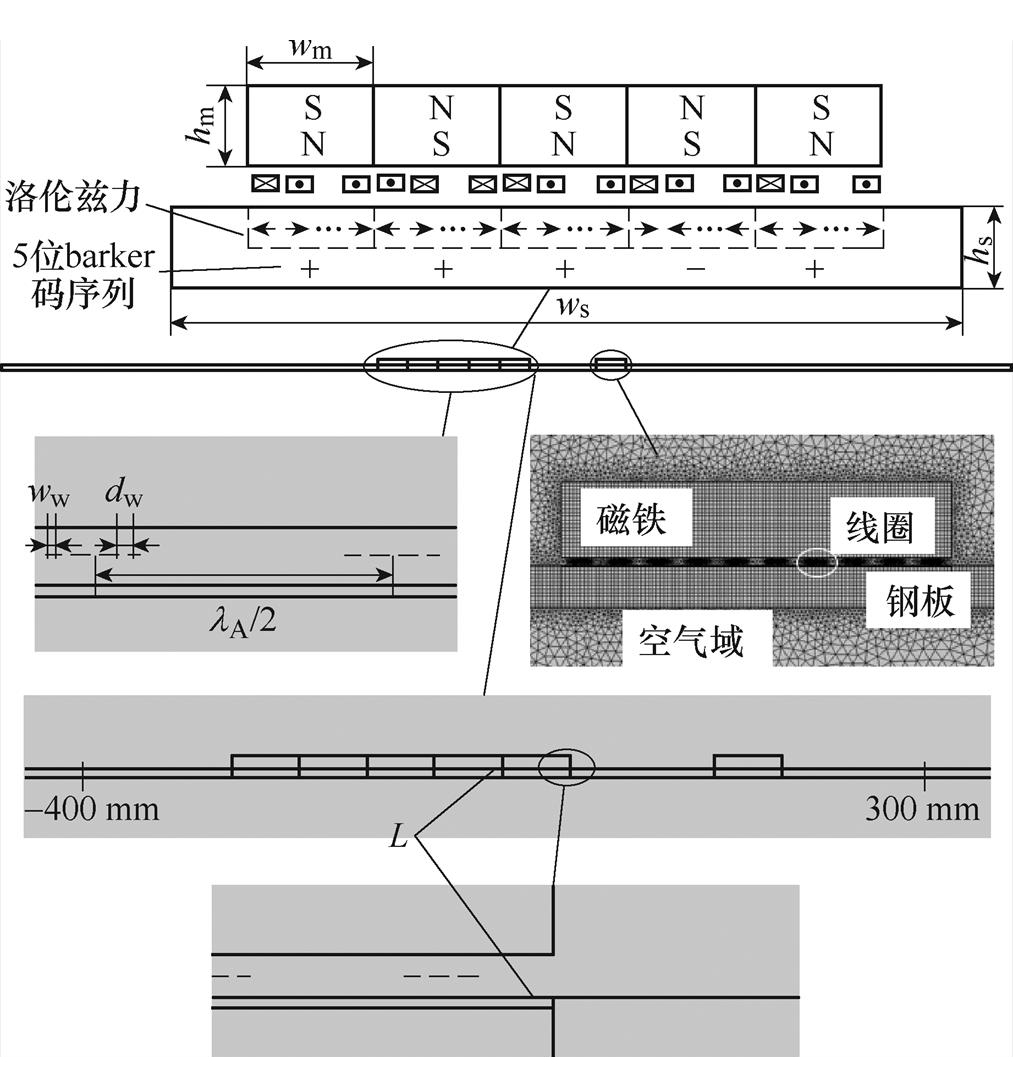
图3 有限元建模示意图
Fig.3 Schematic diagram of finite element model
表1 有限元模型参数
Tab.1 Finite element model parameters
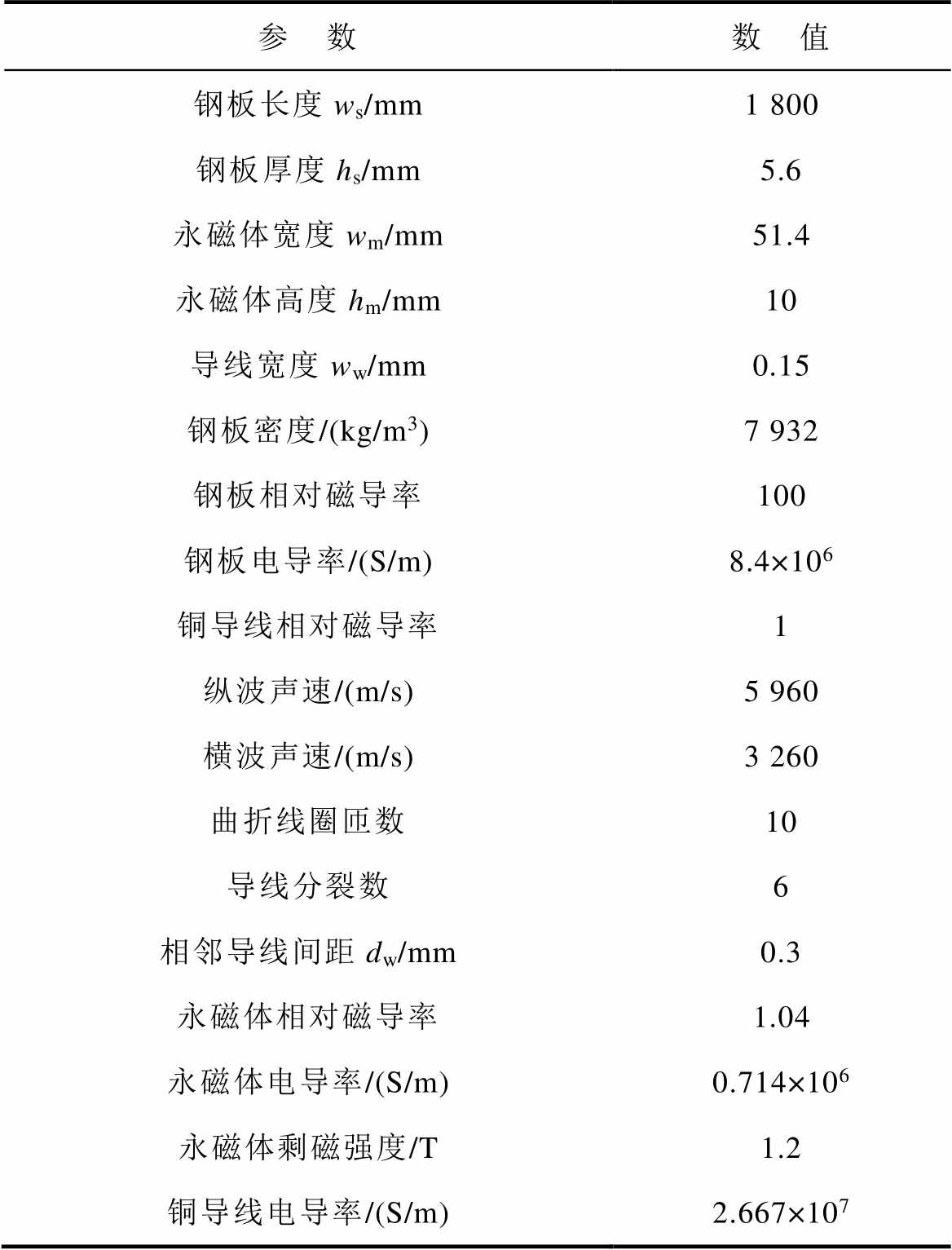
参 数数 值 钢板长度ws/mm1 800 钢板厚度hs/mm5.6 永磁体宽度wm/mm51.4 永磁体高度hm/mm10 导线宽度ww/mm0.15 钢板密度/(kg/m3)7 932 钢板相对磁导率100 钢板电导率/(S/m)8.4×106 铜导线相对磁导率1 纵波声速/(m/s)5 960 横波声速/(m/s)3 260 曲折线圈匝数10 导线分裂数6 相邻导线间距dw/mm0.3 永磁体相对磁导率1.04 永磁体电导率/(S/m)0.714×106 永磁体剩磁强度/T1.2 铜导线电导率/(S/m)2.667×107
图3为5阵元EMAT按照洛伦兹力方向{1, 1, 1, -1, 1}进行排列，可以产生Barker码形式的Lamb波。钢板的杨氏模量为214 GPa，泊松比为0.271。钢板的左右端面设置为低反射边界，用于消除端面反射回波。激励EMAT为多阵元Lamb波EMAT，接收EMAT采用单阵元Lamb波EMAT。EMAT采用六分裂曲折线圈，相邻导线间距为0.3 mm，匝间距为l/2，l 为导波的波长。在曲折线圈上加载的激励电流的函数表达式为
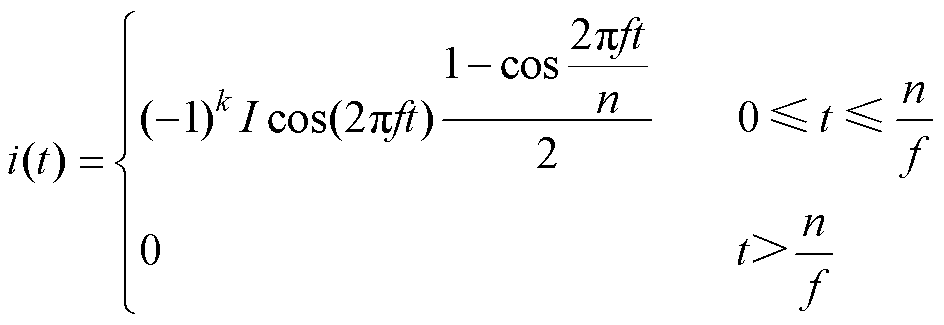（7）
式中，I为激励电流幅值；k为每匝导线的序号；中心频率f为0.24 MHz；n为正弦脉冲串的周期数。
有限元模型中的空气域、永磁体、曲折线圈和钢板试样的最大网格单元大小分别为2 mm、0.5 mm、0.02 mm、0.5 mm。对钢板上边界进行边界层网格细化，第1层厚度为0.005 2 mm，共5层，相邻层网格单元大小增长率为1.2。当瞬态求解器最大计算步长满足fmax/100，最大网格单元大小满足lmin/10时，计算结果收敛。在有限元模型中，设置测点线段L起始于激励EMAT永磁体组的最左侧和终止于接收EMAT永磁体的最右侧，位于钢板试样表面往下0.001 mm。考虑多阵元Lamb波EMAT中曲折线圈导线的趋肤效应和邻近效应，采用单匝线圈模型，对应的控制方程见参考文献[40]。
Lamb波的多模态效应会影响脉冲压缩效果，降低缺陷波信号经脉冲压缩和旁瓣抑制后的SNR和空间分辨率，所以有必要激励单一模态的Lamb波。厚度为5.6 mm的钢板Lamb波频散曲线如图4所示。图4a、图4b分别为相速度、群速度频散曲线，当激励频率为0.24 MHz，可以产生S0、A0两种模态的Lamb波。A0模态波长约为10.28 mm，对应的曲折线圈匝间距为lA/2=5.14 mm。由图5可知，当激励频率为0.24 MHz、永磁体宽度为51.4 mm时，曲折线圈EMAT仅产生单一Lamb模态。
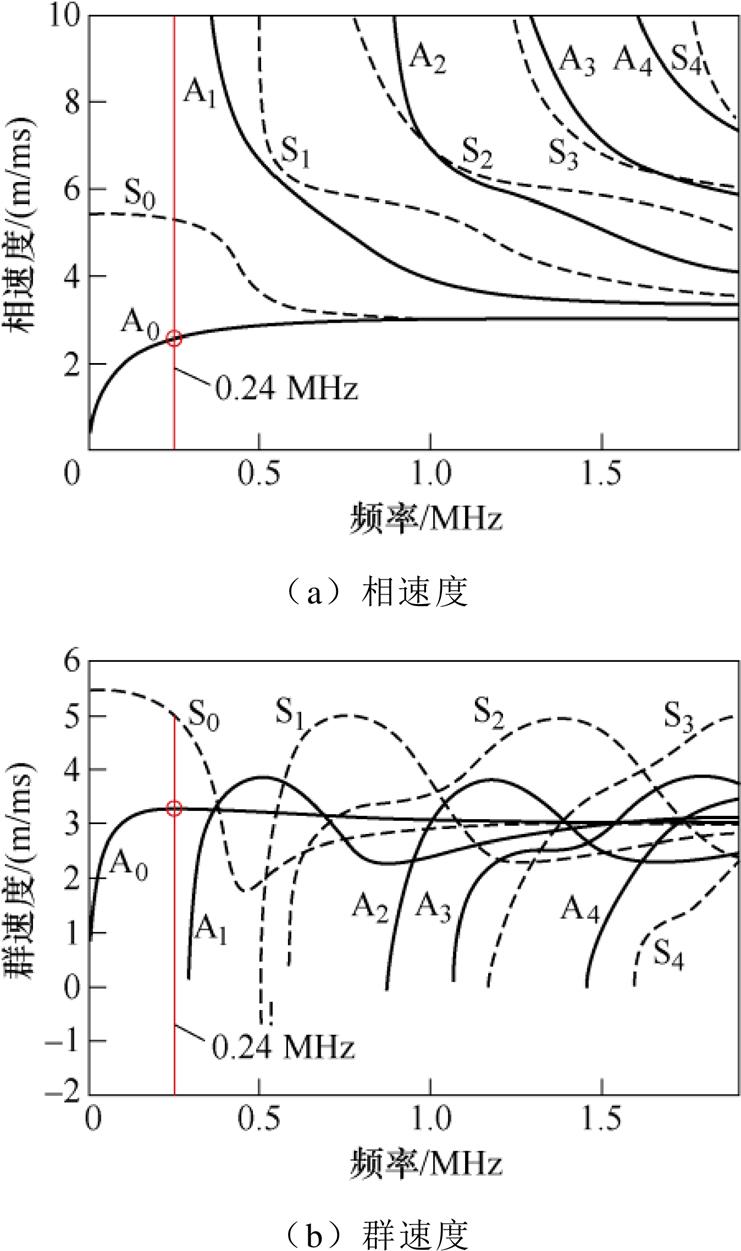
图4 Lamb波在钢板中的频散曲线
Fig.4 Dispersion curves of Lamb wave in steel plate
在基于Barker码脉冲压缩技术的多阵元Lamb波EMAT中，保证每个阵元激励出的Lamb波信号与对应Barker码码元的一致性是提高脉冲压缩效果的关键。由于每个阵元的磁场分布并不均匀，且各个阵元间的磁场分布不相同，位于多阵元EMAT前后两端的磁场和位于中间的磁场分布存在较大差异，脉冲压缩效果并不理想。因此，考虑多阵元EMAT外部增加外置永磁体，使多阵元EMAT的每个阵元磁场分布基本一致，以提高脉冲压缩效果。5位阵元EMAT的三种永磁体配置形式如图6所示。
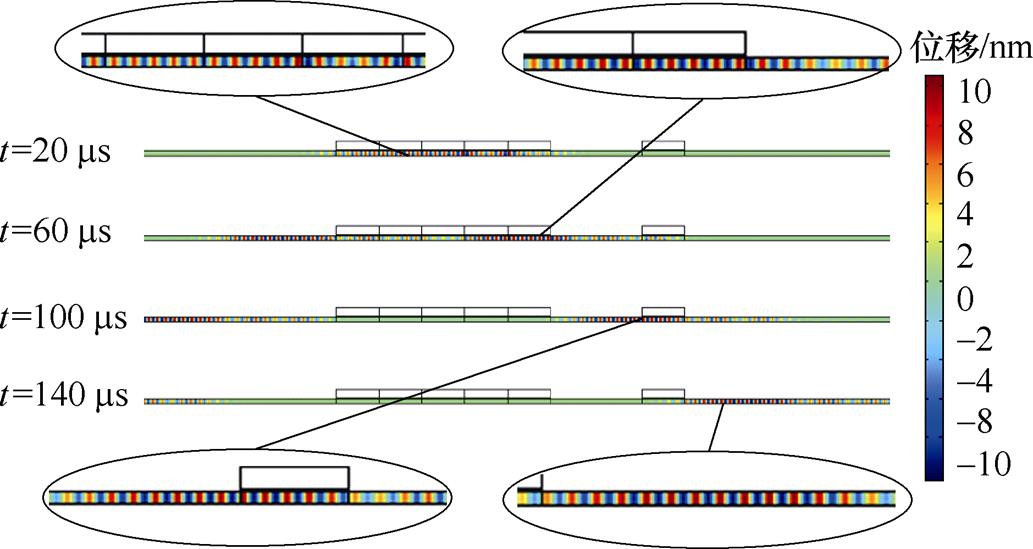
图5 钢板Lamb波传播云图
Fig.5 Lamb wave propagation nephogram of steel plate
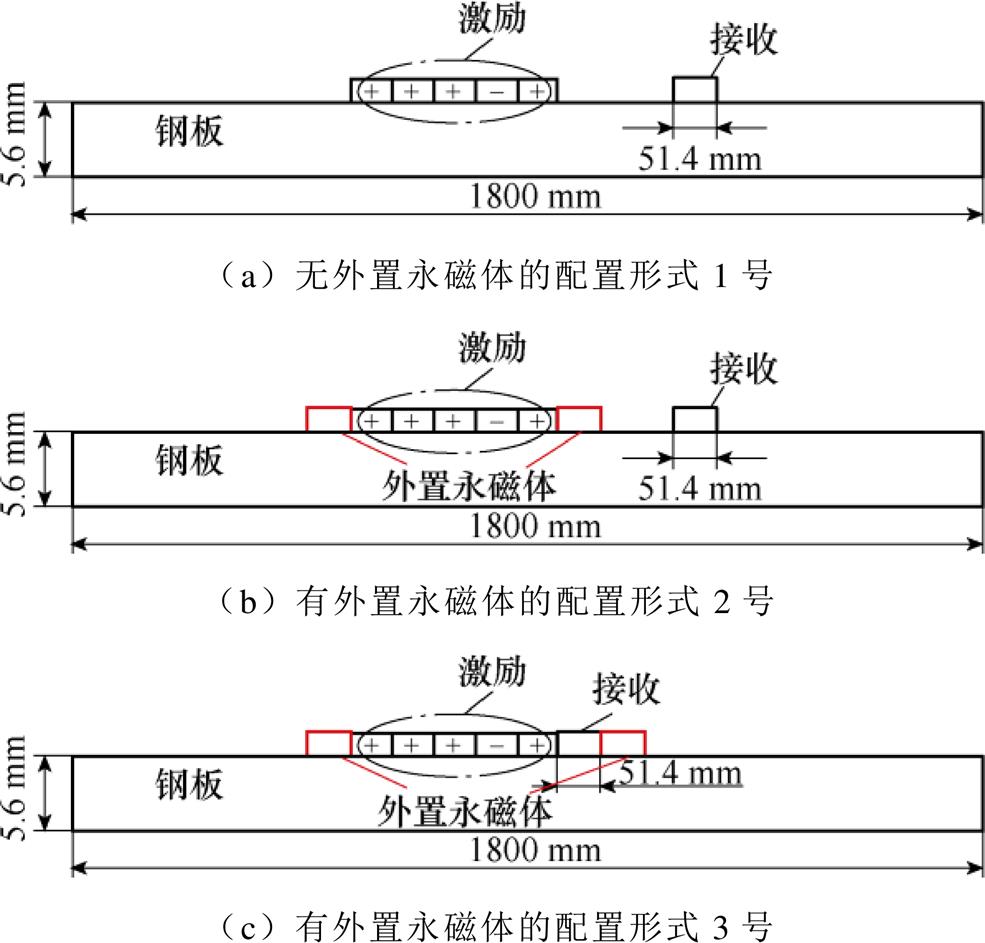
图6 5位阵元EMAT的三种永磁体配置形式示意图
Fig.6 Schematic diagram of three permanent magnet configurations of 5 bit array element EMAT
在多阵元EMAT有限元模型中，当曲折线圈匝数为10匝、tone-burst信号的周期数为8、中心频率为0.24 MHz时，不同永磁体配置形式的多阵元EMAT对应的Lamb波信号、脉压信号和经旁瓣抑制后的脉压信号如图8所示。由图8可知，配置形式2号和配置形式3号的经旁瓣抑制后的脉压信号主旁瓣比（Peak-Side Level, PSL）比配置形式1号分别高出5.85 dB和5.05 dB，说明外置永磁体能够提高经旁瓣抑制后的脉压信号的PSL。配置形式2号的PSL略高于配置形式3号，说明接收EMAT与激励EMAT间隔一定距离可以提高脉压信号的PSL。在线段L（如图3所示）处，三种永磁体配置形式对应的钢板表面磁场分布如图7所示。由图7和图8可知，与配置形式1号相比，配置形式2号通过在5阵元EMAT两侧引入1对永磁体，可以使5阵元激励EMAT中各个阵元（特别是第1阵元和第5阵元）对应的偏置磁场分布更趋于一致，所激励的超声导波波形与Barker码激励信号特征更一致，因此配置形式2号对应的脉冲压缩效果更好。与配置形式2号相比，在配置形式3号中，接收EMAT靠近5阵元激励EMAT，导致接收EMAT对应的偏置磁场出现很大程度的畸变，因此其对应的脉冲压缩效果变差。
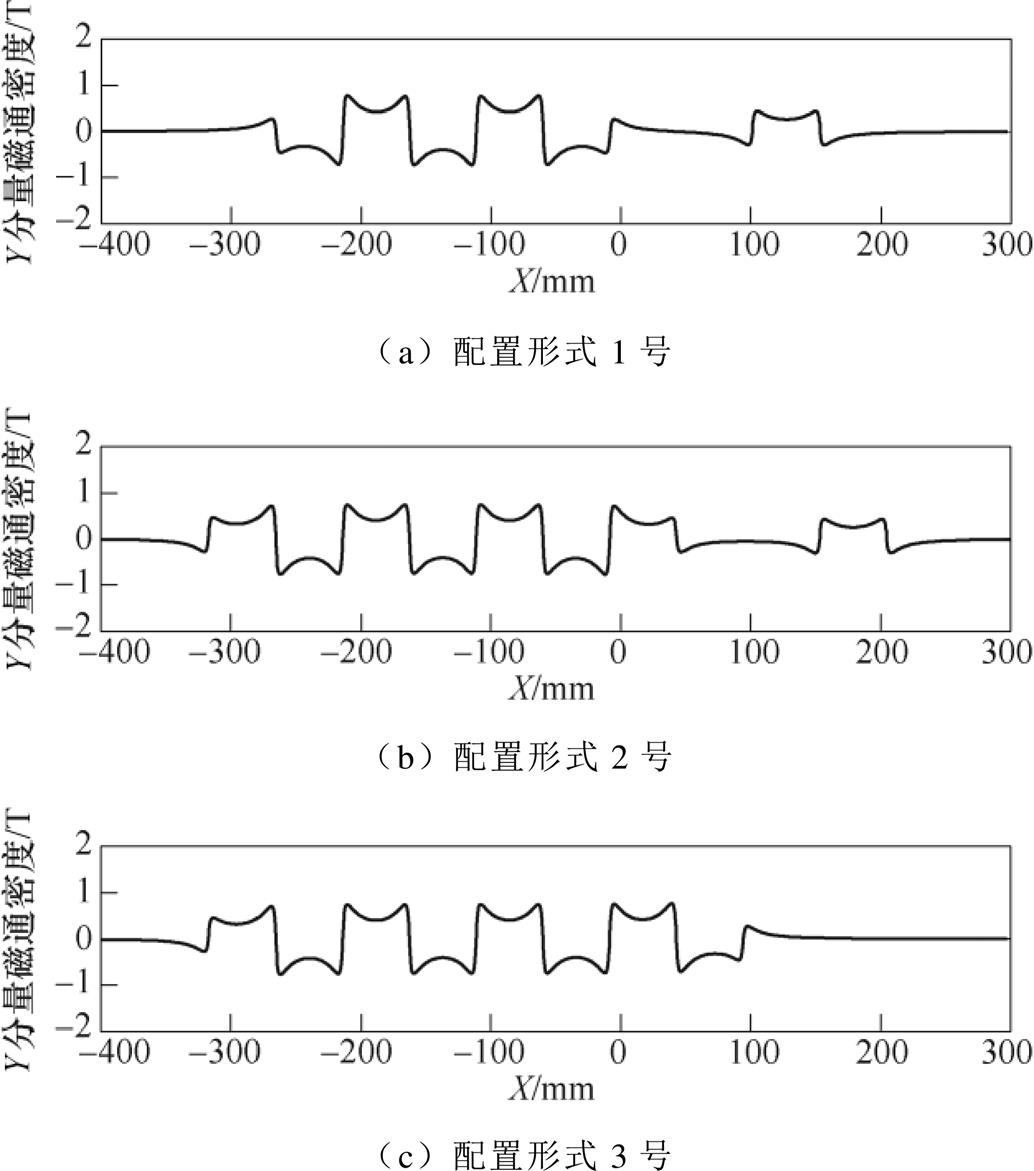
图7 不同永磁体配置形式对应的钢板表面磁场分布
Fig.7 Magnetic field distribution in the steel plate surface corresponding to different permanent magnet configurations
在多阵元Lamb波EMAT有限元模型中，当曲折线圈匝数为10匝、tone-burst信号的周期数为8、中心频率为0.24 MHz时，不同序列长度的多阵元EMAT对应的Lamb波信号、脉压信号和经旁瓣抑制后的脉压信号如图9所示。由图9可知，脉压信号经旁瓣抑制后，PSL可提升11.51～14.74 dB，主瓣宽度由114.42～240.71 ms缩减至70 ms左右，这说明多阵元Lamb波EMAT能提高检测回波的PSL和空间分辨率。当序列长度为5位、7位和13位时，对应的脉冲压缩比分别为1.62、1.95和3.38，PSL分别为29.33 dB、29.72 dB和37.09 dB。序列长度的增加有利于提高多阵元EMAT的脉冲压缩效果。
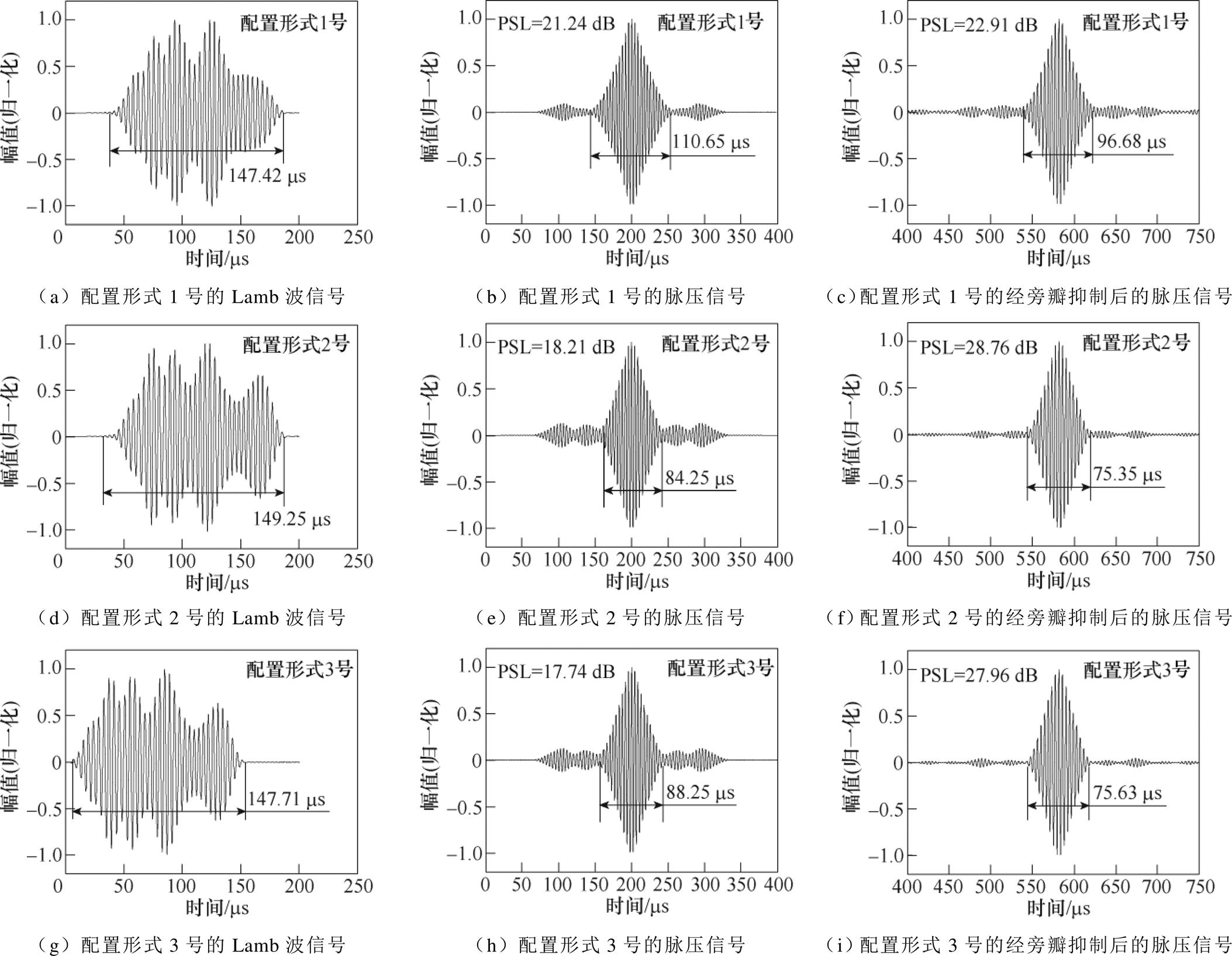
图8 不同永磁体配置形式的Lamb波信号、脉压信号和经旁瓣抑制后的脉压信号
Fig.8 Lamb wave signal, pulse-compressed signal, and the pulse-compressed signal after sidelobe suppression of different permanent magnet configurations
图9 不同序列长度的Lamb波信号、脉压信号和经旁瓣抑制后的脉压信号
Fig.9 Lamb wave signal, pulse-compressed signal, the pulse-compressed signal after sidelobe suppression with different sequence lengths
图10为不同阵元间距对应的钢板表层电涡流密度分布。由图10可知，当改变阵元间距时，第一阵元和第二阵元相邻导线对应的电涡流幅值基本不变（偏差在3%以内），同时第四阵元和第五阵元相邻导线对应的电涡流幅值也基本不变（偏差在2%以内），由此可见，阵元间距对钢板表层电涡流密度分布的影响可以忽略不计。图11为不同阵元间距对应的钢板表面磁场分布，图12为不同阵元间距的Lamb波信号、脉压信号和经旁瓣抑制后的脉压信号，从图11和图12可以看出，随着阵元间距的增加，其钢板表面磁场分布逐渐发生畸变，各个阵元对应的磁场分布越来越不一致，因此经旁瓣抑制后的脉压信号的PSL随着阵元间距的增加逐渐减小，阵元间距10 mm和阵元间距20 mm对应的PSL相较于阵元间距0 mm分别减小了5.42 dB和6.8 dB。考虑到多阵元Lamb波EMAT的体积在实际应用过程中的影响，其阵元间距越小越好。可知，当tone-burst激励信号的周期数为2、5、8、11、14、17时，对应的主瓣宽度逐渐增加，而PSL呈先增长后降低的趋势。周期数为8的tone-burst信号对应的PSL最大，为31.16 dB，此时主瓣宽度较小，为80.65 ms，即不会对信号的空间分辨率产生较大影响，因此多阵元EMAT的tone-burst激励信号的周期数最佳值为8。
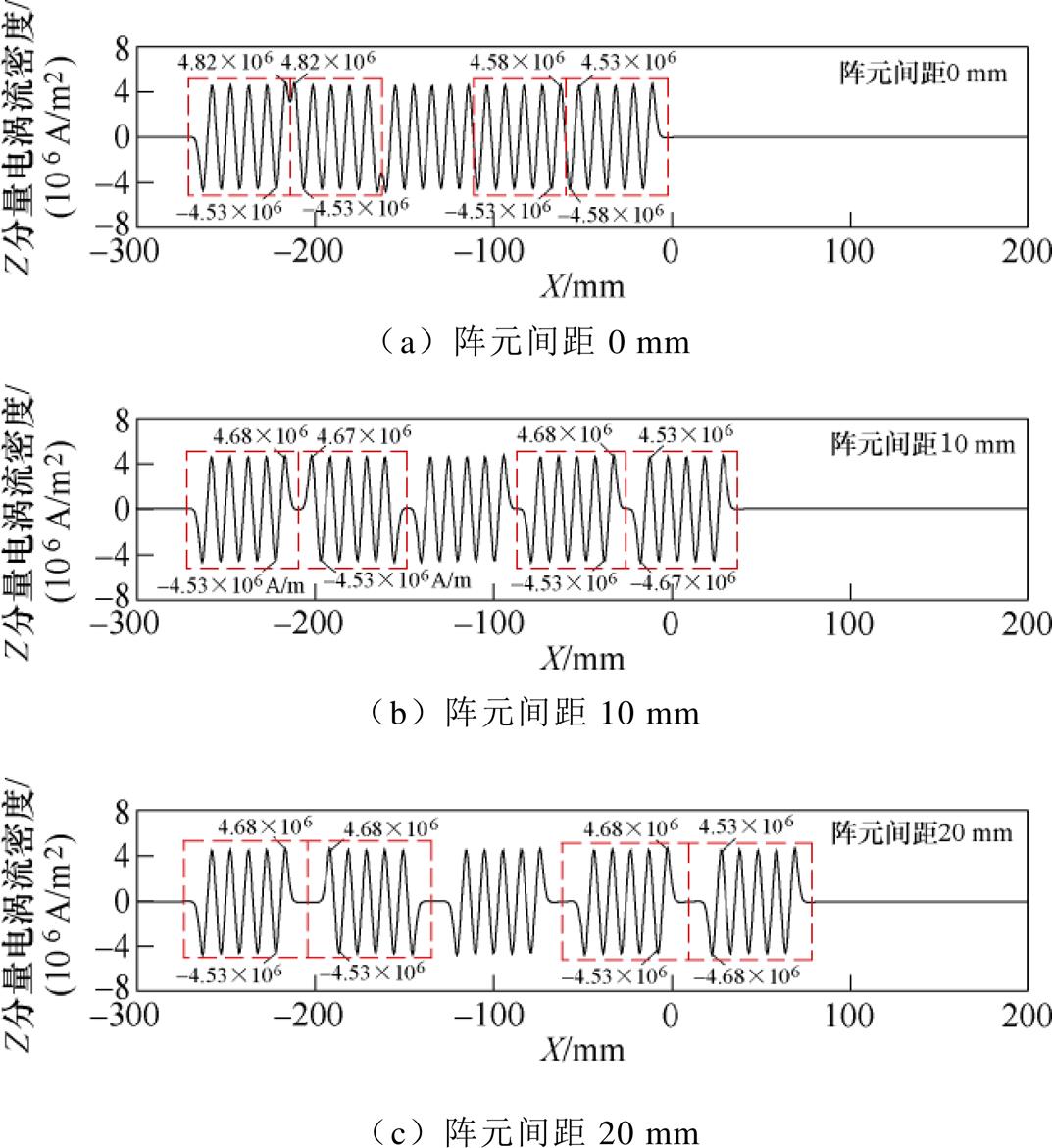
图10 不同阵元间距对应的钢板表层电涡流密度分布
Fig.10 Eddy current density distribution of steel plate surface corresponding to different array element spacing
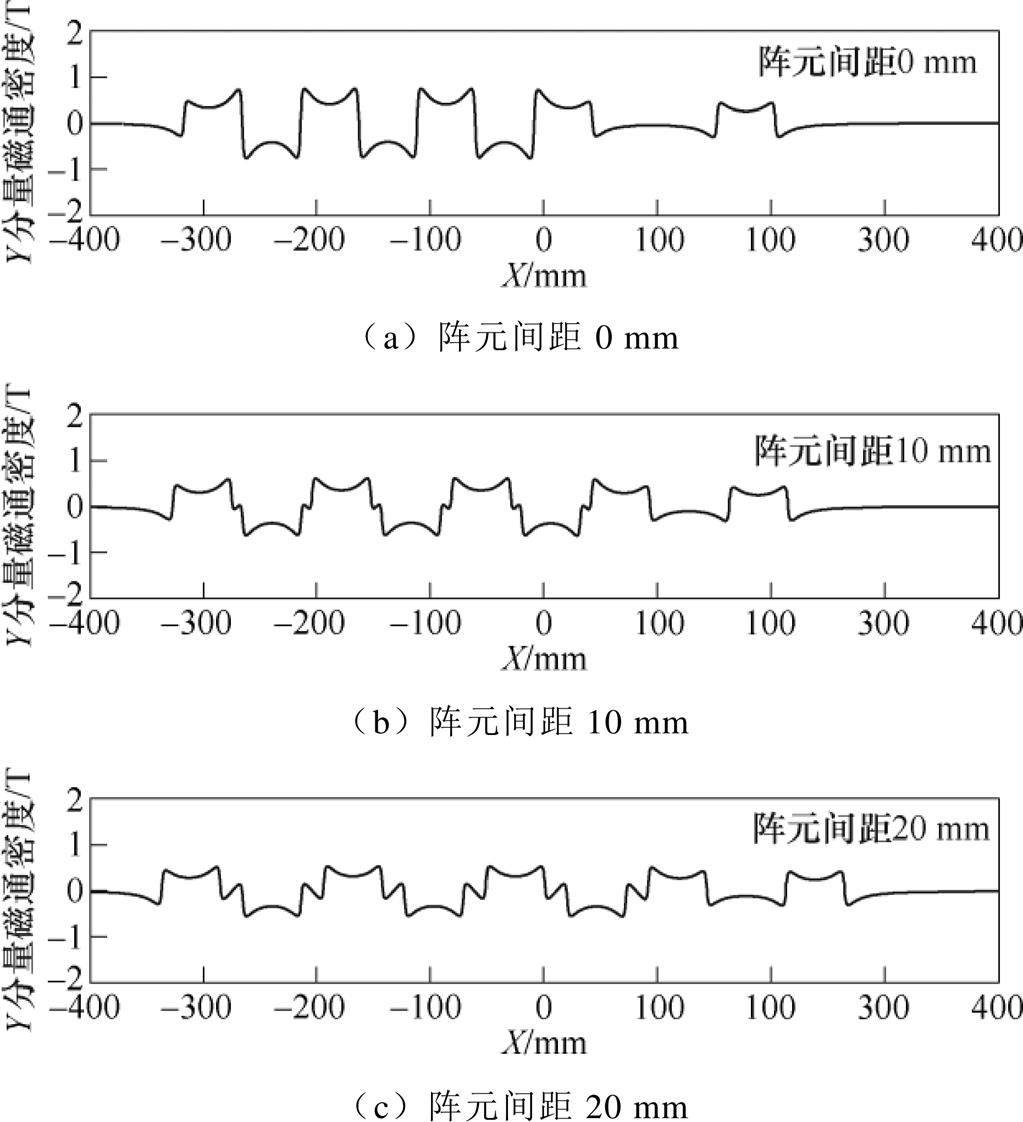
图11 不同阵元间距对应的钢板表面磁场分布
Fig.11 Magnetic field distribution in the steel plate surface corresponding to different array element spacing
采用不同周期数的tone-burst激励信号，得到的经旁瓣抑制后的脉压信号如图13所示。由图13
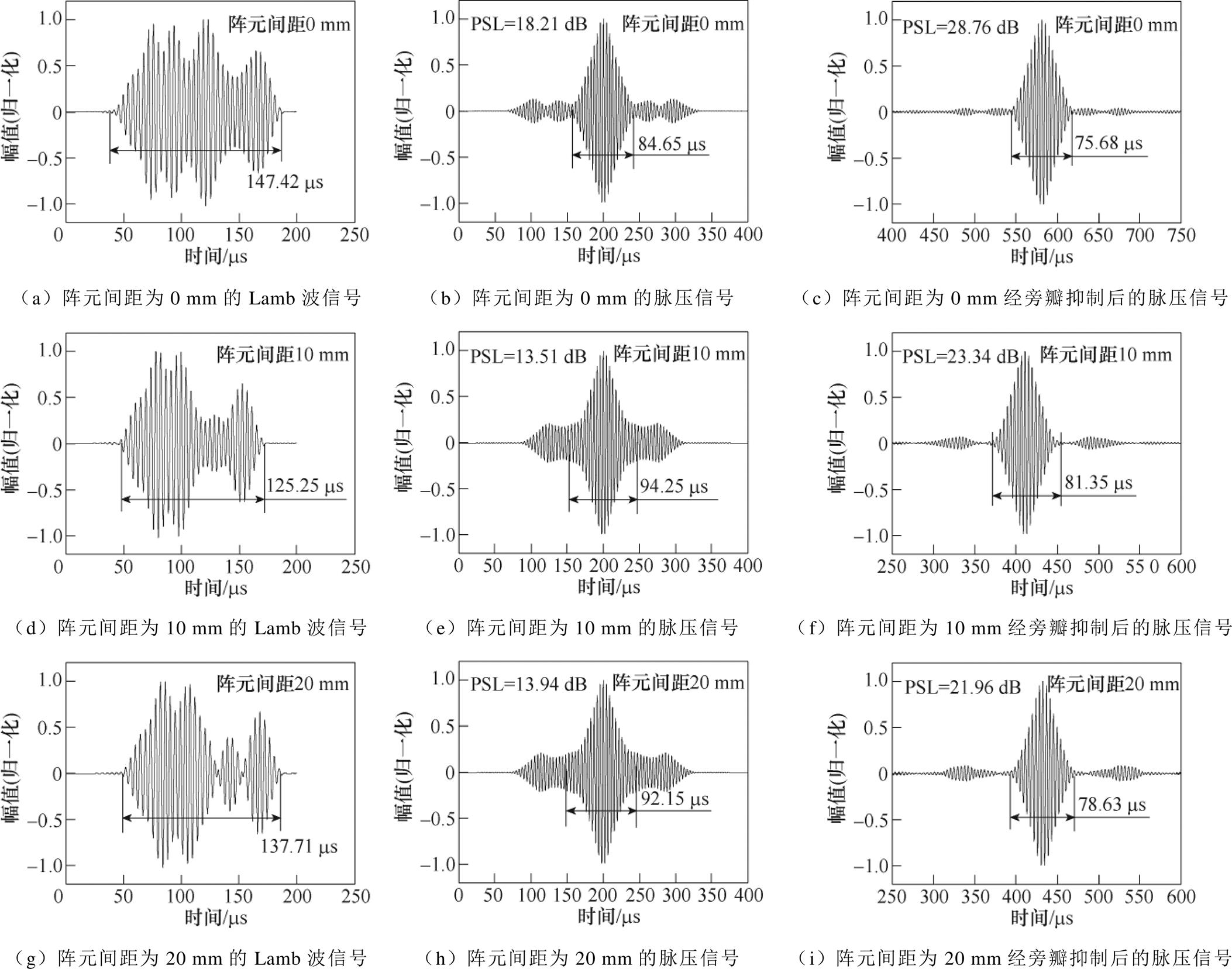
图12 不同阵元间距的Lamb波信号、脉压信号和经旁瓣抑制后的脉压信号
Fig.12 Lamb wave signal, pulse-compressed signal, the pulse-compressed signal after sidelobe suppression with different array element spacing
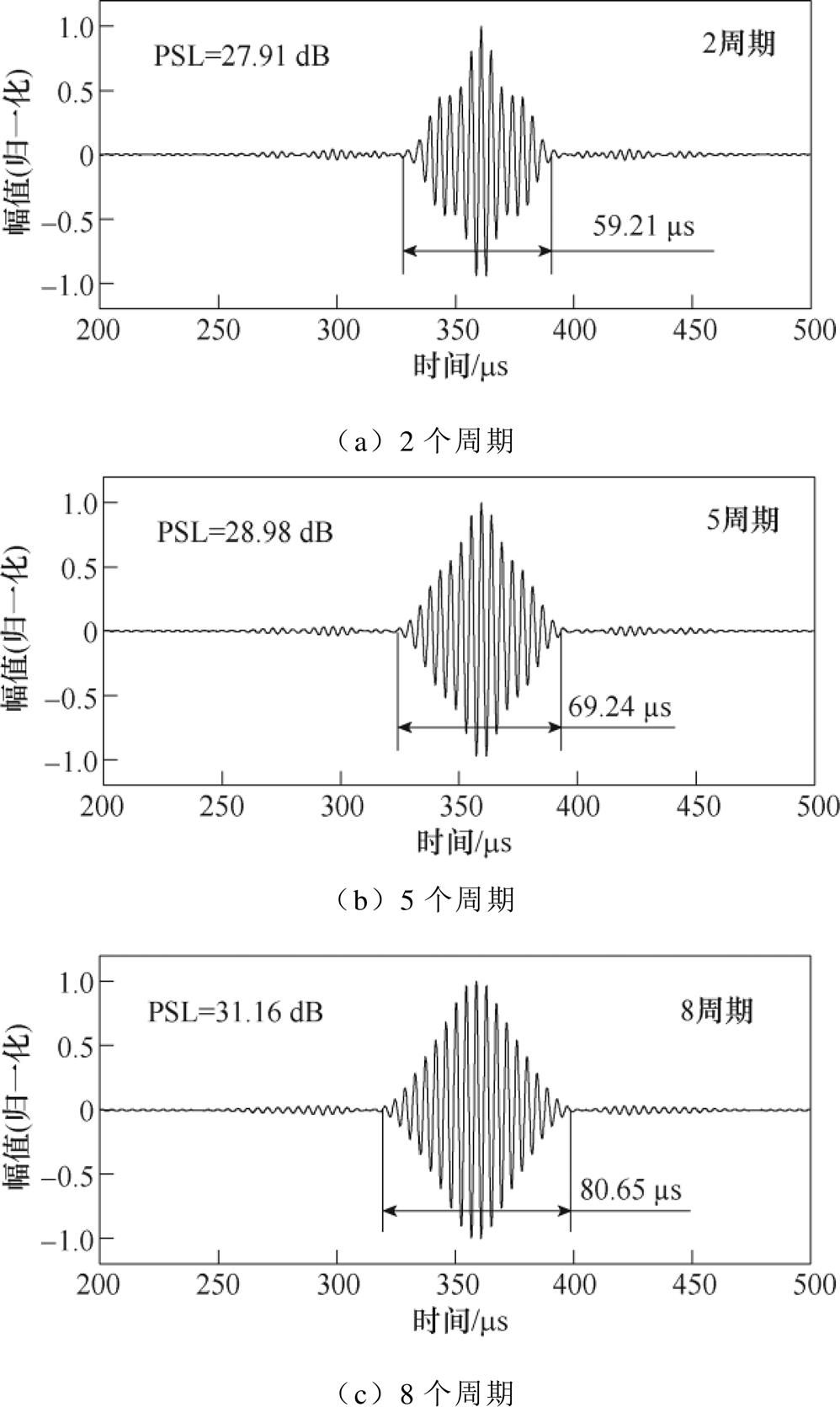
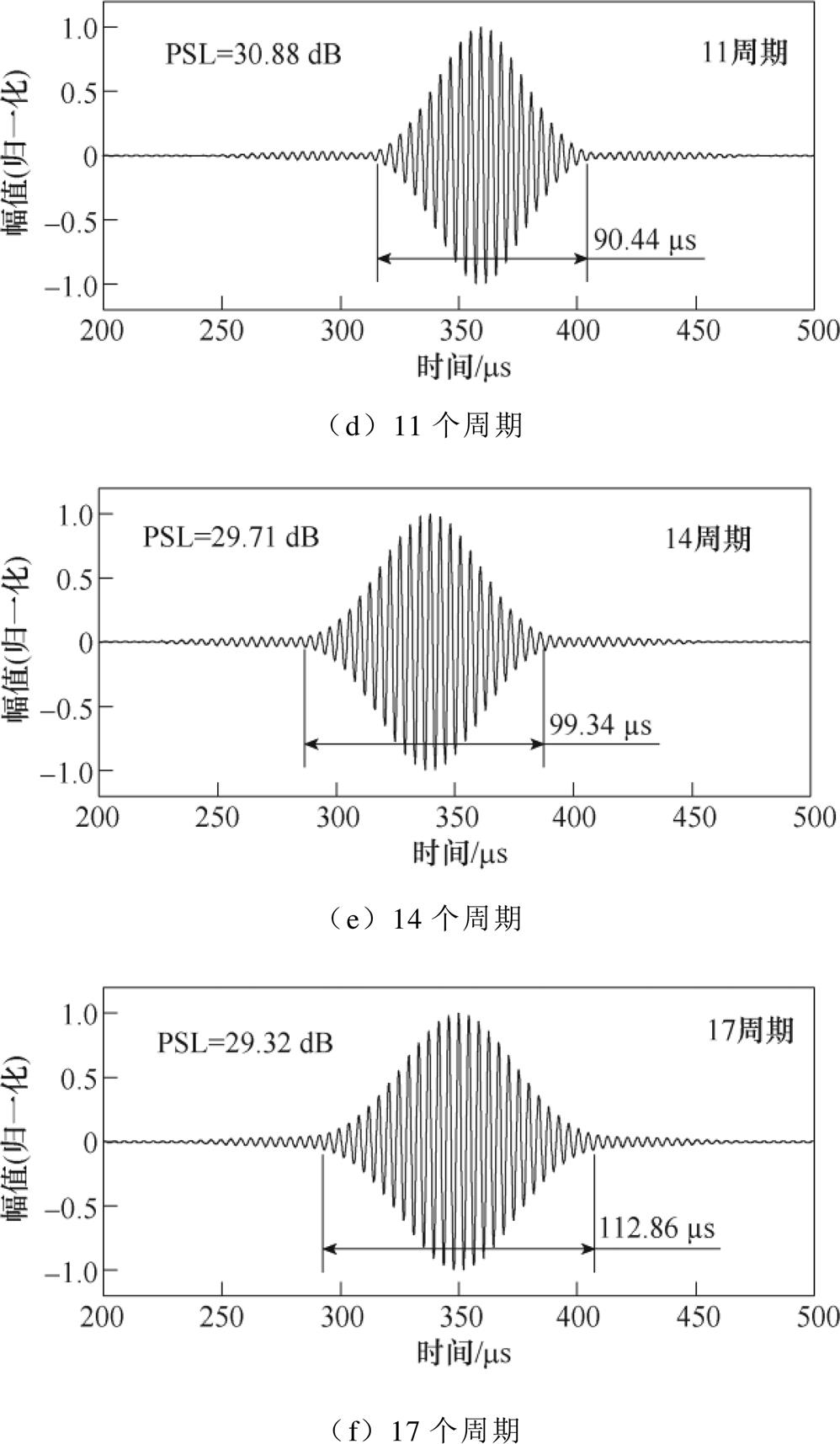
图13 不同tone-burst信号周期数对应的经旁瓣抑制后的脉压信号
Fig.13 Pulse-compressed signal after sidelobe suppression corresponding to different numbers of cycles of the tone-burst signal
曲折线圈匝数不仅会影响Lamb波信号的强度，还会使延时时间发生改变，从而在对Barker码形式的Lamb信号进行旁瓣抑制时，影响其抑制效果。曲折线圈匝数的变化还会影响EMAT的体积大小，从而限制其在现场检测中的应用。分别将曲折线圈匝数设置为4、6、8和10匝，对应的经旁瓣抑制后的脉压信号如图14所示。由图14可知，曲折线圈匝数增加后，经旁瓣抑制后的脉压信号的主瓣宽度和PSL均有不同变化。当曲折线圈匝数为4、6、8和10匝时，4匝对应的PSL最大，为39.41 dB，主瓣宽度最小，为46.41 ms，因此，多阵元EMAT的曲折线圈匝数最佳值为4。
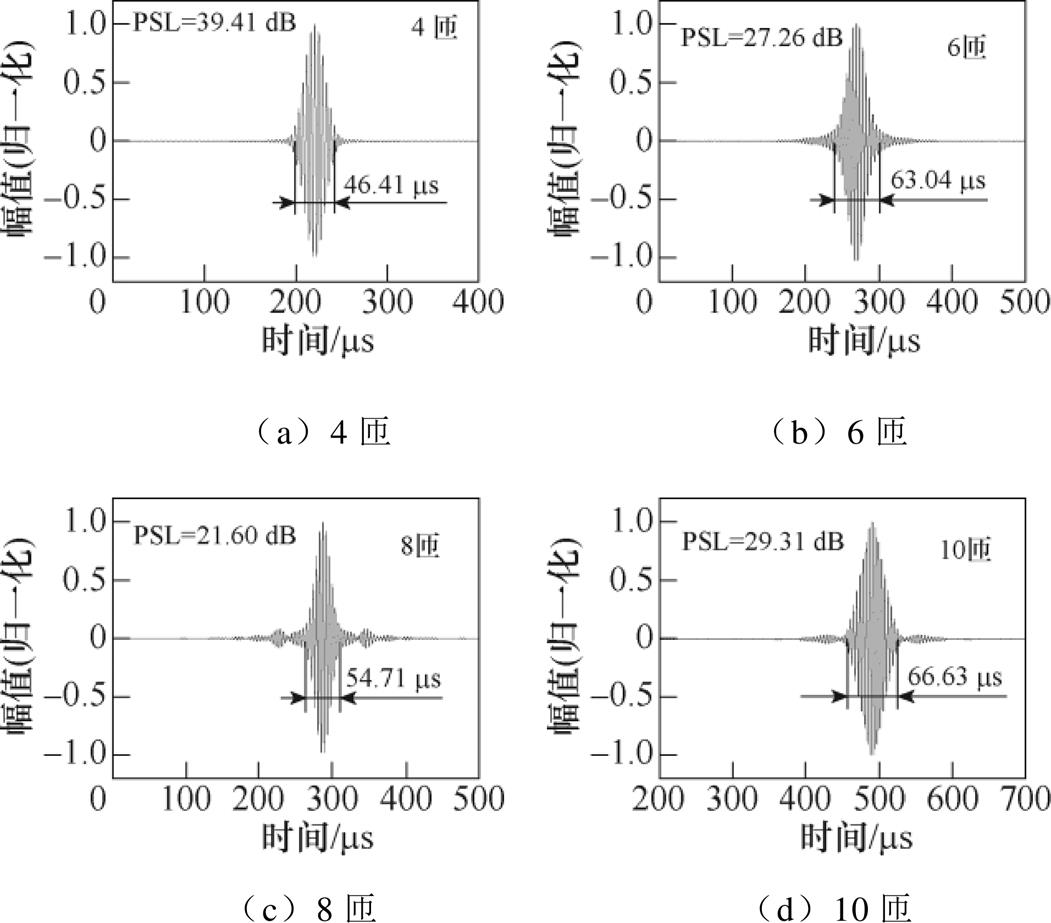
图14 不同线圈匝数对应的经旁瓣抑制后的脉压信号
Fig.14 Pulse-compressed signal after sidelobe suppression corresponding to different coil turns
基于Barker码脉冲压缩技术的钢板多阵元Lamb波EMAT检测实验系统如图15所示。同时，图15还提供了永磁体和曲折线圈的设计参数。信号发生器产生中心频率为0.24 MHz的tone-burst信号，经功率放大器和激励端阻抗匹配器，得到大幅值高频的激励电流，在通过多阵元Lamb波EMAT，激发出Barker码形式Lamb波。Lamb波信号由单阵元EMAT接收，接收到的信号经接收端阻抗匹配器、带通滤波器，后由前置放大器进行放大，再经数据采集卡模数转换后，可在PC上实现数据显示和存储。序列长度是5位的多阵元EMAT示意图如图15所示，试样为45号钢钢板，其长、宽、高分别为1 800 mm、1 200 mm和5.6 mm。
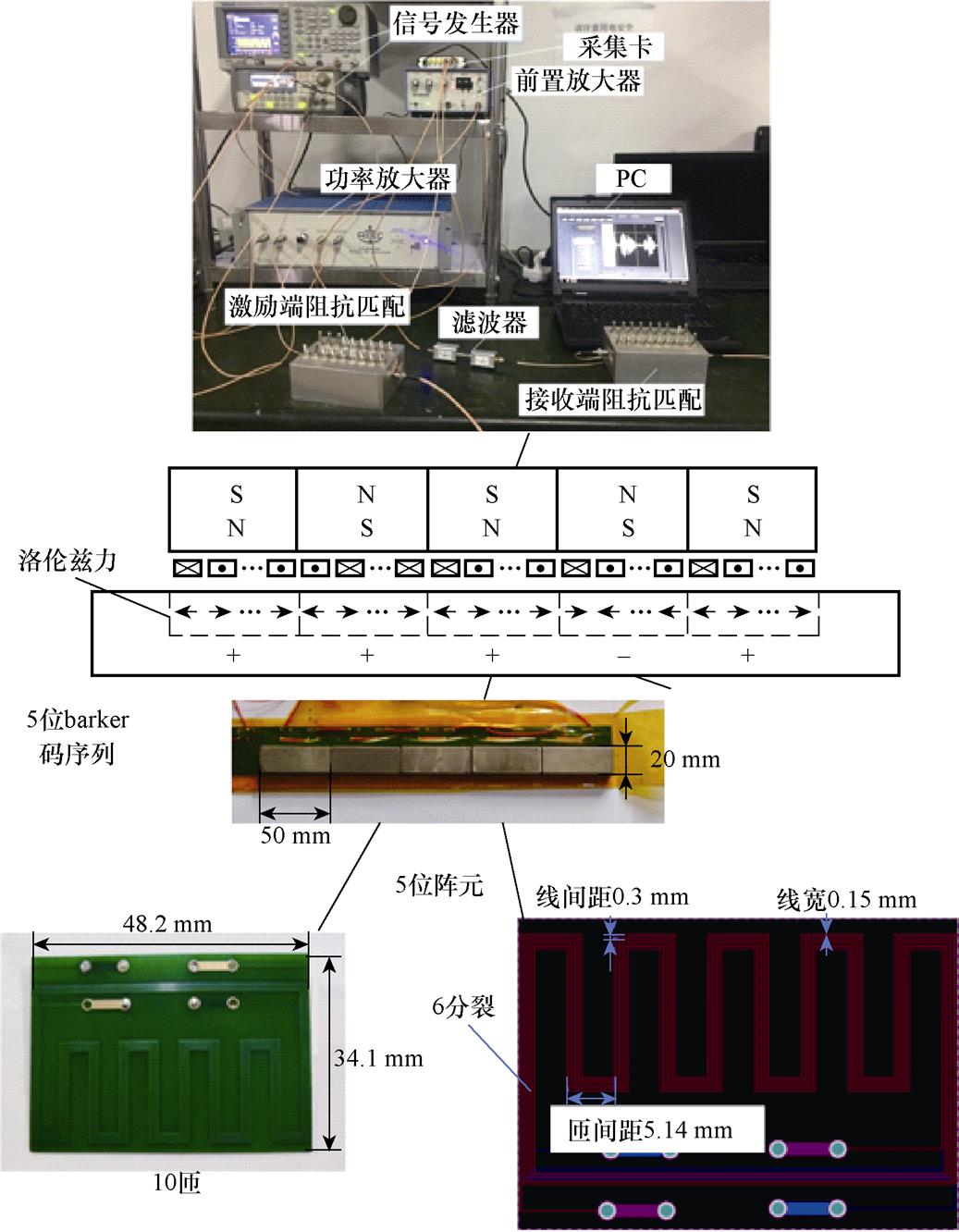
图15 多阵元Lamb波EMAT检测实验系统
Fig.15 Multi-element Lamb wave EMAT experimental system
实验中采用的三种永磁体的配置形式如图6所示，分别采用4匝和10匝曲折线圈配合方形永磁体作为5位和13位多阵元EMAT的单个阵元。图16为有外置永磁体的配置形式3号得到超声波信号。由图16可知，有外置永磁体的配置形式3号并不能获取较好的检测信号。由图7可知，与配置形式2号和配置形式1号相比，在配置形式3号中，由于接收EMAT靠近5阵元激励EMAT，接收EMAT对应的偏置磁场出现很大程度的畸变，因此其对应的脉冲压缩效果最差。
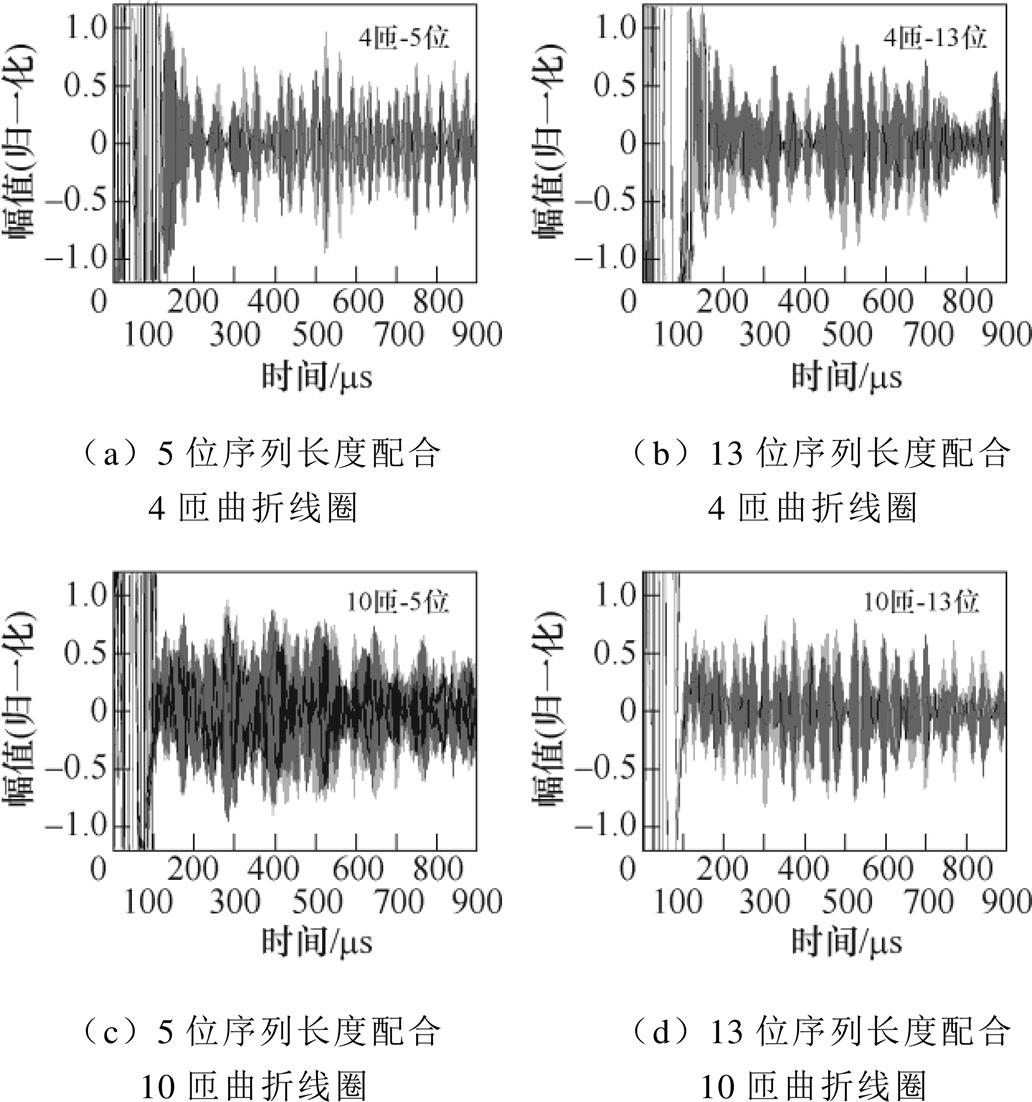
图16 有外置永磁体的配置形式3号对应的超声信号
Fig.16 Ultrasonic signal corresponding to configuration 3号 with external permanent magnets
无外置永磁体的配置形式1号和有外置永磁体的配置形式2号得到的超声波信号如图17所示。由图17可知，这两种配置形式均能得到清晰的直达波，且能分辨直达波与端面回波。直达波经过旁瓣抑制后的脉压信号如图18所示，在多阵元EMAT增加外置永磁体后，与无外置永磁体相比，5位序列长度配合10匝曲折线圈、13位序列长度配合10匝曲折线圈、5位序列长度配合4匝曲折线圈对应的直达波SNR分别提高了7.41 dB、0.4 dB、1.89 dB。通过设置外置永磁体，能够提高经旁瓣抑制后脉压信号的信噪比。
由图18可知，当多阵元Lamb波EMAT为5位序列时，采用10匝曲折线圈对应无外置永磁体和1对外置永磁体的SNR较采用4匝曲折线圈对应的SNR分别提高了0.06 dB、5.58 dB，说明10匝线圈较4匝线圈能取得更好的信噪比。当多阵元Lamb波EMAT采用10匝线圈时，采用13位序列对应无外置永磁体和采用1对外置永磁体对应的SNR较采用5位序列对应的SNR分别提高了9.17 dB、2.16 dB。说明13位序列较5位序列能取得更好的信噪比。综上所述，对于多阵元EMAT，曲折线圈匝数应选择10，Barker序列长度应选择13位。
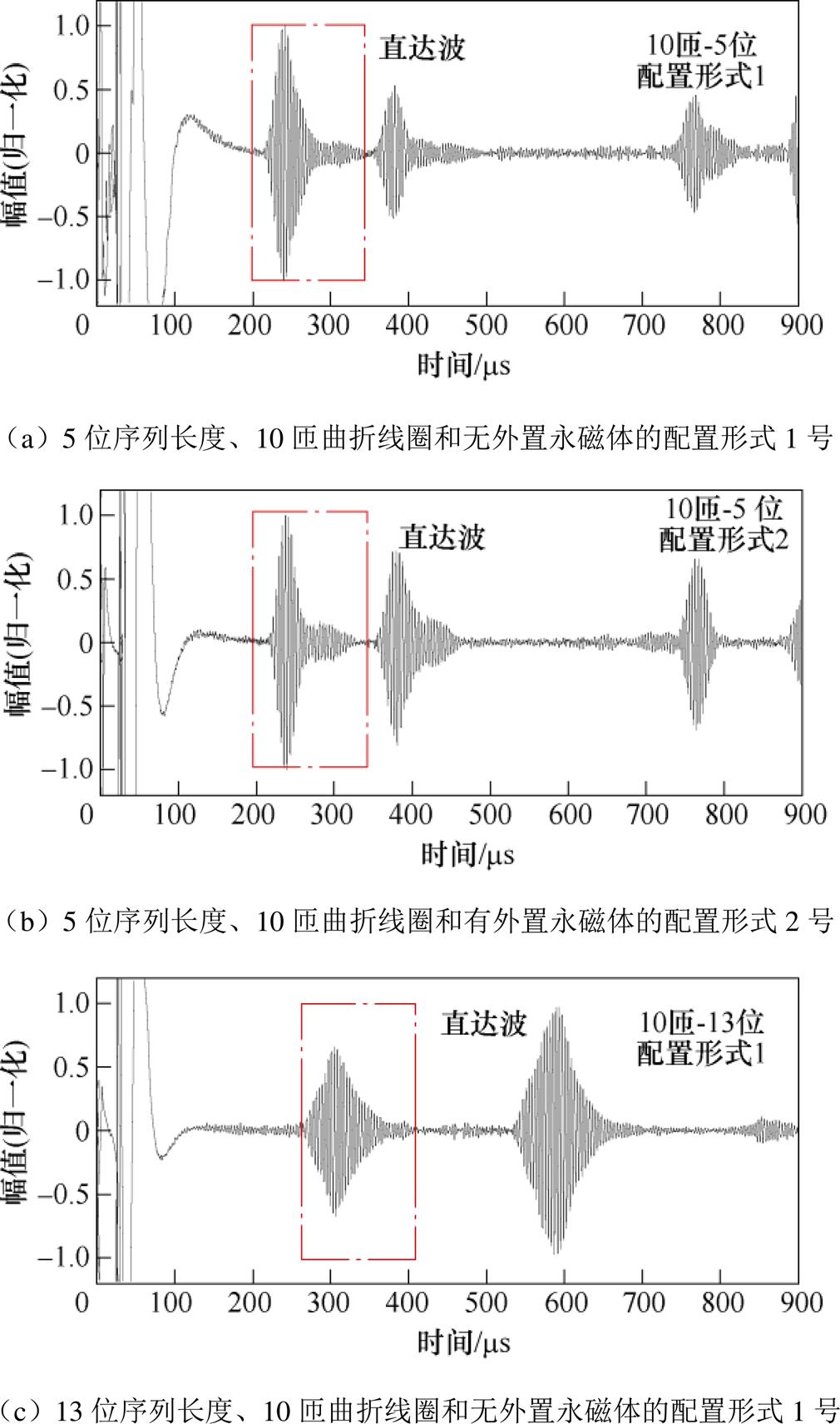
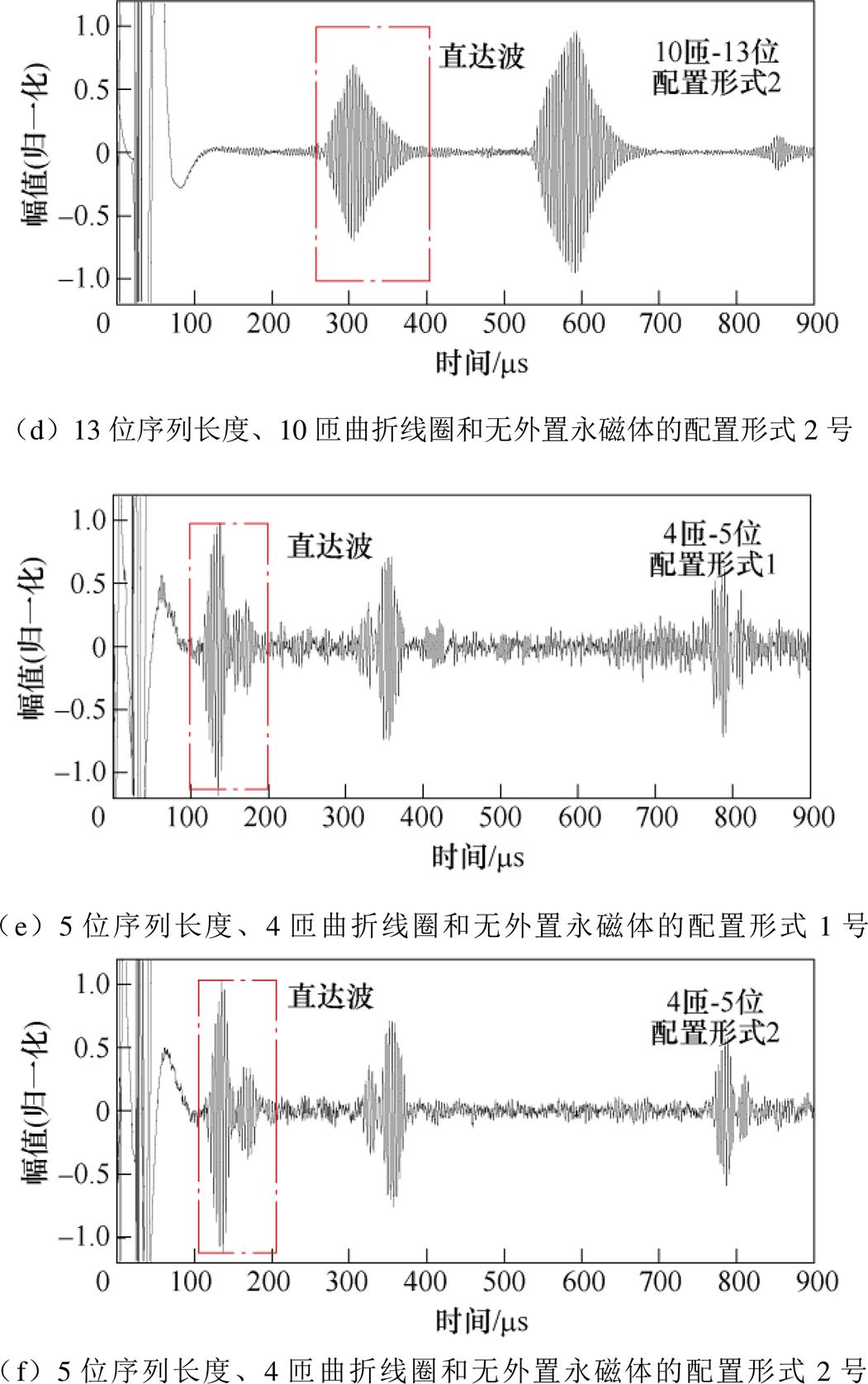
图17 无外置永磁体的配置形式1号和有外置永磁体的配置形式2号的超声波信号
Fig.17 Ultrasonic signal of configuration 1# without external permanent magnet and configuration 2# with external permanent magnets
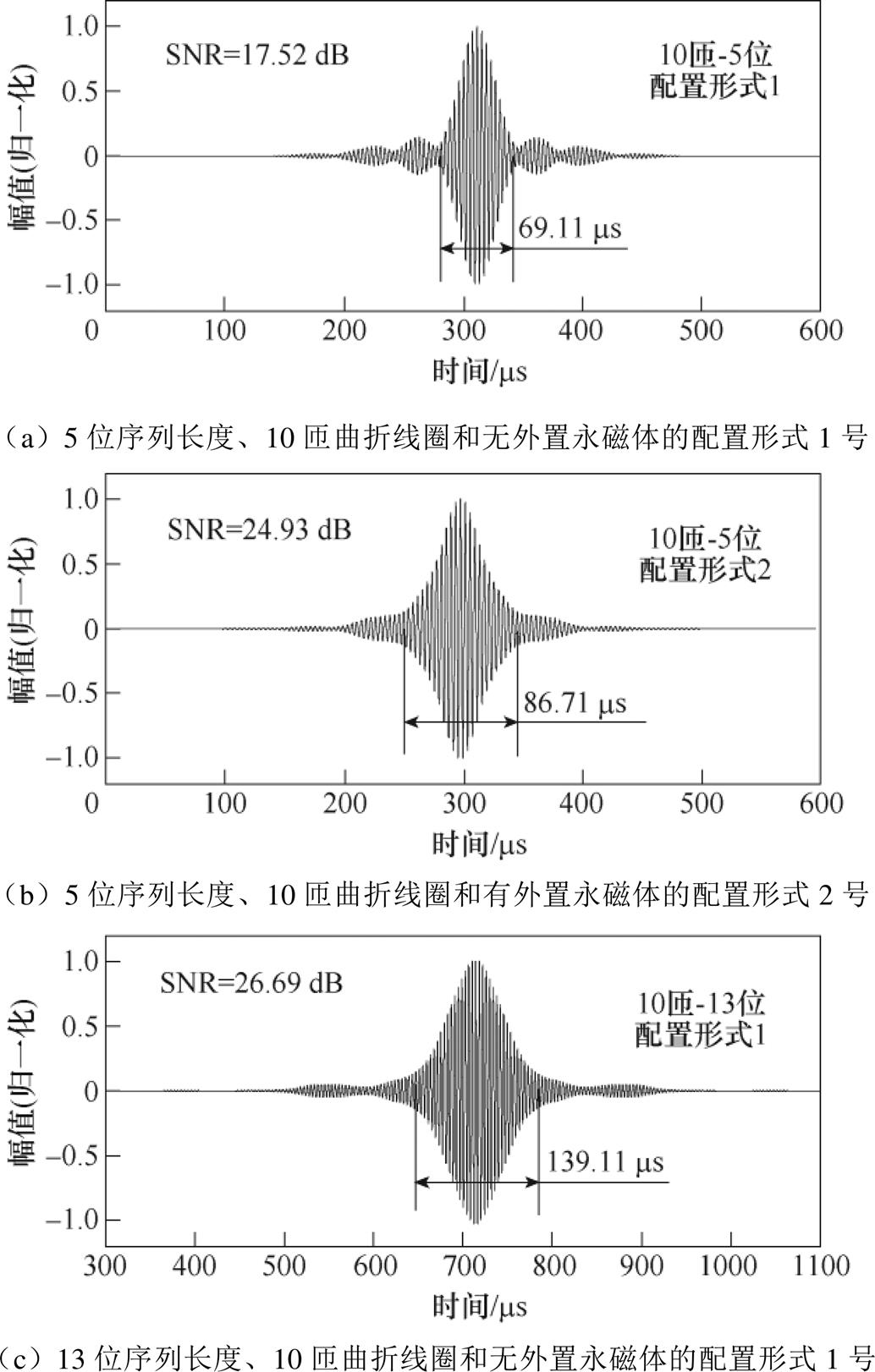
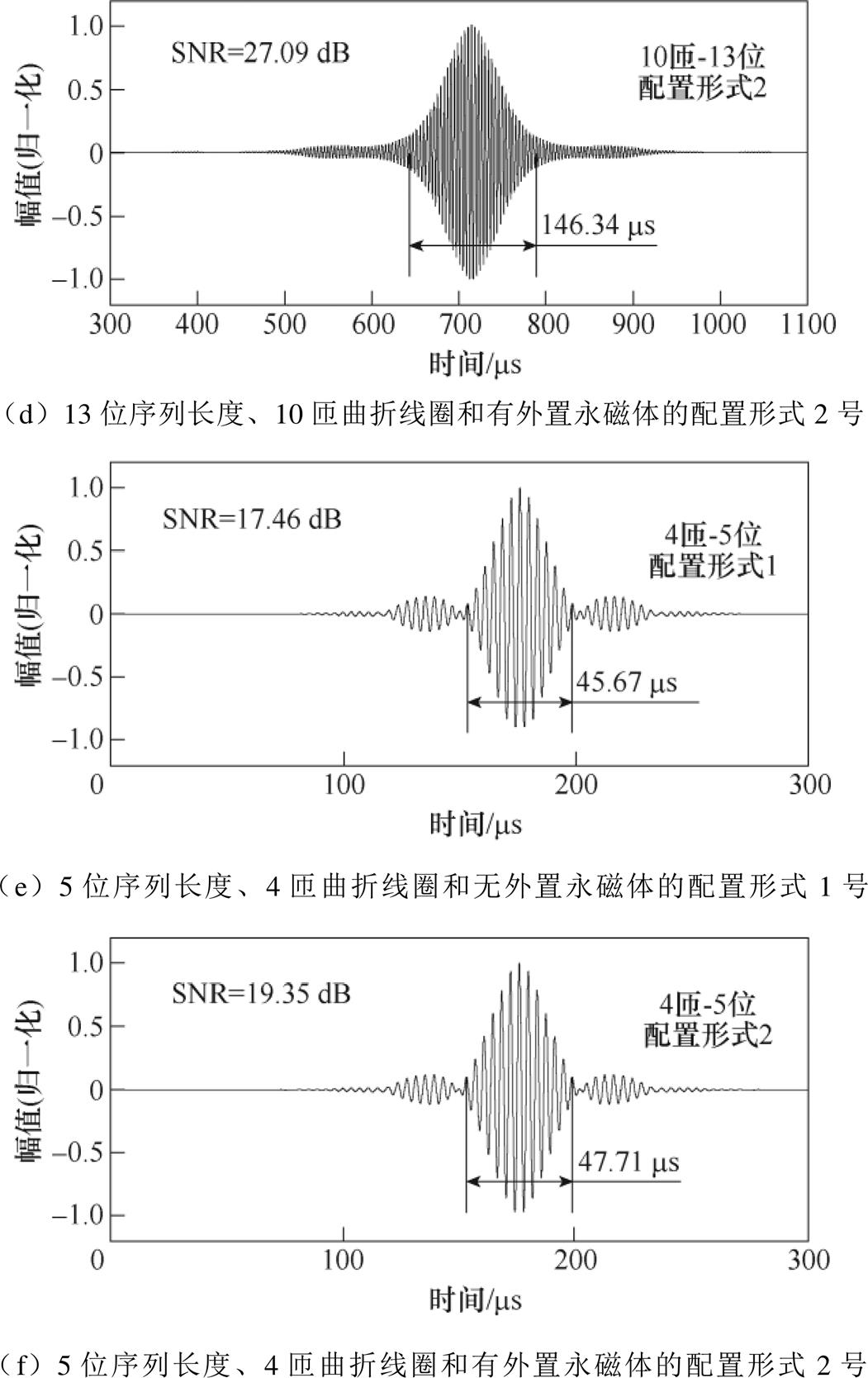
图18 无外置永磁体的配置形式1号和有外置永磁体的配置形式2号对应的经旁瓣抑制后的脉压信号
Fig.18 Pulse-compressed signal after sidelobe suppression corresponding to configuration 1# without external permanent magnets and configuration 2# with external permanent magnets
对于13位序列长度配合4匝曲折线圈的多阵元EMAT来说，其脉冲压缩效果并不理想，考虑通过设置多对外置永磁体，使其内部偏置磁场更加均匀，得到的超声波信号如图19所示。经过旁瓣抑制后的脉压信号如图20所示，可以看出，随着外置永磁体数量逐渐增加，其信噪比也逐渐提高，1对、2对和3对外置永磁体对应的SNR较无外置永磁体的SNR分别提高了0.78 dB、8.66 dB和9.8 dB。这说明采用多对外置永磁体，可以显著提高经旁瓣抑制后脉压信号的信噪比。虽然外置永磁体的对数增加后能够显著提高信噪比，但同时也会增加探头的体积，体积过大会在现场检测中受到极大的限制，实际应用也十分困难，因此外置永磁体的对数选择应综合考虑实际需求。
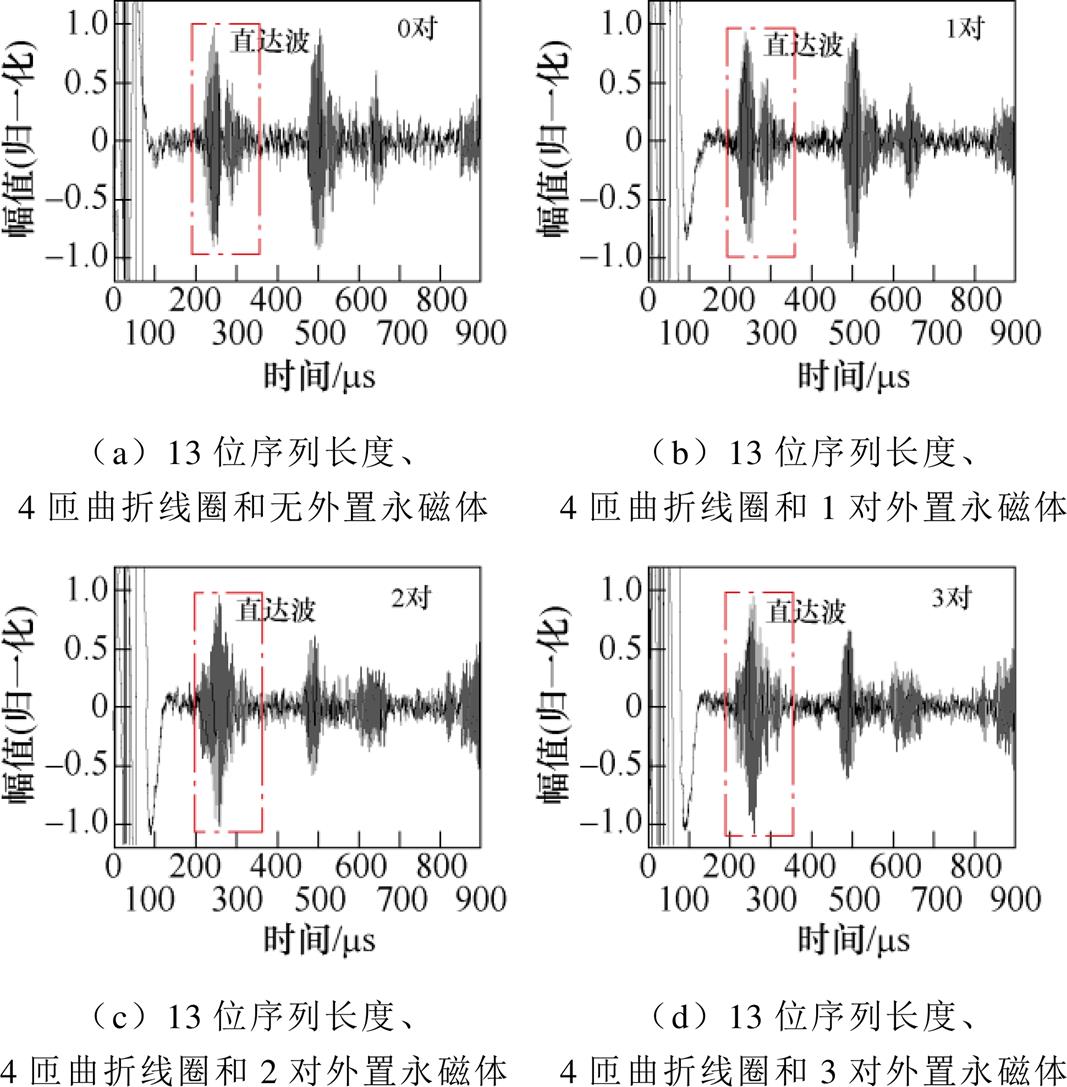
图19 13位序列长度和4匝曲折线圈多阵元EMAT配置不同对数的外置永磁体对应的超声波信号
Fig.19 Ultrasonic signals corresponding to 13 bit sequence length and 4-turn meander line coil multiple array element EMAT with external permanent magnets of different pairs
将不同周期数的tone-burst激励信号分别通入13位序列长度配置10匝曲折线圈的多阵元EMAT，经过旁瓣抑制后的脉压信号如图21所示。随着tone-burst激励信号周期数的增加，经旁瓣抑制后的脉压信号主瓣宽度呈不断增加的趋势，SNR呈先增加后减小的趋势。综合考虑到检测所需的空间分辨率和SNR，应选取11周期的tone-burst信号，对应的主瓣宽度不超过120 ms、SNR＞35 dB。
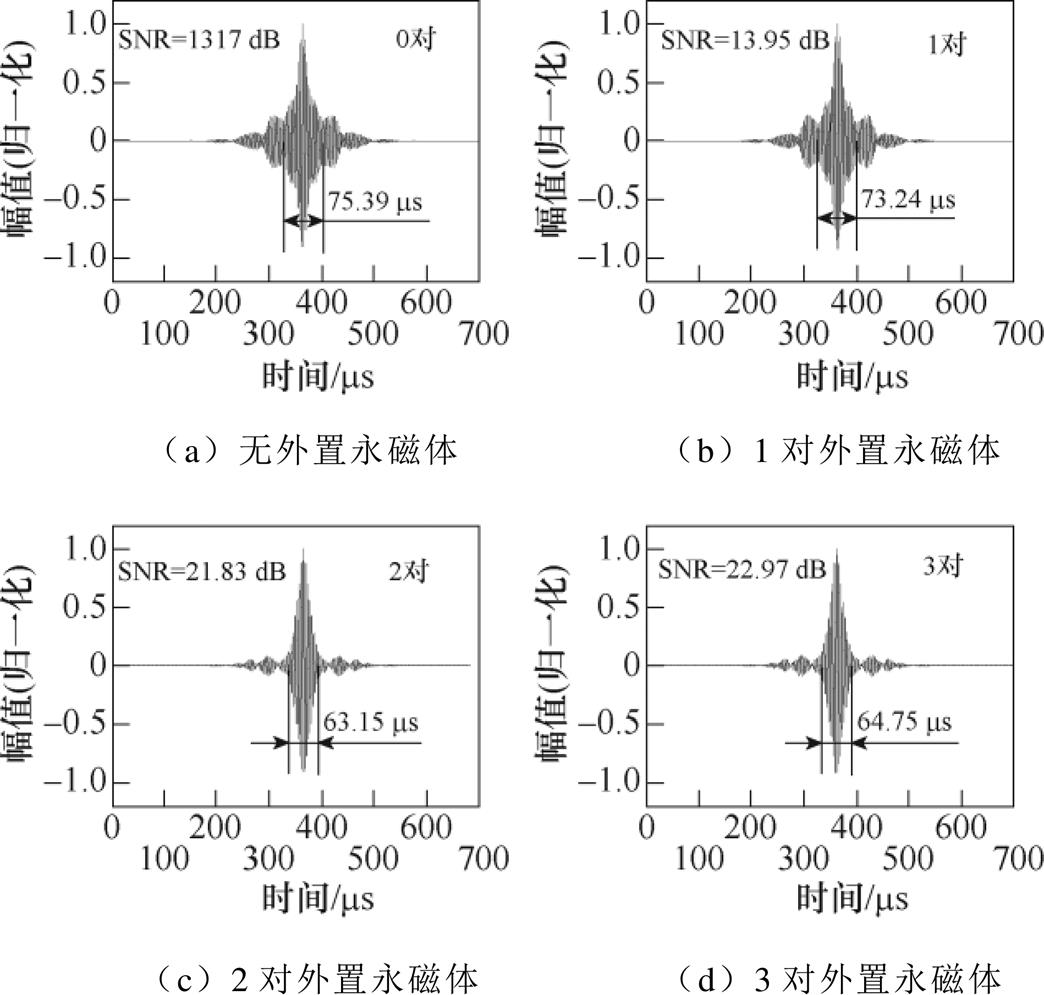
图20 13位序列长度和4匝曲折线圈多阵元EMAT配置不同对数的外置永磁体得到的经旁瓣抑制后的脉压信号
Fig.20 Pulse-compressed signal after sidelobe suppression obtained by 13 bit sequence length and 4-turn meander line coil multiple array element EMAT with external permanent magnets of different pairs
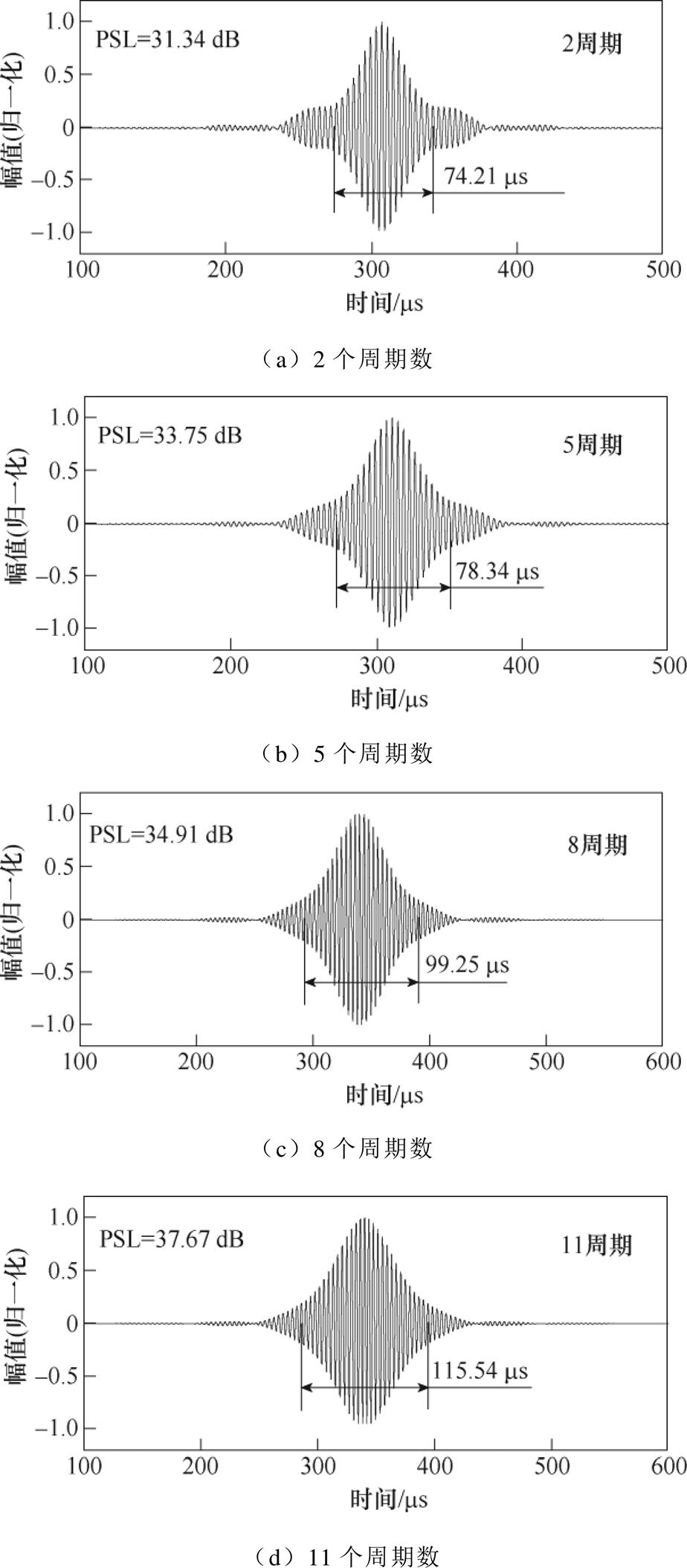
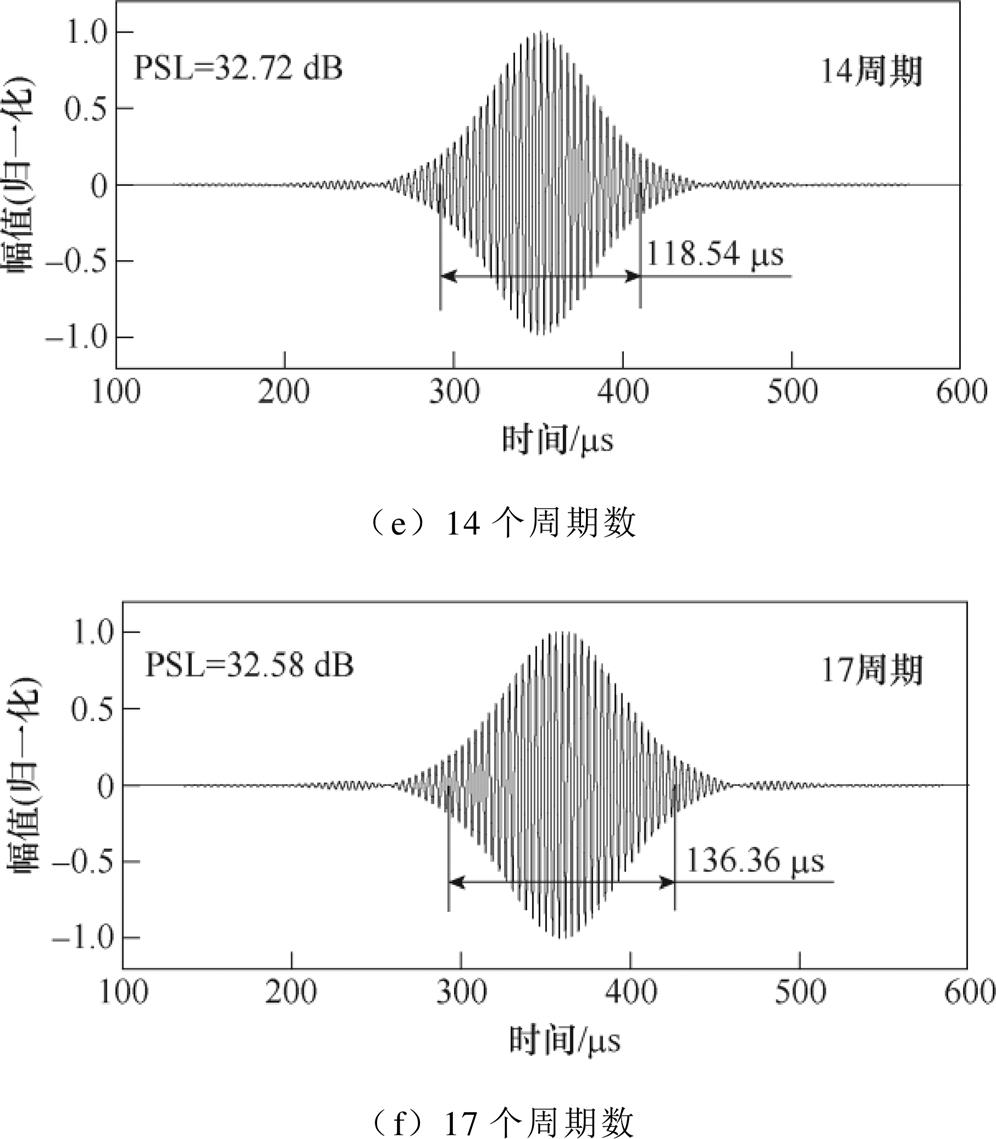
图21 不同周期数的tone-burst激励时经旁瓣抑制后的脉压信号
Fig.21 Pulse-compressed signals after sidelobe suppression when the tone-burst signal with different cycles is used
1）本研究所设计的新型多阵元EMAT，在通入一定周期、频率的tone-burst信号后，根据多阵元EMAT换能机理，能够成功激励出Barker码编码形式的Lamb波。Lamb波信号经过脉冲压缩后，通过计算延时时间并进行旁瓣抑制，可有效地抑制旁瓣。采用基于tone-burst信号激励-Barker码脉冲压缩技术的多阵元Lamb波EMAT可以同时提高超声波信号的信噪比和空间分辨率。
2）在配置了一对外置永磁体的情况下，采用激励EMAT和接收EMAT靠近这一方案时，无法获取良好的超声波信号。采用激励EMAT和接收EMAT间隔一定距离这一方案，能够得到清晰的超声波信号。通过设置外置永磁体，能够提高经旁瓣抑制后脉压信号的SNR；增加外置永磁体对数可以显著提高经旁瓣抑制后脉压信号的SNR。
3）随着激励信号周期数的增加，经旁瓣抑制后的脉压信号主瓣宽度呈不断增加的趋势，检测回波SNR呈先增加后减小的趋势。综合考虑到检测回波的空间分辨率和SNR，多阵元Lamb波EMAT最佳参数为：曲折线圈匝数为10、激励信号周期数为11、Barker序列为13位，并配置3对外置永磁体。
4）将本研究应用于其他厚度的金属板或管的导波检测时，需要保证各个阵元的间距一致，这是脉冲压缩能否成功的关键。阵元间距的一致度越高，其超声波信号的脉冲压缩效果越好。此外，需要保证各个阵元磁场分布的均匀性和一致性，将有利于提高脉冲压缩效果。
参考文献
[1] Vakhguelt A, Kapayeva S D, Bergander M J. Com- bination non-destructive test (NDT) method for early damage detection and condition assessment of boiler tubes[J]. Procedia Engineering, 2017, 188: 125- 132.
[2] 郭俊营, 李忠诚, 李文旭, 等. 美国在役核电厂安全壳钢衬里锈蚀及修复技术研究进展[J]. 建筑结构, 2022, 52(3): 127-134.
Guo Junying, Li Zhongcheng, Li Wenxu, et al. Research progress on corrosion and repair technology of steel linear of containment in US external nuclear power plants[J]. Building Structure, 2022, 52(3): 127-134.
[3] Mažeika L, Raišutis R, Jankauskas A, et al. High sensitivity ultrasonic NDT technique for detecting creep damage at the early stage in power plant steels[J]. International Journal of Pressure Vessels and Piping, 2022, 196: 104613.
[4] Yu Shuo, Jin Hao, Cao Miaofeng. Study on corrosion characteristic of semi-ring steel plate for strength- ening shield tunnel under DC stray current[J]. Con- struction and Building Materials, 2022, 347: 128631.
[5] Su Sanqing, Wang Pu, Shi Pengpeng, et al. Experi- ment and simulation on testing steel plate with corrosion defects via magnetic flux leakage method[J]. Journal of Magnetism and Magnetic Materials, 2022, 560: 169595.
[6] Zhang Yusheng, Ming Hongliang, Tang Lichen, et al. Effect of the frequency on fretting corrosion behavior between Alloy 690TT tube and 405 stainless steel plate in high temperature pressurized water[J]. Tribology International, 2021, 164: 107229.
[7] 徐庆林, 王向军, 张建春, 等. 921A钢板腐蚀电场的Frumkin修正[J]. 电工技术学报, 2020, 35(14): 2951-2958.
Xu Qinglin, Wang Xiangjun, Zhang Jianchun, et al. Frumkin correction of corrosion electric field generated by 921A steel[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 2951-2958.
[8] Singh S, Singh Grewal J, Rakha K. Erosion wear performance of HVOF and cold spray coatings deposited on T-91 boiler steel[J]. Materials Today: Proceedings, 2022, 62: 7509-7516.
[9] Zou D L, Hao Y F, Wu H, et al. Safety assessment of large-scale all steel LNG storage tanks under wind-borne missile impact[J]. Thin-Walled Structures, 2022, 174: 109078.
[10] 刘素贞, 陈云龙, 张闯, 等. 融合多维超声时频域特征的锂离子电池荷电状态估计[J]. 电工技术学报, 2023, 38(17): 4539-4550, 4563.
Liu Suzhen, Chen Yunlong, Zhang Chuang，et al. State of charge estimation of lithium-ion batteries fused with multidimensional ultrasonic time- frequency domain features[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4539-4550, 4563.
[11] 刘素贞, 袁路航, 张闯, 等. 基于超声时域特征及随机森林的磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2022, 37(22): 5872-5885.
Liu Suzhen, Yuan Luhang, Zhang Chuang，et al. State of charge estimation of LiFeO4 batteries based on time domain features of ultrasonic waves and random forest[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5872-5885.
[12] 吴立峰, 刘昊, 林仲钦, 等. 低温环境下锂离子电池荷电状态与超声透射飞行时间的关系研究[J]. 电工技术学报, 2022, 37(21): 5617-5626.
Wu Lifeng, Liu Hao, Lin Zhongqin, et al. Relation- ship between state of charge of lithium-ion battery and ultrasonic transmission flight time at low temperature[J]. Transactions of China Electro- technical Society, 2022, 37(21): 5617-5626.
[13] 刘继伦, 刘素贞, 金亮, 等. 用于测厚和裂纹检测的正交横波电磁超声换能器仿真分析及实验研究[J]. 电工技术学报, 2022, 37(11): 2686-2697.
Liu Jilun, Liu Suzhen, Jin Liang, et al. Simulation and experiment of orthogonal shear waves with electromagnetic acoustic transducer for thickness measurement and crack detection[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2686- 2697.
[14] 蔡智超, 李毅博. 基于Halbach阵列电磁超声纵波换能器优化设计[J]. 电工技术学报, 2021, 36(21): 4408-4417.
Cai Zhichao, Li Yibo. Optimum design of electro- magnetic acoustic longitudinal wave transducer based on Halbach array[J]. Transactions of China Elec- trotechnical Society, 2021, 36(21): 4408-4417.
[15] 蔡智超, 孙翼虎, 赵振勇, 等. 基于时频分析和深度学习的表面粗糙度超声模式识别方法[J]. 电工技术学报, 2022, 37(15): 3743-3752.
Cai Zhichao, Sun Yihu, Zhao Zhenyong, et al. A deep learning-based electromagnetic ultrasonic recognition method for surface roughness of workpeice[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3743-3752.
[16] Zhai Guofu, Liang Bao, Li Xi, et al. High-temperature EMAT with double-coil configuration generates shear and longitudinal wave modes in paramagnetic steel[J]. NDT & E International, 2022, 125: 102572.
[17] Tu Jun, Zhong Zhiwu, Song Xiaochun, et al. An external through type RA-EMAT for steel pipe inspection[J]. Sensors and Actuators A: Physical, 2021, 331: 113053.
[18] Tkocz J, Greenshields D, Dixon S. High power phased EMAT arrays for nondestructive testing of as-cast steel[J]. NDT & E International, 2019, 102: 47-55.
[19] 赵国梁, 刘素贞, 张闯, 等. 变厚板塑性形变超声非线性响应及其实验[J]. 电工技术学报, 2022, 37(20): 5092-5103.
Zhao Guoliang, Liu Suzhen, Zhang Chuang et al. Ultrasonic nonlinear response of plate with varying thickness in plastic deformation and experiment[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5092-5103.
[20] 刘素贞, 王淑娟, 张闯, 等. 钢板电磁超声表面波的仿真分析及缺陷定量检测[J]. 电工技术学报, 2020, 35(1): 97-105.
Liu Suzhen, Wang Shujuan, Zhang Chuang, et al. Simulation analysis of electromagnetic acoustic surface wave of steel plate and quantitative defect detection[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 97-105.
[21] 武建伟. 超声导波技术在管道检测中的试验分析[J]. 电工技术, 2023(3): 148-150.
Wu Jianwei. Analysis of experiment in pipeline detection using ultrasonic guided wave technology[J]. Electric Engineering, 2023(3): 148-150.
[22] 刘素贞, 张严伟, 张闯, 等. 电磁超声管道周向兰姆波仿真分析及缺陷检测特性研究[J]. 电工技术学报, 2017, 32(22): 144-151.
Liu Suzhen, Zhang Yanwei, Zhang Chuang, et al. Research on simulation analysis of electromagnetic ultrasonic circumferential lamb waves and defect feature detection in pipeline[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 144-151.
[23] Seung H M, Park C I, Kim Y Y. An omnidirectional shear-horizontal guided wave EMAT for a metallic plate[J]. Ultrasonics, 2016, 69: 58-66.
[24] Palmer S B, Dixon S. Industrially viable non-contact ultrasound[J]. Insight-Non-Destructive Testing and Condition Monitoring, 2003, 45(3): 211-217.
[25] Ramp H O, Wingrove E R. Principles of pulse com- pression[J]. IRE Transactions on Military Electronics, 1961, MIL-5(2): 109-116.
[26] Fu Juan, Wei Gang, Huang Qinghua, et al. Barker coded excitation with linear frequency modulated carrier for ultrasonic imaging[J]. Biomedical Signal Processing and Control, 2014, 13: 306-312.
[27] Mitsuta H, Sakai Kaoru. High sensitivity detection of ultrasonic signal for nondestructive inspection using pulse compression method[J]. Microelectronics Reliability, 2019, 92: 172-178.
[28] Laureti S, Ricci M, Mohamed M N I B, et al. Detection of rebars in concrete using advanced ultrasonic pulse compression techniques[J]. Ultrasonics, 2018, 85: 31-38.
[29] 时亚, 石文泽, 陈果, 等. 钢轨踏面检测电磁超声表面波换能器优化设计[J]. 仪器仪表学报, 2018, 39(8): 239-249.
Shi Ya, Shi Wenze, Chen Guo, et al. Optimal design of electromagnetic ultrasonic surface wave transducer for rail tread detection[J]. Chinese Journal of Scientific Instrument, 2018, 39(8): 239-249.
[30] 刘素贞, 刘继伦, 张闯, 等. 一种新型窄磁铁聚焦式电磁超声表面波换能器[J/OL]. 中国电机工程学报: 1-13[2023-05-24]. http://kns.cnki.net/kcms/detail/ 11.2107.TM.20220406.1932.004.html.
Liu Suzhen, Liu Jilun, Zhang Chuang, et al. A new electromagnetic acoustic transducer design with narrow magnet for generating focused surface wave[J/OL]. Proceedings of the CSEE: 1-13[2023-05-24]. http://kns.cnki.net/kcms/detail/11.2107.TM.20220406. 1932.004.html.
[31] Gandomzadeh D, Abbaspour-Fard M H. Numerical study of the effect of core geometry on the per- formance of a magnetostrictive transducer[J]. Journal of Magnetism and Magnetic Materials, 2020, 513: 166823.
[32] Kang Lei, Dixon S, Wang Kaican, et al. Enhancement of signal amplitude of surface wave EMATs based on 3-D simulation analysis and orthogonal test method[J]. NDT & E International, 2013, 59: 11-17.
[33] Pei Cuixiang, Zhao Siqi, Xiao Pan, et al. A modified meander-line-coil EMAT design for signal amplitude enhancement[J]. Sensors and Actuators A: Physical, 2016, 247: 539-546.
[34] Sun Mingjian, Shen Yi, Zhang Wei. A wavelet threshold denoising method for ultrasonic signal based on EMD and correlation coefficient analysis[C]//2010 3rd International Congress on Image and Signal Processing, Yantai, China, 2010: 3992-3996.
[35] Nie Zhichao, Wang Kui, Zhao Mingjie. Application of wavelet and EEMD joint denoising in nonlinear ultrasonic testing of concrete[J]. Advances in Materials Science and Engineering, 2018: 1-11.
[36] Si Dan, Gao Bin, Guo Wei, et al. Variational mode decomposition linked wavelet method for EMAT denoise with large lift-off effect[J]. NDT & E International, 2019, 107: 102149.
[37] Hao Kuansheng, Huang Songling, Zhao Wei, et al. Modeling and finite element analysis of transduction process of electromagnetic acoustic transducers for nonferromagnetic metal material testing[J]. Journal of Central South University, 2011, 18(3): 749-754.
[38] Harris F J. On the use of windows for harmonic analysis with the discrete Fourier transform[J]. Proceedings of the IEEE, 1978, 66(1): 51-83.
[39] Miller R. Fundamentals of radar signal processing (richards, M. A.; 2005)[book review[J]. IEEE Signal Processing Magazine, 2009, 26(3): 100-101.
[40] Jafari-Shapoorabadi R, Konrad A, Sinclair A N. Comparison of three formulations for eddy-current and skin effect problems[J]. IEEE Transactions on Magnetics, 2002, 38(2): 617-620.
Abstract Traditional Barker code pulse compression technology is constrained by rated parameters of pulse power amplifiers (duty cycle, maximum pulse width), resulting in reduced pulse compression effectiveness and detection speed. Amulti-element Lamb wave Electromagnetic Acoustic Transducer (EMAT) based on Barker code pulse compression technology is proposed. In this multi-element EMAT, the combination of a permanent magnet and a meander line coil is considered an independent element, and the direction of the Lorentz force is controlled by the magnetic field direction of the permanent magnet and the current direction of the meander line coil in each group of array elements. In this way, the excited Lamb wave phase {0, 180°} is consistent with the Barker code sequence {1, -1}, ultimately generating Lamb waves in Barker code form. A finite element model for the multi-element Lamb wave EMAT detection process is established based on Barker code pulse compression technology with tone-burst excitation. The influence of factors (permanent magnet configuration, array element sequence length, excitation signal cycle count, and meander line coil turns) on peak-side lobe ratio and main lobe width after pulse compression is analyzed.
The results show that configuring external permanent magnets improves the signal-to-noise ratio (SNR) of pulse-compressed signals after side lobe suppression when the multi-element Lamb wave EMAT is excited by tone-burst signals. The SNR of the detection echo can be increased by 9.8 dB when the multi-element EMAT with a four-turn meander line coil and a 13-bit Barker code sequence length is configured with three pairs of external permanent magnets. As the number of excitation signal cycles increases, the main lobe width of the pulse-compressed signal after sidelobe suppression exhibits a continuously increasing trend, and the SNR initially increases and then decreases. As the length of the Barker sequence increases, the SNR of the pulse-compressed signal after sidelobe suppression shows a continuously increasing trend. Considering the spatial resolution and SNR of the detected echo, the optimal parameters of the multi-element Lamb wave EMAT area 10-turn meander line coil, 11 excitation signal cycles, a 13-bit Barker sequence, and a configuration with three pairs of external permanent magnets.
The new multi-element EMAT successfully generates Lamb waves in Barker code form when excited with a tone-burst signal. After the pulse compression, the Lamb wave signal effectively suppresses sidelobes by calculating delay time and performing sidelobe suppression. The multi-element Lamb wave EMAT based on tone-burst excitation and Barker code pulse compression technology improves ultrasonic signals' SNR and spatial resolution. When applied to guided wave detection inmetal plates or pipes with varying thicknesses, maintaining consistent spacing between array elements is crucial for pulse compression effects. Ensuringuniform and consistent magnetic field distribution for each array element is also beneficial.
keywords：Electromagnetic ultrasonic transducer, Barker code pulse compression, multi-element Lamb wave EMAT, signal-to-noise ratio, spatial resolution
国家自然科学基金（52065049, 12064001）、国防基础科研计划（JCKY2022401C005）、江西省主要学科与技术带头人培训计划（20204BCJL22039, 20225BCJ23023）、江西省杰出青年基金（20212ACB214010）、江西省重点研发计划（20212BBE51006, 20223BBE51034）和南昌航空大学研究生创新专项资金（YC2021-S694）资助项目。
收稿日期 2023-03-03
改稿日期 2023-05-06
DOI: 10.19595/j.cnki.1000-6753.tces.230249
中图分类号：TG115.28+5
石文泽 男，1986年生，副教授，研究方向为激光/电磁超声检测。E-mail: 70658@nchu.edu.cn
卢 超 男，1971年生，教授，博士生导师，研究方向为超声检测及仪器等。E-mail: luchaoniat@163.com（通信作者）
（编辑 郭丽军）