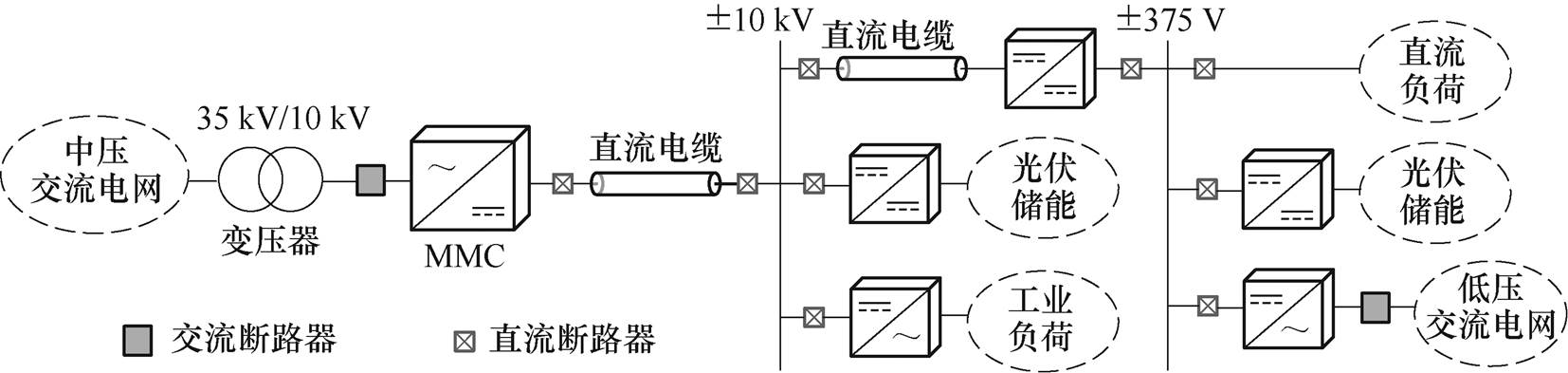
图1 中低压直流配电网示意图
Fig.1 Schematic diagram of medium and low voltage DC distribution network
摘要 随着直流配电网的快速发展与深化应用，准确可靠的故障测距技术对直流故障检修和恢复至关重要。该文提出一种基于固态断路器（SSCB）主动注入式直流故障测距方法。首先，利用SSCB开断主动注入不同脉冲宽度的信号，并检测注入脉冲首末端和反射波首末端的时间差作为注入波形传播时间间隔，能够减小采样频率带来的误差。然后，提取电缆线路电压线模量作为检测量，削弱正负极线路之间的耦合作用，获得稳定波速。最后，基于小波变换原理提出改进自适应模极大值方法来检测脉冲首末端时刻，减小噪声和过渡电阻对测距精度的影响。仿真结果表明，基于SSCB主动注入式测距方法在直流配电网单极接地和极间短路故障情况下均能够实现准确且快速的定位。
关键词：直流配电网 故障测距 固态断路器 主动注入 自适应模极大值
近年来，随着分布式发电、储能技术的快速发展，以及直流负荷数量的增加，电源侧和负荷侧的直流化特征日益显著，直流配电网成为配电系统发展与应用的方向。然而，直流故障易发生，危害大，需要快速隔离。直流配网通常采用地下电缆供电，检修困难且线路较短，阻抗小，难以准确找出故障点。精确的故障测距可有效缩短故障清除时间，减小系统停电损失，提高供电可靠性，对直流配电网的进一步发展至关重要[1-2]。
目前，直流故障测距主要分为被动式和主动式。被动式又包括被动故障分析法与被动行波法。故障分析法是根据线路参数和测量的电压、电流，通过分析计算，求出系统故障距离[3-5]。文献[6]提出一种基于故障极电流谐波量的直流配电网双端故障测距方法，利用故障距离与系统参数及谐波电流间的函数关系，实现故障测距。文献[7-8]利用线路参数构造故障时域微分方程，求解方程实现故障定位。该方法虽然能够识别故障位置，但是可用于故障分析的直流系统故障特征量较少，并且直流线路参数的误差会严重影响故障定位精度，容易受到过渡电阻的影响。被动式行波测距方法利用故障点产生的故障行波到达测量装置的时间差来计算故障距 离[9-11]。由于故障行波波形特征信息单一固定并且能量有限，易受故障线路阻抗影响，故障行波在高阻抗线路中更容易迅速衰减，可能无法检测到波头到达测量装置的时刻，导致故障定位失败。
为克服被动式测距的缺点，部分学者提出一种主动式行波测距方法，利用额外装置或变换器控制主动注入特征信号。文献[12]提出一种将脉冲注入法和单端故障行波法相结合的接地故障测距方案。该方法需要增加额外的脉冲注入设备，增加故障测距的投入成本。文献[13-14]通过控制模块化多电平换流器（Modular Multilevel Converter, MMC）注入脉冲，检测脉冲发出时间和反射脉冲到达测量装置的时间差，实现对MMC型高压直流系统的故障测距。该方法在故障过程中对MMC进行控制，增加控制复杂度，MMC运行存在一定安全隐患。主动式行波测距方法虽然能够在一定程度解决传统被动式行波测距方法中行波特征信息少与能量有限的问题，但是由于其测量原理是基于波速与时间的乘积，仍然容易受到线路波速稳定性与采样频率的影响。
直流系统不存在自然过零点，且故障电流上升速度快、幅值大，对隔离装置快速性和熄弧要求极高。而直流固态断路器（Solid State Circuit Breaker, SSCB）刚好满足上述需求。SSCB由半导体功率器件作为主开关，具有无弧关断、动作速度快及可控性高等优点[15-16]，可以控制其开断注入特征信息丰富、能量大的信号。脉冲注入过程类似于SSCB多次快速重合闸。基于此，本文提出一种基于固态断路器主动注入式直流故障测距方法。
本文首先详细分析基于固态断路器主动注入式的工作原理；接着对双极直流电缆模量进行分析与提取，并基于小波变换原理提出改进自适应模极大值检测方法；然后给出基于SSCB主动注入式直流故障测距的具体流程；最后进行仿真验证。
本文列出一种典型辐射状中低压直流配电网拓扑，其示意图如图1所示，中压直流电压等级为±10 kV，低压直流电压等级为±375 V。换流器采用MMC，出口处配置直流断路器，直流侧电容中性点高阻接地。本文以MMC与±10 kV母线之间的中压直流电缆线路为研究对象，固态断路器安装在MMC直流侧出口处。
图1 中低压直流配电网示意图
Fig.1 Schematic diagram of medium and low voltage DC distribution network
当检测到直流线路发生故障后，控制单元驱动SSCB关断，此时断路器出口端的电压值将在ms级时间内降到0 V，具体SSCB工作原理不是本文研究重点，详见文献[15-16]。因此，可以在直流系统发生故障后，通过控制断路器的关断与导通，制造一个幅值为Vp、宽度为Tp的脉冲信号，继而通过检测脉冲信号离开断路器的时间与脉冲信号反射到断路器的时间之差，来进行直流线路故障测距。
主动注入式测距方法对脉冲存在一定的要求，脉冲的幅值与宽度都会对行波的检测有很大的影响。脉冲宽度与幅值较小，则能量小，传播衰减后不易检测；脉冲宽度过大，会导致线路测距死区增大。因此，本文通过控制断路器导通状态持续时间，来改变注入脉冲宽度。由于断路器中半导体功率开关器件动作速度快，则脉冲下降时间很小，更利于脉冲信号的检测，并且脉冲宽度持续一定时间，导致脉冲幅值Vp能够达到所需要的值。在断路器采样频率满足要求的条件下，注入脉冲宽度需要满足
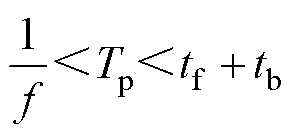（1）
式中，f为采样频率；tf与tb分别为注入脉冲信号前行到故障点时间和从故障点反射到断路器检测点时间。
在断路器出口端制造一个脉冲信号，该脉冲信号将沿线路按照系统潮流流动的方向传播，如图2所示。直流线路具备均匀的分布参数，线路中处处阻抗值近乎相等。当线路中某处发生故障后，此处的阻抗值发生了改变，形成阻抗不连续点，则主动注入的脉冲信号将在此处发生反射和折射。反射波将向母线处断路器传播，折射波将继续向另一端传播。通过检测脉冲在断路器处发出首端时间tis1和末端时间tie1，反射脉冲到达断路器的首端时间trs1和末端时间tre1，可测得故障距离l为
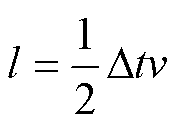（2）
其中
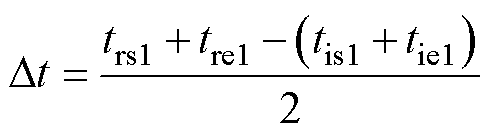（3）
式中，∆t为脉冲信号在直流固态断路器端口与故障点往返传播的时间；v为主动注入脉冲信号的传播速度，本文使用电压的线模量作为实测传播速度。
图2 基于SSCB主动注入脉冲原理
Fig.2 Based on SSCB active injection pulse principle
由式（3）可以看出，为了提高直流线路故障测距精度，需要同时保证脉冲信号时间检测与传播速度测量的准确性。针对这两个方面，本文首先通过一种双极电缆解耦方法获取满足故障测距要求的模量值，然后基于传统小波变换原理提出一种改进自适应模极大值方法来精确检测信号到达断路器的 时间。
目前对于电缆阻抗和导纳参数的准确计算存在一定的误差，很多文献中提到的等效阻抗和导纳参数的计算方法往往不会同时考虑电缆自身各层之间及电缆双极之间的耦合[17]。精确有效地解耦电缆参数对于直流线路故障定位具备重大意义。本文以不带铠装的交联聚乙烯电缆为例，该电缆由导体和护套两层结构组成。如图3所示为单根直流电缆的横截面，Uc和Us分别为导体层与护套层的对地电压；Ic和Is分别为流过导体层和护套层的电流；Ycs和Yse分别为导体层和护套层之间的互相导纳。因此，双极直流电缆有四组电压量和电流量，彼此之间相互耦合。
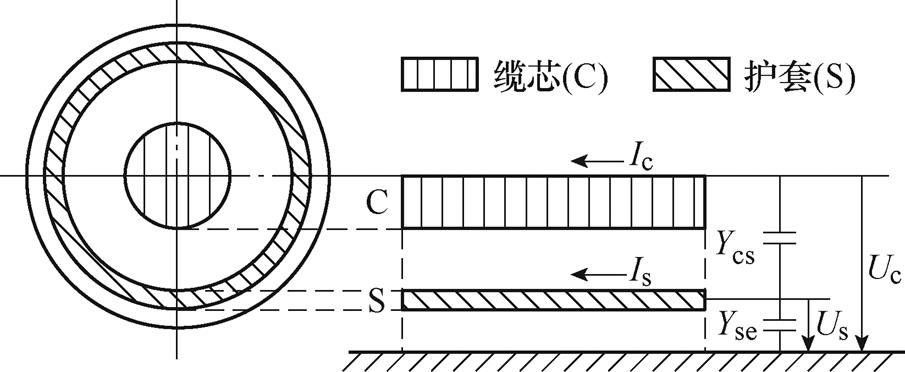
图3 不带铠装的交联聚乙烯电缆横截面
Fig.3 Cross-linked polyethylene cable cross-section without armor
与架空线路相似，直流电缆传输方程为
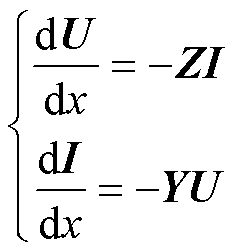（4）
式中，Z、Y分别为双极电缆的串联阻抗矩阵和并联导纳矩阵；U=[ucpucnuspusn]T为电压向量；I= [icpicnispisn]T为电流向量；p、n分别表示直流线路的正、负极。
通常情况下，埋于地下的直流电缆双极之间铺设间距较小，除本极电缆自身各层存在电磁耦合外，双极之间也存在电磁耦合。因此，Z和Y为满秩矩阵，不易求解。需要通过相位模式变换将相空间变量转变为其他空间坐标，并且Z、Y矩阵中的非对角元素变为0以消除双极之间的电磁耦合。新坐标空间中的电压和电流叫做模电压和模电流，则有
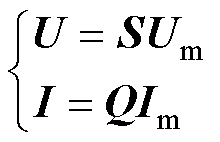（5）
式中，S、Q分别为电压、电流的相模变换矩阵；Um、Im分别为模电压和模电流矩阵。
经过推导，得到模电流和模电压表达式分别为
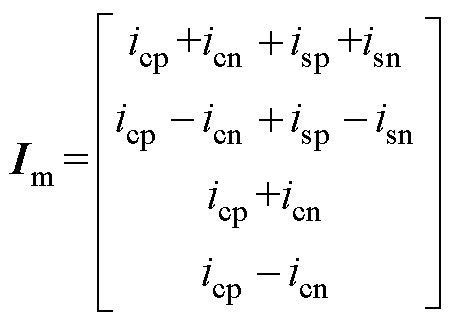（6）
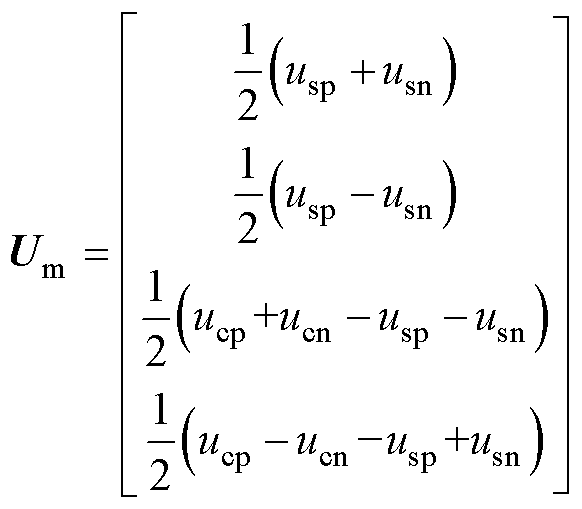（7）
通过分析式（6）和式（7）各模量电压或电流在直流双极电缆中的衰减常数和传播速度，根据实际研究和工程需要，本文选取3、4模量电压作为故障测距的变量，因为3、4模量的衰减常数相对较小，其在电缆中传播速度接近光速且较为稳定。
直流线路故障精确定位的一个前提是行波到达时间的准确提取，常用方法包括阈值法、峰值法及小波变换模极大值法等[18-20]。其中阈值法与峰值法在故障定位时受噪声与电能质量影响较大。而小波变换可以在一定信噪比的波形中检测到信号突变点，用于线路故障测距，具有较高的精度。
若在函数f(x)上的某一点 (x0, y0) 能够满足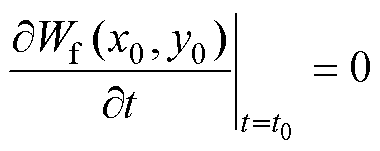
，则该点为小波的局部极值点。若对任意t∈(t0, d) 满足|Wf(x0, t)|≤|Wf(x0, t0)|，则点 (x0, y0) 为小波极大值点，Wf(x0, t0) 为小波变换模极大值。对于一个信号x(t)的某处存在间断点或导数不连续点，则在该点表现为小波变换模极大值点。
然而，在实际应用中，采集到的电压或电流行波难免会掺杂许多噪声或者在系统运行过程中受到信号干扰，虽然小波变换能够在一定程度上滤除噪声恢复原信号，但是仍然有部分噪声或干扰波形没有被滤除，这些将导致在小波变换分析后出现伪极值点，继而导致直流线路故障测距出现较大误差，甚至失败。除此之外，虽然传统行波测距具有一定的抗过渡电阻能力，但当直流故障线路过渡电阻过大时，行波反射系数过小，所测行波信号的奇异性将会很小，会导致小波变换获取的模极大值太小，甚至无法提取。
为了降低伪极值点对故障线路测距精度的影响，本文基于小波变换原理提出一种改进自适应模极大值检测方法：
（1）首先，选择合适的小波函数对采集到的电压行波信号Ur（含噪）进行多尺度小波变换，从时域变换到小波域。本文综合考虑选择二进小波db2，既能够反映信号争议的近似特征，又能很好地反映信号细节的变换。
（2）其次，在各尺度下尽可能提取电压行波信号的小波系数，由于信号和噪声在小波变换各尺度上不同的传播特性，选择一个合适的阈值，用阈值函数对各尺度下的系数进行量化，信号对应的小波系数大于阈值则被保留，噪声对应的小波系数小于阈值则被置零，以此来达到除去噪声的效果。本文选取Minimax阈值，具备一定的自适应性。
（3）再次，用处理后的系数进行小波逆变换来重构电压行波信号Ur，并再次利用二进小波函数db2对重构信号进行小波变换，得到小波的局部模极大值序列。
（4）最后，为了克服极值点过小的影响，进一步提高故障测距的抗过渡电阻能力，本文将利用自适应门槛值在获取的局部极大序列中提取出所需要的模极大值点，继而计算出主动注入脉冲经过故障点反射回断路器的时间。
传统的方法一般都是设定某一恒定的值作为模极大值点选择的门槛值，然而当过渡电阻过大时，其模极大值较小，该方法具有一定的局限性。针对这一问题，本文将设置一个自适应门槛值，并根据过渡电阻的不同，改变这一门槛值的大小。门槛值自适应变化的依据如下。
当直流系统发生故障时，IGBT闭锁，变换器输出侧电容器快速放电。此阶段故障瞬间电压微分是由电压初始值UC0、电流初始值I0、故障处的线路电感L、线路电阻R和过渡电阻Rf共同决定。已知系统运行参数的条件下，由于直流线路电感L和线路电阻R很小，过渡电阻Rf在很大程度上决定了电压微分值的变化。因此，可以通过同一时刻的瞬态电压微分值du(t)/dt来体现过渡电阻Rf的相对大小，Rf越小，变化率越大；反之，亦然。在实际应用中，使用相邻时刻t1和t2的电压变化率作为瞬态电压微分值du(t)/dt，则有
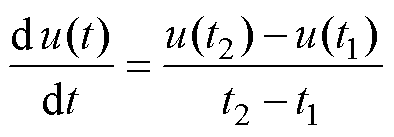（8）
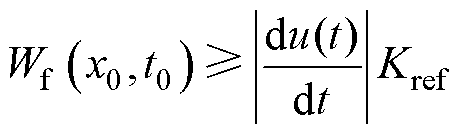（9）
式中，u(t2)和u(t1)为故障发生后t1和t2时刻的瞬态电压值；Kref为门槛参考值，根据系统参数设置，为一常数，取0.98。
根据式（8）和式（9）采用自适应门槛值，可以选取合适的模极大值点，对应的时间即为注入脉冲首端时间tis1和末端时间tie1以及反射波首端时间trs1和末端时间tre1。
基于SSCB主动注入脉冲式直流故障测距的具体流程主要分成两个部分：直流系统正常运行时的电压行波速度v与发生故障后直流线路故障距离l的测量。具体过程分析如下：
1）电压行波速度v测量
行波测距精度的重要影响因素之一就是波速v的确定，即本文所提测距方案实现的第一步。为了提高波速v测量的准确性，依据2.1节分析，选择电压行波线模量作为测量信号，其衰减常数相对较小，在电缆中传播速度接近光速且较为稳定。测速流程如图4所示，由于SSCB的整个动作过程时间极短，在数ms内完成，对于系统正常工作的影响极小，因此该过程在直流系统正常运行状态下进行。通过系统上位机控制SSCB的关断与导通来主动注入一个脉冲信号，经线路传播到另一端，由于阻抗在另一端不连续，该信号又沿着线路反射回SSCB处，整个传播距离为线路全长的两倍即2L，通过式（2）和式（10）测得波速v1。为进一步提高波速v测量的准确性，重复上述操作过程，获得一组波速序列{v1, v2,…, vn}，取平均值来作为最终所测波速v。
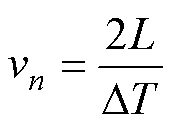（10）
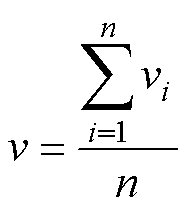（11）
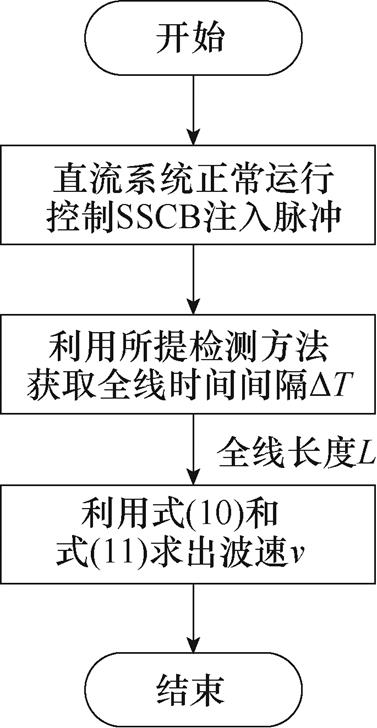
图4 波速v测量流程
Fig.4 Flow chart of wave velocity v measurement
2）直流线路故障测距
当检测到系统发生故障后，在直流侧电容放电阶段快速检测相邻时刻瞬态电压值，计算瞬态电压微分值du(t)/dt，用来设置弹性门槛值|du(t)/dt|Kref，可以有效选取模极大值点。检测完后，上位机控制故障线路上SSCB的关断与导通来主动注入多组不同脉冲宽度的信号，该信号将沿线路向故障点传播，并在故障点发生反射。利用2.2节所提算法检测出脉冲发射首末端时间和反射波首末端时间，结合图4流程测量的波速v，可以通过式（2）和式（3）计算出单次脉冲下线路故障距离l1，重复上述过程，获得一组波速序列{l1, l2,…, lm}，取平均值来作为最终故障距离l，如式（12）所示，故障测距流程如图5所示。
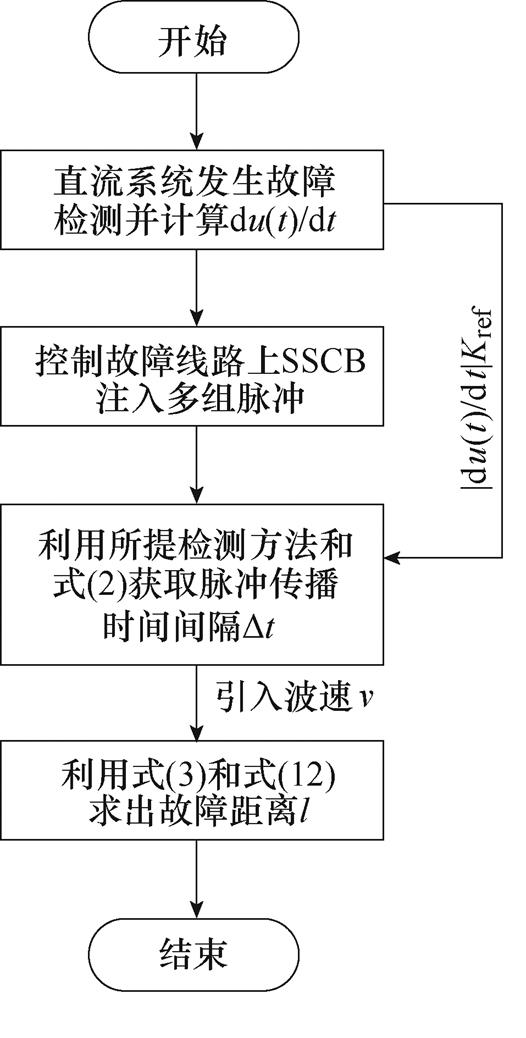
图5 直流线路故障测距流程
Fig.5 Flow chart of DC line fault location
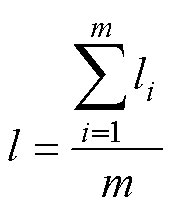（12）
采样频率f、脉冲宽度Tp、注入脉冲次数N等关键参数对于提高测距精度、抗过渡电阻和噪声能力有着重要的作用，其参数优化和选取非常重要。
1）采样频率f
由测距原理式（2）和式（3）可知，采样频率对反射波到达断路器的首端时间trs1和末端时间tre1的准确度影响较大，采样频率越高，则故障测距精度就越高。但是测距精度并不与采样频率成正比，而且采样频率过高也会增加数据处理的难度和成本，以及提高对电压采样传感器的要求。因此，需要根据行波信号的特征和测距原理来合理选择采样频率。一方面，根据傅里叶变换的原理，采样频率至少要满足奈奎斯特采样定理，即采样频率要大于行波信号最高频率的2倍，才能避免混叠现象，即f≥2/Tp（Tp为注入脉冲宽度）；另一方面，考虑到高采样频率电压传感器成本较高以及现有传感技术限制[13, 21-22]。综合考虑，本文的采样频率选定在2/Tp≤f≤300 kHz。
2）脉冲宽度Tp
对于脉冲宽度，除了式（1）约束外，还要考虑固态断路器硬件和注入脉冲能量两个方面。固态断路器在注入信号过程中，虽然在极短时间（ms级）内完成开断动作，但是这也需要一个时间，即决定了脉冲宽度Tp的下限[15-16]。
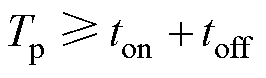（13）
式中，ton和toff分别为固态断路器的开通时间和关断时间。
另一方面，脉冲宽度过小会导致注入信号能量较弱，线路衰减过于严重，导致对反射波检测失 败[23-24]。对于传输线路来说，脉冲宽度越窄、衰减作用越明显。其中，线路传输函数为
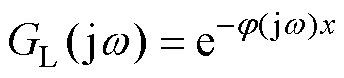（14）
式中，x为线路长度；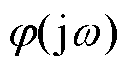
为传输系数，即
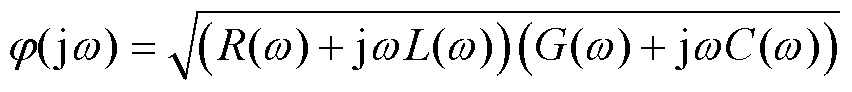（15）
式中，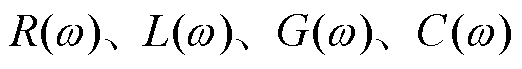
分别为单位长度的电阻、电感、电导和电容。
根据式（14）可知，线路越长，脉冲宽度越窄，信号幅值衰减越显著。以本文的线缆长度为10 km为例，其幅值衰减不超过0.2(pu)的情况下，综合式（1）和式（13），本文脉冲宽度Tp选取在0.025～0.035 ms。
3）注入脉冲次数N
本文注入多组脉冲的宽度等差增加。注入不同脉冲宽度信号目的是减小采样频率、噪声和测量误差带来的影响，提高故障测距精度。根据测距原理式（1）和式（2），可以看出，对反射脉冲到达断路器的首端时间trs1和末端时间tre1的测量准确度将直接影响到测距精度。然而由于采样频率f导致无法采集到任意时刻，且获取的时刻都是采样周期1/f整数倍，这对于整个测距精度的影响较大。因此设计注入N组不同脉冲宽度的信号，每次增加DTp，总增加时间不小于采样周期1/f。假设采样获取的时间值按照超过一半的采样周期1/f加一个完整采样周期的时间，则对于注入脉冲次数N和增加时间DTp，有
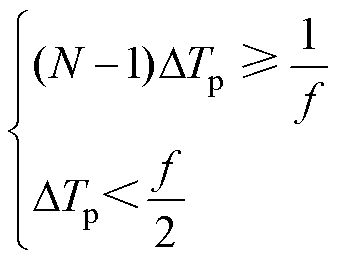（16）
同时按照式（12）计算最终的平均测距结果，理论上注入脉冲次数越多越好，但是考虑在注入脉冲过程中系统处于故障状态，总注入时间不宜过长，并且注入数量过多，也会增加数据处理的难度和成本。综合考虑，本文选取单脉冲注入次数在5～7次。
4）脉冲注入过程的约束条件
将注入过程中MMC直流侧线路电压和线路电流的波动幅度作为对系统负面影响程度的指标，并充分考虑短时间系统可容忍最大短路电压和电流的能力。脉冲注入过程中对系统负面影响的定量表达式为
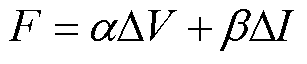（17）
式中，F为脉冲注入过程对系统的负面影响程度；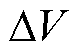
为电压波动幅度；
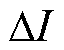为电流波动幅度；a 和b 为权重系数，分别反映了电压、电流波动对系统影响程度的相对重要性，本文选取a、b 均为0.5。
定义约束条件为
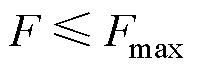（18）
式中，Fmax为系统允许的最大负面影响程度，取决于短时间内系统可容忍最大短路电压和电流能力，不同的直流系统，该值具有一定差异。
本文所提故障测距方法在主动脉冲注入过程中要满足上述约束条件，保证系统的安全。
为了验证所提故障测距方法的有效性，评估测距性能，本文在PSCAD/EMTDC中搭建如图1所示的直流配电系统仿真模型。该仿真以MMC与±10 kV母线之间的直流电缆线路为测试对象，线路长度设为10 km，采样频率设为200 kHz，注入脉冲宽度为0.03 ms，次数为6，满足关键参数选取要求。
故障后控制直流固态断路器开断来主动注入脉冲信号如图6所示。由于固态断路器自身存在缓冲和钳位回路，在主动注入脉冲的开断过程中并不会在断路器两端产生较高的瞬时过冲电压[25]，而注入的电压行波是由于固态断路器开断导致MMC直流侧脉冲能量沿线路往故障点传播形成的，与断路器关断过电压是有区别的。但是，在某些情况下，断路器开断操作导致较高的过冲电压可能会引起系统中的电压行波。线路故障下不同脉冲宽度的多次脉冲如图7所示。由图7可知，故障发生在0.49 s，固态断路器在ms级快速隔离故障点，使得MMC直流侧电压几乎保持稳定。在0.5 s产生主动脉冲信号进行故障测距，图6中第一个波头是断路器主动注入脉冲的入射波，第二个波头为故障点反射波，极性相反。可以看出，本文固态断路器的电压过冲不会影响注入脉冲电压行波的传播和后续故障测距。
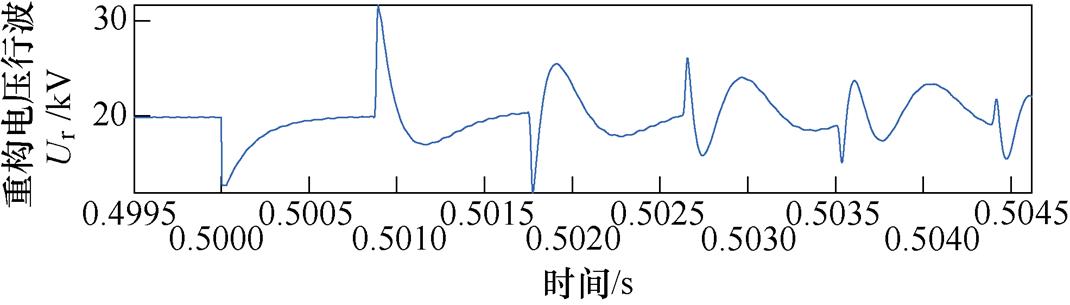
图6 SSCB主动注入脉冲信号
Fig.6 SSCB active injection pulse signal
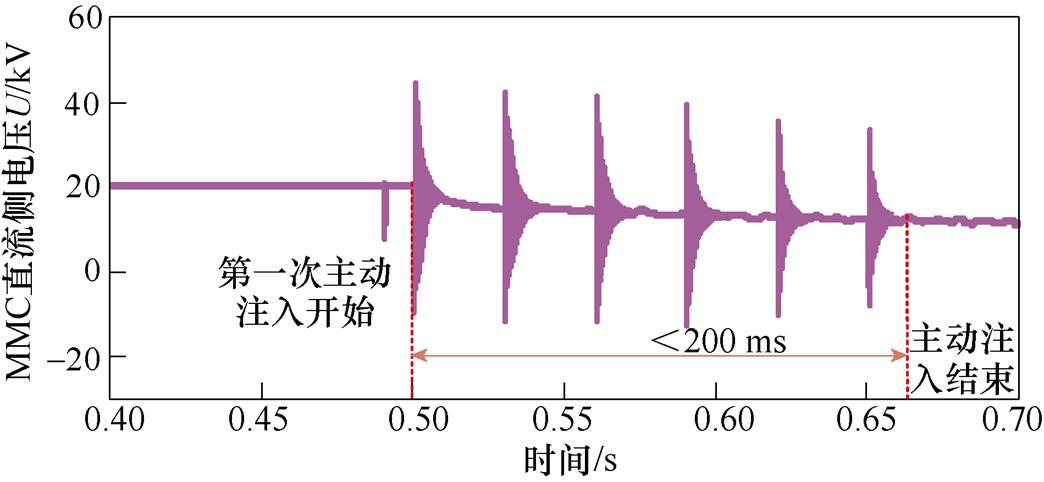
图7 线路故障下不同脉冲宽度的多次脉冲
Fig.7 Multiple pulse diagrams with different pulse widths under line faults
利用直流固态断路器控制的灵活性，产生不同宽度的脉冲信号，主动脉冲注入6次，第一次脉冲宽度Tp=0.03 ms，后面脉冲信号宽度在前一次的基础上增加0.002 ms，整个过程小于200 ms，如图7所示。相邻脉冲时间足够长，每个脉冲的折反射过程不会相互影响。在采样频率固定时，不同脉冲宽度根据式（2）得到的时间会产生一定的差异。每个不同宽度的脉冲都能计算出一个相应故障距离，再利用平均值计算出最终的故障距离，能够在一定程度上减小由于采样频率导致的测距误差问题。
图8为利用所提改进自适应模极大值方法提取模极大值。图中，tis1为直流固态断路器主动注入脉冲电压首端的时刻，tie1为主动注入脉冲电压末端的时刻，tie1-tis1为主动注入脉冲宽度。trs1为注入脉冲电压经过故障点反射回到测量点的电压行波首端的时刻，tre1为注入脉冲电压经过故障点反射回到测量点的电压行波末端的时刻。
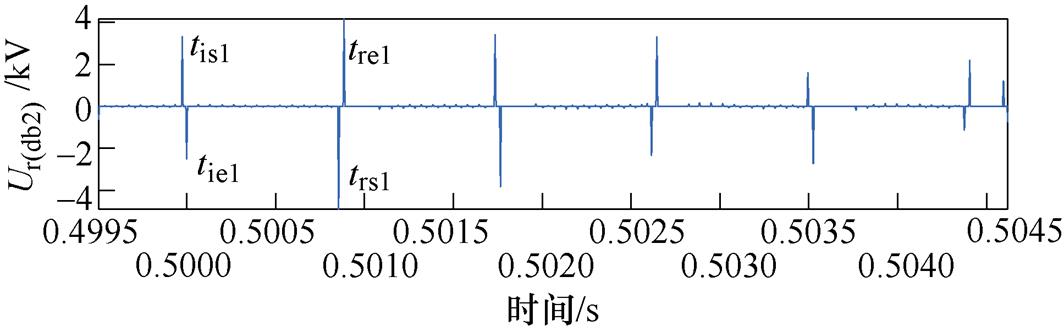
图8 改进自适应方法提取的模极大值
Fig.8 The modulus maximum extracted by improved adaptive method
利用式（2）可以计算出脉冲信号在直流固态断路器端口与故障点往返传播的时间∆t，最后再根据式（10）和式（11）测得的行波速度，计算出多组故障距离，并根据式（12）计算均值作为最终故障测距值。
双极短路故障仿真中，在相同故障距离下，分别设置过渡电阻为0.1、10和100 W 进行故障测距仿真。选取测距相对误差作为算法的测距精度指标[6]，如式（19）所示。双极短路故障测距结果见表1。
（19）
在单极接地故障仿真中，相同故障距离下，分别设置过渡电阻为0.1、10和100 W 进行故障测距仿真。单极接地故障测距结果见表2。
测距结果表明，无论是在单极接地故障还是在双极短路故障下，本文所提方法的测距精度在线路总长为10 km配电网中误差均低于0.55%，可以较为精准地实现短距离配电网故障测距。本文所提方法虽为单端测距方法，在过渡电阻为100 W 时，仍然具有较高的故障测距精度，具备一定程度的抗过渡电阻能力。
表1 双极短路故障测距结果
Tab.1 Bipolar short-circuit fault location results
故障距离/km过渡电阻/W测距结果/km相对误差(%) 0.50.10.5440.44 100.5200.20 1000.5440.44 30.13.0140.14 103.0020.02 1002.9910.09 50.15.0000 105.0000 1004.9880.12 90.19.0070.07 108.9950.05 1009.0070.07
表2 单极接地故障测距结果
Tab.2 Single pole ground fault location results
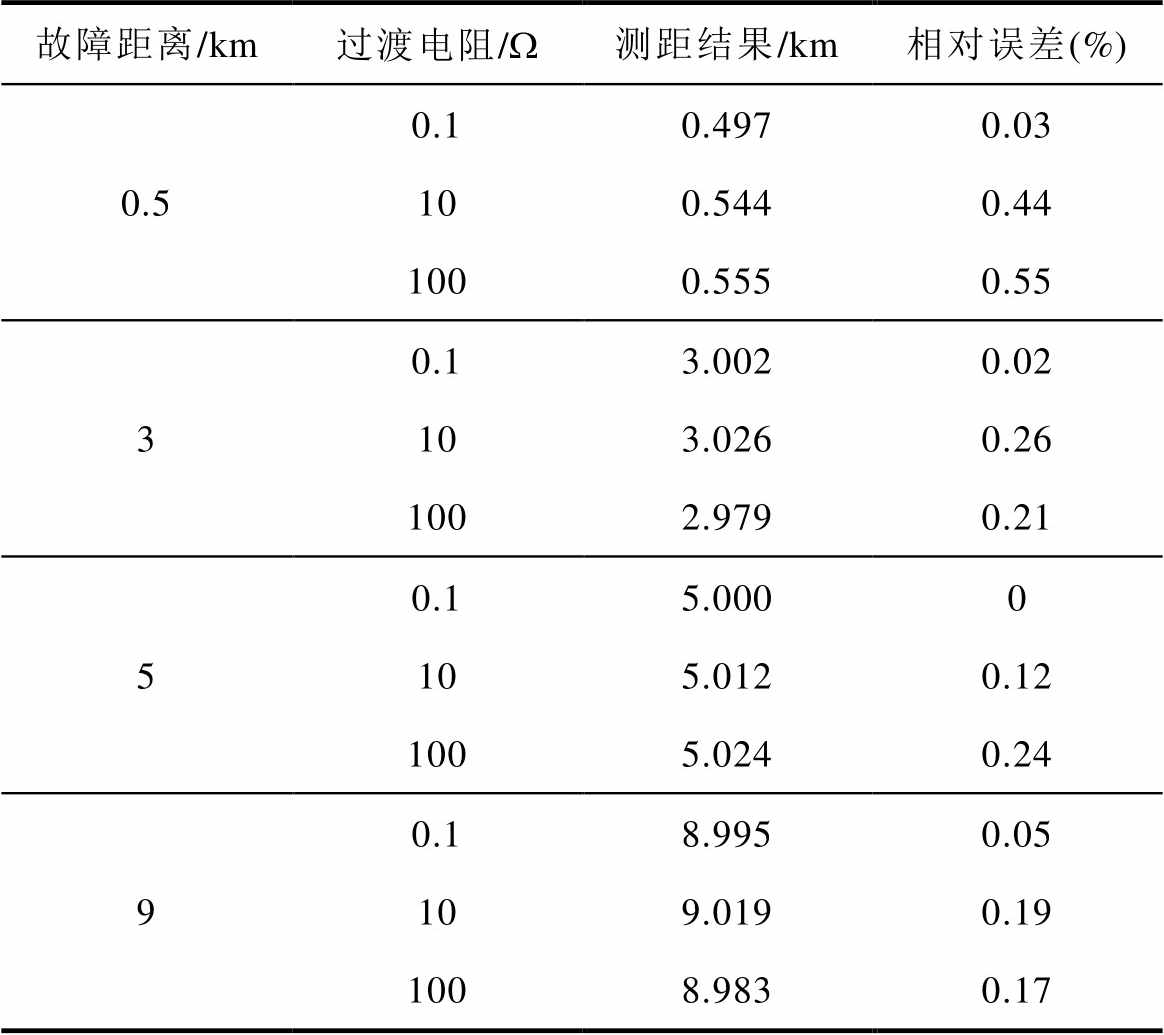
故障距离/km过渡电阻/W测距结果/km相对误差(%) 0.50.10.4970.03 100.5440.44 1000.5550.55 30.13.0020.02 103.0260.26 1002.9790.21 50.15.0000 105.0120.12 1005.0240.24 90.18.9950.05 109.0190.19 1008.9830.17
在行波测距方法中，采样频率是影响故障测距精度的重要因素之一。线路越短，对采样频率要求越高。为验证本文所提方法能够在一定程度上削弱对采样频率的依赖性，对比同类方法文献中的线路
长度和采样频率，同等误差下10 km线路一般行波法的采样频率要高于200 kHz。本文设定采样频率分别为200、150和80 kHz，利用所提方法在过渡电阻为10 W 的双极短路故障下进行故障测距，结果见表3。
表3 不同采样频率下的故障测距结果
Tab.3 Fault location results with different sampling frequencies
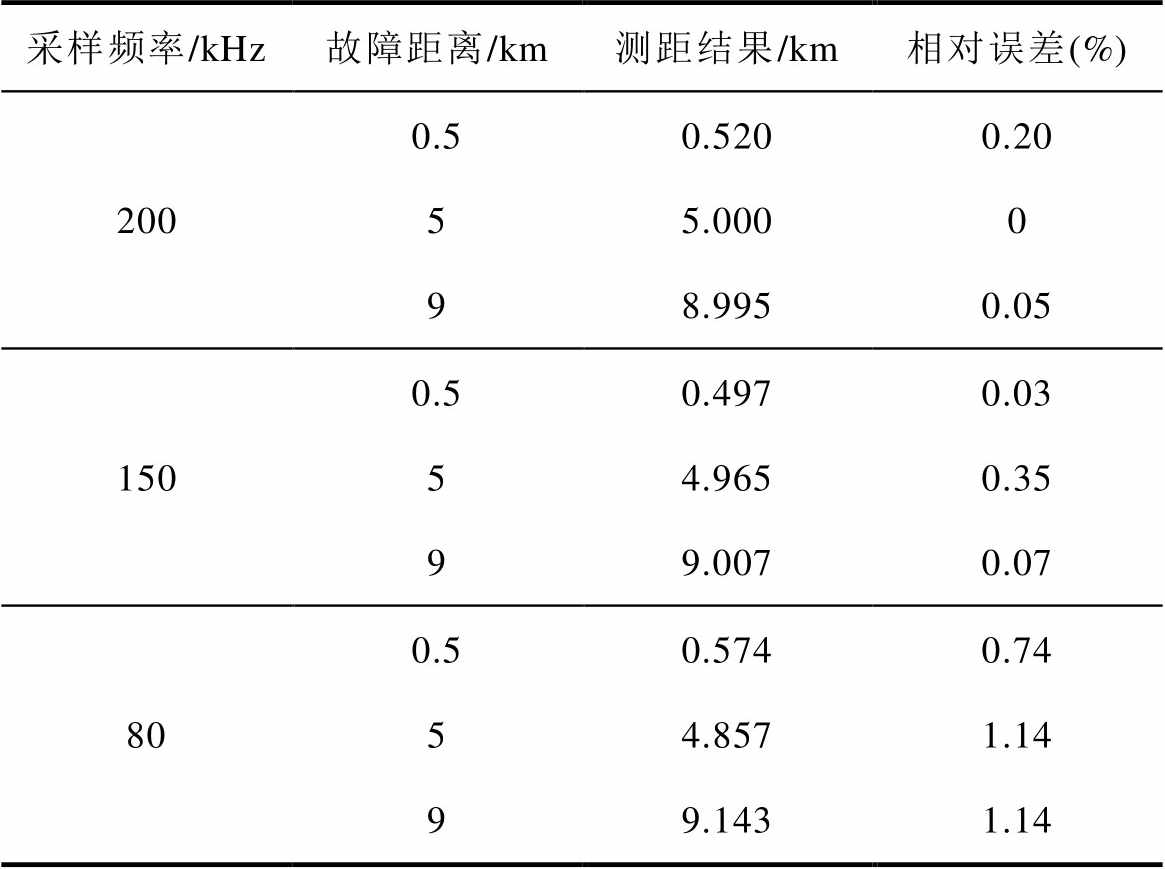
采样频率/kHz故障距离/km测距结果/km相对误差(%) 2000.50.5200.20 55.0000 98.9950.05 1500.50.4970.03 54.9650.35 99.0070.07 800.50.5740.74 54.8571.14 99.1431.14
不同采样频率下的测距结果表明，行波测距方法会受到采样频率的影响，采样频率越小、相对误差越大。但是本文所提方法在80 kHz采样频率下，仍然能够保证故障测距相对误差在1.14%以内，在一定程度降低了对采样频率的依赖。
高斯白噪声对于直流电力系统的影响具有随机性，是干扰直流故障定位的重要影响因素之一。本文加入信噪比（Signal to Noise Ratio, SNR）分别为40、20、5 dB的白噪声，并采用所提方法在过渡电阻为10 W 情况下进行定位，结果见表4。
表4 不同测量噪声下的故障测距结果
Tab.4 Fault location results with different measurement noise
故障类型信噪比/dB故障距离/km测距结果/km相对误差(%) 双极短路故障400.50.5200.20 55.0000 98.9950.05 200.50.5440.44 55.0000 99.0070.07 50.50.5670.67 55.0360.36 98.9360.36 单极接地故障400.50.5440.44 55.0120.12 99.0190.19
（续）
故障类型信噪比/dB故障距离/km测距结果/km相对误差(%) 单极接地故障200.50.5440.44 54.9650.35 99.0190.19 50.50.5550.55 55.0240.24 98.9360.64
在不同信噪比的噪声干扰下，故障测距结果表明，不同故障下，仍然能够实现相对误差低于0.67%的故障测距精度，该方法具备一定的抗噪声能力。但是当信噪比低于5 dB时，噪声对于测距定位影响增大，难以实现高精度的故障测距。
本文提出了一种基于固态断路器的主动注入式直流故障测距方法，控制直流固态断路器的开通与关断来注入不同宽度脉冲信号，并通过检测注入脉冲首、末端时间和反射脉冲首、末端时间，实现直流线路的故障测距。得到以下结论：
1）本文所提出的测距方法在直流配电网发生单极接地故障、极间短路故障情况下，均能实现较高精度的故障测距，无需额外增加设备，操作简单，具备一定的工程应用价值。
2）文中检测不同宽度脉冲发射波首末端与反射波首末端时间差的平均值作为脉冲信号在断路器与故障点之间传播时间，在一定程度上削减了行波测距方法对采样精度的依赖性，在10 km直流配电线路中降低到80 kHz，仍然具有较高的测距精度。
3）基于小波变换原理提出改进自适应模极大值法，将根据故障线路参数自适应设置模极大值选择的门槛值，能够进一步提高本文测距方法的抗过渡电阻和噪声能力，结果表明，在100 W 过渡电阻情况下，仍然能够保证较高的故障测距精度，并且在信噪比达到5 dB时，仍能实现较高的测距精度。
4）本文所提方法是一种单端测距方法，无需进行通信，主要适用于不具备通信功能的应用场合，但是存在近端测距死区的局限性，将会在未来针对此问题开展相关研究。
主要贡献如下：
1）通过一种双极电缆解耦方法提取波速稳定性高的模量值，削弱正负极线路耦合作用。基于传统小波变换理论，提出一种改进自适应模极大值方法来检测脉冲时间，降低伪极点，减小噪声和过渡电阻对故障测距的影响。
2）本文方法注入多组不同脉冲宽度的信号，利用多组发射脉冲信号与反射波的首末端时间差平均值作为故障测距时间，能够在一定程度削弱行波测距对采样频率的依赖，在短距离配电线路中仍然具备较高的故障测距精度。
3）针对现有主动式测距法需额外注入信号装置或MMC注入控制复杂且不够灵活的问题，利用直流固态断路器注入特征脉冲信号，无需额外增加设备，操作简单、安全可靠。
参考文献
[1] 薛士敏, 陈超超, 金毅, 等. 直流配电系统保护技术研究综述[J]. 中国电机工程学报, 2014, 34(19): 3114-3122.
Xue Shimin, Chen Chaochao, Jin Yi, et al. A research review of protection technology for DC distribution system[J]. Proceedings of the CSEE, 2014, 34(19): 3114-3122.
[2] Beheshtaein S, Cuzner R M, Forouzesh M, et al. DC microgrid protection: a comprehensive review[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019(99): 1.
[3] 李晔, 李斌, 刘晓明, 等. 基于反向行波幅值比的对称单极柔性直流系统行波方向保护[J]. 电工技术学报, 2023, 38(9): 2418-2434.
Li Ye, Li Bin, Liu Xiaoming, et al. The direction protection based on the amplitude ratio of the backward traveling wave for the symmetrical mono- pole flexible DC system[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2418-2434.
[4] 葛耀中. 新型继电保护和故障测距的原理与技术[M]. 2版. 西安: 西安交通大学出版社, 2007.
[5] 张广斌, 陈柏宇, 束洪春, 等. 基于时域波形特征认知的输电线路近端故障辨识与定位[J]. 电力系统自动化, 2024, 48(5): 146-156.
Zhang Guangbin, Chen Boyu, Shu Hongchun, et al. Identification and fault location for proximity faults on transmission lines based on the time-domain waveform feature recognition[J]. Automation of Electric Power Systems, 2024, 48(5): 146-156.
[6] 徐峰, 范春菊, 孙秋, 等. 含电力电子变压器的直流配电线路双端故障测距方法[J]. 电力系统及其自动化学报, 2019, 31(10): 73-80.
Xu Feng, Fan Chunju, Sun Qiu, et al. Dual-terminal fault location method for DC distribution lines with power electronic transformer[J]. Proceedings of the CSU-EPSA, 2019, 31(10): 73-80.
[7] 宋国兵, 李德坤, 褚旭, 等. 基于参数识别原理的VSC-HVDC输电线路单端故障定位[J]. 电网技术, 2012, 36(12): 94-99.
Song Guobing, Li Dekun, Chu Xu, et al. One-terminal fault location for VSC-HVDC transmission lines based on principles of parameter identification[J]. Power System Technology, 2012, 36(12): 94-99.
[8] 李博通, 刘涛, 杨昕陆, 等. 故障自清除型直流配电网新型双极短路故障元件识别方法[J]. 电工技术学报, 2022, 37(17): 4423-4434.
Li Botong, Liu Tao, Yang Xinlu, et al. New fault element identification method of bipolar short-circuit fault in DC distribution network with fault self- clearing[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4423-4434.
[9] 李博雅, 杨耀, 杨立红. 高压直流输电线路单端故障测距组合算法[J]. 电力系统保护与控制, 2014, 42(3): 116-121.
Li Boya, Yang Yao, Yang Lihong. A combined method of single-ended fault location for HVDC transmission lines[J]. Power System Protection and Control, 2014, 42(3): 116-121.
[10] 李德坤, 宋国兵, 高淑萍, 等. VSC-HVDC输电线路单端行波自动化故障定位方法研究[J]. 电网技术, 2013, 37(4): 1128-1133.
Li Dekun, Song Guobing, Gao Shuping, et al. Study on automatic fault location for VSC-HVDC trans- mission lines based on one-terminal traveling wave[J]. Power System Technology, 2013, 37(4): 1128-1133.
[11] 张广斌, 束洪春, 于继来, 等. 不依赖双侧时钟同步的输电线双端行波测距[J]. 电工技术学报, 2015, 30(20): 199-209.
Zhang Guangbin, Shu Hongchun, Yu Jilai, et al. Double-ended travelling wave fault location inde- pendent of two side time synchronization[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(20): 199-209.
[12] 张怿宁, 郝洪民, 李京, 等. 脉冲注入法和单端故障行波法相结合的直流输电系统接地极线路故障测距[J]. 电力系统保护与控制, 2017, 45(20): 117-122.
Zhang Yining, Hao Hongmin, Li Jing, et al. Fault location of HVDC grounding electrode lines based on combination of pulse injection method and single- ended fault travelling wave method[J]. Power System Protection and Control, 2017, 45(20): 117-122.
[13] 王帅, 毕天姝, 贾科. 基于主动脉冲的MMC- HVDC单极接地故障测距[J]. 电工技术学报, 2017, 32(1): 12-19.
Wang Shuai, Bi Tianshu, Jia Ke. Single terminal fault location for MMC-HVDC transmission line using active pulse[J]. Transactions of China Electro- technical Society, 2017, 32(1): 12-19.
[14] 宋国兵, 王婷, 张晨浩, 等. 利用全桥MMC注入特征信号的直流自适应重合闸方法[J]. 电网技术, 2019, 43(1): 149-156.
Song Guobing, Wang Ting, Zhang Chenhao, et al. Adaptive auto-reclosing of DC line based on characteristic signal injection with FB-MMC[J]. Power System Technology, 2019, 43(1): 149-156.
[15] He Dong, Shuai Zhikang, Lei Zhiqi, et al. A SiC JFET-based solid state circuit breaker with digitally controlled current-time profiles[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(3): 1556-1565.
[16] Wang Wei, Shuai Zhikang, Duan Hong, et al. A single-drive SiC-JFET-SCM for solid state circuit breaker in MVDC distribution networks[J]. IEEE Transactions on Industrial Electronics, 2023, 70(11): 11121-11131
[17] 杨明嘉, 夏成军, 赖胜杰, 等. 基于线芯-护层过渡电阻无功特性的交叉互联电缆故障测距[J/OL]. 电工技术报, 2023, DOI: 10.19595/j.cnki.1000-6753. tces.222277.
Yang Mingjia, Xia Chengjun, Lai Shengjie, et al. Fault location of cross-connected cables based on reactive power characteristics of core-sheath transi- tion resistance[J/OL]. Transactions of China Elec- trotechnical Society, 2023, DOI: 10.19595/j.cnki. 1000-6753. tces.222277.
[18] 胡昌华, 张军波, 周涛. 基于MATLAB的系统分析与设计-4-小波分析[M]. 西安: 西安电子科技大学出版社, 1999.
[19] 姜涛, 高浛, 李筱静, 等. 基于小波耗散能量谱的电力系统强迫振荡源定位[J]. 电工技术学报, 2023, 38(7): 1737-1750.
Jiang Tao, Gao Han, Li Xiaojing, et al. Forced oscillation source location in power system using wavelet dissipation energy spectrum[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1737-1750.
[20] 崔芮华, 张振, 佟德栓, 等. 基于改进经验小波变换多特征融合的航空交流串联电弧故障检测[J]. 电工技术学报, 2022, 37(12): 3148-3161.
Cui Ruihua, Zhang Zhen, Tong Deshuan, et al. Aviation AC series arc fault detection based on improve empirical wavelet transform multi-feature fusion[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3148-3161.
[21] 赵冠琨, 贾科, 陈金锋, 等. 基于断路器重合闸的柔性直流输电线路单端故障测距方法[J]. 电力系统保护与控制, 2021, 49(7): 48-56.
Zhao Guankun, Jia Ke, Chen Jinfeng, et al. A single terminal fault location method for a DC transmission line based on circuit breaker reclosing[J]. Power System Protection and Control, 2021, 49(7): 48-56.
[22] 吴学斌, 黄治, 邓惟绩. 基于改进变分模态分解的电缆行波故障定位研究[J]. 湖南电力, 2021, 41(3): 1-6, 11.
Wu Xuebin, Huang Zhi, Deng Weiji. Research on cable traveling wave fault location based on improved variational modal decomposition method[J]. Hunan Electric Power, 2021, 41(3): 1-6, 11.
[23] 宋国兵, 侯俊杰, 郭冰. 基于主动探测式的混合MMC直流输电系统单端量故障定位[J]. 电网技术, 2021, 45(2): 730-740.
Song Guobing, Hou Junjie, Guo Bing. Single-ended fault location of hybrid MMC-HVDC system based on active detection[J]. Power System Technology, 2021, 45(2): 730-740.
[24] 陈文, 陈凯平, 夏向阳, 等. 高压直流输电系统输电电缆的故障定位方法[J]. 湖南电力, 2022, 42(6): 123-128.
Chen Wen, Chen Kaiping, Xia Xiangyang, et al. Fault location method of HVDC transmission cable[J]. Hunan Electric Power, 2022, 42(6): 123-128.
[25] Giannakis A, Peftitsis D. Performance evaluation and limitations of overvoltage suppression circuits for low- and medium-voltage DC solid-state breakers[J]. IEEE Open Journal of Power Electronics, 2021, 2: 277-289.
Abstract Accurate and reliable fault location technology is crucial for DC fault repair and recovery with the rapid development and widespread application of DC distribution networks. The passive traveling wave ranging method has the issues of limited energy and insufficient traveling wave characteristic information. The traditional active traveling wave ranging method partially addresses these issues. However, the effects of line wave speed stability and sampling frequency are susceptible. This paper proposes an active injection DC fault location method based on a solid-state circuit breaker (SSCB). First, the SSCB is utilized to interrupt and actively inject signals with different pulse widths. The time difference between the first end of the injected pulse and the first end of the reflected wave is detected as the time interval of injection waveform propagation. This approach reduces errors caused by sampling frequency limitations. Then, the voltage line modulus of the cable line is extracted as the detection quantity, effectively weakening the coupling effect between the positive and negative lines and providing a stable wave speed measurement. Finally, based on the wavelet transform principle, an improved adaptive modulus maximum approach is proposed to detect the first and last moments of the pulse accurately. This approach also mitigates the impact of noise and transition resistance on ranging accuracy.
The simulation results show that the proposed method achieves high fault location accuracy for single-pole ground and bipolar short-circuit faults in a distribution network with a total line length of 10 km. The fault location accuracy is less than 0.55%. Even at a high sampling frequency of 80 kHz in 10 km DC distribution lines, the relative error of fault location remians within 1.14%, which reduces dependence on sampling frequency and enhances the robustness of the method. Moreover, the method exhibits resilience to noise interference at different signal-to-noise ratios. With signal-to-noise ratios of 40 dB, 20 dB, and 5 dB, the fault location accuracy with a relative error of less than 0.67% is consistently achieved. However, when the signal-to-noise ratio drops below 5 dB, the impact of noise on ranging and positioning increases, posing challenges for achieving high-precision fault location.
The following conclusions can be drawn from the simulation analysis. (1) The proposed method achieves high-precision fault location under single-pole ground or inter-pole short-circuit faults in DC distribution networks. It does not require additional equipment and is simple to operate. (2) A detection method is introduced to measure the average time difference between the end of the transmitted pulse wave and the end of the reflected wave of pulses with different widths. This method reduces the dependence on sampling accuracy caused by the traveling wave ranging method. (3) An improved adaptive modulus maximum method is proposed based on the principle of wavelet transform. The method adaptively sets the threshold value for modulus maximum selection based on fault line parameters, enhancing the resistance to transition resistance and noise in the distance measurement method. (4) The proposed single-ended ranging method does not need communication, which is suitable for applications without communication functions. However, it has the limitation of a dead zone in near-end ranges. Future research will focus on addressing this issue.
keywords：DC distribution network, fault location, solid-state circuit breaker, active injection, adaptive modulus maximum
国家自然科学基金项目（52125705）、博士后面上资助项目（2021M701137, 2022M721082）、湖南省青年基金项目（2022JJ40066）、湖南省重点研发计划项目（2023GK2010）和湖南省研究生科研创新项目（CX20220394）资助。
收稿日期 2023-09-23
改稿日期 2023-11-27
DOI: 10.19595/j.cnki.1000-6753.tces.231576
中图分类号：TM614
王 伟 男，1995年生，博士研究生，研究方向直流固态断路器及直流配电网保护。E-mail: wangwei95@hnu.edu.cn
帅智康 男，1982年生，教授，博士生导师，研究方向为新能源并网稳定性分析与控制技术。E-mail: shuaizhikang-001@163.com（通信作者）
（编辑 陈 诚）