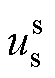 为公共连接点交流电压,
为公共连接点交流电压,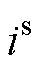 为交流侧电流。
为交流侧电流。摘要 以并网逆变器为功率接口的新能源发电系统在弱电网条件下易发生振荡失稳问题。该文将并网逆变器的控制回路可视化为电路元件组成的虚拟阻抗,基于该电路模型分析了弱电网条件下电流内环与锁相环交互作用导致并网逆变器振荡失稳的机理,在此基础上,提出了基于有源阻尼的稳定控制设计方法,并对不同有源阻尼控制的电路特性以及稳定性提升能力进行了对比分析。研究结果表明,针对锁相环引入负电阻造成的振荡失稳问题,阻抗-高通滤波器型有源阻尼控制策略具有更优的稳定性提升能力。最后通过PSCAD/EMTDC仿真和远宽StarSim控制器硬件在环实验对比了不同有源阻尼控制策略的振荡抑制效果,并验证了阻抗-高通滤波器型有源阻尼控制的动态性能。结果表明,所设计的稳定控制能够在200 ms内有效抑制系统振荡,并且可实现在短路比为1的极弱电网条件下稳定运行。
关键词:并网逆变器 电路等效 振荡稳定性 有源阻尼 虚拟阻抗 稳定控制
以风电、光伏为主的新能源快速发展的同时也引发了一系列新型宽频振荡问题,成为构建新型电力系统的关键技术挑战之一[1-2]。并网逆变器是新能源发电系统与电网的功率接口,也是构成直流微电网的关键装备,其动态特性对并网稳定性具有较大影响[3-4]。
在稳定性分析方面,特征值法[5]和阻抗法[6]是目前分析振荡稳定性的主流方法。特征值法通过建立整个系统的状态空间方程,求解系统特征值进行稳定性评估,并利用参与因子获取影响系统稳定性的主导状态量,但是该方法基于数值解,在揭示振荡机理方面存在不足。阻抗法通过建立源-荷子系统的等效阻抗模型,利用对数频率稳定判据或Nyquist稳定判据分析系统的小扰动稳定性,该方法由于具有紧凑型、模块化表征变流器宽频动态、易于电路互联等优势被广泛采用[6-7]。但是阻抗法主要用于揭示变流器所有控制环节对其端口频率响应特性的集中影响,难以直观体现各个控制环节的作用机制。通过将并网逆变器关键控制环节的数学模型进行等效,得到能够反映控制器物理本质的电路模型,有利于揭示各个环节的交互机理[8-10]。文献[8]对电压源逆变器的电压和电流环PI或PR控制器进行电路等效,揭示了其物理本质,但未考虑锁相环模型。文献[9]利用电流环PI控制器的RC等效电路,揭示了并网变流器在感性弱电网条件下的固有LC振荡现象,并利用相量法分析了锁相环对该固有LC振荡电路的阻尼作用,但没有直观地给出电流环与锁相环交互形成负电阻的物理模型。文献[10]将并网逆变器等效为d通道和q通道的谐波电路,指出q通道低频段的负电阻特性完全由锁相环引入。但dq通道的等效电路缺乏明确的物理含义,如何将并网逆变器各控制环节可视化为有明确物理含义的电路模型仍需进一步研究。
在稳定控制方面,主要包括调整控制参数[11-13]、附加振荡抑制环节[14-22]等。调整控制参数的方式是指对系统原有的控制器参数进行调整,以增大系统在振荡频段的阻尼水平,提升系统的稳定性,适用于中低频段的振荡抑制,但改变控制参数对系统基频控制性能具有较大影响。附加振荡抑制环节的方式是目前抑制振荡的主流方案,通常也称作有源阻尼控制,主要有两种思路:一是阻断振荡传播路 径[14, 21],通过在电压或电流反馈通道上添加滤波器,提供一个振荡频率处的反向电压或电流,切断次同步振荡的传播途径,需要根据具体振荡频率设计相应的控制参数;二是消除振荡源,通过振荡机理分析找到产生振荡的主要原因或主导环节,进而采取相应的措施消除振荡源或增强主导环节的稳定性。根据滤波功能的不同,有源阻尼控制可分为低通、高通、带通、带阻等多种类型[15, 22]。
利用低通滤波器(Low Pass Filter, LPF)可以降低前馈电压控制对变流器的负阻尼效应,从而达到抑制系统高频振荡的目的[15]。高通滤波器(High Pass Filter, HPF)仅允许高于截止频率的振荡分量通过,多用于抑制功率、直流电流和直流电压出现的低频振荡[16, 18]。低通和高通滤波器组合可以形成带通滤波器(Band Pass Filter, BPF)[19]和带阻滤波器结构陷波器(Band Rejection Filter, BRF)。带通/带阻滤波器通过设置中心频率和带宽可以提取或阻断某一特定频段的振荡分量,既可以实现中高频振荡的抑制[20],也可以实现次/超同步振荡的抑制[21-22]。不同滤波器都可以用电阻、电感、电容等电路元件进行等效,但当前鲜有文献从电路角度揭示滤波器在特定频段实现振荡抑制的机理。
综上所述,针对并网逆变器的振荡稳定性分析和有源阻尼控制已有大量研究,但主要针对特定频段振荡的分析与抑制,且多基于状态空间模型或阻抗模型,而缺少能够直观反映不同控制环节作用机制的分析方法和系统性的有源阻尼控制设计方法。为此,本文研究一种基于电路模型的并网逆变器振荡稳定性分析方法,将控制回路可视化为不同序域视角下的电路模型,从电路角度揭示锁相环引入负电阻并导致并网逆变器振荡失稳的机理。在此基础上,提出有源阻尼控制的设计依据,并对不同类型有源阻尼控制的电路特性和稳定性提升能力进行对比分析,最后通过PSCAD/EMTDC仿真和控制器硬件在环实验验证理论分析的正确性。
三相并网逆变器的典型控制结构如图1所示,包含电流内环、锁相环、前馈解耦项、坐标变换、控制延时等环节。图1中,Lg为交流电网电感,Lf为逆变器滤波电感,HI为电流内环PI控制的传递函数,HPLL为锁相环PI控制的传递函数,Gde代表控制延时,以“0”为下标的量代表电压和电流的稳态值,以“c”为上标的量代表控制系下的分量,以“s”为上标的量代表电气系下的分量,us为变流器出口侧交流电压,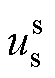 为公共连接点交流电压,
为公共连接点交流电压,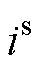 为交流侧电流。
为交流侧电流。
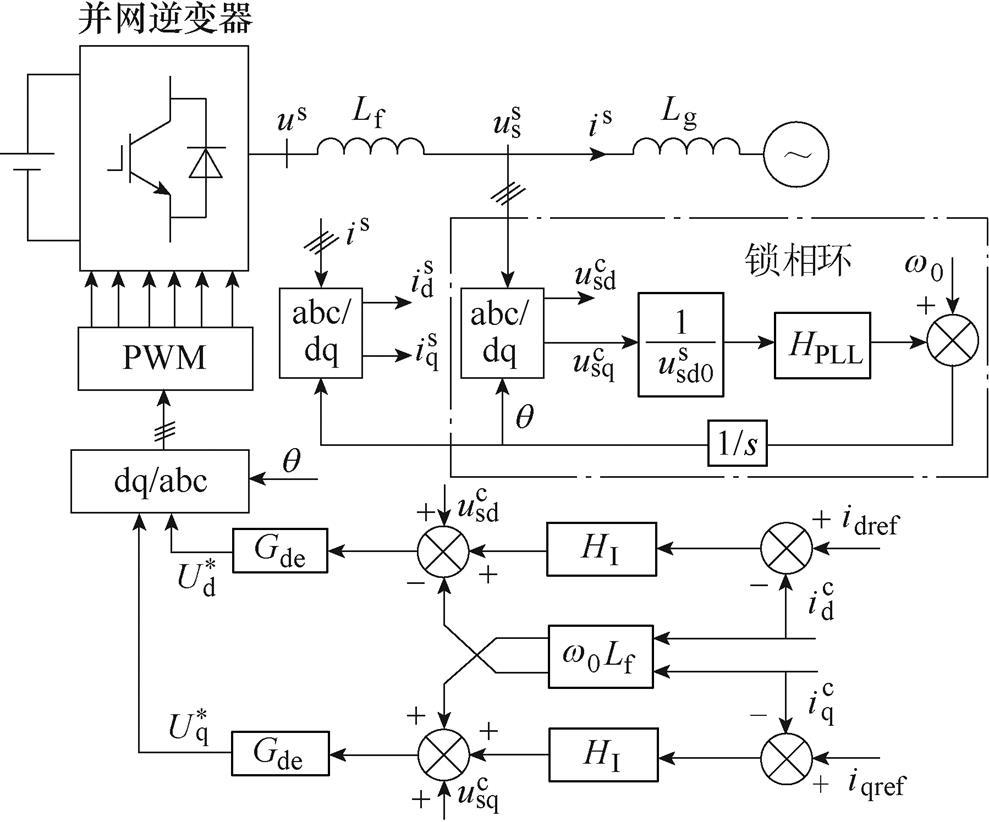
图1 并网逆变器结构示意图
Fig.1 Structure of the grid-connected inverter
能够反映控制器内部动态的交流电压和电流的关系为
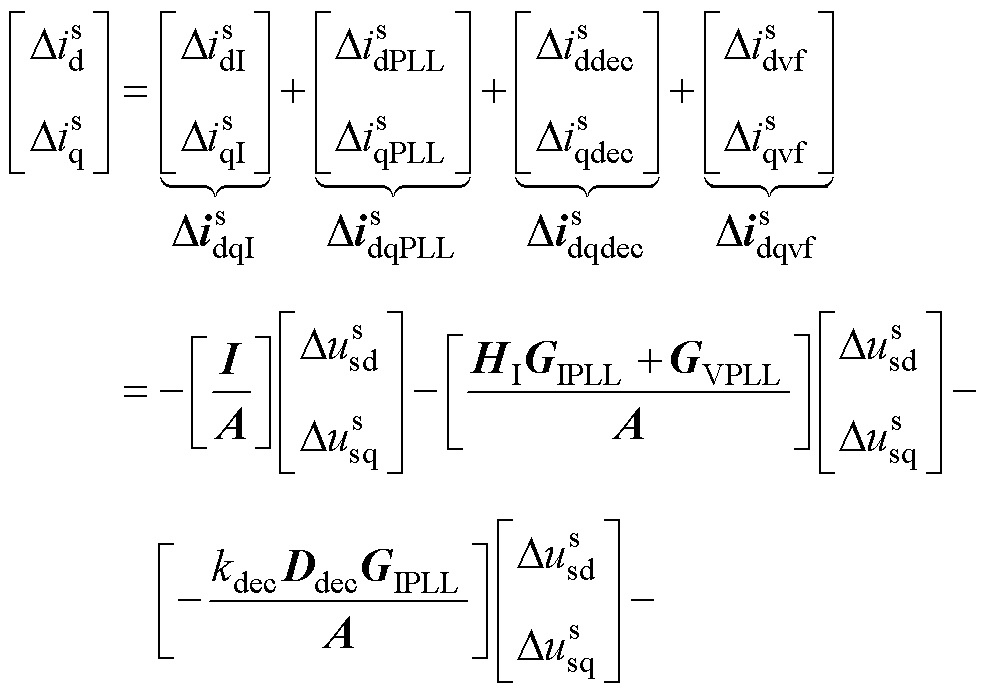
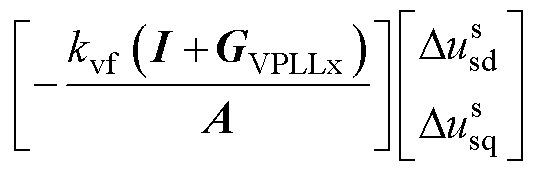 (1)
(1)
式中,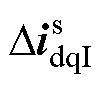 为电流内环控制与滤波电感等效的dq电流分量;
为电流内环控制与滤波电感等效的dq电流分量;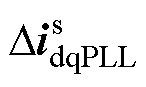 为锁相环等效的dq电流分量,
为锁相环等效的dq电流分量,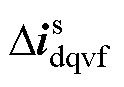 和
和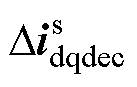 分别为电压前馈和解耦项等效的dq电流分量[23];kvf表示是否考虑电压前馈,等于1代表考虑电压前馈;kdec表示是否考虑解耦项,等于1代表考虑解耦项;加粗的变量代表2维矩阵;I为2阶单位矩阵;A、HI、GIPLL、GVPLL、GVPLLx、Ddec的表达式见附录中式(A1)。
分别为电压前馈和解耦项等效的dq电流分量[23];kvf表示是否考虑电压前馈,等于1代表考虑电压前馈;kdec表示是否考虑解耦项,等于1代表考虑解耦项;加粗的变量代表2维矩阵;I为2阶单位矩阵;A、HI、GIPLL、GVPLL、GVPLLx、Ddec的表达式见附录中式(A1)。
1.2.1 电流内环等效电路
根据式(1)可知,dq域下仅考虑电流内环的并网逆变器电压电流关系如式(2)所示,考虑解耦项,非对角线元素为0,忽略控制延时影响,等效电路模型如图2所示。电流内环比例环节Kpi可以等效为虚拟电阻,积分环节Kii/s可以等效为虚拟电容,AI=Kpi+Kii/s+sLf。
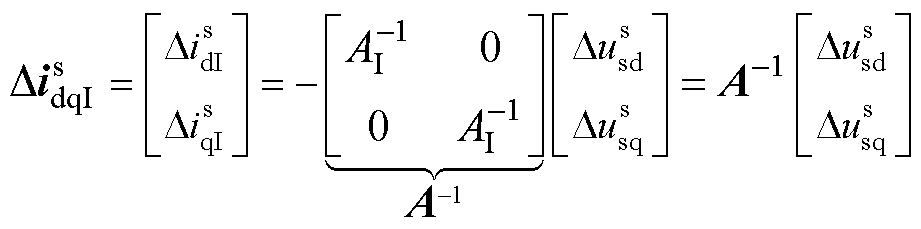 (2)
(2)
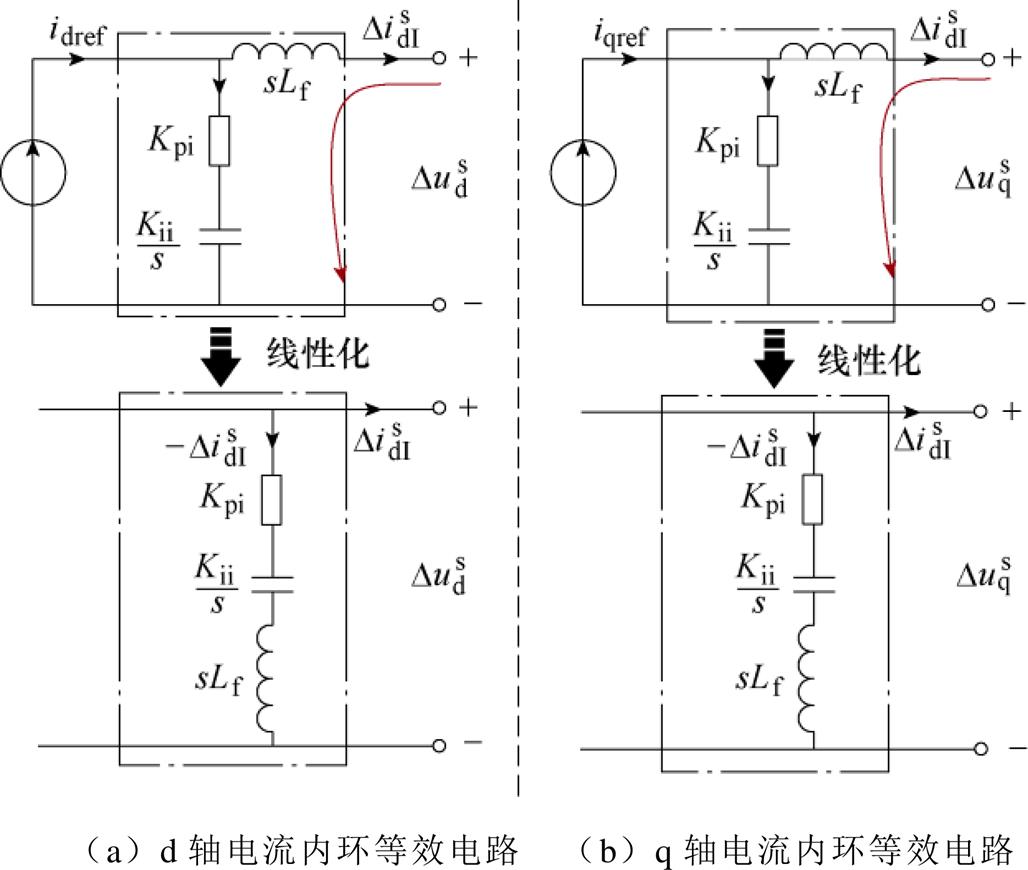
图2 电流内环等效电路示意图
Fig.2 Diagram of the equivalent circuit of the inner current loop control
1.2.2 锁相环等效电路
在锁相环的影响下,并网逆变器电压电流关系如式(3)所示,锁相环在dq域下的等效电路如图3所示,d轴电路等效为q轴电压控制的电流源,q轴等效电路可表示为虚拟电阻Kpi/GPLLq(s)、虚拟电容Kii/GPLLq(s)和虚拟电感sLf/GPLLq(s)串联的形式。GPLLd和GPLLq如式(4)所示。
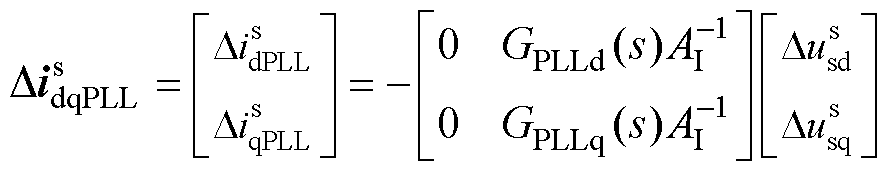 (3)
(3)
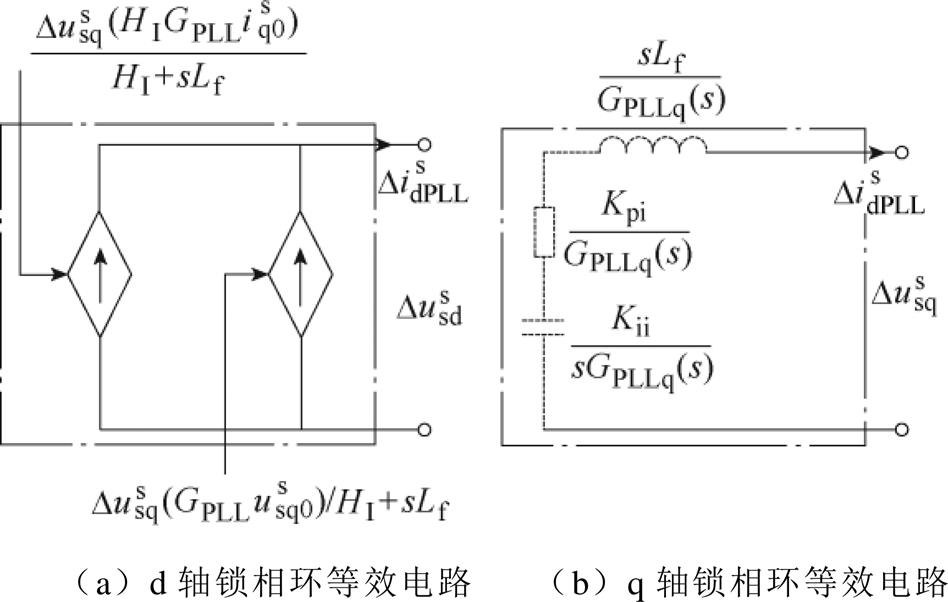
图3 锁相环等效电路示意图
Fig.3 Diagram of the equivalent circuit of the PLL
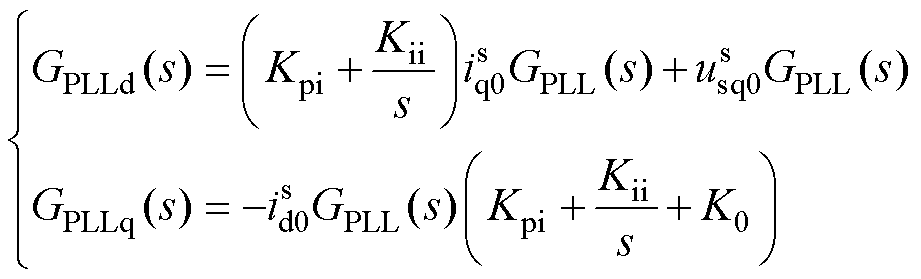 (4)
(4)
式中,K0=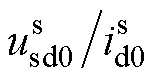 ;GPLL(s)为锁相环闭环传递函数,如附录中式(A1)所示。
;GPLL(s)为锁相环闭环传递函数,如附录中式(A1)所示。
1.2.3 电压前馈/解耦项以及交流电网等效电路
考虑电压前馈和解耦项的并网逆变器电压电流关系如式(5)和式(6)所示,dq域下等效电路如图4所示,电压前馈和解耦项在d轴的电路等效为q轴电压控制的电流源,电压前馈和解耦项在q轴的等效电路由虚拟阻抗构成。
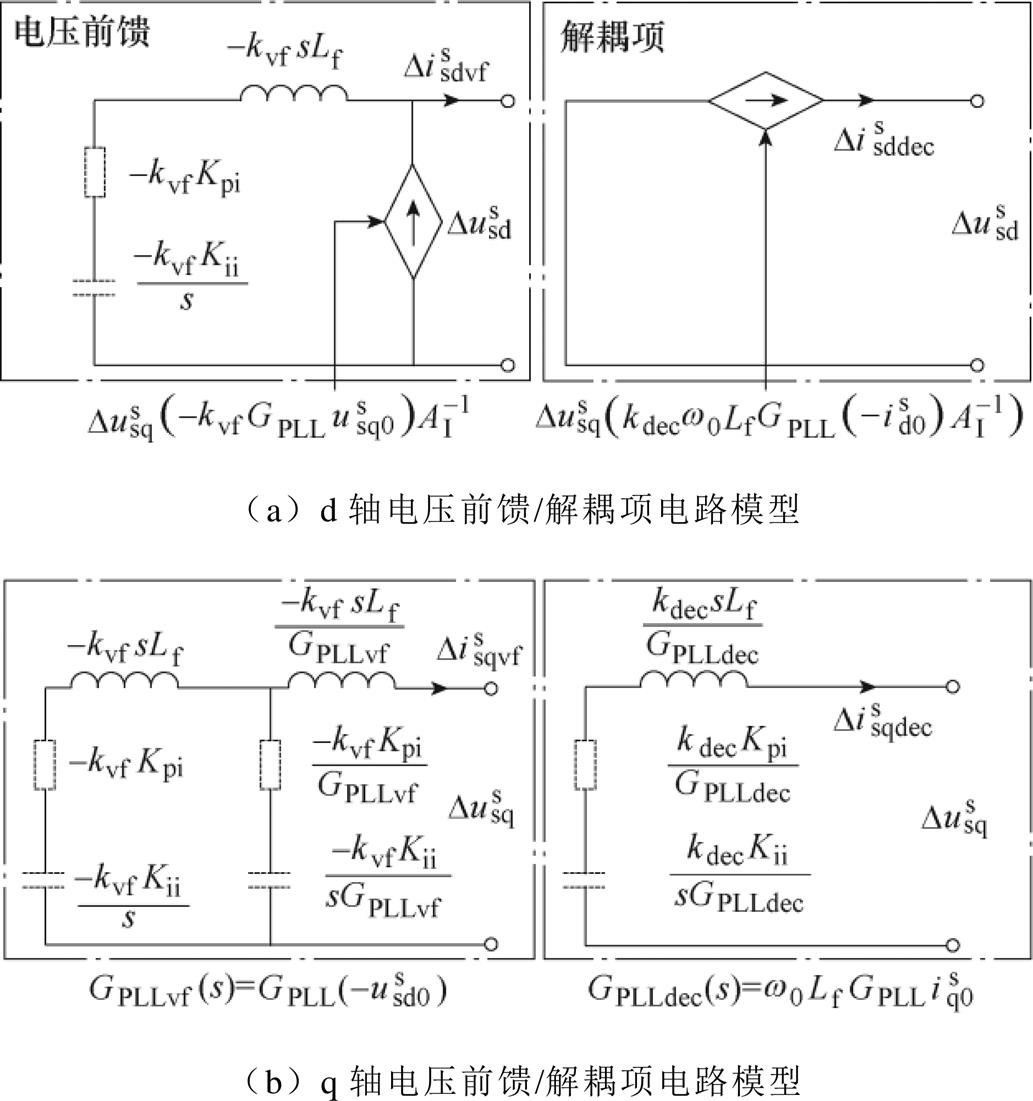
图4 电压前馈和解耦项等效电路示意图
Fig.4 Diagram of the equivalent circuit of the voltage feedforward and decouple term
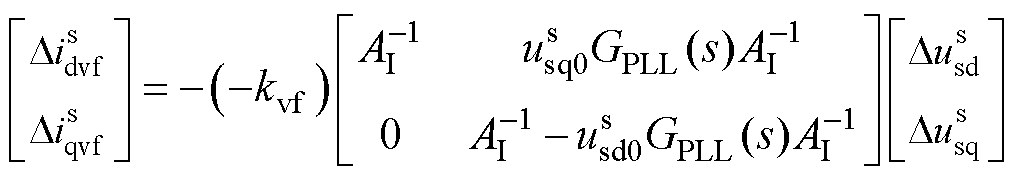 (5)
(5)
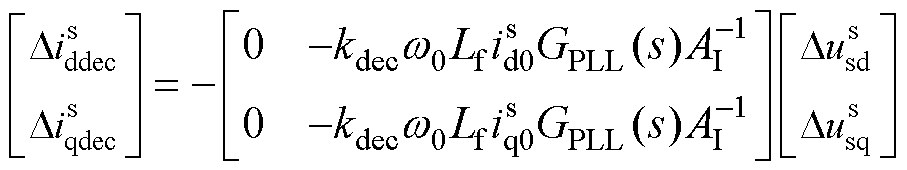 (6)
(6)
交流电网在dq域下的阻抗如式(7)所示,等效电路如图5a所示。
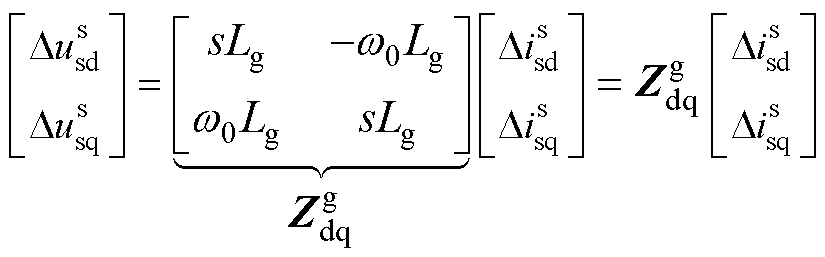 (7)
(7)
根据图2~图4中不同控制环节的等效电路可以得到并网逆变器在dq域下的等效电路模型如图5a所示,根据式(8)和式(9)将dq域下并网逆变器和交流电网的等效电路转换为改进序域下(dq±)的等效电路[24],如图5b所示。
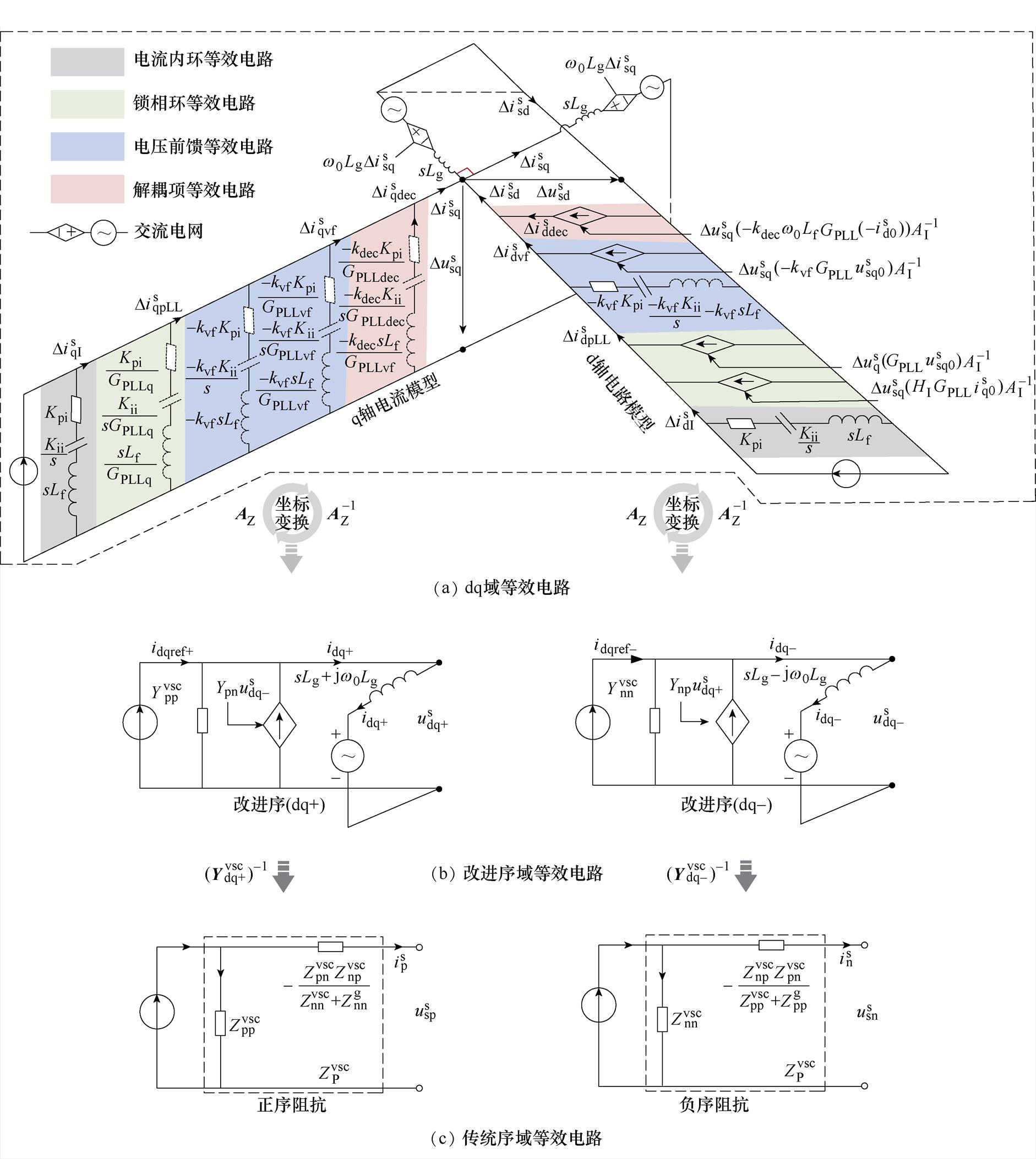
图5 并网逆变器等效电路示意图
Fig.5 Diagram of the equivalent circuit of the grid-connected inverter
改进域下用于表征控制器内部动态的交流电压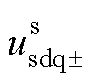 和电流
和电流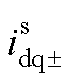 的关系如式(10)所示,图中
的关系如式(10)所示,图中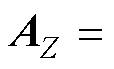
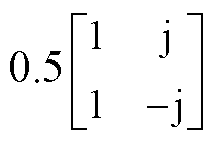 ,
,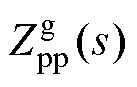 =sLg+jw0Lg,
=sLg+jw0Lg,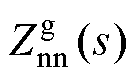 =sLg-jw0Lg。
=sLg-jw0Lg。
根据式(10)~式(12)将改进序域下的并网逆变器等效电路经过频率偏移后(sp=s-jw0,sn= s+jw0)转换为传统序域下的等效电路[25],其中,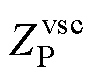 为逆变器正序阻抗,
为逆变器正序阻抗,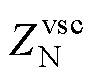 为逆变器负序阻抗。如式(13)和图5c所示,
为逆变器负序阻抗。如式(13)和图5c所示,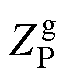 为交流电网正序阻抗,
为交流电网正序阻抗,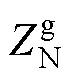 为交流电网负序阻抗。
为交流电网负序阻抗。
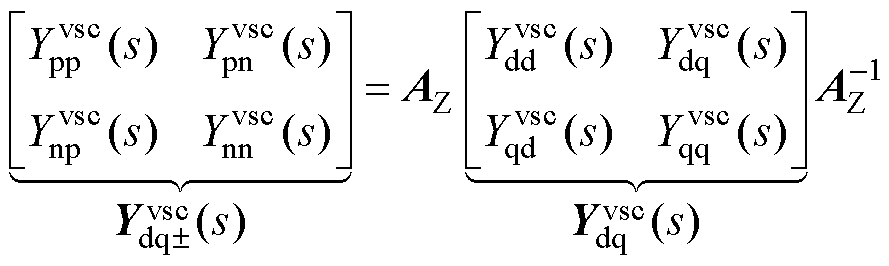 (8)
(8)
式中,Y为导纳,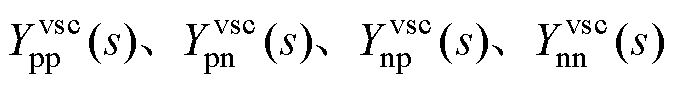 为二维改进序域导纳的四个元素;
为二维改进序域导纳的四个元素;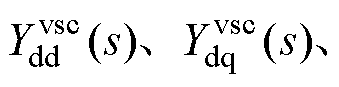
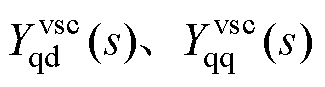 为二维dq域导纳的四个元素。
为二维dq域导纳的四个元素。
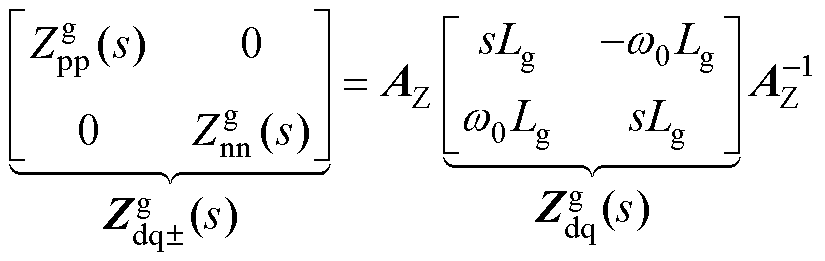 (9)
(9)
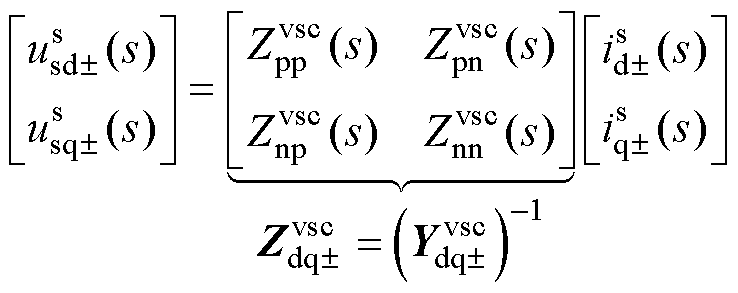 (10)
(10)
式中,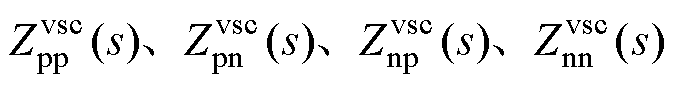 为二维改进序阻抗的四个元素。
为二维改进序阻抗的四个元素。
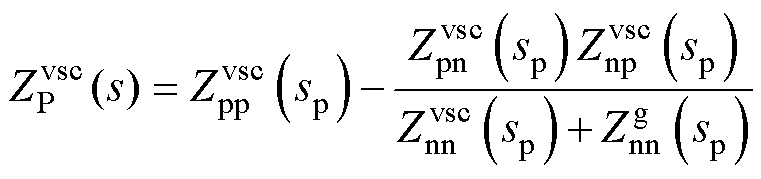 (11)
(11)
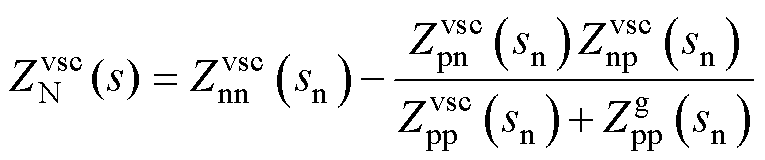 (12)
(12)
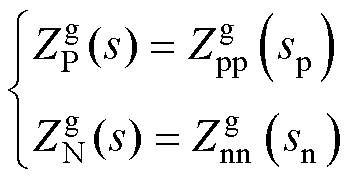 (13)
(13)
根据第1节推导的并网逆变器等效电路模型可知,以下情况下并网逆变器在次/超同步频段不存在负电阻特性或者负电阻:
(1)仅考虑电流内环的情况下,图5所示并网逆变器的等效电路由线性电路元件构成,不存在负电阻。
(2)根据式(1)和式(5)可知,电压前馈主要影响dq域下的对角线元素,如果kvf=1,电压前馈会抵消电流内环在dq轴提供的正电阻,但也可以削弱锁相环在q轴引入的负电阻;如式(14)所示,电压前馈可以改善正负序域阻抗在基频附近的负电阻,但影响较小,本文忽略电压前馈对基频附近负电阻的影响;电压前馈主要会导致中高频段出现负电阻。
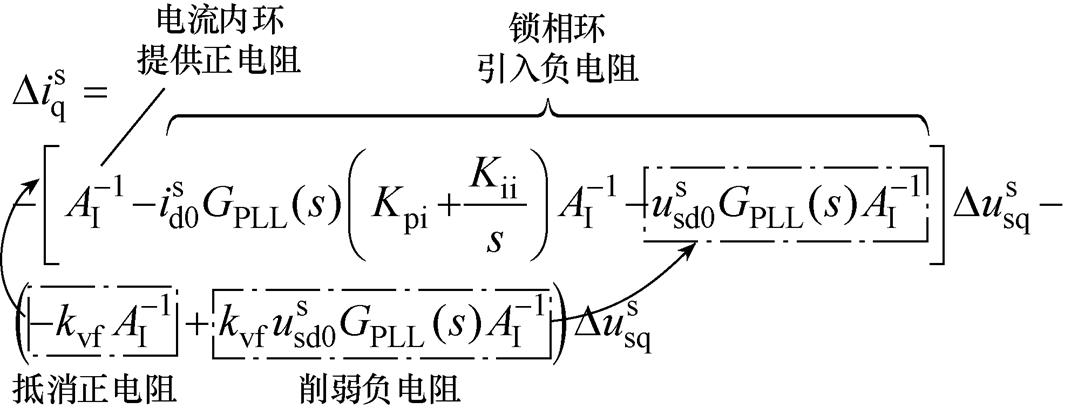 (14)
(14)
(3)忽略解耦项在q轴等效电路形成的负电阻(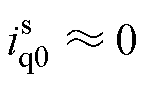 ),解耦项会导致dq域下的非对角线元素Zdq出现负电阻,但是转换到正序阻抗后,解耦项形成的负电阻较小,可以忽略。
),解耦项会导致dq域下的非对角线元素Zdq出现负电阻,但是转换到正序阻抗后,解耦项形成的负电阻较小,可以忽略。
(4)锁相环在q轴的等效电路如图6所示,其中滤波电感与锁相环交互形成的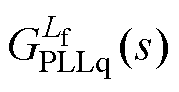 实部恒为正(
实部恒为正(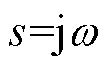 ),不会引入负电阻,如附录中式(A2)所示。
),不会引入负电阻,如附录中式(A2)所示。
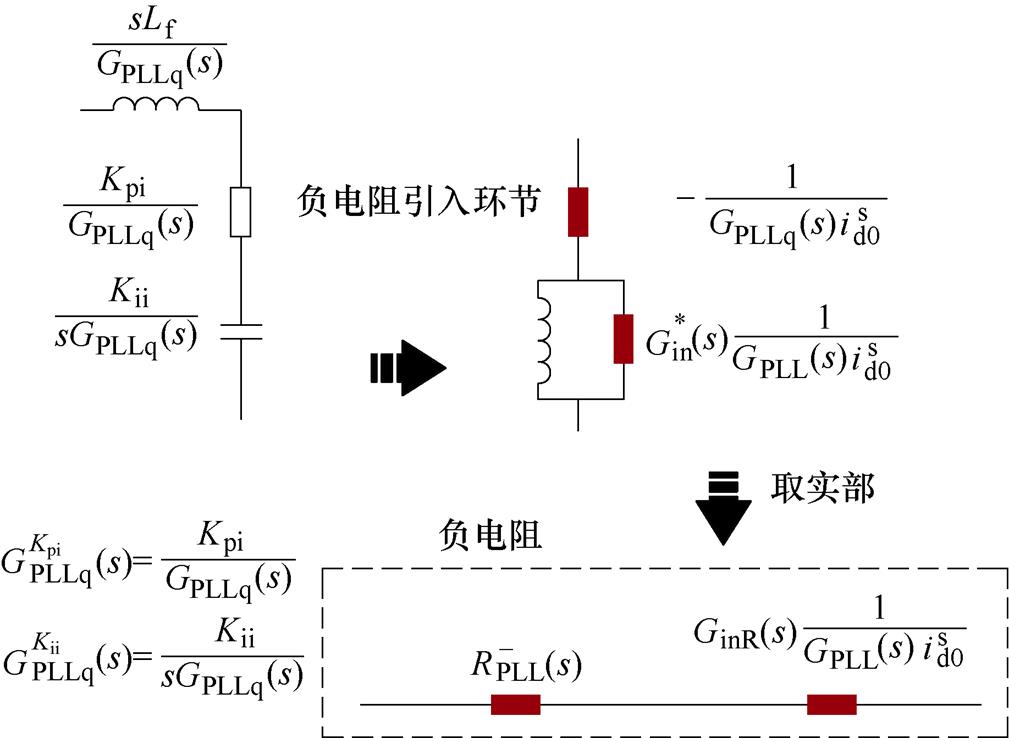
图6 锁相环引入负电阻示意图
Fig.6 Diagram of the negative resistance introduced by PLL
根据图6和式(15)可知,电流内环与锁相环交互形成的虚拟电阻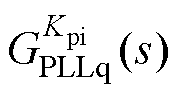 和虚拟电容
和虚拟电容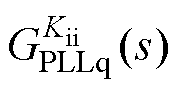 是锁相环在q轴等效电路形成负电阻的根本原因。锁相环主导的
是锁相环在q轴等效电路形成负电阻的根本原因。锁相环主导的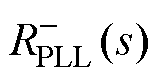 决定了并网逆变器是否存在负电阻,直接主导着负电阻的大小和影响频段。
决定了并网逆变器是否存在负电阻,直接主导着负电阻的大小和影响频段。
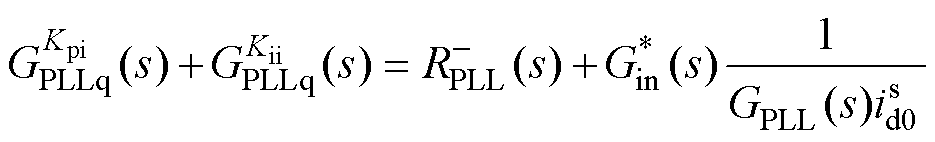 (15)
(15)
其中
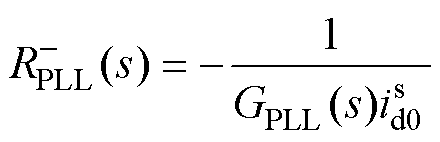 (16)
(16)
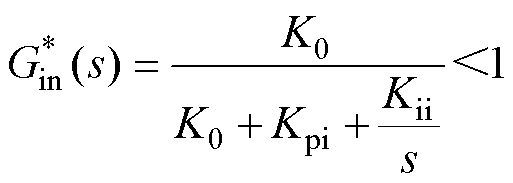 (17)
(17)
锁相环主导的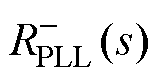 如图7a所示,随着锁相环带宽增加,负电阻影响的频段会在次/超同步频段扩大,频率超过临界值ftPLL后,负电阻的大小和影响频段开始缩小,ftPLL为
如图7a所示,随着锁相环带宽增加,负电阻影响的频段会在次/超同步频段扩大,频率超过临界值ftPLL后,负电阻的大小和影响频段开始缩小,ftPLL为
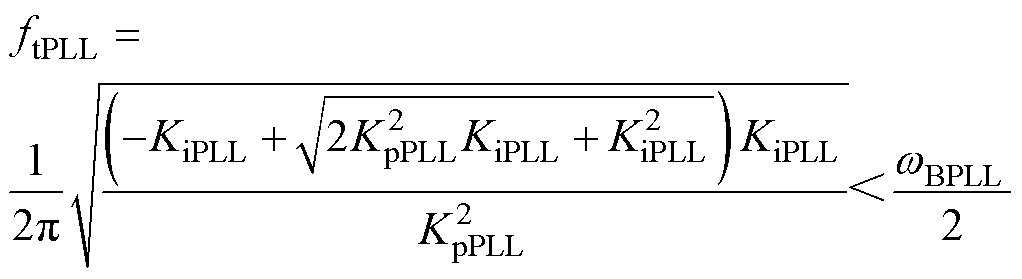 (18)
(18)
式中,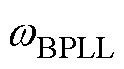 为锁相环带宽;KpPLL为锁相环PI控制的比例系数;KiPLL为锁相环PI控制的积分系数。
为锁相环带宽;KpPLL为锁相环PI控制的比例系数;KiPLL为锁相环PI控制的积分系数。
由式(15)可知,电流内环对负电阻的影响体现在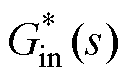 ,
,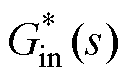 的实部
的实部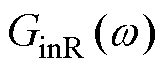 恒为正,即
恒为正,即
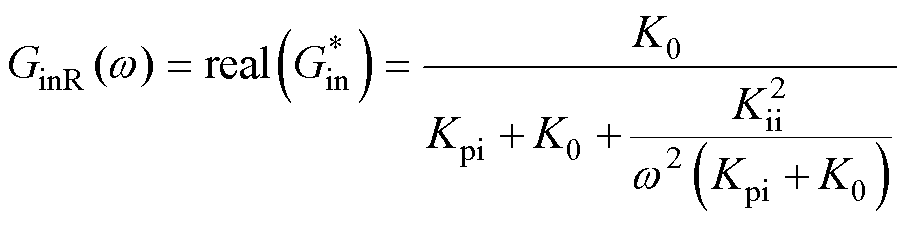 (19)
(19)
根据式(15)可知,锁相环带宽一定时,定义电流内环主导的负电阻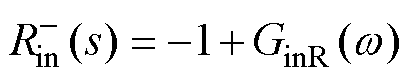 。
。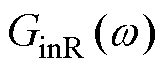 变化导致
变化导致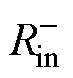 的大小和影响频段改变,在低频段,
的大小和影响频段改变,在低频段,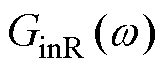 随Kpi变化呈现非单调特性,随Kii增加而降低;在高频段,
随Kpi变化呈现非单调特性,随Kii增加而降低;在高频段,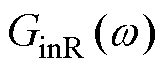 主要受Kpi影响,随Kpi增加而降低。整体上,随着电流内环带宽的增加,负电阻
主要受Kpi影响,随Kpi增加而降低。整体上,随着电流内环带宽的增加,负电阻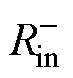 增加且影响的频段扩大,随着频率增加,负电阻
增加且影响的频段扩大,随着频率增加,负电阻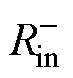 降低,如图7b所示。
降低,如图7b所示。
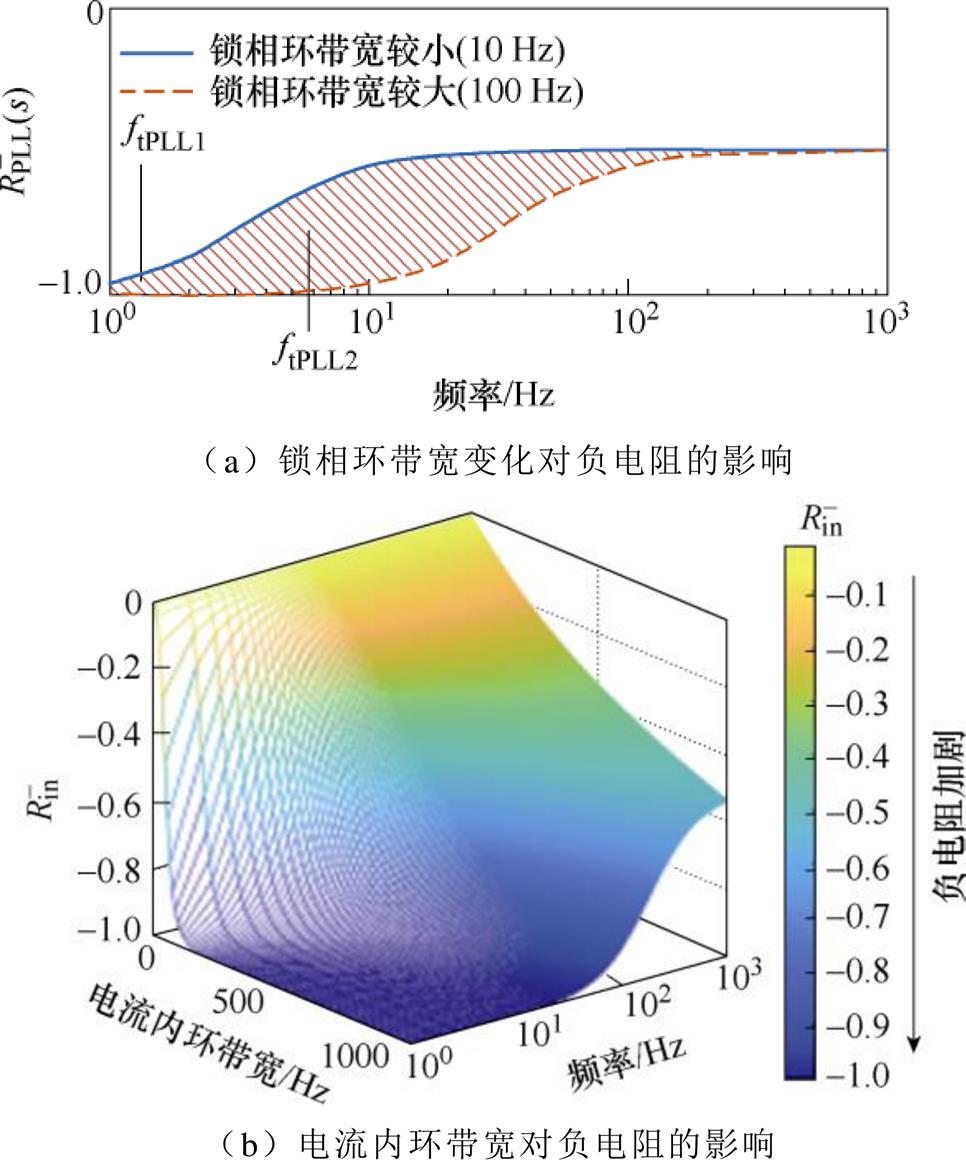
图7 锁相环带宽和电流内环带宽对负电阻的影响
Fig.7 Negative resistance effectd by PLL and the current inner loop
dq域下并网逆变器的负电阻仅在q轴等效电路的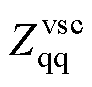 存在[26],如图8a所示,将图6中的负电阻由
存在[26],如图8a所示,将图6中的负电阻由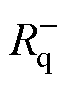 等效代替,且
等效代替,且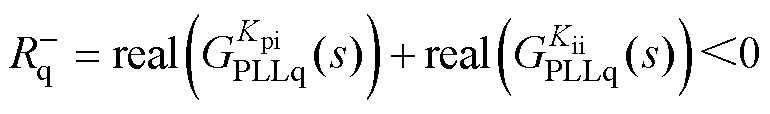 ,
,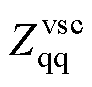 等效为
等效为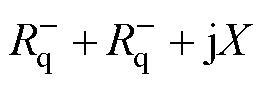 ,
,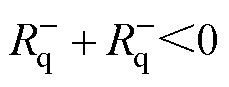 时,经过坐标变换和频率偏移后,dq域下
时,经过坐标变换和频率偏移后,dq域下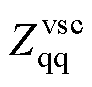 的负电阻引入改进序域的对角线元素中,如图5b和式(20)所示,改进序域的负电阻如图8b所示。
的负电阻引入改进序域的对角线元素中,如图5b和式(20)所示,改进序域的负电阻如图8b所示。
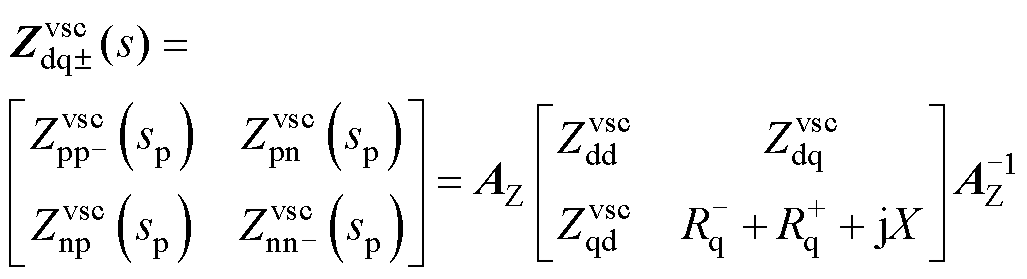 (20)
(20)
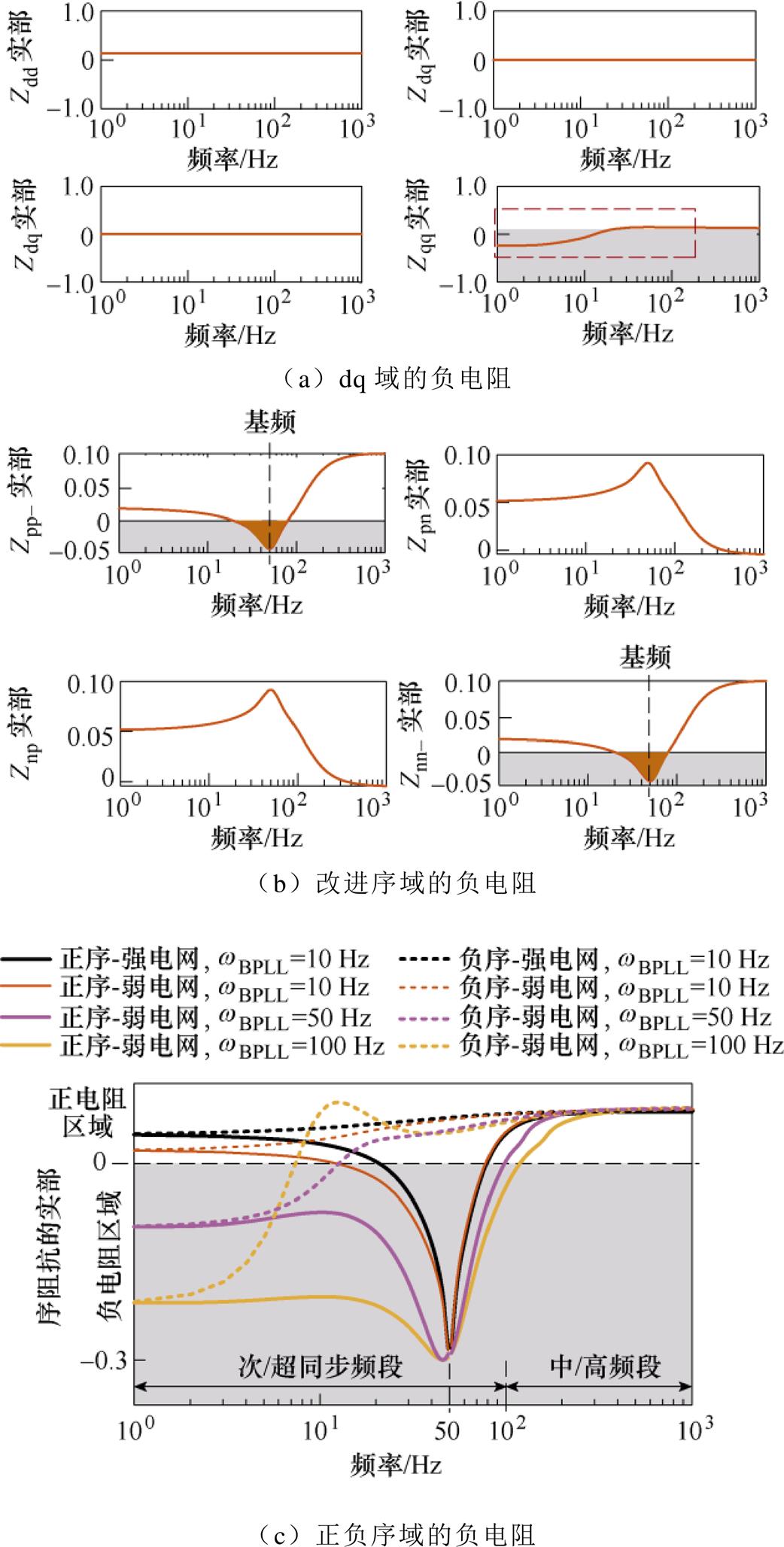
图8 dq域、改进序域、正负序域的负电阻分析
Fig.8 Negative resistance of the dq domian, modified sequence doamin and positive/negative domain
式中,变量具体表达形式见附录中式(A3)和式(A4)。
以正序阻抗为例,结合式(11)和式(20)可得到改进序域非对角线元素的负电阻对正序阻抗的影响,即
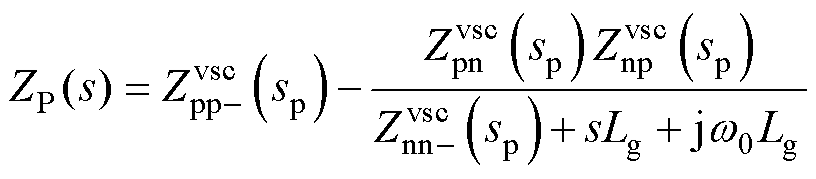 (21)
(21)
正序阻抗实部等效为负电阻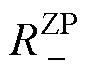 和正电阻
和正电阻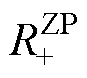 ,即
,即
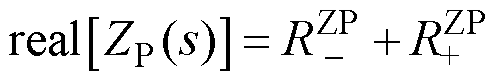 (22)
(22)
电网强度由5降为3,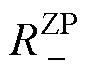 超过
超过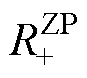 导致正序阻抗在基频附近呈现负电阻特性,弱电网下锁相环带宽增加会造成正序阻抗的负电阻区域继续扩大,如图8c所示。
导致正序阻抗在基频附近呈现负电阻特性,弱电网下锁相环带宽增加会造成正序阻抗的负电阻区域继续扩大,如图8c所示。
电流内环和锁相环交互对负电阻影响表示为
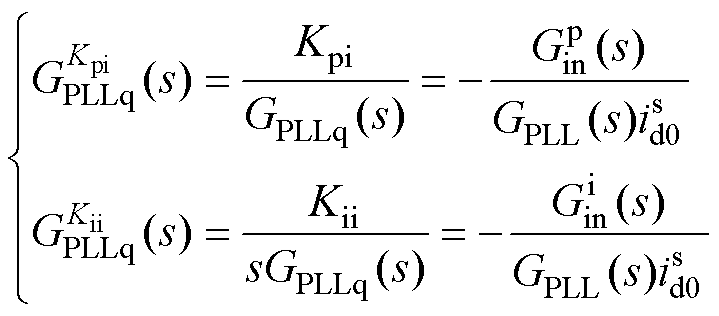 (23)
(23)
其中
 (24)
(24)
 (25)
(25)
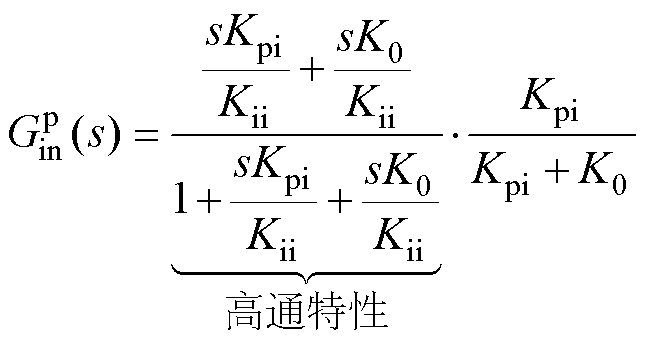
由式(23)可知,电流内环的比例环节Kpi与锁相环交互形成的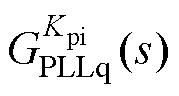 中,
中,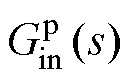 呈现高通滤波器特性。如图9a所示,电流内环带宽增加,
呈现高通滤波器特性。如图9a所示,电流内环带宽增加,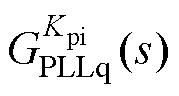 会减小低频段的负电阻而增加高频段的负电阻。随着频率增加,
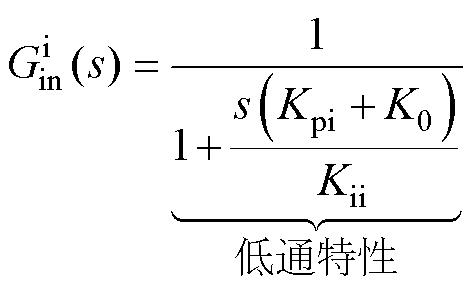
会减小低频段的负电阻而增加高频段的负电阻。随着频率增加,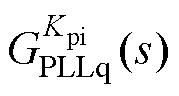 形成的负电阻增加。电流内环的积分环节Kii和锁相环交互形成的
形成的负电阻增加。电流内环的积分环节Kii和锁相环交互形成的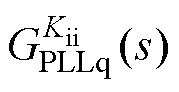 中,
中,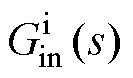 呈现低通滤波器特性。如图9b所示,电流内环带宽增加,
呈现低通滤波器特性。如图9b所示,电流内环带宽增加,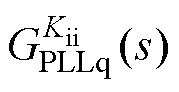 在全频段形成的负电阻增加。随着频率增加,
在全频段形成的负电阻增加。随着频率增加,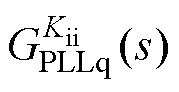 形成的负电阻降低。
形成的负电阻降低。
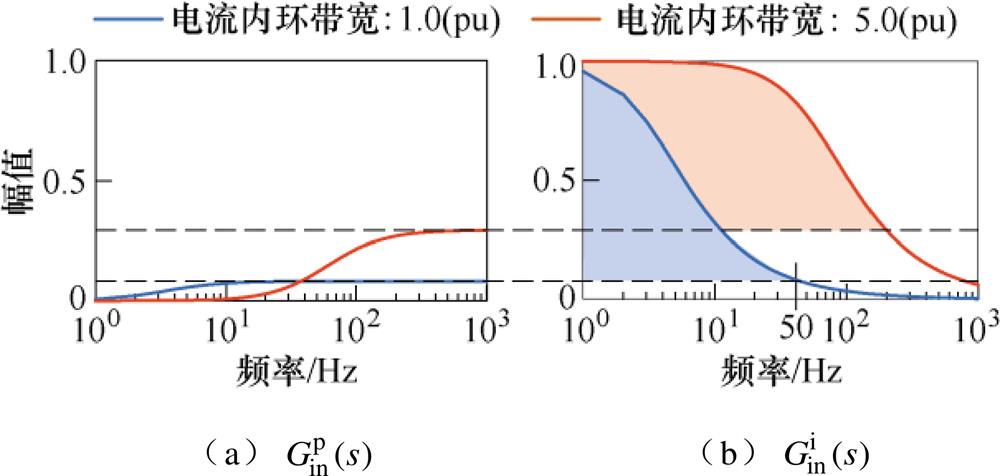
图9 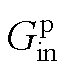 和
和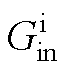 的幅频特性曲线
的幅频特性曲线
Fig.9 Magnitude-frequency characteristics of 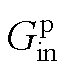 and
and 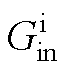
锁相环带宽一定时,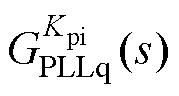 和
和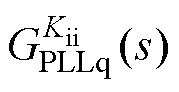 形成的负电阻分别为
形成的负电阻分别为
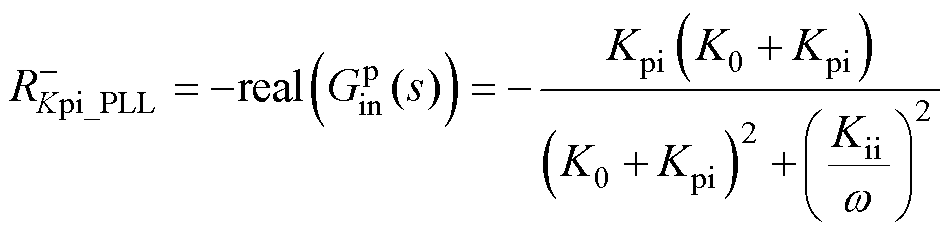 (26)
(26)
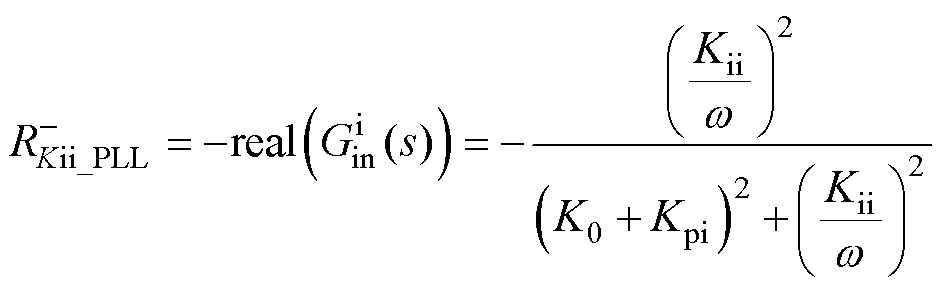 (27)
(27)
式中,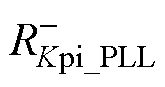 为
为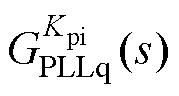 形成的负电阻;
形成的负电阻;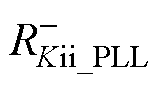 为
为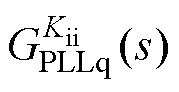 形成的负电阻。
形成的负电阻。
定义电流内环比例Kpi和积分环节Kii对负电阻影响的灵敏度分别为PKpi和PKii,分别表示为
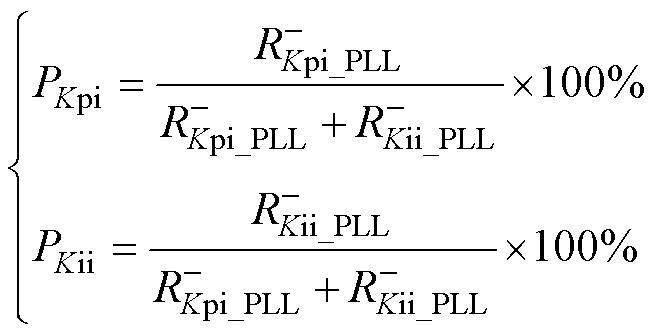 (28)
(28)
由此可得Kpi和Kii对负电阻的灵敏度如图10所示。在次/超同步频段,0.5(pu)电流内环带宽以内,随着频率增加,Kpi逐渐主导负电阻。随着电流内环带宽增加,Kii对负电阻的灵敏度增加,且影响的频段扩大,超过0.5(pu)电流内环带宽后,Kii主导负电阻。结合图9和图10可知,在次/超同步频段,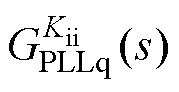 形成的负电阻大于
形成的负电阻大于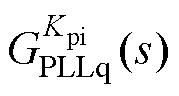 形成的负电阻,Kii对负电阻的影响较大。
形成的负电阻,Kii对负电阻的影响较大。
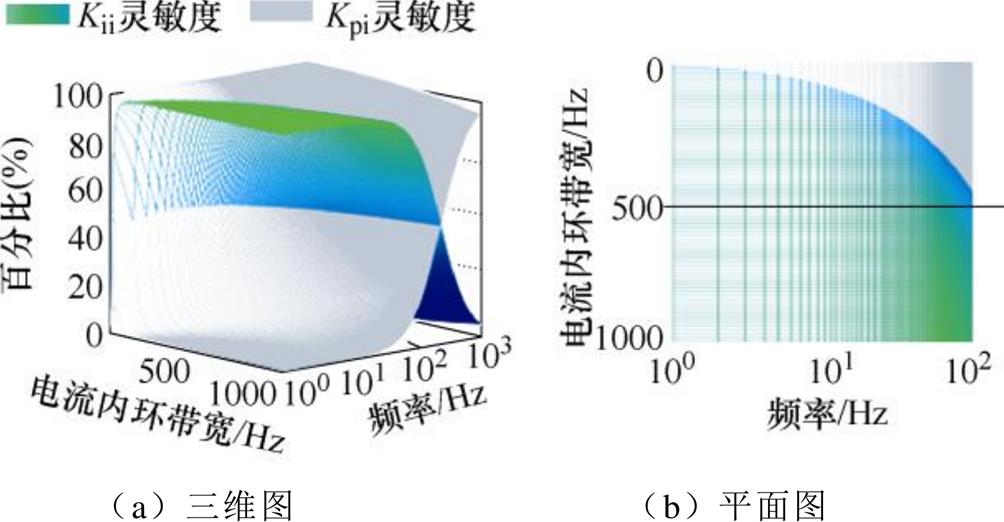
图10 电流内环参数对负电阻的灵敏度
Fig.10 Sensitivity of the negativeresistance related to the current inner loop
综上所述,并网逆变器的电流内环与锁相环交互是q轴等效电路形成负电阻的根本原因,其中锁相环决定了负电阻是否存在并影响其覆盖频段,电流内环的积分系数主导了负电阻的大小。并网逆变器q轴等效电路形成的负电阻经过坐标变化后会导致序域阻抗在基频附近呈现负电阻特性,与弱电网交互易出现振荡失稳现象。
由上述分析可知,锁相环带宽和逆变器功率固定的情况下,电流内环主导了负电阻的大小。在dq域下,将有源阻尼控制GZv(s)通过电流接入电压前馈可以等效影响电流内环主导的负电阻,从而起到降低整个系统负电阻的作用。有源阻尼控制的添加位置和等效电路如图11所示。
虚拟阻抗是最典型的有源阻尼控制策略,虚拟阻抗的结构如图12所示,可以分别由虚拟电阻Rv、虚拟电感Lv或虚拟电容Cv构成,也可以由它们串联构成。
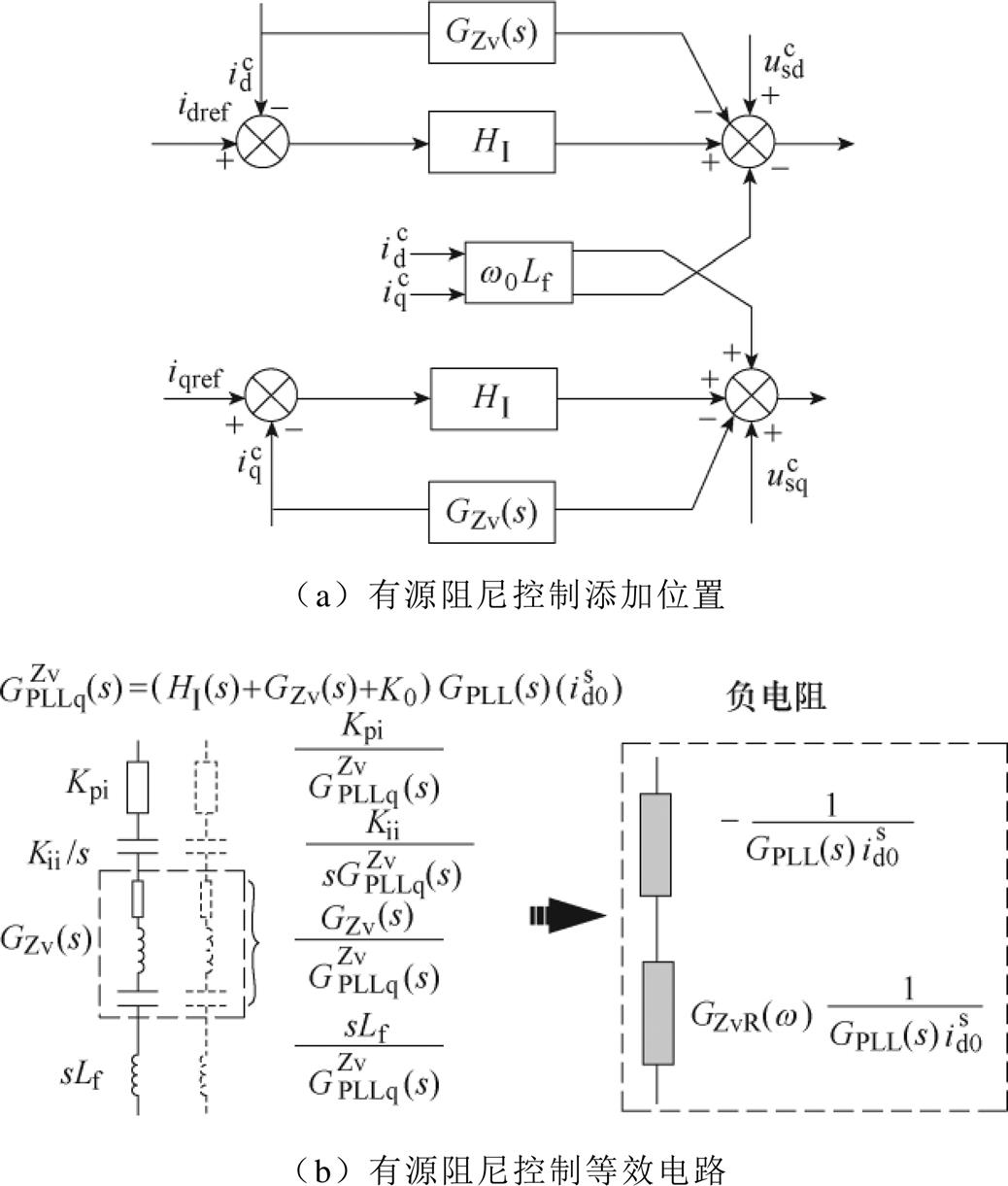
图11 有源阻尼控制添加位置及等效电路示意图
Fig.11 The adding position and the equivalent circuit of the active damping control

图12 虚拟阻抗等效电路示意图
Fig.12 Equivalent circuit diagram of virtualimpedance
如式(29)所示,虚拟阻抗通过影响HKP和HKI来改变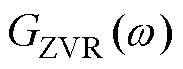 的大小,即等效改变图6和式(19)中
的大小,即等效改变图6和式(19)中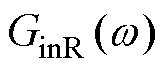 的Kpi和Kii的大小从而影响负电阻
的Kpi和Kii的大小从而影响负电阻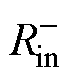 。
。
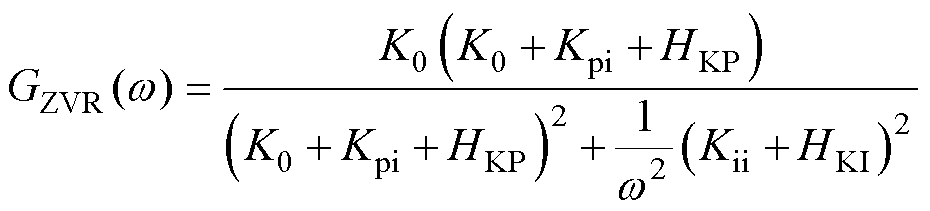 (29)
(29)
其中
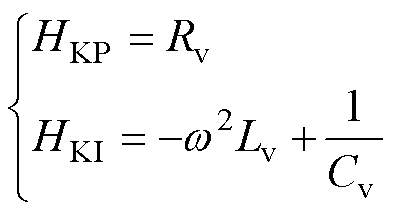 (30)
(30)
根据式(29)可知虚拟阻抗对负电阻的影响规律:
(1)增加虚拟电阻Rv意味着增加Kpi。在不同频段,虚拟电阻对负电阻的抑制能力不同,在低频段呈现非单调性且抑制能力有限;在较高频段,较小的虚拟电阻即可有效的抑制负电阻。在不同的电流内环带宽下,虚拟电阻对负电阻的抑制能力不同。
(2)增加虚拟电感Lv意味着减小Kii。虚拟电感对负电阻的抑制呈现非单调性,通过合理设计虚拟电感的参数可以实现在不同频段抑制负电阻。
(3)增加虚拟电容Cv,Ki呈现减小趋势。电流内环带宽较小时,增加虚拟电容可以在高频段抑制负电阻;电流内环带宽较大时,虚拟电容抑制负电阻的能力降低。
整体而言,仅采用虚拟电阻无法实现全频段抑制负电阻,且呈现非单调特性,参数设计存在困难;虚拟电感通过合理设计参数可以在不同频段抑制负电阻,但是虚拟电感等效为微分环节,在实际控制器中较难实现;虚拟电容对负电阻的抑制能力受限于电流内环带宽的影响,且主要在高频段可以有效抑制负电阻。
基于虚拟阻抗对负电阻的影响规律,根据前文机理分析可知,线性环节自身可以提供一定的正电阻,如何限制锁相环与电流内环交互形成的负电阻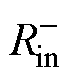 是本节有源阻尼控制设计的主要依据。在锁相环带宽和逆变器功率确定的前提下,为了抑制次/超同步频段的负电阻,有源阻尼控制的设计应满足以下原则,对四个条件的补充说明见附录。
是本节有源阻尼控制设计的主要依据。在锁相环带宽和逆变器功率确定的前提下,为了抑制次/超同步频段的负电阻,有源阻尼控制的设计应满足以下原则,对四个条件的补充说明见附录。
(1)有源阻尼控制传递函数的分子阶数大于等于分母阶数。
(2)加入有源阻尼控制后,式(20)中负电阻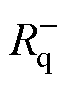 与正电阻
与正电阻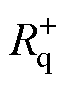 之后大于稳定阈值Rth。
之后大于稳定阈值Rth。
(3)满足并网逆变器的调制度要求。
(4)不影响逆变器的基频控制特性。
在图12虚拟阻抗基础上,将等效电路元件进行串并联可以形成不同的有源阻尼控制结构,不同有源阻尼的表达式及电路等效见表1,低通/高通滤波器的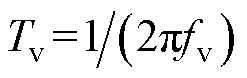 ,
,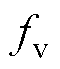 为截止频率。带通/带阻型有源阻尼的
为截止频率。带通/带阻型有源阻尼的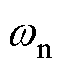 代表滤波器的中心频率,
代表滤波器的中心频率,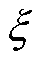 为阻尼比,
为阻尼比,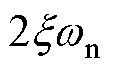 代表带宽。
代表带宽。
表1 不同有源阻尼对比
Tab.1 Comparison of different active damping control methods
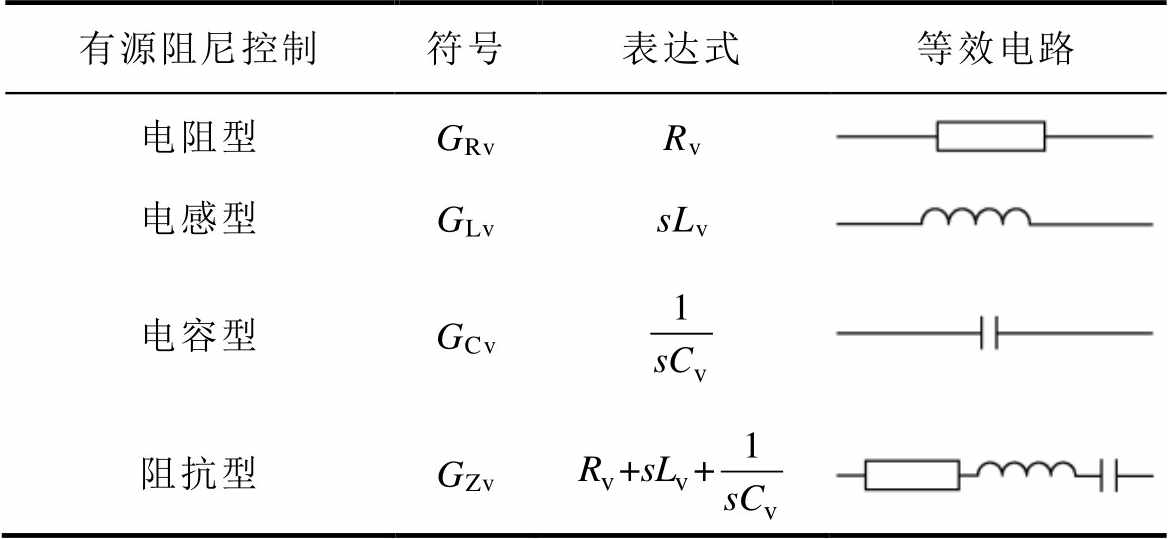
有源阻尼控制符号表达式等效电路 电阻型GRvRv 电感型GLvsLv 电容型GCv 阻抗型GZv
(续)
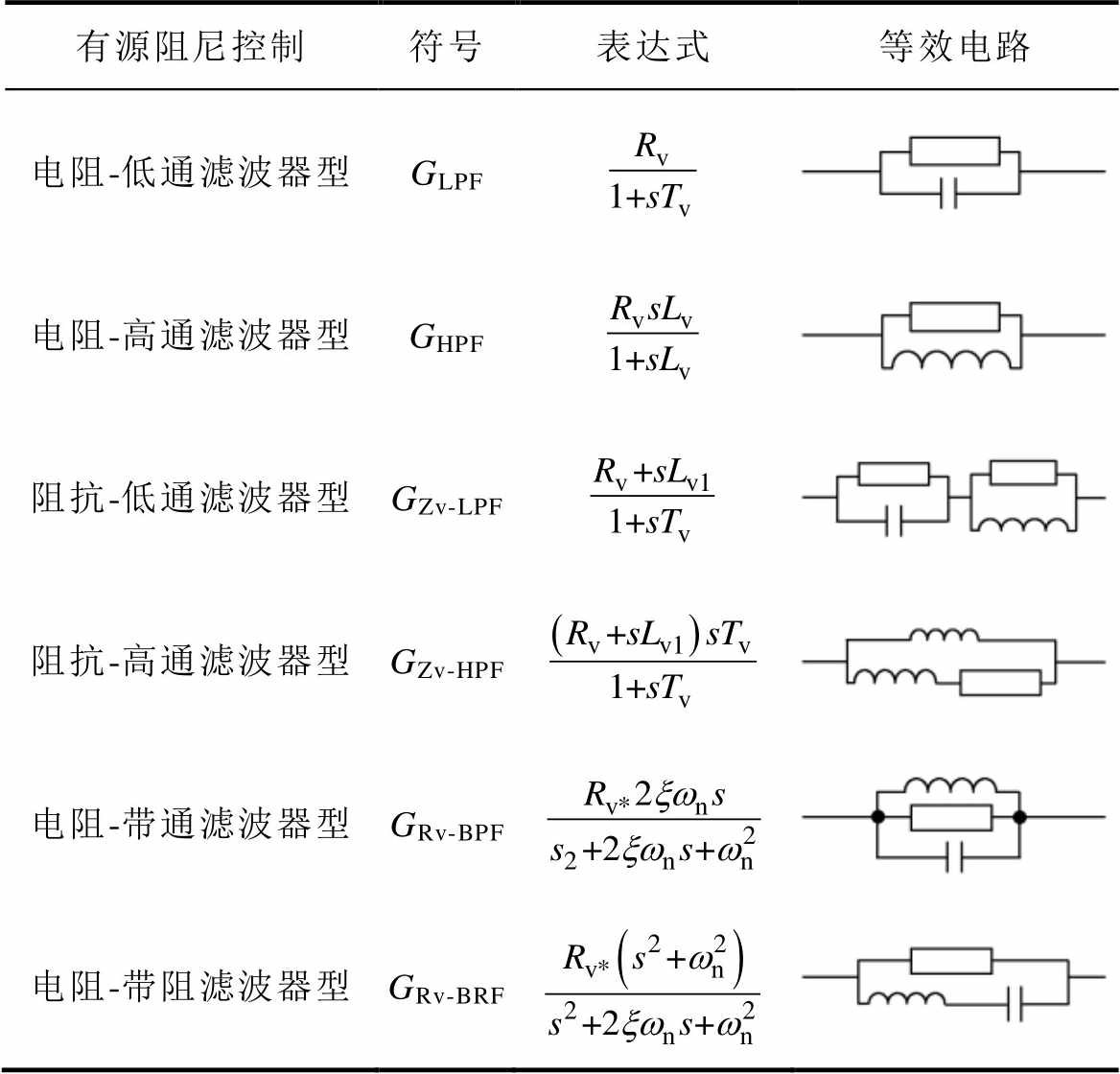
有源阻尼控制符号表达式等效电路 电阻-低通滤波器型GLPF 电阻-高通滤波器型GHPF 阻抗-低通滤波器型GZv-LPF 阻抗-高通滤波器型GZv-HPF 电阻-带通滤波器型GRv-BPF 电阻-带阻滤波器型GRv-BRF
分别将低通、高通、带通、带阻作为滤波器连接图12中的虚拟电阻Rv或者虚拟阻抗Rv+sLv1,接入图11所示的红色虚线区域,有源阻尼控制通过改变式(29)中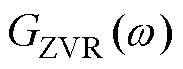 来抑制整体的负电阻,不同有源阻尼等效电路及其对负电阻的影响如图13和图14所示。其中阻抗-低通滤波器可以等效为虚拟电阻、虚拟电感和虚拟电容串联的形式,如图13a所示;根据中心频率的不同,带通滤波器可以等效为虚拟电阻与虚拟电感或虚拟电容串联的形式,如图13b和图13c所示,其中
来抑制整体的负电阻,不同有源阻尼等效电路及其对负电阻的影响如图13和图14所示。其中阻抗-低通滤波器可以等效为虚拟电阻、虚拟电感和虚拟电容串联的形式,如图13a所示;根据中心频率的不同,带通滤波器可以等效为虚拟电阻与虚拟电感或虚拟电容串联的形式,如图13b和图13c所示,其中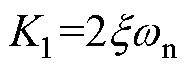 ,
,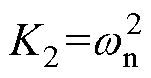 ;阻抗高通滤波器可以等效为虚拟电阻与虚拟电感串联的形式,如图13d所示。不同有源阻尼控制等效电路对
;阻抗高通滤波器可以等效为虚拟电阻与虚拟电感串联的形式,如图13d所示。不同有源阻尼控制等效电路对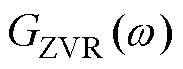 的影响见附录式(A5)~式(A8)。
的影响见附录式(A5)~式(A8)。
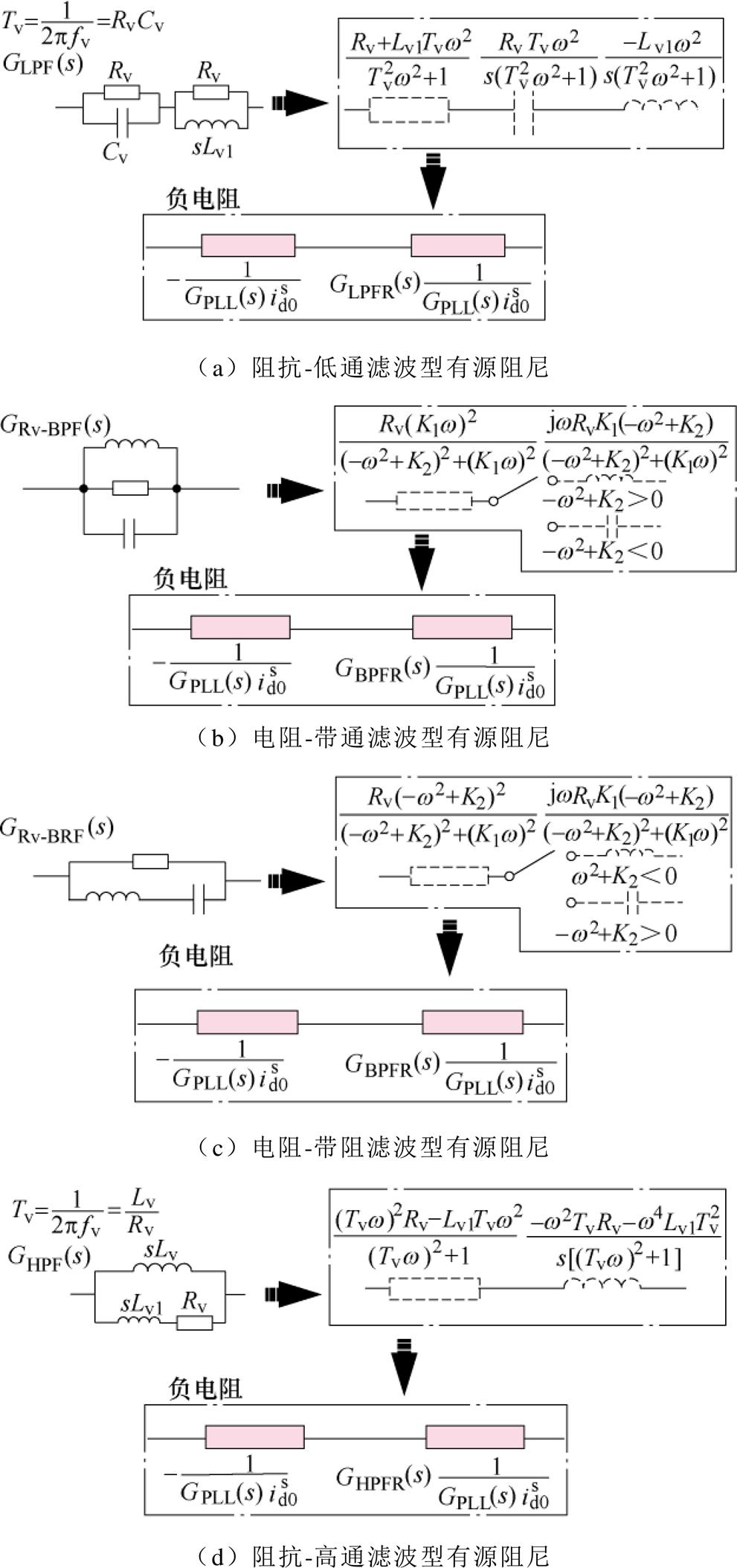
图13 有源阻尼控制接入后的电路等效示意图
Fig.13 Equivalent circuit diagram of active damping control
对于低通滤波器,虚拟电阻和截止频率较低时,高频段对负电阻的抑制能力更强。截止频率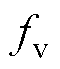 一定时,增加虚拟电阻会导致次/超同步频段对负电阻的抑制能力下降。虚拟电阻一定时,增加截止频率会导致全频段对负电阻的抑制能力下降,在低频段对负电阻的抑制能力降低更明显。如附录中式(A5)所示和图13a所示,仅加入电阻-低通滤波器时(Lv1= 0),Kii被等效增加,不满足有源阻尼设计原则的条件(1),影响规律与加入虚拟电阻或虚拟电容类似。优化为阻抗-低通滤波器后(Lv1=0.1 mH),对负电阻的抑制能力有限,如图14a所示。
一定时,增加虚拟电阻会导致次/超同步频段对负电阻的抑制能力下降。虚拟电阻一定时,增加截止频率会导致全频段对负电阻的抑制能力下降,在低频段对负电阻的抑制能力降低更明显。如附录中式(A5)所示和图13a所示,仅加入电阻-低通滤波器时(Lv1= 0),Kii被等效增加,不满足有源阻尼设计原则的条件(1),影响规律与加入虚拟电阻或虚拟电容类似。优化为阻抗-低通滤波器后(Lv1=0.1 mH),对负电阻的抑制能力有限,如图14a所示。
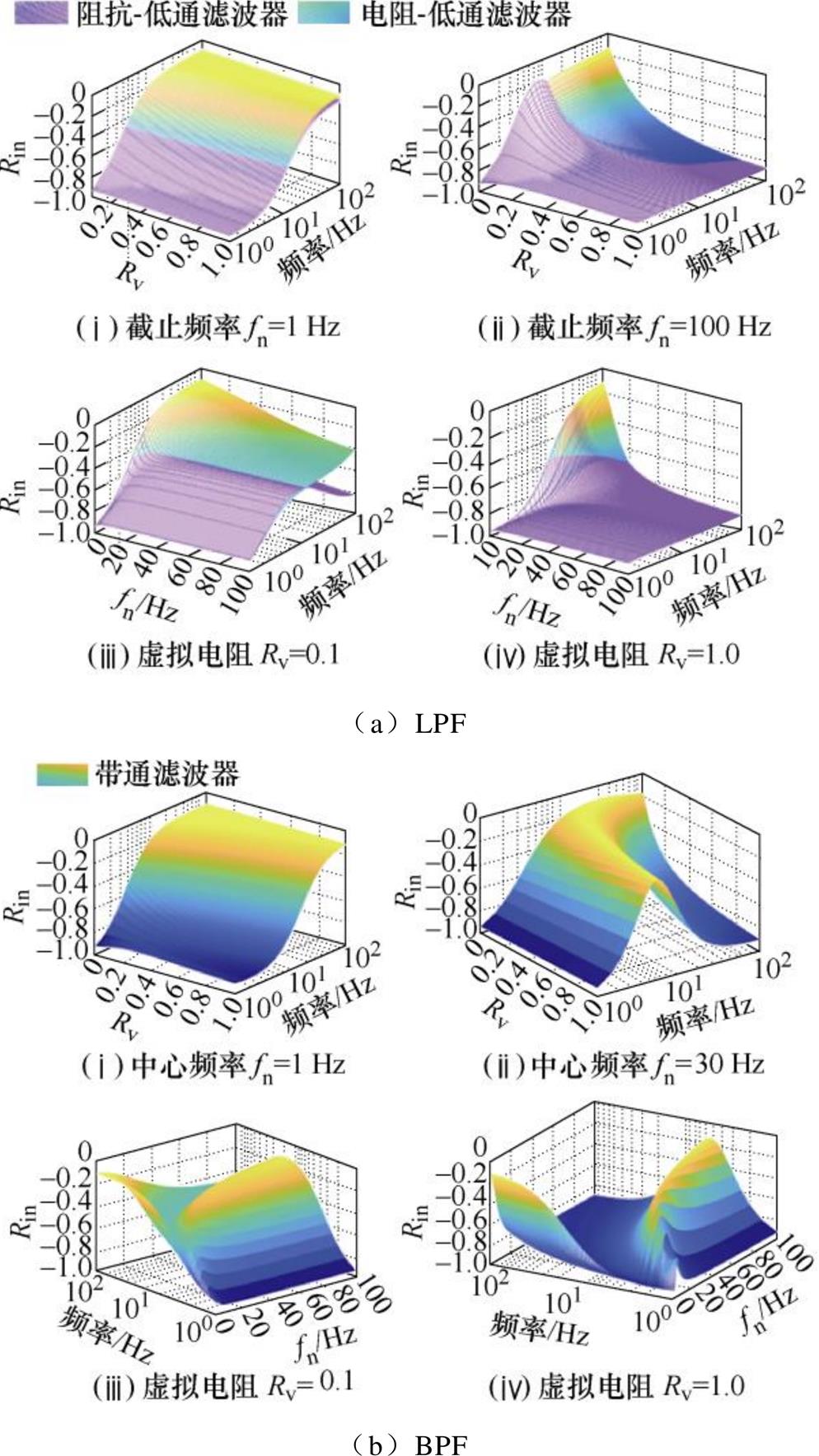
图14 有源阻尼控制对负电阻的抑制能力对比
Fig.14 Comparison of the negative resistance suppression of different active damping control methods
如图13b和图13c所示,对于带通/带阻滤波器,是否满足有源阻尼设计原则的条件(1),与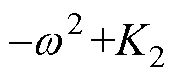 有关,取决于中心频率和目标频段的大小。如图14b所示,带通滤波器的中心频率较低时,高频段对负电阻的抑制能力较强,影响规律与低通滤波器类似。随着中心频率增加,带通滤波器在低频段对负电阻的抑制能力增强,在高频段对负电阻的抑制能力下降,且虚拟电阻增加会降低高频段对负电阻的抑制能力。虚拟电阻一定的情况下,带通滤波器的中心频率变化会对造成负电阻的抑制呈现非单调性,在某些频段难以抑制负电阻。如图14c所示,中心频率较低时,带阻滤波器仅在虚拟电阻较小时在高频段对负电阻有抑制能力。增加中心频率,有利于增强带阻滤波器在特定频段对负电阻的抑制,影响规律与高通滤波器类似。虚拟电阻一定的情况下,带阻滤波器的中心频率变化造成对负电阻的抑制呈现非单调特性,影响规律与高通滤波器和虚拟电感类似。
有关,取决于中心频率和目标频段的大小。如图14b所示,带通滤波器的中心频率较低时,高频段对负电阻的抑制能力较强,影响规律与低通滤波器类似。随着中心频率增加,带通滤波器在低频段对负电阻的抑制能力增强,在高频段对负电阻的抑制能力下降,且虚拟电阻增加会降低高频段对负电阻的抑制能力。虚拟电阻一定的情况下,带通滤波器的中心频率变化会对造成负电阻的抑制呈现非单调性,在某些频段难以抑制负电阻。如图14c所示,中心频率较低时,带阻滤波器仅在虚拟电阻较小时在高频段对负电阻有抑制能力。增加中心频率,有利于增强带阻滤波器在特定频段对负电阻的抑制,影响规律与高通滤波器类似。虚拟电阻一定的情况下,带阻滤波器的中心频率变化造成对负电阻的抑制呈现非单调特性,影响规律与高通滤波器和虚拟电感类似。
对于高通滤波器,截止频率较大时,在次/超同步频段可以通过增加虚拟电阻大小对负电阻实现抑制。虚拟电阻一定时,较高的截止频率有利于抑制次/超同步频段的负电阻。如附录中式(A8)所示和图13d所示,仅加入电阻-高通滤波器后(Lv1=0),Kii被等效减小,满足有源阻尼设计原则的条件(1),影响规律与加入虚拟电阻和虚拟电感类似。优化为阻抗-高通滤波器后(Lv1=0.1 mH),在次/超同步频段对负电阻的抑制能力明显增强,如图14d所示。
由上述分析可知,增强有源阻尼控制的感性有助于抑制锁相环引入的负电阻。不同有源阻尼控制的负电阻抑制能力不同,低通滤波器对低频段负电阻的抑制能力相对较弱,带通/带阻滤波器有利于减小特定频段的负电阻,相对而言,阻抗-高通滤波器型有源阻尼对次/超同步振荡的抑制效果更优。
为了验证不同有源阻尼控制的振荡抑制效果,根据图1在PSCAD/EMTDC中搭建并网逆变器的仿真模型,参数见表2。设置并网逆变器所连交流电网强度在1.0 s由5降为3,35/65 Hz的次/超同步振荡呈现衰减趋势。在此基础上,1.5 s将锁相环带宽从10 Hz增加至50 Hz,35/65 Hz的次/超同步振荡逐渐呈现发散趋势,并网逆变器交流电流以及频谱图如图15a所示。
在2.1 s将阻抗-高通滤波器型有源阻尼投入,根据第3.1节有源阻尼控制设计的依据,虚拟电阻Rv取值为0.1 W,虚拟电感Lv取值为0.1 mH,高通滤波器的截止频率设定为15 Hz,次/超同步振荡被抑制,如图15a所示。在相同虚拟阻抗和截止频率的参数下,2.1 s采用阻抗-低通滤波器型有源阻尼,仅能保证振荡不发散,难以抑制振荡。3.0 s改为阻抗-高通滤波器型有源阻尼,振荡即被抑制,如图15b所示。如果采用虚拟电阻-带阻/带通滤波器型有源阻尼,Rv=0.1 W,中心频率fn=15 Hz。2.1 s和2.5 s分别将虚拟电阻-带阻/带通型有源阻尼投入,但仍难以抑制振荡,仅能保证振荡不发散,如图15c所示(图15虚线表示无振荡抑制的波形,发散趋势)。
表2 并网逆变器参数
Tab.2 Parameters of grid-connected inverter
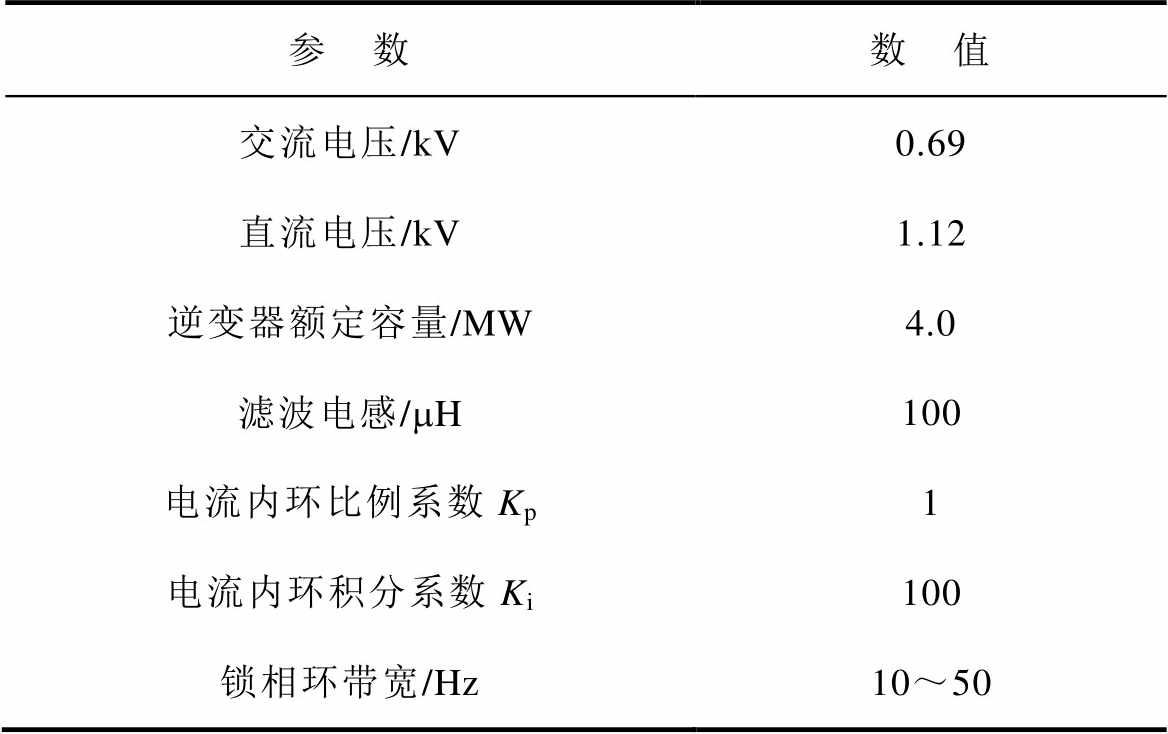
参 数数 值 交流电压/kV0.69 直流电压/kV1.12 逆变器额定容量/MW4.0 滤波电感/mH100 电流内环比例系数Kp1 电流内环积分系数Ki100 锁相环带宽/Hz10~50
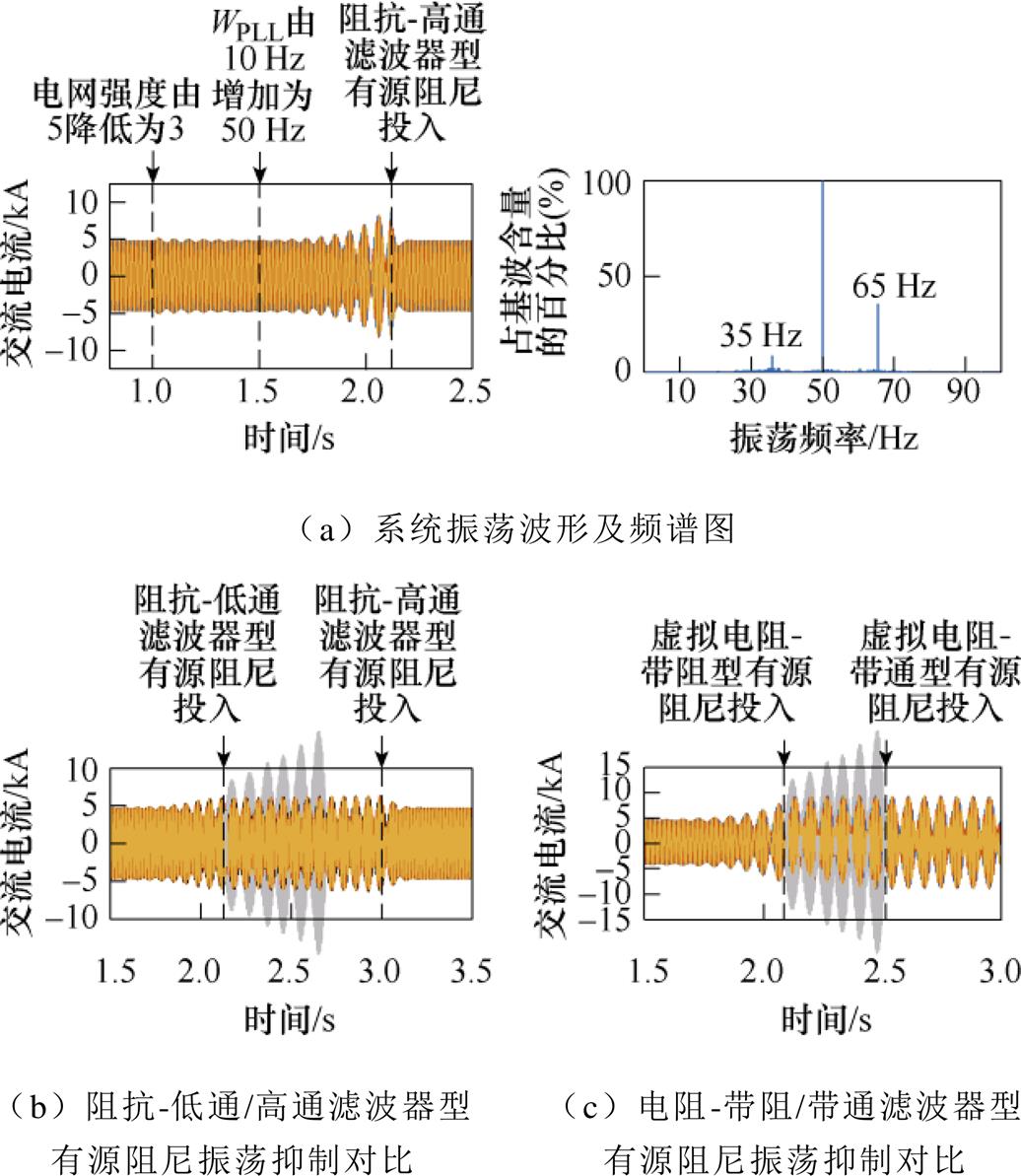
图15 有源阻尼振荡抑制仿真验证
Fig.15 Simulation verification of the oscillation suppressing effectiveness of the active damping
由4.1节可知,在相同参数情况下,阻抗-高通滤波器型有源阻尼的振荡抑制能力更优,为了验证其动态性能,不同电网强度出现功率阶跃时,阻抗-高通滤波器型有源阻尼对功率的影响如图16所示。不采用有源阻尼控制的情况下,随着电网强度变弱,并网逆变器功率阶跃变化时会出现功率大幅振荡甚至发散的现象;而采用阻抗-高通滤波器型有源阻尼控制后,可有效地抑制不同电网强度下功率阶跃变化时的振荡现象,可实现在电网短路比为1的极弱电网条件下稳定运行,显著提升系统的稳定性。
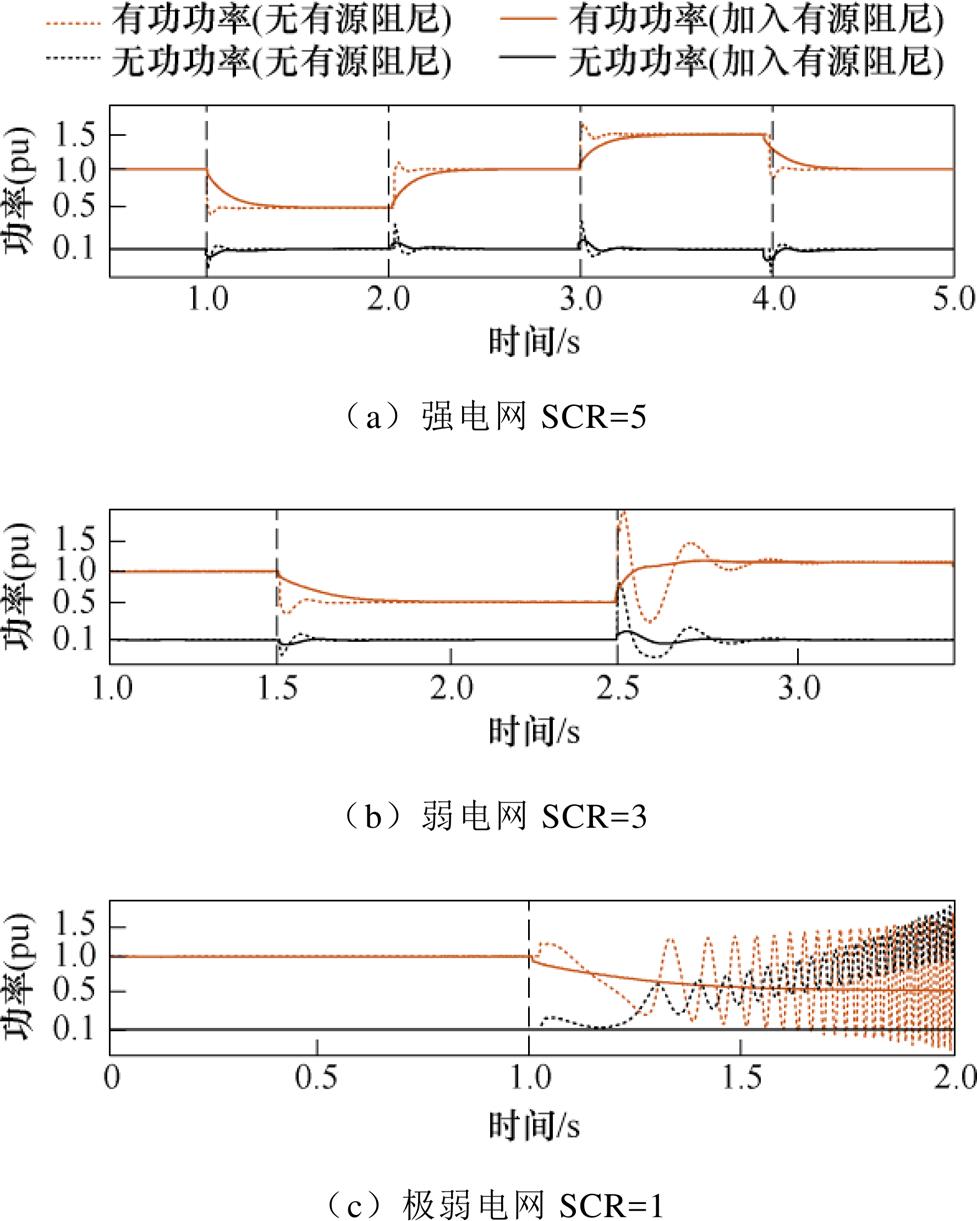
图16 并网逆变器功率阶跃波形
Fig.16 Waveforms of the grid-connected inverter with power changing
基于远宽8020实时仿真平台进行并网逆变器的控制器硬件在环实验,验证本文分析的正确性以及所提方法的有效性。所述实验平台如图17所示,控制器采用远宽MT1070RCP数字控制器。系统参数同表2。
不加任何振荡抑制的情况下,设置并网逆变器锁相环带宽为50 Hz,电网强度变弱后系统出现振荡并呈现发散趋势,如图18a所示;如果加入虚拟电阻-带阻/带通滤波器型有源阻尼,与第4.1节相同的参数下,振荡发散趋势可以被抑制,但仍旧存在振荡,如图18b所示;而采用阻抗-高通滤波器有源阻尼控制后,系统振荡可以在200 ms内被有效抑制,如图18c所示。

图17 控制器硬件在环实时仿真平台实物
Fig.17 Physical diagram of controller hardware-in-the-loop real-time simulation platform
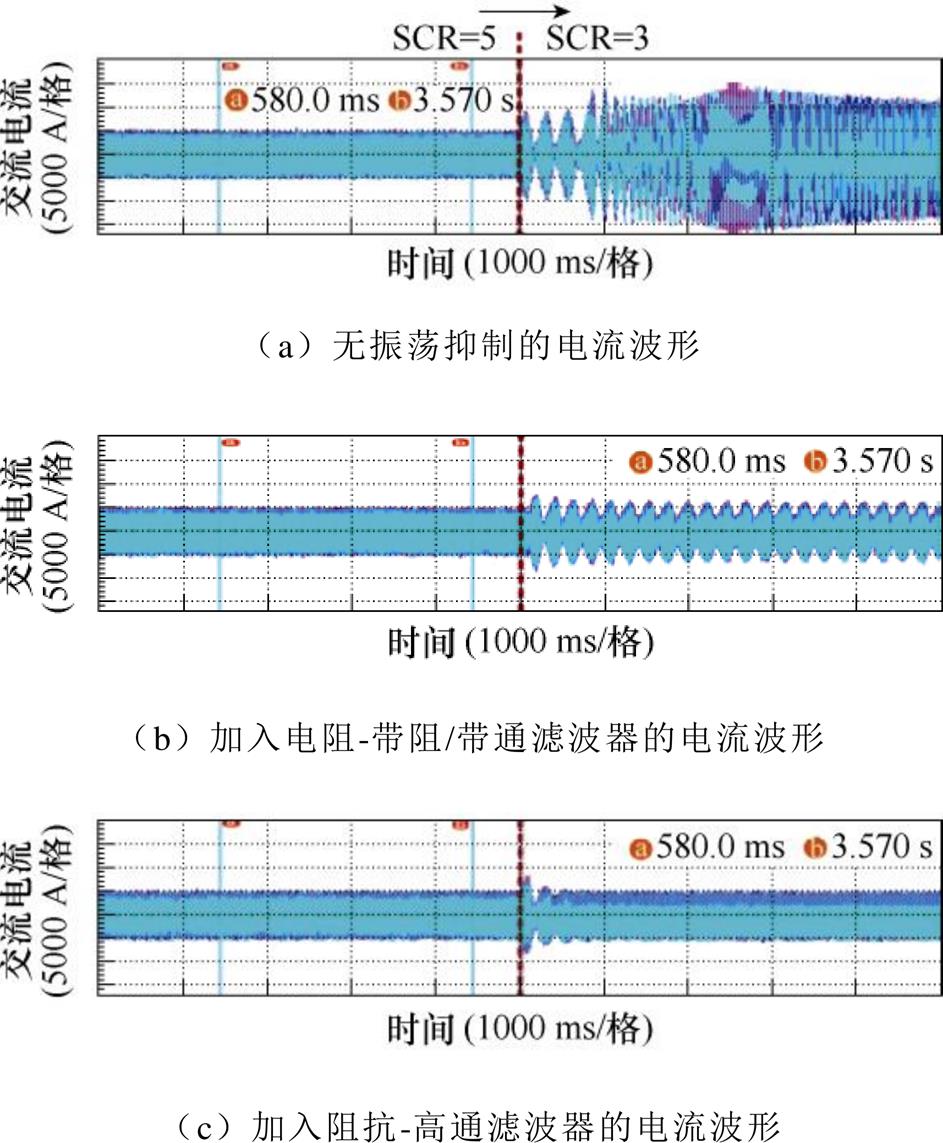
图18 有源阻尼振荡抑制实验验证
Fig.18 Experimentalverification of the oscillation suppressing effectiveness of the active damping
为了验证阻抗-高通滤波器有源阻尼的动态性能,分别设置有功功率从1.0(pu)增加至1.5(pu)。如果不采用任何振荡抑制控制,强电网情况下(SCR= 5),功率阶跃后会出现波动,弱电网情况下(SCR=3)功率阶跃后会出现振荡现象。加入阻抗-高通滤波器有源阻尼后,可以抑制功率阶跃后的振荡,如图19所示。
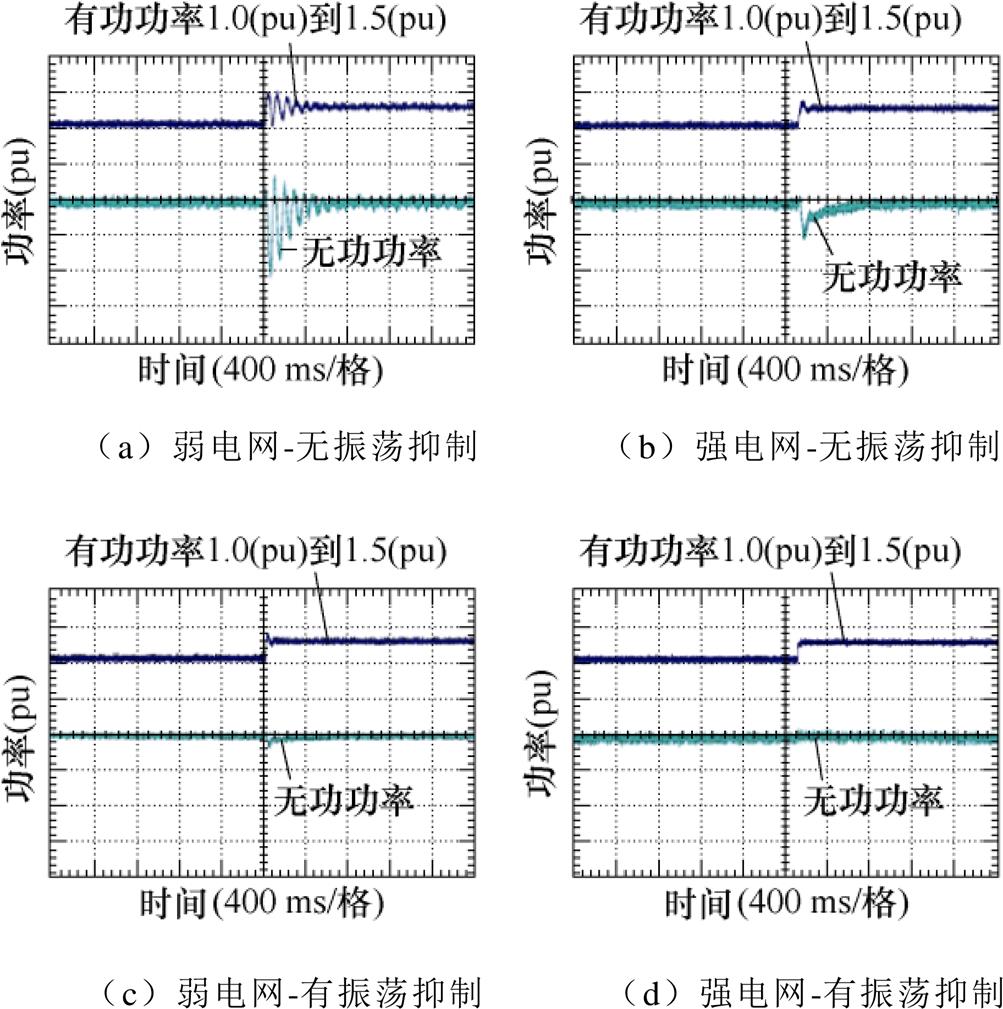
图19 并网逆变器功率阶跃实验波形
Fig.19 Experimental waveforms of the grid-connected inverter with power changing
本文建立了并网逆变器控制器的等效电路模型,揭示了并网逆变器接入弱电网条件下负电阻的产生机制,基于此提出了有源阻尼稳定控制的设计原则。得到的主要结论如下:
1)并网逆变器的电流内环与锁相环交互是q轴等效电路形成负电阻的根本原因,进而导致传统序阻抗在基频附近呈现负电阻特性,在弱电网条件下负电阻特性加剧,易出现次/超同步振荡风险。
2)根据锁相环与电流内环交互形成的电路模型可知,q轴等效电路出现的负电阻中,锁相环决定了负电阻是否存在并影响其覆盖频段,电流内环的积分系数则主要影响负电阻的大小。
3)基于电路模型进行有源阻尼控制参数设计时,增强有源阻尼控制的电感特性可以等效降低电流内环的积分系数对负电阻的灵敏度,进而起到增加系统振荡稳定性的作用。
4)带通/带阻滤波器有利于减小特定频段的负电阻,低通滤波器有利于抑制高频段振荡,高通滤波器有利于抑制低频段振荡。参数相同情况下,阻抗-高通滤波器型有源阻尼对次/超同步振荡的抑制效果更优,且能够显著改善逆变器的动态性能。
附 录
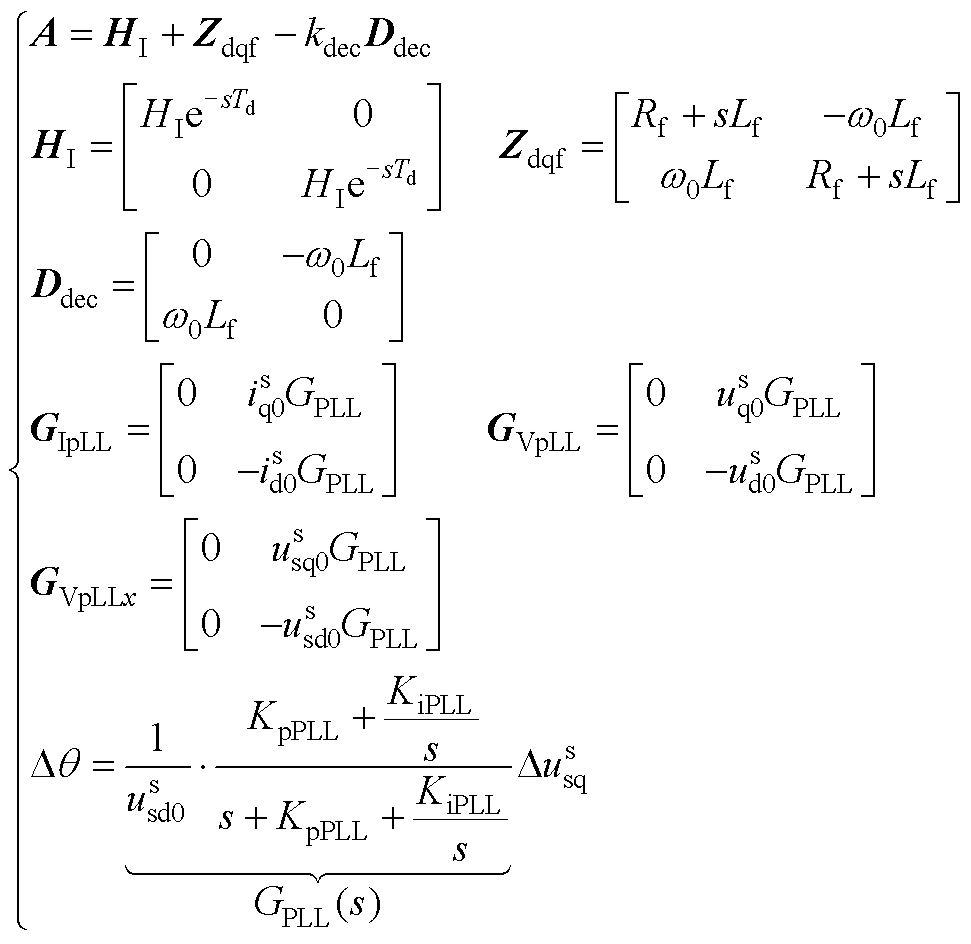 (A1)
(A1)
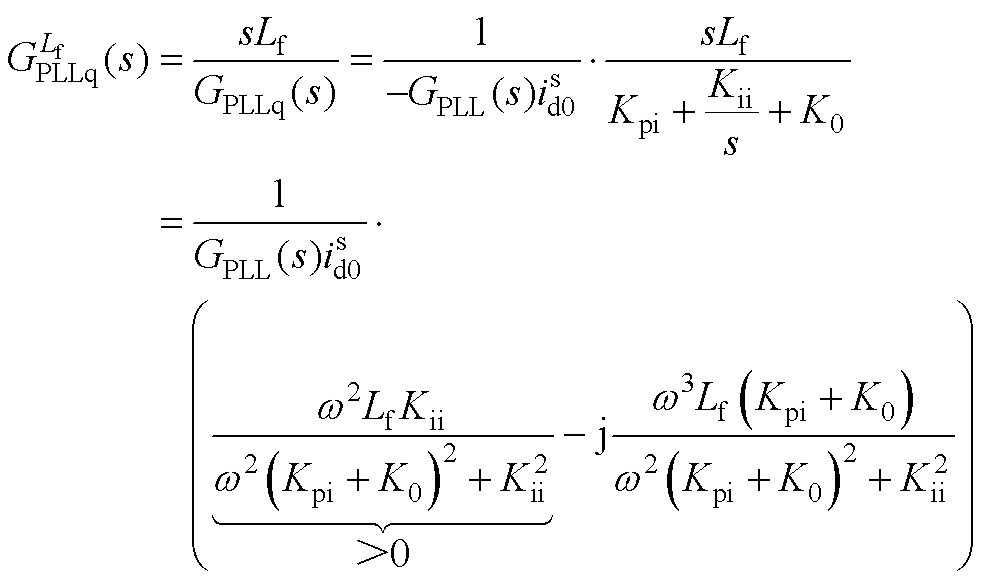 (A2)
(A2)
式(19)中
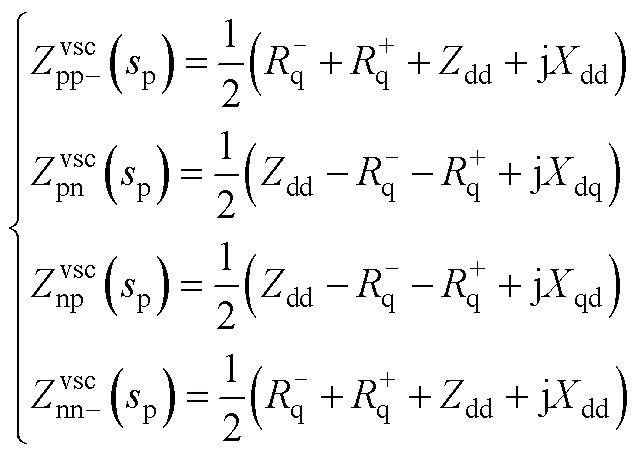 (A3)
(A3)
式(A3)中
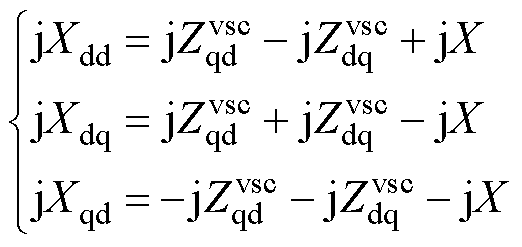 (A4)
(A4)
第3.3节中,将阻抗-低通滤波器代入式(29)后,图13a中GLPFR(s)的HKP和HKI如式(A5)所示;将电阻-带通滤波器代入式(29)后,图13b中GBPFR(s)的HKP和HKI如式(A6)所示;将电阻-带阻滤波器代入式(29)后,图13c中GBRFR(s)的HKP和HKI如式(A7)所示;将阻抗-高通滤波器代入正文式(29)后,图13d中GHPFR(s)的HKP和HKI如式(A8)所示。
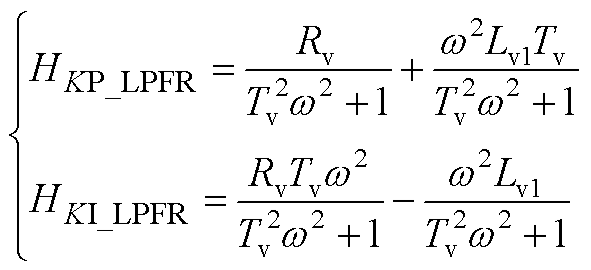 (A5)
(A5)
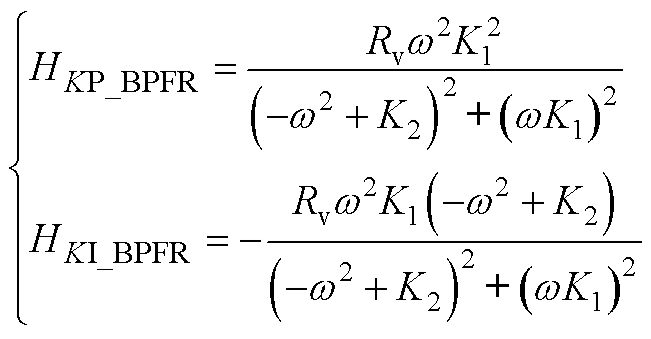 (A6)
(A6)
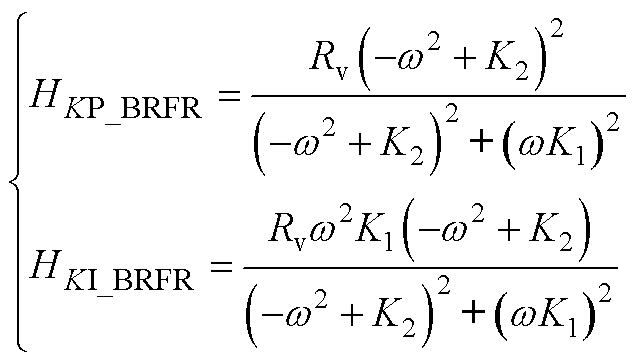 (A7)
(A7)
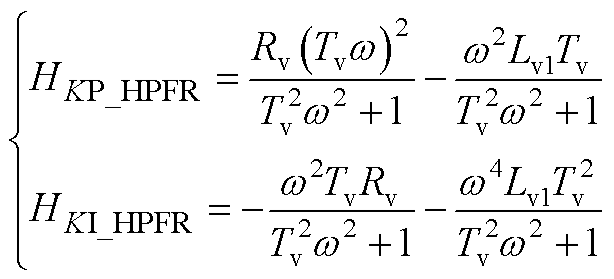 (A8)
(A8)
对正文第3.1节中有源阻尼控制设计原则的补充说明:
对于条件(1),有源阻尼控制的外特性尽可能呈现感性,从而可以等效减小电流内环的积分系数Kii。
对于条件(2),设定逆变器在q轴总的电阻阈值为Rth(Rth的大小或正负取决于逆变器的稳定阈值),加入有源阻尼控制后,正文式(20)中逆变器在q轴总的正电阻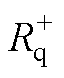 与负电阻
与负电阻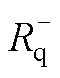 之和大于阈值Rth,Rth约为负电阻的1/2。
之和大于阈值Rth,Rth约为负电阻的1/2。
对于条件(3),并网逆变器调制度约束条件如式(A9)所示,不同调制方式下的逆变器调制度阈值Mth不同。将有源阻尼控制等效为GZv(s)=RAHA(s),RA决定虚拟电阻的最大值,HA(s)代表不同的滤波器,将GZv(s)代入式(A9)可得式(A10)所示的约束条件。如式(A11)所示,虚拟电阻存在上限和下限值,上限值满足调制度阈值限制,其下限值与电流内环和锁相环参数有关。
对于条件(4),需要对有源阻尼控制中的滤波器参数进行合理设计,仅对特定频段的振荡进行抑制,防止对逆变器的基频特性造成影响。
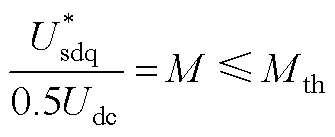 (A9)
(A9)
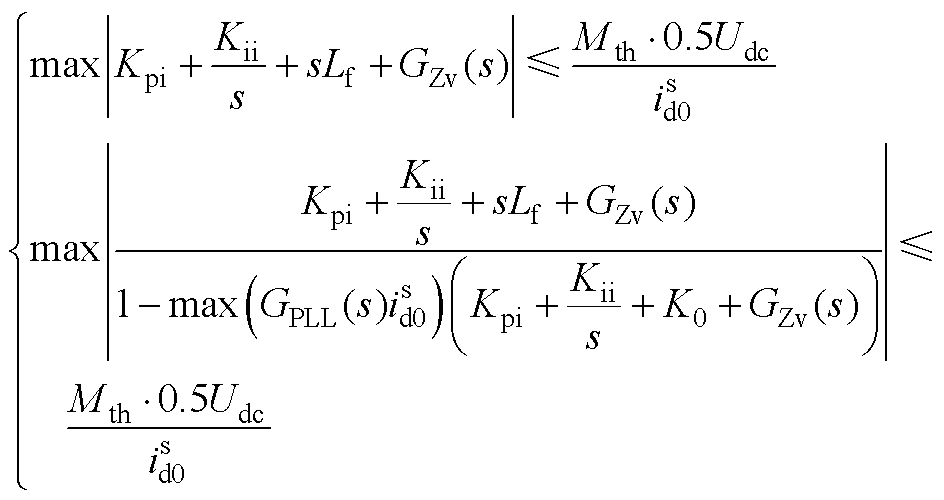 (A10)
(A10)
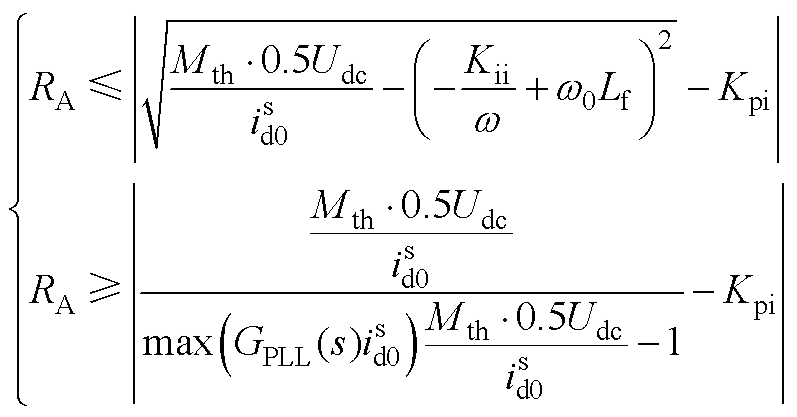 (A11)
(A11)
参考文献
[1] 高本锋, 邓鹏程, 梁纪峰, 等. 光伏电站与弱交流电网间次同步交互作用路径及阻尼特性分析[J]. 电工技术学报, 2023, 38(24): 6679-6694.
Gao Benfeng, Deng Pengcheng, Liang Jifeng, et al. Analysis of path and damping characteristics of subsynchronous interaction between photovoltaic plant and weak AC grid[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6679-6694.
[2] 高磊, 吕敬, 蔡旭. 如东海上风电柔直送出系统的中频振荡特性分析[J]. 电网技术, 2023, 47(9): 3495- 3509.
Gao Lei, Lü Jing, Cai Xu. Analysis of mid-frequency oscillation characteristics in Rudong MMC-HVDC system for offshore wind farms[J]. Power System Technology, 2023, 47(9): 3495-3509.
[3] Li Pengfei, Guo Li, Li Xialin, et al. Reduced-order modeling and comparative dynamic analysis of DC voltage control in DC microgrids under different droop methods[J]. IEEE Transactions on Energy Conversion, 2021, 36(4): 3317-3333.
[4] 刘欣, 郭志博, 贾焦心, 等. 基于单输入单输出等效序阻抗的微网VSG并网稳定性分析及虚拟阻抗设计[J/OL]. 电工技术学报, 2023, DOI: 10.19595/ j.cnki.1000-6753.tces.230077.
Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Microgrid VSG grid-connection stability analysis and virtual impedance design based on single input single-output equivalent sequence impedance[J/OL]. Transactions of China Electrotechnical Society, 2023, DOI: 10. 19595/j.cnki.1000-6753.tces.230077.
[5] 杜步阳, 邵德军, 朱建行, 等. 电压源型变流器并网系统多时间尺度间相互作用[J]. 电工技术学报, 2023, 38(20): 5547-5559.
Du Buyang, Shao Dejun, Zhu Jianhang, et al. The interaction between multiple timescales of the grid-tied voltage source converter[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5547- 5559.
[6] 吕敬, 蔡旭, 张占奎, 等. 海上风电场经MMC- HVDC并网的阻抗建模及稳定性分析[J]. 中国电机工程学报, 2016, 36(14): 3771-3781.
Lü Jing, Cai Xu, Zhang Zhankui, et al. Impedance modeling and stability analysis of MMC-based HVDC for offshore wind farms[J]. Proceedings of the CSEE, 2016, 36(14): 3771-3781.
[7] 王晴, 刘增, 韩鹏程, 等. 基于变流器输出阻抗的直流微电网下垂并联系统振荡机理与稳定边界分析[J]. 电工技术学报, 2023, 38(8): 2148-2161.
Wang Qing, Liu Zeng, Han Pengcheng, et al. Analysis of oscillation mechanism and stability boundary of droop-controlled parallel converters based on output impedances of individual converters in DC micro- grids[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2148-2161.
[8] 曾正, 邵伟华, 宋春伟, 等. 电压源逆变器典型控制方法的电路本质分析[J]. 中国电机工程学报, 2016, 36(18): 4980-4989, 5123.
Zeng Zheng, Shao Weihua, Song Chunwei, et al. Circuit-based analysis of typical control schemes of voltage-source inverter[J]. Proceedings of the CSEE, 2016, 36(18): 4980-4989, 5123.
[9] 张琛, 蔡旭, 李征. 电压源型并网变流器的机-网电气振荡机理及稳定判据研究[J]. 中国电机工程学报, 2017, 37(11): 3174-3183, 3372.
Zhang Chen, Cai Xu, Li Zheng. Stability criterion and mechanisms analysis of electrical oscillations in the grid-tied VSC system[J]. Proceedings of the CSEE, 2017, 37(11): 3174-3183, 3372.
[10] 曾志杰, 肖华锋, 高博, 等. 并网逆变器小信号建模简化方法与应用[J]. 中国电机工程学报, 2020, 40(21): 7002-7012.
Zeng Zhijie, Xiao Huafeng, Gao Bo, et al. Simplified small-signal modeling method of grid-connected inverters and its applications[J]. Proceedings of the CSEE, 2020, 40(21): 7002-7012.
[11] 刘其辉, 洪晨威, 逄思敏, 等. 基于弹性系数的双馈风电机组控制参数对次同步振荡作用分析及调整方法[J]. 电工技术学报, 2022, 37(14): 3528-3541.
Liu Qihui, Hong Chenwei, Pang Simin, et al. Analysis and adjustment method of doubly-fed fan control parameters on subsynchronous oscillation based on impedance elastic sensitivity[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3528- 3541.
[12] Lü Jing, Cai Xu, Molinas M. Optimal design of controller parameters for improving the stability of MMC-HVDC for wind farm integration[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(1): 40-53.
[13] 徐思莹, 王晗, 曹云峰, 等. 稳定边界及多目标约束下自同步电压源双馈风电机组参数整定[J]. 电力系统自动化, 2023, 47(11): 18-28.
Xu Siying, Wang Han, Cao Yunfeng, et al. Parameter tuning for self-synchronous voltage source doubly-fed wind turbines with stability boundary and multi- objective constraint[J]. Automation of Electric Power Systems, 2023, 47(11): 18-28.
[14] 吕敬, 蔡旭. 风电场柔性直流并网系统镇定器的频域分析与设计[J]. 中国电机工程学报, 2018, 38(14): 4074-4085, 4313.
Lü Jing, Cai Xu. Frequency-domain analysis and design of stabilization controllers for wind farm integration through VSC-HVDC system[J]. Pro- ceedings of the CSEE, 2018, 38(14): 4074-4085, 4313.
[15] Zou Changyue, Rao Hong, Xu Shukai, et al. Analysis of resonance between a VSC-HVDC converter and the AC grid[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10157-10168.
[16] 万勋, 李云丰, 彭敏放. 直流输电系统虚拟并联电阻阻尼控制策略研究[J]. 中国电机工程学报, 2018, 38(12): 3471-3480.
Wan Xun, Li Yunfeng, Peng Minfang. Virtual parallel resistor damping control of VSC based HVDC system[J]. Proceedings of the CSEE, 2018, 38(12): 3471-3480.
[17] Li Yunfeng, Tang Guangfu, Ge Jun, et al. Modeling and damping control of modular multilevel converter based DC grid[J]. IEEE Transactions on Power Systems, 2018, 33(1): 723-735.
[18] 季宇, 王东旭, 吴红斌, 等. 提高直流微电网稳定性的有源阻尼方法[J]. 电工技术学报, 2018, 33(2): 370-379.
Ji Yu, Wang Dongxu, Wu Hongbin, et al. The active damping method for improving the stability of DC microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 370-379.
[19] 孙焜, 姚伟, 周毅, 等. 基于SISO序阻抗的直驱风场经柔直输电系统中频振荡机理分析及抑制[J]. 中国电机工程学报, 2023, 43(2): 442-454.
Sun Kun, Yao Wei, Zhou Yi, et al. Mechanism analysis and suppression of medium-frequency oscilla- tion based on the SISO impedance in a PMSG-based wind farm when connected to a VSC-HVDC[J]. Proceedings of the CSEE, 2023, 43(2): 442-454.
[20] 李云丰, 贺之渊, 孔明, 等. 柔性直流输电系统高频稳定性分析及抑制策略(二): 阻尼控制抑制策略[J]. 中国电机工程学报, 2021, 41(19): 6601-6616.
Li Yunfeng, He Zhiyuan, Kong Ming, et al. High frequency stability analysis and suppression strategy of MMC-HVDC systems (part Ⅱ): damping control suppression strategy[J]. Proceedings of the CSEE, 2021, 41(19): 6601-6616.
[21] Rao Yiming, Lü Jing, Zhai Dongling, et al. Adaptive mitigation control for wideband oscillations of offshore wind farms with MMC-HVDC system[J]. CSEE Journal of Power and Energy Systems, DOI: 10.17775/CSEEJPES.2021.06530.
[22] Liu Huakun, Xie Xiaorong, Li Yu, et al. Mitigation of SSR by embedding subsynchronous Notch filters into DFIG converter controllers[J]. IET Generation, Trans- mission & Distribution, 2017, 11(11): 2888-2896.
[23] 薛涛, 吕敬, 王凯, 等. 海上全功率风电机组精细化阻抗建模及机网侧耦合分析[J]. 中国电机工程学报, 2022, 42(12): 4303-4319.
Xue Tao, Lü Jing, Wang Kai, et al. Accurate impedance modeling of an offshore full-power wind turbine system and analysis of the coupling chara- cteristics between machine-and grid-side systems[J]. Proceedings of the CSEE, 2022, 42(12): 4303-4319.
[24] Zong Haoxiang, Lü Jing, Cai Xu, et al. Accurate aggregated modelling of wind farm systems in modified sequence domain for stability analysis[J]. Electric Power Systems Research, 2019, 175: 105928.
[25] Rygg A, Molinas M, Zhang Chen, et al. A modified sequence-domain impedance definition and its equi- valence to the dq-domain impedance definition for the stability analysis of AC power electronic systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1383-1396.
[26] Wen Bo, Boroyevich D, Burgos R, et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.
Abstract The renewable energy power generation systems that utilize grid-connected inverters as the power interface are prone to instability issues when the AC grid is weak. The fundamental reason for the wideband oscillation phenomenon when grid-connected inverters are integrated into AC grids is negative resistance.
Firstly, to understand the mechanism of the negative resistance and propose the effective oscillation suppression methods, this paper visualizes the current-inner loop, phase-locked loop, voltage feedforward, and decoupling terms of the grid-connected inverter in to the equivalent circuit model in the dq-domain, modified-sequence domain and positive/negative-sequence domain. By studying the interaction of control dynamics within the sub-/super-synchronous frequency range, the circuit essence of the negative resistance is revealed.
Secondly, based on the equivalent circuit model of the grid-connected inverter and the inherent essence of the negative resistance, the design principles of active damping control are proposed. Additionally, the optimal location for implementing active damping control is examined. According to the equivalent circuit among various active damping controls, the investigation is conducted to understand the impact of these controls on the negative resistance characteristics.
Finally, the oscillation suppression effects of different active damping control strategies are compared through PSCAD/EMTDC simulations and StarSim controller hardware-in-the-loop experiments. Besides, the dynamic performance of the impedance-high-pass filter type active damping control is validated. It is demonstrated that the system oscillation can be effectively suppressed within 200 ms using the designed control method. Additionally, the grid-connected inverter remains stable under weak grid conditions with SCR=1.
The main conclusions of this paper are as follows:
(1) The interaction between the current inner loop and the phase-locked loop of the grid-connected inverter is the primary cause for the emergence of the negative resistance in the q-axis equivalent circuit. The negative resistance of the q-axis circuit results in the negative resistance characteristic in the traditional sequential-domain impedance, particularly near the fundamental frequency. Under the weak grid scenarios, the negative resistance characteristic becomes more pronounced, elevating the risk of sub-/super-synchronous oscillations.
(2) Based on the circuit model resulting from the interaction between the phase-locked loop and current inner loop, the phase-locked loop determines the existence of negative resistance and its frequency range coverage. The magnitude of the negative resistance is influenced by the integral coefficient of the current inner loop.
(3) When designing the active damping control parameters, it is essential to enhance the inductance characteristics of the active damping control to mitigate the impact of negative resistance caused by the integral coefficient of the current inner loop. Thus, the system oscillatory stability can be improved.
(4) The band-pass filter and band-rejection filter are beneficial for reducing negative resistance within the specific frequency range. Meanwhile, low-pass filters are advantageous for mitigating the high-frequency oscillations, whereas high-pass filters are useful for suppressing low-frequency oscillations. Under the same parameter conditions, the impedance-high pass filter-based active damping control proposed in this paper demonstrates a better suppression effect on sub-/super-synchronous oscillations, resulting in a notable enhancement of the dynamic performance.
keywords:Grid-connected inverter, impedance circuit equivalent, oscillation stability, active damping, virtual impedance, stability control
国家自然科学基金项目(52277195)和国网浙江省电力有限公司科技项目(B3311DS22000K)资助。
收稿日期 2023-08-31
DOI: 10.19595/j.cnki.1000-6753.tces.231442
中图分类号:TM721
高 磊 男,1997年生,博士研究生,研究方向为新能源柔直并网稳定分析与控制。E-mail: gaolei97@sjtu.edu.cn
吕 敬 男,1985年生,工学博士,副教授,研究方向为新能源柔直并网稳定分析与控制。E-mail: lvjing@sjtu.edu.cn(通信作者)
改稿日期 2023-11-02
(编辑 郭丽军)