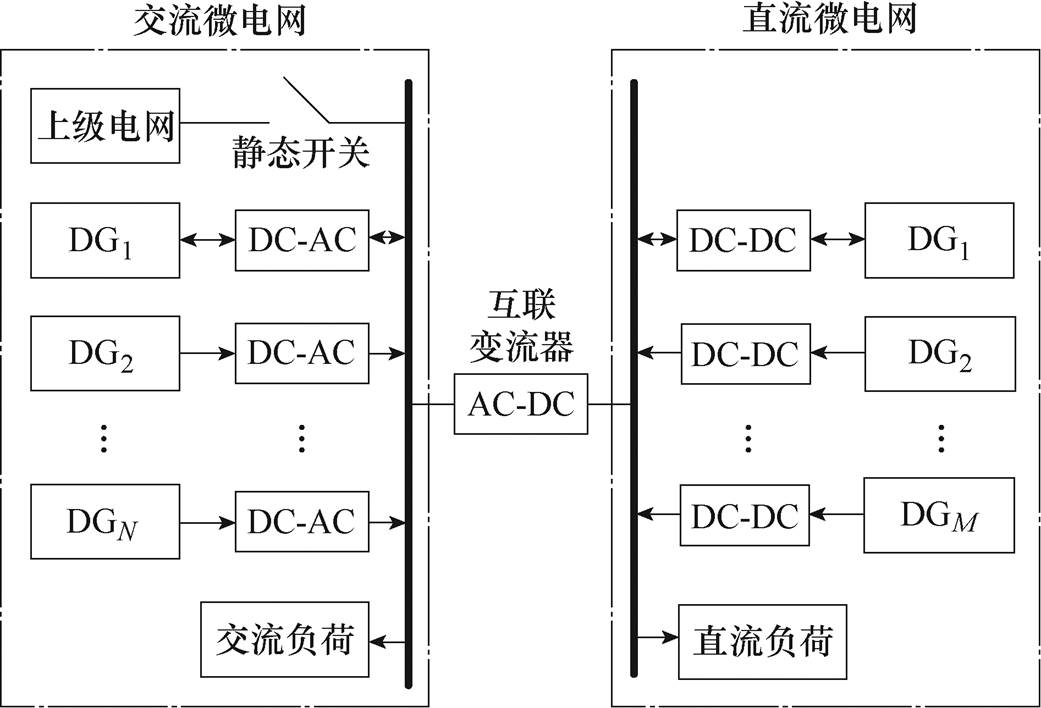
图1 交直流微电网系统结构
Fig.1 The structure of AC-DC microgrid system
摘要 交直流微电网在不同类型电力电子变流器的不同带宽控制环节作用下,容易引发系统发生宽频振荡问题。现有的微电网振荡分析主要基于阻抗分析法和特征分析法,然而这两种方法存在一定的局限性。为此,该文研究了基于频域阻抗网络模型的交直流微电网振荡问题建模与分析方法。首先,建立了交直流微电网在频域下的等效阻抗网络模型,并计算节点频域导纳矩阵及回路频域阻抗矩阵。其次,基于频域模式分析法,建立了交直流微电网的节点/回路振荡参与程度指标以及设备和控制参数的灵敏度指标,给出了振荡的交直流传播特性分析方法,便于明晰系统振荡机理与关键影响因素。最后,通过Matlab/Simulink时域仿真及算例分析验证了上述频域阻抗网络建模和振荡稳定性分析方法的有效性。
关键词:交直流微电网 频域阻抗网络建模 振荡稳定性 频域模式分析
在“双碳”目标背景下[1-2],我国正在建设新型电力系统。微电网是分布式电源的有效组织利用形式,也是新型电力系统的重要组成部分。交直流微电网综合了交流微电网和直流微电网各自的特点和优势,在有效减少多个电源转换环节的同时,为分布式电源(Distributed Generation, DG)的灵活接入和可再生能源的局部消纳提供了有效的解决方案,近年来受到广泛关注[3]。然而,交直流微电网中大量不同类型电力电子变流器在不同带宽控制环节的作用下容易诱发系统宽频带振荡现象,威胁微电网的安全稳定运行[4],如浙江上虞交直流微电网在2019年发生的直流电流增幅振荡现象[5]。因此,亟须开展对交直流微电网振荡问题的研究。
目前,常用的微电网振荡分析方法主要有基于特征分析法和阻抗分析法两种思路[4]。特征分析法基于系统的小信号状态空间模型,通过求解状态矩阵特征根判断系统稳定性。阻抗分析法是将微电网系统划分为等效的源与荷两个子系统,分别建立阻抗模型,通过Nyquist稳定判据或Bode图分析系统的稳定性。下面将分别评述已有文献中对交流微电网、直流微电网以及交直流微电网的振荡问题研究工作。
针对交流微电网,文献[6]以单母线孤岛微电网为研究对象,建立了系统小信号状态空间模型,采用特征分析的方法确定了影响微电网稳定性的主要因素;文献[7]针对两个交流微电网互联系统,分析了多阻抗优化控制的工作机理和优化后的端口阻抗模型,依据阻抗分析法和Nyquist稳定判据,对比分析了优化前后系统的振荡稳定性。针对直流微电网,文献[8]对含有多个恒功率负荷(Constant Power Load, CPL)的系统,将其等效为单个CPL后,通过阻抗法分析指出系统发生振荡与否与CPL数量密切相关;文献[9]通过对系统的特征根和阻抗Bode图进行分析,指出电压控制型电源直流电压控制的带宽过大或过小都有可能导致系统发生振荡现象。针对交直流微电网,文献[10]构建了DC-DC变流器和AC-DC变流器的阻抗模型,通过阻抗Bode图判据可知,当功率从直流微电网流向交流微电网时,存在两个变流器动态交互的现象,导致了振荡失稳;文献[11]构建了交直流微电网的小信号动态模型,通过特征分析法指出当下垂系数变大以及接口变流器PI控制参数变大时,都有可能导致系统振荡失稳。文献[12]在文献[11]基础上进一步分析指出,交流微电网内DG的电压外环和电流内环的比例控制系数变大也可能导致系统失稳。
尽管已有文献对微电网振荡问题做了一定研究,然而在振荡分析方法上,特征分析法和阻抗分析法均存在一定的局限性。基于小信号状态空间建模的特征分析法对于交直流微电网中含结构与参数未知的“黑箱/灰箱”设备时难以处理[13-14],且当系统存在大量建模对象时面临“维数灾”问题[15];基于Nyquist稳定判据的阻抗分析法需要将系统划分出明确的源荷分界点,然而对于复杂网络拓扑的交直流微电网,分界点划分存在困难[16-17]。为此,亟须探索适宜的交直流微电网振荡问题建模分析方法。
基于频域阻抗网络的建模分析方法结合了特征分析法和阻抗分析法的优势,可以有效地解决上述问题[18]。其主要思想为构建系统的频域阻抗网络模型,形成节点频域导纳矩阵,进而求解系统特征根。然而,已有研究大多将该方法运用于纯交流系统以及大电网,例如,文献[19-21]针对大规模风电电力系统开展的宽频振荡问题研究。如何将频域阻抗网络建模分析法应用于交直流微电网,并对系统的振荡机理、关键影响因素以及振荡的交直流传播特性等进行量化分析,都有待深入研究。
为此,本文针对基于频域阻抗网络模型的交直流微电网振荡问题建模与分析方法展开研究。首先,在交流DG/直流DG的阻抗模型推导以及基于所提的三维阻抗统一建模框架推导交直流变流器阻抗模型基础上,构建了考虑交直流耦合互联的系统频域阻抗网络模型及节点频域导纳矩阵;其次,基于频域模式分析法,建立了交直流微电网的节点/回路振荡参与程度指标以及设备和控制参数的灵敏度指标,给出了振荡的交直流传播特性分析方法,以便于揭示系统振荡机理;最后,通过Matlab/Simulink时域仿真和算例分析验证了建模与分析方法的有效性。
交直流微电网的系统结构如图1所示,主要由交流微电网、直流微电网和互联变流器(Interlinking Converter, ILC)三部分组成。其中交流子网由交流分布式电源DG和交流负载构成;直流子网由直流分布式电源DG和直流负载构成;互联变流器用来实现子网之间功率的双向流动。当与上级电网连接的静态开关断开时,交直流微电网处于离网运行状态,需要由分布式电源来维持系统电压和频率[22-23]。本文主要研究的是离网运行模式下的交直流微电网系统。

图1 交直流微电网系统结构
Fig.1 The structure of AC-DC microgrid system
交直流微电网系统频域阻抗网络建模的基本思路为:将系统中各个电力设备建模阻抗模型,随后基于系统拓扑并考虑了交直流耦合情况将各设备阻抗模型互联,构成系统整体的频域阻抗网络模型。本节剩余部分主要介绍交直流微电网内的设备阻抗建模,而系统整体的阻抗网络建模将在第2节中介绍。
本文中交流微电网采用主从控制策略,DG的控制类型包括Vf控制、PQ控制和VdcIq控制方式。其中,Vf控制的DG作为主电源,维持系统频率与电压,而PQ控制和VdcIq控制的DG作为从电源,PQ控制下DG发出指定的有功和无功功率,VdcIq控制下DG发出指定的电流并维持直流电压。VdcIq控制下DG的阻抗建模过程如附录第5节所示,其他控制方式下交流DG的阻抗建模过程和结果受篇幅所限,文中不再赘述。
本文中直流微电网同样采用主从控制策略,DG的控制类型包括电压电流双闭环控制和单电流环控制方式。电压电流双闭环控制的DG作为主电源,维持系统电压;而单电流环控制的DG作为从电源,发出指定的电流。不同控制方式下直流DG的阻抗建模结果受篇幅所限,文中不再赘述。
1.4.1 互联变流器三维阻抗/导纳建模的统一框架
互联变流器是交直流微电网中的核心设备,其VSC电路如图2所示,由于需要同时考虑交直流侧的动态特性,传统仅考虑交流侧动态的二维阻抗模型难以适用,需要建立额外考虑直流侧动态的三维阻抗模型。然而,传统的三维阻抗模型基于传递函数矩阵推导[24-26],当变流器的控制方法改变时需要重新推导,增加了建模的复杂度。为此,本文提出基于状态空间模型的变流器三维阻抗建模统一框架,可灵活应用于不同类型的控制,建模思路简单实用,具体阐述如下。
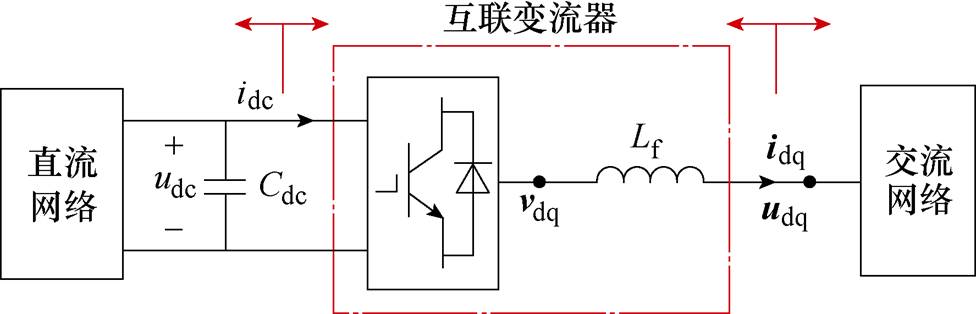
图2 互联变流器VSC电路
Fig.2 VSC circuit diagram of interconnected converter
变流器的三维导纳YVSC(s)见式(1)(阻抗可通过导纳求逆获得,本文以导纳的推导为例)。
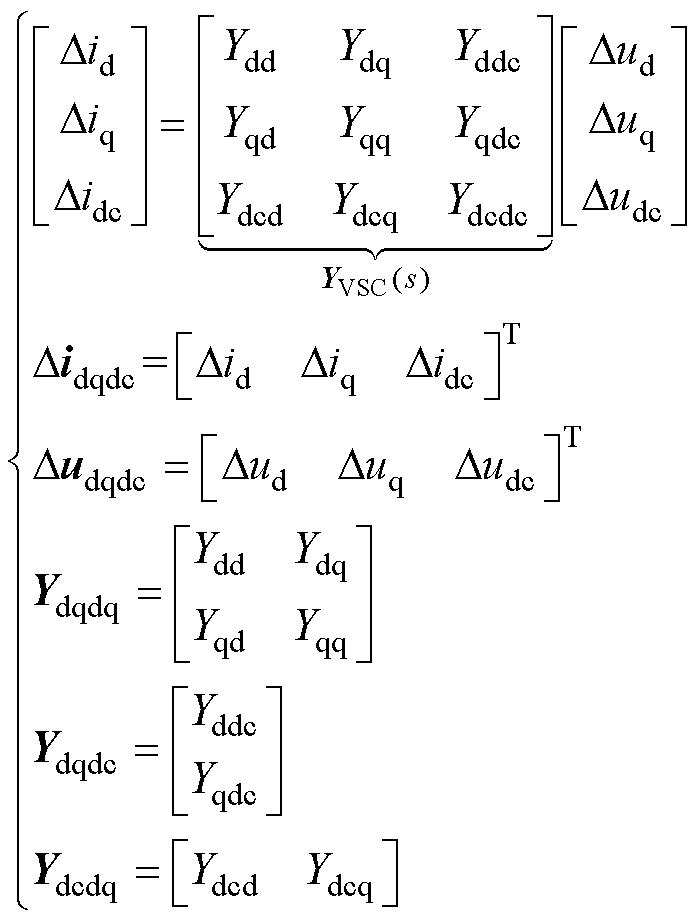 (1)
(1)
式中,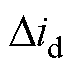 、
、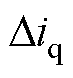 和
和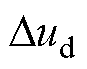 、
、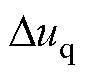 分别为互联变流器交流侧dq轴电流和电压;
分别为互联变流器交流侧dq轴电流和电压;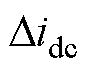 、
、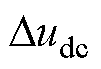 分别为互联变流器直流侧的电流和电压;Ydqdq、Ydcdc分别表示交流侧和直流侧的导纳;Ydqdc、Ydcdq分别为交直流侧的耦合导纳。
分别为互联变流器直流侧的电流和电压;Ydqdq、Ydcdc分别表示交流侧和直流侧的导纳;Ydqdc、Ydcdq分别为交直流侧的耦合导纳。
若互联变流器的小信号状态空间模型可推导为
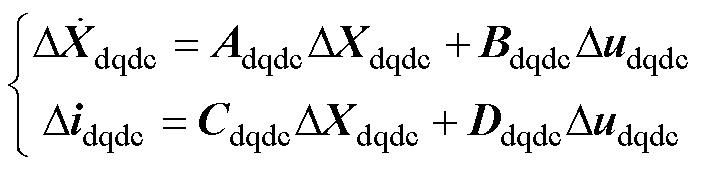 (2)
(2)
式中,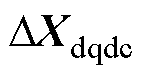 、
、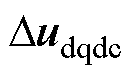 、
、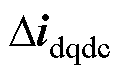 分别为状态、输入、输出矢量的小信号增量;Adqdc、Bdqdc、Cdqdc、Ddqdc分别表示系数矩阵。对式(2)进行Laplace变换,进而在s域内推导
分别为状态、输入、输出矢量的小信号增量;Adqdc、Bdqdc、Cdqdc、Ddqdc分别表示系数矩阵。对式(2)进行Laplace变换,进而在s域内推导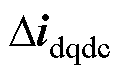 与
与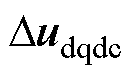 的关系,可得
的关系,可得
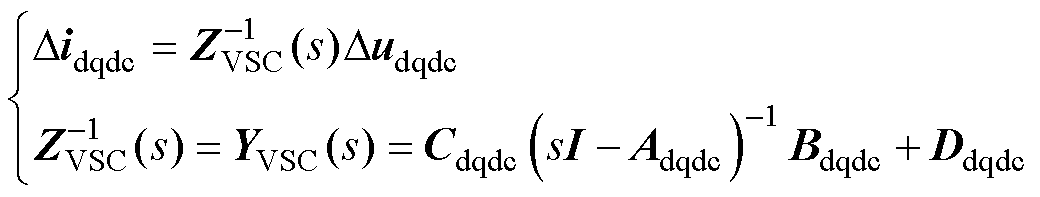 (3)
(3)
式中,ZVSC(s)和YVSC(s)分别为互联变流器在dq坐标系下的三维阻抗和导纳矩阵。
1.4.2 PQ控制下的互联变流器阻抗建模
本文中互联变流器采用PQ控制,用于控制互联变流器传输的有功、无功功率。考虑到互联变流器三维导纳建模过程与二维建模相比多了一个直流侧电流的环节,假设元件为理想元件,根据功率平衡方程,互联变流器交直流侧之间的关系可以表示为
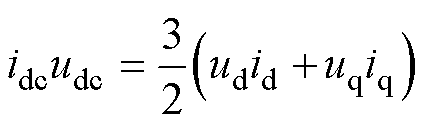 (4)
(4)
对式(4)进行线性化处理,可以得到
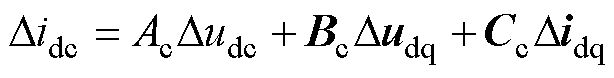 (5)
(5)
功率外环、电流内环、锁相环、电感滤波器等动态建模过程受篇幅所限,不再赘述。
最后,结合上述各个环节的线性化方程,可以得出PQ控制方式下互联变流器的小信号状态空间模型,由式(6)给出。
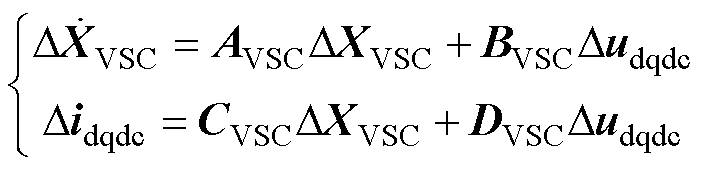 (6)
(6)
式中,AVSC、BVSC、CVSC和DVSC为系数矩阵。
在式(6)中,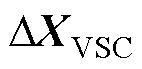 为状态变量向量,表示为
为状态变量向量,表示为
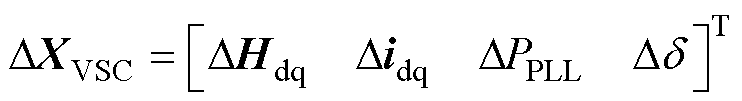 (7)
(7)
式中,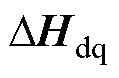 、
、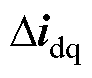 、
、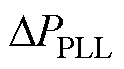 和
和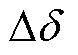 分别为电流控制器、电感滤波器、锁相环以及系统和控制dq坐标系转换的状态变量;
分别为电流控制器、电感滤波器、锁相环以及系统和控制dq坐标系转换的状态变量;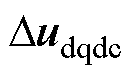 和
和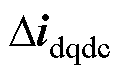 分别为系统dq坐标系下的输入和输出变量。将式(6)变换为s域后,就可得到互联变流器在PQ控制方式下的频域导纳矩阵,即
分别为系统dq坐标系下的输入和输出变量。将式(6)变换为s域后,就可得到互联变流器在PQ控制方式下的频域导纳矩阵,即
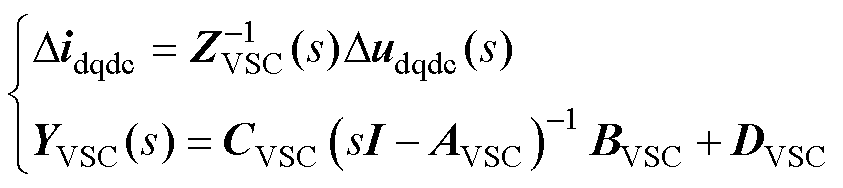 (8)
(8)
其阻抗矩阵为
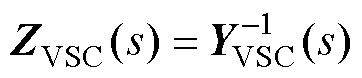 (9)
(9)
需要说明的是,当互联变流器使用其他类型的控制,或互联变流器的交流侧使用LC滤波器时,也可通过式(2)和式(3)所建立的三维导纳统一建模框架灵活方便地建模。
本节将采用频率扫描法[27-28]验证交直流微电网内设备阻抗建模的准确性。具体验证过程为在输入变量处设置扰动变量,分别改变每个扰动变量的频率,通过对变流器的时域仿真测量输出变量的值,得到线性无关的矢量组。随后,通过数学处理,得到相应的交直流微电网内各设备的导纳矩阵,从而绘制相应的Bode图。将理论推导的阻抗模型和扫频得到的导纳矩阵Bode图相比较,验证了交流DG、直流DG以及互联变流器阻抗模型的准确性,具体验证结果详见附录第1节。
需要说明的是,当交直流微电网中包含结构与参数未知的“黑箱/灰箱”设备时,可通过扫频法获得其阻抗特性,随后通过最小二乘法拟合可得到设备的阻抗传递函数,用于后续稳定分析。
首先,构建系统内各设备的阻抗模型,然后根据电路关系形成系统的频域阻抗网络。随后,根据电网络原理,系统的节点频域导纳矩阵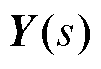 和回路频域阻抗矩阵Z(s)可表示[18]为
和回路频域阻抗矩阵Z(s)可表示[18]为
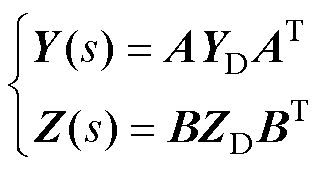 (10)
(10)
式中,A和B分别为节点频域阻抗网络的节点-支路关联矩阵和回路-支路关联矩阵,二者根据电网络原理来定义;YD和ZD分别为支路导纳矩阵和支路阻抗矩阵,均为对角矩阵,其对角元素分别为各支路设备的导纳和阻抗。
根据频域模式分析法,通过求取s域内节点导纳矩阵和回路阻抗矩阵的行列式的零点即可得到系统的全部特征根[18]sm=sm±jwm,即
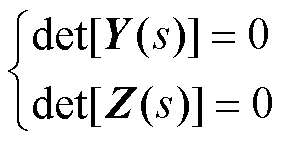 (11)
(11)
式中,det( · )表示矩阵的行列式。基于特征根可得到振荡模式的阻尼比和振荡频率。
下面以图3所示的交直流微电网系统为例给出其频域阻抗网络建模及节点频域导纳矩阵(或回路频域阻抗矩阵)的结果。图3中包含3个交流DG,3个直流DG和1个互联变流器,其控制方式如图3所示。
根据第1节的工作,可以得到s域内系统中各个设备的导纳模型,分别是:①交流微电网中VdcIq控制、Vf控制和PQ控制的DG的导纳模型,即Yinv_VdcIq(s)、Yinv_Vf(s)和Yinv_PQ(s);②直流微电网中3个DG的导纳模型,即YBoost1(s)、YBoost2(s)和YBoost3(s);③互联变流器的三维导纳模型YVSC(s)。其中,为了便于交直流的耦合建模,互联变流器三维导纳模型的等效电路如图4所示[29]。类比无源互感元件,可将交直流侧受控电流源表征的耦合项Ydqdc和Ydcdq表示为交流支路和直流支路之间的互感[29]。Ydqdc代表直流侧对交流侧的影响,而Ydcdq则代表交流侧对直流侧的影响,交直流侧振荡的传播通道由耦合项Ydqdc和Ydcdq构成。
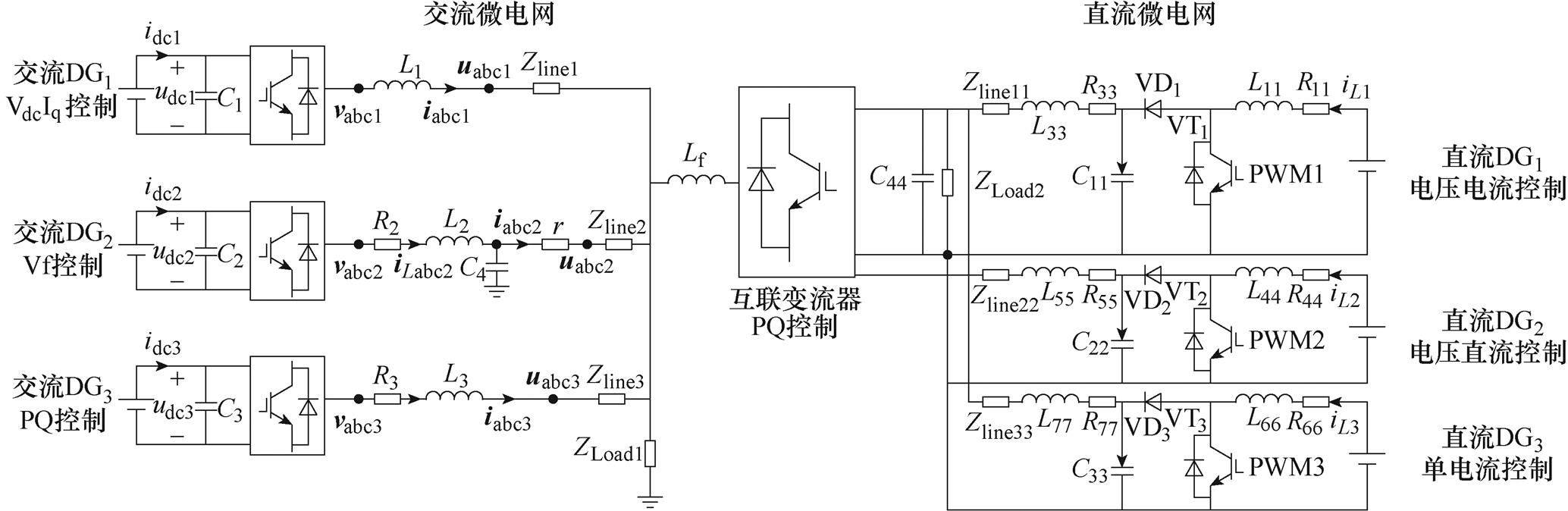
图3 交直流微电网系统拓扑
Fig.3 The topology of AC-DC microgrid system
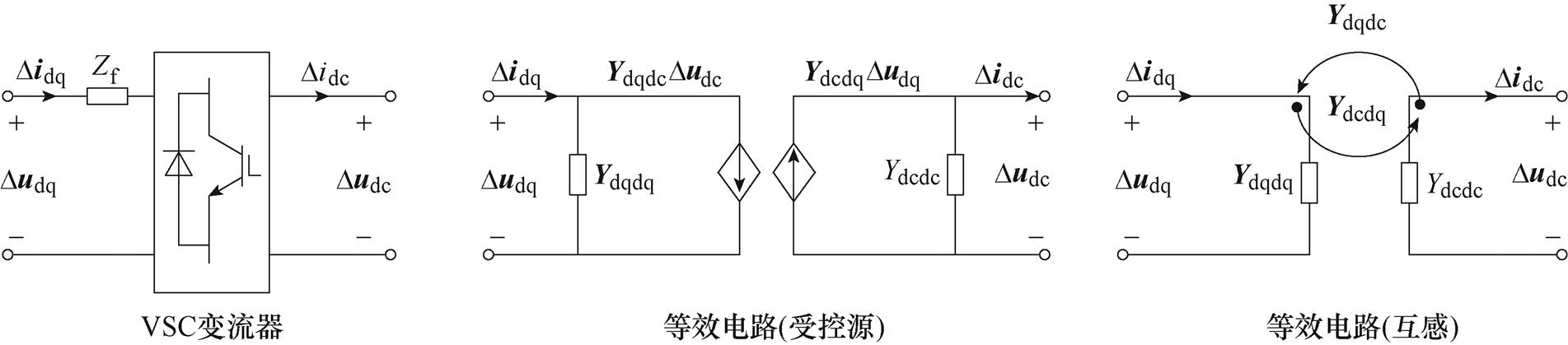
图4 互联变流器等效电路
Fig.4 The equivalent circuit of interconnected converter
进一步地,基于图3和图4,将各个设备的阻抗按照图3所示的系统拓扑连接关系相互连接起来,即可得到交直流微电网系统的整体频域导纳网络,如图5所示。其中,图5a为交直流微电网系统的等效频域导纳网络模型,图5a中,Yline1、Yline2和Yline3分别是交流微电网中的线路导纳,Yline11、Yline22和Yline33分别是直流微电网中的线路导纳,YLoad1和YLoad2分别是交直流微电网中的负载导纳。Ydqdq、Ydcdc分别是互联变流器VSC中交直流侧的等效导纳,Y44是直流侧的电容导纳;其中1、2、3、4、5、6、7、8表示的是系统中的节点编号。图5b为交直流微电网系统的有向图,将在3.1节中详细介绍。
根据节点编号以及电网络拓扑关系,可得到节点-支路关联矩阵A和回路-支路关联矩阵B,如附录第2节中式(A1)所示。随后,可形成支路导纳矩阵YD和支路阻抗矩阵ZD。再者,根据式(10),可得到交直流微电网的系统节点频域导纳矩阵YMG(s)和回路频域阻抗矩阵ZMG(s)。YD、ZD和YMG(s)的结果如式(12)所示,ZMG(s)的结果不再赘述。最后,根据式(11)可计算得到系统的特征根。
由式(12)中的YMG(s)结果可知,互联变流器三维导纳YVSC(s)中的元素Ydqdq、Ydcdq、Ydqdc和Ydcdc体现在YMG的第 (4, 4), (5, 4), (4, 5), (5, 5) 这些位置上。
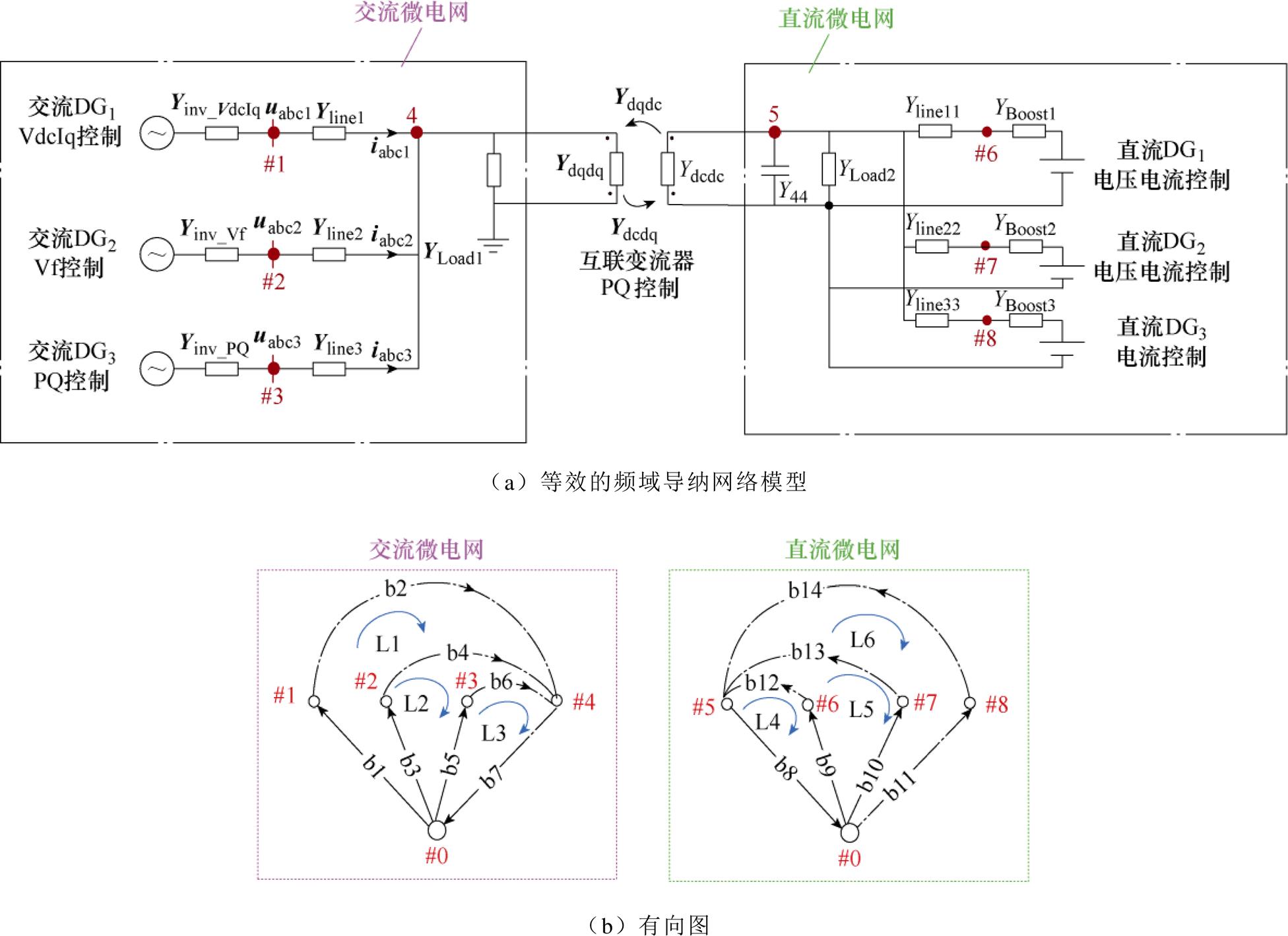
图5 交直流微电网系统的频域等效电路及有向图
Fig.5 Frequencydomain equivalent circuit and directed graph of AC-DC microgrid system
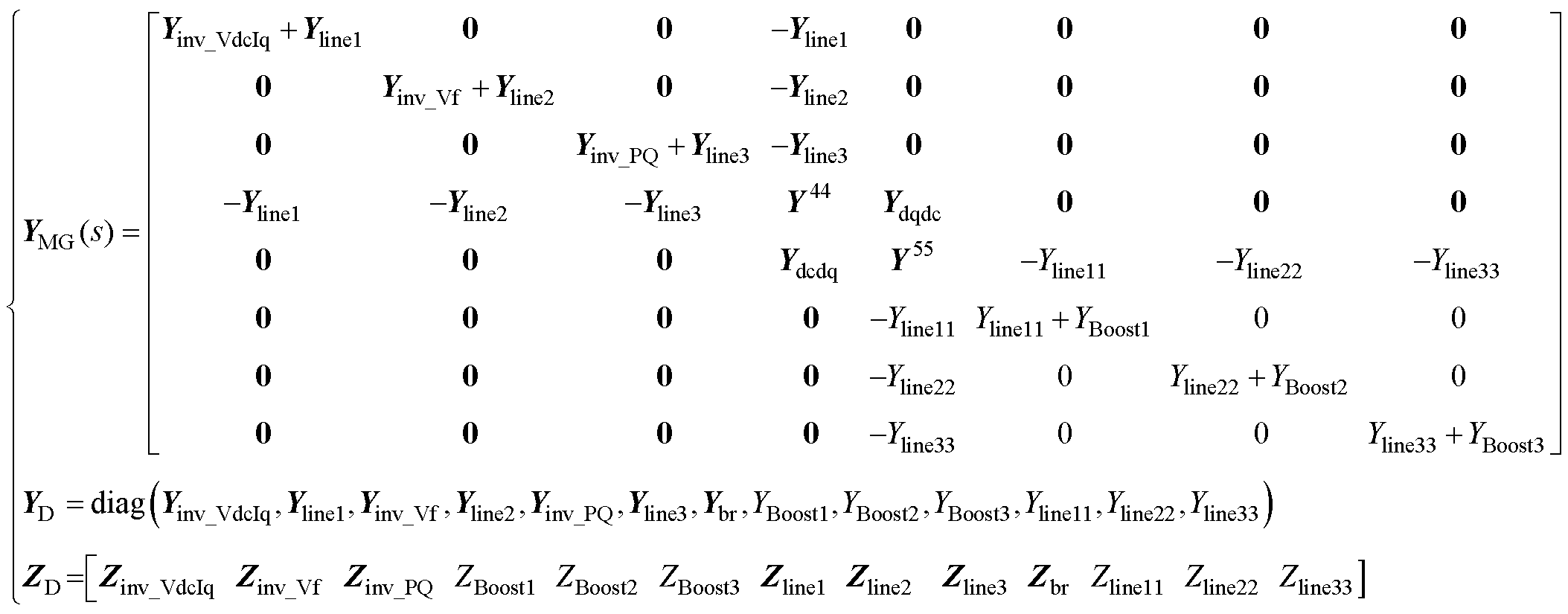 (12)
(12)
其中
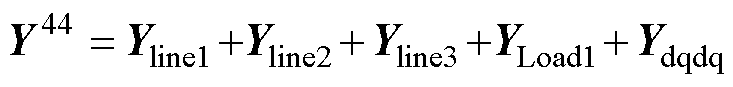
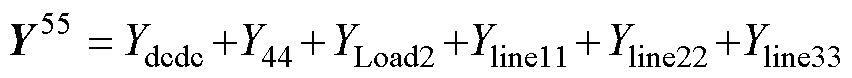
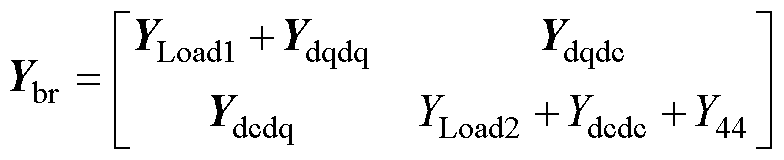
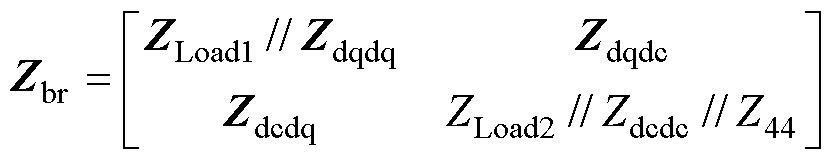
基于第2节获得的系统节点频域导纳矩阵YMG(s)信息,结合频域模式分析方法,针对交直流微电网系统的振荡机理、关键影响因素以及振荡的交直流传播特性等进行量化分析研究。首先,基于系统的频域阻抗网络模型,根据频域模式分析法计算系统的振荡模式,即计算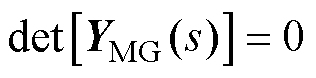 的根;其次,基于所得振荡模式,计算节点/回路的可观度、可控度以及参与因子指标,确定主导节点/回路的位置;进一步地,计算主导节点/回路处的设备和参数灵敏度指标,确定关键设备和关键控制参数;最后,分析系统振荡的交直流传播特性。
的根;其次,基于所得振荡模式,计算节点/回路的可观度、可控度以及参与因子指标,确定主导节点/回路的位置;进一步地,计算主导节点/回路处的设备和参数灵敏度指标,确定关键设备和关键控制参数;最后,分析系统振荡的交直流传播特性。
类比于时域下的模式分析法,在频域模式分析法中也可引入参与因子的概念,用来衡量各节点/回路对振荡模式的参与程度[18]。基于所得振荡模式,参与因子的具体推导过程如附录第6节,由推导过程可得
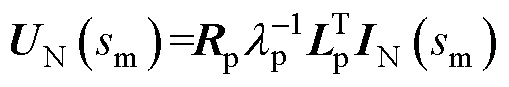 (13)
(13)
式中, 为零特征值
为零特征值 的右特征向量;
的右特征向量;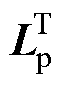 为
为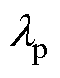 的左特征向量。将
的左特征向量。将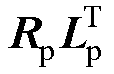 所得矩阵的对角元素用于衡量参与因子(Participation Factor, PF)[18]。同理,回路参与因子与上述推导过程类似,可通过ZMG(s)计算得到相应的右特征向量
所得矩阵的对角元素用于衡量参与因子(Participation Factor, PF)[18]。同理,回路参与因子与上述推导过程类似,可通过ZMG(s)计算得到相应的右特征向量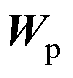 和左特征向量
和左特征向量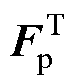 ,具体推导过程不再赘述。
,具体推导过程不再赘述。
节点(node)和回路(loop)对振荡模式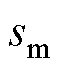 的可观度(Observability, Obs)和可控度(Controllabi- lity, Con)分别为[18]
的可观度(Observability, Obs)和可控度(Controllabi- lity, Con)分别为[18]
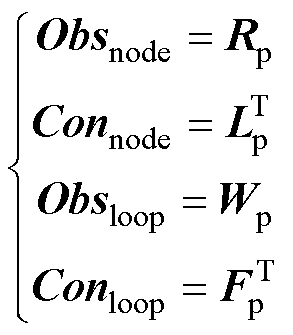 (14)
(14)
节点/回路的可观度反映了各个节点/回路对振荡模式的观测效果;节点/回路的可控度反映了各个节点/回路对振荡模式的激励作用;节点/回路的参与因子则衡量了各个节点/回路对振荡模式的参与程度,根据参与因子大小可以定位主导振荡模式的节点/回路位置(参与因子越大,振荡效果越显著),从而追溯振荡源。
结合如图5b所示的交直流微电网系统的有向图可知,系统中有8个节点(1~8)、6条回路(L1~L6)和14条支路(b1~b14)。
在3.1节中分析了系统中各节点/回路对振荡模式的参与程度,为了进一步分析主导节点/回路处各个设备及其控制参数对于振荡模式的灵敏程度,以便能够定位导致系统发生振荡的关键设备和控制参数,下面引入灵敏度的概念并进行推导[30-31],具体推导过程如附录第7节所示。根据附录式(A17),并联设备对振荡模式的灵敏度为
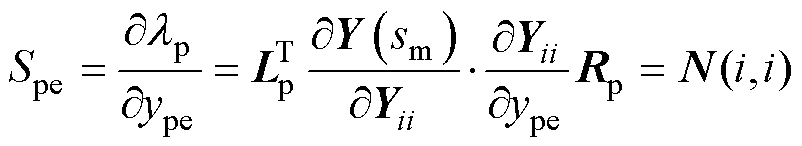 (15)
(15)
式中,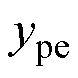 、
、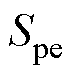 分别为并联设备的导纳和并联设备对振荡模式的灵敏度。
分别为并联设备的导纳和并联设备对振荡模式的灵敏度。
根据附录式(A17),串联设备对振荡模式的灵敏度为
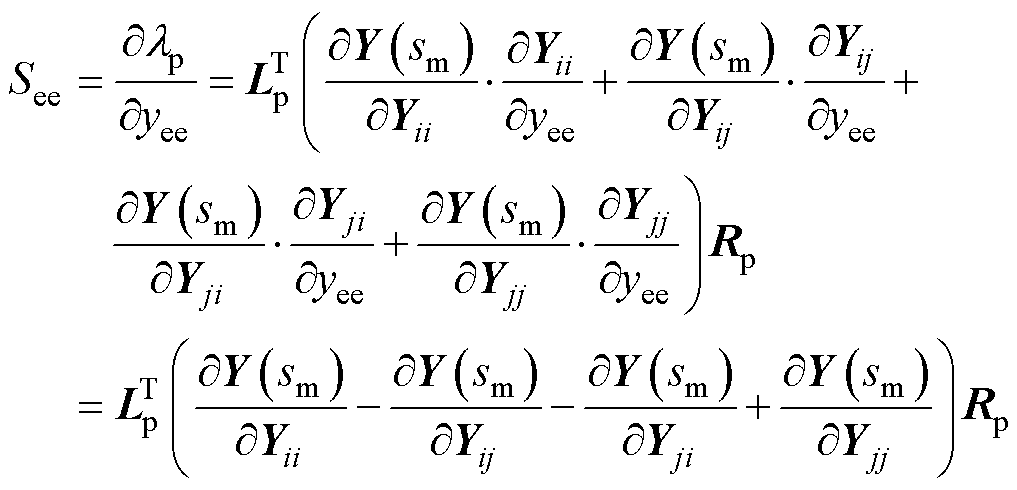
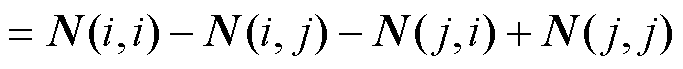 (16)
(16)
式中,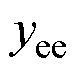 为串联设备的导纳;
为串联设备的导纳; 为串联设备对振荡模式的灵敏度;N为灵敏度矩阵,
为串联设备对振荡模式的灵敏度;N为灵敏度矩阵,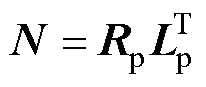 ;N(i, j)表示矩阵的第i行第j列元素。
;N(i, j)表示矩阵的第i行第j列元素。
在得到设备的灵敏度后,进一步根据导数的链式法则,可获得主导节点/回路处各设备参数对振荡模式的灵敏度。
定义系统中某一设备的参数对振荡模式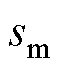 的灵敏度为
的灵敏度为
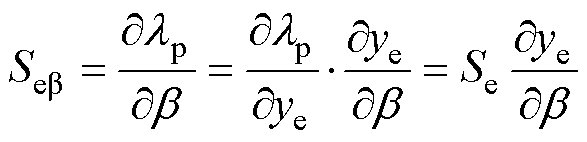 (17)
(17)
式中,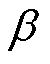 为设备参数;
为设备参数;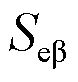 为设备参数对振荡模式的灵敏度。
为设备参数对振荡模式的灵敏度。
根据设备及其参数灵敏度的大小,可以对引发振荡的关键设备和参数进行定位,明晰振荡的关键影响因素。
本节基于文献[29]中的理论方法,进行微电网振荡在交直流之间的传播特性分析。与交流微电网或直流微电网相比,交直流微电网的振荡存在交直流系统中的传播问题。若交流微电网(直流微电网)发生振荡时,只会限制在本区域而不会传播至整个系统,则体现为单网振荡;若交流微电网(直流微电网)发生振荡时,会经过互联变流器传播至直流微电网(交流微电网),从而影响整个系统,则体现为全网振荡特性。
Znode(s)表示交直流微电网的节点阻抗矩阵,Znode(s)为
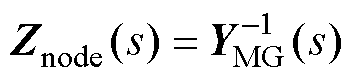 (18)
(18)
基于矩阵理论中的置换矩阵映射关系和节点可观度振荡指标,将整个交直流微电网的节点阻抗矩阵重新排布后,划分为振荡的高风险区域和低风险区域[29],然后列写交直流微电网的电压电流方程,即
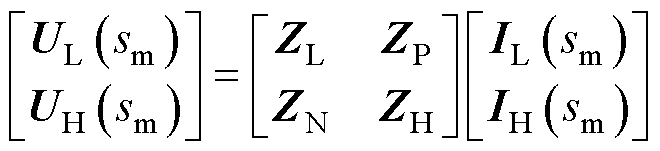 (19)
(19)
式中,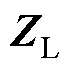 由低风险节点组成,定义为交直流微电网的低风险区域;
由低风险节点组成,定义为交直流微电网的低风险区域; 由高风险节点组成,定义为交直流微电网的高风险区域;
由高风险节点组成,定义为交直流微电网的高风险区域;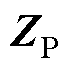 和
和 为两个区域之间的交互耦合项,分别量化低风险区域电压受高风险区域振荡电流的影响和高风险区域电压受低风险区域振荡电流的影响。交直流微电网的单网-全网振荡特性的传播通道主要由系统节点阻抗矩阵中的非对角线耦合元素构成,若发生振荡的区域与之相关的耦合元素为0,系统体现为单网振荡特性;反之,则体现为全网振荡特性。
为两个区域之间的交互耦合项,分别量化低风险区域电压受高风险区域振荡电流的影响和高风险区域电压受低风险区域振荡电流的影响。交直流微电网的单网-全网振荡特性的传播通道主要由系统节点阻抗矩阵中的非对角线耦合元素构成,若发生振荡的区域与之相关的耦合元素为0,系统体现为单网振荡特性;反之,则体现为全网振荡特性。
为了能够准确地界定单网-全网振荡特性,下面给出区域传播强度振荡指标[29],用以量化评估区域之间的振荡交互强度和刻画振荡的传播边界,如
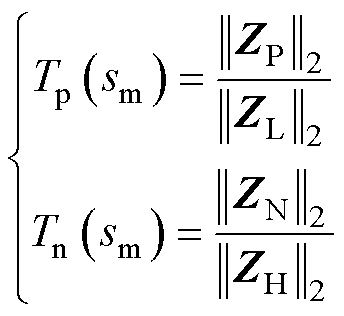 (20)
(20)
式中,若Tp(sm)=0,说明高风险区域的振荡向低风险区域传播的通道被阻断,体现为交直流微电网的单网振荡特性;若Tp(sm)≠0,说明高风险区域的振荡将向低风险区域传播,体现为交直流微电网的全网振荡特性。
本节将基于第3节的交直流微电网振荡稳定性分析方法,对交直流微电网系统的振荡问题进行分析研究,并且在Matlab/Simulink平台上进行时域仿真分析。
在Matlab/Simulink中搭建如图3所示的交直流微电网系统,系统中的关键参数详见附录第3节。系统的等效频域导纳网络模型及相应的节点、支路和回路的定义如图5所示。
在系统正常运行时,基于系统的节点导纳矩阵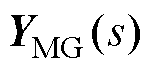 ,通过计算
,通过计算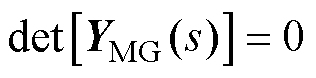 ,就可以获得系统的全部特征根,其中主导模式为s1=-22.84±31.31i和s2=-61.97±576.92i,可知系统稳定。此时系统的时域仿真结果也表明系统能够正常稳定运行,受篇幅所限,不再展示。
,就可以获得系统的全部特征根,其中主导模式为s1=-22.84±31.31i和s2=-61.97±576.92i,可知系统稳定。此时系统的时域仿真结果也表明系统能够正常稳定运行,受篇幅所限,不再展示。
4.1.1 交流微电网参数变化下系统的振荡特性分析
1)根轨迹与时域仿真结果
交流微电网中VdcIq控制的逆变器的电流内环PI控制器比例增益参数Kpi1由2逐渐减少至0.13时,此时的根轨迹变化情况如图6所示,图中起始位置用蓝色圆圈表示,终止位置用黑色叉号表示,黑色的箭头表示根轨迹的方向。从图6中可以看出,Kpi1的变化对多数特征根影响较小,但有一个模态的特征根随着Kpi1的减小明显向虚轴移动,当Kpi1到达0.27时越过虚轴,出现负阻尼特征根,此时系统失稳,失稳模式为s=3.37±64.79i,失稳振荡频率为10.32 Hz。
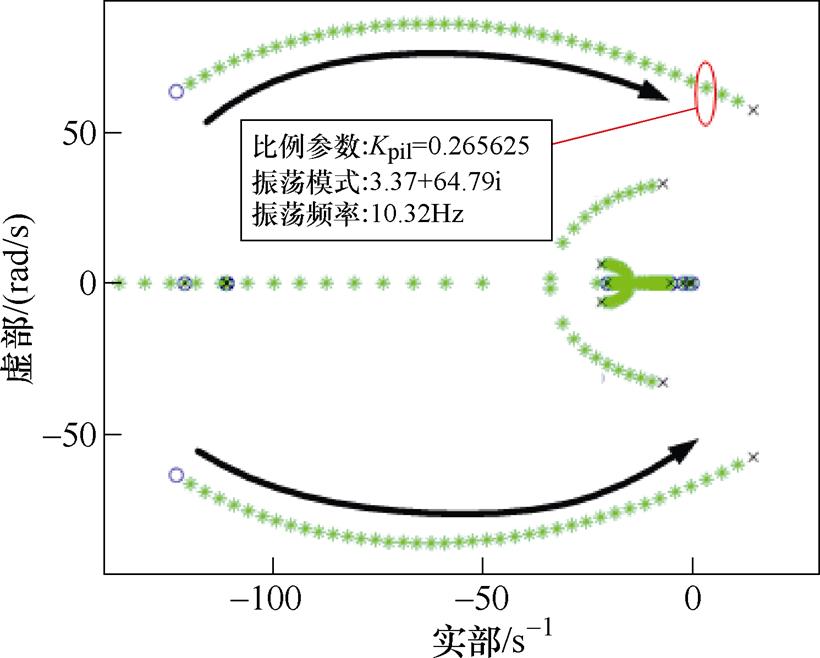
图6 交流微电网中VdcIq控制下逆变器电流内环比例增益参数Kpi1变化的根轨迹
Fig.6 Root trajectory of the variation of the inverter current inner loop proportional gain parameter Kpi1 under VdcIq control in AC microgrids
当Kpi1=0.27时,VdcIq控制的逆变器的输出有功功率如图7所示。可知,此时系统发生振荡失稳,仿真结果中的振荡频率为10.35 Hz,与理论计算得到的振荡频率相对应。
2)参与因子和灵敏度结果
基于3.1节和3.2节中给出的振荡稳定性分析方法,将上述失稳振荡模式代入相关的计算公式中,可以分别获得节点/回路的参与因子和主导振荡节点/回路处的关键设备和参数灵敏度的大小。计算结果分别见表1和表2,可以看出,节点1和回路L1的参与因子最大,而节点5~8和回路L4~L6的参与因子均为0(受篇幅限制,表中未展示),设备Yinv_VdcIq的灵敏度最大,参数Kpv1、Kpi1的灵敏度都比较大。同时,由图5可知,节点1和回路L1均与交流DG1有关,且参数Kpv1、Kpi1为交流DG1的比例增益控制参数,说明系统的失稳振荡是由节点1和回路L1主导,具体地由交流DG1及其参数Kpv1、Kpi1引发。此外,表1和表2还表明,节点3、4与回路2也在一定程度上参与了振荡,说明PQ控制的交流DG3和Vf控制的交流DG2也对振荡有贡献,表明了多台设备参与振荡的动态交互特性;而直流微电网内的节点和回路对振荡参与不高,说明振荡的参与情况主要局限在交流微电网。
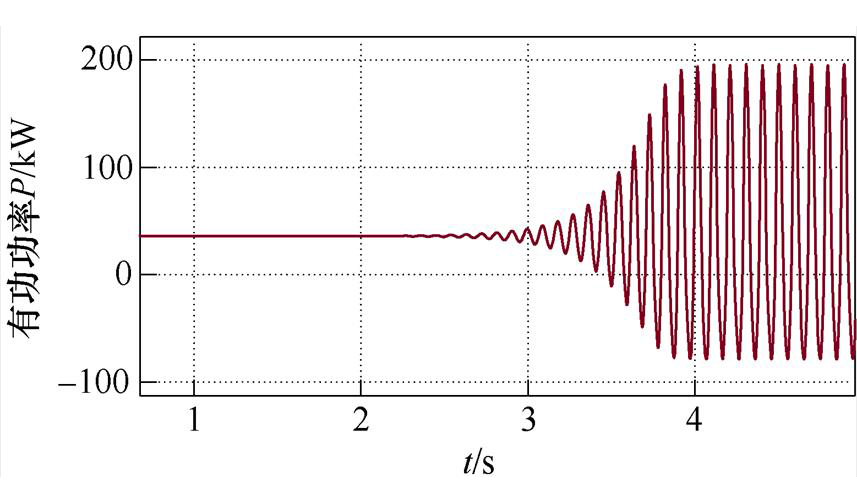
图7 交流微电网中VdcIq控制DG的输出有功功率
Fig.7 VdcIq control of DG output active power in AC microgrid
表1 节点/回路参与因子
Tab.1 Node/loop participation factors
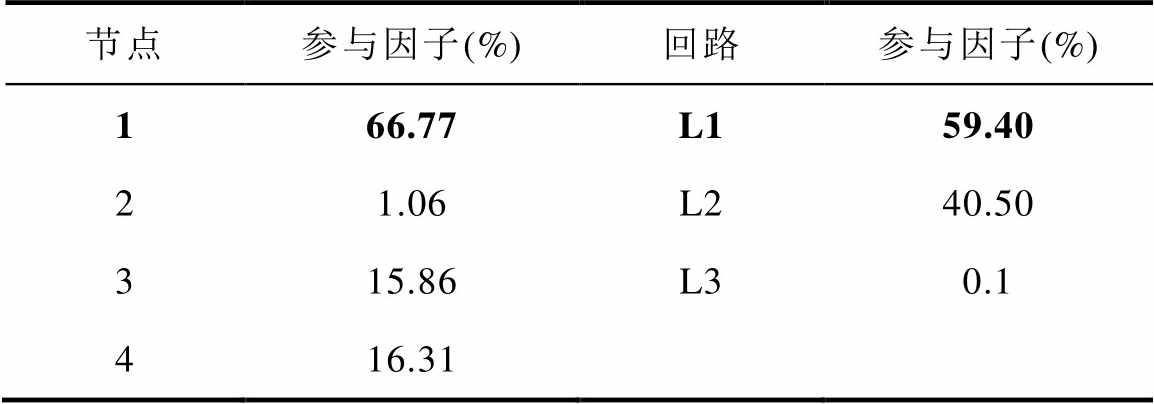
节点参与因子(%)回路参与因子(%) 166.77L159.40 21.06L240.50 315.86L30.1 416.31
表2 设备和设备参数灵敏度
Tab.2 Equipment and equipment parameter sensitivity
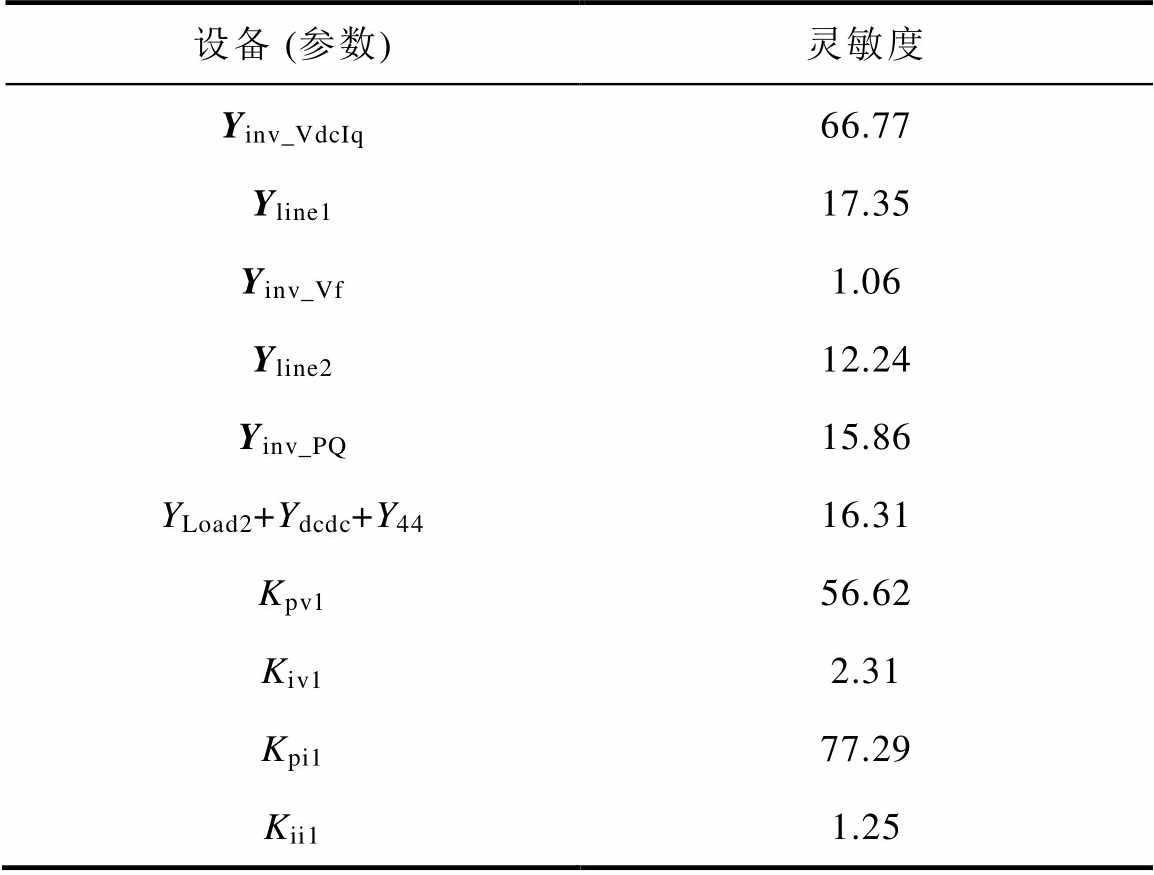
设备 (参数)灵敏度 Yinv_VdcIq66.77 Yline117.35 Yinv_Vf1.06 Yline212.24 Yinv_PQ15.86 YLoad2+Ydcdc+Y4416.31 Kpv156.62 Kiv12.31 Kpi177.29 Kii11.25
4.1.2 直流微电网参数变化下系统的振荡特性分析
直流微电网参数变化下系统的振荡特性分析与交流微电网的类似,具体分析过程详见附录第4节,也可验证所建立模型的准确性、振荡的主导影响因素以及多设备间的动态交互情况。
4.1.3 互联变流器参数变化下系统的振荡特性分析
1)根轨迹与时域仿真结果
当PQ控制下互联变流器的电流内环PI控制器比例增益参数Kpi由10逐渐减少至0.001时,系统的根轨迹变化情况如图8所示。从图8中可以看出,Kpi的变化对多数特征根影响较小,但有两个模态的特征根随着Kpi的减少向虚轴移动,当Kpi到达0.001时接近虚轴,出现弱阻尼特征根,振荡模式为s1= -1.99±205.48i,s2=-1.17±193.18i,振荡频率分别为32.72 Hz和30.76 Hz。
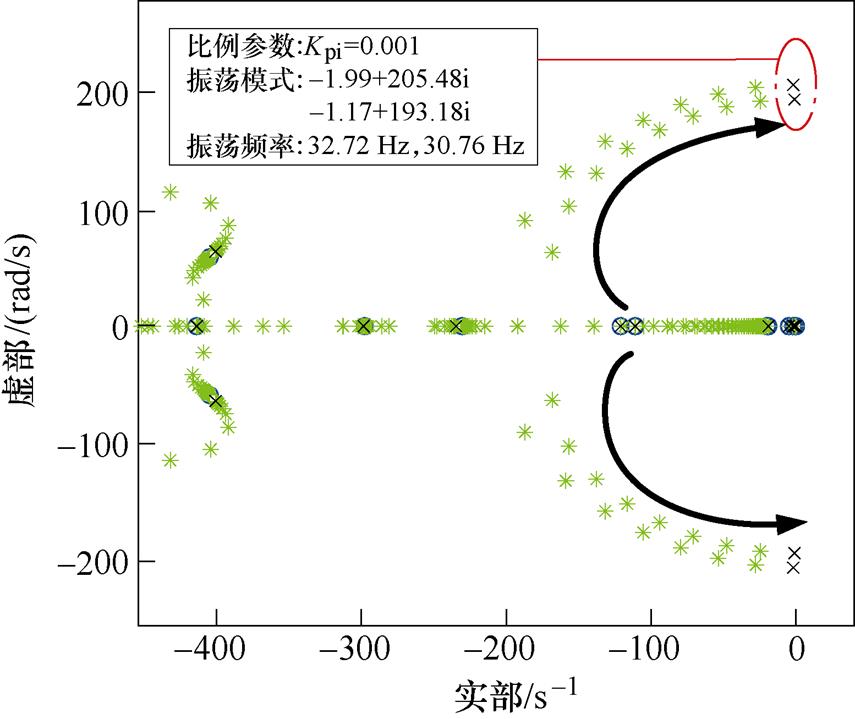
图8 PQ控制下的互联变流器电流内环比例增益参数Kpi变化的根轨迹
Fig.8 Root trajectory of the variation of the interconnected converter current inner loop proportional gain parameter Kpi under PQ control
当Kpi=0.001时,互联变流器的输出有功功率结果如图9所示,可见此时系统处于弱阻尼状态,仿真结果中振荡频率为31.31 Hz,与理论计算得到的振荡频率相对应。
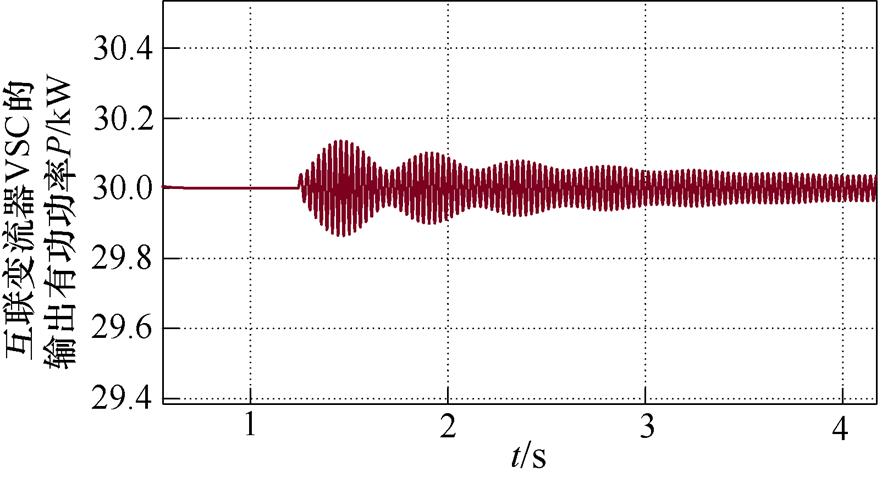
图9 PQ控制下互联变流器VSC的输出有功功率
Fig.9 Output active power of interconnected inverter VSC under PQ control
2)参与因子和灵敏度结果
以上述失稳振荡模式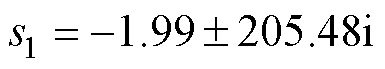 为例,将其代入相关的计算公式中,获得的节点参与因子、关键设备及其控制参数的灵敏度大小分别见表3和表4。
为例,将其代入相关的计算公式中,获得的节点参与因子、关键设备及其控制参数的灵敏度大小分别见表3和表4。
表3 节点参与因子
Tab.3 Node/loop participation factors
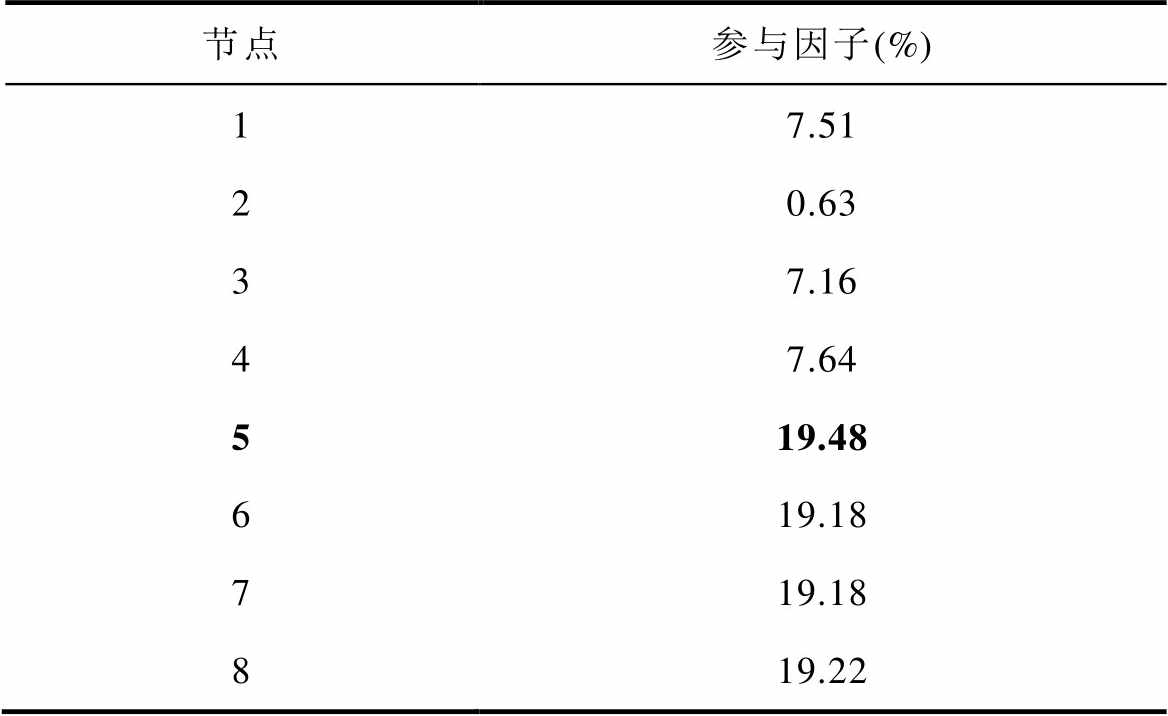
节点参与因子(%) 17.51 20.63 37.16 47.64 519.48 619.18 719.18 819.22
表4 设备/参数灵敏度
Tab.4 Equipment/parameter sensitivity
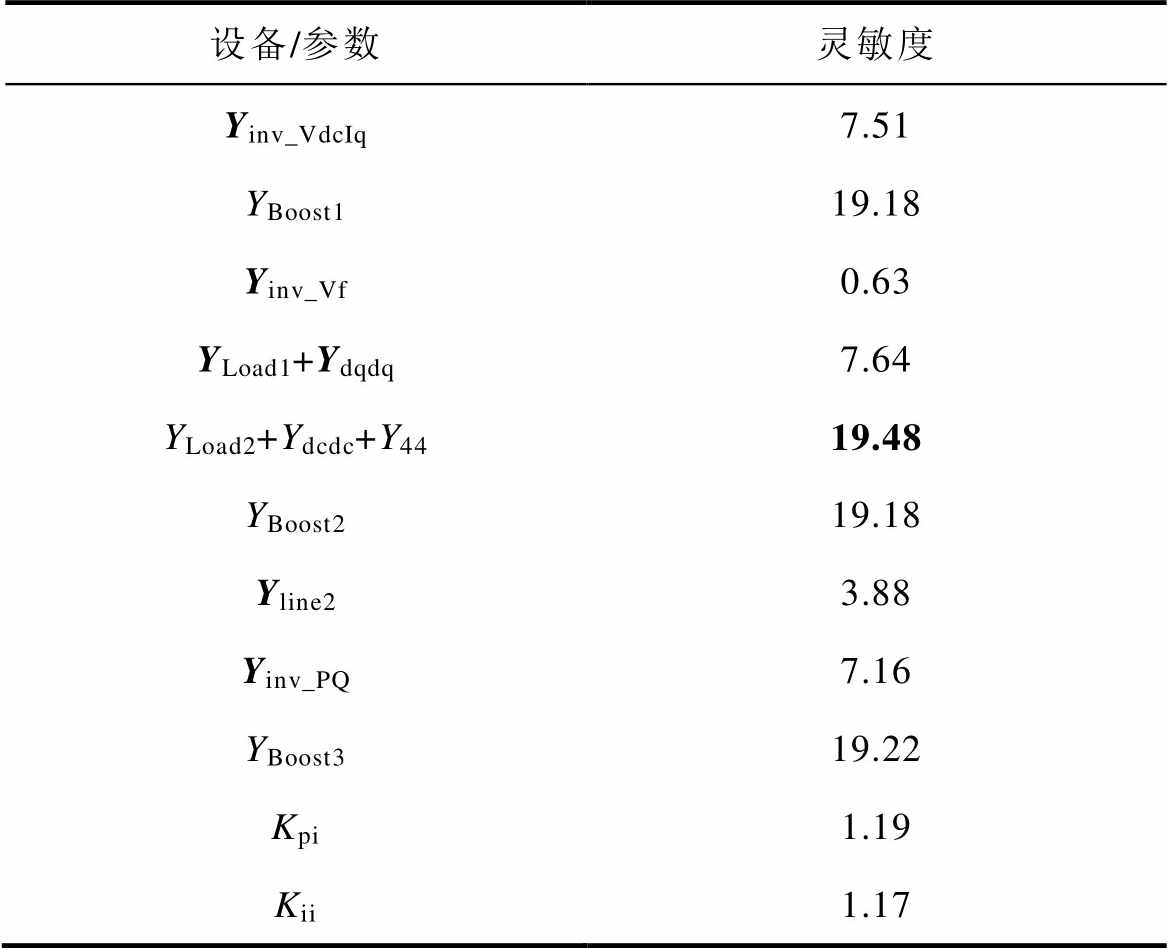
设备/参数灵敏度 Yinv_VdcIq7.51 YBoost119.18 Yinv_Vf0.63 YLoad1+Ydqdq7.64 YLoad2+Ydcdc+Y4419.48 YBoost219.18 Yline23.88 Yinv_PQ7.16 YBoost319.22 Kpi1.19 Kii1.17
由表3、表4可见,节点5的参与因子最大,设备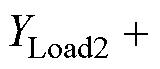
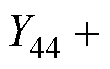
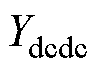 的灵敏度最大,参数Kpi和Kii的灵敏度都比较大,说明它们对系统振荡起主导作用。由此可知,该振荡受互联变流器的直流侧影响最大,且与其电流内环控制参数强相关。由表3和表4还可知,节点6、7、8和
的灵敏度最大,参数Kpi和Kii的灵敏度都比较大,说明它们对系统振荡起主导作用。由此可知,该振荡受互联变流器的直流侧影响最大,且与其电流内环控制参数强相关。由表3和表4还可知,节点6、7、8和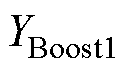 、
、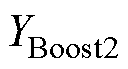 、
、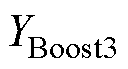 的参与因子和灵敏度均较大,说明该振荡受3个直流DG的影响也较大,但是受交流微电网的影响较小。
的参与因子和灵敏度均较大,说明该振荡受3个直流DG的影响也较大,但是受交流微电网的影响较小。
交直流微电网中其他参数变化下系统的振荡特性分析结果受篇幅所限,文中不再赘述。
本节分析振荡在交直流微电网间的传播特性。单网-全网振荡特性主要表现为振荡模式是否可观,因此首先通过节点可观度振荡指标将系统划分为低风险节点和高风险节点,并且将低风险节点靠前,而高风险节点靠后重新排列。假设设定节点可观度的阈值为0.01,若Obs<0.01,则将此节点定义为低风险节点;反之,则定义为高风险节点;其次通过置换矩阵映射关系来将系统的节点阻抗矩阵重新排布后,划分为低风险区域和高风险区域;最后通过计算振荡传播强度来刻画单网-全网振荡边界。
4.2.1 全网振荡
以图7所示的系统振荡失稳为例,当系统中交流侧VdcIq控制下逆变器的PI参数改变导致系统发生振荡时,交流微电网、直流微电网以及互联变流器的仿真结果如图10所示,可见此时系统在交流侧和直流侧均存在振荡,体现为全网振荡特性。计算此时失稳振荡模式下系统的节点可观度见表5,由表5可知,节点5~8的节点可观度相比于节点1~4的节点可观度极低,且都小于阈值0.01,因此可将节点5~8定义为低风险节点,而剩余节点则定义为高风险节点,得到的置换关系P1和置换矩阵E1如下所示。
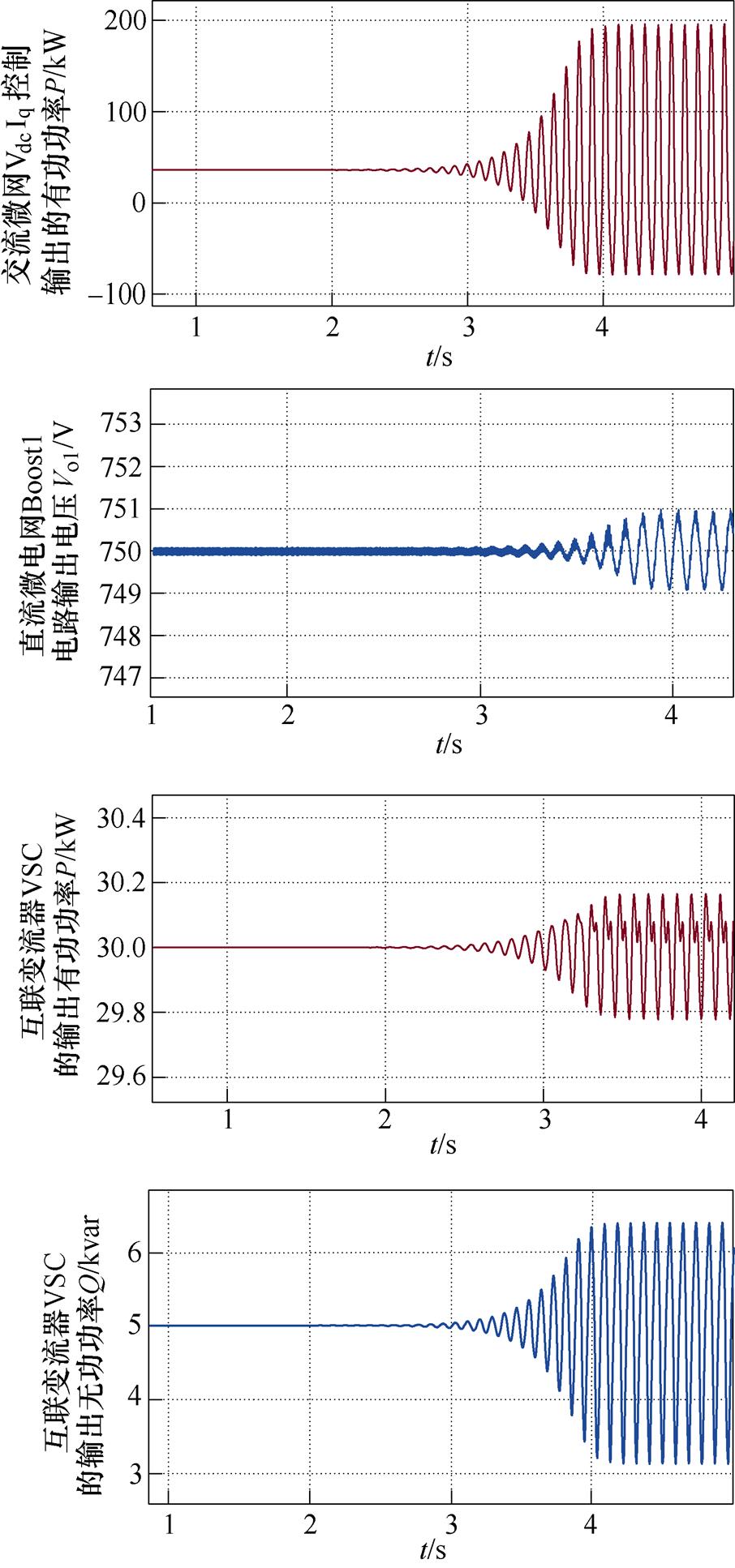
图10 系统全网振荡特性的时域仿真结果
Fig.10 Time domain simulation results of the entire network oscillation characteristics of the system
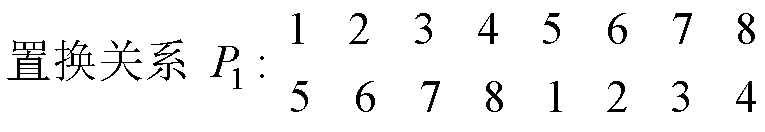
 (21)
(21)
表5 节点可观度
Tab.5 Node observability
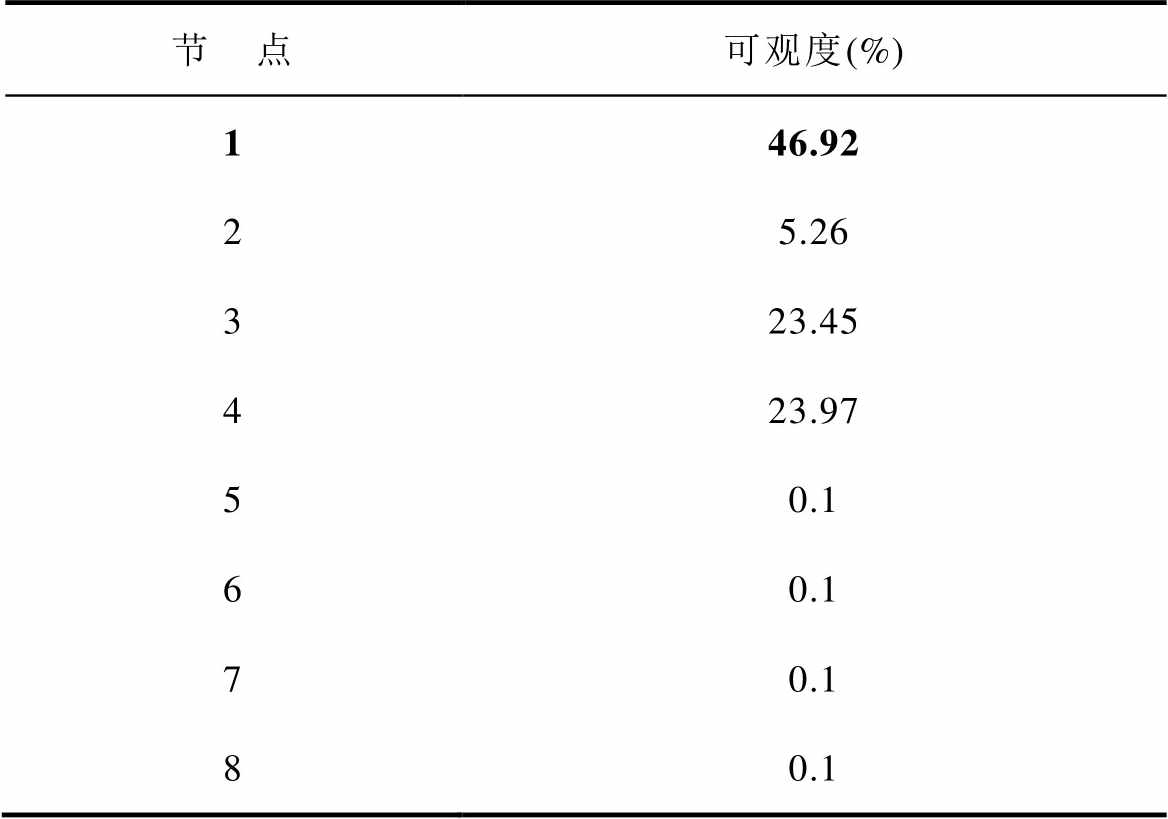
节 点可观度(%) 146.92 25.26 323.45 423.97 50.1 60.1 70.1 80.1
将此置换矩阵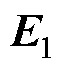 与节点阻抗矩阵Znode(sm)进行式(22)的运算,即可将系统划分为高风险区域和低风险区域,从而获得重新排布后的节点阻抗矩阵ZEnode(sm)。然后根据式(20)计算区域振荡传播强度得到Tp(sm)=3.6×1011≠0,说明高风险区域(交流微电网)的振荡将向低风险区域(直流微电网)传播,系统体现为全网振荡特性,与图10中的时域仿真结果一致。而Tn(sm)=0,说明低风险区域(直流微电网)的振荡不能向高风险区域(交流微电网)反向传播。
与节点阻抗矩阵Znode(sm)进行式(22)的运算,即可将系统划分为高风险区域和低风险区域,从而获得重新排布后的节点阻抗矩阵ZEnode(sm)。然后根据式(20)计算区域振荡传播强度得到Tp(sm)=3.6×1011≠0,说明高风险区域(交流微电网)的振荡将向低风险区域(直流微电网)传播,系统体现为全网振荡特性,与图10中的时域仿真结果一致。而Tn(sm)=0,说明低风险区域(直流微电网)的振荡不能向高风险区域(交流微电网)反向传播。
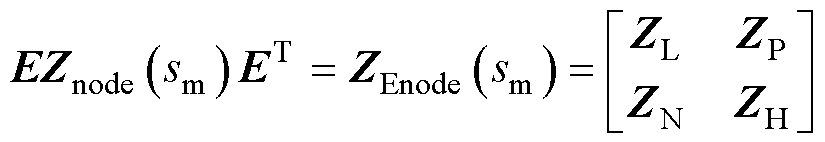 (22)
(22)
4.2.2 单网振荡
以4.1.2节中的系统振荡失稳为例,当系统中直流侧双闭环控制下Boost变换器的PI参数改变导致系统发生振荡时,交流微电网、直流微电网以及互联变流器的仿真结果如图11所示,可见只有直流微电网振荡,而互联变流器和交流微电网均不振荡,说明振荡被局限在了直流微电网内部,无法通过互联变流器向交流微电网传播,体现为单网振荡特性。
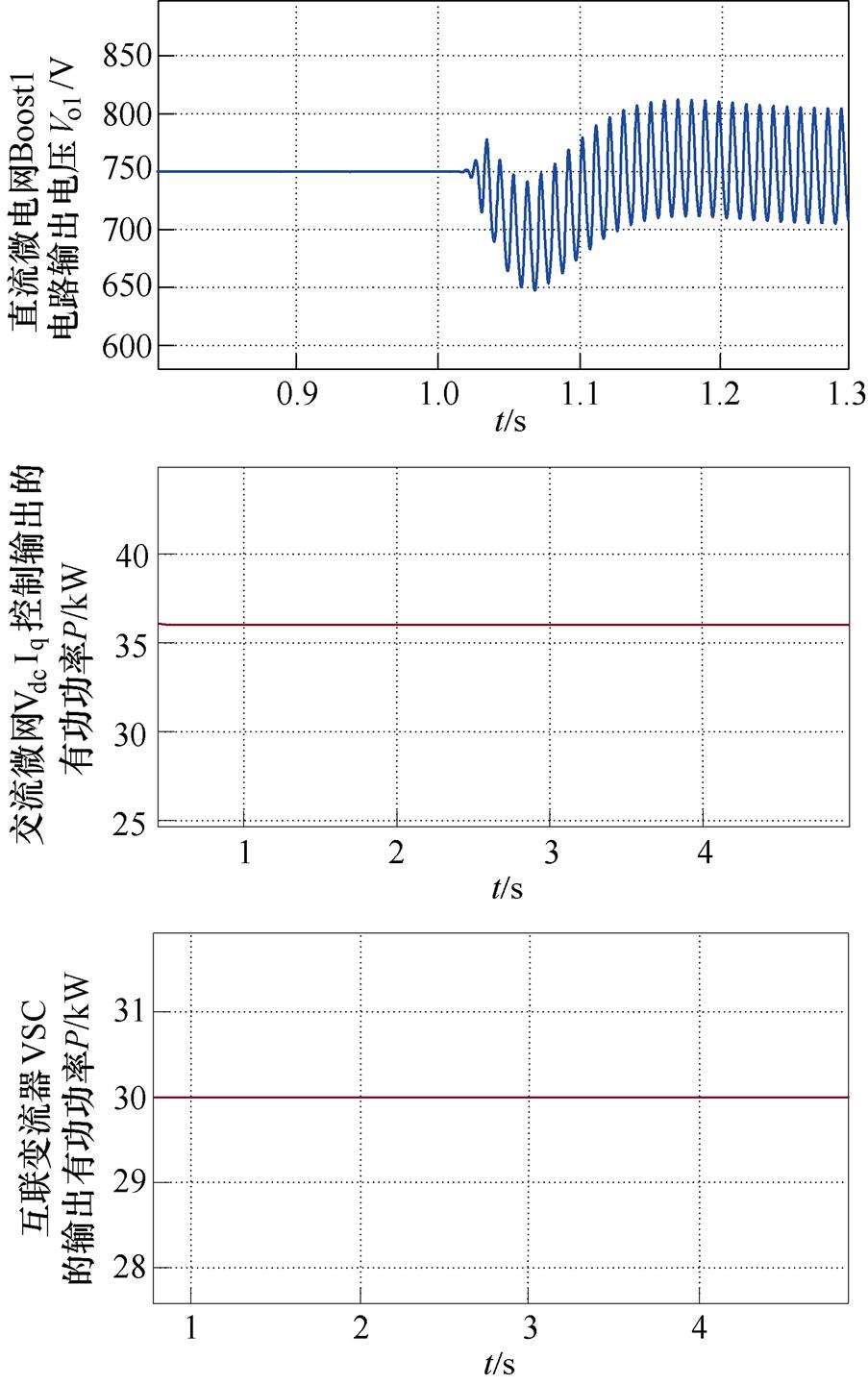
图11 系统单网振荡特性的时域仿真结果
Fig.11 Time domain simulation results of the single network oscillation characteristics of the system
计算此时在失稳振荡模式s2=268.08±867.99i下系统的节点可观度见表6,由表6可知,节点1~4的节点可观度相比于节点5~8的节点可观度极低,且都小于阈值0.01,因此可将节点1~4定义为低风险节点,而剩余节点则定义为高风险节点,同样也可以得到置换关系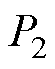 和置换矩阵
和置换矩阵 ,受篇幅所限,不再展示。
,受篇幅所限,不再展示。
表6 节点可观度
Tab.6 Node observability
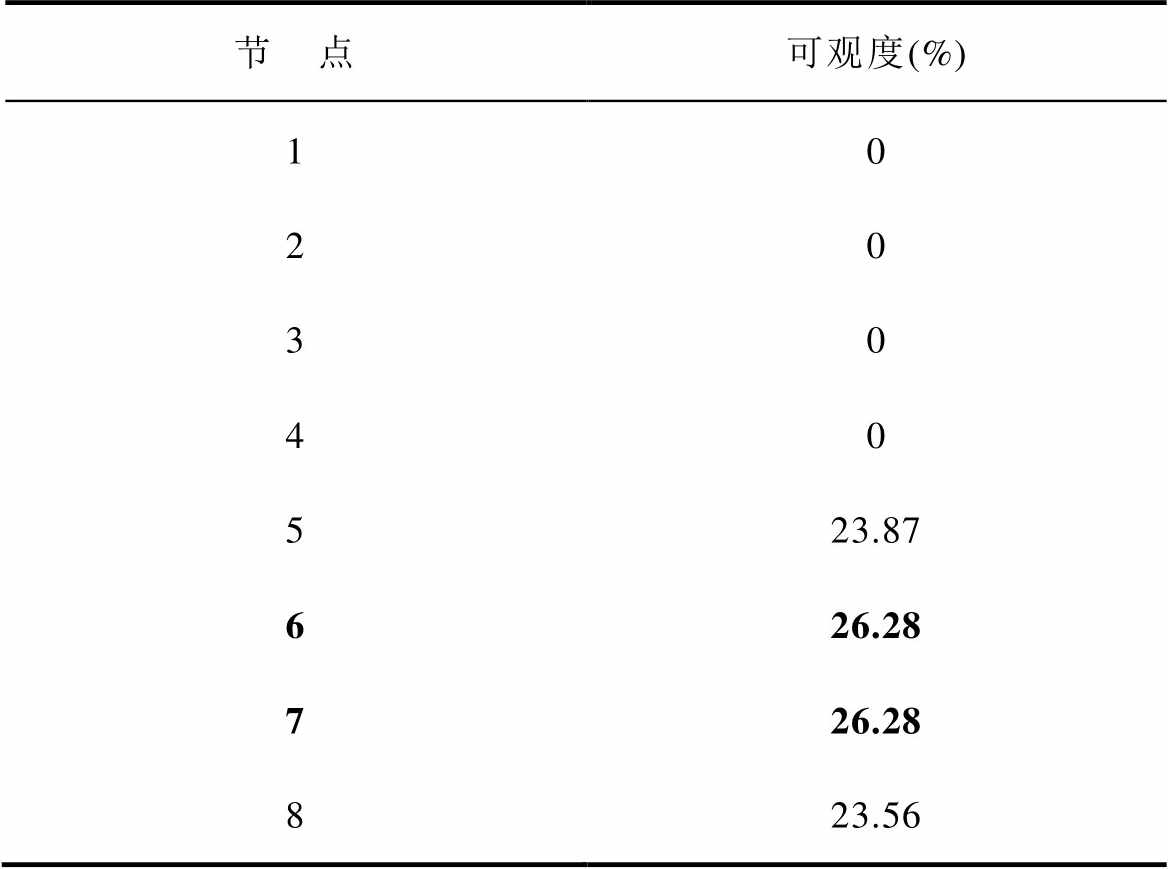
节 点可观度(%) 10 20 30 40 523.87 626.28 726.28 823.56
同理,根据式(20)计算区域振荡传播强度得到Tp(sm)=0,说明高风险区域(直流微电网)的振荡不能向低风险区域(交流微电网)传播,系统体现为单网振荡特性,与图11中的时域仿真结果一致。而Tn(sm)=0.036 1≠0,说明低风险区域(交流微电网)的振荡可以向高风险区域(直流微电网)反向传播。
本文针对基于频域阻抗网络模型的交直流微电网振荡问题建模与分析方法展开研究,对交直流微电网的振荡机理、关键影响因素以及振荡的交直流传播特性进行了量化分析。首先,建立了交直流微电网系统在频域下的等效阻抗网络模型,推导得到了系统的节点频域导纳矩阵。随后,基于频域模式分析法,计算系统在某一振荡模式下的节点/回路参与因子和设备/参数的灵敏度指标,能够有效地定位振荡源与关键参数,揭示多设备参与振荡的动态交互特性。同时,通过分析系统的单网-全网振荡特性,
进一步明晰了系统振荡的交直流传播特性。后续将基于振荡分析结果,进一步关注交直流微电网的振荡抑制控制方法。
附 录
1. 交直流微电网设备阻抗模型的准确性验证结果
受篇幅所限,本文只展示互联变流器VSC的部分准确性验证结果,如附图1所示为互联变流器通过理论推导公式和扫描频率得到的三维导纳矩阵YVSC中的Ydcq和Yqq的Bode图,可知两者一致。
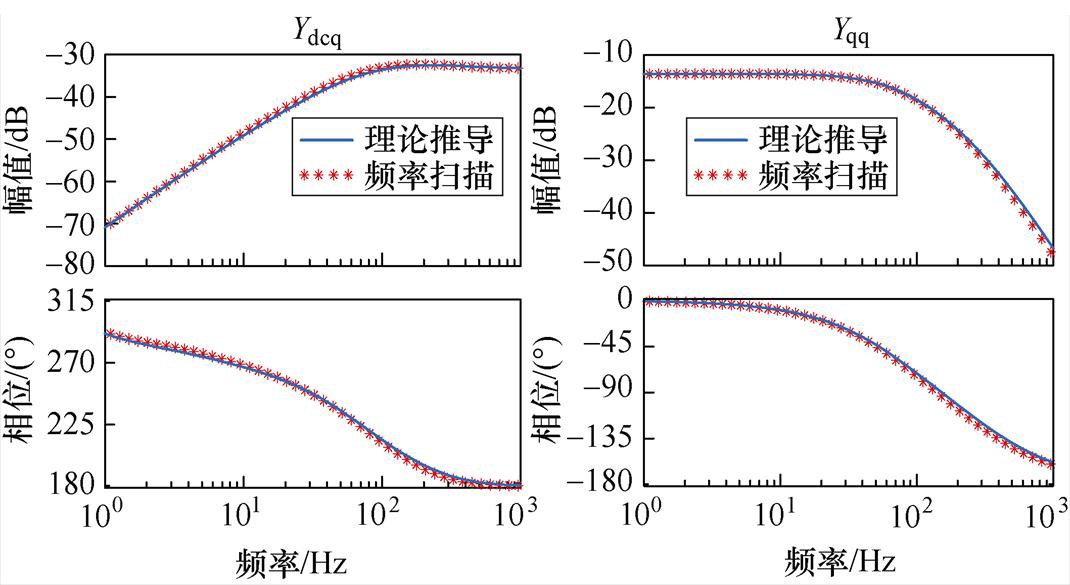
附图1 设备阻抗建模准确性验证Bode图
App.Fig.1 The bode diagram for verifying the accuracy of device impedance modeling
2. 节点-支路关联矩阵与回路-支路关联矩阵
 (A1)
(A1)
3. 仿真系统参数
附表1 交直流微电网的关键运行参数
App.Tab.1 Key operating parameters of AC-DC microgrids
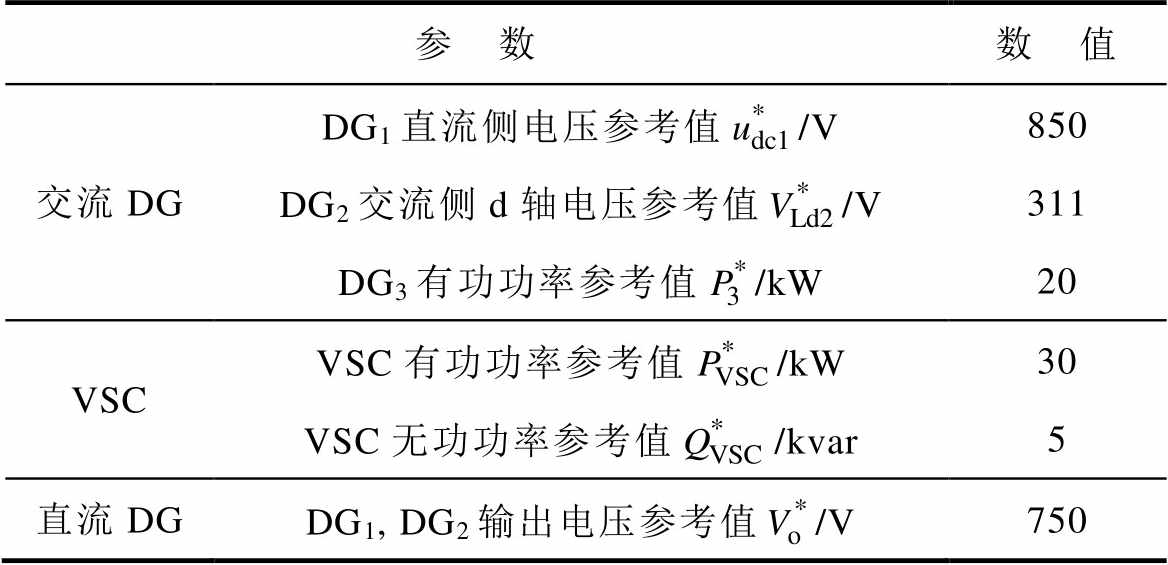
参 数数 值 交流DGDG1直流侧电压参考值/V850 DG2交流侧d轴电压参考值/V311 DG3有功功率参考值/kW20 VSCVSC有功功率参考值/kW30 VSC无功功率参考值/kvar5 直流DGDG1, DG2输出电压参考值/V750
附表2 交直流微电网的关键控制参数
App.Tab.2 Key control parameters of AC-DC microgrids
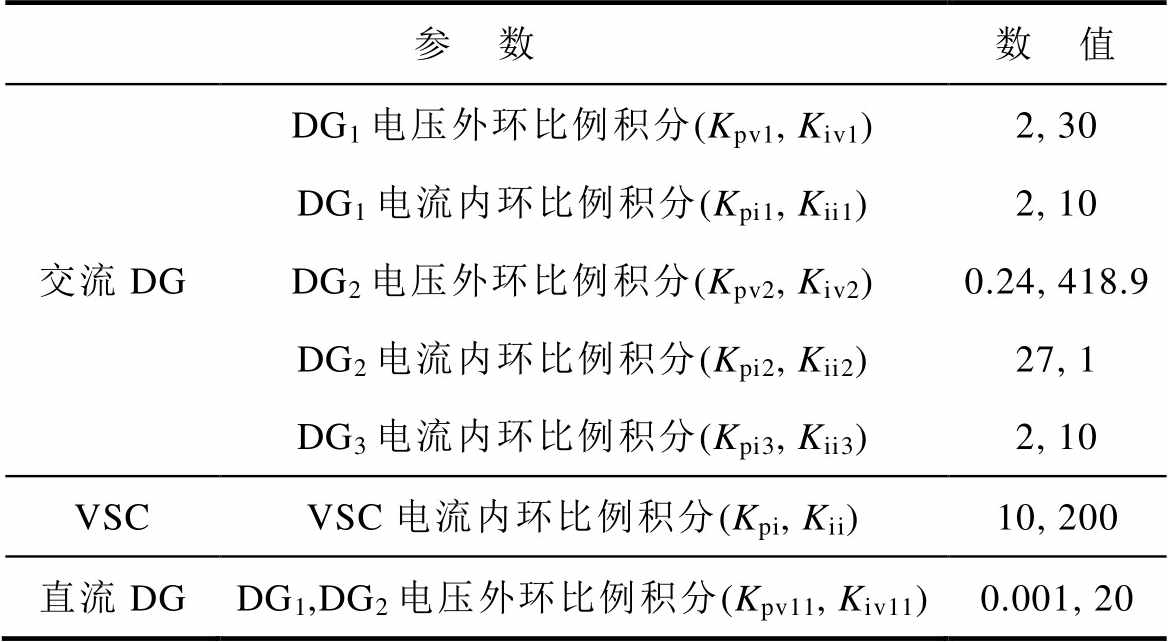
参 数数 值 交流DGDG1电压外环比例积分(Kpv1, Kiv1)2, 30 DG1电流内环比例积分(Kpi1, Kii1)2, 10 DG2电压外环比例积分(Kpv2, Kiv2)0.24, 418.9 DG2电流内环比例积分(Kpi2, Kii2)27, 1 DG3电流内环比例积分(Kpi3, Kii3)2, 10 VSCVSC电流内环比例积分(Kpi, Kii)10, 200 直流DGDG1,DG2电压外环比例积分(Kpv11, Kiv11)0.001, 20
4. 直流微电网参数变化下系统的振荡特性分析
1)根轨迹与时域仿真结果
当直流微电网中双闭环控制下Boost变换器的电压外环PI控制器比例增益参数Kpv11由0.001逐渐增加至1时,系统的根轨迹变化情况如附图2所示。可知,Kpv11的变化对多数特征根影响较小,但有两个模态的特征根随着Kpv11的增加明显向虚轴移动,当Kpv11到达0.20时越过虚轴,出现负阻尼特征根,此时系统失稳,失稳振荡模式为s1=276.07±850.47i,s2=268.08±867.99i,振荡频率分别为135.43 Hz和138.21 Hz。
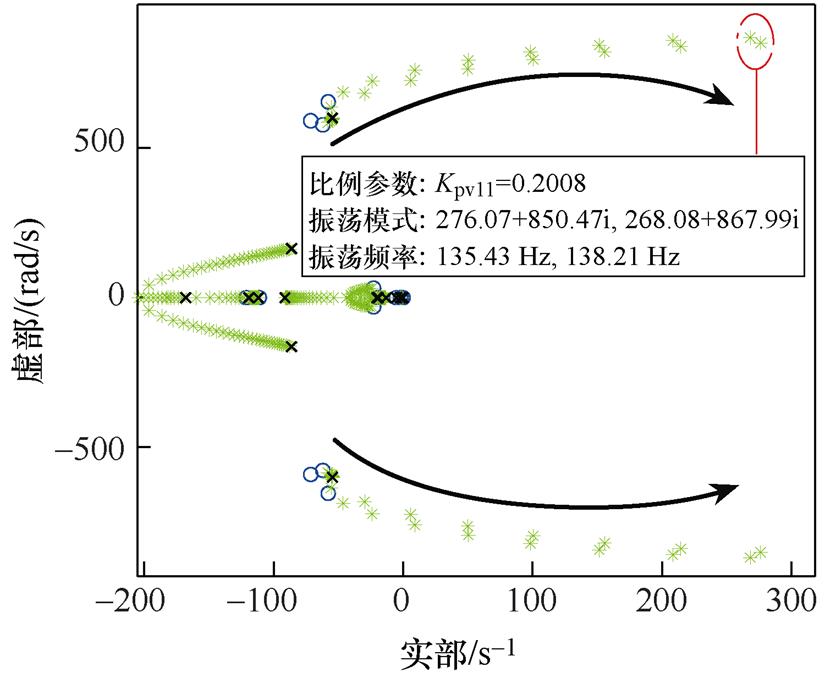
附图2 直流微电网中双闭环控制下Boost变换器电压外环比例增益参数Kpv11变化的根轨迹
App.Fig.2 Root trajectory of the variation of the Boost converter voltage outer loop proportional gain parameter Kpv11 under double closed-loop control in DC microgrids
当Kpv11=0.20时,直流微电网中双闭环控制下Boost变换器的输出电压的时域仿真结果可参考图11。可知,此时系统发生振荡失稳,仿真结果中的振荡频率为139.40 Hz,与理论计算得到的振荡频率相对应。
2)参与因子和灵敏度结果
以上述失稳振荡模式s1=276.07±850.47i为例,将其代入相关的计算公式中,就可以获得节点/回路的参与因子、关键设备及控制参数的灵敏度大小。其中节点6、7参与因子的大小均为50%,而剩余节点的参与因子大小均为0%;回路L4、回路L5的参与因子大小均为50%,而剩余回路的参与因子大小均为0%;设备YBoost1、YBoost2、Yline11、Yline22的灵敏度大小均为50,而剩余设备的灵敏度大小均为0;电压外环的比例增益参数Kpv11和积分增益参数Kiv11的灵敏度大小为分别为395.3和1.37,而电流内环的比例增益参数Kpi11和积分增益参数Kii11的灵敏度大小为分别为454.36和34.30。
可见,节点6、7和回路L4、L5的参与因子最大,设备YBoost1、YBoost2、Yline11和Yline22的灵敏度最大,参数Kpv11、Kpi11的灵敏度都比较大。同时,由图5可知,节点6、7和回路L4、L5分别与直流DG1和DG2有关,且参数Kpv11、Kpi11均为直流DG1和DG2的比例增益控制参数,说明系统的失稳振荡是由节点6、7和回路L4、L5主导,具体地由直流DG1和DG2及其参数Kpv11、Kpi11引发。而交流微电网内的节点和回路对振荡参与程度不高,说明振荡的参与情况主要局限在直流微电网。
5. VdcIq控制下DG的阻抗建模过程
附图3为VdcIq的控制结构。VdcIq控制是通过外部直流电压控制环、内部电流控制环、锁相环和PWM发生器,将逆变器直流侧电压udc1和交流侧q轴电流iq1调节到各自的参考值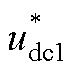 和
和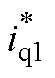 。在附图3中,L1表示逆变器交流侧的滤波电感,vabc1、uabc1、iabc1、udc1和idc1则分别表示逆变器交流侧端口电压、输出电压、输出电流,直流侧电压和电流。下标为d和q的变量表示dq坐标系中相应的分量,PI为PI控制器。
。在附图3中,L1表示逆变器交流侧的滤波电感,vabc1、uabc1、iabc1、udc1和idc1则分别表示逆变器交流侧端口电压、输出电压、输出电流,直流侧电压和电流。下标为d和q的变量表示dq坐标系中相应的分量,PI为PI控制器。
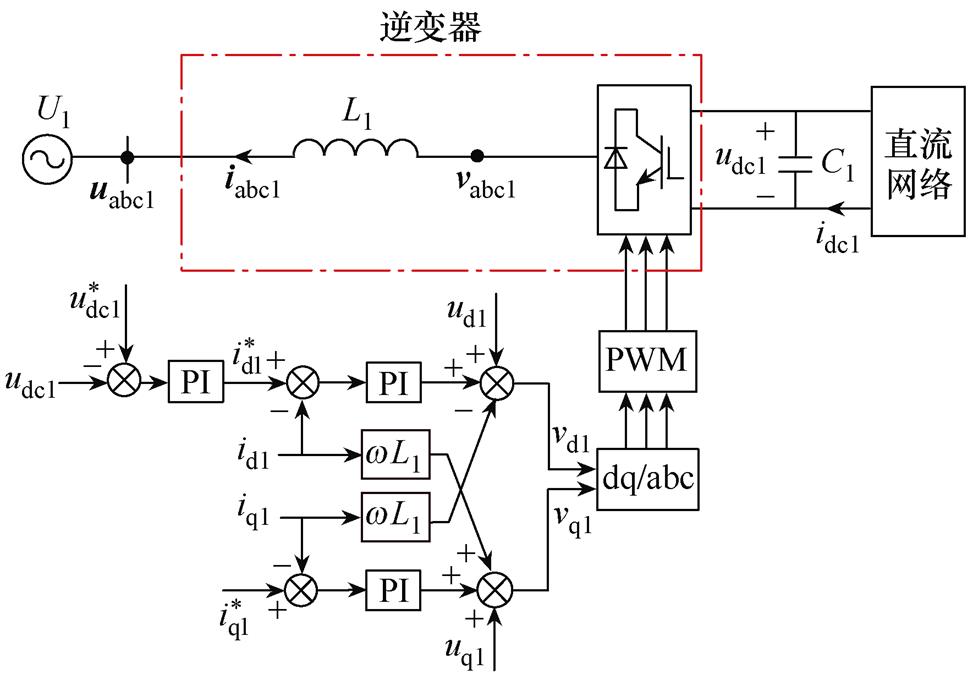
附图3 VdcIq控制结构
Fig.3 The structure diagram of VdcIq control
附图3所示,VdcIq控制方式下逆变器的小信号状态空间建模过程如下所示。
1)直流侧电压控制器环节
VdcIq控制中的直流侧电压控制器由式(A2)给出。
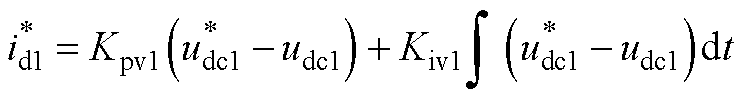 (A2)
(A2)
式中,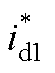 为id1的参考值;Kpv1和Kiv1分别为电压外环的比例和积分增益,式(A2)的线性化处理结果由式(A3)给出。
为id1的参考值;Kpv1和Kiv1分别为电压外环的比例和积分增益,式(A2)的线性化处理结果由式(A3)给出。
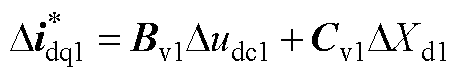 (A3)
(A3)
式中,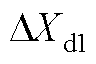 为直流侧电压控制器的状态变量;
为直流侧电压控制器的状态变量;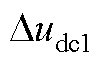 为直流侧电压的状态变量。
为直流侧电压的状态变量。
2)直流侧电容环节
考虑到直流侧电容的动态过程,则有
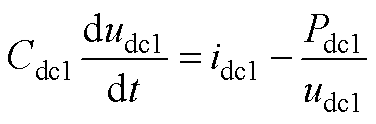 (A4)
(A4)
式中, 为直流侧有功功率,在忽略逆变器开关损耗之后与交流侧有功功率相等,即
为直流侧有功功率,在忽略逆变器开关损耗之后与交流侧有功功率相等,即
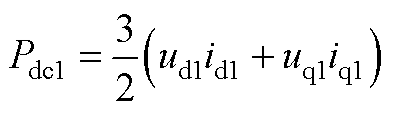 (A5)
(A5)
选取 为状态变量,联立式(A4)和式(A5)并对其结果进行线性化处理,可得
为状态变量,联立式(A4)和式(A5)并对其结果进行线性化处理,可得
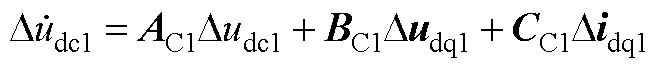 (A6)
(A6)
3)电流控制器环节
VdcIq控制中的电流控制器由式(A7)给出。
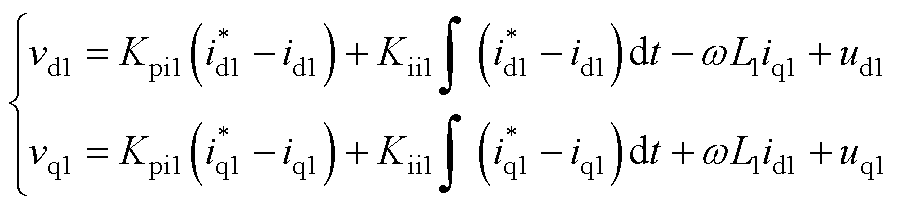 (A7)
(A7)
式中,Kpi1和Kii1分别为电流内环的比例和积分增益,式(A7)的线性化处理结果由式(A8)给出,其中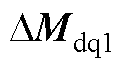 是电流控制器的状态变量。
是电流控制器的状态变量。
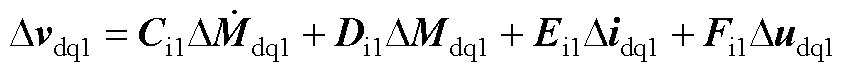 (A8)
(A8)
由于L滤波器、锁相环以及系统和控制dq坐标系动态建模过程和线性化处理结果与上述动态建模过程类似,这里不再赘述。
最后,结合上述各个环节的线性化方程,就可以得出VdcIq控制方式下逆变器的小信号状态空间模型,由式(A9)给出。
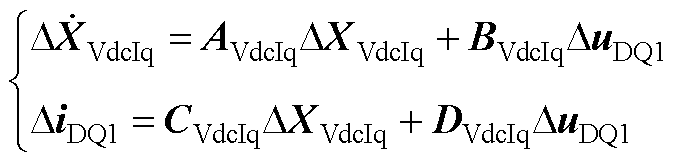 (A9)
(A9)
式中,AVdcIq、BVdcIq、CVdcIq和DVdcIq为系数矩阵;DXVdcIq为状态变量向量,即
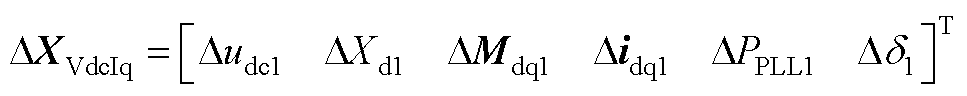 (A10)
(A10)
式中,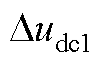 、
、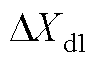 、
、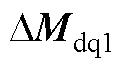 、
、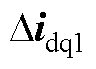 、
、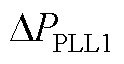 和
和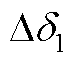 为直流侧电容、直流侧电压控制器、电流控制器、L滤波器、锁相环以及系统和控制dq坐标系转换的状态变量;DuDQ1和DiDQ1分别为系统dq坐标系下的输入和输出变量,Didq1为控制dq坐标系下的输出电流。
为直流侧电容、直流侧电压控制器、电流控制器、L滤波器、锁相环以及系统和控制dq坐标系转换的状态变量;DuDQ1和DiDQ1分别为系统dq坐标系下的输入和输出变量,Didq1为控制dq坐标系下的输出电流。
将式(A9)变换为s域后,就可得到逆变器在VdcIq控制方式下的频域导纳矩阵,即
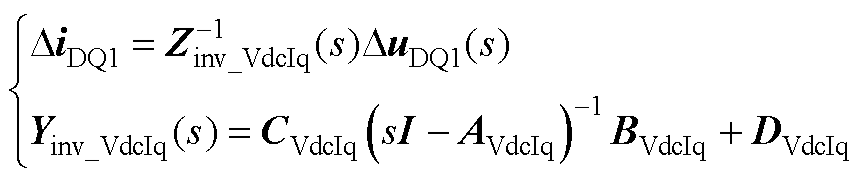 (A11)
(A11)
进而得到其阻抗矩阵为
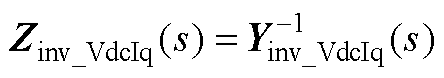 (A12)
(A12)
6. 参与因子的推导过程
参与因子的具体推导过程如下[18]。
以节点导纳矩阵为例,将振荡模式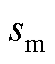 代入节点导纳矩阵中,得到YMG(sm),并将其进行特征值分解可以得到
代入节点导纳矩阵中,得到YMG(sm),并将其进行特征值分解可以得到
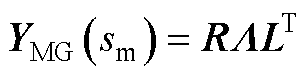 (A13)
(A13)
其中
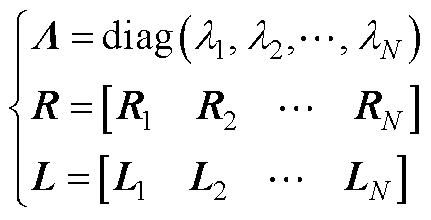 (A14)
(A14)
式中,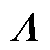 为特征值矩阵;YMG(sm)为对称矩阵;
为特征值矩阵;YMG(sm)为对称矩阵;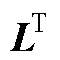 和
和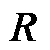 分别为左右特征向量矩阵且互为逆矩阵。由于振荡模式sm是YMG(sm)的行列式零点,因此YMG(sm)存在一个唯一零特征值,记作
分别为左右特征向量矩阵且互为逆矩阵。由于振荡模式sm是YMG(sm)的行列式零点,因此YMG(sm)存在一个唯一零特征值,记作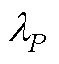 ,而
,而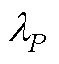 所对应的左右特征向量分别为
所对应的左右特征向量分别为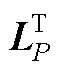 和
和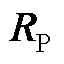 ,将式(A14)代入节点电压方程YMG(s)UN(s)=IN(s)中,可得式(A13)。
,将式(A14)代入节点电压方程YMG(s)UN(s)=IN(s)中,可得式(A13)。
7. 灵敏度的推导过程
定义系统中某一设备对振荡模式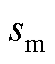 的灵敏度为
的灵敏度为
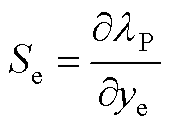 (A15)
(A15)
式中,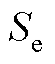 为设备对振荡模式的灵敏度;
为设备对振荡模式的灵敏度;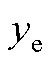 为设备的导纳。
为设备的导纳。
根据特征向量的定义和左右特征向量之间的关系,可以得到
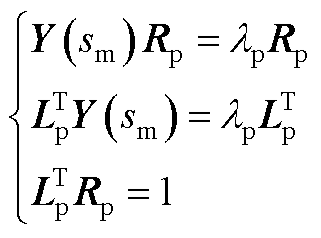 (A16)
(A16)
将式(A16)代入式(A15),可得
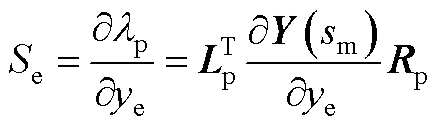 (A17)
(A17)
根据如图5所示的交直流微电网系统的等效导纳网络模型和节点导纳矩阵可知,系统中的设备可以分为两大类:一类是参考节点与节点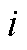 之间的并联设备,其导纳仅出现在节点导纳矩阵的对角元素Yii中;另一类是除参考节点外的节点
之间的并联设备,其导纳仅出现在节点导纳矩阵的对角元素Yii中;另一类是除参考节点外的节点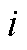 和节点
和节点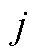 之间的串联设备,其导纳同时出现在节点导纳矩阵的对角元素Yii、Yjj和非对角元素Yij、Yji中。
之间的串联设备,其导纳同时出现在节点导纳矩阵的对角元素Yii、Yjj和非对角元素Yij、Yji中。
参考文献
[1] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677.
Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[2] 张天策, 李庚银, 王剑晓, 等. 基于可行域投影理论的新能源电力系统协同运行方法[J]. 电工技术学报, 2023, DOI: 10.19595/j.cnki.1000-6753.tces.230196.
Zhang Tiance, Li Gengyin, Wang Jianxiao, et al. coordinated operation method of renewable energy power systems based on feasible region projection theory[J]. Transactions of China Electrotechnical Society, 2023, DOI: 10.19595/j.cnki.1000-6753.tces. 230196.
[3] 杨向真, 张徐进博, 杜燕, 等. 考虑直流子网影响的交直流混合微电网谐振特性分析[J]. 高电压技术, 2023, 49(2): 713-726.
Yang Xiangzhen, Zhang Xujinbo, Du Yan, et al. Analysis of resonance characteristics of AC/DC hybrid microgrid considering the influence of DC subgrid[J]. High Voltage Engineering, 2023, 49(2): 713-726.
[4] 吴翔宇, 张晓红, 许寅, 等. 微电网(群)宽频振荡分析和抑制研究进展与展望[J]. 电网技术, 2023, 47(9): 3727-3745.
Wu Xiangyu, Zhang Xiaohong, Xu Yin, et al. Research progress and prospect of wide-band oscillations analysis and suppression for microgrid (clusters)[J]. Power System Technology, 2023, 47(9): 3727-3745.
[5] 吴梦. 交直流混合微电网电能质量与稳定性分析[D]. 北京: 北京交通大学, 2019.
[6] 韩鹏. 交流微电网孤岛运行控制及稳定性研究[D].北京: 中国矿业大学, 2022.
[7] 刘振国, 金铭, 于海, 等. 交流微电网直流互联变流器系统多阻抗优化控制[J]. 中国电力, 2023, 56(2): 93-101, 156.
Liu Zhenguo, Jin Ming, Yu Hai, et al. A multi- impedance optimization control for AC microgrid DC interconnected converter system[J]. Electric Power, 2023, 56(2): 93-101, 156.
[8] 郑凯元, 杜文娟, 王海风. 聚合恒功率负荷对直流微电网稳定性影响的阻抗法分析[J]. 电网技术, 2021, 45(1): 134-148.
Zheng Kaiyuan, Du Wenjuan, Wang Haifeng. DC microgrid stability affected by aggregated constant power loads based on impedance method[J]. Power System Technology, 2021, 45(1): 134-148.
[9] Gao Fei, Bozhko S. Modeling and impedance analysis of a single DC bus-based multiple-source multiple- load electrical power system[J]. IEEE Transactions on Transportation Electrification, 2016, 2(3): 335-346.
[10] 黄旭程, 何志兴, 伍文华, 等. 交直流微电网中变换器级联系统稳定性分析与协同控制[J]. 中国电机工程学报, 2019, 39(5): 1432-1443.
Huang Xucheng, He Zhixing, Wu Wenhua, et al. Stability analysis of converters cascade system in the hybrid AC/DC microgird and coordinative control[J]. Proceedings of the CSEE, 2019, 39(5): 1432-1443.
[11] 胡翔. 交直流混合微电网的建模与稳定性分析[D]. 济南: 山东大学, 2018.
[12] 李晓英. 基于MMC的交直流混合型微电网孤岛运行控制与稳定性分析[D]. 兰州: 兰州理工大学, 2021.
[13] Zhang Haitao, Mehrabankhomartash M, Saeedifard M, et al. Impedance analysis and stabilization of point- to-point HVDC systems based on a hybrid AC-DC impedance model[J]. IEEE Transactions on Industrial Electronics, 2021, 68(4): 3224-3238.
[14] Liu Huakun, Xie Xiaorong. Impedance network modeling and quantitative stability analysis of sub-/ super-synchronous oscillations for large-scale wind power systems[J]. IEEE Access, 1809, 6: 34431-34438.
[15] 王一珺, 王海风. 直流电压动态时间尺度下大规模直驱风电场振荡稳定性及参数稳定域分析[J]. 中国电机工程学报, 2021, 41(增刊1): 92-107.
Wang Yijun, Wang Haifeng. Analysis of oscillation stability and parameter stability region of large-scale direct-drive wind farm under DC voltage dynamic time scale[J]. Proceedings of the CSEE, 2021, 41(S1): 92-107.
[16] 王洋, 杜文娟, 王海风. 多风电场-多机电力系统次同步振荡稳定性分析[J]. 中国电机工程学报, 2019, 39(22): 6562-6572.
Wang Yang, Du Wenjuan, Wang Haifeng. Stability analysis of subsynchronous oscillation in multi- machine power system with multiple wind farms[J]. Proceedings of the CSEE, 2019, 39(22): 6562- 6572.
[17] 朱宇昕, 赵晋斌, 毛玲, 等. 并网系统的广义阻抗比及其稳定性分析与研究[J]. 中国电机工程学报, 2020, 40(22): 7240-7249.
Zhu Yuxin, Zhao Jinbin, Mao Ling, et al. Generalized impedance ratio and stability analysis for grid- connected systems[J]. Proceedings of the CSEE, 2020, 40(22): 7240-7249.
[18] 占颖, 吴琛, 谢小荣, 等. 风电并网系统次同步振荡的频域模式分析[J]. 电力系统自动化, 2020, 44(18): 90-97.
Zhan Ying, Wu Chen, Xie Xiaorong, et al. Frequency domain modal analysis of subsynchronous oscillation in grid-connected wind power system[J]. Automation of Electric Power Systems, 2020, 44(18): 90-97.
[19] 占颖, 谢小荣, 柴炜, 等. 风电次/超同步振荡的安全域分析[J]. 中国电机工程学报, 2022, 42(23): 8446-8454.
Zhan Ying, Xie Xiaorong, Chai Wei, et al. Analyzing the security region of sub/super-synchronous oscillation in wind power integrated systems[J]. Proceedings of the CSEE, 2022, 42(23): 8446-8454.
[20] 杨超然. 新能源电力系统小干扰同步稳定性分析和稳定裕度提升策略研究[D]. 杭州: 浙江大学, 2021.
[21] 邢法财. 含非同步机电源电力系统的宽频谐振问题研究[D]. 杭州: 浙江大学, 2021.
[22] 施静容, 李勇, 贺悝, 等. 一种提升交直流混合微电网动态特性的综合惯量控制方法[J]. 电工技术学报, 2020, 35(2): 337-345.
Shi Jingrong, Li Yong, He Li, et al. A comprehensive inertia control method for improving the dynamic characteristics of hybrid AC-DC microgrid[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 337-345.
[23] 张靖, 张志文, 胡斯佳, 等. 独立微电网风储协同调频的功率柔性分配策略[J]. 电工技术学报, 2022, 37(15): 3767-3780.
Zhang Jing, Zhang Zhiwen, Hu Sijia, et al. A flexible power distribution strategy with wind turbine gen- erator and energy storage for frequency regulation in isolated microgrid[J]. Transactions of China Elec- trotechnical Society, 2022, 37(15): 3767-3780.
[24] 吴天昊, 谢小荣, 姜齐荣, 等. 考虑频率耦合及交直流端口耦合效应的并网变流器三端口导纳模型[J]. 中国电机工程学报, 2022, 42(1): 249-261.
Wu Tianhao, Xie Xiaorong, Jiang Qirong, et al. Three-port admittance modeling of grid-connected converters considering frequency-coupling and AC/DC coupling effects[J]. Proceedings of the CSEE, 2022, 42(1): 249-261.
[25] Zhang Chen, Cai Xu, Molinas M, et al. On the impedance modeling and equivalence of AC/DC-side stability analysis of a grid-tied type-IV wind turbine system[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 1000-1009.
[26] Pedra J, Sainz L, Monjo L. Three-port small signal admittance-based model of VSCs for studies of multi-terminal HVDC hybrid AC/DC transmission grids[J]. IEEE Transactions on Power Systems, 2021, 36(1): 732-743.
[27] 潘鹏宇, 胡海涛, 肖冬华, 等. 高速列车变流器“扫频式”dq阻抗测量中的频率耦合干扰机理及抑制策略[J]. 电工技术学报, 2022, 37(4): 990-999, 1009.
Pan Pengyu, Hu Haitao, Xiao Donghua, et al. Frequency coupling interference mechanism and suppression strategy for frequency-sweeping-based dq impedance measurement of high-speed train con- verter[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 990-999, 1009.
[28] Zhang Qiufang, He Jinghan, Xu Yin, et al. Average- value modeling of direct-driven PMSG-based wind energy conversion systems[J]. IEEE Transactions on Energy Conversion, 2022, 37(1): 264-273.
[29] 宗皓翔, 张琛, 蔡旭. 电力电子主导的交直流混联电网振荡分析与评估[J]. 中国电机工程学报, 2023, 43(10): 3844-3856.
Zong Haoxiang, Zhang Chen, Cai Xu. Oscillation analysis and evaluation of the power electronics- dominated hybrid AC/DC grid[J]. Proceedings of the CSEE, 2023, 43(10): 3844-3856.
[30] 占颖. 大规模风电次/超同步振荡的频域模式分析与安全域研究[D]. 北京: 清华大学, 2022.
[31] 仰彩霞. 基于模态分析法的电力系统谐波谐振问题研究及其灵敏度分析[D]. 武汉: 武汉大学, 2010.
Abstract Microgrids are an effective form of organizing and utilizing distributed power sources, and are also an important component of new power systems. The AC-DC microgrid combines the characteristics and advantages of both AC and DC microgrids. However, under the dynamic interaction between different types of power electronic converters and the power grid, AC-DC microgrids are prone to trigger broadband oscillation problems, seriously threatening the safe and stable operation of the system. The analysis of microgrid oscillation problems in existing studies is mainly based on impedance analysis and feature analysis, but both methods have certain limitations. Therefore, this article conducts research on modeling and analysis methods for oscillation problems in AC-DC microgrids based on frequency domain impedance network models.
Firstly, based on the state space method, impedance models of various devices in the AC-DC microgrid system are established. Then, the various devices in the system are connected according to the topological relationship of the system, and an equivalent impedance network model of the AC-DC microgrid system in the frequency domain is established. Based on the principles of electrical networks, the node frequency domain admittance matrix and loop impedance frequency domain matrix of the system are calculated. Secondly, based on the frequency domain mode analysis method, indicators for the degree of node/loop oscillation participation and sensitivity indicators for equipment and control parameters of the AC-DC microgrid are established. The analysis method for the AC-DC propagation characteristics of oscillation is provided, which facilitates the clarification of the system oscillation mechanism and key influencing factors. Finally, the effectiveness of the above frequency domain impedance network modeling and oscillation stability analysis methods is verified through Matlab/ Simulink time-domain simulation and example analysis.
keywords:AC-DC microgrids, frequency domain impedance network modeling, oscillation stability, frequency domain mode analysis
国家自然科学基金面上项目(52177066)资助。
收稿日期 2023-08-31
改稿日期 2023-09-18
DOI: 10.19595/j.cnki.1000-6753.tces.231432
中图分类号:TM721
吴翔宇 男,1990年生,副教授,硕士生导师,研究方向为微电网运行控制、可再生能源电力系统振荡分析与抑制、韧性电网。E-mail: wuxiangyu@bjtu.edu.cn(通信作者)
张晓红 女,1998年生,硕士研究生,研究方向为微电网(群)稳定分析。E-mail: 21121535@bjtu.edu.cn
(编辑 郭丽军)