图1 直流微电网等效模型
Fig.1 DC microgrid equivalent model
摘要 直流微电网中恒功率负荷（CPL）具有负阻尼特性，该特性会降低系统稳定性。为此，通过在滤波器上添加被动阻尼来增强直流微电网系统的稳定性，并提出一种基于机器学习的方法来检测带被动阻尼直流微电网系统的稳定性。首先，建立带被动阻尼直流微电网系统的小信号模型，以此来确定影响系统稳定性的参数。其次，以所选系统参数为变量建立仿真场景，以此来获取用于机器学习算法训练的数据集。再次，提出一种基于轻量型梯度提升机（LGBM）的直流微电网稳定性检测模型，并采用沙普利加解释法（SHAP）分析所选参数对LGBM预测结果和直流微电网系统稳定性的影响。最后，通过仿真和硬件在环实验验证所提方法的有效性和优越性。
关键词：直流微电网 稳定性检测 被动阻尼 轻量型梯度提升机 沙普利加解释
随着新能源发电技术的发展，微电网因为可以消纳新能源发电而受到广泛关注[1-3]。与交流微电网相比，直流微电网具有效率高、成本低、控制简单、可靠性高等突出优点[2-4]，目前已成功应用于许多场合。然而，电力电子装置的增加以及恒功率负荷（Constant Power Loads, CPL）的负阻抗特性，降低了直流微电网系统的稳定性[5-7]。为此，学者们对直流微电网的稳定性进行了大量研究。
目前，对直流微电网稳定性的研究主要是通过建立机理模型，然后再选择有效的控制理论方法来分析系统的稳定性。此方法可以分为两种类型：小信号和大信号。在小信号分析中，主要利用线性分析工具（Bode图、Nyquist图、Routh-Hurwitz判据和分岔理论）推导出直流链路的局部稳定条件[8-11]。然而，小信号研究只能探索小扰动[12]。与小信号稳定性分析不同，大信号稳定性分析主要通过建立非线性数学模型，然后采用非线性方法来分析直流微电网稳定性，如李雅普诺夫法、势函数理论、波波夫理论等[13-15]。
为了进一步增强直流微电网系统的稳定性，研究人员提出了添加主动阻尼的方法，包括虚拟有源电阻补偿[16]、同步降压电路[17]和输出电流前馈[18]等。但是，这些方法需要复杂的控制算法和信号处理，因此设计较复杂且实现成本较高[19]。此外，这些方法可能还会降低负载性能，对系统的动态响应产生影响[20]。
被动阻尼技术相比于主动阻尼技术在创新性方面略有不足，但被动阻尼通常只需要使用一些简单的被动元件，不需要复杂的控制算法和信号处理技术，因此实现简单、成本较低[21]。文献[11]给出了无源阻尼电路及其优化方法，这些方法可以降低源端的输出阻抗谐振峰值，使源端输出阻抗在全频范围内小于负载端输入阻抗。在直流微电网系统中，为了分析被动阻尼对系统稳定性的影响以及设计被动阻尼参数，所采用的方法、过程与文献[8-15]所提直流微电网稳定性分析法基本一致，均为先建立机理模型，再利用控制理论方法来判断添加被动阻尼后直流微电网系统的稳定性[23]。然而，机理模型往往会忽略部分结构对系统的影响，导致模型误差随着系统维度和复杂度的增加而逐渐增大[22-23]。并且，基于机理模型的分析方法忽视了局部稳定性和整体稳定性的关系，导致结果具有不确定性。
针对上述问题，本文提出一种基于机器学习的方法来检测带被动阻尼直流微电网的稳定性。该方法可以有效改善机理模型误差问题，并且综合考虑了局部与全局稳定的关系，同时可以实现快速、精确地在线检测带被动阻尼直流微电网的稳定状态。首先介绍了样本数据获取方法，包括建立小信号模型、选择仿真变量、构建仿真模型、处理数据等。其次基于轻量级梯度提升机（Light Gradient Boosting Machine, LGBM）给出检测直流微电网稳定性的评估流程。再次利用沙普利加解释法（Shapley Additive explanations, SHAP）分析系统参数对直流微电网系统稳定性以及LGBM预测结果的影响。最后通过仿真和硬件在环实验的结果表明，所提方法可以有效评估在不同结构和阻尼器下直流微电网的稳定性。LGBM的预测准确率可达96.5%以上，较理论方法和传统机器学习算法具有明显优势。
直流微电网级联系统的等效模型如图1所示，其组成包括分布式发电单元、储能单元（Energy Storage, ES）、变流器单元和负载单元等。
图1 直流微电网等效模型
Fig.1 DC microgrid equivalent model
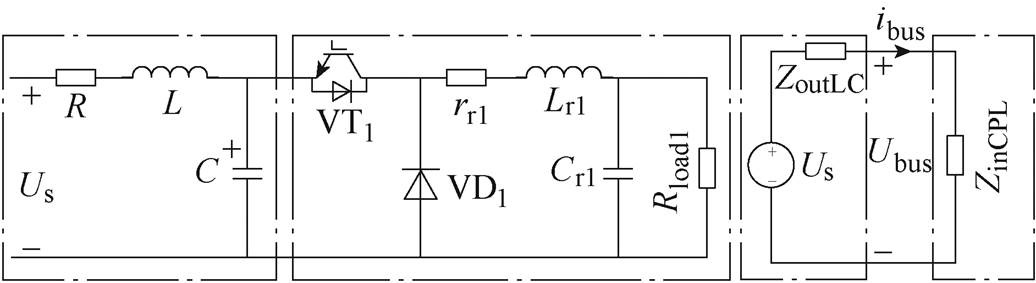
图1中，R、L、C分别为线路电阻、线路电感、母线电容，Lr1、rr1、Cr1分别为负载侧滤波电感、电阻和电容，Rload1为阻性负载，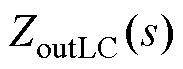
为源端输出阻抗，
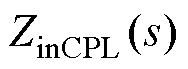负载变换器的输入阻抗，Us为电压源，Ubus为级联母线电压。
Us到Ubus的传递函数表示为
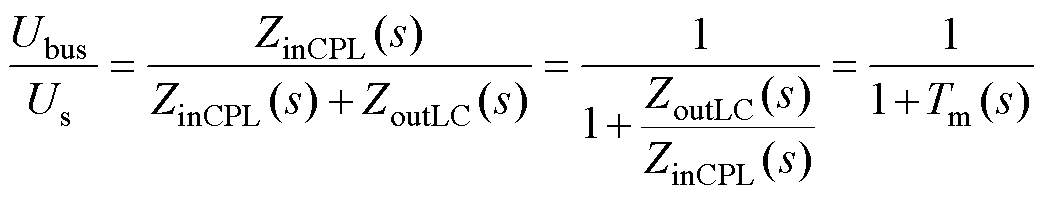（1）
当源端变换器的输出阻抗与负载变换器的输入阻抗不匹配时，由源变换器和负载变换器组成的级联系统会变得不稳定[24]。加入被动阻尼可以有效降低源变换器的输出阻抗，因此可以有效提升直流微电网系统的稳定性。
本文考虑了四种不同的被动阻尼方法[11, 25]：RC并联、RL串联、RL并联和RLC串联阻尼器，其结构如图2所示。基于此结构，分别建立四种阻尼器的仿真场景来构建样本数据库。仿真变量与LGBM的输入特征保持一致，具体包括阻尼器参数、LC滤波器参数和负荷参数，变量选择过程如1.3节所示。
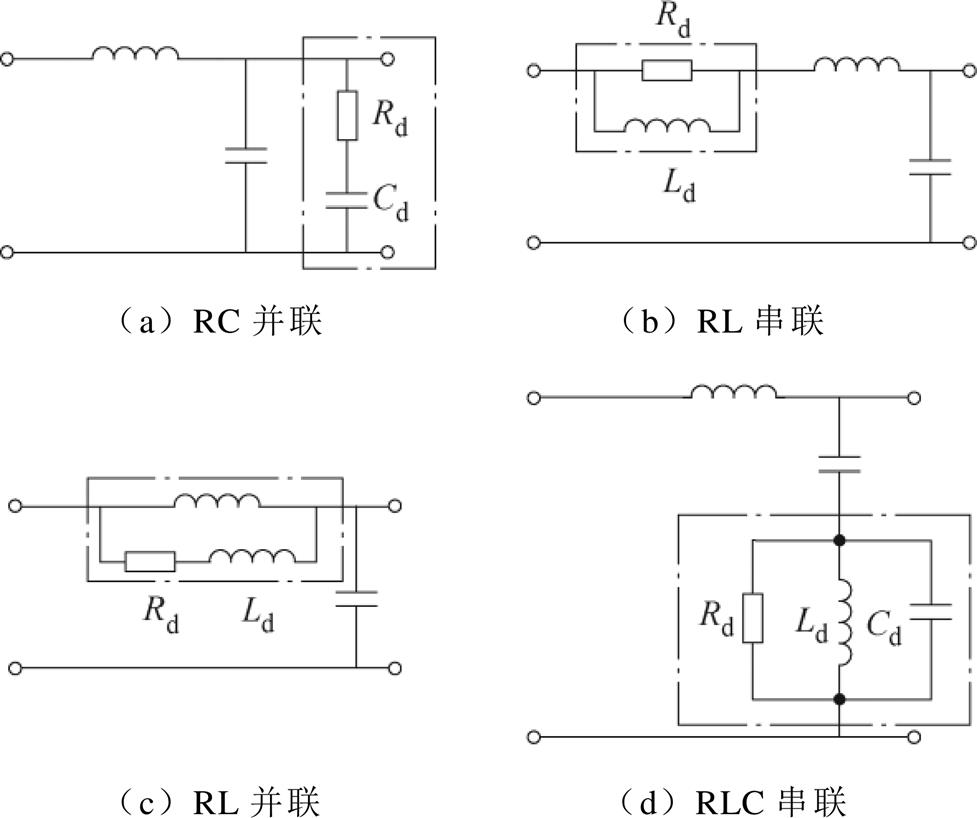
图2 被动阻尼结构
Fig.2 Passive damping structures
由1.1节可知，为保证带被动阻尼直流微电网系统的稳定性，要求系统的阻抗比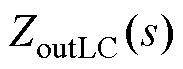
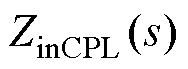满足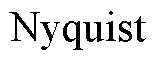
稳定性判据[22]，或者
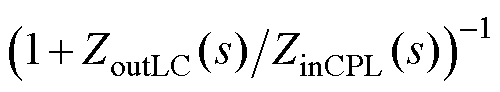的特征多项式满足Routh- Hurwitz判据。当只涉及一个参数时，Nyquist判据更便于应用[9]。对于涉及多个参数的被动阻尼直流微电网电路，为了确定其稳定性条件，本文采用Routh-Hurwitz准则。将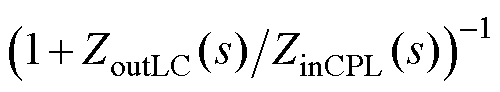的特征多项式写成一般形式为
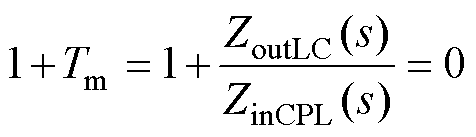（2）
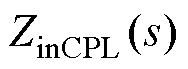式中，和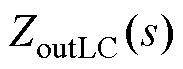分别[11, 26]为
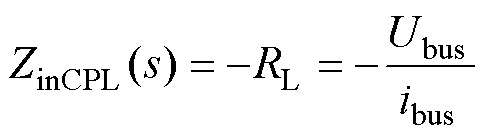（3）
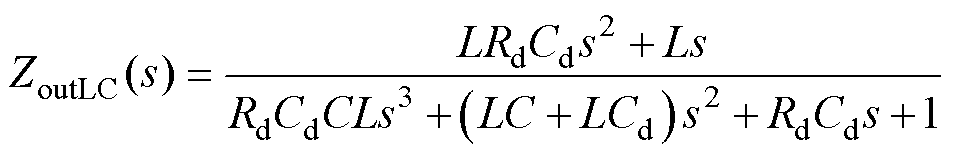（4）
结合式（1）～式（4）可得带RC并联阻尼器直流微电网系统的特征方程如式（5）所示。添加RL并联阻尼器、RL串联阻尼器以及RLC串联阻尼器的直流微电网系统的特征方程如附录所示。
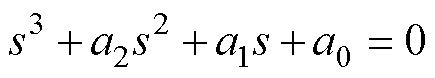（5）
其中
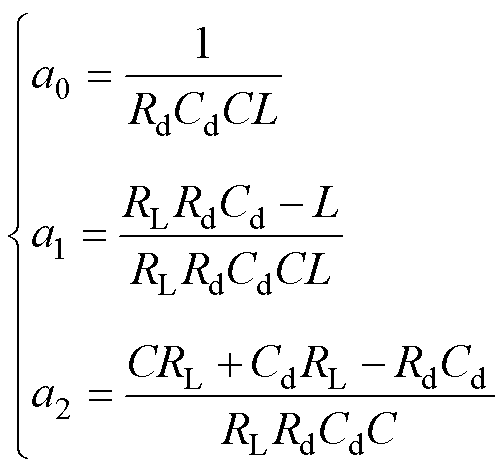（6）
特征方程的参数需要满足Routh-Hurwitz判据
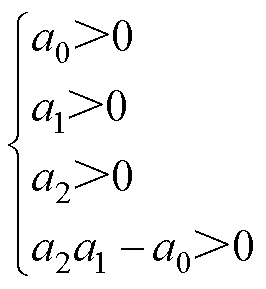（7）
其中
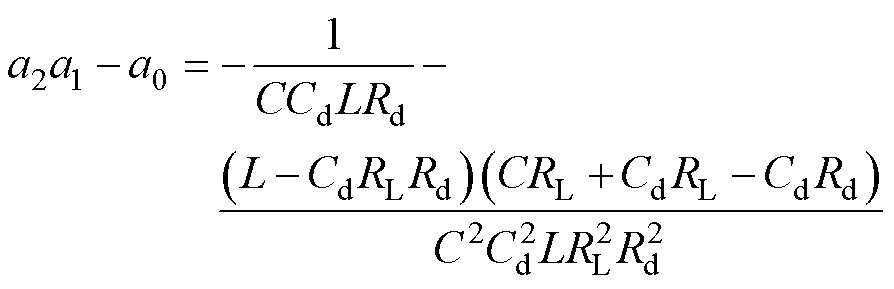（8）
至此，带有RC并联阻尼器的直流微电网的稳定条件证毕。由式（5）～式（8）可以看到，系统参数L、C、Rd、Cd、CPL共同影响直流微电网系统的稳定性，所以本文将上述参数作为LGBM检测直流微电网稳定性的输入特征。在带有其余阻尼器的直流微电网场景中，特征选择过程与上述相同。
在确定LGBM的输入特征后，基于机器学习检测直流微电网稳定性的框架如图3所示。
本文所采用的数据来源于时域仿真。首先确定仿真变量的取值区间。其中，通过参考文献[7, 11] 以及式（5）～式（8）来确定滤波器参数、负荷参数以及阻尼器参数的初始取值区间。在初始区间基础上，再通过时域仿真来确定最终取值区间。
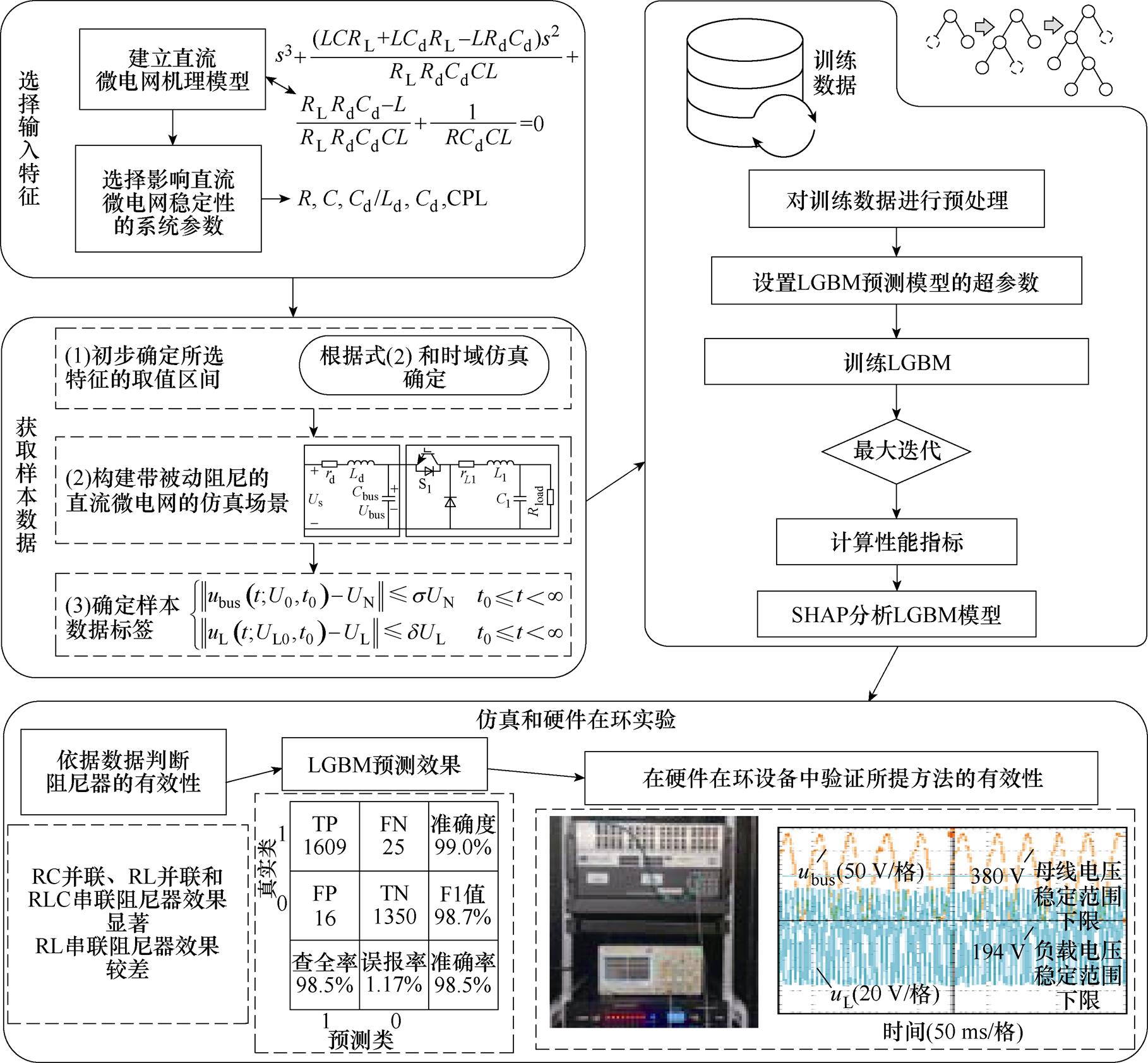
图3 基于机器学习检测直流微电网稳定性的框架
Fig.3 Content structure for detecting DC microgrid stability based on machine learning
为了表征所选参数与直流微电网系统之间的耦合关系，本节基于时域仿真来生成样本数据。带被动阻尼直流微电网的结构如图2和图4所示，系统参数设置见表1，样本数据生成方法为拉丁超立方采样法。
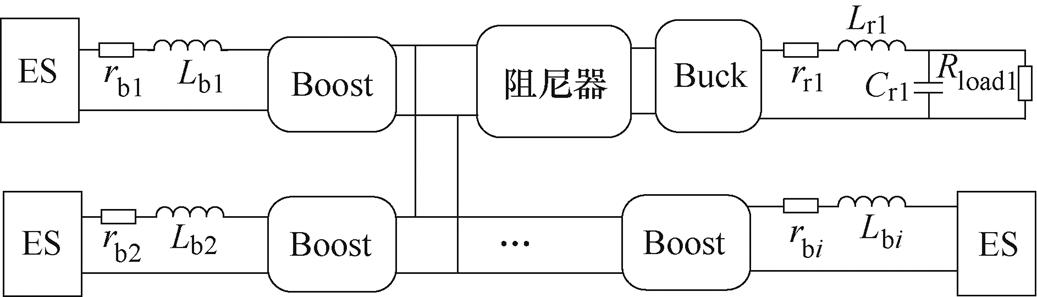
图4 直流微电网结构
Fig.4 DC microgrid structure
表1 直流微电网系统参数
Tab.1 System parameters of the DC microgrid
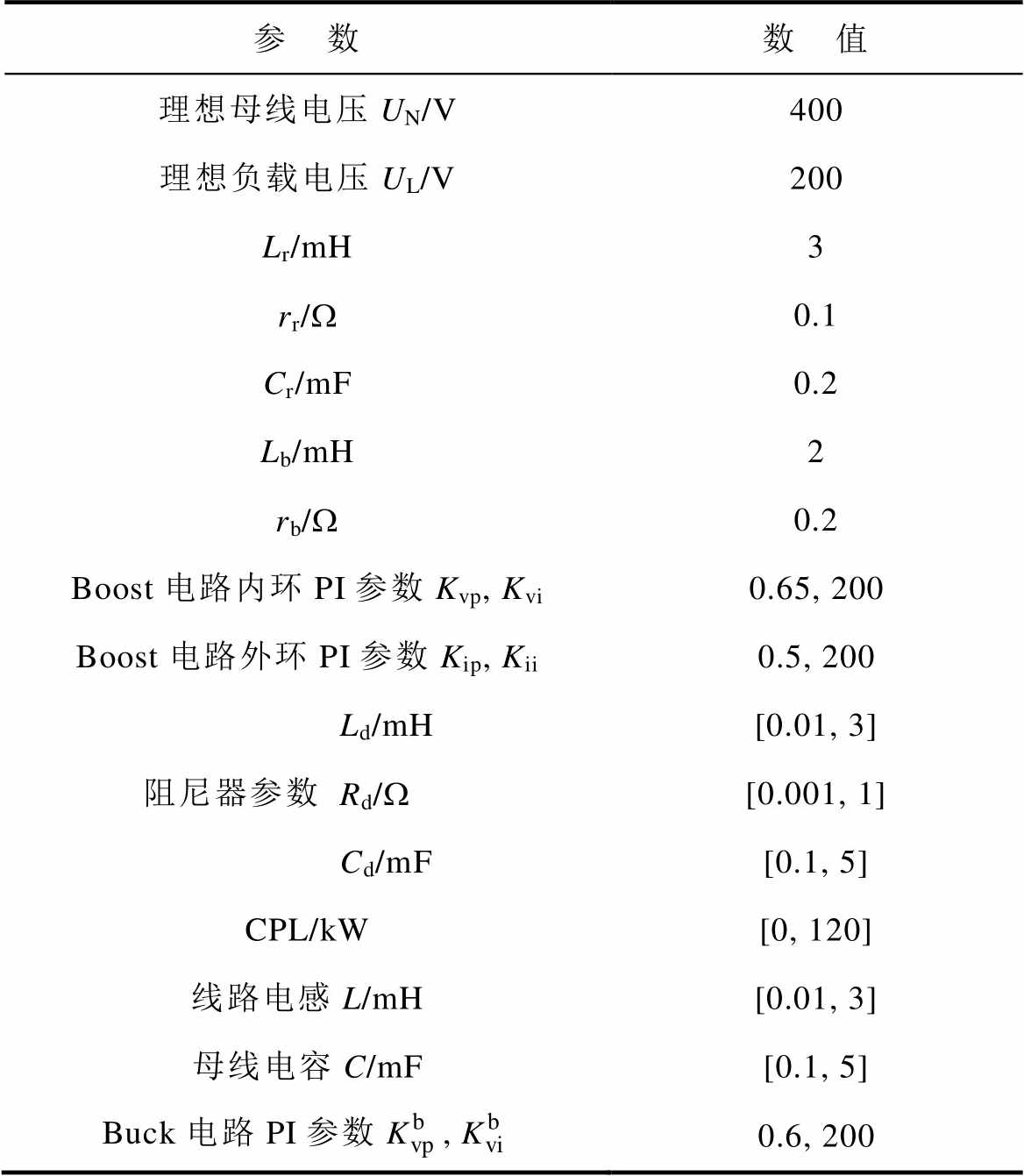
参 数数 值 理想母线电压UN/V400 理想负载电压UL/V200 Lr/mH3 rr/W0.1 Cr/mF0.2 Lb/mH2 rb/W0.2 Boost电路内环PI参数Kvp, Kvi0.65, 200 Boost电路外环PI参数Kip, Kii0.5, 200 Ld/mH[0.01, 3] 阻尼器参数Rd/W[0.001, 1] Cd/mF[0.1, 5] CPL/kW[0, 120] 线路电感L/mH[0.01, 3] 母线电容C/mF[0.1, 5] Buck电路PI参数,0.6, 200
在建立仿真获得初始样本数据后，为了得到用于LGBM训练的样本数据，需要制定直流微电网稳定性标准来为初始样本数据分类。根据理论分析方法，判断系统是否稳定的标准为母线电压和母线电流是否稳定[11, 16]。图5为母线电压和负载电压仿真结果，此时母线电压稳定，但负载电压值已经下降为仅83%的额定值，负载端已经不满足系统稳定运行的要求。因此，上述标准无法全面反映系统的稳定状态，为此，建立了可同时满足局部稳定和全局稳定的直流微电网稳定性准则，即
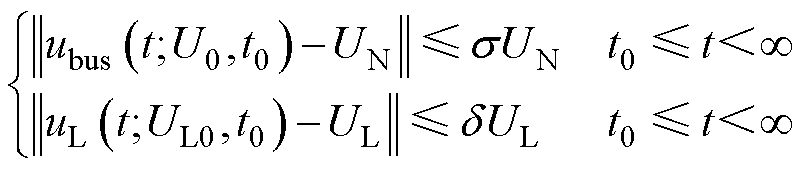（9）
式中，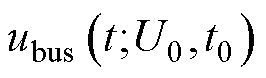
为母线电压的状态；
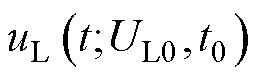为负载电压状态；s 和d 分别为母线电压和负载电压的最大允许偏差范围。
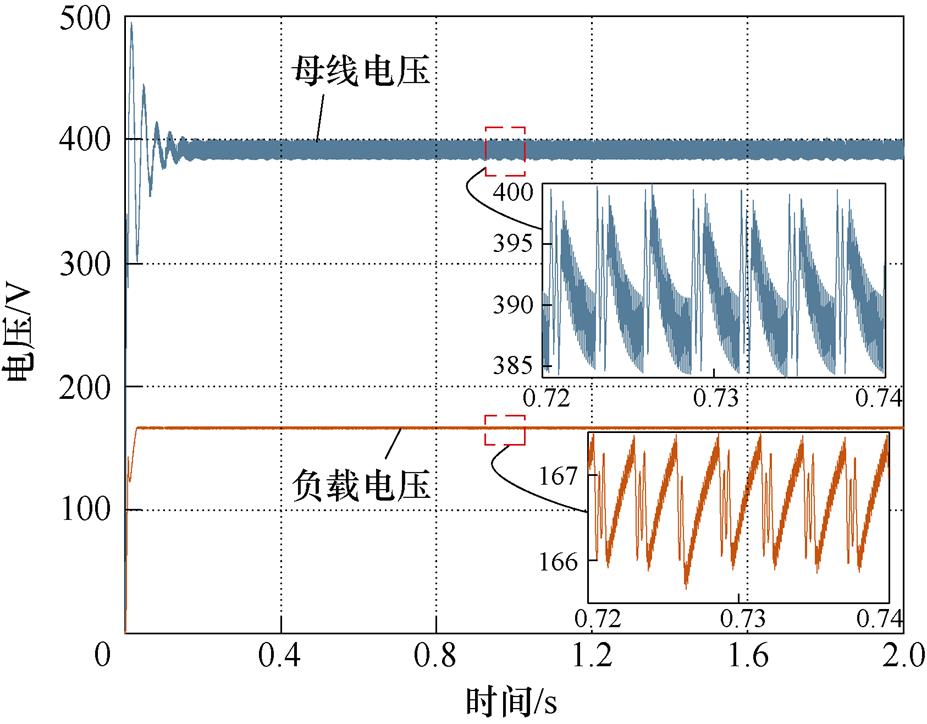
图5 母线电压和负载电压
Fig.5 Bus voltage and load voltage
LGBM是近年来提出的一种数据分类模型。其核心是梯度增强树算法，属于增强算法。增强算法为一种基于弱学习机组合生成强学习机的方法，是目前通用且有效的。该模型提高了每台学习机前一轮训练中分类错误数据的权重，降低了分类结果正确的分类数据的权重。增强算法的原理[27-28]为
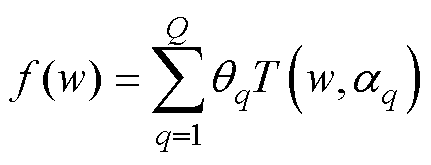（10）
式中，f(w)为强学习者；Q为基础学习器的个数；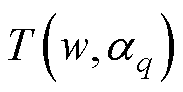
为第q个基础学习器；
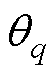为第q个基础学习器的权重；w为样本；
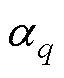为第q个基础学习器的参数。
直流微电网稳定性检测可以看作是一个复杂的回归问题。决策树的线性组合可以很好地拟合L、C、Cd/Ld、Rd、CPL与稳定状态的关系。定义训练样本D1为
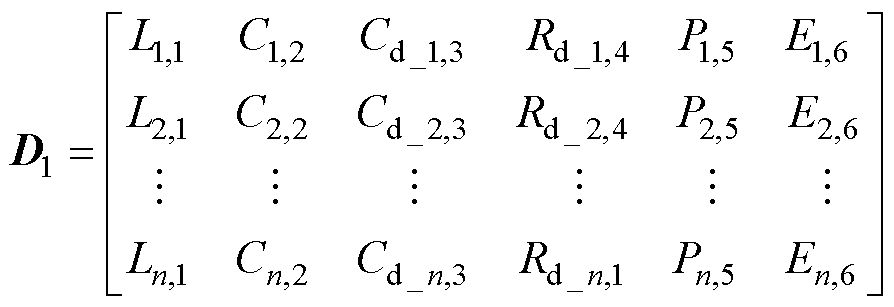（11）
在LGBM迭代中，fq-1(w)被定义为前一个迭代中的强学习器，Ls(P, fq-1(w))被定义为损失函数。定义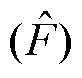
为特性集，E为直流微电网稳定性的状态。然后，利用样本参数和负梯度得到回归树，即基学习器。将每个弱学习器相加得到一个强学习器为
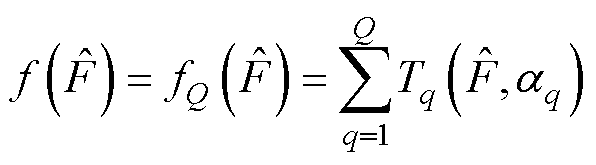（12）
式中，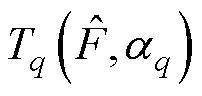
为新学习器的输出，可以表示为
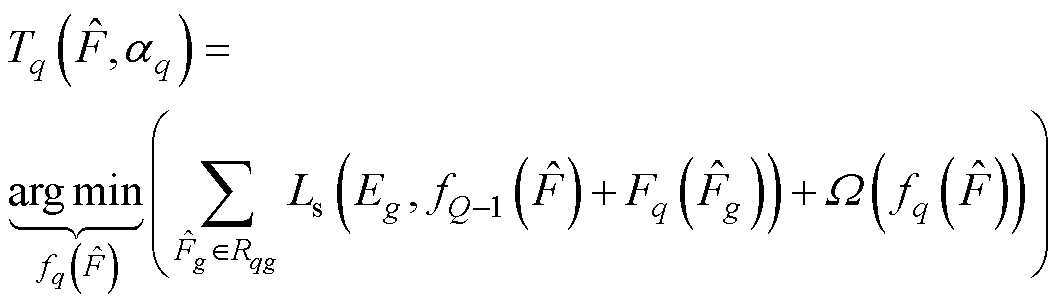（13）
式中，Rqg为对应叶节点的区域；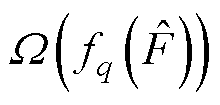
为正则项，可以表示为
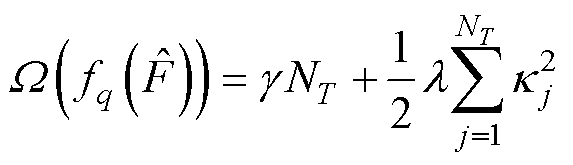（14）
式中，g 为叶子树惩罚正则项；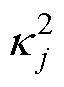
为第j棵树叶子；NT为叶子节点数量；l 为叶权重惩罚项。
SHAP是一种解释机器学习模型的方法[29-30]，该方法从合作博弈论出发来构建加性解释模型，通过计算1.3节所选特征的归因值来反映特征对LGBM模型预测值的贡献程度，用于解释LGBM模型。SHAP把模型解释为所有输入特征的归因值之和，即
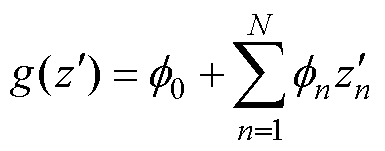（15）
式中，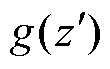
为LGBM模型；N为LGBM的输入特征个数；
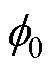为关于直流微电网稳定性训练样本映射的SHAP均值；
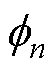为第n个特征对应的SHAP值；
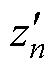为0-1变量，当选择第n个特征时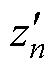=1，不选择第n个特征时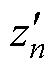=0。
SHAP值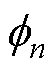定义如下
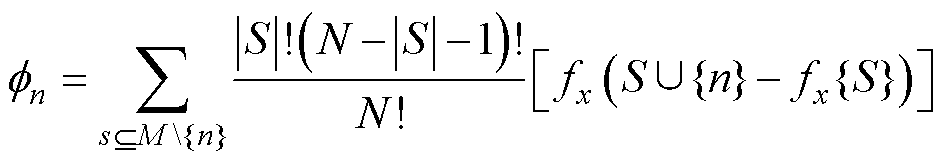（16）
式中，M为在LGBM模型输入特征的集合；S为M的一个序列子集；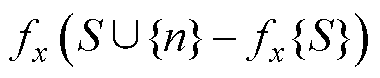
为在第i个特征中加入S特征子集后带来的预测差异。
本文所提LGBM方法在基于Sklearn框架的Python语言中实现，硬件平台设置：CPU为Intel Core i5-7400 4.80 GHz，内存RAM为16 GB，GPU为Nvidia GeFore GTX 3060 4G。
在Matlab2021a中进行时域仿真来生成样本数据集，硬件平台设置：CPU为AMD Ryzen Threadripper 3900X，CPU数量为128，内存RAM为128 GB。
首先通过样本数据来分析四种被动阻尼对提升直流微电网稳定性的效果，评价指标为CPL临界值的大小[13, 23-24]。获取样本数据的仿真结构如图2和图4所示，微源数量为1，系统参数见表1。整理样本数据后可得：在无被动阻尼的直流微电网系统中，CPL临界值为35 kW。添加RC并联阻尼器后，CPL临界值最大提升31 kW，RL并联阻尼器提升的CPL临界值为15 kW，RLC串联阻尼器提升的CPL临界值为22 kW，RL串联阻尼器仅提升CPL临界值3 kW。基于上述结论，后续主要检测具有RC并联阻尼器、RL并联阻尼器和RLC串联阻尼器的直流微电网系统的稳定性。
本文以图2和图4所示的直流微电网结构为例，建立以下两个算例来检验本文所提方法的有效性，案例区分标志为微源的数量和种类。每个案例包含3个场景，分别对应在4.1节选择的三种被动阻尼。
仿真算例1：直流微电网包含4个储能。
场景F1：以L、C、CPL以及RC并联阻尼器参数Cd、Rd为变量进行时域仿真。
场景F2：以L、C、CPL以及RL并联阻尼器参数Ld、Rd为变量进行时域仿真。
场景F3：以L、C、CPL以及RLC串联阻尼器参数Ld、Cd、Rd为变量进行时域仿真。
仿真算例2：直流微电网包含8个储能和1个光伏。
场景F4：以L、C、CPL以及RC并联阻尼器参数Cd、Rd为变量进行时域仿真。
场景F5：以L、C、CPL以及RL并联阻尼器参数Ld、Rd为变量进行时域仿真。
场景F6：以L、C、CPL以及RLC串联阻尼器参数Ld、Cd、Rd为变量进行时域仿真。
为保证样本数据有效性，从生成的训练数据中，随机选取30组数据进行手动检验，以此来验证初始训练数据的有效性。
随后，设置LGBM的参数：迭代次数为100次，学习率为0.05，批次为1批，叶子节点数为21，最大树深为5。
LGBM检测直流微电网稳定性的重点在于减少失稳状态分类为稳定状态的数量，因此本文选择准确率、误报率、准确度、查全率、F1_Score等典型分类评价指标对LGBM方法的学习效果进行分析，结果如图6所示，图中，1代表系统稳定，0代表系统失稳，TN、TP、FP、FN定义为：TN为实际直流微电网系统不稳定，预测结果为系统不稳定；TP为实际直流微电网系统稳定，预测结果为系统稳定；FP为实际直流微电网系统不稳定，预测结果为系统稳定；FN为实际直流微电网系统稳定，预测结果为系统不稳定。
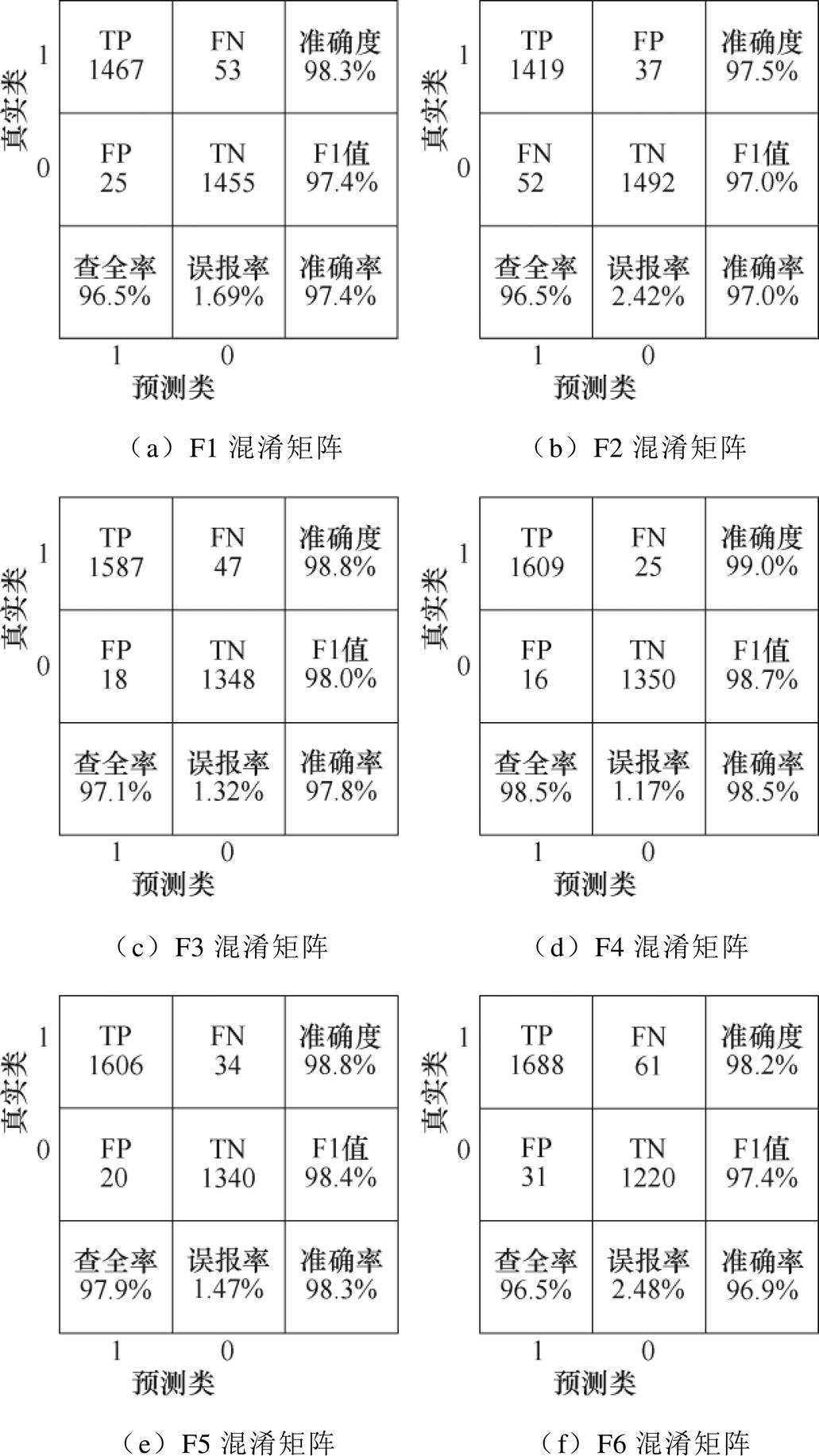
图6 LGBM预测模型在不同场景的混淆矩阵
Fig.6 Confusion matrix of the LGBM prediction model in different scenarios
图6可知，在仿真场景F1～F6中，LGBM方法判断带被动阻尼直流微电网稳定性的准确率依次为97.4%、97.0%、97.8%、98.5%、98.3%、96.9%。将失稳状态识别为稳定状态将会严重影响电力系统的安全性，本文所提方法的误报率仅为1.69%、2.42%、1.32%、1.17%、1.47%、2.48%。上述结果验证了本文方法在检测带被动阻尼直流微电网稳定性的有效性。
以添加RC并联阻尼器的算例为例，分别在场景F1和F4中随机生成两组数据来检验LGBM的学习效果，检验案例如下所述：
检验案例T1：在场景F1中，L=2.36 mH, C= 4.90 mF, Cd=3.10 mF, Rd=0.696 W, CPL=64 kW，预测结果为直流微电网系统失稳。
检验案例T2：在场景F1中，L=0.05 mH, C= 1.96 mF, Cd=1.86 mF, Rd=0.585 W, CPL=55 kW，预测结果为直流微电网系统稳定。
检验案例T3：在场景F4中，L=2.27 mH, C= 3.79 mF, Cd=0.575 mF, Rd=0.239 W, CPL=78 kW，预测结果为直流微电网系统失稳。
检验案例T4：在场景F4中，L=0.95 mH, C= 1.92 mF, Cd=4.23 mF, Rd=0.383 W, CPL=98 kW，预测结果为直流微电网系统稳定。
上述检验案例的仿真结果如图7所示。在检验案例T1中，直流母线电压和负载电压发生振荡，因此系统失稳；在T2中，直流母线电压和负载电压均未发生较大幅度振荡，且未超过电压稳定范围下限，因此系统稳定。同理，在T3中，系统失稳；在T4中，系统稳定。仿真结果与预测结果一致，证明了本文所提方法在检测带被动阻尼直流微电网系统稳定性方面的有效性。
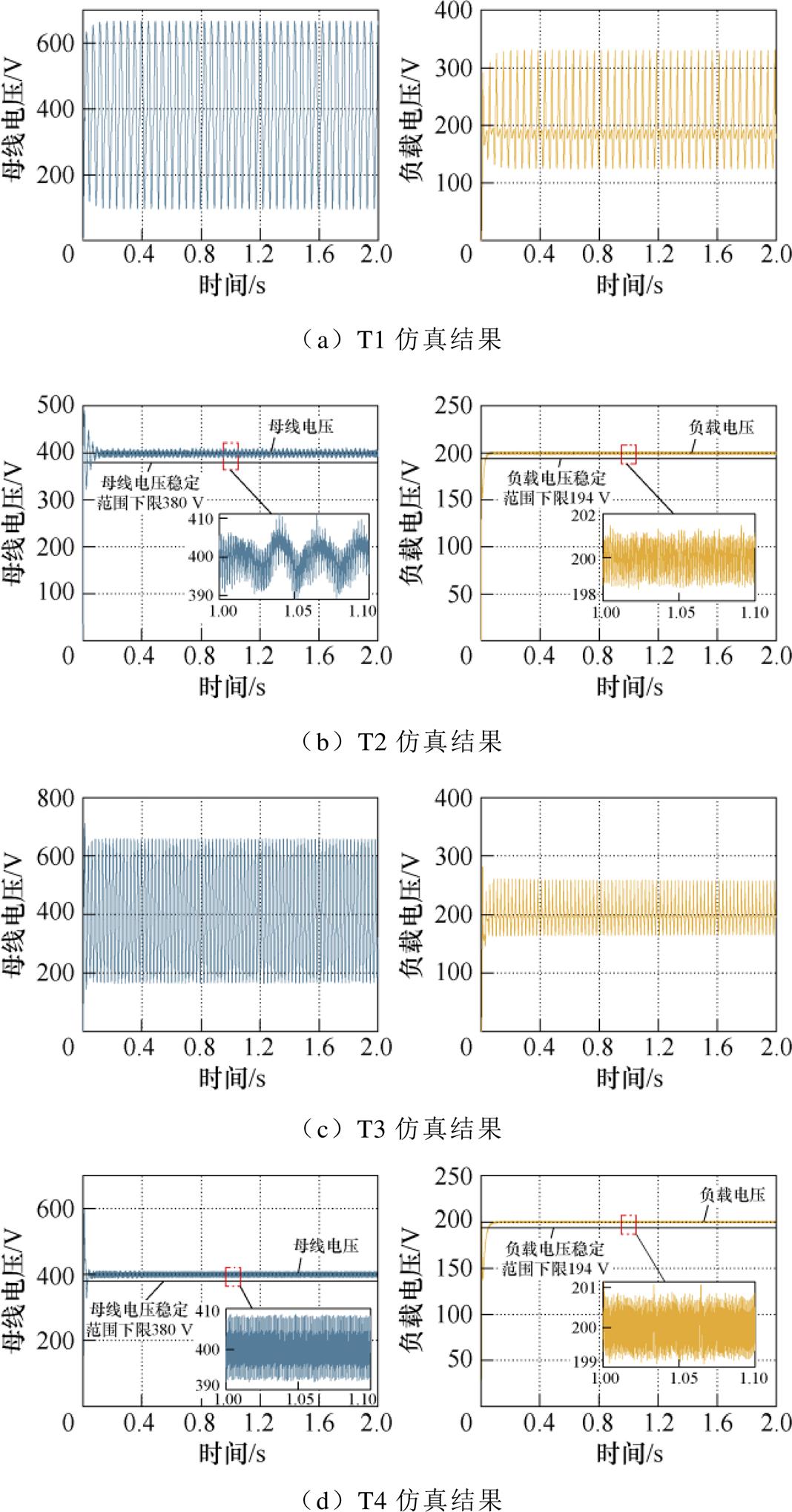
图7 检验案例T1～T4的仿真结果
Fig.7 The simulation results of test case T1 to T4
本文在训练完成LGBM预测模型后，利用SHAP方法可视化所选特征的重要性和特征对预测结果的影响。定义特征值映射的SHAP值为该特征值对预测准确率的影响程度。图8中，横轴从左到右的特征名称顺序对应预测结果重要性的排序。直线柱状图表示该特征的取值越大，LGBM预测结果越趋向为直流微电网系统不稳定，虚线柱状图表示该特征越大，LGBM预测结果越趋向为直流微电网系统稳定。
由图8可知，在场景F4中，CPL对预测结果影响最大；其中CPL和L越大，预测结果越趋向于系统失稳，Rd、Cd、C越大，则预测结果越趋向于系统稳定。同理，在场景F5中，CPL对预测结果影响最大。其中，CPL、L和Ld的取值越大，预测结果越趋向于系统失稳；C和Rd越大，预测结果越趋向于系统稳定。在场景F6中，母线电容C对预测结果影响最大；C、Cd的取值越大，预测结果越趋向于系统稳定；L、Ld、CPL和Rd越大，预测结果越趋向于系统失稳。
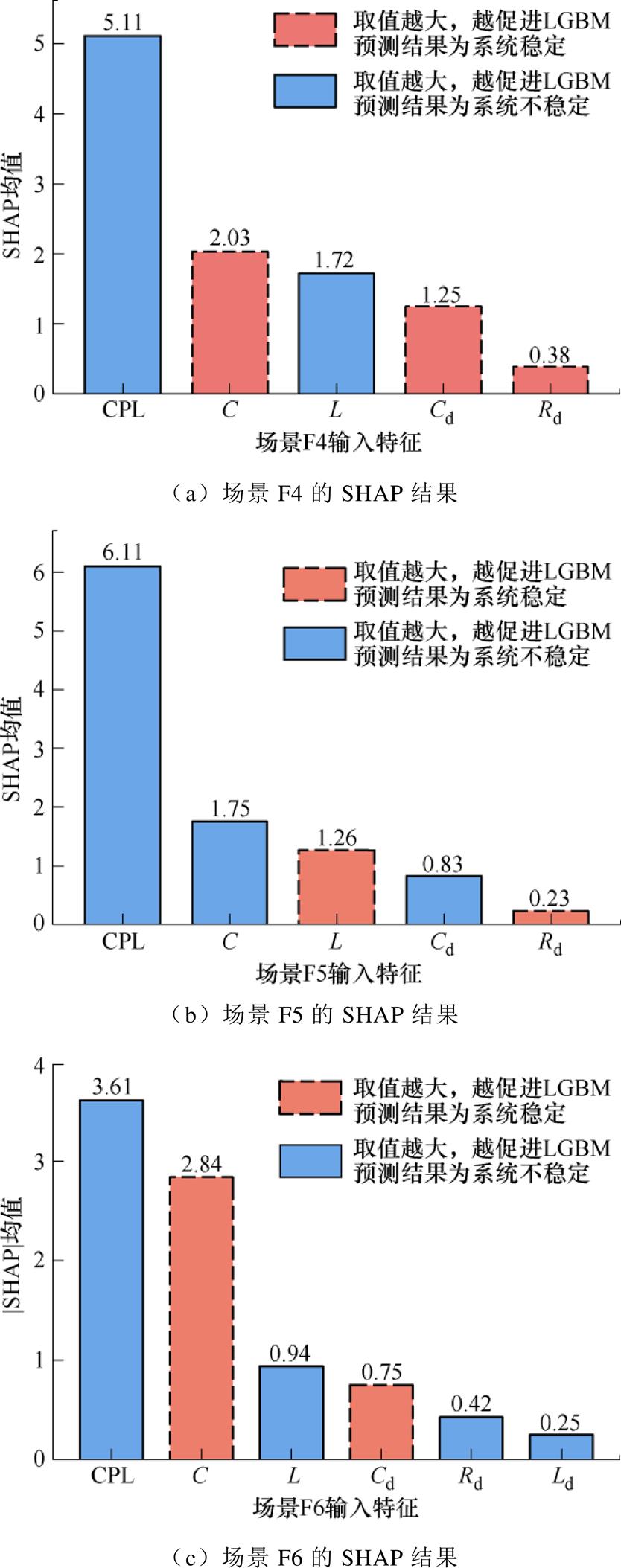
图8 输入特征对LGBM预测直流微电网稳定性的影响
Fig.8 Influence of input characteristics on the stability of LGBM prediction DC microgrid
本文将所提出的LGBM方法与基于机理模型的理论方法、常用机器学习以及常用深度学习算法进行比较。选用的对比算法具体包含决策树（Decision Tree, DT）、随机森林（Random Forest, RF）、极限梯度提升（Extreme Gradient Boosting, XGBoost）算法、朴素贝叶斯（Naive Bayes, NB）、梯度提升树（Gradient Boosting Decision Tree, GBDT）、深度神经网络（Deep Neural Network, DNN）、深度置信神经网络（Deep Belief Networks, DBN）、线性回归（Linear Regression, LR）、Routh-Hurwitz判据九种算法。
不同分类器性能对比结果见表2。可以看到，LGBM相比于DT、RF、NB、GBDT、DBN以及DNN方法，在所有的分类性能指标中明显占优。LGBM与XGBoost和DNN在验证集上准确率较为接近，但LGBM在训练时间上具有明显的优势。最后，基于Routh-Hurwitz数学方法的检测准确率只有50%左右，与之相比，本文所提LGBM具有全面的优势。
综上可知，本文所提LGBM方法在检测带被动阻尼直流微电网性方面具有明显的优势。
表2 不同分类器性能比较
Tab.2 Performance comparison of different classifiers
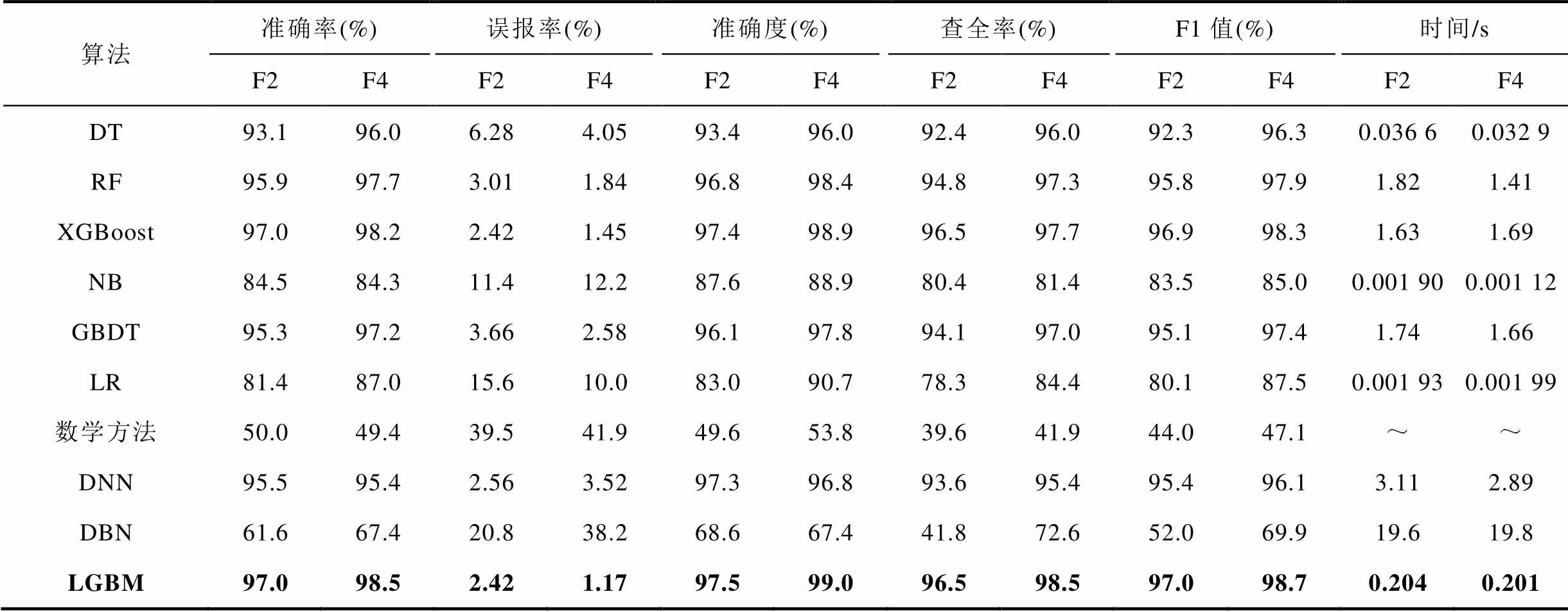
算法准确率(%)误报率(%)准确度(%)查全率(%)F1值(%)时间/s F2F4F2F4F2F4F2F4F2F4F2F4 DT93.196.06.284.0593.496.092.496.092.396.30.036 60.032 9 RF95.997.73.011.8496.898.494.897.395.897.91.821.41 XGBoost97.098.22.421.4597.498.996.597.796.998.31.631.69 NB84.584.311.412.287.688.980.481.483.585.00.001 900.001 12 GBDT95.397.23.662.5896.197.894.197.095.197.41.741.66 LR81.487.015.610.083.090.778.384.480.187.50.001 930.001 99 数学方法50.049.439.541.949.653.839.641.944.047.1～～ DNN95.595.42.563.5297.396.893.695.495.496.13.112.89 DBN61.667.420.838.268.667.441.872.652.069.919.619.8 LGBM97.098.52.421.1797.599.096.598.597.098.70.2040.201
为了进一步验证本文所提LGBM检测带被动阻尼直流微电网稳定性的有效性，本节设置了3个实验算例，如下所述：
实验算例S1：以L、C、CPL以及RC并联阻尼器参数Cd、Rd为变量进行实验。
实验算例S2：以L、C、CPL以及RL并联阻尼器参数Ld、Rd为变量进行实验。
实验算例S3：以L、C、CPL以及RLC串联阻尼器参数Ld、Cd、Rd为变量进行实验。
直流微电网结构如图4所示，实验所用的直流微电网结构包含6个储能系统、1个CPL和1个阻尼器。源变换器是一个Boost变换器，CPL连接Buck变换器。硬件在环设备如图9所示。
图9 硬件在环设备
Fig.9 Hardware-in-the-loop device
在每个实验算例中随机选取15组数据在OP5707硬件在环设备中进行实验，以此来验证训练数据的有效性及最优性。通过对样本数据的学习，直流微电网系统稳定性的预测结果为：实验算例S1～S3的预测准确率为97%以上，并且误报率均小于3%。预测结果证明了所选输入特征组合以及所提LGBM算法的有效性。在3个实验算例中，共随机生成六组数据来检验LGBM学习效果。
检验案例D1： 在实验算例S1中，L=1.41 mH, C= 1.35 mF, Cd=1.50 mF, Rd=0.944 W, CPL=102 kW，预测结果为直流微电网系统不稳定。
检验案例D2：在实验算例S1中，L=1.65 mH, C=1.28 mF, Cd=4.67 mF, Rd=0.678 W, CPL=98 kW，预测结果为直流微电网系统稳定。
检验案例D3：在实验算例S2中，L=1.76 mH, C=1.26 mF, Ld=2.83 mH, Rd=0.221 W, CPL=80 kW，预测结果为直流微电网系统不稳定。
检验案例D4：在实验算例S2中，L=1.36 mH, C=2.08 mF, Ld=2.22 mH, Rd=0.516 W, CPL=88 kW，预测结果为直流微电网系统稳定。
检验案例D5：在实验算例S3中，L=2.21 mH, C=1.37 mF, Ld=1.59 mH, Cd=0.891 mF, Rd=0.441 W, CPL=87 kW，预测结果为直流微电网系统不稳定。
检验案例D6：在实验算例S3中，L=1.13 mH, C=2.15 mF, Ld=1.99 mH, Cd=2.31 mF, Rd=0.312 W，CPL=82 kW。预测结果为直流微电网系统稳定。
将所有检验案例在硬件在环设备中进行检验，结果如图10所示。依据式（10）的直流微电网稳定标准，6个检验案例的预测结果均与实验结果保持一致。由此证明了本文所提LGBM预测方法可以精准地检测直流微电网系统的稳定性。
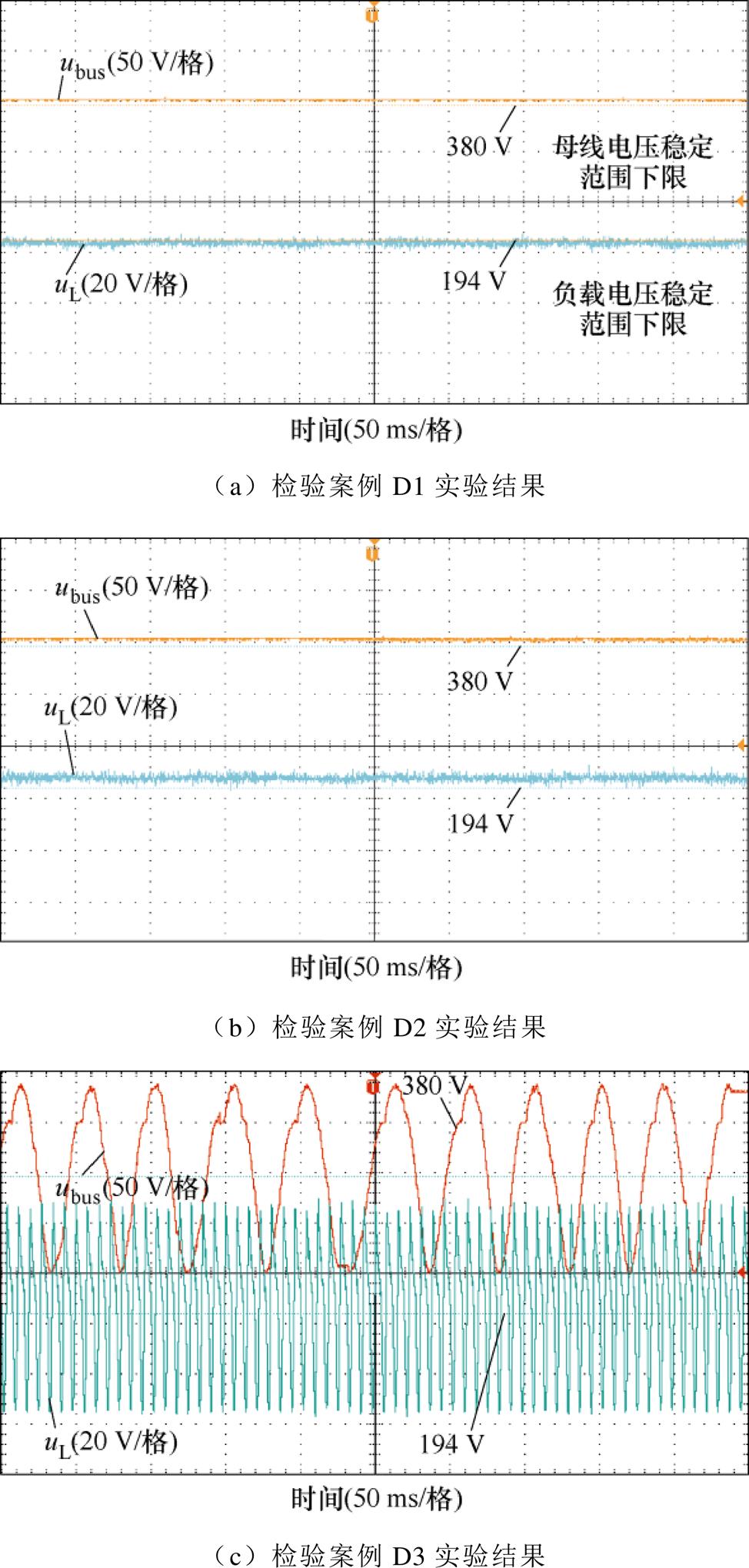
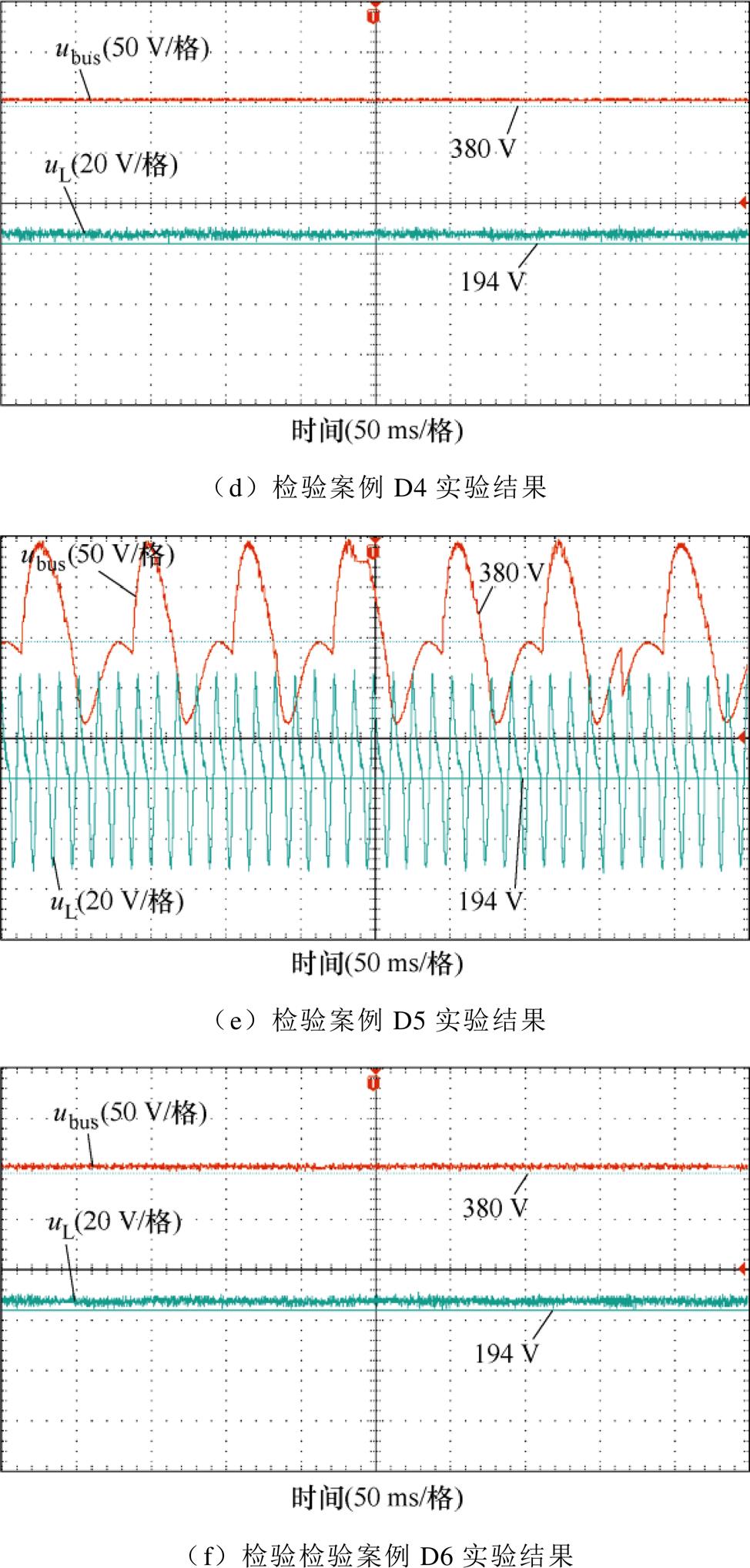
图10 实验结果
Fig.10 Experimental results
针对CPL负阻抗特性导致直流微电网系统失稳的问题，本文提出采用被动阻尼来提升系统稳定性，并基于LGBM方法来检测带被动阻尼直流微电网系统的稳定性。本方法通过时域仿真和硬件在环实验，证明了该方法的有效性和优越性。通过仿真和实验的对比分析，可以得出以下结论。
1）RC并联阻尼器、RL并联阻尼器和RLC串联阻尼器可以显著提升带CPL直流微电网系统的稳定性，然而，串联RL电路提升效果并不理想。
2）与传统理论方法相比，本文所提方法在高维复杂的直流微电网系统中，判断系统稳定状态的准确率依然超过96%，明显优于传统理论方法。与传统机器学习算法相比，在保证较高准确率和较低误报率的同时，显著地减小了计算成本和时间，评价指标均优于传统机器学习算法。
3）通过SHAP方法解释算选输入特征对直流微电网稳定性和LGBM预测结果的影响。结果表明，CPL、电感器件与直流微电网系统的稳定性呈负相关，电容类器件呈正相关；CPL对LGBM算法的预测结果在所有场景中影响最大。
本文采用LGBM预测模型在检测具有被动阻尼直流微电网的稳定性方面取得较好效果。另外，在解决电网中数学模型精度不足、电网参数设计以及充分利用电力数据方面具有较大的发展前景。
附 录
1. 带RL串联阻尼器的直流微电网源端输出阻抗表示为
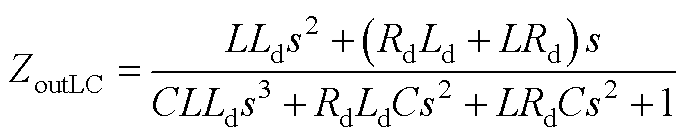（A1）
将式（A1）代入式（4）中，可得直流微电网系统的特征方程为
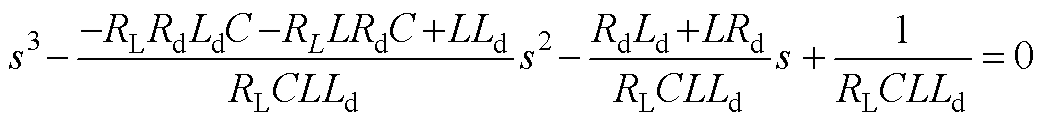（A2）
式（5）中各参数表示为
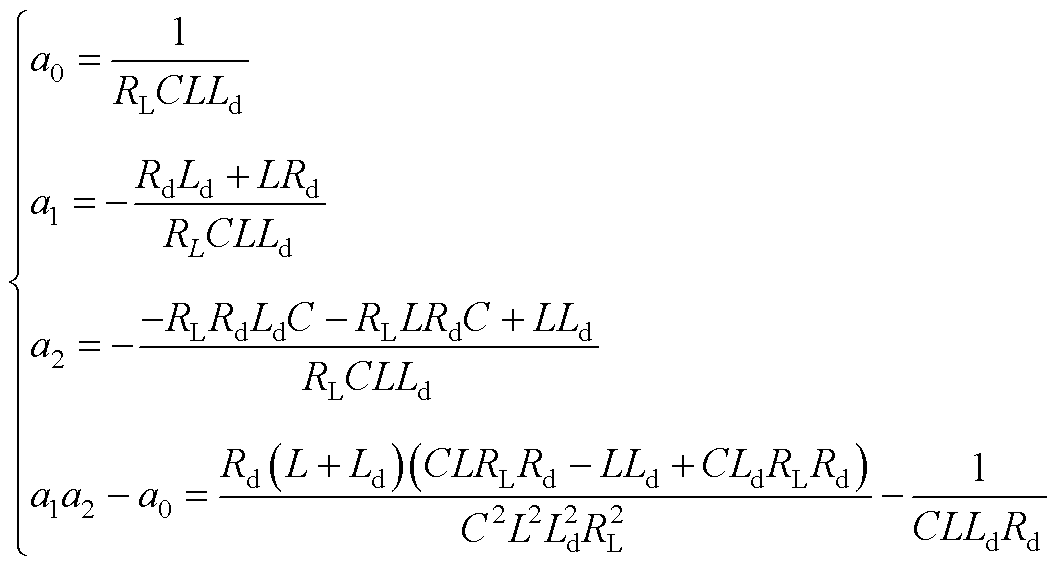（A3）
2. 带RL并联阻尼器的直流微电网源端输出阻抗表示为
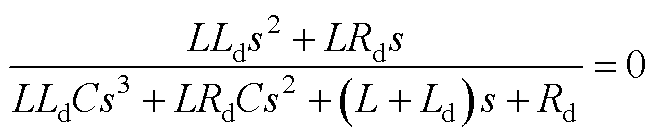（A4）
将式（A4）代入式（4）中，可得直流微电网系统的特征方程为
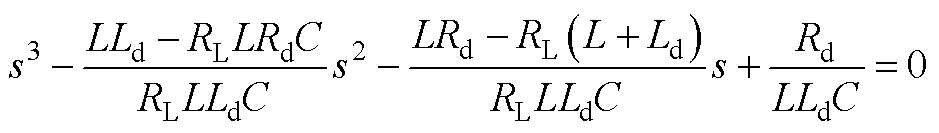（A5）
式（5）中各参数表示为
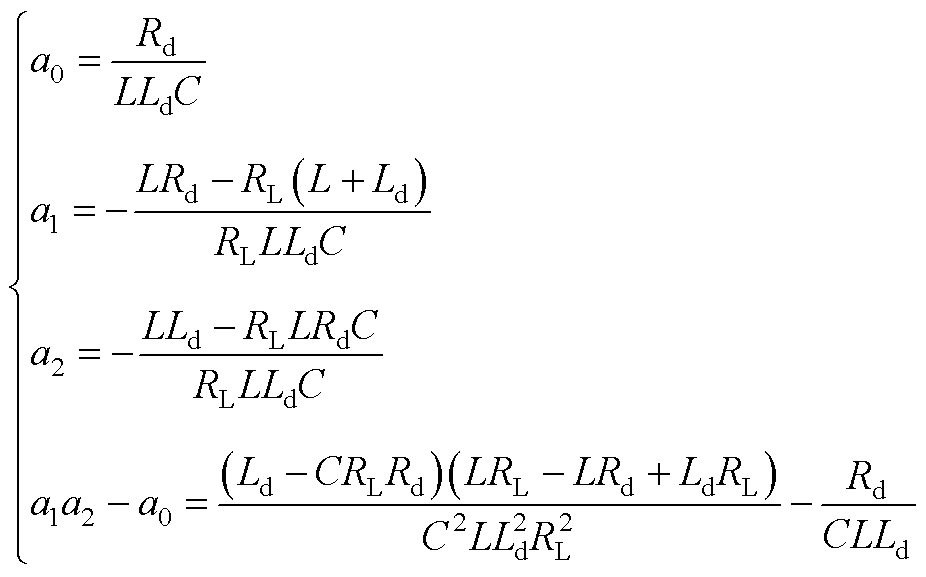（A6）
3. 带RLC串联阻尼器的直流微电网源端输出阻抗表示为
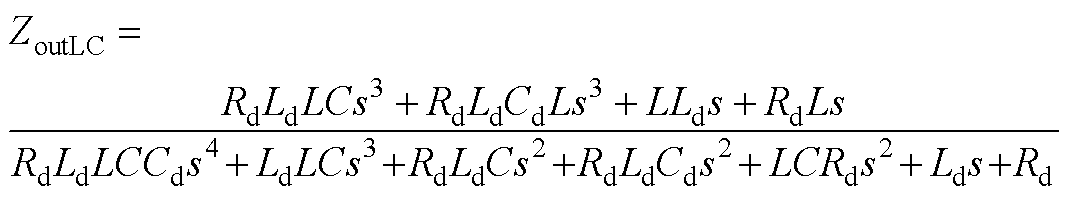（A7）
将式（A7）代入式（4）中，可得直流微电网系统的特征方程为
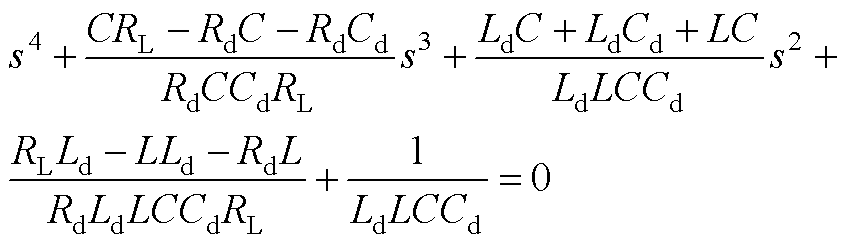（A8）
系统稳定条件为
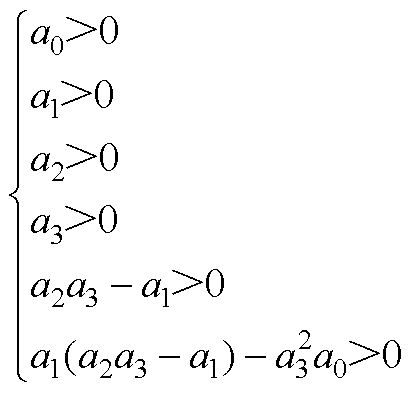（A9）
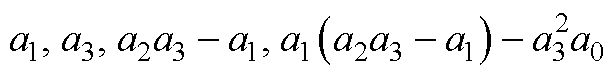计算结果分别为
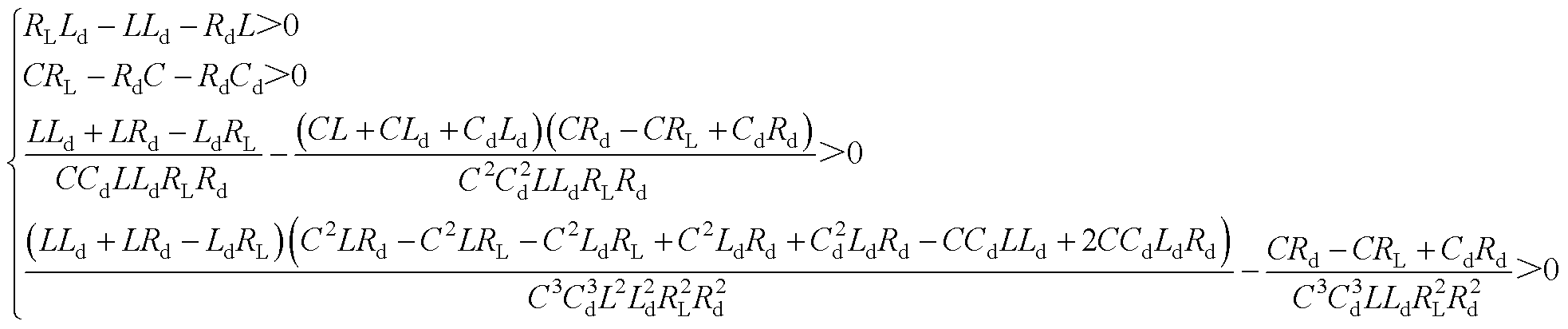（A10）
参考文献
[1] Xia Yanghong, Wei Wei, Long Teng, et al. New analysis framework for transient stability evaluation
of DC microgrids[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 2794-2804.
[2] 陶珑, 王萍, 王议锋, 等. 微电网低压接口变换器的参数寻优自抗扰控制[J]. 电工技术学报, 2022, 37(16): 4202-4211.
Tao Long, Wang Ping, Wang Yifeng, et al. Active disturbance rejection control with automatic optimi- zation for low-voltage interface converter in micro- grid[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4202-4211.
[3] 张伟亮, 张辉, 支娜, 等. 基于节点源荷电流差分的直流微电网储能变换器控制策略[J]. 电工技术学报, 2022, 37(9): 2199-2210.
Zhang Weiliang, Zhang Hui, Zhi Na, et al. Control strategy of DC microgrid energy storage converter based on node differential current[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2199- 2210.
[4] 王晴, 刘增, 韩鹏程, 等. 基于变流器输出阻抗的直流微电网下垂并联系统振荡机理与稳定边界分析[J]. 电工技术学报, 2023, 38(8): 2148-2161.
Wang Qing, Liu Zeng, Han Pengcheng, et al. Analysis of oscillation mechanism and stability boundary of droop-controlled parallel converters based on output impedances of individual converters in DC micro- grids[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2148-2161.
[5] 张辉, 梁誉馨, 孙凯, 等. 直流微电网中多端口隔离型DC-DC变换器的改进虚拟电容控制策略[J]. 电工技术学报, 2021, 36(2): 292-304.
Zhang Hui, Liang Yuxin, Sun Kai, et al. Improved virtual capacitor control strategy of multi-port isolated DC-DC converter in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 292-304.
[6] 张泽华, 宋桂英, 张晓璐, 等. 考虑恒功率负载的直流微电网稳定性与鲁棒性控制策略[J]. 电工技术学报, 2023, 38(16): 4391-4405.
Zhang Zehua, Song Guiying, Zhang Xiaolu, et al. Stability and robustness control strategy of DC microgrid considering constant power load[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(16): 4391-4405.
[7] 谢文强, 韩民晓, 严稳利, 等. 考虑恒功率负荷特性的直流微电网分级稳定控制策略[J]. 电工技术学报, 2019, 34(16): 3430-3443.
Xie Wenqiang, Han Minxiao, Yan Wenli, et al. Hierarchical stability control strategy of DC micro- grid considering constant power load performance[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3430-3443.
[8] 朱晓荣, 李铮, 孟凡奇. 基于不同网架结构的直流微电网稳定性分析[J]. 电工技术学报, 2021, 36(1): 166-178.
Zhu Xiaorong, Li Zheng, Meng Fanqi. Stability analysis of DC microgrid based on different grid structures[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 166-178.
[9] Liu Haiyuan, Guo Wenzhong, Cheng Dong, et al. Stability and bifurcation analysis of DC microgrid with multiple droop control sources and loads[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 2361-2372.
[10] 吴琦, 邓卫, 谭建鑫, 等. 基于下垂控制的多端直流系统稳定性分析[J]. 电工技术学报, 2021, 36(增刊2): 507-516.
Wu Qi, Deng Wei, Tan Jianxin, et al. Stability analysis of multi-terminal DC system based on droop control[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 507-516.
[11] Cespedes M, Xing Lei, Sun Jian. Constant-power load system stabilization by passive damping[J]. IEEE Transactions on Power Electronics, 2011, 26(7): 1832-1836.
[12] Du Yuhua, Men Yuxi, Ding Lizhi, et al. Large-signal stability analysis for inverter-based dynamic micro- grids reconfiguration[J]. IEEE Transactions on Smart Grid, 2023, 14(2): 836-852.
[13] Chang Fangyuan, Cui Xiaofan, Wang Mengqi, et al. Large-signal stability criteria in DC power grids with distributed-controlled converters and constant power loads[J]. IEEE Transactions on Smart Grid, 2020, 11(6): 5273-5287.
[14] 刘宿城, 李响, 秦强栋, 等. 直流微电网集群的大信号稳定性分析[J]. 电工技术学报, 2022, 37(12): 3132-3147.
Liu Sucheng, Li Xiang, Qin Qiangdong, et al. Large signal stability analysis for DC microgrid clusters[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3132-3147.
[15] Jiang Jianbo, Liu Fei, Pan Shangzhi, et al. A conservatism-free large signal stability analysis method for DC microgrid based on mixed potential theory[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11342-11351.
[16] 明佳, 王玉斌, 王璠, 等. 直流微网的大信号稳定性分析及有源阻尼补偿方法[J]. 电工技术学报, 2021, 36(增刊2): 517-529.
Ming Jia, Wang Yubin, Wang Fan, et al. Large-signal stability analysis and active damping compensation methods for DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 517-529.
[17] Wu Mingfei, Lu D D C. A novel stabilization method of LC input filter with constant power loads without load performance compromise in DC microgrids[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4552-4562.
[18] 季宇, 王东旭, 吴红斌, 等. 提高直流微电网稳定性的有源阻尼方法[J]. 电工技术学报, 2018, 33(2): 370-379.
Ji Yu, Wang Dongxu, Wu Hongbin, et al. The active damping method for improving the stability of DC microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 370-379.
[19] Li Xiangke, Zhang Xinan, Jiang Wentao, et al. A novel assorted nonlinear stabilizer for DC-DC multilevel Boost converter with constant power load in DC microgrid[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 11181-11192.
[20] Aldhaheri A, Etemadi A H. Stabilization and per- formance preservation of DC-DC cascaded systems by diminishing output impedance magnitude[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 1481-1489.
[21] 杜镇宇, 阳岳希, 季柯, 等. 张北柔直工程高频谐波振荡机理与抑制方法研究[J]. 电网技术, 2022, 46(8): 3066-3075.
Du Zhenyu, Yang Yuexi, Ji Ke, et al. High frequency harmonic resonance and suppression in Zhangbei project[J]. Power System Technology, 2022, 46(8): 3066-3075.
[22] 黄明增, 胡雅涵, 文云峰, 等. 融合JMIM和NGBoost的电力系统暂态稳定评估方法[J]. 电力系统自动化, 2021, 45(8): 155-165.
Huang Mingzeng, Hu Yahan, Wen Yunfeng, et al. Assessment method of transient stability for power system based on joint mutual information maximi- zation and natural gradient Boosting[J]. Automation of Electric Power Systems, 2021, 45(8): 155-165.
[23] Zhang Yuchen, Xu Yan, Zhang Rui, et al. A missing-data tolerant method for data-driven short- term voltage stability assessment of power systems[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 5663-5674.
[24] Chen Yangfan, Zhang Yu, Qu Erya, et al. Active damping method for LC-DAB system based on a power-based impedance model[J]. IEEE Transactions on Power Electronics, 2023, 38(4): 4405-4418.
[25] Beres R N, Wang Xiongfei, Blaabjerg F, et al. Optimal design of high-order passive-damped filters for grid-connected applications[J]. IEEE Transactions on Power Electronics, 2015, 31(3): 2083-2098.
[26] 滕昌鹏, 王玉斌, 周博恺, 等. 含恒功率负载的直流微网大信号稳定性分析[J]. 电工技术学报, 2019, 34(5): 973-982.
Teng Changpeng, Wang Yubin, Zhou Bokai, et al. Large-signal stability analysis of DC microgrid with constant power loads[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 973-982.
[27] 肖迁, 穆云飞, 焦志鹏, 等. 基于改进LightGBM的电动汽车电池剩余使用寿命在线预测[J]. 电工技术学报, 2022, 37(17): 4517-4527.
Xiao Qian, Mu Yunfei, Jiao Zhipeng, et al. Improved LightGBM based remaining useful life prediction of lithium-ion battery under driving conditions[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4517-4527.
[28] Ye Lin, Dai Binhua, Li Zhuo, et al. An ensemble method for short-term wind power prediction considering error correction strategy[J]. Applied Energy, 2022, 322: 119475.
[29] 郑心仕, 梁寿愚, 苏晓, 等. 基于贝叶斯方法与可解释机器学习的负荷特性分析与预测[J]. 电力系统自动化, 2023, 47(13): 56-68.
Zheng Xinshi, Liang Shouyu, Su Xiao, et al. Characteristic analysis and load forecasting based on Bayesian method and interpretable machine learning[J]. Automation of Electric Power Systems, 2023, 47(13): 56-68.
[30] 顾菊平, 蒋凌, 张新松, 等. 基于特征提取的锂离子电池健康状态评估及影响因素分析[J]. 电工技术学报, 2023, 38(19): 5330-5342.
Gu Juping, Jiang Ling, Zhang Xinsong, et al. Estimation and influencing factor analysis of lithium- ion batteries state of health based on features extraction[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5330-5342.
Abstract In DC microgrids, the negative impedance characteristics of constant power loads (CPL) can reduce system damping, leading to system collapse. To enhance the stability of DC microgrid systems, researchers propose various active damping addition methods, including virtual active resistance compensation, synchronous buck circuit, and output current feedforward, which require complex control algorithms and signal processing. In addition, these methods may reduce load performance and affect the system’s dynamic response. Compared with active dampers, passive damping only requires simple passive components without complex control algorithms and signal processing technology. Accordingly, the implementation is simple, and the cost is low. To analyze the stability of the DC microgrid after adding dampers, traditional methods based on the mechanism model ignore the structure influence, and the model error gradually increases with the increase of system dimension and complexity. Thus, this paper proposes a machine learning-based method to detect the stability of DC microgrids with passive damping. This method can effectively improve the error problem of the mechanism model, comprehensively consider the relationship between local and global stability, and realize the rapid and accurate online detection of the passive damped DC microgrid stable state.
Firstly, this paper establishes an impedance model for the DC microgrid system with passive damping, using the Routh-Hurwitz criterion to determine the parameters that influence system stability. Secondly, simulation scenarios are conducted based on the selected system parameters to obtain sample data for training the machine learning algorithm. A stability detection model based on the light gradient boosting machine (LGBM) is introduced for DC microgrids. The influence of the selected parameters on the LGBM prediction and the stability of the DC microgrid system is further explored using Shapley additive explanations (SHAP). Finally, the effectiveness and superiority of the proposed method are validated through simulations and hardware-in-the-loop experiments.
The results show that the CPL critical value is increased by 31 kW, 15 kW, and 22 kW, respectively, when RC parallel, RL parallel, and RLC series dampers are added to the single energy storage DC microgrid. The RL series damper only improves the CPL critical value by 3kW. After establishing six simulation scenarios with RC parallel, RL parallel, and RLC series dampers, the proposed LGBM achieves prediction accuracy of more than 96.5% and a false alarm rate of less than 2.5% when there is uncertainty in source and load. Compared with traditional mathematical, machine learning, and deep learning methods, the proposed method has advantages in prediction accuracy and computational speed. Among the selected system parameter features, CPL, line inductance, and damper inductance are negatively correlated with the stability of the DC microgrid. In contrast, line capacitance and damper capacitance are positively correlated with the stability of DC microgrids.
The following conclusions can be drawn. (1) RC parallel dampers, RL parallel dampers, and RLC series dampers significantly enhance the stability of the DC microgrid system with CPL. However, the RL series damper does not show an ideal improvement effect. (2) The proposed LGBM model consistently achieves the highest prediction accuracy across multiple scenarios and reduces computational time. (3) The SHAP method effectively explains the impact of each input feature on the stability of the LGBM detection DC microgrid, providing interpretability to the LGBM model.
keywords：DC microgrid, stability detection, passive damping, light gradient boosting machine, Shapley additive explanations
DOI: 10.19595/j.cnki.1000-6753.tces.231393
中图分类号：TM712
国家自然科学基金（52177204）和湖南省自然科学基金（2021JJ30875）资助项目。
收稿日期 2023-08-28
改稿日期 2023-11-13
刘 笑 男，1999年生，硕士研究生，研究方向为微电网稳定性分析。E-mail: lx032230264@163.com
杨 建 男，1978年生，教授，博士生导师，研究方向为电机控制、电力电子等。E-mail: jian.yang@csu.edu.cn（通信作者）
（编辑 陈 诚）