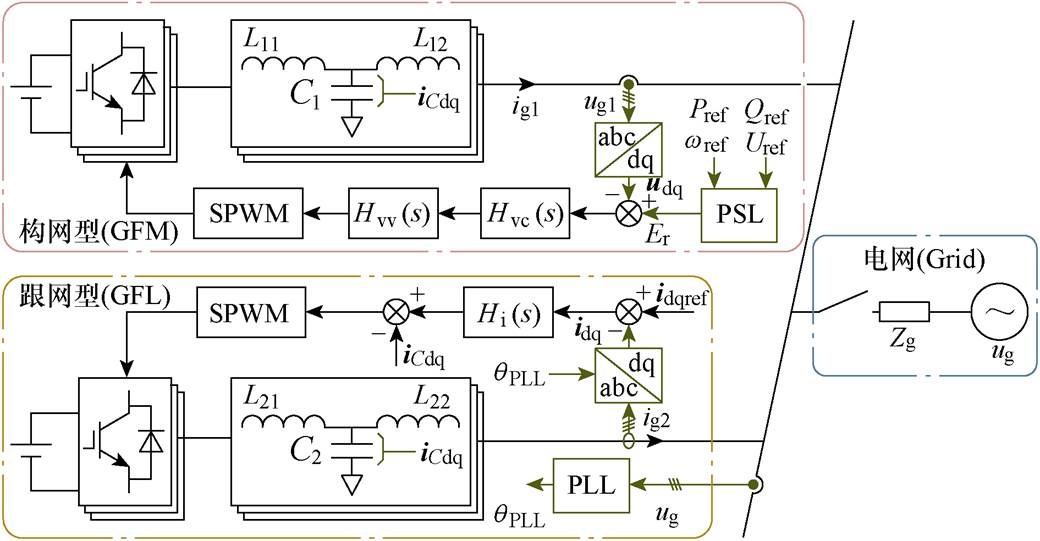
图1 异构逆变器并联系统结构示意图
Fig.1 HIPS structure schematic
摘要 以新能源为主体的新型电力系统正逐步呈现出异构逆变器并联系统特征,即以跟网型与构网型两类逆变器共存的形式呈现。为了全面准确地分析异构逆变器并联系统的稳定性问题,充分计及逆变器间、逆变器与电网间的交互影响,该文建立多逆变器的交互导纳矩阵模型。同时,提出一种基于Gershgorin圆定理的多机稳定性判据,通过引入距离向量函数简化分析过程。然后,基于改进的稳定性判据提出一种参数灵敏度计算方法,并量化分析了系统关键作用因子对异构系统稳定性的影响程度。最后,通过时域仿真算例与实验,验证了理论分析的有效性和稳定性判据的有效性。
关键词:构网型逆变器 跟网型逆变器 异构逆变器并联系统 Gershgorin圆定理 参数灵敏度分析
跟网型逆变器(Grid-Following inverter, GFL)作为新能源接入电力系统的纽带,能够助力实现新能源的最大化利用,但在电网电压和频率支撑方面有诸多局限[1-3]。为此,构网型逆变器(Grid-Forming inverter, GFM)得到广泛关注,且被认为是高比例新能源接入场景下并网逆变器调控方式的大势所 趋[3-4]。这导致以新能源为主体的新型电力系统将在较长时间内出现GFL与GFM共存的调控形式,构成异构逆变器并联系统[5](Heterogeneous Inverters Paralleled System, HIPS)。
异构系统综合了GFL与GFM两种类型逆变器的优势,具备了电压、频率支撑与功率快速响应能力,但无法完全规避这两类逆变器所面临的问题,诸如GFL在弱电网中容易发生高频谐振[6]、GFM在强电网中易发生低频失稳等问题[7]。此外,相较于单逆变器系统,多逆变器并联系统在稳定性分析上需考虑设备间相互作用引发的交互失稳问题[8]。
目前,逆变器并联系统小信号稳定性已有较多研究,但多数聚焦于单类型逆变器并联系统的等效模型[9]、失稳机理[10]、分析工具[11]等方面。其中,针对跟网型逆变器并联系统(Grid-Following inver- ters paralleled system, GFLs)的研究主要集中于锁相环(Phase Locked Loop, PLL)控制[12],构网型逆变器并联系统(Grid-Forming inverters paralleled system, GFMs)研究多数集中于功率同步环(Power Synchronization Loop, PSL)控制,包括下垂控制[13]、虚拟同步电机[10](Virtual Synchronous Generator, VSG)控制等。在系统建模方面,主要有基于频域的阻抗建模与基于时域的状态空间建模两种。文献[9]建立GFLs的诺顿等效电路与节点导纳矩阵,应用模态分析法定性研究了系统参数、控制变量的影响。文献[10]通过建立两台VSG-GFMs小信号状态空间模型,分析了VSG控制参数、电网阻抗等对系统频率稳定性的影响规律。由于多逆变器并联系统模型阶数高、变量参数复杂等问题,导致状态空间法在研究多机系统稳定上存在局限。目前工程上更多是采用阻抗法,常见的有dq轴阻抗模型[14]与静止坐标轴的序阻抗模型[15],其中序阻抗模型具有清晰的物理意义、便于实验测量等优势[16-18]。文献[15]建立了PLL-GFL的序阻抗模型,并研究了PLL等关键参数与系统谐振特性的关系,但没有进一步拓展到多机系统上。文献[19]建立了基于下垂控制GFMs的阻抗模型,分析了下垂系数等关键参数的影响机理。文献[20]则建立可描述VSG动态特性的序阻抗模型,揭示系统与各控制环节、电网阻抗之间的关系。
除上述对单类型逆变器并联系统的特性研究外,也有学者对于这两类逆变器特性开展对比分析。文献[21]分别建立GFL与GFM的谐波线性化模型,分析两者在不同工况下的响应特性。但是,目前对于HIPS的研究相对缺乏,计及逆变器间交互作用的研究甚少。文献[22]建立了HIPS的状态空间矩阵模型,探究了功率渗透率对孤岛系统的影响规律,但所提建模方式状态变量过多,无法进一步推广至多台逆变器并联系统上。综上所述,为表征GFL与GFM的本质特性,需要将PLL的建模统一于GFL序阻抗模型,PSL的建模统一于GFM序阻抗模型中,通过稳定性分析揭示异构系统的谐振机理。
稳定性分析方面,文献[9]应用模态分析法与文献[10]应用特征值分析法,均需要求解矩阵特征值,存在计算冗余复杂等问题。此外,阻抗比判据的应用也较为广泛,其通过系统环路增益的Nyquist曲线是否包围点 (-1, 0),来判断系统稳定状态[23]。相较于Nyquist判据需要求解出每一频率下的特征值,Gershgorin圆判据仅需通过特征值的分布规律即可判断系统稳定性[24]。目前,Gershgorin圆判据在单机系统稳定性分析上应用较多。如文献[24]将Gershgorin圆判据应用在模块化多电平换流器(Modular Multilevel Converter, MMC)系统中,该判据充分考虑了阻抗矩阵中非对角线元素的影响。文献[25]将Gershgorin圆判据应用于双馈感应电机(Doubly Fed Induction Motor, DFIG)系统,并且提出了一个Gershgorin圆判据的广义Nyquist稳定性准则来简化分析过程。因此,鉴于多逆变器并联系统的高阶数及计算复杂问题,Gershgorin圆判据在分析稳定性过程中具有明显优势。
归纳来看,已有研究多集中于单类型逆变器并联系统的稳定性分析,针对不同类型的HIPS稳定机理研究还不够充分,缺乏相应的稳定性判据,且对HIPS多维谐振特性缺乏系统研究。为此,本文首先建立了计及交互作用影响的HIPS交互导纳矩阵,提出了改进Gershgorin圆判据,通过参数灵敏度分析探明了不同工况下系统失稳的主导逆变器,同时阐释了各关键作用因子对系统稳定性的影响规律。最后,通过时域仿真与实验,验证了理论分析的正确性和改进判据的有效性。
HIPS的结构示意图如图1所示,包括GFLs、GFMs以及电网。由图1可知,GFL采用PLL实现同步,Hi(s)为电流环等效传递函数;LCL滤波器由L11、C1、L12构成;iC1为电容电流;ig1为GFM并网电流。此外,GFM采用PSL实现自同步,Pref、Qref、Uref、wref分别为额定有功功率、无功功率、线电压有效值、角频率;其主电路同样采用LCL型滤波器,控制回路由电压环Hvv(s)和电流环Hvc(s)构成,ig2为GFL并网电流;ug为电网电压,Zg为电网等效阻抗。在建立HIPS交互导纳模型时,综合考虑PLL、PSL的影响,以实现对不同类型逆变器进行准确建模。

图1 异构逆变器并联系统结构示意图
Fig.1 HIPS structure schematic
跟网型逆变器的控制结构如图1所示,本文采用典型的基于同步坐标系的PLL和基于dq坐标系下的电流环控制,如附图1所示,锁相环的传递函数HPLL可表示为
 (1)
(1)
忽略频率耦合效应影响,可采用谐波线性化方法对锁相环与电流环进行建模,并考虑控制延时的影响[26-27],本文参考文献[28]详细推导了基于PLL的GFL序阻抗模型,推导过程此处不再赘述,获得的正负序输出导纳YGFLp(s)与YGFLn(s)分别为
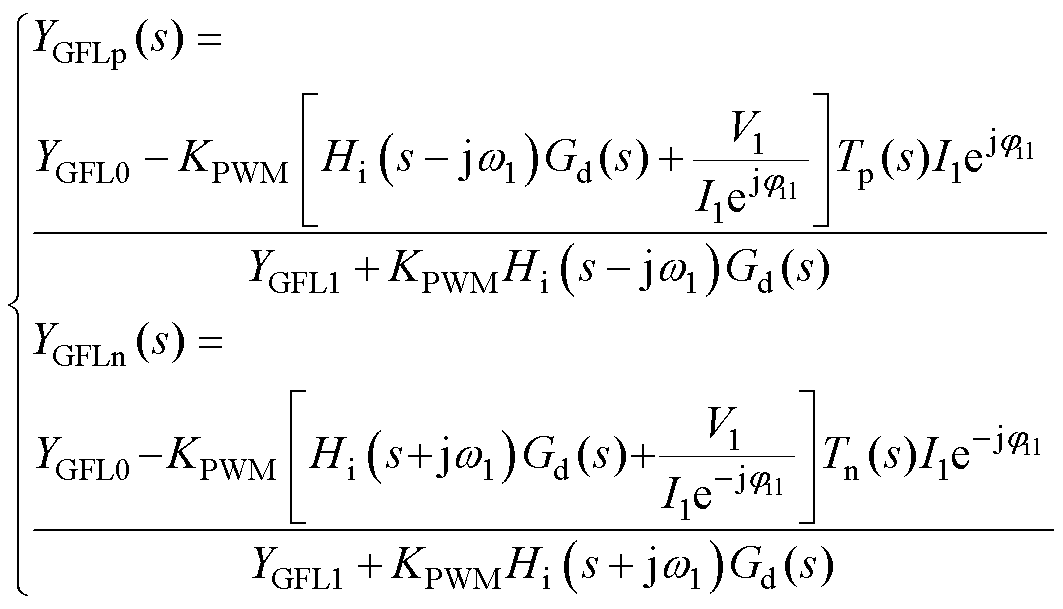 (2)
(2)
式中,I1为基波电流峰值;V1为电网电压峰值;ji1为基波电流相位;w1为基波角频率;KPWM为调制环节的等效系数;电流环采用PI控制器,其传递函数表达式为Hi(s)=Kpi+Kii/s;Tp(s)、Tn(s)分别为qPLL对正、负序电压扰动的闭环传递函数,其表达式详见附录式(A1);变量YGFL0、YGFL1详见附录式(A2);Gd(s)为控制延时环节的等效传递函数,表达式为
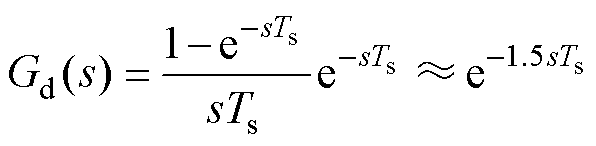 (3)
(3)
式中,Ts为采样周期。进一步地,GFL可简化为诺顿等效模型,如图2所示。
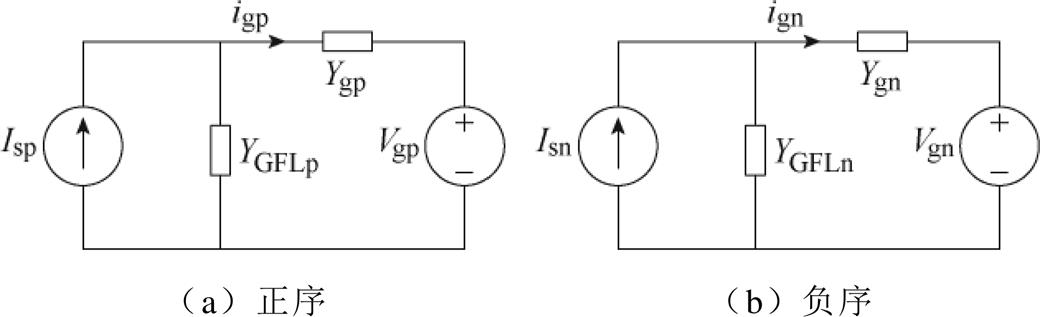
图2 跟网型逆变器序导纳诺顿等效模型
Fig.2 GFL sequential admittance Norton model
构网型逆变器的控制结构如图1所示,功率外环采用典型的下垂控制实现自同步,控制结构如附图2所示。图中的kp、kq分别为有功、无功下垂系数,由下垂控制基本原理可知,其传递函数表达式为
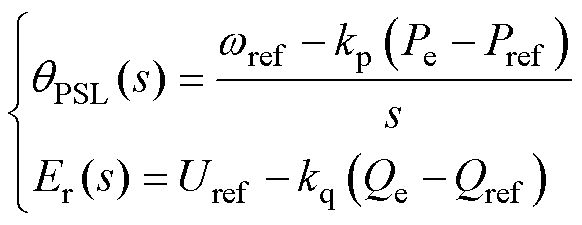 (4)
(4)
构建功率外环控制的GFM阻抗模型,同样考虑系统控制延时的影响,根据文献[19]推导GFM正、负序输出阻抗模型ZGFMp(s)与ZGFMn(s)分别表示为
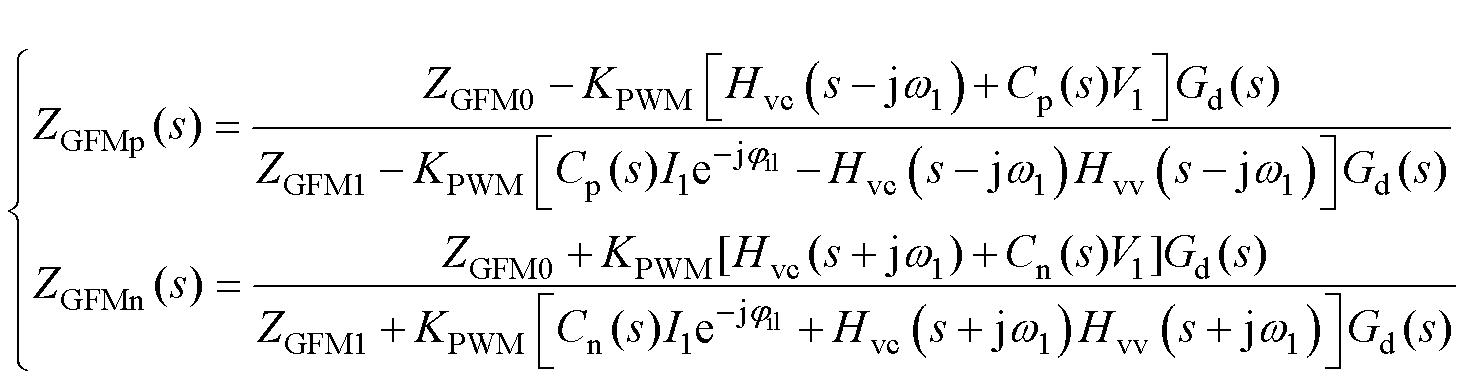 (5)
(5)
式中,电压环表达式为Hvv(s)=Kpvv+Kivv/s;电流环表达式为Hvc(s)=Kpvc+Kivc/s;Cp(s)、Cn(s)、ZGFM0、ZGFM1详见附录式(A3)~式(A6)。其中,Cp(s)、Cn(s)为考虑下垂控制及相位扰动的正、负序调制信号。进一步地,GFM可简化为戴维南电路,如图3所示。
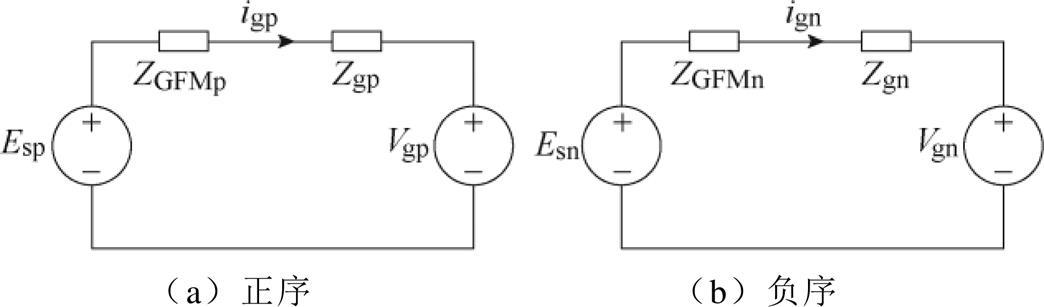
图3 构网型逆变器序阻抗戴维南电路
Fig.3 GFM sequential impedance Thevenin model
由上述建模分析可知,跟网型逆变器可等效为诺顿模型,构网型逆变器可等效为戴维南模型。在并联电路中,导纳的计算更为简单,因此本文将戴维南电路等效为诺顿电路,如图4所示。需要说明的是,本文以逆变器正序导纳为例,对异构系统进行谐振特性研究。
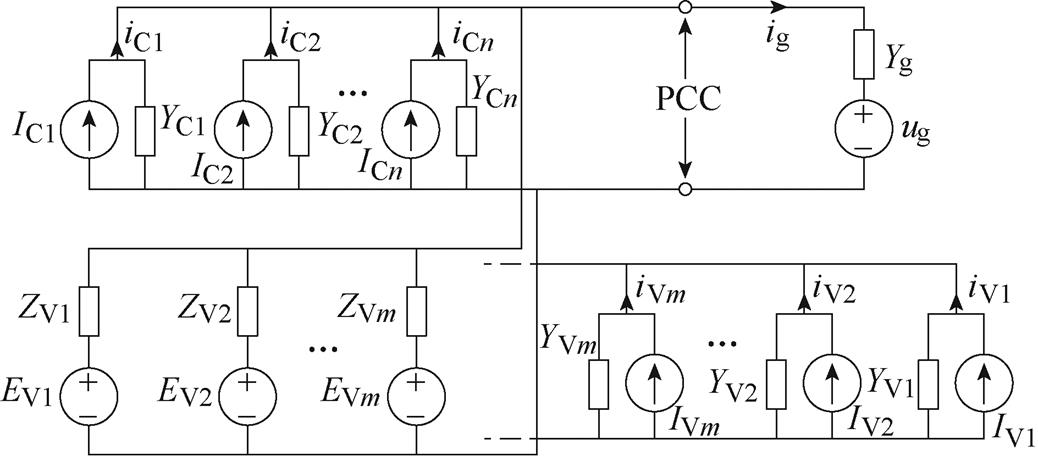
图4 n台跟网型与m台构网型逆变器组成的异构系统
Fig.4 HIPS consisting of n GFL and m GFM
由单逆变器系统拓展至多逆变器并联系统,引入互导纳Yij(i≠j)表示逆变器之间的交互影响;互导纳Yig表示逆变器与电网的交互影响,可构建如图5所示的考虑交互影响的异构系统诺顿电路。
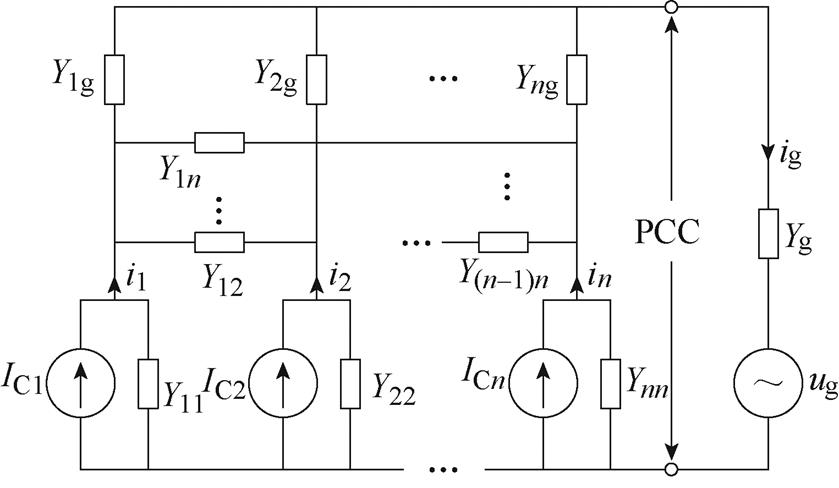
图5 考虑交互作用的异构系统诺顿电路
Fig.5 Norton equivalent circuit for HIPS considering interaction effects
对异构逆变器并联系统设置节点,建立系统导纳矩阵Y为
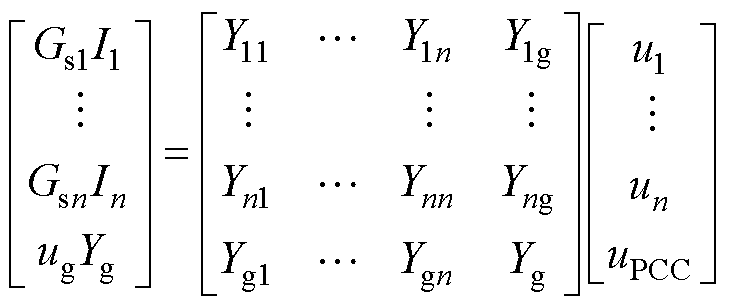 (6)
(6)
其导纳矩阵对应的元素表达式为
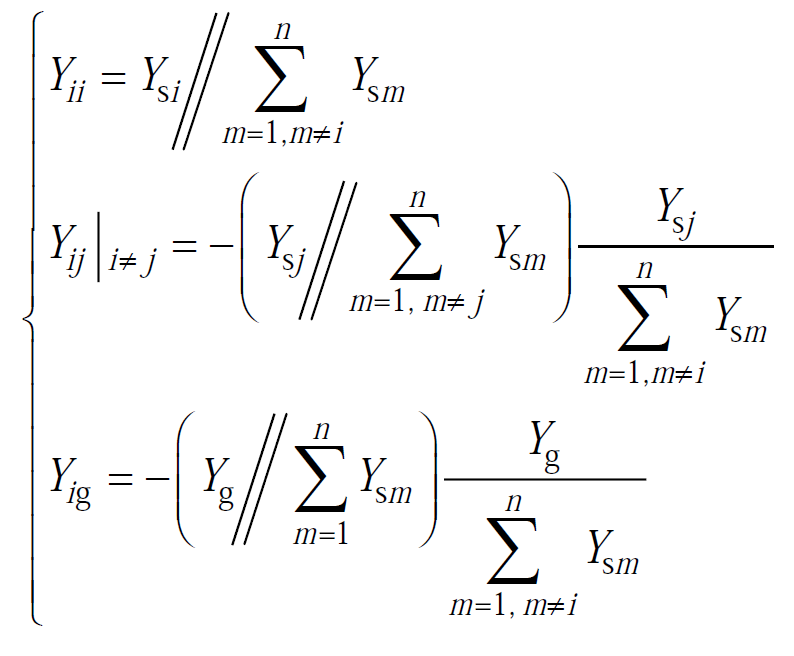 (7)
(7)
本节基于Gershgorin圆定理,提出一种改进的多机系统稳定性分析方法,将Gershgorin圆在复平面上的分布划分为四种类型,并引入距离向量函数F简化分析过程。
Gershgorin圆定理最初应用于判断矩阵特征值分布中。设A为n阶复矩阵,A=[aij]n×n,则矩阵的任一特征值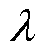 满足式(8),即矩阵特征值均分布于圆域Gi集合中。
满足式(8),即矩阵特征值均分布于圆域Gi集合中。
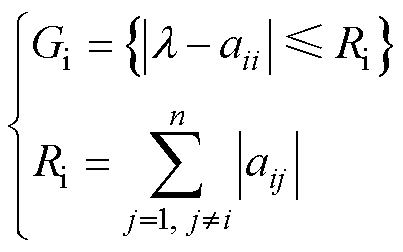 (8)
(8)
式中,Ri为Gershgorin圆半径。Gershgorin圆定理可概括为:以对角线元素为圆心,非对角线元素幅值和为半径。
由Nyquist判据可知,系统的环路增益T=Y/Yg的Nyquist曲线不包围点 (-1, 0) 时,系统处于稳定状态。在判断多逆变器并联系统稳定性时,若只考虑每台逆变器相应的环路增益满足Nyquist判据,不能证明整体系统处于稳态。若以上述多逆变器并联系统的交互导纳矩阵为基础,建立并联系统的环路增益矩阵T,且有
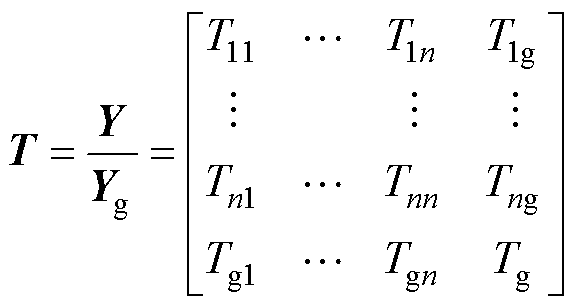 (9)
(9)
矩阵充分考虑了非逆变器自身因素对系统稳定性的影响。相应地,系统环路增益矩阵任一特征值的Nyquist曲线不包围点 (-1, 0) 时,可判断系统处于稳定状态。但是Nyquist判据需求解出每个频率下矩阵的特征值,计算过程冗余复杂。
在Gershgorin圆定理稳定性判据中,环路增益矩阵元素与特征值关系可表示为
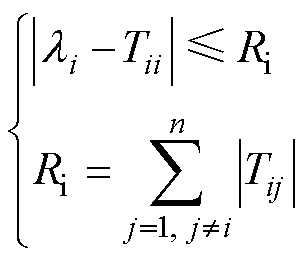 (10)
(10)
以逆变器自身环路增益为圆心,非逆变器自身因素增益幅值和为半径,在复平面上得到不同频率下的Gershgorin圆,如图6所示,若任一Gershgorin圆均不包围点 (-1, 0),则可判断系统处于稳态。

图6 Gershgorin圆示意图
Fig.6 Gershgorin-circle diagram
传统的Gershgorin圆判据虽避免了求解出每个频率下的矩阵特征值,但需绘制出每个频率下的Gershgorin圆域,计算过程同样繁琐。为此,本文提出一种基于Gershgorin圆定理的改进稳定性判据以简化分析过程。
本文所提方法将Gershgorin圆域在复平面上的分布划分为四种类型,如图7、图8所示。SⅣ为设定的禁区范围,将禁区边界与实轴的夹角定义为禁区相位p。
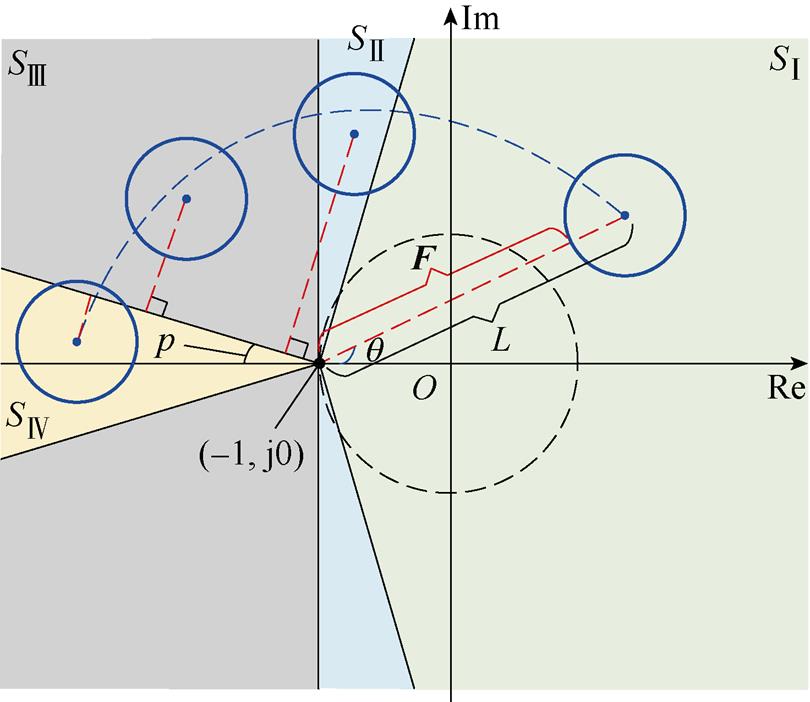
图7 不同Gershgorin圆分布类型
Fig.7 Distribution of different Gershgorin-circle domains
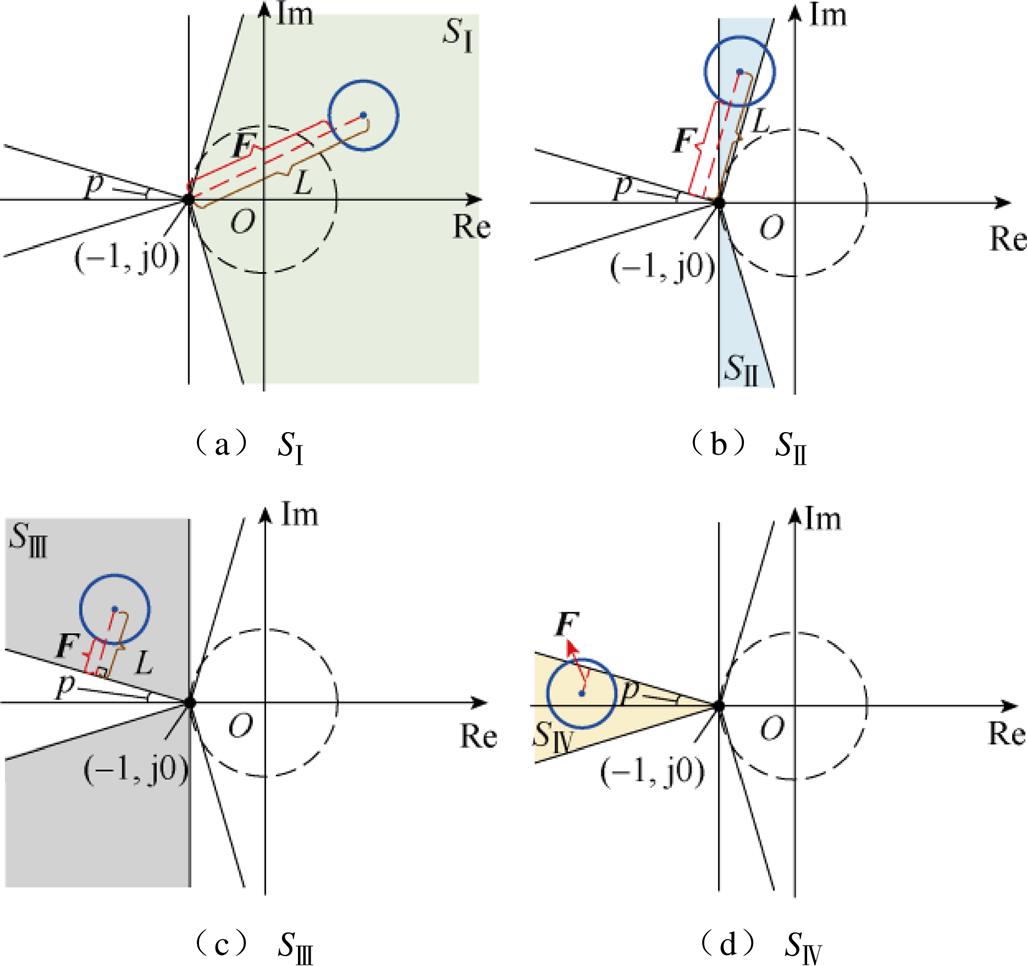
图8 具体区域划分情况
Fig.8 Specific regional divisions
如图8a所示,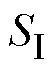 区域可表示为
区域可表示为
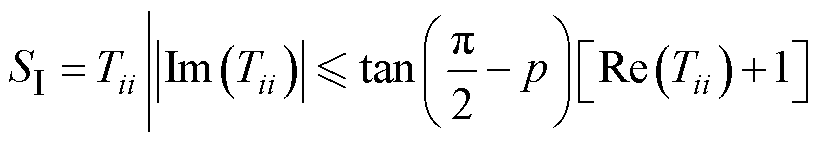 (11)
(11)
则在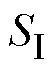 区域上的Gershgorin圆到禁区的距离向量F可表示为
区域上的Gershgorin圆到禁区的距离向量F可表示为
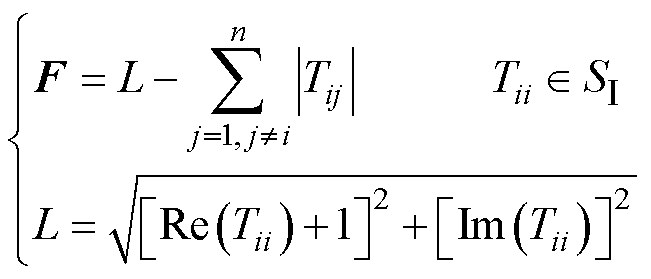 (12)
(12)
式中,L为Gershgorin圆心到禁区的距离。
同理,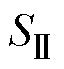 区域可表示为
区域可表示为
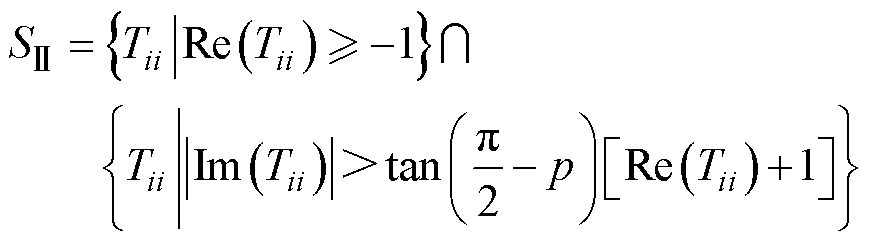 (13)
(13)
在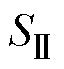 区域上的距离向量F表达式如式(14)所示,其中,q 为距离L与实轴间的夹角。
区域上的距离向量F表达式如式(14)所示,其中,q 为距离L与实轴间的夹角。
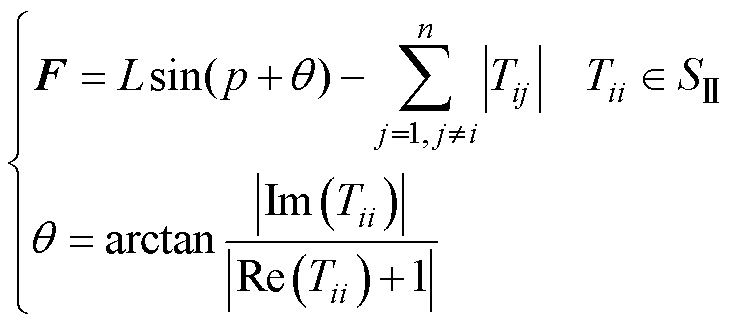 (14)
(14)
如图8c所示,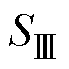 区域与向量F可表示为
区域与向量F可表示为
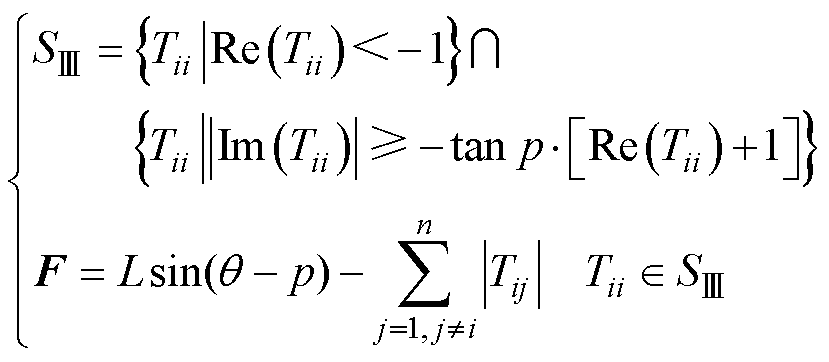 (15)
(15)
此外,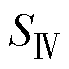 区域与向量F可表示为
区域与向量F可表示为
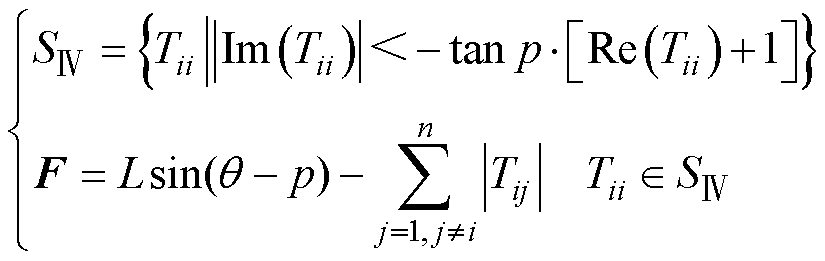 (16)
(16)
综上所述,其对应的Gershgorin圆域到禁区的距离向量F可用于表征系统的稳定性,即
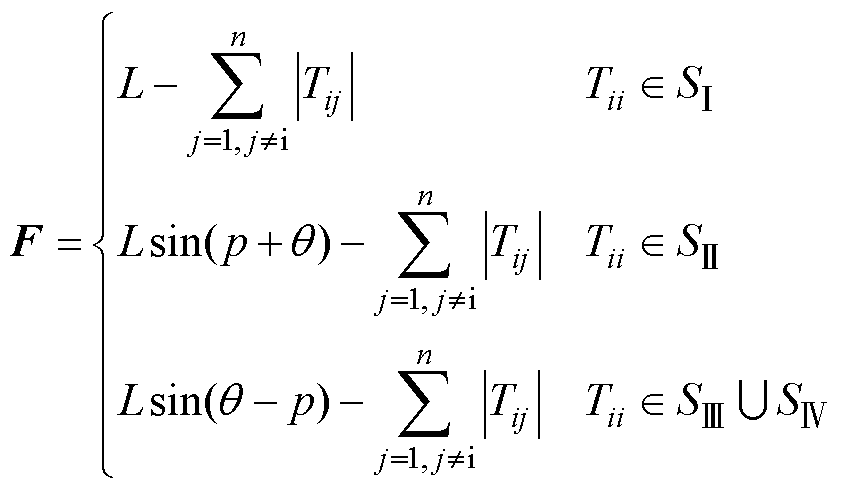 (17)
(17)
其判据可概括为:当且仅当距离向量F小于零时,可以判断系统处于失稳状态。
传统量化分析关键作用参数的影响大多是在求解出系统的特征值矩阵的基础上,进一步对特征值矩阵求相应参数的偏导值,才能求解出参数灵敏度,该过程存在计算复杂且容易出现奇异矩阵等问题。为此,本文提出基于改进Gershgorin圆判据的参数灵敏度分析法。现定义F(s, x)为关于x的分段距离函数,其中x为系统内任意可调参数,满足
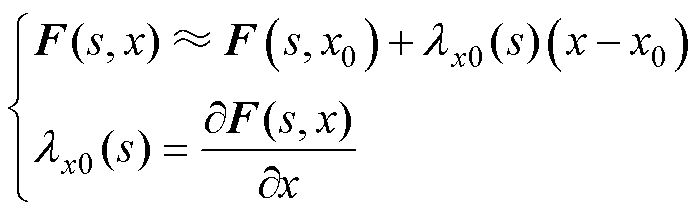 (18)
(18)
式中,x0为参数初始值;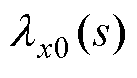 为参数x在x0处的灵敏度函数。
为参数x在x0处的灵敏度函数。
值得注意的是,上述分析是基于线性化分析,对于参数变化量Dx=x-x0取值不宜过大。此外,对关键作用参数灵敏度进行量化分析的结果存在正负,可理解为:若灵敏度为正表征正相关,即增大参数时,其等效负阻抗增大,导致系统失稳风险加剧;若为负,则反之。
本节将应用上述改进Gershgorin圆定理判据对引起异构逆变器并联系统失稳的关键因素进行分析,并对造成失稳的逆变器进行定位。所研究的不同类型逆变器的参数见表1。
表1 不同类型逆变器参数
Tab.1 Parameters of various kinds of inverters
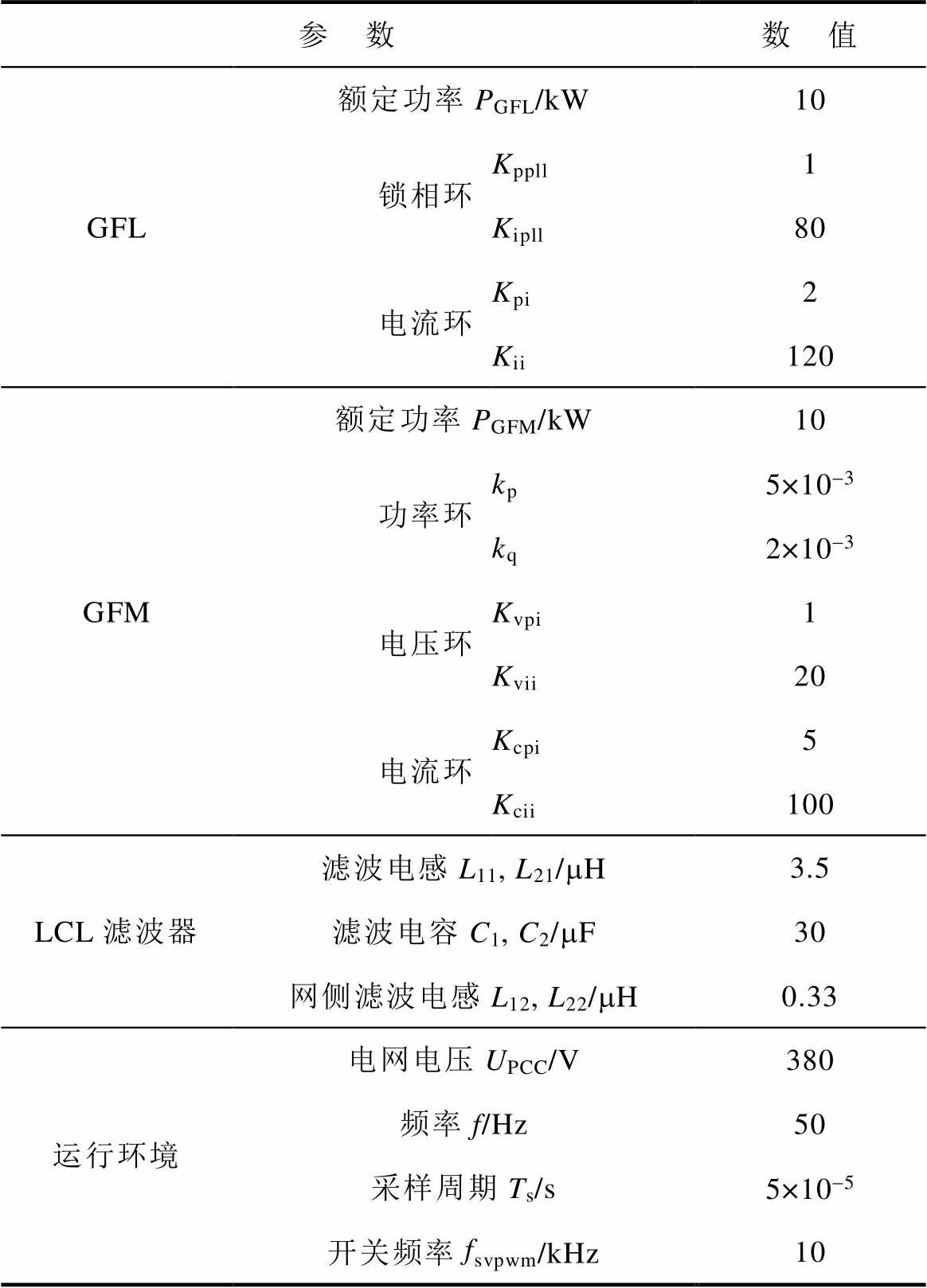
参 数数 值 GFL额定功率PGFL/kW10 锁相环Kppll1 Kipll80 电流环Kpi2 Kii120 GFM额定功率PGFM/kW10 功率环kp5×10-3 kq2×10-3 电压环Kvpi1 Kvii20 电流环Kcpi5 Kcii100 LCL滤波器滤波电感L11, L21/mH3.5 滤波电容C1, C2/mF30 网侧滤波电感L12, L22/mH0.33 运行环境电网电压UPCC/V380 频率f/Hz50 采样周期Ts/s5×10-5 开关频率fsvpwm/kHz10
图9分别给出了两台跟网型逆变器并联系统在不同电网强度下的稳定性分析结果及不同谐振点的关键参数灵敏度分析。本文采用短路阻抗比[29](Short Circuit Ratio, SCR)表征电网强度,可表示为
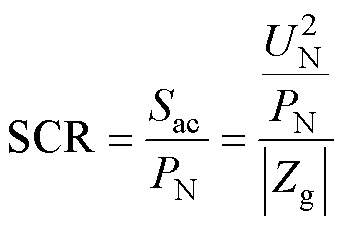 (19)
(19)

图9 不同SCR下GFLs稳定性及参数灵敏度分析
Fig.9 Analysis of stability and sensitivity of parameters of GFLs under different SCRs
由图9a可知,随着电网强度SCR的降低,GFLs稳定性也逐渐降低,其中共出现3处谐振峰,分别视为三种情况,即情况Ⅰ、情况Ⅱ、情况Ⅲ;图9b~图9d分别为上述三种情况下锁相环带宽BPLL-GFL、电流环带宽BCL-GFL灵敏度分析结果,总结如下:
(1)情况Ⅰ:随着电网强度SCR的降低,跟网型逆变器并联系统在低频段的失稳风险加剧;根据参数灵敏度分析可知,诱发低频段失稳的本质原因是电网阻抗的增大导致锁相环失稳。
(2)情况Ⅱ:由于网侧等效电感值增大,其谐振频率向低频处偏移,但系统与电网阻抗间耦合作用增强,导致其失稳风险加剧;引起该频段失稳的本质原因是电网阻抗增大导致锁相环与电流环失稳,因此该谐振可被视为GFLs与电网交互作用结果。
(3)情况Ⅲ:该处出现的谐振失稳点是由逆变器自身LCL谐振所导致,其谐振频率计算如式(20)所示,LCL滤波器与电网阻抗的耦合作用随着电网阻抗的增加而增加;由参数灵敏度分析可知,该点作为逆变器的固有谐振频率,与电流环、锁相环参数影响相关性不高。
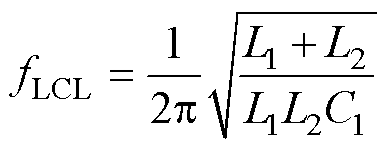 (20)
(20)
综上所述,GFLs在弱电网中极易出现中高频谐振失稳现象,其本质原因是过大的电网阻抗值引发电流环、锁相环失稳,且与滤波器耦合作用增强。
为与GFLs谐振特性分析作对比,本文在相同工况下分析了GFMs稳定性及关键作用参数灵敏度,如图10所示。同时,将图中出现的3次谐振峰,分别定义为情景Ⅰ、情景Ⅱ、情景Ⅲ,并且发现:
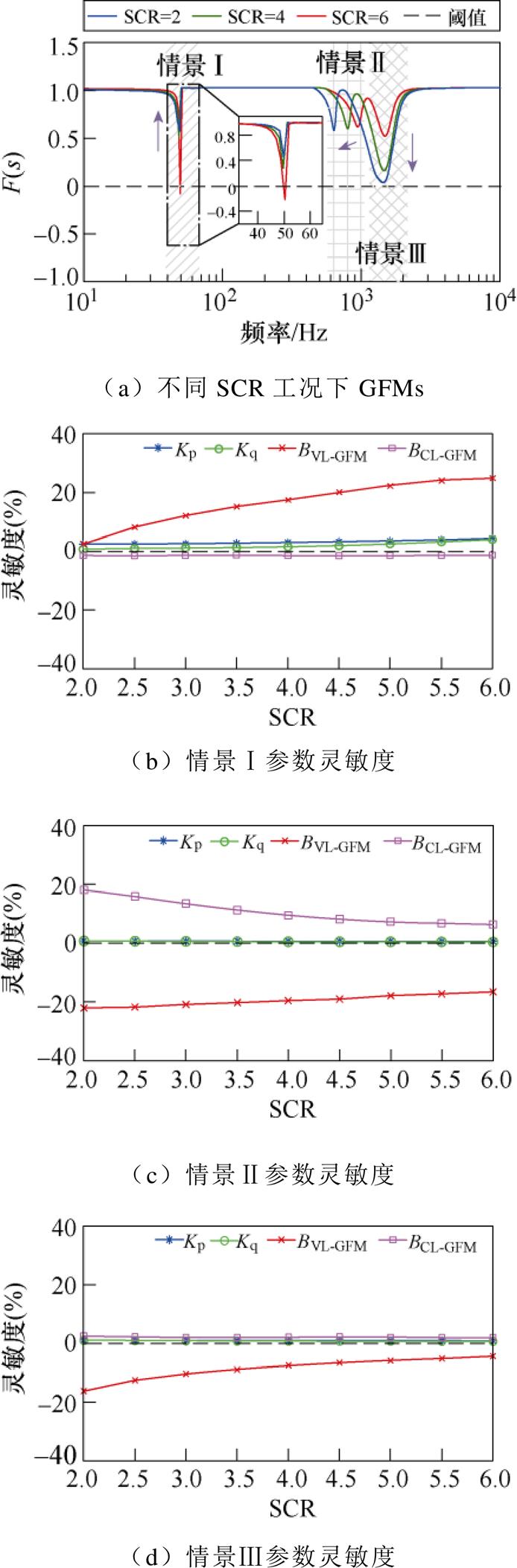
图10 不同SCR下GFMs稳定性及参数灵敏度分析
Fig.10 Analysis of stability and sensitivity of parameters of GFMs under different SCRs
(1)情景Ⅰ:随着电网强度SCR的增强,构网型逆变器并联系统在低频段的失稳风险加剧;根据参数灵敏度分析可知,使低频段失稳的本质原因是过小的电网阻抗导致功率外环与电压环失稳。值得说明的是,根据式(21),在电压Ug不变的情况下,感抗值XL越低时瞬时无功功率值越高,从而导致功率外环受到极大的功率波动引发解列失稳,进一步导致了电压环失稳。
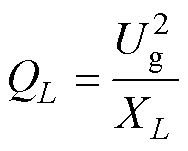 (21)
(21)
(2)情景Ⅱ:随着电网强度SCR的降低,其网侧等效感抗值增大,使该失稳频段向低频处转移,但系统与电网阻抗间耦合作用增强,导致其失稳风险加剧;引起该频段失稳的本质原因是电网阻抗的增大导致电流环失稳。
(3)情景Ⅲ:该谐振点作为构网型逆变器固有LCL谐振点,其失稳风险随着电网阻抗的增加而加剧;根据参数灵敏度可知,电网阻抗的增大有利于电压环稳定。换言之,由于电网阻抗的增大有利于电压环稳定,对中高频段谐振具有抑制作用,使系统在中高频段不易发生谐振失稳。
综上所述,GFMs在强电网中极易发生低频段谐振失稳现象,其本质原因是过小的电网阻抗值引发功率环、电压环失稳。
由跟网型、构网型逆变器组成的异构逆变器并联系统,综合了这两类逆变器的优势,但同时也保留了各类型逆变器在不同SCR工况下存在的失稳风险。为此,本文以HIPS交互导纳模型为基础,通过改进Gershgorin圆判据进行稳定性分析与关键作用参数灵敏度分析。
图11a、图11c、图11e给出了异构系统在不同电网强度SCR工况下的稳定性分析结果,其中出现的3次谐振峰,分别定义为状况Ⅰ、状况Ⅱ、状况Ⅲ,结合图11b、图11d、图11f的关键参数灵敏度分析与上述两类逆变器并联系统作对比,可以发现:
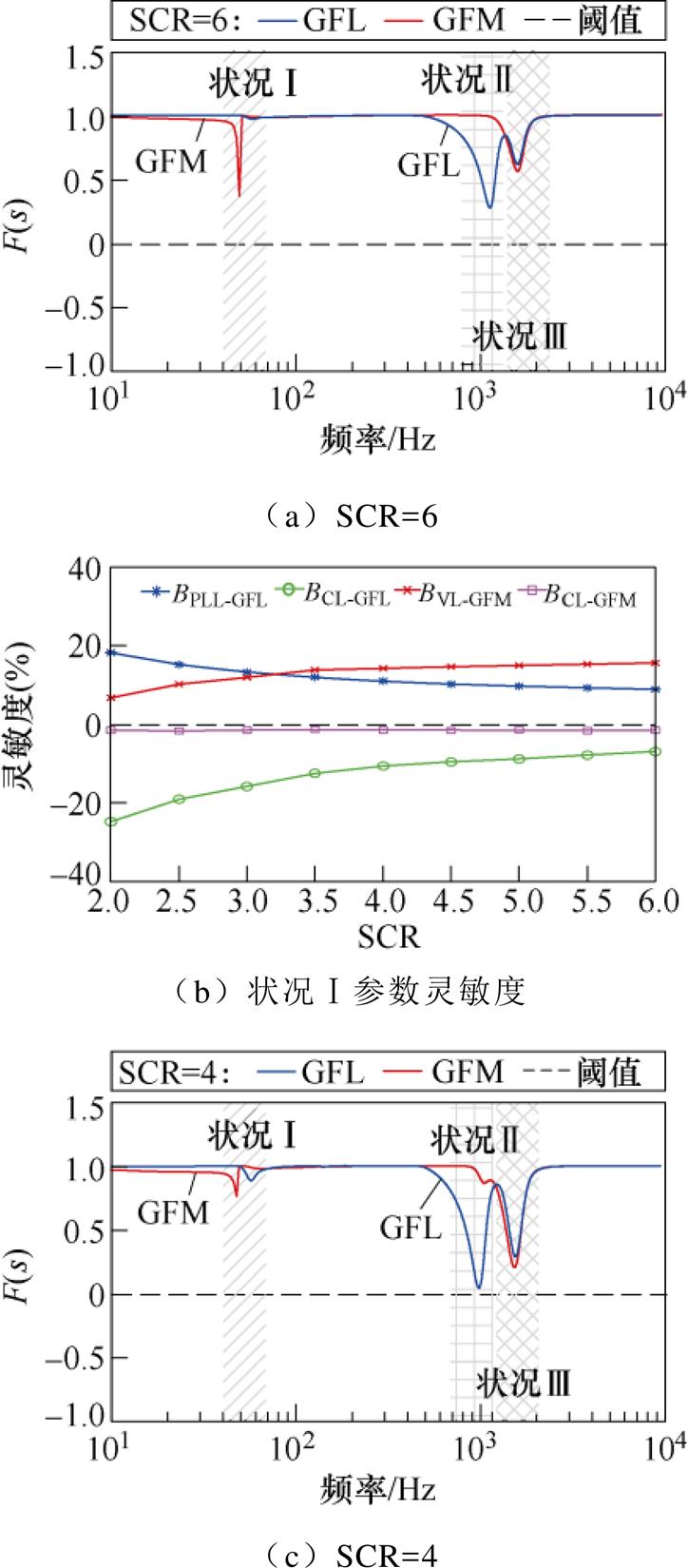
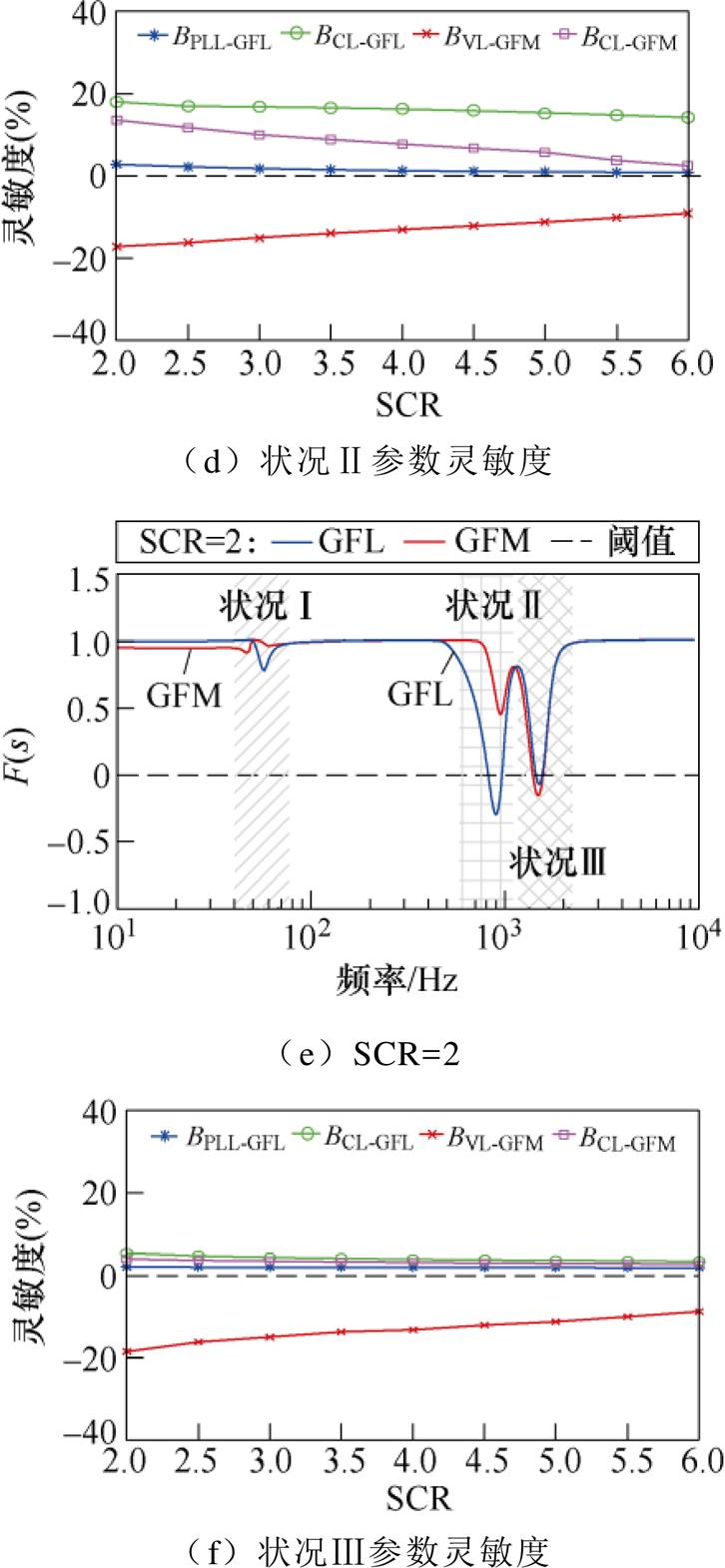
图11 不同SCR下HIPS稳定性及参数灵敏度分析
Fig.11 Analysis of stability and sensitivity of parameters of HIPS under different SCRs
(1)状况Ⅰ:相较于GFM在强电网下的谐振峰值、GFL在弱电网下的谐振峰值,HIPS的谐振峰值显著降低,且均处于稳定状态,这是由于GFL与GFM在稳定性上具有互补特性。在弱电网中,由GFM为GFL提供电压和频率的支撑,削弱电网阻抗的耦合影响;在强电网中,以GFM为视角,其网侧等效感抗随着GFL的接入而增加,根据式(24)可知,感抗值的增加能够降低电网功率波动影响。
(2)状况Ⅱ:电网阻抗的增加会加重系统与电网阻抗间的耦合效应,导致其在中高频段极易发生谐振失稳现象;结合参数灵敏度分析可知,决定该处出现谐振失稳的关键因素是这两类逆变器的电流环带宽,但由于GFM电压环的钳制作用,该处发生谐振失稳的主导因素是GFL的电流环。
(3)状况Ⅲ:与上述分析的两类逆变器并联系统一致,该点作为异构系统的固有LCL谐振频率点;与构网型逆变器并联系统一致的是,导致该处发生谐振失稳的关键因素是GFM的电压环。
综上所述,HIPS在弱电网工况下易发生高频段的谐振失稳,其本质原因在于GFL的电流环与电网阻抗耦合作用加剧;系统在强电网工况下易发生低频段的谐振失稳,其本质原因在于过小的电网阻抗导致GFM的功率环与电压环失稳。
为验证上述理论分析的正确性和所提稳定性判据的有效性,基于Matlab/Simulink搭建了HIPS,各类逆变器参数见表1。同时,通过搭建两台5 kW逆变器并联系统进一步验证该判据的有效性,实验平台如图12所示。

图12 实验平台
Fig.12 Experimental platform
结合第3节GFLs主导参数灵敏度分析可知,影响GFLs稳定性的内在因素包括电流环带宽BCL-GFL与PLL带宽BPLL-GFL。图13分别给出了电流环带宽BCL-GFL、PLL带宽BPLL-GFL与电网强度SCR间的约束关系。由图13可知,BCL-GFL在稳定区域内带宽可调范围远小于BPLL-GFL;且BCL-GFL取值过高或过低时均不利于系统稳定。因此,BCL-GFL是影响GFLs稳定性最主要的因素。
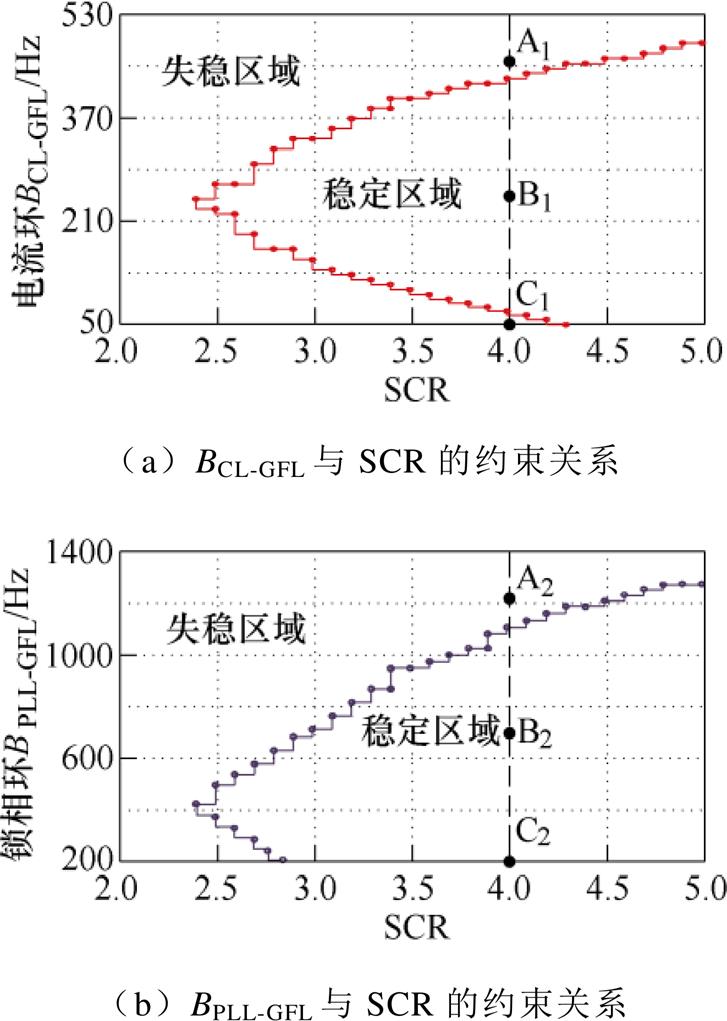
图13 GFLs关键参数与SCR间的约束关系
Fig.13 Constraints between parameters of GFLs and SCR
图14分别给出了电压环带宽BVL-GFM、电流带宽BCL-GFM与电网强度SCR间的约束关系。由图14可知,BVL-GFM是影响GFMs稳定性最主要因素,BVL-GFM在稳定区域内带宽可调范围远小于BCL-GFL。
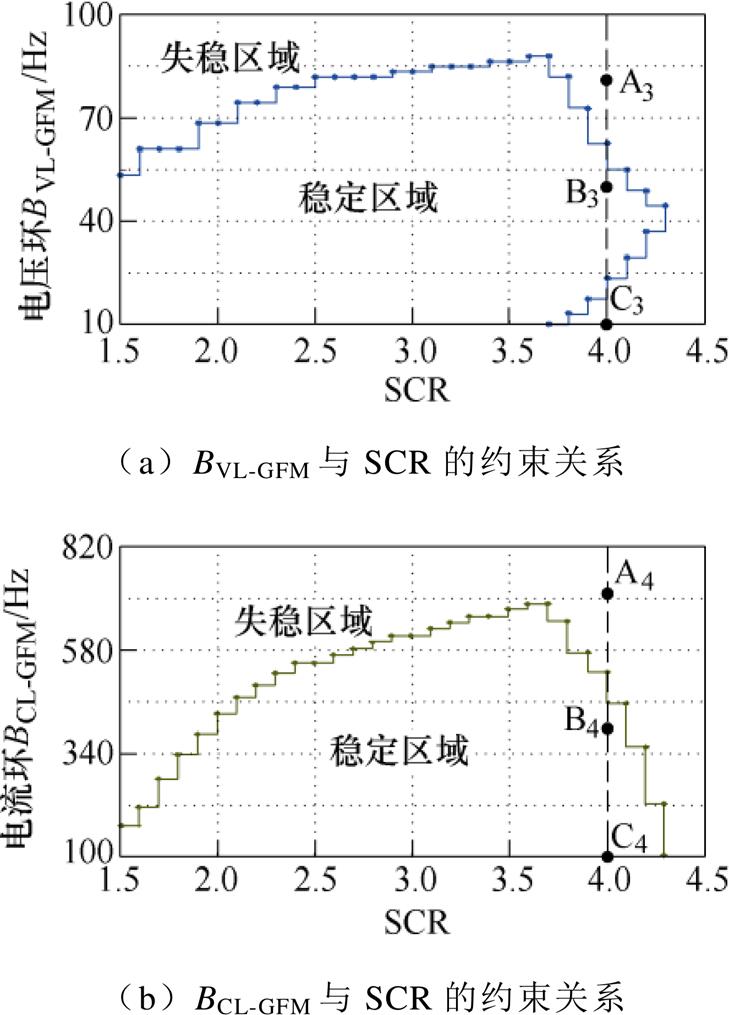
图14 GFMs关键参数与SCR间的约束关系
Fig.14 Constraints between parameters of GFMs and SCR
图15给出了GFLs在不同SCR、电流环带宽BCL-GFL及锁相环带宽BPLL-GFL工况下并网电流的变化情况与快速傅里叶变换(Fast Fourier Transfor- mation, FFT)分析结果,如图15a可知,随着电网强度由SCR=6到SCR=2变化,GFLs出现高频谐振,其中以700 Hz与1 650 Hz最为显著,这与上述稳定性分析结果一致。需要说明的是,案例中BCL-GFL的取值分别对应图13a中SCR=4时的A1、B1、C1;BPLL-GFL的取值分别对应图13b中的A2、B2、C2。根据图15b、图15c对比BCL-GFL与BPLL-GFL的影响可知,影响GFLs稳定性的内在主导因素是BCL-GFL,BCL-GFL过低的情况下,系统容易出现低频振荡,但过高时又容易引发高频谐振。
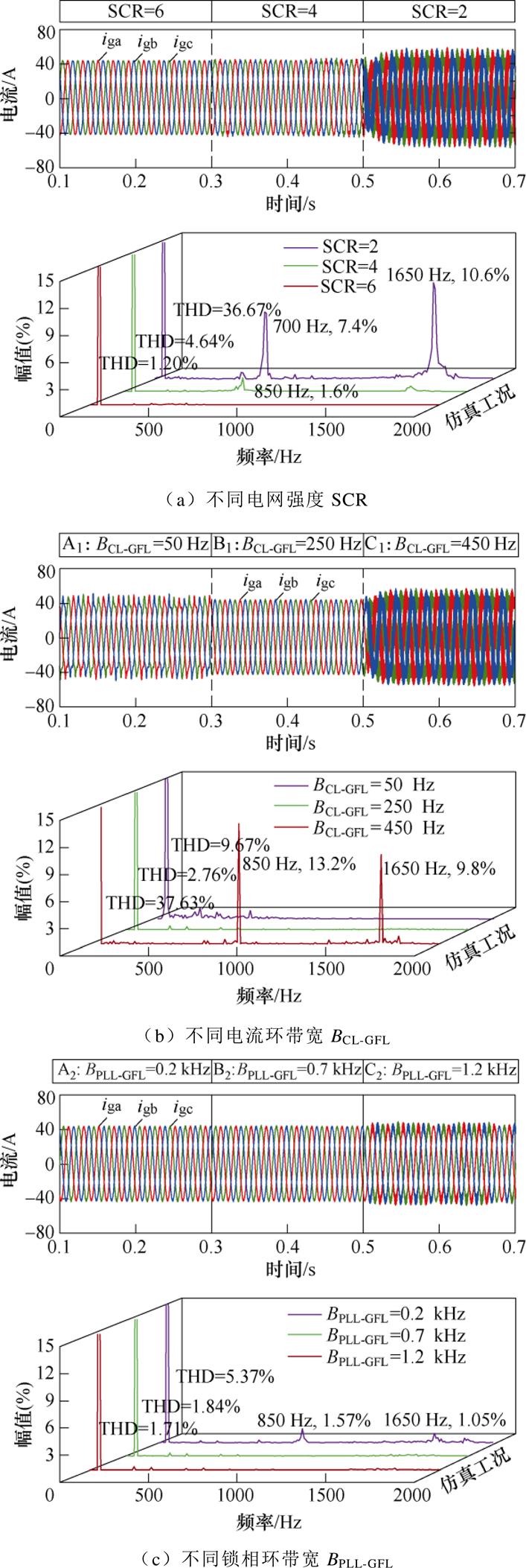
图15 GFLs关键作用因子仿真验证及FFT分析
Fig.15 Simulation validation and FFT analysis of the critical effect factors of GFLs
图16给出了GFMs在不同SCR、电压环带宽BVL-GFM及电流环带宽BCL-GFM工况下并网电流的变化情况与FFT分析结果。可以发现,电网阻抗过低的情况下,容易引起GFMs低频振荡;影响GFMs的关键作用因子是电压环带宽BVL-GFM,其取值过大或过小均不利于系统稳定。
图17分别给出了GFLs与GFMs并网点电压及输出电流在电网强度SCR变化时的实验结果。由图17可知,随着电网强度的减弱,GFLs出现高频谐振;反之,随着电网强度的增强,GFMs因功率波动影响,触发设备保护动作。
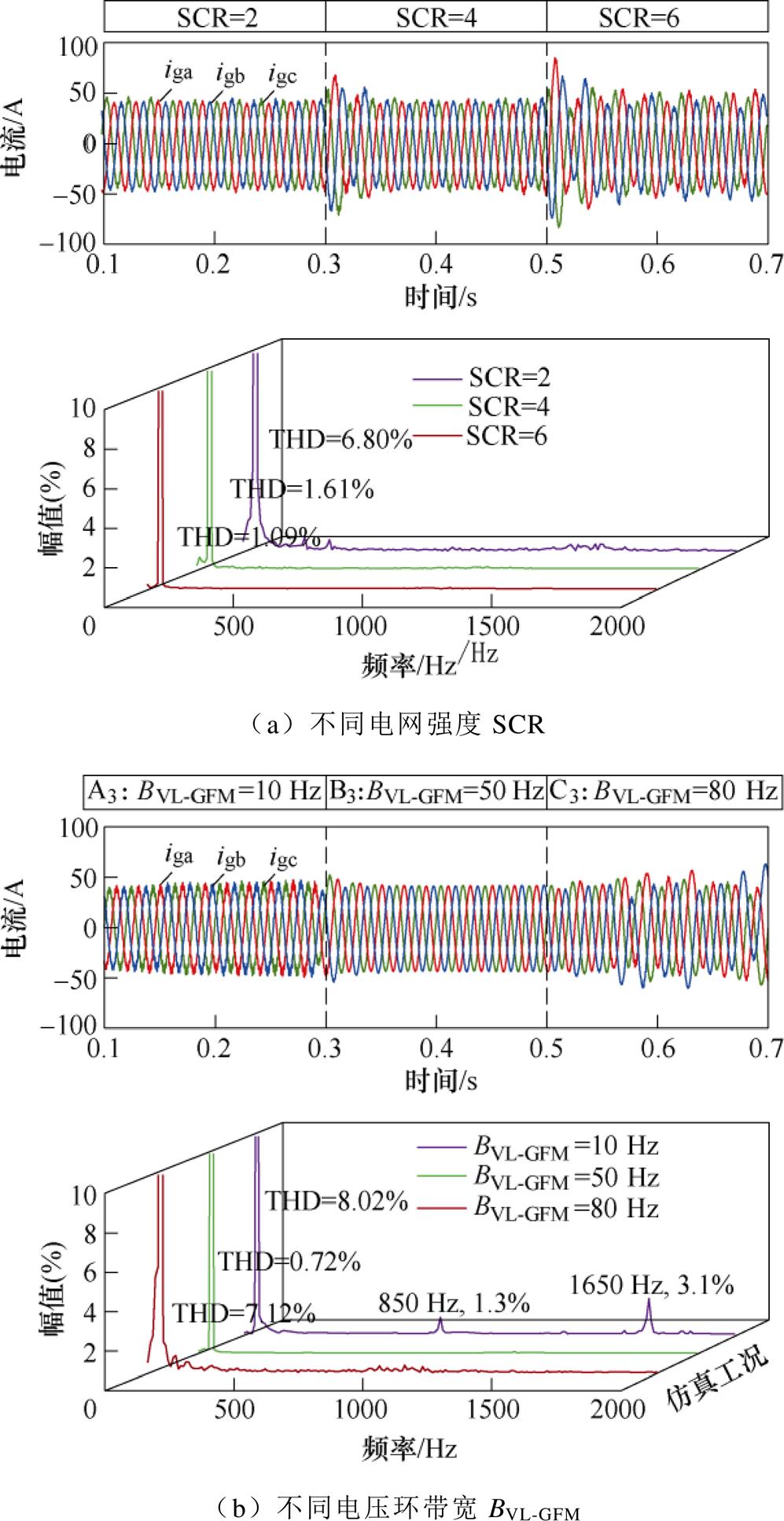
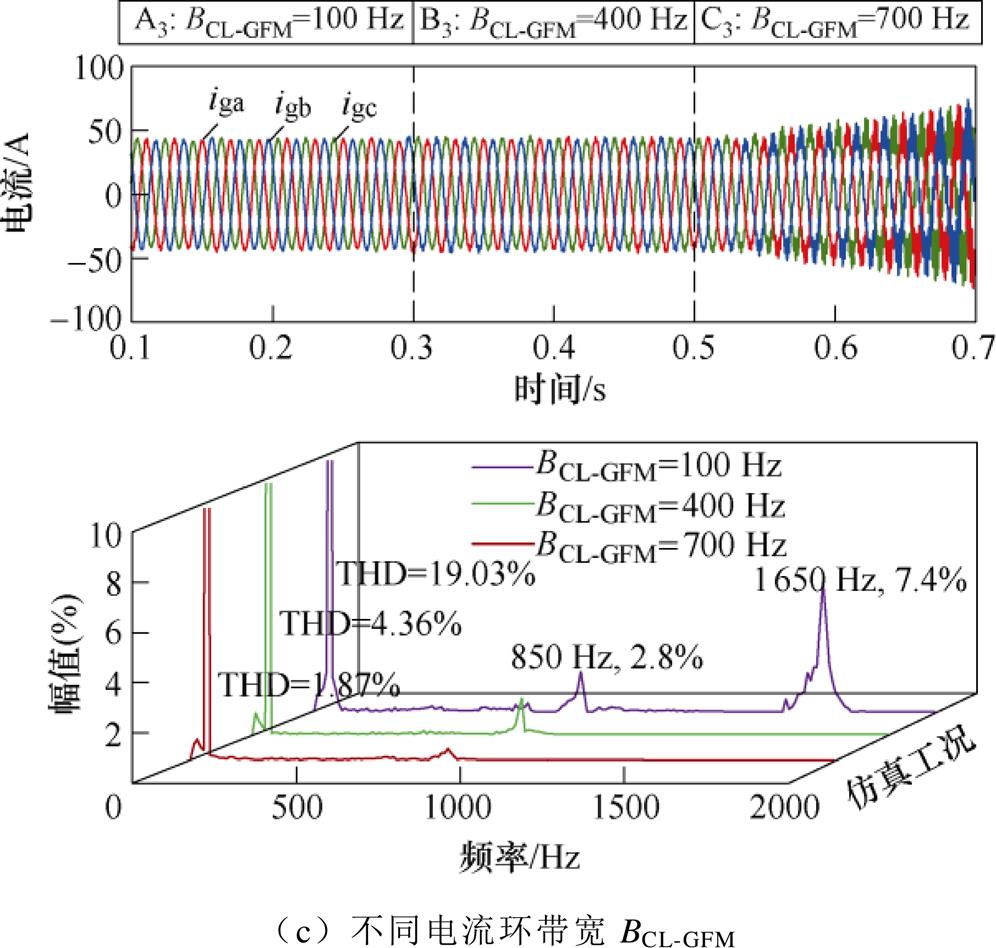
图16 GFMs关键作用因子仿真验证及FFT分析
Fig.16 Simulation validation and FFT analysis of the critical effect factors of GFMs
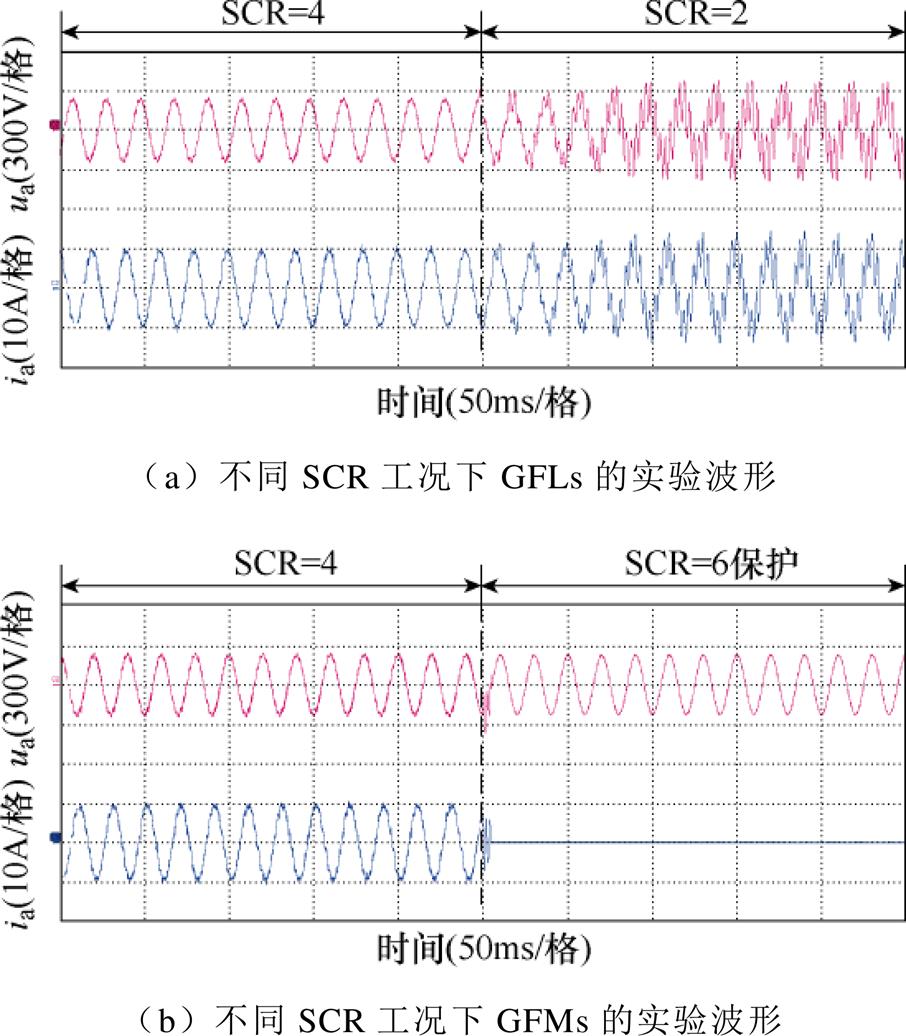
图17 不同SCR工况下逆变器并联系统实验结果
Fig.17 Experimental results of the inverters paralleled system under different SCR conditions
为进一步验证两类逆变器构成的异构系统具有更良好的稳定范围,本文以表1中GFL与GFM逆变器参数搭建HIPS仿真及实验平台,验证HIPS的互补特性。图18、图19分别给出了由HIPS稳态运行切换至GFL、GFM单类型逆变器运行的前后并网电流变化仿真和实验结果。可知,切除GFL实现由HIPS运行到GFM独立运行时,系统出现低频振荡;而由HIPS到GFL独立运行时,系统出现高频谐振。实验结果表明,由GFL与GFM构成的HIPS在一定程度上具有稳定性互补的效果。
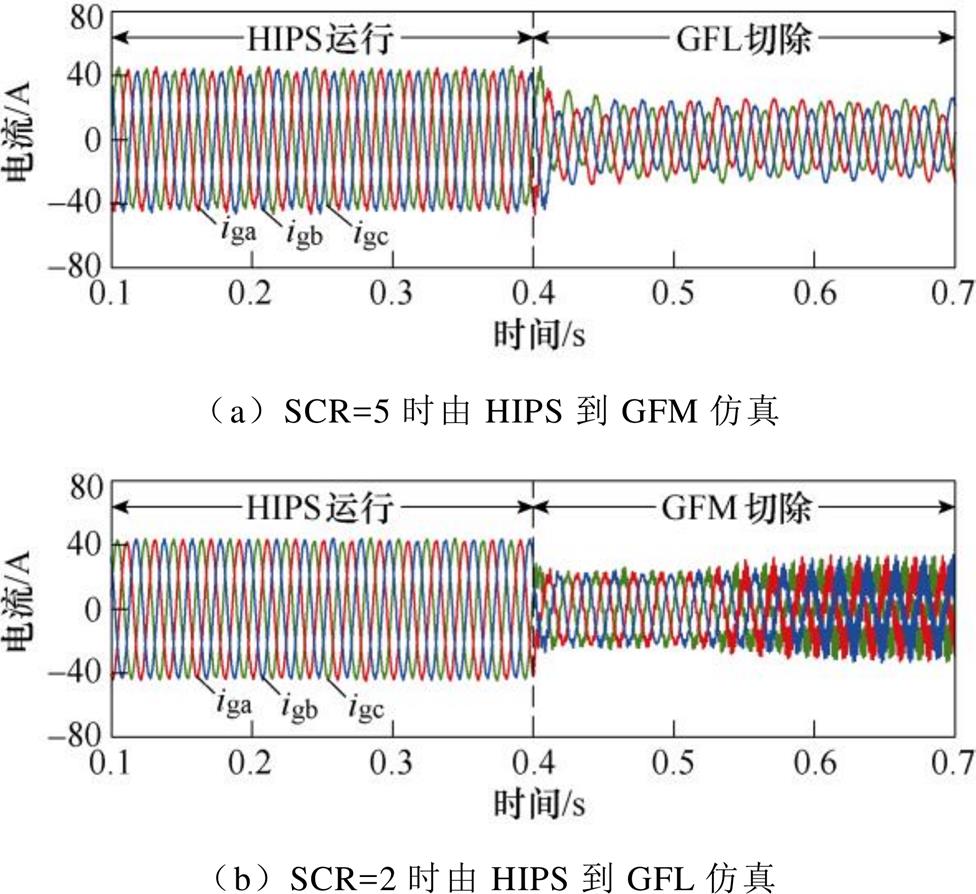
图18 不同工况下逆变器并联系统仿真结果
Fig.18 Simulation results of the inverter paralleled system under different working conditions
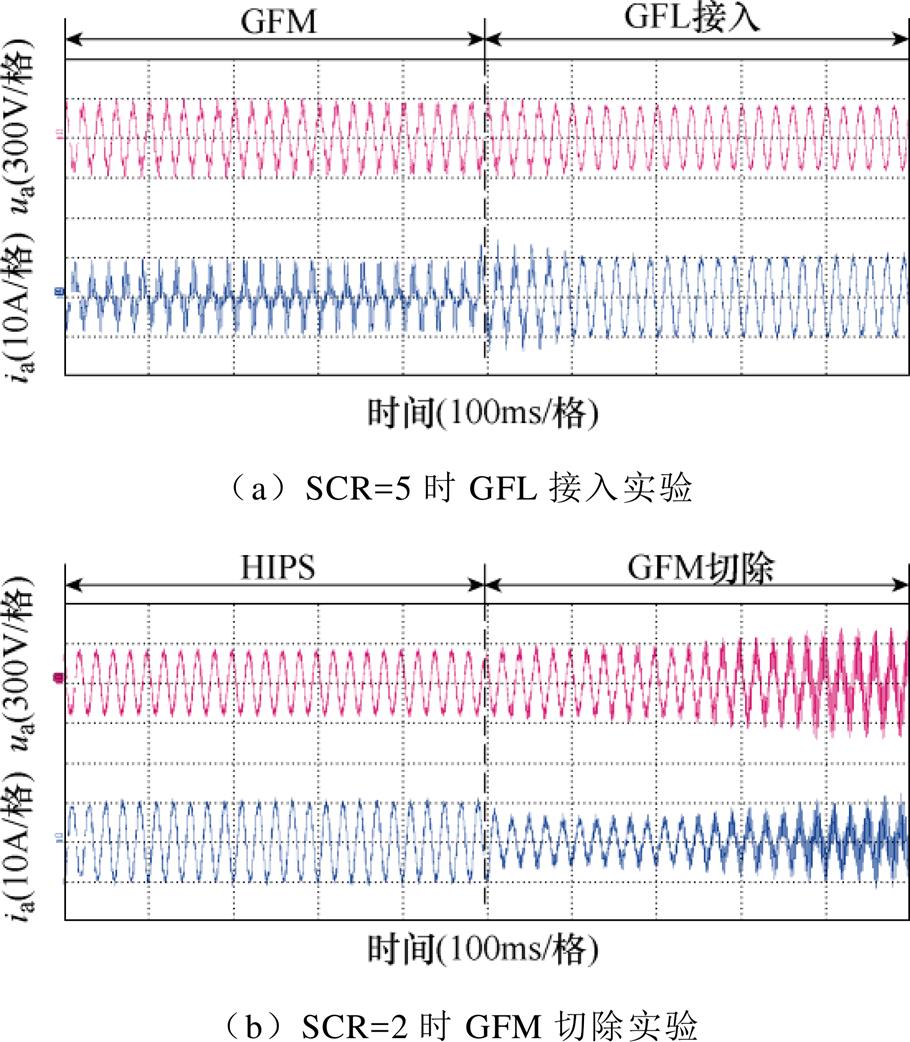
图19 不同工况下逆变器并联系统实验结果
Fig.19 Experimental results of the inverters paralleled system under different conditions
本文应用Matlab中的Profile函数,从计算内存消耗和CPU使用率等方面比较了Nyquist判据[20]、模态分析法[9]和改进Geshgorin圆判据,如图20所示。比较发现:所提出的判据运行内存占用为10 996 KB,峰值内存为1 900 KB,运行时间为1.019 s,CPU使用率为0.2%。其中,运行时间缩短至Nyquist判据的26%,CPU使用率缩短至Nyquist判据的17%,可见改进判据在计算效率方面具有显著优势。
此外,附图3分别给出了Nyquist判据、模态分析法和所提出的改进Gershgorin圆判据在两台逆变器并联系统中的稳定性分析结果。与仅用于直观判断系统稳定性的Nyquist判据和仅用于定位谐振点的模态分析法相比,所提出的改进Gershgorin圆判据既能判断系统的稳定性,又能定位谐振点。
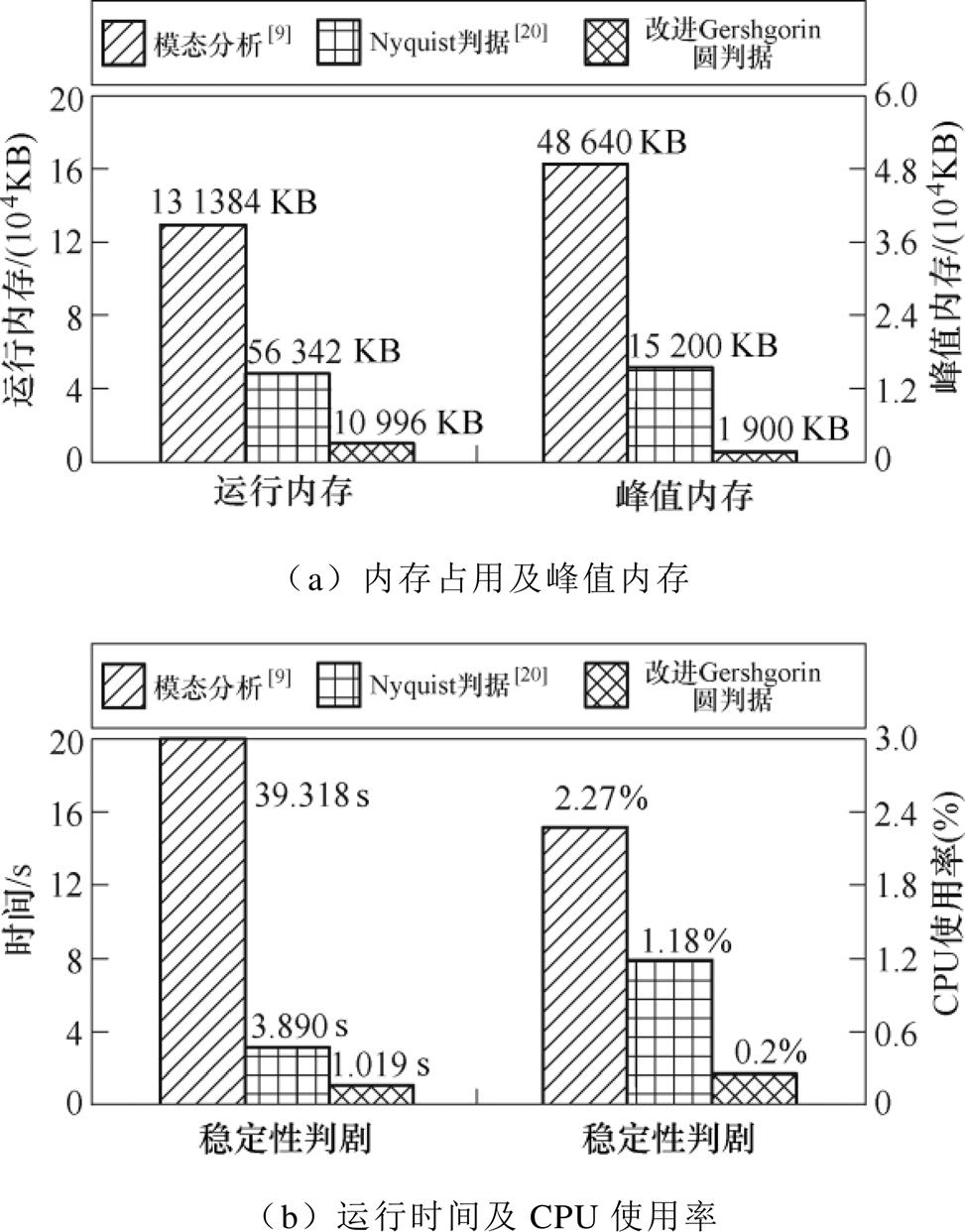
图20 不同稳定性判据的计算效率对比
Fig.20 Comparison of computational efficiency between different stability criteria
本文建立了HIPS的交互导纳矩阵,为分析系统的多维谐振特性奠定了模型基础。同时,为解决现有稳定性分析的繁琐问题,基于Gershgorin圆定理提出一种改进的多机稳定性判据,通过引入距离向量函数F简化分析过程,简化了稳定性判定过程,并且基于该判据能够详细分析各逆变器及关键作用因子对谐振点的影响机理。主要结论如下:
1)提出的改进Gershgorin圆判据可概括为:当且仅当距离向量F小于零时,可以判断系统处于失稳状态。该方法既能判断系统的稳定性,亦能直观地分析系统振荡点。相较于传统的Nyquist判据与模态分析冗余复杂的计算过程,改进Gershgorin圆判据将算法程序的运行时间缩短至Nyquist判据的26%,CPU使用率缩短至Nyquist判据的17%。
2)对比GFLs与GFMs可发现,GFLs在弱电网中出现高频谐振失稳的本质原因是过大的电网阻抗值引发电流环、锁相环失稳;且电网阻抗越大,与LCL滤波器耦合作用越强。而GFMs在强电网中极易发生低频段振荡失稳现象,其本质原因是过小的电网阻抗值引发功率环、电压环失稳。
3)HIPS综合了GFL与GFM的优势,二者在稳定性上具有一定程度的互补特性,可解释为:在弱电网中,由GFM为GFL提供电压和频率的支撑,削弱电网阻抗的耦合影响;在强电网中,GFM的网侧等效感抗值随着GFL接入而增加,感抗值的增加能够降低功率波动影响。
本文聚焦频域下异构系统HIPS的交互导纳矩阵模型及其稳定性分析,并对关键作用因素进行量化分析。下一步将结合实际工程,围绕复杂高阶异构系统的离散域建模问题进行深入研究。
附 录
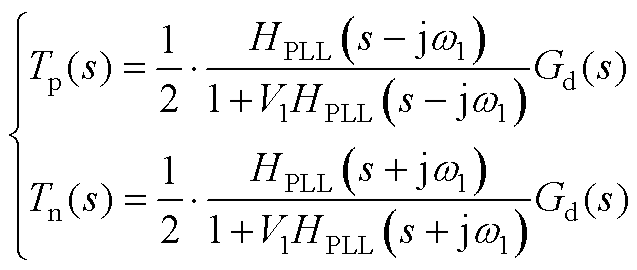 (A1)
(A1)
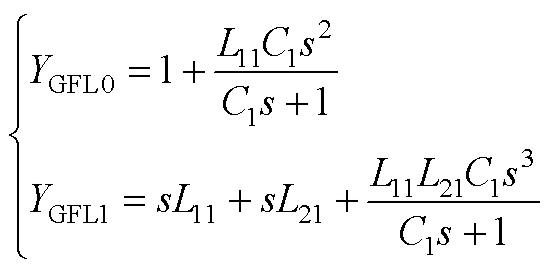 (A2)
(A2)
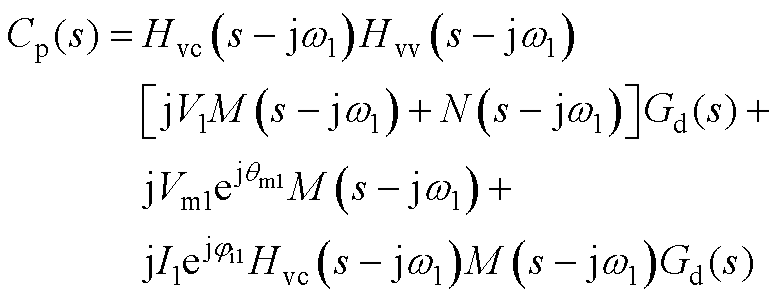 (A3)
(A3)
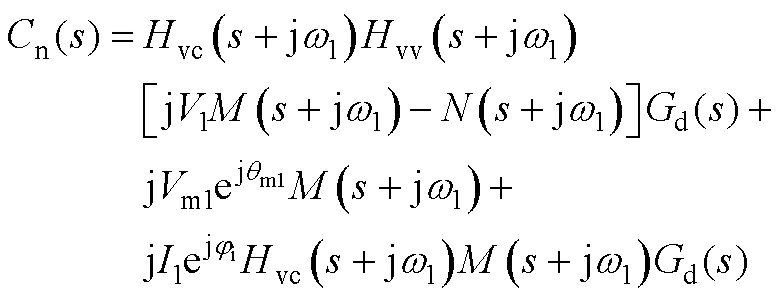 (A4)
(A4)
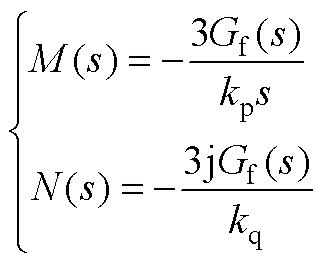 (A5)
(A5)
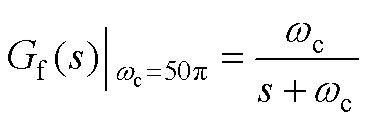 (A6)
(A6)
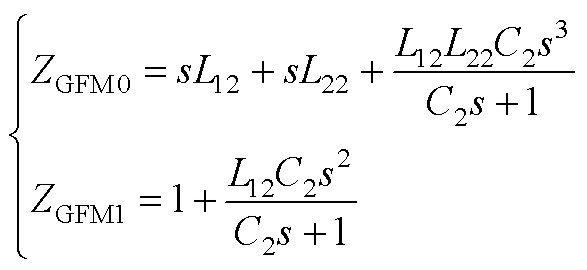 (A7)
(A7)
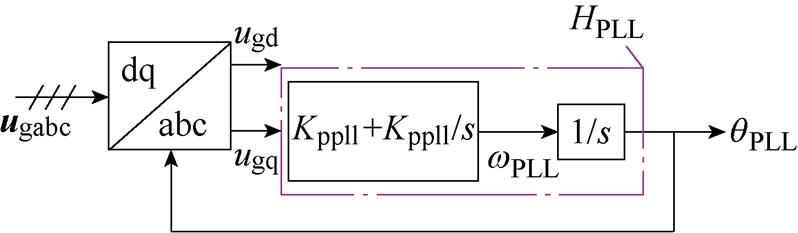
附图1 基于同步坐标系的锁相环结构
App.Fig.1 Structure diagram of SRF-PLL
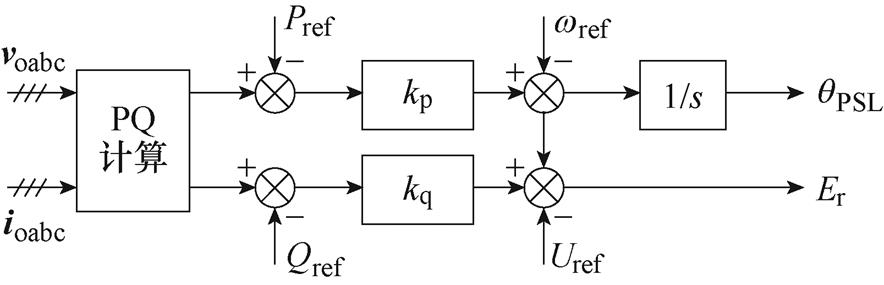
附图2 基于下垂控制的功率外环框图
App.Fig.2 Structure diagram of PSL based on droop control
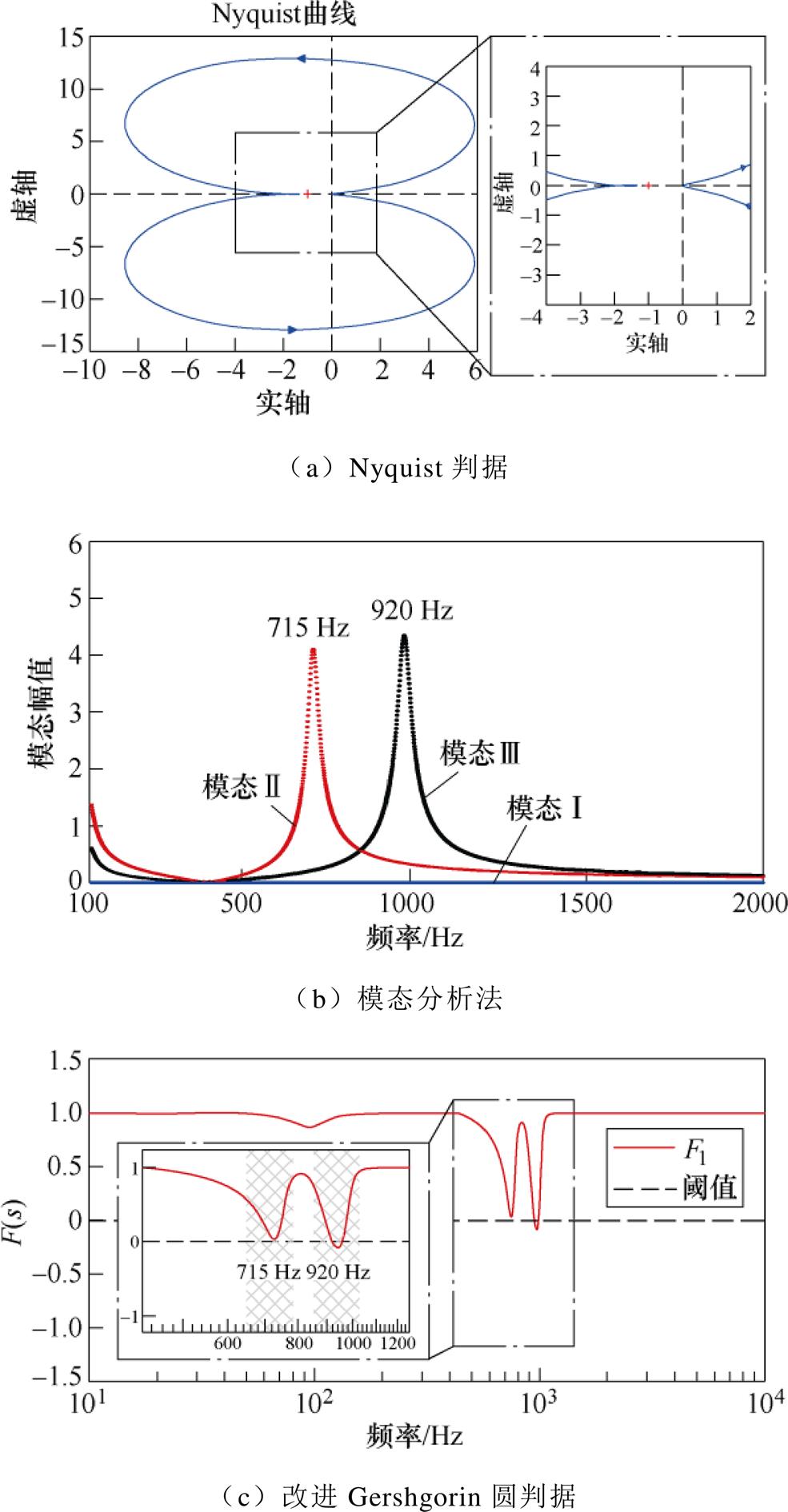
附图3 不同稳定性判据的对比
App.Fig.3 Comparison of different stability criteria
参考文献
[1] Fu Xikun, Sun Jianjun, Huang Meng, et al. Large- signal stability of grid-forming and grid-following controls in voltage source converter: a comparative study[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7832-7840.
[2] Wu Heng, Wang Xiongfei. Passivity-based dual-loop vector voltage and current control for grid-forming VSCs[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 8647-8652.
[3] 张兴, 李明, 郭梓暄, 等. 新能源并网逆变器控制策略研究综述与展望[J]. 全球能源互联网, 2021, 4(5): 506-515.
Zhang Xing, Li Ming, Guo Zixuan, et al. Review and perspectives on control strategies for renewable energy grid-connected inverters[J]. Journal of Global Energy Interconnection, 2021, 4(5): 506-515.
[4] 葛平娟, 肖凡, 涂春鸣, 等. 考虑故障限流的下垂控制型逆变器暂态控制策略[J]. 电工技术学报, 2022, 37(14): 3676-3687.
Ge Pingjuan, Xiao Fan, Tu Chunming, et al. Transient control strategy of droop-controlled inverter con- sidering fault current limitation[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3676- 3687.
[5] 谢震, 杨曙昕, 代鹏程, 等. 构网型全功率风电机组网侧变流器耦合分析及抑制策略[J]. 电工技术学报, 2023, 38(14): 3745-3758, 3768.
Xie Zhen, Yang Shuxin, Dai Pengcheng, et al. Grid-side coupling analysis and suppression strategy of grid-forming full-power wind turbines[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(14): 3745-3758, 3768.
[6] 杨权, 梁永昌, 魏建荣, 等. 多谐波源下分布式电源并网逆变器的谐波抑制策略[J].电工技术学报, 2023, 38(11): 2908-2920.
Yang Quan, Liang Yongchang, Wei Jianrong, et al. Research on harmonic suppression strategy of grid connected inverter under multi-harmonic sources[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2908-2920.
[7] Wang Weiyu, Jiang Lin, Cao Yijia, et al. A parameter alternating VSG controller of VSC-MTDC systems for low frequency oscillation damping[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4609- 4621.
[8] 张占俊, 李建文, 董耀, 等. 弱电网下多逆变器并网谐振失稳分析方法[J]. 电气技术, 2020, 21(10): 21-28.
Zhang Zhanjun, Li Jianwen, Dong Yao, et al. Method of resonance instability analysis of multiple grid- connected inverters in weak grid[J]. Electrical Engineering, 2020, 21(10): 21-28.
[9] Hong Lucheng, Shu Wantao, Wang Jianhua, et al. Harmonic resonance investigation of a multi-inverter grid-connected system using resonance modal analysis[J]. IEEE Transactions on Power Delivery, 2019, 34(1): 63-72.
[10] 涂春鸣, 谢伟杰, 肖凡, 等. 多虚拟同步发电机并联系统控制参数对稳定性的影响分析[J]. 电力系统自动化, 2020, 44(15): 77-86.
Tu Chunming, Xie Weijie, Xiao Fan, et al. Influence analysis of control parameters of parallel system with multiple virtual synchronous generators on stability[J]. Automation of Electric Power Systems, 2020, 44(15): 77-86.
[11] 林顺富, 戴烨敏, 颜昕昱, 等. 基于谐波状态空间理论的LCL型并网逆变器谐波交互及稳定性分析[J]. 电力自动化设备, 2022, 42(6): 76-83.
Lin Shunfu, Dai Yemin, Yan Xinyu, et al. Analysis on harmonic interaction and stability of LCL grid- connected inverter based on harmonic state space theory[J]. Electric Power Automation Equipment, 2022, 42(6): 76-83.
[12] Wang Rui, Zhao Xin, Sun Qiuye, et al. Stability analysis of phase locked loops for AC microgrids with hybrid power sources[J]. IEEE Transactions on Energy Conversion, 2023, 38(2): 1197-1207.
[13] Li Yitong, Gu Yunjie, Timothy C Green. Revisiting grid-forming and grid-following inverters: a duality theory[J]. IEEE Transactions on Power Systems, 2022, 37(6): 4541-4554.
[14] 汪春江, 孙建军, 宫金武, 等. 并网逆变器与电网阻抗交互失稳机理及阻尼策略[J]. 电工技术学报, 2020, 35(增刊2): 503-511.
Wang Chunjiang, Sun Jianjun, Gong Jinwu, et al. Mechanism and damping strategy of interactive instability between grid-connected inverter and grid impedance[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 503-511.
[15] Li Han, Wu Weimin, Huang Min, et al. Design of PWM-SMC controller using linearized model for grid-connected inverter with LCL filter[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 12773-12786.
[16] 胡鹏, 艾欣, 肖仕武, 等. 静止无功发生器序阻抗建模及对次同步振荡影响因素的分析[J]. 电工技术学报, 2020, 35(17): 3703-3713.
Hu Peng, Ai Xin, Xiao Shiwu, et al. Sequence impedance of static var generator and analysis of influencing factors on subsynchronous oscillation[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3703-3713.
[17] 刘一锋, 周小平, 洪乐荣, 等. 虚拟惯性控制的负荷变换器接入弱电网的序阻抗建模与稳定性分析[J]. 电工技术学报, 2021, 36(4): 843-856.
Liu Yifeng, Zhou Xiaoping, Hong Lerong, et al. Sequence impedance modeling and stability analysis of load converter with virtual inertia control connected to weak grid[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 843-856.
[18] 胡宇飞, 田震, 查晓明, 等. 构网型与跟网型变流器主导孤岛微网阻抗稳定性分析及提升策略[J]. 电力系统自动化, 2022, 46(24): 121-131.
Hu Yufei, Tian Zhen, Cha Xiaoming, et al. Impedance stability analysis and promotion strategy of islanded microgrid dominated by grid-connected and grid- following converters[J]. Power System Automation, 2022, 46(24): 121-131.
[19] 陈杰, 闫震宇, 赵冰, 等. 下垂控制三相逆变器阻抗建模与并网特性分析[J]. 中国电机工程学报, 2019, 39(16): 4846- 4856, 4986.
Chen Jie, Yan Zhenyu, Zhao Bing, et al. On the impedance modelling and grid-connected characteri- stics of the three-phase droop controlled inverter[J]. Proceedings of the CSEE, 2019, 39(16): 4846-4856, 4986.
[20] 于彦雪, 关万琳, 陈晓光, 等. 基于序阻抗的虚拟同步机同步频率谐振现象[J]. 电工技术学报, 2022, 37(10): 2584-2595.
Yu Yanxue, Guan Wanlin, Chen Xiaoguang, et al. Synchronous frequency resonance in virtual syn- chronous generator based on sequence-impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2584-2595.
[21] 卫楚奇, 石磊, 周百灵, 等. 电压型与电流型逆变器序阻抗建模与分析[J]. 电力电子技术, 2020, 54(10): 107-110.
Wei Chuqi, Shi Lei, Zhou Bailing, et al. Sequential impedance modeling and analysis of voltage controlled and current controlled inverters[J]. Power Electronics, 2020, 54(10): 107-110.
[22] 李翼翔, 田震, 唐英杰, 等. 考虑构网型与跟网型逆变器交互的孤岛微电网小信号稳定性分析[J]. 电力自动化设备, 2022, 42(8): 11-18.
Li Yixiang, Tian Zhen, Tang Yingjie, et al. Small- signal stability analysis of island microgrid con- sidering interaction between grid-forming converter and grid-following converter[J]. Electric Power Automation Equipment, 2022, 42(8): 11-18.
[23] Yu Jiajun, Wang Shike, Liu Zeng, et al. Accurate small-signal terminal characteristic model and SISO stability analysis approach for parallel grid-forming inverters in islanded microgrids[J]. IEEE Transa- ctions on Power Electronics, 2023, 38(5): 6597-6612.
[24] 徐海亮, 高铭琨, 吴瀚, 等. 海上风电场-MMC互联系统频率耦合建模及稳定性分析[J]. 电力系统自动化, 2021, 45(21): 92-102.
Xu Hailiang, Gao Mingkun, Wu Han, et al. Frequency-coupling modeling and stability analysis of offshore wind farm-modular multilevel converter interconnection system[J]. Automation of Electric Power Systems, 2021, 45(21): 92-102.
[25] Xu Hailiang, Wu Han, Li Zhi, et al. Gershgorin-circle based low-complexity generalized Nyquist stability criterion for DFIG driven wind turbines[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2022, 12(1): 29-40.
[26] Wang Jianguo, Jiu Dun Yan, Jiang Lin, et al. Delay- dependent stability of single-loop controlled grid- connected inverters with LCL filters[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(1): 743-757.
[27] 刘津铭, 陈燕东, 伍文华, 等. 孤岛微电网序阻抗建模与高频振荡抑制[J]. 电工技术学报, 2020, 35(7): 1538-1552.
Liu Jinming, Chen Yandong, Wu Wenhua, et al. Sequence impedance modeling and high-frequency oscillation suppression method for island microgrid[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1538-1552.
[28] 王赟程, 陈新, 陈杰, 等. 基于谐波线性化的三相LCL型并网逆变器正负序阻抗建模分析[J]. 中国电机工程学报, 2016, 36(21): 5890-5898, 6033.
Wang Yuncheng, Chen Xin, Chen Jie, et al. Analysis of positive-sequence and negative-sequence impedance modeling of three-phase LCL-type grid-connected inverters based on harmonic linearization[J]. Pro- ceedings of the CSEE, 2016, 36(21): 5890-5898, 6033.
[29] 徐政. 新型电力系统背景下电网强度的合理定义及其计算方法[J]. 高电压技术, 2022, 48(10): 3805- 3819.
Xu Zheng. Reasonable definition and calculation method of power grid strength under the background of new type power systems[J]. High Voltage Engineering, 2022, 48(10): 3805-3819.
Abstract The modern power system has undergone a significant transformation with the high penetration of new energy sources and power electronic equipment. A distinctive feature of the power supply system dominated by new energy sources is the emergence of the heterogeneous inverter paralleled system (HIPS), characterized by the coexistence of grid-following (GFL) and grid-forming (GFM) inverters. Compared to a single-type multi-inverter paralleled system, HIPS needs to consider the device interactions and uncertainties introduced by differences between inverters. This paper focuses on the multi-dimensional resonance characteristics of HIPS and investigates the effects of interactions between different inverter types on system stability by establishing the HIPS interaction admittance matrix model.
Since the GFL is synchronized by a phase-locked loop (PLL) and the GFM is self-synchronized by a power-synchronized loop (PSL), the effects of PLL, PSL, and delay are comprehensively considered when establishing the HIPS interaction admittance matrix. It enables accurate modeling of different inverter types. An improved Gershgorin-circle stability criterion (GCSC) is proposed. The introduction of a distance vector function F simplifies the analyzing process. A parameter sensitivity calculation method based on GCSC is proposed, and the stability effects of key action factors on HIPS are quantitatively analyzed. Finally, the effectiveness of the theoretical analysis and stability criterion is verified by time-domain simulation arithmetic and experiments.
If the distance vector F is less than zero, the system is judged unstable. This method can determine system stability and visually analyze the oscillation point of the system. Compared to traditional methods such as the Nyquist criterion and modal analysis method, the GCSC reduces algorithm running time to 26% and CPU usage to 17%.
The following conclusions can be drawn. (1) The high-frequency resonant instability of the grid-following inverter paralleled system (GFLs) in a weak grid is primarily caused by the instability of the current loop and PLL triggered by the excessive grid impedance. The current loop bandwidth BCL-GFL has a narrow adjustable range within the stabilization region, which is the most important parameter affecting the stability of GFLs. Moreover, the coupling effect with theLCL filter becomes strong as the grid impedance increases. (2) GFMs are susceptible to low-frequency oscillatory instability in a strong grid, mainly caused by small grid impedance triggering PSL and voltage loop instability. The voltage loop bandwidth BVL-GFM is identified as a crucial parameter. (3) HIPS, integrating GFL and GFM advantages, exhibits complementary stability characteristics. In weak grids, the GFM provides voltage and frequency support for the GFL to weaken the coupling influence of grid impedance. In strong grids, the GFL access increases the grid-side equivalent inductive reactance of the GFM, reducing power fluctuation influence. In addition, the time-domain simulation and experimental results show that the resonance points of the FFT analysis of the grid-connected currents are consistent with the stability analysis results of the GCSC.
Focusing on the HIPS interaction admittance matrix model and its stability analysis, this paper quantitatively analyzes the key action factors. Further research is suggested to delve into discrete-domain modeling problems for complex high-order HIPS considering practical engineering aspects.
keywords:Grid-forming inverter, grid-following inverter, heterogeneous inverter paralleled system, the Gershgorin-circle theorem, parametric sensitivity analysis
DOI: 10.19595/j.cnki.1000-6753.tces.231089
中图分类号:TM464
国家自然科学基金(52077222)和山东省自然科学基金(ZR2020ME202)资助项目。
收稿日期 2023-07-11
改稿日期 2023-08-08
林鸿彬 男,1999年生,硕士研究生,研究方向为新能源并网稳定性问题及控制技术。E-mail: lin_hongbin@126.com
葛平娟 女,1996年生,博士,硕士生导师,研究方向为新能源电力变换与微电网技术。E-mail: gepingjuan@upc.edu.cn(通信作者)
(编辑 陈 诚)