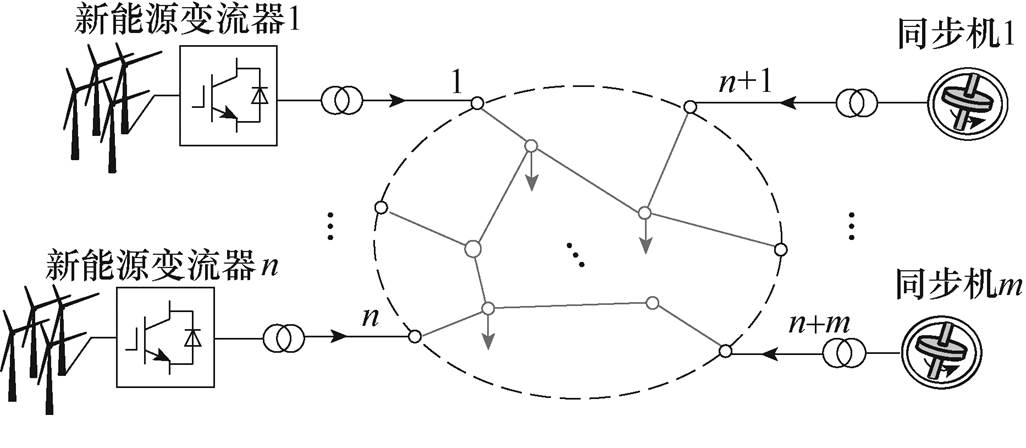
图1 多机系统示意图
Fig.1 Diagram of multi-device system
摘要 低惯量电力系统中跟网型变流器可能会与同步机转子动态产生交互,给系统稳定性分析引入新的问题,仅靠跟网型设备动态和短路比衡量交流系统强度不再准确。为此,该文综合分析系统惯量和短路比对跟网型变流器小干扰同步稳定的影响,提出适用于分析低惯量系统中并网变流器稳定性的方法,所提方法计算量低、物理意义明确。首先,推导变流器和同步机混联系统的闭环模型,并提取出能表征低惯量动态的相互作用系数矩阵,定性分析两类设备间的交互关系。其次,基于模态摄动理论,将原多机系统解耦为稳定性等效的子系统。然后,选取适用于分析小干扰同步稳定问题的相位主导回路,根据该回路提出综合考虑惯量和短路比的稳定性分析方法。最后,基于仿真算例验证了所提低惯量系统中并网变流器小干扰同步稳定性分析方法的有效性。
关键词:低惯量系统 小干扰同步稳定 广义短路比 最小子系统 系统强度
“双碳”背景下,随着新能源的大规模并网,电力系统逐渐演变为低惯量、低短路比的弱交流系统[1](以下简称为“弱交流系统”)。相较于传统电力系统,弱交流系统中源网耦合加剧,动力学行为更加复杂[2-4],并网变流器振荡失稳问题凸显。
在研究系统振荡失稳问题时,系统电压支撑强度(以下简称为“系统强度”)因可用于评估系统的稳定性和响应性能而备受关注[5]。系统强度由电网强度和设备动态共同决定,其中,电网强度描述了不考虑接入设备动态的开环交流电网性能,可通过短路比(Short Circuit Ratio, SCR)指标进行量化评估[6]。对于设备动态方面对系统强度的影响,鉴于目前我国交流系统中新能源机组的锁相同步控制技术较为成熟,在未来一段时间,新能源设备主要以跟网型控制并网(不特殊说明,本文所研究的变流器特指跟网型变流器),组网功能仍主要由同步发电机组承担[7],而同步机的惯量在很大程度上影响着其组网的能力[8]。由此可见,除交流系统短路比外,系统惯量也是衡量系统强度、评估并网变流器稳定性(后文稳定性均指小干扰同步稳定性)的重要指标。
短路比常被用于表征电力电子设备馈入交流系统时交流电网的相对强度,可用于分析交流网络连接特征对系统稳定性的影响[9-12]。变流器单馈入系统中,随着并网线路阻抗增大,短路比减小,锁相环动态和线路动态耦合加剧[13],导致由锁相环主导的系统小干扰同步失稳问题频发。文献[9]提出广义短路比(generalized Short Circuit Ratio, gSCR)的概念,建立了系统稳定性和电网强度之间的显性关系,实现了多变流器并网系统稳定裕度的量化。文献[10]基于模态摄动理论,将广义短路比理论拓展至异构多机系统。然而,上述研究重点关注系统低短路比特性对系统稳定性的影响,分析时通常将同步机等效为理想电压源节点,没有考虑弱交流系统的低惯量特性。
次/超同步频段下,弱交流系统的低惯量特性使得同步机无法等效为理想电压源,可能导致同步机与变流器两类设备的同步环节产生交互耦合[14-19],由此可见,交流系统对并网变流器稳定性的支撑强度还受到系统惯量的影响。针对两机互联系统,文献[16-17]通过时域仿真和特征值分析,研究了同步机惯量常数和网络阻抗对系统稳定性的影响;文献[18]分析了同步机的物理特性和控制参数对电力电子设备稳定性的影响,揭示了两类设备动态的交互路径。针对多机系统,文献[19]建立了系统的详细状态空间模型,通过仿真分析发现,与全电力电子设备电力系统相比,含有小容量同步机的弱交流系统更容易失稳。文献[20]给出了一种便于拓展的多设备统一坐标系建模方法,保留了各设备同步环节的动态,为探索弱交流系统稳定机理提供了一个分析方法。文献[21]针对同步稳定问题,兼顾了各类设备模型的鲁棒性和稳定分析的便捷性,给出了电流源视角下各类设备的统一建模方法。文献[22]针对系统小干扰稳定性提升问题,启发式地分析了惯量对系统稳定性的影响。上述文献基于仿真法或模型解析法探索了低惯量特性对系统稳定性的影响,为分析弱交流系统稳定性提供了一定的模型和理论基础。但基于仿真分析所得结论可能仅适用于特定工况,不利于揭示失稳机理,而且全系统电磁暂态模型仿真计算量过高,尚缺乏有效的全电磁仿真手段[23]。基于模型的解析方法又存在系统全阶模型过于复杂,容易出现“维数灾”问题[24]。此外,上述研究尚未分析弱交流系统多机间耦合机理,也缺少综合考虑弱交流系统低短路比和低惯量特性,以及对系统稳定性的定量化分析。
为此,本文综合分析了系统广义短路比和惯量对跟网型变流器小干扰同步稳定的影响,提出了适用于低惯量多机系统的并网变流器稳定裕度量化方法。首先,推导了变流器和同步机混联运行系统的闭环模型,利用相互作用系数矩阵定性分析了两类设备间的耦合关系;其次,进一步基于模态摄动理论,将多机原系统解耦为稳定性等效的子系统;然后,根据适用于分析系统小干扰同步稳定问题的主导回路,提出了综合考虑惯量和短路比的稳定性分析方法。最后,通过仿真算例验证了所提稳定性分析方法的有效性。
本节首先对要研究的问题及使用的假设条件进行了描述。然后以问题为导向,建立了同步机和变流器混联系统的闭环模型。进一步通过数学变换,分离出系统中两类设备耦合的动态,形成单位相互作用系数矩阵(Unit Interaction Factor Matrix, UIFM),并根据UIFM定性分析了两类设备间的 交互。
考虑图1所示的含n台变流器和m台同步机的多机混联系统,其中节点1~n连接新能源变流器,节点n+1~n+m连接同步机。

图1 多机系统示意图
Fig.1 Diagram of multi-device system
分析并网变流器锁相环主导的系统小干扰稳定性时,由于变流器锁相环动态与同步机摇摆方程动态处于不同时间尺度,可基于奇异摄动定理假设同步机节点电压幅值和相位恒定,即认为同步机节点为无穷大节点[25]。然而低惯量系统中,两类同步环节的带宽可能产生交互耦合,即在锁相环的时间尺度上,同步机无法提供理想的电压支撑能力,不能再简单地将同步机节点视为无穷大节点,需要考虑其动态对并网变流器稳定性的影响。本文聚焦弱交流系统中并网变流器锁相环主导的小干扰同步稳定问题,拟研究问题可归纳为:
(1)弱交流系统中的低惯量特性,是如何诱发并网变流器小干扰失稳的?
(2)如何综合短路比和惯量两个维度,定量化分析弱交流系统的小干扰稳定性、评估系统强度?
为了更好地阐述和论证上述问题,考虑以下合理简化:①网络中电容动态对所研究的锁相环主导的小扰动稳定问题影响较小,各线路的阻感比均相同[5];②考虑负荷为恒电流负荷,在恒功率或恒阻抗负荷时,可以通过端口等值等方法,将负荷等效至设备端口处,进而将其动态归至设备侧进行解 耦[26];③新能源变流器间的动态特性和同步机间的动态特性相似(两类设备各自同构),且同类设备间的相位差较小[9]。当考虑两类设备各自都异构时,可以参考文献[11]的处理方法,本文不再赘述。
按图1中的虚线可将系统模型划分为网络和设备两部分,对应的导纳矩阵分别为YN(s)和YG(s)。根据多变量频域理论,系统闭环模型Ysys(s)表示[27]为
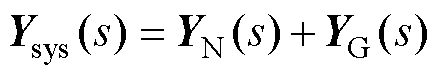 (1)
(1)
1.2.1 设备侧导纳模型
对于小干扰同步稳定问题,设备以电流源形式建模并兼顾了各类设备模型的鲁棒性和稳定分析的便捷性[21],可建立简洁统一的闭环模型。因此,本文设备侧建模以电流源形式建模。
首先建立变流器设备线性化的导纳模型。全局xy坐标系下,第i(i=1~n)台变流器导纳模型GVSC(s)可以表示为
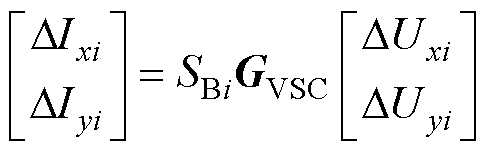 (2)
(2)
其中
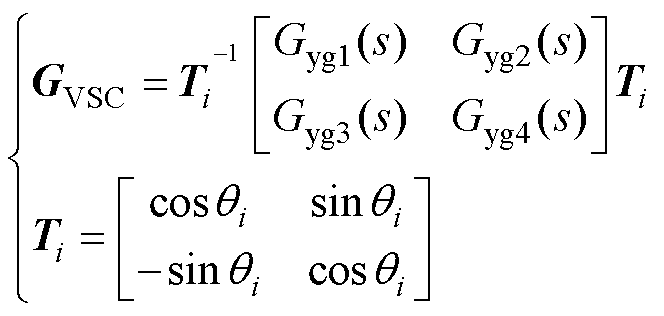 (3)
(3)
式中,Gyg1(s)、Gyg2(s)、Gyg3(s)和Gyg4(s)为变流器在同步dq坐标系下以自身容量标幺后的导纳矩阵元素,推导过程及具体表达式见文献[13];q 为稳态时坐标系间的相位差;SBi为第i台变流器经系统基准容量标幺后的自身额定容量。值得一提的是,同步dq坐标系是稳态时与局部dq坐标系重合的同步旋转坐标系,该坐标系下的导纳模型包含了同步环节(锁相环)的动态,因此仅通过稳态的坐标变换[21]和容量归一化,即可得到全局xy坐标系下变流器设备(i=1~n)导纳矩阵动态。
建立同步机的导纳模型。为了重点分析惯量的耦合作用,本文建立诺顿等效后内电流源端口处的模型,将自身容量标幺下的定子感应电动势的动态LSG归至网络,如附图1所示。由于同步机诺顿等效后为内电流源并联导纳的形式,将LSG归至网络时增加了同步机设备节点的自导纳,增加量为对角矩阵BSG=diag(SBj/LSG),其中对角元素SBj/LSG为比值的形式,表征了考虑容量归算后各节点导纳增加量的有名值。式(4)给出了同步全局xy坐标系下第j(j=n+1~n+m)台同步机内电源端口处的导纳模型,具体推导过程及各元素的表达式如附录式(A1)~式(A8)所示。
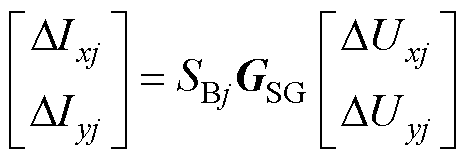 (4)
(4)
结合跟网型变流器和同步机的导纳模型,全局xy坐标系下设备侧动态模型可表示为
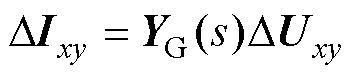 (5)
(5)
其中
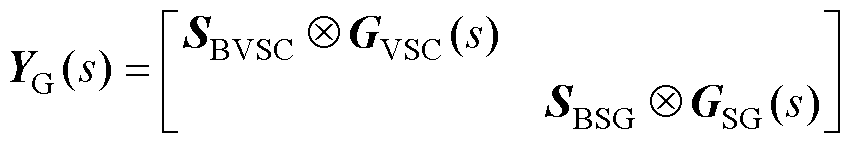
式中,SBVSC=diag(SBi)、SBSG=diag(SBj)分别为变流器和同步机的容量矩阵;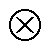 表示Kronecker积。
表示Kronecker积。
1.2.2 交流电网模型
全局xy坐标系下,交流电网动态模型[9](以电流流出变流器为正方向)为
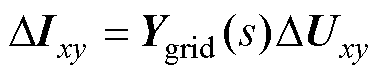 (6)
(6)
其中
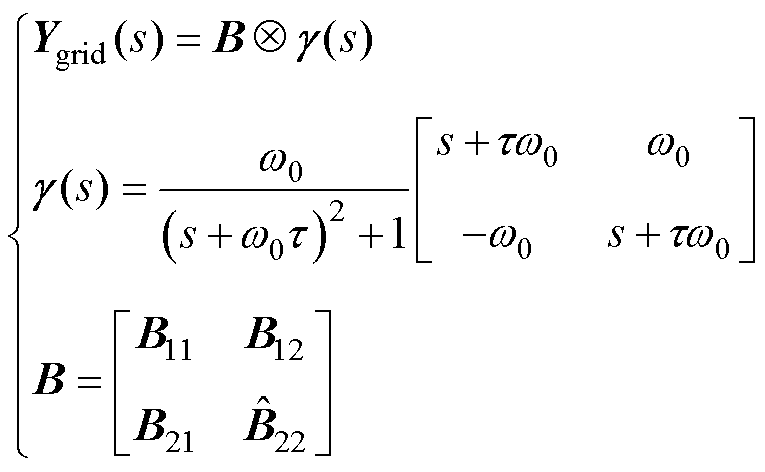 (7)
(7)
式中,D表示变量的微增量;Uxy=[Ux1Uy1Ux2Uy2… Ux(n+m) Uy(n+m)]T、Ixy=[Ix1Iy1Ix2Iy2…Ix(n+m)Iy(n+m)]T分别为设备节点电压和电流的列向量;Ygrid(s)为交流电网的导纳传递函数矩阵;s为拉普拉斯算子;w0=2π f0为工频角速度;t 为线路电阻与电感的比值,t=Rij/Lij;B为消去内部无源节点的工频导纳矩阵; 为考虑了同步机内电抗的子导纳矩阵;B11∈Rn×n、B12∈Rn×m、B21∈Rm×n、B22∈Rm×m为根据设备类型划分的子导纳矩阵。
为考虑了同步机内电抗的子导纳矩阵;B11∈Rn×n、B12∈Rn×m、B21∈Rm×n、B22∈Rm×m为根据设备类型划分的子导纳矩阵。
系统闭环框图如图2所示,对应的矩阵形式的系统闭环模型可表示为
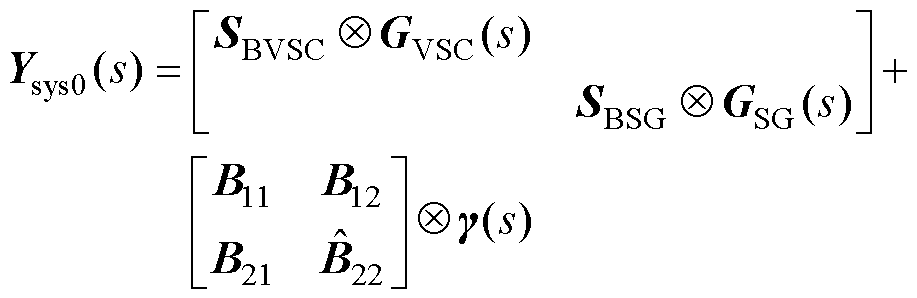 (8)
(8)

图2 多机系统闭环框图
Fig.2 Closed-loop block diagram of multi-device system
求解系统闭环特征方程det(Ysys0(s))=0,即可根据系统是否有特征值实部大于0判断系统稳定性。为了进一步分析同步机动态对并网变流器稳定性的影响,根据网络特征保持的Schur分解[28],可以得到关注变流器稳定问题的闭环模型为
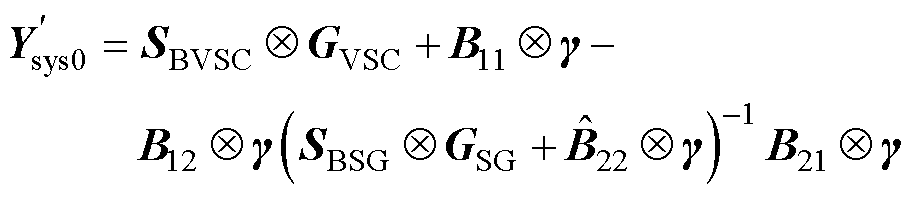 (9)
(9)
为表达简洁,式(9)及本节后文各式隐去了“(s)”。针对本文关注的低惯量场景,考虑系统中的同步机容量较小,根据Neumann级数性质,式(9)可进一步表示为
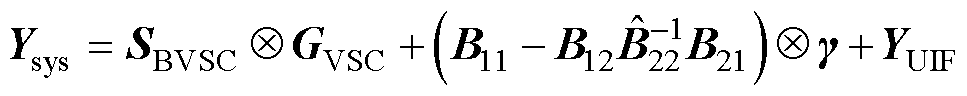 (10)
(10)
其中
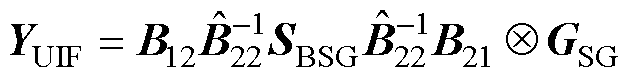 (11)
(11)
式中,YUIF为同步机和变流器的相互作用矩阵,反映了同步机动态对系统闭环特征方程的影响,可用于对系统的定性分析[29]。如当系统中同步机占很大比例时,对应的同步机容量矩阵中各元素SBj较大,此时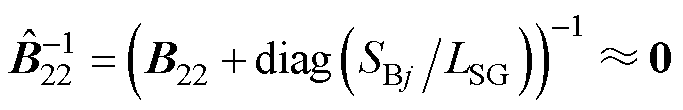 ,对应的系统闭环特征方程可表示为
,对应的系统闭环特征方程可表示为
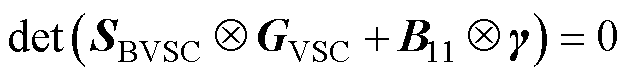 (12)
(12)
而在同步机容量很小时有SBj≈0、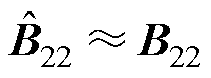 ,对应的系统闭环特征方程可表示为
,对应的系统闭环特征方程可表示为
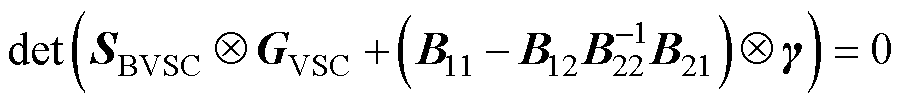 (13)
(13)
由此可见,当不考虑同步机动态的交互耦合时(对应节点变为无穷大或接地节点),系统的闭环特征方程中仅包含变流器和网络动态的交互,与变流器多馈入系统的闭环特征方程相同[10]。此时相互作用矩阵YUIF=0n×n。由此可见,YUIF项包含了同步机和互联两类设备的网络动态,定性地描述了低惯量系统中同步机和变流器动态的交互作用,为低惯量系统的稳定性分析提供了模型基础。此外,整理为YUIF形式的闭环模型式(10),可以通过摄动理论和模态解耦进行降阶,从而能通过低阶等效模型量化分析低惯量对并网变流器稳定性的影响。
在第1节建立的系统闭环模型的基础上,本节首先利用矩阵摄动理论,构造了一个与原系统稳定性分析等效的同构系统;其次通过模态解耦,将构造出的等效同构系统解耦为多个子系统,并给出了主导系统稳定性的子系统(即最弱子系统)的小信号电路模型。由此可提取出影响原复杂系统稳定性的关键因素,并将其具象为子系统中底层元件的 交互。
文献[10]基于广义短路比的概念,给出了一系列将多机同构的系统解耦为等效子系统的方法,进而可以通过分析低阶的子系统,表征原高阶系统的稳定性。根据上述思路,首先需要构造一个与原系统稳定性等效的同构系统。根据矩阵摄动理论[30],可以构造出与式(10)所示原系统稳定性等效的同构系统为
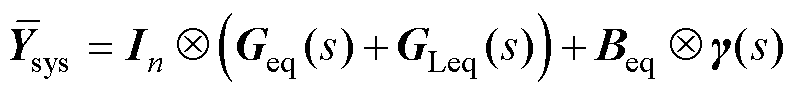 (14)
(14)
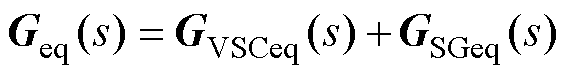 (15)
(15)
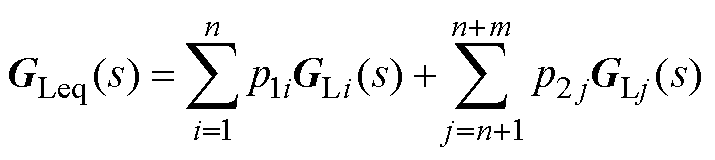 (16)
(16)
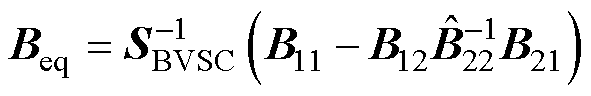 (17)
(17)
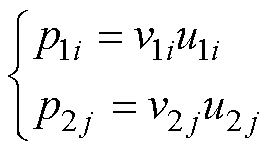 (18)
(18)
其中
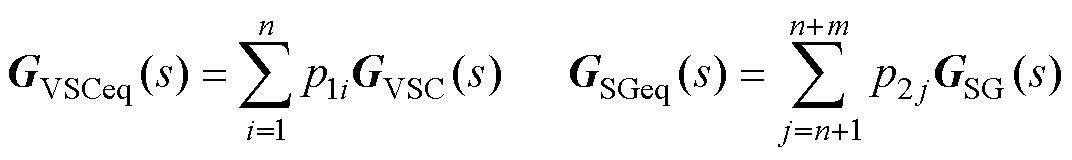
式中,Geq(s)为等效同构设备的导纳模型,由等效变流器模型GVSCeq(s)和等效同步机模型GSGeq(s)求和得到;GLeq(s)为等效负荷的导纳模型,由等效至设备端口的负荷GLi(s)和GLj(s)[26]加权求和得到,在系统中负荷都为恒电流负荷时,该项为0;Beq为拓展导纳矩阵,其物理含义为保留变流器端口网络动态导纳矩阵,具体形式为保留变流器端口导纳矩阵的舒尔补数;p1i和p2j分别为第i台变流器和第j台同步机的权重系数,用于加权得到等效同构设备;u1i和v1i分别为Beq最小特征值l1对应的左右特征向量u1和v1中的第i个元素;u2j和v2j分别为向量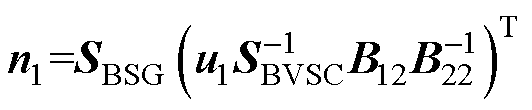 和
和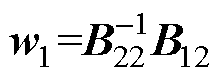 中的第j个元素,j=1~m。表1给出了式(14)~式(18)中各参数和物理量的含义及选取方法。
中的第j个元素,j=1~m。表1给出了式(14)~式(18)中各参数和物理量的含义及选取方法。
表1 等效同构系统中各参量含义及选取方法
Tab.1 Meaning and selection methods of parameters in the equivalent isomorphic system

物理量含义及选取方法 Geq(s)构造的等效同构设备的导纳模型,由等效变流器模型GVSCeq(s)和等效同步机模型GSGeq(s)加权求和得到 GLeq(s)等效负荷的导纳模型,由等效至变流器端口负荷导纳模型GLi(s)和等效至同步机端口负荷导纳模型GLj(s)加权求和得到 Beq拓展导纳矩阵,物理含义为保留变流器端口网络动态导纳矩阵 l1Beq最小特征值,为系统的广义短路比,物理意义为最弱等效子系统中线路等效电感的倒数 p1i变流器设备的加权系数,p1i为第i台变流器设备的加权系数 u1i, v1iBeq最小特征值l1对应的左右特征向量u1和v1中的第i个元素 p2j同步发电机设备的加权系数,p2j为第j台同步机的加权系数 u2j, v2j向量和中的第j个元素
至此,构造出了一个与原异构系统稳定性等效的同构系统式(14),可进一步用于解耦降阶。决定原系统式(10)中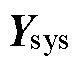 稳定性的主导特征轨迹可以由等效同构系统
稳定性的主导特征轨迹可以由等效同构系统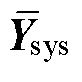 的一阶近似进行表示,且误差为
的一阶近似进行表示,且误差为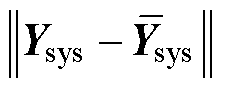 的高阶无穷小。此外,由于两类设备各自同构,式(15)中的等效设备是由两类各自同构的设备加权求和得到,因此将各设备传递函数叠加时仅需直接求和对应的权重即可,保留了设备动态特性。
的高阶无穷小。此外,由于两类设备各自同构,式(15)中的等效设备是由两类各自同构的设备加权求和得到,因此将各设备传递函数叠加时仅需直接求和对应的权重即可,保留了设备动态特性。
对于式(14)中的等效同构系统,可将其解耦为多个独立的子系统[10],重点关注其中主导系统稳定性的最弱子系统,该子系统与原系统稳定性等效,其闭环模型可表示为
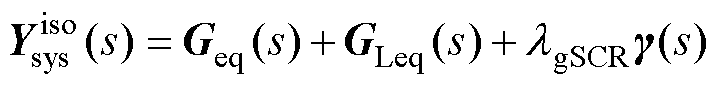 (19)
(19)
式中,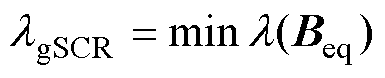 为系统的广义短路比,量化了交流系统的电网强度。与原高阶复杂系统相比,该子系统模型阶数较低且形式清晰,降低了稳定性分析的计算量,便于分析关键参数对系统稳定性的影响,而且可以进一步形成具体的电路模型。结合等效同构模型的具体表达式(15),选取合适的电流正方向后,以设备和网络的电流小信号动态形式写出式(19)模型的闭环特征方程为
为系统的广义短路比,量化了交流系统的电网强度。与原高阶复杂系统相比,该子系统模型阶数较低且形式清晰,降低了稳定性分析的计算量,便于分析关键参数对系统稳定性的影响,而且可以进一步形成具体的电路模型。结合等效同构模型的具体表达式(15),选取合适的电流正方向后,以设备和网络的电流小信号动态形式写出式(19)模型的闭环特征方程为
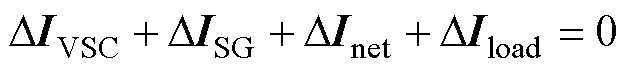 (20)
(20)
式中,DIVSC=GVSCeq(s)DUc为等效变流器模型的电流小信号动态;DISG=GSGeq(s)DUc为等效同步机模型的电流小信号动态;DInet=lgSCRg(s)DUc为流过等效网络模型电流的小信号动态;DIload=GLeqDUc为等效负荷模型的电流小信号动态;DUc为虚拟公共连接点的电压小信号模型。根据基尔霍夫定律,图3给出了解耦子系统对应的小信号电路模型。
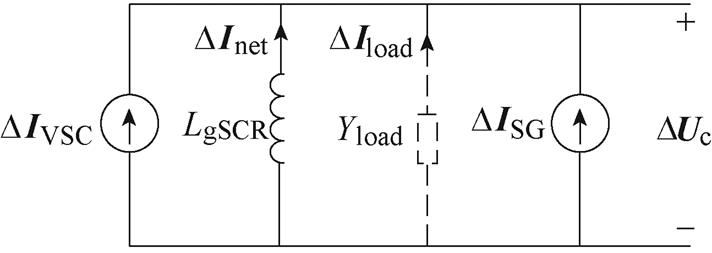
图3 等效子系统的小信号电路模型
Fig.3 Small signal circuit model of the equivalent subsystem
图3中,LgSCR为等效电感,其值可根据广义短路比计算得到,LgSCR=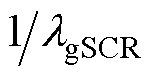 ,虚线部分为考虑系统存在恒阻抗负荷时子系统中的等效负荷,发电设备以电流源形式建模。式(19)中稳定性等效的最小子系统将多机混联的复杂模型简化,保留了影响原系统稳定性的关键因素(各发电设备特性和网络信息),根据式(19)可以得到图3所示的子系统的等效电路模型。从子系统变流器的视角观察,变流器所接入系统的动态由除变流器以外的环节决定,即由组网同步机动态(惯量)和网络动态(短路比)共同决定。此外,原系统中设备投切或网络拓扑变化等变动会导致子系统中等效出的设备和网络的具体参数发生变化,但子系统的结构不变,仍然是图3中电流源互联的形式,这方便进一步分析多机系统的基本耦合机制并提出稳定裕度评估指标。
,虚线部分为考虑系统存在恒阻抗负荷时子系统中的等效负荷,发电设备以电流源形式建模。式(19)中稳定性等效的最小子系统将多机混联的复杂模型简化,保留了影响原系统稳定性的关键因素(各发电设备特性和网络信息),根据式(19)可以得到图3所示的子系统的等效电路模型。从子系统变流器的视角观察,变流器所接入系统的动态由除变流器以外的环节决定,即由组网同步机动态(惯量)和网络动态(短路比)共同决定。此外,原系统中设备投切或网络拓扑变化等变动会导致子系统中等效出的设备和网络的具体参数发生变化,但子系统的结构不变,仍然是图3中电流源互联的形式,这方便进一步分析多机系统的基本耦合机制并提出稳定裕度评估指标。
本节首先选取了适用于分析小干扰同步稳定问题的相位主导回路,得到与最小子系统稳定性等效的单输入单输出(Single-Input Single-Output, SISO)系统,可以通过奈奎斯特判据分析其稳定性;然后建立了衡量系统稳定裕度的指标,并给出了综合考虑系统惯量和短路比的二维稳定运行域计算方法。
第2节建立的子系统模型考虑了设备的详细动态,其中一些环节对于本文关注的小干扰稳定问题影响较小。
首先,为便于揭示耦合机理并分离出惯量和电网强度对变流器小干扰稳定性的影响,对两类设备模型进行一些合理简化。本文关注的变流器小干扰同步失稳问题主要是锁相环与弱电网(低短路比低惯量)相互作用导致的次/超同步振荡。对于变流器,在该振荡模态所在的频段,根据奇异摄动理论,保留决定稳定性的锁相环动态进行建模,忽略功率外环等其他环节的动态,仅保留式(2)中Gyg4(s)的动态[13];对于同步机,为重点关注惯量的影响,采用经典二阶模型[20, 31]。结合附录式(A7)的具体表达式,保留了两类设备基本同步动态性质的子系统简化模型可表示为
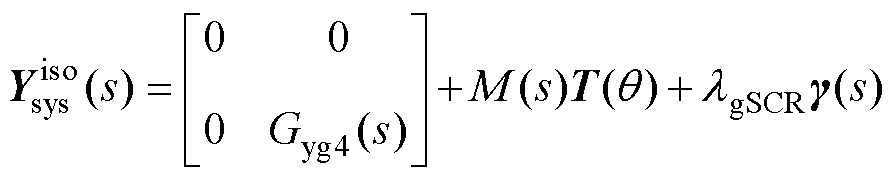 (21)
(21)
式中,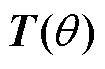 为坐标变换阵,具体形式详见附录式(A8),q=qSgeq-qSGeq,此处将等效变流器的坐标系变换阵归至同步机侧;M(s)=
为坐标变换阵,具体形式详见附录式(A8),q=qSgeq-qSGeq,此处将等效变流器的坐标系变换阵归至同步机侧;M(s)=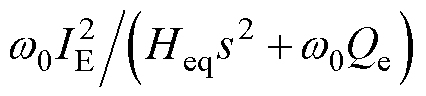 为同步机的角度动态,IE为同步机内电流源的幅值稳态值,Qe为内电流源发出的无功功率稳态值,Heq为通过模态摄动解耦得到的等效同步发电机的惯量,量化了原多机交流系统的惯量水平(以下简称为“系统等效惯量”)。
为同步机的角度动态,IE为同步机内电流源的幅值稳态值,Qe为内电流源发出的无功功率稳态值,Heq为通过模态摄动解耦得到的等效同步发电机的惯量,量化了原多机交流系统的惯量水平(以下简称为“系统等效惯量”)。
选取式(21)中简化系统的主导回路,对于某个环节主导的稳定问题,基于该环节对应的主导回路模型得到的稳定性分析结果的鲁棒性和标称性较好[32]。本文侧重于分析跟网型变流器锁相环动态与弱交流系统耦合导致的小干扰同步稳定问题,变流器模型中的Gyg4(s)元素包含了锁相环动态,反映了变流器的同步动态,因此选取Gyg4(s)同步回路作为主导回路进行分析,对应SISO系统闭环特征方 程为
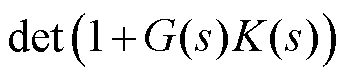 (22)
(22)
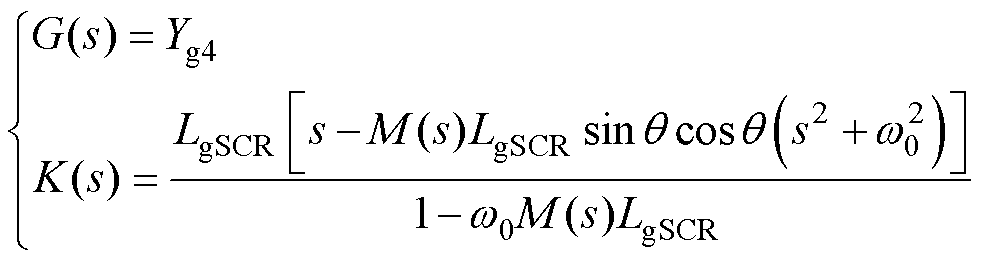 (23)
(23)
式中,G(s)、K(s)分别为系统的前向通路和反馈回路。以变流器端口的视角观察,反馈回路K(s)包含了除变流器外系统其余环节的动态,反映了变流器所接入系统的系统强度。由于K(s)包含了系统的惯量和广义短路比,因此系统强度受到等效惯量和广义短路比的共同影响,其中广义短路比反映了系统的电网强度,惯量项反映了系统的惯量水平。
至此,本节通过数学变换将式(8)所示的多输入多输出(Multiple-Input Multiple-Output, MIMO)系统,转化为稳定性等效的SISO 系统,进而可以通过奈奎斯特稳定判据判断系统的稳定性并量化稳定裕度。
对于如式(22)所示SISO系统,首先通过奈奎斯特稳定判据判断系统的稳定性,在系统稳定时,可以进一步量化系统稳定裕度。控制理论中,一般用灵敏度函数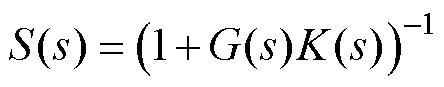 的H∞范数Fs对SISO系统的稳定裕度进行量化,其值越小,稳定裕度越大[27],系统强度越强。
的H∞范数Fs对SISO系统的稳定裕度进行量化,其值越小,稳定裕度越大[27],系统强度越强。
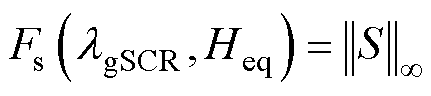 (24)
(24)
根据上述分析,图4给出了多机系统的稳定性分析及稳定裕度评估流程。具体地,首先,计算系统的稳定运行域,由于系统的稳定性受到lgSCR和Heq两个指标影响,在合理范围内遍历两指标的参数值,在不同参数取值的情况下对式(22)应用奈奎斯特判据判断子系统是否稳定,进而形成两个指标共同约束的二维稳定运行域(Feasible Region, FR);其次,对于某运行工况下的多机系统,通过图4所示方法得到该工况下的等效子系统,当该子系统的lgSCR和Heq落在可行域中时,即(lgSCR, Heq)∈FR,系统稳定;最后,在系统稳定时,可以根据稳定裕度函数Fs评估系统强度。
为验证上述理论分析的有效性,基于Matlab/ Simulink平台搭建如附图2所示的两区4机系统和附图3所示的10机39节点系统,选取系统基准容量为100 MV·A,设备关键控制参数、设备容量和交流网络线路参数见附表1~附表5,同步发电机的励磁等控制环节所用参数见文献[31]。
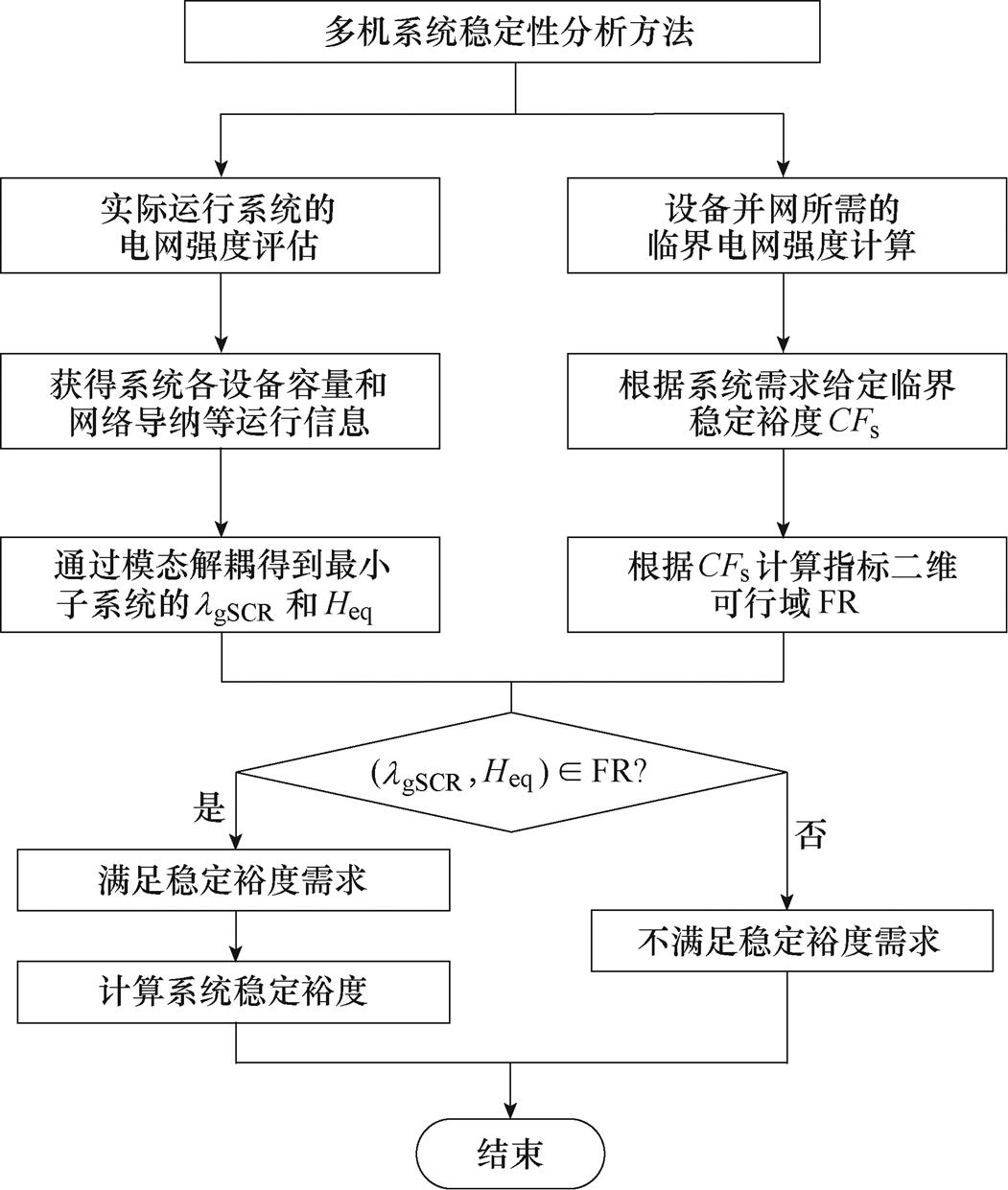
图4 多机系统稳定性分析流程
Fig.4 Flow chart of stability analysis of multi-device system
本节基于两区4机系统验证所提理论分析方法的有效性。
首先,验证第2节中解耦子系统与原系统小干扰稳定的等效性。本文主要关注不同类型设备间的交互,为简化分析,负荷采用恒电流负荷。修改系统网络阻抗和惯量的值,观察原两区4机系统和解耦子系统的主导特征根的变化,其中原系统的特征根通过Matlab/Simulink中搭建模型的状态空间方程计算得到,子系统的特征根通过Matlab中的m文件编程计算得到。两区4机系统等效前后主导特征根对比如图5所示。
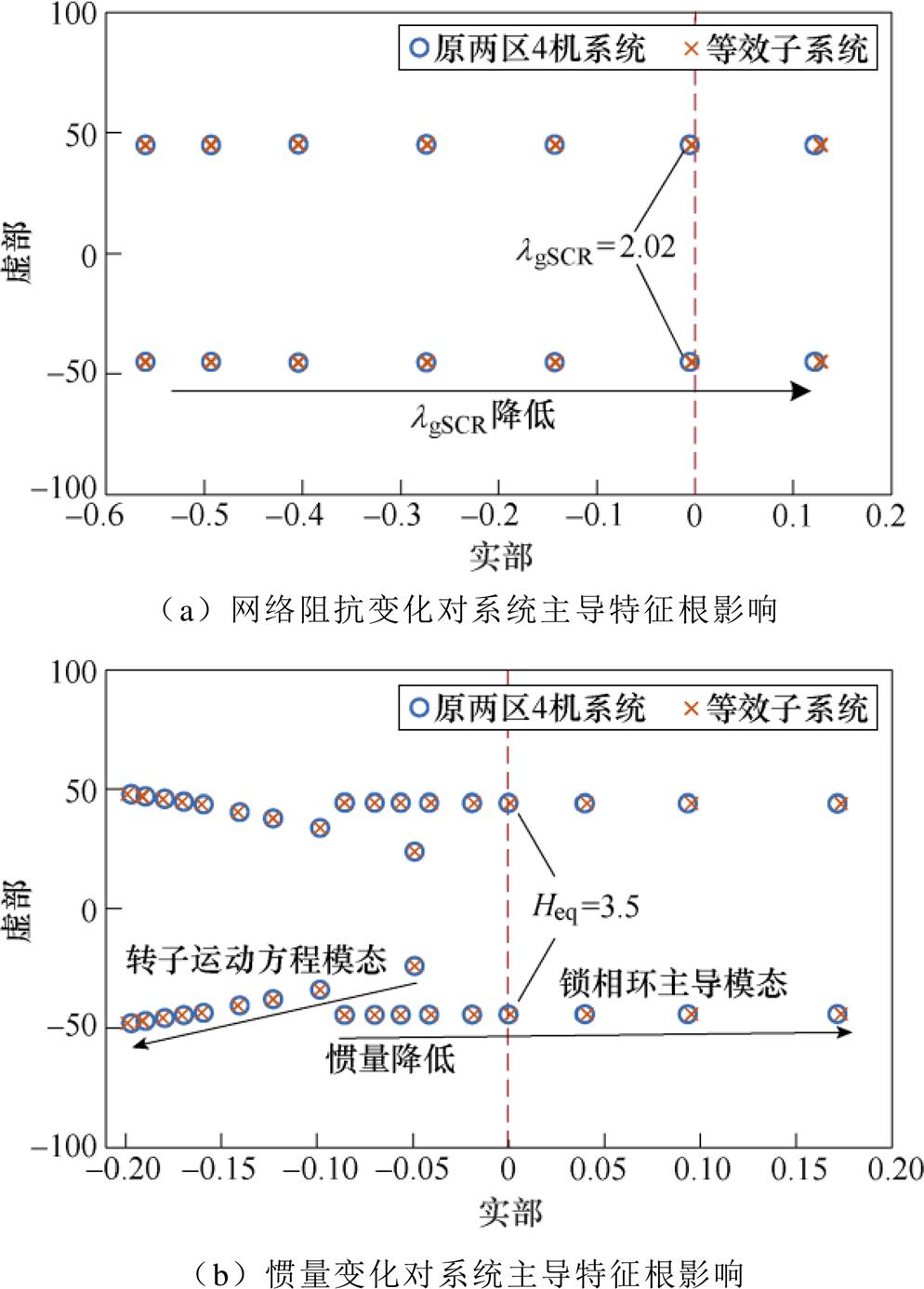
图5 两区4机系统等效前后主导特征根对比
Fig.5 Comparison of dominant roots of two area four machine power system before and after equivalence
图5a给出了Heq=20的高惯量系统中,网络线路电感L36、L46和L56由各自的初始值逐渐增加至初始值的600%,对应广义短路比lgSCR由2.876减小至1.913时,原两区4机系统和解耦子系统的主导特征根的变化,可以看出,电网强度降低,恶化了跟网型变流器小干扰同步稳定性。图5b给出了lgSCR= 2.1的低短路比系统中,各同步机惯量由5降至1.9时,系统主导特征根的变化,随着系统等效惯量降低,图5b中同步机转子运动方程对应模态的振荡频率逐渐增高,增至8 Hz附近(对应特征根虚部为50 rad/s)时,两类设备同步环节动态的带宽产生交互耦合,导致系统发生小干扰失稳。由此可见,低惯量系统的相位动态特性,将会增加锁相环型变流器的失稳风险。在系统强度(网络阻抗和惯量)变化的过程中,原始两区4机系统和等效子系统的主导特征根基本保持一致,验证了子系统和原两区4机系统小扰动稳定的等效性,因此通过模态解耦得到的子系统可以用于分析弱交流系统的稳定性问题。
值得一提的是,上述算例验证了子系统的稳定性与原系统等效,在该方法正确的情况下,可以利用解耦子系统分析各类稳定性问题,例如,同步机调速器与电力电子设备外环的低频段交互[18]、电力电子设备间的交互[33]等。由于本文关注低惯量系统中同步机转子运动动态和跟网型变流器锁相环动态的耦合,对于其他参数的影响不再展开分析。此外,本文所提简化模型式(21)的合理性和准确性验证详见附录第3节。
接下来,验证第3节中选取的同步主导回路分析低惯量系统稳定问题的有效性。在m文件中编写式(22)、式(23)所示SISO系统的闭环模型,并绘制其开环传递函数的奈奎斯特曲线。图6a和图6b分别给出了lgSCR由2.876减小至1.913和惯量由5降至1.9时的奈奎斯特曲线。可以看出,主导回路的稳定性判断结果与系统极点分析所得结果(见图5)一致。进一步地,根据3.2节中式(24)计算图6中稳定系统的裕度,表2给出了系统强度量化结果,Fs的值越小,稳定裕度越大,系统强度越强。
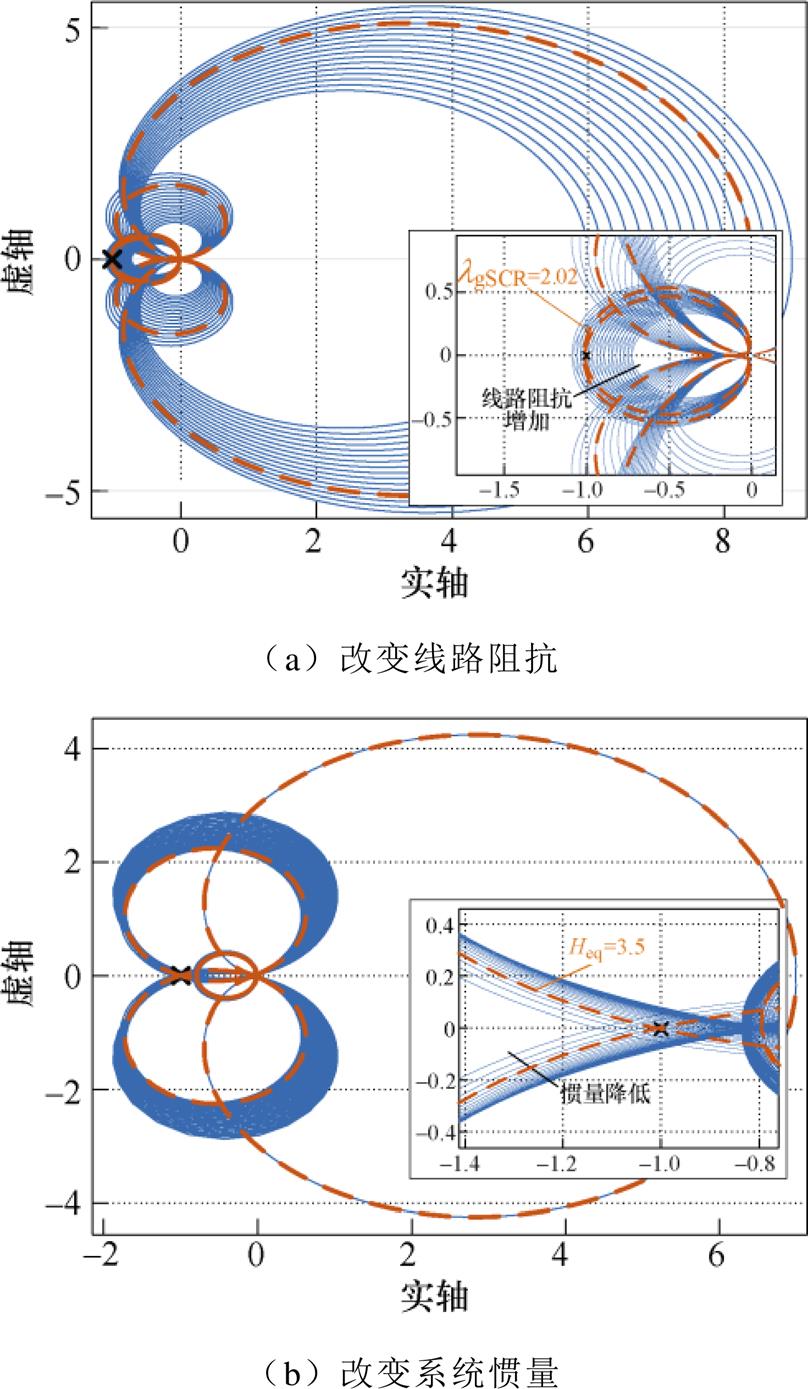
图6 两区4机系统主导回路的奈奎斯特曲线
Fig.6 Nyquist curves of the dominant loop of the two area four machine power system
表2 两区4机系统强度量化结果
Tab.2 Quantitative results of the two area four machine power system strength
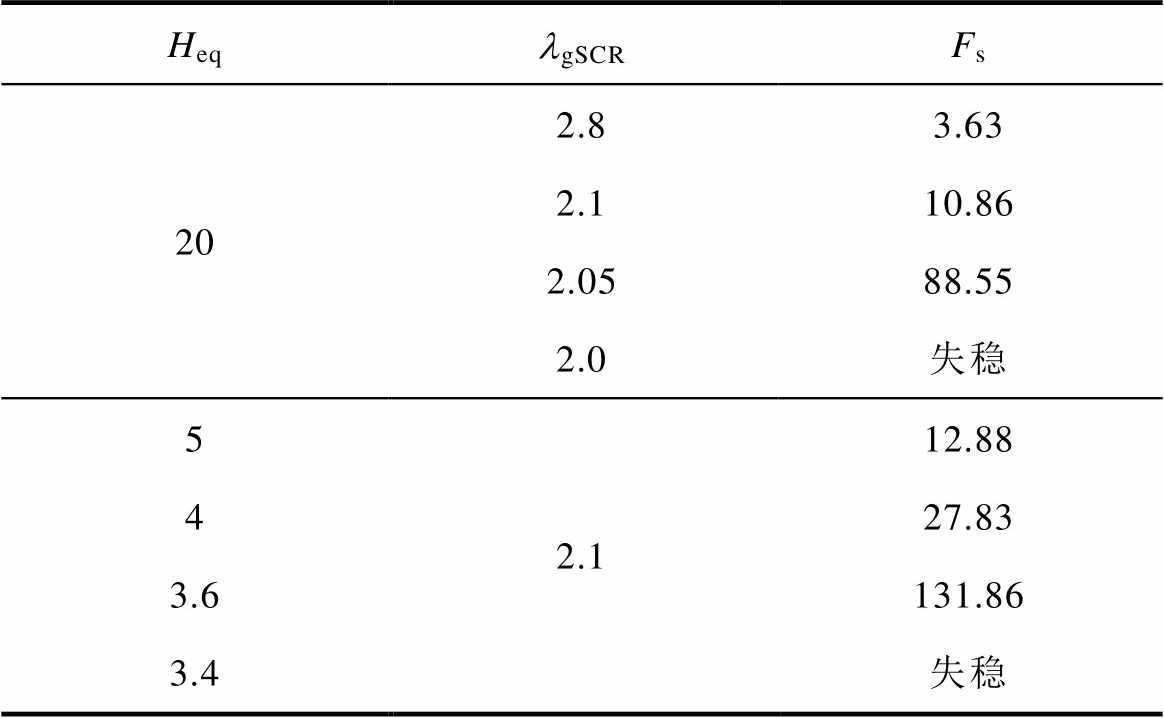
HeqlgSCRFs 202.83.63 2.110.86 2.0588.55 2.0失稳 52.112.88 427.83 3.6131.86 3.4失稳
进一步地,从时域角度验证所提理论的准确性。首先遍历系统等效惯量由1.5~9变化和系统广义短路比由1.9~3.1变化的参数域,根据如图4所示的稳定性分析流程,计算各工况下系统是否稳定,并给出了如图7所示的系统二维稳定运行域。
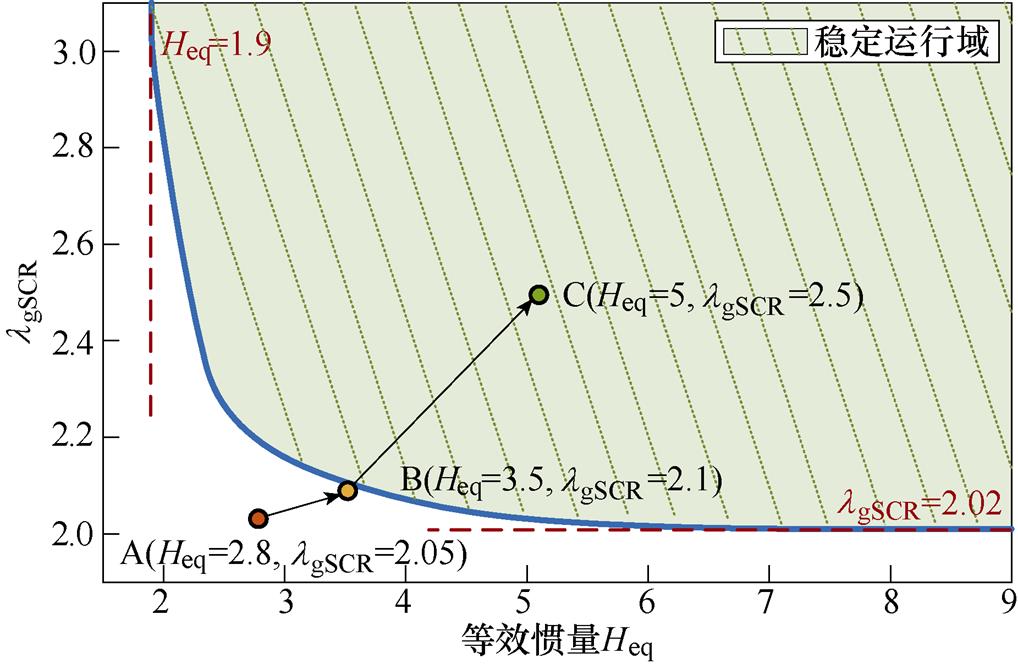
图7 两区4机系统二维稳定运行域
Fig.7 Two-dimensional stable operation domain of two area four machine power system
在Matlab/Simulink中搭建附图2中的两区4机系统的电磁暂态仿真模型。系统的初始工况为图7中的A点,在1.5 s和3 s分别切换至B和C点。系统运行在平衡点的情况下,于0.25 s时在同步机1的转子处施加一转速小扰动时,变流器1端口的有功功率时域仿真波形如图8所示。
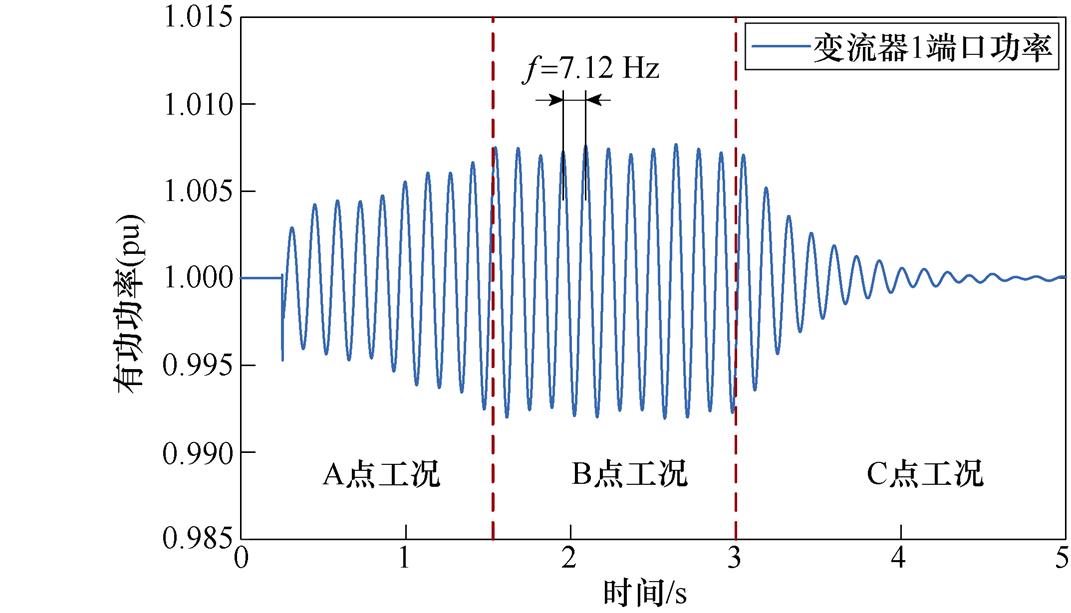
图8 两区4机系统时域仿真波形
Fig.8 Time domain simulation waveform of two area four machine power system
可以看出,在A、B和C三点处对应的工况下,时域波形分别振荡发散、等幅振荡和振荡收敛,与理论计算结果一致。其中,振荡发散的特征根为0.042±44.33i,振荡收敛特征根为-0.091±44.33i,振荡收敛对应特征根实部的绝对值大于振荡发散对应特征根的绝对值,因此收敛速度快于发散的速度,与图8中的仿真结果一致。此外,从曲线中得到的原两区4机系统的振荡频率为7.12 Hz,这与图5b中根据子系统计算得到的临界稳定特征根0.009± 44.33i的振荡频率7.05 Hz基本一致,说明了原始两区4机系统和等效子系统的最弱振荡模式相同。
本节基于IEEE 10机39节点系统,旨在验证本文所提稳定性分析方法的适用性,因此重点对比了最终得到的SISO简化模型和原系统的稳定性等效性。具体地,在模态摄动解耦和主导回路选取后,得到稳定性等效的SISO系统,并对比了Nyquist稳定性判断结果和时域仿真结果。
首先,根据附表5中系统交流网络线路参数,计算出系统的广义短路比lgSCR=2.18。根据图4中的稳定性分析流程,将原多机系统模态解耦为等效子系统并选取同步主导回路进行分析。图9给出了保持网络参数不变(lgSCR=2.18)情况下,等效惯量Heq为2、2.82和4时的系统Nyquist曲线。由图可知,在三种工况下,基于主导回路的稳定性判断结果分别为振荡发散、等幅振荡和振荡收敛。
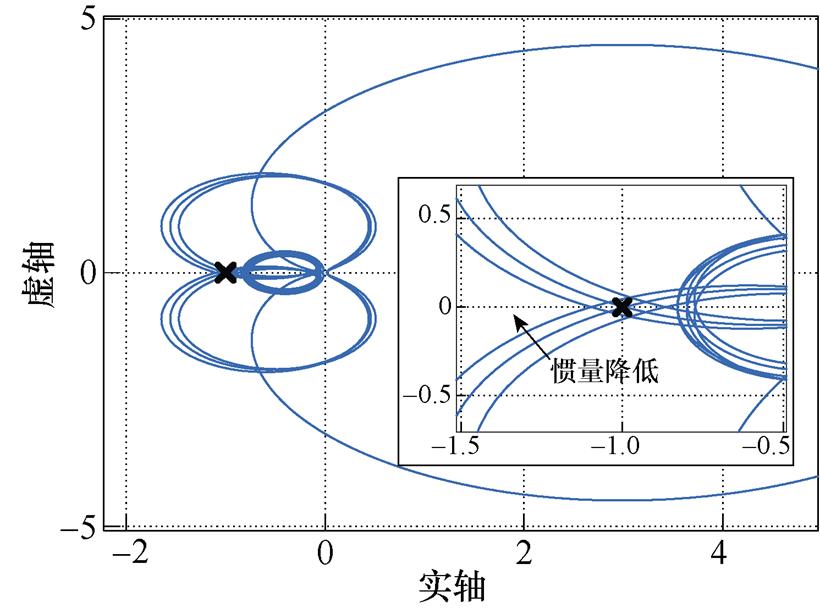
图9 10机39节点系统主导回路的奈奎斯特曲线
Fig.9 Nyquist curves of the dominant loop of the 10-machine 39-bus power system
在系统位于初始工况(lgSCR=2.18, Heq=2)平衡点的情况下,于1 s时在设备1(变流器)的端口处施加一q轴电压小扰动,并在8 s和11 s时将等效惯量设置为Heq=2.82和Heq=4,图10给出了变流器5端口的有功功率时域仿真波形。由图可知,时域仿真结果与理论分析结果一致,这验证了本文所提稳定性分析方法在多机系统中的适用性。
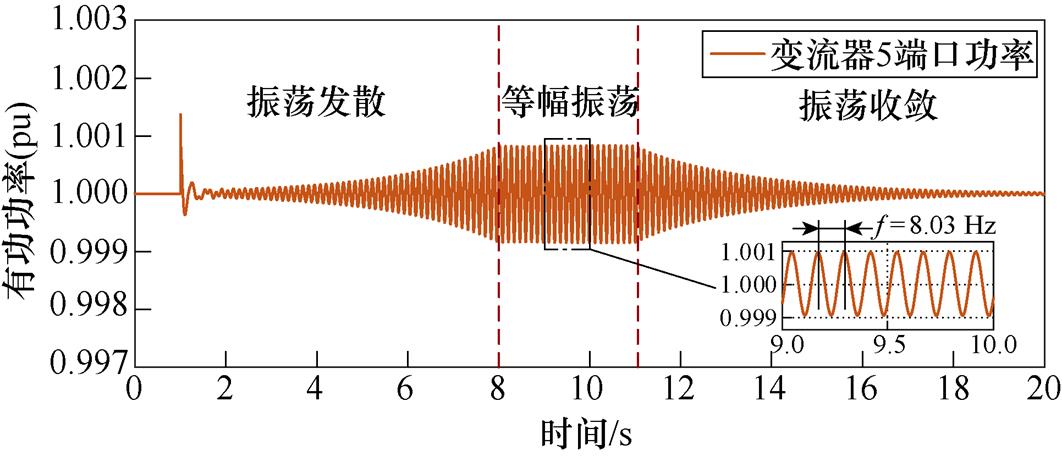
图10 10机39节点系统时域仿真波形
Fig.10 Time domain simulation waveform of the 10-machine 39-bus power system
综上所述,本节从模态理论分析和时域仿真两方面验证了所提模态摄动解耦和基于主导回路的稳定性分析方法的有效性。
本文针对弱交流系统中并网变流器次/超同步振荡问题,综合分析了广义短路比和等效惯量对并网变流器稳定性的影响。主要结论如下:
1)同步机容量小的低惯量系统可以解耦为n个单变流器和单同步机互联的最小子系统,其中最弱子系统与原系统的稳定性等效。
2)弱交流系统中,在设备动态固定的前提下,并网变流器小干扰稳定性由线路连接阻抗和同步机惯量时间常数共同决定,可由广义短路比和系统等效惯量共同约束的二维稳定域刻画,当广义短路比或等效惯量减小时,系统稳定性恶化;反之,则改善。
3)随着同步机容量减小,系统等效惯量水平逐渐降低,两类设备同步环节动态的带宽产生交互耦合,可能诱发并网变流器锁相环主导的次/超同步振荡失稳。
如何综合分析不同环节交互下的系统稳定性问题,是未来主要的工作之一。
附 录
1. 同步机建模及其简化模型
同步发电机定子感应电动势动态可以通过等效电感LSG的动态表示为
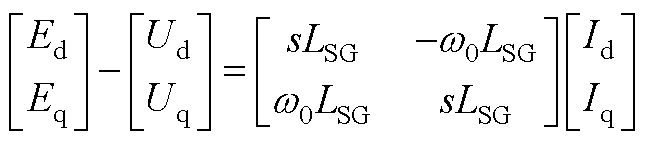 (A1)
(A1)
内电动势的幅值动态为
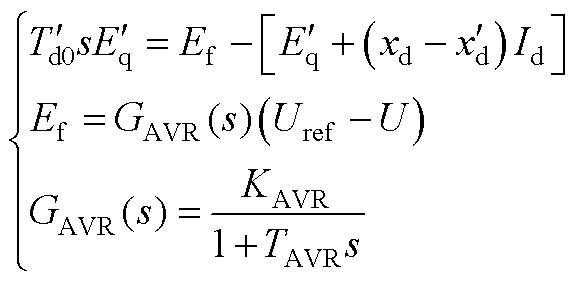 (A2)
(A2)
式中,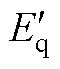 为q轴暂态电动势,为同步机的内电动势;
为q轴暂态电动势,为同步机的内电动势;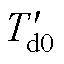 为d轴暂态时间常数;
为d轴暂态时间常数;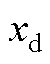 和
和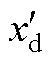 分别为同步电抗及暂态电抗;Ef为励磁电动势;Uref为同步发电机端口电压参考值;
分别为同步电抗及暂态电抗;Ef为励磁电动势;Uref为同步发电机端口电压参考值;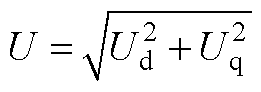 为端口电压实际值,Ud和Uq分别为其d轴和q轴分量;GAVR(s)为励磁系统传递函数,可以由一阶惯性环节近似表示;KAVR为其增益;TAVR为其等效时间常数。
为端口电压实际值,Ud和Uq分别为其d轴和q轴分量;GAVR(s)为励磁系统传递函数,可以由一阶惯性环节近似表示;KAVR为其增益;TAVR为其等效时间常数。
内电动势的相位动态为
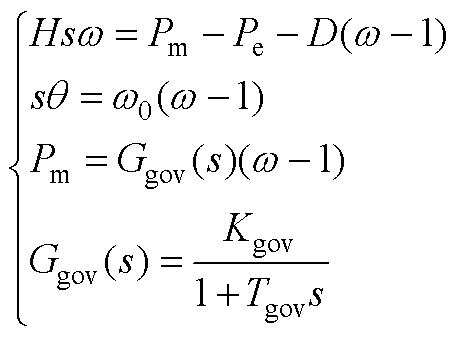 (A3)
(A3)
式中,H、D分别为同步机惯量和阻尼系数;q 、w 分别为转子角与转子转速;w0为系统标称频率;Pe为有功功率;Pm为调速系统机械功率;Ggov(s)为调速器传递函数,可以由一阶惯性环节近似表示;Kgov为其增益;Tgov为其等效时间常数。
根据式(A4)对同步机诺顿等效,附图1给出了等效前后的同步机模型电路。将虚线右侧的定子电感动态归至网络侧。
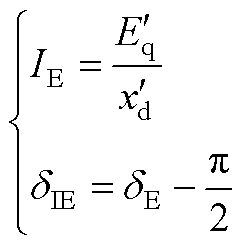 (A4)
(A4)
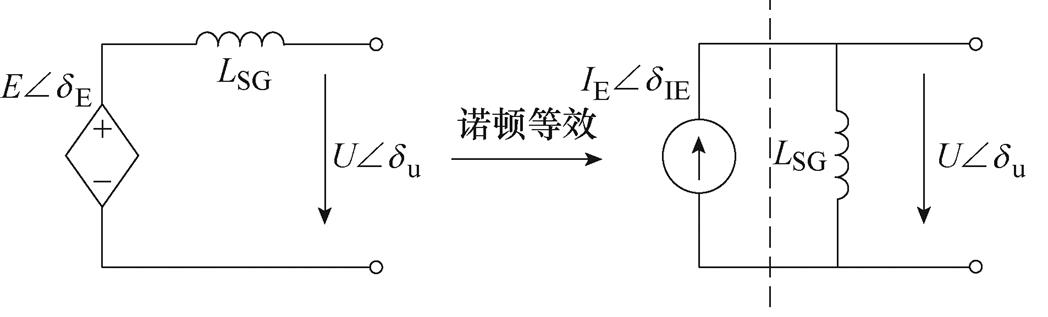
附图1 同步机内部诺顿等效示意图
App.Fig.1 Norton equivalence diagram of a synchronous generator at internal port
线性化式(A1)~式(A4)并联立求解,得到内电流源处的导纳模型为
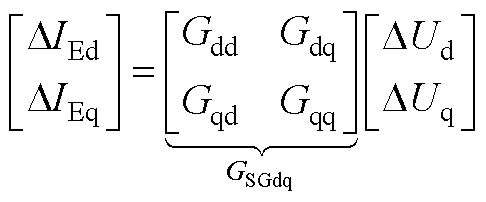 (A5)
(A5)
其中
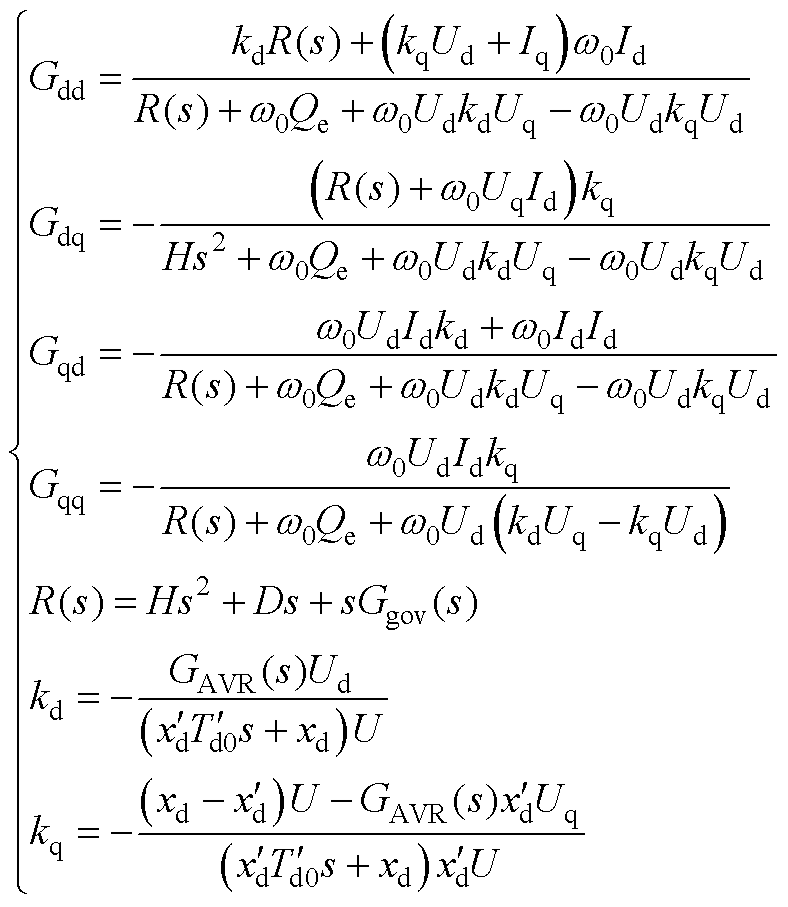 (A6)
(A6)
dq同步坐标系和全局同步坐标系存在稳态相位差q 时,仅需进行式(A7)坐标变换即可。
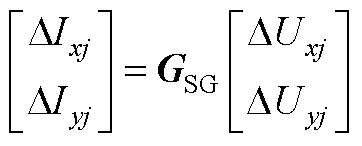 (A7)
(A7)
其中
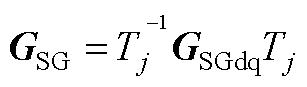
第3节中仅关注相位动态的简化模型为
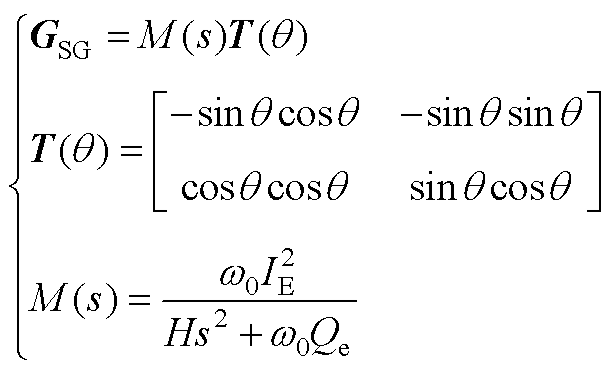 (A8)
(A8)
2. 仿真系统介绍
附表1 设备主要参数
App.Tab.1 Main parameters of devices

设备类型参 数数 值 变流器功率外环PI参数0.5, 40 电流内环PI参数0.5, 40 锁相环PI参数4, 2 100 同步机惯量和阻尼8, 0 定子等效电感(pu)0.1
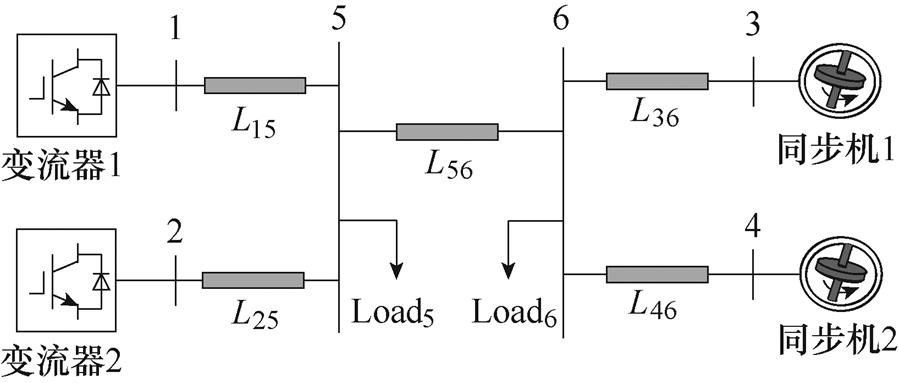
附图2 两区4机系统示意图
App.Fig.2 Topology diagram of a two area four machine power system
附表2 两区4机系统设备容量
App.Tab.2 Device capacity in two area four machine power system

设 备容量(pu) 变流器11.75 变流器21.65 同步机10.25 同步机20.35
附表3 两区4机系统交流网络线路参数
App.Tab.3 Network data of two area four machine power system
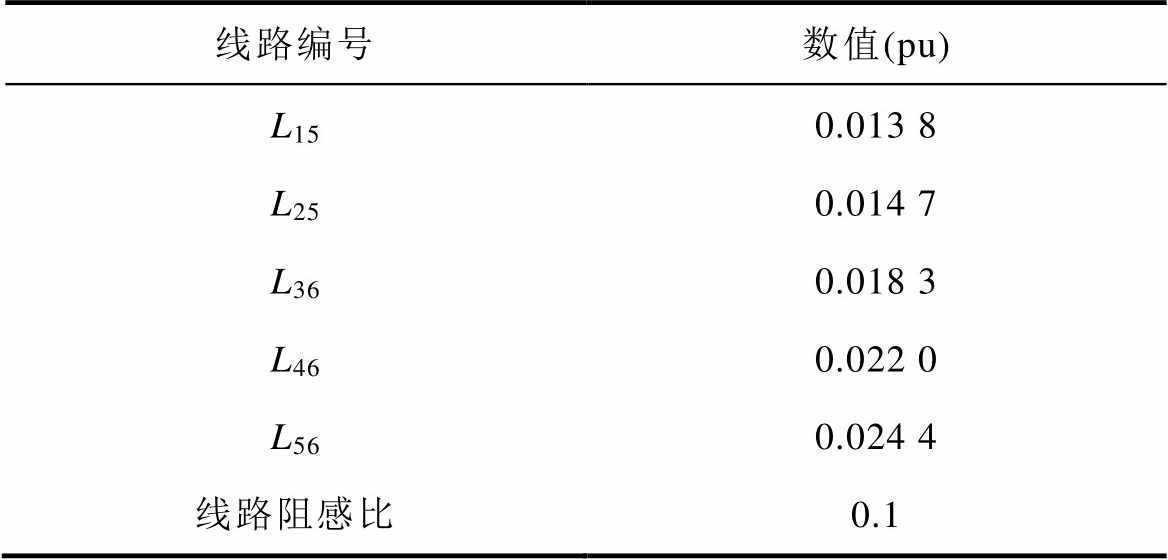
线路编号数值(pu) L150.013 8 L250.014 7 L360.018 3 L460.022 0 L560.024 4 线路阻感比0.1
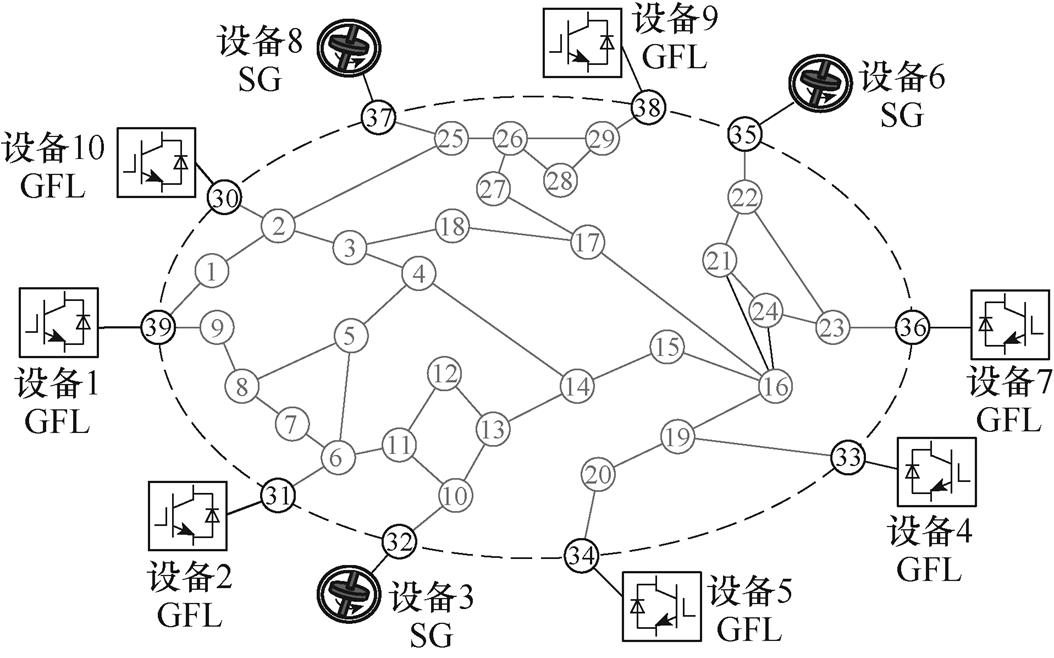
附图3 IEEE 10机39节点系统拓扑
App.Fig.3 Topology diagram of IEEE 10-machine 39-bus power system
附表4 10机39节点系统设备容量
App.Tab.4 Capacity of device in 10-machine 39-bus power system
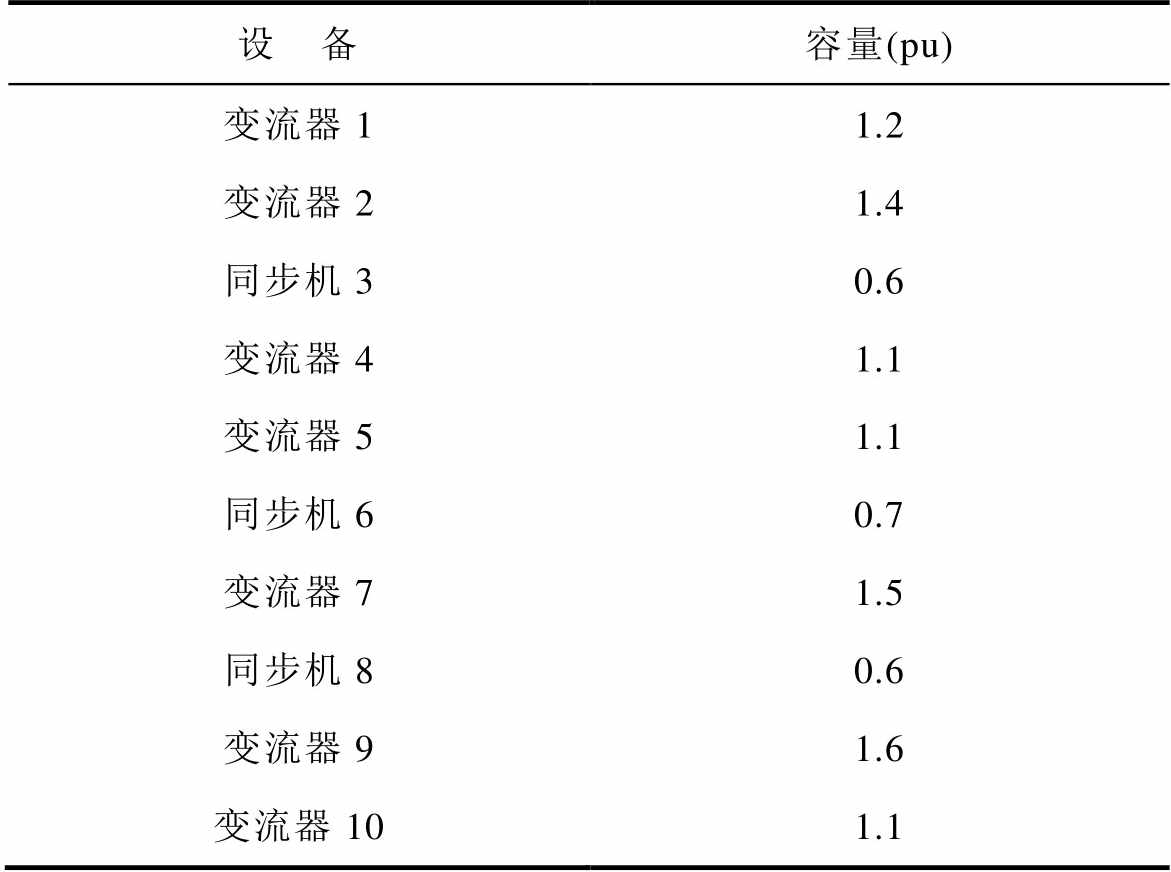
设 备容量(pu) 变流器11.2 变流器21.4 同步机30.6 变流器41.1 变流器51.1 同步机60.7 变流器71.5 同步机80.6 变流器91.6 变流器101.1
3. 简化模型验证
首先,验证所提简化模型的合理性,式(21)中的简化模型忽略了对所关注的主导特征根影响较小的环节。各动态环节对系统小干扰稳定性的影响,可以通过主导特征根的参与因子刻画。具体见附表6,附表6中各环节参与因子为同类型设备对应环节参与因子求和得到。由附表6可知,锁相环动态、转子运动动态和网络动态主导了低惯量系统的小干扰稳定性,因此可以根据3.1节中分析对详细模型进行合理简化。
附表5 10机39节点系统交流网络线路参数
App.Tab.5 Network data of 10-machine 39-bus power system
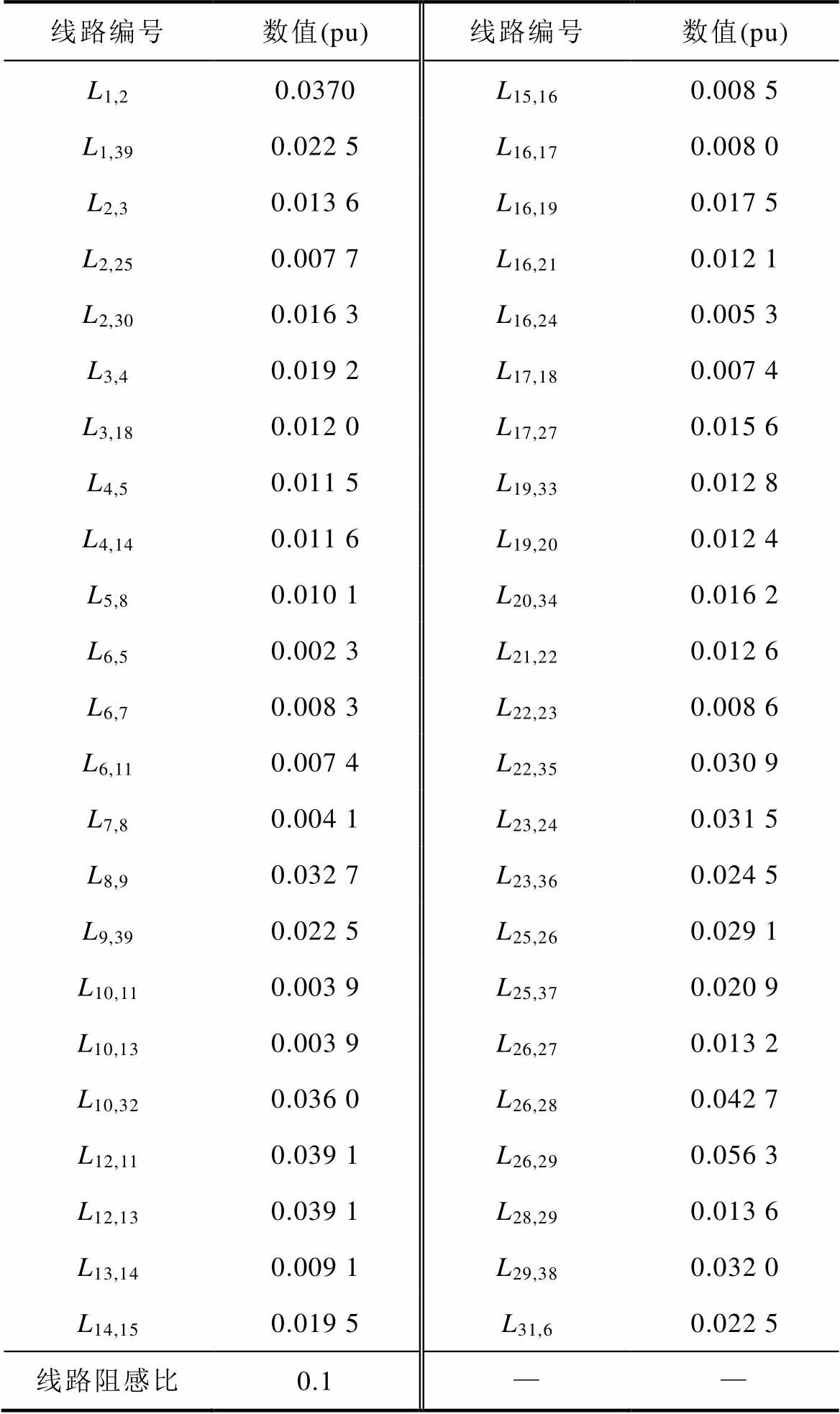
线路编号数值(pu)线路编号数值(pu) L1,20.0370L15,160.008 5 L1,390.022 5L16,170.008 0 L2,30.013 6L16,190.017 5 L2,250.007 7L16,210.012 1 L2,300.016 3L16,240.005 3 L3,40.019 2L17,180.007 4 L3,180.012 0L17,270.015 6 L4,50.011 5L19,330.012 8 L4,140.011 6L19,200.012 4 L5,80.010 1L20,340.016 2 L6,50.002 3L21,220.012 6 L6,70.008 3L22,230.008 6 L6,110.007 4L22,350.030 9 L7,80.004 1L23,240.031 5 L8,90.032 7L23,360.024 5 L9,390.022 5L25,260.029 1 L10,110.003 9L25,370.020 9 L10,130.003 9L26,270.013 2 L10,320.036 0L26,280.042 7 L12,110.039 1L26,290.056 3 L12,130.039 1L28,290.013 6 L13,140.009 1L29,380.032 0 L14,150.019 5L31,60.022 5 线路阻感比0.1——
附表6 主导模态参与因子
App.Tab.6 Participating factors of the dominant modes
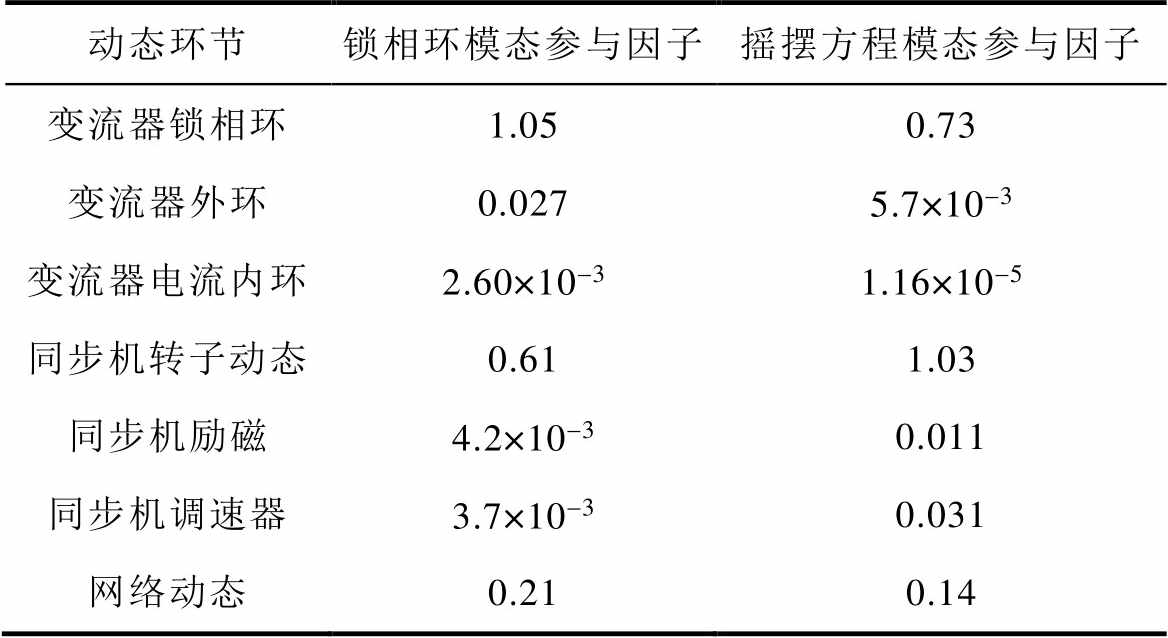
动态环节锁相环模态参与因子摇摆方程模态参与因子 变流器锁相环1.050.73 变流器外环0.0275.7×10-3 变流器电流内环2.60×10-31.16×10-5 同步机转子动态0.611.03 同步机励磁4.2×10-30.011 同步机调速器3.7×10-30.031 网络动态0.210.14
验证简化模型的准确性。附图4进一步给出了根据所建立的简化模型和详细模型得到的系统主导特征根对比,其中简化模型主导特征根是通过编写m文件程序计算得到,详细模型主导特征根通过Simulink线性化得到。可以看出,简化模型与详细模型的主导特征根基本一致,综合上述分析,验证了本文所提简化模型的合理性和准确性。
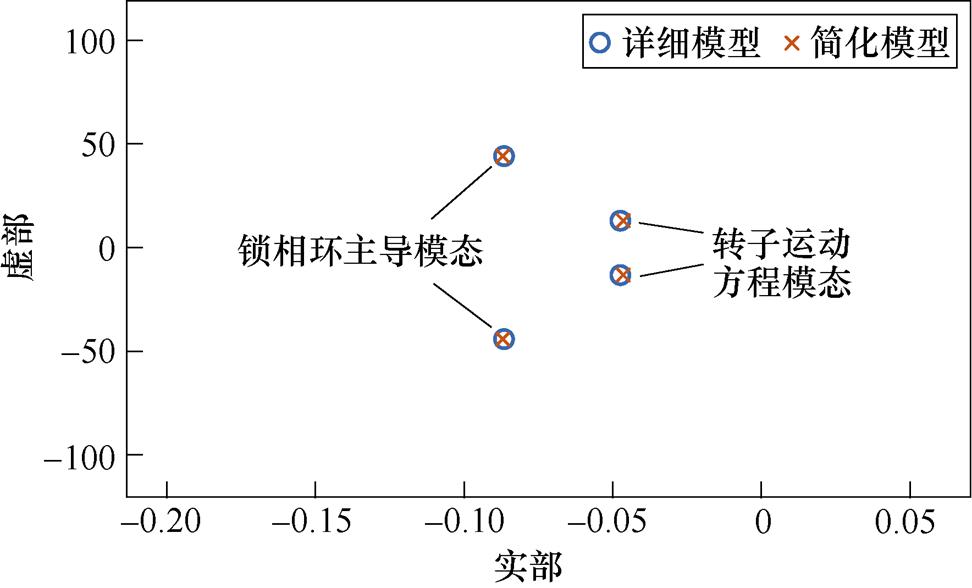
附图4 简化模型与详细模型主导极点对比
App.Fig.4 Dominant pole comparison diagram of simplified model and detailed model
参考文献
[1] 袁小明, 张美清, 迟永宁, 等. 电力电子化电力系统动态问题的基本挑战和技术路线[J]. 中国电机工程学报, 2022, 42(5): 1904-1917.
Yuan Xiaoming, Zhang Meiqing, Chi Yongning, et al. Basic challenges of and technical roadmap to power- electronized power system dynamics issues[J]. Proceedings of the CSEE, 2022, 42(5): 1904-1917.
[2] Hatziargyriou N, Milanović J, Rahmann C, et al. Stability definitions and characterization of dynamic behavior in systems with high penetration of power electronic interfaced technologies[R]. New York, USA: Institute of Electrical and Electronics Engineers, 2020.
[3] Peng Qiao, Jiang Qin, Yang Yongheng, et al. On the stability of power electronics-dominated systems: challenges and potential solutions[J]. IEEE Transa- ctions on Industry Applications, 2019, 55(6): 7657- 7670.
[4] 邵冰冰, 赵峥, 肖琪, 等. 多直驱风机经柔直并网系统相近次同步振荡模式参与因子的弱鲁棒性分析[J]. 电工技术学报, 2023, 38(3): 754-769.
Shao Bingbing, Zhao Zheng, Xiao Qi, et al. Weak robustness analysis of close subsynchronous oscillation modes’ participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.
[5] 周瑀涵, 辛焕海, 鞠平. 基于广义短路比的多馈入系统强度量化原理与方法: 回顾、探讨与展望[J]. 中国电机工程学报, 2023, 43(10): 3794-3811.
Zhou Yuhan, Xin Huanhai, Ju Ping. System strength quantification principle and method of multi-infeed systems based on generalized short-circuit ratio: reviews, discussions and outlooks[J]. Proceedings of the CSEE, 2023, 43(10): 3794-3811.
[6] 于琳, 孙华东, 赵兵, 等. 新能源并网系统短路比指标分析及临界短路比计算方法[J]. 中国电机工程学报, 2022, 42(3): 919-929.
Yu Lin, Sun Huadong, Zhao Bing, et al. Short circuit ratio index analysis and critical short circuit ratio calculation of renewable energy grid-connected system[J]. Proceedings of the CSEE, 2022, 42(3): 919-929.
[7] 郭剑波. 构建新型电力系统是实现能源转型、达成“双碳”目标的有效途径[N]. 国家电网报, 2021- 09-07(5).
[8] 齐磊, 赵巍, 孙孝峰, 等. 低调频容量高比例新能源主导局部电网低频失稳分析[J]. 电力系统自动化, 2022, 46(12): 174-183.
Qi Lei, Zhao Wei, Sun Xiaofeng, et al. Analysis on low-frequency instability of local power grid with low-frequency regulation capacity dominated by high proportion of renewable energy[J]. Automation of Electric Power Systems, 2022, 46(12): 174-183.
[9] 辛焕海, 董炜, 袁小明, 等. 电力电子多馈入电力系统的广义短路比[J]. 中国电机工程学报, 2016, 36(22): 6013-6027.
Xin Huanhai, Dong Wei, Yuan Xiaoming, et al. Generalized short circuit ratio for multi power electronic based devices infeed to power systems[J]. Proceedings of the CSEE, 2016, 36(22): 6013-6027.
[10] 辛焕海, 甘德强, 鞠平. 多馈入电力系统广义短路比: 多样化新能源场景[J]. 中国电机工程学报, 2020, 40(17): 5516-5527.
Xin Huanhai, Gan Deqiang, Ju Ping. Generalized short circuit ratio of power systems with multiple power electronic devices: analysis for various renewable power generations[J]. Proceedings of the CSEE, 2020, 40(17): 5516-5527.
[11] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191.
Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[12] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system[J]. Transactions of China Electro- technical Society, 2023, 38(21): 5758-5770, 5938.
[13] 辛焕海, 李子恒, 董炜, 等. 三相变流器并网系统的广义阻抗及稳定判据[J]. 中国电机工程学报, 2017, 37(5): 1277-1293.
Xin Huanhai, Li Ziheng, Dong Wei, et al. Generalized-impedance and stability criterion for grid-connected converters[J]. Proceedings of the CSEE, 2017, 37(5): 1277-1293.
[14] Pulgar-Painemal H, Wang Yajun, Silva-Saravia H. On inertia distribution, inter-area oscillations and location of electronically-interfaced resources[J]. IEEE Transactions on Power Systems, 2018, 33(1): 995-1003.
[15] Dong Dong, Wen Bo, Boroyevich D, et al. Analysis of phase-locked loop low-frequency stability in three- phase grid-connected power converters considering impedance interactions[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 310-321.
[16] Ding Lizhi, Lu Xiaonan, Tan Jin. Small-signal stability analysis of low-inertia power grids with inverter-based resources and synchronous con- densers[C]//2022 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), New Orleans, LA, USA, 2022: 1-5.
[17] Ding Lizhi, Lu Xiaonan, Tan Jin. Comparative small-signal stability analysis of grid-forming and grid-following inverters in low-inertia power systems[C]//IECON 2021-47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 2021: 1-6.
[18] 徐李清, 郭春义, 杨硕. 联接低惯量交流系统的MMC与发电机之间的低频交互振荡模式研究[J]. 中国电机工程学报, 2023, 43(9): 3402-3415.
Xu Liqing, Guo Chunyi, Yang Shuo. Research on low frequency interactive oscillation mode between generator and MMC connected to low inertia AC system[J]. Proceedings of the CSEE, 2023, 43(9): 3402-3415.
[19] Markovic U, Stanojev O, Aristidou P, et al. Understanding small-signal stability of low-inertia systems[J]. IEEE Transactions on Power Systems, 2021, 36(5): 3997-4017.
[20] Gu Yunjie, Li Yitong, Zhu Yue, et al. Impedance- based whole-system modeling for a composite grid via embedding of frame dynamics[J]. IEEE Transactions on Power Systems, 2021, 36(1): 336- 345.
[21] 庄可好, 辛焕海, 高晖胜, 等. 双轴励磁电流源同步机视角下跟网/构网设备建模及其互联系统同步稳定性分析[J]. 中国电机工程学报, 2023, 43(20): 7759-7773.
Zhuang Kehao, Xin Huanhai, Gao Huisheng, et al. Modeling of grid-forming and grid-following devices from the perspective of dual excitation current sources synchronous generator and synchronous stability analysis of interconnected systems[J]. Proceedings of the CSEE, 2023, 43(20): 7759-7773.
[22] 花赟玥, 杨超然, 何国庆, 等. 考虑小干扰稳定和频率稳定的虚拟惯量配置分析[J]. 清华大学学报(自然科学版), 2021, 61(5): 437-445.
Hua Yunyue, Yang Chaoran, He Guoqing, et al. Virtual inertia configuration analysis considering small-signal stability and frequency stability[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(5): 437-445.
[23] 陈国平, 李明节, 董昱, 等. 构建新型电力系统仿真体系研究[J]. 中国电机工程学报, 2023, 43(17): 6535-6551.
Chen Guoping, Li Mingjie, Dong Yu, et al. Research on the simulation technology architecture for the new-type power system[J]. Proceedings of the CSEE, 2023, 43(17): 6535-6551.
[24] Du Wenjuan, Dong Wenkai, Wang Haifeng. A method of reduced-order modal computation for planning grid connection of a large-scale wind farm[J]. IEEE Transactions on Sustainable Energy, 2020, 11(3): 1185-1198.
[25] Yang Chaoran, Huang Linbin, Xin Huanhai, et al. Placing grid-forming converters to enhance small signal stability of PLL-integrated power systems[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3563-3573.
[26] Tu Jing, Zhou Ming, Cui Hantao, et al. An equivalent aggregated model of large-scale flexible loads for load scheduling[J]. IEEE Access, 2019, 7: 143431- 143444.
[27] Skogestad S, Postelethwaite I. Multivariable feedback control[M]. New York: Wiley Publishing, 1996.
[28] 袁辉, 辛焕海, 王冠中, 等. 含SVG的新能源多馈入系统振荡分析和广义短路比计算[J]. 电力系统自动化, 2021, 45(14): 38-46.
Yuan Hui, Xin Huanhai, Wang Guanzhong, et al. Analysis on oscillation of multi-infeed system with renewable energy and static var generator and calculation of its generalized short-circuit ratio[J]. Automation of Electric Power Systems, 2021, 45(14): 38-46.
[29] Gao Huisheng, Wang Guanzhong, Li Zhiyi, et al. Assessing interaction strength between synchronous generator and LCC-HVDC in AC/DC systems[C]// 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2020: 1-5.
[30] Stewart G W, Sun Jiguang. Matrix perturbation theory[M]. Boston: Academic Press, 1990.
[31] 高晖胜. 新能源电力系统模态频率: 定义、分析与控制[D]. 杭州: 浙江大学, 2022.
Gao Huisheng. Modal frequency in renewable- integrated power system: definition, analysis and control[D]. Hangzhou: Zhejiang University, 2022.
[32] 宫泽旭, 艾力西尔·亚尔买买提, 辛焕海, 等. 新能源电力系统并网设备小扰动稳定分析(一): 机理模型与稳定判据适用性[J]. 中国电机工程学报, 2022, 42(12): 4405-4419.
Gong Zexu, Yaermaimaiti Ailixier, Xin Huanhai, et al. Small signal stability analysis of equipment in renewable energy power system (part I): mechanism model and adaptation of stability criterion[J]. Proceedings of the CSEE, 2022, 42(12): 4405-4419.
[33] 高本锋, 王义, 范辉, 等. 基于阻尼路径的新能源经LCC-HVDC送出系统次同步交互作用分析方法[J]. 电工技术学报, 2023, 38(20): 5572-5589.
Gao Benfeng, Wang Yi, Fan Hui, et al. A sub- synchronous interaction analysis method of renewable energy generations integrated with LCC-HVDC system based on damping path[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5572- 5589.
Abstract With the widespread integration of renewable energy sources, the power system is transitioning into a weak AC system characterized by low inertia and a reduced short-circuit ratio. Compared to conventional power systems, the interaction between sources and grids becomes more intricate in weak AC systems, resulting in complex dynamic behaviors. The challenge of oscillation instability in grid-connected inverters is accentuated in low-inertia power systems. In such systems, grid-following inverters may interact with the dynamics of synchronous machine rotors, posing new challenges for stability analysis. Relying solely on the dynamics and short-circuit ratio of grid-following devices is insufficient to assess the strength of the AC system. This paper addresses the small-signal oscillation instability in the sub-synchronous frequency range. The impact of the system's generalized short-circuit ratio and inertia on the small-disturbance synchronous stability of grid-following inverters are analyzed. The proposed stability margin quantification method is designed for grid-connected inverters in low-inertia multi-machine systems with low computational complexity and clear physical significance.
This paper initially establishes a closed-loop model for the hybrid system of synchronous machines and inverters. The dynamic coupling of the two types of devices is separated by mathematically transforming the closed-loop model. A unit interaction factor matrix (UIFM) is generated, including the dynamics of synchronous machines and the interconnected network of the two types of devices. This matrix qualitatively describes the interaction between the dynamics of synchronous machines and inverters in low-inertia systems, providing a model foundation for stability analysis.
The matrix perturbation theory is employed for the closed-loop model, constructing an isomorphic system equivalent to the original system's stability. Modal decoupling is then applied to break down the constructed equivalent isomorphic system into multiple subsystems. The small-signal circuit model of the dominant subsystem is provided. Key factors affecting the stability of the original complex system are extracted, concretizing the interaction of bottom-layer components in the subsystem.
Since the minimal subsystem remains a two-dimensional multiple-input, multiple-output (MIMO) system, this paper selects a phase-dominant loop suitable for analyzing small-disturbance synchronous stability problems. The result in a single-input, single-output (SISO) system is equivalent to the stability of the minimal subsystem. The stability of this system is analyzed using the Nyquist criterion, and stability margin indicators are established. A two-dimensional stable operating region calculation method, considering both system inertia and short-circuit ratio, is provided. Finally, using the Matlab/Simulink platform, the effectiveness of the proposed analysis method is validated using a two-area, four-machine system and a 10-machine 39-bus system.
keywords:Low inertia system, small-disturbance synchronization stability, generalized short-circuit ratio, minimum subsystem, system strength
国家电网有限公司科技资助项目(52094023001W)。
收稿日期 2023-09-01
改稿日期 2023-12-05
DOI: 10.19595/j.cnki.1000-6753.tces.231434
中图分类号:TM712
胡 光 男,1999年生,博士研究生,研究方向为新能源并网稳定分析。E-mail: 12110056@zju.edu.cn
辛焕海 男,1981年生,教授,博士生导师,研究方向为交直流系统稳定分析与控制、新能源并网稳定分析与控制。E-mail: xinhh@zju.edu.cn(通信作者)
(编辑 陈 诚)