
图1 PEM电解水制氢系统主要生产环节[14,24]
Fig.1 Main links of hydrogen production system with PEM electrolyzers[14,24]
摘要 随着可再生能源发电及电解制氢技术的发展,基于质子交换膜(PEM)技术的可再生能源制氢将成为氢能供应的主要手段之一。新能源发电具有随机性和波动性,现有多堆PEM电解制氢系统功率分配策略难以在功率波动场景下保证系统高效运行。对此,该文首先建立了包含主要能耗环节的制氢系统整体效率模型,探究了制氢效率与电流密度、温度的特性关系。然后,根据该效率特性提出了基于功率-温度自适应控制的多堆PEM电解制氢系统效率优化策略,包含离线优化与在线控制两部分:离线优化部分根据制氢系统效率模型预先制定不同电解总功率下的电解槽功率及温度设定方案;在线控制部分根据离线优化方案、制氢功率进行电解槽功率和温度调节。最后,采用实际风电功率进行算例分析,结果表明,相比于传统的功率平均分配策略和链式分配策略,该文提出的效率优化策略将产氢量分别提高了6.4%和5.7%。
关键词:质子交换膜电解槽 电解制氢 新能源发电 效率优化 自适应控制
随着现代社会对清洁能源的重视,氢能在能源、交通等领域不断普及[1-2]。预计到2050年,氢能在全球终端能源消费量中的占比可达到25%[3]。可再生能源发电制氢已成为实现“双碳”目标、推动能源供给可持续发展的重要途径。
电解水制氢技术主要有碱性电解、质子交换膜(Proton Exchange Membrane, PEM)电解及高温固体氧化物电解技术。近年来,PEM电解技术逐步成熟,呈现出电流密度高、响应速度快的优势,适应功率波动的制氢场景[4-5]。多堆PEM电解制氢成为有效消纳富余可再生能源的重要手段,其运行方式从配合新能源消纳的被动负载逐步转换为与电力系统双向互动的柔性负载。在电力系统运行经济性方面,文献[6-8]在区域电网经济调度研究中通过优化电解制氢功率计划,提升了可再生能源消纳水平。在电力系统动态性能控制方面,通过控制电解制氢系统中的电力电子换流器,可以在电力系统动态过程中提供电压[9]/频率[10]支撑,以及平抑功率波动[11-12]。上述研究使电解制氢系统运行或控制更加灵活,但缺少对电解制氢系统自身能耗特性的关注。
对于大型PEM电解制氢系统,电能成本约占全生命周期成本的70%[13],提升能耗效率对于降低制氢成本至关重要。文献[14]详细地分析了电解制氢系统中的电解、干燥、压缩等环节的能耗,得出不同条件下的经济运行点,为提升电解制氢效率提供了理论指导。文献[15]建立电解槽动态模型,探究了不同压强下电解槽电压特性及能耗特性。文献[16]探究了电解槽压强、PEM膜厚度对制氢全过程效率的影响,得到不同电解电流密度下的最优压强设定值。文献[17]探究了温度和压强变化对电解效率的影响,并通过温度与压强优化得到最佳运行效率。文献[18]在风氢系统优化配置中考虑电解效率,提出了风氢系统容量配置方法。文献[19]分析了温度对电解率的影响,并对电解槽温度进行了自适应温度控制,使电解槽运行于最佳温度点。上述研究着眼于电解槽本体效率特性,但未将制氢系统中辅助设备的能耗特性考虑在内,也未考虑多电解槽之间的功率分配问题。
在多堆电解槽功率分配方面,文献[20-21]针对碱性电解槽动态响应慢的问题,提出适用于可再生能源制氢的碱性电解槽定期轮值策略,从而兼顾电解槽寿命和制氢效率。文献[22]充分利用PEM电解槽良好的变载能力,提出根据可再生能源出力逐级启动电解槽的链式分配策略,降低系统的控制复杂度。文献[23]提出多堆PEM电解槽统一控制结构,多组电解槽并列于同一条直流母线,无需独立的功率控制器,并依靠电解槽相同的外特性实现制氢功率的平均分配。上述多堆电解槽控制策略具有操作简便、可实施性强的优势,适用于制氢功率相对恒定的场景。然而其设置方式相对主观,在可再生能源出力频繁波动时,难以保证系统的高效运行。
综上所述,现有针对多堆PEM电解槽制氢效率提升的研究还不够完善,需进一步探究电解制氢系统的整体效率特性,提出适用于可再生能源制氢场景的多堆电解槽功率分配方法。对此,本文对电解制氢系统主要能耗环节进行了详细分析,建立了包含换流器、电解槽、多级压缩机的整体效率模型,并基于该模型从优化和控制两个层面提出了基于功率-温度自适应控制的多堆PEM电解系统效率优化方法。该方法首先通过离线优化预先制定不同电解功率下的电解槽功率及温度设定方案;其次,在线控制换流器占空比及循环水阀门开度,实现电解槽功率和温度调节,从而使电解槽在不同的制氢负载下最大化制氢效率;最后,通过实时数字仿真平台RT-LAB与热力瞬态仿真工具TRNSYS进行了联合仿真验证,并与传统功率分配策略进行对比,验证了本文所提效率优化方法的有效性。
PEM电解制氢的主要生产环节[14,24]如图1所示。在阴极生成的氢气经过气液分离、干燥、压缩后进行存储或管道运输。对于大规模PEM电解制氢系统,电解过程中产生大量热量,为防止PEM过热老化损坏,需要将水进行循环流动并采用换热器散热。在整个制氢流程中,主要耗能环节有电解槽制氢、整流器耗能及压缩耗能,干燥、循环冷却等辅助环节耗能占比通常低于3%[25-26]。因此,本文分别对电解、压缩、换流器三个主要能耗环节进行效率分析,以获得表征效率特性的数学模型。

图1 PEM电解水制氢系统主要生产环节[14,24]
Fig.1 Main links of hydrogen production system with PEM electrolyzers[14,24]
大型电解槽通常由多个电解小室串联而成。单个电解小室的电解电压可以分解为能斯特电压(Nernst voltage)、活化过电势(activation overpotential)、欧姆过电势(Ohmic overpotential)三个部分[17,27],即
 (1)
(1)
其中
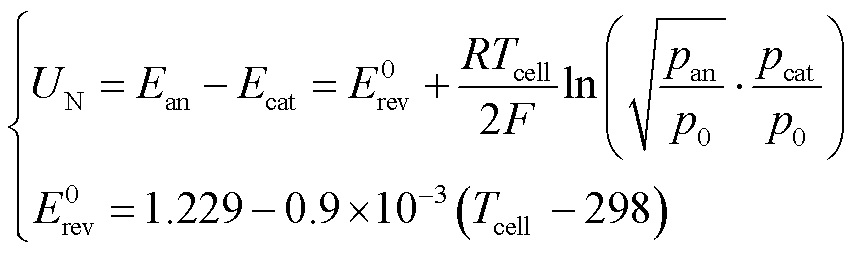 (2)
(2)
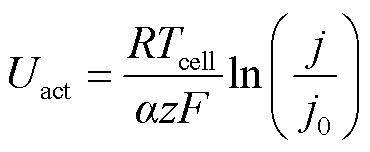 (3)
(3)
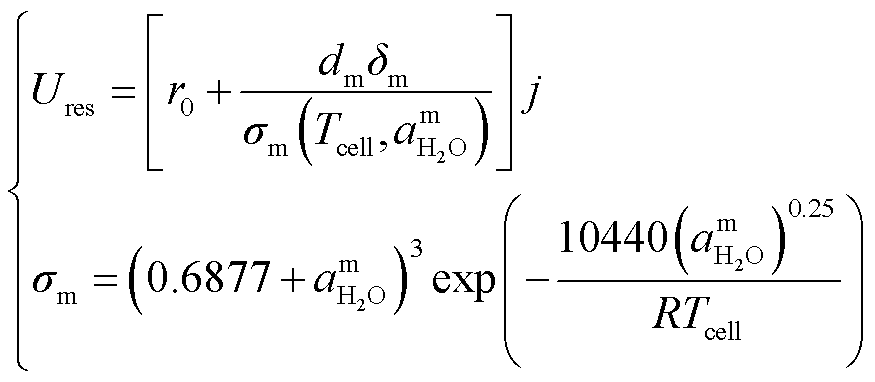 (4)
(4)
式中,Ucell和Tcell分别为单个电解小室的电压和温度;UN为能斯特电压;Uact为活化过电势;Ures为欧姆过电势;Ean为阳极电势;Ecat为阴极电势;E0 rev为可逆电压;R为理想气体常数;F为法拉第常数;z为转移电子摩尔数;α为电荷转移系数;j为电流密度;j0为交换电流密度;pan和pcat分别为阳极和阴极压强;p0为参考压强;dm、δm、σm分别为质子交换膜厚度、膨胀系数、电解膜电导率;am H2O为质子交换膜中的水分活度;r0为电解液电阻。
电解制氢本身为吸热反应。在标准状况下,当电解电压达到理论分解电压1.23 V时,电解反应开始发生,并需要从外部吸收热量48.6 kJ/mol。然而在该电压下,电解反应非常缓慢。工业生产中为了提升制氢速率,通常会提升电解电流,将不可避免地增加欧姆过电势并释放出焦耳热。当电压达到热中性电压1.48 V时,焦耳热与电解吸收热量动态平衡,电解反应表现出既不发热也不吸热。此后继续提升电流,电解速率将加快,需要采取散热措施。
电解效率存在不同的定义方式。若将电解效率定义为反应所生成氢气的低热值与消耗电量的比值,则由上述分析可知,电解效率模型可以采用两阶段效率函数表示:在电解电压低于热中性电压1.48 V时,电解消耗的电能完全转化为氢气中的化学能和增加的水蒸气中的焓值,并且需要从外部吸收热量,这一阶段电解效率可用热力学效率计算,如式(5)所示;当电压高于热中性电压1.48 V时,电能传输产生的热量高于电解吸收的热能,需要采用散热措施以保证电解温度恒定,该阶段电解效率可用电压效率计算,如式(7)所示。
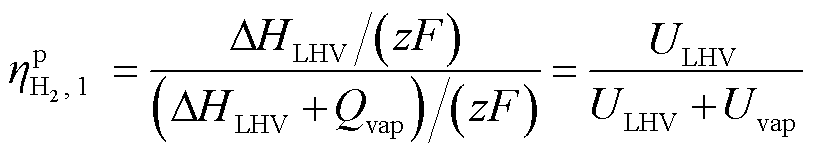 (5)
(5)
 (6)
(6)
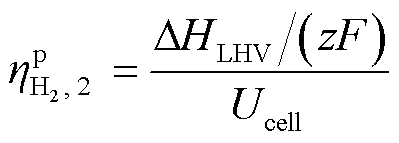 (7)
(7)
式中,ηp H2,1为电解电压小于热中性电压时的热力学效率;ΔHLHV为氢气低热值;ULHV为氢气低热值对应的电压;Qvap为生成每摩尔氢气时附加生成水蒸气增加的内能;Uvap为加热水导致温度上升后饱和水蒸气焓值对应的电压;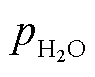 、
、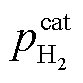 、
、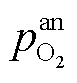 分别为水蒸气分压、氢气分压、氧气分压;ΔHvap为水蒸气焓值;ηp H2,2为电解电压大于热中性电压时的电压效率。
分别为水蒸气分压、氢气分压、氧气分压;ΔHvap为水蒸气焓值;ηp H2,2为电解电压大于热中性电压时的电压效率。
另一方面,由于氢气分子直径很小,反应生成的部分氢气会透过质子交换膜到阳极发生逆反应,降低氢气产量。考虑这部分损失后的效率称为法拉第效率ηF H2,可表示为
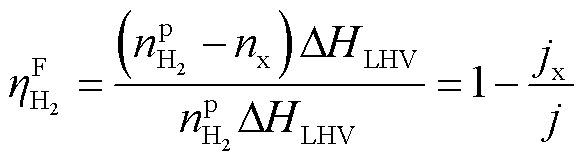 (8)
(8)
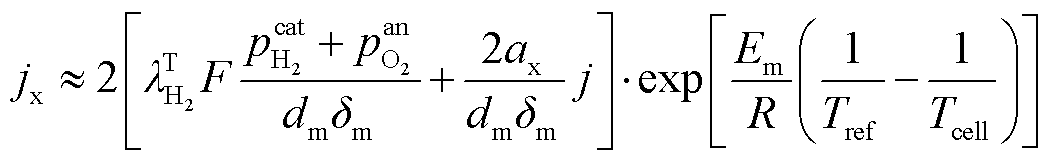 (9)
(9)
式中,Tref为电解液参考温度;np H2为发生逆反应之前的制氢速率;nx为逆反应消耗的氢气速率;jx为逆反应电流密度;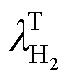 为PEM渗透系数;ax为电流密度对渗透系数的影响因子;Em为逆反应过程的活化能。根据法拉第定律,nx与jx成正比,因此法拉第效率可以表示为1-jx/j。
为PEM渗透系数;ax为电流密度对渗透系数的影响因子;Em为逆反应过程的活化能。根据法拉第定律,nx与jx成正比,因此法拉第效率可以表示为1-jx/j。
综上所述,电解槽效率ηELE可以表示为
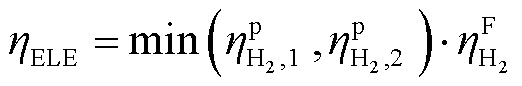 (10)
(10)
由于电解槽电压受到电流密度和电解温度的双重影响,可基于电解效率模型,得到考虑产氢效率和法拉第效率的电解效率曲面,如图2所示。由图2可知,热力学效率随着电流密度的增大而增大,而电压效率随着电流密度的增大而降低。在电流密度为1~2 A/cm2的范围内,热力学效率曲面ηp H2,1和电压效率曲面ηp H2,2相交。因此,电解效率在电流密度较小的范围(约1 A/cm2以内)时较低,并随着电流密度的增大而快速增大,最终电解效率随着电流密度的增加而降低。此外,电解效率也受到电解温度的影响。在电流密度很低时受温度影响较小;而当电流密度较大时,随着温度的增加而提高。

图2 考虑产氢效率与法拉第效率的电解效率曲面
Fig. 2 Electrolytic efficiency surfaces considering the hydrogen production efficiency and Faraday efficiency
氢气压缩是电解制氢系统中不可忽视的能耗环节。氢气的储运压强通常维持在数MPa至数十MPa范围内,其与电解槽压强之间存在很大的压强差。大规模电解制氢系统一般采用多级压缩、级间冷却的方式降低压缩能耗[28],如图3a所示。单级压缩并冷却后,氢气恢复至初始温度,随后进入下一级压缩。图3b中阴影部分即为通过多级压缩方式降低的功耗。假设电解槽内部压强恒定,则单级压缩功耗及压缩级数由式(11)和式(12)给出。采用多级压缩时,当每一级压缩比相同时所消耗的压缩能量最小[29-30]。因此,可以得出多级压缩的效率模型,如式(13)所示。
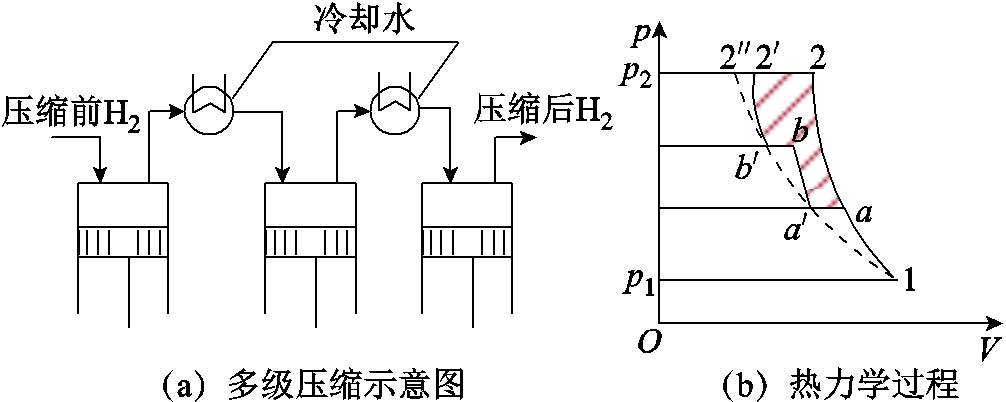
图3 多级压缩示意图及热力学过程
Fig.3 Diagram of multistage compression and its thermodynamic process
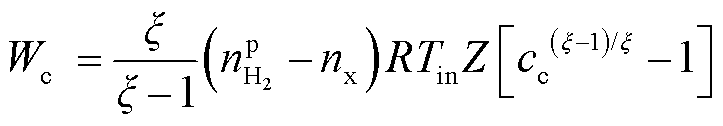 (11)
(11)
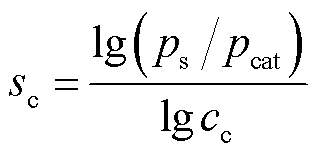 (12)
(12)
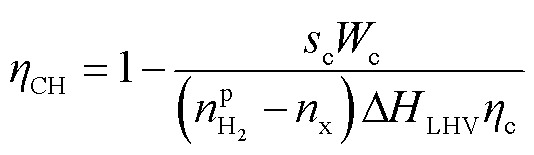 (13)
(13)
式中,Wc为单级压缩作用在氢气上的有效功率;ξ为氢气的绝热指数;Tin为氢气压缩前的温度;Z为压缩因子;cc为单级压缩比;sc为压缩级数;ps为储氢压强;ηc为压缩机工作效率;ηCH为氢气多级压缩过程的整体效率。
电解制氢负荷属于典型低电压大功率直流负载,正常运行中换流器必不可少[31-32]。以电解系统中广泛使用的Buck降压换流器为例分析DC-DC降压变流器的运行效率。Buck电路功率损耗主要包含通态损耗、开通损耗和关断损耗[33],即
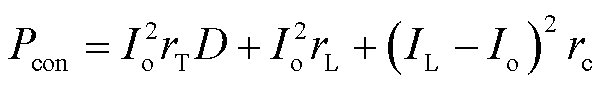 (14)
(14)
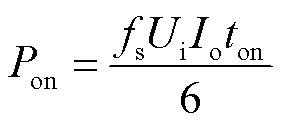 (15)
(15)
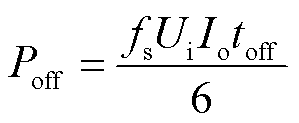 (16)
(16)
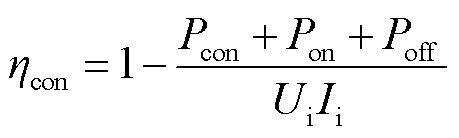 (17)
(17)
式中,Pcon为换流器通态损耗;Pon为开通损耗;Poff为关断损耗;D为占空比;Io为负载电流;rT为MOSFET导通电阻;rL为电感直流电阻;rc为电容器等效串联电阻;fs为开关频率;Ui和Ii分别为输入端电压和电流;ton和toff分别为MOSFET开通时间和关断时间;ηcon为降压换流器效率。
基于上述分析,包含主要功率损耗环节的整体效率模型ηtotal为
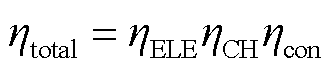 (18)
(18)
为了进一步探究与电解槽效率特性相适应的自适应控制策略,以额定功率为2 MW的电解制氢系统为例,绘制电解效率关于电流密度和电解温度的曲面,如图4所示。电解槽运行及辅助设备参数分别见表1和表2[17,34]。表中,1 bar=0.1 MPa。
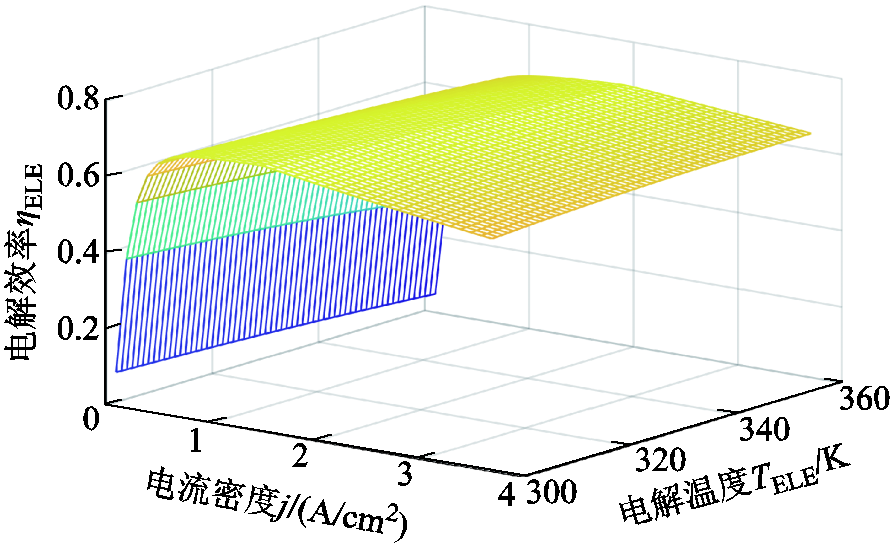
图4 计及主要能耗环节的电解效率曲面
Fig.4 Efficiency surface of electrolysis system considering main energy consumption links
表1 电解槽运行参数
Tab.1 Operating parameters of electrolyzers
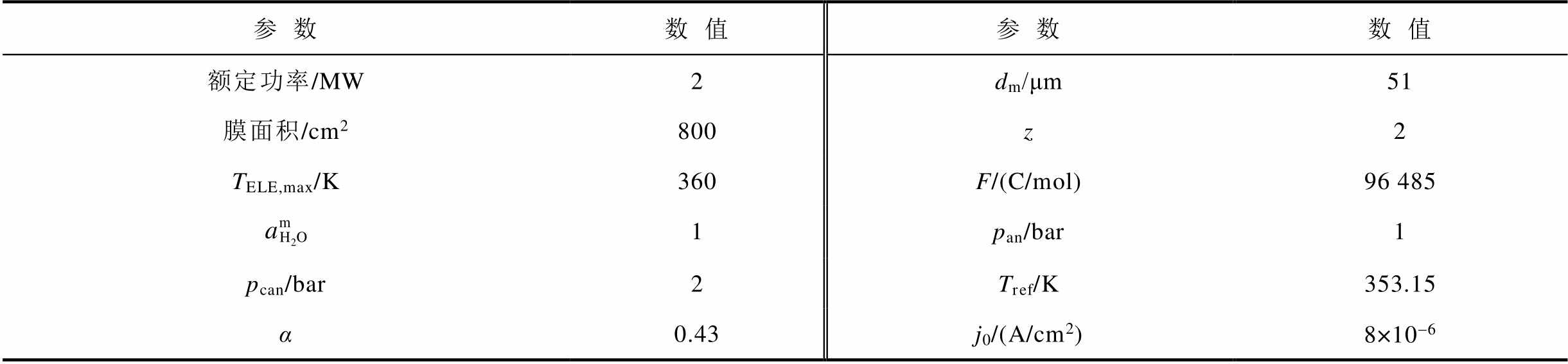
参数数值参数数值 额定功率/MW2dm/μm51 膜面积/cm2800z2 TELE,max/K360F/(C/mol)96 485 1pan/bar1 pcan/bar2Tref/K353.15 α0.43j0/(A/cm2)8×10-6
表2 辅助设备参数
Tab.2 Auxiliary equipment parameters

参数数值参数数值 ηc0.825ξ1.4 Tin/K300cc2.75 ps/bar200/Pa47 948 rT/mΩ100fs/kHz200 rL/mΩ80ton/ns6 rc/mΩ3toff/ns6
由图4可知,电解效率并非随着电流密度、电解温度单调变化。当电解温度固定时,电解效率随着电流密度的增加先增大后降低,最大效率点出现在1.5~2 A/cm2范围内,数值约为0.6~0.7。当电流密度固定时,在电流密度小于1.5 A/cm2时,电解效率随着温度的上升而下降;当电流密度超过1.5 A/cm2后,电解效率随着温度的升高而升高。在实际制氢系统中,通常会通过提升电解温度来提升电解效率,但为了防止电解膜高温老化,电解温度应当保持在360 K以下[35]。
由于电解温度影响,电解效率曲面在电解效率ηtotal-电流密度j平面上的投影是一条宽度随电流密度变化而变化的区间,如图5阴影部分所示。区间的宽度表示温度对电解效率影响的程度。阴影区间宽度越大,表示该电流密度下温度对电解效率影响越大。该区间上限表示在电解温度可灵活调节情况下的电解槽最大效率曲线ηTbest。为方便对比,同时给出了电解系统常用的固定温度360 K下的制氢效率曲线ηT360。将ηTbest通过图4所示的电解系统效率曲面可对应得到最佳电解温度Tbest。可以看出,最佳电解效率并非总是在最高电解温度下实现。当电流密度较低时,最佳电解温度相对较低,这是由于电流密度较低时,温度升高将大大降低法拉第效率。当电流密度超过1.5 A/cm2时,最佳电解温度随着电流密度增大而增大。
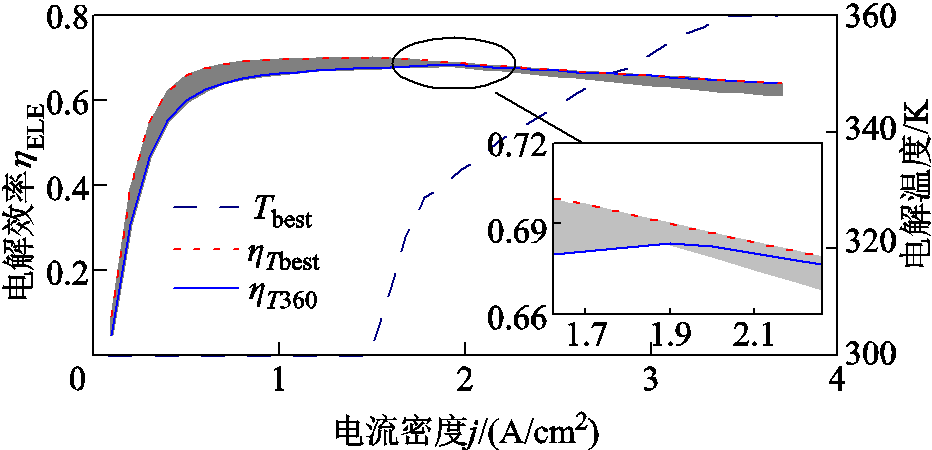
图5 电解效率曲面投影及效率峰值对应的温度曲线
Fig.5 Surface projection of electrolysis efficiency and temperature curve corresponding to peak efficiency
基于上述分析,对于大规模可再生能源电解制氢系统,当可再生能源功率波动时,合理调整电解槽功率分配以及电解温度,可以提升电解效率。电解功率可以通过调节DC-DC换流器实现,电解槽运行温度可以通过循环水流速进行调节。
现有制氢功率分配策略通常基于固定场景设定,在可再生能源出力频繁波动的场景下,难以保证系统处于高效的状态。对此,需探索一种能够根据可再生能源实际出力自适应调节电解槽状态的控制策略。
图6给出了电解功率-温度可控的可再生能源制氢的系统结构,其中多组电解槽通过DC-DC换流器并联在直流母线上,每组电解槽通过独立的换流器进行功率控制,并通过冷却功率可控的换热器进行温度调节。电解槽功率参考值由自适应控制器确定,温度参考值可根据最大效率曲面获得。考虑到电解系统效率模型计算相对复杂,在线实时优化难以在有效时间内完成,因此将功率自适应分配策略分为离线优化和在线控制两个部分:离线优化实现功率-温度参考值生成;在线控制实现基于功率-温度参考值的自适应调节控制。以下进行详细论述。
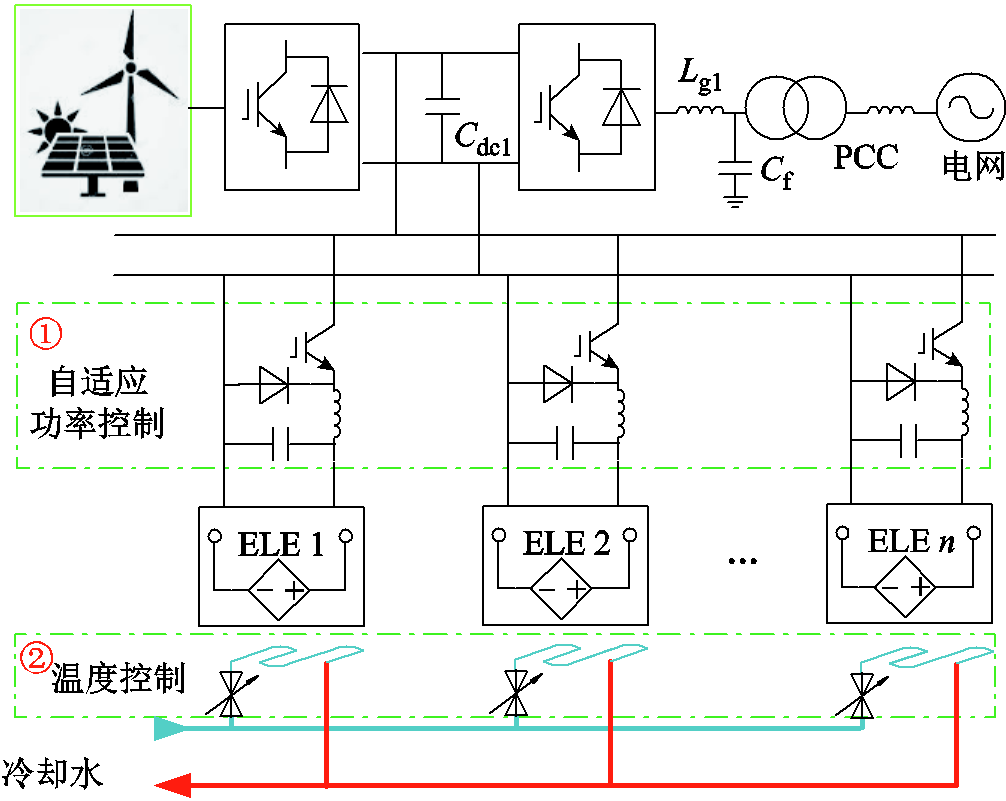
图6 电解功率-温度可控的多电解槽制氢系统结构
Fig.6 System structures of the multi-stack hydrogen production with controllable power and temperature
电解制氢系统结构通常不会随时改变,因此可预先计算出制氢总功率从最小值到最大值变化时的电解槽功率和温度设定方案,形成离线数据表。在实时运行中只需根据实际制氢总功率查表得到电解槽功率和温度参考值。PEM电解槽功率可以在s级时间范围内完成调节,而电解槽温度变化则相对较慢,需要min级时间完成调节[26]。因此,离线优化环节分别以最小化制氢功率损耗、最小化温度调节量为目标进行两阶段优化。在第一阶段实现最大化制氢效率,如式(19)所示。
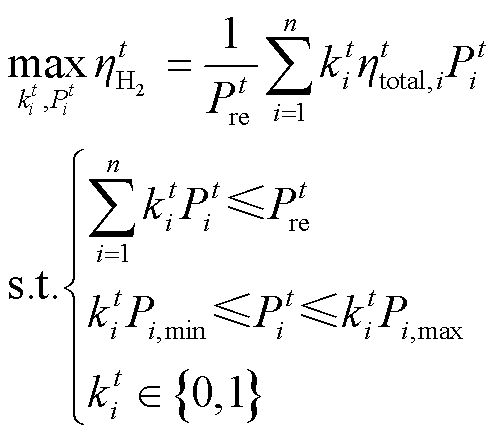 (19)
(19)
式中,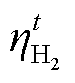 为第t个时段整个电解制氢系统的效率;Pt re为第t个时段制氢总功率;Pt i和kt i分别为第i个电解槽第t个时段功率与启停状态;Pi,max和Pi,min分别为第i个电解槽的运行功率上、下限;n为电解槽台数。
为第t个时段整个电解制氢系统的效率;Pt re为第t个时段制氢总功率;Pt i和kt i分别为第i个电解槽第t个时段功率与启停状态;Pi,max和Pi,min分别为第i个电解槽的运行功率上、下限;n为电解槽台数。
由于第一阶段通常会存在多种电解槽功率分配或启停方案,为尽快达到高效制氢状态,第二阶段以最小化温度调整为目标确定电解槽制氢功率,如式(20)所示。
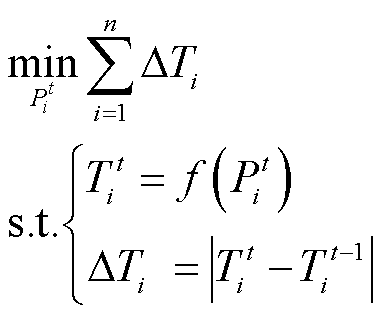 (20)
(20)
式中,f(Pt i)为电解槽最佳功率-温度对应曲线,可由图5中最优温度曲线Tbest分段线性化得到;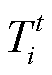 为第i个电解槽时段t的温度;ΔTi为第i个电解槽相邻两个时段的温度调节量。
为第i个电解槽时段t的温度;ΔTi为第i个电解槽相邻两个时段的温度调节量。
上述两阶段优化模型普遍适用于多堆PEM电解制氢系统。实际的制氢系统中通常由多台规格相同的电解槽构成,这种情况下制氢功率分配变得相对简单。可证明,对于一个由n台电解槽构成的电解系统,如果已开启j(j=2,…, n)台电解槽,将电解功率平均分配给j台电解槽时的效率大于其他分配方案,证明过程见附录,则不同电解功率下最大化制氢效率问题转变为电解槽开启台数问题。
设Pj-1,j表示开启j-1台电解槽与j台电解槽的启停临界功率(即当制氢功率为Pj-1, j时,开启j-1台电解槽与开启j台电解槽效率相同),则只需在离线优化阶段计算出各个临界启停功率Pj-1,j,便可以根据实际制氢功率所属范围确定电解槽开启台数。临界启停功率可以通过式(21)获得。
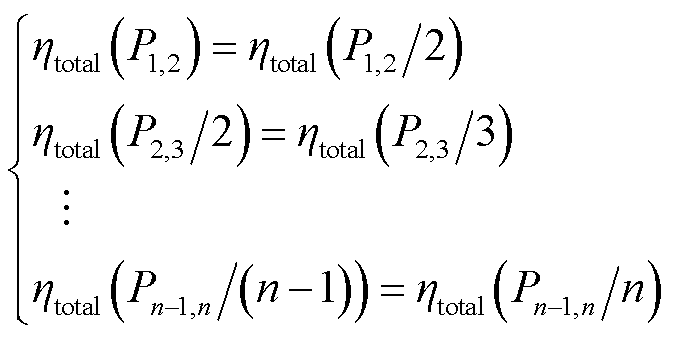 (21)
(21)
图7给出了由n台相同规格电解槽构成的制氢系统在不同制氢功率下的分配方案。在该分配方案下,当制氢总功率PELE满足Pj-1,j<PELE≤Pj, j+1时,每台电解槽的功率为PELE/j。该方案可能导致不同电解槽的运行时间不均衡。为避免其使用寿命快速降低,可定期对相同规格的电解槽进行轮换[20]。
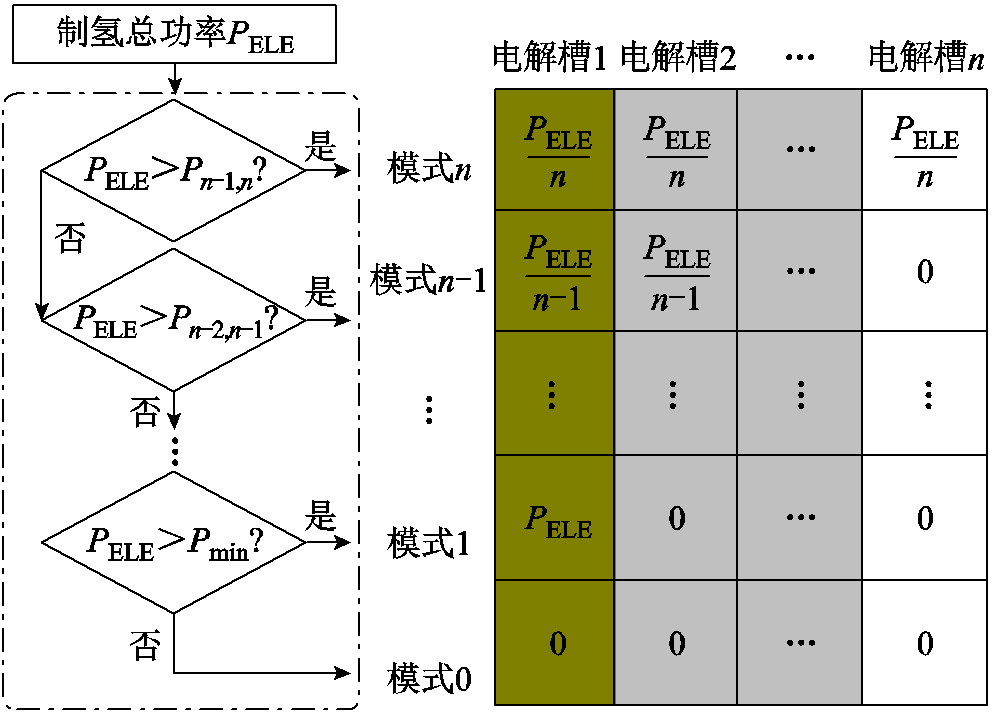
图7 相同规格电解槽启停策略
Fig.7 Startup and shutdown strategy of electrolyzers with the same model
在线控制阶段,基于离线控制的参考指标对电解功率和温度进行实时控制。电解功率采用双闭环PI控制策略,如图8下部所示,其中外环为功率环,内环为电流环。电解槽温度通过调节换热器阀门开度进行控制,在满足电解槽散热约束的情况下,散热功率由换流器低温侧液体流量进行调节,如图8上部所示。忽略电解槽与环境之间的被动散热,则电解槽-换热器温度模型[36]为
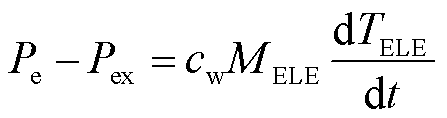 (22)
(22)
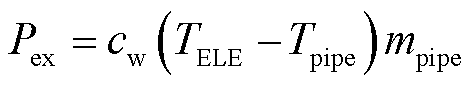 (23)
(23)
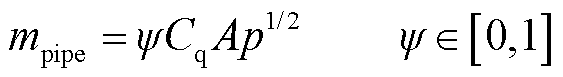 (24)
(24)
式中,Pe为由于焦耳效应引起的电加热功率;Pex为换热器带走的热功率;TELE为电解槽温度;MELE为电解槽内电解液的总质量;cw为水的比热容;Cq为阀门流量系数,取0.82;A为阀门的流通面积;ψ为阀门开度;p为阀门两侧压强差;Tpipe为电解槽补水温度;mpipe为电解液循环的质量流量。由式(22)可知,电解槽温度属于一阶惯性环节,因此可以采用PI控制器进行温度控制。
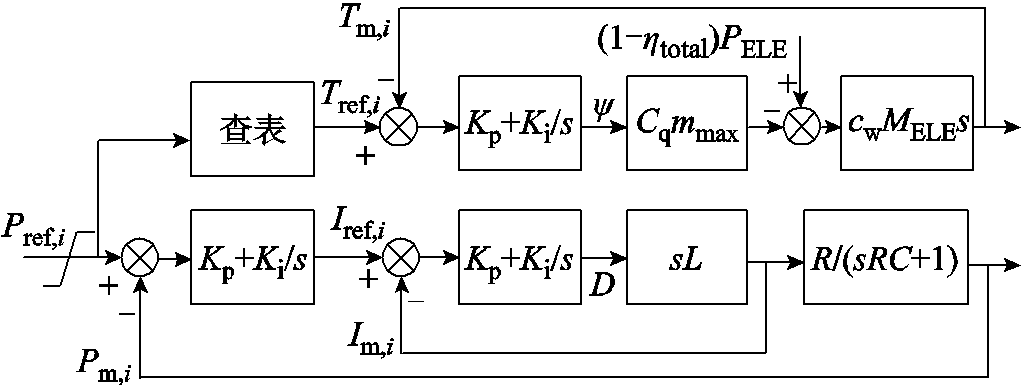
图8 电解槽功率-温度控制图
Fig. 8 Electrolyzer power and temperature control
经过上述分析,得到由离线优化和在线控制两部分构成的电解制氢系统功率-温度控制策略,如图9所示。离线优化阶段,根据系统结构、设备参数构建系统效率模型,基于该模型获得电解功率从最小值到最大值的电解槽功率分配以及温度设定方案;在线控制阶段,基于系统当前制氢总功率,结合离线优化阶段预先制定的功率-温度设定方案,获取对应电解槽功率及温度,然后通过Buck电路和阀门控制器生成PWM调制信号及阀门开度信号。
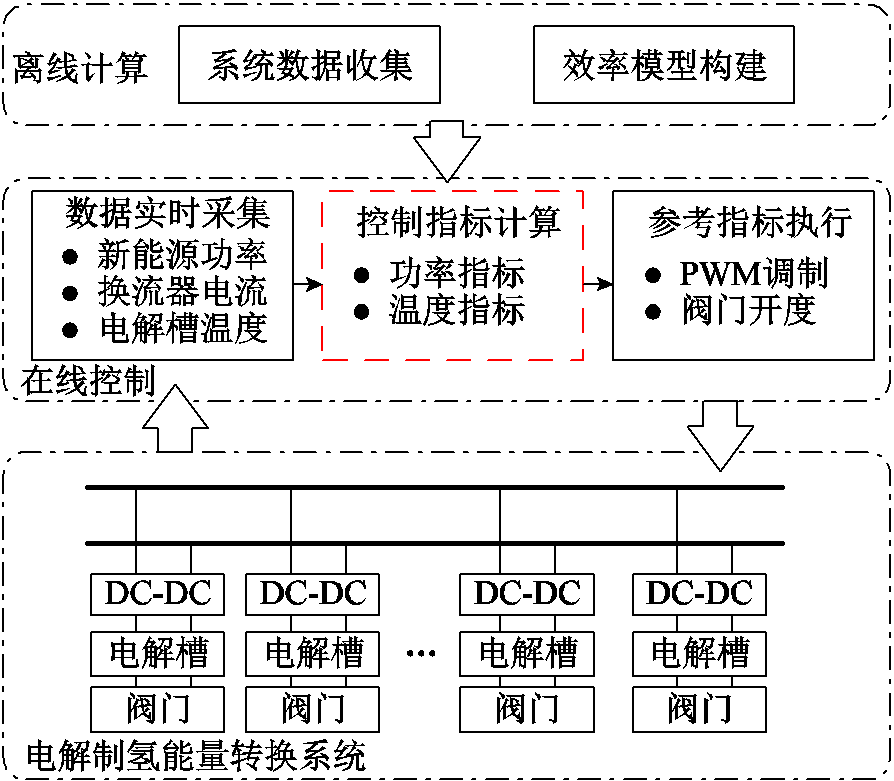
图9 基于功率-温度自适应控制的效率优化策略
Fig.9 Efficiency optimization strategy based on power-temperature adaptive control
为验证本文所提出的基于功率-温度自适应控制的效率优化策略的正确性,采用实时联合仿真平台进行验证。功率-温度自适应控制策略基于RT-LAB OP5600实时仿真平台搭建,多电解槽制氢系统基于热力瞬态实验平台TRNSYS构建。通过RT-LAB内置的socket接口与TRNSYS下的type155与Matlab COM模块实现通信。实时仿真系统设置如图10所示。为方便描述,将平均分配策略、链式分配策略、基于功率自适应控制的效率优化策略、基于功率-温度自适应控制的效率优化策略分别用策略1~策略4表示;前三种控制策略采用固定电解温度360 K,策略4的温度根据图5中最佳电解温度曲线Tbest设定。电解功率设置为从0开始逐渐增加至满载,得到的分配结果及效率曲线如图11和图12所示。
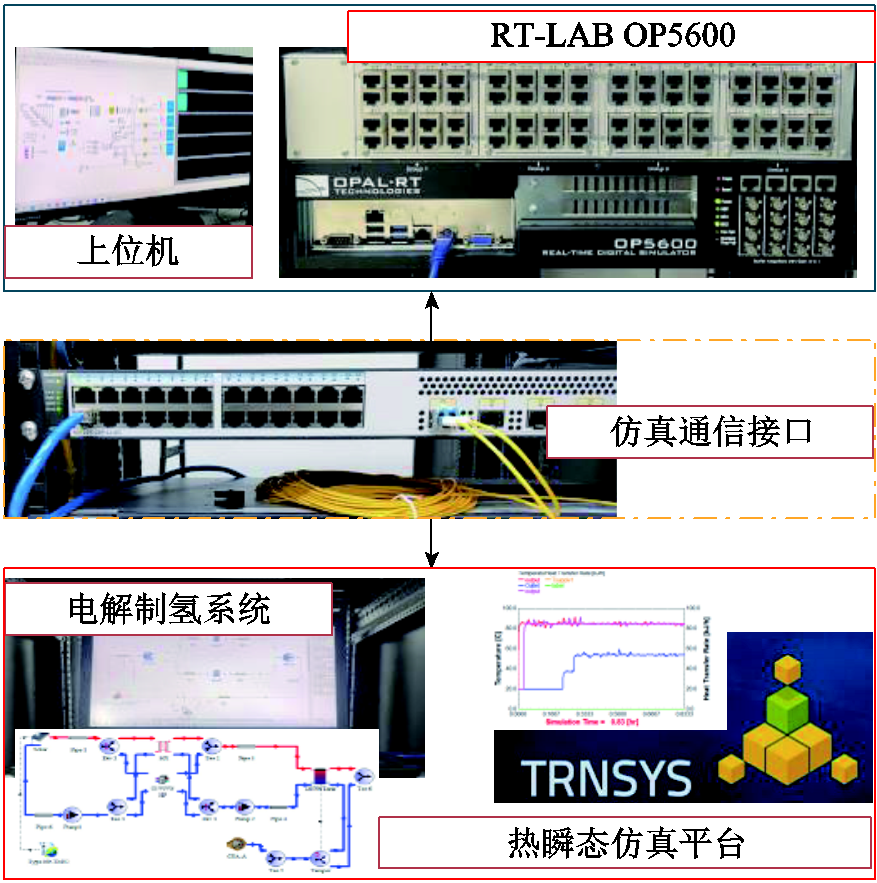
图10 实时仿真系统设置
Fig.10 Diagram of real-time simulation system settings
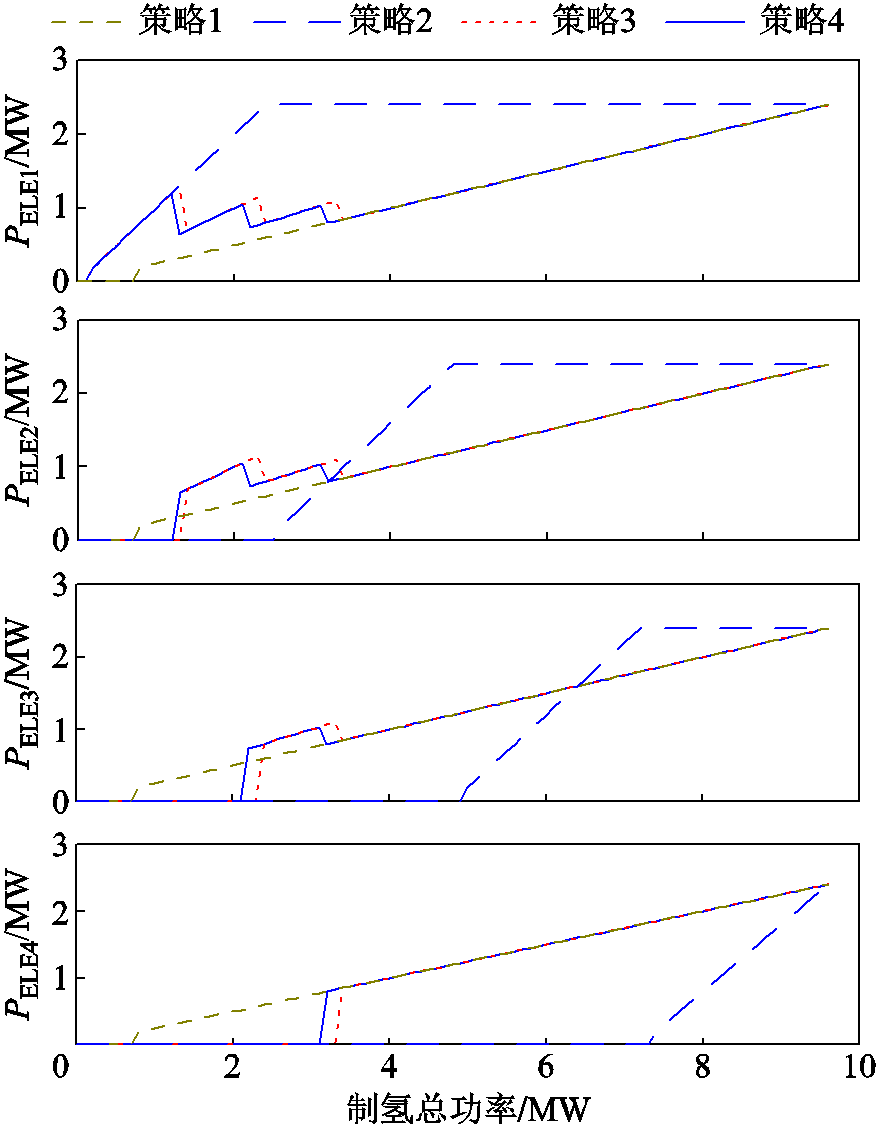
图11 不同策略下电解槽功率分配曲线
Fig.11 Electrolyzer distribution under different control strategies
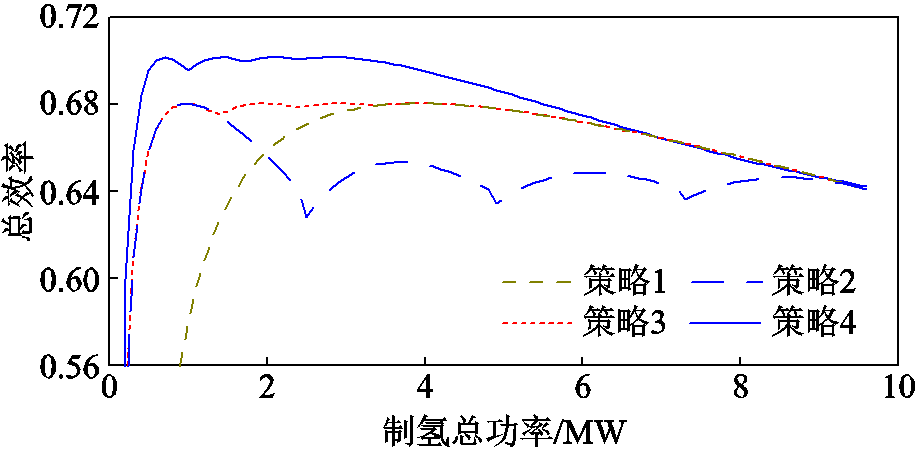
图12 不同策略的制氢效率曲线
Fig.12 Efficiency curves under different control strategies
图11表示当制氢总功率从0升至最大负载时,4台电解槽(ELE1~ELE4)在不同策略下的功率分配情况。由图11可知,采用平均分配策略(策略1)的制氢系统,在制氢总功率较小时无法启动,降低了低功率场景下新能源的利用率;链式分配策略(策略2)可根据制氢功率逐级启动电解槽,对低功率利用效率高;采用功率自适应控制策略(策略3和4),在总制氢功率为0~4 MW范围内,逐级开启电解槽,使制氢效率曲线较大范围地维持在最高效的区间。与温度恒定的功率自适应控制策略(策略3)相比,功率-温度自适应控制策略(策略4)使制氢效率最高点向左偏移,较为提前启动下一级电解槽。
上述分析可以从图12的制氢总效率曲线上体现:采用平均分配策略时,电解槽在1 MW制氢功率以内不会启动,因此低功率范围利用率低,但是高功率范围利用率相对较高;链式分配策略的效率最高峰覆盖范围较小,在系统没有满载的时候,效率低于其他三种策略;采用功率自适应分配策略时,控制器可以根据制氢总功率的变化自适应地分配电解槽运行功率,从而使制氢系统更大范围地运行于最佳效率区间。与平均分配策略相比,功率自适应控制策略提升了对低功率的利用效率;与链式分配策略相比,功率自适应控制策略可以使整个制氢功率范围的效率提升。功率-温度自适应控制策略由于同时优化功率和温度,效率在0~5 MW范围内相对于仅考虑功率优化的策略3提升约2%;随着制氢功率的增加,效率优势逐渐降低,制氢功率达到7 MW后,优化后的温度上升至360 K,策略3和策略4效率曲线重合。
综上所述,链式分配策略适用于制氢功率较低的场景;平均分配策略适用于制氢功率较大的场景;基于功率自适应控制的效率优化策略兼具前两种策略的优势,从低负载区间到高负载区间均保持较高的制氢效率;而基于功率-温度自适应控制的效率优化策略通过功率和温度的双重控制,可在0%~70%负载区间内进一步提升制氢效率。
本文所提效率优化策略适用于风电、光伏等可再生能源制氢场景,以风电制氢为例进行有效性验证。制氢系统由额定容量为4×2 MW、过载率为120%的PEM电解槽构成,功率由装机容量为10 MW的风电场提供。基于风电场一年实测数据,采用Kantorovich距离[37]将历史数据削减为低、中、高三种典型风电出力场景,对应概率分别为0.6、0.2、0.2。为便于描述,将三种风功率场景分别表示为场景1~场景3,典型制氢功率曲线如图13所示。
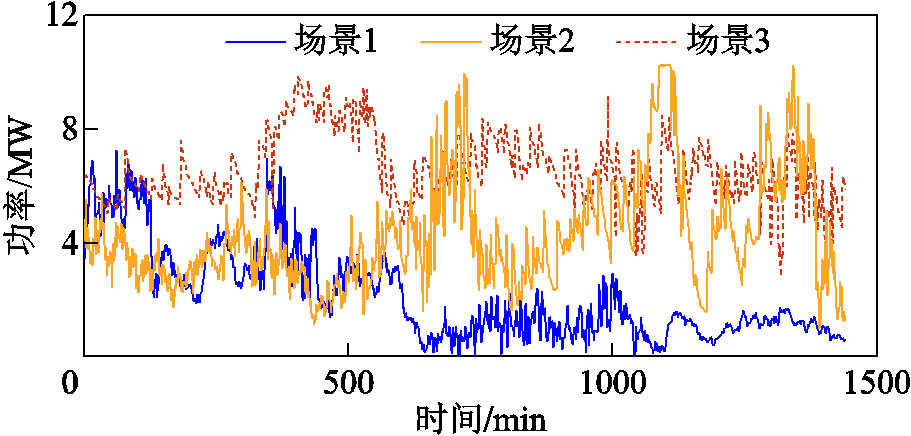
图13 典型制氢功率曲线
Fig.13 Typical hydrogen production power profiles
图14和图15分别给出了场景1下四种制氢策略的功率分配方案及制氢效率曲线。从功率分配方案可以看出:策略1由于采用平均分配策略,在制氢总功率较低时段,例如,600 min时,每台电解槽分配的功率不满足最小运行功率,系统停止制氢,降低了新能源利用率;策略2采用链式开启策略,整体功率始终没有达到开启第4台电解槽的阶段;策略3和4采用了最大化制氢效率策略,在高功率时段启用了四台电解槽。在四种控制策略中,后三种策略都可以根据风功率变化调整电解槽的启停。由图15可以看出,采用功率-温度自适应控制策略后,除了在1 100 min时总效率较低外,基本上可全过程保持最高的电解效率;功率自适应控制策略与功率平均分配策略效率曲线在大部分时段重合,在总制氢功率很低的时段,平均分配策略导致电解槽停止运行,而功率自适应分配策略还能使得电解槽保持较高的运行效率;链式分配策略根据制氢功率的大小调整电解槽启停,因此可以利用较低的制氢功率,减少了停机的情况。但链式分配策略没有进行效率优化,在风功率出力较大的时段(0~600 min)内,运行效率低于其他三种分配策略。
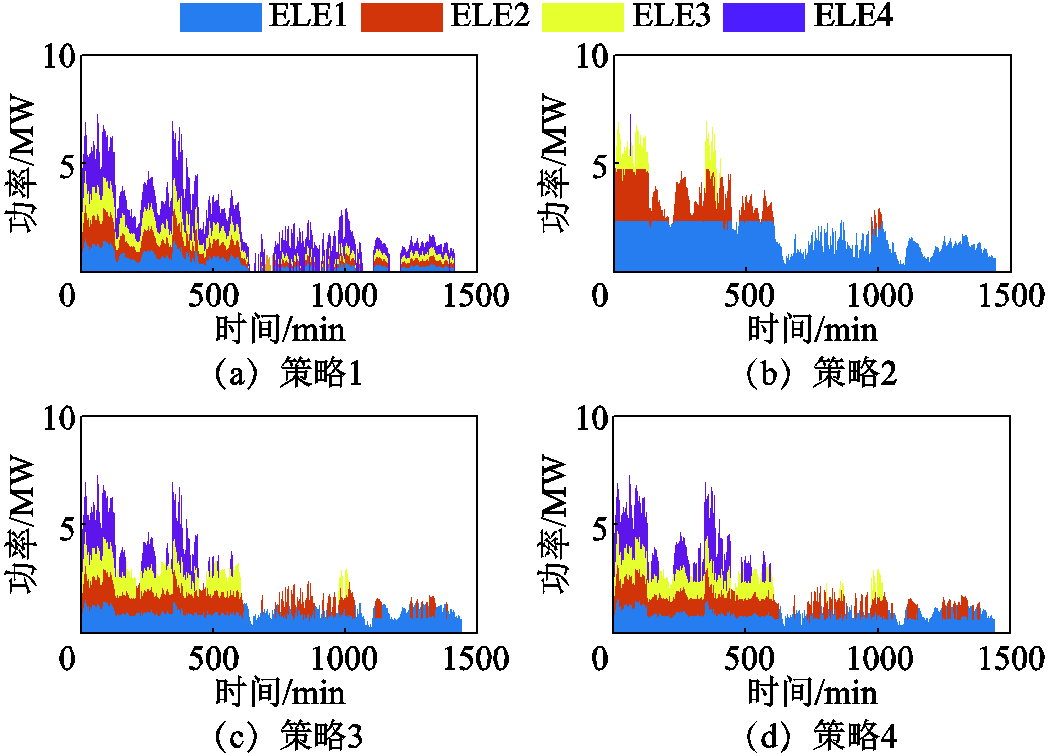
图14 场景1下四种策略电解槽功率分配情况
Fig.14 Power distribution of electrolyzers with four strategies under Scenario 1
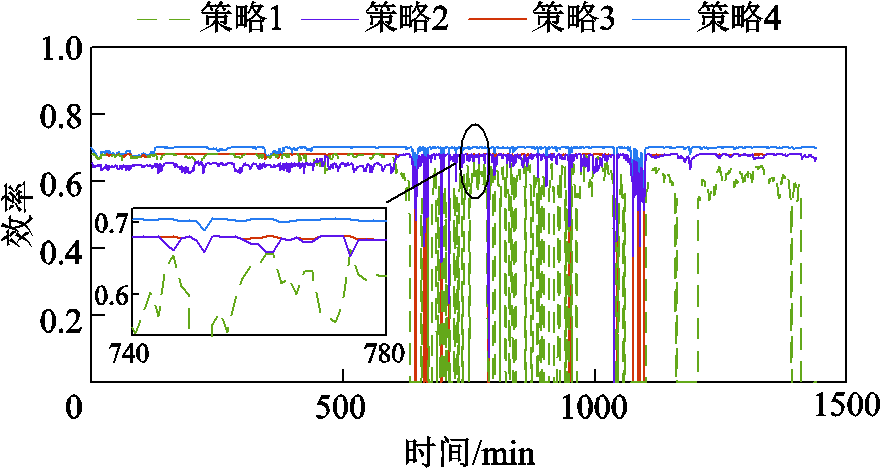
图15 场景1下四种策略制氢效率
Fig.15 Overall hydrogen production efficiencies of four strategies under Scenario 1
图16和图17分别给出了场景2下四种制氢策略的功率分配方案及制氢效率曲线。在场景2下,由于功率未下降至最低范围,采用策略1的四台电解槽未退出运行,但每台电解槽分配到的制氢功率很低;相比之下,策略2采用了链式分配策略,因此只有很短时段开启3号和4号电解槽;策略3和策略4的电解槽功率分配基本相同。在功率较高的1 100~1 200 min范围内,由于控制策略1、3、4的控制信号相同(每台电解槽的功率和温度指标相同),因此其效率也相同。可以看出,采用功率-温度自适应控制策略的电解槽,其效率在制氢高功率时段与其他三种策略相同,而在低、中制氢功率范围内,制氢效率明显提升。
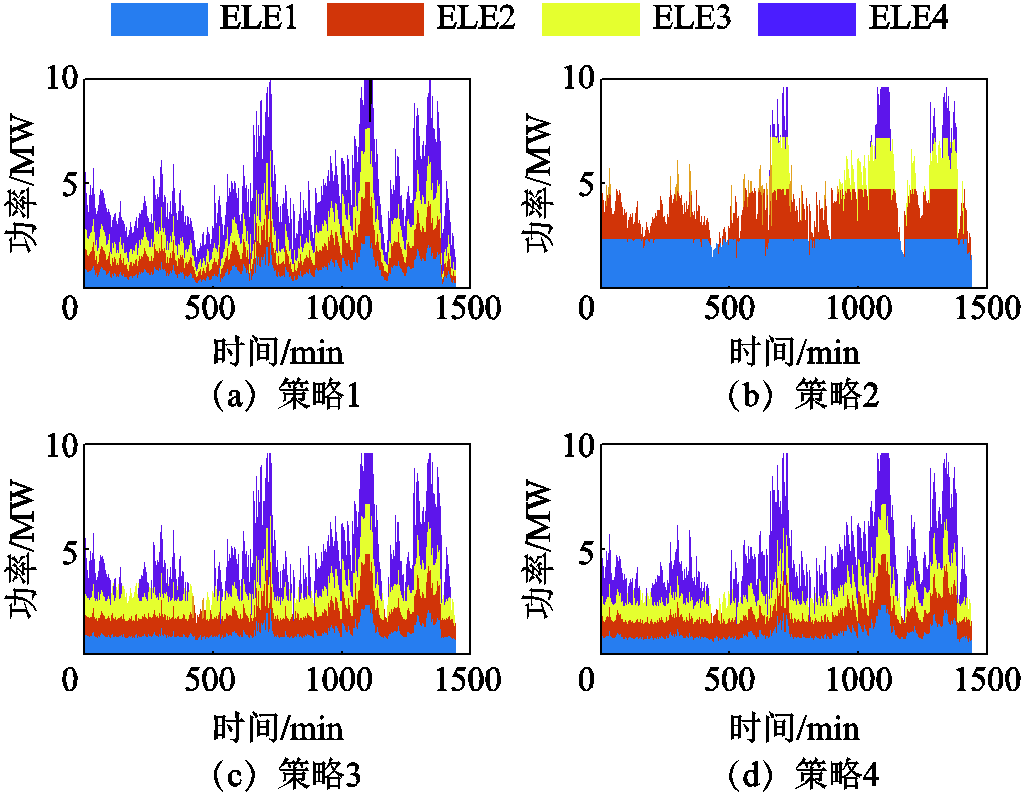
图16 场景2下四种策略电解槽功率分配情况
Fig.16 Power distribution of electrolyzers with four strategies under Scenario 2
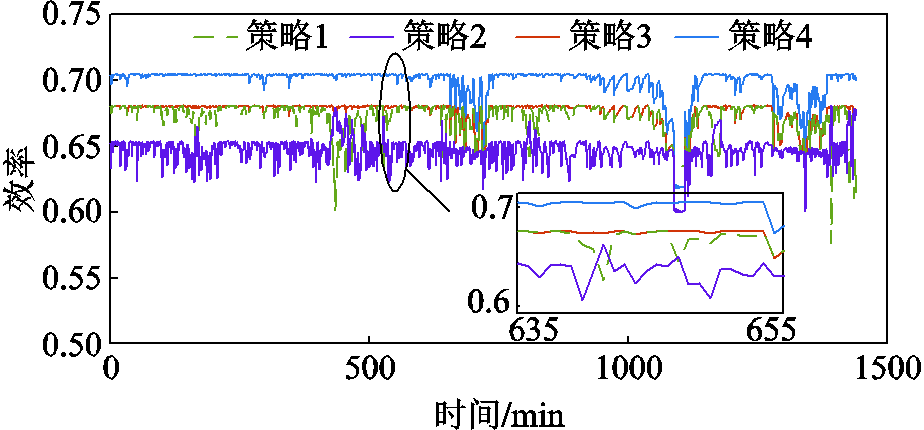
图17 场景2下四种策略制氢效率
Fig.17 Overall hydrogen production efficiencies of four strategies under Scenario 2
图18和图19分别给出了场景3下四种制氢策略的功率分配方案及制氢效率曲线。由于制氢功率全时段都很高,控制策略1、3、4的功率分配结果相同;而链式分配策略难以使电解槽功率相同,因此在400~500 min功率高峰范围内启动了4号电解槽。在电解效率方面,控制策略1和3的功率和温度指标相同,因此两条效率曲线重合;由于控制策略4采用了温度自适应控制,部分时段的温度指标与策略1和3不同,效率也略高于其他两种控制策略。
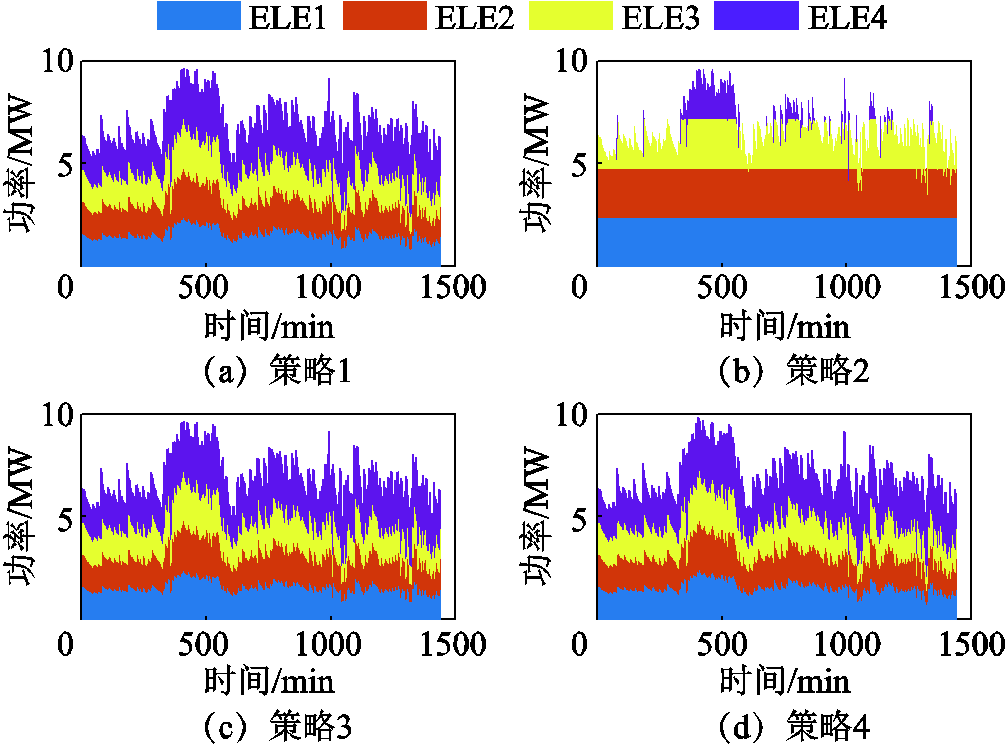
图18 场景3下四种策略电解槽功率分配情况
Fig.18 Power distribution of electrolyzers with four strategies under Scenario 3
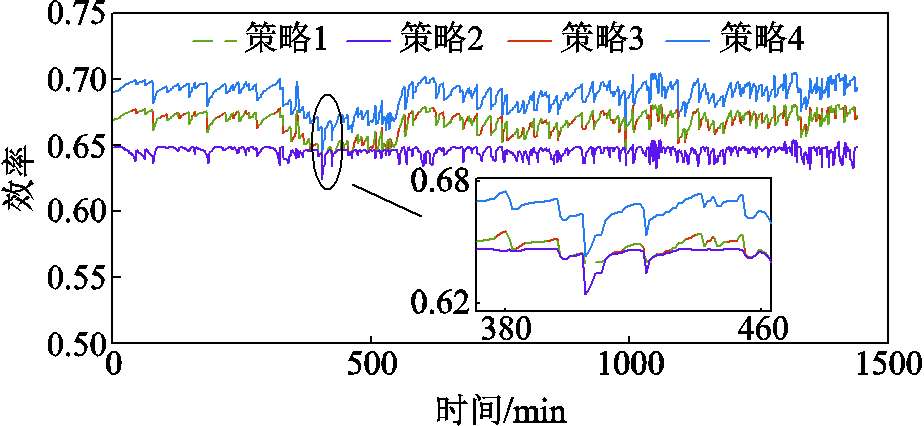
图19 场景3下四种策略制氢效率
Fig.19 Overall hydrogen production efficiencies of four strategies under Scenario 3
表3给出了三种典型场景下四种控制策略的制氢总量。相比于传统的平均分配策略,功率-温度自适应控制在三种场景下可以分别提升制氢量约9.8%、1.6%、0.9%;相对于链式分配策略,可分别提升6.2%、5.7%、4.1%。考虑到三个场景的概率分别为0.6、0.2、0.2,功率-温度自适应控制策略相对于平均分配策略增加制氢量6.4%,相对于链式分配策略增加制氢量5.7%。
表3 不同场景/策略下的制氢总量
Tab.3 Total hydrogen production under different scenarios and strategies(单位:kg)

场景策略1策略2策略3策略4 1970.61 003.81 040.71 065.7 22 039.81 961.72 041.02 073.3 33 117.83 022.93 117.83 146.6
本文建立了包含主要能耗环节的电解制氢系统效率模型,分析了电解制氢系统最优效率与电解功率、温度的关系,提出了基于离线优化与在线控制的多堆PEM电解制氢系统效率优化策略。通过算例分析,得到以下结论:
1)制氢效率受到电解功率和温度的双重影响,升高电解温度并不一定会提高制氢效率,其最优取值需在制氢效率曲面上依据电解功率对应确定。
2)相对于平均分配策略和链式分配策略,本文提出的功率-温度自适应控制策略既可以充分利用低功率高效制氢,又可以在较大功率范围内保持高效率,因此适用于制氢功率波动的场景。
3)在实际风电制氢场景下,相对于传统的平均控制策略和链式分配策略,本文提出的功率-温度自适应控制策略分别提升产氢量6.4%和5.7%。
由不同场景下的制氢效率曲线可知,优化后的系统效率维持在70%左右,而大量的能量在电解、压缩等环节以热能形式耗散。因此,下一步计划开展电解制氢系统与区域供热系统耦合运行的相关研究,实现氢/热联供,提升可再生能源利用效率。
附 录
以两台电解槽为例证明,其功率分配示意图如附图1所示。若两台电解槽分配的功率不相同,设其分别为P1和P2,对应的制氢量分别为F(P1)和F(P2),设F(P4)为两台电解槽的平均产氢量,即
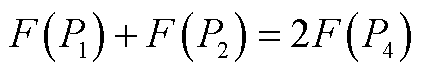 (A1)
(A1)

附图1 两台电解槽功率分配示意图
App.Fig.1 Power distribution of 2 electrolytic cells
令P3为平均分配的功率,则有
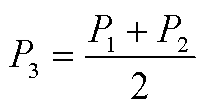 (A2)
(A2)
即对应的产氢量为2F(P3)。根据制氢量-功率曲线,有
 (A3)
(A3)
因此,两台电解槽功率平均分配的产氢量大于不平均分配的产氢量。类似地,如果启动j台电解槽,则平均分配的产氢量大于其他分配策略。
参考文献
[1] 王雨晴, 王文诗, 徐心竹, 等. 面向低碳交通的含新能源汽车共享站电-氢微能源网区间-随机混合规划方法[J]. 电工技术学报, 2023, 38(23): 6373-6390. Wang Yuqing, Wang Wenshi, Xu Xinzhu, et al. Hybrid interval/stochastic planning method for new energy vehicle sharing station-based electro-hydrogen micro-energy system for low-carbon transportation[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6373-6390.
[2] 吴孟雪, 房方. 计及风光不确定性的电-热-氢综合能源系统分布鲁棒优化[J]. 电工技术学报, 2023, 38(13): 3473-3485. Wu Mengxue, Fang Fang. Distributionally robust optimization of electricity-heat-hydrogen integrated energy system with wind and solar uncertainties[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3473-3485.
[3] 刘玮, 万燕鸣, 熊亚林, 等. 碳中和目标下电解水制氢关键技术及价格平准化分析[J]. 电工技术学报, 2022, 37(11): 2888-2896. Liu Wei, Wan Yanming, Xiong Yalin, et al. Key technology of water electrolysis and levelized cost of hydrogen analysis under carbon neutral vision[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2888-2896.
[4] Han Bo, Steen S M, Mo Jingke, et al. Electrochemical performance modeling of a proton exchange membrane electrolyzer cell for hydrogen energy[J]. International Journal of Hydrogen Energy, 2015, 40(22): 7006-7016.
[5] 李军舟, 赵晋斌, 曾志伟, 等. 具有动态调节特性的光伏制氢双阵列直接耦合系统优化策略[J]. 电网技术, 2022, 46(5): 1712-1721. Li Junzhou, Zhao Jinbin, Zeng Zhiwei, et al. Optimization strategy of photovoltaic hydrogen production dual array direct coupling system with dynamic regulation characteristics[J]. Power System Technology, 2022, 46(5): 1712-1721.
[6] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516. Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in industrial park integrated energy system based on stackelberg game[J]. Transactions of China Electro-technical Society, 2021, 36(3): 507-516.
[7] 鲁明芳, 李咸善, 李飞, 等. 季节性氢储能-混氢燃气轮机系统两阶段随机规划[J]. 中国电机工程学报, 2023, 43(18): 6978-6992. Lu Mingfang, Li Xianshan, Li Fei, et al. Two-stage stochastic programming of seasonal hydrogen energy storage and mixed hydrogen-fueled gas turbine system[J]. Proceedings of the CSEE, 2023, 43(18): 6978-6992.
[8] Huang Chunjun, Zong Yi, You Shi, et al. Economic model predictive control for multi-energy system considering hydrogen-thermal-electric dynamics and waste heat recovery of MW-level alkaline electro-lyzer[J]. Energy Conversion and Management, 2022, 265: 115697.
[9] Nguyen T T, Kim H M. Cluster-based predictive PCC voltage control of large-scale offshore wind farm[J]. IEEE Access, 2020, 9: 4630-4641.
[10] Kumar S S, Nirmal Mukundan C M, Jayaprakash P. Modified LMS control for a grid interactive PV–fuel cell–electrolyzer hybrid system with power dispatch to the grid[J]. IEEE Transactions on Industry Applications, 2022, 58(6): 7907-7918.
[11] Abdelghany M B, Faisal Shehzad M, Liuzza D, et al. Modeling and optimal control of a hydrogen storage system for wind farm output power smoothing[C]// 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Korea (South), 2020: 49-54.
[12] Huang Chunjun, Zong Yi, You Shi, et al. Cooperative control of wind-hydrogen-SMES hybrid systems for fault-ride-through improvement and power smoothing[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 1-7.
[13] Guerra O J, Eichman J, Kurtz J, et al. Cost competitiveness of electrolytic hydrogen[J]. Joule, 2019, 3(10): 2425-2443.
[14] Tjarks G, Gibelhaus A, Lanzerath F, et al. Energetically-optimal PEM electrolyzer pressure in power-to-gas plants[J]. Applied Energy, 2018, 218: 192-198.
[15] Correa G, Marocco P, Muñoz P, et al. Pressurized PEM water electrolysis: dynamic modelling focusing on the cathode side[J]. International Journal of Hydrogen Energy, 2022, 47(7): 4315-4327.
[16] Scheepers F, Stähler M, Stähler A, et al. Improving the efficiency of PEM electrolyzers through membrane-specific pressure optimization[J]. Energies, 2020, 13(3): 612.
[17] Scheepers F, Stähler M, Stähler A, et al. Temperature optimization for improving polymer electrolyte membrane-water electrolysis system efficiency[J]. Applied Energy, 2021, 283: 116270.
[18] 邓智宏, 江岳文. 考虑制氢效率特性的风氢系统容量优化[J]. 可再生能源, 2020, 38(2): 259-266. Deng Zhihong, Jiang Yuewen. Optimal sizing of a wind-hydrogen system under consideration of the efficiency characteristics of electrolysers[J]. Renewable Energy Resources, 2020, 38(2): 259-266.
[19] Keller R, Rauls E, Hehemann M, et al. An adaptive model-based feedforward temperature control of a 100 kW PEM electrolyzer[J]. Control Engineering Practice, 2022, 120: 104992.
[20] 沈小军, 聂聪颖, 吕洪. 计及电热特性的离网型风电制氢碱性电解槽阵列优化控制策略[J]. 电工技术学报, 2021, 36(3): 463-472. Shen Xiaojun, Nie Congying, Lü Hong. Coordination control strategy of wind power-hydrogen alkaline electrolyzer bank considering electrothermal charac-teristics[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 463-472.
[21] 唐司航. 基于风电功率最值预测的电解槽阵列轮换控制策略研究[D]. 石家庄: 河北科技大学, 2022. Tang Sihang. Research on control strategy of alkaline electrolyzer array with rotation mode based on best value forecast for wind power[D]. Shijiazhuang: Hebei University of Science and Technology, 2022.
[22] 卢昕宇, 杜帮华, 赵波, 等. 基于链式分配策略的风氢耦合系统设计与控制[J]. 太阳能学报, 2022, 43(6): 405-413. Lu Xinyu, Du Banghua, Zhao Bo, et al. Design and control of wind-hydrogen coupled system based on chain distribution strategy[J]. Acta Energiae Solaris Sinica, 2022, 43(6): 405-413.
[23] Luxa A, Jöres N, Yáñez C, et al. Multilinear modeling and simulation of a multi-stack PEM electrolyzer with degradation for control concept comparison[C]// Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications, Lisbon, Portugal, 2022: 52-62.
[24] Bareiß K, de la Rua C, Möckl M, et al. Life cycle assessment of hydrogen from proton exchange membrane water electrolysis in future energy systems[J]. Applied Energy, 2019, 237: 862-872.
[25] Sakas G, Ibáñez-Rioja A, Ruuskanen V, et al. Dynamic energy and mass balance model for an industrial alkaline water electrolyzer plant process[J]. International Journal of Hydrogen Energy, 2022, 47(7): 4328-4345.
[26] Tiktak W J. Heat management of PEM electrolysis[D]. Delft: Delft University of Technology, 2019.
[27] Zheng Yi, You Shi, Bindner H W, et al. Optimal day-ahead dispatch of an alkaline electrolyser system concerning thermal–electric properties and state-transitional dynamics[J]. Applied Energy, 2022, 307: 118091.
[28] 游双矫. 中石油为雄安新区供氢方式优化的研究[D]. 北京: 中国石油大学(北京), 2020. Yon Shuangjiao. Research on optimization of hydrogen supplies for Xiongan New Area by CNPC[D]. Beijing: China University of Petroleum, 2020.
[29] 徐卫君, 张伟, 胡宇涛, 等. 先进绝热压缩空气储能多能流优化调度模型[J]. 电工技术学报, 2022, 37(23): 5944-5955. Xu Weijun, Zhang Wei, Hu Yutao, et al. Multi energy flow optimal scheduling model of advanced adiabatic compressed air energy storage[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5944-5955.
[30] Skorek-Osikowska A, Bartela Ł, Katla D, et al. Thermodynamic assessment of the novel concept of the energy storage system using compressed carbon dioxide, methanation and hydrogen generator[J]. Fuel, 2021, 304: 120764.
[31] 张理, 韩民晓, 范溢文. 多相堆叠交错并联制氢变换器控制策略与特性分析[J]. 电工技术学报, 2023, 38(2): 485-495. Zhang Li, Han Minxiao, Fan Yiwen. Control strategy and characteristic analysis of multi-phase stacked interleaved buck converter for hydrogen production[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 485-495.
[32] 任洲洋, 王皓, 李文沅, 等. 基于氢能设备多状态模型的电氢区域综合能源系统可靠性评估[J]. 电工技术学报, 2023, 38(24): 6744-6759. Ren Zhouyang, Wang Hao, Li Wenyuan, et al. Reliability evaluation of electricity-hydrogen regional integrated energy systems based on the multi-state models of hydrogen energy equipment[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6744-6759.
[33] Ayachit A, Kazimierczuk M K. Averaged small-signal model of PWM DC-DC converters in CCM including switching power loss[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2019, 66(2): 262-266.
[34] Talebian I, Alavi P, Marzang V, et al. Analysis, design, and investigation of a soft-switched buck converter with high efficiency[J]. IEEE Transactions on Power Electronics, 2022, 37(6): 6899-6912.
[35] Yigit T, Selamet O F. Mathematical modeling and dynamic Simulink simulation of high-pressure PEM electrolyzer system[J]. International Journal of Hydrogen Energy, 2016, 41(32): 13901-13914.
[36] Rizwan M, Alstad V, Jäschke J. Design considerations for industrial water electrolyzer plants[J]. International Journal of Hydrogen Energy, 2021, 46(75): 37120-37136.
[37] 宋天昊, 李柯江, 韩肖清, 等. 储能系统参与多应用场景的协同运行策略[J]. 电力系统自动化, 2021, 45(19): 43-51. Song Tianhao, Li Kejiang, Han Xiaoqing, et al. Coordinated operation strategy of energy storage system participating in multiple application scenarios[J]. Automation of Electric Power Systems, 2021, 45(19): 43-51.
Abstract With the growing focus of human society on low-carbon energy, the proportion of hydrogen energy in power systems is increasing and the hydrogen production system from water electrolysis is evolving towards a larger capacity and multiple stacks. Water electrolysis based on the proton exchange membrane (PEM) technology using renewable energy is a promising means of promoting the consumption of renewable energy and building a low-carbon power system. However, the randomness and volatility of renewable energy pose challenges to the efficient operation of a multi-stack PEM electrolytic hydrogen production system under fluctuating power scenarios. To enhance the efficiency of hydrogen production systems with multi-stack PEM electrolyzers, this research proposes an efficiency optimization strategy with power-temperature adaptive control. The research work is described as follows:
Firstly, an overall efficiency model of the hydrogen production system is established. The relationship between optimal system efficiency and the electrolytic power and temperature is analyzed. It reveals that the optimal electrolytic efficiency might not be achieved at the upper limits of electrolytic temperature. When the current density is low, the optimal electrolytic temperature is relatively low due to the significant reduction in Faraday efficiency caused by temperature rise. However, when the current density exceeds 1.5 A/cm2, the optimal electrolysis temperature increases with the increase of current density. Therefore, to improve the electrolytic efficiency when the power of renewable energy fluctuates, it is necessary to properly adjust the electrolytic power and temperature of the electrolyzers.
Secondly, offline optimization and online control are employed to enhance electrolytic efficiency. The offline optimization involves a two-stage optimization model, where the first stage optimizes the startup and shutdown status, electrolysis power, and temperature settings of different electrolyzers to maximize hydrogen production efficiency. In the second stage, a specific power-temperature implementation scheme is determined for the electrolyzers, to achieve rapid temperature adjustment when there are multiple solutions in the first stage. In the online control section, the dynamic models of the power and temperature control of the electrolyzers are established, respectively. Based on the current total power of hydrogen production and the power-temperature setting scheme determined in the offline optimization stage, the PWM modulation signal and the valve opening signal are generated by the buck and the valve controllers, respectively.
Finally, to verify the effectiveness of the proposed efficiency enhancement strategy, a comparison is made between the proposed method and the existing average allocation strategy and chain allocation strategy. The analysis shows that the efficiency of hydrogen production is affected by both electrolytic power and temperature. Increasing the electrolysis temperature does not necessarily improve the hydrogen production efficiency, and its optimal value should be determined based on the electrolysis power. Compared with the average allocation strategy and the chain allocation strategy, the power-temperature adaptive control strategy proposed in this research can make full use of low renewable energy efficiently, while maintaining high efficiency over a large power range, making it suitable for hydrogen production with power fluctuations. In actual scenarios of hydrogen production from wind power, the proposed power-temperature adaptive control strategy can increase hydrogen production by 6.4% and 5.7%, respectively, compared with the average allocation strategy and chain allocation strategy.
keywords:Proton exchange membrane elecrolyzers, power to hydrogen, renewable energy power generation, efficiency optimization, adaptive control
DOI:10.19595/j.cnki.1000-6753.tces.230113
中图分类号:TQ116.2; TM73
国家自然科学基金资助项目(52077136,U2166201)。
收稿日期 2023-02-01
改稿日期 2023-03-13
韩鹏飞 男,1993年生,博士研究生,研究方向为可再生能源发电制氢系统优化与控制等。E-mail:han_pf@sjtu.edu.cn
徐潇源 男,1989年生,副教授,研究方向为电力系统不确定性分析、电力系统优化运行等。E-mail:xuxiaoyuan@sjtu.edu.cn(通信作者)
(编辑 李 冰)