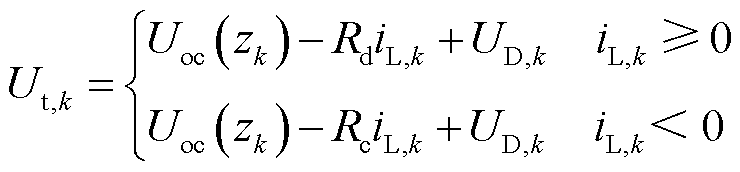 (1)
(1)
摘要 动力电池是电动汽车的技术瓶颈,其状态的高精度估计一直是行业的技术难点,不准确的状态估计值易造成安全隐患,并加速动力电池系统老化。然而,动力电池每用必衰、时变非线性、环境敏感性等特点导致对其状态的实时精准估计极具挑战性。该文针对锂离子动力电池峰值功率估计的问题,提出基于多时间尺度滑动窗口的双扩展卡尔曼滤波(DEKF)算法,基于峰值功率测试结果更新模型参数库,实现了参数的缓时变估计。评价指标显示,动力电池全寿命、全电量区间内,变温度等条件下的验证结果表明所提算法能够准确估计电池参数和功率状态,电压误差小于40 mV。
关键词:电动汽车 锂离子电池 峰值功率估计 双扩展卡尔曼滤波算法 滑动窗口
环境污染和能源短缺是全球亟待解决的热点问题之一,加快开发电动汽车己成为全球共识[1-3]。作为电动汽车的动力源,车用电池系统在安全、工作性能和寿命等方面的局限制约了电动汽车的发展[4-5]。目前,生产厂家普遍选用锂离子动力电池,主要因为其具有电压高、比能量大、体积小、质量轻等优点[6-7]。为了最大程度地保证电池高效且安全的工作,需要设计电池管理系统(Battery Management System, BMS)来控制和保护电池[8]。为了保证BMS能够安全、高效、准确地运行,及时作出合理的决策,电池状态估计方法需要具有足够的准确性、稳定性和高适应性[9-13]。
功率状态(State of Power, SOP)估计是BMS的主要功能之一,与电池荷电状态(State of Charge, SOC)、健康状态(State of Health, SOH)、温度以及模型参数有着紧密的联系,但比SOC估计变化更快,其在线实时估计可用于能量管理策略的合理制定[14]。SOP有多种定义方式,其中实用意义更强的是恒功率形式持续的动态最大峰值功率,影响着驱动、制动、能量分配等控制策略的制定[15]。现有的SOP估计方法分为三类:特性图谱法、基于数据驱动的方法和多约束估计法。特征图谱法通过离线测试的数据表,以数据插值的方式实现功率能力的在线预测。基于数据驱动的方法将电池看作一黑箱,以峰值功率作为输出,其影响因素作为输入,通过对大量数据进行训练,实现峰值功率预测[16],预测精度与电池本身特点无关,单纯依靠数据的可靠度,从而建立抽象的电池模型[17]。由于数据驱动方法高度依赖培训数据的质量和数量,并且很难直接收集一系列用于训练的连续参考SOP,因此很少有人将这些方法应用于在线SOP估计。多约束估计法是基于动态的电池参数模型,根据多个约束指标求取峰值电流,最终将峰值电流与估计端电压的乘积作为峰值功率[18],其精度受到所选择模型拟合精度和参数在线辨识精度的影响[19]。当前,常用的约束指标包括端电压、SOC、温度、电流和设计功率等。WangYujie等[20-21]基于戴维南模型估计了磷酸铁锂电池和超级电容器混合系统在连续时间内的峰值功率。TanYaqian等[22]基于双极化模型对各种约束条件下的三元锂离子电池进行SOC和SOP联合估计,最大SOP估计误差减小。Chen Wenxin等[23]基于新的多模型融合等效电路模型,估算了锂离子电容器的SOP,但仅在电流和电压限制下讨论了放电SOP。参数在线辨识方法通常分为基于定义的特征提取方法[24-25]、基于数据驱动的方法[22]和基于模型的方法[23]。综上可知,电池系统参数和状态的准确估计对于电池功率状态的评估有重要意义。
实车应用时,状态估计方法一般难以得到精确且与实际相符的峰值功率。因此,本文首先在不同温度、不同工况、不同老化状态的情况下开展了大量电芯、模组和电池包实验,建立了兼具高预测精度和低计算量的电池单体模型和双特征单体均匀分布的电池包模型,实施单体模型到系统算法的拓展。其次,提出了基于多时间尺度滑动窗口的双扩展卡尔曼滤波(Double Extend Kalman Filter, DEKF)算法,基于峰值功率测试结果更新模型参数库,实现了参数的缓时变估计,提升了算法估计峰值功率的精度和鲁棒性,完成了电池系统全寿命、全电量、多温度、多工况情况下的模型参数和功率状态估计。最终,通过硬件在环验证,证明了其有效性和精确性。
电池模型的建立遵循一般规律,主要包括四个步骤,分别是电池模型选择、辨识数据测试、模型参数辨识、验证数据测试。本文选择建立了12种常见的等效电路模型[28],完成美国电池测试手册中的混合功率脉冲特征(Hybrid Pulse Power Characteristic, HPPC)测试,针对测试数据用Matlab内置遗传算法辨识电池模型参数,再进行模拟电动汽车形式工况的动力电池城市道路循环(Urban Dynamometer Driving Schedule, UDDS)和动态应力测试(Dynamic Stress Test, DST),验证电池模型拟合精度,筛选出合适的电池模型。
经过对比分析,一阶RC模型具有相对较高的电压预测精度和相对较少的计算量,适合作为参数状态协同估计算法的模型。该模型是OCV-SOC插值表格、欧姆内阻、一阶RC网络结构的组合,内阻大小与电流方向有关,其电路原理如图1所示,计算式为
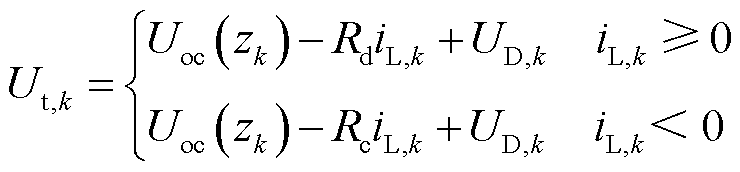 (1)
(1)
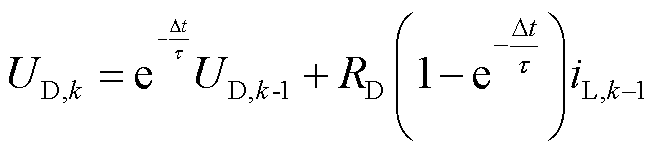
式中,Ut,k、zk、iL,k分别为电池终端电压、SOC、电流;Uoc(zk)是以二维插值表格形式描述开路电压和SOC的关系;Rd和Rc分别为放电和充电欧姆内阻;Δt为采样间隔;UD,k为极化电压;RD和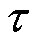 分别为极化内阻和时间常数;下标k代表迭代次数。
分别为极化内阻和时间常数;下标k代表迭代次数。
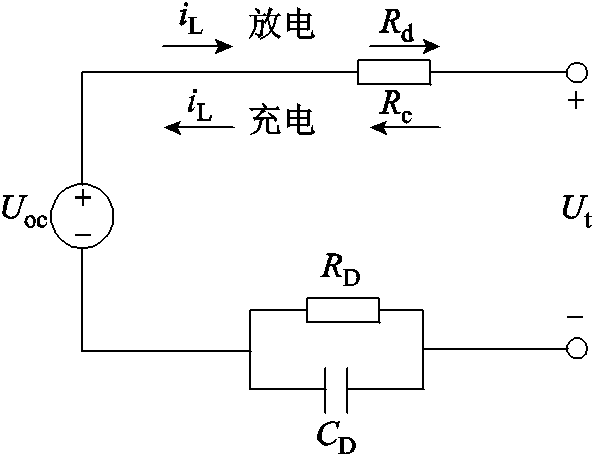
图1 电芯模型原理图
Fig.1 Schematic diagram of cell model
在电池单体模型的基础上,建立了具有双特征单体均匀分布的电池包模型。其中,双特征单体是指电池包中实时最高单体电压和最低单体电压,其所属单体编号是变化的。同时,并联环节视作大单体,模型参数随着电池特性发生倍率变化。基于电池单体均匀分布的假设,输入最高、最低单体电压和总电压,计算全部单体电压的数据,简化电池系统计算公式,实现了从单体模型到系统模型的转变。
根据经典的电池状态和参数估计算法推导计算出的峰值功率往往变化过快,与实际情况不符,存在较大的估计误差。针对锂离子动力电池系统峰值功率估计研究的常见问题,本文提出了基于多时间尺度滑动窗口的DEKF算法,基于峰值功率测试结果更新模型参数库,实现了参数的缓时变估计,提升了算法估计峰值功率的精度和鲁棒性。
针对一阶RC等效电路模型,将k+1时刻的开路电压在k时刻进行一阶泰勒展开,得到动力电池电压计算模型为
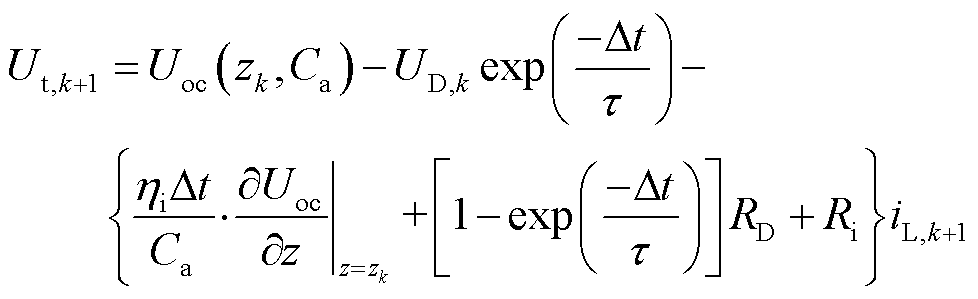 (2)
(2)
式中,Ca为电池的最大可用容量;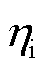 为电池的库仑效率,在这里
为电池的库仑效率,在这里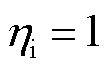 ;RD为极化内阻;Ri为欧姆内阻;
;RD为极化内阻;Ri为欧姆内阻;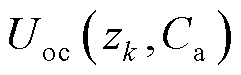 是在Uoc(zk)基础上描述了开路电压与SOC和最大可用容量之间的关系。
是在Uoc(zk)基础上描述了开路电压与SOC和最大可用容量之间的关系。
任意时刻动力电池的电流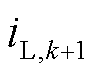 可计算为
可计算为
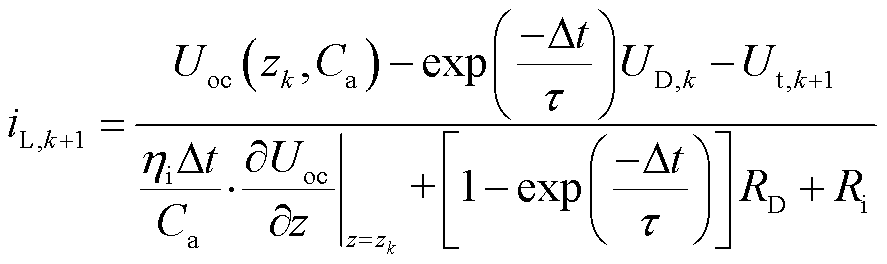 (3)
(3)
任意时刻动力电池的功率Pk+1可计算为
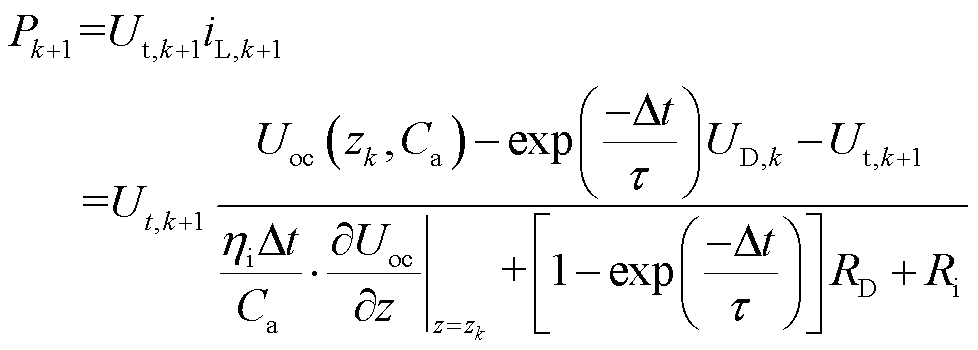 (4)
(4)
在持续时间 (L为持续时间间隔数)内,将动力电池预测模型视为定常系统,即模型参数保持不变,则有
(L为持续时间间隔数)内,将动力电池预测模型视为定常系统,即模型参数保持不变,则有
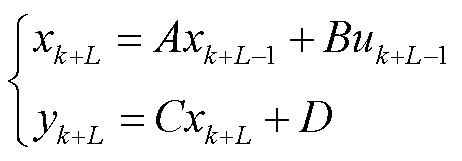 (5)
(5)
式中,u、x、y分别为输入量(电流)、状态量(极化电压)、输出量(测量值端电压)。其中,A、B、C、D视为常数,只与k时刻的模型参数有关,可表达为
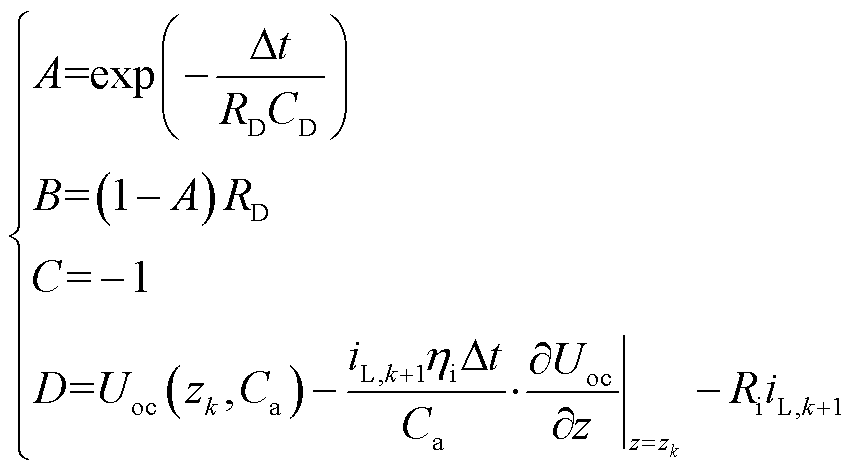 (6)
(6)
式中,CD为极化电容。
在进行恒功率推导的过程中,需要消除电流的影响,根据电流、电压、功率三者的关系进行替换,得到
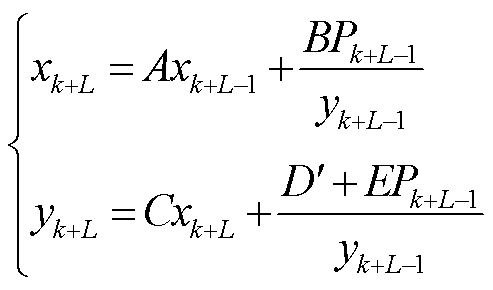 (7)
(7)
其中
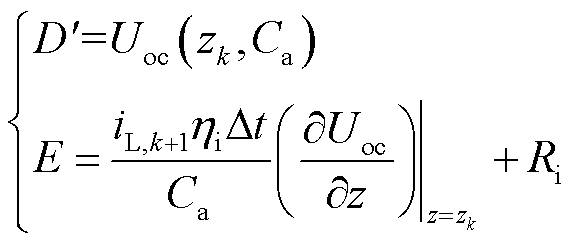
式中,P为输入量(恒功率);A、B、C、![]() 、E视为常数,只与k时刻的模型参数有关。
、E视为常数,只与k时刻的模型参数有关。
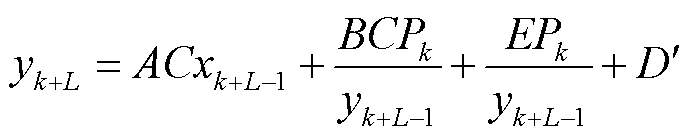 (8)
(8)
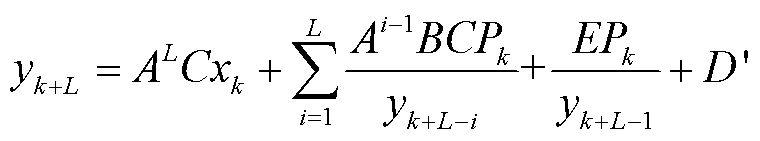 (9)
(9)
由式(8)和式(9)可知,k+L时刻的端电压与k时刻的模型参数,以及期间内所有的端电压值、功率值有关,难以消除中间端电压量测值的影响,无法直接计算恒功率形式的预测电压和最大峰值功率。
为了解决这个问题,进行如下分析:已知k时刻的模型参数、k+L时刻的端电压;求解k时刻的持续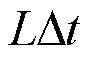 时间的恒功率最大峰值功率。
时间的恒功率最大峰值功率。
由上述基础公式可知,k+L时刻的端电压很难与k时刻的持续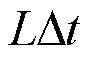 时间的恒功率最大峰值功率有直接、简单的关系,需要逐步正向推导,才能由功率推导出预测电压。
时间的恒功率最大峰值功率有直接、简单的关系,需要逐步正向推导,才能由功率推导出预测电压。
考虑到峰值功率的大小与端电压的高低有着正相关的关系,所以可以使用二分法,选取一定的峰值功率大小,将求得相应的端电压与目标端电压进行比较,再用二分法修正峰值功率大小,达到不断接近真实峰值功率的目的。恒功率峰值功率算法流程如图2所示。首先,根据设备和电池限定的最大峰值功率,计算k时刻的最大峰值功率先验值,将k时刻的参数与极化电压作为输入,计算k+L时刻的预测电压,根据预测电压与电池下截止电压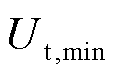 (若为充电,则为上截止电压
(若为充电,则为上截止电压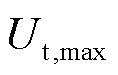 )之差,判断是否小于设定值,重新计算峰值功率或直接输出。
)之差,判断是否小于设定值,重新计算峰值功率或直接输出。
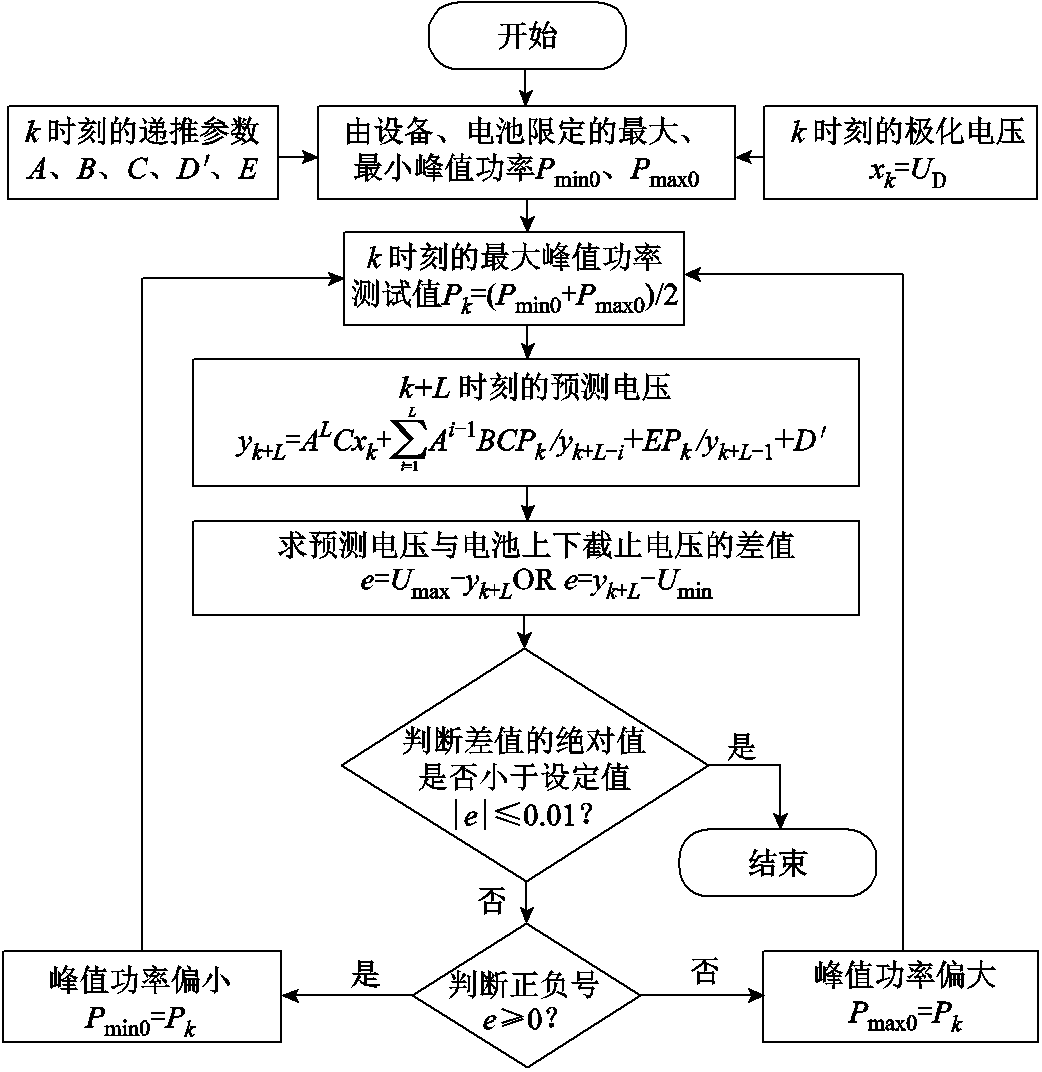
图2 恒功率峰值功率算法
Fig.2 Constant power peak power algorithm
2.2.1多时间尺度滑动窗口DEKF算法实施动力电池峰值功率估计
为便于分析,将非线性离散系统转换为描述包含隐含状态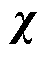 和参数
和参数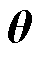 的系统,即
的系统,即
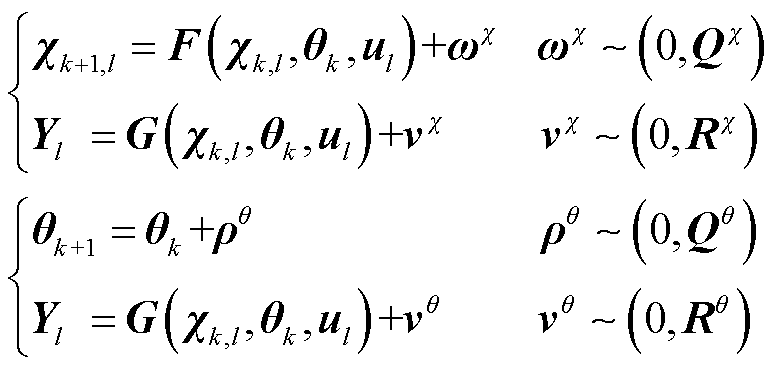 (10)
(10)
式中,F、G为描述系统信息的系数矩阵;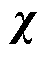 为系统的状态;u为系统的输入信息(控制矩阵);Y为系统的观测矩阵(测量矩阵);下标k、l分别描述宽尺度与窄尺度下的系统时间;
为系统的状态;u为系统的输入信息(控制矩阵);Y为系统的观测矩阵(测量矩阵);下标k、l分别描述宽尺度与窄尺度下的系统时间;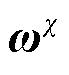 和
和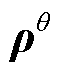 分别为系统状态和参数白噪声,其协方差分别为
分别为系统状态和参数白噪声,其协方差分别为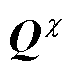 和
和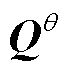 ;其中,上标
;其中,上标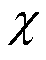 代表系统状态的信息,上标
代表系统状态的信息,上标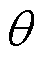 代表参数的信息;
代表参数的信息;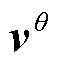 为测量白噪声,其协方差
为测量白噪声,其协方差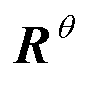 。使用状态观测器EKFc估计系统的状态、参数观测器EKFθ估计系统参数。
。使用状态观测器EKFc估计系统的状态、参数观测器EKFθ估计系统参数。
2)矩阵定义
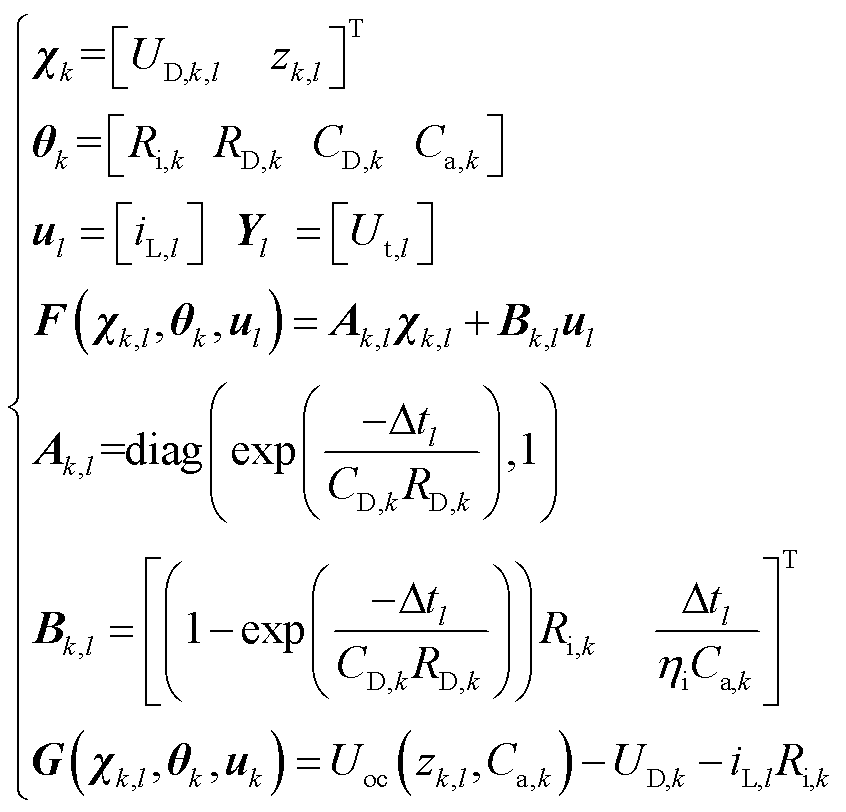 (11)
(11)
3)滑动窗口长度设定为300个采样点,则
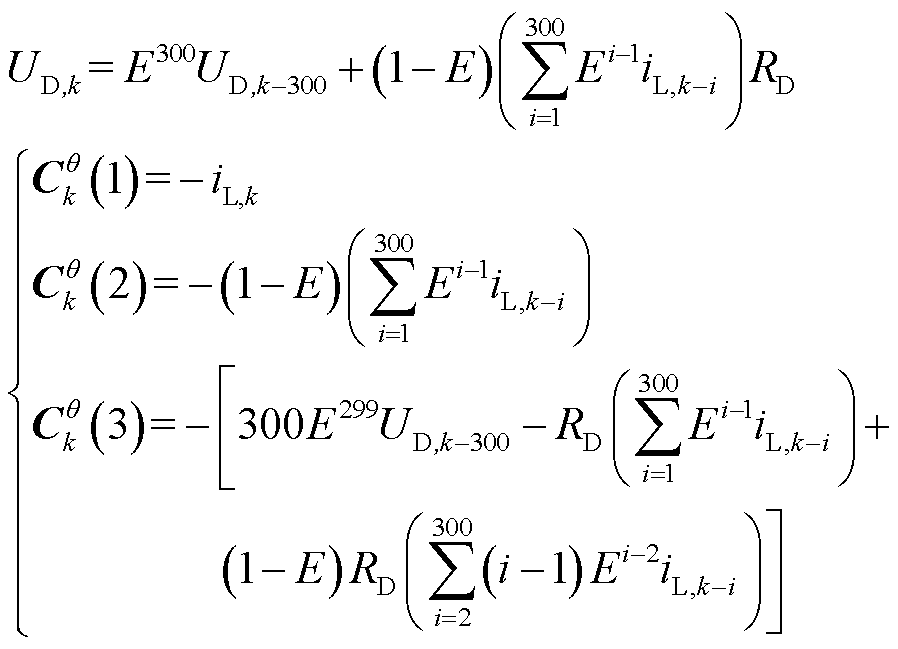 (12)
(12)
式中, 为参数观测器EKFθ的雅可比矩阵,
为参数观测器EKFθ的雅可比矩阵,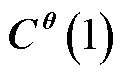 、
、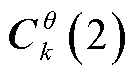 、
、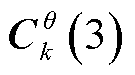 是其三个分量。
是其三个分量。
4)初始化
需要初始化的参数信息包括: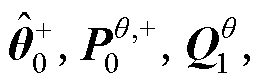
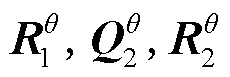 ;需要初始化的状态信息包括:
;需要初始化的状态信息包括: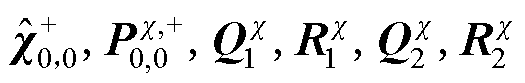 。其中,上标“^”代表该参数或状态的估计值,上角标“-”代表先验估计值,上角标“+”代表后验修正值。第一行代表系统参数的初始信息,第二行代表系统状态的初始信息;下角标“1”代表最高电压单体,下角标“2”代表最低电压单体。
。其中,上标“^”代表该参数或状态的估计值,上角标“-”代表先验估计值,上角标“+”代表后验修正值。第一行代表系统参数的初始信息,第二行代表系统状态的初始信息;下角标“1”代表最高电压单体,下角标“2”代表最低电压单体。
一般来说,初始化参数调试完毕后,不需要再对初始参数进行修改。实车应用时,可以在BMS断电前,适当存储当前的电池状态和参数,下次车辆起动时,再载入相关的参数,提高算法的鲁棒性。
5)参数EKF的宽尺度时间更新
宽尺度范围内,参数变化相对状态变化慢。
 (13)
(13)
6)状态EKF的窄尺度时间更新
窄尺度范围内,只有状态发生变化。
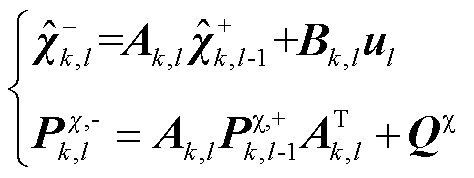 (14)
(14)
7)状态EKF的窄尺度测量更新
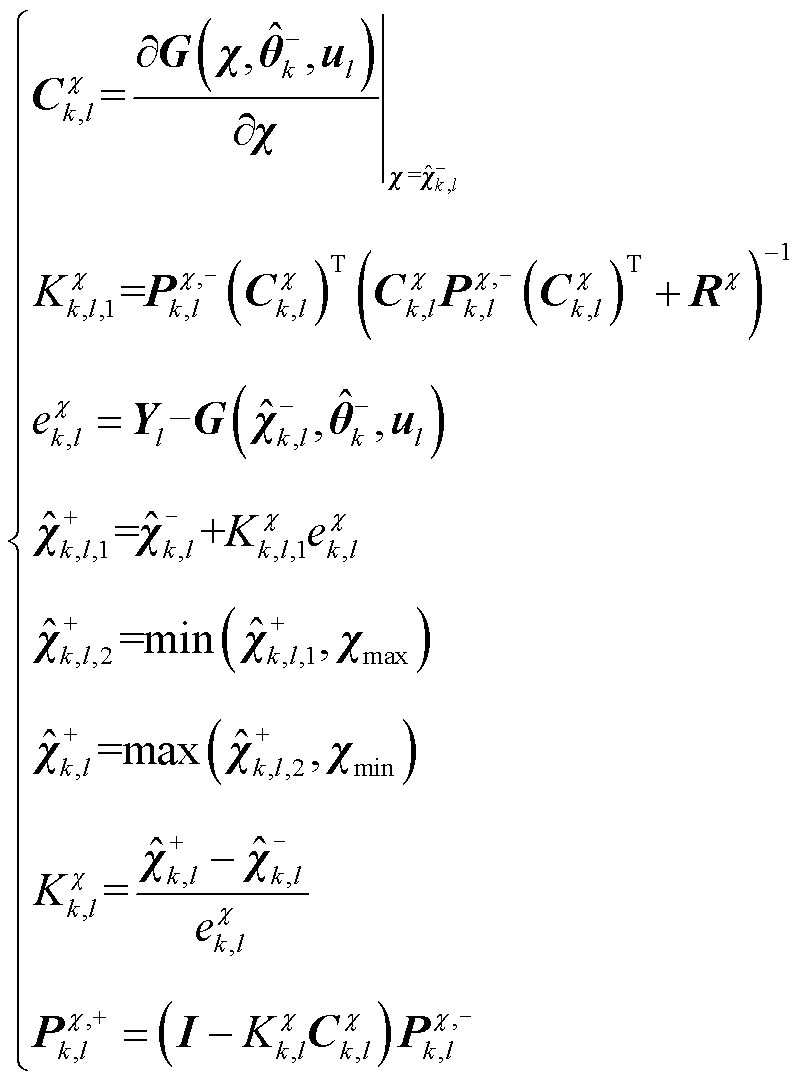 (15)
(15)
返回前一步,直到宽时间尺度+1,进入下一步更新宽尺度的参数。
8)参数EKF的宽尺度测量更新
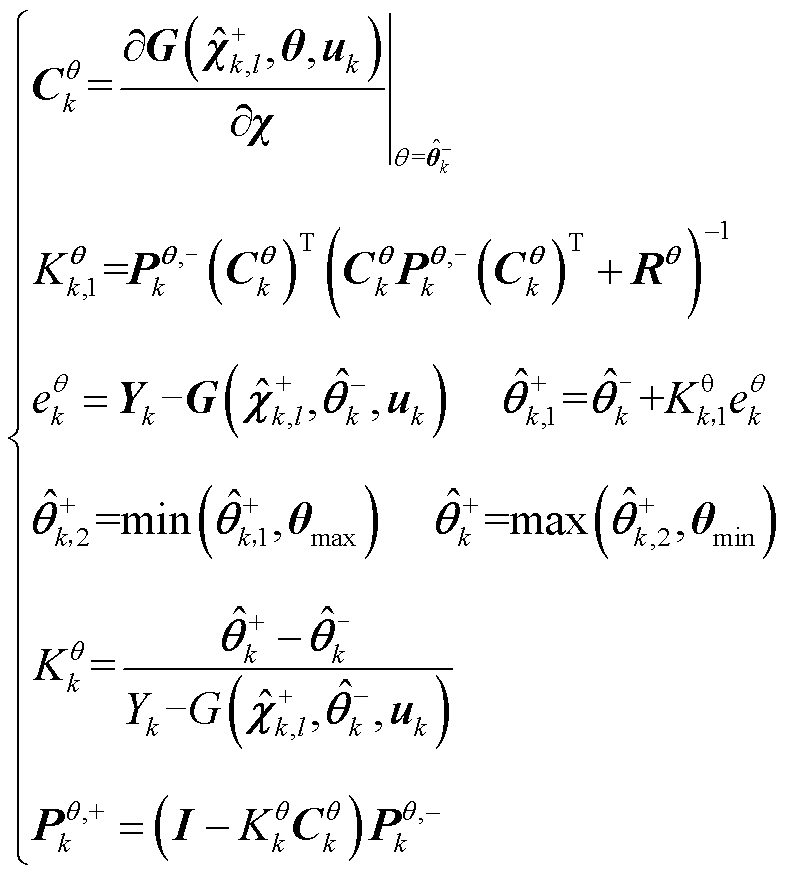 (16)
(16)
9)电池包级别的SOC及SOP输出
首先针对最高和最低电压等效单体,分别实施前述8个步骤,得到两组实时模型参数和状态。然后基于输出的单体电池容量和单体电池SOC,按照定义计算得到电池包级别的SOC。其次基于实时模型参数,按照峰值功率定义得到电池包最大充电和放电峰值电流,再分析得到加载峰值电流后的瞬时电压、持续预测电压和功率等效电压,最终计算得到电池包级别的SOP。每一个数据点都可以根据当前的状态和参数计算出SOP,此处使用当前电压估计的误差对极化电压进行修正。
电池包可充电容量Cad,pack和可放电容量Cac,pack分别为
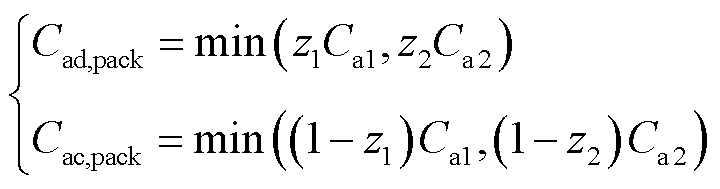 (17)
(17)
电池包SOC输出为
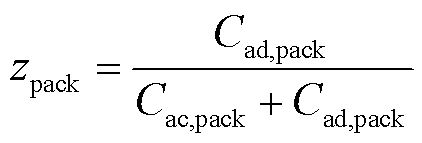 (18)
(18)
输出单体电压峰值电流为
 (19)
(19)

式中,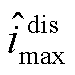 为达到电池下截止电压前所允许释放的最大电流;
为达到电池下截止电压前所允许释放的最大电流;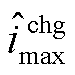 为达到电池上截止电压前所允许充入的最大电流;上角标“dis”代表放电过程,上角标“chg”代表充电。
为达到电池上截止电压前所允许充入的最大电流;上角标“dis”代表放电过程,上角标“chg”代表充电。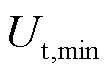 为电池的下截止电压,
为电池的下截止电压, 为电池的上截止电压,
为电池的上截止电压,![]() 、
、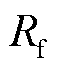 为中间变量。
为中间变量。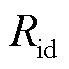 为放电过程的欧姆内阻,Ric为充电过程的欧姆内阻。
为放电过程的欧姆内阻,Ric为充电过程的欧姆内阻。
电池包电流为
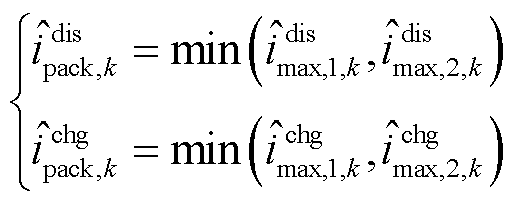 (20)
(20)
式中,电流项下角标“1”表示最高电压单体,下角标“2”表示最低电压单体;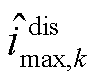 、
、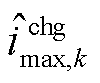 根据式(20)计算。
根据式(20)计算。
电池单体瞬时电压为
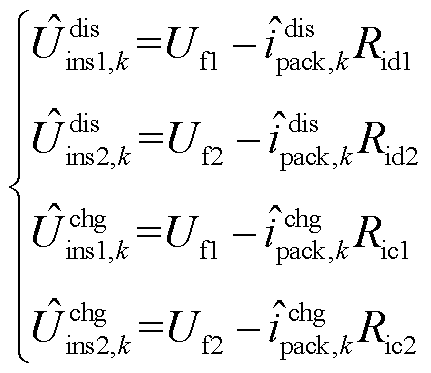 (21)
(21)
式中,![]() 、
、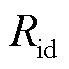 根据式(19)计算;
根据式(19)计算;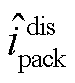 、
、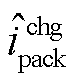 根据式(20)计算。
根据式(20)计算。
电池单体预测电压为
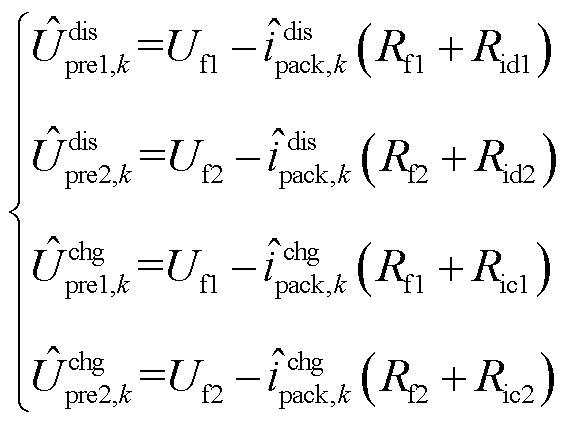 (22)
(22)
电池单体等效电压为
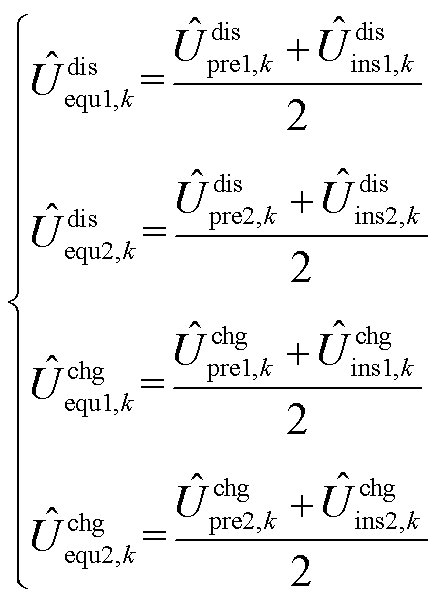 (23)
(23)
电池包内单体分布系数为
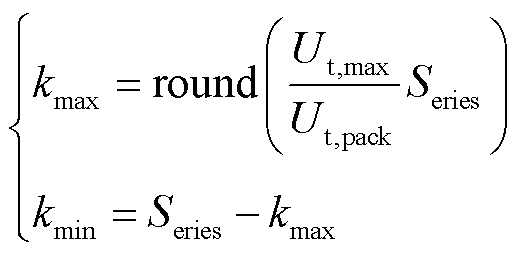 (24)
(24)
式中,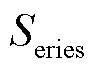 为电池包内电池单体的数量。
为电池包内电池单体的数量。
电池包SOP输出为
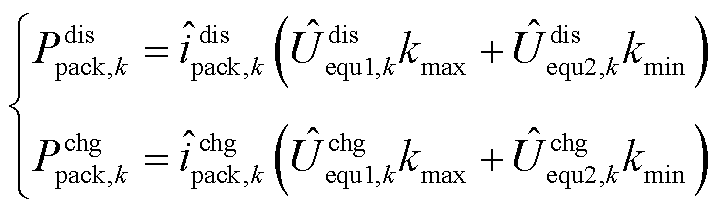 (25)
(25)
硬件在环仿真的特点是在系统仿真框架之中引入了硬件物理实物,更好地模拟实际情况,是纯数字仿真的升华。与纯数字仿真相比,硬件在环仿真能够验证原理算法的实时性,同时也提高了仿真过程的真实性,能够更全面地验证原理算法的有效性。在产品的开发过程中,由于硬件在环仿真更接近实际情况,测试结果具有很高的可靠度。
动力电池系统硬件在环仿真试验台架主要由若干个ARBIN多通道的100A或300A大倍率充放电机、调温范围为-40~80℃的可程控式恒温温箱、可设计动力电池充放电策略的ARBIN主控界面上位机、基于LabVIEW设计的用于显示采集数据和算法仿真实时结果的监测界面、为电路板供电的12V恒压源、装载有前文设计的核心算法程序的MPC5644主控板、装载辅助采集电压和均衡程序的采集均衡板、霍尔电流传感器以及试验对象等组成。其中,试验对象主要包括三元材料50A·h的电池单体、12串电池模组。试验台架整体构成如图3所示。

图3 硬件在环试验台架
Fig.3 Hardware-in-the-loop test bench
试验数据来源于多个三元材料容量50 A·h的锂离子动力电池单体、电池模组。其中,动力电池单体和模组在初次特性测试的基础上,分类筛选需要进行测试的具有代表性的单体和模组,然后按照试验要求和流程完成了为期半年的全寿命、多温度的功率预测验证、老化循环测试试验,获取了大量的试验数据。峰值功率验证试验采用国标GB/T 31467中提出的SOP测试方法,该方法要求调整电池系统至指定SOC和温度状态,静置足够长的时间,然后在该状态下多次测试电池系统不同峰值功率所能持续的最长时间,记录对应的恒功率值和持续时间,重复至少5次测试,同时保证待求持续时间左右两端的记录时间至少各有2个,进而拟合得到峰值功率与持续时间的关系曲线。峰值功率测试流程如图4所示。测试结果如图5所示。
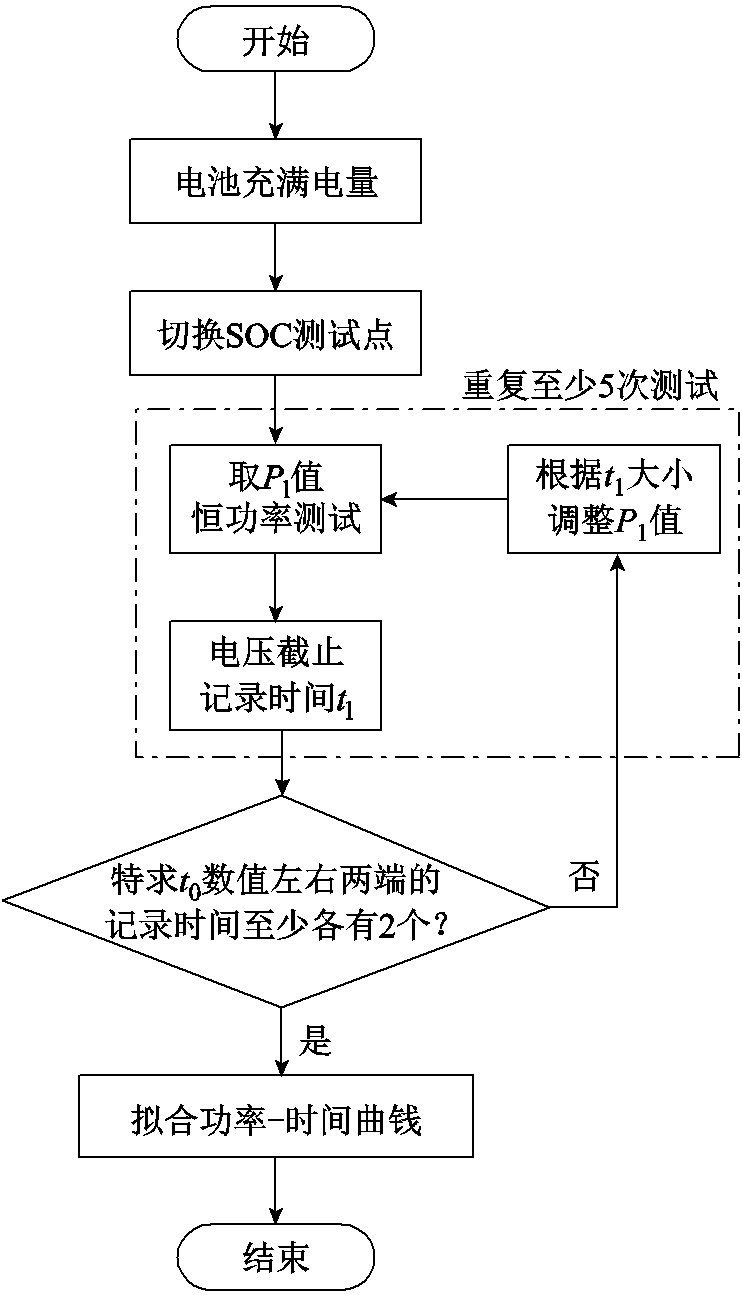
图4 峰值功率测试流程
Fig.4 Peak power test flow chart
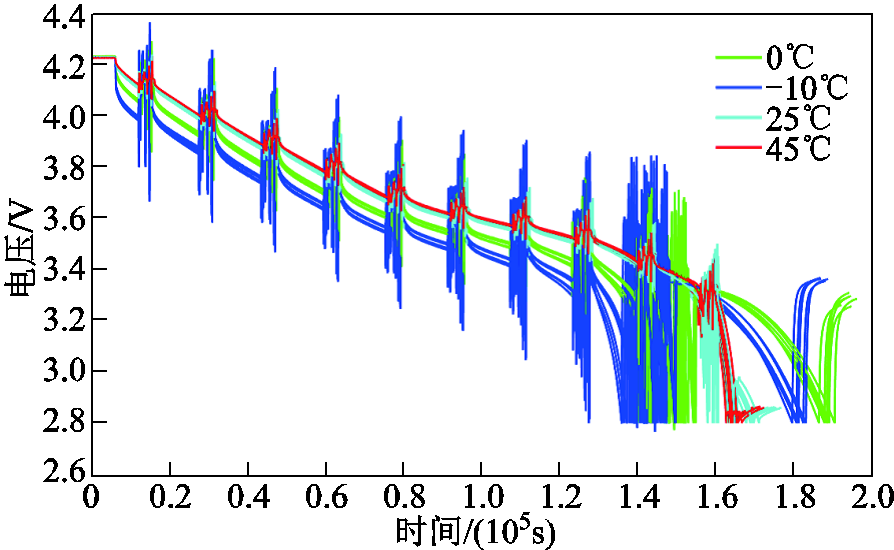
图5 恒功率验证试验数据
Fig.5 Constant power verification experimental data
恒功率HPPC验证试验步骤如下:
(1)调节温度至指定值,分别为-10℃、0℃、25℃和45℃,保温至少2 h。
(2)静置10 min,循环次数=1。
(3)15A放出5%SOC的电量,调整至待测试的SOC点。
(4)60s UDDS放电工况,用于DEKF在线参数辨识。
(5)100W放电30s,静置40s。
(6)100W充电30s,静置1min。
(7)200W放电10s,静置40s。
(8)200W充电10s,静置1min。
(9)300W放电5s,静置40s。
(10)300W充电5s,静置1min。
(11)15A放出10%SOC,调整至下一个待测试的SOC点。
(12)循环次数+1,若循环次数小于或等于10,则返回步骤(4);否则进行步骤(13)。
(13)静置1min,2.5A放到下截止电压,静置10min。
本文试验数据是来源于新鲜和老化的3并150A×h电池包各一个,新鲜和老化的3并150A×h电池包主要用于电池包级别的算法验证。
新鲜电池包数据包括14组,数据中包括40℃、25℃、6℃和0℃四种环境温度,以及新欧洲城市循环(New Europe Driving Cycle, NEDC)、UDDS、US06、世界轻型汽车测试循环工况(World Light Vehicle Test Cycle, WLTC)四种工况,如图6所示,颜色表示不同的试验数据,虚线是最低电压、实线是最高电压。各条曲线的图例用字母D加数字的格式代表,具体含义见表1。
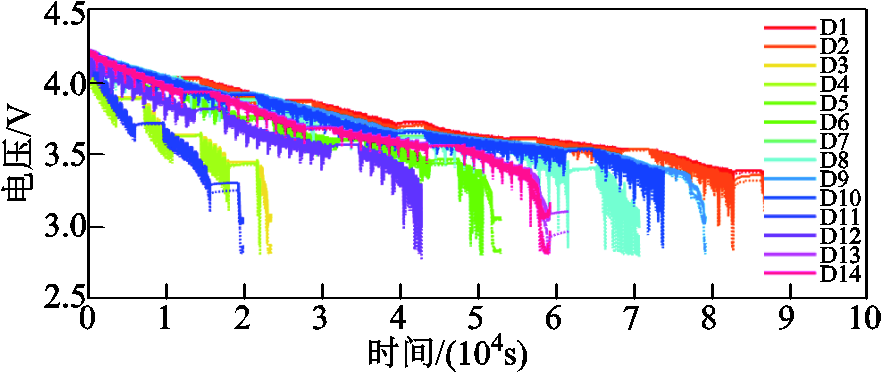
图6 新鲜电池包实验数据
Fig.6 Experimental data of fresh battery pack
表1 新鲜电池包数据图例含义
Tab.1 Legend meaning of fresh battery pack data

工况温度/℃图例 NEDC0D12 6D13 25D14 40D10
(续)
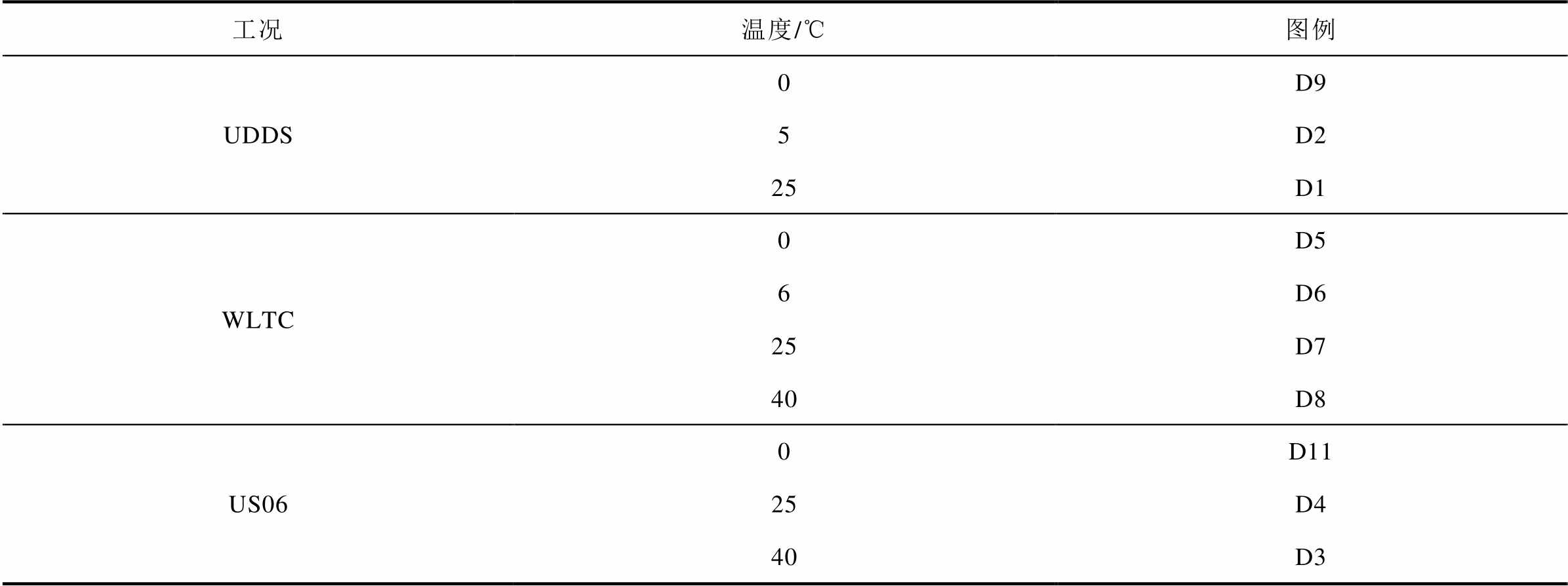
工况温度/℃图例 UDDS0D9 5D2 25D1 WLTC0D5 6D6 25D7 40D8 US060D11 25D4 40D3

图7 老化电池包实验数据
Fig.7 Experimental data of aging battery pack
老化电池包数据包括四组,数据中包括25℃充电数据、0℃长时间反复充放电测试数据、-10℃NEDC测试数据、25℃US06测试数据。如图7所示,颜色表示不同的试验数据,虚线是最低电压、实线是最高电压。上述四组数据在图7中分别由编号D1、D2、D3、D4表示。
3.3.1 新鲜电池包数据验证结果
数据来源:1个新鲜电池包的测试数据,共14组,数据中包括40℃、25℃、6℃和0℃四种环境温度,以及NEDC、UDDS、US06、WLTC四种工况。
算法设置:针对不同的数据,初始SOC相对真实SOC初值误差下偏30%,初始容量相对真实容量初始误差下偏1A×h,其他参数调试完成以后保持不变,同时适用于全部14组数据。
结果说明:全部14组数据的SOC误差均满足要求,最大误差为2.192%。SOC误差变化如图8和表2所示。在图8中,各条曲线的图例含义见表1。
3.3.2 老化电池包数据验证结果
数据来源:1个老化电池包的测试数据,共4组,数据中包括25℃充电数据、0℃长时间反复充放电测试数据、-10℃NEDC测试数据、25℃US06测试数据。
表2 新鲜电池包数据验证结果
Tab. 2 Verification results of fresh battery pack data
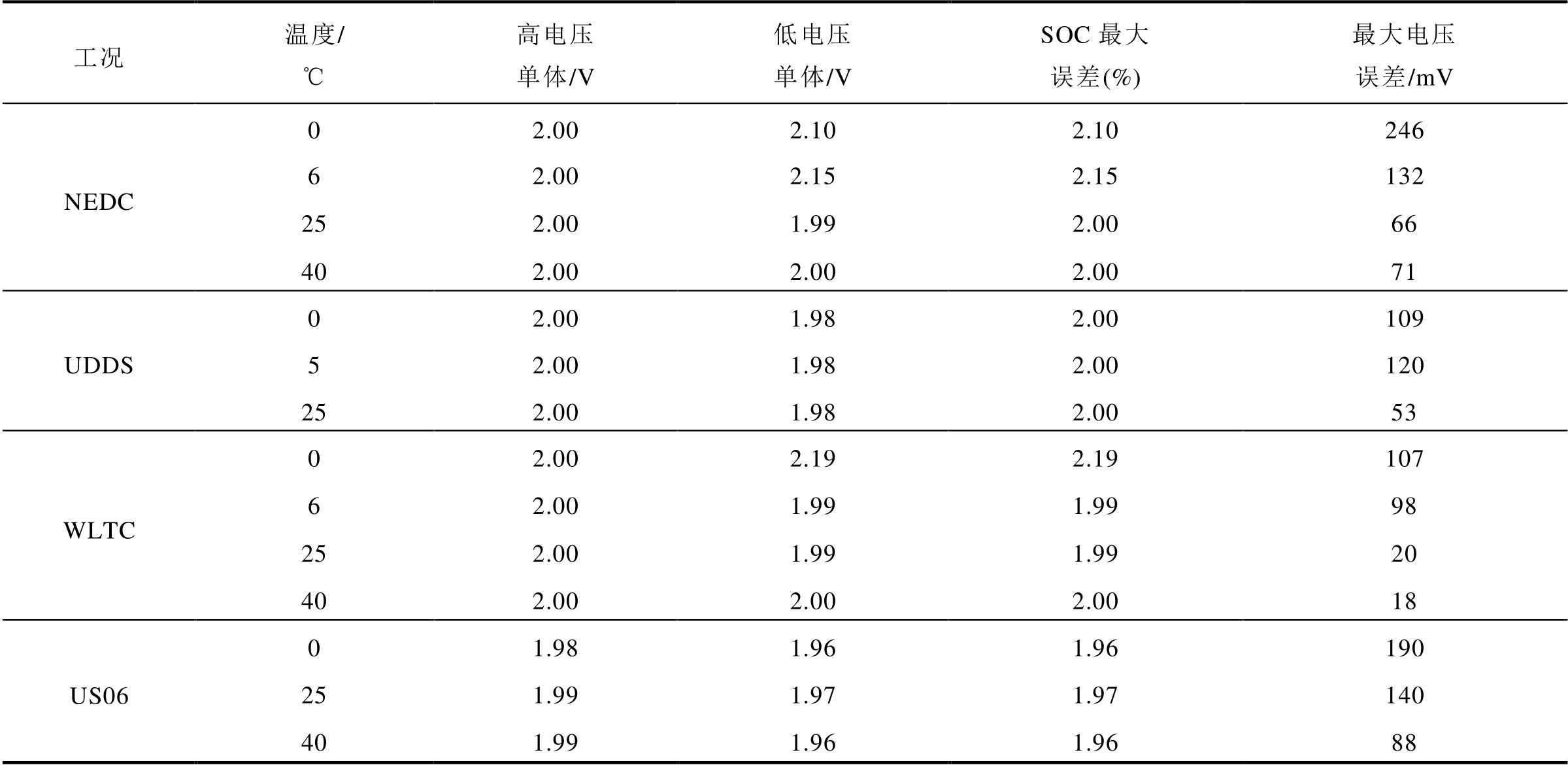
工况温度/℃高电压单体/V低电压单体/VSOC最大误差(%)最大电压误差/mV NEDC02.002.102.10246 62.002.152.15132 252.001.992.0066 402.002.002.0071 UDDS02.001.982.00109 52.001.982.00120 252.001.982.0053 WLTC02.002.192.19107 62.001.991.9998 252.001.991.9920 402.002.002.0018 US0601.981.961.96190 251.991.971.97140 401.991.961.9688
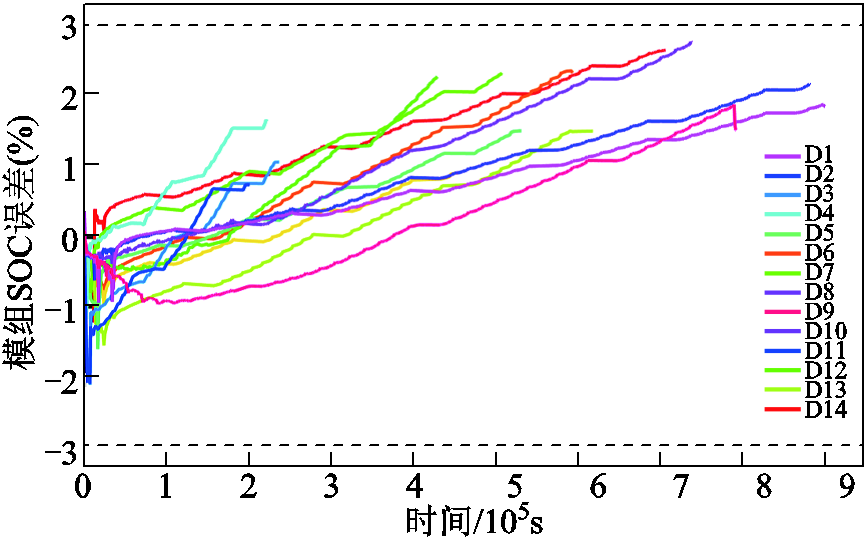
图8 新鲜电池包数据验证结果
Fig.8 Verification results of fresh battery pack data
算法设置:针对SOC较高的数据,初始SOC相对真实SOC初值误差下偏30%,针对SOC较低的数据,初始SOC相对真实SOC初值误差上偏30%,初始容量相对真实容量初始误差下偏1A×h,其他参数调试完成以后保持不变,适用于全部4组数据。
结果说明:全部4组数据的SOC误差均满足要求,最大误差为2.82%。SOC误差变化如图9和表3所示。各条曲线在图中的图例与图7相同。
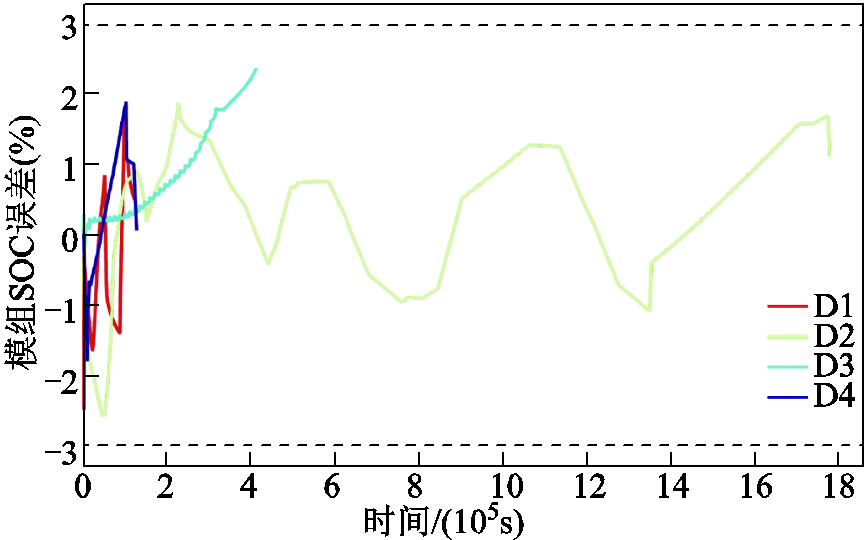
图9 老化电池包数据验证结果
Fig.9 Verification results of aging battery pack data
表3 老化电池包数据验证结果
Tab.3 Verification results of aging battery packs

试验数据D1D2D3D4 单体电芯容量真值48.65A×h48.85A×h 算法单体电芯容量47.65A×h47.85A×h SOC初始真值(%)00100100 算法SOC初始值(%)30307070 高压单体SOC误差(%)2.842.912.201.11 低压单体SOC误差(%)2.582.532.671.92 最大SOC误差(%)2.822.762.661.83 最大端电压误差/mV80212291114
3.2.3 SOP峰值功率验证结果
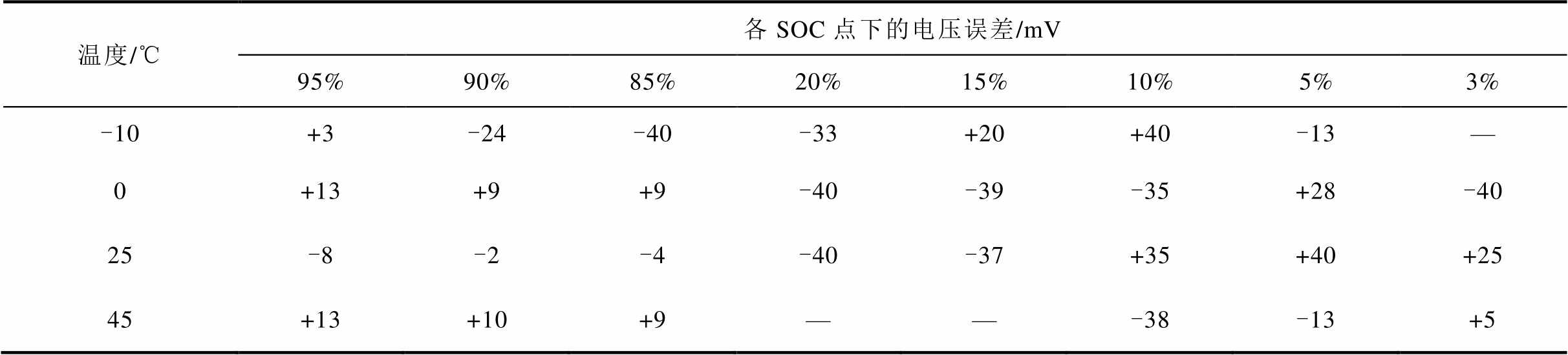
SOP各项评价指标实测结果见表4。在高SOC点(95%、90%、85%)进行充电峰值功率测试电压误差,正号表示超出电池电压上限即峰值功率偏大,负号表示与电池电压上限的差距即峰值功率偏小;在低SOC点(20%、15%、10%、5%、3%)进行的放电峰值功率测试电压误差,正号表示超出电池电压下限即峰值功率偏大,负号表示距离电池电压下限的差距即峰值功率偏小。其中空缺结果为测试设备或电池本身条件限制而无法进行测试的数据点。由表4可知,电池系统SOP算法精度在全部测试的4个温度点8个SOC点中的电压误差均在40 mV以内,可以认为SOP算法精度基本满足要求。
表4 SOP各项评价指标实测结果
Tab.4 Measured results of SOP evaluation indexes
温度/℃各SOC点下的电压误差/mV 95%90%85%20%15%10%5%3% -10+3-24-40-33+20+40-13— 0+13+9+9-40-39-35+28-40 25-8-2-4-40-37+35+40+25 45+13+10+9——-38-13+5
本文针对锂离子动力电池系统状态估计的问题,在电池单体一阶RC模型基础上,建立了具有双特征单体均匀分布的电池包模型;提出了基于多时间尺度滑动窗口的DEKF算法,基于峰值功率测试结果更新模型参数库,实现了参数的缓时变估计;搭建了硬件在环验证平台,在动力电池系统全寿命、全电量区间内,以及变温度等条件下的验证结果表明:改进后的DEKF算法是有效的,具有高精确度和鲁棒性,SOC估计误差小于3%,SOP等效电压误差小于40 mV。在-20℃以下的环境中,电池极化显著增大,传统的等效电路模型近乎失效,后续工作将围绕改进-20℃下的电池模型展开,来实现全温度区间的SOP准确估计。
参考文献
[1] 高德欣, 王义, 郑晓雨, 等. 基于深度学习的电动汽车充电状态监测与安全预警方法[J]. 电机与控制学报, 2023, 27(7): 122-132. Gao Dexin, Wang Yi, Zheng Xiaoyu, et al. Electric vehicle charging status monitoring and safety warning method based on deep learning[J]. Electric Machines and Control, 2023, 27(7): 122-132.
[2] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725. Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703-1725.
[3] 肖迁, 穆云飞, 焦志鹏, 等. 基于改进LightGBM的电动汽车电池剩余使用寿命在线预测[J]. 电工技术学报, 2022, 37(17): 4517-4527. Xiao Qian, Mu Yunfei, Jiao Zhipeng, et al. Improved LightGBM based remaining useful life prediction of lithium-ion battery under driving conditions[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4517-4527.
[4] 孙金磊, 唐传雨, 李磊, 等. 基于状态与模型参数联合估计的老化电池可充入电量估计方法[J]. 电工技术学报, 2022, 37(22): 5886-5898. Sun Jinlei, Tang Chuanyu, Li Lei, et al. An estimation method of rechargeable electric quantity for aging battery based on joint estimation of state and model parameters[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5886-5898.
[5] 杨镜司, 秦文萍, 史文龙, 等. 基于电动汽车参与调峰定价策略的区域电网两阶段优化调度[J]. 电工技术学报, 2022, 37(1): 58-71. Yang Jingsi, Qin Wenping, Shi Wenlong, et al. Two-stage optimal dispatching of regional power grid based on electric vehicles' participation in peak-shaving pricing strategy[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 58-71.
[6] Lu Languang, Han Xuebing, Li Jianqiu, et al. A review on the key issues for lithium-ion battery management in electric vehicles[J]. Journal of Power Sources, 2013, 226: 272-288.
[7] Han Xuebing, Lu Languang, Zheng Yuejiu, et al. A review on the key issues of the lithium ion battery degradation among the whole life cycle[J]. eTransportation, 2019, 1: 100005.
[8] Hannan M A, Lipu M S H, Hussain A, et al. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: challenges and recommendations[J]. Renewable and Sustainable Energy Reviews, 2017, 78: 834-854.
[9] He Hongwen, Xiong Rui, Fan Jinxin. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach[J]. Energies, 2011, 4(4): 582-598.
[10] Lin Cheng, Zhang Xiaohua, Xiong Rui, et al. A novel approach to state of charge estimation using extended Kalman filtering for lithium-ion batteries in electric vehicles[C]//2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 2014: 1-6.
[11] 陈铖. 车用锂离子电池容量和荷电状态的多尺度联合估计研究[D]. 北京: 北京理工大学, 2016.Chen Cheng. Research on the multi-scale estimation of the lithium-ion battery capacity and SOC for electric vehicles[D]. Beijing: Beijing Institute of Technology, 2016.
[12] 熊瑞. 基于数据模型融合的电动车辆动力电池组状态估计研究[D]. 北京: 北京理工大学, 2014. Xiong Rui. Estimation of battery pack state for electric vehicles using model-data fusion approach[D]. Beijing: Beijing Institute of Technology, 2014.
[13] 刘素贞, 袁路航, 张闯, 等. 基于超声时域特征及随机森林的磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2022, 37(22): 5872-5885. Liu Suzhen, Yuan Luhang, Zhang Chuang, et al. State of charge estimation of LiFeO4 batteries based on time domain features of ultrasonic waves and random forest[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5872-5885.
[14] Pan Rui, Wang Yujie, Zhang Xu, et al. Power capability prediction for lithium-ion batteries based on multiple constraints analysis[J]. Electrochimica Acta, 2017, 238: 120-133.
[15] Sun Fengchun, Xiong Rui, He Hongwen, et al. Model-based dynamic multi-parameter method for peak power estimation of lithium–ion batteries[J]. Applied Energy, 2012, 96: 378-386.
[16] Guo Ruohan, Shen Weixiang. A data-model fusion method for online state of power estimation of lithium-ion batteries at high discharge rate in electric vehicles[J]. Energy, 2022, 254: 124270.
[17] Tang Xiaopeng, Liu Kailong, Liu Qi, et al. Comprehensive study and improvement of experimental methods for obtaining referenced battery state-of- power[J]. Journal of Power Sources, 2021, 512: 230462.
[18] Li Bowen, Wang Shunli, Fernandez C, et al. A linear recursive state of power estimation method based on fusion model of voltage and state of charge limitations [J]. Journal of Energy Storage, 2021, 40: 102583.
[19] Wu Muyao, Qin Linlin, Wu Gang. State of power estimation of power lithium-ion battery based on an equivalent circuit model[J]. Journal of Energy Storage, 2022, 51: 104538.
[20] Wang Yujie, Pan Rui, Liu Chang, et al. Power capability evaluation for lithium iron phosphate batteries based on multi-parameter constraints estim- ation[J]. Journal of Power Sources, 2018, 374: 12-23.
[21] Wang Yujie, Zhang Xu, Liu Chang, et al. Multi-timescale power and energy assessment of lithium-ion battery and supercapacitor hybrid system using extended Kalman filter[J]. Journal of Power Sources, 2018, 389: 93-105.
[22] Tan Yaqian, Luo Maji, She Liyang, et al. Joint estimation of ternary lithium-ion battery state of charge and state of power based on dual polarization model[J]. International Journal of Electrochemical Science, 2020, 15(2): 1128-1147.
[23] Chen Wenxin, Xu Cheng, Chen Manlin, et al. A novel fusion model based online state of power estimation method for lithium-ion capacitor[J]. Journal of Energy Storage, 2021, 36: 102387.
[24] 王洪利. 电动汽车动力电池组上位机监控及管理平台设计[D]. 天津: 天津大学, 2014. Wang Hongli. Design of monitoring and management platform for upper computer of electric vehicle power battery pack[D]. Tianjin: Tianjin University, 2013.
[25] Gong Xianzhi, Xiong Rui, Mi C C. Study of the characteristics of battery packs in electric vehicles with parallel-connected lithium-ion battery cells[C]// 2014 IEEE Applied Power Electronics Conference and Exposition - APEC, Fort Worth, TX, USA, 2014: 3218-3224.
[26] Lin J C. Development of a two-staged balancing scheme for charging lithium iron cells in series[J]. IET Electrical Systems in Transportation, 2016, 6(3): 145-152.
[27] 彭飞. 锂离子电池状态估算方法研究与实现[D]. 成都: 电子科技大学, 2014. Peng Fei. Research And Realization of state estimation for lithium-ion batteries[D]. Chengdu: University of Electronic Science and Technology of China, 2014.
[28] Hu Xiaosong, Li Shengbo, Peng Huei. A comparative study of equivalent circuit models for Li-ion batteries[J]. Journal of Power Sources, 2012, 198: 359-367.
Abstract State of Power (SOP) estimation is one of the core functions of battery management system (BMS). Current SOP estimation methods are mainly divided into three categories: characteristic map method, data-driven method and multi-constraint model-based estimation method. However, in practical applications, traditional SOP estimation methods are generally difficult to obtain accurate and realistic peak power. Therefore, a large number of battery cell, module and battery pack experiments are carried out under different temperatures, different working conditions and different aging states in this paper. A battery cell model and battery pack model with dual-characteristic cells uniformly distributed are established to implement the expansion of the cell model to the system algorithm, which is high prediction accuracy and low calculation amount. In addition, a double Kalman filter (DEKF) algorithm based on multi-time scale sliding windows is proposed. The model parameter library is updated based on the peak power test results, which realizes the slow time-varying estimation of the parameters and improves the accuracy and robustness of the algorithm to estimate the peak power.
Firstly, an equivalent circuit model (ECM) is established as the battery model in this paper. Then, by comparing 12 common ECMs in terms of modeling accuracy and computational complexity, the Thevenin model is finally selected to simulate battery characteristics, due to the relatively high voltage prediction accuracy and relatively small amount of calculation. Based on the battery cell model, a battery pack model with dual characteristic cells uniformly distributed is established. The two characteristic cells are the real-time highest cell voltage and the lowest cell voltage in the battery pack. The cell numbers of characteristic cells are hence changeable. At the same time, the parallel link is regarded as a large cell, and the model parameters change with the battery characteristics. Based on the assumption of uniform distribution of battery cells, the highest and lowest cell voltage and battery pack voltage are used as input. The calculation formula of the battery system is simplified, and the transformation from the single model to the system model is realized. For the Thevenin model, the open-circuit voltage at time k+1 is taken as the first-order Taylor expansion at time k, and the power battery voltage calculation model is obtained. Considering that the peak power has a positive correlation with the terminal voltage, the dichotomy method is used to try to select a certain peak power. By comparing the corresponding terminal voltage with the target terminal voltage, the dichotomy method is used to correct the peak value Power level, to achieve the purpose of constantly approaching the real peak power. Finally, a hardware-in-the-loop (HIL) simulation platform was built. The experimental objects mainly included 50 A×h three-cell battery cells and 12-string battery modules. On the basis of the initial characteristic test of power battery cells and modules, representative cells and modules that need to be tested are classified and screened, and then a half-year full-life and multi-temperature power prediction is completed in accordance with the experimental requirements and procedures verification and aging cycle test experiments are conducted, and a large amount of experimental data is obtained. The results show that the improved DEKF algorithm is effective, has high accuracy and robustness, and the SOC estimation error is less than 3%. Effective voltage error is less than 40mV.
keywords:Electric vehicle, lithium ion battery, peak power estimation,double Kalman filter (DEKF) algorithm, sliding window
DOI:10.19595/j.cnki.1000-6753.tces.230086
中图分类号:TM912
国家自然科学基金资助项目(52107222)。
收稿日期 2023-01-13
改稿日期 2023-05-26
李 强 男,1985年生,高级工程师,研究方向为新能源汽车电控系统开发。E-mail: li-qiang@weichai.com
杨瑞鑫 男,1988年生,副研究员,硕士生导师,研究方向为新能源汽车电池管理。E-mail: yangruixin@bit.edu.cn(通信作者)
(编辑 郭丽军)