图1 试验设备
Fig.1 Test equipment
摘要 滤波算法中观测方程的准确性在电池状态评估中起着决定性作用。然而，该文通过试验发现，由于温度、工作电流和荷电状态（SOC）的影响，即使使用精度较高的电池模型，扩展卡尔曼滤波（EKF）算法中观测方程的输出值与实际电压之间仍会存在较大误差，即产生了较大的新息。该文提出一种基于观测方程重组的增强型扩展卡尔曼滤波（E-EKF）算法。该算法的核心思想是利用具有温度、SOC和电流自适应能力的误差修正策略对观测方程进行重组，实现算法中新息的降低，进而提高SOC估计的准确性。使用两种不同温度下的典型工况试验对E-EKF算法的性能进行了验证。试验结果表明，该算法能够适应不同的温度和工况，并具有较高的SOC估计精度。
关键词：扩展卡尔曼滤波算法 误差修正方程 观测方程重组 SOC估计
锂离子电池具有能量密度高、续航能力强等特点，能够满足不同设备对储能装置的需求，在航空航天、军事装备、电动汽车等领域有诸多应用[1-4]。虽然锂离子电池性能优越，但是过度充放电会对其循环寿命造成不可逆转的损害[5-6]。因此，为了保证电池组始终处于安全、健康的工作状态，有必要对电池荷电状态（State of Charge, SOC）进行快速且准确的在线估计。
目前，文献中SOC的估计方法大致可分为三类，分别是基于原理、基于模型和基于数据驱动。基于原理的方法是指通过求解开路电压（Open Circuit Voltage, OCV）、内阻等一些与SOC相关的参数，然后结合公式或曲线拟合获得实时SOC。具体来说，该方法可以通过安时积分计算、开路电压测量或内阻监测实现[7-8]。基于模型的方法，如卡尔曼滤波（Kalman Filter, KF）和扩展卡尔曼滤波（Extended Kalman Filter, EKF）等，将电池等效电路模型与滤波算法相结合，利用所建状态空间方程中观测值的更新，实现SOC的实时估计[9-10]。基于数据驱动的方法是指通过大量数据训练模型，然后在输入（如电压、电流）和输出（如SOC）之间建立抽象的映射关系[11-12]。目前常用的算法有神经网络、支持向量机和随机森林等[13-14]。相比于其他两种方法，基于模型的SOC估计方法因其在多变的电池工作条件下具有更强的鲁棒性和更高的准确性而被广泛研究[15-16]。
为了进一步完善滤波算法，提高SOC估计精度，研究者们在卡尔曼滤波算法的基础上不断进行改进，最终设计出具有更高精度的SOC估计算法。文献[17]针对自适应扩展卡尔曼滤波（Adaptive Extended Kalman Filter, AEKF）算法运行初期收敛速度缓慢的问题，提出了一种模糊自适应扩展卡尔曼滤波算法，改善了算法的收敛速度，提高了SOC在线估计的实用性。文献[18]提出了一种改进的自适应扩展卡尔曼滤波算法，利用遗忘因子Sage-Husa EKF对测量噪声的统计特性进行自适应修正，并根据创新量对误差协方差矩阵进行自适应修正，最终实现了SOC估计精度和鲁棒性的提高。文献[19]提出了一种基于n阶等效电路模型的自适应无迹卡尔曼滤波SOC估计方法。该方法通过对系统噪声协方差和测量噪声协方差的实时更新，提高了协方差的精度，进而提高了SOC估计的准确性。文献[20]针对扩展卡尔曼滤波算法对电池数学模型精确的高度依赖与动态电池模型难以精确获得之间的矛盾，提出一种完全数据驱动的基于改进EKF算法的动力电池全生命周期SOC估计方法。仿真结果表明，该方法具有较好的鲁棒性和实用性。
通过上述分析可知，目前以提高观测方程准确性作为滤波算法改进方向的研究相对较少。然而，SOC的估计精度在很大程度上受到观测方程准确性的影响。因此，为了提高算法的估计精度，有必要对观测方程进行详细研究。基于以上原因，论文通过分析EKF观测方程输出电压误差影响因素，提出一种误差修正策略，进一步利用该策略对原算法中的观测方程进行干预，构成增强型扩展卡尔曼滤波（Enhanced Extended Kalman Filter, E-EKF）算法。在多种环境温度下，开展两种典型工况对E-EKF性能进行验证，结果表明，提出的误差修正策略具有较强的温度和工况适应性，能够有效提高观测方程精度和SOC估计精度。
本文首先介绍论文所采用数据相关的试验设计，给出电池采用的ECM模型原理，并对观测方程输出误差影响因素进行分析；然后构建误差修正函数，生成E-EKF算法，最后对所提算法的性能进行了验证与分析。
试验研究对象为圆柱型锂离子电池LR18650SZ，其额定容量为2 400 mA·h，标称电压为3.6 V。试验测试设备为Neware的电池测试系统CT—4008，其电流范围为50 mA～10 A，电压范围为25 mV～5 V。电流和电压的精度均为满量程的±0.1%。测试电池被放置在多禾DHT环境试验箱中，以模拟温度的变化。试验设备如图1所示。
在现有的电池等效电路模型（Equivalent Circuit Model, ECM）中，OCV的估算是建模过程的基础和核心，对ECM的精度有很大影响。当电池长时间静置时，其端电压被认为是一个不变的量，此时的电压称为开路电压。在实际运行中，电池组通常不会长期处于静置状态，因此有必要对电池的OCV进行估计。OCV-SOC试验的具体步骤如下：
图1 试验设备
Fig.1 Test equipment
（1）电池采用恒流恒压模式充电。
（2）以0.5C的倍率和总容量的10%为单位对电池进行放电，然后再静置1 h，直到电压达到放电截止电压。
（3）放电结束后静置1 h，与放电过程类似，对电池进行充电，直到电压达到充电截止电压。
在每次静置结束时获得的OCV被定义为放电/充电OCV。
在实践中，电池的充放电电流并不是恒定的，因此研究不同工况下电池的充放电特性具有实际意义。动态应力测试（Dynamic Stress Test, DST）包括电动汽车的简单加速和减速，是电池常见的有代表性的试验条件之一。US06包含了电动汽车运行过程中可能出现的高速、高加速和快速波动。该工况下的电流变化比DST的电流变化更剧烈，可以反映出电池更复杂的工作状态。因此，本文选择DST和US06来模拟电池的实际工作环境，其电流曲线如图2所示。
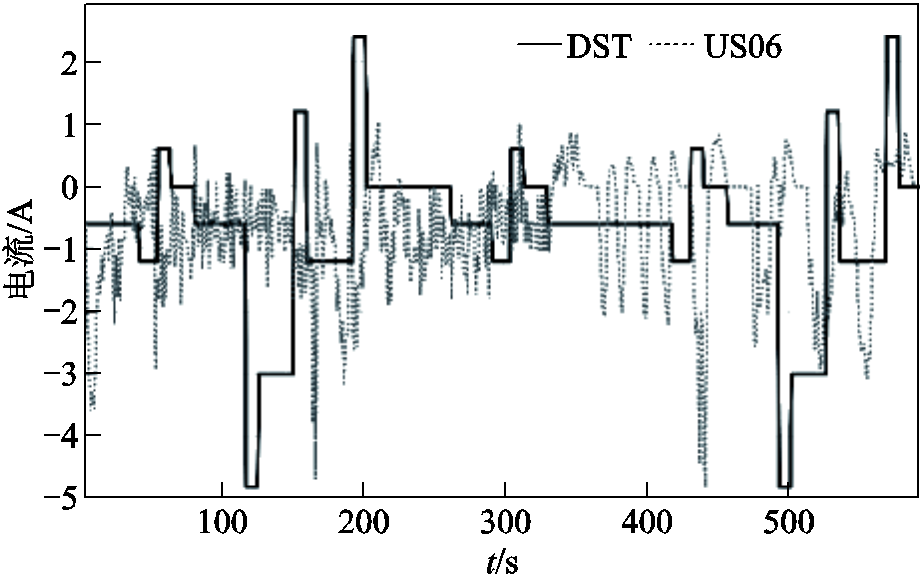
图2 工况电流曲线
Fig.2 Working current curves
为了防止过充过放导致锂离子电池使用寿命缩短，一般将SOC为20%～80%的区间作为电池的最佳工作区间[21]。因此，本节将在SOC为20%～80%的区间内对EKF算法进行分析研究。
锂离子电池ECM整体建模的主要挑战包括两大方面：模拟电池的极化效应和迟滞效应。极化效应的模拟可以通过在模型中加入RC并联网络解决。网络的阶次越高，模拟效果越好，但随着阶次的增加，需要辨识的参数就越多，过拟合问题就会变得更严重，从而降低模型参数辨识的可靠性[22-23]。迟滞效应的模拟可以通过在模型中加入零状态或单状态迟滞子模型解决[24-26]。与零状态迟滞子模型相比，单状态迟滞子模型具有更好的迟滞模拟效果。
综上所述，本文在充分考虑精度要求和参数辨识的复杂性后，选用以一阶RC模型为基础的单状态迟滞模型作为EKF算法的结合模型，模型结构如图3所示。Ul为电池的端电压；Up为RC并联网络的端电压；Uoc为电池开路电压；H为迟滞子模型；Rs为电池内阻，它描述了电池的静态特性；Rp和Cp分别是电池的极化电阻和极化电容，描述了电池的动态特性；I为电流。其中迟滞子模型H的方程按照文献[27]进行设计。
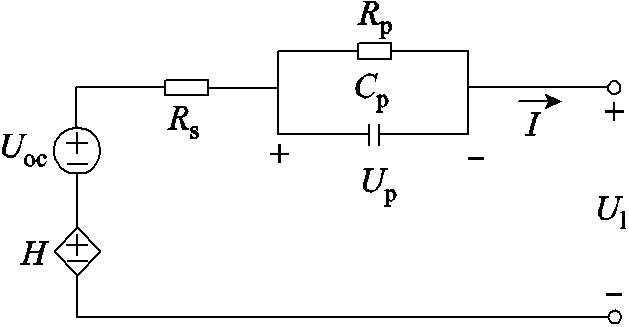
图3 单状态迟滞模型
Fig.3 Single-state hysteresis model
EKF算法中每一次SOC的估计值都要通过新息和卡尔曼增益矩阵进行调整修正。因此，通过提高算法中观测方程的准确性实现新息的降低，同样是提高算法SOC估计精度的有效手段之一。
观测方程的精度通常受参数辨识算法和温度等状态量的影响。其中，温度等状态量一方面直接对观测方程的精度产生影响；另一方面通过影响模型中的参数间接干扰观测方程。实时在线参数辨识方法可以解决温度等对模型参数的影响。因此，本文忽略温度等因素的间接影响，只分析参数辨识算法和温度等状态量的直接影响。
2.2.1 参数辨识算法的影响分析
参数是影响观测方程精度的因素之一，可以采用离线或在线辨识方法进行获取。然而，离线法不能随电池工作状态的变化调整参数辨识结果，鲁棒性差。因此，目前通常采用在线参数辨识方法。据此，本节将在SOC为20%～80%区间内以一阶RC模型为基础，分析常用的在线参数辨识方法EKF和遗忘因子递推最小二乘（Recursive Least Squares of Forgetting Factor, FFRLS）对算法中观测方程的影响。
图4展示了在不同温度和工况下使用不同参数辨识方法时，观测方程输出电压误差的概率密度分布。根据图4a～图4d可知，在同样的温度和工况下，观测方程输出的电压误差概率密度分布极为相似。根据图4e和图4f可知，虽然在40℃两种工况下，不同参数辨识算法产生的概率密度分布有所不同，但概率密度较大的误差范围是极为相似的。这说明观测方程的误差概率密度分布受辨识方法影响很小。
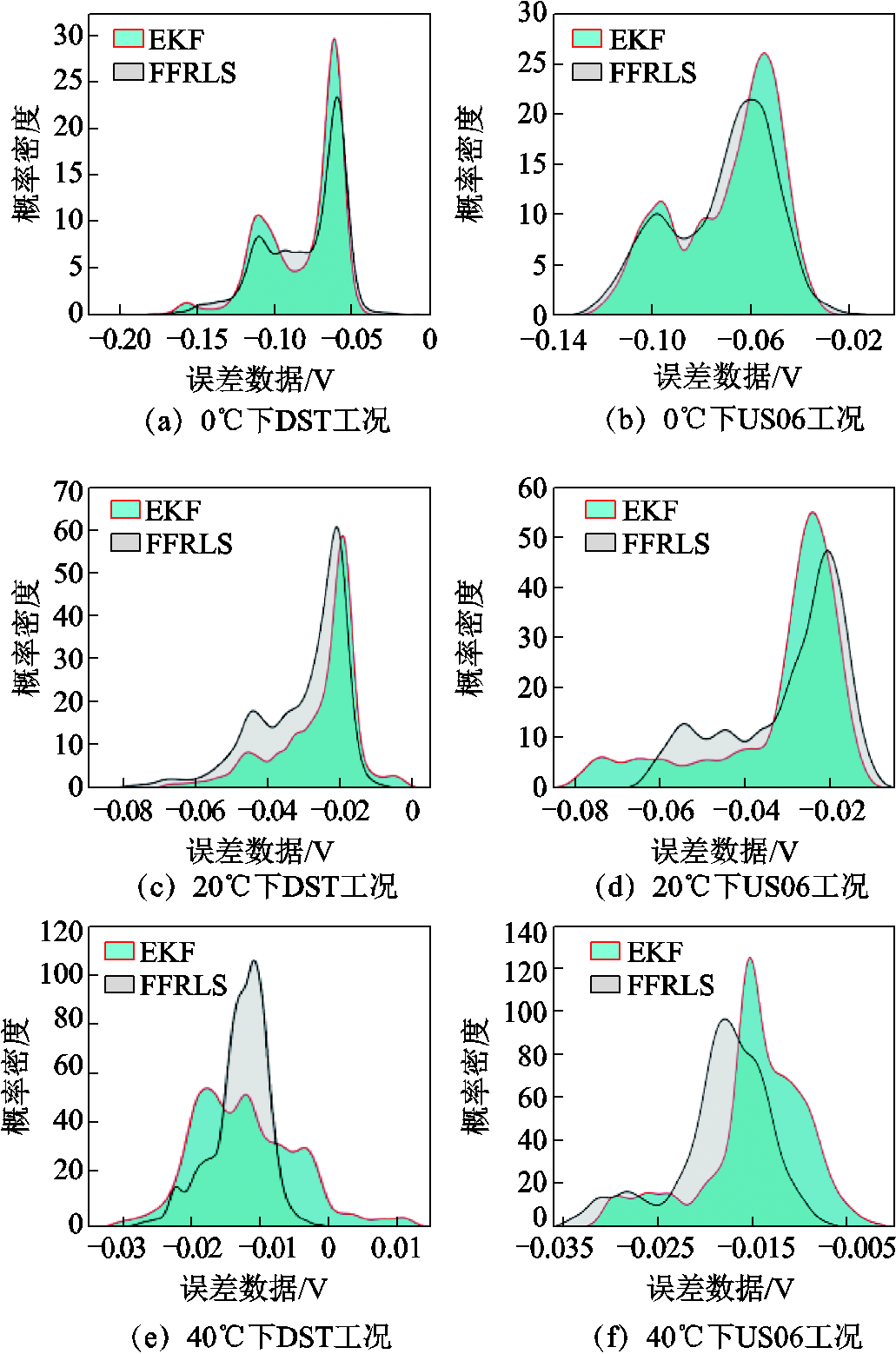
图4 观测方程输出电压误差的概率密度分布
Fig.4 Probability density plot of the output voltage error of the observation equation
根据上述分析可知，在试验所用的温度和工况下，不同参数辨识方法下的观测方程输出误差十分接近。同种温度和工况下，两种参数辨识算法产生的观测方程输出误差平均值相差均不超过15%。与此同时，不同参数辨识方法下观测方程输出误差的概率密度分布规律也大致相同。据此可得结论：参数辨识方法对观测方程输出结果精度的影响很小，可以忽略不计。
2.2.2 不同状态量的影响分析
为探寻其他影响观测方程精度的状态量，设计了不同温度下（0℃、20℃、40℃）的DST工况试验。
图5为20%～80%SOC区间内，观测方程在DST工况下产生的输出电压误差数据曲线。其中，输出电压误差数据为实际电压与输出电压的差值。总误差为观测方程产生的实际误差。
图5 观测方程在DST工况下的输出电压误差数据
Fig.5 Output voltage error data of the observation equation in the DST operating condition
根据图5a和图5b可知：误差分布并不固定，其数值会随着SOC的变化波动；不同工作电流下误差随SOC变化的趋势与总误差相似； SOC-误差平面内，不同电流下的误差曲线在误差轴上的位置不同。根据图5c可知：输出电压在整体上高于实际电压，但二者之间的误差并不固定；误差的极值点基本出现在电流变化的时刻。根据图5d可知：①温度和误差曲线之间存在较为稳定的变化规律——温度越高，观测方程在同一SOC下产生的误差越接近于0；②SOC固定时，误差在数值上随着温度的变化波动。上述分析表明观测方程产生的误差主要受三个状态量的影响，即电流、SOC和温度。
综上所述，当电池模型固定后，观测方程的精度可以认为与模型和参数辨识方法无关，此时仅需考虑电流、SOC和温度的影响。据此，应进一步分析电流、SOC和温度与误差之间的变化规律，并在此基础上实现观测方程精度的提升，最终构成E-EKF算法。
从上述试验结果中可以看出，电流、SOC和温度是影响误差的主要因素。为了削弱这三种状态量对观测方程精度的负面影响，本文在SOC为20%～80%的区间内建立了一种E-EKF算法。具体的算法建立过程分为两部分：一方面，在分析影响因素和观测方程产生误差之间相互关系的基础上，建立了具有温度、SOC和工作电流自适应能力的误差修正函数；另一方面，利用所建立的修正函数重组算法中的观测方程，完成E-EKF算法的构建。
3.1.1 考虑温度因素的SOC-误差关系建模
根据上述对误差影响因素的分析可知，在不同的温度下，SOC对误差的影响是不同的。因此，在建立SOC-误差关系的数学模型时，有必要考虑温度的影响。
图6中灰色数据点为观测方程在0℃、20℃和40℃的DST工况中产生的输出电压误差数据。在综合考虑数学模型精度和复杂性的基础上，本文选用二阶多项式对数据进行拟合，以表达误差变化趋势，如图6中黑色曲线所示，从而分析不同温度下误差曲线的变化规律。
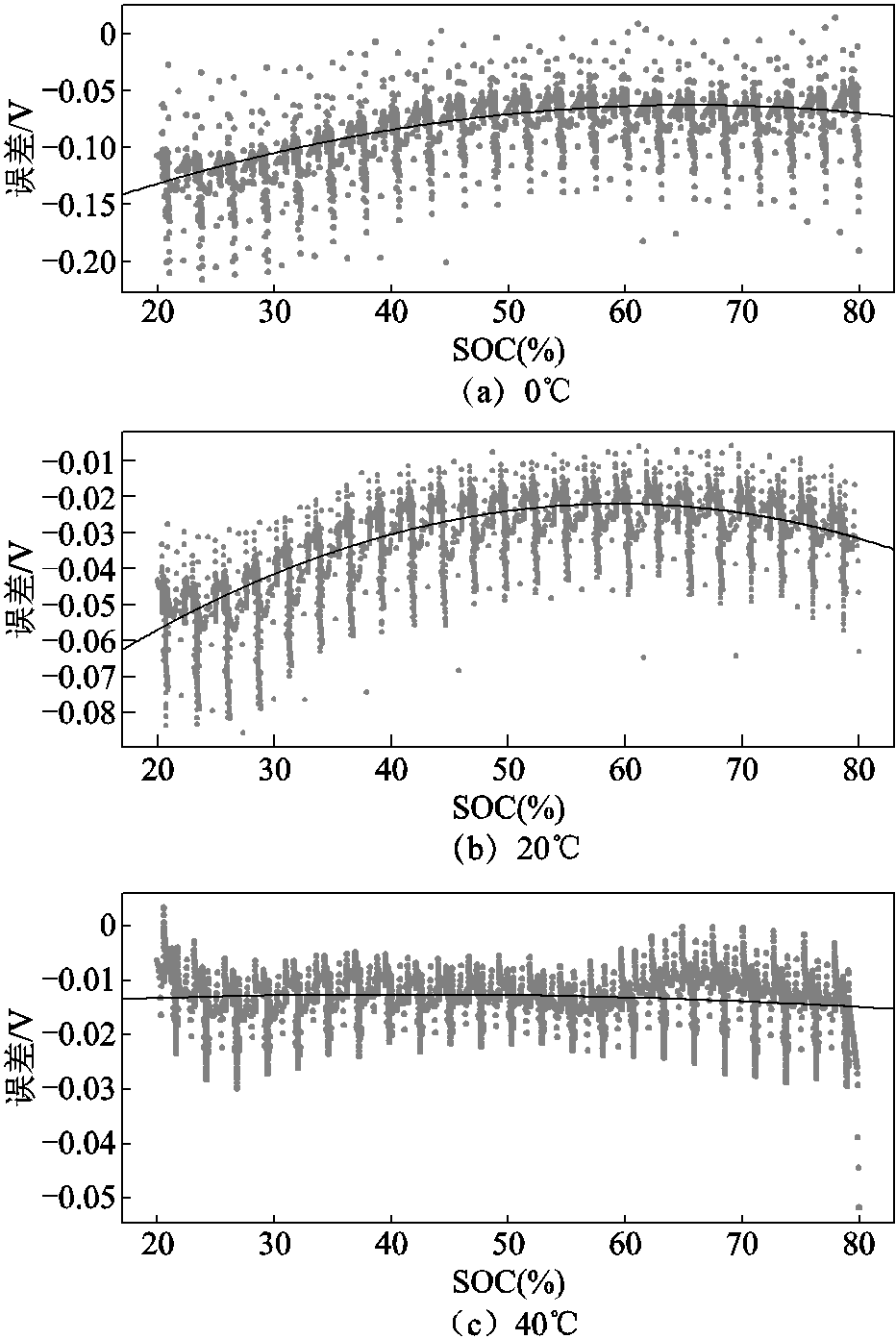
图6 观测方程在DST工况下产生的端电压误差曲线
Fig.6 The terminal voltage error curves generated by the observation equation in the DST operating condition
二阶多项式数学关系模型为
（1）
式中，E为误差；P1、P2、P3为使数据吻合而选择的常量。
根据图6c可以发现，SOC在20%～25%区间内，由于误差随SOC的增加明显下降，导致二阶多项式的趋势在40℃时发生改变。考虑到提高某特定温度下误差变化趋势的精度会导致数学模型的整体适用性下降。因此选择降低40℃时误差变化趋势的精度，以SOC在25%～80%区间内的误差变化趋势代替。此时，误差曲线在0℃、20℃和40℃的变化趋势相似。利用Matlab中的cftool工具箱进行二阶多项式拟合，数据记录于表1。
根据2.2.2节中分析可知，温度和SOC会影响误差曲线的变化趋势，而温度和工作电流则会影响误差曲线在误差轴上的位置。对于二阶多项式而言，P1和P2决定了曲线的变化趋势，P3决定了曲线的位置。据此，可以得出结论：P1和P2受温度和SOC的影响，P3受温度和工作电流的影响。由于P3的影响因素包含工作电流，其分析将于3.1.2节进行。
表1 式（1）中参数
Tab.1 Parameters in Equ.(1)
温度/℃P1P2P3 0-0.358 30.437 4-0.191 2 20-0.219 80.255 5-0.092 4 40-0.024 60.015 9-0.011 3
由表1可知，参数与温度之间存在稳定的变化规律：P1与温度呈正相关，P2与温度呈负相关。根据表1中参数与温度之间的关系，可以拟合出一条抛物线，如图7所示。得到相应的二阶多项式数学关系模型为
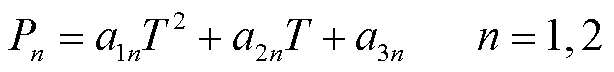（2）
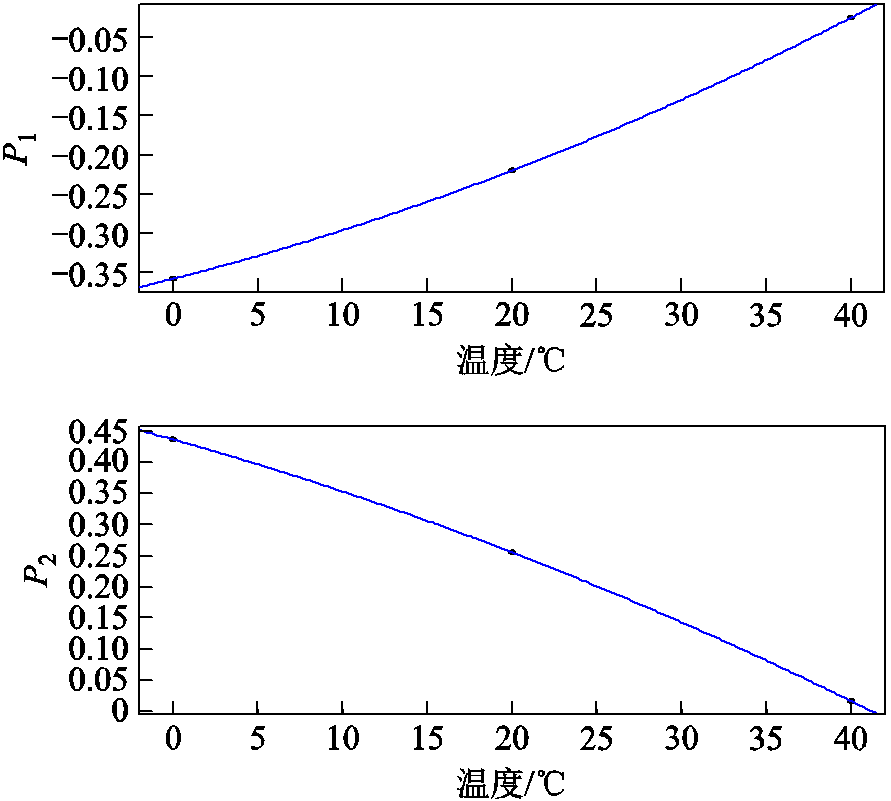
图7 参数-温度关系曲线
Fig.7 Parameter-temperature relationship curves
至此，P1和P2参数已具备温度自适应能力。
3.1.2 考虑温度的工作电流-误差关系建模
为了分析工作电流和误差之间的关系，本节将总误差按工作电流的不同进行拆分，如图5b所示。根据上述分析可知，不同工作电流下误差曲线和总误差曲线具有相同的P1和P2参数。同时工作电流的变化仅对P3产生影响，并且影响程度随着温度改变。据此，应建立一种考虑温度和工作电流的P3数学模型，以提高式（1）对误差的修正能力。
利用式（1）计算不同温度和工作电流下的P3数据，并记录于表2。一般情况下，电流倍率越大，观测方程误差越大。从表2可以看出，在各种温度下，基本满足随电流倍率增大，与电流相关的P3的绝对值呈增长趋势。为了体现该规律，本文采用二阶多项式拟合负电流下的电流-P3曲线，并以x=0为轴对称到正电流侧，所得曲线如图8所示。公式为
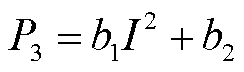（3）
式（3）中参数见表3。
表2 不同温度不同电流下的P3数据
Tab.2 P3 data at different temperatures and currents
电流/A0℃20℃40℃ 2.4-0.195 5-0.100 0-0.015 3 1.2-0.194 2-0.089 3-0.009 2 0.6-0.170 4-0.082 6-0.004 1 -0.6-0.173 7-0.087 1-0.009 2 -1.2-0.203 1-0.096 7-0.014 3 -3.0-0.207 1-0.094 1-0.014 5 -4.8-0.206 2-0.097 5-0.019 0
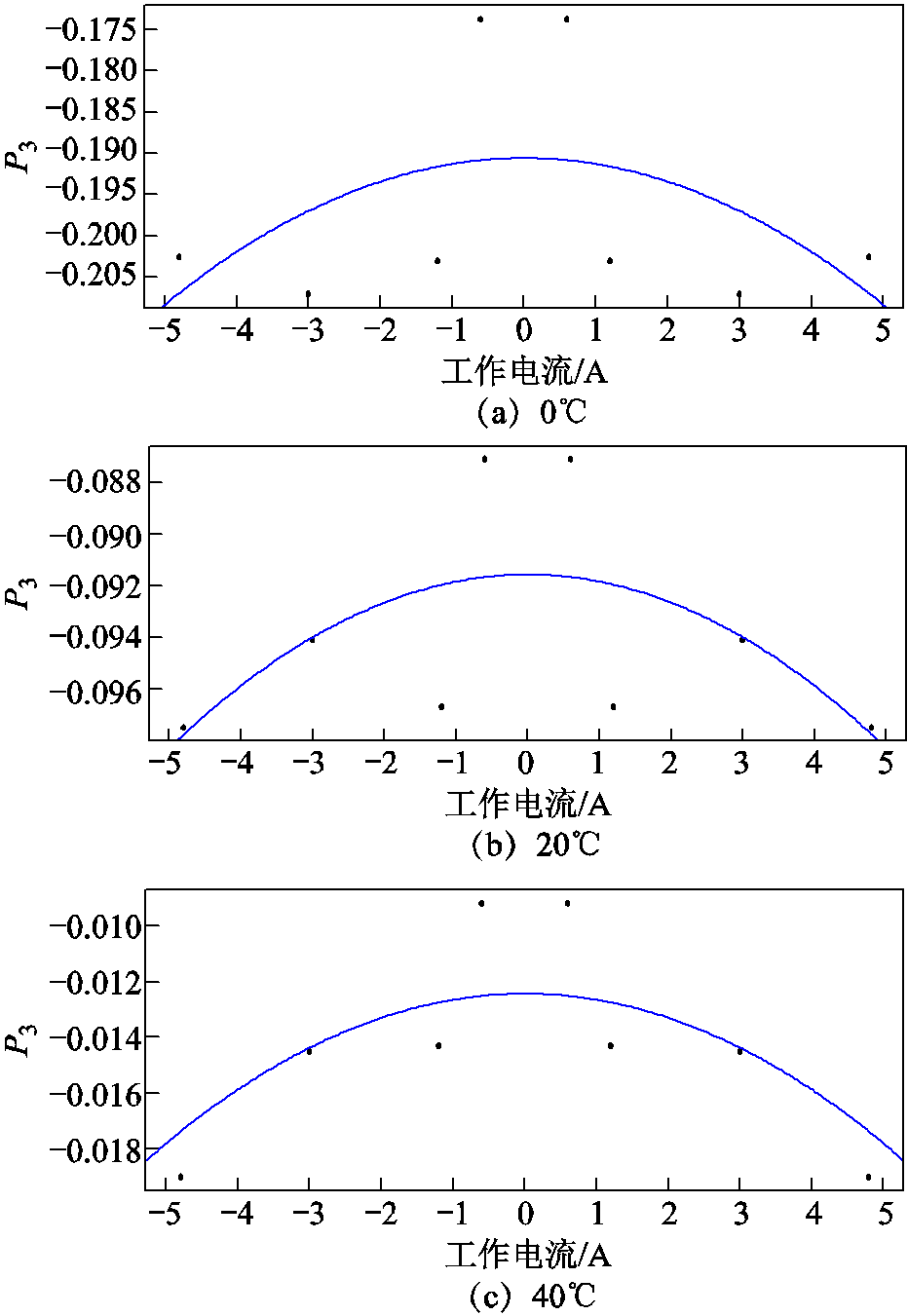
图8 不同温度下的P3-电流曲线
Fig.8 P3-current curves at different temperatures
表3 式（3）中参数
Tab.3 The parameters in Equ.(3)
T/℃b1/10-4b2/10-2 0-8.711-19.02 20-2.686-9.158 40-2.137-1.308
分析表3中数据可以发现，式（3）中的两个参数与温度之间存在明显的变化规律，即参数b1和b2与温度呈正相关。根据表中参数和温度的数据，可以拟合出一条抛物线，如图9所示。得到相应的二阶多项式数学关系模型为
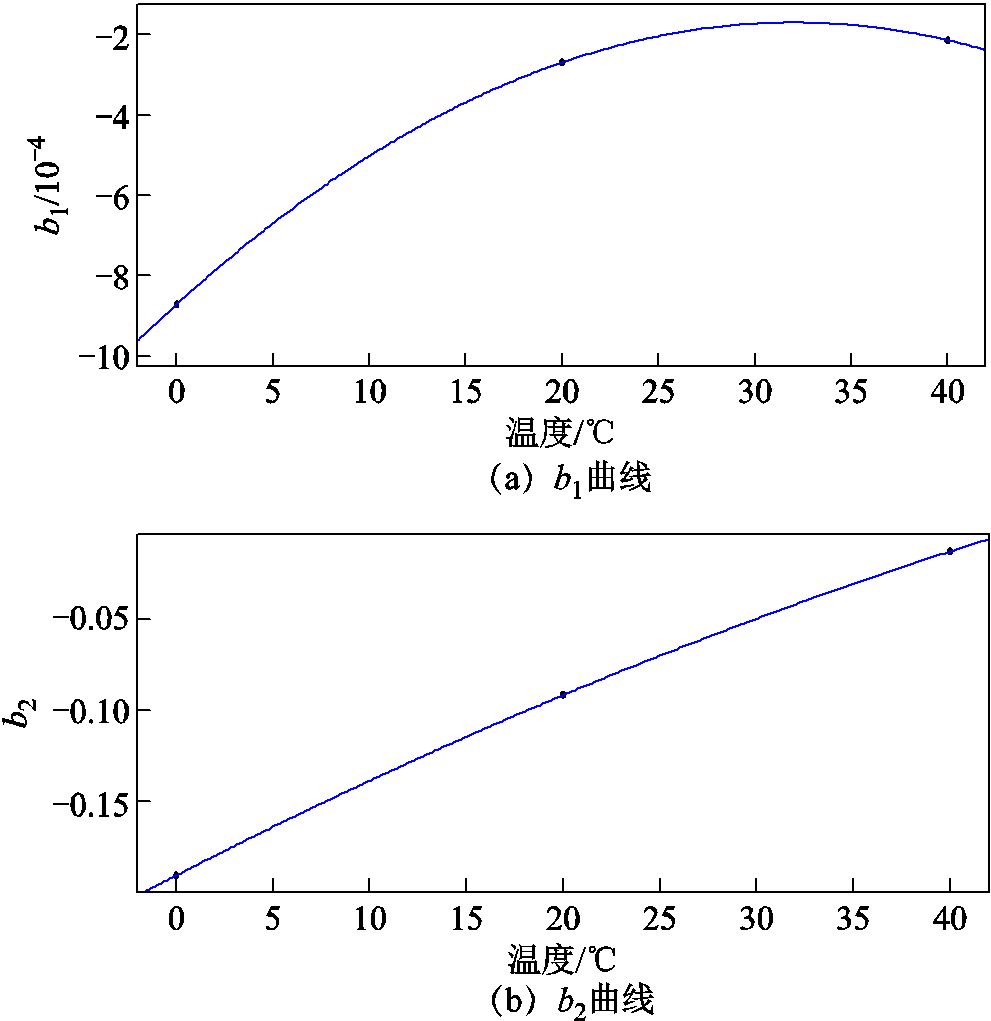
图9 参数-温度关系曲线
Fig.9 Parameter-temperature relationship curves
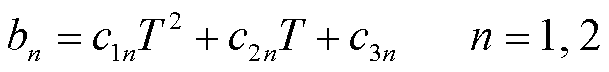（4）
将式（4）代入式（3），参数P3即可具备温度、工作电流自适应能力。至此，考虑温度、SOC和工作电流因素的误差修正方程已设计完成。将P1、P2和P3代入式（1）中，即可实现方程的温度、SOC和电流自适应能力。公式为
(5)
动力锂离子电池一般的电量应用区间是SOC= 20%～80%。因此本文的研究重点是在该SOC区间内设计E-EKF算法，另外两端的SOC区间直接沿用EKF算法进行SOC估计工作。
EKF算法即使与精度足够的模型相结合，其观测方程也会产生较大的输出误差，进而导致SOC估计精度下降。为了解决这一问题，本文建立了一种具有自适应能力的误差修正函数，并以此为基础，完成了观测方程的重组。重组后的方程如式（6）所示。利用重组的观测方程代替原方程，即可完成增强型EKF（E-EKF）算法的构建。
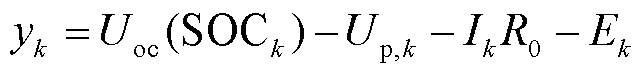（6）
式中，
为式（5）所示的误差修正方程。
误差修正方程的温度、SOC和电流自适应能力使重组后的观测方程可以在不同温度和工作条件下具备更高的输出电压精度。这一进步实现了算法中新息的降低，从而提高了SOC的估计精度。
为了验证误差修正函数的有效性和E-EKF算法的性能，本节使用前文提到的DST和US06工况，以0℃、10℃、20℃、25℃、30℃和40℃作为试验温度，平均误差作为衡量标准，首先对比了E-EKF和EKF的观测方程精度，然后对比了E-EKF、EKF和AEKF[8, 17]的SOC估计精度。其中，0℃、20℃和40℃下DST工况的试验数据被用于训练E-EKF算法。平均误差计算公式为
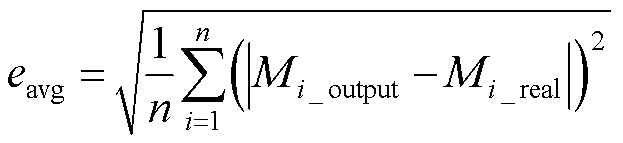（7）
式中，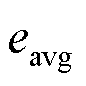
为平均误差；
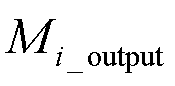和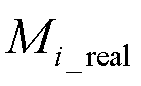
分别为第i时刻的输出值和实际值；n为误差个数。
以25℃为例，对比不同工况中EKF和E-EKF算法观测方程的输出情况。为了防止数据过于密集导致图片内容不可阅读，本文选取算法部分工作情况进行对比，如图10所示。根据图10a和图10b可知，在25℃下的两种工况中，E-EKF算法中观测方程的输出电压更接近实际电压。根据图10c和图10d可知，E-EKF算法中观测方程产生的输出电压误差在整体上更接近于0。
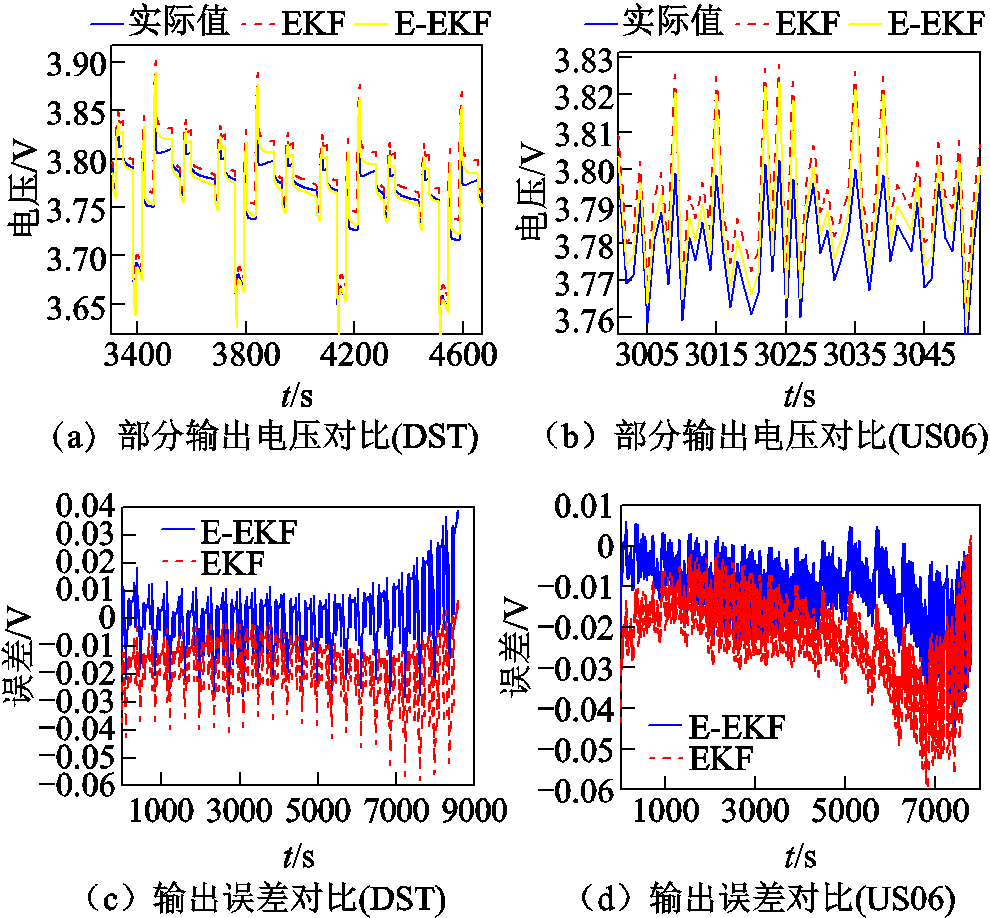
图10 两种算法中观测方程在25℃下的输出情况对比
Fig.10 Comparison of the output of observation equations of the two algorithms at 25℃
以平均误差作为衡量标准，记录两种算法在两种工况下的观测方程输出电压误差数据，见表4。对结果进行分析：①在DST和US06工况下，E-EKF中观测方程产生的平均误差均小于EKF。具体来说，在所有试验温度和工况下，E-EKF中观测方程产生的平均误差平均值与EKF相比，DST工况下降低了71.85%，US06工况下降低了60.92%；②电池活性随温度降低而减弱，相比高温条件，低温时极化电压变化较快，这是导致模型在低温时误差相对较大的重要原因；③忽略SOC工作区间、电流倍率和环境温度影响，会给锂电池建模带来较大误差，论文通过修正电池模型观测方程，提高了模型对这些影响因素的适应性，进而提高了模型精度。
表4 两种算法在两种工况下的观测方程输出电压误差
Tab.4 The output voltage error of observation equation of two algorithms under two working conditions（单位：V）
温度DSTUS06 EKFE-EKFEKFE-EKF 0℃0.078 30.017 20.069 10.024 1 10℃0.047 20.011 90.046 00.016 1 20℃0.031 50.008 10.028 90.011 2 25℃0.017 90.008 30.021 40.009 5 30℃0.017 40.006 40.012 30.008 5 40℃0.012 10.005 40.017 30.006 9 平均值0.034 10.009 60.032 50.012 7
图11和图12分别给出10℃、25℃和30℃下（构建E-EKF时未使用的温度），EKF、AEKF 和本文的E-EKF 算法在DST 和US06 工况下的SOC估计结果和误差。所有温度下的平均误差情况见表5。对结果进行分析：①三种算法在不同温度的两种工况下都能较好地估计电池SOC。②电流倍率、SOC工作区间、环境温度会影响电池内部电化学参数变化率，因此，不同工况、不同温度下SOC估计误差会有存在一定差异。③E-EKF估计SOC产生的平均误差均小于EKF。具体来说，E-EKF估计SOC时产生的平均误差平均值与EKF相比，DST工况降低了18.12%，US06工况降低了73.64%。④E-EKF估计SOC时产生的平均误差在大多数情况下都小于AEKF，仅在0℃和20℃的DST工况下的误差略大于AEKF。总体而言，在所有试验温度下，E-EKF估计SOC时产生的平均误差平均值与AEKF相比，DST工况下降低了6.15%，US06工况下降低了30.00%。
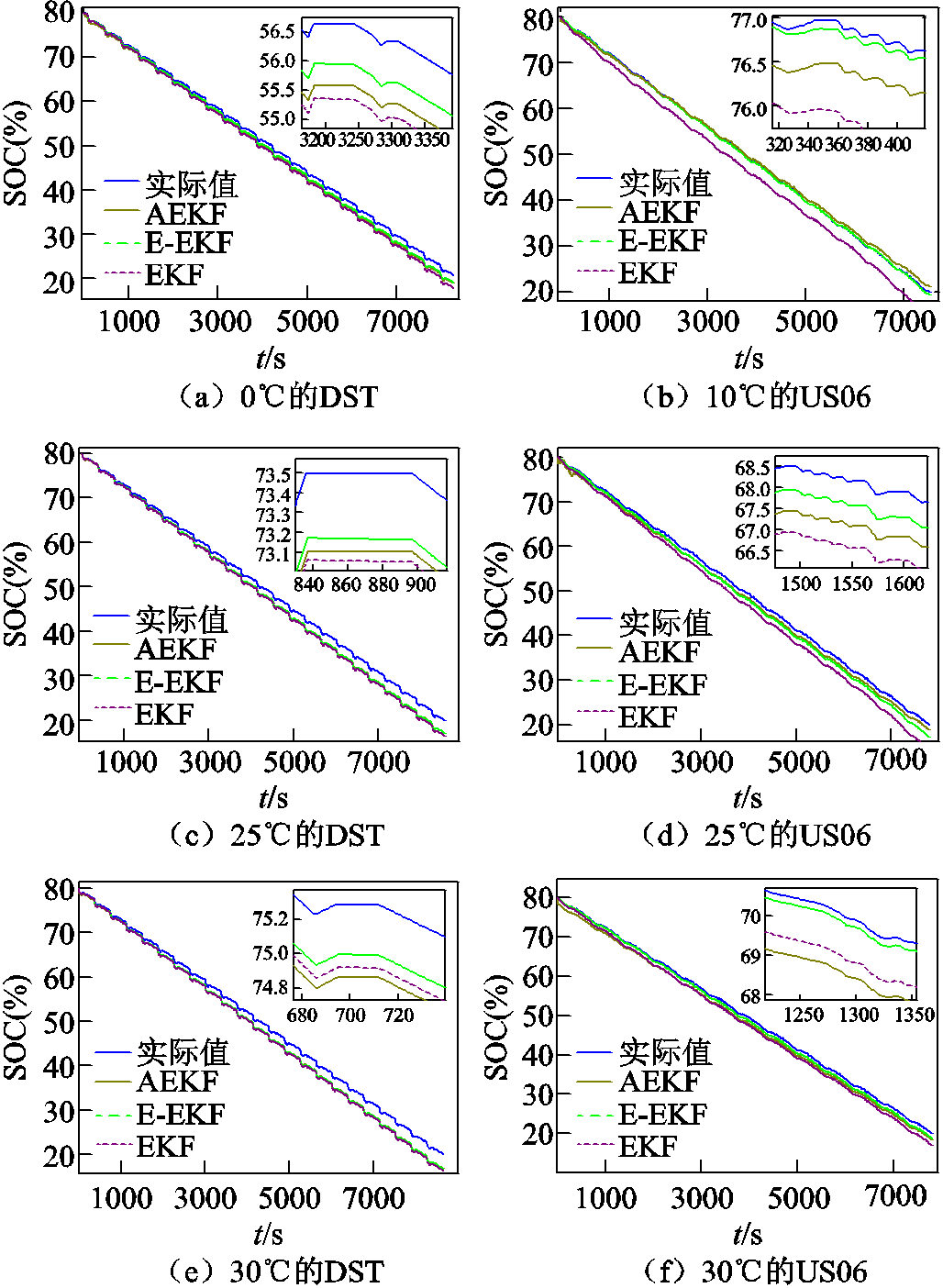
图11 不同温度和工况下三种算法的SOC估计情况
Fig.11 SOC estimation of three algorithms at different temperatures and working conditions
图12 不同温度和工况下三种算法的SOC估计误差
Fig.12 SOC estimation errors of the three algorithms under different temperature and working conditions
表5 三种算法在不同工况下的SOC估计误差数据
Tab.5 SOC estimation error data for the three algorithms under different operating conditions
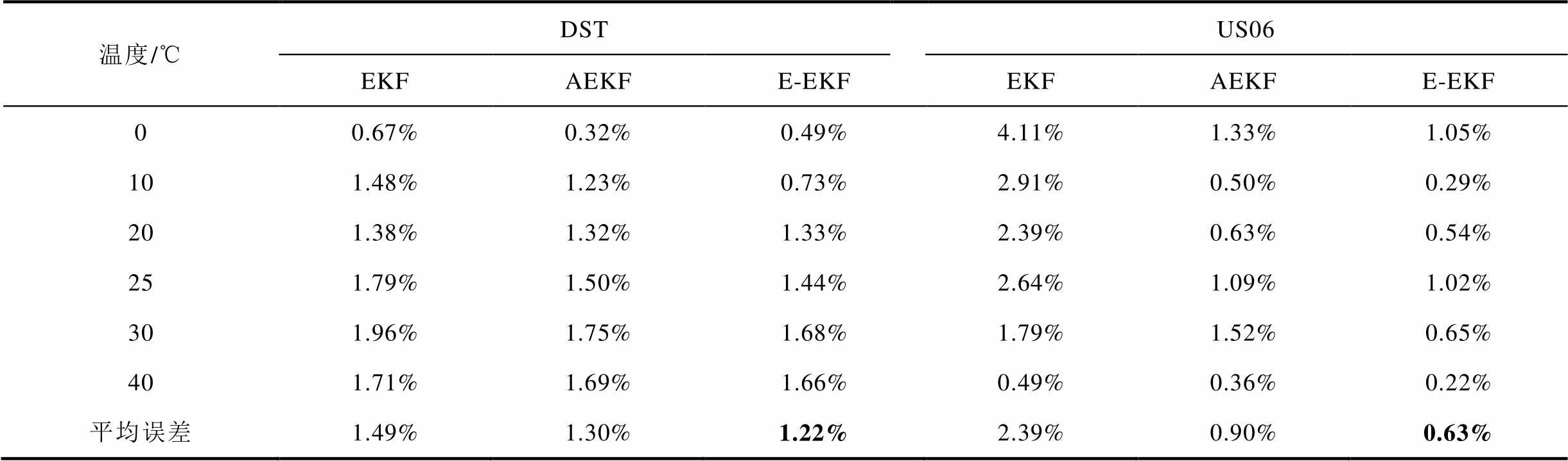
温度/℃DSTUS06 EKFAEKFE-EKFEKFAEKFE-EKF 00.67%0.32%0.49%4.11%1.33%1.05% 101.48%1.23%0.73%2.91%0.50%0.29% 201.38%1.32%1.33%2.39%0.63%0.54% 251.79%1.50%1.44%2.64%1.09%1.02% 301.96%1.75%1.68%1.79%1.52%0.65% 401.71%1.69%1.66%0.49%0.36%0.22% 平均误差1.49%1.30%1.22%2.39%0.90%0.63%
综上所述，在所有测试温度下的两种工况中，E-EKF在整体上具有比EKF更高的观测方程精度和比EKF、AEKF更高的SOC估计精度，尤其是在动态较强的US06工况下，由于E-EKF提高了对SOC工作区间、电流倍率和环境温度的适应性，SOC估计性能明显有较大提升。
本文针对EKF算法中观测方程输出精度不足的问题，提出了一种基于观测方程重组的增强型扩展卡尔曼滤波算法。首先，通过分析不同因素对观测方程的影响，筛选出相关性较强的状态量（温度、SOC和工作电流），并以此为基础建立了一种具有温度、SOC和电流自适应能力的误差修正方程。然后，利用所建立的误差修正方程对观测方程进行重组，构成E-EKF算法。最后，使用两种不同温度下的典型工况对比了EKF、AEKF和E-EKF的性能。试验结果表明，本文提出的E-EKF对不同的温度和工况具有普遍适应性，能够有效提升SOC估计精度。
参考文献
[1] 郭向伟, 邢程, 司阳, 等. RLS锂电池全工况自适应等效电路模型[J]. 电工技术学报, 2022, 37(16): 4029-4037. Guo Xiangwei, Xing Cheng, Si Yang, et al. RLS adaptive equivalent circuit model of lithium battery under full working condition[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4029-4037.
[2] 刘海东, 周萍, 周正, 等. 锂离子电池开路电压快速估计研究[J]. 机械工程学报, 2022, 58(8): 227-235, 243. Liu Haidong, Zhou Ping, Zhou Zheng, et al. Fast estimation of open circuit voltage for lithium-ion batteries[J]. Journal of Mechanical Engineering, 2022, 58(8): 227-235, 243.
[3] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725. Wu Longxing, Pang Hui, Jin Jiamin, et al. Overview of estimation methods of state of charge of lithium-ion batteries based on electrochemical model[J]. Tran-sactions of China Electrotechnical Society, 2022, 37(7): 1703-1725.
[4] Wu Longxing, Liu Kai, Pang Hui, et al. Online SOC estimation based on simplified electrochemical model for lithium-ion batteries considering current bias[J]. Energies, 2021, 14(17): 5265.
[5] 骆凡, 黄海宏, 王海欣. 基于电化学阻抗谱的退役动力电池荷电状态和健康状态快速预测[J]. 仪器仪表学报, 2021, 41(9): 172-180. Luo Fan, Huang Haihong, Wang Haixin. Rapid prediction of the state of charge and state of health of decommissioned power batteries based on electrochemical impedance spectroscopy[J]. Chinese Journal of Scientific Instrument, 2021, 41(9): 172-180.
[6] Liu Xingtao, Li Kun, Wu Ji, et al. An extended Kalman filter based data-driven method for state of charge estimation of Li-ion batteries[J]. Journal of Energy Storage, 2021, 40: 102655.
[7] Huang Congsheng, Cheng Zheyuan, Chow M Y. A robust and efficient state-of-charge estimation methodology for serial-connected battery packs: most significant cell methodology[J]. IEEE Access, 2021, 9: 74360-74369.
[8] 郝文美, 张立伟, 彭博, 等. 动车组钛酸锂电池荷电状态估计[J]. 电工技术学报, 2021, 36(增刊1): 362-371. Hao Wenmei, Zhang Liwei, Peng Bo, et al. State of charge estimation of lithium titanate battery for electric multiple units[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 362-371.
[9] Hua Xiao, Zhang Cheng, Offer G. Finding a better fit for lithium ion batteries: a simple, novel, load dependent, modified equivalent circuit model and parameterization method[J]. Journal of Power Sources, 2021, 484: 229117.
[10] 巫春玲, 胡雯博, 孟锦豪, 等. 基于最大相关熵扩展卡尔曼滤波算法的锂离子电池荷电状态估计[J]. 电工技术学报, 2021, 36(24): 5165-5175. Wu Chunling, Hu Wenbo, Meng Jinhao, et al. State of charge estimation of lithium-ion batteries based on maximum correlation-entropy criterion extended Kalman filtering algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5165-5175.
[11] Shu Xing, Li Guang, Zhang Yuanjian, et al. Stage of charge estimation of lithium-ion battery packs based on improved cubature Kalman filter with long short-term memory model[J]. IEEE Transactions on Transportation Electrification, 2021, 7(3): 1271-1284.
[12] 周才杰, 汪玉洁, 李凯铨, 等. 基于灰色关联度分析-长短期记忆神经网络的锂离子电池健康状态估计[J]. 电工技术学报, 2022, 37(23): 6065-6073. Zhou Caijie, Wang Yujie, Li Kaiquan, et al. State of health estimation for lithium-ion battery based on gray correlation analysis and long short-term memory neural network[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6065-6073.
[13] 黄凯, 丁恒, 郭永芳, 等. 基于数据预处理和长短期记忆神经网络的锂离子电池寿命预测[J]. 电工技术学报, 2022, 37(15): 3753-3766. Huang Kai, Ding Heng, Guo Yongfang, et al. Prediction of remaining useful life of lithium-ion battery based on adaptive data preprocessing and long short-term memory network[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3753-3766.
[14] Yang Fangfang, Zhang Shaohui, Li Weihua, et al. State-of-charge estimation of lithium-ion batteries using LSTM and UKF[J]. Energy, 2020, 201: 117664.
[15] Jiang Bo, Dai Haifeng, Wei Xuezhe, et al. Joint estimation of lithium-ion battery state of charge and capacity within an adaptive variable multi-timescale framework considering current measurement offset[J]. Applied Energy, 2019, 253: 113619.
[16] Guo Yuanjun, Yang Zhile, Liu Kailong, et al. A compact and optimized neural network approach for battery state-of-charge estimation of energy storage system[J]. Energy, 2021, 219: 119529.
[17] 宫明辉, 乌江, 焦朝勇. 基于模糊自适应扩展卡尔曼滤波器的锂电池SOC估算方法[J]. 电工技术学报, 2020, 35(18): 3972-3978. Gong Minghui, Wu Jiang, Jiao Chaoyong. SOC estimation method of lithium battery based on fuzzy adaptive extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3972-3978.
[18] Zhang Zhiyong, Jiang Li, Zhang Liuzhu, et al. State-of-charge estimation of lithium-ion battery pack by using an adaptive extended Kalman filter for electric vehicles[J]. Journal of Energy Storage, 2021, 37: 102457.
[19] Lin Xinyou, Tang Yunliang, Ren Jing, et al. State of charge estimation with the adaptive unscented Kalman filter based on an accurate equivalent circuit model[J]. Journal of Energy Storage, 2021, 41: 102840.
[20] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707. Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[21] Roy A, Patil R B, Sen R. The effect of fast charging and equalization on the reliability and cycle life of the lead acid batteries[J]. Journal of Energy Storage, 2022, 55: 105841.
[22] Lai Xin, Meng Zheng, Wang Shuyu, et al. Global parametric sensitivity analysis of equivalent circuit model based on Sobol’ method for lithium-ion batteries in electric vehicles[J]. Journal of Cleaner Production, 2021, 294: 126246.
[23] 吴健, 尹泽, 李豪, 等. 基于分数阶理论的锂离子电池高频等效电路模型[J]. 电工技术学报, 2021, 36(18): 3902-3910. Wu Jian, Yin Ze, Li Hao, et al. High-frequency equivalent circuit model of lithium-ion battery based on fractional order theory[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3902-3910.
[24] Movahedi H, Tian Ning, Fang Huazhen, et al. Hysteresis compensation and nonlinear observer design for state-of-charge estimation using a nonlinear double-capacitor Li-ion battery model[J]. IEEE/ASME Transactions on Mechatronics, 2022, 27(1): 594-604.
[25] Tran M K, Mevawala A, Panchal S, et al. Effect of integrating the hysteresis component to the equivalent circuit model of Lithium-ion battery for dynamic and non-dynamic applications[J]. Journal of Energy Storage, 2020, 32: 101785.
[26] Plett G L. Extended Kalman filtering for battery management systems of liPB-based HEV battery packs[J]. Journal of Power Sources, 2004, 134(2): 277-292.
[27] Barai A, Widanage W D, Marco J, et al. A study of the open circuit voltage characterization technique and hysteresis assessment of lithium-ion cells[J]. Journal of Power Sources, 2015, 295: 99-107.
Abstract：Lithium-ion batteries play a crucial role in energy storage, aerospace, new energy vehicles and other fields. However, over-charging and over-discharging will cause irreversible damage, consequently, to ensure the reliable and safe operation of batteries, it is very necessary to accurately estimate the state of charge (SOC) in real time. Considering that the observation equation of the dynamical system is an important factor affecting the SOC estimation result, an adaptive error correction strategy is put forward in the paper, furthermore, the observation equation is reconstructed. Combined with the extended Kalman filter (EKF), the enhanced EKF is established to estimate SOC.
Here, the widely used first-order RC model is adopted as the battery equivalent circuit model (ECM). In addition, it mainly studies the commonly used 20%～80% SOC working range.
Firstly, the effects of the parameter identification method, ambient temperature, SOC and current ratio on the offset between the output of the observation equation and the true measurement value are studied. The results show that: (1) at the same temperature and working condition, the probability density distribution of the output error of the observation equation produced by the two parameter identification methods (Recursive least squares of forgetting factor (FFRLS) and EKF) is very similar, more specifically, the difference of the average output error of them is less than 15%. (2) Temperature has a great influence on the output error of observation equation. Generally, the lower the temperature, the greater the output error. The higher the temperature, the closer and smaller the errors under the same SOC. (3) In general, the larger the current rate, the larger the output error of the observation equation. The extreme point of output error basically occurs when the current rate changes. (4) The output error of observation equation fluctuates with SOC, and its distribution has no obvious rule. Base on the experimental analysis, it is inferred that, the output error of the observation equation is mainly affected by the battery rate, temperature and SOC, and is less affected by the parameter identification algorithm, so it will be ignored in the paper. Secondly, according to the output error distribution and analysis results, an adaptive error correction model is generated, which is a second-order polynomial about SOC. In which, the coefficients of secondary and primary terms are affected by temperature and SOC, while the coefficient of the constant term are affected by temperature and current rate. As a result, the error correction model can adapt to current rate, SOC and temperature in practical applications. Finally, the adaptive error correction model is used to reconstruct the observation equation, combined with the EKF (named E-EKF) to update the SOC in real time.
DST and US06 conditions are used to verify the validity of the adaptive error correction model and the performance of E-EKF algorithm. In which, DST conditions at 0℃, 20℃and 40℃are used to train the adaptive error correction model, and US06 and DST at 0℃, 10℃, 20℃, 25℃, 30℃ and 40℃ are used to test the model. On the one hand, the accuracy of the observation equation of E-EKF and EKF is obtained, the results show that, compared with EKF, the average output error generated by the observed equation in E-EKF is reduced by 71.84% in DST condition and 60.92% in US06 condition. On the other hand, the SOC estimation accuracy of E-EKF, EKF and adaptive EKF (AEKF) is obtained. The results show that, compared with EKF and AEKF, the average SOC estimation error of E-EKF is reduced by 18.12% and 6.15% in DST condition and 73.64% and 30.00% in US06 condition respectively.
In summary, current rate, SOC working range and ambient temperature which influence the performance of Lithium-ion batteries are dynamic change in practical applications. Ignoring these factors, when using EKF to estimate SOC, there will be a large error (that is, a large innovation) between the output of the observation equation and the measurement value, resulting in lower SOC estimation accuracy. The adaptive error correction model proposed can help to reduce the innovation, so as to improve the accuracy of SOC estimation.
keywords：Extended Kalman filter algorithm (EKF), error correction strategy, reconstruction of observation equation, SOC estimation
DOI: 10.19595/j.cnki.1000-6753.tces.230061
中图分类号：TM912
河北省自然科学基金面上资助项目（E2019202328）。
收稿日期 2023-01-13
改稿日期 2023-02-28
黄 凯 男，1980年生，博士，副教授，硕士生导师，研究方向为储能与动力电池组测试与建模、电池组性能状态预测与可靠性估计。E-mail：huangkai@hebut.edu.cn
郭永芳 女，1979年生，博士，副教授，硕士生导师，研究方向为智能算法、锂离子电池建模与寿命估计。E-mail：guoyongfang@hebut.edu.cn（通信作者）
（编辑 郭丽军）