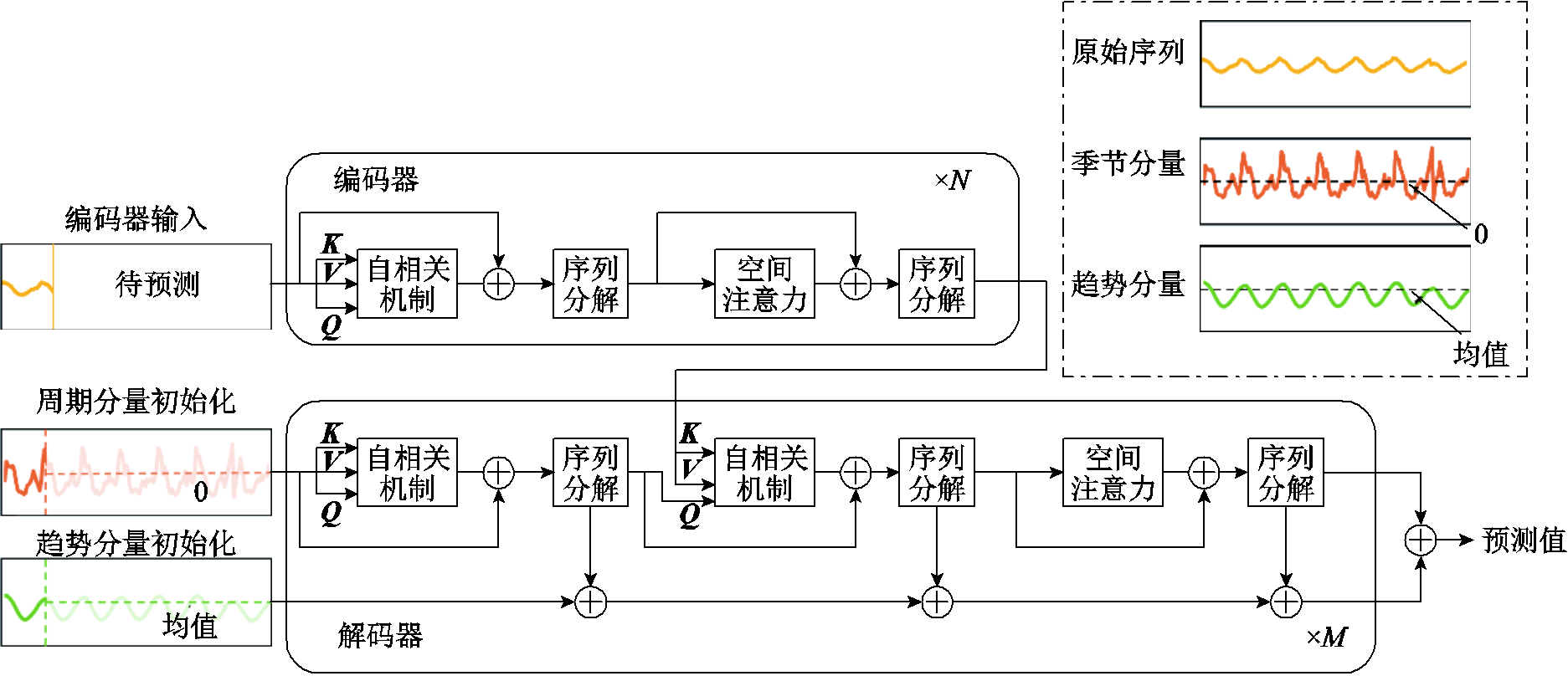
图1 STformer模型架构
Fig.1 Architecture of Stformer
摘要 针对在低压台区海量高波动用户负荷预测场景下，传统探索单个用户时间特征的负荷预测方法存在无法学习用户之间的空间相关性、无法实现多用户共同预测的问题，该文提出一种基于时空注意力机制的Transformer负荷预测模型（STformer），提供精准的台区多用户短期负荷预测。首先，改进传统Transformer模型，嵌入序列分解模块、自相关计算模块和空间注意力模块。其中，序列分解模块可以将波动较大的用户负荷曲线分解为相对平稳的多个子序列，有助于更好地提取负荷曲线的时间依赖性和周期因子；自相关计算是一种改进的注意力机制，可以挖掘多个历史同时期子序列的时间相关性；空间注意力机制可以提取台区多用户之间的动态空间相关性。然后，利用蒙特卡洛随机失活方法（MC dropout）将STformer拓展到台区多用户负荷概率预测。最后，采用真实台区多用户负荷数据集进行验证，与多种负荷预测模型进行对比，证明STformer模型可有效提高短期多用户负荷点预测和概率预测的精确性和鲁棒性。
关键词：多用户负荷预测 时空相关性 Transformer模型
在“碳达峰·碳中和”目标的指导下，大量用户侧分布式电源从低压配电台区入网，加剧了能源消耗模式的波动性和不确定性[1]。面对高波动的负荷曲线，在未来几分钟或几小时内对低压台区单个用户进行准确且高效的短期电力负荷预测对需求侧响应、可再生能源消纳具有重要价值[2-3]。此外，智能电表等装置在用户侧的广泛使用一方面为电力企业分析台区用户用电行为之间的关联提供了数据基础[4]；另一方面也带来了海量用户的负荷预测需求[5]，这意味着传统仅针对单个对象的预测方法无法满足海量用户的新形势。因此，需要一个针对多用户的负荷预测模型，方便、高效、精确地完成海量用户的点预测和概率预测任务。
目前，一方面由于用户级数据的缺乏；另一方面由于系统级负荷序列更为平稳，周期性规律较强，导致负荷预测的研究主要集中在系统级，即针对台区的总负荷进行预测。经典机器学习方法如多元线性回归（Logistic Regression, LR）[6-7]、支持向量机（Support Vector Regression, SVR）[8-10]、随机森林[11]、前馈神经网络（Feedforward Neural Network, FNN）等都在系统级负荷预测领域证明了其有效性。然而，由于用户用电行为具有主观性和随机性，易受气象条件、市场电价等因素影响，与系统级负荷相比，用户级负荷往往更不规则，波动性更大。因此，提供精准的用户级负荷预测仍然为一项极大的挑战。
随着智能电表等设备的发展，学者们将目光越来越聚焦于用户侧。近年来，深度学习模型在负荷预测领域受到广泛关注，循环神经网络（Recurrent Neural Network, RNN）[12-14]、卷积神经网络（Convolutional Neural Network, CNN）[15-17]、Transformer等模型进一步提升了负荷预测模型的性能和精准度。现有的用户负荷预测方法大多是针对单个用户的时间序列使用深度学习模型进行预测，例如，文献[18]以向量自回归模型、高斯过程回归模型和长短期记忆网络（Long Short Term Memory network, LSTM）异构模型为基础模型，基于权重系数进行组合预测。文献[19]利用气象及环境信息预测单个用户的负荷信息，采用CNN提取特征并输入RNN中进行预测。文献[20]通过特征工程框架，使用基于机器学习的增强方法提高单个住宅短期负荷预测的准确性。然而，上述方法都是对单个用户的时间特征进行建模而忽略了多用户间的空间相关性。同一区域内的用户共享着相同的地理空间、气象条件、节假日信息、电价政策等综合因素，用户用电行为之间往往会存在一定的时空相关性。若能充分挖掘这种时空相关性，将对短期用户负荷的建模产生极为积极的意义。
目前已有少量文献对考虑时空相关性的用户负荷预测进行了初步的探索。时空电力负荷预测倾向于使用所有用户的信息来训练模型，通过提取不同用户单元之间的潜在依赖关系来提高整体预测精度，不同用户间的潜在依赖关系在一定程度上也反映了外因的影响，这样能在缺少外部数据的情况下得到比较精确的预测结果。例如，文献[21]提出一种基于CNN和LSTM的混合模型，融合多个用户之间的长期变化趋势和短期负荷相似性；文献[22-23]提出一种基于图神经网络（Graph WaveNet, GWN）的短期居民负荷预测方法，利用“图学习”的方法描述用户负荷的时空相关性。上述方法在面对多用户负荷预测时都取得了相比于传统方法更为优秀的效果。然而，应当注意到已有的时空方法只能提供确定性预测，无法提供概率预测。概率预测以预测区间、概率密度函数等形式呈现，可以帮助运营商制定基于风险的决策。近年来，面对电网高比例渗透新能源带来的不确定性，概率预测在市场交易、运行调度等环节发挥着越来越大的作用。
Transformer模型[24]是一种完全基于注意力机制的编码器-解码器结构，其直接输出预测长度的预测序列，允许对序列进行相关性建模而不考虑它们之间的距离，因此适用于台区多用户负荷预测问题。但是，标准的Transformer模型无法捕捉序列之间的空间相关性，无法处理高波动性序列，所以需要对标准Transformer模型作一定的修改。
针对上述问题，本文首先提出一种基于时空注意力机制的Transformer负荷预测模型（Spatial-Temprol Transformer, STformer）。通过改进标准的Transformer自注意力机制，为每个编码器和解码器嵌入三种模块：序列分解模块、自相关计算模块和空间注意力模块，有效提取高波动性居民用户之间的动态时空依赖关系。然后，利用蒙特卡洛随机失活方法（MC dropout）将STformer拓展到概率预测领域。该方法不需要对STformer进行额外修改，但使得STformer具备了同时输出点预测和概率预测结果的能力。概率预测提供的不确定性信息可以帮助电力运营商作出基于风险的决策。
针对台区多用户负荷预测时空依赖关系复杂的问题，提出一种新的预测方法——基于时空注意力机制的Transformer（STformer），模型架构如图1所示。
模型设计遵循编码器-解码器结构。编码器/解码器包含序列分解模块、自相关模块和空间注意力模块，目的是进行过去/未来的周期信息建模和空间信息建模。此外，解码器还可累积趋势分量，进行趋势信息的建模。具体措施如下：
图1 STformer模型架构
Fig.1 Architecture of Stformer
1）打破序列分解的预处理惯例，并将其改造为模型的基本内部块，赋予模型复杂时间序列的渐进分解能力。一方面可以将受新能源接入影响波动较大的用户负荷曲线分解为相对平稳的多个子序列；另一方面解决了未来预测负荷以及中间隐藏变量难以分解的问题，有利于消除干扰信息，细化预测结果。
2）设计基于序列周期性的自相关机制，使用快速傅里叶变换（Fast Fourier Transform, FFT）代替矩阵乘法，降低输入数据带来的大计算量。
3）利用池化、卷积等操作设计空间注意力模块，挖掘与利用多用户负荷之间的复杂空间关系。
1.1.1 编码器
编码器的输入Xenc由用户负荷序列Xin和时间编码结果T经过数值嵌入后相加得到。其中，数值嵌入操作是为方便后续的残差连接及模型堆叠，将数据由d维的输入空间投影到dmodel维的模型空间以对齐模型的数据维度。编码器侧重于周期性分量的建模和空间信息建模，经过序列分解得到的趋势分量被丢弃。编码器的输出包含过去的周期性信息和空间信息，将作为交叉信息输入解码器中帮助解码器完善预测结果。
1.1.2 解码器
解码器分为两部分，上半部分用于周期信息建模的堆积式自动相关机制和空间相关性的提取；下半部分用于趋势信息的积累。解码器的输入为Xdes和Xdet两个序列。Xdes和Xdet的前半部分为Xin后半部分进行分解后所得到的周期分量Xens和趋势分量Xent。Xdes和Xdet的后半部分分别为长度为Lpre的0占位符和平均值占位符和。Xdes和Xdet变换到dmodel维度再分别和dmodel维度的时间信息相加作为解码器的两个输入。每个解码器层包含内部的自相关可以细化预测中的周期性信息，编码器-解码器自相关有助于利用过去的周期性信息，空间注意力模块可以提取空间相关性。同时，解码器还从中间的隐藏变量中提取潜在的趋势，使STformer能够逐步细化趋势预测。
如图1所示，序列分解模块被集成到框架的内部，而不是在数据预处理过程中应用时间序列分解。这种渐进分解的结构可以分解历史数据、未来数据和中间隐藏变量，并且捕捉趋势部分和季节部分潜在的未来交互。这种分解模块通过移动平均的方法实现，先通过一个平均池化层得到趋势部分，再减去趋势部分得到季节部分。对时间序列X进行分解可以表示为
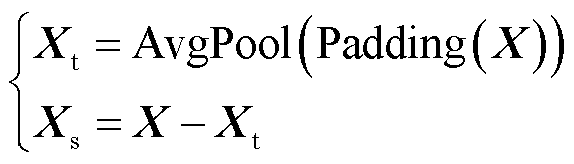（1）
式中，Xt和Xs分别为趋势部分和季节部分，Xt, Xs∈RT×d；AvgPool(·)为平均池化，等价于对序列进行滑动平均；Padding(·)为对输入进行填充，以确保输入输出序列长度一致。整个分解过程可以表示为
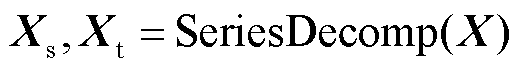（2）
式中，SeriesDelomp(·)为序列分解过程。
空间注意力模块如图2所示，由卷积操作和空间注意力操作两部分构成。首先使用卷积操作对时序分解后的季节性部分进行深层次特征挖掘；然后对挖掘的特征作空间注意力操作。空间注意力操作可以定位空间中有效的信息并进行特征加权，学习重要的空间特征。
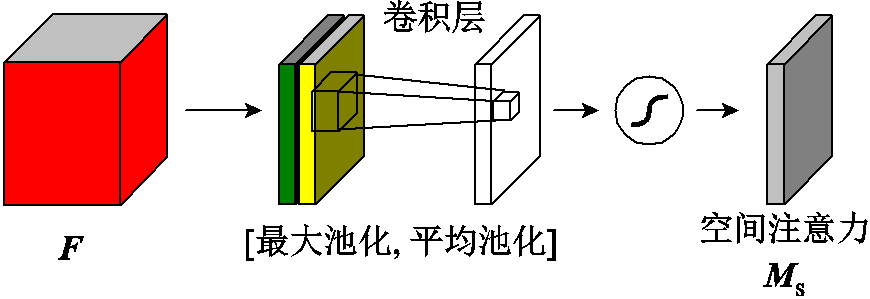
图2 空间注意力模块
Fig.2 Spatial attention model
首先，将解码器第二个序列分解块分解出的季节性部分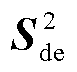
通过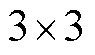
的卷积核进行卷积操作fconv转换成特征图F。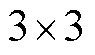的卷积核具有较小的计算复杂度，能够更快地训练和推理，其计算过程表示为
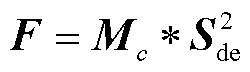（3）
式中，*代表卷积运算；Mc为用到的c个卷积滤波器。
然后，将原始特征中的空间信息变换到另一个空间中并保留关键信息，计算式为
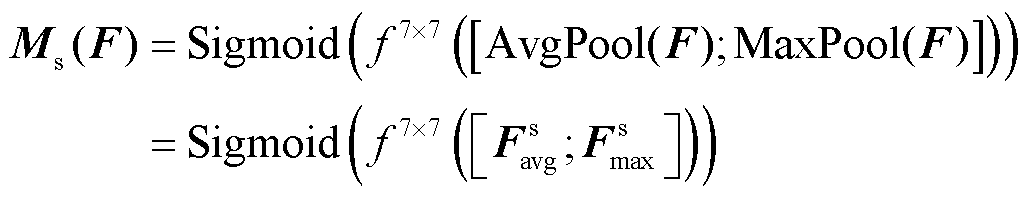(4)
式中，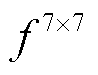
为参考文献[25]设计的滤波器大小为7×7的卷积运算；
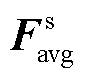和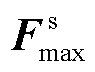
分别为对F进行一个通道维度的平均池化AvgPool(F)和最大池化MaxPool(F)得到的通道描述；Ms(F)为空间注意力图，用来描述空间中特征图的重要位置信息。
自相关机制首先通过计算序列自相关来发现基于周期的相关性，然后通过时间延迟聚合来聚合相似的子序列。自相关机制如图3所示，利用快速傅里叶变换计算自相关系数R(τ)，它反映了时间延迟的相似性。再根据选定的延迟τ将相似的子过程滚动到相同的指数，并通过R(τ)进行聚合。
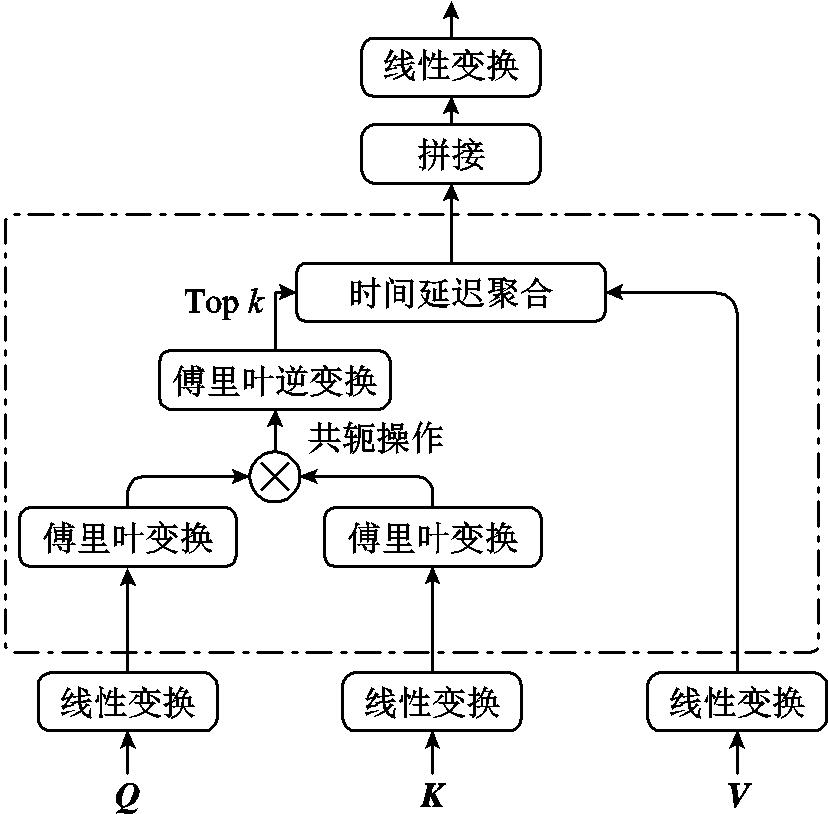
图3 自相关机制
Fig.3 Autocorrelation mechanism
1.4.1 傅里叶简化自相关计算
自相关的概念来自信号分析，表示的是同一个时间序列在任意两个不同时刻的取值之间的相关程度。本文采用维纳-辛钦定理简化了自相关的运算。维纳-辛钦定理在傅里叶光学领域被提出，它指出任意一个均值为常数的广义平稳随机过程的功率谱密度是其自相关函数的傅里叶变换。这种自相关的高效计算可以实现O(Llog2L)的复杂度，其中L为序列长度。对于序列分解块分解出的周期分量Xs，先经过投影得到查询向量Q、被查询信息与其他信息的相关性向量K、被查询信息向量V，自相关系数R(τ)简化计算过程为
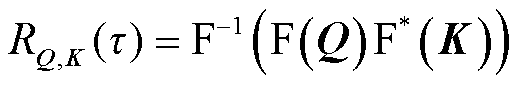（5）
式中，F为傅里叶变换；上标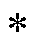
代表共轭。使用自相关系数R(τ)作为估计周期长度τ的非标准化置信度。
1.4.2 时间延迟聚合
时间延迟聚合如图4所示。首先根据傅里叶变换得到的自相关系数RQ,K(τ)选定时间延迟τ1, τ2,…, τk；然后用Softmax函数对置信度聚合子序列RQ,K(τ1), RQ,K(τ2),…, RQ,K(τk)进行归一化；接着根据τ1, τ2,…, τk滚动序列V，该操作基于选定的延迟将相似的子序列对齐；最后用V滚动后的序列和对应的归一化后的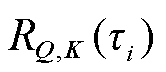
相乘，进行聚合。
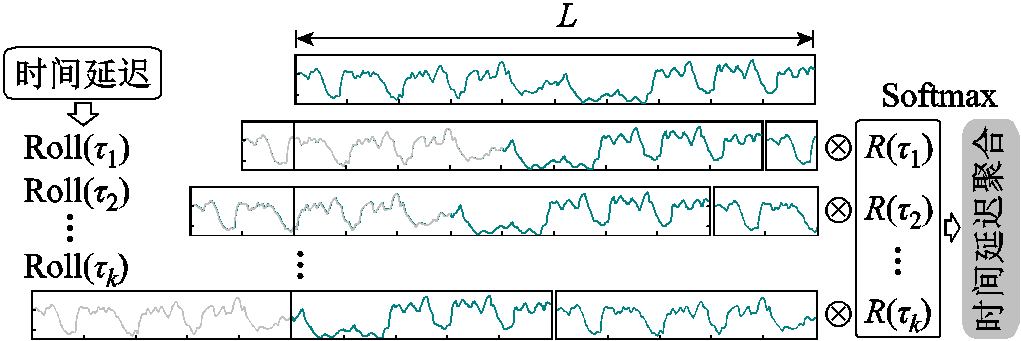
图4 时间延迟聚合
Fig.4 Time delay aggregation
捕捉模型中的不确定性是实现时间序列的概率预测的一种方法[26]。贝叶斯概率理论是解释模型不确定性的有效工具，但它通常需要高昂的计算成本，因此选择使用基于神经网络的MC dropout方法近似贝叶斯理论[27]降低计算成本。具体过程如下：
给定一组N个观测值X={x1, x2,…, xN}和预测值Y={y1, y2,…, yN}，设f W(·)为参数为W的神经网络。贝叶斯推断旨在找到模型参数后验分布p(W|X,Y)。当测试样本x*输入训练模型时，通过计算边缘化后验分布获得预测值的概率分布为
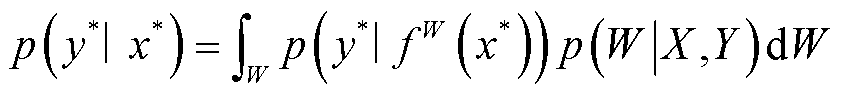（6）
式中，y*为测试集的输出。
预测分布的方差量化了预测不确定性，其可以使用总方差定律进一步分解为
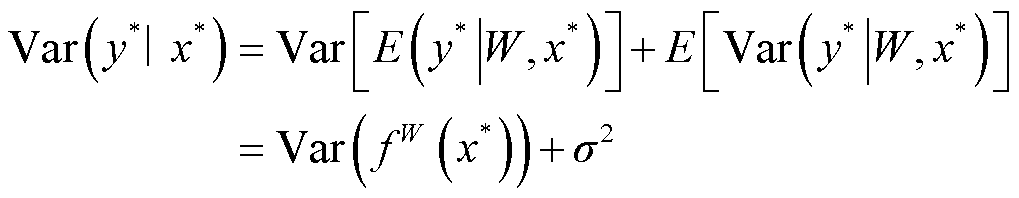(7)
式中，Var(·)为方差函数；E(·)为期望函数。其中方差被分解为两项：Var(f W(x*))反映了模型不确定性；σ2反映了数据生成过程中的内部噪声。估计模型不确定性的关键是后验分布p(W|X,Y)，也称为贝叶斯推断。在这里，使用MC dropout来近似模型不确定性。具体过程如下：给定一个新的输入x*，计算每一层具有随机失活的神经网络的输出。该随机前馈重复B次，得到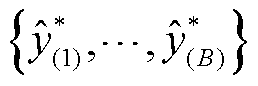
。然后通过样本方差来近似模型不确定性，得到
（8）
其中
此时，根据式（8），式（7）可以近似为
（9）
根据文献[26]，可以使用一个独立的验证集来估计σ2。本文中用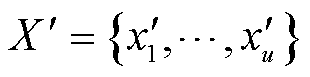
和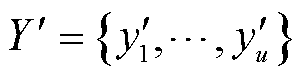
表示验证集，并通过式（10）估计σ2，得到
（10）
式中，
为在训练数据集上训练的STformer模型；β为使用验证集来估计的参数；u为验证集中的数据量。
本文使用来自东南某省真实的台区用户负荷数据验证提出模型的有效性。为了检测模型在不同数据集上的泛化性能，分别对A、B两个居民台区的数据集建立预测模型。每个台区的数据集中包括多条用户的历史负荷信息和日期信息，对同一台区的多用户之间采用基于时空注意力机制的方法进行联合预测。两个台区分别有131个用户和138个用户，采样周期为1 h，时间跨度为2021年4月1日至2022年3月31日。首先每次从中选取10%作为测试集，相当于十折交叉验证；然后取剩下的80%作为训练集和10%作为验证集，每次随机划分训练集和验证集。
本文数据是d个用户一年的负荷数据和对应的日期数据。先进行数据预处理，将数据划分为训练集、验证集和测试集，并且将负荷数据进行标准化。此外还将时间信息解析为4列数据（包括一天中的第几个小时、一星期中的第几天、一个月中的第几个星期、节假日），数据范围为(0,1)。
针对点预测和概率预测选择不同的评价指标在测试集上衡量模型的预测性能，是交叉验证的平均。
1）点预测
使用平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）、平均绝对误差（Mean Absolute Error, MAE）作为度量来计算模型的预测误差，计算公式分别为
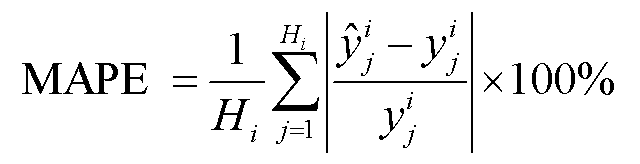（11）
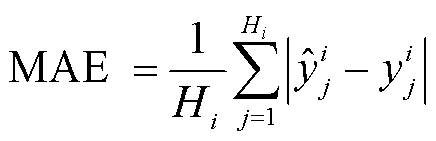（12）
式中，Hi为第i个用户包含的样本个数；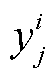
为第i个用户第j个样本的实际值；
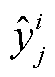为相应的预测值。
为了比较在单个用户上的预测效果，计算每个用户的MAPE和MAE的平均值，分别记作Avgr. MAPE和Avgr.MAE；为了比较在总体用户上的预测效果，计算所有用户的总预测值与总真实的MAPE和MAE，分别记作Aggr.MAPE和Aggr.MAPE。
2）概率预测
使用弹球损失（Pinball）和Winkler来量化MC dropout短期用户负荷概率预测性能，Pinball和Winkler都可以综合评估概率预测的区间可靠性和区间宽度。Pinball表达式为
（13）
式中，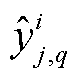
为第q个分位数的负荷预测值；
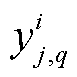为实际观测到的负荷值。对于(1-α)×100%预测区间（α为在统计推断中允许错误发生的概率），Winkler指标定义为
（14）
式中，Lj和Uj分别为预测区间（Prediction Interval, PI）的下限和上限；δ为区间宽度，δ=Uj-Lj。
本文选择了两个机器学习模型——支持向量回归（Support Vector Regression, SVR）、线性回归（Linear Regression, LR）和五个深度学习模型——FNN、LSTM、卷积门控循环单元（Convolutional Neural Network-Gate Recurrent Unit, CNN-GRU）、GWN、Transformer与所提出的模型进行比较。上述网络模型中，FNN模型的隐藏层数为3，隐藏层神经元个数分别设置为40、40、20；SVR模型的核函数采用径向基函数，惩罚参数为5；LSTM模型隐藏层神经元个数为512，使用Adam优化器来训练，
初始学习率为0.001；CNN-GRU模型的卷积层数为3，GRU层数为1，全连通层数为1，卷积核大小为(2, 1)；GWN模型的层数为8，其膨胀因子为1、2、1、2、1、2、1、2；Transformer及其改进算法的主要超参数见表1。所有程序在配置RTX A5000显卡、16核 Intel(R) Xeon(R) Platinum 8350C CPU的计算机上利用python实现。
表1 STformer主要参数
Tab.1 Main parameters used in STformer
参数数值 编码器数量2 解码器数量1 批量大小128 向量维度512 学习率0.000 1 最大迭代次数60 多头注意力数量8
3.3.1 台区单个用户的预测效果
表2列出了不同模型在两个台区预测结果的Avgr.MAPE、Avgr.MAE，图6a和图6c列出了不同模型在每个具体用户上的MAPE值。由表2可以看出，在A台区和B台区中预测效果最差的三个模型是FNN、SVR、LR，这是因为它们不善于提取输入输出之间的复杂映射关系。相比之下，LSTM和CNN-GRU的预测效果优于上述三个算法。这主要归功于LSTM网络模型能较好地提取负荷序列的时间特征；CNN-GRU可以通过CNN捕捉空间特征，而GRU可以在CNN的基础上进一步捕捉负荷序列的时间变化规律。本文提出的STformer模型通过时间注意力机制提取用户的时间变化规律，通过空间注意力机制提取多个用户之间的空间依赖性，最终STformer在所有的场景下都取得了最好的预测结果。具体来说，与FNN、SVR、LR、LSTM、CNN-GRU、GWN、Transformer相比，本文所提出的方法在A台区15个用户上得到的Avgr.MAPE分别减少了22.38%、24.10%、25.25%、22.38%、22.51%、20.29%、16.54%；对B台区15个用户的预测结果得到的Avgr.MAPE分别减少了24.92%、31.08%、32.18%、20.90%、27.7%、8.71%、6.95%。这体现了STformer模型在多用户短期负荷预测方面的准确度，说明在实际工程应用中该模型可以为决策者提供可靠的预测结果。
表2 提前1h点预测性能
Tab.2 Point forecasting performance summary 1 h ahead
区域算法Aggr.MAPE(%)Avgr.MAPE(%)Aggr.MAEAvgr.MAE A台区FNN3.485.7283.161.19 SVR3.645.8587.361.22 LR3.745.9490.901.36 LSTM3.415.7281.551.18 CNN-GRU2.925.7370.281.16 GWN3.495.5783.931.17 Transformer2.855.3267.671.13 STformer2.214.4457.570.92 B台区FNN5.789.6353.520.77 SVR6.6910.4960.830.82 LR7.0010.6664.610.85 LSTM5.049.1449.420.76 CNN-GRU4.8110.0051.140.84 GWN4.337.9247.110.70 Transformer4.137.7744.940.68 STformer3.647.2340.320.61
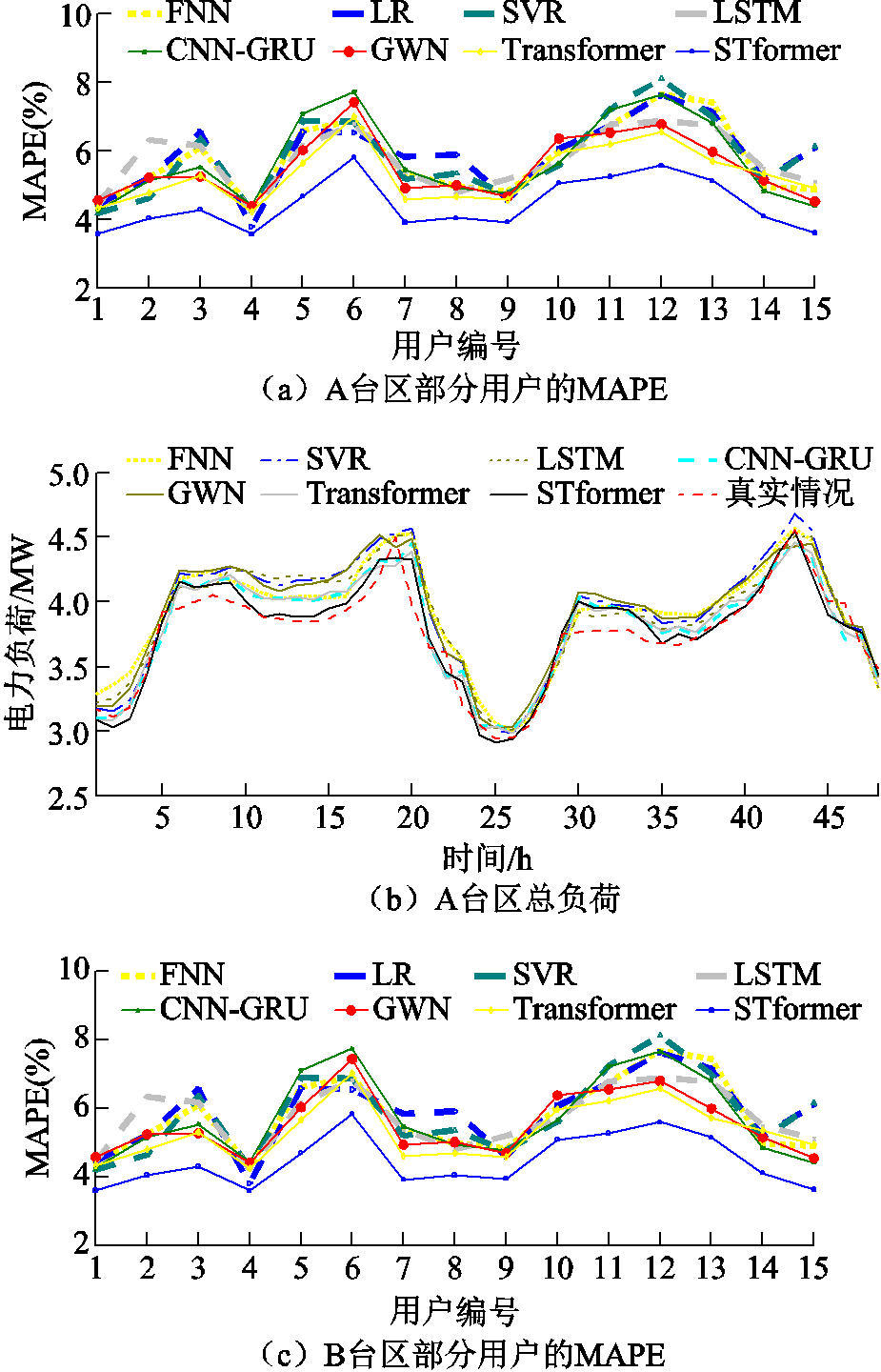
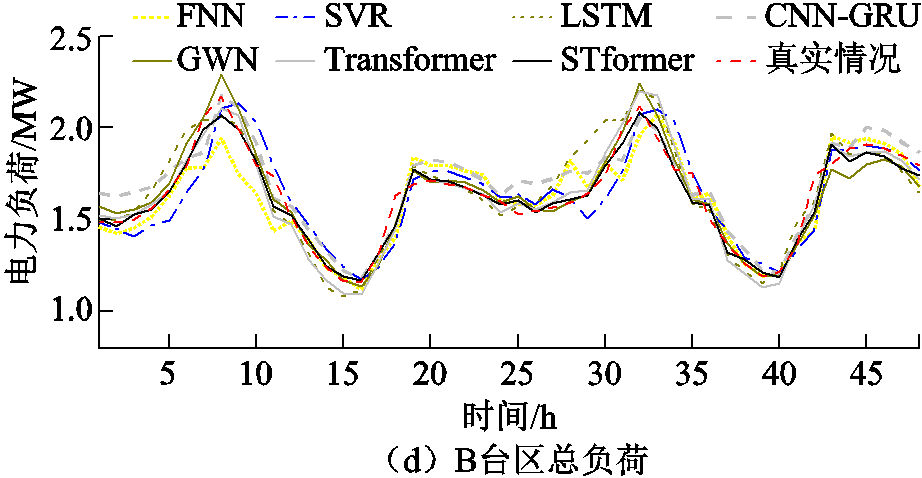
图5 各种模型在提前1 h点预测上的表现
Fig.5 Performance of various models in point prediction 1 h ahead
由图6a和图6c可以看出，尽管在每个用户上，预测结果的MAPE有一定波动，但是本文提出的模型在每个用户的预测准确度均优于其他对比方法。说明本文提出的方法可以有效地提取多个用户之间的空间相关性，并利用这种空间信息提高每个用户的预测准确度。
3.3.2 台区用户总负荷的预测效果
本节评估了模型在预测总负荷（同一台区所有用户的总功率）方面的性能。图6b和图6d绘制了采用不同算法时，A、B两个台区1 h前负荷的预测结果和真实曲线，此处使用了两天的预测结果进行展示。可以看到，STformer的总负荷预测值更接近真实值。例如，图6b中[10, 15]、[35, 40]的时间步长间隔直观地证明了STformer在总负荷预测中的性能优于其他模型。从图6d也可以看出，该模型总体上对实际负荷曲线的拟合度更高，特别是在上升沿中。综合来看，STformer在总负荷预测中的性能优于其他模型。此外，表2中STformer模型在总负荷预测结果的Aggr.MAPE和Aggr.MAE始终优于其他对比模型。这说明所提出的STformer模型不仅可以为台区单个用户提供精准的负荷预测结果，而且可以为台区总负荷预测提供优秀的预测结果。
使用A、B两个台区2021—2022年的负荷数据来验证基于MC dropout方法的短期多用户负荷概率预测的有效性。随机失活比p=0.1被添加到所有的dropout层，式（8）由模型迭代500次估计（B=100），β的估计值为0.81。
为了量化MC dropout在解决短期负荷概率预测上的性能，采用Pinball、50%预测区间的Winkler评分、90%预测区间的Winkler评分来评估所提出的方法的覆盖率和间隔宽度。在A、B两个台区的负荷数据集上实现STformer模型，并将结果与分位数回归神经网络（Quantile Regression Neural Network, QRNN）[28]和稀疏高斯过程回归（Sparse Gaussian Process Regression, SGPR）[29]进行比较。其中，QRNN是一种基于神经网络的分位数回归方法，其做法是将标准的神经网络L1损失函数替换为Pinball损失函数；SGPR在传统的高斯过程基础上增加了诱导点机制，可以有效地缓解高斯过程的计算负担。提前1 h概率预测评价指标见表3。从表3中可以看出，与现有方法相比，所提出的具有MC dropout的STformer模型在Pinball和两个Winkler分数上表现更好，可提供更好的概率预测结果。通过对具有MC dropout的神经网络进行抽样，可以得出结论，所提出的具有MC dropout的STformer模型能很好地捕捉短期负荷预测任务的不确定性。
表3 提前1 h概率预测评价指标
Tab.3 Comparison of probabilistic prediction indexes 1 h ahead
地点算法PinballWinkler(50%)Winkler(90%) A台区QRNN0.518 54.797 810.060 9 SGPR0.412 23.795 07.306 3 本文0.370 13.285 05.715 0 B台区QRNN0.404 83.629 17.373 4 SGPR0.348 83.133 26.767 7 本文0.310 22.722 45.934 1
图6显示了A、B两个台区的两个用户1 h前负荷预测的五天预测值、真实值、95%预测区间、80%预测区间和70%预测区间。结果表明，所提出的具有MC dropout的STformer模型的预测区间对真实值具有可靠的覆盖率，并且提供了较窄的预测区间，尤其是在一些波峰和波谷的地方，这对电力系统的稳定运行至关重要。
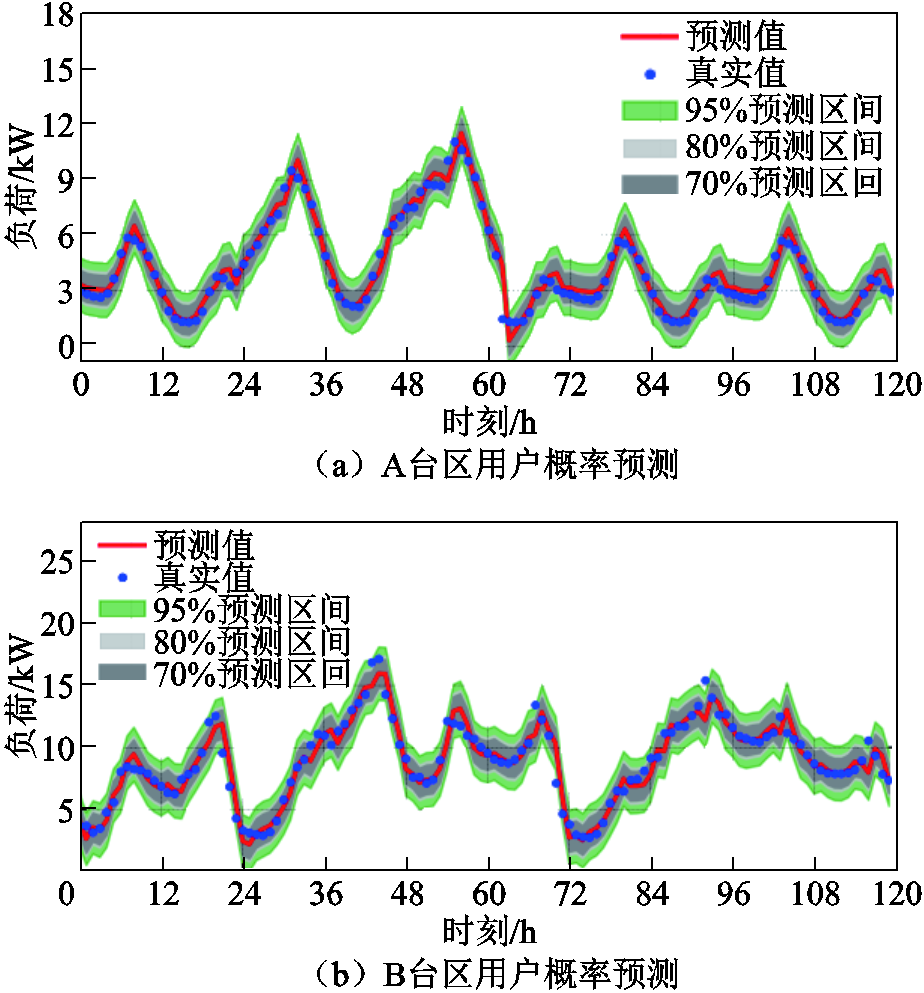
图6 提前1 h概率预测结果
Fig.6 Probabilistic forecasting results one hour ahead
为了证明本文所提出的模型在多步预测上的性能，本文进行了日前负荷预测，预测结果和概率预测评价指标分别见表4和表5。表4中的MPE为平均相对误差，即日前负荷预测MAPE的平均值；MAXE为日前负荷预测MAPE的最大值[30]。前缀Aggr代表台区总负荷的评估指标，Avgr代表单个用户负荷的评估指标。从表4和表5可以看出，本文所提出的模型在日前负荷点预测和概率预测上都取得了最好的效果。
表4 日前负荷点预测性能
Tab.4 Point forecasting performance summary one day ahead
区域算法Aggr.MPE(%)Avgr.MPE(%)Aggr.MAXE(%)Avgr.MAXE(%) A台区FNN13.2919.6820.8928.43 SVR15.2325.9524.7533.7 LR15.1423.2723.2130.68 LSTM8.2014.9113.5624.85 CNN-GRU6.5210.859.7118.57 GWN7.9112.7410.2217.42 Transformer4.419.236.8413.21 STformer3.256.215.798.73
表5 日前负荷概率预测评价指标
Tab.5 Comparison of probabilistic forecasting indexes one day ahead
区域算法PinballWinkler(50%)Winkler(90%) A台区QRNN1.442 312.065 128.327 6 SGPR1.089 68.253 919.542 4 本文0.594 25.376 29.853 2
本文还通过消融实验比较了不同模块对实验效果的影响。分别利用完整的STformer、删除空间注意力模块的STformer、删除自相关模块的STformer、删除时间序列分解模块的STformer进行了提前1 h负荷预测。随机选择A台区的三个用户进行MAE和MAPE计算，四个模型之间的比较结果如图7所示。
从图7中可以发现：①删除任何一个模块都会导致模型性能下降，说明每一个模块都有助于预测准确度和模型鲁棒性的提高；②与其他模型相比，删除空间注意力模块的STformer性能下降幅度最大，这说明空间注意力模块所提供的空间信息在模型中起重要作用，空间信息也可以降低过拟合问题的风险，从而提高模型预测的准确性；③删除自相关模块的STformer和删除序列分解模块的STformer的性能优于删除空间注意力模块的STformer，但相较于完整的STformer准确性仍然有所下降。自相关机制使得模型可以从历史数据中学到负荷行为信息，时序分解块本身也可以细化预测结果，这都对未来序列预测起到了正面作用。
图7 不同模型的效果
Fig.7 Effects of different modules
本文还验证了FFT的加入给模型推理速度带来的变化。将基于自相关的模型和基于自我注意的模型在训练阶段的内存和运行时间进行比较，结果见表6。针对内存效率，在STformer中将自相关模块替换为自注意力，并记录内存。针对运行时间，本文将自相关和自注意力机制执行103次以获得每步的执行时间。可以看出，自相关模型的傅里叶变换方法降低了计算复杂度，从而提高了模型的计算速度。主要原因是在传统自注意力机制计算中，计算相似度的操作是一个关于Q、K、V的矩阵乘法操作，计算复杂度为O(L3)。然而，FFT可以将矩阵乘法的计算复杂度降为O(Llog2L)，因此利用FFT改进后的自注意力机制，即自相关机制，可以加快模型的计算速度。
表6 模型效率分析
Tab.6 Model efficiency analysis
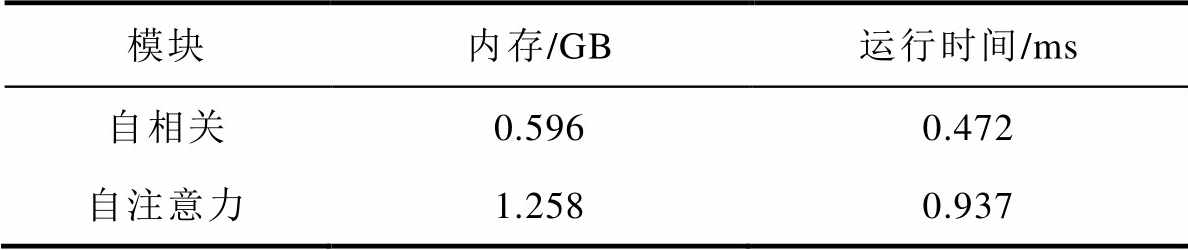
模块内存/GB运行时间/ms 自相关0.5960.472 自注意力1.2580.937
面向台区多用户的短期负荷预测问题，本文提出一种基于时空注意力机制的Transformer模型，通过在Transformer模型的编码器和解码器中嵌入时序分解模块、空间注意力模块、自相关计算模块，使其具有捕捉动态时空相关性的能力。其中，时序分解模块可以简化时间模式；空间注意力模块可以用来获取多个用户之间的动态空间相关性；自相关计算可以挖掘多个历史同时期子序列的时间相关性。本文还利用MC dropout方法将STformer拓展到台区多用户的负荷概率预测。与其他模型相比，该模型提高了海量用户负荷和总负荷的点预测精度，也提高了海量用户负荷的概率预测精度。
参考文献
[1] 张勇军, 羿应棋, 李立浧, 等. 双碳目标驱动的新型低压配电系统技术展望[J]. 电力系统自动化, 2022, 46(22): 1-12. Zhang Yongjun, Yi Yingqi, Li Licheng, et al. Prospect of new low-voltage distribution system technology driven by carbon emission peak and carbon neutrality targets[J]. Automation of Electric Power Systems, 2022, 46(22): 1-12.
[2] van der Meer D W, Munkhammar J, Widén J. Probabilistic forecasting of solar power, electricity consumption and net load: investigating the effect of seasons, aggregation and penetration on prediction intervals[J]. Solar Energy, 2018, 171: 397-413.
[3] 康重庆, 夏清, 张伯明. 电力系统负荷预测研究综述与发展方向的探讨[J]. 电力系统自动化, 2004, 28(17): 1-11. Kang Chongqing, Xia Qing, Zhang Boming. Review of power system load forecasting and its development[J]. Automation of Electric Power Systems, 2004, 28(17): 1-11.
[4] Wang Yi, Chen Qixin, Hong Tao, et al. Review of smart meter data analytics: applications, methodologies, and challenges[J]. IEEE Transactions on Smart Grid, 2019, 10(3): 3125-3148.
[5] Fekri M N, Grolinger K, Mir S. Distributed load forecasting using smart meter data: federated learning with recurrent neural networks[J]. International Journal of Electrical Power & Energy Systems, 2022, 137: 107669.
[6] 朱天怡, 艾芊, 贺兴, 等. 基于数据驱动的用电行为分析方法及应用综述[J]. 电网技术, 2020, 44(9): 3497-3507. Zhu Tianyi, Ai Qian, He Xing, et al. An overview of data-driven electricity consumption behavior analysis method and application[J]. Power System Technology, 2020, 44(9): 3497-3507.
[7] 陈锦鹏, 胡志坚, 陈纬楠, 等. 二次模态分解组合DBiLSTM-MLR的综合能源系统负荷预测[J]. 电力系统自动化, 2021, 45(13): 85-94. Chen Jinpeng, Hu Zhijian, Chen Weinan, et al. Load prediction of integrated energy system based on combination of quadratic modal decomposition and deep bidirectional long short-term memory and multiple linear regression[J]. Automation of Electric Power Systems, 2021, 45(13): 85-94.
[8] 赵登福, 庞文晨, 张讲社, 等. 基于贝叶斯理论和在线学习支持向量机的短期负荷预测[J]. 中国电机工程学报, 2005, 25(13): 8-13. Zhao Dengfu, Pang Wenchen, Zhang Jiangshe, et al. Based on Bayesian theory and online learning SVM for short term load forecasting[J]. Proceedings of the CSEE, 2005, 25(13): 8-13.
[9] Lee J, Cho Y. National-scale electricity peak load forecasting: traditional, machine learning, or hybrid model?[J]. Energy, 2022, 239: 122366.
[10] 高亚静, 孙永健, 杨文海, 等. 基于新型人体舒适度的气象敏感负荷短期预测研究[J]. 中国电机工程学报, 2017, 37(7): 1946-1955. Gao Yajing, Sun Yongjian, Yang Wenhai, et al. Weather-sensitive load’s short-term forecasting research based on new human body amenity indicator[J]. Proceedings of the CSEE, 2017, 37(7): 1946-1955.
[11] 吴潇雨, 和敬涵, 张沛, 等. 基于灰色投影改进随机森林算法的电力系统短期负荷预测[J]. 电力系统自动化, 2015, 39(12): 50-55. Wu Xiaoyu, He Jinghan, Zhang Pei, et al. Power system short-term load forecasting based on improved random forest with grey relation projection[J]. Automation of Electric Power Systems, 2015, 39(12): 50-55.
[12] 王琛, 王颖, 郑涛, 等. 基于ResNet-LSTM网络和注意力机制的综合能源系统多元负荷预测[J]. 电工技术学报, 2022, 37(7): 1789-1799. Wang Chen, Wang Ying, Zheng Tao, et al. Multi-energy load forecasting in integrated energy system based on ResNet-LSTM network and attention mechanism[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1789-1799.
[13] Tang Xianlun, Dai Yuyan, Wang Ting, et al. Short-term power load forecasting based on multi-layer bidirectional recurrent neural network[J]. IET Generation, Transmission & Distribution, 2019, 13(17): 3847-3854.
[14] 王增平, 赵兵, 纪维佳, 等. 基于GRU-NN模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(5): 53-58. Wang Zengping, Zhao Bing, Ji Weijia, et al. Short-term load forecasting method based on GRU-NN model[J]. Automation of Electric Power Systems, 2019, 43(5): 53-58.
[15] 张昆明, 蔡珊珊, 章天晗, 等. 考虑多维时域特征的行业中长期负荷预测方法[J]. 电力系统自动化, 2023, 47(20): 104-114. Zhang Kunming, Cai Shanshan, Zhang Tianhan, et al. Medium-and long-term industry load forecasting method considering multi-dimensional temporal features[J]. Automation of Electric Power Systems, 2023, 47(20): 104-114.
[16] 赵洋, 王瀚墨, 康丽, 等. 基于时间卷积网络的短期电力负荷预测[J]. 电工技术学报, 2022, 37(5): 1242-1251. Zhao Yang, Wang Hanmo, Kang Li, et al. Temporal convolution network-based short-term electrical load forecasting[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1242-1251.
[17] Jalali S M J, Ahmadian S, Khosravi A, et al. A novel evolutionary-based deep convolutional neural network model for intelligent load forecasting[J]. IEEE Transactions on Industrial Informatics, 2021, 17(12): 8243-8253.
[18] Yu Yang, Fan Jinfu, Wang Zhongjie, et al. A dynamic ensemble method for residential short-term load forecasting[J]. Alexandria Engineering Journal, 2023, 63: 75-88.
[19] Sajjad M, Ahmad Khan Z, Ullah A, et al. A novel CNN-GRU-based hybrid approach for short-term residential load forecasting[J]. IEEE Access, 2020, 8: 143759-143768.
[20] Forootani A, Rastegar M, Sami A. Short-term individual residential load forecasting using an enhanced machine learning-based approach based on a feature engineering framework: a comparative study with deep learning methods[J]. Electric Power Systems Research, 2022, 210: 108119.
[21] Jiang Lianjie, Wang Xinli, Li Wei, et al. Hybrid multitask multi-information fusion deep learning for household short-term load forecasting[J]. IEEE Transactions on Smart Grid, 2021, 12(6): 5362-5372.
[22] 董雷, 陈振平, 韩富佳, 等. 基于图卷积神经网络与K-means聚类的居民用户集群短期负荷预测[J]. 电网技术, 2023, 47(10): 4291-4301. Dong Lei, Chen Zhenping, Han Fujia, et al. Short-term load forecasting of residential user groups based on graph convolutional neural network and K-means clustering[J]. Power System Technology, 2023, 47(10): 4291-4301.
[23] 张鹏飞, 胡博, 何金松, 等. 基于时空图卷积网络的短期空间负荷预测方法[J]. 电力系统自动化, 2023, 47(13): 78-85. Zhang Pengfei, Hu Bo, He Jinsong, et al. Short-term spatial load forecasting method based on spatio-temporal graph convolutional network[J]. Automation of Electric Power Systems, 2023, 47(13): 78-85.
[24] 李云松，张智晟. 考虑综合需求响应的Trans-GNN综合能源系统多元负荷短期预测[J/OL]. 电工技术学报, 2023: 1-11. https://doi.org/10.19595/j.cnki. 1000-6753.tces.231267. Li Yunsong，Zhang Zhisheng. Trans-GNN based multi load short-term forecasting of integrated energy system considering integrated demand response [J/OL]. Transactions of China Electrotechnical Society, 2023: 1-11. https://doi.org/10.19595/j.cnki. 1000-6753.tces. 231267.
[25] Woo S, Park J, Lee J Y, et al. CBAM: convolutional block attention module[C]//Proceedings Part Ⅶof Computer Vision-ECCV 2018, Munich, Germany, 2018: 3-19.
[26] Zhu Lingxue, Laptev N. Deep and confident prediction for time series at Uber[C]//2017 IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 2017: 103-110.
[27] Gal Y, Ghahramani Z. Dropout as a Bayesian approximation: representing model uncertainty in deep learning[C]//ICML'16: Proceedings of the 33rd International Conference on International Conference onMachine Learning, New York, NY, USA, 2016: 1050-1059.
[28] Zhang Wenjie, Quan Hao, Srinivasan D. An improved quantile regression neural network for probabilistic load forecasting[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 4425-4434.
[29] Wen Honglin, Ma Jinghuan, Gu Jie, et al. Sparse variational Gaussian process based day-ahead pro-babilistic wind power forecasting[J]. IEEE Transactions on Sustainable Energy, 2022, 13(2): 957-970.
[30] 储晨阳, 秦川, 鞠平, 等. 基于优化稀疏编码的超短期负荷滚动多步预测[J]. 电工技术学报, 2021, 36(19): 4050-4059. Chu Chenyang, Qin Chuan, Ju Ping, et al. Multi-step rolling ultra-short-term load forecasting based on the optimized sparse coding[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4050-4059.
Abstract With a large number of customer-side distributed power sources entering the network from low-voltage distribution stations and the widespread use of devices such as smart meters on the customer side, a load forecasting model for multiple users is needed to facilitate point forecasting and probabilistic tasks for a large number of users efficiently and accurately. Traditional methods of customer load forecasting model the temporal characteristics of individual customers and are unable to learn the problems of spatial correlation between customers and the inability to achieve forecasts for multiple customers. Customers in the same region share the same geographic space, weather conditions, holiday information, tariff policies, and other comprehensive factors, and there is often a certain amount of spatial and temporal correlation between customers' electricity consumption behavior. If this spatial-temporal correlation can be fully explored, it will have extremely positive implications for modeling short-term customer loads. A small body of literature has already explored the initial exploration of customer load forecasting, taking spatial-temporal correlation into account. However, the existing spatio-temporal methods can only provide deterministic forecasts, not probabilistic ones. To address these issues, this paper proposes a multi-customer short-term load forecasting model for station areas. Learning spatial-temporal correlation information from historical load data can perform accurate multi-user short-term load point forecasts and probabilistic forecasts for station areas.
Firstly, three modules are embedded for each encoder and decoder by improving the standard Transformer self-attention mechanism: sequence decomposition module, autocorrelation calculation module, and spatial attention module to effectively extract the dynamic spatio-temporal dependencies among highly volatile residential users. Among them, the sequence decomposition module can decompose highly volatile subscriber load curves into relatively smooth multiple sub-series, which helps to extract better the time dependence and period factor of load curves; the autocorrelation calculation is an improved attention mechanism that can mine the time dependence of multiple historical contemporaneous sub-series; and the spatial attention mechanism can extract the dynamic spatial support among multiple users in a station area. The STformer model is then extended to the field of probabilistic forecasting using a Monte Carlo stochastic deactivation method (MC dropout). This method does not require additional modifications to STformer but allows STformer to output both point prediction and probabilistic prediction results. Finally, the STformer model with MC dropout is used to forecast the station customer load, and both point and probabilistic forecasts are output.
In this paper, the model's validity is verified using one-hour-ahead load forecasting and day-ahead load forecasting using accurate station customer load data from a province in the southeast. The proposed STformer model has a MAPE of 4.44% for each user and 2.21% for the total load in station area A. The probabilistic forecast evaluation index pinball is 0.370 1; the average relative error MPE for each user and 3.25% for the total load in station area A is 6.21%. is 3.25%, and the probabilistic forecast assessment index pinball is 0.594 2. This paper also compares the effects of different modules on the experimental results through ablation experiments. This paper also verifies the change in model inference speed brought about by the addition of FFT, comparing the running memory and time of the autocorrelation-based model with that of the self-attentive-based model during the training phase.
The following conclusions can be drawn from the simulation analysis: (1) Compared with other baselines, the STformer model proposed in this paper extracts the temporal variation pattern of users through the temporal attention mechanism and the spatial dependency between multiple users through the spatial attention mechanism, which ultimately achieves the best prediction results in all scenarios. (2) Each module of STformer contributes to the improvement of prediction accuracy and model robustness. The spatial attention module has the greatest impact on the prediction accuracy of STformer, and the Fourier transform method of the autocorrelated model reduces the computational complexity and thus accelerates the computational speed of the model. (3) The prediction intervals of the proposed STformer model with MC dropout have reliable coverage of the true values and provide narrower prediction intervals, especially at some peaks and troughs, which are critical for the temperature operation of power systems.
keywords：Multi-customers load forecasting, spatial-temporal correlation, Transformer model
DOI:10.19595/j.cnki.1000-6753.tces.230110
中图分类号：TM743
国家电网公司总部科技项目“基于智能量测的低压高渗透率分布式光伏接入可测可控技术研究”（5700-202255222A-1-1-ZN）资助。
收稿日期 2023-02-01
改稿日期 2023-07-02
赵洪山 男，1965年生，教授，博士生导师，研究方向为电力系统动态分析与控制、电力负荷预测等。E-mail：zhaohshcn@126.com
吴雨晨 女，1998年生，硕士研究生，研究方向负荷预测和人工智能技术。E-mail：wyc@ncepu.edu.cn（通信作者）
（编辑 李 冰）