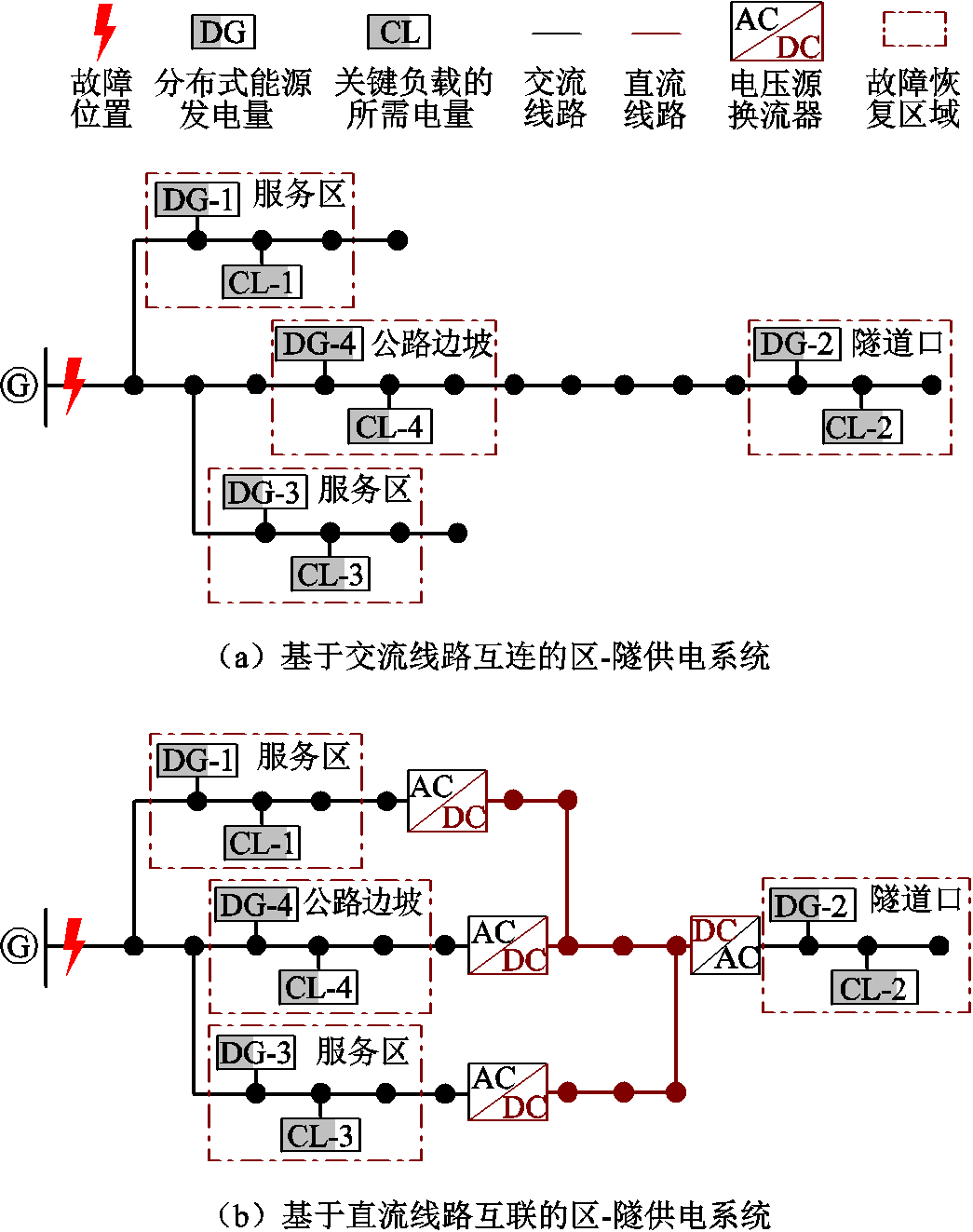
图1 不同拓扑结构的故障恢复区域
Fig.1 Fault recovery area with different topologies
摘要 在“双碳”目标下,以服务区光伏车棚、光伏隧道为代表的能源交通融合供电场景逐步普及,这使得形态开放且布局分散的区-隧供电系统在面临极端灾害或人为攻击时更为脆弱。为此,该文提出一种基于直流线路互联的区-隧供电系统弹性恢复策略。根据灾害前对直流线路的改造与韧性加固计划,首先,提出了基于直流线路被优先遍历的可行拓扑搜索策略,用于保障所提系统在极端灾害后的有效互联;其次,基于对故障负荷重要级权重的多层级分类策略,该文先后以重要负荷恢复量最大化和系统额外损耗最小化为目标构建了故障恢复目标函数,共同保证极端灾害发生后系统基于稀缺分布式能源的最大弹性恢复;再次,基于传统二阶锥松弛方法可能挣脱原始约束的缺陷,提出通过约束额外损耗中流经电流分量实现对混合整数二阶锥规划问题的收敛,确保所提模型在不同初始条件下的稳定适用;最后,通过涵盖区-隧供电系统的改进IEEE 123节点配电网进行仿真,验证了所提策略的有效性。
关键词:区-隧供电系统 直流线路互联 深度优先遍历 弹性恢复
随着我国经济社会的发展,道路交通的能源消耗规模持续扩大[1]。为契合能源转型目标,充分开发公路交通运输系统的服务区、沿线边坡或隧道口隔离带等区域可用空间资源,通过安装光伏发电组件,以构建清洁、绿色和高弹性的能源交通融合供电系统成为未来发展趋势[2]。随着能源交通融合供电系统的逐步普及和交通负荷的多样化需求增长,公路交通系统的供用电特性也在经历从传统大电网支撑交流负荷向分布式能源支撑交/直流负荷的形态转变[3]。因此,任意能源交通融合供电系统都可以被视为交/直流混合微电网。
考虑到单个能源交通融合供电系统的出力局限性和可再生能源的发电间歇性,联合成对服务区,以及双洞隧道隔离带等多个能源交通融合供电系统分布式能源供电能力的区-隧供电(District-Tunnel Power Supply, DTPS)系统,不仅能够实现多区域间的源荷互济,而且能够有效提升供电可靠性。进一步,联合多个能源交通融合供电系统分布式能源供电能力的DTPS系统也可以被视为交/直流混合微电网集群。然而,与交/直流混合微电网集群不同的是,所提DTPS系统表现出其独有的特征[4-6],即在分布上,呈现单区域内源荷聚集、多区域间布局分散;在属性上,呈现单区域内负荷权重基本一致、多区域间负荷权重差异明显;在性能上,呈现单区域内可用源出力有限、多区域间可用源协同脆弱等。此外,DTPS系统还面临由交通系统故障与能源系统故障所导致的双威胁,以及由分布式能源发电随机与交通负荷用电随机所导致的双波动。随着近年来极端自然灾害或网络攻击等高冲击-小概率事件所导致大停电事故的频繁发生,如何提升以区-隧为代表的交通能源供电系统的弹性恢复性能成为亟须解决的问题[7]。
当前,针对联合多个能源交通融合供电系统分布式能源供电能力的DTPS系统研究尚不完善,相关研究成果也多集中于对单一交通能源供电区域的优化规划[8-9]、优化调度[10-12]等。在针对能源交通融合供电系统的弹性恢复方面,文献[13]针对单一自给自足的能源交通融合供电系统,提出一种旨在增强公路运输能源系统应对持续冻雨灾害极端天气灾害的两阶段弹性增强方法,该方法将储能电池预先充电以支持系统运行,提出减少甩负荷的应急响应以实现系统的弹性恢复。文献[14]针对能源和交通一体化系统,提出一种考虑综合能源系统和输电网的灾后弹性恢复策略,该策略在第一阶段通过配置天然气和燃气轮机,进而采用单一能量流构造树约束以提升负载恢复量,并在第二阶段通过分配移动储能的最优路径来弥补电力需求的短缺。此外,文献[15]则针对电-气-热-交通的城市能源系统,提出一种协同储能车紧急供电、维修人员调度、拓扑重构的协同优化模型。尽管上述研究均为实现能源交通融合供电系统在极端灾害下的弹性恢复给出了解决方案,然而其研究思路均集中于实现单个区域内可用资源的最大程度利用或多源之间的路径规划,且解决方案仍需要在满足辐射状约束下实施,这使得系统在任一线路损坏时的可行拓扑缩减,进而限制弹性恢复性能。
此外,在针对多个供电区域互联的弹性恢复方面,现有研究试图通过灵活控制可用区域的边界范围以提升孤岛微电网的供电能力及负载的恢复能力[16],或通过控制自动开关设备的开断状态来动态构建系统可用拓扑[17],或通过控制智能开关状态以动态调整微电网的连接边界[18]。然而,上述解决方案均需要满足配电系统严格的辐射状约束,且考虑极端灾害下DTPS系统各区域可能出现的故障电流增加或相位差增加,这可能使基于开关设备互联的孤岛微电网电能质量降低。相比之下,直流线路具有更高的线路传输能力、更小的压降和线路功率损耗[19-20],并可在环路模式下运行,而不考虑频率和电压相位的影响等优势[21],因此针对传统交流配电网为避免环网运行而所需遵循的辐射状约束限制,可以通过额外增加一条直流链路来避免[22-23]。进一步,若所提DTPS系统能够基于直流线路实现多区域分散能源交通融合系统的有效互联,并避免交流配电网的辐射状约束,将能够为提升系统的弹性恢复性能提供新思路。然而,无论是现有针对交通能源系统的弹性恢复策略[13-15],还是现有针对交/直流混合微电网的弹性恢复策略[24-26],均没有考虑基于直流线路互联的恢复策略,而传统适用于交流配电网的恢复方案被继续使用,必将限制所提系统的弹性恢复潜力。
综上所述,若要提升DTPS系统在应对极端灾害事件下的弹性恢复能力,主要还存在两个挑战:
(1)松弛辐射状约束的可行拓扑生成。尽管极端灾害后系统可用基础设施大面积受损,然而在现有包含直流线路的混合配电网中,其故障恢复仍是在满足辐射状约束条件下实现的,这将限制极端灾害下系统的可行恢复方案。因此,如何充分挖掘自身架构或功能实现对可行拓扑的扩展是其一大挑战。
(2)实现弹性恢复的能源系统调度。考虑极端灾害后系统分布式电源可用出力被缩减,现有基于故障负荷节点权重系数的功率恢复策略均没有考虑极端灾害下相同权重系统故障负荷不能被完全恢复的情景,进而限制系统弹性指数。因此,如何利用自身分布式电源出力实现对重要故障负荷的优先恢复是其另一大挑战。
基于上述研究存在的不足,本文提出了基于直流线路互联的DTPS系统弹性恢复策略。首先,提出直流线路被优先遍历的可行拓扑搜索策略,该策略基于对不同类型分布式电源至故障负荷节点的可行路径搜索,有效避免了辐射状约束对系统可行解的限制,从而获得系统所有可行拓扑;其次,建立用于DTPS系统弹性提升的故障恢复目标函数,该目标函数在基于权重因子完成对所有故障负荷功率分配的基础上,以系统额外损耗最小为目标保证了稀缺分布式电源的利用效率;再次,以流经电流最小为目标对混合整数二阶锥规划进行二次收敛,填补了传统二阶锥松弛规划最优解脱离非线性约束的缺陷;最后,涵盖改进IEEE 123节点的配电系统验证了所提恢复策略的有效性。
本文所提DTPS系统拓扑结构如图1所示。图1中,“区”:高速公路服务区,作为提供交通服务的重要能源节点,其供电来源严重依赖大电网。在交通能源融合背景下,服务区停车场、停车棚、建筑屋顶等空间资源能够为分布式光伏发电系统的开发提供场地,以替代或减少大电网的出力。
“隧”:高速公路隧道,作为维持交通安全的关键能源节点,在交通中占据着重要供电类型地位。在交通能源融合背景下,双洞隧道口间隔、公路边坡、匝道等空间资源能够为分布式光伏发电、风力发电的开发提供布局场地。

图1 不同拓扑结构的故障恢复区域
Fig.1 Fault recovery area with different topologies
“DTPS系统”:联合成对服务区及双洞隧道隔离带等公路交通多区域分布式能源供电能力的供电系统,以高速公路服务区与隧道为主要场景,以公路交通用电设备为主要负荷,并同时包含交流和直流供电类型。
在极端灾害发生后,上层电网通常会失去供电能力。在如图1a所示基于交流线路的恢复拓扑中,基于服务区及隧道等区域分布式电源的分布特征可形成四个用于故障负荷恢复的孤岛微电网。然而受限于交流配电网的辐射状约束限制,各孤岛微电网之间不存在可用的恢复路径。因此在极端灾害发生后,尽管隧道口间隔和公路边坡的分布式能源发电量大于关键负载的所需电量,但其剩余发电量却不能被用于其他孤岛微电网的故障负荷恢复。由此可知,基于辐射状约束的故障恢复策略不仅会造成稀缺分布式资源的浪费和关键负荷的恢复指数,而且会导致系统的运行可靠性普遍较低。
一个有效的解决方案是将地理上相邻的孤岛微电网整合并形成联合多微电网的供电系统,从而实现多供电区域之间的能量调度与电力交互。此外,由于直流线路可以在环路模式下运行,因此通过额外增加直流线路能够避免传统交流配电网在辐射状约束拓扑下运行的限制。对此,如图1b给出了基于直流线路互联的DTPS系统拓扑结构。
基于该结构,直流线路能够为所有独立的孤岛微电网提供互联通道,并利用电压源转换器(Voltage Source Converter, VSC)实现DTPS系统内多供电微电网的协同,进而使得系统内分布式能源发电量可以被整合以共同承担系统内故障负荷的恢复。尽管极端灾害后稀缺分布式能源的发电量可能仍不足以承担所有故障负荷恢复所需,但基于结构的恢复策略却能通过有效协同各孤岛微电网的供电能力,从而避免稀缺分布式能源的浪费。
需要说明的是,在用于互联所有孤岛微电网的VSC设备中,应确保至少有一个VSC设备工作在恒定的直流电压控制模式,以确保DTPS系统在失去大电网供电后仍能稳定运行;而剩余VSC设备工作在PQ控制模式,以确保DTPS系统内各孤岛微电网可以根据其盈余状态而灵活调整电力传输方向。
极端灾害事件发生后,系统可被利用的拓扑结构通常被大规模破坏。对于采用辐射状拓扑运行的DTPS系统,其恢复策略需要在满足严格辐射状约束限制下实施。基于断线解环思想的辐射状约束模型[27]为
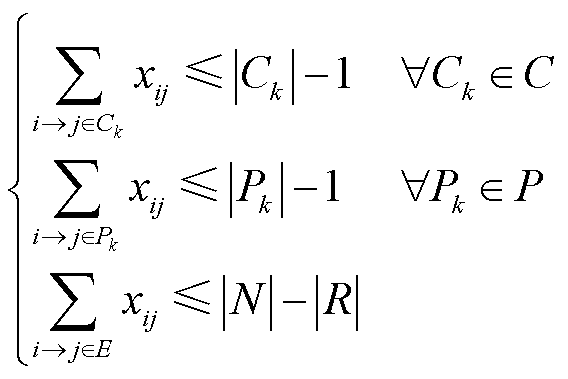 (1)
(1)
式中,i、j分别为系统中的节点;xij为无方向的0-1决策变量,若节点i和j相连,则xij=1,否则为0;Ck、Pk分别为图中任一环、根节点之间的任一路径;E为所有可能线路构成的边集集合;C、P、N、R分别为网络中所有供电环路构成的集合、根节点之间所有路径构成的集合、所有节点的集合和所有根节点构成的集合。
基于深度优先遍历策略,极端灾害发生后DTPS系统基于传统辐射状约束和基于直流线路互联松弛下的可行解空间如图2所示。在各孤岛微电网基于交流线路互联的辐射状拓扑约束条件下,各孤岛微电网内的可用分布式电源仅可恢复该孤岛内的故障负荷。此外,由于各孤岛微电网间无可用互联路径,因此多孤岛间的可用分布式电源因无法协同而使得本就稀缺的可用分布式电源无法得到充分利用,造成系统弹性恢复能力较低。
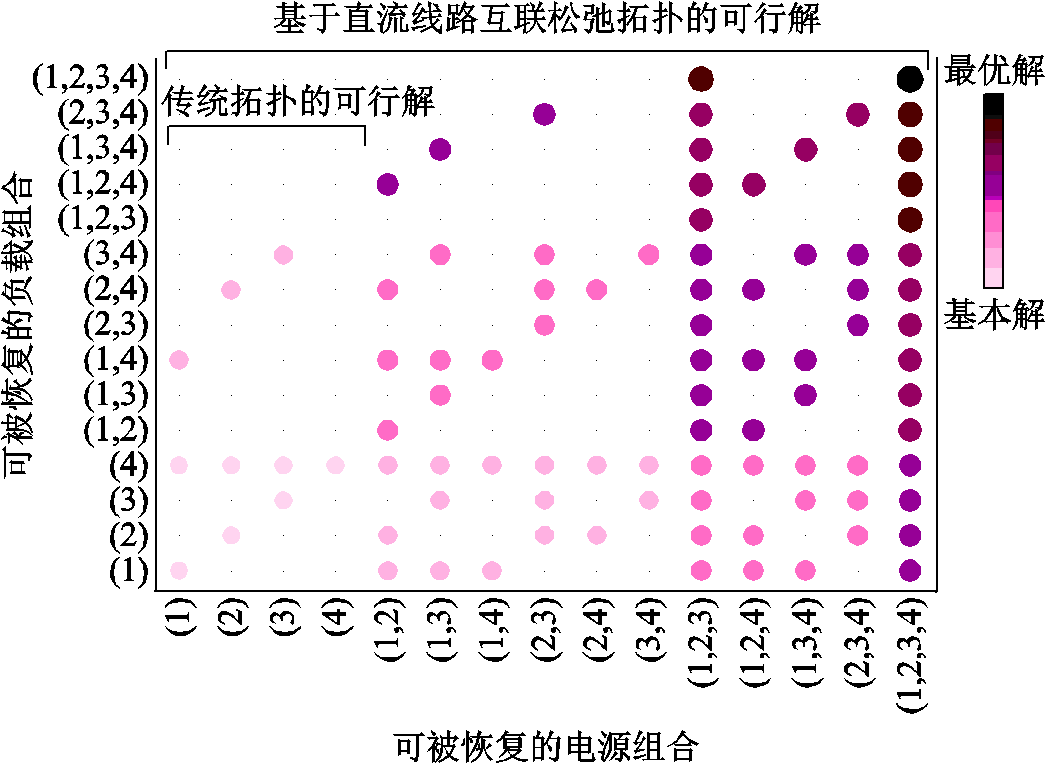
图2 不同拓扑结构的可行解空间
Fig.2 Feasible solutions space for different topologies
与基于交流线路互联不同,由于直流线路可以在闭环模式下运行,因此额外增加一条直流链路可以避免传统交流系统所需遵循的辐射状约束限制,并使系统可行拓扑结构数量呈指数增长。进一步,由于各孤岛微电网之间的互联被保证,因此极端灾害发生后系统可用分布式能源可以在多孤岛微电网之间交互,并使得故障负荷可以被最大程度恢复。综上所述,基于直流线路互联的拓扑恢复策略不仅能够减少系统稀缺可用分布式能源的浪费,而且能够最大限度地提升系统的弹性恢复性能。
为充分发挥所提DTPS系统基于直流线路的物理互联和能量互补优势,本文提出了基于直流线路被优先遍历的可行拓扑搜索策略。该策略基于对分布式能源所并入线路类型的差异,并利用深度优先遍历法分别给出了不同类型分布式能源到故障负荷节点的可行路径搜索策略。在此搜索过程中,不同类型分布式能源到故障负荷节点的可行拓扑结构可以被确定。
具体搜索过程可以描述为:使用具有n个节点的无向图G=〈V, E〉表示DTPS系统,并确定极端灾害后的可用电源点集和故障负荷点集,用非空有穷集合V表示,然后以电源点集中的元素为起点,以负荷点集中的元素为目标点,并从电源点集中任一元素开始向相邻点移动,如果达到目标点集中任一元素,则返回上一个十字路口并选择另一移动方向,并在到达目标点集中任一元素后返回,重复该过程,直至遍历所有可行路径,用边集E表示。
根据分布式电源所并入DTPS系统的线路类型差异,本文将包含所有分布式电源点的集合VSource分为三类,即接入直流线路的分布式电源点集合VDC Source、接入交流线路但有可连直流线路的分布式电源点集合VAC Source-1、接入交流线路且无可连直流线路的分布式电源点集合VAC Source-2,因此有
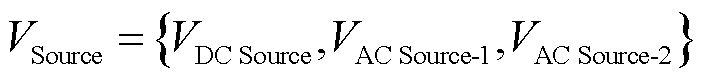 (2)
(2)
1.3.1 以VDC Source为起点的可行拓扑搜索
当以接入直流线路的所有分布式电源点集合VDC Source中的任一节点为起点,故障负荷节点集合VLoad中的任一节点为目标点,其节点集合和电气距离矩阵分别为
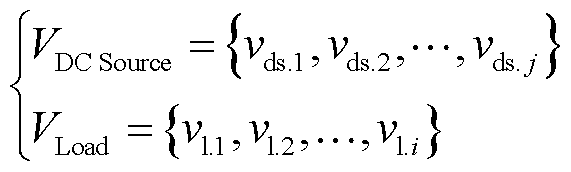 (3)
(3)
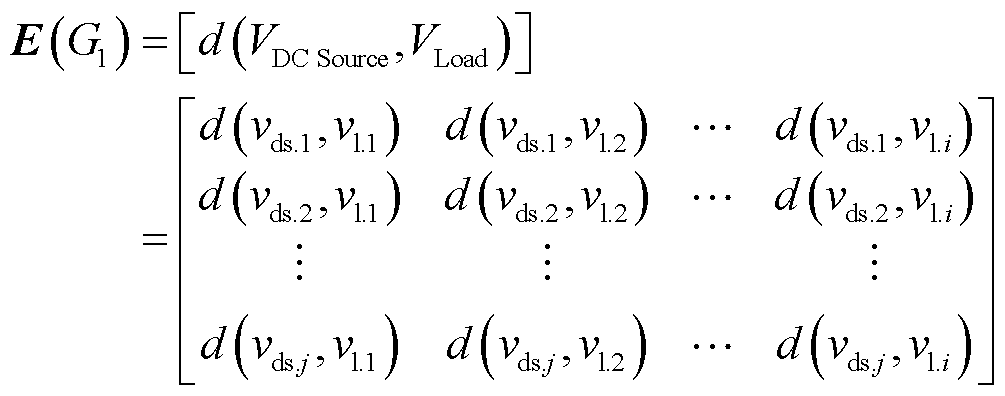 (4)
(4)
式中,vds.1, vds.2,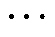 , vds.j为集合VDC Source中的所有分布式电源节点;vl.1, vl.2,
, vds.j为集合VDC Source中的所有分布式电源节点;vl.1, vl.2,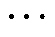 , vl.i为集合VLoad中的所有故障负荷节点;d(vds.j, vl.i)为集合VDC Source中任一节点j到集合VLoad中任一节点i的电气距离。
, vl.i为集合VLoad中的所有故障负荷节点;d(vds.j, vl.i)为集合VDC Source中任一节点j到集合VLoad中任一节点i的电气距离。
1.3.2 以VAC Source-1为起点的可行拓扑搜索
在分布式电源接入交流线路但有可连直流线路情况下,直流线路能够为多孤岛微电网的协同互济提供无约束、小损耗的弹性通道。因此在极端灾害发生后,基于直流线路互联松弛能够实现多孤岛分布式能源的充分利用。定义其搜索策略为:优先确定“VAC Source-1至直流线路”的最短电气距离,再确定“直流线路至VLoad”的最短电气距离,从而完成对可行拓扑的搜索。考虑到DTPS系统的负荷节点较多且供电路径更长,持续的直流线路搜索不仅消耗搜索时间,而且会限制系统恢复性能。
对此,本文提出将“VAC Source-1中任一分布式电源节点至直流线路”的最短电气距离路径集合定义为与集合VAC Source-1中分布式电源节点一一对应的关键电源点集合VAC Point。在此基础上,基于集合VAC Source-1的故障恢复策略可通过集合VAC Point完成,即搜索“集合VAC Point中所有节点至集合VLoad”的最短电气距离路径进而确定集合VAC Source-1经直流线路到达集合VLoad的可行拓扑。
基于上述讨论,以关键电源点集合VAC Point中任一节点为起点,故障负荷节点集合VLoad中任一节点为目标点的节点集合和电气距离矩阵分别为
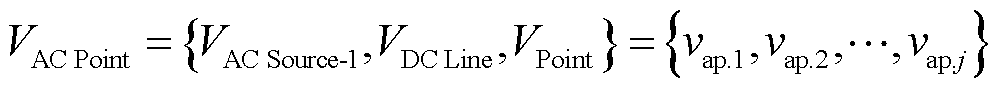 (5)
(5)
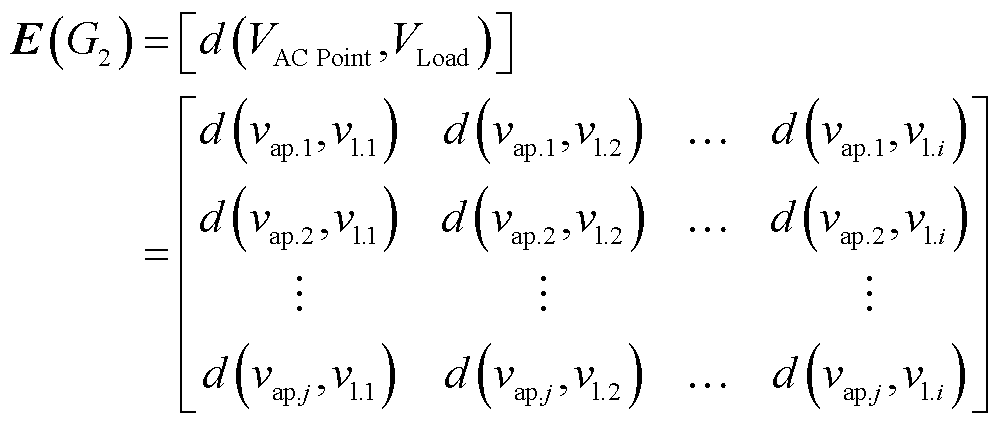 (6)
(6)
式中,vap.1, vap.2,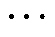 , vap.j为集合VAC Point中的所有关键电源节点;VPoint为接入交流线路分布式电源与直流线路的连接点;d(vap.j, vl.i)为集合VAC Point中任一节点j到集合VLoad中任一节点i的电气距离。
, vap.j为集合VAC Point中的所有关键电源节点;VPoint为接入交流线路分布式电源与直流线路的连接点;d(vap.j, vl.i)为集合VAC Point中任一节点j到集合VLoad中任一节点i的电气距离。
根据最短路径原理,从式(6)中取电气距离最短的路径,即可得到以直流线路为核心,连接集合VAC Source-1中所有分布式电源节点至集合VLoad中所有故障负荷节点的可行拓扑。
1.3.3 以VAC Source-2为起点的可行拓扑搜索
然而在实际供电系统中,并不能保证所有接入交流线路的分布式电源都能搜索到与之相连的直流线路。因此,需要建立以接入交流线路且无可连直流线路的分布式电源集合VAC Source-2中任一节点为起点,故障负荷集合VLoad中任一节点为目标点的节点集合和电气距离矩阵,分别为
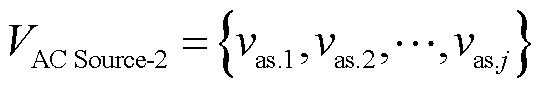 (7)
(7)
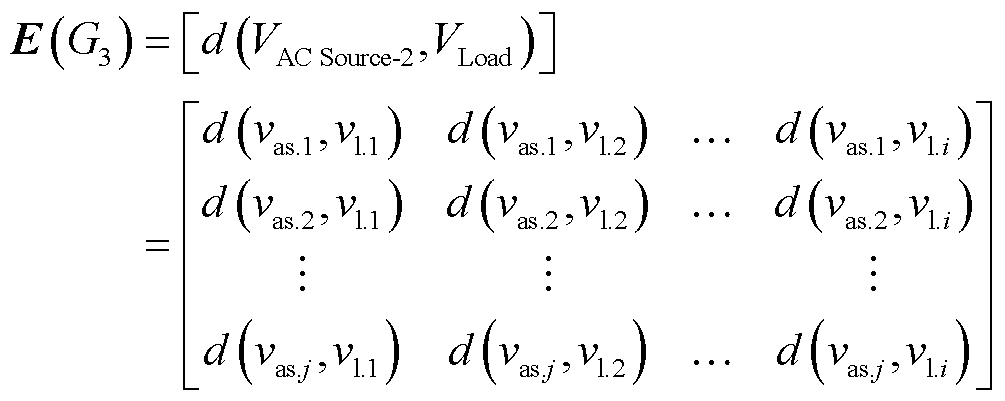 (8)
(8)
式中,vas.1, vas.2,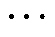 , vas.j为集合VAC Source-2中的所有分布式电源节点;d(vas.j, vl.i)为集合VAC Source-2中任一节点j到集合VLoad中的任一节点i的电气距离。
, vas.j为集合VAC Source-2中的所有分布式电源节点;d(vas.j, vl.i)为集合VAC Source-2中任一节点j到集合VLoad中的任一节点i的电气距离。
根据上述对不同类型分布式电源到故障负荷节点的可行路径搜索策略,可以搜索出多个可行拓扑。然而,可行拓扑的存在只能说明分布式电源节点到故障负荷节点的物理连接。进一步,以第2节所提基于多层级故障负荷重要级分类的弹性恢复策略,并在满足潮流运行约束验证的基础上,即可筛选出可行的恢复拓扑。最后以系统拓扑损耗最小为目标,通过对比所有可行恢复拓扑的弹性恢复指数即可确定用于DTPS系统的最优恢复拓扑。
为确保所提DTPS系统在极端灾害发生后能够利用稀缺性可调度能源实现对重要负荷的最大程度持续供电。本文先后以重要负荷恢复量 最大化和直流线路接入所导致系统额外损耗
最大化和直流线路接入所导致系统额外损耗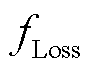 最小化为目标,可建立弹性恢复目标函数为
最小化为目标,可建立弹性恢复目标函数为
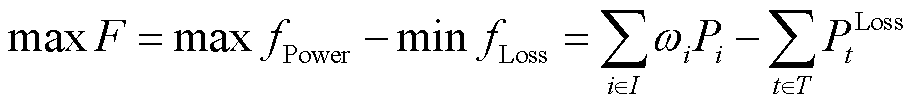 (9)
(9)
式中,F为系统的恢复目标;I为所有故障负荷i的集合;ωi为故障负荷i的权重系数;Pi为故障负荷i的实际恢复功率;PLoss t为t时刻系统的损耗功率。
2.1.1 多层级的负荷恢复策略
为限制极端自然灾害下分布式电源对重要负荷的优先供电,本文对上述一级、二级和三级负荷的重要级权重关系规定为
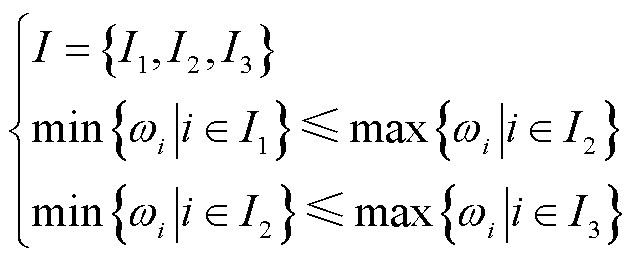 (10)
(10)
式中,I1、I2和I3分别为一级、二级和三级故障负荷节点集合。
考虑到极端事件发生后,系统本就稀缺的可调度能源很难保证同等优先级负荷的完全恢复。因此,为使所提系统目标函数的弹性指数最大化,本文在同等权重级别负荷的基础上,提出增加价值因子系数,即负荷完全恢复实际所需功率越高则其价值因子系数越高,反之越低。
假设极端故障发生后,DTPS系统中稀缺可被调度能源仅能满足集合I1中故障负荷节点的完全恢复,集合I2中故障负荷节点的部分恢复,而集合I3中的故障负荷节点均无法恢复。在不能被完全恢复的集合I2中,本文引入负荷价值因子对该集合内所有故障负荷节点按降序再次排列。假设剩余可调度能源仅能满足集合I2中第i21~i2m-1故障负荷节点的完全恢复,第i2m个故障负荷节点的部分恢复,而剩余第i2m+1~i2n故障负荷节点均无法恢复。此时,集合I1中所有故障负荷节点以及集合I2中第i21~i2m-1故障负荷节点的实际恢复功率均为该节点的需求功率;第i2m个故障负荷节点的实际恢复功率为系统剩余可调度功率;而集合I2中第i2m+1~i2n故障负荷节点以及集合I3中所有故障负荷节点的实际恢复功率均为0。基于上述分析,可得所有故障负荷节点的实际恢复功率如图3所示。
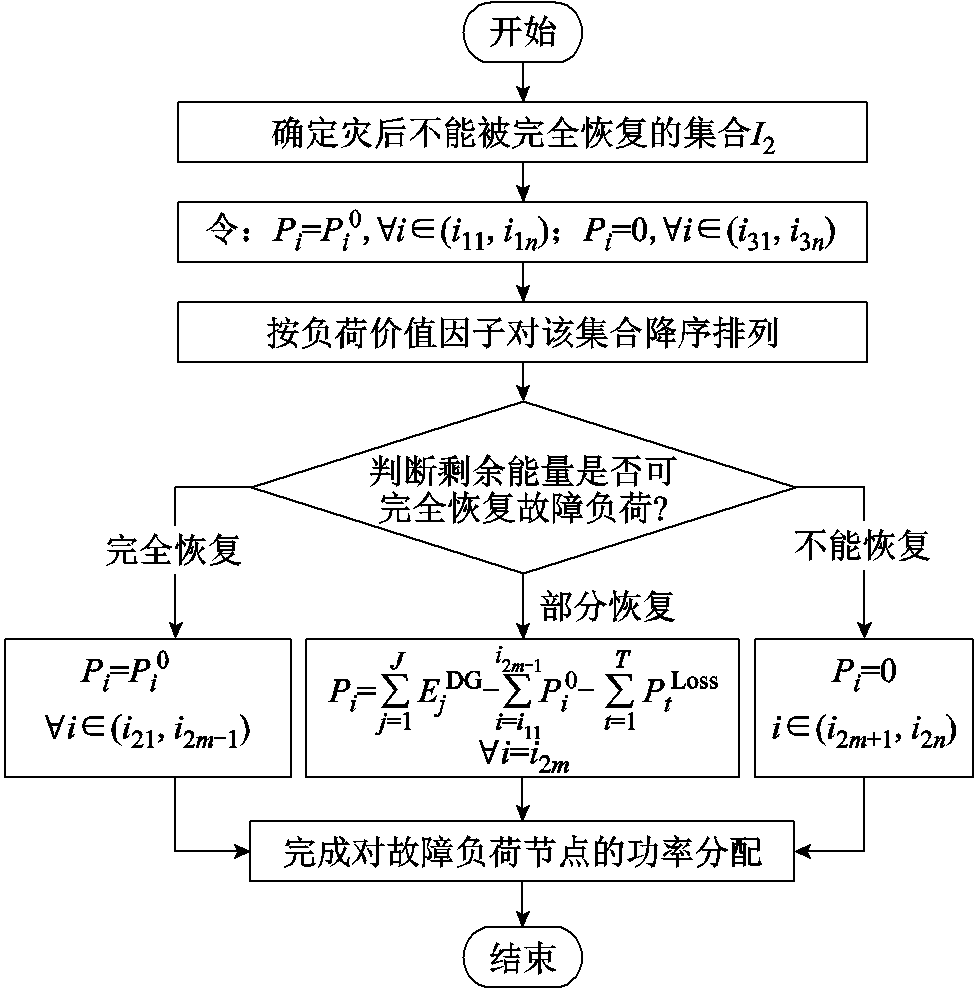
图3 多层级故障负荷的功率分配策略
Fig.3 Power recovery strategy for multi-level fault load
进一步,本文所提以重要负荷恢复量最大化的弹性恢复目标函数可以被优化为
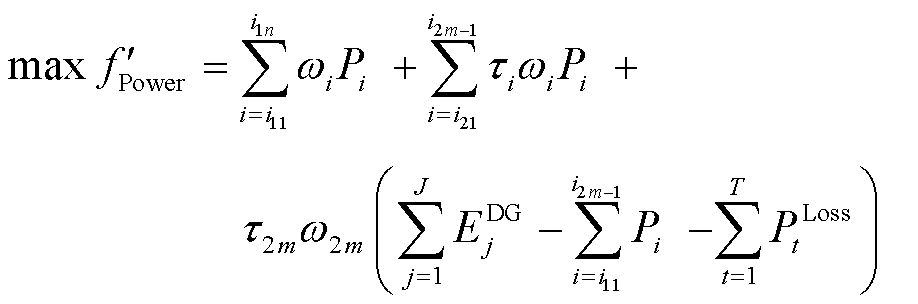 (11)
(11)
式中,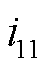 和
和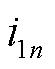 分别为集合
分别为集合 中权重级别最高和最低的故障负荷点;
中权重级别最高和最低的故障负荷点;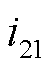 为
为 中权重级别最高的故障负荷点;
中权重级别最高的故障负荷点; 为
为 中被部分恢复的负荷节点;τi为I2集合中所有故障负荷节点的价值因子系数,本文定义该系数在[ωi, (ωi+1-ωi)/2]范围内等差取值;
中被部分恢复的负荷节点;τi为I2集合中所有故障负荷节点的价值因子系数,本文定义该系数在[ωi, (ωi+1-ωi)/2]范围内等差取值;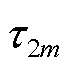 为第
为第 个负荷的价值因子系数;ω2m为故障负荷
个负荷的价值因子系数;ω2m为故障负荷 的权重系数;EDG j为系统电源节点j的分布式能源总出力。
的权重系数;EDG j为系统电源节点j的分布式能源总出力。
2.1.2系统额外损耗最小化
为保证DTPS系统弹性指数F的最大化,本文再次以所提系统额外损耗最小为目标补充目标函数。在本文中,考虑所提系统的额外损耗包括线路自身的损耗和流经VSC额外增加的损耗,其目标函数为
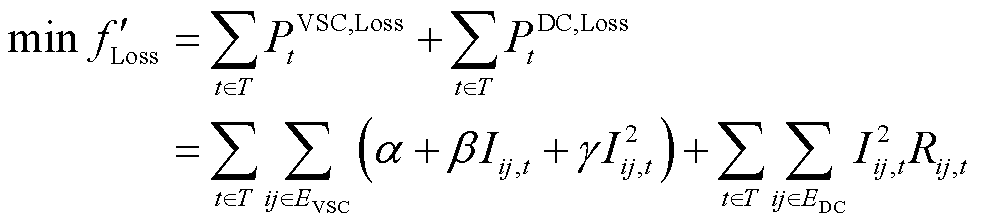 (12)
(12)
式中,PVSC,Loss t和PDC,Loss t分别为t时刻流经VSC设备和直流线路的功率损耗值;α、β和γ分别为与VSC设备容量SN及直流线路电压Vdc相关的损耗系数,α=0.11SN,β=0.003Vdc,γ=0.003 V2 dc/SN;Iij,t为t时刻支路电流幅值;Rij,t为t时刻的直流线路电阻。
在包含分布式电源的DTPS系统中,各区域交流支路和直流支路、VSC换流站的潮流约束均可表示为Distflow潮流方程形式,这在诸多恢复策略中已经被广泛讨论,本文不再赘述。在本文所提极端灾害的负载策略中,要求所有稀缺性分布式可用能源都能够被充分利用直至恢复过程完成,因此所有分布式电源的出力被约束。
对于柴油发电机,其出力约束是确保在故障发生s个小时后发电机燃料储备可以被完全利用,即
 (13)
(13)
式中,EDG i,t为i节点柴油发电机在t时刻的可用出力;EDG,max i和EDG,min i分别为i节点柴油发电机的最大和最小可用出力。
对于风机发电系统,出力约束是保持发电机运行在最佳叶尖速比,确保系统工作在最大功率输出状态,可表示为
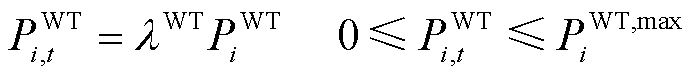 (14)
(14)
式中,PWT i,t为i节点风力发电机组在t时刻的输出功率;PWT,max i为i节点风力发电机组的最大输出功率;λWT为与风速相关的功率输出值。
对于光伏系统,出力约束是保持光伏系统最高电压和电流值,确保系统工作在最大功率输出状态,可表示为
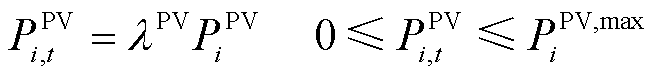 (15)
(15)
式中,PPV i,t为i节点光伏系统在t时刻的输出功率;PPV,max i为i节点光伏系统的最大输出功率;λPV为与光照辐射量相关的功率输出值。
对于储能系统,其出力约束是确保故障后s个小时内储能设备的能量值被充分利用,可表示为
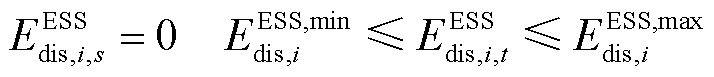 (16)
(16)
式中,EESSdis,i,s为i节点储能在s个小时后能够释放的能量;EESSdis,i,t为i节点储能在t时刻的释放能量;EESS,maxdis,i和EESS,mindis,i分别为i节点储能释放功率的上、下限。
此外,交流支路、直流支路及VSC换流站的潮流约束分别为
 (17)
(17)
式中,UAC,i,t、UDC,i,t、UVSC,i,t分别为节点i处的交流、直流和流经VSC的电压值;IAC,i,t、IDC,i,t、IVSC,ij,t分别为节点i处的交流、直流和VSC的电流值;PAC,ij,t、PDC,ij,t、PVSC,ij,t及QAC,ij,t、QDC,ij,t、QVSC,ij,t分别为t时刻以节点i为起点、节点j为终点的交流支路、直流支路和流经VSC的有功功率和无功功率。
由于上述目标函数中有关于分布式电源的供电恢复策略和系统潮流约束在极坐标下均呈现非线性和非凸性。为此,引入中间变量将上述问题转换为混合整数二阶锥规划(Mixed Integer Second-Order Cone Programming, MISOCP)问题能够获得最优解,即将复杂的优化模型转换为锥模型,从而将最优解的搜索空间限制在有限的凸锥范围内。基于交流、直流和VSC约束条件的松弛目标为
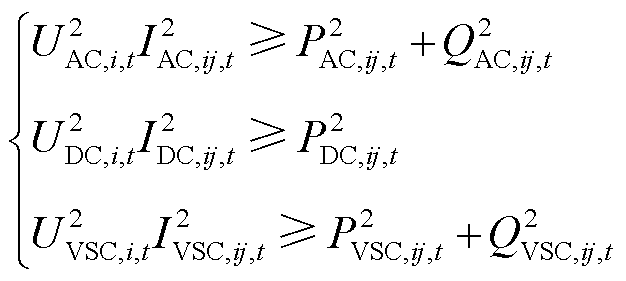 (18)
(18)
基于MISOCP的目标函数松弛过程极大程度地扩展了可行解的范围,然而这也可能导致部分解脱离原始约束条件的限制。因此如果能够反过来对目标函数进行收敛,则可以保证系统最优解满足原始非线性限制。为将式(18)中所示交流、直流和VSC松弛目标方程的误差尽可能趋于零,可利用本文所提网络损耗最小化的目标函数对其进行反向收敛。由于网络损耗是由流经线路电流所决定,因此当电流达到最小值时,使用MISOCP即可保证所得解为原始目标函数的最优解。
根据所提基于直流线路互联的DTPS系统弹性提升策略,在综合分布式能源所并入线路类型的差异基础上,基于深度优先遍历法对不同类型分布式能源到故障负荷节点的可行路径进行搜索,并在搜索过程中,获得连接不同类型分布式能源到故障负荷节点的可行拓扑结构。进一步,基于搜索到的多个可行拓扑,以基于多层级故障负荷重要级分类的弹性恢复策略为目标,并在满足潮流运行约束验证的基础上,筛选出可行恢复拓扑。最后,以系统拓扑损耗最小为目标完成对所有可行恢复拓扑的对比,确定最优恢复拓扑。其流程如图4所示。
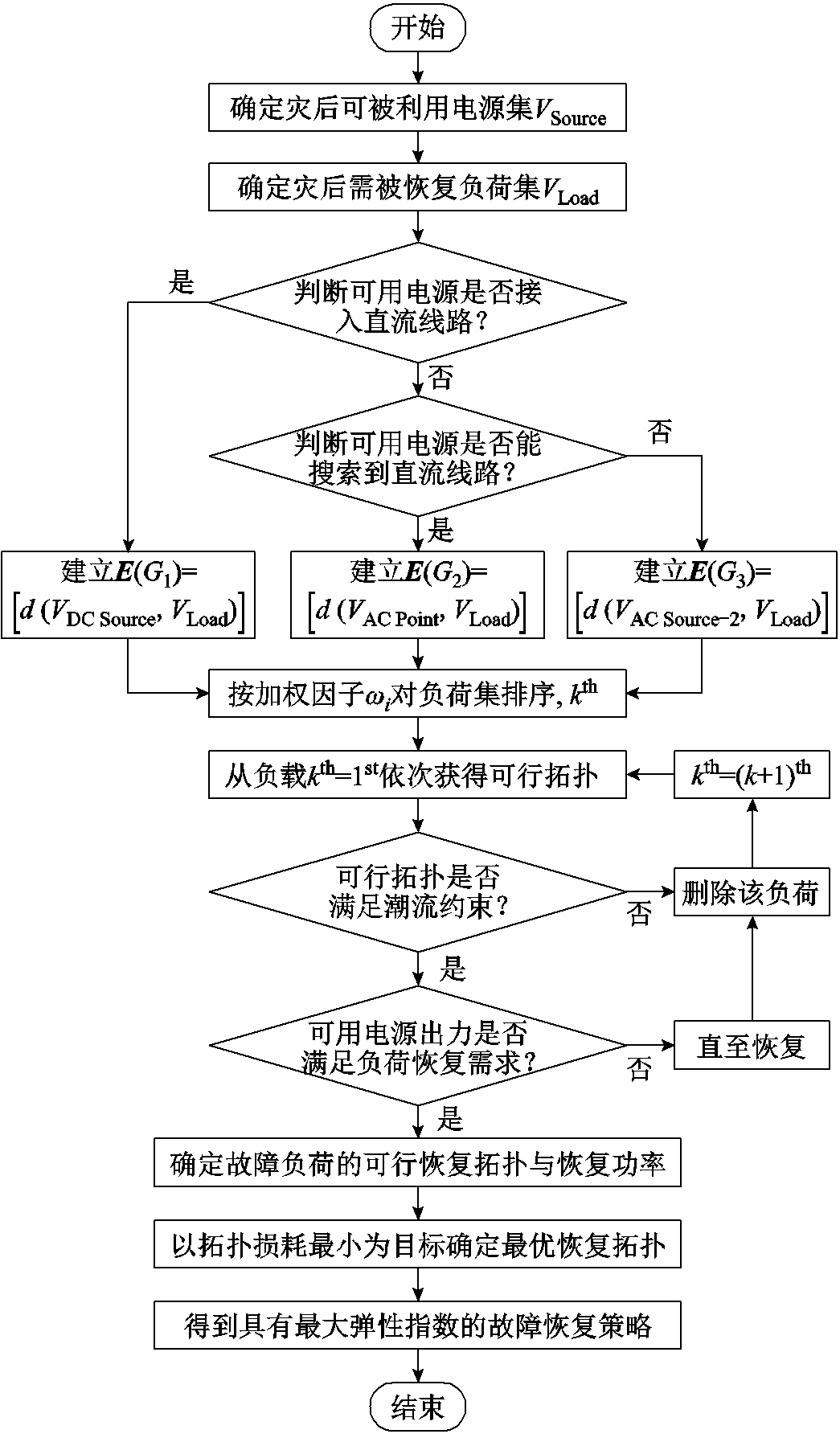
图4 基于直流线路互联的弹性恢复策略流程
Fig.4 Recovery strategy flowchart based on DC line interconnection relaxation
(1)确定灾后可用的分布式电源集和故障负载集。将极端灾害发生后可被利用分布式电源所在节点确定为可用分布式电源集,并将灾后失去供电并需要被恢复的负荷节点确定为故障负荷集。
(2)利用深度优先遍历法确定直流线路被优先遍历的可行拓扑搜索策略。依次判断灾后可用分布式电源集中的各电源节点是否接入直流线路,若接入直流线路,则建立该直流线路上可用电源到故障负荷节点之间的电气距离矩阵E(G1);若电源节点没有接入直流线路,则再次判断该电源节点是否可搜索到直流线路,若能够搜索到直流线路,则构造与分布式电源一一对应的关键交流电源点集合,并建立该集合到故障负荷节点之间的电气距离矩阵集E(G2),否则建立该电源节点到故障负荷节点之间的电气距离矩阵集E(G3)。基于上述操作,即可完成所有分布式电源到故障负荷节点之间可行拓扑的搜索。
(3)确定故障负荷的恢复顺序。按加权因子ωi对需要被恢复的所有故障负荷节点进行排序,得到kth,并从第kth=1st依次确定故障负荷节点的可行拓扑。
(4)完成对可行拓扑的潮流约束及功率分配。从kth=1st开始依次判断该故障负荷节点的可行拓扑是否满足潮流约束,若满足则进入下一步,若不满足则直接删除该故障负荷节点,则开始对故障负荷kth=(k+1)th进行约束判定;进一步判断可用分布式电源出力是否能够满足故障负荷节点的功率恢复需求,若满足,则记录该拓扑为可行恢复拓扑,若不满足,则在完成对所有可行拓扑对该负荷的kth故障恢复后删除该负载,并开始对故障负荷kth=(k+1)th进行约束判定。以此确定所有故障负荷节点的可行恢复拓扑,并完成功率分配。
(5)以最小化DTPS系统损耗为目标确定故障恢复策略。以最小化系统损耗为目标对DTPS系统中所有可行恢复拓扑进行筛选,并在满足潮流约束条件下确定最优恢复拓扑,进而基于该拓扑确定具有最大弹性指数的系统恢复策略。
为验证所提基于直流线路互联的DTPS系统弹性提升策略的有效性,本文以包含服务区、隧道用电场景的改进IEEE 123节点配电网为基础拓扑,在Matlab R2021B环境下利用YALMIP工具包调用CPLEX 12.6求解器完成对所提恢复策略的建模及求解,所采用的计算机配置为Inter Core i5-8250U@1.60 GHz,8 GB内存。假设极端灾害事件为台风,则基于DTPS系统的改进IEEE 123节点配电系统拓扑结构及台风行动轨迹如图5所示。
在台风灾害发生后,位于节点1处的总变电站失去供电能力,且随着台风实时路径的变化信息,节点14与节点19、节点36-120、节点102-122之间的支路受台风攻击后断开。对此,台风灾害事件发生后,DSTP系统剩余可用的分布式能源包括:位于节点8、28和76处的三台柴油发电机,位于节点54和108处的两套光伏、储能发电系统,以及位于节点47处的风力发电系统。台风灾害事件发生后,所有可用分布式能源的供电容量见表1。

图5 改进的IEEE123节点配电系统
Fig.5 Improved IEEE 123-node distribution system
表1 灾后可用分布式电源数据
Tab.1 Available distributed power data after a disaster

电源类型功率类型节点位置有功功率/ (kW·h)最大功率/kW 可调度源柴油发电机83 600 600 柴油发电机283 600600 柴油发电机764 400600 光伏-储能547 000400 光伏-储能1082 800300 不可调度源风力发电471 800200
台风灾害后,包含I1、I2和I3类负载在内的所有临界负载所需的供电容量见表2。其中,I1、I2和I3类负载的权重系数分别设定为10、5和1。
表2 故障负载所需电量数据
Tab.2 Required power data of fault load

负载类型节点位置所需功率/kW I1类负载162 520 312 180 871 340 1042 500 1231 840 I2类负载32 360 232 300 422 340 653 600 1012 080 1172 100 I3类负载51 860 121 920 211 800 251 600 331 640 491 380 603 000 821 500 962 500 1142 280
在台风灾害发生前,假设节点53-67之间的交流线路均被改造为直流线路且加固,且在其与交流线路的连接处,节点53与节点119、节点40与节点63、节点61与节点118,以及节点64与节点102之间增加VSC并加固,默认加固设备能够在台风灾害时保持稳定运行。在台风灾害发生后,剩余分布式电源的可用恢复策略涵盖三种类型,如图6所示。类型a中,电源节点28断开与其他电源连接,且无可连直流线路,因此该电源仅支持独立恢复;类型b中,接入直流线路的电源节点54能够通过VSC设备直接与其他可用电源连接,可实现与其他可用电源的联合恢复;类型c中,接入交流线路的电源节点8、47、76及108可以被连接到直流线路,因此可通过搜索包含直流线路的路径实现与剩余可用电源的联合恢复。
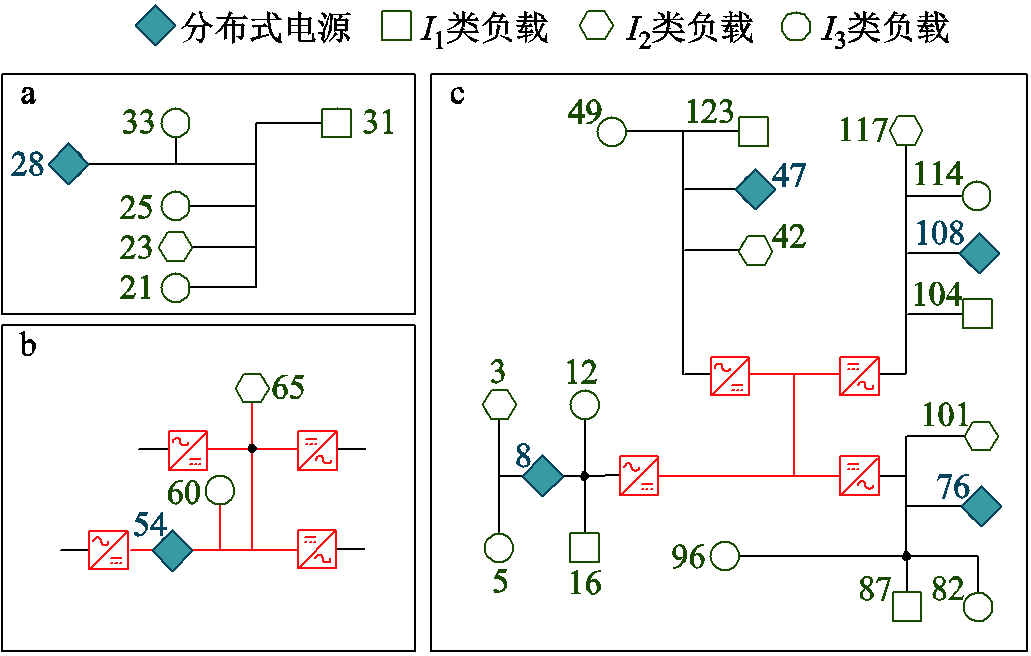
图6 分布式电源的接入类型
Fig.6 Connection types for distributed power sources
基于上述三种电源连接类型所示单元和多电源拓扑连接方案,本文分别对比了台风灾害攻击下使用传统恢复策略和所提恢复策略时系统的弹性恢复能力。其中,单电源拓扑在传统恢复策略和所提恢复策略下的故障节点恢复结果如图7所示。
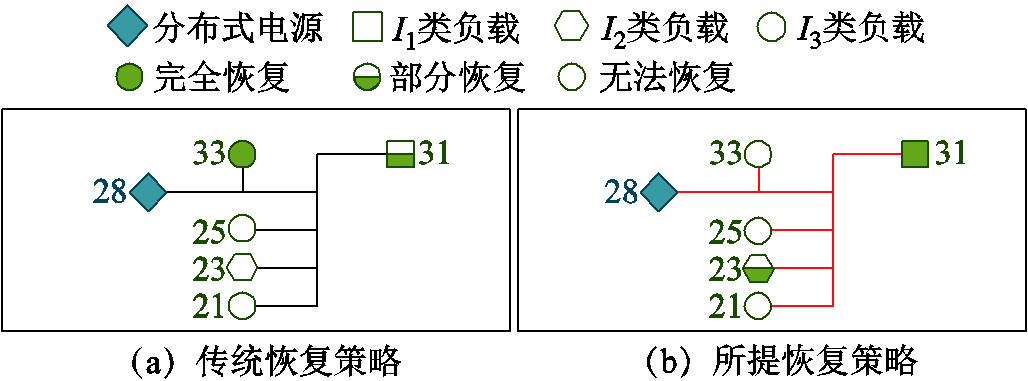
图7 单电源拓扑的恢复结果
Fig.7 Recovery result of single power supply topology
由图7a可知,I3类负载CL-33可以被完全恢复,I1类负载CL-31部分恢复,总恢复时间约为5.54 h,而剩余负载均不能恢复。由图7b可知,I1类负载CL-31可以被优先完全恢复,I2类负载CL-23被部分恢复,总恢复时间约为5.43 h。尽管该拓扑的辐射状约束均被松弛,但受单个电源出力限制,仍有多个负载无法恢复。
受所恢复负载供电类型的权重因子差异,使用本文所提策略能够尽可能地利用稀缺分布式电源实现更高权重因子负载的恢复,从而提升系统弹性指数。因此,相较传统故障恢复策略的弹性指数约为9 150.14 kW·h,采用本文所提故障恢复策略的弹性指数被提升至11 978.15 kW·h。由于更高权重因子负载被优先恢复,因此使用本文所提策略可将系统弹性指数提升30.91%,故障恢复时间缩短0.11 h。单电源拓扑结构分别使用传统恢复和所提恢复策略的弹性指数和恢复时间如图8所示。
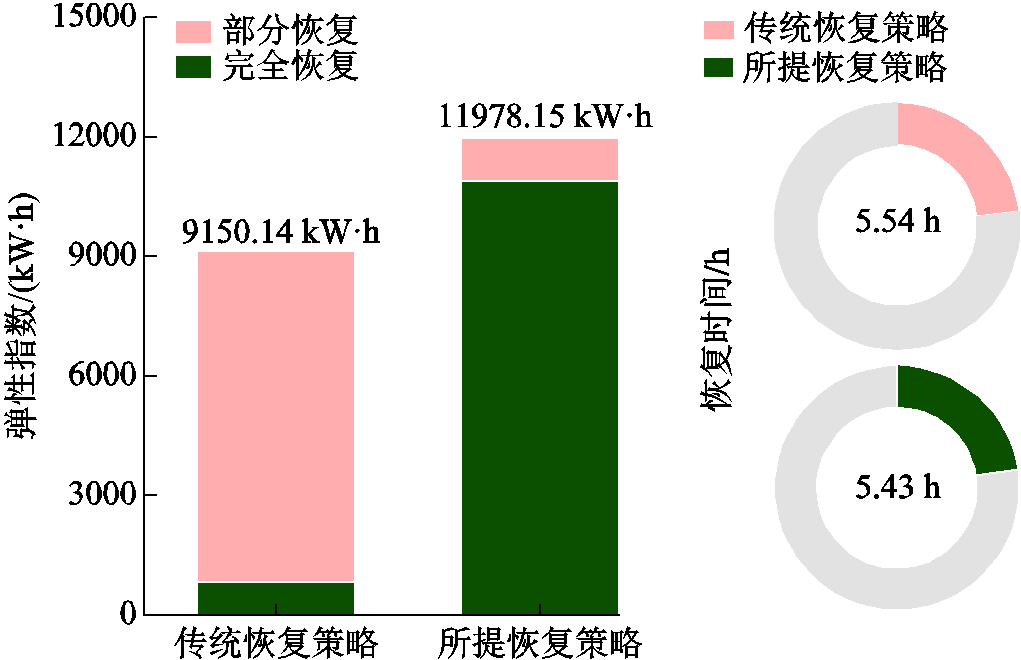
图8 单电源拓扑的弹性指数和恢复时间
Fig.8 Resilience indes and recovery times of single power supply topology
多电源拓扑在传统恢复和所提恢复策略下的故障节点恢复效果如图9所示。

图9 多电源拓扑的恢复结果
Fig.9 Recovery results of multi power supply topology
由图9a可知,各类负载的恢复结果仅受该负载所连接电源的出力影响。其中,由于I1类负载 CL-42完全恢复所需的能量为2 340 kW·h,受辐射状约束只能连接至容量为1 800 kW·h的单电源WT-47,因此CL-42只能被部分恢复,恢复时间约为8.17 h。单电源DG-8、PE-108和DG-76的出力除可完全恢复CL-16、CL-104、CL-87和CL-82外,能够部分恢复CL-12、CL-114和CL-96,总恢复时间约为17.07 h。然而,总能量为7 000 kW·h的单电源PE-54在完成对CL-65和CL-60的完全恢复后仍有剩余能量,但却无法供给于权重因子较高的负载,诸如I1类负载CL-42、CL-96。由于该拓扑结构下各电源间无法互联进而导致可用分布式电源出力的浪费,且该恢复策略对负载的恢复顺序无约束,因此更高权重因子的负载无法得到优先恢复,系统弹性指数约为48 928.98 kW·h,总恢复时间约为17.19 h。
相反,基于本文所提由所有电源总出力和负载权重因子共同作用下的故障恢复结果如图9b所示。其中,I1类负载CL-16、CL-42、CL-96和CL-114可以被优先完全恢复,总恢复时间约为10.35 h。在I1类负载被恢复基础上,剩余电源却不能完全恢复所有I2类负载,其中CL-65和CL-104可被完全恢复,CL-3被部分恢复,总恢复时间约为15.9 h。此外,CL-101、CL-123及剩余I3类负载均不能被恢复。在该拓扑下,由于所有电源与负载相连,因此所有分布式电源的出力被集中,并可以尽可能多地恢复权重因子更高的重要负载,从而最大化拓扑的弹性指数,约为68 540.95 kW·h。相较于传统恢复策略,本文所提故障恢复策略可将弹性指数提升40.09%,故障恢复时间缩短1.29 h。多电源拓扑使用传统策略和所提策略的弹性指数和恢复时间如图10所示。
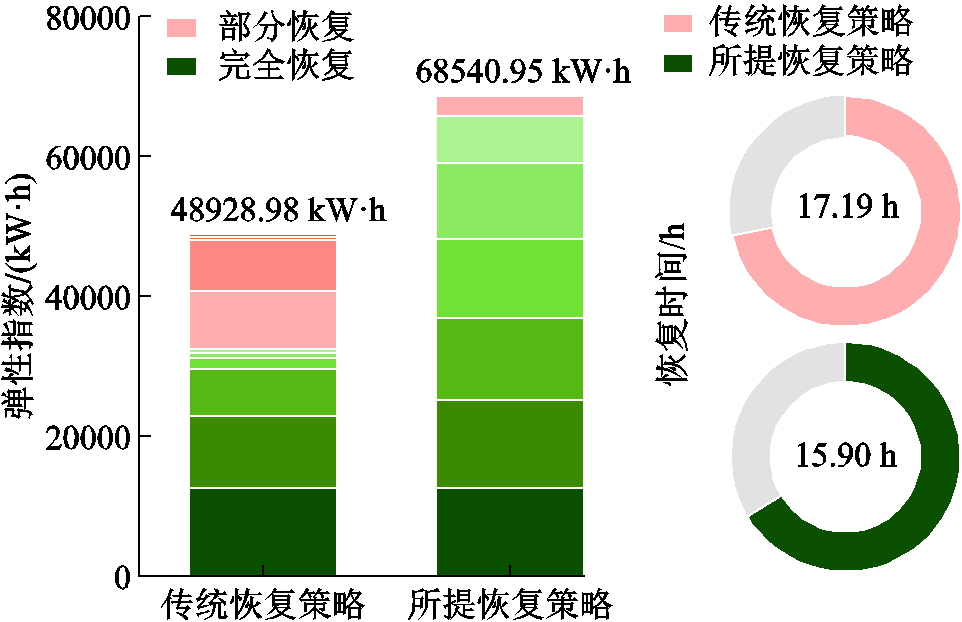
图10 多电源拓扑的弹性指数及恢复时间
Fig.10 Resilience indes and recovery times of multi power supply topology
综上所述,本文所提故障恢复策略可将所有可用电源及负载互联,并将极端灾害故障下稀缺分布式电源供给权重因子更高的负载;相反,传统方法因没有考虑这种互联能力从而造成稀缺分布式能源的被浪费和更高权重负载的被忽视。因此,基于本文所提直流线路被优先遍历的恢复策略不仅能够有效降低系统的传输损耗,而且大大缩短了负载的故障恢复时间。
在台风灾害发生后,系统故障的初始状态受故障随机性影响存在诸多不确定性,例如:台风灾害的发生位置、可用电源的出力分配等。为证明所提互联方案和故障弹性恢复策略的恢复效果,本文假设并对比了两种故障初始状态下的弹性指数。
案例Ⅰ:故障灾害位置发生转移。该案例下,假设台风导致配电网节点9-10、节点68-98间线路断开。此时,I3类负载CL-12断开与可调度源DG-8的连接,转而连接至不可调度源WT-47;I2类负载CL-101断开与可调度源DG-76的连接,转而连接至电源PE-108;除此之外,系统剩余初始条件均不变。传统和所提恢复策略在多电源拓扑下的恢复结果分别如图11a和图11b中所示。
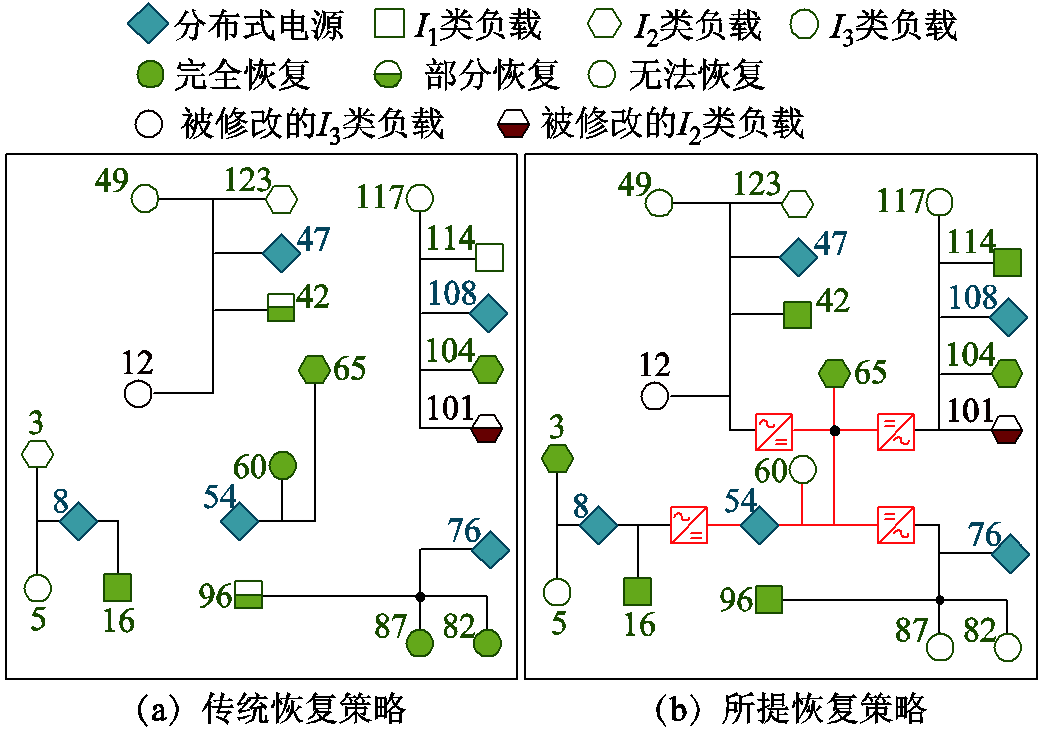
图11 案例Ⅰ的拓扑恢复结果
Fig.11 Topology recovery results in CaseⅠ
根据图11所示恢复结果可知,I3类负载CL-12在由单电源DG-8部分恢复转移至电源WT-47无法被恢复后,DG-8的剩余供电能力被用于供给权重因子更高的I2类负载CL-3,这使得弹性指数增加 1 601.61 kW·h。进一步,I2类负载CL-101失去单电源DG-76的供给而被电源PS-108部分恢复后,使I1类负载CL-114无法恢复,并使故障弹性系数降低312.96 kW·h。因此,使用传统方法的弹性指数被提升至50 217.63 kW·h,较初始案例弹性指数增长 1 288.65 kW·h。由于本文所提恢复策略严格保证了权重因子较高负荷的优先恢复,因此使用本文所提恢复策略的弹性指数仍为68 540.95 kW·h,高于传统恢复策略。
案例Ⅱ:部分电源出力发生变化。该案例下,假设电源DG-8和DG-76的初始可用电源出力发生变化,即DG-8和DG-76在极端灾害下的发电容量分别为3 600 kW·h和4 400 kW·h。除此之外,系统可用电源总出力及剩余初始条件均不变。传统和所提恢复策略在多电源拓扑下的恢复结果分别如图12a和图12b所示。
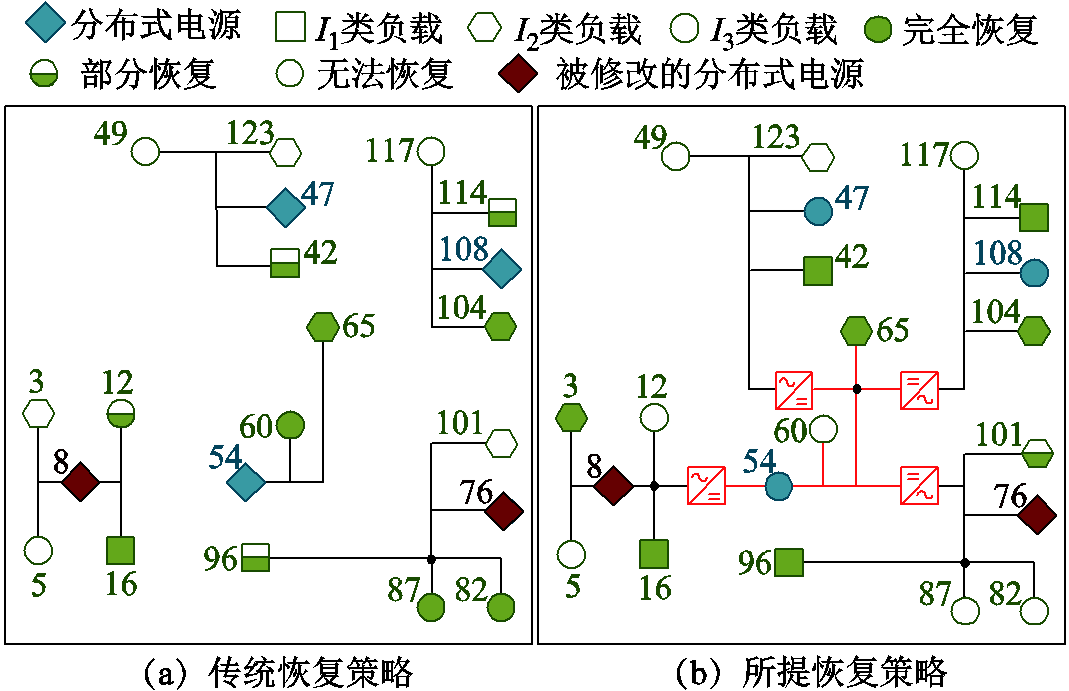
图12 案例Ⅱ的拓扑恢复结果
Fig.12 Topology recovery results in CaseⅡ
根据图12所示恢复结果可知,由于传统恢复策略下单电源DG-76发电容量的降低,I1类负载CL-96可被恢复的能量被削减,进而造成弹性指数降低3 897.83 kW·h。此外,由于单电源DG-8发电容量的提升,I3类负载CL-12可被恢复的能量会被提升,但由于CL-12的权重系数更小,仅使弹性恢复指数提升451.3 kW·h。综合上述变化,使用传统恢复策略的弹性指数为45 482.45 kW·h,较初始案例的弹性恢复指数下降3 446.53 kW·h。由于本文所提恢复策略仅受系统总出力影响,因此其弹性指数不受初始条件变化,始终保持为68 540.95 kW·h,远高于传统恢复策略。
综合上述两种案例恢复结果,图13给出了两种案例下不同恢复策略的弹性指数对比。由图13可知,相较于初始案例,在系统故障灾害位置发生变化案例下使用传统恢复策略能够使系统弹性指数提升2.56%,而部分电源出力变化但系统总出力不变案例下则使系统弹性指数降低7.04%。相较于传统恢复策略在不同初始条件下的弹性指数取决于负载所连接电源出力的限制,由于本文所提恢复策略不仅保证了系统多电源之间的协同互济,且多层级的故障恢复顺序保证了重要负载的优先恢复,因此即使初始条件突变,仍能够保证稳定较高的弹性指数。

图13 不同初始条件下的弹性指数
Fig.13 Resilience index under different initial conditions
本文提出了一种极端灾害下基于直流线路互联的DTPS系统弹性恢复策略,所提策略不仅能够有效提升DTPS系统的弹性恢复指数,而且能够有效缩短系统恢复时间。具体成果如下:
1)本文提出了基于直流线路互联的深度优先遍历策略,有效拓展了系统故障状态下的可行恢复拓扑。与传统恢复策略相比,所提策略有效提升了系统所有单电源的互联效率,且基于直流线路优先遍历的拓扑搜索策略有效提升了系统的可行解空间。此外,有目标性的配电设备加固计划能够降低安装成本。
2)本文提出了重要负荷优先恢复量最大和配电网额外损耗最小的弹性恢复策略。验证结果表明,本文所提恢复策略在弹性指数和恢复时间上明显优于传统恢复策略。初始条件下,所提恢复策略在单电源和多电源拓扑下的弹性指数可较传统恢复策略提升30.91%和40.09%,恢复时间缩短了0.11 h和1.29 h。
3)本文所提弹性恢复策略可在系统初始条件变化时保证弹性指数的稳定性,并被拓展于交直流混合微电网。验证结果表明,在多电源拓扑故障灾害位置发生转移、可用电源出力发生变化等初始条件突变情况下,所提恢复策略的弹性指数仍分别较传统恢复策略提升36.49%和55.70%。
参考文献
[1] 杨勇平, 武平, 程鹏, 等. 我国陆路交通能源系统发展战略研究[J]. 中国工程科学, 2022, 24(3): 153-162. Yang Yongping, Wu Ping, Cheng Peng, et al. Development strategy for energy system of land transport in China[J]. Strategic Study of CAE, 2022, 24(3): 153-162.
[2] 贾利民, 师瑞峰, 吉莉, 等. 我国道路交通与能源融合发展战略研究[J]. 中国工程科学, 2022, 24(3): 163-172. Jia Limin, Shi Ruifeng, Ji Li, et al. Road transportation and energy integration strategy in China[J]. Strategic Study of CAE, 2022, 24(3): 163-172.
[3] 马静, 徐宏璐, 马瑞辰, 等. 能源交通融合下的弹性公路能源系统发展技术要点及展望[J]. 电网技术, 2023, 47(3): 885-896. Ma Jing, Xu Honglu, Ma Ruichen, et al. A review on the development of resilient highway energy system under the integration of energy and transportation[J]. Power System Technology, 2023, 47(3): 885-896.
[4] 贾利民, 程鹏, 张蜇, 等. “双碳”目标下轨道交通与能源融合发展路径和策略研究[J]. 中国工程科学, 2022, 24(3): 173-183. Jia Limin, Cheng Peng, Zhang Zhe, et al. Integrated development of rail transit and energies in China: development paths and strategies[J]. Strategic Study of CAE, 2022, 24(3): 173-183.
[5] 陈冲, 贾利民, 赵天宇, 等. 去碳化导向的轨道交通与新能源融合发展: 形态模式、解决方案和使/赋能技术[J]. 电工技术学报, 2023, 38(12): 3321-3337. Chen Chong, Jia Limin, Zhao Tianyu, et al. Decarbonization-oriented rail transportation and renewable energy integration development-configurations, solutions, and enabling/empowering technologies[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3321-3337.
[6] 江里舟, 别朝红, 龙涛, 等. 能源交通一体化系统发展模式与运行关键技术[J]. 中国电机工程学报, 2022, 42(4): 1285-1301. Jiang Lizhou, Bie Zhaohong, Long Tao, et al. Development model and key technology of integrated energy and transportation system[J]. Proceedings of the CSEE, 2022, 42(4): 1285-1301.
[7] 王守相, 刘琪, 赵倩宇, 等. 配电网弹性内涵分析与研究展望[J]. 电力系统自动化, 2021, 45(9): 1-9. Wang Shouxiang, Liu Qi, Zhao Qianyu, et al. Connotation analysis and prospect of distribution network elasticity[J]. Automation of Electric Power Systems, 2021, 45(9): 1-9.
[8] 王雨晴, 王文诗, 徐心竹, 等. 面向低碳交通的含新能源汽车共享站电-氢微能源网区间-随机混合规划方法[J]. 电工技术学报, 2023, 38(23): 6373-6390. Wang Yuqing, Wang Wenshi, Xu Xinzhu, et al. Hybrid interval/stochastic planning method for new energy vehicle sharing station-based electro-hydrogen micro-energy system for low-carbon transportation[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6373-6390.
[9] 李珂, 邵成成, 王雅楠, 等. 考虑电-气-交通耦合的城市综合能源系统规划[J]. 中国电机工程学报, 2023, 43(6): 2263-2273. Li Ke, Shao Chengcheng, Wang Yanan, et al. Optimal planning of urban integrated energy systems considering electricity-gas-transportation interactions[J]. Proceedings of the CSEE, 2023, 43(6): 2263-2273.
[10] 王丰, 杨函煜, 李林溪, 等. 考虑氢能交通运输时空特性的电-氢综合能源系统协同优化方法[J]. 电力系统自动化, 2023, 47(19): 31-43. Wang Feng, Yang Hanyu, Li Linxi, et al. Collaborative optimal method for electricity-hydrogen integrated energy system considering spatial-temporal characteristics of hydrogen transportation[J]. Automation of Electric Power Systems, 2023, 47(19): 31-43.
[11] 倪萌, 王蓓蓓, 朱红, 等. 能源互联背景下面向高弹性的多元融合配电网双层分布式优化调度方法研究[J]. 电工技术学报, 2022, 37(1): 208-219. Ni Meng, Wang Beibei, Zhu Hong, et al. Study of two-layer distributed optimal scheduling strategy for highly elastic multi-resource fusion distribution network in energy interconnection environment[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 208-219.
[12] 蔡胜, 谢云云, 张玉坪, 等. 考虑孤岛微网建立过程功率冲击的弹性配电网主动预防调度[J]. 电工技术学报, 2023, 38(23): 6419-6432. Cai Sheng, Xie Yunyun, Zhang Yuping, et al. Proactive scheduling of resilient distribution systems considering power impact during islanded microgrid formation process[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6419-6432.
[13] Chen Fangjian, Xia Mingchao, Chen Qifang, et al. Resilience enhancement method against persistent extreme weather with low temperatures in self-sustained highway transportation energy system[J]. IEEE Transactions on Industry Applications, 2024, 60(1): 996-1009.
[14] Jiang Xinyi, Chen Jian, Chen Ming, et al. Multi-stage dynamic post-disaster recovery strategy for distribution networks considering integrated energy and transportation networks[J]. CSEE Journal of Power and Energy Systems, 2020, 7(2): 408-420.
[15] 陶然, 赵冬梅, 徐辰宇, 等. 考虑电-气-热-交通相互依存的城市能源系统韧性评估与提升方法[J]. 电工技术学报, 2023, 38(22): 6133-6149. Tao Ran, Zhao Dongmei, Xu Chenyu, et al. Resilience assessment and enhancement methods for urban energy system considering electricity-gas-heat-transport interdependency[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6133-6149.
[16] 李振坤, 周伟杰, 钱啸, 等. 有源配电网孤岛恢复供电及黑启动策略研究[J]. 电工技术学报, 2015, 30(21): 67-75. Li Zhenkun, Zhou Weijie, Qian Xiao, et al. Distribution network restoration and black start based on distributed generators[J]. Transactions of China Electrotechnical Society, 2015, 30(21): 67-75.
[17] Chen Chen, Wang Jianhui, Qiu Feng, et al. Resilient distribution system by microgrids formation after natural disasters[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 958-966.
[18] Kim Y J, Wang Jianhui, Lu Xiaonan. A framework for load service restoration using dynamic change in boundaries of advanced microgrids with synchronous-machine DGs[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 3676-3690.
[19] Wang Xu, Li Zhiyi, Shahidehpour M, et al. Robust line hardening strategies for improving the resilience of distribution systems with variable renewable resources[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 386-395.
[20] 郭慧, 汪飞, 顾永文, 等. 基于电压分层控制的直流微电网及其储能扩容单元功率协调控制策略[J]. 电工技术学报, 2022, 37(12): 3117-3131. Guo Hui, Wang Fei, Gu Yongwen, et al. Coordinated power control strategy for DC microgrid and storage expansion unit based on voltage hierarchical control[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3117-3131.
[21] Sciano D, Raza A, Salcedo R, et al. Evaluation of DC links on dense-load urban distribution networks[J]. IEEE Transactions on Power Delivery, 2016, 31(3): 1317-1326.
[22] Kallel R, Boukettaya G. An energy cooperative system concept of DC grid distribution and PV system for supplying multiple regional AC smart grid connected houses[J]. Journal of Building Engineering, 2022, 56: 104737.
[23] Celli G, Pilo F, Pisano G, et al. Meshed vs. radial MV distribution network in presence of large amount of DG[C]//IEEE PES Power Systems Conference and Exposition, New York, NY, USA, 2005: 709-714.
[24] 傅守强, 陈翔宇, 张立斌, 等. 面向韧性提升的交直流混合配电网协同恢复方法[J]. 中国电力, 2023, 56(7): 95-106. Fu Shouqiang, Chen Xiangyu, Zhang Libin, et al. Coordinated restoration method of hybrid AC/DC distribution networks for resilience enhancement[J]. Electric Power, 2023, 56(7): 95-106.
[25] 尹航, 刘友波, 高红均, 等. 含分布式储能系统的交直流混合配电网负荷恢复策略[J]. 电力自动化设备, 2021, 41(8): 25-32. Yin Hang, Liu Youbo, Gao Hongjun, et al. Load recovery strategy of AC/DC hybrid distribution network with distributed energy storage systems[J]. Electric Power Automation Equipment, 2021, 41(8): 25-32.
[26] 金国彬, 李双, 李国庆, 等. 考虑电动汽车集群时空能量可调控特性的交直流混合配电网紧急优化调度[J]. 电力自动化设备, 2023, 43(7): 102-109. Jin Guobin, Li Shuang, Li Guoqing, et al. Emergency optimal dispatch of AC/DC hybrid distribution network considering spatio-temporal energy controllable characteristics of electric vehicle clusters[J]. Electric Power Automation Equipment, 2023, 43(7): 102-109.
[27] 王颖, 许寅, 和敬涵, 等. 基于断线解环思想的配电网辐射状拓扑约束建模方法[J]. 中国电机工程学报, 2021, 41(7): 2395-2404. Wang Ying, Xu Yin, He Jinghan, et al. Radiality constraint modelling method in distribution network based on cutting-line and opening-loop idea[J]. Proceedings of the CSEE, 2021, 41(7): 2395-2404.
Abstract To realize the goal of energy transition, it has become a future trend to fully develop the available space resources of highways and build a clean energy power supply system. Considering the limitations of a single power supply system and the intermittency of power generation, district-tunnel power supply (DTPS) systems that include multiple service areas or tunnel power supply systems have higher reliability. However, due to the dual threats of transportation and energy systems, as well as the dual fluctuations of distributed generation and traffic load electricity consumption, the proposed regional tunnel power supply system has a higher risk when facing extreme natural disasters and human attacks. Experts and scholars have conducted research on the resilience of multi-area systems. However, existing recovery strategies are all implemented under radial constraints, which often leads to the waste of scarce distributed resources. To address these issues, this paper proposes an elastic recovery strategy based on DC line interconnection.
First, based on the pre-disaster DC line renovation and reinforcement plan, a deep priority traversal strategy for DC lines is proposed to ensure effective interconnection of the system in extreme events. Second, based on multi-level classification strategy, a two-stage fault recovery objective function is constructed to ensure the recovery index of the power system based on scarce distributed energy after extreme disasters, including priority recovery of important loads and minimization of additional losses. In addition, based on the traditional second-order cone relaxation method, a convergence strategy for solving mixed integer second-order cone programming problems is proposed, which can overcome the limitations of original constraints and ensure the stable use of the proposed model under different initial conditions. Final, the improved IEEE 123-node power supply system covering DTPS system scenarios verified the stable applicability of the proposed strategy.
The verification results indicate that although the total power output of the system under a single power supply topology is limited, compared with traditional recovery strategies, the proposed strategy can still improve the elasticity index by 30.91% and shorten the recovery time by 0.11 h. In a multi power topology, the proposed recovery strategy can recover loads with higher weight factors and ensure the maximum utilization of scarce distributed energy, thereby increasing the system elasticity index by 40.09% and shortening the recovery time by 1.29 h. In addition, compared to traditional recovery strategies where sudden changes may lead to an increase or decrease in the recovery index, the proposed strategy always ensures a stable and high recovery index.
In summary, the following conclusions can be drawn: (1) Compared to traditional fault recovery strategies, the topology structure based on DC line interconnection can effectively improve the feasible solution space of the system, and reduce the installation cost of the system through targeted reinforcement plans. (2) The proposed fault recovery strategy is significantly superior to traditional strategies in terms of recovery index and recovery time. (3) The proposed resilience recovery strategy remains stable under different initial conditions and can be extended to hybrid AC/DC microgrids.
keywords:District-tunnel power supply system, DC line interconnection, depth-first traverse, resilience recovery
DOI:10.19595/j.cnki.1000-6753.tces.230769
中图分类号:TM619
国家重点研发计划资助项目(2021YFB1600202)。
收稿日期 2023-05-26
改稿日期 2023-11-10
孔惠文 女,1994年生,博士研究生,研究方向为新能源电力系统的分析、稳定与控制,综合交通与能源系统等。E-mail:hwkong@ncepu.edu.cn
马 静 男,1981年生,教授,博士生导师,研究方向为电力系统分析、稳定与控制等。E-mail:hdmajing@163.com(通信作者)
(编辑 赫 蕾)