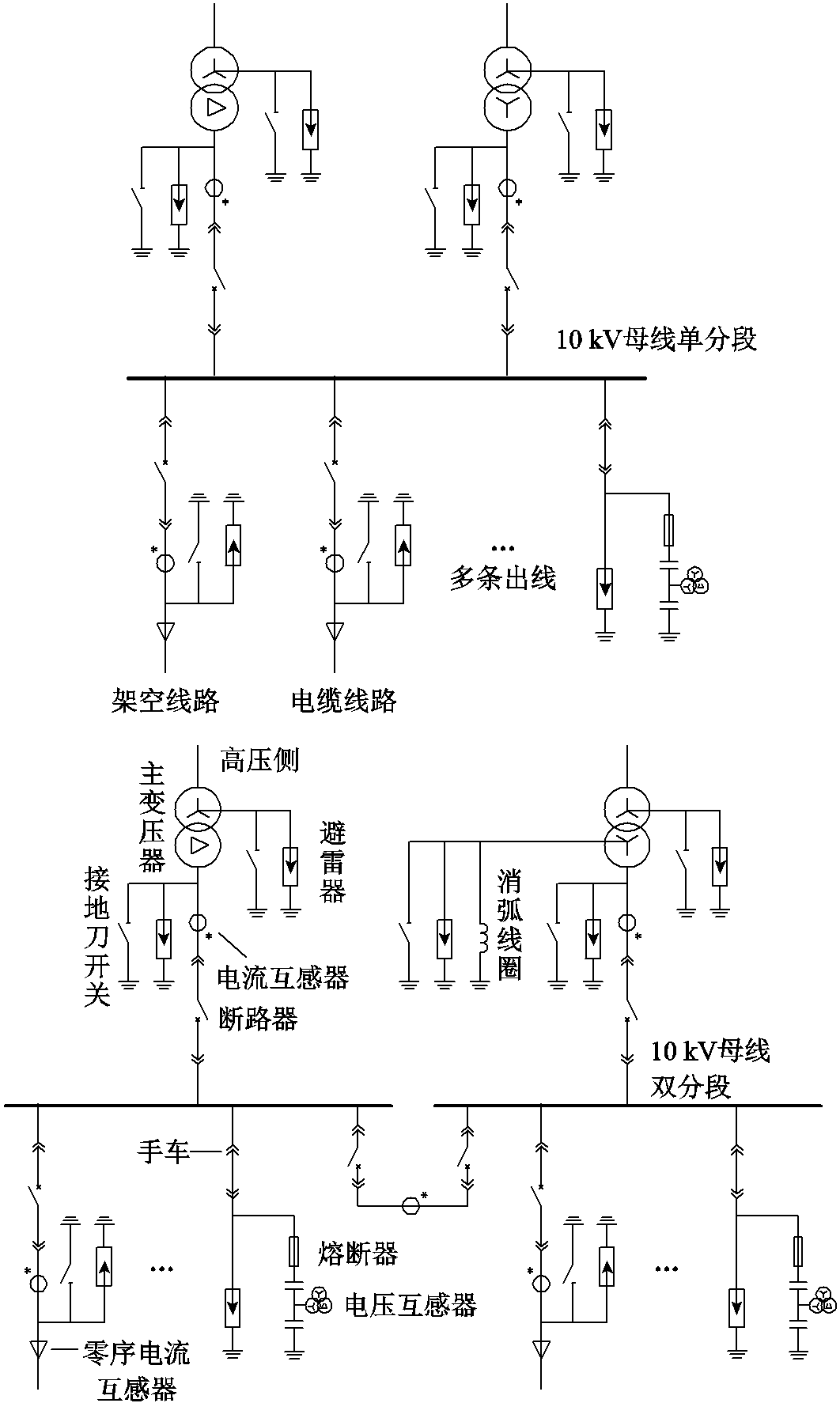
图1 典型10 kV母线系统
Fig.1 Typical 10 kV busbar system
摘要 受母线并联电容器对于线模行波的高频滤波作用的启发,该文跳出基于零模行波设计选线方法的视角,提出利用变电站边界特性的配电网线模行波选线方法。首先,研究证实了电子式电压互感器、金属氧化物避雷器与母线其余设备杂散电容共同组成的智能变电站线路边界具备强健的高频滤波特性,其对于线模行波的折射衰减作用为后续选线方法的设计奠定了基础;然后,基于健全线路与故障线路上线模行波高频瞬时能量的差异构造了选线新判据,其在高阻故障与小相角接地故障等工况下具备较高的灵敏度;最后,基于PSCAD/EMTDC仿真平台验证了所提选线方法的有效性、灵敏性与可靠性,该方法以线模行波作为所选模量,为故障选线问题的解决提供了全新的思路。
关键词:配电网 故障选线 线模行波 边界特性 高频瞬时能量
目前,我国中压配电网通常采用中性点非有效接地方式,当发生单相接地故障时,如何准确地选线是业内长期面临的技术难题[1]。虽然近年来随着基于暂态法选线装置的推广应用,实际选线成功率已有较大程度的提升,但当发生高阻故障与小相角接地故障时,由于系统故障特征十分微弱[2-3],仍易导致现有的各种选线方法失效。
相较于易受系统接地方式影响的稳态量选线方法[4-5]、耐受过渡电阻能力较差的注入式选线方法[6-7]及工程应用较为困难的人工智能选线方法[8-9],暂态行波选线方法因具有故障特征明显、不受接地方式影响、耐受过渡电阻能力强等突出优势而成为当前关注热点[10-12]。起初,有研究学者提出可通过比较线路电流的初始极性与幅值来实现选线[13],但该方法严重依赖初始波头,在近距离故障时效果不佳;其后,利用单相反、正向行波积分比值的方法开始出现[14],其可靠地延长了判据有效时间,大幅缩小了选线死区,但在架空-电缆混联线路中灵敏性不足;在此基础上,又有学者提出了利用故障电流方向行波能量的选线方法[15],有效地解决了特殊故障工况下行波积分比值方法灵敏度不高、准确度较低的难题。除此之外,也有学者尝试将相关性分析引入配电网故障选线领域[16-17],其实现简单,实用性强,但实际应用效果有待工程检验。
应特别注意到,上述既有的暂态行波选线方法均需基于零模行波的精确检测与特征提取,如此考虑的最重要的原因是当变电站低压母线上装设并联补偿电容器时,线模行波因受电容器高频滤波作用的影响而使得健全线路上的暂态行波信号十分微弱,由此将导致前述暂态行波选线方法的误判率大大增加。而零模行波因无法在不接地电容器组内形成回路而几乎不受影响,由此得以成为配网选线领域中行波模量的主流选择[14,16]。虽然基于零模行波设计的选线方法在实际应用中取得了良好的应用效果,但也仍存在以下问题:①当长线路末端发生高阻故障与小相角接地故障时,信号特征较为微弱,又因零模行波衰减较快,安装于变电站的选线装置可能难以准确检测到零模行波;②目前配网线路较多只安装了两相电流互感器,导致零模行波难以获取[18]。因此,上述弊端将成为制约当前基于零模选线方法性能进一步提高的掣肘。
线模行波相比零模行波衰减慢,其在故障选线领域中的应用潜力尚未发掘,假如能够充分调动线模行波在故障选线中的作用,其与零模行波相互协同则有望更为完整地反映故障特征,为运维人员的最终选线决策提供更为可靠的依据。因低压母线上并联补偿电容器对于线模行波的高频滤波作用,健全线路与故障线路上的线模行波存在显著差异,所以可设计基于线模行波的选线方法。但若变电站母线上未安装并联补偿电容器或其未投入运行时,健全线路和故障线路上的线模行波是否仍具有明显的差异则需进行深入分析。国家电网公司于2009年提出坚强智能电网的计划后[19],传统的配网变电站逐步向智能变电站升级演变,其改造措施包括:采用电子式电压互感器(Electronic Voltage Transformer, EVT)取代传统的电磁式电压互感器[20],而EVT与并联补偿电容器均属于容性设备,故其均能对高频分量行波产生对地滤波作用。如果能够证实EVT与金属氧化物避雷器(Metal-Oxide Arrester, MOA)等基础容性元件和母线其余设备杂散电容共同组成的配网母线滤波边界可以形成与并联电容器相类似的高频滤波作用,则无论并联补偿电容器投入与否,健全线路与故障线路上线模行波的显著差异都将存在,进而可为基于线模行波的故障选线方法奠定设计基础。但是,如何深入分析并清晰地构建变电站低压侧的高频滤波特性,以及如何基于健全线路与故障线路上线模行波的差异构造单相接地故障选线方法,目前均尚未有研究。
精确分析线模行波在变电站线路边界处的传输过程是厘清健全线路与故障线路上线模行波差异的关键,也是后续设计故障选线方法的基础。
典型10 kV母线系统如图1所示。智能变电站内的10 kV母线通常采用母线单分段或双分段接线形式,其一般接有两条主变进线及若干条电缆或架空线路出线,低压侧中性点采用不接地或经消弧线圈接地两种方式。母线上主要连接EVT、MOA、电流互感器、接地刀开关、手车、熔断器、断路器、变压器等基础设备,以及可能连接并联电容器等补偿设备,但其未必投入运行。
现主要针对母线上的基础设备,按照其自身的宽频暂态特性进行如下划分:
1)设备的高频滤波特性主要取决于其对地杂散电容。该类设备主要包括电流互感器、接地刀开关、手车、熔断器、断路器、变压器及母线本身,其绝缘子或设备外壳等的对地杂散电容会对故障行波的传播造成影响,但由于其数值一般较小,故作用较为有限。为简化分析,可将上述设备整体的高频滤波效应等效为等值杂散电容CB,文献[16]指出,10 kV配电网母线对地杂散电容CB大约为0.1~5 nF。

图1 典型10 kV母线系统
Fig.1 Typical 10 kV busbar system
2)设备的高频滤波特性主要取决于其自身的主电容。该类设备主要包括EVT和MOA,其等效结构中均包含主电容,而电容的高频低阻特性会为故障行波高频分量的传输提供对地流通通路,且其数值一般远大于其余设备的杂散电容大小,故对于行波传输的影响较为显著。因此,EVT和MOA主电容的频率特性在分析母线边界滤波性能时应当被准确评估。
当前智能变电站内安装的EVT主要采用电容分压或阻容分压两种形式,现暂以阻容分压型EVT为例,其等效结构与暂态电路如图2所示[21-22]。图2a中,C1和C2分别为高低压分压电容;R1和R2分别为C1和C2的并联高阻,用以提升电压的量测精度;运放电路并联于C2和R2两端,用以输出数字式或模拟式二次电压信号。图2b中,Lk1和Lk2分别为C1和C2的寄生电感;Ck1和Ck2分别为C1和C2的对地杂散电容。由于运放电路的输入阻抗高达kΩ数量级,其在高频下可近似看作被低压分压电容C2的高频极小阻抗短接,因此在EVT的暂态电路中可不计及运放电路的影响。
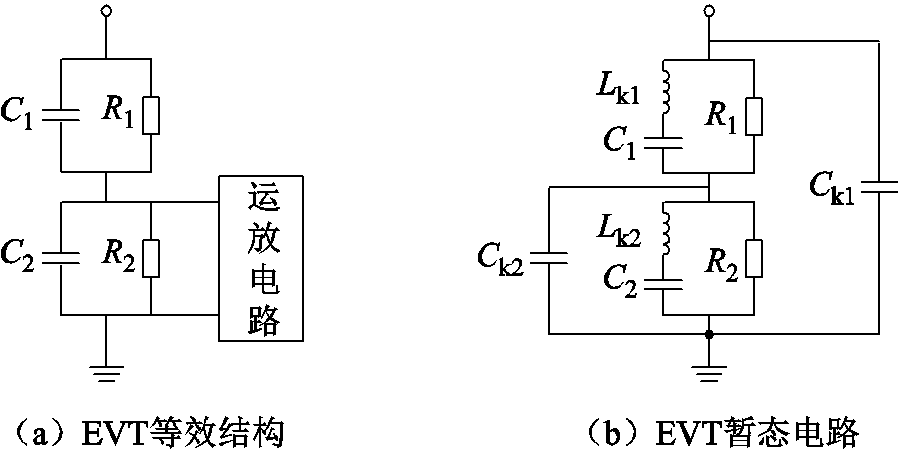
图2 EVT的等效结构与暂态电路
Fig.2 The equivalent structure and transient circuit of EVT
MOA具备优良的伏安非线性特性,当其工作于电力系统正常运行电压或故障低压状态时主要呈现出电容性,流过其自身的电流仅为mA级别。MOA的等效结构与暂态电路如图3所示[23-24]。图3a中,Cb为MOA氧化锌阀片的固有电容;Rb为MOA氧化锌阀片的等效高阻;上下所接的电极与法兰均为MOA的物理组成结构。图3b中,Lb为固有电容Cb的寄生电感;Cz1、Cz2、Cz3分别为MOA电极的对地杂散电容、各相MOA的耦合电容及法兰和设备外壳等的对地杂散电容;Rw为接地电阻。
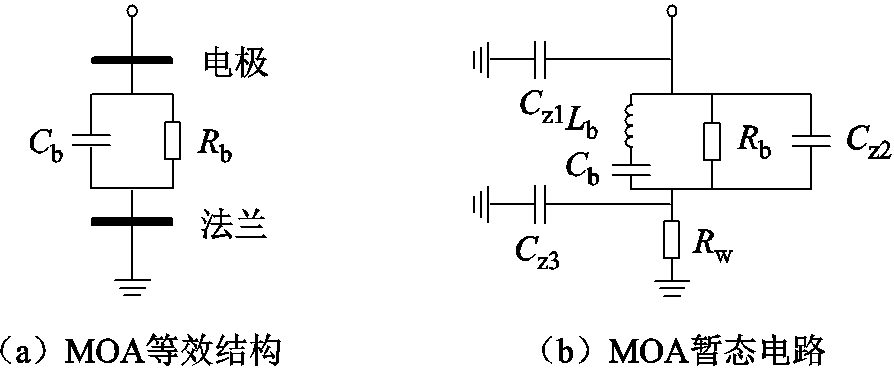
图3 MOA的等效结构与暂态电路
Fig.3 The equivalent structure and transient circuit of MOA
基于以上分析,可将EVT、MOA及母线其余设备杂散电容CB共同作为线路边界,现分析其对故障行波传播的影响,即线路边界折射系数的频率特性。
假设于电缆或架空线路上发生故障,故障初始行波到达母线系统后将进行能量的重新分配,现暂以图1中的10 kV单母线分段接线为例,可知共计1组EVT、n+4组MOA及母线其余设备杂散电容CB将对故障行波产生影响,而后故障行波继续传输至母线其余分支出线上,其中,10 kV变电站通常存在多达4~10回的进出线(不包括主变压器支路),n为母线总分支出线数目,n=1,2,…,9,下同。由于变压器的等值阻抗呈感性,其在高频下可处理为开路,故变压器所连接下级线路的波阻抗及中性点可能连接的消弧线圈等均不会对故障行波产生影响。假设除了故障线路外,母线系统上还剩n1条架空线路和n2条电缆线路,满足n1+n2=n,则根据彼得逊法则,可得故障初始电压行波传输至母线系统时的集中参数等效电路如图4所示。
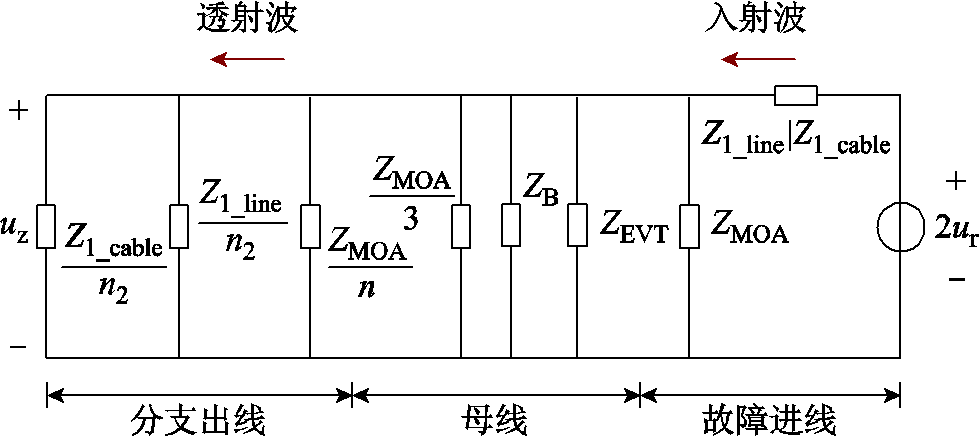
图4 行波传播等效电路
Fig.4 The equivalent circuit of travelling waves propagation
图4中,ur为电压入射波;uz为电压折射波;Z1_line和Z1_cable分别为架空线路和电缆线路的线模波阻抗,Z1_line|Z1_cable表示故障线路要么为架空线路,要么为电缆线路;ZEVT、ZMOA、ZB分别为EVT、MOA以及母线其余设备杂散电容CB的等值阻抗;图中部分阻抗分母处的字符意为该阻抗所对应的并联数目,例如ZMOA/n表示分支出线处共有n个ZMOA并联。由此,可求得折射波的运算微分解为
 (1)
(1)
式中,H(s)为行波信号经线路边界的折射系数,其表达式为
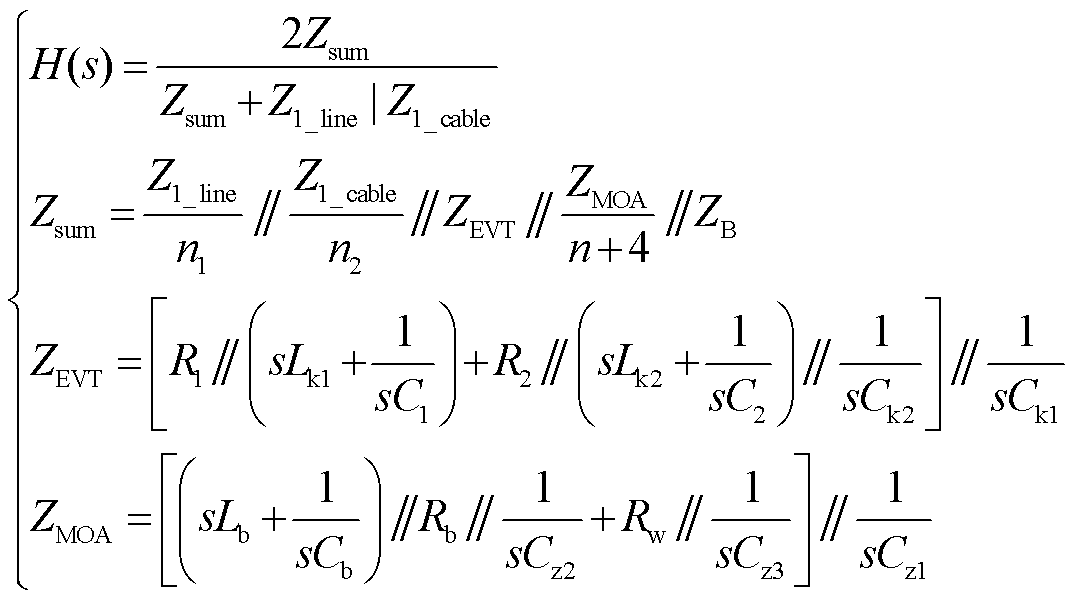 (2)
(2)
式中,“//”表示阻抗的并联运算。
根据附录仿真章节的10 kV输电线路结构可计算得出架空线路的波阻抗Z1_line=341 Ω,电缆线路的波阻抗Z1_cable=53 Ω;考虑母线其余设备杂散电容CB的取值范围为0.1~5 nF;EVT和MOA的暂态电路相关参数见附表1(部分参数来源于实际厂商产品)[21-24]。将上述参数代入式(2)后,可得到不同线路边界下折射系数的幅频特性如图5所示。
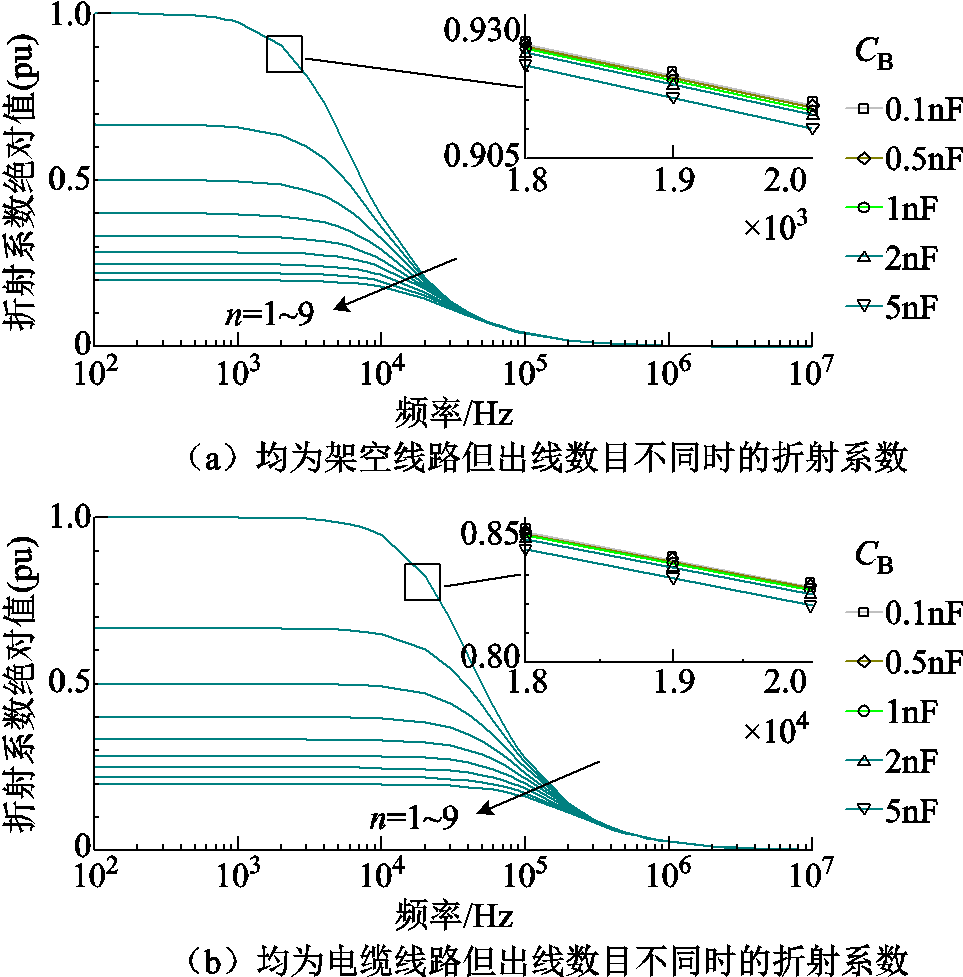
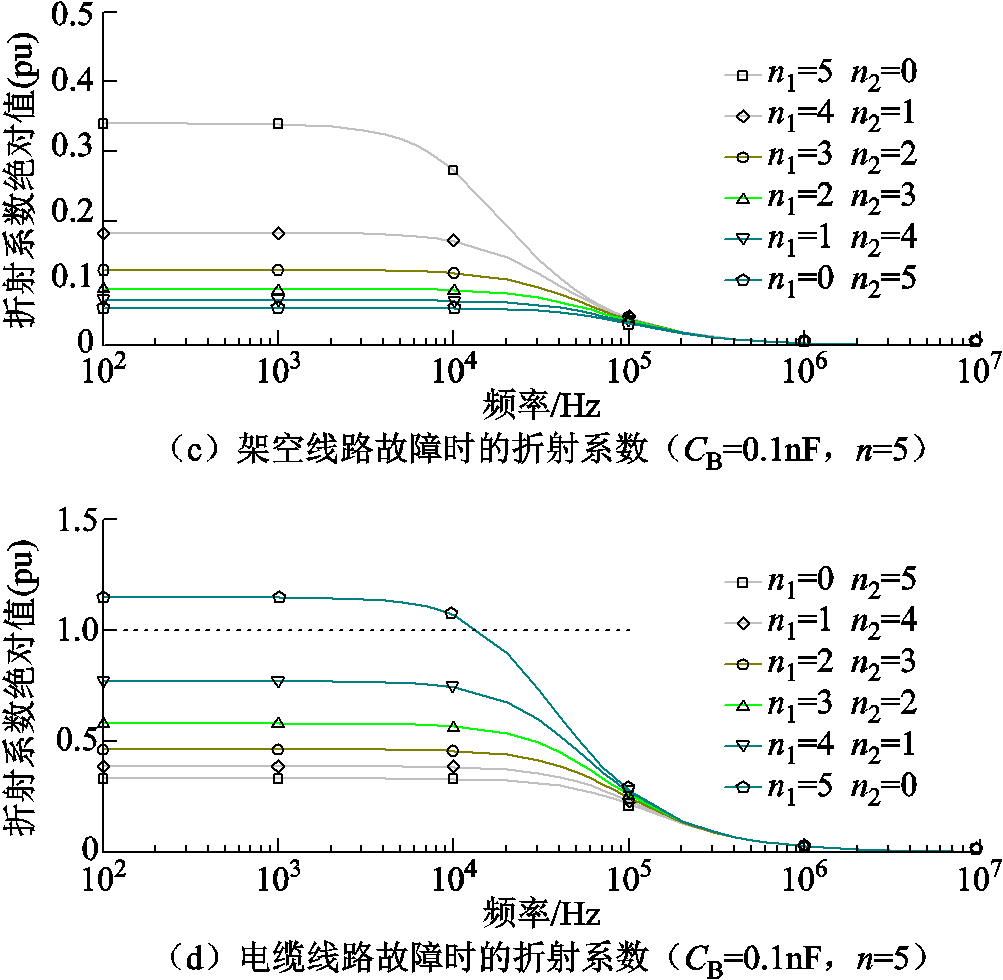
图5 不同线路边界下线模行波折射系数幅频特性曲线
Fig.5 The amplitude-frequency curve of refractive coefficients on line mode traveling waves under different configurations of line boundary
分析可得以下结论:
1)杂散电容CB的取值变化几乎不影响折射系数幅频特性曲线的分布情况,这主要是因为CB的数值较为微小,对于线路边界高频滤波衰减作用的贡献十分有限,但这也从侧面反映出智能变电站所组成的线路边界的折射衰减作用具有较强的鲁棒性。
2)当线路边界的所有出线均为架空线路或者电缆线路时,随着出线数目的增多,线路边界对于104 Hz以下的低频暂态行波的折射衰减作用逐渐增强,但线路边界对于105 Hz以上的高频暂态行波的折射衰减作用则不受出线数目的影响,其始终维持在较高水平。
3)无论故障发生于架空线路还是电缆线路,线路边界对于高频暂态行波始终具有可观的折射衰减作用,而其对于低频暂态行波的折射作用则需视具体情形而定,存在折射行波大于入射行波的可能性。
现进一步分析当母线系统上连接并联电容器时的情况,其中电容器组的接线方式如图6所示[25],其由手车、断路器、放电线圈、接地刀开关、串联空心电抗器、避雷器、电容器组、电流互感器等设备构成。放电线圈用于使电容器组从电力系统中切除后的剩余电荷迅速泄放;空心电抗器用于限制电容器合闸涌流与抑制电网奇次谐波;每相电容器平均分为两组,构成双星形不接地接线,其两中性点串联的电流互感器用于监测电容器组是否正常运行。
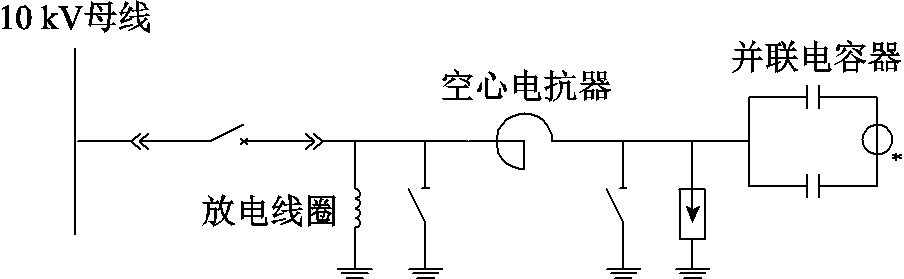
图6 10 kV电容器组一次接线方式
Fig.6 Primary wiring diagram of 10 kV capacitor bank
现以图5c故障发生在架空线路上(CB=0.1 nF)为例,考虑每相电容器组的额定容量为8 106 kvar,空心电抗器取12%的串抗率,可得到此时线路边界折射系数的幅频特性如图7所示。分析图7可知,此时线路边界对于高低频暂态行波的折射衰减作用均十分强烈,线模行波将主要存在于故障线路与电容器上,而健全线路检测得到的线模行波则十分微弱,该分析结果与文献[14,16]所得结论一致。
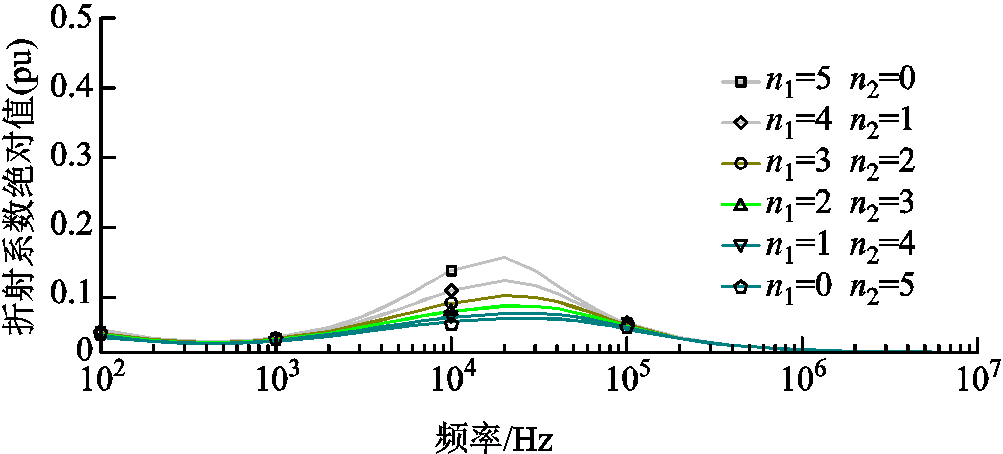
图7 并联电容器组下的线模行波折射系数幅频特性曲线
Fig.7 The amplitude-frequency curve of refractive coefficients on line mode traveling waves under shunt capacitor bank
此外,线路边界对于零模行波的折射衰减作用与图5近似,详细波形如附图2所示,而由于并联电容器采用不接地形式,零模行波无法在电容器内形成对地回路,因此其影响可以忽略。当智能变电站内安装的EVT采用电容分压形式,或母线系统采用双分段接线形式时,所得结论与以上分析近乎一致,限于篇幅不再赘述。
综上所述,对于105 Hz左右的频带而言,10 kV智能变电站母线系统对于线模行波始终具备强健的高频滤波衰减特性,且该衰减作用几乎与母线系统运行方式无关,具有优异的鲁棒特征,由此可为后续配电网线模行波故障选线方法的设计奠定可靠的理论基础。
根据1.2节的理论分析推导可知,母线系统的强烈折射衰减作用将导致故障线路上的行波分量远远超过健全线路,由此可设计区分故障线路与健全线路的全新选线方法。
根据1.2节的分析结论,本文预选取105 Hz左右的频带行波作为研究对象。但是,在高阻故障与小相角接地故障下,故障行波信号相对微弱,高频暂态行波更是极低,此时继续辨识行波的极性与幅值将可能导致误判概率增高,而基于反正行波积分比值的方法也将可能因反正行波十分接近而导致选线方法的灵敏性严重不足。为此,本文选取行波能量作为选线判据的度量指标,并借鉴Teager能量算子引入“瞬时能量”的概念[26],即以信号瞬时幅值与瞬时频率二次方的乘积作为全新的能量计算方式,其计算公式为
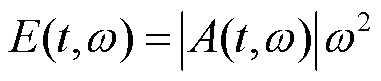 (3)
(3)
式中,E(t, ω)为行波信号在t时刻ω频段下的瞬时能量;A(t, ω)为行波信号在t时刻ω频段下的瞬时幅值。
Teager能量算子能够凸显非平稳信号的幅值突变特征,其与瞬时能量计算公式的联系可详见文献[26]。利用式(3)能够提升高频分量在能量计算中的有效占比,从而有望提升高阻故障与小相角接地故障等工况下选线判据的灵敏度。现基于线模电流行波和波阻抗构造初始正向电压行波信号,并详细分析其在健全线路与故障线路中瞬时能量的特征差异,从而以此设计配电网故障选线判据,具体阐述如下。
1)对于线路故障的判据分析
规定由母线指向线路为正方向,则对于健全线路而言,结合式(3)可将其初始正向电压行波信号的瞬时能量表示为
 (4)
(4)
式中,En为健全线路初始正向电压行波的瞬时能量;H(ω)为母线线路边界的折射系数;Γ(ω)为线路传输函数; 为Γ(ω)的具象表达式;γ(ω)为模量传输系数;
为Γ(ω)的具象表达式;γ(ω)为模量传输系数;![]() 为故障点至母线线路边界的距离;if(ω)为故障线路初始反向电流行波;If为初始反向电流行波if(ω)的幅值;Zf为故障线路波阻抗。
为故障点至母线线路边界的距离;if(ω)为故障线路初始反向电流行波;If为初始反向电流行波if(ω)的幅值;Zf为故障线路波阻抗。
对于故障线路而言,结合式(3)可将其初始正向电压行波信号的瞬时能量表示为
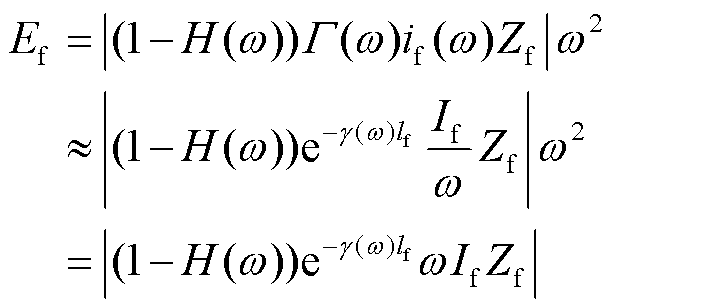 (5)
(5)
式中,Ef为故障线路初始正向电压行波的瞬时能量。
现以图5c故障发生在架空线路上(CB=0.1 nF),故障距离为10 km,n1=4,n2=1为例,根据附录中仿真章节的10 kV输电线路结构能够得到架空线路的线路传输函数,从而可得健全线路与故障线路中初始正向电压行波信号在不同频段下的瞬时能量分布示意曲线如图8所示。
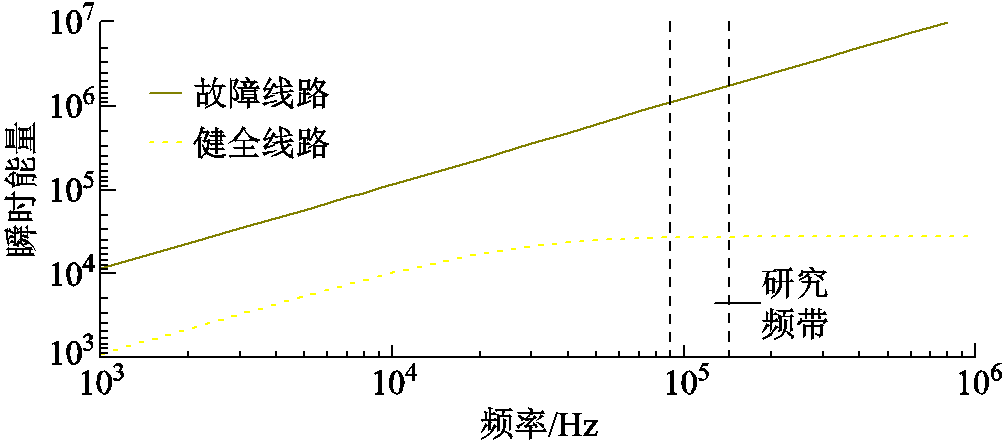
图8 健全线路与故障线路上的瞬时能量分布曲线
Fig.8 The distribution curve of instantaneous energy under normal lines and faulty lines
由图8可知,由于线路边界对于高频分量强烈的折射衰减作用,导致健全线路上的高频瞬时能量远远低于故障线路。进一步分析可知,故障相角、过渡电阻以及线路波阻抗仅会改变式(4)、式(5)中线路上初始电流行波的幅值,但不会影响图8中各条线路上研究频带内瞬时能量的相对大小关系。同时观察可知,此时行波高频分量在瞬时能量计算中的贡献程度显著提高,从而有望提升高阻故障与小相角接地故障下选线判据的灵敏度。
此外,由于线模行波在配网输电线路上的传输衰减十分有限,因此不同故障距离下的瞬时能量分布情况与图8近似。同时,当线路构成为图5中其余工况时,上述所得结论仍然成立,限于篇幅不再赘述。由于故障发生后,被约束在故障线路上的高频瞬时能量远远超过健全线路,因而可设计故障选线判据如下:
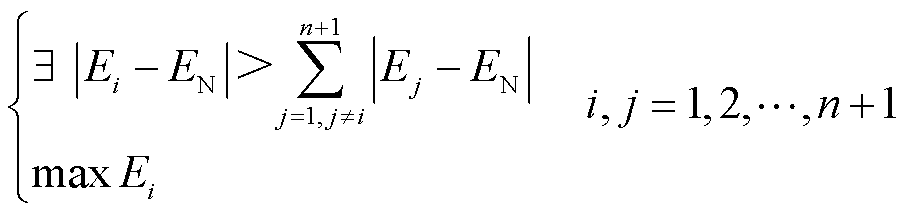 (6)
(6)
式中,∃意为数学逻辑运算符号“存在”;Ei、Ej分别为第i条和第j条线路上研究频带内的高频瞬时能量;EN为所观察的高频瞬时能量中的中位数,如遇偶数则取最中间两个数值的平均数。
由式(6)可知,若存在第i条线路的正向电压行波高频瞬时能量的中位数绝对偏差大于其余所有线路之和,则判定发生线路故障,且第i条线路为故障线路,其余线路为健全线路。上述证明过程见附录。
2)对于母线故障的判据分析
当发生母线故障时,由于所有线路均与母线相连,因此各条线路上感受到的因电压突变产生的初始正向电压行波近似相等,结合式(3)可将其在各条线路上的瞬时能量表示为
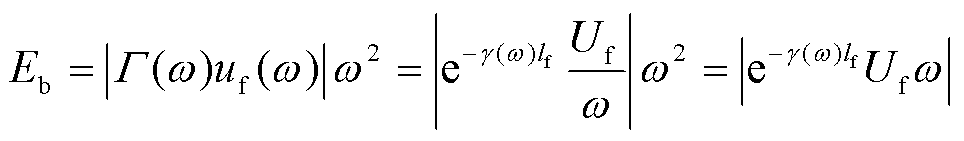 (7)
(7)
式中,Eb为母线故障时线路初始正向电压行波的瞬时能量;uf(ω)为母线故障时线路初始正向电压行波;Uf为初始正向电压行波uf(ω)的幅值。
仍然以图5c故障发生在架空线路上(CB=0.1 nF),故障距离为10 km,n1=4,n2=1为例,可将母线故障时各条线路中初始正向电压行波信号在不同频段下的瞬时能量分布示意曲线绘制如图9所示。
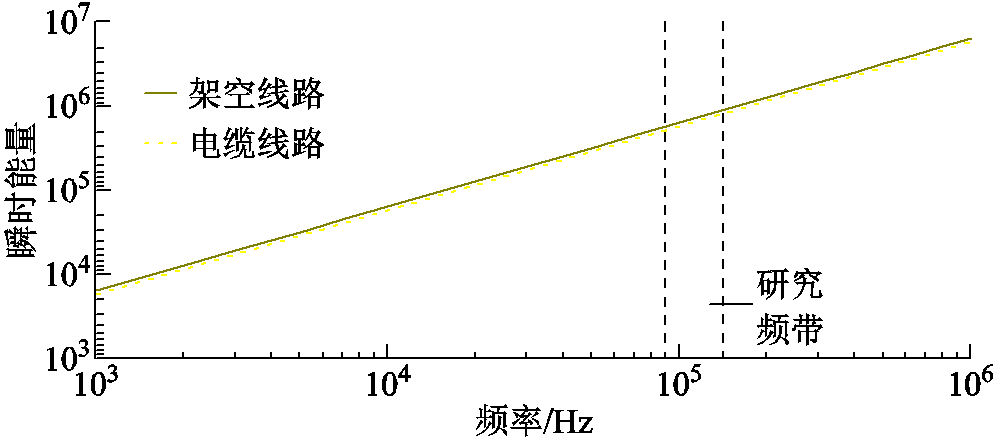
图9 母线故障时各条线路上的瞬时能量分布曲线
Fig.9 The distribution curve of instantaneous energy of each line under busbar fault
由图9可知,各条线路上研究频带内的高频瞬时能量的大小近乎一致,故而能够与线路故障实现明显区分,因而可设计出母线故障判据,即
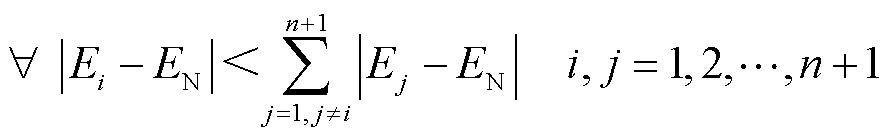 (8)
(8)
式中,∀表示数学逻辑运算符号“任意”。
由式(8)可知,若满足任意第i条线路的正向电压行波高频瞬时能量的中位数绝对偏差均小于其余所有线路之和,则判定发生母线故障。
综上所述,各条线路中正向电压行波信号的高频瞬时能量在线路故障与母线故障时存在显著差异,因此本文选取正向电压行波信号作为故障选线的依据。本文未采用目前业界主流电流行波信号的方式,其主要原因是:当发生线路故障时,故障线路中正向电流行波信号的高频瞬时能量大于健全线路;当发生母线故障时,由于各条线路波阻抗存在差异,各条线路正向电流行波信号中的高频瞬时能量不尽相同,故而,若采用正向电流行波信号的高频瞬时能量,则在线路故障与母线故障时无法可靠区分。
此外,本文优先选取线模行波作为所提选线方法研究参量的原因主要包括以下几个方面:①由1.2节分析可知,在母线并联电容器投入运行后,线路边界对于线模行波的折射衰减作用相比零模行波将更为强健,换而言之,此时故障线路与健全线路上线模行波的高频瞬时能量差异相比零模行波将更为显著,本文方法采用线模行波将具备更高的灵敏性与可靠性;②当配网线路只安装两相电流互感器时,零模行波难以获取,而线模行波的获取则几乎不受影响;③当较长线路末端发生故障时,由于零模行波衰减较快,在保护安装处可能无法有效采集到零模高频分量,而相比之下线模行波衰减较慢,本文方法采用线模行波相比零模行波在上述故障工况下更具优势。
本文所提的配电网故障选线方法流程如图10所示。
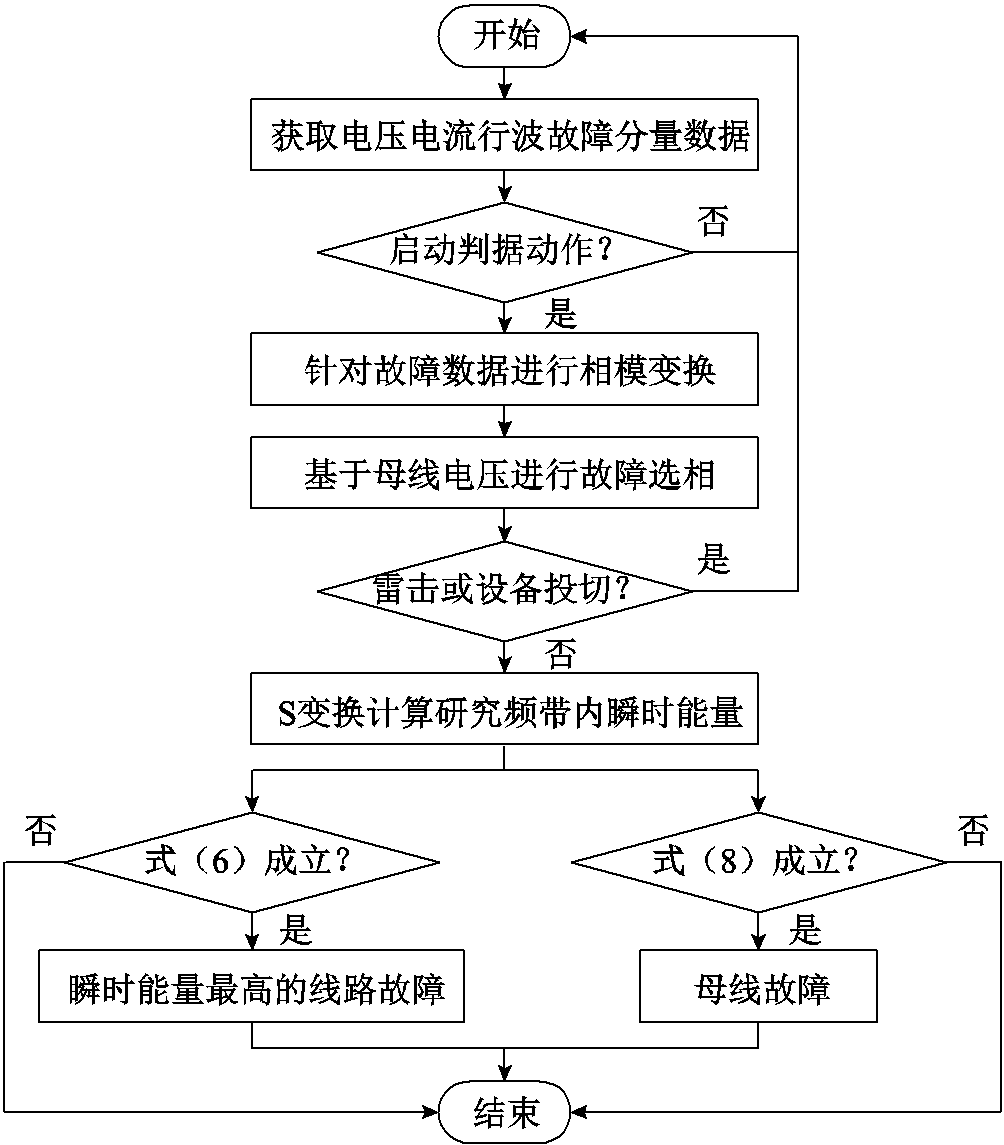
图10 配电网故障选线流程
Fig.10 The algorithm flow chart of the fault line selection in the distribution network
具体实现步骤阐述如下:
(1)获取各条线路故障前后各工频一周波的三相电流数据和母线电压数据,并求取其各自故障行波。
(2)当母线零序电压瞬时值大于设定阈值KrelUN时,立即启动故障选线,其中,Krel为可靠启动系数,UN为母线额定电压。
(3)对电压、电流数据进行凯伦贝尔相模变换,其计算公式为
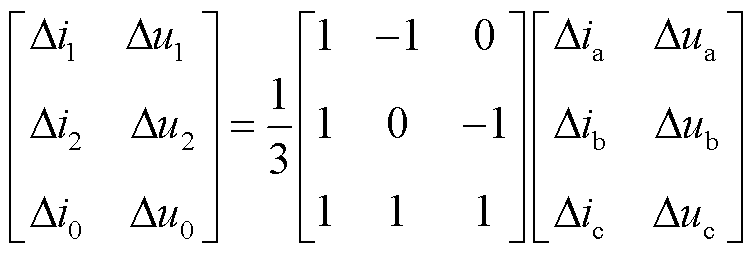 (9)
(9)
式中,Δi1、Δi2、Δi0和Δu1、Δu2、Δu0分别为电流和电压故障行波的1模、2模、0模数据;Δia、Δib、Δic和Δua、Δub、Δuc分别为电流和电压故障行波的a相、b相、c相数据。
(4)利用母线三相电压进行故障选相。根据故障选相结果,当发生a相或b相故障时,可选取1模或2模电流作为研究对象;当发生c相故障时,选取2模电流作为研究对象。
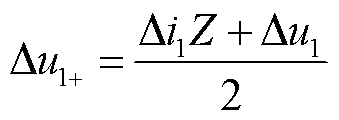 (10)
(10)
式中,Δu1+为正向电压行波1模行波;Z为线路波阻抗,其求取方式可参考文献[27]。
(5)基于波形特性差异可有效辨识雷击故障[28],基于合闸后暂态电流自振荡频率差异等可有效区分设备投切产生的瞬时放电干扰[29],从而能够避免雷击故障、设备投切等非线路故障扰动对于本文所提选线方法可靠性的影响。
(6)当线路故障发生后,本文选取S变换计算各条线路研究频带内电压行波的瞬时能量,其计算公式为
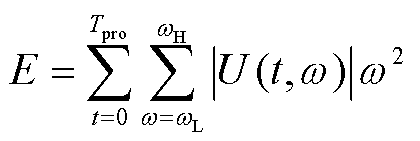 (11)
(11)
式中,E为保护采样窗长内总频带能量;Tpro为保护采样时间窗长;ωL为频带范围下限;ωH为频带范围上限;U(t, ω)为初始正向电压行波在t时刻ω频段下的瞬时幅值。
(7)将所得的电压行波瞬时能量代入式(6)与式(8)分别进行判断:当式(6)成立时,则判定发生线路故障,并确定瞬时能量含量最高的线路为故障线路;当式(8)成立时,则判定发生母线故障。
2.3.1 高频信号的传变特性分析
实际工程案例中,故障行波频率大多集中在8~200 kHz[15],而无论是电磁式、电子式抑或是光学式电流互感器,均能够可靠传变几百kHz的高频信号。电子式电压互感器同样具备优良的传变特性,其截止频率甚至高达10 MHz[20]。因此,智能变电站内的电压、电流互感器采集的暂态行波信号能够满足故障选线流程的数据要求。
2.3.2 采样窗长的理论选取依据
故障行波的高频瞬时能量主要集中在初始正向行波中,这是因为后续的多次折反射过程将导致其快速衰减。虽然2.1节仅分析了初始正向电压行波的高频瞬时能量,但其实所有后续的正向电压行波仍然满足上述所分析的边界折反射规律,亦即适用于本文所提判据。由式(11)可知,瞬时能量的计算方式是采样时间段内的所有能量之和,因此计算所得的高频瞬时能量将随着保护采样时间窗长Tpro的增大而增大,并逐渐趋于稳定值。基于上述分析,为了保证选线判据的可靠性,规定保护采样时间窗长至少包含初始正向行波和第二次正向行波,即
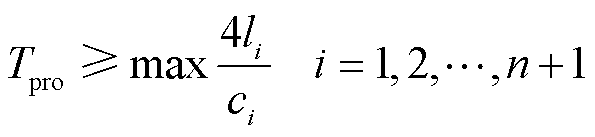 (12)
(12)
式中,li为第i条线路的输电长度;ci为第i条线路中线模行波的传输速度。
由式(12)可知,在适当延长采样数据窗长的情况下,累计计算的高频瞬时能量能够扩大故障线路与健全线路之间计算结果的差异,但过长的采样数据窗长也会给保护装置硬件增加计算负担,采样时间窗长的合理选取需协调上述两者之间的矛盾。
2.3.3 线路边界的鲁棒强度检验
现以图5a中当CB=0.1 nF,出线分支数量n=5时,100 kHz下所对应的折射系数绝对值为研究对象。以附表1中的所有参数为参考值,并考虑其上下浮动变化10%时折射系数绝对值的变化程度,不同参数数值下折射系数变化程度如图11所示。

图11 不同参数数值下折射系数变化程度
Fig.11 The variation of refraction coefficient with different parameter values
由图11可知,智能变电站线路边界的折射系数主要受EVT的参数C1的影响,而其余参数的影响微乎其微,这主要是由元件各参数的数量级差异以及其串并联后的主导关系造成的。此外,工程实证经验表明,当EVT的部分分压电容发生受潮、老化、温升甚至击穿时,其主电容参数仍然能够保持在额定值附近[30],由此表明,智能变电站线路边界的高频滤波特性不易受外界环境的影响,其能够为故障选线方法的可靠性提供有效保障。
基于PSCAD/EMTDC仿真软件平台搭建如图12所示的10 kV配电网输电系统,并搭建如图2所示的母线系统。其中,输电线路结构详见附图1;考虑母线其余设备杂散电容CB的取值为0.1 nF;110 kV/10 kV变压器中性点采用不接地方式;母线系统共接6条出线,L1、L2为架空线路,L3、L4为电缆线路,L5为架空-电缆混联线路,L6为含有分支的架空线路;输电线路末端均采用10 kV/0.4 kV变压器与负荷相连,所有负荷均以(4+j1)MV·A消耗功率来模拟。

图12 10 kV配电网输电系统
Fig.12 Transmission system of 10 kV distribution network
仿真模型采用500 kHz采样率。根据2.3节的理论分析,经仿真初步测试后确定,截取初始波头到达后的200 μs时间窗长计算故障后各条线路出口的电压行波高频瞬时能量。
现于线路L2处设置故障,故障相角θ为90°,过渡电阻Rf为0 Ω,故障距离lf为5 km,此时健全线路L1和故障线路L2上正向电压行波信号频谱能量的分布规律如图13所示。
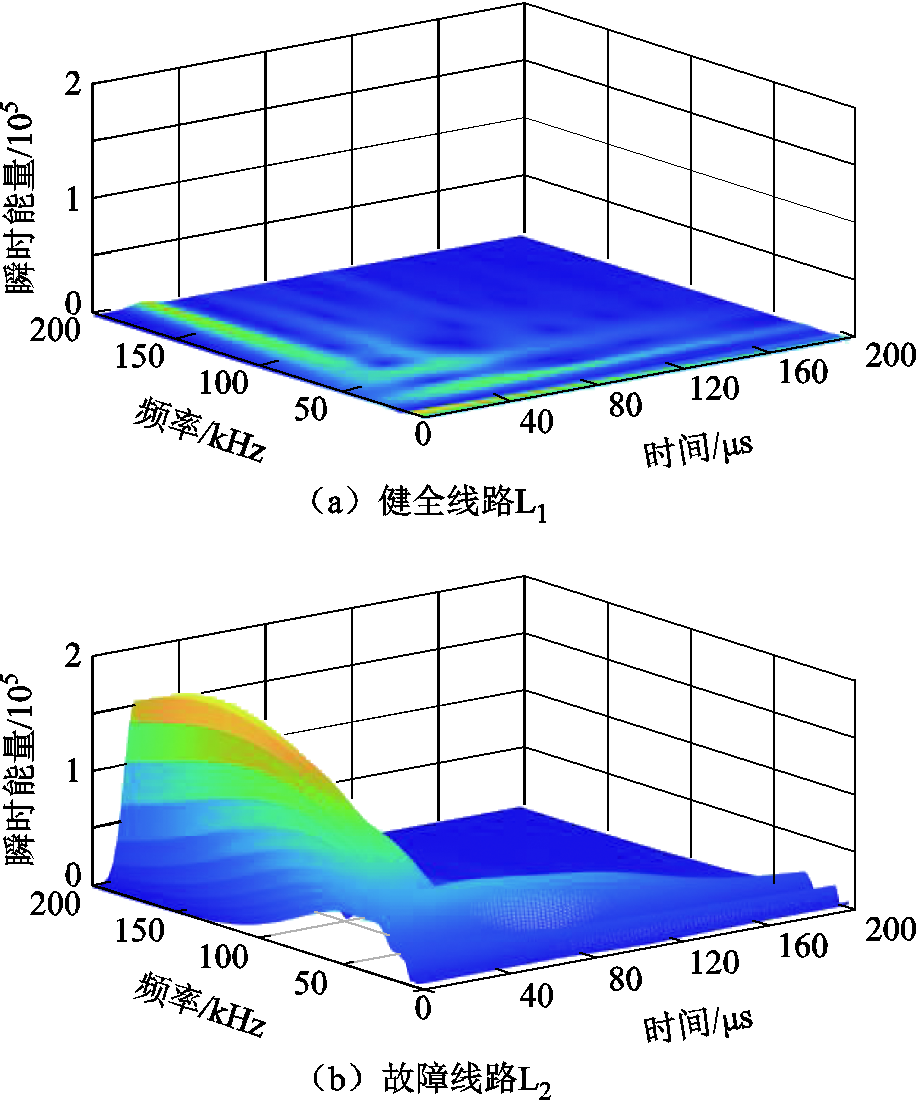
图13 故障暂态行波信号频谱特性
Fig.13 Spectrum characteristics of fault transient traveling waves
分析可得以下结论:
(1)故障线路与健全线路上的高频瞬时能量存在明显的区分,这从侧面证实了本文所研究的线路边界具备强健的高频滤波衰减特性。
(2)故障线路上的行波信号主要分布在1~ 200 kHz之间,且本文基于Teager能量算子放大了高频分量在行波信号频谱特性中的占比,使得高频瞬时能量大多集中在100~200 kHz之间。
(3)值得注意的是,本文图12仿真系统对应于图5c中n1=2,n2=3的情形,此时线路边界效应十分强健,因此图13中故障线路与健全线路上的高频瞬时能量在全频带下均存在明显区分。但为使得研究频带的选取不受母线系统运行方式的影响,根据图13所示的高频瞬时能量分布区域,以及图5、 图7所示的线路边界幅频特性曲线可知,本文所提选线方法的研究频带宜选择为100~200 kHz。考虑避免高频干扰信号的影响,本文最终选取100~ 125 kHz作为选线方法研究频带。
为了严格且全面地验证本文所提故障选线方法的有效性,现设置如下仿真条件:
(1)故障相别以A相短路接地为例。
(2)根据实际经验总结,考虑单相短路接地时的最小故障相角θ为5°,此外,设置故障相角θ在10°~90°之间以每10°递增。
(3)根据实际经验总结,设置过渡电阻Rf在0~2 kΩ之间以每200 Ω递增。
(4)由于仿真平台可设置的最近故障位置受限于采样率的大小,因此设置最近故障位置lf为0.5 km,此外,设置故障位置lf在线路全长间以每1 km递增。
现根据上述仿真条件设置如下四类仿真场景,并求取各条线路出口的电压行波高频瞬时能量,以验证线路故障时选线方法的有效性。
(1)设置线路L2故障,故障相角θ为50°,过渡电阻Rf为200 Ω,故障距离lf为6 km,此时故障选线结果如图14a所示。
(2)设置线路L4故障,过渡电阻Rf为0 Ω,故障距离lf为4 km,此时不同故障相角下的故障选线结果如图14b所示。
(3)设置线路L5故障,故障相角θ为90°,过渡电阻Rf为1 kΩ,此时不同故障距离下的故障选线结果如图14c所示。
(4)设置线路L6故障,故障相角θ为10°,故障距离lf为9 km,此时不同过渡电阻下的故障选线结果如图14d所示。
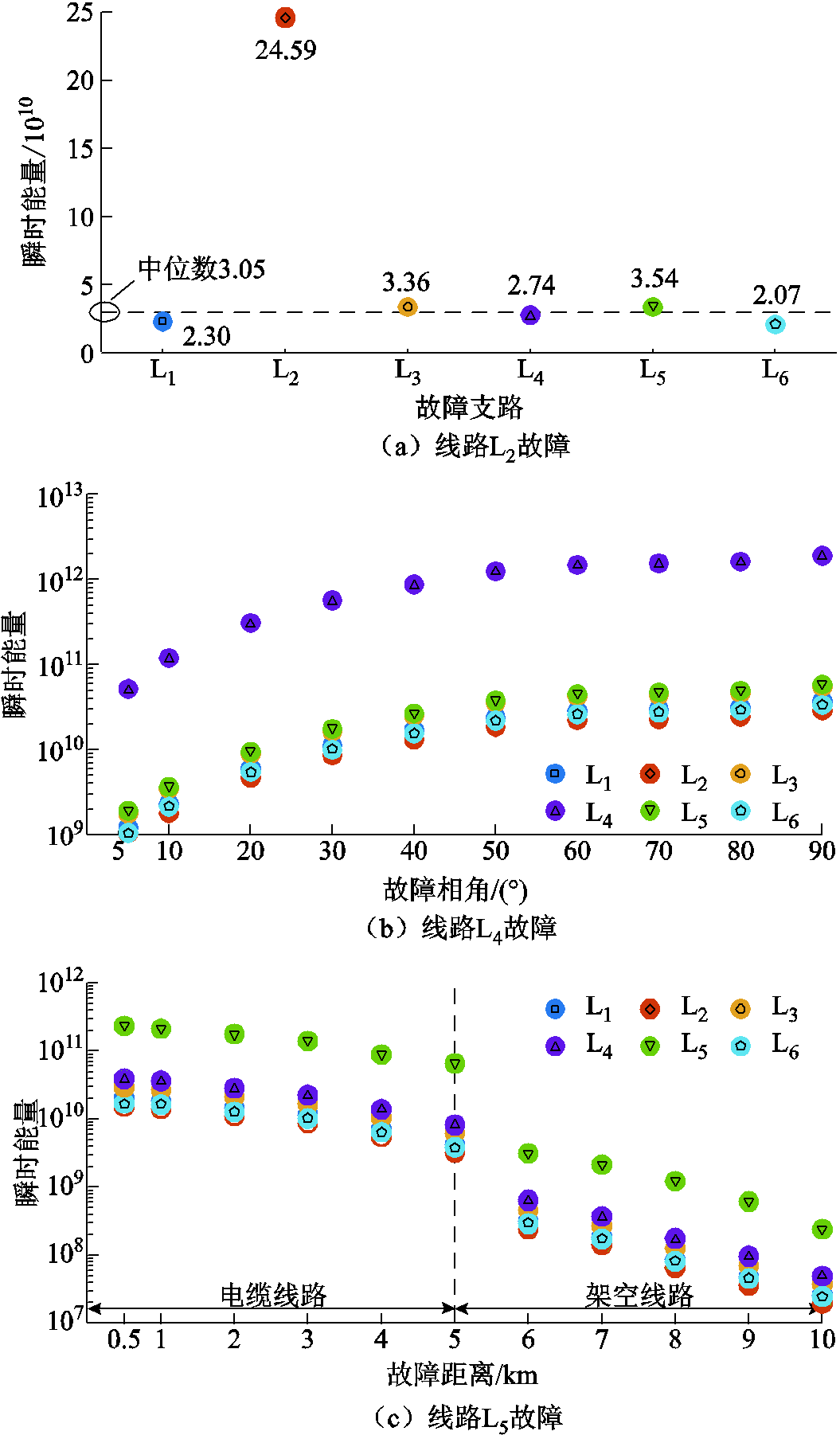
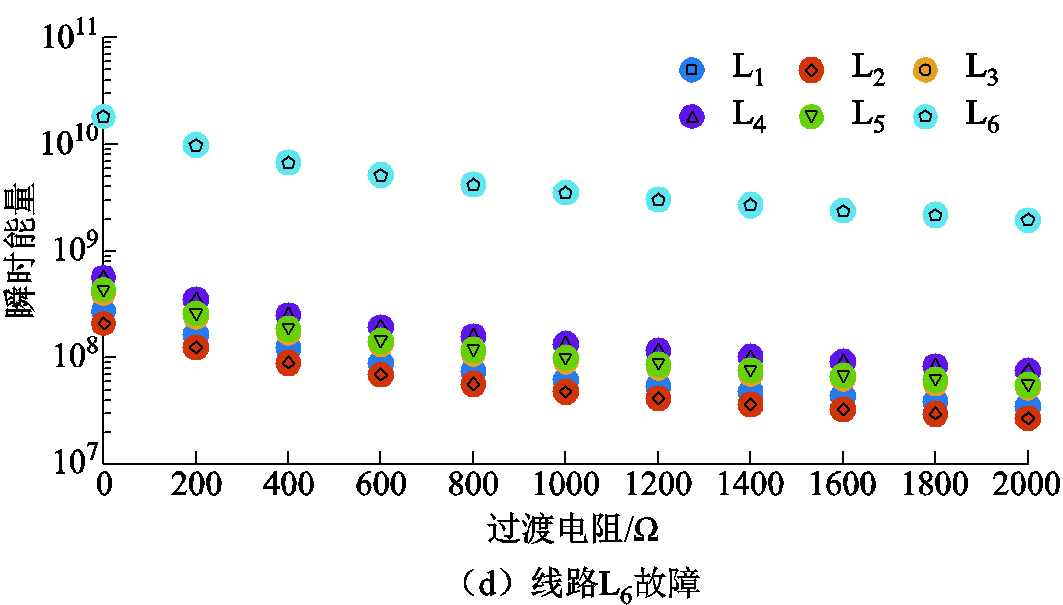
图14 线路故障时选线判据动作情况
Fig.14 The action results of faulty line selection criterion in case of line faults
现根据图14所示的选线结果,分析可得以下结论:
(1)以线路L2故障为例,此时线路L2的正向电压行波高频瞬时能量的中位数绝对偏差为21.54×1010,而其余所有线路的中位数绝对偏差之和为2.84×1010,因此式(6)成立,判定L2线路发生故障。
(2)当故障发生后,各条线路上正向电压行波的高频瞬时能量随着故障相角的增大而增大,随着故障距离、过渡电阻的增大而减小。由图14b~图14d可知,在不同的故障相角、故障距离、过渡电阻之下,本文所提的选线方法均能够可靠识别故障线路,故障线路与健全线路上的高频瞬时能量存在明显的区分。此外,由图14c可知,即使在近距离0.5 km的故障工况下,所提选线方法同样能够可靠动作。
(3)由于架空线路与电缆线路的波阻抗不相等,导致在架空-电缆混联的线路L5的架空线路上出现故障时,行波高频分量在传输进入电缆线路时便发生了衰减,因此在架空-电缆线路连接点前后分别发生故障时,线路上所测量得到的正向电压行波的高频瞬时能量存在较大的突变,但由于本文是利用母线系统的高频衰减特性进行故障选线的,因此故障产生的行波分量在经过母线系统后,均存在故障线路上的行波高频瞬时频带能量大于健全线路,故障行波在连接点前后的突变不会影响本文所提选线方法的可靠动作。以上分析同样适用于解释含有分支的架空线路L6在分支节点前后发生故障时的场景。
同样根据3.2节仿真条件设置如下两类仿真场景,并求取各条线路出口的电压行波高频瞬时能量,以验证母线故障时选线方法的有效性。
(1)设置母线故障处的过渡电阻Rf为400 Ω,此时不同故障相角下的故障选线结果如图15a所示。
(2)设置母线故障处的故障相角θ为90°,此时不同过渡电阻下的故障选线结果如图15b所示。
分析图15可知,不同于线路故障工况,母线故障下各条线路中的正向电压行波高频瞬时能量近似相等,其满足式(8)所示的任意线路正向电压行波高频瞬时能量的中位数绝对偏差均小于其余所有线路之和,因此能够有效识别出母线故障,且本文所提选线方法在母线不同故障过渡电阻与不同故障相角下均能够可靠动作。
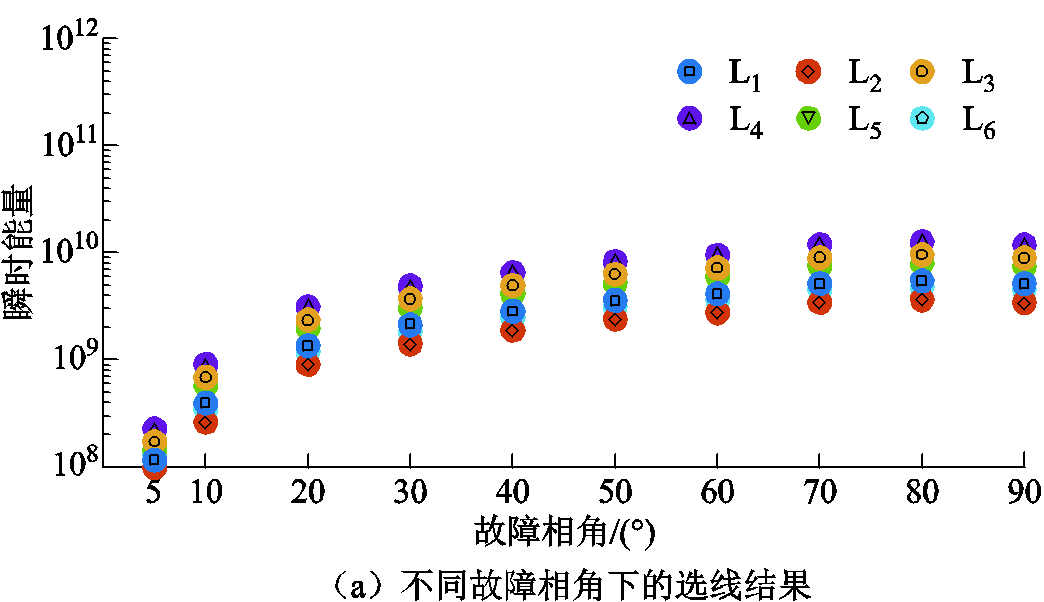

图15 母线故障时选线判据动作情况
Fig.15 The action results of faulty line selection criterion in case of busbar fault
3.4.1 母线并联补偿电容器的影响
由前述理论分析可知,当母线系统上连接并联补偿电容器时并不会影响本文所提故障选线判据的可靠性。现于线路L1和L3处设置故障,故障相位θ=40°,过渡电阻Rf=600 Ω,故障距离lf=5 km,母线不同补偿方式下的故障选线结果见表1。
表1 基于母线并联补偿电容器的选线结果
Tab.1 Simulation results based on busbar shunt capacitor

补偿方式故障线路高频瞬时能量选线结果 无补偿L1[12.43, 1.10, 1.59, 1.59, 1.58, 0.93]×109L1 L3[1.09, 0.84, 55.97, 1.62, 1.60, 0.96]×109L3 电容器补偿L1[90 133, 3.22, 4.71, 4.72, 4.63, 2.77]×105L1 L3[3.08, 2.40, 61 755, 4.59, 4.59, 2.75]×105L3
分析表1数据可知,本文所提选线方法完全适用于母线并联电容器的配电网,且在补偿电容器投入后,故障线路与健全线路上的高频瞬时能量的区分程度相比无补偿时更加明显,推测可知此时线模行波将主要存在于故障线路上,而健全线路检测得到的线模行波则将十分微弱,这与1.2节的理论分析相符。
3.4.2 中性点不同接地方式的影响
配电网系统中性点接地方式主要包括消弧线圈接地和不接地两种方式。现于线路L2和L4处设置故障,故障相角θ=70°,过渡电阻Rf=1.8 kΩ,故障距离lf=1 km,中性点不同接地方式下的故障选线结果见表2。
表2 基于中性点不同接地方式的选线结果
Tab.2 Simulation results based on different neutral grounding modes

接地方式故障线路高频瞬时能量/108选线结果 消弧线圈接地L2[4.69, 37.99, 6.87, 6.89, 6.87, 4.19]L2 L4[2.49, 1.92, 3.66, 128.61, 3.66, 2.27]L4 不接地L2[1.78, 14.43, 2.60, 2.68, 2.61, 1.59]L2 L4[0.91, 0.72, 1.34, 47.11, 1.34, 0.83]L4
根据理论分析可知,由于变压器的等值阻抗呈感性,其在高频下可近似处理为开路,故变压器中性点连接方式几乎不会对线模故障行波的传输过程产生影响,高频瞬时能量仍然集中约束在故障线路上,因此本文所提选线方法的可靠性与中性点接地方式无关。
3.4.3 不同程度噪声干扰的影响
在工程应用中,需考虑外界噪声干扰对接地选线结果的影响。现于线路L5和L6处设置故障,故障相角θ=30°,过渡电阻Rf=1.2 kΩ,故障距离lf=0.5 km,不同随机白噪声干扰下的故障选线结果见表3。
表3 基于不同程度噪声干扰的选线结果
Tab.3 Simulation results based on different levels of noise
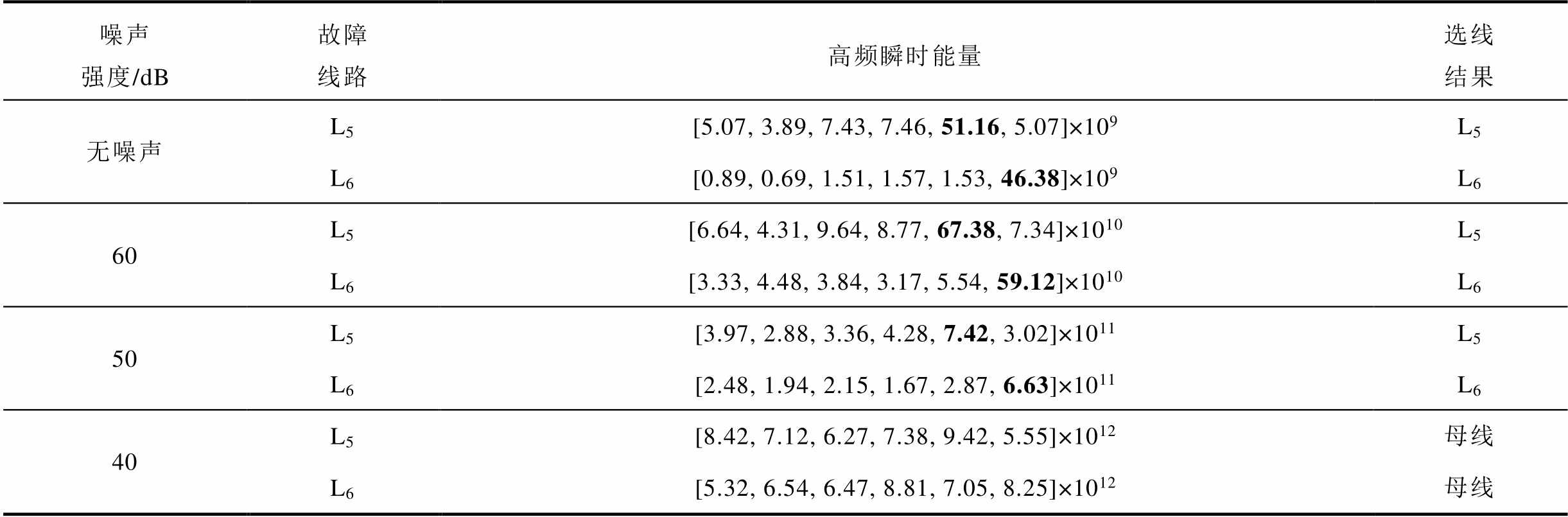
噪声强度/dB故障线路高频瞬时能量选线结果 无噪声L5[5.07, 3.89, 7.43, 7.46, 51.16, 5.07]×109L5 L6[0.89, 0.69, 1.51, 1.57, 1.53, 46.38]×109L6 60L5[6.64, 4.31, 9.64, 8.77, 67.38, 7.34]×1010L5 L6[3.33, 4.48, 3.84, 3.17, 5.54, 59.12]×1010L6 50L5[3.97, 2.88, 3.36, 4.28, 7.42, 3.02]×1011L5 L6[2.48, 1.94, 2.15, 1.67, 2.87, 6.63]×1011L6 40L5[8.42, 7.12, 6.27, 7.38, 9.42, 5.55]×1012母线 L6[5.32, 6.54, 6.47, 8.81, 7.05, 8.25]×1012母线
分析表3数据可知,本文所提故障选线方法本身具有一定程度的抗噪能力,但由于瞬时能量计算方式放大了噪声信号,因此随着信噪比的降低,计算所得的高频瞬时能量严重偏离实际值,可能会导致本选线方法甚至出现误判。在实际应用中,应综合考虑硬件屏蔽与隔离、软件滤波算法等降噪措施,以有效提高选线方法的可靠程度。同时后续还需进一步研究本文所提选线方法在抗干扰方面的改进方案。
3.4.4 间歇性电弧接地故障的影响
根据弧光接地现象和电弧特征,可在PSCAD仿真模型中搭建Mayr电弧模型[16],其表达式为
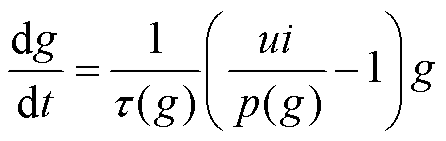 (13)
(13)
式中,g为单位长度电弧导数,其为时间t的函数;τ(g)为电弧惯性时间常数;p(g)为单位长度电弧能量损耗;u为电弧电压;i为电弧电流。
通过控制τ(g)和p(g)可实现电弧的熄灭与重燃特性,从而验证本文所提方法的适应性。现于线路L1处设置电弧故障,故障相角θ=90°,故障距离lf=8 km,故障选线结果见表4。
表4 基于电弧故障的选线结果
Tab.4 Simulation results based on arc fault

τ(g)/10-5p(g)/10-4高频瞬时能量/109选线结果 510[23.15, 2.91, 3.56, 3.54, 3.55, 2.83]L1 1010[21.87, 2.74, 3.39, 3.36, 3.38, 2.61]L1 205[19.95, 2.54, 3.21, 3.17, 3.21, 2.44]L1 503[18.36, 2.40, 3.07, 3.03, 3.07, 2.36]L1
分析表4数据可知,本文所提选线方法能够可靠适应于间歇性电弧故障。这是因为电弧产生的高频分量在经过母线系统后,均存在故障线路上的行波高频瞬时频带能量大于健全线路。本文所提选线方法在电弧故障下具有较好的选线效果。
3.4.5 末端高阻接地的影响
在3.2节与3.3节的仿真验证中,仅分析了2 kΩ过渡电阻工况下的选线性能,现探究本文所提选线方法能够耐受过渡电阻的能力上限。现于线路L2末端位置处设置故障,故障相角θ=20°,故障距离lf=10 km,并考虑60 dB的噪声环境,不同过渡电阻下的故障选线结果见表5。
表5 基于线路末端高阻接地的选线结果
Tab.5 Simulation results based on high resistance grounding at the end of line

过渡电阻/kΩ高频瞬时能量/109选线结果正确与否 2.0[3.38, 10.98, 2.71, 2.81, 3.06, 3.41]L2正确 2.5[3.12, 7.83, 2.91, 3.50, 3.89, 3.50]L2正确 3.0[3.72, 5.89, 3.59, 2.76, 3.43, 3.18]L2正确 3.5[3.87, 3.98, 3.33, 2.82, 3.64, 2.61]母线错误
分析表5数据可知,本文所提选线方法能够耐受过渡电阻的能力上限约为3 kΩ。同时,随着过渡电阻的不断增大,故障行波幅值逐渐减小,计算所得的高频瞬时能量同样逐渐减小,在考虑噪声干扰的误差情况下,健全线路与故障线路上的高频瞬时能量区分程度逐渐降低,所提选线方法的可靠性能严重下降。
3.4.6 波阻抗测量误差的影响
由式(10)可知,本文所提选线方法需要准确测量输电线路线模波阻抗,但因计算误差等因素影响,测量所得的波阻抗数值未必准确,现分析其对本文所提选线方法可靠性能的影响。现于线路L3处设置故障,故障相位θ=80°,过渡电阻Rf =100 Ω,故障距离lf =4 km,当线路L2和线路L3的波阻抗存在一定测量偏差时,故障选线结果见表6。其中,ZL2和ZL3分别为线路L2和线路L3波阻抗的测量值。
表6 基于波阻抗测量误差的选线结果
Tab.6 Simulation results based on measurement error of surge impedance

ZL2/ ΩZL3/Ω高频瞬时能量/1013选线结果 33951[1.27, 1.19, 7.50, 1.32, 1.93, 1.23]L3 34052[1.27, 1.19, 7.66, 1.32, 1.93, 1.23]L3 34153[1.27, 1.19, 7.81, 1.32, 1.93, 1.23]L3 34355[1.27, 1.19, 8.12, 1.32, 1.93, 1.23]L3
分析表6数据可知,波阻抗测量误差对于健全线路的高频瞬时能量而言几乎不产生影响,这是因为线路边界强健的折射衰减作用使得健全线路上的行波电流十分微弱,由式(10)可知,此时波阻抗对于正向电压行波的影响非常小;故障线路的高频瞬时能量将随着测量波阻抗的增大而逐渐增大,但在上述工况下所提选线方法仍然能够可靠识别故障线路。考虑到波阻抗测量误差通常较小,因此其并不会对本文所提选线方法的可靠性能造成太大的干扰。
基于零模暂态行波构造的故障选线判据形式多样,其中利用反正向零模电流行波积分比值的选线方法属于当前主流选线方法。现于线路L2末端处设置故障,故障相位θ=10°,过渡电阻Rf=2 kΩ,以线路L1和线路L2为例,反正向行波积分比值方法与本文所提方法的选线对比结果如图16所示。
分析图16可知,由于配电网母线线路边界的衰减特性,健全线路上的线模、零模行波信号均十分微弱,因此对于反正向行波积分比值方法而言,此时健全线路上分解所得反正向零模电流行波十分接近,积分比值近乎为1,因此导致此时该方法灵敏度严重不足,对于健全线路的误判概率大大增加;而本文方法仅提取了正向电压行波,其在健全线路与故障线路上的区分十分显著,计算得到此时故障线路的高频瞬时能量为6.09×106,健全线路的高频瞬时能量为4.16×105,本文方法能够可靠实现故障选线。
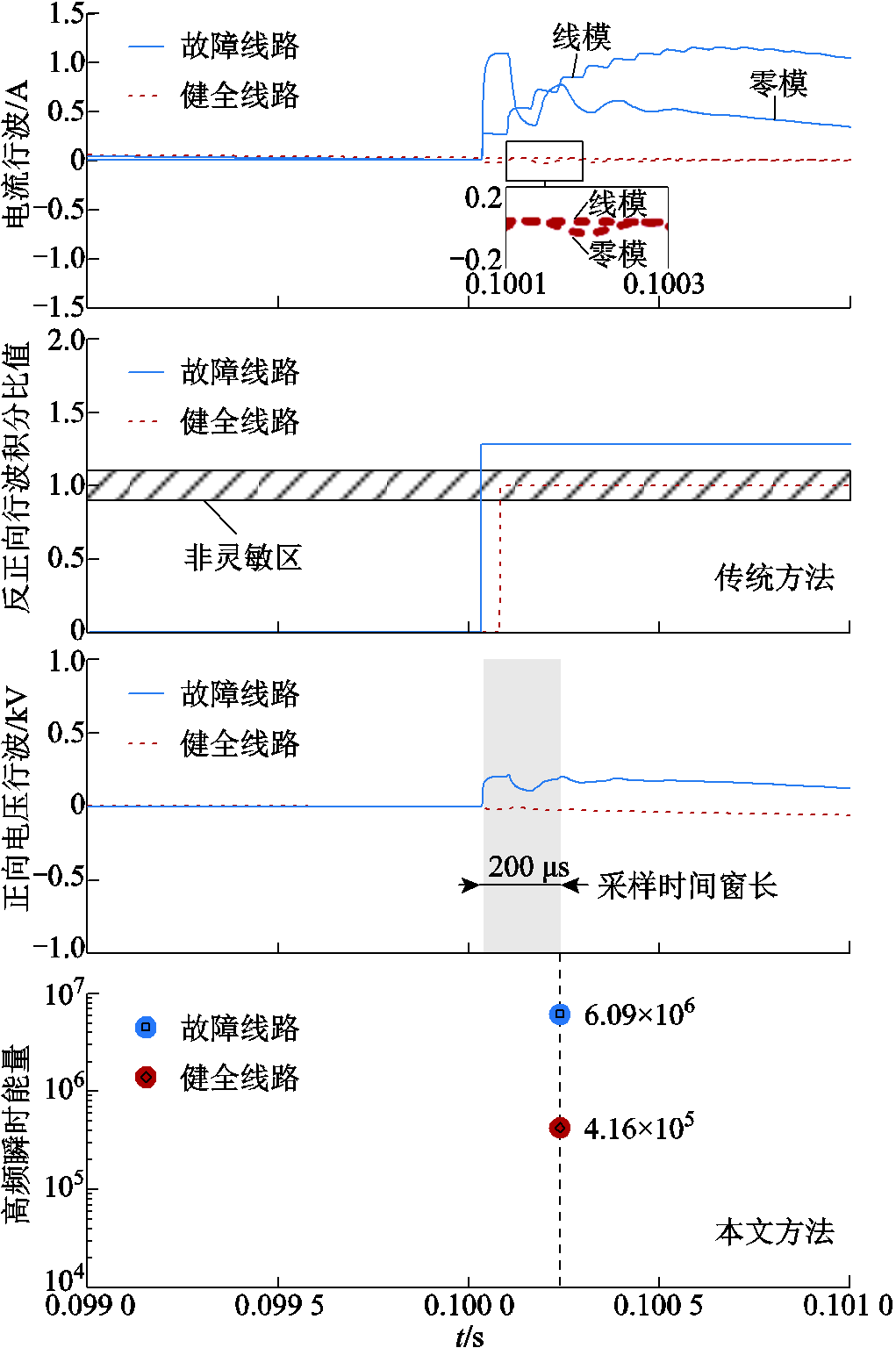
图16 不同选线方法性能结果对比
Fig.16 The performance comparison of different faulty line selection criterions
但是,反正向行波积分比值方法相比本文所提方法而言,其又具备无需故障选相,选线具备自具性(自具性:仅利用本支路故障特征进行故障选线,不与其他支路相比较[15])等优点,因此,本文所提的线模选线方法与基于零模的选线方法均拥有其相对的优势条件,两者相互补强能够更加完整地反映故障特征,这为未来行波选线法的多判据智能融合提供了更多的故障辨识视角。
本文研究发现线模电压行波因线路边界衰减作用而导致健全线路和故障线路上的高频瞬时能量存在特征差异,并基此设计了选线判据。通过理论分析和大量仿真算例可得如下结论:
1)信号选取:基于线模行波的选线方法不受系统接地方式与运行状态的影响,获取方式简单,故障特征明显,其可与基于零模行波的选线方法协同工作以增强对于故障信息的全局把握。
2)判据设计:利用Teager能量算子能够显著强化健全线路与故障线路在高阻故障与小相角接地故障下高频瞬时能量的差异性,有效提升选线判据的灵敏性与可靠性。
3)故障判定:本文所提故障选线方法动作速度快,抗噪性能好,算法原理简单,物理意义明确,无需人工设置阈值,不受补偿电容器的影响,在3 kΩ高阻接地故障与电弧故障下均能实现配电网可靠选线。
本文所提选线方法仅适用于安装了EVT的智能变电站,智能变电站作为坚强智能电网的重要基础和支撑,已成为我国当前变电站建设与改造的主体形式,也为本文所提选线新方法的广泛应用提供了实际基础。此外,本文的未来工作展望是将尝试获取实际配电网故障录波数据,从而对所研究的线路边界效应及选线方法的有效性进行充分验证。
附 录
1. 系统仿真参数
附表1 EVT和MOA暂态电路参数
App.Tab.1 The transient circuit parameters of EVT and MOA

参数数值参数数值 C1/μF0.22Lb/μH0.15 C2/nF2.00Cb/pF1000 R1/MΩ40Rb/MΩ100 R2/MΩ20Cz1/pF63 Lk1/μH0.5Cz2/pF21 Lk2/μH0.2Cz3/pF32 Ck1/pF94Rw/Ω10 Ck2/pF14
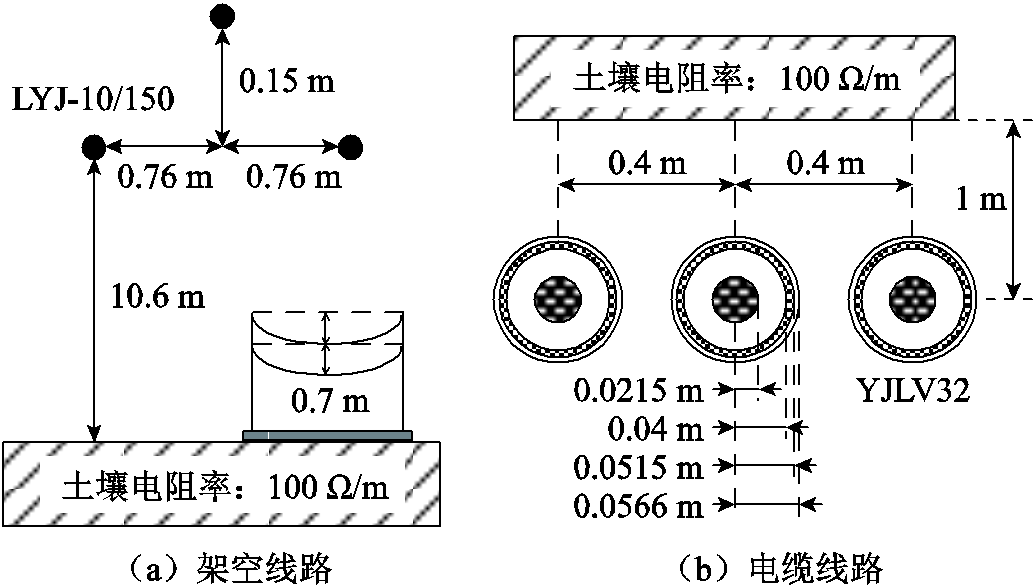
附图1 输电线路结构参数
App.Fig.1 The transmission line configuration parameters
2. 零模行波折射系数幅频特性曲线
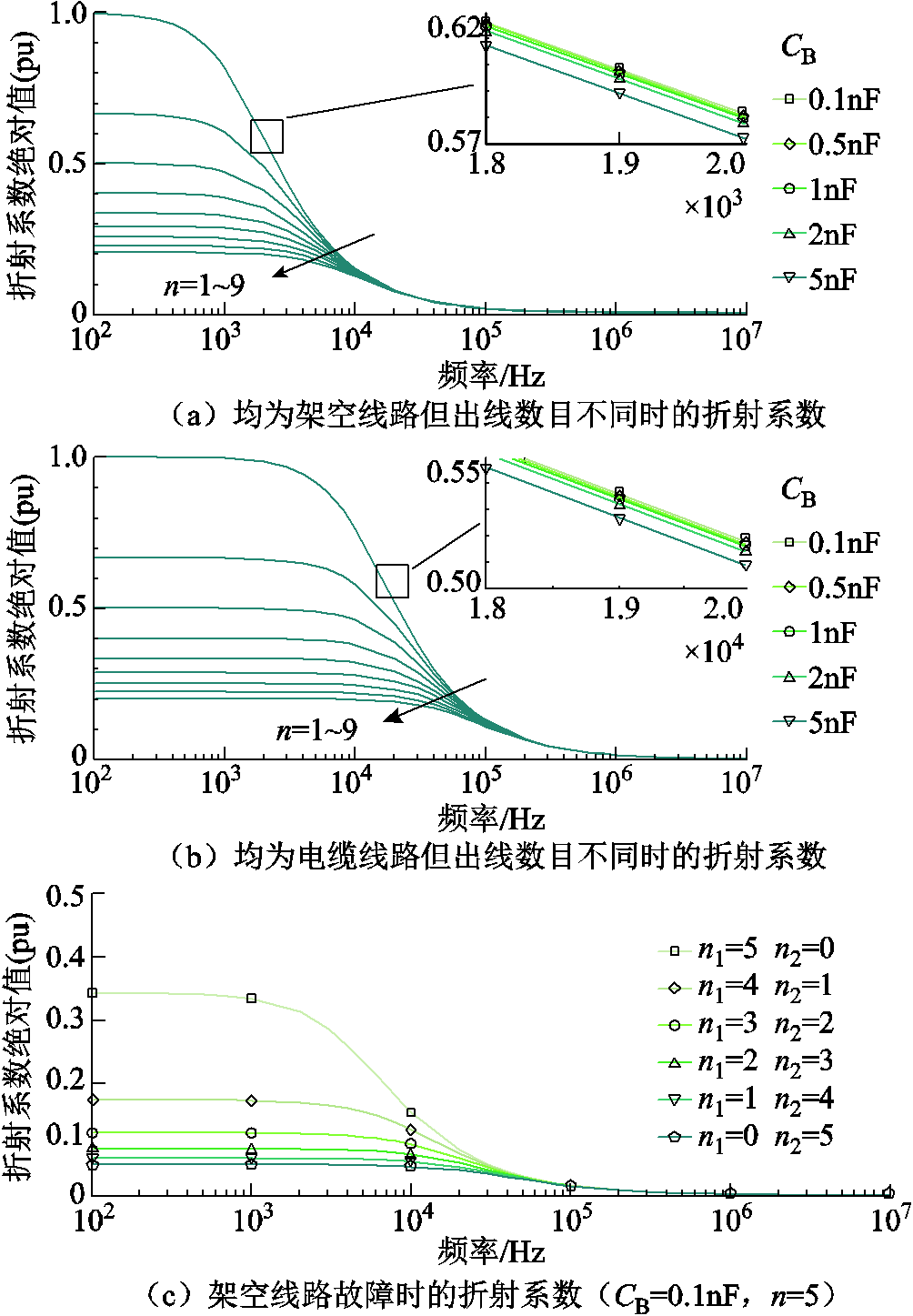
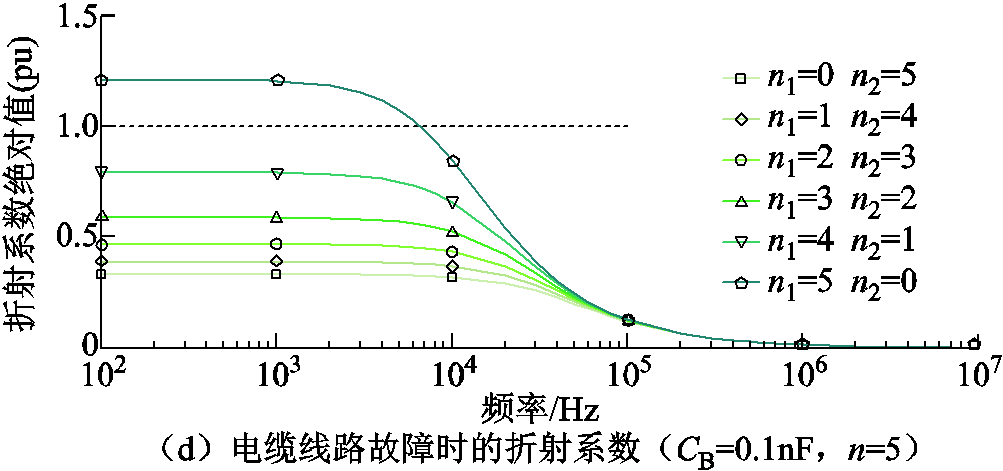
附图2 不同线路边界下零模行波折射系数幅频特性曲线
App.Fig.2 The amplitude-frequency curve of refractive coefficients on zero mode traveling wave under different configurations of line boundary
3. 选线判据证明过程
假设健全线路上研究频带内的高频瞬时能量分别为E1,E2,…,En,n为母线总分支出线数目,n=1, 2, …, 9。由于故障发生后,健全线路上的初始正向电压行波信号近似相等,即研究频带内的高频瞬时能量近似相等,因此可认为E1,E2,…,En服从正态分布,并记其平均值为EAVE。由图8和仿真结果可知,在所选研究频带内故障线路上的高频瞬时能量远远大于健全线路,可认为两者相差近一个数量级,因此将故障线路上研究频带内的高频瞬时能量记为Em,并满足Em≈10EAVE。此外,将E1,E2,…,En,Em的中位数记为EMID。
假设式(6)所示的不等式关系不成立,则
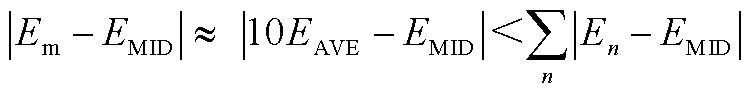 (A1)
(A1)
由于正态分布是单峰对称分布,其中位数与平均数均位于对称中心,两者是相等的。因此E1,E2,…,En的平均值与E1, E2,…,En,Em的中位数近似相等,即EAVE≈EMID,因此式(A1)可变形为
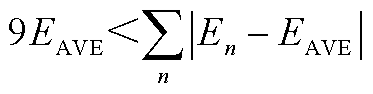 (A2)
(A2)
由于任意的En≥0,根据正态分布规律,E1,E2,…,En的取值均在集合[0,2EAVE]内。当n=9且En均取为0或2EAVE时,式(A2)的不等式左右两边相等,式(A2)不成立,且此时En的取值分布与正态分布的3σ原则相违背,即En的取值本应集中在EAVE附近,其中,σ为正态分布的标准差。当n<9时,则式(A2)更无成立的可能性。因此式(A1)的不等式关系不成立,即发生线路故障时,存在某一条线路的正向电压行波高频瞬时能量的中位数绝对偏差大于其余所有其余线路之和,且该条线路为故障线路。
参考文献
[1] 秦苏亚, 薛永端, 刘砾钲, 等. 有源配电网小电流接地故障暂态特征及其影响分析[J]. 电工技术学报, 2022, 37(3): 655-666. Qin Suya, Xue Yongduan, Liu Lizheng, et al. Transient characteristics and influence of small current grounding faults in active distribution network[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 655-666.
[2] 王晓卫, 刘伟博, 郭亮, 等. 基于不同时段内积投影的灵活接地系统高阻故障选线方法[J]. 电工技术学报, 2024, 39(1): 154-167. Wang Xiaowei, Liu Weibo, Guo Liang, et al. High impedance fault line selection method based on inner product projection of different time periods for flexible grounding systems[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 154-167.
[3] 刘宝稳, 曾祥君, 马宏忠, 等. 参数不对称配电线路的等效模型与接地故障检测方法[J]. 电力系统自动化, 2022, 46(13): 159-167. Liu Baowen, Zeng Xiangjun, Ma Hongzhong, et al. Equivalent model and grounding fault detection method for distribution lines with asymmetry parameters[J]. Automation of Electric Power Systems, 2022, 46(13): 159-167.
[4] 金涛, 褚福亮. 基于暂态非工频零序电流的含DG新型配电网的接地选线方法[J]. 电工技术学报, 2015, 30(17): 96-105. Jin Tao, Chu Fuliang. A fault line-selection method in new distribution network with DG based on transient non-power frequency zero sequence current[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 96-105.
[5] 林湘宁, 高艳, 刘沛, 等. 基于零序补偿导纳的小电流接地系统单相故障保护新方法[J]. 中国电机工程学报, 2006, 26(10): 45-49. Lin Xiangning, Gao Yan, Liu Pei, et al. A novel method to identify the single phase-to-earth fault in the neutral un-effectual grounded system using the zero-sequence compensated admittance[J]. Proceedings of the CSEE, 2006, 26(10): 45-49.
[6] 叶雨晴, 马啸, 林湘宁, 等. 基于SOP的主动式谐振接地配电网单相接地故障区段定位方法[J]. 中国电机工程学报, 2020, 40(5): 1453-1465. Ye Yuqing, Ma Xiao, Lin Xiangning, et al. Active fault locating method based on SOP for single phase grounding faults in the resonant grounding distribution network[J]. Proceedings of the CSEE, 2020, 40(5): 1453-1465.
[7] 刘宝稳, 曾祥君, 张慧芬, 等. 注入电流馈线分布特征及其在接地故障检测中的应用[J]. 电网技术, 2021, 45(7): 2731-2740. Liu Baowen, Zeng Xiangjun, Zhang Huifen, et al. Distribution model of injection current in feeder and its application in single phase to ground fault detection[J]. Power System Technology, 2021, 45(7): 2731-2740.
[8] 喻锟, 胥鹏博, 曾祥君, 等. 基于模糊测度融合诊断的配电网接地故障选线[J]. 电工技术学报, 2022, 37(3): 623-633. Yu Kun, Xu Pengbo, Zeng Xiangjun, et al. Grounding fault line selection of distribution networks based on fuzzy measures integrated diagnosis[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 623-633.
[9] 陈奎, 韦晓广, 陈景波, 等. 基于样本数据处理和ADABOOST的小电流接地故障选线[J]. 中国电机工程学报, 2014, 34(34): 6228-6237. Chen Kui, Wei Xiaoguang, Chen Jingbo, et al. Fault line detection using sampled data processing and ADABOOST for small current grounding system[J]. Proceedings of the CSEE, 2014, 34(34): 6228-6237.
[10] 张淑清, 马跃, 李盼, 等. 基于改进的广义谐波小波包分解和混沌振子的小电流接地系统故障选线[J]. 电工技术学报, 2015, 30(3): 13-20, 43. Zhang Shuqing, Ma Yue, Li Pan, et al. Application of improved generalized harmonic wavelet packet decomposition and chaos oscillator to fault line detection in small current grounding system[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 13-20, 43.
[11] 汤涛, 黄纯, 江亚群, 等. 基于馈线零序阻抗特性的谐振接地故障选线方法[J]. 电工技术学报, 2016, 31(20): 192-201. Tang Tao, Huang Chun, Jiang Yaqun, et al. A method of fault line selection in resonant earthed system based on zero sequence impedance characteristic of lines[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 192-201.
[12] 王侃, 施慎行, 杨建明, 等. 基于暂态行波的接地选线装置及其现场试验[J]. 电力自动化设备, 2008, 28(6): 118-121. Wang Kan, Shi Shenxing, Yang Jianming, et al. Transient-traveling-wave-based grounding line selector and its field tests[J]. Electric Power Automation Equipment, 2008, 28(6): 118-121.
[13] 施慎行, 董新洲. 基于单相电流行波的故障选线原理研究[J]. 电力系统保护与控制, 2008, 36(14): 13-16. Shi Shenxing, Dong Xinzhou. Study of fault line selection using single-phase current traveling waves[J]. Power System Protection and Control, 2008, 36(14): 13-16.
[14] 姜博, 董新洲, 施慎行. 基于单相电流行波的配电线路单相接地故障选线方法[J]. 中国电机工程学报, 2014, 34(34): 6216-6227. Jiang Bo, Dong Xinzhou, Shi Shenxing. A method of single phase to ground fault feeder selection based on single phase current traveling wave for distribution lines[J]. Proceedings of the CSEE, 2014, 34(34): 6216-6227.
[15] 王建元, 朱永涛, 秦思远. 基于方向行波能量的小电流接地系统故障选线方法[J]. 电工技术学报, 2021, 36(19): 4085-4096. Wang Jianyuan, Zhu Yongtao, Qin Siyuan. Fault line selection method for small current grounding system based on directional traveling wave energy[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4085-4096.
[16] 邓丰, 梅龙军, 唐欣, 等. 基于时频域行波全景波形的配电网故障选线方法[J]. 电工技术学报, 2021, 36(13): 2861-2870. Deng Feng, Mei Longjun, Tang Xin, et al. Faulty line selection method of distribution network based on time-frequency traveling wave panoramic waveform[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2861-2870.
[17] 郭谋发, 刘世丹, 杨耿杰. 利用时频谱相似度识别的配电线路接地选线方法[J]. 中国电机工程学报, 2013, 33(19): 183-190, 4. Guo Moufa, Liu Shidan, Yang Gengjie. A novel approach to detect fault lines in distribution network using similarity recognition based on time-frequency spectrum[J]. Proceedings of the CSEE, 2013, 33(19): 183-190, 4.
[18] 董新洲, 毕见广. 配电线路暂态行波的分析和接地选线研究[J]. 中国电机工程学报, 2005, 25(4): 1-6. Dong Xinzhou, Bi Jianguang. Analysis on transient traveling wave and study on fault line selection for distribution lines[J]. Proceedings of the CSEE, 2005, 25(4): 1-6.
[19] 庞红梅, 李淮海, 张志鑫, 等. 110 kV智能变电站技术研究状况[J]. 电力系统保护与控制, 2010, 38(6): 146-150. Pang Hongmei, Li Huaihai, Zhang Zhixin, et al. Research situation of 110 kV smart substation technology[J]. Power System Protection and Control, 2010, 38(6): 146-150.
[20] 田志国, 朱明东, 池立江, 等. 阻容分压型电子式电压互感器暂态特性研究[J]. 自动化仪表, 2022, 43(4): 27-32. Tian Zhiguo, Zhu Mingdong, Chi Lijiang, et al. Research on transient characteristics of resistor-capacitor voltage dividing electronic transformers[J]. Process Automation Instrumentation, 2022, 43(4): 27-32.
[21] 熊江咏, 杨桂平, 郭毅, 等. ECT与EVT在智能配电设备一二次融合中相融性分析[J]. 电力电容器与无功补偿, 2019, 40(1): 108-114. Xiong Jiangyong, Yang Guiping, Guo Yi, et al. Compatibility analysis of ECT and EVT in primary & secondary fusion of intelligent power distribution equipment[J]. Power Capacitor & Reactive Power Compensation, 2019, 40(1): 108-114.
[22] Ye Ziyang, Liu Kun, Zhang Jiefu, et al. Simulation analysis and measurement verification of CVT dielectric loss for its on-line monitoring[C]//2019 IEEE Sustainable Power and Energy Conference, Beijing, China, 2020: 2743-2746.
[23] 贾立莉, 王平, 律方成. 基于EMTP仿真的智能变电站地电位升安全限值的计算[J]. 电瓷避雷器, 2019(2): 52-58. Jia Lili, Wang Ping, Lü Fangcheng. Calculation of safety limit value of grounding potential rise in intelligent substation based on EMTP simulation[J]. Insulators and Surge Arresters, 2019(2): 52-58.
[24] 黄建国, 陈亮, 董莉娜, 等. 变电站用10kV避雷器运行状态在线监测装置的研制[J]. 电瓷避雷器, 2012(4): 85-90. Huang Jianguo, Chen Liang, Dong Lina, et al. Development of on-line monitoring device for 10kV MOA used in substation[J]. Insulators and Surge Arresters, 2012(4): 85-90.
[25] 黄伟明. 某10 kV并联电容器组频繁故障的分析与处理[J]. 电力电容器与无功补偿, 2021, 42(4): 115-119. Huang Weiming. Analysis and treatment on frequent fault of 10 kV shunt capacitor bank[J]. Power Capacitor & Reactive Power Compensation, 2021, 42(4): 115-119.
[26] 祝小彦, 王永杰. 基于MOMEDA与Teager能量算子的滚动轴承故障诊断[J]. 振动与冲击, 2018, 37(6): 104-110, 123. Zhu Xiaoyan, Wang Yongjie. Fault diagnosis of rolling bearings based on the MOMEDA and Teager energy operator[J]. Journal of Vibration and Shock, 2018, 37(6): 104-110, 123.
[27] 陈洋, 黄纯, 陈为熙, 等. 基于测量波阻抗的母线保护新方法[J]. 电网技术, 2012, 36(5): 198-203. Chen Yang, Huang Chun, Chen Weixi, et al. A new method of bus protection based on measuring wave impedance[J]. Power System Technology, 2012, 36(5): 198-203.
[28] 司大军, 束洪春, 陈学允, 等. 输电线路雷击的电磁暂态特征分析及其识别方法研究[J]. 中国电机工程学报, 2005, 25(7): 64-69. Si Dajun, Shu Hongchun, Chen Xueyun, et al. Analysis of electromagnetic transient characteristics of lightning stroke on transmission lines and research on its identification method[J]. Proceedings of the CSEE, 2005, 25(7): 64-69.
[29] 段建东, 罗四倍, 张保会, 等. 超高速保护中合闸于故障线路的识别方法[J]. 中国电机工程学报, 2007, 27(10): 78-84. Duan Jiandong, Luo Sibei, Zhang Baohui, et al. Study of discriminating approach for switching into fault line in ultra-high-speed protection[J]. Proceedings of the CSEE, 2007, 27(10): 78-84.
[30] 王俊波, 李慧, 邱太洪. 基于数据挖掘的CVT电容元件击穿故障分析[J]. 电力电容器与无功补偿, 2019, 40(3): 96-100. Wang Junbo, Li Hui, Qiu Taihong. Breakdown fault analysis of CVT capacitor elements based on data mining[J]. Power Capacitor & Reactive Power Compensation, 2019, 40(3): 96-100.
Abstract Currently, the distribution network system usually adopts a neutral non-effective grounding method. How to accurately select the faulty line has been a problem for a very long time. In recent years, with the widespread application of line selection devices based on the transient-based method, the success rate of fault line selection has improved significantly. However, when high resistance faults and small phase angle grounding faults occur, the weak fault characteristics still easily cause the failure of various existing line selection methods.
It should be noted that the above existing transient-based line selection methods are all based on the zero mode traveling waves. The main reason for such consideration is that when the substation busbar is equipped with parallel shunt capacitors, the line mode traveling waves on the normal line is very weak due to the high-frequency filtering effect of the shunt capacitors while zero mode traveling waves are almost unaffected because they cannot loop in an ungrounded capacitor bank. Although the line selection methods based on zero mode traveling waves have achieved good results in practical applications, the following problems still exist: (1) Because zero mode traveling wave attenuates quickly, it may be very difficult to extract the zero mode traveling waves accurately when high resistance fault and small phase angle grounding fault occur at the end of a long feeder. (2) Currently, only two-phase current transformers are installed in many distribution network system, which makes it difficult to obtain zero mode traveling waves. Therefore, the above drawbacks will become a constraint to improve further the performance of the current line selection methods based on the zero mode traveling waves.
Inspired by the high-frequency filtering effect of busbar shunt capacitors on line mode traveling waves, this paper skipped the perspective of faulty line selection method design based on zero mode traveling waves and proposes a new method using line mode traveling waves based on the substation boundary characteristics in the distribution network. Firstly, the researches confirm that the smart substation line boundary composed of the electronic voltage transformers, the metal-oxide arresters, and the remaining apparatus’s stray capacitance has strong high-frequency filtering characteristics, and its refraction attenuation effect is almost independent of the busbar system operation mode, which is of excellent robustness and can lay a foundation for the design of the proposed line selection method. Then, based on the Teager energy operation, a new line selection criterion is constructed based on the difference of the high-frequency instantaneous energy of the line mode traveling waves between the normal line and the faulty line, which has high sensitivity under the conditions of high resistance faults and small phase angle grounding faults.
Finally, the proposed method is based on the PSCAD/EMTDC platform to verify its effectiveness, sensitivity, and reliability. It can accurately identify the fault line and reliably distinguish the busbar fault. Otherwise, the proposed fault line selection method has fast operation speed, strong anti-noise performance, simple algorithm principle, clear physical meaning, no manual threshold setting, and is unaffected by shunt capacitors. It can realize reliable line selection under arc faults and 3 kΩ high resistance faults in the distribution network. Indeed, the proposed line selection method only applies to the smart substation installed with the electronic voltage transformers. But luckily, the smart substation has become the main construction form of the current substation, which provides a practical basis for the wide application of the proposed new line selection method.
keywords:Distribution network, faulty line selection, line mode traveling wave, boundary characteristic, high-frequency instantaneous energy
DOI:10.19595/j.cnki.1000-6753.tces.230157
中图分类号:TM773
国家重点研发计划(2021YFB2401000)和国家电网有限公司总部科技项目(SGSDDKK00WJJS2200105)资助。
收稿日期 2023-02-14
改稿日期 2023-04-16
吴宇奇 男,1997年生,博士研究生,研究方向为新型电力系统保护与控制等。E-mail:798893267@qq.com
李正天 男,1979年生,博士,副教授,研究方向为继电保护、微电网及配电自动化等。E-mail:453874933@qq.com(通信作者)
(编辑 赫 蕾)