
图1 配电网真型实验现场接线
Fig.1 The wiring diagram of field experiment
摘要 现有各类高阻接地故障模型缺乏对故障发展全过程的物理解释,难以准确模拟故障的非线性特征。该文根据现场录波数据,深入研究高阻接地故障的物理过程,归纳可知故障电流波形的非线性畸变来源于两个方面:空气间隙击穿引起的非线性与接地介质本身的非线性。据此提出高阻接地故障的故障电阻由电弧电阻和接地电阻串联组成,进而建立基于动态电阻串联的高阻接地故障新模型。首先,利用汤逊原理分析空气介质击穿过程中动态电弧的产生,建立了故障点指数电弧模型;然后,研究故障电流在土壤中的流散过程,结合土壤电阻率变化规律,求解接地电阻随故障电流变化的表达式,建立接地电阻模型;最后,在PSCAD中将二者串联,搭建高阻接地故障新模型,结合现场故障数据并与其他模型对比,验证了该文所提模型能更准确地表征不同接地介质下高阻接地故障的非线性特征,为后续研究高阻接地故障辨识提供更精确的数据支撑。
关键词:配电网 高阻接地故障 电弧电阻 接地电阻 非线性特征
配电线路因遭受雷击、大风等会造成线路断线或垂落,进而与高阻抗接地介质接触,引发高阻接地故障(High Impedance Fault, HIF)。高阻接地故障的故障电阻可达上千欧姆,故障电气特征非常微弱,在实际工程环境中难以被检测[1-3],导致故障特征的辨析难度增加[4-5],继电保护方案失效。配电网长期带高阻接地故障运行,引发“伤人、起火、停电”等事故的概率居高不下,对人民群众生命财产的安全产生了极大威胁[6]。因此在缺少故障实测数据的背景下[7],对高阻接地故障进行精确建模,是后续研究高阻接地故障可靠检测算法、故障成因辨识、故障定位等的关键前提。
高阻接地故障的故障电流波形在过零点处发生非线性畸变这一特征已经得到了国内外研究学者的广泛认同,但目前对高阻接地故障模型的研究通常是将故障支路的过渡电阻看作线性电阻[8-9],无法反映高阻接地故障波形的非线性特性。因此,需要针对故障波形的非线性特征对高阻接地故障模型进行深入研究。考虑到高阻接地故障通常伴随着非线性电弧,基于电弧弧隙能量热平衡理论的电弧模型被相继提出,其中包括基于Mayr方程的电弧模型[10]、基于Cassie方程的电弧模型[11]、在电缆内部的稳态间歇性电弧模型[12]等。然而,Mayr电弧模型仅适用于模拟电弧电阻的高阻态,即电弧熄弧状态;Cassie电弧模型仅适用于模拟电弧电阻的低阻态,即电弧燃弧状态,此类模型不完全适用于分析电弧燃弧、熄弧的整个阶段。此外,文献[13]将Mayr和Cassie方程结合,提出通过过渡函数将二者串联组合的电弧模型;文献[14]基于大量故障电弧实验的数学分析,提出Mayr-Schwarz电弧数学模型。此类组合模型与仅基于Mayr或Cassie方程的单一电弧模型相比,更契合实际高阻接地故障工况,但其表达式包含更多电弧参数的电弧电导微分方程,需要进行复杂的迭代微分计算,难以直接应用于高阻接地故障的检测、测距算法中。
配电网发生高阻接地故障时,导线与高阻抗接地介质形成电气连接,导体与接地介质的空气间隙击穿和高阻抗固体接地介质的非线性是导致故障波形产生非线性畸变的主要原因[1,15]。研究学者认为高阻接地故障中非线性电弧的成因源于高电压对空气间隙的击穿,并对基于空气介质击穿原理的高阻接地故障模型进行了深入探索。文献[16]通过阐述短空气间隙中气体放电机理的汤逊原理,分析电弧的产生过程,得到交流电压下电弧电压和电弧电流的表达式,搭建了故障点对数电弧模型;文献[17]发现电弧间隙长度会影响波形畸变程度,在汤逊原理的基础上,搭建了考虑间隙长度的电弧模型。与基于电弧弧隙能量热平衡理论的电弧模型相比[10-14],基于空气间隙击穿的电弧模型可以更好地描述故障波形在过零点附近的非线性畸变特性。然而上述故障建模方法通常认为高阻接地故障过渡电阻是由电弧电阻和一个线性塔基电阻串联组成,忽略了接地介质的非线性特征。文献[18]对高阻抗接地介质的电流随电场强度的变化曲线进行分段线性拟合,构建电导与电压的函数关系,进而建立了高阻接地故障非线性电阻模型,但未考虑导线与接地介质之间的空气间隙击穿过程。综上所述,现有各种高阻接地故障建模方法并未充分考虑高阻接地故障的整个物理发展过程,物理机理解释不足,难以精确模拟高阻接地故障的实际工况。
针对以上问题,本文通过进行高阻接地故障现场实验,分析故障特性,揭示电弧和接地介质是导致高阻接地故障波形出现明显非线性畸变特征的主要因素。进一步地,研究电弧和接地介质参与的高阻接地故障的物理发展过程,发现高阻接地故障的故障电阻由空气间隙击穿产生的电弧电阻和故障电流在土壤介质中流散产生的接地电阻串联组成。在此基础上,深入分析电弧电阻和接地电阻的动态变化规律,确定电弧电阻和接地电阻的函数表达式。最后,根据高阻接地故障的实际物理过程,建立了基于动态电阻串联的高阻接地故障等效模型,并在不同接地介质条件下利用波形相关系数将仿真波形与现场实测波形进行对比,验证了本文所提故障模型可以准确地模拟高阻接地故障的非线性特征,与现有高阻接地故障模型相比具有优越性。
在1:1真型配电网实验室中进行高阻接地故障现场实验,获取并分析现场实验波形,对高阻接地故障特性进行深入探讨。真型配电网实验室采用400 V电源,通过升压变压器将电压提升至10 kV,由接地变压器引出系统中性点经消弧线圈接地,设置其脱谐度为-10%。在配电网10 kV母线接入4条出线,其中包括两条架空线路L1、L2,两条电缆线路L3、L4,并在各出线首端安装录波装置,获取各出线的电压和电流波形。配电网真型实验室现场接线如图1所示。

图1 配电网真型实验现场接线
Fig.1 The wiring diagram of field experiment
由于接地介质类型繁多,受现场实验成本限制,无法对所有介质进行高阻接地故障现场实验。根据湖南省第二次土壤普查结果,全省共有红土壤860.72万hm2,占全省土壤面积的51%[19],其样本如图2所示。因此,本文选取红土壤作为典型接地介质,在出线L4上距离母线2 km处设置经红土壤接地的高阻接地故障实验,获取故障电压、电流波形,研究高阻接地故障的非线性特征。

图2 红土壤样本
Fig.2 The laterite soil
在高阻接地故障现场实验录波数据中截取一定时间窗内的故障电压和电流波形,并在过零点附近局部放大,如图3所示。
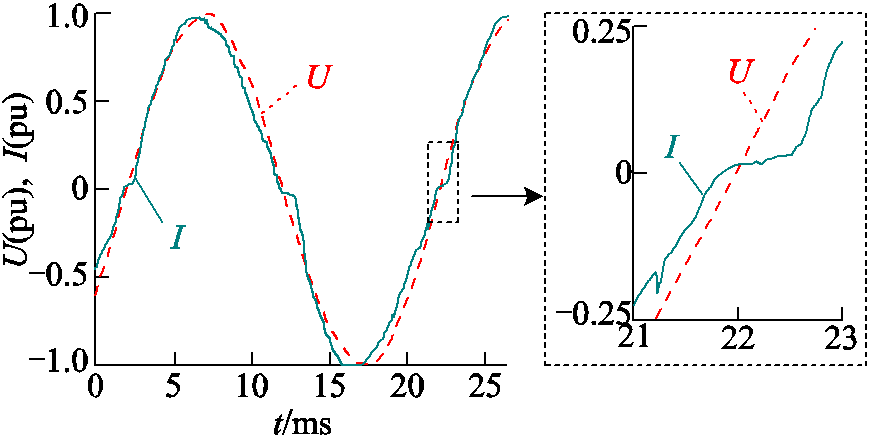
图3 高阻接地故障现场实验波形
Fig.3 The fault waveform of HIF field experiment
由此可知,故障电压波形的非线性畸变特征微弱,波形接近于正弦曲线。而故障电流波形在过零点附近出现明显的畸变:故障电流波形的斜率在即将过零点的时刻突然降低,波形变得平缓,故障电流幅值维持在较低的水平,表现出与水平零轴近似平行的趋势;直至过零点后的某一时刻,故障电流波形的斜率恢复,故障电流幅值开始跃升,随电压正弦变化。将高阻接地故障电流波形的这一非线性特性称为“零休”畸变。
故障电流波形产生“零休”畸变主要包括两个原因。一方面,由于导线与接地介质的空气间隙发生击穿,导致故障波形出现非线性畸变。在配电线路发生高阻接地故障的过程中,当交流电压即将过零时,空气间隙的电离逐渐减弱,空气间隙恢复绝缘,电弧熄灭,弧阻突增,故障电流会先于电压降低到零点,短暂“零休”一段时间;故障点电压过零后逐渐增大,对空气间隙的电离逐渐增强,电弧重新燃烧,弧隙又从绝缘介质转变为导体,故障电流经短暂“零休”后恢复,随故障电压正弦变化,直至下一次过零点时电弧熄灭,再次“零休”。另一方面,土壤是一种复杂的电介质,其导电特性受到众多因素的共同影响,土壤介质本身就具备非线性的特点[20]。发生高阻接地故障时,故障线路经电弧与非线性土壤介质产生电气连接,故障电流注入土壤并在土壤中散流,在土壤中施加了与电流相关的时变电场。土壤介质本身的非线性在该时变电场的作用下凸显,导致故障电流波形产生非线性畸变。
根据图3所示的故障电压、电流波形,绘制对应的伏安特性曲线如图4a所示。高阻接地故障的伏安特性曲线以过零点为中心,对称分布在第一、三象限,在坐标轴上整体呈现为闭环磁滞回线状。当电压、电流距离过零点较远时,伏安特性曲线的斜率稳定;即将过零点时,曲线斜率增大,并维持到过零点后一段时间,曲线斜率又恢复到稳定值。
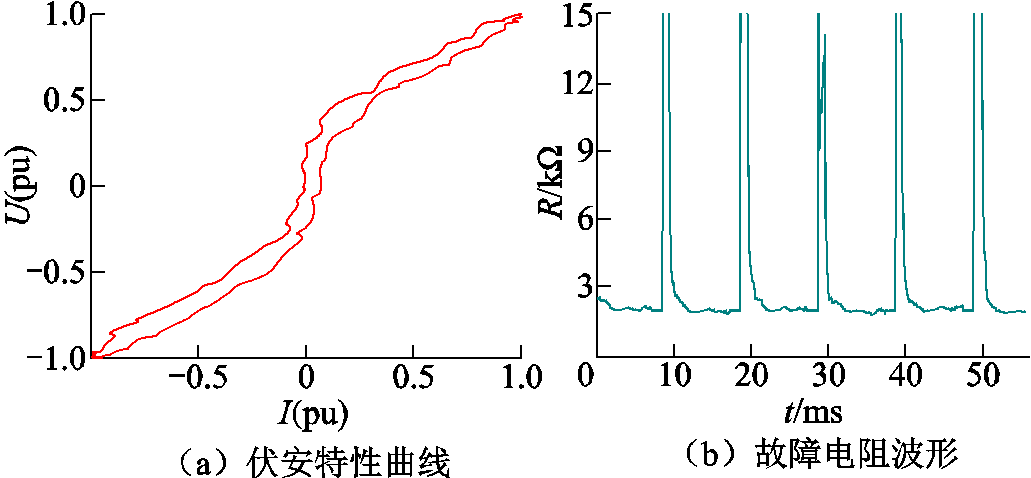
图4 现场实验伏安特性曲线与故障电阻
Fig.4 Volt-ampere characteristics and fault impedance variationof HIF field experiment
根据现场故障电压和电流波形可以计算得到故障电阻波形,如图4b所示。由于测量电流值接近零时,计算得到过渡电阻阻值极大,失去实际意义,因此只截取了阻值在15 kΩ以下的部分。伏安特性曲线斜率的变化也可以反映故障电阻的动态变化规律:当故障电压、电流幅值较低时,伏安特性曲线的斜率较高,故障电阻在过零点附近时刻呈高阻态;随着电压和电流逐渐升高,伏安特性曲线斜率变化减缓,故障电阻减小,呈现低阻态,并将在低阻态维持一段时间,直至下一个过零点出现,过渡电阻将再次呈现高阻态。根据上述分析可知,伏安特性曲线和故障电阻的变化规律与故障电流波形在过零点附近发生“零休”畸变的规律一致,呈现明显的周期性变化特征。
综上所述,受电弧和接地介质的影响,高阻接地故障的故障波形出现明显的非线性畸变特征,导致伏安特性曲线和故障电阻波形均出现非线性畸变。因此,高阻接地故障过渡电阻明显区别于线性电阻,仅用线性电阻代替故障过渡电阻无法精确表征故障波形畸变。对此,需要重点研究电弧和接地介质参与的高阻接地故障的物理发展过程,从而建立基于实际物理过程的高阻接地故障新模型,精确地描述故障波形的非线性特征。
配电线路中高阻接地故障发生的主要形式为馈线断线后跌落,经高阻抗接地介质接地,故障电流由馈线注入大地。对高阻接地故障的物理发展过程进行深入研究,揭示其过渡电阻的组成,建立基于实际物理过程的高阻接地故障新模型。
若故障发生后配电线路与土壤未直接接触,两者之间存在空气间隙。当导线距离土壤较远时,空气间隙的长度较大,电源电压不足以击穿空气间隙;当导线距离土壤很近时,空气间隙长度非常小,若电压超过一定值,空气间隙将被击穿产生电弧,进而形成电弧电阻Rarc,电流通过电弧通道注入土壤。
若故障发生后导线与土壤直接接触,根据电接触理论,由于土壤表面粗糙,导线将通过土壤表面多个微小凸起的接触点与土壤连接,称这些接触点为导电斑。导电斑与土壤直接相互接触区域为真正的电接触面积,多个导电斑电阻并联组成接触电阻。电接触面积越大,导电斑数量越多,并联接触电阻越小。而导线与土壤之间的电接触面积非常小,总的并联接触电阻很大[20]。在导线与土壤直接接触时,接触面内、凸起以外存在长度极短、电场强度极大的空气间隙,当电源电压高于空气介质的击穿电压时,导线与接触面之间的空气间隙被击穿,产生电弧,也将形成电弧电阻Rarc。此时电弧电阻与接触电阻并联[21],而接触电阻远大于电弧电阻,因此,并联电阻阻值近似等于电弧电阻阻值,接触电阻可忽略。
因此,无论导线与土壤是否直接接触,只要电源电压大于空气间隙击穿电压,均会形成电弧电阻Rarc,其阻值与电弧燃弧或熄弧的状态相关,随系统工频动态变化。
在故障电弧产生之后,电弧通道将导线和土壤连接在一起,故障电流通过电弧通道流入大地。由于电弧与土壤的接触面积非常小,相当于一个在地表面的点电流源向土壤中注入电流。土壤是一种复杂的多态复合介质,土壤颗粒表面覆有水膜,其颗粒之间也具有空气间隙。当故障电流注入土壤介质中时,电流将沿土壤颗粒表面的水膜及空气间隙发生散流,在土壤内部形成电流散流通道。设地面为无限大平面,土壤为该无限大平面下方均匀、各向同性的半无限大介质,则高阻接地故障向地中注入的故障电流将以地面上的点电流源为中心,在土壤中向各个方向呈辐射状流散至无穷远。在高阻接地故障发生时,故障电流向地中流散过程中遇到的土壤电阻即为接地电阻Rc,其阻值随向地中注入的故障电流幅值动态变化。
经上述故障机理分析,得到高阻接地故障物理发展过程的示意图如图5所示。由此可知,高阻接地故障的故障电阻Rf由电弧电阻Rarc和接地电阻Rc两部分串联而成,二者都随故障电流If、故障电压Uf时刻动态变化。
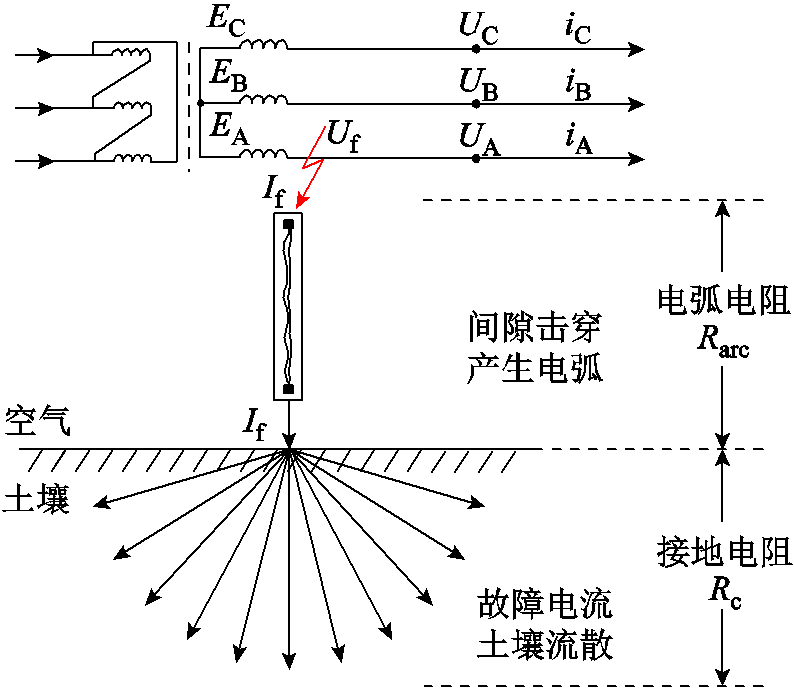
图5 高阻接地故障物理发展过程示意图
Fig.5 Physical development process of HIF
根据高阻接地故障的物理发展过程,提出电弧电阻和接地电阻串联的高阻接地故障动态电阻串联模型如图6所示。电弧电阻和接地电阻分别对应高阻接地故障的空气间隙击穿过程和故障电流在土壤中的散流过程,具有明确的物理意义。
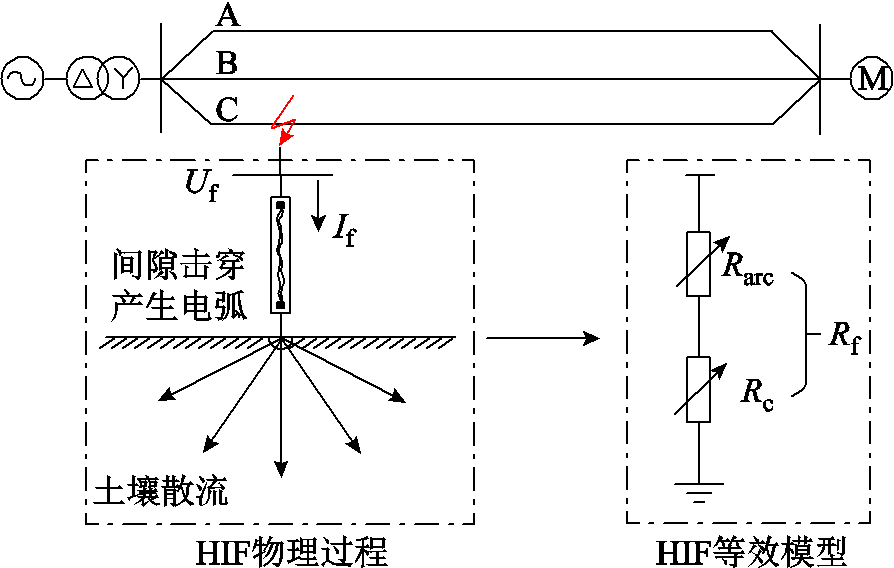
图6 高阻接地故障动态电阻串联模型
Fig.6 Dynamic impedance series model of HIF
电弧的产生源于空气间隙击穿,根据短空气间隙中气体放电的汤逊原理,研究故障点电弧的产生过程。空气间隙中的自由电子在电场作用下不断加速运动,与气体的分子和原子发生碰撞,导致空气电离,产生新电子。空气中自由电子的数目持续增加,进而发展为电子崩[22]。电弧电流可以根据自由电子的定向运动来表征,如式(1)所示。
 (1)
(1)
式中,Is为在很小的电场强度下,由外电离因素引起的饱和电流;α为碰撞电离系数,表示单位电子由阴极向阳极运动1 cm时,发生的平均碰撞电离次数;d为空气间隙的长度。
根据汤逊理论,在一定气压下,碰撞电离系数α与电场强度E、温度T的函数关系[23]为
其中,在气压一定时,对于确定的气体类型,系数b1和b2在E和T值一定范围内为常数。
在热电离状态下,电弧表面的温度会达到 3 000~4 000 K。假设温度T取3 000 K,b1和b2在一定条件下为常数,式(2)可整理为α关于E的指数函数。该电弧温度下,平均电场强度E约为5 kV/cm,此时α与E可近似呈一次函数关系[16],有
 (3)
(3)
将式(3)代入式(1)中,可得空气间隙中电弧电流和电弧电压的表达式为
 (4)
(4)
式中,U为电弧电压,U = Ed;IP=IseBd。
由于交流电压的极性会发生变化,令UP=1/k,可将式(4)进一步转换为
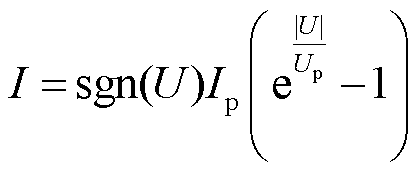 (5)
(5)
由于指数函数在(0, 0)点处按级数展开时,其收敛域为实数域,不易发散,可将指数式(5)整理为
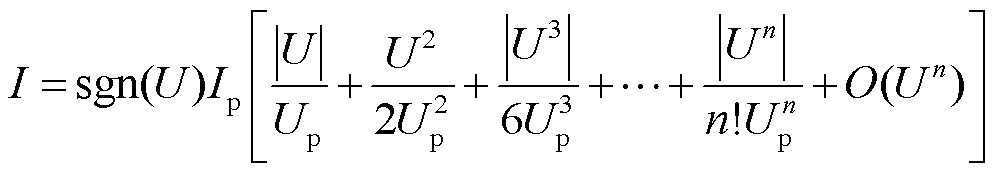 (6)
(6)
式中,O(Un)为指数函数在(0, 0)点处按级数展开时的高阶无穷小余项。根据式(6)可以得到电弧电压U和电弧电流I的函数关系,从而构造电弧电阻模型。U、I的非线性特征随着n的增加越发明显,电弧电阻也出现明显的动态的非线性变化。在实际应用的过程中,根据需求对模型的展开级数进行调整,准确模拟空气间隙击穿过程中电弧的非线性特征。
此外,在空气介质击穿的瞬间,电弧的温度较高且耗散速度较慢,电弧的高温状态会导致电弧电阻的阻值发生变化。这就使得当电弧电阻最小时,电压和电流不能同时达到峰值点,二者产生一定的相位差,故障电流滞后于故障电压,导致通过现场实验获取的高阻接地故障伏安特性曲线出现明显的闭环特征。因此,本文在式(6)所示的电弧模型中设置一定的旋转角度θ,使得电弧电流和电弧电压保持一定的相位差,更契合实际故障工况。
当高阻接地故障发生时,故障电流通过电弧通道流入大地,接地电阻可认为是故障电流经电弧通道流入土壤的散流电阻。将电弧弧柱视为圆柱、电弧通道的中心视作球心,接地电阻Rc即为从电弧边界至无穷远处半球壳的体电阻,其阻值可直接由包围在电弧通道外的一连串厚度为dr的半球壳体电阻串联求得,表示为
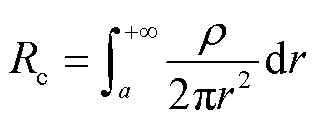 (7)
(7)
式中,ρ为土壤电阻率,与接地电阻密切相关;r为电流流散半径;a为电弧半径,与电弧电流大小密切相关。对于空气中自由燃烧的电弧,一般认为电弧半径a与电弧电流的二次方根成正比[24],即
 (8)
(8)
3.2.1 接地电阻的组成
假设导线跌落到土壤电阻率为ρ的均匀土壤,在故障电流流散的过程中,电场强度始终满足
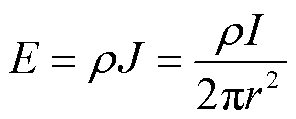 (9)
(9)
式中,J为该区域的电流密度;I为流入地中的电流,由于接地电阻和电弧电阻串联,所以也指电弧电流。
由式(9)可知,电场强度与土壤流散半径的二次方成反比,越靠近故障电流流入的区域,电流流散半径越小,电场强度越大。在距离电弧很近的区域,当故障电流增大到某一值时,该区域的电场强度将大于土壤的临界击穿场强,土壤将被击穿;随着电流流散半径的增大,地中电场强度逐渐减小,电场强度将小于土壤的临界击穿场强。根据电场强度大小,土壤可被分为击穿区域与非击穿区域两部分。相应地,接地电阻也被分为击穿区域电阻与非击穿区域电阻两部分。
在土壤的击穿区域部分,其土壤电阻率与初始电阻率ρ0相比大大减小。根据大量的试验数据,可将击穿区域的土壤电阻率ρ1设定为7%ρ0[25],将击穿区域对应的接地电阻设为Rc1。在土壤的非击穿区域部分,施加的电场使得土壤颗粒间的空气间隙产生局部放电,地中土壤电阻率也发生变化。局部放电的程度与电场强度大小相关,因此,非击穿区域的土壤电阻率ρ2会随着电场强度的变化而变化。将非击穿区域对应的接地电阻设为Rc2。
根据以上分析,随着流散半径的增大,电场强度逐渐减小,假定临界击穿场强对应的土壤击穿半径为rc,以击穿半径为界,土壤被分为击穿区域与非击穿区域,接地电阻可视作由击穿区域电阻Rc1和非击穿区域电阻Rc2串联组成,接地电阻的组成如图7所示,则式(7)可进一步推导为
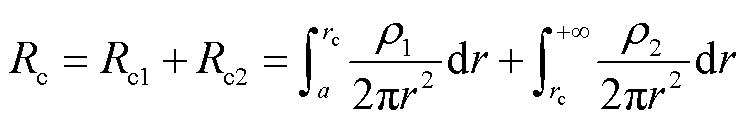 (10)
(10)
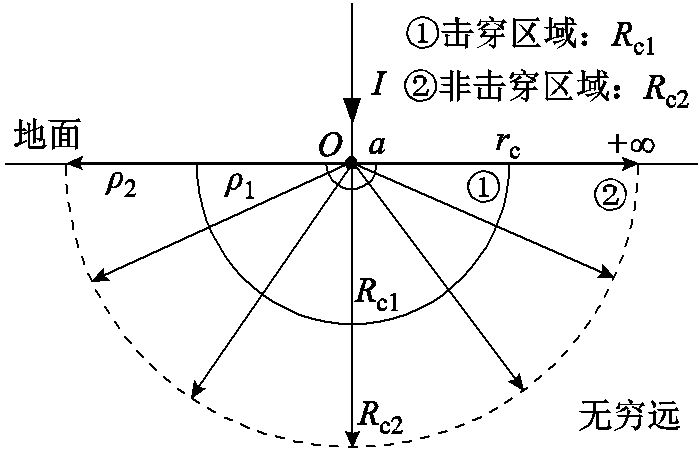
图7 接地电阻的组成
Fig.7 Construction of grounding impedance
土壤的临界击穿场强与土壤原始电阻率呈正相关[26],由于高阻抗接地介质的土壤电阻率均在数百Ω·m以上,临界击穿场强可达数百甚至上千kV/m[27],而配电系统电压等级不高,高阻接地故障电流往往仅为数A[28]。分析式(9)可知,故障电流仅为数A时,若要使故障时地中电场强度达到数百甚至上千kV/m数量级,土壤流散半径r应小于0.01 m,即仅有极少一部分土壤被击穿。且击穿区域的土壤电阻率ρ1仅为7%ρ0,计算得到这一极少部分击穿区域的电阻阻值远远小于故障过渡电阻。因此,计算接地电阻时可将所有区域都近似认为非击穿区域,忽略击穿区域,得到接地电阻的表达式为
 (11)
(11)
由式(11)可知,为了求取非击穿区域的接地电阻,需要明确非击穿区域的土壤电阻率与电流流散半径的关系。根据上述分析,非击穿区域的土壤电阻率与地中电场强度相关,电场强度又与电流流散半径成反比。因此,需要对其进行进一步探究,从而推导出非击穿区域土壤电阻率ρ2与电流流散半径r的函数关系,构造接地电阻模型。
3.2.2 接地电阻模型
由前文分析可知,故障电流注入土壤时,非击穿区域的土壤电阻率ρ2会随着电场强度的变化而变化。本文以红土壤接地介质为例,深入研究接地电阻模型。根据相关文献,得到红土壤的非击穿区域土壤电阻率随电场强度的变化曲线如图8所示[29]。
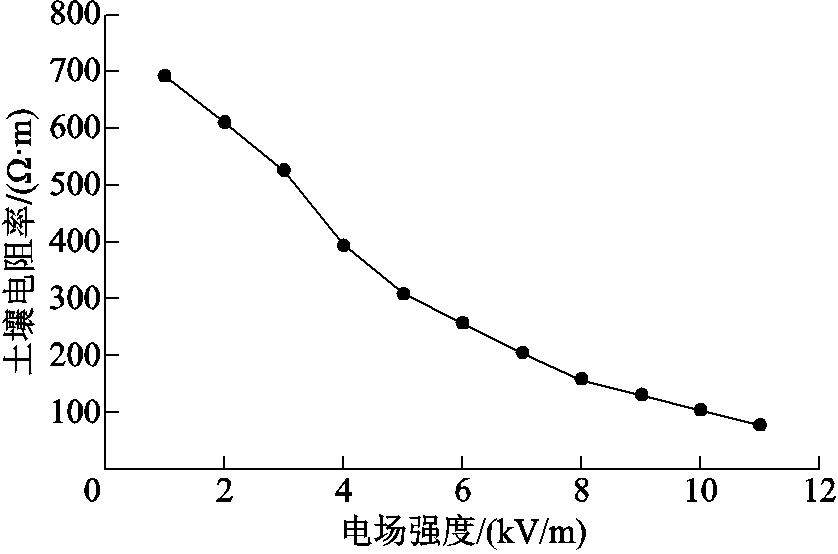
图8 土壤电阻率与电场强度的关系
Fig.8 Relationship between soil resistivity and electric field intensity
随着电场强度的增大,非击穿区域的土壤电阻率非线性减小,与电场强度呈指数函数关系,有
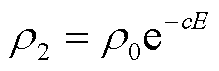 (12)
(12)
式中,c为常数。将式(9)代入式(12)中,可得
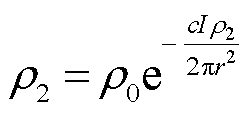 (13)
(13)
该方程为超越方程,电阻率ρ2无法通过初等函数来表示,给电阻率的分析带来困难。对于同一类型的土壤,初始电阻率ρ0相同,电阻率与故障电流及其流散半径有关,可以利用数学分析软件对超越方程进行数值求解,通过生成大量的原始数据对数值解进行拟合,进而得到土壤电阻率与故障电流及其流散半径的表达式。
根据图8所示的红土壤非击穿区域的土壤电阻率随电场强度变化曲线,可拟合得到式(12)中c和ρ0的值。在故障电流相同时,随着电流流散半径的增大,电场强度逐渐减小,土壤电阻率非线性增加,土壤电阻率随流散半径的变化曲线如图9所示;在电流流散半径相同的区域,随着故障电流的增大,
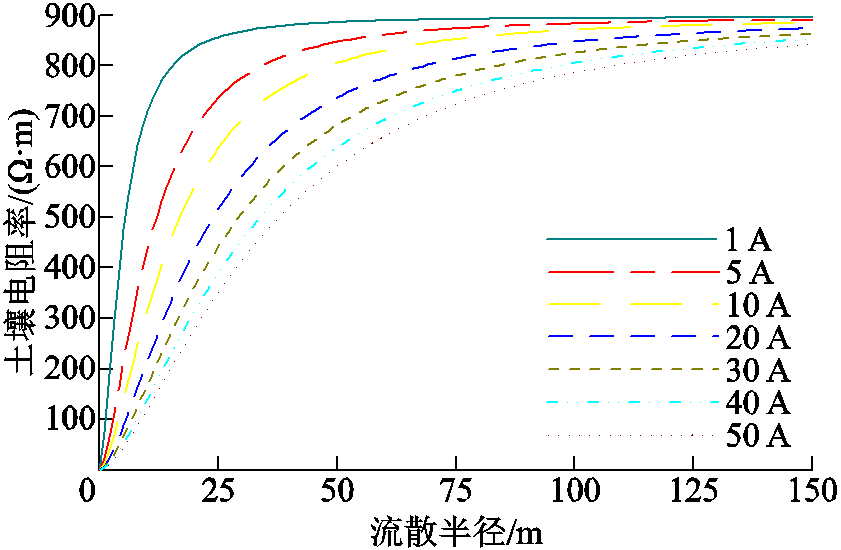
图9 土壤电阻率随流散半径的变化曲线
Fig.9 Variation of soil resistivity with dispersion radius
该区域的电场强度逐渐增大,土壤电阻率非线性减小,土壤电阻率随电流的变化曲线如图10所示。
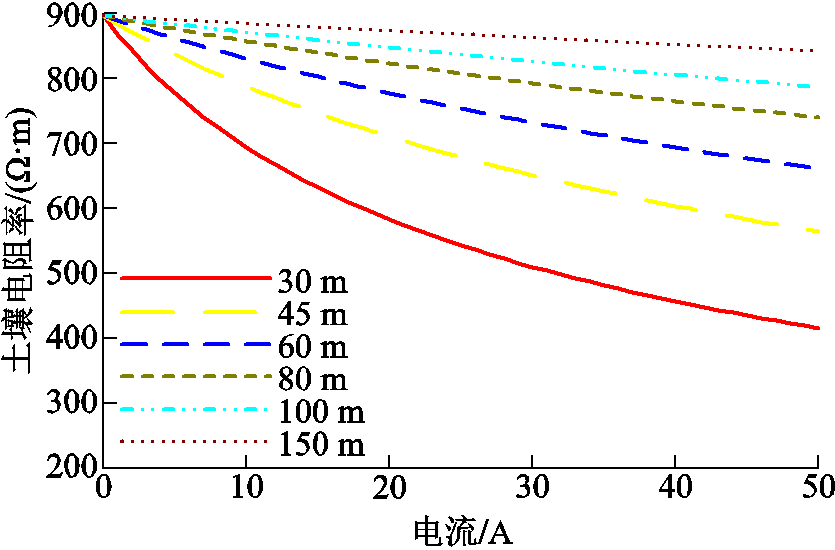
图10 土壤电阻率随电流的变化曲线
Fig.10 Variation of soil resistivity with fault current
基于土壤电阻率随半径和电流的变化规律,可以推算出多个土壤电阻率的函数表达式。为了进一步确定土壤电阻率与电流和半径的最终函数关系,对土壤流散半径从1~150 m每隔1 m取一次值,故障电流从1~50 A每隔1 A取一次值,根据式(13)计算生成共7 500组土壤电阻率的原始数据。再利用1stopt软件对原始数据进行拟合,将拟合精度最好的函数表达式确定为土壤电阻率的最终表达式。拟合精度采用相关系数评估,如式(14)所示。
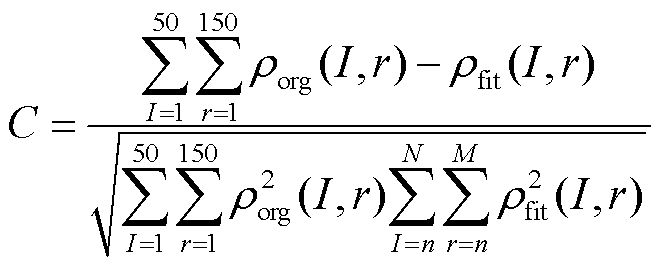 (14)
(14)
式中,ρorg(I, r)为原始数据;ρfit(I, r)为拟合数据。
将多个函数表达式与原始数据进行拟合,最终得到土壤电阻率与电流和流散半径的最优函数表达式为
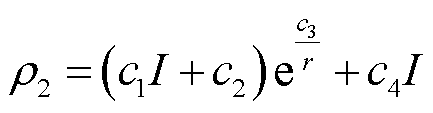 (15)
(15)
式中,c1、c2、c3和c4为拟合参数,接地介质不同,其原始土壤电阻率不同,土壤电阻率随地中电场强度变化特性也各有差异,因此拟合所得上述四个参数对应的值也不同。此外,非击穿区域的散流半径r取值范围为电弧半径a至无穷远处,土壤电阻率的计算可以不考虑电弧半径为0的情况。此时,根据式(13)生成的原始土壤电阻率数据与式(15)计算所得拟合土壤电阻率数据的三维曲面如图11所示,二者相似程度较高,相关系数C可达0.96。因此,得到的最终表达式可以准确表达出土壤电阻率随故障电流与土壤流散半径变化的关系。
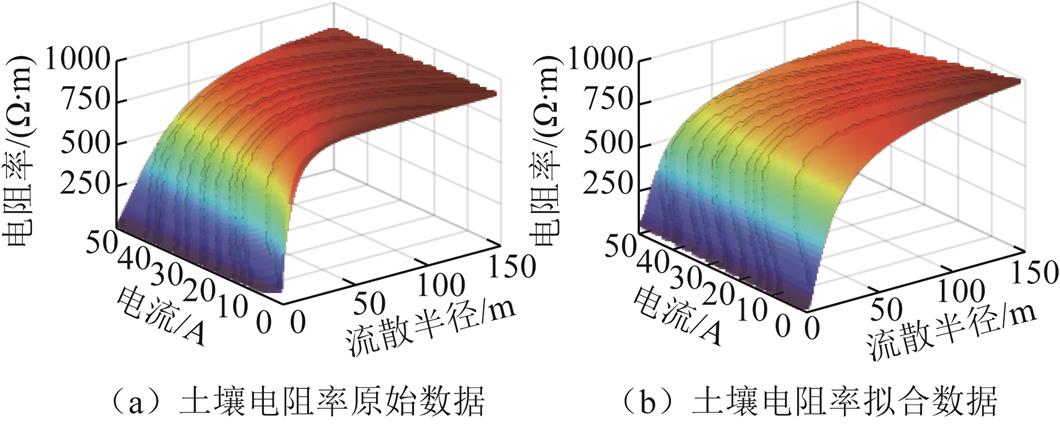
图11 土壤电阻率原始数据与拟合数据对比
Fig.11 Comparison of original and fitting data
将式(15)代入式(11),考虑到交流信号与接地电阻的极性,整理得到非击穿区域电阻Rc2和最终接地电阻Rc分别为
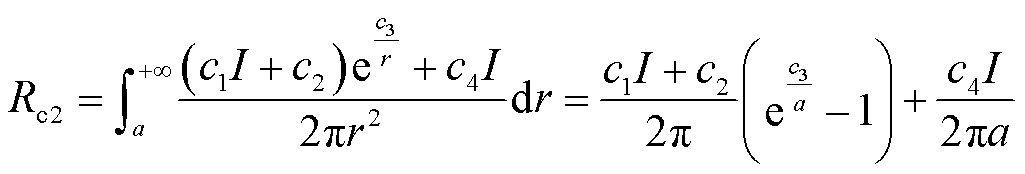 (16)
(16)
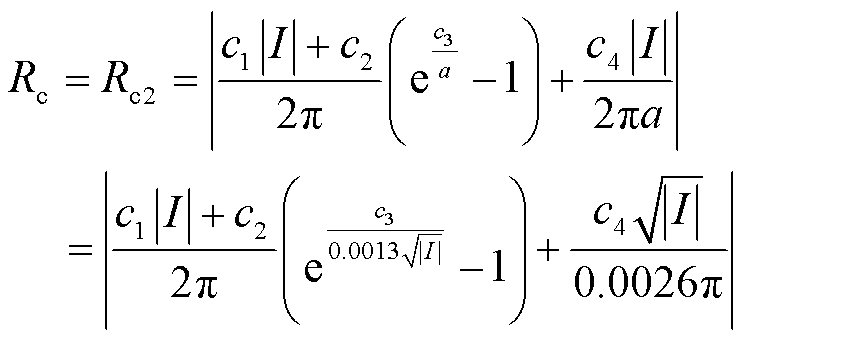 (17)
(17)
由此可知,接地电阻为与故障电流相关的非线性电阻,随故障电流周期性动态变化。通过调节c1、c2、c3和c4的值,可以得到不同接地介质的接地电阻随电流的变化规律。此外,在系统过零点附近,电源电压几乎全加在电弧电阻Rarc上[30],故此时可忽略接地电阻Rc。因此,式(17)可以不考虑电流在系统过零点时的情形,即I≠ 0。但由于维持电弧放电通道的条件仍成立,接地电阻在过零点后增大。
综上所述,高阻接地故障的故障电阻由电弧电阻和接地电阻串联组成。因此,将式(6)所示的电弧电阻模型与式(17)所示的接地电阻模型串联,以此构建基于动态电阻串联的高阻接地故障模型。该模型从高阻接地故障实际物理过程出发,充分考虑了高阻接地故障电阻由电弧和接地介质造成的非线性故障特性,符合实际高阻接地故障的故障工况。
在PSCAD中搭建了如图12所示的10 kV中性点经消弧线圈接地的配电网仿真模型。配电系统包含L1~L4共4条馈线(2条纯架空线路,2条纯电缆线路),馈线后接入负载。配电网模型中消弧线圈的具体参数及馈线长度设置如图12所示,采样率设为0.2 MHz。
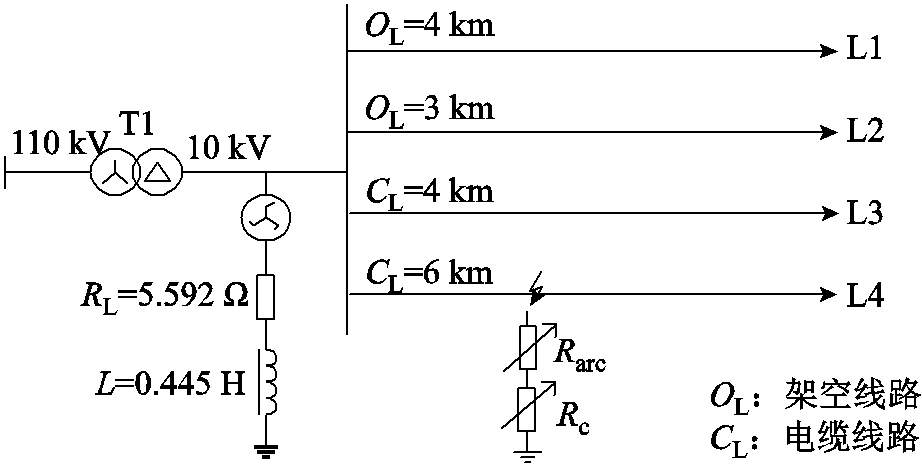
图12 10kV配电网高阻接地故障仿真模型
Fig.12 The simulation model of 10kV distribution network with HIF
搭建动态电阻串联的高阻接地故障模型,接入配电网仿真模型,模拟图1中高阻接地故障现场实验:设置电弧电阻模型参数Ip、Up和接地电阻模型参数c1、c2、c3、c4见表1。采集故障点电压、电流录波数据,根据式(6)和式(17)分别计算电弧电阻与接地电阻,将二者串联后经可控断路器接入配电线路L4馈线距离母线2 km处,模拟配电网在红土壤接地介质发生高阻接地故障的场景。将仿真波形与现场实验波形进行比较,验证本文所提高阻接地故障模型的有效性。
表1 高阻接地故障模型参数
Tab.1 The parameters of HIF model

模型参数 电弧电阻模型Ip = 0.000 2 A Up =1 000 V 接地电阻模型c1= −0.636 6 c2 = 1 051.45 c3 = −12.830 9 c4 = −3.133 2
在10 kV配电网仿真模型中进行高阻接地故障仿真,得到的故障电压、电流波形如图13所示。

图13 所提高阻接地故障模型故障电压、电流波形
Fig.13 Fault waveforms of proposed HIF model
由此可知,故障电流波形过零点附近出现明显的非线性“零休”畸变,这符合高阻接地故障的动态物理过程:当系统电压在过零点附近时,空气间隙未被击穿,电弧处于灭弧阶段,电弧弧阻呈高阻态;且此时故障电压幅值相对较低,故障电流注入土壤后地中电场强度并不高,土壤电阻率将维持在相对较高的水平,故障电流散流路径的电导降低,此时故障电流的幅值低于过零点附近标准的正弦波,使得故障电流中包含谐波。因此,空气间隙未被击穿的过程与电流在土壤中散流产生的谐波会导致故障电流波形在过零点附近发生非线性的“零休”畸变。综上所述,本文提出的高阻接地故障模型符合高阻接地故障的物理发展过程,能够准确反映出现场故障波形的非线性畸变特征。
同时,将图13与图3的现场实验波形进行对比,利用波形相关系数量化仿真故障电流波形和现场实验故障电流波形的相似程度。计算得到二者的波形相关系数高达0.976 2,说明故障仿真波形与现场实验波形一致,验证了本文所提模型可以模拟高阻接地故障的实际故障工况。
根据仿真所得的高阻接地故障电压和电流波形,计算得到伏安特性曲线,如图14所示,并将其与图4a所示现场实验获取的伏安特性曲线进行对比。仿真所得的伏安特性曲线的磁滞特征显著,具有明显的闭环特性,且曲线在过零点附近曲线斜率较大,而之后随着电压、电流的增大,伏安特性曲线斜率逐渐降低至稳定,这与现场实验获取的伏安特性曲线整体趋势一致。
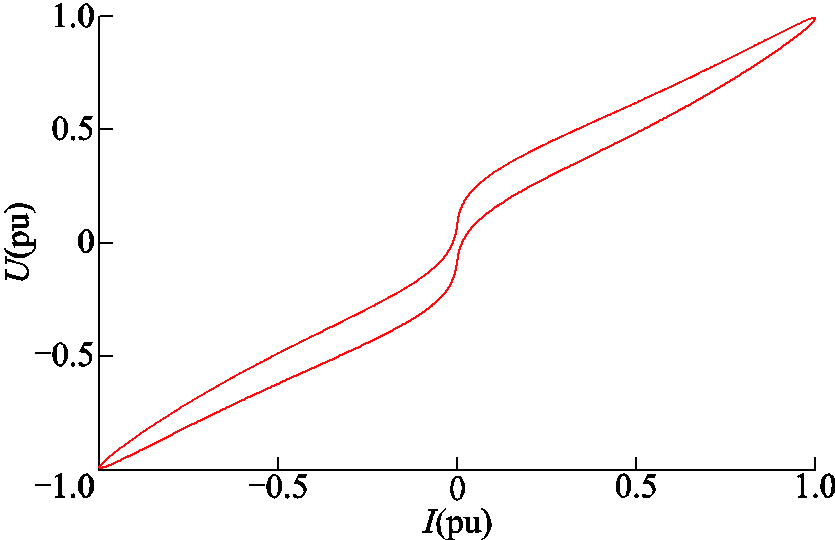
图14 所提高阻接地故障模型伏安特性曲线
Fig.14 Volt-ampere characteristic of proposed HIF model
仿真获取电弧电阻与接地电阻波形如图15a与图15b所示。当故障电流过零点时,电弧绝缘未被击穿,电弧电阻极大且远远大于接地电阻,此时电压全部加于空气间隙,可忽略接地电阻;而故障电流升高后,电弧绝缘逐渐被击穿,电弧电阻迅速下降,而接地电阻逐渐升高。当空气间隙被完全击穿时,电弧电阻最小,约为1 700 Ω,此时接地电阻将达到最大值990 Ω。
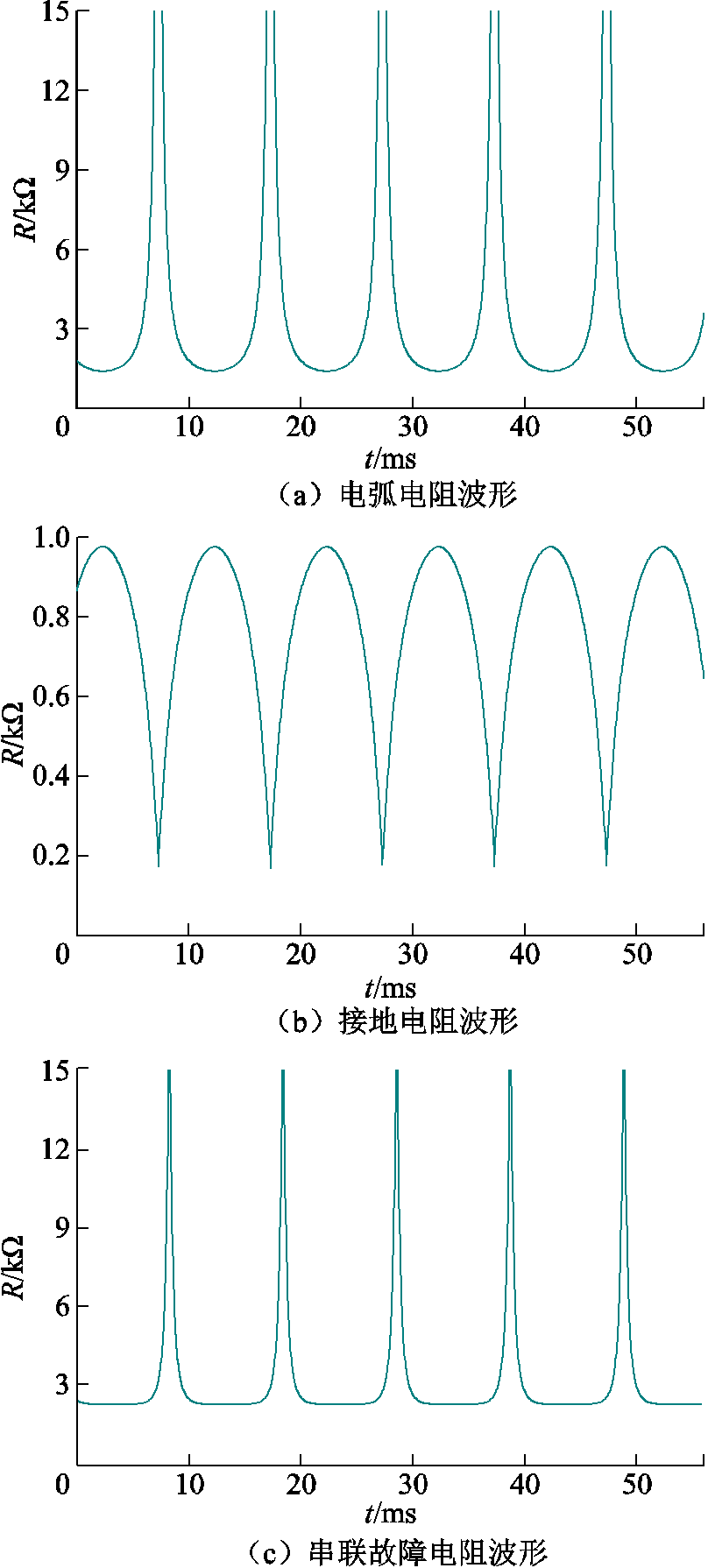
图15 所提高阻接地故障模型故障电阻变化规律
Fig.15 Fault impedance variation of proposed HIF model
将二者串联,绘制出故障电阻波形,如图15c所示。由此可知,故障电阻波形具有尖峰突起,底部平滑的特征:在系统电压过零点附近,故障电流波形产生“零休”畸变,此时故障电阻阻值激增,波形上产生尖峰突起;而随着电流的逐渐增大,故障电阻减小,当电流幅值达到最大值附近时,故障电阻稳定在相对较小的阻值,接近于线性电阻。与图4b对比可知,仿真所得故障电阻波形可以较好地拟合现场实验所获取的故障电阻变化规律。
为验证所提高阻接地故障模型在不同接地介质下的效果,依托图1所示的现场实验平台,进行配电线路经细沙、碎石等典型介质接地的高阻接地故障现场实验。由于各类接地介质的地电特性不同,故障电流波形非线性畸变程度各有差异,设置不同介质的接地电阻模型参数见表2。
表2 不同介质的接地电阻模型参数
Tab.2 The parameters of grounding impedance model in different media

接地电阻模型参数数值 细沙碎石 c1-0.600 3-38.125 c2264.421 46 998.846 2 c3-6.914 3-26.523 5 c4-1.119 1-11.618 6
图16、图17将不同接地介质下高阻接地故障现场试验波形与故障模型仿真波形进行对比。由此可知,现场故障波形与仿真波形畸变程度基本一致,经计算得到电流波形相关系数分别为0.969 3和0.965 8,说明所提故障模型能较为准确地描述不同接地介质下高阻接地故障的非线性特征。

图16 现场实验与模型的电压、电流波形对比(细沙)
Fig.16 Comparison of fault waveforms between field experiment and HIF simulation (micro sand)
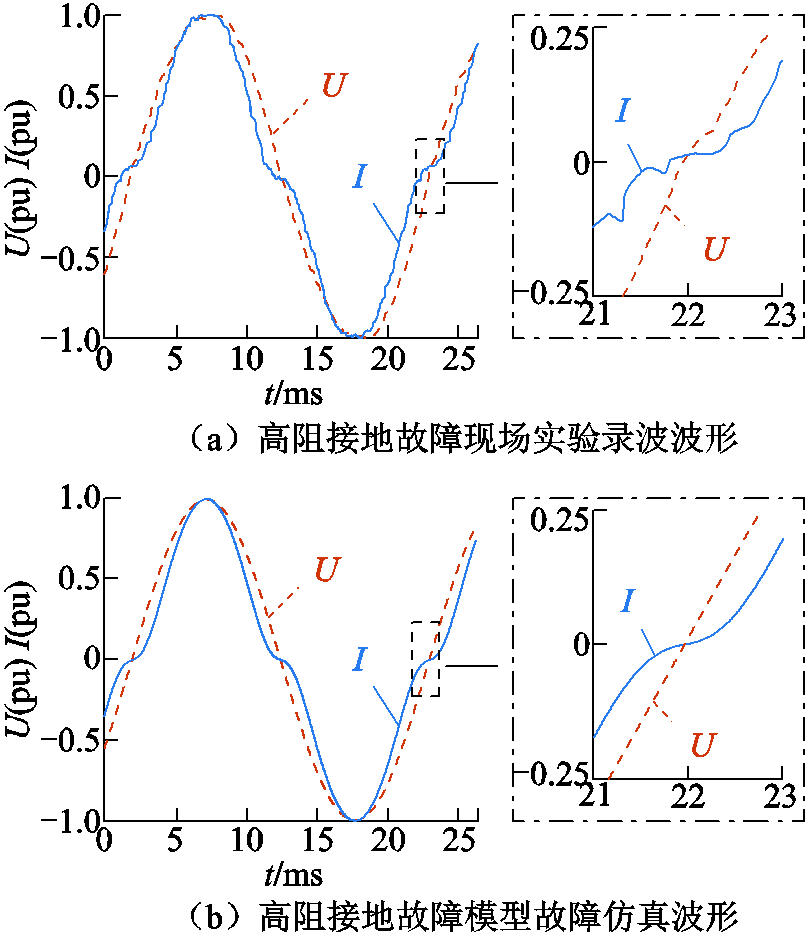
图17 现场实验与模型的电压、电流波形对比(碎石)
Fig.17 Comparison of fault waveforms between field experiment and HIF simulation (gravel)
经过一系列仿真波形与现场实验波形的对比分析,本文提出的高阻接地故障模型仿真所得到的故障电流电压波形与现场试验波形基本一致,且仿真所得的伏安特性曲线与故障电阻波形也与现场实验一致,均能准确体现其非线性特性。因此,本文所提的高阻接地故障模型能够精确地描述不同接地介质下高阻接地故障的动态物理过程,与实际高阻接地故障工况相符,具有较强的实用性。
现有典型的高阻接地故障模型包括文献[10-11]分别提出的基于Mayr电弧、基于Cassie电弧方程串联固定电阻的高阻接地故障模型,文献[16]提出基于汤逊原理的对数电弧模型串联固定电阻的高阻接地故障模型,文献[18]提出基于介质击穿原理的高阻接地故障模型等。将本文所提基于动态电阻串联的高阻接地故障模型与上述现有典型故障模型进行对比,选取合适的参数对各类故障模型进行仿真,进一步验证本文所提高阻接地故障模型的优越性。
现有高阻接地故障模型仿真得到的故障波形如图18所示,将这一系列故障仿真波形与现场高阻接地故障实验波形进行对比。
对比可知,以上四种高阻接地故障模型均能在一定程度上体现出故障电流的非线性畸变。但由于现有模型缺乏对高阻接地故障完整物理诠释,其仿真故障波形在非线性畸变的形状、零休期时长、故障电压电流相位差等因素上与现场实验故障波形均存在差异,并不能完全准确地反映高阻接地故障的特征。
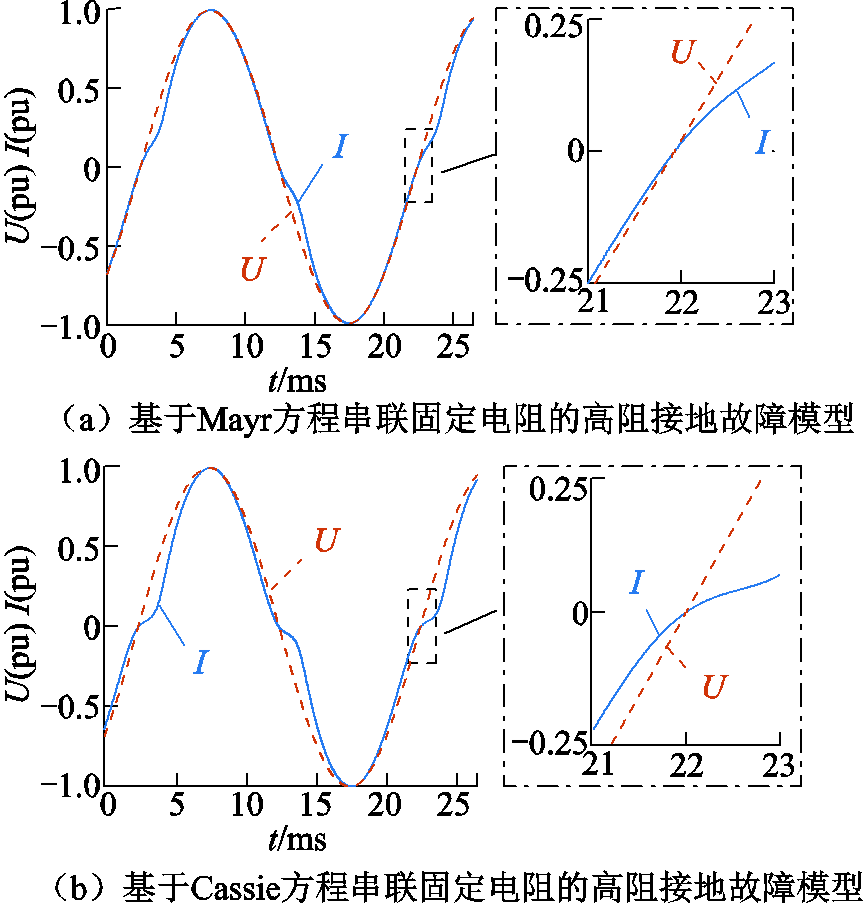
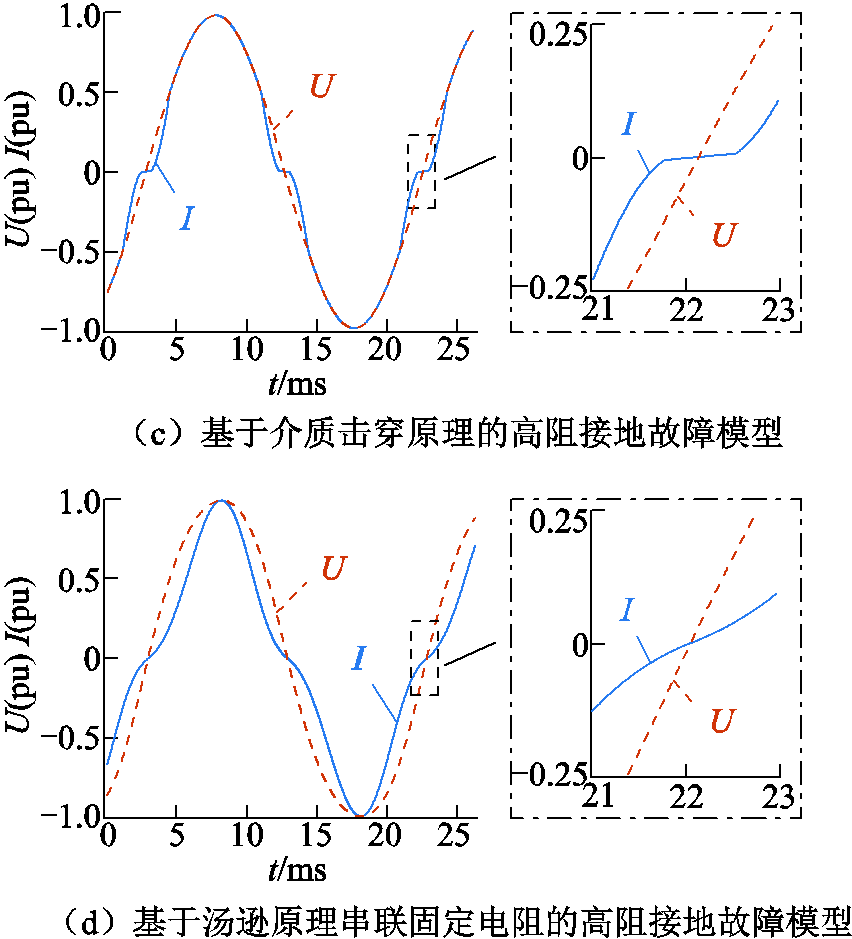
图18 现有高阻接地故障模型电压、电流故障波形
Fig.18 The fault waveforms of existing HIF model
同样,用波形相关系数量化各种高阻接地故障模型电流故障波形与现场实验波形的相似程度,各模型参数及相关系数结果见表3。
表3 故障模型与现场实验电流波形相关系数
Tab.3 The correlation coefficient between HIF models and field experiment current waveform

高阻接地故障模型相关模型参数电流波形相关系数 基于动态电阻串联见表10.976 2 基于Mayr方程串联固定电阻Ploss=25 000,τm=600 μs0.919 7 基于Cassie方程串联固定电阻ec=3 000,τc=750 μs0.918 8 基于介质击穿原理u1=2 000,u2=8 000,g1=0.000 1,g2=0.0020.925 6 基于汤逊原理串联固定电阻IP=0.000 2 A,UP=1 000 V0.903 7
由此可知,本文提出的基于动态电阻串联的高阻接地故障模型仿真所得故障电流波形与现场实验波形的相关系数高达0.976 2,而现有其他高阻接地故障模型仿真所得故障电流波形与现场实验波形的相关系数最高仅为0.925 6。换言之,与其他高阻接地故障模型相比,本文所提高阻接地故障模型得到的故障波形更接近于现场实验波形。因此,基于动态电阻串联的高阻接地故障模型对实际故障的模拟精度优于现有其他高阻接地故障模型,能更好地体现高阻接地故障的非线性畸变特征,具有优越性。
本文从分析配电网高阻接地故障电流、电压波形的畸变特征入手,研究高阻接地故障的动态物理过程,以此为基础提出了一种动态电阻串联的高阻接地故障模型,并得出以下结论:
1)配电网高阻接地故障现场实验表明,受电弧和接地介质的影响,高阻接地故障的电流波形具有明显的非线性畸变特征,伏安特性曲线呈明显的磁滞回线状,故障电阻阻值呈周期性变化。
2)研究高阻接地故障发生时空气间隙击穿与电流在土壤中流散的动态物理过程,发现高阻接地故障电阻由电弧电阻和接地电阻组成。本文提出一种基于电弧电阻和接地电阻两个动态电阻串联的高阻接地故障模型,分别对应间隙击穿和土壤流散过程,具有明确物理意义。
3)在PSCAD中搭建基于动态电阻串联的配电网高阻接地故障模型并进行仿真,并采用波形相关系数量化仿真波形和现场实验波形的相似程度。结果表明本文所提故障模型可以准确地模拟现场实际工况,验证了本文所提模型的准确性;且将其与现有高阻接地故障模型进行对比,本文所提模型仿真波形与现场实验波形的波形相关系数最高,进一步验证了本文所提模型的精确性。
4)对于类型繁多的土壤介质,土壤电阻率随电场强度的变化曲线存在固有差异,还未有文献对此展开深入研究,本文所提模型尚具有一定局限性。因此,下一步将根据地电阻率随电场强度的变化规律对各类复杂土壤进行分类,进一步研究土壤散流时外加电场对黏土、腐殖土、砂土等接地介质土壤电阻率、介电系数、导电离子浓度等地电参量的作用机理,进而构建更为精确、全面的高阻接地故障模型,为后续从机理层面对高阻接地故障辨识提供新思路。
参考文献
[1] 王宾, 崔鑫, 董新洲. 配电线路弧光高阻故障检测技术综述[J]. 中国电机工程学报, 2020, 40(1): 96-107, 377. Wang Bin, Cui Xin, Dong Xinzhou. Overview of arc high impedance grounding fault detection technologies in distribution system[J]. Proceedings of the CSEE, 2020, 40(1): 96-107, 377.
[2] 邓丰, 徐帆, 冯思旭, 等. 基于行波全波形能量分布特征的高阻接地故障检测方法[J]. 中国电机工程学报, 2022, 42(22): 8177-8190. Deng Feng, Xu Fan, Feng Sixu, et al. High-resistance grounding fault detection method based on energy distribution characteristics of traveling wave full waveform[J]. Proceedings of the CSEE, 2022, 42(22): 8177-8190.
[3] 喻锟, 胥鹏博, 曾祥君, 等. 基于模糊测度融合诊断的配电网接地故障选线[J]. 电工技术学报, 2022, 37(3): 623-633. Yu Kun, Xu Pengbo, Zeng Xiangjun, et al. Grounding fault line selection of distribution networks based on fuzzy measures integrated diagnosis[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 623-633.
[4] 邓丰, 梅龙军, 唐欣, 等. 基于时频域行波全景波形的配电网故障选线方法[J]. 电工技术学报, 2021, 36(13): 2861-2870. Deng Feng, Mei Longjun, Tang Xin, et al. Faulty line selection method of distribution network based on time-frequency traveling wave panoramic waveform[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2861-2870.
[5] 王建元, 朱永涛, 秦思远. 基于方向行波能量的小电流接地系统故障选线方法[J]. 电工技术学报, 2021, 36(19): 4085-4096. Wang Jianyuan, Zhu Yongtao, Qin Siyuan. Fault line selection method for small current grounding system based on directional traveling wave energy[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4085-4096.
[6] 国网陕西电力公司. 6·18西安变电站爆炸事故报告[R]. 西安: 国网陕西电力公司, 2016.
[7] 邵庆祝, 崔鑫, 谢民, 等. 弧光高阻接地故障建模及数据修正算法[J]. 电力系统自动化, 2021, 45(11): 120-125. Shao Qingzhu, Cui Xin, Xie Min, et al. Modeling and data correction algorithm for arc high resistance grounding fault[J]. Automation of Electric Power Systems, 2021, 45(11): 120-125.
[8] 龙毅, 欧阳金鑫, 熊小伏, 等. 基于零序功率变化量的配电网单相高阻接地保护[J]. 电工技术学报, 2019, 34(17): 3687-3695. Long Yi, Ouyang Jinxin, Xiong Xiaofu, et al. Protection principle of single-phase high resistance fault for distribution network based on zero-sequence power variation[J]. Transactions of China Electrote-chnical Society, 2019, 34(17): 3687-3695.
[9] 薛永端, 汪洋, 徐丙垠. 小电阻接地系统高灵敏度阶段式零序过电流保护[J]. 中国电机工程学报, 2020, 40(19): 6217-6227. Xue Yongduan, Wang Yang, Xu Bingyin. High sensitive zero-sequence stage current protection for low-resistance grounding system[J]. Proceedings of the CSEE, 2020, 40(19): 6217-6227.
[10] Mayr O. Beiträge zur theorie des statischen und des dynamischen lichtbogens[J]. Archiv Für Elektrotechnik, 1943, 37(12): 588-608.
[11] Cassie A M. Arc rupture and circuit severity: a new theory[R]. Paris, France: CIGRE Report No. 102, 1939: 1-16.
[12] 李露露, 李永培, 周新月, 等. 10kV交联聚乙烯电缆内部多形态间歇性电弧故障建模[J]. 电工技术学报, 2022, 37(23): 6104-6115. Li Lulu, Li Yongpei, Zhou Xinyue, et al. Modeling of multi-modality intermittent arc fault in 10kV XLPE cable[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6104-6115.
[13] 杨明波, 龙毅, 樊三军, 等. 基于组合Mayr和Cassie电弧模型的弧光接地故障仿真及分析[J]. 电测与仪表, 2019, 56(10): 8-13. Yang Mingbo, Long Yi, Fan Sanjun, et al. Simulation and analysis of arc grounding fault based on combined Mayr and Cassie arc models[J]. Electrical Measurement & Instrumentation, 2019, 56(10): 8-13.
[14] 刘艳丽, 郭凤仪, 李磊, 等. 一种串联型故障电弧数学模型[J]. 电工技术学报, 2019, 34(14): 2901-2912. Liu Yanli, Guo Fengyi, Li Lei, et al. A kind of series fault arc mathematical model[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2901-2912.
[15] Jeerings D I, Linders J R. Unique aspects of distribution system harmonics due to high impedance ground faults[J]. IEEE Transactions on Power Delivery, 1990, 5(2): 1086-1094.
[16] 孙月琴, 倪江, 王宾, 等. 应用于输电线路单端测距的高阻接地故障电弧模型分析[J]. 电力系统自动化, 2016, 40(22): 86-92. Sun Yueqin, Ni Jiang, Wang Bin, et al. Transmission line high-impedance fault modeling analysis for single-end fault location[J]. Automation of Electric Power Systems, 2016, 40(22): 86-92.
[17] 王宾, 梁晨光, 李凤婷. 计及间隙长度的弧光接地故障建模及单端测距[J]. 中国电机工程学报, 2019, 39(4): 1001-1009. Wang Bin, Liang Chenguang, Li Fengting. Arc modeling and single-end fault location for arc grounding fault in transmission line considering arc gap length[J]. Proceedings of the CSEE, 2019, 39(4): 1001-1009.
[18] 王宾, 耿建昭, 董新洲. 基于介质击穿原理的配电线路高阻接地故障精确建模[J]. 电力系统自动化, 2014, 38(12): 62-66, 106. Wang Bin, Geng Jianzhao, Dong Xinzhou. High-impedance fault modeling based on solid dielectric electrical breakdown theory[J]. Automation of Electric Power Systems, 2014, 38(12): 62-66, 106.
[19] 张杨珠, 周清, 黄运湘, 等. 湖南土壤分类的研究概况与展望[J]. 湖南农业科学, 2014(9): 31-34, 38. Zhang Yangzhu, Zhou Qing, Huang Yunxiang, et al. General situations and prospects of soil classification in Hunan Province[J]. Hunan Agricultural Sciences, 2014(9): 31-34, 38.
[20] 陈先禄, 刘渝根, 黄勇. 接地[M]. 重庆: 重庆大学出版社, 2002.
[21] 赵玉林. 高电压技术[M]. 北京: 中国电力出版社, 2008.
[22] 梁曦东, 陈昌渔, 周远翔. 高电压工程[M]. 北京: 清华大学出版社, 2003.
[23] 冯允平. 高电压技术中的气体放电及其应用[M]. 北京: 水利电力出版社, 1990.
[24] 李润昌, 刘洪顺, 娄杰, 等. 特高压无补偿线路潜供电弧电气特征与弧柱形态[J]. 高电压技术, 2018, 44(4): 1359-1366. Li Runchang, Liu Hongshun, Lou Jie, et al. Investigation on electrical characteristics and arc column morphology of secondary arc on UHV transmission lines[J]. High Voltage Engineering, 2018, 44(4): 1359-1366.
[25] 李景丽, 袁涛, 杨庆, 等. 考虑土壤电离动态过程的接地体有限元模型[J]. 中国电机工程学报, 2011, 31(22): 149-157. Li Jingli, Yuan Tao, Yang Qing, et al. Finite element model of grounding system considering soil dynamic ionization[J]. Proceedings of the CSEE, 2011, 31(22): 149-157.
[26] 崔韬. 配电线路高阻接地故障检测技术的研究[D]. 北京: 清华大学, 2009.
[27] 郑智慧, 邢鹏翔, 蓝磊, 等. 输电杆塔接地体对埋地油气管道的临界击穿场强试验研究[J]. 电瓷避雷器, 2020(3): 81-85, 91. Zheng Zhihui, Xing Pengxiang, Lan Lei, et al. Experimental study on grounding device of transmission tower lightning discharge to underground oil-gas pipeline[J]. Insulators and Surge Arresters, 2020(3): 81-85, 91.
[28] 程杨. 杆塔接地装置的仿真计算与测量研究[D]. 武汉: 华中科技大学, 2012.
[29] 郭蕾, 古维富, 刘彬, 等. 杆塔接地装置的冲击阻抗建模及应用[J]. 电工技术学报, 2020, 35(10): 2239-2247. Guo Lei, Gu Weifu, Liu Bin, et al. Impulse impedance modeling and application of tower grounding device[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2239-2247.
[30] 梁栋, 徐丙垠, 唐毅, 等. 10kV架空导线单相触树接地故障模型及其检测方法[J]. 中国电机工程学报, 2021, 41(15): 5221-5232. Liang Dong, Xu Bingyin, Tang Yi, et al. Model and detection method for tree-contact single-phase-to-ground faults on 10kV overhead lines[J]. Proceedings of the CSEE, 2021, 41(15): 5221-5232.
Abstract High impedance fault (HIF) may occur in distribution lines owning to harsh weather condition, which is difficult to be detected due to its over thousands of ohms impedance, posing a huge hazard to human and electric equipment. Therefore, the safety risks and the lack of actual HIF data make it essential to require an accurate HIF model. However, only based on heat balance or dielectric breakdown theories, existing HIF models fail to capture nonlinear characteristics due to the insufficient physical interpretation of HIF. Thus, considering the entire fault physical process, a HIF model based on dynamic impedance in series is proposed. By comparing it with other models, the simulation results verify that the proposed model characterizes HIF nonlinear characteristics under various grounding media with higher accuracy.
The HIF experiments under laterite soil had been carried out in the 1:1 real distribution network testing field. Based on the recorded waveforms, the HIF physical processes are analyzed, specifically including the arc ignition and extinction characteristics and the current dispersion in soil. The findings suggest that the nonlinearity of grounding medium and air breakdown process are the primary contributors to the nonlinear distortion of fault current waveforms. Correspondingly, it can be revealed that the HIF fault impedance is composed of arc impedance and ground impedance in series. On this basis, a new HIF model based on dynamic impedance in series is proposed. Firstly, the Thompson Theory is utilized to describe the arc ignition and extinction characteristics in air breakdown process, based on which the dynamic exponential arc impedance model can be established. Secondly, with the analysis of the fault current dispersion process, the variation curve of soil resistivity with electric field intensity is obtained, then the grounding impedance can be calculated to establish the grounding impedance model. Though the analysis of grounding impedance only takes laterite soil as an example,it is worth noting that this is just an approach to calculate grounding impedance, which is not limited by the types of grounding medium. In principle, the approach applies to all grounding media. Ultimately, the new HIF model is obtained by connecting these two impedance models in series. The new HIF model takes the entire HIF physical processes into consideration, featuring specific physical significance.
To validate the effectiveness of the proposed HIF model, a large number of HIF simulations were carried out and the simulated waveforms were compared with the field experimental waveforms using waveform correlation coefficients. Firstly, the simulated waveforms and Voltage-Ampere characteristics curve are similar to the field testing recorded data. Furthermore, for HIF occurring under laterite soil, gravel, and micro sand, the fault current waveform correlation coefficients between simulated and real testing data are 0.9762, 0.9693, and 0.9658 respectively. The simulation results verified that the proposed model exhibits outstanding performance. Secondly, the fault current waveform correlation coefficient of proposed model reaches 0.976 2, compared with only up to 0.925 6 for other existing HIF models. In other words, proposed model can better reflect the nonlinear distortion characteristics of HIF faults with higher accuracy, which demonstrates the superiority of proposed model.
The following conclusions can be drawn from the theoretical and experimental analysis: (1) The real field HIF experiments indicate that the fault current waveform and volt-ampere characteristics curve exhibit obvious non-linear distortion, and the fault impedance fluctuates periodically. (2) The HIF physical process including air breakdown and soil current dispersion are analyzed. Correspondingly, the fault impedance can be composed of arc impedance and grounding impedance. On this basis, a new HIF model based on the dynamic arc and grounding impedance in series is proposed, which features characterizing HIF physical process. (3) The proposed model is constructed in PSCAD. Comparing it with field experiments and other HIF models, the simulation results verify that the proposed model can more accurately characterize the HIF nonlinear features under various grounding media, providing more precise HIF data for subsequence research. (4) However, the proposed HIF model has certain limitations due to the diversity of grounding media. Therefore, the upcoming research will focus on classifying these various grounding media, aiming at constructing a more accurate and comprehensive HIF model.
keywords:Distribution network, high impedance fault, arc impedance, grounding impedance, nonlinear characteristics
DOI:10.19595/j.cnki.1000-6753.tces.230065
中图分类号:TM77
国家自然科学基金(52077008)、湖南省自然科学基金杰出青年项目(2022JJ10048)和湖南省湖湘青年科技创新人才项目(2021RC3097)资助。
收稿日期 2023-01-17
改稿日期 2023-04-08
钟逸涵 男,1998年生,硕士研究生,研究方向电力系统保护控制。E-mail:515089370@qq.com
邓 丰 女,1983年生,副教授,博士生导师,研究方向电力系统微机保护、故障行波保护和故障定位。E-mail:df_csust@126.com(通信作者)
(编辑 赫 蕾)