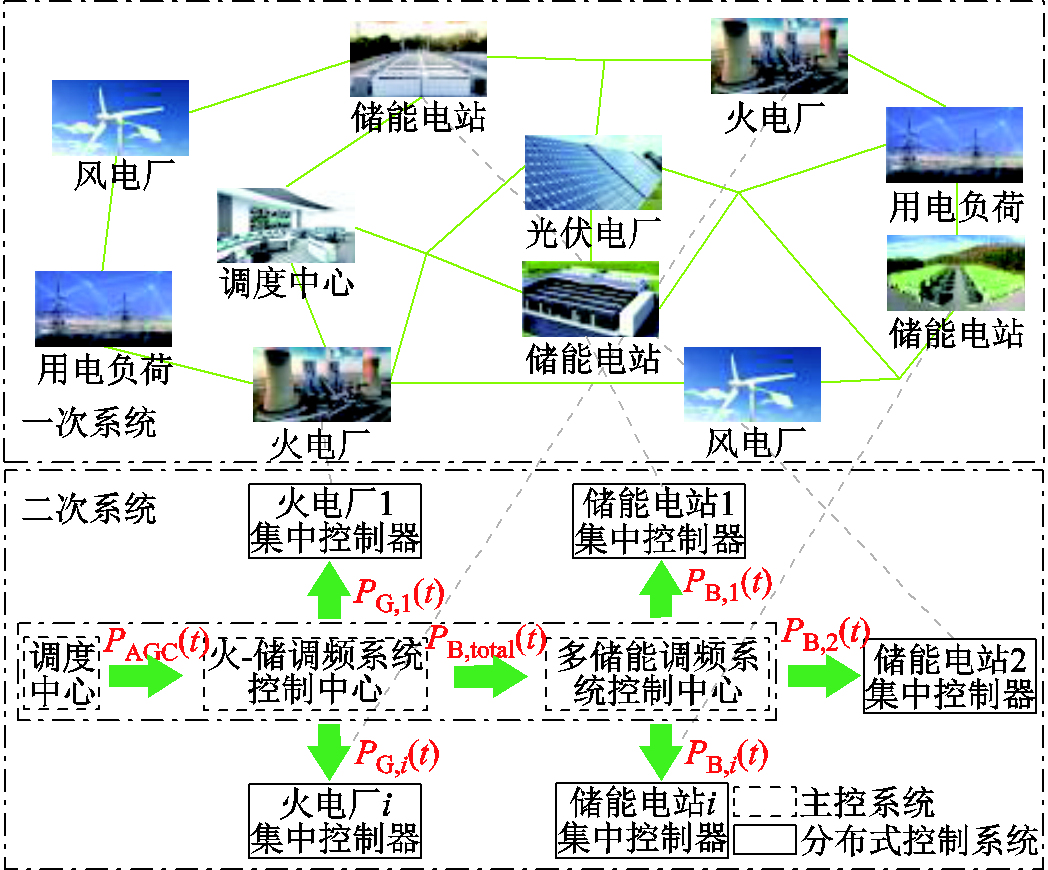
图1 多火-储联合调频系统示意图
Fig.1 Schematic diagram of multi thermal power-energy storage combined frequency modulation system
摘要 针对分布于区域电网不同网络节点的多座储能电站参与电网调频功率调度问题,该文提出一种基于集合经验模态分解(EEMD)和多目标遗传算法(MOGA)的火-多储系统调频功率双层优化策略。该策略包含火-储调频功率优化层和多储能电站调频功率优化层:上层计及火-储调配资源各自优势及剩余调频能力,构建火-储调频功率优化分配模型,完成火-储调频功率的分配;下层引入关于调频成本和荷电状态(SOC)的自适应权重系数,以调频成本最低和SOC均衡为优化目标,完成调频功率在多储能电站之间的分配。仿真结果表明,所提策略可以提升区域电网调频效果并降低调频成本,均衡控制多个储能电站的调频成本和SOC,可以防止经济性较好的储能电站长期处于SOC越限边缘状态,提升储能电站参与调频的积极性和可持续性。
关键词:多火电储能系统 二次调频 双层优化控制 多目标遗传算法(MOGA) 自适应权重系数
近年来,为积极响应绿色低碳发展号召,全力推动能源产业转型升级,我国风光等可再生能源装机容量不断增加[1]。然而,随着新能源渗透率的提高,电力系统将面临惯性下降、调频容量不足等因素带来的调频压力问题[2-3]。储能因其响应速度快、控制精度高的特点,在响应调频指令、改善电网频率质量等方面具有突出表现[4]。
随着储能技术发展以及国家政策支持,电网侧安装运行的储能电站项目数量和容量激增,成为传统机组之外电网调频功率容量的另一重要来源。但是目前储能的造价运行成本仍然较高,如何协调区域内各调频资源(火电机组和储能电站)的联合最优调度,充分发挥传统机组调频成本优势和储能调频性能优势,成为当下亟须解决的工程问题[5-8]。
目前,国内外关于火电、储能的联合调频已经取得了一定的研究成果。文献[9]以火电机组跟随自动发电控制(Automatic Generation Control, AGC)指令偏差值作为储能出力指令辅助火电机组调频;文献[10]提出基于传统机组和储能剩余调频功率的动态比例分配策略,并计及了储能的荷电状态(State of Charge, SOC)恢复。以上策略并未考虑火电机组和电池储能调频性能的差异,易过高或过低利用储能,导致电网调频成本升高或调频性能改善不明显。为此,文献[11]采用传统滤波的方法将调频需求分解为低频和高频部分,分别由储能和火电机组承担,充分发挥各种调频资源的优势,但是其分解效果在一定程度上由滤波器的截止频率和时滞特性决定;为避免滤波参数选取准确性对调频效果的影响,文献[12-13]利用变分模态分解对区域控制误差调频信号进行分解,并按高低频分配调频指令,改善了火储系统的调频性能,降低了火电机组磨损。
可以看出,现阶段国内外已有的火储联合调频控制策略多是从源侧出发,储能仅作为火电机组参与调频的辅助设备。但是随着网侧大容量独立储能电站并网数量的增加,区域内多个储能电站整体的可调频功率和容量有望超过火电机组的可调频功率和容量或与其持平,有必要从网侧角度来考虑区域内整体AGC指令如何在火电机组整体和储能电站整体之间进行分配。另外,因为需要联合多个储能电站进行调频,如何协调区域内所有储能电站,实现区域内多储能电站参与调频的经济性和持续性的均衡仍有待进一步研究。
目前,针对分布于区域电网中不同网络节点的多座储能电站共同参与电力系统调频这一问题,还缺乏有效的调控手段。文献[14]提出一种基于主控中心的多储能电站控制方法,能够较好地保持区域内系统频率稳定,但是需要复杂分组;文献[15]以调频总成本和SOC惩罚最低为目标,采用二次规划的方法求解,来优化各储能电站的出力;文献[16]以调频成本最低为目标对多储能电站调频功率进行分配,并计及各储能电站单元内部的SOC均衡恢复;文献[17]兼顾考虑SOC和充放电成本,以区域控制偏差(Area Control Error, ACE)作为输入量,采用动态比例的方式将调频信号在蓄电池和超级电容器之间进行优化分配。
以上文献均将储能电站看成独立的个体,从多储能电站的调频成本和个体储能电站的SOC约束两个方面对调频指令进行分配,但是仅考虑个体储能电站自身的SOC限制,不考虑多个储能电站之间SOC的相互约束,容易造成某个储能电站SOC状态过高或过低,从而提前失去调频能力的问题;并且多个储能电站参与电力系统调频时,对于储能电站调频成本和SOC恢复两个目标的需求也不是一成不变的,应该根据系统运行状态进行权重调整。
根据上述分析,本文工作的创新点如下:①基于集合经验模态分解(Ensemble Empirical Mode Decomposition, EMMD)构建时空滤波器,构建了计及区域内火电机组和多储能电站整体剩余调频功率的分配模型,避免了传统滤波器滞后和重复调节的同时提高区域内调频资源的利用水平;②综合考虑多个储能电站的经济性和可持续性,构建计及储能电站调频成本和SOC均衡恢复的多储能电站调频功率分配模型,在降低调频成本的同时提高调频可持续性;③构建计及网络安全约束的调频功率再分配模型及考虑网络运行状态的多目标函数自适应权重系数,基于多目标遗传算法(Multi-Objective Genetic Algorithm, MOGA)求解,降低了多目标问题Pareto最优解选取的人为影响权重,并保障电网安全稳定运行。
综上所述,针对含多个储能电站的区域电网调频调度问题,本文提出基于集合经验模态分解和多目标遗传算法的火-多储系统调频功率双层优化策略:在火-多储调频功率优化层,基于集合经验模态分解,构建时空滤波器,将调频需求分解为低/高频分量,分别由火电整体和多储能整体承担,并以经济性最优为目标分配各火电机组承担的调频功率;多储能电站调频功率优化层以调频成本最低和SOC均衡恢复构成多目标函数,以多目标遗传算法进行模型求解,构建关于系统运行状态的自适应权重系数,确定各储能电站承担的调频功率,在降低多储能电站整体调频成本的同时,提高调频的可持续性,最后基于实际运行数据对所提模型进行验证。
本文主要研究新型电力系统下火电机组和储能电站联合参与电网二次调频的功率分配问题,包括火-储调频功率分配、多火电机组调频功率分配和多储能电站调频功率分配三部分内容。其中区域内包含用电负荷、新能源机组、多个不同类型的火电机组和储能电站,其结构如图1所示。

图1 多火-储联合调频系统示意图
Fig.1 Schematic diagram of multi thermal power-energy storage combined frequency modulation system
首先,调度中心通过监测区域电网频率波动,并根据定频率控制模式计算出各调频资源需要调整的出力总量,有
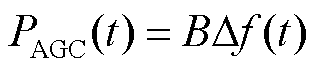 (1)
(1)
式中,PAGC(t)为t时刻区域内总调频功率指令;B为频率偏差系数;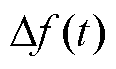 为t时刻区域电网频率偏差。
为t时刻区域电网频率偏差。
然后,该调频指令经时空滤波器分解后,经由火-储联合调频系统控制中心和多储能电站调频系统控制中心计算后得到各调频资源的调频功率指令为
 (2)
(2)
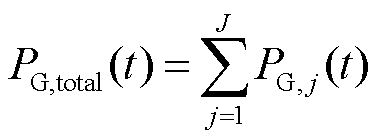 (3)
(3)
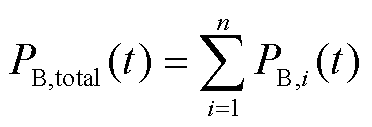 (4)
(4)
式中,PG,total(t)为t时刻火电机组整体所分配的调频功率;PB,total(t)为t时刻多储能电站整体所分配的调频功率;PG,j(t)为t时刻火电机组j所分配的调频功率;PB,i(t)为t时刻储能电站i所分配的调频功率,包含t时刻储能电站i的充电功率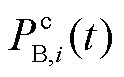 和放电功率
和放电功率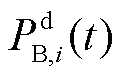 。本文中,
。本文中,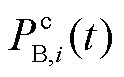 为“负”,
为“负”,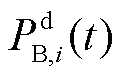 为“正”,三者关系为
为“正”,三者关系为
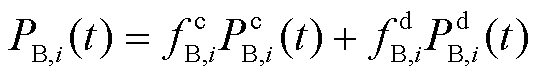 (5)
(5)
式中,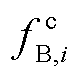 、
、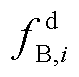 分别为t时刻储能电站i的充放电信号,其值确定方法为
分别为t时刻储能电站i的充放电信号,其值确定方法为
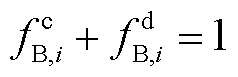 (6)
(6)
式中,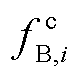 、
、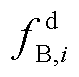 为0或1的整数,并且不能同时等于1。当PAGC(t)为正值时,
为0或1的整数,并且不能同时等于1。当PAGC(t)为正值时,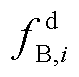 取值为1,表示储能电站i在该时刻放电;当PAGC(t)为负值时,
取值为1,表示储能电站i在该时刻放电;当PAGC(t)为负值时,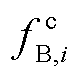 取值为1,表示储能电站i在该时刻充电。
取值为1,表示储能电站i在该时刻充电。
针对网侧各调频资源(火电机组和储能电站)成本/性能的差异,本文提出基于集合经验模态分解和多目标遗传算法的火-多储系统调频功率双层优化策略,包括火-储调频功率优化层和多储能电站调频功率优化层,其框架如图2所示。

图2 双层优化控制策略框图
Fig.2 Block diagram of two-layer optimal control strategy
(1)火-储调频功率优化层构建了时空滤波器,将区域总AGC指令在火电机组整体和储能电站整体之间分配,并构建了多台火电机组之间调频功率的经济分配模型,完成调频功率的初次分配。
(2)多储能电站调频功率优化层提出多个储能电站之间调频功率的优化分配模型,将火-多储调频功率优化层分配得到的多储能电站整体需响应的AGC指令在多个储能电站之间进行再分配,综合考虑不同储能电站的调频成本、储能电站自身以及多储能电站整体的SOC约束,以整体调频成本最低和SOC均衡恢复为多目标,实现多座储能电站的最优调频出力分配。
本文所提双层优化模型可以实现火-储调频功率的分层优化,既能充分发挥火电机组和电池储能各自的调频优势,又能均衡恢复多个储能电站的SOC,保证区域电网整体的调频质量和经济性。
当调频调度指令发生阶跃变化时,电池储能对该指令的响应速度可以达到火电机组的100倍左右[4],因此对于火储联合调频系统,可以让火电机组承担变化较平稳的调频信号,储能系统承担变化较频繁的调频信号,从而充分发挥两种不同调频资源在调频性能和调频经济性方面的优势。
集合经验模态分解可以根据输入信号的极大值
特征尺度为准则,将原始信号分解为多组信号,分解后的信号称为原始信号的固有模态函数分量(Intrinsic Mode Functions, IMF),通过EEMD方法分解原始信号的结果[18]为
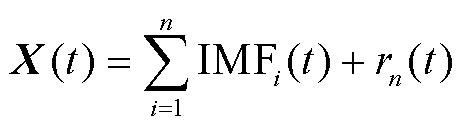 (7)
(7)
式中,X(t)为原始信号;IMFi(t)为原始信号经EEMD分解分解后的固有模态分量;rn(t)为分解余项;n为固有模态分量个数。
如式(7)所示,原始信号经EEMD分解后,可以得到频率逐渐降低的IMF分量,根据IMF分量的特征,构建一种基于原始信号不同周期特征尺度的时空滤波器。
低通时空滤波器可以表示为
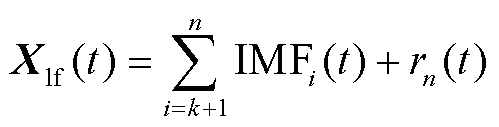 (8)
(8)
高通时空滤波器可以表示为
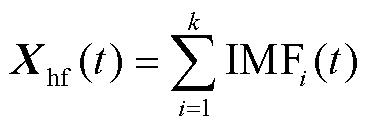 (9)
(9)
式中,Xlf(t)为原始信号的低频信号;Xhf(t)为原始信号的高频信号;k为时空滤波器的阶数。
时空滤波器在AGC控制系统中的作用是将区域总AGC信号分解为火电机组整体和储能电站整体需承担的调频功率指令。时空滤波器的输入为持续的AGC信号。时空滤波器会将输入的AGC信号存储划分为与时间窗口长度相同的数据段,在每个数据段结束时会基于设定的滤波阶数将区域AGC信号进行分解,得到当前时刻火电机组整体及储能电站整体需承担的二次调频功率指令。该指令传输至火电机组调频功率分配控制中心和多储能调频系统控制中心进行计算后得到各调频电源的调频调度指令。各调频资源的调频调度指令持续时间与电网AGC的命令发送周期相同,当下一个时间窗口计时结束后,时空滤波器会完成第二次AGC信号的分解,经上述两个控制中心计算后更新各调频电源的调频调度指令。
时空滤波器的运行需设定滤波阶数和时间窗口长度,滤波阶数的选取与火电机组的运行状态有关,在3.2节火-储调频功率分配中进行介绍;时间窗口长度定义为每个AGC信号数据段中采样点个数与采样点时间间隔的乘积,所选取的时间窗口长度应在保证分解效果的同时尽可能提高分解效率,同时要考虑数据采集环节的运行特性,以满足AGC系统的实时在线要求,时间窗口长度的确定方法为
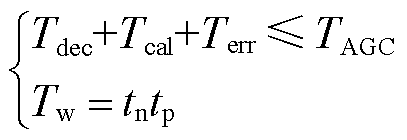 (10)
(10)
式中,Tdec为时间窗口长度为Tw下的分解耗时;Tw为时间窗口长度,本文选定为5 min,即每次需要4个历史数据以及1个当前采样数据;Tcal为分解后的AGC指令经火电机组和储能电站控制中心计算出各调频资源的调频调度指令所需时间;Terr为预留的计算时间误差裕度;TAGC为AGC的时间性能要求;tn为采样点个数;tp为采样点时间间隔。
在3.1节构建时空滤波器基础上,还需要确定滤波阶数k才能完成火-储调频指令的分配。考虑火电机组和电池储能两者在调频性能和调频经济性存在的差异,本文以火电机组可平稳最大出力为目标确定滤波阶数,确定方法如下。
首先,计算时空滤波器所有阶数下可能的分解重构结果,并记录每一种结果下火电机组整体需承担调频功率的最大值,即
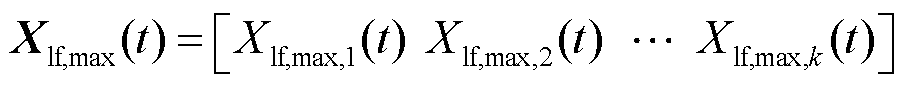 (11)
(11)
式中,Xlf,max(t)为火电机组整体承担的调频功率最大值矩阵;Xlf,max,k(t)为时空滤波器阶数为k时火电机组整体承担的调频指令最大值。
然后,计算每一种结果下火电机组整体需承担的调频功率最大值与爬坡速率最大值的方均根值,选取方均根值最小时所对应的阶数为时空滤波器的阶数。
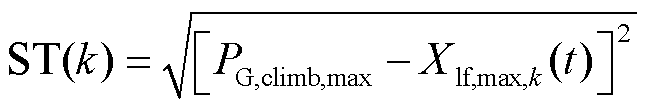 (12)
(12)
式中,ST(k)为滤波阶数选择函数;PG,climb,max为多台火电机组整体的最大爬坡速率。
确定时空滤波器的参数后,可以将区域总AGC指令分解为低频和高频两部分,分别由火电机组整体和储能电站整体承担,有
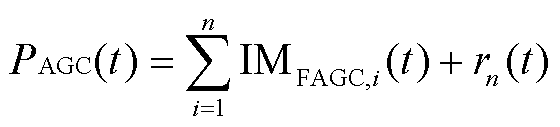 (13)
(13)
式中,IMFAGC,i(t)为区域总AGC指令经EEMD分解后的固有模态分量。
火电机组整体承担的AGC指令为
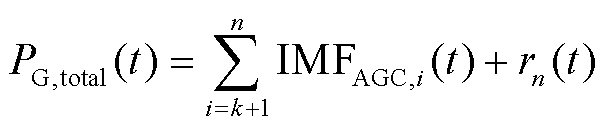 (14)
(14)
储能电站整体承担的AGC指令为
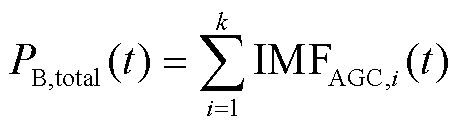 (15)
(15)
为避免火电机组整体或储能电站整体的调频功率指令在某些极端点超过其最大可出力限值,对上述两种调频资源分配的调频功率指令进行修正调整,基本思想如下:当火电机组整体承担的调频功率越限,储能电站整体承担的调频功率未越限时,储能电站整体承担的调频功率按其最大可接受能力累加火电机组整体调频功率越限部分;当火电机组整体承担的调频功率未越限,储能电站整体承担的调频功率越限时,火电机组整体承担的调频功率按其最大可接受能力累加储能电站整体调频指令越限部分;当火电机组和储能电站整体承担的调频功率均越限时,按其最大输出能力参与电网调频。火-储调频功率优化层的控制流程如图3所示。
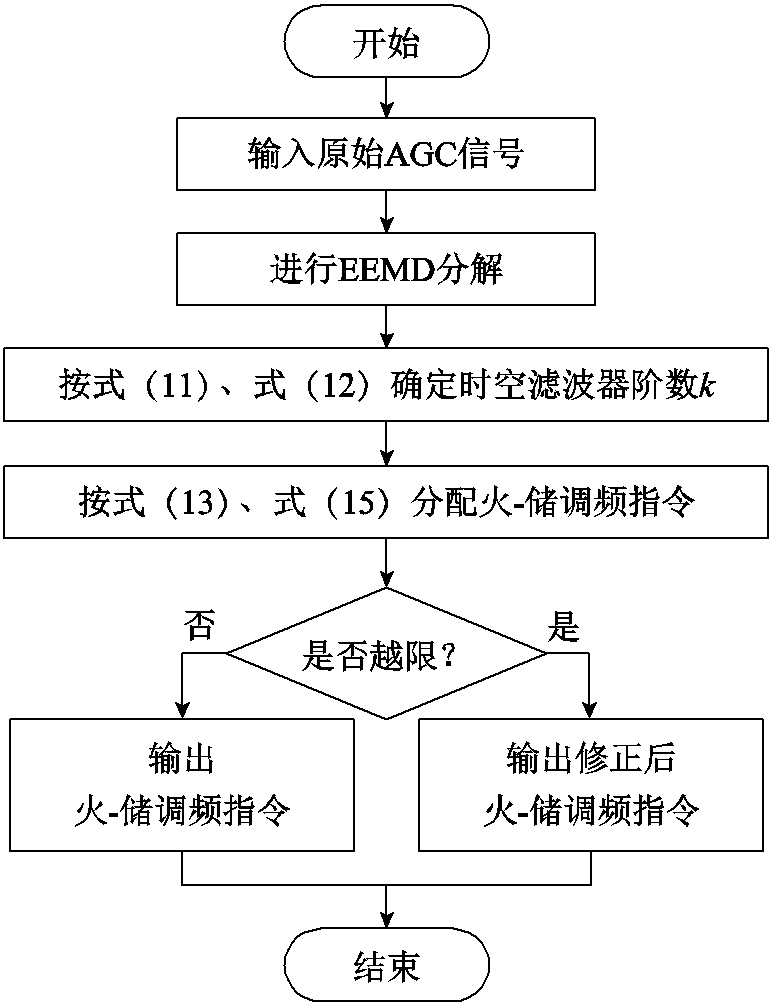
图3 火-储调频功率分配策略流程
Fig.3 Schematic diagram of power distribution strategy for fire storage frequency modulation
为实现多台火电机组的调频功率分配,本文构建了火电机组调频功率经济分配模型,其核心分配思想为:以火电机组整体的经济性为首要目标,以各台火电机组的剩余调频容量为次要目标,各台火电机组与调度指令相同方向的剩余容量越大,该台火电机组的抗拒系数就越小,其被调度的优先级就越高;反之,该台火电机组的抗拒系数就越大,其被调度的优先级就越低。
火电机组调频功率经济分配模型的构建过程为
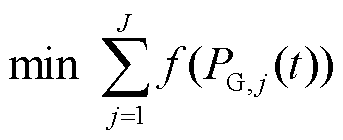 (16)
(16)
式中,f(PG,j(t))为t时刻火电机组j的调频成本,包括煤耗成本、碳捕集成本和机组磨损成本。
火电机组调频成本的函数表达式为
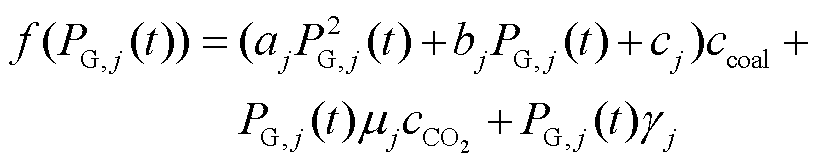 (17)
(17)
式中,aj、bj、cj为机组j的煤耗系数;μj为机组j的碳排放量系数;ccoal为煤耗成本参数;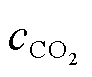 为碳捕集成本;γj为机组j的磨损成本系数。
为碳捕集成本;γj为机组j的磨损成本系数。
火电机组的调频调度需满足以下约束:
1)调频功率平衡约束
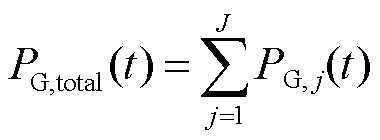 (18)
(18)
2)机组出力上、下限约束
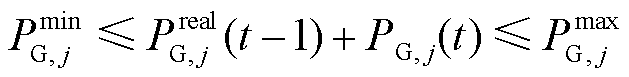 (19)
(19)
式中,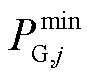 、
、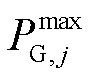 分别为机组j的最小、最大出力限值;
分别为机组j的最小、最大出力限值;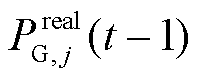 为上一时刻机组j的实际出力值。
为上一时刻机组j的实际出力值。
3)机组爬坡约束
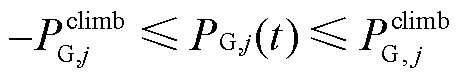 (20)
(20)
式中,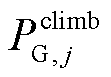 为机组j的爬坡速率。
为机组j的爬坡速率。
为避免经济性较好的火电机组长期运行于满载状态而增加额外的机组磨损,模型中加入了可以改变机组参与调频意愿的抗拒系数,机组出力越接近额定限值,抗拒系数就越大,机组参与调频的意愿就越低,抗拒系数为
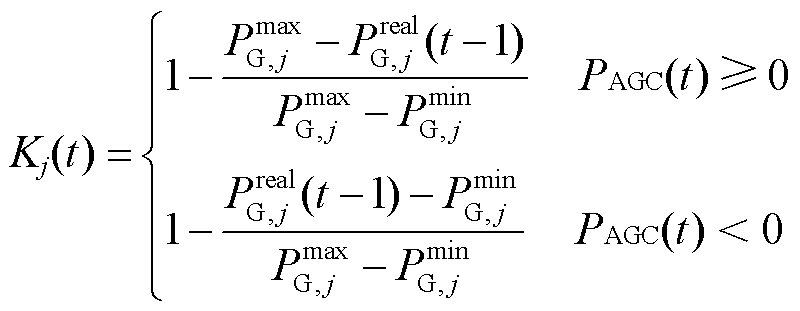 (21)
(21)
式中,Kj(t)为机组j在t时刻的抗拒系数。
为削弱不同火电机组额定容量的差异对抗拒系数的影响,对抗拒系数进行归一化处理,有
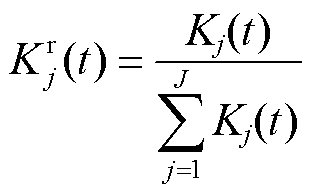 (22)
(22)
式中,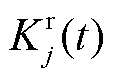 为t时刻机组j归一化后的抗拒系数。
为t时刻机组j归一化后的抗拒系数。
考虑抗拒系数后火电机组调频功率经济分配模型的目标函数为
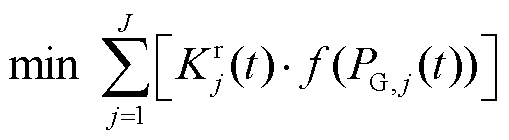 (23)
(23)
为在多储能电站整体经济运行的基础上进行SOC均衡恢复,本文建立了考虑不同类型储能电站调频成本和SOC恢复的两个目标函数,从而达到均衡控制的目的,属于多目标优化模型。
4.1.1 目标函数
储能电站参与电网调频服务时,要考虑其容量投资成本和能量损失成本。另外,储能电站调频时需要频繁改变出力大小和出力方向,会造成其寿命衰减,因此对于储能电站参与调频的成本函数建模中必须考虑其寿命折损成本,本文构建的储能电站调频成本为
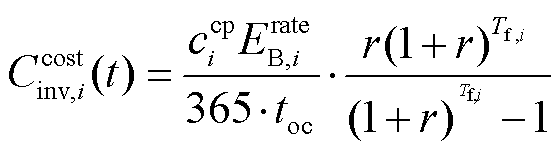 (24)
(24)
 (25)
(25)
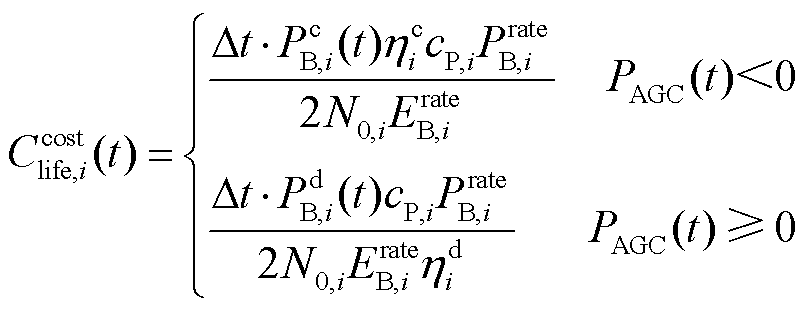 (26)
(26)
式中, 、
、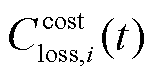 、
、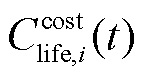 分别为储能电站i的容量投资成本、能量损失成本、寿命折损成本[19];
分别为储能电站i的容量投资成本、能量损失成本、寿命折损成本[19];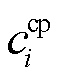 、se、cP,i分别为储能电站i的单位容量成本、上网电价、单位功率成本;
、se、cP,i分别为储能电站i的单位容量成本、上网电价、单位功率成本;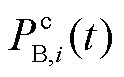 、
、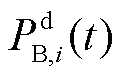 、
、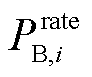 分别为储能电站i在t时刻的充电功率、放电功率、额定功率;
分别为储能电站i在t时刻的充电功率、放电功率、额定功率;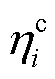 、
、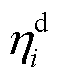 分别为储能电站i的充、放电效率;
分别为储能电站i的充、放电效率; 为储能电站i的额定容量;r为年利率,取8%;Tf,i为储能电站i的浮充寿命;No,i为储能电站i在满充满放情况下的循环次数;toc为调度次数;
为储能电站i的额定容量;r为年利率,取8%;Tf,i为储能电站i的浮充寿命;No,i为储能电站i在满充满放情况下的循环次数;toc为调度次数; 为优化周期。
为优化周期。
储能电站参与调频的成本函数为
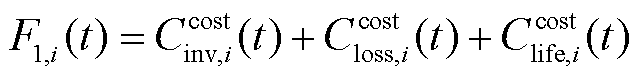 (27)
(27)
式中,F1,i(t)为t时刻储能电站i的调频成本。
若区域内含有n个储能电站,则t时刻关于多储能电站整体调频成本的目标函数为
 (28)
(28)
式中,F1(t)为t时刻多储能电站整体的调频成本。
多储能电站联合参与电网调频时,如果只考虑调频成本,会使经济性较好的储能电站充放电优先级过高,长时间运行于SOC限值边界,而经济性较差的储能电站一直不动作,导致多个储能电站SOC的不均衡,不利于提高储能电站参与调频的积极性和可持续性。因此在储能电站参与电网调频时,还要考虑单个储能电站以及多个储能电站SOC的均衡恢复。储能电站i的SOC控制模型需要考虑各储能电站当前时刻以及上一时刻的SOC值,即
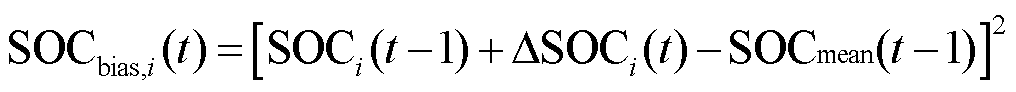 (29)
(29)
式中,SOCbias,i(t)为储能电站i的SOC偏差;SOCi(t-1)为储能电站i上一时刻的SOC;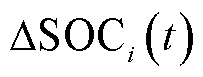 为储能电站i在当前时刻的SOC变化量;SOCmean(t-1)为上一时刻多个储能电站的SOC均值。SOC控制模型各部分的计算方法为
为储能电站i在当前时刻的SOC变化量;SOCmean(t-1)为上一时刻多个储能电站的SOC均值。SOC控制模型各部分的计算方法为
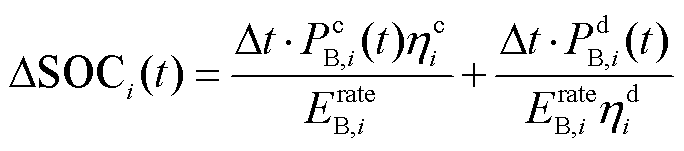 (30)
(30)
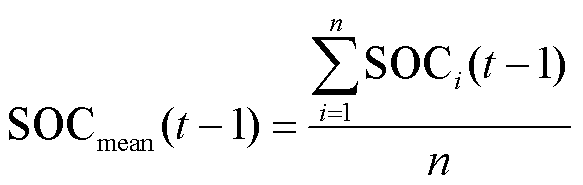 (31)
(31)
因此,t时刻控制多储能电站整体SOC均衡恢复的目标函数为
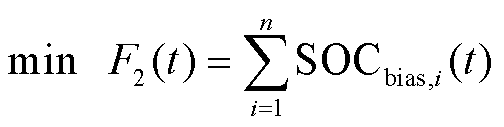 (32)
(32)
式中,F2(t)为t时刻多储能电站整体的SOC偏差。
4.1.2 约束条件
1)调频功率平衡约束
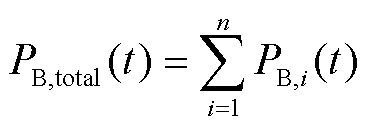 (33)
(33)
2)储能电站额定功率约束
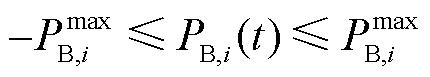 (34)
(34)
式中,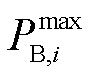 为储能电站i的最大功率限值。
为储能电站i的最大功率限值。
3)储能电站SOC约束
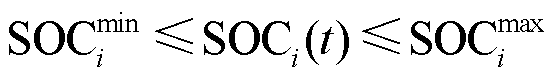 (35)
(35)
式中, 、
、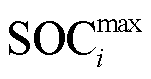 分别为储能电站i允许运行的最小、最大SOC边界。
分别为储能电站i允许运行的最小、最大SOC边界。
4.1节构建的多储能电站调频功率分配模型属于多目标问题。本文基于多目标遗传算法对该模型进行求解,建立了综合考虑调频需求大小和SOC均衡偏差程度的自适应权重系数,以从Pareto解集中选取最优折中解。求解方法分为以下几步:
1)基于多目标遗传算法求取Pareto前沿,将当前时刻最优解集中每一组解的目标函数用模糊隶属度函数表示其满意度,定义为
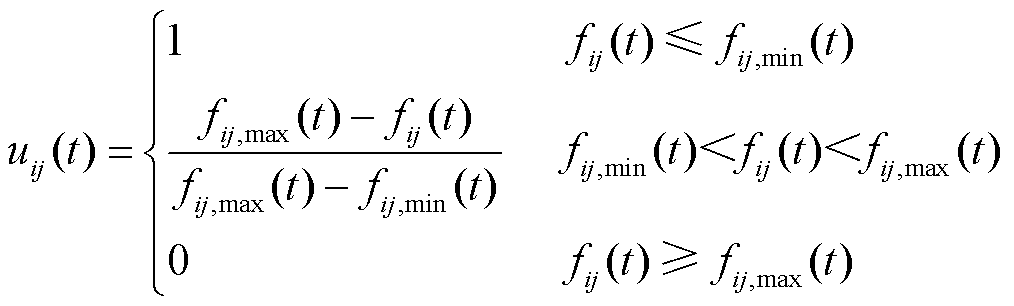 (36)
(36)
式中,uij(t)为t时刻第i组解第j个目标函数的满意度值;fij(t)为t时刻第i组解第j个目标函数的值;fij,max(t)为t时刻第i组解第j个目标函数的最大值;fij,min(t)为t时刻第i组解第j个目标函数的最小值。
根据式(36)可以求得t时刻Pareto解集中每组解的目标函数满意度矩阵为
 (37)
(37)
2)考虑电力系统频率调整需求紧急程度和多储能电站SOC整体偏差程度,构建两个目标函数关于系统状态的自适应权重系数矩阵。
 (38)
(38)
式中,V(t)为t时刻多目标函数关于系统状态的自适应权重系数矩阵;v1(t)为t时刻多储能电站调频成本目标函数的权重系数;v2(t)为t时刻多储能电站SOC综合偏差目标函数的权重系数;v1(t)、v2(t)的确定方法如下所示。
(1)v1的确定
电力系统的调频成本除了与各储能电站的参数相关外,还与调频需求的大小有关。调频需求越大,调频成本越高,则越应该注重对于调频成本的控制。为此,v1(t)由各优化周期调频需求紧急程度的函数确定,即
 (39)
(39)
式中,ARR为调频需求紧急程度;ARRA和ARRE分别为调频需求紧急程度的较低值和较高值。
(2)v2的确定
定义各个储能电站SOC与多储能电站整体SOC平均值的偏差之和为SOCtotal。v2(t)的取值由SOCtotal(t)的函数确定,有
 (40)
(40)
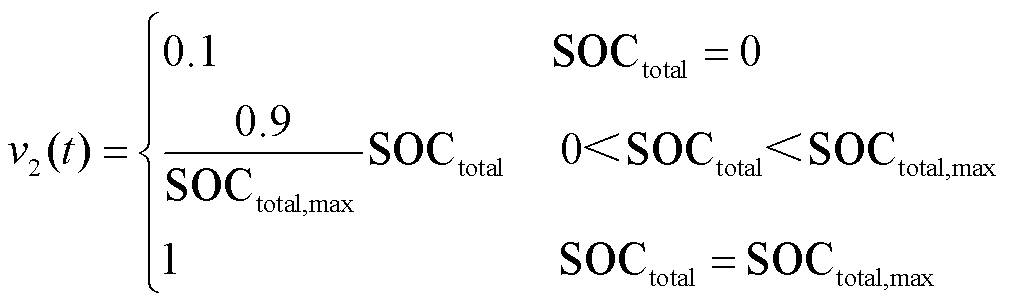 (41)
(41)
式中,SOCtotal,max为各个储能电站SOC与多储能电站整体SOC平均值偏差之和的最大值。
3)求取t时刻的综合满意度矩阵,基于第1)步和第2)步,综合满意度矩阵为
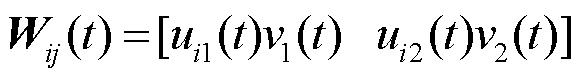 (42)
(42)
根据综合满意度矩阵Wij(t)可以求取t时刻Pareto解集中每组解各目标函数的综合满意度。选取该时刻综合满意度之和最大的一组解作为该时刻各储能电站的最优调频功率指令。
区域电网进行二次调频时,调度中心对调频资源的调度会改变输电线路潮流分布,输电线路面临功率越限的风险,而网络安全是电力系统运行的最基本要求。因此,在调频功率传输的过程中线路功率不应超过其最大限值。因本文主要研究电力系统的调频调度策略,只考虑输电线路有功功率约束。
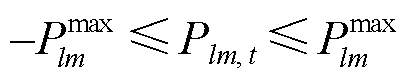 (43)
(43)
式中,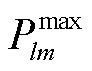 为线路lm传输有功功率的上限;
为线路lm传输有功功率的上限;![]() 为线路lm在t时段由节点l流向节点m的有功功率,计算方法[20]为
为线路lm在t时段由节点l流向节点m的有功功率,计算方法[20]为
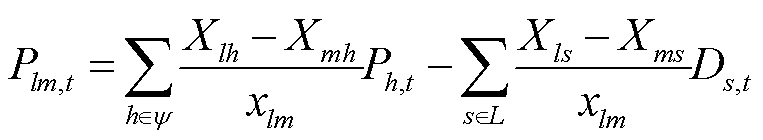 (44)
(44)
式中,Xlh、Xmh、Xls、Xms为网络拓扑的节点h阻抗矩阵元素;xlm为线路lm的电抗值;Ph,t为t时刻电源节点h的有功功率;Ds,t为t时刻负荷节点s的有功功率集合;y为电源节点集合;L为负荷节点集合。
考虑电网的实际运行情况,输电线路不会轻易过载,所以很多时候网络安全约束是不起作用的。为提高求解效率,采用“校验-添加”的思想对线路输电有功约束,即:首先不考虑网络安全约束,对本文构建的双层优化模型求解一次,得到各调频资源的初始调度指令;然后用这组解进行网络安全检验,若线路有功均不越限,则求解结束,下发调度指令;否则以式(16)~式(23)和式(24)~式(28)构建计及输电线路有功功率约束的调频功率经济再分配模型,求解并更新各调频资源的调度指令。
前文所描述的火-多储调频功率双层优化分配策略流程如图4所示。
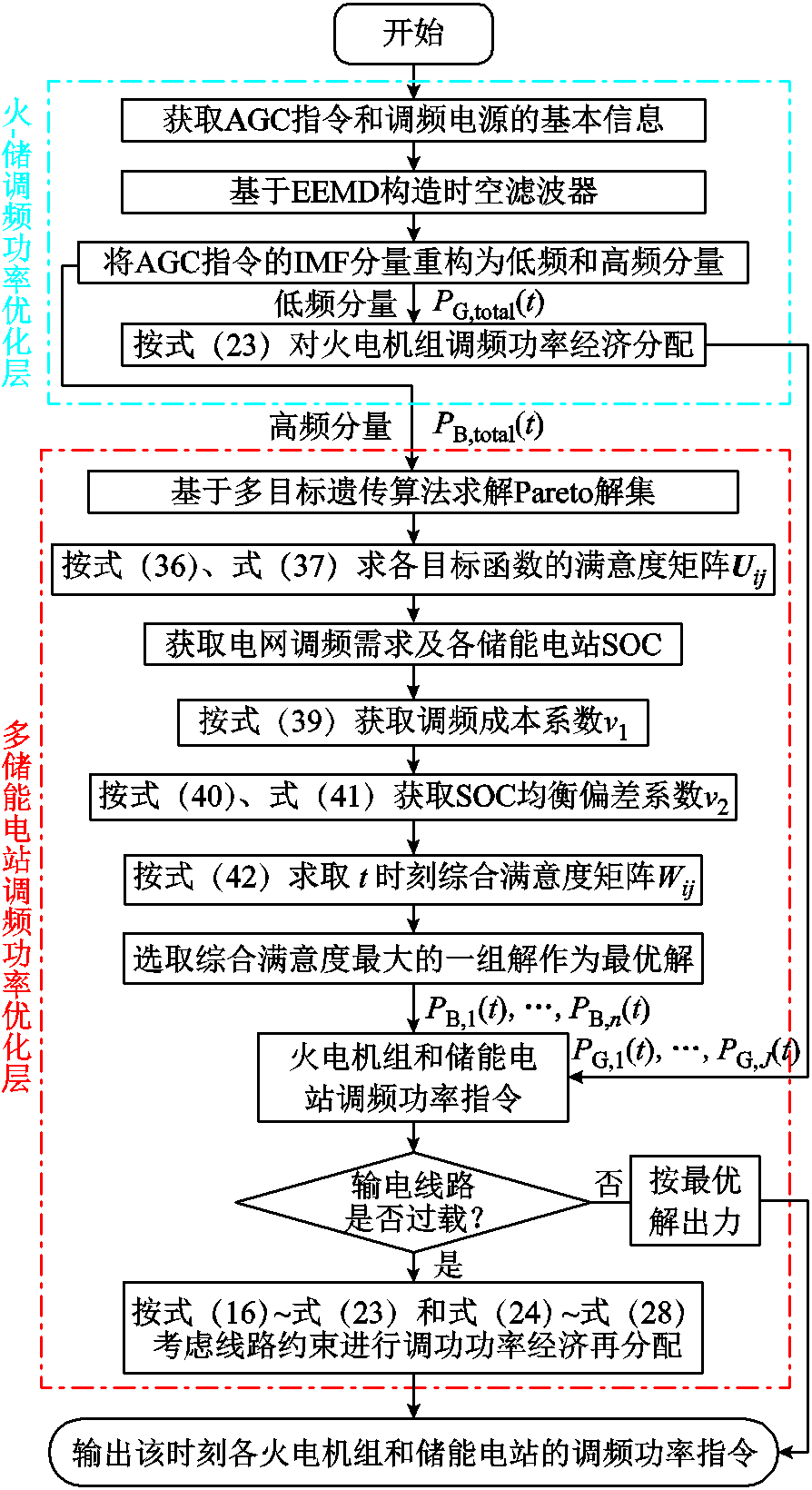
图4 双层优化控制策略流程
Fig.4 Flow chart of two-layer optimal control strategy
1)机组偏离调度次数
当PAGC(t)PG(t)<0或|PAGC(t)|<|PG(t)|时,记Tdev(t)=1,否则Tdev(t)=0。
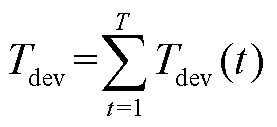 (45)
(45)
式中,T为优化调度次数。Tdev用于评价火电机组承担的二次调频功率跟随原始AGC指令的能力,Tdev越小,跟随能力越强。
2)单位能耗成本
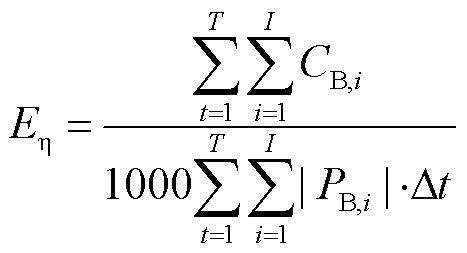 (46)
(46)
式中,I为储能电站数量;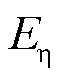 为总调度周期内多储能整体的单位能耗成本,元/(kW·h)。
为总调度周期内多储能整体的单位能耗成本,元/(kW·h)。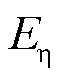 用于评价多储能整体的能源利用效果,越小利用效果越好。
用于评价多储能整体的能源利用效果,越小利用效果越好。
3)多储能电站整体SOC均衡程度
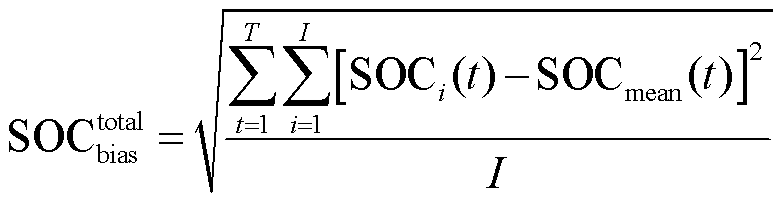 (47)
(47)
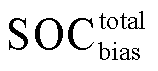 用于评价各储能电站SOC与多储能电站整体SOC平均值的综合偏差程度,
用于评价各储能电站SOC与多储能电站整体SOC平均值的综合偏差程度,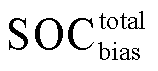 越小说明多储能整体参与调频的可持续性越强。
越小说明多储能整体参与调频的可持续性越强。
4)频率偏差的方均根值
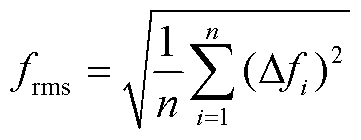 (48)
(48)
系统频率偏差的方均根值frms越小,说明频率波动越小,策略调频效果越好。
为验证本文所提策略的有效性,在IEEE 14节点测试系统对图1所示的区域电网调频功率分配问题展开分析。该区域包含位于网络不同节点的两台火电机组和三座储能电站。火电机组和储能电站的参数分别见表1和表2 [6]。
其他参数说明如下:
(1)火电机组1的调整范围为180~600 MW,爬坡速率为18 MW/min,初始出力为450 MW。
(2)火电机组2的调整范围为90~300 MW,爬坡速率为9 MW/min,初始出力为150 MW。
表1 火电机组参数
Tab.1 Thermal power unit parameters

参数数值 火电机组1火电机组2 a/[kg·(MW2/h)]0.2260.588 b/[kg·(MW/h)]30.4265.12 c/(kg/h)786.80451.32 μ/[kg/(kW·h)]0.750.72 γ/[元/(MW·h)]83.563.5 cco2/(元/t)8080 ccoal/(元/t)700700
表2 储能电站参数
Tab.2 Parameters of energy storage power station

参数数值 储能电站1储能电站2储能电站3 额定功率/MW151010 额定容量/(MW·h)151010 功率成本/(元/kW)2 5001 5001 500 容量成本/[元/(kW·h)]5 0001 2004 000 充放电效率0.830.900.95 浮充寿命121010 循环寿命2 0002 8002 500 SOC限值0.1/0.90.1/0.90.1/0.9 初始SOC0.70.50.3
5.2.1 火电机组指令跟随性能及经济性分析
利用上述算例系统,取某地区实际AGC数据进行仿真,比较本文策略和传统滤波策略下火-储调频功率分配效果。两种策略下火电机组整体需要响应的AGC指令如图5所示,储能电站整体需要响应的AGC指令如图6所示。
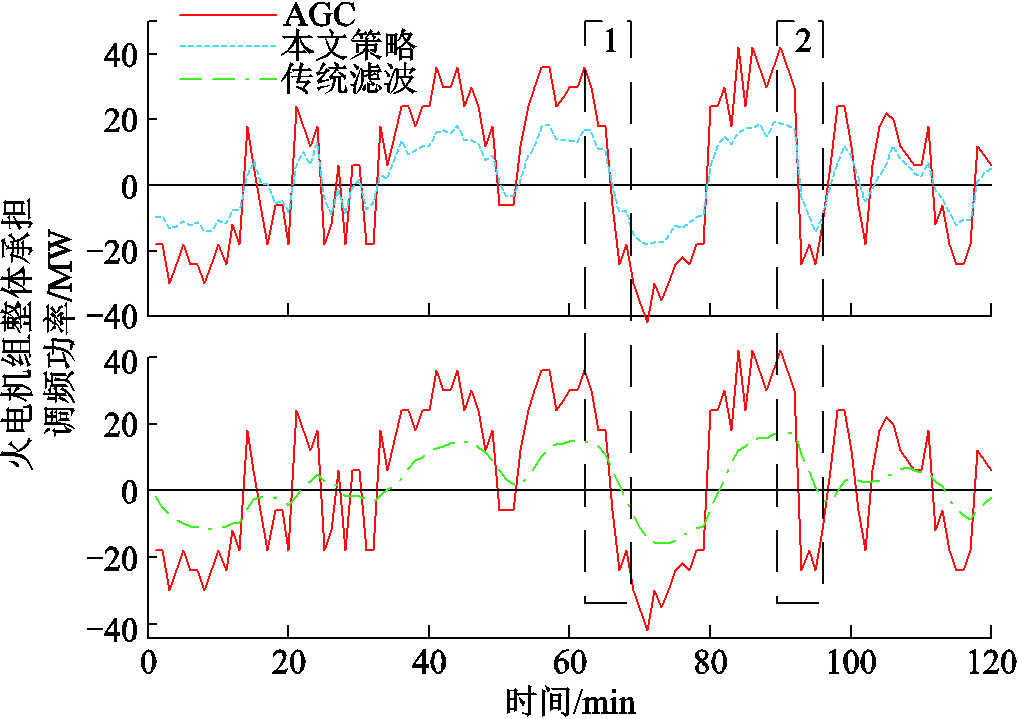
图5 不同策略下火电机组整体AGC指令跟随曲线
Fig.5 Command following performance curves of thermal power units under different strategies

图6 不同策略下储能电站整体承担的AGC指令曲线
Fig.6 Overall AGC command curves of energy storage power stations under different strategies
由图5可知,本文策略和传统滤波策略下,火电机组整体需响应的二次调频调度指令变化幅度较小、频率较低,利于火电机组对二次调频功率指令的跟随。
由图6可知,本文策略下储能整体需承担的AGC指令低于传统滤波策略,本文策略下储能整体需要响应的调频功率累加为1 327.35 MW;传统滤波策略下储能整体需要响应的调频功率累加为1 735.52 MW。原因是在区域总AGC指令波动较为频繁、幅度较大的时间段内,传统滤波策略下需要储能电站发出(吸收)更多的功率来弥补火电机组偏离调度功率的差值。
不同策略下火电机组整体跟随原始AGC指令的性能指标见表3。本文策略下火电机组偏离调度次数为10次,较传统滤波策略降低了64.29%;偏离调度的惩罚容量为1.27 MW·h,较传统滤波策略降低了6.35 MW·h。本文策略下火电机组整体承担的AGC指令跟随原始AGC指令的性能要优于传统滤波策略,下面分析具体原因。
表3 不同策略下火电机组整体的AGC指令跟随情况
Tab.3 Overall AGC command following performance of thermal power units under different strategies

方法偏离调度次数偏离调度惩罚容量/(MW·h)最大偏离功率/ MW 传统滤波287.6234.68 本文策略101.2718.19
传统滤波策略下火电机组跟随AGC指令的效果低于本文策略的原因是传统滤波器因其固有特性会产生过渡带较长、信号失真的问题,不太适用于对高频信号的分解,而在本文策略下原始AGC指令会分解成一系列和输入信号具有相同时间尺度的数据序列,分解后的AGC指令序列与原始AGC指令序列相比具有更强的规律性和可处理性。如图5虚线框1和虚线框2标注所示,在AGC指令波动幅度较大或频率较高的时间段内,本文策略下火电机组整体承担的调度指令仍然可以较好地跟随原始AGC指令,但是传统滤波策略下则存在失真和滞后现象,造成较长时间段内火电机组整体承担的二次调频功率偏离原始AGC指令。
每台火电机组所需承担的二次调频指令如图7所示。在初始时刻,计及剩余调频容量后由经济性较好的火电机组1优先被调度中心调用,当火电机组1不满足调频需求时,由火电机组2进行补足;并且成本抗拒系数会一直介入火电机组调频功率分配策略,避免经济性较好的火电机组长期运行于满载状态而增加额外的磨损成本。
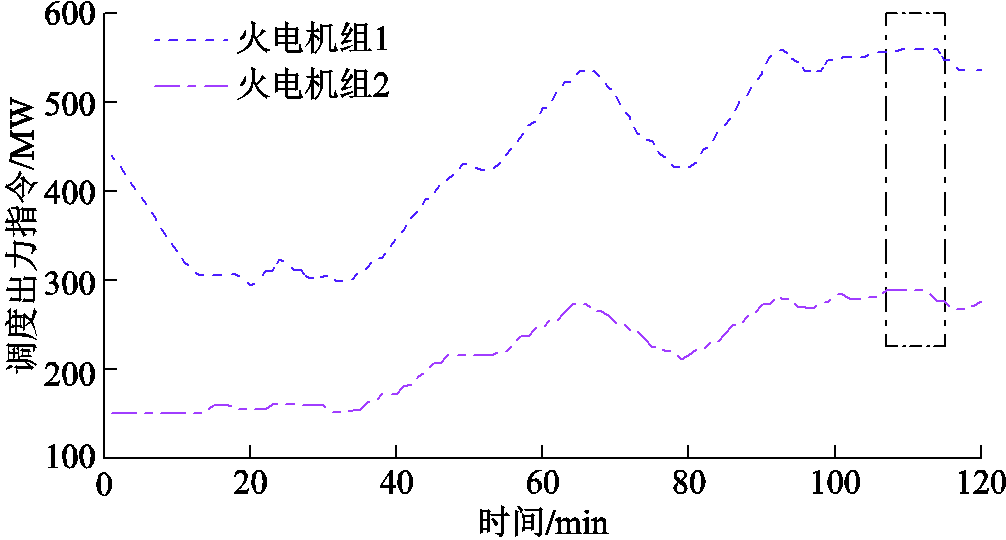
图7 火电机组调频功率调度曲线
Fig.7 Frequency regulation power dispatch curves of thermal power units
表4为不同策略下火电机组整体的调频成本,本文策略下火电机组整体的调频成本为15 158.34元,比例分配策略下为15 613.44元,本文策略较比例分配策略下调频成本降低了2.91%。另外,本文策略下机组磨损成本也低于比例分配策略,有利于延长火电机组运行寿命。
表4 不同策略下火电机组的调频成本
Tab.4 Frequency modulation costs of thermal power units under different strategies(单位:元)

参数数值 本文策略比例分配 煤耗成本2 329.192 398.17 碳捕集成本11 349.6311 725.72 机组磨损成本1 479.521 489.55 总调频成本15 158.3415 613.44
综上所述,针对火-多储整体的调频调度问题,本文策略下各调频资源拥有较好的调频指令跟随效果,可以充分发挥火电机组和储能电站两种调频资源的优势,并且拥有较好的经济性。
5.2.2 多储能电站调频经济性及SOC分析
本文策略下多储能电站整体需承担的AGC指令如图6所示,采用本文策略以及动态容量比例分配策略(下文简称比例分配策略)将其在多个储能电站之间进行调频功率分配,结果及分析如下。
综合满意度系数曲线如图8所示,w1和w2分别是目标函数1和目标函数2的综合满意度系数,其本身是调频需求和各储能电站与多储能电站整体SOC均值的偏差之和的函数,并且呈正相关。多储能电站整体的调频需求和SOC分别如图6和图10所示。
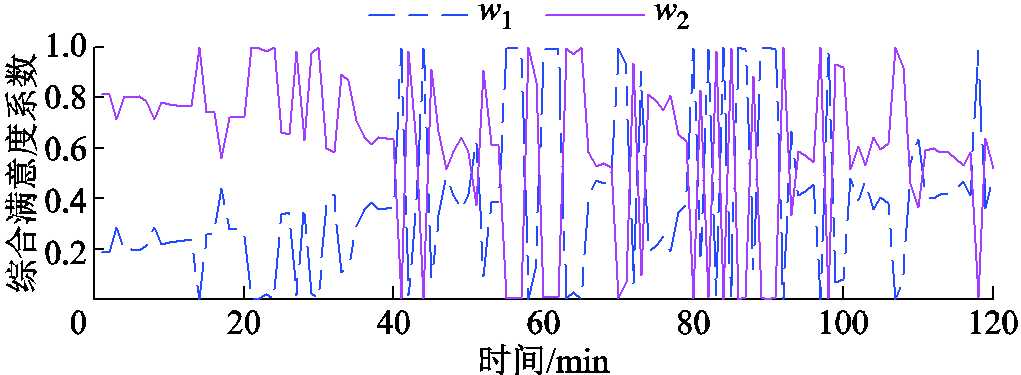
图8 综合满意度系数曲线
Fig.8 Comprehensive satisfaction coefficient curves
在调频调度初期,各储能电站与多储能电站整体SOC均值的偏差之和最大,达到了0.40,而总的调频需求并不高,所以此时w1远小于w2,控制策略更侧重于多储能电站SOC的均衡恢复;在调频调度运行至41、46 min等时刻时,各储能电站与多储能电站整体SOC均值的偏差之和较小,而总的调频需求较大,此时w1远大于w2,控制策略更侧重于降低多储能电站的调频成本,与分析结果一致。
不同策略下多储能电站整体的调频成本见表5,本文策略下为14 531.21元,比例分配策略下为 14 815.00元,本文策略下的总调频成本较比例分配策略下降低了1.92%,具体原因分析如下。
表5 不同策略下多储能电站的调频成本
Tab.5 Frequency modulation costs of multiple energy storage stations under different strategies(单位:元)

策略储能电站容量投资能量损失寿命折损电站调频成本总调频成本 本文储能电站12 272.17664.934 570.077 507.1714 531.21 储能电站2408.30368.391 822.942 599.63 储能电站31 361.00250.372 813.044 424.41
(续)

策略储能电站容量投资能量损失寿命折损电站调频成本总调频成本 比例分配储能电站12 272.17779.755 270.078 321.9914 815.00 储能电站2408.30402.481 991.002 800.78 储能电站31 361.00190.352 140.883 692.23
不同策略下各储能电站的调频里程见表6。由表6可知,本文策略下储能电站1的调频里程较比例分配策略低16.30%;储能电站2的调频里程较比例分配策略低8.50%;储能电站3的调频里程较比例分配策略高31.67%;本文策略下对经济性较差的储能电站1的调用次数少于比例分配策略。
表6 不同策略下各储能电站的调频里程
Tab.6 Frequency modulation mileage of each energy storage station under different strategies(单位:MW)

策略储能电站1储能电站2储能电站3 本文387.17399.29564.05 比例分配462.59436.37428.39
不同策略下储能电站的调频里程构成如图9所示。在调频调度的初始时刻,调频调度中心需要各储能电站进行充电,在本文策略下,由于各储能电站SOC整体均衡度较差,更侧重控制各储能电站的SOC恢复,此时储能电站3的SOC接近下限,考虑到SOC的均衡恢复,仅由储能电站3进行充电;在3~17 min时,调频调度中心需要各储能电站进行充电,本文策略仍然侧重储能电站整体的SOC恢复,由于仅靠储能电站3的不能满足调频需求,此时由经济性较好的储能电站2进行补充充电,而储能电站1此时的SOC较高,仍然不动作;在80~90 min时,如图10所示,此时多储能电站整体的SOC较为均衡,本文策略更注重调频成本的控制,优先由储能电站1和2进行放电。本文策略下,各储能电站的初始SOC对调频策略的影响较小,可以在降低调频成本的基础上均衡恢复各储能电站的SOC。而在比例分配策略下,各储能电站的出力受其初始SOC的影响较大,当调频调度中心需要储能电站放电时,优先由储能电站1放电;当调频调度中心需要储能电站充电时,优先由储能电站3充电。
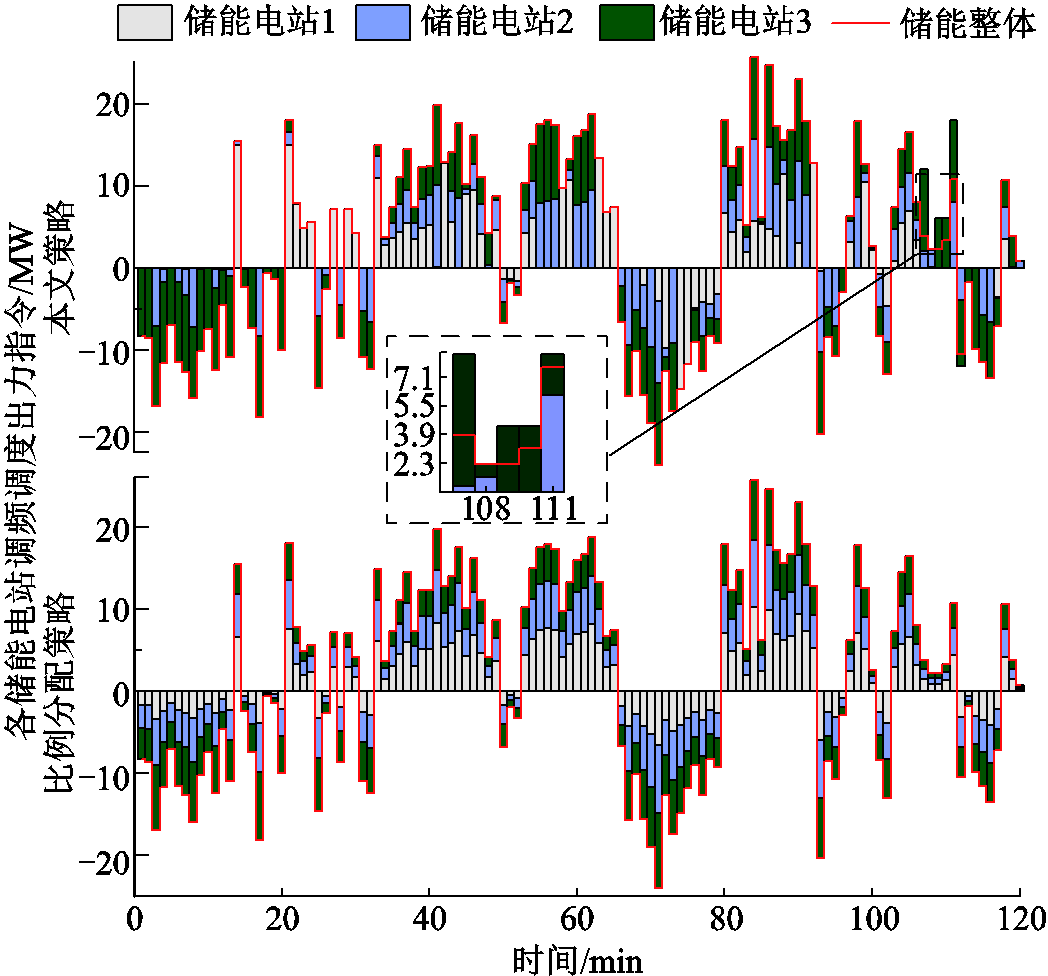
图9 不同策略下各储能电站出力构成情况
Fig.9 Output composition of each energy storage station under different strategies
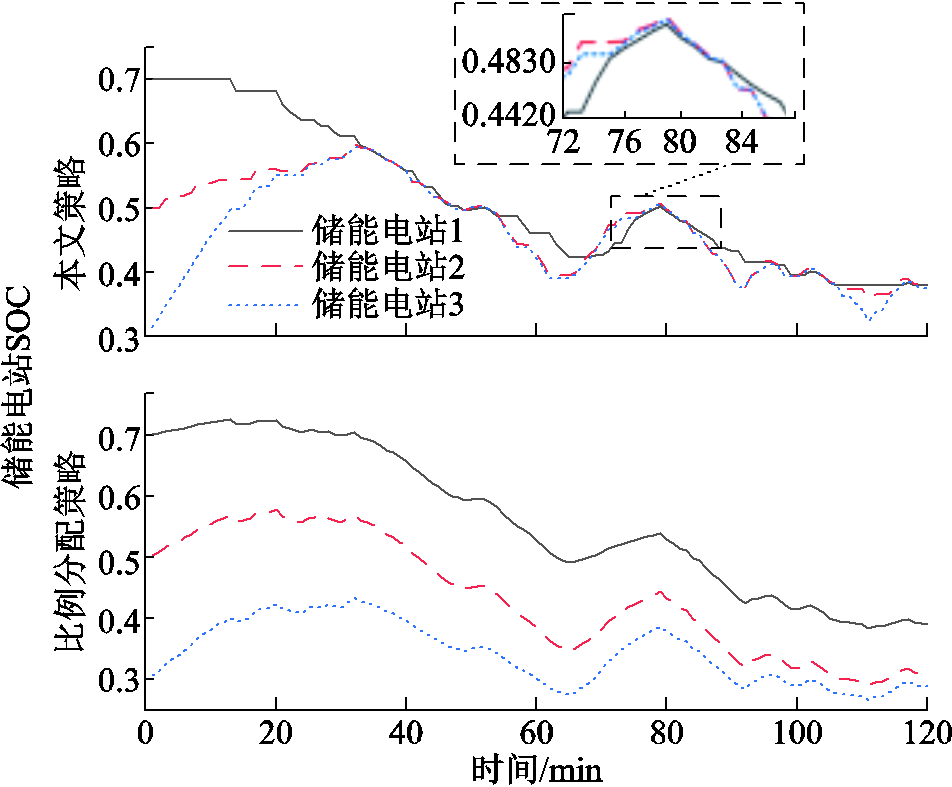
图10 不同策略下各储能电站SOC变化曲线
Fig.10 Variation curves of SOC of various energy storage power stations under different strategies
为了更加直观地比较两种方案的调频经济性,分别计算两种策略下的单位能耗成本指标。本文策略下为0.645 6元/(kW·h),比例分配策略下为0.669 7元/(kW·h),本文策略较比例分配策略在整个调频调度周期的单位能耗成本降低了3.60%。
不同策略下各储能电站SOC变化曲线如图10所示。本文策略下各储能电站SOC最低值为0.314 4,比例分配策略下各储能电站SOC最低值为0.266 1,较本文策略下降低了15.36%。本文策略下可以保持多个储能电站SOC的一致性,维持多储能电站整体的电量平衡,比例分配策略下则无法保持储能电站SOC的一致性,若进行更长时间的工作,储能电站3的SOC可能会达到其下限值,从而提前退出调频服务。
不同策略下各储能电站的SOC指标见表7,SOCi,bias为各储能电站自身的SOC偏差评价指标,是储能电站i在整个调频调度周期下各时刻SOC与0.5的平方偏差的方均根,越小越好。可以看到,本文策略下储能电站1~3的SOC都优于比例分配策略,本文策略下各储能电站自身的SOC偏差指标之和为0.27,比例分配策略下为0.414,该指标在本文策略下优于比例分配策略34.78%;对于多储能整体SOC均衡程度指标,本文策略下为0.079,比例分配策略下为0.167,本文策略下具有显著提升,利于提升多储能电站整体的调频可持续性。
表7 储能电站SOC均衡效果
Tab.7 SOC balancing effect of energy storage station

策略储能电站SOCi,biasSOCtotal,bias 本文储能电站10.1100.079 储能电站20.075 储能电站30.085 比例分配储能电站10.1350.167 储能电站20.115 储能电站30.164
综上所述,本文所提多储能电站调功率分配策略可以根据系统状态协调控制储能电站调频成本降低和SOC恢复这两个目标:当调频需求较大时,由调频成本较低的储能电站优先充放电;当多储能电站SOC偏差较大时,由SOC较差的储能电站优先充放电。本文策略下可以充分调动不同调频成本及SOC储能电站的调频积极性,有利于提升储能电站参与调频的可持续性。
5.2.3 网络安全约束和通信时滞对策略的影响
当电网频率发生波动后,调度中心需要综合考虑各种因素来调度区域内的多种调频资源,包括网络安全约束和通信时滞等因素。为验证本文策略在上述因素影响下的有效性,在上述算例条件下进行分析,考虑网络安全约束前后的输电线路有功功率如图11所示,不同通信时滞下电网的频率偏差如图12所示。
考虑输电线路有功功率传输约束前后线路1-2和线路7-9的稳态有功功率如图11所示。如果不考虑线路有功约束,在108~115 min这段时间线路1-2有功功率会越限;在107~114 min这段时间线路7-9有功功率会越限;而在本文策略下,因为计及网络安全约束,如果初次调频调度结果后验发现线路有功功率越限的情况,则会对调频功率进行再分配,如图7和图9所示,在107~115 min时间段内,火电机组不动作,储能电站整体最终调频指令高于初次调频调度结果,保证了输电线路有功功率不超过最大限值,防止输电线路事故的发生。

图11 输电线路有功功率曲线
Fig.11 Active power curves of transmission line
不同通信时滞下电网频率偏差如图12所示,可以发现,当通信时滞为0.1 s时,对频率偏差的控制效果影响很小;当通信时滞增加到1 s时,对频率偏差的控制效果影响就较为明显;如果通信时滞继续增大,则对电网频率的控制效果影响将会越大。
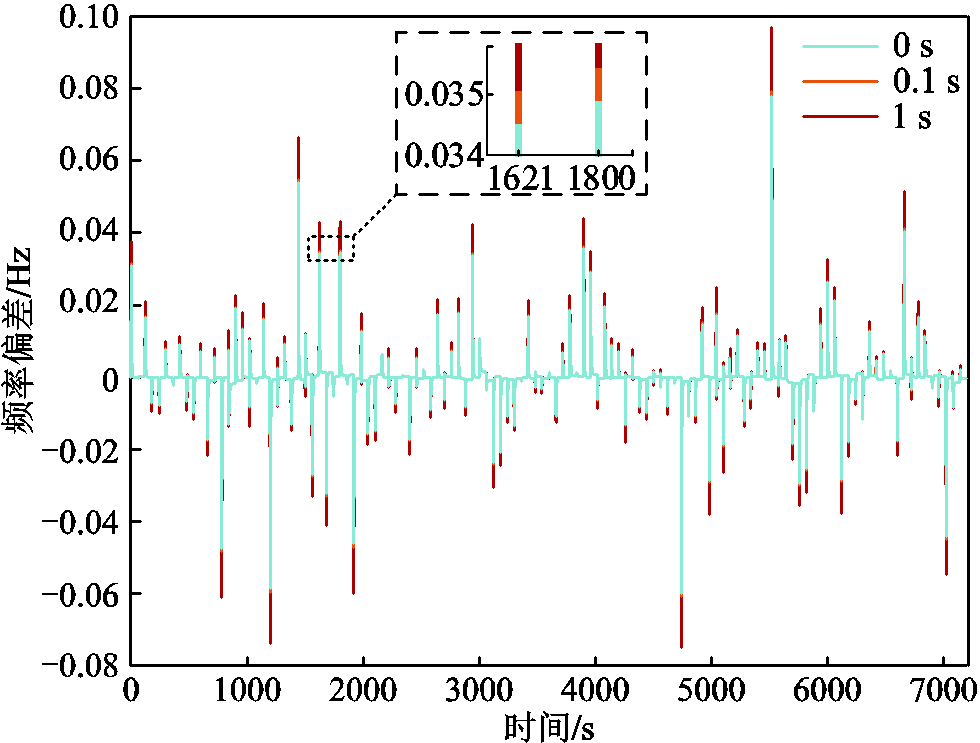
图12 不同通信时滞下的频率偏差曲线
Fig.12 Frequency deviation curves under different communication delays
不同通信时滞下的调频效果指标见表8。无通信时滞下的Dfrms为0.003 6 Hz;通信时滞为1 s时Dfrms为0.004 1 Hz;存在1 s通信时滞较无通信时滞时调频性能下降了13.89%。因此,通信设备传输数据的快速性、准确性对电网频率调控非常重要。
表8 不同通信时滞下的调频效果指标
Tab.8 Frequency modulation performance indicators under different communication delays

通信延时/sfmax/HzDfmax/HzDfrms/Hz 050.0780.0780.003 6 0.150.0790.0790.003 6 150.0970.0970.004 1
实际大规模电力系统中,火电机组和储能电站的数量往往较多,除了考虑上述两个因素对本文策略的影响外,还要满足大规模电力系统相对于小系统对实时求解提出的更高要求。本文所提双层模型各模块在不同规模系统下的求解耗时如图13所示。
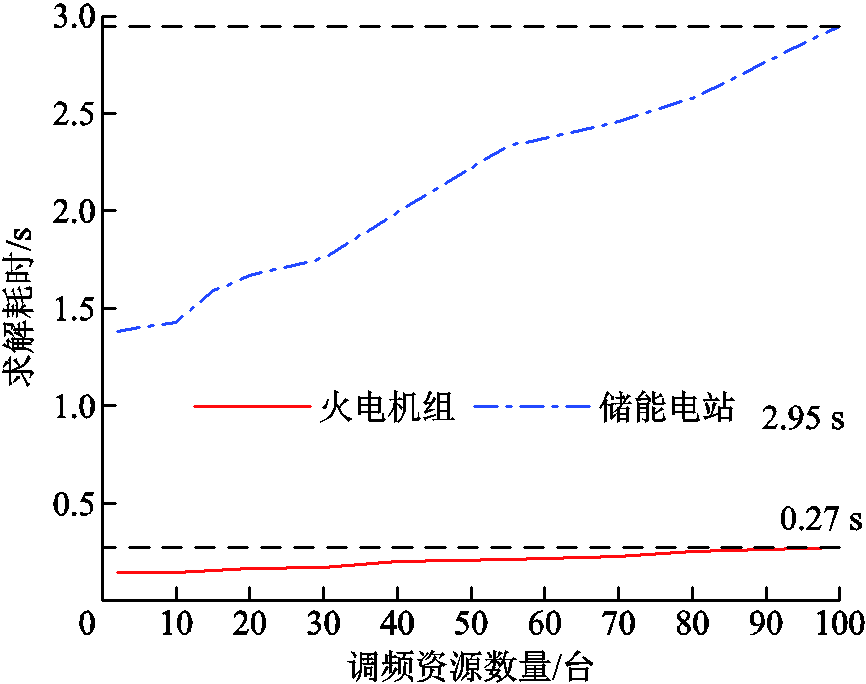
图13 各模块在不同规模系统下的求解耗时曲线
Fig.13 Solution time curve of each module in different scale systems
可以发现,电力系统中火电机组和储能电站数量从2台增加到100台的过程中,两个模块的求解耗时均不超过3.0 s,是满足AGC控制周期的时间性能要求的。
综上所述,在制定电网调频调度策略时,应该考虑多种因素对调频调度结果的联合影响,从而保证电网稳定安全运行。
为了充分发挥火电机组和储能电站两种不同调频资源的优势,在降低整体调频成本的基础上实现多储能电站SOC的均衡恢复,本文提出了计及网络安全约束的火-多储系统调频功率双层优化策略,并进行了仿真验证,得到如下结论:
1)本文构建的火-储调频功率分配模型可以将原始AGC指令分解为火电机组整体和储能电站整体需承担的AGC指令,分解后的信号对原始信号具有较好的跟随效果。本文策略下火电机组承担的调频信号跟随原始调频信号的效果比传统滤波策略高64.29%。
2)本文所提调频功率双层优化模型能够提升区域电网整体调频经济性,相较于按容量比例分配策略火电机组调频成本降低了2.91%,同时机组磨损也略有降低;相较于按比例分配策略,储能电站整体的单位能耗成本降低了3.60%。
3)本文所提多储能电站调频功率分配模型可以协调各储能电站的调频成本和SOC恢复。在整体调频成本降低的基础上,各储能电站SOC保持效果优于比例分配策略34.78%;多储能电站整体SOC均衡效果优于比例分配策略52.69%。有利于提升储能电站参与电力系统调频的积极性和可持续性。
电力系统往往不是独立存在的,并不能仅在一个区域电网内考虑电力系统的调频调度问题,下一步将对研究对象进行扩充,研究两个或多个含火-多储系统的互联区域电网的调频调度问题。
参考文献
[1] Pan Yuling, Dong Feng. Dynamic evolution and driving factors of new energy development: fresh evidence from China[J]. Technological Forecasting and Social Change, 2022, 176: 121475.
[2] 马伟明. 关于电工学科前沿技术发展的若干思考[J]. 电工技术学报, 2021, 36(22): 4627-4636. Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.
[3] 李军徽, 冯喜超, 严干贵, 等. 高风电渗透率下的电力系统调频研究综述[J]. 电力系统保护与控制, 2018, 46(2): 163-170. Li Junhui, Feng Xichao, Yan Gangui, et al. Survey on frequency regulation technology in high wind penetration power system[J]. Power System Protection and Control, 2018, 46(2): 163-170.
[4] 王凯丰, 谢丽蓉, 乔颖, 等. 电池储能提高电力系统调频性能分析[J]. 电力系统自动化, 2022, 46(1): 174-181. Wang Kaifeng, Xie Lirong, Qiao Ying, et al. Analysis of frequency regulation performance of power system improved by battery energy storage[J]. Automation of Electric Power Systems, 2022, 46(1): 174-181.
[5] 李军徽, 侯涛, 穆钢, 等. 电力市场环境下考虑风电调度和调频极限的储能优化控制[J]. 电工技术学报, 2021, 36(9): 1791-1804. Li Junhui, Hou Tao, Mu Gang, et al. Optimal control strategy for energy storage considering wind farm scheduling plan and modulation frequency limitation under electricity market environment[J]. Transactions ofChina Electrotechnical Society, 2021, 36(9): 1791-1804.
[6] 李建林, 马会萌, 惠东. 储能技术融合分布式可再生能源的现状及发展趋势[J]. 电工技术学报, 2016, 31(14): 1-10, 20. Li Jianlin, Ma Huimeng, Hui Dong. Present development condition and trends of energy storage technology in the integration of distributed renewable energy[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 1-10, 20.
[7] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677. Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[8] Aghamohammadi M R, Abdolahinia H. A new approach for optimal sizing of battery energy storage system for primary frequency control of islanded microgrid[J]. International Journal of Electrical Power & Energy Systems, 2014, 54: 325-333.
[9] 丁冬, 刘宗歧, 杨水丽, 等. 基于模糊控制的电池储能系统辅助AGC调频方法[J]. 电力系统保护与控制, 2015, 43(8): 81-87. Ding Dong, Liu Zongqi, Yang Shuili, et al. Battery energy storage aid automatic generation control for load frequency control based on fuzzy control[J]. Power System Protection and Control, 2015, 43(8): 81-87.
[10] 李建林, 屈树慷, 马速良, 等. 电池储能系统辅助电网调频控制策略研究[J]. 太阳能学报, 2023, 44(3): 326-335. Li Jianlin, Qu Shukang, Ma Suliang, et al. Research on frequency modulation control strategy of auxiliary power grid in battery energy storage system[J]. Acta Energiae Solaris Sinica, 2023, 44(3): 326-335.
[11] 胡泽春, 谢旭, 张放, 等. 含储能资源参与的自动发电控制策略研究[J]. 中国电机工程学报, 2014, 34(29): 5080-5087. Hu Zechun, Xie Xu, Zhang Fang, et al. Research on automatic generation control strategy incorporating energy storage resources[J]. Proceedings of the CSEE, 2014, 34(29): 5080-5087.
[12] 于会群, 林涛, 戚明鑫. 基于SSA-VMD和双层模糊控制的火储联合调频策略[J/OL]. 电源学报, 2023: 1-15. http://kns.cnki.net/kcms/detail/12.1420. TM.20221202.1543.003.html. Yu Huiqun, Lin Tao, Qi Mingxin, et al. Combined frequency regulation strategy of thermal power and energy storage based on ssa-vmd and double-layer fuzzy control[J/OL]. Journal of Power Supply, 2023: 1-5. http://kns.cnki.net/kcms/detail/12.1420. TM. 20221202. 1543.003.html.
[13] 李卫国, 焦盘龙, 刘新宇, 等. 基于变分模态分解的储能辅助传统机组调频的容量优化配置[J]. 电力系统保护与控制, 2020, 48(6): 43-52. Li Weiguo, Jiao Panlong, Liu Xinyu, et al. Capacity optimization configuration of energy storage auxiliary traditional unit frequency modulation based on variational mode decomposition[J]. Power System Protection and Control, 2020, 48(6): 43-52.
[14] Lee S J, Kim J H, Kim C H, et al. Coordinated control algorithm for distributed battery energy storage systems for mitigating voltage and frequency deviations[J]. IEEE Transactions on Smart Grid, 2016, 7(3): 1713-1722.
[15] 张圣祺, 袁蓓, 徐青山, 等. 规模化储能参与下的电网二次调频优化控制策略[J]. 电力自动化设备, 2019, 39(5): 82-88, 95. Zhang Shengqi, Yuan Bei, Xu Qingshan, et al. Optimal control strategy of secondary frequency regulation for power grid with large-scale energy storages[J]. Electric Power Automation Equipment, 2019, 39(5): 82-88, 95.
[16] 李军徽, 侯涛, 严干贵, 等. 计及调频成本和荷电状态恢复的多储能系统调频功率双层优化[J]. 中国电机工程学报, 2021, 41(23): 8020-8033. Li Junhui, Hou Tao, Yan Gangui, et al. Two-layer optimization of frequency modulation power in multi-battery energy storage system considering frequency modulation cost and recovery of state of charge[J]. Proceedings of the CSEE, 2021, 41(23): 8020-8033.
[17] 王炜, 李政, 刘宏伟, 等. 基于禁忌搜索的混合储能辅助电网AGC策略研究[J]. 电气传动, 2022, 52(5): 39-46. Wang Wei, Li Zheng, Liu Hongwei, et al. Research on AGC strategy of hybrid energy storage auxiliary power grid based on tabu search[J]. Electric Drive, 2022, 52(5): 39-46.
[18] 葛乐, 袁晓冬, 王亮, 等. 面向配电网优化运行的混合储能容量配置[J]. 电网技术, 2017, 41(11): 3506-3513. Ge Le, Yuan Xiaodong, Wang Liang, et al. Capacity configuration of hybrid energy storage system for distribution network optimal operation[J]. Power System Technology, 2017, 41(11): 3506-3513.
[19] 陈浩, 贾燕冰, 郑晋, 等. 规模化储能调频辅助服务市场机制及调度策略研究[J]. 电网技术, 2019, 43(10): 3606-3617. Chen Hao, Jia Yanbing, Zheng Jin, et al. Research on market mechanism and scheduling strategy of frequency regulation auxiliary service of large-scale energy storage[J]. Power System Technology, 2019, 43(10): 3606-3617.
[20] 黄庶, 林舜江, 刘明波. 含风电场和抽水蓄能电站的多目标安全约束动态优化调度[J]. 中国电机工程学报, 2016, 36(1): 112-121.Huang Shu, Lin Shunjiang, Liu Mingbo. Multi-objective security constrained dynamic optimal dispatch with wind farms and pumped storage stations[J]. Proceedings of the CSEE, 2016, 36(1): 112-121.
Abstract Aiming at the power scheduling problem of frequency modulation involving multiple energy storage stations distributed in different network nodes of regional power grid, a two-layer optimization strategy for frequency modulated power of thermal generation and multi-storage system based on ensemble empirical mode decomposition (EEMD) and multi-objective genetic algorithm (MOGA) is proposed. This strategy includes a thermal power-energy storage frequency modulation power optimization layer and a multi energy storage power station frequency modulation power optimization layer: The upper layer counts the respective advantages of thermal power-energy storage allocation resources as well as the residual frequency modulation capacity of thermal power units and energy storage, constructs the optimization distribution model of thermal power-energy storage frequency modulation power, and completes the distribution of thermal power-energy storage frequency modulation power. The lower layer introduces the adaptive weight coefficient about frequency modulation cost and state of charge (SOC) comprehensive state, takes frequency modulation cost and SOC comprehensive state as the optimization objective, and completes the distribution of frequency modulation power among multiple energy storage systems.
In order to verify the effectiveness of the above control strategies, this paper takes an actual AGC command from a certain location in China for simulation analysis. The specific conclusions are as follows:
Firstly, the thermal power-energy storage frequency modulation power allocation model constructed in this article can decompose the original AGC instructions into the AGC instructions that the thermal power unit as a whole and the energy storage power station as a whole need to bear. The decomposed signal has a good tracking effect on the original signal. The frequency modulation signal borne by the thermal power unit under this strategy follows the original frequency modulation signal, which is 64.29% higher than the traditional filtering strategy.
Secondly, the dual level optimization model for frequency regulation power proposed in this article can improve the overall frequency regulation economy of the regional power grid. Compared with the capacity proportion allocation strategy, the frequency regulation cost of thermal power units is reduced by 3.00%, and the unit wear is also slightly reduced; Compared to the proportional allocation strategy, the overall unit energy consumption cost of energy storage plants has been reduced by 3.6%.
Finally, the frequency modulation power allocation model proposed in this article can coordinate the frequency modulation cost and SOC recovery of each energy storage station. On the basis of reducing the overall frequency regulation cost, the SOC maintenance effect of each energy storage station is 34.78% better than the proportional allocation strategy; The overall SOC balance effect of multiple energy storage power stations is 52.69% better than the proportional allocation strategy.
Keywords:Multi thermal power-energy storage system, secondary frequency modulation, two-layer optimal control, multi-objective genetic algorithm(MOGA), adaptive weight coefficient
DOI:10.19595/j.cnki.1000-6753.tces.230186
中图分类号:TM73
国家电网有限公司科技项目资助(5108-202299257A-1-0-ZB)。
收稿日期 2023-02-21
改稿日期 2023-08-23
李翠萍 女,1982年生,副教授,硕士生导师,研究方向为储能技术在电力系统中的应用。E-mail:licuipingabc@163.com
李军徽 男,1976年生,教授,博士生导师,研究方向为新能源发电联网运行关键技术和储能技术的应用。E-mail:lijunhui@neepu.edu.cn(通信作者)
(编辑 赫 蕾)