图1 构网型直驱风电机组主拓扑及控制结构
Fig.1 Main topology and control structure of grid-forming D-PMSG
摘要 针对构网型直驱永磁同步风电机组在弱电网下的次同步振荡问题，该文提出了基于不确定性和扰动估计器（UDE）的附加阻尼支路振荡抑制策略。首先，网侧变流器采用虚拟同步机（VSG）技术，并基于谐波线性化理论建立了网侧变流器序阻抗模型；其次，深入分析引入电压-电流双闭环控制对弱电网下构网型直驱永磁同步风电机组产生次同步振荡的影响特性，提出了电流环引入UDE附加阻尼支路的振荡抑制策略，并基于UDE的附加阻尼控制采用滤波带宽思想对系统扰动进行估计，通过动态电压补偿方式实现阻尼支撑，可有效抑制次同步振荡，提升系统鲁棒性；最后，通过时域仿真验证了所提振荡抑制方法的有效性。
关键词：直驱永磁同步风电机组 次同步振荡 虚拟同步发电机 不确定性和扰动估计器附加阻尼
在“碳达峰·碳中和”的战略背景下，我国目前新能源发电比例已达到历史新高。随着风电装机容量持续增长，近年来偏远地区直驱风电场与弱电网交互产生次同步振荡问题日益突出。直驱永磁同步风电机组（Direct-drive Permanent Magnet Synchronous Generator, D-PMSG）与弱电网交互过程中，其等效容性与弱电网感性发生谐振，在负阻尼作用下谐振发散产生次同步振荡[1-4]。相较于传统的轴系动态主导的次同步振荡，新型电力系统下的振荡现象往往始于小信号负阻尼发散，终于非线性持续振荡，表现出振荡频率范围宽的特点[5-7]。
国内外学者围绕弱电网下直驱风电机组的并网稳定性及振荡机理开展了大量研究，并取得了丰硕成果。文献[8]结合直驱永磁同步风电机组阻抗模型在频域的分布特点对弱电网下的次同步振荡机理和特性进行了深入分析，其中网侧变流器（Grid Side Converter, GSC）双闭环控制参数以及电流环与锁相环交互对系统产生次同步振荡的影响尤为突出。文献[9-10]围绕锁相环主导的次同步振荡特性进行研究，重点分析了弱电网下锁相环对D-PMSG产生次同步振荡的影响机理。文献[11]利用根轨迹法对网侧变流器电流环主导下的次同步振荡特性进行了深入研究，其中电流环q轴在特定频段范围内呈现出负电阻特性，进而容易引发次同步振荡风险。为避免直接使用锁相环带来的负阻尼效应，并向系统提供惯量支撑，有学者将构网型虚拟同步机（Virtual Synchronous Generator, VSG）控制技术应用到直驱永磁同步风电机组[12-13]。
阻抗分析法因易于工程测量以及形式简单等特点在新能源并网稳定性分析中得到广泛应用。其中序阻抗建模对新能源并网宽频振荡中的频率耦合特征有着清晰的描述。该方法基于谐波线性化理论将交流信号转换为频域中的直流信号，可通过阻抗测量进行修正，相较于dq阻抗法具有表达物理意义明确、适应性强等特点[14-16]。文献[17]基于谐波线性化理论建立序阻抗模型，对虚拟同步机电压-电流双闭环控制模式下的频率耦合振荡特性进行了深入分析。文献[18-19]通过序阻抗建模对虚拟同步机控制技术在弱电网下的稳定性以及影响稳定性的因素进行了研究。文献[20]通过伯德图分别对有、无电压-电流双闭环模式下VSG弱电网的稳定性进行了对比分析。双闭环有利于提高电压控制精度并发挥限幅作用，但其自身等效的容性和负阻尼特性使系统在特定频段范围内的谐振容易发散并引发次同步振荡。文献[21]提出了电压环附加阻尼控制策略，通过传统移相补偿控制原理对系统电压进行补偿，进而实现对振荡的抑制效果。但是当系统受到外界扰动或工况发生变化时，基于移相补偿原理的传统型附加阻尼控制因参数无法实时调节而影响补偿效果。文献[22]将附加阻尼控制应用于高压直流输电模块化多电平换流器（Modular Multilevel Converter, MMC）控制策略中，在传统移相补偿控制基础上，通过对极点进行优化配置提升系统振荡抑制能力。文献[23]采用多通道附加阻尼控制，可实现双馈风电系统多种振荡模态的同时抑制效果。文献[24]提出了基于自适应振荡选频方法的附加阻尼控制策略。该方法可有效避免移相补偿环节，提升振荡抑制精度，但系统鲁棒性和适应复杂工况能力有待提升。基于上述研究，本文提出在电流环引入基于不确定性和扰动估计器（Uncertainty and Disturbance Estimator, UDE）的附加阻尼支路次同步振荡抑制策略。
UDE控制理论是在鲁棒控制理论基础上提出的，主要是为了解决控制系统中存在的参数不确定性及外部扰动带来的问题。该方法核心思想是利用带通滤波器对一定带宽范围内的扰动和不确定性进行估计，对次同步范围内的振荡扰动估计具有较好的适应性[25-26]。为提升D-PMSG系统惯量支撑能力，本文首先在网侧变流器采用构网型虚拟同步机控制技术，并基于谐波线性化理论建立网侧变流器序阻抗模型；其次，在深入分析引入电压-电流双闭环对系统稳定性影响的基础上，构建基于UDE的附加阻尼支路控制数学模型；最后，通过时域仿真验证所提控制策略的有效性。
构网型直驱永磁同步风电机组由机侧变流器（Machine Side Converter, MSC）、网侧变流器及滤波器等部分组成，主拓扑及控制结构如图1所示。机组GSC采用功率外环、电压-电流内环的构网型虚拟同步机控制策略；而MSC则采用电压-电流双闭环的传统矢量控制策略。
图1 构网型直驱风电机组主拓扑及控制结构
Fig.1 Main topology and control structure of grid-forming D-PMSG
VSG控制策略模拟同步机中的机械特性和电磁特性，分别由有功环和无功环以及电压-电流双闭环构成，其控制结构如图1所示。文中将功率环生成的Edref和Eqref直接作为调制信号进行控制的模式称为“开环模式”，而将Edref和Eqref作为电压-电流双闭环给定值进行控制的模式称为“双闭环模式”。
引入转子运动状态方程为
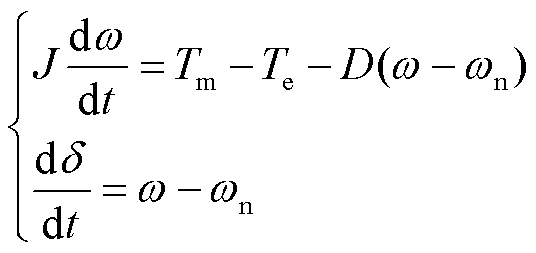（1）
式中，Tm、Te分别为机械转矩、电磁转矩，Tm=Pm/w，Te=Pe/w，Pm、Pe分别为机械功率、电磁功率，w为转子角频率；δ、wn分别为电压相位及电网额定角频率；J、D分别为转动惯量和阻尼系数。通过该环节可实现对系统的惯量支撑。
为实现输出无功功率控制，模拟同步发电机励磁调压功能，表示为
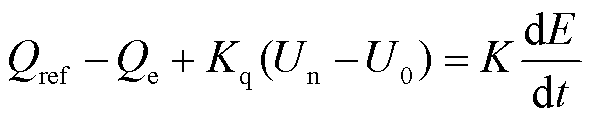（2）
式中，Qe与Qref分别为无功输出值和无功设定值；Un与U0分别为端电压额定峰值和实际峰值；E为网侧逆变器桥臂电势幅值；Kq、K分别为无功下垂系数和无功调节系数。
当变流器端口施加频率为fp的电压扰动分量时，系统会产生频率为fp的电流扰动分量响应，并在频率耦合效应下产生频率为fp-2f0的负序耦合电流扰动分量。频率为fp的电流扰动分量与频率为fp-2f0的负序耦合电流扰动分量成对出现，且关于基频f0对称。基于谐波线性化理论将输出三相交流信号转换成频域直流信号，建立网侧变流器序阻抗模型。以A相为例，其输出电压、电流及滤波电感电流分别为
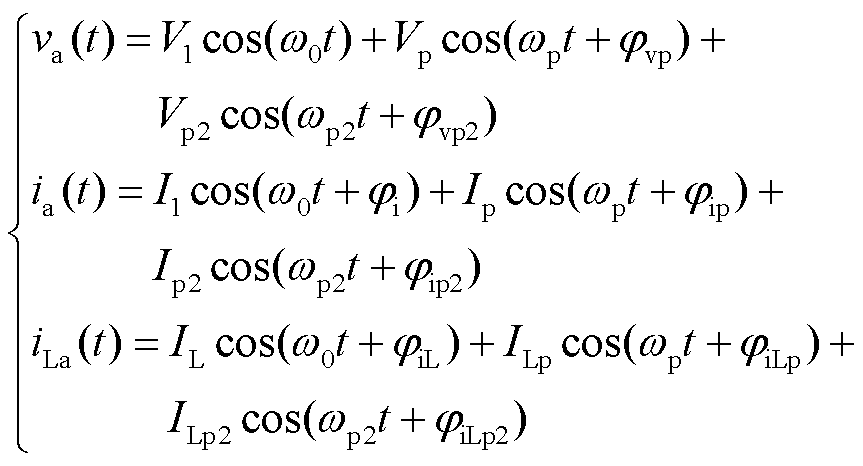（3）
式中，V1、I1和IL分别为输出基波电压、电流和滤波电感电流幅值；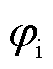
和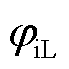
分别为输出基波电流和滤波电感电流初相位；ω0为额定角频率；Vp、Ip和ILp分别为正序扰动频率下输出电压、电流和滤波电感电流幅值；ωp为正序扰动角频率；
、
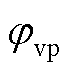和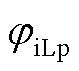
分别为正序扰动频率下输出电压、电流和滤波电感电流初相位；Vp2、Ip2和ILp2分别为负序耦合频率下输出电压、电流和滤波电感电流幅值；jvp2、jip2和jiLp2分别为负序耦合频率下输出电压、电流和滤波电感电流初相位；ωp2为负序耦合角频率。式（3）的频域表达式见附录式（A1）。
VSG桥臂电势与输出端电压电势差可表示为
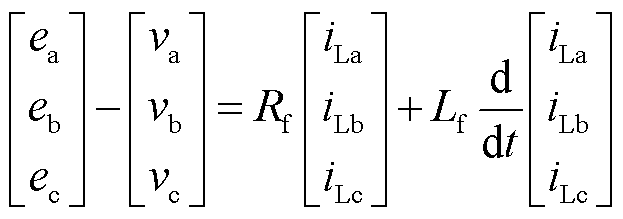（4）
式中，Rf、Lf分别为网侧变流器滤波电阻和滤波电感。
αβ坐标系下，系统输出有功、无功功率为
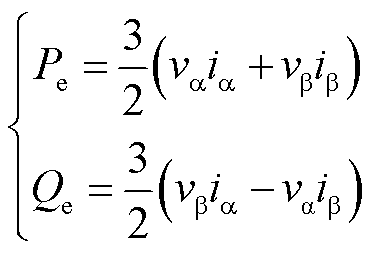（5）
式中，va、vb、ia、ib分别为αβ坐标系下系统输出端电压、输出电流，其频域表达式分别见附录式（A2）和式（A3）。
依据式（5）利用频域卷积定理，忽略二倍频分量，可得有功功率、无功功率频域表达式分别为
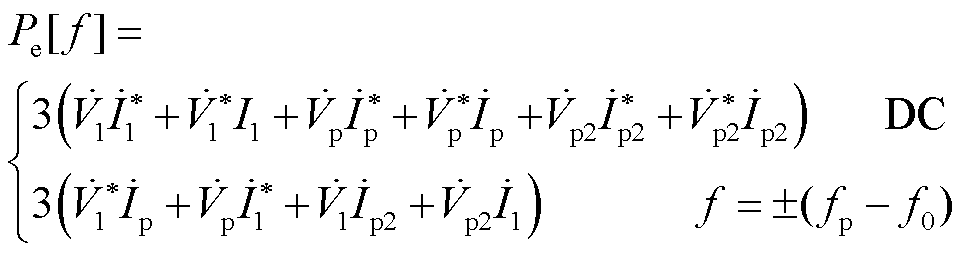（6）
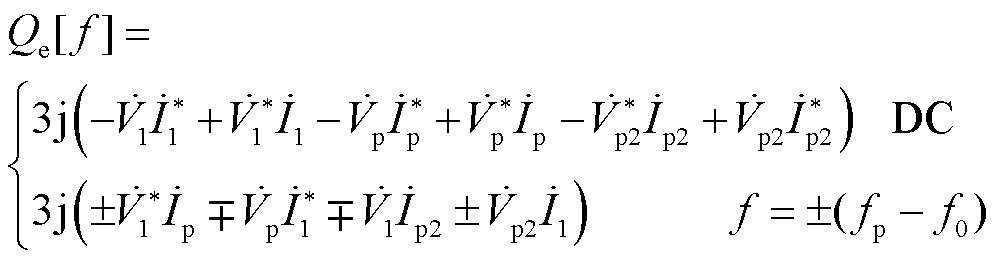（7）
式中，上标“*”表示复数的共轭。
根据式（1）可以得到VSG输出相位为
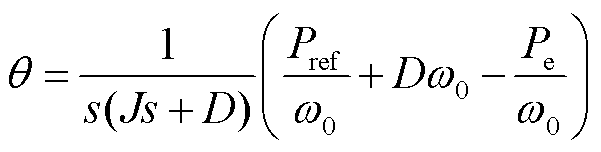（8）
式中，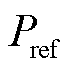
为有功功率参考值。
通过Laplace变换将式（8）变换到频域，然后将式（6）代入并忽略小信号二次项，得到VSG输出相位频域表达式为
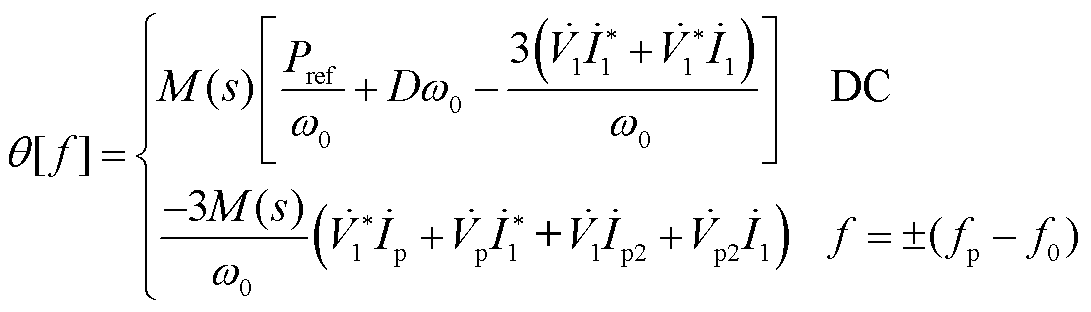（9）
其中
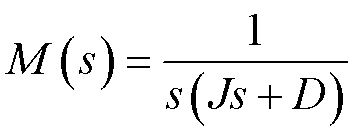
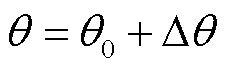
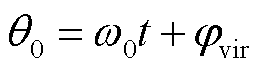
式中，Δθ为电压扰动下对应小信号分量；jvir为VSG初相位。
通过Laplace变换将式（2）变换到频域，然后将式（7）代入并忽略小信号二次项，得到网侧逆变器桥臂电势幅值E的频域表达式为
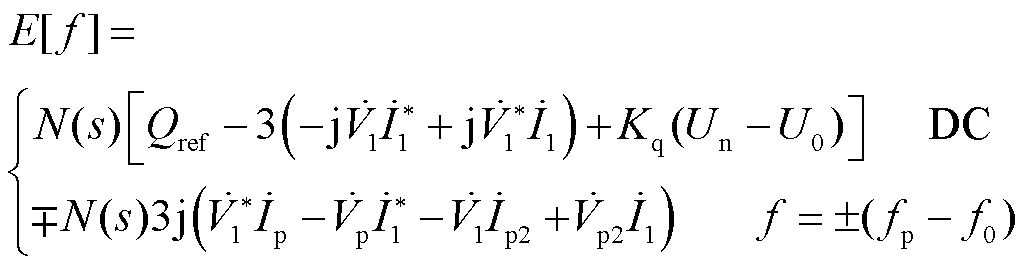（10）
其中
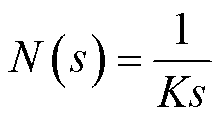
电压外环参考指令频域表达式为
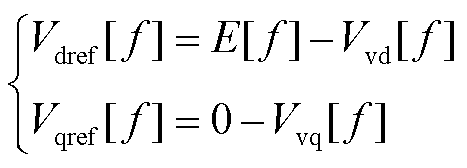（11）
式中，Vvd、Vvq为虚拟阻抗压降，其频域表达式分别为
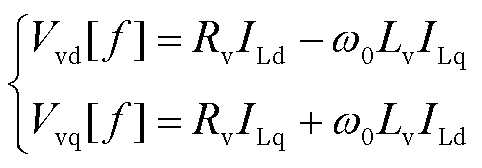（12）
式中，Rv、Lv分别为虚拟电阻和虚拟电感。
将系统三相输出端电压进行Park变换，得到两相dq坐标系下的电压信号。三角函数及Park变换矩阵频域表达式见附录式（A4）～式（A10）。
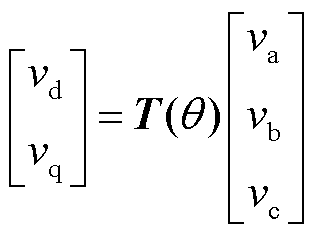（13）
将式（13）通过Laplace变换得到输出电压在dq坐标系下的频域表达式为
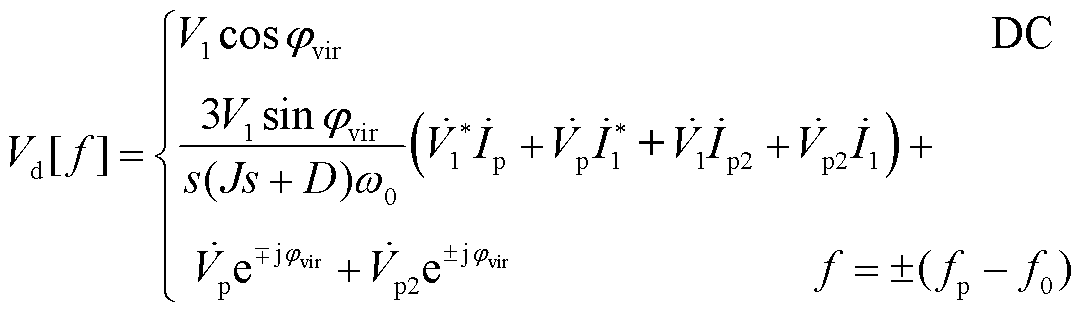（14）
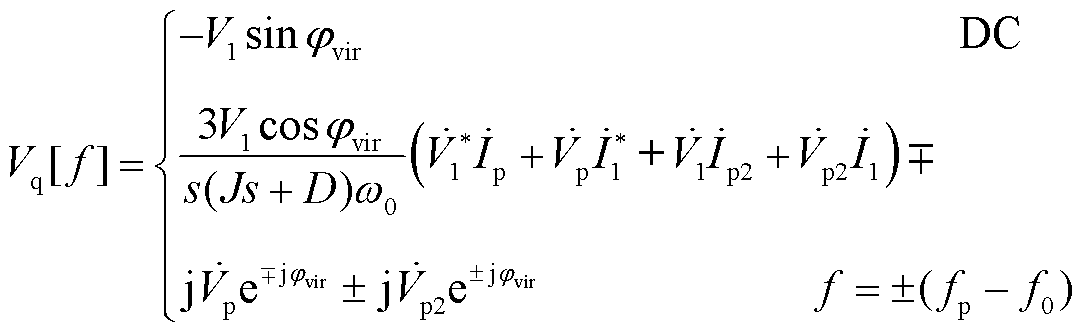（15）
同理可得电感电流频域表达式，见附录式（A11）和式（A12）。
dq坐标系下调制波信号可表示为
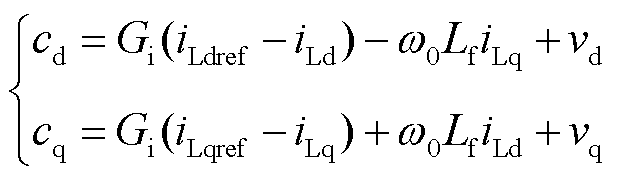（16）
其中
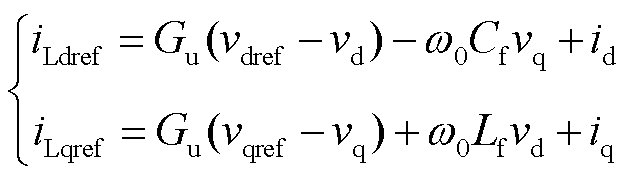（17）
式中，Lf、Cf分别为网侧变流器滤波电感和电容；Gu、Gi分别为电压外环和电流内环PI控制器。
VSG的A相桥臂电势表达式为
（18）
式中，Vdc为直流侧电压；Km为调制系数；Ca为式（16）Park反变换得到的A相调制信号。
图2为忽略耦合影响下频率扰动小信号电流响应，其表达式为
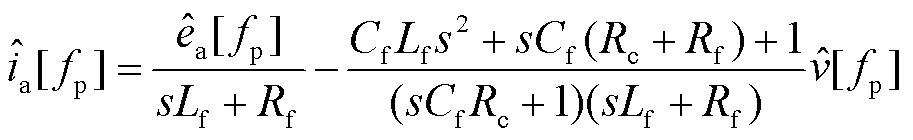（19）
式中，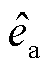
、
、
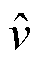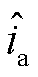分别为桥臂电动势、输出电压、输出电流小信号分量；Rc、Rf均为滤波电阻。
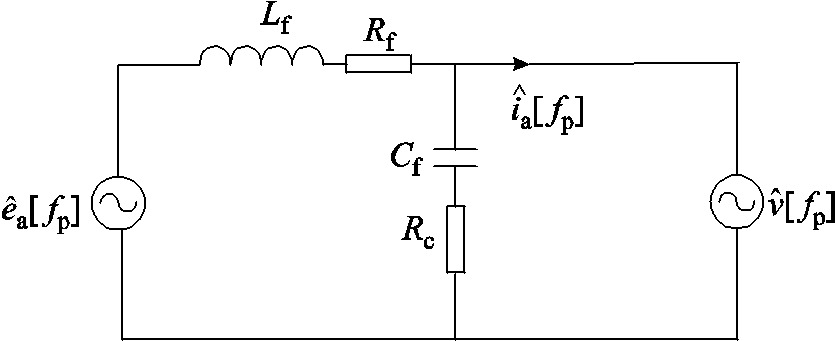
图2 电流频域响应等效电路
Fig.2 Current frequency domain response equivalent circuit
序阻抗频域表达式为
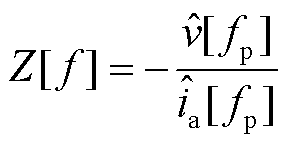（20）
将式（19）代入式（20），忽略耦合影响，可得到双闭环模式下正、负序阻抗表达式为
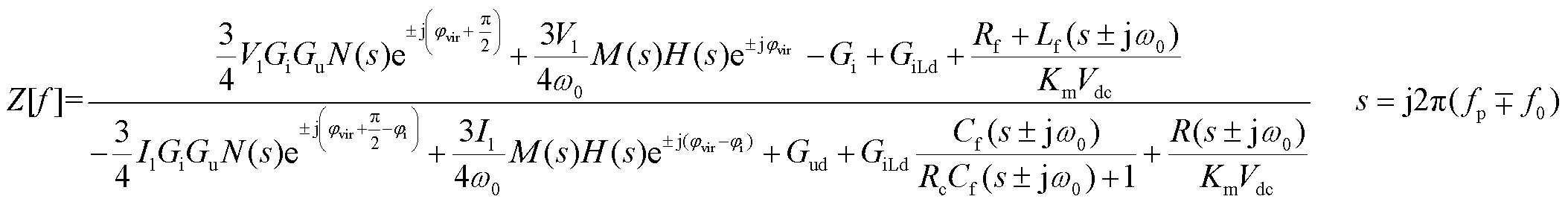（21）
其中
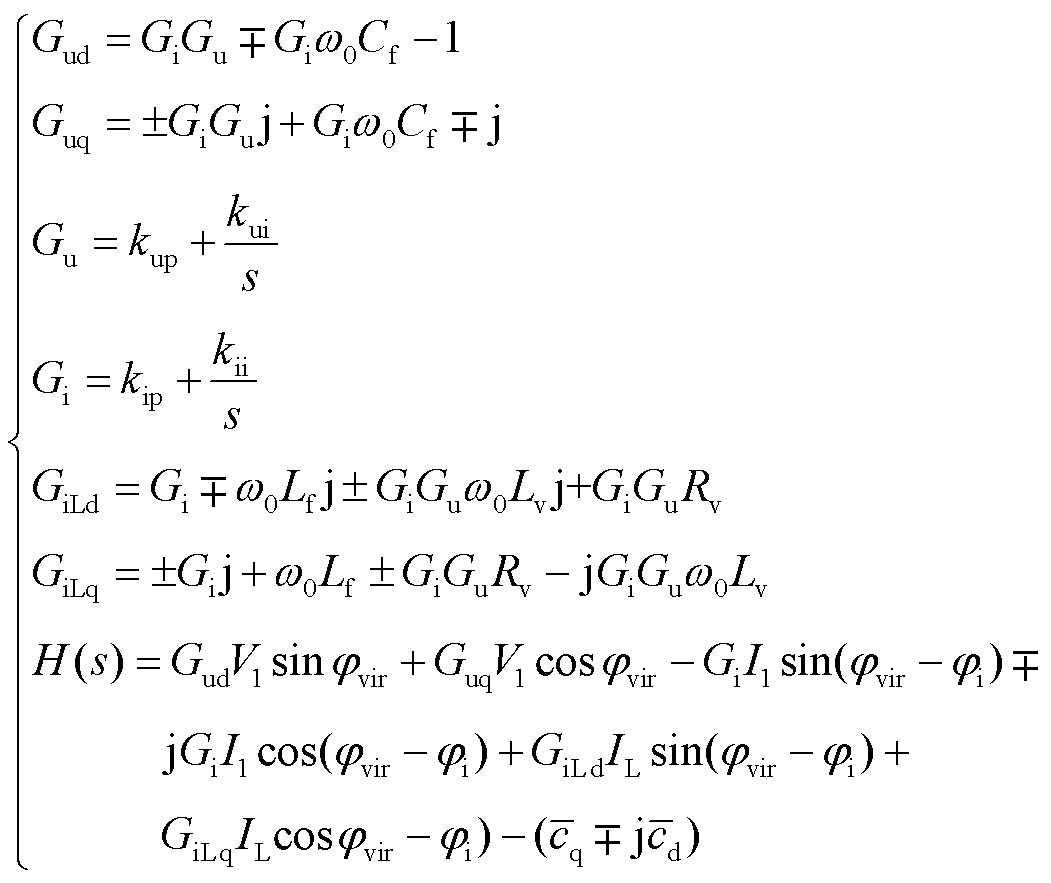
式中，kup、kui分为别电压外环PI控制比例系数和积分系数；kip、kii分别为电流内环PI控制比例系数和积分系数；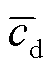
、
为调制信号稳态值。
同理，可得到开环模式下正、负序阻抗表达式为
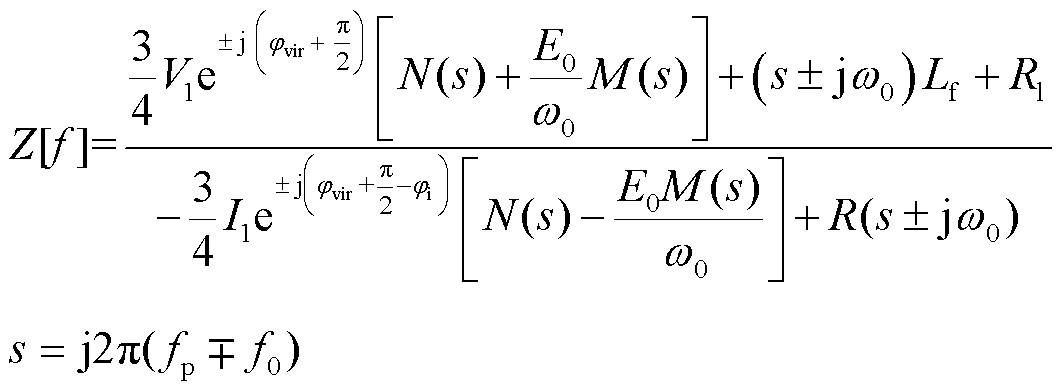(22)
其中
式中，E0为桥臂电动势稳态幅值。
设置电网阻抗值为0.17 mH，短路比（Short Circuit Ratio, SCR）小于3，模拟弱电网工况。双闭环PI控制参数取值分别为kup=15、kui=350、kip=2、kii=200。通过伯德图对VSG有、无双闭环条件下的系统稳定性进行分析，开环模式下序阻抗伯德图如图3所示。由图3b可知，当VSG采用开环控制模式时，VSG正序阻抗在100 Hz以内均呈现感性，负序阻抗随着频率增大由容性逐渐变为感性；100 Hz之后正、负序阻抗曲线重合且呈感性；而在1 000 Hz附近系统因为输出滤波电容影响再次呈现容性。从相频特性曲线可以看出，VSG正、负序阻抗在次/超同步频段整体呈现为感性，与同步发电机相似。从图3a可以看出，VSG序阻抗与弱电网阻抗在100 Hz以内无交点，系统稳定。
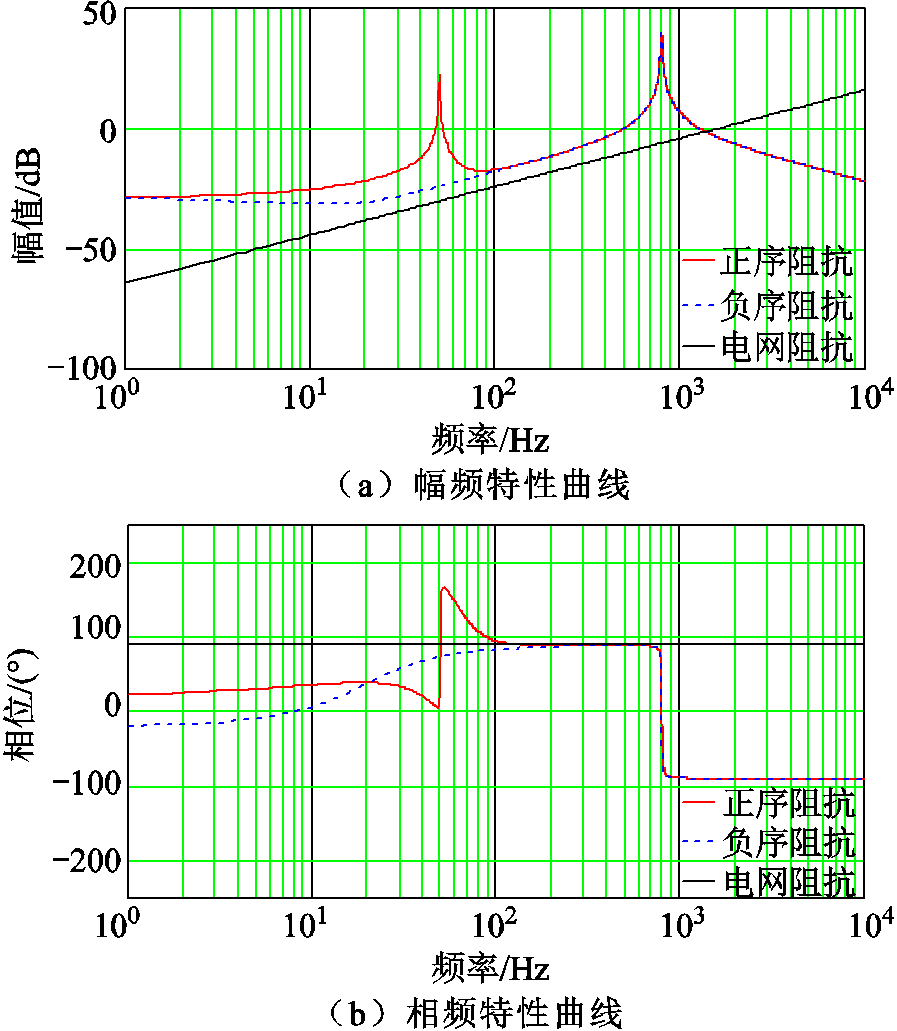
图3 开环模式下序阻抗伯德图
Fig.3 Sequence impedance Bode diagram in open loop mode
双闭环模式下序阻抗伯德图如图4所示。从图4b可知，引入电压-电流双闭环控制策略后，VSG负序阻抗在100 Hz以内呈现感性，而正序阻抗则整体呈现容性，尤其是在20～44 Hz范围内正序阻抗相位低于-90°，呈现出负电阻+容性的特征。从图4a中可以看出，VSG正序阻抗与弱电网阻抗曲线在30 Hz处存在交点，该交点处频率即为D-PMSG系统与弱电网交互产生的谐振频率。从相频特性曲线可知，30 Hz处VSG正序阻抗与弱电网阻抗相位差超过180°，系统失去稳定性。因此，引入电压-电流双闭环使构网型直驱风电系统在次同步频率范围内呈现容性且局部出现负阻尼特征，存在引发次同步振荡风险。
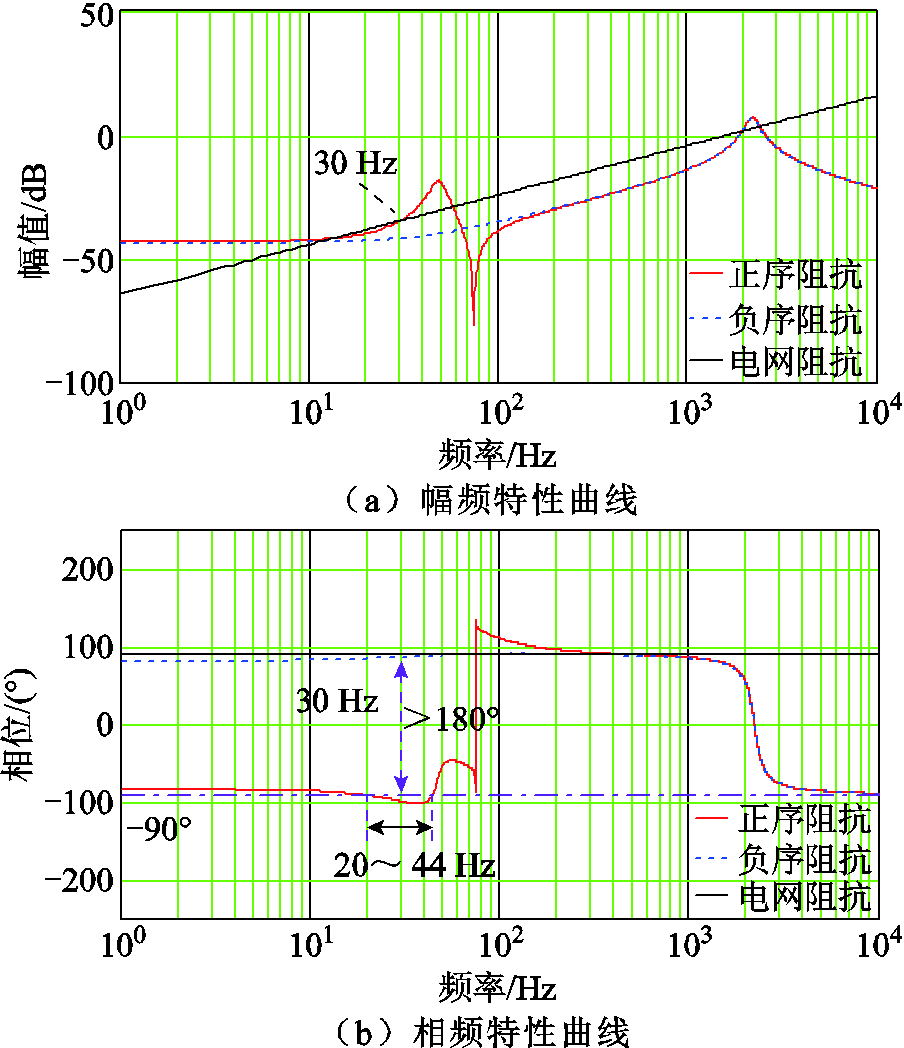
图4 双闭环模式下序阻抗伯德图
Fig.4 Sequence impedance Bode diagram in double closed-loop mode
以3 MW构网型直驱风电系统为例，对有、无电压-电流双闭环模式弱电网下系统运行稳定性进行时域仿真分析。
弱电网条件下，有、无双闭环模式输出有功功率如图5所示，0.8 s时刻将电网电感从正常值切换至0.17 mH，模拟弱电网工况。切换至弱电网工况后，开环模式下有功功率曲线出现短暂小幅波动然后收敛至稳定状态；而双闭环模式下有功功率曲线出现了发散振荡，系统失去稳定。对双闭环条件下系统输出有功功率和电流振荡进行快速傅里叶变换（Fast Fourier Transform, FFT）分析，得到电压谐波扰动下，有功及输出电流响应分量如图6所示。从图6b中可知，输出电流响应分别出现了30 Hz和70 Hz的振荡谐波分量。其中30 Hz分量处于负阻尼区间内，使D-PMSG与弱电网交互谐振发散，引发次同步振荡。而开环模式下，系统整体呈现感性，与弱电网难以产生交互谐振，因此失稳风险较低，时域仿真结果与稳定性分析保持一致。针对该负阻尼所引发次同步振荡问题，本文提出在电流环引入UDE附加阻尼支路的振荡抑制策略。
图5 弱电网条件下，有无双闭环模式输出有功功率
Fig.5 The active power curve with and without double closed-loop mode under weak grid
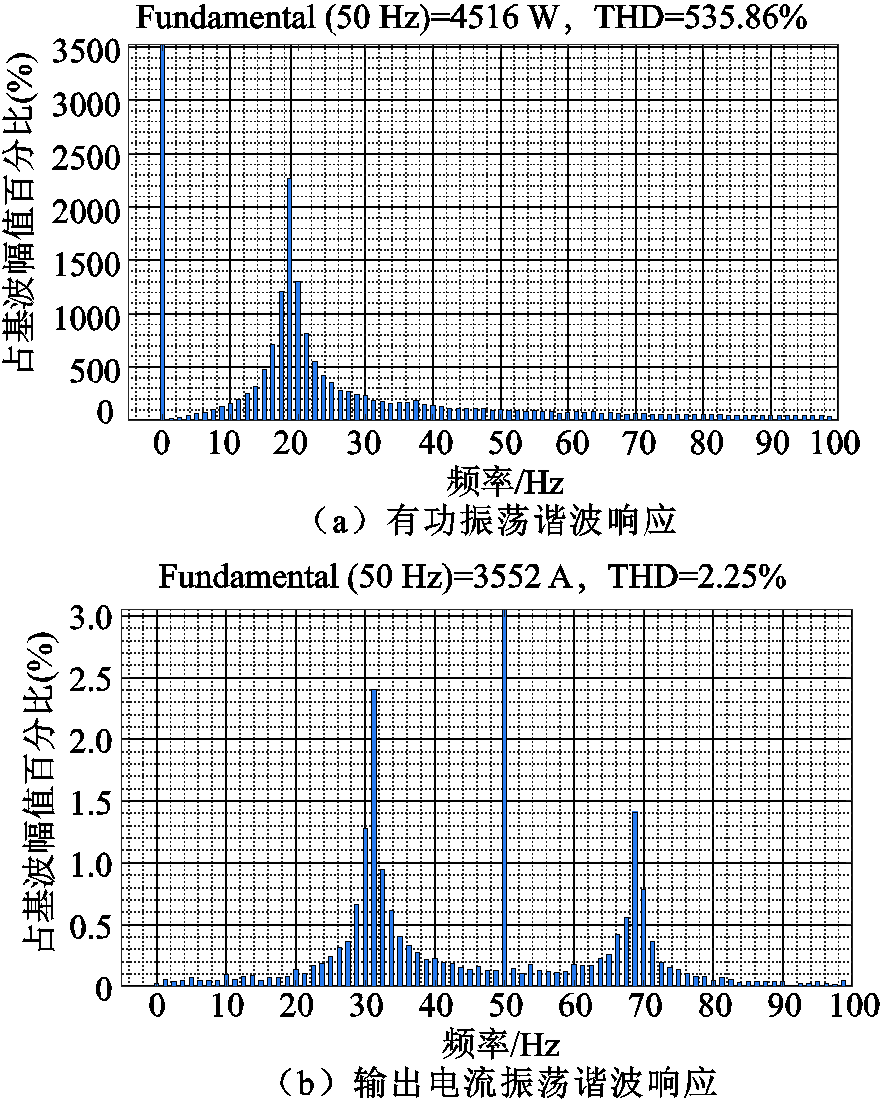
图6 电压谐波扰动下，有功及输出电流响应分量
Fig.6 Active power and output current response component under voltage harmonic disturbances
UDE控制理论在解决因参数不确定性和外部扰动造成系统振荡问题方面具有明显优势，有着较强的系统鲁棒性，本节对该理论原理作简要介绍。
考虑一阶动态系统
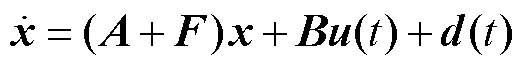（23）
式中，x为控制状态量，x=[x1 x2 …xn]T；u(t)为系统控制输入，u(t)=[u1(t) u2(t) …un(t)]T；A为已知的状态量系数矩阵；F为未知的状态量系数矩阵；B为控制系数矩阵，且满足列满秩；d(t)为外部扰动。
设置参考模型，通过调整系统控制输入u(t)，使系统状态量x渐近跟踪参考模型状态量xm，其表达式为
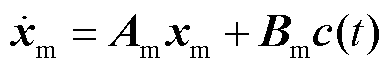（24）
式中，c(t)为参考模型给定量；Am、Bm分别为参考模型状态量系数矩阵和控制系数矩阵。
为获得期望控制性能，需使状态误差快速收敛至0，其表达式为
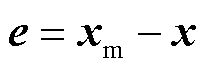（25）
选择合适控制输入u(t)使得式（26）成立。
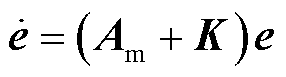（26）
式中，K为误差反馈增益，K＜0；Am＜0。
联立式（23）～式（26），可得
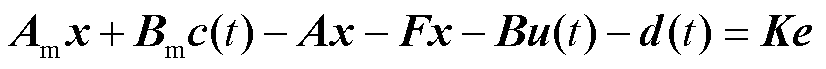（27）
故可得控制输入u(t)表达式为
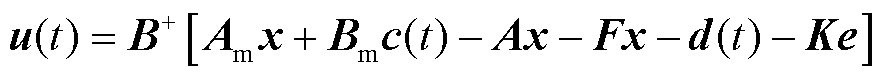（28）
式中，B+为B的伪逆矩阵，B+=(BTB)-1BT。
即最终需满足式（29）成立。
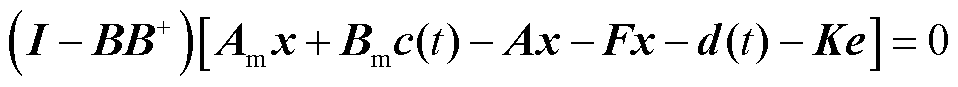（29）
将式（28）进行拉氏变换，可得
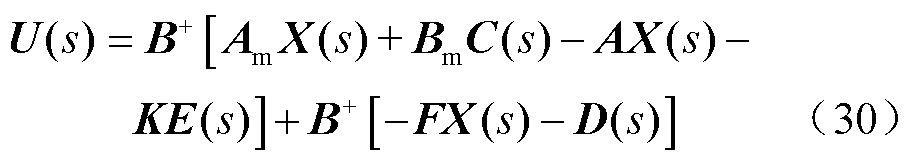
依据式（30）可知
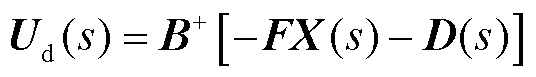（31）
式中，Ud(s)为不确定性和外部扰动总和。
UDE控制理论将系统中的不确定性和扰动等效为集总扰动，选择具有合适带宽的滤波器对该集总扰动进行估计[27]。滤波器设计要求自身带宽能够覆盖集总扰动带宽，且尽可能地在带宽范围内保持单位增益输出，而在范围以外增益为0。
假如存在具有单位增益的滤波器Gf(s)满足严格正实稳定且具有合适的带宽，那么UDE可以表示为
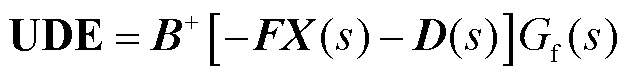（32）
于是，基于UDE的控制规律可以表示为
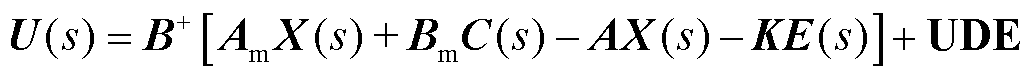（33）
依据式（33）可得控制规律最终表达式为
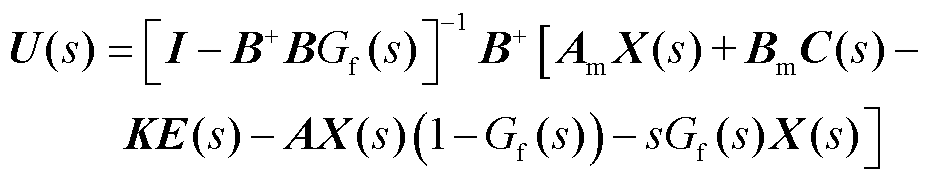(34)
基于UDE理论的控制结构如图7所示。
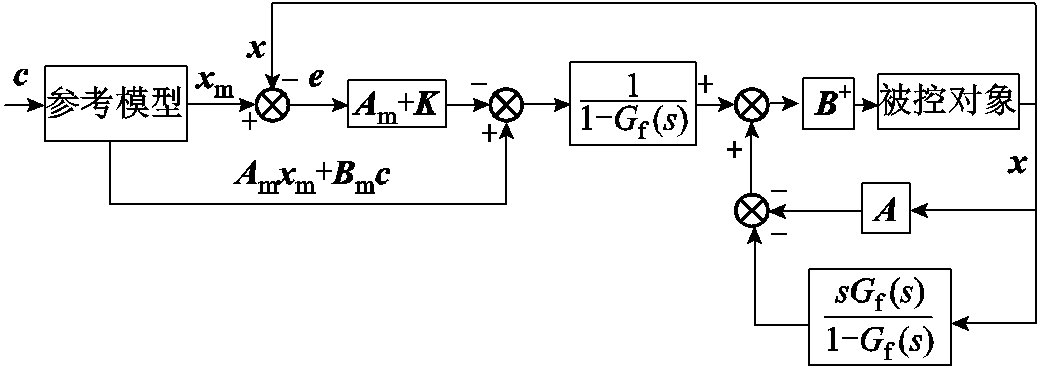
图7 UDE控制结构
Fig.7 Structure of UDE-based controller
3.2.1 传统附加阻尼控制设计
在电力系统中，传统附加阻尼支路由增益环节、隔直环节及相位补偿环节组成，其控制结构如图8所示。
图8 传统附加阻尼控制结构
Fig.8 Structure of traditional supplementary damping control
1）增益环节设计。由于不同工况下，系统出现振荡的幅度不一样，为实现更好地控制性能，通过增益环节来调节输出信号幅值，实现调整输出补偿电压的目的。文中设计增益系数Ksso取值为0.034。
2）隔直环节设计。该环节主要是通过带通滤波器提取振荡谐波电流信号，对提取的振荡谐波信号进行处理分析，为移相补偿控制提供数据支持。考虑到次同步振荡谐波电流频率范围多为10～50 Hz，这里滤波时间Tw取值为1/(20p) s。
3）相位补偿环节设计。该环节是由超前、滞后部分组成，主要完成对电压相位偏移的补偿，进而实现对次同步振荡的抑制。该环节按照式（35）进行整定计算。
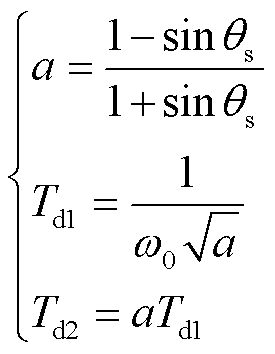（35）
式中，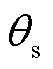
为次同步振荡频率对应相位；Td1、Td2分别为超前、滞后时间常数，分别取值为2.297 s和0.213 s。
由于传统附加阻尼控制需要频繁修改参数且鲁棒性差，该控制方法难以适应新型电力系统复杂工况。
3.2.2 UDE附加阻尼控制器建模
以VSG定子电压-电流方程为基础，将电感电流作为控制变量，桥臂电势作为控制输入（电压补偿），建立UDE附加阻尼控制数学模型[28]。dq坐标系下定子电压-电流一阶状态方程为
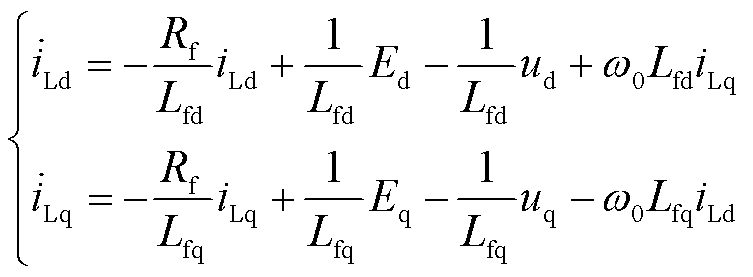（36）
依据式（36）可得矩阵表达式为
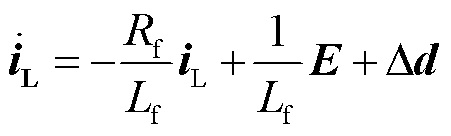（37）
式中，iL为控制状态量，iL=[iLd iLq]T；E为控制输入，E=[Ed Eq]T；Δd为集总扰动，Δd=[Δid Δiq]T，其中
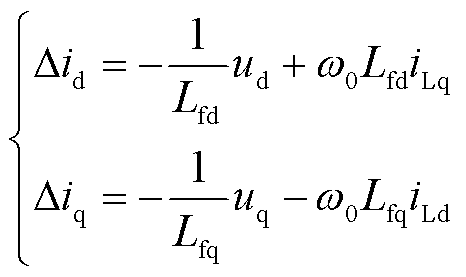（38）
式（38）中多项式分母电感Lf不为零，可认为Δd是有界的。选择合适的控制输入（电压补偿量）E，使电感电流iL能够精确地跟踪不含有振荡谐波分量的参考输入指令iLref的变化。
因此，跟踪误差e=iLref- iL需要满足
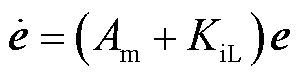（39）
式中，KiL为误差反馈增益，其带宽要小于滤波器带宽，KiL＜0；Am＜0。
联立式（37）和式（39）可得
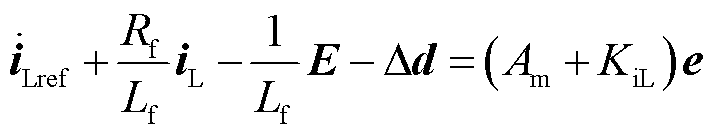（40）
故控制输入E需满足
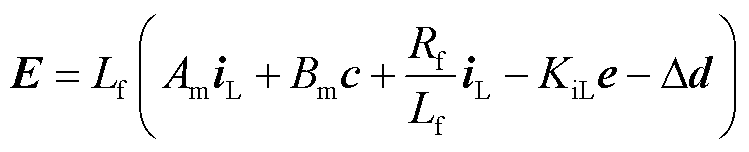（41）
其中
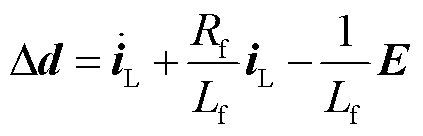
式中，c为参考模型中电感电流设定值iLref。
选择合适的带宽滤波器对集总扰动进行估计，有
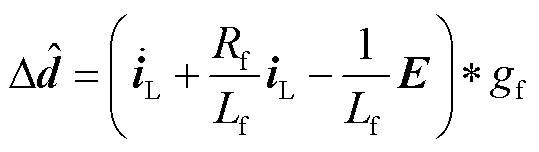（42）
式中，“*”为卷积计算符号；gf为带通滤波器Gf(s)的单位脉冲响应。
用式（42）替换式（41）中的Dd，可得
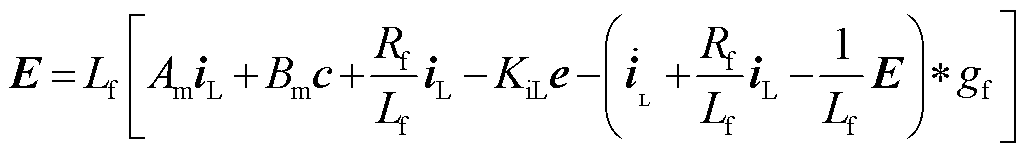（43）
则UDE附加阻尼支路控制数学模型可表示为
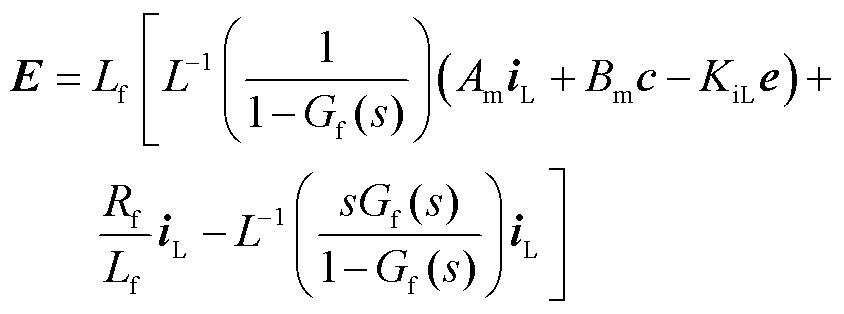(44)
式中，L-1(·)为反拉普拉斯变换。
式（44）中不再包含不确定性和未知扰动项。将式（44）代入式（16），推导可得引入UDE附加阻尼支路后正、负序阻抗表达式，见附录式（A13）。
3.2.3 UDE对系统稳定性影响及参数设计
引入UDE附加阻尼支路前后的VSG系统稳定性对比如图9所示。引入UDE附加阻尼支路后，100 Hz以上频段范围曲线与图4几乎重合，而100 Hz以内频段曲线整体上移，负阻尼区间急剧缩小，大大降低了系统次同步振荡风险。从图9a的幅频特性曲线可以看出，引入附加阻尼支路后系统与电网阻抗在30 Hz处有交点，相频特性曲线显示30 Hz处相位差小于180°，系统稳定。因此，通过引入UDE附加阻尼支路可有效抑制弱电网下D-PMSG系统次同步振荡，提升系统稳定性。
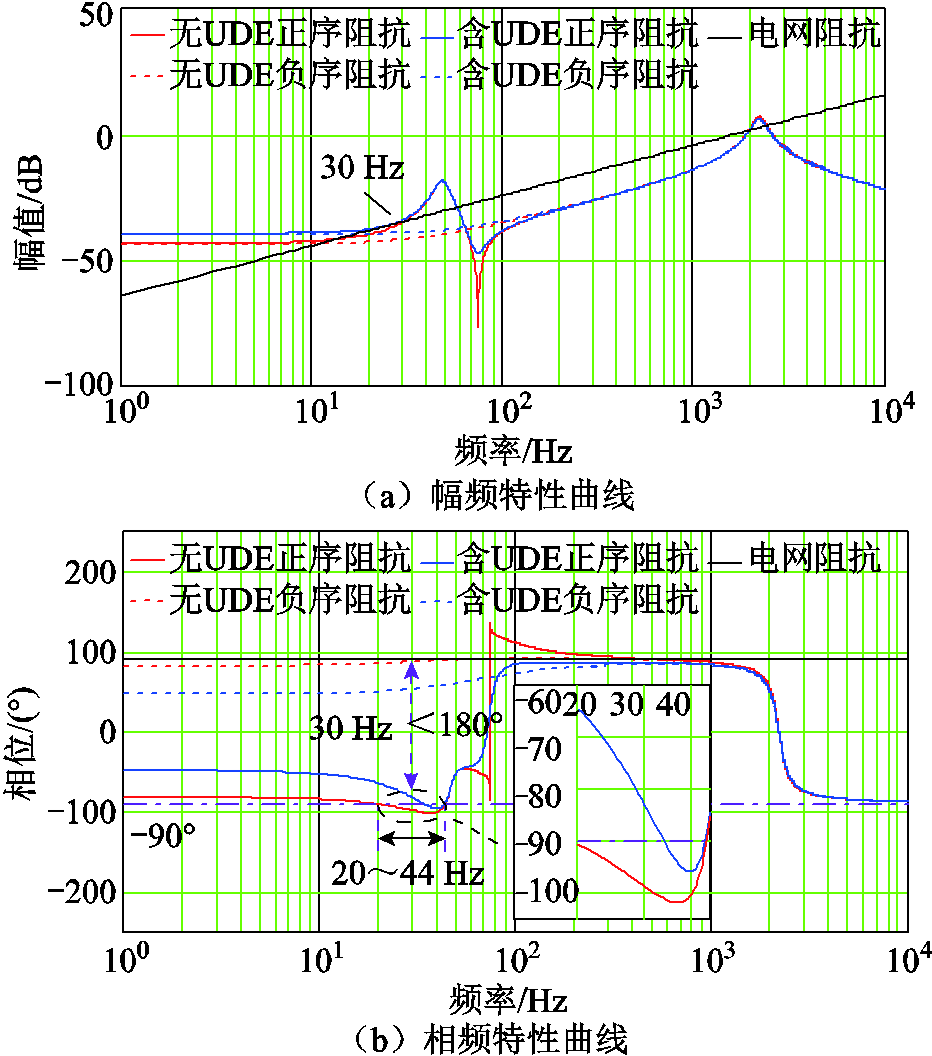
图9 含UDE双闭环模式下序阻抗对比
Fig.9 Sequence impedance comparison in double closed-loop mode with UDE branch
影响UDE控制器性能的参数主要有参考模型状态系数Am、控制系数Bm、误差反馈增益KiL及滤波带宽wf。Am和Bm主要用于设置参考模型，以获得期望的控制性能。从附图1和附图2可知，该参数对VSG系统稳定性影响极小，文中设置Am=-Bm，取值为-10p。KiL用于调节UDE控制器自身稳定性，其取值要小于滤波带宽。附图3中的相频特性曲线显示，随着KiL增大，系统负阻尼区间呈缩小趋势，有利于系统稳定性，但影响并不明显。综合考虑自身稳定性，设置KiL=-20p。
由于影响系统振荡不确定性和外部扰动多为低频范围，本文选择一阶低通滤波器Gf(s)= 1/(Ts+1)。
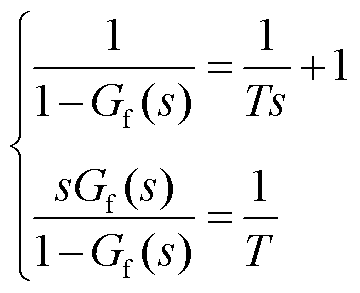（45）
式中，T为响应时间常数，T=1/wf，wf为UDE滤波带宽，其取值需覆盖系统中集总扰动频带上限。
附图4显示，随着wf增大，系统负阻尼区间明显缩小，系统稳定性提升。但随着wf的增大，UDE控制性能受噪声的影响也越大。考虑到交互谐振在次/超同步范围内成对出现，且在极端条件下负阻尼区间可能延伸至超同步范围，集总扰动频带上限设置为100 Hz。综合考虑滤波带宽wf取值为300p。
将式（44）的数学模型以附加阻尼支路形式引入双闭环电流环中，其控制框图如图10所示。图10中补偿电压Ed、Eq即为UDE附加阻尼支路控制输入，通过调整控制输入实现电感电流与参考值的稳定跟踪，进而起到振荡抑制效果。该控制方法具备较好的阻尼支撑能力，通过选取合适参考模型、误差反馈增益以及滤波带宽参数，可实现一定频段范围内的振荡抑制，具有较好的适应性。
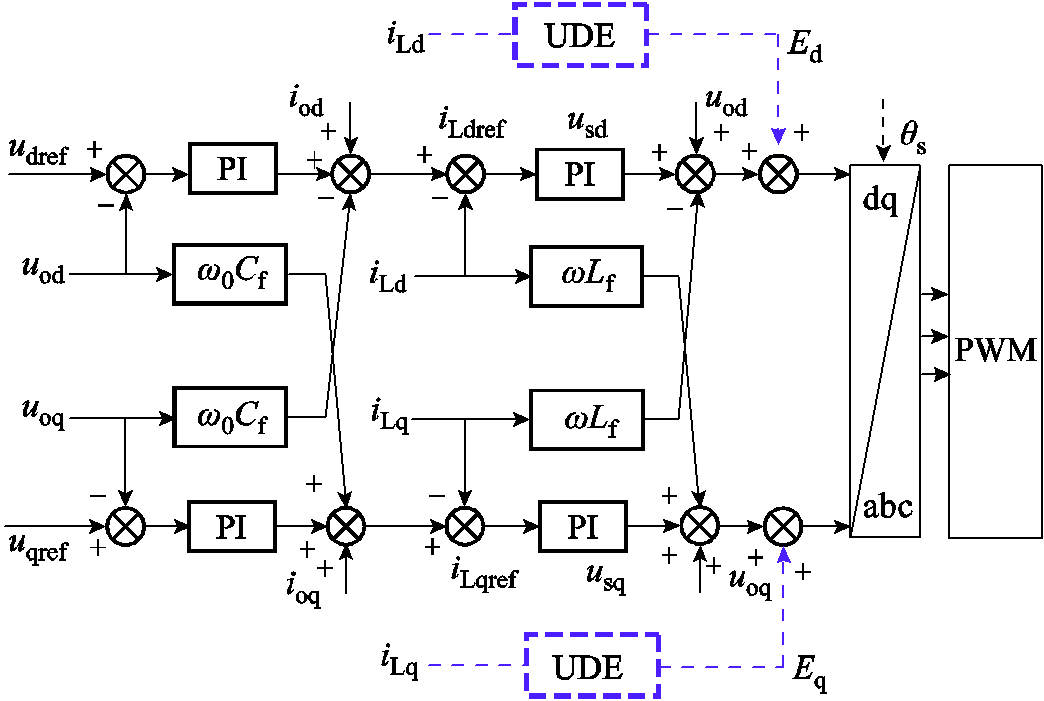
图10 基于UDE的附加阻尼支路控制框图
Fig.10 UDE-based supplementary damping branch control block diagram
本文搭建了单台3 MW构网型直驱永磁同步风电机组并网模型，通过时域仿真对基于UDE附加阻尼支路的振荡抑制策略进行验证。系统并网模型如图11所示，参数见表1，时域仿真实验操作如下所述。
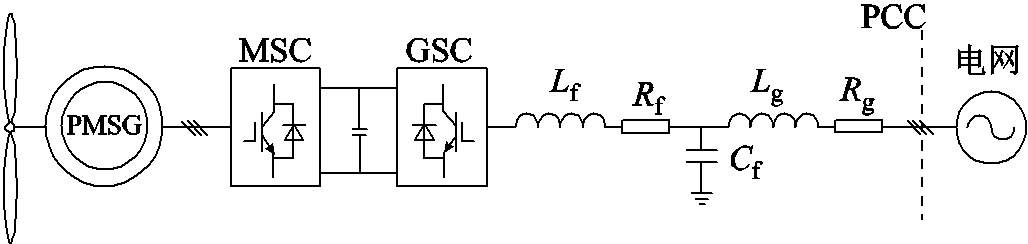
图11 直驱风电机组并网主拓扑
Fig.11 Main topology of grid-connected D-PMSG
表1 直驱永磁同步风电机组系统参数
Tab.1 System parameters of D-PMSG
参数数值参数数值 额定容量Sn/(MV·A)3.0滤波电感Lf/mH0.2 额定电压Un/V690滤波电容Cf/μF200 额定频率f/Hz50滤波电阻Rf/W0.003 直流侧电压Udc/V1 200转动惯量J/(kgm2)0.5 无功调节系数K350阻尼系数D/[Nm/(rad/s)]200 滤波带宽wf/(rad/s)300π状态系数Am-10π 误差反馈增益KiL-20π控制系数Bm10π
1）设置不同电网强度工况。风电机组正常并网后，0.8 s时刻设置电网电感由正常值分别切换到0.17 mH、0.22 mH模拟不同程度的弱电网振荡；1.8 s时刻分别投切基于移相控制和UDE控制的两种附加阻尼控制支路；3.0 s时刻电网电感恢复正常，观察振荡抑制效果。
2）设置不同阶跃扰动工况。风电机组正常并网后，0.8 s时刻设置电网电感由正常值切换到0.17 mH，模拟弱电网振荡；1.8 s时刻UDE附加阻尼控制支路投入使用，同时设置电网电压和有功指令阶跃扰动；2.5 s时刻扰动结束；3.0 s时刻电网电感恢复正常，观察振荡抑制效果。
4.2.1 不同电网强度下振荡抑制仿真结果
不同阻抗工况条件下功率曲线如图12所示。电网电感设置为Z1=0.17 mH时，风电机组输出电流出现30 Hz振荡，而有功、无功功率则出现20 Hz振荡。传统附加阻尼控制参数按照该振荡频率进行整定计算，此时短路比SCR＜3。从图12可知，0.8 s时刻系统开始出现振荡，1.8 s时刻附加阻尼控制支路投入使用，有功功率和无功功率分别从最大振荡幅值0.5 MW和0.4 Mvar衰减并收敛至稳定值。从仿真曲线对比可以看出，有功功率、无功功率在两种附加阻尼支路控制作用下均实现了较好的振荡抑制效果，且含UDE附加阻尼支路的振荡抑制收敛速度明显快于传统型。
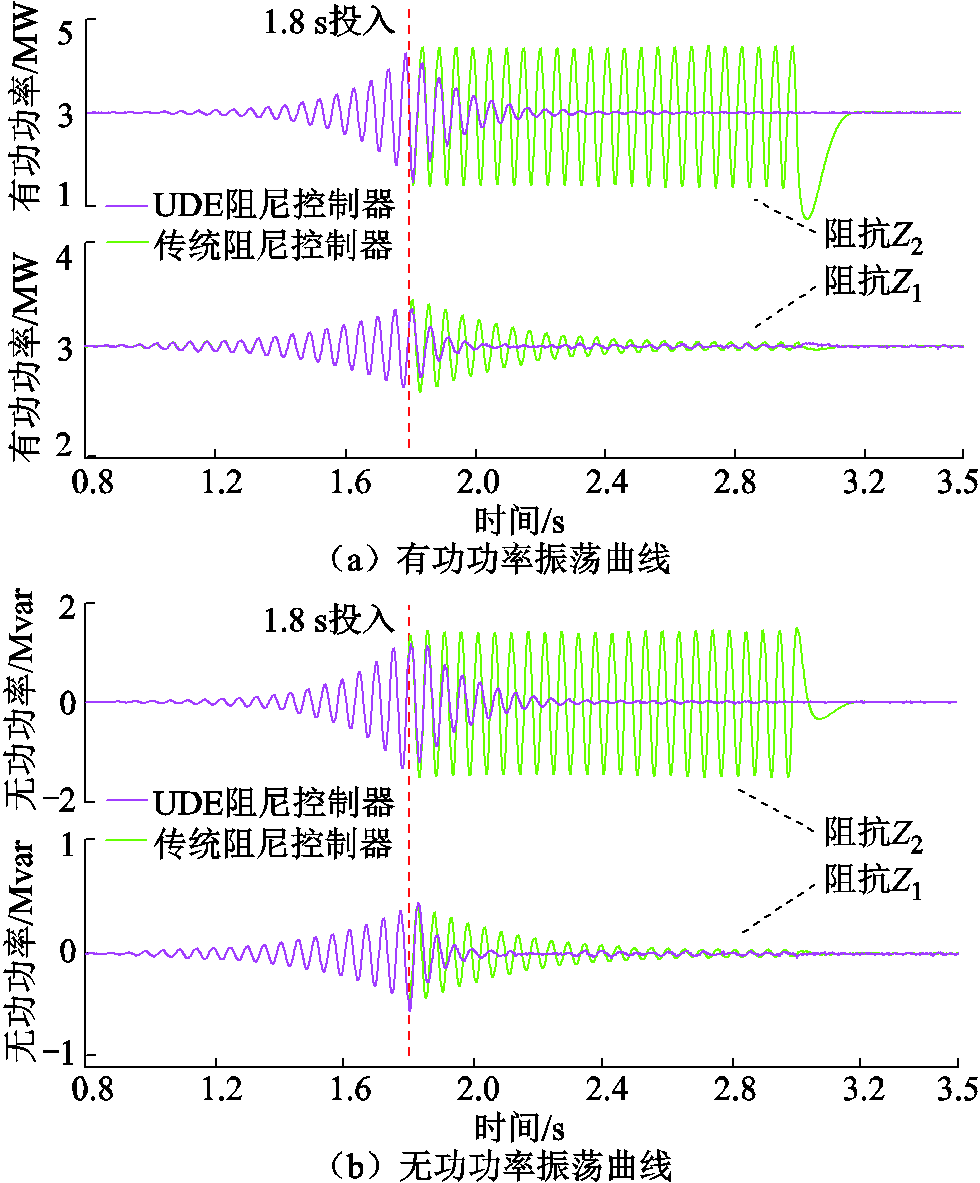
图12 不同阻抗工况条件下功率曲线
Fig.12 Power curves under different impedance conditions
当电网电感设置为Z2=0.22 mH时，传统附加阻尼支路控制下出现了等幅振荡，振荡抑制失败。而在UDE附加阻尼支路控制下，有功功率和无功功率经过几个周波的调整快速收敛至稳定状态。不同电网阻抗下振荡频率也在发生变化，而基于UDE的附加阻尼支路控制均保持了较好的振荡抑制效果，表现出良好的适应性。基于UDE的附加阻尼控制将外部扰动和不确定性作为集总扰动，采用具有合适带宽的滤波器估计该扰动，当系统扰动频率在滤波器带宽范围内时，系统能实现一定电网强度范围内的振荡抑制效果。该控制方法有效解决了传统附加阻尼支路控制必须频繁更改控制参数的问题，提升了适应新型电力系统复杂工况的能力。
4.2.2 电网电压阶跃扰动下仿真结果
电压阶跃扰动工况下功率曲线如图13所示，0.8 s时刻电网电感切换为0.17 mH，系统出现振荡；1.8 s时刻UDE附加阻尼控制支路投入使用，同时施加幅度为5%的额定电压阶跃扰动。从图13中有功功率和无功功率曲线可以看出，施加扰动后系统通过短暂调整达到稳定状态，表现出较好的振荡抑制效果。受无功影响下垂系数影响，无功功率幅值下降至-1.4 Mvar，但其振荡抑制效果依然明显。基于UDE的附加阻尼支路控制在电压阶跃扰动下使系统振荡趋于平稳状态所用调整时间较无扰动情况下仅多了几个周波。
图13 电压阶跃扰动工况下功率曲线
Fig.13 Power curves under voltage step disturbance condition
4.2.3 有功指令阶跃扰动下仿真结果
有功指令阶跃扰动工况下功率曲线如图14所示，当0.8 s时刻电网电感切换为0.17 mH时，系统出现振荡；1.8 s时刻投切UDE附加阻尼控制支路，同时刻施加1 MW的有功指令阶跃扰动。从图14中有功功率、无功功率曲线可以看出，在有功指令阶跃扰动下，系统通过短暂调整达到平稳状态。虽然系统输出有功功率出现幅度为1 MW的阶跃响应，但系统输出有功功率依然表现出较好的振荡抑制效果。在扰动切除时刻，系统出现较大幅度振荡，在UDE附加阻尼控制作用下快速收敛至稳定状态，表现出较好的抗干扰能力。
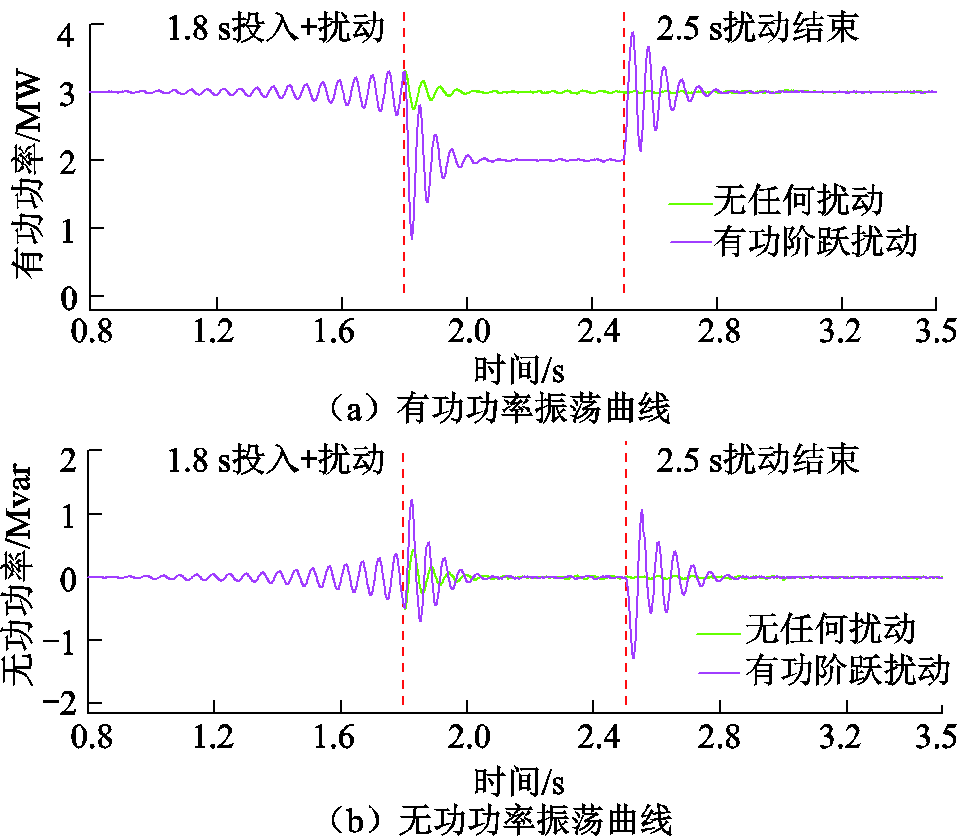
图14 有功指令阶跃扰动工况下功率曲线
Fig.14 Power curves under active command step disturbance condition
本文针对构网型直驱永磁同步风电机组与弱电网交互产生次同步振荡问题，提出了基于UDE附加阻尼支路的振荡抑制策略，并通过时域仿真实验得出以下结论：
1）基于谐波线性化理论，推导了网侧变流器频域的序阻抗模型。引入双闭环控制后，构网型直驱风电系统在特定频段产生的负阻尼+容性特征与弱电网交互易引发次同步振荡。
2）利用滤波带宽思想建立了UDE附加阻尼支路控制模型，实现了一定电网强度范围内的次同步振荡抑制，有效地解决了传统附加阻尼控制必须频繁更改控制参数的问题，提升了系统适应复杂工况的能力。
3）在电网电压和有功指令阶跃扰动下，系统均能保持较好的次同步振荡抑制效果，抗干扰能力明显提升，具有较好的系统鲁棒性。
附 录
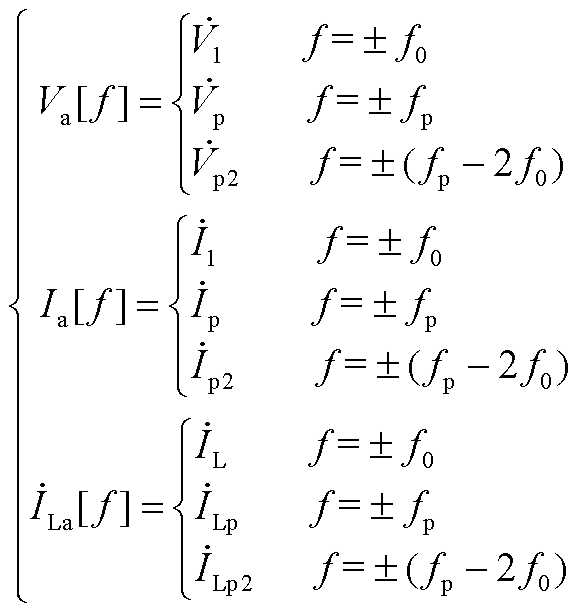（A1）
其中
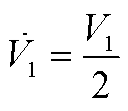
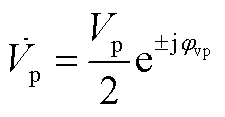
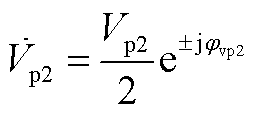
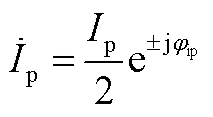
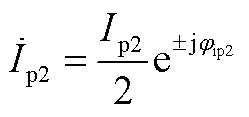
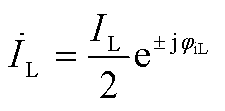
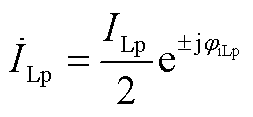
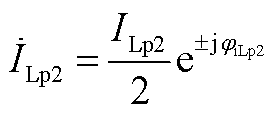
αβ坐标系下，系统输出端电压、输电流频域表达式为
（A2）
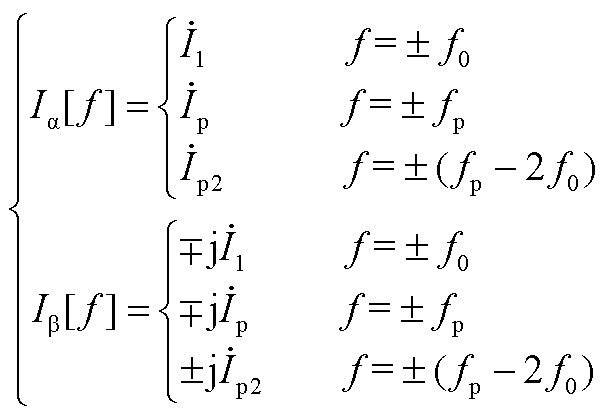（A3）
根据三角函数关系可知
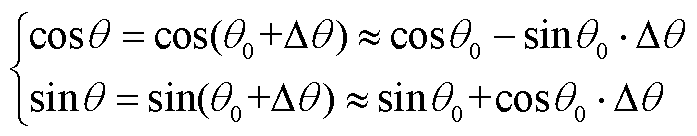（A4）
将式（A4）进行拉氏变换可得
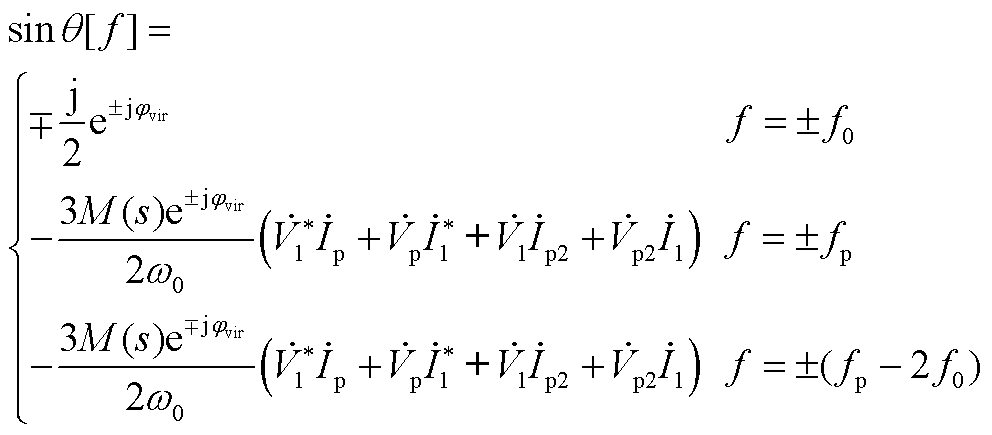（A5）
（A6）
Park变换矩阵表达式为
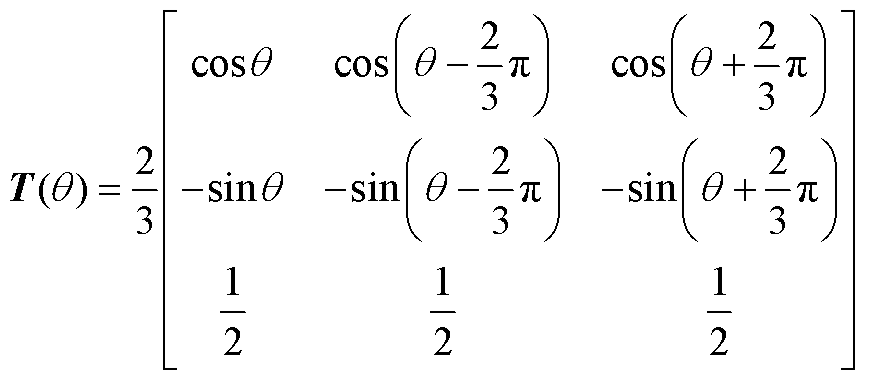（A7）
将Park变换矩阵进行线性化处理得到
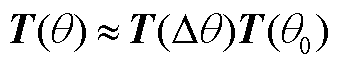（A8）
式中，T(Δθ)、T(θ0)分别为扰动量、基频分量部分对应变换矩阵，其表达式分别为
（A9）
（A10）
电感电流频域表达式为
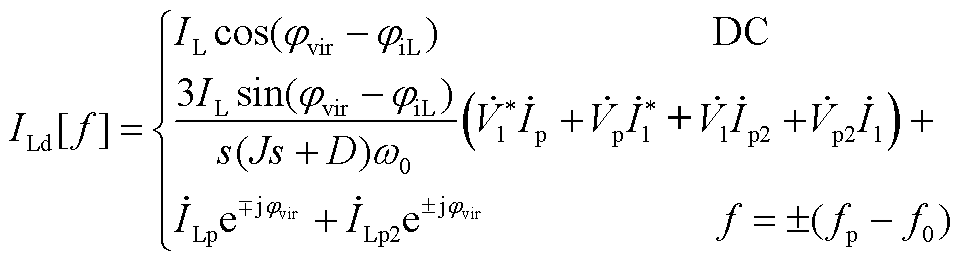（A11）
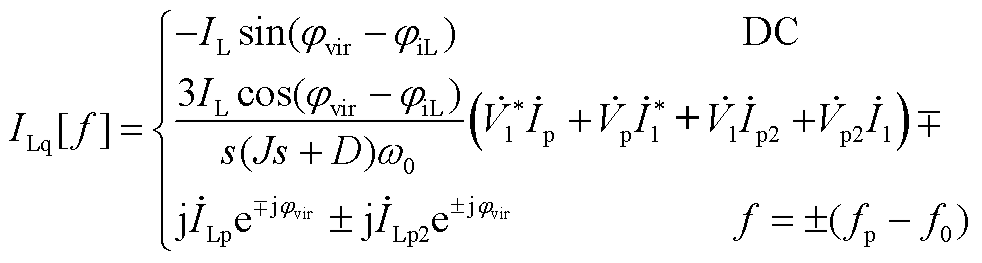（A12）
引入UDE附加阻尼支路后VSG正、负序阻抗表达式为
（A13）
其中
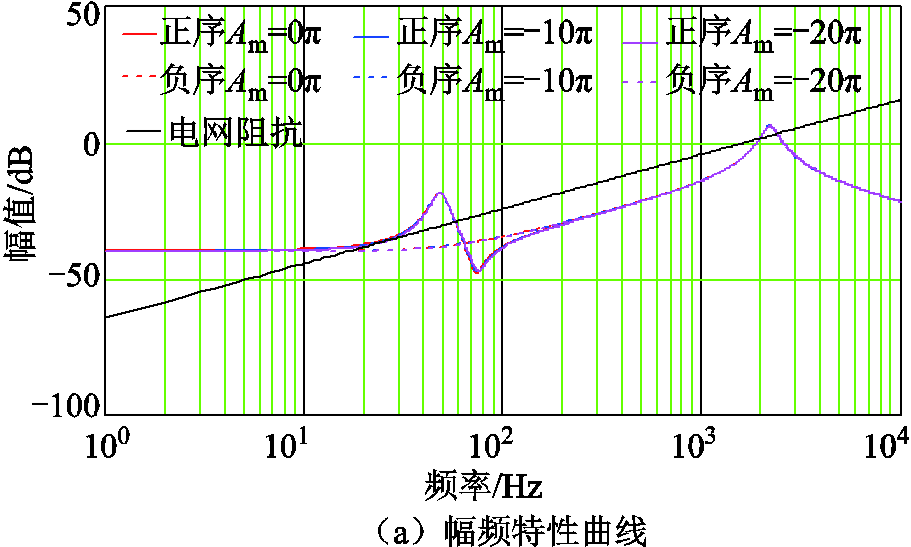
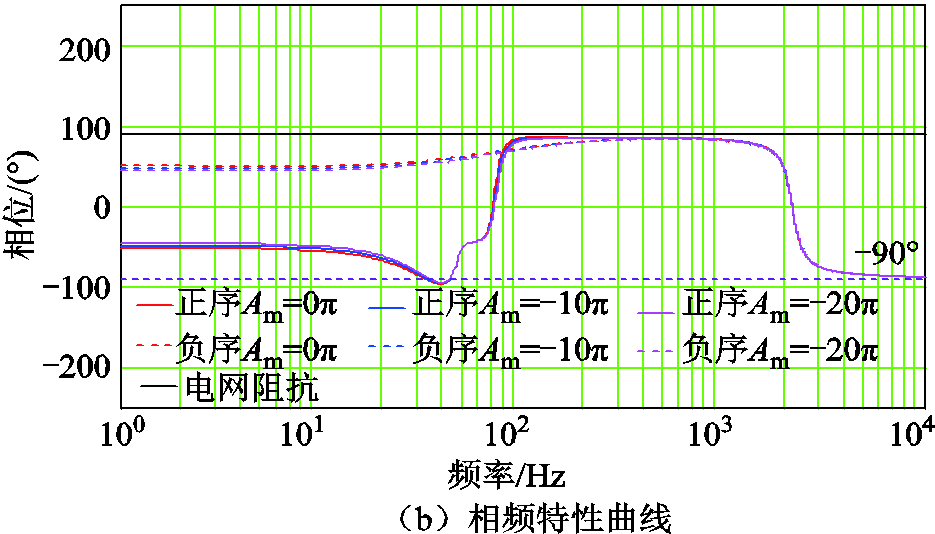
附图1 Am对系统稳定性影响
App.Fig.1 The influence of Am on system stability
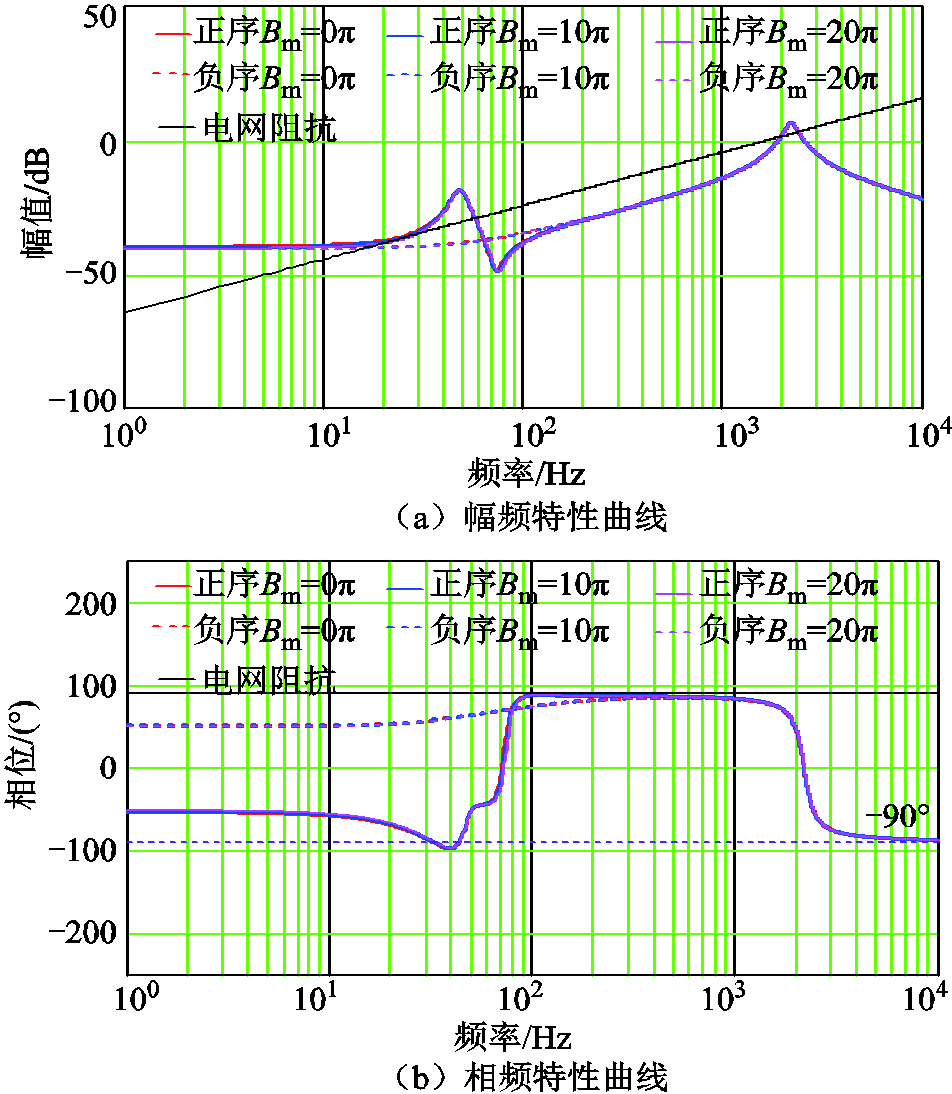
附图2 Bm对系统稳定性影响
App.Fig.2 The influence of Bm on system stability
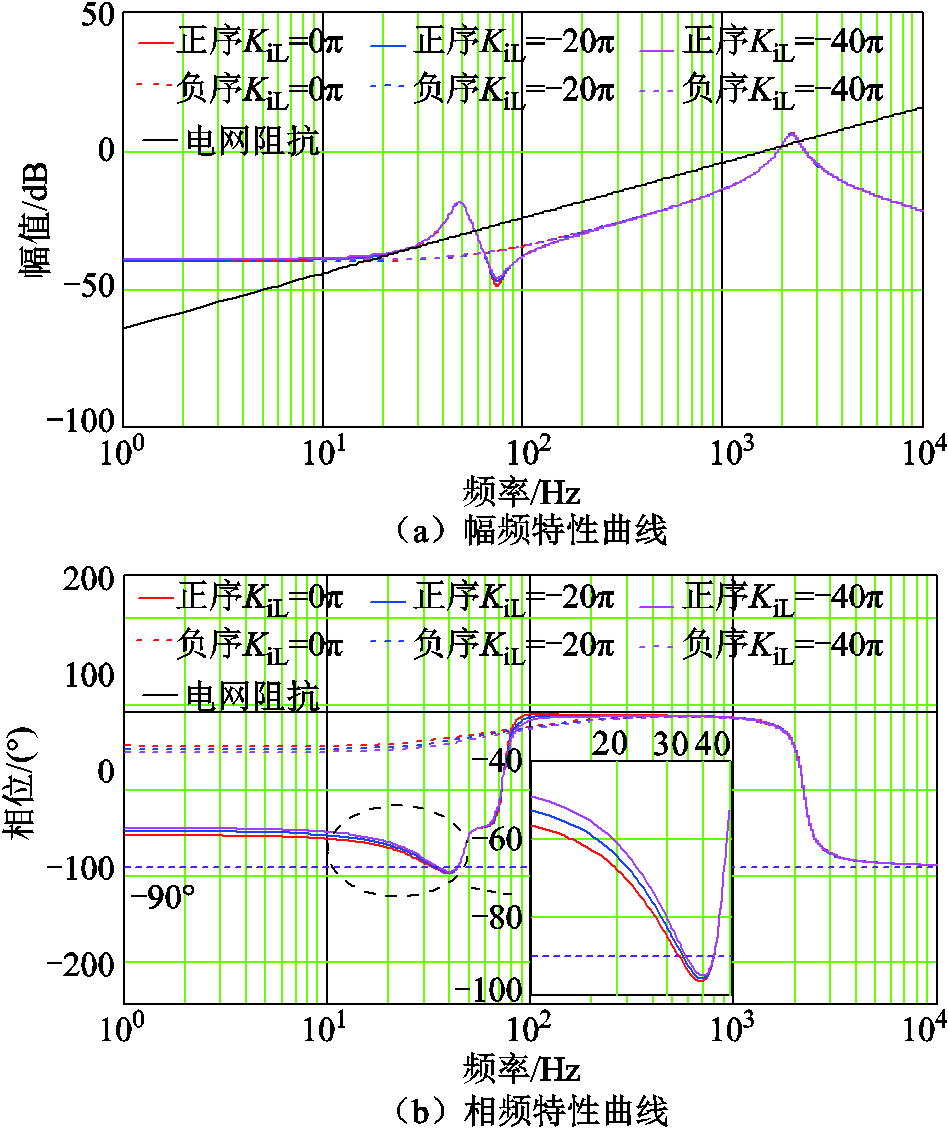
附图3 KiL对系统稳定性影响
App.Fig.3 The influence of KiL on system stability
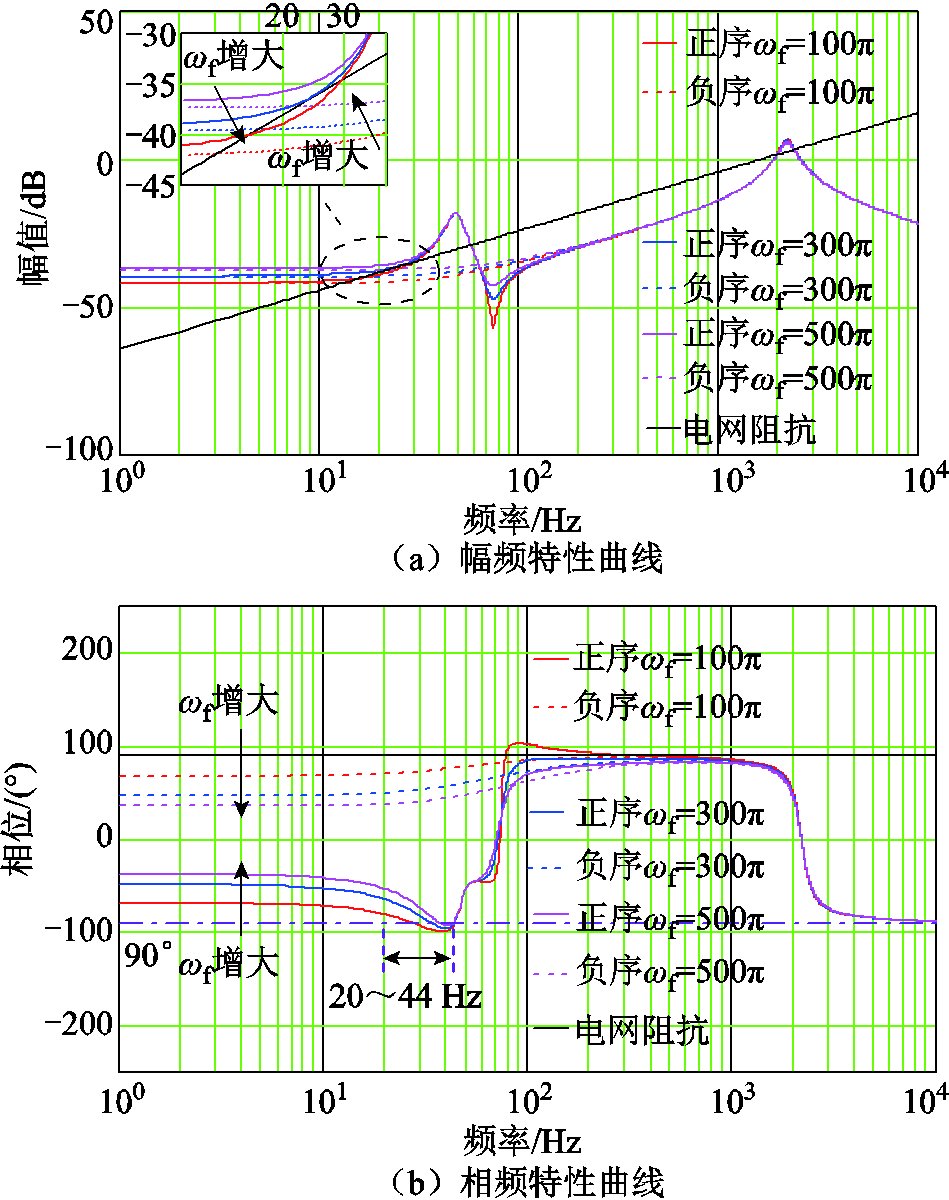
附图4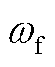 
对系统稳定性影响
App.Fig.4 The influence of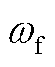 on system stability
参考文献
[1] 高本锋, 王义, 范辉, 等. 基于阻尼路径的新能源经LCC-HVDC送出系统次同步交互作用分析方法[J]. 电工技术学报, 2023, 38(20): 5572-5589. Gao Benfeng, Wang Yi, Fan Hui, et al. A sub-synchronous interaction analysis method of renewable energy generations integrated with LCC-HVDC system based on damping path[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5572-5589.
[2] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191. Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[3] Li Yin, Fan Lingling, Miao Zhixin. Wind in weak grids: low-frequency oscillations, subsynchronous oscillations, and torsional interactions[J]. IEEE Transactions on Power Systems, 2020, 35(1): 109-118.
[4] 邵冰冰, 赵峥, 肖琪, 等. 多直驱风机经柔直并网系统相近次同步振荡模式参与因子的弱鲁棒性分析[J]. 电工技术学报, 2023, 38(3): 754-769. Shao Bingbing, Zhao Zheng, Xiao Qi, et al. Weak robustness analysis of close subsynchronous oscillation modes’ participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.
[5] Yan Gangui, Hu Wenbo, Jia Qi, et al. Analysis of subsynchronous oscillation of direct drive PMSG based wind farm under low operating condition[J]. Journal of Electrical Engineering & Technology, 2021, 16(1): 1-13.
[6] 宫泽旭, 艾力西尔·亚尔买买提, 辛焕海, 等. 新能源电力系统并网设备小扰动稳定分析(二): 导出机理与稳定性分类探讨[J]. 中国电机工程学报, 2022, 42(14): 5126-5140. Gong Zexu, Yaermaimaiti Ailixier, Xin Huanhai, et al. Small signal stability analysis of grid-connected equipment in power system (part Ⅱ): discussion on mechanism derivation and classification of stability[J]. Proceedings of the CSEE, 2022, 42(14): 5126-5140.
[7] 李龙源, 付瑞清, 吕晓琴, 等. 接入弱电网的同型机直驱风电场单机等值建模[J]. 电工技术学报, 2023, 38(3): 712-725. Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al. Single machine equivalent modeling of weak grid connected wind farm with same type PMSGs[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 712-725.
[8] 李光辉, 王伟胜, 刘纯, 等. 直驱风电场接入弱电网宽频带振荡机理与抑制方法(一)：宽频带阻抗特性与振荡机理分析[J]. 中国电机工程学报, 2019, 39(22): 6547-6562. Li Guanghui, Wang Weisheng, Liu Chun, et al. Mechanism analysis and suppression method of wideband oscillation of PMSG wind farms connected to weak grid (partⅠ): analysis of wideband impedancecharacteristics and oscillation mechanism[J]. Proceedings of the CSEE, 2019, 39(22): 6547-6562.
[9] 王旭斌, 杜文娟, 王海风. 直驱风电并网系统中锁相环引起次同步振荡的开环模式谐振机理分析[J]. 中国电机工程学报, 2018, 38(7): 1935-1950, 2209.Wang Xubin, Du Wenjuan, Wang Haifeng. Mechanism analysis of open-loop modal resonance on subsyn-chronous oscillations caused by PLL in power systems with integrated PMSGs[J]. Proceedings of the CSEE, 2018, 38(7): 1935-1950, 2209.
[10] 杜步阳, 邵德军, 朱建行, 等. 电压源型变流器并网系统多时间尺度间相互作用[J]. 电工技术学报, 2023, 38(20): 5547-5559. Du Buyang, Shao Dejun, Zhu Jianhang, et al. The interaction between multiple timescales of the grid-tied voltage source converter[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5547-5559.
[11] 吕佃顺, 许洪华, 马强, 等. 直驱变流器接入弱电网次同步振荡机理分析[J]. 太阳能学报, 2021, 42(5): 423-429. Lü Dianshun, Xu Honghua, Ma Qiang, et al. Analysis of sub-synchronous oscillation mechanism of direct-drive wind turbine inverter connected to weak power system[J]. Acta Energiae Solaris Sinica, 2021, 42(5): 423-429.
[12] Zhong Qingchang, Weiss G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[13] Imai H, Orihara D, Iioka D, et al. A novel virtual synchronous generator control of PMSG-based wind generation system to enhance transient stability of power system[C]//2018 IEEE Electronic Power Grid (eGrid), Charleston, SC, USA, 2018: 1-6.
[14] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146. Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impedance [J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[15] Cespedes M, Sun Jian. Impedance modeling and analysis of grid-connected voltage-source converters [J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1254-1261.
[16] Kazem Bakhshizadeh M, Wang Xiongfei, Blaabjerg F, et al. Couplings in phase domain impedance modeling of grid-connected converters[J]. IEEE Transactions on Power Electronics, 2016, 31(10): 6792-6796.
[17] 杜燕, 赵韩广, 杨向真, 等. 考虑频率耦合效应的虚拟同步发电机序阻抗建模[J]. 电源学报, 2020, 18(6): 42-49. Du Yan, Zhao Hanguang, Yang Xiangzhen, et al. Sequence impedance modeling of virtual synchronous generator considering frequency coupling effect[J]. Journal of Power Supply, 2020, 18(6): 42-49.
[18] 伍文华, 周乐明, 陈燕东, 等. 序阻抗视角下虚拟同步发电机与传统并网逆变器的稳定性对比分析[J]. 中国电机工程学报, 2019, 39(5): 1411-1421. Wu Wenhua, Zhou Leming, Chen Yandong, et al. Stability comparison and analysis between the virtual synchronous generator and the traditional grid-connected inverter in the view of sequence impedance[J]. Proceedings of the CSEE, 2019, 39(5): 1411-1421.
[19] 伍文华, 陈燕东, 周乐明, 等. 虚拟同步发电机接入弱电网的序阻抗建模与稳定性分析[J]. 中国电机工程学报, 2019, 39(6): 1560-1571, 1853. Wu Wenhua, Chen Yandong, Zhou Leming, et al. Sequence impedance modeling and stability analysis for virtual synchronous generator connected to the weak grid[J]. Proceedings of the CSEE, 2019, 39(6): 1560-1571, 1853.
[20] Xu Yunyang, Nian Heng, Wang Yangming, et al. Impedance modeling and stability analysis of VSG controlled grid-connected converters with cascaded inner control loop[J]. Energies, 2020, 13(19): 5114.
[21] 周佩朋, 宋瑞华, 李光范, 等. 直驱风电机组次同步振荡阻尼控制方法及其适应性[J]. 电力系统自动化, 2019, 43(13): 177-184. Zhou Peipeng, Song Ruihua, Li Guangfan, et al. Damping control method of subsynchronous oscillation for direct drive wind turbine generator and its adaptability[J]. Automation of Electric Power Systems, 2019, 43(13): 177-184.
[22] Guo Chunyi, Xu Liqing, Yang Shuo, et al. A supplementary damping control for MMC-HVDC system to mitigate the low-frequency oscillation under low inertia condition[J]. IEEE Transactions on Power Delivery, 2023, 38(1): 287-298.
[23] 李生虎, 张奥博, 夏伟健, 等. 并网DFIG多通道附加阻尼控制器设计及其控制参数整定[J]. 电力自动化设备，2023，43(7) : 73-79. Li Shenghu, Zhang Aobo, Xia Weijian, et al. Design of and parameter setting for multi-band supplementary damping controllers of DFIG-integrated system[J]. Electric Power Automation Equipment，2023，43(7) : 73-79.
[24] 王杨, 杨汉芦, 肖先勇, 等. 双馈风机附加次同步阻尼控制器抑制方法分析与优化设计[J]. 电力自动化设备, 2022, 42(8): 184-190. Wang Yang, Yang Hanlu, Xiao Xianyong, et al. Mitigation method analysis and optimization design of doubly-fed induction generator additional subsyn-chronous damping controller[J]. Electric Power Automation Equipment, 2022, 42(8): 184-190.
[25] Zhong Qingchang, Wang Yeqin, Ren Beibei. UDE-based robust droop control of inverters in parallel operation[J]. IEEE Transactions on Industrial Electro-nics, 2017, 64(9): 7552-7562.
[26] Ren Jianjun, Ye Yongqiang, Xu Guofeng, et al. Uncertainty-and-disturbance-estimator-based current control scheme for PMSM drives with a simple parameter tuning algorithm[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5712-5722.
[27] Wang Yeqin, Ren Beibei, Zhong Qingchang. Bounded UDE-based controller for input constrained systems with uncertainties and disturbances[J]. IEEE Tran-sactions on Industrial Electronics, 2021, 68(2): 1560-1570.
[28] 陈建, 任永峰, 云平平, 等. 基于UDE的虚拟同步发电机功频振荡抑制策略[J]. 太阳能学报, 2022, 43(12): 220-226. Chen Jian, Ren Yongfeng, Yun Pingping, et al. Power-frequency oscillation suppression strategy of virtual synchronous generator based on UDE[J]. Acta Energiae Solaris Sinica, 2022, 43(12): 220-226.
Abstract Under the background of continuous growth of wind power installed capacity, grid-forming converters are used to solve the problem of system inertia loss caused by high proportion of power electronic equipment in wind power system. During the interaction between the grid-forming direct-drive permanent magnet synchronous generator (D-PMSG) and the weak grid, its equivalent capacitance and the weak grid inductance produce resonance. Especially in remote areas, the sub-synchronous oscillation occurs with the resonance diverging under condition of negative damping. Compared with the traditional sub-synchronous oscillation dominated by shafting dynamics, the oscillation phenomenon in the new power system often begins with small signal negative damping divergence and ends in nonlinear continuous oscillation, which shows the characteristics of wide oscillation frequency range. In order to solve the problem of sub-synchronous oscillation caused by the lack of damping, an oscillation suppression strategy of supplementary damping branch based on uncertainty and disturbance estimator (UDE) in grid-forming D-PMSG is proposed.
The sequence impedance model of grid-side converter is established, and the stability of virtual synchronous generator (VSG) with or without voltage-current double closed-loop is analyzed. The sequence impedance of VSG without voltage-current double closed-loop is inductive as a whole, which is similar to the characteristics of traditional synchronous generator. Under this mode, there is no interactive resonance with the weak grid, and the system stability is good, but it cannot achieve accurate voltage regulation and current limiting. The positive sequence impedance of VSG with voltage-current double closed-loop is capacitive as a whole, and the negative damping characteristics appear locally, which has the risk of sub-synchronous oscillation. In order to improve the damping characteristics of grid-forming D-PMSG, the UDE supplementary damping branch is introduced into current loop. The mathematical model of UDE damping controller is established, and the VSG sequence impedance model after introducing UDE controller is derived. The influence of UDE controller parameters on system stability is analyzed based on sequence impedance model with UDE. The parameters of reference model and error feedback gain are mainly used to improve the performance of the controller itself, which has little influence on the stability of VSG. The filter bandwidth of UDE controller has a great influence on the stability of the system. Increasing the filter bandwidth can improve the damping characteristics, but it is more affected by noise. Therefore, the choice of filter bandwidth needs to be compromised. After introducing the UDE supplementary damping branch, the negative damping interval of the VSG is sharply reduced, and the stability of the system is significantly improved.
Conclusions can be drawn that: (1) The sequence impedance model of VSG in the frequency domain is derived. After introducing double closed-loop control, the grid-forming D-PMSG presents negative damping and capacitive characteristics in a specific frequency band, and the sub-synchronous oscillation occurs under interaction with the weak grid. (2) The UDE supplementary damping branch control model is established with the idea of filter bandwidth, which can suppress the sub-synchronous oscillation effectively within a certain range of grid strength. This method solves the problem that the traditional supplementary damping control must change the control parameters frequently, and improves the ability of the system to adapt to complex working conditions. (3) Under the step disturbance of grid voltage and active power command, the system can also suppress sub-synchronous oscillation well, which presents obvious anti-interference ability and good system robustness.
keywords：Direct-drive permanent magnet synchronous generator, sub-synchronous oscillation, virtual synchronous generator, uncertainty and disturbance estimator, supplementary damping
DOI:10.19595/j.cnki.1000-6753.tces.230153
中图分类号：TM712
国家自然科学基金（51967016, 51567020）和内蒙古自治区自然科学基金（2022LHQN05001）资助项目。
收稿日期 2023-02-13
改稿日期 2023-03-09
陈 建 男，1987年生，博士研究生，研究方向为新能源并网稳定性分析与控制。E-mail：chenjian19870612@163.com
任永峰 男，1971年生，博士，教授，博士生导师，研究方向为新型电力系统、综合能源系统、氢能储能技术。E-mail：renyongfeng@vip.sina.com（通信作者）
（编辑 李 冰）