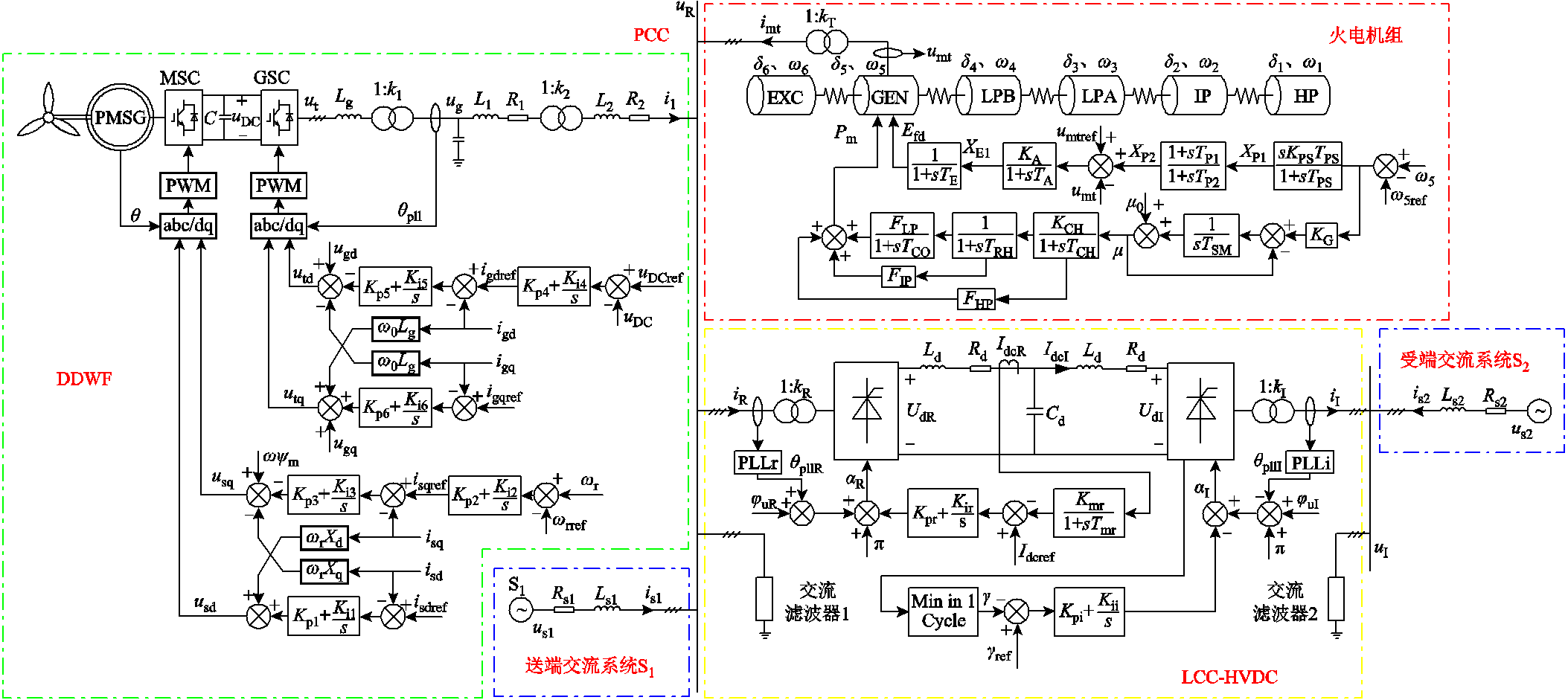
图1 DDWF与火电打捆经LCC-HVDC送出系统结构
Fig.1 Structure of the DDWF-thermal bundled system transmitted via LCC-HVDC
摘要 火电机组与电网换相换流器高压直流输电（LCC-HVDC）间的次同步交互作用会引发火电机组轴系扭振（SSTI），而直驱风电场（DDWF）接入LCC-HVDC送端对SSTI阻尼特性的影响与机理尚未明确，相关研究有待开展。针对上述问题，该文基于DDWF与火电打捆经LCC-HVDC送出系统，采用模块化建模法建立了小信号模型，使用特征值法分析了DDWF的接入与参数变化对LCC-HVDC引起的火电机组SSTI阻尼的影响；同时，针对特征值分析结果进行了机理分析。研究结果表明，DDWF会与火电机组共同承担LCC-HVDC的功率波动，削弱火电机组与LCC-HVDC间的次同步交互作用，从而增大SSTI阻尼，降低SSTI风险；当DDWF的容量增大、风速提升时，SSTI阻尼增大；当DDWF与LCC-HVDC整流站间电气距离增大时，SSTI阻尼降低；当LCC-HVDC整流侧由定电流控制转为定功率控制，或逆变侧由定电压控制转为定关断角控制时，SSTI阻尼降低。基于PSCAD/EMTDC平台进行了时域仿真，验证了特征值分析与机理分析的正确性。
关键词：电网换相换流器高压直流输电 直驱风电场 特征值分析 轴系扭振 风火打捆
近年来，我国新能源发电水平持续提升，发电量及占比不断增加，逐渐从补充电源过渡为主力电源[1-7]，截至2022年6月30日，全国风电总装机容量高达3.42亿kW[8]。在“十四五”大环境下，我国风电总装机容量将保持逐年递增的发展趋势[9-10]，一方面，我国风电基地主要集中在西部、北部与东部沿海地区，与火电基地分布地区重叠，两者均存在通过大容量、远距离输电系统送至中部与东部负荷中心的客观需求[11]；另一方面，直驱永磁同步发电机凭借效率高、故障率低的优点，逐渐成为风力发电系统的主流机型[12-13]。因此，直驱风电场（Direct-Drive Wind Farm, DDWF）与火电打捆经电网换相换流器高压直流输电（Line-Commutated-Converter based High Voltage Direct Current, LCC-HVDC）送出系统凭借输送容量大、成本低、技术成熟等优势，逐渐成为我国风电资源外送的主要形式之一。
现有研究表明，火电机组与LCC-HVDC间的次同步交互作用会引发火电机组轴系扭振（Sub-Synchronous Torsional Interaction, SSTI），进而引起火电机组转子轴系疲劳累积[14-16]。当火电经LCC-HVDC送出系统送端接入风电基地，或新建的LCC-HVDC送端交流母线同时处于风电基地和火电基地附近时，会构成三者间电气距离较近的场景，此时风电场对LCC-HVDC引起的火电机组SSTI影响将不可忽略。
目前，风火打捆经直流送出系统的SSTI问题研究集中于双馈式风力发电机[17-23]。文献[20]采用时域仿真法分析了风火打捆经直流送出系统的SSTI机理，研究结果表明，双馈风机的功率快速调节作用能够削弱火电机组与LCC-HVDC控制器间的次同步交互作用；文献[20-22]采用特征值法分析了双馈风机的接入对火电经LCC-HVDC送出系统SSTI阻尼的影响；文献[23]采用信号注入法研究了双馈风机群控制参数、运行风速、并网台数等因素对火电机组SSTI各模式阻尼特性的影响规律。但由于直驱风机与双馈风机在结构、动态特性等方面差异较大，上述文献对DDWF与火电打捆经LCC-HVDC送出系统的SSTI问题参考价值有限。
针对DDWF与火电打捆经LCC-HVDC送出系统的SSTI问题，现有文献主要存在以下两种形式：①LCC-HVDC与火电机组间的次同步交互作用引发火电机组SSTI；②由DDWF引发的次同步功率流入火电机组，进而引发SSTI[24]。文献[24]初步解释了DDWF与火电打捆经LCC-HVDC送出系统SSTI的原理，分析了由风电场引发的系统次同步功率振荡激发火电机组SSTI；文献[25]通过阻尼重构法分析了单一工况下DDWF与LCC-HVDC的接入对火电SSTI阻尼的影响。现有文献尚未从振荡特征结构角度分析DDWF并网与运行参数变化对LCC-HVDC与火电机组间SSTI阻尼的影响。
本文使用特征值法结合PSCAD/EMTDC时域仿真验证，通过参与因子分离LCC-HVDC引发的火电机组SSTI模态，进而分析DDWF并网与参数变化对SSTI各振荡模态阻尼特性的影响与机理。首先，基于DDWF与火电打捆经LCC-HVDC送出系统的数学模型，采用分块化建模方法在Matlab/ Simulink中建立系统的小信号模型，并通过阶跃响应验证小信号模型的正确性；然后，对比求解LCC-HVDC送端接入或不接入DDWF两种工况下小信号模型的特征值，分离出系统的SSTI模态，明确DDWF并网对火电机组SSTI阻尼的影响，并基于时域仿真验证理论分析；最后，分别针对风速、风电场容量、风电场与LCC-HVDC整流站间的电气距离及LCC-HVDC控制方式变化分析系统运行方式对SSTI阻尼特性的影响。
DDWF与火电打捆经LCC-HVDC送出系统结构如图1所示。系统主要分为五个子系统：火电机组、DDWF、LCC-HVDC、交流系统S1和交流系统S2。鉴于本文主要研究DDWF对LCC-HVDC与火电机组轴系间SSTI的影响，交流系统不作为重点研究对象，因此可将交流系统S1、S2进行戴维南等效，送端交流系统S1在稳态工况下输出有功功率100 MW。图1中us1、us2分别为交流系统S1、S2的无穷大母线处电压；is1、is2分别为交流系统S1、S2的线路电流。
图1 DDWF与火电打捆经LCC-HVDC送出系统结构
Fig.1 Structure of the DDWF-thermal bundled system transmitted via LCC-HVDC
火电机组稳态输出功率为800 MW，包括同步发电机、轴系、调速器、励磁系统与电力系统稳定器（Power System Stabilizer, PSS）、变压器等模块，其中，轴系采用六质量块模型，含高压缸（High Pressure, HP）、中压缸（Intermediate Pressure, IP）、低压缸A（Low Pressure A, LPA）、低压缸B（LPB）、发电机（Generator, GEN）、励磁机（Exciter, EXC）。对于多机系统，当机组间扭振频率接近时，火电机组间振荡模式主要体现在各机组之间，与外部网络基本无关[26]；当机组间扭振频率差超过0.3 Hz时，火电机组之间不产生扭振相互作用[27]，因此，多类型火电机组建模对本文研究结果影响较小。为充分提高仿真效率，本文火电机组采用单一类型的机组模型，并通过同调等值聚合为单机等值模型。图1中火电机组子系统各变量定义如下：imt为定子绕组电流；umt为发电机端口电压；d1～d6、w1～w6分别为高压缸、中压缸、低压缸A、低压缸B、发电机、励磁机的转子角度与角速度；Pm、Efd分别为发电机的输入功率与励磁电压；m为汽轮机汽门开度；XP2为附加到励磁系统的控制信号；XE1、XP1为励磁系统与PSS控制器的中间变量。
LCC-HVDC使用CIGRE标准模型，稳态输送功率1 000 MW，整流站与逆变站分别采用定电流控制策略与定关断角控制策略[28]。图1中LCC-HVDC子系统各变量定义如下：uR、juR分别为交流公共连接点（Point of Common Coupling, PCC）处电压及其相角；qpllR为整流侧锁相环输出相角；iR为由PCC注入整流器的交流电流；UdR、IdcR分别为整流器的直流侧电压与直流侧电流；uI、juI分别为受端交流母线电压及其相角；qpllI为逆变侧锁相环输出相角；iI为逆变器流入受端交流母线的交流电流；UdI、IdcI分别为逆变器的直流侧电压与直流侧电流；aR为整流器触发角；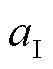
与g 分别为逆变器的触发角与关断角。
DDWF额定风速10 m/s，额定输出有功功率 100 MW。DDWF主要由永磁同步发电机、机侧换流器（Machine-Side Convertor, MSC）、网侧换流器（Grid-Side Convertor, GSC）、交流滤波器、测量与控制系统等模块构成。其中，MSC采用定d轴电流和定发电机转速控制策略，GSC采用定q轴电流和定直流电压控制策略。风机经变压器升压至 35 kV后汇集，再经变压器升压至345 kV后通过交流输电线路接入PCC。现有研究表明，针对风电并网系统的次同步振荡问题，风电场将作为一个整体与系统其他元件进行动态交互[29]，基于风电场单机等值聚合模型得到的分析结果对实际工程仍具有重要的参考价值。故本文中DDWF采用聚合等值模型表示。图1中DDWF子系统各变量定义如下：usd、usq和isd、isq分别为MSC交流出口电压和电流d、q轴分量；q 为永磁发电机转子角度；uDC为直流电容电压；utd、utq和igd、igq分别为GSC交流出口电压、电流d、q轴分量；qpll为锁相环输出的风机出口电压相角；ugd、ugq为风机出口处电压的d、q轴分量；il为DDWF输电线路电流。系统各元件的主要参数详见附表1，控制参数详见附表2。
DDWF与火电打捆经LCC-HVDC送出系统模型结构如图1所示。其中，DDWF的数学模型主要包括：风机轴系模型、永磁同步风力发电机模型、换流器及其控制器模型、直流电容模型、锁相环模型。火电机组的数学模型主要包括同步发电机模型、调速器及PSS模型、励磁控制器模型、轴系质量块模型。LCC-HVDC的数学模型主要包括：晶闸管换流器模型、控制器模型、直流输电线路模型、锁相环模型。
鉴于本文的研究重点是DDWF并网与系统运行方式对SSTI阻尼的影响，受篇幅限制，火电机组的数学模型详见文献[28]，LCC-HVDC的数学模型详见文献[30]，DDWF的数学模型详见文献[31]，此处不再赘述。
2.2.1 小信号模型的建立
鉴于本文所研究的系统拓扑较为复杂，传统方法计算难度大、出错率高且灵活性差，因此采用模块化建模的方式更加简便。建模过程中，首先单独建立各个元件的状态空间子模型，再通过接口联系各个子模型，得到完整的系统小信号模型。
对2.1节中建立的数学模型进行潮流计算，得到系统稳态工作点，在此工作点对上述数学模型进行线性化处理。依据线性化处理得到的微分方程组，在Matlab/Simulink中分别搭建各子模块的状态空间模型。各子模块的状态空间方程为
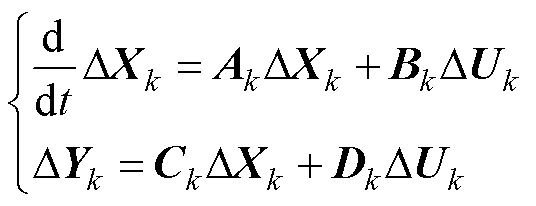（1）
式中，k为模块编号；DXk、DUk、DYk分别为模块k的状态变量、输入变量与输出变量；Ak、Bk、Ck、Dk分别为模块k的系统矩阵、输入矩阵、输出矩阵与直联矩阵。本文中各元件对应的子系统在建立数学模型时分别采用独立的坐标系：火电机组与送端交流系统在xy坐标系下建模；LCC-HVDC在极坐标系下建模；DDWF在dq坐标系下建模。系统中的每个元件子模块都建立之后，需要将各个模块通过输入信号ΔUk与输出信号ΔYk连接到一起，形成闭环系统，此时需要将LCC-HVDC与DDWF的数学模型转换到xy坐标下，即进行坐标变换。dq坐标系、极坐标系与xy坐标系之间的变换关系[32]为
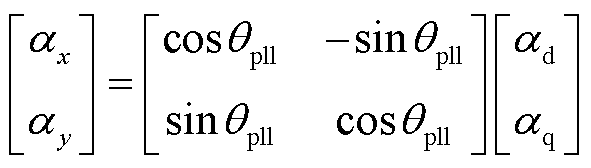（2）
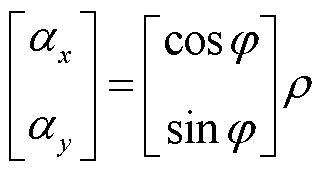（3）
式中，a为某一变量，本文中指电压或电流，ax、ay分别为变量a的xy轴分量；ad、aq分别为a的dq轴分量；r、j分别为a在极坐标系下的幅值与相角。
根据2.1节所介绍的系统结构与参数，结合式（2）、式（3），在Matlab/Simulink中搭建各元件子模块的状态空间模型。各个模块的输入输出接口对应的状态变量与模块连接拓扑结构如图2所示。系统对应的小信号模型为
（4）
式中，ΔX为系统全部状态变量组成的向量，按照状态变量所属子模块可分为15组，见表1； DU为输入变量，ΔU=[Δωrref Δisdref Δigqref ΔuDCref]T。
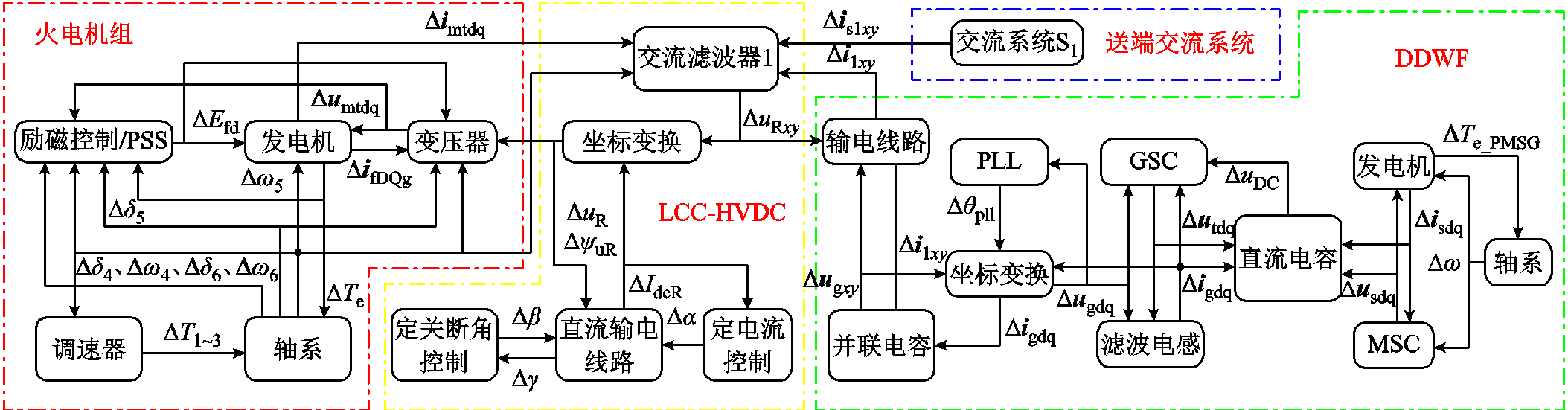
图2 小信号模型子模块连接示意图
Fig.2 Small signal model sub-module connection diagram
表1 系统状态变量组别
Tab.1 Classification of state variables
子系统组别子模块组别状态变量编号 火电机组发电机ΔXgen1～6 励磁系统与PSSΔXEX7～10 轴系ΔXmass11～22 调速器ΔXTUR23～26 LCC-HVDC直流输电系统ΔXHVDC27～33 DDWF滤波电容ΔXC34、35 锁相环ΔXPLL36、37 网侧换流器控制ΔXGSC38～40 永磁同步发电机ΔXG41、42 轴系ΔXM43 机侧换流器控制ΔXMSC44～46 直流电压ΔXDC47 滤波电感ΔXL48、49 线路电流ΔXRL50、51 交流系统S1交流系统ΔXAC52～55
2.2.2 小信号模型的验证
在各类电力系统次同步振荡分析方法中，时域仿真法的精度较高[16]，而阶跃响应曲线能够反映系统的稳态和动态特性。因此，本节对本文所研究系统的小信号模型与电磁暂态模型的阶跃响应进行对比，以验证小信号模型的正确性[16]。
根据第1节中介绍的系统结构及各元件参数，在PSCAD/EMTDC仿真平台中搭建对应的电磁暂态模型。分别对小信号模型与电磁暂态模型进行时域仿真。仿真运行时间到达5.0 s时，将DDWF的GSC控制器外环直流电压指令值uDCref由5 kV阶跃至5.5 kV，系统其他参数不变，得到PSCAD/EMTDC 电磁暂态模型与小信号模型的阶跃响应曲线。小信号模型与PSCAD/EMTDC电磁暂态模型的阶跃响应对比如图3所示。
由图3可知，对于DDWF、LCC-HVDC与火电机组子系统中的状态变量，小信号模型与电磁暂态模型的阶跃响应曲线均基本一致，动态响应相似，对比结果充分验证了所建立小信号模型的正确性。
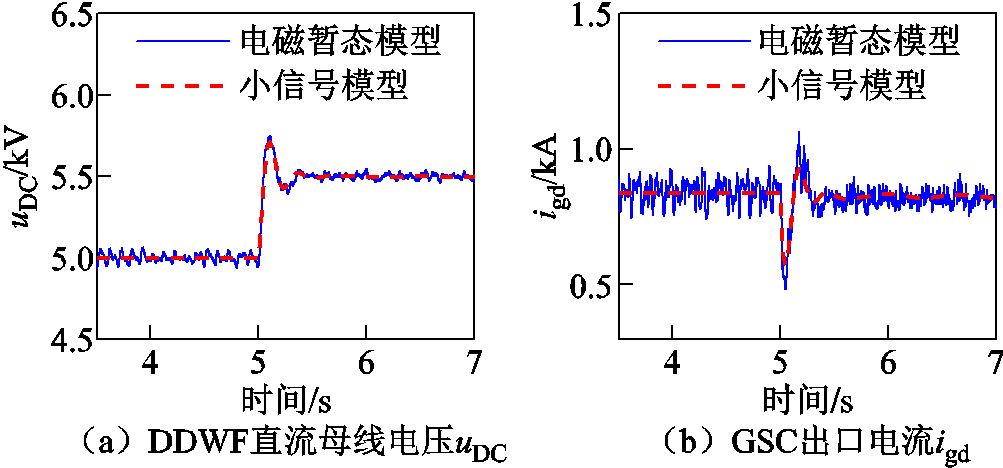
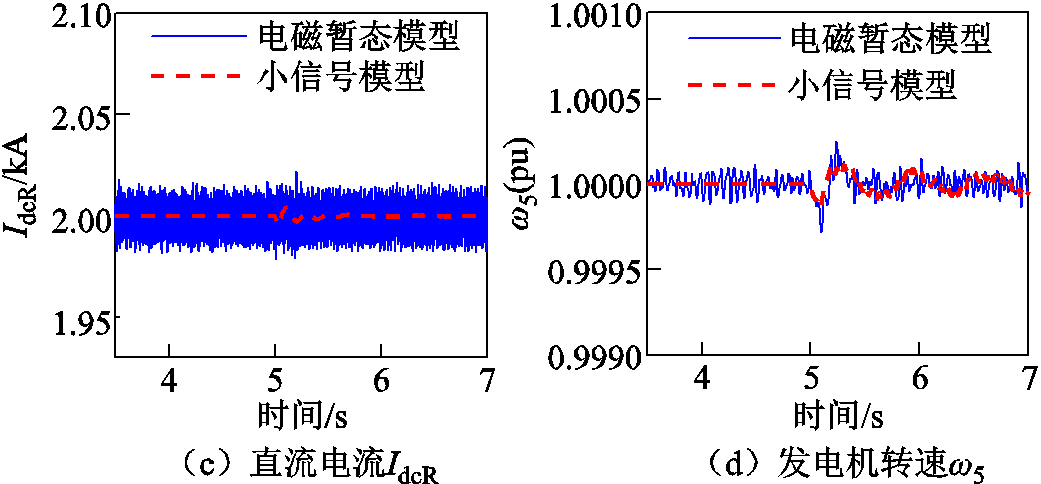
图3 阶跃响应对比
Fig.3 Step response comparition
本节主要分析DDWF接入LCC-HVDC送端对LCC-HVDC引起的火电机组SSTI阻尼特性的影响。首先，求取系统小信号模型特征值，并计算各次同步振荡模态的频率与阻尼比，通过参与因子计算分离出SSTI模态；然后，在PSCAD/EMTDC中进行时域仿真，监测火电机组轴系中的次同步分量；最后，综合特征值与时域仿真结果分析DDWF并网对SSTI阻尼的影响，并对其进行机理分析。
为了评估DDWF并网对LCC-HVDC与火电机组间SSTI的影响，本文在以下两种工况下进行模态分析与时域仿真等工作。
工况A：DDWF不接入PCC，火电机组出力800MW，送端交流系统出力200 MW。
工况B：DDWF接入PCC，火电机组、DDWF和送端交流系统S1出力分别为800 MW、100 MW和100 MW。
采用第2节所建立的小信号模型分别对上述两种工况进行特征值求解，分别计算各特征值对应的频率与阻尼比，筛选出次同步振荡模态，结果见表2。
表2 特征值计算结果及其对应阻尼比
Tab.2 Eigenvalue calculation consequence and corresponding damping ratio
工况振荡模态特征值振荡频率/Hz阻尼比(%) A12.437 0×10-2+j99.1115.77-2.458 9×10-2 22.773 3×10-4+j127.0220.22-2.183 3×10-4 3-1.560 5×10-3+j160.6125.569.716 2×10-4 4-3.691 1×10-3+j202.9832.311.818 4×10-3 53.391 8×10-6+j298.1847.46-1.137 5×10-6
（续）
工况振荡模态特征值振荡频率/Hz阻尼比(%) B12.231 9×10-2+j99.1115.77-2.251 9×10-2 21.692 4×10-4+j127.0220.22-1.332 4×10-4 3-1.767 6×10-3+j160.6125.561.100 6×10-3 4-3.916 7×10-3+j202.9832.311.929 6×10-2 52.944 7×10-6+j298.1847.46-9.875 8×10-7
由表2可知，对于工况A和工况B，系统均存在5个次同步振荡模态，其中，模态1、模态2与模态5的特征值实部为正数，为不稳定振荡模态；模态3、4的特征值实部为负数，为稳定振荡模态。以下通过参与因子确定与上述各次同步振荡模态联系紧密的状态变量，以此分析各模态是否属于SSTI。工况B的参与因子分析结果如图4所示，工况B的各振荡模态的相关状态变量见表3。其中，DXmass=[Dd1 Dd2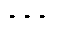
Dd6 Dw1 Dw2 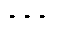Dw6]T，表示火电机组轴系模块状态变量集合；DXgen=[Dimtd Dif DiD Dimtq Dig DiQ]T，表示同步发电机状态变量集合。工况A的参与因子分析结果与工况B类似，详见附录B，此处不再赘述。
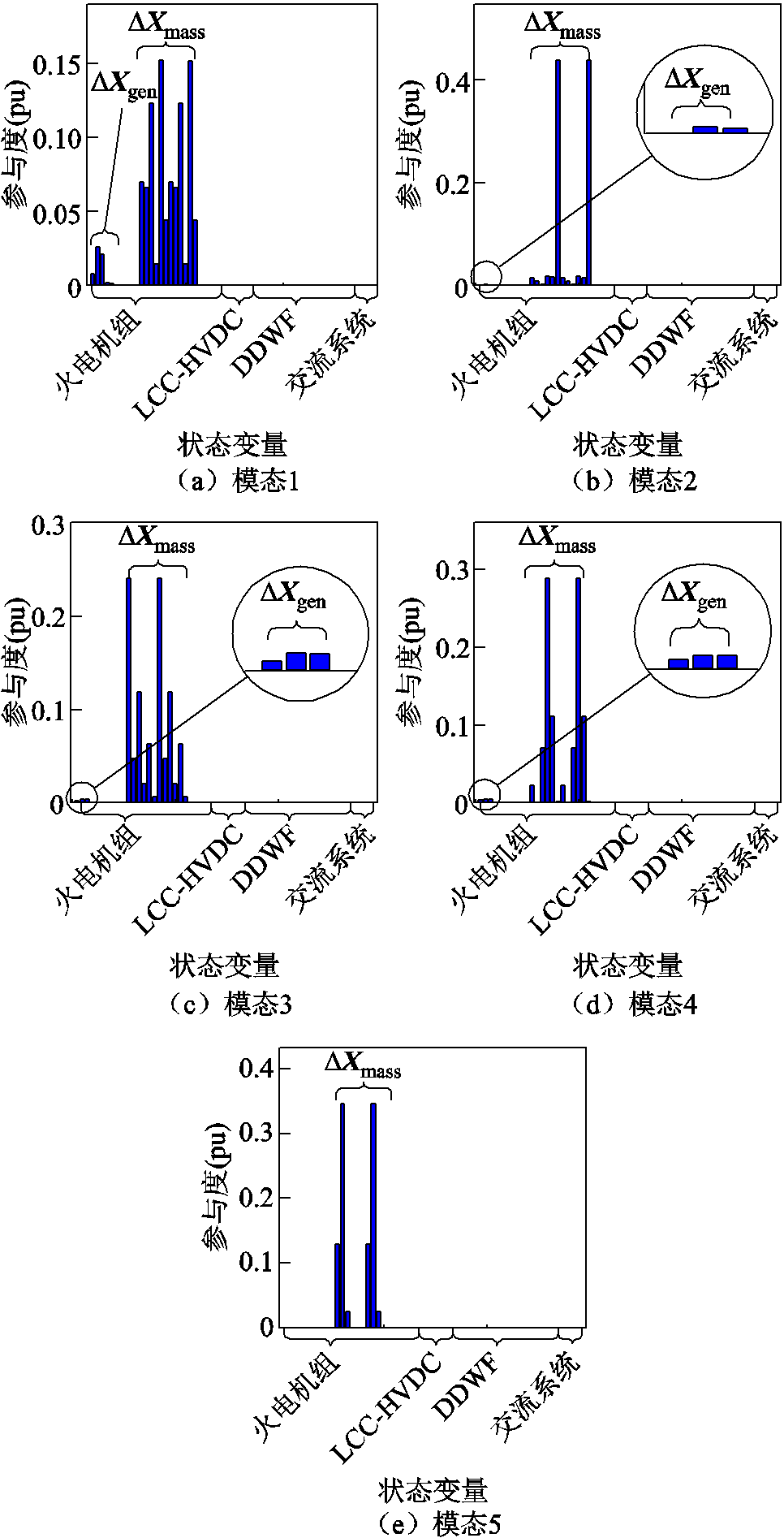
图4 工况B下各次同步振荡模态参与因子
Fig.4 Participation factor of each subsynchronous oscillation mode in Case B
表3 工况B振荡模态参与因子
Tab.3 Participation factor of each oscillation mode in Case B
振荡模态相关状态变量相关状态变量所属系统 1Dd1～Dd6、Dw1～Dw6、Dimtdq、Dif、DiD、Dig火电机组轴系、发电机 2Dd1～Dd6、Dw1～Dw6、Dif、DiD火电机组轴系、发电机 3Dd1～Dd6、Dw1～Dw6、Dimtd、Dif、DiD火电机组轴系、发电机 4Dd1、Dd3～Dd6、Dw1、Dw3～Dw6、Dimtd、Dif、DiD火电机组轴系、发电机 5Dd1～Dd3、Dw1～Dw3火电机组轴系
如图4可知，模态5为火电机组轴系参与的振荡模态，模态1、模态2、模态3与模态4为轴系与发电机共同参与的振荡模态。因此，特征值分析结果中的5个振荡模态均为SSTI。对比表2中工况A与工况B的各对应振荡模态可知，DDWF的接入使各振荡模态的特征值实部减小、虚部大小不变，振荡频率不变、阻尼比增加，系统SSTI阻尼增加，振荡风险降低。
在PSCAD/EMTDC中对上述特征值分析结果进行时域仿真验证。时域仿真主要包括LCC-HVDC整流站交流侧三相短路故障、非对称短路故障及直流闭锁故障。受限于文章篇幅，以三相短路故障仿真为例进行说明：设定总仿真时长50 s，PCC在t =10 s时发生三相接地短路故障，持续时间0.1s。图5a、图5b分别为工况A、B下发电机转子角速度ω5的快速傅里叶变换（Fast Fourier Transform, FFT）结果。
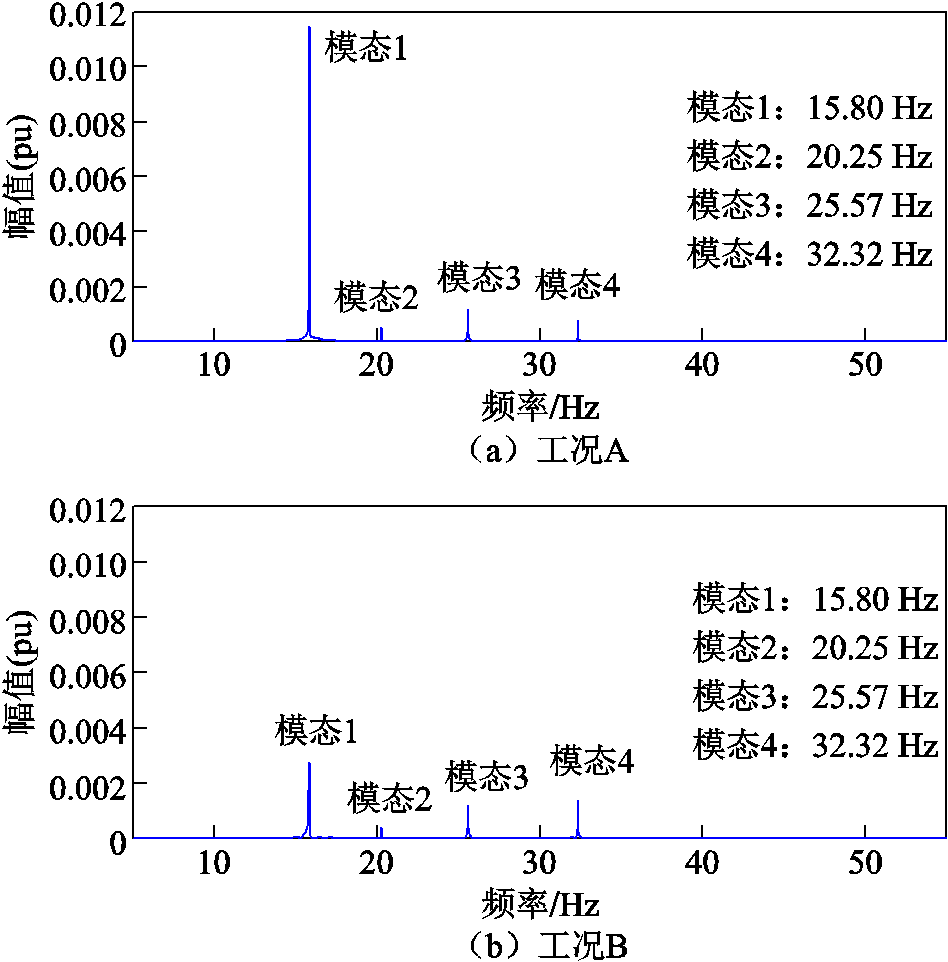
图5 火电机组转子角速度FFT结果
Fig.5 FFT result of rotor angular velocity of TG
由图5a、图5b可知，故障发生后，系统中出现15.80、20.25、25.57、32.32 Hz四种频率的次同步电气量，分别与3.1节中的特征值分析结果的模态1～4相匹配。由于Dw5对模态5的参与度可以忽略不计，因此发电机转子的时域仿真结果中难以观测到模态5对应的47.46 Hz分量。为了更直观地对比工况A、B下各振荡模态的阻尼大小，使用带通滤波器分离w5的各频率分量，结果如图6所示。
图6 火电机组转子角速度各频率分量
Fig.6 Rotor angular velocity frequency components of TG
由图6可知，相对工况A，在工况B中DDWF接入LCC-HVDC送端后，火电机组转子角速度的15.80 Hz与25.57 Hz分量由发散转变为衰减；20.25 Hz分量等幅振荡的幅值降低；32.32 Hz分量衰减速度略有提高，SSTI阻尼提升，与上述特征值分析结果一致。
从上述分析可知，将DDWF并网可以缓解火电机组与LCC-HVDC间的SSTI。根据文献[33]，火电机组与LCC-HVDC间的次同步交互作用越强，越容易引起SSTI。LCC-HVDC整流侧定电流控制器带宽通常在10～20 Hz范围[28]，在该带宽内，系统存在一定的负阻尼，因此，本文中的模态1、模态2为重点研究对象。
SSTI作用机理如图7所示。以工况A下SSTI模态1为例，系统中出现诸如短路的扰动时，火电机组转子中会出现15.80 Hz的次同步分量，进而引发PCC处电压有效值出现15.80 Hz的扰动，由于LCC-HVDC整流侧控制器的快速响应，触发角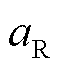
跟随uR变化，引起直流电流IdcR中出现15.80 Hz分量，导致直流输送功率发生振荡，进而影响火电机组的功率与电磁转矩，最终与火电机组转子受到的扰动形成正反馈。
图7 轴系扭振作用机理
Fig.7 The mechanism diagram of SSTI
当DDWF接入LCC-HVDC送端后，火电机组与LCC-HVDC间的交互作用会引起DDWF输出功率变化。当输出功率偏离给定值时，DDWF的GSC控制器会对功率偏差做出快速响应，根据系统运行条件快速调节有功功率与无功功率输出，缓解外部扰动引起的功率波动。DDWF并网提升火电机组SSTI阻尼的原理如图8所示，在此过程中，DDWF会与火电机组共同承担LCC-HVDC的功率波动，削弱火电机组与LCC-HVDC间的次同步交互作用，从而增强火电机组SSTI阻尼。
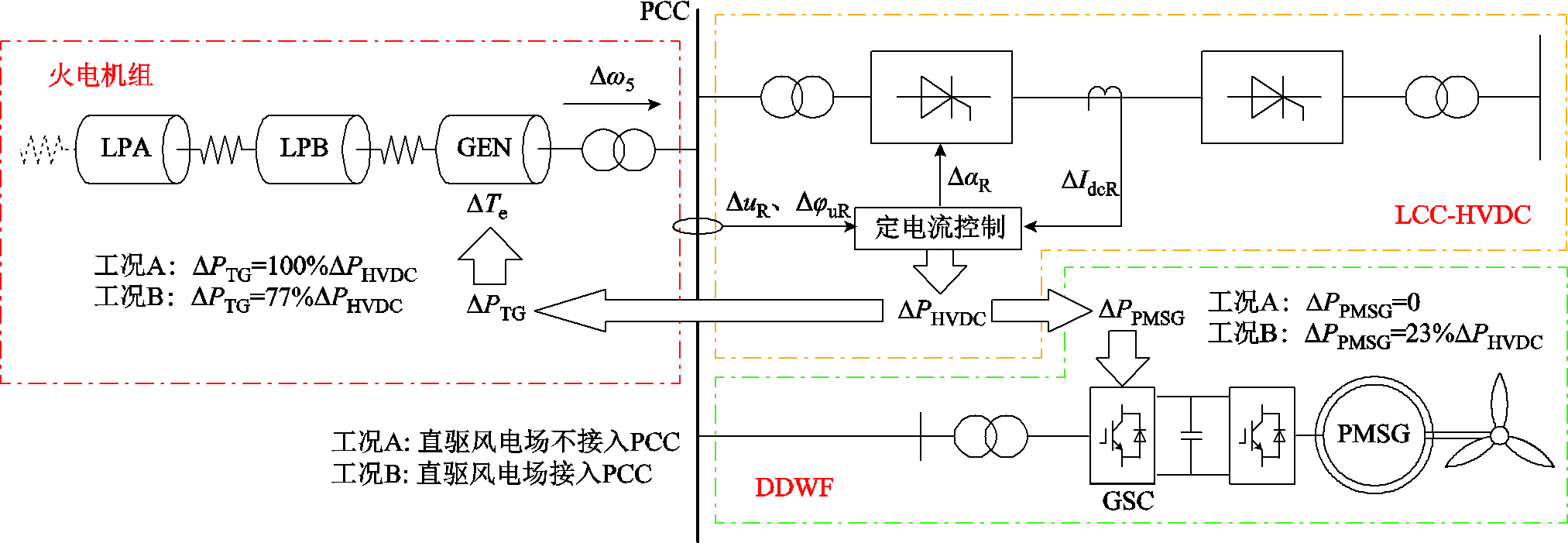
图8 DDWF并网提升火电机组SSTI阻尼的原理
Fig.8 Schematic diagram of DDWF integration raising SSTI damping of thermal generator
为验证上述机理分析的有效性，在PSCAD/ EMTDC中分别监测工况A下由PCC注入火电机组、工况B下由PCC注入火电机组与DDWF的电流，对故障发生后的电流有效值进行FFT，可以观测到模态1对应的次同步分量。将模态1频率下的FFT结果转换为相量，结果见表4。
表4 由PCC注入各支路的模态1对应电流相量
Tab.4 Subsynchronous current phasor of Model 1 from PCC
工况支路电流相量 A火电机组0.008 050 kA∠76.38° B火电机组0.005 342 kA∠73.14° DDWF0.001 631 kA∠59.15°
由表4可知，工况B下由PCC注入DDWF与火电机组的次同步电流相位接近，两者幅值比约为1:3.3，说明DDWF并网后吸收了部分LCC-HVDC的功率波动，有效地削弱了火电机组与LCC-HVDC间的次同步交互作用，改善了SSTI阻尼，验证了上述机理分析的正确性。
本节通过改变风火打捆经LCC-HVDC送出系统的运行方式对系统振荡模态进行影响因素分析，主要包括以下四个方面：风电场风速、风电场容量、风电场与LCC-HVDC整流站之间的电气距离、LCC-HVDC控制方式。
由于频率与LCC-HVDC整流站定电流控制器带宽相近的模态更容易引发不稳定振荡[28]，模态3、模态4及模态5不作为本文的主要研究对象。在以下研究中，仅分析模态1与模态2的振荡影响因素。
保持模型其他参数不变，以0.5 m/s为步长将风速从6 m/s增加至12 m/s，修改受风速影响的电气量初值，求解小信号模型的特征值，得到SSTI模态1、模态2的阻尼比变化曲线如图9所示。
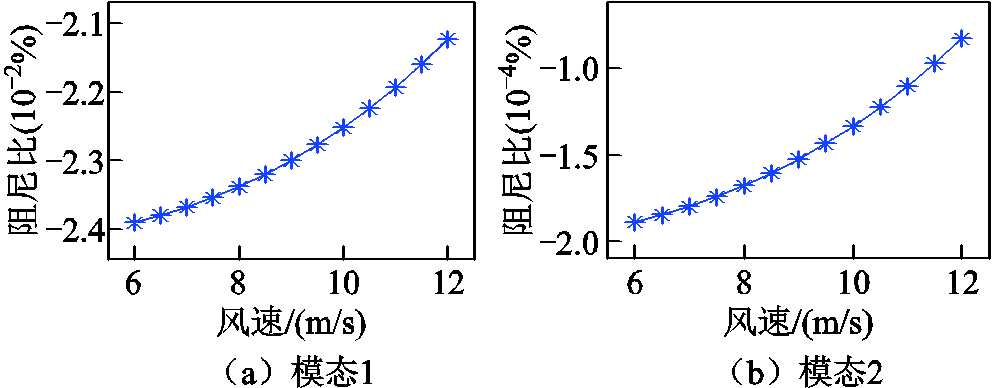
图9 风速变化对SSTI阻尼的影响
Fig. 9 Influence of wind speed variation on SSTI damping
由图9可知，随着风速提升，系统SSTI的模态1与模态2阻尼增加。对上述计算结果进行时域仿真验证，在PSCAD/EMTDC中将风速分别设定为6、8、10 m/s，系统其他参数不变，得到故障后火电机组轴系模态1与模态2对应转速分量如图10所示。
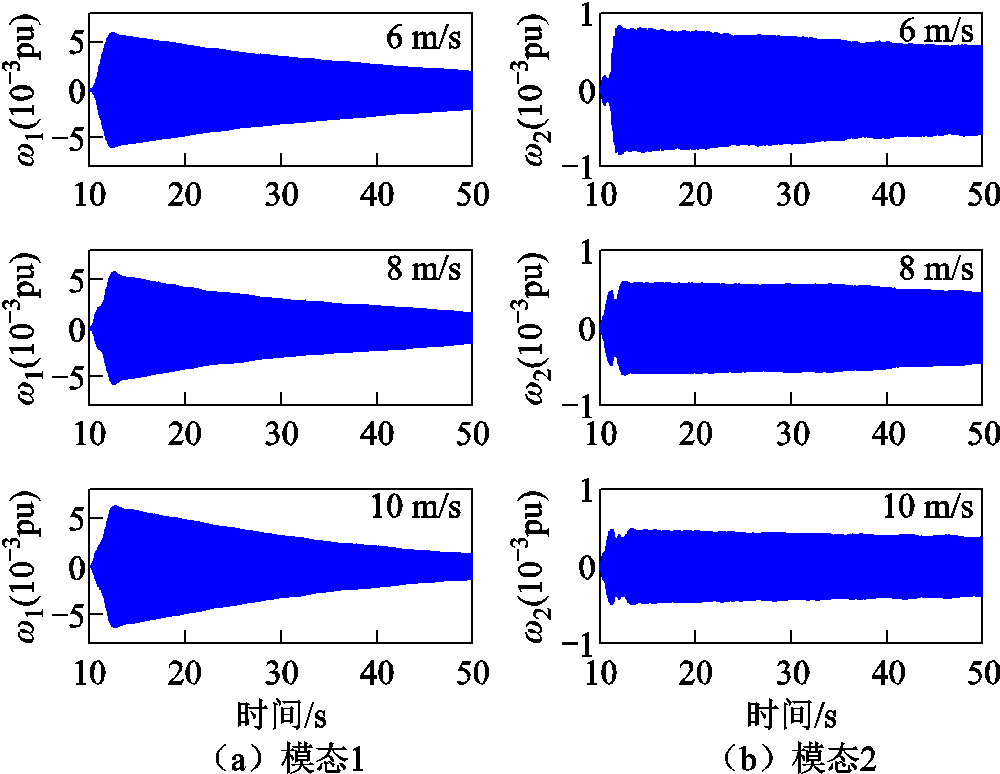
图10 风速变化时的仿真结果
Fig.10 Simulation results of wind speed variation
由图10可知，随着风速增加，模态1对应的转速分量衰减速度提高，阻尼增加；模态2对应转速的等幅振荡幅值减小，阻尼增加。时域仿真结果与特征值分析结果一致，验证了特征值分析结果的正确性。
此结论可以解释为：当风速增大时，每台风机输出有功功率增加，各风机的GSC功率调节范围变大，DDWF承担了更多LCC-HVDC的功率波动，削弱了火电机组与LCC-HVDC间的次同步功率交互，进而提升了SSTI阻尼。
保持其他参数不变，以7 MW为步长将DDWF容量由30 MW增加至100 MW，并修改受DDWF容量影响的电气量初值，分别求解小信号模型特征值，得到SSTI模态1、模态2的阻尼比曲线如图11所示。
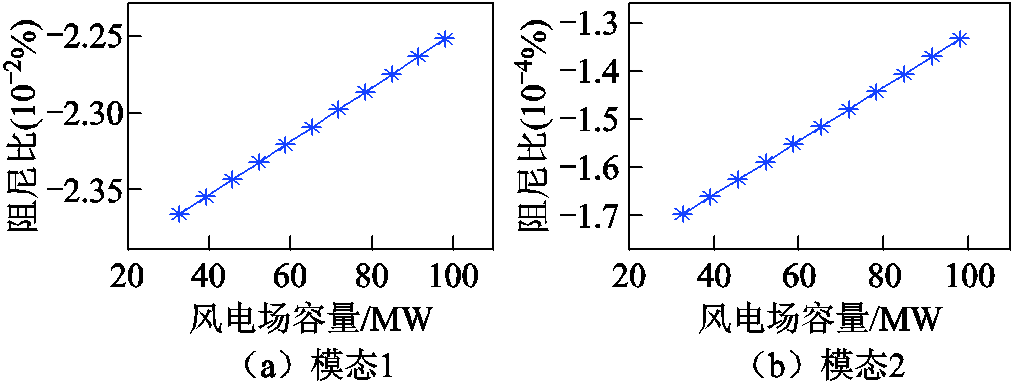
图11 风电场容量对SSTI阻尼的影响
Fig.11 Influence of wind farm capacity on SSTI damping
由图11可知，随着风电场容量提升，SSTI的模态1、模态2阻尼均有增加。对上述特征值分析进行时域仿真验证：通过改变风机台数将风电场容量分别设定为33、66、100 MW，系统中的其他参数不变，得到火电机组轴系模态1与模态2对应转速分量如图12所示。
图12 风电场容量变化时的仿真结果
Fig.12 Simulation results of wind farm capacity variation
由图12可知，随着风电场容量增加，火电机组轴系模态1转速分量由等幅振荡逐渐转变为收敛振荡，阻尼增加；模态2转速分量为等幅振荡，幅值降低，阻尼增加。时域仿真结果与特征值分析结果一致。
此结论可以解释为：当风电场容量增大时，DDWF输出有功功率增加，功率调节范围变大，承担了更多LCC-HVDC的功率波动，削弱了火电机组与LCC-HVDC间的次同步功率交互，进而提升了SSTI阻尼。
保持系统其他参数不变，通过调节线路阻抗的方式改变DDWF与LCC-HVDC整流站间的电气距离。以0.03(pu)为步长，将线路阻抗由0.2(pu)扩大至0.5(pu)，求解小信号模型特征值，得到阻尼比曲线如图13所示。
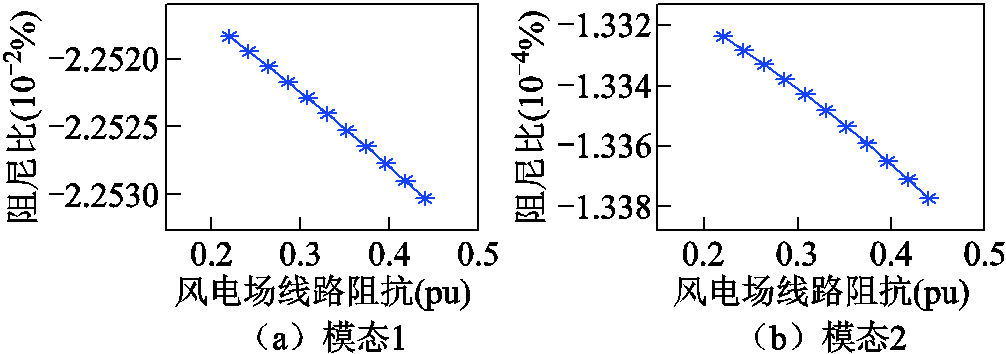
图13 DDWF线路阻抗对SSTI阻尼的影响
Fig.13 Influence of transmission line impedance of DDWF on SSTI damping
由图13可知，随着DDWF输电线路阻抗增大，系统SSTI模态1、模态2阻尼均降低。对上述计算结果进行时域仿真验证，将风电场输电线路阻抗分别设定为0.11(pu)、0.22(pu)与0.33(pu)，监测火电机组轴系中模态1与模态2的转速分量，结果如图14所示。
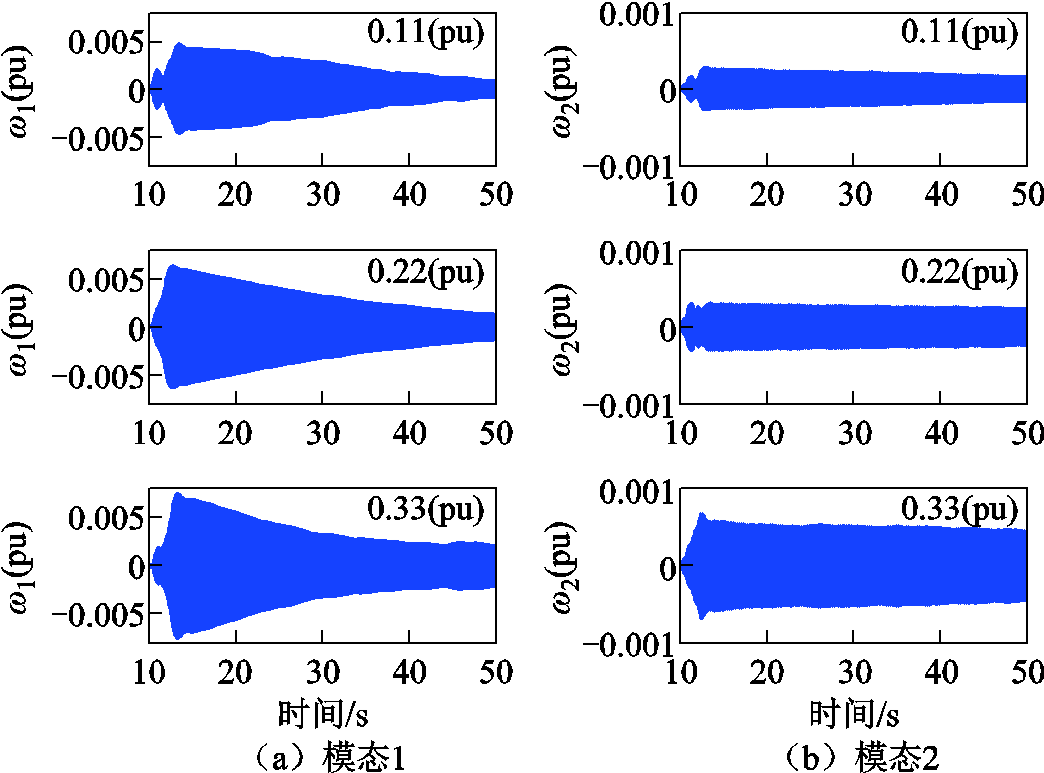
图14 DDWF线路阻抗变化时的仿真结果
Fig.14 Simulation results of DDWF transmission line impedance variation
由图14可知，随着DDWF线路阻抗增大，火电机组轴系模态1对应的转速分量衰减速度降低，阻尼降低；模态2对应的转速分量振荡幅值增大，阻尼降低。时域仿真结果与特征值分析结果一致。
此结论可解释为：DDWF与LCC-HVDC间电气距离提升时，系统强度减弱，GSC对外部功率波动的响应速度降低，SSTI阻尼降低。
为了对比整流侧定电流控制与定功率控制、逆变侧定关断角控制与定电压控制对SSTI阻尼的影响，本文将LCC-HVDC设定以下三种运行方式：
方式1：整流侧采用定功率控制，逆变侧采用定直流电压控制。
方式2：整流侧采用定电流控制，逆变侧采用定直流电压控制。
方式3：整流侧采用定电流控制，逆变侧采用定关断角控制。
设定总仿真时长35 s，初始状态系统以方式2运行，仿真时长34 s；仿真运行至10 s时PCC发生三相短路故障；仿真运行至20 s时，将控制模式分别切换为方式1、方式2（保持）、方式3，监测火电机组轴系中模态1与模态2的转速分量，结果如图15所示。
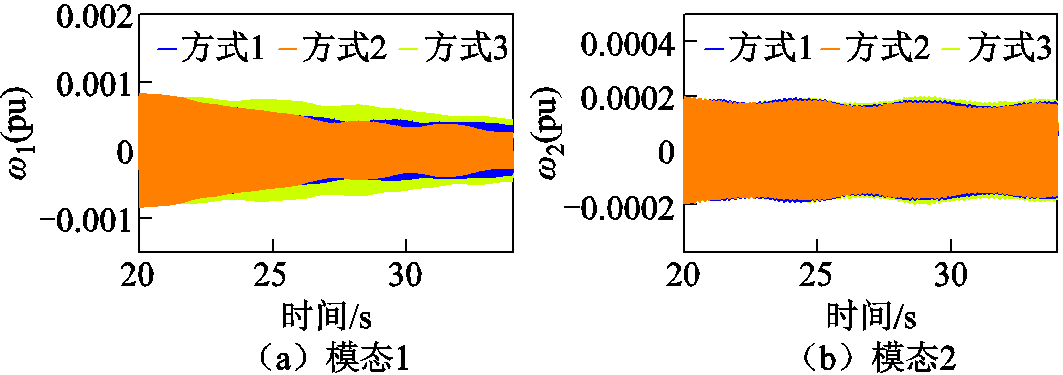
图15 LCC-HVDC控制方式变化时的仿真结果
Fig.15 Simulation results of LCC-HVDC control mode variation
由图15可知，当LCC-HVDC整流侧由定电流控制变为定功率控制，或逆变侧由定直流电压控制变为定关断角控制时，模态1对应的转速分量衰减速度降低，阻尼降低；模态2对应的转速分量振荡幅值略有增大，阻尼降低。此结论可解释为：整流侧定功率控制将功率给定值Pdref除以逆变侧直流电压作为电流给定值，直流电压与直流电流扰动量会在PI控制器输入端叠加，等效于增加了次同步频率下定电流控制器的增益，引起如图7中系统SSTI回路正反馈作用增强，SSTI阻尼降低。逆变侧采用定直流电压控制时，直流电流会削弱注入PI控制器的直流电压扰动信号；逆变侧采用定关断角控制时，直流电流会加剧注入PI控制器的关断角扰动信号，系统对扰动的降解能力变差，系统的SSTI阻尼相对于定直流电压控制时有所降低。
本文通过特征值法分析了DDWF的接入对火电经LCC-HVDC送出系统的轴系扭振模态影响，并针对风火打捆经LCC-HVDC送出系统在不同参数下的阻尼特性进行了分析，其中，主要研究结果如下：
1） 针对DDWF与火电机组打捆经LCC-HVDC送出系统，建立了系统的PSCAD/EMTDC时域仿真模型，并采用分块建模方法建立了系统的小信号模型；通过与电磁暂态模型的阶跃响应对比，验证了小信号模型的正确性。
2）当DDWF未接入系统时，火电机组与LCC-HVDC间的次同步交互作用会加剧外部扰动，火电机组存在SSTI风险；DDWF接入LCC-HVDC送端后，GSC的快速响应可以替代火电机组承担部分直流功率的变化，减轻火电机组与LCC-HVDC间的次同步交互作用，间接提升系统阻尼，降低系统振荡风险。
3）DDWF的容量增大、风速提升时，SSTI阻尼提升；DDWF与LCC-HVDC整流站间电气距离增大时，系统阻尼降低；LCC-HVDC整流侧定电流控制的SSTI阻尼较定功率控制大，逆变侧定直流电压控制的SSTI阻尼较定关断角控制大。该结论对实际工程具有一定理论指导意义。
附 录
1. DDWF与火电经LCC-HVDC送出系统参数
附表1 主要元件参数
App.Tab.1 Main component parameters
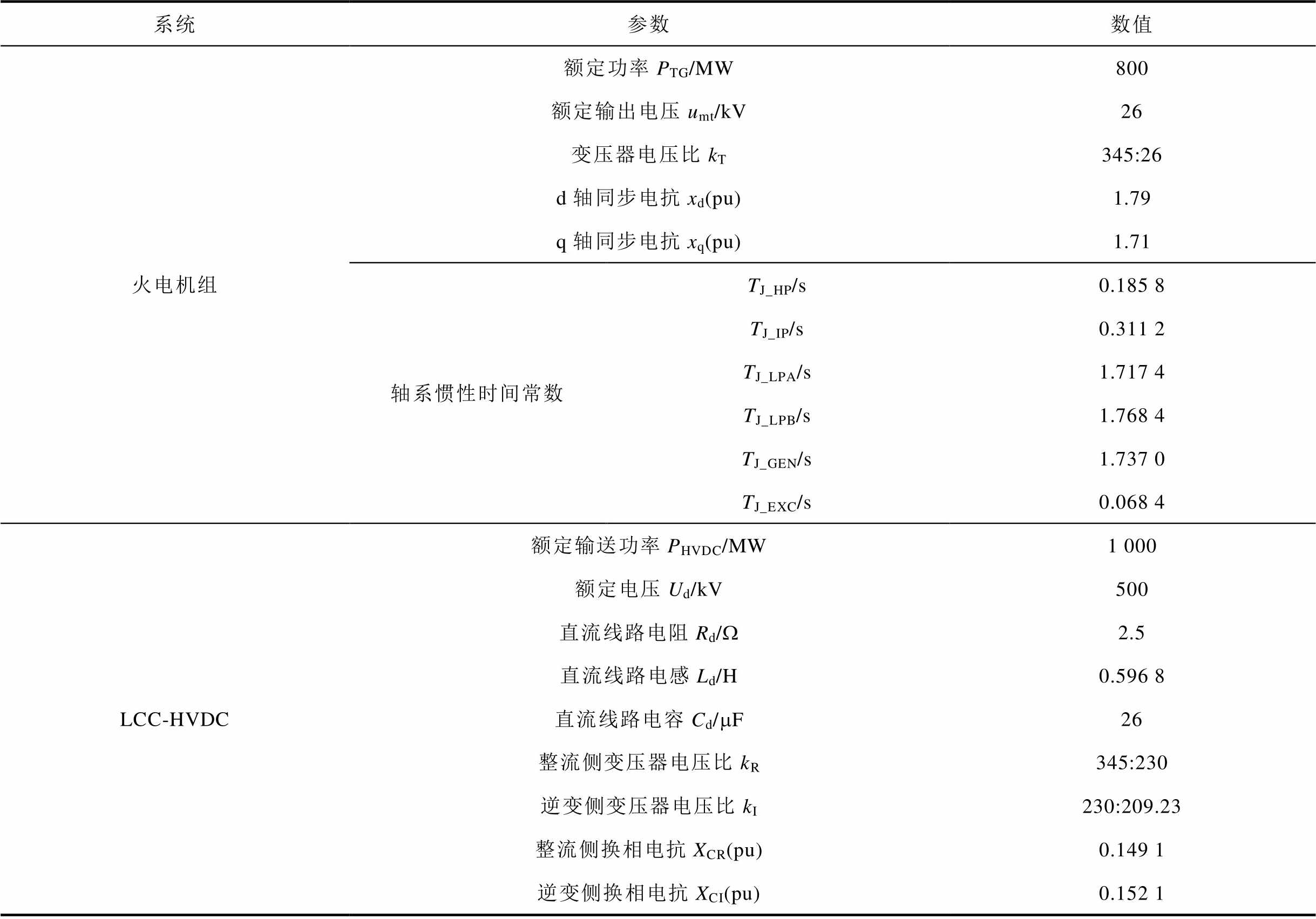
系统参数数值 火电机组额定功率PTG/MW800 额定输出电压umt/kV26 变压器电压比kT345:26 d轴同步电抗xd(pu)1.79 q轴同步电抗xq(pu)1.71 轴系惯性时间常数TJ_HP/s0.185 8 TJ_IP/s0.311 2 TJ_LPA/s1.717 4 TJ_LPB/s1.768 4 TJ_GEN/s1.737 0 TJ_EXC/s0.068 4 LCC-HVDC额定输送功率PHVDC/MW1 000 额定电压Ud/kV500 直流线路电阻Rd/W2.5 直流线路电感Ld/H0.596 8 直流线路电容Cd/mF26 整流侧变压器电压比kR345:230 逆变侧变压器电压比kI230:209.23 整流侧换相电抗XCR(pu)0.149 1 逆变侧换相电抗XCI(pu)0.152 1
（续）
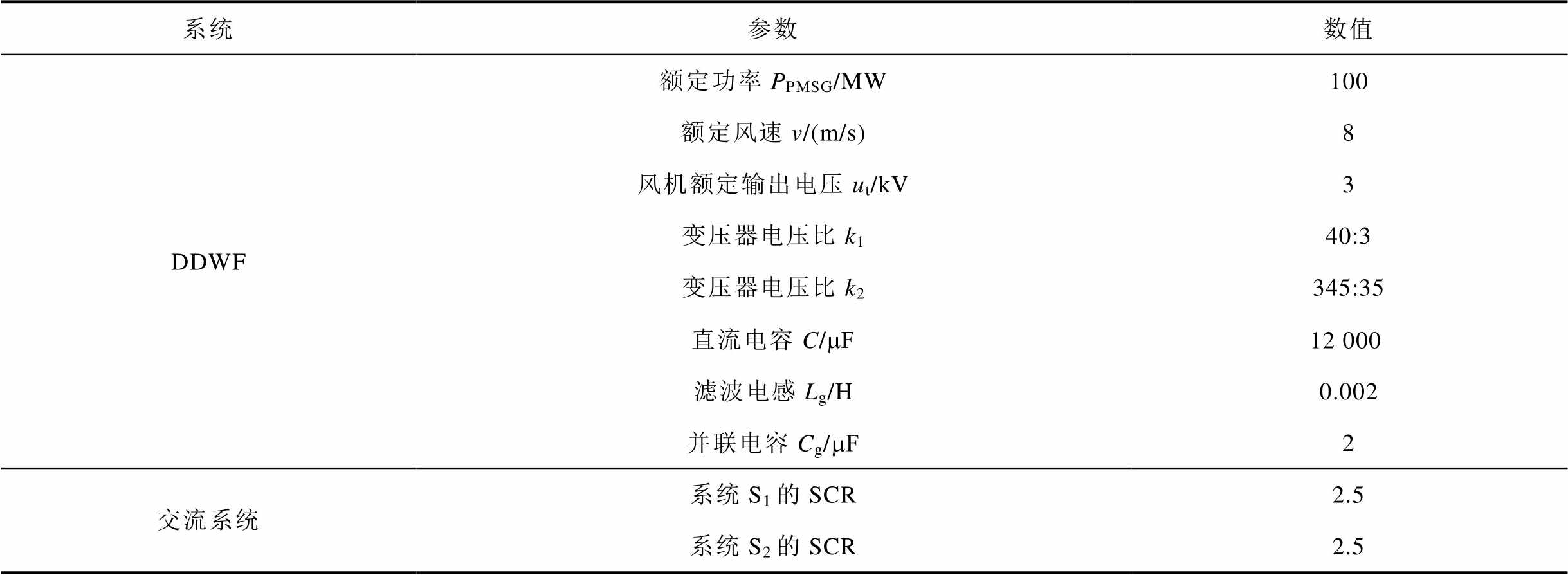
系统参数数值 DDWF额定功率PPMSG/MW100 额定风速v/(m/s)8 风机额定输出电压ut/kV3 变压器电压比k140:3 变压器电压比k2345:35 直流电容C/mF12 000 滤波电感Lg/H0.002 并联电容Cg/mF2 交流系统系统S1的SCR2.5 系统S2的SCR2.5
附表2 控制器参数
App.Tab.2 Controller parameters
控制器参数数值 火电机组励磁与PSS励磁调节增益系数KA50 励磁调节时间常数TA0.01 励磁机时间常数TE0.002 转速偏差放大倍数KPS3 隔直环节时间常数TPS0.125 移相环节时间常数TP17 移相环节时间常数TP20.05 火电机组汽轮机与调速器高压缸功率比例FHP0.3 中压缸功率比例FIP0.26 低压缸功率比例FLP0.44 蒸汽容积时间常数TCH0.3 再热蒸汽容积时间常数TRH7 交叉管时间常数TCO0.2 增益系数KCH0.933 转速调节放大倍数KG20 油动积分时间常数TSM0.5 LCC-HVDC定电流控制比例系数kpR0.4 积分系数kiR58.823 5 LCC-HVDC定关断角控制比例系数kpI0.750 6 积分系数kiI18.382 4 DDWF机侧换流器比例系数kp11 积分系数ki15 比例系数kp20.4 积分系数ki22.5 比例系数kp31 积分系数ki35
（续）
控制器参数参数值 DDWF网侧换流器比例系数kp40.2 积分系数ki420 比例系数kp50.6 积分系数ki52.5 比例系数kp60.6 积分系数ki62.5
2. 工况A的参与因子分析结果
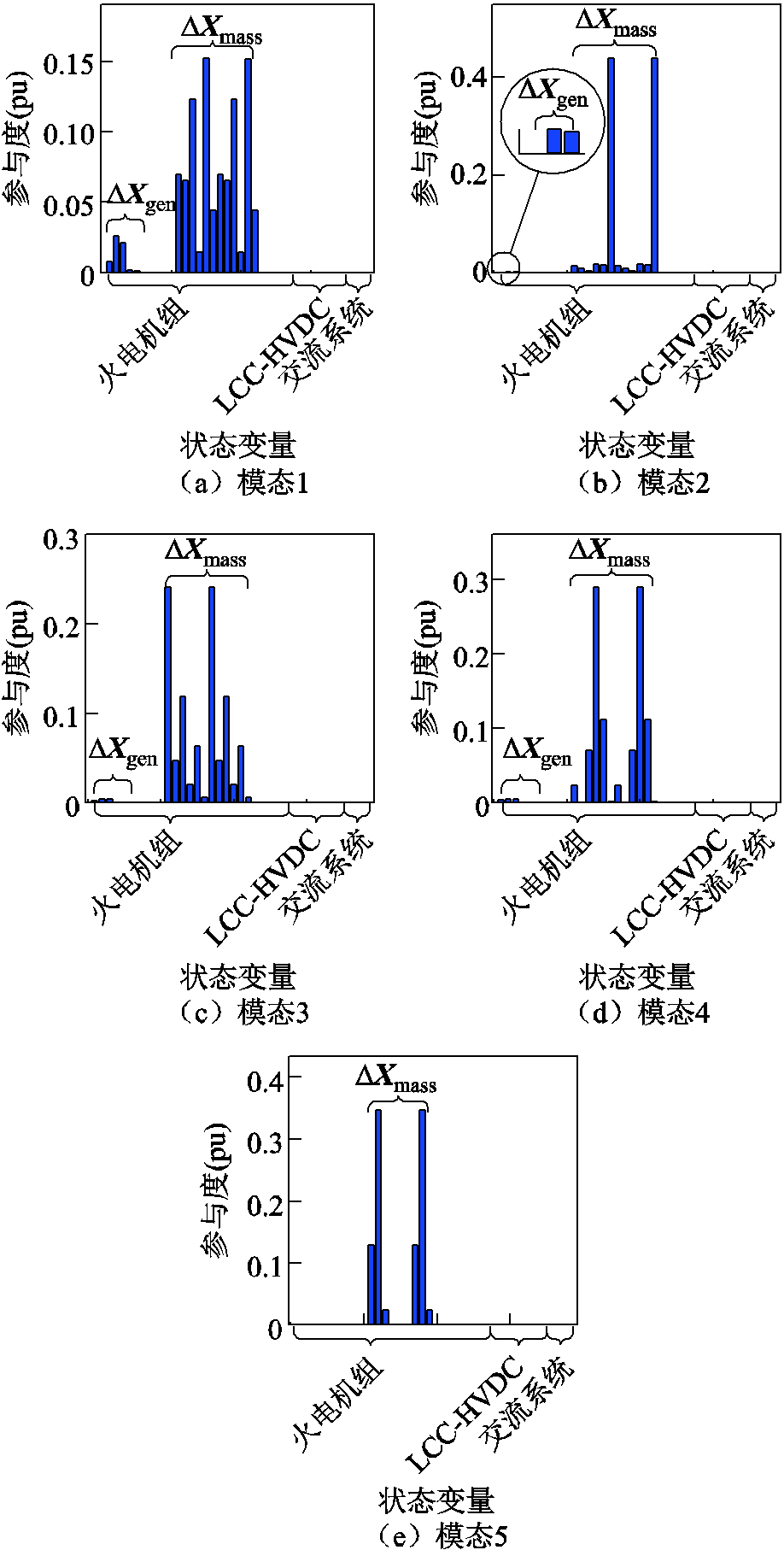
附图1 工况A下各次同步振荡模态的参与因子
App.Fig.1 Participation factor of each subsynchronous oscillation mode in Case A
参考文献
[1] 孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822. Meng Peiyu, Xiang Wang, Pan Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4808-4822.
[2] 朱东海, 邹旭东, 胡家兵, 等. 双馈风电机组无撬棒故障穿越技术研究综述[J]. 电工技术学报, 2022, 37(19): 4895-4910. Zhu Donghai, Zou Xudong, Hu Jiabing, et al. Review of crowbarless fault ride through technology for doubly-fed induction generator-based wind turbines[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4895-4910.
[3] 顾雪平, 白岩松, 李少岩, 等. 考虑风电不确定性的电力系统恢复全过程两阶段鲁棒优化方法[J]. 电工技术学报, 2022, 37(21): 5462-5477. Gu Xueping, Bai Yansong, Li Shaoyan, et al. Two stage robust optimization method for the whole-process power system restoration considering wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5462-5477.
[4] 赵倩, 陈芳芳, 甘露. 基于改进粒子群算法优化支持向量机的风电功率预测[J]. 电气技术, 2020, 21(12): 12-16. Zhao Qian, Chen Fangfang, Gan Lu. Wind power prediction based on support vector machine trained by improved particle swarm optimization[J]. Electrical Engineering, 2020, 21(12): 12-16.
[5] 董文凯, 任必兴, 王海风, 等.适用于系统次同步振荡分析的风电场等值建模方法综述[J]. 电力工程技术, 2022, 41(4): 33-43. Dong Wenkai, Ren Bixing, Wang Haifeng, et al. Small-signal equivalent modeling methods of the wind farm and its application in sub-synchronous oscillations analysis of gird-connected wind power systems[J]. Electric Power Engineering Technology, 2022, 41(4): 33-43.
[6] 陶玉波, 陈昊, 秦晓辉, 等. 短期风电功率预测概念和模型与方法[J]. 电力工程技术, 2018, 37(5): 7-13. Tao Yubo, Chen Hao, Qin Xiaohui, et al. A review of the short-term wind power forecasting theory, model and approach[J]. Electric Power Engineering Technology, 2018, 37(5): 7-13.
[7] 吴熙, 关雅静, 宁威, 等. 双馈风机转子侧变换器参数对次同步振荡的交互影响机理及其应用研究[J]. 电网技术, 2018, 42(8): 2536-2544. Wu Xi, Guan Yajing, Ning Wei, et al. Mechanism of interactive effect of RSC Parameters in DFIG on SSO and its application[J]. Power System Technology, 2018, 42(8): 2536-2544.
[8] 国家能源局. 国家能源局2022年三季度网上新闻发布会文字实录 [EB/OL]. [2022-08-02]. http:// www.nea.gov.cn/2022-08/02/c_1310648934.htm. National Energy Administration. Transcript of the National Energy Administration's online press conference in the third quarter of 2022 [EB/OL]. [2022-08-02]. http://www.nea.gov.cn/2022-08/02/c_ 1310648934.htm.
[9] 辛保安, 单葆国, 李琼慧, 等. “双碳”目标下“能源三要素”再思考[J]. 中国电机工程学报, 2022, 42(9): 3117-3126. Xin Baoan, Shan Baoguo, Li Qionghui, et al. Rethinking of the “Three Elements of Energy” toward carbon peak and carbon neutrality [J]. Proceedings of the CSEE, 2022, 42(9): 3117-3126.
[10] 王倩, 孙大卫, 盛四清, 等. 内禀自同步虚拟同步发电机对系统低频振荡特性的影响[J]. 太阳能学报, 2021, 42(12): 410-418. Wang Qian, Sun Dawei, Sheng Siqing, et al. Effect of virtual synchronous generator on low frequency oscillation characteristics of system[J]. Acta Energiae Solaris Sinica, 2021, 42(12): 410-418.
[11] 郭小江, 赵丽莉, 汤奕, 等. 风火打捆交直流外送系统功角暂态稳定研究[J]. 中国电机工程学报, 2013, 33(22): 19-25, 6. Guo Xiaojiang, Zhao Lili, Tang Yi, et al. Study on angle transient stability for wind-thermal-bundled power transmitted by AC/DC system[J]. Proceedings of the CSEE, 2013, 33(22): 19-25, 6.
[12] 于洋, 徐政, 徐谦, 等. 永磁直驱式风机采用混合直流并网的控制策略[J]. 中国电机工程学报, 2016, 36(11): 2863-2870. Yu Yang, Xu Zheng, Xu Qian, et al. A control strategy for integration of permanent magnet direct-driven wind turbines through a hybrid HVDC system[J]. Proceedings of the CSEE, 2016, 36(11): 2863-2870.
[13] 周佩朋, 李光范, 宋瑞华, 等. 直驱风机与静止无功发生器的次同步振荡特性及交互作用分析[J]. 中国电机工程学报, 2018, 38(15): 4369-4378, 4637. Zhou Peipeng, Li Guangfan, Song Ruihua, et al. Subsynchronous oscillation characteristics and interactions of direct drive permanent magnet synchronous generator and static var generator[J]. Proceedings of the CSEE, 2018, 38(15): 4369-4378, 4637.
[14] 周长春, 徐政. 由直流输电引起的次同步振荡的阻尼特性分析[J]. 中国电机工程学报, 2003, 10(23): 6-10. Zhou Changchun, Xu Zheng. Damping analysis of subsynchronous oscillation caused by HVDC[J]. Proceedings of the CSEE, 2003, 10(23): 6-10.
[15] Chao Hong, Rao Hong. The study of SSTI between Guizhou-Guangdong II ±500 kV DC transmission link and steam-turbine-generators near the rectifier terminal[C]//2006 International Conference on Power System Technology, Chongqing, China, 2006: 1-6.
[16] 程时杰, 曹一家, 江全元. 电力系统次同步振荡的理论与方法[M]. 北京: 科学出版社, 2009.
[17] 刘青, 徐宏璐, 朱益莹, 等. 风火联运经直流外送系统的次同步振荡抑制研究[J]. 电力电容器与无功补偿, 2020, 41(4): 200-205. Liu Qing, Xu Honglu, Zhu Yiying, et al. Study on sub-synchronous oscillation suppression of wind⁃thermal power bundled transmission system[J]. Power Capacitor & Reactive Power Compensation, 2020, 41(4): 200-205.
[18] 杨秀, 李增尧, 胡浩然, 等. 不同输电方式下风电接入对传统火电次/超同步振荡影响研究[J/OL]. 电测与仪表, 2022, https://kns.cnki.net/kcms/detail/23. 1202. TH.20220525.1206.004.html. Yang Xiu, Li Zengyao, Hu Haoran, et al. Research on wind power integration on Sub/Super-synchronous oscillation of thermal power plants under different transmission modes[J/OL]. Electrical Measurement & Instrumentation, 2022, https://kns.cnki.net/kcms/detail/ 23. 1202.TH.20220525.1206.004.html.
[19] 赵书强, 张学伟, 高本锋, 等. 风火打捆经直流送出的次同步振荡分析与抑制措施[J]. 电工电能新技术, 2017, 36(3): 41-50. Zhao Shuqiang, Zhang Xuewei, Gao Benfeng, et al. Analysis and countermeasure of sub-synchronous oscillation in wind-thermal bundling system sent out via HVDC transmission[J]. Advanced Technology of Electrical Engineering and Energy, 2017, 36(3): 41-50.
[20] Gao Benfeng, Hu Yunting, Song Ruihua, et al. Impact of DFIG-based wind farm integration on sub-synchronous torsional interaction between HVDC and thermal generators[J]. IET Generation, Transmission & Distribution, 2018, 12(17): 3913-3923.
[21] 张学伟. 风火打捆送出系统的次同步振荡问题研究[D].保定: 华北电力大学, 2017.
[22] 张瑞雪. 风火打捆经直流送出系统的次同步振荡研究[D]. 保定: 华北电力大学, 2019.
[23] 王俊茜, 贾祺, 刘侃, 等. 基于信号注入法的风火打捆经直流外送系统次同步扭振分析[J]. 电力系统保护与控制, 2021, 49(17): 109-120. Wang Junxi, Jia Qi, Liu Kan, et al. Analysis of sub-synchronous torsional mode of wind-thermal bundled system transmitted via HVDC based on a signal injection method[J]. Power System Protection and Control, 2021, 49(17): 109-120.
[24] 杨尉薇, 朱玲, 李威, 等. 风火打捆直流送出系统次同步振荡及传播特性研究[J]. 电力系统保护与控制, 2019, 47(20): 58-64. Yang Weiwei, Zhu Ling, Li Wei, et al. Study on subsynchronous oscillation and propagation character-ristics of wind-fire bundled sending system[J]. Power System Protection and Control, 2019, 47(20): 58-64.
[25] Zhang Meiqing, Yuan Xiaoming, Hu Jiabing. Mechanism analysis of subsynchronous torsional interaction with PMSG-based WTs and LCC-HVDC[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2):1708-1724.
[26] 张鹏. 交直流系统次同步振荡建模与机理分析[D]. 北京: 华北电力大学, 2014.
[27] 韩俊. 基于状态空间法的多机系统次同步谐振研究[D]. 杭州: 浙江大学, 2011.
[28] Kundur P. Power system stability and control[M]. New York: McGraw-Hill, 1994.
[29] Wu Meng, Xie Le, Cheng Lin, et al. A study on the impact of wind farm spatial distribution on power system sub-synchronous oscillations[J]. IEEE Trans-actions on Power Systems, 2016, 31(3): 2154-2162.
[30] 郭春义, 宁琳如, 王虹富, 等. 基于开关函数的LCC-HVDC换流站动态模型及小干扰稳定性[J]. 电网技术, 2017, 41(12): 3862-3870. Guo Chunyi, Ning Linru, Wang Hongfu, et al. Switching-function based dynamic model of LCC-HVDC station and small signal stability analysis[J]. Power System Technology, 2017, 41(12): 3862-3870.
[31] 邵冰冰, 赵书强, 裴继坤, 等. 直驱风电场经VSC-HVDC并网的次同步振荡特性分析[J]. 电网技术, 2019, 43(9): 3344-3355. Shao Bingbing, Zhao Shuqiang, Pei Jikun, et al. Subsynchronous oscillation characteristic analysis of grid-connected DDWFs via VSC-HVDC system[J]. Power System Technology, 2019, 43(9): 3344-3355.
[32] 高本锋, 崔意婵, 李蕴红, 等. D-PMSG经LCC-HVDC送出系统的次同步振荡特性分析[J]. 中国电机工程学报, 2022, 42(6): 2084-2096. Gao Benfeng, Cui Yichan, Li Yunhong, et al. Analysis of subsynchronous oscillation characteristics of D-PMSG integrated with LCC-HVDC system[J]. Proceedings of the CSEE, 2022, 42(6): 2084-2096.
[33] IEEE Std 1204-1997, IEEE guide for planning DC links terminating at AC locations having low short-circuit capacities[M]. New York: IEEE PES, 1997.
Abstract The sub-synchronous interaction between the thermal generator and the LCC-HVDC (line-commutated-converter based high voltage direct current) will cause the sub-synchronous torsional interaction (SSTI) of the thermal generator shaft system, which in turn causes the fatigue accumulation of the thermal generator rotor shaft system. When the thermal generator is connected to the DDWF (direct-drive wind farm) through the LCC-HVDC sending end, or the new LCC-HVDC sending end AC bus is near the DDWF and thermal generator base at the same time, it will constitute a scene with a close electrical distance between the three. At this time, the influence of DDWF on the SSTI of thermal generator caused by LCC-HVDC can not be ignored.
Firstly, based on the mathematical model of DDWF and thermal power bundled through LCC-HVDC transmission system, the small signal model of the system is established in Matlab/Simulink by block modeling method, and the correctness of the small signal model is verified by step response. Secondly, the eigenvalues of the small signal model under the two conditions of LCC-HVDC sending end access or no access to DDWF are compared and solved, and the SSTI mode of the system is separated. The influence of DDWF grid connection on SSTI damping of thermal generator is clarified, and the theoretical analysis is verified based on time domain simulation. Finally, the influence of system operation mode on SSTI damping characteristics is analyzed for wind speed, wind farm capacity, electrical distance between wind farm and LCC-HVDC rectifier station and LCC-HVDC control mode.
When the DDWF is connected to the LCC-HVDC sending end, the interaction between the thermal power unit and the LCC-HVDC will cause the DDWF output power to change. When the output power deviates from the given value, the GSC controller of DDWF will respond quickly to the power deviation, adjust the active and reactive power output quickly according to the system operating conditions, and alleviate the power fluctuation caused by external disturbance. In this process, DDWF will share the power fluctuation of LCC-HVDC with thermal power units, weaken the sub-synchronous interaction between thermal power units and LCC-HVDC, and enhance the SSTI damping of thermal power units. The simulation results of typical systems show that about 27 % of the sub-synchronous current in LCC-HVDC is absorbed after DDWF is incorporated into the LCC-HVDC transmission system.
The main results of this paper are as follows: (1) The PSCAD / EMTDC time domain simulation model of the system is established for the DDWF and thermal power units bundled by LCC-HVDC transmission system, and the small signal model of the system is established by block modeling method. The correctness of the small signal model is verified by comparing with the step response of the electromagnetic transient model. (2) When DDWF is not connected to the system, the sub-synchronous interaction between the thermal power unit and LCC-HVDC will aggravate the external disturbance, and the thermal power unit has SSTI risk. After DDWF is connected to the sending end of LCC-HVDC, the fast response of GSC can replace the thermal power unit to bear part of the DC power change, reduce the sub-synchronous interaction between the thermal power unit and LCC-HVDC, indirectly improve the system damping and reduce the risk of system oscillation. (3) When the capacity of DDWF increases and the wind speed increases, the damping of SSTI increases. When the electrical distance between DDWF and LCC-HVDC rectifier station increases, the system damping decreases. The SSTI damping of LCC-HVDC rectifier side constant current control is larger than that of constant power control, and the SSTI damping of inverter side constant DC voltage control is larger than that of constant turn-off angle control.
Keywords：Line-commutated-converter based high voltage direct current (LCC-HVDC), direct-drive wind farm (DDWF), eigenvalue analysis, sub-synchronous torsional interaction(SSTI), wind-thermal bundled
DOI:10.19595/j.cnki.1000-6753.tces.230016
中图分类号：TM712
国家重点研发计划资助项目（2021YFB2400800）。
收稿日期 2023-01-16
改稿日期 2023-03-16
高本锋 男，1981年生，副教授，研究方向为高压直流输电和电力系统次同步振荡。E-mail：gaobenfeng@126.com
董涵枭 男，2000年生，硕士研究生，研究方向为电力系统次同步振荡。E-mail：hanxiao_dong@126.com（通信作者）
（编辑 赫 蕾）