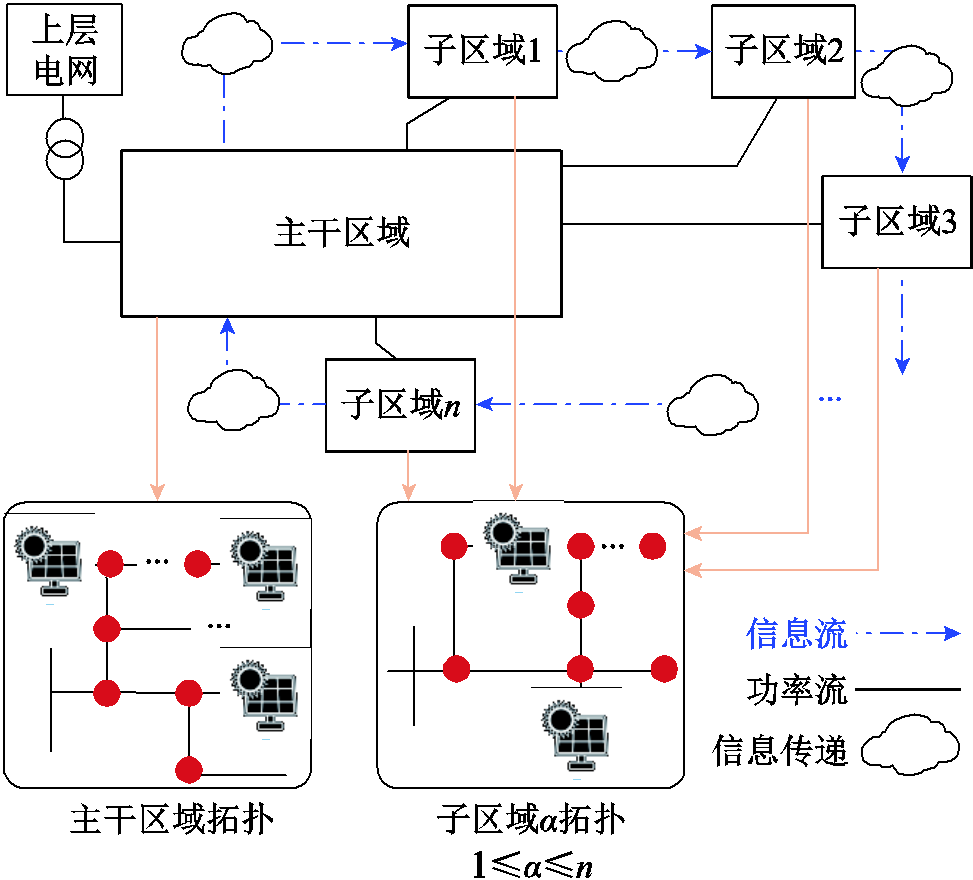
图1 多区域配电网的结构示意图
Fig.1 Structure diagram of multi area distribution network
摘要 针对配电网随机潮流算法中需要对节点功率注入进行大量模拟所引起的计算效率低的问题，提出一种基于区域间场景等值的配电网随机潮流加速算法。首先，从配电网的拓扑连接规律出发，将各区域内节点功率注入对其他区域潮流的影响转换为对边界量的影响，并由此建立了基于边界量的多区域潮流模型；其次，提出一种区域间场景等值方法，快速等值引起其他区域相同潮流变化的功率注入场景；再次，设计了一种随机潮流的分布式求解算法，在求解过程中各区域通过交换边界等值场景集并结合局部功率注入信息重新构造潮流方程，分布式地求解各区域内的随机潮流；最后，通过IEEE 118节点测试系统进行算例分析，验证了所提方法的准确性，且该方法能够显著提高计算效率。
关键词：配电网 场景等值 分布式光伏 随机潮流
在“双碳”战略目标的驱动下，配电网中分布式光伏的渗透率不断提高，截至2022年9月底，我国分布式光伏装机规模已达到1.42亿kW[1]。“容量小、数量多”的分布式光伏已规模化进入用户侧，出力的不确定性和间歇性使得潮流分布发生显著变化，配电网面临的随机性挑战越发突出[2-5]。随机潮流作为定量分析不确定因素对配电系统运行状态影响的重要基础工具，可以有效地获得系统状态变量的概率分布，对运行人员和网络中自动化设备的正确控制存在重要意义[6-8]。
目前常见的随机潮流算法包括模拟法、点估计法、解析法等，其本质是将功率注入空间中的不确定性映射到系统运行过程中状态变量的不确定性。以半不变量方法为代表的解析法通常利用随机量的半不变量性质及其与概率分布的函数关系得到系统潮流结果的概率特征[9-10]，为了提高拟合精度，研究的重点主要集中在对其应用的级数展开方法进行分析比较和改进。文献[11]对比分析了在不同系统中Cornish-Fisher和Gram-Charlier级数展开的概率潮流计算结果。文献[12]采用Cornish-Fisher级数展开提高了非正态分布下曲线拟合的精度。为了解决级数展开负尾部效应等精度问题，文献[13]应用了C型Gram-Charlier 级数拟合状态变量概率分布。
点估计法可以通过非线性潮流方程的计算，输出随机变量的统计矩，无需进行大规模统计实验和交流潮流线性化处理，但其精度会随着输入随机变量的维数或矩的阶数的增加而下降[14]。文献[15]计及多维风电场之间风速的相关性，利用Copula函数拟合风速的联合分布函数作为输入量，提出一种基于Rosenblatt变换的概率潮流三点估计法。文献[16]则利用Nataf变换及逆变换建立多维标准正态空间与多维非正态空间的关系，提出可以处理非正态分布随机变量相关性的概率潮流三点估计法。将Nataf变换与点估计法相结合，对于不同的概率分布均可得到较为准确的估计结果。文献[17]针对配电系统中三相不平衡性显著的问题，利用Gauss-Hermite求积与正态变换技术选取输入变量的估计节点和权重，结果表明其适用于含有非正态分布或相关性不确定变量的配电网。
模拟法是指由蒙特卡洛及优化抽样次数而衍生的算法，在采样规模足够大的情况下能够得到相对准确的结果，常作为验证其他方法的基准[18]。文献[19]提出基于聚类抽样的随机潮流计算方法，其核心思想是对基于历史数据采用蒙特卡洛法产生的大量样本进行聚类，并对计算结果的平均概率密度信息进行统计处理，可为电网调度计划的制定和运行分析提供决策依据。然而，由于在大规模系统中要求解数量庞大的确定性潮流，巨大的计算成本和长时间运行难以满足实时调度需求。
目前，随机潮流算法在国内外已经有了深入的挖掘，取得了良好的研究成果。但由于配电网中各节点的潮流关系是相互耦合的，具体来说是指每个节点的功率注入会引起配电网所有节点电压与支路功率的变化。因此，传统基于采样及优化抽样次数的随机潮流算法往往需要将信息集中到一台计算机上统一处理，从而增大了计算负担，使得其在实际应用中具有挑战性。
针对如何加速随机潮流计算的问题，部分学者从机器学习等其他角度来提升计算效率。文献[20]考虑到大量样本的模拟计算可以被表述为机器学习问题，采用深度神经网络来逼近潮流计算，并根据物理潮流方程进行训练。文献[21]提出了一种新的GPU加速算法，通过将巨大的计算负担转移给GPU以一种更快的方式求解随机潮流，结果显示比基于CPU的算法快两个数量级。
上述研究对随机潮流加速算法做了一系列有益的探索，但现有研究未考虑配电网的拓扑连接结构对随机潮流计算的简化。根据上述分析，本文的创新点总结如下：①从配电网的拓扑连接规律出发，建立了通过边界量来相互影响的多区域潮流模型；②提出了一种区域间场景等值方法，可基于现有以节点注入功率为研究对象的场景缩减方法，通过等值引起其他区域相同边界量的功率注入场景进一步实现场景的缩减；③设计了一种分布式求解方法，能够在已知各区域传递的边界量和内部随机信息的条件下，实现随机潮流的加速求解。
本文设计了基于区域间场景等值的配电网随机潮流加速算法：首先，根据配电网开环运行的辐射状结构特点划分为若干区域，并根据其拓扑连接规律将区域间的潮流作用转换为对其边界量的影响，由此构建了含边界量的多区域潮流模型。然后，提出了一种区域间场景等值的方法，各区域在不同功率注入场景下等值引起其他区域相同边界量变化的场景。据此，设计了一种随机潮流的分布式算法，各区域通过边界等值信息的交换和局部信息重新构造潮流方程并进行确定性的计算，完成配电网随机潮流的分布式求解。
多区域配电网的结构示意图如图1所示，根据配电网的辐射状结构特点，可将其划分为1个主干区域和n个子区域，根节点包含在主干区域内。主干区域和各子区域在拓扑上相互连接，光伏电源以分散的方式接入。
图1 多区域配电网的结构示意图
Fig.1 Structure diagram of multi area distribution network
配电网潮流模型采用Distflow模型，表达式为
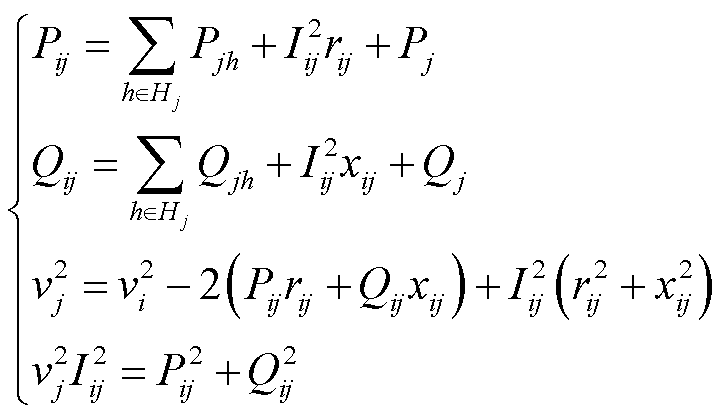（1）
式中，下标i、j为配电网的节点编号；ij为配电网线路编号；vi为节点i的电压幅值；Pj、Qj分别为节点注入的有功功率、无功功率；Pij和Qij分别为线路ij的始端有功功率和无功功率；Hj为在节点j下游与其相连的节点集合；rij和xij分别为线路ij的电阻和电抗；Iij为流过线路ij的电流。
对图1所示的多区域配电网拓扑结构，式（1）的潮流模型可更改为
（2）
式中，Un为第n个区域内的节点电压矩阵，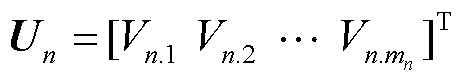
, 
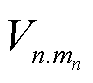为第n个区域内第mn节点的电压，mn为区域n内的节点个数；U0为主干区域的节点电压矩阵；FU为由潮流方程决定的配电网节点注入功率与各节点电压的函数关系；S0.i为主干区域节点i的注入功率矩阵，
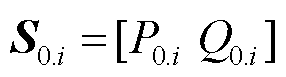, P0.i和Q0.i分别为主干区域内节点i注入的有功功率、无功功率。随机注入功率S0.i采用场景法，可以表示为
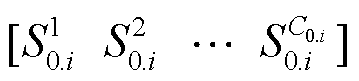，C0.i为主干区域内第i个节点注入功率可能出现的场景数。主干区域内各节点功率注入场景的总数为C0个，子区域n内各节点功率注入场景总数为
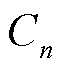个。
各区域可结合文献[22]所证明的拓扑连接规律，将区域间的潮流作用替换为对边界量的影响。具体可以分为以下三种情况：①子区域内功率注入对主干区域潮流的影响表现为子区域功率注入先影响该子区域的边界注入功率，进一步影响主干区域的潮流；②主干区域内功率注入对子区域的影响表现为主干区域功率注入先影响子区域边界节点电压，进一步影响子区域内的潮流；③子区域内随机功率注入对其他子区域的潮流影响表现为子区域先影响该子区域的边界注入功率，进而影响到其他子区域的边界节点电压，最后影响其他子区域内的潮流。
基于上述各区域间潮流作用的特有规律，可将子区域的边界电压与主干区域对子区域的边界注入功率定义为边界量，并在此基础上得到含边界量的配电网多区域潮流模型。
对主干区域有：主干区域的潮流状态是各子区域边界注入功率和主干区域内功率注入的函数，有
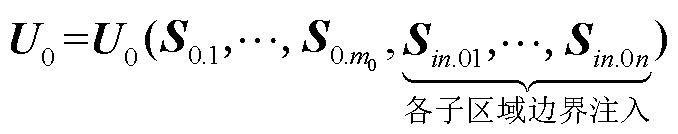（3）
对子区域有：子区域内的潮流方程是其边界电压和内部注入功率的函数。而与主干区域不同的是，子区域的边界电压并不恒定，受配电网所有节点功率注入的变化而变化。因此，以子区域n为例，其潮流方程可表示为
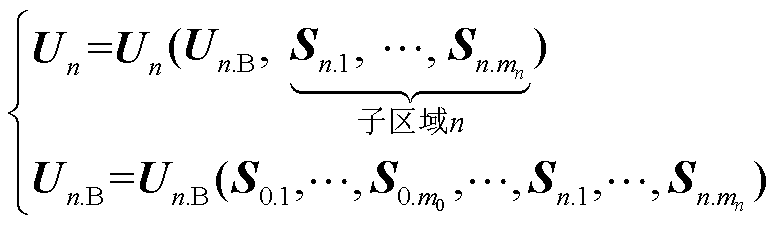（4）
式中，Un.B为子区域n的边界电压。
式（3）、式（4）构成的模型是一个多区域互联、通过边界量来相互影响的配电网潮流模型。对该模型，本节所设计的加速算法思路如下：首先，在各区域内基于配电网拓扑结构，等值内部节点注入功率引起相同边界量的场景，实现场景数量的简化。然后，结合各区域间交换等值后的场景信息与自身的局部信息矩阵求解潮流结果，可以一种近乎分布式的方式加速配电网随机潮流的求解。
配电网各区域可以采用主流的方法如聚类法等手段来缩减区域内的场景。然而，这种方法在节点数过多的系统中应用后，可能仍面临着计算效率低的问题，难以满足实时调度的需要。对此，基于现有对节点注入功率场景缩减方法，提出一种区域间场景等值的方法。
配电网各区域可以根据拓扑连接结构，将区域内功率注入对其他区域边界量影响相同的场景进行等值，进一步减少所需计算的场景数量，达到简化随机潮流计算的目的，根据这一思路，可得到如下的区域间场景等值方法。
2.1.1 子区域不同功率场景对主干区域的等值
以子区域n为例进行说明。在主干区域注入功率不变的情况下，将子区域n中的所有注入场景代入潮流方程（1）中，可以得到子区域n在不同场景下的边界注入功率矩阵，如式（5）所示。
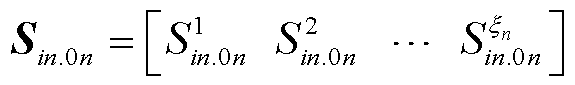（5）
式中，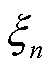
为子区域n边界注入功率的场景个数。
在式（5）中，如果存在两个场景对子区域n的边界注入功率满足式（6），即当它们之间的差值很小时（对应图2中的场景2和3），认为这两个场景是等值的。
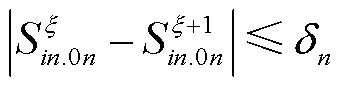（6）
式中，
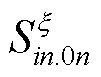为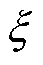
场景下子区域n的边界注入功率；
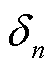为子区域内两个边界功率注入场景间的差值。子区域注入功率对主干区域的场景等值示意图如图2所示。
2.1.2 主干区域内不同功率场景对子区域的等值
由于子区域以主干区域为媒介与其他子区域相连，在进行主干区域对子区域的场景等值时必然既包含其他子区域的边界注入功率，又包含主干区域自身的功率注入。
在子区域n内部节点注入功率不变的条件下，将主干区域内所有功率注入场景代入潮流方程（1）中，可以得到子区域n的边界电压矩阵为
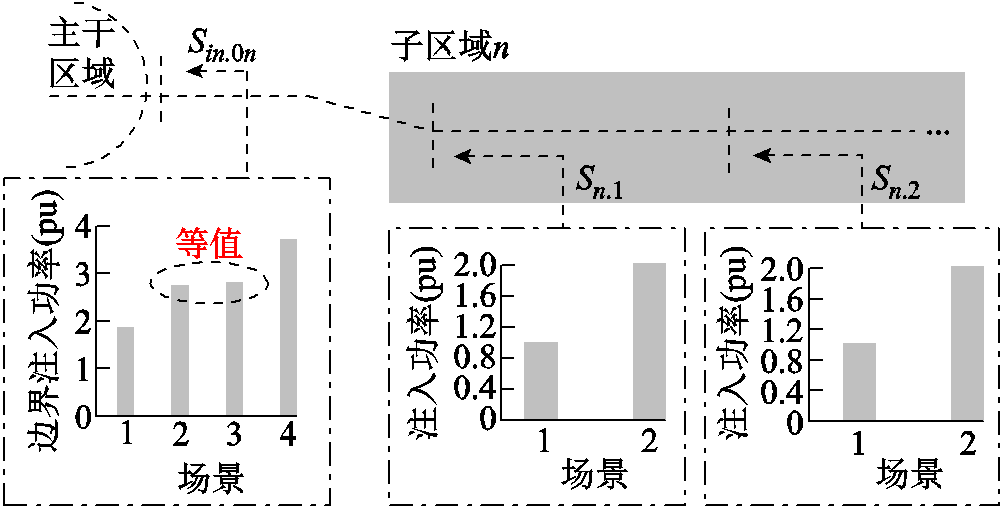
图2 子区域注入功率对主干区域的场景等值示意图
Fig.2 Schematic diagram of scene equivalence of sub area injection power to trunk area
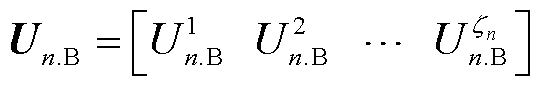（7）
式中，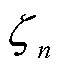
为子区域n边界电压的场景个数。
式（7）中，如果有两个场景对子区域n的边界电压满足式（8），即它们的平方差很小时（对于图3中的场景2和3），这两个场景是等值的。
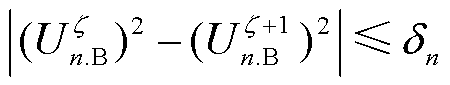（8）
式中，
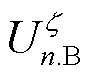为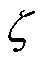
场景下子区域n的边界电压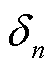；为主干区域内功率注入场景之间对子区域n边界电压影响的差值。主干区域对子区域n的场景等值示意图如图3所示。
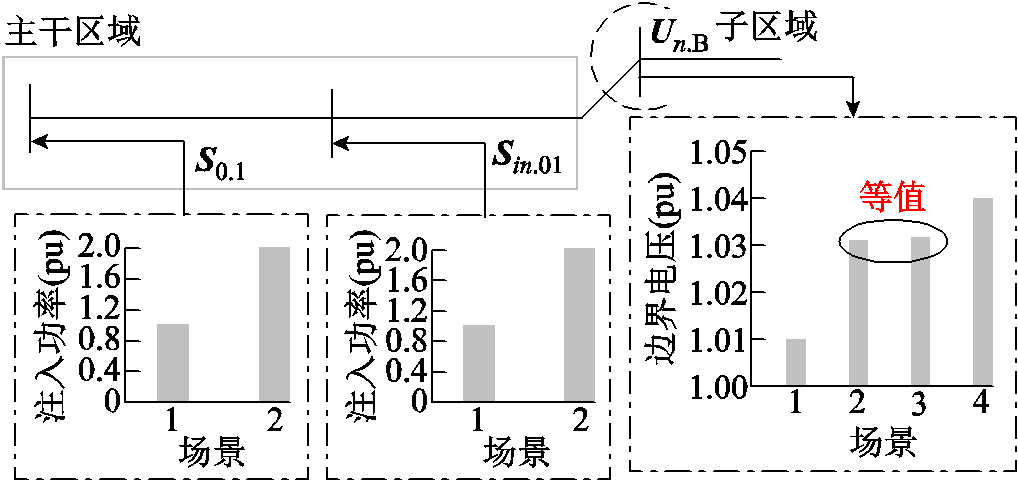
图3 主干区域对子区域n的场景等值示意图
Fig.3 Scene equivalence between main area and sub area n
2.1.3 区域划分方式对场景等值效果的影响
采用区域间场景等值处理可以大量缩减随机潮流计算所需的场景数量。而区域的不同划分方式会改变区域的规模和数量，进而对区域间场景等值的效果产生影响。在此，首先对配电网作合理的假设，进而讨论区域划分方式的不同对场景等值效果的影响。最后，为了提升区域间场景等值效果，给出区域划分的具体原则。
假设 配电网被划分为n个子区域和1个主干区域，根节点位于主干区域内，主干区域与各子区域在拓扑上相互关联。区域n进行场景等值总体时间为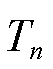
，单次潮流计算的时间为
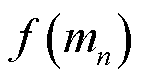，各区域内节点注入功率的可能为
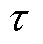种。
在上述假设下，不同的区域划分方式在配电网中主要体现在：①划分区域的规模不同；②划分区域的数量不同。以子区域n为例，其场景等值所需的计算时间与单次潮流计算的时间和自身规模大小（包含的节点数量）相关，总体计算时间为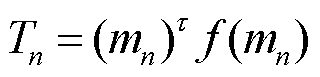
。
增大区域规模会增加单次潮流计算的时间与计算次数，进一步增加区域间场景等值的计算时间。为了保证各区域在每次计算时间的基本一致，避免个别区域计算时间较长影响总计算时间的情况出现，在区域划分时使其规模尽可能相同。
在满足区域规模尽可能相同的前提下，区域划分的数量越多，区域的规模就越小，则各子区域所需的单次潮流计算时间就越短，这使得分布式随机潮流计算的效率更高。由上述分析，为取得更好的场景等值效果，区域划分的原则如下：①根节点位于主干区域内，主干区域与各子区域在拓扑上相互关联；②在保证区域的规模尽可能一致的前提下，使区域划分的数量尽可能多。
在上述区域间场景等值处理的基础上，进一步阐释配电网各区域如何以一种分布式的方式，根据区域内自身随机功率注入信息和区域间交换的等值场景信息重新构造潮流方程，进而实现随机潮流的加速求解。
2.2.1 主干区域的随机潮流求解
子区域基于2.1节所提的区域间场景等值方法，将等值后的边界注入功率传递至主干区域。进一步，将潮流方程（1）中各子区域内部节点注入功率用边界注入功率代替，可在主干区域内构造新的潮流方程，其中方程（1）的前两式替换为式（9），后两式不变。
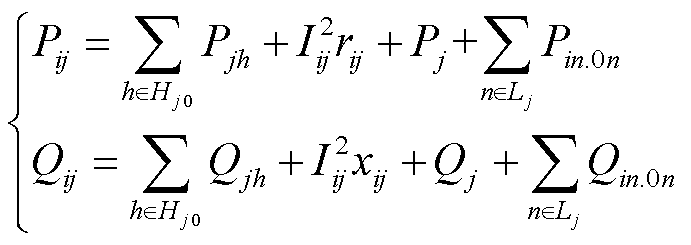（9）
式中，Hj0为主干区域内节点j下游与其相连的节点集合；Pin.0n为主干区域对子区域n的边界注入有功功率；Qin.0n为主干区域对子区域n的边界注入无功功率；Lj为节点j下游与其相连的子区域编号集合。
基于上述构造的潮流方程，将各子区域转递的边界注入功率信息和自身内部的随机功率注入信息形成主干区域的功率注入场景集合，并将该场景代入式（9）中，采用牛顿迭代法进行求解可得到主干区域的随机潮流计算结果。
2.2.2 子区域的随机潮流求解
子区域的自身局部信息是该区域各节点注入功率场景的所有可能组合，以子区域n为例，其局部信息示意图如图4所示。
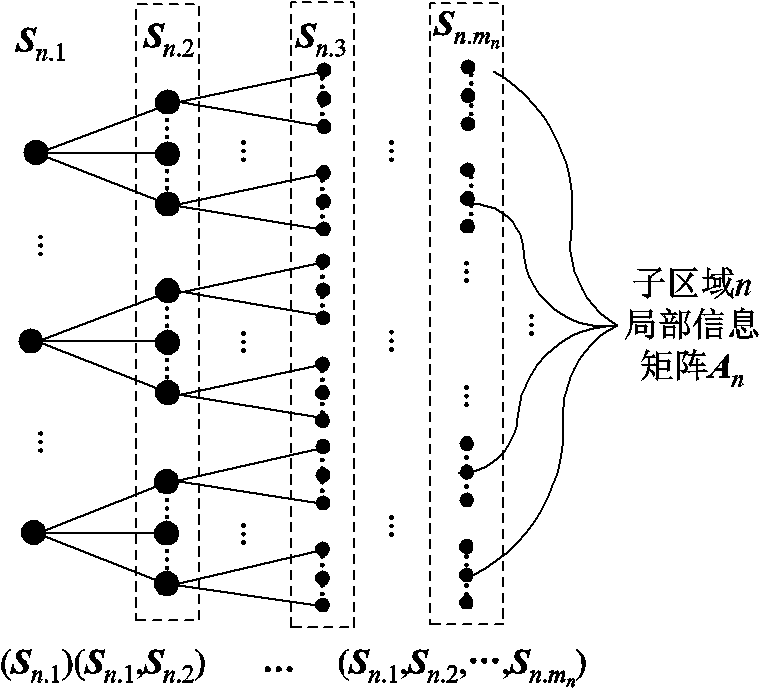
图4 子区域n局部信息示意图
Fig.4 Local information of sub region n
子区域n的局部信息可表示为
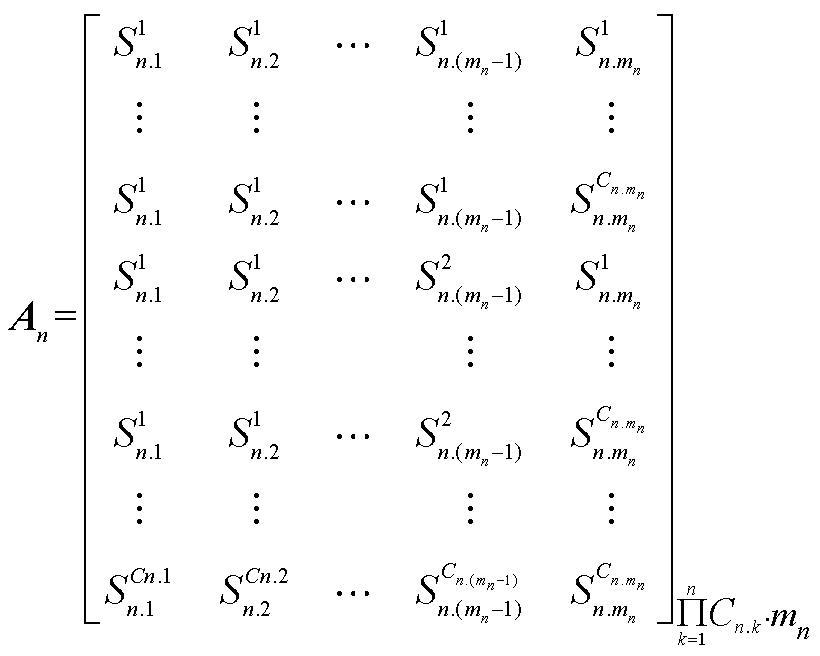（10）
式中，Cn.i为子区域n内节点i功率注入的场景总数。
当主干区域和其他子区域注入功率确定时，将式（4）中边界电压Un.B在子区域n内部的各个功率注入点进行一阶泰勒展开，如式（11）所示。
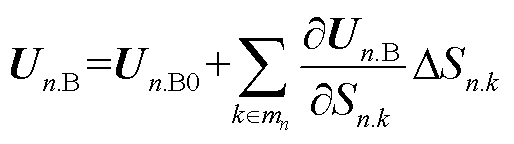（11）
式中，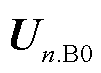
为子区域n的边界电压一阶泰勒展开后的基准值；
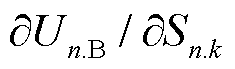为一阶泰勒展开项系数；
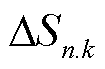为子区域n内第k个节点注入功率的变化量。
经此处理，可将子区域的边界电压分为配电网各节点功率注入时所引起的基准值Un.B0和子区域内部功率注入所引起的变化值两部分。
进一步，子区域n结合文献[20]所提的前推回代的灵敏度计算方法，引入子区域n内各节点功率注入对其边界电压的灵敏度，代入式（11）中可得子区域n不同功率注入下的边界电压。
此时，可以将边界电压作为根节点，在子区域的拓扑结构下重新构造潮流方程，采用牛顿迭代法进行求解可得子区域的随机潮流计算结果。
配电网分布式随机潮流算法的流程如图5所示。
具体步骤如下：
（1）在配电网区域划分的基础上，对随机功率注入的样本进行分区，并在各区域设置等值场景功率距离和等值场景电压距离。
（2）各个子区域结合自身内部节点随机功率注入计算其边界量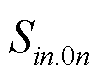
,并将等值后的等值场景信息发送给主干区域。
（3）主干区域接受到所有子区域发送的等值场景后，整理信息并构造潮流方程式（9），进一步结合自身内部随机功率注入进行确定的潮流计算，并汇总主干区域潮流结果。
（4）主干区域对各个子区域进行功率注入场景的等值，并将等值后的场景集合发送给各个子区域。
（5）各子区域采用前推回代的灵敏度计算方法求解式（10），并结合主干区域发送的等值信息计算边界电压，根据内部的随机功率注入信息计算随机功率注入下的潮流并汇总潮流结果。
本节分析本文所提方法对提升随机潮流求解速度的有效性。
假设 节点数量为N的配电网中各节点有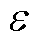
种功率注入的可能场景，且不考虑各节点出力的相关性。
采用蒙特卡洛方法对配电网的随机潮流进行模拟时，所计算的场景数量如式（12）所示，所需计算的场景数量为节点功率注入可能的场景为底的指数函数。随着节点数量的增加，呈现出指数增长的趋势。
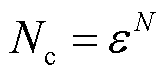（12）
式中，Nc为用蒙特卡洛模拟所需计算的场景数量。
采用本文所提方法时，由于配电网被划分为1个主干区域和n个子区域，主干区域与各子区域是串行计算，各子区域是并行计算的。因此所需的潮流计算次数为
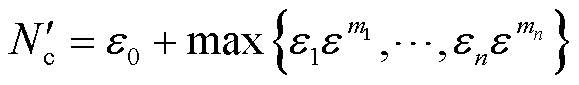（13）
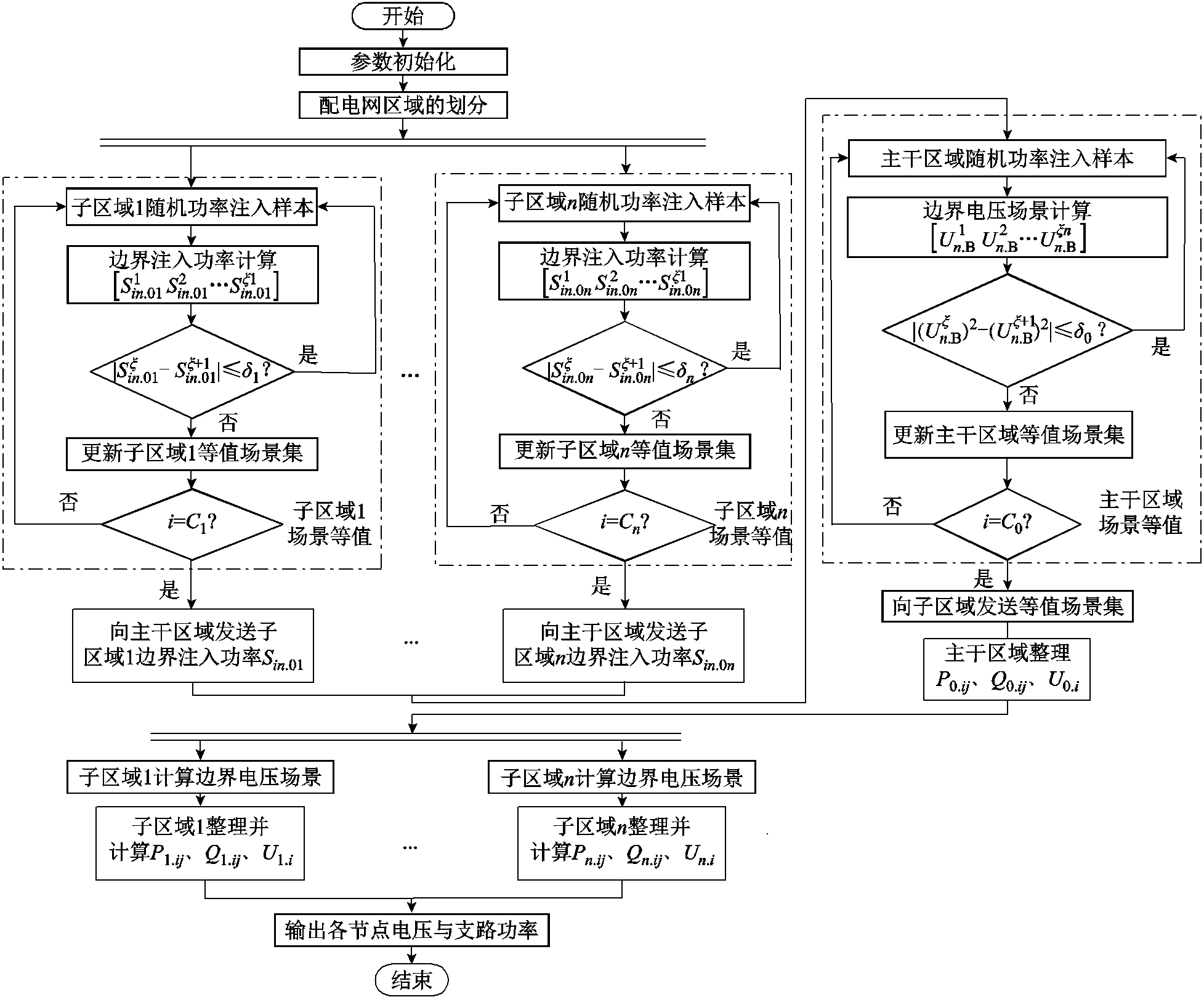
图5 随机潮流分布式计算流程
Fig.5 Flow chart of distributed calculation of stochastic power flow
式中，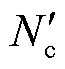
为采用本文所提方法所需的潮流计算次数；
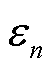为主干区域对子区域n等值之后的边界量场景个数；
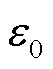为主干区域所需的潮流计算次数。
进一步，如式（14）所示，由形式上可看出采用本文所提方法需要的潮流计算次数远小于蒙特卡洛模拟。
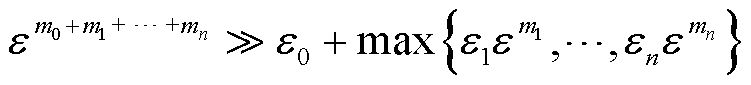（14）
综上所述，分布式随机潮流计算降低了传统集中式的以指数形式增加的场景数量，可在相同的时间约束下求解更多的场景，从而提升了求解效率。
在本节中，将介绍在IEEE 118节点测试系统中得到的数值结果，算例拓扑结果如图6所示。配电网在节点6、22、64、83接入4 MW的光伏电源；在节点37、46、54、62接入3.5 MW的光伏电源；在节点69、77、95、99接入3 MW的光伏电源。由于光伏电站正常工作时，功率因数通常在0.95以上，因此本文只考虑光伏电站发出的有功功率，并且输出的有功功率按照最大功率跟踪原则进行选取。蒙特卡洛的取样精度和本文所提方法的精度相同。
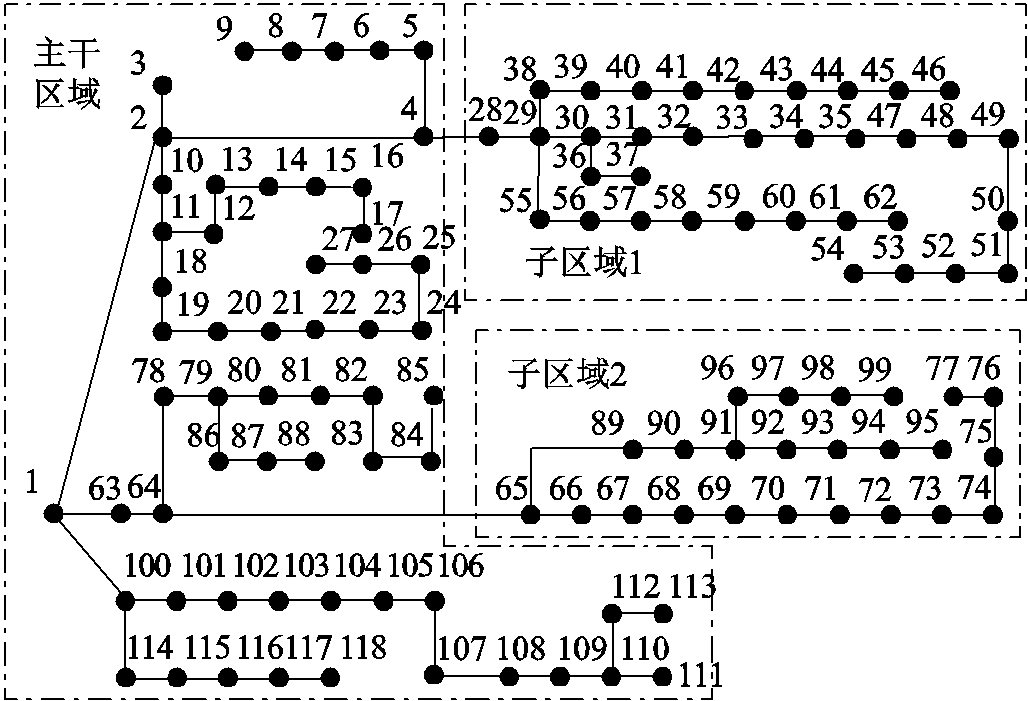
图6 IEEE 118算例系统拓扑结果
Fig.6 IEEE 118 example system topology
基于配电网的分区准则，将系统划分为1个主干区域和2个子区域：节点28～62所构成的区域被划分为子区域1，通过线路4～28与主干区域相连；节点65～77、89～99所构成的区域被划分为子区域2，通过线路64、65与主干区域相连；剩余的部分就构成了主干区域，且根节点位于主干区域内。
设置子区域1和2对主干区域注入功率等值场景差值分别为0.2 MW、0.25 MW，主干区域对子区域1和2的边界电压场景差值为0.001 4(pu)。
上述设置的12个光伏电站的出力采用随机采样方法，出力如图6所示。假设光伏电站间出力互不相关。
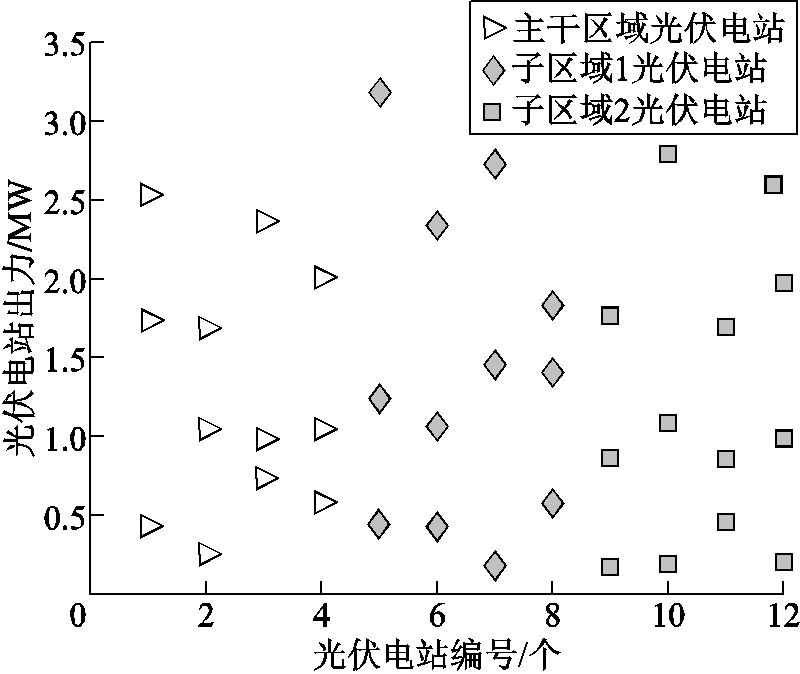
图7 各光伏电站出力散点图
Fig.7 Output of each photovoltaic power station
本文所提出的配电网随机潮流加速算法分别在基于边界量的区域划分和区域间的场景等值引入了近似误差，下面在IEEE 118测试系统中分别讨论这两部分误差。
4.2.1 基于边界量的区域划分误差分析
以集中式求解IEEE 118系统的电气量为基准，与基于边界量的多区域潮流模型计算结果进行对比。主干区域、子区域1和子区域2的误差分布如图8～图10所示。由图8可以发现，主干区域内有功功率与节点电压的偏差均较小。由图9和图10可以发现，子区域内电压的偏差与主干区域相比较大，这是因为基于边界量的多区域潮流模型在计算子区域潮流时，仅对子区域边界电压进行了一阶泰勒展开，忽略了高次项。
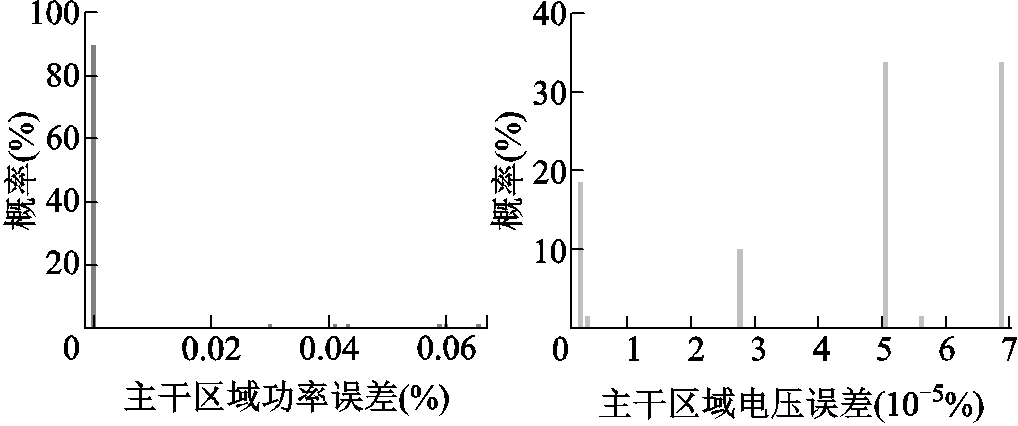
图8 基于边界量区域划分主干区域误差
Fig.8 Error of dividing trunk region based on boundary quantity
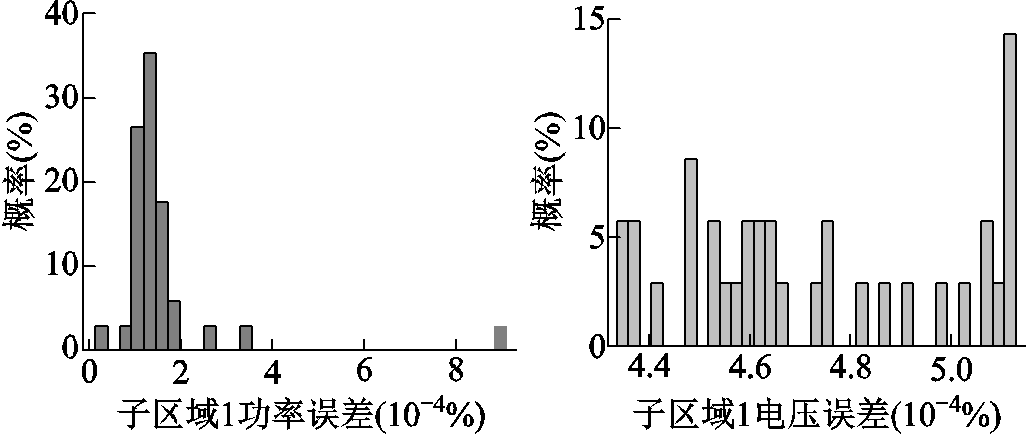
图9 基于边界量区域划分子区域1误差
Fig.9 Sub region 1 error based on boundary quantity region division
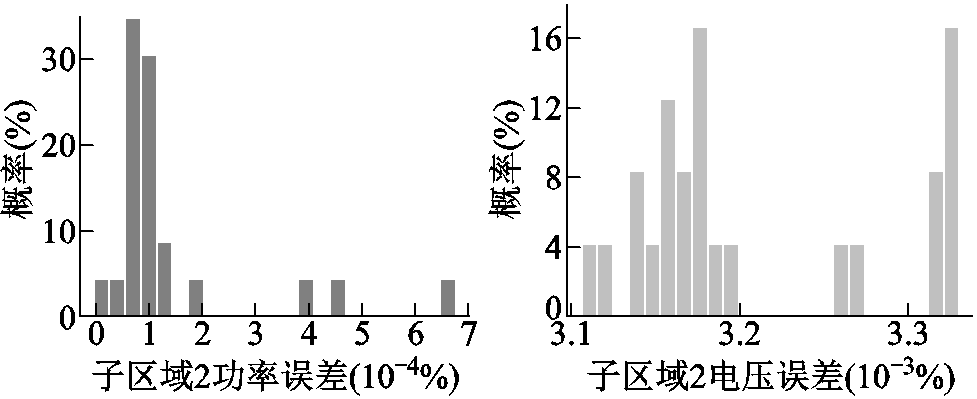
图10 基于边界量区域划分子区域2误差
Fig.10 Sub region 2 error based on boundary quantity region division
4.2.2 区域间场景等值的误差分析
本小节将分析如何通过基于边界量划分的多区域潮流模型，在各区域的不同功率注入场景下等值引起其他区域相同边界量变化的场景，进而实现简化随机潮流所需计算场景数量这一过程，并对其产生的误差进行分析。
1）子区域1对主干区域场景等值
首先，假设主干区域和子区域2内功率注入场景不变，计算子区域1内所有光伏功率注入场景下的边界注入功率并对其进行排序。然后，从边界注入功率的最小值按照所设置的功率等值场景差值依次递增，并以最大的边界注入功率作为最后的聚类中心。最终聚类结果如图11所示。由结果可以看出81个边界功率注入场景被聚类成23类，有效地降低了所计算的场景数量。
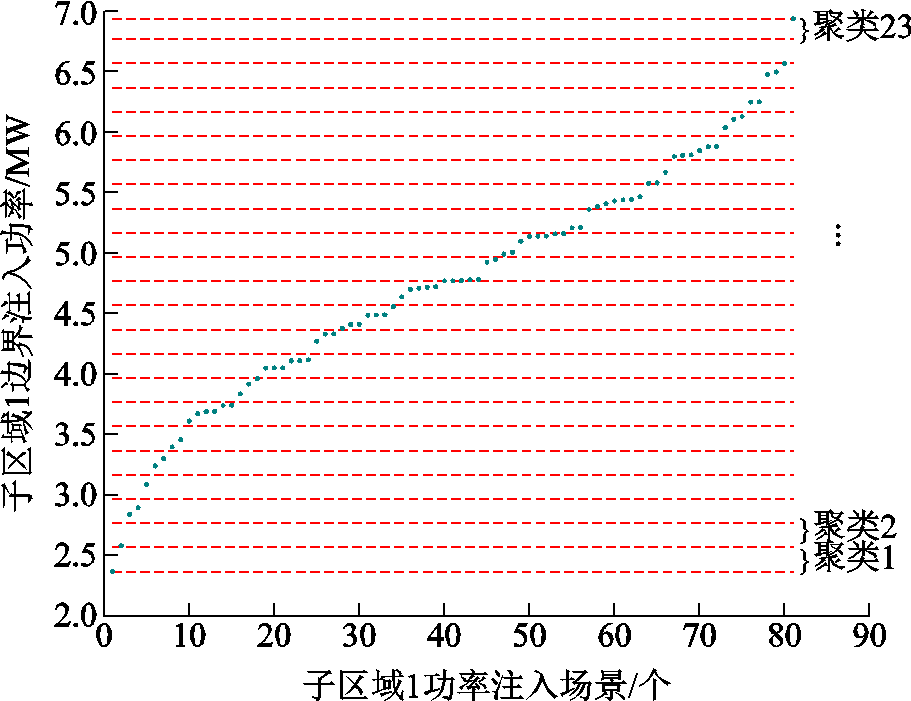
图11 子区域1边界注入功率散点图
Fig.11 Sub region 1 boundary injection power scatter
进一步，以主干区域内各节点电压和支路功率为分析对象，将聚类后的边界量场景代入主干区域重新构造的潮流方程中，并采用牛拉法进行求解，计算结果与蒙特卡洛模拟的对比见表1。
表1 子区域1对主干区域场景等值对比
Tab.1 Scenario equivalence between sub region 1 and main region
本文方法计算场景数量蒙特卡洛模拟所需计算的场景数量主干区域电气量与蒙特卡洛模拟相比的最大误差(%) 2381节点电压0.069 支路功率0.98
从表1中看出，所提方法在子区域对主干区域场景等值时具有较高的精度，同时也除去了冗余的边界量场景。在实际应用过程中，可以根据需要来选择合适的聚类方法。
2）主干区域对子区域1的场景等值
假设子区域2和主干区域的光伏的功率注入场景不变，计算主干区域内所有光伏功率注入场景下子区域1的边界电压的二次方，并对其进行排序。然后，从最小值按照所设置的功率等值场景差值依次递增，并以最大的边界电压二次方（子区域1的边界量）作为最后的聚类中心。聚类结果如图12所示，由结果可以看出81个边界量被聚类成7类，有效地降低了所计算的场景数量。
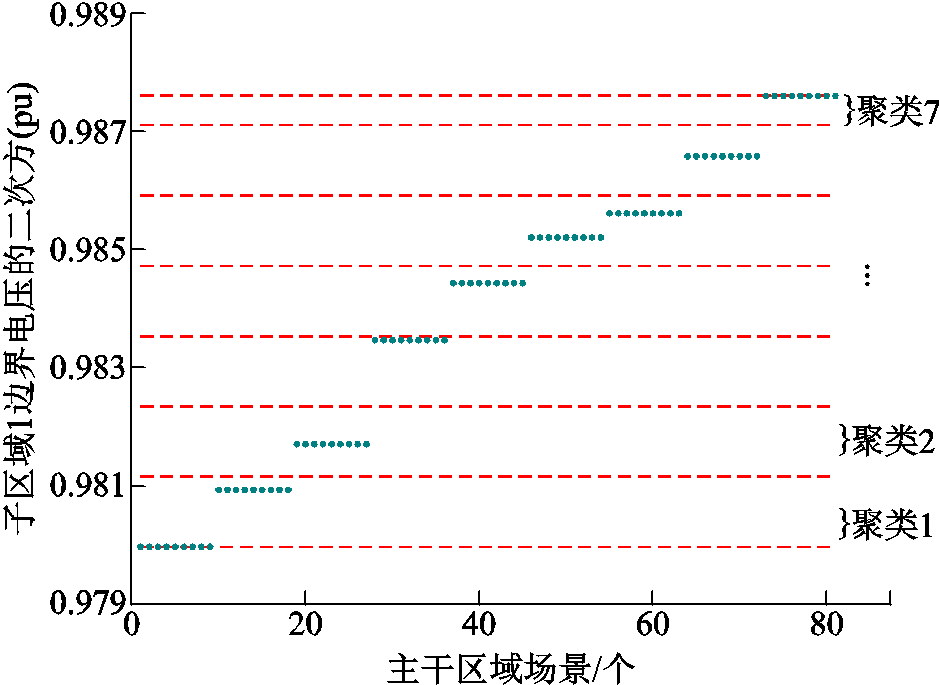
图12 主干区域功率注入下子区域1边界量
Fig.12 Backbone area power injection sub area 1 boundary amount
值得注意的是，在图12的排序结果中发现，每一簇的边界量中有9个场景中子区域1的边界电压是一致的。这是由于主干区域节点64和83的光伏注入功率只会影响线路1～63上传输的功率，并不会对主干区域内线路1、2之后的线路上传输的功率产生影响。因此，节点64和83的光伏注入功率场景对子区域1的边界电压影响是一致的。
接着，以子区域1各节点电压和支路功率为分析对象。设置聚类后的边界电压为根节点电压，代入子区域重新构造的潮流方程中并采用牛拉法进行求解，计算结果与蒙特卡洛模拟的对比见表2。
表2 主干区域对子区域1场景等值对比
Tab.2 Scenario equivalence between main region and sub region 1
本文方法计算场景数量蒙特卡洛模拟所需计算的场景数量子区域1电气量与蒙特卡洛模拟相比的最大误差(%) 781节点电压0.058 支路功率0.003
从表2中可以看出，采用本文所提方法在主干区域对子区域场景等值时具有较高的精度，同时也除去了冗余的边界量场景。在实际应用过程中，可以根据需要来选择合适的聚类方法。
4.2.3 与传统场景缩减方法的对比分析
在传统场景缩减方法中，k-means算法由于聚类效果好、聚类速度快的优点得到了广泛应用[23]。本小节从计算精度和时间两个角度，对比分析区域间场景等值方法与k-means算法的计算结果，验证所提方法的优越性。
需要注意的是，传统k-means算法的缩减效果对聚类中心数量的选取较为敏感。据此，本文根据不同k值下误差二次方和的变化趋势，采用肘部法则来确定最优聚类中心个数，避免过小或者过大的聚类数量影响场景缩减的效果[24]。
1）子区域1对主干区域场景等值的对比分析
假设子区域1的节点37、46、54和62的随机功率注入如图13a所示，分别采用100种场景进行刻画。进一步采用k-means方法对其进行聚类，并依据肘部法则确定最优的聚类中心个数，各节点在不同k值下的误差平方和如图13b所示。
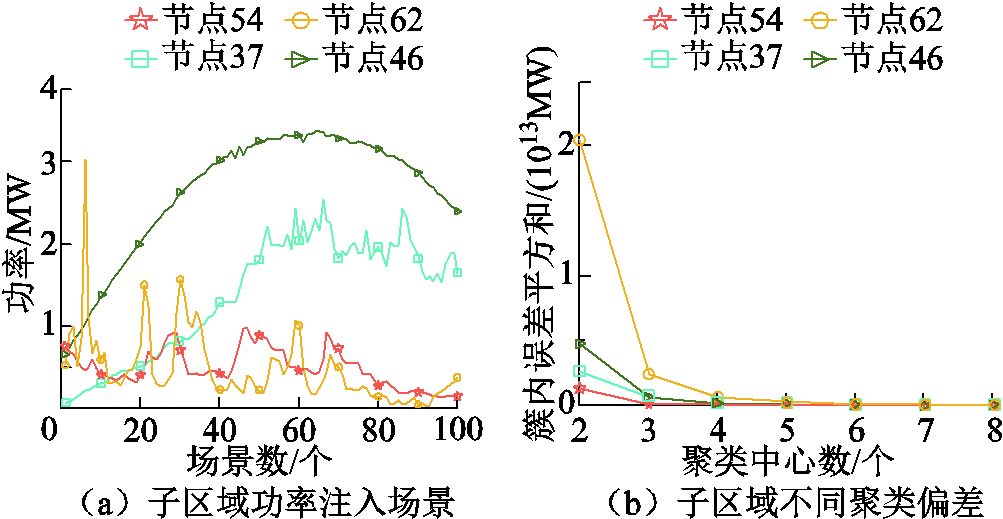
图13 子区域1节点注入及k-means聚类误差平方和
Fig.13 Sub region 1 node injection and k-means clustering error sum of squares
子区域1中各节点随机功率注入场景的最优聚类中心数与聚类结果见表3。
表3 子区域1中k-means聚类结果
Tab.3 k-means clustering results in sub region 1
节点最优聚类中心数/个聚类结果 3730.522、0.978、0.186 4631.229、0.632、1.585 5430.643、0.102、0.353 6231.652、0.244、0.968
进一步，按照本文所提方法在传统场景缩减方法在表3结果的基础之上采用本文所提方法进行场景等值，等值过程如图14所示。
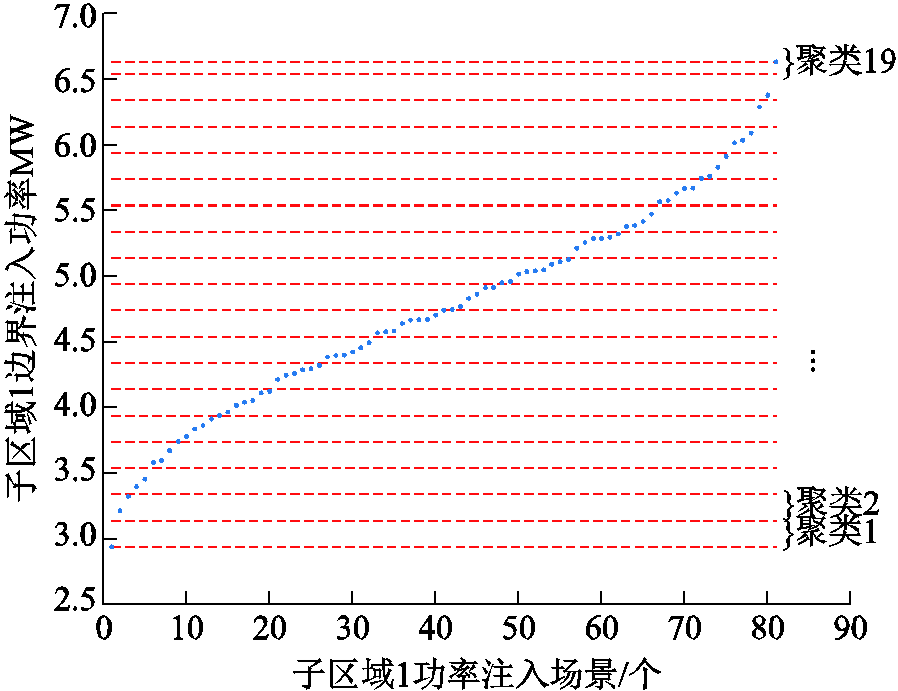
图14 子区域1边界功率等值
Fig.14 Subregion 1 boundary power equivalence
进一步将等值后的场景代入新构建的潮流方程中，计算主干区域的潮流量，统计对比结果见表4。
表4 基于k-means子区域1对主干区域场景等值对比
Tab.4 k-means based scenario equivalence of sub region 1 to backbone region
本文方法计算场景数量k-means聚类后所需计算场景数量主干区域电气量最大误差(%) 1981节点电压0.056 支路功率0.67
从表4中看出，所提方法在k-means场景缩减的基础上，进一步等值了引起边界量相同的场景，大大降低了所需计算的场景数量，且具有较小的误差。证明了所提方法在场景等值时的有效性。
2）主干区域对子区域1场景等值的对比分析
假设主干区域内的节点6、22、64和83的随机功率注入如图15a所示。采用k-means方法对其进行聚类，并依据肘部法则确定最优的聚类中心个数，各节点在不同聚类中心数下的误差平方和如图15b所示。
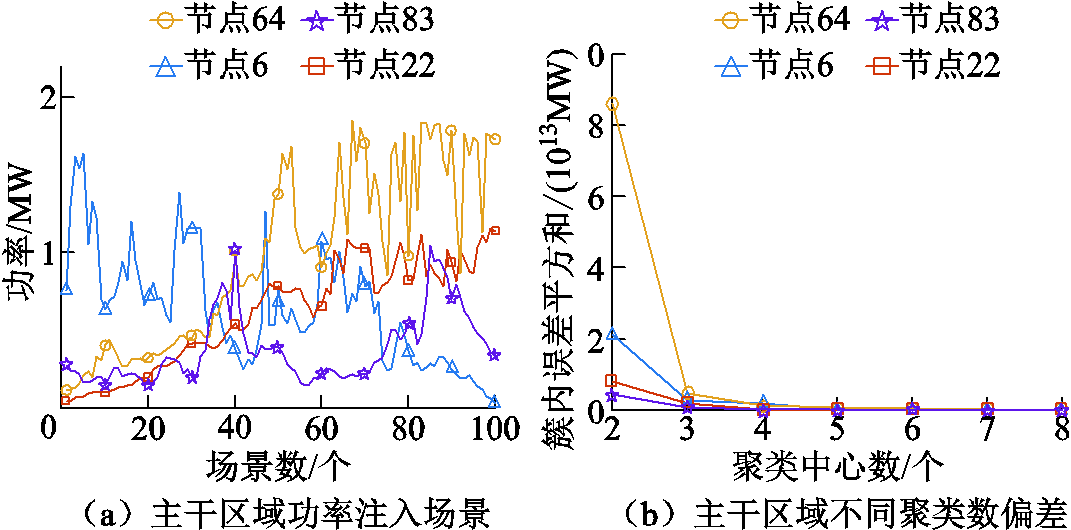
图15 主干区域1节点注入及k-means聚类过程
Fig.15 backbone area node injection and k-means clustering process
主干区域中各节点随机功率注入场景的最优聚类中心数与聚类结果见表5。
表5 主干区域中k-means聚类结果
Tab.5 k-means clustering results in backbone area
节点聚类中心数/个聚类结果 631.405、0.449、0.999 2230.906、0.154、0.509 6431.668、0.352、0.997 8330.249、0.898、0.542
由表5可以看出，使用k-means方法大量缩减了节点注入功率的场景数量。进一步，按照本文所提方法在传统场景缩减方法（表5结果）的基础之上进行场景等值，等值过程如图16所示。
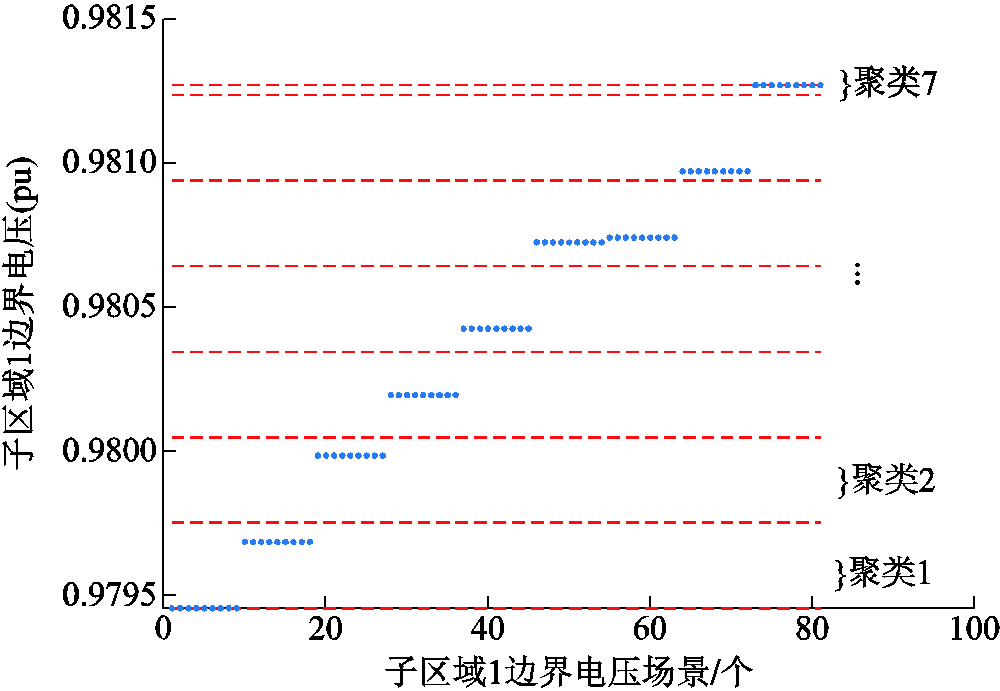
图16 子区域1边界电压等值
Fig.16 Subregion 1 boundary voltage equivalence
进一步将等值后的场景代入新构建的潮流方程中，在子区域1中的统计对比结果见表6。
从表6中看出，所提方法在k-means场景缩减的基础上，进一步等值了引起边界量相同的场景，大大降低了所需计算的场景数量，且具有较小的误差。
表6 基于k-means子区域1对主干区域场景等值对比
Tab.6 k-means based scenario equivalence of backbone region to sub region 1
本文方法计算场景数量k-means聚类后场景数量子区域1电气量最大误差(%) 781节点电压0.035 支路功率0.003
基于上述主干区域对子区域和子区域对主干区域的场景缩减效果分析，所提方法能够在现有考虑节点注入功率场景缩减的基础上，进一步对引起相同边界量的场景进行等值，证明了所提方法在场景等值时的有效性。
本小节对随机潮流分布式求解的计算结果进行准确性分析。基于图6光伏电站的所有出力场景，以312次（即531 441次）蒙特卡洛模拟为基准，并认为其结果是准确的，对比分析本文所提分布式随机潮流算法在分别在主干区域、子区域1和子区域2中计算时的准确性。
各区域分布式计算的收敛曲线如图17～图19所示。其中，图17a、图18a、图19a是一种功率注入场景下，采用牛拉法时各区域内节点电压二次方的收敛过程图，图17b、图18b、图19b为该区域所有场景下潮流计算的收敛曲线。
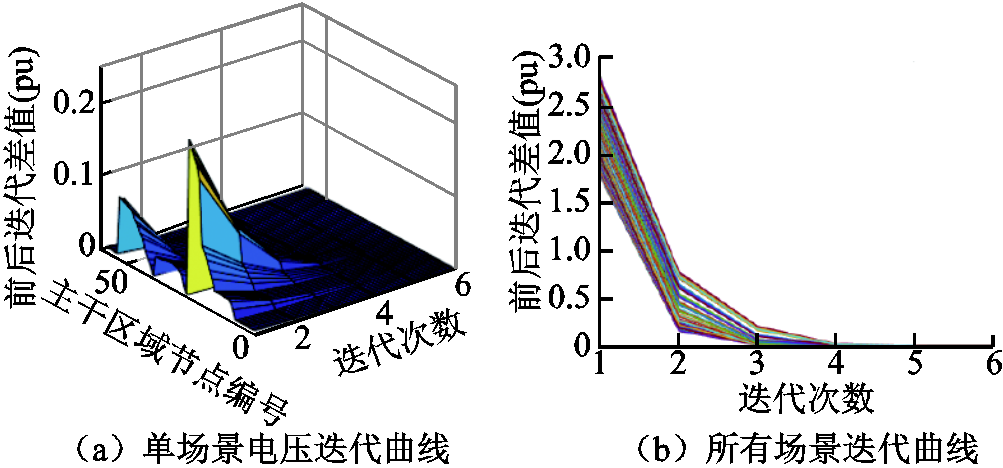
图17 主干区域迭代收敛曲线
Fig.17 Iterative convergence curve in the trunk region
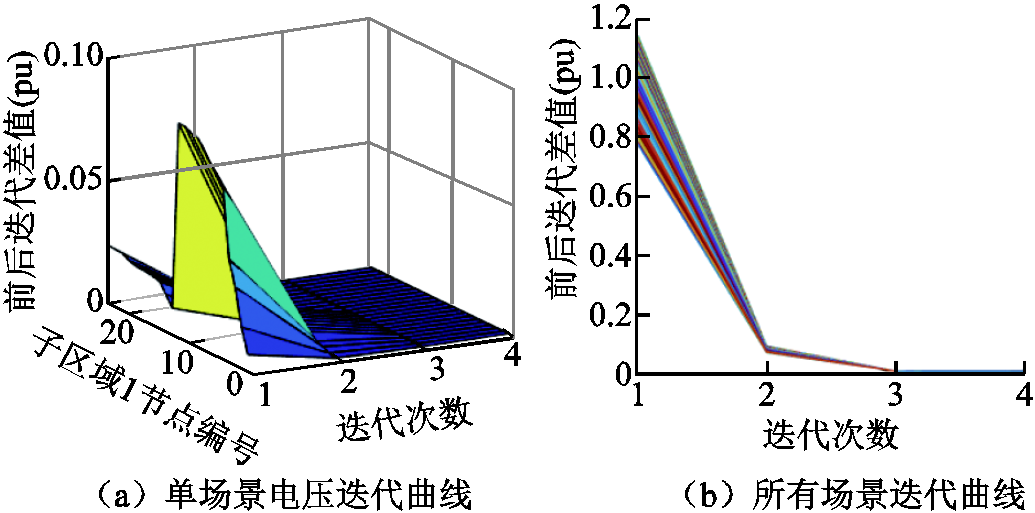
图18 子区域1迭代收敛曲线
Fig.18 Iterative convergence curve for subdomain 1
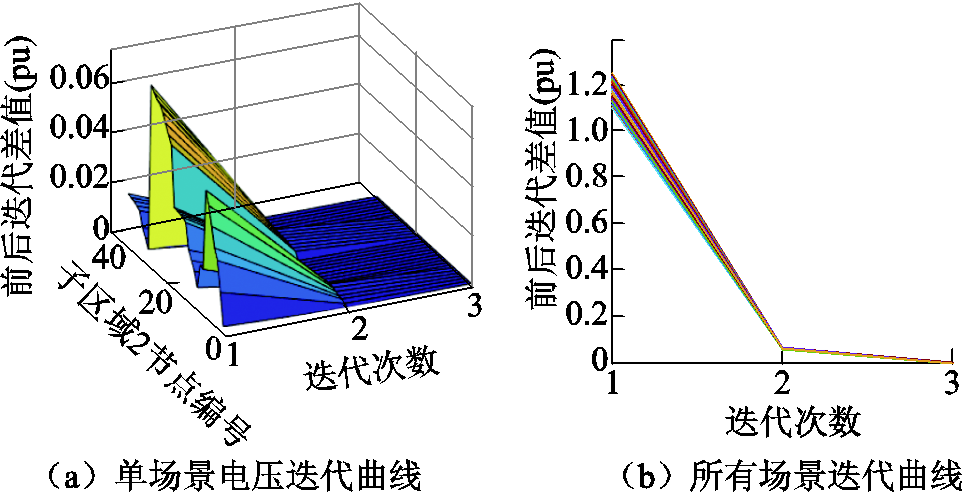
图19 子区域2迭代收敛曲线
Fig.19 Iterative convergence curve for subdomain 2
各区域迭代收敛后，分别统计本文所提方法与蒙特卡洛模拟的误差。主干区域、子区域1和子区域2内各节点电压和支路功率的计算误差如图20～图22所示。
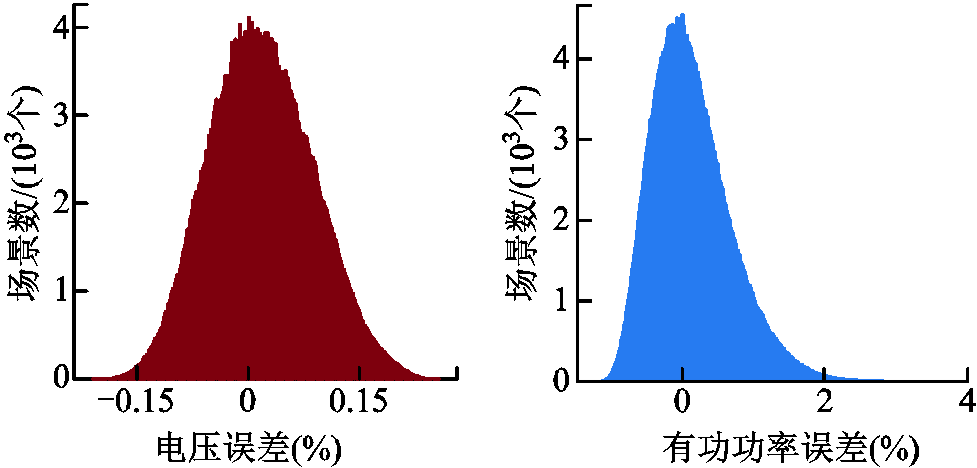
图20 主干区域所有节点电压与有功功率误差
Fig.20 Error diagram of voltage and power of all nodes in in trunk area
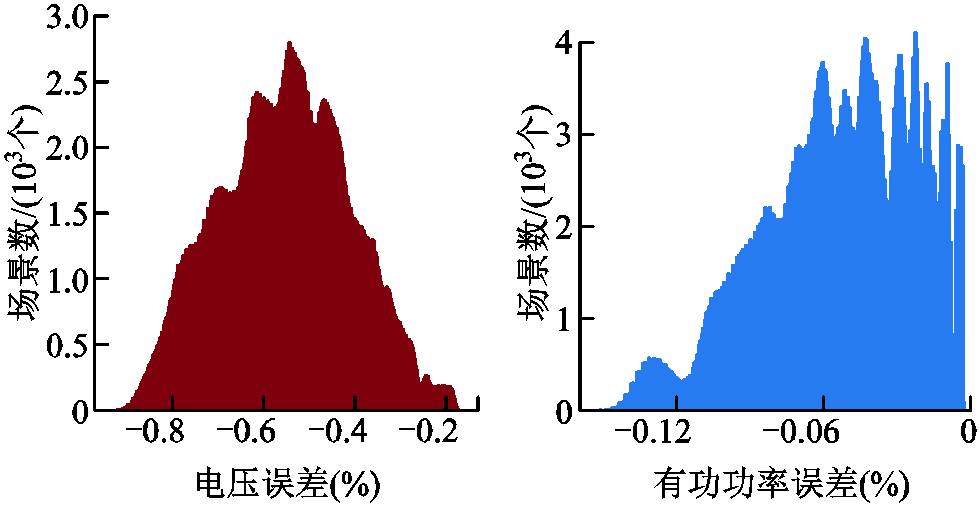
图21 子区域1所有节点电压与有功功率误差
Fig.21 Error diagram of voltage and power of all nodes in sub area 1
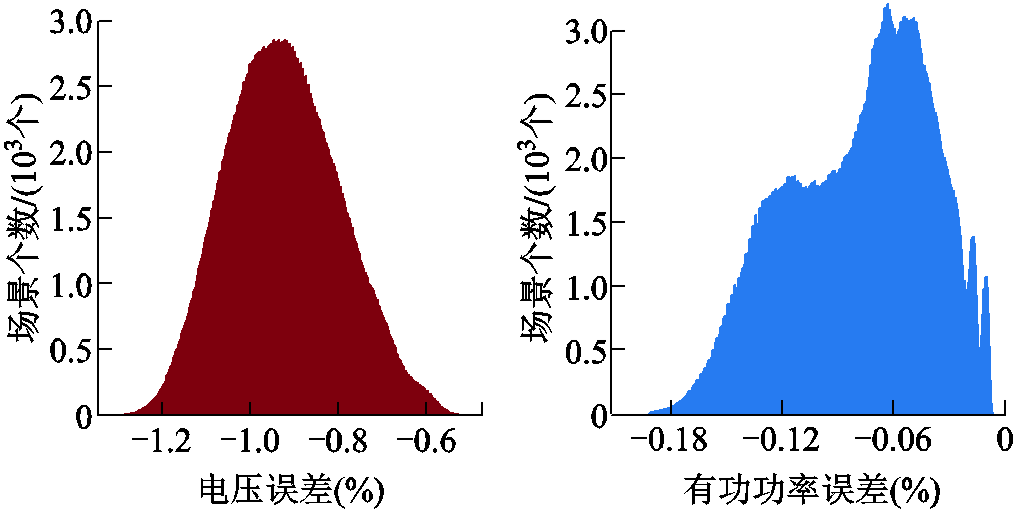
图22 子区域2所有节点电压与有功功率误差
Fig.22 Error diagram of voltage and power of all nodes in sub area 2
上述误差D的计算公式为
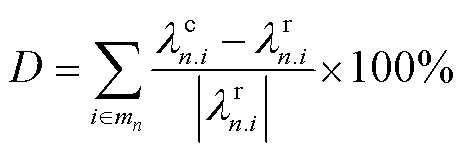（15）
式中，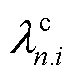
为区域间场景等值下配电网区域n第i个节点电气量的计算值；
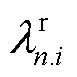为蒙特卡洛模拟下配电网区域n第i个节点电气量的计算值；mn为区域n的节点数目。
由图21和图22可以发现，子区域1和2的电压和有功功率误差均为负值。电压误差为负主要由以下两方面决定：一方面，在子区域对主干区域的场景等值过程中，选取了偏大的等值边界注入功率，导致主干区域流过的功率偏大，进而子区域的边界电压更小；另一方面，由于对子区域的边界电压进行了一阶泰勒展开忽略了高次项，也进一步降低了子区域电压的值。子区域1和2的有功误差功率为负，这是由于子区域是以边界节点为根节点进行潮流计算的，而边界节点电压值低于蒙特卡洛模拟的值，导致子区域各个线路传输的功率值增大。进一步，由于线路功率出现反送，其值为负值。由此代入式（15）后，有功功率的误差仍为负值。
对比图21和图22中不同子区域的误差结果，可以看出子区域2的误差要高于子区域1的误差。这是由于各子区域分别以边界节点的一阶泰勒展开值作为根节点，结合自身局部功率注入信息求解潮流结果。而与子区域1相比，子区域2离配电网的根节点更远，导致使用偏导数求得的边界电压值与真实值的偏差更大。因此，子区域2的有功功率与电压偏差均大于子区域1。
对比图20～图22的误差结果可以看出，主干区域电压的误差较小、有功功率的误差较大，而子区域电压的误差较大、有功功率的误差较小。这是由于在进行边界量的等值时，子区域对主干区域是边界注入功率的等值，而主干区域对子区域是边界电压的等值，因此导致产生上述结果。
综上所述，各区域所有场景下电压与支路功率的误差均较小，验证了所提分布式算法计算随机潮流时的有效性。
本小节分析所提方法在提升计算效率上的有效性。所有计算结果均通过一台计算机硬件配置为3.10GHz Intel(R) Core(TM) i5-11300H CPU，16 GB RAM求解的得出，运行软件为Matlab 9.9.0.1467703。加速比SA定义为
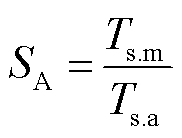（16）
式中，Ts.m为蒙特卡洛模拟需要的计算时间；Ts.a为本文所提方法需要的计算时间。
经统计，采用蒙特卡洛模拟和本文所提方法的计算时间见表7。
表7 计算时间对比表
Tab.7 Calculation time comparison
参数蒙特卡洛模拟本文所提方法 场景/个531 441434 97 时间/s42 517.283 752.73
由于本文所提方法将所计算的场景数量从原来的指数型增加变为了加法，因此加速比为11.32，在计算效率上高于蒙特卡洛模拟方法。
为解决配电网随机潮流算法中需要大量节点功率注入样本模拟导致求解效率低的问题，提出一种区域间场景等值的配电网随机潮流加速算法，通过算例进行验证，结论如下：
1）从配电网的拓扑连接规律出发，将区域间的潮流作用转换为对边界量的影响。进一步，基于现有以节点注入功率为研究对象的场景缩减方法，通过等值引起其他区域相同边界量的功率注入场景，有效地减少了在传递过程中的冗余信息，达到简化随机潮流计算的目的。
2）所提的配电网随机潮流分布式算法，不需要对所有节点随机功率注入样本进行集中处理和统一计算，仅通过各区域内部的功率样本和交换的等值场景信息，即可求解随机潮流结果。
3）相比现有的集中式随机潮流算法，分布式随机潮流算法能够在相同的时间约束下计算更多样本，有效加速了配电网随机潮流的计算速度。
下一步工作可将点估计方法与本文所提区域间场景等值方法进行结合，提升其计算精度并丰富配电网的区域划分方法。
参考文献
[1] 国家能源局. 2022年前三季度光伏发电建设运行情况[EB/OL]. [2022-10-17]. http://www.nea.gov.cn/ 2022-10/27/c_1310671519.htm.
[2] 王晨旭, 唐飞, 刘涤尘, 等. 基于双层代理模型的概率-区间潮流计算及灵敏度分析[J]. 电工技术学报, 2022, 37(5): 1181-1193. Wang Chenxu, Tang Fei, Liu Dichen, et al. Probabilistic-interval power flow and sensitivity analysis using double layer surrogate method[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1181-1193.
[3] 郑重, 苗世洪, 李超, 等. 面向微型能源互联网接入的交直流配电网协同优化调度策略[J]. 电工技术学报, 2022, 37(1): 192-207. Zheng Zhong, Miao Shihong, Li Chao, et al. Coordinated optimal dispatching strategy of AC/DC distribution network for the integration of micro energy Internet[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 192-207.
[4] 倪萌, 王蓓蓓, 朱红, 等. 能源互联背景下面向高弹性的多元融合配电网双层分布式优化调度方法研究[J]. 电工技术学报, 2022, 37(1): 208-219. Ni Meng, Wang Beibei, Zhu Hong, et al. Study of two-layer distributed optimal scheduling strategy for highly elastic multi-resource fusion distribution network in energy interconnection environment[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 208-219.
[5] 朱俊澎, 黄勇, 马良, 等. 基于不确定性最优潮流的配电网分布式发电消纳能力评估[J]. 电力系统自动化, 2022, 46(14): 46-54. Zhu Junpeng, Huang Yong, Ma Liang, et al. Assessment on distributed generation accomodation capability for distribution network based on uncertain optimal power flow[J]. Automation of Electric Power Systems, 2022, 46(14): 46-54.
[6] 赵平, 赵期期, 艾小猛. 考虑极限场景的主动配电网重构与无功电压调整联合鲁棒优化[J]. 电工技术学报, 2021, 36(增刊2): 496-506. Zhao Ping, Zhao Qiqi, Ai Xiaomeng. Network reconfiguration and reactive power voltage regulation coordinated robust optimization for active distribution network considering extreme scenarios[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 496-506.
[7] 王海鑫, 袁佳慧, 陈哲, 等. 智慧城市车-站-网一体化运行关键技术研究综述及展望[J]. 电工技术学报, 2022, 37(1): 112-132. Wang Haixin, Yuan Jiahui, Chen Zhe, et al. Review and prospect of key techniques for vehicle-station-network integrated operation in smart city[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 112-132.
[8] Prusty B R, Jena D. A critical review on probabilistic load flow studies in uncertainty constrained power systems with photovoltaic generation and a new approach[J]. Renewable and Sustainable Energy Reviews, 2017, 69: 1286-1302.
[9] Lin Chaofan, Bie Zhaohong, Pan Chaoqiong, et al. Fast cumulant method for probabilistic power flow considering the nonlinear relationship of wind power generation[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2537-2548.
[10] 高元海, 王淳. 级数展开法拟合概率潮流分布函数的局限及改进[J]. 中国电机工程学报, 2021, 41(17): 5900-5911. Gao Yuanhai, Wang Chun. Limitation analysis and improvement for series expansion methods to fit the distribution function of probabilistic power flow[J]. Proceedings of the CSEE, 2021, 41(17): 5900-5911.
[11] 郭效军, 蔡德福. 不同级数展开的半不变量法概率潮流计算比较分析[J]. 电力自动化设备, 2013, 33(12): 85-90, 110. Guo Xiaojun, Cai Defu. Comparison of probabilistic load flow calculation based on cumulant method among different series expansions[J]. Electric Power Automation Equipment, 2013, 33(12): 85-90, 110.
[12] 陈朝宽, 张靖, 何宇, 等. 基于Cornish-Fisher级数和半不变量法的含光伏配电系统风险评估[J]. 电力自动化设备, 2021, 41(2): 91-96. Chen Chaokuan, Zhang Jing, He Yu, et al. Risk assessment of distribution system with photovoltaic based on Cornish-Fisher series and cumulant method[J]. Electric Power Automation Equipment, 2021, 41(2): 91-96.
[13] 柳志航, 卫志农, 高昇宇, 等. 源-荷互动环境下含高比例风电并网的自适应线性化概率潮流计算[J]. 电网技术, 2019, 43(11): 3926-3937. Liu Zhihang, Wei Zhinong, Gao Shengyu, et al. Adaptive-linearized probabilistic power flow calculation for power grid integrated with high proportion wind power in source-load interactive environment[J]. Power System Technology, 2019, 43(11): 3926-3937.
[14] Sheng Hao, Wang Xiaozhe. Probabilistic power flow calculation using non-intrusive low-rank approximation method[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3014-3025.
[15] 苏晨博, 刘崇茹, 李至峪, 等. 基于贝叶斯理论的考虑多维风速之间相关性的概率潮流计算[J]. 电力系统自动化, 2021, 45(3): 157-165. Su Chenbo, Liu Chongru, Li Zhiyu, et al. Bayesian theory based calculation of probabilistic power flow considering correlation between multi-dimensional wind speed[J]. Automation of Electric Power Systems, 2021, 45(3): 157-165.
[16] 张立波, 程浩忠, 曾平良, 等. 基于Nataf逆变换的概率潮流三点估计法[J]. 电工技术学报, 2016, 31(6): 187-194. Zhang Libo, Cheng Haozhong, Zeng Pingliang, et al. A three-point estimate method for solving probabilistic load flow based on inverse Nataf transformation[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 187-194.
[17] 李钰洋, 王增平. 基于高斯求积的智能配电网三相概率潮流点估计法[J]. 电网技术, 2022, 46(2): 709-717. Li Yuyang, Wang Zengping. Three-phase probabilistic load flow for smart distribution network based on gauss-quadrature-based point estimate method[J]. Power System Technology, 2022, 46(2): 709-717.
[18] 方斯顿, 程浩忠, 徐国栋, 等. 基于Nataf变换含相关性的扩展准蒙特卡洛随机潮流方法[J]. 电工技术学报, 2017, 32(2): 255-263. Fang Sidun, Cheng Haozhong, Xu Guodong, et al. A Nataf transformation based on extended quasi Monte Carlo simulation method for solving probabilistic load flow problems with correlated random variables[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 255-263.
[19] 谢桦, 任超宇, 郭志星, 等. 基于聚类抽样的随机潮流计算[J]. 电工技术学报, 2020, 35(23): 4940-4948. Xie Hua, Ren Chaoyu, Guo Zhixing, et al. Stochastic load flow calculation method based on clustering and sampling[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4940-4948.
[20] Yang Yan, Yang Zhifang, Yu Juan, et al. Fast calculation of probabilistic power flow: a model-based deep learning approach[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2235-2244.
[21] Zhou Gan, Bo Rui, Chien L, et al. GPU-accelerated algorithm for online probabilistic power flow[J]. IEEE Transactions on Power Systems, 2018, 33(1): 1132-1135.
[22] 朱星旭, 韩学山, 杨明, 等. 含分布式光伏与储能配电网时变最优潮流追踪的分布式算法[J]. 中国电机工程学报, 2019, 39(9): 2644-2658. Zhu Xingxu, Han Xueshan, Yang Ming, et al. A distributed algorithm for time-varying optimal power flow tracking in distribution networks with photovoltaics and energy storage[J]. Proceedings of the CSEE, 2019, 39(9): 2644-2658.
[23] Sannigrahi S, Ghatak S R, Acharjee P. Multi-scenario based Bi-level coordinated planning of active distribution system under uncertain environment[J]. IEEE Transactions on Industry Applications, 2020, 56(1): 850-863.
[24] 杨俊闯, 赵超. K-Means聚类算法研究综述[J]. 计算机工程与应用, 2019, 55(23): 7-14, 63. Yang Junchuang, Zhao Chao. Survey on K-Means clustering algorithm[J]. Computer Engineering and Applications, 2019, 55(23): 7-14, 63.
Abstract In the stochastic power flow algorithm of distribution network, the power injection needs a lot of simulation, which will lead to the problem of low computational efficiency. In recent years, scholars have made some achievements in the research of scene reduction, but the designed methods may still face the problem of low computational efficiency after being implemented in systems with too many nodes. Therefore, this paper proposes a stochastic power flow acceleration algorithm for distribution networks based on inter-regional scenario equivalence. Based on the existing mainstream scenario reduction method, the stochastic power flow calculation is further accelerated by adding scenarios that lead to the injection of the same boundary quantity in other regions.
Firstly, based on the topology connection law of distribution network, the influence of power injection scenarios in each region on power flow in other regions is transformed into the influence on its boundary quantities, and the multi-regional power flow model that affects each other through boundary quantities is established. Secondly, an inter-regional scenario equivalence method is proposed, which can quickly equalize scenarios that cause the same power flow change in other regions. Then, a distributed solution algorithm for stochastic power flow is designed. Each region completes the distributed solution of stochastic power flow by exchanging boundary equivalent scenarios and combining local power injection information.
According to this method, the IEEE 118 node test system is solved with partition and stochastic power flow. Simulation results show that the proposed distributed algorithm converges in all regions. In terms of calculation accuracy, the maximum errors of voltage and active power between the scene equivalent imitation method proposed in the main region and the Monte Carlo simulation method are 0.069% and 0.98% respectively, while the maximum errors of voltage and active power between the scene equivalent imitation method proposed in the sub-region and the Monte Carlo simulation method are 0.058% and 0.003% respectively. It can be considered that the calculation results are consistent. In terms of computational efficiency, the number of scenarios required by Monte Carlo simulation and distributed solution algorithms is 531 441 and 43 497, respectively. Compared with Monte Carlo simulation, the acceleration ratio of distributed solution method is 11.32, which effectively reduces the simulation scenarios required by stochastic power flow.
Through the example analysis, the following conclusions can be drawn: (1) By merging the power injection scenarios that cause the same boundary quantity in other regions, the redundant information in the transmission process can be effectively reduced. (2) The proposed stochastic power flow distributed algorithm does not require centralized processing and unified calculation of the stochastic power flow injection samples of each node, but only needs to solve the stochastic power flow results through the power flow samples of each region and exchange the equivalent scenario information. (3) Compared with the existing centralized stochastic power flow algorithm, the distributed stochastic power flow algorithm can calculate more samples under the same time constraint. In the next step, the point estimation method can be combined with the proposed inter-zone scenario equivalence method to improve its calculation accuracy and enrich the distribution network region division method.
keywords：Distribution network, scene equivalent, distributed photovoltaic, distributed, stochastic power flow
内蒙古自治区科学技术厅揭榜挂帅项目（2022JBGS0044）和东北电力大学博士科研启动基金（BSJXM-2021102）资助。
收稿日期 2023-02-14
改稿日期 2023-04-20
DOI:10.19595/j.cnki.1000-6753.tces.230156
中图分类号：TM711
李军徽 男，1976年生，教授，博士生导师，博士，研究方向为新能源发电运行与控制，储能技术在电力系统中的应用。E-mail：lijunhui@neepu.edu.cn
朱星旭 男，1989年生，讲师，硕士生导师，研究方向为电力系统运行与控制。E-mail：neduzxx@163.com（通信作者）
（编辑 赫 蕾）