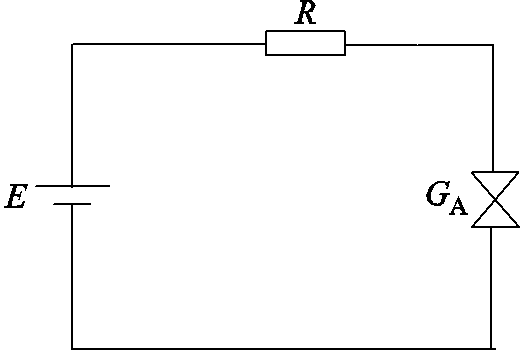
图1 电阻性火花试验等效电路
Fig.1 Equivalent circuit of resistive spark test
摘要 区别于电感性和电容性本质安全电路,电阻性本质安全电路的电弧放电波形因具有三种类型一直无法被准确描述,且电阻性电路本质安全判据的不完善描述会导致实际运行条件下爆炸事故的多发性。对此,该文首先考虑电阻性本质安全电路的放电过程及波形特征,基于函数型数据分析回归算法,建立了高维、参数强相关、适用范围广的电阻性电路电弧放电数学模型,并基于模型建立了相应的本质安全能量判据;然后采用该模型模拟电阻性电路放电过程并提出了一种电弧放电波形分类方法,发现在特定电路参数条件下,当电路正常工作电流I≤0.15 A或I≥0.6 A时,电弧放电基本呈现典型放电形式;最后搭建火花放电试验平台,验证了所建电弧模型的可行性与预测效果的准确性。
关键词:电弧放电数学模型 本质安全 函数型数据 能量判据
应用于煤炭、石油、化工等爆炸性气体环境的电气设备必须满足电气防爆要求,且须对弱电设备优先设计成为本质安全型。研究本质安全(以下简称本安)电路的理论基础是电弧放电引燃机理、电弧放电数学模型和本质安全判据。本安电路电弧放电属于低能(mJ级)电弧放电,其过程复杂,同时受到电气参数、环境参数和检测装置等因素的影响[1-2]。目前,对电路安全性能的评估和研究的常用方法主要包括:使用IEC火花试验装置进行放电试验,根据试验结果直接判断,以及通过建立电弧放电数学模型来设定能量判据和功率判据。这些方法在评估电路安全性能中起着关键作用,有助于确保电路在各种条件下的稳定性和可靠性。
最基本的本安电路按性质可分为电感性电路、电容性电路与电阻性电路。其中,电感性电路电弧放电的数学模型研究居多,包括放电电流线性衰减模型[3]、放电电流抛物线模型、放电电流幂函数模型、静态伏安特性模型[4]和动态伏安特性模型[5]等。文献[6]根据电弧能量平衡理论结合最小二乘法,建立Mayr动态电弧电阻模型。文献[7]将电感性电路电弧放电与统计学相结合,发现放电时间的双正态分布规律。文献[8]基于椭圆积分法,推导电感性电路试验电极的微观表面形貌、发射电流密度、焦耳热和热传导效应等因素与电弧特性的关系并建立模型。文献[9]考虑极间场增强因子作用,建立甲烷-空气混合气体电感分断建弧过程的电子漂移扩散模型和非电子组分重物质输运模型。
对于电容性本质安全电路,现阶段放电模型包括文献[10]提出的电势电容等效模型,以及文献[11]应用Matlab中Cftool工具箱,提出的最小点燃曲线数值化电容性电路放电模型等。文献[12]利用最小二乘法得到了放电持续时间与电容之间的数学表达式,建立了电容性电路短路放电电流和电压模型。文献[13]通过分析IEC火花试验波形提出了电容性电路放电指数模型,得到了电容性电路放电电流、放电电压的数学表达式。文献[14]综合考虑了电路中线路的电感、电容、电阻参数,建立了与实际电路一致的电容等效电路模型。文献[15]利用Fluent软件建立电容性电路放电间隙电压、电流数学模型,拟合出最小点火半径与有效点燃能量之间的函数关系式。文献[16]基于Fowler-Nordheim理论分析一次放电火花电压变化特性,建立放电电压指数模型,推导了火花功率与初始电压、放电电阻、放电时间的函数关系。文献[17]采用等效电荷法,建立了电容短路后火花放电的二维PIC/MCC(particle in cell with Monte Carlo collision)模型。
区别于电感性和电容性本质安全电路,电阻性本质安全电路的电弧放电波形因具有三种类型一直无法被准确描述。文献[18]仅模仿电感性电路的放电电流抛物线模型对电阻性电路电弧放电的三种形式进行了简单描述。
上述研究表明,目前对于电阻性本质安全电路的电弧放电模型的研究还不完善,试验波形和理论分析表明,电阻性电路电弧放电的数据特征是高维度的,且电路参数的影响及环境的影响呈现出高度相关性,以往的建模手段无法直接探究模型数值解。此外,通过建立的单一电压或电流模型而推导出的相关表达式可能因简化而存在误差,并且本安非爆炸性评价方法理论缺少对电阻性电路本安判据的描述,致使其在实际工作中因参数不合理而引起的爆炸事故的可能性大大增加。
电弧放电是本质安全理论中最常见的放电形式,其主要出现在小电流、低电压的本质安全电路中。电路触电断开瞬间,接触压力降低且电极接触面减小。当电极上的电流电压与接触点熔点相当时,电极间形成液态金属滴。随着电极继续拉开,液态金属滴在两极间形成金属桥,引发电弧[19]。电阻性火花试验等效电路如图1所示,图中E为电源电压,R为电路电阻,GA表示放电电弧。

图1 电阻性火花试验等效电路
Fig.1 Equivalent circuit of resistive spark test
电阻性电路的电弧发生形式主要分为以下两种:
1)电阻性电路的断路火花。电阻为线性元件无法储能,电源能量即为火花能量的来源。电路断开时,电极接触面迅速减小,导致电流密度增大,电极间的电压随电阻增大,电极熔化形成液态金属桥。
2)电阻性电路的闭合火花。当电源电压较高时,电极因电路的闭合接近,接触瞬间空气击穿电离;当电源电压较低时,则不会产生电流。这就导致即使运行电压低于最小建弧电压,电路仍会产生电弧。
以往研究认为,电阻性电路的放电模型可由电感性电路放电模型简化得到[20]。但由于电路性质发生变化,模型的简化并不适用。IEC火花试验装置的电极断开时,低能电弧放电存在三种具有本质性区别的放电形式[18],目前尚未有文献对其机理进行合理解释,本文分别对三种形式电弧的形成与熄灭过程进行描述。电阻性电路放电实验波形的三种形式分别如图2~图4所示。
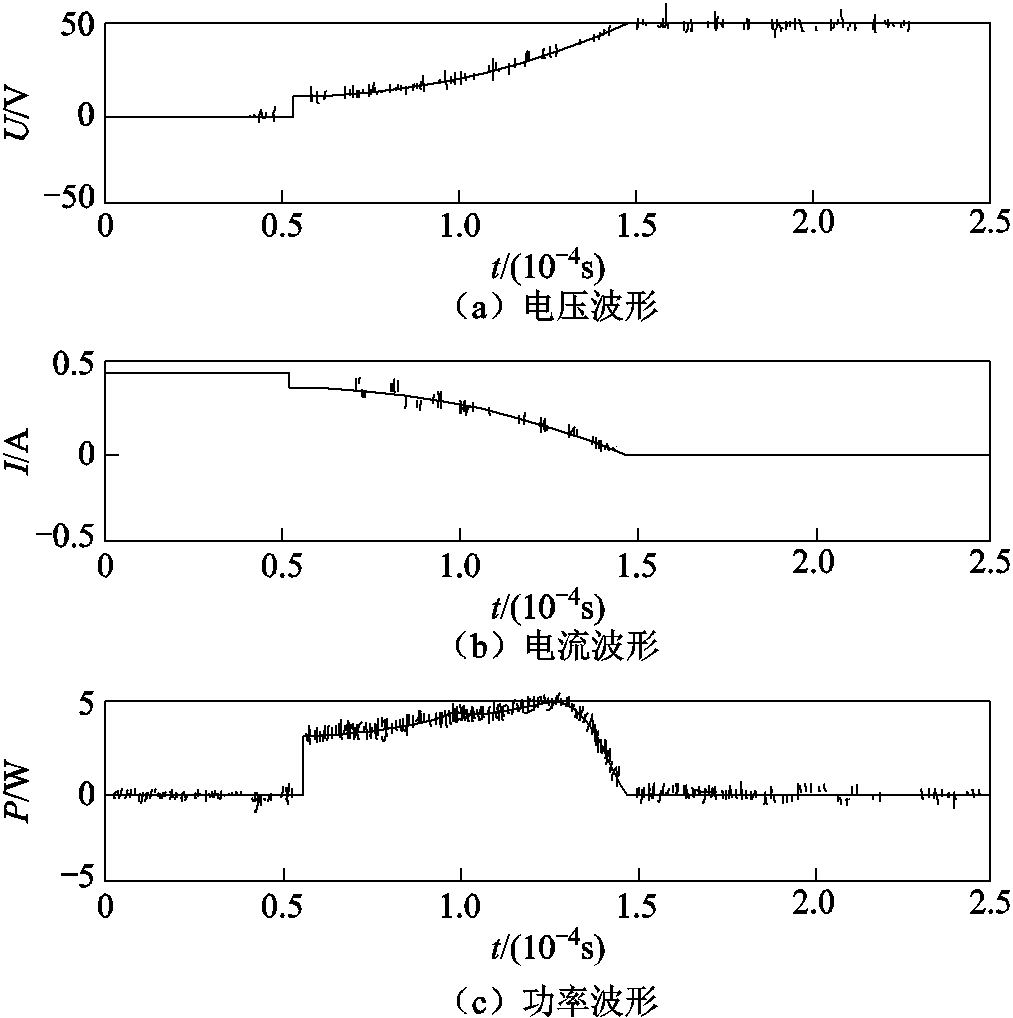
图2 电阻性电路放电实验波形第一种形式
Fig.2 The first case of resistance circuit discharge test waveforms
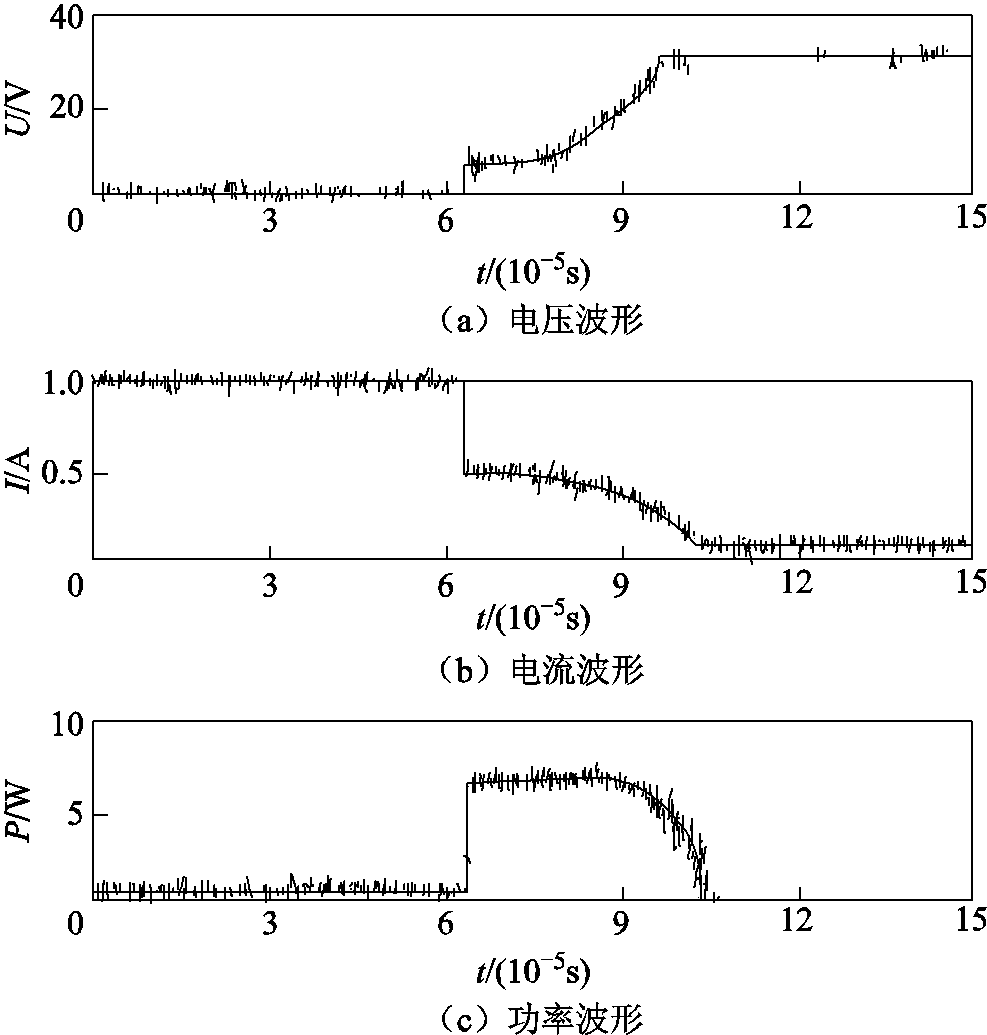
图3 电阻性电路放电实验波形第二种形式
Fig.3 The second case of resistance circuit discharge test waveforms
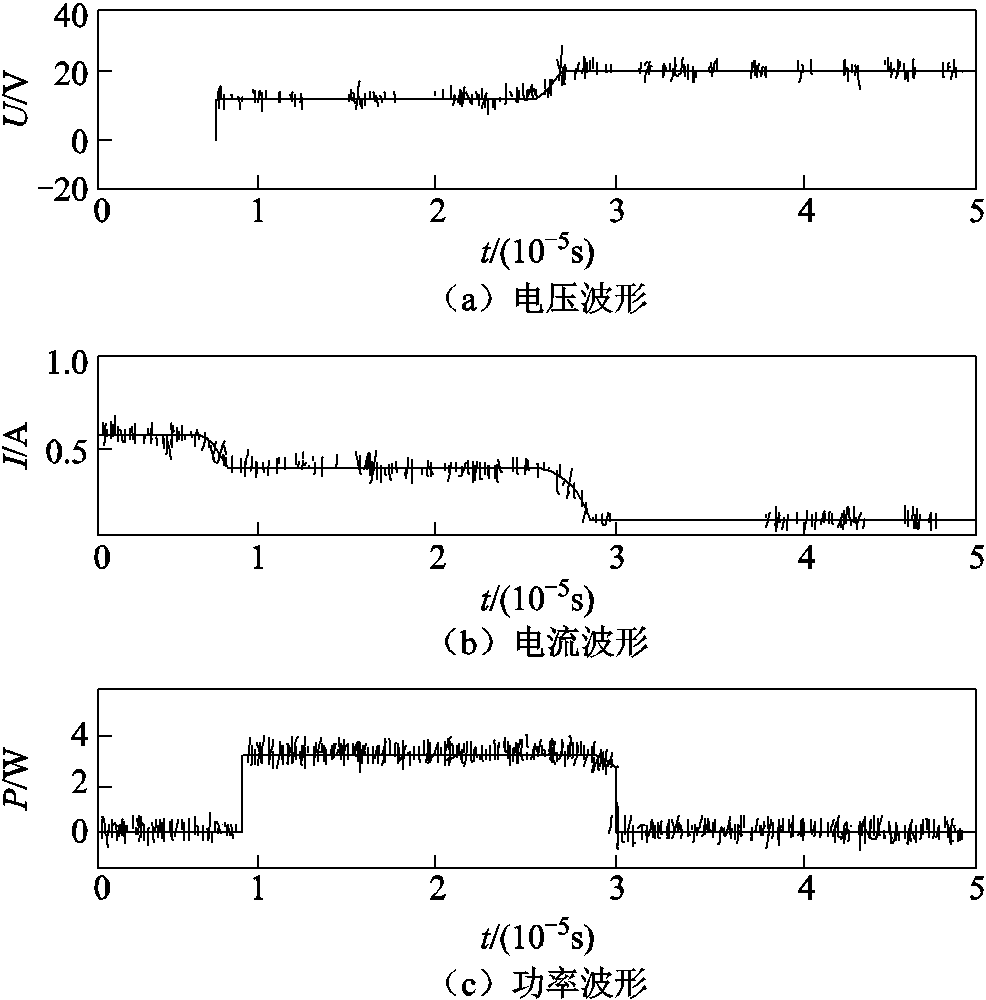
图4 电阻性电路放电实验波形第三种形式
Fig.4 The third case of resistance circuit discharge test waveforms
第一种放电形式是电极间电压首先突变为最小建弧电压,电流服从欧姆定律重新分配;之后电弧电压持续上升而电流持续下降;末期电弧电压快速升到电源电压,而电流快速下降为零。这种放电形式出现的概率为70%,且最容易引起爆炸,属于该类型电路低能电弧放电的典型形式。其放电电压U、电流I与功率P随时间t变化的波形如图2所示。
第二种放电形式是瞬间成弧后,电弧电压上升,电流下降,在整个放电时间内电弧功率逐渐降低,初期几乎没有变化,后期迅速降低到零值。在此情形下,放电时间相对较长,并且发生概率约为25%,其放电电流、电压与功率如图3所示。
第三种放电形式是瞬间成弧后,在放电过程中,电弧电压、电流基本恒定,直至放电完毕,此时电弧电压突然升到电源电压,电弧电流突然降为零,放电时间小,功率基本不变,其发生概率仅为5%,且不会引起爆炸。其放电电流、电压与功率如图4所示。
函数型数据分析(Functional Data Analysis, FDA)[21]回归算法无需对数据采集频率做任何限制,即可将动态函数曲线转换为“原始数据”,具备无限维的空间特征,其描述了如何使用数据光滑后的函数型数据进行建模,并提供其回归系数函数的估计算法和解的表示,具有更强的普适性。其算法流程如图5所示。
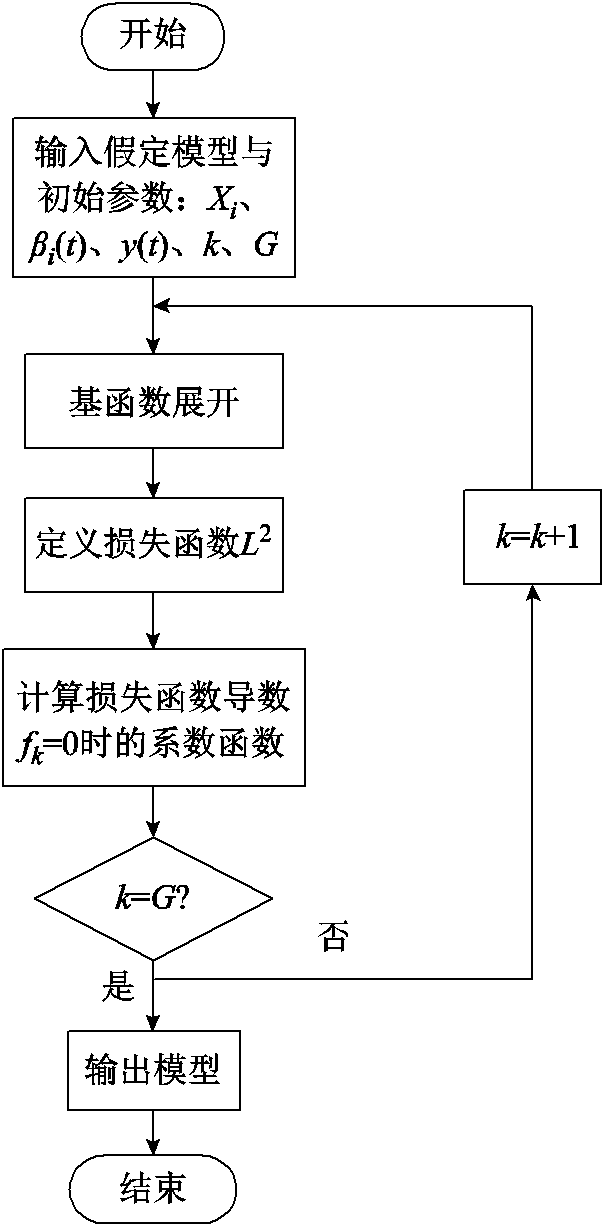
图5 函数数据分析回归算法流程
Fig.5 Flow chart of regression algorithm for functional data analysis
FDA算法具体计算步骤如下:
1)假定初始函数型数据回归模型为式(1),设定模型优化次数为G,此时的迭代次数k=1。
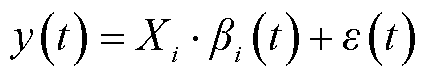 (1)
(1)
式中,y(t)为响应变量;bi(t)为p维未知的函数形系数;Xi为第i个特征量(协变量);Xi×b(t)为效应函数,代表不同协变量所占响应变量的权重;e(t)为误差函数,通常假设e(t)的均值为0。
2)求解系数函数与响应变量在Hilbert空间存在的最优傅里叶基函数(Fourier basis function)展开式[22]。对于给定的函数X(t),其傅里叶基函数展开式为
式中,φl(t)为关于t的基函数,l=1, 2,…, K,φ2r-1(t)= sin(rωt),φ2r(t)=cos(rωt);cl为傅里叶基函数的展开系数;K为基函数个数。K的选取决定了模型的拟合是否平滑,较大的K值可以显著地提高离散数据的平滑度,但存在丢失有用噪声的风险;过小的K值会使被展开函数的一些重要拟合信息被错过。
3)采用最小二乘准则定义损失函数,确定系数函数组成的系数矩阵。
4)计算损失函数导数fk=0时的模型系数函数。
5)判断此时的优化次数k与设置优化次数G是否相等。
6)若k=G,则输出模型,算法结束;若k¹G,则令k=k+1,将此时的系数函数作为模型的新参数,返回步骤2)计算,直至k=G。
通过以上算法,可以揭示电弧放电更深层级的动态演化规律,剖析高维复杂数据下电阻性电路放电的本质特征,建立更合理、更直观的放电模型。
本节基于上述函数型数据分析回归算法,结合电阻性电路电弧放电特性,详细阐述放电电弧电压的数学模型建模过程。
影响电阻性电路放电电弧特性的主要可控因素即电路的电参数(电源电压E、电阻R)。给定参数E和R,组成N个试验取值数对(En, Rn),n=1, 2,…, N;对应每一个(En, Rn),测得其开路电弧电压试验波形,在每一条波形特定节点上有限维取值,由离散数据重构隐含在其中的连续本征函数un(t),由此共得到N组电压样本数据(En, Rn; un(t))。取一组样本,以理想直流电压源与电路电阻的非时变性和插值法重构后电弧电压函数的非线性特征为基础,假定初始模型类型为标量协变量,响应变量为函数的函数型数据模型进行优化,优化次数G=100,初始模型公式为
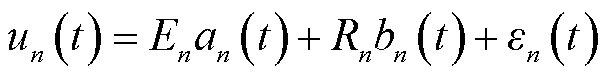 (3)
(3)
式中,an(t)、bn(t)分别为协变量E和R关于t的未知系数函数;en(t)为关于t的误差函数。式(3)中,理想电源电压E与电阻R不受时间t变化影响,即设E、R为标量协变量,电弧电压u(t)为函数型响应变量。
将系数函数与响应变量函数展开成最优傅里叶基函数形式分别为
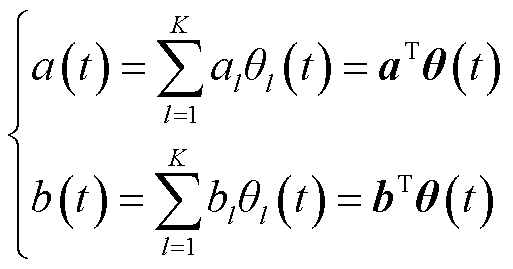 (4)
(4)
![]() (5)
(5)
式中,θ(t)=[θ1(t) θ2(t) … θK(t)]为a(t)、b(t)的最优傅里叶基函数展开式;aT、bT、cT分别为展开系数al、bl、cl组成的系数矩阵的转置;φ(t)=[φ1(t) φ2(t) … φK(t)]为u(t)的最优傅里叶基函数展开式;l代表展开的第l个基函数,l=1, 2,…, K。
为方便记录,记
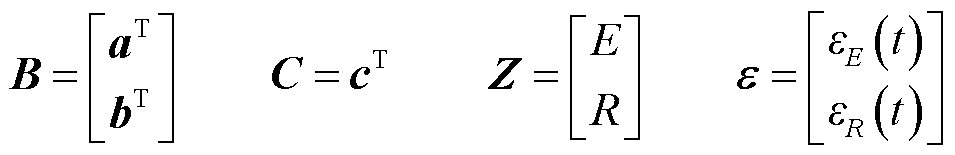
即B、C分别为aT与bT、cT组成的系数矩阵;e为误差函数组成的矩阵。
利用最小二乘准则定义的损失函数LMSSE确定系数函数的系数矩阵B,可得到一个简单的线性光滑器为
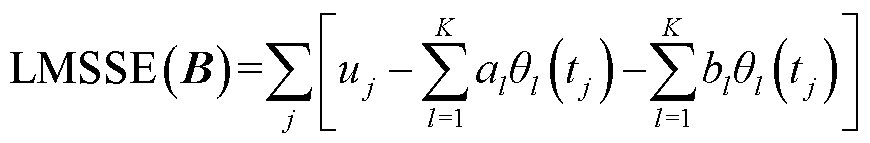 (6)
(6)
式中,j为第j组样本组数。
令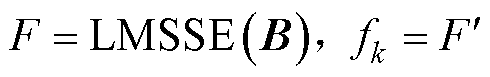 ,当
,当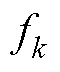 =0时,有
=0时,有
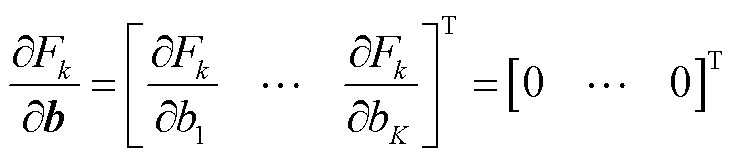 (7)
(7)
定义三个矩阵表示基函数矩阵,分别为
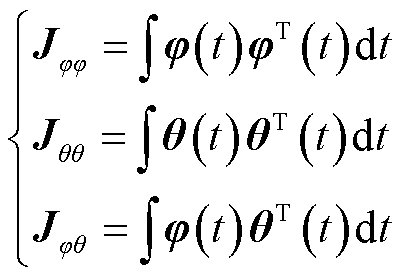 (8)
(8)
为了可读性,省略时间变量t和微分记号dt(后文中也有相应的省略),则式(8)简化表示为
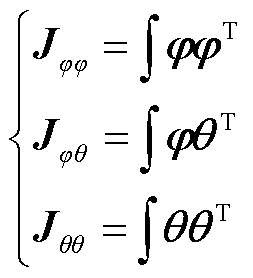 (9)
(9)
根据矩阵的迹的性质以及Kronecker乘积性质,使用矩阵按行拉直运算vec(·)可得
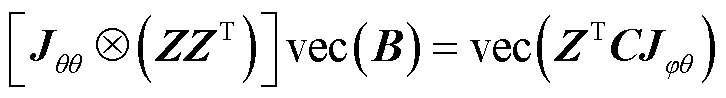 (10)
(10)
式中,“ ”为Kronecker乘积。
”为Kronecker乘积。
解得系数矩阵B为
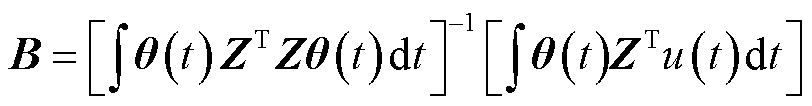 (11)
(11)
因此,经过第一次优化的系数函数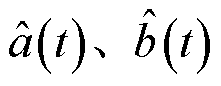 表达式为
表达式为
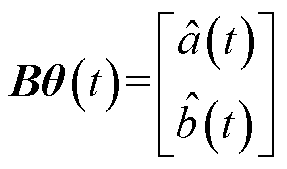 (12)
(12)
此时,令优化次数k=k+1,更新模型系数函数,直至k=100。
遍历其余样本数据,得到N组电压模型为
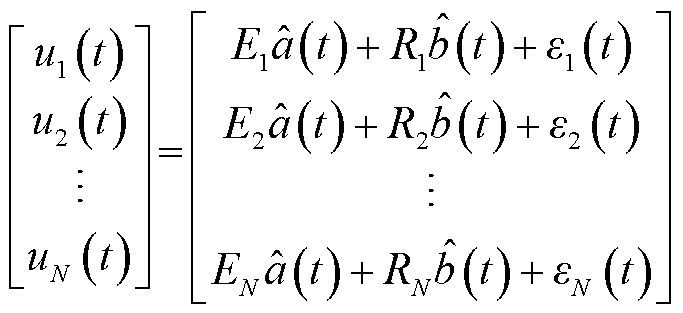 (13)
(13)
输出以E、R和t为变量的电弧电压函数型数据分析回归模型为
 (14)
(14)
放电电流数据与放电电压数据特征相近,电弧电流模型的建模过程与电弧电压相同,本文对其进行简要描述。测得N组电流样本数据(En, Rn; in(t)),n=1, 2,…, N。
输入初始参数与模型得到
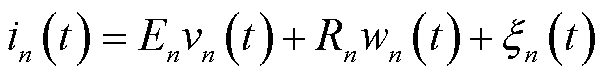 (15)
(15)
式中,v(t)为电源电压变量E的系数函数;w(t)为电阻变量R的系数函数;ξ(t)为随机误差函数。
模型式(15)中函数的最优傅里叶基函数展开式为
 (16)
(16)
![]() (17)
(17)
式中,vT、wT、dT分别为展开系数vl、wl、dl组成的系数矩阵的转置。
记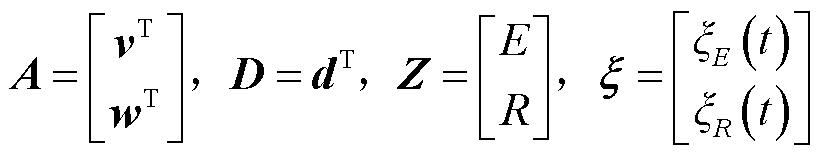 ,即A、D分别为vT与wT、dT组成的系数矩阵,x为误差函数组成的矩阵。
,即A、D分别为vT与wT、dT组成的系数矩阵,x为误差函数组成的矩阵。
定义系数矩阵A的最小二乘损失函数为
 (18)
(18)
令 ,当
,当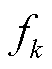 =0时,系数函数的系数矩阵A的解为
=0时,系数函数的系数矩阵A的解为
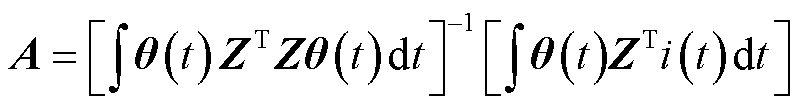 (19)
(19)
同理,遍历N组样本则可建立以E、R和t为变量的放电电弧电流i(t)模型为
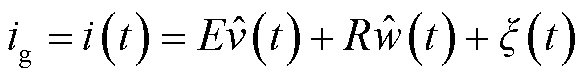 (20)
(20)
通过IEC火花试验装置进行爆炸性检测试验,对检测条件要求较高,且成本较高、周期长、不确定因素多,这些局限最终会大幅降低本安产品的生产效率。本安非爆炸评价方法虽然不能完全替代爆炸性评价的方法,但利用计算机辅助[23-24]研究电路的本质安全性能判别,对设计与检测本质安全电路具有重要的指导意义。相关文献提出基于电感性电路放电电流衰减模型的功率判据,对常用的能量判别式做了补充。然而,目前尚缺乏一个独立的、完备的电阻电路模型和基于该模型的判据。
为了深入研究电弧的能量变化规律,对电阻性电路进行准确的本安性能评价,本文利用函数型数据分析回归算法将不同特征的动态函数曲线转换为“原始数据”进行分析,从理论上提出一种独立于电压和电流模型的功率模型,以降低由于电压和电流模型约束而导致的本安性能评估的误差。
基于试验所测得的N组电弧电压ug与N组电流ig波形数据,以纯电阻电路功率定义式为依据,计算每一组样本功率p与时间变量t的函数关系,并绘制波形曲线,在每一条波形特定节点上有限维取值,得到N组功率样本数据(En, Rn; pn(t)),n=1, 2,…, N。
值得注意的是,功率波形与电压、电流波形特征显然不同,但这并不影响函数型数据回归模型的形式,通过模型系数函数b(t)的自适应过程,能够使最终的模型与波形保持一致。因此,本文提出的函数型数据分析回归算法对电弧功率模型的建立依旧是可行的。
设初始模型及系数函数为
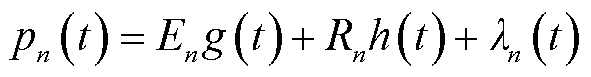 (21)
(21)
式中,g(t)为电源电压变量E的系数函数;h(t)为电阻变量R的系数函数;λ(t)为随机误差函数。
利用基函数展开系数函数与响应函数可得
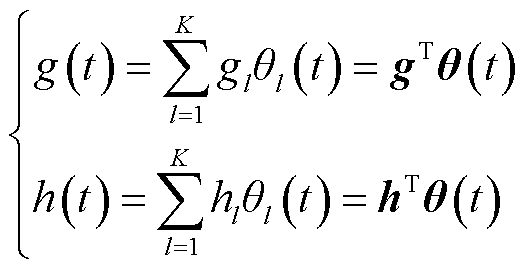 (22)
(22)
![]() (23)
(23)
式中,gT、hT、mT分别为系数gl、hl、ml组成的系数矩阵的转置。
记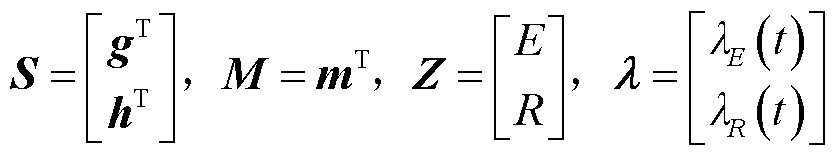 。
。
定义功率模型系数矩阵S的损失函数为
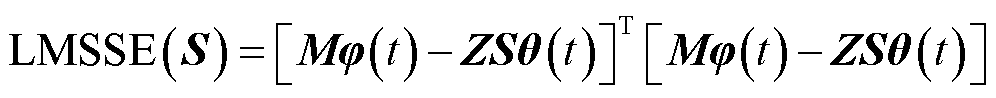 (24)
(24)
令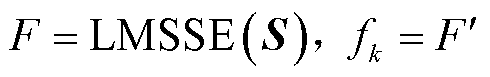 ,当
,当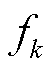 =0时,系数函数的系数矩阵S的解为
=0时,系数函数的系数矩阵S的解为
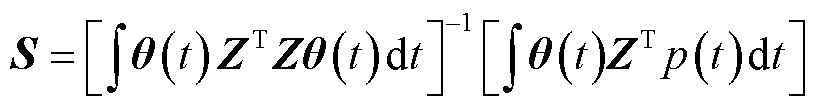 (25)
(25)
同理,遍历N组样本则可建立以E、R和t为变量的放电电弧功率p(t)模型为
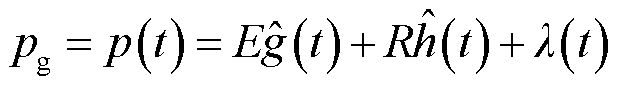 (26)
(26)
基于前文所建立的功率模型,设电弧放电时间为T,则电弧放电能量Wg表达式为
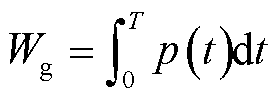 (27)
(27)
将式(27)展开得到
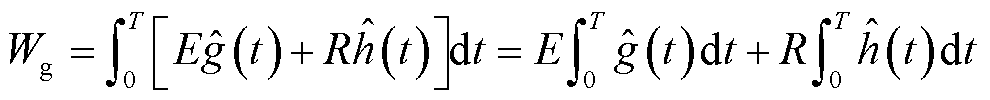 (28)
(28)
根据式(28),结合最小点燃能量,可以建立简单电阻性电路本安性能判据为
 (29)
(29)
式中,Wmin为火花试验装置的最小点燃能量[25],mJ;a为能量损耗系数,取值为3[26];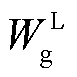 为混合气体爆炸的临界放电能量,mJ。
为混合气体爆炸的临界放电能量,mJ。
故能量判据为
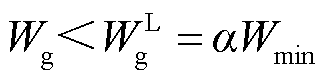 (30)
(30)
为验证所得数学模型,本文基于IEC标准火花试验装置对不同电源电压与电阻进行电弧放电试验,对比实测值与仿真模型之间的差异。按照标准直流电阻性电路拓扑连接电路。被试电路接入火花试验装置电极,将电路参数调整到规定的安全系数后,判定在电极系统的规定转数内是否打出火花。两接触电极之一是由带有两道槽的旋转镉电极盘组成;另一个接触电极由四根钨丝组成,钨丝直径为0.2 mm,并固定在圆周直径为50 mm的极握上(极握用黄铜材料制造)。旋转极握使钨丝电极在开槽的镉盘上滑动,极握与镉盘之间的距离为10 mm。钨丝的自由长度为11 mm,其不与镉盘接触时,垂直于镉盘表面。驱动镉盘和极握的两轴相隔31 mm,并且两轴之间和试验装置底盘之间相互绝缘。电流通过轴系上的滑动电极流进和流出,两轴由不导电的齿轮啮合起来,齿轮传动比为50:12。用电机带动的极握转速为80 r/min。开通电源后镉盘与钨丝装置以相同且均匀的转速接触、断开打火放电。
试验电路系统选用UT37014型直流稳压电源,DLM3034型示波器用于电弧波形的采集。将所述火花装置的正、负极连接到示波器的第一通道测定电弧电压;示波器第二通道连接电阻两端的正负极测量电弧电流。试验采样频率设定为12.5 kHz。试验数据列于表1中。
表1 电阻电路电弧放电试验数据
Tab.1 Resistance circuit arc discharge test data sheet

样本集E/VR/Ω 训练集2420, 25, 30, 40, 60, 80, 120 2730, 60, 90, 120, 150, 200 3020, 25, 30, 40, 60, 80, 120, 150, 300 3640, 60, 90, 120, 180, 240 检验集4840, 60, 90, 120, 180, 240, 360, 450
试验共记录36组不同电路条件样本类型。其中,训练集共28组样本类型,用于算法程序以训练最优模型;检验集共8组样本类型,用于检验模型是否准确。每组样本类型的电弧电压、电流波形重复测量五次,试验共记录360组波形。根据示波器信号合成取得36组对应的功率波形共计180组。
将试验收集的训练集数据导入Matlab进行仿真分析,根据2.1节所提出的函数型数据分析回归算法编写程序,训练三种(电压、电流、功率)模型。
插值法处理后的训练集电弧电压、电弧电流及功率平滑曲线分别如图6~图8所示。
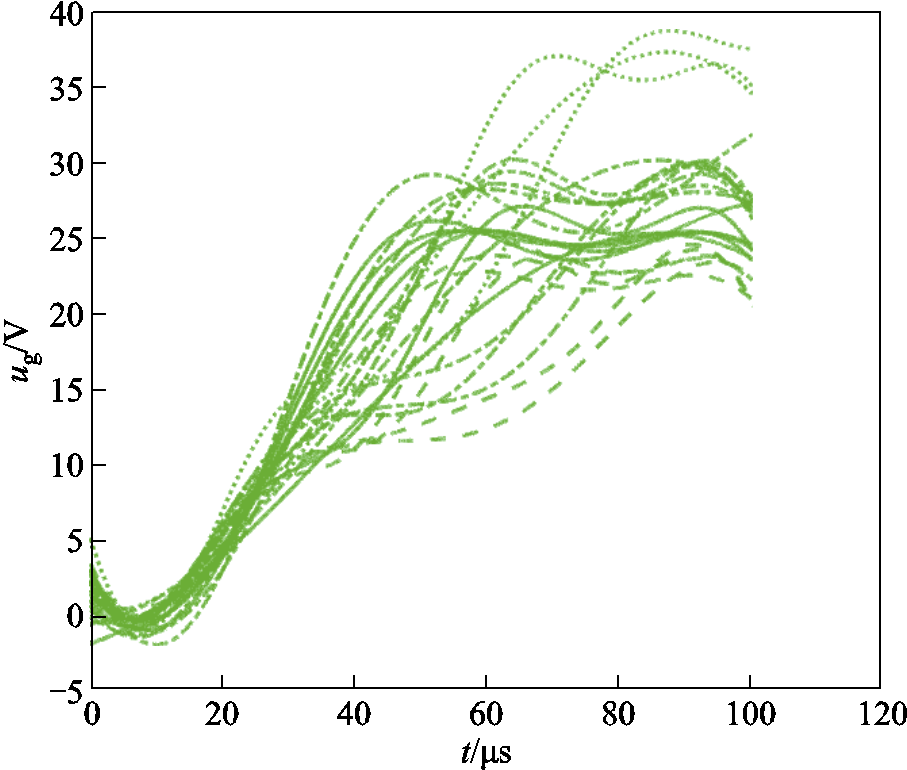
图6 电阻性电路电弧电压样本拟合曲线
Fig.6 Arc voltage sample fitting curves of resistive circuit
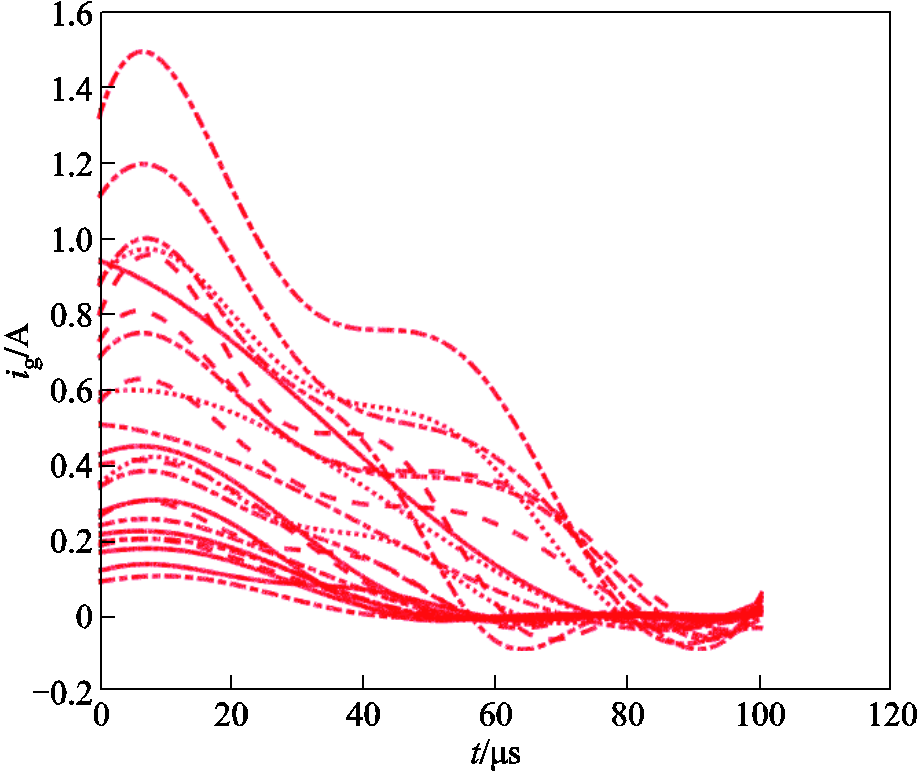
图7 电阻性电路电弧电流样本拟合曲线
Fig.7 Arc current sample fitting curves of resistive circuit
以文献[18]提出的放电形式一在放电试验中出现的次数最多、形式二次之、形式三出现的次数最少的结论为依据。本文在此基础上整合出电压、电流与功率波形与放电形式类型一致的样本组,对其电弧放电不同形式可能出现的先决条件进行初步研究。分类形式见表2。其中ug/S1、ug/S2、ug/S3分
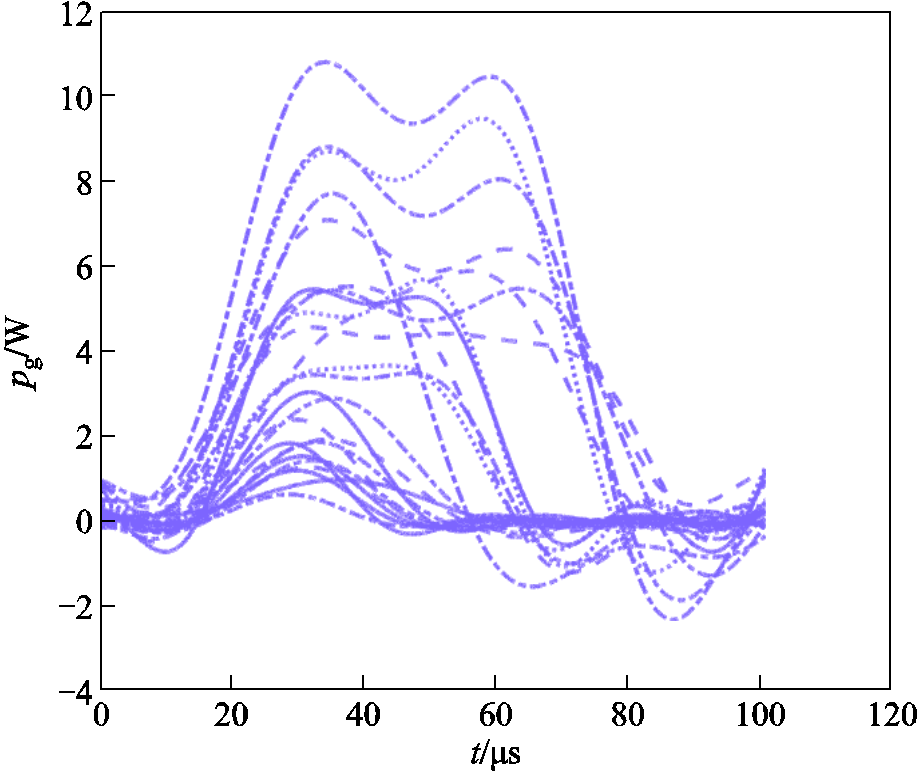
图8 电阻性电路电弧功率样本拟合曲线
Fig.8 Arc power sample fitting curves of resistive circuit
别表示在此电路参数条件下电弧电压波形属于放电的第一、二、三种形式;ig与pg分类形式与ug同理。
从表2可看出,放电形式一在放电试验中出现的次数最多、形式二次之、形式三出现次数最少,结果与文献[18]结论相符。结合表2,交叉对比电压、电流及功率波形,整合三种电参数波形均符合同一种放电特征的样本组,绘制不同放电形式出现概率与电路正常工作电流I的关系如图9所示。
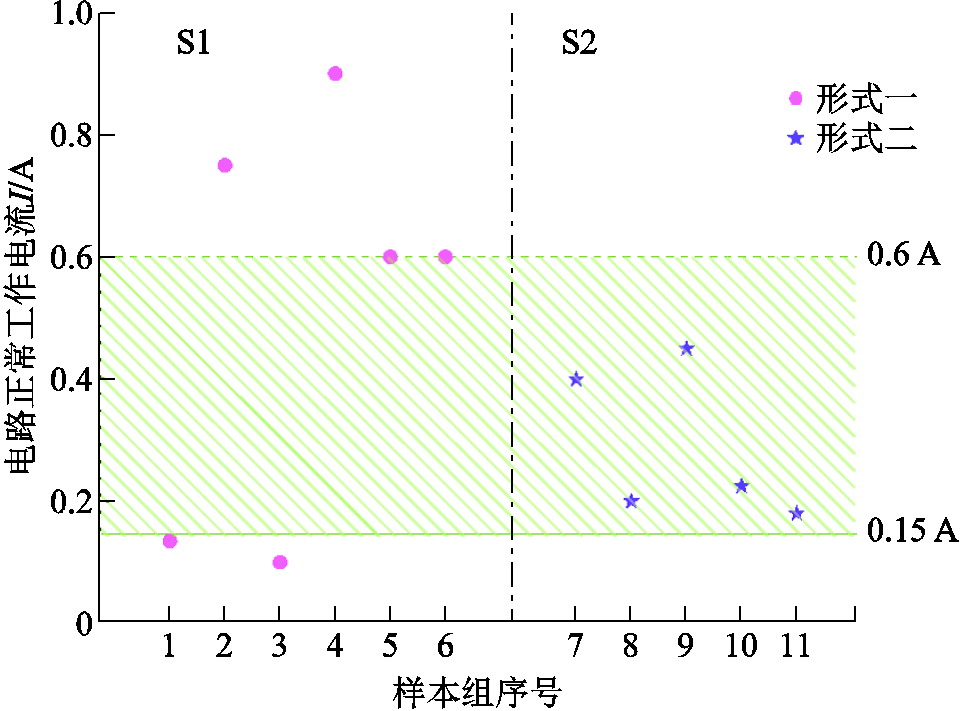
图9 电阻性电路电弧放电形式分类
Fig.9 Classification of arc discharge of resistive circuit
表2 不同电路参数下的电压、电流、功率分类形式
Tab.2 Voltage, current and power classification table under different circuit parameters

E/VR/Ω ug/S1ug/S2ug/S3ig/S1ig/S2ig/S3pg/S1pg/S2pg/S3 2420, 30, 4025, 60, 1208020, 30, 4025, 60, 120804025, 30, 60, 12020, 80 2730, 90, 20060, 120, 150—30, 90, 20060, 120, 150—30, 90, 20060, 120, 150— 3020, 25, 40, 60, 80, 120, 150, 30030—20, 40, 60, 80, 30025, 30, 120, 150—30, 40, 60, 80, 120, 150, 30020, 25— 3640, 6090—40, 6090—40, 60, 90—— 4860, 90, 120, 180, 36040—60, 90, 120, 180, 36040—60, 90, 120, 180, 36040—
由上述图表分析可知,当电源电压参数范围为24 V≤E≤48 V且电阻范围为20 W≤R≤360 W时,电弧第一种放电形式在放电试验中出现的概率最大,第三种形式出现概率最小,这与前人结论相符。相同参数范围内,图9中阴影区域表示电弧放电第二种形式可能出现的范围,放电第一种形式出现在空白区域的概率较大。从电路正常工作电流角度分析可知,当电流值I≤0.15 A或I≥0.6 A时,电弧放电表征为第一种放电形式,这时电路电弧的放电时间长,功率前期上升,能量也随之增大,容易引起爆炸;当正常工作电流值0.15 A<I<0.6 A时,电弧放电表征趋向于第二种放电形式,这时电弧的放电时间虽长,但前期功率基本不变,后期迅速下降。
需要特别说明的是,第三种形式出现的概率未能与电路电流表现出直接关系,其他试验条件下的放电形式分类与正常工作电流关系也仍需进一步探究。
为判断所提出的基于函数型数据分析回归算法建立的模型是否适用于电弧放电的所有形式,执行仿真程序进行模型训练。由于样本数据数量庞大无法呈现全部仿真结果,本文选取部分结果进行讨论。部分模型训练结果与分类形式如图10所示。
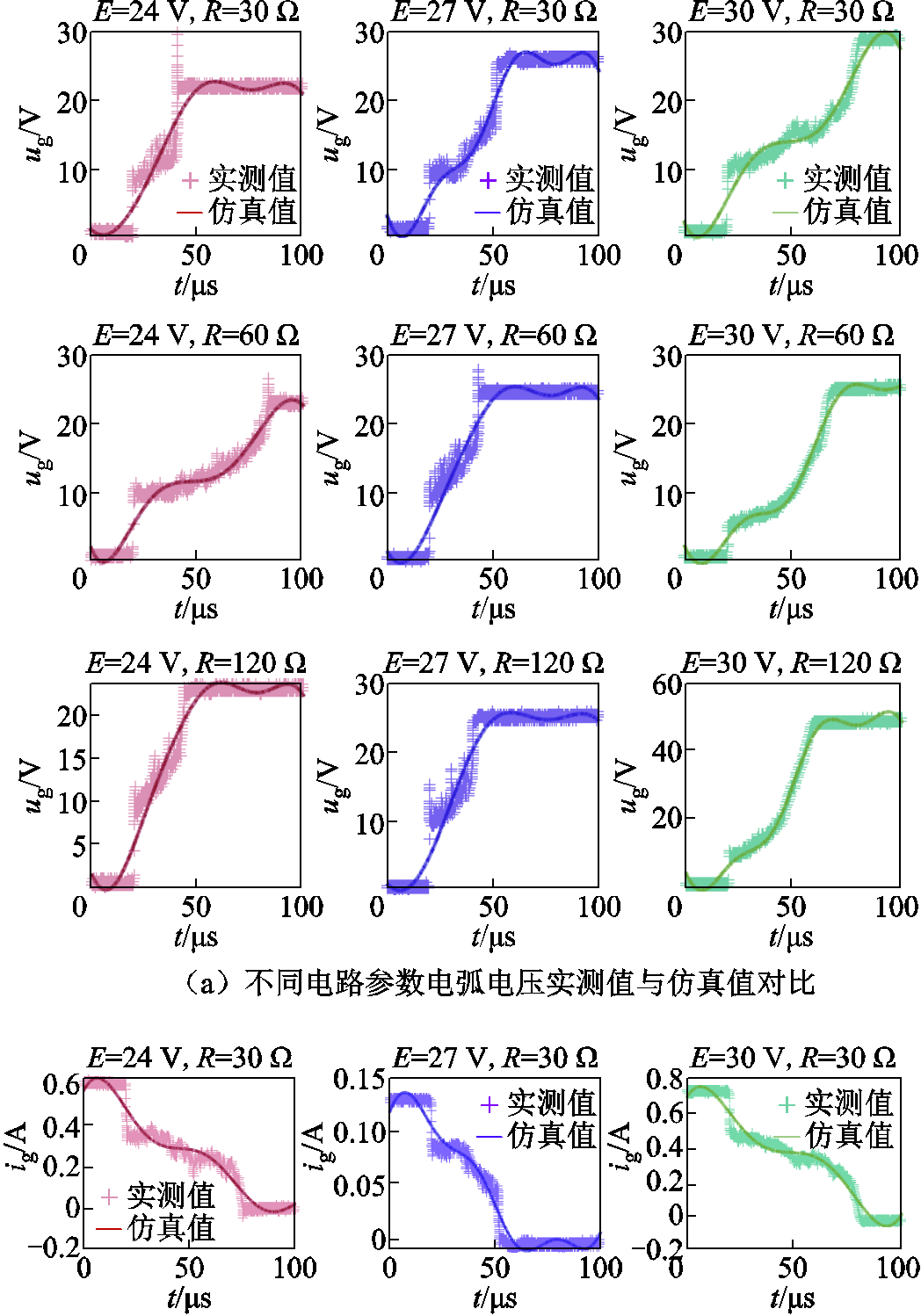
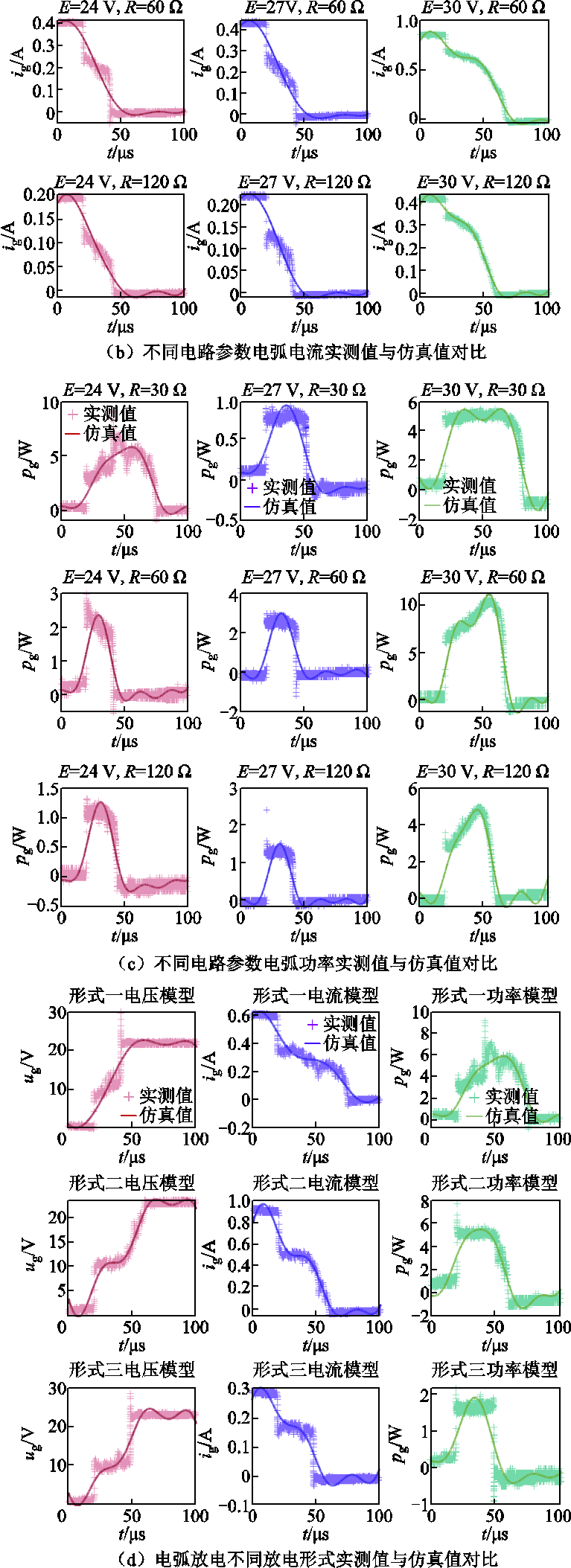
图10 部分模型训练结果与分类形式实测值与仿真值对比
Fig.10 Comparison between test value and simulation value of some model training results and classification
观察试验数据与仿真数据对比曲线不难发现,在不同电路参数条件下,对于趋势有所差异的放电电弧电压、电流及功率波形,仿真值与实测值基本吻合。通过训练的模型可以清晰地区分电阻性电路电弧放电的三种形式,说明函数数据分析回归算法所建立的数学模型具有较好的普适性。
函数型数据分析回归算法建立数学模型的自适应过程的复杂程度决定了模型与实测值的误差大小,本文采取最小二乘优化准则求解出的电压模型系数函数a(t)、b(t)以及电流模型系数函数v(t)、w(t)的95%置信区间范围如图11所示。
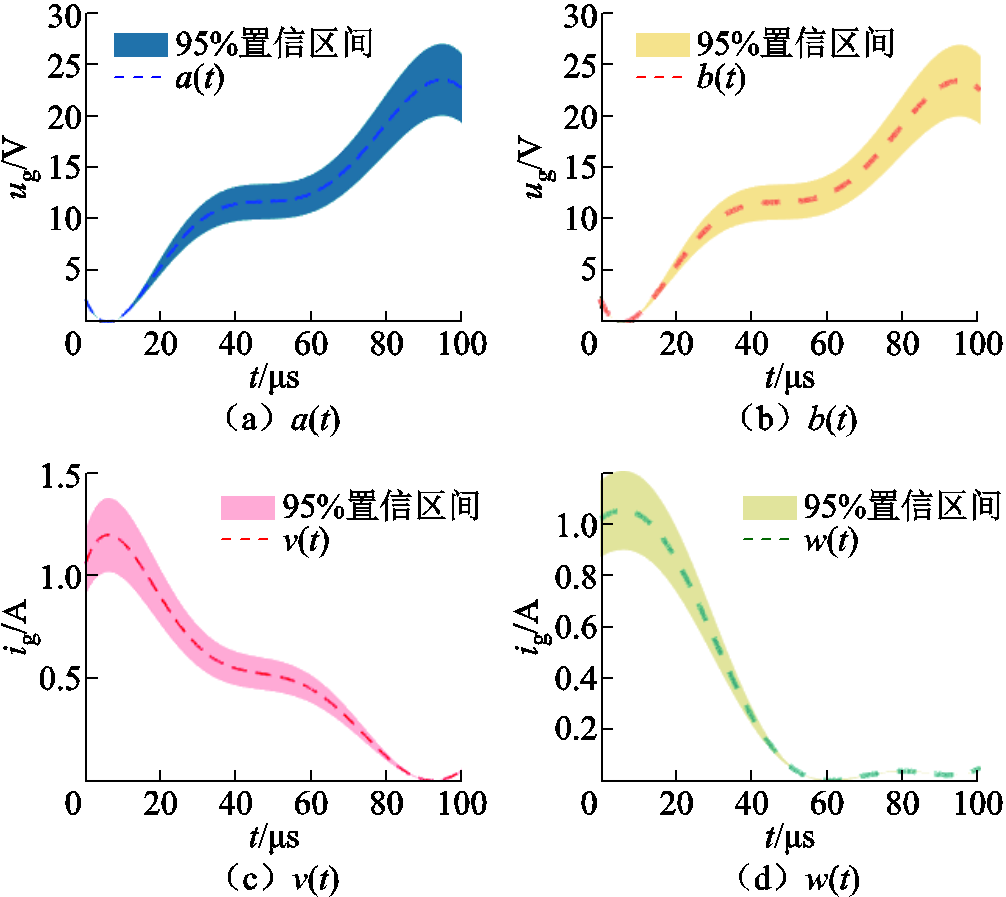
图11 电压与电流模型系数函数95%置信区间
Fig.11 95% confidence interval of voltage model and current model
由图11可以看出,电压与电流模型的系数函数根据各自协变量初始值的不同,其置信区间范围有所差别。
为深入探究所提模型描述实际波形的准确程度,本文利用回归评价指标均方误差(Mean Square Error, MSE)、方均根误差(Root Mean Square Error, RMSE)、平均绝对误差(Mean Absolute Error, MAE)、决定系数(R2)表征模型式(14)、式(20)、式(26)训练过程存在的误差。将训练样本组按分类代入电压、电流、功率模型进行回归计算,并绘制折线图如图12所示。
对比电压、电流及功率模型的各类指标分析得出,电压与功率模型的MSE、MAE计算值较大,则实际值与理论值之间的误差较大;电流模型的MSE、MAE计算值较小,其系数函数的自适应过程好。电流模型的驯化程度优于电压与功率模型。
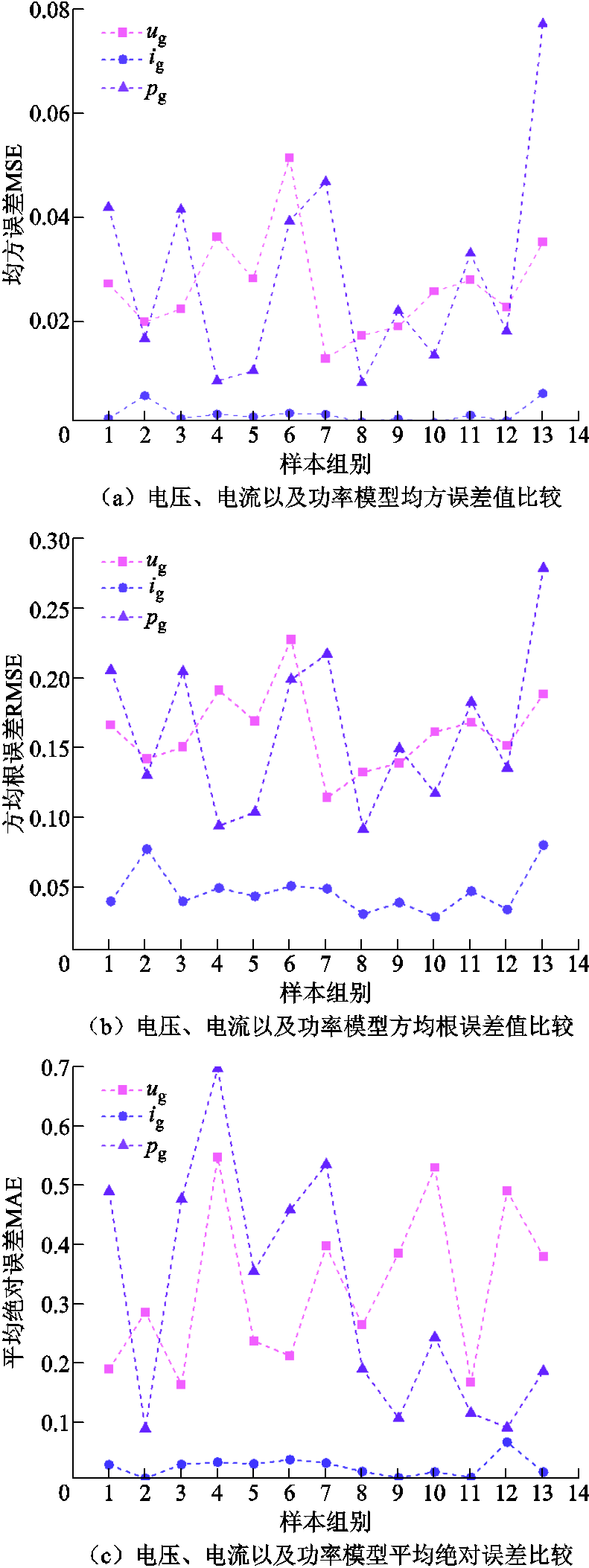
图12 模型回归指标对比
Fig.12 Comparison of model regression indicators
表3分别列出了少数样本组三种模型的决定系数。其中,决定系数最小为0.790 1,最大为1,其余均在0.8~0.99范围内浮动,说明在本文的试验条件下,至少有80%的实际数据可以被所建模型所描述,证明了函数型数据分析回归模型的可行性。但考虑到工程环境的复杂性与多变性,模型实际应用的误差范围有待进一步精确。
表3 三种模型决定系数计算结果对比表
Tab.3 Comparison table of determination coefficient calculation results of three models
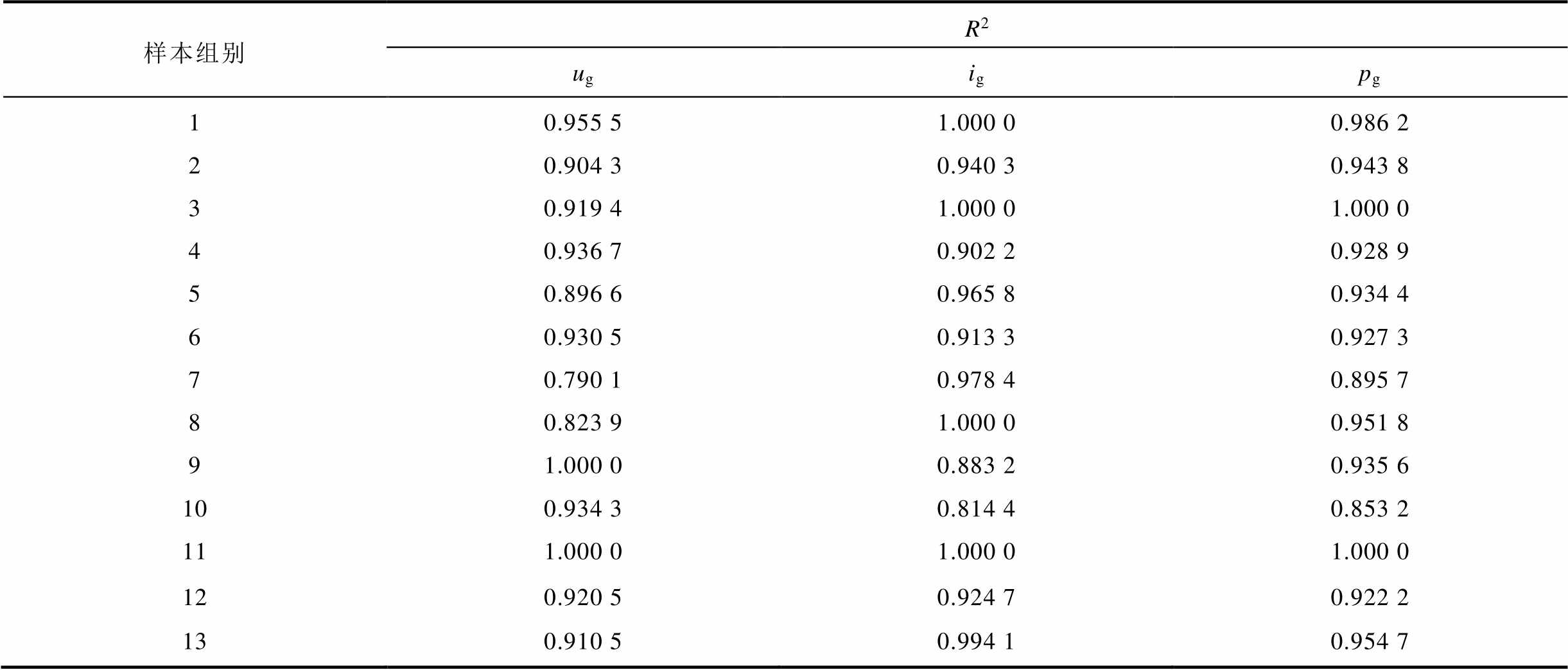
样本组别R2 ugigpg 10.955 51.000 00.986 2 20.904 30.940 30.943 8 30.919 41.000 01.000 0 40.936 70.902 20.928 9 50.896 60.965 80.934 4 60.930 50.913 30.927 3 70.790 10.978 40.895 7 80.823 91.000 00.951 8 91.000 00.883 20.935 6 100.934 30.814 40.853 2 111.000 01.000 01.000 0 120.920 50.924 70.922 2 130.910 50.994 10.954 7
与传统电弧解析模型不同的是,本文采用的函数型数据分析回归算法所建立的放电模型不仅反映了变量E、R与u(t)、i(t)、p(t)的高维函数关系,同时能对电弧电压、电流进行数值模拟,从而实现对本安和非本安状态的判定和预报。以电阻性电路火花放电试验检验集样本作为实际值,对模型预测值与其之间的误差进行检测,根据回归指标表征模型预测效果。电弧模型预测值与实际值对比如图13所示。
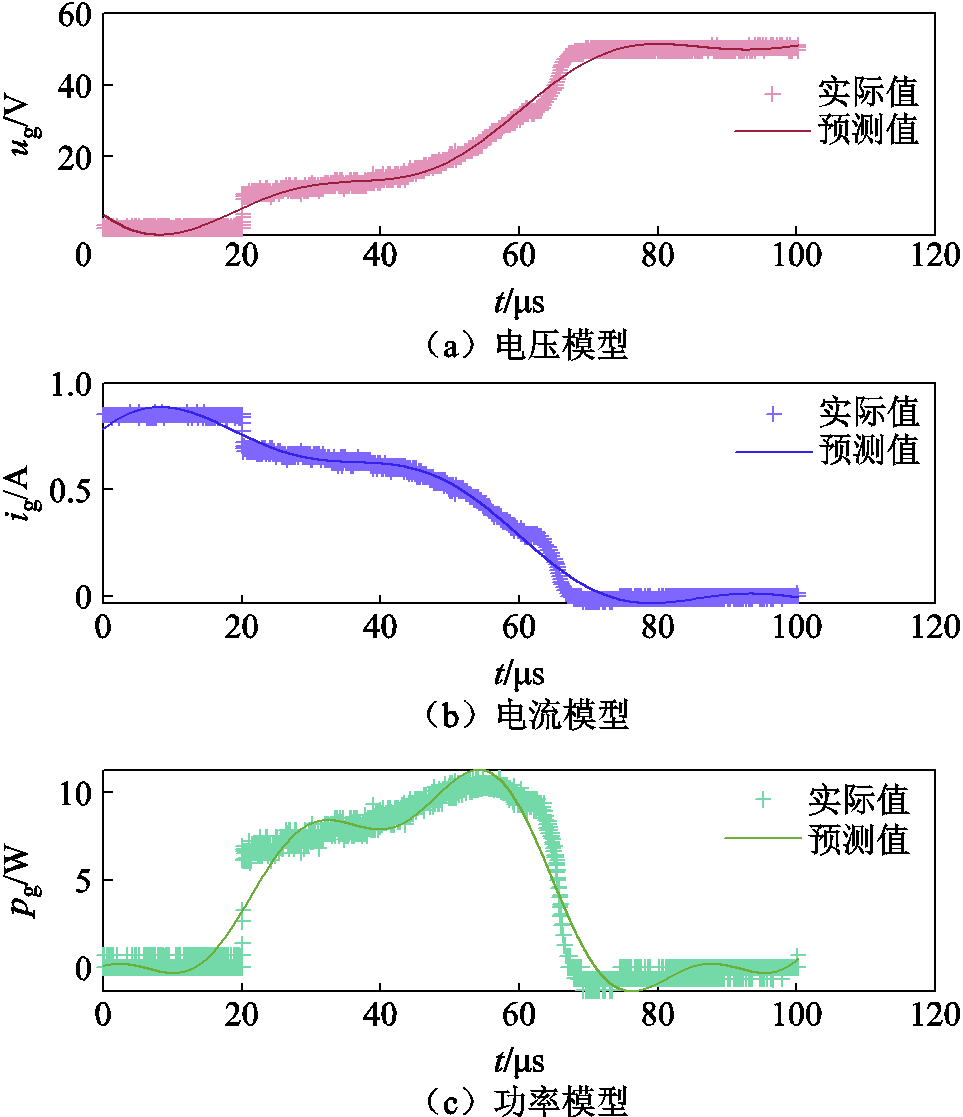
图13 检验样本电弧模型预测值与实际值对比
Fig.13 Comparison between predicted value and true value of arc model of test sample
由图13可看出,模型预测值与实际值存在偏差,但趋势相同且偏差不大。检验样本组模型的回归指标计算值见表4~表6。
表4 检验样本组电弧电压模型回归指标计算值
Tab.4 The model regression indicators of the arc voltage model of the sample group were tested
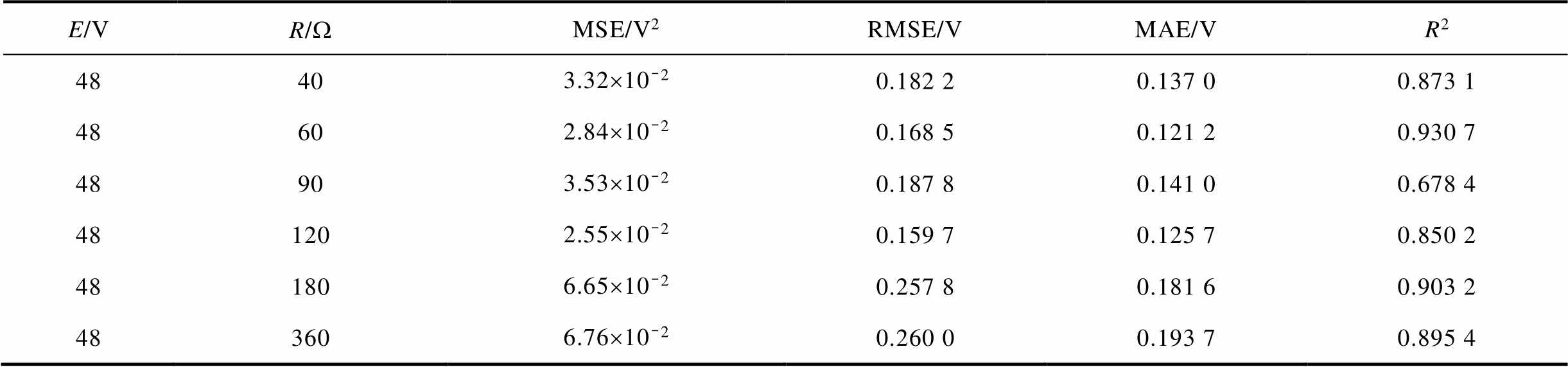
E/VR/WMSE/V2RMSE/VMAE/VR2 48403.32´10-20.182 20.137 00.873 1 48602.84´10-20.168 50.121 20.930 7 48903.53´10-20.187 80.141 00.678 4 481202.55´10-20.159 70.125 70.850 2 481806.65´10-20.257 80.181 60.903 2 483606.76´10-20.260 00.193 70.895 4
表5 检验样本组电弧电流模型回归指标计算值
Tab.5 The model regression indicators of the arc current model of the sample group were tested

E/VR/WMSE/A2RMSE/AMAE/AR2 48402.31´10-40.015 20.035 90.841 2 48609.09´10-40.030 20.021 60.954 7 48905.08´10-40.022 50.016 90.893 6 481201.69´10-40.053 00.010 00.741 6 481802.38´10-40.015 40.011 30.913 0 483601.39´10-40.011 80.008 80.879 5
表6 检验样本组电弧功率模型回归指标计算值
Tab.6 The model regression indicators of the arc power model of the sample group were tested

E/VR/WMSE/W2RMSE/WMAE/WR2 48402.97´10-20.172 31.250 00.854 7 48609.37´10-30.096 80.671 30.924 0 48904.37´10-20.209 00.493 70.903 7 481202.00´10-20.141 40.343 50.655 8 481801.41´10-20.118 70.278 10.934 5 483607.22´10-30.085 00.190 80.889 1
检验集六组样本类别中,电流模型的MSE与MAE值小于其他模型,这说明电流模型仿真出的预测值与实际值之间的误差较小。除电压模型第三组(E=48 V, R=90 W)样本类型和电流、功率模型第四组(E=48 V, R=120 W)样本类型外,其余组的R2均在0.84~0.96之间,表明在本文所进行试验的试验条件下,至少有84%的实际数据可以被电弧电压、电流及功率模型预测。
本文对电阻性电路电弧放电特性曲线进行深入分析,推断放电阶段电弧各波形出现的电路参数条件,综合考虑电阻电路电源电压和电阻对时间变量t的影响,提出了一种将不同特征动态函数曲线转换为“原始数据”进行分析的函数型数据分析思想。通过函数型数据分析回归算法建立了高维且参数强相关、适用范围广的电阻性电路电弧放电数学模型,具体结论如下:
1)对提出的放电模型进行不同电路参数下的仿真分析,搭建试验平台将试验结果与之进行对比。结果证明了所提出的函数型数据分析电弧模型的准确性和可行性,并基于功率模型与最小点燃曲线建立了电阻性电路本安能量判据。
2)当电源电压参数为24 V≤E≤48 V且电阻范围为20 W≤R≤360 W时,根据电阻性电路电弧放电三种形式将试验数据分类,探究不同形式出现可能的电路参数条件。从电路正常工作电流角度分析可知,当电流值I≤0.15 A或I≥0.6 A时,电弧放电表征为功率前期上升;当正常工作电流值0.15 A<I<0.6 A时,电弧放电表征为前期功率基本不变,后期迅速下降。但其他电路参数形式下的放电形式分类与正常工作电流关系仍需进一步探究。
基于函数型数据分析回归算法建立电阻性电路电弧放电数学模型发现,电弧放电不同形式的放电条件规律有利于本质安全电路的优化设计。建立电阻电路的本安能量判据,有利于完善本质安全非爆炸性评价方法。但这种本质安全性能评估判据的使用需要大量试验数据验证作为支撑,后续还需要开展更详细的试验以验证前述理论分析。
参考文献
[1] 皇金锋, 李林鸿, 任舒欣, 等. 考虑滤波电容等效串联电阻的输出本质安全型Buck-Boost变换器分析与设计[J]. 电工技术学报, 2021, 36(8): 1658-1670. Huang Jinfeng, Li Linhong, Ren Shuxin, et al. Analysis and design of an intrinsically safe Buck-Boost converter on considering of the filter capacitor with equivalent series resistance[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1658-1670.
[2] 朱林, 刘树林, 刘柏清, 等. 本质安全低压直流电路放电理论及数值研究综述[J]. 工矿自动化, 2022, 48(8): 16-25. Zhu Lin, Liu Shulin, Liu Boqing, et al. Review of discharge theory and numerical research on intrinsically safe low voltage DC circuits[J]. Journal of Mine Automation, 2022, 48(8): 16-25.
[3] 柯拉夫钦克B C, 谢洛夫B N, 叶雷金A T, 等. 安全火花电路[M]. 张丙军, 译. 北京: 煤炭工业出版社, 1981.
[4] Uber C, Hilbert M, Felgner A, et al. Electrical discharges caused by opening contacts in an ignitable atmosphere - part I: analysis of electrical parameters at ignition limits[J]. Journal of Loss Prevention in the Process Industries, 2019, 61: 114-121.
[5] 孟庆海, 胡天禄, 牟龙华. 本质安全电路低能电弧放电特性及参数[J]. 电工技术学报, 2000, 15(3): 28-30, 35. Meng Qinghai, Hu Tianlu, Mu Longhua. Low energy arc discharge characteristic and parameters of intrinsically safe circuits[J]. Transactions of China Electrotechnical Society, 2000, 15(3): 28-30, 35.
[6] 赵永秀, 刘树林, 马一博. 爆炸性试验电感电路分断放电特性分析与建模[J]. 煤炭学报, 2015, 40(7): 1698-1704. Zhao Yongxiu, Liu Shulin, Ma Yibo. Analysis and modeling of inductor-disconnected-discharged chara-cteristics based on explosive test[J]. Journal of China Coal Society, 2015, 40(7): 1698-1704.
[7] 孟庆海, 王进己. 本质安全电感电路电弧放电时间双正态分布[J]. 电工技术学报, 2017, 32(2): 119-124. Meng Qinghai, Wang Jinji. Dual normal distribution of arc discharge time for inductive intrinsically safe circuits[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 119-124.
[8] 赵永秀, 刘树林, 王瑶, 等. 安全火花试验电极热场致发射模型和温度效应的数值模拟研究[J]. 电工技术学报, 2019, 34(20): 4179-4187. Zhao Yongxiu, Liu Shulin, Wang Yao, et al. Research on numerical simulation of thermal field electron emission and temperature effect for safety spark test electrode[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4179-4187.
[9] 赵永秀, 张颖, 田江晖. 爆炸性环境电感分断建弧机理及影响因素[J]. 高电压技术, 2022, 48(9): 3765-3775. Zhao Yongxiu, Zhang Ying, Tian Jianghui. Arcing mechanism and influencing factors on inductor- disconnected-discharge in explosive environment[J]. High Voltage Engineering, 2022, 48(9): 3765-3775.
[10] 康骞, 许春雨, 田慕琴, 等. 电势电容电路短路火花放电影响因素分析[J]. 工矿自动化, 2020, 46(8): 38-43, 63. Kang Qian, Xu Chunyu, Tian Muqin, et al. Analysis of influencing factors of short-circuit spark discharge in electric potential capacitance circuit[J]. Industry and Mine Automation, 2020, 46(8): 38-43, 63.
[11] 王玉婷, 刘树林, 马一博, 等. 简单电容电路最小点燃电压曲线的数值化研究[J]. 电工技术学报, 2014, 29(增刊1): 345-350. Wang Yuting, Liu Shulin, Ma Yibo, et al. Research on digitization of the minimum ignition voltage curve of simple capacitive circuit[J]. Transactions of China Electrotechnical Society, 2014, 29(S1): 345-350.
[12] 刘树林, 钟久明, 樊文斌, 等. 电容电路短路火花放电特性及其建模研究[J]. 煤炭学报, 2012, 37(12): 2123-2128. Liu Shulin, Zhong Jiuming, Fan Wenbin, et al. Short circuit discharge characteristics of the capacitive circuit and its mathematical model[J]. Journal of China Coal Society, 2012, 37(12): 2123-2128.
[13] 刘建华. 爆炸性气体环境下本质安全电路放电理论及非爆炸评价方法的研究[D]. 徐州: 中国矿业大学, 2008. Liu Jianhua. A study on discharge theory and non-explosion evaluating method of the intrinsically safe circuits for explosive atmospheres[D]. Xuzhou: China University of Mining and Technology, 2008.
[14] 赵永红. 容性本安电路放电模型及放电特性分析[J]. 煤炭工程, 2021, 53(6): 172-175. Zhao Yonghong. Discharge model and characteristic analysis of capacitive intrinsic safety circuit[J]. Coal Engineering, 2021, 53(6): 172-175.
[15] 刘树林, 于昌隆. IEC安全火花试验装置点燃因素研究[J]. 西安科技大学学报, 2023, 43(1): 167-174. Liu Shulin, Yu Changlong. Study on igniting factors of IEC safety spark test apparatus[J]. Journal of Xi’an University of Science and Technology, 2023, 43(1): 167-174.
[16] 宋璐雯, 刘树林. 电极移动速度对电容短路火花放电特性的影响[J]. 西安科技大学学报, 2022, 42(4): 826-832. Song Luwen, Liu Shulin. Effect of electrode moving speed on the spark discharge characteristics of capacitor short circuit[J]. Journal of Xi’an University of Science and Technology, 2022, 42(4): 826-832.
[17] 王党树, 栾哲哲, 古东明, 等. 基于电荷等效法的电容短路放电微观特性数值模拟研究[J]. 电工技术学报, 2021, 36(13): 2684-2696. Wang Dangshu, Luan Zhezhe, Gu Dongming, et al. Numerical simulation research on microscopic characteristics of capacitor short-circuit discharge based on charge equivalent method[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2684-2696.
[18] 刘建华, 王崇林, 姜建国. 直流电阻性本质安全电路低能电弧放电分析[J]. 中国矿业大学学报, 2003, 32(4): 440-442, 451. Liu Jianhua, Wang Chonglin, Jiang Jianguo. Analysis of low-energy arc discharge of D.C. resistive intrinsically safe circuits[J]. Journal of China University of Mining & Technology, 2003, 32(4): 440-442, 451.
[19] 巩泉役, 彭克, 陈羽, 等. 基于电弧随机性和卷积网络的交流串联电弧故障识别方法[J]. 电力系统自动化, 2022, 46(24): 162-169. Gong Quanyi, Peng Ke, Chen Yu, et al. Identification method of AC series arc fault based on randomness of arc and convolutional network[J]. Automation of Electric Power Systems, 2022, 46(24): 162-169.
[20] 刘树林, 郝雨蒙, 李艳, 等. 基于最大功率的本安Buck变换器设计方法[J]. 电工技术学报, 2021, 36(3): 542-551. Liu Shulin, Hao Yumeng, Li Yan, et al. Design methods of intrinsically safe Buck converter based on the maximum output power[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 542-551.
[21] Baranowski J, Grobler-Dębska K, Kucharska E. Recognizing VSC DC cable fault types using Bayesian functional data depth[J]. Energies, 2021, 14(18): 5893.
[22] Guo Yi, Tierney S, Gao Junbin. Robust functional manifold clustering[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(2): 777-787.
[23] 王英, 曹丽, 陈小强, 等. 考虑双弓间距的双弓网Habedank电弧数学模型研究[J]. 高压电器, 2021, 57(11): 18-26. Wang Ying, Cao Li, Chen Xiaoqiang, et al. Research on Habedank arc mathematics model of double pantograph-catenary considering double pantographs interval[J]. High Voltage Apparatus, 2021, 57(11): 18-26.
[24] 郝莎, 徐建源, 林莘, 等. 基于隔离开关结构和操作特性的电弧放电模型研究与应用[J]. 高压电器, 2022, 58(4): 131-136. Hao Sha, Xu Jianyuan, Lin Xin, et al. Research and application of arc discharge model based on the structure and operation characteristics of discon-nector[J]. High Voltage Apparatus, 2022, 58(4): 131-136.
[25] 国家市场监督管理总局, 国家标准化管理委员会. 爆炸性环境第4部分:由本质安全型“i”保护的设备: GB/T 3836.4—2021[S]. 北京: 中国标准出版社, 2021.
[26] 孟庆海, 牟龙华, 王崇林, 等. 本质安全电路的功率判别式[J]. 中国矿业大学学报, 2004, 33(3): 292-294. Meng Qinghai, Mu Longhua, Wang Chonglin, et al. Electric power criterion of intrinsic safe circuits[J]. Journal of China University of Mining & Technology, 2004, 33(3): 292-294.
Abstract Different from the traditional inductive and capacitive intrinsically safe circuits, the resistive intrinsically safe circuit is difficult to describe accurately due to its three different discharge waveforms. The experimental waveform and theoretical analysis show that the arc of the resistive circuit has multi-dimensional characteristics, and there is a strong correlation between it and environmental factors. It is difficult to solve it directly by traditional modeling methods, which makes the intrinsic safety criterion of the resistive circuit lack a complete theoretical system, resulting in multiple accidents in the actual operating environment. In order to solve such problems, this paper proposes a discharge model based on functional data analysis regression algorithm on the basis of studying the arc discharge characteristic curve of resistive intrinsically safe circuit, and establishes the arc discharge energy criterion of resistive intrinsically safe circuit based on this model.
Firstly, the functional data analysis regression algorithm framework is constructed, and the mathematical models of arc discharge voltage and current are established respectively based on the three essential different discharge waveform characteristics of low energy arc discharge when the electrode of IEC spark test device is disconnected. Secondly, a power model independent of voltage and current model is proposed theoretically. Based on the power model, the energy criterion of resistive intrinsically safe circuit is supplemented. The model is simulated by Matlab software and a classification method of arc discharge waveform is proposed. Finally, a spark discharge test platform is built to verify the feasibility of the arc model and the accuracy of the prediction effect. The model does not require any restrictions on the frequency of data acquisition, and converts the dynamic function curve into 'original data', which has infinite dimensional spatial characteristics and reduces the error caused by the simplification of the formula in the derivation process. The comparison between the experimental data and the simulation results shows that under the experimental conditions carried out in this paper, at least 80% of the actual data of the three different discharge waveforms can be described by the model, which proves the feasibility and universality of the functional data analysis regression model. The evaluation of the prediction effect of the discharge model established by the functional data analysis regression algorithm shows that at least 84% of the actual data can be predicted by the arc voltage, current and power model under the test conditions in this paper. It solves the problem that the arc discharge waveform of resistive intrinsically safe circuit cannot be accurately described because of three types. In addition, the model is used to explore the circuit parameter conditions of three cases of arc discharge in resistive circuits. It is found that under the condition of the power supply voltage parameter of 24 V≤E≤48 V and the resistance range of 20 W≤R≤360 W, when the normal working current of the circuit is I≤0.15 A or I≥0.6 A, the arc discharge is characterized by an early increase in power; when the normal operating current value is 0.15 A<I<0.6 A, the arc discharge is characterized by the initial power basically unchanged and the later rapid decline.
Through simulation and experimental results, the following conclusions are drawn: (1) The proposed functional data analysis arc model solves the problem that the arc discharge waveform of the resistive intrinsically safe circuit cannot be accurately described due to three types. (2) The proposed model uses the idea of functional data analysis to transform the dynamic function curves of different characteristics into 'original data' for analysis, which reduces the error caused by formula simplification. (3) Compared with the traditional model, the proposed model can predict the discharge arc voltage and current values at different discharge times, which solves the problem that the traditional model cannot explore the numerical solution.
keywords:Arc discharge mathematical model, intrinsic safety, functional data, energy criterion
国家社会科学基金重点资助项目(20BTJ046)。
收稿日期 2023-02-14
改稿日期 2023-04-22
DOI:10.19595/j.cnki.1000-6753.tces.230161
中图分类号:TD685; TM133
朱 冉 女,1999年生,硕士研究生,研究方向为电气安全技术。E-mail:2602440779@qq.com
孟庆海 男,1986年生,研究员,研究方向为电气安全技术。E-mail:mengqinghai@ncut.edu.cn(通信作者)
(编辑 李 冰)