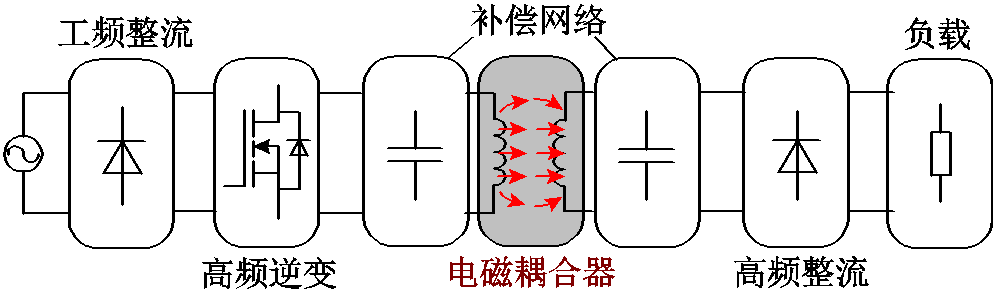
图1 磁耦合谐振式WTP系统示意图
Fig.1 Schematic diagram of magnetically coupled resonant WTP system
摘要 电磁耦合器是实现无线电能传输（WPT）技术的核心元件，其工作温度决定了系统运行的稳定性与使用寿命。为此该文以抗偏移能力强的旋转式电磁耦合器为研究对象，针对该电磁耦合器在非正弦激励下损耗及温度精确计算的问题，同时为避免大量实验数据繁琐采集过程，利用瞬态电磁-热流场双向间接耦合方法，建立考虑绝缘引起的匝间距及温度对材料属性影响的三维电磁场仿真模型，而后将电磁损耗计算结果作为载荷耦合至热流场中并建立对应关系，实现对热点温度计算。仿真与实验结果表明，物理模型的热点温度与测量值最大误差为5.15%，仿真得出的温升分布规律能较准确地展示实际情况，验证了物理仿真模型的合理性，可为旋转式电磁耦合器的散热设计提供依据，在工程应用中具有一定指导意义。
关键词：无线电能传输 旋转式电磁耦合器 多物理场耦合 温升特性 电磁损耗
自主式水下航行器（Autonomous Underwater Vehicles, AUV）是目前人类探索海洋资源的重要设备之一，而采用有线输电方式是限制其应用范围和发展的关键问题[1-2]。无线电能传输（Wireless Power Transfer, WPT）技术采用非物理接触传能方式，同时具有高自动化程度以及安全性、强灵活性和适用性等特点，可作为AUV可靠的供电方式[3-5]。典型的磁耦合谐振式WPT系统示意图如图1所示，其中电磁耦合器是实现WPT的核心组件，用于进行原、副边间“电-磁-电”能量转换传输。
图1 磁耦合谐振式WTP系统示意图
Fig.1 Schematic diagram of magnetically coupled resonant WTP system
为减小暗流及水压对电磁耦合器原、副边对位的影响，AUV大多采用笼状对接系统。本文设计的笼状对接无线充电装置如图2所示。其中电磁耦合器原边安装于笼状对接装置中，副边安装于AUV机身处。随着系统频率和容量的不断提升、整机体积的不断缩小，电磁耦合器的损耗和温升问题逐渐明显，其温升过高不仅会加快整机系统的绝缘老化速度、增大组件的热应力，影响系统使用寿命，同时系统中电子器件的参数也会因为周围温度变化发生漂移，进一步影响系统效率和运行稳定性[6-9]。因此，精确预估高频电磁耦合器线圈绕组及磁心损耗、研究正常模态下电磁耦合器温升分布，对AUV的散热设计及提高WPT系统的可靠性至关重要。
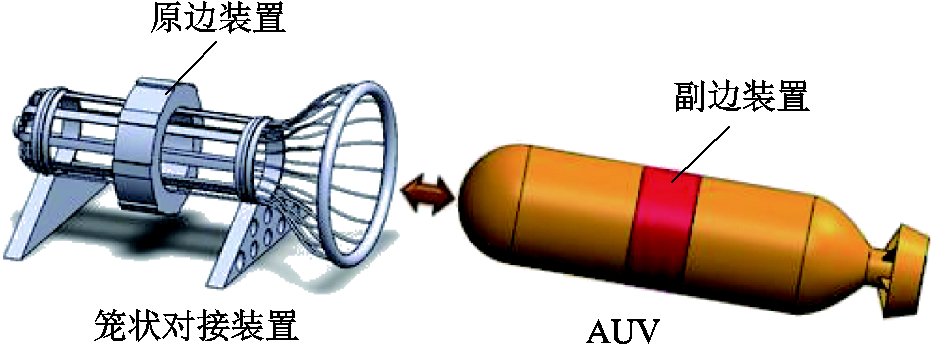
图2 AUV对接系统示意图
Fig.2 Schematic diagram of AUV docking system
为减小高频环境下电磁耦合器的磁心损耗，WPT系统通常采用磁滞回线狭长、磁导率较高的软磁材料，同时利用多股绞合Litz线绕制线圈绕组来降低由趋肤效应引起的涡流损耗[10-11]。将线圈绕组简化为整块体积相同的导体是目前常用的建模方法，该方法能极大降低建模难度、缩短计算时间，但在高频电磁场中的计算精度往往难以保证。文献[12-13, 16-18]均采用简化模型，忽略由于绝缘层厚度引起的匝间距对电磁耦合器电阻等参数的影响。文献[12]使用频域求解器对轴式松耦合变压器进行电磁损耗计算，忽略经高频逆变器之后高次谐波对损耗计算结果的影响；文献[13]采用高磁导率、低损耗的磁条增大原、副边之间耦合系数，但在计算损耗时默认Litz线圈交流电阻等于直流电阻。目前，电磁耦合器温升计算方法主要包括等效热网络法和数值计算法。等效热网络法通常是根据研究对象的热流路径建立热回路模型，对各组件发热损耗功率进行计算及设置。如果建立正确的热回路模型并设置合理的功率添加方法，电磁耦合器的温升分布规律就比较容易得到。文献[14]研究空气中磁耦合器的热回路模型和加热机理，计算各部件发热功率并定性地给出温度分布，实验结果与理论分析吻合度较高；文献[15]为提高热模型精度，利用仿真与实验相结合的方法确定研究对象的表面传热系数，结果表明，根据实验测算建立的热模型有足够高的工程精度。由于等效热网络法基于大量实验数据测算，同时建模过程繁琐，因此不适合多参数复杂模型计算。有限元法考虑磁心材料的非线性及导体各向异性参数的影响，可极大地提高计算精度且能够直观地得到空间内磁场与温升分布，在工程计算中逐渐得到应用。文献[16]对通入相反电流的两个铜导体提出电-磁-热分析模型，但该结果仅适用于二维模型计算；文献[17]提出一种精确测量磁耦合器损耗的实验方法，但仅在特定温度下进行测量对比，并且缺少在系统运行时磁耦合器各部件温度分布；文献[18]通过多物理场耦合研究了工作频率及温度对车用平板式电磁耦合器材料特性的影响规律。虽然在文章中讨论模型各部分的发热量，但并未给出各部件的温升分布。
针对上述问题，本文首先建立了考虑旋转式电磁耦合器线圈绝缘层的三维电磁场仿真模型，同时考虑电磁材料属性的温度效应，基于三维瞬态场仿真得到电磁组件损耗非均匀分布。采用电磁-热流场间接耦合计算方法求解自然对流下电磁耦合器的稳态温升分布，最终搭建一套带有红外热成像仪的WPT系统样机对电磁耦合器进行温升测试，验证仿真模型的合理性与准确性。
结合笼状对接无线充电系统外形，为减小由于对位偏差对系统传输功率带来的影响，本文研究对象为环型磁心结构的旋转式电磁耦合器，如图3所示。其主要由环形磁心及多芯Litz线圈绕组构成，原边线圈紧贴原边环形磁心的内侧，副边线圈紧贴副边环形磁心外侧。副边线圈嵌套于原边线圈内，原、副边磁心由TDK PC_40铁氧体构成。为使得原边线圈与磁心紧密贴合，利用3D打印定制原边紧固件。考虑到用于磁心与线圈间的紧固件、垫板等部件由树脂材料构成，对磁场分布基本没有影响，故在电磁场中建模时可忽略。实验样机具体参数见表1。
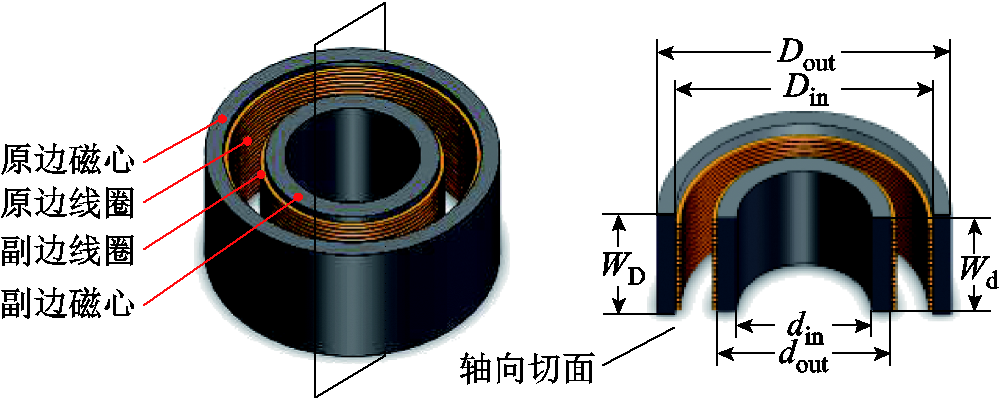
图3 旋转式电磁耦合器示意图
Fig.3 Schematic diagram of rotary electromagnetic coupler
表1 实验样机具体参数
Tab.1 Specific parameters of experimental prototype
参数数值 原边侧磁心截面积/mm21 193 磁心窗高WD/mm79 磁心内径Din/mm142 磁心外径Dout/mm162 线圈匝数22 副边侧磁心截面积/mm2734 磁心窗高Wd/mm73 磁心内径din/mm74 磁心外径dout/mm96 线圈匝数22 利兹线截面半径1.56 规格/mm0.1 mm×500
针对旋转式电磁耦合器电磁损耗精确计算问题，本文考虑了由绝缘引起的匝间距对计算电磁耦合器高频交流电阻的影响，同时考虑到多芯Litz线难以精细化建模，根据等效电阻不变的原则，利用孔隙率系数将多芯Litz线圈简化为截面积相同的方形导体[19]。
图4为求解旋转式电磁耦合器三维磁-热-流耦合计算流程。首先对三维电磁模型设置与温度相关的材料属性，在初始温度下计算电磁耦合器的损耗密度；其次采用间接耦合方式将电磁损耗作为热流场激励，利用网格-节点单元对应关系对流热场模型的流体、传热及能量方程进行耦合分析，计算出三维模型的表面传热系数；然后，根据温度结果反馈至电磁场中得到对应的材料系数后，再反复迭代计算；最后，当迭代步数内监测点的相邻两步间温度差值小于1 K时，终止迭代并得到电磁耦合器稳态温升分布。
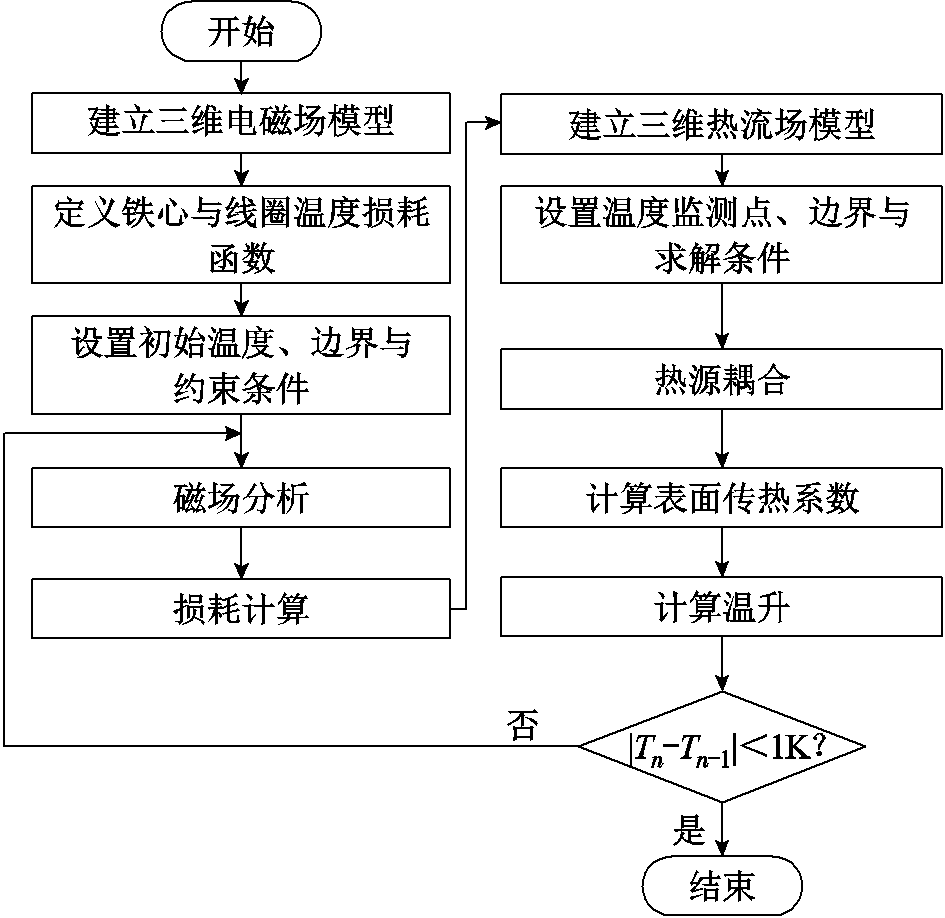
图4 多场耦合计算流程
Fig.4 Multi-field coupling calculation flow chart
经过高频逆变后电磁耦合器原边线圈接入电流为非正弦，因此采用瞬态电磁场计算方法求解。在理论分析时忽略位移电流及引线电流对交变磁场的影响，同时认为电磁材料属性均为各向同性。利用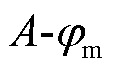
位组对旋转式电磁耦合器瞬态磁场建立的控制方程及Neumann边界条件为
（1）
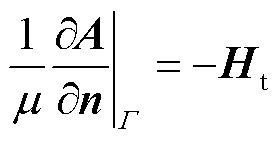（2）
式中，A为矢量磁位；Ax、Ay、Az分别为矢量磁位在x、y、z方向的分量；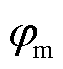
为标量电势；m为磁导率；s为电导率；J为随时间变化的非正弦矢量传导电流密度；t为时间；n为边界的外法向矢量；Ht为磁场强度的法向分量。
电磁耦合器的电磁损耗是产生温升的主要原因，其主要包括线圈损耗和磁心损耗。
2.2.1 线圈损耗计算
线圈损耗是由于线圈中通入电流引起的损耗，通常是电磁耦合器损耗产生的主要来源，高频情况下可分解为趋肤效应损耗和邻近效应损耗。为减小趋肤效应损耗，WPT系统常采用多芯绞合型Litz线绕制线圈。根据Litz线的空间结构分析可知，当流经频率较高的电流时，单匝Litz线电阻Rcon包括因自身电流产生的趋肤效应电阻Rskin和组成Litz线的细线间由于邻近效应产生的内部感应电阻Rin_pro。WPT中谐振线圈的交流电阻还应包括由相邻其他线匝流经交流电，使本线匝中产生的匝间感应电阻Rturn_pro，以及系统中其他线圈流经交流电产生的交变磁场在本线圈中产生的线圈间感应电阻Rcoil_pro。因此单个谐振线圈的总电阻Rcoil的表达式为
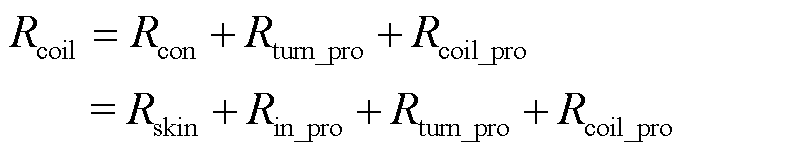(3)
假设除了该待求线圈外，系统中还存在M个其他线圈，同时认为Litz线中每股细线导通电流及物理参数均相等，忽略线圈弯曲部分的内外半径延展导致的轻微变化，根据文献[20]式（3），Rskin、Rin_pro、Rturn_pro和Rcoil_pro分别为
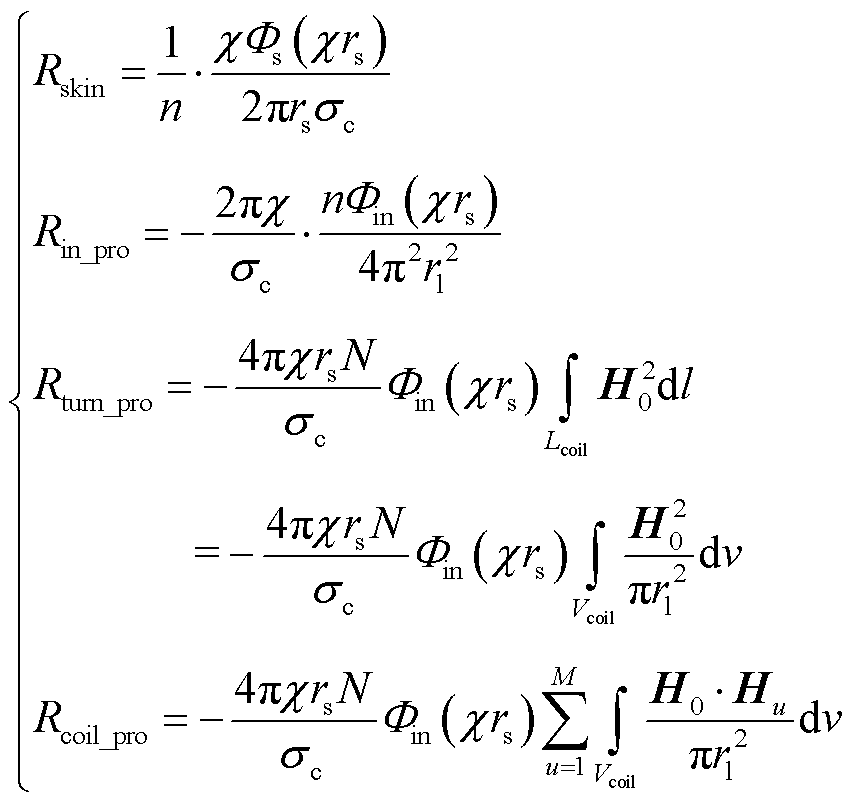（4）
式中，N为线圈匝数；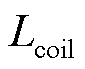
为单匝Litz线长度；
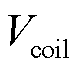为单匝Litz线体积；H0为线圈中通入幅值为1 A正弦交流电时的磁场强度；Hu为在待求线圈与其他线圈u中通入幅值为1 A电流、剩余线圈短路时，在待求线圈中的磁场强度；理想情况下认为每股细线中的磁场强度相等，因此对线圈二次方电场强度的线积分可用线圈截面按照面积平均的二次方电场强度的体积分来等效；n为组成单匝Litz线的细线股数；c为圆导体在高频基波下归一化厚度，即c= (wm0mcsc)1/2；rs为单股细线的标称半径；
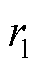为Litz线半径；
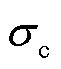为铜的电导率；
、
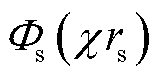为中间变量，表示为
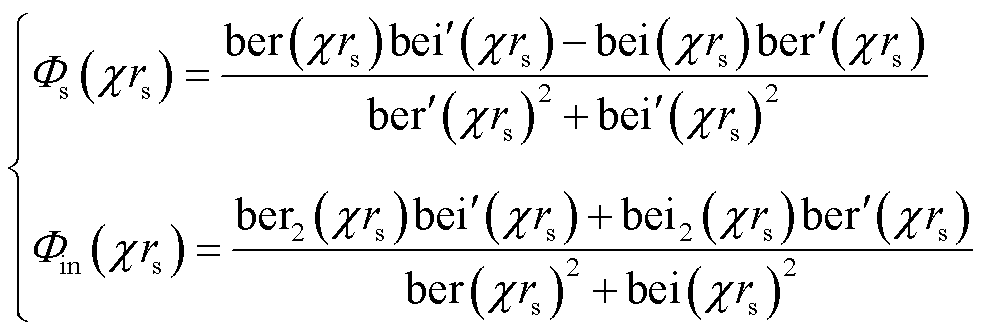（5）
式中，ber和bei分别为第一类零阶Kelvin函数的实部与虚部；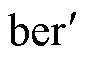
和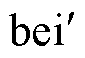
分别为第一类一阶Kelvin函数的实部和虚部；ber2与bei2分别为第一类二阶Kelvin函数的实部与虚部。上述分析基于Ferreira公式对单根孤立圆导线进行研究推导，在实际工程应用中，由于式（5）包含较为复杂的Kelvin函数，因此本文利用Lammeraner & Stafl公式简化线圈电阻的计算过程，即
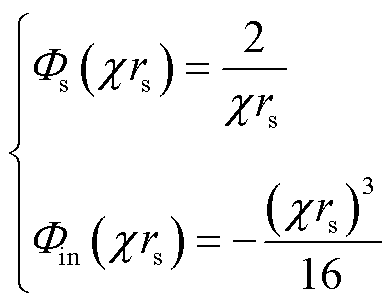（6）
当系统工作在谐振点附近且系统中仅存在一对谐振线圈时，副边线圈中感应电流与原边线圈中的发射电流的相位差为p/2，故可推导出谐振线圈间的感应耦合电阻为零。至此，在本文研究的系统中单个线圈的损耗计算公式为
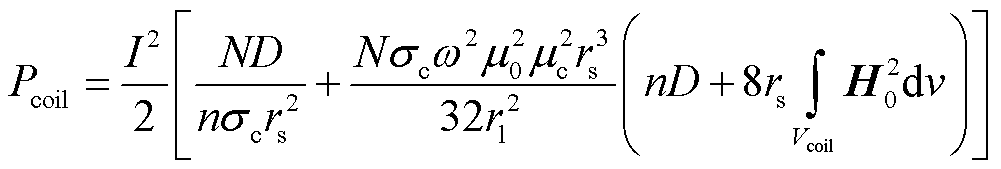（7）
式中，I为通入线圈的电流；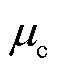
为Litz线的磁导率。温度对线圈损耗的影响主要通过改变铜材料的电导率、增大线圈单位长度电阻产生。在一般温度范围内，计及温度的线圈电导率sc为
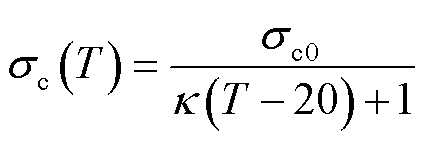（8）
式中，T为温度；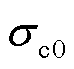
为参考温度（20℃）下铜材料的电导率，取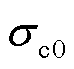= 5.8×107 S/m；k为铜材料的温度补偿系数，取0.003 93。
2.2.2 磁心损耗计算
为提高WPT系统的传输能力，通常会在电磁耦合器中加入铁氧体等磁心材料用以配合谐振线圈来提高系统互感，但与此同时也会引入磁心损耗。磁心损耗通常与磁心的物理参数、工作频率以及磁感应强度等相关，可用带温度系数的修正Steinmetz公式进行计算。
（9）
式中，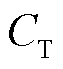
、
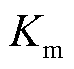、x及y为通过实验修正得到的系数，其中，CT的取值与磁心的工作温度有关；f为当前系统工作频率；Vcore为磁心体积；Bm为磁感应强度最大值。Steinmetz公式在正弦激励下计算磁心损耗的准确度非常高，对于非正弦激励可配合使用傅里叶级数分解法分解为各谐波分量，再进行求解加和得到总的磁心损耗。
由于电磁耦合器的磁心、线圈、紧固件表面与周围空气间均存在温度差，热量会从温度高的部分流向温度低的部分以达到热稳定。在自然对流冷却方式下，电磁耦合器的传热方式主要包括热传导、热对流及热辐射三种方式。考虑到原边线圈与原边磁心、副边线圈与副边磁心均为紧密贴合方式，因此对于原边磁心、线圈和紧固件，以及副边磁心和线圈接触面间的稳态热传导过程可根据傅里叶定律进行描述为
（10）
式中，lx、ly、lz为固体介质沿x、y、z方向的导热系数；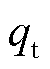
为固体介质间用于导热的热流密度。
电磁耦合器的热量来源于磁心以及线圈产生的电磁损耗，温度升高致使其周围空气介质的密度减小。根据阿基米德定律可知，电磁耦合器中绝大部分热量通过周围空气循环散失。考虑到三维热流场模型中的NS方程具有高度非线性且相互作用非常复杂，故在大范围内对空气进行自然对流散热计算时，动量守恒方程可利用Boussinesq近似简化分析。在开放空间的流体场内，对电磁耦合器自然对流传热过程建立控制方程为
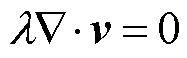（11）
流体场中质量守恒、动量守恒及能量守恒方程分别为
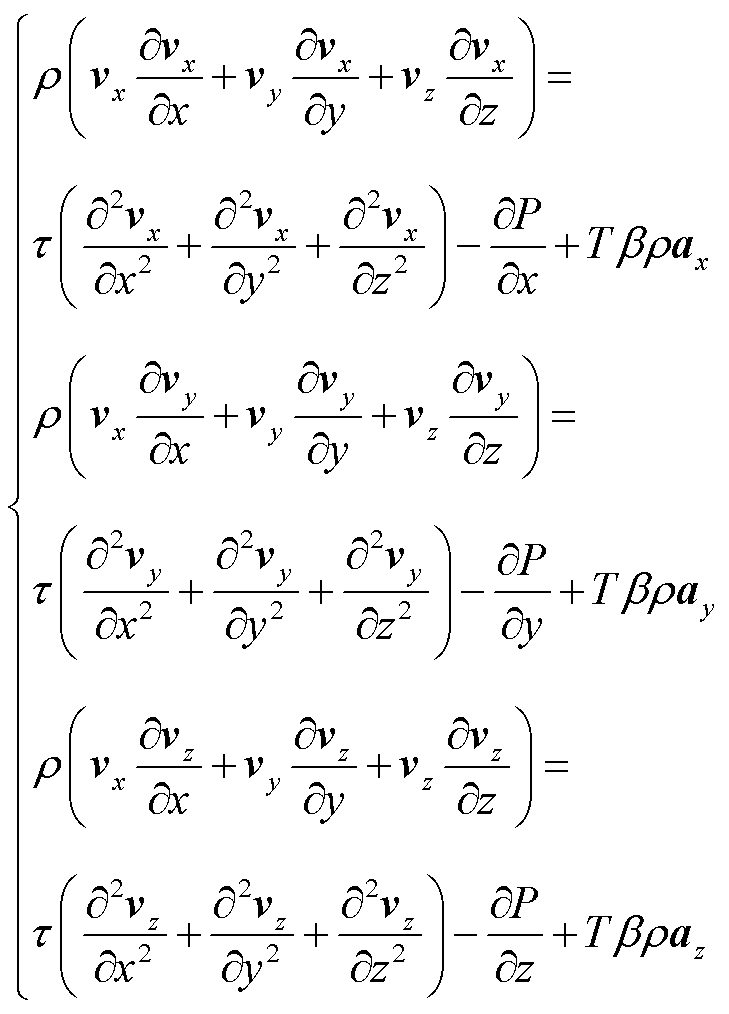（12）
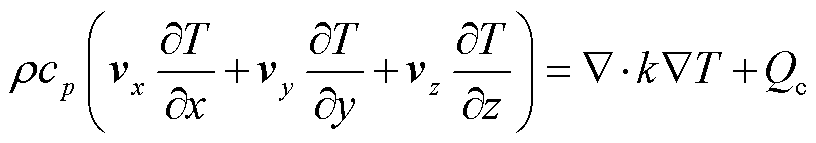（13）
式中，vx、vy、vz分别为流体速度在x、y、z轴方向的分量；r为流体的体积密度；t为流体的动力粘度；P为流体受到的压力；b为流体的热膨胀系数；ax、ay、az分别为体积力在x、y、z轴方向的加速度；cp为比定压热容；k为流体介质导热系数；Qc为流体的内热源，即在忽略黏性耗散、辐射时，损耗热量流向空气中的部分。
在电磁耦合器中，紧固件与副边线圈绝缘、副边磁心外侧无线圈接触部分之间存在辐射换热过程。本文基于面-面辐射方式，利用Stefan-Boltzmann方程对该过程进行描述为
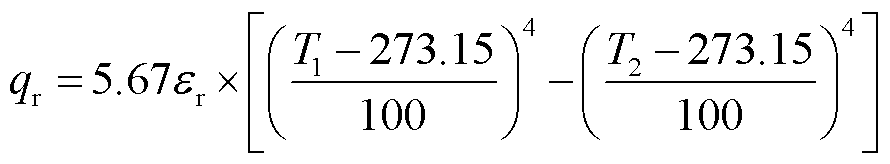（14）
其中，面等效发射率er为
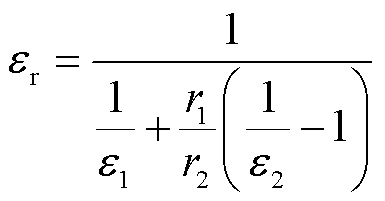（15）
式中，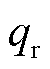
为辐射散热的热流密度；T1、T2分别为两相对辐射面的温度；
、
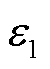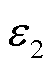分别为两相对辐射面的发射率；
、
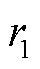分别为两相对辐射面的半径。以电磁耦合器为原点，在较大范围内求解热力学及流体问题的边界约束为
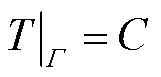（16）
（17）
式中，该范围边界温度T设为常数C；该范围流体边界设置为无滑移条件，对照电磁耦合器应用位置而言，气流速度在x、z方向无加速度，仅存在沿y轴负方向的重力加速度g。
本文采用Matlab Simulink搭建WPT系统中DC-DC变换电路，模拟移相全桥控制下电流波形。考虑到旋转式电磁耦合器电流波形为非正弦，因此选择Ansys Maxwell瞬态场求解器求解电磁损耗。得到的电磁耦合器磁场分布情况如图5所示。
图5 电磁耦合器磁场分布
Fig.5 Magnetic field distribution of electromagnetic coupler
观察图5可以发现，电磁耦合器的磁场分布基本呈上下对称，磁场强度沿磁心中心位置向端部逐渐衰减。副边磁心中间位置磁力线分布最密，最大磁感应强度位于贴近副边线圈几何中心的磁心表面处，约为5.32×10-2 T。根据文献[21]可得到旋转式电磁耦合器最大磁感应强度，在此本文不再过多赘述。最大磁感应强度计算公式为
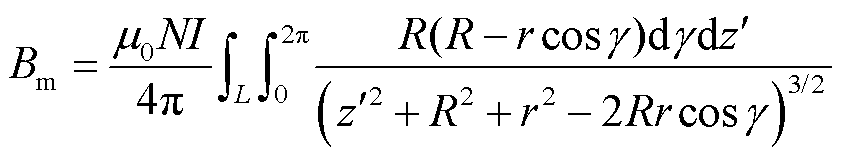（18）
式中，N为线圈匝数；R为原边磁心内边缘半径；r为副边磁心外边缘半径；L为线圈高度。代入相应数据可计算出旋转式电磁耦合器最大磁感应强度Bmax=5.18×10-2 T，与瞬态电磁场所得最大磁感应强度数值的差值控制在误差范围内。
图6为电磁耦合器在一周期内损耗密度的分布情况。通过观察图5和图6a可以发现，旋转式电磁耦合器磁心的平均损耗密度分布与磁感应强度分布具有相同特性。副边磁心靠近中间位置在一周期内损耗最大，原、副边磁心平均损耗密度沿中心位置向端部衰减，副边磁心单位面积的平均损耗密度高于原边磁心。从图6b可以看出，副边线圈的平均损耗密度高于原边线圈，线圈的平均损耗密度Pcoil计算公式为
（19）
式中，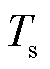
为电磁耦合器工作的一周期；i(t)为线圈内流经的总电流；Rcoil可通过式（3）计算得到。根据式（19）计算得到20℃时原、副边线圈在一周期内的平均损耗分别为0.381 W、3.133 W，有限元仿真得到原、副边线圈在一周期内的平均损耗分别为0.392 W、3.241 W，误差分别为2.9%、3.4%，验证了本文电磁场三维模型的准确性。
图6 电磁耦合器损耗密度分布
Fig.6 Magnetic field distribution of electromagnetic coupler
电磁耦合器中每个部件产生的电磁损耗将会以热能的形式消散，并最终表现为温度升高。相较于电磁场中三维模型，线圈、磁心表面间的绝缘材料以及用于固定线圈和磁心的紧固件对热流场分析影响较大，因此应考虑在内。求解电磁耦合器的三维热流场模型如图7所示，其中忽略基座和紧固件中对散热影响较小的部分。
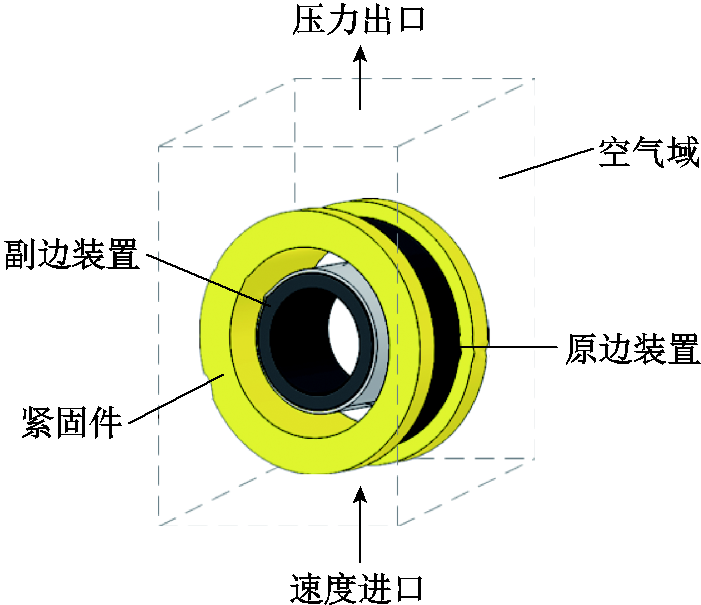
图7 热流场模型
Fig.7 Heat flow field model
本文根据文献[22]中的变压器温度场模型建立方法对单层多匝线圈电磁耦合器热流场模型进行简化，如图8所示。对Litz线单股外部绝缘及单根外侧尼龙丝一起等效，根据等效导热系数计算公式
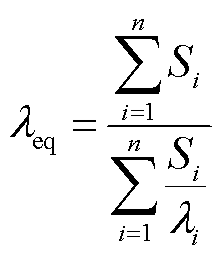（20）
式中，leq为等效导热系数；Si和li分别为各绝缘材料截面积及相应的导热系数。电磁耦合器中磁心、铜线、环氧改性漆、复合聚氨酯漆、PLA塑胶和尼龙丝的导热系数分别为27.2、387.6、0.21、0.23、0.226和0.25 W/(m·℃)。
图8 线圈等效模型
Fig.8 Coil equivalent model
将电磁损耗计算结果间接耦合至热流场中作为初始热源，模拟自然对流情况下旋转式电磁耦合器达到稳态时的温升变化，以实验测试环境为参考值，设置初始环境温度为20℃，空气相对压强为0 Pa。为减少热流场迭代步数和增强计算收敛性，在重力方向的入口速度设置为0.005 m/s。
图9给出了电磁耦合器稳态温升与流速分布结果，可以看出旋转式电磁耦合器温升随纵向高度增加呈上升趋势。外部气体主要从x轴方向进入，由于受电磁耦合器嵌套式结构影响，原、副边间气道内空气径向流通路径受阻，导致气流流速较低，降低对流换热速率，使内侧磁心及线圈温度较高。从图9a中可以看出，线圈温度整体高于磁心温度，这是由于线圈的发热功率远高于磁心。每匝线圈作为独立发热源而言，由于外侧环绕线圈的散热较好，靠近中间位置的线圈散热受到外侧线圈热源的影响使得温度略高。线圈紧密环绕在磁心表面，并且在建模时已经假设线圈与磁心接触良好，结合图9b和图9c可以观察到，越靠近线圈、周围空气流速越高的位置，温度越高；与线圈距离较远、周围空气流速低的位置，温度越低，磁心的温升分布特点符合热力学定律。同时，由于紧固件的存在使得原边磁心和原边线圈增大了与紧固件之间的传导热源，降低和消除了与空气之间的对流热源。紧固件作为非导磁性材料不产生能量损耗，因此其发热功率为零，图9a中所示紧固件的温升主要来源于原边线圈和原边磁心的热传导。
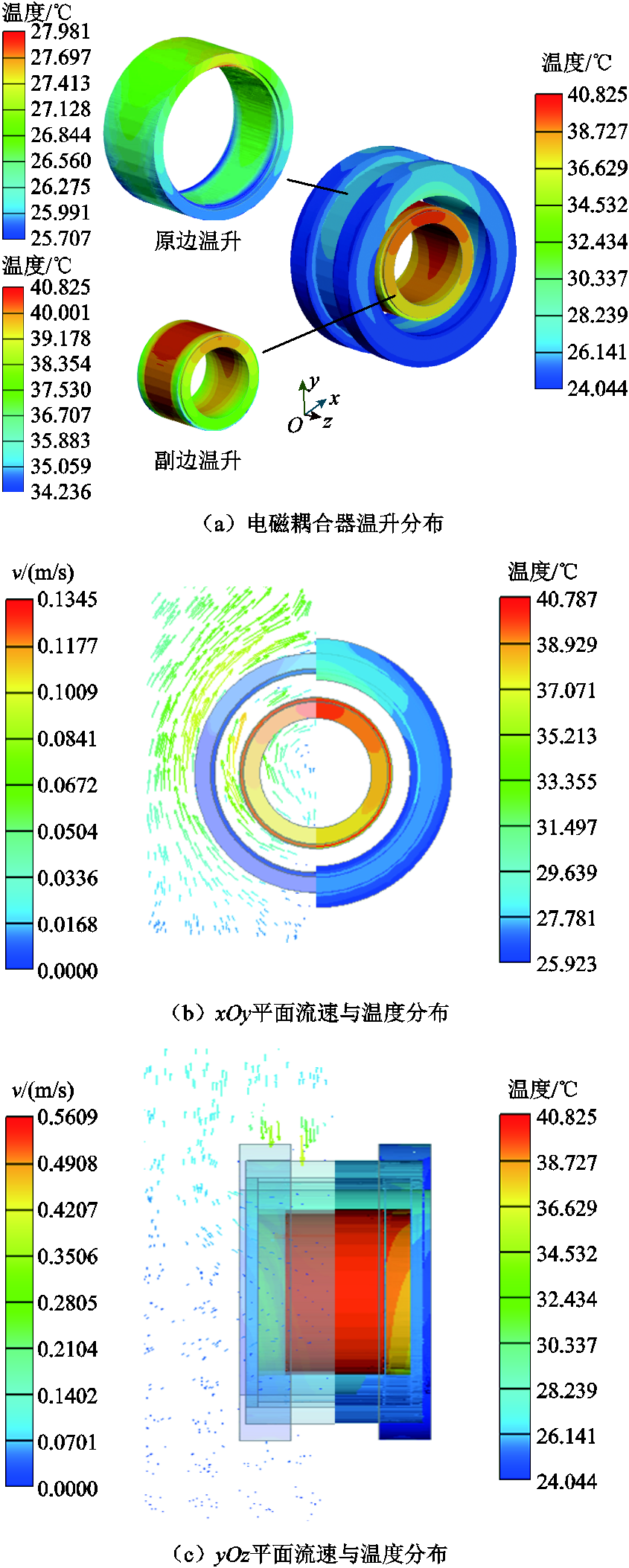
图9 电磁耦合器温度与流速分布结果
Fig.9 Temperature and velocity distribution results of electromagnetic coupler
旋转式电磁耦合器副边磁心温度分布如图10所示，其热点温度出现在副边线圈顶部对应区域，相比环境温度的最高温升大约为21℃；最低温度位于磁心边缘处，与副边线圈轴向距离最小值为 1.3 mm，温差大约为3℃，平均温度为39.6℃。副边磁心最高温升产生的原因一部分来自自身的铁心，另一部分来自于副边高温线圈的热传导。温度不均匀分布对电磁耦合器参数计算增加不确定性，同时长期过热容易引发磁心变形或损坏。因此当旋转式电磁耦合器应用于大功率情况时，在研发设计初期应考虑副边磁心的温升情况。
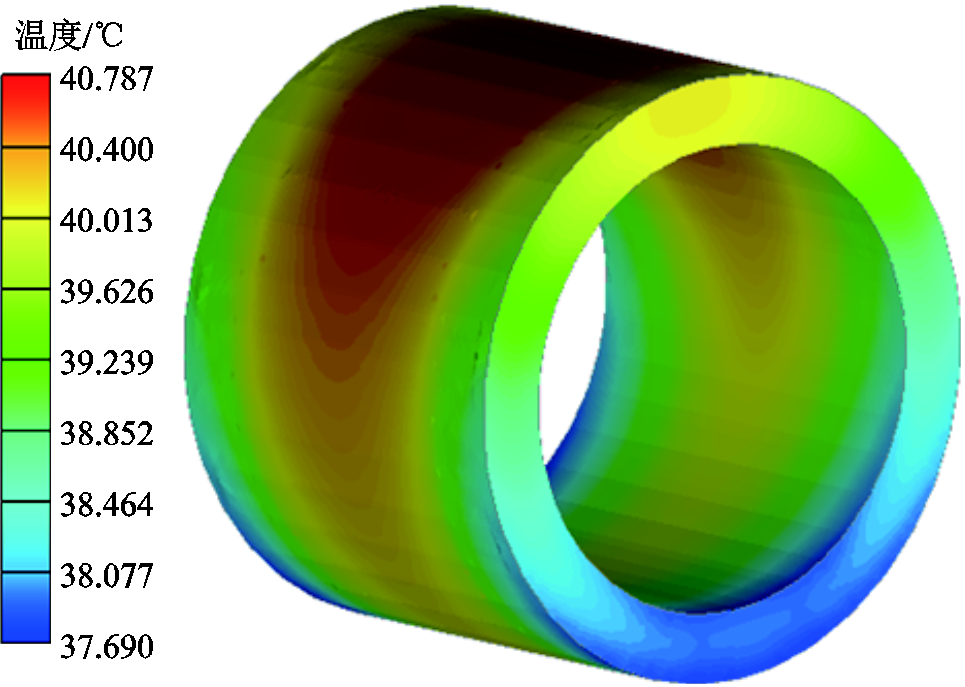
图10 副边磁心温升分布
Fig.10 Temperature rise distribution of inner magnetic core
为验证旋转式电磁耦合器多物理场耦合仿真模型的合理性与仿真结果的准确性，本文以环境温度为20℃，谐振频率为50 kHz，最大稳定输出功率为1 kW的无线电能传输系统电磁耦合器进行温度分布的实验测试。搭建图11所示的无线电能传输系统实验平台，利用LW-1001KD为系统提供工频整流后的100 V直流电压输入，通过RIGOL DS7024示波器采集原、副边线圈输出电压、电流波形，同时JT6343A作为直流负载，同步显示系统输出功率。采用红外热成像仪实时观测电磁耦合器整体的温升变化过程，配合使用K型热电偶多通道测温仪和红外测温枪可更加直观地监测在仿真中出现的局部热点。
图11 WPT系统实验平台
Fig.11 WPT system experimental platform
通过LCR测试仪测量旋转式电磁耦合器参数见表2，其中原、副边线圈自感分别为161.2 mH、152.4 mH，互感为133.1 mH，电阻值分别为70.9 mW、64 mW，与电磁仿真中数值偏差均小于10%，验证了建模方法的有效性。其中存在误差的主要原因有：①在仿真建模中忽略Litz线内部绞合结构，采用简化模型会使得仿真值与实际测量值产生偏差；②物理模型中材料属性默认为各向同性对参数的计算也会产生影响。
表2 旋转式电磁耦合器仿真与测量参数比较
Tab.2 Comparison of simulation and measurement parameters of rotary electromagnetis coupler
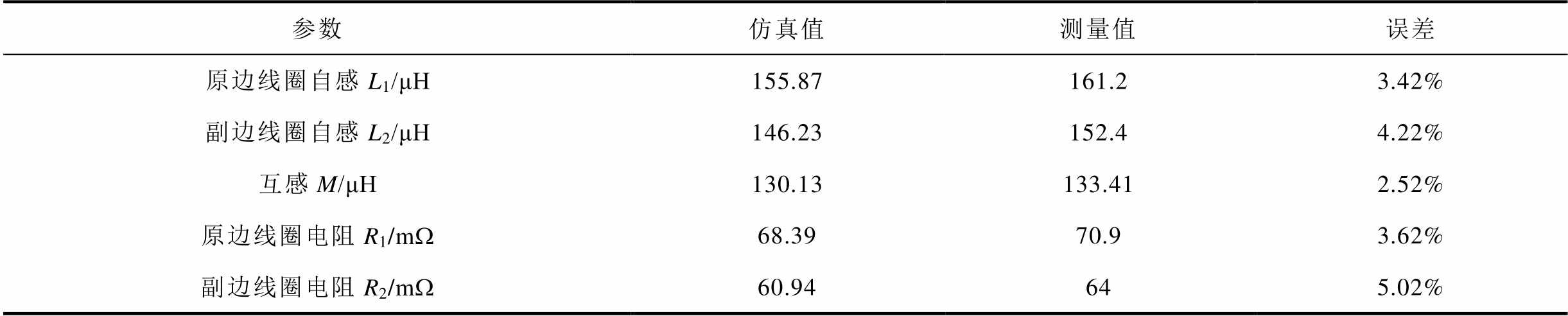
参数仿真值测量值误差 原边线圈自感L1/μH155.87161.23.42% 副边线圈自感L2/μH146.23152.44.22% 互感M/μH130.13133.412.52% 原边线圈电阻R1/mW68.3970.93.62% 副边线圈电阻R2/mW60.94645.02%
图12为功率分析仪采集到的数据，由图12可知，输入功率Pdc为645 W时，输出功率PL为525 W，且原边电流Idc有效值约为6.34 A，副边电流IL有效值约为 16.18 A，其有效值约为原边电流有效值的 2.5倍。根据损耗计算公式可知，旋转式电磁耦合器副边产生的损耗将大于原边，即旋转式电磁耦合器副边产生的发热功率将大于原边。
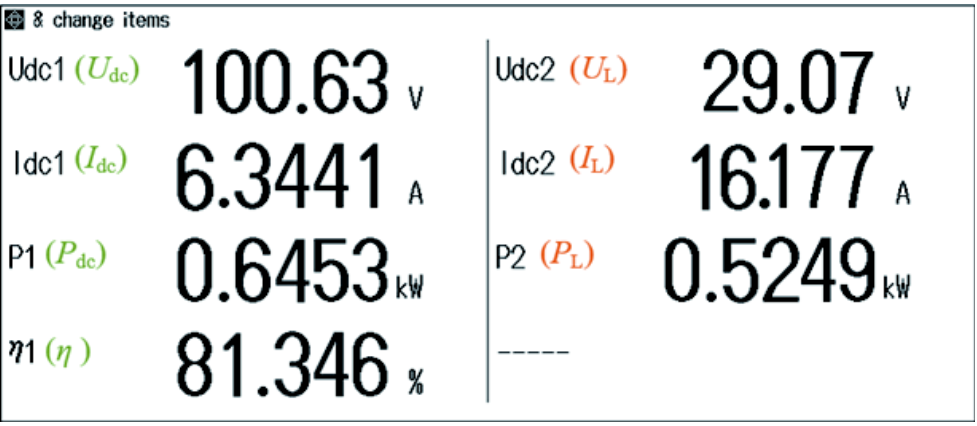
图12 功率分析仪采集数据
Fig.12 Power analyzer data
根据3.3节热流场模拟结果选择各部件的温度测量位置，采用多路测温仪对选择热点进行温度测量。温升测试的结果可以明确系统中发热最为严重的部分，从而在系统优化时多加考虑，因此选取仿真中各部件的最高温度点。分别选择原边磁心外侧顶端中心位置，副边磁心内侧顶端中心位置，原、副边线圈轴向中心位置，即从外向内的第11、12匝线圈间作为温度测量点，如图13所示。
图13 松耦合变压器各部件测温位置
Fig.13 Temperature measurement position of each component of Loose coupling transformer
使用FLUKE红外热成像仪拍摄电磁耦合器的稳态温升分布，如图14所示。热电偶多路测温仪记录了在谐振状态下的系统运行20 min后的实验值，测量结果与仿真值大致相同，见表3。造成温度误差的主要原因有：
（1）为使铜线圈的热源体积密度相同，将其简化为与铜材料体积相同的薄板式结构，忽略每匝绕线间的尼龙纤维对线圈的散热影响。
（2）三维热流场仿真中模拟的自然对流属于理想状态，实际状况下的实验平台无法完全满足条件。仿真温度与实测值偏差≤6%，满足工程计算需要，验证了建模方法的合理性。
图14 红外线稳态温升分布结果
Fig.14 Infrared steady-state temperature rise distribution results
表3 热点温度仿真与实验结果
Tab.3 Hot spot temperature simulation and experimental results
部件位置温度/℃误差(%) 仿真值测量值 原边磁心中部27.228.65.15 原边线圈中部27.929.14.3 副边磁心中部40.441.83.47 副边线圈中部40.742.33.93
鉴于电磁耦合器的工作温度是决定WPT系统稳定运行的关键因素，本文建立了考虑绝缘引起匝间距的旋转式电磁耦合器三维电磁场仿真模型，并对其磁场与损耗进行计算和分析。采用磁-热-流多物理场耦合方法计算自然状态下表面传热系数，实现对电磁耦合器的温升计算，最终通过所搭建的实验平台验证理论分析的正确性，可得到以下结论：
1）旋转式电磁耦合器磁心的平均损耗密度与磁感应强度的分布呈正相关，靠近线圈轴向中心位置的磁感应强度最高，损耗密度最大，端部最小，基本呈递减规律分布。
2）旋转式电磁耦合器高温区域位于副边线圈顶端，最高温度仿真值与测量值分别为40.7℃和42.3℃，误差为3.93%，副边线圈自身最大温差约6.6℃。由于磁心的存在使得电磁耦合器极大地减小了漏磁，在提高传输效率时也引入了损耗，受制于嵌套结构的影响，在线圈高温传导下产生局部过热，其最高温度相比于环境温度高22.3℃。
3）考虑材料属性温度效应的多物理场耦合计算，克服传统磁路法计算不准确的问题，能够更好地研究旋转式电磁耦合器的温升分布。通过对电磁耦合器的温升测试，验证了建模方法的合理性与结果的准确性。
本文的分析计算可为无线充电系统旋转式电磁耦合器的损耗计算及温升分布研究提供理论依据。后续将开展对旋转式电磁耦合器应用于水下大功率下的温升试验，以及针对高温部分展开散热优化研究。基于本文模型，可以对AUV的传输特性随温度的变化趋势展开深入分析，本文的多物理场耦合分析也为AUV的结构设计提供思路。
参考文献
[1] Zeng Yingqin. Lu Conghui, Liu Renzhe, et al. Liu, Wireless power and data transfer system using multidirectional magnetic coupler for swarm AUVs[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 1440-1444.
[2] 闫争超, 胡谦宇, 赵晨旭, 等. 水下航行器感应式无线电能传输技术研究综述[J/OL]. 中国电机工程学报, 2022: 1-16[2023-02-15]. https://kns.cnki.net/ kns8/defaultresult/index. Yan Zhengchao, Hu Qianyu, Zhao Chenxu, et al. Summary of research on induction radio energy transmission technology for underwater vehicles[J/OL].Proceedings of the CSEE, 2022: 1-16[2023-02-15] https:// kns.cnki.net/kns8/defaultresult/index
[3] Yan Zhengchao, Zhang Yiming, Zhang Kehan, et al. Underwater wireless power transfer system with a curly coil structure for AUVs[J]. IET Power Electronics, 2019, 12(10): 2559-2565.
[4] Qiao Kangheng, Sun Pan, Rong Enguo, et al. Anti-misalignment and lightweight magnetic coupler with H‐shaped receiver structure for AUV wireless power transfer[J]. IET Power Electronics, 2022, 15(16): 1843-1857.
[5] Gerasimov V A,Komlev A V, Filozhenko A Y. improving the quality of the underwater robot’s contactless battery charging system[C]// Journal of Physics: Conference Series, 2021, 2096(1): 012107-. DOI:10.1088/1742-6596/2096/1/012107.
[6] Chae D J, Kim Y S. Analysis for electrical and thermal hazard in kW-class wireless power transmission environment[C]// 2018 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (Wow), Montreal, QC, Canada, 2018. DOI:10.1109/ WoW.2018.8450930.
[7] Hwang K, Chung S, Yoon U, et al. Thermal analysis for temperature robust wireless power transfer systems[C]//2013 IEEE Wireless Power Transfer (WPT), Perugia, Italy, 2013.DOI:10.1109/WPT.2013. 6556879.
[8] Li Yang, Zhao Jingtai, Yang Qingxin, et al. A novel coil with high misalignment tolerance for wireless power transfer[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-4.
[9] Campi T, Cruciani S, De Santis V, et al. EMF safety and thermal aspects in a pacemaker equipped with a wireless power transfer system working at low frequency[J]. IEEE Transactions on Microwave Theory and Techniques, 2016, 64(2): 375-382.
[10] 陈庆彬, 范峰, 汪金帅, 等. 无线电能传输磁耦合系统Litz线圈交流电阻精确评估方法[J]. 电工技术学报, 2022, 37(24): 6294-6305. Chen Qingbin, Fan Feng, Wang Jinshuai, et al. Accurate evaluation method for AC resistance of Litz coil of radio energy transmission magnetic coupling system [J].Transactions of China Electrotechnical Society, 2022, 37(24): 6294-6305.
[11] 张献, 韩大稳, 沙琳, 等. 一种共享磁通多耦合模式的无线电能传输系统抗偏移方法[J]. 电工技术学报, 2022, 37(21): 5359-5368. Zhang Xian, Han Dawen, Sha Lin, et al. An anti-offset method for radio energy transmission system with shared magnetic flux multi-coupling mode[J] Transactions of China Electrotechnical Society, 2022, 37(21): 5359-5368.
[12] 赵蒙蒙, 李岩松, 丰江波, 等. 轴式松耦合变压器的热行为特性及影响因素[J]. 电测与仪表, 2019, 56(7): 22-29. Zhao Mengmeng, Li Yansong, Feng Jiangbo, et al. Thermal behavior characteristics and influence factors of shaft-type loosely coupled transformer[J]. Electrical Measurement and Instrumentation, 2019, 56(7): 22-29.
[13] Wang Shuo, Dorrell David G. Loss analysis of circular wireless EV charging coupler[J]. IEEE Transactions on Magnetics, 2014, 50(11): 1-4.
[14] Liang Ce,Yang Guang, Yuan Feng, et al. Modeling and analysis of thermal characteristics of magnetic coupler for wireless electric vehicle charging system[J]. IEEE Access, 2020, 8: 173177-173185.
[15] 毛行奎, 陈为. 开关电源高频功率平面变压器热设计研究[J]. 电工电能新技术, 2007, 26(4): 21-25. Mao Xingkui, Chen Wei. Research on thermal design of high frequency power plane transformer for switching power supply[J]. New Electrical Energy Technology, 2007, 26(4): 21-25.
[16] Zhu Tianxin, Feng Panshang, Li Xuekun, et al. The study of the effect of magnetic flux concentrator to the induction heating system using coupled electromagnetic-thermal simulation model[C]//International Conference on Mechanical and Automation Engineering, Jiujiang, China,2013: 123-127.
[17] Kalra G R, Pearce M G S, Kim S, et al. A power loss measurement technique for inductive power transfer magnetic couplers[J]. IEEE Journal of Emerging and Selected Topics in Industrial Electronics, 2020, 1(2): 113-122.
[18] Tiemann M, Saifo M, Clemens M, et al. Magnetic and thermal coupled field analysis of wireless charging systems for electric vehicles[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-4.
[19] Kazimierczuk M. High-frequency magnetic components[M]. 2nd ed. Chichester, UK: John Wiley & Sons, 2014.
[20] Liu Jiangtao, Deng Qijun, Czarkowski D, et al. Frequency optimization for inductive power transfer based on AC resistance evaluation in Litz-wire coil[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2355-2363.
[21] 程志远, 陈坤, 李东东, 等. 旋转式无线充电系统偏移特性研究[J]. 电工技术学报, 2021, 36(22): 4648-4657. Cheng Zhiyuan, Chen Kun, Li Dongdong, et al. Research on the offset characteristics of rotary wireless charging system[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4648-4657.
[22] 李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491. Li Yongjian, Yan Xinxiao, Zhang Changgeng, et al. Transformer loss calculation and hot spot prediction based on magnetic-thermal-current coupling model[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4483-4491.
Abstract Electromagnetic couplers are the core components of wireless power transfer (WPT), and their operating temperature determines the stability and service life of the system operation. Therefore, accurately estimating the coil winding and magnetic core losses of high-frequency electromagnetic couplers and studying the temperature rise distribution of electromagnetic couplers under normal modes are crucial for the heat dissipation design of underwater autonomous vehicles and improving the reliability of WPT systems. To address these issues, this article takes the rotary electromagnetic coupler with strong resistance to radial offset as the research object and establishes a three-dimensional electromagnetic thermal field simulation model that considers the influence of insulation induced turn spacing and temperature on material properties, achieving accurate calculation of hot spot temperature.
Firstly, theoretical analysis is conducted on the temperature rise of the electromagnetic coupler, which involves calculating the loss of the electromagnetic coupler, and then loading the loss as a heat source into the heat flow field to obtain the temperature distribution of the electromagnetic coupler; Secondly, based on the temperature rise principle of electromagnetic couplers and strictly following the temperature rise calculation process, the finite element Ansys Maxwell simulation software is used to solve the electromagnetic loss and hot spot distribution. In the simulation software, the first step is to calculate coil losses and magnetic core losses.Then, using the transient electromagnetic field heat flow field bidirectional indirect coupling method, a three-dimensional electromagnetic field simulation model is established. Finally, the electromagnetic loss calculation results are coupled as loads into the heat flux field and corresponding relationships are established to obtain the hot spot distribution of the rotating electromagnetic coupler.
The simulation results show that the magnetic field distribution of the electromagnetic coupler is basically symmetrical from top to bottom, and the magnetic field intensity gradually decreases along the center position of the magnetic core towards the end. The maximum magnetic density is located on the surface of the magnetic core close to the geometric center of the secondary coil. The average loss density distribution of the electromagnetic coupler has the same characteristics as the magnetic induction intensity distribution. At 20 ℃, the average loss errors of the primary and secondary coils within one cycle were obtained through theoretical analysis and finite element simulation, which were 2.9% and 3.4%. The experimental results show that the deviation between the parameters measured by the LCRand the numerical values in simulation is less than 10%. The thermocouple multi-channel thermometer records the temperature of the system when it reaches steady state at 20 ℃. The high-temperature area is located at the top of the secondary coil, and the deviation between the simulated temperature of the hot spot and the measured value is less than 6%, verifying the rationality of the modeling method.
The following conclusions can be drawn through experimental analysis:(1) The average loss density of the magnetic core of the rotating electromagnetic coupler is positively correlated with the distribution of magnetic induction intensity; (2) The relative position of the coil, flow velocity, and convective heat transfer coefficient all have an impact on the operating temperature of the system. At the same time, due to the influence of the nested structure, local overheating will occur under the high temperature conduction of the coil, resulting in the severe temperature rise area of the rotating electromagnetic coupling concentrated in the middle of the LCT; (3) In order to simulate the temperature rise distribution of rotary electromagnetic couplers more accurately, in addition to considering the turn spacing caused by insulation, the temperature effect of material properties should also be considered.
keywords：Wireless power transfer (WPT), rotary electromagnetic coupler, multi-physical field coupling, temperature rise characteristic, electromagnetic loss
国家自然科学基金资助项目（51877129）。
收稿日期 2023-02-17
改稿日期 2023-04-01
DOI: 10.19595/j.cnki.1000-6753.tces.230205
中图分类号：TM724
程志远 男，1977年生，博士，高级工程师，研究方向为无线电能传输、高压电缆无线取电。E-mail：chengzhiyuan@126.com
李东东 男，1976年生，博士，教授，研究方向为风力发电与电力系统稳定控制、智能用电等。0E-mail：powerldd@163.com（通信作者）
（编辑 郭丽军）