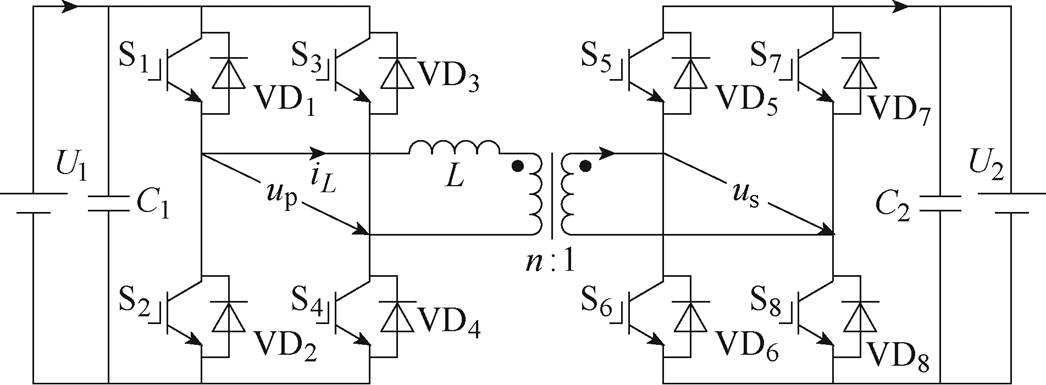
图1 DAB变换器拓扑
Fig.1 Topology of dual-active-bridge converter
摘要 针对双有源桥（DAB）变换器宽电压范围应用，该文研究一种全工况连续、表达形式统一、计算量小的三移相（TPS）调制策略，并分析其功率传输特性及软开关性能。结合工程应用中的非理想因素，对TPS调制不同开关模式下的死区效应及其边界进行研究，给出DAB宽电压范围运行时避免电压跌落和极性反转的约束条件。针对死区引入的移相比损失、软开关范围减小等问题，提出一种基于开关脉冲调整的死区补偿策略以补偿移相比损失，重新获取全工况软开关范围，降低死区引入的附加电流应力及损耗、提升效率。最后通过仿真和实验验证所提策略的有效性。
关键词：双有源桥变换器 宽电压范围运行 三移相（TPS）调制 死区效应 死区补偿
电力电子变压器（Power Electronic Transformer, PET）是智能电网、能源互联网等场合中实现功率变换、能量多向传输的关键设备[1-4]。双有源桥（Dual-Active-Bridge, DAB）变换器因具有高频隔离、结构对称、易于实现软开关等优势，已成为高压大容量模块化PET的核心功率电路[5-8]。在可再生能源和储能设备接入等场合，DAB变换器的输入输出电压和功率宽范围变化，对低损耗、低电流应力的调制策略提出了新需求。同时，死区、开关振荡、脉冲延迟等非理想因素的负面影响也亟待解决[9-10]。
DAB变换器的三移相（Triple-Phase-Shift, TPS）调制策略具有三个控制自由度，是移相调制的最基本形式，单移相（Single-Phase-Shift, SPS）、扩展移相和双移相调制均可认为是TPS调制的一种特殊情况。由于自由度多、工作模式复杂，TPS调制目前仍没有统一的应用标准[11-13]。许多学者基于TPS调制原理提出了多种优化调制策略[14-19]，但对于工程应用而言，仍存在全工况不连续、控制算法复杂等问题。如文献[15-16]仅对轻载工况进行了优化，没有覆盖全输出功率范围；文献[17-18]以消除回流功率为约束，在全工况内的优化效果不够理想；文献[19]得到了TPS调制下传输功率和电流的统一模型，但调制策略的全工况表达不连续，模式划分较为复杂，计算量大。
在实际应用中，众多非理想因素会削弱DAB运行效率和性能。如器件寄生电容与变压器漏感在死区期间谐振引入额外损耗，开关器件驱动脉冲的延迟和振荡造成电压波形畸变等。特别是在DAB的高频链路中，死区的负面效应将严重影响变换器的软开关性能及效率。死区效应的分析与补偿已成为DAB变换器工程应用中不可忽视的因素[20]。
文献[21-23]针对不同调制策略，阐明了相位漂移、移相误差、电压跌落和电压极性反转等死区效应及产生机理，并修正了功率传输模型，但均没有提出死区补偿的方法。部分文献指出通过理论计算对变换器参数进行设计，可以避免死区期间的电压畸变[24-26]，或通过定量补偿移相比和占空比的方法抑制死区效应[27-28]。然而以上方法只对固定输出电压的工况有效。当DAB变换器全功率范围运行且输入输出电压宽范围变化时，随着工作点的改变，死区效应不尽相同，移相比损失也随之变化。因此，简单地采用参数约束或定量补偿不能在宽电压全功率范围内取得较好的效果。
综上所述，对于DAB变换器宽电压范围运行，现有调制策略计算量大、全工况不连续，死区效应分析不全面、补偿策略适用范围窄。针对这一现状，本文研究了一种宽电压范围TPS调制策略，对其传输功率特性及软开关性能进行了分析；结合死区等非理想因素，研究了不同工况下死区效应的产生机理及边界，明确了避免电压跌落和极性反转的参数约束；在此基础上提出了基于开关脉冲调整的死区补偿策略；最后搭建仿真模型和1.5 kW实验平台对调制策略、死区效应及其补偿效果进行了验证。
双有源桥变换器拓扑如图1所示，图中，L为变压器漏感和外部附加电感之和，n为变压器匝比，U1和U2为变换器两端直流电压，C1、C2分别为变换器输入端支撑电容和输出端滤波电容，S1～S4、S5～S8分别为一次侧和二次侧H桥开关管。定义DAB变换器电压比m=nU2/U1。up、us分别为变压器一次侧和二次侧H桥输出电压，通过控制up、us之间的移相角即可调节传输功率的大小和方向。当DAB变换器接储能负载时，负载电压宽范围变化，变压器两侧电压不匹配程度高，DAB回流功率和电流应力增大、软开关范围减小、损耗增加，因此对其优化调制策略提出了挑战。
图1 DAB变换器拓扑
Fig.1 Topology of dual-active-bridge converter
为减小DAB变换器的回流功率，在每个开关周期中，变压器传输功率应尽量大、通过漏感转移的功率应尽量小。因此在每种开关模式内，变压器一次和二次电压矩形波应尽量重叠。由此可知DAB变换器在全工况TPS调制策略下存在两种可行的开关模式如图2所示。图中，iL为电感电流，Ths为开关周期Ts的一半，D1、D2为半个开关周期内一次侧和二次侧H桥电压占空比，Df为移相占空比。
基于以上两种开关模式，参考文献[29]以电流应力最小为目标，建立并求解评价函数，得到全工况内的优化调制策略及传输功率模型见表1。表中，P=Po/Pn为输出功率标幺值，Po为变换器实际输出功率，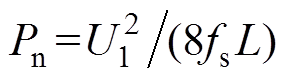
为功率标幺时的基准值。
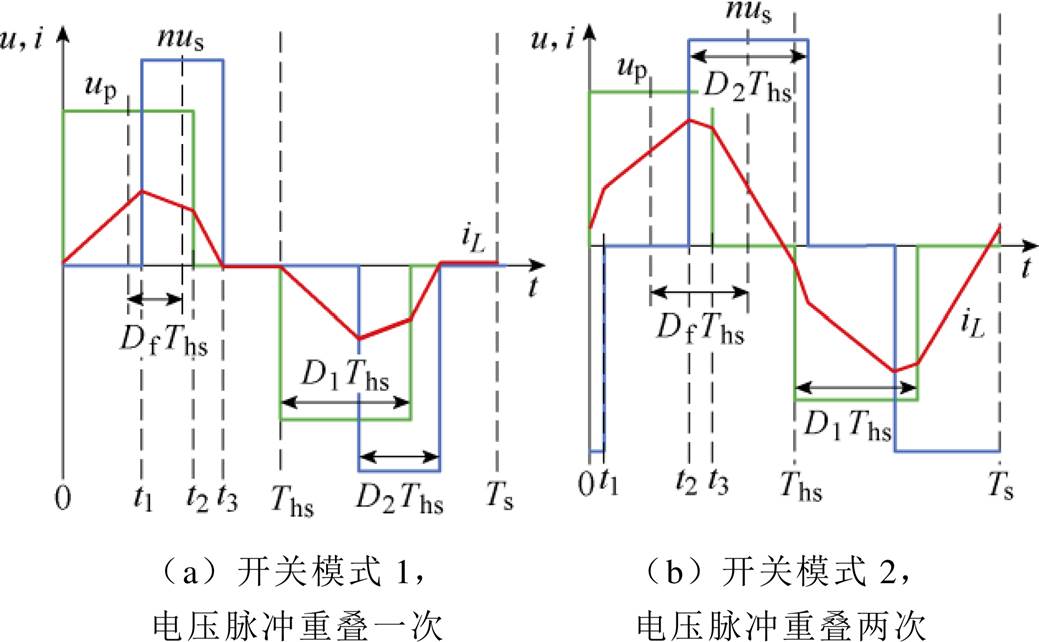
图2 DAB的全工况TPS优化调制策略
Fig.2 Three-phase-shift optimal modulation strategy of DAB in full operating range
表1 全工况TPS调制策略及传输功率模型
Tab.1 TPS modulation strategy and power transmission model in full operating range
m开关模式1开关模式2 m＜1 m=1 m＞1
不考虑死区等非理想因素，变换器工作模式可由输出功率P和电压比m按表1中的关系确定，可得到宽电压范围（m∈[0.5, 1.5]）、全工况（输出功率P∈[0, 1]）内变换器开关模式分布如图3所示。
图3中，工作点低于切换边界时，变换器工作在开关模式1；反之，工作在开关模式2。m=1时D1=D2=1，TPS调制退化为SPS调制，将其绘制为间断点。
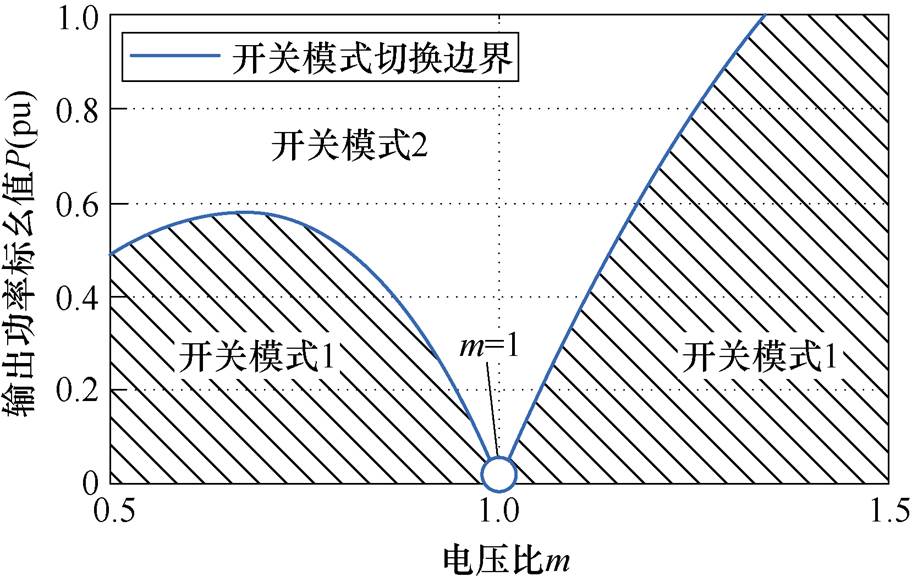
图3 无死区时全工况范围内开关模式分布
Fig.3 Switching mode distribution in full operating range without dead band
根据传输功率计算模型，可得TPS策略全工况内有功功率传递特性如图4所示。模式切换点以下曲线为开关模式1，切换点以上为开关模式2。
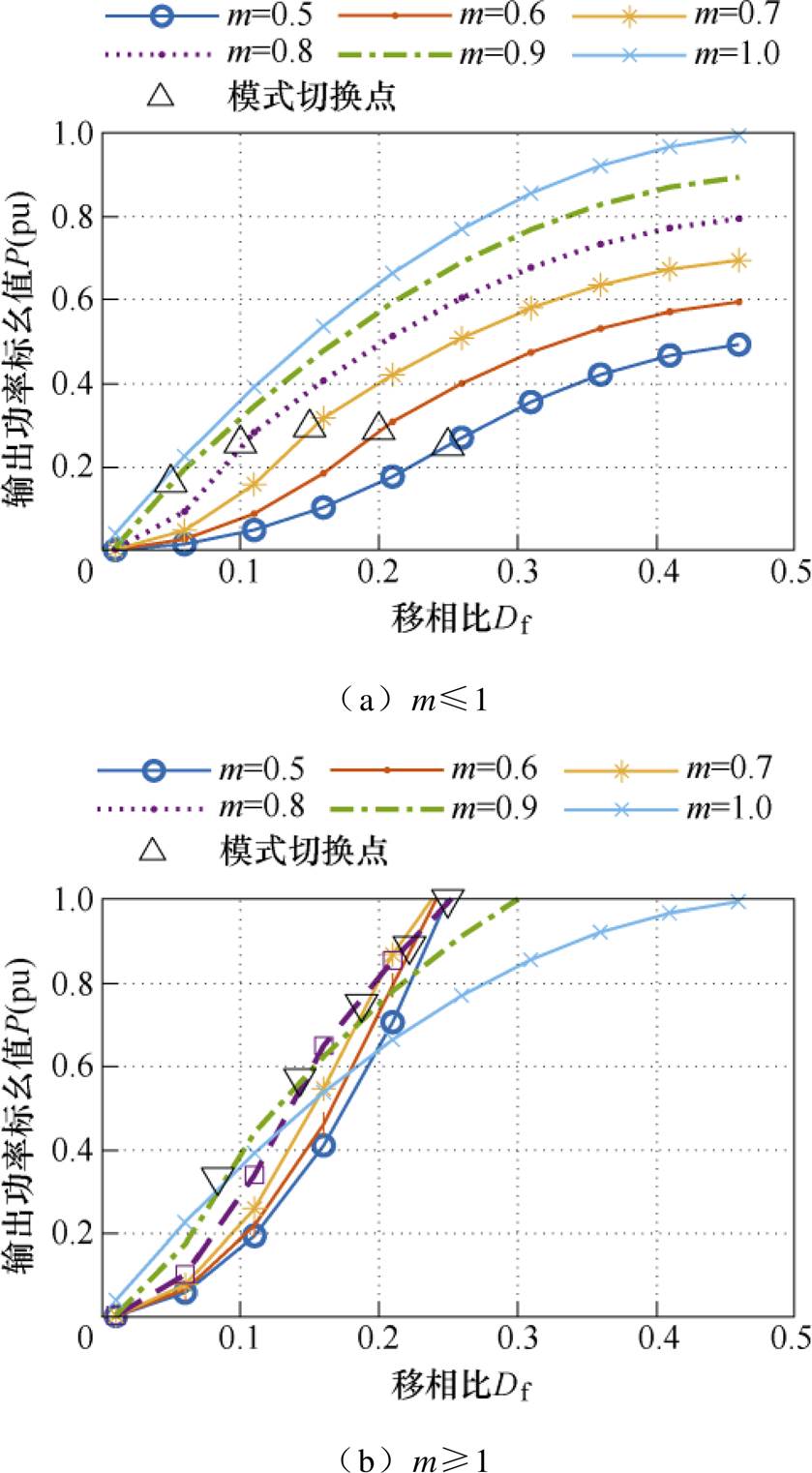
图4 TPS调制下全工况功率传输特性
Fig.4 Power transmission under TPS modulation
由图4可知，对于DAB宽电压范围运行，本文采用的全工况TPS优化调制策略的计算简单、表达形式统一，可以实现两种开关模式的平滑切换和全功率范围内的连续调节。
为评估采用TPS调制策略后的DAB电气特性，以所有器件关断电流之和，即变换器总开关电流Isw衡量开关损耗；以电感电流有效值Irms衡量导通损耗；以电感电流最大值Imax衡量电流应力。所有电流值对In=U1/(4fsL)进行标幺化，可得全工况内各电气量时域表达式见表2。
由表2中电气量关系绘制TPS与SPS调制的电流应力及开关电流对比如图5、图6所示。图中，实线为TPS调制下电流值，虚线表示相同条件下SPS调制的电流值。可知TPS调制策略可以减小电压不匹配时的电流应力和开关电流，有效降低器件损耗。
表2 TPS调制策略全工况电气量表达式
Tab.2 Electrical parameters of TPS modulation in full operating range
开关模式开关模式1m=1开关模式2 m＜1m＞1m＜1m＞1 输出功率范围P(pu) 电感电流最大值Imax 总关断电流Isw 电感电流有效值Irms
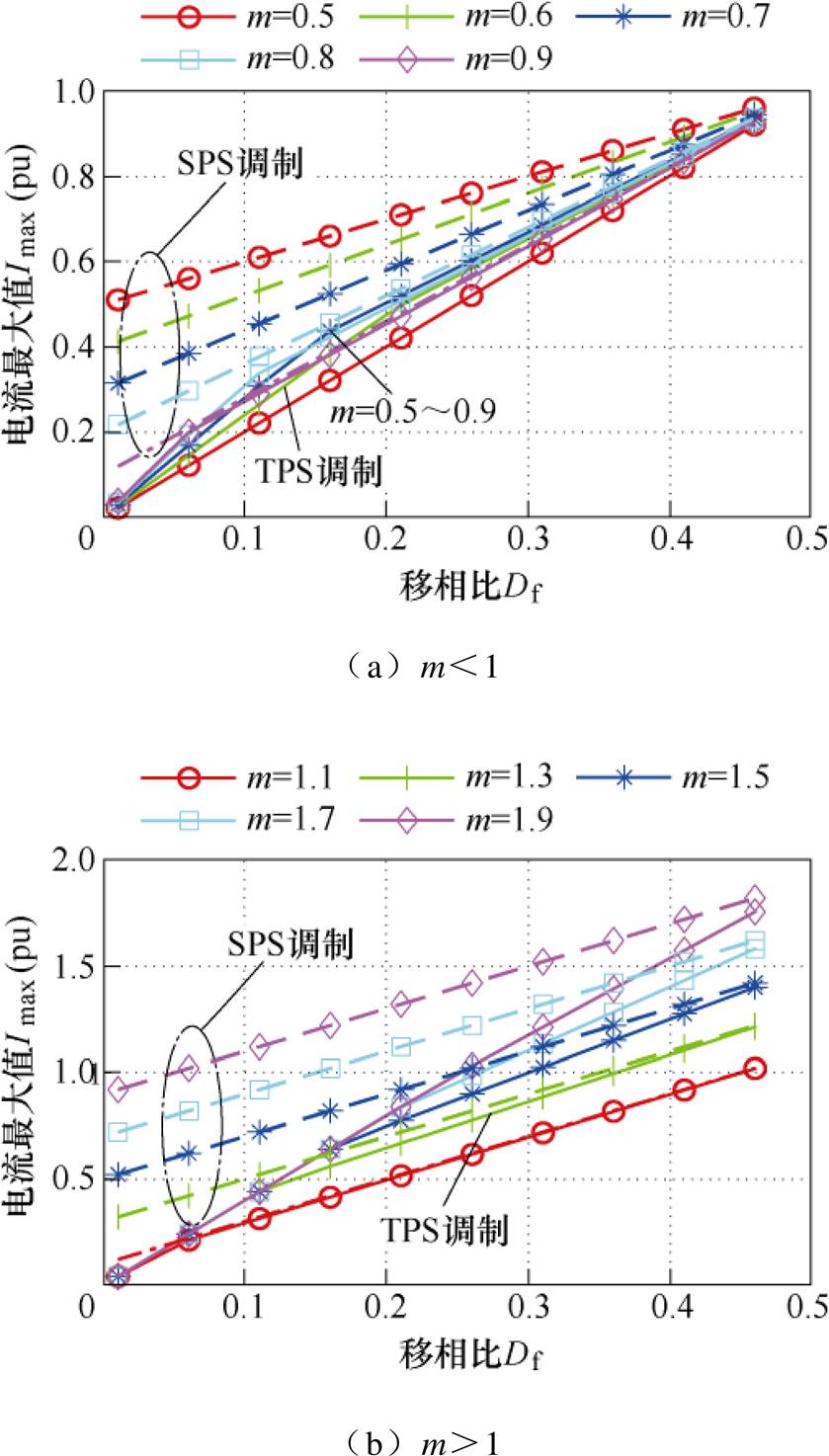
图5 TPS调制与SPS调制电流应力对比
Fig.5 Current stress comparison of TPS and SPS
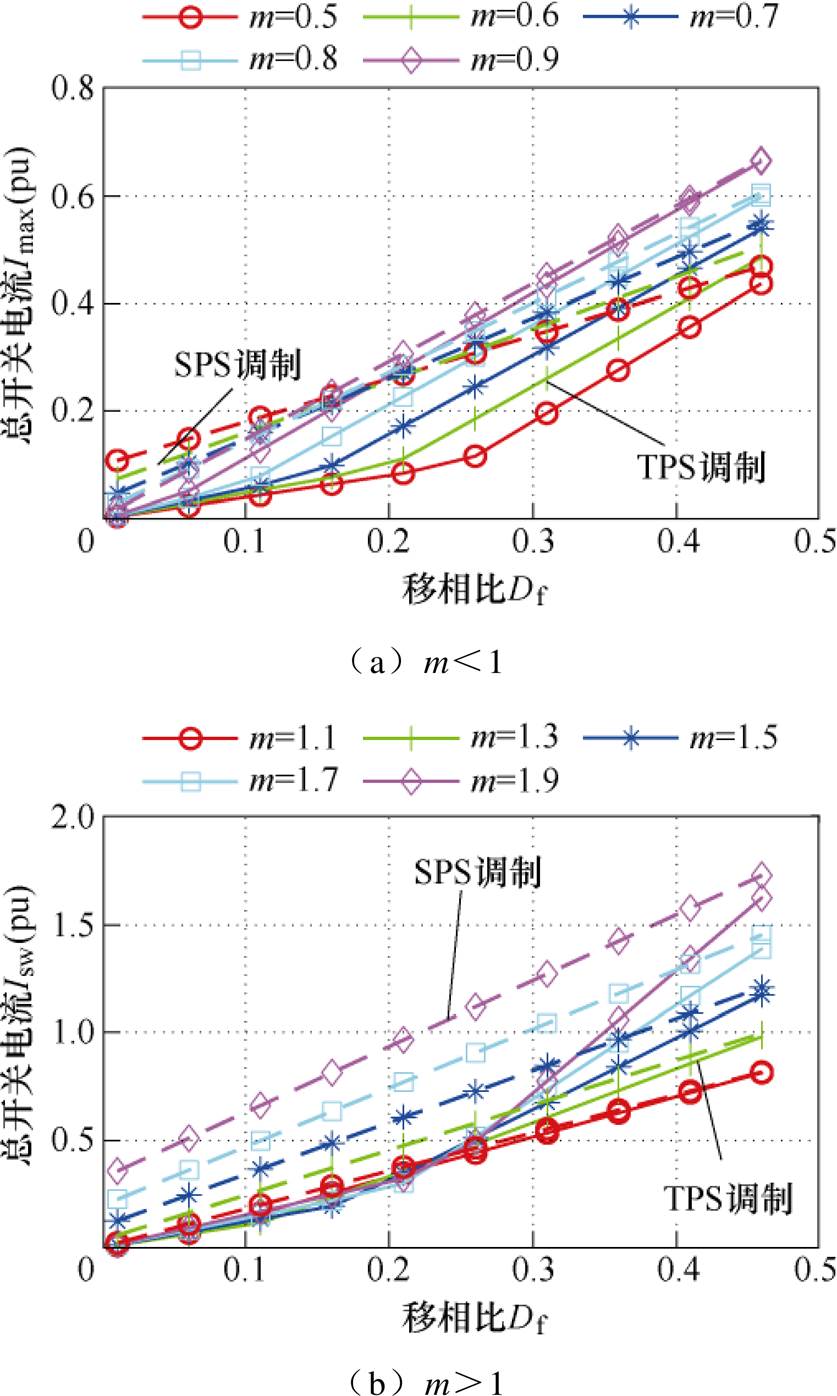
图6 TPS调制与SPS调制开关电流对比
Fig.6 Switching current comparison of TPS and SPS
基于TPS调制在全工况内的不同开关模式可计算各开关器件动作时刻关断电流见表3。在不考虑死区效应时，由电流值分析可得到TPS调制策略的软开关特性。
表3 全工况TPS调制策略下器件关断电流
Tab.3 Turn-off current of devices under the full operating range TPS modulation strategy
工况一次侧关断电流二次侧关断电流 开关模式1m＜1 m＞1 m=1 开关模式2m＜1 m＞1
由表3可知，不考虑非理想因素时，采用全工况TPS调制策略，可获得全工况开关器件零电压开通和部分工况零电流关断。可以在宽电压范围工况中保证变换器的软开关性能，降低开关损耗。
在实际应用中，死区、脉冲延迟、开关振荡及器件寄生参数等非理想因素均会对变换器的开关特性带来影响，造成电压电流波形畸变，进而威胁其稳定运行。
图7为DAB工作在开关模式1下引入死区前后的理论波形。其中实线为理想波形，虚线为加入死区后的波形，电感电流与x轴围成的三角形阴影部分为DAB的正向传输功率。由图可知，死区的加入使电压脉宽和传输功率减小，产生了回流功率和电流尖峰，控制器需要更高的移相比Df以达到所需传输功率。
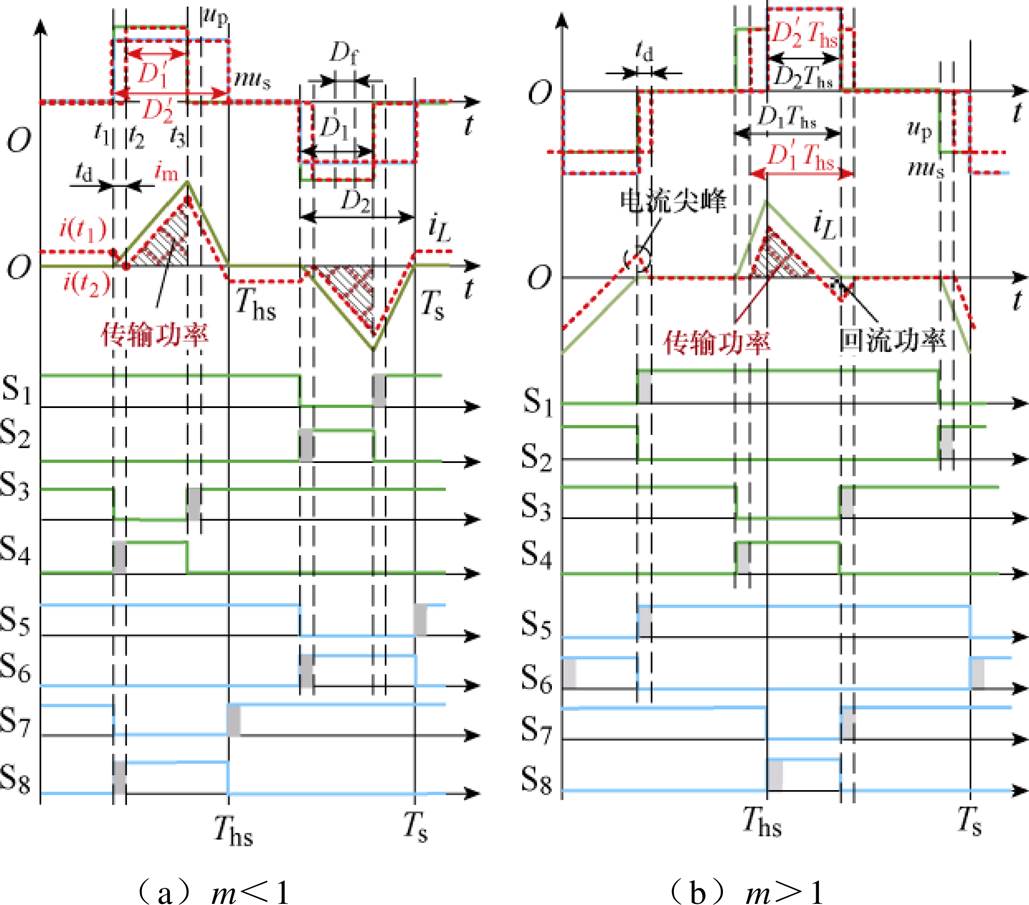
图7 开关模式1引入死区前后理论波形
Fig.7 Theoretical waveforms in mode 1 before and after considering dead band
相同工况下Df实际值高于理论值的部分称为移相比损失DDf。移相比损失造成TPS调制的开关模式切换边界改变，使DAB实际工作模式与理论出现差异。设理想条件下模式切换边界上的移相比为Df_edg，功率为Pedg。受死区影响后的边界移相比下移，变为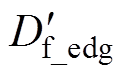
，则有
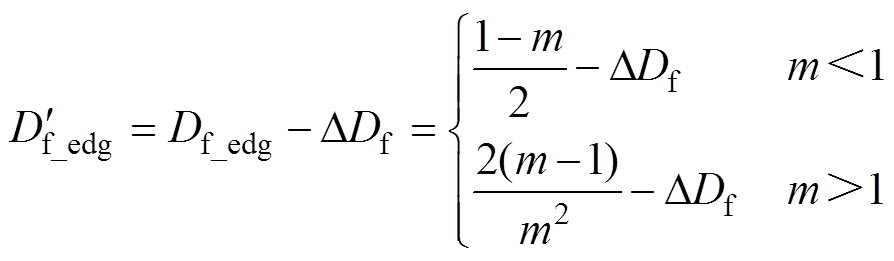（1）
将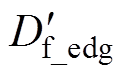代入表1的传输功率公式可求得受死区影响后的传输功率边界
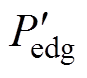，切换边界变化如图8所示。
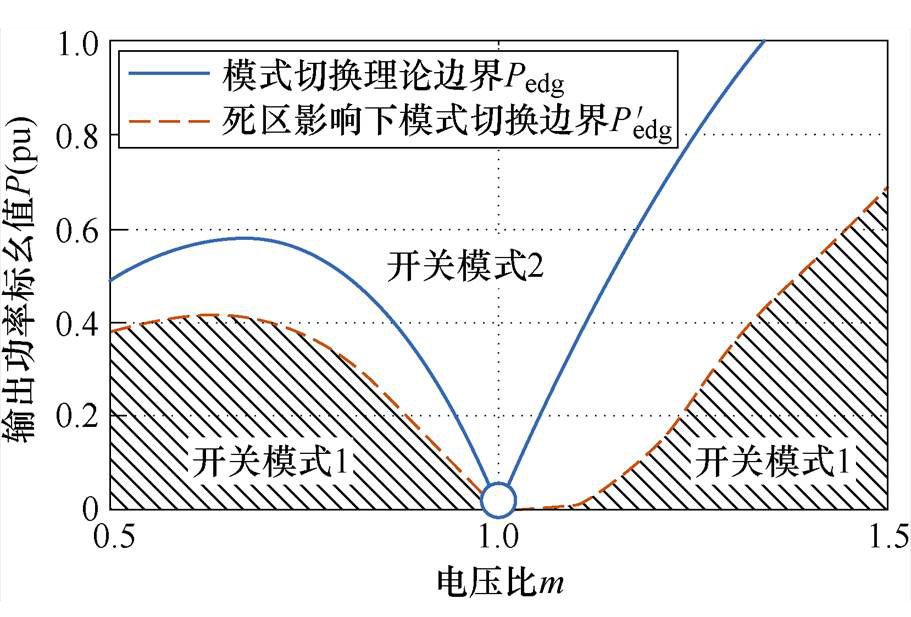
图8 考虑死区前后的开关模式边界
Fig.8 Switching mode boundary before and after considering dead band
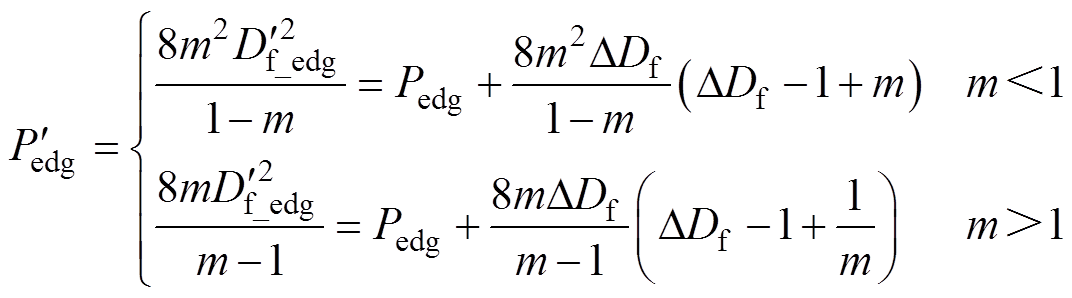（2）
由图8可知考虑死区后，由于全工况内移相比损失DDf不同，不同工况开关模式切换边界移动的距离不同，因此死区对移相比损失的影响表现出非线性。
由于引入死区后电感电流波形发生变化，开关时刻的电流值改变，TPS调制的软开关性能受到影响。设引入死区后移相比和脉宽分别为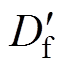
、
、
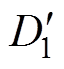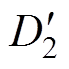，由图7a可得，m＜1时引入死区后一个周期内电感电流变化，解得各时刻关断电流为
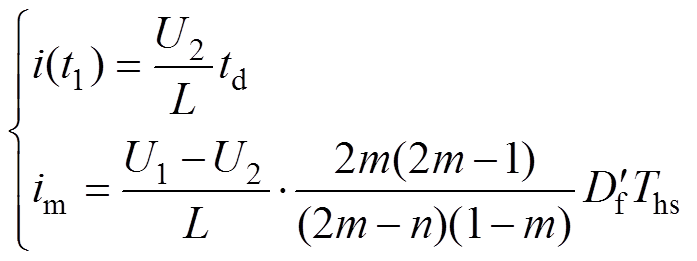（3）
同理由图7b可求得升压工况各时刻关断电流，得到开关模式1中引入死区前后零电压软开关（Zero Voltage Switching, ZVS）、零电流软开关（Zero Current Switching, ZCS）的性能及变化见表4加粗部分。
由表4可知，开关模式1中引入死区后，在降压工况中，一次侧H桥软开关性能不变，二次侧所有开关由零电流关断变为硬关断；升压工况中，一次侧H桥软开关性能不变，二次侧S6、S8由零电流关断变为硬关断。同时，死区带来的电流尖峰和电流零区间偏置会增加开关器件的电应力及导通损耗，降低变换器效率。
表4 开关模式1引入死区前后软开关性能对比
Tab.4 Soft switching performance in mode 1 before and after considering dead band
开关模式1m＜1m＞1 无死区引入死区后无死区引入死区后 S1, S3ZVS开通 ZCS关断ZVS开通 ZCS关断ZCS开通 ZCS关断ZCS开通 ZCS关断 S2, S4ZCS开通硬关断ZCS开通硬关断ZCS开通 ZCS关断ZCS开通 ZCS关断 S5, S7ZCS开通ZCS关断ZVS开通硬关断ZCS开通硬关断ZVS开通硬关断 S6, S8ZCS开通ZCS关断ZCS开通硬关断ZVS开通ZCS关断ZVS开通硬关断
对于开关模式2，死区的引入不会影响调制策略原有的软开关性能，但会产生其他死区效应，2.3节对此进行了分析。
在开关模式2中，死区的引入使电压电流波形发生畸变，在m＜1和m≥1工况下会分别出现电压跌落和电压极性反转现象，开关模式2不同工况下死区效应波形如图9所示。以图9a中m＜1工况为例对变换器半个周期内的开关模态及换相过程进行分析，m＞1和m=1时类似。
图10为前半个周期t0～t5（对应[0, Ths]）内第一个开关模态示意图，以此类推可得到各模态期间的电感电流变化如式（4）所示，uL为电感两端电压。可知一次电压跌落和极性反转引入了附加模态，使开关器件换相次数增加，变换器的回流功率和器件损耗增加。
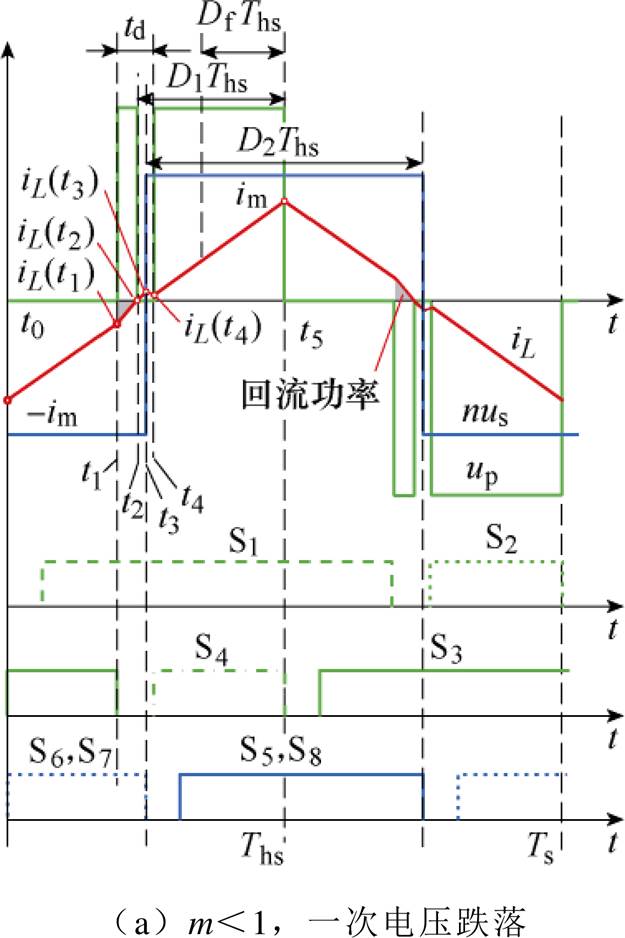
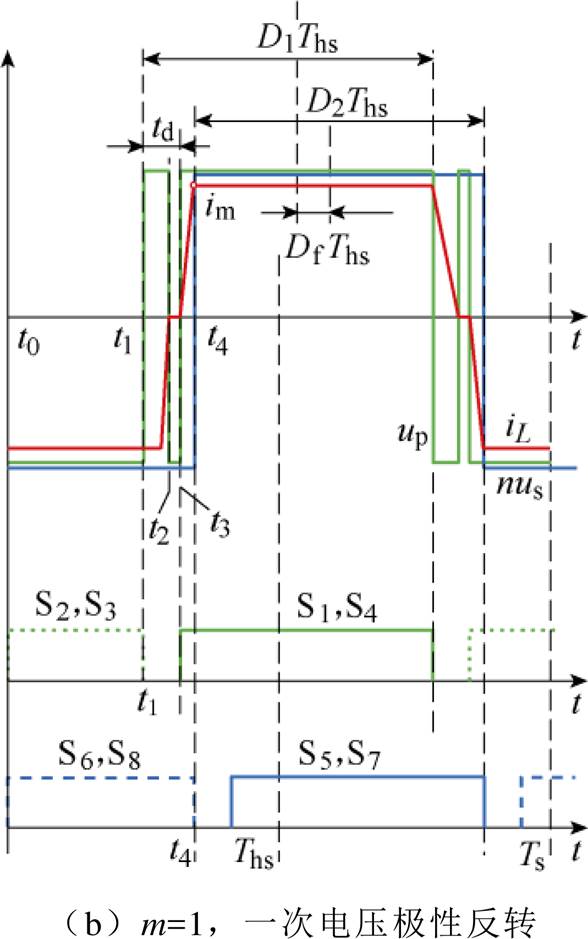
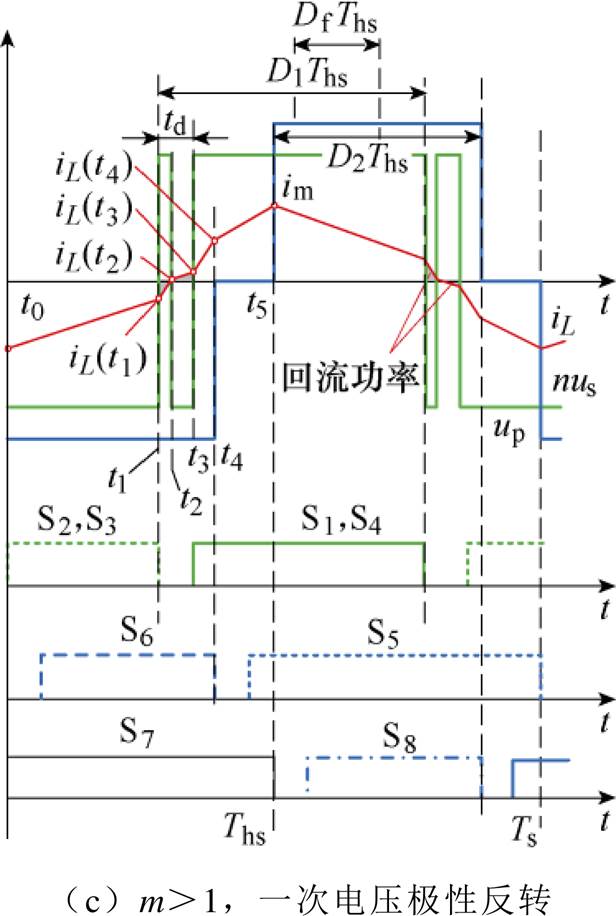
图9 开关模式2不同工况下死区效应波形
Fig.9 Waveforms of dead band effects of mode 2 in different working conditions
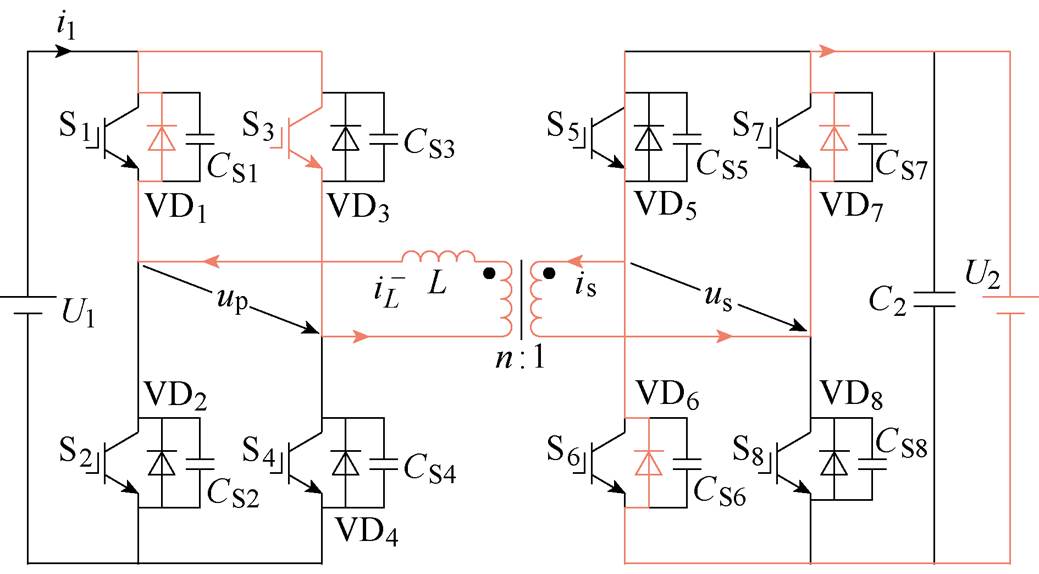
图10 m＜1开关模式1在[t0, t1]期间的开关模态
Fig.10 Switching state during [t0, t1] in mode 1 m＜1
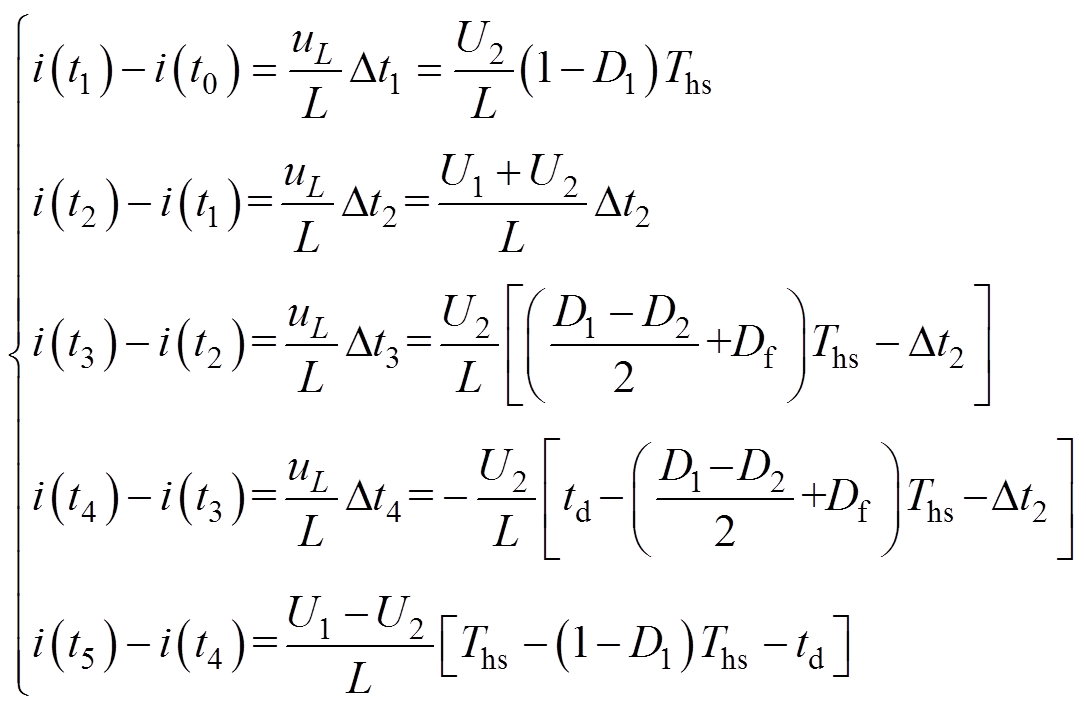（4）
由DAB的对称性可知i(t0)=-im、i(t5)=im。在图9a中要使电压不发生跌落，需使电感电流在进入死区之前减小到0或在死区之内保持为0，即满足下列不等式之一
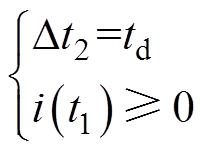（5）
联立式（4）、式（5）解得开关模式2在m＜1时不发生电压跌落的约束条件为
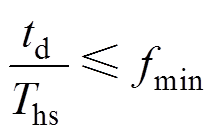（6）
其中
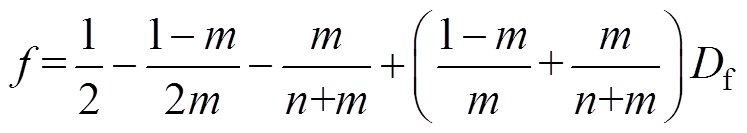（7）
同理由图9b、图9c可得m=1和m＞1工况的电流模型，代入不等式（5）进行计算，得到m=1工况下不发生极性反转的约束条件为
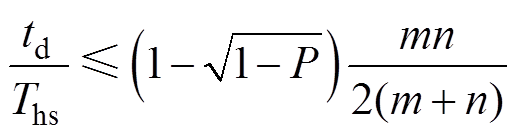0＜P≤1 （8）
m＞1工况电压极性不发生反转的约束条件为
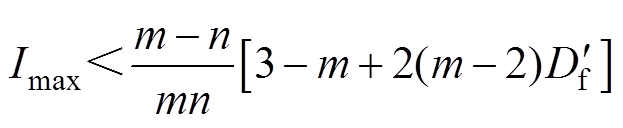（9）
由式（9）可知，m＞1时是否发生极性反转与死区时间无关，仅由变换器的工况决定。
由于开关管和反并联二极管存在寄生电容，开关切换过程中伴随着寄生电容充放电过程，因此在研究死区期间的开关动作时需要考虑寄生电容充放电时间的约束。以图10为例，开关模态1切换至模态2时，一次侧H桥右桥臂由S3导通变为S4的反并联二极管（VD4）导通。一次侧寄生电容CS3充电至母线电压U1，CS4放电至0。对变换器电路进行分析可得下管寄生电容上的电压变化方程为
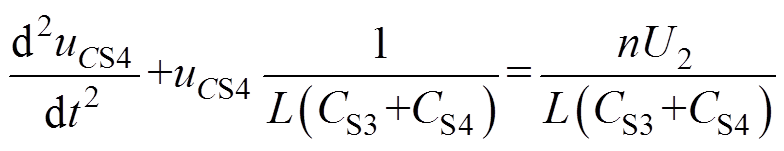（10）
求解方程可得到uCS4表达式为
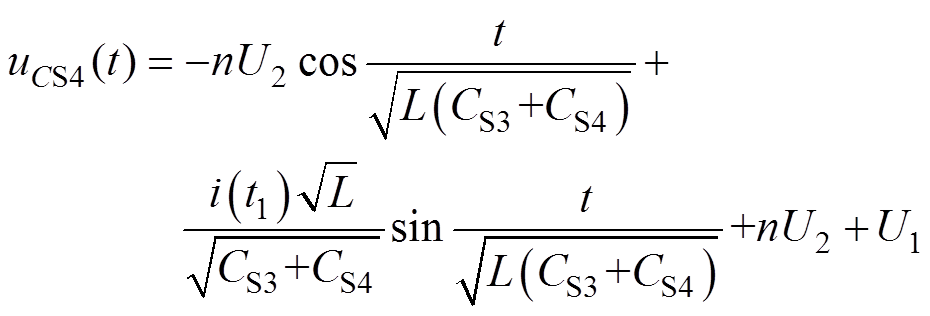（11）
式中，i(t1)为放电开始时刻的电感电流，令uCS4=0可求出电容充放电时间tv。
同理可对全工况内每个开关模态切换时的充放电过程进行分析，寄生电容充放电时间tv应满足
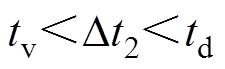（12）
式（12）表示电容放电时间tv对死区时间td的约束，寄生电容参数可以通过变换器所用开关器件的数据手册求得。
综上所述，TPS调制策略在全工况内避免电压跌落和极性反转的边界条件见表5。
表5 全工况内死区效应边界条件
Tab.5 Restriction conditions of dead band effects in full operating range
工况边界条件 m＜1 m=1 m＞1 寄生电容充放电时间约束
在DAB的宽电压范围TPS调制策略中引入死区后，出现了移相比损失、软开关性能改变、一次电压跌落和极性反转等死区效应。其中，电压跌落和极性反转可以通过表5的约束条件避免，但移相比损失等效应则需要通过死区补偿策略进行补偿。
分析移相比损失的产生机理可知，采用传统的脉冲上升沿延迟产生死区的方法，电压脉宽被死区时间占用。脉宽和移相比等效减小，导致传输功率不足，是产生移相比损失的最主要原因，由此带来了电流畸变和软开关性能改变等效应。
因此本文从调整开关脉冲的角度出发进行死区补偿，在DAB变压器一次侧H桥中采用S1、S3管提前关断、延迟开通的方法产生死区，其原理如图11所示。
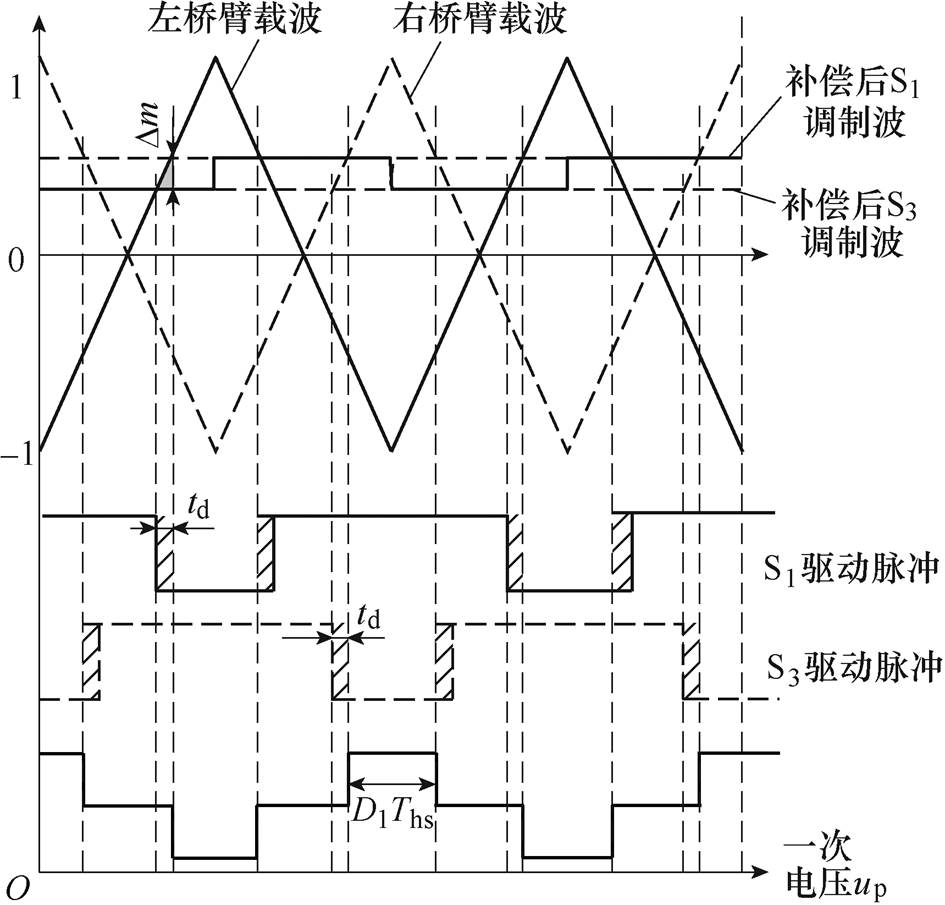
图11 本文提出的死区补偿策略原理
Fig.11 Principle of the proposed dead-time compensation strategy
在图11的阴影三角形中，死区时间为td，调制波所需要补偿的值为Dm，由三角形相似原理可知
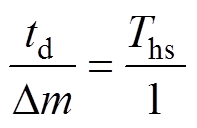
补偿后的调制波mmodu可表示为
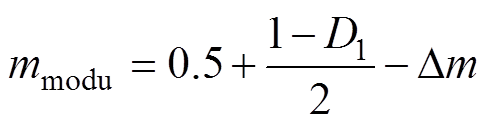（13）
在PI调节器输出的调制比基础上每半个周期按照式（13）更新S1、S3的调制波，即可实现其提前关断，同时采用上升沿延迟的方法实现延迟开通。由图11可知采用此方法后，死区被调整到脉冲占空比之外，可避免死区时间对电压脉宽的占用。
以m＜1开关模式1为例分析死区补偿策略效果，其死区补偿前后的理论波形如图12所示。
同理可对m＞1时开关模式1的死区补偿效果进行分析，得到死区补偿前后软开关性能变化见表6加粗部分。可知采用死区补偿策略后开关模式1的零电流区间恢复，在升压和降压工况中均可保证控制策略原有的软开关性能。
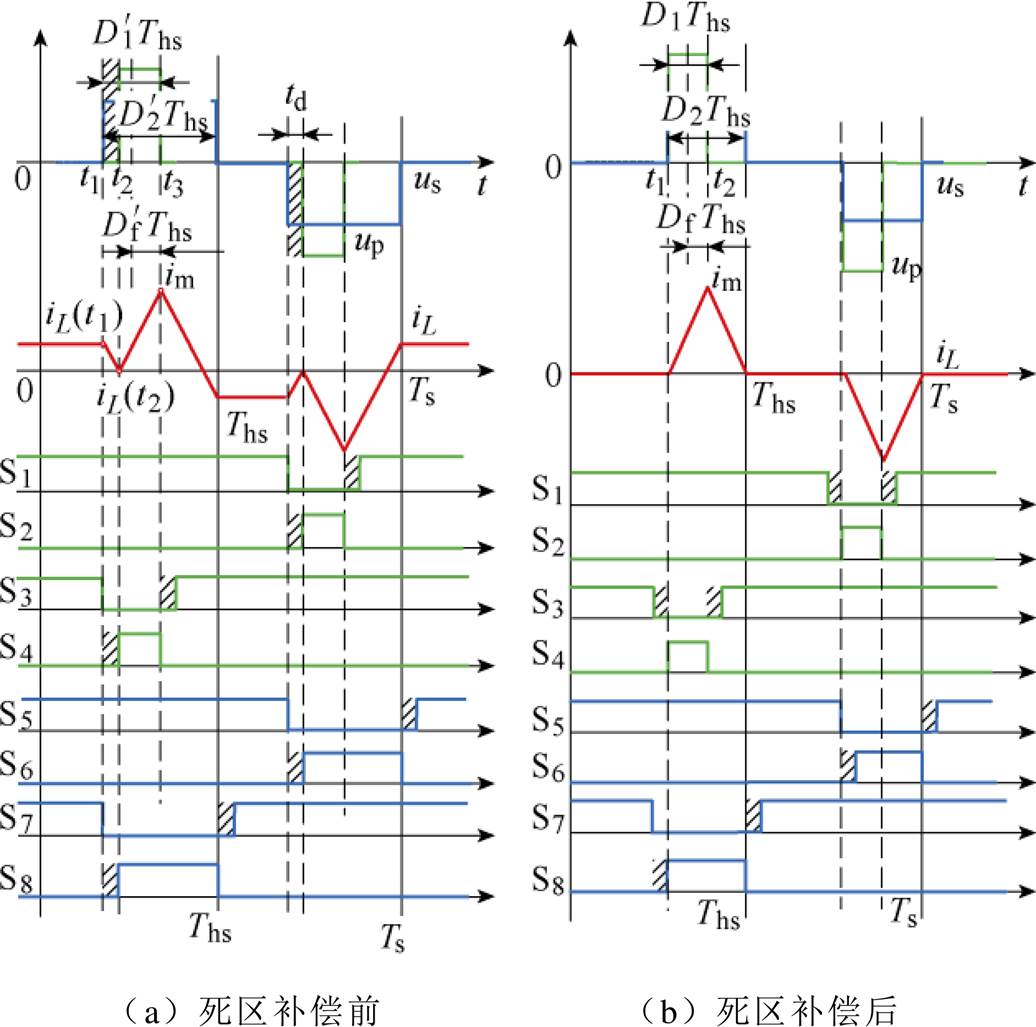
图12 m＜1，开关模式1下死区补偿前后理论波形
Fig.12 Theoretical waveforms in mode 1 m＜1 before and after dead-time compensation
表6 开关模式1死区补偿前后软开关性能
Tab.6 Soft switching performance in mode 1 before and after dead-time compensation
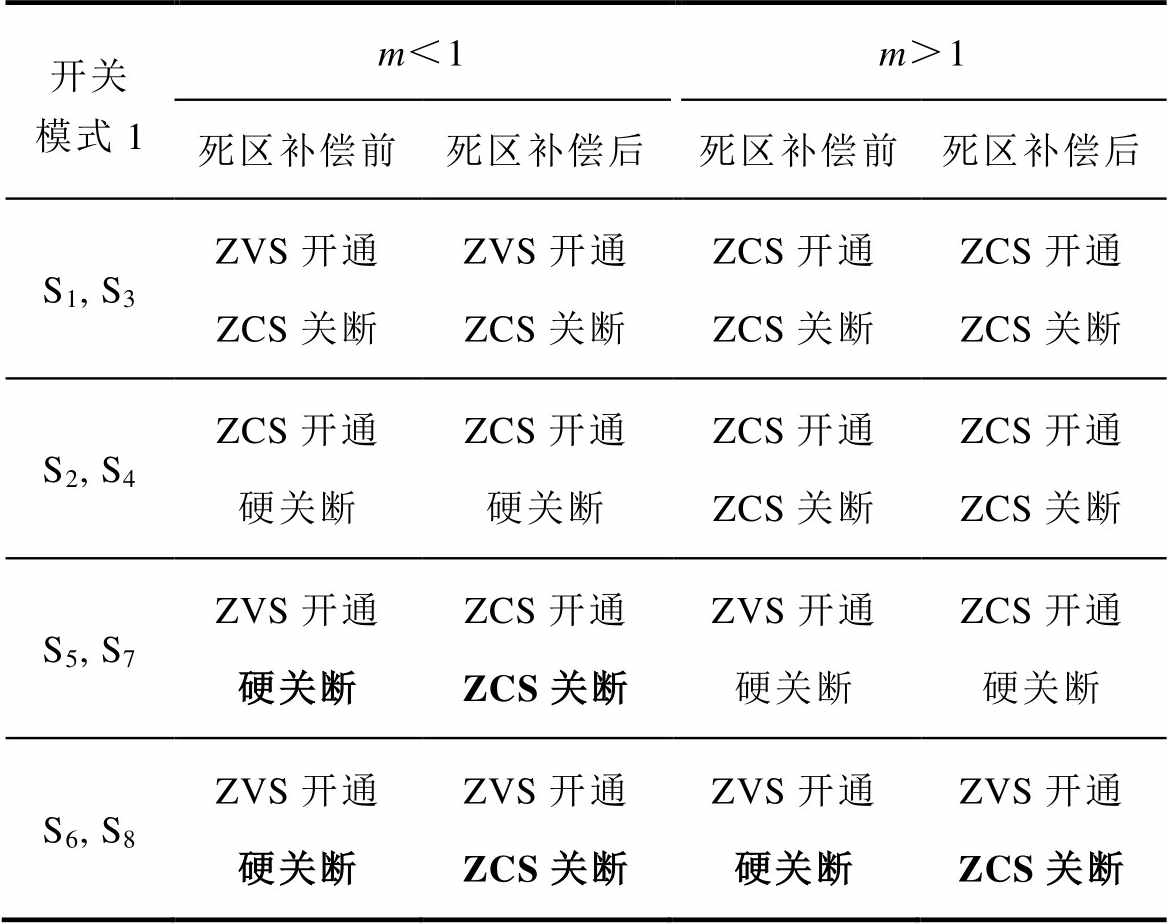
开关模式1m＜1m＞1 死区补偿前死区补偿后死区补偿前死区补偿后 S1, S3ZVS开通ZCS关断ZVS开通 ZCS关断ZCS开通 ZCS关断ZCS开通 ZCS关断 S2, S4ZCS开通硬关断ZCS开通硬关断ZCS开通 ZCS关断ZCS开通 ZCS关断 S5, S7ZVS开通硬关断ZCS开通ZCS关断ZVS开通硬关断ZCS开通硬关断 S6, S8ZVS开通硬关断ZVS开通ZCS关断ZVS开通硬关断ZVS开通ZCS关断
依照此法对死区补偿策略在全工况内的补偿效果进行分析，可得全工况死区补偿效果如图13所示。可知在宽电压全功率范围内，本文所提的死区补偿策略在开关模式1的所有工况中可以减小损耗、提高变换器效率，获得较好的补偿效果；开关模式2的部分工况补偿后损耗减小、效率提高，少数工况死区补偿前后效果相当，个别工况会出现负效果。在实际应用中可以参考理论分析的补偿效果，合理设置死区补偿策略的应用范围。
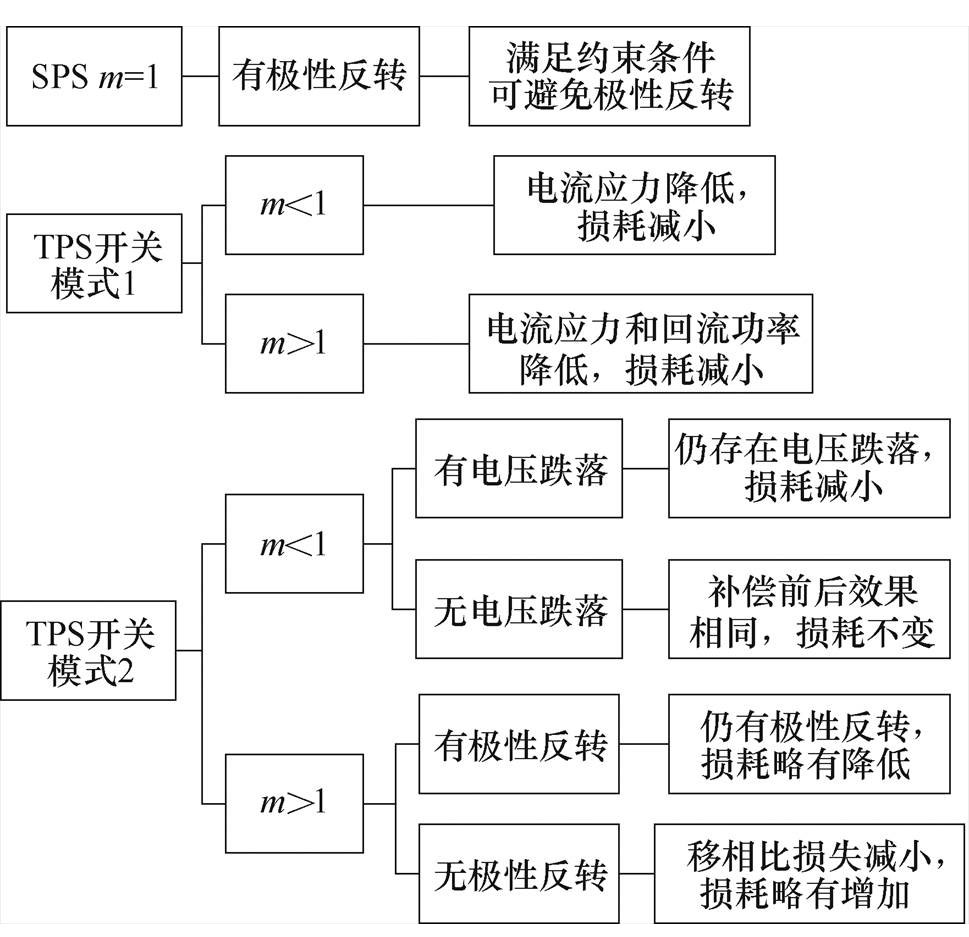
图13 全工况死区补偿策略效果
Fig.13 Effectiveness of dead-time compensation strategy in full operating range
为了验证DAB变换器宽电压范围全工况的死区效应及死区补偿策略，搭建PLECS仿真模型及图14所示的DAB测试平台，主要参数见表7。
图14 1.5 kW DAB变换器测试平台
Fig.14 Experimental platform of 1.5 kW DAB converter
以m＜1正向功率变换为例，TPS调制在两种开关模式下的理想仿真波形如图15所示。可知在理想条件下，开关模式1下输出功率和电感电流均较小，除一次侧S2、S4管以外，其他开关均可实现软开关。开关模式2下变换器输出功率大，电感储能多，电感电流大，所有开关均为ZVS开通，硬关断。升压工况同理。
表7 DAB仿真及实验平台参数
Tab.7 Parameters of simulation and experimental platform of DAB
参 数数 值 输入电压U1/V200 变压器匝数比n1:1 死区时间td/ms2 输入电容C1/mF180 额定功率Pn/kW1.5 输出电压U2/V100～300 开关频率fs/kHz20 电压比m0.5～1.5 输出电容C2/mF100 总漏感L/mH85
两种开关模式引入死区后的实验波形如图16、图17所示。将实验波形与理想仿真波形对比可知，在开关模式1中，死区引入了移相比误差，导致电流断续期间电感电流非零、部分器件软开关失效、开关电流应力增加等现象。在开关模式2中，软开关性能不受死区的影响，与仿真分析结果一致。
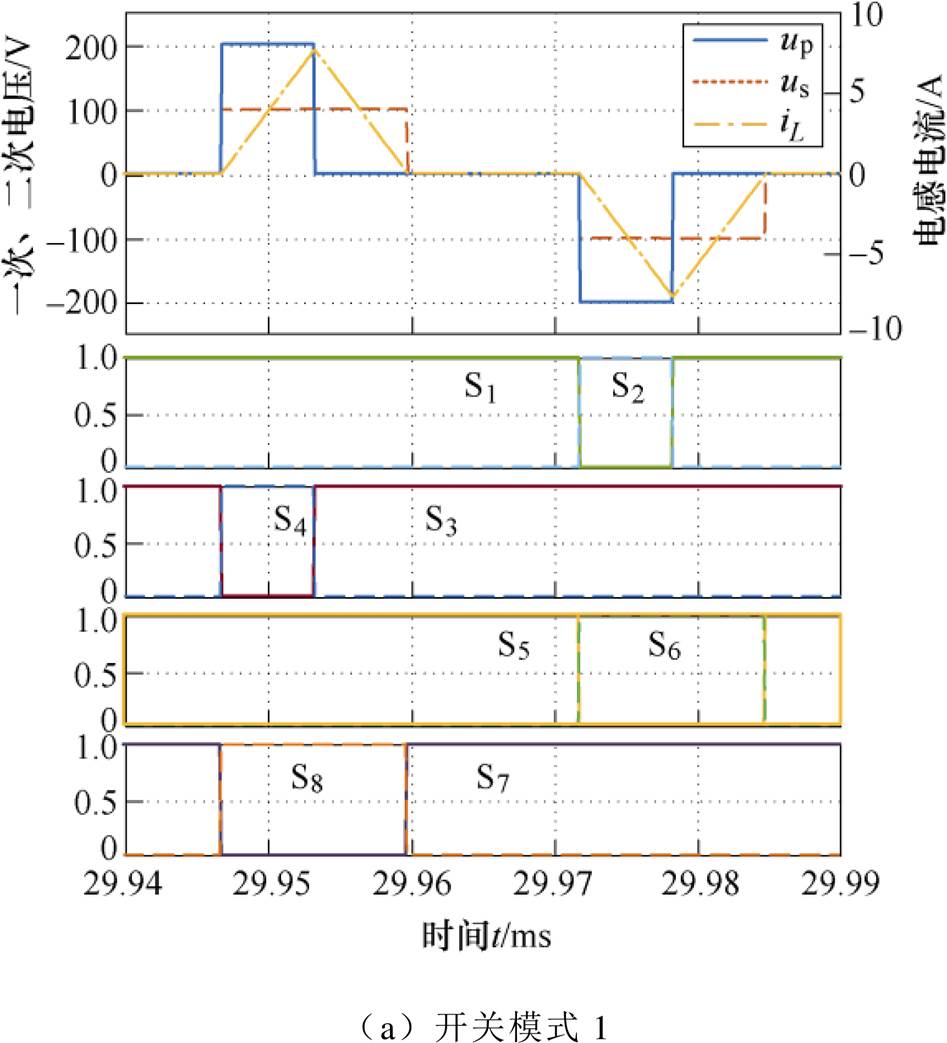
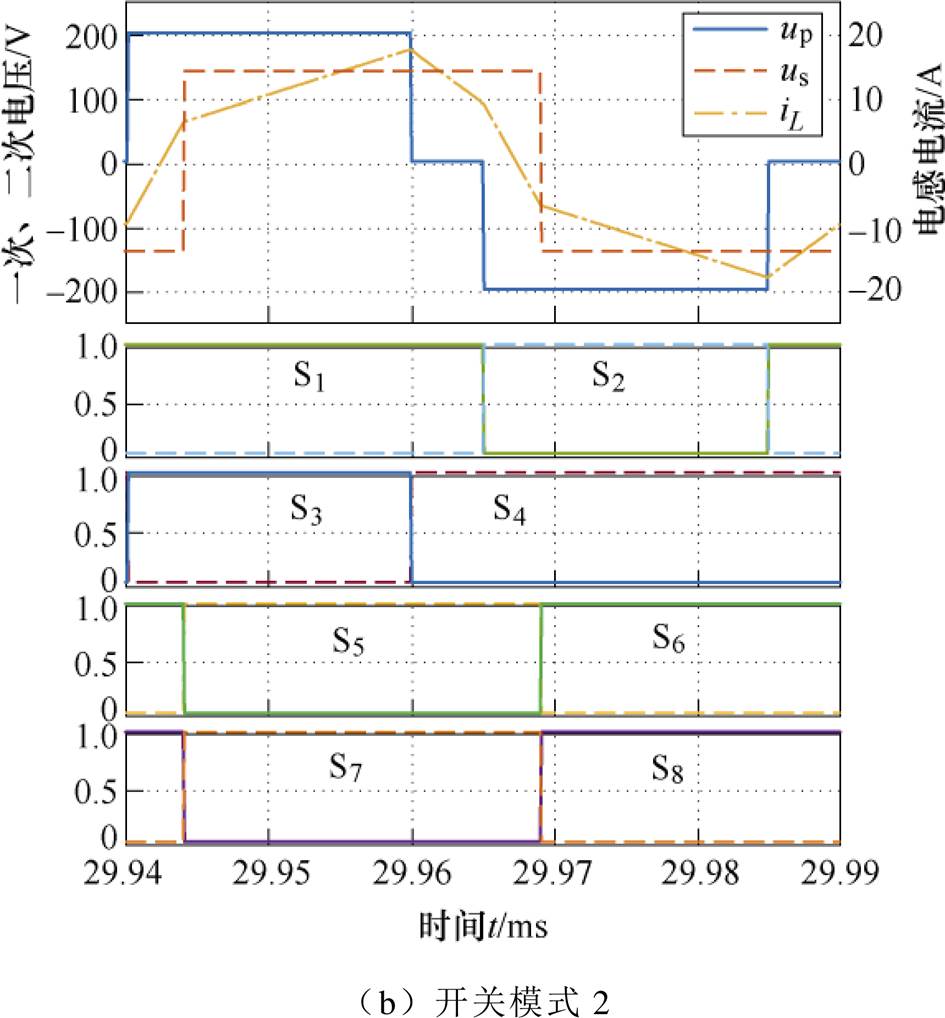
图15 无死区理想情况下m＜1仿真波形
Fig.15 Simulation waveforms when m＜1 in ideal condition without dead band
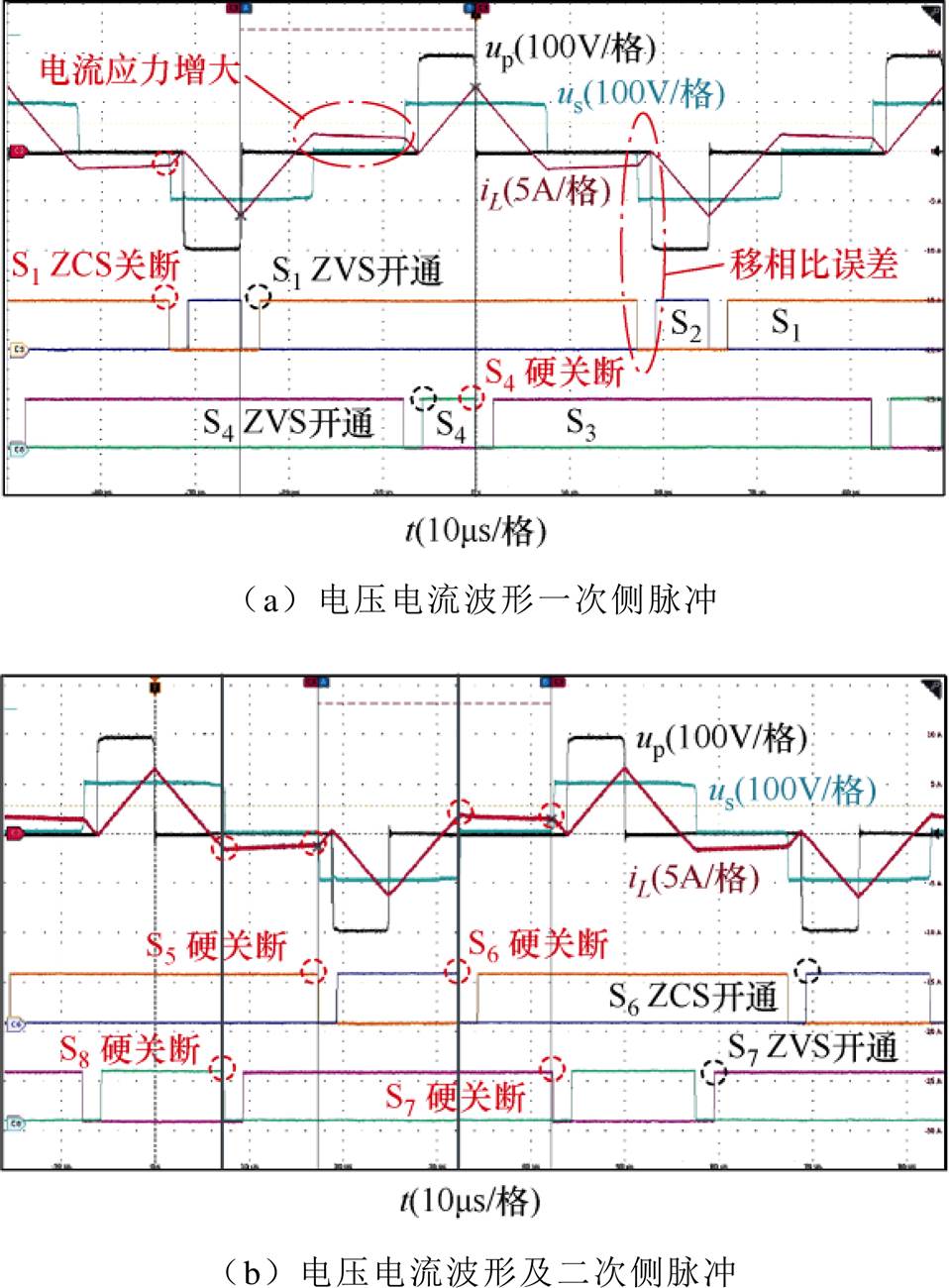
图16 有死区时m＜1开关模式1实验波形
Fig.16 Experimental waveforms in mode 1 with dead band when m＜1
由实验结果可知，本文采用的TPS调制策略具有全范围软开关性能，且可以实现宽电压全功率范围的连续调节，但软开关特性会受到死区效应的影响。
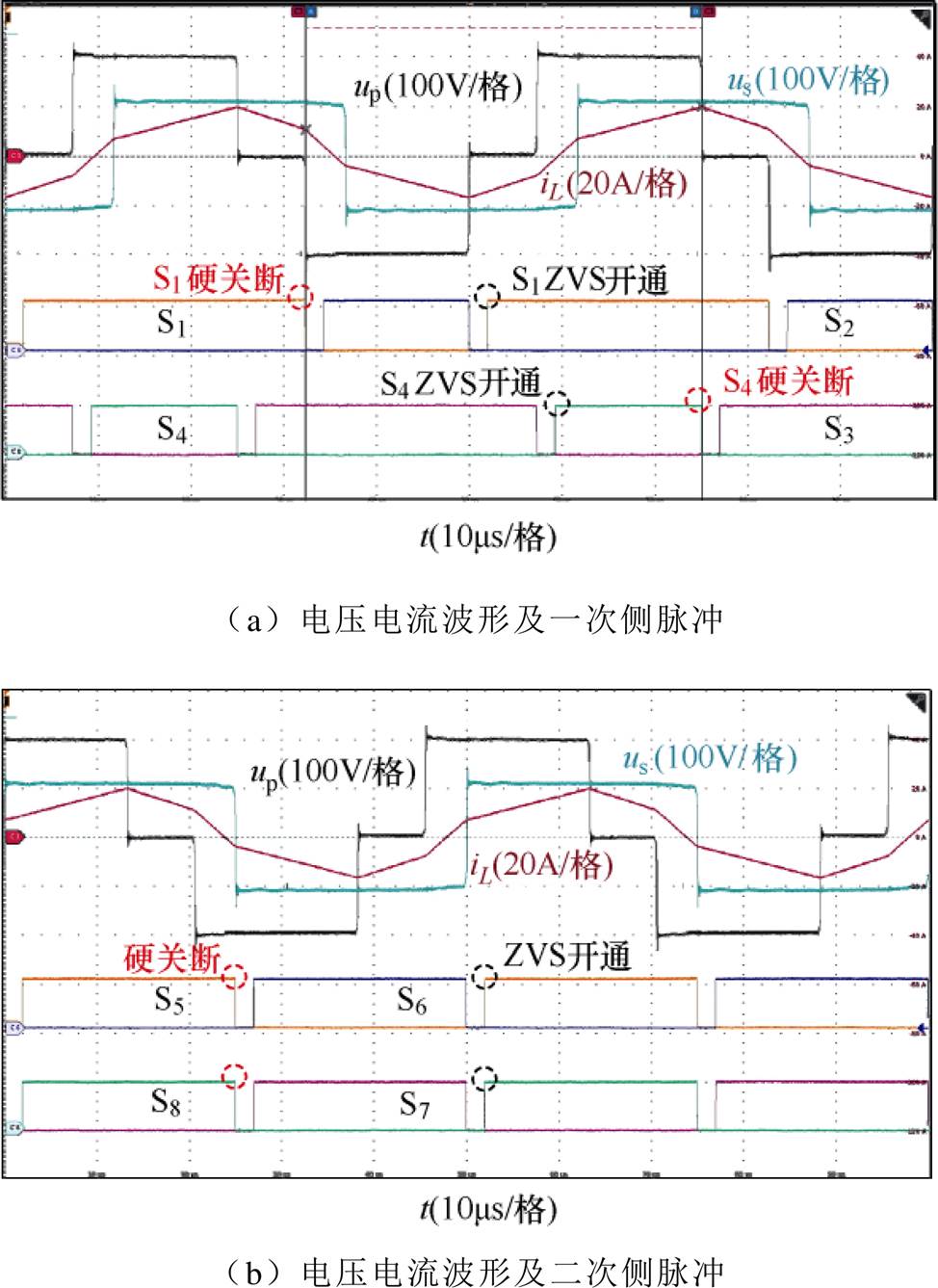
图17 有死区时m＜1开关模式2实验波形
Fig.17 Experimental waveforms in mode 2 with dead band when m＜1
本节分别对开关模式2的降压和升压工况进行实验，验证此工况下的死区效应及其边界条件。
4.2.1 电压跌落
在m＜1开关模式2下选取工况1（m=0.8、Po= 1 200 W）、工况2（m=0.7、Po=750 W）验证其死区效应。通过计算可知工况1不满足约束条件式（6），工况2处于模式切换边界上，由于移相比损失的影响，满足约束条件式（6），实验波形如图18所示。
由图18可知，工况1在S1、S2和S3、S4切换的死区时间内电流过零，一次侧发生了电压跌落，工况2中无电压跌落，表明2.3节所得边界条件的准确性。实验数据见表8，其中误差一栏为实验值与理论无死区时计算值的差值，即电流值对m=1、Po=Pn=1.5 kW的额定工况下的电流值计算百分比，Df及D1、D2对其最大值0.5取百分比。
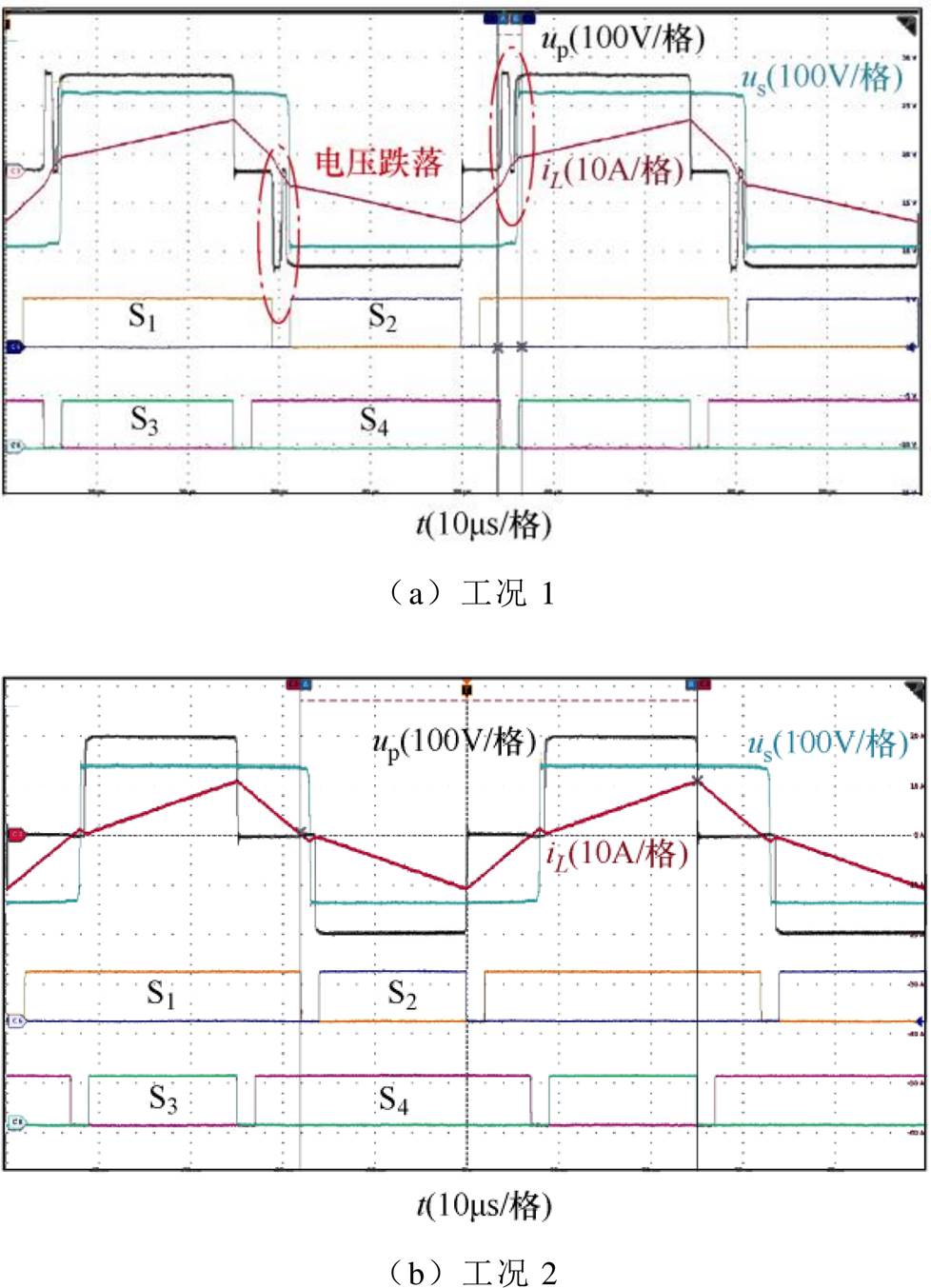
图18 m＜1，开关模式2 实验波形
Fig.18 Experimental waveforms in mode 2 when m＜1
表8 m＜1，开关模式2死区效应实验数据
Tab.8 Experimental data with dead band effect in m＜1 mode 2
参数工况1工况2 理论实验误差(%)理论实验误差(%) Df0.1610.1763.00.1400.1736.6 D10.8300.8402.00.6520.72013.6 D2110.00.931113.8 IL-max/A12.4312.773.911.2411.391.7 Uo/V160157.5—140137.2— Po/W1 2001 182—750723.8—
由实验数据可知，引入死区后实验中电流应力相对理论计算提高1 %～3 %。工况1中移相比和电压脉宽误差小于3 %；工况2位于模式切换边界附近，D2实验值为1，表明变换器进入开关模式2，此时移相比损失造成变换器工作模式与理论分析不同，电压脉宽与理论值的误差高达13.8 %。
4.2.2 电压极性反转
由2.3节理论分析可知，m＞1时开关模式2下是否发生极性反转与死区时间无关，仅由变换器的工况决定。图19为仿真得到的m＞1工况下死区效应的分布，其中x轴为输出功率标幺值，y轴为电压比m，z轴为实际输出功率Po。z轴为0表示该工况会发生电压极性反转；不为0的点如（0.6, 1.3, 900）则表示在输出功率为900 W（即60 %额定功率）、电压比m=1.3的工况下不会发生极性反转。
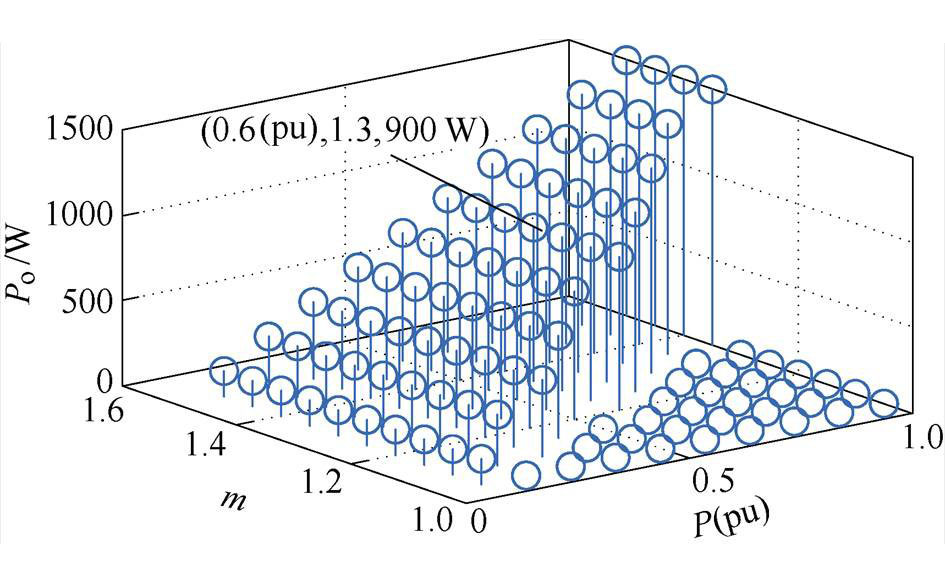
图19 m＞1 不同工况下死区效应分布
Fig.19 Dead band effects distribution in different working conditions when m＞1
选取工况3（m=1.25、Po=1.2 kW）、工况4（m=1.4、Po=1.2 kW）验证m＞1开关模式2下的死区效应。由计算可知工况3不满足约束条件式（9），工况4满足约束条件，实验波形如图20所示。
由实验结果可知，工况3在死区时间内出现电压极性反转，工况4满足约束条件式（9），无极性反转现象，与2.3节理论分析的边界条件吻合。
在开关模式1下采用死区补偿策略，以降压工况为例，其实验波形如图21所示。
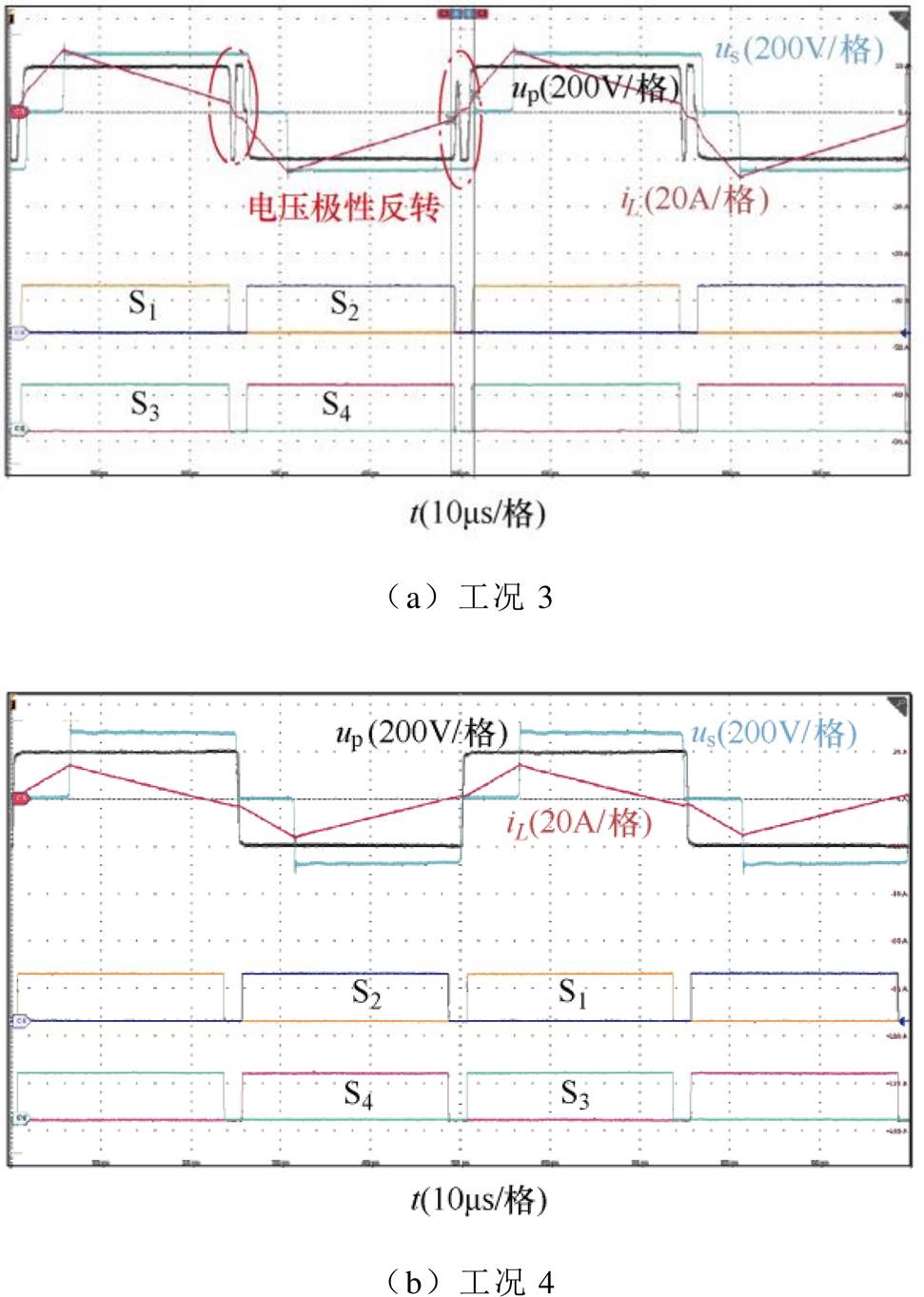
图20 m＞1，开关模式2实验波形
Fig.20 Experimental waveforms in mode 2 when m＞1
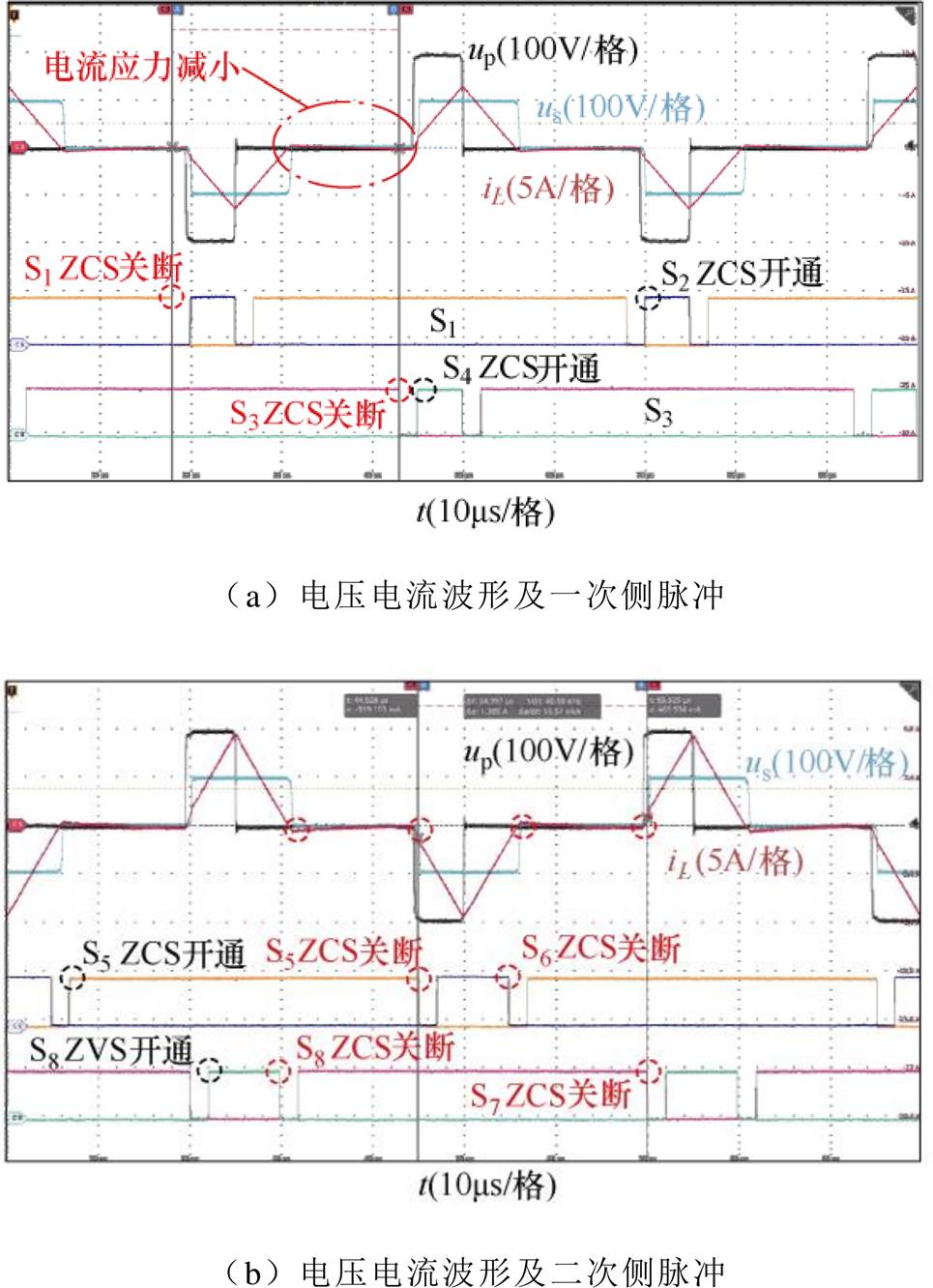
图21 m＜1开关模式1 死区补偿后实验波形
Fig.21 Experimental waveforms in mode 1 after dead-time compensation when m＜1
由实验波形可知，该工况下采用死区补偿策略后，移相比损失消除，一次侧H桥软开关性能不变，二次侧所有开关恢复ZCS关断。实验结果表明，死区补偿后该工况下电流应力减小2 %～3 %，效率提高3.03 %。同理可对升压工况下的死区补偿效果进行验证，所得实验数据表明死区补偿后电流应力减小15 %～17 %、效率提高3.5 %。一次侧H桥软开关性能不变，二次侧S6、S8恢复ZCS关断，与表6理论分析效果一致。
综上所述，在开关模式1下，死区补偿策略可以补偿死区导致的电压脉宽减小和移相比损失等问题，避免软开关失效，减小电流应力和损耗。
随后在输出电压宽范围变化（m=0.5～1.5）、全功率（Po=(10 %～100 %)Pn）范围内采用死区补偿策略，通过实验测定死区补偿前后的变换器效率，可得到不同工况下死区补偿的效率提升效果如图22所示。
由实验结果可知，相比死区补偿之前，开关模式1在降压工况下效率提高0.5 %～3 %；升压工况下效率提高3 %～7 %。开关模式2中，中高输出功率工况的效率较补偿之前略有提高，在少数较高输出功率场合，死区补偿后的效率低于补偿之前，全工况内的补偿效果与图13一致。
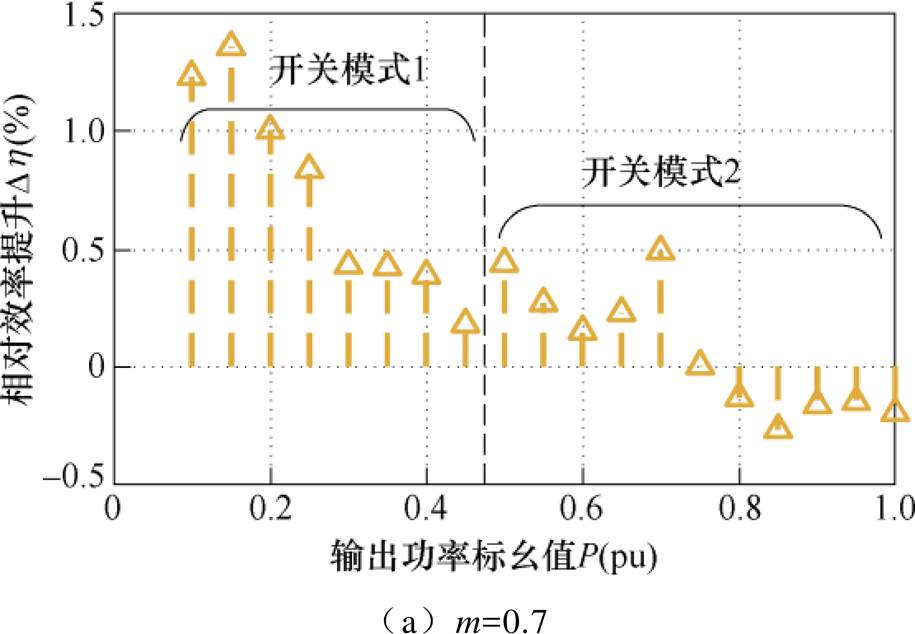
图22 全工况死区补偿效率提升值
Fig.22 Efficiency increase after dead-time compensation in full operating range
本文针对DAB变换器宽电压全功率范围运行下的TPS调制策略及其死区效应和补偿问题进行了研究。所采用的TPS调制侧策略具有表达形式统一、计算简单、开关模式平滑切换等特性；分析了非理想因素对TPS调制效果的影响，针对不同开关模式下的电压跌落和极性反转等死区效应给出约束条件，为宽电压范围DAB变换器的参数设置提供了参考；提出了一种基于开关脉冲调整的死区补偿策略，可以避免死区带来的移相比损失和软开关失效等问题，减小器件损耗，提高变换器效率；所提补偿策略不需要改变系统的控制架构及调制算法，易于工程实现。最后通过仿真和实验证明所提TPS策略及其死区补偿方法的有效性。
参考文献
[1] 林霖, 裴忠晨, 蔡国伟, 等. 混合式隔离型模块化多电平变换器[J]. 电工技术学报, 2021, 36(16): 3319-3330.
Lin Lin, Pei Zhongchen, Cai Guowei, et al. Hybrid isolated modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3319-3330.
[2] 刘计龙, 朱志超, 肖飞, 等. 一种面向舰船综合电力系统的模块化三端口直流变换器[J]. 电工技术学报, 2020, 35(19): 4085-4096.
Liu Jilong, Zhu Zhichao, Xiao Fei, et al. A modular three-port DC-DC converter for vessel integrated power system[J]. Transactions of China Electro- technical Society, 2020, 35(19): 4085-4096.
[3] 赵先浩, 谢红福, 刘飞, 等. 基于多端口电能路由器的楼宇直流微电网研究与应用[J]. 电气技术, 2022, 23(8): 75-83.
Zhao Xianhao, Xie Hongfu, Liu Fei, et al. Research and application of building DC microgrid based on multi port power router[J]. Electrical Engineering, 2022, 23(8): 75-83.
[4] 马伟明. 关于电工学科前沿技术发展的若干思考[J]. 电工技术学报, 2021, 36(22): 4627-4636.
Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.
[5] 高范强, 李子欣, 李耀华, 等. 面向交直流混合配电应用的10kV-3MV·A四端口电力电子变压器[J]. 电工技术学报, 2021, 36(16): 3331-3341.
Gao Fanqiang, Li Zixin, Li Yaohua, et al. 10kV- 3MV·A four-port power electronic transformer for AC-DC hybrid power distribution applications[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3331-3341.
[6] 张航, 李子欣, 高范强, 等. 一种混合模块型直流变压器冗余设计及控制策略[J]. 电工技术学报, 2022, 37(2): 409-423.
Zhang Hang, Li Zixin, Gao Fanqiang, et al. A redundant design and control strategy of hybrid modular DC transformer[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 409-423.
[7] Liu Tao, Yang Xu, Chen Wenjie, et al. Design and implementation of high efficiency control scheme of dual active bridge based 10 kV/1 MW solid state transformer for PV application[J]. IEEE Transactions on Power Electronics, 2019, 34(5): 4223-4238.
[8] 赵彪, 安峰, 宋强, 等. 双有源桥式直流变压器发展与应用[J]. 中国电机工程学报, 2021, 41(1): 288-298, 418.
Zhao Biao, An Feng, Song Qiang, et al. Development and application of DC transformer based on dual- active-bridge[J]. Proceedings of the CSEE, 2021, 41(1): 288-298, 418.
[9] Bai Hua, Mi C C, Gargies S. The short-time-scale transient processes in high-voltage and high-power isolated bidirectional DC-DC converters[J]. IEEE Transactions on Power Electronics, 2008, 23(6): 2648-2656.
[10] 汪涛, 骆仁松, 张茂强, 等. 考虑死区效应的双有源桥直流变压器损耗优化[J]. 电力系统自动化, 2023, 47(6): 197-205.
Wang Tao, Luo Rensong, Zhang Maoqiang, et al. Loss optimization of DC transformer based on dual active bridge considering dead-zone effect[J]. Auto- mation of Electric Power Systems, 2023, 47(6): 197-205.
[11] Krismer F, Kolar J W. Accurate small-signal model for the digital control of an automotive bidirectional dual active bridge[J]. IEEE Transactions on Power Electronics, 2009, 24(12): 2756-2768.
[12] Krismer F, Kolar J W. Closed form solution for minimum conduction loss modulation of DAB con- verters[J]. IEEE Transactions on Power Electronics, 2012, 27(1): 174-188.
[13] Zhao Biao, Song Qiang, Liu Wenhua, et al. Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power-conversion system[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4091-4106.
[14] Gong Linxiao, Jin Xinyu, Xu Junzhong, et al. A dynamic ZVS-guaranteed and seamless-mode-transition modulation scheme for the DAB converter that maximizes the ZVS range and lowers the inductor RMS current[J]. IEEE Transactions on Power Electronics, 2022, 37(11): 13119-13134.
[15] 黄珺, 王跃, 李卓强, 等. 基于三重移相控制的双主动全桥直流变换器优化调制策略[J]. 中国电机工程学报, 2016, 36(6): 1658-1666.
Huang Jun, Wang Yue, Li Zhuoqiang, et al. Optimized modulation scheme of dual active bridge DC-DC converter based on triple-phase-shift con- trol[J]. Proceedings of the CSEE, 2016, 36(6): 1658-1666.
[16] Huang Jun, Wang Yue, Li Zhuoqiang, et al. Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidire- ctional DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4169-4179.
[17] Wu Fengjiang, Feng Fan, Gooi H B. Cooperative triple-phase-shift control for isolated DAB DC-DC converter to improve current characteristics[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 7022-7031.
[18] Li Xiaoguang, Wu Fengjiang, Yang Guijie, et al. Improved modulation strategy for single-phase isolated quasi-single-stage AC-DC converter to improve current characteristics[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4296-4308.
[19] 童安平, 杭丽君, 李国杰. 三重移相控制下DAB变换器全局优化控制策略及分析[J]. 中国电机工程学报, 2017, 37(20): 6037-6049.
Tong Anping, Hang Lijun, Li Guojie. Global optimized control strategy of dual active bridge converter controlled by triple-phase-shift modulation scheme and its analysis[J]. Proceedings of the CSEE, 2017, 37(20): 6037-6049.
[20] 胡钰杰, 李子欣, 赵聪, 等. 基于MOSFET的串联谐振双有源桥死区振荡机理分析及抑制[J]. 电工技术学报, 2022, 37(10): 2549-2558.
Hu Yujie, Li Zixin, Zhao Cong, et al. Mechanism analysis and suppression of oscillation in dead time of series resonant dual active bridge based on MOSFET[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2549-2558.
[21] Zhao Biao, Song Qiang, Liu Wenhua, et al. Dead-time effect of the high-frequency isolated bidirectional full-bridge DC-DC converter: comprehensive theore- tical analysis and experimental verification[J]. IEEE Transactions on Power Electronics, 2014, 29(4): 1667-1680.
[22] Song Chaochao, Chen Alian, Pan Yiwei, et al. Modeling and optimization of dual active bridge DC-DC converter with dead-time effect under triple- phase-shift control[J]. Energies, 2019, 12(6): 973.
[23] 宋超超. 双有源桥式DC-DC变换器优化控制策略研究[D]. 济南: 山东大学, 2019.
[24] Song Chaochao, Chen Alian, Chen Jie, et al. Dead- time effect analysis of dual active bridge DC-DC converter with dual-phase-shift control[C]//2017 Chinese Automation Congress (CAC), Jinan, China, 2018: 6545-6550.
[25] 刘海洋, 崔淑梅, 孙赫阳. 开关缓冲电容与死区效应对双有源桥式变换器传输功率影响[J]. 高电压技术, 2023, 49(2): 727-737.
Liu Haiyang, Cui Shumei, Sun Heyang. Impact of snubber capacitance and dead-time effects on dual active bridge converters power transmission[J]. High Voltage Engineering, 2023, 49(2): 727-737.
[26] 杨喆明, 付超, 石新春, 等. 死区影响下双有源桥DC/DC电压极性反转分析[J]. 电力电子技术, 2017, 51(2): 19-21.
Yang Zheming, Fu Chao, Shi Xinchun, et al. The analysis for voltage polarity reversal based on dead-time of dual active bridge DC/DC converters[J]. Power Electronics, 2017, 51(2): 19-21.
[27] Takagi K, Fujita H. Dynamic control and dead-time compensation method of an isolated dual-active- bridge DC-DC converter[C]//2015 17th European Conference on Power Electronics and Applications (EPE'15 ECCE-Europe), Geneva, Switzerland, 2015: 1-10.
[28] Luo Suhua, Wu Fengjiang, Wang Guizhong. Effect of dead band and transient actions on CTPS modulation for DAB DC-DC converter and solutions[J]. IEEE Transactions on Transportation Electrification, 2021, 7(3): 949-957.
[29] 任强, 艾胜. 全工况范围的DAB三自由度优化控制策略[J]. 中国电机工程学报, 2020, 40(11): 3613- 3622.
Ren Qiang, Ai Sheng. A three degree freedom optimal control strategy of dual-active-bridge converters for full range operations[J]. Proceedings of the CSEE, 2020, 40(11): 3613-3622.
Abstract Dual-active-bridge (DAB) converters are commonly adopted in large-capacity modular power electronic transformers (PET) due to their high-frequency galvanic isolation, symmetrical structure, and inherent soft switching performance. For renewable energy and energy storage equipment applications, the DAB converter operates in the wide input-to-output voltage range, requiring new modulation strategies with lower loss and lower current stress. Meanwhile, the nonideal issues, such as dead band effects, switching waveforms oscillation, and pulses delay, remain to be settled. For DAB converters operating in a wide voltage range, the existing multi- phase-shift modulation strategies still have large computation and discontinuous operating range problems. Moreover, the dead band effects need to be further analyzed, and the dead-time compensation strategies may not be suitable for the wide operating range. Therefore, this paper proposes a three-phase-shift (TPS) modulation strategy for a wide operating range and a dead-time compensation strategy.
Firstly, the optimal algorithm of the wide voltage range TPS modulation strategy is presented, and its power transmission characteristic is evaluated. Based on the model of leakage inductance current, the electrical parameters of TPS modulation in full operating range could be obtained. The current stress characteristics are compared between the TPS modulation and single-phase-shift (SPS) modulation. The switching current model describes the soft switching characteristics in different switching modes. Secondly, considering the non-ideal factors, the dead band effects in different switching modes are elaborated, including phase-shift duty cycle loss, switching mode boundary change, soft switch performance failure, and voltage polarity reversal and voltage sag phenomena in the transformer primary side. Regarding the voltage distortion, by calculating the commutation process and switch states during the dead band, the boundary of voltage polarity reversal and voltage sag are derived. Thirdly, a dead-time compensation strategy based on switching pulses adjustment is proposed regarding the phase-shift duty cycle loss and soft switch performance failure. By adjusting the drive pulses of diagonal switches in the primary H-bridge, the inherent soft switch characteristics in mode 1 can be restored, and the switching loss and current stress of switches can be reduced.
Finally, the theoretical analysis and the proposed strategy are verified by PLECS simulation and the 1.5 kW DAB converter experiment platform, where two 600 V IGBT half-bridge modules are applied. The following conclusions can be drawn from the simulation and experimental results: (1) The wide voltage range TPS modulation strategy adopted in this paper has full-range soft switching performance and can realize continuous regulation in the full power range. In switching mode 1, S2 and S4 are the hard turn-off and zero-voltage turn-on, and other switches are zero-current turn-on and -off. In mode 2, all switches are zero-voltage turn-on and hard turn-off. (2) The experimental waveforms in different working conditions can verify the correctness of the dead band effect boundary conditions in the whole operating range derived from the theoretical calculation. According to the experimental data, the phase-shift duty cycle loss and the voltage pulse loss caused by the dead band could be compensated by the proposed compensation strategy, restore the soft switching performance, and reduce the current stress and switching loss of switching devices. (3) In the wide voltage and full power range, the result shows that the proposed strategy can improve the converter’s efficiency in all working conditions of switching mode 1 and most working conditions of mode 2. At the same time, without changing the control architecture and modulation algorithm of the system, the proposed dead-time compensation strategy is easily implemented in engineering.
keywords：Dual-active-bridge (DAB) converter, wide voltage range operation, three-phase-shift (TPS) modulation, dead band effect, dead-time compensation
DOI: 10.19595/j.cnki.1000-6753.tces.222342
中图分类号：TM46
国家自然科学基金资助项目（51907199）。
收稿日期 2022-12-21
改稿日期 2023-02-27
康 薇 女，1998年生，博士研究生，研究方向为双有源桥变换器调制控制策略与优化设计。E-mail: kangxiaodouxjtu@163.com
任 强 男，1989年生，助理研究员，研究方向为电力电子电能变换技术。E-mail: im_qiangren@126.com（通信作者）
（编辑 陈 诚）