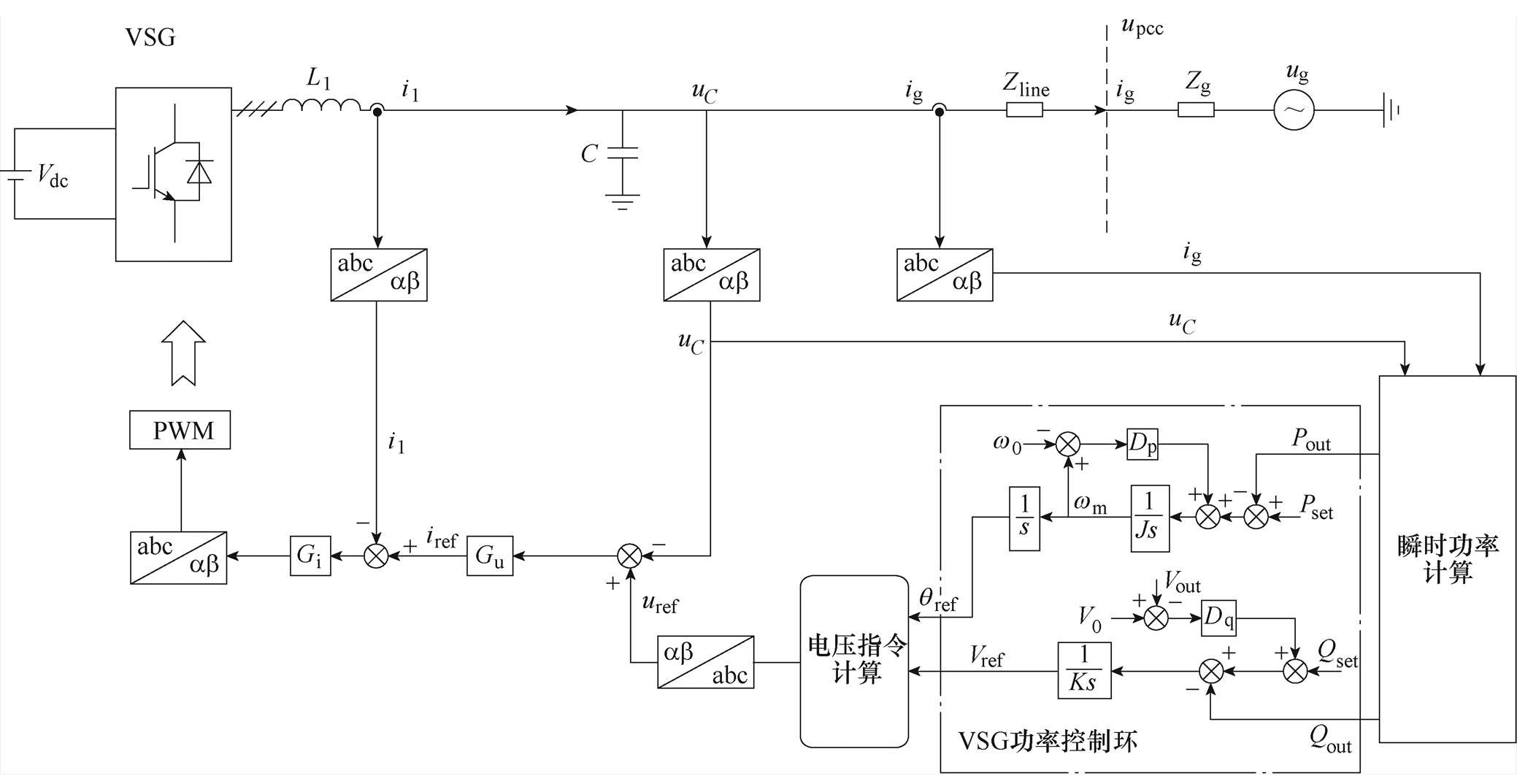
图1 传统VSG控制框图
Fig.1 Control diagram of conventional VSG
摘要 当虚拟同步机(VSG)接入畸变电网时,其输出电流质量恶化。现有基于公共耦合点(PCC)电压采样的各种谐波治理方案受限于线路阻抗的大小而抑制效果不佳。为此,该文提出一种电压-电流级联闭环控制策略实现了VSG基波电压和线路谐波电流的协调闭环控制。在基波频率下,VSG跟随功率控制回路的基波电压指令实现功率传输;在谐波频率下,通过单个一阶复矢量滤波器对谐波电流总和进行整体提取,并采用闭环输出谐波电压补偿的参考量,从而等效增强了谐波电压补偿量的参考信号,大幅提升了VSG输出电流的谐波抑制效果。相比于现有方案,该方法克服了由于线路阻抗过低而抑制效果不佳的问题,能在不增加额外电感器件的条件下提高VSG在畸变电网下的输出电流质量。最后,该文搭建15 kW的样机进行实验,并与现有的三类方法进行对比,较为全面地验证了该方法的有效性且增强了谐波的抑制效果。
关键词:虚拟同步机 谐波抑制 阻抗重塑 电能质量
近年来,人们对传统能源的成本、安全和温室气体排放的关注度日益提高,大量分布式能源通过并网逆变器等电力电子设备接入电网,使能源结构得以优化,为加速向绿色能源转型带来了新的机遇[1]。
随着基于电流控制的电流源型逆变器(Current- Controlled Inverter, CCI)在电力系统中的渗透率越来越高,也给电网的运行带来了新的挑战[2]。CCI在电力系统中等效为电流源[3],通过向电网注入恒定的有功和无功电流从而实现功率的传输。然而CCI缺乏对电网运行的考虑,只负责向电网提供高质量的电流,并不参与电网的电力调节,这使得电力系统的惯性降低,系统频率和电压稳定性下降,因而大大增加了系统发生大规模故障进而解列的风险。因此,更希望并网逆变器能像传统的同步发电机一样,积极参与电网的电力调节,基于这一思想,虚拟同步机(Virtual Synchronous Generator, VSG)控制的概念应运而生[4]。相比于CCI,VSG模拟了同步发电机的基本行为,包括下垂机制和惯性特性,其在电力系统中等效为电压源,根据电网电压的频率和幅值自动改变其有功功率和无功功率[5],进而起到对电网的支撑作用。同时,VSG模拟的惯性特性对电网的总惯性也有贡献,其有助于提高暂态频率稳定性,增强了分布式能源接入电网的友好性,因此,近年来VSG受到了广泛的关注。
目前,针对VSG的相关研究主要集中在功率暂态特性改善[6-7]、稳定性分析[8-11]和参数设计[12-14]、功率解耦[15]以及电网故障状态下的稳定性[16]等方面。然而,当传统VSG接入有电压畸变的电网时,并网电流将严重畸变,这意味着VSG在为电网提供惯性的同时,也成为了谐波源,使电能质量恶化,这是不可取的,为此,需要引入额外的谐波抑制方案来改善VSG的输出电流质量。
IEEE标准[17]中规定了对公共耦合点(Point of Common Coupling, PCC)并网电压和电流的谐波抑制要求,同时也指出PCC电压的畸变源自其所连接的各个谐波电流源汇流后流入大电网等效电感时造成的谐波电压降。为保证PCC电压不越限,就需要对PCC上并联的非线性负载和VSG等谐波电流源进行治理。对于非线性负载,可以通过有源滤波器(Active Power Filter, APF)来实现谐波的就地治理;而对于VSG这个新兴的谐波电流源,则需要引入额外的谐波抑制方案来改善VSG的输出电流质量。
值得注意的是,基于电压控制的VSG与CCI的控制结构不同[18],由于没有输出电流闭环控制回路,VSG很难直接调节输出谐波电流,谐波电流属于开环控制,其大小与VSG等效谐波输出阻抗有关,为此针对CCI的谐波抑制方案难以应用于VSG[19]。现有VSG的主要谐波抑制方案主要依托PCC电压采样,通过PCC电压前馈或反馈的方式提高并网电流质量。文献[20-21]推导了基于电压控制的电压源型逆变器的PCC电压前馈函数,将PCC电压前馈至控制器输出侧,能在一定程度上抑制谐波电流。然而,在考虑数字延时的情况下,前馈函数中的高阶前馈函数难以在实际应用中实现,具有局限性。文献[22]通过PCC电压正反馈的方式大大增加了逆变器的谐波输出阻抗,提高了并网电流质量。然而过大的反馈系数会带来稳定性和过调制等问题,谐波抑制效果欠佳。文献[23-24]利用多谐振控制器作为电压闭环控制器,无稳态误差跟踪PCC处的电网谐波电压分量,减小了PCC处与逆变器之间的谐波电压差,保证了输出电流的质量。然而,上述基于PCC电压采样的控制策略无法直接调节VSG的输出谐波电流,抑制效果依赖PCC谐波电压测量的准确度,而且需要对PCC电压的谐波分量分别进行提取,对于PCC电压畸变率较低的强电网,谐波分量提取困难;并且在多数工程应用中,线路阻抗较小,PCC电压和电容电压的谐波采样分量近似相等,这将导致谐波电压闭环控制失效,补偿效果受限。为此,文献[25]针对线路阻抗低造成的谐波抑制效果降低这一问题,提出了一种开环电压控制的谐波抑制方案,避免了电压闭环控制的同时在PCC与VSG之间增加额外的滤波电感,人为地增加了PCC和滤波电容之间的阻抗,克服了上述缺陷的同时提高了谐波电流抑制能力。然而,该方案需要增加额外的电感器件,难以推广应用。文献[26-27]通过多个二阶广义积分器来分离各次谐波电流分量,然后通过增加各次谐波虚拟阻抗实现了输出谐波电流的抑制;但是为了保证系统稳定性[28],虚拟阻抗取值不能无限增大,从而将限制其谐波抑制效果。
上述所有的VSG的谐波电流抑制方法[20-27]以及本文将提出的方法,其物理实质都是通过不同的方法直接或间接地使得VSG的内电压(滤波电容电压)产生一个与PCC的谐波电压相同的谐波电压。于是在两个电压间的电感两侧没有谐波电压差,就没有谐波电流。可见在谐波电流完全抑制时,VSG内电压(电容电压、输出电压)的谐波是必须完全跟随网侧PCC的电压谐波的。
总的来说,现有基于PCC电压采样的各种谐波电流抑制方案,由于PCC与VSG电容的电压谐波采样差值较小,易受干扰,造成谐波抑制效果不佳的问题。因此在现有方法基础上,需要找到一种合适的VSG输出谐波电流抑制方案以进一步改进其在畸变电网条件下的并网电流质量。本文提出了一种电压-电流级联闭环控制策略,所提方案在基波频率下,VSG跟随功率控制回路的基波电压指令;在谐波频率下,通过单个一阶复矢量滤波器整体提取谐波总和并闭环输出谐波电压补偿的参考量,从而不需要额外电感即可增大PCC与VSG电容之间的谐波电压差值,以改进VSG谐波电流抑制效果。本文的主要贡献如下:
1)本文提出的方法,通过单个一阶复矢量滤波器对谐波电流之和进行整体提取后,通过多谐振闭环控制,生成VSG谐波电压补偿的参考量;从而增强了谐波电压补偿量的参考信号,大幅提升了VSG输出电流谐波的抑制效果。
2)本文方法较之现有基于虚拟阻抗的方法,既可以达到无穷大虚拟阻抗的谐波抑制效果,也避免了虚拟阻抗取值过大时存在失稳问题。
3)通过将本文方法、原始VSG、基于PCC电压采样的方法、基于虚拟阻抗的方法进行对比实验,较为全面地验证了本文方法的有效性且增强了谐波抑制效果。
图1为VSG的拓扑结构和控制框图。图中,Vdc为直流侧电压,i1、ig分别为逆变器侧电流和网侧电流,uC、upcc、ug分别为电容电压、PCC处电压和电网电压,L1、C分别为逆变器侧电感和滤波电容,Zline、Zg分别为VSG与PCC接入之间的线路阻抗和电网阻抗,由于线路电阻和电网电阻较小,一般呈感性,满足Zline(s)=sLline,Zg(s)=sLg。
控制系统首先通过输出侧电流ig和电容电压uC进行功率计算,为功率控制器提供输出有功功率和无功功率计算值,其中三相瞬时实时功率在静止坐标系下的计算方程为

图1 传统VSG控制框图
Fig.1 Control diagram of conventional VSG
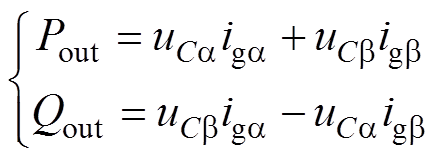 (1)
(1)
式中,Pout、Qout分别为控制器计算的有功输出和无功输出;下标a、b 表示输出侧电流与电容电压所在的静止坐标系。
功率控制器在接收到有功功率和无功功率的反馈后,采用VSG控制算法来调节有功和无功输出,并为电压控制环提供电压参考指令值。由图1可知,VSG的有功和无功控制方程分别为
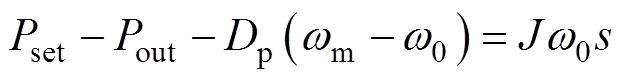 (2)
(2)
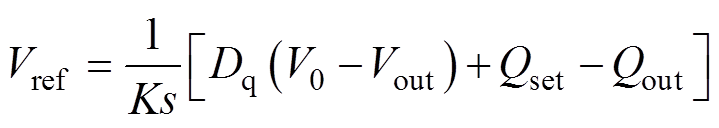 (3)
(3)
式中,Pset、Qset分别为有功输入和无功输入参考值;wm为逆变器输出电压角频率;w0为电网电压的基波角频率;Dp和J分别为VSG有功控制环的阻尼系数和惯性系数;K为励磁调节系数;V0为额定输出电压幅值;Dq为无功回路的下垂系数。
对于VSG而言,电压控制一般采用双环控制结构,其中电压通常采用电容电压闭环,保证输出电压跟随功率环电压指令,采用PR控制器,用Gu表示;逆变器侧电流采用P控制器闭环,用Gi表示,实现电流的快速跟踪,Gpwm为数字系统固有延时环节。由于功率控制环设计带宽远低于电压/电流控制环[13],因此在分析电压控制环时,功率外环给的参考指令值可以视为定值。
由图1可得电压闭环传递函数为
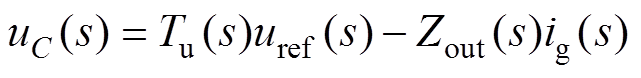 (4)
(4)
式中,uref(s)为电压参考指令;Tu(s)为参考电压的传递函数;Zout(s)为VSG等效输出阻抗,分别表示为
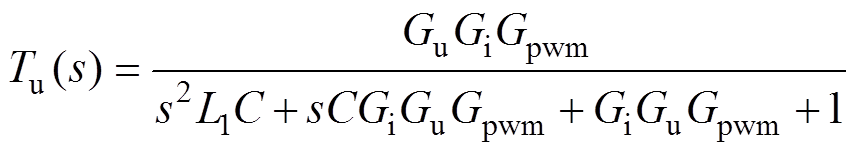 (5)
(5)
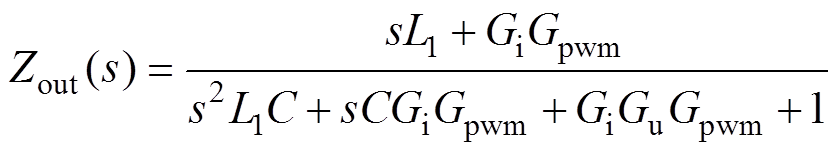 (6)
(6)
根据式(4),可得VSG等效电路模型,如图2a所示。假设电网存在谐波电压,可将其分解为图2b和图2c的基波和谐波等效电路模型。图中uref.1和uref.h、Zout.1和Zout.h、Zline.1和Zline.h、Zg.1和Zg.h、upcc.1和upcc.h、ug1和ugh分别为电压参考指令值、VSG等效输出阻抗,线路阻抗、电网阻抗、PCC电压以及电网电压的基波分量和谐波分量。
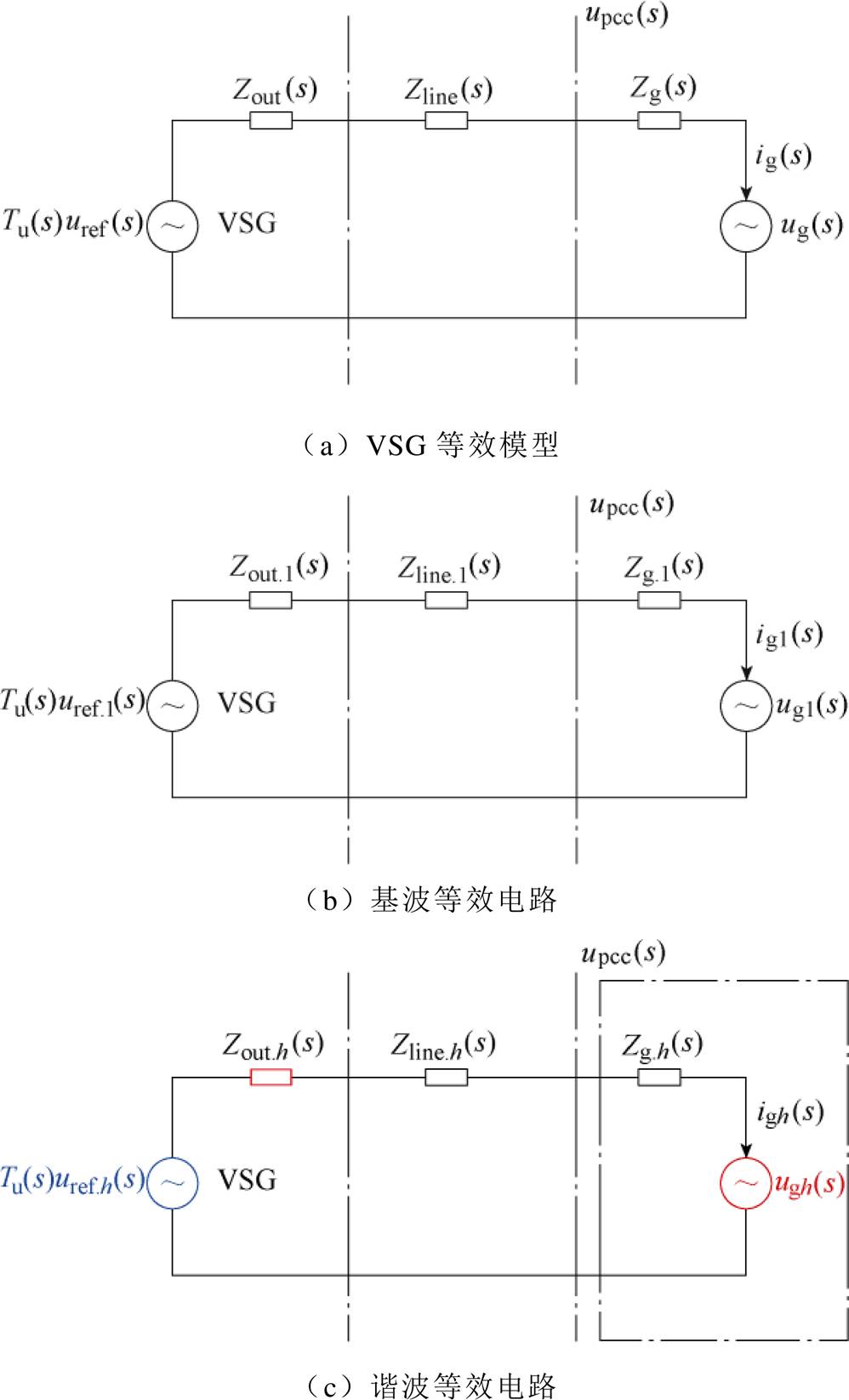
图2 VSG电路模型
Fig.2 VSG circuit model
由线性叠加原理,VSG的输出电流可表示为
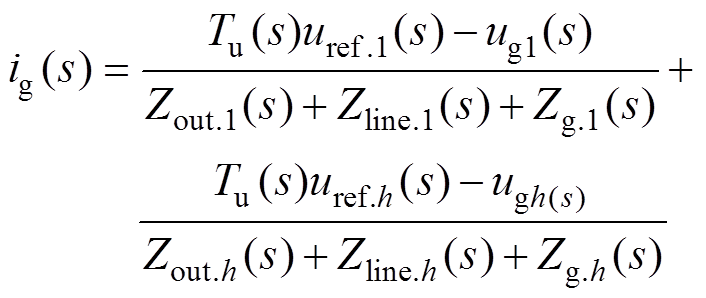 (7)
(7)
式中,下标1、h分别为基波分量和谐波分量。
由于VSG功率控制器输出的电压参考指令值中仅包含保证系统功率传输的基波电压幅值和相位信息,电压参考指令值中仅含基波分量,不含谐波分量,即uref.1=uref,uref.h=0,因此VSG的输出谐波电流的数学表达式为
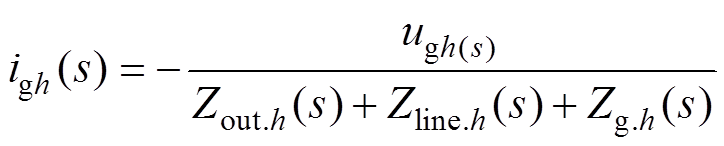 (8)
(8)
可以发现,对于VSG而言,输出谐波电流属于开环控制,当VSG接入畸变电网时,输出电流会受到畸变电网电压的严重影响,其谐波含量大小与输出阻抗Zout的大小有关。为此,在式(8)的基础上,绘制了igh/ugh与输出阻抗Zout的关系,如图3a所示,阻抗Zout的Bode图如图3b所示。由于线路阻抗较小,因此取电网阻抗Zg=jw0.002 W,Zline=0。
图3a说明,在考虑网侧畸变电压时,往往需要通过增大VSG的输出阻抗来保证输出电流的电能质量。然而传统VSG控制方案的等效谐波输出阻抗Zout的Bode图在各频段都处于较小值,如图3b所示。这意味着,VSG虽然为电网提供了惯性支撑,但当电网存在大量背景谐波时,VSG却成为了谐波源,向电网注入了大量谐波电流,为此,需要引入额外的谐波抑制方案以保证VSG输出电流质量。
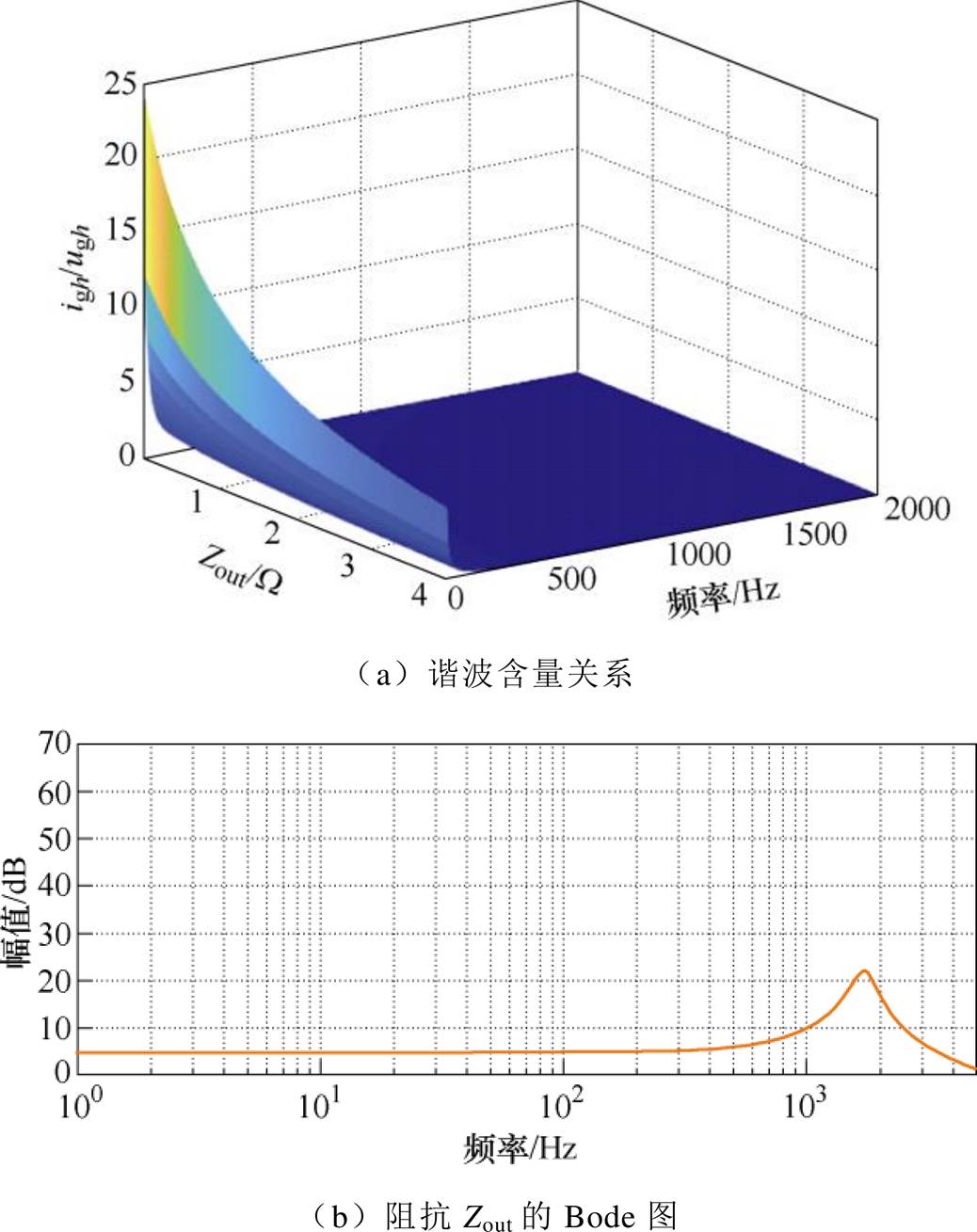
图3 VSG输出阻抗
Fig.3 Output impedance of VSG
由于VSG功率环只是为了保证常规策略中的基波电压控制性能,所以VSG在谐波域属于开环控制。为此,有学者提出通过PCC谐波电压反馈的方式,使uref.h=upcc.h,通过多谐振控制器GRu无静差追踪PCC谐波电压以减小VSG与PCC之间的谐波电压差,从而降低VSG并网谐波电流含量。
然而由于线路阻抗过小以及电压传感器对谐波电压检测精度的问题,将导致PCC谐波电压分量与电容电压谐波分量近似相等,由此将使电压/电流闭环控制失效,从而导致谐波抑制效果不佳。针对现有主流基于PCC电压采样的谐波抑制方案受到线路阻抗大小限制的问题,本文提出了一种电压-电流级联闭环控制方案,方案控制框图如图4所示。
相比于图1,图4保留了传统VSG的基波电压控制回路,它通过调节输出电压来控制VSG的输出功率,体现了VSG的频率支撑特性。新增加的框线是本文提出的方法,其在输出电流反馈回路中加入了一阶复矢量滤波器H(s),利用其在f0处增益为1且无相移的特性进行谐波电流总和的整体提取,并通过比例谐振控制器kp+GRi生成VSG谐波电压补偿的参考分量uref.h,然后通过多谐振控制器GRu实现PCC谐波电压跟踪,减小输出谐波电流,从而实现了系统对谐波电流的闭环控制。其中谐波电流外环电流参考指令iref.h=0,H(s)的时域表达式如式(9)所示,其在ab 坐标下的实现方式如图中点画线所示。
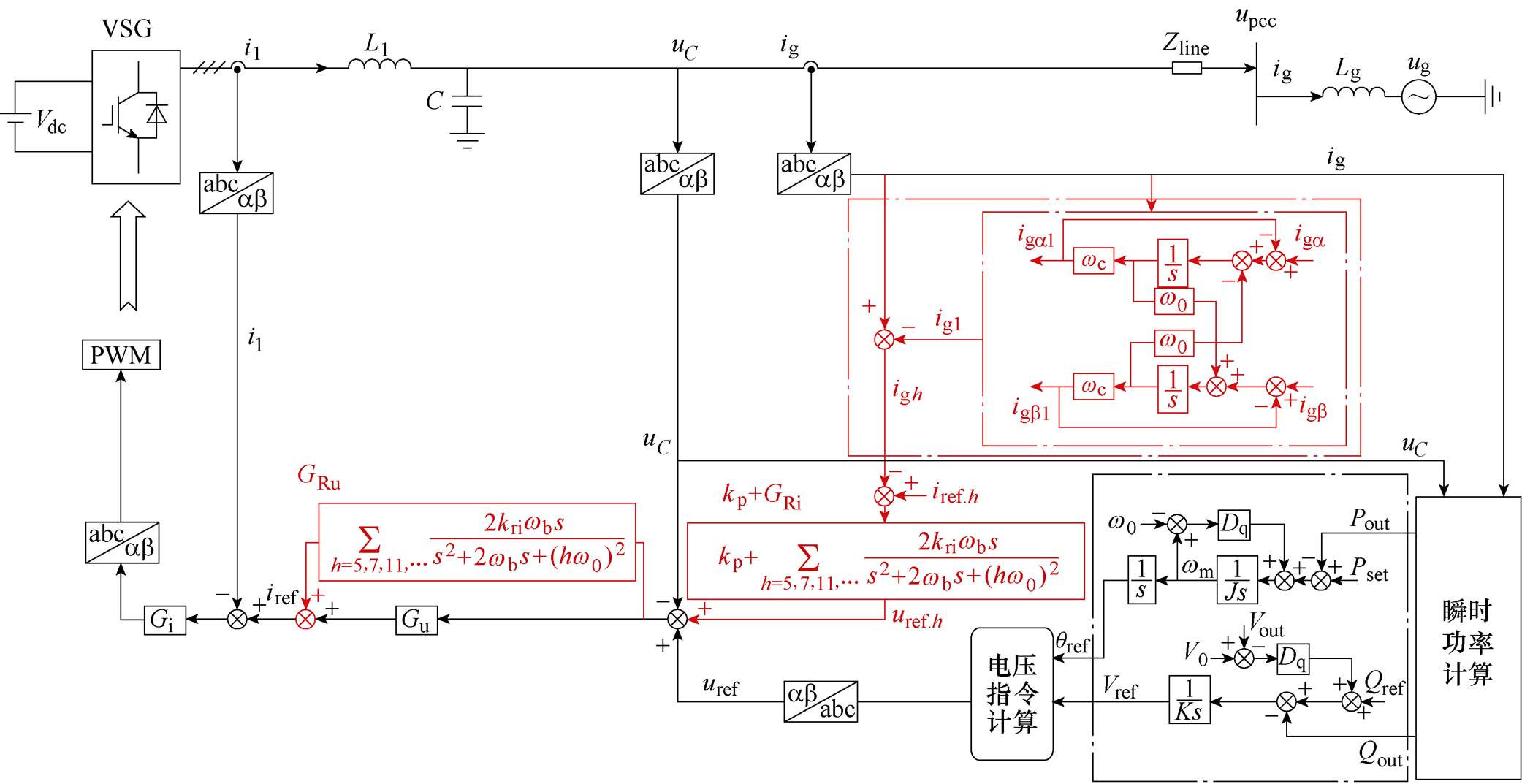
图4 电压-电流级联闭环控制方案
Fig.4 Voltage-current cascade closed loop control block diagram
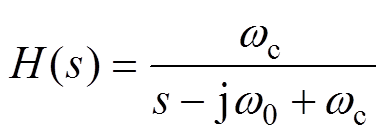 (9)
(9)
式中,w0=2pf0,这里取f0=50 Hz;wc为滤波器截止角频率。
为了保证系统对谐波电流的有效控制以及谐波参考电压值的无静差跟踪,在电压环和谐波电流环中引入了多谐振控制器GRu和kp+GRi,利用谐振控制器在谐波频率处高增益的特点提高对并网谐波电流的控制性能,使系统可以有效跟踪谐波参考分量,改善并网电流质量,保证VSG有功特性的同时,解决了VSG在接入畸变电网时输出电流质量畸变的问题,其传递函数表达式分别为
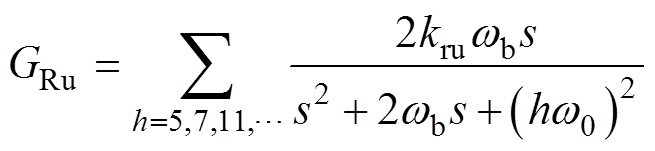 (10)
(10)
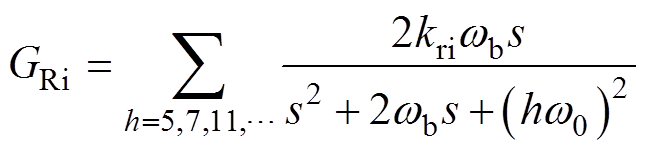 (11)
(11)
式中,kRu、kRi为谐振控制器增益系数;wb为控制器带宽。
加入电压-电流级联闭环控制后,VSG的输出电压传递函数为
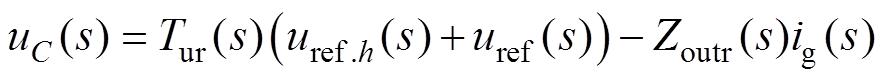 (12)
(12)
式中,uref.h(s)为谐波电流闭环控制提供的谐波电压参考值;Tur(s)和Zoutr(s)分别为电压-电流级联控制方案中参考电压到输出电压的传递函数以及输出电流到输出电压的传递函数,即
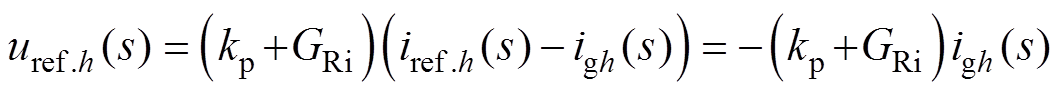 (13)
(13)
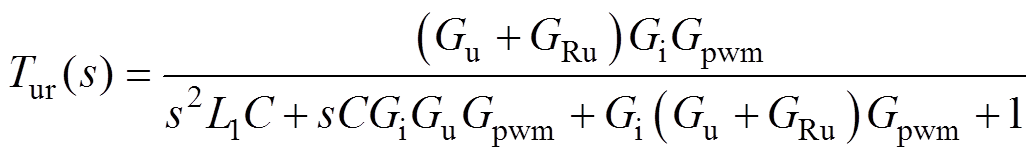 (14)
(14)
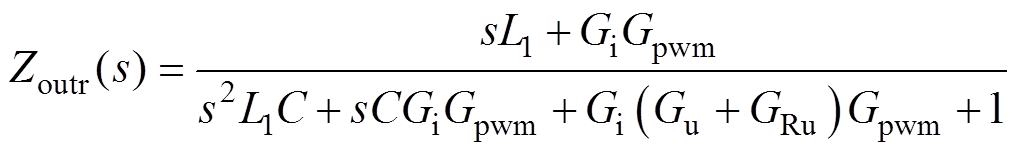 (15)
(15)
所以对于电压-电流级联闭环控制方案而言,并网谐波电流表达式为
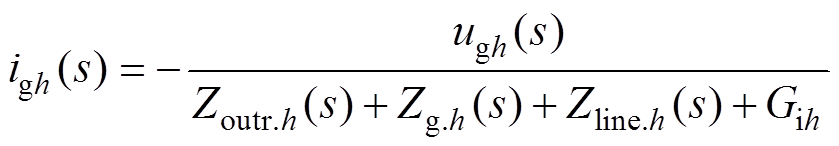 (16)
(16)
式中,Gih为谐波电流igh(s)到输出电压uC的传递函数,具体表示为
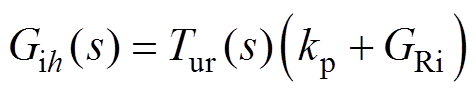 (17)
(17)
相比于式(8),式(16)在分母上引入了一个额外的阻抗分量Gih,表明电压-电流级联闭环控制方案的输出阻抗在原来的基础上增加了Gih项,相当于串联了阻抗为Gih的电路元件,由此电压-电流级联闭环控制方案的等效电路模型如图5所示。图中,Ztotal.u为改进方案下的等效谐波输出阻抗。
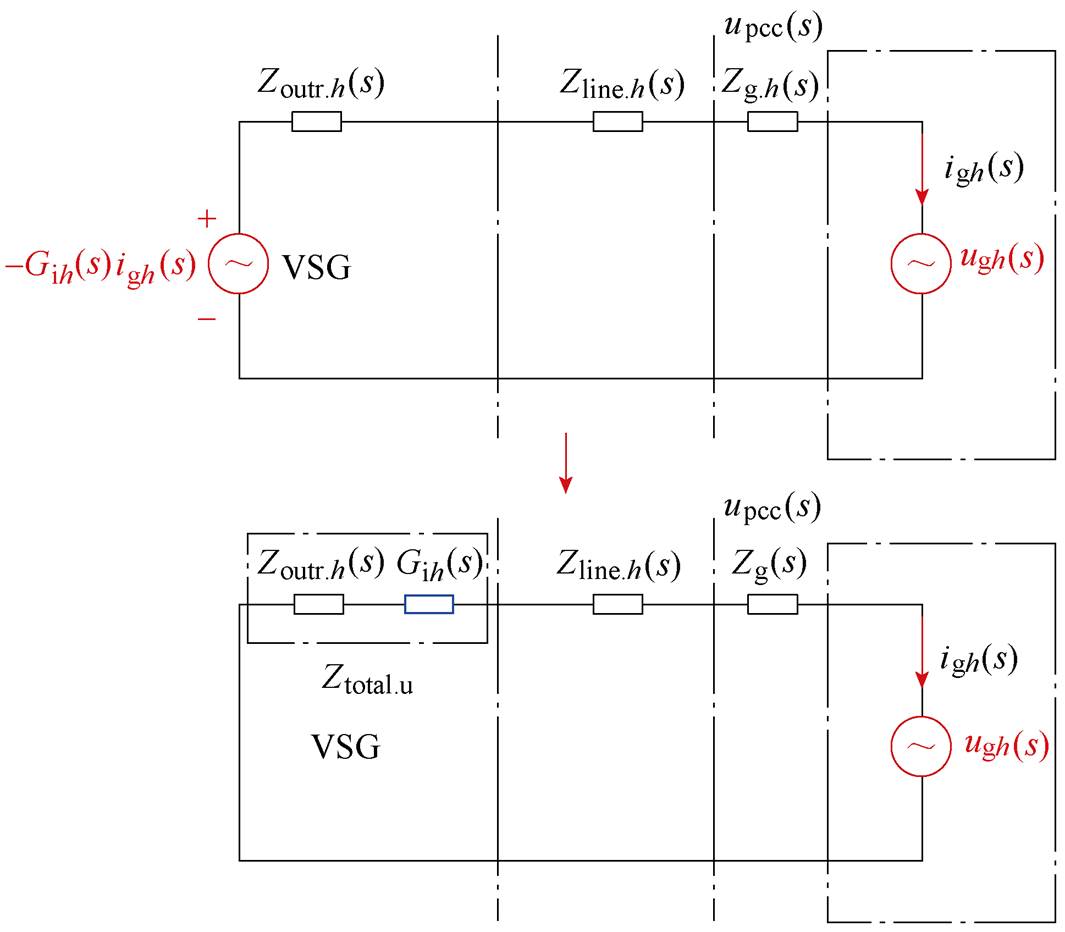
图5 改进VSG方案等效电路模型
Fig.5 Improved VSG circuit model
图6为改进前后的等效输出阻抗Bode图。可以发现,所提方案的输出阻抗Ztotal.u在5、7、11、13次等谐波频率处相比于传统输出阻抗都有大幅增加,这得益于多谐振控制器在谐波频率处高增益的特点,增加了Gih在谐波频率处的幅值,从而提高了等效谐波输出阻抗Ztotal.u的阻抗,根据第1节中对传统VSG接入畸变电网时,其输出谐波电流与畸变电网电压的关系分析可知,igh/ugh与输出阻抗Zout呈正相关,输出阻抗越大,电网谐波电压对并网电流的影响越小,因此电压-电流级联闭环控制方案能够有效降低网侧畸变电压对输出电流的影响。
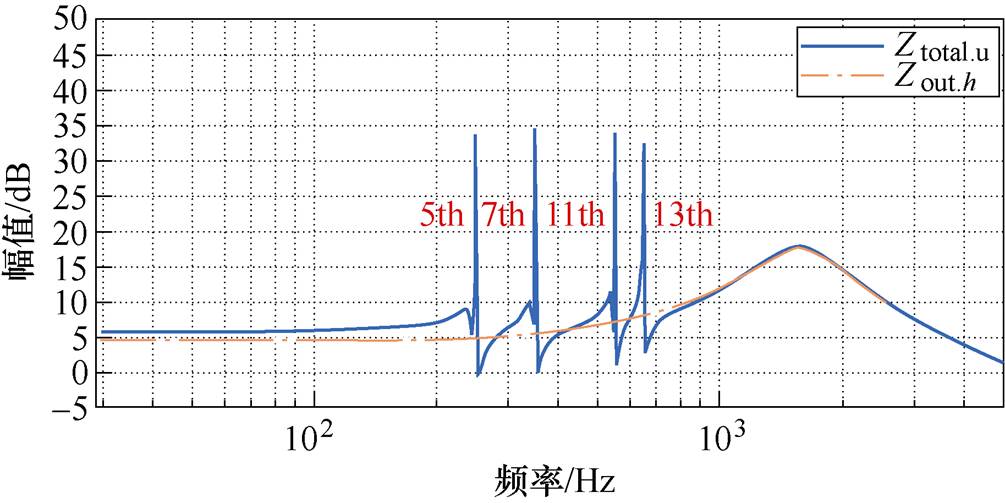
图6 改进VSG等效输出阻抗Bode图
Fig.6 Improved VSG equivalent output impedance Bode diagram
传统VSG控制方法、现有的基于PCC电压采样的方法以及本文电压-电流级联闭环控制方法的控制框图的对比如图7所示。
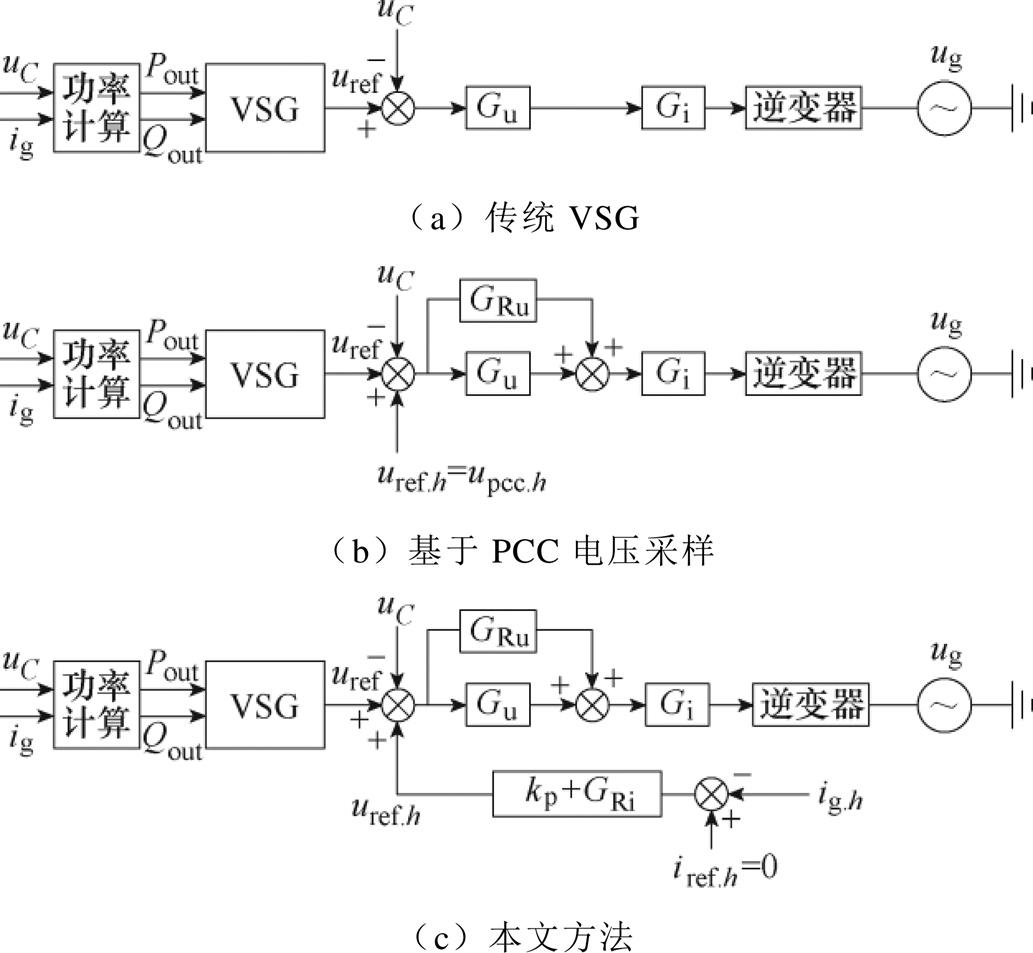
图7 控制方案的对比
Fig.7 Comparison of control schemes
从图7可以直观地看出三种方法的递进式改进的关系。首先,基于PCC电压采样的方法是在传统VSG的控制架构上增加了PCC谐波电压反馈,再通过多谐振控制器GRu追踪PCC谐波电压,以减小VSG与PCC之间的谐波电压差,从而降低VSG输出谐波电流。但是这类方法面临线路阻抗大小限制的问题,由于线路阻抗过小,导致PCC谐波电压分量与电容电压谐波分量近似相等,谐波电压补偿量信号太弱,从而导致谐波抑制效果不佳,为此需要采取额外增加电感的方式来放大该信号。
本文方法则是将图7b中的PCC采样提取的谐波电压补偿量信号的开环方式改为从电流采样来获取谐波电流,并通过比例谐振控制器来获取这个谐波电压补偿量信号;或者说只要还存在着谐波电流偏差,就会产生足够大的谐波电压补偿量信号;其本质上是把原本开环获取的谐波电压补偿信号换成了一个增益极大的闭环,放大了电压谐波参考信号指令值,从而解决了由于线路阻抗过小带来的谐波抑制效果不佳的问题,大幅提升了VSG输出电流谐波的抑制效果。
根据上述三种方法递进式改进的关系,可以看出三种方法的VSG控制包括内部的电压环控制的控制参数设计是相同的,可按照文献[12-13]进行。这部分的控制只是为了保证常规策略中的基波电压控制性能。而基于PCC电压采样的方法所增加的谐振控制器GRu作为谐波电压环的控制器,其参数设计整定可遵照常规谐振控制方法[14]进行;而本文方法同样用到相同的GRu和控制参数设计。图7c中本文方法新增的控制环路,是把谐波电流转化为谐波电压补偿量信号的比例谐振控制器kp+GRi;这部分控制参数设计可以通过常规的比例谐振控制器设计方法[29]。上述控制参数的设计结果见表1,将用于接下来的分析与实验。
表1 控制参数
Tab.1 Control parameters
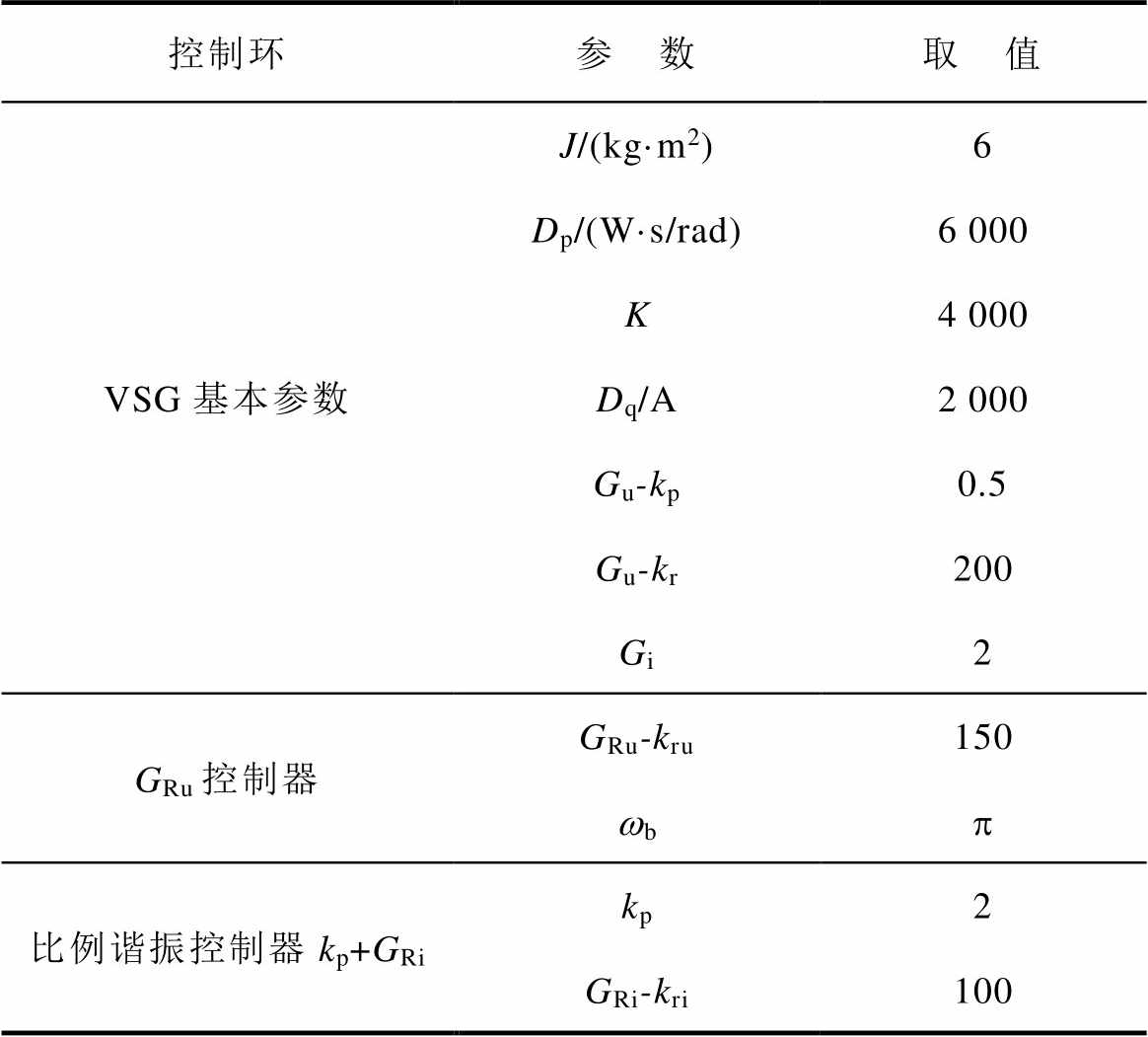
控制环参 数取 值 VSG基本参数J/(kg·m2)6 Dp/(W·s/rad)6 000 K4 000 Dq/A2 000 Gu-kp0.5 Gu-kr200 Gi2 GRu控制器GRu-kru150 wbp 比例谐振控制器kp+GRikp2 GRi-kri100
本文方法将VSG传统的基波控制方案转变成基波电压控制和谐波电流级联控制,提出了电压-电流级联闭环控制方案;在基波频率下,VSG跟随功率控制回路的基波电压指令实现闭环控制,保证了VSG对电网的支撑作用;在谐波频率下,通过对谐波总和进行整体提取,并采用闭环控制输出谐波电压补偿的参考量,从而等效于增强了谐波电压补偿量的参考信号,大幅提升了VSG输出电流谐波的抑制效果。以下将从基波电压控制和谐波电流控制两个方面来分析系统稳定性。
2.2.1 基波电压控制回路
作为VSG加入本文电压-电流级联的谐波闭环控制环节后的传递函数,式(12)的基波电压分量可表示为
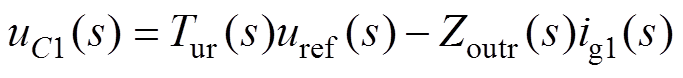 (18)
(18)
式中,下标1表示基波分量。
为进行弱电网条件下的稳定性分析,将电网视为电流源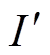 与电网阻抗并联的诺顿等效模型,则式(18)可表示为
与电网阻抗并联的诺顿等效模型,则式(18)可表示为
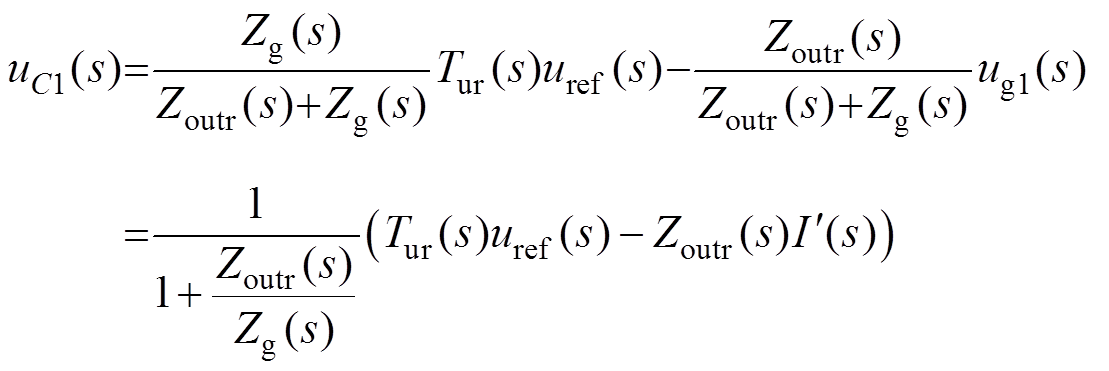
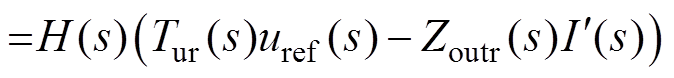 (19)
(19)
其中
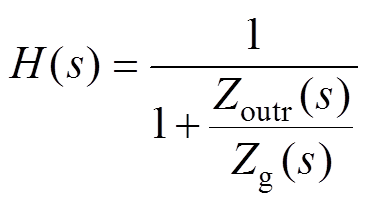 (20)
(20)
式中,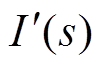 =ug(s)/Zg(s)。
=ug(s)/Zg(s)。
根据文献[30]基于阻抗的电压源和电流源型逆变器并网稳定性判据可知,为保证VSG控制的逆变器接入畸变电网时的稳定性,需要满足以下两点判据:
(1)在强电网(Zg=0)的情况下,并网逆变器设计为稳定系统,系统要保证其电压跟踪性能,同时保证电压源的电压性能,即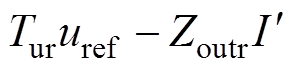 在右半平面不存在极点。
在右半平面不存在极点。
(2)在弱电网(Zg≠0)的情况下,并网逆变器等效输出阻抗与电网阻抗之比满足Nyquist稳定判据。
为分析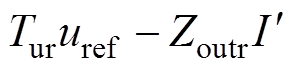 ,Tur闭环表达式(14)对应的开环传递函数(参考电压到输出电压)为
,Tur闭环表达式(14)对应的开环传递函数(参考电压到输出电压)为
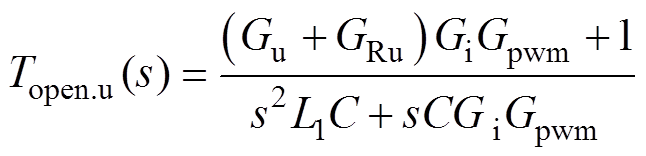 (21)
(21)
根据式(21)可得电压-电流级联闭环控制方案中基波电压开环传递函数Bode图,如图8所示。系统的剪切频率为2 541 Hz,相位裕度为32.1 °,根据Nyquist稳定性判据可知,系统保持稳定。幅频曲线中,50 Hz基频处增益为68 dB,这意味着本文方法可以实现基频电压指令的无静差跟踪。同时由于多谐振控制器GRu在谐振频率处高增益的特点,也使得电压开环传递函数在谐波频率处具有相当高的增益,能有效跟踪谐波电流闭环控制输出的谐波电压参考分量。
上述分析证明所提控制方案在接入强电网(Zg=0)时,基波电压稳定,即 不存在右半平面极点,满足稳定性判据(1)。
不存在右半平面极点,满足稳定性判据(1)。
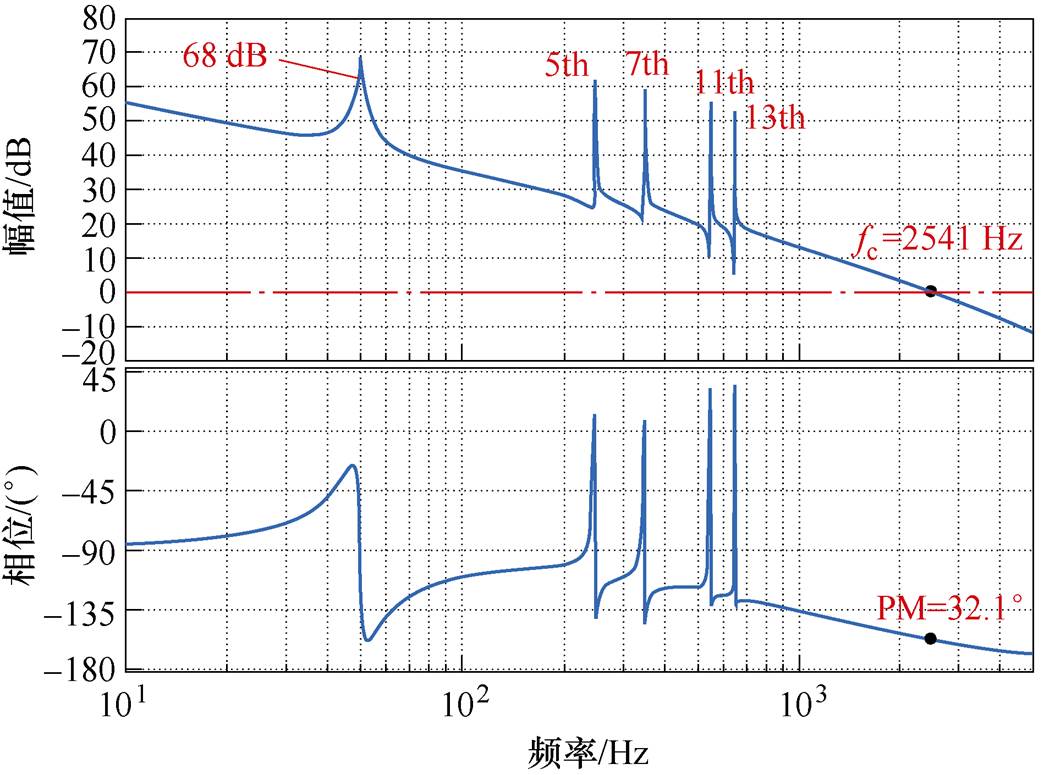
图8 Topen.u的Bode图
Fig.8 Bode diagram of Topen.u
在弱电网条件下,观察式(19)发现,H可以等效为前向通路传递函数为1,反馈通路传递函数为Zoutr/Zg的闭环负反馈控制系统传递函数,其中Zoutr/Zg为该系统的等效环路增益。因此,如果Zoutr/Zg满足Nyquist稳定判据,则H稳定。采用Bode图进行分析时,这要求Zoutr与Zg的幅频曲线交叉点的相位差应在±180 °之间。
根据式(15),绘制了输出阻抗Zoutr与网侧电感的Bode图,如图9所示,其中点画线和虚线分别表示网侧电感为1~2 mH。
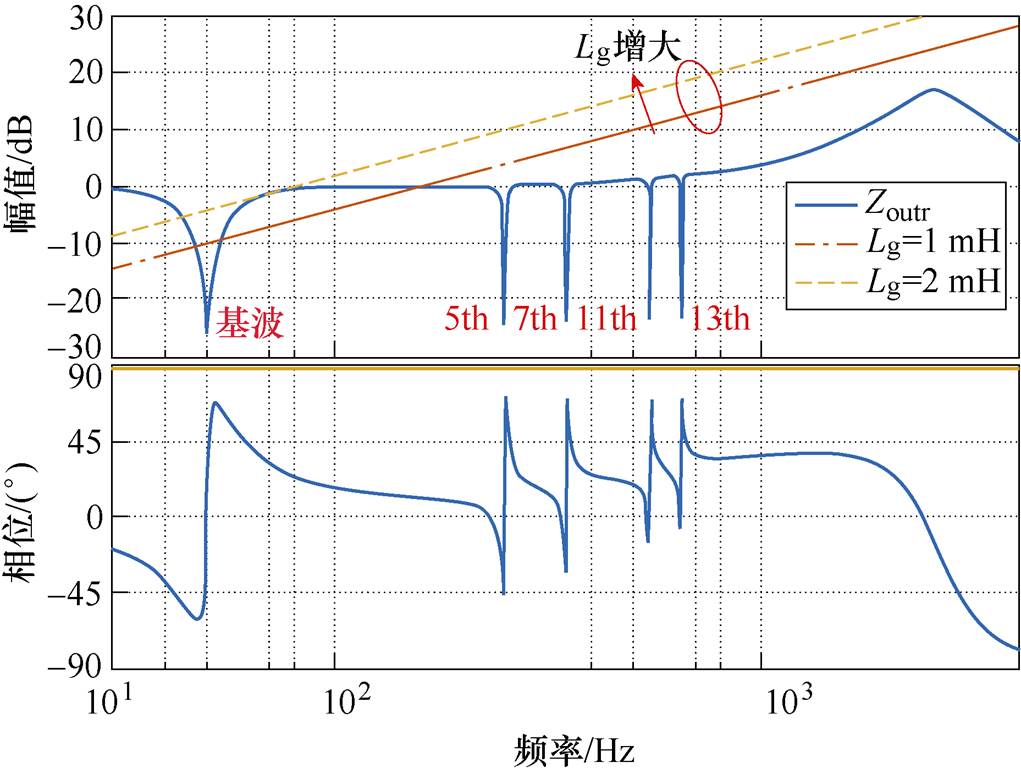
图9 Zoutr的Bode图
Fig.9 Bode diagram of Zoutr
可以发现,本文方法中其等效基波输出阻抗Zoutr始终在±90 °之间,这表明当VSG接入Lg大范围变化的弱电网系统时,输出阻抗与网侧阻抗的幅频曲线交叉点的相位差始终小于180 °,系统在基波频率下保持稳定。
2.2.2 谐波电流控制回路
同理根据式(12),忽略扰动项uref,可得系统输出谐波电流的闭环传递函数为
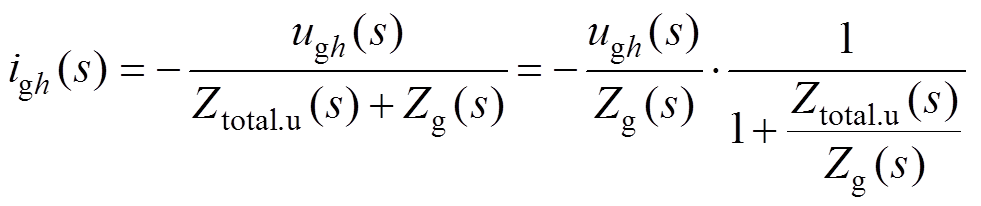
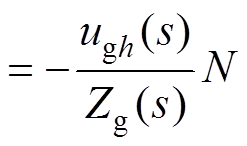 (22)
(22)
其中
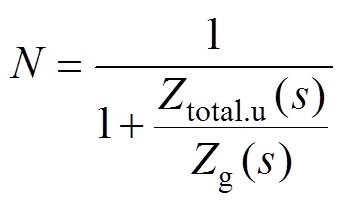 (23)
(23)
根据前述的稳定性判据,此时VSG的谐波电流稳定性取决于N是否稳定。同理,绘制了等效谐波输出阻抗Ztotal.u与网侧电感(1~2 mH)的Bode图,如图10所示。
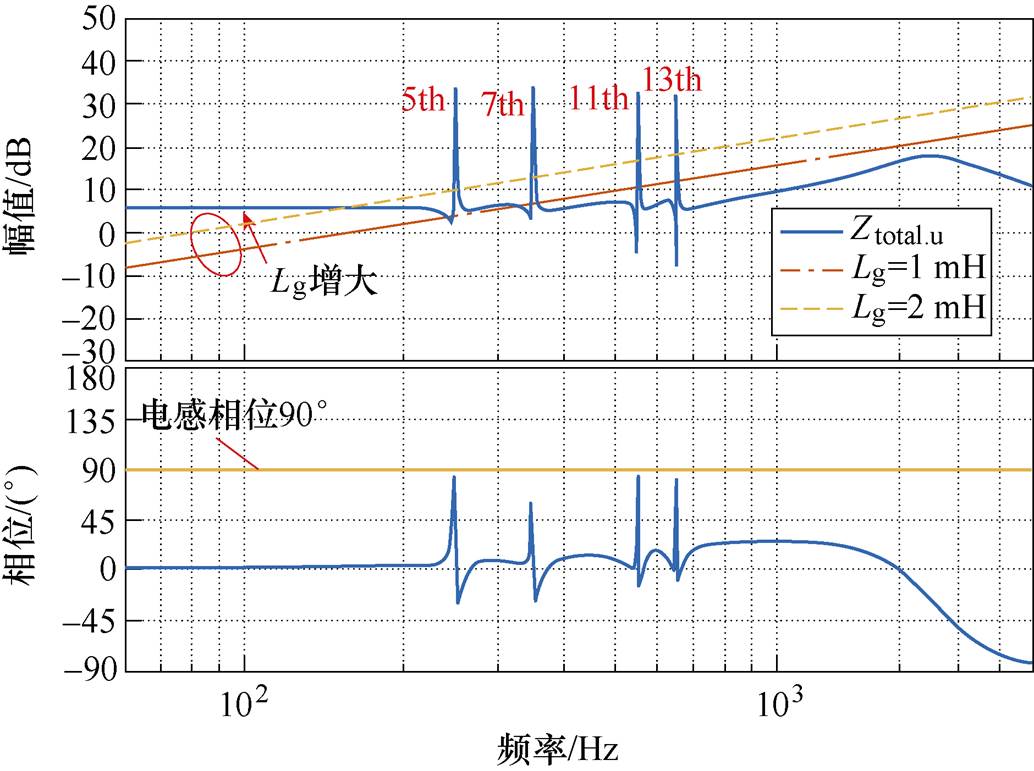
图10 Ztotal.u的Bode图
Fig.10 Bode diagram of Ztotal.u
从图10中可以发现,不管网侧阻抗如何变化,等效谐波输出阻抗与网侧阻抗交叉截点频率处的相位差始终小于180 °,保证了谐波频率下并网谐波电流控制的稳定性。
以上分析说明本文所提电压-电流级联闭环控制方案保证了基波电压的控制稳定性的同时,也保证了谐波电流控制环的稳定性。
为了验证所提方法的有效性,在实验室搭建了一台15 kW的基于VSG控制的并网逆变器,通过实验验证了本文所提谐波电流抑制策略的正确性。
实验平台如图11所示,VSG逆变器部分由基于IGBT的三桥臂逆变器结合LC滤波器实现,由Kratzer高压双向功率直流源供电,通过外接电感实现对线路阻抗的模拟,其中实验平台的实验参数见表2。输出侧通过隔离变压器、断路器接入电网,控制程序通过TMS320F28335实现,并利用CAN通信与示波器对实验过程中的电压、电流、功率及频率等信号进行实时观测。

图11 实验设备
Fig.11 Laboratory equipment
逆变器与电网之间的三相隔离变压器采用传统的Yd联结,逆变器侧为三角形联结,网侧为星形联结,因此不考虑3次倍频谐波分量。但考虑到电网中含有大量5、7、11、13、17和19次谐波,因此,着重对比了不同方案下上述谐波次电流含量大小变化情况。
表2 VSG实验参数
Tab.2 Experimental parameters of VSG
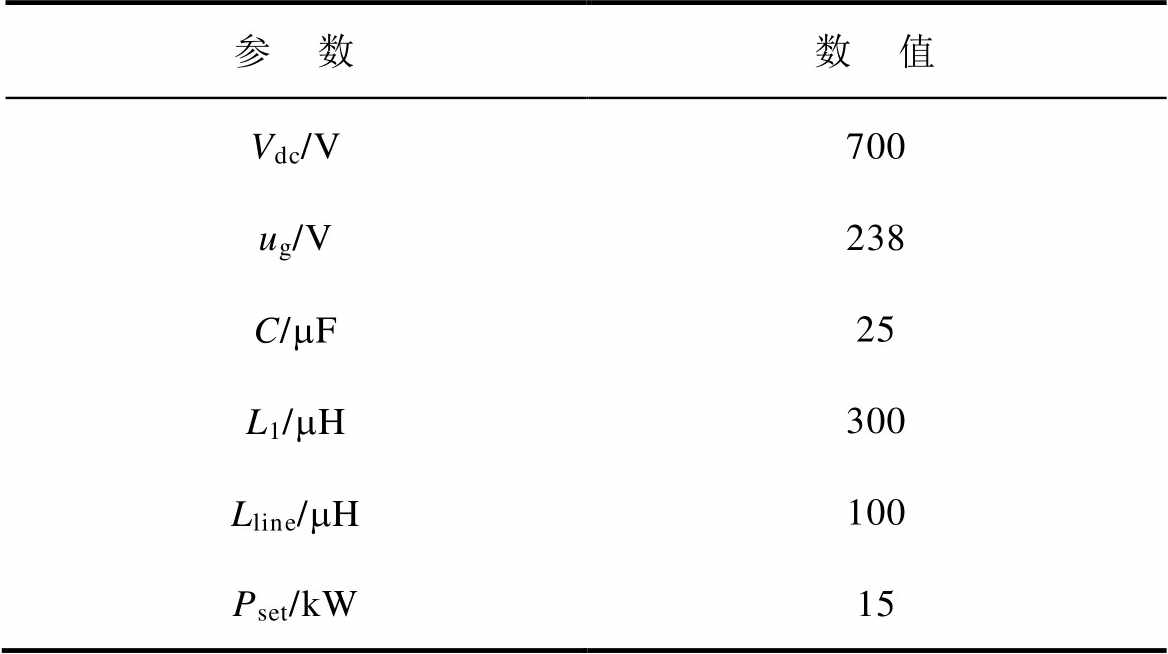
参 数数 值 Vdc/V700 ug/V238 C/mF25 L1/mH300 Lline/mH100 Pset/kW15
首先针对VSG的功率暂态响应特性,比较了传统VSG、现有基于PCC电压采样的方法与本文方法在0~15 kW输出功率突变的过程中,系统的谐波抑制能力以及动态跟踪能力。图12为实验结果,图12a~图12c分别为传统VSG、基于PCC电压采样方法和本文方法。
根据实验结果的功率阶跃,可以发现三种谐波电流抑制方法都能够准确跟踪输出指令功率,说明三种方法在基波频率下都具备支撑电网电压和频率的VSG特性。

图12 功率指令突变效果对比
Fig.12 Power command mutation effect comparison chart
将电流波形放大,可以发现,在暂态与稳态过程中,传统VSG的并网输出谐波电流已经发生了严重的畸变。基于PCC电压采样方法的谐波较之传统VSG有所改善。而本文方法则在暂态和稳态过程中皆保持了最好的正弦度。这得益于本文方法在谐波频率下实现了网侧谐波电流的直接闭环控制,所以在暂态和稳态过程中,谐波抑制效果更好,且一致。
在此基础上,为了验证本文提出方案对VSG输电流的改进效果,分别做了传统VSG与本文方法的并网实验。图13为两种控制方案在PCC与VSG之间线路阻抗为100 mH时的谐波电流实验波形效果对比,相较于传统VSG方案,本文方法总谐波畸变率(Total Harmonic Distortion, THD)由9.72%变为3.68%,具有明显的改善效果。通过图14的谐波对比柱状图可以发现,传统VSG输出电流中含有大量5、7、11、13次谐波,其中5、7、11次谐波分别达到了6.77%、4.35%和3.40%,THD为9.72%;而使用本文方法后,各次谐波都得到了大幅度的抑制,5、7、11次谐波分别降低到了0.48%、0.21%和0.52%,THD降低为3.68%,得到了良好的改善。实验结果证明改进方案能有效改善VSG接入畸变电网时的输出电流质量。
为了进一步验证本文方法的有效性,将再次与在不同线路阻抗下基于PCC电压采样的谐波电流抑制方案进行实验对比。将原来为100 mH的Lline串联了500 mH和1 500 mH的电感进行了测试。图15、图16分别为两组实验的输出电流和PCC电压波形,可以发现,本文方法在Lline=100 mH(见图13b)、600 mH和1 600 mH的情况下输出电流分别为3.68%、3.29%和2.68%。相比基于PCC电压采样的谐波抑制方案而言,本文方法获得的输出电流THD明显降低,证明了本文所提VSG谐波抑制方案的优越性。同时可以看出,本文方法较之基于PCC电压采样的方法,其受到线路阻抗变化的影响更小。
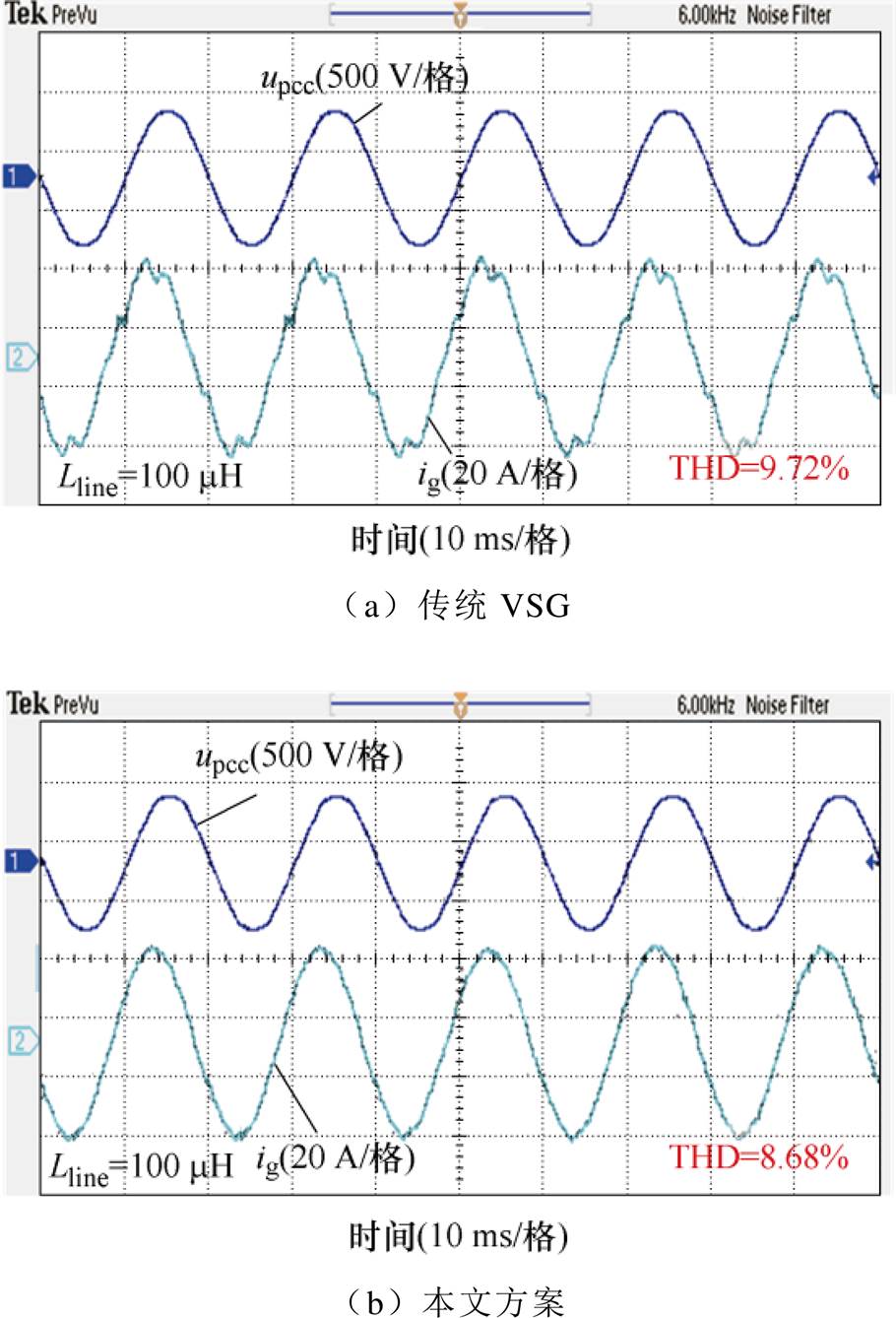
图13 PCC与VSG之间线路电感Lline=100 mH时的实验结果
Fig.13 Experimental results when the line impedance between PCC and VSG is 100 mH
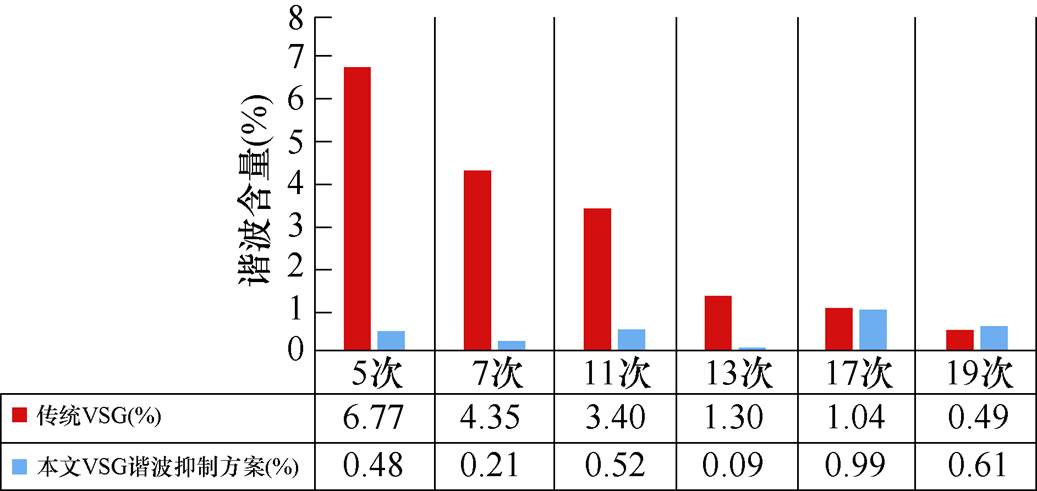
图14 各次谐波对比(Lline=100 mH)
Fig.14 Comparison of harmonics (Lline=100 mH)
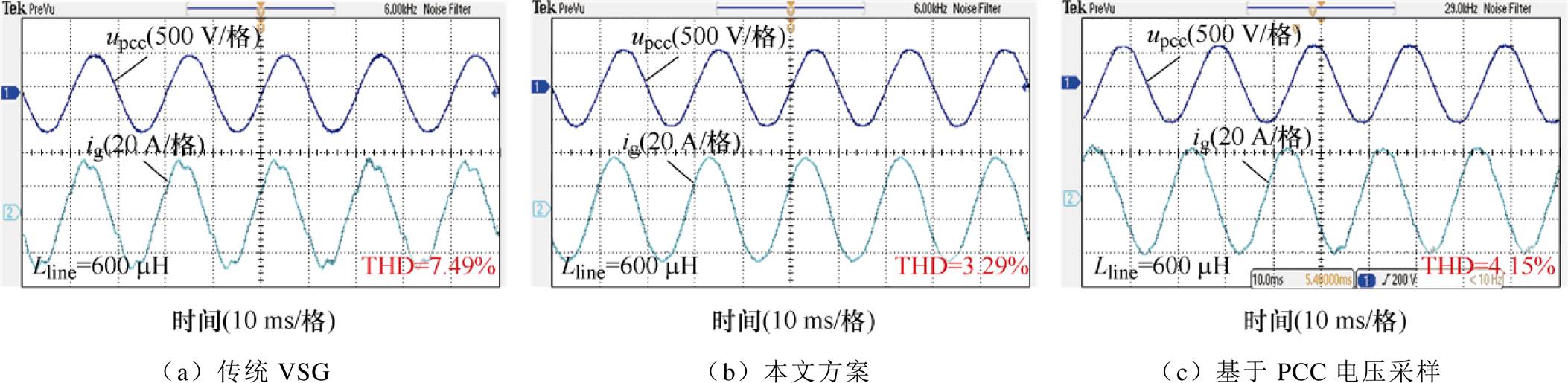
图15 PCC与VSG之间线路阻抗为600 mH时的实验结果
Fig.15 Experimental results when the line impedance between PCC point and VSG is 600 mH
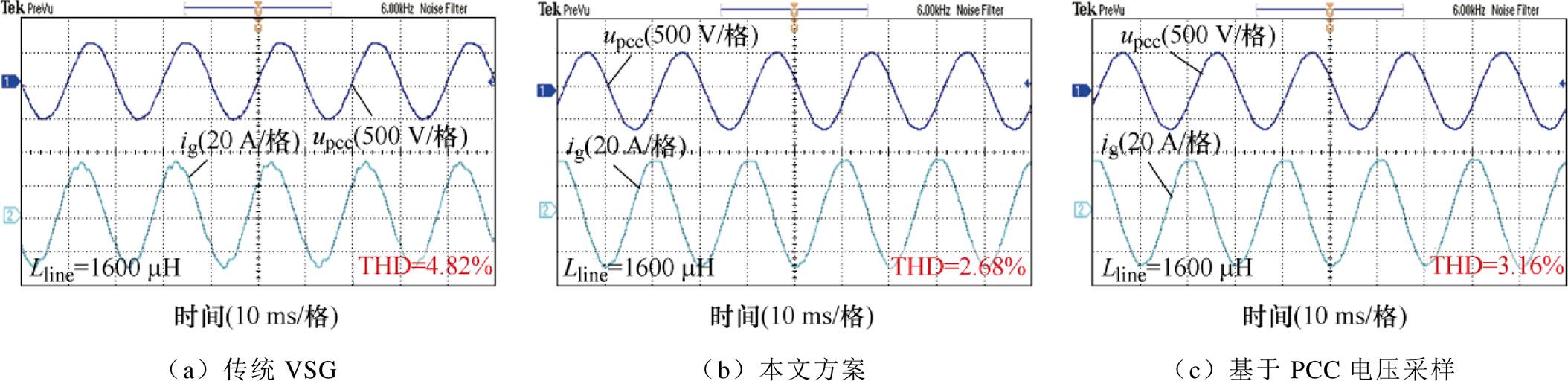
图16 PCC与VSG之间线路阻抗为1 600 mH时的实验结果
Fig.16 Experimental results when the line impedance between PCC point and VSG is 1 600 mH
通过进行基于PCC电压采样的方法的补充实验来分析其受到线路阻抗影响的情况如图17所示。图17a是Lline=100 mH时的结果,THD高达4.52%。图17b与图16c相同,即当Lline达1 600 mH时,此时THD降为3.16%。因此,现有基于PCC电压采样的对比方案需要在较大Lline接入条件下才能有效抑制电流谐波,亦或像文献[25]一样额外接电感以提高谐波抑制效果。

图17 基于PCC谐波电压采样的谐波抑制方案
Fig.17 Harmonic suppression schemes based on harmonic voltage sampling at PCC
图18a归纳对比了三种VSG方法的各次谐波的抑制效果,图18b归纳了在不同线路阻抗下基于PCC电压采样的谐波抑制效果。显而易见,本文方法较之现有的基于PCC电压采样的方案,克服了由于PCC接入线路阻抗过小导致的谐波抑制效果不佳的问题,通过网侧谐波电流闭环直接控制方案在线路阻抗很小的情况下即可达到很好的谐波抑制效果。
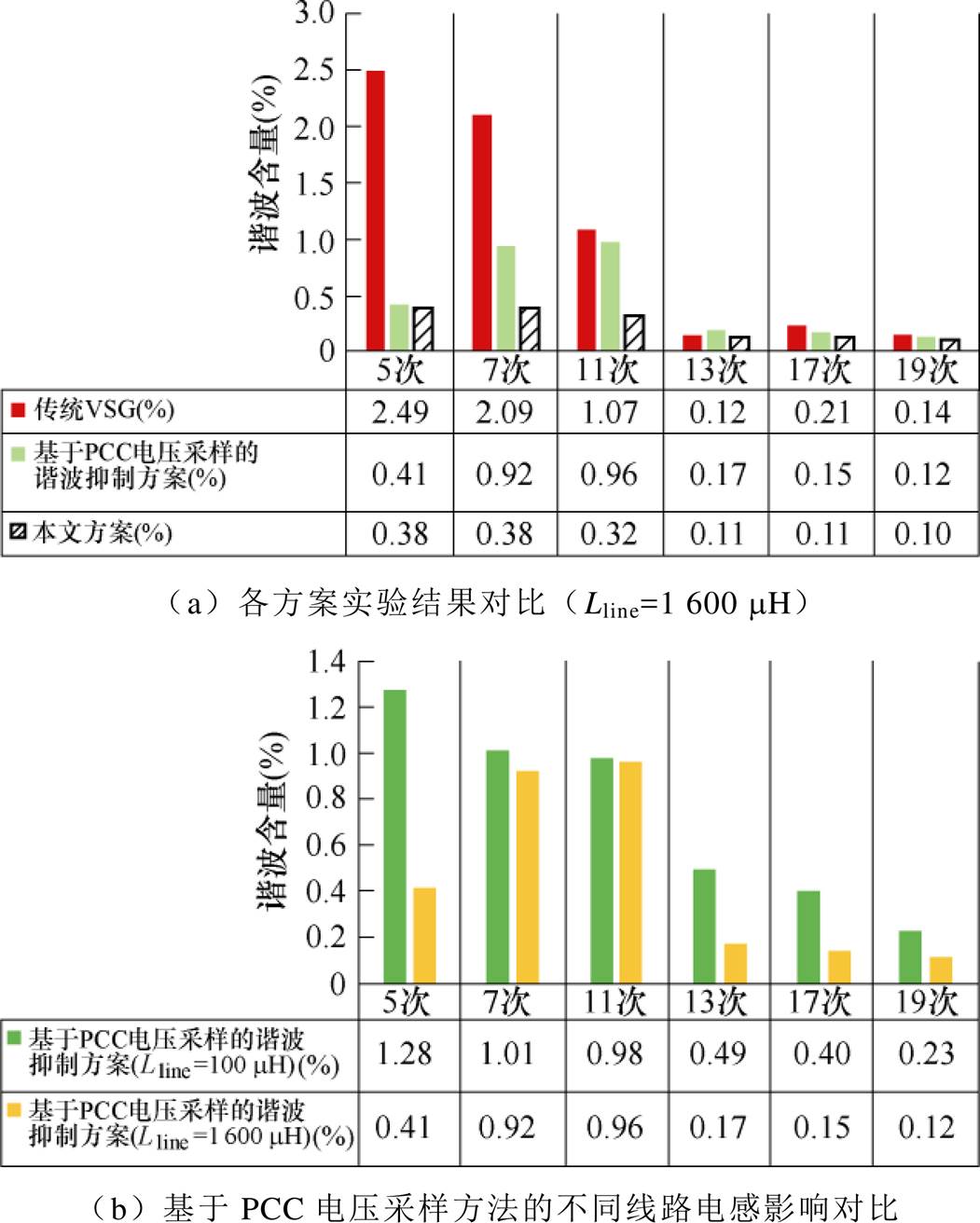
图18 各次谐波抑制效果
Fig.18 Harmonic suppression effect
本文方法较之与基于虚拟阻抗的方法[26-27],既可以达到无穷大虚拟阻抗的谐波抑制效果,也避免了虚拟阻抗取值过大时存在的失稳问题。
以下采用本文实验系统的同样参数对文献[26-27]中虚拟阻抗方法进行实验,首先通过实验获取各次谐波的最大虚拟阻抗,对5、7、11次谐波逐个不断增加其虚拟阻抗直至失稳振荡,从而得到各次谐波对应的最大可用的虚拟阻抗,以使现有虚拟阻抗方法在实际运行时可以达到最好的谐波抑制效果,从而能够公平地与本文方法进行比较。图19为增大虚拟阻抗的临界失稳实验结果。
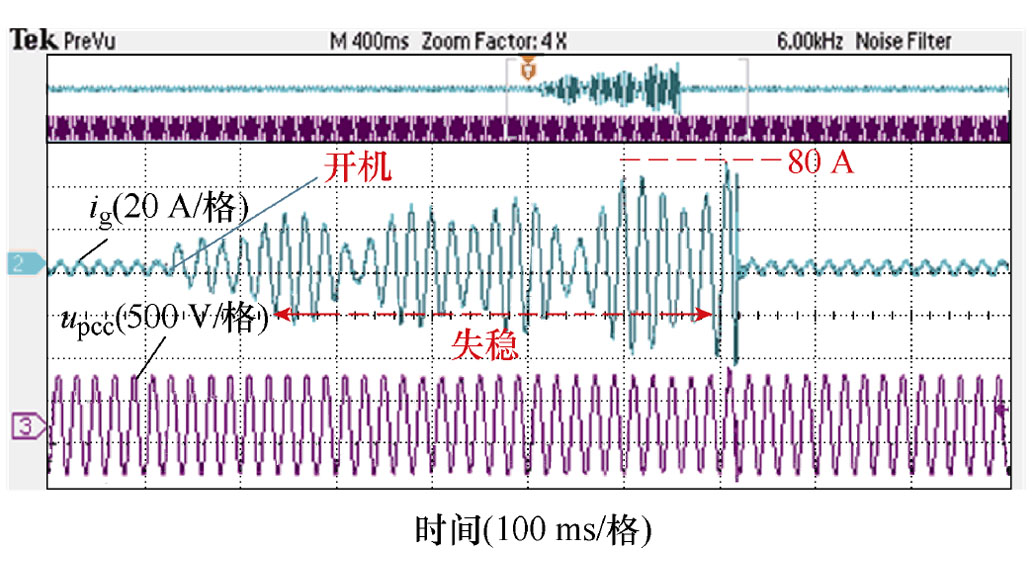
图19 增大虚拟阻抗的临界失稳实验结果
Fig.19 Experimental results of critical instability
图20中虚拟阻抗谐波抑制方法的实验采用与图16b中本文方法完全一样的实验条件;同时,采用图19所示的实验结果获取在不失稳前提下的最大虚拟阻抗值,以获取最佳抑制效果。显然,本文方法的谐波电流抑制效果更好(THD=2.68%小于3.58%)。
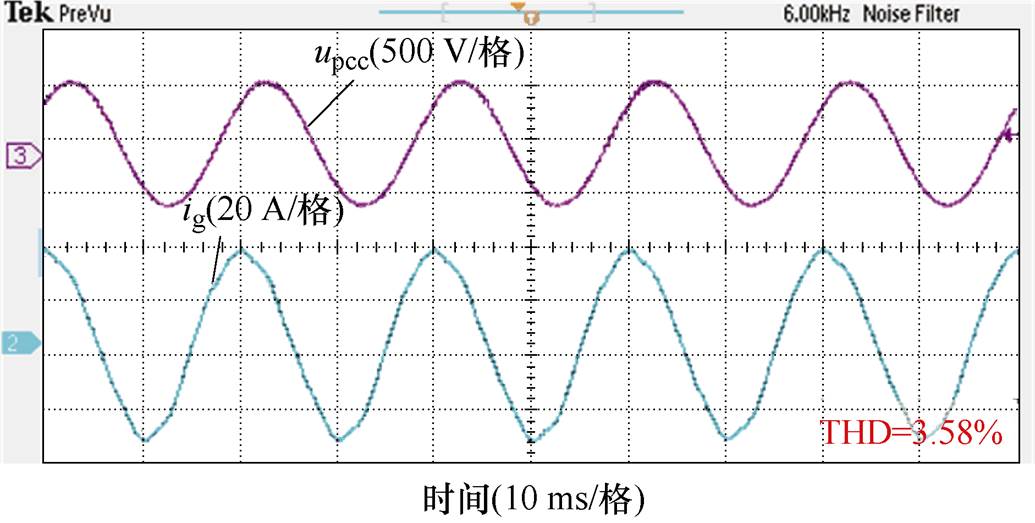
图20 最大虚拟阻抗下的谐波抑制效果
Fig.20 Maximum virtual impedance suppression scheme
针对虚拟同步机的输出电流谐波问题,现有多数抑制方法都是基于PCC电压采样来生成谐波电压补偿参考量,但抑制效果受限于线路阻抗的大小。本文提出的电压-电流级联闭环控制策略,通过对谐波电流总和进行整体提取,并采用闭环输出谐波电压补偿的参考量,从而在物理意义上等效于增强了谐波电压补偿量的参考信号,大幅提升了VSG输出电流谐波的抑制效果,克服了由于线路阻抗过低对抑制效果的限制,能在不增加额外电感的条件下提高VSG在畸变电网下的输出电流质量。通过搭建15 kW的样机平台,将本文方法与传统VSG、基于PCC电压采样的方法和基于虚拟阻抗的方法进行对比实验,较为全面地验证了本文方法的有效性,且谐波抑制效果更佳。
参考文献
[1] 王成山, 李琰, 彭克. 分布式电源并网逆变器典型控制方法综述[J]. 电力系统及其自动化学报, 2012, 24(2): 12-20.
Wang Chengshan, Li Yan, Peng Ke. Overview of typical control methods for grid-connected inverters of distributed generation[J]. Proceedings of the CSU- EPSA, 2012, 24(2): 12-20.
[2] Mohandes B, EI Moursi M S, Hatziargyriou N, et al. A review of power system flexibility with high penetration of renewables[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3140-3155.
[3] Wang Baochao, Xu Yongxiang, Shen Zhaoyuan, et al. Current control of grid-connected inverter with LCL filter based on extended-state observer estimations using single sensor and achieving improved robust observation dynamics[J]. IEEE Transactions on Indu- strial Electronics, 2017, 64(7): 5428-5439.
[4] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339- 2359.
Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage- source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2359.
[5] 高海力, 谭建成. 大型光储联合虚拟同步发电机技术综述[J]. 电气技术, 2018, 19(1): 1-4, 9.
Gao Haili, Tan Jiancheng. The overview of the VSG technology of grid connected large-scale PV-storage hybrid system[J]. Electrical Engineering, 2018, 19(1): 1-4, 9.
[6] D'Arco S, Suul J A. Equivalence of virtual syn- chronous machines and frequency-droops for converter-based microgrids[J]. IEEE Transactions on Smart Grid, 2014, 5(1): 394-395.
[7] Shuai Zhikang, Shen Chao, Liu Xuan, et al. Transient angle stability of virtual synchronous generators using Lyapunov’s direct method[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 4648-4661.
[8] 刘一锋, 周小平, 洪乐荣, 等. 虚拟惯性控制的负荷变换器接入弱电网的序阻抗建模与稳定性分析[J]. 电工技术学报, 2021, 36(4): 843-856.
Liu Yifeng, Zhou Xiaoping, Hong Lerong, et al. Sequence impedance modeling and stability analysis of load converter with virtual inertia control con- nected to weak grid[J]. Transactions of China Elec- trotechnical Society, 2021, 36(4): 843-856.
[9] 姜卫同, 胡鹏飞, 尹瑞, 等. 基于虚拟同步机的变流器暂态稳定分析及混合同步控制策略[J]. 电力系统自动化, 2021, 45(22): 124-133.
Jiang Weitong, Hu Pengfei, Yin Rui, et al. Transient stability analysis and hybrid synchronization control strategy of converter based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2021, 45(22): 124-133.
[10] 颜湘武, 张伟超, 崔森, 等. 基于虚拟同步机的电压源逆变器频率响应时域特性和自适应参数设计[J].电工技术学报, 2021, 36(增刊1): 241-254.
Yan Xiangwu, Zhang Weichao, Cui Sen, et al. Frequency response characteristics and parameter tuning of voltage-sourced converters under VSG control[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 241-254.
[11] 于彦雪, 关万琳, 陈晓光, 等. 基于序阻抗的虚拟同步机同步频率谐振现象[J]. 电工技术学报, 2022, 37(10): 2584-2595.
Yu Yanxue, Guan Wanlin, Chen Xiaoguang, et al. Synchronous frequency resonance in virtual syn- chronous generator based on sequence-impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2584-2595.
[12] 余裕璞, 顾煜炯, 和学豪. 逆变器电压电流双闭环控制系统设计[J]. 电力科学与工程, 2019, 35(3): 1-7.
Yu Yupu, Gu Yujiong, He Xuehao. Design of voltage and current double closed-loop control system for inverter[J]. Electric Power Science and Engineering, 2019, 35(3): 1-7.
[13] 吴恒, 阮新波, 杨东升, 等. 虚拟同步发电机功率环的建模与参数设计[J]. 中国电机工程学报, 2015, 35(24): 6508-6518.
Wu Heng, Ruan Xinbo, Yang Dongsheng, et al. Modeling of the power loop and parameter design of virtual synchronous generators[J]. Proceedings of the CSEE, 2015, 35(24): 6508-6518.
[14] Chen Xinran, Ruan Xinbo, Yang Dongsheng, et al. Step-by-step controller design of voltage closed-loop control for virtual synchronous generator[C]//7th Annual IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 2015: 3760- 3765.
[15] 姜静雅, 王玮, 吴学智, 等. 基于自适应无功功率补偿的虚拟同步机功率解耦策略[J]. 电工技术学报, 2020, 35(13): 2747-2756.
Jiang Jingya, Wang Wei, Wu Xuezhi, et al. Power decoupling strategy in virtual synchronous generator based on adaptive reactive power compensation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2747-2756.
[16] 葛平娟, 肖凡, 涂春鸣, 等. 考虑故障限流的下垂控制型逆变器暂态控制策略[J]. 电工技术学报, 2022, 37(14): 3676-3687.
Ge Pingjuan, Xiao Fan, Tu Chunming, et al. Transient control strategy of droop-controlled inverter con- sidering fault current limitation[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3676- 3687.
[17] IEEE Std 519-2014 IEEE recommended practice and requirements for harmonic control in electric power systems[S]. IEEE, 2014.
[18] Liu Baojin, Liu Zeng, Liu Jinjun, et al. An adaptive virtual impedance control scheme based on small-AC- signal injection for unbalanced and harmonic power sharing in islanded microgrids[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 12333-12355.
[19] Wu Wenhua, Zhou Leming, Chen Yandong, et al. Sequence-impedance-based stability comparison between VSGs and traditional grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 46-52.
[20] 耿乙文, 田芳芳, 孙帅, 等. 一种基于虚拟同步发电机的电流谐波抑制方法[J]. 电工技术学报, 2018, 33(5): 1040-1050.
Geng Yiwen, Tian Fangfang, Sun Shuai, et al. A method of current harmonics suppression based on VSG[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1040-1050.
[21] 徐健, 曹鑫, 郝振洋, 等. 基于电网谐波电压前馈的虚拟同步整流器电流谐波抑制方法[J]. 电工技术学报, 2022, 37(8): 2018-2029.
Xu Jian, Cao Xin, Hao Zhenyang, et al. A harmonic- current suppression method for virtual synchronous rectifier based on feedforward of grid harmonic voltage[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2018-2029.
[22] He Jinwei, Li Yunwei, Munir M S. A flexible harmonic control approach through voltage-controlled DG-grid interfacing converters[J]. IEEE Transactions on Industrial Electronics, 2012, 59(1): 444-455.
[23] 冯伟, 孙凯, 关雅娟, 等. 孤立微电网中基于输出电压复合控制的电压源型并网逆变器谐波电流抑制策略[J]. 电工技术学报, 2016, 31(7): 72-80.
Feng Wei, Sun Kai, Guan Yajuan, et al. A harmonic current suppression strategy for voltage source grid- connected inverters based on output voltage hybrid control in islanded microgrids[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 72-80.
[24] Zhao Xin, Meng Lexuan, Xie Chuan, et al. A unified voltage harmonic control strategy for coordinated compensation with VCM and CCM converters[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 7132-7147.
[25] 周杰, 刘傲洋, 罗皓文, 等. 虚拟同步机接入弱电网的电能质量新问题及谐波抑制方法[J]. 智慧电力, 2021, 49(2): 83-90.
Zhou Jie, Liu Aoyang, Luo Haowen, et al. Power quality issues and harmonic suppression method of virtual synchronous generator connected to weak grid[J]. Smart Power, 2021, 49(2): 83-90.
[26] Liu Baojin, Liu Jinjun, Liu Zeng. Improvement of grid current quality for droop-controlled grid- connected inverters under distorted grid conditions[C]// 11th IEEE Energy Conversion Congress and Expo- sition, Baltimore, MD, USA, 2019: 2560-2565.
[27] Savaghebi M, Jalilian A, Vasquez J C, et al. Secondary control for voltage quality enhancement in microgrids[J]. IEEE Transactions on Smart Grid, 2012, 3(4): 1893-1902.
[28] He Jinwei, Li Yunwei. Analysis, design, and imple- mentation of virtual impedance for power electronics interfaced distributed generation[J]. IEEE Transa- ctions on Industry Applications, 2011, 47(6): 2525- 2538.
[29] 阮新波, 王学华, 潘冬华. LCL型并网逆变器的控制技术[M]. 北京: 科学出版社, 2015.
[30] Sun Jian. Impedance-based stability criterion for grid- connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
Abstract With the increasing amount of renewable energy sources and energy storage devices in the power grid, more power electronic inverters get tied to the grid as current sources. As a result, the overall grid rotary inertia and frequency stability will decrease. So Virtual Synchronous Generators (VSG) schemes are being implemented in grid-tied inverters. VSGs are inverters in voltage source control mode. Particularly, its output voltage vector instantaneous angle is obtained by the rotor dynamics equation of the virtual synchronous generator to provide inertia and frequency support to the grid, just as the rotary synchronous generators. However, when VSG is connected to the grid, even a slight amount of grid voltage distortion would induce significant harmonics currents. Therefore, various VSG harmonic current suppression schemes are introduced.
Existing VSG harmonic current suppression methods are mainly based on PCC voltage feedback, whose voltage harmonics get extracted and added to the VSG output voltage commands. Therefore, the line connecting VSG and PCC would have no net harmonic voltage across, and no harmonic current would be induced. However, the existing methods based on PCC voltage feedback have practical limitations. As the line impedances are usually small, it only takes a tiny amount of harmonic voltage difference to induce a significant amount of harmonic currents. Slight noises and nonlinearity in the feedback path will introduce harmonic voltage difference and large harmonic current. Therefore, some paper proposes adding extra inductors in series with the PCC connecting line, but extra volume and cost are incurred.
This paper introduces a VSG output harmonic current closed loop to receive the voltage harmonic signal feedback. Therefore, the noises and the nonlinearity in the previous open-loop PCC harmonic voltage feedbacks can be eliminated, and the VSG output voltage can accurately track the voltage harmonics at the PCC point. As a result, the output current harmonics suppression is more effective.
This paper first establishes the impedance model of VSG and analyzes the output current harmonics. To implement this closed-loop control scheme, the sum of all orders of the harmonics is first extracted from the VSG output current feedbacks by a first-order complex vector filter and fed through a proportional-resonant control loop to generate the VSG harmonic voltage reference. The enhancement of the harmonic loop impedance with the proposed method is analyzed in detail and compared with the existing methods. Moreover, this paper further analyzes the system stability of the proposed method for both fundamental frequency voltage control and harmonic current control, using the impedance-based stability criterion of the voltage-source inverter. Compared with the existing harmonic current suppression methods using virtual impedance, the proposed scheme can suppress the harmonic current with much larger loop gains than the virtual impedance-based method.
Finally, a 15 kW VSG prototype is built to verify the proposed method compared with the conventional VSG and two harmonic current suppression methods based on PCC voltage feedback and the virtual impedance, respectively. The method proposed in this paper significantly improves VSG output current THD. Besides, it is noted that the harmonic suppression effect of the proposed method is much less susceptible to the low impedance value of the PCC connection line than the PCC voltage feedback-based method. In addition, the best suppression effect can be realized using the maximum virtual impedance value without instability.
keywords:Virtual synchronous generators (VSG), harmonic suppression, impedance reshaping, power quality
DOI: 10.19595/j.cnki.1000-6753.tces.222327
中图分类号:TM464; TM341; TM762
重庆市研究生科研创新资助项目(CYB21018)。
收稿日期 2022-12-17
改稿日期 2023-02-08
徐 菘 男,1997年生,硕士研究生,研究方向为新能源发电及电能质量控制。E-mail: 278398646@qq.com
陆 帅 男,1975年生,博士生导师,教授,研究方向为电力电子技术和电驱动、着重于高功率密度技术研究,应用于混合动力、纯电动汽车和可再生能源微电网系统。E-mail: Lushuai1975@gmail.com(通信作者)
(编辑 陈 诚)