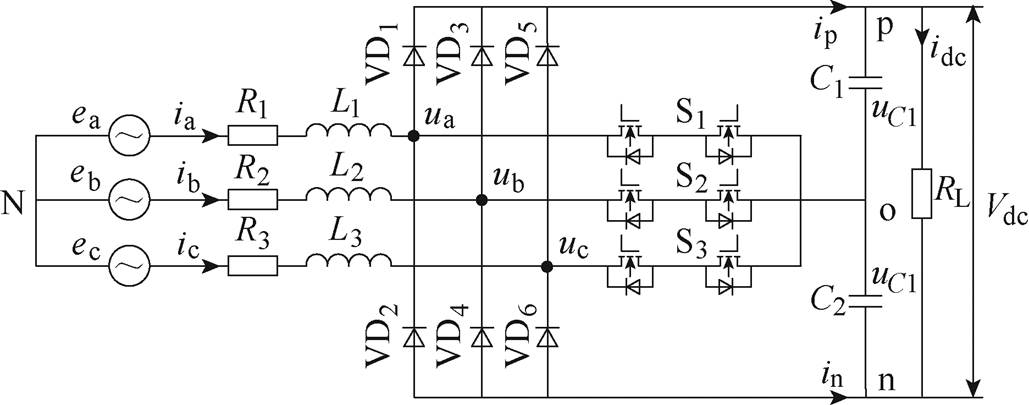
图1 三相Vienna整流器主电路拓扑
Fig.1 The topology of the three-phase Vienna rectifier
摘要 三相Vienna整流器具有不需要考虑开关死区、可靠性高等优点,但参数易受外部扰动影响而导致控制性能下降。针对这些问题,该文提出一种基于自适应超螺旋滑模观测器的无模型预测电流控制策略(ASTSMO-MFPCC)。首先,通过分析三相Vienna整流器参数失配数学模型,构建不依赖系统物理参数的超局部模型。其次,设计超螺旋滑模观测器估计超局部模型中的动态部分,有效抑制系统扰动影响。同时,设计自适应增益,动态调整超螺旋滑模观测器参数,解决增益选择难题。最后,构建离散化预测模型和成本函数,实现无模型预测电流控制算法。仿真与实验结果表明,所提策略具有良好的鲁棒性和动稳态性能。
关键词:Vienna整流器 超螺旋滑模观测器 无模型预测电流控制
近年来,三相Vienna整流器广泛应用于通信电源、风力发电、电力传动等领域。Vienna整流器具有同一桥臂开关驱动信号之间无死区、可靠性高、输入电流谐波含量低等优点,已成为三相功率因数校正领域的研究热点[1-3]。
三相Vienna整流器传统的控制方法主要有滞环控制、单周期控制、比例积分(Proportional Integral, PI)控制等控制算法。文献[4]将直流侧中点电压偏差引入滞环电流闭环控制中,控制简单、响应快速,但工作频率变化大、滤波器设计困难。文献[5]提出在传统单周期控制策略中引入谐振控制器,可以有效抑制输入不平衡引起的单周期控制的三相Vienna整流器输入电流中的3次谐波分量,改善输入电流品质,但对电流的采样精度有较高要求。文献[6]采用级联式非线性PI控制器,系统响应快速且易于实现,具有较强的抗扰能力,但控制器参数多、整定复杂。
随着控制理论的发展以及对Vienna整流器研究工作的深入,许多高级非线性的控制方法也逐渐被应用到Vienna整流器的控制中,如滑模控制(Sliding Mode Control, SMC)、自抗扰控制(Active Disturbance Rejection Control, ADRC)、模型预测控制(Model Predictive Control, MPC)等[7]。SMC因其结构简单、鲁棒性强、收敛速度快等优点得到广泛应用,文献[8]将SMC应用到Vienna整流器电压外环,提升了整流器抗扰动的能力。然而传统的SMC由于趋近律的离散性,不可避免地存在抖振问题,严重影响控制效果。文献[9]将模糊控制与SMC结合,提出了一种模糊趋近律,改善了动态性能,减弱了抖振,但同时也使得控制器复杂,降低了鲁棒性。高阶滑模控制继承了传统滑模鲁棒性强、结构简单、易于实现等优点,同时还可以有效抑制抖振,成为当下解决滑模抖振问题的有效手段。文献[10]将二阶滑模用在电机转子位置观测中,保证观测器稳定的同时有效抑制了抖振,但二阶滑模需要用到滑模面导数的信息,增加了控制难度。超螺旋滑模(Super-Twisting Sliding Mode, STSM)是一种二阶滑模,也是唯一一种仅需要用到滑模面信息,不需要滑模面各阶导数信息的高阶滑模[11]。文献[12]将STSM应用到Buck-Boost型电源变换器中,改善其存在的间歇性扰动问题,取得了不错的控制效果。文献[13]通过设计Lyapunov函数证明了STSM算法的稳定性,然而得到的稳定性条件与系统不确定性的界有关,一般很难得到准确值,具有一定的局限性。
MPC因其原理简单、响应快速、易于实现多目标优化等优点受到学界广泛关注[14]。有限集模型预测控制(Finite Control Set Model Predictive Control, FCS-MPC)根据整流器的离散特性,将可能输出的电压矢量作为控制集,通过列举搜索算法,选出最优的电压矢量作为输出,控制过程直观,并且能够通过在成本函数中加入中点电位约束项,实现中点电位与交直轴电流的同时优化,不需要设计调制算法,简化了控制结构,易于应用在三电平整流器的控制中[15-16]。
模型预测控制的基础是被控对象的数学模型,所以对模型参数的准确度有较高的要求,然而三相Vienna整流器在实际工况下会受到各种扰动的影响,导致难以获得精确参数,为此国内外的学者提出过许多解决办法。文献[17]提出一种基于在线扰动补偿的级联式无差拍控制策略,通过龙伯格观测器对扰动进行估计和补偿,实现整流器有功功率和无功功率的解耦控制,但系统运行仍然依赖模型参数。法国学者M. Fliess提出的无模型控制为解决MPC模型参数扰动问题提供了新思路[18]。文献[19]提出一种无模型预测电流策略,通过递归最小二乘算法来识别具有外部输入的自回归模型的参数,可准确预测受控变量,但算法中含有高阶矩阵的运算,计算量较大。文献[20]提出一种通过预测电流梯度实现无模型控制的方法,有效地解决了电流差分方法更新滞后带来的问题,但该方法对电流采样的精度要求较高。
为进一步提升三相Vienna整流器在复杂环境下的控制性能,本文提出一种基于自适应超螺旋滑模观测器的无模型预测电流控制策略。首先,构建包含模型电感、电阻等参数扰动项的超局部模型,增强系统在参数失配时的鲁棒性,解决MPC依赖物理参数问题。其次,设计超螺旋滑模观测器估计超局部模型中的动态部分,解决传统滑模观测器由于抖振作用造成的系统动稳态性能下降问题。同时设计自适应增益矩阵,动态调整观测器参数,抑制动态部分边界不确定对系统的影响,保证预测模型准确性。最后,通过仿真和实验,验证所提算法的有效性和稳定性。
Vienna整流器的主电路拓扑如图1所示,ea、eb、ec为三相输入电压;ia、ib、ic为三相输入电流;L1、L2、L3为升压电感,L1=L2=L3=L;R1、R2、R3为等效电阻,R1=R2=R3=R;VD1~VD6为6个快速恢复二极管;C1、C2为直流侧滤波电容,容值为C;uC1、uC2分别为两个电容上的电压;RL为负载电阻;Vdc为直流侧电压;S1、S2、S3为三组反向串联开关管。

图1 三相Vienna整流器主电路拓扑
Fig.1 The topology of the three-phase Vienna rectifier
根据Vienna整流器在连续电流模式下的工作过程,其在三相静止坐标系下的数学模型为
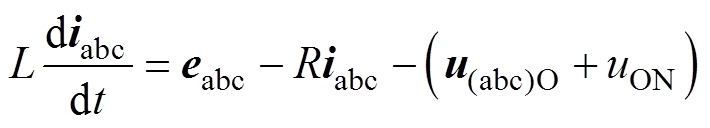 (1)
(1)
式中,iabc为三相电流;eabc为网侧电压;u(abc)O为a、b、c和O之间的电压;uON为O和N之间的电压。
将式(1)变换到两相旋转坐标系下,可得到
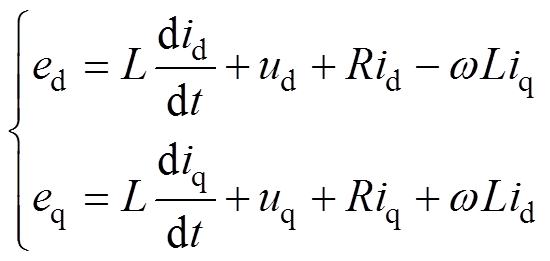 (2)
(2)
式中,ed、eq分别为整流器输出电压在d、q轴下的分量;ud、uq分别为网测电压在d、q轴下的分量;id、iq分别为网侧电流在d、q轴下的分量;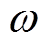 为交流角频率。
为交流角频率。
整流器在实际工况运行中,由于温度变化等外部扰动影响,实际电感和电阻值会发生变化,造成系统模型参数与实际值不匹配,进而导致预测控制系统性能下降。利用一阶前向欧拉法对式(2)离散化可得一个控制周期d、q轴电流变化量为
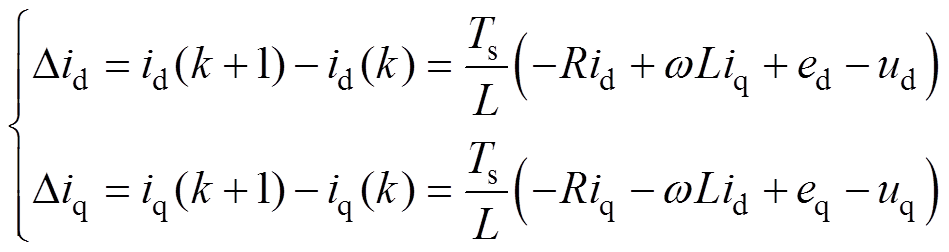 (3)
(3)
由式(3)可知,电感参数变化将直接影响d、q轴电流的变化量,当电感值变化两倍时,Did、Diq将变化为原来的1/2,因此可知,当电感参数不匹配时会对预测控制产生较大影响。而实际系统中等效电阻很小,其参数变化对系统带来的影响很有限。
为确保控制器的良好性能,分析Vienna整流器在参数失配时的数学模型,表达式为
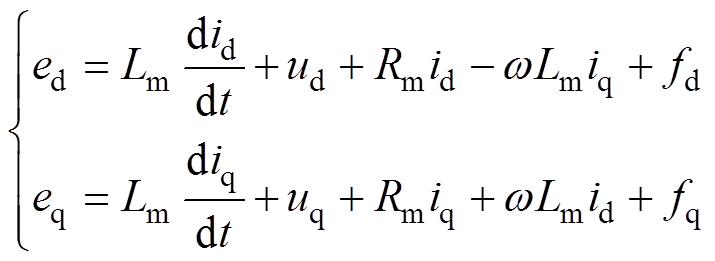 (4)
(4)
式中,Lm和Rm分别为电感和电阻的标称值;fd和fq为参数变换带来的扰动量,其值为
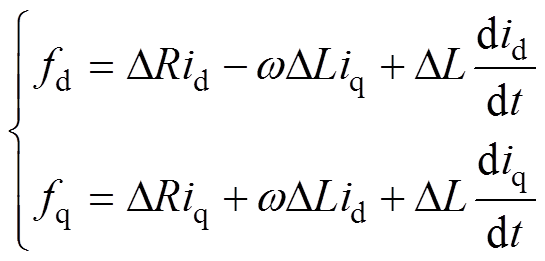 (5)
(5)
式中,DL、DR分别为电感、电阻的摄动值。
Vienna整流器的开关状态和电流极性决定其网侧端电压。如果中点电压保持平衡,则x相端电压可表示为
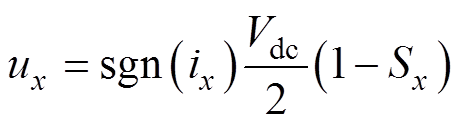 (6)
(6)
式中,Sx为开关函数,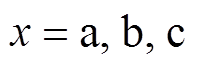 ,当x相开关导通时,Sx=1;关断时,Sx=0。Sgn( · )为符号函数,当ix>0时,sgn(ix)=1;当ix<0时,则sgn(ix)=0。
,当x相开关导通时,Sx=1;关断时,Sx=0。Sgn( · )为符号函数,当ix>0时,sgn(ix)=1;当ix<0时,则sgn(ix)=0。
则三相Vienna整流器的参考电压矢量表示为
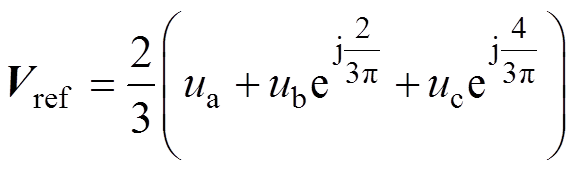 (7)
(7)
Vienna整流器电压矢量及电平状态如图2所示。
基于超局部的无模型预测控制原理是局部建模,并从输入和输出信息两方面对其进行实时更新。单输入单输出系统的一阶超局部模型表示为
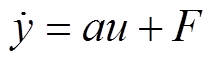 (8)
(8)
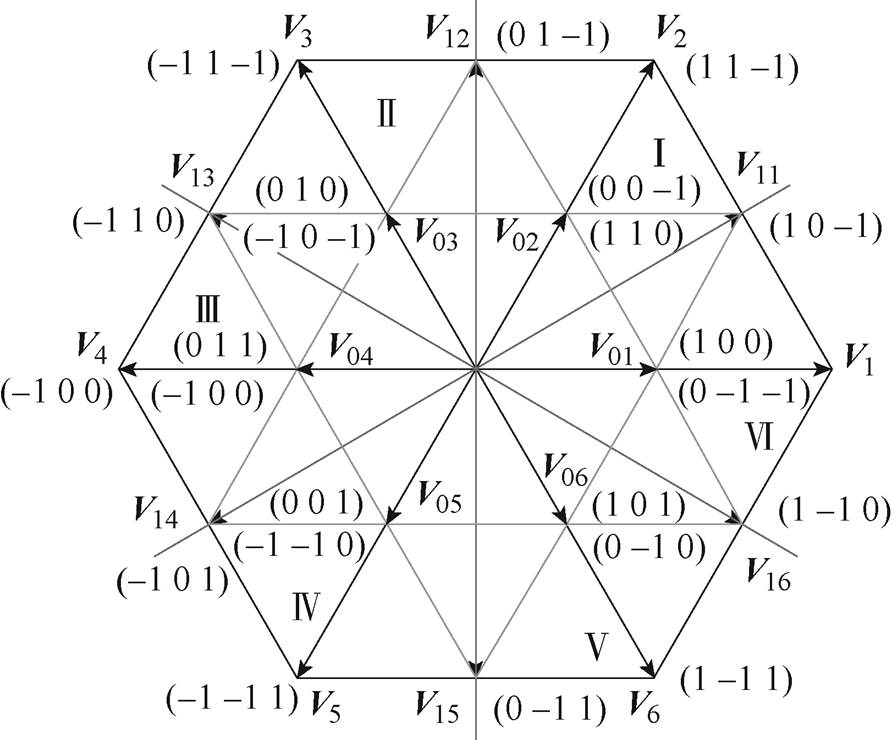
图2 Vienna整流器电压矢量
Fig.2 Voltage vector of Vienna rectifier
式中,u和y分别为系统的输入和输出;a为非物理常数增益,使au和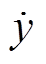 保持相同的阶数;F为超局部模型参数,代表系统动态部分。
保持相同的阶数;F为超局部模型参数,代表系统动态部分。
根据超局部模型构建原理,并结合式(4)和式(8),构造出Vienna整流器电流环的一阶超局部模型为
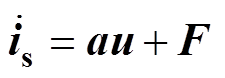 (9)
(9)
式中,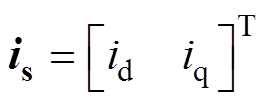 ;
;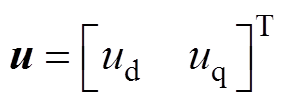 ;
;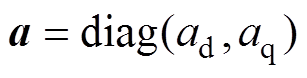 ,
,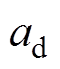 、
、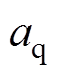 为待设计的电流系数,一般为
为待设计的电流系数,一般为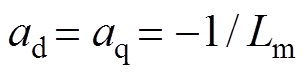 ,其值并不需要很精确;
,其值并不需要很精确;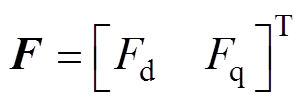 ,Fd和Fq为需要估计的动态部分。
,Fd和Fq为需要估计的动态部分。
为了能够得到FCS-MPC需要的下一时刻预测值,对被控对象的数学模型进行离散化,工程上常利用一阶前向欧拉法离散化整流器数学模型,即
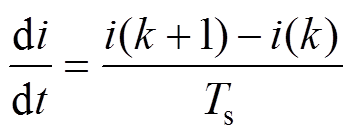 (10)
(10)
式中,Ts为系统采样周期。
利用该方法对式(9)进行离散化,同时考虑到Vienna整流器有两个直流侧母线电容,为三电平整流器,因此需要预测中点电位的变化。得到Vienna整流器离散的电流以及中点电位预测模型,即
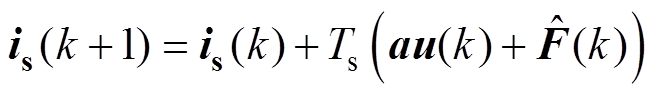 (11)
(11)
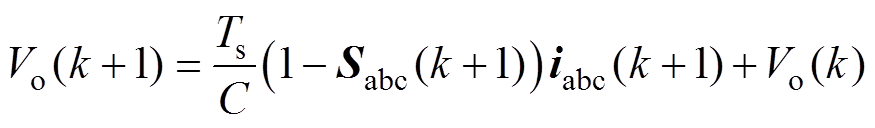 (12)
(12)
式中,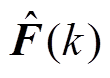 为F在kTs时刻的估计值;
为F在kTs时刻的估计值;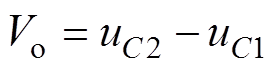 为上下电容电压差;
为上下电容电压差;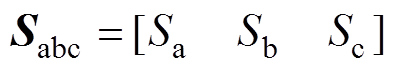 为三相开关管开关状态。
为三相开关管开关状态。
由于在离散控制系统中,实际输出电压与参考电压之间有一拍延迟,为了弥补这一影响,需要对预测模型进行延迟补偿,补偿后的方程为
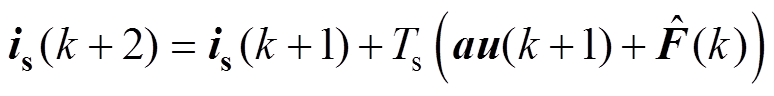 (13)
(13)
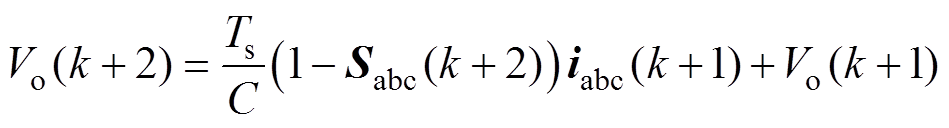 (14)
(14)
通过合理设计成本函数,可以实现FCS-MPC对多目标的优化。本文为实现控制器对电流和中点电位的控制,设计以电流误差和中点电位差为约束的成本函数g,表达式为
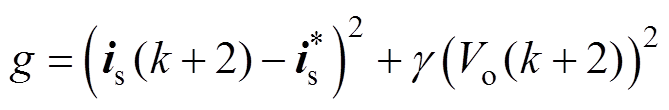 (15)
(15)
式中,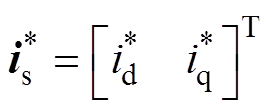 为整流器d、q轴电流参考值;
为整流器d、q轴电流参考值;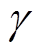 为成本函数的权重系数。
为成本函数的权重系数。
三相Vienna整流器由于受电流极性的限制,相同的开关状态在不同电流极性下对应不同的电压矢量。因此在每个时刻,共有8个备选电压矢量可供选择,结合式(13)~式(15),遍历所有可选电压矢量,选择最优的电压矢量作为预测控制器的输出。相比于其他三电平整流器需要遍历27次电压矢量,三相Vienna整流器有限集模型预测控制可以在更小计算量下实现三电平的功能。
对超局部模型中动态部分的准确估计是实现无模型预测控制器良好控制性能的关键,文献[21]采用滑模观测器估计动态部分,但将滑模抖振引入了控制系统,影响系统动稳态性能。超螺旋滑模算法是由学者Levant提出的一种二阶滑模算法,通过将传统滑模算法中不连续的高频切换项从信号u转移至其导数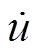 中,在保留传统滑模鲁棒性强优点的同时,有效地削弱了系统的抖振,传统的超螺旋滑模算法为
中,在保留传统滑模鲁棒性强优点的同时,有效地削弱了系统的抖振,传统的超螺旋滑模算法为
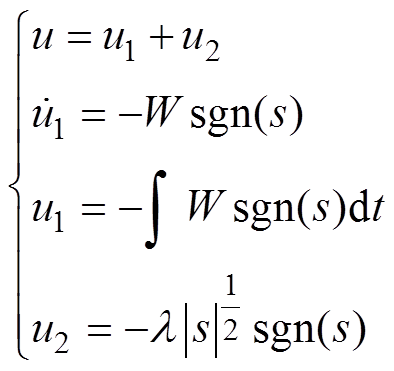 (16)
(16)
式中,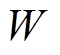 、
、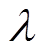 为算法中的可调参数。
为算法中的可调参数。
超螺旋滑模算法在设计时仅需要用到滑模面的信息,并且当系统关于滑模变量的相对阶为1时可以直接应用。不过由于系统中动态部分F的边界通常难以精确获得,使得超螺旋滑模算法的参数选取变得困难。
为实现Vienna整流器无模型预测电流控制良好的控制性能,本节在设计超螺旋滑模观测器对动态部分F进行估计的基础上,设计自适应算法[22],将观测器的增益设计成与整流器d、q轴电流观测误差有关的自适应增益,当不确定扰动导致出现观测误差时增益自动调整,直至误差被消除,抑制了动态部分边界不确定对系统的影响,有效地提升了观测器的抗干扰能力。设计出的自适应超螺旋滑模观测器表达式为
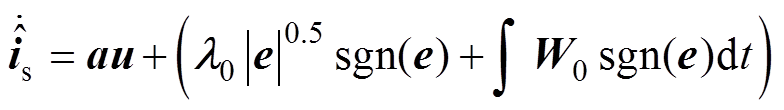 (17)
(17)
式中,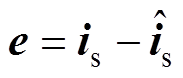 为整流器d、q轴电流观测误差;
为整流器d、q轴电流观测误差;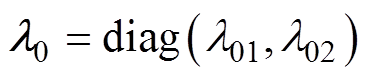 和
和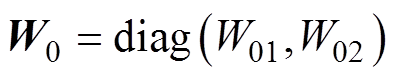 为自适应增益矩阵;
为自适应增益矩阵;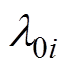 和
和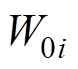 (i=1, 2)为关于观测误差
(i=1, 2)为关于观测误差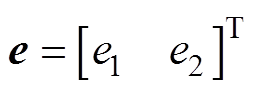 的函数,其表达式为
的函数,其表达式为
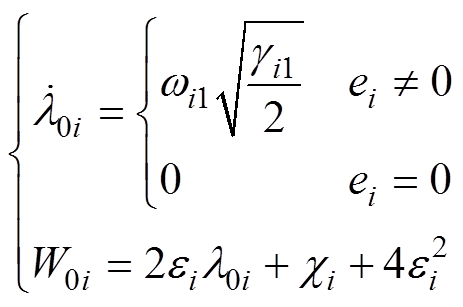 (18)
(18)
式中,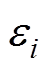 、
、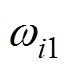 、
、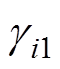 和
和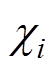 均为正常数。根据式(18)设计的自适应超螺旋滑模观测器结构框图如图3 所示。
均为正常数。根据式(18)设计的自适应超螺旋滑模观测器结构框图如图3 所示。
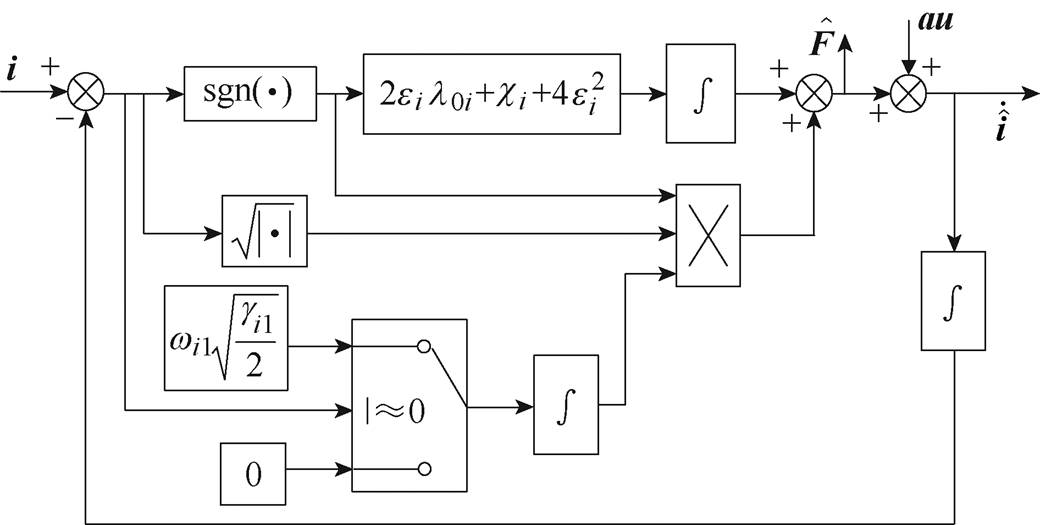
图3 自适应超螺旋滑模观测器结构框图
Fig.3 Adaptive super-twisting sliding mode observer
当观测器达到稳定时,动态部分F的估计值可表示为
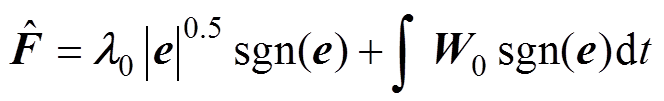 (19)
(19)
将式(9)和式(17)相减,可得观测器误差方程为
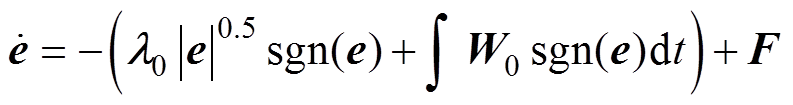 (20)
(20)
为了简化证明过程,将上述误差方程分为d轴和q轴误差方程,本节将对d轴观测器误差方程进行证稳,q轴的证稳过程与d轴相同。d轴观测器误差方程可表示为
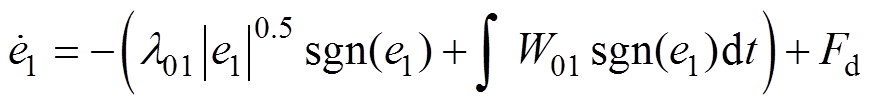 (21)
(21)
式中,e1为d轴观测误差;Fd为未知部分在d轴的分量。
将式(24)改写为状态方程的形式为
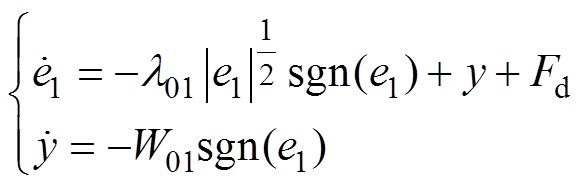 (22)
(22)
为便于Lyapunov函数分析,取新的状态变量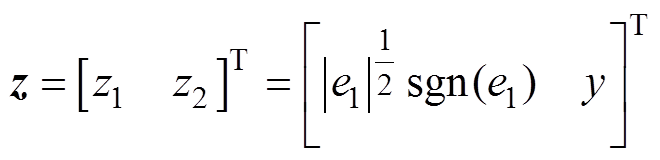 ,将式(22)重写为
,将式(22)重写为
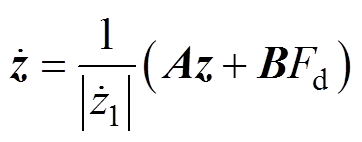 (23)
(23)
其中
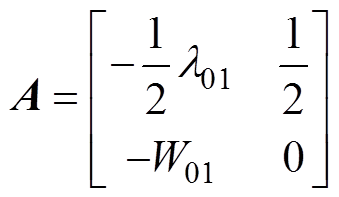
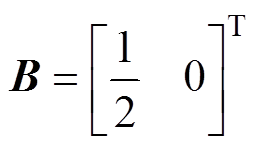
设计的Lyapunov函数表示为
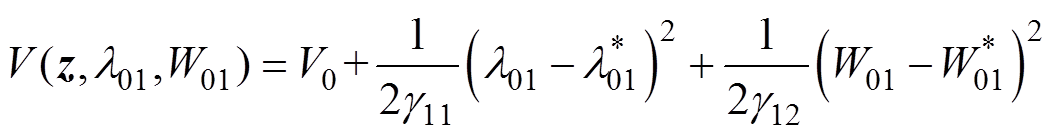 (24)
(24)
式中,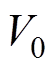 =
=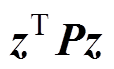 ,
,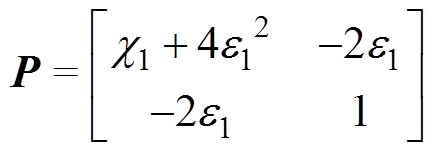 ;
;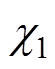 、
、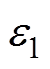 、
、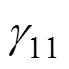 、
、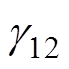 、
、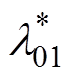 、
、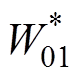 均为正常数。
均为正常数。
对函数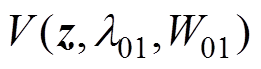 求导可得
求导可得
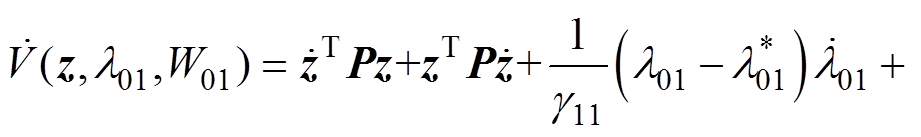
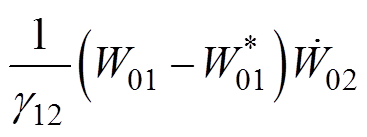 (25)
(25)
结合式(23),式(25)的前两项可以表示为
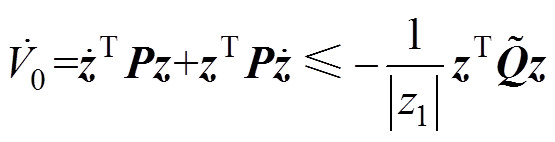 (26)
(26)
考虑到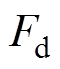 有界,即
有界,即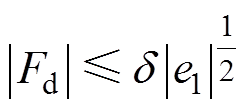 ,
, 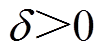 。对称矩阵
。对称矩阵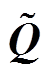 可表示为
可表示为
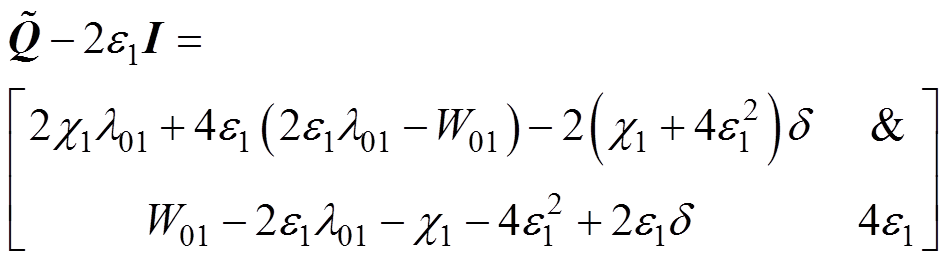 (27)
(27)
其中
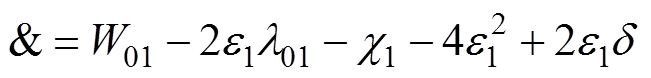
为保证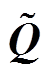 正定且最小特征值
正定且最小特征值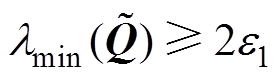 ,可得
,可得
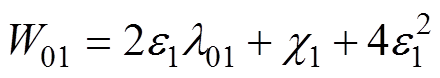 (28)
(28)
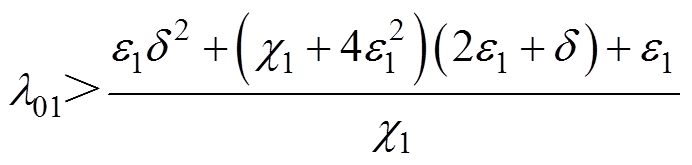 (29)
(29)
通过式(26)和式(27)可得
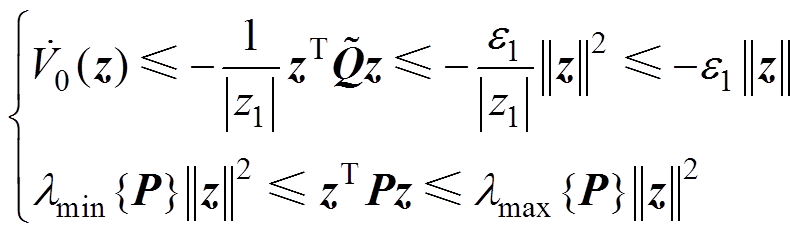 (30)
(30)
根据式(30)中的不等关系能够推导出
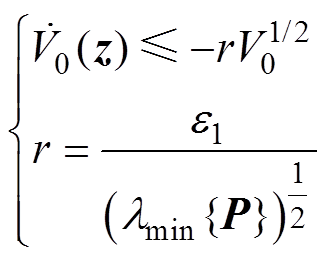 (31)
(31)
通过式(31),可以将式(25)改写为
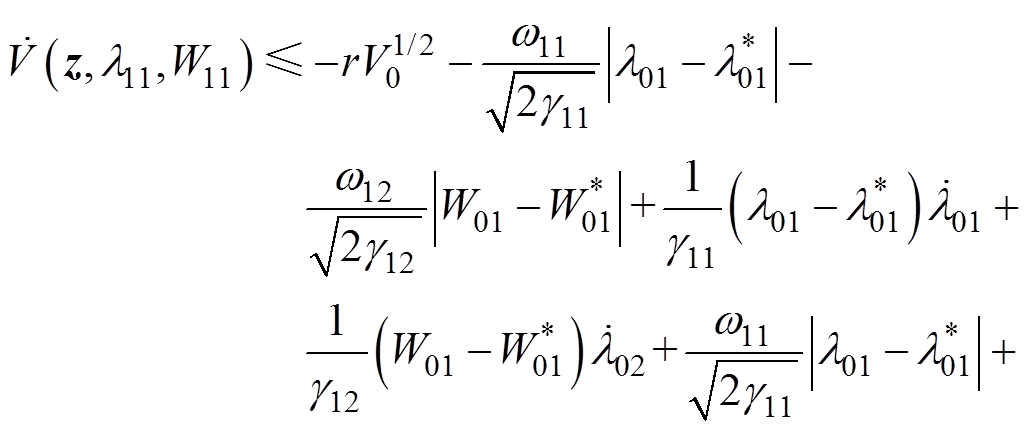
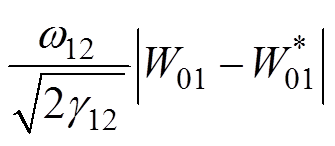 (32)
(32)
根据基本不等式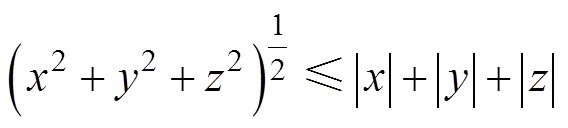 ,式(32)前三项可表示为
,式(32)前三项可表示为
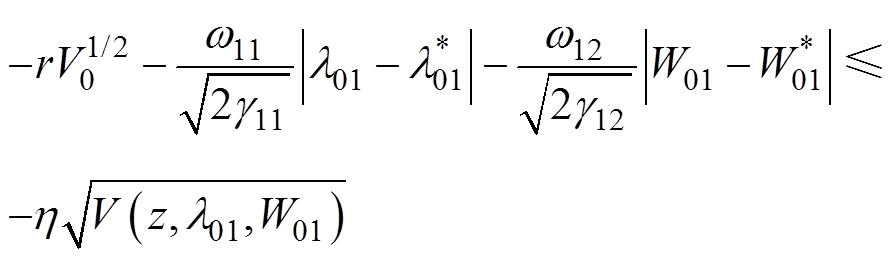 (33)
(33)
式中,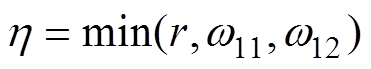 ,
,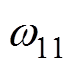 、
、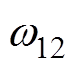 为正常数。
为正常数。
假设采用自适应律式(18)时,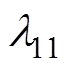 和
和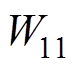 均有界,根据式(33),式(32)可以改写为
均有界,根据式(33),式(32)可以改写为
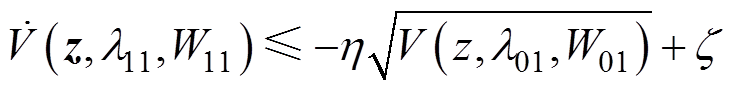 (34)
(34)
其中
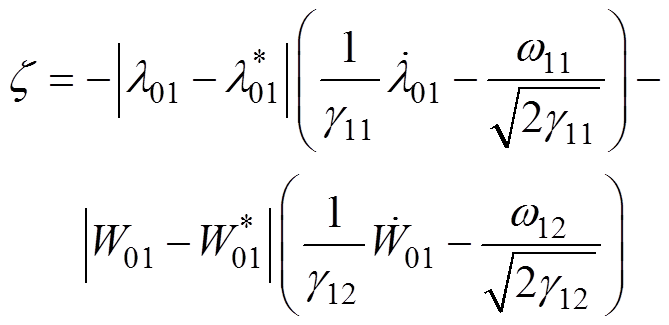 (35)
(35)
为了得到有限时间收敛性质,令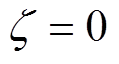 ,从而得到增益
,从而得到增益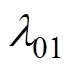 和
和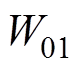 的自适应律为
的自适应律为
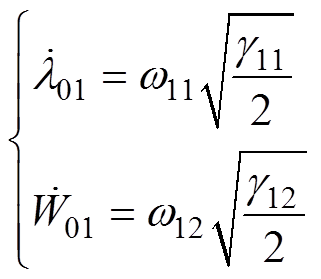 (36)
(36)
选取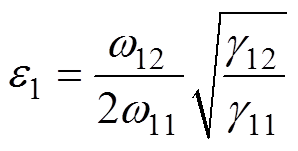 ,可使式(34)和式(26)一致。此时式(34)可以写成
,可使式(34)和式(26)一致。此时式(34)可以写成
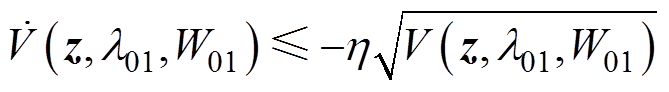 (37)
(37)
故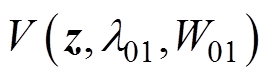 和
和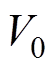 都能够在有限时间内收敛到0,所以状态观测误差
都能够在有限时间内收敛到0,所以状态观测误差 和其导数
和其导数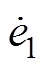 能够在有限时间收敛到0,即上述设计的自适应超螺旋滑模观测器是在有限时间内稳定的。
能够在有限时间收敛到0,即上述设计的自适应超螺旋滑模观测器是在有限时间内稳定的。
将稳定后自适应超螺旋滑模观测器得到的动态部分估计值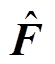 代入预测电流表达式中,并进行延迟补偿得
代入预测电流表达式中,并进行延迟补偿得
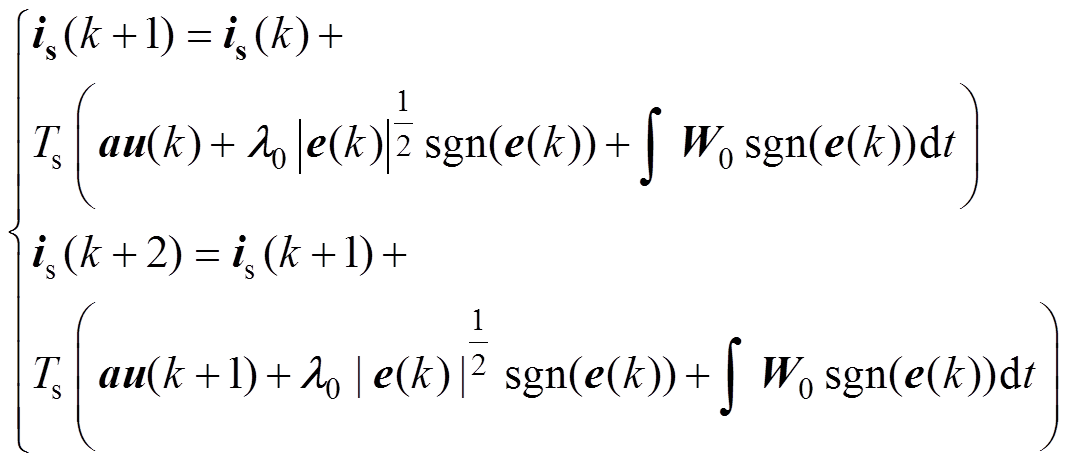 (38)
(38)
最后将式(38)结合成本函数进行遍历寻优,得
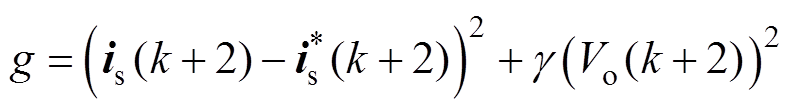 (39)
(39)
综上所述,所提出的基于自适应超螺旋滑模观测器的Vienna整流器无模型预测电流控制(Model Free Predictive Current Control based on Adaptive Super-Twisting Sliding Mode Observer, ASTSMO- MFPCC)系统框图如图4所示。其控制流程如下:首先通过自适应超螺旋滑模观测器估计Vienna整流器电流环超局部模型中的动态部分F;然后将估计值代入预测方程中得出下一时刻的预测值,同时结合成本函数对预测值遍历寻优;最后选出使成本函数最小的电压矢量作为内环控制器输出。该算法运行时不需要整流器系统精确物理参数,具有很强的鲁棒性。
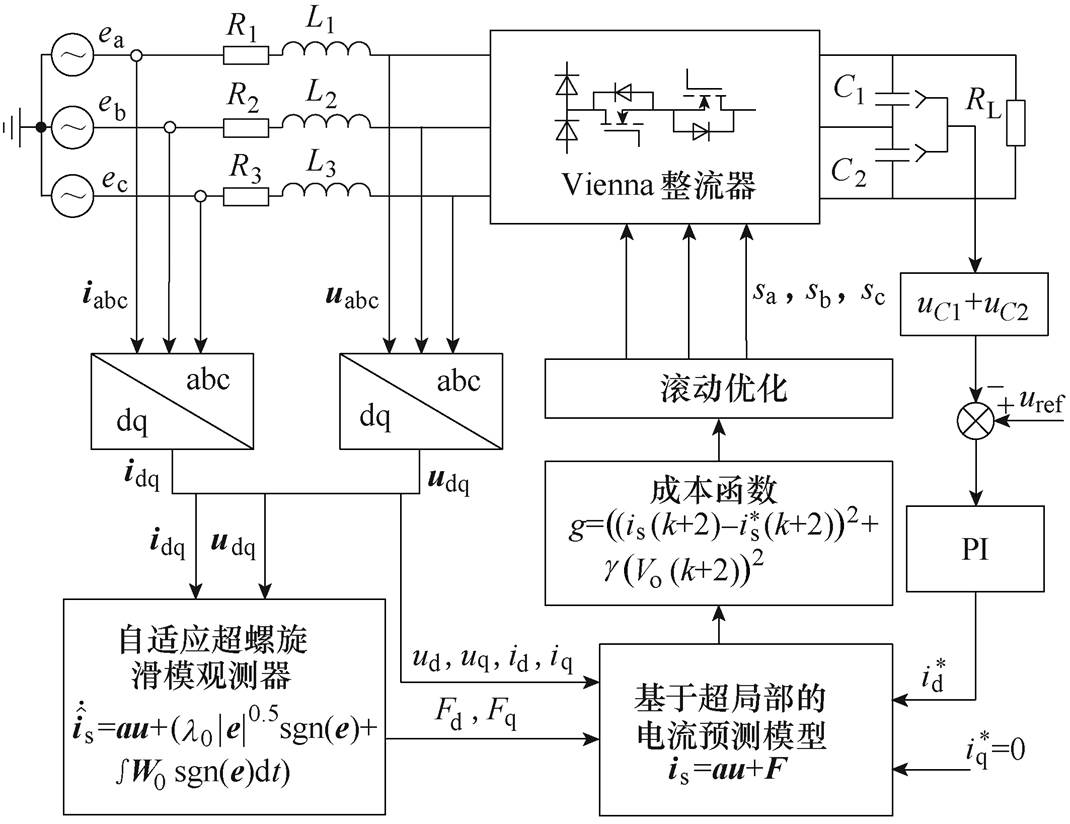
图4 ASTSMO-MFPCC控制系统框图
Fig.4 Block diagram of the ASTSMO-MFPCC control system
为了对所提算法有效性进行验证,在Matlab/ Simulink仿真环境下搭建模型,并与基于传统滑模观测器的无模型预测电流控制(MFPCC based on Sliding Mode Observer, SMO-MFPCC)算法对比,两种算法外环PI控制器参数设置相同,相关仿真参数见表1。
表1 仿真参数
Tab.1 Simulation parameters

参 数数 值 滤波器电感L/mH10 直流侧电容C1, C2/mF2 350 负载电阻RL/W100 控制器更新频率fs/kHz20 电网线电压有效值E/V100 电网电压频率fg/Hz50
图5为整流器负载突变仿真结果,在0.4 s时负载由100 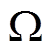 突变为50
突变为50 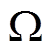 ,SMO-MFPCC算法的母线电压降落了4.8 V,经过约38 ms达到稳态值,本文所提的ASTSMO-MFPCC算法的母线电压降落了3.5 V,经过约32 ms到达稳态值;在0.6 s时负载由50
,SMO-MFPCC算法的母线电压降落了4.8 V,经过约38 ms达到稳态值,本文所提的ASTSMO-MFPCC算法的母线电压降落了3.5 V,经过约32 ms到达稳态值;在0.6 s时负载由50 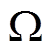 突变为100
突变为100 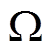 ,SMO-MFPCC算法的母线电压上升了4.9 V,经过约36 ms达到稳态值,ASTSMO-MFPCC算法的母线电压上升了3.4 V,经过约27 ms到达稳态值。仿真结果表明,ASTSMO- MFPCC算法的电压波动更小,调节速度更快。从图5c可知,在发生负载变化时,ASTSMO-MFPCC算法中的自适应超螺旋观测器可以跟踪干扰变化动态调整增益,保证了系统的响应速度与鲁棒性。
,SMO-MFPCC算法的母线电压上升了4.9 V,经过约36 ms达到稳态值,ASTSMO-MFPCC算法的母线电压上升了3.4 V,经过约27 ms到达稳态值。仿真结果表明,ASTSMO- MFPCC算法的电压波动更小,调节速度更快。从图5c可知,在发生负载变化时,ASTSMO-MFPCC算法中的自适应超螺旋观测器可以跟踪干扰变化动态调整增益,保证了系统的响应速度与鲁棒性。
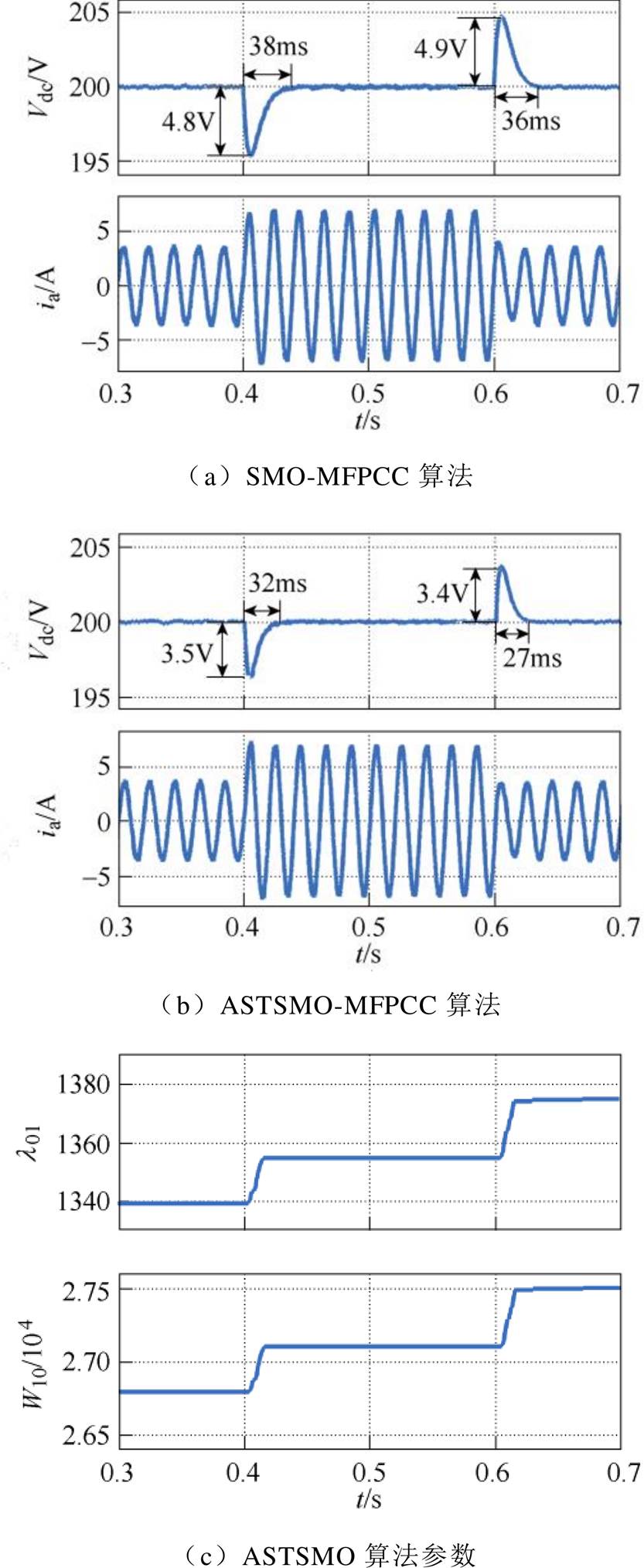
图5 负载突变仿真结果
Fig.5 Simulation results of load mutation
图6为整流器电感参数突变仿真结果,电感标称值Lm=10 mH,为了验证两种算法在电感参数失配时的效果,将控制器中的电感参数按照0.5Lm Lm
Lm 2Lm的规律变化。在0.4 s时电感参数从5 mH突变到10 mH,SMO-MFPCC算法的d轴电流上升了0.83 A,调节时间约为31 ms,本文所提的ASTSMO-MFPCC算法d轴电流上升了0.61 A,调节时间约为18 ms;在0.5 s时电感参数从10 mH突变到20 mH,SMO-MFPCC算法的d轴电流上升了0.31 A,调节时间约为25 ms,而ASTSMO-MFPCC算法的d轴电流几乎没有变化。仿真结果表明,面对电感变化时ASTSMO-MFPCC算法具有更好的效果。比较图6a和图6b可知,滑模观测器观测出的Fd、Fq存在较大的抖振,ASTSMO-MFPCC算法中的自适应超螺旋观测器可以有效的解决传统滑模带来的抖振问题。
2Lm的规律变化。在0.4 s时电感参数从5 mH突变到10 mH,SMO-MFPCC算法的d轴电流上升了0.83 A,调节时间约为31 ms,本文所提的ASTSMO-MFPCC算法d轴电流上升了0.61 A,调节时间约为18 ms;在0.5 s时电感参数从10 mH突变到20 mH,SMO-MFPCC算法的d轴电流上升了0.31 A,调节时间约为25 ms,而ASTSMO-MFPCC算法的d轴电流几乎没有变化。仿真结果表明,面对电感变化时ASTSMO-MFPCC算法具有更好的效果。比较图6a和图6b可知,滑模观测器观测出的Fd、Fq存在较大的抖振,ASTSMO-MFPCC算法中的自适应超螺旋观测器可以有效的解决传统滑模带来的抖振问题。
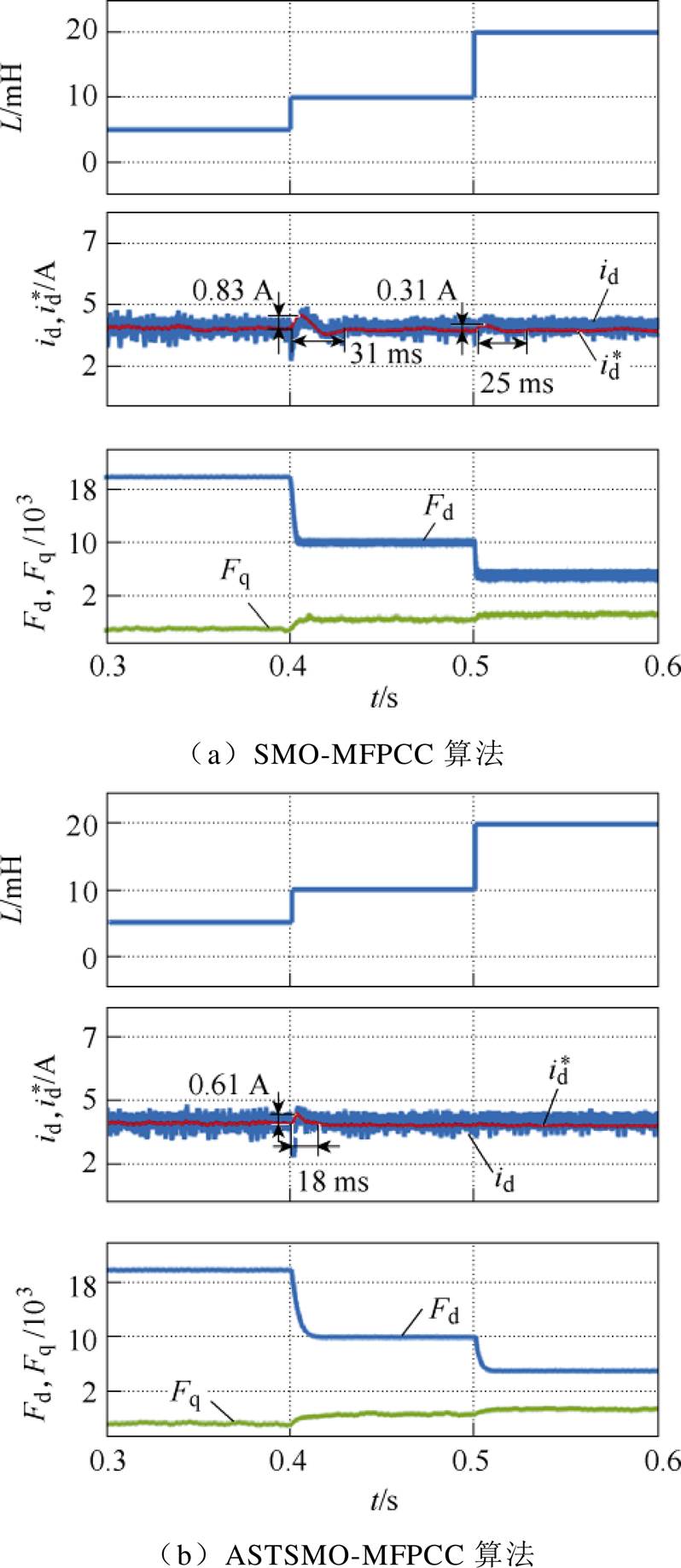
图6 电感参数突变仿真结果
Fig.6 Simulation results of inductor parameter mutation
为进一步验证所提算法的有效性,建设Vienna整流器实验平台进行测试,如图7所示。采用的主控芯片是TI公司的TMS32F28335芯片,功率器件选用IXYS公司的MOSFET整流模块,通过泰克MDO4054B-3示波器测量相应数据,实验参数与仿真一致。

图7 Vienna整流器实验平台
Fig.7 Experiment platform of Vienna rectifier
为验证算法在稳态时的控制性能,设置负载为100  ,母线电压为200 V的稳态实验,实验结果如图8和图9所示。从图8a和图9a可知,两种算法在达到稳态时均实现了单位功率因数运行,并且直流侧电压均可以准确跟踪参考值。图8b和图9b为两种算法a相电流的频谱分析,SMO-MFPCC算法a相电流总谐波畸变率(Total Harmonic Distortion, THD)为6.70%,而本文所提的ASTSMO-MFPCC算法a相电流THD仅为4.26%,实验结果表明,ASTSMO-MFPCC算法电流谐波含量更低,对电网的影响更小,有效保证了输入电流质量。
,母线电压为200 V的稳态实验,实验结果如图8和图9所示。从图8a和图9a可知,两种算法在达到稳态时均实现了单位功率因数运行,并且直流侧电压均可以准确跟踪参考值。图8b和图9b为两种算法a相电流的频谱分析,SMO-MFPCC算法a相电流总谐波畸变率(Total Harmonic Distortion, THD)为6.70%,而本文所提的ASTSMO-MFPCC算法a相电流THD仅为4.26%,实验结果表明,ASTSMO-MFPCC算法电流谐波含量更低,对电网的影响更小,有效保证了输入电流质量。
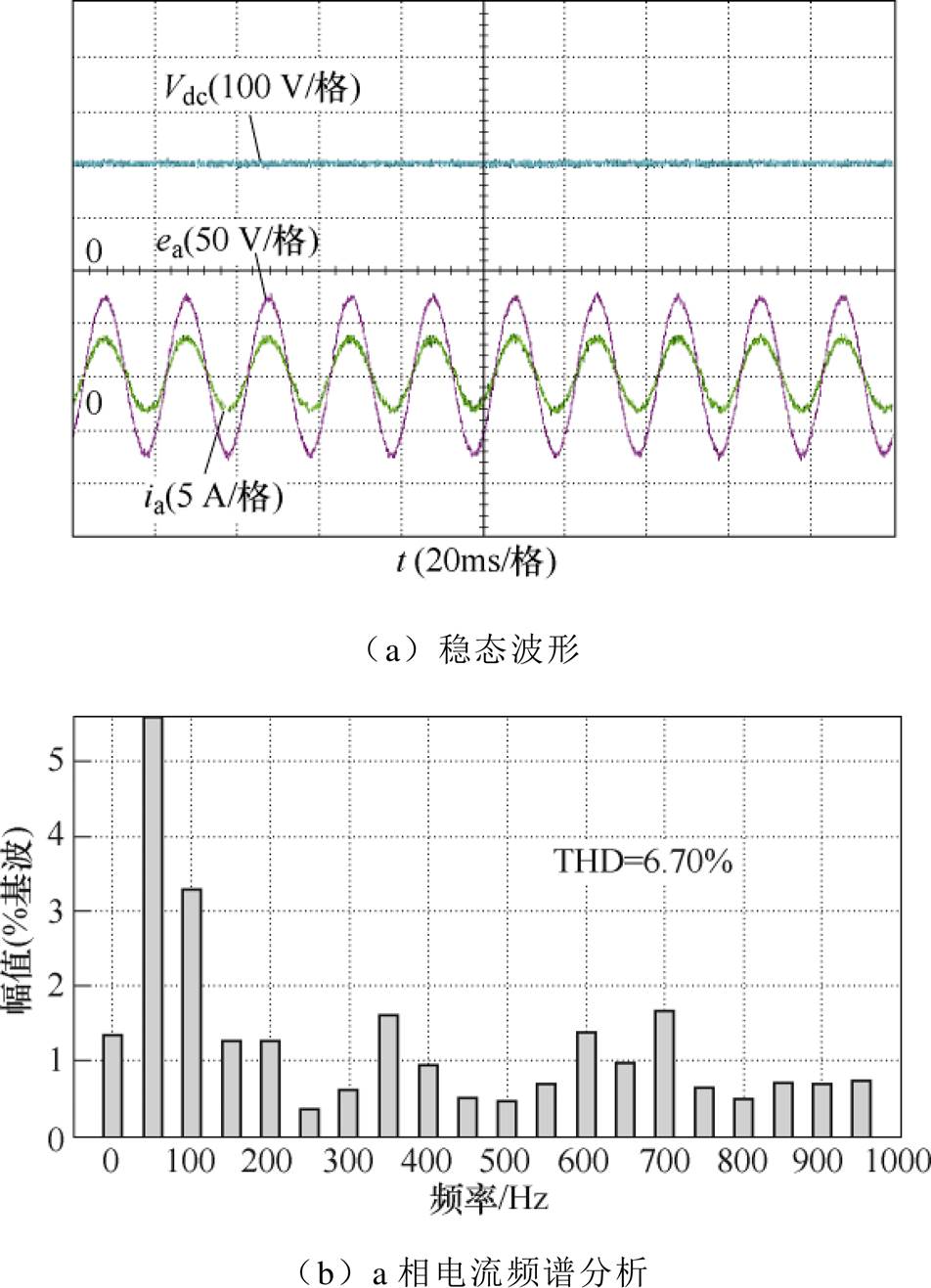
图8 SMO-MFPCC算法稳态实验结果
Fig.8 Steady-state experimental results of SMO-MFPCC algorithm
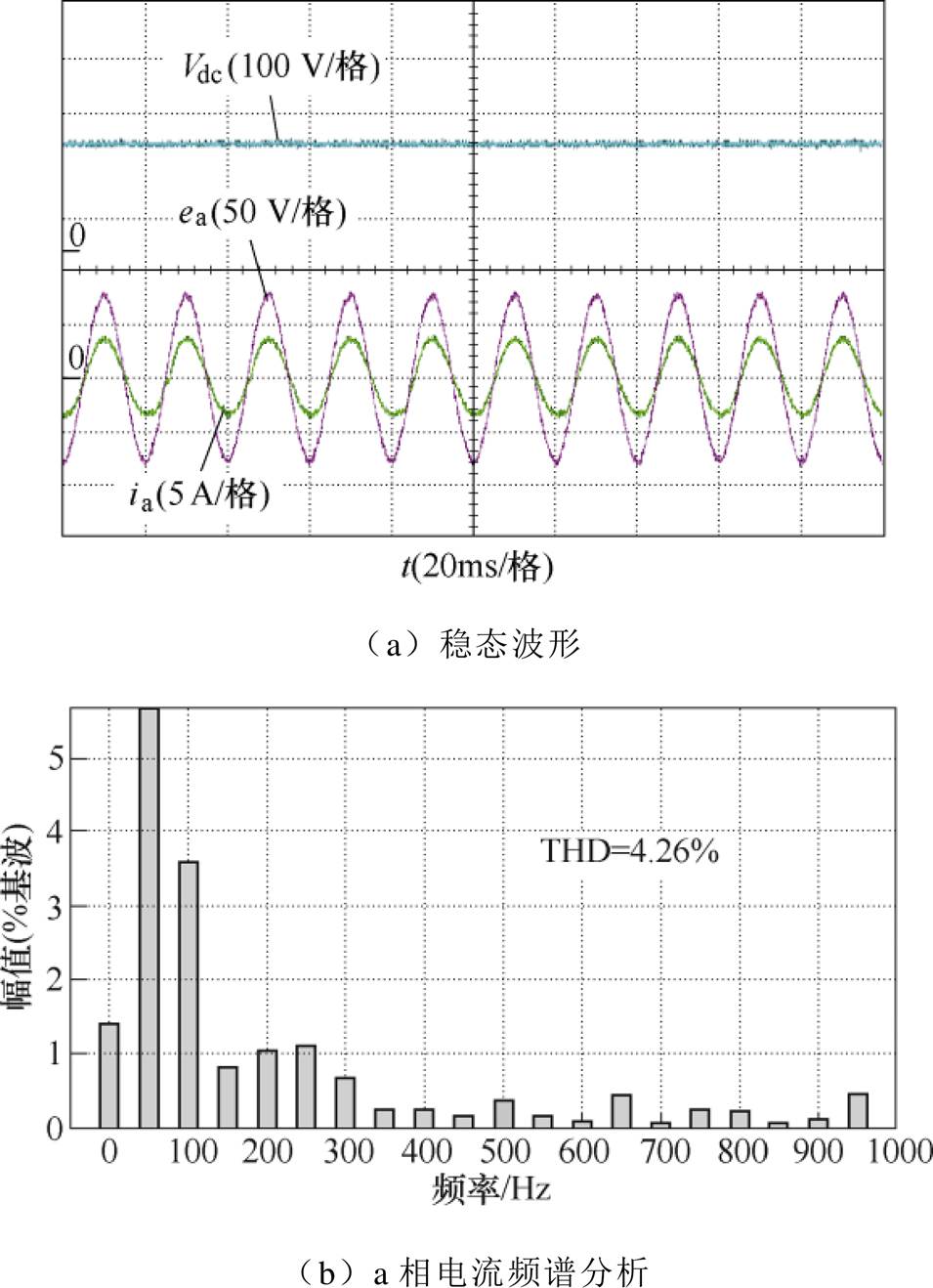
图9 ASTSMO-MFPCC算法稳态实验结果
Fig.9 Steady-state experimental results of ASTSMO-MFPCC algorithm
5.2.1 母线电压阶跃实验
为比较两种算法在参考电压突变时的控制性能,设计参考电压跃变实验。将参考电压先从200 V升压到250 V,经过0.5 s后,再从250 V降为220 V。图10为参考电压阶跃响应实验结果,在两次跃变后,SMO-MFPCC算法到达稳态时间分别约为167 ms和96 ms,ASTSMO-MFPCC算法到达稳态时间分别约为153 ms和89 ms。结果表明,ASTSMO-MFPCC算法具有更快的动态响应。
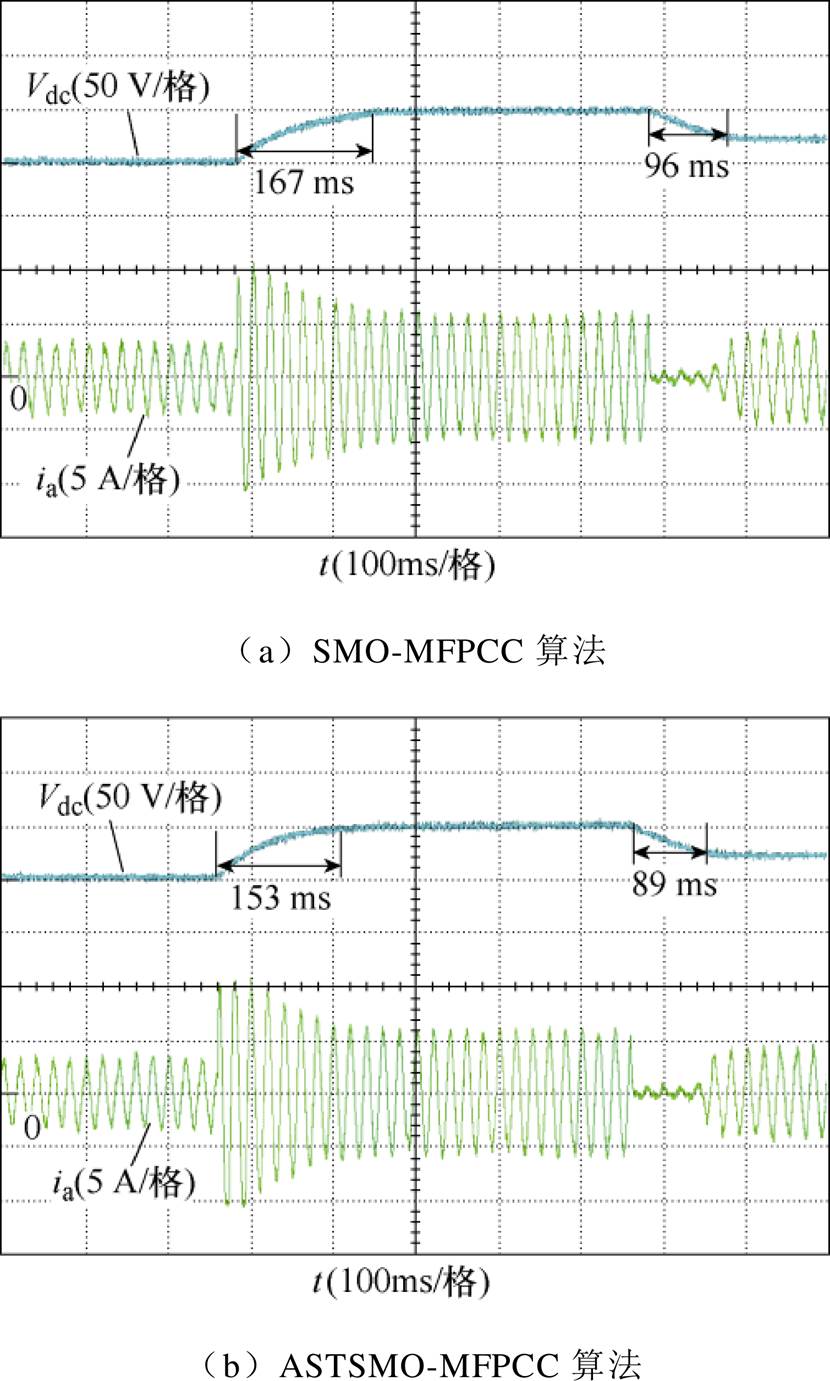
图10 参考电压阶跃响应实验结果
Fig.10 Experimental results of reference voltage step response
5.2.2 加减载实验
为验证所提算法的抗扰动能力,对Vienna整流器进行负载突变实验,图11为实验结果。整流器负载由100  加载到50
加载到50  后,SMO-MFPCC算法的母线电压降落了16 V,调节时间约为137 ms,ASTSMO-MFPCC算法的母线电压降落了7 V,调节时间约为121 ms;当负载由50
后,SMO-MFPCC算法的母线电压降落了16 V,调节时间约为137 ms,ASTSMO-MFPCC算法的母线电压降落了7 V,调节时间约为121 ms;当负载由50  减载到100
减载到100  后,SMO-MFPCC算法的母线电压升高了18 V,调节时间约为135 ms,ASTSMO-MFPCC算法的母线电压升高了6 V,调节时间约为123 ms。实验结果表明,相比于SMO-MFPCC算法,ASTSMO-MFPCC算法具有更强的抗负载扰动能力。
后,SMO-MFPCC算法的母线电压升高了18 V,调节时间约为135 ms,ASTSMO-MFPCC算法的母线电压升高了6 V,调节时间约为123 ms。实验结果表明,相比于SMO-MFPCC算法,ASTSMO-MFPCC算法具有更强的抗负载扰动能力。
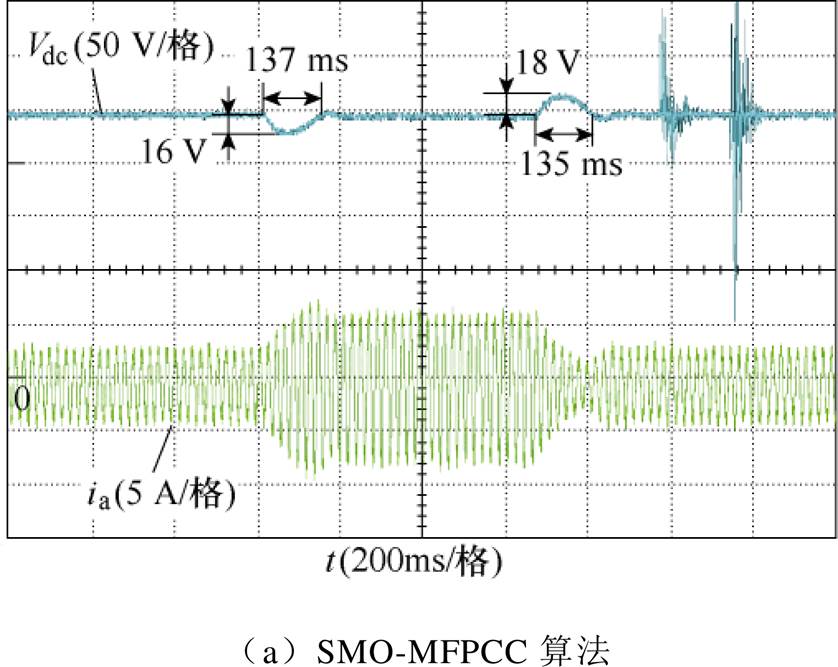
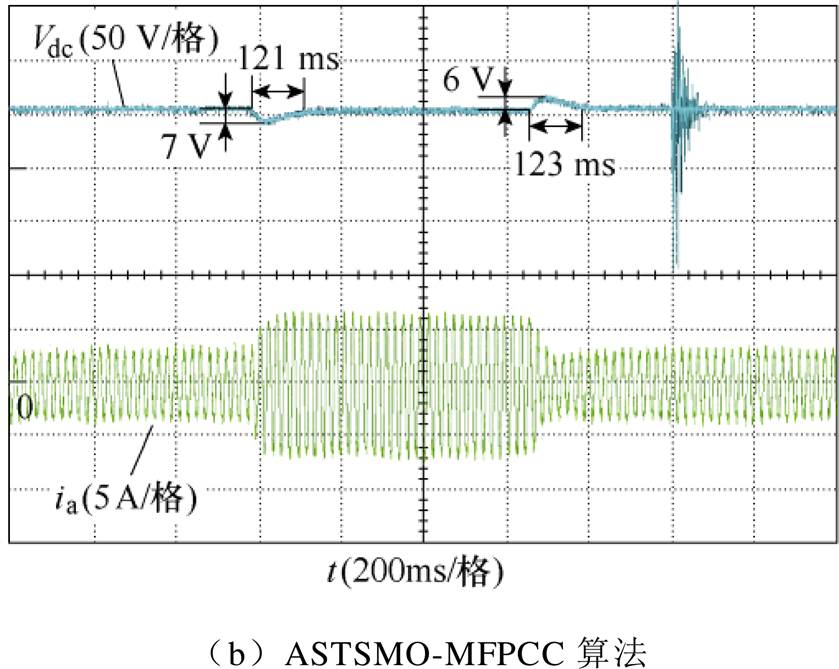
图11 负载突变实验结果
Fig.11 Experimental results of load mutation
为比较两种控制算法在模型参数发生变化时的控制效果,设置模型参数阶跃变化实验,实验将控制器中的电感参数值从0.5Lm跃变为Lm,再从Lm跃变为2Lm。电感参数失配实验结果如图12所示,在电感参数变化时,SMO-MFPCC算法的d轴电流有着明显的变化,且经过较长时间恢复稳定,而ASTSMO-MFPCC算法在参数变化时d轴电流并无明显变化。电感参数在2Lm时,SMO-MFPCC算法稳定后的电流波动约为2.7 A,ASTSMO-MFPCC算法稳定后的电流波动约为2.1 A。结果表明,ASTSMO- MFPCC算法相较SMO-MFPCC算法具有更强的鲁棒性。
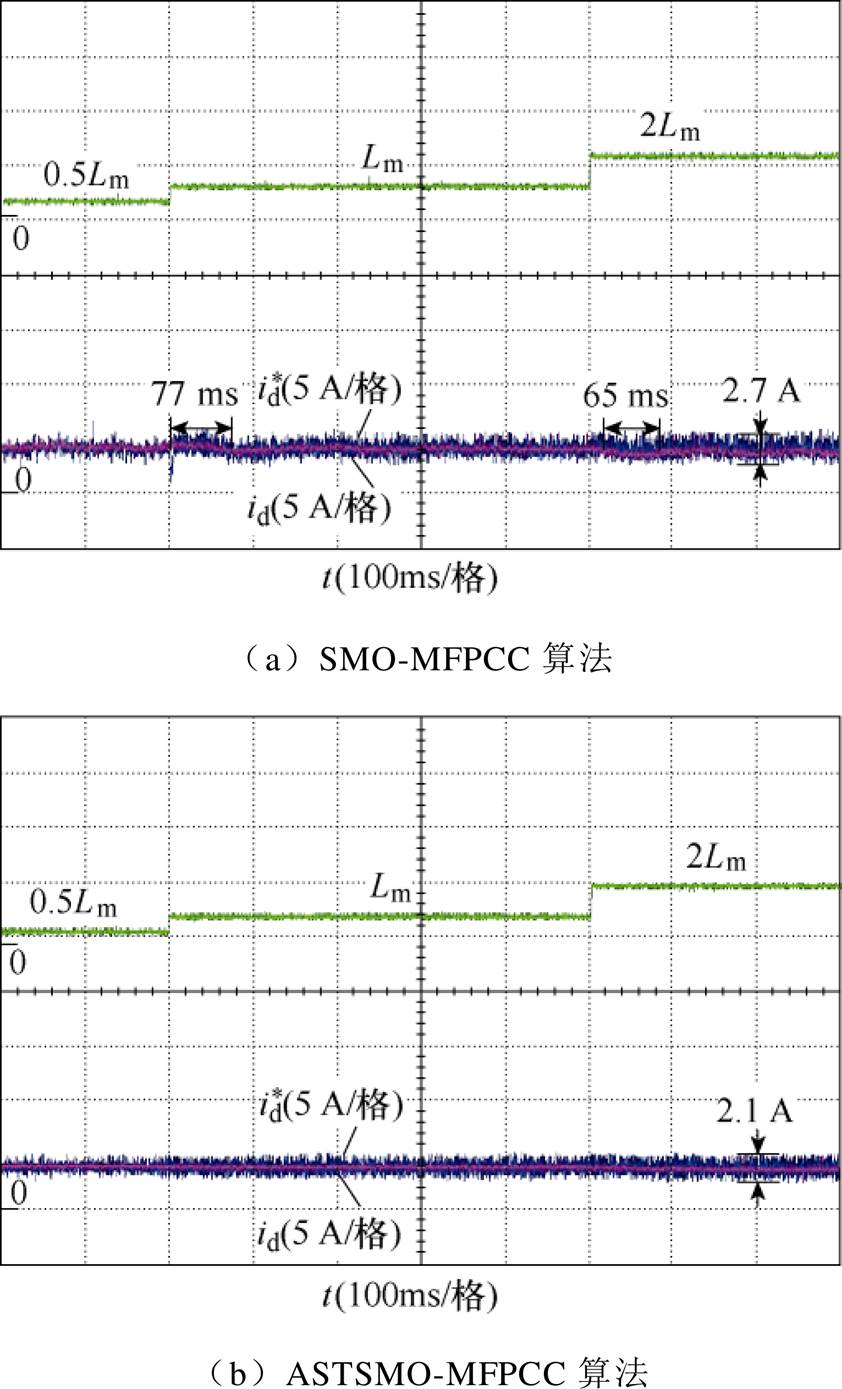
图12 参数失配实验结果
Fig.12 Experimental results of parameter mismatch
表2给出了两种控制算法在不同工况下的性能对比,由表2可知,所提出的ASTSMO-MFPCC算法相比SMO-MFPCC算法在上述工况下存在明显优势。
本文针对三相Vienna整流器在复杂环境下参数失配造成的控制性能下降问题,提出基于自适应超螺旋滑模观测器的无模型预测电流控制策略。该策略将无模型控制思想应用到预测控制系统设计中,使系统运行时不依赖精确的整流器物理参数。通过设计超螺旋滑模观测器观测超局部模型动态部分,解决传统滑模观测器由于抖振作用造成的系统动稳态性能下降问题,提高了系统扰动抑制能力。同时设计自适应增益,动态调整观测器参数,可以有效地简化增益选择。仿真与实验结果验证了所提方法具有更强的鲁棒性和更优的动稳态性能。
表2 控制性能对比
Tab.2 Control performance comparison
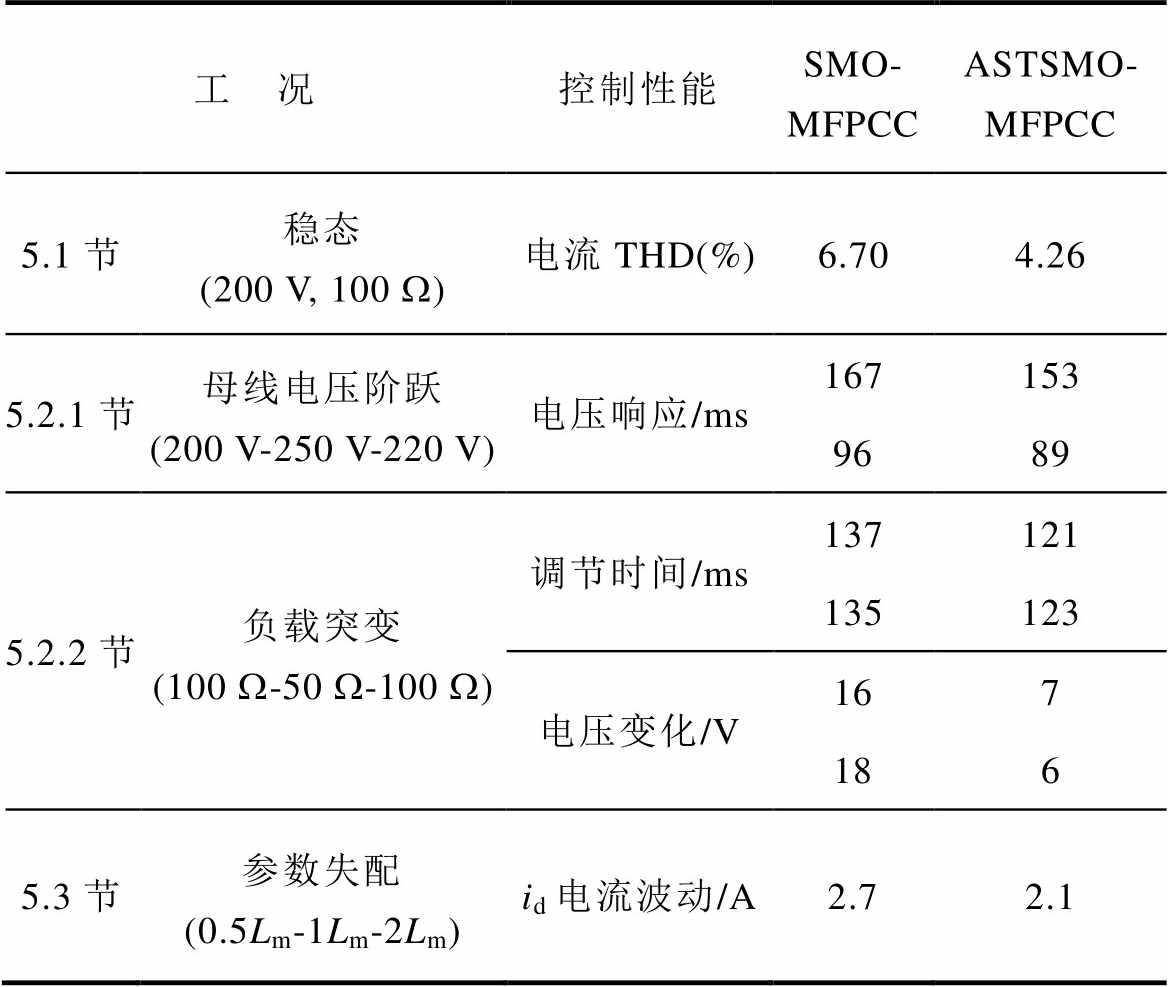
工 况控制性能SMO- MFPCCASTSMO- MFPCC 5.1节稳态 (200 V, 100 W)电流THD(%)6.704.26 5.2.1节母线电压阶跃 (200 V-250 V-220 V)电压响应/ms167153 9689 5.2.2节负载突变 (100 W-50 W-100 W)调节时间/ms137121 135123 电压变化/V167 186 5.3节参数失配 (0.5Lm-1Lm-2Lm)id电流波动/A2.72.1
参考文献
[1] Singh B, Singh B N, Chandra A, et al. A review of three-phase improved power quality AC-DC con- verters[J]. IEEE Transactions on Industrial Electro- nics, 2004, 51(3): 641-660.
[2] Chen Hao, Aliprantis D C. Analysis of squirrel-cage induction generator with Vienna rectifier for wind energy conversion system[J]. IEEE Transactions on Energy Conversion, 2011, 26(3): 967-975.
[3] Kolar J W, Zach F C. A novel three-phase utility interface minimizing line current harmonics of high- power telecommunications rectifier modules[J]. IEEE Transactions on Industrial Electronics, 1997, 44(4): 456-467.
[4] Foureaux N C, Oliveira J H, de Oliveira F D, et al. Command generation for wide-range operation of hysteresis-controlled Vienna rectifiers[J]. IEEE Transa- ctions on Industry Applications, 2015, 51(3): 2373- 2380.
[5] 韦徵, 陈新, 陈杰, 等. 输入电压不平衡时三相PFC整流器改进单周期控制策略研究[J]. 电工技术学报, 2014, 29(10): 65-72.
Wei Zheng, Chen Xin, Chen Jie, et al. Modified one-cycle controlled three-phase PFC rectifier under unbalanced input-voltage conditions[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 65-72.
[6] 郭文杰, 林飞, 郑琼林. 三相电压型PWM整流器的级联式非线性PI控制[J]. 中国电机工程学报, 2006, 26(2): 138-142.
Guo Wenjie, Lin Fei, Zheng Qionglin. The cascaded nonlinear PI control for three-phase votagle source PWM rectifier[J]. Proceedings of the CSEE, 2006, 26(2): 138-142.
[7] Xu Bo, Liu Kaipei, Ran Xiaohong. Computationally efficient optimal switching sequence model predictive control for three-phase Vienna rectifier under balanced and unbalanced DC links[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 12268-12280.
[8] 马辉, 谢运祥. 基于滑模变结构的Vienna整流器新型双闭环控制策略研究[J]. 电工技术学报, 2015, 30(12): 143-151.
Ma Hui, Xie Yunxiang. A novel dual closed-loop control strategy based on sliding-mode variable structure of Vienna-type rectifier[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 143- 151.
[9] Qiu Xiaonan, Li Yinghui, Xu Haojun, et al. A dual closed-loop control strategy research based on sliding mode control for Vienna rectifier[C]//2021 Inter- national Conference on Control Science and Electric Power Systems (CSEPS), Shanghai, 2021: 20-24.
[10] Liang Donglai, Li Jian, Qu Ronghai. Sensorless control of permanent magnet synchronous machine based on second-order sliding-mode observer with online resistance estimation[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3672-3682.
[11] Chalanga A, Kamal S, Fridman L M, et al. Imple- mentation of super-twisting control: super-twisting and higher order sliding-mode observer-based app- roaches[J]. IEEE Transactions on Industrial Electro- nics, 2016, 63(6): 3677-3685.
[12] 吴宇, 皇甫宜耿, 张琳, 等. 大扰动Buck-Boost变换器的鲁棒高阶滑模控制[J]. 中国电机工程学报, 2015, 35(7): 1740-1748.
Wu Yu, Huangfu Yigeng, Zhang Lin, et al. A robust high order sliding mode for Buck-Boost converters with large disturbances[J]. Proceedings of the CSEE, 2015, 35(7): 1740-1748.
[13] Moreno J A, Osorio M. A Lyapunov approach to second-order sliding mode controllers and obser- vers[C]//2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 2009: 2856-2861.
[14] Vazquez S, Rodriguez J, Rivera M, et al. Model predictive control for power converters and drives: advances and trends[J]. IEEE Transactions on Indu- strial Electronics, 2017, 64(2): 935-947.
[15] Wang Fengxiang, Xie Haotian, Chen Qing, et al. Parallel predictive torque control for induction machines without weighting factors[J]. IEEE Transa- ctions on Power Electronics, 2020, 35(2): 1779- 1788.
[16] Rodriguez J, Kazmierkowski M P, Espinoza J R, et al. State of the art of finite control set model predictive control in power electronics[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 1003-1016.
[17] 余晨辉, 汪凤翔, 林贵应. 基于在线扰动补偿的三电平PWM整流器级联式无差拍控制策略[J]. 电工技术学报, 2022, 37(4): 954-963.
Yu Chenhui, Wang Fengxiang, Lin Guiying. Cas- caded deadbeat control strategy with online dis- turbance compensation for three-level PWM rectifier[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 954-963.
[18] Fliess M, Join C. Model-free control[J]. International Journal of Control, 2013, 86(12): 2228-2252.
[19] González-Castaño C, Flores-Bahamonde F, Young H, et al. Model-free predictive control based on ARX representation: a comparative assessment with proportional-integral regulator[C]//2021 IEEE Inter- national Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 2022: 953-958.
[20] Ma Chenwei, Li Huayu, Yao Xuliang, et al. An improved model-free predictive current control with advanced current gradient updating mechanism[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 11968-11979.
[21] 赵凯辉, 周瑞睿, 冷傲杰, 等. 一种永磁同步电机的有限集无模型容错预测控制算法[J]. 电工技术学报, 2021, 36(1): 27-38.
Zhao Kaihui, Zhou Ruirui, Leng Aojie, et al. Finite control set model-free fault-tolerant predictive control for permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(1): 27-38.
[22] Shtessel Y B, Moreno J A, Plestan F, et al. Super-twisting adaptive sliding mode control: a Lyapunov design[C]//49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 2011: 5109-5113.
Abstract The three-phase Vienna rectifier is widely used in communication power supply, wind power generation, and electric drive due to its advantages of no dead zone between the same switch bridge, high reliability, and low harmonic content of input current. The traditional control methods applied in Vienna rectifiers mainly include proportional-integral (PI), single-period control, etc. These traditional control methods have simple principles and convenient designs. However, with the increasing requirement of Vienna rectifier performance and the increasing complexity of the application, the traditional control method is difficult to obtain a satisfactory control effect. In order to improve the control performance of the Vienna rectifier under the complex environment, a model-free predictive current control strategy based on adaptive super-twisting sliding mode observer (ASTSMO-MFPCC) is proposed.
Firstly, an ultra-local model independent of system physical parameters is constructed by analyzing the mathematical model under the condition of model mismatch. Secondly, a super-twisting sliding mode observer is designed to estimate the unknown part of the ultra-local model, which can effectively suppress the influence of system disturbance. At the same time, an adaptive gain was designed to dynamically adjust the parameters of the super-twisting sliding mode observe to solve the gain selection problem. Finally, a two-step predictive cost function is constructed to realize the model-free predictive current control. To validate the performance of ASTSMO-MFPCC, a model-free predictive current control algorithm based on traditional sliding mode observer (SMO-MFPCC) is realized and compared under steady-state, dynamic, and parameter mismatch conditions. The simulation and experimental results show that the bus voltage of the ASTSMO-MFPCC algorithm can reach the steady state faster, and the amplitude of voltage change is small in the given voltage and load mutation experiments. From the simulation results of load mutation, it can be found that the observer parameters can adjust adaptively after the load changes. In the steady-state experiment, the A-phase current THD of SMO-MFPCC is 6.7%, while that of the ASTSMO-MFPCC algorithm is only 4.26%. In the parameter mismatch experiment, the D-axis current of SMO-MFPCC has a significant change and needs a long time to stabilize, and the current fluctuation is as high as 2.7 A. The ASTSMO-MFPCC has a smaller change in D-axis current, and the current fluctuation is only 2.1 A. According to the simulation results of inductance parameter mutation, the chattering observed by the adaptive super-twisting sliding mode observer is significantly smaller.
Simulation and experimental results verify the feasibility and correctness of the proposed method, and the following conclusions are drawn: (1) This strategy combines model-free control with predictive control so that the system is independent of the exact physical parameters of the rectifier during operation. (2) The control performance degradation problem of a system caused by the chattering of the traditional sliding mode observer is solved, and the disturbance suppression ability is improved. At the same time, the adaptive gain is designed, and the observer parameters are adjusted dynamically to simplify the gain selection effectively. (3) The comprehensive comparison with the SMO-MFPCC method confirms that the ASTMO-MFPCC strategy has better dynamic and stable performance and anti-interference ability.
keywords:Vienna rectifier, super-twisting sliding mode observer, model-free predictive current control
DOI: 10.19595/j.cnki.1000-6753.tces.222213
中图分类号:TM46
国家自然科学基金项目(52277070)和福建省科技计划项目对外合作项目(2021I0039)资助。
收稿日期 2022-11-25
改稿日期 2022-12-24
汪凤翔 男,1982年生,研究员,博士生导师,研究方向为电机驱动与电力电子。E-mail: fengxiang.wang@fjirsm.ac.cn
于新红 男,1989年生,工程师,研究方向为电力电子技术。E-mail: xinhong.yu@fjirsm.ac.cn(通信作者)
(编辑 陈 诚)