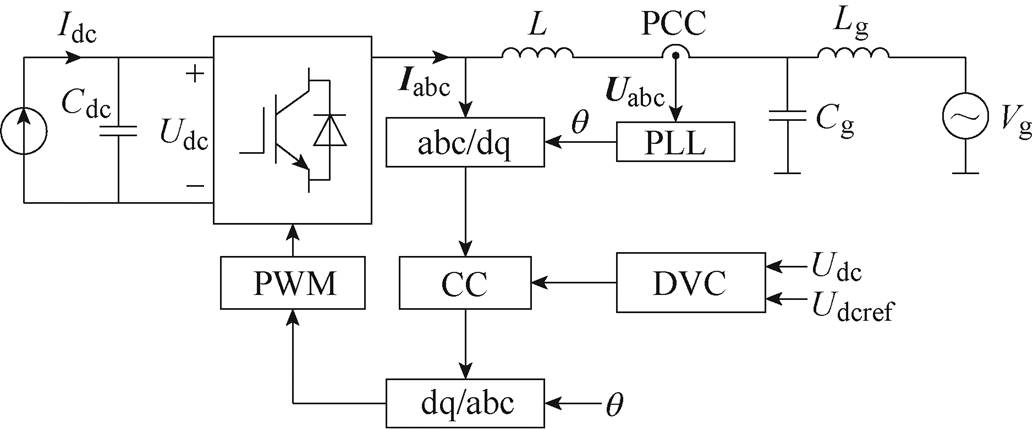
图1 GTC单线结构框图
Fig.1 One-line diagram of a GTC
摘要 三相并网变流器的不对称控制结构会导致频率耦合效应,降低其接入弱电网的稳定裕度,增加了阻抗分析的复杂度。首先,该文提出一种三相并网变流器的对称控制策略,以消除由锁相环和直流电压环引起的频率耦合效应。该控制策略通过在控制环路中引入直流电压环q轴补偿,以形成对称的直流电压闭环结构,同时引入对称锁相环,消除传统锁相环的非对称动态特性。因此,三相并网变流器可建模为单输入单输出的阻抗复矢量形式,进而可采用标准奈奎斯特准则进行阻抗稳定性分析,能够直观地说明控制器对系统阻抗特性的主导作用。然后,对并网变流器的阻抗特性进行分析,得出弱电网中对称锁相环的带宽对系统稳定性有着至关重要的影响,并且,不同运行工况也会改变并网变流器的阻抗特性,进而影响系统的稳定性。最后,仿真和实验结果验证了所提控制策略对频率耦合效应抑制的有效性以及阻抗特性分析的准确性。
关键词:三相并网变流器 频率耦合 对称控制 弱电网 稳定性分析
随着高比例新能源电力系统的发展,三相并网变流器(Grid-Tied Converters, GTCs)被广泛用于风能、太阳能以及储能系统的电网接口[1]。然而,可再生能源通常远离负荷,长距离的输电线路和大容量的变压器降低了电网强度[2]。在弱电网中,GTCs的宽频带控制动态和无源滤波器与电网阻抗间的复杂交互作用会导致诸多的谐振和稳定性问题,对电力系统的安全运行提出了挑战[3-4]。
并网频率耦合问题引发了国内外学者的广泛关注[5-7]。由于GTCs的直流电压控制器(DC-link Voltage Controller, DVC)只控制d轴电流参考值,而锁相环(Phase Locked Loop, PLL)只控制q轴电压,这种不对称的控制结构导致GTCs是镜像频率耦合(Mirror Frequency Coupled, MFC)系统[8]。当向MFC系统中注入某一频率的电压谐波时,除产生同频率的电流谐波外,还会产生关于基频对称的镜像谐波分量,即频率耦合效应[9]。并且,随着电网强度的降低,控制系统与弱电网的交互作用的增强加剧了频率耦合效应。由于谐波耦合分量的存在,电力系统可能发生次同步振荡,甚至造成同步发电机切机,使系统失稳[10-11]。
此外,当建立GTCs的阻抗模型分析系统的交互稳定性问题时[12-13],由于频率耦合效应的单输入多输出特性,GTCs的dq阻抗和ab阻抗均需要用多输入多输出(Multiple-Input Multiple-Output, MIMO)的2阶矩阵表示[14],显著增加了阻抗分析与控制器设计的复杂性。并且,MIMO系统需要利用广义奈奎斯特判据(Generalized Nyquist Criterion, GNC)评估系统稳定性,仅能用于稳定性的判别而无法深入分析振荡的形成机理[15-16]。当系统需要采用阻抗重塑等稳定性增强技术时,频率耦合特性将使得虚拟阻抗的参数整定变得困难,不易实现[17]。文献[18]提出了统一阻抗建模理论,该理论表明,当系统中频率耦合效应被消除时,阻抗矩阵可以降阶为单输入单输出(Single-Input Single- Output, SISO)的阻抗复矢量。因此,有必要研究GTCs的频率耦合抑制方法并建立GTCs的SISO阻抗模型分析阻抗特性。
文献[19]将GTCs导纳矩阵近似为SISO系统,该方法利用数学变换将矩阵非对角元素变为对角元素,且没有抑制频率耦合的影响,降低了稳定性判别的准确性。文献[20]提出了一种不对称的电流控制方法来消除PLL引起的不对称效应。文献[21]提出了一种对称锁相环(Symmetric PLL, SPLL)结构,通过同时跟踪公共耦合点(Point of Common Coupling, PCC)电压的相位和幅值,引入复矢量角的概念,有效地消除了由PLL控制结构不对称导致的频率耦合效应。文献[17]将SPLL用于双馈风机(Doubly Fed Induction Generator, DFIG)中,抑制了频率耦合特性,系统被降阶为SISO模型,并提出了改进的阻抗重塑策略。文献[22]将SPLL用于单相并网逆变器中,建立了SISO导纳模型,进行了面向控制器设计的导纳特性分析,并提出了一种前置滤波器来抑制SPLL的负电阻效应。然而,这些研究只考虑了PLL动态的影响,而没有解决DVC引起的不对称性问题。为此,文献[23]提出了一种解耦控制策略来改善DVC动态影响,但是需要在控制中引入小信号量,实现困难,且其抑制效果和滤波器性能有关,在基频附近的抑制效果不佳。目前,易于控制系统实现的含DVC外环的GTCs全频段频率耦合消除方法还有待进一步研究。
基于上述研究现状,本文提出了一种GTCs的对称控制策略。首先,提出直流电压环q轴补偿方法以消除DVC导致的d轴不对称,引入SPLL以消除PLL导致的q轴不对称,从而将GTCs建立为镜像频率解耦系统,有效地抑制了频率耦合效应。然后,建立GTCs的SISO复矢量导纳模型,从而能够准确判别系统稳定性并揭示振荡的形成机理,为控制器的设计提供导向。根据该模型,分析了电网短路比(Short Circuit Ratio, SCR),SPLL和DVC控制参数变化对系统稳定性的影响,分析了不同控制器对不同频段导纳特性的主导作用,比较了不同运行工况对导纳特性的影响。最后,仿真和实验结果验证了所提对称控制策略的有效性。
GTC的单线结构框图如图1所示。交流侧通过电感滤波器连接到LC型电网,其中,L为滤波电感,Lg和Cg分别为电网电感和电网电容。直流侧由电容Cdc并联直流电流源组成。Iabc和Uabc分别为三相PCC电流和电压。Udc和Idc分别为直流侧电容电压和电流源注入电流。DVC和电流控制器(Current Controller, CC)均在dq轴下使用PI控制,DVC输出CC的d轴电流参考值。PLL追踪PCC电压相位与电网同步。

图1 GTC单线结构框图
Fig.1 One-line diagram of a GTC
GTC小信号模型如图2所示,图中考虑了DVC和PLL的动态过程对系统的影响,本节中的小信号模型的推导及下述矩阵表达式均来自于文献[12, 24-25]。为表述清晰,下标“0”表示稳态值;D 表示小信号量。
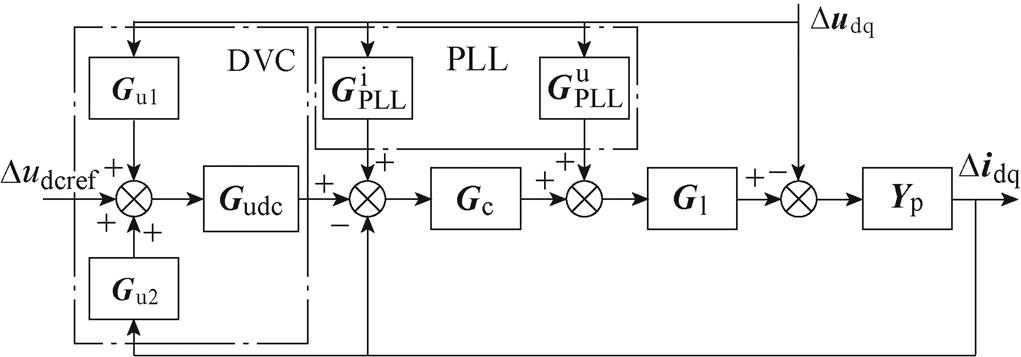
图2 GTC小信号模型
Fig.2 The small-signal model of GTC
为降低dq轴电流间的交叉耦合,本文采用电流解耦控制策略。因此,dq轴下滤波器导纳矩阵可表示为
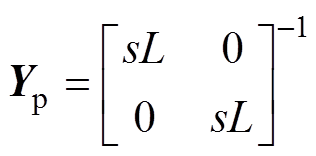 (1)
(1)
根据滤波器中电压与电流的关系,可以得到dq轴下GTC的输出电流为
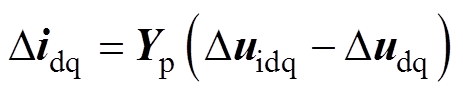 (2)
(2)
式中,Didq=[Did Diq]T为dq轴PCC电流;Duidq=[DuidDuiq]T为dq轴GTC端口输出电压;Dudq=[Dud Duq]T为dq轴PCC电压。
当不考虑前馈回路时,外环输出Didqref =[Didref, Diqref]T作为内环的参考电流,内环输出Duidq作为PWM的参考电压,表示为
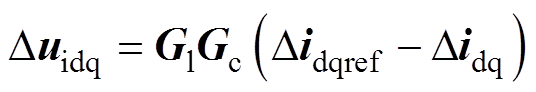 (3)
(3)
式中,Gl为时延环节的传递函数矩阵,包含1.5个采样周期Ts,即
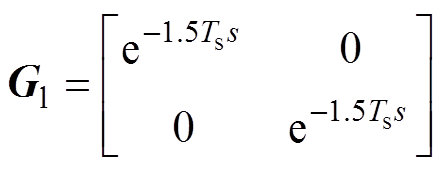 (4)
(4)
Gc为CC的PI控制器,Kpc和Kic分别为其比例增益和积分增益,其表达式为
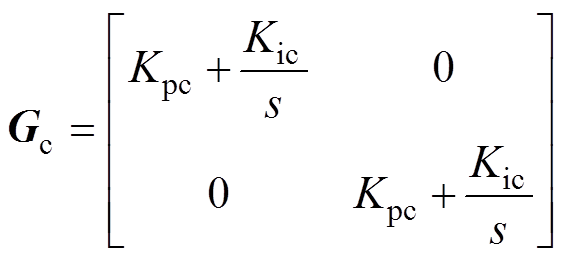 (5)
(5)
Gudc为DVC的PI控制器,Kpu和Kiu分别为其比例增益和积分增益,其表达式为
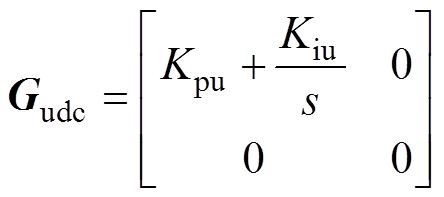 (6)
(6)
图2中,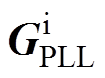 和
和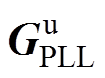 用来表示PLL小信号扰动对控制系统坐标变换的影响。对于传统的同步参考坐标系锁相环(Synchronous Reference Frame PLL, SRF-PLL),其通过PI控制器调节PCC的q轴电压实现GTC与电网的同步。SRF-PLL的闭环传递函数表示为
用来表示PLL小信号扰动对控制系统坐标变换的影响。对于传统的同步参考坐标系锁相环(Synchronous Reference Frame PLL, SRF-PLL),其通过PI控制器调节PCC的q轴电压实现GTC与电网的同步。SRF-PLL的闭环传递函数表示为
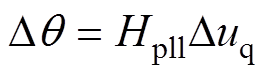 (7)
(7)
其中
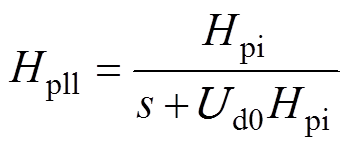
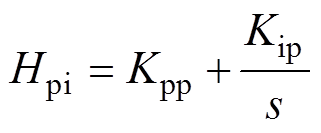
式中,Ud0为PCC稳态电压幅值;Kpp和Kip分别为锁相环的比例增益和积分增益;Hpi为PLL的PI控制器;Dq 为锁相环的输出。
PLL对电流和端口输出电压的动态影响可由两个不对称矩阵表示为
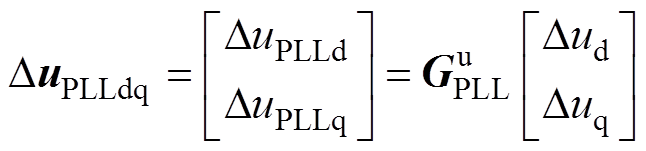 (8)
(8)
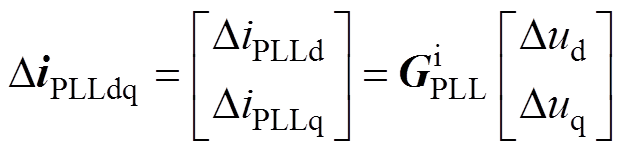 (9)
(9)
其中
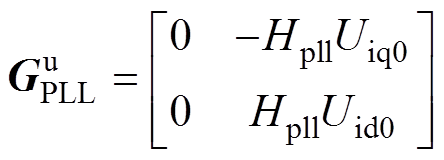
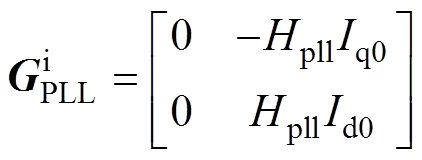
式中,Idq0=[Id0 Iq0]T和Uidq0=[Uid0 Uiq0]T分别为电流和端口输出电压的dq轴稳态幅值。
因此,当考虑PLL前馈回路时,式(3)被重写为
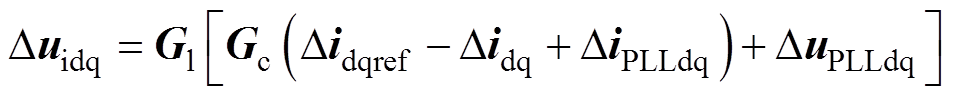 (10)
(10)
本文中,外环采用DVC控制,根据有功功率平衡规则,并考虑滤波器中的瞬时功率损耗[24],DVC动态的影响Gu1和Gu2可分别表示为
 (11)
(11)
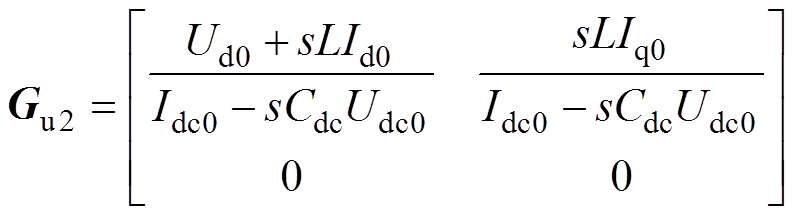 (12)
(12)
式中,Idc0和Udc0分别为直流电流和电压的稳态值。因此,当GTC运行于单位功率因数状态时,参考电流表示为
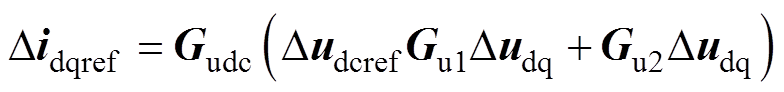 (13)
(13)
式中,Dudcref=[Dudcref 0]T为直流电压参考值。
根据图2框图,GTC的闭环响应可以写为
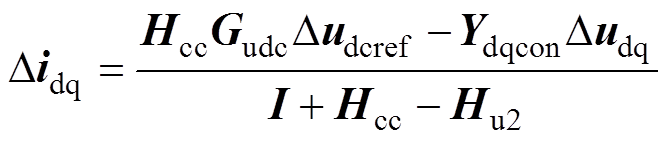 (14)
(14)
其中
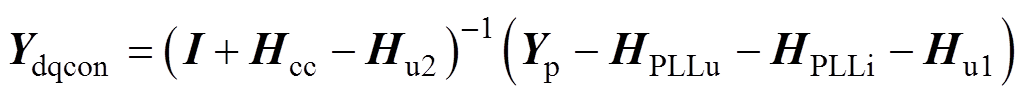
式中,I为单位矩阵;Ydqcon为GTC的输出导纳矩阵;Hcc、Hu1、Hu2、HPLLu和HPLLi如式(15)所示;Hu1, Hu2, HPLLu和HPLLi的详细表达式如附录式(A1)~式(A4)所示。
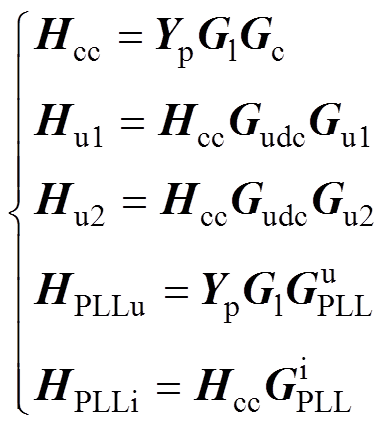 (15)
(15)
为了直观地分析GTC的导纳特性,将其导纳模型由2阶实矩阵Ydqcon等效变换为能够直接揭示频率耦合特性的2阶复矢量矩阵Y±,con[18]。变换过程表示为
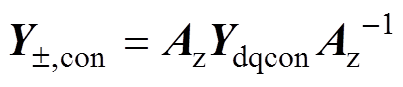 (16)
(16)
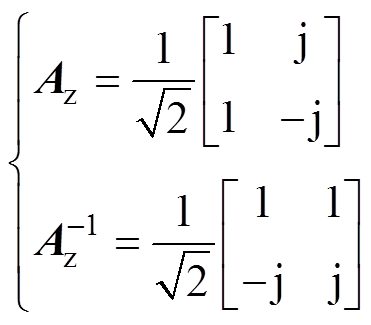 (17)
(17)
文献[18]中指出,对角元素相同,非对角元素互为相反数的2阶实矩阵被定义为对称矩阵。其中,对称矩阵经过式(16)的线性变换后,所生成的2阶复矢量矩阵中对角线元素互为共轭,非对角线元素为0。此时,系统完全解耦,不存在频率耦合效应,且导纳特性可以根据降阶的SISO复矢量获得。而对于非对称矩阵,其经过复等效变换后得到的复矢量矩阵中会产生非零的副对角线元素,这将导致双频模型被引入系统中,产生频率耦合现象。
根据前述分析,由于DVC和SRF-PLL自身控制的不对称性,Hu1、Hu2、HPLLu、HPLLi均为不对称矩阵。因此,Ydqcon也不对称,这表明在采用传统控制方案的GTC中,频率耦合效应是不可避免的。为了进一步说明频率耦合效应,在时域仿真中按图1所示结构搭建单机并网系统,仿真参数见表1,并向PCC中注入80 Hz和110 Hz的扰动电压(幅值为基频的10%)。PCC电流的快速傅里叶(Fast Fourier Transform, FFT)分析如图3所示。可以看出,对于频率fp1=80 Hz和fp2=110 Hz两个给定输入扰动,产生了频率为2f1-fp1=20 Hz和|2f1-fp2|=10 Hz的两个耦合输出扰动,f1为电网基频。
表1 GTC仿真参数
Tab.1 Simulation parameters of GTC
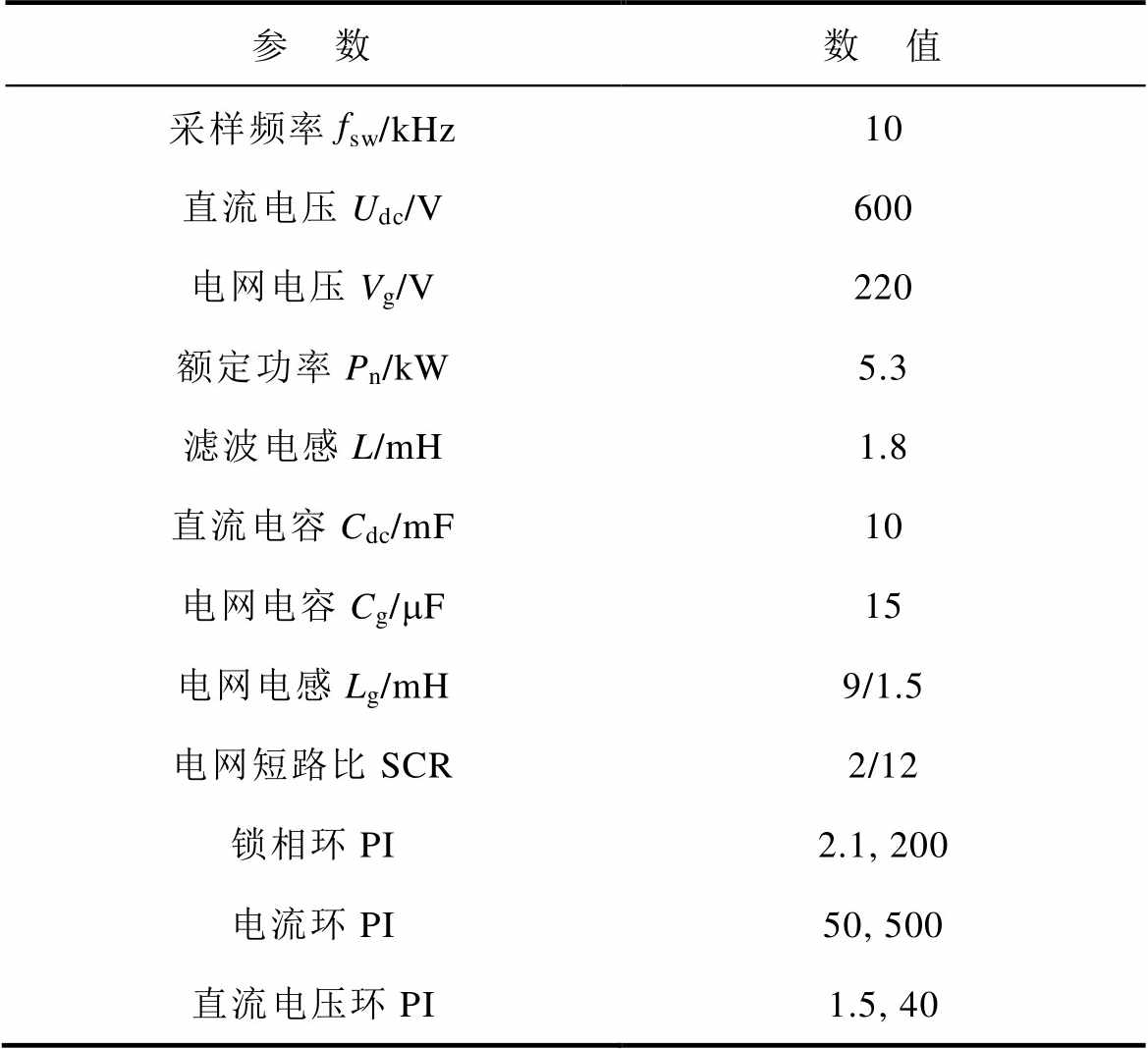
参 数数 值 采样频率fsw/kHz10 直流电压Udc/V600 电网电压Vg/V220 额定功率Pn/kW5.3 滤波电感L/mH1.8 直流电容Cdc/mF10 电网电容Cg/mF15 电网电感Lg/mH9/1.5 电网短路比SCR2/12 锁相环PI2.1, 200 电流环PI50, 500 直流电压环PI1.5, 40
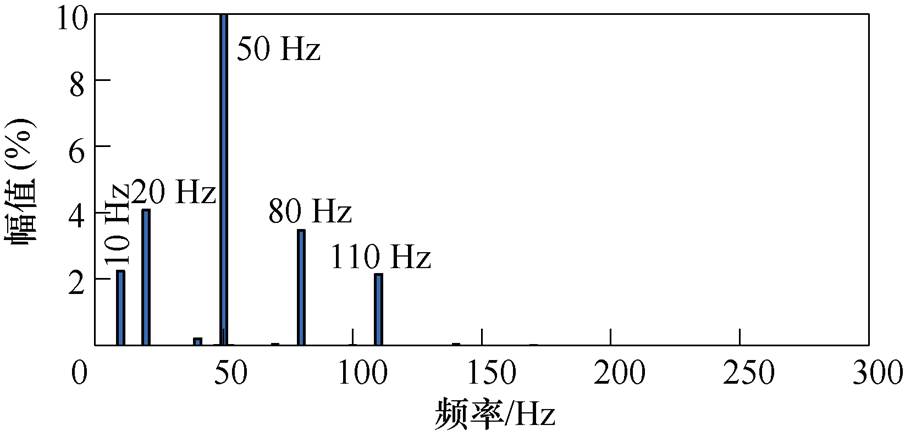
图3 传统控制策略PCC电流的FFT分析
Fig.3 FFT analysis of PCC current based on conventional control strategy
为了消除GTC中的频率耦合效应,本节提出了一种对称控制策略以减小DVC和SRF-PLL造成的不对称影响。
由式(6)可知,DVC只控制d轴分量,使得Gu1、Gu2和Gudc为不对称矩阵,从而发生频率耦合现象。为了抑制DVC的这种不对称动态,本节提出一种q轴补偿方法。为了表述清晰,将Hu1和Hu2改写为
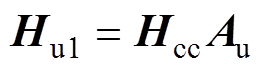 (18)
(18)
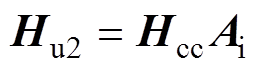 (19)
(19)
其中
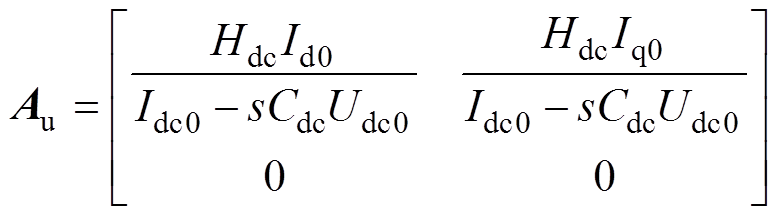
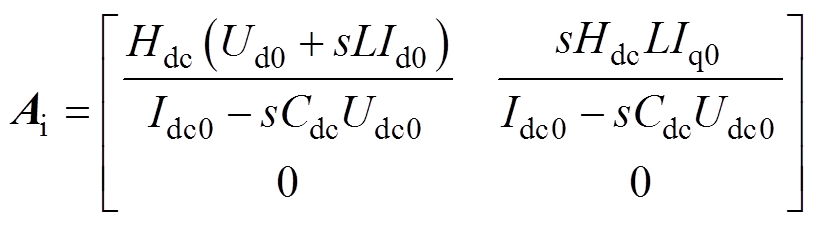
式中,Hdc=Kpu+Kiu/s。
根据图2,DVC控制结构的不对称性会同时影响系统的前馈回路和反馈回路。因此,针对DVC的q轴补偿由两部分组成,即q轴前馈补偿和q轴反馈补偿。提出了分别针对Au和Ai的两个补偿矩阵Gsh1和Gsh2,表示为
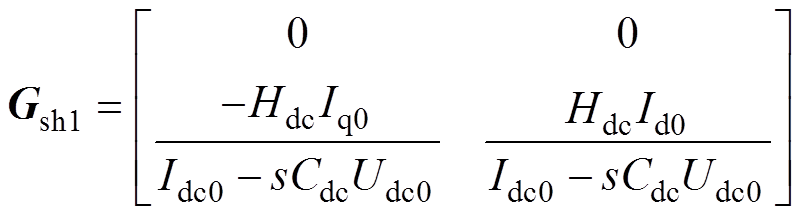 (20)
(20)
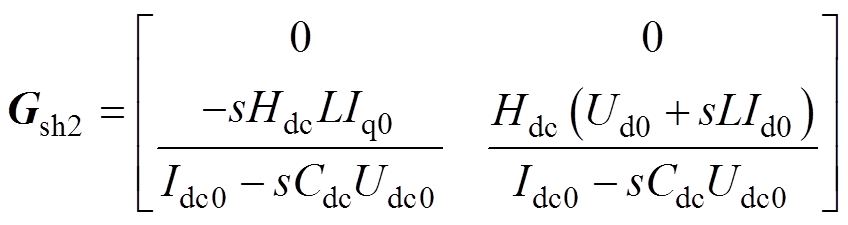 (21)
(21)
显然,当式(20)和式(21)分别被引入系统的前馈和反馈中时,Au和Ai被补偿为对称矩阵,由DVC导致的频率耦合效应被抑制。补偿过程表示为
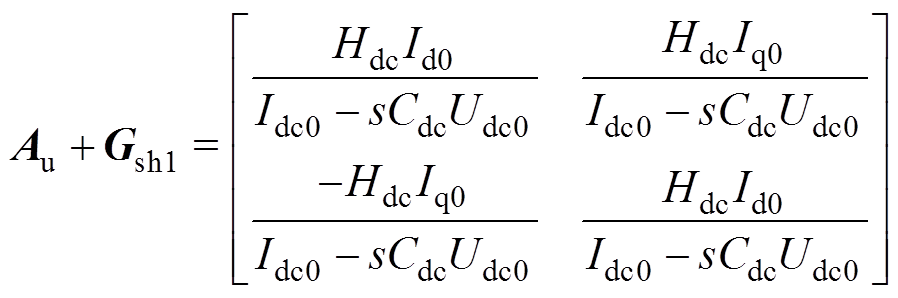 (22)
(22)
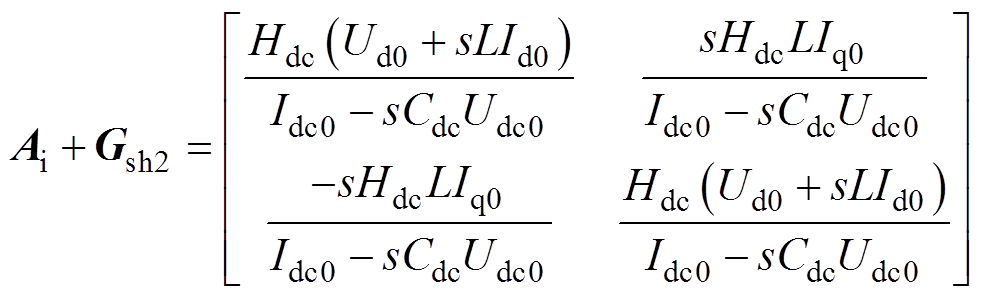 (23)
(23)
补偿后,q轴电流的参考值重塑为Direqref,即
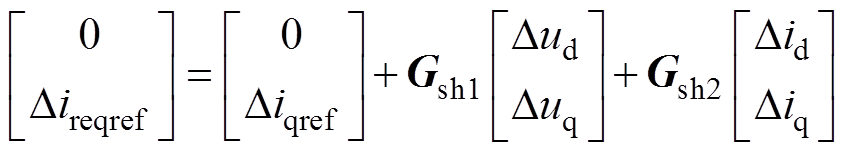 (24)
(24)
为进一步说明所提控制策略的正确性,根据式(11)和式(12),将补偿前的直流电压表示为复矢量形式Dudc,即
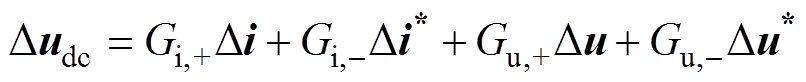 (25)
(25)
其中
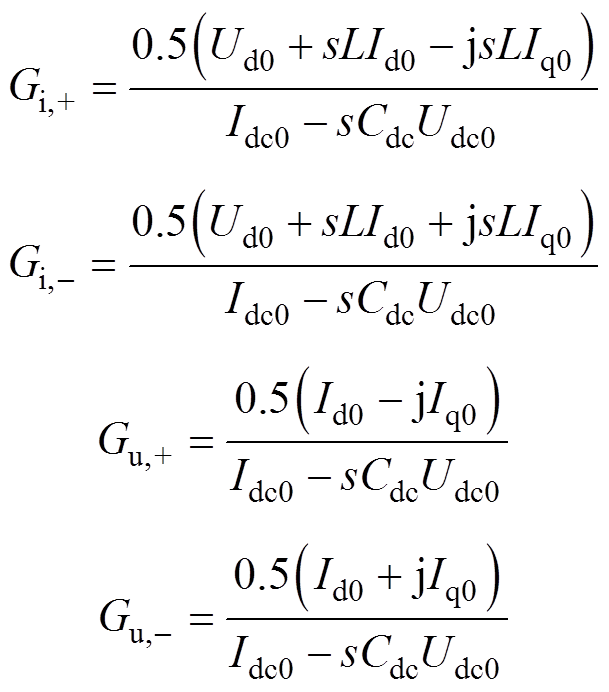
式中,Di=Did+jDiq和Du=Dud+jDuq分别为Didq、Dudq的复矢量形式;上标“*”表示复共轭。可以看出,补偿前的直流电压同时受到Di、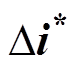 、Du和
、Du和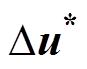 影响,这是一个双频扰动模型。由于共轭分量的引入,在dq坐标下,频率为fp的谐波与频率为- fp的谐波总是耦合产生的,当变换至ab(abc)坐标时,则同时存在fp+f1和- fp+f1频率的谐波,由此导致频率耦合效应。抑制频率耦合的关键在于消除共轭分量的引入。
影响,这是一个双频扰动模型。由于共轭分量的引入,在dq坐标下,频率为fp的谐波与频率为- fp的谐波总是耦合产生的,当变换至ab(abc)坐标时,则同时存在fp+f1和- fp+f1频率的谐波,由此导致频率耦合效应。抑制频率耦合的关键在于消除共轭分量的引入。
根据式(16)、式(20)和式(21),将q轴补偿后的直流电压表示为复矢量形式Dudcs,即
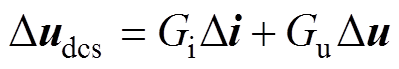 (26)
(26)
其中
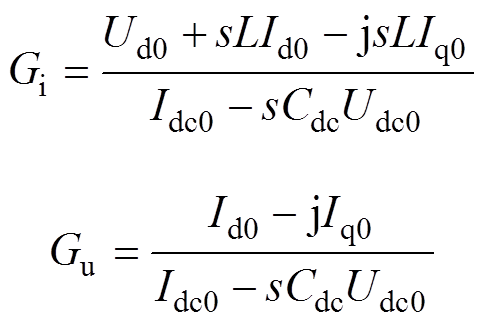
根据式(26)可以看出,补偿后的直流电压仅受到Di和Du影响,不会引入共轭分量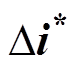 和
和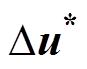 。这表明,所提出的q轴补偿方法可以完全补偿直流电压环dq轴输出的不对称,电流参考值被补偿为完整的复矢量。此时,DVC动态的输入与输出间仅存在单一频率的响应,是一个严格解耦的单频模型,由DVC导致的频率耦合效应被有效抑制。
。这表明,所提出的q轴补偿方法可以完全补偿直流电压环dq轴输出的不对称,电流参考值被补偿为完整的复矢量。此时,DVC动态的输入与输出间仅存在单一频率的响应,是一个严格解耦的单频模型,由DVC导致的频率耦合效应被有效抑制。
图1中,传统的SRF-PLL仅利用q轴电压实现相位跟踪,这导致HPLLu和HPLLi均为不对称矩阵。为了抵消这种控制结构的不对称性,采用SPLL结构[21],其控制结构如图4所示。与SRF-PLL不同,SPLL中包含两条控制回路,同时控制PCC的d轴和q轴电压实现相位同步。其中,q轴控制回路与SRF-PLL功能相同,d轴控制回路跟踪PCC电压的额定值Un。因此,SPLL的输出是一个复矢量相位,即qdq=qd+jqq。采用复矢量相位进行坐标变换能够有效消除SRF-PLL导致的频率耦合效应。根据复矢量等效原理,当采用SPLL结构时,式(8)和式(9)改写为
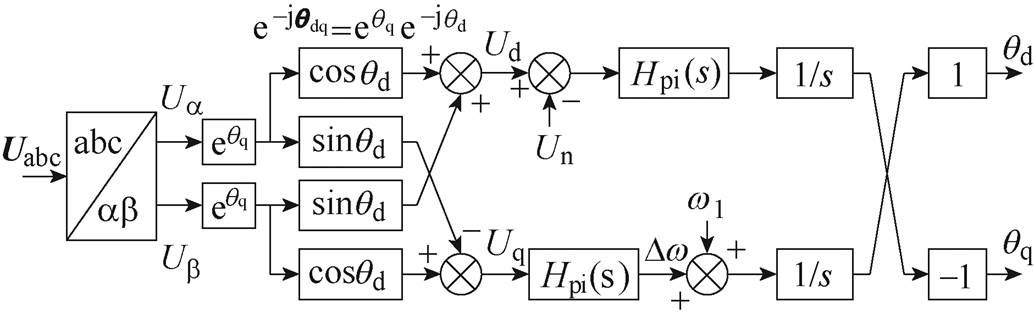
图4 SPLL控制结构
Fig.4 Control structure of SPLL
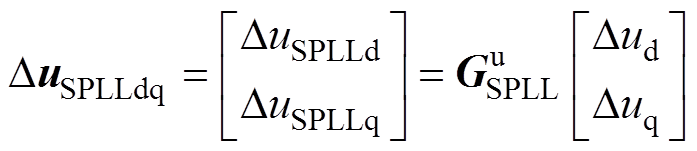 (27)
(27)
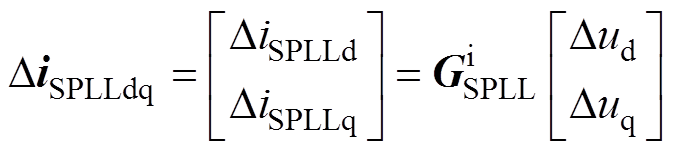 (28)
(28)
其中
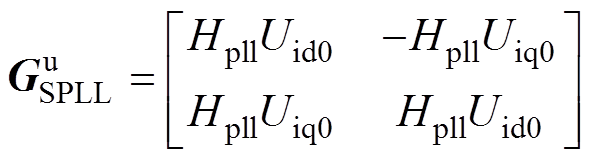
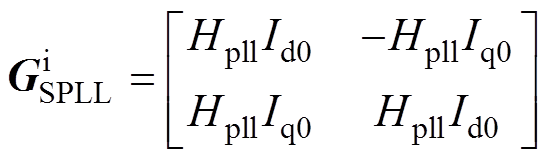
可以看出,SPLL小信号动态对电流和端口输出电压的影响均由对称矩阵表示,PLL环节的控制不对称性被消除。同样地,将SRF-PLL动态变换为复矢量形式,则式(8)和式(9)可分别表示为
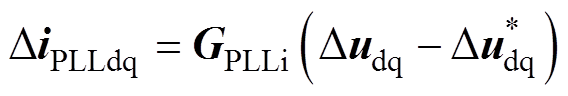 (29)
(29)
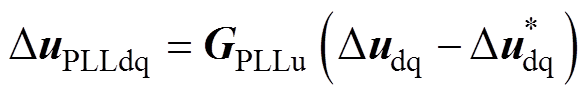 (30)
(30)
其中
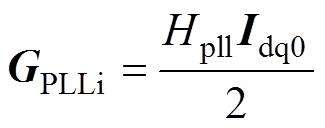
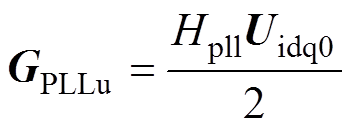
式中,DiPLL=DiPLLd+jDiPLLq;DuPLL=DuPLLd+jDuPLLq;I0= Id0+jIq0;Ui0=Uid0+jUiq0。与DVC相似,由于SRF-PLL仅利用q轴电压追踪电网相位,这种不对称会引入共轭分量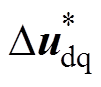 ,导致频率耦合效应。当采用SPLL结构时,SPLL动态的复矢量形式表示为
,导致频率耦合效应。当采用SPLL结构时,SPLL动态的复矢量形式表示为
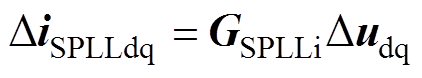 (31)
(31)
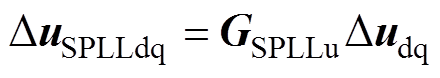 (32)
(32)
其中
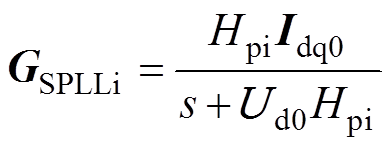
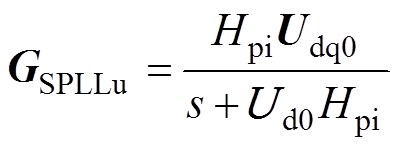
式中,DiSPLL=DiSPLLd+jDiSPLLq;DuSPLL=DuSPLLd+jDuSPLLq。SPLL结构通过引入d轴控制回路将PLL输出相位重塑为完整复矢量,不会引入共轭分量,有效地抑制了由PLL动态导致的频率耦合。
根据上述分析,推导了考虑SPLL和q轴补偿的对称输出导纳模型为
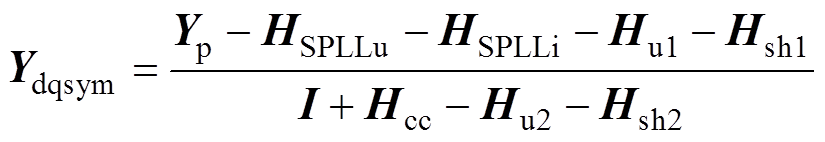 (33)
(33)
其中
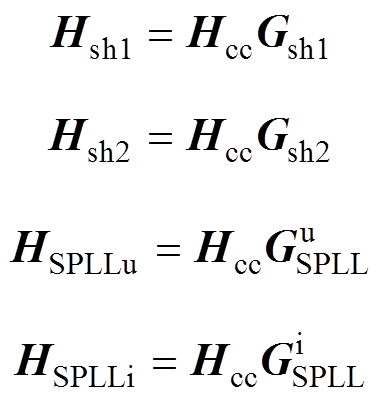
通过比较Ydqcon和Ydqsym可见,Ydqcon中不对称矩阵Hu1、Hu2、HPLLu、HPLLi分别被Ydqsym中的对称矩阵Hu1+Hsh1、Hu2+Hsh2、HSPLLu、HSPLLi所替代。因此,采用对称控制策略后,导纳矩阵变为对称矩阵,频率耦合效应被消除。图5给出了基于对称控制的GTC小信号模型。
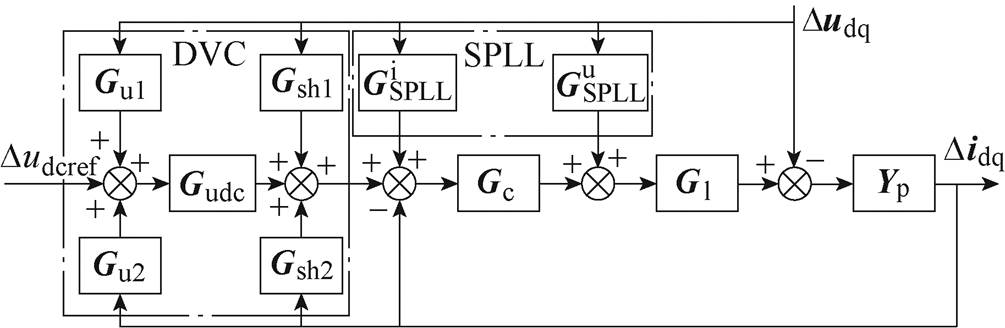
图5 基于对称控制的GTC小信号模型
Fig.5 The small-signal model of GTC based on symmetric control strategy
在时域仿真中搭建基于对称控制策略的GTC单机并网系统以验证所提方法的有效性。为了更加关注于GTC导纳的频率特性,本节采用单位功率因数运行方式。GTC的dq导纳模型扫频结果如图6所示,从图中可以看出,频率扫描结果与理论分析结果吻合良好。
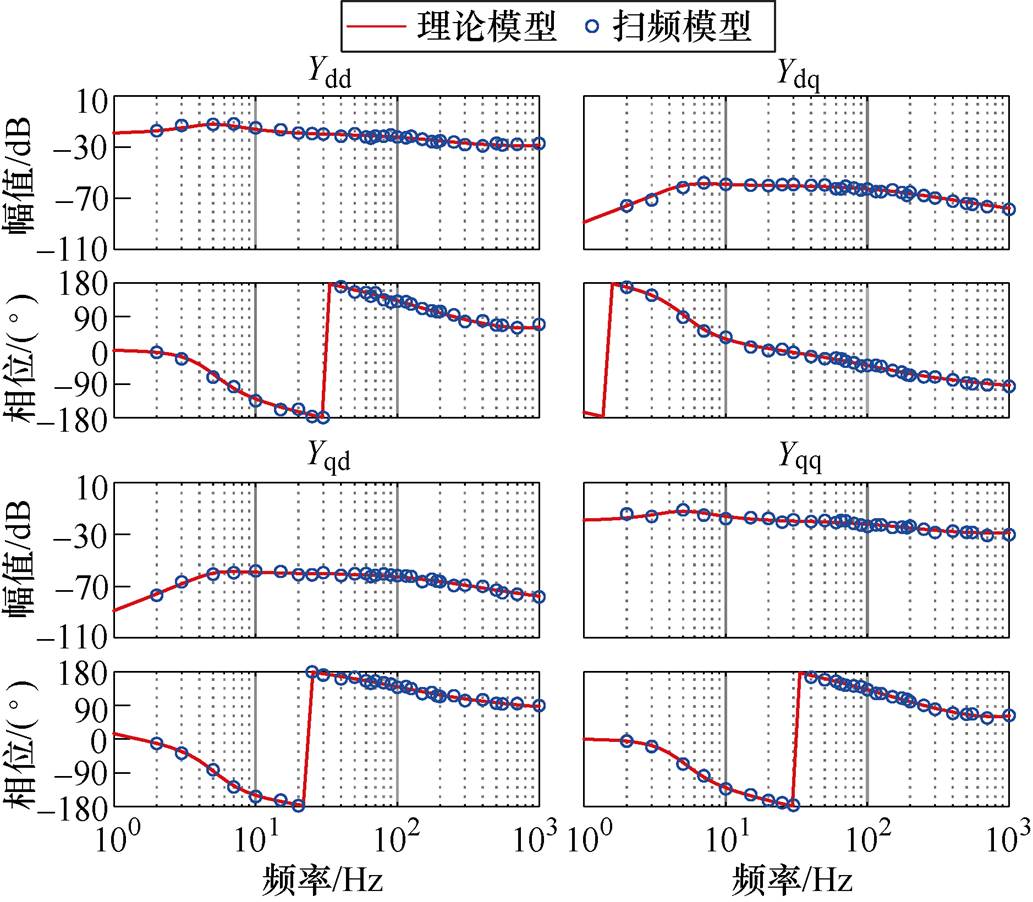
图6 GTC对称dq导纳模型验证
Fig.6 Validation of the symmetric dq-frame admittance model for GTC
由图6可以看出,对角线元素Ydd和Yqq相位、幅值均相等,非对角线元素Ydq和Yqd幅值相等,相位相反。为了简洁,令Yd=Ydd=Yqq, Yq=-Ydq=Yqd。因此,采用对称控制策略后,GTC的dq导纳矩阵变为对称矩阵。为了验证频率耦合抑制效果,与图3相同,向PCC注入fp1=80 Hz和fp2=110 Hz的谐波扰动(幅值为基频的10%),其输出电流的FFT分析如图7所示。从图7中可以看出,20 Hz和10 Hz的耦合分量被明显抑制,频率耦合效应被消除。
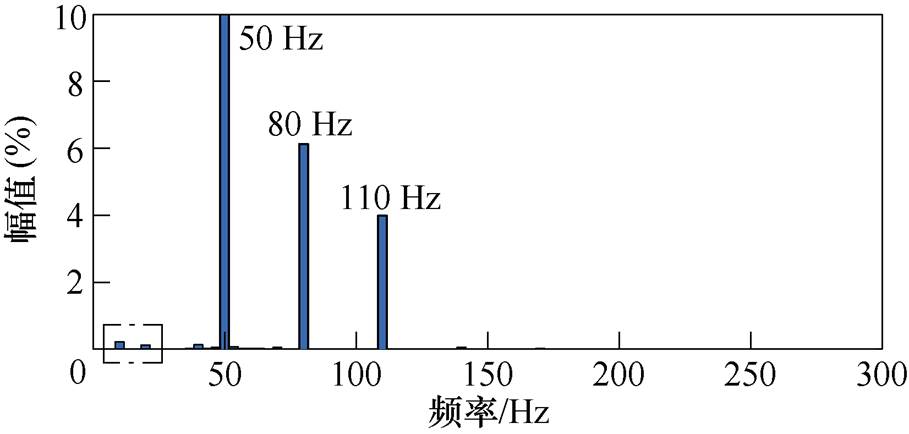
图7 对称控制策略PCC电流的FFT分析
Fig.7 FFT analysis of PCC current based on symmetric control strategy
为了研究q轴补偿对系统稳态性能的影响,图8给出了谐波注入前后q轴参考电流的变化情况。从图8中可以看出,当系统处于稳态运行时,q轴补偿控制输出为0,q轴参考电流保持稳态值不变。当并网系统中存在振荡时,该方法对振荡导致的控制输出不对称进行补偿,此时q轴参考电流将存在波动。因此,引入的q轴补偿控制不会影响系统的稳态运行。
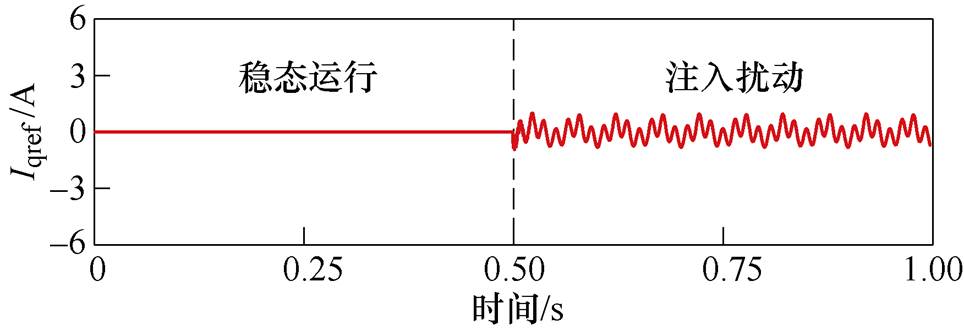
图8 q轴参考电流变化
Fig.8 The variation of the q-axis current reference
为了研究对称控制策略对系统动态性能的影响,图9给出了系统稳定运行时直流电压的阶跃响应。在1 s时,直流电压由600 V切换至640 V,两种控制策略的上升时间分别为Dt1=59.7 ms, Dt2= 59.9 ms,可以看出,所提控制策略对上升时间几乎没有影响,并且两种控制策略下直流母线电压超调量基本相同。因此,所提出的控制策略不会劣化系统的动态性能。
综上所述,对称控制策略能够在不影响系统稳态和动态性能的条件下消除频率耦合效应。并且,基于统一阻抗建模方法,对称的导纳矩阵可以降阶为SISO的导纳复矢量,简化了GTC并网系统的稳定性分析过程,能够直观地分析振荡的形成机理。
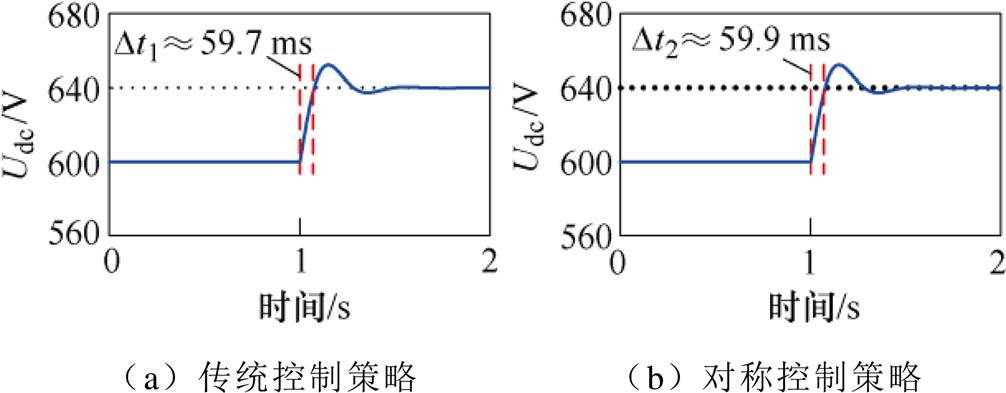
图9 直流电压动态性能比较
Fig.9 Comparison of the DC-link voltage dynamic performance
根据式(16),将导纳矩阵Ydqsym转化为复传递函数矩阵Y±,sym。Y±,sym中非对角线元素为0,对角线元素互为共轭,则Y±,sym表示为
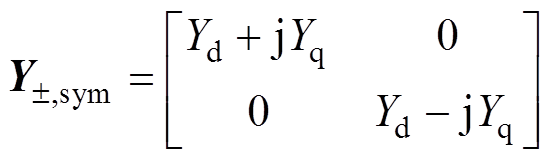 (34)
(34)
将式(34)降阶为SISO导纳复矢量,即Yp=Yd+ jYq,则GTC导纳特性可根据该复矢量获得。同时,由于电网导纳对称,其复矢量形式为
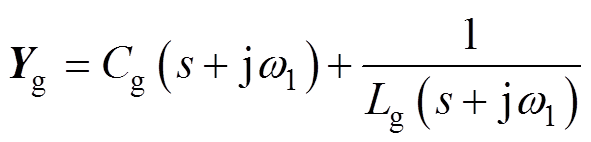 (35)
(35)
式中,w1=2pf1。当导纳比Yp/Yg满足Nyquist稳定性判据时,GTC并网系统稳定。与GNC相比,该方法能够更加直观地获取系统的稳定裕度、导纳特性和振荡频率等信息。本文选取相位裕度(Phase Margin, PM)作为稳定裕度,表示为
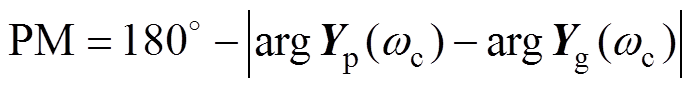 (36)
(36)
式中,wc=2pfc,fc为Yp和Yg的幅频特性曲线交点处的频率(以下简称为交点频率)。
Yp和Yg的频率特性如图10所示。图10中可以看出,Yp在低频段呈现明显的负电阻特性。随着频率增加,Yp逐渐呈电感特性,这是因为控制器的带宽有限,其在中高频段对GTC导纳特性的影响可以忽略不计。在强电网条件(SCR=12)下,Yp和Yg的幅频特性曲线在500 Hz频率范围内无交点,这表明系统是稳定的。当电网SCR降低至2时,Yp和Yg的幅频特性曲线在156 Hz处相交,此时相位裕度PM=-21°,系统失稳,且存在156 Hz的振荡。
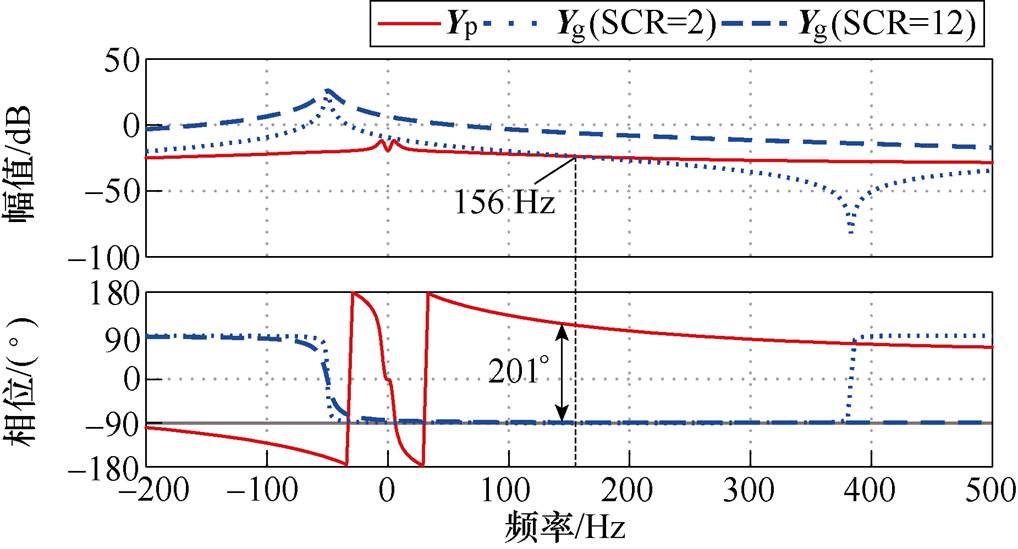
图10 Yp和Yg的频率特性
Fig.10 Bode diagrams of the admittances Yp and Yg
为了分析SPLL带宽对系统稳定性的影响,图11给出了fbw1=113 Hz和fbw2=65 Hz两种SPLL带宽下Yp的伯德图。图11中可以看出,当fbw从65 Hz增加到113 Hz时,交点频率从224 Hz降低到156 Hz,系统的PM从18.5°下降到-21°,系统发生振荡。进一步分析可知,随着SPLL带宽的增加,Yp相位大于90°的负电阻频段明显扩大,导致振荡风险。
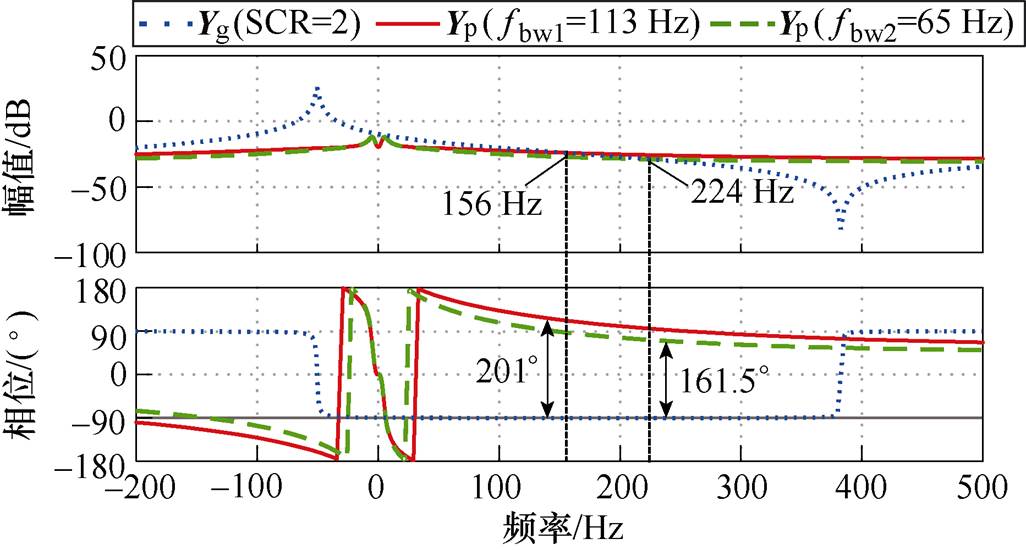
图11 不同SPLL带宽时Yp的频率特性
Fig.11 Bode diagrams of Yp with different SPLL bandwidths
为了分析DVC控制参数对系统稳定性的影响,图12给出了Kpu1=1.5和Kpu2=3.5两种不同比例增益下Yp的伯德图。为了更全面地说明DVC动态在稳定与失稳两种情况下的性能表现,选择了fbw1和fbw2两种锁相环带宽。在失稳条件下,由图12a可知,Kpu从1.5增加到3.5时,PM从-21°下降到-22.9°。在稳定条件下,由图12b可知,Kpu的增加使PM从18.5°下降到17.9°。所以,DVC比例增益的增大同样不利于系统稳定,但是与SPLL的带宽增加相比,该影响相对较小。可以认为,当DVC带宽远小于SPLL和电流环时,其控制参数的变化几乎不会导致并网系统的稳定状态发生变化。
进一步分析可知,Kpu的增加使Yp呈负电阻部分的相频特性曲线出现偏移,但是这种偏移只对小于交点频率的频段明显,对交点频率处的影响可以忽略不计。如图12所示,两种情况下,增加Kpu导致交点频率处相位分别增加1.9°和0.6°,系统PM变化不大。
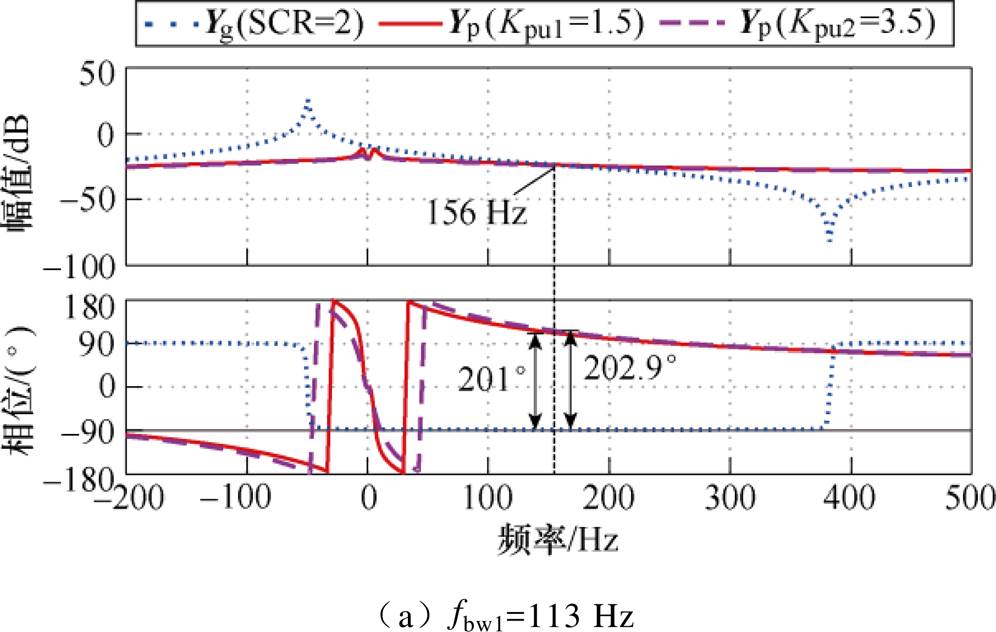
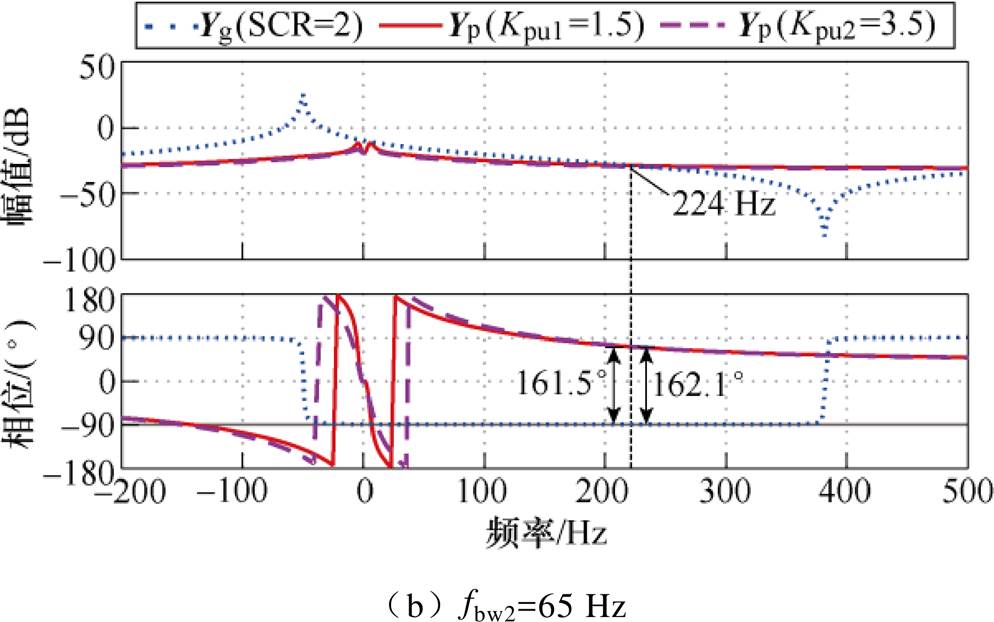
图12 不同Kpu时Yp的频率特性
Fig.12 Bode diagram of Yp with different Kpu
综上所述,在控制系统中,SPLL带宽的增加不利于GTC接入弱电网时的同步稳定性,导致振荡风险。当DVC带宽远小于SPLL和电流环时,其比例增益的增加也会恶化同步稳定性,但是通常这种影响可忽略不计。
图13给出了当SPLL带宽fbw2=65 Hz时,GTC向电网中注入不同无功功率时Yp伯德图的变化。从图13中可以看出,当GTC向电网中注入容性无功时(Iqref1=10 A),Yp的负电阻现象更加显著,交点频率增加至236 Hz,系统PM由18.5°降为-3.7°,系统中将产生236 Hz的谐波。当GTC向电网中注入感性无功时(Iqref2=-10 A),Yp的负电阻现象被明显抑制,相位整体降低,交点频率降低至198 Hz,系统PM增加至31.7°,稳定性进一步增强。
此外,该现象还表明,感性无功的注入有助于提高SPLL带宽的最大允许值,而容性无功的注入则相反,这为PLL带宽的设计提供了一种新思路。
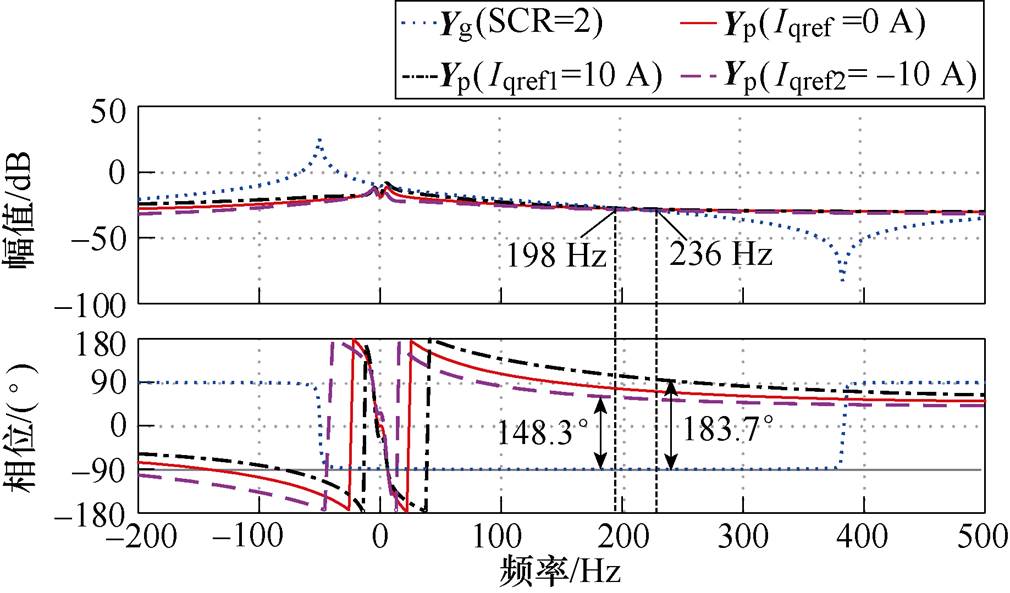
图13 不同Iqref时Yp的频率特性
Fig.13 Bode diagram of Yp with different Iqref
综上所述,运行工况也会对GTC的同步稳定产生重要影响。容性无功的注入会削弱稳态性能带来的振荡风险,而感性无功的注入则有助于增强稳定性。
为了进一步分析Yp的导纳特性,根据叠加原理,将图5中的小信号模型分解为Ydqp、Ydqspll、Ydqdvc三个子系统,则Ydqsym可以写为
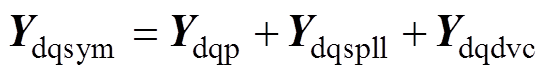 (37)
(37)
式中,Ydqp为GTC的开环导纳;Ydqspll为SPLL动态引入的并联导纳;Ydqdvc为DVC动态引入的并联导纳。各子系统小信号框图如图14所示。

图14 GTC子系统小信号框图
Fig.14 The small-signal model of GTC subsystem
从图14中可以看出,SPLL和DVC子系统均引入了电压前馈回路,这将改变GTC的导纳特性。为了进一步分析各个子系统对导纳特性的影响程度,将Ydqp、Ydqspll、Ydqdvc变换为复矢量,即Ypp、Ypspll、Ypdvc,其伯德图如图15所示。
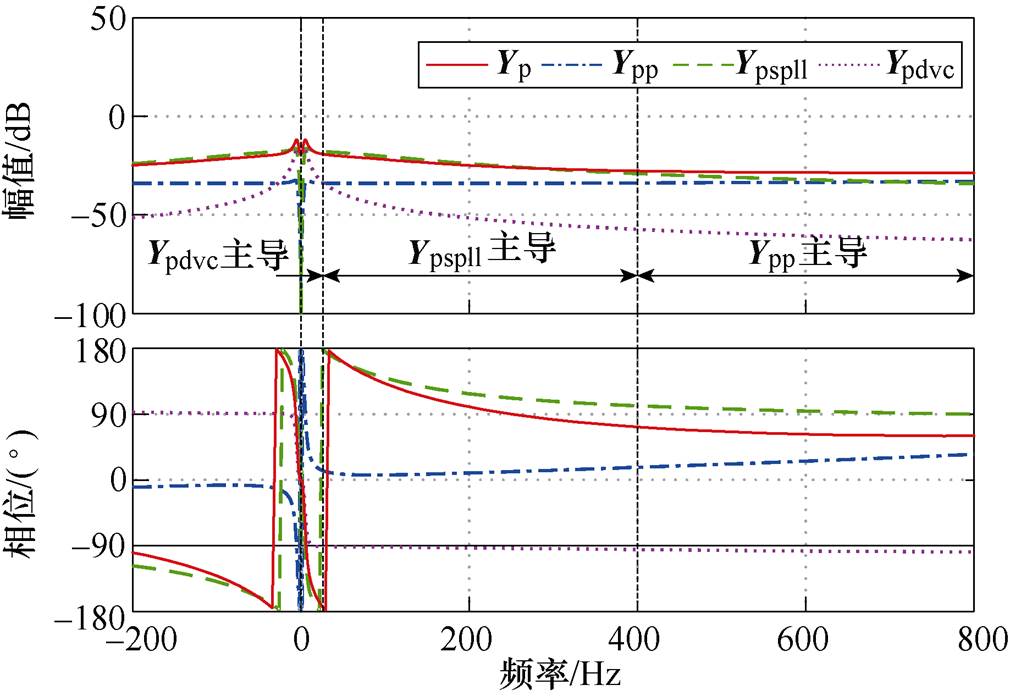
图15 GTC子系统伯德图
Fig.15 Bode diagram of GTC subsystem
根据图15可知,在不同的频段范围内,Yp的导纳特性由不同的子系统主导,这揭示了GTC产生振荡的原因,可以总结为以下三条结论。
首先,由于DVC带宽较小,Ypdvc主导Yp在0~15 Hz之间的导纳特性,随着频率的增加,Ypdvc的影响可以忽略不计。因此,DVC比例参数的增大导致Yp相频特性曲线在0 Hz附近发生偏移,而不影响交点频率的相频特性。
其次,Ypspll的幅值在15~400 Hz范围内趋近于Yp,这说明SPLL在该频段内主导导纳特性。并且Ypspll的相位在该频段内始终大于90°,这导致GTC呈现负电阻特性。SPLL带宽的增加会进一步增加Ypspll的相位,进而降低系统PM。因此,SPLL引入的并联导纳是控制器导致振荡的根本原因,这为稳定性增强控制策略提供了理论依据。
最后,当频率大于400 Hz时,Ypp的幅值逐渐趋近于Yp,这表明高频段的导纳特性主要由滤波器等无源元件主导,控制器的影响可以忽略。从图15中可以发现,Ypp的相位始终分布于[0°, 90°],Yp呈现阻感性,此时PM>0,系统能够维持稳定。
综上所述,GTC控制系统诱发振荡的根本原因是SPLL在中低频段引入的负电阻效应。这种负电阻效应显著降低了系统PM,不利于系统的稳定运行。
为了进一步验证所提控制方法的有效性,搭建了如图16所示的单机并网装置。实验中,交流测试电网环境由Chroma 61704模拟,背靠背变流器中前级AC-DC变流器模拟直流电流源以向直流侧注入电流,后级DC-AC变流器以维持直流母线电压稳定,实现功率由直流侧到模拟电网侧传输。控制系统采用快速原型控制器MT1050。
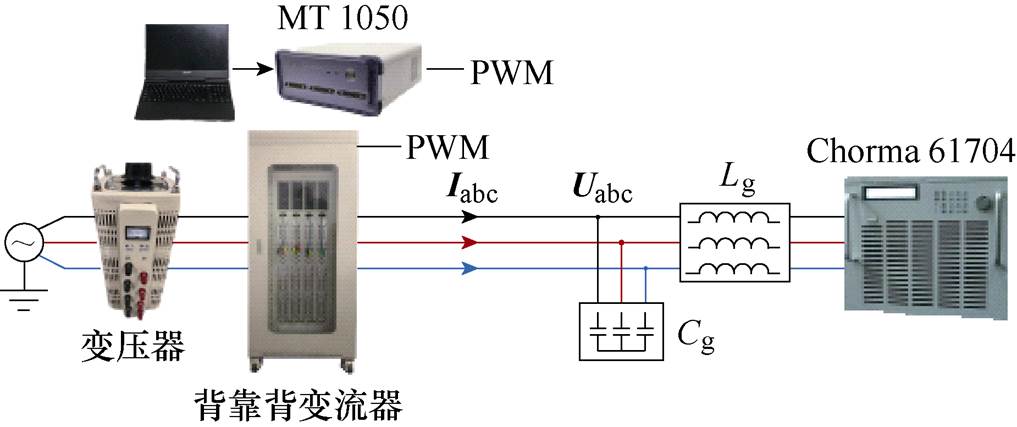
图16 实验平台
Fig.16 Experimental setup
图17为电网SCR=12,Kpu1=1.5时,65 Hz和113 Hz两种SPLL带宽下,采用对称控制策略的三相并网电流波形和直流电压波形。可以看出,两种带宽的波形都是稳定的。这表明在强电网中,控制参数变化时,GTC仍然能够稳定运行,具有良好的鲁棒性,系统允许带宽较大的SPLL。
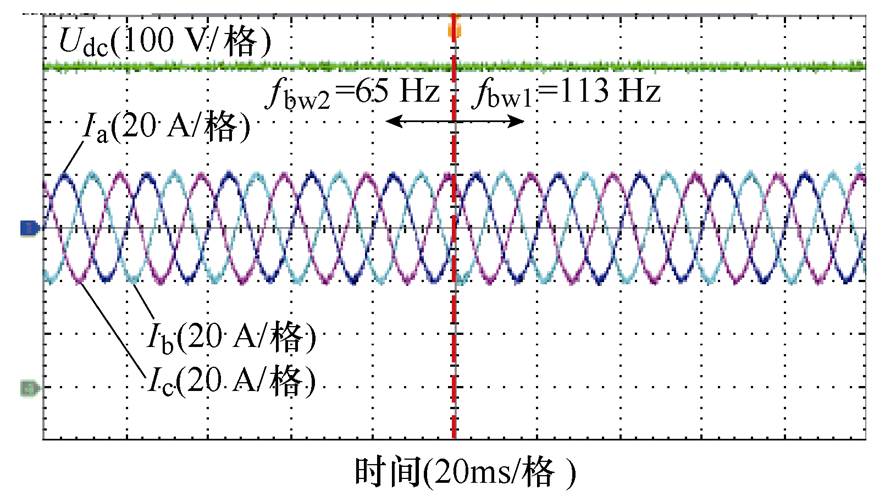
图17 SCR=12时采用对称控制方案的实验波形
Fig.17 Experimental waveforms of symmetric control scheme when SCR=12
图18为电网SCR=2,SPLL带宽为65 Hz,Kpu2= 3.5时,采用对称控制策略的三相并网电流波形和直流电压波形。可见,在弱电网中,低带宽的SPLL同样不会导致系统振荡,DVC比例增益的变化对系统同步稳定性影响较小,系统仍能稳定运行。
图19a为电网SCR=2,SPLL带宽为113 Hz,Kpu1=1.5时,采用对称控制策略的三相并网电流波形和直流电压波形。实验结果表明,在弱电网中,高带宽的SPLL会导致系统失稳。图19b为三相并网电流的FFT频谱。由于dq轴和ab 轴间存在50 Hz的频移,并网电流在ab 轴中的振荡频率为207 Hz,这与图10理论分析一致。频谱图中谐波分量不存在耦合,这表明频率耦合被有效抑制。并且,交流侧的总谐波畸变率(Total Harmonic Distortion, THD)约为13.35%,直流侧的THD约为0.61%。
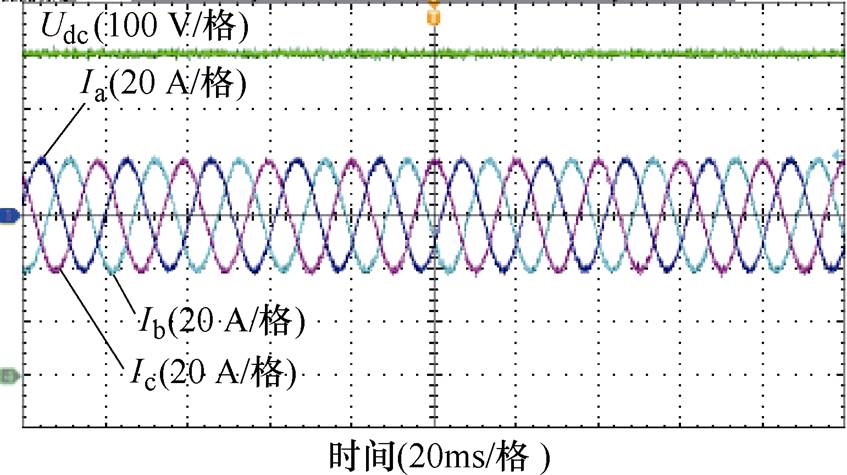
图18 SCR=2, fbw2=65 Hz, Kpu2=3.5时实验波形
Fig.18 Experimental waveforms when fbw2=65 Hz, Kpu2=3.5 and SCR=2
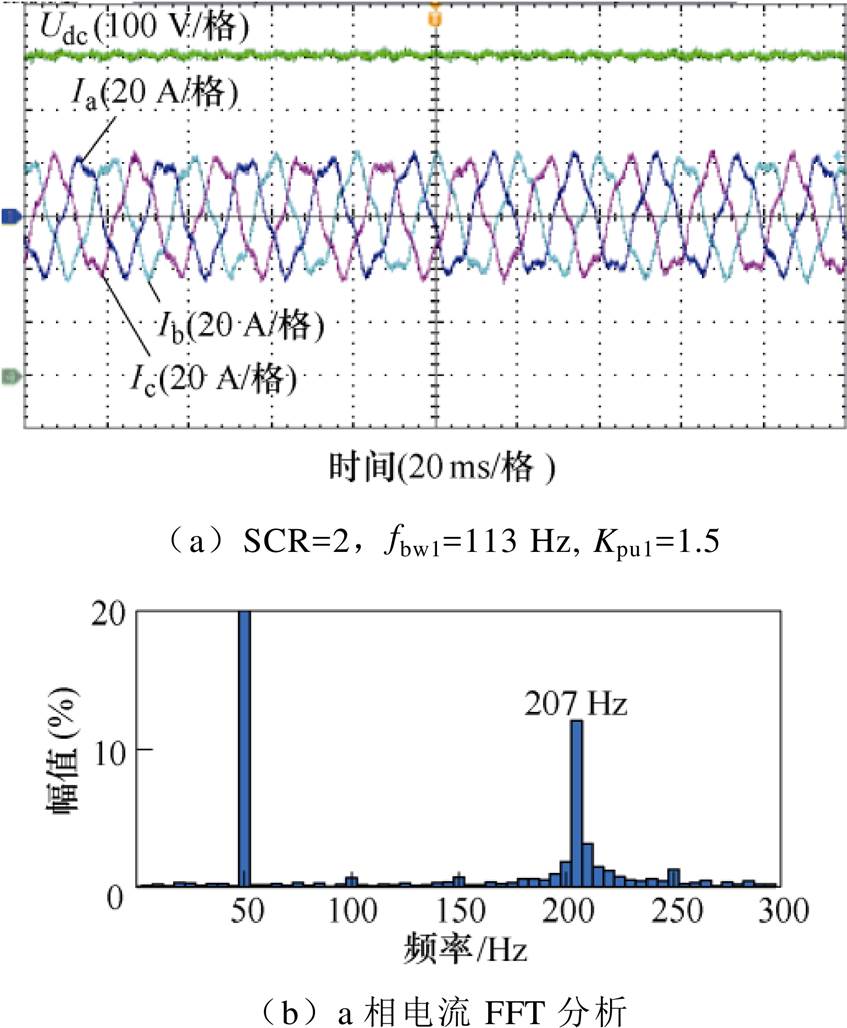
图19 SCR=2, fbw1=113 Hz, Kpu1=1.5时实验波形
Fig.19 Experimental waveforms when fbw1=113 Hz, Kpu1=1.5 and SCR=2
图20为电网SCR=2,SPLL带宽为65 Hz,Kpu1=1.5时,GTC注入无功功率条件下的实验波形。根据图20a可知,容性无功注入下,系统发生振荡,并网电流波形中存在284 Hz的谐波。交流侧THD约为10.21%,直流侧THD约为0.43%。由图20b可知,感性无功注入下,系统能够保持稳定,交流侧THD约为1.63%,直流侧THD约为0.04%。实验结果验证了图13分析的准确性。
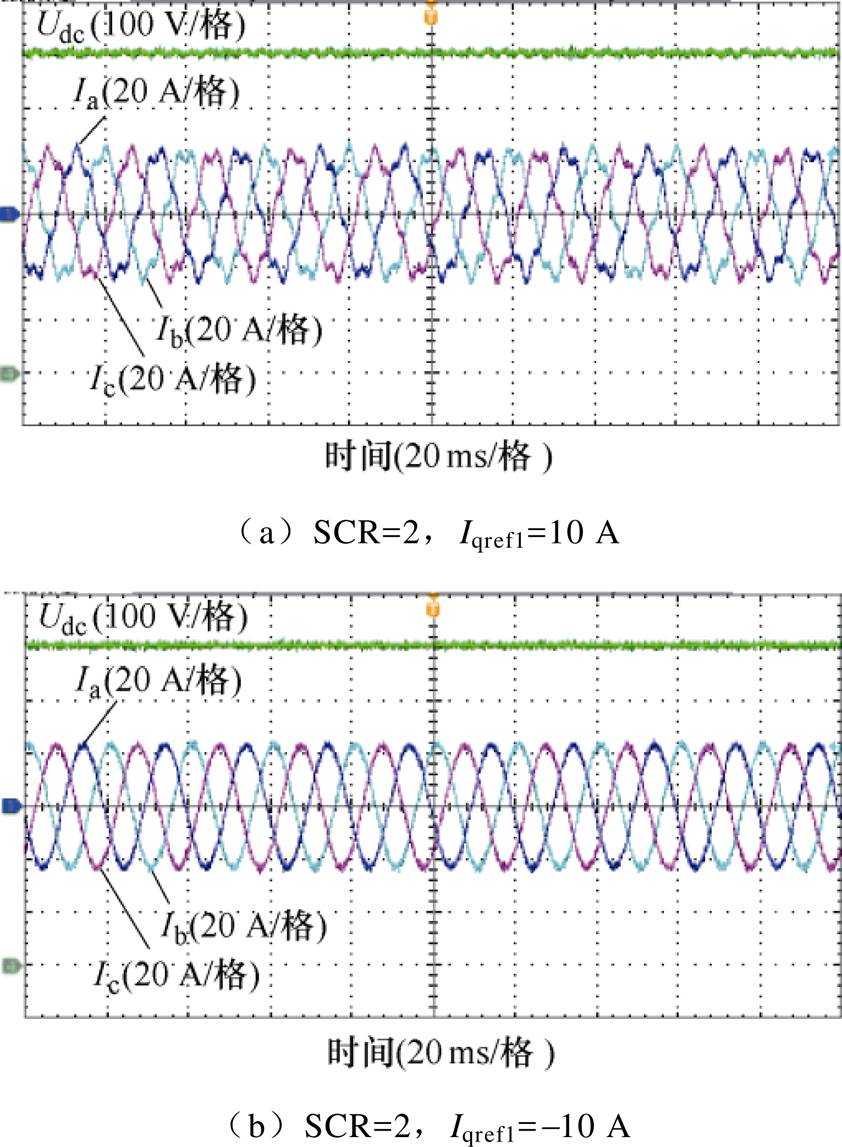
图20 无功功率注入的实验波形
Fig.20 Experimental waveforms of reactive power injection
为了验证所提控制策略的鲁棒性,使电网电压骤降至0.7(pu)。当SPLL带宽分别为fbw1=113 Hz和fbw2=65 Hz,电网SCR=2时,实验波形如图21所示。可以看出,对于一个失稳系统,电网电压发生骤降会改变其振荡频率;而对于稳定系统,电网电压骤降后系统仍然能维持稳定。这表明启用对称控制策略并不会影响电网电压骤降情况下系统的稳定状态,所提方法具有良好的鲁棒性。
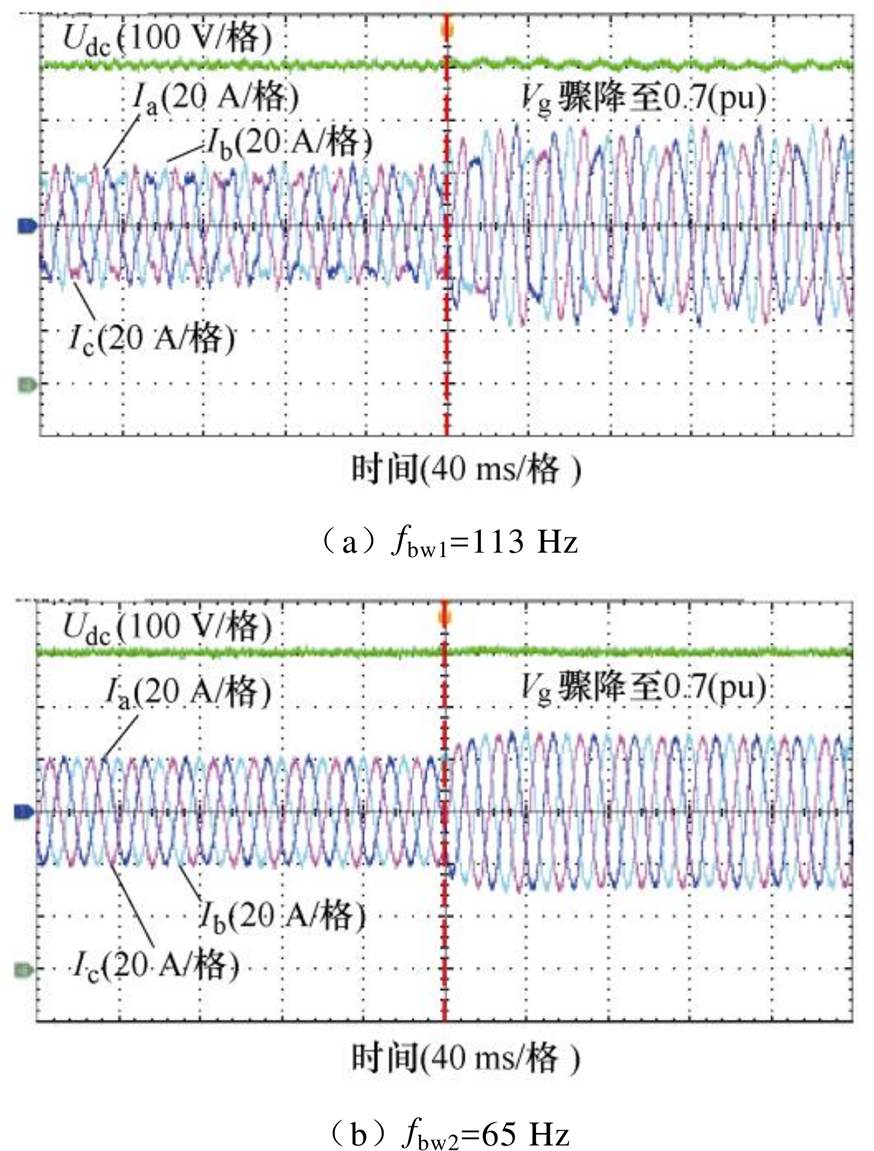
图21 电网电压骤降时的实验波形
Fig.21 Experimental waveforms of grid voltage dips
为了分析所提控制策略对动态性能的影响,在实验中设置了40 V的直流电压阶跃,实验波形如图22所示。可以看出两种控制策略下直流电压的上升时间分别为Dt1=47 ms和Dt2=49 ms,表明对称控制策略不会影响系统的动态性能,这与图9的仿真结果一致。
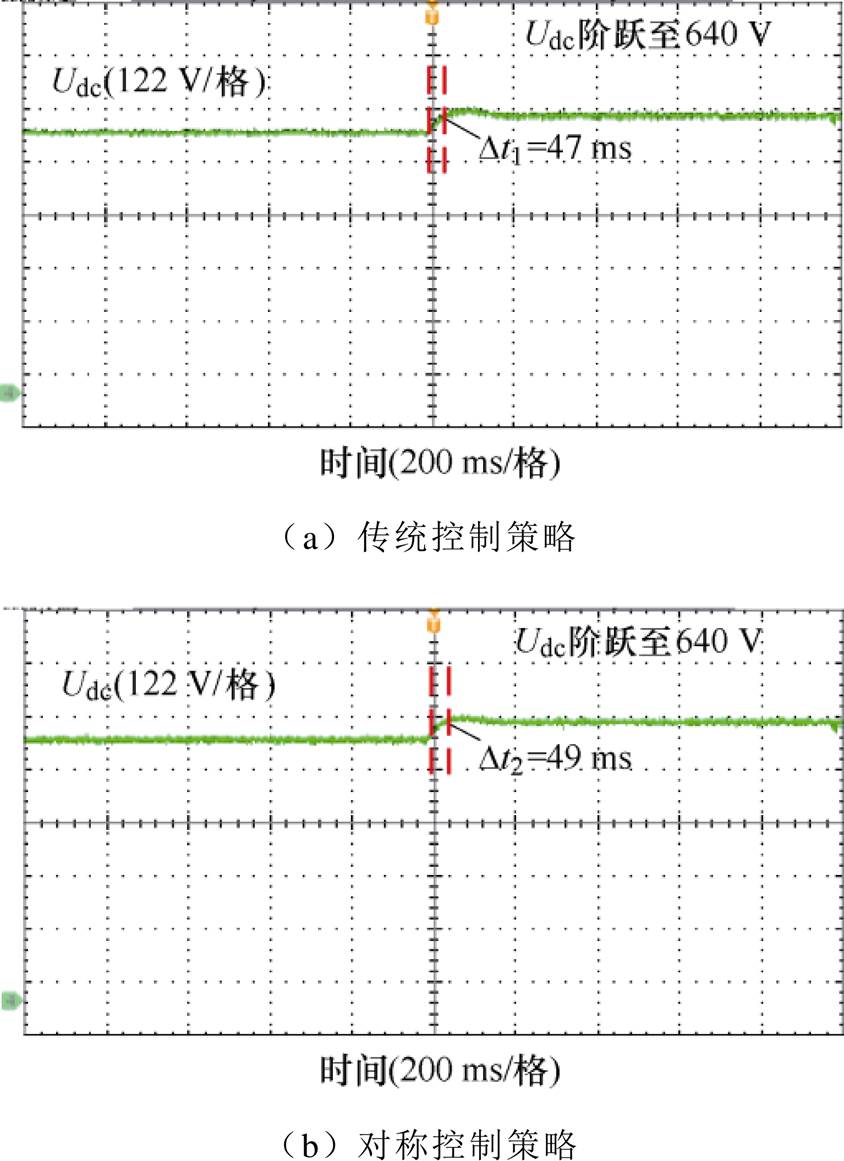
图22 直流电压阶跃实验波形
Fig.22 Experimental waveforms of DC-link voltage step
本文提出了一种对称控制策略,解决了因SRF- PLL和DVC控制结构的不对称导致的GTC频率耦合问题。首先,引入电压环q轴补偿和SPLL,将GTC的dq轴导纳矩阵补偿为对称矩阵,实现了GTC的频率解耦控制。进而将GTC的dq轴导纳矩阵降阶为SISO的复矢量模型,更加直观地分析了GTC的导纳特性和振荡的形成机理,并得到如下结论:
1)在弱电网中,DVC仅在直流频率附近主导GTC的导纳特性,其参数变化对系统稳态性能影响不大;SPLL仅在中低频段主导GTC的导纳特性,其带宽增加会导致负电阻效应加剧,进而降低系统的PM,导致系统振荡;在高频段,GTC的导纳特性主要由无源元件主导,控制器影响可以忽略。
2)不同运行工况也会改变GTC的稳态特性,其中容性无功的注入不利于并网系统的稳定,而感性无功的注入则与之相反。
结合SISO导纳特性的GTC稳定性增强控制策略将在后续工作中开展相关研究。
附 录
令Kpic=Kpc+Kic/s,Kpiu=Kpu+Kiu/s。Hu1、Hu2、HPLLu、HPLLi表达式分别为
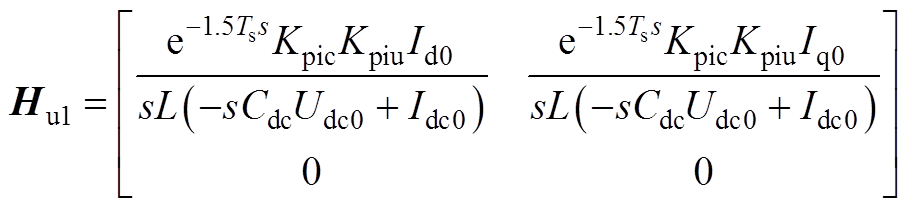 (A1)
(A1)
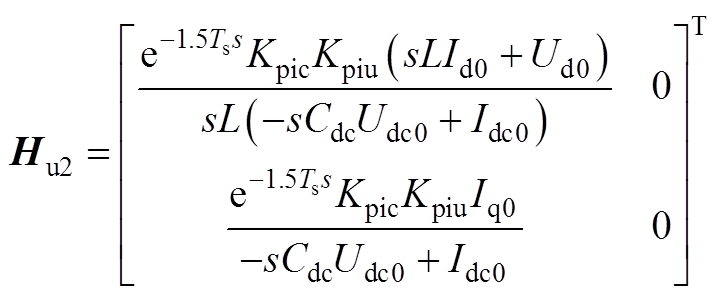 (A2)
(A2)
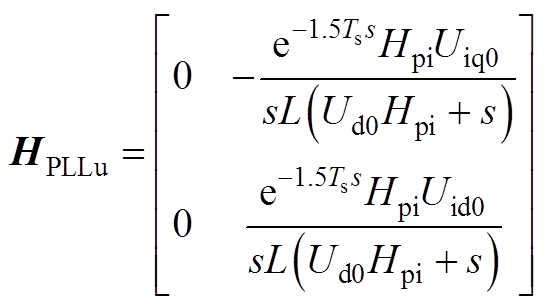 (A3)
(A3)
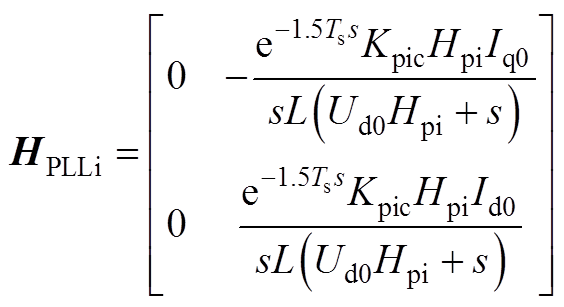 (A4)
(A4)
参考文献
[1] 沈姝衡, 方天治, 章益凡. 高带宽数字控制LCL型并网逆变器及其提高并网系统鲁棒性的谐振抑制技术研究[J]. 电工技术学报, 2022, 37(21): 5548- 5561.
Shen Shuheng, Fang Tianzhi, Zhang Yifan. A high- bandwidth digital-control LCL-type grid-tied inverter and resonance-suppressing technique for improving the robustness of grid-connected system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(21): 5548-5561.
[2] 于彦雪, 马慧敏, 陈晓光, 等. 弱电网下基于准静态模型的混合控制微电网逆变器同步稳定性研究[J]. 电工技术学报, 2022, 37(1): 152-164.
Yu Yanxue, Ma Huimin, Chen Xiaoguang, et al. Synchronous stability research of inverters in hybrid microgrid based on the quasi-static models under weak grid[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 152-164.
[3] 吴滨源, 李建文, 李永刚, 等. 用于谐波劣化分析的并网逆变器阻抗灰箱拟合方法[J]. 电工技术学报, 2022, 37(4): 942-953.
Wu Binyuan, Li Jianwen, Li Yonggang, et al. A gray-box fitting method of grid-connected inverters impedance for the analysis of harmonic degra- dation[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 942-953.
[4] Wang Xiongfei, Blaabjerg F. Harmonic stability in power electronic-based power systems: concept, modeling, and analysis[J]. IEEE Transactions on Smart Grid, 2018, 10(3): 2858-2870.
[5] 吴天昊, 谢小荣, 姜齐荣, 等. 考虑频率耦合及交直流端口耦合效应的并网变流器三端口导纳模型[J]. 中国电机工程学报, 2022, 42(1): 249-261.
Wu Tianhao, Xie Xiaorong Jiang Qirong, et al. Three-port admittance modeling of grid-connected converters considering frequency-coupling and AC/ DC coupling effects[J]. Proceedings of the CSEE, 2022, 42(1): 249-261.
[6] 刘威, 谢小荣, 黄金魁, 等. 并网变流器的频率耦合阻抗模型及其稳定性分析[J].电力系统自动化, 2019, 43(3): 138-146.
Liu Wei, Xie Xiaorong, Huang Jinkui, et al. Frequency-coupled impedance model and stability analysis of grid-connected converter[J]. Automation of Electric Power Systems, 2019, 43(3): 138-146.
[7] Xu Yunyang, Nian Heng, Wang Tao, et al. Frequency coupling characteristic modeling and stability analysis of doubly fed induction generator[J]. IEEE Transactions on Energy Conversion, 2018, 33(3): 1475-1486.
[8] Rygg A, Molinas M, Zhang Chen, et al. A modified sequence-domain impedance definition and its equivalence to the dq-domain impedance definition for the stability analysis of AC power electronic systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1383-1396.
[9] Kazem Bakhshizadeh M, Wang Xiongfei, Blaabjerg F, et al. Couplings in phase domain impedance modeling of grid-connected converters[J]. IEEE Transactions on Power Electronics, 2016, 31(10): 6792-6796.
[10] 刘其辉, 洪晨威, 逄思敏, 等. 基于弹性系数的双馈风电机组控制参数对次同步振荡作用分析及调整方法[J]. 电工技术学报, 2022, 37(14): 3528-3541.
Liu Qihui, Hong Chenwei, Pang Simin, et al. Analysis and adjustment method of doubly-fed fan control parameters on subsynchronous oscillation based on impedance elastic sensitivity[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3528- 3541.
[11] 张骞, 边晓燕, 徐鑫裕, 等. 基于SVD-Prony及主成分回归的次同步振荡阻尼特性影响因素研究[J]. 电工技术学报, 2022, 37(17): 4364-4376.
Zhang Qian, Bian Xiaoyan, Xu Xinyu, et al. Analysis of influencing factors on damping characteristics of subsynchronous oscillation based on singular value decomposition-Prony and principal component regression[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4364-4376.
[12] Wen Bo, Boroyevich D, Burgos R, et al. Analysis of d-q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.
[13] Sun Jian. Impedance-based stability criterion for grid- connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
[14] Harnefors L, Wang Xiongfei, Chou S, et al. Asymmetric complex-vector models with application to VSC-grid interaction[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1911-1921.
[15] 徐海亮, 高铭琨, 吴瀚, 等. 海上风电场-MMC互联系统频率耦合建模及稳定性分析[J]. 电力系统自动化, 2021, 45(21): 92-102.
Xu Hailiang, Gao Mingkun, Wu Han, et al. Frequency-coupling modeling and stability analysis of offshore wind farm-modular multilevel converter interconnection system[J]. Automation of Electric Power System, 2021, 45(21): 92-102.
[16] 辛焕海, 李子恒, 董炜, 等. 三相变流器并网系统的广义阻抗及稳定判据[J]. 中国电机工程学报, 2017, 37(5): 1277-1293.
Xin Huanhai, Li Ziheng, Dong Wei, et al. Generalized-impedance and stability criterion for grid-connected converters[J]. Proceedings of the CSEE, 2017, 37(5): 1277-1293.
[17] Hu Bin, Nian Heng, Li Meng, et al. Impedance-based analysis and stability improvement of DFIG system within PLL bandwidth[J]. IEEE Transactions on Industrial Electronics, 2022, 68(6): 5803-5814.
[18] Wang Xiongfei, Harnefors L, Blaabjerg F. Unified impedance model of grid-connected voltage-source converters[J]. IEEE Transactions on Power Elec- tronics, 2018, 33(2): 1775-1787.
[19] Chou S, Wang Xiongfei, Blaabjerg F. Two-port network modeling and stability analysis of grid- connected current-controlled VSCs[J]. IEEE Transa- ctions on Power Electronics, 2020, 35(4): 3519- 3529.
[20] Du Xiong, Wang Guoning, Shi Ying, et al. Using asymmetric current controller to improve the stability of grid-inverter system due to PLL effect[C]//IEEE 18th Workshop on Control and Modeling for Power Electronics (COMPEL), Stanford, USA, 2017: 1-7.
[21] Yang Dongsheng, Wang Xiongfei, Liu Fangcheng, et al. Symmetrical PLL for SISO impedance modeling and enhanced stability in weak grids[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1473-1483.
[22] Lin Jianheng, Su Mei, Sun Yao et al. Frequency coupling suppression control strategy for single-phase grid-tied inverters in weak grid[J]. IEEE Transactions on Industrial Electronics, 2022, 69(9): 8926-8938.
[23] Zhang Xueguang, Fu Sida, Chen Wenjia, et al. A Symmetrical control method for grid-connected converters to suppress the frequency coupling under weak grid conditions[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13488-13499.
[24] Yazdani A, Iravani R. An accurate model for the DC-side voltage control of the neutral point diode clamped converter[J]. IEEE Transactions on Power Delivery, 2006, 21(1): 185-193.
[25] Gong Hong, Wang Xiongfei, Harnefors L. Rethinking current controller design for PLL-synchronized VSCs in weak grids[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 1369-1381.
Abstract With the development of renewable energy power systems, three-phase grid-tied converters (GTCs) are widely used as grid-tied interfaces of wind, solar, and battery systems. Because renewable sources are distributed in remote areas, long-distance transmission lines result in a weak grid. In the weak grid, the asymmetric control structure of a three-phase gird-tied converter leads to frequency coupling, which is not conducive to the stability of the system and the design of the controller. Therefore, a symmetric control strategy is proposed to compensate for the asymmetry of the dq axis caused by the phase-locked loop (PLL) and DC-link voltage control (DVC). Then, the frequency coupling effect is eliminated, and GTCs are modeled as a single-input and single-output (SISO) admittance complex vector. The stability analysis based on the SISO admittance can reveal the inducement of system oscillation and simplify the parameters design of the controller.
Firstly, the dq-frame admittance model of the DVC-embedded GTC with the conventional control strategy is developed, and the instantaneous power balance of the filter is considered for accuracy. Then, the unified impedance modeling approach transforms the real admittance matrix into the complex admittance. Since the dq axis is asymmetric, the complex conjugate components of the PCC voltage and current are introduced, and the frequency coupling effect is inevitable. Consequently, the symmetric PLL (SPLL) and the q-axis compensation of DVC are introduced. Compared with the synchronous reference frame PLL (SRF-PLL), SPLL controls the q-axis and d-axis of common coupling (PCC) voltage points. Therefore, the output of the SPLL is a complex vector angle that tracks the amplitude and phase of the PCC voltage. For DVC, to compensate for the asymmetry of q-axis control, q-axis voltage feedforward compensation and q-axis current feedback compensation are introduced, respectively, effectively eliminating the conjugate components of the DVC. Moreover, the accuracy of the symmetric control model is verified by the sweep frequency method. The sweep frequency results show that the diagonal elements are equal, and the off-diagonal elements are opposite in the dq-frame admittance matrix. In other words, GTC becomes a symmetric system, and the frequency coupling is suppressed. The simulation results demonstrate that the proposed scheme does not affect the dynamic and steady-state performance of the system.
Besides, based on the SISO model, the admittance characteristics of GTC are analyzed. The influencing factors of the admittance characteristics are divided into two parts, namely, the control parameters and the operating conditions. In the control system, high-bandwidth SPLL can cause the system to oscillate, while the DVC parameter changes have little effect on stability. Furthermore, oscillations are triggered when inductive reactive power is injected into the system, while the opposite is true when capacitive reactive power is injected. Further analysis shows that the SPLL dominates the GTC phase characteristics in the low-frequency band. The parallel admittance introduced by the SPLL dynamics has a negative resistance effect, significantly reducing the system stability margin. The experimental results verify the effectiveness of the proposed symmetric control strategy and the accuracy of the theoretical analysis.
The conclusions of this paper can be summarized as follows: (1) By introducing the SPLL and q-axis compensation of DVC, the frequency coupling effect of GTC is eliminated. (2) Based on the analysis of SISO admittance characteristics, SPLL dominates the frequency characteristics of GTC in the low-frequency band, and its negative resistance characteristics lead to system instability. (3) Different operating conditions affect the admittance characteristics of GTC. The injection of inductive reactive power is detrimental to system stability, and the injection of capacitive reactive power is the opposite.
keywords:Three-phase grid-tied converter, frequency coupling, symmetric control, weak grid, stability analysis
DOI: 10.19595/j.cnki.1000-6753.tces.222388
中图分类号:TM46
国家重点研发计划资助项目(2021YFB2601600, 2021YFB1600203)。
收稿日期 2023-01-03
改稿日期 2023-03-06
王 震 男,1996年生,博士研究生,研究方向新能源并网技术、能源交通融合。E-mail: wangzhen@ncepu.edu.cn
程 鹏 男,1988年生,博士,副研究员,硕士生导师,研究方向为新能源电力系统、新能源动力系统。E-mail: p.cheng@ncepu.edu.cn(通信作者)
(编辑 陈 诚)