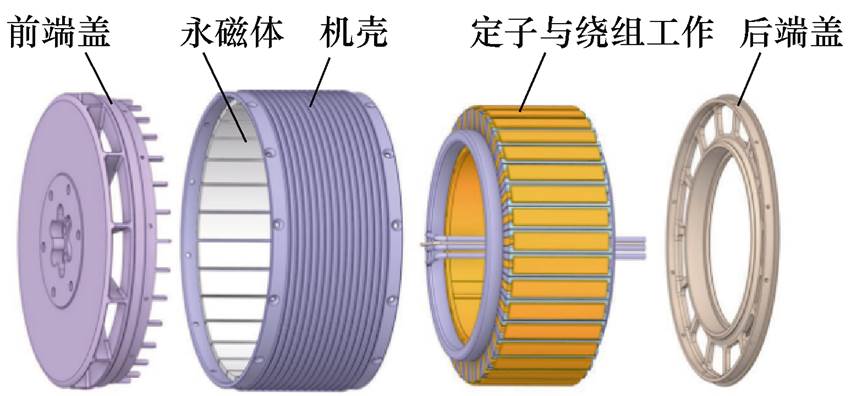
图1 17 kW表贴式PMSM-3D结构模型
Fig.1 17 kW surface-mounted PMSM-3D structure model
摘要 随着无人机的迅速发展，噪声问题影响消费者体验及AI交互、语音识别等技术，限制了无人机应用潜力。该文针对一台17 kW无人机用外转子永磁同步电机进行研究。为降低电机尖端振动噪声，且保留原电机电磁性能，重点提出优化磁极和定子开槽的方法。具体以平均转矩、转矩脉动等作为约束条件，构建多目标优化数学模型，并利用混合粒子群优化算法求解。该文深入探讨磁极参数、定子开槽对低阶次径向气隙磁通密度空间谐波特征的影响。并对电机转子模态仿真，以研究径向电磁力与空间模态的作用机理。在多转速情况下，以巡航转速为重点，分析整体电机电磁振动噪声特征。最后，仿真和实验结果表明，电机在巡航转速下的尖端噪声显著减小。验证了优化结构对无人机电机尖端振动噪声有明显抑制作用，对解决无人机噪声问题具有重要意义。
关键词：无人机外转子永磁同步电机 电磁振动噪声 巡航转速 混合粒子群优化算法
多旋翼无人机（Unmanned Aerial Vehicle, UAV）在政府公共服务和民用领域中发挥着日益重要的作用[1]。随着无人机技术的不断发展，其电机转速、功率和拉力也不断提高，导致振动、噪声和声音平顺性（Noise Vibration Harshness, NVH）问题日益严重。无人机的运行噪声不仅对消费者体验产生负面影响，还会干扰操作人员和周围环境，限制无人机在语音识别技术和人工智能交互等领域的应用潜力[2-3]。
因此，研究无人机噪声问题具有重要意义。特别是针对无人机的巡航噪声进行降噪优化，以减少其对人们生活的影响。在噪声问题中，无人机的噪声主要来自高速旋转的螺旋桨和永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）的电磁噪声。针对螺旋桨噪声产生机理和抑制方法的研究已经取得了显著成果，使螺旋桨噪声得到了有效改善[4]。因此，近年来，无人机电机辐射的噪声引起了越来越多的关注，成为一个新的研究重点。
在无人机降噪的研究中，文献[4]通过圆柱形微穿孔板吸收器与碳纤维多孔材料耦合的复合吸音结构降低了小型四旋翼无人机电机的噪声。文献[5]设计了一种用于无人机的无刷电机减振固定结构，通过优化定子齿轭参数和绕组排布策略，采取一体化处理的机座和固定底座，加强支撑定子铁心并填充缓冲材料，同时在模块之间设置弹性连接，以达到减少低阶径向激振力波。本研究是一款无人机外转子PMSM，故可参考PMSM的振动噪声研究。径向电磁力是中小功率电机电磁噪声的主要来源。文献[3-9]都对径向电磁力引起的振动和噪声给予了很大关注。文献[6]针对瓦片形磁极永磁电机中2p阶径向电磁力波引起的振动问题，提出了优化磁极参数的方法，但没有实验验证。文献[7]采用极间虚齿结构削弱表贴式PMSM的六倍频振动噪声，并通过实验验证了理论和有限元模型的正确性。文献[8]研究了电机的充磁方式对振动噪声的影响，发现在一定范围内气隙磁通密度3次谐波存在最优值，可减小电机振动噪声。文献[9]研究了一台40极240槽斜槽PMSM，发现零阶径向力引起的齿槽频次振动大于力波次数为极数40的2倍频径向振动。目前，国内外已有许多学者对电机振动噪声的削弱方法进行研究。文献[10]研究了隔离分数槽集中绕组永磁同步电机中不同设计参数对NVH性能的影响，并提出了集中单位力响应法来分析电磁和结构影响，用于NVH性能优化决策。文献[11-12]探讨了电机在不完全对称情况下对振动噪声产生的影响。文献[11]通过对受偏心率影响的电磁因素进行研究分析，构建了电机的整体结构模型，并将电磁特性分析结果应用于机械系统进行振动分析。文献[12]提出一种分段交错不等磁极的削弱方法，该方法有效保证了电机转矩密度。文献[13-17]致力于通过PMSM的结构优化来减少电机振动噪声。文献[13]基于结构优化的方法，研究了两相电流和电磁力诱导典型工况下的共振降噪。文献[14]提出一种新型定转子结构，通过仿真对比优化前后电机的电磁振动噪声，并发现电机结构优化后整体性能得到改善。文献[15]提出一种混合磁极转子结构来削弱低阶电磁激振力谐波分量进而抑制电磁振动。文献[16]针对内置式多层磁钢的PMSM，提出通过优化电机转子结构来抑制电机振动噪声的方法，并分析了极槽配合对振动噪声的影响。文献[17]以8极48槽永磁同步电机为例，建立了单层和双层永磁体两种内置式转子的有限元模型，通过仿真分析比较了两种电机的电磁振动噪声特性。上述对电磁振动噪声的削弱方法，主要对电机的几何结构进行优化。其他方法则主要关注电流激励对电磁振动噪声的影响。文献[18]以电动大巴车用72槽12极内置式PMSM为研究对象，采用定子绕组注入13次谐波电流的方法，削弱0阶径向电磁力波引起的振动噪声。文献[19]介绍了注入磁链谐波的方法，相对于传统磁场定向控制，该方法可降低电机的总声压级约10 dB。文献[20]分析磁致伸缩效应对铁心振动的影响，通过谐波电流注入法削弱电机的4倍频法向电磁力，进而抑制电机的4倍电频率振动。
综上所述，目前针对抑制电机电磁振动噪声的方法研究颇多，但是一些降噪方法会降低电机输出转矩或者提高制造成本和复杂性。本文针对一台17 kW无人机用表贴式PMSM，通过解析计算和有限元分析电机径向气隙磁通密度的频率特征与电机噪声。并在保持与原电机输出转矩几乎一致的基础上，提出一种优化磁极参数与定子开槽结构来抑制电机振动噪声。对比分析优化前后电机电磁性能和噪声特性变化。最后，通过实验验证了优化后结构对电机噪声具有削弱效果，同时证明了仿真结果的有效性。
PMSM的噪声辐射与电磁振动之间存在很强的关联性[21]。实践证明，通过优化电磁设计、改善电机磁通密度和电磁力波，可以有效改善电机的振动噪声性能。因此，针对PMSM的磁通密度、电磁力波和电磁振动噪声展开研究，将有助于揭示电机振动噪声的内在规律，对于电机噪声的抑制具有重要的理论意义和实用价值。
图1所示为无人机用17 kW表贴式外转子PMSM-3D结构模型，由前、后端盖、机壳、永磁体、定子以及定子绕组组成。
图1 17 kW表贴式PMSM-3D结构模型
Fig.1 17 kW surface-mounted PMSM-3D structure model
在17 kW的PMSM中，气隙磁场主要由永磁体（Permanent Magnet, PM）场和电枢反应（Armature Reaction, AR）场组成。定子开槽的效果始终作为相对渗透函数引入。当忽略磁路的饱和度时，由此产生的径向气隙磁通密度Br可以表示为
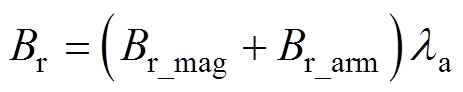（1）
式中，Br_mag为径向PM场气隙磁通密度；Br_arm为径向AR场气隙磁通密度；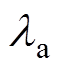
为相对磁导率实部。
其中，外转子PMSM的PM场径向气隙磁通密度表达式为
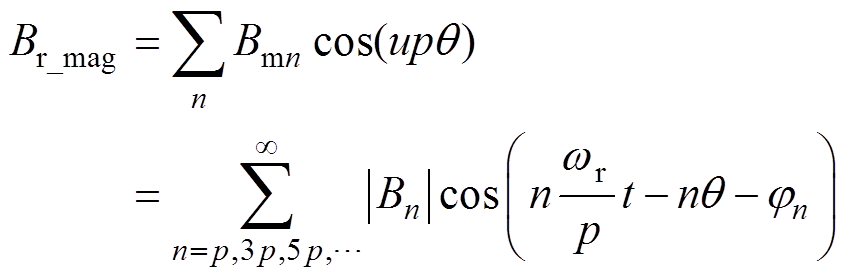（2）
式中，p为磁极对数；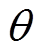
为空间机械角度；Bmn为n次PM场谐波幅值；|Bn|为n阶气隙磁通密度谐波幅值；jn为n阶谐波相位；u为PM场的空间阶数，且为奇数，
；
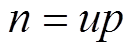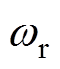为角速度；t为时间。为了便于叙述，下文均以谐波的空间阶数代指相应谐波。
表贴式外转子永磁体和气隙结构模型如图2所示。通过如图2所示的几何关系，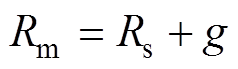
，
，
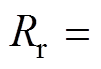
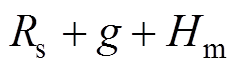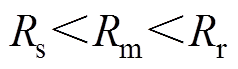。其中，Rs为定子半径；Rm为转子内径，Rr为电机轴心到PM外表面半径，g为气隙长度；Hm为PM厚度。推导出其在气隙区域中的磁场分量的径向气隙磁通密度表达式[22]为
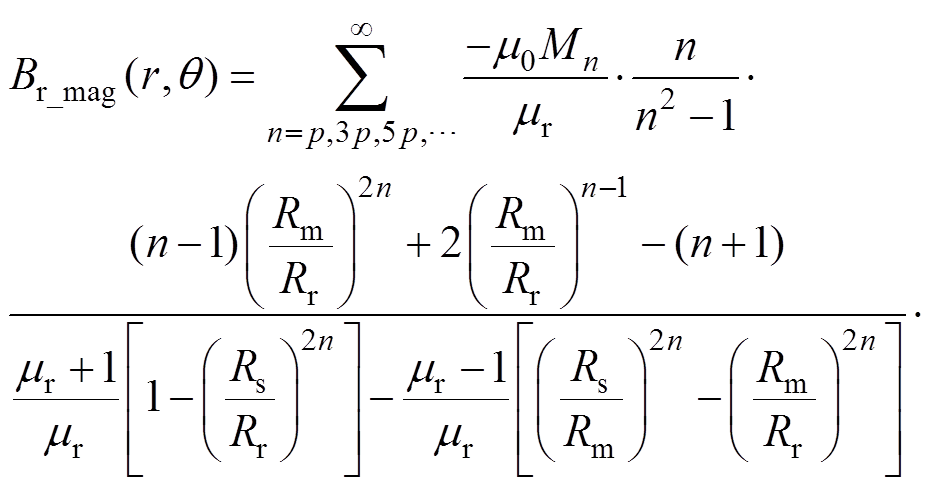
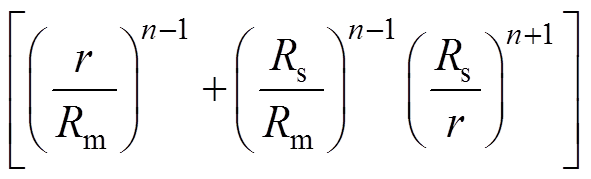（3）
其中
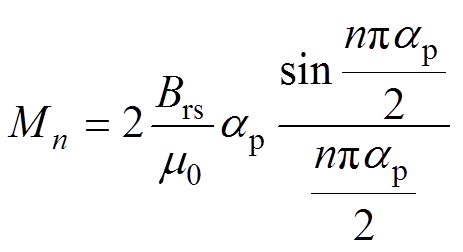（4）
式中，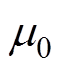
为真空磁导率，
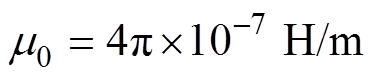；mr为相对磁导率；Brs为永磁体剩磁；
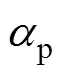为极弧系数。
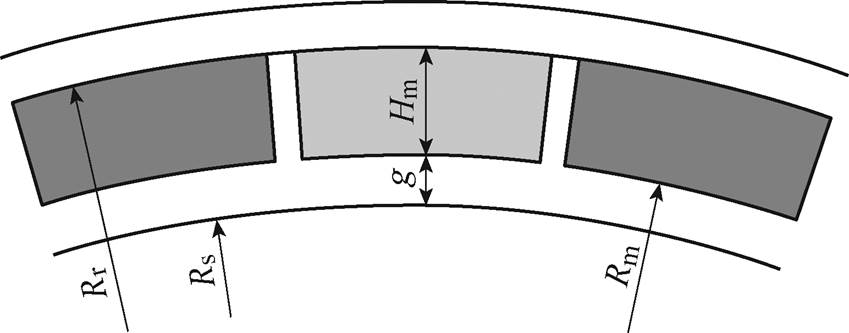
图2 表贴式外转子永磁体和气隙结构模型
Fig.2 Model of permanent magnet and air gap structure of surface-mounted external rotor
在转子坐标中，Br_arm和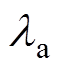可以表示为傅里叶级数的形式，有
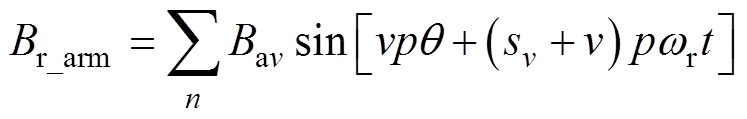（5）
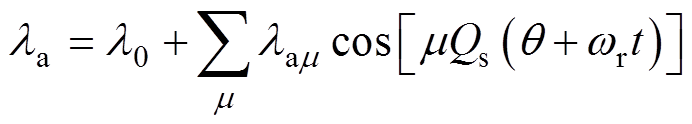（6）
式中，Qs为槽数；v、m 为电枢反应场的不同谐波阶数；sv为旋转方向；Bav为vp次AR场谐波幅值；l0为相对磁导率的直流分量；lau为mQs阶次相对磁导率幅值。
对于具有不同槽极组合和双层绕组的永磁同步电机，有
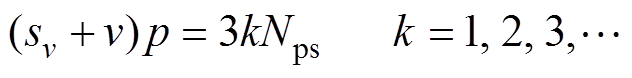（7）
其中
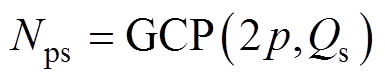
式中，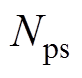
为极数和槽数的最大公约数。
根据麦克斯韦应力张量法[23-24]，忽略切向磁通密度分量，导致永磁体表面产生噪声的径向电磁力波可以表示为
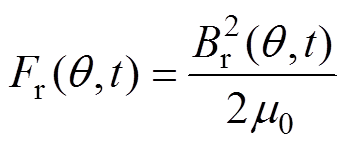（8）
将式（2）、式（5）、式（6）代入式（8），则有
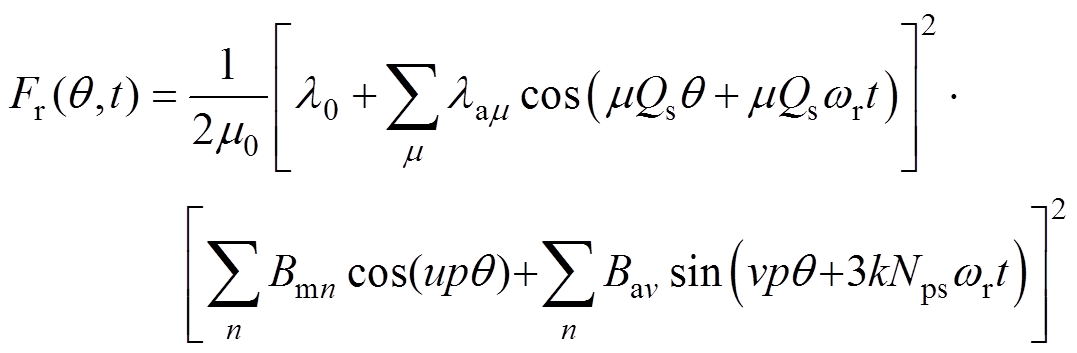（9）
根据多项式乘法规则，将式（9）展开可得到九项，根据来源可分为六类。利用三角函数的乘积求和公式推导得到这6个力源的振幅、频率，见表1，表中，fr为转子的旋转频率。
表1 径向电磁力密度的来源、振幅和频率
Tab.1 Sources, amplitudes and frequencies of radial electromagnetic force densities
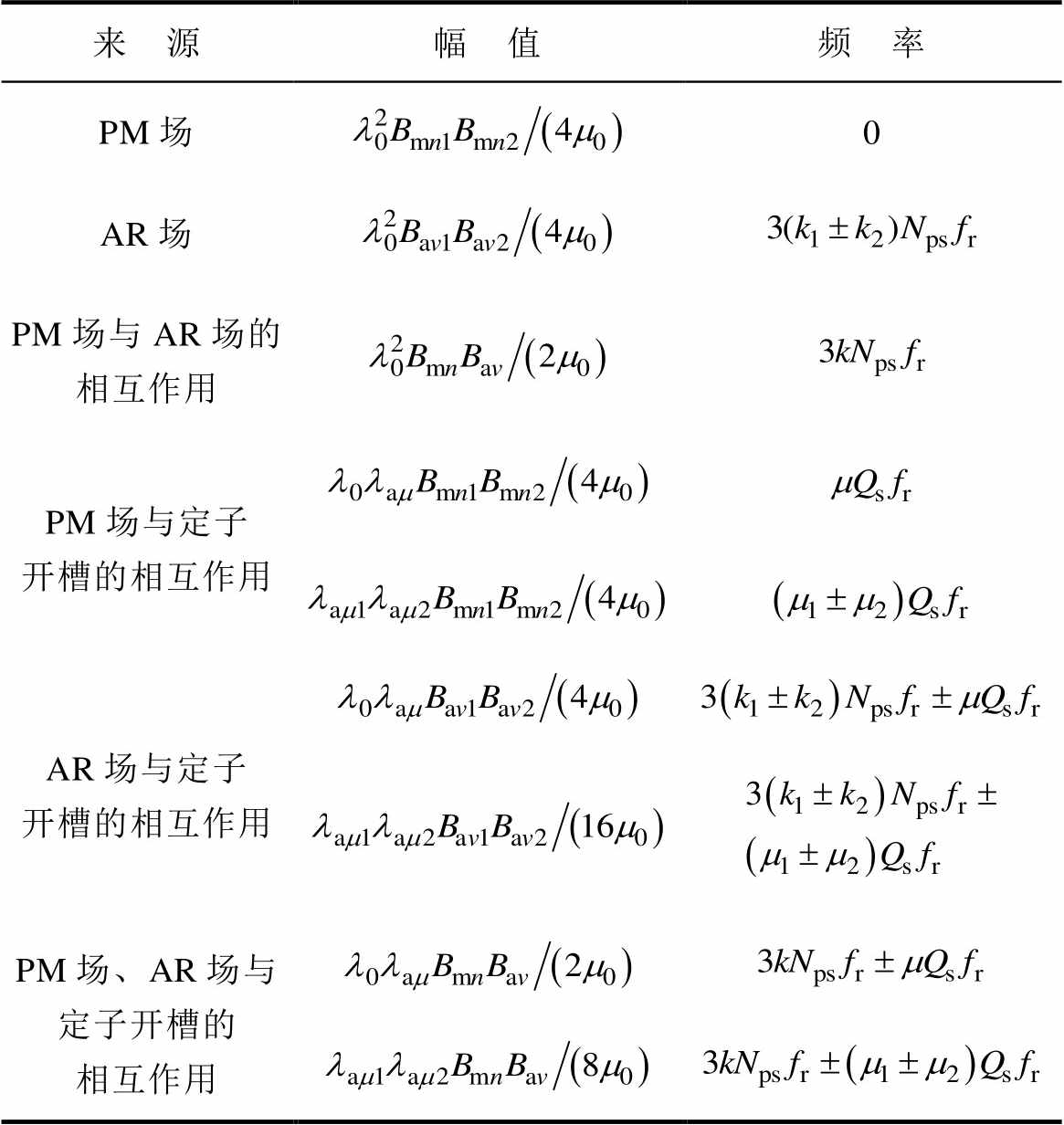
来 源幅 值频 率 PM场0 AR场 PM场与AR场的相互作用 PM场与定子开槽的相互作用 AR场与定子开槽的相互作用 PM场、AR场与定子开槽的相互作用
从表1可以看出，负载下的径向电磁力频率等于3kNps fr。当内转子电机通正弦电流激励时，作用在定子表面的径向电磁力的频率等于2kNps fr。因此，外转子PMSM辐射噪声的频率特性与内转子PMSM是不同的。但是，这两种PMSM的空间特征是相同的。空载下的径向电磁力频率等于mQs fr，来自永磁场和定子开槽的相互作用。考虑通过优化磁极参数、调整槽口大小改变各次气隙磁通密度谐波的幅值和分布，进而改变径向电磁力波各谐波力分量，最终达到减小电机电磁振动及噪声的目的。
本研究采用的电机为无人机用外转子PMSM，样机基本参数见表2，永磁体采用径向充磁方式。
表2 无人机用外转子PMSM基本数据
Tab.2 Basic data of external rotor PMSM for drones
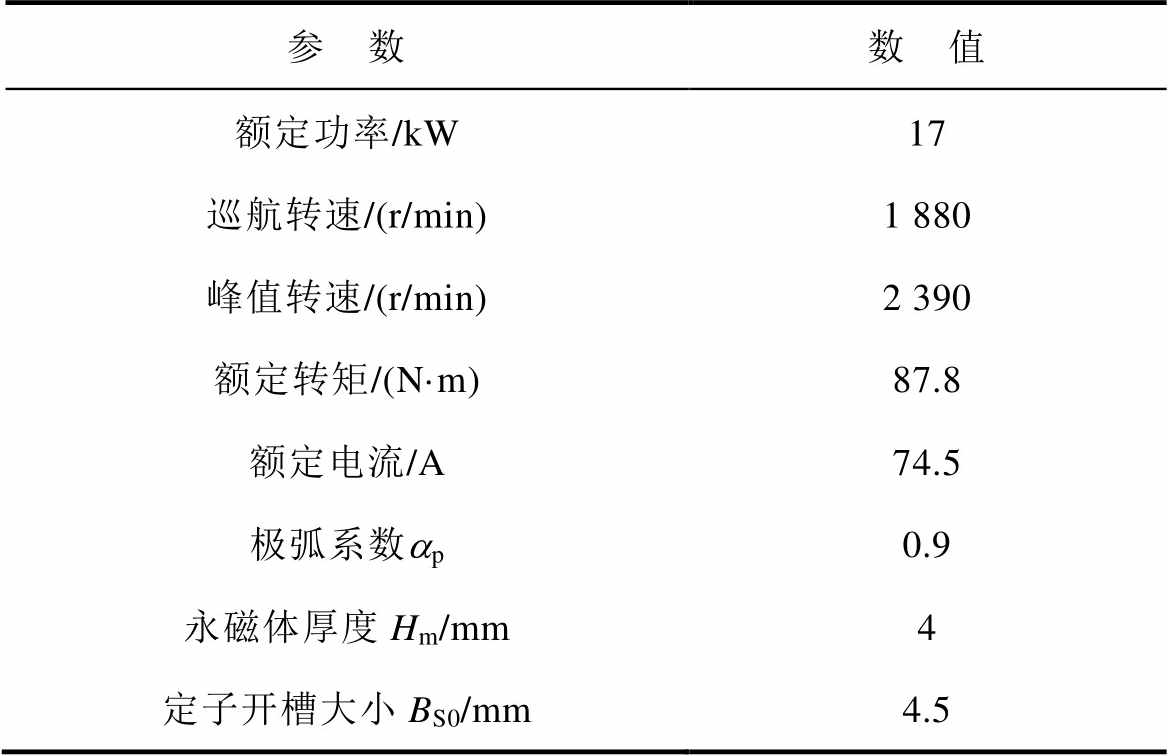
参 数数 值 额定功率/kW17 巡航转速/(r/min)1 880 峰值转速/(r/min)2 390 额定转矩/(N·m)87.8 额定电流/A74.5 极弧系数ap0.9 永磁体厚度Hm/mm4 定子开槽大小BS0/mm4.5
由于径向气隙磁通密度、径向电磁力是产生电机振动噪声的原因[25]，故优先分析磁极参数、槽口大小对径向气隙磁通密度、径向电磁力的影响。在众多径向气隙磁通密度谐波分量中，对电机电磁振动噪声起决定作用的主要为空间阶次较低、幅值较大的谐波分量[26]。
首先对电机巡航转速下径向气隙磁通密度进行快速傅里叶变换（Fast Fourier Transform, FFT）分析，如图3所示。由于电机采用分数槽设计，气隙磁通密度谐波分量较整数槽电机更加丰富，会产生分数次谐波。但从图3可以观察到分数次谐波幅值并不高，所在区域为低幅值谐波区域；低次谐波中，3、5次谐波幅值较大，对所产生的电磁振动噪声影响较大，其余次谐波幅值较低；高次谐波相互作用产生的谐波因其幅值较小，对基波影响不大。且外转子机壳振动形变与力波空间阶次的四次方成反比，高阶力波所激发的电磁振动噪声较小，故可忽略不计。
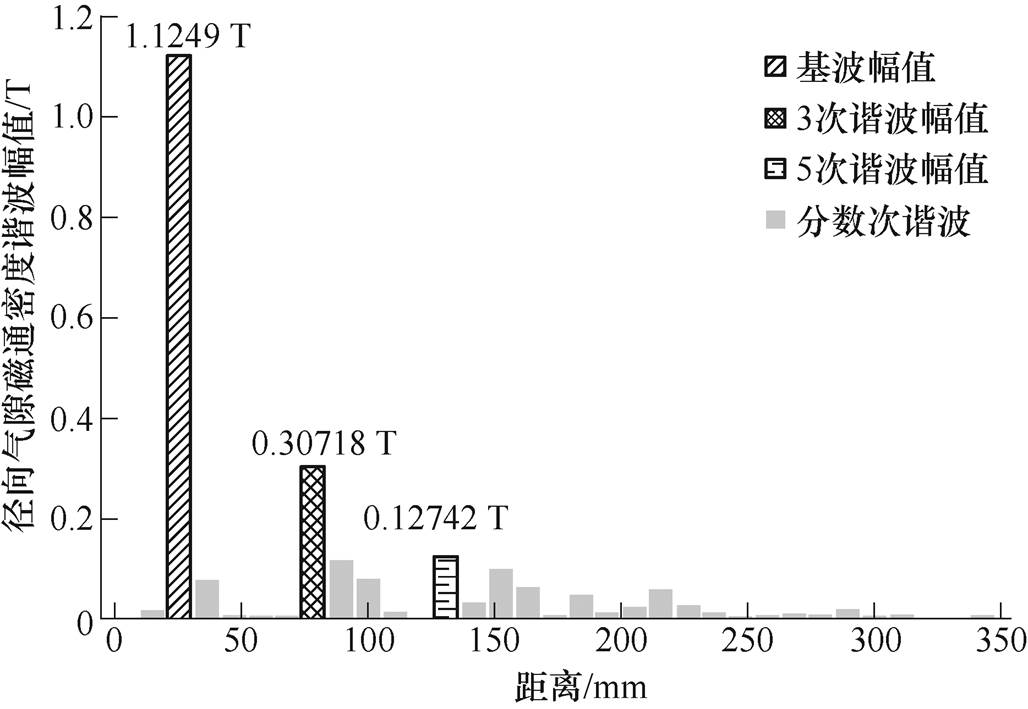
图3 电机径向气隙磁通密度FFT分析
Fig.3 FFT analysis of motor radial air gap magnetization
综上所述，需探究极弧系数、磁极厚度以及定子开槽大小与3、5次径向气隙磁通密度幅值的关系。最终通过优化三者的结构参数，降低3、5次径向气隙磁通密度幅值以减小电机振动噪声。
1.2.1 极弧系数、磁极厚度与定子开槽对气隙磁通密度基波幅值影响
为了研究极弧系数ap、磁极厚度Hm与定子开槽大小BS0对气隙磁通密度基波幅值Br1的影响，以ap、Hm与BS0为输入变量，Br1为输出变量。计算不同ap、Hm、BS0下各次谐波的幅值。三者与Br1的关系如图4所示。
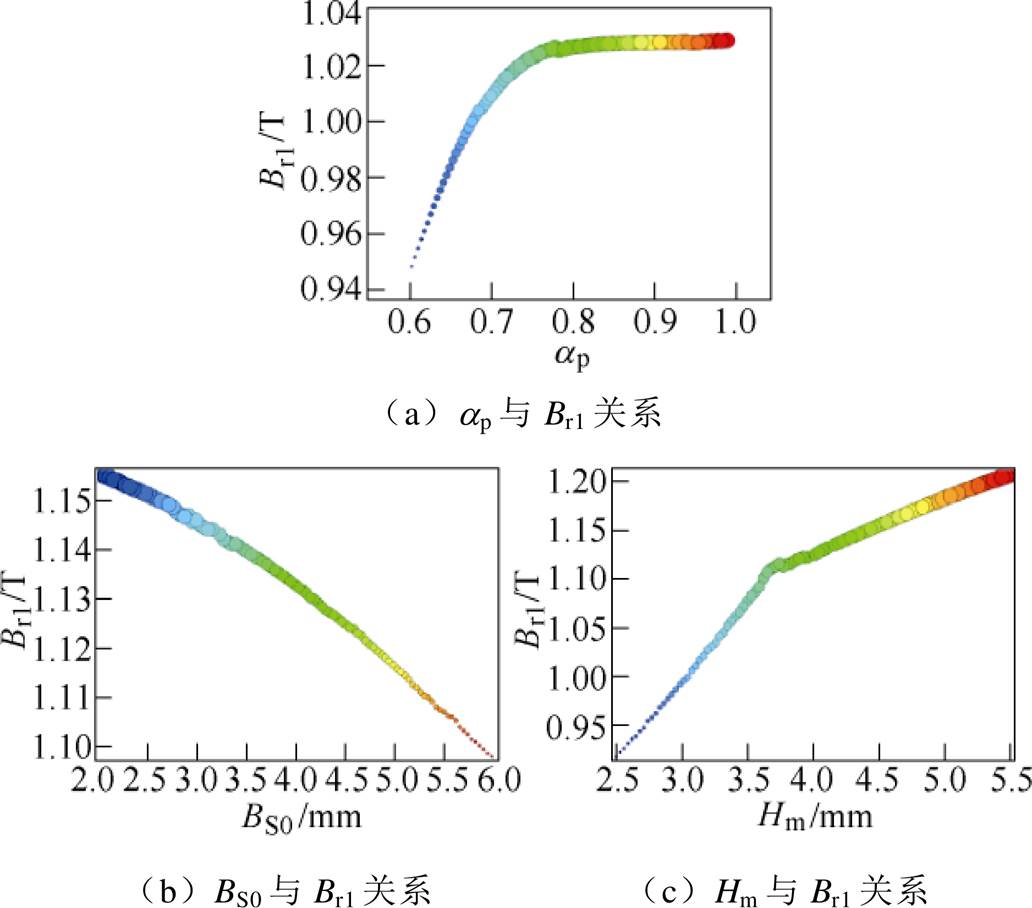
图4 各参数与Br1关系
Fig.4 Relationship diagram between various parameters and Br1
由图4可知，随着极弧系数ap与磁极厚度Hm的增加，Br1呈现出增长的趋势；当ap达到0.8后，其增长率趋于稳定；当Hm达到3.7 mm后，基波幅值增长率变小，但依旧呈正线性相关。而当定子开槽BS0增加时，Br1呈现出负增长的趋势。
1.2.2 极弧系数对气隙磁通密度3、5次谐波幅值影响
为了研究极弧系数ap对低次谐波的影响，以ap为输入变量，气隙磁通密度3次谐波幅值Br3与5次谐波幅值Br5为输出变量。由图4可知，当ap取值过小时，不仅会影响基波气隙磁通密度幅值，而且会降低电机整体性能，例如电机转矩。原电机电磁方案极弧系数为0.9，故选取ap=0.6～0.99进行计算，磁极厚度、定子开槽大小与原始样机相同。利用公式计算径向充磁时不同极弧系数下3、5次谐波的幅值。ap与输出变量的关系如图5所示。
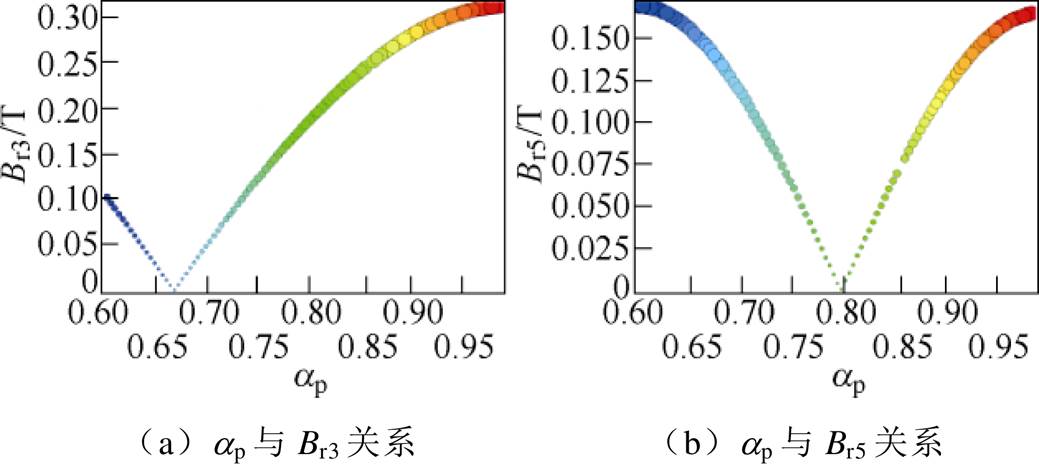
图5 极弧系数与3、5次谐波关系
Fig.5 Plot of polar arc factor versus 3rd and 5th harmonics
由图5可知，随着ap的增加，空间气隙磁通密度谐波幅值Br3与Br5都呈现出先减小再增大的趋势。当ap在0.67附近时，Br3达到最小；当极弧系数在0.8附近时，Br5达到最小。
1.2.3 磁极厚度对气隙磁通密度3、5次谐波幅值 影响
磁极厚度Hm取值过小会导致气隙磁通密度基波幅值过小，由于气隙长度限制，Hm取值不宜过大，故取Hm=2.5～5.5 mm，充磁方向为径向充磁，极弧系数、定子开槽大小与原方案一致。与1.2.2节类似，计算不同极弧系数下3、5次谐波的幅值。磁极厚度与低次谐波影响计算结果如图6所示。
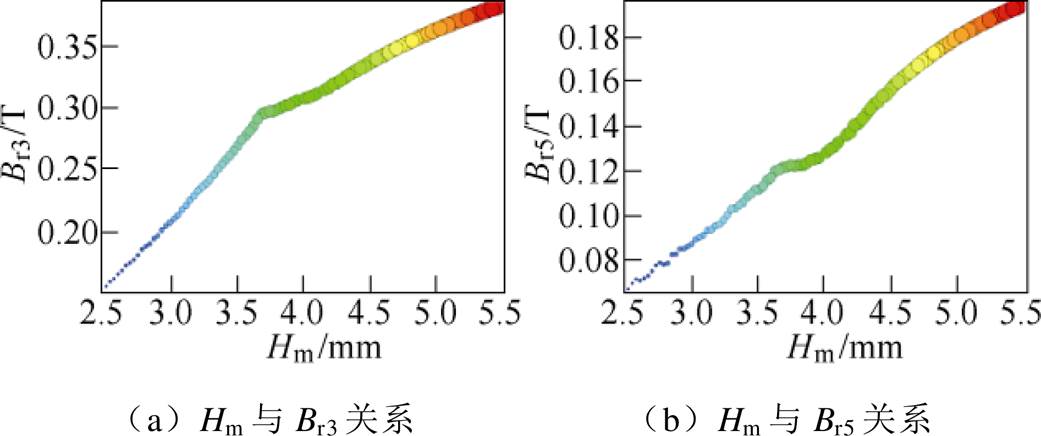
图6 Hm与3、5次谐波关系
Fig.6 Hm versus 3rd and 5th harmonics
由图6可知，随着Hm的增加，空间气隙磁通密度的3次谐波幅值Br3与5次谐波幅值Br5都呈现正相关的趋势。
1.2.4 定子开槽对3、5次气隙磁通密度谐波幅值影响分析
与1.2.3节类似，取BS0=2～6 mm进行计算分析，极弧系数、永磁体厚度与原方案一致。计算径向充磁时不同极弧系数下3次谐波与5次谐波的幅值。BS0对3、5次谐波幅值影响计算结果如图7所示。
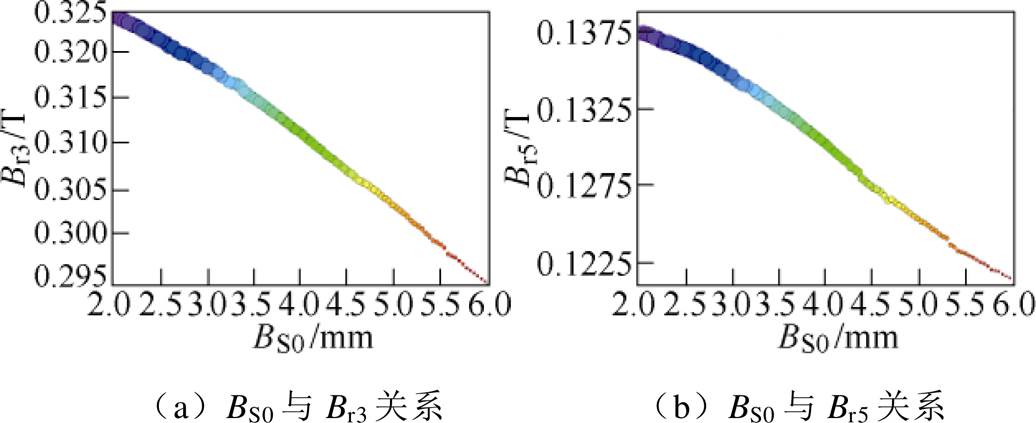
图7 定子开槽与3、5次谐波关系
Fig.7 Stator slotting versus 3rd and 5th harmonics
由图7可知，随着BS0的增加，空间气隙磁通密度的3次谐波幅值Br3与5次谐波Br5幅值呈现负相关关系。
17 kW无人机用外转子PMSM，电机为分数槽双层绕组设计，具有15对极和36个定子槽。对于30极/36槽的PMSM，其极数和槽数的最大公因式Nps=6。在电磁力的分析上可以认为该PMSM由6个5极/6槽电机组成。在借助Maxwell设计电机时，设计为1/6电磁模型，图8为1/2电磁结构模型。
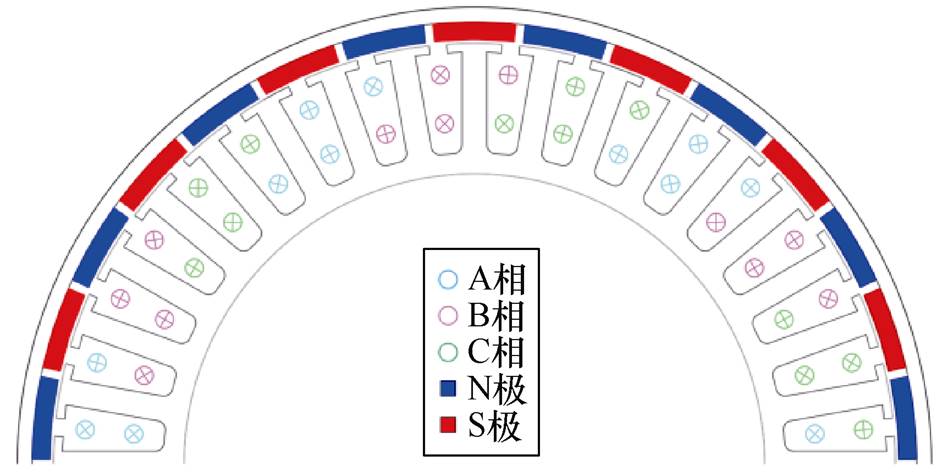
图8 电机电磁结构模型
Fig.8 Motor electromagnetic structure model
分析电机在空载工况与额定电流负载工况下的径向气隙磁通密度。借助有限元仿真软件计算空载和带载情况下，径向气隙磁通密度在一个电周期内空间一周的二维时空分布，结果如图9所示。
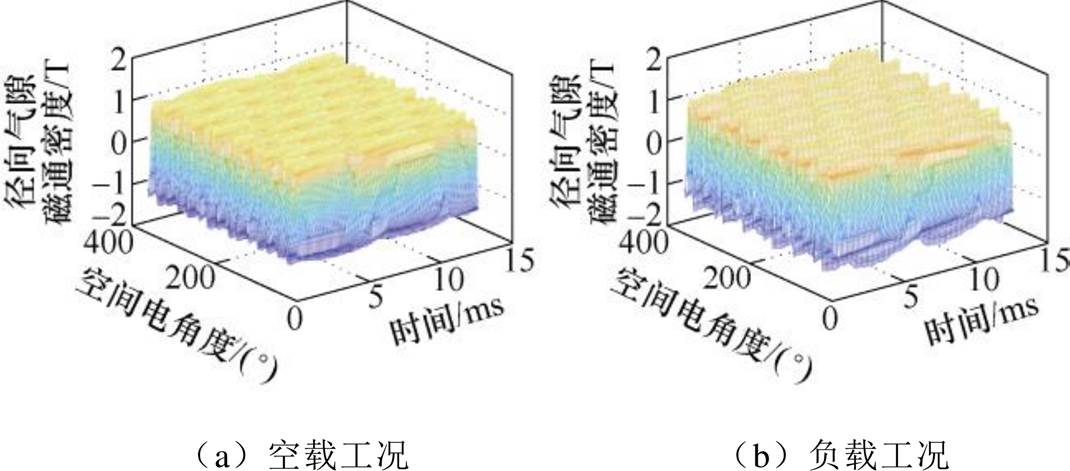
图9 径向气隙磁通密度分析
Fig.9 Radial air gap magnetic density analy
对上述计算的径向气隙磁通密度在一个电周期内空间一周的二维时空分布进行二维FFT分解，结果如图10所示。
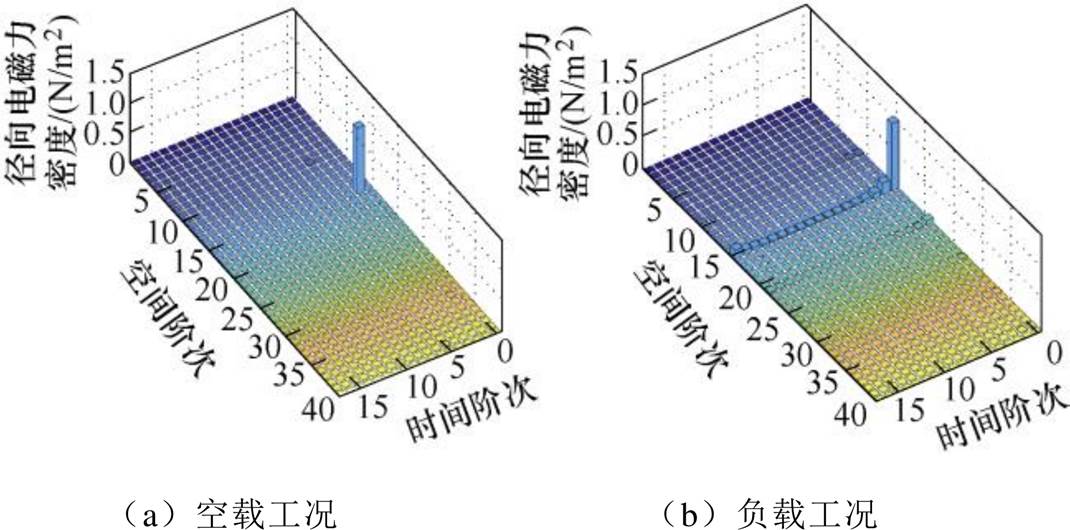
图10 径向气隙磁通密度FFT分析
Fig.10 Radial air gap magnetic density FFT analysis
由图10可知，径向气隙磁场的空间基波、3次及5次谐波幅值较高，由于AR场的介入，负载工况下的径向气隙磁场谐波更加丰富。
建立多物理场模型来计算PMSM的振动和噪声。首先，建立二维电磁有限元模型，计算永磁体表面的节点力，三维完整模型中的节点力是根据PMSM的周期性获得的，并假设电磁力在轴向上均匀分布。然后，建立PMSM三维结构模型，进行模态仿真，节点力通过插值从电磁模型加载到结构模型。这样，就考虑到了电磁力的不均匀分布。最后，采用模态叠加法计算振动和噪声。PMSM噪声计算的一般过程如图11所示。
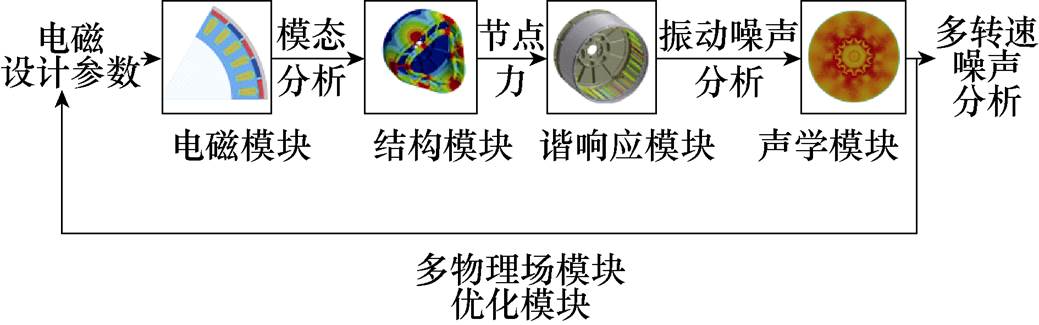
图11 PMSM的噪声计算程序
Fig.11 Noise calculation program for PMSM
电机的电磁噪声除了与气隙磁场产生的电磁力波频率、阶数和幅值有关之外，还与电机的结构固有模态有关。外转子电机电磁噪声主要由电机转子及壳体的振动产生。因此，提前通过仿真预估转子的固有频率，并将电磁力频率和转子固有频率错开，是减小电磁噪声的有效手段。
借助Workbench平台搭建电磁-结构耦合分析模型。构建了一个精确的有限元结构模型来预测转子的振动。转子结构由转子外壳、PM、内端和外端盖组成。图12为电机实物图与有限元结构模型。
图12 PMSM转子模型
Fig.12 PMSM rotor model
当电机径向力波频率与转子的某阶固有频率相等或相近时，就会引起共振。此时，即使径向力波的幅值不大，也会导致转子较大的振动，进而产生较大的电磁噪声。对电机噪声而言，最重要的是空间振型六阶以下的固有模态与固有频率。其对应的电磁力波频率波形，分别如图13和图14所示，图中，r为空间阶次，m为时间阶次。
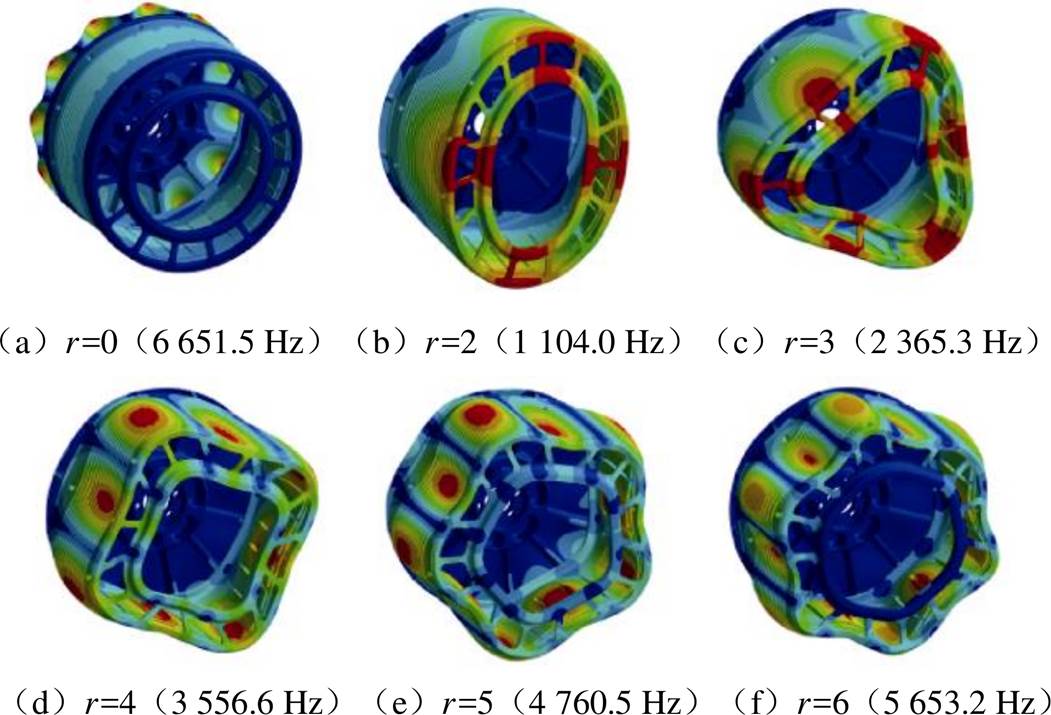
图13 电机转子固有模态
Fig.13 Inherent modes of the motor rotor
图14 电磁力波频率波形
Fig.14 Electromagnetic force waves frequency waveform
由于Nps=6，能引起电机共振的模态为空间r=6阶与空间r =0阶。通过解析法计算径向电磁力频率。在全工况转速下，得到转子与转子、定子与转子、定子与定子相互作用产生的径向电磁力波和空间6阶、空间0阶模态作用曲线。
电磁力波与模态空间交互图如图15所示。图中，f为电流频率。由图15可知，5 600 Hz频率线分别与空间6阶14f、16f、20f、22f相交，6 500 Hz频率线分别与空间0阶12f、18f、24f相交，这些交点是电磁力频率与模态频率接近的点，有可能会产生共振以及尖端噪声。
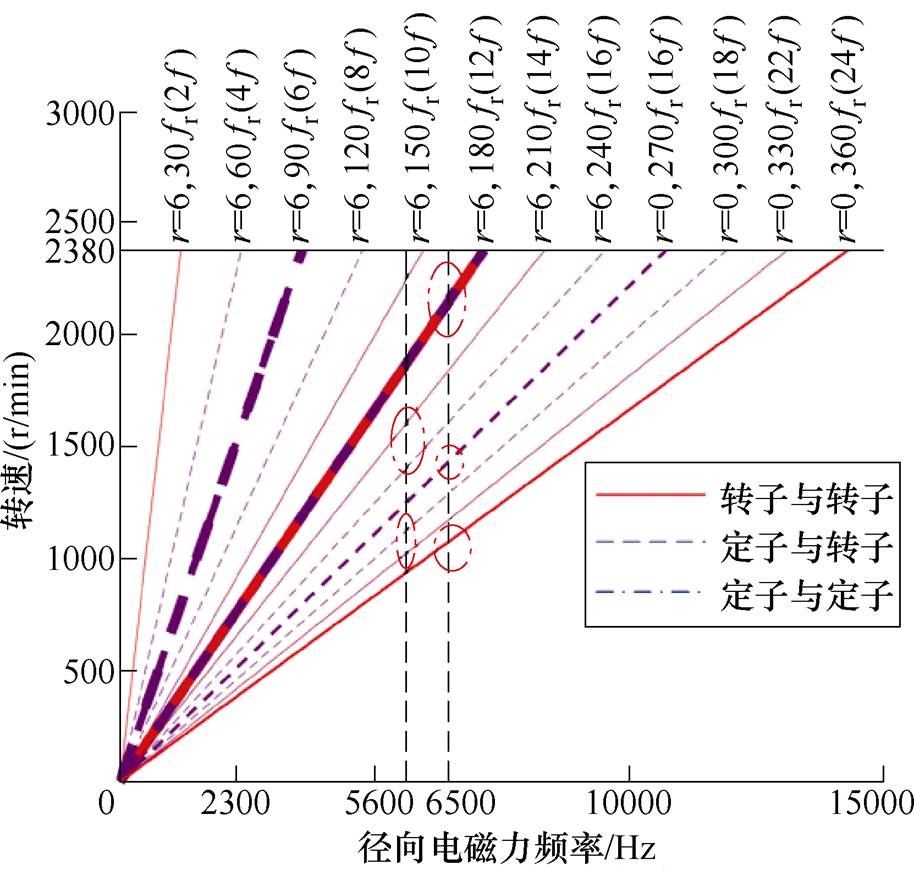
图15 电磁力波与模态空间交互图
Fig.15 Electromagnetic force waves interacting with the modal space
为更好地了解该电机的振动噪声特性，对电机进行振动噪声仿真。首先建立电机声场模型。声场共分为最外层的物理层区域和内侧的声学区域。为了便于网格剖分，将最外侧的物理层区域进行分割。图16所示为导入巡航转速点1 880 r/min的声场模型。
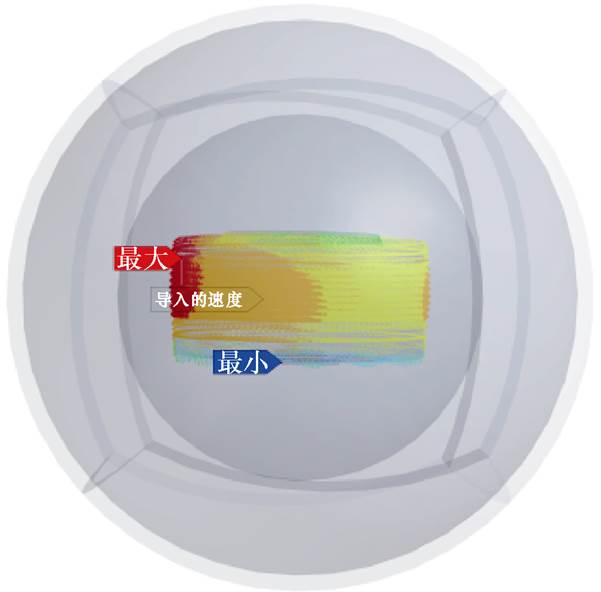
图16 声场模型
Fig.16 Sound field model
在额定电流下，设置电机转速从低转速130 r/min到峰值转速2 380 r/min，共10个步长，对电机空载和负载两种情况进行多工况全速域噪声分析。图17所示分别为电机在空载和额定负载工况下的等效辐射功率级瀑布图。
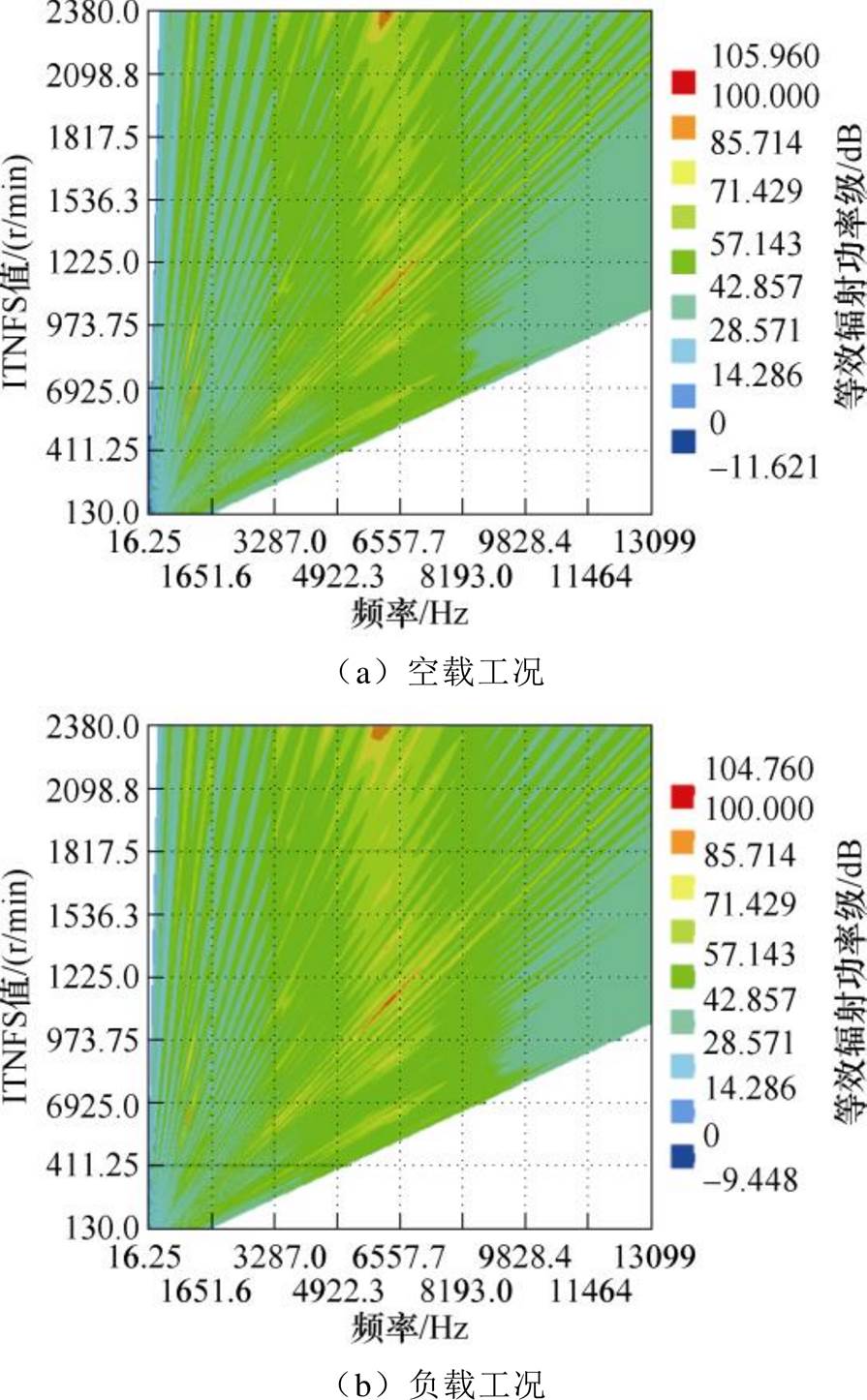
图17 等效辐射功率级瀑布图
Fig.17 Waterfall diagram of equivalent radiated power levels
由图17可知，多转速下在6 500 Hz左右，电机空载和带载的噪声频率带最为明显，这与2.1节电磁力波仿真结果保持一致。在带载情况下的噪声比空载的噪声稍丰富，二者等效辐射功率瀑布图波形几乎一致。
由于无人机长时间处于巡航工作状态下，故对巡航转速进行声仿真是必要的。图18所示为电机在巡航转速下空载和额定负载工况进行噪声仿真。由图18可知，电机在6 500 Hz附近出现较大的噪声带，出现尖端噪声，且超过70 dB。分别对应空间模态为6阶与0阶。可以看出，空间0阶模态对电机噪声的影响最大，且在6 580 Hz处出现最大噪声为74.22 dB。空载与带载情况下的噪声波形几乎一致，空载噪声比带载情况低2～3 dB，且在噪声带处的尖端噪声差异很小。
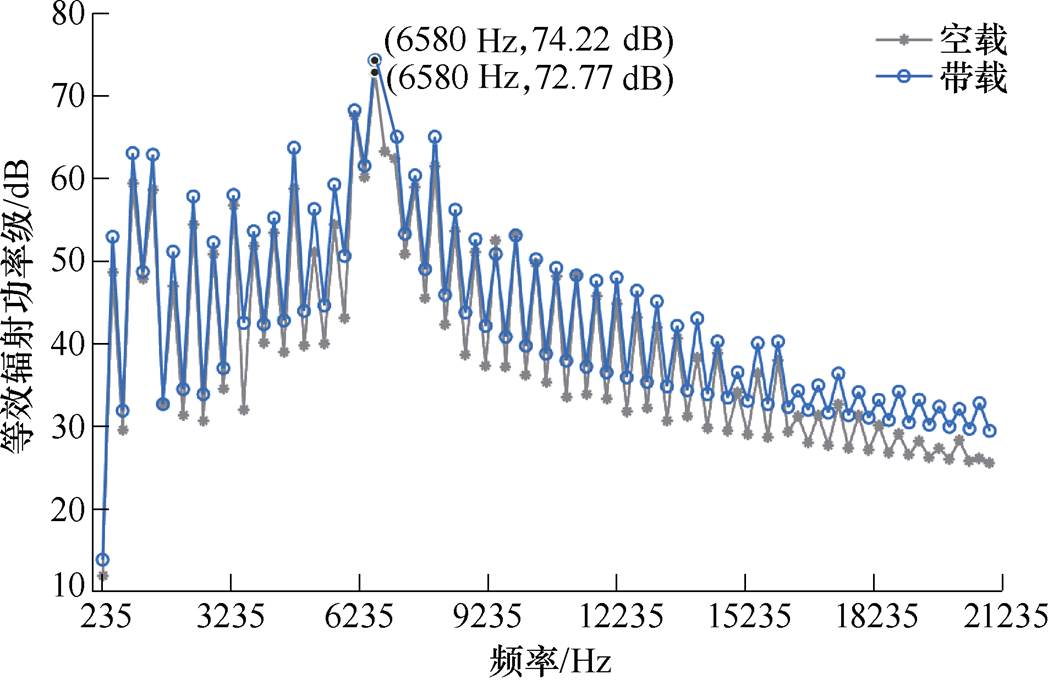
图18 巡航转速等效辐射功率级
Fig.18 Cruise speed equivalent radiated power level
根据图18，噪声带对应的声压级数值较大。且人耳长时间处于大于70 dB的环境中会受到较大的损伤。因此，需要采用合适方法对该电机的噪声进行优化。
首先确定优化目标以及输入参数，引入综合优化目标函数来评估电机的性能。在径向充磁条件下，以3、5次径向气隙磁通密度谐波为优化目标，ap、Hm以及BS0作为输入参数变量，最小化径向气隙磁通密度谐波幅值为优化目标，借助解析法建立目标函数表达式。
对于目标函数约束条件，优化设计需要保证电机转矩性能，转矩性能变化必然会影响到电机的工作性能。因此，约束条件必须满足以下两个要求：①输入参数的范围必须在设计参数的最大值和最小值范围内；②在不影响平均转矩Tavg与转矩脉动t 条件下，对输入电机结构参数进行优化。
综合考虑，本文选择了Tavg变化范围不大于1%且t 值小于等于原方案值（3.56%），径向气隙磁通密度基波幅值误差范围不超过3%作为约束条件。目标函数与约束条件表达式为
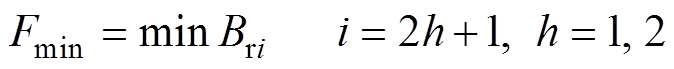（10）
（11）
其中
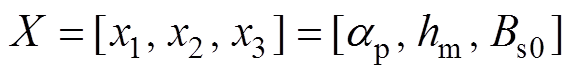
式中，Tcons为原方案平均转矩；tcons为原方案转矩脉动；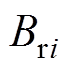
为i阶次谐波幅值；
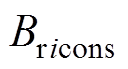为原方案i阶次谐波幅值。原方案设计参数的初始值和优化约束范围见表3。
表3 原方案参数初始值与优化约束范围
Tab.3 Initial values of the original scheme parameters and optimized constraint ranges
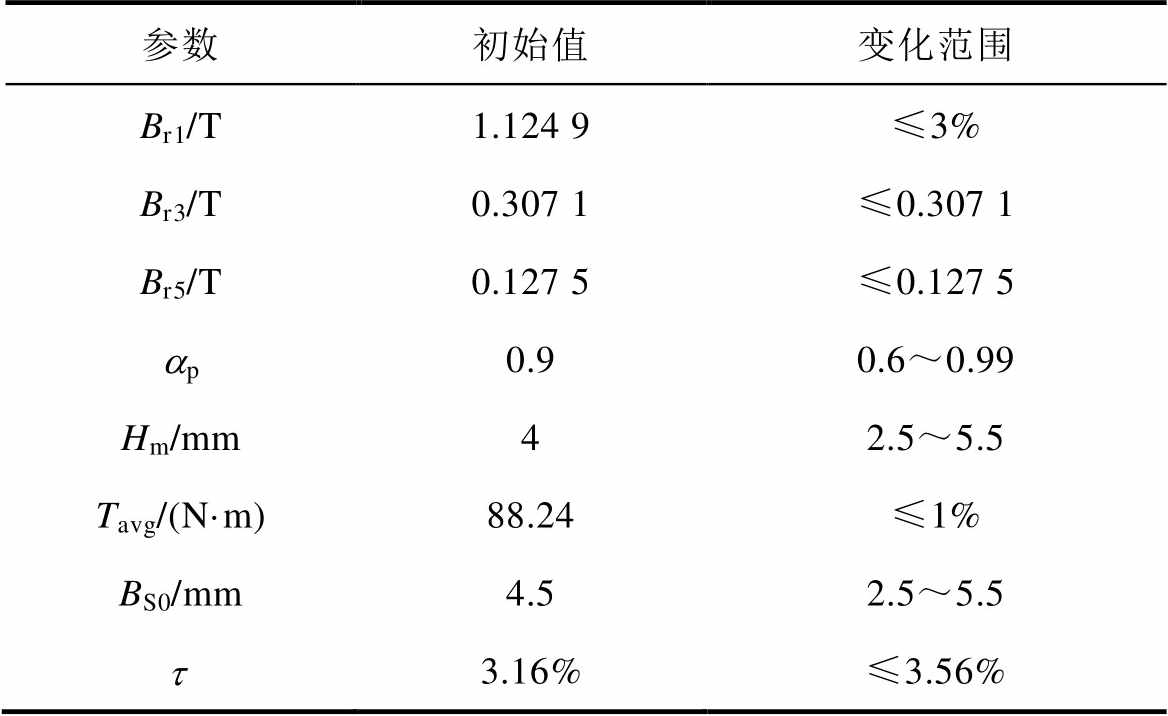
参数初始值变化范围 Br1/T1.124 9≤3% Br3/T0.307 1≤0.307 1 Br5/T0.127 5≤0.127 5 ap0.90.6～0.99 Hm/mm42.5～5.5 Tavg/(N·m)88.24≤1% BS0/mm4.52.5～5.5 t 3.16%≤3.56%
为了更好地体现输入参数与优化量之间的关系。引入灵敏度矩阵M为
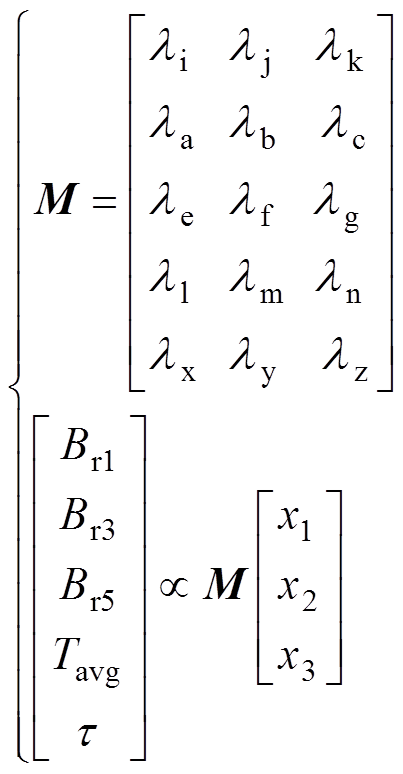（12）
式中，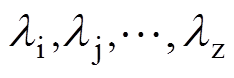
分别为设计参数x1、x2与x3对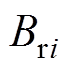、Tavg与t 的灵敏度因子。借用软件求得灵敏度矩阵M见表4。
表4 灵敏度矩阵
Tab.4 Sensitivity matrix
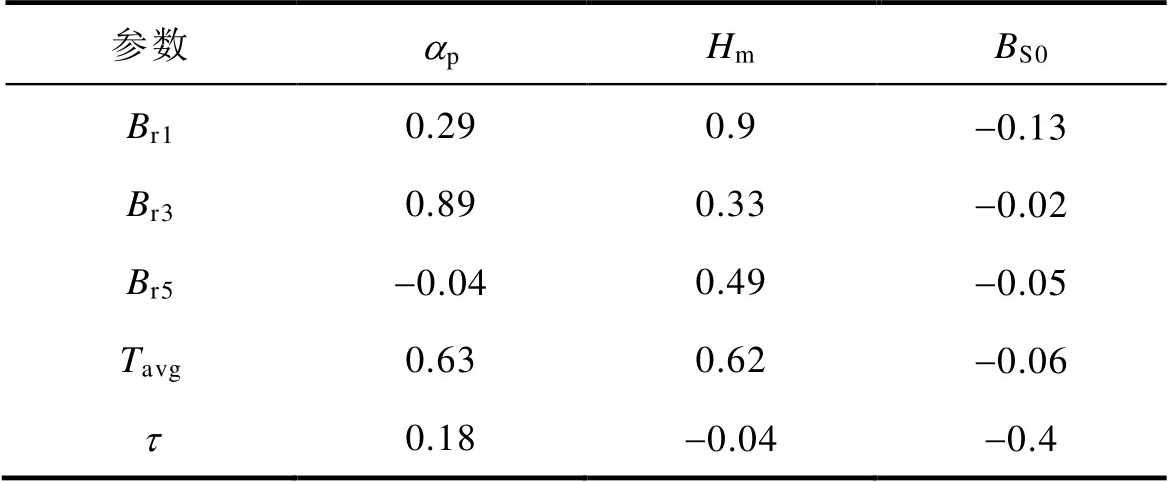
参数apHmBS0 Br10.290.9-0.13 Br30.890.33-0.02 Br5-0.040.49-0.05 Tavg0.630.62-0.06 t0.18-0.04-0.4
灵敏度绝对值越大，则表示设计参数对输出参数的影响越大。由表4可知，极弧系数ap对Br3的灵敏因子达到了0.89，永磁体厚度Hm对Br1、Br5的灵敏因子分别达到了0.9和0.49；Hm与ap对平均转矩的灵敏因子分别达到了0.62、0.63；BS0对转矩脉动的灵敏因子达到了-0.4。
对于多目标优化问题，采用混合粒子群优化算法对电机进行参数优化求解。在设计空间均匀选取了9 900个优化数据样本点阵。最后在约束条件下，求解得到如图19所示优化结果。
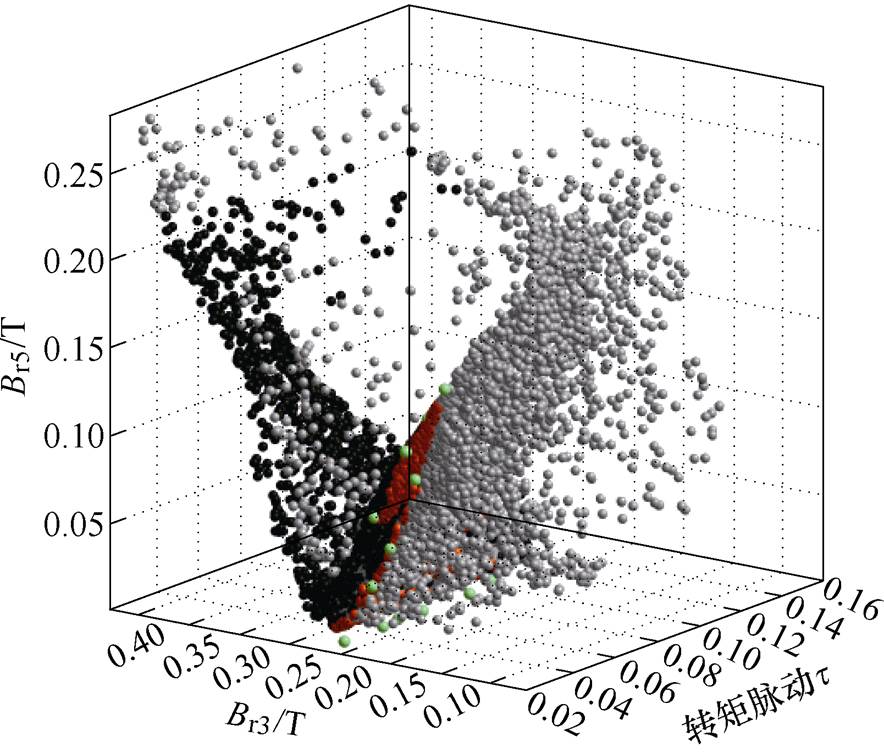
图19 数据点优化结果
Fig.19 Data point optimization results
图19中，灰色数据点为不满足约束条件的优化点；黑色数据点为满足样本优化约束条件的优化点；红色区域为帕累托最优解集；绿色数据点为验证设计点。最终筛选出3个备选优化方案，见表5。
表5 结构优化方案
Tab.5 Optimization plan for rotor magnetic pole
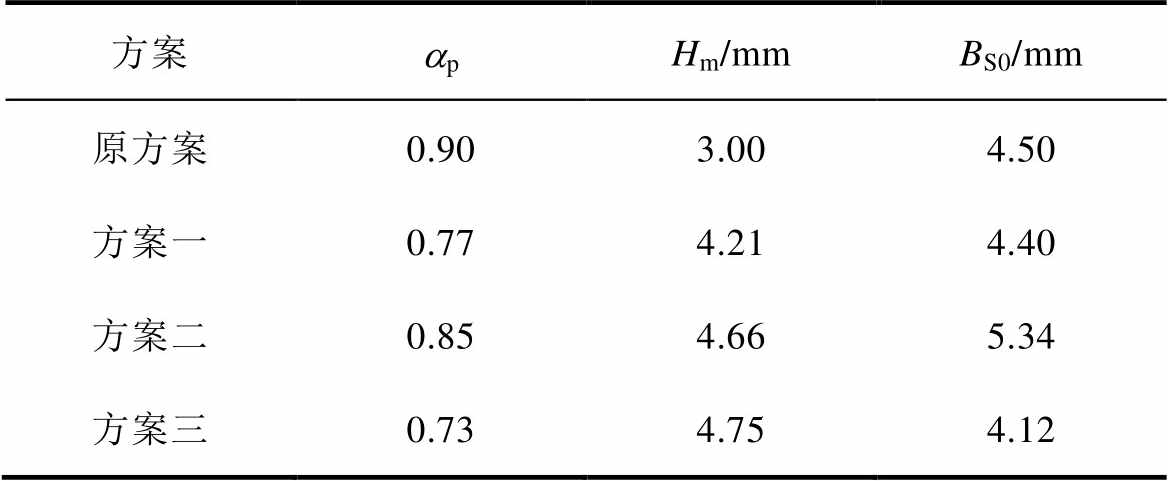
方案apHm/mmBS0/mm 原方案0.903.004.50 方案一0.774.214.40 方案二0.854.665.34 方案三0.734.754.12
建立不同方案下电机转子结构有限元仿真模型，对径向气隙磁通密度进行傅里叶变换分解得到其谐波分布如图20所示，为方便观察，分数次谐波未显示。
各方案基波幅值Br1基本保持不变，方案一比原方案的径向气隙磁通密度3阶、5阶分量幅值下降了45.57%、60.92%；方案二保持3阶幅值分量与原方案基本持平，5阶分量幅值下降了30.79%；方案三保持5阶幅值分量与原方案基本持平，3阶分量幅值下降61.59%。
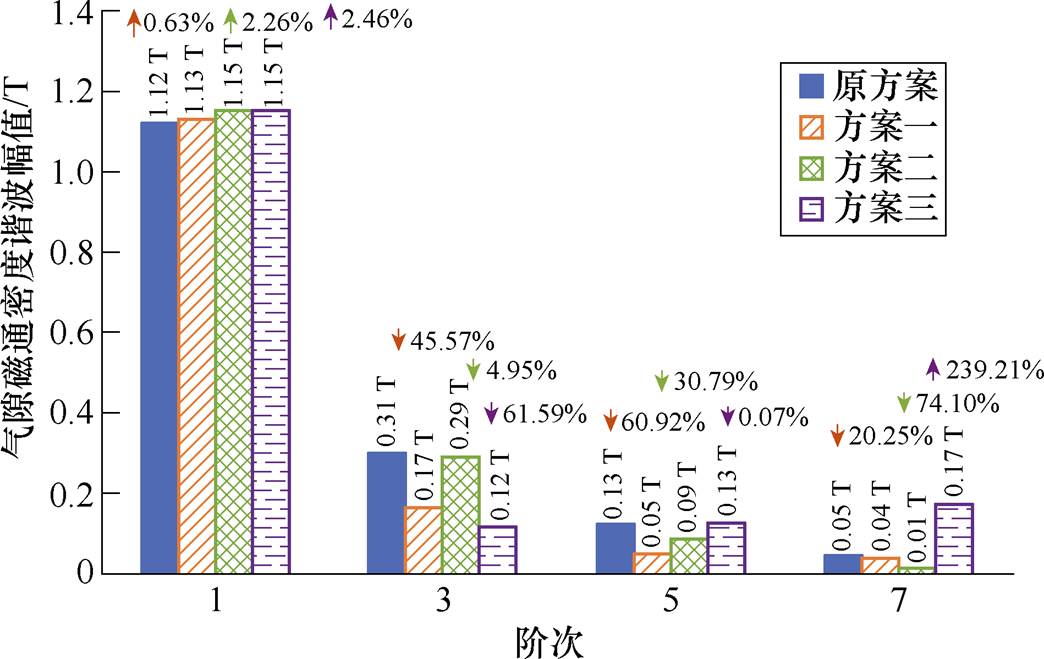
图20 径向气隙磁通密度谐波对比
Fig.20 Radial air gap flux density harmonic comparison
通过仿真得到各方案下径向电磁力密度时空分布，并对其进行快速傅里叶分解，图21所示为前三整数阶电磁力峰值FFT对比。在0阶径向电磁力分量中，方案一与方案三的电磁力幅值下降分别为5.88%、1.84%；在2阶分量中，各个方案均有不同程度下降，依次为33.03%、5.83%、39.38%；对于径向电磁力4阶分量，方案一和方案二的幅值分别下降6.81%、23.68%，方案三的幅值略微上升。由于电机振动时动态形变的振幅与电磁激振力空间阶数的4次方成反比，故径向电磁力0阶分量在电机中起重要作用，因此方案一对于电磁激振力的抑制效果最佳。
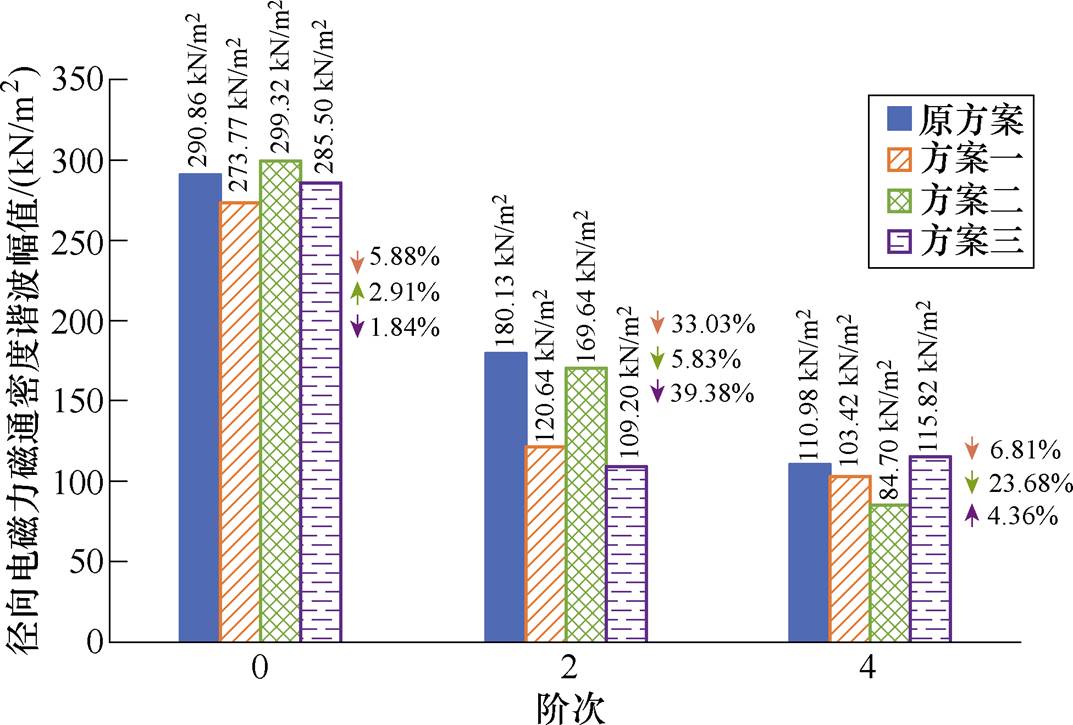
图21 径向电磁激振力FFT优化前后对比
Fig.21 Comparison before and after FFT optimization of radial electromagnetic excitation force
构建各个方案下的新结构电机磁-结构固耦合模型，计算其声功率级。针对电机转子以及定子槽口进行优化设计，在振动噪声有限元计算中忽略了电机的定子部分，对转子磁极部分重新进行建模。各方案下电机巡航转速等效辐射功率级如图22所示，图中标注的数据点为原方案在不同频率点的声功率级。
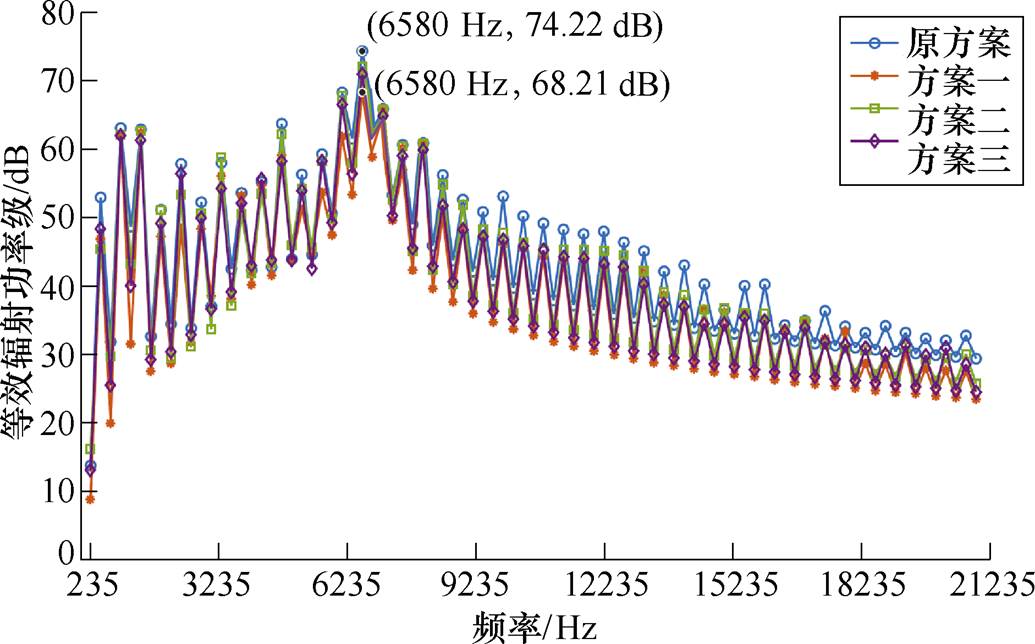
图22 巡航转速等效辐射功率级优化对比
Fig.22 Comparison of cruise speed equivalent radiated power level optimization
相较于原方案，新方案的各个噪声带处的尖端噪声幅值均有不同程度的降低，其中方案一取得最小值，该结构下的最大声功率幅值相较于原结构降低了约6 dB，且在不同的频率点处的振动噪声幅值亦有明显下降，电机噪声抑制效果明显。
在巡航转速与额定电流下，电机各个方案的转矩波形如图23所示。转矩波动系数t 为
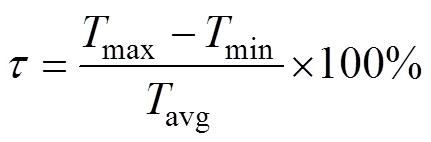（13）
式中，Tmax、Tmin分别为电磁转矩的最大、最小值。由图23可知，各结构下电机Tavg的数值接近，但方案三的转矩波动降幅达45%；方案一次之，转矩波动降幅达32%。可以看出，本文优化的电机结构在不同程度上提高了电机转矩性能。
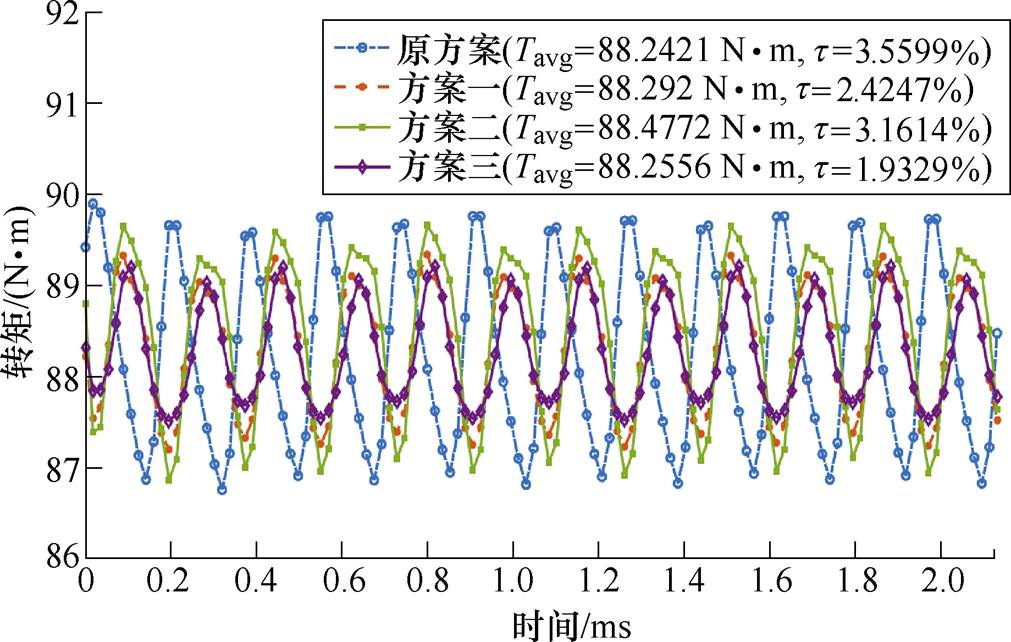
图23 瞬态转矩优化前后对比
Fig.23 Transient torque optimization before and after comparison
结合上述各方案对于等效辐射声功率级的优化结果可知，方案一对电机综合性能的提升最为显著，因此可将其确定为电机转子优化与定子开槽大小的最终方案。
为了验证分析理论及方法的正确性，对电机仿真结果进行实验验证。实验分两个步骤进行验证。第一步验证巡航转速下的噪声是否优化，第二步验证巡航转速下的转矩脉动是否降低。
由仿真结果可知，在带载和空载情况下的噪声波形及空间特性十分接近，故只对空载情况下电机巡航转速噪声进行验证。噪声测试的实验平台与数据采集平台分别如图24、图25所示。电机被放在消声室内，共5个测试点，麦克风置于离电机机壳表面1 m位置。实验中采用LMS系统采集数据，利用Testlab软件进行数据分析。
图24 电机噪声测试消音室平台
Fig.24 Motor noise test silencer room platform
图25 电机噪声测试数据采集平台
Fig.25 Motor noise test data acquisition platform
在巡航转速下，噪声实验结果如图26所示。可以看出，实验与仿真结果存在一定误差，这主要是因为进行有限元仿真时，对模型进行了适当的简化和等效，且未考虑机械结构及固定方式等因素的影响。但误差在可接受的范围内，实验与仿真声功率趋势基本一致，且峰值噪声频率带6 600 Hz附近。因此有限元结果与实验结果的对比，可验证理论分析及仿真结果的有效性。
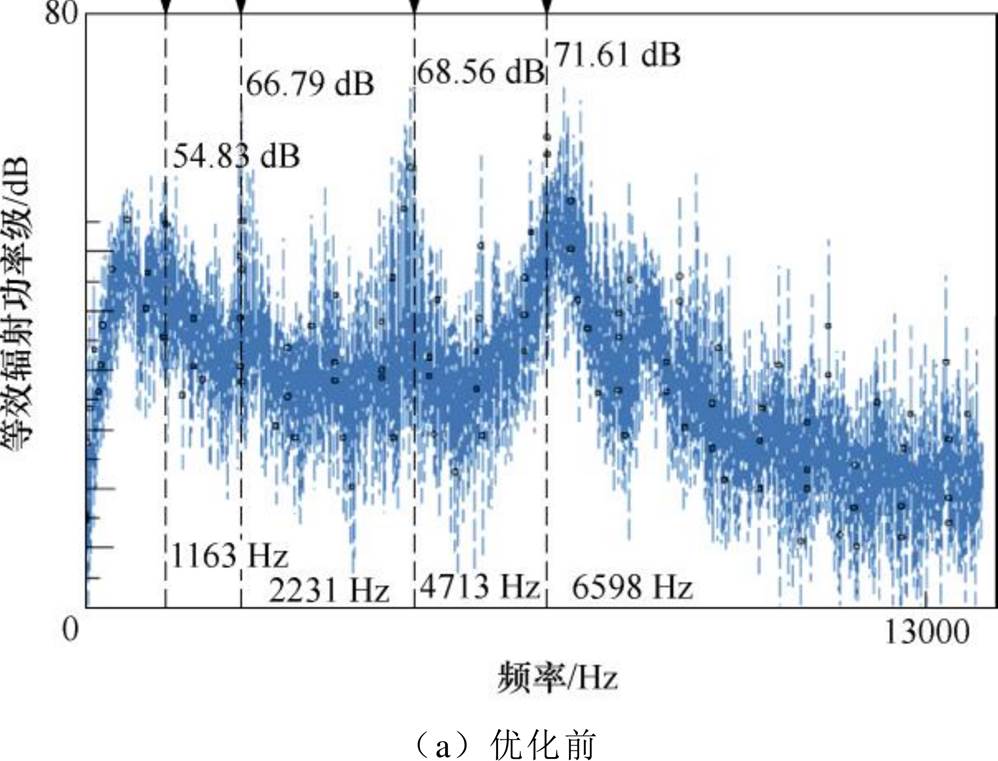
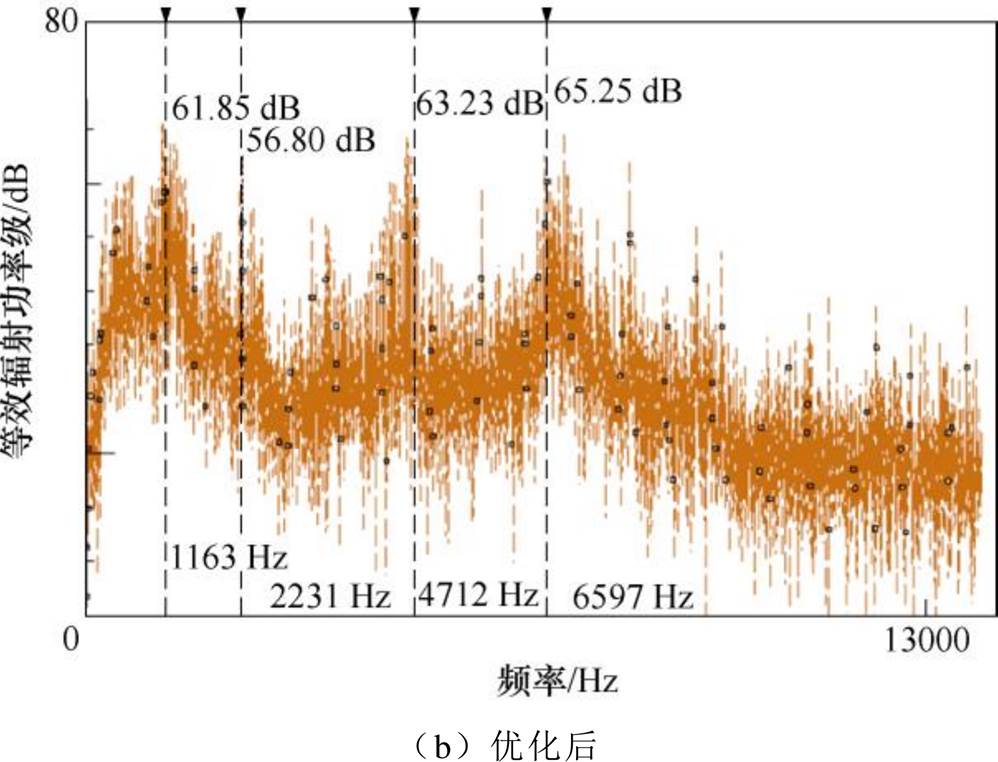
图26 巡航转速下电机噪声优化对比
Fig.26 Comparison of motor noise optimization at cruising speeds
电机在6 600 Hz噪声带的最大尖端电磁振动噪声由最初的71.61 dB降低至65.25 dB，降低了6.36 dB，下降了约8.9%。此外，在2 200 Hz噪声带的最大噪声由最初的66.79 dB降低至56.80 dB，降低了9.99 dB，下降了约15.0%；在4 700 Hz噪声带的最大噪声由最初的68.56 dB，降低至63.23 dB降低了5.33 dB，下降了约7.8%。虽然，在1 100 Hz附近最大噪声有小幅度上升，但电机在巡航状态下的电机电磁噪声整体降低。
进一步验证电机转矩性能。测试平台与内部连接平台分别如图27、图28所示。为确保安全，电机被置于箱内。当电机达到巡航转速，每5 s采集一次转矩数据。
在巡航转速下，转矩实验结果如图29所示。仿真中各个方案的平均转矩数值接近，实验中的原方案平均转矩为87.436 4 N·m，优化方案为87.556 8 N·m，平均转矩几乎不变。仿真中原方案转矩波动为3.56%，实验中为3.30%；优化方案转矩波动为2.42%，实测结果为2.16%。转矩波动整体下降了34.5%。可以看出，实验与仿真结果的误差很小，可验证电磁仿真结果的有效性。
图27 电机转矩测试实验
Fig.27 Motor torque test experiment
图28 内部17 kW电机连接平台
Fig.28 Internal 17 kW motor connection platform
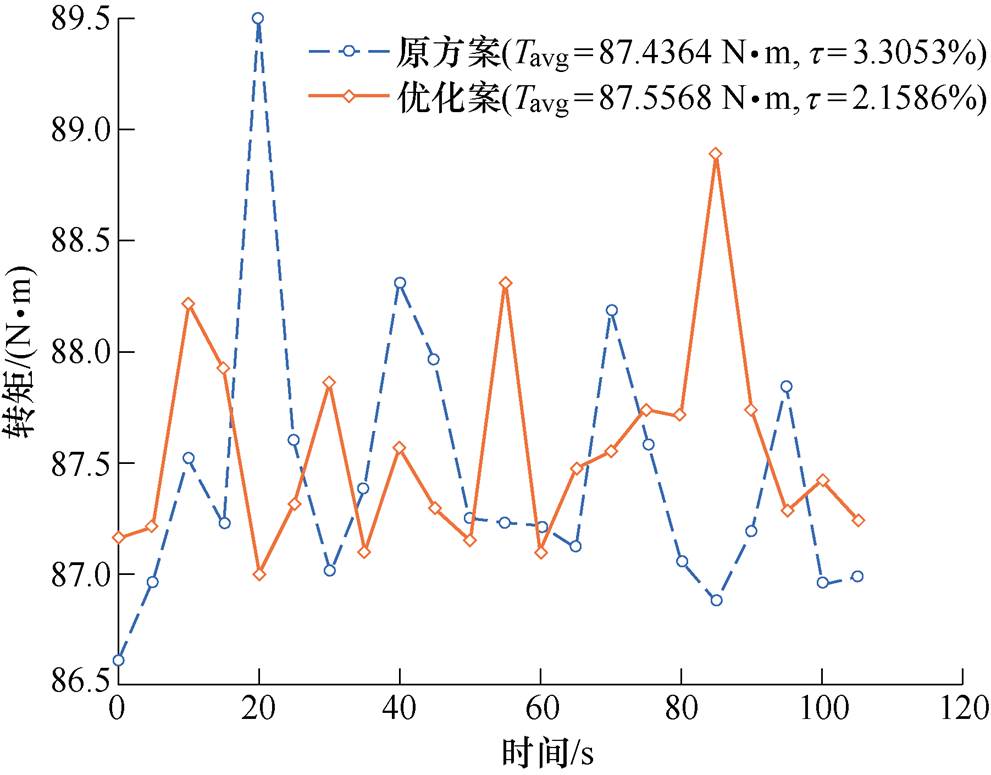
图29 巡航转速下电机转矩测试数据对比
Fig.29 Comparison of motor torque test data at cruise speeds
本文推导了表贴式永磁电机空间径向气隙磁通密度与磁极参数的函数关系。分析了磁极参数、定子开槽对径向气隙磁通密度谐波幅值的影响，研究转子模态与电磁力作用机理。采用了混合粒子群优化算法对结构参数进行优化。最后对优化样机进行了噪声实验，降低了无人机巡航转速下的尖端噪声，验证了仿真及理论的正确性。所得结论可对降低无人机电机尖端噪声提供参考。
1）与现有的电机结构优化方法相比，本文在保持电机输出平均转矩情况下，降低了电机的转矩 波动。
2）本文以17 kW无人机用36极/30槽外转子电机为例，优化极弧系数、永磁体厚度以及开槽参数，降低3、5次气隙磁通密度谐波的幅值，从而有效地削弱径向电磁力及其引起的振动噪声峰值。在实验结果中，巡航转速尖端噪声下降约6 dB。
参考文献
[1] 王科雷, 周洲, 马悦文, 等. 垂直起降固定翼无人机技术发展及趋势分析[J]. 航空工程进展, 2022, 13(5): 1-13.
Wang Kelei, Zhou Zhou, Ma Yuewen, et al. Development and trend analysis of vertical takeoff and landing fixed wing UAV[J]. Advances in Aeronautical Science and Engineering, 2022, 13(5): 1-13.
[2] 陈鹏, 陈洋, 王威. 无人机声学定位技术综述[J]. 华南理工大学学报(自然科学版), 2022, 50(12): 109-123.
Chen Peng, Chen Yang, Wang Wei. Review for UAV acoustic positioning[J]. Journal of South China University of Technology (Natural Science Edition), 2022, 50(12): 109-123.
[3] 潘嘉琦, 曹科才, 丁嘉存, 等. 基于维纳滤波的无人机语音系统的设计与实现[J]. 计算机与数字工程, 2021, 49(10): 2161-2167.
Pan Jiaqi, Cao Kecai, Ding Jiacun, et al. Design and implementation of UAV phonetic system based on Wiener filtering[J]. Computer & Digital Engineering, 2021, 49(10): 2161-2167.
[4] Xu He, Kong Deyi, Qian Yujie, et al. Motor noise reduction of unmanned aerial vehicles[J]. Applied Acoustics, 2022, 198: 108979.
[5] 臧渊, 齐亨通, 周洁. 多旋翼无人机电机减振加固结构设计[J]. 科技创新与应用, 2022, 12(31): 89-92, 98.
Zang Yuan, Qi Hengtong, Zhou Jie. Structural design of motor vibration reduction and reinforcement for multi-rotor UAV[J]. Technology Innovation and Application, 2022, 12(31): 89-92, 98.
[6] 刘慧娟, 卜斌彬, 郭跃. 削弱表贴式永磁电机2p阶径向电磁力波幅值的磁极设计方法[J]. 微特电机, 2023, 51(4): 8-14.
Liu Huijuan, Bu Binbin, Guo Yue. A magnetic pole optimization method to suppress the amplitude of 2p-order radial electromagnetic force of surface mount permanent magnet motor[J]. Small & Special Electrical Machines, 2023, 51(4): 8-14.
[7] 李泽星, 夏加宽, 刘铁法, 等. 基于极间虚齿的表贴式永磁电机六倍频振动噪声的削弱[J]. 电工技术学报, 2023, 38(5): 1287-1298.
Li Zexing, Xia Jiakuan, Liu Tiefa, et al. Reduction of six times frequency vibration and noise of surface- mounted permanent magnet synchronous machines with interpolar virtual teeth[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1287-1298.
[8] 乔鸣忠, 卢希浩, 张弛. 气隙磁密3次谐波对电机振动噪声的影响[J]. 国防科技大学学报, 2023, 45(3): 92-98.
Qiao Mingzhong, Lu Xihao, Zhang Chi. Influence of third order harmonic of air gap flux density on motor vibration and noise[J]. Journal of National University of Defense Technology, 2023, 45(3): 92-98.
[9] 吕长朋, 李明勇, 陈辉. 永磁电机零阶径向力引起的齿槽频次振动[J]. 中国电机工程学报, 2021, 41(19): 6778-6787.
Lü Changpeng, Li Mingyong, Chen Hui. Cogging frequency vibration of permanent magnet motor caused by zeroth-order radial magnetic forces[J]. Proceedings of the CSEE, 2021, 41(19): 6778-6787.
[10] Das S, Chowdhury A, Wan Zhao, et al. Sensitivity analysis based NVH performance evaluation in permanent magnet synchronous machines using lumped unit force response[C]//2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 2020: 802-807.
[11] Bang T K, Shin K H, Lee Y G, et al. Comparative study of NVH of permanent magnet machines according to rotor eccentricity with fractional pole/ slot combinations[J]. IEEE Transactions on Applied Superconductivity, 2022, 32(6): 1-7.
[12] 李泽星, 夏加宽, 刘铁法, 等. 基于分段交错不等磁极的表贴式永磁电机极频振动的削弱[J]. 电工技术学报, 2023, 38(4): 945-956.
Li Zexing, Xia Jiakuan, Liu Tiefa, et al. Reduction of pole-frequency vibration of surface-mounted per- manent magnet synchronous machines with piecewise stagger unequal poles[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 945-956.
[13] Cheng Ziran, Ruan Lin, Huang Shoudao, et al. Research on noise reduction of 3.6 MW evaporative cooling wind motor induced by electromagnetic and two-phase flow resonance based on stator optimi- zation[J]. Processes, 2021, 9(4): 669.
[14] 刘畅, 邱鑫, 杨建飞, 等. 永磁同步电机电磁振动噪声优化方法研究[J]. 微特电机, 2023, 51(4): 20- 25, 31.
Liu Chang, Qiu Xin, Yang Jianfei, et al. Research on optimization method of electromagnetic vibration noise of permanent magnet synchronous motor[J]. Small & Special Electrical Machines, 2023, 51(4): 20-25, 31.
[15] 陈少先, 丁树业, 申淑锋, 等. 船舶用表贴式永磁同步电机的电磁振动分析与抑制[J]. 电工技术学报, 2023, 38(5): 1275-1286, 1298.
Chen Shaoxian, Ding Shuye, Shen Shufeng, et al. Analysis and suppression of electromagnetic vibration of surface mounted permanent magnet synchronous motor for ships[J]. Transactions of China Electro- technical Society, 2023, 38(5): 1275-1286, 1298.
[16] 韩雪岩, 张新刚, 朱龙飞, 等. 内置式多层磁钢永磁同步电机振动噪声抑制措施[J]. 电机与控制学报, 2021, 25(8): 67-75.
Han Xueyan, Zhang Xingang, Zhu Longfei, et al. Measures to reduce vibration and noise of interior permanent magnet synchronous motor with multilayer permanent magnets[J]. Electric Machines and Control, 2021, 25(8): 67-75.
[17] 谢颖, 辛尉, 蔡蔚, 等. 内置式永磁同步电机不同转子拓扑结构的电磁性能及电磁振动噪声分析[J]. 电机与控制学报, 2023, 27(1): 110-119.
Xie Ying, Xin Wei, Cai Wei, et al. Electromagnetic performance and electromagnetic vibration noise analysis of different rotor topologies of interior permanent magnet synchronous motor[J]. Electric Machines and Control, 2023, 27(1): 110-119.
[18] 钱喆, 刘同鑫, 邓文哲, 等. 电流谐波注入的车用永磁同步驱动电机振动噪声抑制[J]. 电机与控制学报, 2022, 26(7): 115-124.
Qian Zhe, Liu Tongxin, Deng Wenzhe, et al. Vibration and noise suppression of permanent magnet synchronous drive motor with harmonic current injection[J]. Electric Machines and Control, 2022, 26(7): 115-124.
[19] Harries M, Woerndle A, De Doncker R W. Low vibrations and improved NVH in permanent magnet synchronous machines due to injection of flux-linkage harmonics[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(2): 1649- 1657.
[20] 刘睿松, 董婷. 谐波电流注入下永磁直线同步电机振动分析[J]. 微特电机, 2023, 51(8): 16-21.
Liu Ruisong, Dong Ting. Vibration analysis of permanent magnet linear synchronous motor under harmonic current injection[J]. Small & Special Electrical Machines, 2023, 51(8): 16-21.
[21] Liu Feng, Wang Xiuhe, Xing Zezhi, et al. Reduction of cogging torque and electromagnetic vibration based on different combination of pole arc coefficient for interior permanent magnet synchronous machine[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(4): 291-300.
[22] Du Jianmin, Li Yan, Yu Zhanyang, et al. Research on radial electromagnetic force and vibration response characteristics of squirrel-cage induction motor fed by PWM inverter[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 1-4.
[23] Hong Jianfeng, Wang Shanming, Sun Yuguang, et al. Piecewise stagger poles with continuous skew edge for vibration reduction in surface-mounted PM synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 8498-8506.
[24] 夏加宽, 康乐, 詹宇声, 等. 表贴式三相永磁同步电机极槽径向力波补偿模型及参数辨识[J]. 电工技术学报, 2021, 36(8): 1596-1606.
Xia Jiakuan, Kang Le, Zhan Yusheng, et al. The model of pole slot radial force wave compensation for surface-mounted three-phase permanent magnet syn- chronous motor and parameter identification[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1596-1606.
[25] 张洪涛. 永磁同步电机噪声分析及优化[J]. 防爆电机, 2023, 58(5): 20-23.
Zhang Hongtao. Noise analysis and optimization of PMSM[J]. Explosion-Proof Electric Machine, 2023, 58(5): 20-23.
[26] 康乐, 夏加宽, 苏航, 等. 表贴式永磁电机各次电流引起径向振动的机理分析及综合抑制策略[J]. 电工技术学报, 2022, 37(18): 4638-4650.
Kang Le, Xia Jiakuan, Su Hang, et al. Mechanism analysis and comprehensive suppression strategy of radial vibration induced by each current of surface magnet motor[J]. Transactions of China Electro- technical Society, 2022, 37(18): 4638-4650.
Abstract In unmanned aerial vehicle (UAV) noise fields, extensive research on propeller noise generation mechanisms and suppression methods has achieved remarkable results. The noise radiated by UAV motors has become a new research focus. The study addresses a 17 kW UAV with a surface-mounted external rotor permanent magnet synchronous motor. The existing methods reduce the motor output torque but increase manufacturing complexity. Therefore, the paper proposes an optimization method for pole and stator slotting parameters to improve the motor vibration noise without reducing the output torque.
Since radial air-gap flux density and radial electromagnetic force cause motor vibration noises, the space harmonic characteristics of the radial air-gap flux density are analyzed according to the effects of the magnetic pole and stator slotting parameters on the amplitude of low-order radial air-gap flux density. Rotor modal simulation is carried out to investigate the mechanism of the radial electromagnetic force and the motor space modes. Then, the characteristics of electromagnetic vibration noises at multiple speeds are analyzed, focusing on the vibration noise at a cruising speed of 1 880 r/min. A multi-objective optimization mathematical model is established using a hybrid particle swarm optimization algorithm, taking the average torque, torque pulsation, and flux density fundamental wave amplitude as the constraints. After comparing three alternatives, Scheme 1 is selected as the optimization scheme. The simulation shows that the amplitude of the 3rd and 5th-order components of the radial air gap magnetization is decreased by 45.57% and 60.92% compared with the original scheme. The magnitude of the radial electromagnetic force decreases by 5.88% in the fundamental component, 33.03% in the 2nd component, and 6.81% in the 4th component. The torque fluctuation of Scheme 1 decreases by 32% when the average torque is almost unchanged.
Experimental results show that after structure optimization, the electromagnetic vibration tip noise at the cruising speed is reduced by 6.36 dB from the initial 71.61 dB to 65.25 dB, and the overall performance of the motor vibration noise is improved at multiple speeds. The optimized structure significantly suppresses the UAV motor tip vibration noise at the cruising speed. In addition, the average torque is 87.44 N·m for the original scheme and 87.56 N·m for the optimized scheme, and the average torque is almost constant. The torque pulsation is 3.30%, and the torque fluctuation of the optimized scheme is 2.16%. The overall decrease in torque fluctuation is 34.5%. The optimized structure reduces the tip noise of the motor and optimizes the torque pulsation.
keywords：Unmanned aerial vehicle (UAV) outer rotor permanent magnet synchronous motor, electro- magnetic vibration noise, cruise speed, hybrid particle swarm optimization algorithm
DOI: 10.19595/j.cnki.1000-6753.tces.231228
中图分类号：TM351
国家自然科学基金资助项目（51877059）。
收稿日期 2023-07-31
改稿日期 2023-08-30
刘栋良 男，1977年生，教授，硕士生导师，研究方向为电机及其控制、新能源及电力电子/电动汽车驱动系统、电动航空驱动系统、电动船舶推进系统。E-mail: LiuDL@hdu.edu.cn
詹成根 男，1997年生，硕士研究生，研究方向为电动航空驱动系统。E-mail: 1376438612@qq.com（通信作者）
（编辑 崔文静）