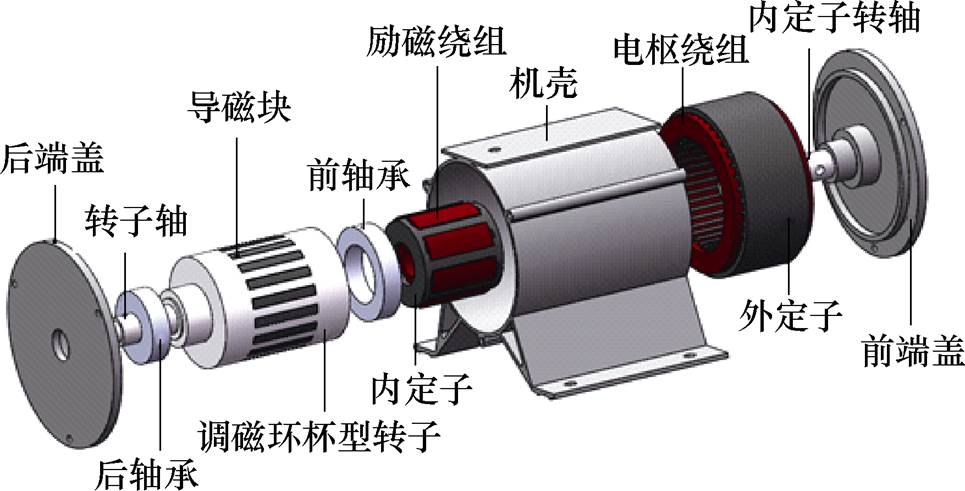
图1 DS-EEFMM样机结构
Fig.1 Configuration of DS-EEFMM prototype
摘要 准确获得电机结构的模态分析结果是研究电磁噪声的前提条件。该文以一台双定子电励磁场调制电机为研究对象，首先，利用有限元软件对影响其模态分析的弹性模量展开研究，探索弹性模量变化对各阶固有频率的相对影响率大小，找到外定子、电枢绕组、机壳和端盖的弹性模量变化对模态分析结果的影响规律，由此明确参数调整的方向性。然后，采用锤击法进行模态实验，并获得外定子、外定子组件以及整机模态实验结果与仿真结果二者误差的大小。最后，根据二者误差大小及参数调整的方向性，选择合适的弹性模量调整值将其误差均调整到4%以内，从而得到精确的模态仿真结果，进而有利于后续该电机电磁噪声的分析。
关键词：双定子电励磁场调制电机 有限元模态分析 弹性模量调整规律 模态实验
双定子电励磁场调制电机（Double-Stator Electric- Excitation Field-Modulated Machine, DS-EEFMM）为基于磁场调制原理[1-4]提出的一种低速直驱电机。该电机的工作谐波磁场经调磁环转子调制产生后，与电枢谐波磁场之间相互作用产生较高的电磁转矩密度[5-6]。但是丰富的谐波磁场之间的相互作用又会产生较高的电磁力密度，作用在铁心上使其产生径向振动进而产生剧烈的电磁噪声[7-9]。电机的振动噪声不仅会污染环境，还会影响人们的身心健康，更严重的还会造成安全事故。因此，有必要研究双定子电励磁场调制电机的振动噪声响应。
模态分析是电机振动与噪声分析中的重要一部分，通常是将解析计算、有限元分析、模态实验相结合来得到模态分析结果。文献[10]利用解析计算的方法，将定子视为均匀的圆柱体，通过计算动能和势能来研究固有频率。文献[11]充分考虑了定子齿、机壳和端盖的复杂结构，提高了解析计算定子固有频率的准确性，除此之外，解析计算的方法还可以用来分析电机结构参数对电机固有频率的影响。定子铁心叠压系数对固有频率的影响较大，不同的叠压系数会使得定子铁心的整体刚度不同，考虑叠压效应会减小固有频率计算结果与实际结果之间的偏差[12]。文献[13]中，通过多组模态实验证明了绕组是否浸漆对定子固有频率有较大影响，铁心加未浸漆绕组其低阶径向固有频率会下降，而加浸漆绕组会使固有频率明显增加。文献[14]研究了具有集中绕组的永磁同步电机定子系统的精确建模和固有频率，并通过修正公式和经验系数来确定定子的等效材料参数，从而设定了定子铁心弹性模量。文献[15-16]考虑了机壳和端盖对小型异步电机固有频率的影响，得出了机壳和端盖对电机的模态分析结果影响较大的结论。如前所述，考虑定子铁心的叠压效应、绕组是否浸漆以及机壳和端盖的影响对电机的模态分析至关重要。
准确获得DS-EEFMM的模态分析结果，需要对外定子、电枢绕组、机壳和端盖赋予相应的等效材料参数，例如杨氏模量、剪切模量、泊松比和质量密度等。现阶段对于电机组件材料参数的确定大多是通过模态实验对仿真结果进行参数调整，使二者误差收敛到合理误差范围之内[17-21]。文献[22]提出了一种定子系统等效材料参数校正方法，并获得了较为精确的结果，虽然此方法可以获得准确度较高的定子-绕组模态分析结果，但是由于整机各结构材料参数调整对其各阶固有频率的影响是一个综合效果，与单个结构的贡献并不是线性关系，若不能明确指出其方向性，会使整机参数调整困难，难以将其各阶误差调整到满足要求的误差范围之内。
为解决上述问题，本文以双定子电励磁场调制电机为研究对象，首先建立新的等效模型并研究各结构弹性模量变化对各阶固有频率的相对影响率大小，由此明确外定子、电枢绕组、机壳和端盖弹性模量调整的方向性。然后通过锤击法得到外定子、外定子组件以及整机的模态实验结果，对比仿真结果后得到二者误差大小。最后根据二者误差大小以及参数调整的方向性，将外定子组件以及整机模态分析结果误差调整到与外定子相同的误差范围之内。
DS-EEFMM样机结构如图1所示，外定子放置电枢绕组、通过过盈配合的方式固定在外壳内表面；内定子放置励磁绕组、通过内定子轴固定在前端盖；由铁磁段与非铁磁段组成的调磁环杯型转子位于内外定子之间，两端分别通过轴承固定在前后端盖上。DS-EEFMM的具体参数尺寸见表1。
图1 DS-EEFMM样机结构
Fig.1 Configuration of DS-EEFMM prototype
由于该电机结构部件较多，采用整体3D有限元模型进行模态分析时会导致模型剖分困难，大幅增加仿真所需要的时间，因此需要建立新的等效模型。考虑到内定子、励磁绕组、内定子轴、调磁环转子等结构通过端盖直接与机壳相连，而机壳对电机的模态分析影响相对较大，因此将DS-EEFMM的结构部件分为三部分等效，依次为外定子、电枢绕组、外壳组成的外定子组件；内定子、励磁绕组、内定子轴和前端盖组成的内定子组件；由调磁环杯型转子、前后轴承、转子轴和后端盖组成的调磁环杯型转子组件。因此，在搭建模型的过程中，可将内定子、励磁绕组、内定子轴以附加质量的形式等效到前端盖。同样地，将调磁环杯型转子等结构等效到后端盖。
表1 DS-EEFMM样机设计参数
Tab.1 Key parameters of the proposed DS-EEFMM
参 数数 值 外定子槽数42 内定子槽数8 励磁绕组极对数4 电枢绕组极对数14 调磁环极对数18 外定子外径/mm145 外定子内径/mm95.6 内定子外径/mm78 内定子内径/mm36 调磁环杯型转子外径/mm94.6 调磁环杯型转子内径/mm79 电枢长度/mm60 额定转矩/(N·m)4 额定频率/Hz50 相数3
DS-EEFMM三部分组件及其等效后的模型如图2所示。等效原则是：等效后的前后端盖对整机的影响应与等效前的内定子组件和调磁环杯型转子组件对整机的影响保持一致。据此，建立DS- EEFMM的等效模型，用于后续外定子、外定子组件以及整机模态分析。
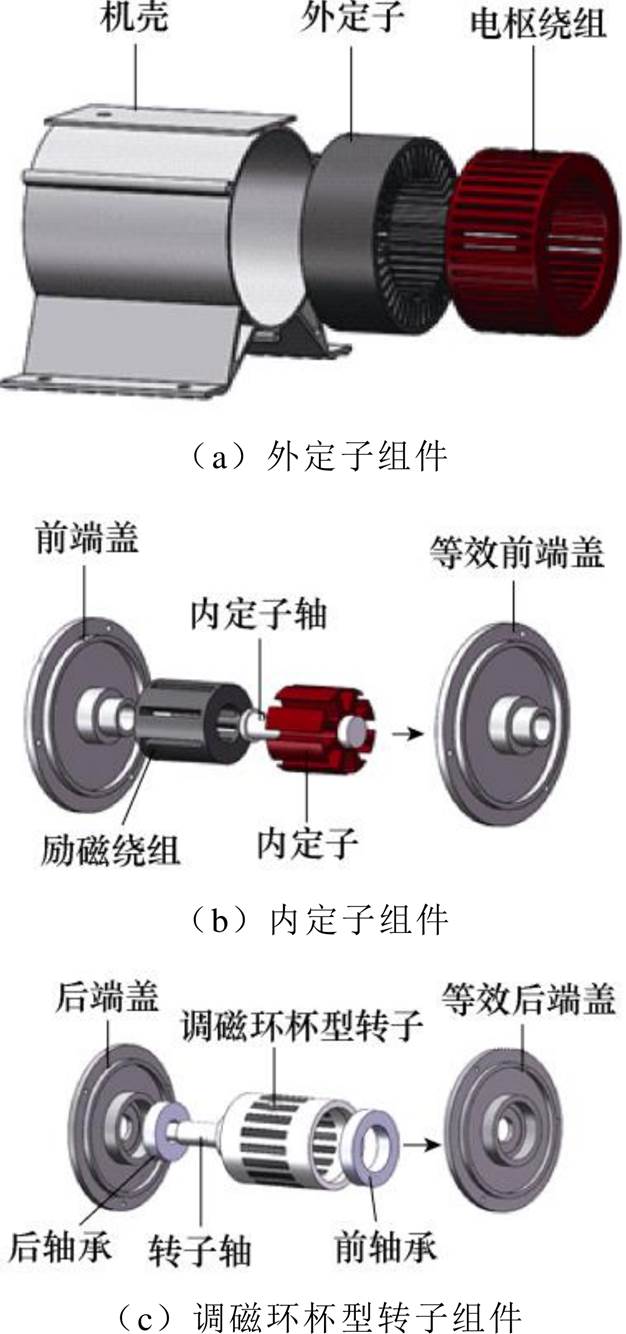
图2 DS-EEFMM 三组件
Fig.2 Three parts of DS-EEFMM
电机结构的模态分析遵循动力学平衡方程[10]，有
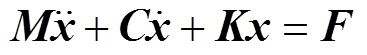（1）
式中，M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；x为位移矩阵；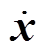
为速度矩阵；
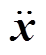为加速度矩阵；F为激振矩阵。
电机的模态分析属于无阻尼分析，阻尼矩阵C为零，激振矩阵在模态分析中也为零。在特定条件下，体系按同一频率做减振运动，位移矩阵可表示为
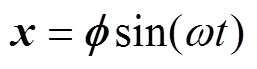（2）
联立式（1）与式（2），整理可得
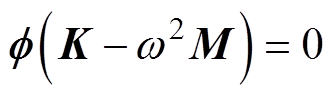（3）
式中，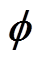
为模态振型；
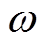为角频率。则电机结构的固有频率可以表示为
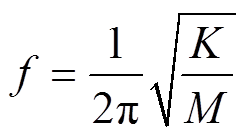（4）
对于定子结构来说，定子铁心的刚度Ks和质量Ms分别表示[23]为
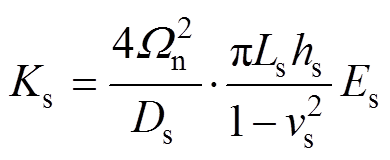（5）
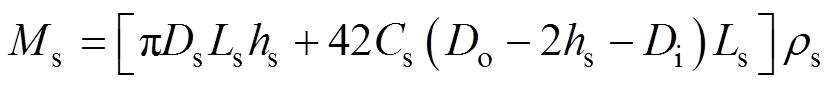（6）
式中，Es、vs、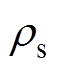
分别为铁心材料的弹性模量、泊松比和质量密度，上述为材料参数；Ds为定子铁心直径；Ls为定子轴向长度；hs为铁心轭高；Cs为齿宽；Do与Di分别为定子铁心内、外径；
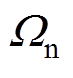为与Ds和hs有关的参数，上述参数可归类为结构参数。
结构参数按照电机实际结构来确定，本文将其设为定值。考虑到泊松比较小，调整范围有限，故也将其设为定值，因此定子结构固有频率可以表示为
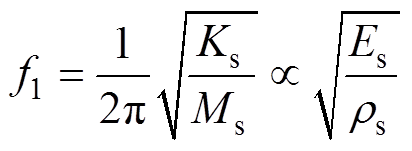（7）
对于绕组结构的固有频率可表示为式（4），质量和刚度同样由材料参数和结构参数决定。而定子-绕组系统的集中刚度与集中质量分别为两个子系统的集中刚度与质量之和，其固有频率可表示为
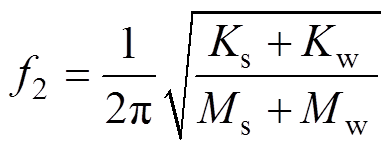（8）
式中，Kw和Mw分别为绕组的刚度和质量。同样可将其结构参数和泊松比设为定值，则式（8）可以表示为
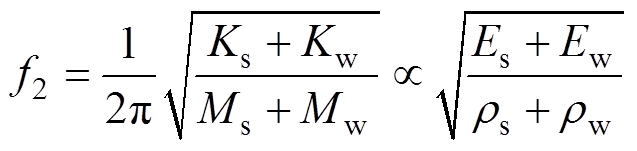（9）
式中，Ew、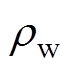
分别为绕组的弹性模量和质量密度。同样地，将定子-绕组-机壳系统表示为
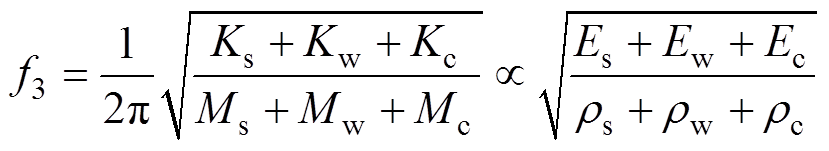（10）
式中，Kc、Mc分别为机壳的刚度和质量；Ec、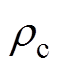
分别为机壳的弹性模量和质量密度。
由式（10）可以得到定子模态频率与各结构弹性模量参数之间的函数关系。当结构材料确定以后，其弹性模量也随之确定，但是无论解析计算或有限元计算，二者均是基于理想条件下建立的，以此确定的弹性模量参数得到的计算结果往往与实际结果之间存在不小的误差。对于有限元模型来说，一般需要调整定子铁心和绕组等各向异性参数，而考虑到整机模型中机壳与端盖等结构对定子模态影响较大，仍需对机壳和端盖弹性模量参数进行调整，由此得到较为精确的仿真结果。
由上述分析可知，电机结构的固有频率主要受弹性模量和质量密度的影响。由于质量密度的设定可根据各结构的实际质量与实际体积得到，因此在本文中，不再对其进行后续调整。本节主要分析各向异性材料参数对固有频率的影响，包括杨氏模量E与剪切模量G，也为需要进行调整的关键参数。
电机中，各向异性材料主要包括外定子和电枢绕组材料，其弹性模量的z方向与x、y方向特性不同，因此这两个部件需要确定4个关键参数，即x, y, z方向的杨氏模量Ex=Ey，Ez和xOy, xOz, yOz平面的剪切模量Gxy，Gxz=Gyz。而各向同性材料则包括机壳和端盖，各方向材料特性相同，只需要确定E与G两个关键参数即可。
鉴于电机的振动主要来源于定子的径向形变，故对电机部件进行模态分析时，以低阶径向模态为主要研究目标。
首先，对外定子结构进行分析，赋予其相应的弹性模量初始值。外定子结构如图3所示，由硅钢片沿z轴方向叠压而成，xOy平面可视为各向同性材料[24]，按照硅钢片弹性模量参数进行取值，即：Ex=Ey=206 GPa，Gxy=80 GPa，并且取泊松比v=0.3。
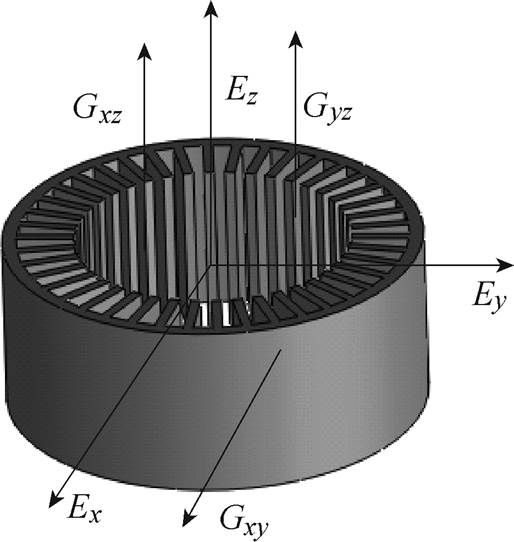
图3 外定子结构
Fig.3 Configuration outer stator
Ez的取值按照复合材料弹性参数的计算方法确定[14]，即
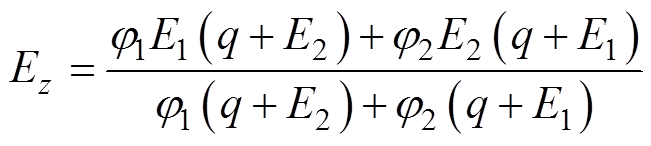（11）
式中，E1为硅钢片杨氏模量；E2为绝缘材料杨氏模量；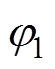
、
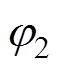为两种材料所占体积比，由硅钢片系数决定；q为经验拟合常数，其近似值为
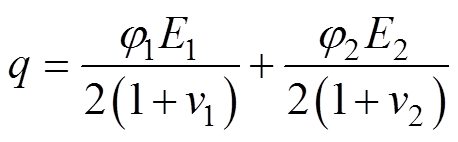（12）
式中，v1、v2为两种材料的泊松比。考虑到叠片系数为0.96，E2=1.9 GPa，v2=0.35，由式（11）与式（12）得Ez=180 GPa。
Gxz=Gyz的取值对电机轴向模态影响较大，对径向模态影响很小，并且由于z方向的叠片效应，其值要小于Gxy，因此在本文中将其设为0.9Gxy[12]，即Gxz=Gyz=72 GPa。
在初始值基础上，通过调整弹性模量的值来寻找其对各阶固有频率的影响规律。其中，Gxy与Ex存在固定关系，即
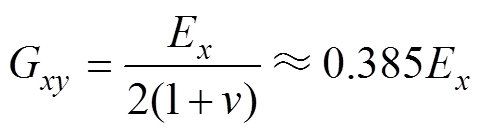（13）
此外，设定Gxz=Gyz=0.9Gxy，即
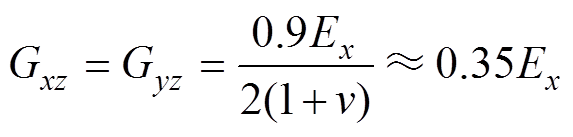（14）
对式（11）与式（12）进行分析，由于E1远大于E2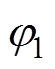，约为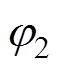的十几倍，而泊松比差别不大，所以式（12）与式（11）可以近似表示为
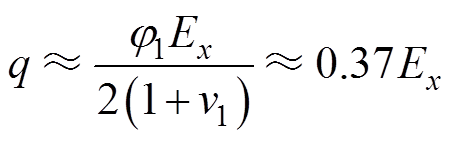（15）
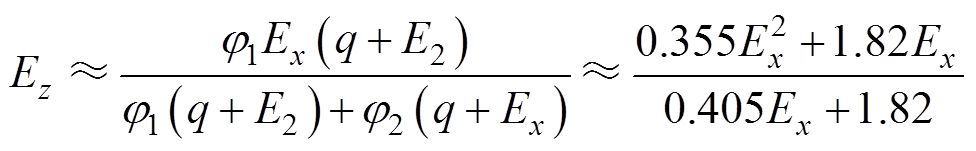
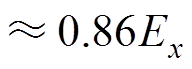（16）
由此可得外定子弹性模量之间的取值关系，即Ez、Gxy、Gxz=Gyz的取值与Ex=Ey直接相关。因此，在对弹性模量进行参数调整时，可以选择调整其中的一个参数而固定其他参数的方式进行调整，定义为单参数调整。也可以利用弹性模量之间的取值关系同时调整2～4个参数，定义为组合参数调整。
利用有限元对比分析这两种调整方式发现，当不同的弹性模量参数变化对外定子各阶固有频率的影响相同时，组合调整比单独调整时对模态频率的相对影响率更大。于是，根据对各阶固有频率影响的不同及其相对变化率的大小，得到如图4～图6所示的三种调整规律，折线图和柱形图分别为参数每调整10%时各阶固有频率的大小及其相对变化率。
（1）调整方式1。按照Ex=Ey，Ez=0.86Ex，Gxy= 0.385Ex，Gxz=Gyz=0.35Ex同时调整4个参数，其调整规律如图4所示。
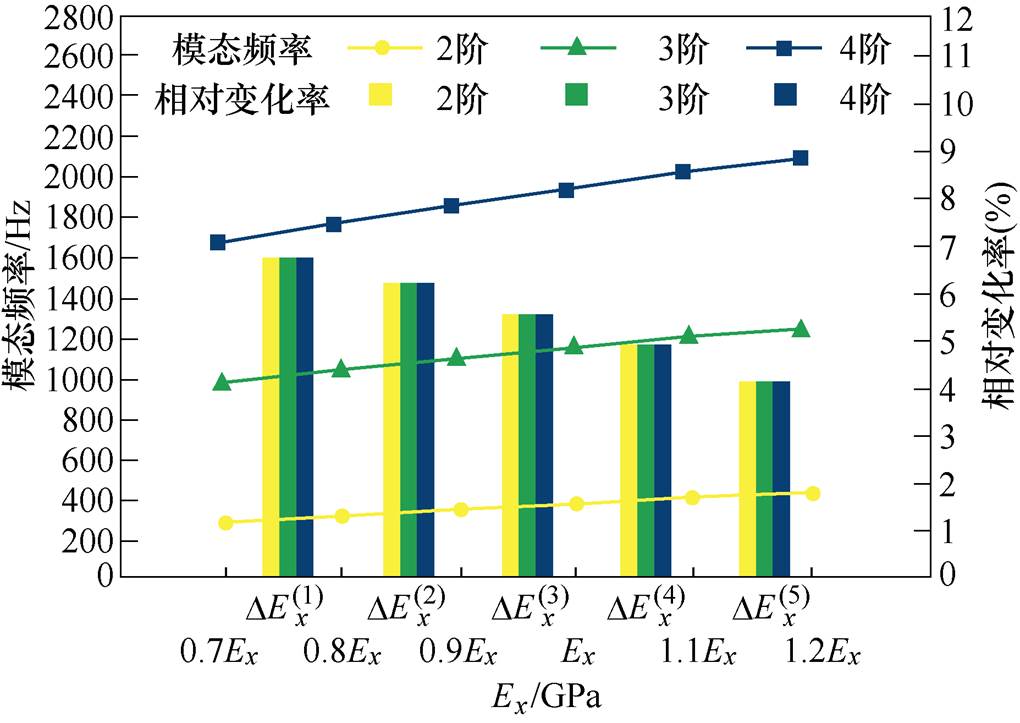
图4 外定子调整规律1
Fig.4 The first regulation rule of outer stator
（2）调整方式2。同时调整Ex=Ey，Ez=0.86Ex两个参数，并且固定Gxy=80 GPa，Gxz=Gyz=72 GPa，其调整规律如图5所示。
（3）调整方式3。同时调整Ex=Ey，Gxz=Gyz=0.35Ex两个参数，并且固定Ez=180 GPa，Gxy=80 GPa，其调整规律如图6所示。
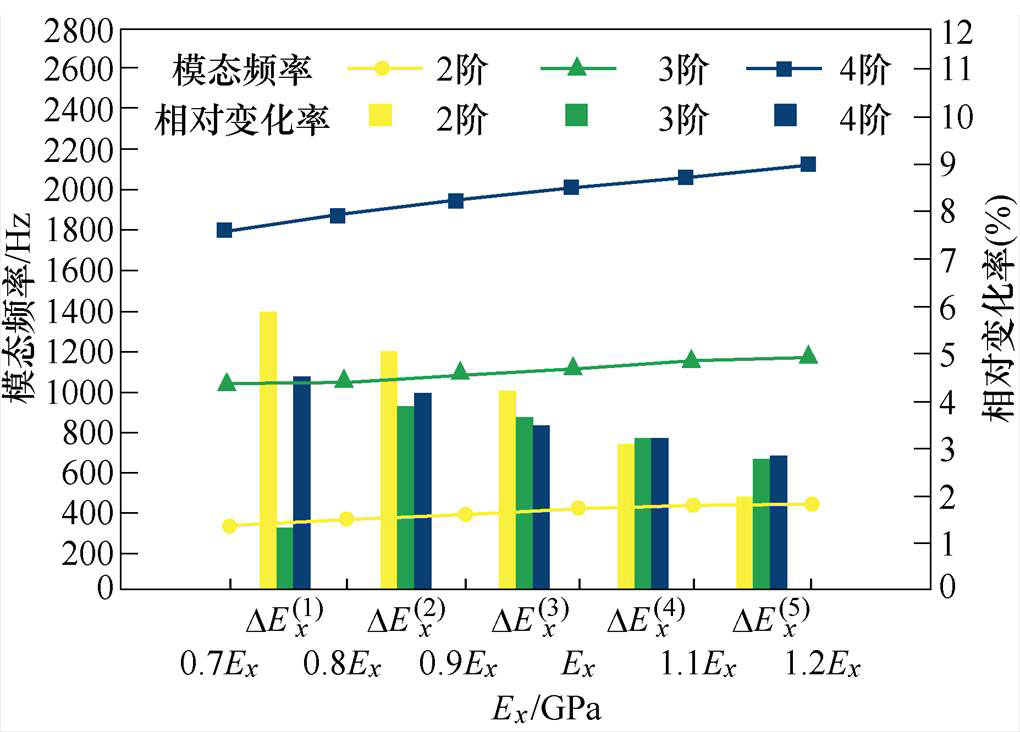
图5 外定子调整规律2
Fig.5 The second regulation rule of outer stator
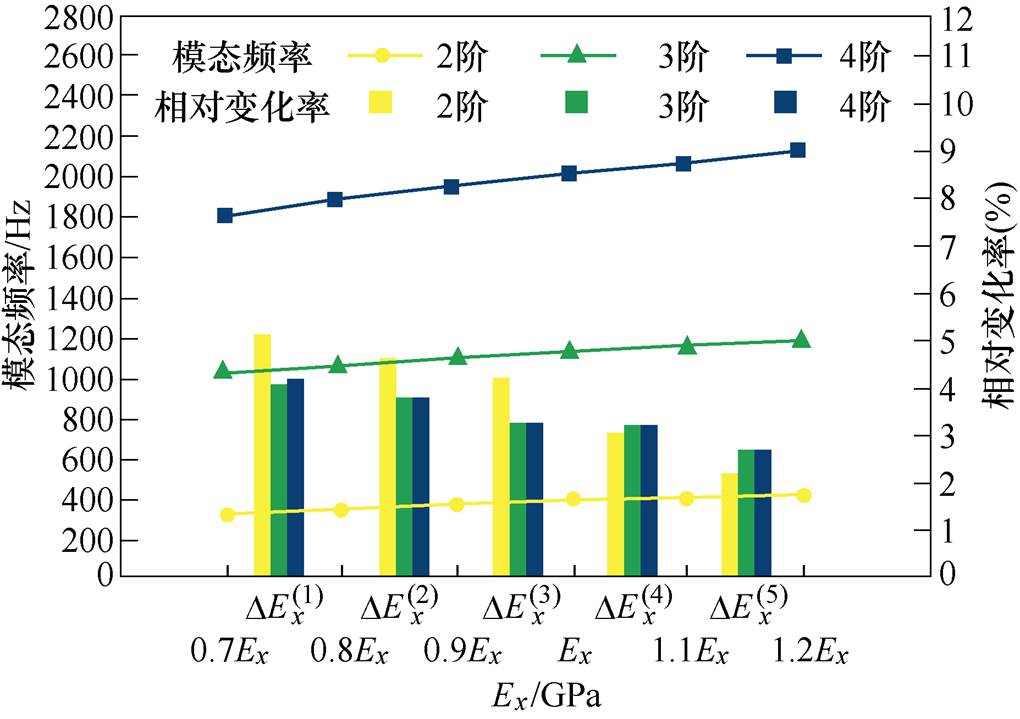
图6 外定子调整规律3
Fig.6 The third regulation rule of outer stator
可见，方式1得到的调整规律1对各阶的相对影响较大，并且变化规律相同。方式2和方式3在初始值以上与以下范围调整变化规律则不同。方式2在初始值以下调整对2阶固有频率影响最大，4阶次之，对3阶影响相对较小；在初始值以上调整，对2阶影响相对较小，对3、4阶影响相对较大。方式3在初始值以下调整对2阶影响较大，对3、4阶影响相对较小，但变化率相同；而在初始值以上调整，影响规律则相反。得到上述调整规律后，就可以在初始值的基础上，按照各阶误差大小进行弹性模量参数调整。
绕组弹性模量参数的设定与其是否浸漆关系较大。文献[13, 19]中对于浸漆绕组杨氏模量x、y方向的取值为9.5 GPa，大约为实心铜杨氏模量的1/10，z方向的取值要大于x、y方向。而对未浸漆绕组x、y方向，杨氏模量的取值要明显小于浸漆绕组，大约为实心铜杨氏模量的1/1 000[22]。剪切模量的取值方法与外定子一致，质量密度同样由电枢绕组实际质量与建模体积确定。
根据DS-EEFMM实际结构分析，本电机绕组的存在会使外定子固有频率降低，即其对外定子质量的影响大于刚度，可以选择将绕组等效为外定子齿的附加质量。而考虑到绕组弹性模量变化对外定子固有频率影响较大，因此有必要对绕组的调整规律进行分析。但是需要注意的是，无论怎么调整绕组的弹性模量，仍要保证绕组对外定子质量的影响大于刚度。根据文献[22]将绕组的初始参数设为：Ex=Ey=140 MPa，Ez=180 MPa，Gxy=55 MPa，Gxz= Gyz=50 MPa，v=0.3，该值使外定子的固有频率降低，并且通过有限元分析发现，Ez与Ex=Ey之间的差距不能太大，否则会使绕组端部出现无意义的振型。因此，为了便于分析，设
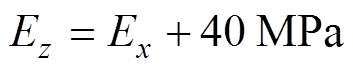（17）
同样地，根据不同弹性模量参数变化对各阶固有频率的影响及其相对变化率大小，得到如图7～图10所示的四种调整规律，其中折线图与柱形图分别为所选参数每调整20 MPa时各阶固有频率的大小及其相对变化率。
（1）调整方式1。设Ex取值范围为80～180 MPa，按照Ex=Ey，Ez=Ex+40 MPa，Gxz=Gyz=0.35Ex，Gxy= 0.385Ex同时调整4个参数，得到的调整规律如图7所示。
图7 绕组调整规律1
Fig.7 The first regulation rule of winding
（2）调整方式2。同时调整Ex=Ey，Ez=Ex+40 MPa两个参数并且固定Gxy=55 MPa，Gxz=Gyz=50 MPa，其调整规律如图8所示。
（3）调整方式3。设Gxy在取值范围30～130 MPa内进行调整，并且固定Ex=Ey=140 MPa，Ez=180 MPa，Gxz=Gyz=50 MPa，其调整规律如图9所示。
（4）调整方式4。设Gxz=Gyz在取值范围为25～125 MPa进行调整，且固定Ex=Ey=140 MPa，Ez= 180 MPa，Gxy=55 MPa，其调整规律如图10所示。
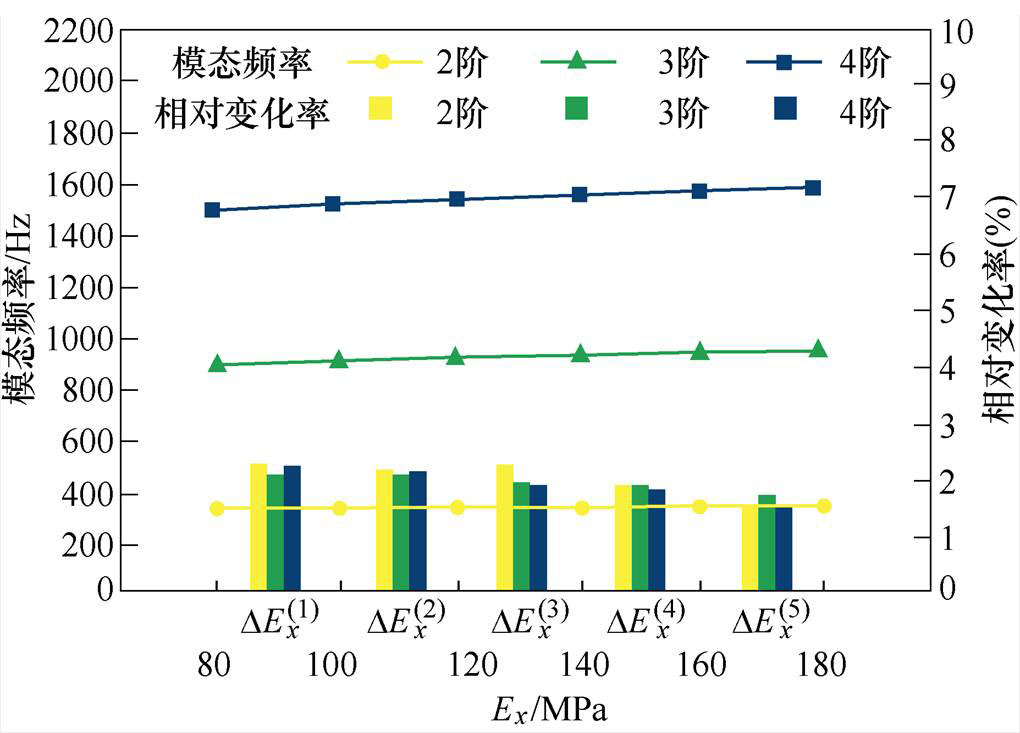
图8 绕组调整规律2
Fig.8 The second regulation rule of winding
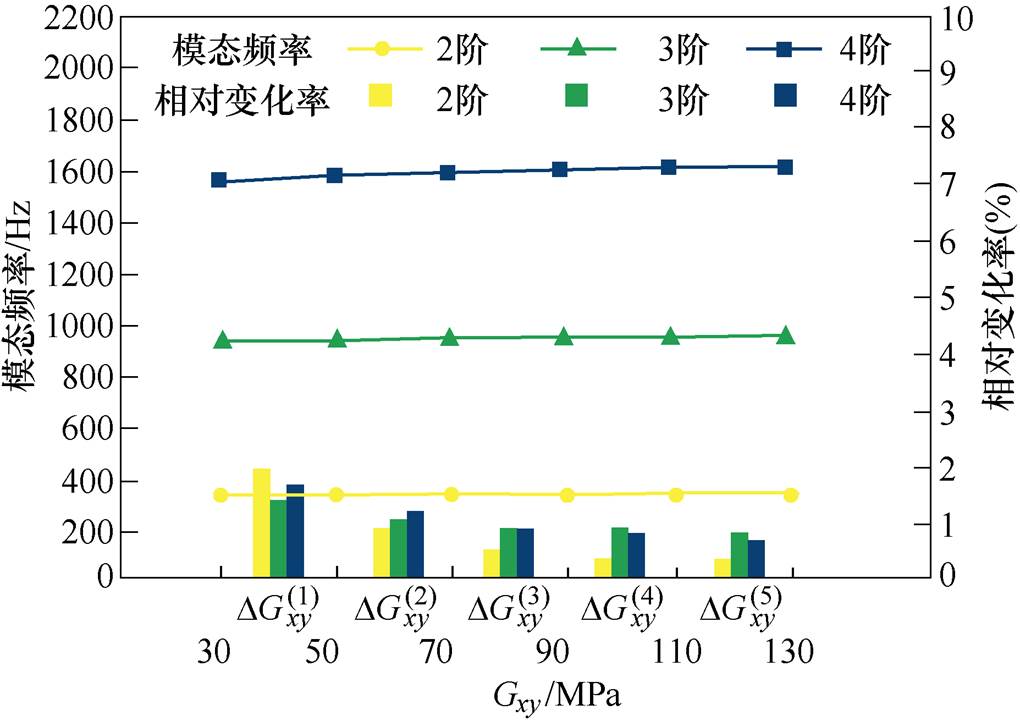
图9 绕组调整规律3
Fig.9 The third regulation rule of winding
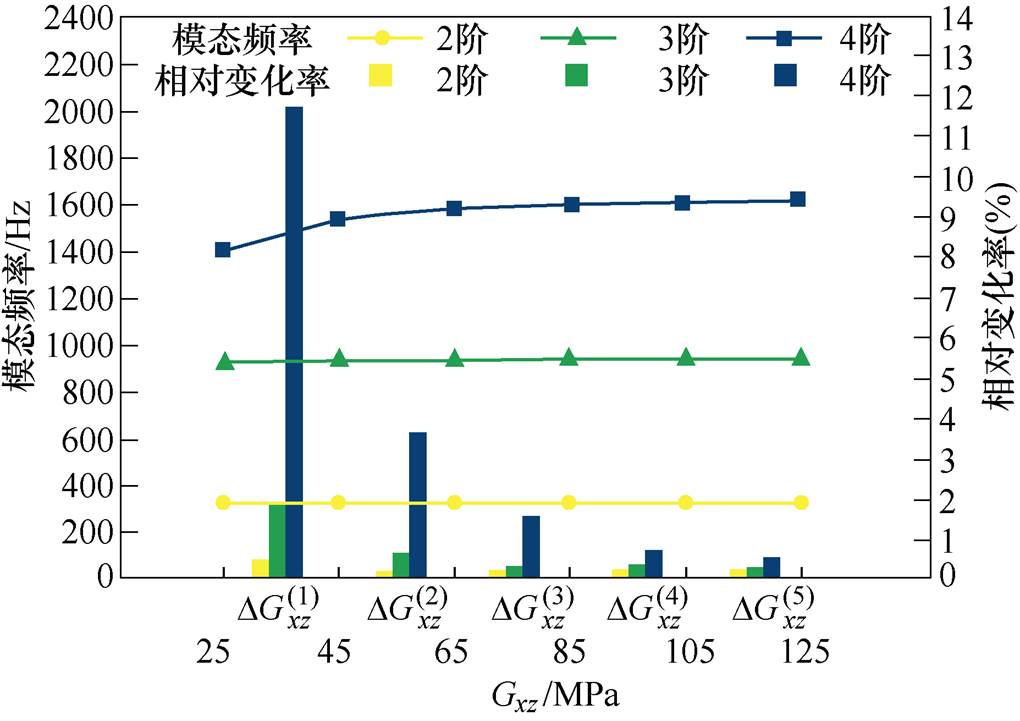
图10 绕组调整规律4
Fig.10 The fourth regulation rule of winding
由此可得，调整方式1对4阶固有频率影响明显大于2、3阶。方式2各阶整体变化规律大致相同，对2阶影响稍大。方式3中Gxy在初始值以下调整对2阶影响较大；在初始值以上调整对2阶影响较小。在方式4中，几乎不对2、3阶产生影响，并且Gxz=Gyz在25～65 MPa范围内变化时，对4阶影响较大。
DS-EEFMM的机壳材料为铝合金，视为各向同性材料，其弹性模量的取值按照铝合金的材料属性选取，即E=71 GPa，G=27 GPa，v=0.33，质量密度同样按实际建模体积与实际质量确定。
通过有限元分析发现，杨氏模量的调整范围在60～110 GPa比较合理，否则会出现4阶振型不明显现象。通过调整机壳的杨氏模量得到机壳对外定子模态频率的影响规律如图11所示。
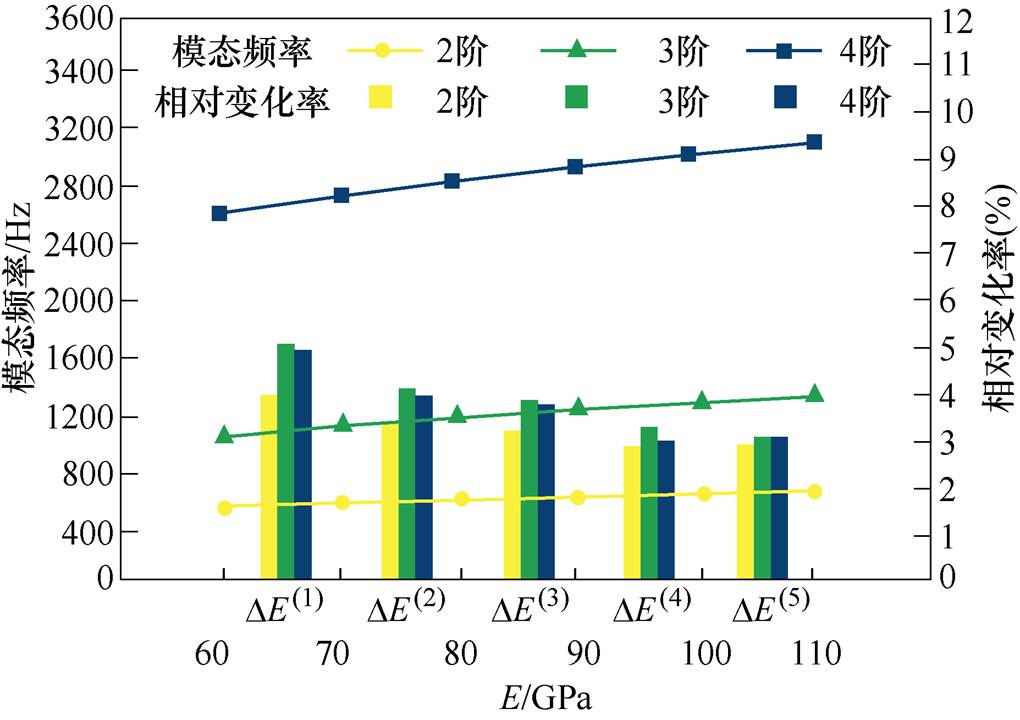
图11 机壳调整规律
Fig.11 The regulation rule of casing
由此可得，机壳杨氏模量的变化对3、4阶固有频率的影响规律相同，对2阶固有频率的影响要小于3、4阶。除此之外，由于端盖通过与机壳相连来影响定子模态频率。对端盖做简要分析后，发现其影响规律与机壳相似，但对固有频率的相对影响率要小，因此不再继续分析端盖弹性模量变化对定子固有频率的影响规律。
在弹性模量参数调整之前需要搭建模态测试平台得到模态实验结果，并作为参数调整依据。本节分别进行外定子、外定子组件、整机三组模态实验来对弹性模量进行调整，根据有限元材料参数设置初始值时与实验值误差的大小，利用弹性模量不同的调整方式得到的调整规律，选取适当调整值，从而使2、3、4阶模态分析仿真结果与实验结果的误差均在4%以内。
DS-EEFMM模态测试平台如图12所示，通过软尼龙绳悬挂电机结构对其进行自由状态下的零阻尼模态测试。采用力锤作为激振设备使待测电机结构产生振动信号，之后通过加速度传感器采集电机结构振动时的加速度信号，并输出至振动信号分析仪中进行信号分析，最后经振动分析软件中的频响函数、相干函数等计算处理后，得到待测电机结构的模态振型及固有频率。
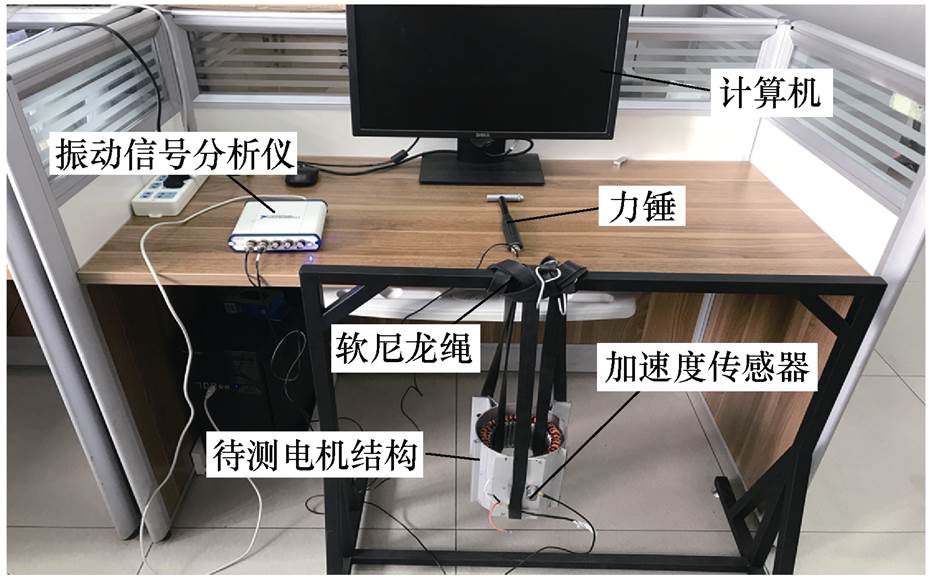
图12 模态测试平台
Fig.12 Modal test platform
对外定子模态仿真模型设置初始参数后得到仿真结果。根据搭建的模态测试平台进行外定子模态实验，得到2、3、4阶模态振型和固有频率。外定子材料设置初始参数时仿真结果与实验结果对比见表2。
表2 外定子有限元初始值与实验值对比
Tab.2 Comparison between initial finite element valueand experimental value of outer stator
阶数固有频率/Hz误差(%) 有限元实验值 2423.5382.310.8 31 1261 090.53.3 42 008.81 896.45.9
从表2可以看出，各阶的有限元值均大于实验值，需要将弹性模量的初始值向下调整。2阶误差较大，3阶误差较小，根据3.1节得到的外定子弹性模量调整规律，可以采用方式2进行调整，但直接运用方式2调整范围太大，不易获取合适的调整值。因此先用方式1将Ex向下调整16 GPa，使各阶误差整体减小，再用方式2将Ex向下调整12 GPa，经过两次调整从而将各阶误差调整到4%以内。
最后，得到外定子模态实验结果与有限元仿真结果见表3，可以看出，外定子各阶固有频率误差均处于4%以内，误差较小，从而获得了较为精确的外定子有限元模态分析结果。
表3 外定子模态实验结果与有限元结果对比
Tab.3 Comparison between modal test results and finite element results of outer stator
阶数固有频率/Hz误差(%) 模态实验有限元仿真 23.5 382.3395.5 3-3.1 1 090.51 056.2 4-0.65 1 896.41 884
对于外定子组件弹性模量的调整，需要在初始值的基础上，对外定子、绕组和机壳分别选择一个合适的调整值，以此来观察每个部件弹性模量参数调整对外定子组件固有频率影响的大小，并且根据该影响率以及各部件弹性模量均为调整值时与实验值各阶固有频率的误差大小，来选择合适的结构进行精确调整，从而将外定子组件模态分析结果误差同样调整到4%以内。外定子组件设置初始参数时模态分析仿真结果与实验结果对比见表4。
表4 外定子组件有限元初始值与实验值对比
Tab.4 Comparison between initial finite element value and experimental value of outer stator group
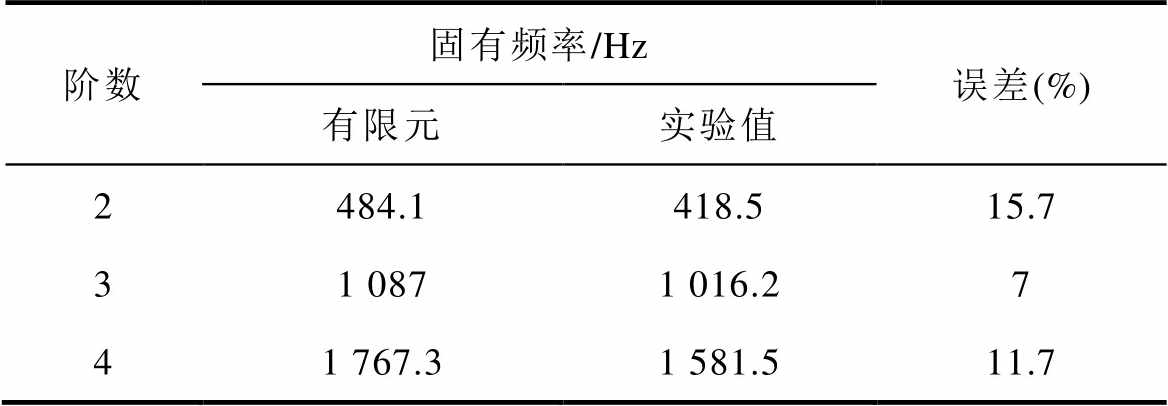
阶数固有频率/Hz误差(%) 有限元实验值 2484.1418.515.7 31 0871 016.27 41 767.31 581.511.7
由表4可知，当外定子组件仿真模型弹性模量均为初始值时，仿真结果大于实验结果且各阶误差较大。因此，对于各结构调整值的设定，绕组按照对各阶固有频率相对影响率较大的调整方式1来选取，设Ex向下调整30 MPa；而外定子则选择4.1节中所分析的第二次调整值；机壳则设E向下调整9 GPa。外定子、电枢绕组、机壳的弹性模量调整值见表5。
表5 外定子组件弹性模量调整值
Tab.5 Adjustment value of elastic modulus of outer stator group
结构部件杨氏模量/MPa剪切模量/MPa 外定子Ex=Ey=1.78×105Gxy=7.3×104 Ez=1.53×105Gxz=Gyz=6.6×104 电枢绕组Ex=Ey=110Gxy=45 Ez=150Gxz=Gyz=40 机壳E=6.2×104G=2.3×104
外定子、绕组和机壳分别设定弹性模量调整值时，相对各结构均设置初始值时各阶固有频率的减小率如图13所示。可以看出，调整电枢绕组弹性模量对外定子组件的4阶固有频率影响要明显大于2、3阶，而调整外定子与机壳弹性模量时对2、3阶的影响要比4阶更加明显。
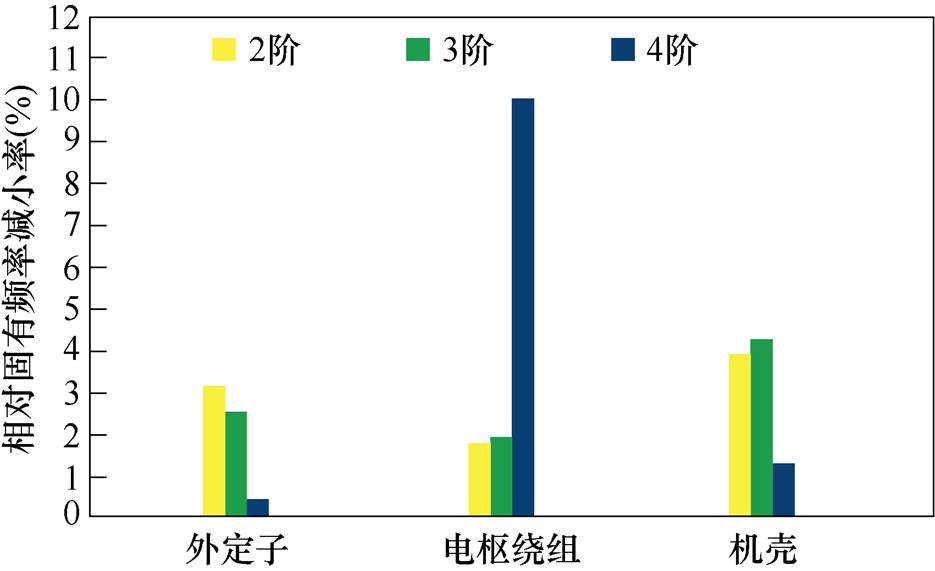
图13 各结构对外定子组件固有频率影响大小
Fig.13 Impact of each structure on natural frequency of outer stator group
外定子、电枢绕组和机壳弹性模量均设为如表5所示的调整值时，外定子组件仿真结果与模态实验结果对比见表6。其中，2阶误差较大，而3、4阶固有频率误差在合理的误差范围内。
表6 外定子组件有限元调整值与实验值对比
Tab.6 Comparison between finite element adjustment value and experimental value of outer stator group
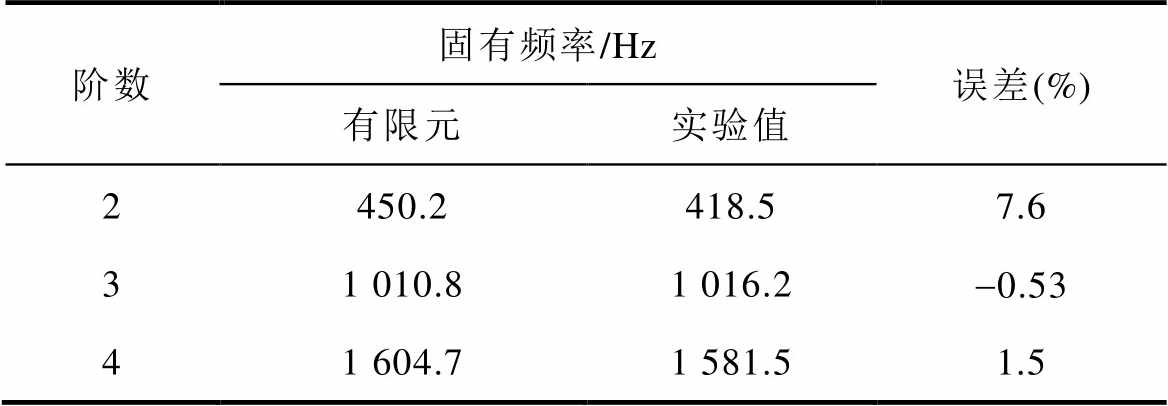
阶数固有频率/Hz误差(%) 有限元实验值 2450.2418.57.6 31 010.81 016.2-0.53 41 604.71 581.51.5
由图13可知，选择调整外定子与机壳均可将2阶误差调整到合理范围以内。但调整机壳弹性模量对3阶影响更大，因此选用外定子进行调整，并在其第二次调整值的基础上运用方式1向下调整28 GPa。最后根据外定子弹性模量设置第三次调整值，绕组和机壳设置第一次调整值时外定子组件模态实验结果与仿真结果对比见表7，由此看出，各阶模态分析结果均处于所设定的较小误差范围之内。
表7 外定子组件模态实验结果与有限元结果对比
Tab.7 Comparison between modal test results and finite element results of outer stator group
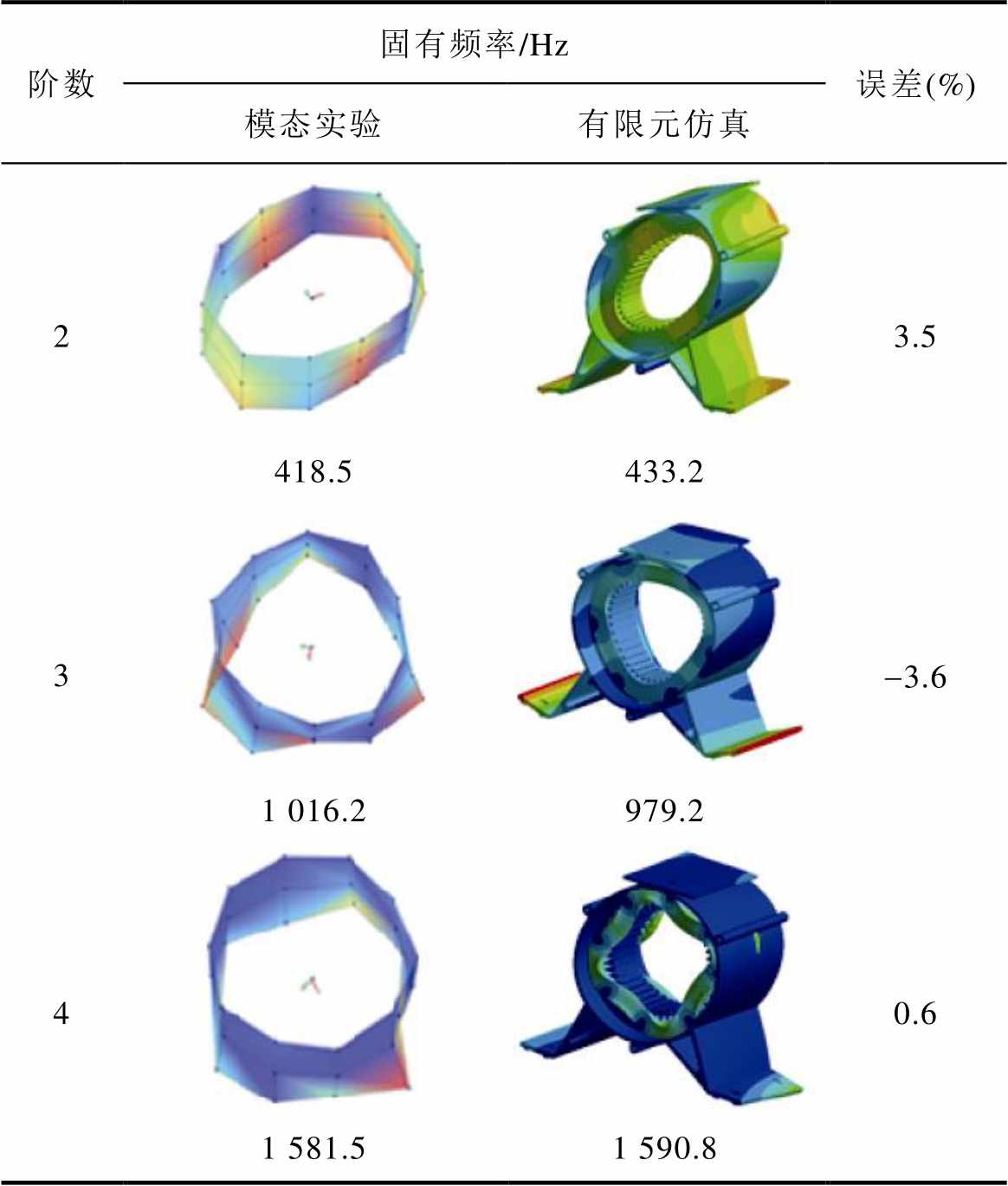
阶数固有频率/Hz误差(%) 模态实验有限元仿真 23.5 418.5433.2 3-3.6 1 016.2979.2 40.6 1 581.51 590.8
根据第1节中所建立的整机等效模型进行模态参数调整。在Ansys有限元软件中，将整机模型的前后端盖与机壳之间的连接方式选择No Separation连接，并且将机壳、前后端盖与6个螺栓之间的接触方式设为Bonded连接，以此来模拟实际端盖与机壳之间的装配情况。等效前端盖的质量密度按照内定子组件的实际质量与前端盖的建模体积确定。等效后端盖的质量密度按照调磁环杯型转子组件的实际质量与后端盖的建模体积确定。将等效前后端盖的弹性模量同样视为各向同性，材料属性与铝合金相同。
整机模态分析有限元模型设置初始参数时仿真结果与实验结果对比见表8。
对于整机模态分析弹性模量的调整，同样是在初始值的基础上给外定子、电枢绕组、机壳和前后端盖设置一个调整值，由此分别分析各结构设为调整值时对整机各阶固有频率的相对影响率大小。但是不同于外定子组件的是，整机模型只需根据设置初始值时仿真结果与实验结果的各阶误差大小，来选择合适的结构部件继续调整，从而将各阶误差调整到较小误差范围以内。外定子、绕组和机壳的调整值分别选择4.2节所设置的调整值。各结构分别设置调整值时对整机各阶固有频率的相对减小率如图14所示。
表8 整机有限元初始值与实验值对比
Tab.8 Comparison between initial finite element value and experimental value of overall prototype
阶数固有频率/Hz误差(%) 有限元实验值 2726.7651.611.5 312681 168.48.5 41 772.31 734.12.2
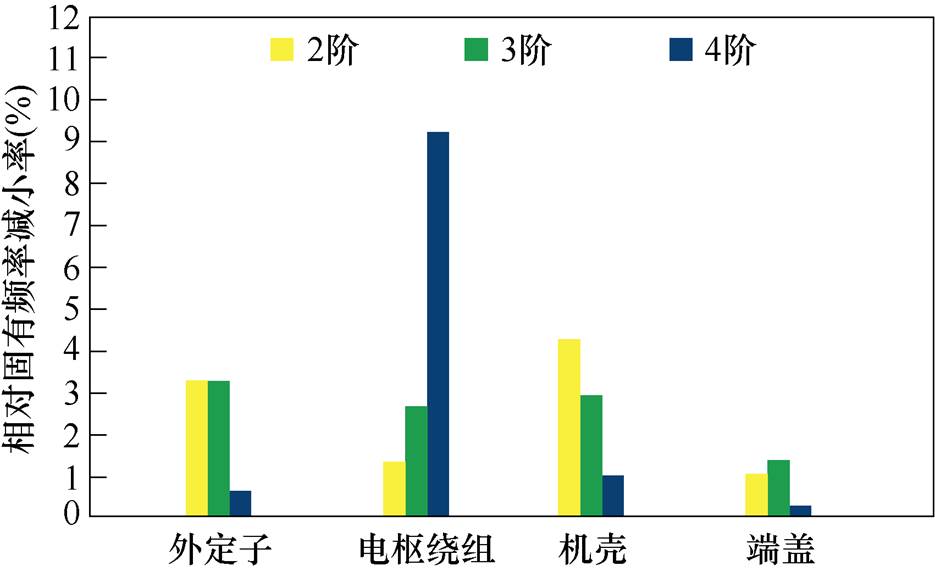
图14 各结构对整机固有频率影响大小
Fig.14 Impact of each structure on natural frequency of overall prototype
从图14可以看出，调整外定子、机壳和端盖的弹性模量对整机4阶模态频率影响较小，对2、3阶影响相对较大，而调整绕组反之。由表8可知，整机模型参数设置初始值时，4阶模态频率在合理的误差范围之内，所以不适合选用电枢绕组参数进行调整，由此选用外定子加机壳的组合方式进行调整，最后再利用端盖进行微调，从而使各阶误差降到较小误差范围之内。
因此，外定子选用前述外定子以及外定子组件模态实验所确定的弹性模量调整值，并且将机壳和前后端盖均向下调整9 GPa，以此来达到减小误差的目的。整机模态实验结果与仿真结果对比见表9。为了更清晰地展现整机模态，表9中仿真模型隐藏了前后端盖。可以看到，整机有限元模态分析结果误差均处于4%以内，从而证明了所提出的弹性模量调整方法可以得到较为精确的整机模态分析结果。最后得到整机模型弹性模量参数见表10。
表9 整机模态实验结果与有限元结果对比
Tab.9 Comparison between modal test results and finite element results of overall prototype
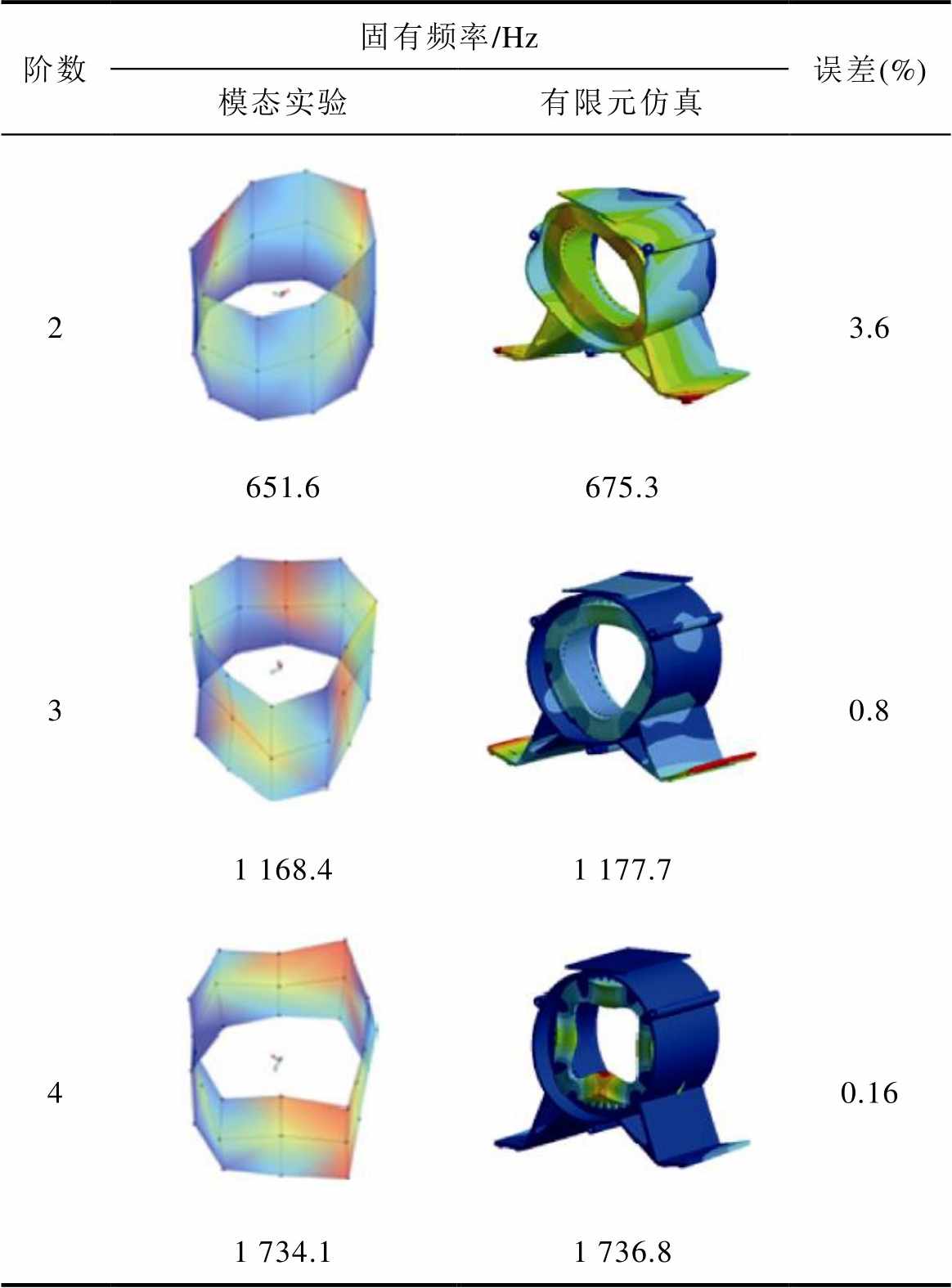
阶数固有频率/Hz误差(%) 模态实验有限元仿真 23.6 651.6675.3 30.8 1 168.41 177.7 40.16 1 734.11 736.8
表10 整机模型弹性模量参数
Tab.10 Elastic modulus parameters of the overall prototype
结构部件杨氏模量/MPa剪切模量/MPa 外定子Ex=Ey=1.5×105Gxy=5.8×104 Ez=1.3×105Gxz=Gyz=5.3×104 电枢绕组Ex=Ey=140Gxy=55 Ez=180Gxz=Gyz=50 外壳E=6.2×104G=2.33×104 前后端盖E=6.5×104G=2.44×104
本文提出了一种用于模态分析的双定子电励磁场调制电机的弹性模量调整方法。通过外定子、外定子组件和整机模态实验来验证此调整方法可以有方向性地确定各结构弹性模量的调整值，从而得到较为精确的有限元模态分析结果。最后达到三组模型的实验与仿真的各阶误差均在4%以内，具有较高的准确度。
由于整机模型结构较多，在弹性模量调整之前需要对电机结构进行合理等效。通过研究发现，外定子、机壳和等效端盖的弹性模量调整对整机各阶固有频率的影响规律相似，表现为对2、3阶的影响明显大于4阶，而电枢绕组则反之。由此可根据整机模型设置初始值时与实验值固有频率误差的大小，选取合适的结构对其弹性模量进行调整，从而明确了整机参数调整的方向性，可使其有限元模态分析结果处于较小误差范围之内。
参考文献
[1] Cheng Ming, Han Peng, Hua Wei. General airgap field modulation theory for electrical machines[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6063-6074.
[2] 黄海林, 李大伟, 曲荣海, 等. 磁齿轮复合永磁电机拓扑及应用综述[J]. 电工技术学报, 2022, 37(6): 1381-1397.
Huang Hailin, Li Dawei, Qu Ronghai, et al. A review of magnetic geared machines: topologies and appli- cations[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1381-1397.
[3] Zhu Z Q, Liu Yue. Analysis of air-gap field modulation and magnetic gearing effect in fractional- slot concentrated-winding permanent-magnet syn- chronous machines[J]. IEEE Transactions on Indu- strial Electronics, 2017, 65(5): 3688-3698.
[4] 王于涛, 隋义, 刘国鹏, 等. 横向错位磁场调制型无刷双转子电机的工作机理与性能分析[J]. 电工技术学报, 2022, 37(22): 5677-5686.
Wang Yutao, Sui Yi, Liu Guopeng, et al. Operating principle and performance analysis of transverse- dislocated magnetic-field modulated brushless double- rotor machine[J]. Transactions of China Electro- technical Society, 2022, 37(22): 5677-5686.
[5] 鲍晓华, 朱然, 刘佶炜, 等. 基于相位分析的双定子低速大转矩永磁同步电动机转矩脉动研究[J]. 电工技术学报, 2022, 37(22): 5660-5669.
Bao Xiaohua, Zhu Ran, Liu Jiwei, et al. Torque ripple analysis of dual-stator surface mounted low-speed high-torque permanent magnet synchronous motors based on phase analysis[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5660-5669.
[6] 李祥林, 李金阳, 杨光勇, 等. 电励磁双定子场调制电机的多目标优化设计分析[J]. 电工技术学报, 2020, 35(5): 972-982.
Li Xianglin, Li Jinyang, Yang Guangyong, et al. Multi-objective optimization analysis of electric- excitation double-stator field-modulated machine[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 972-982.
[7] Wang Yubin, Zhao Chenchen, Li Xianglin. Vibration and noise analysis of flux-modulation double stator electrical-excitation synchronous machine[J]. IEEE Transactions on Energy Conversion, 2021, 36(4): 3395-3404.
[8] 肖阳, 宋金元, 屈仁浩, 等. 变频谐波对电机振动噪声特性的影响规律[J]. 电工技术学报, 2021, 36(12): 2607-2615.
Xiao Yang, Song Jinyuan, Qu Renhao, et al. The effect of harmonics on electromagnetic vibration and noise characteristic in inverter-duty motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(12): 2607-2615.
[9] 罗玉涛, 卢若皓. 基于结构参数分级优化的电机电磁噪声抑制[J]. 电工技术学报, 2021, 36(14): 2957- 2970.
Luo Yutao, Lu Ruohao. Hierarchical optimization of structural parameters for motor electromagnetic noise suppression[J]. Transactions of China Electrotech- nical Society, 2021, 36(14): 2957-2970.
[10] 诸自强, 陈永校. 电机定子固有频率及其模态的有限元法分析[J]. 电工技术学报, 1987, 2(4): 39-46.
Zhu Ziqiang, Chen Yongxiao. The analysis of natural freqencies and modes of electrical machine stators by finite element method[J]. Transactions of China Electrotechnical Society, 1987, 2(4): 39-46.
[11] Xing Zezhi, Wang Xiuhe, Zhao Wenliang, et al. Calculation method for natural frequencies of stator of permanent magnet synchronous motors based on three-dimensional elastic theory[J]. IEEE Transa- ctions on Energy Conversion, 2021, 36(2): 755-766.
[12] 王天煜, 王凤翔. 大型异步电动机定子振动与模态分析[J]. 中国电机工程学报, 2007, 27(12): 41-45.
Wang Tianyu, Wang Fengxiang. Vibration and modal analysis of stator of large induction motors[J]. Proceedings of the CSEE, 2007, 27(12): 41-45.
[13] 李晓华, 黄苏融, 张琪. 电动汽车用永磁同步电机定子结构固有频率分析[J]. 中国电机工程学报, 2017, 37(8): 2383-2391.
Li Xiaohua, Huang Surong, Zhang Qi. Analysis of natural frequencies of stator structure of permanent magnet synchronous motors for electric vehicles[J]. Proceedings of the CSEE, 2017, 37(8): 2383-2391.
[14] Chai Feng, Li Yi, Pei Yulong, et al. Accurate modelling and modal analysis of stator system in permanent magnet synchronous motor with con- centrated winding for vibration prediction[J]. IET Electric Power Applications, 2018, 12(8): 1225-1232.
[15] 代颖, 崔淑梅, 宋立伟. 车用电机的有限元模态分析[J]. 中国电机工程学报, 2011, 31(9): 100-104.
Dai Ying, Cui Shumei, Song Liwei. Finite element method modal analysis of driving motor for electric vehicle[J]. Proceedings of the CSEE, 2011, 31(9): 100-104.
[16] 谢颖, 王严, 吕森, 等. 小型异步电机模态计算与试验分析[J]. 电工技术学报, 2015, 30(16): 1-9.
Xie Ying, Wang Yan, Lü Sen, et al. Modal calculation and test of small asynchronous motor[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 1-9.
[17] Wang Shanming, Hong Jianfeng, Sun Yuguang, et al. Analysis of zeroth-mode slot frequency vibration of integer slot permanent-magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2020, 67(4): 2954-2964.
[18] Lin Fu, Zuo Shuguang, Deng Wenzhe, et al. Modeling and analysis of electromagnetic force, vibration, and noise in permanent-magnet synchronous motor con- sidering current harmonics[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7455-7466.
[19] 吴建华. 基于物理模型开关磁阻电机定子模态和固有频率的研究[J]. 中国电机工程学报, 2004, 24(8): 109-114.
Wu Jianhua. Study on the stator mode shapes and natural frequencies of switched reluctance motor based on real structual model[J]. Proceedings of the CSEE, 2004, 24(8): 109-114.
[20] 左曙光, 张耀丹, 阎礁, 等. 考虑定子各向异性的永磁同步电机振动噪声优化[J]. 西安交通大学学报, 2017, 51(5): 60-68.
Zuo Shuguang, Zhang Yaodan, Yan Jiao, et al. Optimization of vibration and noise in permanent magnet synchronous motor considering stator anisotropy[J]. Journal of Xi’an Jiaotong University, 2017, 51(5): 60-68.
[21] 邓文哲, 左曙光, 孙罕, 等. 考虑定子铁芯和绕组各向异性的爪极发电机模态分析[J]. 振动与冲击, 2017, 36(12): 43-49.
Deng Wenzhe, Zuo Shuguang, Sun Han, et al. Modal analysis of a claw-pole alternator considering orthotropy of the stator core and windings[J]. Journal of Vibration and Shock, 2017, 36(12): 43-49.
[22] Yin Hongbin, Ma Fangwu, Zhang Xueyi, et al. Research on equivalent material properties and modal analysis method of stator system of permanent magnet motor with concentrated winding[J]. IEEE Access, 2019, 7: 64592-64602.
[23] Yu Yinquan, Bi Chao, Jiang Quan, et al. Prediction of vibration in PM synchronous motor based on calculation of stator natural frequency[J]. Micro- system Technologies, 2015, 21(12): 2803-2810.
[24] Liu Feng, Wang Xiuhe, Xing Zezhi, et al. Reduction of cogging torque and electromagnetic vibration based on different combination of pole arc coefficient for interior permanent magnet synchronous machine[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(4): 291-300.
Abstract Modal analysis is an important part of motor vibration and noise analysis. To accurately obtain the results of motor modal analysis, it is necessary to assign corresponding elastic modulus parameters to the stator, armature winding, casing, end cover, and other structures. When the structural material is determined, its elastic modulus is also determined. Analytical and finite element calculations are based on ideal conditions, and there is often a significant error between the calculated and actual results based on the determined elastic modulus. The structure of the entire machine model, such as the casing and end cover, greatly affects the stator modal. For a finite element model, adjusting anisotropic parameters like the stator core and winding is necessary.
At this stage, the determination of the elastic modulus of the motor structure is mainly done through modal experiments to adjust the parameters of the simulation results. Their errors converge to a reasonable error range. Although this method can obtain stator modal analysis results with high accuracy, the influence of parameter adjustment on each order of natural frequencies is not linear. Suppose its directionality cannot be clearly pointed out, it is difficult to adjust the parameters of the stator assembly and the entire machine. As a result, adjusting the errors of each order is difficult. Therefore, a double-stator electric-excitation field-modulated machine is taken as the research object. First, the initial values of the material parameters of each structure are determined, and the elastic modulus that affects its modal analysis is studied using finite element software. The relative influence rate of the elastic modulus changes in the outer stator, armature winding, casing, and end cover on each order of natural frequency is observed. According to the value relationship between elastic modulus, distinct adjustment methods were identified: three for the outer stator, four for the armature winding, and singular for the casing and end cover, thereby clarifying the directionality of elastic modulus adjustment for each structure. After that, the hammer method was used to conduct modal experiments on the outer stator, the outer stator assembly, and the entire machine. The error magnitude between modal experimental results and simulation results was obtained. Finally, the elastic modulus of the outer stator, armature winding, casing, and end cap was adjusted based on the error magnitude and the directionality for elastic modulus adjustments.
Due to the complexity of the entire machine’s structure, it is necessary to appropriately equate the motor structure before adjusting the elastic modulus. It is found that modifying the elastic modulus of the outer stator, casing, and equivalent end cover has a similar effect on the natural frequencies across various orders of the entire machine. The effects on the 2nd and 3rd orders are significantly greater than the 4th order, and the armature winding has an opposite effect. Therefore, according to the error between the finite element modal analysis and experimental results obtained with the initial elastic modulus, the elastic modulus adjustment values for the outer stator and armature windings, determined through modal experiments, are selected. The elastic modulus of the casing and end cover is directly adjusted to minimize errors. The error of the finite element modal analysis results for the entire machine is within 4%. It proves that the proposed elastic modulus adjustment method can obtain more accurate modal analysis results for the entire machine, thereby facilitating the electromagnetic noise prediction and analysis of the motor.
keywords：Double-stator electric-excitation field-modulated machine, finite element modal analysis, adjustment rule of elastic modulus, modal experiment
DOI: 10.19595/j.cnki.1000-6753.tces.230052
中图分类号：TM356
国家自然科学基金资助项目（52130706）。
收稿日期 2023-01-13
改稿日期 2023-03-15
宋春同 男，1997年生，硕士研究生，研究方向为特种电机的电磁噪声分析。E-mail: songchuntong2021@163.com
王玉彬 男，1974年生，教授，博士生导师，研究方向为特种电机设计及其控制。E-mail: wangyubin@upc.edu.cn（通信作者）
（编辑 崔文静）