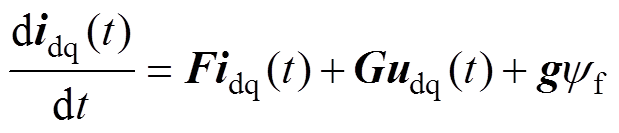 (1)
(1)
摘要 高速电驱动场合会受到开关频率的限制,低载波比特性凸显,由此引起的控制延迟问题影响了内置式永磁同步电机(IPMSM)矢量控制系统性能。基于扩展电动势的建模方案能够获得IPMSM的对称化模型,有利于离散化分析和设计,以提升低载波比运行性能。扩张状态观测器(ESO)能够实现扩展电动势和扰动的集总观测,然而低载波比延迟问题影响了估算性能。该文在离散域中分析延迟影响,设计和对比研究了几种延迟影响抑制方案,即延迟校正扩张状态观测器,提升了估计精度。基于此,设计了IPMSM离散域电流控制方案,显著提升了电流响应特性。通过电动汽车驱动实验平台验证了该文的分析和设计。
关键词:内置式永磁同步电机 数字控制延迟 扩张状态观测器 离散域设计
内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM)高功率密度、高效率和宽调速范围的优点,使其广泛应用于新能源电动汽车、重型机械等工业场合[1]。为提升功率密度,电机转速不断增高,但受限于损耗和散热条件,开关频率提升有限,低载波比问题愈发明显[2]。逆变器输出电压精度降低,数字控制延迟问题凸显,对电流控制提出挑战。因此,如何克服控制延迟影响,提升控制性能是当前高性能控制算法研究的热点[3]。
转子磁链定向同步旋转坐标系(dq坐标系)PI控制,不仅具有较好的控制性能,而且易于工程实现,因而得到广泛应用。但是,随电机转速的提升、载波比的下降,实际运行性能明显下降。其原因主要有三个方面:dq轴间交叉耦合加剧、离散化误差增加、控制延迟加大[4-6]。针对dq轴电流交叉耦合问题,前馈、反馈、内模及复矢量等方法被引入[7-10],以期实现dq轴间的解耦控制。然而,电流控制器通常是基于连续域设计,再通过欧拉、双线性变换(Tustin)等方法进行离散化数字实现。低载波比下离散化误差增加,影响解耦效果和控制性能[11]。针对离散化误差问题,文献[12]直接在离散域中进行控制器设计,提升了低载波比控制性能。但这些基于模型的设计方案对系统内外扰动抑制能力不 足[13-14],尤其在高速低载波比工况下,运行性能依然欠佳。扰动观测器实现对扰动量的估计与补偿,构成复合控制,将有利于控制性能的提升。
目前,应用较广的扰动观测器有未知输入观测器(Unknown Input Observer, UIO)、扰动观测器(Disturbance Observer, DOB)、摄动观测器(Pertur- bation Observer, POB)及扩张状态观测器(Extended State Obsever, ESO)等。其中,ESO是韩京清教授在20世纪90年代首次提出的[15],采用和UIO类似的思路,将系统外部扰动和内部不确定性作为系统的“总扰动”,并将其设为新的状态进行估计。相比UIO、DOB和POB等扰动观测器而言,ESO理论上可以独立于对象模型和扰动模型,具有扰动观测能力强、参数依赖度低的优点,近来受到关注并成为研究的热点[16-19]。
ESO能够实现对系统内外部扰动的快速观测,将其应用在数字控制系统中,可以削弱控制延迟的影响,从而提高系统稳定性和动态性能[20-21]。但是由于控制延迟的存在,被控对象的输出信号时间上滞后于输入信号,导致传统ESO两路输入不同步,尤其在低载波比工况下,延迟较大,造成的观测误差较大[22-23]。对此,文献[24]通过Pade近似将控制延迟表示为一阶惯性环节,从而采用高阶ESO处理时滞对象,有效提高了ESO观测性能。文献[25]考虑控制延迟,通过对ESO输入施加延时环节,实现观测器输入量的同步。文献[26]则将ESO与Smith预估器结合,通过输出预测的方式,实现ESO输入信号的同步。
然而,以上观测器均是基于连续域设计,延迟难以准确处理,且数字化实现时受到离散化误差的影响。因此,本文在离散域中直接设计扩张状态观测器,对数字控制延迟产生的影响进行分析,总结归纳出多种考虑数字延迟的时延型ESO,并基于此,提出了基于延迟校正扩张状态观测器的IPMSM电流控制方案。与传统方案相比,所提方案提升了电流环的稳定裕度,改善了电流信号的跟踪性能和抗扰性能。
IPMSM在同步旋转坐标系下的数学模型为
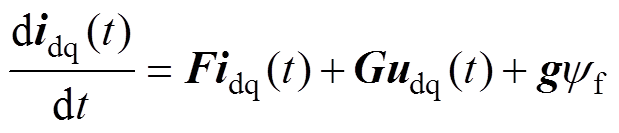 (1)
(1)
其中
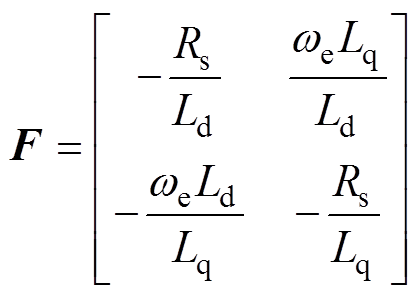
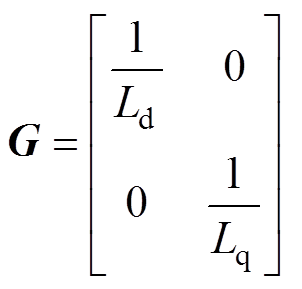
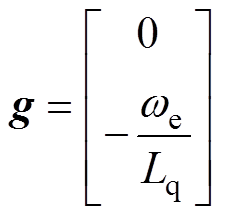
式中,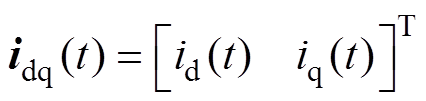 为定子电流向量,
为定子电流向量, 、
、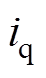 分别为d、q轴电流;
分别为d、q轴电流;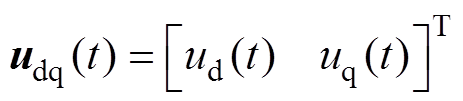 为定子电压向量,
为定子电压向量,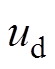 、
、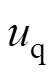 分别为d、q轴电压;F、G、g为系数矩阵;Ld、Lq分别为d、q轴电感;
分别为d、q轴电压;F、G、g为系数矩阵;Ld、Lq分别为d、q轴电感;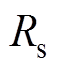 为定子电阻;
为定子电阻;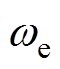 为转子电角速度;
为转子电角速度;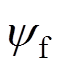 为永磁体磁链。
为永磁体磁链。
对IPMSM而言,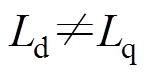 ,状态矩阵不对称。为使式(1)对称,降低数字实现计算量,可借助扩展反电动势的概念将模型对称化改造,即
,状态矩阵不对称。为使式(1)对称,降低数字实现计算量,可借助扩展反电动势的概念将模型对称化改造,即
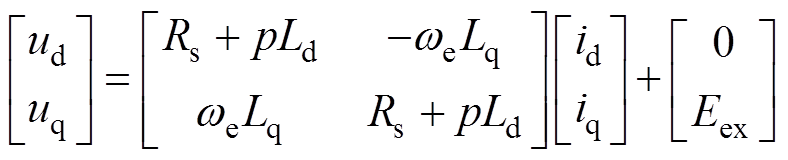 (2)
(2)
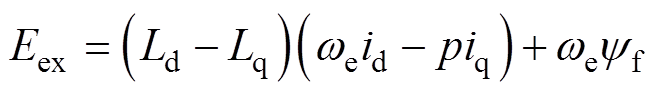 (3)
(3)
式中,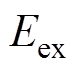 为IPMSM扩展反电动势;p为微分算子。
为IPMSM扩展反电动势;p为微分算子。
对式(2)所示的对称化模型可采用复矢量进行描述,从而在形式上为一阶方程,便于设计和分析。复矢量形式为
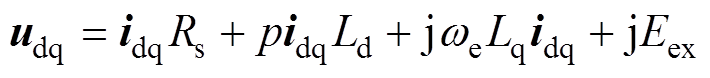 (4)
(4)
式中,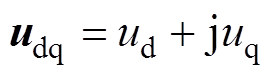 为定子电压矢量;
为定子电压矢量;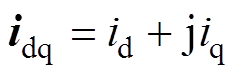 为定子电流矢量。
为定子电流矢量。
实际运行中,IPMSM定子电阻Rs,交直轴电感Ld、Lq会受温度和磁饱和的影响而发生改变。考虑这些不确定性和外部扰动Ddq,则式(4)可表示为
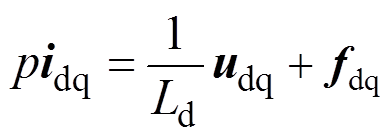 (5)
(5)
式中,fdq为整体扰动,即
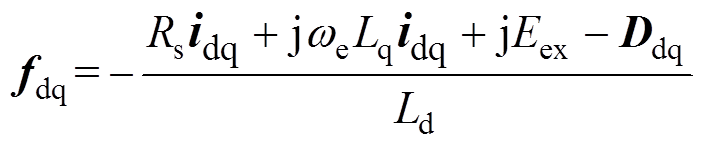 (6)
(6)
将整体扰动fdq作为一个新状态,则可将状态向量扩张为xdq=[idq fdq]T。以udq为控制输入,ydq为输出变量,并令b0=1/Ld,则扩张后的状态空间模型可表示为
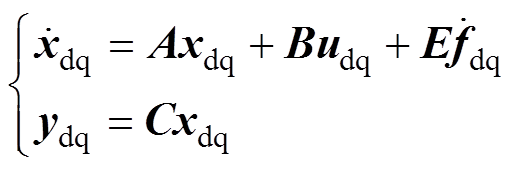 (7)
(7)
其中
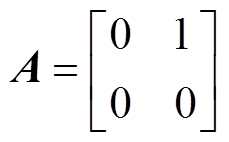
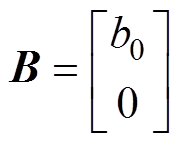
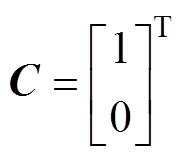
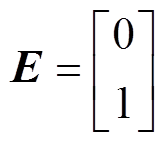
式中, 为整体扰动
为整体扰动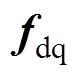 的微分,
的微分,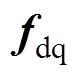 未知且通过观测器校正项可以进行估计补偿,因而后续推导中略去
未知且通过观测器校正项可以进行估计补偿,因而后续推导中略去 。为了设计离散型ESO,假设采样时间足够小,以至于扰动fdq在两个相邻采样周期内变化不是很大,式(8)成立。
。为了设计离散型ESO,假设采样时间足够小,以至于扰动fdq在两个相邻采样周期内变化不是很大,式(8)成立。
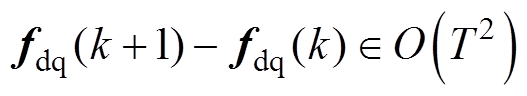 (8)
(8)
式中,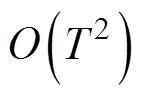 为误差的阶;k为周期数。
为误差的阶;k为周期数。
对式(7)进行离散化,假设采样时间为Ts,采用Zero-Order-Hold(ZOH)来离散对象模型,记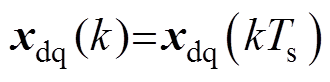 ,
, ,
,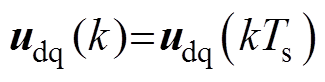 ,
,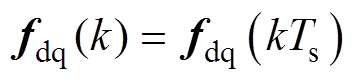 ,离散化后得
,离散化后得
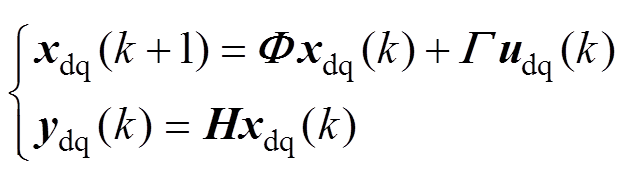 (9)
(9)
其中


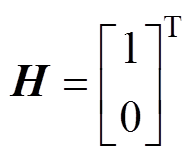
式中,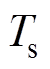 为采样周期。
为采样周期。
针对离散状态方程式(9),可设计状态观测器为
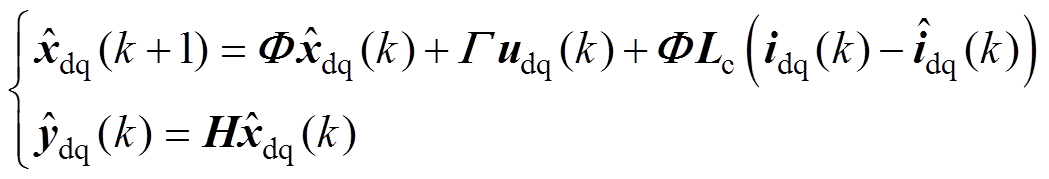 (10)
(10)
式中,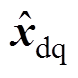 和
和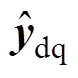 分别为xdq和ydq的估计值;Lc=[Lc1 Lc2]T为误差校正增益,其中,Lc1、Lc2为校正增益。
分别为xdq和ydq的估计值;Lc=[Lc1 Lc2]T为误差校正增益,其中,Lc1、Lc2为校正增益。
定义状态误差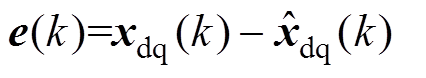 ,将式(9)减去(10)得误差方程为
,将式(9)减去(10)得误差方程为
 (11)
(11)
其中
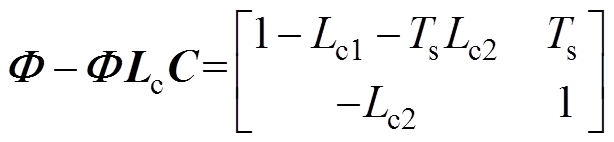
为获得较好的误差收敛特性,校正增益取Lc1= 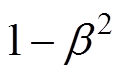 、Lc2=
、Lc2=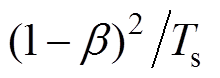 ,其中
,其中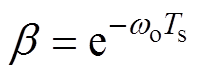 ,
,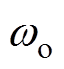 为观测带宽。式(11)所示误差方程的特征多项式为
为观测带宽。式(11)所示误差方程的特征多项式为
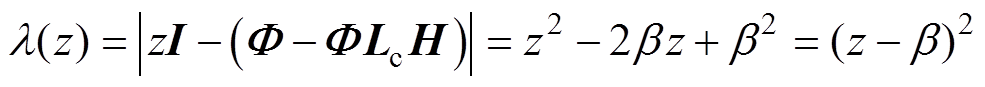 (12)
(12)
显然,只要满足条件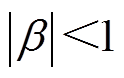 ,则观测器特征根全部位于单位圆内,且误差校正增益只与
,则观测器特征根全部位于单位圆内,且误差校正增益只与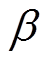 相关,简化了参数整定过程。图1中给出了观测器的结构框图,由于在设计时没有考虑延迟的影响,为便于描述这里将其命名为无延时ESO。
相关,简化了参数整定过程。图1中给出了观测器的结构框图,由于在设计时没有考虑延迟的影响,为便于描述这里将其命名为无延时ESO。
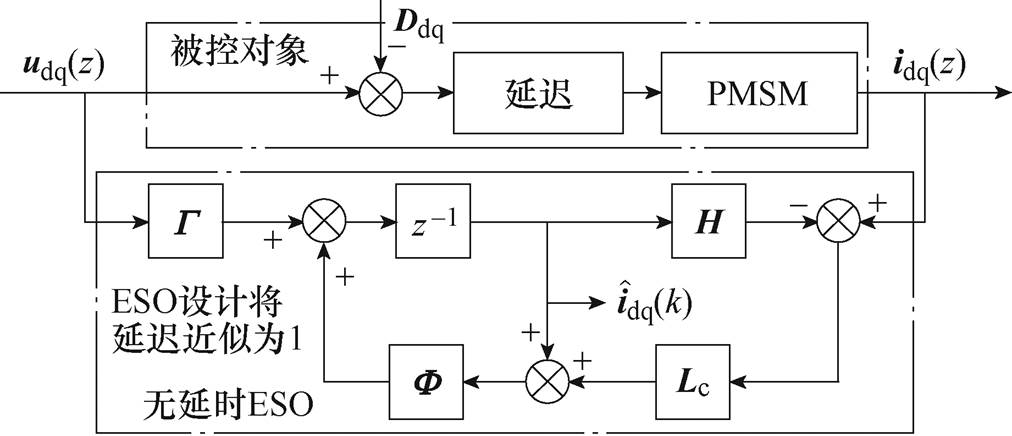
图1 无延时ESO结构框图
Fig.1 Block diagram of ESO without time-delay considered
图2为IPMSM电流环数字控制系统原理框图。数字控制延迟主要分为采样-计算延迟和脉冲宽度调制(Pulse Width Modulation, PWM)延迟两部分,在图2中,分别用z-1和ZOH表示。PWM延迟的零阶保持特性为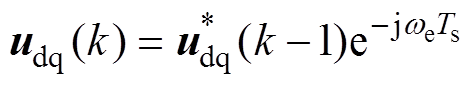 ,在控制器输出端加入
,在控制器输出端加入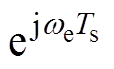 环节,可以对其相位滞后
环节,可以对其相位滞后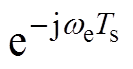 进行补偿,补偿后的电压矢量在同步旋转坐标系下满足
进行补偿,补偿后的电压矢量在同步旋转坐标系下满足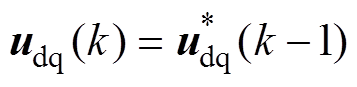 。
。
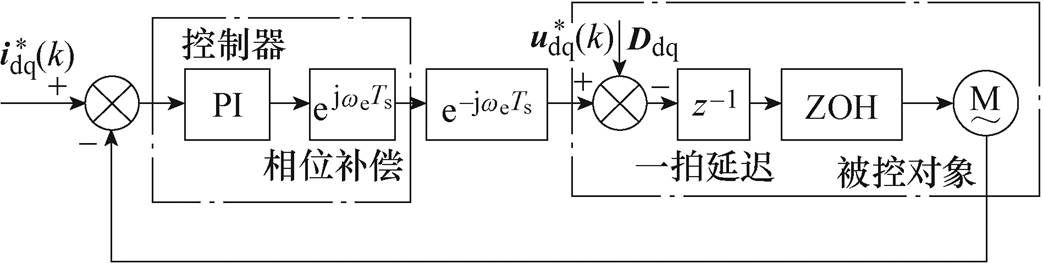
图2 IPMSM电流环数字控制系统
Fig.2 Digital current control system of IPMSM
数字控制的延迟作用使得当前拍采样获得的电流实际上是上一拍控制电压作用的结果,即当前拍采样获得的电流实际上为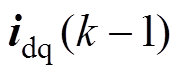 ,相比输入信号
,相比输入信号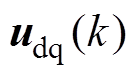 滞后一个采样周期Ts。对ESO而言,控制电压和输出电流为其输入信号,如图3所示。两个信号的不同拍,必将影响观测性能,尤其在低载波比场合下,影响更为突出,甚至造成系统不稳定。
滞后一个采样周期Ts。对ESO而言,控制电压和输出电流为其输入信号,如图3所示。两个信号的不同拍,必将影响观测性能,尤其在低载波比场合下,影响更为突出,甚至造成系统不稳定。
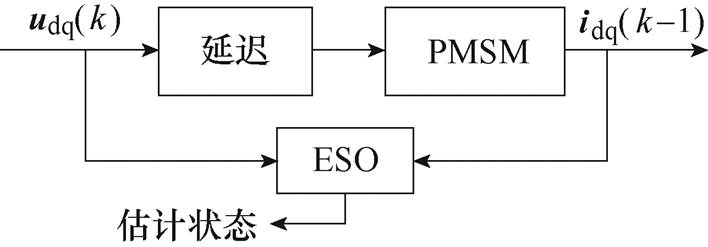
图3 延迟对ESO输入信号的影响
Fig.3 Effects of delay on ESO inputs
考虑到电流的延迟,可将式(10)所示ESO重新表述为
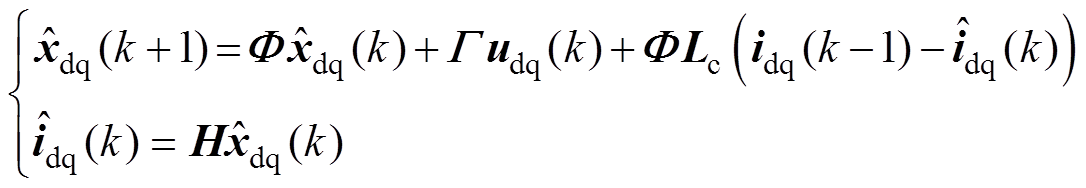 (13)
(13)
图4展示了采样周期对ESO的性能的影响,IPMSM参数将在实验部分给出。
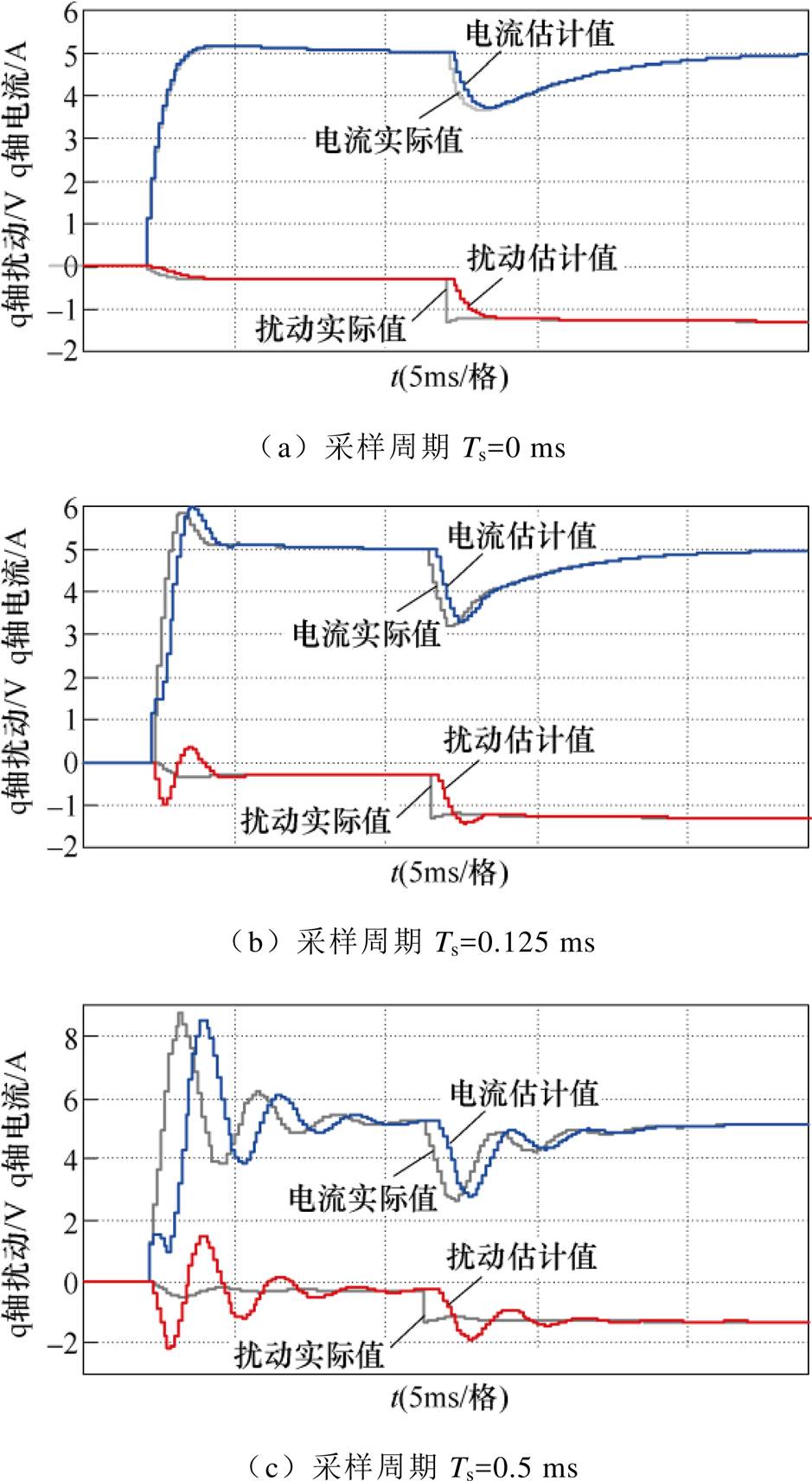
图4 延迟对观测器性能的影响
Fig.4 Effects of delay on ESO performance
由图4不难发现,随着采样周期的增加,延迟增大,不仅观测误差增加,而且动态响应过程变差,甚至存在振荡的风险。
通过第1节的分析不难发现,数字控制延迟导致信号滞后,造成观测器的两路输入信号不同步,制约了ESO的观测性能。因此,本节考虑数字延迟对ESO进行设计。为便于叙述,这里将考虑延迟的ESO称为“时延型ESO(Delay ESO, DESO)”。
目前,针对数字延迟引发ESO输入信号不同步的问题,多采用延迟近似建模或Smith预估的方案。文献[24]通过将延迟环节近似为线性环节,进而将时滞对象转换为无时滞的高阶对象,再进行ESO设计。延迟近似建模方法有Pade近似、泰勒展开、全极点近似等。为方便ESO增益参数整定,本文采用Pade近似将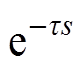 近似为一阶惯性环节,有
近似为一阶惯性环节,有
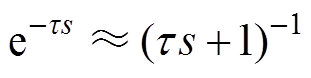 (14)
(14)
式中,t 为时间常数。
为在对象模型中包含延迟环节,将状态向量扩充为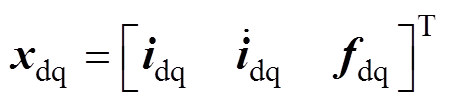 ,则考虑延迟后,被控对象模型可重新表述为
,则考虑延迟后,被控对象模型可重新表述为
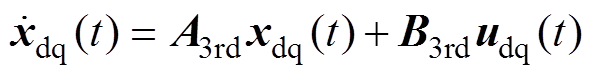 (15)
(15)
其中
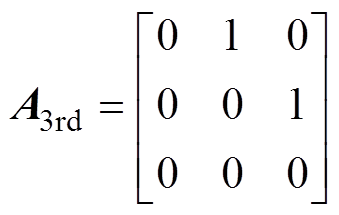
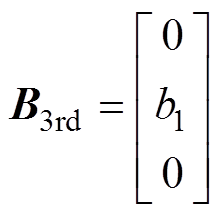
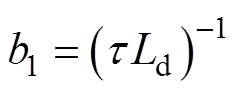
对应的ZOH离散化模型为
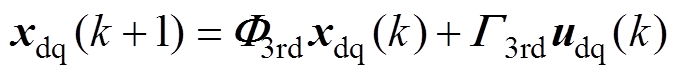 (16)
(16)
其中
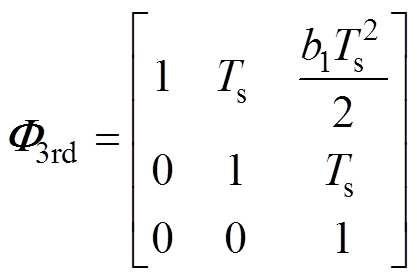
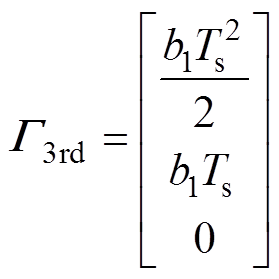
于是,ESO可设计为
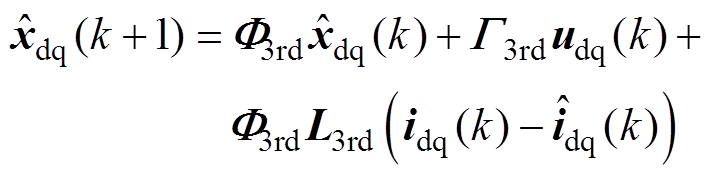 (17)
(17)
对应的结构框图如图5所示。为便于表述,本文将这种通过延迟近似建模提升ESO阶次的处理方案称为“模型法DESO(Model-DESO, M-DESO)”。
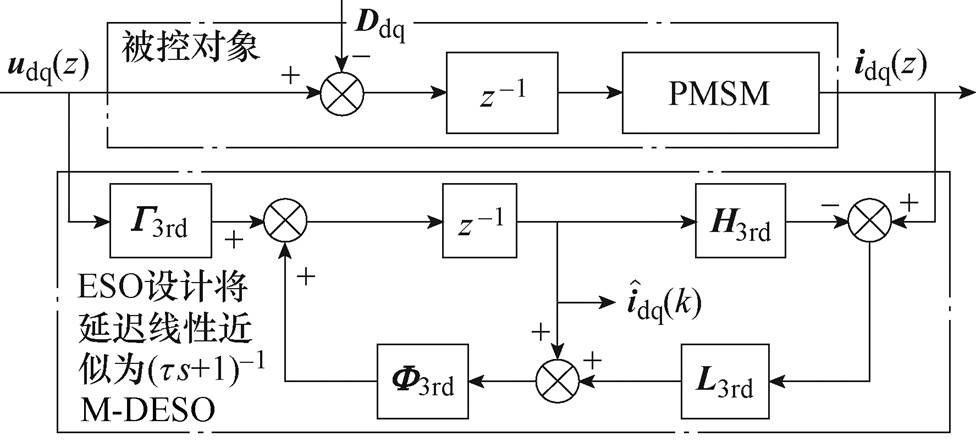
图5 模型法DESO结构框图
Fig.5 Block diagram of M-DESO
同样,将极点配置在单位圆内的同一位置,即将其特征多项式配置为
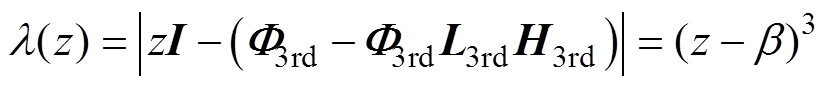 (18)
(18)
其中
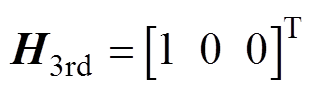
计算可得误差校正增益矩阵为
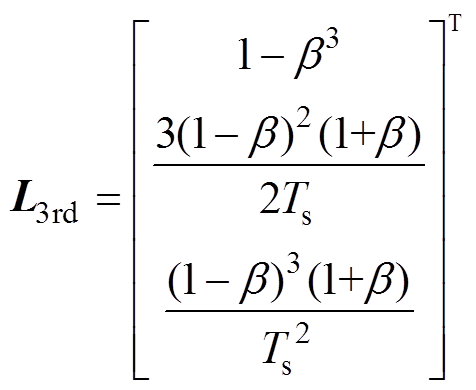 (19)
(19)
除了对延迟环节进行近似建模外,也可通过信号处理的手段解决ESO输入信号不同步问题。文献[26]采用Smith预估器方案对电流采样信号进行一拍超前预估,使其与电压信号匹配,以克服延迟对观测器带来的不利影响。本文将基于Smith预估器所设计的ESO记为“Smith-DESO”。
采用零阶保持器法对复矢量电机模型式(4)离散化,将扩展反电动势Eex视为扰动项,可得永磁同步电机离散化模型为
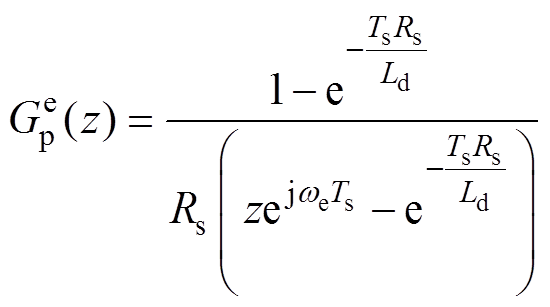 (20)
(20)
Smith预估器的表达式为
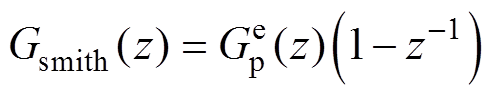 (21)
(21)
将Smith预估器所获得的一拍预测电流记为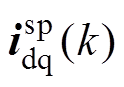 ,对应的ESO结构框图如图6所示。
,对应的ESO结构框图如图6所示。
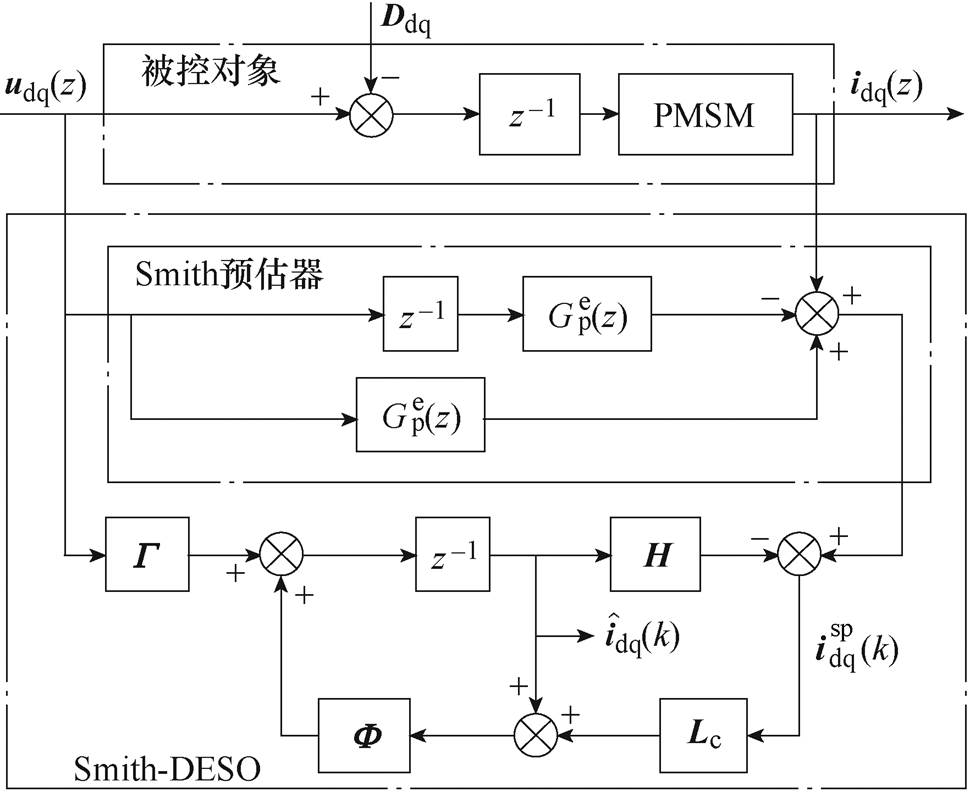
图6 Smith-DESO结构框图
Fig.6 Block diagram of Smith-DESO
就扰动观测精度而言,数字延迟对ESO的影响主要在于控制电压和采样电流作为ESO的两路输入信号不同步。实际上,通过控制电压的一拍滞后,也能实现与电流信号的同步。图7中给出了控制电压一拍延迟方案ESO结构框图。本文将其命名为“电压延迟DESO(Voltage delay-DESO, Ud-DESO)”。
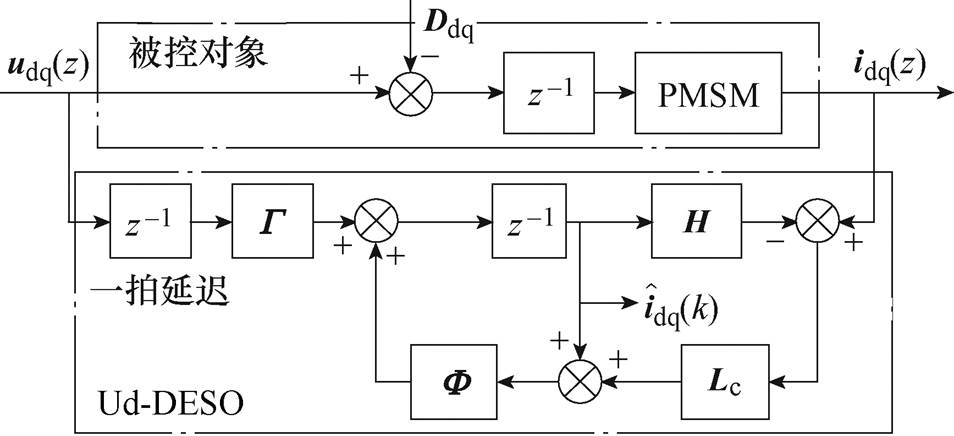
图7 电压延迟DESO结构框图
Fig.7 Block diagram of Ud-DESO
综上所述,基于对ESO基本结构与时滞对象的理解与认识,Smith-DESO和Ud-DESO就是针对时滞对象特性进行延迟校正。其基本思路是在普通线性ESO的基础上,在ESO的信号输入端增加一个Smith预估模块,预测得到电流信号idq(k-1)的下一拍电流idq(k)(见图8a),或者对控制信号udq(k)在进入扩张状态观测器之前延迟一拍(见图8b),使得进入ESO的信号udq和idq得到了同步。
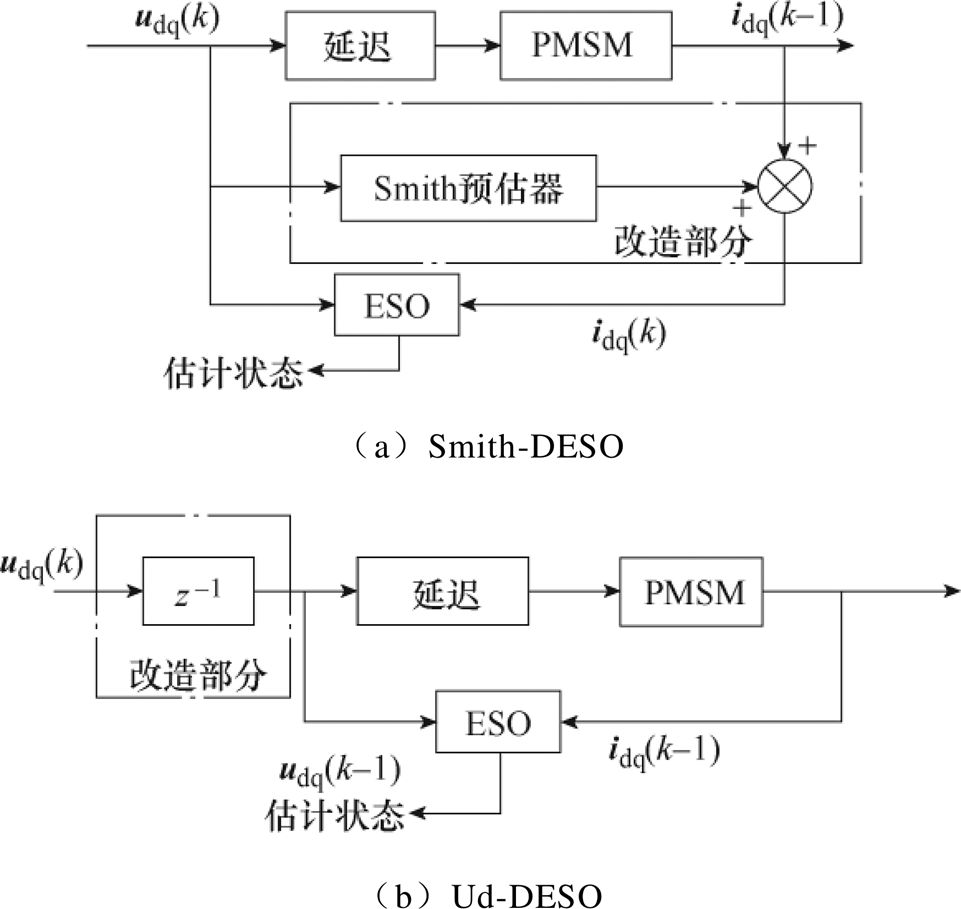
图8 改造后的时延型ESO结构框图
Fig.8 Block diagram of the modified DESO
此时,ESO估计的系统状态和扰动就都具有明确物理意义,即ESO的输入/输出具有了因果逻辑上的同步关系,预期可以产生较为有效的控制效果。但是,从图8b中可以看出,Ud-DESO的信号匹配整体滞后一拍。因此,虽然Ud-DESO解决了信号不同步问题,但是在相同带宽下,由于输入信号滞后一拍,观测性能改善不明显。对此,后续可以通过提高观测带宽来提高观测速度,以发挥Ud-DESO方案的性能优越性。
为了验证上述DESO对时滞对象的观测效果﹐本节将结合仿真对其性能进行研究,仿真参数与实验部分相同。为避免电流控制因素影响,仿真采用相同的电流控制方案,且ESO独立于控制系统运行,即观测结果暂不参与控制。首先设置无延时ESO、M-DESO、Smith-DESO、Ud-DESO四种观测器的观测带宽 均为4 800 rad/s,结果如图9所示。
均为4 800 rad/s,结果如图9所示。
可以看出,在相同带宽下,Smith-DESO的观测性能最好,M-DESO相对较差,无延时ESO和Ud-DESO性能较为接近,说明:通过Smith预估消除一拍延迟使得输入信号同步,可以有效提升观测器性能;M-DESO,由于近似误差存在,观测效果不理想;Ud-DESO虽然也解决了信号不同步问题,但是电压整体延迟一拍,因此在相同观测带宽下,Ud-DESO方案性能改善不明显,优势未得以展现。
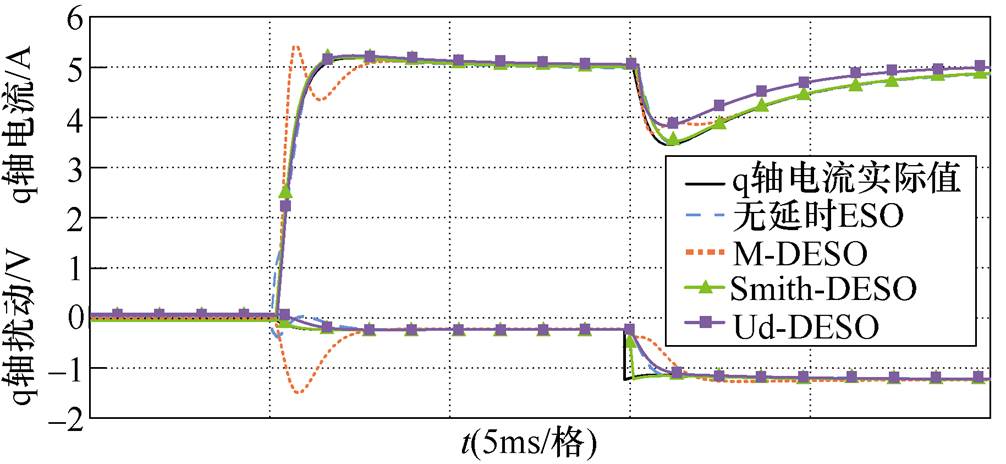
图9 不同ESO对q轴的观测结果
Fig.9 Estimating results of the q-axis ESOs
通过控制理论知识可知,增大观测器带宽能更好地跟踪扰动,但同时也会放大输出干扰。无延时ESO、M-DESO未从理论上解决信号不同步问题,因此观测带宽受限。随着带宽增大,观测器波形会出现较大纹波,稳定性明显变差甚至发散。而Smith-DESO、Ud-DESO由于从理论上解决了两路输入信号同步,可以通过提高观测带宽提升观测器的动态性能,并具有良好的稳定性。为了更好地发挥各ESO方案的优势,除相同观测带宽下的研究对比外,本文还将各方案的观测带宽 设置为其允许带宽最大值进行研究对比,具体参数见表1。表中,wc为控制带宽,Kp、Ki分别为控制器比例、积分参数。
设置为其允许带宽最大值进行研究对比,具体参数见表1。表中,wc为控制带宽,Kp、Ki分别为控制器比例、积分参数。
表1 ESO带宽选择
Tab.1 Selection of ESO band widths

观测器控制器参数观测带宽/(rad/s) 无延时ESO=1 200 rad/sKp=1.248Ki=724 800 M-DESO4 800 Smith-DESO24 000 Ud-DESO24 000
2.2.1 IPMSM标称参数观测性能对比
假设IPMSM模型精确,对q轴分别施加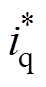 =5 A的电流阶跃指令,d=-5 V的外部扰动。q轴ESO观测结果如图10所示。
=5 A的电流阶跃指令,d=-5 V的外部扰动。q轴ESO观测结果如图10所示。
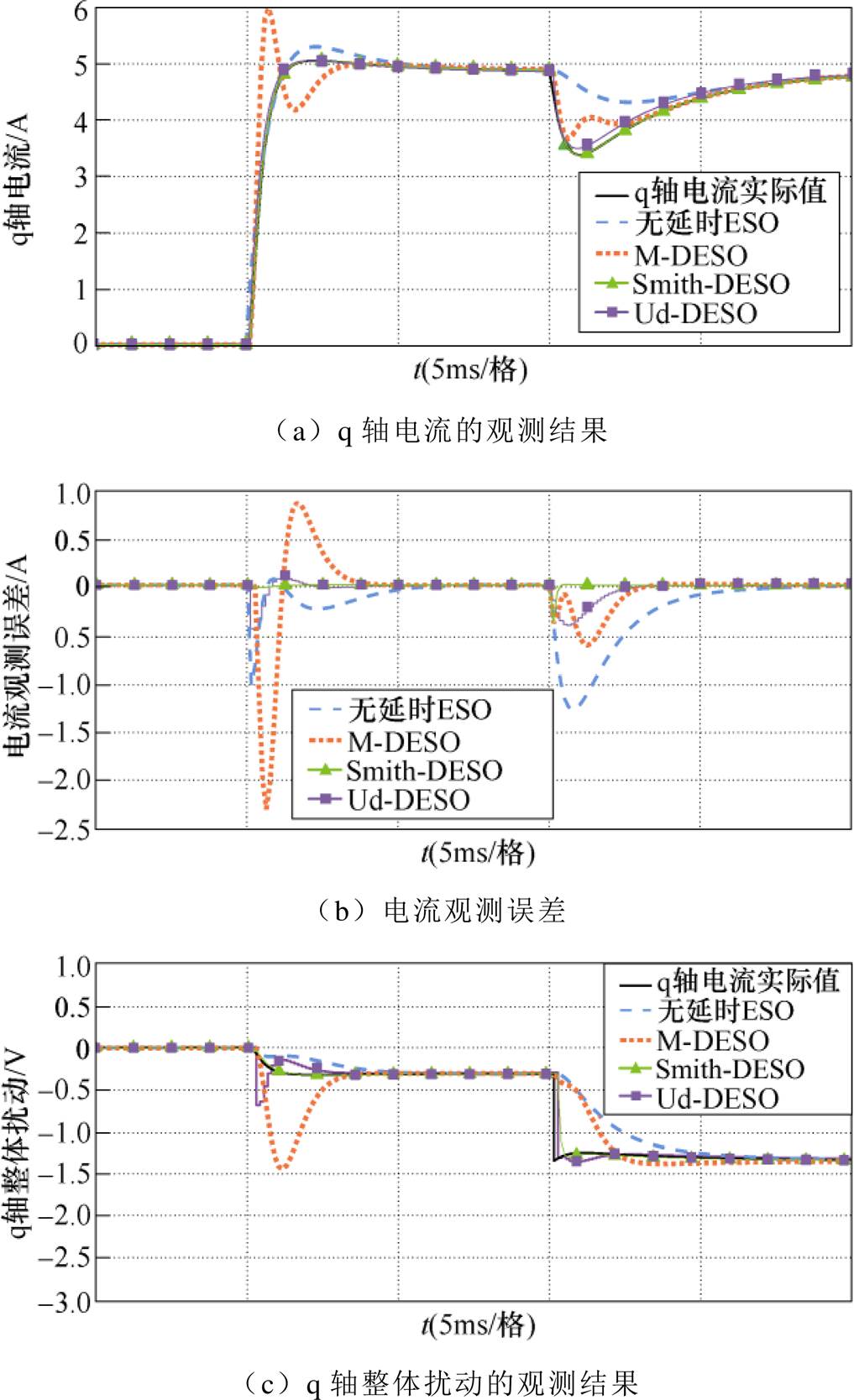
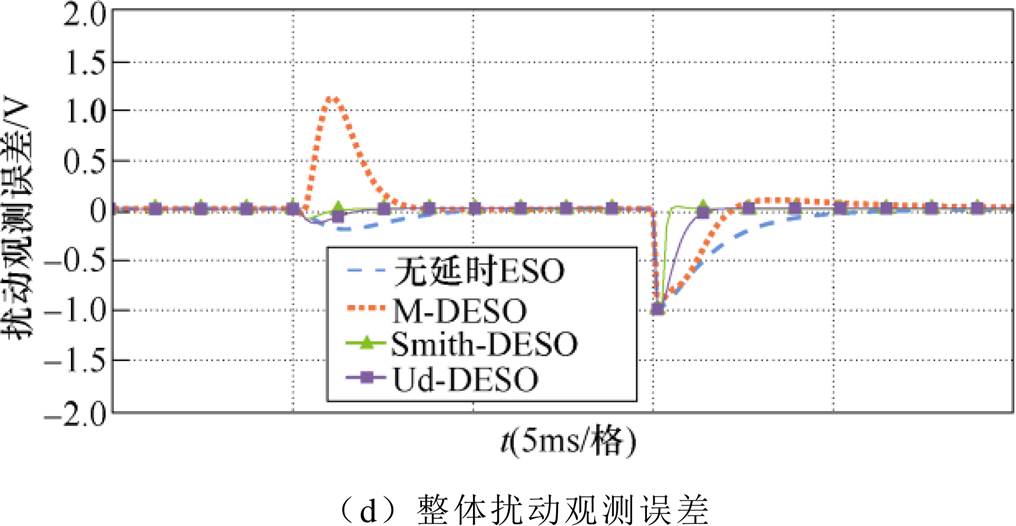
图10 标称参数下q轴ESO观测结果对比
Fig.10 Comparison of the estimating results of the q-axis ESOs under nominal parameters
由图10可以看出,在指令阶跃和施加外部扰动时,无延时ESO和M-DESO的瞬时误差较大。Smith-DESO和Ud-DESO则具有较好的扰动观测性能,观测误差较小。这表明通过改造ESO结构,使得输入信号同步,可以有效提高观测性能,实现更好的扰动估计。Smith-DESO和Ud-DESO动态特性明显好于无延时ESO或M-DESO。
2.2.2 IPMSM参数偏差时仿真对比
假设实际运行时观测器中使用的电感参数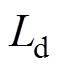 分别设为标称参数
分别设为标称参数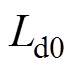 的0.5倍和2倍,q轴扰动观测结果如图11、图12所示。
的0.5倍和2倍,q轴扰动观测结果如图11、图12所示。
不难看出,当电机电感参数发生变化时,无延时ESO和M-DESO也存在一定的振荡,误差增大。Smith-DESO虽然仍然能够实现状态量的估计,但调节时间和扰动的恢复时间最长,表明Smith-DESO对模型参数偏差较为敏感。而Ud-DESO能够较为快速、平稳地跟踪q轴变量。因此,在参数失配时,相比于其他三种ESO,Ud-DESO仍然能够保持良好的扰动观测能力。
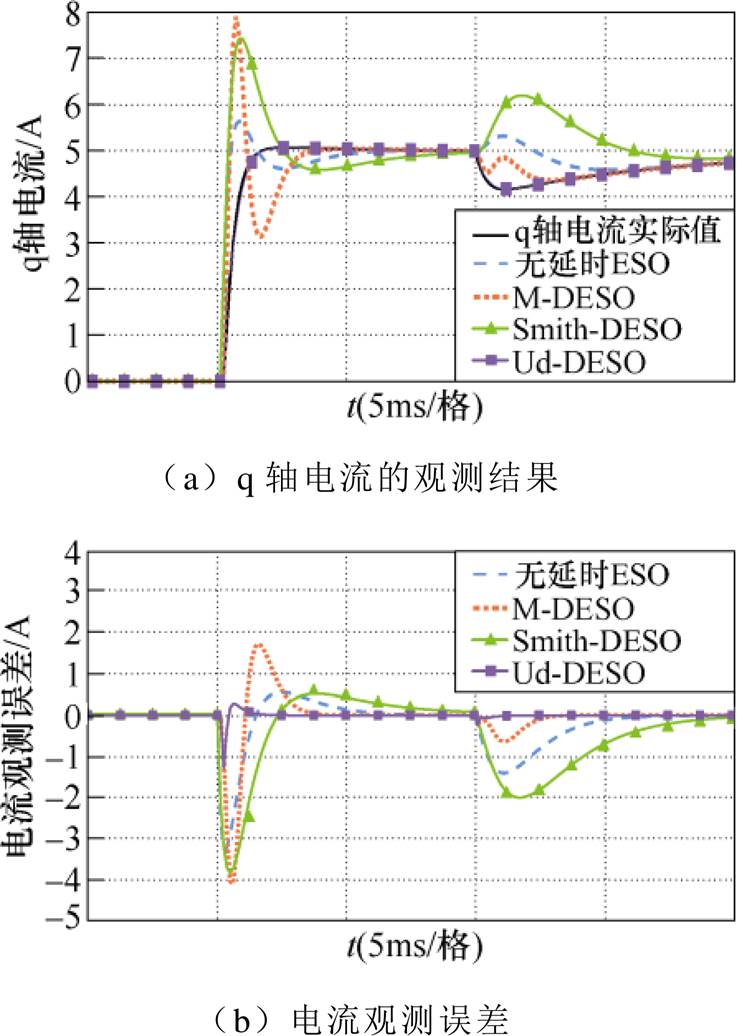
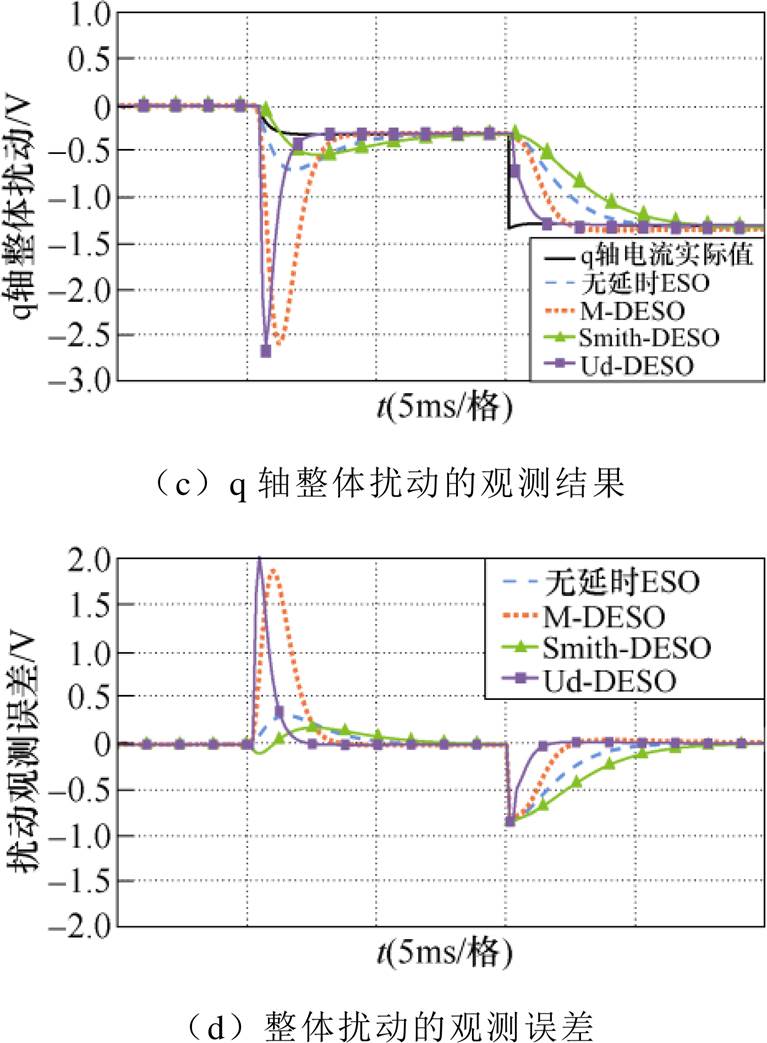
图11 Ld=0.5Ld0时q轴ESO的观测结果
Fig.11 Estimating results of the q-axis ESOs under Ld=0.5Ld0
综上所述,由于数字延迟存在,传统无延时ESO输入信号不同步,观测性能较差;M-DESO近似延迟环节设计观测器,但存在近似误差,电流跟踪和抗扰性能不理想;四种ESO中,Smith-DESO方案波形跟踪性能最优,观测误差最小,但其观测结果较为依赖电机参数;Ud-DESO观测性能稍弱,但对电机电感参数鲁棒性更好。
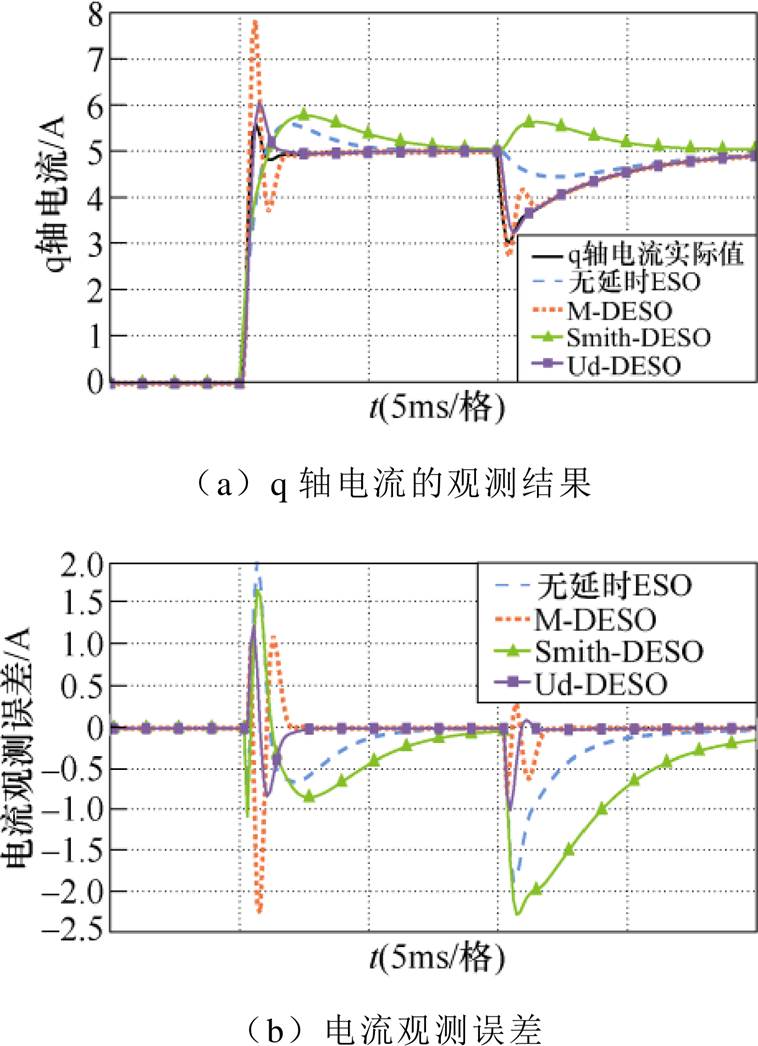
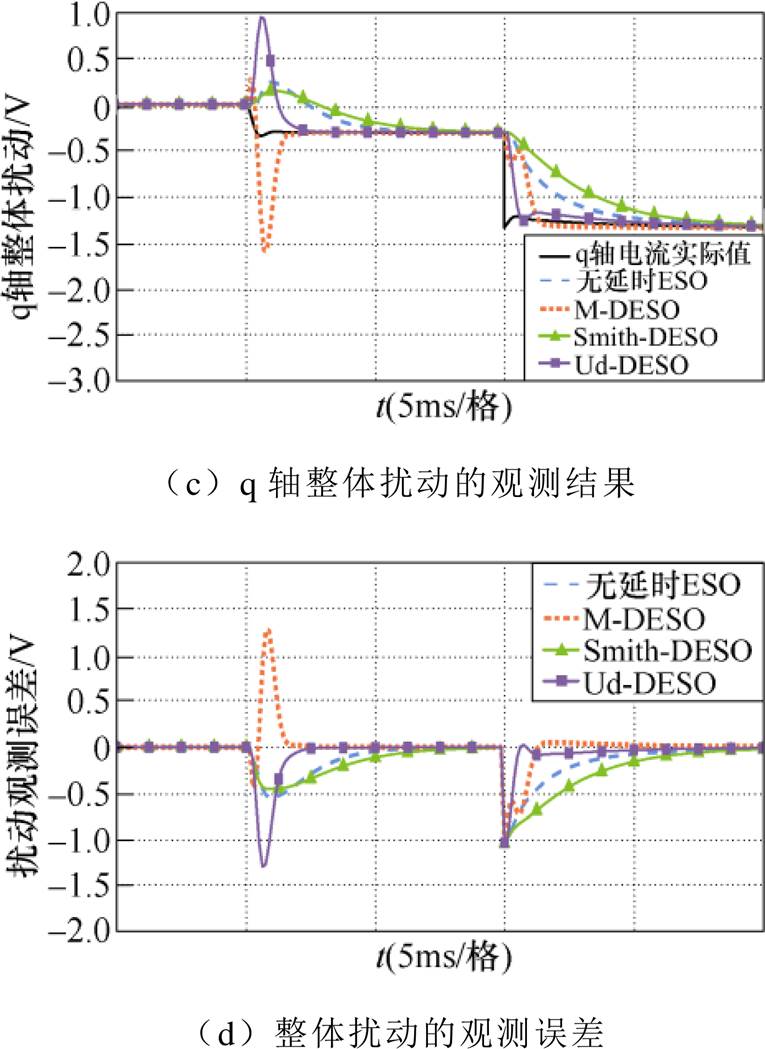
图12 Ld=2Ld0时,不同ESO对q轴的观测结果
Fig.12 Estimating results of the q-axis ESOs under Ld=2Ld0
第2节针对数字延迟产生的信号不同步问题,设计和对比了几种时延型ESO方案,提升了观测器的观测性能。本节重点就其中两种观测性能较好的Smith-DESO和Ud-DESO,设计了基于DESO的IPMSM离散域电流控制策略。
图13中给出了两种基于Smith-DESO、Ud- DESO的电流控制策略原理框图。
根据ESO的状态空间模型,可将观测器估计状态与输入信号的关系描述为
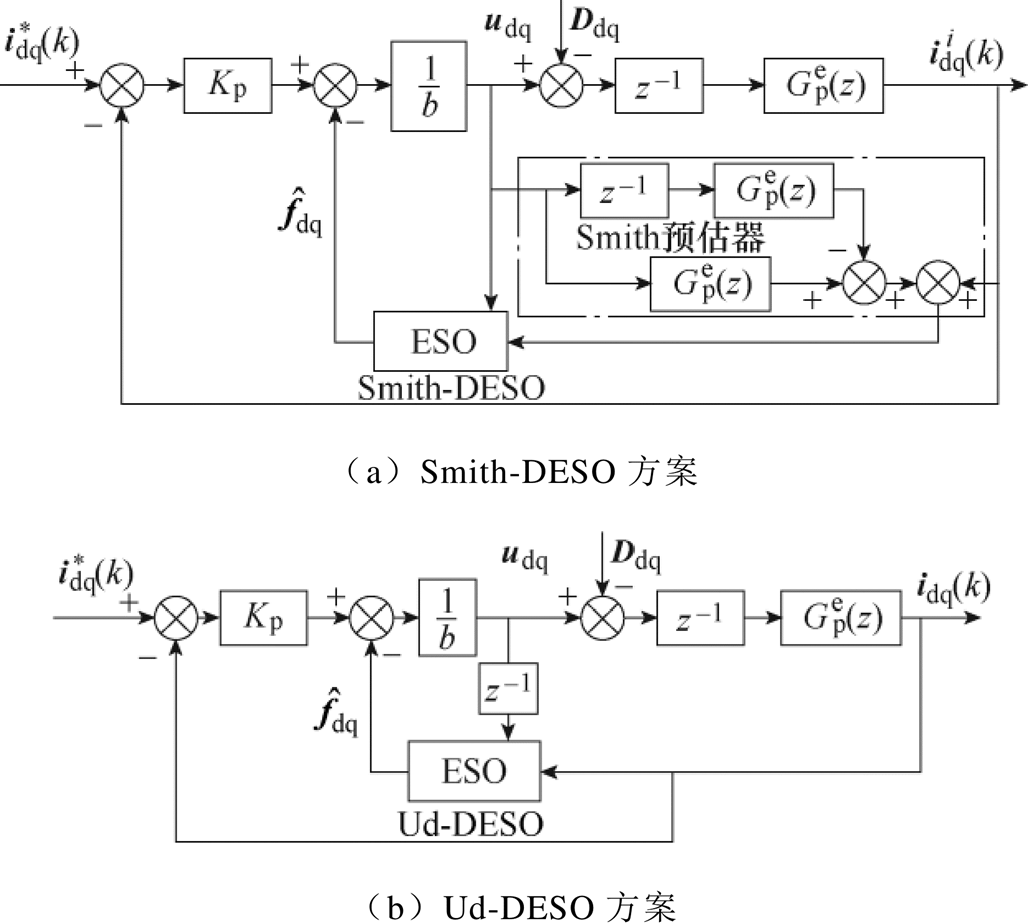
图13 基于ESO的IPMSM电流控制策略
Fig.13 Current control strategies of IPMSM based on ESOs
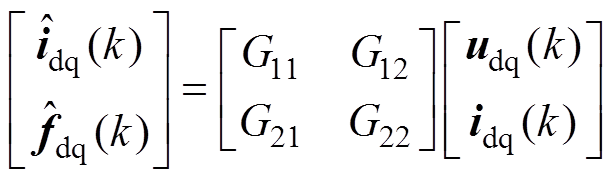 (22)
(22)
式中,系数矩阵表达式见附录。
结合式(20)和式(22),可将图13中三种电流控制方案等效为反馈控制结构,如图14所示。基于此,可以获得各电流控制方案的传递函数。
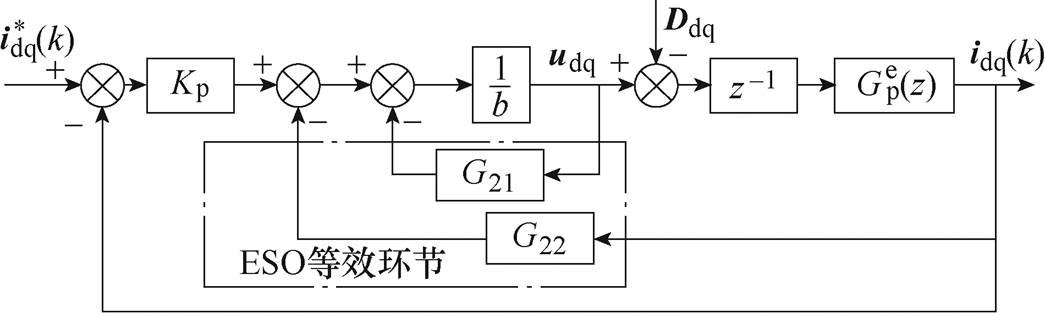
图14 基于ESO的IPMSM电流控制的等效框图
Fig.14 Equivalent diagrams of IPMSM current control strategies based on ESOs
无延时ESO方案闭环传递函数为
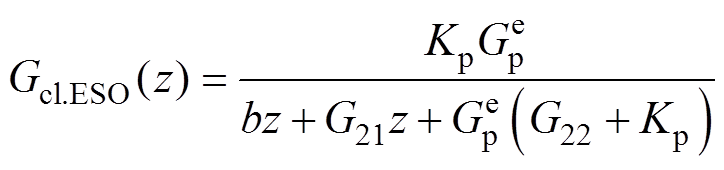 (23)
(23)
Smith-DESO方案闭环传递函数为
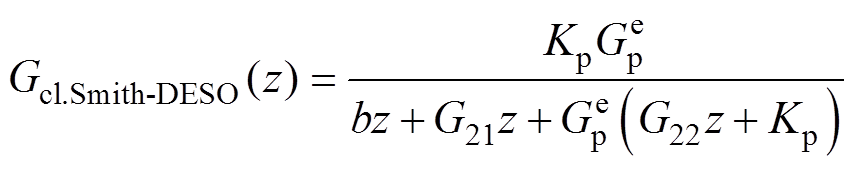 (24)
(24)
Ud-DESO方案闭环传递函数为
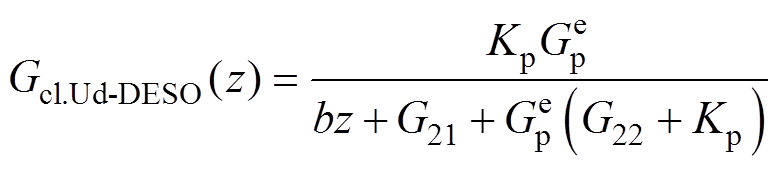 (25)
(25)
根据上述电流控制策略的离散域闭环传递函数,可以通过零极点分布图分析闭环控制系统稳定性。图15为电机运行频率从0~800 Hz变化时,各电流控制策略零极点的变化轨迹。运行频率fe= 0 50
50 800 Hz,开关频率fs=4 000 Hz,Kp=1 000。
800 Hz,开关频率fs=4 000 Hz,Kp=1 000。
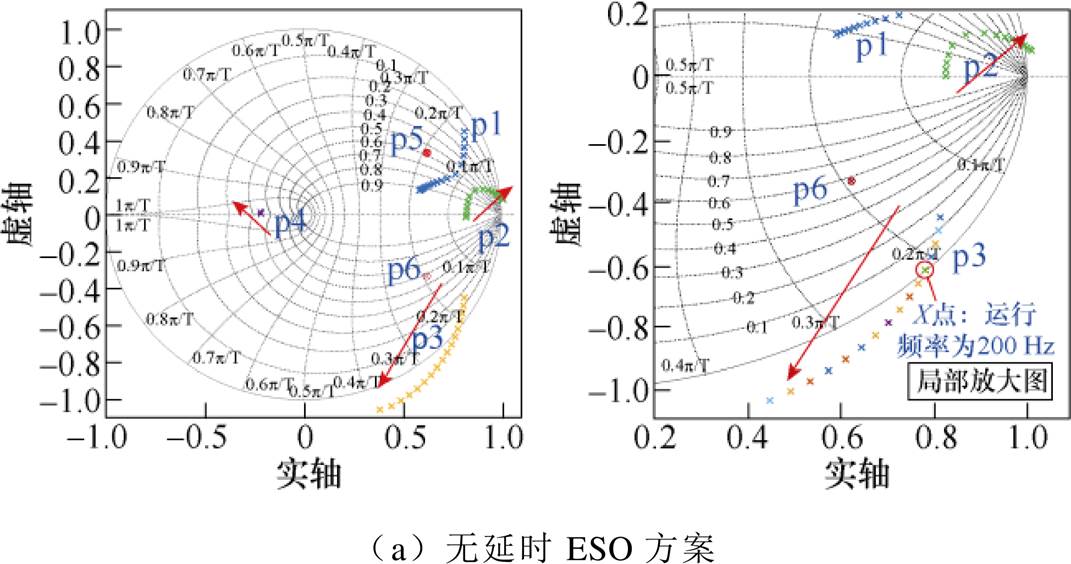
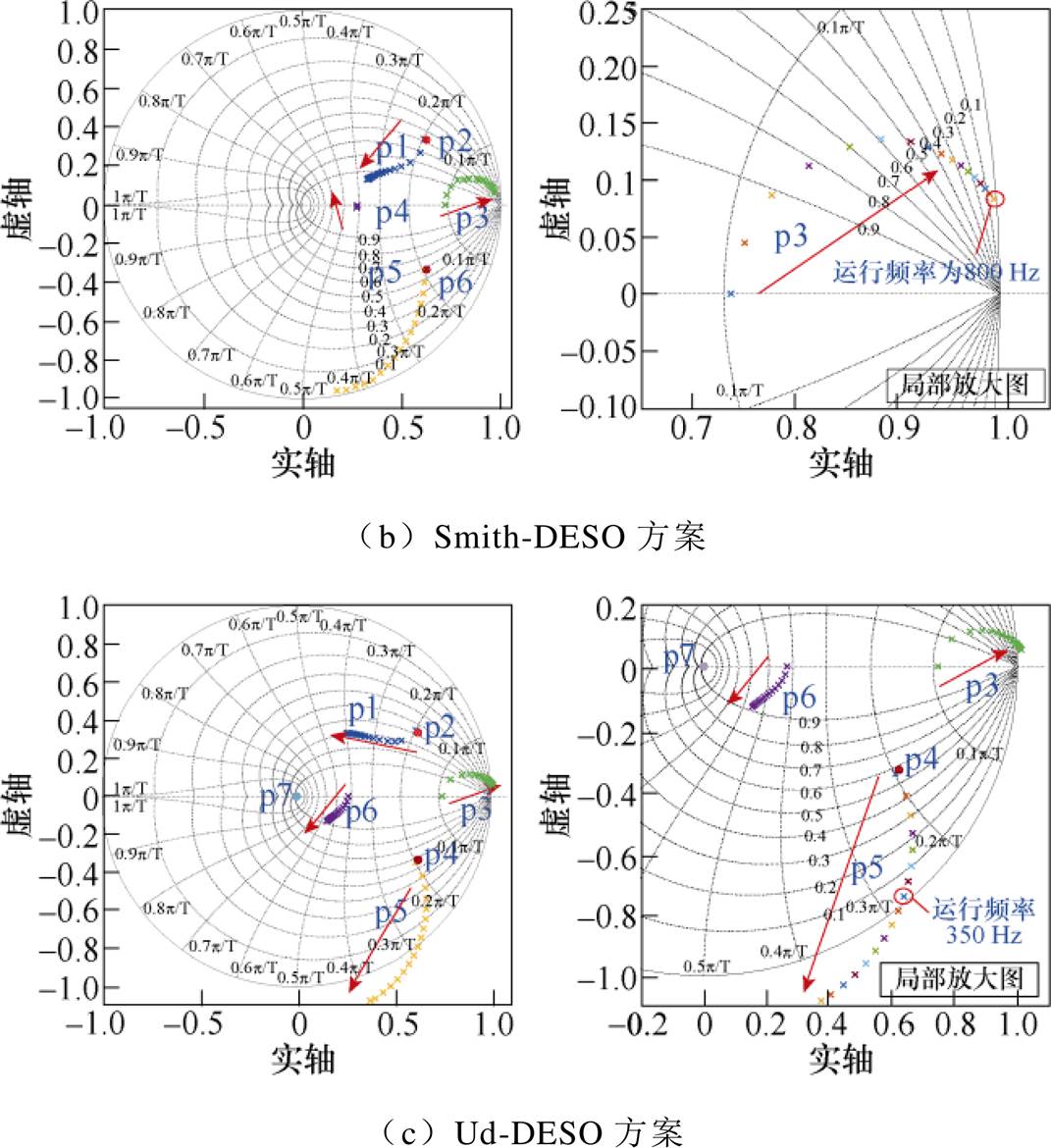
图15 电流控制闭环零极点随运行频率变化趋势
Fig.15 Locus of the poles and zeros of the current closed-loop control strategies with operating frequency increasing
由图15a不难看出,无延时ESO方案的极点p2和p3随运行频率增加,逐渐向单位圆外移动,稳定裕度逐渐降低。由局部放大图可见,点X处于临界稳定点,此时电机运行频率为200 Hz,即载波比低于20便出现不稳定现象。
而由图15b、图15c可知,基于DESO的电流控制策略闭环极点虽然随着运行频率增加,也会向单位圆外移动,但迁移幅度明显减小,稳定性远优于无延时ESO方案。其中Smith-DESO方案在运行频率800 Hz(载波比为5)时,仍然保持稳定,说明该策略可以更好抵消延迟环节对观测器的影响,有助于提升低载波比下运行稳定性。
为验证所提方案的抗扰性能,该部分对系统抗扰特性进行分析。传统PI控制中外部扰动到输出电流的传递函数为
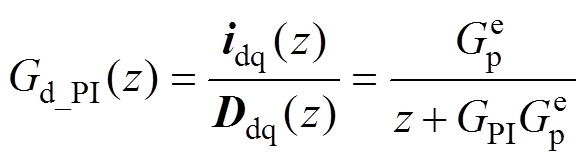 (26)
(26)
式中,GPI为PI控制器的传递函数。
类似地,可以求得基于各种ESO扰动补偿的电流环扰动传递函数分别为
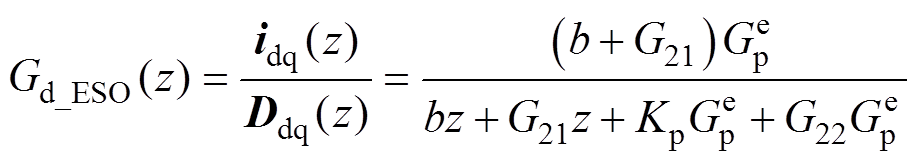 (27)
(27)
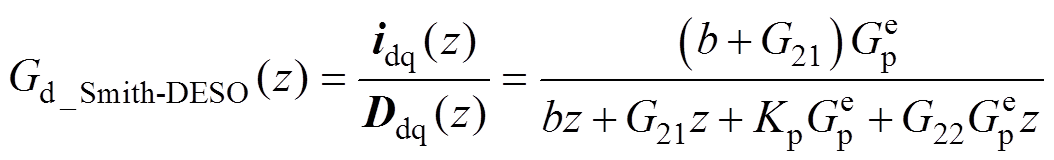 (28)
(28)
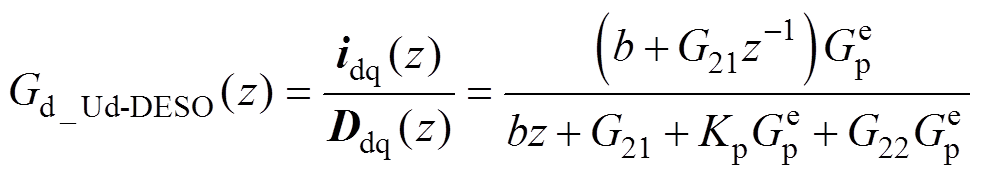 (29)
(29)
图16中绘制了基波频率为零时,各扰动传递函数的阶跃响应曲线。从图中看出,ESO控制策略能够快速抑制外部扰动,抗扰特性明显优于传统PI控制器。其中,Smith-DESO能够快速抑制阶跃扰动,扰动响应时间由传统PI控制的50 ms缩小至2.5 ms,抗扰性显著提高。
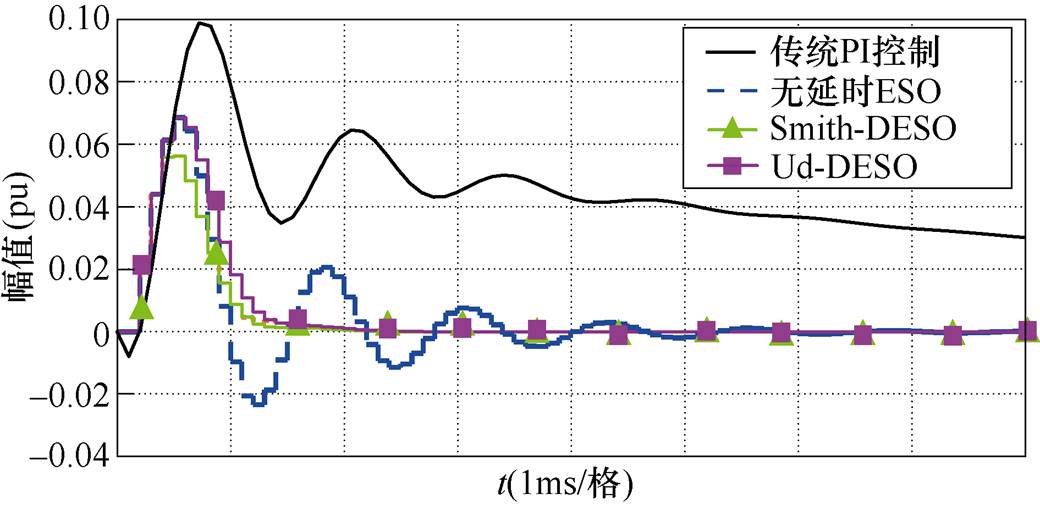
图16 扰动传递函数单位阶跃抗扰响应曲线
Fig.16 Step response of the disturbance transfer functions
以TI公司TMS320F28379为核心控制器,搭建了相应的实验平台来验证基于延迟校正扩张状态观测器的离散域电流控制策略对IPMSM的控制效果。实验平台结构框图如图17所示,其对应的实物如图18所示,所用电机参数见表2。逆变器主电路由三菱IPM功率模块PM100CLA120构成,开关频率设定为4 kHz,采样频率为8 kHz。直流母线电压设为580 V,由直流电压柜提供。拖动机组中三相异步电机作为负载电机,由商用变频器进行控制,拖动机组运转或加载。
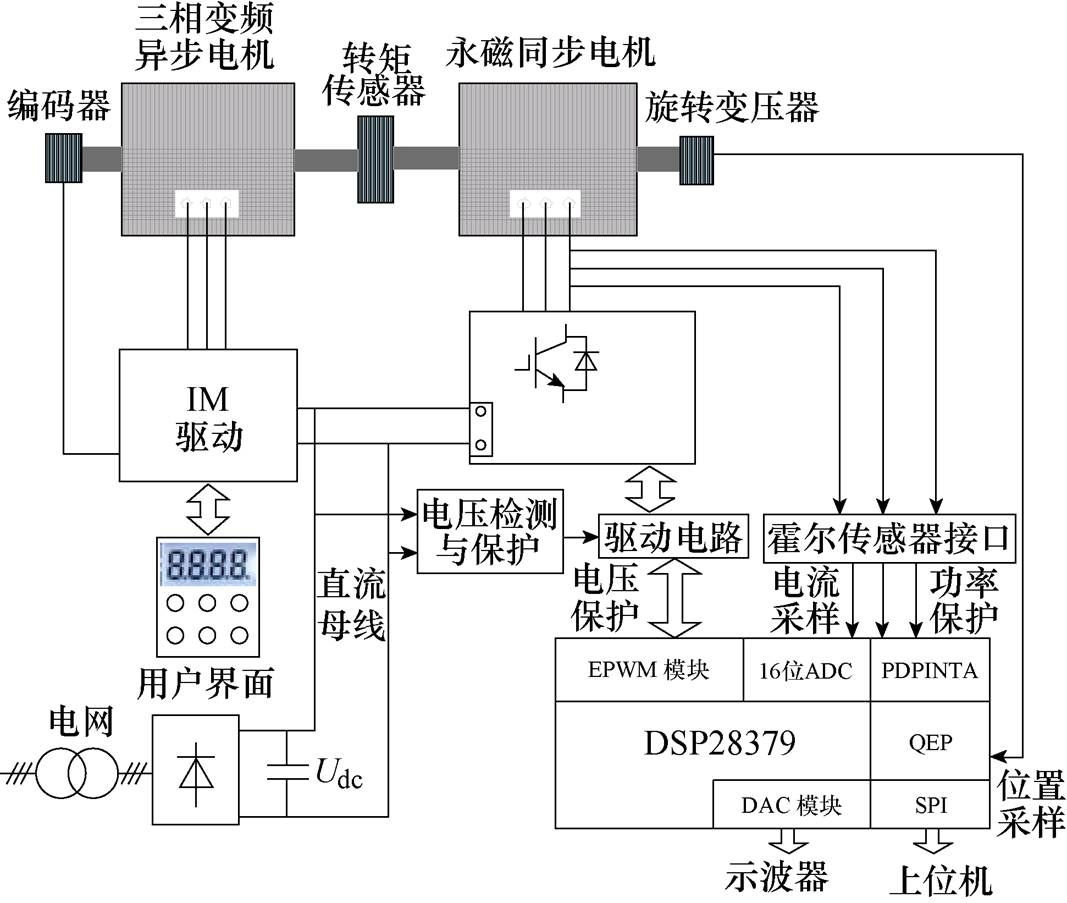
图17 实验平台结构框图
Fig.17 Block diagram of the experimental platform

图18 实验平台实物
Fig.18 Experimental platform
图19中给出四种基于ESO的IPMSM电流控制策略的电流阶跃响应,电机转速n=3 000 r/min,q轴电流阶跃幅值为90 A。
表2 永磁同步电机参数
Tab.2 Parameters of PMSM
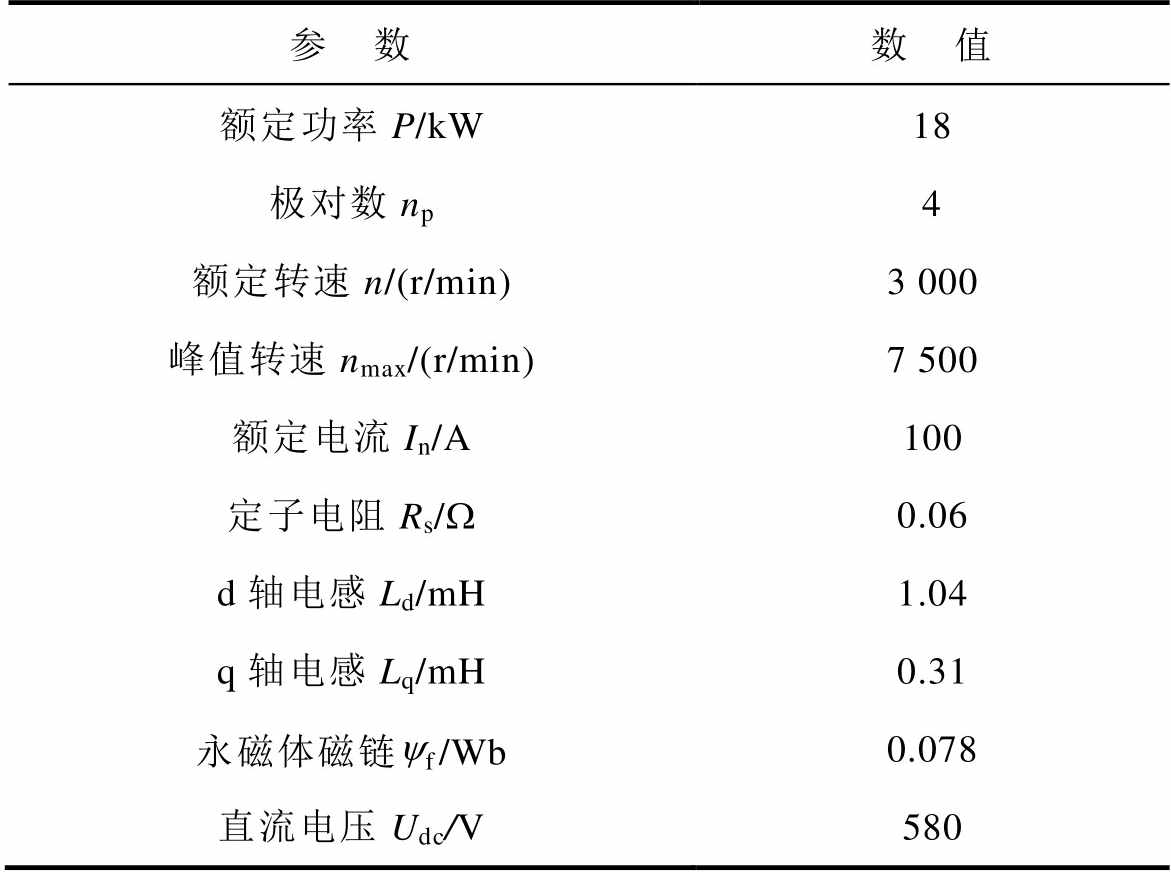
参 数数 值 额定功率P/kW18 极对数np4 额定转速n/(r/min)3 000 峰值转速nmax/(r/min)7 500 额定电流In/A100 定子电阻Rs/W0.06 d轴电感Ld/mH1.04 q轴电感Lq/mH0.31 永磁体磁链yf/Wb0.078 直流电压Udc/V580
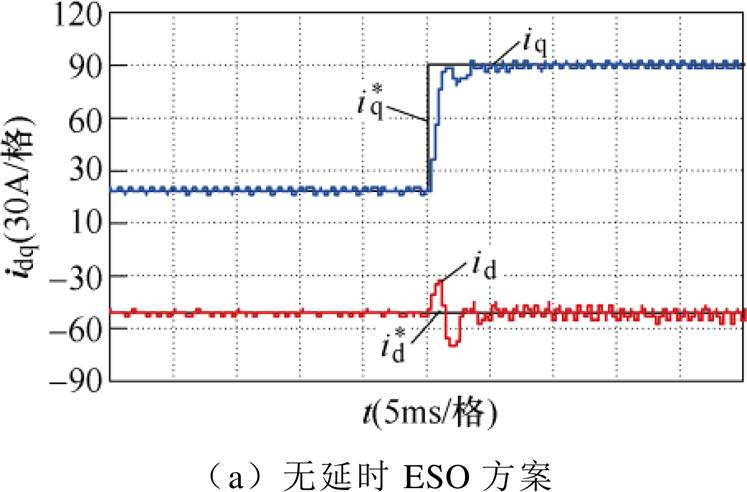
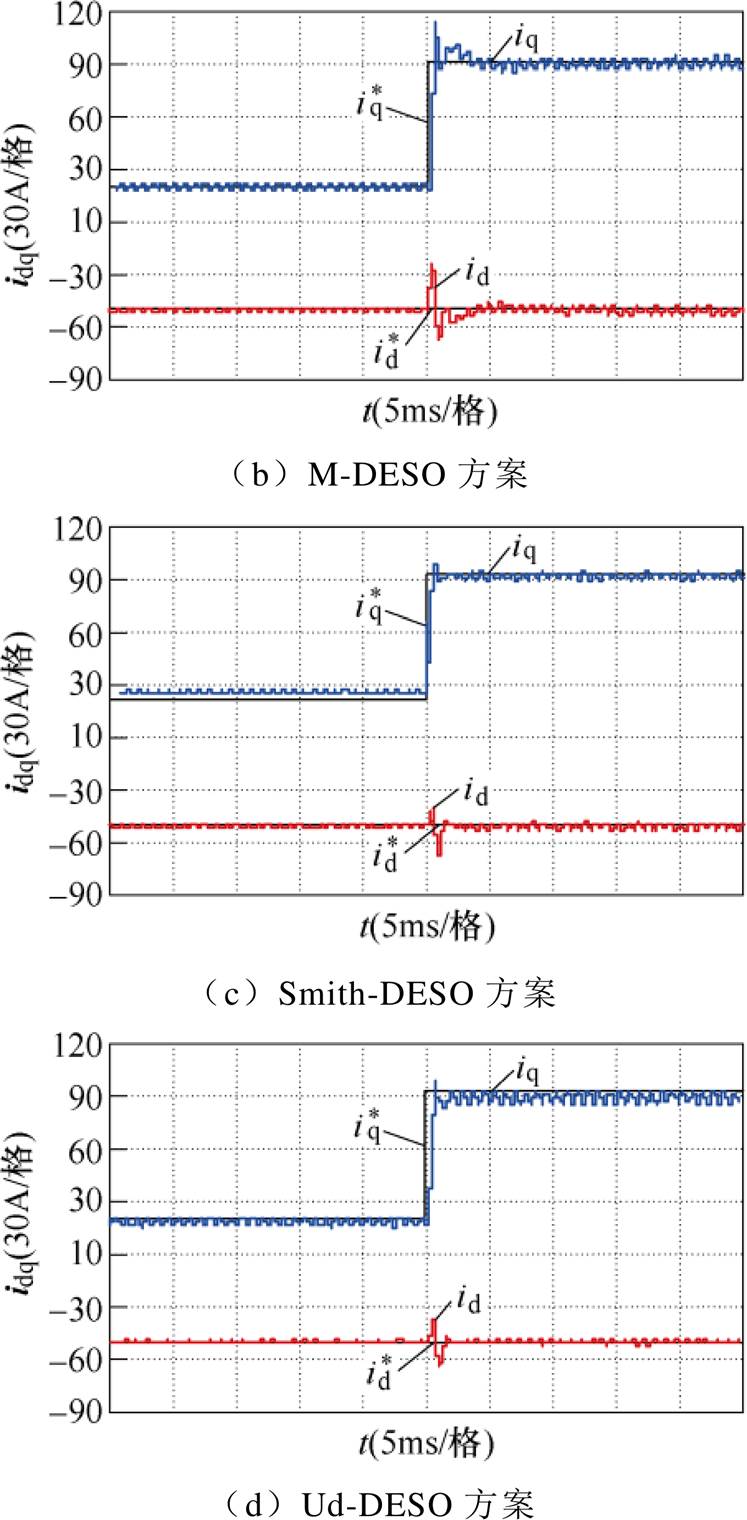
图19 电流响应实验结果
Fig.19 Experimental results of the current step responses
通过实验不难发现,四种方案中,Smith-DESO和Ud-DESO方案动态性能相对较好。
为进一步验证所提策略的抗扰性能,在q轴电压指令处施加阶跃扰动信号d=20 V,图20记录了不同控制策略下的电流抗扰性能。受到扰动后,各方案的恢复时间依次为2.3、4.7、0.9和1.2 ms。Smith-DESO和Ud-DESO方案恢复速度相对较快,抗扰动性能更强,实验结果与理论分析一致。
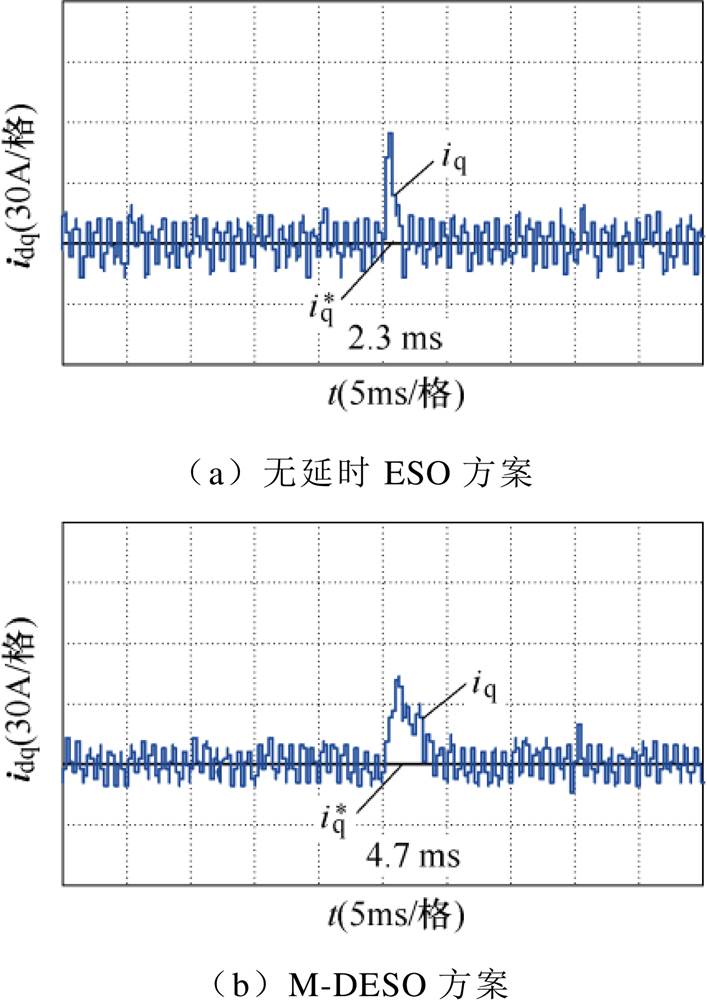
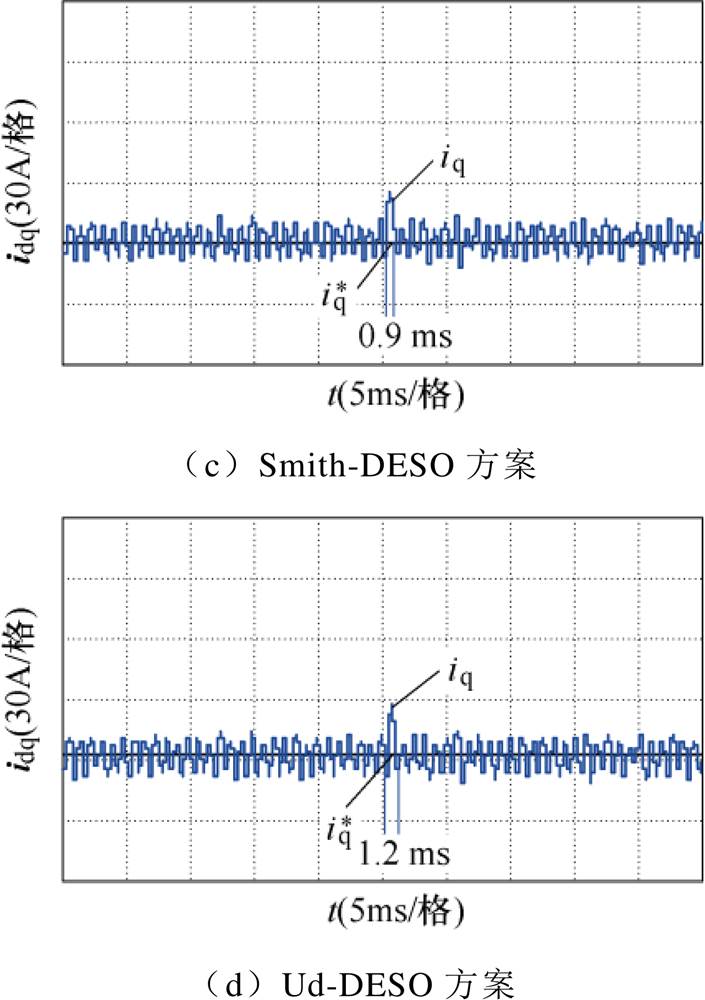
图20 电流抗扰响应实验结果
Fig.20 Experimental results of the disturbance responses
为检测以上方案对参数变化的鲁棒性,将观测器中使用的电感参数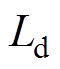 分别设为标称参数
分别设为标称参数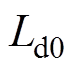 的0.5倍和2倍,在图21中记录了四种电流控制策略在参数偏差情况下的电流阶跃响应波形。
的0.5倍和2倍,在图21中记录了四种电流控制策略在参数偏差情况下的电流阶跃响应波形。
由图21可知,当电感参数发生变化时,无延时ESO和M-DESO方案动态性能较差,出现响应速度过慢或明显超调的情况。相对而言,Smith-DESO和Ud-DESO方案虽然q轴电流到达稳态的时间有所增加,但相对于前两种,电流到达稳态的时间更短,瞬时超调更小。
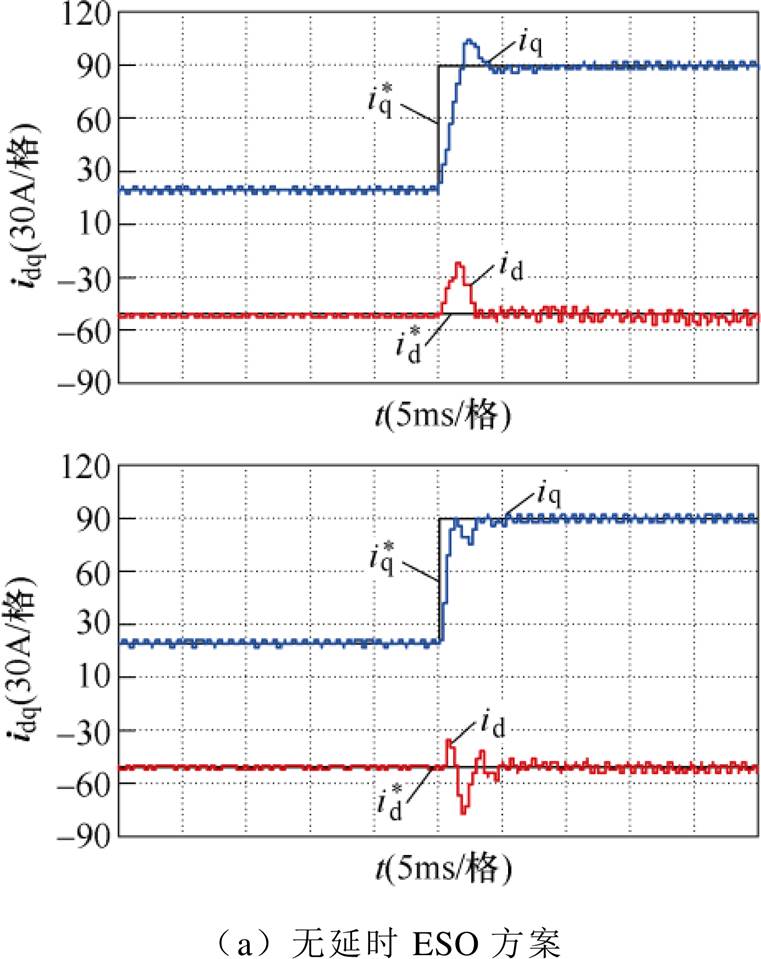
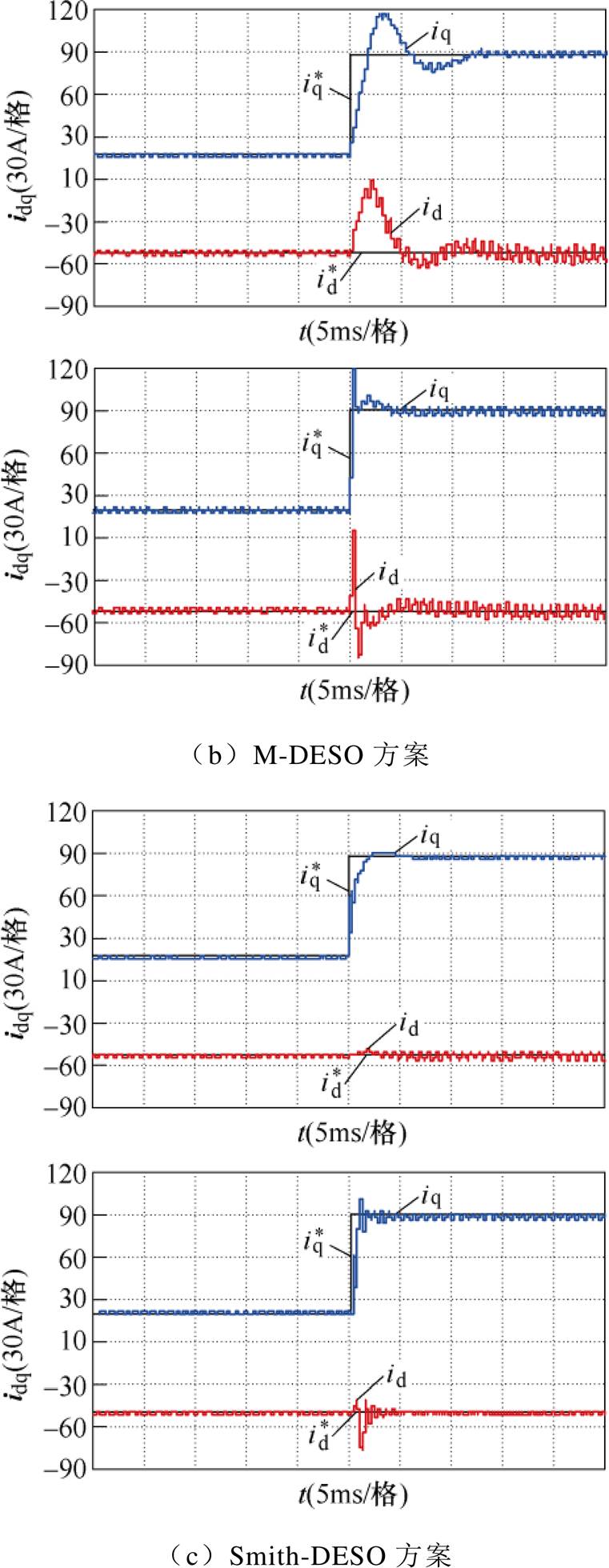
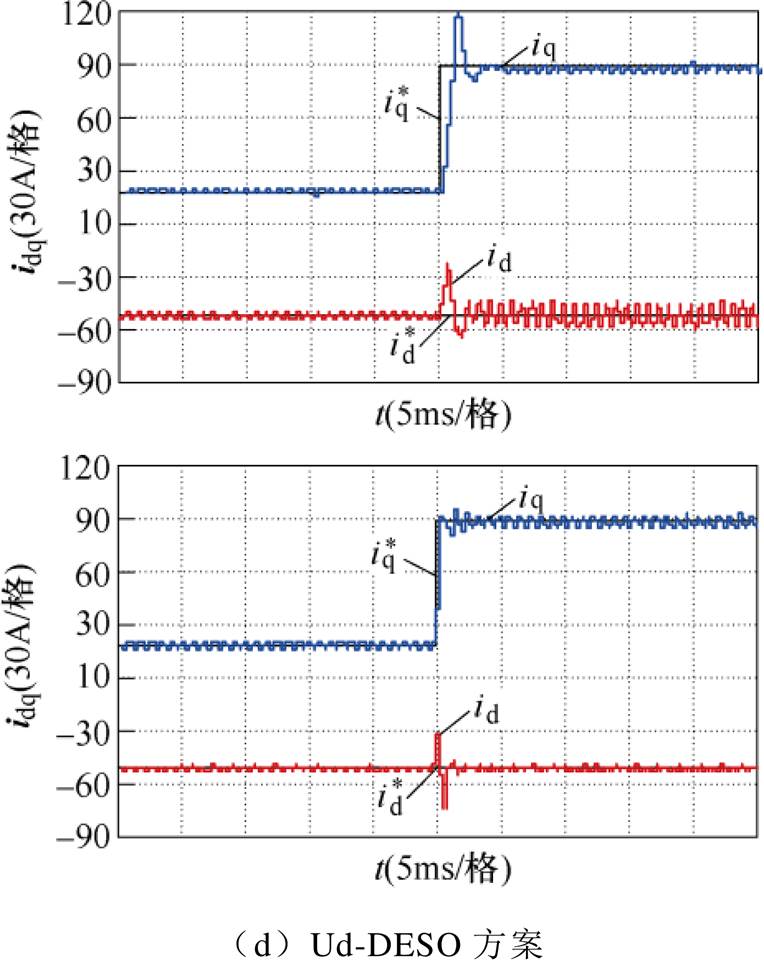
图21 参数偏差时电流阶跃响应
Fig.21 Step response under parameter mismatch
综合理论分析和实验结果,四种电流控制策略的优缺点列于表3中。
表3 基于各种ESO的电流控制策略性能对比
Tab.3 Performance comparison of current control strategies based on each ESOs

控制方案稳定载波比N(倍)抗扰性/ ms动态性能/ms电感偏差(倍) 无延时ESO202.32.60.5~1.7 M-DESO13.34.73.90.7~1.6 Smith-DESO40.91.10.4~2.1 Ud-DESO11.41.21.20.3~2.6
当电机参数准确时,Smith-DESO方案系统稳定性最好,动态性能和抗扰性能最佳。随着电机运行频率上升时,该策略在载波比较低(实验可做到6 000 r/min,载波比为10)的工况下,仍能良好运行。当参数存在偏差时,电压延迟DESO方案表现出更好的参数鲁棒性,控制性能相对较好。
本文考虑数字延迟对观测器的影响,对比分析了几种延迟校正方案,并针对内置式永磁同步电机,设计了相应的离散域电流控制策略。理论分析和实验研究表明:
1)传统无延时ESO受数字控制延迟影响,导致ESO输入信号不同步,观测性能较差;M-DESO存在近似误差,电流跟踪和抗扰性能改善不理想。
2)Smith-DESO稳定性和动态性能最好,但观测效果对电机参数具有较强的依赖性;Ud-DESO受电感参数失配的影响比Smith-DESO小,鲁棒性较强,但观测速度稍慢。
附录 等效方程系数
ESO等效方程为
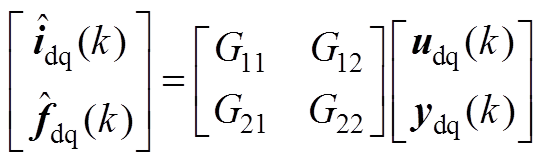 (A1)
(A1)
其中,变换矩阵系数分别为
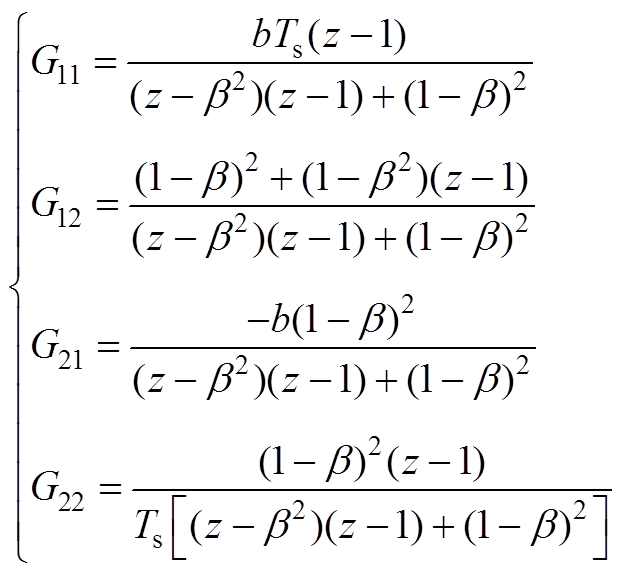 (A2)
(A2)
模型法DESO等效方程为
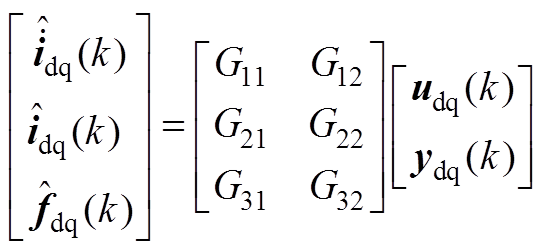 (A3)
(A3)
其中,变换矩阵系数分别为
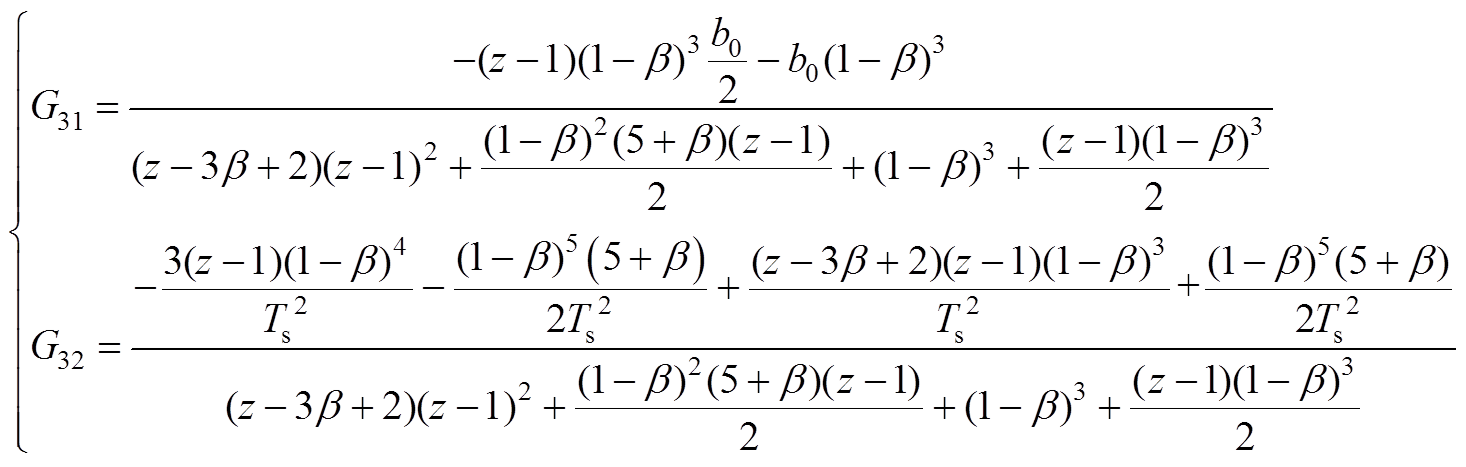 (A4)
(A4)
参考文献
[1] Gerada D, Mebarki A, Brown N L, et al. High-speed electrical machines: technologies, trends, and deve- lopments[J]. IEEE Transactions on Industrial Elec- tronics, 2014, 61(6): 2946-2959.
[2] Walz S, Lazar R, Buticchi G, et al. Dahlin-based fast and robust current control of a PMSM in case of low carrier ratio[J]. IEEE Access, 2019, 7: 102199- 102208.
[3] Herbst G. Practical active disturbance rejection control: bumpless transfer, rate limitation, and incremental algorithm[J]. IEEE Transactions on Industrial Electronics, 2016, 63(3): 1754-1762.
[4] Holtz J, Oikonomou N. Fast dynamic control of medium voltage drives operating at very low switching frequency-an overview[J]. IEEE Transactions on Industrial Electronics, 2008, 55(3): 1005-1013.
[5] Morimoto S, Sanada M, Takeda Y. Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulator[J]. IEEE Transactions on Industry Applications, 1994, 30(4): 920-926.
[6] Briz F, Degner M W, Lorenz R D. Analysis and design of current regulators using complex vectors[J]. IEEE Transactions on Industry Applications, 2000, 36(3): 817-825.
[7] Diab A M, Bozhko S, Guo Feng, et al. Fast and simple tuning rules of synchronous reference frame proportional-integral current controller[J]. IEEE Access, 2021, 9: 22156-22170.
[8] Harnefors L, Nee H P. Model-based current control of AC machines using the internal model control method[J]. IEEE Transactions on Industry Appli- cations, 1998, 34(1): 133-141.
[9] 刘宇博, 王旭东, 周凯. 基于滑模观测器的永磁同步电机电流偏差解耦控制[J]. 电工技术学报, 2020, 35(8): 1642-1652.
Liu Yubo, Wang Xudong, Zhou Kai. Current deviation decoupling control with a sliding mode observer for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1642-1652.
[10] 吴为, 丁信忠, 严彩忠. 基于复矢量的电流环解耦控制方法研究[J]. 中国电机工程学报, 2017, 37(14): 4184-4191, 4298.
Wu Wei, Ding Xinzhong, Yan Caizhong. Research on control method of current loop decoupling based on complex vector[J]. Proceedings of the CSEE, 2017, 37(14): 4184-4191, 4298.
[11] Hoffmann N, Fuchs F W, Kazmierkowski M P, et al. Digital current control in a rotating reference frame- part I: system modeling and the discrete time-domain current controller with improved decoupling capa- bilities[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 5290-5305.
[12] Kim H, Degner M, Guerrero J M, et al. Discrete-time current regulator design for AC machine drives[C]// 2009 IEEE Energy Conversion Congress and Expo- sition, San Jose, CA, USA, 2009: 1317-1324.
[13] Li Silong, Sarlioglu B, Jurkovic S, et al. Analysis of temperature effects on performance of interior permanent magnet machines for high variable temperature applications[C]//IEEE Transactions on Industry Applications, 2017: 4923-4933.
[14] Diab A, Rashed M, Li Jing, et al. Performance analysis of PMSM for high-speed starter-generator system[C]//2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS- ITEC), Nottingham, UK, 2019: 1-7.
[15] Han Jingqing. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.
[16] 李思毅, 苏健勇, 杨贵杰. 基于自抗扰控制的永磁同步电机弱磁控制策略[J]. 电工技术学报, 2022, 37(23): 6135-6144.
Li Siyi, Su Jianyong, Yang Guijie. Flux weakening control strategy of permanent magnet synchronous motor based on active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6135-6144.
[17] 朱良红, 张国强, 李宇欣, 等. 基于级联扩张观测器的永磁电机无传感器自抗扰控制策略[J]. 电工技术学报, 2022, 37(18): 4614-4624.
Zhu Lianghong, Zhang Guoqiang, Li Yuxin, et al. Active disturbance rejection control for position sensorless permanent magnet synchronous motor drives based on cascade extended state observer[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4614-4624.
[18] 朱进权, 葛琼璇, 张波, 等. 考虑悬浮系统影响的高速磁悬浮列车牵引控制策略[J]. 电工技术学报, 2022, 37(12): 3087-3096.
Zhu Jinquan, Ge Qiongxuan, Zhang Bo, et al. Traction control strategy of high-speed maglev considering the influence of suspension system[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3087-3096.
[19] 刘春强, 骆光照, 涂文聪, 等. 基于自抗扰控制的双环伺服系统[J]. 中国电机工程学报, 2017, 37(23): 7032-7039, 7095.
Liu Chunqiang, Luo Guangzhao, Tu Wencong, et al. Servo systems with double closed-loops based on active disturbance rejection controllers[J]. Pro- ceedings of the CSEE, 2017, 37(23): 7032-7039, 7095.
[20] Diab A M, Bozhko S, Galea M, et al. Stable and robust design of active disturbance-rejection current controller for permanent magnet machines in transportation systems[J]. IEEE Transactions on Transportation Electrification, 2020, 6(4): 1421- 1433.
[21] 韩京清. 时滞对象的自抗扰控制[J]. 控制工程, 2008, 15(增刊2): 7-10, 18.
Han Jingqing. Auto-disturbances rejection control for time-delay systems[J]. Control Engineering of China, 2008, 15(S2): 7-10, 18.
[22] Li Longfei, Xiao Jie, Zhao Yun, et al. Robust position anti-interference control for PMSM servo system with uncertain disturbance[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2020, 4(2): 151-160.
[23] 章回炫, 范涛, 边元均, 等. 永磁同步电机高性能电流预测控制[J]. 电工技术学报, 2022, 37(17): 4335-4345.
Zhang Huixuan, Fan Tao, Bian Yuanjun, et al. Predictive current control strategy of permanent magnet synchronous motors with high performance[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4335-4345.
[24] 王丽君, 李擎, 童朝南, 等. 时滞系统的自抗扰控制综述[J]. 控制理论与应用, 2013, 30(12): 1521- 1533.
Wang Lijun, Li Qing, Tong Chaonan, et al. Overview of active disturbance rejection control for systems with time-delay[J]. Control Theory & Applications, 2013, 30(12): 1521-1533.
[25] Zheng Qinling, Gao Zhiqiang. Predictive active disturbance rejection control for processes with delay[C]//Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 2013: 4108-4113.
[26] 唐德翠, 高志强, 张绪红. 浊度大时滞过程的预测自抗扰控制器设计[J]. 控制理论与应用, 2017, 34(1): 101-108.
Tang Decui, Gao Zhiqiang, Zhang Xuhong. Design of predictive active disturbance rejection controller for turbidity[J]. Control Theory & Applications, 2017, 34(1): 101-108.
Abstract As to high-speed electric drives, the ratio of the switching to the fundamental frequencies is low due to the limited switching frequency allowed. As a result, the control delay negatively affects the vector control performance of the IPMSM heavily. However, the traditional control strategy usually ignores the delay, and when the motor speed increases and the carrier ratio decreases, the actual performance decreases significantly. There are three main reasons: cross-coupling between d-q axes, discretization error, and control delay. To address these problems, several schemes, i.e., delay-corrected extended state observers (ESOs), are designed and compared. Consequently, the estimating accuracy is enhanced. Based on the proposed ESOs, this paper proposes several current control strategies of IPMSM, producing an improved current response.
Firstly, the extended back EMF (EEMF) based IPMSM model was built, and ESOs can estimate the EEMF and other disturbances as a whole. It allows a symmetric model of the IPMSM, which is beneficial to analysis and design in the discrete-time domain, enhancing the performance in low-ratio applications. Secondly, this paper analyzes delay effects in discrete fields. Several delay effect suppression strategies are designed to improve the estimation accuracy, namely the delay-corrected ESO. Finally, based on the proposed ESOs, the IPMSM discrete-domain current control strategies are designed, significantly improving the current response characteristics. The EV-driven experimental platform verifies the analysis and design.
Simulation results of the observer performance show that as the delay increases, the traditional ESO increases the error, worsens the dynamic response process, and even has the risk of oscillation. Under the same bandwidth, Smith-DESO has the best observation performance, the model DESO (M-DESO) is poor, and the observation results of the traditional ESO and voltage delay DESO (Ud-DESO) are close. If the observation bandwidth continues to increase, the stability of traditional ESO and M-DESO will become significantly worse. However, Smith-DESO and Ud-DESO can still have good stability due to the synchronization of the two input signals. Smith-DESO scheme remains stable when the operating frequency is 800Hz (the carrier ratio is 5). The disturbance suppression time is reduced from 50 ms (controlled by the traditional PI scheme) to 2.5 ms, indicating that the strategy can better offset the delay impact on the observer, which helps to improve the operation stability and disturbance resistance performance under the low carrier ratio.
The following conclusions can be drawn from theoretical analysis and experimental research: (1) Traditional non-delay ESO is affected by the control delay, and the ESO input signal is unsynchronized and has poor observation performance. M-DESO is designed by the approximate delay, but there is an approximate error, and current tracking and disturbance performance is not ideal. (2) Smith-DESO has the best stability and dynamic performance, but the observation effect depends on the motor parameters. Ud-DESO is less affected by the inductive parameter mismatch than Smith-DESO, but the observation speed is slightly slower. (3) The proposed current control strategies of the IPMSM suppress the delay impact on the observer, which quickly estimates and compensates for internal and external disturbances. It helps to improve motor stability and dynamic performance under low ratios.
keywords:Interior permanent magnet synchronous motor; digital control delay; extended state observer; discrete domain design
DOI: 10.19595/j.cnki.1000-6753.tces.222286
中图分类号:TM351
安徽省科技重大专项(202003a05020029)和台达电力电子科教发展计划项目(DREK2020004)资助。
收稿日期 2022-12-12
改稿日期 2023-01-16
朱玉璞 男,1996年生,硕士,研究方向为永磁同步电机驱动控制。E-mail: zhuyupu_hfut@163.com(通信作者)
杨淑英 男,1980年生,教授,博士生导师,研究方向为风力发电系统、电驱动系统。E-mail: yangsyhfah@163.com
(编辑 崔文静)