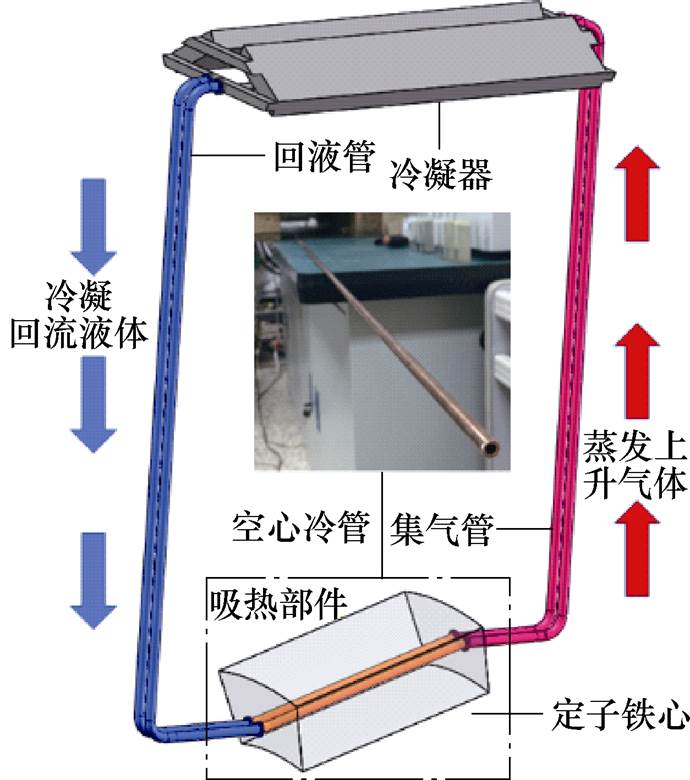
图1 穿管式蒸发冷却风力发电机冷却系统循环示意图
Fig.1 Schematic diagram of cooling system circulation of stator axial pipe evaporative cooling wind generators
摘要 采用自循环式蒸发冷却技术是提升大容量风力发电机组散热能力和可靠性的一种经济且有效的方式，然而在传统电机的分析设计和性能预测过程中，往往会忽略定子局部穿管结构的改变对电机电磁性能的影响，同时也会忽略这部分接触热阻在热传导过程中对电机冷却性能的影响。对此，该文首先基于风力发电机的运行特性和单元灵敏度方法分析了定子铁心穿管结构对电机电磁及冷却性能的影响，然后通过小倾角自循环管道换热实验以及接触热阻温升实验对空心圆铜管的换热能力以及接触热阻进行了分析和测试，最后建立了以电磁及传热性能为优化目标的铁心穿管结构优化策略，并以一台10 MW永磁直驱式风力发电机为研究对象，对定子铁心穿管结构开展了优化设计研究。通过优化方案的有限元分析验证说明，提出的优化策略可以准确且有效地满足电机电磁和冷却性能的设计要求，同时从电磁和散热两个维度来评估，所提出的优化策略同样适用于相同应用场景下的其他永磁同步电机。
关键词：蒸发冷却风力发电机 定子铁心穿管冷却 电磁及冷却特性 接触热阻 单元灵敏度分析 优化设计
近些年来，伴随着可再生能源领域的飞速发展，风力发电技术作为清洁能源产业中重要的组成部分，目前已经越来越受到世界各个国家的重视[1]。同时，风力发电机作为新能源电机系统中的核心机械-电磁能量转换部件，其技术水平和创新理论也亟待进一步提升和发展[2]。然而，伴随着风电机组单机容量不断提升，其面临的损耗和发热问题也愈发严重，过高的运行温度将加速电机内绝缘材料的热老化过程，从而影响其使用寿命和力学性能[3]，这将对风力发电机的安全运行带来严重的危害，同时也将不利于其轻量化和小型化发展[4]。因此，针对这些挑战，目前新理论和新技术的研究已变得迫在眉睫。对此，应用我国自主研发的蒸发冷却技术可以大幅度地提高发电机组的冷却效率[5]，其使用的不燃不爆冷却工质也可以从根本上避免由冷却系统泄露而造成的短路风险。整套系统具有维护简单、无需泵驱动运行、安全可靠等诸多优点，目前已经在诸多电气领域成功应用[6-7]，同时也是未来大容量风电机组冷却方案的理想选择[8]。
近些年来，国内外许多学者已经在风力发电机的电磁及冷却性能的分析建模以及优化问题上做了大量的研究，同时也取得了诸多成果。文献[9]考虑变流器影响的同时基于改进后的遗传算法对直驱式风力发电机的电磁参数进行了优化设计研究。文献[10]基于混合遗传算法实现了对直驱式风力发电机单位能源成本的优化设计分析。文献[11]基于不同永磁体的运行温度对海上直驱式风力发电机组的单位能源成本进行了优化研究。文献[12]基于磁通密度分布的二维解析计算模型对直驱式风力发电机的电磁参数进行了优化设计，然而这些研究中并没有考虑电磁设计参数对电机冷却性能的影响。文献[13-14]对蒸发冷却风力发电机的冷却特性以及小倾角自循环冷却系统的流动性能进行了研究，然而并没有考虑冷却结构参数对发电机电磁性能的影响。文献[15-16]建立了永磁风力发电机全域二维电磁场分析计算模型，并基于电磁损耗，建立了自然风冷下电机的二维温度场分析计算模型，实现了对不同转速下电机的温升预测。文献[17]基于磁-热双向耦合机理建立了电机二维电磁场-热传导耦合分析模型，并对电机的温升进行了分析。这些研究虽然考虑了发电机电磁场与温度场间的耦合影响关系，然而却忽略了传热路径上局部接触热阻对热传导过程的影响，因此在发电机性能精准建模分析和预测过程中，有必要综合考虑以上的全部影响因素，对电机性能进行全面分析。
目前，蒸发冷却风力发电机通常可以采用绕组直接内冷[18]或定子全浸式冷却技术[19]，与上述两者不同，定子穿管式蒸发冷却技术的冷源布置在铁心轭部，电机绕组和铁心中产生的热量需要通过定子铁心穿管导出至外界，因此在电机的分析设计过程中不仅需要考虑冷却结构对电机电磁及冷却性能的影响作用，还需要计及冷却管和铁心壁面的接触热阻对整个热传导过程的影响。
鉴于此，本文分析了定子穿管结构对风力发电机电磁及冷却性能的影响，基于设计单元的电磁-传热灵敏度分析提出了一种电磁-冷却性能协同优化策略，通过实验测定了空心冷却管与铁心交界面之间的接触热阻，分析了小倾角自循环特性下空心冷却管的换热特性。最后以一台10 MW直驱式风力发电机作为研究对象，对定子铁心穿管方案开展了优化设计研究，并通过有限元仿真分析软件对优化结果的正确性和有效性进行了分析验证。本文中得出的实验结果和提出的优化策略可以为今后大容量蒸发冷却风力发电机的性能分析和优化设计研究提供参考和依据。
水平轴风力发电机通常设计成卧式倾斜3°～5°仰角的形式，这种小倾角环境为自循环蒸发冷却系统的布置和运行提供了有利的条件[20]。轴向穿管式风力发电机的蒸发冷却系统由定子段冷却管、上升集气管、冷凝回流管、冷凝器以及管内循环流动的冷却工质组成，如图1所示。在运行过程中，液态工质在定子段吸收铁心和绕组中产生的热量后开始汽化，汽化后的工质经集气管送至冷凝器进行冷却，冷凝后的工质基于自身重力回流至底部定子段空心冷却管内，重新参与循环。
图1 穿管式蒸发冷却风力发电机冷却系统循环示意图
Fig.1 Schematic diagram of cooling system circulation of stator axial pipe evaporative cooling wind generators
由于蒸发冷却风力发电机的运行原理和拓扑结构与传统的风力发电机基本一致，因此本文以一台10 MW外转子表贴式永磁风力发电机的物理模型作为研究对象，其主要电磁参数见表1。
表1 10 MW蒸发冷却永磁风力发电机主要电磁参数
Tab.1 Main electromagnetic parameters of a 10 MW evaporative cooling permanent magnet wind generator
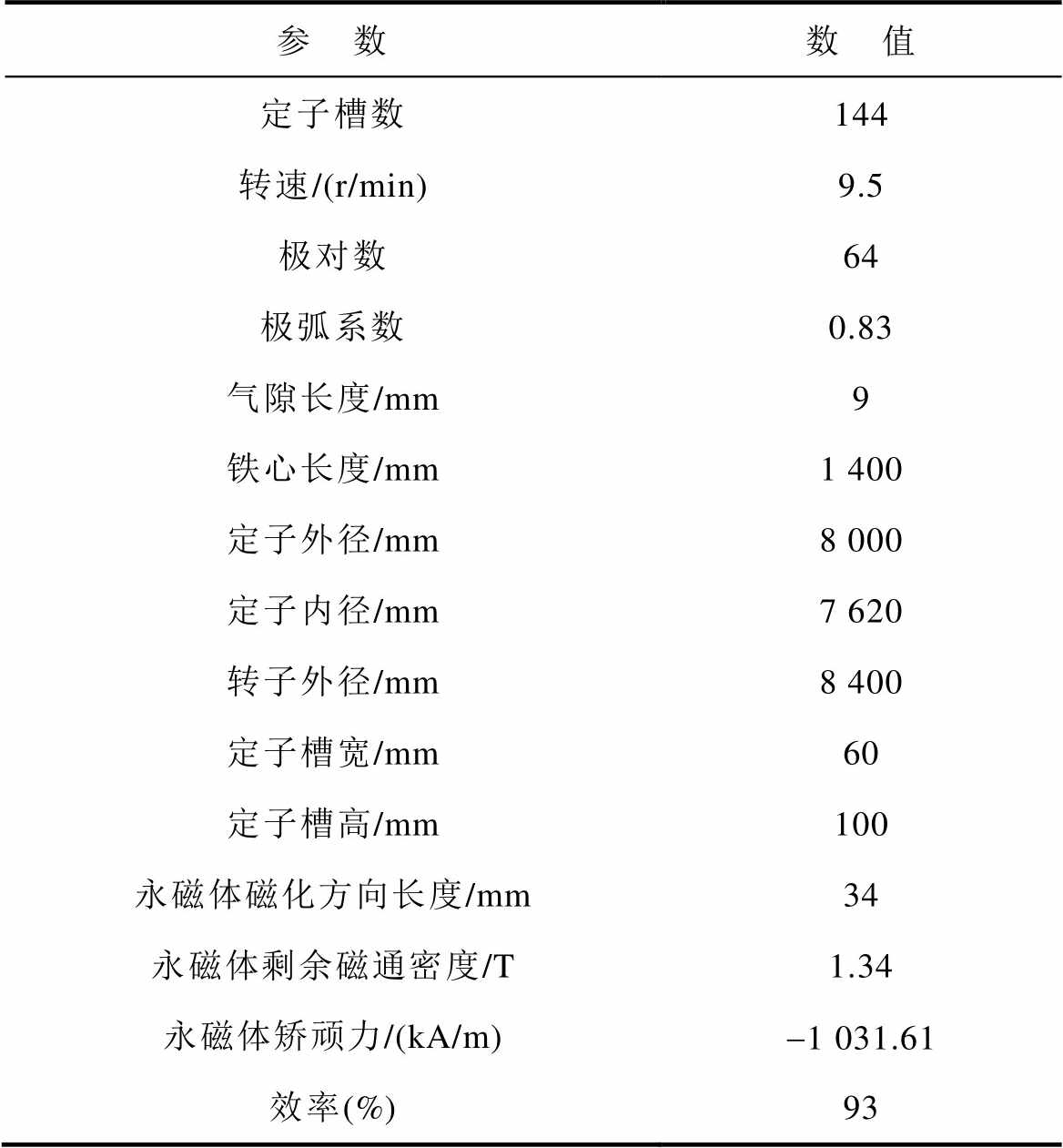
参 数数 值 定子槽数144 转速/(r/min)9.5 极对数64 极弧系数0.83 气隙长度/mm9 铁心长度/mm1 400 定子外径/mm8 000 定子内径/mm7 620 转子外径/mm8 400 定子槽宽/mm60 定子槽高/mm100 永磁体磁化方向长度/mm34 永磁体剩余磁通密度/T1.34 永磁体矫顽力/(kA/m)-1 031.61 效率(%)93
当定子轭部开孔后，由于开孔区域的气隙磁导率远低于铁心电工钢片，将导致轭部原本均匀分布的磁力线沿开孔边缘绕行[21]，定子穿管式风力发电机磁力线及磁通密度分布云图如图2所示，继而对电机的主磁路产生影响。
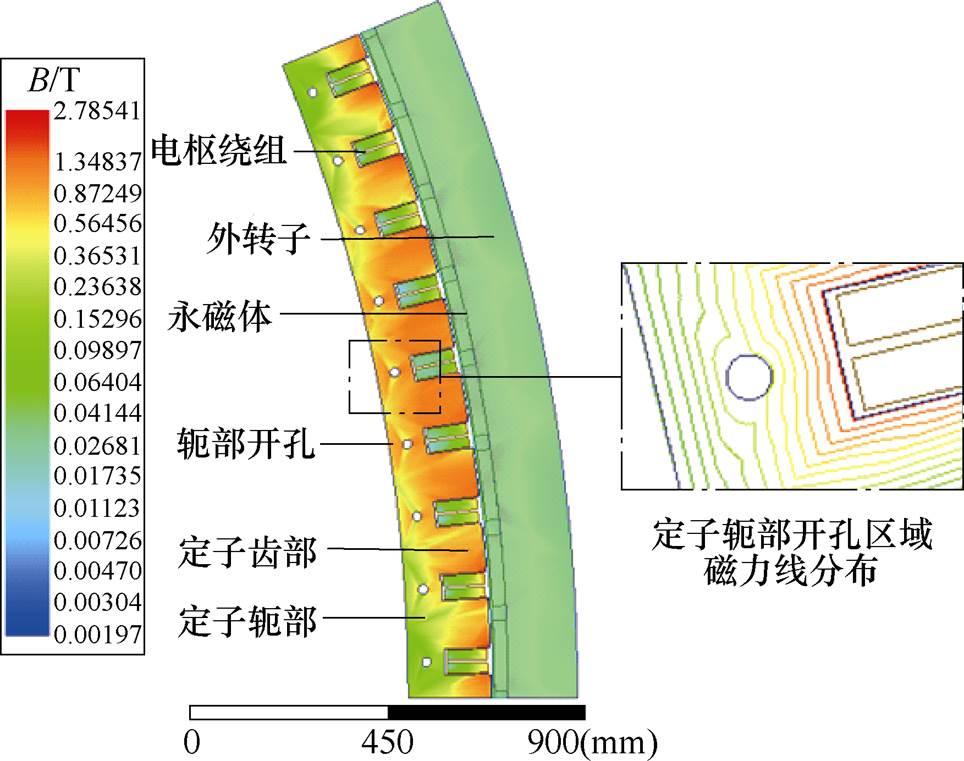
图2 定子穿管式风力发电机磁力线及磁通密度分布云图
Fig.2 Magnetic field line and density distribution cloud diagram of stator axial pipe wind generators
定子轭部开孔区域的增加等效于轭部有效磁通面积的减少、磁通密度和铁耗的增加。轭部铁心饱和后将导致主磁路的磁阻增加[22]，永磁体中进入主磁路的磁通减少，永磁体的利用率降低，从而对发电机的运行性能带来不利的影响。
以上述10 MW直驱式风力发电机作为研究对象，在每个定子槽顶部中心位置布置单根冷却管的工况下，空载气隙磁通密度随开孔尺寸和位置的变化趋势见表2。可知，空载气隙磁通密度随开孔半径的增大而减小，同时也随开孔位置而变化，因此应综合考虑铁心穿管方案对电机电磁性能的影响。
表2 空载气隙磁通密度随开孔尺寸和位置的变化关系
Tab.2 The relationship between the maximum magnetic density of no-load yoke and the opening size and position
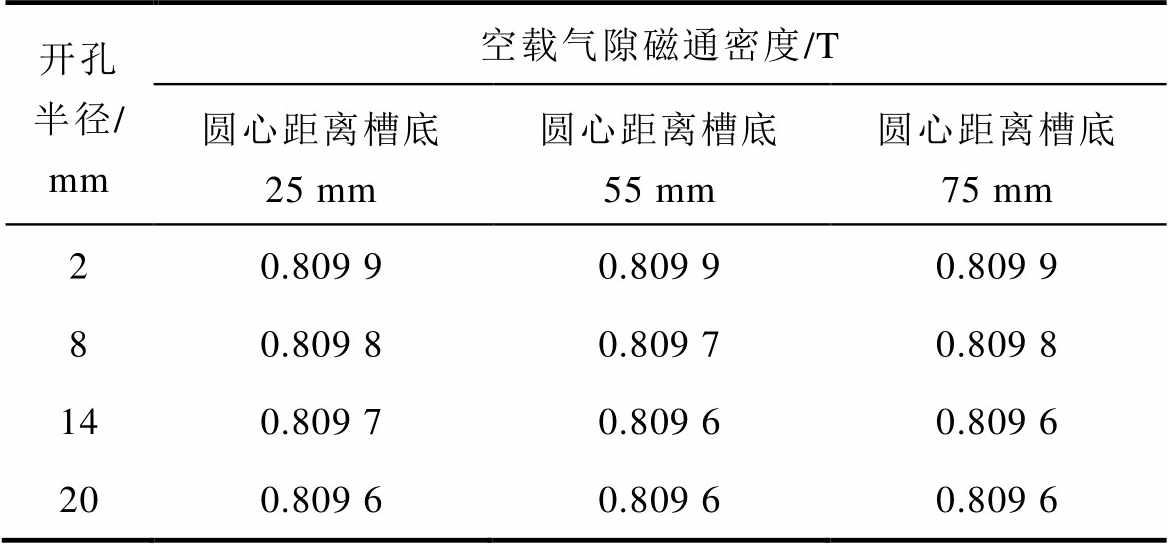
开孔半径/ mm空载气隙磁通密度/T 圆心距离槽底 25 mm圆心距离槽底 55 mm圆心距离槽底 75 mm 20.809 90.809 90.809 9 80.809 80.809 70.809 8 140.809 70.809 60.809 6 200.809 60.809 60.809 6
在运行过程中，永磁直驱式风力发电机通过背靠背的双脉冲宽度调制（Pulse Width Modulation, PWM）变流器与电网相连[9]，在机侧变流器采用定子直轴电流Id=0的控制策略下，发电机的等效电路和稳态运行向量如图3所示。
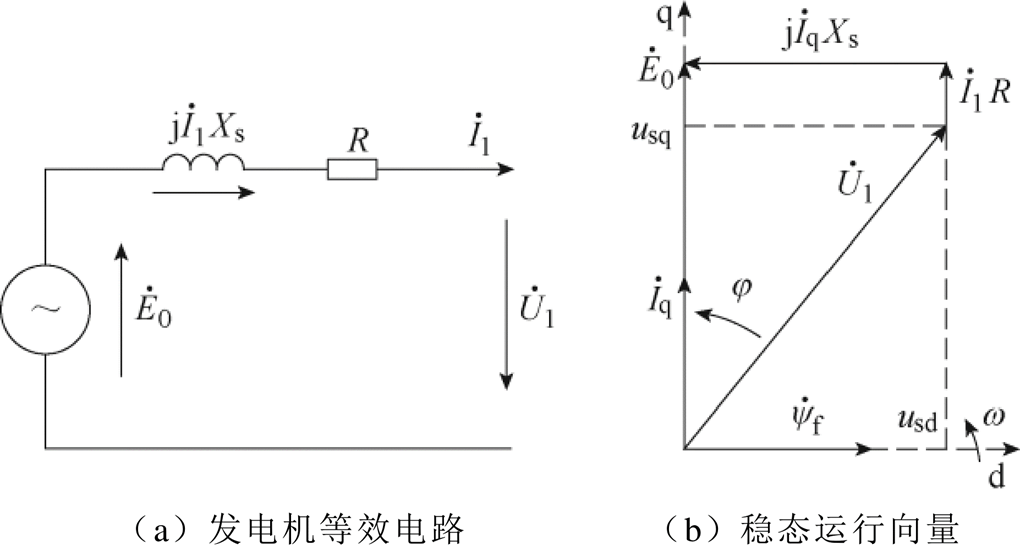
图3 风力发电机运行等效电路及稳态运行向量
Fig.3 Equivalent circuit and steady-state operation vector diagram of wind generators
由图3b可知，在忽略定子电阻R时发电机的相电流为
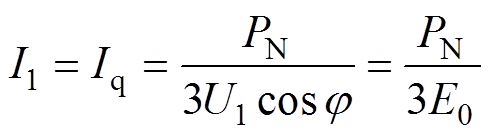（1）
式中，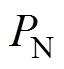
为发电机电磁功率；
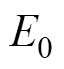为空载反电动势；
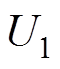为定子相电流；
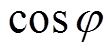为功率因数；
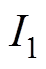和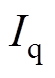
分别为定子相电流和定子交轴电流。
永磁同步发电机的空载反电动势为
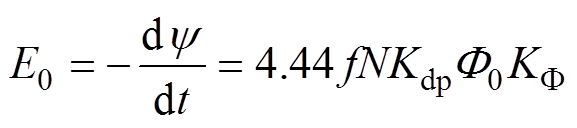（2）
式中，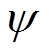
为单相绕组空载磁链；
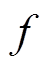为发电机频率；
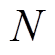为每相绕组匝数；
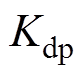为绕组系数；
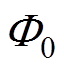为每极空载气隙磁通；
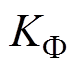为空载磁通波形系数。
由上述分析可知，在电机主要设计尺寸和转速不变的情况下，主磁路磁阻的增加将引起发电机空载气隙磁通密度和反电动势的减少以及运行电流的升高，继而引起绕组铜耗和温升的增加，从而影响发电机的安全运行和发电输出性能。
在忽略电机轴向温度梯度变化的前提下，风力发电机的定子径向稳态温度场分布规律满足含内热源的二维物体稳态热传导方程，其控制方程为
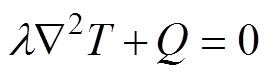（3）
式中，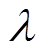
为材料的导热系数；
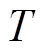为温度场分布；
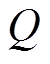为内热源的体热源密度。
因此，其温度场分布可以通过微分方程进行求解。同样，基于传热学基本理论可以分析得到定子绕组热源在传热路径上的各部分热阻[23-24]为
（4）
式中，R为热阻，下标为各部分热阻名称；h为等效对流换热系数；Sv、Sc为接触面面积；l为传导方向长度；Sd为传导方向的横截面积；rc为接触热阻。
从上述分析可知，定子绕组传热路径中的传热热阻由换热系数、传热距离、对流换热系数、换热面积和接触热阻等多个因素所决定，因此作为其中的关键影响因素，接触热阻以及自循环流动状态下工质的对流换热系数需通过具体实际工况下的对应实验来进行测定。因此，为了减少定子绕组热源传热路径上的热阻，也同样应综合考虑冷却管布置数量、尺寸和位置对发电机冷却性能的影响。
由上述分析可知，定子冷却管结构会对电机的电磁和冷却性能产生影响，然而这类非线性优化问题很难基于传统算法进行求解。拓扑优化算法则是基于单元灵敏度对结构方案进行寻优[25]，在考虑设计单元对性能影响的同时避免了对复杂非线性方程组的求解，因此能够适用于此类优化问题的求解。
拓扑优化算法的核心思想为：以最小化电机轭部等效磁阻作为优化目标，在优化过程中逐步“删除”灵敏度较低的单元，则可以在最大程度地减少每一步迭代对优化目标的影响，最终得到最优的设计结果。因此，为了简化计算，本文在优化分析过程中采用相同尺寸且互不重叠的均分网络对定子轭部设计区域进行划分，如图4所示。
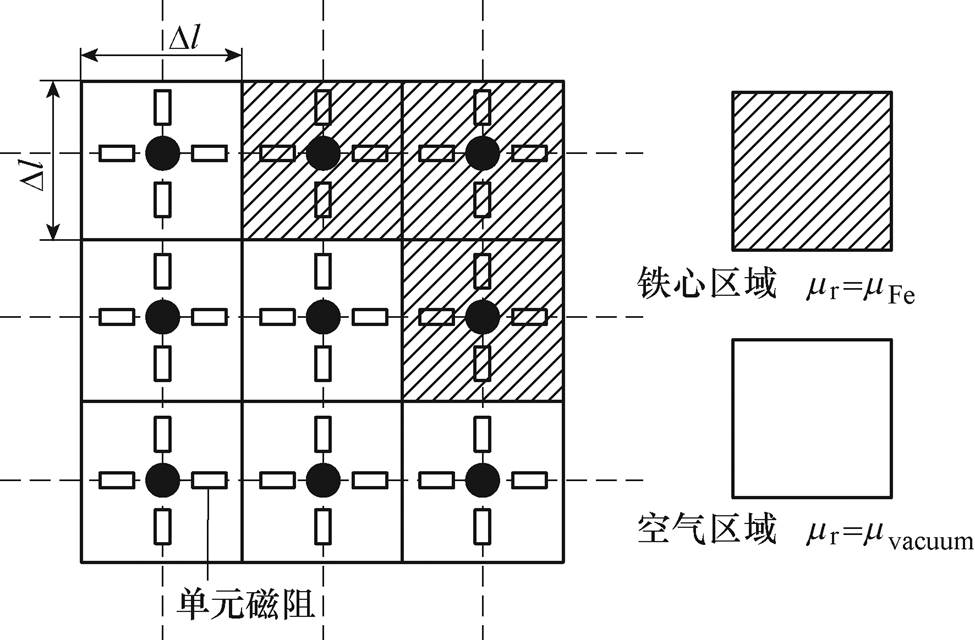
图4 单元灵敏度分析区域网格划分示意图
Fig.4 Schematic diagram of grid division for element sensitivity analysis area
类比于电路分析中的“节点电压法”可得设计区域内单元节点的磁导矩阵控制方程[26]为
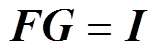（5）
式中，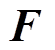
为节点磁动势矩阵；
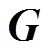为节点磁导矩阵；
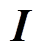为流入节点内的磁通源矩阵。
为了简化分析，将定子轭部区域的复杂磁阻网络简化等效为两节点i和j之间的等效磁阻。当令节点j的基准磁动势为0时，基于二端口电阻等效理论和磁导矩阵控制方程可将n个纯磁阻连接的磁导矩阵简化为n-1阶矩阵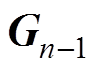
，有
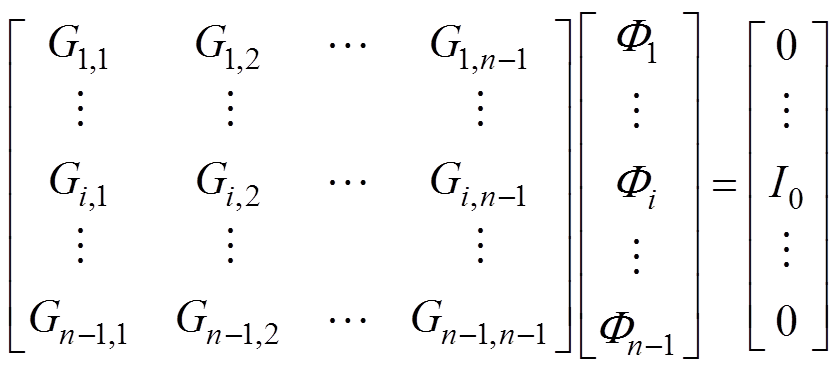（6）
式中，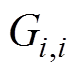
为单元节点i的自磁导；
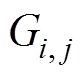为单元节点i和j的互磁导；
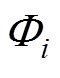为节点i的磁动势；
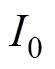为流入节点i的磁通源。
基于磁导矩阵可得节点i的磁动势为
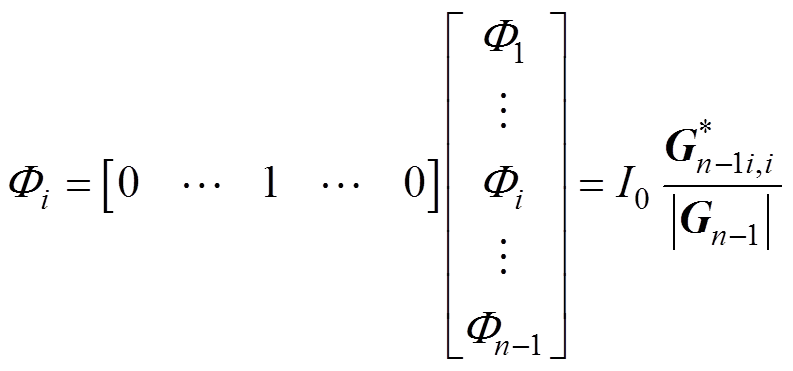（7）
式中，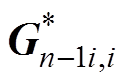
的意义为矩阵
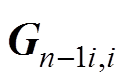的伴随矩阵。则节点i和节点j之间的等效磁阻为
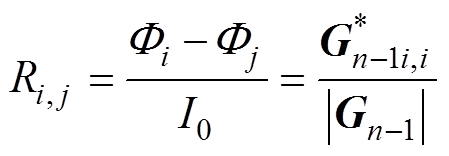（8）
忽略某一单元e磁导率的改变对外磁通源以及其余单元磁导率的影响，则单元e磁导率变化对定子轭部等效磁阻的影响可以近似表示为
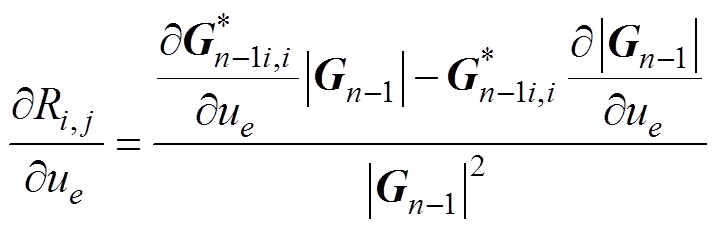（9）
式中，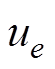
为单元节点e的磁导率。
于是式（9）中任意单元e的电磁灵敏度可以用于评估该单元属性转变后对定子轭部磁阻产生的 影响。
与磁阻矩阵单元灵敏度分析相似，传热矩阵单元灵敏度分析同样将定子轭部设为优化区域，采用相同尺寸的网格单元对设计区域进行划分。
对于稳态热传导问题，基于有限体积法可得设计区域内单元节点的传热矩阵控制方程[27]为
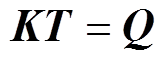（10）
式中，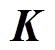
为节点热传导矩阵；
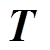为节点温度矩阵；
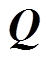为节点热载荷矩阵。
忽略单元变化对热载荷的影响，则单元e发生变化后新系统的平衡方程变为
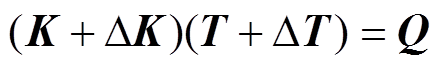（11）
式中，
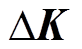与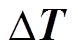
分别为节点热传导矩阵和节点温度矩阵的变化量。
忽略高阶项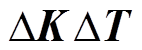
，则系统温度项的变化为
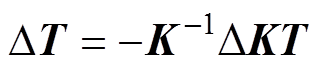（12）
因此，绕组单元某节点k的温度由铁心单元e变为空气而引起的改变为
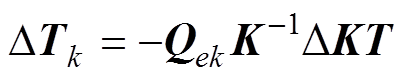（13）
式中，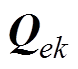
为仅第k项为1，其余项均为0的行向量。
于是式（13）中的传热灵敏度可以用于评估单元e对绕组节点k冷却性能的影响。
对于风力发电机自循环冷却系统而言，空心管道的冷却性能将直接决定电机的散热能力，同时也会对电机方案的设计、冷却工质的用量以及铁心穿管的优化方案产生影响。因此，为了获得其实际运行工况下的准确传热特性，需要对其开展实验进行测定和分析。
作为自循环冷却系统中的核心换热工质，实验中采用的相变换热工质的主要物性参数见表3。
表3 冷却工质的主要物性参数
Tab.3 Main physical parameters of cooling medium
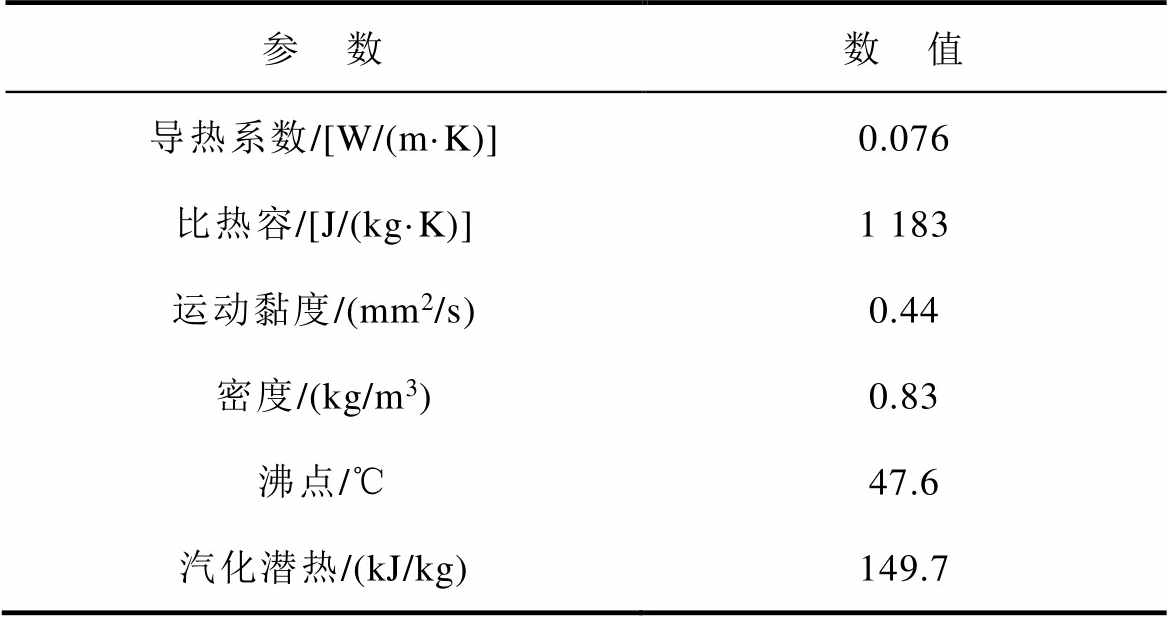
参 数数 值 导热系数/[W/(m·K)]0.076 比热容/[J/(kg·K)]1 183 运动黏度/(mm2/s)0.44 密度/(kg/m3)0.83 沸点/℃47.6 汽化潜热/(kJ/kg)149.7
基于5°小倾角自循环式冷却系统实验台，本文对单根长度为1 500 mm的空心冷却管开展了冷却性能实验测试分析，其实验原理如图5所示。在实验过程中放置冷凝器的高度位置为900 mm，铜管倾斜低端为回液口，高端为出气口，空心铜管的内径和外径分别为2.5 mm和4 mm。在回液口至出气口间铜管外壁面处沿程均布了11个T型热电偶（相邻间隔150 mm）用于测试整体的温度变化趋势，并依次标记为1～11号。测试前采用Fluke9171干式温度校验炉对T型热电偶进行了校准，并使用Fluke2686A数据采集器收集处理热电偶在实验过程中产生的温度信号。
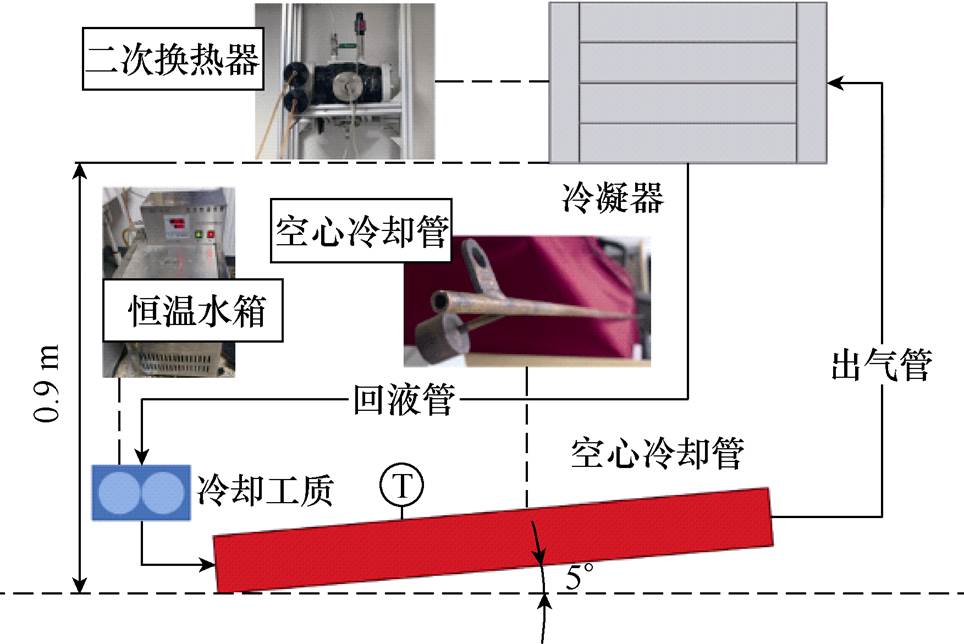
图5 空心冷却铜管小倾角自循环冷却性能测试平台
Fig.5 Small dip angle self-circulation cooling performance test platform for hollow cooling copper tubes
实验过程中的铜管损耗由交流电源产生，以作为恒定的热负荷（热流密度）输入条件，并采用Fluke345电流钳对输入的电流信号进行收集和处理，转换为相应的实验热负荷数值。冷却管外壁面包有保温层以保证绝热边界条件。实验过程中采用恒温水箱以保证工质进水口温度恒定为20℃，冷凝器容量足够大且自循环系统在实验过程中运行在常压的状态下。待自循环系统经加热达到稳定状态后，对铜管外壁面的温度值进行采集和校准，最终得到其外壁面沿程各点温度随铜管附加热流密度的变化趋势如图6所示。
由于自循环系统在高于极限热流密度时出气口附近铜管壁面温度将骤升[28]，为了在温度可控的前提下探究电机电流密度的最大取值，从而为电磁设计提供参考，因此在设计过程中应以极限热流密度，即以图6中热流密度的最大值（8 303 W/m2）作为边界条件对其进行约束。
冷却工质在空心铜管段吸热后将发生相变沸腾，工质在空心铜管不同段存在着不同种类的流型，不同流型下的两相流具有完全不同的流动和传热特性，流型变化以及密度波的不稳定性造成了如图6所示的温度变化趋势[29]。因此，为了简化分析，以铜管外壁面沿程平均温升，即沿程11个均布热电偶温度的平均值作为基准，基于空心铜管加载的热流密度与空心铜管温度与入水口温度之差的比值可以拟合得到工质沸腾换热系数随热流密度的变化趋势，如图7所示。
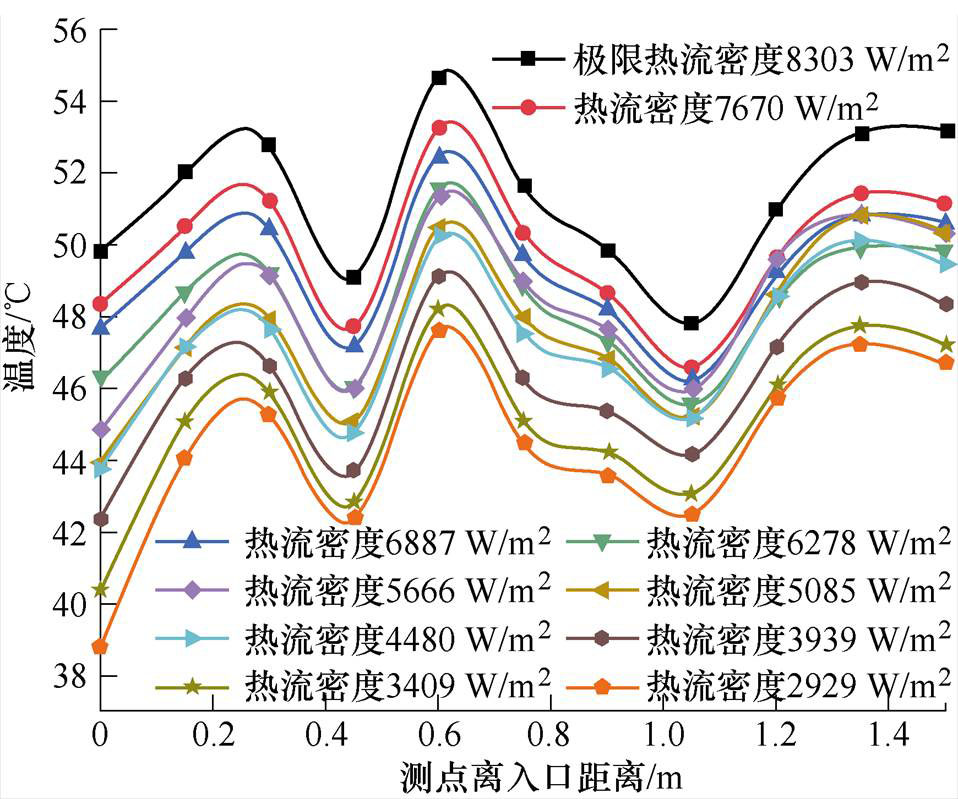
图6 空心铜管沿程温度随热负荷变化曲线
Fig.6 Temperature curves of hollow cooling copper tubes varies with thermal load
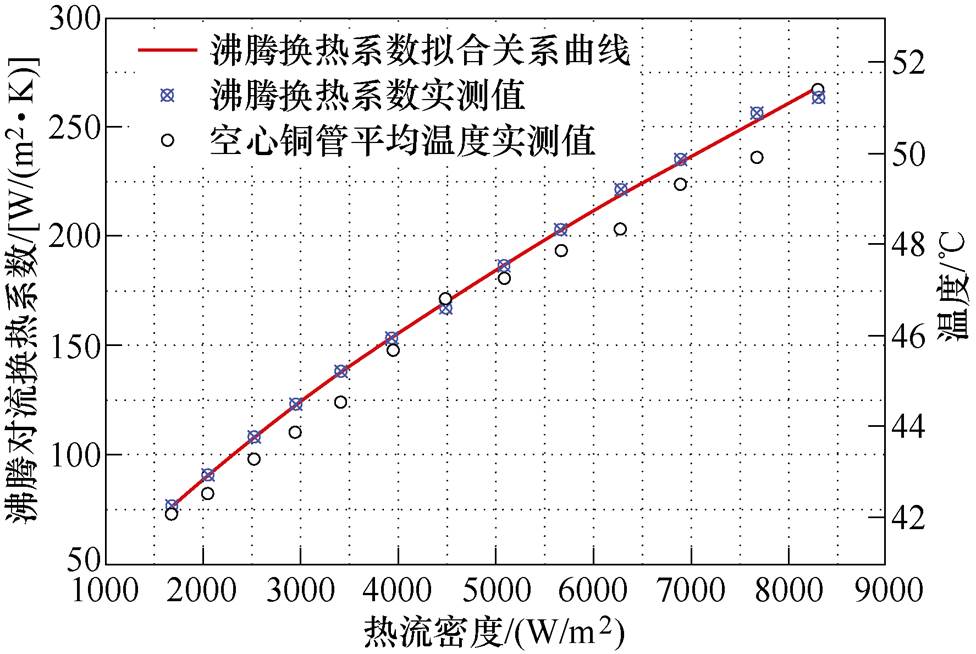
图7 空心铜管沸腾换热系数同热流密度的拟合曲线
Fig.7 The fitting curve of boiling heat transfer coefficient and heat flux of hollow copper tubes
图7中沸腾换热系数拟合曲线的表达式为
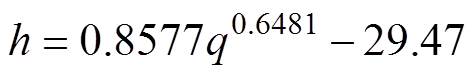（14）
式中，h为对流换热系数；q为热流密度。
拟合曲线的标准差为2.05，确定系数R-square为0.999 1，误差范围满足工程设计所需的精度要求。拟合曲线的变化趋势与以往矩形空心导线换热能力的实验研究结论相符[30]，因此可以用于表征空心铜管的对流换热特性。
在未完全接触界面之间存在接触热阻，这将增加热量传递的阻力[23]，因此为了研究表面粗糙度对接触热阻的影响，本文中以孔/轴的配合精度为H7/ h7作为参考基准，对内孔粗糙度为Ra3.2 mm的硅钢片DW470-50以及外壁面粗糙度分别为Ra1.6 mm、Ra3.2 mm及Ra6.3 mm的一组空心紫铜管进行接触热阻测试实验，其测试实验原理如图8所示。
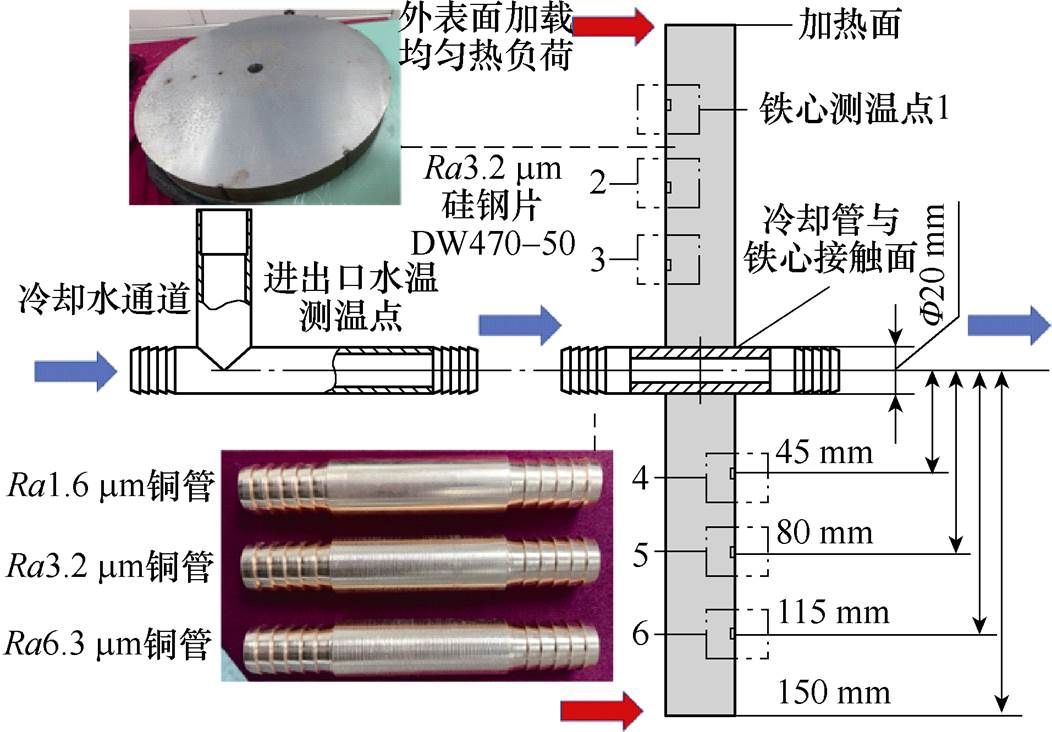
图8 空心管道与铁心壁面接触热阻测试实验原理
Fig.8 Experimental schematic diagram of thermal resistance test between hollow pipe and core wall
由接触热阻定义可知，空心管道外壁面与铁心内壁面交界处的接触热阻为
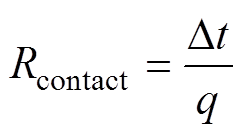（15）
式中，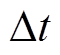
为接触面两侧的温差。
图8中，测试硅钢片的外径r1=150 mm，内径r2=10 mm，两端面测温点以硅钢片中心为原点呈对称分布，任一端面测温点由内至外距圆心的垂直距离分别为45、80和115 mm，最外层轴向表面采用聚酰亚胺加热薄膜均匀加热，以此作为第二类传热边界条件（热流密度边界条件）。基于式（3）可得硅钢片的稳态径向温度分布规律为
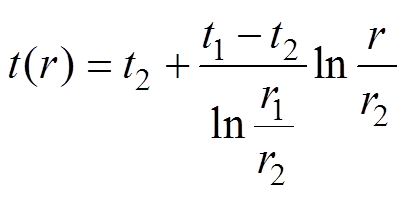（16）
式中，t1为r1处稳定温度；t2为r2处稳定温度。
实验过程中采用保温棉等绝热材料对加热实验台轴向外侧与空气接触的散热区域进行隔热处理，以确保铁心硅钢片外径向内径的热流传递为单一径向方向，如图9所示。铁心温度由埋置在铁心侧面小孔（半径为2 mm，深度为2 mm）内的1～6号PT100测得，进出口水温由与冷却水道封装成一体的铠装PT100直接测得。图9中，将进出水口温测点分别标记为7号和8号，采用测量误差为±0.5%的BREMEN电磁流量计采集管路内冷却水的进口流量，其中空心铜管的内径和外径分别为6 mm和10 mm，接触面的长度为30 mm，接触面的缝隙处采用卡夫特k-5211导热硅脂进行填充。
图9 空心管道与铁心壁面接触热阻实验平台
Fig.9 Thermal resistance test platform for contact between hollow pipe and core wall
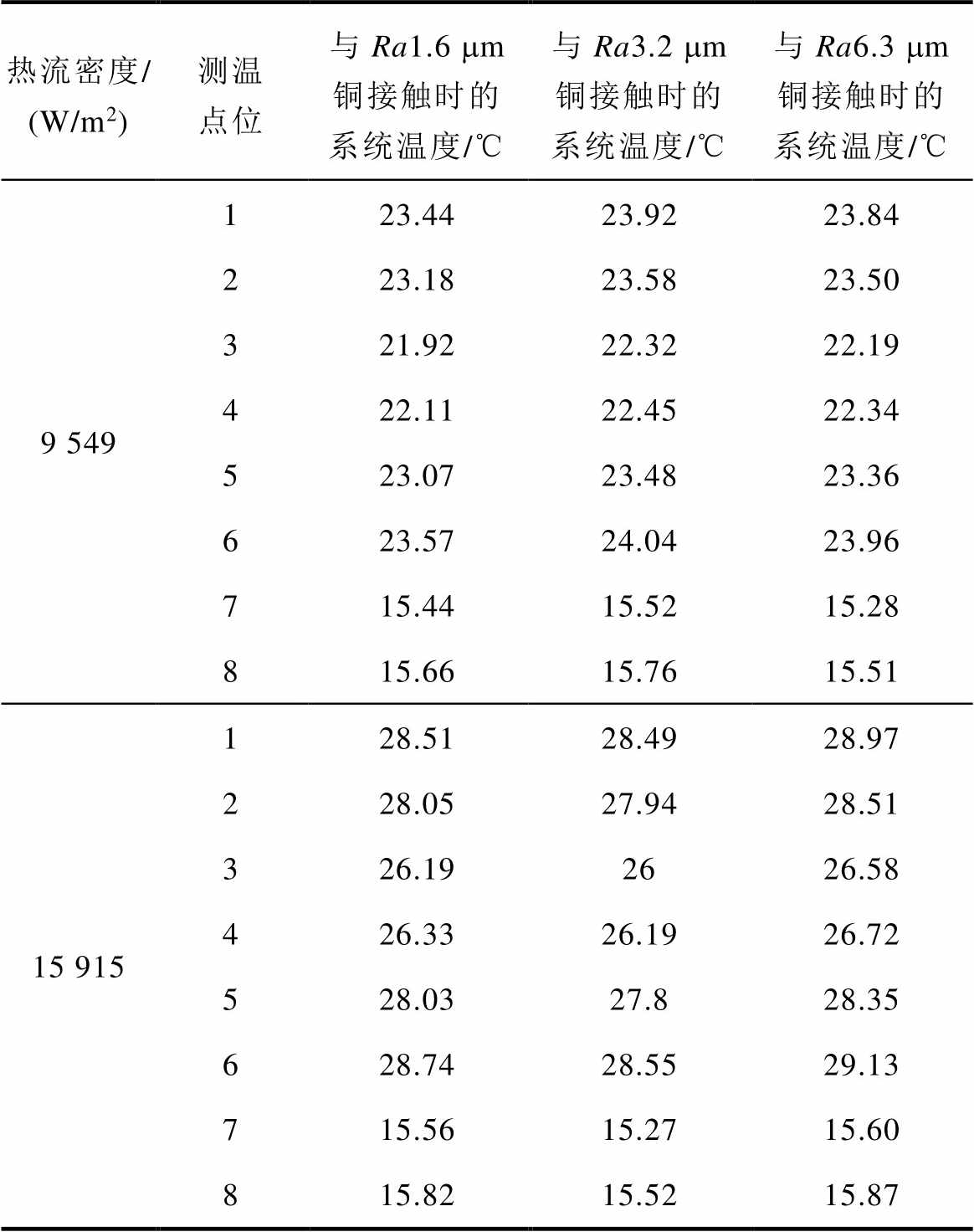
当冷却水的流速为1.4 L/h，系统温度达到稳定时，实验系统内各点的温度实验结果见表4。
表4 不同粗糙度配合下的系统温度分布实验结果
Tab.4 Experimental results of temperature distribution of heating models with different roughness
热流密度/ (W/m2)测温点位与Ra1.6 mm铜接触时的系统温度/℃与Ra3.2 mm铜接触时的系统温度/℃与Ra6.3 mm铜接触时的系统温度/℃ 9 549123.4423.9223.84 223.1823.5823.50 321.9222.3222.19 422.1122.4522.34 523.0723.4823.36 623.5724.0423.96 715.4415.5215.28 815.6615.7615.51 15 915128.5128.4928.97 228.0527.9428.51 326.192626.58 426.3326.1926.72 528.0327.828.35 628.7428.5529.13 715.5615.2715.60 815.8215.5215.87
基于进出口平均水温以及冷却水流速可得此工况下空心铜管内工质的雷诺数Re=1 592，小于临界雷诺数Rec=2 300，属于层流传热。因此，采用齐德-泰特（Sieder-Tate）公式可得层流换热工况下管道内工质的平均数努塞尔Nu[23]为
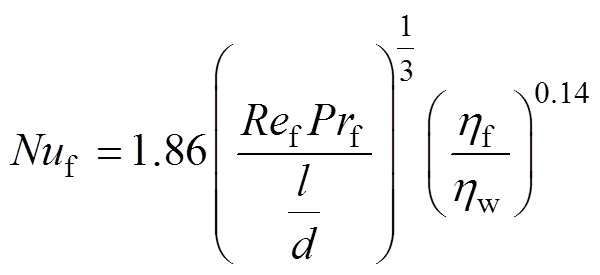（17）
式中，Nu为努塞尔数；Pr为普朗特数；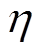
为动力黏度；下标f、w分别表示以流体平均温度及壁面温度来计算流体的运动黏度；l为管的长度；d为管的当量直径。
继而可得空心铜管表面的对流换热系数为
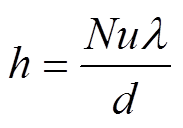（18）
基于平均水温、对流换热系数和热流密度可得空心铜管内壁面温度，继而拟合得到空心铜管外壁面温度；以铁心对称两侧面的温度平均值为基准可以拟合得到定子径向的温度分布，继而获得铁心内壁面温度。综上所述，以表面粗糙度配合均为Ra3.2 mm的铜管/铁心配合工况为基准，拟合得到的实验系统整体的温度分布曲线如图10所示。
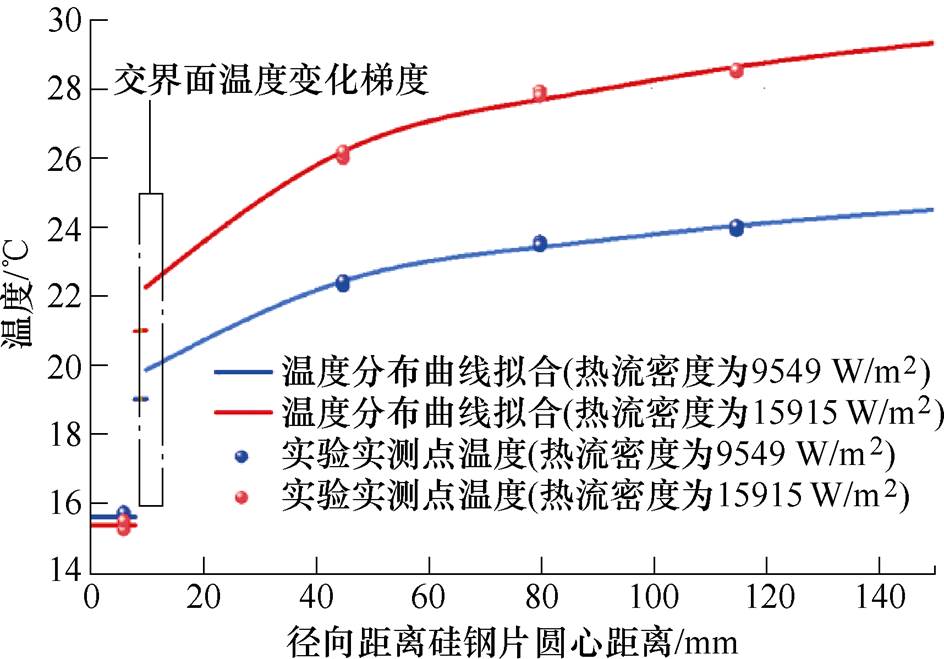
图10 接触热阻实验平台系统温度分布曲线拟合
Fig.10 Temperature distribution curves fitting of contact thermal resistance test platform system
从拟合结果中可知，测试温度与预测模型相符，因此说明了上述模型可以准确地反映系统内的温度分布。基于此模型，通过接触面两侧的温度梯度以及加载的热流密度可得到不同表面粗糙度配合下的铜管外表面与铁心内壁面的接触热阻值，结果见表5。
基于传热学可知[23]，在常规压力和表面粗糙度配合工况下，不锈钢/不锈钢的接触热阻为 (2.2～5.88)×10-4 m2·K/W，铜/铜的接触热阻为 (0.25～2.5)×10-4 m2·K/W。从分析结果中可知，采用导热硅脂填充后的空心铜穿管与硅钢片的表面交界面处具有较低的接触热阻，因此能够说明本文中提出的定子铁心穿管冷却结构具有良好的导热性能，同时也具有良好的冷却应用前景。
表5 不同粗糙度配合下的接触热阻测试实验结果
Tab.5 Experimental results of contact thermal resistance test with different roughness
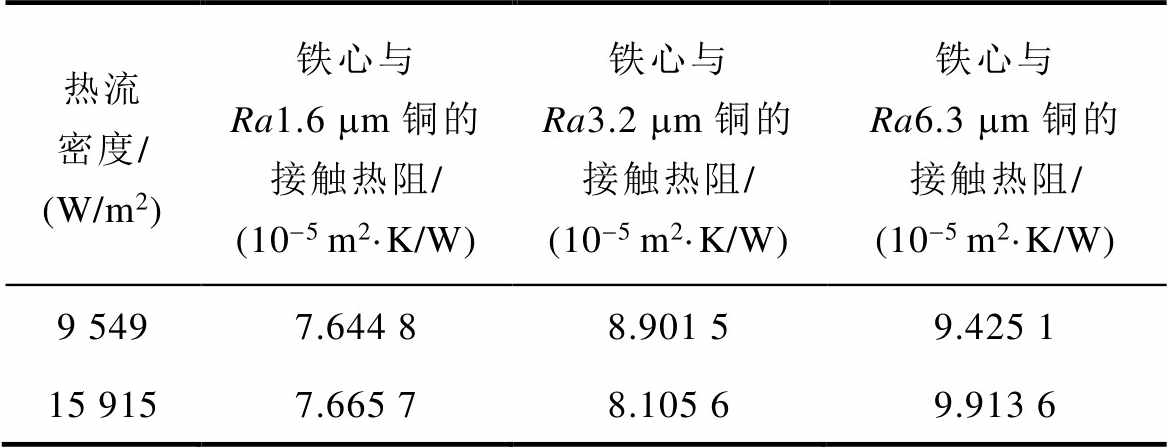
热流密度/ (W/m2)铁心与Ra1.6 mm铜的接触热阻/ (10-5 m2·K/W)铁心与Ra3.2 mm铜的接触热阻/ (10-5 m2·K/W)铁心与Ra6.3 mm铜的接触热阻/ (10-5 m2·K/W) 9 5497.644 88.901 59.425 1 15 9157.665 78.105 69.913 6
基于上述分析，本文以定子轭部单元密度作为设计变量，以发电机电磁和传热性能作为优化目标建立的优化模型为
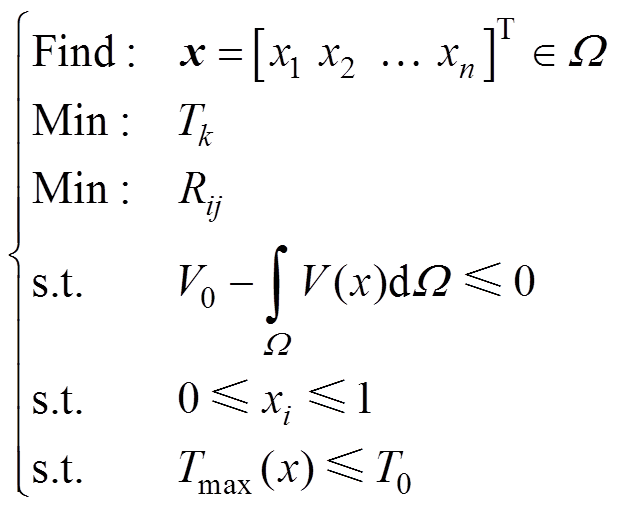（19）
式中，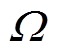
为定子轭部设计区域；
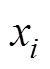为单元密度，在本文中只有0或1两种状态，0代表空气单元，1代表铁心单元；n为设计单元总数；Rij为定子轭部等效磁阻；Tk为绕组节点k的温度；V0为定子轭部区域体积约束；T0为绕组最高温度约束。
为了在优化过程中对管径r进行统一，同时避免开孔位置与设计边界以及相邻孔发生干涉，因此本文基于单元灵敏度过滤技术[29]将过滤函数和惩罚因子定义为
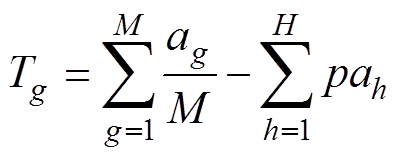（20）
式中，Tg为过滤后的单元灵敏度；M为以单元g为圆心过滤半径范围r内的单元总数；ag为以单元g为圆心过滤半径范围r内的单元灵敏度；H为以单元g为圆心过滤半径范围r内的设计区域和空气区域边缘单元总数；ah为以单元g为圆心过滤半径范围r内的设计区域和空气区域边缘单元灵敏度；p为干涉区域惩罚因子，本文中取为500。
为了同步表征设计单元的电磁及传热性能，本文在优化过程中采用归一化策略将多目标优化模型转换为单目标优化问题进行求解，统一后的单元电磁-传热灵敏度偏差值如式（21）所示，偏差值越小，表示单元同时具有更好的电磁和冷却特性。
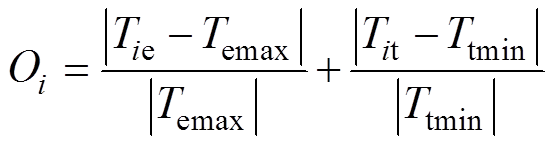（21）
式中，Oi为单元i归一化后的电磁-传热灵敏度偏差值；Tie为单元i过滤后的电磁灵敏度；Temax为设计区域单元中最大的非正数电磁灵敏度；Tit为单元i过滤后的传热灵敏度；Ttmin为设计区域单元中最小的非正数传热灵敏度。
基于上述分析建立的定子铁心穿管方案优化设计迭代流程如图11所示，其中单个槽下的冷却管以槽中心呈对称分布，以实现发电机定子温度场的均匀分布。
在实际运行工况与实验工况基本相同的假设前提下，本文通过式（14）来计算仿真分析过程中工质的对流换热系数。在定子径向温度场有限元分析过程中，本文中假设定子绕组和铁心发热均匀，绕组和铁心径向的导热系数设置为398 W/(m·K)和40 W/(m·K)，基于等效导热系数 [0.15 W/(m·K)] 来计及绕组中的绝缘材料及其间的接触热阻对定子绕组温度的影响[31]。
考虑到电机结构的对称性分布，在优化过程中选取8极9槽下的单元电机作为研究对象，对9个轭部区域中相同位置下的单元灵敏度进行了平均化处理。其中，单个定子轭部优化设计区域的尺寸为170 mm×90 mm，为了在保证分析精度的同时减少优化迭代流程，将定子轭部单元尺寸设置为10 mm× 10 mm，单元划分总数为153，如图12所示。
当空心冷却管与铁心壁面的接触面表面粗糙度均为Ra3.2 mm，绕组最高温升约束为130℃（B级绝缘等级），冷却铜管壁厚为2 mm，单个槽轭部布置偶数个冷却管，自循环系统热负荷初选为7 000 W/m2的前提下，基于上述优化策略得到的10 MW直驱式风力发电机的冷却管优化布置方案如图13所示。其中优化方案一为单个定子槽轭部布置4根管径为20 mm的冷却管，优化方案二为单个定子槽轭部布置6根管径为14 mm的冷却管，优化方案三为单个定子槽轭部布置8根管径为10 mm的冷却管。
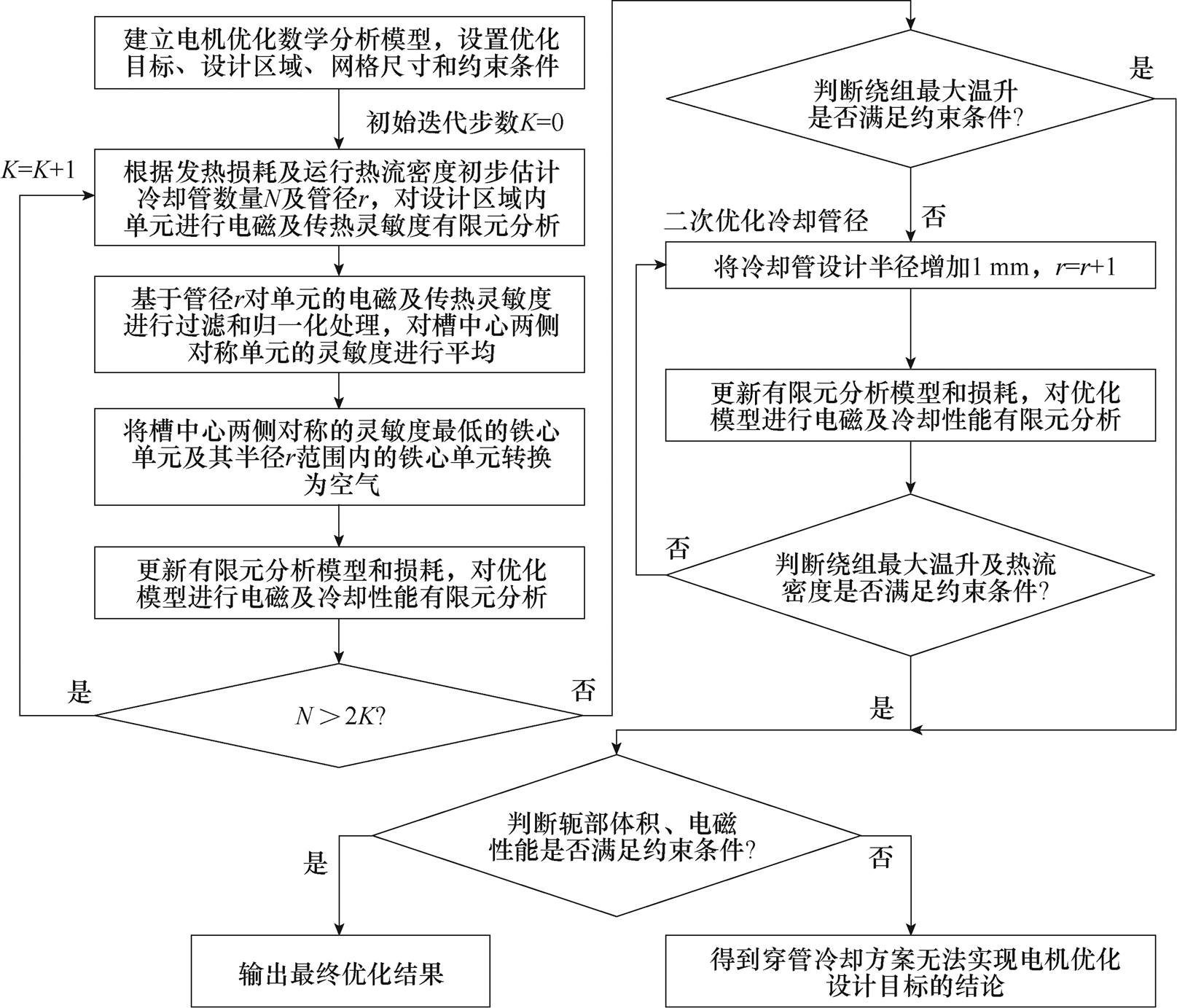
图11 铁心穿管冷却方案优化设计迭代流程
Fig.11 Iterative process of optimization design of core pipe cooling scheme
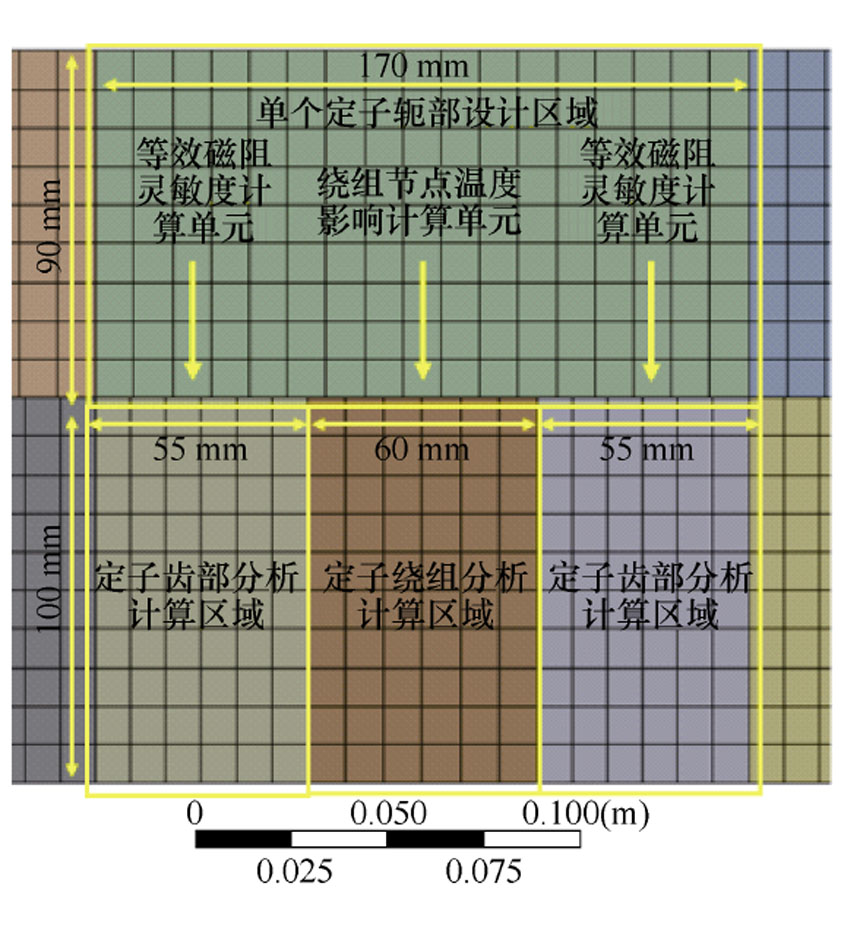
图12 单个定子槽轭部优化设计区域示意图
Fig.12 Schematic diagram of optimization analysis of single stator slot yoke region
为了验证优化结果的电磁输出性能，本文基于Maxwell2021R1有限元仿真软件中的2D瞬态磁场求解器对电机模型进行了有限元分析。当电机额定输出电磁功率为10 MW，相电压设置为3 300 V，铁心材料设置为DW465-50，对电机模型施加周期对称边界条件，对转子外径施加矢量磁位边界条件，对定子绕组施加电流源激励的条件下，基于有限元分析得到的优化方案在空载和负载下的电磁输出特性见表6。
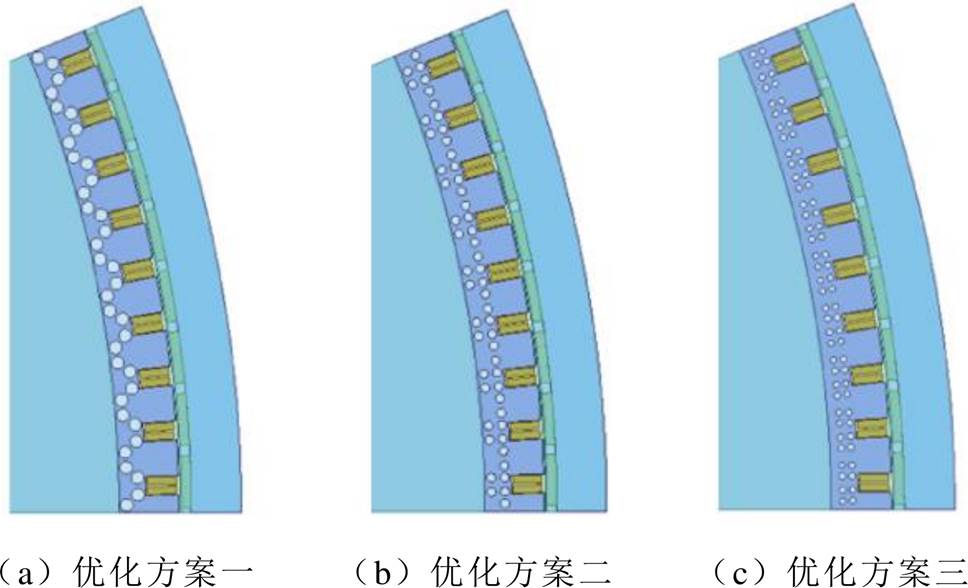
图13 10 MW风力发电机定子轭部冷却管优化方案
Fig.13 Optimization scheme of stator yoke cooling pipe for 10 MW direct-drive wind generators
为了验证优化结果的传热特性和冷却性能，本文基于ANSYS2021R1有限元分析软件中的Steady- Sate Thermal稳态热求解模块对三种优化方案中的定子径向温度场进行了有限元分析。基于工质的对流换热系数对冷却管内表面施加第三类边界条件（对流换热边界条件），对定子上下外边界施加绝热边界条件，对定子左右外边界施加相同的绝热（对称）边界条件，对空心铜管与铁心壁面的交界面施加接触热阻，基于额定负载特性下的电机损耗对铁心和绕组施加内热源激励，将工质换热温度设置为20℃，对模型赋予相应的材料属性后求解温度场得到的仿真分析结果如图14所示。
表6 优化方案电磁输出性能有限元分析结果
Tab.6 Finite element simulation results of electromagnetic performance of optimization scheme
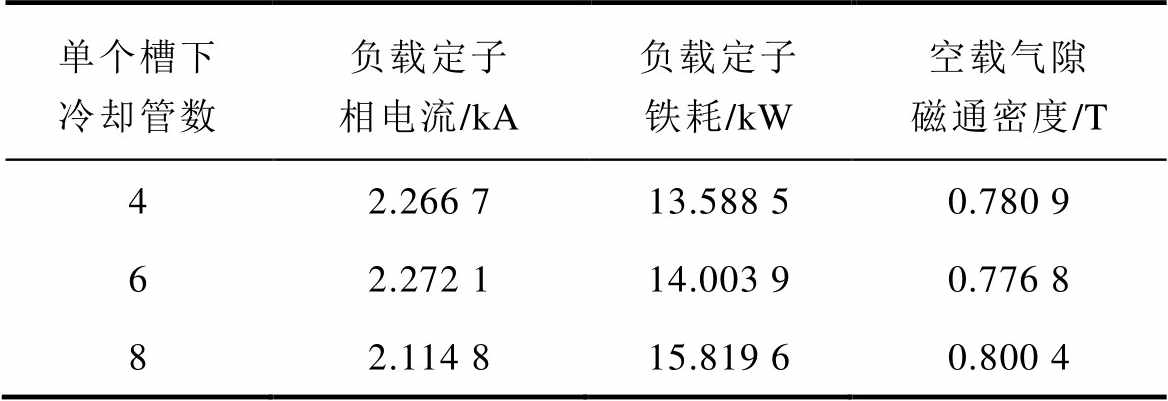
单个槽下冷却管数负载定子相电流/kA负载定子铁耗/kW空载气隙磁通密度/T 42.266 713.588 50.780 9 62.272 114.003 90.776 8 82.114 815.819 60.800 4
从温度场有限元仿真结果验证中可知，三种优化方案均能满足绕组最大温升约束的要求，不同优化方案中的定子温度场分布趋势基本相同，呈现为较为均匀的对称分布，靠近冷却管附近的绕组温度较低，冷却性能较好，因此证明了本文中提出的优化策略和冷却方案的可行性和有效性。同时，基于电磁和传热性能分析可知，优化方案三在降低电机运行损耗的同时能够满足绕组的最大温升和散热要求，因此是三种方案中最合适的选择，而不同的冷却管布置方案也会对不同结构尺寸电机的电磁和冷却性能产生不同的影响，在电机参数的优化设计过程中应予以权衡考虑。
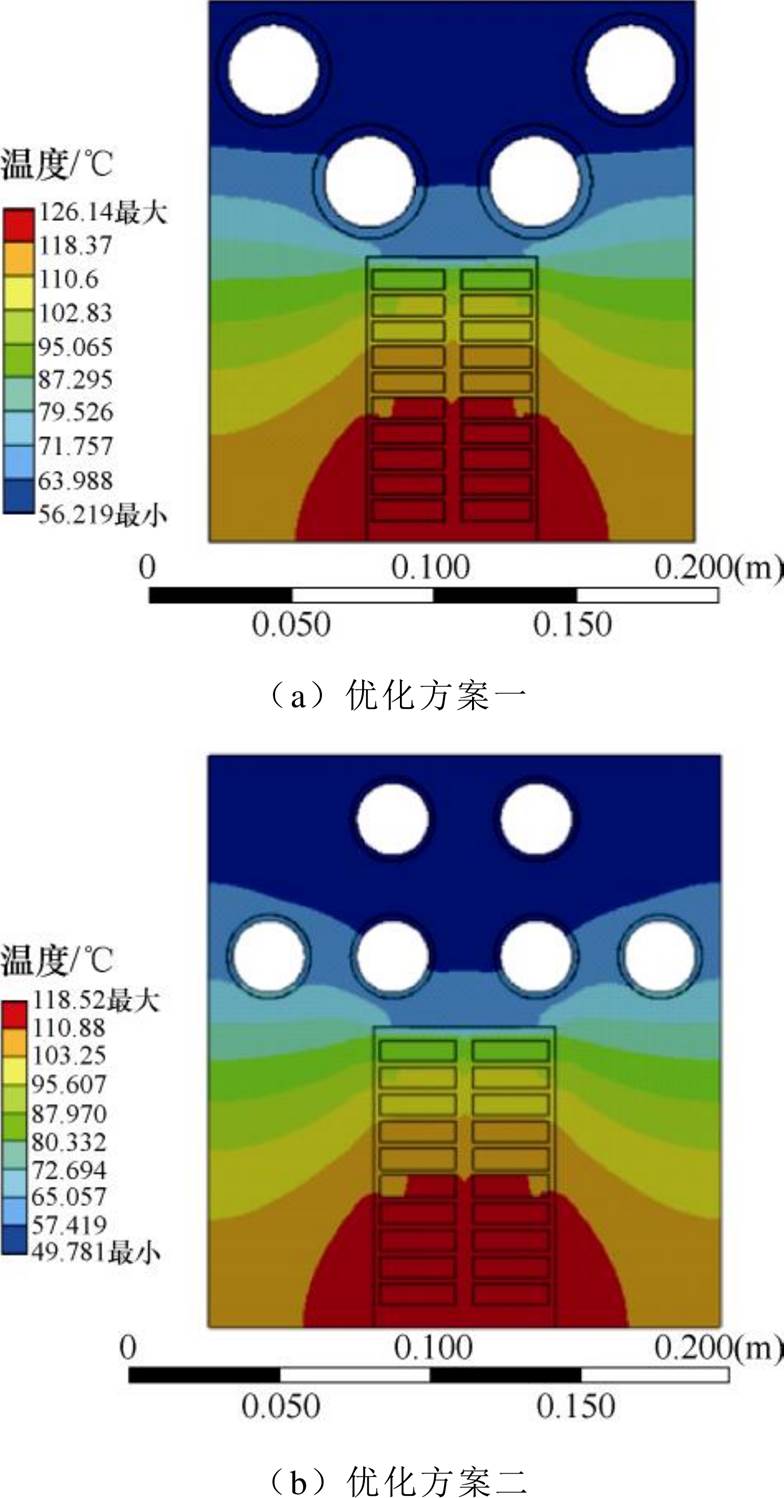
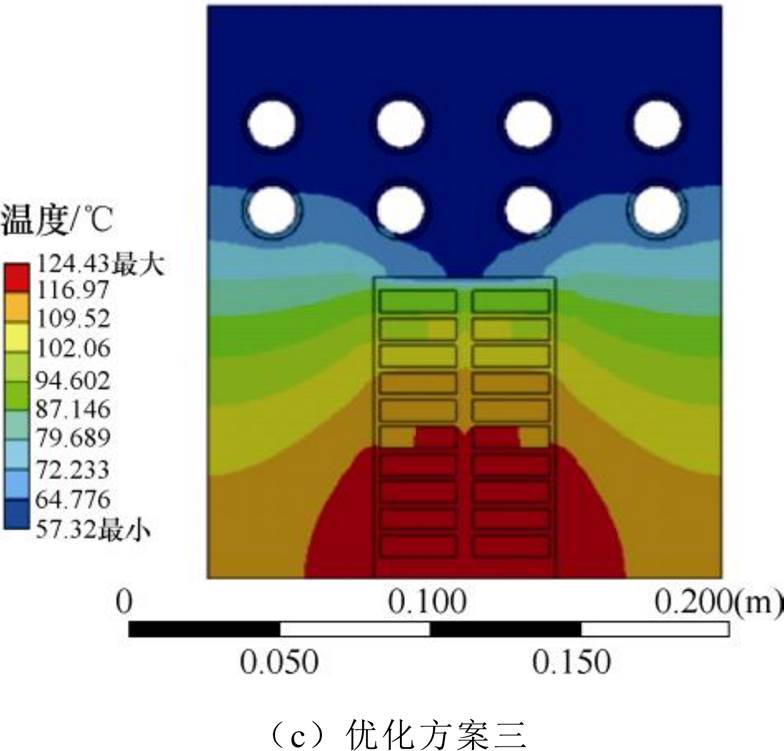
图14 定子轭部冷却管优化方案温度场有限元验证
Fig.14 Finite element verification of temperature field of stator yoke cooling pipe optimization scheme
本文基于设计单元的电磁-传热灵敏度分析以及冷却性能测试实验对蒸发冷却风力发电机定子铁心穿管结构的优化布置策略以及电磁-传热特性进行了分析和研究，所得到的结论如下：
1）本文基于风力发电机的运行特性以及小倾角自循环系统的结构布置形式，分析了定子铁心穿管结构位置尺寸对风力发电机电磁及冷却性能的影响关系，基于单元灵敏度分析建立了定子穿管区域单元对电机电磁-冷却特性的影响分析模型，能够基于灵敏度分析设计单元对电机电磁及冷却性能的影响。
2）本文基于小倾角自循环实验平台以及接触热阻测试平台对铁心穿管的冷却性能和接触热阻进行了实验测试研究，测得了实验过程中小倾角自循环冷却系统的极限运行热流密度为8 303 W/m2，分析得到了铁心穿管冷却性能与其加载的热流密度之间的关系。通过建立的实验系统温度预测模型得到了配合精度为H7/h7的工况下，不同壁面表面粗糙度配合和运行热流密度下的铜管与铁心壁面的接触热阻。分析结果表明，本文中提出的新技术具有良好的导热性能，同时实验结果能够为其他同类型接触条件下的冷却技术提供设计参考和依据。
3）本文建立了考虑电磁-传热影响特性的蒸发冷却风力发电机定子铁心穿管优化策略，基于优化策略对一台10 MW直驱式风力发电机进行了三种不同冷却布置方案的优化设计研究，基于有限元仿真验证了三种优化方案均能满足电机电磁及绕组最大温升约束的要求，说明了本文中优化方案和冷却技术的可行性和有效性。本文中的优化方法和策略能够为定子穿管式风力发电机的优化设计提供参考，同时也能够为今后定子穿管式风力发电机在结构多参数权衡选择时提供参考和依据。
参考文献
[1] Yaramasu V, Wu Bin, Sen P C, et al. High-power wind energy conversion systems: state-of-the-art and emerging technologies[J]. Proceedings of the IEEE, 2015, 103(5): 740-788.
[2] 边春元, 邢海洋, 李晓霞, 等. 基于速度变化率的无位置传感器无刷直流电机风力发电系统换相误差补偿策略[J]. 电工技术学报, 2021, 36(11): 2374- 2382.
Bian Chunyuan, Xing Haiyang, Li Xiaoxia, et al. Compensation strategy for commutation error of sensorless brushless DC motor wind power generation system based on speed change rate[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2374- 2382.
[3] 高俊国, 孟睿潇, 胡海涛, 等. 电机定子绝缘老化寿命预测研究进展[J]. 电工技术学报, 2020, 35(14): 3065-3074.
Gao Junguo, Meng Ruixiao, Hu Haitao, et al. Research progress on prediction of aging life of motor stator insulation[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3065-3074.
[4] 丁树业, 孙兆琼, 徐殿国, 等. 3 MW双馈风力发电机传热特性数值研究[J]. 中国电机工程学报, 2012, 32(3): 137-143, 4.
Ding Shuye, Sun Zhaoqiong, Xu Dianguo, et al. Numerical investigation of heat transfer for 3 MW doubly-fed wind generators[J]. Proceedings of the CSEE, 2012, 32(3): 137-143, 4.
[5] 顾国彪, 阮琳. 蒸发冷却技术在水轮发电机领域的应用和发展[J]. 中国电机工程学报, 2014, 34(29): 5112-5119.
Gu Guobiao, Ruan Lin. Applications and deve- lopments of the evaporative cooling technology in the field of hydrogenerators[J]. Proceedings of the CSEE, 2014, 34(29): 5112-5119.
[6] 熊斌, 阮琳, 顾国彪, 等. 蒸发冷却技术在高电荷态ECR离子源磁体上的应用: LECR4[J]. 电工技术学报, 2015, 30(10): 219-225.
Xiong Bin, Ruan Lin, Gu Guobiao, et al. Application of evaporative cooling technology in magnet of high charge state ECR ion source-LECR4[J]. Transactions of China Electrotechnical Society, 2015, 30(10): 219-225.
[7] 张玉斌, 温英科, 阮琳. 全浸式蒸发冷却IGBT电热耦合模型研究[J]. 电工技术学报, 2022, 37(15): 3845-3856.
Zhang Yubin, Wen Yingke, Ruan Lin. Research on electrothermal coupling model of fully-immersed evaporative cooling IGBT[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3845-3856.
[8] 王海峰, 李旺, 顾国彪, 等. 风力发电机自循环蒸发内冷系统稳定性的研究[J]. 物理学报, 2016, 65(3): 030501.
Wang Haifeng, Li Wang, Gu Guobiao, et al. Static bifurcation analysis of natural circulation inner evaporative cooling system in wind turbine[J]. Acta Physica Sinica, 2016, 65(3): 030501.
[9] 高剑, 黄守道, 张文娟, 等. 基于变流器控制策略的直驱永磁风力发电机优化设计[J]. 电工技术学报, 2013, 28(7): 103-109.
Gao Jian, Huang Shoudao, Zhang Wenjuan, et al. Optimal design for permanent magnet wind power generators based on converter controlling algo- rithm[J]. Transactions of China Electrotechnical Society, 2013, 28(7): 103-109.
[10] McDonald A, Bhuiyan N A. On the optimization of generators for offshore direct drive wind turbines[J]. IEEE Transactions on Energy Conversion, 2017, 32(1): 348-358.
[11] Bhuiyan N A, McDonald A. Optimization of offshore direct drive wind turbine generators with con- sideration of permanent magnet grade and tempera- ture[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 1105-1114.
[12] Penzkofer A, Atallah K. Analytical modeling and optimization of pseudo-direct drive permanent magnet machines for large wind turbines[J]. IEEE Transa- ctions on Magnetics, 2015, 51(12): 1-14.
[13] Li Wang, Wang Haifeng. Steady-state thermal simu- lation of the stator coil of the evaporative inner cooling system in wind turbines[C]//2012 IEEE 6th International Conference on Information and Auto- mation for Sustainability, Beijing, 2013: 248-251.
[14] 李旺, 王海峰, 顾国彪. 风力发电机自循环蒸发内冷系统的静态分岔分析[J]. 电工电能新技术, 2015, 34(4): 6-11.
Li Wang, Wang Haifeng, Gu Guobiao. Static bifurcation analysis on natural circulation inner evaporative cooling system in wind turbines[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(4): 6-11.
[15] 李伟力, 仝世伟, 程鹏. 离网型永磁同步发电机电磁场和温度场数值计算与分析[J]. 中国电机工程学报, 2010, 30(30): 107-113.
Li Weili, Tong Shiwei, Cheng Peng. Calculation and analysis of electromagnetic and temperature fields in off-grid type permanent magnet synchronous gen- erator[J]. Proceedings of the CSEE, 2010, 30(30): 107-113.
[16] 李伟力, 程鹏, 张美巍, 等. 1.5MW永磁风力发电机电磁场与温度场计算与分析[J]. 电机与控制学报, 2010, 14(12): 52-57, 62.
Li Weili, Cheng Peng, Zhang Meiwei, et al. Electro- thermal analysis and calculation of a 1.5MW per- manent magnet wind generator[J]. Electric Machines and Control, 2010, 14(12): 52-57, 62.
[17] 温彩凤, 汪建文, 孙素丽. 基于热电磁耦合的永磁风力发电机涡流损耗分析[J]. 太阳能学报, 2015, 36(9): 2278-2284.
Wen Caifeng, Wang Jianwen, Sun Suli. Analysis of eddy current losses in permanent magnet wind generator based on electromagnetic-thermal coupling method[J]. Acta Energiae Solaris Sinica, 2015, 36(9): 2278-2284.
[18] Cheng Ziran, Ruan Lin, Gao Jian, et al. Multi- objective optimization of stator direct cooling for direct-drive permanent-magnet wind generators[C]// 2022 IEEE International Conference on Power Systems Technology (POWERCON), Kuala Lumpur, Malaysia, 2022: 1-6.
[19] Cheng Ziran, Ruan Lin, Huang Shoudao, et al. Research on noise reduction of 3.6 MW evaporative cooling wind motor induced by electromagnetic and two-phase flow resonance based on stator optimi- zation[J]. Processes, 2021, 9(4): 669.
[20] Yan Jing, Yu Shunzhou, Cao Rui. Research on the temperature distribution of the hollow conductors in the self-circulating evaporative inner cooling system for high power rectifier equipment[J]. Journal of Physics: Conference Series, 2021, 1748(5): 052023.
[21] 窦润田, 李永建, 张献, 等. 受工艺孔影响的变压器铁心损耗计算与分析[J]. 电工技术学报, 2022, 37(12): 2909-2923.
Dou Runtian, Li Yongjian, Zhang Xian, et al. Calculation and analysis of transformer core loss due to technological hole[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 2909-2923.
[22] 毕刘新, 王善铭, 夏永洪. 表贴式永磁电机漏磁导的解析计算[J]. 清华大学学报(自然科学版), 2010, 50(4): 525-528.
Bi Liuxin, Wang Shanming, Xia Yonghong. Calcu- lation of leakage permeance in a surface-mounted permanent magnet machine[J]. Journal of Tsinghua University (Science and Technology), 2010, 50(4): 525-528.
[23] 杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 2006.
[24] 骆凯传, 师蔚, 张舟云. 基于温度实验的永磁同步电机损耗分离方法[J]. 电工技术学报, 2022, 37(16): 4060-4073.
Luo Kaichuan, Shi Wei, Zhang Zhouyun. Method of loss separation of permanent magnet synchronous motor based on temperature experiment[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(16): 4060-4073.
[25] Liu Chengsi, Xu Yongxiang, Zou Jibin, et al. Permanent magnet shape optimization method for PMSM air gap flux density harmonics reduction[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(4): 284-290.
[26] 佟文明, 姚颖聪, 李世奇, 等. 考虑磁桥不均匀饱和的内置式永磁同步电机等效磁网络模型[J]. 电工技术学报, 2022, 37(12): 2961-2970.
Tong Wenming, Yao Yingcong, Li Shiqi, et al. Equivalent magnetic network model for interior permanent magnet machines considering non-uniform saturation of magnetic bridges[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 2961- 2970.
[27] 刘硕, 方国东, 王兵, 等. 近场动力学与有限元方法耦合求解热传导问题[J]. 力学学报, 2018, 50(2): 339-348.
Liu Shuo, Fang Guodong, Wang Bing, et al. Study of thermal conduction problem using coupled peridy- namics and finite element method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(2): 339-348.
[28] 鲁钟琪. 两相流与沸腾传热[M]. 北京: 清华大学出版社, 2002.
[29] Sigmund O, Petersson J. Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima[J]. Structural Optimization, 1998, 16(1): 68-75.
[30] 国建鸿, 傅德平, 袁建华, 等. 300MW汽轮发电机强迫循环蒸发冷却定子绕组温升计算[J]. 中国电机工程学报, 2008, 28(26): 92-97.
Guo Jianhong, Fu Deping, Yuan Jianhua, et al. Calculation of temperature distribution of larger evaporative cooling turbo-generator with forced inner cooling system[J]. Proceedings of the CSEE, 2008, 28(26): 92-97.
[31] 李晔, 李琦, 范涛, 等. 电传动车辆用永磁电机定子绕组等效导热系数获取方法[J]. 兵工学报, 2021, 42(10): 2215-2222.
Li Ye, Li Qi, Fan Tao, et al. Acquisition method for equivalent thermal conductivity coefficient of stator winding of permanent magnet motor[J]. Acta Armamentarii, 2021, 42(10): 2215-2222.
Abstract In recent years, with the rapid development of renewable energy, the capacity of wind generators has increased, and the problems of loss and heating are becoming more and more serious. Excessive operating temperatures will harm the safe operation of wind generators. Evaporative cooling technology can greatly improve the generator’s cooling efficiency. The whole system has many advantages, such as simple maintenance, safety, reliability, and more. Many scholars have researched electromagnetic and cooling performance analysis modeling and wind generator optimization. However, the influence of small changes in the stator’s local structure on electromagnetic performance and the contact thermal resistance on cooling performance is often ignored. Therefore, a collaborative optimization strategy of electromagnetic and cooling performance is proposed based on the electromagnetic and heat transfer sensitivity analysis of the design unit. Through experiments, the thermal contact resistance between the hollow cooling tube and the core interface is measured, and the heat transfer characteristics of the hollow cooling tube under the self-circulation characteristics of a small dip angle are analyzed. The optimization design of a 10 MW direct drive wind turbine is carried out.
Firstly, the influence of the stator core’s cooling pipe structure on electromagnetic and cooling performance of wind generators is analyzed based on the operating characteristics of wind generators and the element sensitivity method. Secondly, the heat transfer capacity and contact thermal resistance of hollow round copper pipe are analyzed and tested through the heat transfer experiment of self-circulating pipe with a small dip angle and the temperature rise experiment of contact thermal resistance. Thirdly, the optimization model of the stator core cooling structure is established. Finally, the optimization design of the stator core cooling structure is studied and verified by finite element analysis.
The self-recirculating cooling system with a small dip angle experiment shows that the critical heat flux of a 1 500 mm hollow copper tube is 8 303 W/m2 when the condenser height is 900 mm, and the inlet temperature of cooling water is 20℃. The variation trend of the convective heat transfer coefficient of the evaporative cooling medium with heat flux is revealed by experiments, and the standard deviation of the fitted curve is 2.05. The contact thermal resistance experiment shows that when the hole/shaft matching accuracy is H7/h7, the roughness of DW470-50 is Ra3.2 mm, the heat flux is 9 549 W/m2, the contact thermal resistance between the iron core and the hollow copper tube with the roughness of Ra1.6 mm, Ra3.2 mm, and Ra 6.4 mm is 7.644 8×10-5 m2·K/W, 8.901 5×10-5 m2·K/W, and 9.425 1×10-5 m2·K/W, respectively. Finally, evaporation cooling wind generators of three different configurations using stator core pipe structures are optimized based on the sensitivity analysis strategy.
The following conclusions can be drawn from the simulation analysis: (1) The established influence analysis model can analyze the influence of the stator cooling tube’s design elements on the electromagnetic and cooling performance of wind generators. (2) Based on the small-dip self-circulation test platform and the contact thermal resistance test platform, the relationship between the cooling performance of the core tube and the loaded heat flux is obtained. It shows that wind generators’ new evaporative cooling technology has good thermal conductivity. (3) The finite element simulation method verifies that the three optimization schemes can meet the requirements of electromagnetic and winding maximum temperature rise constraints.
keywords：Evaporative cooling wind generators, stator core cooling pipe structure, electromagnetic and cooling characteristics, thermal contact resistance element, sensitivity analysis, optimization design
DOI: 10.19595/j.cnki.1000-6753.tces.230024
中图分类号：TK89
国家自然科学基金资助项目（U22A20219）。
收稿日期 2023-01-09
改稿日期 2023-02-06
程自然 男，1993年生，博士研究生，研究方向为电力设备新技术、电机设计及优化。E-mail: chengziran1993@hun.edu.cn
阮 琳 女，1976年生，研究员，博士生导师，研究方向为电力设备新技术、大电机内综合物理场仿真研究和流体流动与传热分析。E-mail: rosaline@mail.iee.ac.cn（通信作者）
（编辑 崔文静）