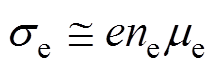（1）
摘要 现有电弧炉模型主要关注电弧内部与外部特性的联系，割裂了电弧内部微观下电气与物理的耦合影响，难以体现电弧的电热物理本质，导致仿真精度有所欠缺。针对上述问题，该文提出一种改进的新型交流电弧炉模型。首先，在电子连续性方程的基础上，构建电弧的电气特性模型；其次，根据弧柱磁压缩力平衡方程和瞬时能量平衡方程分别构建电弧的压强、温度等物理参数模型，推导得到电弧内部的电气特性与物理参数之间的耦合机理，得到两者的耦合模型；然后，基于电弧炉变压器二次侧额定电流和最大电弧温度之间的关系，利用麻雀搜索算法对电弧温度曲线进行辨识，确定物理模型的各个参数；最后，依据50 t、55 t炼钢交流电弧炉的现场实测数据，在Matlab/Simulink平台上搭建模型并验证模型的正确性。仿真结果表明，所提模型更符合交流电弧炉实际运行过程中的物理本质，能更精确地反映其谐波、电压波动特性。
关键词：交流电弧炉 电弧温度 麻雀算法 电气特性 物理参数
电弧炉以其较低的投资费用、较优的冶炼质量以及较低的碳排放等优势，在国内外冶金企业中得到广泛的应用[1]。但电弧炉的冶炼过程中随机性强，具有强时变非线性的特点[2]，产生的大量谐波会加剧电力系统设备的热效应，降低其使用寿命；电压偏差及波动会使得变电站的保护频繁启动，造成安全隐患[3-4]。因此，交流电弧炉的精确建模对研究电弧炉在电网产生的电能质量影响，制定相关治理措施具有重要意义。
电弧炉的非线性主要是由于电弧的随机性导致。随机理论是表征电弧随机性的有效建模方法之一。文献[5-7]将带通高斯白噪声或带通白噪声叠加在电弧半径、电弧电压或电弧弧长等静态电弧参数上，以此得到电弧炉冶炼过程中的非线性时变特征，但随机理论仅是机械地在静态电弧参数上叠加随机信号，难以解释其内在的机理过程以及外在特性。后续研究表明，电弧炉的电压、电流波动与混沌系统的外在表现较为接近，应用混沌理论建立的模型比随机理论更接近电弧现象的本质[8]。文献[9]首次使用混沌动力学描述电弧炉的非线性特性，在此基础上，文献[10-13]采用蔡氏电路产生的低频混沌电路信号对电弧半径或电弧电压进行调制，得到具有双吸引子混沌现象的电弧炉模型，但该方法需要大量的电压电流实测数据进行参数辨识，工程适用性较差。文献[14]将实际的电弧炉U-I特性曲线分段线性化来模拟交流电弧炉的波动特性，但该拟合方法较为粗糙，忽略了电弧的热惯性。文献[15]基于电弧的物理特性进行了理论上的初步探讨，在考虑电弧弧柱热惯性的基础上将弧柱电阻等效为线性时变电阻，但该方法将电弧温度视作调制的倍频余弦信号，难以准确反映温度对电弧弧柱的影响。文献[16]基于电子连续性方程构建电弧的确定性模型，并考虑电弧半径、弧长对电子密度的影响，得到交流电弧炉外部特性与内部微观特性有机结合的通用模型，该模型虽在电弧微观上有一定深入，但其将温度、压强等参数视作常数，没有考虑电弧参数变化对其物理过程的影响，难以准确反映冶炼过程中电弧的时变特性与其电热物理本质。
现有研究表明，电弧的物理状态不是静止的，电弧温度与电弧电流有密切联系，其会随着电流的变化呈现典型的倍频交变特性，电弧的压强大小也会随着电流以及弧长的变化呈现相关性特征[17]，同时，电弧温度与压强的变化也会反过来影响电子密度进而反映到电弧电压、电流上[18]，即电弧的电气量与物理参数之间呈现出耦合影响[19]。上述模型主要将电弧视作非线性电气元件，便于和电弧炉电气系统联合求解。但是难以反映电弧内部粒子之间的微观动态形成机理，不能完全描述电弧的时变特征，割裂了电弧弧柱中电压、电流与电弧温度、压强等参数之间的耦合影响，与实际有一定偏离，导致构建的仿真模型未能准确反映其电能质量特性。
本文中，将电弧的电压、电流定义为电气特性，将表征电弧状态的温度、压强定义为物理参数，并针对以上问题，提出一种基于电气特性-物理参数耦合的交流电弧炉模型，揭示了电弧炉冶炼过程中的电压、电流等电气特性与电弧的温度、压强等物理参数的动态耦合关系。首先，基于电弧的电子连续性方程构建电气特性模型，考虑电弧炉冶炼过程中电气量对物理过程中电弧温度、压强等物理参数影响的机理；其次，计及电弧的磁压缩与瞬时能量平衡过程中电弧温度、压强的变化对电弧电气特性的影响，构建电气特性-物理参数耦合的电弧炉模型；进一步地，基于实际电弧炉变压器参数构建电弧温度曲线，并使用麻雀搜索算法对电弧温度进行辨识，以确定模型参数；最后，以福建某50 t、55 t交流电弧炉实测数据为例，在Matlab/Simulink软件中，验证了模型的正确性。
本文所提出的交流电弧炉通用模型由电气特性模型与物理参数模型两部分构成。电气特性模型通过电弧内部微观特性来表征电弧炉的强时变非线性，与此同时，电弧的电气量会对电弧的温度、压强等物理参数产生影响，构建物理参数模型得到冶炼过程中电弧温度、压强的累积效应反映到电弧电气量的变化特性，考虑两者的密切联系与相互影响，从而建立电弧电气特性与物理参数之间的耦合模型。
对于任何电弧等离子体，产生的电流可由来自电子的电流和来自离子的电流两个基本项组成[18]。而在电弧放电过程中，电子的迁移速度远大于离子的迁移速度。因此，在电中性条件下[20]，弧柱电导率可近似认为主要由电子密度和电子迁移率决定。
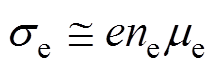（1）
式中，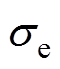
为弧柱电导率；e为电子电荷；ne为电子密度；
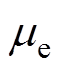为电子迁移率，现有研究表明电子迁移率在电弧燃烧时稳定分布，可近似视为常数[16, 21]。
为研究电弧放电的最基本特性，可忽略电子和离子的扩散，利用电子连续性方程求解电子密度[16]，即
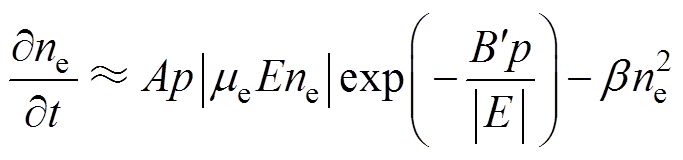（2）
式中，p为弧柱压强；E为弧柱中的电场强度；A、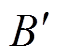
为经验常数；
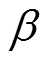为电子复合系数，在准中性区域中，假定空气由21%的氧气和79%的氮气组成，电子复合系数[18]可简化为
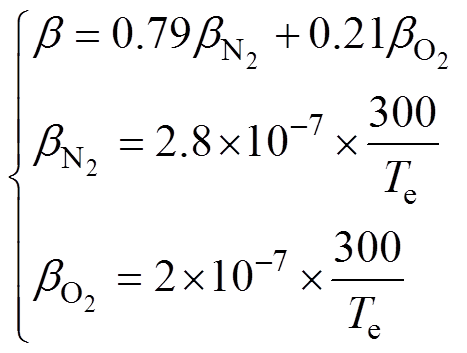（3）
式中，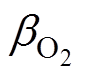
、
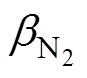分别为氧气和氮气的电子复合系数；Te为电子温度。值得注意是，在电弧环境中，是满足局部热力学平衡条件的，可认为电子温度Te与电弧温度T相等，即：Te=T [21]，则式（3）可化简为
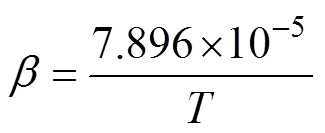（4）
根据欧姆定律的微分形式，可以得到
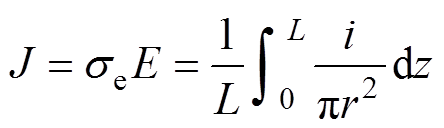（5）
式中，J为电弧弧柱的平均电流密度；L为电弧弧长；i为电弧电流；r为电弧半径，其变化规律可表示为
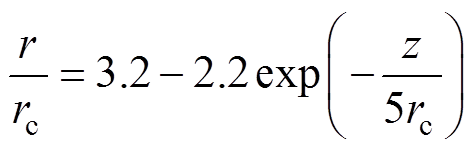（6）
式中，rc为阴极斑点半径；z为电弧的轴向坐标。
定义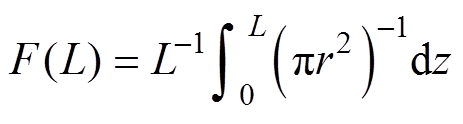
，则式（5）可表示为
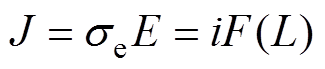（7）
对电弧弧柱中的电场强度轴向方向进行积分得到电弧电压为
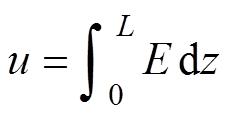（8）
联立式（1）～式（8）可得到电弧的电气特性方程为
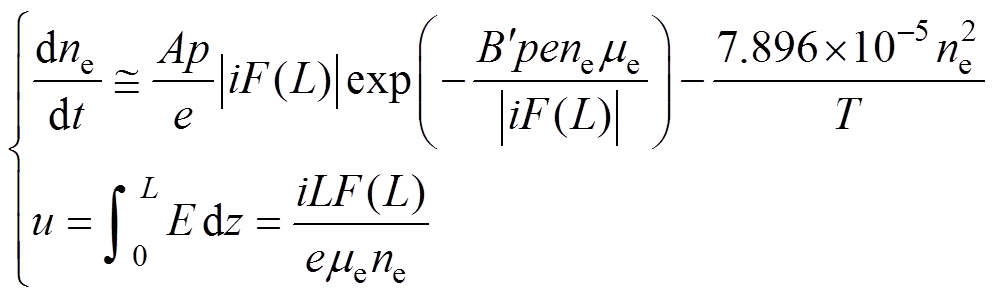（9）
式中，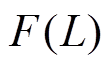
用于反映弧长的影响，可表示[28]为
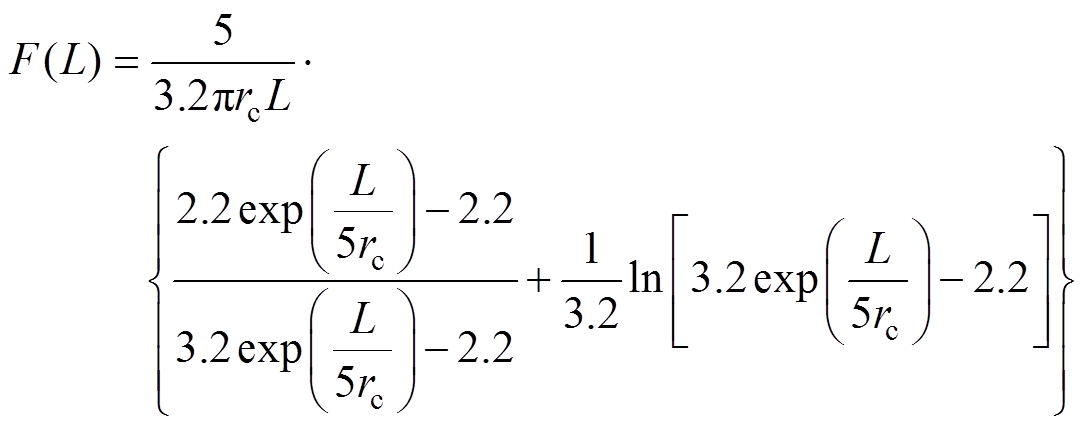（10）
现有研究表明，电弧炉的弧长在实际运行过程中会呈现出周期性、准周期性或随机性的波动[16]，可用式（11）进行模拟。
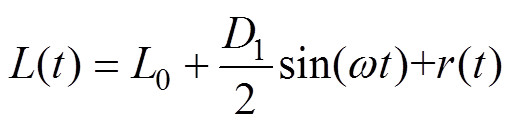（11）
式中，D1对应于弧长的最大变化值，可由电弧电压的变化范围来确定；r(t)为带通高斯白噪声，由高斯白噪声和带通滤波器得到；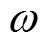
为正弦信号的激励频率，通常选用人眼对电压波动所产生的闪变最为敏感的频率，即为8.8 Hz；L0为理想弧长，其大小与电弧电压有关。具体参数确定方法详见文献[16]。
电弧现象在本质上是电物理与热物理的一个综合过程，并且在大多情况下，热物理过程起着决定性的作用[22]。基于瞬时能量平衡方程[20]可表征出交流电弧放电过程中的物理特性，该式适用于电弧弧柱的所有体积元。
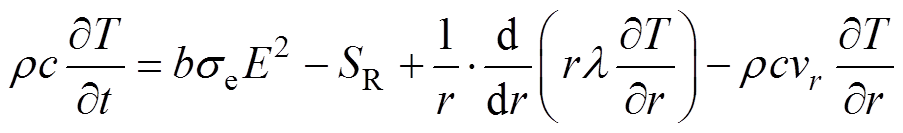（12）
式中，左边项是电弧单位体积的热容量时间变化率，右边项依次为电场引起的输入能量、辐射源项、热传导项以及径向对流引起的单位体积净能量损失；b为模型参数；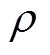
为密度，取1.293 kg/m3；c为比热容，在电弧环境中，一般取0.998 kJ/(kg·K)；SR为辐射源项；
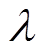为导热系数；vr为等离子体的径向速度分量。
在电弧环境中，电弧弧柱的磁场会对弧柱产生一个压缩力，导致弧柱半径收缩，从而影响电弧电阻。表明电弧属于弹性导体，其形状会受到环境压强的影响[17]。对弧柱构建力平衡方程以研究压强对电弧的影响[23]。
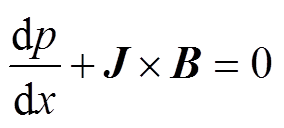（13）
式中，x为电弧弧柱的径向坐标；B为弧柱磁感应强度；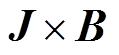
表示洛伦兹力。
依据安培环路定律，可对磁感应强度进行求 解，有
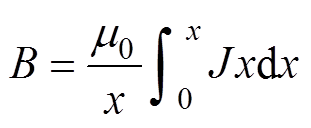（14）
式中，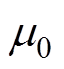
为真空磁导率。
将式（14）代入式（13），并对式（13）两边从弧柱边缘向弧柱内部积分，可得到磁压缩对弧柱径向距离x处的压强为
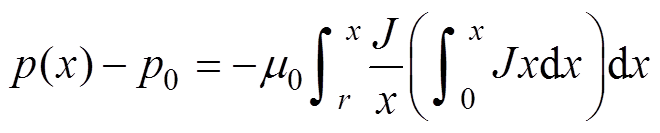（15）
式中，p(x)为弧柱内径向距离x处的压强；p0为弧柱边缘处压强。
将式（7）的平均电流密度代入式（15），整理得到磁压缩附加压强与电弧电流、弧长的关系为
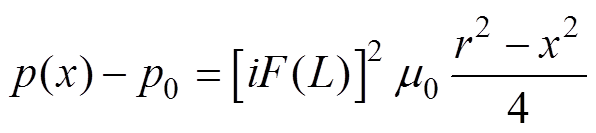（16）
当径向距离为零时，即可得到弧轴处的附加压强为
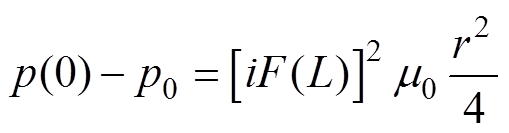（17）
电弧稳定燃烧时，电弧弧柱的压强较为稳定均匀，可近似取弧柱压强为弧轴处压强，即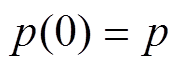
。
对于大电流电弧，对流引起的能量损失占电弧能量平衡的5%左右，其散失能量的90%是通过辐射散热完成，这部分能量对电弧炉作业具有支配作用[24-26]。因此，本文关注最主要的辐射散热为
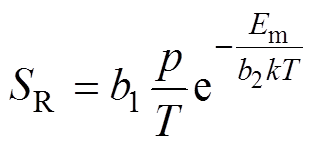（18）
式中，b1、b2为待确定参数，其大小与电弧炉的容量有关；k为玻耳兹曼常数；Em为受激原子的高能级平均值。
联立式（7）、式（12）～式（18），得到交流电弧的物理参数方程为
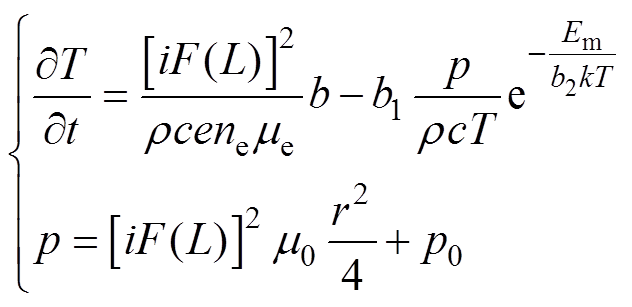（19）
电子连续性方程体现的电场特性与欧姆定律组成电弧的电气特性模型，瞬时能量平衡方程与磁场产生的磁压缩力平衡方程构成电弧的物理参数模型，其中的能量转移会非常强烈地影响电场和磁场，而电磁场又通过电弧电导进行加热，作为能量源反过来影响温度场[19]。
电弧的电气特性模型与物理参数模型较为完整地反映了等离子体中温度场、电场以及磁场之间重要耦合效应，正是这些耦合效应导致了电弧的形成。图1给出了电气特性模型与物理参数模型之间的耦合关系。
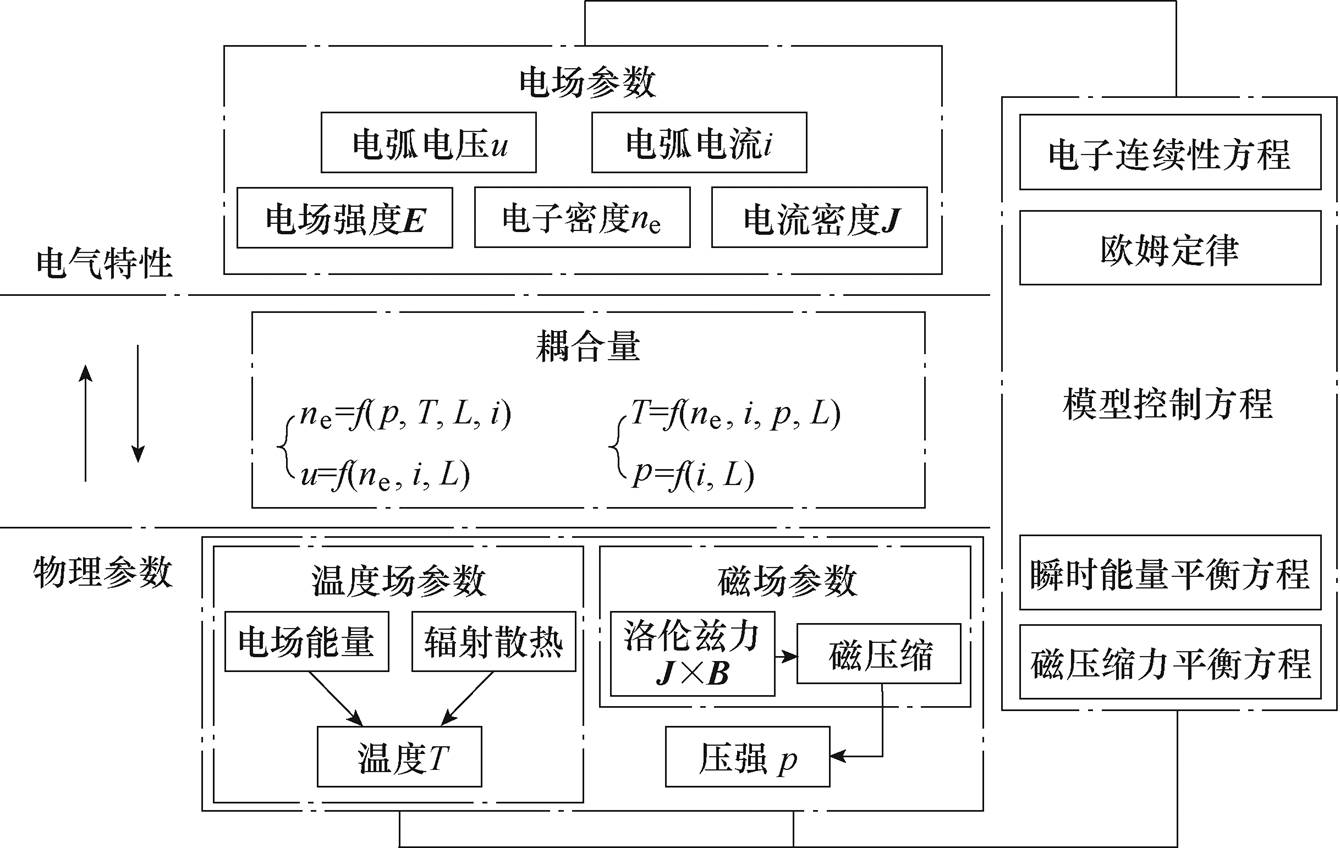
图1 电气特性-物理参数耦合关系
Fig.1 Diagram of the coupling between physical and electrical characteristic models
模型建立后，为了获得数值解，必须给定边界条件。现有研究表明，电弧在正常工作状态下呈现为典型的“长钟型（钟罩型）”[27]，如图2所示。因此本文模型的边界条件建立在以下计算区域。图2中，ABCDEF为等离子体电弧在空气中的导电区域，其中AB为阴极斑区域；BE为电弧；DEF为阳极表面。为了简化计算，认为正常工作状态下电弧是稳定的，维持为长钟型，且无偏弧情况。
由此可得到计算区域的边界条件见表1[28]。
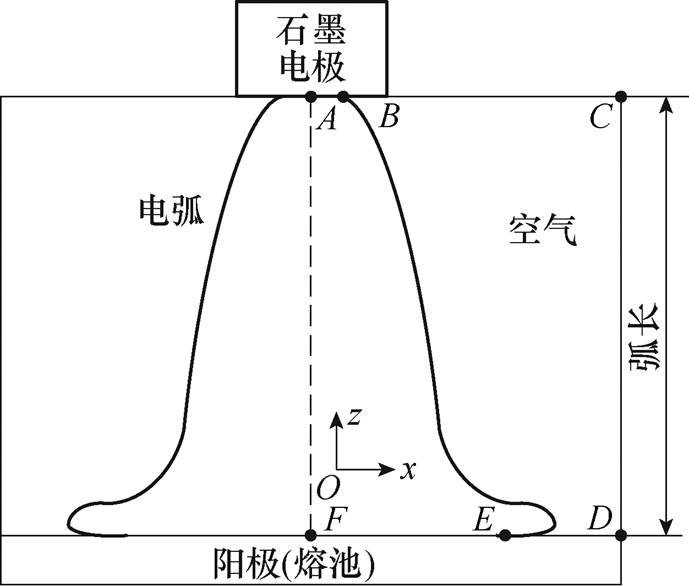
图2 电弧等离子体计算区域
Fig.2 Arc plasma calculation area
表1 电弧等离子体的边界条件
Tab.1 Boundary conditions of arc plasma
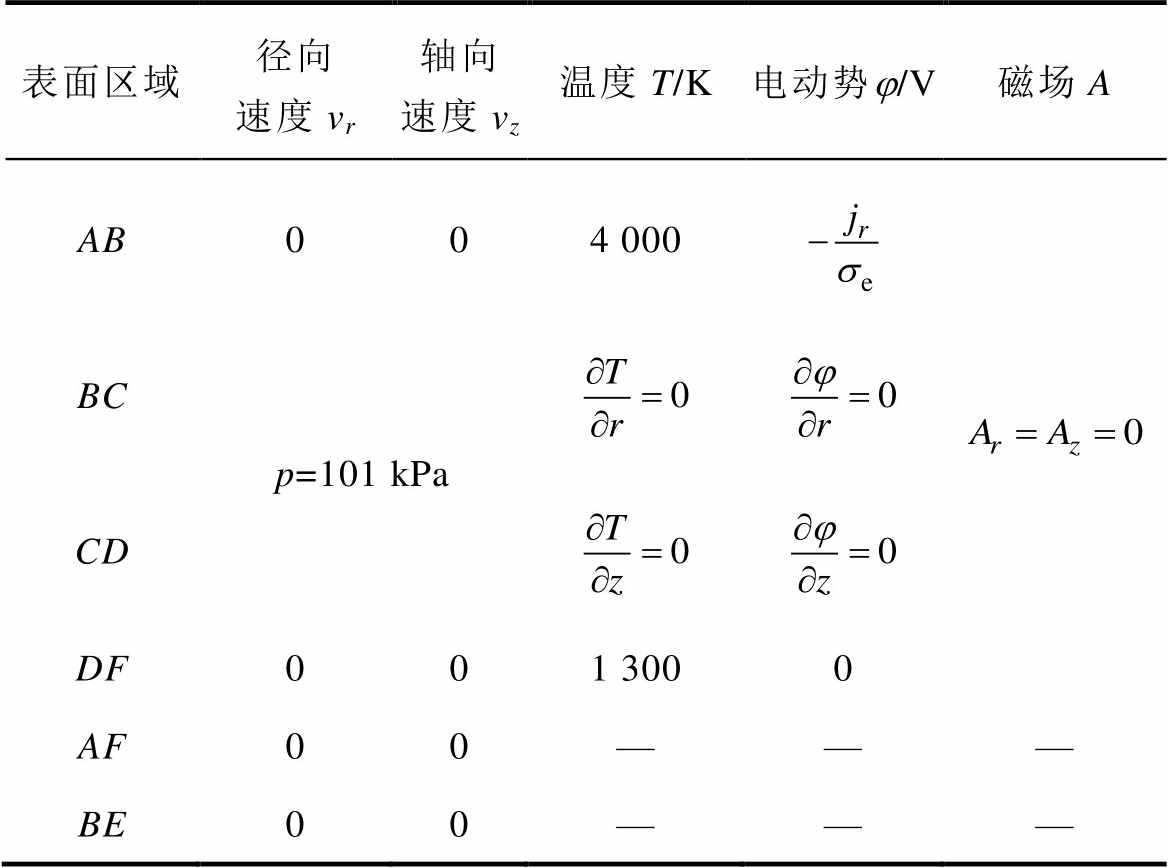
表面区域径向速度vr轴向速度vz温度T/K电动势j/V磁场A AB004 000 BCp=101 kPa CD DF001 3000 AF00——— BE00———
本文所提出的电气特性-物理参数耦合模型以文献[16]的电子连续性方程为基础构建电气特性模型，以弧长变化模型来表征电弧的不确定性，以确定性模型表征电弧的非线性，如图3所示；以电弧的磁压缩力平衡方程和瞬时能量平衡方程构建物理参数模型，以此反映温度、压强对电弧确定性模型的影响，如图4所示。
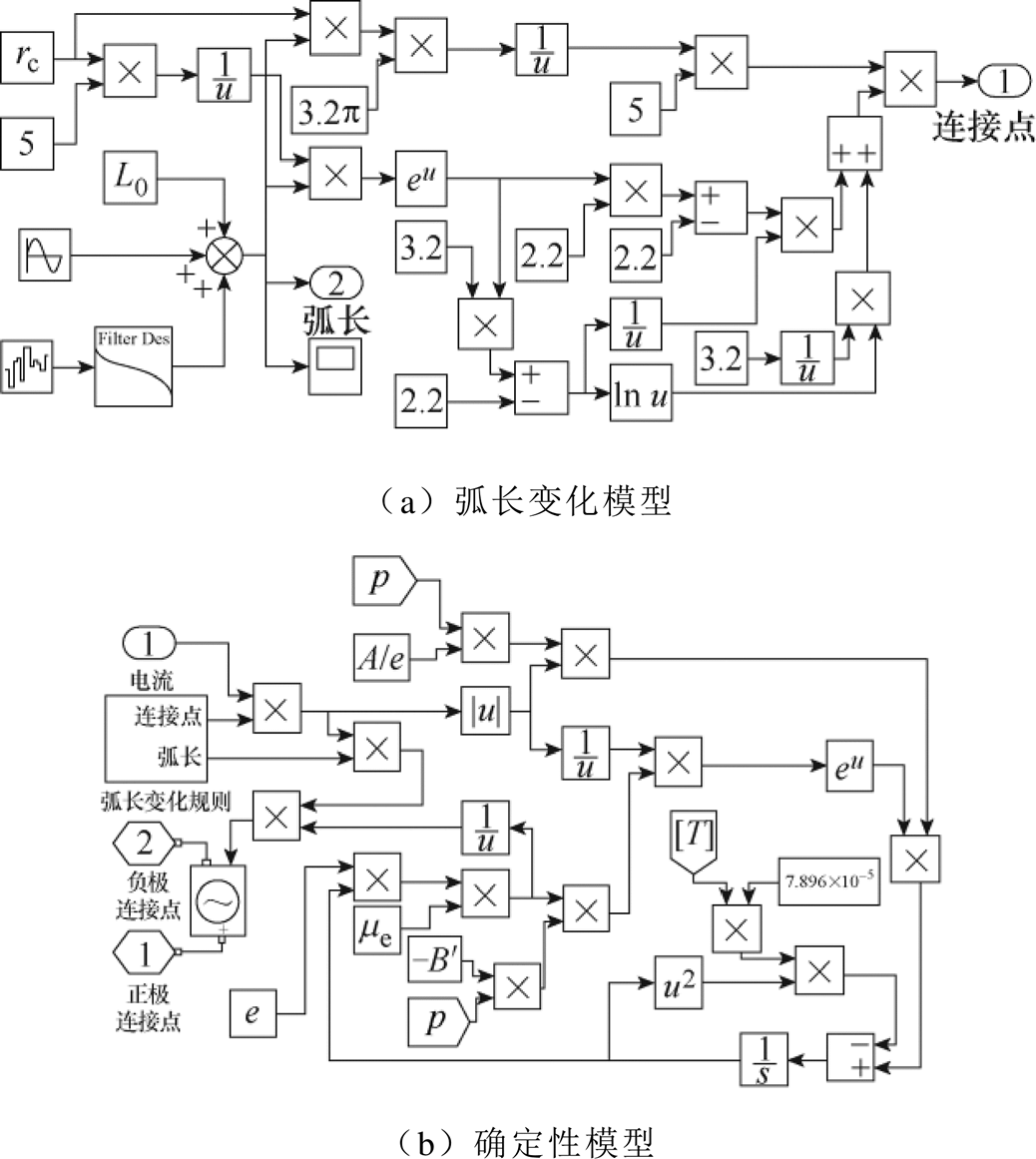
图3 电气特性模型
Fig.3 Electrical characteristic model
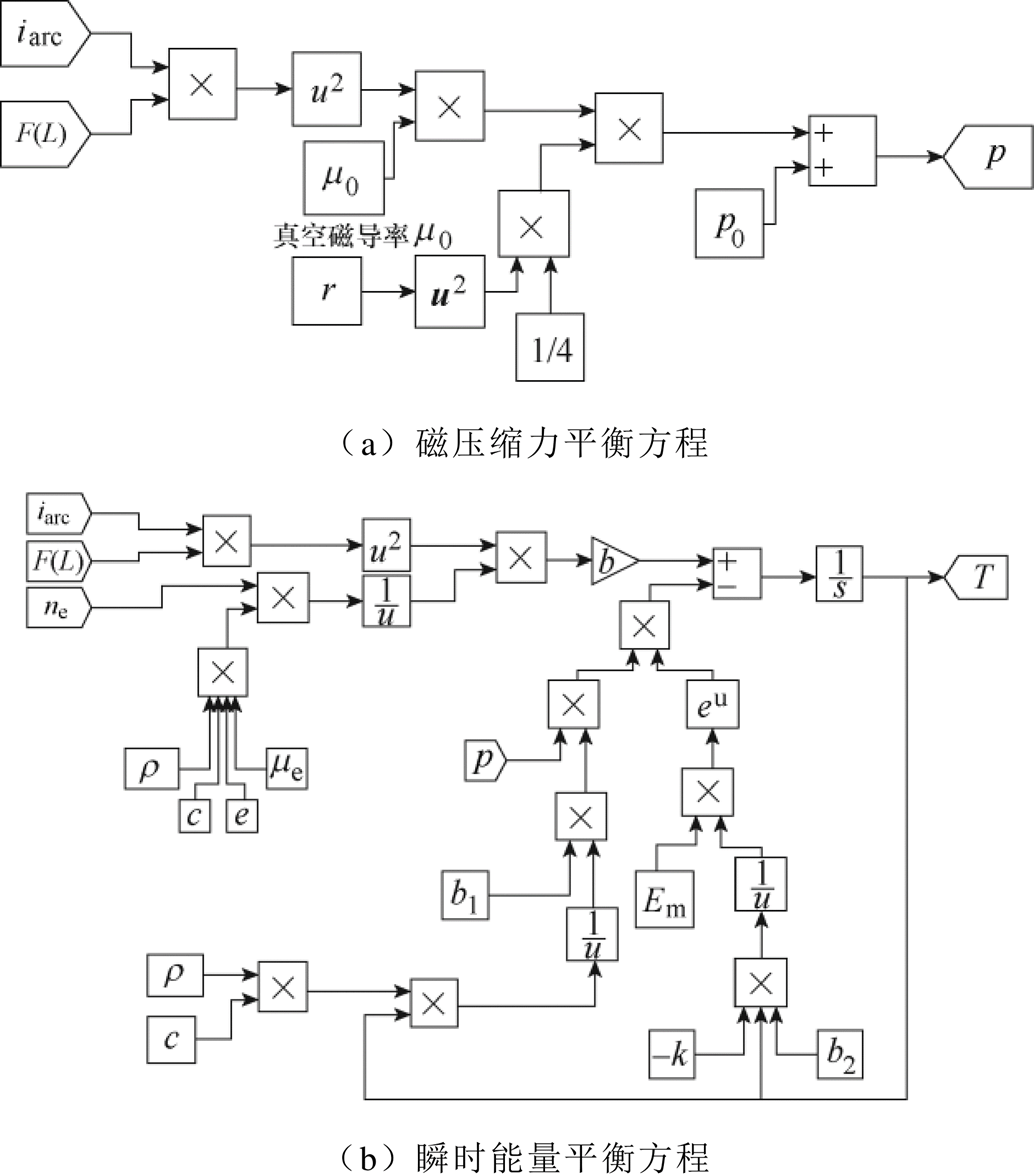
图4 物理参数模型
Fig.4 Physical parameter model
耦合模型中包含电子密度、电弧电压、电弧电流、温度、弧长和反映热惯性影响等因素的多个参数，若想准确确定这些参数，需要大量的测试数据，由于电弧炉工作的特殊性和已有测试手段的局限性，难以准确获取模型的所有参数。因此，只能从工程应用的角度对模型中的各个参数进行近似估算及辨识，以确定电弧炉模型的各个参数。
本文使用的电气特性模型参数可参照文献[16]进行估算，而在物理参数模型中的温度场参数b、b1和b2还未确定。针对待确定的参数，本文使用麻雀搜索算法[29]（Sparrow Search Algorithm, SSA）对电弧温度进行参数辨识。麻雀搜索算法（SSA）是一种新的元启发式算法，相较于目前的灰狼优化算法、粒子群算法、引力搜索算法等[30-34]其他算法，具有更强的逃离局部极值能力和全局搜索能力。它模拟了麻雀群体在抗捕食的过程中，为获取食物个体位置不断逼近食物的过程。发现者位置x的更新方式可表示为
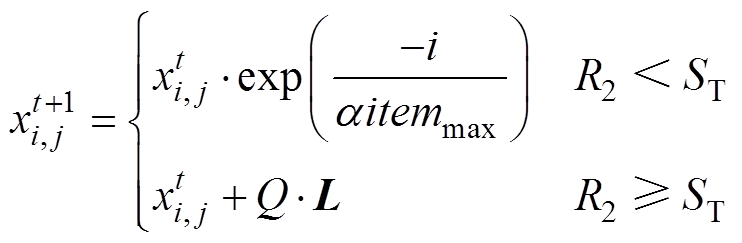（20）
式中，t为当前迭代数；i=1, 2, 3,…, P，P为发现者的数量；j=1, 2, 3,…, d，d为待优化问题变量的维数；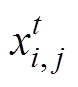
为第i个个体在第t次迭代中第j维的位置信息；itemmax为最大的迭代次数，为一常数；
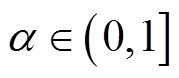是一个随机数；R2为一个在[0, 1]上的随机数，用于表示发现者麻雀对危险的警觉程度；ST∈[0.5, 1]表示安全值；Q为满足正态分布的随机数；L为一个元素均为1的d维行向量。
对于麻雀中的加入者，其位置更新方式为
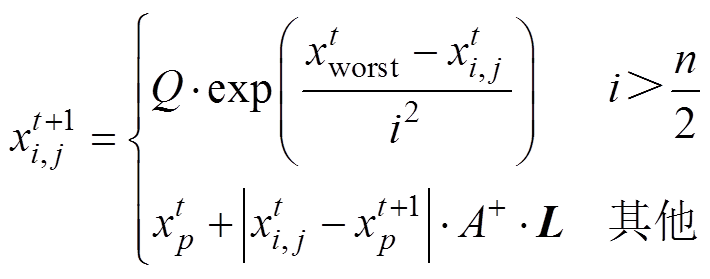（21）
式中，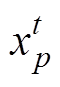
为第t次迭代中发现者所占据的最优位置，
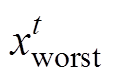为第t次迭代中全局最差的位置；A+=AT(AAT)-1，其中A为元素随机赋值为1或-1的d维行向量。
处于群体边缘处的麻雀作为警戒者，其位置更新方式为
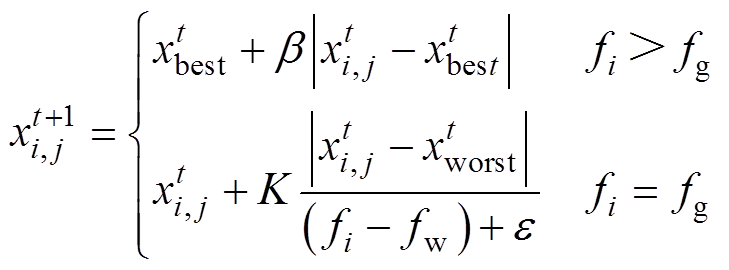（22）
式中，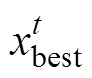
为第t次迭代中全局的最优位置；i∈[P+1, n]，n为麻雀的总数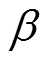；为服从标准正态分布的随机数，用于控制步长；K∈[-1, 1]为一个随机数；
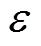为用于防止分母为零的最小常数；fi为当前麻雀个体的适应度值，fg和fw分别为当前的最优和最差的适应度值。
现有文献证明，在不同大小的电流下，弧柱温度的变化曲线是类似的[26]。因此本文基于Bowman在电流为8 A、15 A、25 A时对碳电极交流电弧温度测量得到的若干结果[32]，得到真实情况下的电弧温度曲线特征，结合实际电弧炉变压器二次侧的额定电流与文献[28]中不同电弧电流大小下电弧最大温度的计算结果，构建符合电弧炉实际工况下的电弧温度曲线，并使用SSA算法对所构建的电弧温度曲线进行辨识，以使得模型的电弧温度仿真计算结果与实际情况相近。本文使用文献[15]所提出的余弦函数来近似设定需要逼近的电弧温度曲线。
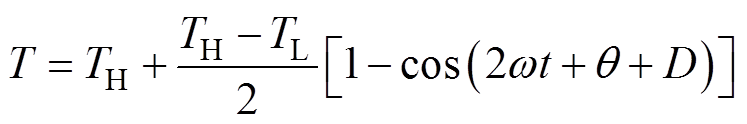（23）
式中，TL为弧柱温度的最小值，其取值范围在7 000～8 000 K；TH为弧柱温度的最大值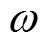；为外加激励的角频率；
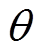为电弧电流过零点时滞后于外加激励的相角；D为反映弧柱热惯性的影响，由于D的存在使得电弧温度的最大值不出现在电弧电流的最大值处，而是要滞后一个角度，其取值范围在-10°～-30°。
电弧电流与最大电弧温度TH之间的对应关系见表2[28]，基于麻雀算法的参数辨识流程如图5所示。
表2 最大电弧温度与电流的对应关系
Tab.2 The relationship between maximum arc temperature and current
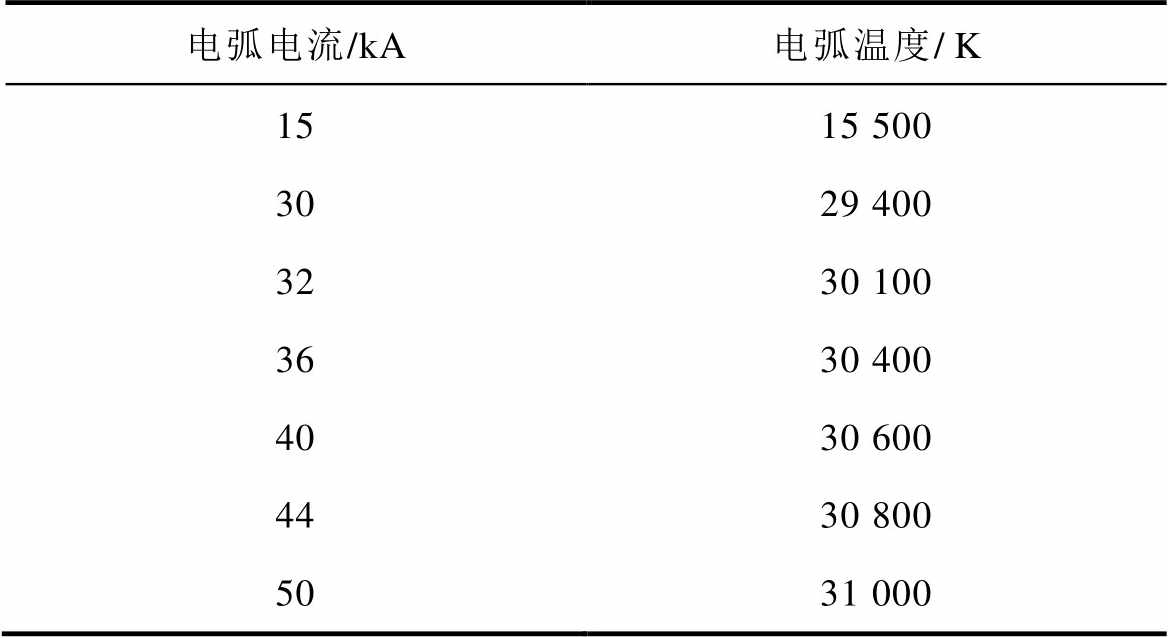
电弧电流/kA电弧温度/K 1515 500 3029 400 3230 100 3630 400 4030 600 4430 800 5031 000
本文以福建的50 t和55 t炼钢电弧炉实测数据进行算例验证，以验证模型的正确性与适用性。鉴于电弧炉仅在熔化期具有严重的电能质量问题且对电弧炉设备的考核也多在熔化期进行，因此本文算例重点针对电弧炉熔化期进行验证。且出于设备稳定生产要求以及人员安全性考虑，一般难以对炉变低压进行测试，因此本文使用电弧炉变压器高压侧数据并基于变压器谐波传递特性将其折算至低压侧[36-37]。
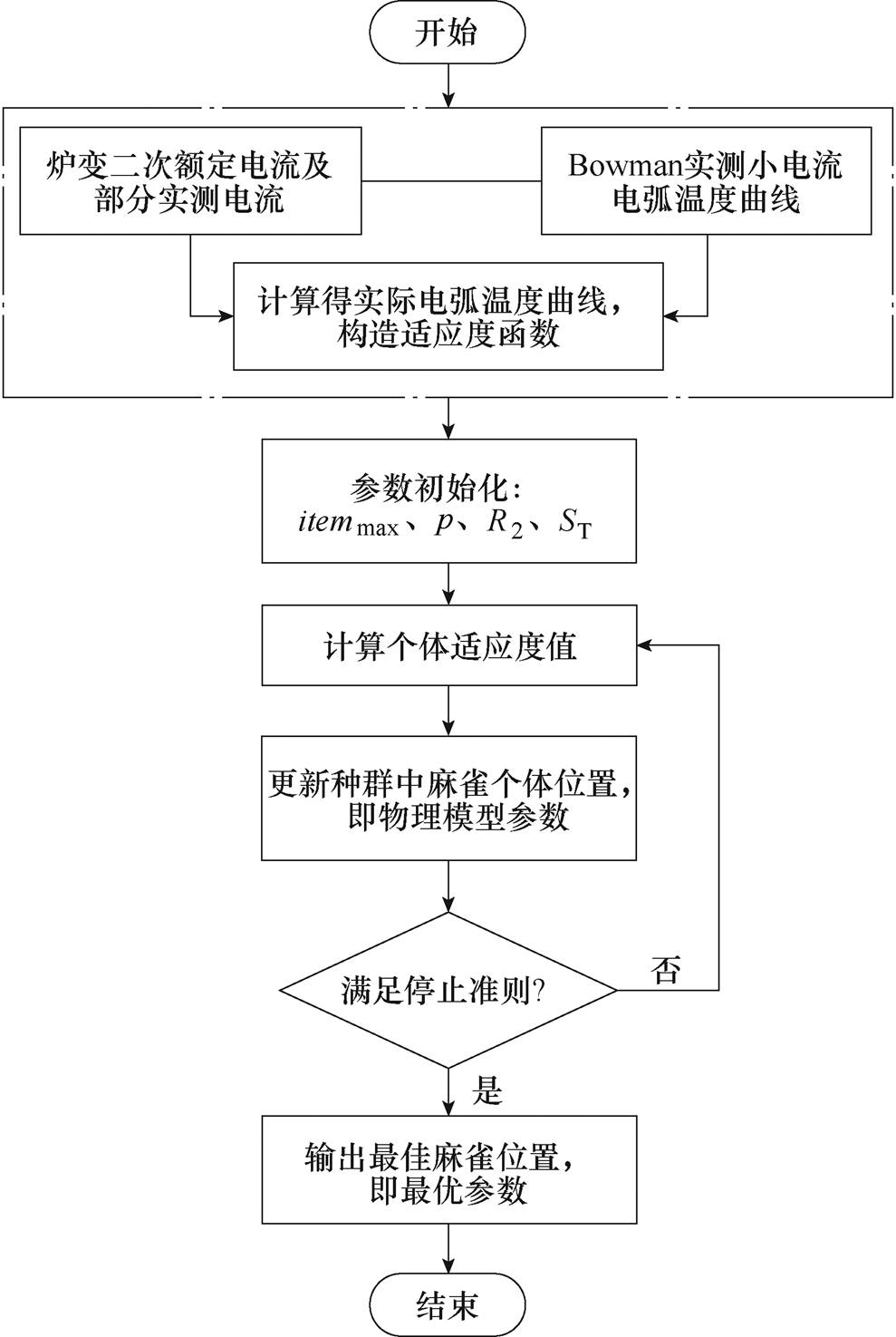
图5 基于麻雀算法的电弧温度辨识流程
Fig.5 The flow chart of arc temperature identification based on the sparrow algorithm
本文以福建某50 t炼钢交流电弧炉负荷为例，图6为其供电系统的等效电路。钢厂的主变压器T1将110 kV高压电网电压转换为35 kV；T2为电弧炉变压器，其设备型号为HSSPZ-22000/35；rd为短网阻抗，rd=0.4 mW；Xd为短网的电抗（自感和互感之和），Xd=3 mW。电弧炉变压器的参数见表3。
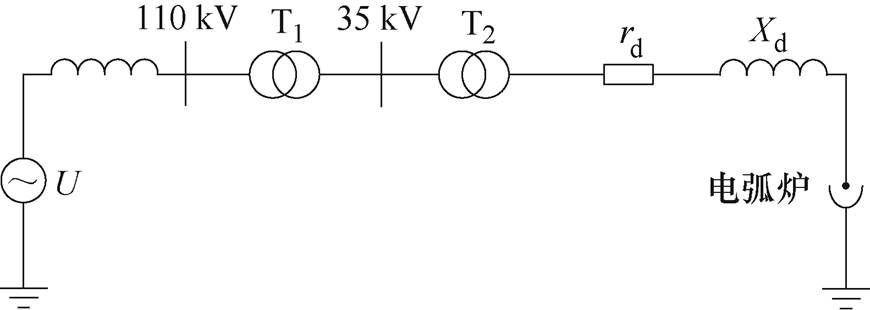
图6 50 t交流电弧炉供电系统等效电路
Fig.6 Equivalent circuit of 50 t AC electric arc furnace power supply system
表3 HSSPZ-22000/35电弧炉变压器参数
Tab.3 Arc furnace transformer parameters of HSSPZ-22000/35
参 数数 值 负载损耗/kW189.7 空载损耗/kW20.4 阻抗电压(%)8.7 空载电流(%)0.398 炉变二次额定电流/kA35.88
依据图6所示的等效电路，在Matlab/Simulink软件中进行仿真。其中，电弧炉数学模型中电气特性模型的仿真参数可通过文献[16]的参数估算方法进行确定，取值为A=1.105 9×1011；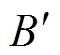
=0.079 9；rc= 0.016 5 m；L0=0.20 m。物理参数模型使用SSA算法对电弧温度进行辨识，辨识曲线如图7所示，所得参数为b=3.572 7×10-5；b1=2.046 9×104；b2= 71.018 1，构建的50 t交流电弧炉的仿真模型如图8所示。
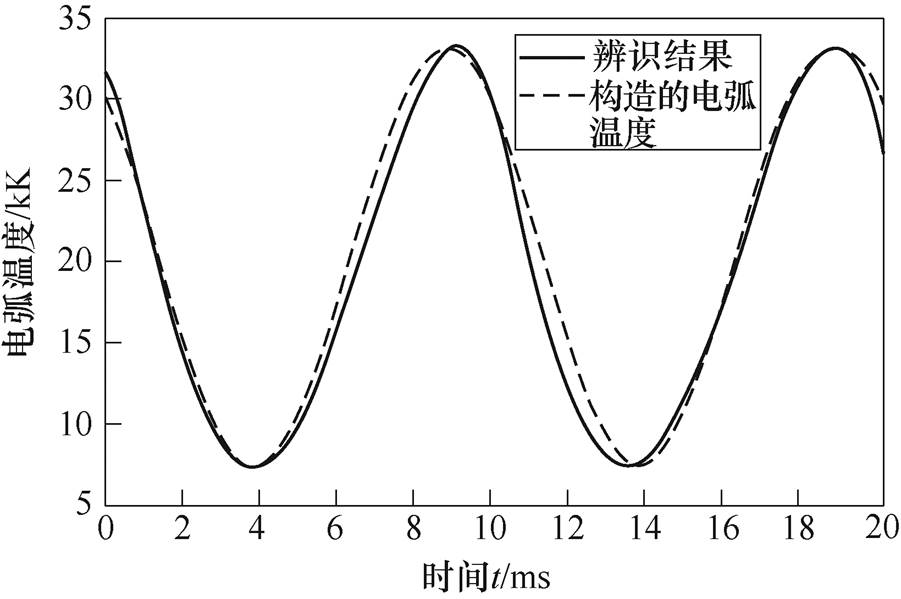
图7 基于SSA的电弧温度辨识曲线
Fig.7 Arc temperature identification curve based on SSA
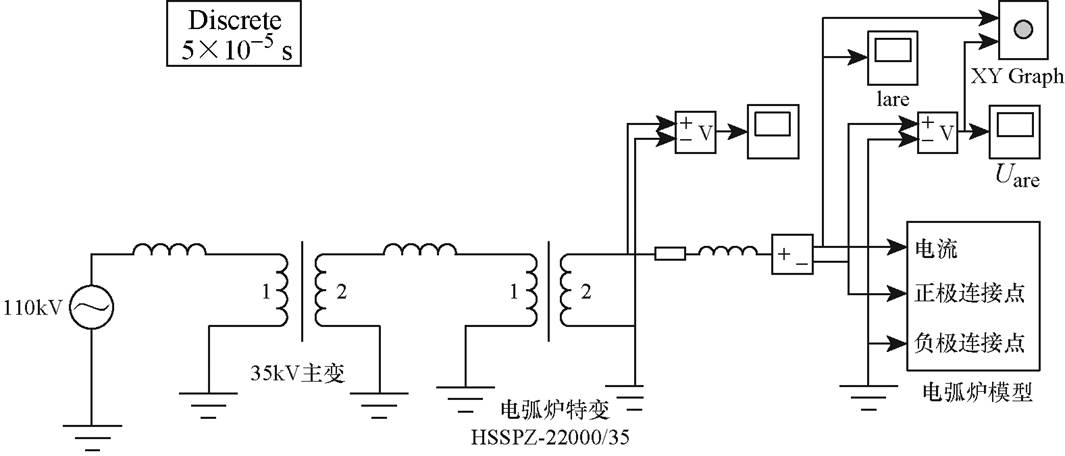
图8 50 t交流电弧炉仿真电路
Fig.8 Simulation circuit of 50 t AC electric arc furnace
在电弧炉实际运行过程中，由于电弧的随机性，电弧炉的每个交流电周期的伏安特性曲线并不一致，图9为仿真得到的50 t炼钢交流电弧炉的U-I特性曲线。从图9中可以看出，考虑了电弧电流、弧长变化以及物理参数的耦合影响后，所建立的模型能够反映电弧电流和电弧电压之间呈现的高度强时变非线性特征，与电弧炉实际冶炼过程中的特性基本一致。
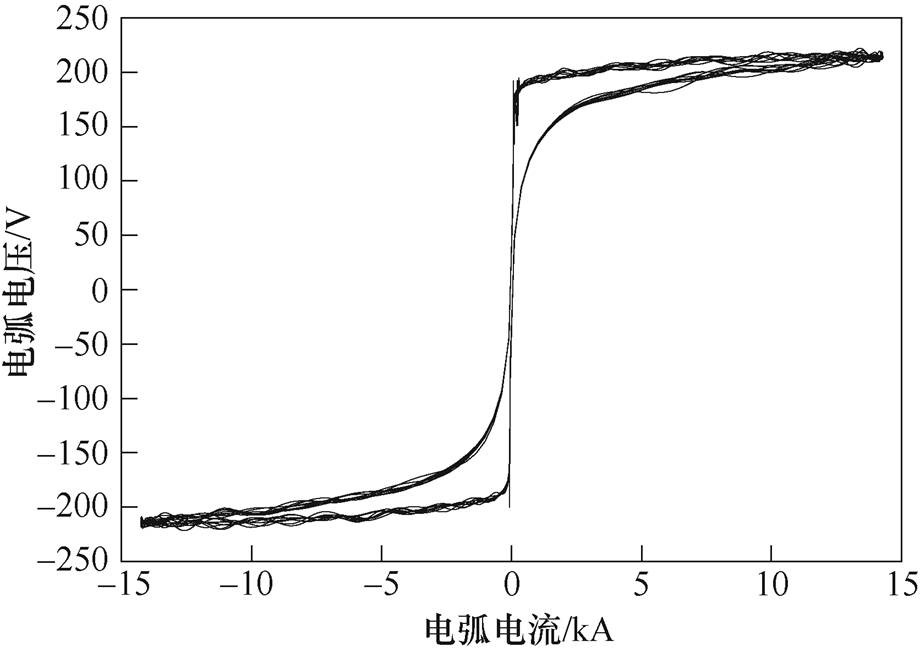
图9 50 t交流电弧炉U-I特性曲线
Fig.9 U-I characteristic of 50 t electric arc furnace
图10为仿真所得的50 t交流电弧炉的电弧电压和电弧电流。由图10可以看出，由于电弧温度的交变特性以及压强的变化影响，电弧电流和电弧电压呈现明显的畸变特征，并且电弧电压还存在明显的随机波动。综上所述，本文所建立的电弧炉模型能够更切合实际地体现电弧炉冶炼过程中的高度非线性和随机特性。
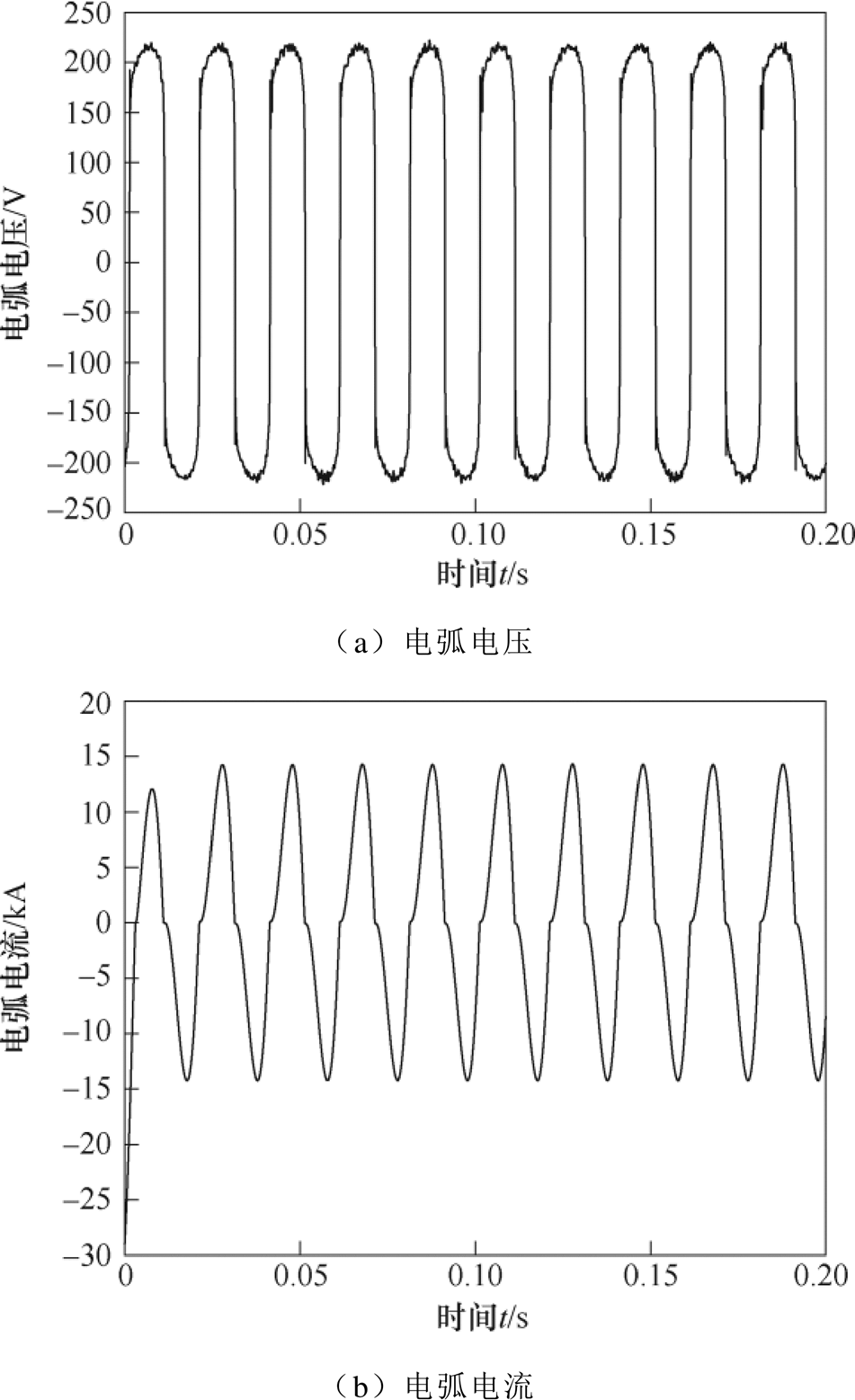
图10 50 t交流电弧炉仿真结果
Fig.10 Simulation results of 50 t AC electric arc furnace
1）谐波含量的对比分析
50 t交流电弧炉的实际电弧电压、电流数据通过故障录波器（采样频率12.6 kHz）采集得到。并在此基础上，利用Matlab/Simulink软件分别搭建文献[16]模型和本文方法模型，并使用软件的快速傅里叶变换（Fast Fourier Transform, FFT）分析功能对电弧炉电弧电压及电弧电流的各次谐波含量进行计算，表4及表5给出了两种方法的仿真谐波含量与实测的对比结果。
表4 50 t交流电弧炉的谐波电压分析结果
Tab.4 Harmonic voltage of 50 t AC electric arc furnace
谐波次数方法畸变率(%) 仿真电压实测电压绝对误差 3文献[16]28.3027.890.41 本文方法27.680.21 5文献[16]15.7114.521.19 本文方法14.700.18 7文献[16]9.779.760.01 本文方法9.840.08 9文献[16]7.416.261.15 本文方法6.810.55 THD文献[16]36.4636.330.13 本文方法36.180.15
表5 50 t交流电弧炉的谐波电流分析结果
Tab.5 Harmonics current of 50 t AC electric arc furnace
谐波次数方法畸变率(%) 仿真电流实测电流绝对误差 3文献[16]17.1417.080.06 本文方法17.070.01 5文献[16]5.725.740.02 本文方法5.210.53 7文献[16]2.642.880.24 本文方法2.800.08 9文献[16]1.491.370.12 本文方法1.460.09 THD文献[16]18.4418.280.16 本文方法18.110.17
根据两种方法的仿真结果与实测的对比，从表4和表5可知，本文所提出的交流电弧炉模型具有更高的精度。各次的谐波电压畸变率误差值不超过0.55%，谐波电压总畸变率误差值仅为0.15%。各次谐波电流畸变率的仿真精度在整体上更具优势，谐波电流总畸变率误差值不超过0.17%。
2）电压波动对比及分析
根据GB/T 12326-2008《电能质量 电压波动和闪变》，电压波动定义为电压方均根曲线上相邻两个极值电压之差。根据以上定义，电压波动的计算公式为
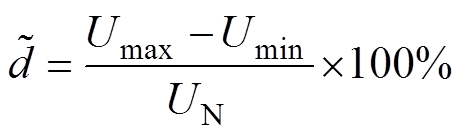（24）
根据式（24）将仿真模型中电压波动状况与实测测量值进行对比，见表6。
表6 50 t交流电弧炉电压波动状况
Tab.6 Voltage fluctuation of 50 t AC electric arc furnace
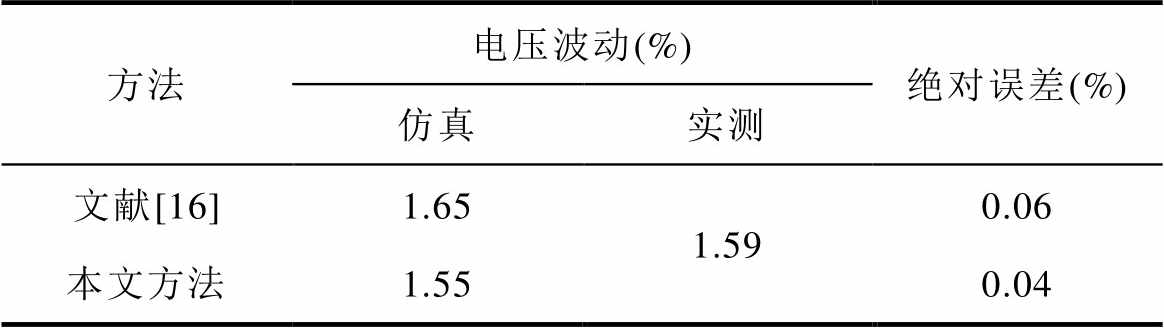
方法电压波动(%)绝对误差(%) 仿真实测 文献[16]1.651.590.06 本文方法1.550.04
由表6可知，本文方法与文献[16]方法对电压波动的仿真精度基本一致，但本文所建立的模型对谐波和电压波动的仿真效果上误差均较小。
图11为电弧电流及电弧温度的仿真结果，可以看出：交流电弧的温度随电流的变化而变化，呈现交变特性，且为二倍频的关系。由于电弧的热惯性，当电弧电流达到最大值Imax时，电弧温度滞后一定时间才达到最大值Tmax。图12为电弧压强的仿真结果，可以看出：电弧弧柱的压强并不是一直处于一个大气压下，而是会在1～1.7个大气压范围内波动。
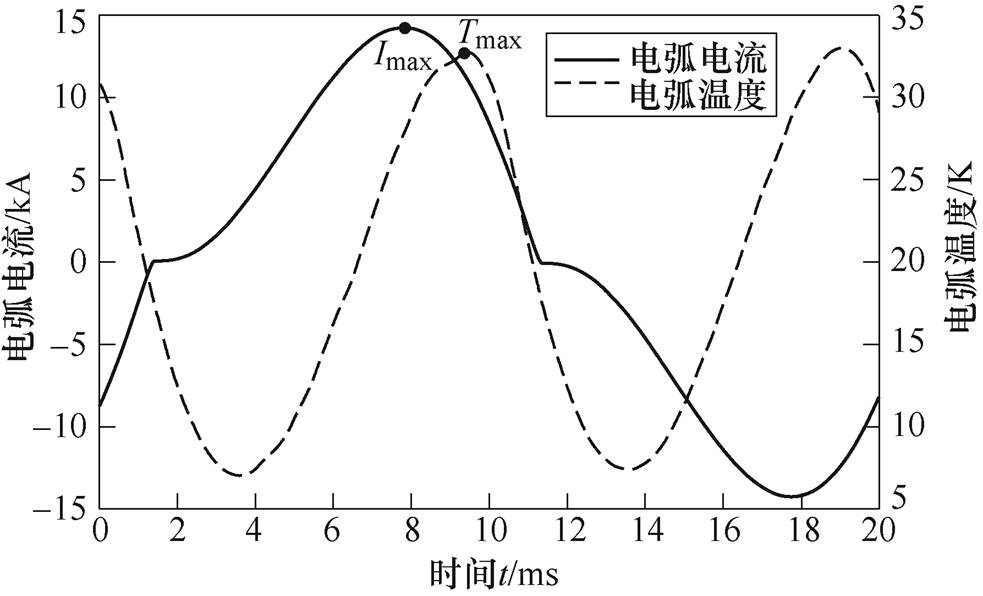
图11 电弧电流及电弧温度仿真结果
Fig.11 Simulation results of arc current and arc temperature
为进一步验证模型在不同型号电弧炉的适用性，本文使用福建某五金铸造的55 t炼钢交流电弧炉为例进行验证。图13为该负荷的供电方式，电弧炉变压器型号为HSSPZ-38000/35，rd=0.4 mW，Xd= 3 mW，电弧炉变压器的参数见表7。鉴于该负荷加装了静止无功补偿器（Static Var Generator, SVG）治理装置，在此仅验证谐波电流的仿真效果。
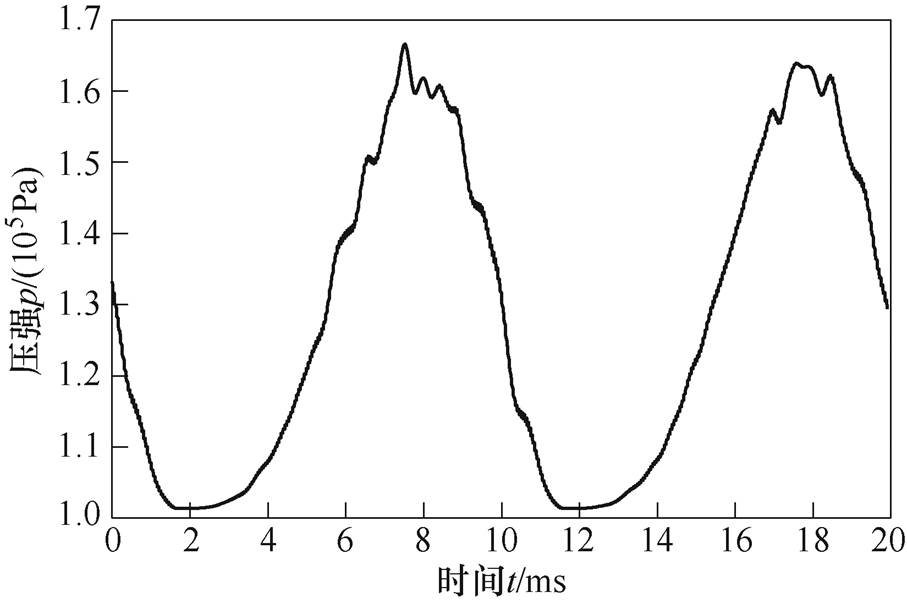
图12 电弧压强变化曲线仿真结果
Fig.12 Simulation results of arc pressure variation curve
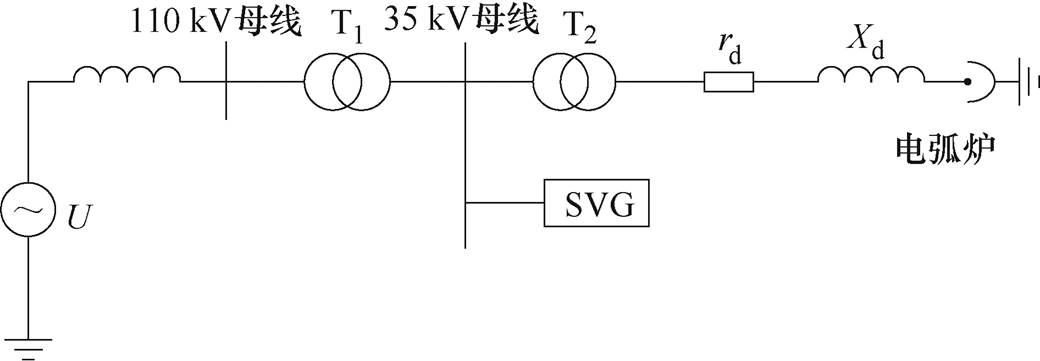
图13 55 t交流电弧炉供电示意图
Fig.13 Power supply diagram of 55 t AC arc furnace
表7 HSSPZ-38000/35电弧炉变压器参数
Tab.7 Arc furnace transformer parameters of HSSPZ-38000/35
参 数数 值 负载损耗/kW280 空载损耗/kW27 阻抗电压(%)8.10 空载电流(%)0.24 炉变二次额定电流/kA40
构建的交流电弧炉仿真模型如图14所示。文献[16]模型使用的参数为：A=5.562 5×1010；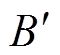
= 0.047 8；rc=0.015 7 m；L0=0.647 5 m；
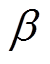=1.847 9× 10-9。在A、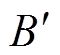、rc、L0确定的基础上使用本文方法构建仿真模型，b=9.891 6×10-4；b1=5.042 8×105；b2=117.919 8。
仿真所得55 t交流电弧炉的谐波电流曲线如图15所示。其中，实际电弧电流通过德维创电能质量分析仪（采样频率为20 kHz）采集得到。根据文献[16]方法和本文方法构建55 t交流电弧炉模型，分别对实测和仿真的谐波电流各次含有率及总畸变率进行计算，对比结果见表8。
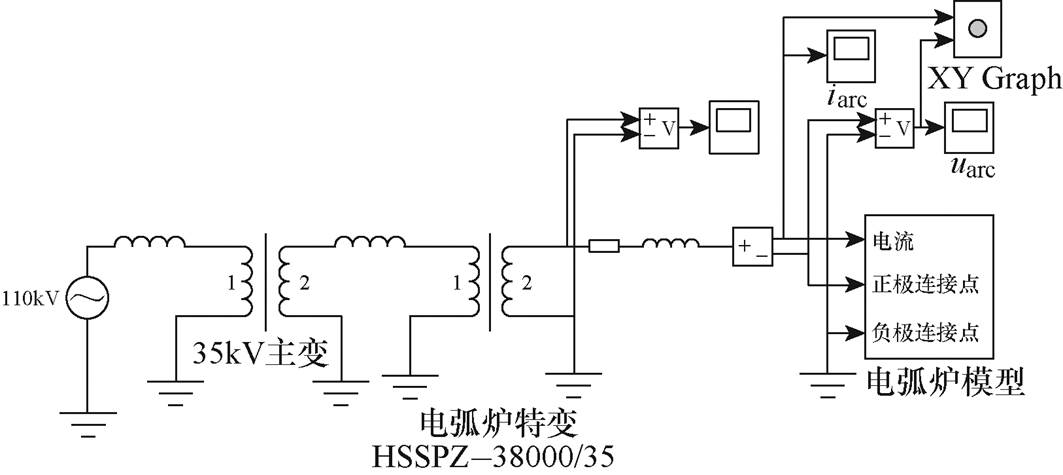
图14 55 t炼钢交流电弧炉仿真电路
Fig.14 Simulation circuit of 55 t AC electric arc furnace
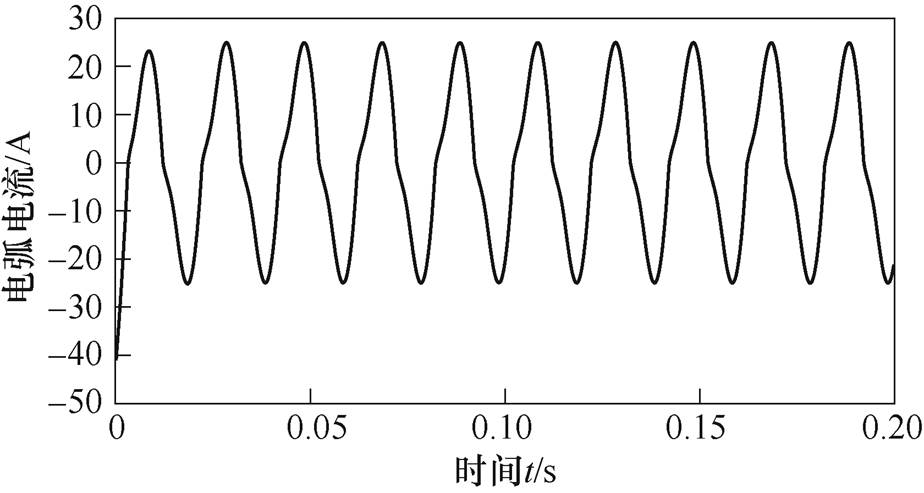
图15 55 t交流电弧炉电弧电流仿真结果
Fig.15 Simulation results of arc current of 55 t AC arc furnace
表8 55 t交流电弧炉的电流谐波状况
Tab.8 Current harmonics of 55 t AC electric arc furnace
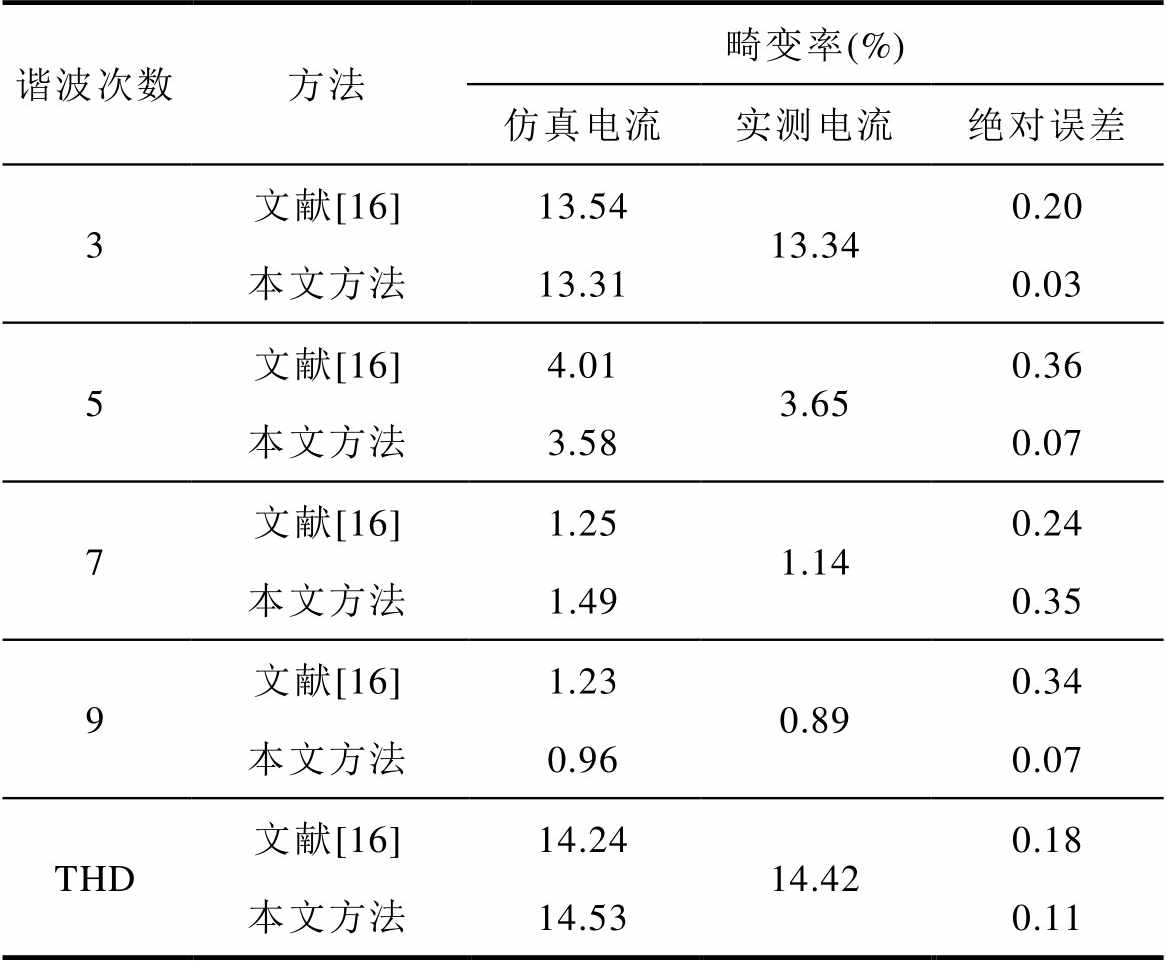
谐波次数方法畸变率(%) 仿真电流实测电流绝对误差 3文献[16]13.5413.340.20 本文方法13.310.03 5文献[16]4.013.650.36 本文方法3.580.07 7文献[16]1.251.140.24 本文方法1.490.35 9文献[16]1.230.890.34 本文方法0.960.07 THD文献[16]14.2414.420.18 本文方法14.530.11
根据表8结果可知，本文构建的模型可适应不同型号容量的电弧炉仿真，并且使用本文方法在仿真精度上具有更小的误差。
本文提出一种基于电弧的电气特性与物理参数耦合的交流电弧炉模型，并通过50 t及55 t炼钢交流电弧炉实测数据进行验证，得到以下结论：
1）揭示了电弧微观特性下压强、电弧温度等物理参数与电压、电流等电气特性的耦合机理，充分考虑了电弧的热惯性，在此基础上构建的电弧炉模型，更贴近交流电弧炉实际运行过程中的特征，对电弧炉的谐波电压、电流以及电压波动等电能质量特性的仿真精度有更进一步的提高，且能应用于不同型号电弧炉的仿真研究，具有较好的适用性。
2）本文方法在确定模型时仅需炉变低压侧额定电流参数以及炉变高压侧数周波录波电流，即可确定模型的全部参数，便于从工程角度确定电弧温度，具有较强的工程实用性和可移植性。
参考文献
[1] 朱荣, 魏光升, 张洪金. 近零碳排电弧炉炼钢工艺技术研究及展望[J]. 钢铁, 2022, 57(10): 1-9.
Zhu Rong, Wei Guangsheng, Zhang Hongjin. Research and prospect of EAF steelmaking with near-zero carbon emissions[J]. Iron and Steel, 2022, 57(10): 1-9.
[2] Collantes Bellido R, Gomez T, Identification and modelling of a three phase arc furnace for voltage disturbance simulation[J].IEEE Transactions on Power Delivery, 1997, 12(4): 1812-1817.
[3] 林海雪. 电弧炉的有功功率冲击对发电机组的影响[J]. 中国电机工程学报, 2014, 34(增刊1): 232-238.
Lin Haixue. Influence of active power impact caused by EAF on the generating sets[J]. Proceedings of the CSEE, 2014, 34(S1): 232-238.
[4] 林才华, 张逸, 黄道姗, 等. 低频间谐波检测分析与治理技术研究综述[J]. 供用电, 2019, 36(9): 59-65.
Lin Caihua, Zhang Yi, Huang Daoshang, et al. A summary of research on low frequency inter-harmonic detection analysis and governance technology[J]. Distribution and Utilization, 2019, 36(9): 59-65.
[5] 王晶, 束洪春, 林敏, 等. 用于动态电能质量分析的交流电弧炉的建模与仿真[J]. 电工技术学报, 2003, 18(3): 53-58.
Wang Jing, Shu Hongchun, Lin Ming, et al. Modeling and simulation of AC arc furnace for dynamic power quality studies[J]. Transactions of China Electro- technical Society, 2003, 18(3): 53-58.
[6] 王育飞, 潘艳霞, 姜建国. 基于MATLAB的交流电弧炉随机模型与仿真[J]. 高电压技术, 2008, 34(5): 973-977.
Wang Yufei, Pan Yanxia, Jiang Jianguo. Stochastic model of AC electric arc furnace based on MATLAB[J]. High Voltage Engineering, 2008, 34(5): 973-977.
[7] 王琰, 毛志忠, 李妍, 等. 用于电压波动研究的交流电弧炉电弧模型[J]. 电网技术, 2010, 34(1): 36-40.
Wang Yan, Mao Zhizhong, Li Yan, et al. An electric arc model of AC electric arc furnace for research on voltage fluctuation[J]. Power System Technology, 2010, 34(1): 36-40.
[8] KingP E, Ochs T L, Hartman A D. Chaotic responses in electric arc furnaces[J]. Journal of Applied Physics, 1994, 76(4): 2059-2065.
[9] O'Neill-Carrillo E, Heydt GT, Kostelich EJ, et al. Nonlinear deterministic modeling of highly varying loads[J]. IEEE Transactions on Power Delivery, 1999, 14(2): 537-542.
[10] 宁元中, 梁颖, 吴昊. 电弧炉的混合仿真模型[J]. 四川大学学报(工程科学版), 2005, 37(1): 85-89.
Ning Yuanzhong, Liang Ying, Wu Hao. Circuit model of arc furnace for mixed-discipline simulation[J]. Advanced Engineering Sciences, 2005, 37(1): 85-89.
[11] Ozgun O, Abur A. Flicker study using a novel arc furnace model[J]. IEEE Transactions on Power Delivery, 2002, 17(4): 1158-1163.
[12] 王育飞, 姜建国. 用于电能质量研究的新型交流电弧炉混沌模型[J]. 中国电机工程学报, 2008, 28(10): 106-110.
Wang Yufei, Jiang Jianguo. A novel chaotic model of AC electric arc furnace for power quality study[J]. Proceedings of the CSEE, 2008, 28(10): 106-110.
[13] 林才华, 张逸, 邵振国, 等. 用于低频非平稳间谐波研究的超高功率电弧炉模型[J]. 中国电力, 2020, 53(11): 1-8.
Lin Caihua, Zhang Yi, Shao Zhenguo, et al. An ultra-high-power electric arc furnace model for low- frequency non-stationary inter-harmonics studies[J]. Electric Power, 2020, 53(11): 1-8.
[14] 祁碧茹, 肖湘宁. 用于电压波动研究的电弧炉的模型和仿真[J]. 电工技术学报, 2000, 15(3): 31-35.
Qi Biru, Xiao Xiangning. Modeling and simulation of an arc furnace for voltage fluctuation investigation[J]. Transactions of China Electrotechnical Society, 2000, 15(3): 31-35.
[15] 刘小河, 程少庚, 苏文成. 电弧炉电气系统的谐波分析研究[J]. 电工技术学报, 1994, 9(2): 21-26, 10.
Liu Xiaohe, Cheng Shaogeng, Su Wencheng. Harmonic analysis of electric systems of arc furnace[J]. Transactions of China Electrotechnical Society, 1994, 9(2): 21-26, 10.
[16] 张逸, 林才华, 邵振国, 等. 基于电子连续性方程的新型交流电弧炉通用模型[J]. 中国电机工程学报, 2021, 41(21): 7425-7434.
Zhang Yi, Lin Caihua, Shao Zhenguo, et al. A novel general model of AC electric arc furnace based on electron continuity equation[J]. Proceedings of the CSEE, 2021, 41(21): 7425-7434.
[17] 曹振. 电弧炉电弧模型的研究[D]. 辽宁: 东北大学, 2009.
[18] Underwood T, Roy S, Glaz B. Physics based lumped element circuit model for nanosecond pulsed dielectric barrier discharges[J]. Journal of Applied Physics, 2013, 113(8): 083301.
[19] 徐龙, 李秋菊, 马文会, 等. 三维非轴对称直流电弧射流过程数值模拟[J]. 昆明理工大学学报(自然科学版), 2021, 46(4): 18-26.
Xu Long, Li Qiuju, Ma Wenhui, et al. Numerical simulation of 3D non-axisymmetric DC arc jet process[J]. Journal of Kunming University of Science and Technology(Natural Sciences), 2021, 46(4): 18-26.
[20] 过增元, 赵文华. 电弧和热等离子体[M]. 北京: 科学出版社, 1986.
[21] Lowke J J. Simple theory of free-burning arcs[J]. Journal of Physics D: Applied Physics, 1979, 12(11): 1873-1886.
[22] 赵永秀, 刘树林, 马一博. 爆炸性试验电感电路分断放电特性分析与建模[J]. 煤炭学报, 2015, 40(7): 1698-1704.
Zhao Yongxiu, Liu Shulin, Ma Yibo. Analysis and modeling of inductor-disconnected-discharged charac- teristics based on explosive test[J]. Journal of China Coal Society, 2015, 40(7): 1698-1704.
[23] Abid F, Niayesh K, Jonsson E, et al. Arc voltage characteristics in ultrahigh-pressure nitrogen including supercritical region[J]. IEEE Transactions on Plasma Science, 2018, 46(1): 187-193.
[24] Latham D J. A channel model for long arcs in air[J]. The Physics of Fluids, 1980, 23(8): 1710.
[25] 于丰, 毛志忠. 电弧炉系统电弧模型的建立与参数辨识[J]. 东北大学学报(自然科学版), 2013, 34(2): 178-181.
Yu Feng, Ma Zhizhong. An arc model for arc furnace system and parameter identification[J]. Journal of Northeastern University (Natural Science), 2013, 34(2): 178-181.
[26] 王其平, 电器电弧理论[M]. 北京: 机械工业出版社, 1991.
[27] 姚聪林, 朱红春, 姜周华, 等. 电弧炉内长电弧等离子体的数值模拟[J]. 工程科学学报, 2020, 42(增刊1): 60-67.
Yao Conglin, Zhu Hongchun, Jiang Zhouhua, et al. Numerical simulation of a long arc plasma in an electric arc furnace[J]. Chinese Journal of Engin- eering, 2020, 42(S1): 60-67.
[28] 王丰华. 电弧炉建模研究及其应用[D]. 上海: 上海交通大学, 2006.
[29] Xue J K, Shen B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science and Control Engineering, 2020, 8(1): 22-34.
[30] Zhang C L, Ding S F. A stochastic configuration network based on chaotic sparrow search algorithm[J]. Knowledge-Based Systems, 2020, 8(1): 22-34.
[31] 薛建凯. 一种新型的群智能优化技术的研究与应用[D]. 上海: 东华大学, 2020.
[32] 李婕, 杨淑英, 谢震, 等. 基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识[J]. 电工技术学报, 2022, 37(18): 4604-4613.
Li Jie, Yang Shuying, Xie Zhen, et al. Online para- meter identification of permanent magnet syn- chronous motor based on fast particle swarm optimization algorithm with effective information iterated[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4604-4613.
[33] 刘廷章, 张子恒. 基于循环迭代粒子群算法对电动汽车无线充电系统的联合参数在线辨识[J]. 电工技术学报, 2022, 37(18): 4548-4564.
Liu Tingzhang, Zhang Ziheng. Online identification of joint parameters of electric vehicle wireless charging system based on loop-iteration particle swarm optimization[J]. Transactions of China Elec- trotechnical Society, 2022, 37(18): 4548-4564.
[34] 葛磊蛟, 赵康, 孙永辉, 等. 基于孪生网络和长短时记忆网络结合的配电网短期负荷预测[J]. 电力系统自动化, 2021, 45(23): 41-50.
Ge Leijiao, Zhao Kang, Sun Yonghui, et al. Short- term load forecasting of distribution network based on combination of siamese network and long short-term memory network[J]. Automation of Electric Power System, 2021, 45(23): 41-50.
[35] Bowman B, Edels H. Radial temperature measure- ments of alternating current arcs[J]. Journal of Physics D: Applied Physics, 1969, 2(1): 53-63.
[36] 贾静然, 段晓波, 卢锦玲, 等. 变压器的谐波传递特性研究[J]. 中国电力, 2017, 50(1): 92-96, 157.
Jia Jingran, Duan Xiaobo, Lu Jinling, et al. Research on harmonic transfer characteristics of transformer[J]. Electric Power, 2017, 50(1): 92-96, 157.
[37] 胡雪凯, 张乾, 田广, 等. 双绕组变压器谐波传递特性研究[J]. 河北电力技术, 2021, 40(3): 62-66,71.
Hu Xuekai, Zhang Qian, Tian Guang, et al. Research on harmonic transfer characteristics of double winding transformer[J]. Heibei Electric Power, 2021, 40(3): 62-66, 71.
Abstract Accurate modeling of electric arc furnaces (EAF) is important for studying the impacton power quality of EAF and developing relevant management measures in the power grid. However, the existing research mainly treats the electric arc as a nonlinear electrical component, neglecting the coupling of electric and physical parameters in the electric arc. Thus, reflecting the electro thermal physical nature of the arc is challenging, resulting in a deficiency in simulation accuracy.
This paper proposes an improved AC arc furnace model. The voltage and current of the arc are defined as electrical characteristics, while the temperature and pressure that characterize the arc state are defined as physical parameters. The coupling mechanism between the electrical and physical parameters is determined based on the electronic continuity equation, Ohm's Law, the magnetic compression force balance equation, and the instantaneous energy balance equation. A general model is constructed that reflects harmonics and voltage fluctuations of AC electric arc furnaces more accurately. Its mathematical expressions are given as follows:
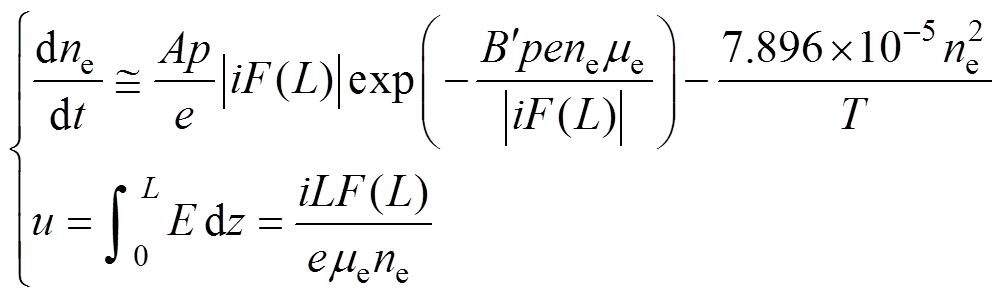(A.1)
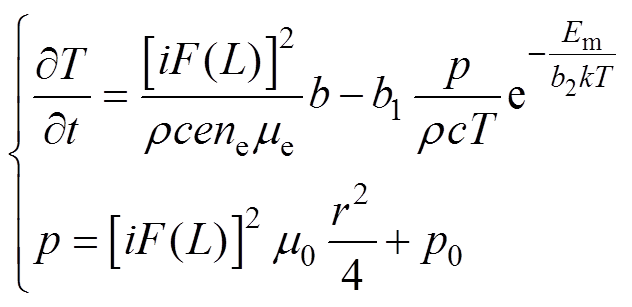(A.2)
For the unknown parameters in the models: A, 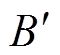, rc; and L0 can be estimated and determined through mechanistic analysis; b, b1, and b2 can be identified using arc furnace transformer parameters and existing arc temperature-related research to construct an arc temperature curve. The data amount is reduced, making it more practical for engineering applications.
Measured data from two steel mills’ 50t and 55t electric arc furnaces are used to verify the model. The results indicate that the simulated AC arc temperature varies with the arc current, exhibiting an alternating characteristic and a double-frequency relationship. The thermal inertia of the arc induces a lad in the peak temperature relative to the peak current. The pressure in the arc column fluctuates around atmospheric pressure. Furthermore, considering the arc’s electrical-physical coupling characteristics, the simulation accuracy of the electrical characteristics, such as harmonic voltage, harmonic current, and voltage fluctuations, has been further improved compared to existing methods.
keywords：AC electric arc furnace, arc temperature, sparrow search algorithm, electrical characteristic, physical parameters
DOI: 10.19595/j.cnki.1000-6753.tces.230034
中图分类号：TF748.41
国家自然科学基金资助项目（51777035）。
收稿日期 2023-01-09
改稿日期 2023-07-29
徐云聪 男，1999年生，硕士研究生，研究方向为电能质量分析。E-mail: 1360397798@qq.com
张 逸 男，1984年生，博士，副教授，研究方向为电能质量、主动配电网以及电力数据分析等。E-mail: zhangyi@fzu.edu.cn（通信作者）
（编辑 郭丽军）