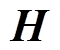 可以表示为
可以表示为摘要 为了解决矢量积分方程法计算舰船感应磁场时效率较低和计算量较大的问题,提出一种基于简化标量磁位的积分方程正演模型,并引入多层自适应交叉近似(MLACA)算法,不仅能够保证磁场计算精度,还能大幅减少计算机的内存需求和计算时间。数值仿真表明,使用基于MLACA的标量积分方程法能够快速获取高精度的铁磁物体感应磁场。针对舰船铁磁材料的磁性参数不易获取的问题,基于磁场实测值和正演耦合模型,以磁场拟合度、磁化率先验分布和光滑约束条件为目标函数建立磁化率反演模型,并采用模拟退火(SA)算法优化得到等效磁化率的空间分布。球壳数值仿真和船模试验结果表明,磁化率反演优化模型有效可行,其中球壳磁场的预测误差为2.2%,船模磁场的预测误差约为4.8%。
关键词:舰船磁场 简化标量磁位 多层自适应交叉近似 模拟退火法 等效磁化率
大多数舰船由铁磁材料制成,在地磁场的磁化作用和其他因素的影响下会产生舰船磁场,成为被攻击或监视的信号源,因此,全面、准确地了解和掌握舰船磁场的空间分布特性是实施磁防护措施的重要前提,也是磁隐身技术的一项重要研究内容[1-2]。舰船磁场按照产生机理可以分为铁磁性磁场、涡流磁场、杂散磁场和极低频磁场等。而铁磁性磁场又包含了感应磁场和固定磁场两类[3]。获取舰船固定磁场和感应磁场的一般做法是利用舰船下方的磁传感器阵列直接测量舰船在不同外磁场作用下产生的磁场并进行分解计算[3],但是该方法要求舰船左右大致对称,且在测量过程中舰船的位置不能出现较大偏移,测得的也仅为有限的磁场信息。若想得到舰船的空间磁场分布,还需要利用有限的测量点磁场值再次进行延拓和换算。针对测量法这一弊端和通用性不够的问题,需要研究数值建模方法来计算得到更加精确的舰船全空间磁场。舰船感应磁场与地磁场的大小、方向以及材料磁导率等因素有关,对于非规则的铁磁物体来说,可以使用等效源法[3-6]、边界元法[7]、有限元法[8]和积分方程法[9]等数值方法进行建模。因此,本文主要研究舰船感应磁场的建模和计算方法,进而为舰船磁性设备的位置选定、磁性处理、消磁系统设计等提供帮助。
舰船感应磁场的计算归结为开域问题,而对于开域的静磁场计算问题来说,由于积分方程法仅需对铁磁区进行离散,且不需要考虑边界条件和可以求解连续函数等的优点,受到广泛关注和应用。国内,Fan Mingwu等[10]提出了三维静磁场的矢量积分方程法;倪振群等[11]将该方法应用于舰船感应磁场的计算;周国华等[12]、郭成豹等[13]、朱武兵等[14]使用非规则体单元、面单元对舰船几何结构进行网格离散,研发了用于计算舰船感应磁场的工具包;何保委等[15]使用标量磁位建模提升了求解精度。针对在感应磁场求解过程中铁磁物体磁化率难以确定的问题,郭成豹等提出了利用试验样品的磁性参数替代的方法[16],周国华等则提出一种利用粒子群算法对磁化率进行优化的模型[17],为舰船感应磁场的正演计算奠定了基础。国外,C. W. Trowbridge等[18]早在1970年间就将积分方程法用于求解物体的电磁场;O. Chadebec等[19]首次将积分方程法引入薄壳体舰船模型的闭环消磁算法建模当中;S. Guerin[20]和Y. Vuillermet[21]研究对比了以磁化强度、点磁荷、切向磁偶极子为磁源的感应磁场建模方法。近年来,法国Grenoble Alpes大学的研究团队陆续提出了新的关于积分方程法的加速改进算法和耦合算法[22-24],在减少网格数量的同时提升了磁场计算精度。总的来说,积分方程法已经广泛应用于磁场计算领域,但是求解时间过长和对计算机配置要求较高等问题还有待进一步改善。
本文以舰船感应磁场的计算为研究背景,提出一种改进型标量积分方程法。首先,通过选取三角形单元离散薄壳体,依据插值原理[25]将计算点由单元中心点转移至节点,推导得到了基于标量磁位的积分方程公式。其次,在求解稠密耦合系数矩阵的逆运算时,为减少计算机的内存需求和计算时间,引入了通用性较强的多层自适应交叉近似(Multi- Level Adaptive Cross Approximation, MLACA)算法和广义最小残差(Generalized Minimal Residual, GMRES)法,将源点和场点按照相对位置进行分组计算。由于感应磁场正演需要已知铁磁材料的磁性参数,考虑到临近单元的磁化率应当平滑过渡。然后,基于磁场实测值和正演耦合算法建立了等效磁化率的反演模型,以磁场拟合度、磁化率先验分布和光滑约束条件构建目标函数,采用模拟退火(Simulated Annealing, SA)算法对磁化率寻优求解,在具有磁场解析解的铁质球壳上进行数值仿真对比验证。最后,将本文所提出的高精度感应磁场建模方法应用于一艘磁性参数未知的缩比船模进行试验研究,通过将测量值和实测值进行比较,最后得出结论。
铁磁性舰船受地磁场磁化后,在空间任意一点P产生的磁场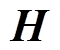 可以表示为
可以表示为
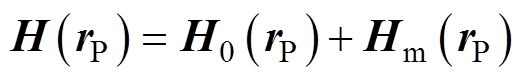 (1)
(1)
式中,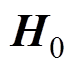 为地磁场;
为地磁场;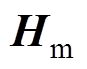 为附加场(感应磁场);
为附加场(感应磁场);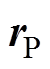 为场点P的位置矢量。由于舰船的源区和场域均不包含自由电流,可以引入标量磁位
为场点P的位置矢量。由于舰船的源区和场域均不包含自由电流,可以引入标量磁位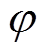 [26],从而得到
[26],从而得到
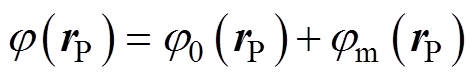 (2)
(2)
式中,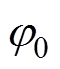 和
和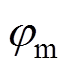 分别为地磁场的标量磁位和简化标量磁位。根据电磁场相关理论[27],简化标量磁位
分别为地磁场的标量磁位和简化标量磁位。根据电磁场相关理论[27],简化标量磁位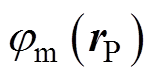 可以表示为
可以表示为
 (3)
(3)
式中,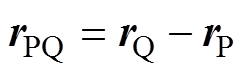 ,
,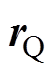 为源点Q的位置矢量;
为源点Q的位置矢量;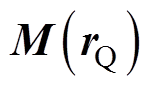 为源点(舰船)的磁化强度;
为源点(舰船)的磁化强度;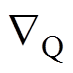 为散度算子;
为散度算子;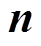 为舰船表面的外法向;
为舰船表面的外法向;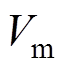 和
和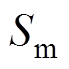 分别为舰船占据的空间和外表面。
分别为舰船占据的空间和外表面。
在舰船内部,假设船体铁磁材料各向同性,即
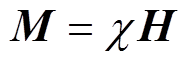 (4)
(4)
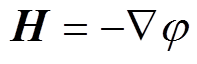 (5)
(5)
式中,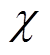 为舰船铁磁材料的磁化率;
为舰船铁磁材料的磁化率; 为梯度算子。式(3)~式(5)组成了求解舰船感应磁场的基本公式,但由于方程中被积函数
为梯度算子。式(3)~式(5)组成了求解舰船感应磁场的基本公式,但由于方程中被积函数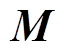 和积分结果
和积分结果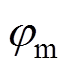 有关,属于第二类Fredholm积分方程[28],通常情况下将舰船离散为若干个单元进行求解,地磁场作用下的舰船离散单元模型和感应磁场方向如图1所示。
有关,属于第二类Fredholm积分方程[28],通常情况下将舰船离散为若干个单元进行求解,地磁场作用下的舰船离散单元模型和感应磁场方向如图1所示。
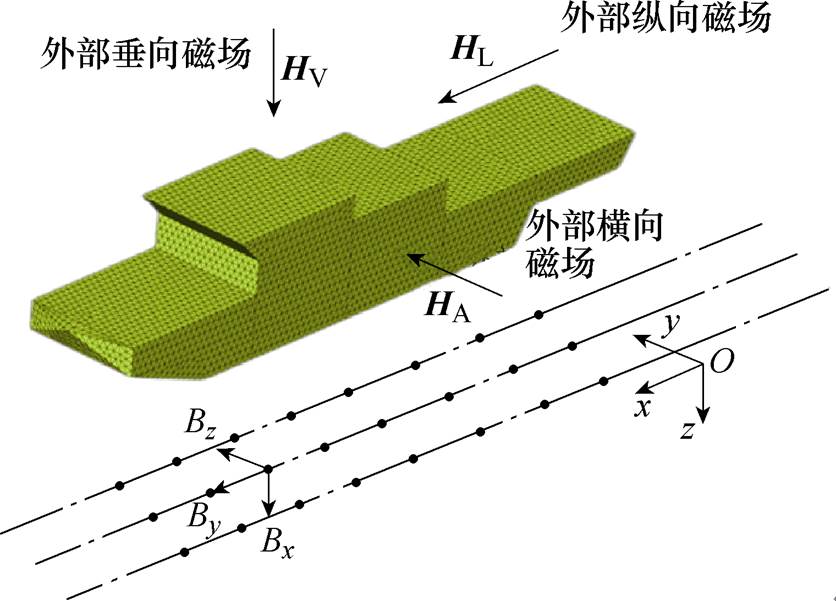
图1 地磁场作用下的舰船离散单元模型和感应磁场方向
Fig.1 The discrete element model and induced magnetic field of ship under the influence of geomagnetic field
根据积分方程法原理,在舰船被离散化后,由于离散单元极小,此时每个单元内部的磁性参数(磁化强度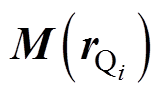 )变化量极小,可以看作常数,因此
)变化量极小,可以看作常数,因此
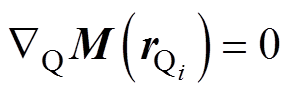 (6)
(6)
基于叠加定理,空间任意一点的磁位为所有离散单元在该点产生的磁位的代数和。联立式(3)~式(6),可以得到
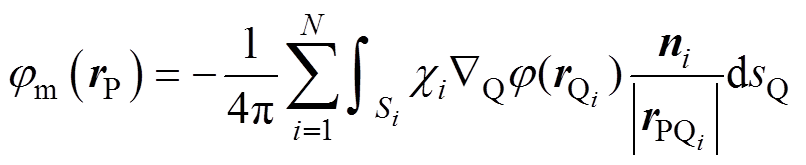 (7)
(7)
式中,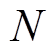 为离散单元的数量;
为离散单元的数量;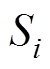 为第i个离散单元的外表面;
为第i个离散单元的外表面;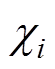 为第i个离散单元的磁化率;
为第i个离散单元的磁化率;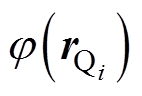 为第i个离散单元的标量磁位;
为第i个离散单元的标量磁位;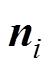 为第i个离散单元表面的外法向;
为第i个离散单元表面的外法向;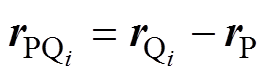 为第i个离散单元到场点的位置矢量。为求得每个离散单元内部的标量磁位,根据点匹配法[14]依次将场点P取为各单元中心点,联立式(2)和式(7)可以得到以标量磁位为待求量的代数方程组为
为第i个离散单元到场点的位置矢量。为求得每个离散单元内部的标量磁位,根据点匹配法[14]依次将场点P取为各单元中心点,联立式(2)和式(7)可以得到以标量磁位为待求量的代数方程组为
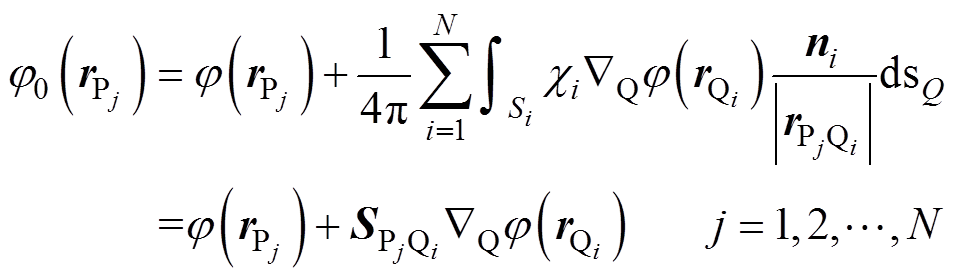 (8)
(8)
标量磁位积分方程法的关键在于求解式(8)中的耦合系数矩阵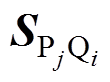 。对于离散单元数量较多的几何模型,多个耦合系数合成了大型非对称稠密矩阵,求解时间和计算机的内存消耗会随着单元数量的增加而急剧增加。针对舰船壳体、甲板和舱壁等主要结构属于薄壳体(长度和宽度远远大于厚度)的特点,本文选取了面单元对薄壳体结构进行离散化,具有以下优势:
。对于离散单元数量较多的几何模型,多个耦合系数合成了大型非对称稠密矩阵,求解时间和计算机的内存消耗会随着单元数量的增加而急剧增加。针对舰船壳体、甲板和舱壁等主要结构属于薄壳体(长度和宽度远远大于厚度)的特点,本文选取了面单元对薄壳体结构进行离散化,具有以下优势:
(1)从离散单元来看,使用面单元要比体单元更加适应薄壳体的剖分。
(2)对于同一艘舰船或者薄壳体,使用面单元离散后的单元数量相比较于体单元数量能够大幅减少,从而提高求解速度、降低计算机的内存需求。
不失一般性,采用如图2所示的三棱柱作为离散单元,此时式(8)仍然适用,并且可以转化为
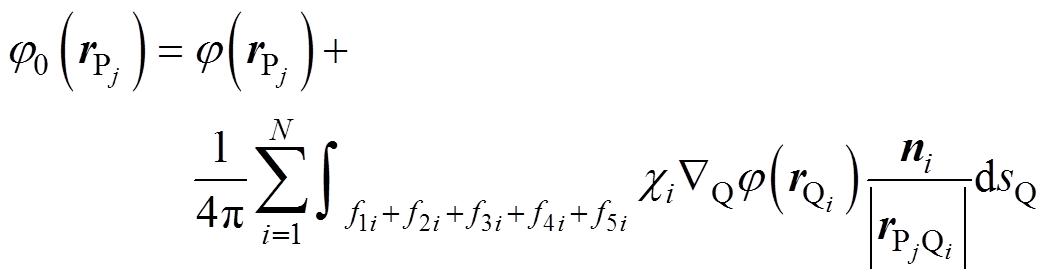 (9)
(9)
式中,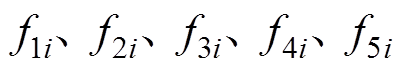 分别为三棱柱单元的五个外表面。当三棱柱的两个三角形间距e缩小到一定程度时,退化为三角形壳单元。对壳单元来说,由于面
分别为三棱柱单元的五个外表面。当三棱柱的两个三角形间距e缩小到一定程度时,退化为三角形壳单元。对壳单元来说,由于面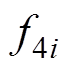 和
和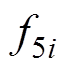 的外法线方向相反,因而有
的外法线方向相反,因而有
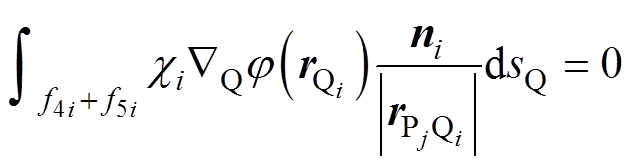 (10)
(10)
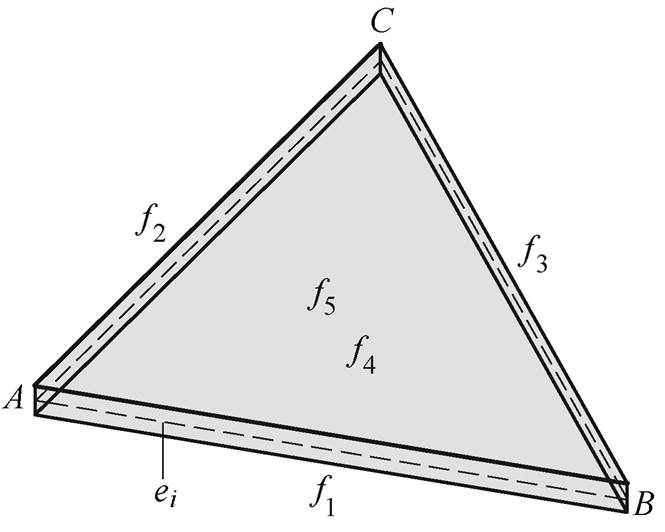
图2 三棱柱离散单元
Fig.2 The triangular prism discrete element
考虑到薄壳体结构的厚度ei相比于长度和宽度都小得多,因此可以使用三角形面单元对舰船的薄壳体结构进行离散,从而得到
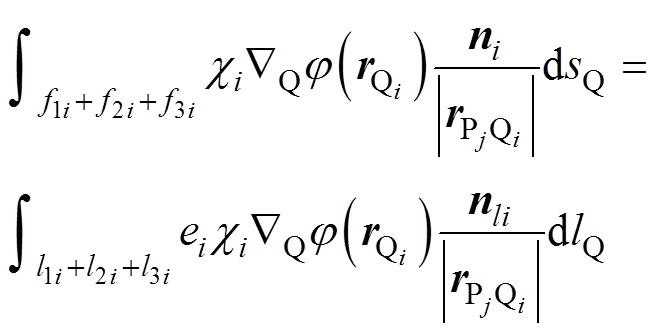 (11)
(11)
式中,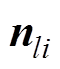 为面单元边线的外法向,或是三棱柱单元表面
为面单元边线的外法向,或是三棱柱单元表面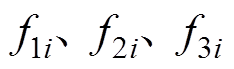 的外法向;
的外法向;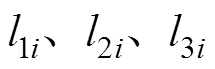 为三角形单元的各边长。联立式(9)~式(11)可以得到
为三角形单元的各边长。联立式(9)~式(11)可以得到
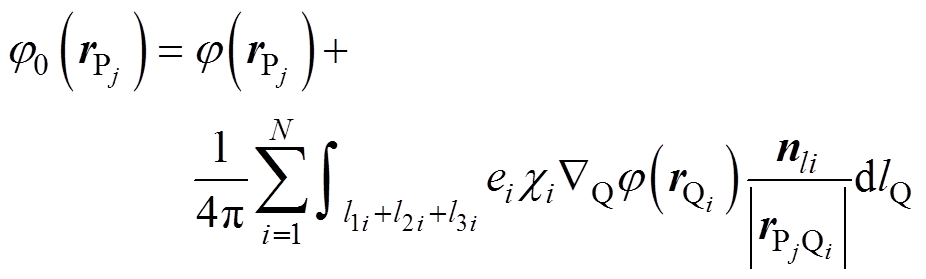
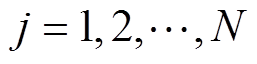 (12)
(12)
观察式(12)的被积函数,需要对未知的标量磁位求梯度,因此需要消去该梯度算子。基于三角形单元的线性插值原理[25],可以将单元内部的标量磁位用插值函数和节点标量磁位来表示,即
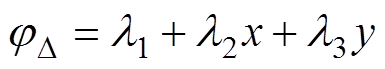 (13)
(13)
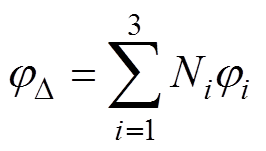 (14)
(14)
式中,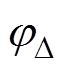 为三角形单元内部任意点的磁位;(x, y)为该点坐标;
为三角形单元内部任意点的磁位;(x, y)为该点坐标;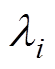 为待定常数;
为待定常数;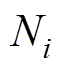 为基函数;
为基函数;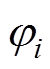 为节点磁位。式(13)表明,单元内任意点的标量磁位可以由该点坐标和待定系数来表示;式(14)表明,单元内任意点的标量磁位可以由节点磁位和插值函数表示。此时将节点坐标分别代入式(13)得
为节点磁位。式(13)表明,单元内任意点的标量磁位可以由该点坐标和待定系数来表示;式(14)表明,单元内任意点的标量磁位可以由节点磁位和插值函数表示。此时将节点坐标分别代入式(13)得
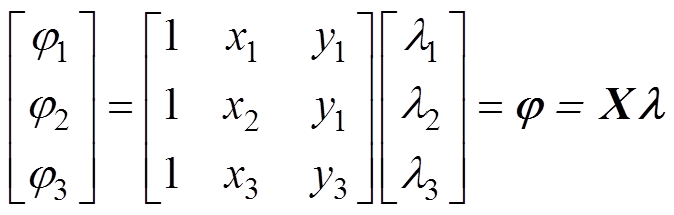 (15)
(15)
联立式(12)~式(15),可以得到
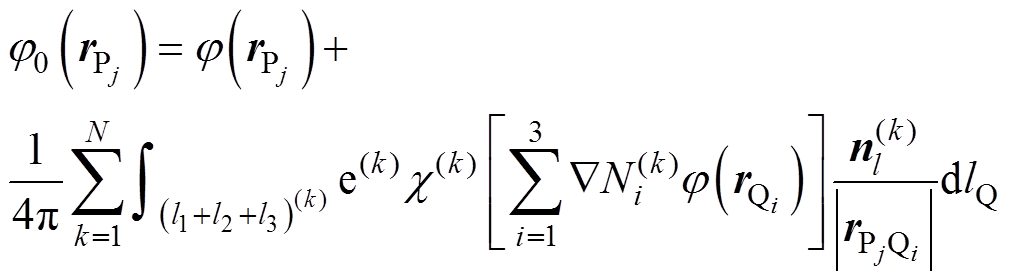 (16)
(16)
式中,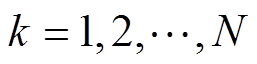 为单元上标;
为单元上标;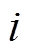 和
和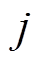 均为节点下标;插值函数
均为节点下标;插值函数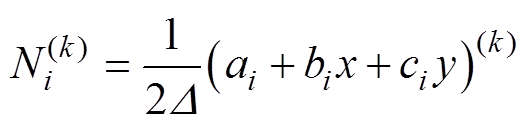 ,
,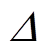 为
为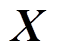 的行列式,
的行列式,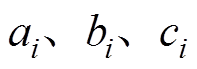 分别为
分别为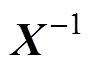 的代数余子式。为了使等号左右两边格式统一,对式(16)进行变形,得到
的代数余子式。为了使等号左右两边格式统一,对式(16)进行变形,得到
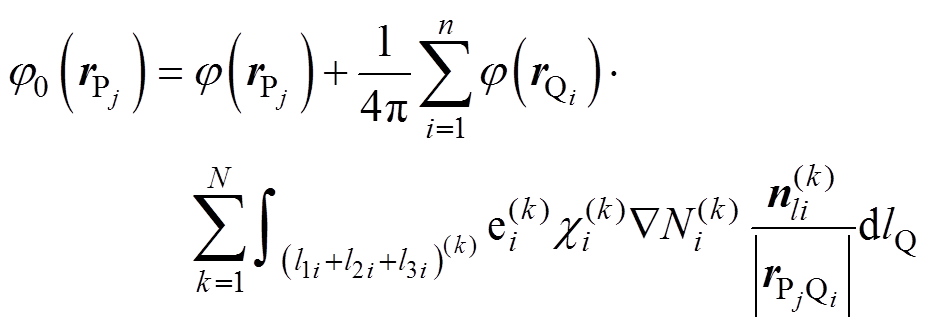 (17)
(17)
式中,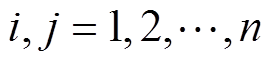 ,
,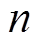 为离散单元的总节点数。由于被积函数当中
为离散单元的总节点数。由于被积函数当中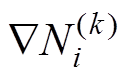 为常量,式(17)当中仅有
为常量,式(17)当中仅有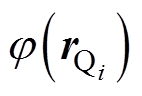 为未知数,最终得到的矩阵表达式为
为未知数,最终得到的矩阵表达式为
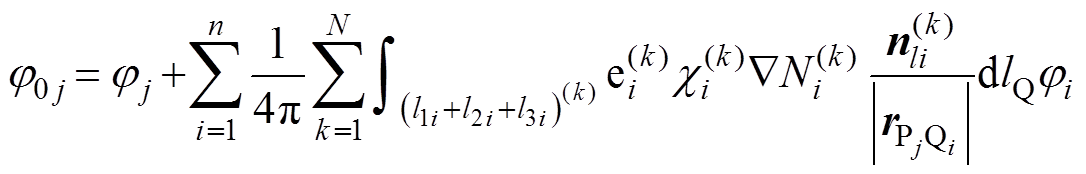
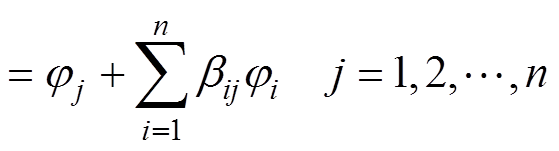 (18)
(18)
式(5)和式(18)组成了基于面单元求解舰船感应磁场的标量磁位积分方程法公式。首先以地磁场作为左端的输入项,通过求解该代数方程组可以得到每个离散单元的标量磁位,然后再求解空间任意场点的磁场值。
为了求解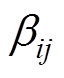 ,不妨在每个三角形单元分别建立以A为原点,以边线AB为x轴,以面法向为z轴的局部坐标系
,不妨在每个三角形单元分别建立以A为原点,以边线AB为x轴,以面法向为z轴的局部坐标系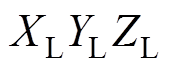 ,如图3所示。此时动点q仅在线段AB上,因此式(18)的被积函数可以表示为
,如图3所示。此时动点q仅在线段AB上,因此式(18)的被积函数可以表示为
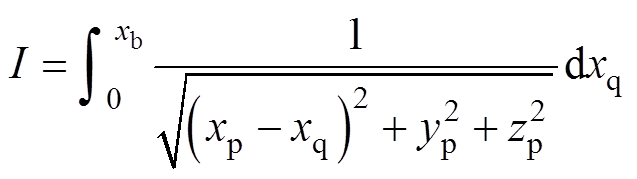 (19)
(19)
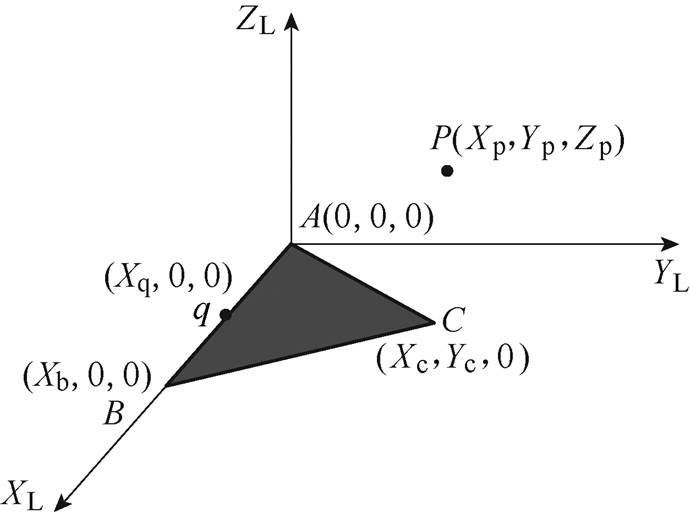
图3 三角形面单元局部坐标系
Fig.3 The local coordinate system of triangular face element
定积分 的原函数不易求得,可以采用高斯数值积分公式进行求解,之后将求解结果转换到全局坐标系,转换矩阵[12]为
的原函数不易求得,可以采用高斯数值积分公式进行求解,之后将求解结果转换到全局坐标系,转换矩阵[12]为
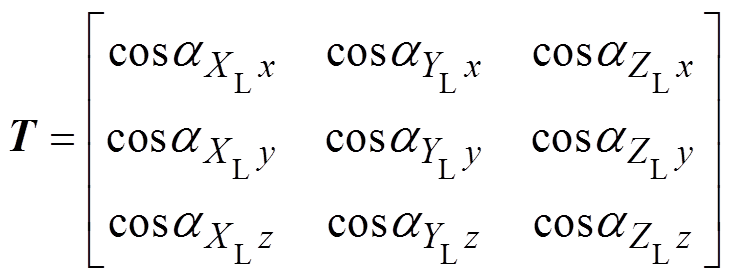 (20)
(20)
式中,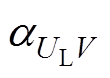 为局部坐标系的
为局部坐标系的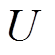 轴与全局坐标系的
轴与全局坐标系的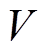 轴的夹角,
轴的夹角,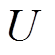 =
=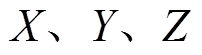 ,
,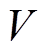 =
= 。全局坐标系和局部坐标系的位置关系如图4所示。
。全局坐标系和局部坐标系的位置关系如图4所示。
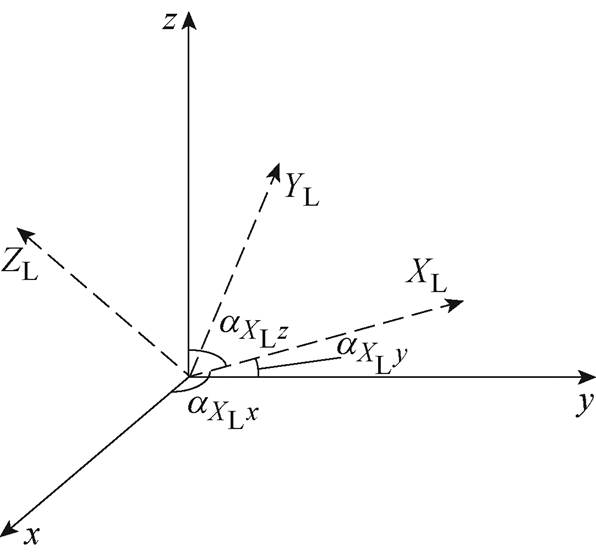
图4 局部坐标系和全局坐标系的相对位置
Fig.4 The relative position of the local coordinate and global coordinate system
至此,基于标量磁位的薄壳体感应磁场正演建模方法和公式已经给出。为了体现标量建模方法相比于矢量建模方法的优越性,参照式(18),直接给出以磁感应强度为待求量的积分方程作为后续对比研究,其表达式为
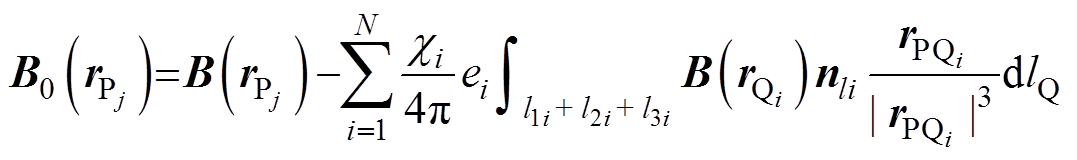 (21)
(21)
标量积分公式最终可以化简为如 的表达式,由于系数矩阵
的表达式,由于系数矩阵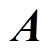 是非对称稠密矩阵,直接求逆具有
是非对称稠密矩阵,直接求逆具有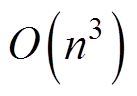 的计算复杂度和
的计算复杂度和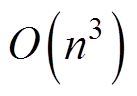 的存储复杂度,普通计算机采用常规的求解方法只能解决节点自由度在数千以内的小规模磁场问题且非常耗时。为实现大型舰船的感应磁场建模问题,本文引入了多层自适应交叉近似算法[28],可以有效地加速求解速度和降低计算机的内存需求。
的存储复杂度,普通计算机采用常规的求解方法只能解决节点自由度在数千以内的小规模磁场问题且非常耗时。为实现大型舰船的感应磁场建模问题,本文引入了多层自适应交叉近似算法[28],可以有效地加速求解速度和降低计算机的内存需求。
MLACA为一种矩阵压缩算法,它将离散单元划分为近场组和远场组两类,对于近场组的单元采用直接计算方法,对于远场组的单元采用两个满秩矩阵的乘积来近似表示,其原理为
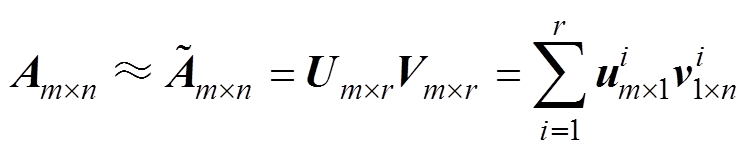 (22)
(22)
式中,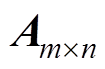 为精确计算的矩阵;
为精确计算的矩阵;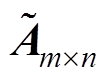 为近似矩阵;
为近似矩阵;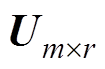 和
和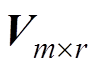 为两个满秩的稠密矩阵;
为两个满秩的稠密矩阵;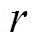 为
为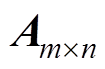 的有效秩;
的有效秩;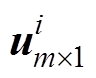 和
和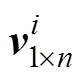 分别为
分别为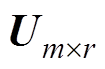 和
和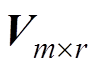 为对应的列向量和行向量。
为对应的列向量和行向量。
为了使得近似矩阵尽量逼近精确矩阵,定义残差计算公式为
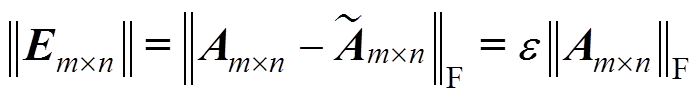 (23)
(23)
式中,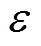 为给定的精度控制常数;
为给定的精度控制常数;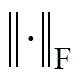 为矩阵的Frobenus范数。由式(22)可知,MLACA算法使用
为矩阵的Frobenus范数。由式(22)可知,MLACA算法使用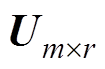 和
和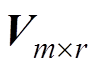 来近似逼近
来近似逼近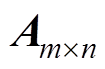 ,存储量由
,存储量由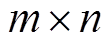 变成了
变成了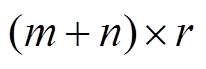 ,极大地减少了内存需求。
,极大地减少了内存需求。
MLACA算法的优点在于它是纯数学方法,不会涉及积分方程核函数的展开和变换,所以适用于各种不同核函数的积分方程组,通用性较强,直接给出MLACA算法应用于标量磁位积分方程法的磁场正演流程[29]。
1)网格离散。对铁磁目标进行几何建模和网格剖分,获取单元和节点的信息。
2)建立八叉树。将铁磁目标所占空间按照八叉树模式划分为多个小区域,以层数L=2为例,铁磁区域空间一共划分成了64个小立方体,每个立方体包含了一组场点或源点的集合,若64组点的集合相互作用,得到的是一个64×64的矩阵块。在该矩阵中,近场区为位于对角线的矩阵块,是满秩矩阵;远场区为非对角线的矩阵块,是低秩矩阵。按照近场区和远场区的划分,分别采用直接求解方法和调用MLACA算法求解系数矩阵。
3)对远场区调用MLACA算法。
(1)初始化行下标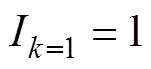 和精度控制常数
和精度控制常数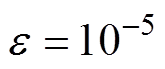 。
。
(2)调用标量积分方程法,计算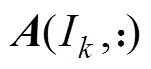 ,使得误差矩阵
,使得误差矩阵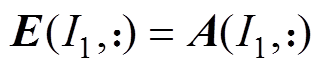 。
。
(3)寻找列下标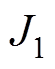 ,使得
,使得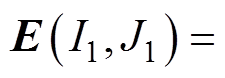
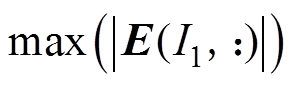 ,从而确定
,从而确定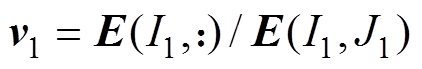 。
。
(4)调用标量积分方程法,计算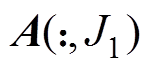 ,使得误差矩阵
,使得误差矩阵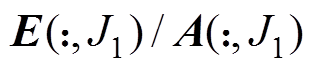 ,确定
,确定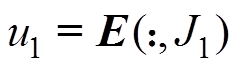 。
。
(5)计算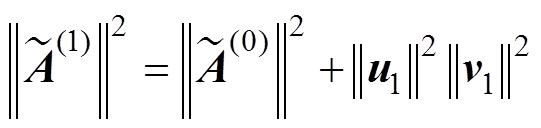 ,若满足
,若满足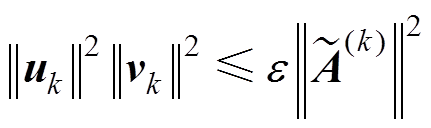 条件,MLACA算法结束;若不满足,开始进行下一次迭代;以下是迭代过程。
条件,MLACA算法结束;若不满足,开始进行下一次迭代;以下是迭代过程。
(6) 令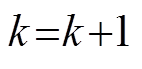 ,寻找行下标
,寻找行下标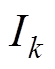 ,使得
,使得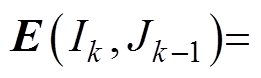
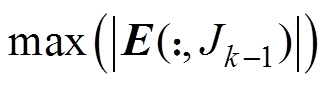 。
。
(7)更新误差矩阵的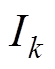 行,使得
行,使得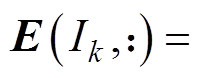
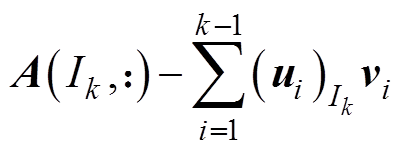 。
。
(8)寻找列下标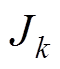 ,使得
,使得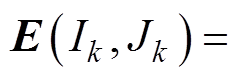
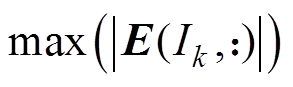 ,从而确定
,从而确定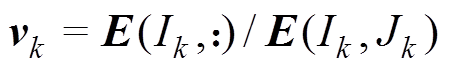 。
。
(9)更新误差矩阵的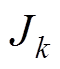 列,使得
列,使得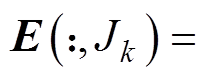
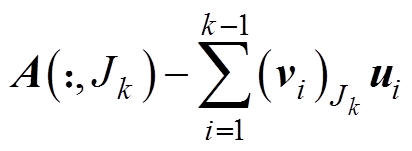 ,确定
,确定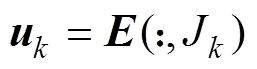 。
。
(10)计算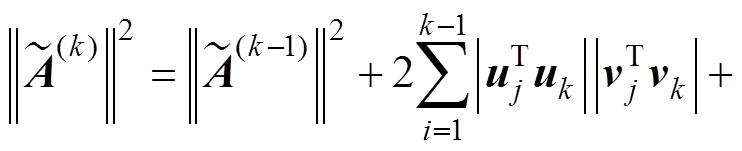
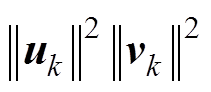 ,转步骤(5)进行判别是否需要进行下一步迭代。
,转步骤(5)进行判别是否需要进行下一步迭代。
(11)输出矩阵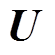 和
和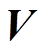 。
。
4)采用广义最小残差(GMRES)法求解式(18),输出值为单元节点的标量磁位。
由算法流程可以看出,MLACA算法不需要知道原精确矩阵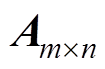 的所有值便可以得到近似矩阵
的所有值便可以得到近似矩阵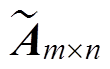 ,每次迭代过程需要
,每次迭代过程需要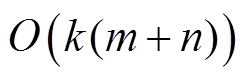 的计算复杂度和存储复杂度,最终的计算复杂度仅为
的计算复杂度和存储复杂度,最终的计算复杂度仅为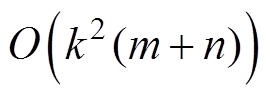 ,远远低于直接进行逆运算。
,远远低于直接进行逆运算。
为了检验标量磁位积分方程法结合MLACA算法的应用效果,本文给出了具有磁场解析解的铁质球壳算例进行验证。为了排除网格疏密带来的影响,分别采用不同的网格密度对球壳模型进行剖分,用于检验所提出算法的计算精度、运行速度以及对计算机所消耗内存的压缩程度。
铁质球壳模型及测量点示意图如图5所示,外径为10 m,厚度为0.01 m,材料磁导率为61。外磁场大小Bez=36 000 nT,方向竖直向下。以球壳模型的中心点为原点建立三维直角坐标系(竖直向下为z轴正方向),测量点的范围为x∈[-30, 30 ] m,步长为1 m;y∈[-10, 10] m,步长为10 m;z=15 m。
球壳模型在垂向外磁场的作用下,三分量感应磁场的解析结果可以表示为
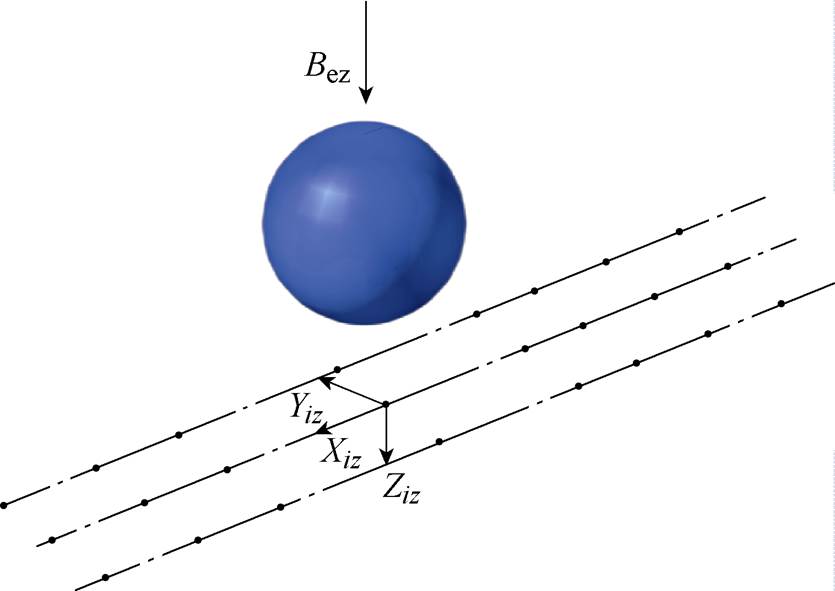
图5 铁质球壳模型及测量点示意图
Fig.5 The schematic diagram of iron spherical shell model and measurement point position
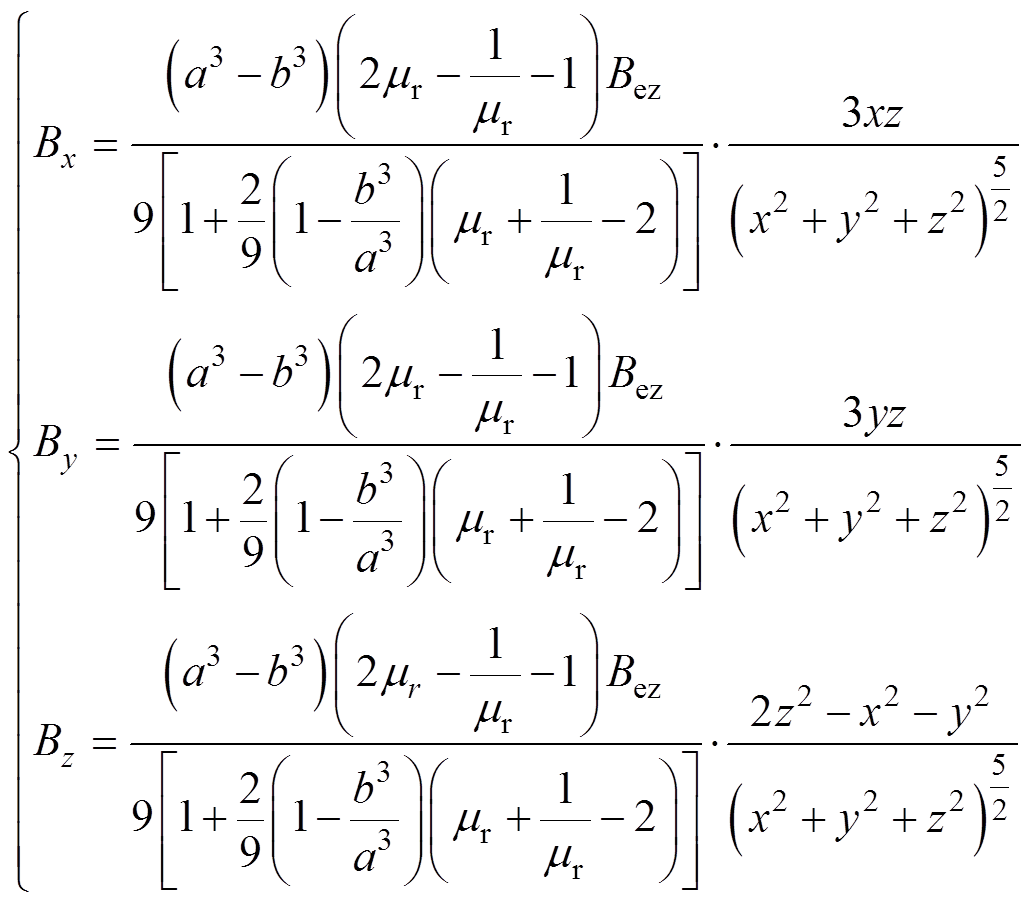 (24)
(24)
式中,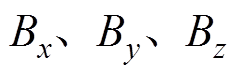 分别为球壳的三分量感应磁场;
分别为球壳的三分量感应磁场;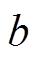 和
和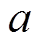 分别为球壳的内、外径;
分别为球壳的内、外径;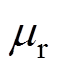 为材料磁导率;(x, y, z)为测量点的坐标。
为材料磁导率;(x, y, z)为测量点的坐标。
根据式(18)和式(22),分别使用基于MLACA的标量积分方程法(Scalar Integral Equation Method, SIEM)和矢量积分方程法(Vector Integral Equation Method, VIEM)求解不同网格密度球壳下方测量点的感应磁场。以磁场解析解为理论值,评估不同方法计算得到的磁场的平均相对误差。
为保证使用不同算法进行比较的公平性,本文使用的编程软件统一为Matlab 2020,选用的计算机平台为搭载12核心的Core i7 10 750H型处理器,主频为2.6 GHz,RAM为32 GB的笔记本,计算结果见表1,当网格密度模式为3号时,球壳模型的磁场三分量结果如图6所示。
对于球壳模型来说,根据表1和图6的数据可以得出以下结论:
(1)网格密度越高,积分方程法的磁场计算误差越小,说明适当增加离散单元的数量可以得到高精度的铁磁物体感应磁场,但是当网格密度增加到一定程度时,计算精度提高的不明显。
表1 使用积分方程法计算不同网格密度球壳模型磁场的结果
Tab.1 The calculation results of spherical shell models with different mesh densities utilizing integral equation method

网格模式网格数节点数平均相对误差(%)计算时间/s内存需求/MB VIEMSIEM+ MLACAVIEMSIEM+ MLACAVIEMSIEM+ MLACA 1116601.071.012220.1 24662350.390.37117201 31 1925980.260.2556251093 42 5781 2910.190.182439447113 55 1542 5790.170.179423401 81850 66 6483 3260.160.161 5475393 11682 79 0564 5300.160.162 8959845 742151
(2)本文使用了MLACA算法压缩内存(层数为6)和加速计算后,SIEM+MLACA相比较VIEM节省了内存消耗约97%,节省了计算时间约65%。
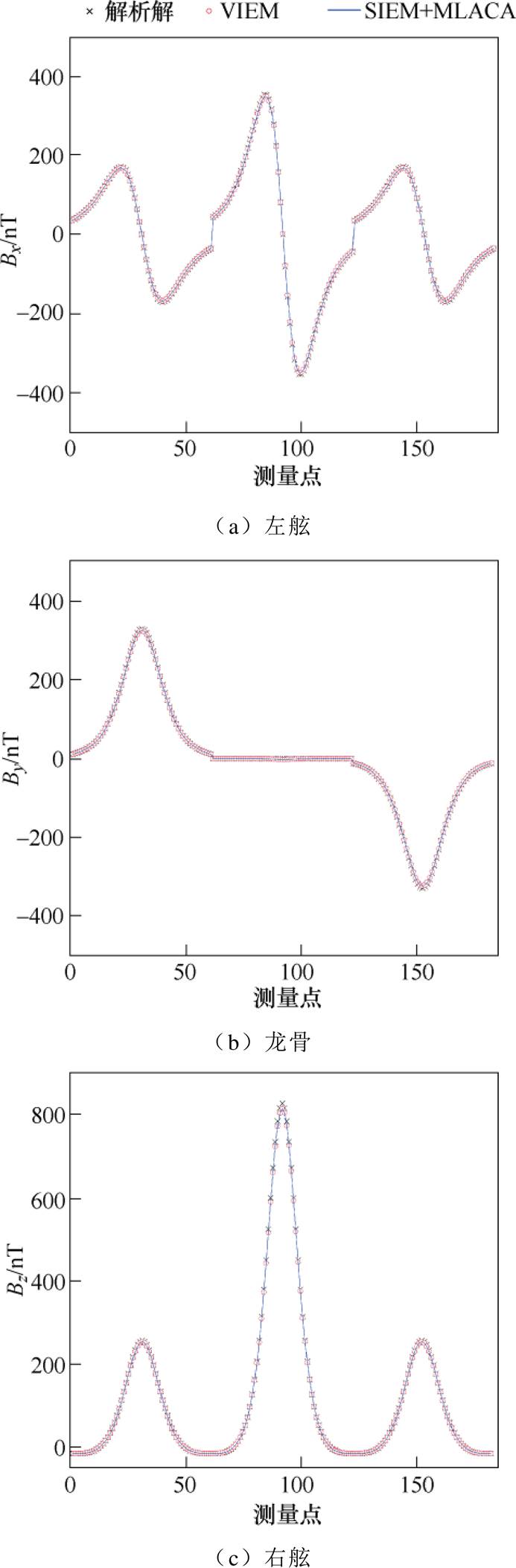
图6 铁质球壳磁场计算结果比较
Fig.6 The comparison of magnetic field calculation results of iron spherical shell
(3)在相同网格密度的情况下,基于MLACA的SIEM在保证计算精度不变的前提下,能够大幅减少计算时间和降低计算机的内存需求,验证了MLACA算法的有效性。
根据积分方程法原理可知,计算物体感应磁场的前提是获得材料的磁化率(或磁导率)。对于一般的铁磁性材料来说,可以通过查阅磁化率曲线或者采取样品试验的方法来获取磁化率[17],但由于舰船铁磁材料的多样性以及船体需要经过多次的高温锻造和冲击试验,意味着舰船磁化率不是一个常数,而是一个与空间位置相关的变量。
等效磁化率是指在建模过程中铁磁材料相对于测量点或者计算点所“表现”出来的磁化率参数。考虑到舰船已经被离散为N个单元,等效磁化率记为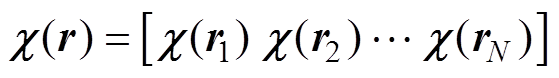 。为了能够获取不同舰船铁磁材料的磁性参数,本节假定舰船在弱磁(地磁场)条件下磁化率为线性模型,以舰船模型的磁场实测值为输入,基于标量磁位积分方程法和MLACA算法,建立舰船铁磁材料的等效磁化率反演模型。
。为了能够获取不同舰船铁磁材料的磁性参数,本节假定舰船在弱磁(地磁场)条件下磁化率为线性模型,以舰船模型的磁场实测值为输入,基于标量磁位积分方程法和MLACA算法,建立舰船铁磁材料的等效磁化率反演模型。
首先假设在某一磁化状态下K个测量点获取的舰船三分量感应磁场为
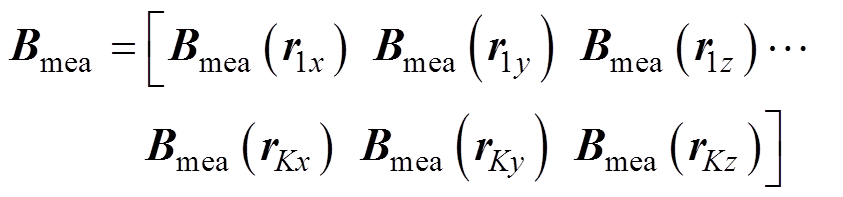 (25)
(25)
在反演模型中,通常根据磁场计算值和测量值的拟合程度来寻找合适的磁化率分布,令拟合函数为
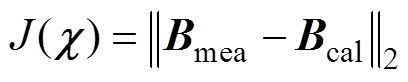 (26)
(26)
式中, 为磁感应强度的计算值,其各分量取决于磁化率,函数
为磁感应强度的计算值,其各分量取决于磁化率,函数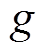 的表达式由式(18)决定;
的表达式由式(18)决定;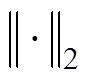 为二范数。若
为二范数。若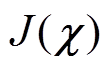 趋近无穷小,说明磁场计算值和测量值之间拟合程度较高,此时磁化率的解记为
趋近无穷小,说明磁场计算值和测量值之间拟合程度较高,此时磁化率的解记为
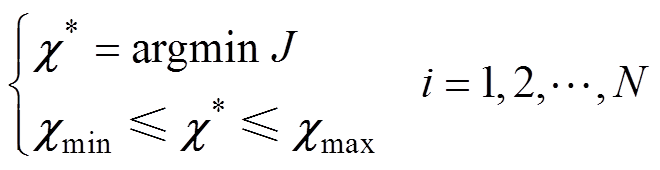 (27)
(27)
式中,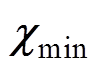 和
和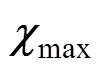 为磁化率设定的最小值和最大值。
为磁化率设定的最小值和最大值。
在实际磁场测量过程中,测量值包含了噪声,这些噪声通常来源于测量设备、测量环境和人为因素等,可以给定一个容差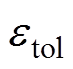 作为截止条件,此时磁场拟合度的可接受范围表示为
作为截止条件,此时磁场拟合度的可接受范围表示为
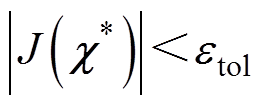 (28)
(28)
根据式(27)和式(28)可以得到众多符合截止条件的空间磁化率分布,然而对于物体“真实”的磁化率来说,该方法得到的解可能是众多局部最优解的其中一个。为确保得到拟合度和稳定性较好的等效磁化率,加入两个约束条件来减少解空间的维度,从而改善反演结果的质量。
(1)约束条件1:在磁化率反演过程中,使用上一次反演结果作为下一次反演的先验值,把上一次的反演值记为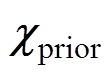 。
。
(2)约束条件2:等效磁化率的分布应当符合物理客观规律和满足平滑性准则,即不允许某一单元的磁化率无限大,也不允许相邻单元的磁化率发生突变。具体实现办法是使用有限差分格式[30]使得相邻单元的磁化率过渡更加平滑,具体表达式为
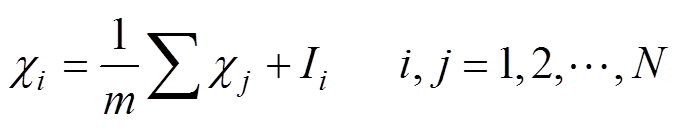 (29)
(29)
式中,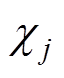 为
为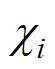 的所有临近单元(共享一条边的两个单元);
的所有临近单元(共享一条边的两个单元);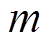 为临近单元个数;
为临近单元个数;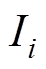 为修正值,保证相邻网格的磁化率光滑过渡。将模型的光滑约束用矩阵形式表示为
为修正值,保证相邻网格的磁化率光滑过渡。将模型的光滑约束用矩阵形式表示为
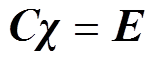 (30)
(30)
式中,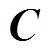 为光滑度矩阵;
为光滑度矩阵; 取决于修正值。联立式(27)~式(30),得到等效磁化率的最终解为
取决于修正值。联立式(27)~式(30),得到等效磁化率的最终解为
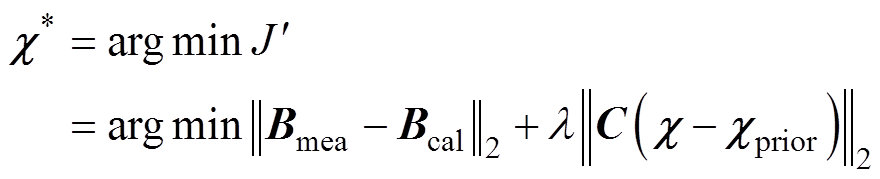 (31)
(31)
式中,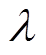 为正则化权重,设定光滑约束的占比为总目标函数的5%。
为正则化权重,设定光滑约束的占比为总目标函数的5%。
模拟退火算法借鉴于高温固体的退火过程,当固体的温度较高时,由于内能较大,固体内部的粒子处于快速且无序的运动状态[31]。在温度缓慢降低的过程中,由于内能减小,粒子缓慢趋于有序。最终,在固体处于常温时,内能达到最小,此时粒子状态最为稳定。SA算法由两层循环组成,内外层循环分别是同一温度下寻找局部最优解和温度冷却过程中寻找全局最优解,它是通过在内循环搜索解的过程中赋予一定的概率来跳出局部最优解从而达到全局寻优的目的[32]。下面直接给出由SA算法对磁化率进行反演建模的流程,如图7所示。
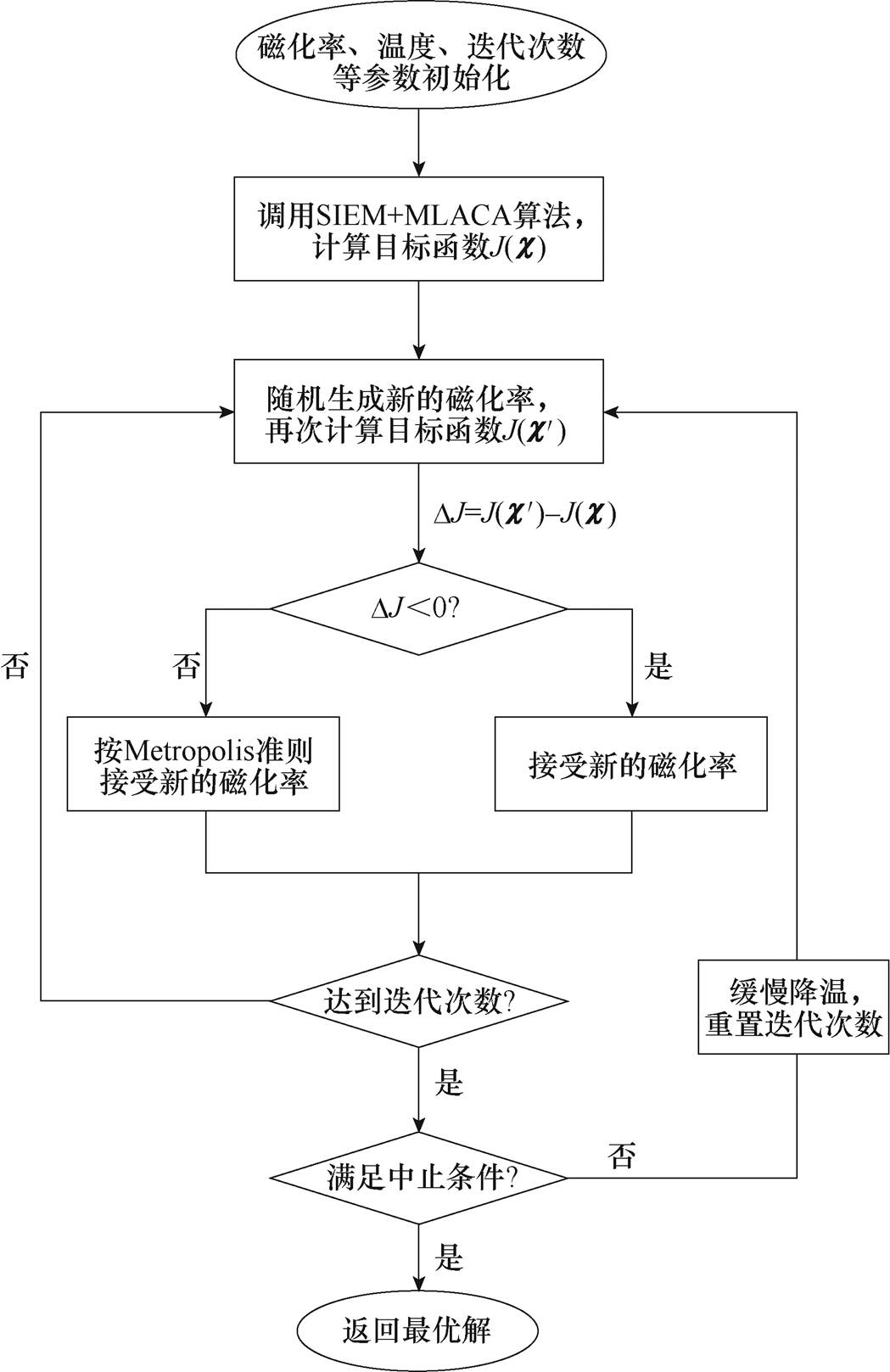
图7 模拟退火法用于反演磁化率的流程
Fig.7 The flow of magnetic susceptibility inversion using simulated annealing method
将SIEM+MLACA方法获得的铁质球壳磁场三分量作为输入,使用SA算法对铁磁球壳的磁化率进行反演优化,使用和不使用约束条件前后的磁化率光滑度对比结果如图8所示。可以看出,增加了5%的光滑度约束之后,相邻单元的磁化率过渡更加平滑,说明了约束方程的作用。
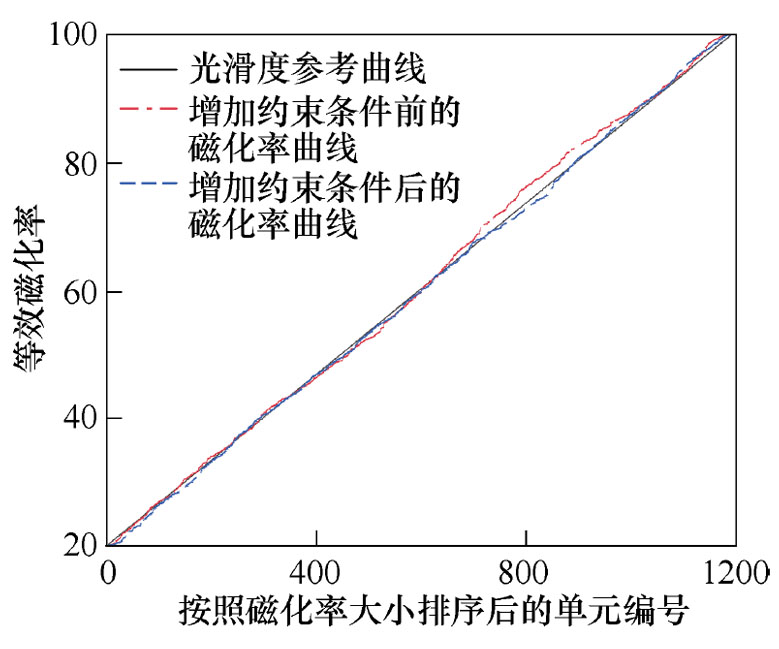
图8 优化前后的磁化率曲线光滑度对比
Fig.8 The comparison of the smoothness of magnetic susceptibility curves before and after optimization
基于反演优化得到的等效磁化率对球壳在25 m深度的五条测线的磁场进行预测,结果如图9所示。与“真实磁化率”计算得到的磁场解析值进行对比,预测磁场的平均相对误差仅为2.2%,证明所获取的等效磁化率是相对准确的。
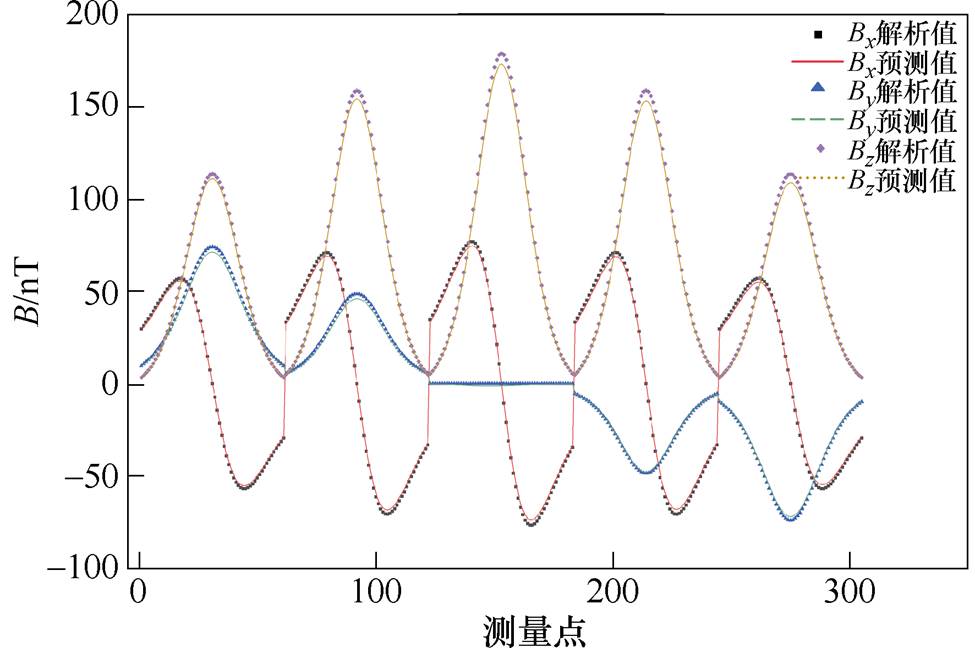
图9 基于等效磁化率的球壳模型磁场预测值和解析值比较(左舷-龙骨-右舷)
Fig.9 The comparison of predicted magnetic field values based on equivalent magnetic susceptibility and analytical magnetic field values of spherical shell model (port-keel-starboard)
为验证所提出的等效磁化率反演优化方法在工程上的实用,以一磁性参数未知的缩比船模(见图1)为试验研究对象,通过测量其感应磁场求解得到等效磁化率分布,并将其用于预测其他深度的感应磁场,从而验证等效磁化率的稳定性。
船模磁场测量示意图如图10所示,船模长度为L=2.75 m,宽度为W=0.5 m,厚度为e=0.8 mm,在船模下方设置上层磁传感器阵列z1和下层磁传感器阵列z2,分别作为磁场测量平面和磁场预测平面。此外,为了排除环境磁场的影响,在远离船模的地方设置了单个传感器用于监测环境磁场的变化,所使用的传感器为高精度三分量磁通门传感器,测量分辨率为1 nT。船模所在试验环境的磁场水平分量为34 200 nT,垂向分量为35 000 nT,通过逐点测量法获取船模下方的垂向感应磁场,测量点的范围为x∈[-L, L],步长为L/60;y∈[-W, W],步长为W;z1=1.3 W,z2=2 W。
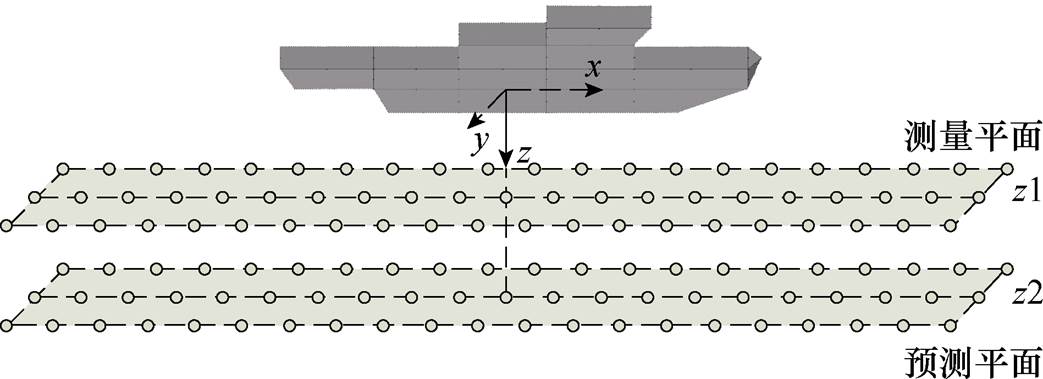
图10 磁性船模测量磁场测量示意图
Fig.10 The schematic diagram of magnetic field measurement experiment of magnetic ship model
在兼顾计算时间和磁场精度的前提下,将试验船模几何模型离散为3 988个三角形单元,1 835个节点。使用SA算法进行等效磁化率反演优化求解时,设定参数如下:初始温度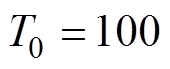 ,温度衰减系数
,温度衰减系数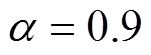 ,最大迭代次数和每个温度下的迭代次数均为
,最大迭代次数和每个温度下的迭代次数均为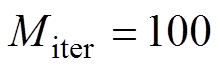 ,容差
,容差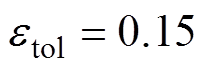 。一般用于制作缩比船模的钢材磁导率大致在100~180之间,因此本文选择的磁化率范围是
。一般用于制作缩比船模的钢材磁导率大致在100~180之间,因此本文选择的磁化率范围是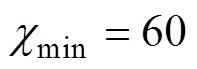 ,
,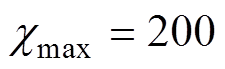 。
。
将船模在z1平面测量的磁场值作为输入,通过反演优化模型求解得到其等效磁化率分布,根据磁场拟合值判断等效磁化率是否合理,然后将其用于预测z2平面的船模磁场。船模在z1平面的磁场拟合效果和z2平面的磁场预测值和实测值的对比结果如图11所示。
由图11看出,磁场拟合值和预测值都和实测值比较吻合,其误差分别为5.1%和4.8%,表明本文所提出方法得到的等效磁化率是有效的,可用于舰船感应磁场的高精度建模。从整个测量和计算的过程来看,试验结果的误差主要来源以下方面:
(1)测量误差:主要包括测传感器自身的测量误差、使用逐点测量法测量船磁时的人为操作引入的误差以及试验环境变化带来的偶然误差。
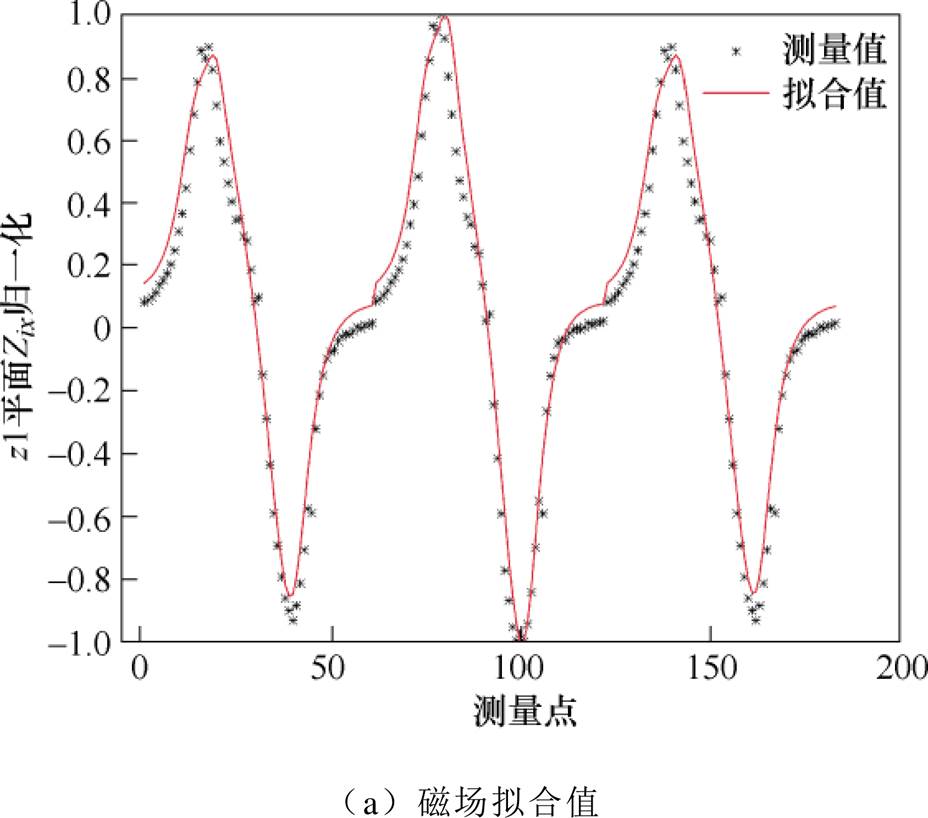
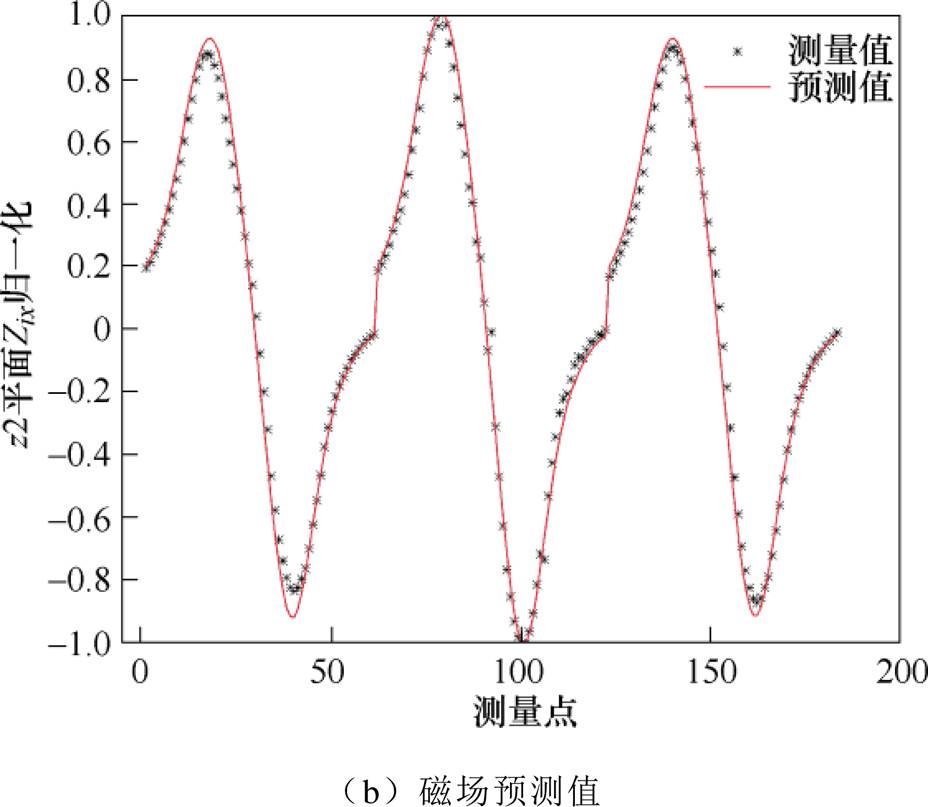
图11 磁性船模磁场拟合值和磁场预测值与实测值比较(左舷-龙骨-右舷)
Fig.11 The comparison of fitting and predicted magnetic field values with measured values of magnetic ship model (port-keel-starboard)
(2)计算误差:考虑到计算时间不宜过长,船模的剖分单元不能无限多,但理论上只有离散单元足够小、足够多时,每个单元才可以被看作均匀磁化体,但是这种做法会导致计算量急剧增加。
(3)模型误差:船模受地磁场磁化时,实际磁化率仍会有微小变化,但是本文为了求解等效磁化率,认为磁化率在弱磁环境中基本不变,这种线性化处理方式引入了误差。
本文首先提出了一种结合多层自适应交叉近似算法的改进型标量积分方程法,用于快速高效获取高精度的舰船感应磁场。其次通过建立以磁场拟合度、磁化率先验分布和平滑约束条件为目标函数的等效磁化率反演模型,并使用模拟退火算法进行优化求解,解决了工程中铁磁物体磁化率不易获取的难题,得出以下结论:
1)球壳数值仿真表明,所提出的铁磁物体感应磁场正演模型高效准确。当几何模型的网格密度较小时,基于MLACA法的标量积分方程法微弱提高了磁场计算精度;随着网格密度增大,该方法在保持计算精度的同时,大幅减少了计算时间和计算机的内存消耗。
2)球壳数值仿真和缩比船模试验研究结果表明,等效磁化率反演模型有效可行,其中船模试验结果的磁场拟合误差和预测误差约为5.0%,表明所提出的感应磁场正演模型和等效磁化率反演优化模型可以用于大型舰船的高精度磁场建模,能够为舰船铁磁设备安装位置的确定和消磁绕组的设计提供 依据。
参考文献
[1] Holmes J J. Reduction of a ship's magnetic field signatures[M]. Maryland, USA: Morgan & Claypool Publishers, 2008.
[2] 刘大明. 舰船消磁理论与方法[M]. 北京: 国防工业出版社, 2011.
[3] 郭成豹, 殷琦琦. 舰船磁场磁单极子阵列法建模技术[J]. 物理学报, 2019, 68(11): 106-115.
Guo Chengbao, Yin Qiqi. Magnetic monopole array model for modeling ship magnetic signatures[J]. Acta Physica Sinica, 2019, 68(11): 106-115.
[4] 戴忠华, 周穗华, 张晓兵. 多目标优化的舰船磁场建模方法[J]. 物理学报, 2021, 70(16): 147-159.
Dai Zhonghua, Zhou Suihua, Zhang Xiaobing. Multi- objective optimization of ship magnetic field mode- ling method[J]. Acta Physica Sinica, 2021, 70(16): 147-159.
[5] 刘琪, 孙兆龙, 姜润翔, 等. 一种舰船下方磁场的信号重构及换算方法[J]. 电工技术学报, 2022, 37(15): 3723-3732.
Liu Qi, Sun Zhaolong, Jiang Runxiang, et al. A signal reconstruction and conversion method of magnetic field under ship[J]. Transactions of China Electro- technical Society, 2022, 37(15): 3723-3732.
[6] 刘芙妍, 颜冰. 磁偶极子阵列模型的适用性研究与优化分析[J]. 物理学报, 2022, 71(12): 36-48.
Liu Fuyan, Yan Bing. Applicability and optimization analysis of magnetic dipole array model[J]. Acta Physica Sinica, 2022, 71(12): 36-48.
[7] 徐庆林, 王向军, 张建春, 等. 921A钢板腐蚀电场的Frumkin修正[J]. 电工技术学报, 2020, 35(14): 2951-2958.
Xu Qinglin, Wang Xiangjun, Zhang Jianchun, et al. Frumkin correction of corrosion electric field gen- erated by 921A steel[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 2951-2958.
[8] 饶凡, 吴旭升, 高嵬, 等. 两极永磁电机静态内外磁场研究[J]. 电工技术学报, 2021, 36(14): 2936- 2944.
Rao Fan, Wu Xusheng, Gao Wei, et al. Study on internal and external magnetic field of static two-pole permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2936-2944.
[9] Chadebec O, Coulomb J L, Janet F. A review of magnetostatic moment method[J]. IEEE Transactions on Magnetics, 2006, 42(4): 515-520.
[10] Fan Mingwu, Shao Hanguang, Wang Jingguo. Some experiences of using integral equation method to calculate magnetostatic fields[J]. IEEE Transactions on Magnetics, 1985, 21(6): 2185-2187.
[11] 倪振群, 蔡雪祥, 翁行泰. 舰船主甲板模型感应磁场的计算[J]. 上海交通大学学报, 1996, 30(7): 83-88.
Ni Zhenqun, Cai Xuexiang, Weng Xingtai. Com- putation of inductive magnetic field induced by vessel’s main deck model[J]. Journal of Shanghai Jiaotong University, 1996, 30(7): 83-88.
[12] 周国华, 肖昌汉, 刘胜道, 等. 基于六面体单元表面磁场积分法求解三维静磁场[J]. 电工技术学报, 2009, 24(3): 1-7.
Zhou Guohua, Xiao Changhan, Liu Shengdao, et al. 3D magnetostatic field computation with hexahedral surface integral equation method[J]. Transactions of China Electrotechnical Society, 2009, 24(3): 1-7.
[13] 郭成豹, 刘大明. 薄钢壳物体磁特征建模研究[J]. 兵工学报, 2012, 33(8): 912-915.
Guo Chengbao, Liu Daming. Modeling of magnetic signatures of thin-sheet objects[J]. Acta Armamentarii, 2012, 33(8): 912-915.
[14] 朱武兵, 庄劲武, 赵文春, 等. 载体感应磁场的改进积分方程法[J]. 国防科技大学学报, 2018, 40(3): 101-106.
Zhu Wubing, Zhuang Jinwu, Zhao Wenchun, et al. Modified integral equation method for carrier’s induced magnetic field solving[J]. Journal of National University of Defense Technology, 2018, 40(3): 101- 106.
[15] 何保委, 周国华, 刘胜道, 等. 标量磁位积分方程法计算舰艇三维静磁场[J/OL]. 兵工学报, 2022, http://kns.cnki.net/kcms/detail/11.2176.TJ.20221027.1405.004.html.
He Baowei, Zhou Guohua, Liu Shengdao, et al. Ship’s 3D magnetostatic field computation utilizing integral equation method of scalar magnetic potential[J]. Acta Armamentarii, 2022, http://kns.cnki.net/kcms/detail/ 11.2176.TJ.20221027.1405.004.html.
[16] 郭成豹, 张晓锋, 肖昌汉, 等. 薄钢板船舶磁性的物理模型和数值模拟混合建模[J]. 哈尔滨工程大学学报, 2008, 29(3): 247-250.
Guo Chengbao, Zhang Xiaofeng, Xiao Changhan, et al. Magnetization determination of ships made of thin steel sheets by combining the physical model and numerical calculations[J]. Journal of Harbin Engin- eering University, 2008, 29(3): 247-250.
[17] 周国华, 肖昌汉, 闫辉, 等. 一种弱磁作用下铁磁物体感应磁场的计算方法[J]. 哈尔滨工程大学学报, 2009, 30(1): 91-95.
Zhou Guohua, Xiao Changhan, Yan Hui, et al. A method to calculate the induced magnetic field of ferromagnetic objects in a weak magnetic field[J]. Journal of Harbin Engineering University, 2009, 30(1): 91-95.
[18] Trowbridge C W. Progress in magnet design by computer[C]//Proceedings of 4th Conference Mag- netostatic Technology, NewYork, USA, 1972: 555- 565.
[19] Chadebec O. Modelling of magnetic field induced by shells-identification of the magnetisation application to the closed loop degaussing of a ferromagnetic hull[D]. Grenoble, France: Institut National Polyte- chnique de Grenoble, 2001.
[20] Guerin S. Magnetic source identification measurement robustness and optimization- application to ship magnetization reconstruction[D]. Grenoble, France: Institut National Polytechnique de Grenoble, 2005.
[21] Vuillermet Y. Closed loop degaussing applied to double hull submarine Magnetization identification from near magnetic field measurements[D]. Grenoble, France: Institut National Polytechnique de Grenoble, 2008.
[22] Le-Van V. Developement of magnetostatic volume integral formulations[D]. Grenoble, France: Univer- site Grenoble Alpes, 2015.
[23] Chavin-Collin G, Bannwarth B, Cavallera D, et al. An integral face formulation for thin non-conductive magnetic regions[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-4.
[24] Chavin-Collin G. Identification de l’aimantation de tôles ferromagnétiques soumises à des champs magnétiques faibles et à de fortes contraintes mécaniques: application à l’immunisation magnétique des sous-marins en boucle fermée[D]. Grenoble, France: Universite Grenoble Alpes, 2020.
[25] 谢德馨, 杨仕友. 工程电磁场数值分析与优化设计[M]. 2版. 北京: 机械工业出版社, 2017.
[26] Le-Van V, Bannwarth B, Carpentier A, et al. The adaptive cross approximation technique for a volume integral equation method applied to nonlinear magnetostatic problems[J]. IEEE Transactions on Magnetics, 2014, 50(2): 445-448.
[27] 周耀忠, 张国友. 舰船磁场分析计算[M]. 北京: 国防工业出版社, 2004.
[28] 陈杰, 鲁习文. 舰船感应磁场预测的一种新方法[J]. 物理学报, 2010, 59(1): 239-245.
Chen Jie, Lu Xiwen. A new method for predicting the induced magnetic field of naval vessels[J]. Acta Physica Sinica, 2010, 59(1): 239-245.
[29] 裴亚杰. 电磁场积分方程自适应交叉近似算法的研究[D]. 南京: 南京邮电大学, 2011.
[30] Vijn A R P J. Development of a closed-loop degaussing system towards magnetic unobservable vessels[D]. Delft, Netherlands: Delft University of Technology, 2021.
[31] 何保委, 刘胜道, 周国华, 等. 基于多目标模拟退火法的垂向检测线圈改进[J]. 华中科技大学学报(自然科学版), 2021, 49(12): 46-50.
He Baowei, Liu Shengdao, Zhou Guohua, et al. Improvement of vertical detecting coil based on multi-objective simulated annealing method[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2021, 49(12): 46-50.
[32] 陈龙, 易琼洋, 贲彤, 等. 全局优化算法在Preisach磁滞模型参数辨识问题中的应用与性能对比[J]. 电工技术学报, 2021, 36(12): 2585-2593, 2606.
Chen Long, Yi Qiongyang, Ben Tong, et al. Appli- cation and performance comparison of global optimization algorithms in the parameter identi- fication problems of the Preisach hysteresis model[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2585-2593, 2606.
Abstract Mastering the distribution of a ship’s induced magnetic field is an important issue for implementing magnetic stealth technology, and the integral equation method is one of the main methods to calculate the ship’s induced magnetic field. The integral equation method only needs to discretize the ferromagnetic region and does not need to consider the boundary conditions, so it has been widely concerned and applied. The traditional vector integral equation for modeling induced magnetic fields has the problems of low efficiency and an enormous computational burden. Considering that there are many discrete elements of large ferromagnetic objects such as ships, the coupling coefficient between elements forms a huge asymmetric dense matrix. As a result, the computing time and memory requirement will increase sharply with the increase of the number of elements. Therefore, a scalar magnetic potential integral equation method based on surface elements is proposed. Since the integral equation method needs to obtain the magnetic susceptibility of ferromagnetic materials, the equivalent magnetic susceptibility inversion model is established based on a multi-level adaptive cross approximation (MLACA) algorithm.
Firstly, the scalar magnetic potential integral formula based on triangular surface elements is derived. According to the principle of linear interpolation, the scalar magnetic potential of the center point of discrete elements is expressed by interpolation function and node scalar magnetic potential, and the elements’ coupling coefficient matrix is obtained by establishing a local coordinate system. Therefore, the scalar integral method of surface elements is obtained for solving the ship’s induced magnetic field. Secondly, the MLACA algorithm is introduced to guarantee the accuracy of magnetic field calculation and reduce the memory requirement and computing time of the computer. Finally, aiming at the problem that the magnetic parameters of ferromagnetic materials of ships are not easy to obtain, a magnetic susceptibility inversion model is established based on the measured magnetic field values and the forward coupling model. The magnetic field fitting degree, prior distribution of magnetic susceptibility, and smooth constraint are the objective function. The spatial distribution of equivalent magnetic susceptibility is optimized by simulated annealing (SA) algorithms.
A numerical simulation of the spherical iron shell shows that the proposed scalar magnetic potential coupling forward modeling method can efficiently obtain the ship’s induced magnetic field with high precision. For the same discrete elements, compared with the vector method, the scalar method can save about 97% of the memory consumption and 65% of the computing time, which verifies the effectiveness of the scalar magnetic potential integral equation method based on the MLACA algorithm. According to the inversion model, the equivalent magnetic susceptibility of the spherical iron shell is optimized by the SA algorithm, which is utilized to predict the spherical shell of other positions, and the average relative error is only 2.2%. After using of smooth constraint condition, the equivalent magnetic susceptibility obtained is smoother.
In order to verify the practicability of the proposed forward modeling method and magnetic susceptibility inversion method in engineering, an experimental scheme was designed for a reduced-scale ship model with unknown magnetic parameters. Firstly, the equivalent magnetic susceptibility distribution of the ship model is obtained by measuring the magnetic field of the ship model at the z1 plane, and it is used to predict the induced magnetic field at the z2 plane. The magnetic field fitting and prediction errors of the ship are about 5.0%, indicating that the proposed forward modeling model of induced magnetic field and the inverse optimization model of equivalent magnetic susceptibility can be used for induced magnetic field modeling of large ships with high precision and can provide support for the implementation of magnetic stealth technology on ships.
keywords:Ship magnetic field, reduced scalar magnetic potential, multi-level adaptive approximate cross, simulated annealing method, equivalent magnetic susceptibility
DOI: 10.19595/j.cnki.1000-6753.tces.222204
中图分类号:TM153
国家自然科学基金资助项目(51377165, 52207020)。
收稿日期 2022-11-22
改稿日期 2022-12-29
何保委 男,1995年生,博士研究生,研究方向为电磁环境与防护技术。E-mail: hebaowei188@163.com
刘月林 女,1989年生,硕士,讲师,研究方向为电磁环境与防护技术。E-mail: mooncake1024@163.com(通信作者)
(编辑 陈 诚)