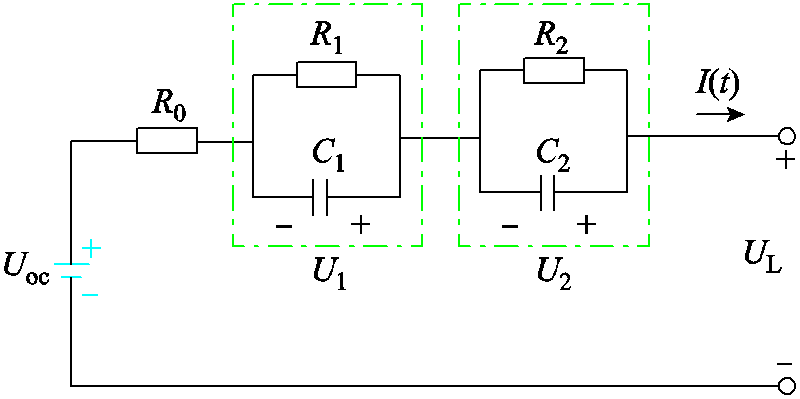
图1 锂离子二阶RC电池等效电路模型
Fig.1 Second-order RC equivalent circuit model of lithium-ion battery
摘要 传统最小二乘法（LS）用于锂离子电池模型在线参数辨识精度低，通过带遗忘因子递推最小二乘算法能够有效地提高辨识精度，但固定的遗忘因子影响模型动态特性。遗忘因子的自适应处理能提高算法对动态系统的参数辨识能力，而目前的自适应方法容易忽略模型参数的稳定性，同时方法待定系数范围较大且难以确认。为了得到高精度且稳定性良好的模型参数，该文设计了一种精度和稳定性兼优且更简单的自适应遗忘因子递推最小二乘（AFFRLS）改进方法，并与其他AFFRLS、可变遗忘因子递推最小二乘（VFFRLS）进行仿真对比分析。结果表明，改进的AFFRLS能够在模型精度和参数稳定性取得更好的平衡，且对不同的在线工况具有良好的适用性。
关键词：锂离子电池模型 参数辨识 最小二乘法 自适应遗忘因子
锂离子电池为新能源汽车提供主要动力来源，具有能量密度大、输出电压高等特点。实际应用中，掌握电池荷电状态（State of Charge, SOC）对电池的管理和控制至关重要。锂电池充放电过程具有动态非线性特性，内部伴随着复杂的电化学反应，并受到外部因素的影响，导致准确地估算SOC成为难题[1]。
目前国内外学者通过模型方法模拟电池内部电动力过程和电化学反应过程，常见的模型有：等效电路模型（Equivalent Circuit Model, ECM）[2-3]、电化学模型（Electrochemical Model, EM）[4]、电化学阻抗模型（Electrochemical Impedance Model, EIM）[5]。其中EM模拟准确度更高，但结构复杂，估算参数较多；ECM由电压源、电阻、电容组合表示，结构比EM简单；EIM模拟电池动态特性良好，但参数的获取依赖精密仪器，难以在线应用。综合模拟精度和模型复杂度，二阶RC等效电路模型常被用来研究电池内部电动力过程和电化学反应过程。获得高精度的模型参数是建立模型的关键，辨识模型参数有离线和在线辨识方法[6]。离线方法通过实验获取模型参数，但参数结果难以反映电池时变特性；在线方法利用电池工况测量的端电压和输出电流，通过算法辨识模型参数，辨识结果精度更高，动态特性良好。
常见的在线参数辨识算法有遗传算法（Genetic Algorithm, GA）[7]、递推最小二乘算法（Recursive Least Square, RLS）[8]、粒子群算法（Particle Swarm Optimization, PSO）[9]、扩展卡尔曼滤波（Extended Kalman Filter, EKF）[10]等。其中，GA辨识精度和收敛速度与算法参数有关，算法易陷入局部最优。RLS结构简单，但辨识误差较大。PSO用于参数辨识，与RLS和EKF相比，准确度较低[11]。而EKF需要计算雅可比矩阵，计算量较大。为了进一步提高RLS辨识精度，不少研究对RLS进行了优化。例如，带遗忘因子最小二乘（Forgetting Factor Recursive Least Square, FFRLS）通过遗忘因子来调整新旧数据的比例，降低旧数据占比，加快算法收敛速度[1,12]。基于傅里叶变换的偏置补偿递推最小二乘对系统噪声进行补偿[13]，精度较高，但收敛速度不及FFRLS。用于分数阶的重复预测递推最小二乘，通过修正分数阶导数的近似误差，来提高辨识精度，算法结构复杂[14]。解耦加权递推最小二乘将模型的快、慢动态参数进行辨识[15]，计算量比FFRLS大。递推扩展最小二乘[16]引入遗忘因子和噪声估计，但结构比FFRLS复杂。FFRLS用于在线参数辨识，精度高，结构简单，易于在微控制器实现应用。电池充放电过程中的电压电流动态变化，固定的遗忘因子影响参数辨识结果的时变性和辨识精度。因此，对遗忘因子作动态处理，通过改变遗忘因子的权重来适应系统的动态变化[17]，文献[18]提出了可变遗忘因子递推最小二乘（Variable Forgetting Factor Recursive total Least Squares, VFFRLS），通过修正误差实时改变遗忘因子大小。文献[19]通过模拟退火算法优化FFRLS，实现遗忘因子动态变化，但计算较为复杂。文献[20]设计了一种自适应表达式，通过修正误差对遗忘因子作自适应处理，与VFFRLS对比有更高的精度和响应速度。文献自适应遗忘因子最小二乘（Adaptive Forgetting-Factor Least Square, AFFRLS）方法中的待定系数影响算法对误差的跟踪能力，其待定系数取值范围较大，给实际应用带来一定困难。且现有自适应方法容易忽略模型的参数稳定性，而辨识参数波动过大容易引起算法发散。因此，本文设计了一种精度和稳定性兼优且更简单的自适应遗忘因子递推最小二乘改进方法。
本文在锂离子电池二阶RC等效电路模型的基础上，首先通过电池动态应力测试（Dynamic Stress Test, DST）、美国联邦城市运行工况（Federal Urban Driving Schedule, FUDS）动态工况数据，分析缓变与剧变工况下不同遗忘因子对FFRLS辨识参数稳定性和精度的影响；然后利用固定遗忘因子值的FFRLS仿真表现，选择合适的遗忘因子取值范围；再将本文改进的AFFRLS用于在线参数辨识，通过两种不同动态工况验证算法的辨识精度和参数稳定性；最后将本文改进的AFFRLS与文献提及的VFFRLS[18]、自适应遗忘因子递推最小二乘[20]进行对比分析。仿真结果表明，本文改进的AFFRLS在不同工况具有良好的适用性，在缓变和剧变工况下的精度都优于文献[18,20]中自适应遗忘因子最小二乘方法，且参数稳定性优于FFRLS取固定遗忘因子λ值为0.980、0.985的辨识结果。
ECM通过电压源、电阻和电容的组合建立物理模型，模拟电池内部复杂的电化学现象。选择的二阶RC等效电路模型包括电压源、内阻、两个RC并联网络。锂离子二阶RC电池等效电路模型如图1所示[20]。图1中，Uoc为开路电压，UL为端电压，I(t)为输出电流，R0为内阻；R1、C1分别为电化学极化电阻和电化学极化电容，其乘积表示电池内部动态特性较长的时间常数；R2、C2分别为浓差极化电阻和浓差极化电容，其乘积表示电池动态特性较短的时间常数。模型在电池放电时I(t)为正，充电时为负。
图1 锂离子二阶RC电池等效电路模型
Fig.1 Second-order RC equivalent circuit model of lithium-ion battery
由基尔霍夫定律，等效电路可表示为
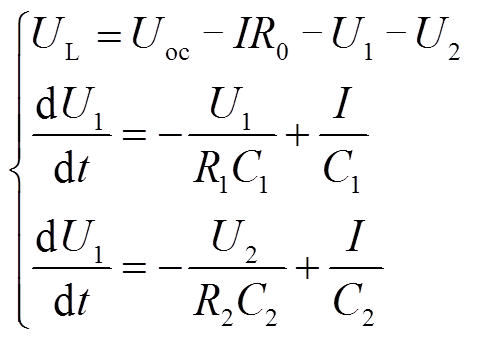（1）
对式（1）进行拉氏变换得到
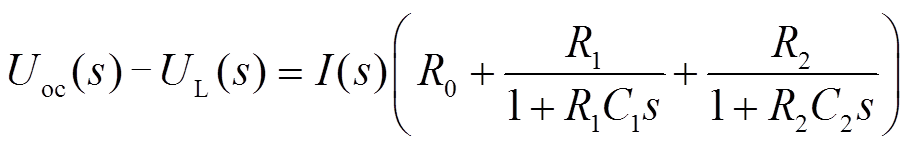（2）
令时间常数τ1=R1C1、τ2=R2C2，化简得
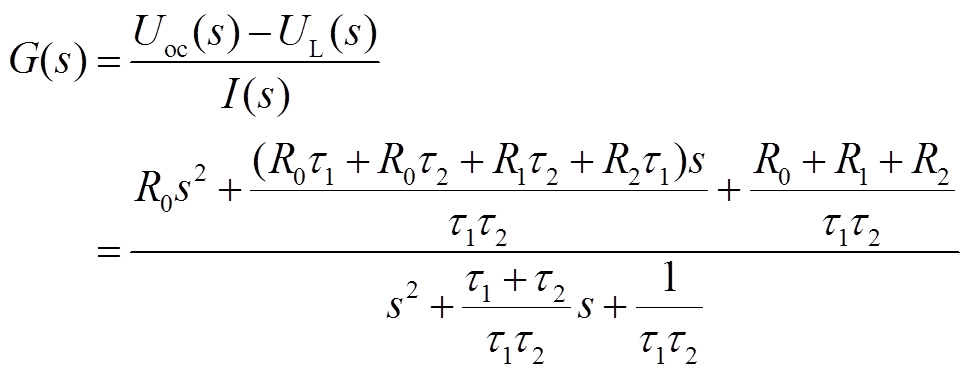（3）
进一步作双线性变换，令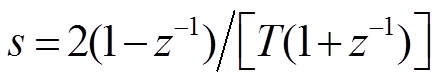
，得到离散传递函数为
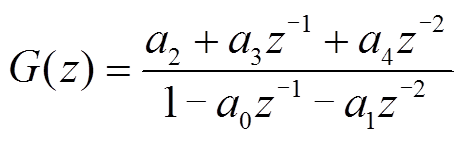（4）
式中，а0、а1、а2、а3、а4为常数。
LS方法简单，计算耗时短，辨识易于实现，目前在线性系统、非线性系统均有应用。算法核心是使预测数据和实际数据之间误差平方和最小[18]。算法简单描述如下。
对于线性系统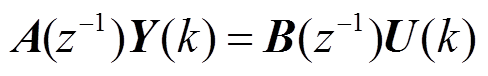
，其中Y(k)为系统输出，U(k)为系统输入，该系统差分方程表示为
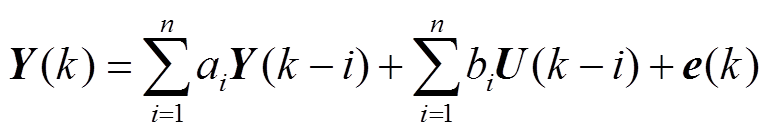（5）
式中，e(k)为系统测量误差向量。
令待估计参数向量为
θ(k)=[a1 a2 … an b1 b2 … bn]T
输入数据量为
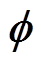(k)=
[Y(k-1) Y(k-2) … Y(k-n) U(k-1) U(k-2) … U(k-n)]T
将式（5）写成最小二乘形式为
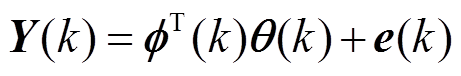（6）
经过N次观测，取评价指标函数J为
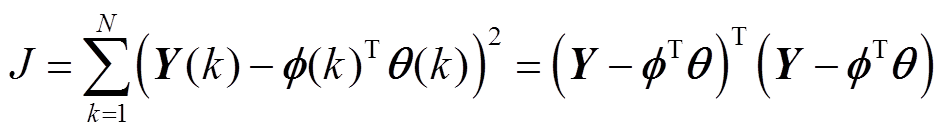
为得到参数向量LS最优估计值，取J最小，令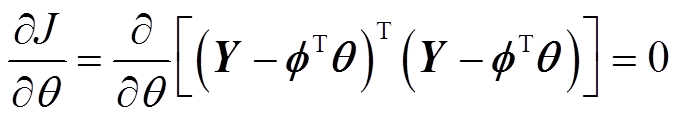
，则
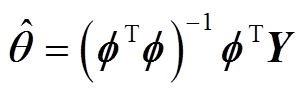（7）
当输入数据量较大时，常把式（7）用递推形式表示，即递推最小二乘（RLS），表达式为
（8）
式中，Kk为增益；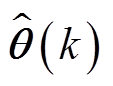
为k时刻估计值；P(k)为误差协方差；I为单位矩阵。
令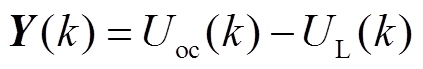
，二阶RC等效电路模型的差分方程表示为
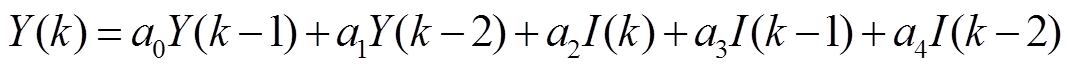（9）
则模型参数关系为最小二乘式，可表示为
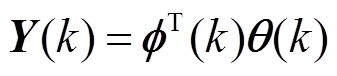（10）
将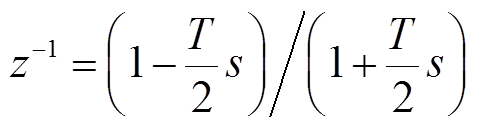
代入式（4），并与式（3）对比得到参数关系式（11），
、
、
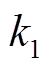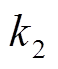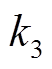为中间变量，即
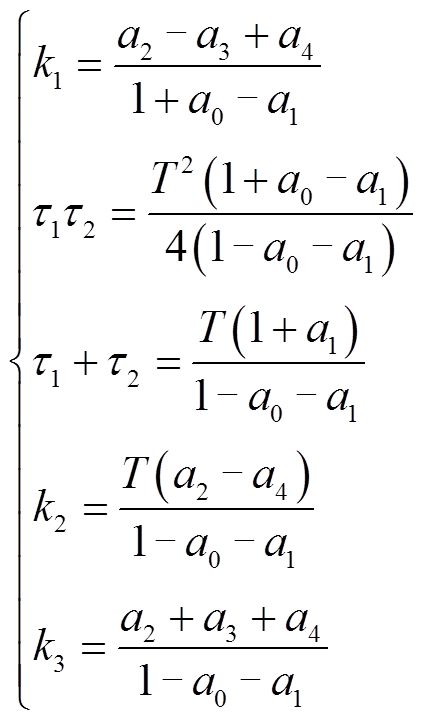（11）
由式（11）得到模型参数表达式为
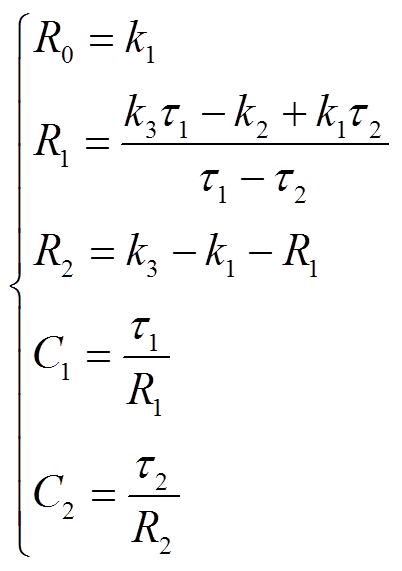（12）
传统RLS辨识模型参数时，随着递推过程旧数据不断累积，新数据的修正作用受到影响。为了降低旧数据的比例，引入遗忘因子λ，FFRLS表达式为
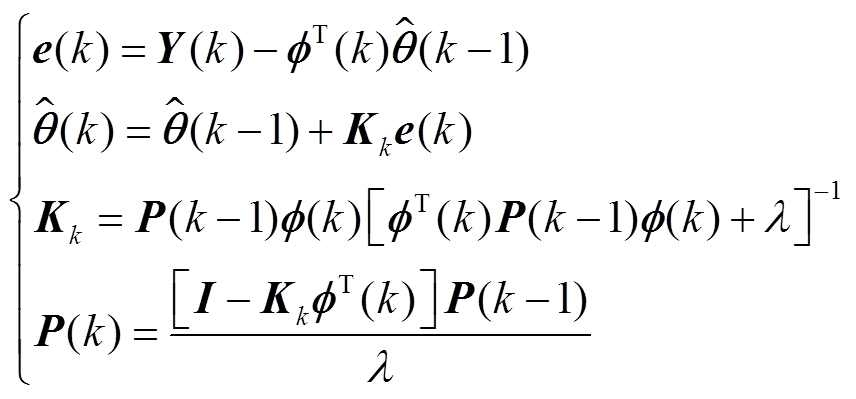（13）
式中，e(k)为预测误差。λ取值范围一般在0.95～1，当λ=1时，算法回到最初的RLS。
当e(k)较小时，说明辨识结果接近真实值，此时希望提高参数稳定性；当e(k)较大时，算法对系统跟踪能力较差，需要降低λ值来提高算法精度，加快算法收敛速度。自适应方法将λ值随系统动态变化而变化，能有效提高算法对动态系统时变参数的跟踪能力和算法精度。
文献[18]基于可变遗忘因子策略，提出了一种VFFRLS算法，根据误差大小变化来调整λ值。λ值更新表达式为
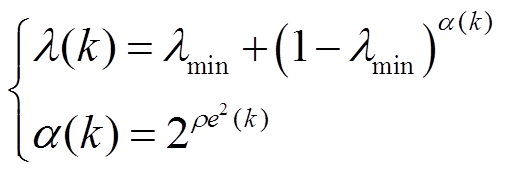（14）
式中，ρ为待定系数，ρ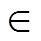
[104, 5×104]；λmin为预期最小λ值。
当e2(k)趋于0时，λ值趋于1；当e2(k)趋于无穷时，λ值趋于λmin[18]。可变遗忘因子策略能够实现λ值自适应变化，且方法简单。但λ趋于最小值的速度受ρ值大小影响，对系数取值要求较高。ρ值与λmin取合理范围，其算法参数辨识效果会更好。
文献[20]提出的AFFRLS在e(k)大于预测允许误差时，λ值趋于λmin；相应地，小于预测允许误差时，λ值变大。表达式为
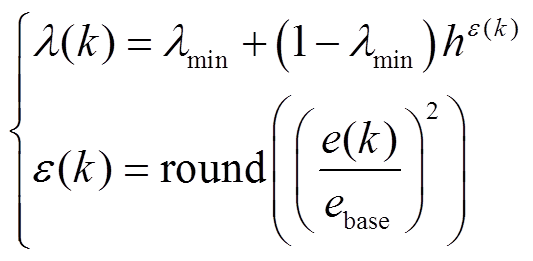（15）
式中，ebase为允许误差；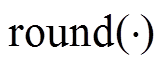
为取整函数；h为灵敏度系数，能够改变λ值对误差的敏感程度，取值在0和1之间。h接近1时，λ值变化速度缓慢，相对地，h越接近0，λ值变化速度越快。综合考虑快速性和准确性，h值一般取0.9[20]。
上述自适应方法容易忽略参数结果的稳定性问题，且参数待定系数需进一步确认。本文寻求算法辨识精度和稳定性的平衡，将在缓变和剧变工况数据下进行仿真分析。当e(k)较大时，希望λ值快速接近最小值，提高辨识精度；而e(k)在误差允许范围内，λ值应当趋于最大值，提高参数稳定性。为了实现上述目的，本文提出了一种新的改进AFFRLS，表达式为
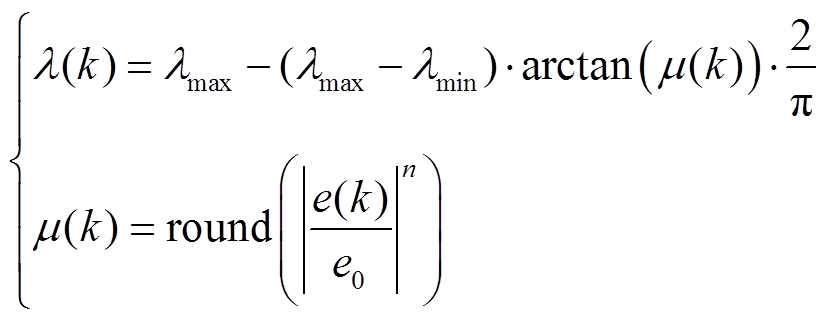（16）
式中，λmax为预期最大λ值。通过式（16）将λ值限制在最大、最小值之间，能取到最大值。e0为预设基准误差，当e(k)＜e0时，通过n次方将比值缩小，n一般取2或4，λ快速接近λmax；当e(k)＞e0时，比值将进一步被放大，加快趋于λmin的取值速度。取整函数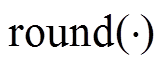能实现数值匹配的梯度变化，减少中间过渡值。
当修正误差e(k)与e0比值在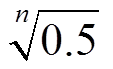
和1之间时，λ值为
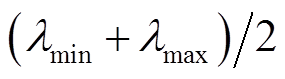；比值在0到
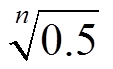时，λ值得到1；比值大于1时，λ取值范围在λmin和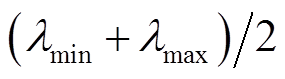之间梯度变化，且通过n次方将λ快速自适应变化接近λmin。与文献VFFRLS、文献AFFRLS相比，本文改进的AFFRLS避免了待定系数的选值过程，方法更为简单。
改进的AFFRLS参数辨识流程如图2所示。首先由测量数据组成f(k)，结合式（13）和式（10）计算增益、预测端电压及预测误差，并更新参数向量。将参数向量通过式（11）和式（12）计算得到模型参数，后由式（16）自适应更新算法λ值。
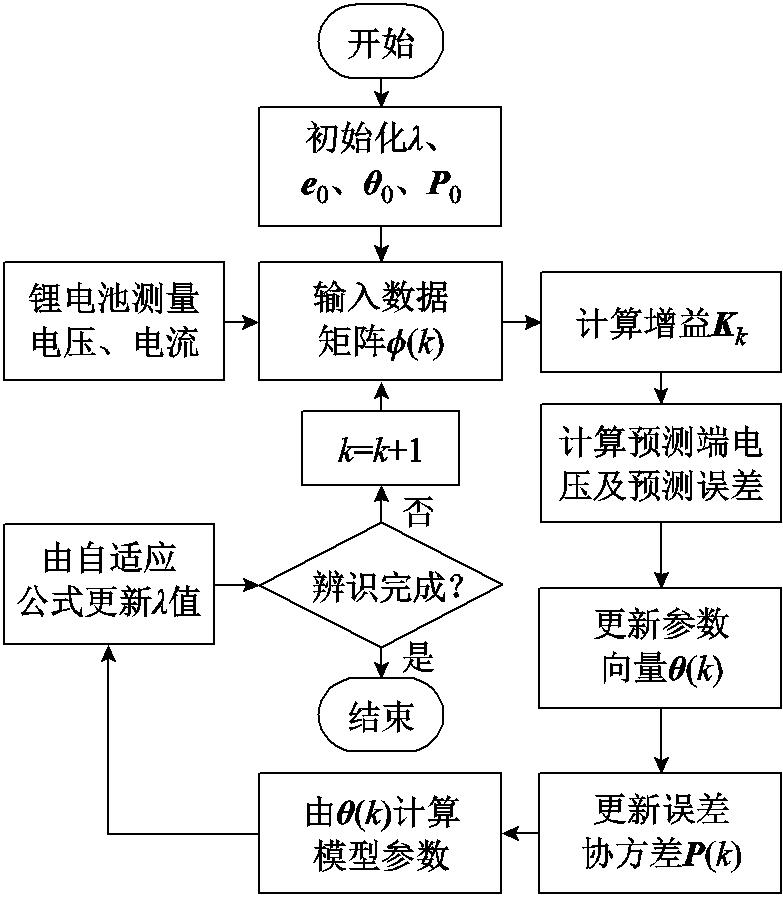
图2 改进AFFRLS方法参数辨识流程
Fig.2 Parameter identification flow chart of the improved AFFRLS
首先利用DST和FUDS工况数据对不同λ值下FFRLS进行在线参数辨识，分析缓变和剧变工况下不同λ值对辨识结果的影响。
本文数据集来自马里兰大学高级生命周期工程研究中心[21]，测试电池为18650镍钴锰酸锂/石墨锂离子单体电池，容量为2 A∙h，实验表明增量开路电压（Open Circuit Voltage, OCV）实验建立的OCV-SOC关系更准确，OCV-SOC仿真数据选取25℃增量OCV实验数据。选取25℃实验环境下DST、FUDS实验数据用于模型在线辨识。模型辨识精度通过实测端电压和模拟端电压的平均绝对误差（Mean Absolute Error, MAE）、方均根误差（Root Mean Squared Error, RMSE）和最大绝对误差值（Maximum absolute Error, ME）衡量。
选取的DST实验数据集在电池放电至SOC为80%基础上静置2 h，再以一定规律的充放电电流周期性循环模拟动态工况，单次循环时间为360 s。取遗忘因子λ分别为0.980、0.985、0.990、0.995、1，对DST实验数据进行仿真分析，参数辨识结果如图3所示。
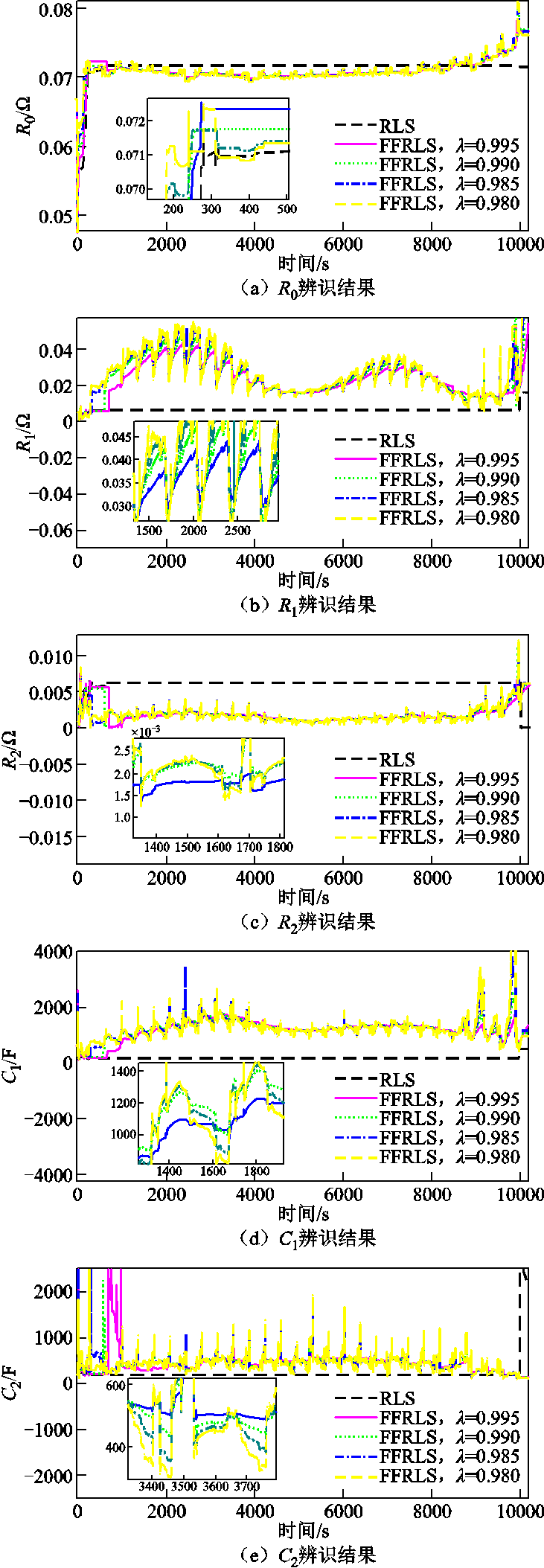
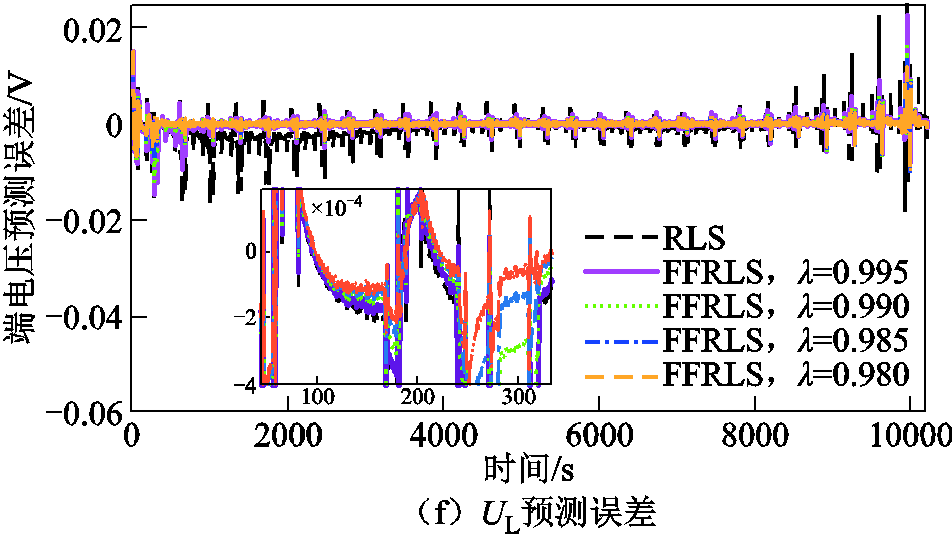
图3 DST工况下不同λ值参数辨识结果
Fig.3 Parameter identification results of different λ values via DST
由图3a～图3e参数辨识结果可知，λ=1时，图形趋于一条直线，参数稳定；λ=0.980时，算法最快收敛，整体上图形波动幅度最大，参数波动反映了模型参数随电压电流变化而变化的时变特性。其中图3a～图3e的图形趋势显示，随着λ值减小参数图形波动逐渐变大，参数稳定性下降。误差图3f为基于模型参数的预测端电压与实测端电压误差的时间变化曲线，可以看出，λ=0.980时误差分布最接近0点，λ=1时误差曲线在0点上下波动最明显。
估算端电压与实测端电压误差见表1。由表1可以得到，λ越接近1，误差越大；MAE随λ减小而减小，但从0.995到0.980变化逐渐不明显；RMSE随着λ减小而减小，变化幅度随之变小；最大误差随着λ减小而持续减小。从误差数据来看，λ越接近0.980，估计精度越高。λ减小时，旧数据在迭代过程的修正误差比重下降，新数据比重增加，算法对系统时变参数的跟踪能力得到加强。
表1 DST工况下端电压估算结果
Tab.1 Results of terminal voltage estimation via DST
辨识方法MAE/mVRMSE/mVME/V λ=0.9800.247 0 0.583 9 0.011 9 λ=0.9850.271 1 0.653 5 0.013 5 λ=0.9900.310 8 0.774 7 0.016 2 λ=0.9950.398 1 0.993 4 0.022 5 RLS1.6 2.5 0.046 1
从辨识结果来看，对于参数R0、R1、R2、C1、C2的辨识，随着λ减小，算法收敛速度加快，精度逐渐提高，参数时变特性更好。但参数波动过大易引起算法发散。可见取合适的λ值对参数估算有着重要意义。
FUDS实验是在电池满电状态放电至SOC为80%，后静置2 h，以1 372 s剧烈变化的充放电电流开展。FUDS相比DST工况电池动态变化更剧烈，通过FUDS工况数据验证不同λ值下FFRLS对复杂在线工况的辨识能力。
FUDS与DST工况辨识结果规律表现一致，图形在此省略。FUDS仿真显示，λ越小，收敛速度越快，参数曲线动态特性越明显，λ取0.980时误差分布最接近0点，而λ取1时误差波动最明显。
FUDS工况下端电压估算结果见表2，可知FUDS工况下不同λ值误差规律与DST工况下一致，整体上λ越小，误差越小。最大绝对误差在λ取0.980～0.990时无明显变化，此时取λ=0.990对系统电压电流剧烈变化跟踪能力较好。表2与表1对比可得，表2中MAE与RMSE数值更大，差值小于0.24 mV，说明对于急剧变化的系统，FFRLS估算精度有所下降。
表2 FUDS工况下端电压估算结果
Tab.2 Results of terminal voltage estimation via FUDS
辨识方法MAE/mVRMSE/mVME/V λ=0.9800.377 9 0.722 00.009 5 λ=0.9850.411 7 0.803 10.009 6 λ=0.9900.462 8 0.934 30.009 6 λ=0.9950.562 0 1.2 0.010 4 RLS1.8 2.5 0.030 8
由DST和FUDS仿真结果来看，对于不同动态工况，λ值减小，参数的精度得到提高，但稳定性有所下降。当修正误差较大时，通过减小λ值来增强算法对动态参数的跟踪能力；当修正误差较小时，应令λ值趋于1提高参数稳定性。对λ值动态匹配能够在算法辨识的精度和稳定性中寻求平衡，并能提高不同工况下的适用性。
第3节得到了不同λ值下FFRLS对在线参数辨识结果的影响规律，综合考虑精度和稳定性，λ值取0.980～1。本节对本文改进AFFRLS、文献[18]中VFFRLS、文献[20]中AFFRLS进行仿真分析。首先通过DST工况数据进行在线参数辨识，仿真结果如图4所示。
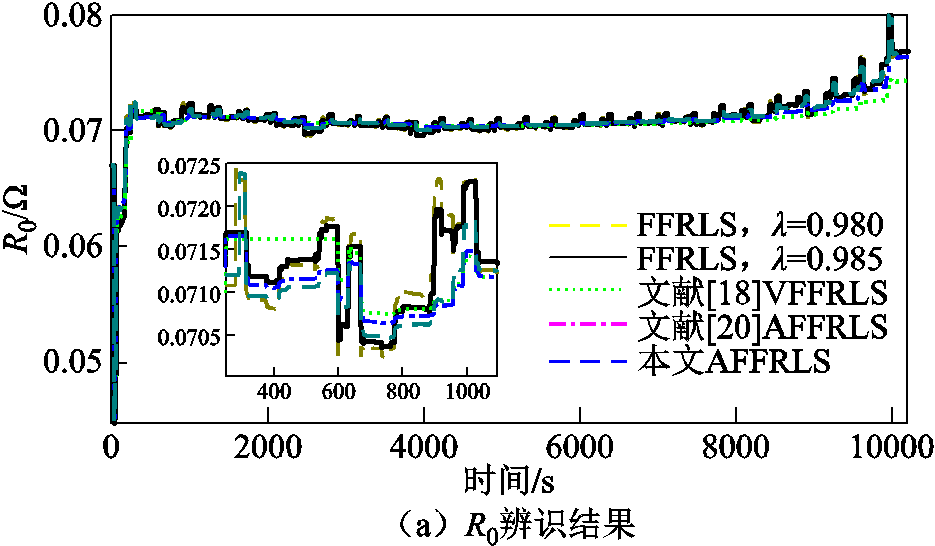
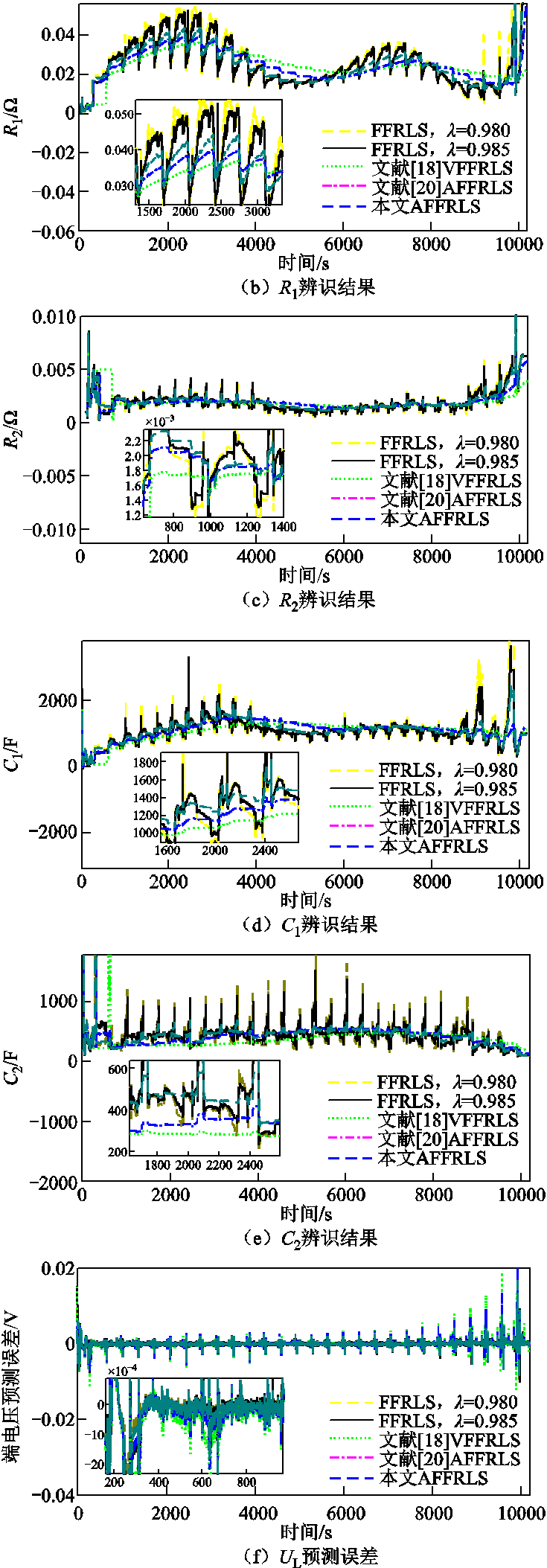
图4 DST工况下辨识参数对比
Fig.4 Comparison of identification parameters via DST
由图4a～图4e可以看出，VFFRLS图形走势最平缓，图形波动最小，参数动态特性较差；固定值下FFRLS方法参数波动最大。另由图4f中UL预测误差可知，估算前期和后期本文AFFRLS改进方法出现的误差峰值更小，误差波动小于文献方法。
图4f误差曲线中，在算法开始阶段，受参数初始值设定不当的影响，预测误差出现短暂波动，但随迭代过程逐渐得到修正。从276～8 898 s数据点，本文改进AFFRLS辨识绝对误差小于5 mV，大部分预测误差小于1 mV。电压、电流输入数据平稳性越差，误差短期内增大越明显。如在数据点1 383 s与1 384 s处，电流变化差值为3 A，1 384 s处本文改进AFFRLS预测端电压误差为-3.598 6 mV，文献AFFRLS为-3.944 1 mV，VFFRLS为-4.130 4 mV，本文改进AFFRLS较文献两种方法分别提高了8.8%、12.9%。算法后期锂电池荷电状态减小，电压、电流波动变大，误差明显增大。如数据点9 932 s和9 933 s差值为3.5 A，9 933 s处本文改进AFFRLS预测误差为16.854 0 mV，文献自适应FFRLS为25.685 0 mV，VFFRLS为38.483 1 mV，此时改进的AFFRLS预测误差比文献自适应FFRLS和VFFRLS分别提高34.4%和56.2%。可见数据平稳性下降时，本文AFFRLS辨识精度优于文献方法，有效地降低了算法对数据平稳性的依赖。
图4f在预测误差小于1 mV的时间段内，三种自适应方法趋于相同的最大λ值，此时三种自适应方法具有相似的辨识表现。以5 000～5 200 s数据点为例，该时间段内本文改进AFFRLS的预测端电压MAE为0.124 3 mV，ME为0.851 6 mV；文献自适应FFRLS的预测端电压MAE为0.138 5 mV，ME为0.894 6 mV；VFFRLS预测端电压MAE为0.146 3 mV，ME为0.931 1 mV。此时本文改进AFFRLS预测准确度较文献自适应FFRLS、VFFRLS仍得到提升，MAE分别提升了10.3%、15%，ME分别提升4.8%、8.5%。三种自适应方法整体辨识误差见表3。
表3 DST工况下变遗忘因子方法辨识误差对比
Tab.3 Identification error comparison of variable forgetting factor methods via DST
辨识方法MAE/mVRMSE/mVME/V 文献[19]VFFRLS0.373 6 0.926 4 0.038 5 文献[20]AFFRLS0.319 0 0.720 30.025 7 本文AFFRLS0.284 40.621 40.016 8
从表3可知，三种变遗忘因子方法中本文AFFRLS精度最高。由图4a～图4e可知，本文改进AFFRLS得到的模型参数动态特性优于文献自适应方法，其对动态系统的时变跟踪能力更强。与λ值为0.980和0.985的FFRLS参数图形对比，本文AFFRLS稳定性更好。因此，可以认为提出的方法具备较高的辨识准确度和良好的稳定性。
FUDS仿真结果如图5所示。从图5a～图5e可知，提出的AFFRLS辨识结果稳定性要优于λ值为0.980和0.985的FFRLS。图5f与图4f对比，FUDS较DST工况电压、电流变化更为剧烈，此时FUDS工况下端电压预测误差短期内出现增大较DST工况更加频繁。例如，电流在9 432 s和9 433 s差值为3.75 A，算法预测误差大幅增大。9 433 s处改进的AFFRLS预测误差为3.100 6 mV，文献自适应FFRLS为5.666 1 mV，VFFRLS为10.105 1 mV，此时本文改进AFFRLS预测误差比文献方法分别提高了45.3%、69.3%。FUDS工况下短期数据大幅变化时，本文改进AFFRLS辨识准确度仍优于文献两种自适应方法。
图5f中短期内三种方法取得相近的预测误差曲线，本文改进AFFRLS比文献方法仍有小幅度提升。以5 900～6 100 s数据点为例，本文改进AFFRLS端电压预测误差MAE为0.199 1 mV，ME为0.797 mV；文献自适应FFRLS对应MAE为0.226 7 mV，ME为0.808 3 mV；VFFRLS对应MAE为0.217 6 mV，ME为0.820 8 mV。该时间段本文改进AFFRLS端电压预测误差MAE较文献自适应FFRLS、VFFRLS分别提升了12.2%、8.5%，ME分别提升1.4%、2.9%。
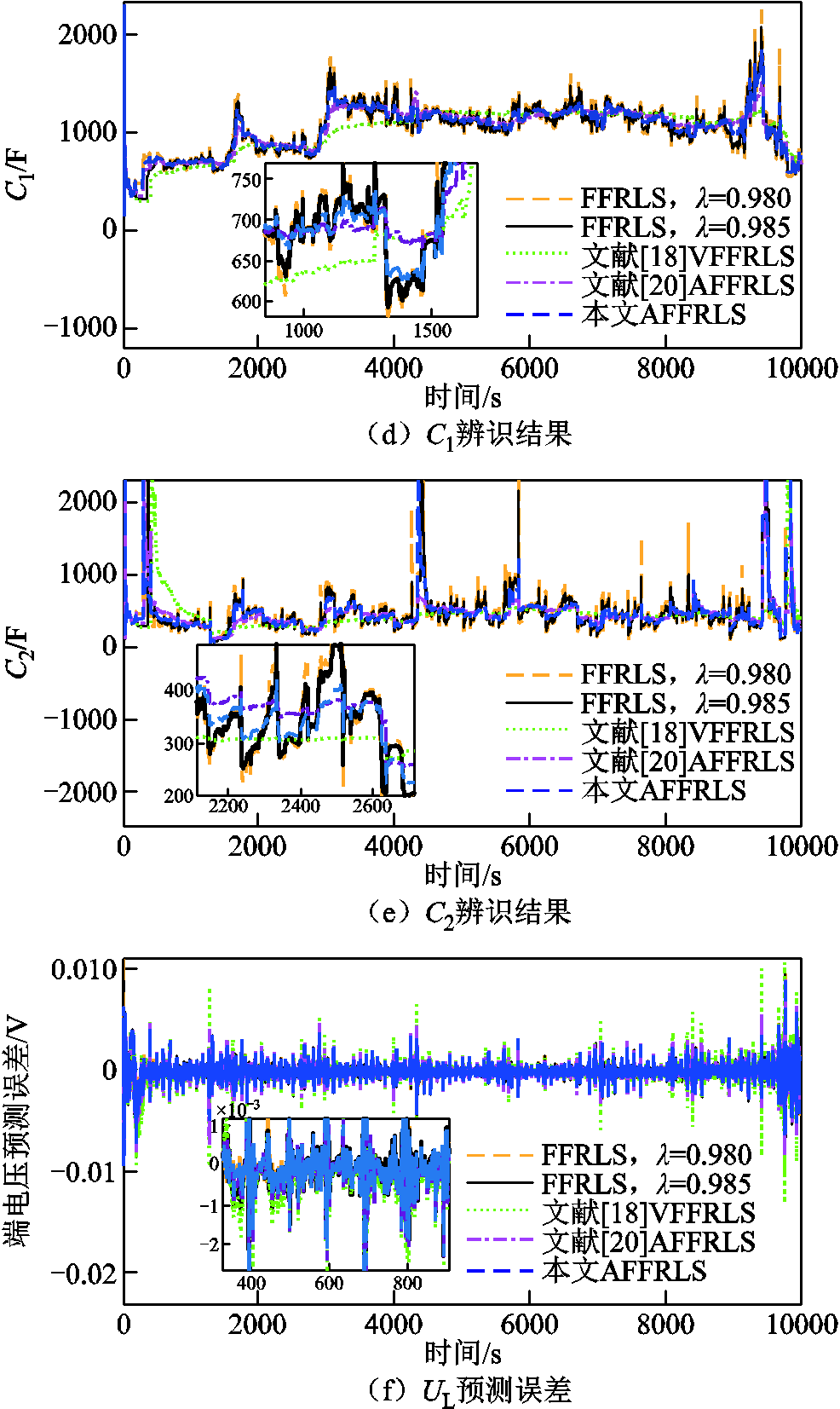
图5 FUDS工况下辨识参数对比
Fig.5 Comparison of identification parameters via FUDS
由图5a～图5e，剧变工况下VFFRLS辨识参数最为平缓。从表4误差结果来看，提出的AFFRLS精度最高，其MAE与表2中λ值取0.985时接近，RMSE介于λ值为0.980和0.985之间。综合DST和FUDS工况仿真结果来看，提出的AFFRLS方法精度最高，稳定性优于λ为0.980和0.985的FFRLS方法，且在缓变和剧变工况下都做到了精度上的提高。
表4 FUDS工况下变遗忘因子方法辨识误差对比
Tab.4 Identification error comparison of variable forgetting factor methodsvia FUDS
辨识方法MAE/mVRMSE/mVME/V 文献[18]VFFRLS0.524 8 0.974 0 0.012 9 文献[20]AFFRLS0.447 4 0.808 60.009 5 本文AFFRLS0.415 40.747 90.009 5
图6呈现了三种自适应方法λ值与误差关系，VFFRLS方法在DST和FUDS工况下，λ值随误差变化最缓慢，本文AFFRLS对误差跟踪能力更好。基于相同预设基准误差，本文自适应方法能快速识别系统动态变化，降低自适应方法对数据平稳性的依赖，有效提高辨识精度。与另外两种自适应方法相比，改进的AFFRLS有良好的仿真效果。
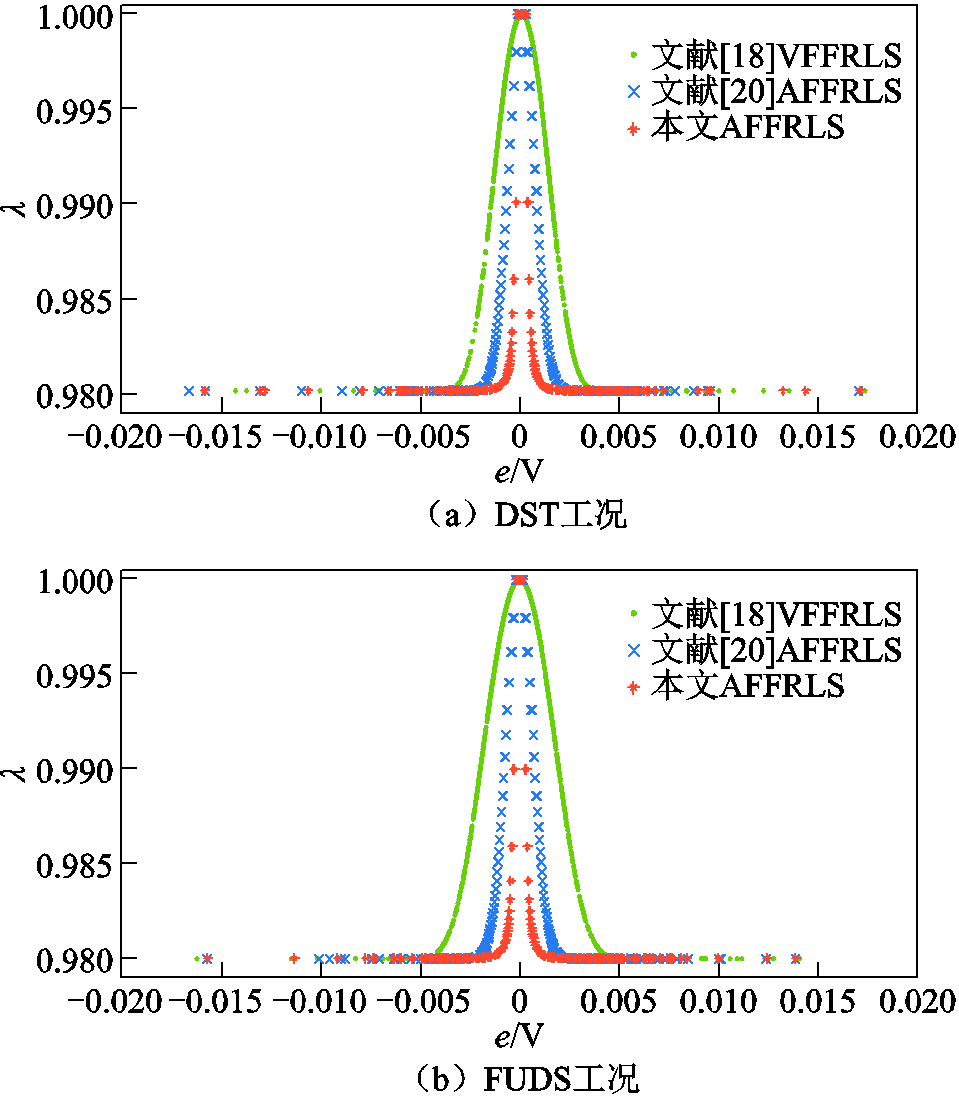
图6 DST与FUDS工况下λ值与误差关系
Fig.6 λ values and errors relation via DST and FUDS
DST与FUDS工况变遗忘因子方法计算时间对比见表5。表5中，T1表示算法平均计算时间，T2表示预测误差达到连续3次小于e0所需时间，DST和FUDS两种工况下ebase=e0。仿真在Matlab 2021a平台，CPU为I5-7300HQ_@2.5 GHz环境中进行，时间数据取20次仿真平均值。由表5可知，两种工况下T1基本一致。DST缓变工况开始阶段电压、电流波动较平缓，三种方法T2无明显差别，但本文改进AFFRLS在FUDS剧变工况下T2较文献[18]VFFRLS、文献[20]AFFRLS分别提高了40.1%、15.4%。可见本文改进AFFRLS算法收敛速度更快，对误差的跟踪能力更好。且本文改进AFFRLS避免了EKF的雅可比矩阵计算、GA和PSO繁琐的迭代过程，用于在线参数辨识时计算速度更快。
图7所示为DST与FUDS工况下本文改进AFFRLS算法λ值随时间的分布，整体上FUDS剧变工况在0.980附近分布点更多。算法前期，误差波动大，λ值分布基本接近0.980，此时算法可以获得更高的精度和更快的收敛速度，对误差变化更敏感，DST工况和FUDS工况都出现较大波动。算法中期，参数辨识基本稳定，随着电流变化幅度e(k)出现短暂波动，此时λ值分布在(0.980, 0.99]之间；误差与基准误差比值低于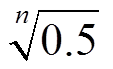
时，λ值为1，此时参数结果较为稳定。算法后期电池能量匮乏，电压波动大，e(k)值变大，且FUDS比DST工况表现更为剧烈，此时FUDS工况λ值大部分接近0.980，DST工况在9 700～9 900 s以1为主， 9 900～10 000 s开始波动，λ值回落到接近0.980区域。
表5 DST与FUDS工况变遗忘因子方法计算时间对比
Tab.5 Calculation time comparison of variable forgetting factor methodsvia DST and FUDS
辨识方法DST-T1/ msDST-T2/ msFUDS-T1/ msFUDS-T2/ ms 文献[18]VFFRLS0.003 40.488 80.003 31.428 7 文献[20]AFFRLS0.003 20.488 40.003 30.998 6 本文AFFRLS0.003 20.488 40.003 30.844 6
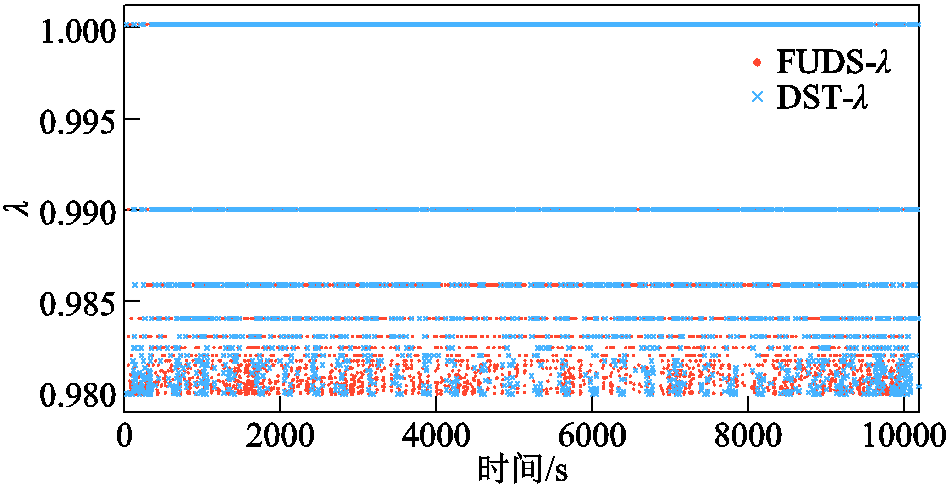
图7 DST与FUDS工况下λ值与时间关系
Fig.7 Relationship between λ values and times via DST and FUDS
从图7中λ值随时间分布情况可知，FUDS工况下λ值以接近0.980区域分布点居多，DST则以λ取1为主。可见对于DST和FUDS工况，提出的AFFRLS有着不同的自适应表现，对e(k)具有良好的跟随性。
在线参数辨识方法能够获得动态特性良好的电池模型，FFRLS用于在线参数辨识方法简单，易于工程应用，但单一的遗忘因子影响算法对动态系统的时变跟踪能力。固定值的FFRLS仿真结果表明，λ值接近1，模型参数精度低、时变特性较差；λ值减小，模型精度提高，对系统动态变化跟踪性能更好。但参数波动过大易引起算法发散。可见取合适的λ值对模型参数精度和稳定性有重要意义。
为了获得高精度且稳定性良好的参数辨识结果，设计了一种AFFRLS改进方法，与文献AFFRLS、VFFRLS进行仿真对比分析，结果表明，本文AFFRLS精度最高，辨识结果较文献方法动态特性更好；相比固定λ值取0.980、0.985的FFRLS参数辨识结果，本文AFFRLS稳定性更好。从λ值和误差关系来看，本文AFFRLS能够快速识别误差变化。且本文AFFRLS在DST和FUDS工况参数辨识有不同的自适应表现，对误差有着良好的跟踪能力。
本文AFFRLS改进方法结构简单，计算速度快，用于锂离子电池模型参数辨识时，能够在精度和稳定性上取得更好的平衡，对于不同的工况具有良好的适用性。将本文AFFRLS与卡尔曼滤波方法结合进行锂电池SOC预测，能够提高SOC的预测精度，且有利于避免模型参数剧烈变化带来的算法发散问题。所研究的改进方法可为进一步利用AFFRLS和无迹卡尔曼滤波进行荷电状态评估提供支撑。
参考文献
[1] 庞辉, 郭龙, 武龙星, 等. 考虑环境温度影响的锂离子电池改进双极化模型及其荷电状态估算[J]. 电工技术学报, 2021, 36(10): 2178-2189. Pang Hui, Guo Long, Wu Longxing, et al. An improved dual polarization model of Li-ion battery and its state of charge estimation considering ambient temperature[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2178-2189.
[2] 郭向伟, 邢程, 司阳, 等. RLS锂电池全工况自适应等效电路模型[J]. 电工技术学报, 2022, 37(16): 4029-4037. Guo Xiangwei, Xing Cheng, Si Yang, et al. RLS adaptive equivalent circuit model of lithium battery under full working condition[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4029-4037.
[3] You H W, Bae J I, Cho S J, et al. Analysis of equivalent circuit models in lithium-ion batteries[J]. AIP Advances, 2018, 8(12): 125101.
[4] Han Xuebing, Ouyang Minggao, Lu Languang, et al. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part I: Diffusion simplification and single particle model[J]. Journal of Power Sources, 2015, 278: 802-813.
[5] Xu Jun, Mi C C, Cao Binggang, et al. A new method to estimate the state of charge of lithium-ion batteries based on the battery impedance model[J]. Journal of Power Sources, 2013, 233: 277-284.
[6] Ettihir K, Boulon L, Agbossou K. Optimization-based energy management strategy for a fuel cellbattery hybrid power system[J]. Applied Energy, 2016, 163: 142-153.
[7] He Lin, Wang Yangyang, Wei Yujiang, et al. An adaptive central difference Kalman filter approach for state of charge estimation by fractional order model of lithium-ion battery[J]. Energy, 2022, 244: 122627.
[8] 谷苗, 夏超英, 田聪颖. 基于综合型卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2019, 34(2): 419-426. Gu Miao, Xia Chaoying, Tian Congying. Li-ion battery state of charge estimation based on comprehensive Kalman filter[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 419-426.
[9] 黄凯, 郭永芳, 李志刚. 基于信息反馈粒子群的高精度锂离子电池模型参数辨识[J]. 电工技术学报, 2019, 34(增刊1): 378-387. Huang Kai, Guo Yongfang, Li Zhigang. High precision parameter identification of lithium-ion battery model based on feedback particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 378-387.
[10] 张彩萍, 姜久春. 用基于遗传优化的扩展卡尔曼滤波算法辨识电池模型参数[J]. 吉林大学学报(工学版), 2012, 42(3): 732-737. Zhang Caiping, Jiang Jiuchun. Identification of battery model parameters by extended Kalman filter algorithm based on genetic optimization[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(3): 732-737.
[11] Zhang Shuzhi, Zhang Xiongwen. A comparative study of different online model parameters identification methods for lithium-ion battery[J].Science China Technological Sciences, 2021, 64(10): 2312-2327.
[12] 陈玉珊, 秦琳琳, 吴刚, 等. 基于渐消记忆递推最小二乘法的电动汽车电池荷电状态在线估计[J]. 上海交通大学学报, 2020, 54(12): 1340-1346. Chen Yushan, Qin Linlin, Wu Gang, et al. Online state of charge estimation for battery in electric vehicles based on forgetting factor recursive least squares[J]. Journal of Shanghai Jiao Tong University, 2020, 54(12): 1340-1346.
[13] Wei Zhongbao, Meng Shujuan, Xiong Binyu, et al. Enhanced online model identification and state of charge estimation for lithium-ion battery with a FBCRLS based observer[J]. Applied Energy, 2016, 181: 332-341.
[14] Sun Xiangdong, Ji Jingrun, Ren Biying, et al. A novel online identification algorithm of lithium-ion battery parameters and model order based on a fractional order model[J]. IET Renewable Power Generation, 2021, 15(11): 2396-2408.
[15] Zhang Cheng, Allafi W, Dinh Q, et al. Online estimation of battery equivalent circuit model parameters and state of charge using decoupled least squares technique[J]. Energy, 2018, 142: 678-688.
[16] Feng Tianheng, Yang Lin, Zhao Xiaowei, et al. Online identification of lithium-ion battery parameters based on an improved equivalent-circuit model and its implementation on battery state-of-power prediction[J]. Journal of Power Sources, 2015, 281: 192-203.
[17] 谢文超, 赵延明, 方紫微, 等. 带可变遗忘因子递推最小二乘法的超级电容模组等效模型参数辨识方法[J]. 电工技术学报, 2021, 36(5): 996-1005. Xie Wenchao, Zhao Yanming, Fang Ziwei, et al. Variable forgetting factor recursive least squales based parameter identification method for the equivalent circuit model of the supercapacitor cell module[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 996-1005.
[18] Lao Zizhou, Xia Bizhong, Wang Wei, et al. A novel method for lithium-ion battery online parameter identification based on variable forgetting factor recursive least squares[J]. Energies, 2018, 11(6): 1358.
[19] Wang Hao, Zheng Yanping, Yu Yang. Lithium-ion battery SOC estimation based on adaptive forgetting factor least squares online identification and unscented Kalman filter[J]. Mathematics, 2021, 9(15): 1733.
[20] Sun Xiangdong, Ji Jingrun, Ren Biying, et al. Adaptive forgetting factor recursive least square algorithm for online identification of equivalent circuit model parameters of a lithium-ion battery[J]. Energies, 2019, 12(12): 2242.
[21] Zheng Fangdan, Xing Yinjiao, Jiang Jiuchun, et al. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries[J]. Applied Energy, 2016, 183: 513-525.
Abstract Offline and online methods are used to identify model parameters, but the model dynamic characteristic obtained by the online method is better. The recursive least squares method is simple and often used for online parameter identification of lithium-ion battery models. However, the least square method(RLS) has a low identification accuracy. Thus, the forgetting factor recursive least square method was proposed to improve the accuracy of parameter identification. To improve the dynamic identification ability, the variable forgetting factor least square (VFFRLS) method and adaptive forgetting factor recursive least square (AFFRLS) method appear. Yet the current adaptive methods tend to ignore the stability of model parameters, and the undetermined coefficient range of this method is large and difficult to confirm. The model parameter changes drastically, and it is easy to cause the divergence of the algorithm. This paper proposes a simpler AFFRLS method without an undetermined coefficient to address these issues. And it takes into account the accuracy and stability of the model.
Firstly, based on dynamic stress testing (DST) and Federal City Operating Conditions (FUDS) data, the FFRLS method with fixed forgetting factor value is simulated and analyzed, and the influence trend of different forgetting factors on the accuracy and stability of model parameters is obtained. Secondly, the proposed AFFRLS method is compared with other AFFRLS and VFFRLS, and the stability and accuracy of the identification parameters are analyzed. Finally, the error tracking ability and convergence speed of the three adaptive methods are analyzed, and the adaptive performance of the proposed AFFRLS to DST and FUDS conditions are analyzed.
The FFRLS simulation results with fixed forgetting factor(λ) value show that when λ value decreases, the algorithm has better tracking ability for time-varying parameters, the convergence speed is accelerated, and the identification accuracy is effectively improved. However, when the λ value decreases, the parameter changes drastically, and the stability decreases. It can be seen that obtaining the appropriate λ value is important for the identification ability of the adaptive methods. The results of the three adaptive methods simulations show that the improved AFFRLS in this paper has better tracking ability for time-varying parameters and high model accuracy. And it has better stability of the parameter obtained by FFRLS with fixed λ values of 0.980 and 0.985. It can be seen that the proposed AFFRLS can achieve a better balance between accuracy and stability.The relationship between the λ value and the error of the adaptive methods shows that the improved AFFRLS can track the error variation better. By comparing the operation time with the three methods, the results show that the proposed AFFRLS has a faster convergence rate. According to the relationship between λ value and time in DST and FUDS conditions, the improved AFFRLS method has the majority of λ value near 0.980 in the FUDS condition, and the majority of λ value is 1 in the DST condition.
The simulation analysis shows that: (1) The proposed AFFRLS method can improve the accuracy of thealgorithm and take the stability of model parameters into consideration, and it has a good balance between algorithm accuracy and parameter stability. Applying the proposed AFFRLS method and Kalman filter to predict the state of charge can improve the prediction accuracy. (2) The proposed AFFRLS method has better tracking ability for error variation and faster convergence speed. (3) The proposed method can improve the algorithm's accuracy under both slow and drastic conditions, so it's suitable for different online conditions.
Keywords：Lithium-ion battery model, parameter identification, least square method, adaptive forgetting factor
DOI: 10.19595/j.cnki.1000-6753.tces.222214
中图分类号：TM912
国家自然科学基金项目（61741126）和广西自然科学基金项目（2022GXNSFAA035533）资助。
收稿日期 2022-11-24
改稿日期 2023-02-28
范兴明 男，1978年生，教授，博士生导师，研究方向为智能化电器和高电压新技术。E-mail：fanxm_627@163.com
张 鑫 女，1976年生，硕士，高级实验师，研究方向为智能化电器。E-mail：zhangxin_wt@163.com（通信作者）
（编辑 郭丽军）