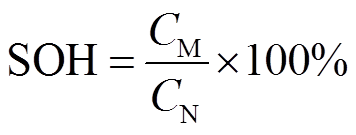 (1)
(1)
摘要 实时准确地评估电动汽车锂电池健康状态(SOH)对电动汽车的稳定行驶至关重要。因此,该文提出一种基于锂电池日常片段充电数据和双扩展卡尔曼滤波-小波神经网络-小波长短时记忆神经网络(DEKF-WNN-WLSTM)的电池全充时间估计模型,进而提高了片段充电数据评估电池健康状态的准确度。首先,设计双扩展卡尔曼滤波预测-校正算法,分别用来估计片段充电数据对应的全充时间和校正扩展卡尔曼滤波的状态初值,以提高估计的准确性。然后,设计了小波神经网络-小波长短时神经网络来学习扩展卡尔曼滤波递推过程的观测值。最后,通过实验仿真,验证了所提算法在锂电池健康状态实时估算中的准确性和有效性。
关键词:电池健康状态 片段数据 双扩展卡尔曼滤波 小波神经网络 小波长短时记忆神经网络
由于锂电池具有重量轻、寿命长、效率高、成本低等优点,是电动汽车的主要动力来源[1],因此对于电动汽车的锂电池进行性能评价具有重要意义。通常情况下,锂电池通过电池管理系统(Battery Management System, BMS)进行性能评价[2]。BMS的评价指标主要包括荷电状态(State of Charge, SOC)、剩余使用寿命(Remaining Useful Life, RUL)和健康状态(State of Health, SOH)[3-5]。一般来说,SOH描述电池长期的状态变化,因此获得准确的SOH估计值对于电池长期安全稳定的使用至关重要。
主要的SOH评估方法可以分为三类:直接测量法、基于经验的方法和数据驱动方法。典型的直接测量法是通过累积电流积分测量电池的SOH[6]。但在实际应用中,该方法对电流采样精度敏感,应用效果不佳。电化学阻抗谱(Electrochemical Impedance Spectroscopy, EIS)是另一种直接方法[7-8],通过分析电池在不同频率下的交流阻抗谱,得到电池内部的化学状态,进而评价电池的外部特征。然而电池内部参数的采集需要特殊且昂贵的设备,且参数分析过程复杂。基于经验的方法包括周期计数法、面向事件的累积法、安时法以及加权安时法等[9]。然而,在实际应用中,电池的工作条件往往与标准工作条件不一致,这将导致较大的估计误差。最后一个主流的方法是数据驱动方法,该方法通过学习隐藏于数据中的信息来估计SOH,不需要电池系统的先验知识。因此,数据驱动方法可以避免模型获取困难的问题,是一种更加实用的估计方法。
支持向量机(Support Vector Machine, SVM)是一种常用的数据驱动算法,它通过核函数将低纬度空间的非线性问题映射到高纬度空间[10]的线性问题来估计SOH,但该方法不易选择合适的核函数且对交叉训练和正则化方法依赖程度高。相关向量机(Relevance Vector Machine, RVM)的原理与支持向量机大致相同,不同的是其网络权值是用稀疏贝叶斯理论结构获得的[11]。然而,由于RVM模型的稀疏矩阵,RVM对训练数据的需求较高且预测结果的稳定性较差。高斯过程回归(Gaussian Process Regression, GPR)是另一种基于贝叶斯框架的估计方法[12-13],但该算法中超参数较多,训练中调整过程繁琐。基于神经网络的方法作为一种高效的数据驱动方法,正在成为电池性能评估的主流方法[14-18]。其中,小波神经网络(Wavelet Neural Network, WNN)结合自学习和非线性函数逼近能力,具有精度高和细节描述能力强的优点[19-20]。J. Zhang等提出了将离散小波多分辨率分解与多层感知器相结合的四层小波神经网络,与反向传播神经网络(Back Propagation Neural Networks, BPNN)相比具有较好的预测性能。但该方法局限于多分辨率分析,结构不灵活且鲁棒性不强[21]。Xia Bizhong等通过引入小波伸缩因子和小波平移因子,调整小波神经网络的结构,使网络具有较强的鲁棒性[22]。但由于它只是一个三层网络,其估计精度远远低于深度网络。与BPNN相比,循环神经网络(Recurrent Neural Network, RNN)可以保存输入数据与SOH值之间的信息,因此常被用于SOH估计[23]。但由于梯度消失和梯度爆炸的问题,RNN无法用于长期估计。为了解决这一问题,引入了长短时记忆神经网络(Long Short Term Memory, LSTM)[24-26]。LSTM具有单元状态,可以保存输入和输出之间的重要信息。然而,由于LSTM的单元特性,当测试数据与训练数据之间的相关性不高时,其估计效果不好,意味着该方法的鲁棒性不强。
因此,本文设计了一种小波神经网络和小波长短时记忆神经网络(Wavelet LSTM, WLSTM)。该网络包括输入层、两个隐藏层和输出层。双隐层由WNN层和WLSTM层组成,WLSTM层的激活函数用Morlet小波函数代替。因此,该网络同时具有WNN和LSTM的优点。
此外,为了能够更安全稳定地使用纯电力电动汽车,随时了解电池当前时刻的健康状态是十分有必要的,即实时估计电池的SOH。然而,锂电池是一个机制复杂、内部状态未测量的综合系统,SOH的在线估计通常依赖电池模型和关键参数之间的拟合关系。电池模型参数反映电池内部的动态响应,并会随着电池的退化而发生相应的变化。程泽等[27]在二阶RC网络等效电路模型的基础上,联合Sage-Husa自适应滤波思想,设计了自适应平方根无迹卡尔曼滤波(Adaptive Square Root Unscented Kalman Filter, ASRUKF)算法;通过对电池参数的实时更新,实现电池SOH的实时估计,虽然不涉及电化学分析过程,但是其电池特性变化的分析过程依旧较复杂。
王萍等[28]提出了一种基于数据驱动和经验模型结合的在线实时估计方法。其实时估计的核心为在固定循环次数下,利用观测器对模型的参数进行更新。该方法虽然实现了预测SOH的实时性,减少了监测器的负荷,但每次的参数更新需要离线操作,具有一定的不便性。
周頔等[29]用扩展卡尔曼滤波和高斯过程回归(Extended Kalman Filter and Gaussian Process Regression, EKF-GPR),不需要完成整个充放电操作,仅对日常片段充电数据进行处理,通过估计片段数据的全充时间,进而得到电池在当前时刻的SOH,实现了电池的实时估计,该方法的平均绝对误差在2%以下,短期内的评估值基本满足现实要求,解决了短时间内的动力电池锂电池健康状态的实时估计问题,具有一定的应用价值,但长期的预测精度不理想。
为了解决实时估计的精度问题,本文设计了双扩展卡尔曼滤波-小波神经网络-小波长短时记忆神经网络(DEKF-WNN-WLSTM)模型,用一次全充数据和三次片段数据分别训练两个WNN-WLSTM网络,然后将两个训练好的网络融入DEKF中,为EKF的循环递推提供相应的输出值。此外,构建双EKF实现电池全充时间的实时估计,其中第一个EKF用于估计片段数据对应的全充时间;第二个EKF用来估计当前循环下电池全充时间的估计值与真实值的误差,并实时修正当前循环次数下估计的全充时间,进而为下次循环中第一个EKF提供较准确的状态初值。实验结果表明,本文所提算法的平均绝对误差远远低于EKF-GPR,并且随着循环次数的增加,DEKF-WNN-WLSTM的累积误差也远远低于后者。
一般情况下,SOH的定义为
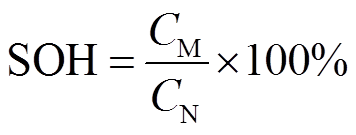 (1)
(1)
式中,CM为测量放电容量;CN为电池标称放电容量。该公式表示锂电池在标准条件下从充满状态以一定倍率放电到截止电压所放出的容量与其所对应的标称容量的比值[29]。
考虑到通过电池释放电量离线测试电池的SOH费时且操作不便,同文献[29],本文采用充电数据代替放电数据估算SOH,可用测量充电容量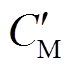 与标称充电容量
与标称充电容量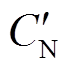 的比值来判断电池健康状况下降后的状态,衡量电池的健康程度,即
的比值来判断电池健康状况下降后的状态,衡量电池的健康程度,即
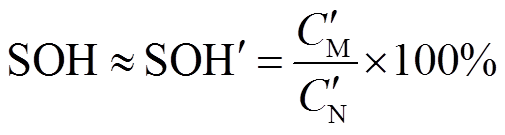 (2)
(2)
用充电数据估算SOH具有简便快捷的显著优势,并且由文献[29]可知:充电容量计算的SOH和放电容量计算的SOH具有一致性,因此,本文采用片段充电数据作为输入,估计电池的全充时间,进而估算电池的健康状态是合理的。
电池容量是指在某种条件下,活性物质参加电化学反应所释放电量的多少,有时也会将电池所能充入的最大电量作为电池容量。相同地,基于恒流充电的动力电池SOC计算公式为
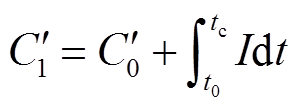 (3)
(3)
式中,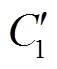 为电池充电容量;
为电池充电容量;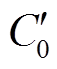 为初始容量;I为电池充电电流;
为初始容量;I为电池充电电流;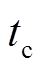 为电池充电时从初始时刻
为电池充电时从初始时刻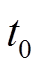 充电到截止电压所需的时间。若电池从零容量开始充电,则式(3)修改为
充电到截止电压所需的时间。若电池从零容量开始充电,则式(3)修改为
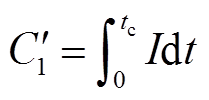 (4)
(4)
基于式(4),定义基于充电容量的SOH为
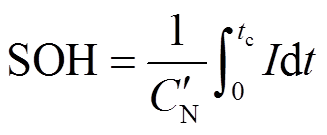 (5)
(5)
该方法可以简便地计算动力电池的SOC和SOH,缺点是电池需要从零容量充电至截止电压,该过程费时且不方便。
通常情况下,在充电效率一定时,电池从零容量开始充电至充满状态所用的时间越长,电池的容量也就越大。随着电池不断的循环充放电,其恒流充电时间在不断缩短[30],这与SOH整体下降的趋势一致。而在本文中,由式(5)可知,SOH和电池的充电时间成正比,二者具有较强的相关性,基于此,只要得到电池的全充时间,即可得到电池的SOH。
由于电动汽车在实际的使用情况较复杂,其动力电池的充电情况往往是片段的,而非完全充电,例如,SOC从30%或50%充至80%或100%的充电情况,就无法根据充电情况判断出电池的实时全充时间和可用容量。本文基于该情况,同文献[29],构建利用从任意的起始SOC值处进行恒流充电至100%这样的片段数据,估计锂电池当前的全充时间,进而计算电池当前时刻的SOH。
本节主要介绍基于DEKF-WNN-WLSTM算法并使用片段数据对电池的实时全充时间t进行预测。
扩展卡尔曼滤波算法是由卡尔曼滤波转变而来,其核心在于对非线性系统的局部线性化。该算法的实质是基于递归估算的最优自适应算法。EKF是广泛使用的非线性系统的最优状态估计算法[31]。一般情况下,扩展卡尔曼滤波由状态方程和测量方程组成,算法方程为
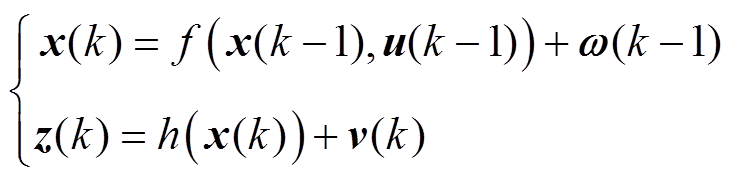 (6)
(6)
式中,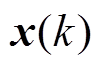 、
、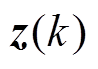 分别为k时刻系统的状态向量和量测向量;
分别为k时刻系统的状态向量和量测向量;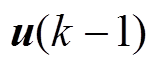 为
为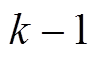 时刻控制输入向量;
时刻控制输入向量;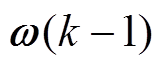 为系统噪声;
为系统噪声;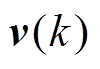 为量测噪声;
为量测噪声;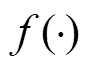 和
和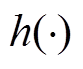 为非线性函数。利用一阶泰勒展开式使系统的非线性状态空间方程转换为线性的状态空间方程,再结合使用卡尔曼滤波算法可以实现扩展卡尔曼滤波的循环递推。
为非线性函数。利用一阶泰勒展开式使系统的非线性状态空间方程转换为线性的状态空间方程,再结合使用卡尔曼滤波算法可以实现扩展卡尔曼滤波的循环递推。
小波神经网络以全连接网络和小波理论为基础,用小波分析理论构建并改进神经网路结构,与通常使用的全连接神经网络相比(如BPNN),其激活函数被一组小波函数代替,这些函数由Morlet小波母函数产生[22]。
一般的三层小波神经网络结构如图1所示:该网络包含K个输入节点,L个隐藏层节点,K个输出节点。网络参数由两个权重参数![]() 和
和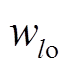 、小波伸缩因子
、小波伸缩因子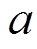 以及小波平移因子
以及小波平移因子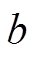 组成,这些参数在网络的学习过程中会持续不断地变化以寻求最优解。网络输出值
组成,这些参数在网络的学习过程中会持续不断地变化以寻求最优解。网络输出值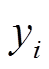 和输入值
和输入值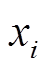 之间的关系可以描述为
之间的关系可以描述为
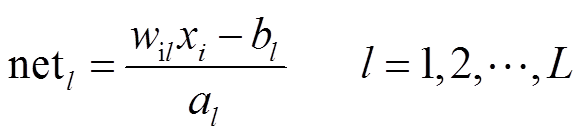 (7)
(7)
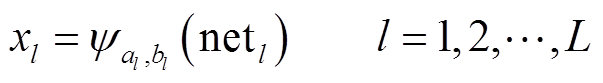 (8)
(8)
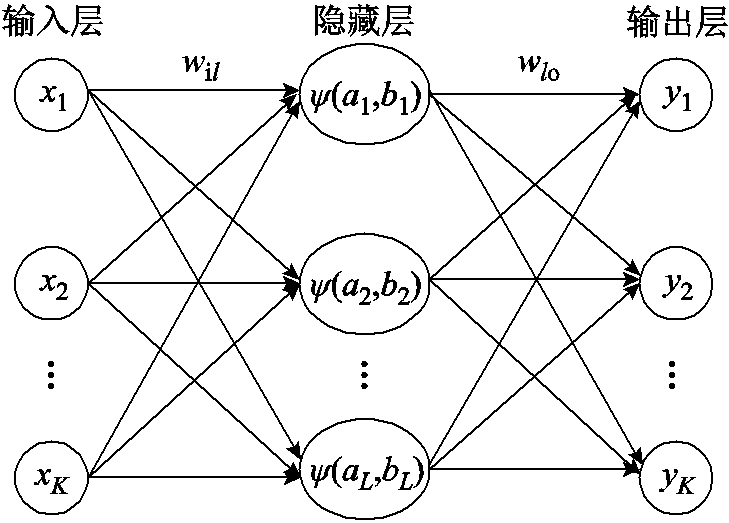
图1 三层小波神经网络结构
Fig.1 Schematic structure of the WNN
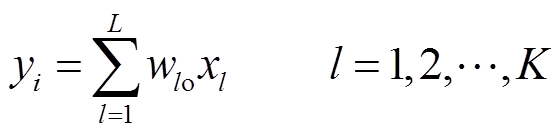 (9)
(9)
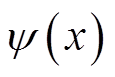 是Morlet小波函数的生成函数,通常在神经网络中作为激活函数被广泛应用,其表达式为
是Morlet小波函数的生成函数,通常在神经网络中作为激活函数被广泛应用,其表达式为
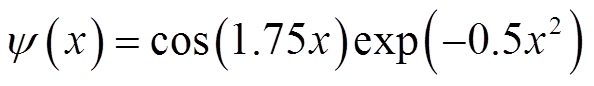 (10)
(10)
相比于循环神经网络(RNN)存在梯度消失和梯度爆炸等问题,长短时记忆神经网络在处理具有时间序列特性的数据时具有明显的优势,因为后者有一个可以保存重要的信息记忆状态。图2描述了长短时记忆神经网络的细胞结构,它用遗忘门、输入门、输出门和记忆单元训练网络。
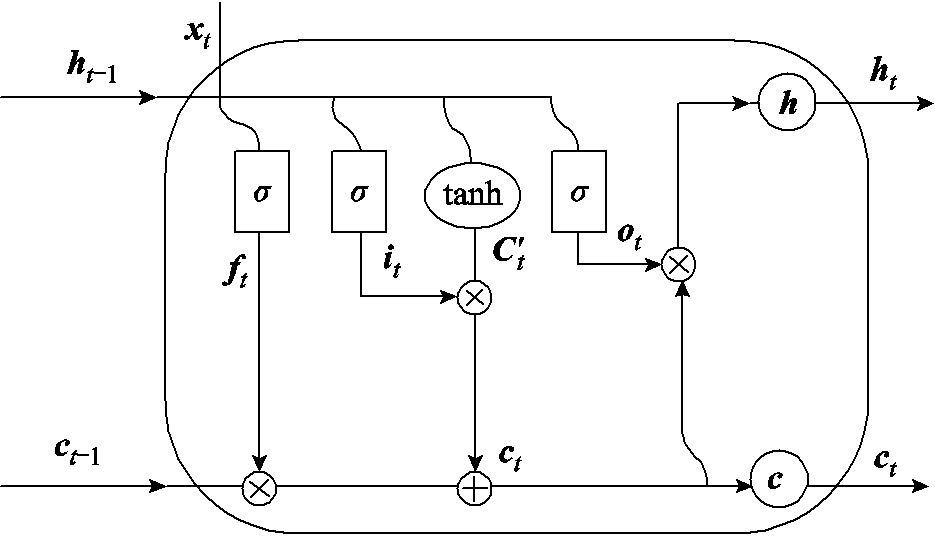
图2 LSTM的细胞结构示意图
Fig.2 Schematic structure of the LSTM cell
该过程可以用公式表示为
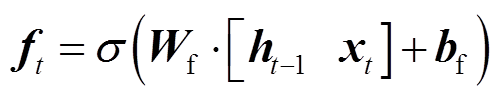 (11)
(11)
式中,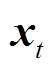 和
和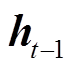 分别为当前t时刻的输入状态和上一时刻隐藏层的输出状态;
分别为当前t时刻的输入状态和上一时刻隐藏层的输出状态;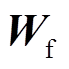 、
、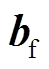 和
和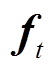 分别为遗忘门的权重项、偏置项及输出项;
分别为遗忘门的权重项、偏置项及输出项;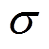 指代Sigmoid激活函数。图2中的输入门
指代Sigmoid激活函数。图2中的输入门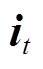 可表示为
可表示为
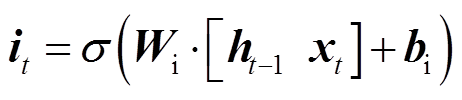 (12)
(12)
式中,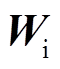 、
、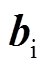 和
和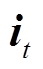 分别为输入门的权重项、偏置项和输出项。图2中输出门
分别为输入门的权重项、偏置项和输出项。图2中输出门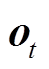 可描述为
可描述为
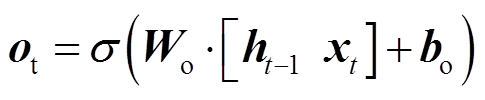 (13)
(13)
式中,![]() 、
、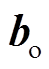 和
和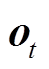 分别为输出门的权重项、偏置项及输出项。第四个值
分别为输出门的权重项、偏置项及输出项。第四个值![]() 计算式为
计算式为
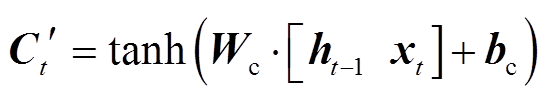 (14)
(14)
式中,变量![]() 和
和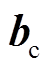 分别为单元状态的权重项和偏置项;
分别为单元状态的权重项和偏置项;![]() 和tanh为候选单元状态及tanh激活函数。
和tanh为候选单元状态及tanh激活函数。
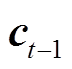 和
和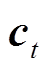 分别指代上一时刻及当前时刻的单元状态,表示为
分别指代上一时刻及当前时刻的单元状态,表示为
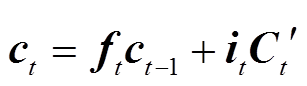 (15)
(15)
最后获得输出ht为
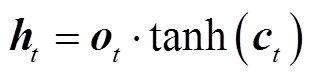 (16)
(16)
式中,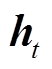 为隐藏层在当前时刻的输出。
为隐藏层在当前时刻的输出。
为了进一步提高网络的估计性能,本文设计了基于LSTM和WNN的双隐层小波神经网络-小波长短时记忆神经网络。该网络既具有WNN鲁棒性强的优点[22],又保留了LSTM能保存重要数据信息的能力,具有较好的预测性能,其结构示意图如图3所示。与图1所示的WNN结构类似,WNN-WLSTM在WNN单元之后增加了小波长短时记忆层(WLSTM)组成另一个隐藏层。新结构共有四层,包括输入层、隐藏层一(即WNN层)、隐藏层二(即WLSTM层)和输出层。第一个隐藏层的输出记作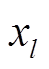 ,该层的输出与输入数据
,该层的输出与输入数据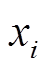 的关系可以用式(7)和式(8)描述。
的关系可以用式(7)和式(8)描述。
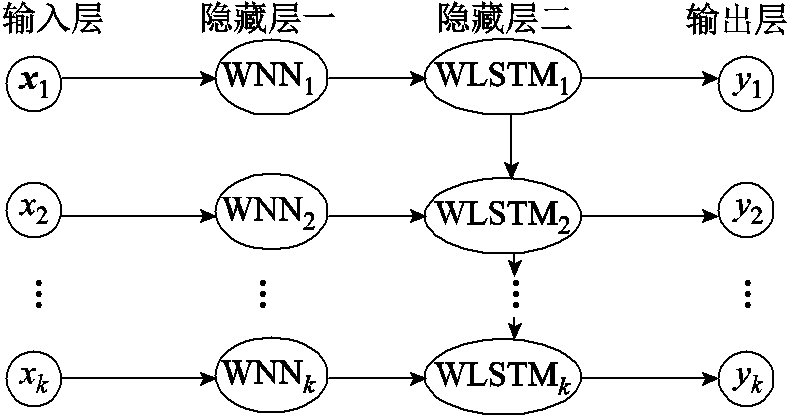
图3 WNN-WLSTM结构示意图
Fig.3 Structure of the WNN-WLSTM
隐藏层一和一般的全连接层相比,其输出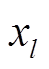 是隐藏层二的既定的输入数据,由全连接隐藏层一的小波基函数线性叠加近似而成。
是隐藏层二的既定的输入数据,由全连接隐藏层一的小波基函数线性叠加近似而成。
隐藏层二是小波长短时记忆层,该层的激活函数是Morlet小波函数,因此,修改后的LSTM层公式(11)~式(14)和式(16)为
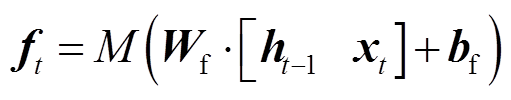 (17)
(17)
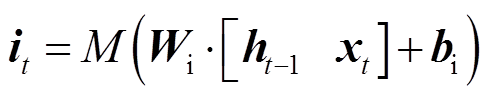 (18)
(18)
 (19)
(19)
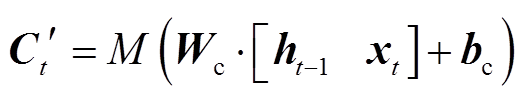 (20)
(20)
 (21)
(21)
M在式(17)~式(21)中为Morlet小波函数。此外,因为式(16)中没有激活函数,所以WLSTM层依旧采用原公式。
调整后的WLSTM层依旧可以提取数据间的时间序列特征,实验表明WNN-WLSTM能够为扩展卡尔曼滤波提供较为准确的测量值。
损失函数用于量化模型预测值与实测值之间的差异,并根据差异更新网络的各项参数,本文所用的损失函数为
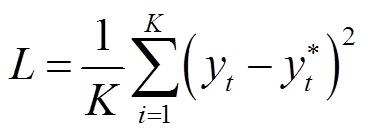 (22)
(22)
式中,K、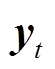 和
和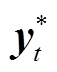 分别为数据总个数、t时刻的真实值和估计值。
分别为数据总个数、t时刻的真实值和估计值。
最小化损失函数是由优化器确定的,本文选择RMSprop优化器。
本文用小波神经网络-小波长短时记忆神经网络学习两个扩展卡尔曼滤波的量测方程,训练数据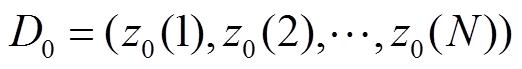 为扩展卡尔曼滤波的量测值,对于小波神经网络-小波长短时神经网络一(WNN-WLSTM1)和小波神经网络-小波长短时神经网络二(WNN-WLSTM2),N分别为全充数据和前三次片段数据中的采样样本总数,xp(k)、zp(k)分别为当前p次循环数下的第k个状态量和量测量,同时也是WNN-WLSTM的测试输入值,
为扩展卡尔曼滤波的量测值,对于小波神经网络-小波长短时神经网络一(WNN-WLSTM1)和小波神经网络-小波长短时神经网络二(WNN-WLSTM2),N分别为全充数据和前三次片段数据中的采样样本总数,xp(k)、zp(k)分别为当前p次循环数下的第k个状态量和量测量,同时也是WNN-WLSTM的测试输入值,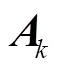 为扩展卡尔曼滤波的初始状态矩阵。该网络将状态方程和量测方程分别表示为
为扩展卡尔曼滤波的初始状态矩阵。该网络将状态方程和量测方程分别表示为
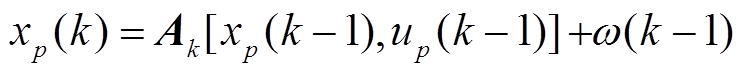 (23)
(23)
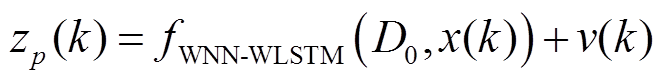 (24)
(24)
式中,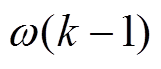 、
、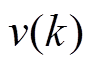 分别为两种噪声,这里假设两种噪声服从高斯分布。
分别为两种噪声,这里假设两种噪声服从高斯分布。
本文提出的算法将WNN-WLSTM融入扩展卡尔曼滤波中,采用两个WNN-WLSTM网络以及双卡尔曼滤波提高系统模型预测性能,模型的流程如图4所示,其中t为循环的次数上限。
(1)初始化参数:恒流充电电流I,恒压充电截止电压V,初次循环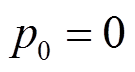 ,初始恒流充电下的全充数据
,初始恒流充电下的全充数据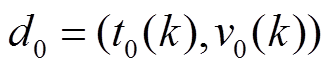 ,
,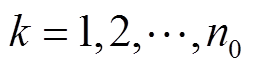 ,
,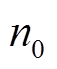 为在恒流I充电下电池达到截止电压V时的总采样时间点数,
为在恒流I充电下电池达到截止电压V时的总采样时间点数,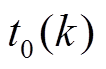 是等间隔采样的离散相对时间,采样时间间隔
是等间隔采样的离散相对时间,采样时间间隔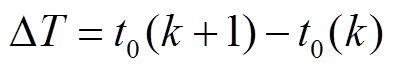 为常数,
为常数,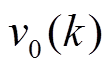 表示第k个采样点的电压;扩展卡尔曼滤波一(
表示第k个采样点的电压;扩展卡尔曼滤波一(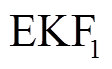 )以及扩展卡尔曼滤波二(
)以及扩展卡尔曼滤波二(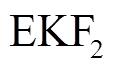 )的初始状态矩阵分别为
)的初始状态矩阵分别为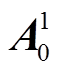 和
和![]() 。
。
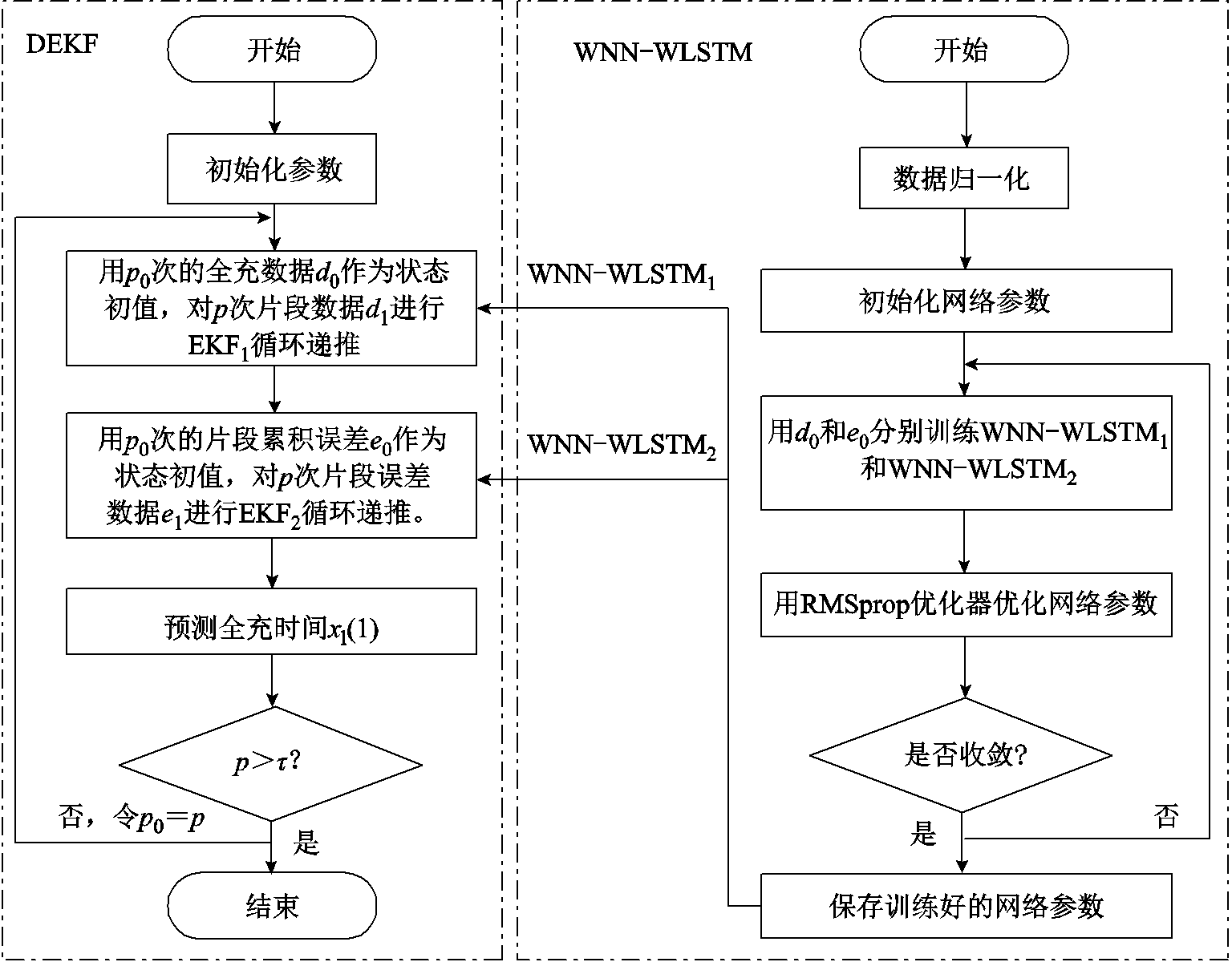
图4 DEKF-WNN-WLSTM流程
Fig.4 The flow chart of DEKF-WNN-WLSTM
步骤(2)~(4)为训练阶段:该阶段训练两个WNN-WLSTM。
(2)训练WNN-WLSTM1:用恒流充电的全充数据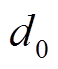 对小波神经网络-小波长短时记忆神经网络(图3所示)进行训练,通过反向传播得到并保存更新后的网络参数,进而得到最优训练后的网络WNN-WLSTM1。
对小波神经网络-小波长短时记忆神经网络(图3所示)进行训练,通过反向传播得到并保存更新后的网络参数,进而得到最优训练后的网络WNN-WLSTM1。
(3)提取WNN-WLSTM2的训练数据:提取前三次的片段数据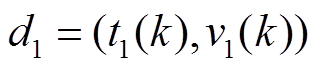 ,
,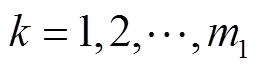 ,利用
,利用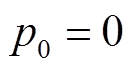 次的全充数据
次的全充数据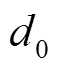 作为状态的初值,状态向量初始化为
作为状态的初值,状态向量初始化为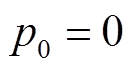 次的全充时间
次的全充时间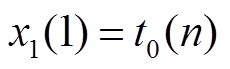 ,对前三次片段数据进行扩展卡尔曼滤波-小波神经网络-小波长短时记忆神经网络(EKF-WNN-WLSTM)循环递推,并保存状态方程和测量方程每次输出的状态值和测量值
,对前三次片段数据进行扩展卡尔曼滤波-小波神经网络-小波长短时记忆神经网络(EKF-WNN-WLSTM)循环递推,并保存状态方程和测量方程每次输出的状态值和测量值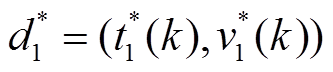 ,
,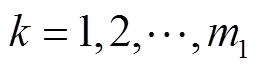 ,最后用
,最后用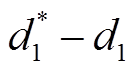 得到WNN-WLSTM2的训练数据
得到WNN-WLSTM2的训练数据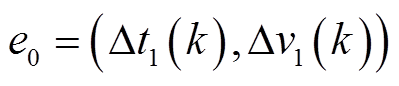 ,
,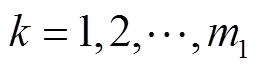 。
。
状态方程为
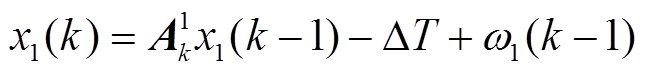 (25)
(25)
测量方程为
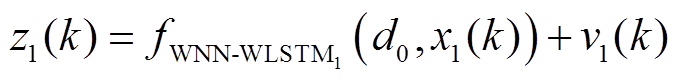 (26)
(26)
式中,WNN-WLSTM1表示利用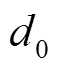 做小波神经网络-小波长短时神经网络一训练并预测状态
做小波神经网络-小波长短时神经网络一训练并预测状态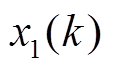 的电压值
的电压值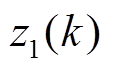 。
。
(4)训练WNN-WLSTM2:利用训练数据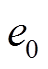 对小波神经网络-小波长短时记忆神经网络(图3所示)进行训练,通过反向传播得到并保存更新后的网络参数,进而得到最优训练后的网络
对小波神经网络-小波长短时记忆神经网络(图3所示)进行训练,通过反向传播得到并保存更新后的网络参数,进而得到最优训练后的网络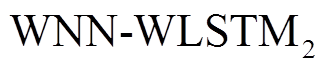 ;
;
步骤(5)~(10)为测试阶段该阶段,融合WNN-WLSTM和DEKF,估计片段数据对应的全充时间
(5)扩展卡尔曼滤波一:提取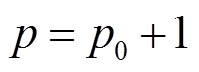 次的片段数据
次的片段数据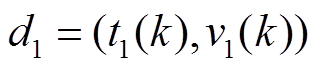 ,
,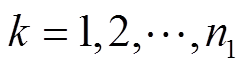 ,利用
,利用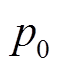 次的全充数据
次的全充数据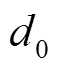 作为状态的初值,状态向量初始化为
作为状态的初值,状态向量初始化为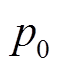 次的全充时间
次的全充时间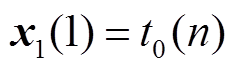 ,对p次的片段数据进行
,对p次的片段数据进行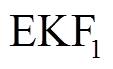 循环递推,估计第p次恒流充电所需要的全充时间,状态方程和测量方程如式(25)和式(26)所示。
循环递推,估计第p次恒流充电所需要的全充时间,状态方程和测量方程如式(25)和式(26)所示。
(6)扩展卡尔曼滤波一:循环递推
预测:
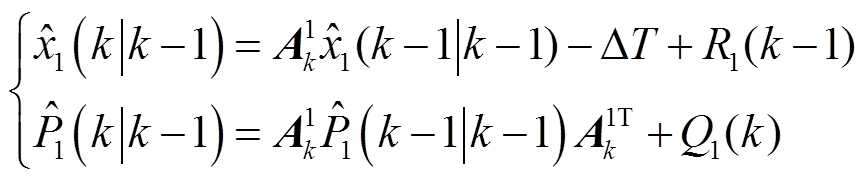
式中,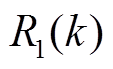 和
和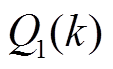 分别为噪声
分别为噪声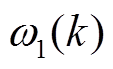 和
和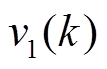 的协方差。
的协方差。
利用差商近似雅可比矩阵更新模型为
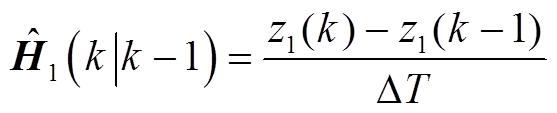
计算增益:
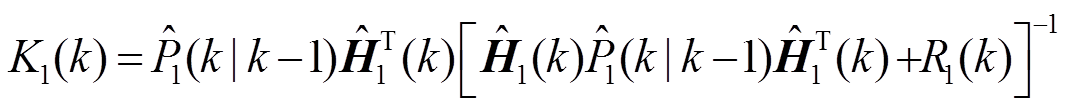
更新状态:
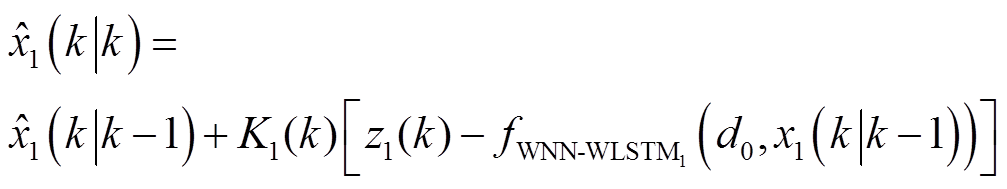
更新协方差:
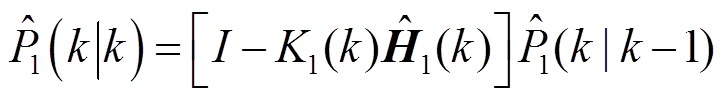
(7)扩展卡尔曼滤波二:提取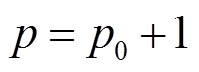 次
次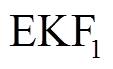 的状态和测量误差数据
的状态和测量误差数据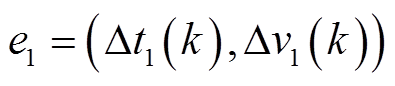 ,
,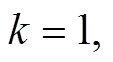
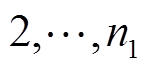 ,利用
,利用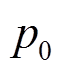 次时的片段累积误差
次时的片段累积误差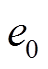 作为状态的初值,状态向量初始化为
作为状态的初值,状态向量初始化为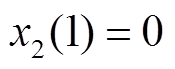 ,对p次的片段数据进行
,对p次的片段数据进行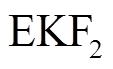 循环递推,估计第p次恒流充电
循环递推,估计第p次恒流充电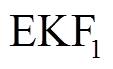 预测的全充时间与真实的全充时间的误差。
预测的全充时间与真实的全充时间的误差。
状态方程:

测量方程:
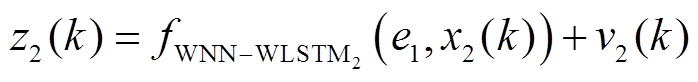
式中,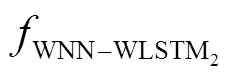 表示利用
表示利用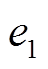 做小波神经网络-小波长短时神经网络二训练并预测状态
做小波神经网络-小波长短时神经网络二训练并预测状态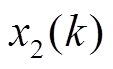 的误差电压值
的误差电压值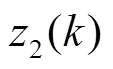 ;
; 为
为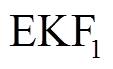 估计相邻两次全充时间的差值。
估计相邻两次全充时间的差值。
(8)扩展卡尔曼滤波二:循环递推
预测:
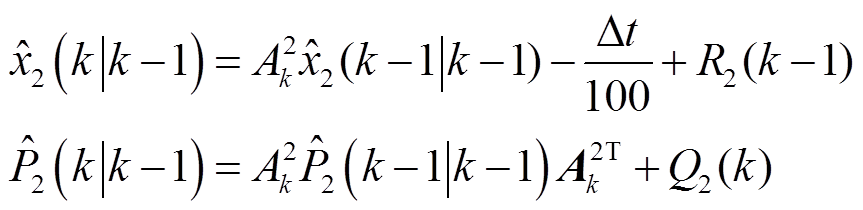
利用差商近似雅可比矩阵进行更新模型:
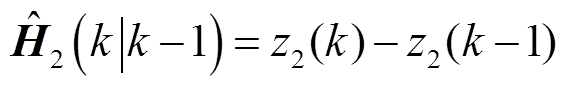
计算增益
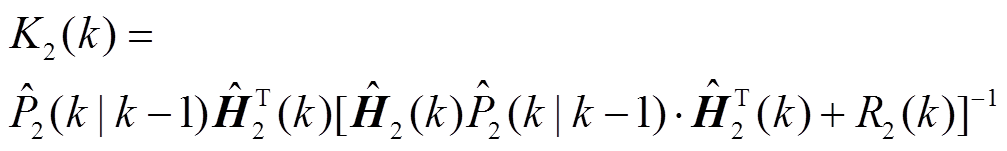
更新状态
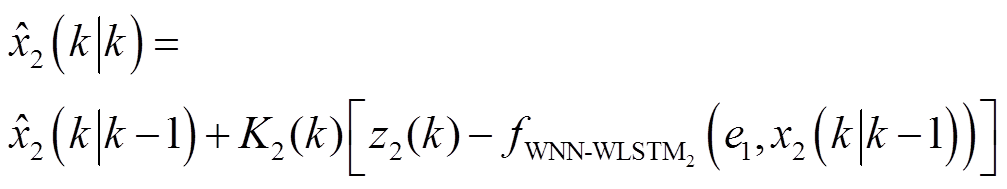
更新协方差
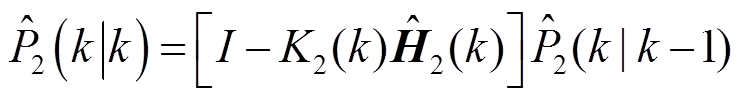
式中,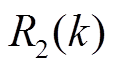 和
和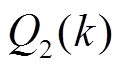 分别为噪声
分别为噪声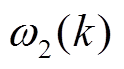 和
和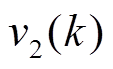 的协方差。
的协方差。
(9)预测全充时间与真实的全充时间的误差
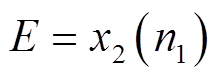
(10)预测全充时间:计算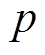 次片段数据的全充时间为
次片段数据的全充时间为
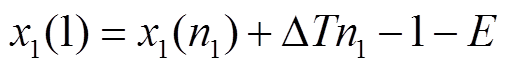
(11)更新循环:令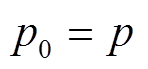 ,
,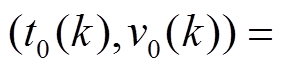
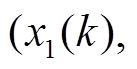
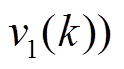 ,重复步骤(5)~步骤(10)。
,重复步骤(5)~步骤(10)。
为了展示所提算法的有效性,本文选用深圳新威尔电子公司提供的三元锂电池充放电数据库进行实验,该电池首先在2 100 mA的恒流条件下充电,直到电池电压达到8.4 V;然后在恒流2 100 mA水平下放电,直到电池电压达到5.6 V,如图5和图6所示。实验首先验证了DEKF-WNN-WLSTM算法的有效性,然后和EKF-GPR算法做对比,验证本文算法准确性,最后用DEKF算法估计的全充时间评估电池的健康状态。
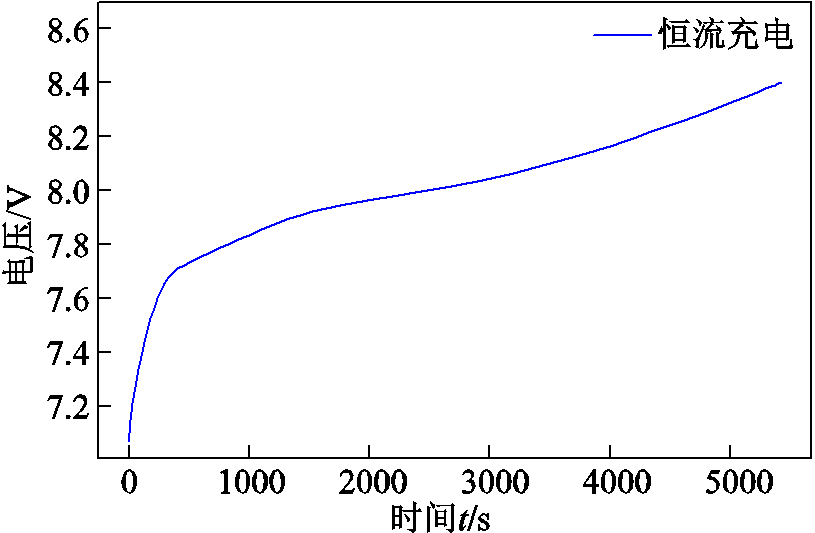
图5 恒流充电模式
Fig.5 The constant current charging mode
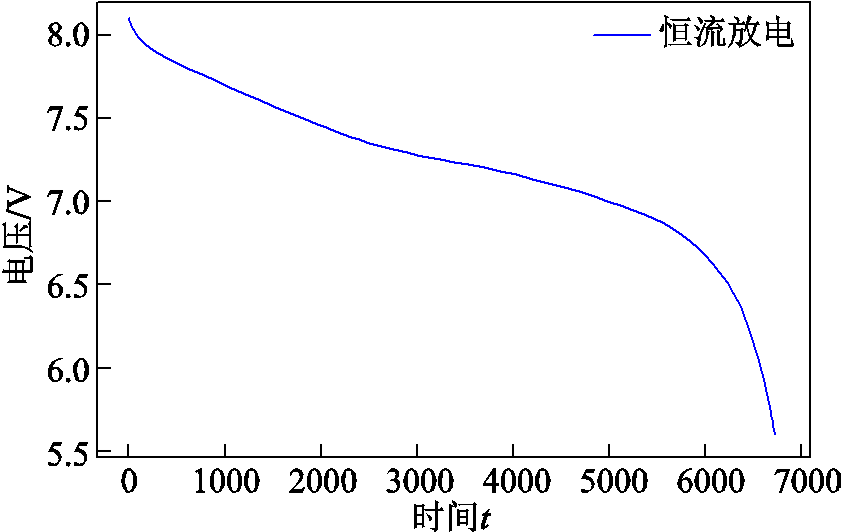
图6 恒流放电模式
Fig.6 The constant current discharging mode
实验硬件设施采用Inter(R) Core(TM) i5-7200u CPU @ 2.50 GHz处理器,Windows7旗舰版64位操作系统和8 GB运行内存。编程软件为Matlab 2018和Python 3.8,其中Python以深度学习框架Keras为支撑,实现了基于TensorFlow的WNN-WLSTM仿真模型的构建,为Matlab构建的双卡尔曼滤波模型提供相应的测量值。
图7是估计的全充时间和真实的全充时间对比图,可以看到,除个别变化较快的周期外,二者变化情况基本完全一致。这说明本文提出的DEKF-WNN-WLSTM算法能够在较低的误差范围内利用日常片段充电数据估计电池的全充时间。
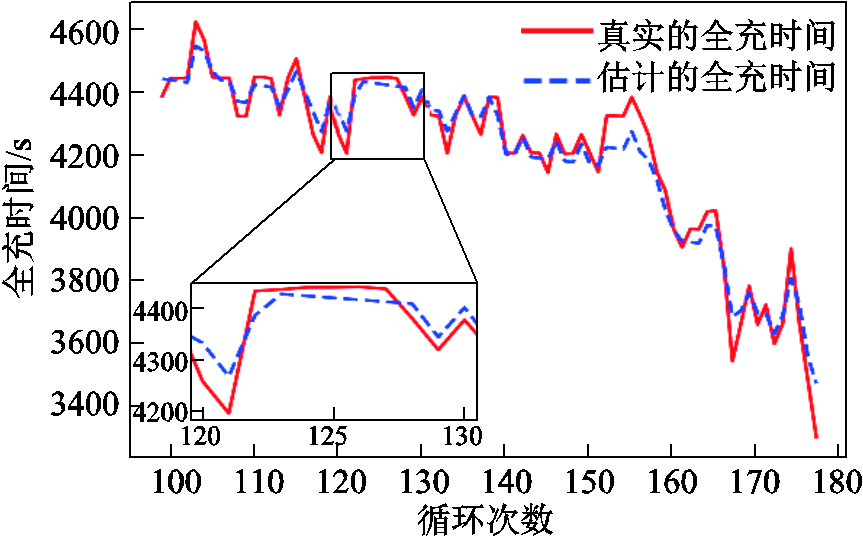
图7 估计的全充时间和真实的全充时间
Fig.7 The estimated whole charging time and true whole charging time
图8~图10分别为本文算法估计的绝对误差、相对误差及相对误差绝对值。根据图10可以计算得到,整个80次预测结果的平均相对误差为0.010 1。由于电池的初始充放电数据不稳定,本文舍弃前100次的电池数据,选用第100次循环数据作为初始全充数据。从图8~图10中可以得到,前50次循环中估计全充时间的误差全部小于2%,大多数时刻小于1%。由于对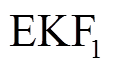 的状态初值进行了一定的修正,50~78次之间的误差也在4%以内,验证了本文算法的准确性和有效性。
的状态初值进行了一定的修正,50~78次之间的误差也在4%以内,验证了本文算法的准确性和有效性。
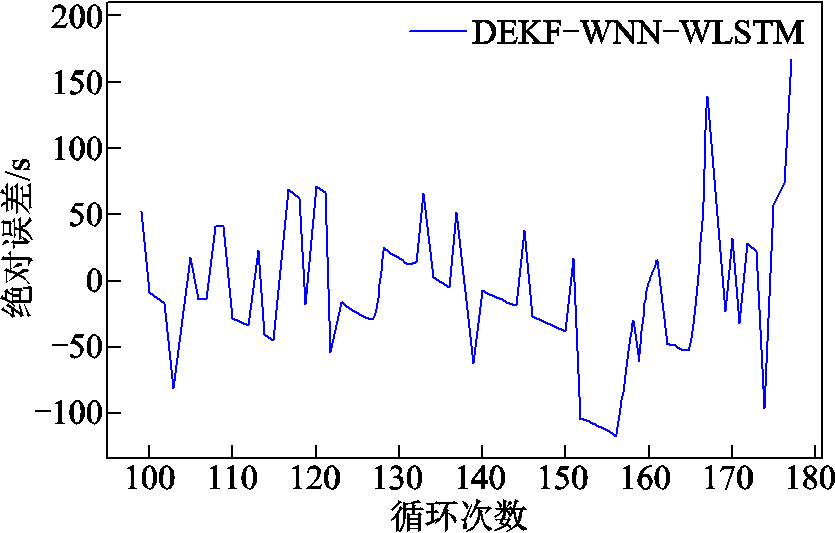
图8 估计全充时间的绝对误差
Fig.8 Absolute error of estimated full charge time
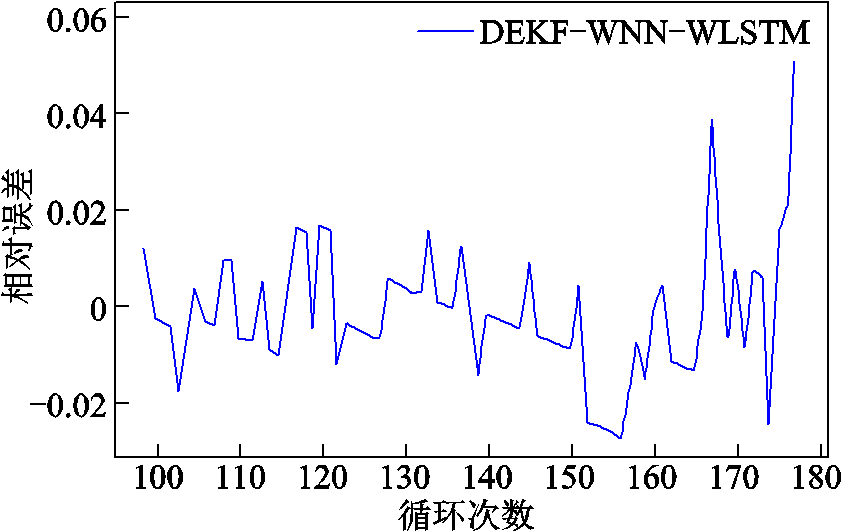
图9 估计全充时间的相对误差
Fig.9 Relative error of estimated full charge time
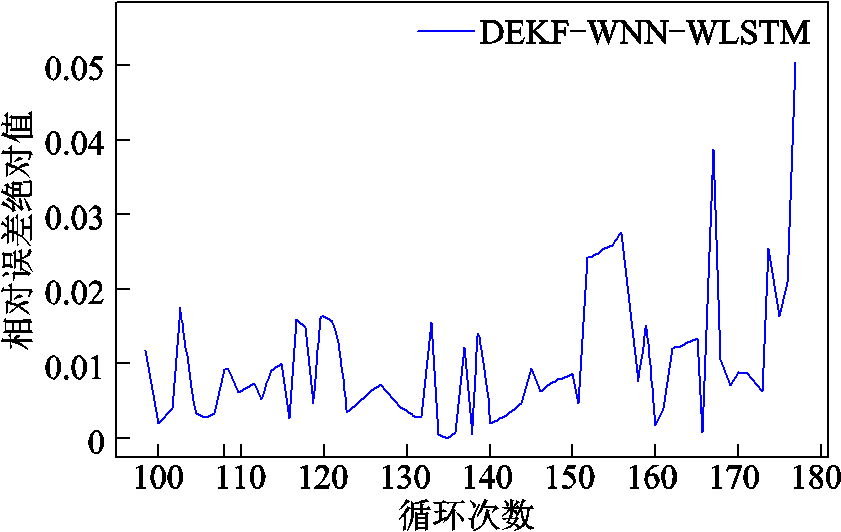
图10 估计全充时间的相对误差绝对值
Fig.10 Absolute value of relative error of estimated full charge time
为了进一步证明所提方法的预测性能,本节与周頔等[29]提出的基于EKF-GPR方法进行比较。图11为两种方法估计和真实的全充时间对比图。从图中可以看到:本文所提的算法相比于EKF-GPR更接近真实值,尤其是在循环次数为125~135和170~180时。这说明随着循环次数的增加,DEKF-WNN-WLSTM方法能够缓解一定的误差增长,在不人为进行一次全放全充操作以更新初始全充时间值的条件下,本文所提方法具有更好的估计效果。
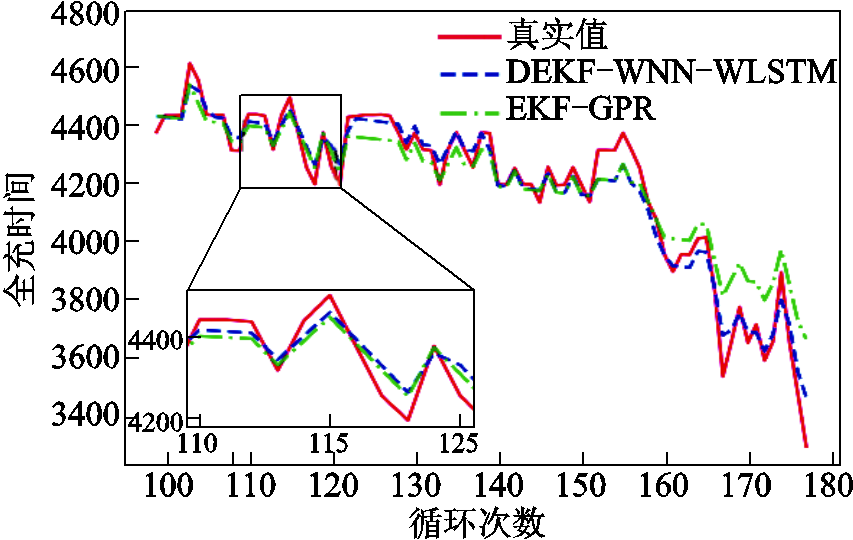
图11 两种估计方法的结果比较
Fig.11 Comparison results of the two estimation methods
表1为两种方法的平均相对误差,DEKF-WNN-WLSTM的平均相对误差为0.010 1,低于EKF-GPR的0.017 6,进一步说明本文所提方法的准确性高。
表1 两种方法的平均相对误差
Tab.1 The average relative error of the two methods

指标EKF-GPRDEKF-WNN-WLSTM 平均相对误差0.017 60.010 1
图12~图14分别为两种估计方法的绝对误差、相对误差和相对误差绝对值。可以发现:DEKF-WNN-WLSTM相对于EKF-GPR而言,其误差曲线普遍低于后者,尤其是循环次数在165~180之间时,二者的误差曲线相差最远,这说明本文方法具有较好的预测能力。
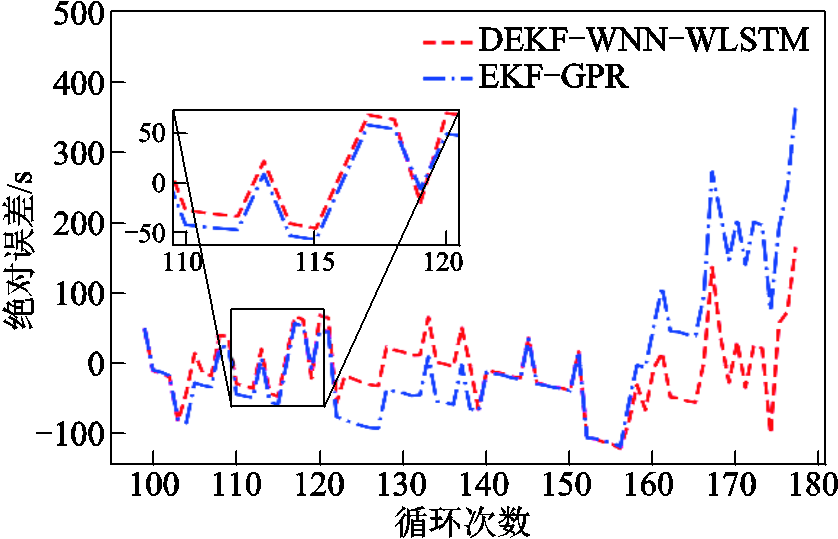
图12 两种方法的绝对误差
Fig.12 Absolute error of the two methods
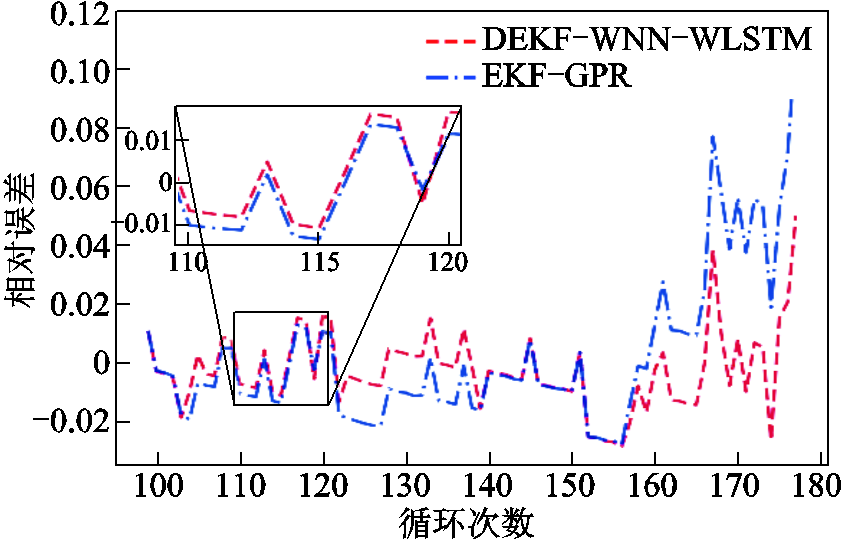
图13 两种方法的相对误差
Fig.13 Relative error of the two methods
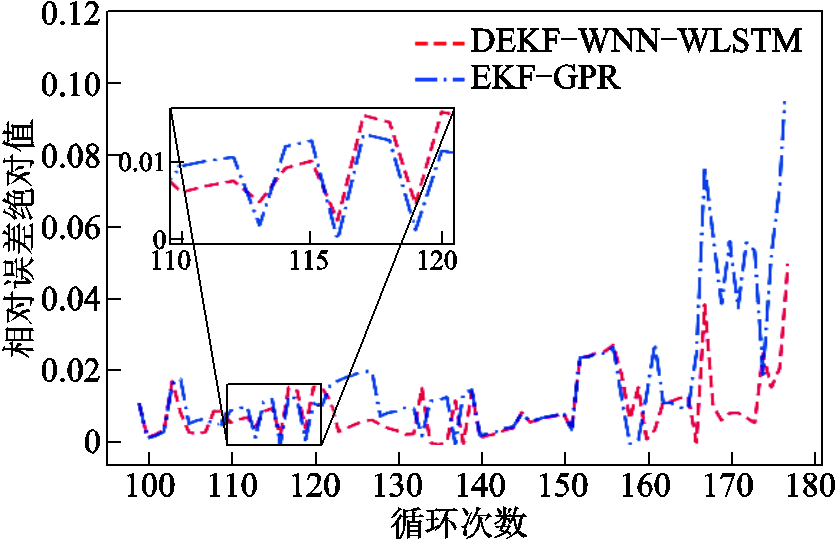
图14 两种方法的相对误差绝对值
Fig.14 Absolute value of relative error of the two methods
本文采用式(3)所示的基于充电容量评估电池SOH的模型。由式(2)和式(3)可得电池的SOH为
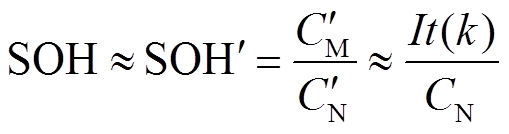
式中,t(k)为第k次循环的全充时间。
因为恒流充电电流I和放电标称容量CN为常数,所以电池实时的SOH和电池的全充时间成正比。由图7可知,估计的电池SOH曲线和估计的全充时间成正比,同样具有整体下降局部再升性。假设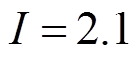 A,
A,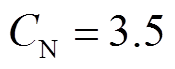 A·h,则本文方法估计的SOH如图15所示;两种方法估计的SOH如图16所示。
A·h,则本文方法估计的SOH如图15所示;两种方法估计的SOH如图16所示。
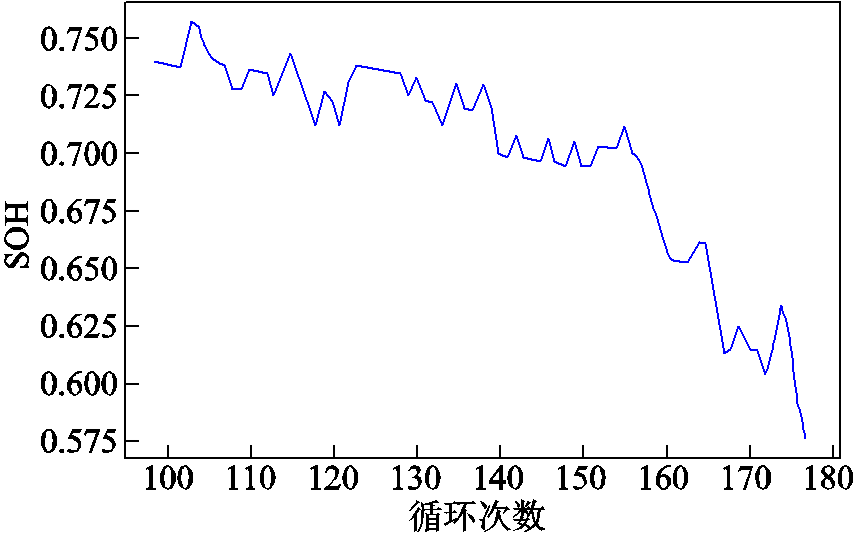
图15 本文方法估计的SOH
Fig.15 The estimated SOH of the proposed method
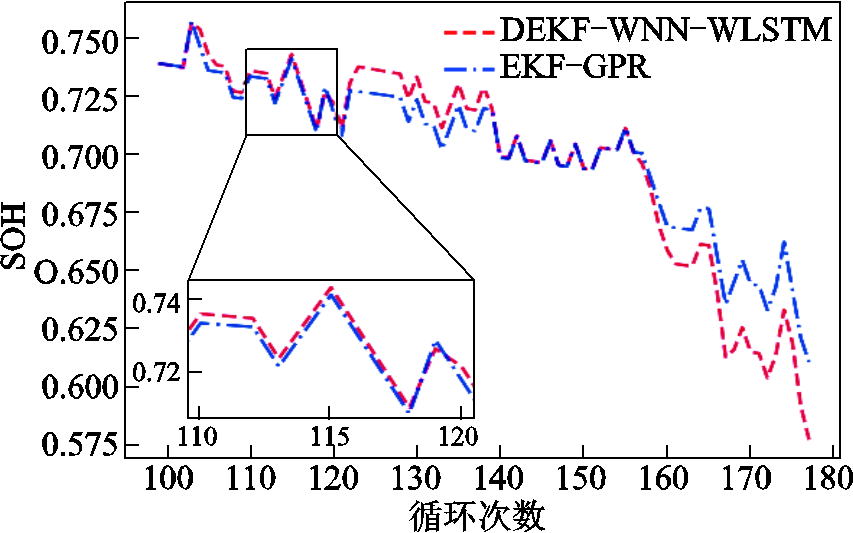
图16 两种方法估计的SOH
Fig.16 The estimated SOH of the two methods
本文提出了基于DEKF-WNN-WLSTM和日常片段充电数据的锂电池健康状态估计算法,其核心为利用小波神经网络-小波长短时记忆神经网络优秀的学习和预测性能,去学习扩展卡尔曼滤波的量测方程,在一定的噪声假设下,可以实现电池健康状态的实时预测,有利于电池的维护以及电动汽车在现实生活中的广泛使用。实验仿真结果表明,相比于EKF-GPR电池SOH实时估计模型,本文所提方法能够有效缓解误差的累积,且短期内的预测值和真实值的差异基本可以控制在1%左右。最后,利用充电容量估算SOH模型,实现了电池SOH的实时评估。
参考文献
[1] Al-Ghussain L, Darwish Ahmad A, Abubaker A M, et al. An integrated photovoltaic/wind/biomass and hybrid energy storage systems towards 100% renewable energy microgrids in university campuses[J]. Sustainable Energy Technologies and Assessments, 2021, 46: 101273.
[2] Guo Yuanjun, Yang Zhile, Liu Kailong, et al. A compact and optimized neural network approach for battery state-of-charge estimation of energy storage system[J]. Energy, 2021, 219: 119529.
[3] Zhang Zhengxin, Si Xiaosheng, Hu Changhua, et al. Degradation data analysis and remaining useful life estimation: a review on Wiener-process-based methods[J]. European Journal of Operational Research, 2018, 271(3): 775-796.
[4] Hu Xiaosong, Feng Fei, Liu Kailong, et al. State estimation for advanced battery management: key challenges and future trends[J]. Renewable and Sustainable Energy Reviews, 2019, 114: 109334.
[5] Shrivastava P, Soon T K, Bin Idris M Y I, et al. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries[J]. Renewable and Sustainable Energy Reviews, 2019, 113: 109233.
[6] Chen Zheng, Xue Qiao, Xiao Renxin, et al. State of health estimation for lithium-ion batteries based on fusion of autoregressive moving average model and Elman neural network[J]. IEEE Access, 2019, 7: 102662-102678.
[7] Lyu Chao, Zhang Tao, Luo Weilin, et al. SOH estimation of lithium-ion batteries based on fast time domain impedance spectroscopy[C]//2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi'an, China, 2019: 2142-2147.
[8] Kwiecien M, Badeda J, Huck M, et al. Determination of SoH of lead-acid batteries by electrochemical impedance spectroscopy[J]. Applied Sciences, 2018, 8(6): 873.
[9] Sauer D U, Wenzl H. Comparison of different approaches for lifetime prediction of electrochemical systems—using lead-acid batteries as example[J]. Journal of Power Sources, 2008, 176(2): 534-546.
[10] Zhang Ji’ang, Wang Ping, Gong Qingrui, et al. SOH estimation of lithium-ion batteries based on least squares support vector machine error compensation model[J]. Journal of Power Electronics, 2021, 21(11): 1712-1723.
[11] Wang Shuai, Zhang Xiaochen, Chen Wengxiang, et al. State of health prediction based on multi-kernel relevance vector machine and whale optimization algorithm for lithium-ion battery[J]. Transactions of the Institute of Measurement and Control, 2021, DOI: 101177/01423312211042009.
[12] 杨胜杰, 罗冰洋, 王菁, 等. 基于容量增量曲线峰值区间特征参数的锂离子电池健康状态估算[J]. 电工技术学报, 2021, 36(11): 2277-2287. Yang Shengjie, Luo Bingyang, Wang Jing, et al. State of health estimation for lithium-ion batteries based on peak region feature parameters of incremental capacity curve[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2277-2287.
[13] 韩乔妮, 姜帆, 程泽. 变温度下IHF-IGPR框架的锂离子电池健康状态预测方法[J]. 电工技术学报, 2021, 36(17): 3705-3720. Han Qiaoni, Jiang Fan, Cheng Ze. State of health estimation for lithium-ion batteries based on the framework of IHF-IGPR under variable temperature[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3705-3720.
[14] 李超然, 肖飞, 樊亚翔, 等. 基于卷积神经网络的锂离子电池SOH估算[J]. 电工技术学报, 2020, 35(19): 4106-4119. Li Chaoran, Xiao Fei, Fan Yaxiang, et al. An approach to lithium-ion battery SOH estimation based on convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4106-4119.
[15] 郭永芳, 黄凯, 李志刚. 基于短时搁置端电压压降的快速锂离子电池健康状态预测[J]. 电工技术学报, 2019, 34(19): 3968-3978. Guo Yongfang, Huang Kai, Li Zhigang. Fast state of health prediction of lithium-ion battery based on terminal voltage drop during rest for short time[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3968-3978.
[16] Fan Yaxiang, Xiao Fei, Li Chaoran, et al. A novel deep learning framework for state of health estimation of lithium-ion battery[J]. Journal of Energy Storage, 2020, 32: 101741.
[17] Bonfitto A. A method for the combined estimation of battery state of charge and state of health based on artificial neural networks[J]. Energies, 2020, 13(10): 2548.
[18] Zhang Sihan, Hosen M S, Kalogiannis T, et al. State of health estimation of lithium-ion batteries based on electrochemical impedance spectroscopy and backpropagation neural network[J]. World Electric Vehicle Journal, 2021, 12(3): 156.
[19] Chang Chun, Wang Qiyue, Jiang Jiuchun, et al. Lithium-ion battery state of health estimation using the incremental capacity and wavelet neural networks with genetic algorithm[J]. Journal of Energy Storage, 2021, 38: 102570.
[20] Jia Jianfang, Wang Keke, Pang Xiaoqiong, et al. Multi-scale prediction of RUL and SOH for lithium-ion batteries based on WNN-UPF combined model[J]. Chinese Journal of Electronics, 2021, 30(1): 26-35.
[21] Zhang J, Gao X P, Li Y Q. Efficient wavelet networks for function learning based on adaptive wavelet neuron selection[J]. IET Signal Processing, 2012, 6(2): 79.
[22] Xia Bizhong, Cui Deyu, Sun Zhen, et al. State of charge estimation of lithium-ion batteries using optimized Levenberg-Marquardt wavelet neural network[J]. Energy, 2018, 153: 694-705.
[23] Chang Wen-Yeau, Chang Po-Chuan. Application of radial basis function neural network, to estimate the state of health for LFP battery[J]. International Journal of Electrical and Electronics Engineering (IJEEE), 2018, 7(1): 1-6.
[24] 周才杰, 汪玉洁, 李凯铨, 等. 基于灰色关联度分析-长短期记忆神经网络的锂离子电池健康状态估计[J]. 电工技术学报, 2022, 37(23): 6065-6073. Zhou Caijie, Wang Yujie, Li Kaiquan, et al. State of health estimation for lithium-Ion battery based ongray correlation analysis and long short-term memory neural network[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6065-6073.
[25] 黄凯, 丁恒, 郭永芳, 等. 基于数据预处理和长短期记忆神经网络的锂离子电池寿命预测[J]. 电工技术学报, 2022, 37(15): 3753-3766. Huang Kai, Ding Heng, Guo Yongfang, et al. Prediction of remaining useful life of lithium-ion battery based on adaptive data preprocessing and long short-term memory network [J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3753-3766.
[26] Kim S J, Kim S H, Lee H M, et al. State of health estimation of Li-ion batteries using multi-input LSTM with optimal sequence length[C]//2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, Netherlands, 2020: 1336-1341.
[27] 程泽, 杨磊, 孙幸勉. 基于自适应平方根无迹卡尔曼滤波算法的锂离子电池SOC和SOH估计[J]. 中国电机工程学报, 2018, 38(8): 2384-2393. Cheng Ze, Yang Lei, Sun Xingmian. Estimation of SOC and SOH of Li-ion battery based on adaptive square root unscented Kalman filter algorithm[J]. Proceedings of the CSEE, 2018, 38(8): 2384-2393.
[28] 王萍, 弓清瑞, 张吉昂, 等. 一种基于数据驱动与经验模型组合的锂电池在线健康状态预测方法[J]. 电工技术学报, 2021, 36(24): 5201-5212. Wang Ping, Gong Qingrui, Zhang Jiang, et al. An online state of health prediction method for lithium batteries based on combination of data-driven and empirical model[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5201-5212.
[29] 周頔, 宋显华, 卢文斌, 等. 基于日常片段充电数据的锂电池健康状态实时评估方法研究[J]. 中国电机工程学报, 2019, 39(1): 105-111. Zhou Di, Song Xianhua, Lu Wenbin, et al. Real-time SOH estimation algorithm for lithium-ion batteries based on daily segment charging data[J]. Proceedings of the CSEE, 2019, 39(1): 105-111.
[30] Yang Duo, Zhang Xu, Pan Rui, et al. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve[J]. Journal of Power Sources, 2018, 384: 387-395.
[31] Julier S J, Uhlmann J K. New extension of the Kalman filter to nonlinear systems[C]//AeroSense '97. Proc SPIE 3068, Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, USA, 1997, 3068: 182-193.
Abstract As a clean technology to solve carbon emissions, electric vehicles have been widely used in modern vehicles. Due to its high energy density, light weight, long life and low self discharge, lithium-ion batteries have become the main energy storage equipment of electric vehicles. Real time and accurate evaluation of the state of health (SOH) of the lithium batteries is critical to the stable driving of electric vehicles. However, most traditional SOH forecast methods are offline, which makes it difficult to obtain the SOH of the batteries in real time. Recently, some methods were presented to forecast the SOH of lithium-ion batteries, but most of them suffered from inconvenient adjustment of battery model parameters and accumulation of errors. To address these issues, this paper proposes a battery full charging time estimation model and dual extended Kalman filters-wavelet neural network-wavelet long short-term memory neural network (DEKF-WNN-WLSTM). By taking the daily segment charging data of lithium batteries as input, to predict the full time charging of the battery, and then get the SOH in real time.
Firstly, based on the strong robustness of wavelet neural network (WNN) and the ability of long short term memory (LSTM) to extract the time series features of the data, the neural network of WNN-WLSTM is designed. Secondly, two WNN-WLSTM networks are trained with one full charging data and three fragment data of lithium batteries, respectively. Thirdly, a real-time estimation algorithm named DEKF is constructed, in which the first EKF is used to estimate the full charging time corresponding to the segment data, and the second EKF is used to predict the error between the estimated and measured battery full charging time under the current cycle. Then the two trained networks are integrated into DEKF to provide corresponding output values for the cyclic recursion of EKF. Finally, a real-time SOH estimation model based on daily segment charging data is designed. The segment data from constant current charging to full charging at any time is used as the input of DEKF-WNN-WLSTM, to estimate the current full charging time of lithium batteries, then calculate the SOH of the battery at the current time. In this real-time model, the WNN-WLSTM alleviates the inconvenient adjustment of battery model parameters problem, addresses the long-term dependence problem. The DEKF uses the daily segment charging data as the input, which extends the practical application of the model.
Simulation results on the actual battery charging and discharging data show that, the mean relative error of the predictions for the entire 80 cycles is 0.010 1, the estimated error for the first 50 cycles is completely less than 2%, and less than 1% at most times. The comparison between DEKF-WNN-WLSTM and extended Kalman filter and Gaussian process regression (EKF-GPR) shows that, the mean relative error of EKF-GPR is 0.017 6, which is higher than DEKF-WNN-WLSTM, especially in the 170~180 cycles, which indicates that the model of DEKF-WNN-WLSTM can alleviate certain error growth with the increase of cycles. The proposed method has a better estimation effect under the condition that no artificial full recharge operation is performed to update the initial full charging time value.
The following conclusions can be drawn from the simulation analysis: (1)The proposed method integrates WNN-WLSTM neural network, which address the problems of long-term dependence and the inconvenient adjustment of battery model parameters. (2) Compared with EKF-GPR, the DEKF-WNN-WLSTM not only improves the prediction accuracy, but also alleviates the error accumulation. (3) The proposed model only needs the daily segment charging data. In this sense, it is practical in the real world.
keywords:State of health, segment data, dual extended Kalman filter, wavelet neural network, wavelet long short-term memory
DOI:10.19595/j.cnki.1000-6753.tces.222241
中图分类号:TM911
黑龙江省自然科学基金联合引导项目(LH2022F032)和山东省自然科学基金联合基金培育项目(ZR2022LLZ003)资助。
收稿日期 2022-12-28
改稿日期 2023-02-14
宋显华 女,1981年生,博士,副教授,博士生导师,研究方向为机器学习和智能状态监测、图像安全和量子计算等。E-mail:songxianhua@hrbust.edu.cn(通信作者)
姚全正 男,1997年生,硕士研究生,研究方向为机器学习以及电动汽车动力电池健康状态评估。E-mail:2311884748@qq.com
(编辑 郭丽军)