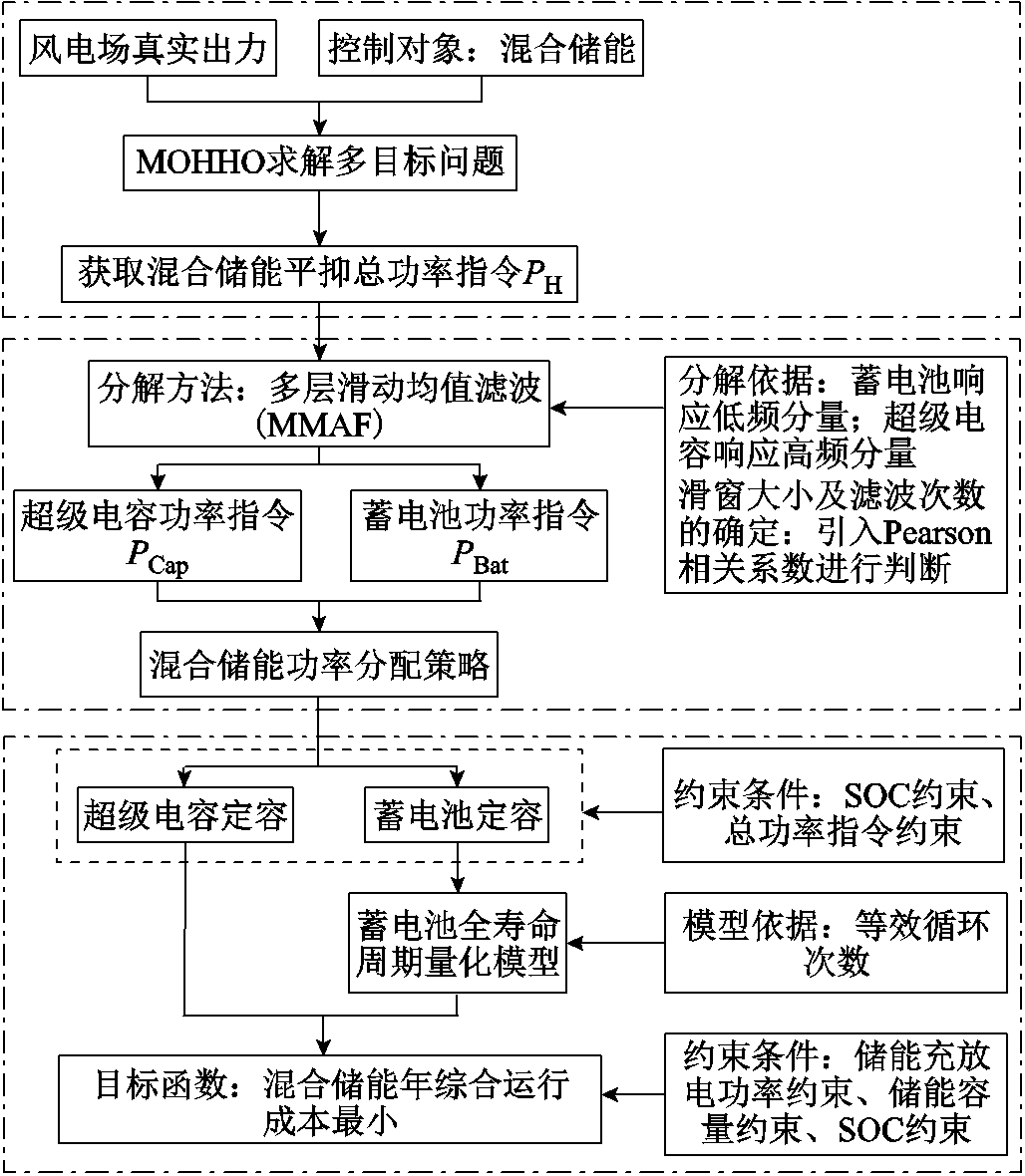
图1 基于MMAF的混合储能功率分配方法及定容研究框架
Fig.1 Hybrid energy storage power allocation method and constant capacity research framework based on MMAF
摘要 为了解决混合储能系统功率分配时因模态混叠导致功率分配不精确、储能系统成本过高的问题,提出一种多次滑动均值滤波(MMAF)的功率分配方法用于削弱模态混叠现象,降低混合储能成本。首先,获取满足平抑要求的混合储能最小总功率指令,采用MMAF算法对其进行滤波,获得蓄电池与超级电容各自的功率指令,引入Pearson相关系数量化模态混叠现象,作为判断滤波次数和每次滤波滑窗大小的指标,将蓄电池和超级电容各自的功率指令作为储能定容的可行域,考虑电池荷电状态约束求取储能适配的最小额定功率和额定容量;然后,基于等效运行时间建立蓄电池全寿命周期量化模型,为经济性分析提供依据;最后,以改进的混合储能全寿命周期成本模型验证了该文方法可以有效地限制模态混叠,降低混合储能系统成本。
关键词:混合储能 功率分配 模态混叠 多次滑动均值滤波(MMAF)算法 蓄电池全寿命周期量化模型
高比例风电接入电网,由于其自身的波动性和随机性会对电力系统造成冲击[1]。储能设备对电能具有时空转移和灵活调度的能力,在风电场侧配置储能设备是解决风电波动的一个可行方案[2-3]。蓄电池作为能量型储能的代表具有储能能量密度大、存储能力强等特性,但由于其存在功率密度小、使用寿命短等缺陷,不宜高频率地切换充放电状态[4-5]。超级电容作为功率型储能,具有功率密度大、响应时间短、使用寿命长等优点[6-7]。将二者结合组成的混合储能系统可以形成优势互补[8-9],克服单一储能的劣势,提高风电平抑效率[10]。但是如何将混合储能总功率精确地分配给蓄电池和超级电容却是一个亟须解决的问题。混合储能总功率分配不准确引起混合储能系统定容不合理从而导致混合储能系统成本高的问题成为阻碍储能行业发展的重要因素[11-13]。如何通过精准分配混合储能总功率来合理定容以实现经济效益最大化已成为近年来众多学者研究的重大课题[14-16]。
国内外研究人员针对上述问题开展了许多研究,得到了一些结论。文献[17]采用经验模态分解(Empirical Mode Decomposition, EMD)对混合储能总功率进行分析,按照不同的截止频率将总功率分配给蓄电池和超级电容。但EMD分解后各模态易发生混叠且分解过程中易存在噪声,这对后续混合储能的经济性分析十分不利。为了限制模态混叠,文献[18-19]提出了基于变分模态分解(Variational Modal Decomposition, VMD)的频域分析方法用于对混合储能总功率进行分解。虽然VMD在一定程度上限制了模态混叠,但其并不能在所有非平稳信号上直接使用,且分解层数的选择有较大的主观性,因此文献[20]提出了一种采用智能算法对VMD参数寻优的混合储能功率分配策略。这种方法在一定程度上克服了VMD参数选取的人为性,但寻优算法无法保证优化所得的参数是全局最优解,进而也无法判断是否最大化地避免了模态混叠。文献[21-23]则直接从储能定容入手,建立风光储系统,以经济成本为目标探究了不同场景下混合储能定容配置问题。文献[24]基于合作博弈建立了共享储能的运行机制,分析了不同合作模式下的收益,以此规划储能的容量配置。文献[25]通过模型预测控制(Model Predictive Control, MPC)建立了混合储能动态功率分配策略并获得了较好的功率分配效果。文献[26]利用动态小波对混合储能系统功率进行分配,克服了传统小波不能根据时序自适应地调整小波参数的局限性,但并没有对动态小波分解后各模态是否发生混叠做进一步分析。文献[27]改进了一阶低通滤波器,在功率分配之前加入判断指令以减少因模态混叠使混合储能功率误分配的情况。
尽管已经有众多研究人员针对此类问题进行探究,但现阶段仍存在如下问题:①在对混合储能总功率分配时缺少可以量化模态混叠的指标;②由于风电出力的不确定性,现有功率分配方法并不能对所有非平稳信号都有较好的分解效果。
滑动均值滤波(Moving Average Filtering, MAF)因其原理简单、适用性强的优势近年来被广泛应用于平滑风功率波动中[28]。本文提出一种基于多次滑动均值滤波(Multiple Moving Average Filtering, MMAF)的混合储能系统功率分配方法及定容策略。首先,获取混合储能总功率指令,通过MMAF对混合储能总功率进行分解,同时引入Pearson相关系数判断滤波次数与滑窗大小,根据功率分配结果对混合储能系统进行定容;然后,基于等效运行时间建立了蓄电池全寿命周期量化模型,为混合储能经济性分析提供理论依据;最后,通过改进的混合储能全寿命周期成本(Life Cycle Cost, LCC)模型验证了本文方法能够更好地量化并限制模态混叠,降低混合储能系统的综合成本。本文的整体框架如图1所示。

图1 基于MMAF的混合储能功率分配方法及定容研究框架
Fig.1 Hybrid energy storage power allocation method and constant capacity research framework based on MMAF
用于平滑风功率波动的混合储能系统结构拓扑如图2所示,其功率流关系为
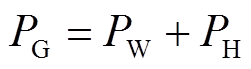 (1)
(1)
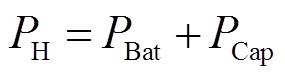 (2)
(2)
式中,PBat为蓄电池的有功出力;PCap为超级电容的有功出力;PH为混合储能的有功出力;PW为风电原始功率;PG为风电并网功率。
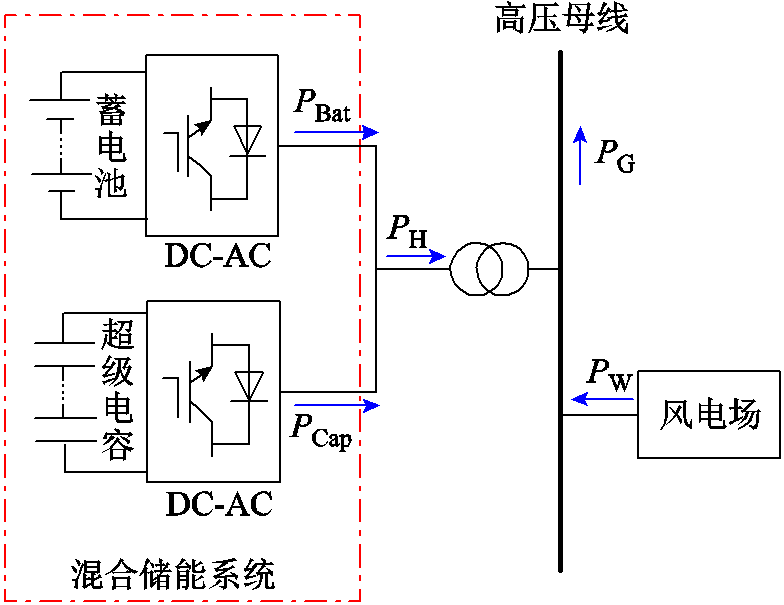
图2 平滑风功率的混合储系统结构拓扑
Fig.2 Topology diagram of hybrid storage system with smooth wind power
为了平抑风电并网功率波动,以混合储能系统作为研究对象。在求解混合储能总功率指令PH时将混合储能系统(Hybrid Energy Storage System, HESS)看作整体,不考虑蓄电池与超级电容各自的运行状态,通过定义式(3)~式(9)所示的多目标函数获取满足平抑要求的HESS最小出力指令。
1)目标Ⅰ:功率波动绝对值均值
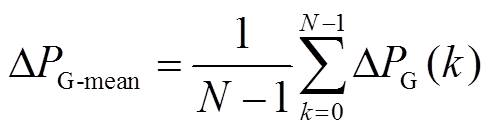 (3)
(3)
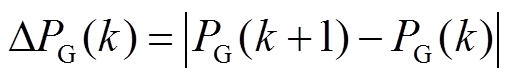 (4)
(4)
式中,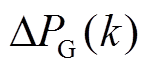 为k时刻风电并网功率波动的绝对值;
为k时刻风电并网功率波动的绝对值;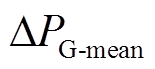 为风电并网功率波动绝对值均值;N为调度日内采样点个数;T为一个调度日时长。
为风电并网功率波动绝对值均值;N为调度日内采样点个数;T为一个调度日时长。
2)目标Ⅱ:储能充放电总能量
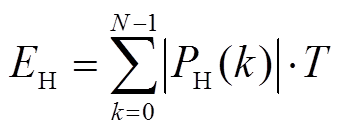 (5)
(5)
式中,EH为混合储能在整个控制周期内吞吐能量的总值。
3)目标Ⅲ:储能出力能力评价系数
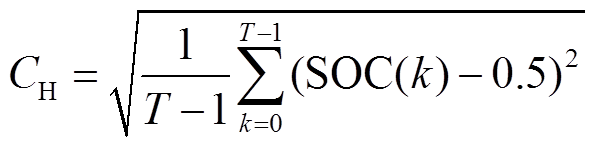 (6)
(6)
式中,SOC(k)为k时刻混合储能的荷电状态。
4)目标Ⅳ: 储能进入死区时间
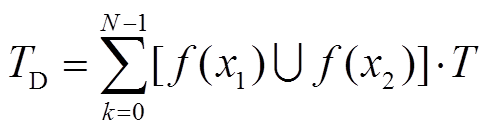 (7)
(7)
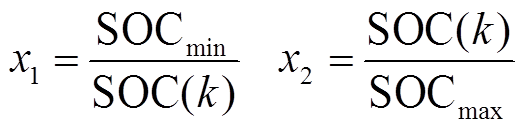 (8)
(8)
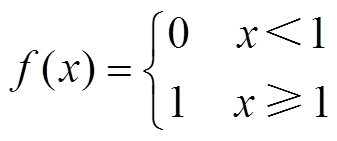 (9)
(9)
式中,TD为控制周期内储能装置由于荷电状态(State of Charge, SOC)越限而无法吞吐能量的时间,即死区时间;SOCmax和SOCmin分别为储能电池荷电状态的上限和下限。
上述四个目标函数均会影响HESS的运行状态。通过多目标哈里斯鹰算法(Multi Objective Harris Hawks Optimizer, MOHHO)[29]求取在四个目标值最小时的HESS总功率指令PH,为后续分析如何将HESS总功率指令分配给蓄电池与超级电容以实现混合储能系统成本最低提供数据基础。
近些年常见的储能功率分配方法有EMD、VMD等。这些方法普遍存在的问题是信号分解层数需要依靠经验判断,主观性较强,分解后所得各模态的频谱时常发生混叠,对功率分配及储能设备的健康运行极其不利。针对上述问题,本文借鉴模态分解中“多层分解”的思想,采用MMAF对混合储能总功率指令进行多次滤波,同时引入Pearson相关系数作为判断滑窗大小与滤波次数的一项重要指标,避免主观地选择滤波参数,以达到最大程度抑制模态混叠的目的。
MAF本质属于低通滤波,因其原理简单,易于实现等优点,被广泛应用于信号处理领域。将混合储能总功率指令作为输入信号,通过MMAF可以获得相应的低频分量和高频分量。本文重点对每次滤波后获取的低频分量进行处理,最大限度地剔除混杂在低频分量中的高频分量。取最后一次滤波所得低频分量作为蓄电池的功率指令,总功率指令与最终所得的低频分量做差即可得到高频分量,以此作为超级电容的功率指令。MMAF算法功率分配原理如图3所示。
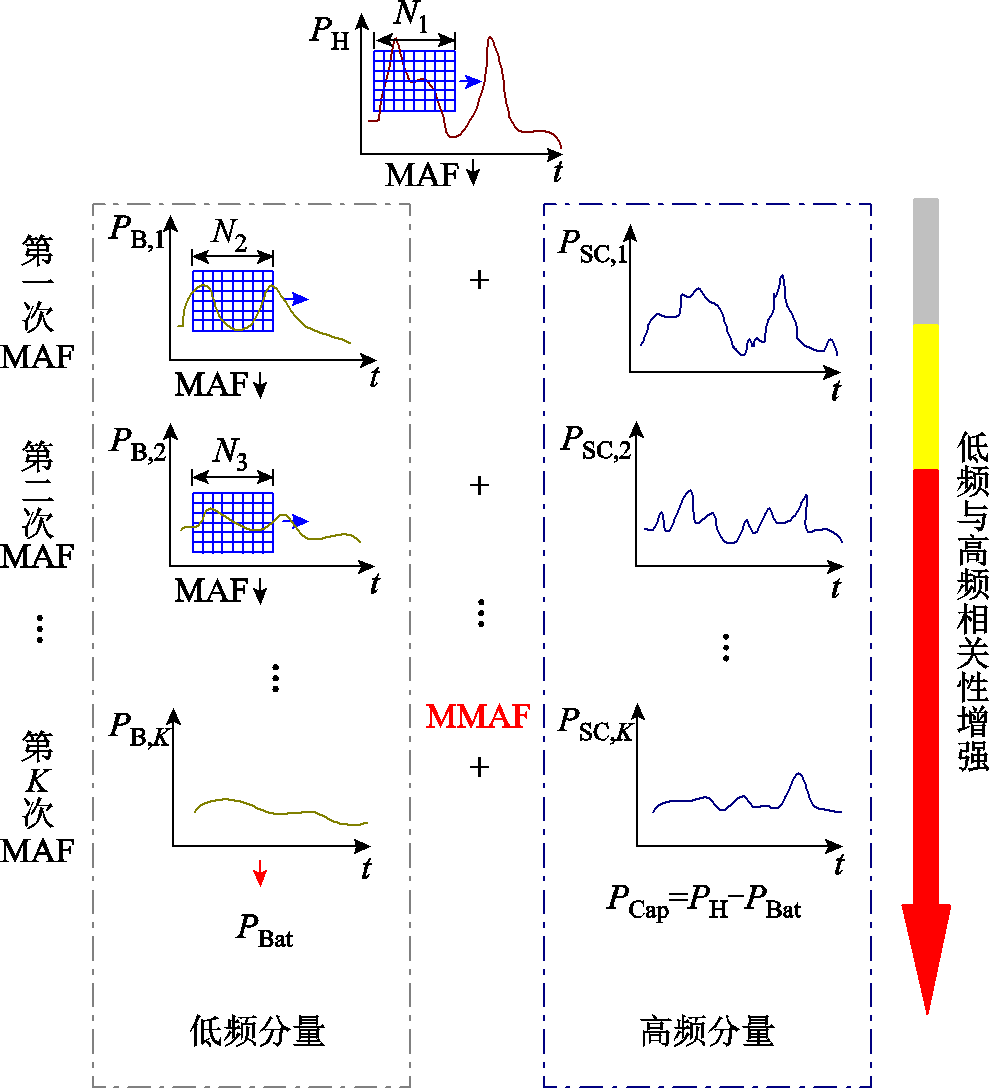
图3 MMAF算法功率分配功率原理
Fig.3 Schematic diagram of MMAF algorithm power distribution
设第x次MAF的窗口大小为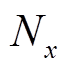 ,且
,且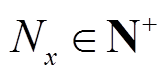 ,假设在每个
,假设在每个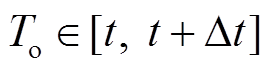 时段内(
时段内(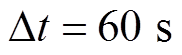 )混合储能总功率指令用
)混合储能总功率指令用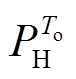 表示,则由递推归纳可得第一次滤波后在
表示,则由递推归纳可得第一次滤波后在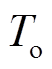 区间内蓄电池预分配的功率指令为
区间内蓄电池预分配的功率指令为
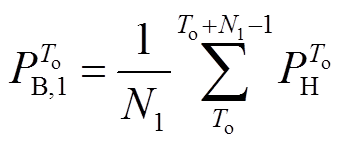 (10)
(10)
式中,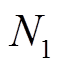 为第一次MAF的窗口大小;
为第一次MAF的窗口大小;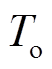 为混合储能的控制步长(min-1);
为混合储能的控制步长(min-1);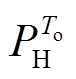 为
为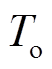 时刻混合储能总功率指令;
时刻混合储能总功率指令;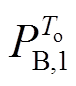 为第一次滤波后
为第一次滤波后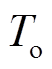 时段蓄电池预分配的功率指令。
时段蓄电池预分配的功率指令。
经过一次MAF后混合储能总功率指令中大多数高频信号被分离,此时认为滤出的低频分量中仍存在部分高频分量,即存在模态混叠现象。因此对第一次滤波后得到的低频信号进行第二次MAF,并以此类推至第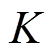 次,有
次,有
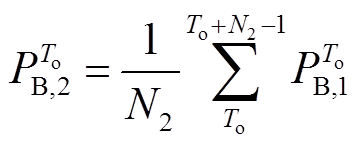 (11)
(11)
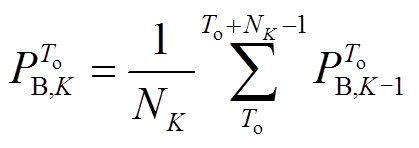 (12)
(12)
式中,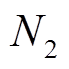 为第二次MAF的窗口大小;
为第二次MAF的窗口大小;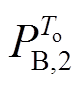 为第二次滤波后
为第二次滤波后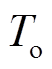 时段蓄电池预分配的功率指令;
时段蓄电池预分配的功率指令;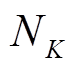 为第
为第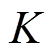 次MAF的窗口大小;
次MAF的窗口大小;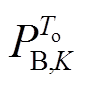 为第K次滤波后
为第K次滤波后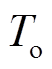 时段蓄电池预分配的功率指令。
时段蓄电池预分配的功率指令。
经第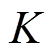 次MAF后所得到的低频分量认为已经较好地分离了所有的高频分量,将此时的低频信号作为蓄电池最终分得的功率指令。经过MMAF后确定的蓄电池和超级电容的功率指令分别为
次MAF后所得到的低频分量认为已经较好地分离了所有的高频分量,将此时的低频信号作为蓄电池最终分得的功率指令。经过MMAF后确定的蓄电池和超级电容的功率指令分别为
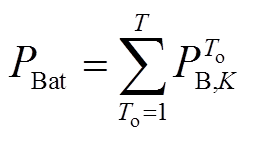 (13)
(13)
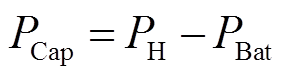 (14)
(14)
2.2.1 滑窗大小N的确定
滑动窗口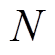 的大小对滤波效果有直接影响。
的大小对滤波效果有直接影响。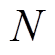 选择不合理,会导致滤波后的低频分量中包含部分高频分量的模态,即发生模态混叠。本文通过穷举
选择不合理,会导致滤波后的低频分量中包含部分高频分量的模态,即发生模态混叠。本文通过穷举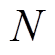 的大小求取在每一窗口大小下滤波得到的低频分量与高频分量的相关性,取相关系数最小时对应的滑动窗口作为第一次滤波的窗口大小
的大小求取在每一窗口大小下滤波得到的低频分量与高频分量的相关性,取相关系数最小时对应的滑动窗口作为第一次滤波的窗口大小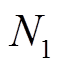 。同理可得第二次~第K次的滑动窗口大小
。同理可得第二次~第K次的滑动窗口大小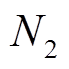 ~
~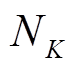 。
。
记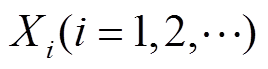 为滑窗大小
为滑窗大小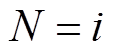 时滤波获取的低频信号,
时滤波获取的低频信号,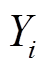 为对应的高频信号。则将
为对应的高频信号。则将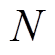 遍历后每个滑窗大小下产生的低频与高频信号的Pearson相关系数可定义为
遍历后每个滑窗大小下产生的低频与高频信号的Pearson相关系数可定义为
 (15)
(15)
式中,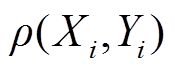 为
为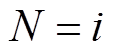 时低频分量与高频分量的Pearson相关系数;
时低频分量与高频分量的Pearson相关系数;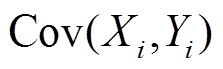 为
为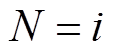 时低频分量与高频分量的协方差;
时低频分量与高频分量的协方差;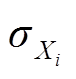 、
、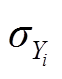 分别为
分别为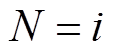 时低频分量与高频分量的标准差。
时低频分量与高频分量的标准差。
2.2.2 滤波次数K的确定
模态混叠会造成混合储能总功率指令分配的不准确性,导致混合储能系统成本的增加和储能电池的老化。若要最大程度地限制模态混叠现象,则有必要对MMAF的滤波次数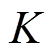 进行合理选择。为了将模态混叠程度量化表示,以及为
进行合理选择。为了将模态混叠程度量化表示,以及为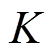 的选择提供理论依据,定义式(16)所示的Pearson相关系数。
的选择提供理论依据,定义式(16)所示的Pearson相关系数。
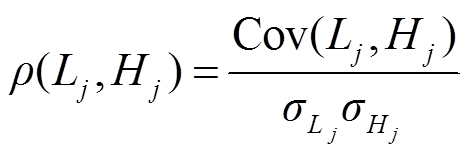 (16)
(16)
式中,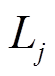 和
和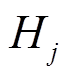
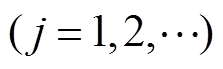 分别为
分别为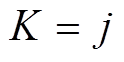 时滤波产生的低频分量和高频分量;
时滤波产生的低频分量和高频分量;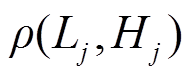 为
为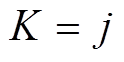 时滤波后产生的低频分量与高频分量的Pearson相关系数;
时滤波后产生的低频分量与高频分量的Pearson相关系数;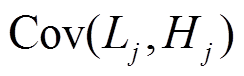 为
为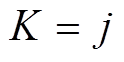 时低频分量和高频分量的协方差;
时低频分量和高频分量的协方差;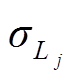 、
、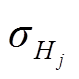 分别为
分别为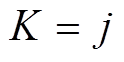 时低频分量与高频分量的标准差。
时低频分量与高频分量的标准差。
由第2.1节理论分析可知,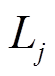 为在第
为在第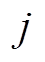 次滤波后蓄电池预分配的功率指令,
次滤波后蓄电池预分配的功率指令,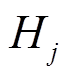 为在第
为在第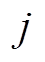 次滤波后超级电容预分配的功率指令。通过式(10)~式(16)的推导与分析可知,
次滤波后超级电容预分配的功率指令。通过式(10)~式(16)的推导与分析可知,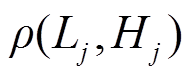 越大,说明第
越大,说明第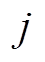 次滤波获得的高频分量与低频分量的相关性越大。若此时
次滤波获得的高频分量与低频分量的相关性越大。若此时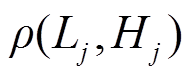 大到一定程度,表明经过第
大到一定程度,表明经过第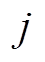 次滤波分离出的高频分量已经与低频分量有了非常强的相关性,可以认为第
次滤波分离出的高频分量已经与低频分量有了非常强的相关性,可以认为第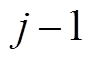 次滤波所得的低频分量中已经不存在高频分量,滤波次数
次滤波所得的低频分量中已经不存在高频分量,滤波次数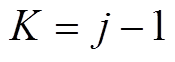 最大程度地限制了模态混叠现象。
最大程度地限制了模态混叠现象。
储能定容包括对储能电池额定功率与额定容量的配置。储能定容方案的合理性及精确性直接影响其经济性。本文以获取的蓄电池与超级电容各自分配的功率指令为基础,综合考虑储能电池荷电状态的限制,分别对蓄电池与超级电容进行定容规划。定容策略框架如图4所示。
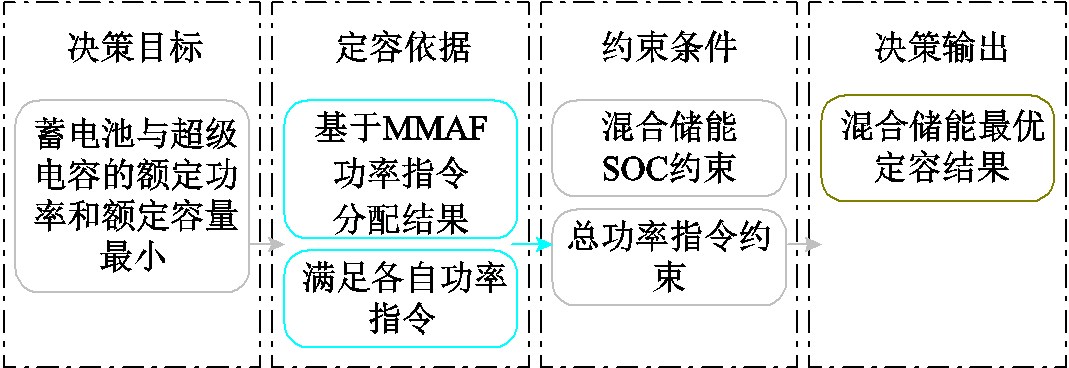
图4 混合储能定容策略框图
Fig.4 Block diagram of hybrid energy storage constant capacity strategy
在平滑风功率的场景下,对储能电池的功率而言,当电池充电时,需要在规定的时间内将其对应的功率指令全部吸收;当电池放电时,需要在规定的时间内将其对应的功率指令全部释放。则其额定功率最小值应满足任意时刻的功率指令需求,即不小于在第2节中分配的功率指令最大值。在储能电池的一个调度日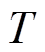 内可表述为:
内可表述为: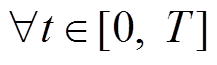 ,
,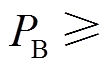
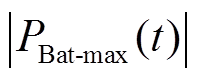 。若考虑储能变流器的工作效率和储能建设成本,则蓄电池满足功率指令需求的最小额定功率
。若考虑储能变流器的工作效率和储能建设成本,则蓄电池满足功率指令需求的最小额定功率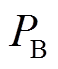 可按式(17)进行配置。
可按式(17)进行配置。
 (17)
(17)
式中,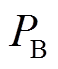 为蓄电池应配置的额定功率;
为蓄电池应配置的额定功率;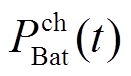 和
和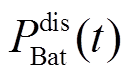 分别为
分别为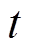 时刻蓄电池的充、放电功率指令;
时刻蓄电池的充、放电功率指令;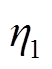 和
和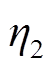 分别为双向DC-DC和双向DC-AC转换器的工作效率,本文取80%;
分别为双向DC-DC和双向DC-AC转换器的工作效率,本文取80%;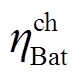 和
和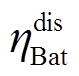 分别为蓄电池的充、放电效率,本文取90%。
分别为蓄电池的充、放电效率,本文取90%。
同理超级电容的最小额定功率配置方式为
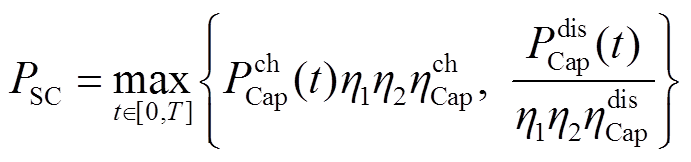 (18)
(18)
式中,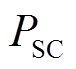 为超级电容应配置的额定功率;
为超级电容应配置的额定功率;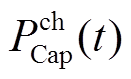 和
和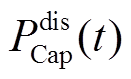 分别为
分别为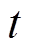 时刻超级电容的充、放电功率指令;
时刻超级电容的充、放电功率指令;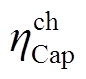 和
和 分别为超级电容的充、放电效率,本文取90%。
分别为超级电容的充、放电效率,本文取90%。
储能容量反映的是储能设备吞吐电量多少的能力。储能设备某一时刻剩余容量占额定容量的百分比用荷电状态表征,有
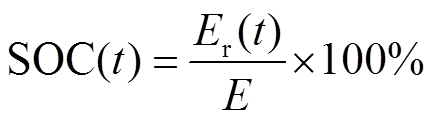 (19)
(19)
式中,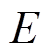 为储能电池的额定容量;
为储能电池的额定容量;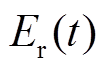 为
为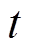 时刻储能电池剩余的容量。
时刻储能电池剩余的容量。
基于式(19)可分别建立储能电池充放电时SOC的动态递推关系式。
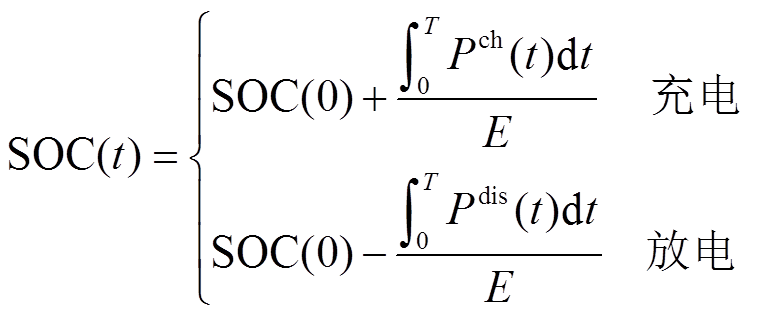 (20)
(20)
式中,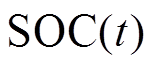 为
为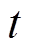 时刻电池的荷电状态;
时刻电池的荷电状态;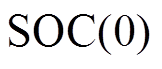 为初始时刻电池的荷电状态;
为初始时刻电池的荷电状态;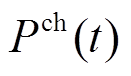 和
和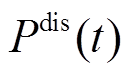 分别为
分别为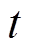 时刻电池的充、放电功率。
时刻电池的充、放电功率。
在储能电池正常运行的过程中,其额定容量的最小值应满足任意时刻的能量吞吐需求,同时还要满足SOC的约束关系,即
 (21)
(21)
将式(20)代入式(21)中可得
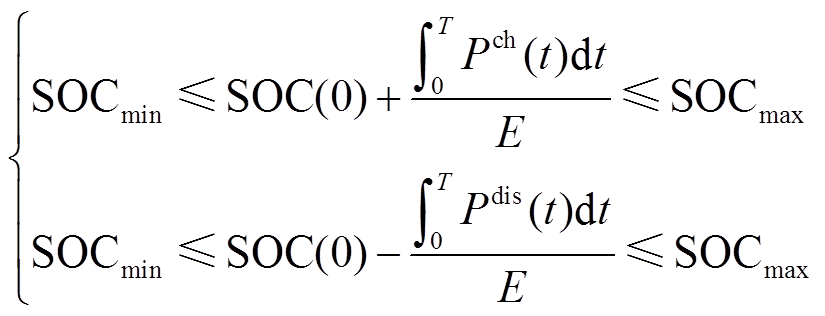 (22)
(22)
通过式(22)可求解出充电过程与放电过程中储能额定容量的取值范围,即
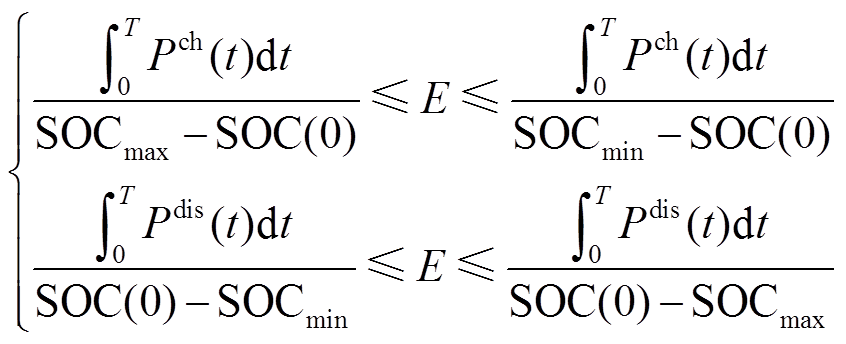 (23)
(23)
在储能电池的充电(放电)过程中,其SOC逐渐上升(下降),如若要满足式(21)的约束,则充、放电过程中储能的额定容量均应满足不等式(23)中的最小值,即
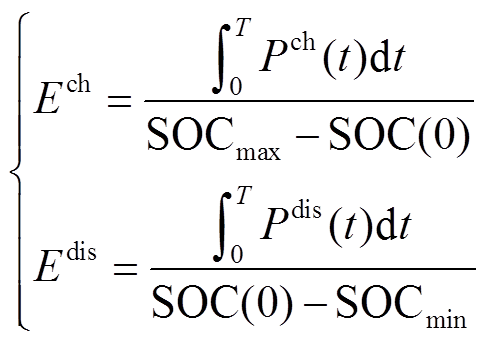 (24)
(24)
式中,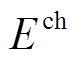 为满足充电过程的储能电池的额定容量;
为满足充电过程的储能电池的额定容量;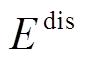 为满足放电过程的储能电池的额定容量。
为满足放电过程的储能电池的额定容量。
在实际过程中,储能电池的额定容量既要满足充电过程的容量需求,又要满足放电过程中的容量需求,因此取式(24)的最大值作为最终确定的储能电池额定容量,即
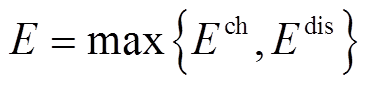 (25)
(25)
基于上述分析和理论推导可知,蓄电池和超级电容的最小适配额定容量分别为
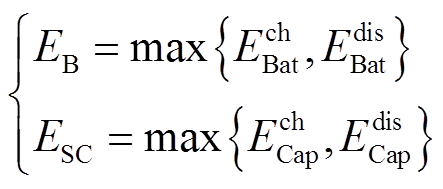 (26)
(26)
本文以铅酸电池作为电化学储能的代表,建立电池全寿命周期量化模型。由于超级电容的循环次数一般为几十万次到几百万次,远远超过蓄电池的循环次数,因此本文将超级电容的使用寿命设为固定值。一般的蓄电池实际循环次数由式(27)的Gaussian寿命函数进行拟合。
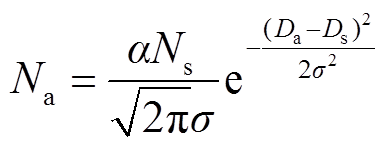 (27)
(27)
式中,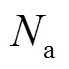 为蓄电池实际循环次数;
为蓄电池实际循环次数;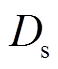 为蓄电池的额定放电深度;
为蓄电池的额定放电深度;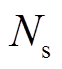 为在额定放电深度下对应的蓄电池循环次数,即额定循环次数;
为在额定放电深度下对应的蓄电池循环次数,即额定循环次数;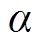 为拟合系数;
为拟合系数;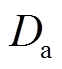 为在运行过程中蓄电池的实际放电深度,有
为在运行过程中蓄电池的实际放电深度,有
 (28)
(28)
式中,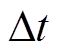 为蓄电池放电时间区间。
为蓄电池放电时间区间。
传统的蓄电池循环寿命模型由放电深度的幂函数拟合,即
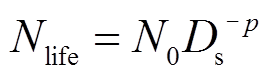 (29)
(29)
式中,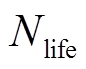 为蓄电池寿命周期内全部的循环次数;
为蓄电池寿命周期内全部的循环次数;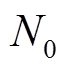 为蓄电池以100%放电深度运行时的循环次数;
为蓄电池以100%放电深度运行时的循环次数;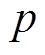 为拟合系数。
为拟合系数。
传统模型以最大放电深度下对应的循环次数代替蓄电池运行周期内的全部循环次数,模型的精确性有待提高[30]。为此,本文提出一种新的蓄电池储能全寿命周期量化模型。由面向事件的蓄电池寿命模型(式(30))可知[31],电池实际放电量在使用中实时变化且不易准确测量,而电池循环次数一般由生产厂家直接提供,相对较为准确,因此可采用循环次数代替其中的电池放电量,得到在每一时刻实际放电深度下对应的循环次数(式(31))。
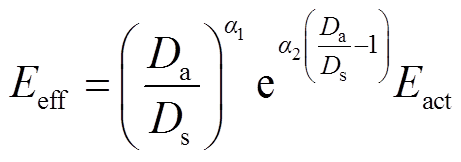 (30)
(30)
式中,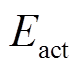 为蓄电池实际放电量;
为蓄电池实际放电量; 为换算到额定放电深度时的有效放电电量;
为换算到额定放电深度时的有效放电电量;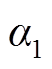 与
与 为拟合系数。
为拟合系数。
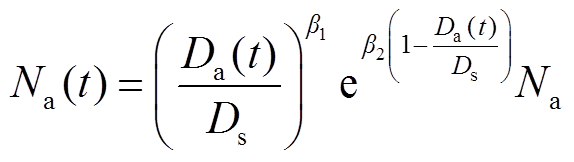 (31)
(31)
式中,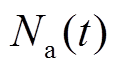 为每一时刻蓄电池实际放电深度下的循环次数;
为每一时刻蓄电池实际放电深度下的循环次数;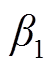 与
与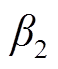 为拟合系数。
为拟合系数。
受电力系统分析中“标幺值”这一概念的启发,对式(31)做进一步改进。通过雨流计数法将得到的蓄电池每时刻实际放电深度下对应的循环次数乘以比例系数折算到在额定放电深度下的等效循环次数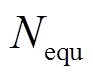 ,即
,即
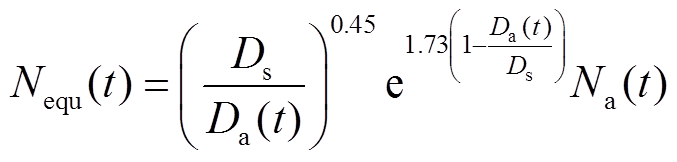 (32)
(32)
折算后的蓄电池寿命模型不仅考虑了循环次数对电池寿命折损的累加效应,而且克服了传统模型中用最大放电深度下的循环次数代替全寿命周期循环次数的局限性。
故在蓄电池的运行周期内,其实际循环寿命可通过对等效循环次数求和,以等效运行时间表示为
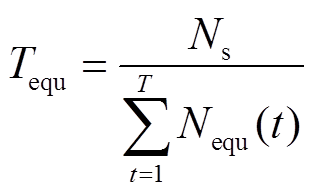 (33)
(33)
式中,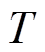 为蓄电池的一个调度日时长;
为蓄电池的一个调度日时长;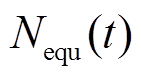 为
为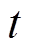 时刻蓄电池折算到额定放电深度下的等效循环次数。从式(33)可以看出,
时刻蓄电池折算到额定放电深度下的等效循环次数。从式(33)可以看出,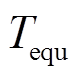 反映了蓄电池使用寿命的长短,无量纲。
反映了蓄电池使用寿命的长短,无量纲。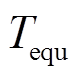 越小,表明蓄电池实际循环次数越多,使用寿命越短;
越小,表明蓄电池实际循环次数越多,使用寿命越短;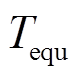 越大,表明蓄电池实际循环次数越少,使用寿命越长。
越大,表明蓄电池实际循环次数越少,使用寿命越长。
为了提高所建蓄电池储能全寿命周期量化模型的鲁棒性,现对模型做如下假设:
(1)假设蓄电池储能所处密闭空间内的温度和湿度均恒定。
(2)假设标准情况下蓄电池储能的额定循环次数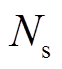 与标准情况下蓄电池储能的额定放电深度
与标准情况下蓄电池储能的额定放电深度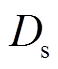 不随电池的使用时间而变化。
不随电池的使用时间而变化。
(3)假设蓄电池储能的充放电效率在运行过程中保持不变。
(4)假设蓄电池储能不发生自放电现象。
传统的混合储能LCC模型中电池维护成本通常为
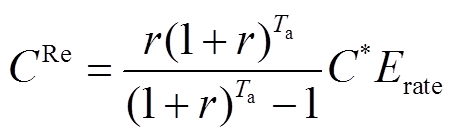 (34)
(34)
式中,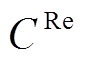 为电池年维护成本;
为电池年维护成本;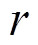 为贴现率;
为贴现率;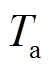 为电池使用寿命;
为电池使用寿命;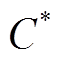 为电池的单位维护成本;
为电池的单位维护成本;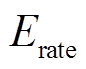 为电池的额定容量。
为电池的额定容量。
从式(34)可以看出,传统的混合储能LCC模型中单位维护成本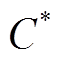 不随时间的改变而改变,且从如图5所示的电池维护成本曲线可以看出,传统电池维护成本曲线随使用时间线性增加,这与储能电池实际运行情况不符。随着电池使用年限的增长,电池老化加快导致的累积效应应使其维护成本每隔Y年比前一个Y年增加更多,且应为非线性增加(图5中红色虚线)。基于此本文在对混合储能系统做经济性评估时改进了传统混合储能的LCC模型,有
不随时间的改变而改变,且从如图5所示的电池维护成本曲线可以看出,传统电池维护成本曲线随使用时间线性增加,这与储能电池实际运行情况不符。随着电池使用年限的增长,电池老化加快导致的累积效应应使其维护成本每隔Y年比前一个Y年增加更多,且应为非线性增加(图5中红色虚线)。基于此本文在对混合储能系统做经济性评估时改进了传统混合储能的LCC模型,有
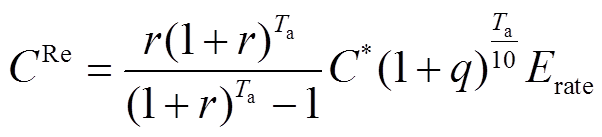 (35)
(35)
在电池年维护成本中添加“电池维护成本增量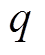 ”这一因子,用来描述每隔十年由于电池不断老化的累积效应所带来维护成本的非线性增加现象,以便更加符合储能电池在实际运行过程中的情况,提高LCC模型的可实用性。
”这一因子,用来描述每隔十年由于电池不断老化的累积效应所带来维护成本的非线性增加现象,以便更加符合储能电池在实际运行过程中的情况,提高LCC模型的可实用性。
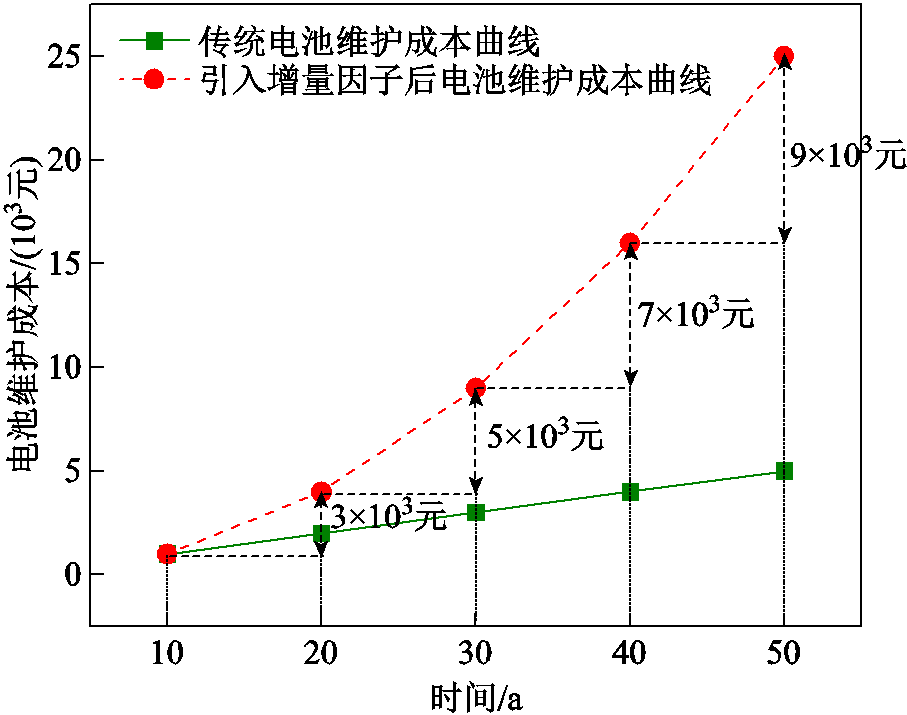
图5 电池维护成本曲线
Fig.5 Battery maintenance cost curve
改进后的混合储能LCC模型各部分表达式如下。
1)蓄电池年综合成本
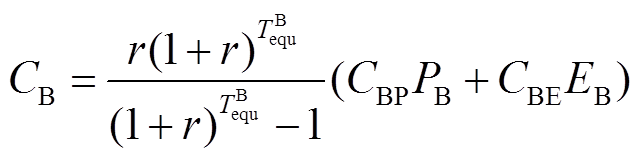 (36)
(36)
式中,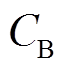 为蓄电池的年综合成本;
为蓄电池的年综合成本;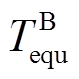 为蓄电池的等效运行时间,由式(33)确定;
为蓄电池的等效运行时间,由式(33)确定;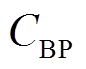 与
与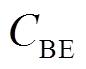 分别为蓄电池的单位功率成本和单位容量成本;
分别为蓄电池的单位功率成本和单位容量成本;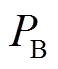 与
与 分别为蓄电池的额定功率和额定容量。
分别为蓄电池的额定功率和额定容量。
2)蓄电池年维护成本
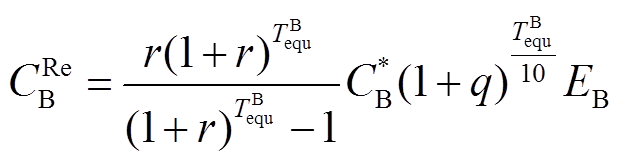 (37)
(37)
式中,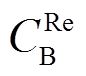 为蓄电池的年维护成本;
为蓄电池的年维护成本;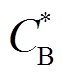 为蓄电池的单位维护成本;
为蓄电池的单位维护成本;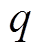 为每十年储能电池维护成本的增量百分比。
为每十年储能电池维护成本的增量百分比。
3)超级电容年综合成本
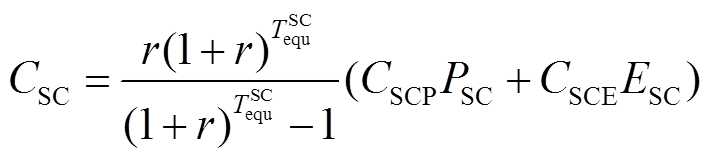 (38)
(38)
式中,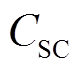 为超级电容的年综合成本;
为超级电容的年综合成本;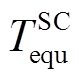 为超级电容的等效运行时间,为固定值;
为超级电容的等效运行时间,为固定值;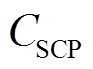 与
与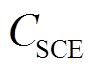 分别为超级电容的单位功率成本和单位容量成本;
分别为超级电容的单位功率成本和单位容量成本;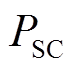 与
与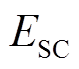 分别为超级电容的额定功率和额定容量。
分别为超级电容的额定功率和额定容量。
4)超级电容年维护成本
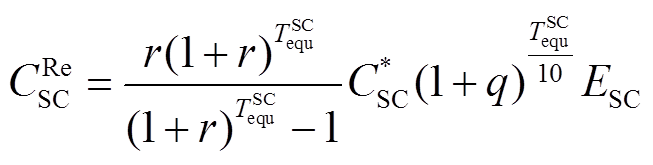 (39)
(39)
式中,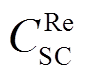 为超级电容的年维护成本;
为超级电容的年维护成本;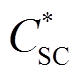 为超级电容的单位维护成本。
为超级电容的单位维护成本。
结合式(36)~式(39)可得混合储能系统全寿命周期成本为
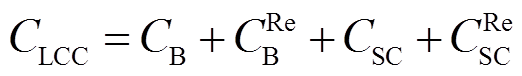 (40)
(40)
式中,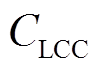 为混合储能系统的全寿命周期成本。
为混合储能系统的全寿命周期成本。
本文以某100 MW级风电场一天的连续风电功率数据为实验数据,采样时间间隔为1 min,共1 440个采样点。获得满足在风电平抑要求的混合储能总功率指令序列如图6a所示,平抑后风电并网功率波动如图6b所示,满足我国GB规定的100 MW风电场1 min有功功率波动最大值不得超过10 MW的限制。储能系统相关参数见表1[32]。
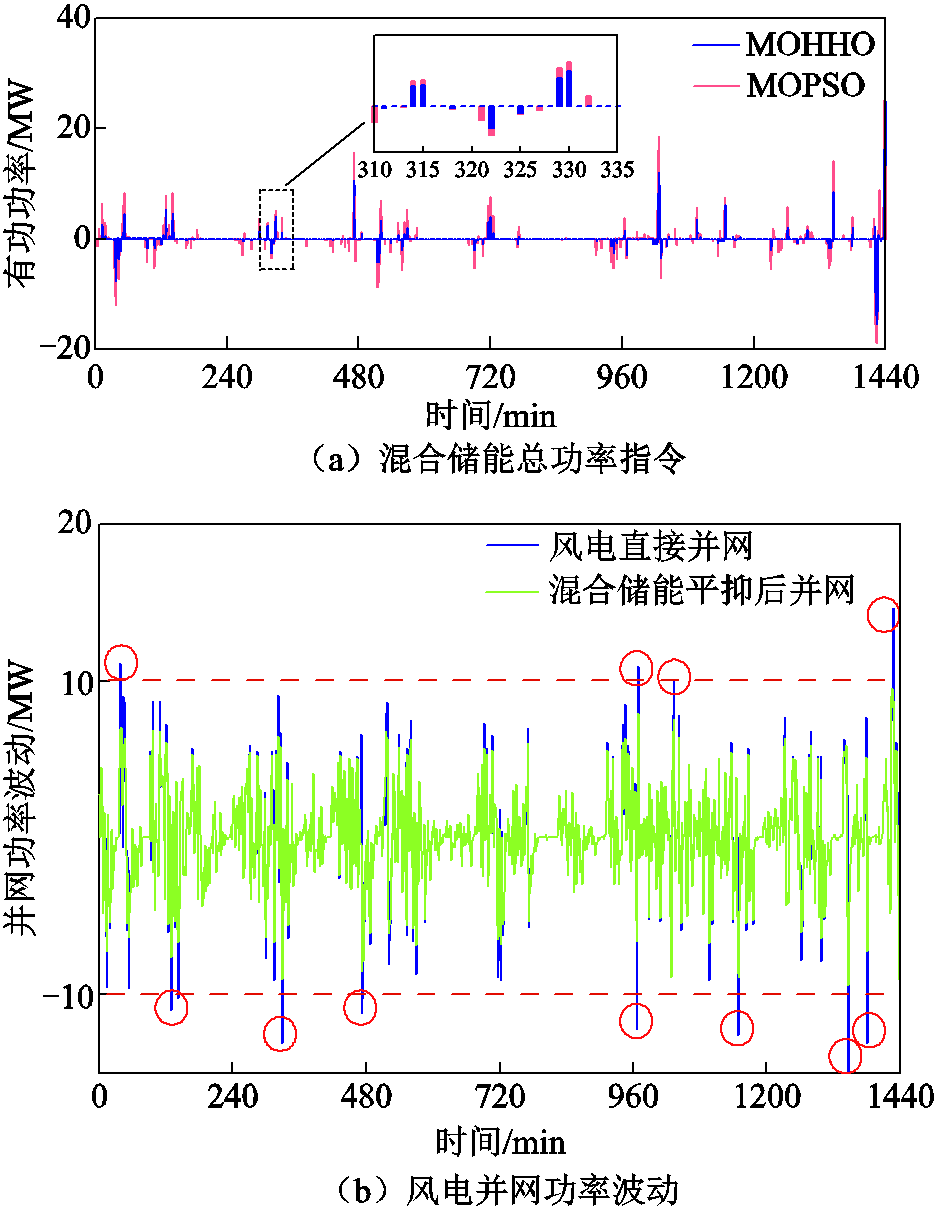
图6 混合储能总出力与平抑效果
Fig.6 Hybrid energy storage total output and flattening effect diagram
图6a展示了不同算法对混合储能总功率指令的求取结果。可以看出,MOHHO算法相较于MOPSO算法可以获得更小的储能出力,因此本文后续均以MOHHO算法获得的混合储能总功率指令进行分析与讨论。
图6b展示了风电并网功率波动情况。从中可以看出,未经平抑的风电并网功率部分时刻的波动值已经超出10 MW,经过HESS平抑后的风电并网功率波动有了明显减小,且1 min内波动均未超过 10 MW,符合我国相应风电场装机容量GB规定的1 min风电有功功率并网波动要求。
表1 储能相关参数
Tab.1 Relevant parameters of energy storage

储能参数数值 蓄电池单位功率成本/(万元/MW)270 单位容量成本/[万元/(MW∙h)]64 单位维护成本/[万元/(MW∙h)] 0.005 荷电状态上限0.8 荷电状态下限0.2 贴现率r(%)10 运维成本增量(%)20 额定循环次数350 超级电容单位功率成本/(万元/MW)150 单位容量成本/[万元/(MW∙h)]2 700 单位维护成本/[万元/(MW∙h)]0.005 荷电状态上限0.8 荷电状态下限0.2 贴现率(%)10 运维成本增量(%)20 使用寿命30
MMAF滑动窗口大小及滤波次数的不同对模态混叠程度均有直接影响,继而蓄电池和超级电容所分配的功率指令就会有相应的变化,影响储能电池的使用寿命及最终混合储能额定功率和容量的配置。
为了尽可能地避免模态混叠,本文通过引入Pearson相关系数作为判断最优滑窗大小与最优滤波次数的一项指标。在不断增大滑窗大小N时,取相关系数最小时对应的滑动窗口作为当前滤波的窗口大小,直至将N遍历完全。获取了最优滑窗大小N之后,再对滤波次数进行遍历,求出每次滤波后的低频分量与高频分量的Pearson相关系数。
本文算例预设滑窗大小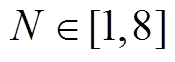 且
且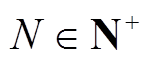 ,滤波次数
,滤波次数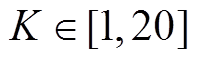 且
且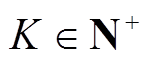 。实验得出的滤波次数和滑窗大小与Pearson相关系数的关系如图7a所示。
。实验得出的滤波次数和滑窗大小与Pearson相关系数的关系如图7a所示。
从图7a可以看出,实验得出的最优滑窗大小不随滤波次数的改变而改变,即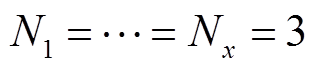 。滤波次数
。滤波次数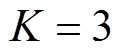 时曲线出现了明显拐点,
时曲线出现了明显拐点,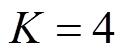 时滤波后的低频分量和高频分量的Pearson相关系数的增量相较于
时滤波后的低频分量和高频分量的Pearson相关系数的增量相较于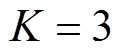 时有了明显的放缓。这表明
时有了明显的放缓。这表明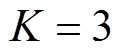 时滤波所得的低频分量中大多数的高频分量已经被滤除。由Pearson相关系数得知此时的
时滤波所得的低频分量中大多数的高频分量已经被滤除。由Pearson相关系数得知此时的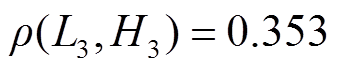 ,两者属于弱相关,判断此时仍有少量高频分量混杂在低频分量中。因此为了最大程度地削弱模态混叠以获取最佳的混合储能功率分配指令,达到最低的综合成本,继续增大滤波次数。当滤波次数K达到14次时,可以发现继续增加滤波次数时Pearson相关系数的变化趋势趋于水平,且第14次滤波后的高、低频分量间的Pearson相关系数(
,两者属于弱相关,判断此时仍有少量高频分量混杂在低频分量中。因此为了最大程度地削弱模态混叠以获取最佳的混合储能功率分配指令,达到最低的综合成本,继续增大滤波次数。当滤波次数K达到14次时,可以发现继续增加滤波次数时Pearson相关系数的变化趋势趋于水平,且第14次滤波后的高、低频分量间的Pearson相关系数(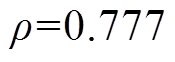 )已经达到了强相关。这表明第14次被滤波的信号中已经几乎不含有高频分量。由递推式(12)可知第14次被滤波的信号正是第13次滤波后所得到的低频分量。由此可以推断出第13次滤波后所得的低频分量中已经不包含高频分量,因此通过Pearson相关系数确定的最优滤波次数为
)已经达到了强相关。这表明第14次被滤波的信号中已经几乎不含有高频分量。由递推式(12)可知第14次被滤波的信号正是第13次滤波后所得到的低频分量。由此可以推断出第13次滤波后所得的低频分量中已经不包含高频分量,因此通过Pearson相关系数确定的最优滤波次数为 。
。
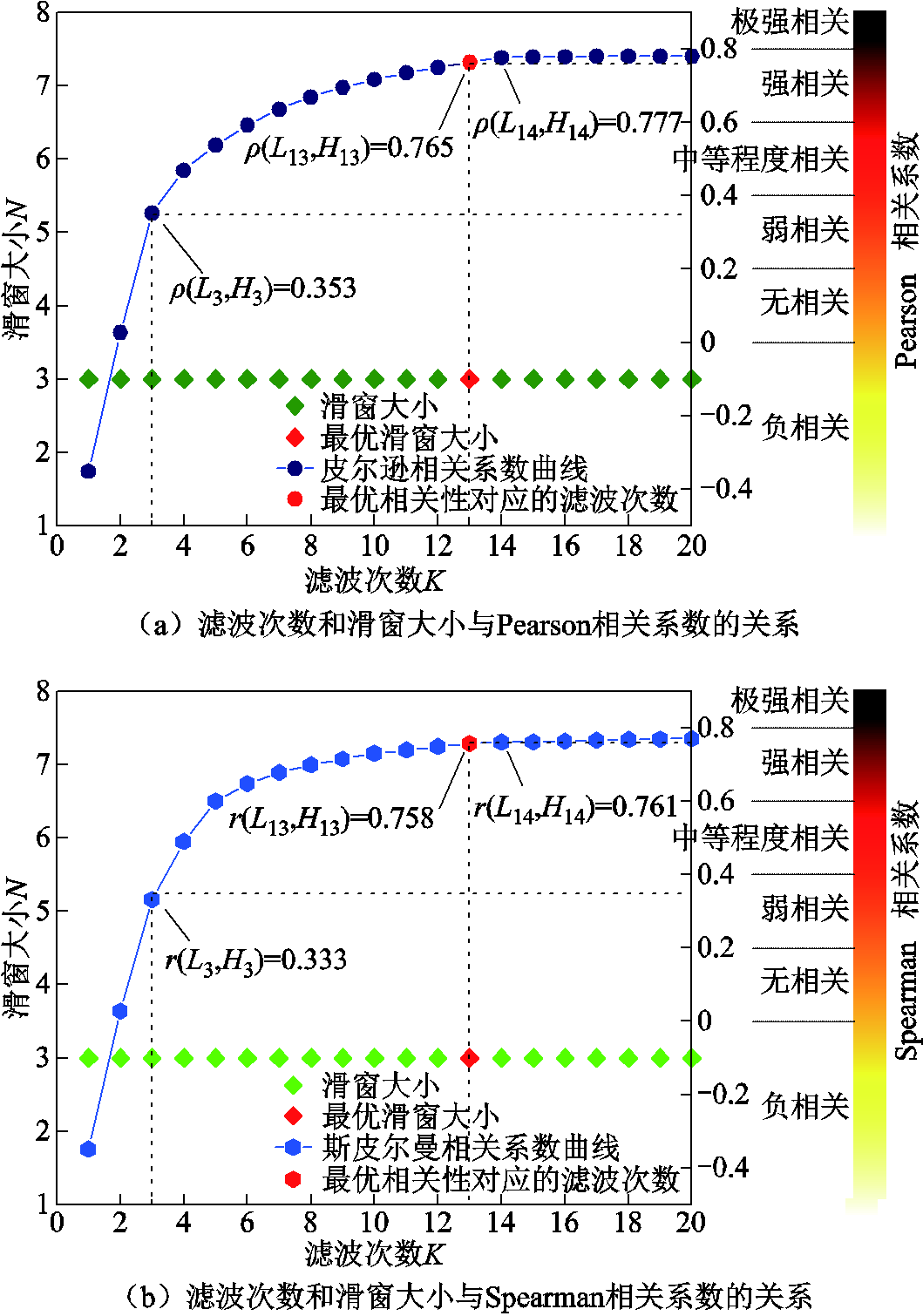
图7 滤波次数和滑窗大小与不同类相关系数间的关系
Fig.7 The relationship between filtering frequency, sliding window size, and correlation coefficients of different types
由于Pearson相关系数只能评估变量间的线性关联度,一般对变量间的单调关联性表现较差;且Pearson相关系数的使用前提是变量需近似服从正态分布。但是随着滤波次数的增加,无法得知每次滤波后低频和高频信号是否近似正态分布,因此算例通过Spearman相关系数再次对MMAF方法的相关参数进行确定。滤波次数和滑窗大小与Spearman相关系数的关系如图7b所示。通过图7b可知,当滤波次数K达到14次时,高低频分量间的Spearman相关系数(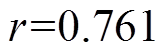 )达到了强相关,再继续增加滤波次数后,Spearman相关系数几乎不再发生变化。这表明第14次滤波得到的低频分量与高频分量有极强的单调趋势,可以认为第14次被滤波的信号中已经不含有高频分量。而第14次被滤波的信号由前文分析可知是第13次滤波后所得到的低频分量。因此通过Spearman相关系数确定的最优滤波次数为13次。最优滑窗大小也并没有随滤波次数的增加而改变。这与通过Pearson相关系数确定的最优解一致。Pearson相关系数保证了变量间线性关联度的准确性;Spearman相关系数保证了变量间单调关联性的准确性。算例从变量间的线性、单调性关联度两个角度证明了最优解选择的合理性,也证明了在确定MMAF方法的相关参数时仅通过Pearson相关系数是完全可行的。
)达到了强相关,再继续增加滤波次数后,Spearman相关系数几乎不再发生变化。这表明第14次滤波得到的低频分量与高频分量有极强的单调趋势,可以认为第14次被滤波的信号中已经不含有高频分量。而第14次被滤波的信号由前文分析可知是第13次滤波后所得到的低频分量。因此通过Spearman相关系数确定的最优滤波次数为13次。最优滑窗大小也并没有随滤波次数的增加而改变。这与通过Pearson相关系数确定的最优解一致。Pearson相关系数保证了变量间线性关联度的准确性;Spearman相关系数保证了变量间单调关联性的准确性。算例从变量间的线性、单调性关联度两个角度证明了最优解选择的合理性,也证明了在确定MMAF方法的相关参数时仅通过Pearson相关系数是完全可行的。
图8a展示了混合储能总功率指令的频谱图。从中可以看出未,经分解的HESS总功率频谱较为杂乱,高低频混杂在一起,这对混合储能系统的使用寿命和经济性十分不利。
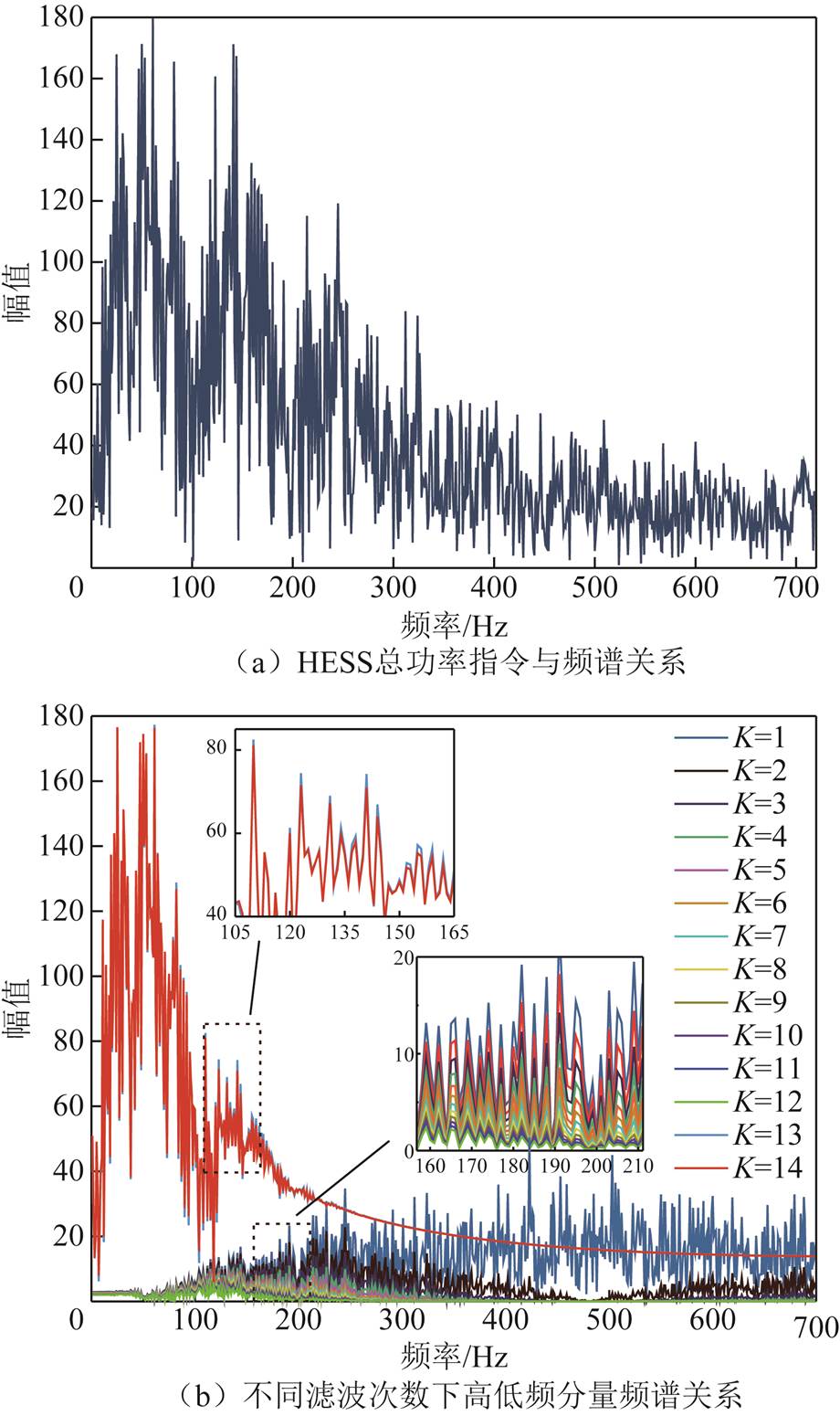
图8 混合储能系统功率指令频谱关系
Fig.8 Spectral relationship of power command in hybrid energy storage system
图8b展示了不同滤波次数时所得的高低频分量间的频谱关系。从图8b中可以看出,随着滤波次数的增加,高、低频分量的模态也逐渐分开。当 时低频分量与高频分量几乎已经完全分离,从图中也可以看出存留在低频分量里的也仅是高频分量的基波,对功率指令的分配及后续混合储能经济性的分析并不能产生实质性影响。为了进一步说明最优的滤波次数为13次,对第14次滤波得到的信号进行了模态分析,发现
时低频分量与高频分量几乎已经完全分离,从图中也可以看出存留在低频分量里的也仅是高频分量的基波,对功率指令的分配及后续混合储能经济性的分析并不能产生实质性影响。为了进一步说明最优的滤波次数为13次,对第14次滤波得到的信号进行了模态分析,发现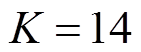 时所得信号模态(图8b中深红色曲线)与
时所得信号模态(图8b中深红色曲线)与 时所得信号模态(图8b中浅蓝色曲线)几乎完全重合,没有发生明显分离的趋势。说明经过第13次滤波后低频分量中的高频分量已经被完全滤除。结合图7的分析,进一步证明了
时所得信号模态(图8b中浅蓝色曲线)几乎完全重合,没有发生明显分离的趋势。说明经过第13次滤波后低频分量中的高频分量已经被完全滤除。结合图7的分析,进一步证明了 是滤波次数的最优解。
是滤波次数的最优解。
5.2.1 HESS总功率指令的分配结果
通过上述实验得知:当MMAF的滑窗大小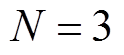 ,滤波次数
,滤波次数 时,可以最大程度地避免模态混叠。因此本算例采用
时,可以最大程度地避免模态混叠。因此本算例采用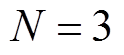 、
、 作为混合储能最优功率指令分配的滤波参数。
作为混合储能最优功率指令分配的滤波参数。
当采用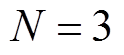 、
、 的MMAF对混合储能总功率指令进行滤波时,蓄电池与超级电容各自分得的功率指令如图9所示。从图9可以看出,蓄电池分配的功率指令波动较平稳,波动频率较低;超级电容分配的功率指令则波动较剧烈,波动频率较高,符合两种储能电池的功率特性,验证了本文所提方法的有效性。
的MMAF对混合储能总功率指令进行滤波时,蓄电池与超级电容各自分得的功率指令如图9所示。从图9可以看出,蓄电池分配的功率指令波动较平稳,波动频率较低;超级电容分配的功率指令则波动较剧烈,波动频率较高,符合两种储能电池的功率特性,验证了本文所提方法的有效性。
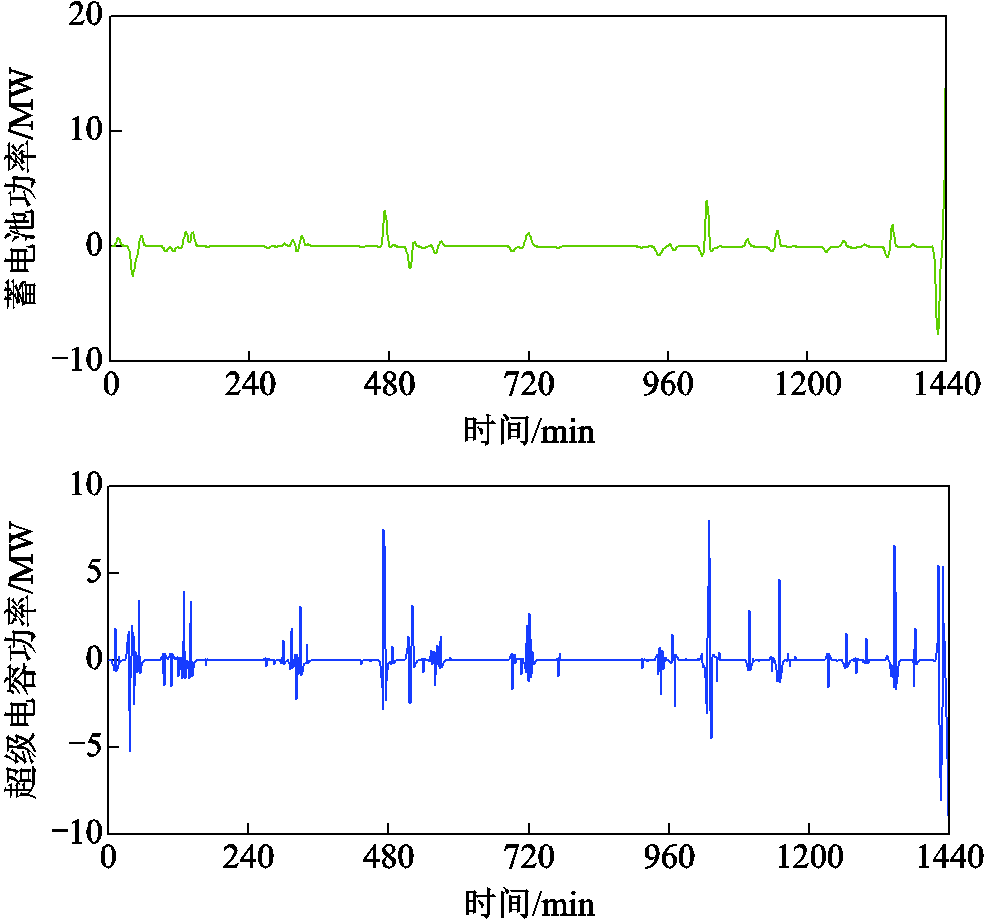
图9 MMAF蓄电池与超级电容的功率指令
Fig.9 Power command of battery and super capacitor in MMAF method
图10展示了在本文所提MMAF方法下蓄电池在一个调度日内的实际放电深度。
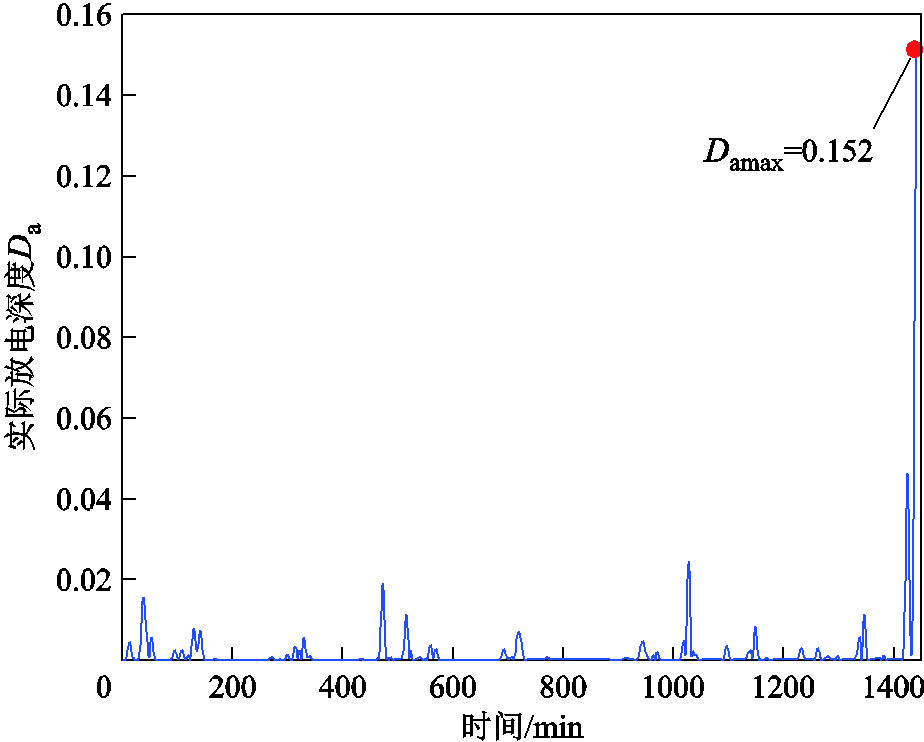
图10 MMAF蓄电池放电深度变化
Fig.10 Variation diagram of battery discharge depth in MMAF method
从图10可以看出,蓄电池在整个调度日内的最大放电深度仅为15.2%,所有时段的放电深度均在25%以下,处于浅循环放电状态。电池的浅循环放电状态可大大增加蓄电池的使用寿命,从而降低了因寿命问题而更换储能电池所带来的额外成本。
5.2.2 混合储能的定容优化结果
我国多个省市发布最新相关文件,明确新能源整体配储标准:每100MW风电场按不低于其装机容量的10%~20%配建储能系统。但由于地理位置差异等因素,导致有些风能资源匮乏的地区并不需要建设与标准等规模大小的储能设备,否则会使得混合储能系统整体的经济性较差。
对上述问题本文采取了针对性的混合储能定容优化方案。为了检验本文所提方案的有效性及建立蓄电池储能全寿命周期量化模型的准确性,分不同场景对比了不同储能组合方案下储能设备的使用寿命与储能的LCC;对比了本文定容方法与标准配置方案下的经济性差异,结果见表2与表3。
表2 MMAF实验结果
Tab.2 Experimental results of MMAF

参数数值 /(MW∙h)2.72 /MW1.6833 /(MW∙h)1.62 /MW1.6424 19.9 /万元565.2
表3 单一储能实验结果
Tab.3 Single energy storage experiment results

参数数值 /(MW∙h)20 /MW20 6.5 /万元1 446.3 /(MW∙h)20 /MW20 /万元6 046.5
按照规定,本文算例中100MW风电场应配置10 ~20MW∙h的储能。表2的实验结果得出满足当前混合储能总功率指令要求的最小定容参数,表明蓄电池和超级电容的额定功率和额定容量并不需要按标准配置即可满足当前的总平抑功率指令需求,避免了因储能配置与实际情况不适配而导致的经济性差的现象。验证了本文提出的混合储能总功率指令分配方法与定容策略高度匹配。
为了更好地说明混合储能系统在响应功率指令时较单一储能有更显著的经济性,本文使蓄电池与超级电容分别各自响应混合储能总功率指令。在“单一储能实验”这组对比实验中,储能按照风电场装机容量的20%进行定容。
通过表2和表3两组实验结果对比可知相较于单一储能,由蓄电池和超级电容组成的混合储能系统全寿命周期成本最优,LCC相比于单蓄电池和单超级电容分别降低了60%和90%;使用单一超级电容储能进行功率指令的响应时经济性最差,这是由于超级电容的单位容量成本过高导致;使用单一蓄电池储能进行功率指令的响应时经济性也较差,而且相比较于混合储能系统,蓄电池的等效运行时间从19.9降至6.5。这是由于在使用单一蓄电池储能响应功率指令时蓄电池充放电深度增加,频繁地进行充放电状态切换,大大影响了其使用寿命,最终导致了成本的升高。
为了进一步说明本文MMAF方法多次滤波对降低混合储能经济性的显著性,现对混合储能总功率指令只进行一次MAF分析混合储能的LCC,以此验证本文多次滤波的必要性,结果如图11、图12、表4所示。
结合图11和表4的实验数据可以看出,只经过一次MAF获取的蓄电池和超级电容功率指令由于存在模态混叠,使得原本应分配给超级电容的功率指令分配给了蓄电池。如图11中480 min和1 000 min时,蓄电池分得的功率指令明显高于图9中对应时刻的功率指令,而图11中超级电容此刻对应的功率指令要比图9中小很多。与表2的实验数据相比,由于存在模态混叠现象,蓄电池响应了部分高频分量指令从而影响了其使用寿命,致使其等效运行时间从19.9减少至19.2。图11展示了单次MAF蓄电池放电深度变化情况。需要说明的是由于混合储能总功率指令在1 440min的信号不含高频分量的原因才导致了通过MAF方法与MMAF方法得到的蓄电池最大放电深度相同。另外通过图10与图12对比分析可以看出,其余采样点时单次MAF时蓄电池的放电深度普遍要高于MMAF时蓄电池的放电深度,这也是导致单次MAF蓄电池寿命减少的一个原因。此外由于MMAF模态混叠程度较MAF时有了大幅削弱,因此LCC也从566.2万元减少至565.2万元,验证了本文MMAF方法降低混合储能成本的必要性。
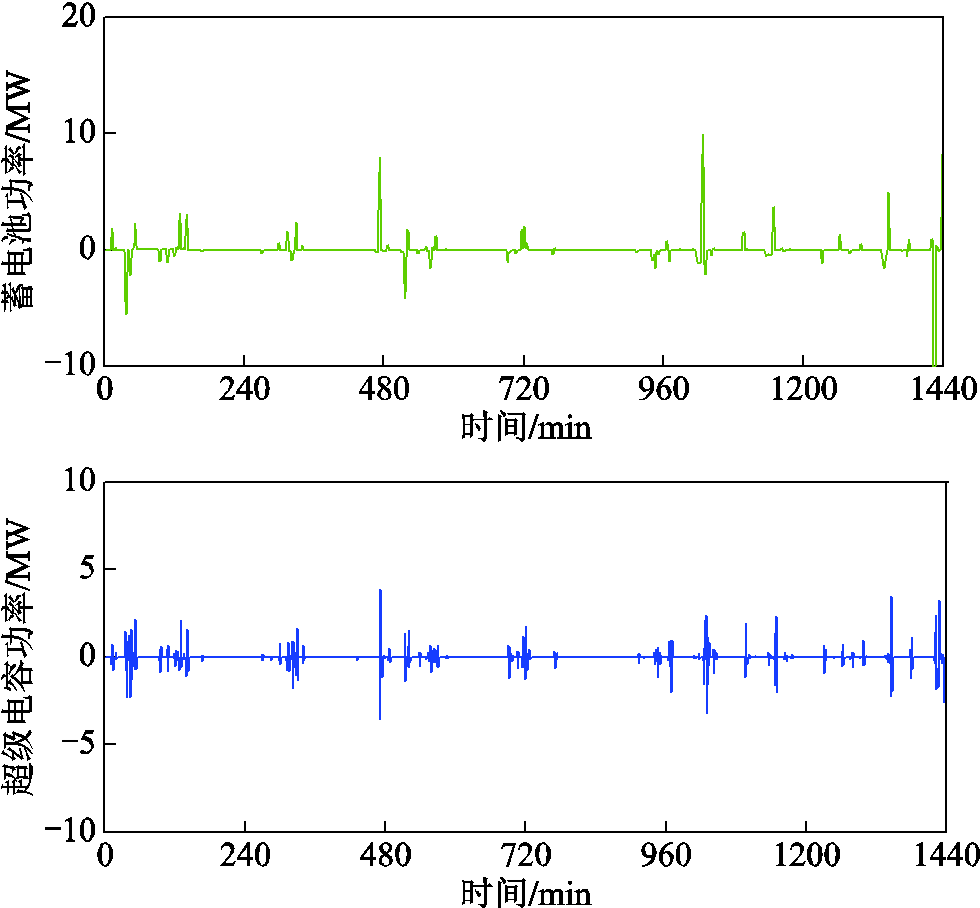
图11 单次MAF蓄电池与超级电容的功率指令
Fig.11 Power command of single MAF battery and super capacitor
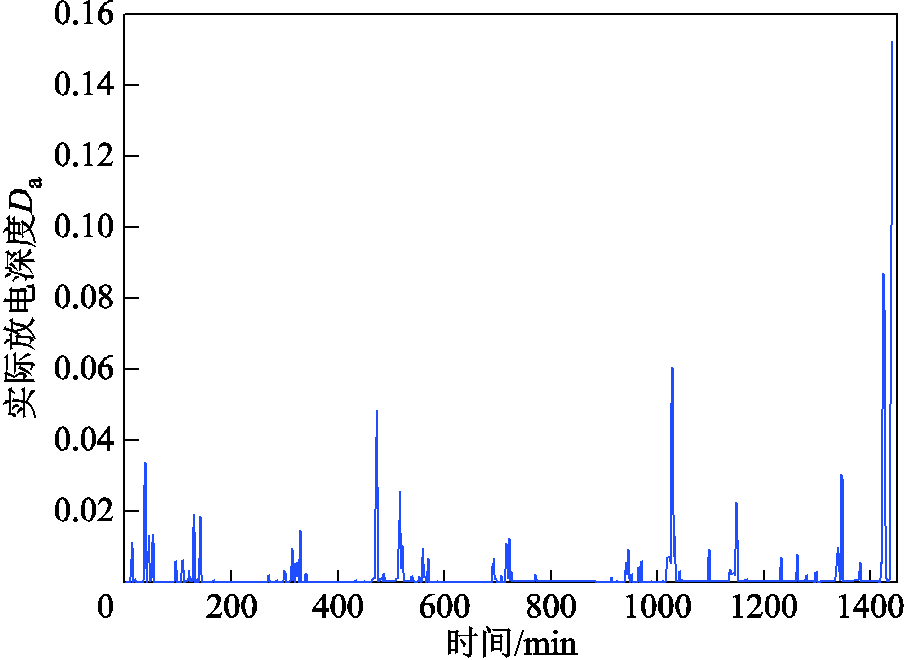
图12 单次MAF蓄电池放电深度变化
Fig.12 Discharge depth change diagram of single MAF battery
表4 单次MAF实验结果
Tab.4 Single MAF experiment results

参数数值 /(MW∙h)2.72 /MW1.683 3 /(MW∙h)1.62 /MW1.642 4 19.2 /万元566.2
为了说明MMAF方法较其他方法的优势,将本文混合储能功率分配方法与EMD、VMD、小波变换方法进行比较,得到如图13所示结果。
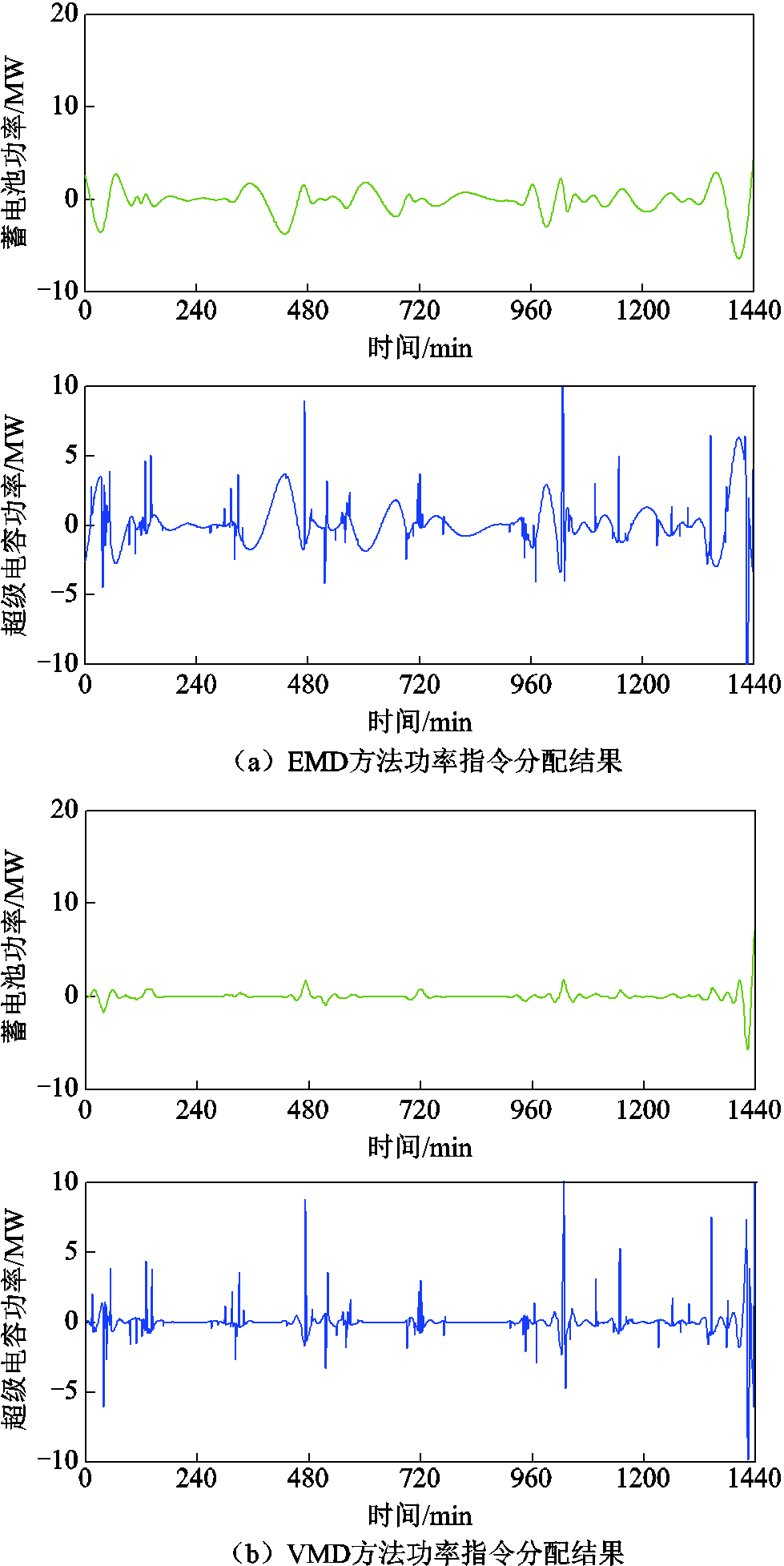
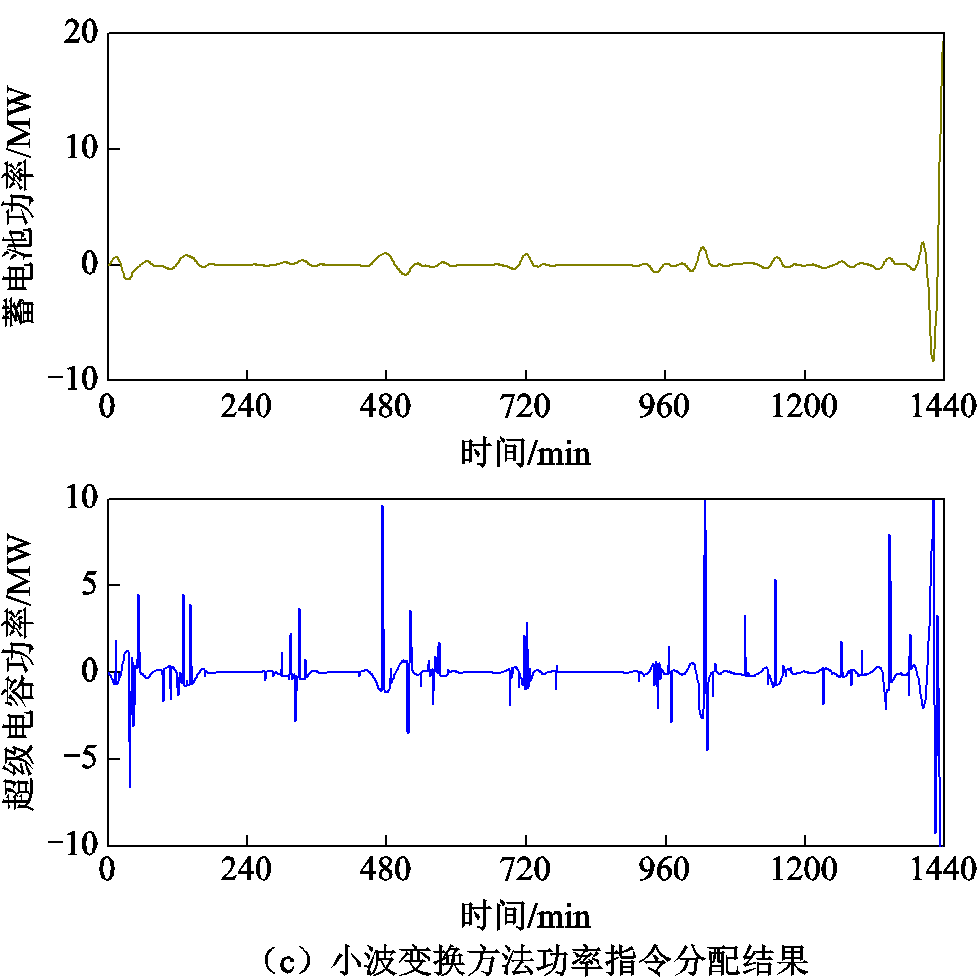
图13 传统方法下混合储能功率分配结果
Fig.13 Figure of hybrid energy storage power allocation results under traditional methods
不同功率分配方法下HESS成本见表5。通过所有实验结果横向比较可以看出,本文MMAF方法比EMD方法获取的混合储能LCC降低了87.6%、比VMD方法获取的LCC降低了3.3%、比WT方法获取的LCC降低了56.8%。证实了本文提出的MMAF方法在功率分配时能够更好地削弱模态混叠现象,更加精确地分离高低频分量,从而定容时可以依据功率分配结果最小化混合储能的额定功率和容量。将储能功率分配问题与定容问题联合考虑,求得了混合储能LCC的最优解。
为了更好地契合混合储能系统在实际运行工况中的某些特殊情况,以蓄电池为例,对其发生放电越限情况时HESS总功率指令如何分配做了进一步研究。定义混合储能中电池发生放电越限现象时的工况为“故障工况”。需要指出的是:不同于正常工况,故障工况下HESS的经济效益将不再是首要目标,如何将蓄电池因放电越限而无法响应的这部分功率指令进行再分配才是重中之重。因为一旦蓄电池因放电越限而无法响应本身的功率指令时就会造成风电平抑效果变差,风电波动的增大严重时有可能导致风机脱网,造成更大的经济损失。故本节不再对HESS的经济性做分析,而是更关注于故障工况下的HESS功率指令的分配情况。
表5 不同功率分配方法下HESS成本的对比
Tab.5 Comparison of HESS cost under different power allocation methods

方法/(MW∙h)/MW/(MW∙h)/MW/万元降低百分比(%) EMD13.91446.119314.71242.663520.84 551.187.6 VMD1.79361.98681.67442.17627.2584.63.3 WT4.69372.87063.88474.063818.51 307.156.8 MMAF2.721.68331.621.642419.9565.2—
放电越限现象可以通过电池的SOC曲线很好地表征。本文规定蓄电池和超级电容的SOC上限为80%,下限为20%,因此当蓄电池放电使得SOC低于20%时即认为发生了放电越限现象。
由于本文算例所用的HESS总功率指令较为平缓,混合储能系统在整个调度日内没有出现“故障工况”。因此本文在研究故障工况时采用另外一组HESS总功率指令作为研究数据,如图14所示。
以蓄电池为例,其在故障工况时HESS功率指令分配场景及机理如下:
1)同正常工况,通过MMAF对混合储能总功率指令进行滤波,Pearson相关系数作为判断滤波参数的指标,获得蓄电池与超级电容各自的功率指令。
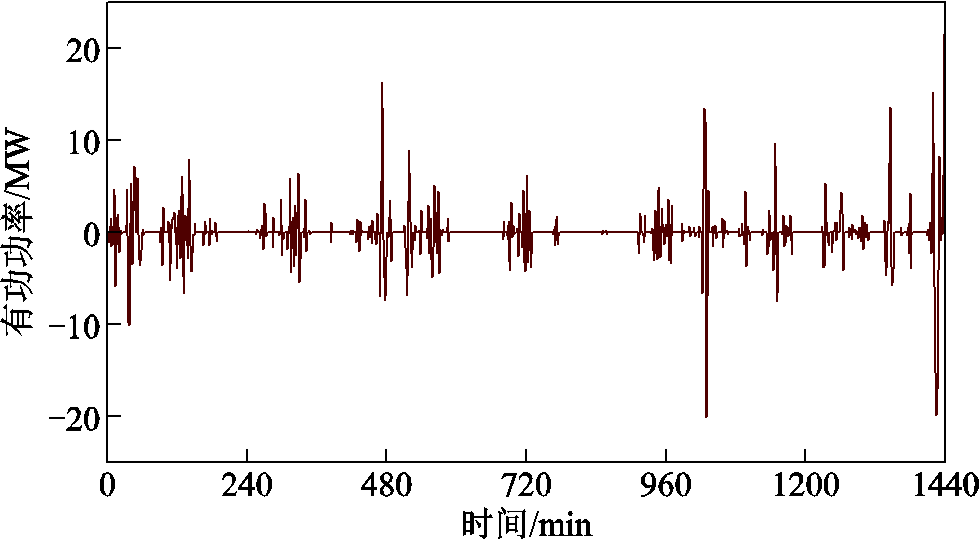
图14 混合储能总功率指令
Fig.14 Hybrid energy storage total power command
2)蓄电池在自身分得的功率指令下进行充放电,部分时刻出现深度放电致使其SOC低于下限(20%),此时蓄电池进入“故障工况”。
3)当蓄电池SOC首次降至下限时,即刻起令蓄电池实际输出功率Pbat=0,原本由蓄电池响应的放电功率指令全部由超级电容承担,直到后续时刻风电出力过多时需要给HESS充电以满足平抑需求。
4)优先向蓄电池充电以帮助其快速恢复SOC。在恢复过程中,蓄电池的SOC会第二次升至下限,即刻起不再对蓄电池实际输出功率做限制,恢复蓄电池与超级电容各自原本分得的功率指令。
5)蓄电池SOC一次在下降的过程中达到下限值,一次在恢复的过程中达到下限值。记蓄电池SOC两次达到下限值的时间区间为一个完整的故障工况运行时间,作为一次故障工况修复的标志。恢复到正常工况后,进入步骤1)。
需要说明的是:本文仅以蓄电池放电越限为例,当超级电容放电越限时由蓄电池对其功率指令进行响应,机理与上述完全一致,由于篇幅有限,本文不再赘述。对于蓄电池与超级电容同时发生放电越限的情况属于小概率事件,不属于本文研究重点,故不再对其讨论。
图15给出了调度日内局部时段的故障工况运行过程中蓄电池与超级电容各自SOC的变化趋势,以此更加直观地展示上述机理。
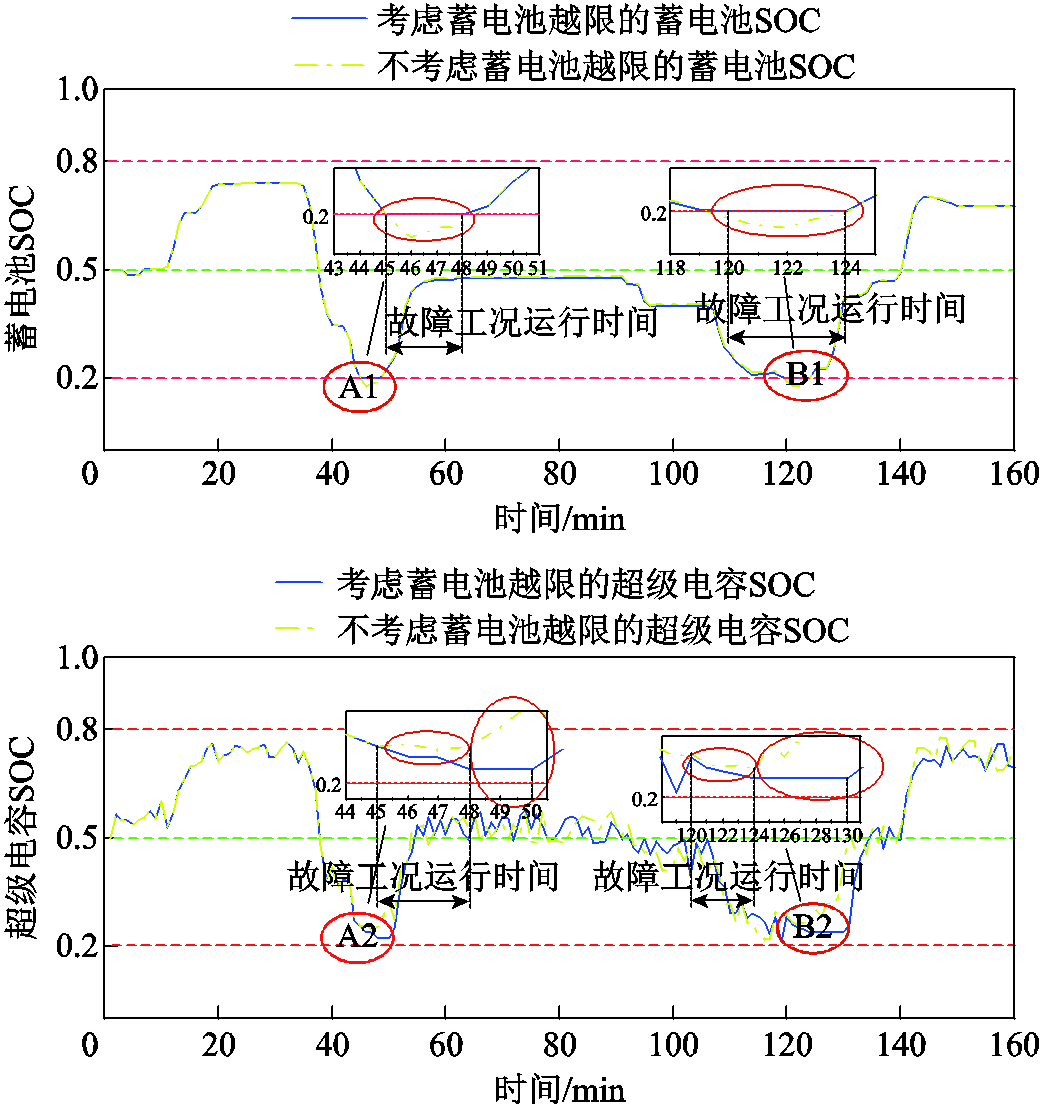
图15 故障工况下蓄电池和超级电容SOC曲线
Fig.15 SOC curve of battery and supercapacitor under fault condition
从图15可以看出在选取的时域段内共发生了两次蓄电池放电越限的现象:A1时段和B1时段。由局部放大图可知对于A1时段,在45 min时蓄电池的SOC降至0.2,此时若不考虑蓄电池放电越限,其SOC曲线对应图中绿色点画线。可以看出,蓄电池将继续向外输出功率,这极大地损害了电池寿命。若此时考虑蓄电池放电越限,其SOC曲线对应图中蓝色实线。可以看出在45 min,由于放电越限迫使此时的蓄电池实际输出功率Pbat=0,因此后一小段时间内蓄电池的SOC也一直维持在0.2。在故障工况运行时间内蓄电池的功率指令由超级电容进行响应,对应的超级电容SOC曲线是A2时段。由A2时段的放大图可知,由于此时的超级电容需要承担部分蓄电池的放电功率指令,因此超级电容在45 min时的SOC曲线较未考虑蓄电池放电越限情况下的SOC曲线进一步下降。48 min时需要向HESS充电,通过A1时段可以看出,蓄电池的SOC曲线逐步上升。此时从A2时段超级电容的SOC变化趋势可以看出:在不考虑蓄电池放电越限情况下的超级电容SOC在48 min已经开始上升,说明48 min时超级电容已经开始充电;而考虑了蓄电池放电越限情况下的超级电容SOC在蓄电池充电过程中保持不变,说明此过程超级电容并未得到充电,其在50 min才首次充电出现SOC上升的趋势,体现了当蓄电池SOC过低时优先向蓄电池充电的原则。同理对于B1和B2时段,在故障工况运行时间内蓄电池SOC始终保持在0.2,没有再进行放电行为,而当需要向HESS充电时,不考虑蓄电池放电越限情况下的超级电容SOC在124 min已经开始上升,说明124 min时超级电容已经开始充电;而考虑了蓄电池放电越限情况下的超级电容则是在130 min才首次充电出现SOC上升的趋势,同样体现了蓄电池优先充电的原则。
故障工况时经过这种功率分配机理后的HESS功率分配结果如图16所示。
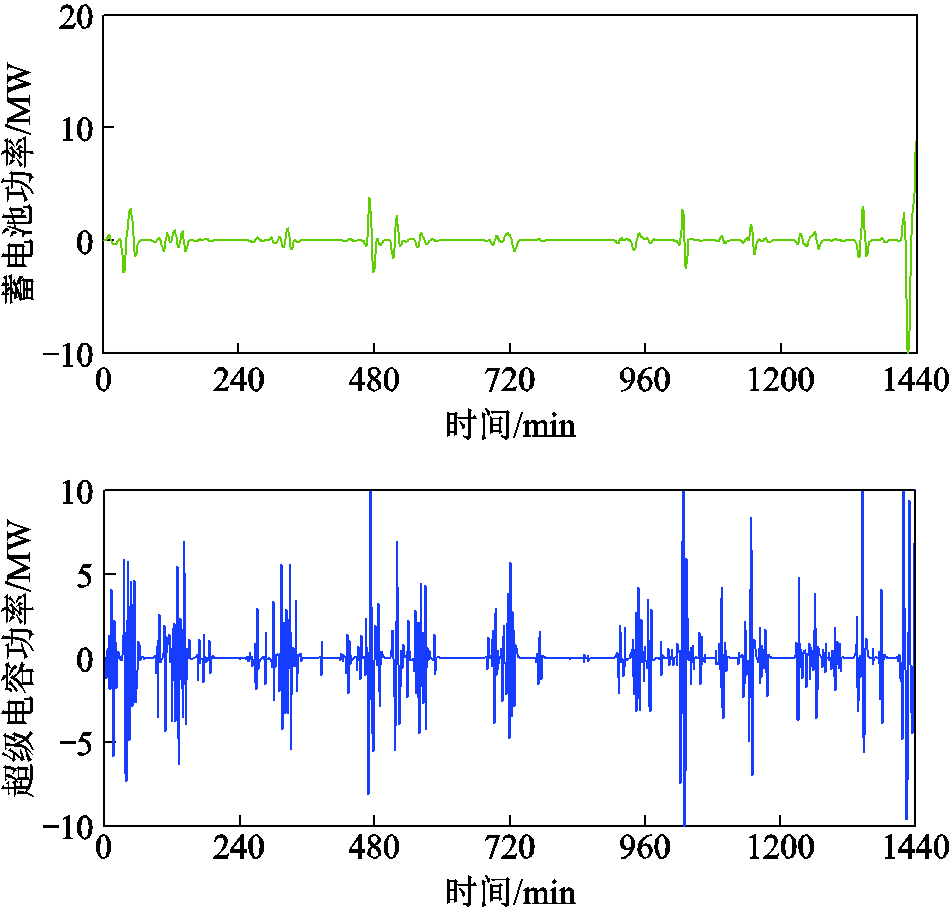
图16 故障工况时功率指令分配结果
Fig.16 Power command distribution result under fault condition
图16中的功率分配结果符合两种储能电池的功率特性。需要说明的是由于超级电容在调度日内会承担一些蓄电池的功率指令,因此图16中故障工况时超级电容实际响应的功率幅值更大一些。
图17展示了故障工况时MMAF分解后各模态的频谱关系。
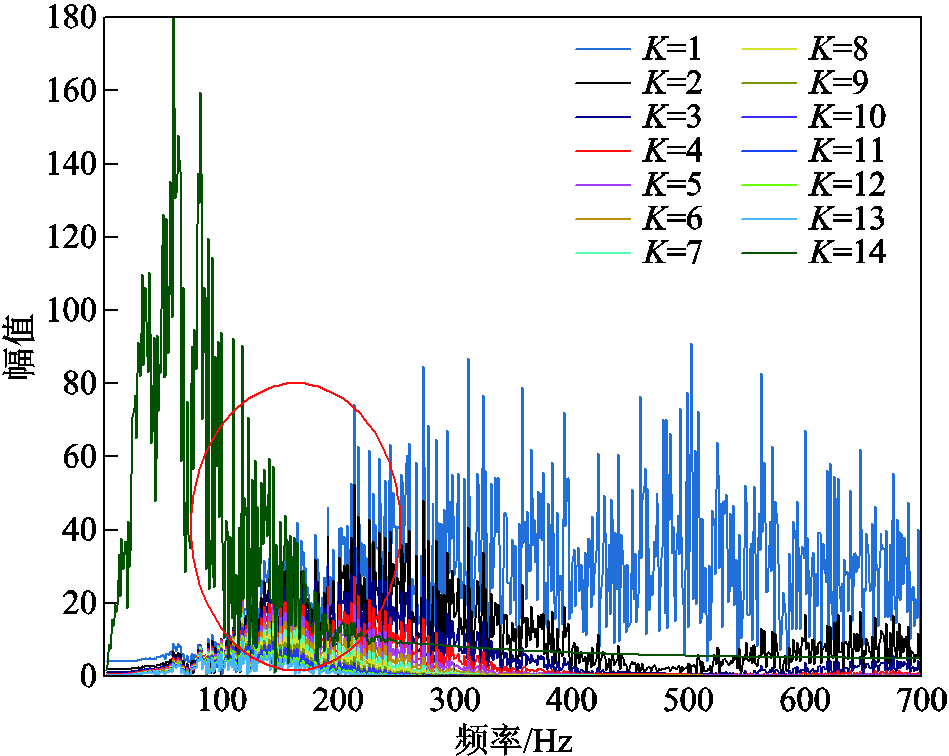
图17 故障工况时MMAF分解后各模态的频谱
Fig.17 Spectrum diagram of each mode after MMAF decomposition under fault condition
从图17的各模态频谱关系中可以明显看出,故障工况时由于超级电容承担了相当一部分因蓄电池放电越限而本应该由蓄电池承担的功率指令,因此不可避免地出现了模态混叠现象(图中红色圈内),这也符合故障工况时设定的HESS功率指令分配的机理。在故障工况下虽然出现了模态混叠,但通过这种“互为备用”的机理避免了功率指令因电池放电越限而无法响应的情况,从而避免了因放电越限而没有电池响应功率指令导致风电无法平抑现象的发生,遏制了由于风功率波动较大导致风机脱网的可能。因此与风机脱网带来的经济损失与电力事故相比,故障工况下模态混叠导致的HESS成本增加就显得微不足道了。
本文针对平抑风电波动的混合储能系统功率分配不精确、成本过高的问题,采用引入Pearson相关系数的MMAF方法得出蓄电池与超级电容各自分配的功率指令,并基于分配结果对混合储能进行了定容,得到如下结论:
1)引入Pearson相关系数的MMAF为滤波参数的选取提供了理论支撑,有效地减弱了模态混叠现象,实现了高精度的功率分配。
2)采用MMAF处理混合储能功率分配问题及定容问题时混合储能系统的LCC相较于传统EMD、VMD、WT方法分别降低87.6%、3.3%、56.8%,在保证蓄电池使用寿命的同时,为解决风电场侧混合储能电站的功率分配与容量配置问题提供了新思路。
参考文献
[1] 刘其辉, 逄思敏, 吴林林, 等. 大规模风电汇集系统电压不平衡机理、因素及影响规律[J]. 电工技术学报, 2022, 37(21): 5435-5450. Liu Qihui, Pang Simin, Wu Linlin, et al. The mechanism, factors and influence rules of voltage imbalance in wind power integration areas[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5435-5450.
[2] 顾雪平, 白岩松, 李少岩, 等. 考虑风电不确定性的电力系统恢复全过程两阶段鲁棒优化方法[J]. 电工技术学报, 2022, 37(21): 5462-5477. Gu Xueping, Bai Yansong, Li Shaoyan, et al. Two stage robust optimization method for the whole-process power system restoration considering wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5462-5477.
[3] de Siqueira L M S, Peng Wei. Control strategy to smooth wind power output using battery energy storage system: a review[J]. Journal of Energy Storage, 2021, 35: 102252.
[4] 齐先军, 郑夕炜, 王晓蓉, 等. 基于时频分析的改进小波包风电功率波动平抑方法[J]. 太阳能学报, 2022, 43(7): 302-309. Qi Xianjun, Zheng Xiwei, Wang Xiaorong, et al. Improved wavelet packet method of smoothing wind power fluctuations based on time-frequency analysis[J]. Acta Energiae Solaris Sinica, 2022, 43(7): 302-309.
[5] 李政, 刘宏伟, 康健, 等. 混合储能参与自动发电控制容量优化配置[J]. 电气技术, 2021, 22(9): 34-40. Li Zheng, Liu Hongwei, Kang Jian, et al. Participation of hybrid energy storage in capacity optimization configuration of automatic generation control system[J]. Electrical Engineering, 2021, 22(9): 34-40.
[6] Wang Huaqing, Xie Zhuoshi, Pu Lei, et al. Energy management strategy of hybrid energy storage based on Pareto optimality[J]. Applied Energy, 2022, 327: 120095.
[7] Zhou Shiyao, Chen Ziqiang, Huang Deyang, et al. Model prediction and rule based energy management strategy for a plug-in hybrid electric vehicle with hybrid energy storage system[J]. IEEE Transactions on Power Electronics, 2021, 36(5): 5926-5940.
[8] Xu Yanhui, Xu Yijia, Huang Yan. Generation of typical operation curves for hydrogen storage applied to the wind power fluctuation smoothing mode[J]. Global Energy Interconnection, 2022, 5(4): 353-361.
[9] Jin He, Liu Pei, Li Zheng. Dynamic modeling and design of a hybrid compressed air energy storage and wind turbine system for wind power fluctuation reduction[J]. Computers & Chemical Engineering, 2019, 122: 59-65.
[10] 孙玉树, 唐西胜, 孙晓哲, 等. 基于MPC-HHT的多类型储能协调控制策略研究[J]. 中国电机工程学报, 2018, 38(9): 2580-2588, 2826. Sun Yushu, Tang Xisheng, Sun Xiaozhe, et al. Research on multi-type energy storage coordination control strategy based on MPC-HHT[J]. Proceedings of the CSEE, 2018, 38(9): 2580-2588, 2826.
[11] 袁铁江, 张昱, 栗磊, 等. 计及功率密度约束含氢储能的预装式多元储能电站容量优化配置研究[J]. 电工技术学报, 2021, 36(3): 496-506. Yuan Tiejiang, Zhang Yu, Li Lei, et al. Capacity optimization configuration of pre-installed multi-energy storage power station considering power density constrained hydrogen storage[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 496-506.
[12] 李奇, 赵淑丹, 蒲雨辰, 等. 考虑电氢耦合的混合储能微电网容量配置优化[J]. 电工技术学报, 2021, 36(3): 486-495. Li Qi, Zhao Shudan, Pu Yuchen, et al. Capacity optimization of hybrid energy storage microgrid considering electricity-hydrogen coupling[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 486-495.
[13] 钱韦廷, 赵长飞, 万灿, 等. 基于概率预测的混合储能平抑风电波动随机优化调控方法[J]. 电力系统自动化, 2021, 45(18): 18-27. Qian Weiting, Zhao Changfei, Wan Can, et al. Probabilistic forecasting based stochastic optimal dispatch and control method of hybrid energy storage for smoothing wind power fluctuations[J]. Automation of Electric Power Systems, 2021, 45(18): 18-27.
[14] 李建林, 牛萌, 周喜超, 等. 能源互联网中微能源系统储能容量规划及投资效益分析[J]. 电工技术学报, 2020, 35(4): 874-884. Li Jianlin, Niu Meng, Zhou Xichao, et al. Energy storage capacity planning and investment benefit analysis of micro-energy system in energy interconnection[J]. Transactions of China Electrote-chnical Society, 2020, 35(4): 874-884.
[15] Yang Yuqing, Bremner S, Menictas C, et al. Modelling and optimal energy management for battery energy storage systems in renewable energy systems: a review[J]. Renewable and Sustainable Energy Reviews, 2022, 167: 112671.
[16] 李建林, 李雅欣, 刘海涛, 等. 计及储能电站安全性的功率分配策略研究[J]. 电工技术学报, 2022, 37(23): 5976-5986. Li Jianlin, Li Yaxin, Liu Haitao, et al. Research on power distribution strategy considering the safety of energy storage power station[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5976-5986.
[17] 郭玲娟, 魏斌, 韩肖清, 等. 基于集合经验模态分解的交直流混合微电网混合储能容量优化配置[J]. 高电压技术, 2020, 46(2): 527-537. Guo Lingjuan, Wei Bin, Han Xiaoqing, et al. Capacity optimal configuration of hybrid energy storage in hybrid AC/DC micro-grid based on ensemble empirical mode decomposition[J]. High Voltage Engineering, 2020, 46(2): 527-537.
[18] 李亚楠, 王倩, 宋文峰, 等. 基于变分模态分解和Hilbert变换的平滑风电出力混合储能容量优化配置[J]. 电测与仪表, 2019, 56(1): 82-88, 95. Li Yanan, Wang Qian, Song Wenfeng, et al. Capacity configuration of hybrid energy storage for smoothing wind power outputs based on variational mode decomposition and Hilbert transform[J]. Electrical Measurement & Instrumentation, 2019, 56(1): 82-88, 95.
[19] 李鑫, 王娟, 邱亚, 等. 基于VMD的混合储能容量优化配置[J]. 太阳能学报, 2022, 43(2): 88-96. Li Xin, Wang Juan, Qiu Ya, et al. Optimal allocation of hybrid energy storage capacity based on variational mode decomposition[J]. Acta Energiae Solaris Sinica, 2022, 43(2): 88-96.
[20] 杜佳耘, 雷勇, 李永凯, 等. 基于参数优化变分模态分解的混合储能功率分配策略[J]. 现代电力, 2021, 38(1): 51-59. Du Jiayun, Lei Yong, Li Yongkai, et al. Hybrid energy storage strategy based on parameter optimized variational mode decomposition[J]. Modern Electric Power, 2021, 38(1): 51-59.
[21] 李建林, 郭斌琪, 牛萌, 等. 风光储系统储能容量优化配置策略[J]. 电工技术学报, 2018, 33(6): 1189-1196. Li Jianlin, Guo Binqi, Niu Meng, et al. Optimal configuration strategy of energy storage capacity in wind/PV/storage hybrid system[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1189-1196.
[22] Zhu Honglu, Hou Ruyin, Jiang Tingting, et al. Research on energy storage capacity configuration for PV power plants using uncertainty analysis and its applications[J]. Global Energy Interconnection, 2021, 4(6): 608-618.
[23] Hou Hui, Xu Tao, Wu Xixiu, et al. Optimal capacity configuration of the wind-photovoltaic-storage hybrid power system based on gravity energy storage system[J]. Applied Energy, 2020, 271: 115052.
[24] 王再闯, 陈来军, 李笑竹, 等. 基于合作博弈的产销者社区分布式光伏与共享储能容量优化[J]. 电工技术学报, 2022, 37(23): 5922-5932. Wang Zaichuang, Chen Laijun, Li Xiaozhu, et al. Capacity optimization of distributed PV and shared energy storage of prosumer community based on cooperative game[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5922-5932.
[25] Ye Lin, Zhang Cihang, Tang Yong, et al. Hierarchical model predictive control strategy based on dynamic active power dispatch for wind power cluster integration[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4617-4629.
[26] Guo Tingting, Liu Youbo, Zhao Junbo, et al. A dynamic wavelet-based robust wind power smoothing approach using hybrid energy storage system[J]. International Journal of Electrical Power & Energy Systems, 2020, 116: 105579.
[27] 陈亚爱, 林演康, 王赛, 等. 基于滤波分配法的混合储能优化控制策略[J]. 电工技术学报, 2020, 35(19): 4009-4018. Chen Yaai, Lin Yankang, Wang Sai, et al. Optimal control strategy of hybrid energy storage based on filter allocation method[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4009-4018.
[28] 张明龙, 张振宇, 高源, 等. 基于变分模态分解的暂态扰动波形去噪算法[J]. 电力系统保护与控制, 2022, 50(8): 43-49. Zhang Minglong, Zhang Zhenyu, Gao Yuan, et al. Transient disturbance waveform denoising algorithm based on variational mode decomposition[J]. Power System Protection and Control, 2022, 50(8): 43-49.
[29] Omar A I, Ali Z M, Al-Gabalawy M, et al. Multi-objective environmental economic dispatch of an electricity system considering integrated natural gas units and variable renewable energy sources[J]. Mathematics, 2020, 8(7): 1100.
[30] 葛玉友, 尚策. 寿命约束的储能规划[J]. 中国电机工程学报, 2020, 40(19): 6150-6161. Ge Yuyou, Shang Ce. Energy storage planning constrained by its life[J]. Proceedings of the CSEE, 2020, 40(19): 6150-6161.
[31] 丁明, 吴杰, 张晶晶. 面向风电平抑的混合储能系统容量配置方法[J]. 太阳能学报, 2019, 40(3): 593-599. Ding Ming, Wu Jie, Zhang Jingjing. Capacity optimization method of hybrid energy storage system for wind power smoothing[J]. Acta Energiae Solaris Sinica, 2019, 40(3): 593-599.
[32] 马兰, 谢丽蓉, 叶林, 等. 基于混合储能双层规划模型的风电波动平抑策略[J]. 电网技术, 2022, 46(3): 1016-1029. Ma Lan, Xie Lirong, Ye Lin, et al. Wind power fluctuation suppression strategy based on hybrid energy storage Bi-level programming model[J]. Power System Technology, 2022, 46(3): 1016-1029.
Abstract When the hybrid energy storage system (HESS) allocates power in the scenario of suppressing wind power fluctuations, the power distribution is inaccurate due to mode aliasing, which leads to the poor economy of the hybrid energy storage system. To address these issues, this paper suggests a method of multiple moving average filtering (MMAF) to decompose the total power command of hybrid energy storage.
Firstly, the minimum flat total power command of hybrid energy storage meeting the flat requirements was obtained, and the obtained total power command of hybrid energy storage was filtered through MMAF to make the battery respond to the filtered low frequency part and the supercapacitor respond to the high frequency part. Pearson correlation coefficient was used as the index to quantify modal aliasing, and Pearson correlation coefficient was used as the basis to determine the optimal filtering sliding window size and the optimal filtering times to ensure that the maximum limit of modal aliasing can be achieved under the sliding window size and filtering times. Taked the power command of the battery and the supercapacitor as the feasible region of the energy storage capacity, the minimum rated power and rated capacity of the hybrid energy storage system can be determined by comprehensively considering the battery state of charge (SOC) constraints. Secondly, based on the equivalent operating time, a quantitative model of battery life cycle was established, which provided a basis for the economic analysis of hybrid energy storage system. The cumulative effect of battery charging and discharging on its life loss was considered in the model, and the actual number of battery cycles was converted into the equivalent number of cycles at the rated discharge depth. Finally, the incremental factor of battery maintenance cost was introduced into the hybrid energy storage life cycle cost model (LCC) to describe the nonlinear increase of maintenance cost caused by the cumulative effect of battery aging every ten years, so as to better conform to the actual operation of the energy storage battery and improve the practicability of the LCC model. The effectiveness of the proposed method to reduce the comprehensive cost of hybrid energy storage was verified by simulation experiments.
According to the actual simulation experiment, the method in this paper can well smooth the power fluctuation of wind power grid connection, made it meet the grid connection requirements, and the hybrid energy storage configuration result was better than other configuration methods. The simulation results under different working conditions showed that MMAF method can ensure the battery operation life during power distribution, and can minimize the mode aliasing phenomenon and reduce the comprehensive cost of hybrid energy storage. Under normal working conditions, the LCC of MMAF was reduced by 87.6% compared with the empirical mode decomposition method (EMD). Compared with the variational mode decomposition method (VMD), the LCC of MMAF was reduced by 3.3%. Compared with the wavelet transform (WT) method, the LCC of MMAF was reduced by 56.8%. In case of failure, the battery and supercapacitor form a standby working mode for each other. The total power command of mixed energy storage was redistributed by MMAF method, which avoided the situation that the power command cannot respond due to battery failure, curbs the possibility of wind turbine disconnection, and avoided greater economic losses.
Keywords:Hybrid energy storage, power distribution, mode aliasing, MMAF algorithm, quantitative model of battery life cycle
DOI:10.19595/j.cnki.1000-6753.tces.222348
中图分类号:TM711
国家自然科学基金联合基金重点资助项目(U21A20485)。
收稿日期 2022-12-21
改稿日期 2023-02-12
田博文 男,1997年生,硕士研究生,研究方向为新能源侧储能优化配置与控制。E-mail:932725835@qq.com
张志禹 男,1966年生,博士,教授,研究方向为电网信息处理与深度学习。E-mail:zhangzhiyu@xaut.edu.cn(通信作者)
(编辑 赫 蕾)