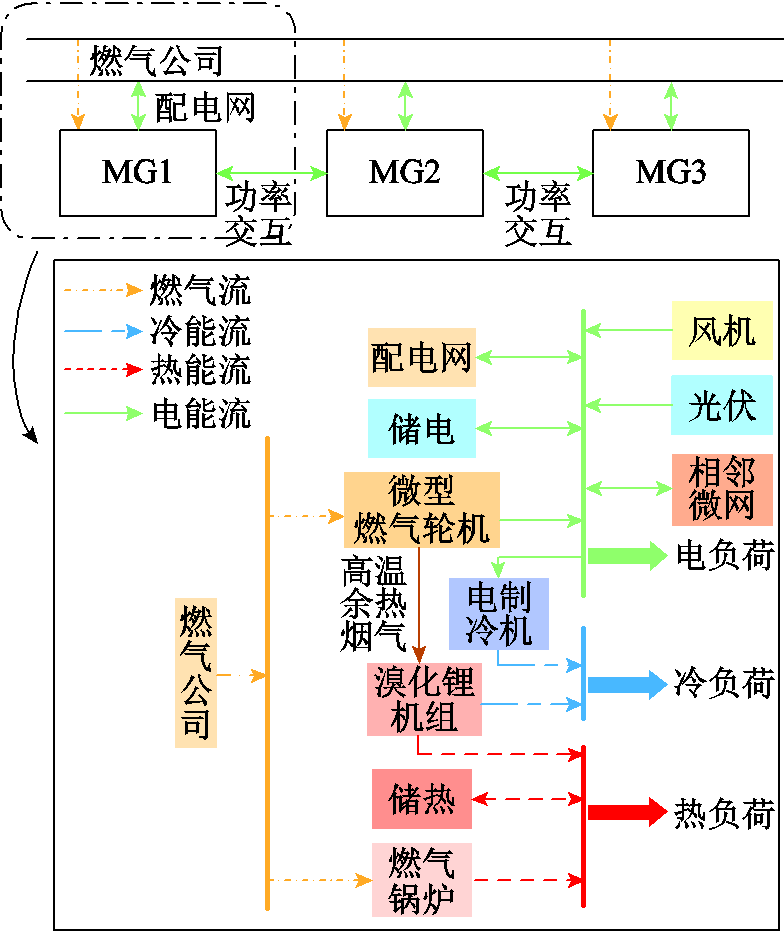
图1 多微网系统结构示意图
Fig.1 Schematic diagram of multi-microgrid
摘要 构建多微网系统是消纳可再生能源、提升电网稳定性的有效方式。通过各微网的协调调度,可有效提升微网的运行效益以及可再生能源的消纳水平。现有多微网优化问题场景多元,变量众多,再加上源荷不确定性及多微网主体的数据隐私保护等问题,为模型的高效求解带来了巨大挑战。为此,该文提出了一种分层约束强化学习优化方法。首先,构建了多微网分层强化学习优化框架,上层由智能体给出各微网储能优化策略和微网间功率交互策略;下层各微网以上层策略为约束,基于自身状态信息采用数学规划法对各微网内部的分布式电源出力进行自治优化。通过分层架构,减小通信压力,保护微网内部数据隐私,充分发挥强化学习对源荷不确定性的自适应能力,大幅提升了模型求解速度,并有效兼顾了数学规划法的求解精度。此外,将拉格朗日乘子法与传统强化学习方法相结合,提出一种约束强化学习求解方法,有效地解决了传统强化学习方法难以处理的约束越限问题。最后通过算例验证了该方法的有效性和优势。
关键词:多微网系统 分层约束强化学习 不确定性 数据隐私保护
在“双碳”目标背景下,新能源渗透率逐渐升高。多微网系统作为一种包含可再生能源、多能负荷、分布式储能等的综合集成单元,可以通过微网内多能互补和微网间协调优化,在增强配电网系统供电可靠性和促进可再生能源就地消纳等方面发挥显著作用[1-4]。然而多微网系统规模较大,同时由于可再生能源出力的波动性、不同能源形式之间的耦合性等,其调度优化问题面临着重大挑战,因此寻找能够实现高效能量管理的优化策略对于提高系统性能十分必要。
针对多微网系统的优化调度问题,文献[5]计及微网间的功率交互,建立了多微网系统经济调度模型,并验证了多微网协调运行相较于独立运行可有效减少运行成本;文献[6]则建立了光伏余电上网的微网决策模型,采用序列二次规划算法进行求解,并通过算例验证了模型及算法的有效性。此外,其他常用算法如遗传算法[7-8]、粒子群算法[9-10]、差分进化算法[11]、目标级联法[12]及交替方向乘子法[13-14]等也已应用于多微网优化问题中。然而以上方法均依赖系统的精细建模及源荷的精准预测,难以针对源荷随机变化动态响应,当源荷随机波动时,相应的模型、预测器和求解器均需要进行重设。
深度强化学习(Deep Reinforcement Learning, DRL)通过与环境的交互试错寻找最优策略,不依赖源荷的精准预测,而且对于源荷的不确定性具有良好的自适应能力[15-16]。因此近期有学者开始关注基于数据驱动的DRL方法,并将其应用于微电网的优化问题中。文献[17-18]采用了Q-learning算法有效求解微网系统调度优化问题,然而当特征量增多时,该方法将面临维数灾难的问题[19];文献[19]则提出一种改进的竞争Q网络算法,基于多参数动作探索机制以解决原算法稳定性低和维度灾难等问题,但该算法需要对动作空间进行离散化处理,继而影响求解精度。文献[20-22]则将连续空间的强化学习算法应用于综合能源微网优化问题中,详细设计了智能体的动作空间、状态空间和奖励函数,并通过算例验证了算法的有效性。文献[23]建立了基于博弈论的多微网系统协同优化模型,并将博弈论与强化学习算法相结合,通过Nash-Q算法求得博弈均衡解,实现各微网的电能互补和在线优化。文献[24]为了缩减强化学习的动作空间,对微网优化调度进行分层处理,通过上层强化学习智能体求解储能策略,下层求解器求解其余分布式电源出力的方法简化动作空间,从而提升收敛速度,但只针对单微网优化问题,且采用离散空间无法实现连续控制。此外,上述基于强化学习的微网系统优化中,将强化学习问题描述为马尔科夫决策过程(Markov Decision Process, MDP),优化问题中的约束条件,均通过向奖励函数中添加惩罚项实现。这种方法属于“软约束”施加方式,模糊了目标和约束之间的界限,收敛速度较慢,且需要人工反复调试惩罚系数以保证训练效果。若惩罚系数过大,则会导致策略过于保守,难以学习到最优策略;反之,则导致约束难以得到严格满足,影响系统安全运行。
针对以上问题,本文提出一种面向多微网的分层约束强化学习优化方法。首先,提出一种多微网系统分层强化学习优化框架,将多微网优化问题分为上下两层求解,上层无需获取各微网的所有运行状态信息,由智能体基于净负荷预测信息和储能状态信息,给出各微网内储能优化策略和微网间功率交互策略;下层各微网以上层策略为约束,基于自身状态信息通过数学规划法对微网内部设备出力进行自治优化。该框架利用上下层之间的协同实现多微网系统的整体优化,充分发挥了强化学习基于数据驱动原理可自适应源荷随机性的优势,并有效兼顾了数学规划法的求解精度。并基于该分层框架提出一种约束强化学习求解方法,该方法融合了深度强化学习方法和拉格朗日乘子法,将约束优化问题转换为无约束优化问题,驱使智能体在严格满足约束的前提下寻找最优策略。相比于传统集中式优化方法,本文方法不仅可根据源荷波动动态响应,满足在线优化的要求,同时也无需聚合所有微网状态信息,保护了微网数据隐私;相比于传统强化学习方法,有效地解决了难以处理的约束越限问题,且收敛速度和精度均显著提升。最后,通过算例分析验证了本文方法的有效性以及其较传统集中式优化和DRL方法的优势。
本研究面向多微网系统,以含多种能源形式耦合的冷热电联供型微网为例,其内部能源形式包括冷、热、电和气。图1展示了微网内的能量流向及多微网系统的结构。

图1 多微网系统结构示意图
Fig.1 Schematic diagram of multi-microgrid
微网(Microgrid)用MG表示,为不失一般性,图1中给出了较普遍的冷热电联供型微网能量流动关系,实际不同微网的组成并非完全相同。微网内电负荷除了由微型燃气轮机(Micro-Turbine, MT)消耗天然气供给,还可由分布式可再生能源、配电网、邻近微网和蓄电池(Battery, BT)供给,其中与配电网、邻近微网和蓄电池之间的能量为双向交互;热负荷部分由燃气锅炉(Gas Boiler, GB)、燃气和储热槽(Heat Storage, HS)供给,同时溴化锂机组吸收MT发电产生的高温余热烟气制热供给;冷负荷部分由溴化锂机组吸收高温余热烟气制冷供给,部分由电制冷机(Electric Cooler, EC)消耗电能制冷供给。在同一区域内,邻近的微网可以互联形成多微网系统,微网之间通过联络线进行能量交互。微网内设备模型见附录。
深度强化学习过程可描述为一个马尔科夫决策过程,由状态空间 、动作空间
、动作空间 、奖励函数
、奖励函数 、状态转移概率
、状态转移概率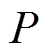 及折扣系数
及折扣系数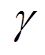 组成。智能体通过和环境的不断交互学习得到使奖励最大化的序列动作。而多微网优化过程是一个典型的序贯决策问题,因此,多微网优化问题十分适合采用强化学习方法求解。
组成。智能体通过和环境的不断交互学习得到使奖励最大化的序列动作。而多微网优化过程是一个典型的序贯决策问题,因此,多微网优化问题十分适合采用强化学习方法求解。
为简化强化学习动作空间及奖励函数的复杂设计,保证算法的可靠收敛,本文提出一种多微网系统分层强化学习优化框架,将多微网优化问题分解为上下两层求解,上层智能体模型充分考虑时间相关性及整个决策周期的综合累计回报,仅需基于各微网的预测净负荷和储能(含储电和储热)状态信息,制定微网间的交互策略及储能优化策略并下发至下层;下层各微网则以上层策略为约束采用数学规划法求解内部设备的最优出力,同时向上层反馈奖励信号值指导上层策略更新,避免了上层智能体的无效探索。利用上下层的协同实现多微网系统的全局优化,不仅充分发挥了强化学习可自适应源荷随机性的优势,同时也有效兼顾了数学规划法的求解精度。多微网系统分层强化学习框架示意图如图2所示。
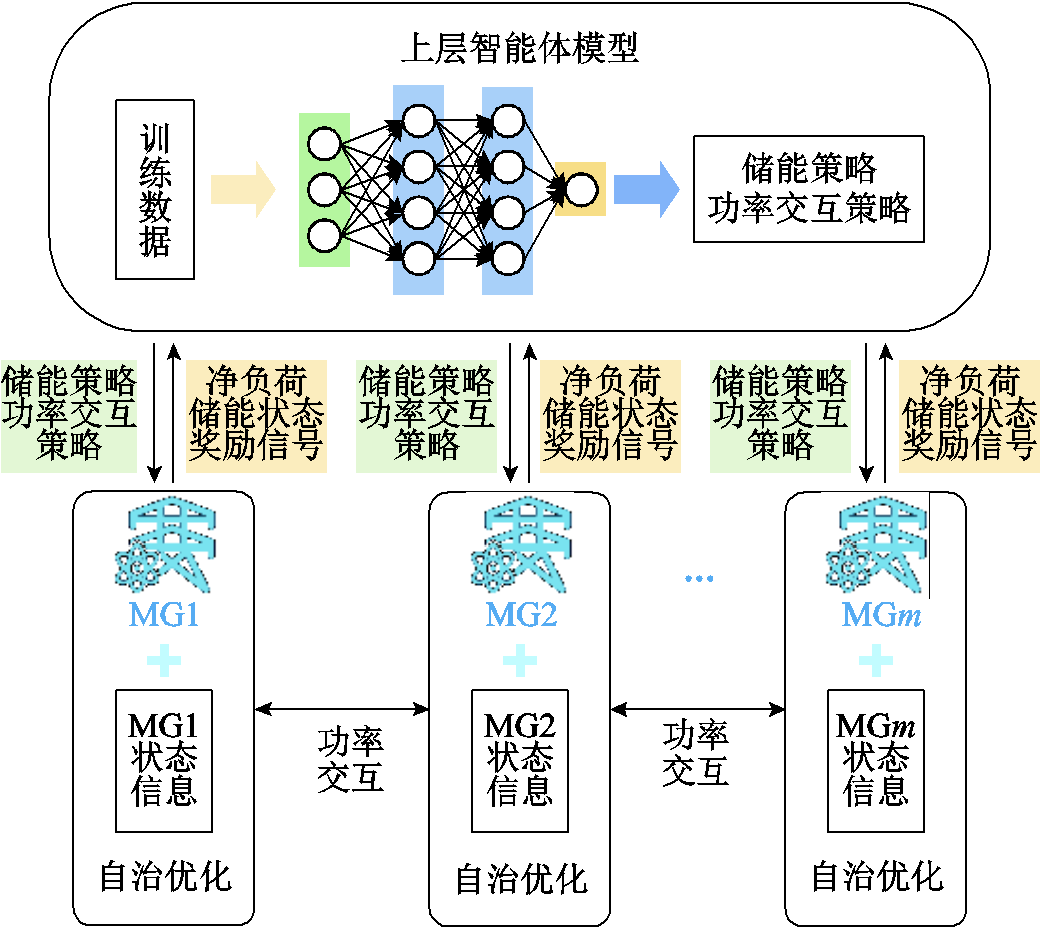
图2 多微网系统分层强化学习框架示意图
Fig.2 Schematic diagram of hierarchical reinforcement learning framework for multi-microgrid system
通过分层优化架构,大大简化了智能体动作空间维度和奖励函数的复杂设计。而且上层策略给定后,多微网优化任务被分解为多个子微网自治优化问题,各微网可基于上层策略快速得出各时间断面的设备最优出力,因此大大缩小了下层优化问题的规模,从而实现下层模型的快速求解。此外,在通信方面,上层仅需获取各微网的净负荷预测信息、储能状态信息及各微网反馈的奖励信号,无需额外的微网内部状态信息。而下层各微网之间不进行信息交互,仅基于自身状态信息进行优化,有效地减小了通信压力并保护了各微网内部数据隐私,在稳态和故障等不同情况下,也能实现与其他微网的交互与应急处置。训练完成的模型通过读取当前状态空间即可给出优化策略。
2.2.1 智能体状态空间
智能体的状态空间用于表征环境的状态信息,状态空间包含了智能体决策所需的信息,智能体基于当前状态做出相应动作并与环境进行交互。本文模型的状态空间如式(1)所示,包括各微网的储能荷电状态、储热状态、分时电价信息以及冷、热、电净负荷功率,其中净负荷信息由各微网上传,通过负荷预测值减去新能源出力预测值得到。通过分层设计,智能体仅需要获取基本的状态信息用于辅助决策,无需获得微网内设备的详细运行状态信息。
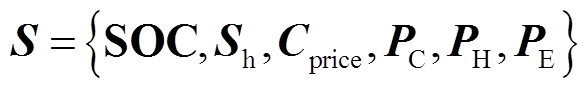 (1)
(1)
式中,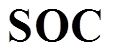 为储电的荷电状态;
为储电的荷电状态;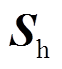 为储热状态;
为储热状态;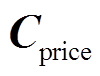 为分时电价信息;
为分时电价信息;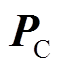 为冷净负荷预测功率;
为冷净负荷预测功率;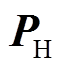 为热净负荷预测功率;
为热净负荷预测功率;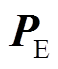 为电净负荷预测功率。其中可再生能源和冷热电负荷均为预测功率,为增强模型应对源荷不确定性的能力,在训练过程中将预测功率叠加预测误差作为状态量。
为电净负荷预测功率。其中可再生能源和冷热电负荷均为预测功率,为增强模型应对源荷不确定性的能力,在训练过程中将预测功率叠加预测误差作为状态量。
2.2.2 智能体动作空间
智能体的动作空间为上层模型中的相关控制变量,包括各微网间的交互功率、各微网的储电充放功率和储热吸收、释放的热功率,即
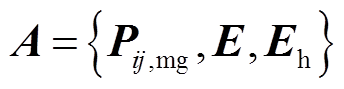 (2)
(2)
式中,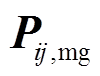 为相邻微网i、j间的交互功率;
为相邻微网i、j间的交互功率;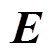 为蓄电池充放电功率;
为蓄电池充放电功率;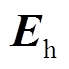 为储热吸收、释放的热功率。
为储热吸收、释放的热功率。
2.2.3 智能体奖励函数
奖励函数是智能体基于当前环境状态选择对应动作并作用于环境后反馈的奖励信号。奖励函数用于指导智能体策略的趋优更新,通过持续的学习使得策略的累计奖励最大化。本文的优化目标选取为最小化运行成本和环境污染物排放(通过折算成本计算),因此奖励函数即为多微网系统的综合优化目标,由于强化学习目标是累计奖励最大化,故添加负号。
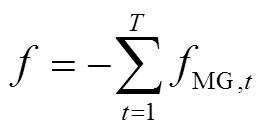 (3)
(3)
式中,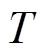 为调度总时段数;
为调度总时段数;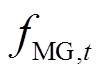 为多微网系统在
为多微网系统在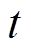 时段的综合目标函数,由下层模型自治优化后向上层传递。
时段的综合目标函数,由下层模型自治优化后向上层传递。
2.2.4 智能体动作约束
智能体动作约束包括荷电量状态约束式(4)、充放电功率约束式(5)、调度周期始末能量平衡约束式(6)、充放电转换约束式(7)及各微网的功率交互约束式(8)。储热作为储能设备同样需要满足容量、功率、工作状态约束。与蓄电池类似,此处不再赘述。
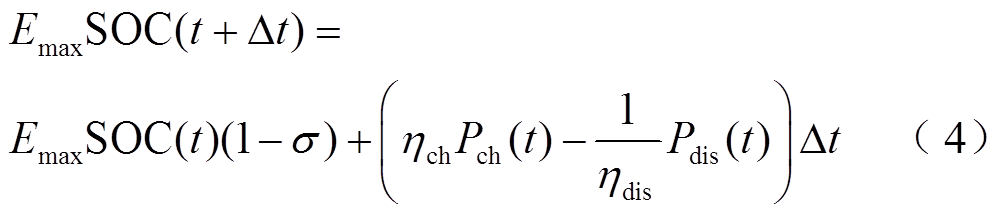
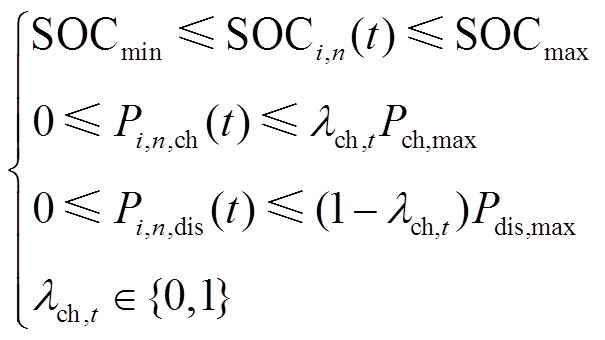 (5)
(5)
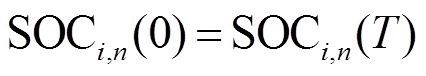 (6)
(6)
 (7)
(7)
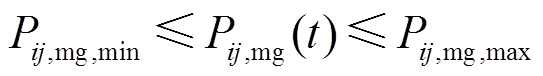 (8)
(8)
式中,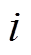 和
和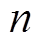 分别为微网编号和设备编号;
分别为微网编号和设备编号;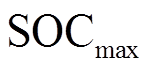 、
、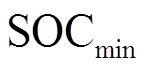 分别为蓄电池荷电状态的上、下限;
分别为蓄电池荷电状态的上、下限;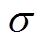 为蓄电池的自放电系数;
为蓄电池的自放电系数;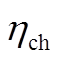 、
、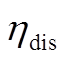 分别为蓄电池的充、放电效率;
分别为蓄电池的充、放电效率;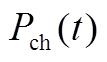 、
、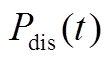 分别为蓄电池的充、放电功率;
分别为蓄电池的充、放电功率;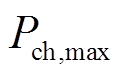 、
、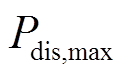 分别为蓄电池最大充、放电功率;
分别为蓄电池最大充、放电功率;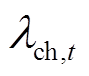 为蓄电池在
为蓄电池在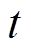 时段的充放电状态系数;
时段的充放电状态系数;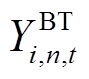 为蓄电池的充放电转换系数;
为蓄电池的充放电转换系数;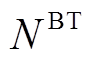 为蓄电池的最大充放电转换次数;
为蓄电池的最大充放电转换次数;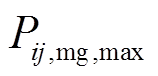 、
、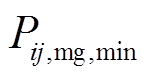 分别为微网
分别为微网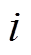 与微网
与微网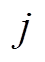 交互功率的上、下限。
交互功率的上、下限。
为保证输出动作的上、下限约束,本文将输出动作经过tanh函数限制在[-1,1]之间,再通过线性变换即可满足式(4)、式(8)的上、下限约束。对于式(5)~式(7),传统的强化学习方法通过向奖励函数中添加惩罚项的形式处理约束,但这种将奖励和约束统一建模为奖励函数的方式模糊了目标和约束的界限,需要人为设置惩罚系数。若惩罚系数过大,则会导致智能体难以学习到最优策略;若系数太小,则易使得策略难以满足安全约束。因此,为避免上述问题,本文将拉格朗日乘子法与传统强化学习方法相结合,将约束优化问题转换为无约束问题进行求解,在满足安全约束的前提下寻找最优策略,从而避免将约束以惩罚项的形式加入奖励中,该部分内容将在第3节进行详细介绍。
2.3.1 目标函数
下层各微网获取上层策略后,各个微网可实现独立并行求解,无需获取其他微网的任何运行状态进行优化,因此下层为各微网的自治优化模型,模型目标为最小化微网运行成本和环境污染物排放,其中环境污染物排放通过折算成本计算。此外,为有效保护各微网数据隐私,各微网的目标中还引入了常数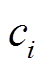 。由于上层智能体下发策略后只需根据下层奖励信号的变化趋势即可学习最优策略,并不关注具体的成本值。与优化问题中目标函数中的常数不影响优化结果相似,在本文这种固定步长(调度周期固定)的强化学习问题中,向每个即时奖励中添加常数并不影响智能体的寻优[25]。加入
。由于上层智能体下发策略后只需根据下层奖励信号的变化趋势即可学习最优策略,并不关注具体的成本值。与优化问题中目标函数中的常数不影响优化结果相似,在本文这种固定步长(调度周期固定)的强化学习问题中,向每个即时奖励中添加常数并不影响智能体的寻优[25]。加入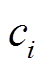 构建伪成本信号,既不影响训练过程,也能保护微网的成本隐私,
构建伪成本信号,既不影响训练过程,也能保护微网的成本隐私,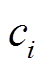 由各个微网自行设置(本文在[-10,10]之间随机选取)。目标函数表达式为
由各个微网自行设置(本文在[-10,10]之间随机选取)。目标函数表达式为
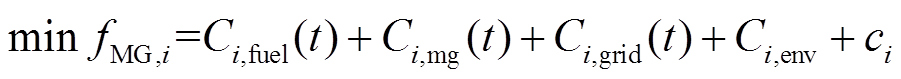 (9)
(9)
式中,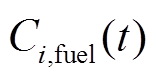 、
、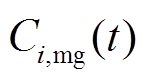 、
、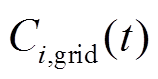 分别为微网
分别为微网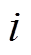 在
在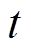 时段内的燃气成本、相邻微网交互成本及配电网交互成本,各成本的计算表达式分别如式(10)~式(12);
时段内的燃气成本、相邻微网交互成本及配电网交互成本,各成本的计算表达式分别如式(10)~式(12);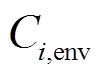 为各微网的环境污染折算成本,相关模型和参数来源于文献[26]。
为各微网的环境污染折算成本,相关模型和参数来源于文献[26]。
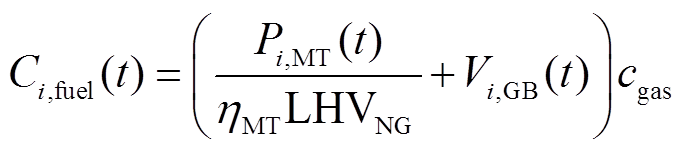 (10)
(10)
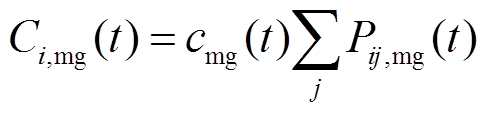 (11)
(11)
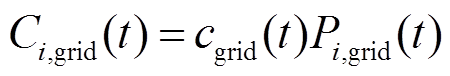 (12)
(12)
式中,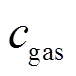 为天然气价格;
为天然气价格;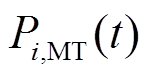 为
为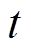 时段微网
时段微网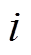 的MT输出电功率;
的MT输出电功率;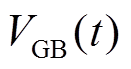 为
为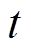 时段内微网
时段内微网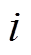 的GB耗气量;
的GB耗气量;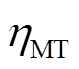 为发电效率;
为发电效率;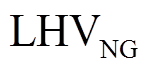 为天然气热值。
为天然气热值。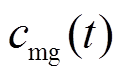 、
、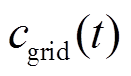 分别为
分别为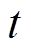 时段相邻微网间的电能交易价格及微网与配电网之间电能交易价格;
时段相邻微网间的电能交易价格及微网与配电网之间电能交易价格;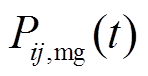 、
、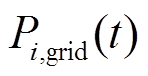 分别为
分别为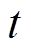 时段微网
时段微网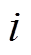 与微网
与微网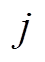 之间及微网
之间及微网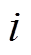 与配电网之间的交互电量。
与配电网之间的交互电量。
2.3.2 能量平衡约束
多微网系统内的冷、热、电负荷与出力应满足实时平衡约束,即
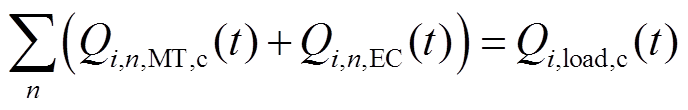 (13)
(13)
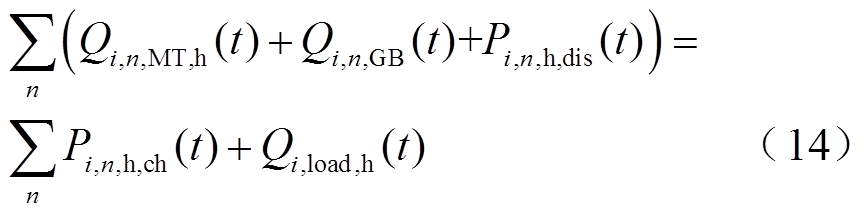
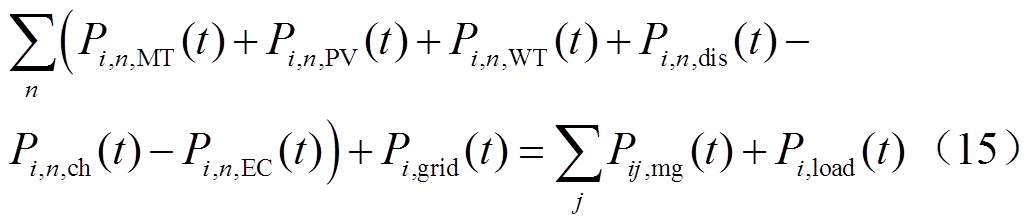
式中, 、
、 、
、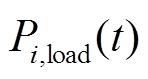 分别为
分别为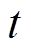 时段微网
时段微网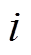 的冷负荷、热负荷和电负荷;
的冷负荷、热负荷和电负荷; 、
、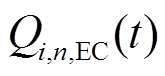 分别为微网
分别为微网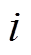 内编号为
内编号为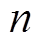 的MT和EC在
的MT和EC在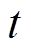 时段内的制冷功率;
时段内的制冷功率;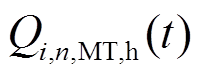 、
、 分别为微网
分别为微网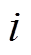 内编号为
内编号为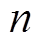 的MT、GB在
的MT、GB在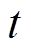 时段内的制热功率;
时段内的制热功率;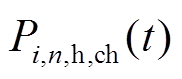 、
、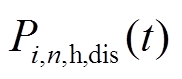 分别为微网
分别为微网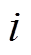 内编号为
内编号为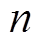 的HS在
的HS在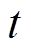 时段内的充、放热功率;
时段内的充、放热功率;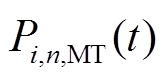 、
、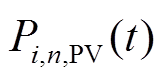 、
、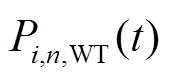 、
、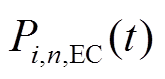 分别为微网
分别为微网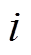 内编号为
内编号为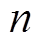 的MT、PV、WT、EC输出或消耗的电功率;
的MT、PV、WT、EC输出或消耗的电功率;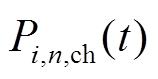 、
、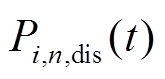 分别为ES的充、放电功率。
分别为ES的充、放电功率。
2.3.3 运行约束
除了微网内的能量平衡约束,为保证多微网系统的安全运行,还需满足设备运行约束及功率交互约束,由于各微网距离较近,因此不考虑线路损耗。
1)微型燃气轮机运行约束
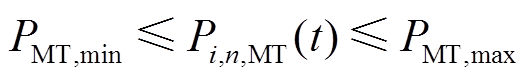 (16)
(16)
式中,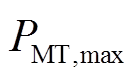 、
、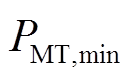 分别为燃气轮机出力的上、下限。
分别为燃气轮机出力的上、下限。
2)燃气锅炉运行约束
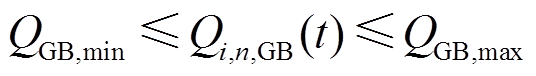 (17)
(17)
式中,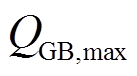 、
、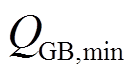 分别为燃气锅炉输出热功率的上、下限。
分别为燃气锅炉输出热功率的上、下限。
3)电制冷机运行约束
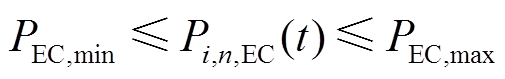 (18)
(18)
式中,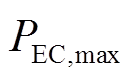 、
、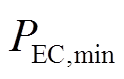 分别为电制冷机输入电功率功率的上、下限。
分别为电制冷机输入电功率功率的上、下限。
4)功率交互约束
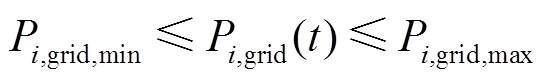 (19)
(19)
式中,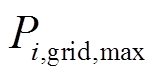 、
、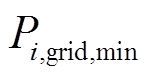 分别为微网
分别为微网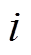 与配电网交互功率的上、下限。
与配电网交互功率的上、下限。
在模型训练过程中,上、下层模型需通过信息交互完成多微网系统的协同优化。下层各微网需要将微网内部的净负荷信息及储能状态上传至上层用于决策,同时在训练过程中,还需将式(9)中的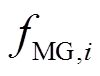 反馈给上层智能体以指导智能体的策略更新;而上层智能体则充分考虑时间相关性及整个决策周期的综合累计回报,将储能策略和微网交互功率下发至下层模型,从而使下层各微网以上层策略为约束进行自治优化。
反馈给上层智能体以指导智能体的策略更新;而上层智能体则充分考虑时间相关性及整个决策周期的综合累计回报,将储能策略和微网交互功率下发至下层模型,从而使下层各微网以上层策略为约束进行自治优化。
在本文模型的信息交互中,上层智能体仅获取各微网的净负荷预测信息、储能状态信息及各微网反馈的奖励信号,并向下层传递储能策略和微网交互策略。而下层各微网之间不进行信息交互,仅通过上层给定策略进行功率交互,并基于自身状态信息进行优化。因此有效地减少了多微网设备众多造成的通信压力,并保护了各微网内部数据隐私。
采用强化学习方法解决多微网系统优化问题的一个难点就是如何处理运行约束。在传统的强化学习方法中,通常采用罚函数法将约束建模为马尔科夫决策过程(Constraint Markov Decision Process, CMDP)中的负奖励,然而如何设计合适的罚函数是该方法的难点。此外,这种方法模糊了目标与约束之间的界限,难以确定合适的惩罚系数平衡目标和约束之间的关系。若惩罚系数过小,智能体给出的动作难以满足运行约束;若系数过大,则可能导致智能体对约束的过度惩罚,难以学习到较好的调度策略,而且即使设置较大的惩罚系数,也无法保证策略严格满足约束。
为了解决上述问题,本文基于CMDP[27],通过CMDP对考虑约束的强化学习问题进行数学描述。基于CMDP数学理论,结合强化学习方法,构建了一种约束强化学习算法求解多微网系统优化问题。与传统强化学习算法建模为MDP不同,约束强化学习算法采用CMDP建模。CMDP更好地描述了包含约束的强化学习问题,要求智能体在满足安全约束的前提下寻找最优策略,其除了由状态空间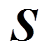 、动作空间
、动作空间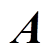 、奖励函数
、奖励函数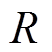 、状态转移概率
、状态转移概率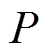 及折扣系数
及折扣系数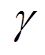 组成以外,还存在一个辅助成本函数
组成以外,还存在一个辅助成本函数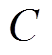 和安全阈值
和安全阈值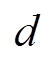 。
。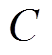 用于表征智能体策略对于约束的满足程度,
用于表征智能体策略对于约束的满足程度,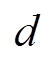 则为可接受的违反约束阈值。
则为可接受的违反约束阈值。
在CMDP中,智能体在每个时间断面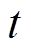 ,通过观察系统状态
,通过观察系统状态 选择相应的动作
选择相应的动作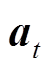 。随后通过与环境交互得到奖励值
。随后通过与环境交互得到奖励值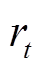 及辅助成本值
及辅助成本值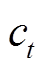 。与此同时,环境状态将根据状态转移概率
。与此同时,环境状态将根据状态转移概率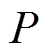 变化为状态
变化为状态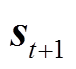 。
。
智能体的目标为在辅助成本(表征约束越限情况)满足安全阈值的前提下,寻找最优策略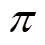 ,以最大化整个时间序列的累计奖励,有
,以最大化整个时间序列的累计奖励,有
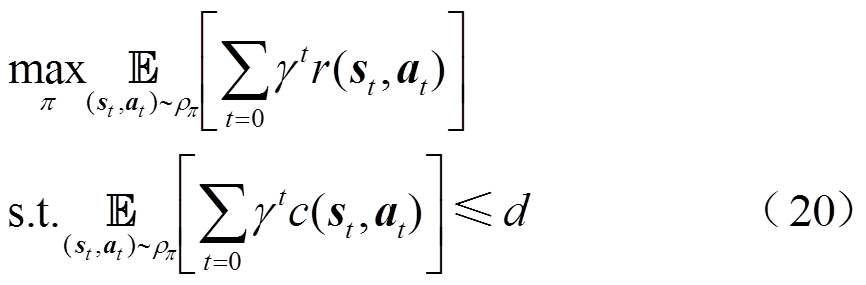
式中,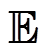 为期望;
为期望;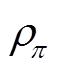 为策略
为策略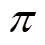 的轨迹分布;
的轨迹分布;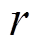 为奖励函数;
为奖励函数;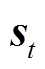 为
为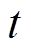 时间断面的状态;
时间断面的状态;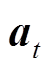 为
为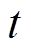 时间断面的动作;
时间断面的动作;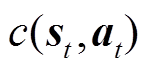 为辅助成本函数,反映了策略给出的动作对于约束的满足情况。例如,当智能体给出的动作不满足约束时,
为辅助成本函数,反映了策略给出的动作对于约束的满足情况。例如,当智能体给出的动作不满足约束时,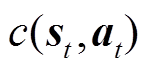 =1;当满足约束时,
=1;当满足约束时,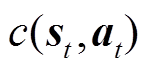 =0。因此,可以设置安全阈值
=0。因此,可以设置安全阈值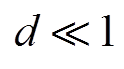 以驱使智能体给出的动作满足约束。
以驱使智能体给出的动作满足约束。
通过CMDP框架,充分考虑了强化学习过程中的约束问题,避免了奖励函数的复杂设计及惩罚系数的反复调整,最大程度减少了人为干预,有效地解决了传统MDP难以平衡目标和安全约束的问题。为了求解CMDP,可采用拉格朗日松弛技术,将带约束的优化问题转换为无约束优化问题。具体来说引入以下拉格朗日函数。
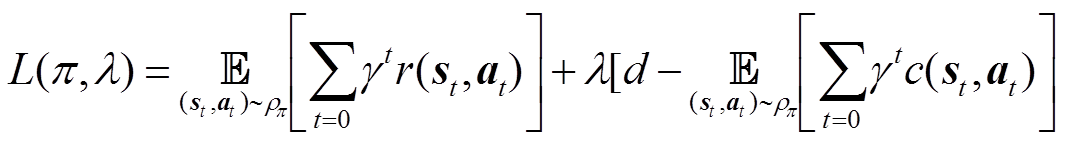 (21)
(21)
式中,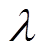 为拉格朗日乘子。通过拉格朗日松弛,上述优化问题转换为如下min-max问题,可采用原始对偶优化方法,即利用策略梯度上升和对偶梯度上升轮流更新原始域参数和对偶域参数进行求解[28]。
为拉格朗日乘子。通过拉格朗日松弛,上述优化问题转换为如下min-max问题,可采用原始对偶优化方法,即利用策略梯度上升和对偶梯度上升轮流更新原始域参数和对偶域参数进行求解[28]。
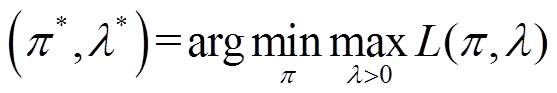 (22)
(22)
传统的SAC(soft actor critic)算法[29]在电力系统优化调度中已有应用,并已验证具有较强的寻优能力和较好的鲁棒性。然而SAC算法是基于MDP问题进行设计的,算法目标是找到使累计奖励最大的策略。本文采用CMDP对约束强化学习过程建模,要求智能体能在辅助成本(表征约束越限情况)满足安全阈值的前提下,寻找最优策略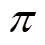 ,以最大化整个时间序列的累计奖励。尽管传统的SAC方法可以采用向奖励中添加惩罚项的方式处理约束,但这种方式模糊了智能体目标和约束的界限,学习的策略要么过于保守,要么难以保证约束完全得到满足,而且惩罚项的设计也十分复杂。因此本节在SAC算法的基础上,结合拉格朗日乘子法提出一种Lagrangian-SAC(LSAC)算法进行求解。下面将对算法进行详细介绍。
,以最大化整个时间序列的累计奖励。尽管传统的SAC方法可以采用向奖励中添加惩罚项的方式处理约束,但这种方式模糊了智能体目标和约束的界限,学习的策略要么过于保守,要么难以保证约束完全得到满足,而且惩罚项的设计也十分复杂。因此本节在SAC算法的基础上,结合拉格朗日乘子法提出一种Lagrangian-SAC(LSAC)算法进行求解。下面将对算法进行详细介绍。
3.2.1 算法目标
SAC算法的最终目标为使累计奖励最大的同时,保证策略的熵最大化,以增强算法的寻优能力和鲁棒性,即
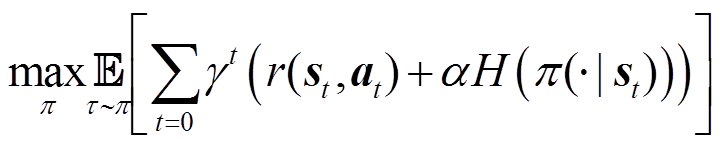 (23)
(23)
式中,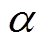 为温度系数(
为温度系数(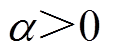 ),用于确定策略熵项相对于奖励重要性的比重;
),用于确定策略熵项相对于奖励重要性的比重; 为在状态
为在状态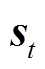 下策略采取动作的熵,其计算方式为
下策略采取动作的熵,其计算方式为
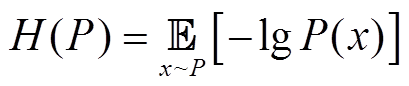 (24)
(24)
在LSAC算法中,为保证系统安全,需要在满足约束的前提下寻找策略以最大化算法目标,因此采用拉格朗日乘子法将约束优化问题转换为无约束优化问题(如3.1节所述),算法目标变为
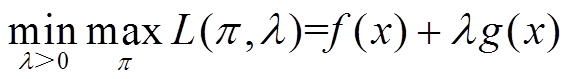 (25)
(25)
其中
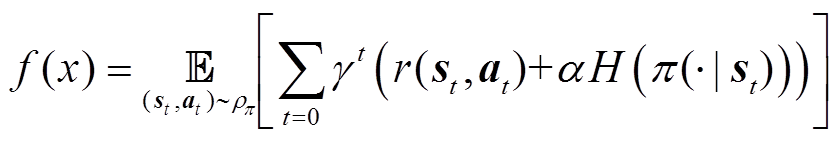 (26)
(26)
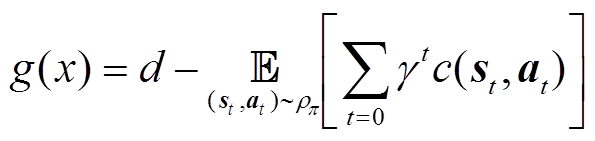 (27)
(27)
在本文中,相关动作约束即为式(5)~式(7)和储热约束,因此,将辅助成本函数定义为
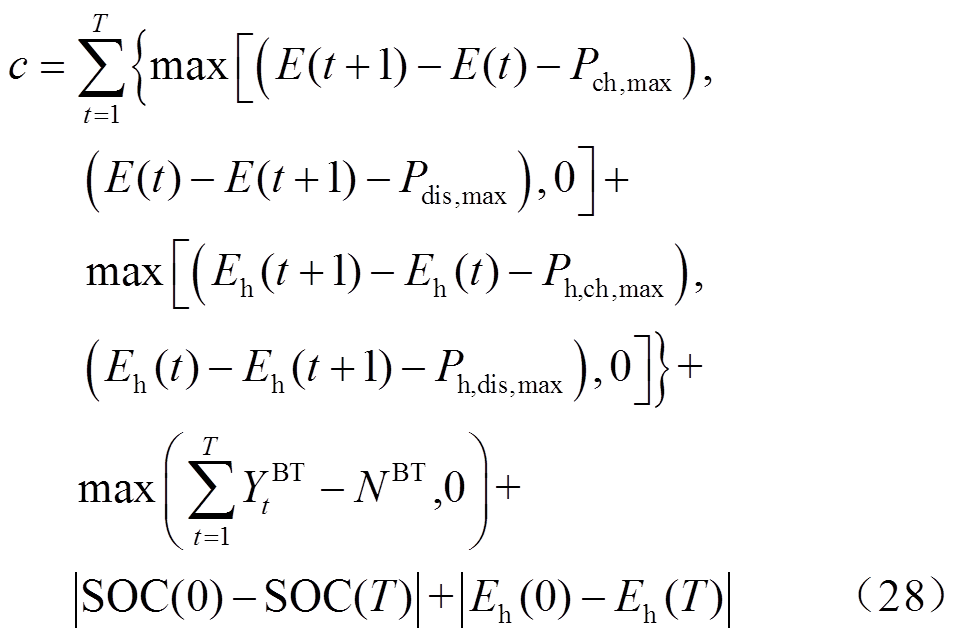
3.2.2 智能体迭代策略
SAC算法中的柔性策略迭代分为柔性策略评估和柔性策略改进两部分,可参考文献[29],此处不再赘述。
在LSAC中,为求解式(25)的极大极小问题,采用原始对偶优化方法交替更新策略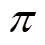 和拉格朗日乘子
和拉格朗日乘子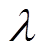 。LSAC中引入辅助成本
。LSAC中引入辅助成本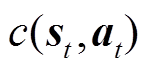 的状态-动作值函数
的状态-动作值函数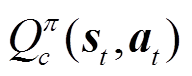 ,其计算推导过程与
,其计算推导过程与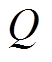 函数[29]类似,有
函数[29]类似,有
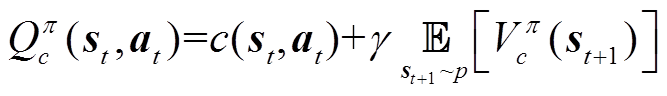 (29)
(29)
式中,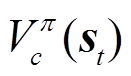 为状态
为状态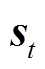 的辅助成本状态值函数。
的辅助成本状态值函数。
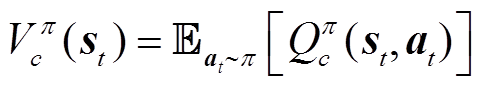 (30)
(30)
引入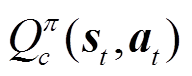 后,LSAC的策略改进过程变为
后,LSAC的策略改进过程变为
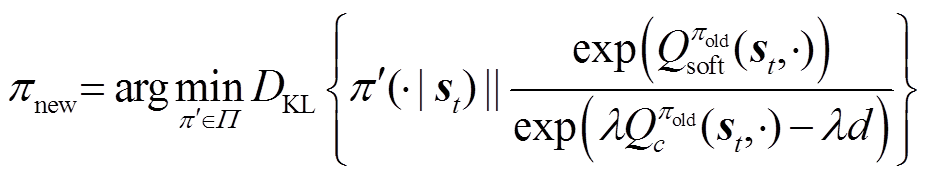 (31)
(31)
式中,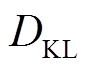 为KL散度;
为KL散度;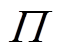 为策略分布的集合;
为策略分布的集合;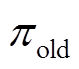 和
和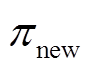 分别为改进前、后的策略;
分别为改进前、后的策略;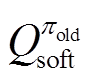 和
和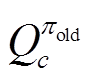 分别为策略改进前的
分别为策略改进前的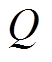 函数和辅助成本
函数和辅助成本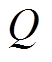 函数。
函数。
3.2.3 智能体网络构建
为将柔性策略迭代过程拓展到更实用的函数近似过程,本文采用神经网络参数化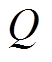 函数、辅助成本
函数、辅助成本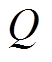 函数和策略分布。
函数和策略分布。
柔性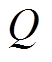 函数的网络参数可通过最小化贝尔曼残差的方式训练得到
函数的网络参数可通过最小化贝尔曼残差的方式训练得到
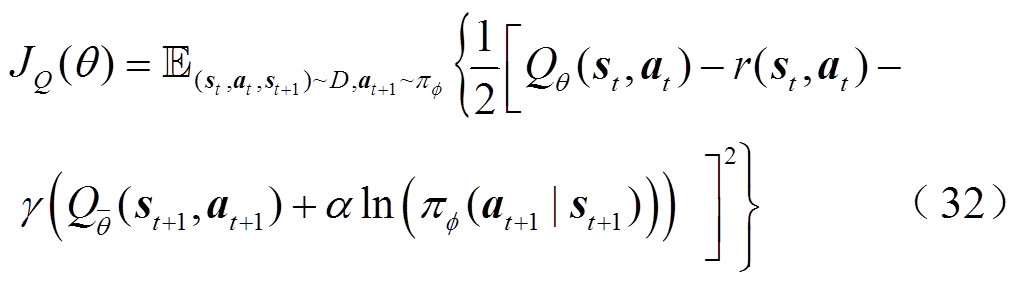
式中,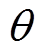 为
为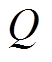 函数网络的参数;
函数网络的参数;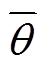 为目标
为目标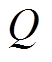 函数网络的参数,通过式(33)更新,其中
函数网络的参数,通过式(33)更新,其中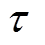 为软更新系数,本文模型中取0.005;
为软更新系数,本文模型中取0.005;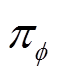 为当前策略分布;
为当前策略分布;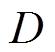 为经验回放单元[30]。为增强网络训练速度和稳定性,本文引入两个
为经验回放单元[30]。为增强网络训练速度和稳定性,本文引入两个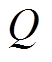 函数网络并进行独立训练,在训练过程中选择更小的值作为目标
函数网络并进行独立训练,在训练过程中选择更小的值作为目标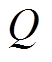 网络的
网络的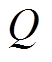 值。
值。
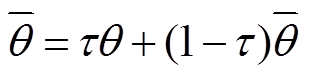 (33)
(33)
辅助成本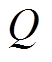 函数的网络参数更新过程与
函数的网络参数更新过程与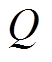 函数类似,有
函数类似,有
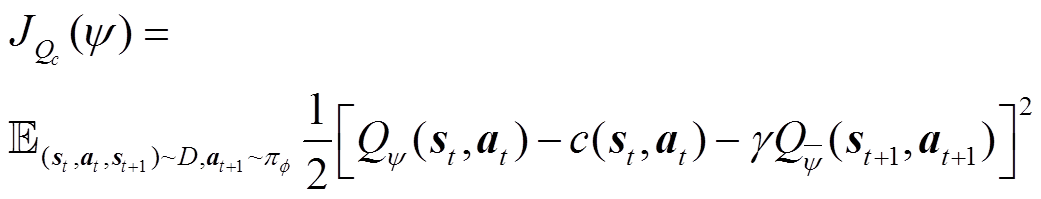 (34)
(34)
式中,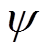 为辅助成本
为辅助成本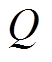 函数网络的参数;
函数网络的参数;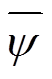 为目标
为目标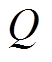 函数网络的参数,采用式(33)的方式软更新,在实践中同样引入了两个辅助成本
函数网络的参数,采用式(33)的方式软更新,在实践中同样引入了两个辅助成本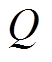 函数网络独立训练。
函数网络独立训练。
策略分布网络的参数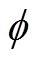 通过最小化其KL散度更新,即
通过最小化其KL散度更新,即
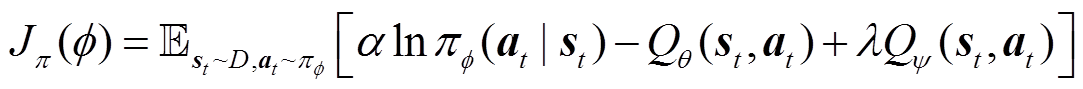 (35)
(35)
其中动作采用了再参数化以减少梯度估计的方差,有
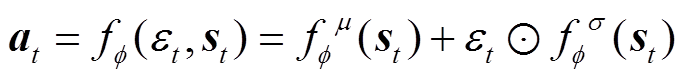 (36)
(36)
式中,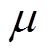 和
和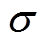 分别为策略分布网络输出的均值和方差;
分别为策略分布网络输出的均值和方差;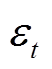 为噪声,从标准正态分布采样得到;
为噪声,从标准正态分布采样得到; 为元素积。
为元素积。
本文通过自动调整拉格朗日乘子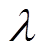 来求解CMDP问题,无需额外的超参数调整,通过最小化损失函数式(37)更新。
来求解CMDP问题,无需额外的超参数调整,通过最小化损失函数式(37)更新。
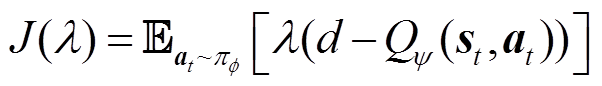 (37)
(37)
温度系数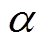 表示策略熵相对于奖励的重要性权重,在训练过程中奖励不断变化,采用定值的
表示策略熵相对于奖励的重要性权重,在训练过程中奖励不断变化,采用定值的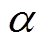 会导致训练的不稳定。本文构建了一个温度系数网络使
会导致训练的不稳定。本文构建了一个温度系数网络使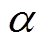 根据策略空间的探索程度自动调整,采用最小化损失函数式(38)的形式进行自适应更新。
根据策略空间的探索程度自动调整,采用最小化损失函数式(38)的形式进行自适应更新。
 (38)
(38)
式中,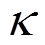 为最小期望熵的超参数。
为最小期望熵的超参数。
此外,由于SAC算法可处理离散动作空间问题[31],通过将连续动作空间离散化或在神经网络输出层中将连续动作和离散动作分别输出,本文方法也可解决混合动作空间策略生成问题[32],只需对网络更新过程进行相应修改即可。而由于本文研究的多微网优化问题涉及的均为连续动作空间,因此在算法设计上均是基于连续空间。
LSAC算法的网络结构如图3所示。与SAC算法类似,其内部含有一个策略分布网络和两个表征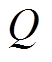 函数的值网络,以及为提高训练稳定性的两个目标值网络。不同的是LSAC算法基于CMDP框架,引入了辅助成本
函数的值网络,以及为提高训练稳定性的两个目标值网络。不同的是LSAC算法基于CMDP框架,引入了辅助成本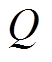 函数,因此LSAC的内部还存在两个辅助值网络及两个目标辅助值网络(图3中红实线框标出)。
函数,因此LSAC的内部还存在两个辅助值网络及两个目标辅助值网络(图3中红实线框标出)。
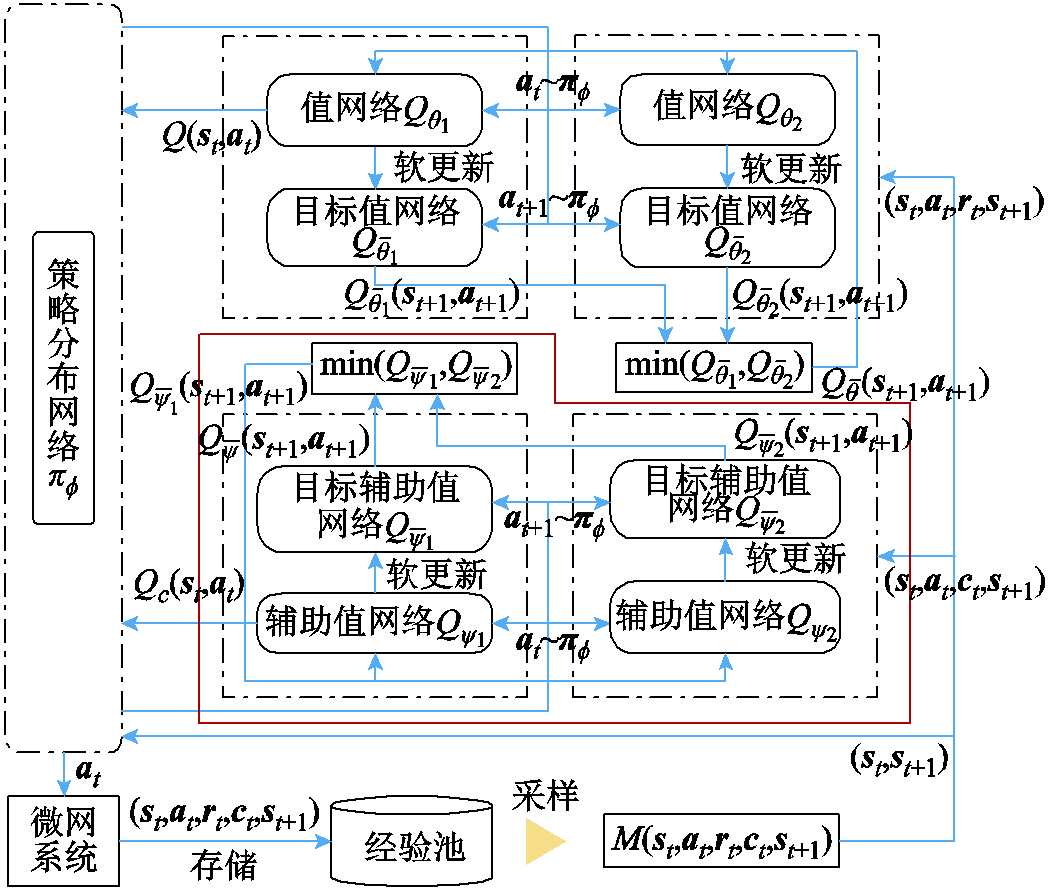
图3 LSAC算法网络结构
Fig.3 The network structure of LSAC
在LSAC算法的网络中,共存在三类神经网络,分别是用于参数化策略分布、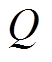 函数和辅助成本
函数和辅助成本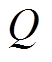 函数的策略分布网络、值网络,以及辅助值网络。其中值网络和辅助值网络均由两组结构相同的神经网络构成,在训练过程中选择值较小的一个网络,且采用软更新的方式更新参数,以增加网络训练速度和稳定性[29]。在训练过程中,首先智能体获取当前时刻的状态
函数的策略分布网络、值网络,以及辅助值网络。其中值网络和辅助值网络均由两组结构相同的神经网络构成,在训练过程中选择值较小的一个网络,且采用软更新的方式更新参数,以增加网络训练速度和稳定性[29]。在训练过程中,首先智能体获取当前时刻的状态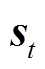 ,并由策略分布网络输出动作
,并由策略分布网络输出动作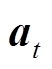 ;同时微网系统基于策略
;同时微网系统基于策略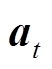 进行状态转移至
进行状态转移至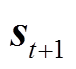 ,再将
,再将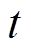 时刻的即时奖励
时刻的即时奖励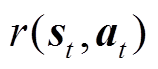 和辅助成本
和辅助成本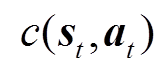 反馈给智能体;智能体将经验数据
反馈给智能体;智能体将经验数据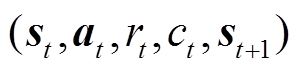 存储至经验回放单元。在网络参数更新过程中,从经验回放单元采样,并根据式(32)~式(38)对参数进行更新。
存储至经验回放单元。在网络参数更新过程中,从经验回放单元采样,并根据式(32)~式(38)对参数进行更新。
分层约束强化学习模型将多微网系统的优化任务进行分解,实现多微网优化任务的简化求解,利用上下层的协同完成模型的训练,并通过LSAC算法解决传统强化学习方法难以处理约束的问题。其具体步骤如下:
1)初始化值网络、辅助值网络、策略分布网络、温度系数网络参数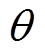 、
、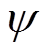 、
、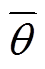 、
、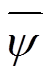 、
、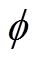 、
、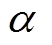 。
。
2)从状态空间初始化多微网系统状态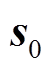 。
。
3)基于当前状态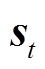 给出当前时间断面的调度动作
给出当前时间断面的调度动作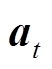 (即储能优化策略和微网间交互策略),并下发至多微网系统。
(即储能优化策略和微网间交互策略),并下发至多微网系统。
4)下层各子微网系统接收上层的储能优化策略及微网间交互策略,同时基于自身状态信息进行自治优化,通过求解器得到当前时间断面微网内设备的最优出力策略,更新系统的状态至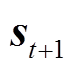 ,并将伪成本信号
,并将伪成本信号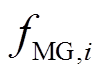 反馈给上层智能体。
反馈给上层智能体。
5)将经验数据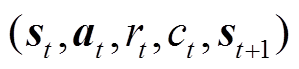 存储至经验回放单元,若经验样本量小于设定值,则转至步骤3)。
存储至经验回放单元,若经验样本量小于设定值,则转至步骤3)。
6)从经验回放单元中批量抽取样本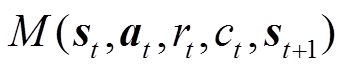 ,并通过策略网络得到
,并通过策略网络得到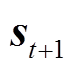 状态下的策略动作
状态下的策略动作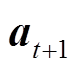 。
。
7)通过式(32)、式(34)更新值网络、辅助值网络参数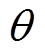 、
、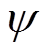 ;通过式(35)、式(37)、式(38)更新策略网络参数
;通过式(35)、式(37)、式(38)更新策略网络参数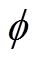 、拉格朗日乘子
、拉格朗日乘子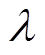 及温度系数
及温度系数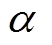 。
。
8)通过式(33)软更新目标值网络、目标辅助值网络参数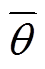 和
和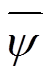 。
。
9)若还未到达末时间断面,则进入下个时间断面,令t=t+1,转至步骤3)。
10)若算法收敛或已到最大训练回合数,则输出模型;否则,转至步骤2),进入下一训练回合。
多微网系统分层约束强化学习流程如图4所示。

图4 多微网系统分层约束强化学习流程
Fig.4 Constraint hierarchical reinforcement learning flow chart of multi-microgrid system
本文采用包含同一区域内三个微网的多微网系统进行算例验证分析[5]。电价采用附表1中的分时电价。为防止出现从配电网购电倒卖的情况,向配电网购电的价格高于向配电网售电的价格,相邻微网之间的购售电价相同,且与向配电网售电价格一致。微网内相同类型的设备参数见附表2。由于电能的产消较为灵活,MT采用以热定电的方式运行。微网系统中储能、可控分布式电源和不可控分布式电源的容量比例大致是1:1.2:2。天然气气价为3.05元/m3,低位热值取9.78 kW∙h/m3,燃气管道的流量上限远大于设备额定运行的需求量,因此不考虑流量上限。储能荷电量状态限制在0.1~0.9之间,其初始荷电量状态 。智能体策略网络和值网络隐藏层均为2层,采用ReLU函数,每层神经元个数为128。其余相关超参数设置见附表3。
。智能体策略网络和值网络隐藏层均为2层,采用ReLU函数,每层神经元个数为128。其余相关超参数设置见附表3。
针对上述多微网系统优化问题采用分层约束强化学习算法(Bi-LSAC)进行模型训练,将训练过程中的累积奖励函数绘制曲线如图5所示。从图5中可看出,训练过程初期,由于智能体探索的随机性较强,易产生较不合理的调度结果,奖励值较小。随着训练的进行,智能体与环境的交互经验逐渐增加,其给出的动作所产生的奖励值也逐渐升高,并于1 700轮左右收敛,奖励值不再上升,由于训练过程中源荷的随机波动存在小幅振荡。从图5中奖励函数曲线的变化趋势可以看出模型收敛性较好,且收敛较快。
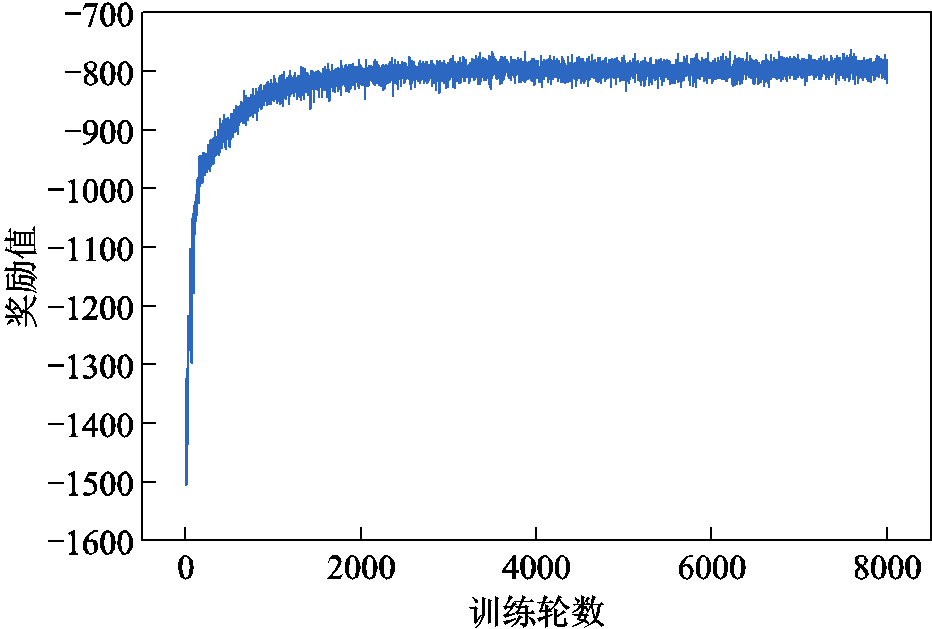
图5 奖励函数曲线
Fig.5 Reward function curve
训练过程中智能体决策动作的约束越限曲线如图6所示。可以看出,除训练初期由于智能体随机探索造成的约束越限以外,动作的约束越限值始终为0,表明本文方法可良好应对强化学习的动作约束问题,保证智能体在满足约束的前提下寻找最优策略。
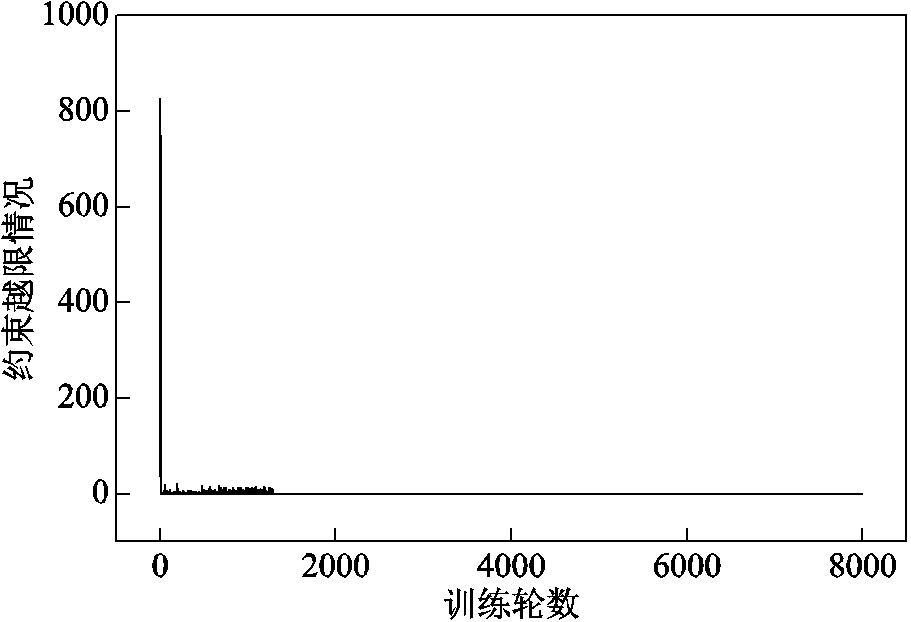
图6 约束越限曲线
Fig.6 Constraint violation curve
为进一步验证本文所提方法的有效性,本文采用Bi-LSAC算法针对多微网协同运行场景、多微网独立运行场景及联络线故障断开场景进行求解,并对相应的优化结果进行分析比较。
4.3.1 多微网协同运行模式
在多微网协同运行模式下,微网1内的冷、热、电能流动情况如图7所示。从图7a中可以看出,微网1内的冷负荷主要由电制冷机及微型燃气轮机余热烟气制冷供给,在0:00—7:00和23:00—24:00两个电价低谷时段,通过电制冷机将富余的可再生能源及从配电网购买的电能转换供给冷负荷。而在7:00—23:00时段电价升高,微型燃气轮机启动,部分冷负荷由微型燃气轮机燃气余热制冷供给。从图7b可以看出,微网1内的热负荷由燃气锅炉和微型燃气轮机交替供给,在0:00—7:00和23:00—24:00时段,热负荷均由燃气锅炉供给,微型燃气轮机处于停机状态,这是由于此时电价较低,相比采用微型燃气轮机进行冷热电联供,通过可再生能源及从配电网购电供电制冷,采用燃气锅炉制热收益更高;而在7:00—23:00时段,随着电价升高,通过微型燃气轮机消耗天然气对系统内的冷热电负荷联供以减少系统购电,从而降低系统运行成本。同时当微型燃气轮机供热大于微网内热负荷时,热储能将剩余热量进行储存,在系统供热不足时补充供给热负荷。
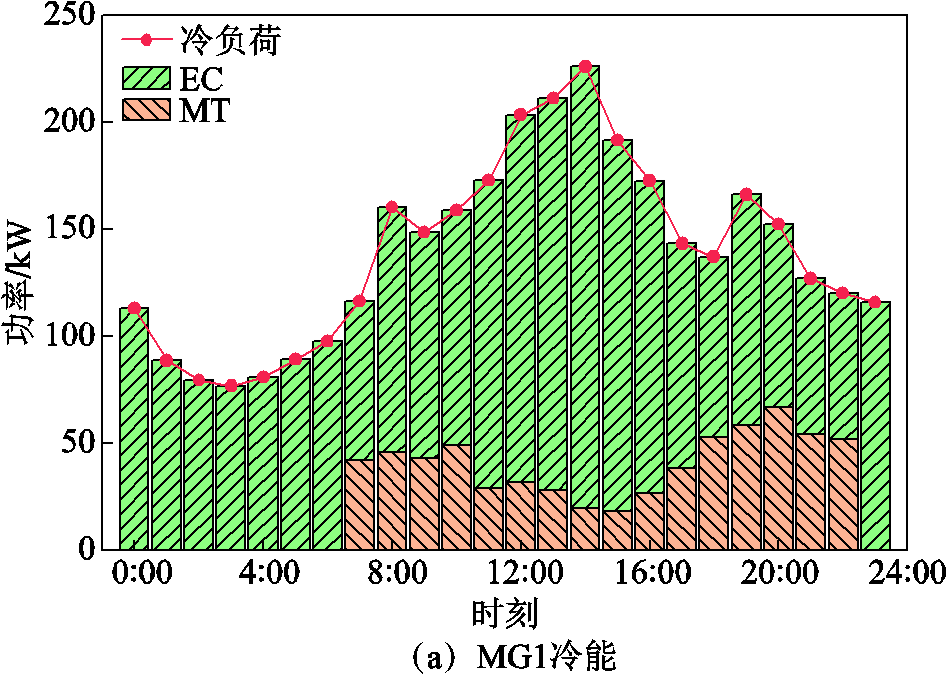
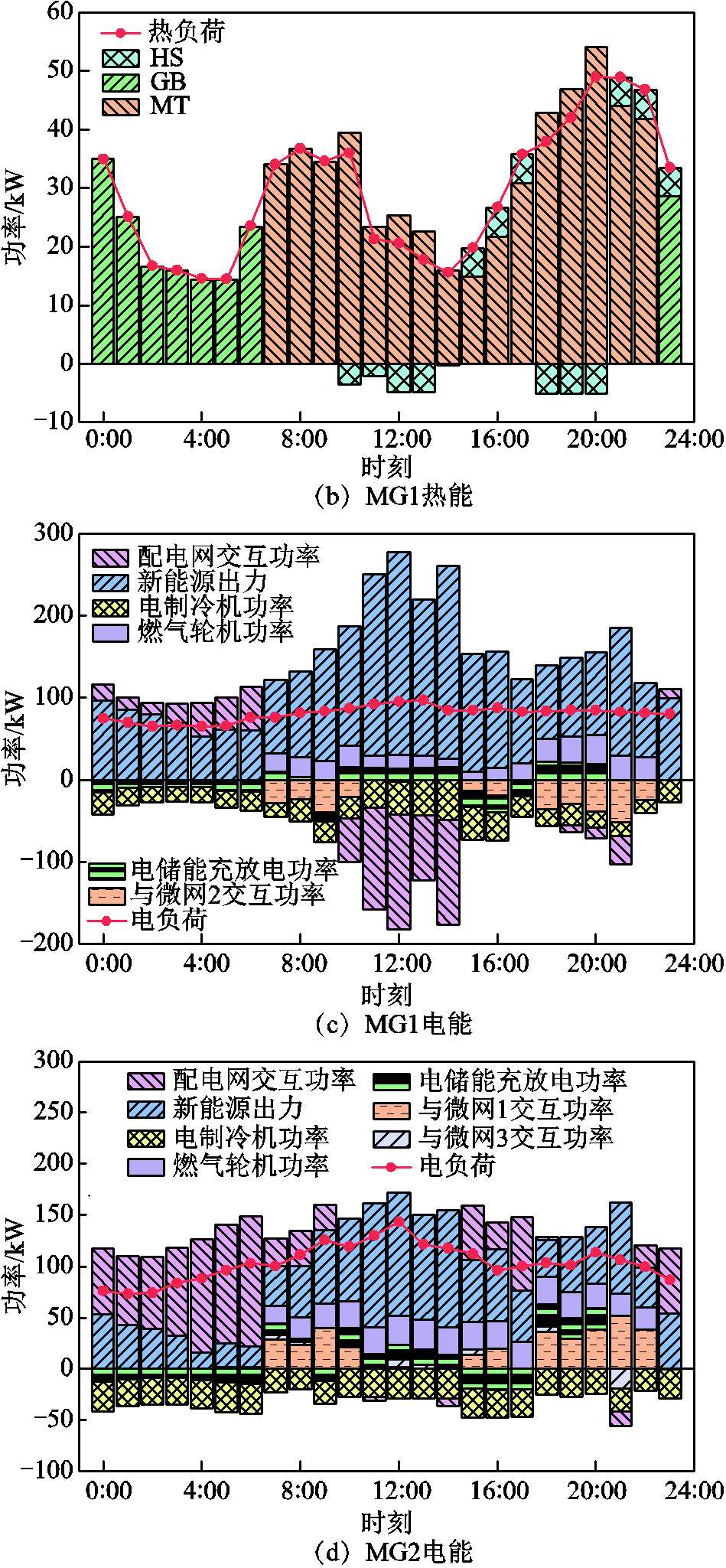
图7 Bi-LSAC的优化调度结果
Fig.7 Optimized scheduling results of Bi-LSAC
图7c、图7d给出了微网1和微网2内的电能流动情况。可以看出,电能的供需两端实现了实时平衡。不论是微网1还是微网2,其储能跟随电价引导进行充放电,在谷电价时段充电作为备用,在峰电价时段放电以减少系统运行成本。在谷电价时段,两微网主要通过可再生能源及向配电网购电供给电负荷;而在7:00—23:00时,电价升高,燃气轮机开始工作,用于供给电负荷以减少用电成本。此外,微网1内的可再生能源在大多数时段均大于系统内负荷需求,是典型的多电型微网;而微网2与之相反,是典型的缺电型微网。因此微网1消纳富余可再生能源的方式除了供储能充电、通过电制冷机转冷及向配电网售电以外,还可通过联络线向微网2输送电能用于供给微网2内缺额电量;而微网2为减少系统运行成本,当自身用电需求无法满足时,优先从相邻微网购电,再考虑向配电网购电。
本文方法得到的运行成本与基于完美预测信息的集中式优化结果比较见表1。基于完美预测信息的集中式优化结果,是指源荷预测出力与实际值无偏差的理想条件下,收集各微网全局状态信息进行集中优化求解得到的结果(即基于实际值得到的集中式优化最优解)。为保证条件一致进行验证,本文方法也基于预测值直接进行测试,差距在0.03%左右,验证了本文所提方法的有效性。
表1 最优解与Bi-LSAC结果比较
Tab.1 Results comparison between the optimal solution and Bi-LSAC

算法运行成本/元 完美预测信息最优解840.042 7 Bi-LSAC840.297 5
4.3.2 协同运行与独立运行模式对比分析
为验证多微网协同优化相比独立运行的优势。设置各微网通过联络线交互协同优化和各微网间联络线断开独立运行两种场景进行对比。图8给出了在两种场景下多微网系统与配电网的交互电量水平。从图8中可以直观看出,多微网协同运行场景下,通过各微网互为备用,有效减少与配电网的交互功率水平,从而降低高可再生能源渗透率对配电网的影响。且通过微网间交互,可有效减少多微网系统的购电成本及污染物排放,相关结果见表2。无交互场景下的运行成本为921.963 8元,相比协同运行增加了9.72%,而污染排放量则相比增加了46.24%。
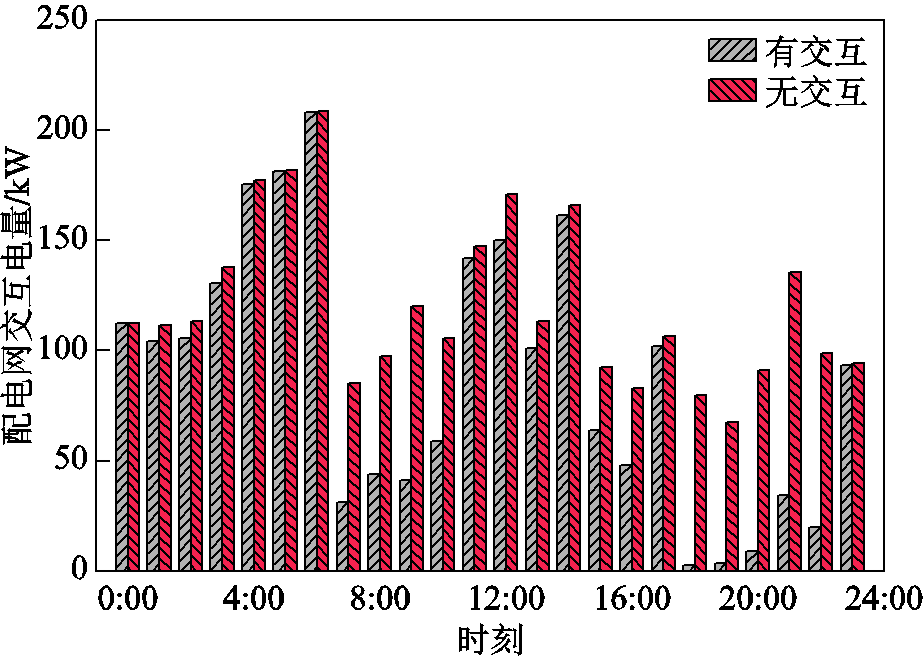
图8 协同运行和独立运行模式的配电网交互水平
Fig.8 Interaction power of distribution network between cooperative and independent operation modes
表2 协同运行和独立运行模式结果比较
Tab. 2 Results comparison between cooperative and independent operation modes

场景运行成本/元污染排放量/kg 独立运行921.963 82 045.509 6 协同运行840.297 51 398.691 8
4.3.3 联络线故障场景分析
为验证模型的拓展性,考虑微网1与微网2之间联络线因故障断开的场景。在该场景下,两微网交互功率值即为0,下层模型同样可通过自治优化完成微网内的优化调度,图9给出了在该场景下微网1的电能流动情况,在该种情况下由于联络线断开,无法通过向相邻微网供电消纳微网1内的富余电量,因此富余电量转由向配电网售出,所提模型在该场景下同样可完成系统的调度优化。此外,针对孤网运行场景,与上述联络线故障场景类似,只需将下层模型参数进行调整,将配电网的交互功率设置为0,即可完成多微网系统孤网运行的调度优化。
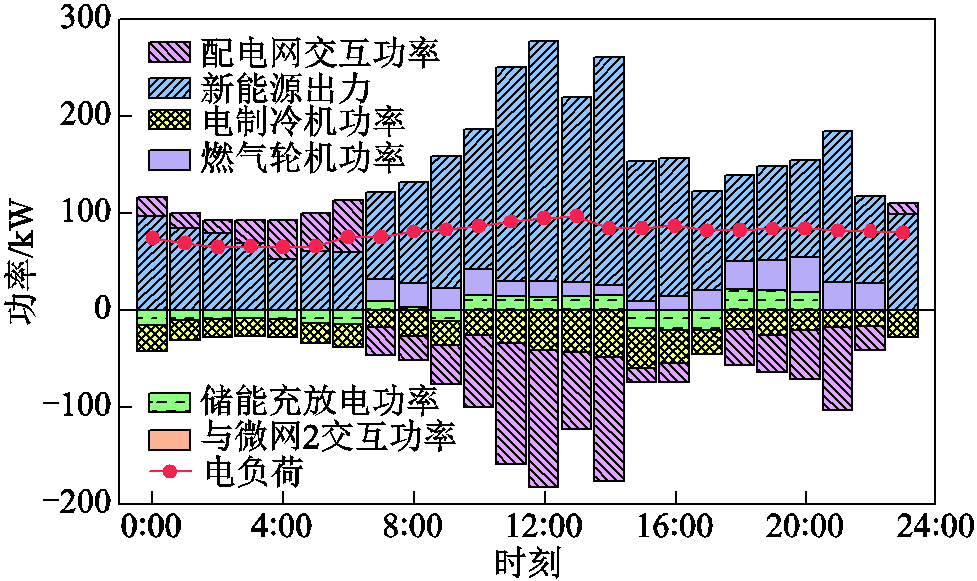
图9 联络线故障情况下微网1电能流动情况
Fig.9 The flow of electric energy in microgrid 1 when the tie line is disconnected
4.4.1 优化效果对比分析
本文利用所提基于分层约束强化学习模型的多微网系统优化方法对优化变量进行了分层处理,在下层采用数学规划法求解部分不具有时间关联性的动作变量,降低了强化学习奖励函数设计及动作空间的复杂性。为验证该方法(Bi-LSAC)相比单层强化学习方法在收敛速度和精度方面的优越性,采用SAC方法解决上述多微网系统优化调度问题,并与本文方法进行对比,两种方法训练过程中的运行成本曲线如图10所示。从图10中可以看出,采用DDPG(deep deterministic policy gradient)和SAC方法收敛速度较慢且波动性相对较大,分别在大约7 500和7 000轮左右时运行成本曲线收敛,而本文方法收敛迅速,大约在1 700轮左右即可收敛;而且DDPG和SAC方法最终收敛到的运行成本也明显高于本文方法。三种方法的结果对比见表3,Bi-LSAC方法相比于DDPG和SAC方法给出的调度成本分别降低了18.12%和12.42%,验证了本文方法在收敛速度及优化能力方面的优越性。
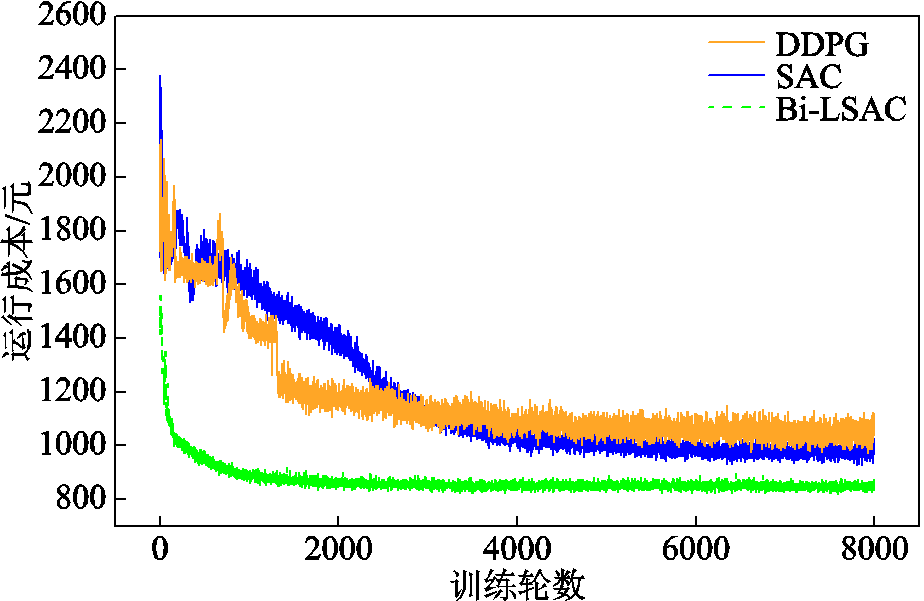
图10 传统强化学习方法和Bi-LSAC的运行成本曲线
Fig. 10 The operational cost curves between traditional reinforcement learning and Bi-LSAC
表3 SAC与Bi-LSAC方法比较
Tab. 3 Comparison of SAC and Bi-LSAC

算法收敛轮数运行成本/元 DDPG7 500992.586 4 SAC7 000944.623 1 Bi-LSAC1 700840.297 5
4.4.2 策略约束越限对比分析
除了采用分层优化框架,本文提出的Bi-LSAC方法通过将传统强化学习算法与拉格朗日乘子法相结合,将约束问题转换为无约束问题,避免了将约束以惩罚项的形式加入奖励,使智能体在满足约束的前提下寻找最优策略。图11给出了本文方法与传统方法在训练过程中的约束越限情况。从图11中可以看出,传统方法将约束以惩罚项的形式加入奖励中,使得目标与越限惩罚的界限模糊,收敛较为困难,尽管越限程度随着训练进行有所减少,但始终无法保证约束完全得到满足;而本文方法除在智能体随机探索初期有一定约束越限行为,后续训练过程中智能体动作越限值始终为0,验证了本文方法可有效处理强化学习约束问题。
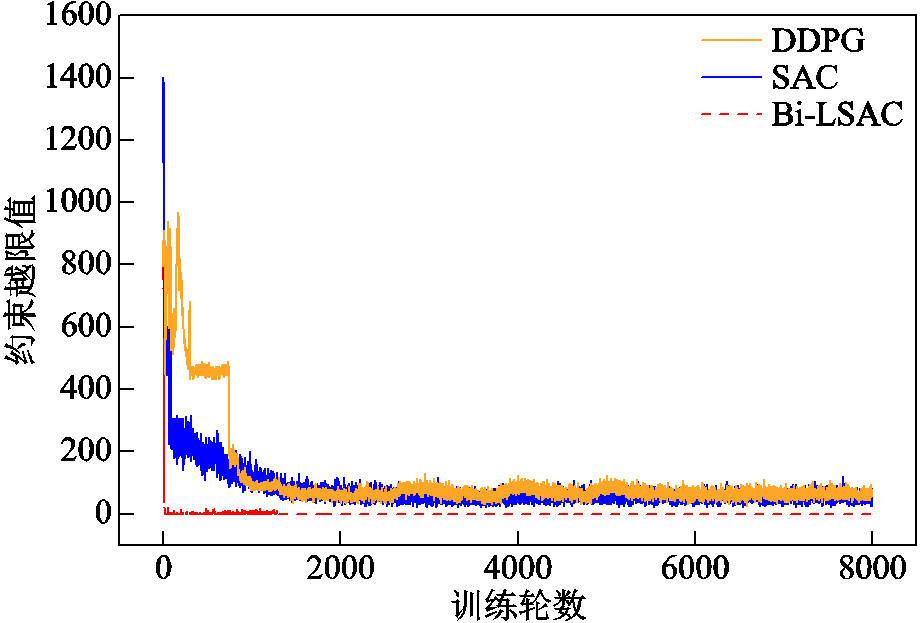
图11 传统强化学习方法和Bi-LSAC的约束越限情况
Fig.11 The constraint violation curves between traditional reinforcement learning and Bi-LSAC
4.5.1 计算结果和效率对比分析
本文方法通过灵活调整训练过程中与环境交互的步长,可应用于不同时间尺度的优化调度问题。为验证本文所提方法的优越性,调度周期选取24 h,相邻时间断面间隔为5 min,采用集中式优化方法解决上述多微网优化问题,将多微网优化问题转换为混合整数线性规划问题,利用CPLEX求解器进行求解并与本文方法进行比较。本文方法基于数据驱动,可根据实际数据在s级内给出调度结果,满足在线优化要求。两种方法的对比见表4。可以看出,本文方法在基于不完全信息的情况下,即可得到与基于全局信息的集中式优化趋于一致的结果,差距仅为0.023%,且决策时间为ms级别,相比于集中式min级的决策时间,可有效满足在线优化的要求。同时,图12给出了随着微网数量增加两种方法在决策时间上的变化情况。从图12中可以看出,随着微网数量增加,本文方法仍可在s级内给出调度结果,而集中式优化随着微网数量增加计算复杂度呈指数增长,计算效率大幅下降。
表4 集中式优化与Bi-LSAC方法比较
Tab.4 Comparison of centralized optimization and Bi-LSAC

算法运行成本/元决策时间/s 集中式优化800.674 9435.175 4 Bi-LSAC800.865 20.192 0
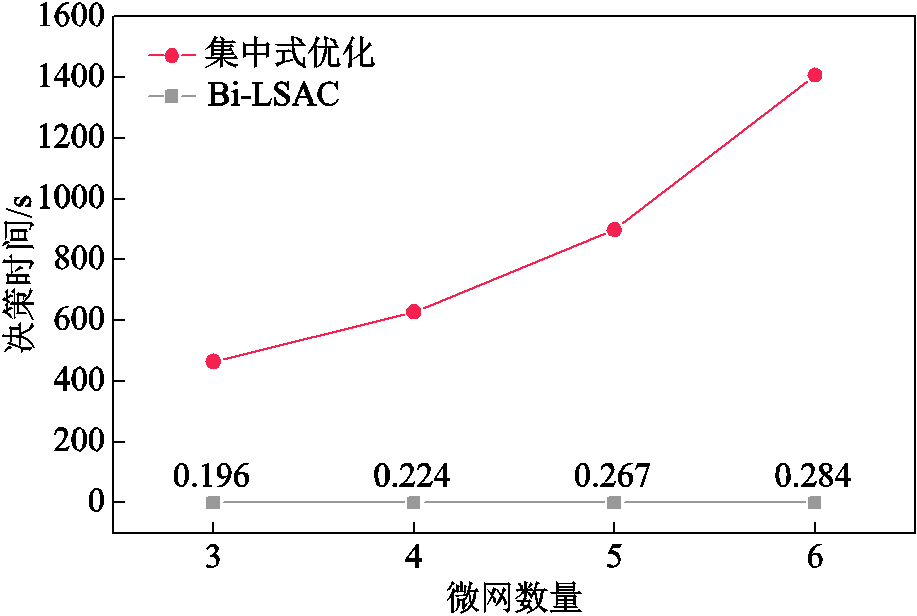
图12 集中式优化和Bi-LSAC方法决策时间对比
Fig.12 Comparison of decision time between centralized optimization and Bi-LSAC
4.5.2 数据传输对比分析
在数据传输和信息交互方面,本文所提方法只需由各微网向上层智能体传递少量关键状态信息(即净负荷及储能状态)进行决策,无需上传微网内的其余状态信息;各微网之间则不进行任何信息交互,其交互功率由上层智能体自适应决策给出,因而可有效降低通信压力,并保护各微网内部的数据隐私。图13给出了集中式优化与本文方法数据传输量的对比。集中式优化需聚合多微网系统全局信息用于决策,而本文方法相比于集中式优化通信量减少约93.46%,基于局部信息即可完成多微网系统的全局优化,大大降低了通信压力,同时有效保护了数据隐私。
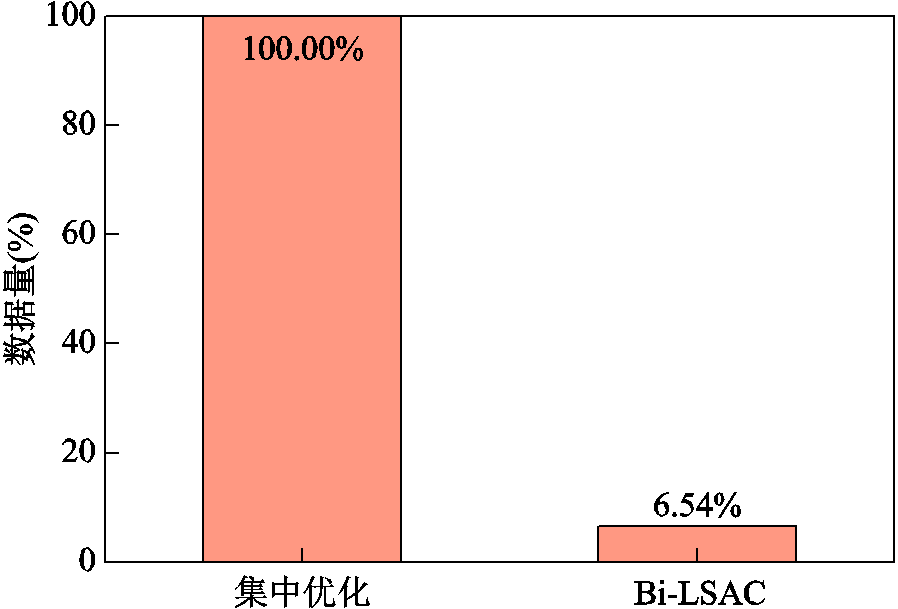
图13 集中式优化和Bi-LSAC方法信息传输量对比
Fig. 13 Comparison of data transmission volume between centralized optimization and Bi-LSAC
强化学习模型可以自适应源荷的随机性波动,在源荷波动时,无需重新对模型进行训练,根据训练好的模型即可实时给出调度结果。为验证本文所提方法应对源荷不确定性的能力,选取不同场景对模型进行随机性测试。固定随机变量中冷热电负荷的波动性水平不变,其标准差为期望值的5%,而风、电和光伏出力的标准差分别为期望值的10%、15%、20%,基于可再生能源和负荷的基准功率,从每一种波动性水平的概率分布中抽样生成150个场景集,随机选取20个场景进行测试。图14给出了微网1风电波动性水平为20%时所生成的150个场景。
图15给出了新能源出力波动性为10%时,测试结果与传统优化求解结果的比较情况,三种波动性水平下的平均测试结果见表5。从测试结果中可以看出,面对不同波动性水平的场景,传统优化受求解速度限制,难以满足在线优化的实时性要求,对于源荷的随机波动,需通过实时市场向配电网购售电满足实时平衡。而本文所提方法能在线给出优化调度策略,在波动性水平分别为10%、15%、20%时,传统优化求解得到的平均成本与本文方法求解结果的差距分别在7.82%、10.33%、13.53%左右,验证了本文方法在应对源荷随机性方面的优越性。
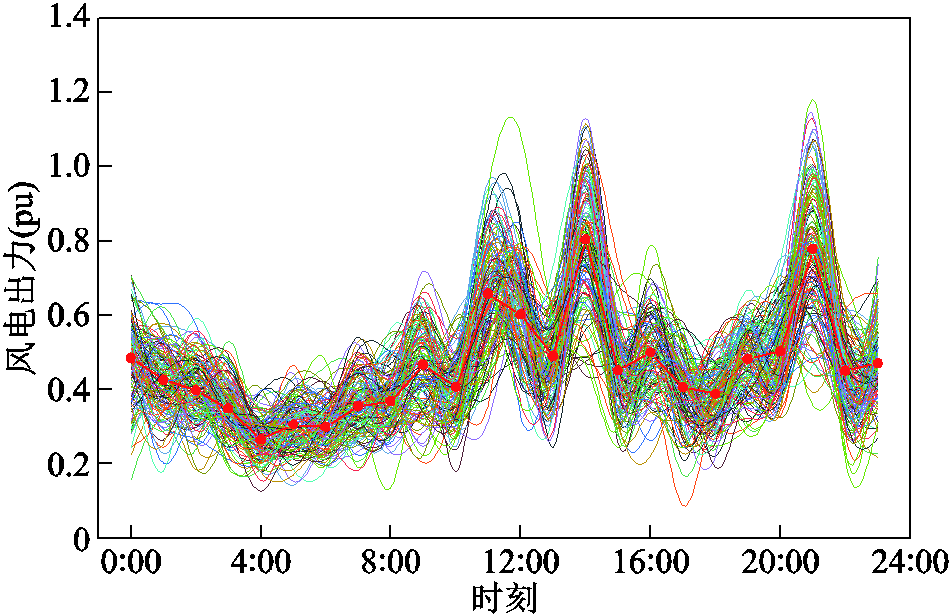
图14 波动性水平为20%时的风电场景
Fig.14 Wind scenarios with volatility levels of 20%
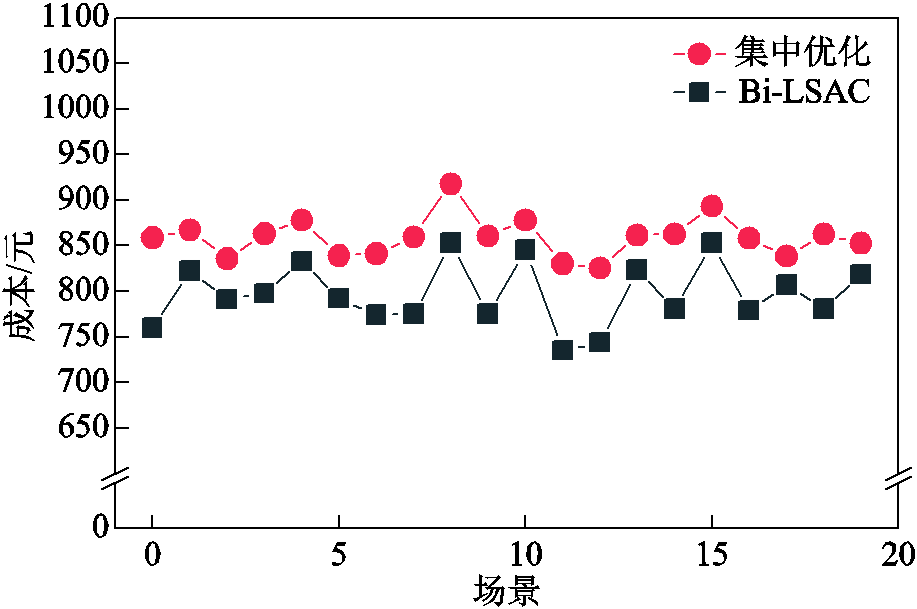
图15 Bi-LSAC和传统优化在不同随机场景的成本比较
Fig.15 Comparison of costs under different scenarios between centralized optimization and Bi-LSAC
表5 不同源荷波动性水平下测试结果比较
Tab.5 Comparison of test results under different volatility levels of power and loads

波动性水平(%)Bi-LSAC/元传统优化/元 10797.151 7859.480 0 15821.542 8906.378 1 20867.157 3984.520 8
本文以多微网系统为研究对象,设计了一种分层优化框架,基于该框架,将数据驱动方法与数学规划法结合,构建了一种分层强化学习求解方法;并将拉格朗日乘子法与传统强化学习方法SAC算法结合设计了LSAC算法,以解决传统强化学习难以处理约束的问题,最终通过算例得到以下结论:
1)通过分层设计实现多微网优化任务的简化求解,各微网之间不进行信息交互,仅需上传净负荷及储能关键状态信息,并基于自身状态信息独立并行求解,然后利用上下层的协同实现多微网系统的整体优化。通过算例验证了本文所提方法在基于局部状态信息的情况下,可即时给出与最优解趋于一致的调度结果。
2)本文所提方法将数据驱动与传统方法相结合,简化了强化学习动作空间及奖励设计的复杂性。在充分发挥强化学习快速求解能力的同时,有效地兼顾了数学规划法的求解精度,可针对多微网优化问题实现高效求解。算例结果表明,相比于传统强化学习方法在收敛速度和精度上均有较大提升。
3)本文构建了基于拉格朗日乘子法的约束强化学习算法,通过将约束问题转换为无约束问题,避免了将约束以惩罚项的形式加入奖励函数中,解决了传统强化学习难以处理约束的问题。算例表明,所提方法可保证智能体在满足约束的前提下寻找最优策略,避免了传统强化学习方法由于人工设置惩罚系数造成的难以满足约束及收敛困难等问题。
4)模型具有良好的鲁棒性,可有效应对源荷随机性,并自适应快速决策各微网的功率交互,不依赖于源荷的精确建模,相较于传统优化方法避免了反复的迭代过程,根据源荷状态即可实时给出调度结果。
附 录
1. 微型燃气轮机
MT是实现冷热电气多种能源形式耦合的核心设备,其耗气量及排出的余热烟气热量均与发电功率成正比,模型为
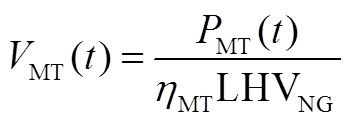 (A1)
(A1)
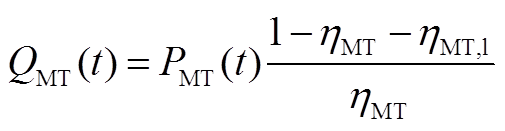 (A2)
(A2)
式中,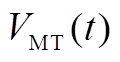 为MT在
为MT在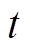 时段内的耗气量;
时段内的耗气量;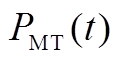 为MT在
为MT在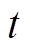 时段内的发电功率;
时段内的发电功率;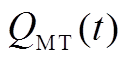 为MT在
为MT在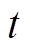 时段内的余热烟气热量;
时段内的余热烟气热量;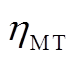 为发电效率;
为发电效率;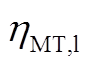 为MT的热损失系数;
为MT的热损失系数; 为天然气热值。
为天然气热值。
2. 溴化锂机组(Lithium Bromide unit, LB)
MT排出的部分高温余热烟气经溴化锂机组收集后可用于制冷和供热。
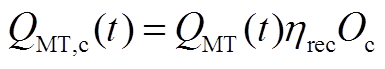 (A3)
(A3)
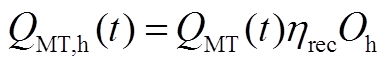 (A4)
(A4)
式中,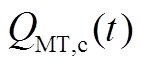 为溴化锂机组在
为溴化锂机组在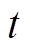 时段内的制冷功率;
时段内的制冷功率;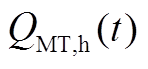 为溴化锂机组在
为溴化锂机组在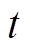 时段内的制热功率;
时段内的制热功率;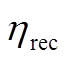 为溴化锂机组的烟气回收率;
为溴化锂机组的烟气回收率; 、
、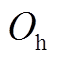 分别为溴化锂机组的制冷系数和制热系数。
分别为溴化锂机组的制冷系数和制热系数。
3. 燃气锅炉
燃气锅炉通过燃烧天然气向系统供热,其模型为
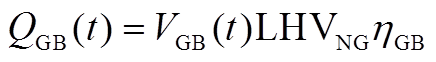 (A5)
(A5)
式中,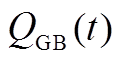 为GB在
为GB在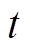 时段内输出的热功率;
时段内输出的热功率;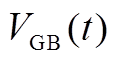 为GB在
为GB在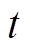 时段内的耗气量;
时段内的耗气量;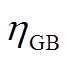 为GB的制热效率。
为GB的制热效率。
4. 电制冷机
电制冷机通过消耗电能进行制冷,其制冷功率与输入电功率有关,即
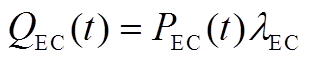 (A6)
(A6)
式中,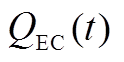 为EC在
为EC在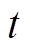 时段内的制冷功率;
时段内的制冷功率;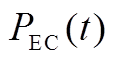 为EC在
为EC在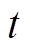 时段内输入的电功率;
时段内输入的电功率;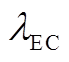 为EC的制冷能效比。
为EC的制冷能效比。
5. 蓄电池模型
蓄电池可通过充放电消纳微网内出力或供给微网内电负荷,其模型为
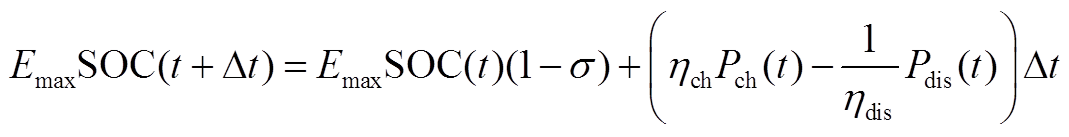 (A7)
(A7)
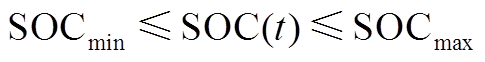 (A8)
(A8)
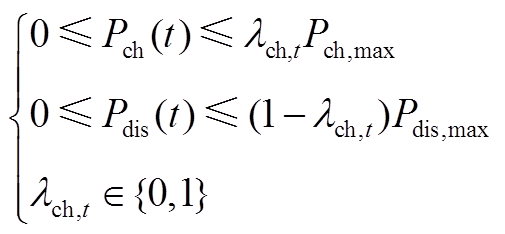 (A9)
(A9)
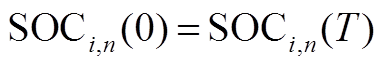 (A10)
(A10)
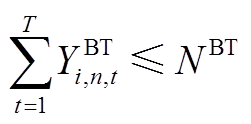 (A11)
(A11)
式中,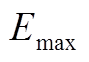 为储能容量;
为储能容量;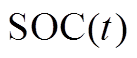 为蓄电池在
为蓄电池在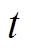 时段的荷电状态;
时段的荷电状态;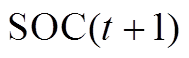 为蓄电池在
为蓄电池在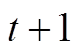 时段的荷电状态;
时段的荷电状态;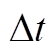 为时间间隔;
为时间间隔;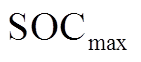 、
、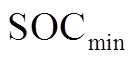 分别为蓄电池荷电状态的上、下限;
分别为蓄电池荷电状态的上、下限;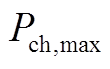 、
、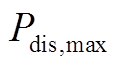 分别为蓄电池最大充、放电功率;
分别为蓄电池最大充、放电功率;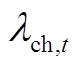 为蓄电池在
为蓄电池在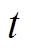 时段的充放电状态系数;
时段的充放电状态系数;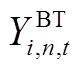 为蓄电池的充放电转换系数;
为蓄电池的充放电转换系数;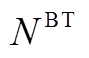 为蓄电池的最大充放电转换次数。
为蓄电池的最大充放电转换次数。
6. 储热槽模型
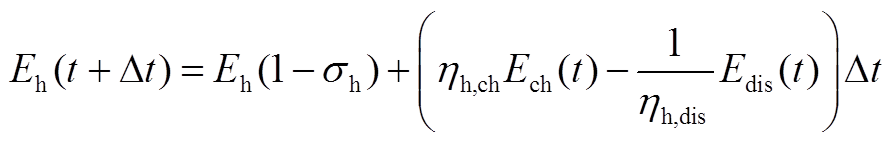 (A12)
(A12)
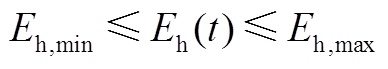 (A13)
(A13)
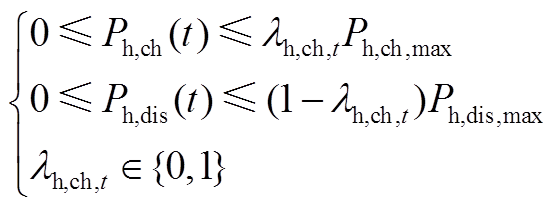 (A14)
(A14)
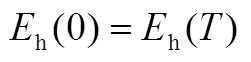 (A15)
(A15)
式中,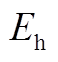 为储热槽蓄热量;
为储热槽蓄热量;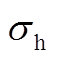 为散热系数;
为散热系数;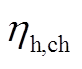 、
、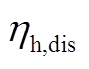 分别为蓄热槽的充、放热效率;
分别为蓄热槽的充、放热效率;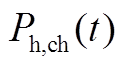 、
、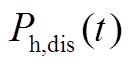 分别为储热槽在
分别为储热槽在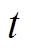 时段的充、放热功率;
时段的充、放热功率;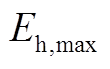 、
、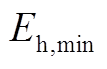 分别为储热槽蓄热的上、下限;
分别为储热槽蓄热的上、下限;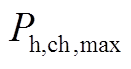 、
、 分别为蓄电池最大充放热功率;
分别为蓄电池最大充放热功率;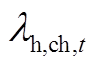 为储热槽在
为储热槽在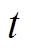 时段的充放热状态系数。
时段的充放热状态系数。
7. 分布式可再生能源
本文研究的微网内分布式电源包括风力发电和光伏发电,风力发电和光伏发电的出力可表述为预测出力叠加预测误差,其中风、光出力的预测误差符合正态分布。
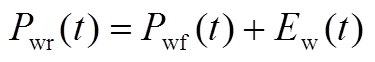 (A16)
(A16)
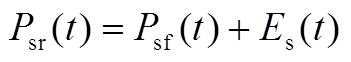 (A17)
(A17)
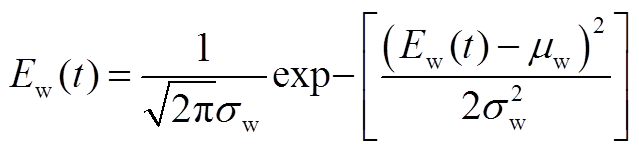 (A18)
(A18)
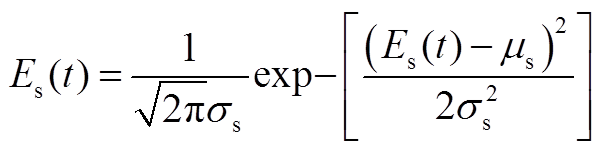 (A19)
(A19)
式中,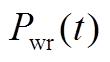 、
、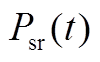 分别为在
分别为在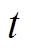 时段内风电、光伏出力的实际值;
时段内风电、光伏出力的实际值;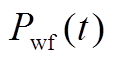 、
、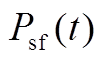 分别为在
分别为在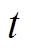 时段内风电、光伏出力的预测值;
时段内风电、光伏出力的预测值;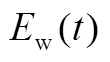 、
、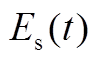 分别为在
分别为在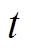 时段内风电、光伏出力的预测误差;
时段内风电、光伏出力的预测误差;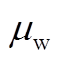 、
、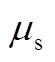 、
、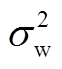 、
、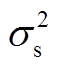 分别为风电、光伏出力的预测均值和方差。
分别为风电、光伏出力的预测均值和方差。
附表1 分时电价
App.Tab.1 Time-of-use electricity price
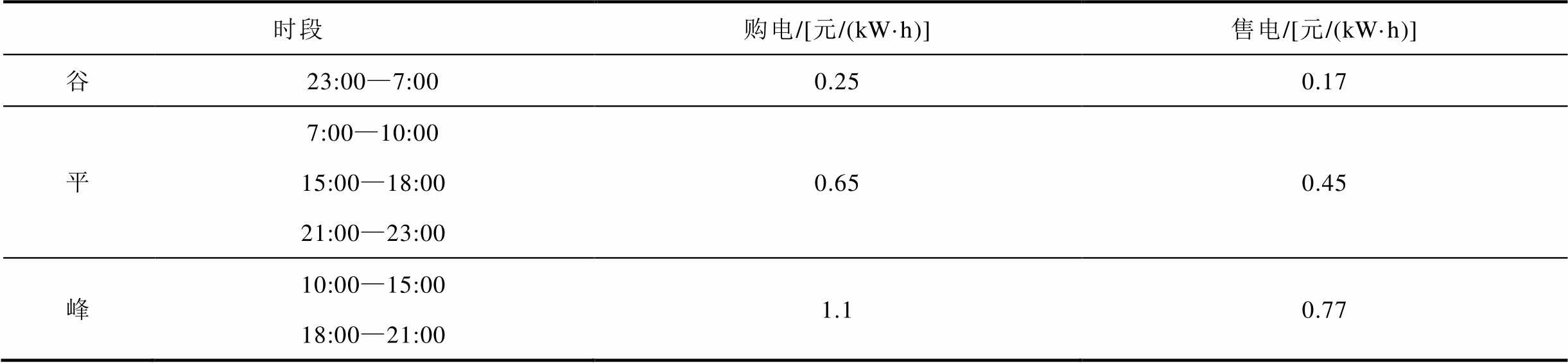
时段购电/[元/(kW·h)]售电/[元/(kW·h)] 谷23:00—7:000.250.17 平7:00—10:0015:00—18:0021:00—23:000.650.45 峰10:00—15:0018:00—21:001.10.77
附表2 微网设备参数
App.Tab.2 Parameters of microgrid equipment

参数数值 微型燃气轮机最大发电功率/kW120 微型燃气轮机发电效率0.35 微型燃气轮机热损失系数0.05 溴化锂机组烟气回收率0.75 溴化锂机组制冷系数1.45
(续)

参数数值 溴化锂机组制热系数1.17 燃气锅炉最大输出功率/kW50 燃气锅炉制热效率0.9 电制冷机最大输入功率/kW100 电制冷机制冷能效比4.24 蓄电池容量/(kW·h)100 蓄电池荷电状态0.1~0.9 蓄电池自放电系数0 蓄电池充放电效率0.9 蓄电池最大充放电功率/kW20 储热槽最大储热量/(kW·h)50 储热槽自散热系数0.005 储热槽充放热效率0.9 储热槽最大充放热功率/kW5 与配电网最大交互功率/kW300 与微网最大交互功率/kW100
附表3 神经网络超参数
App.Tab.3 Neural network hyperparameters

超参数数值 折扣因子学习率软更新系数经验回放单元容量采样样本数0.993×10-40.00520 00064
参考文献
[1] 蔡瑶, 卢志刚, 孙可, 等. 计及源荷不确定性的独立型交直流混合微网多能源协调优化调度[J]. 电工技术学报, 2021, 36(19): 4107-4120. Cai Yao, Lu Zhigang, Sun Ke, et al. Multi-energy coordinated optimal scheduling of isolated AC/DC hybrid microgrids considering generation and load uncertainties[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4107-4120.
[2] 靳小龙, 穆云飞, 贾宏杰, 等. 融合需求侧虚拟储能系统的冷热电联供楼宇微网优化调度方法[J]. 中国电机工程学报, 2017, 37(2): 581-591. Jin Xiaolong, Mu Yunfei, Jia Hongjie, et al. Optimal scheduling method for a combined cooling, heating and power building microgrid considering virtual storage system at demand side[J]. Proceedings of the CSEE, 2017, 37(2): 581-591.
[3] 张释中, 裴玮, 杨艳红, 等. 基于柔性直流互联的多微网集成聚合运行优化及分析[J]. 电工技术学报, 2019, 34(5): 1025-1037. Zhang Shizhong, Pei Wei, Yang Yanhong, et al. Optimization and analysis of multi-microgrids integration and aggregation operation based on flexible DC interconnection[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1025-1037.
[4] 刘志坚, 刘瑞光, 梁宁, 等. 含电转气的微型能源网日前经济优化调度策略[J]. 电工技术学报, 2020, 35(增刊2): 535-543. Liu Zhijian, Liu Ruiguang, Liang Ning, et al. Day-ahead optimal economic dispatching strategy for micro energy-grid with P2G[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 535-543.
[5] 王守相, 吴志佳, 庄剑. 考虑微网间功率交互和微源出力协调的冷热电联供型区域多微网优化调度模型[J]. 中国电机工程学报, 2017, 37(24): 7185-7194, 7432. Wang Shouxiang, Wu Zhijia, Zhuang Jian. Optimal dispatching model of CCHP type regional multi-microgrids considering interactive power exchange among microgrids and output coordination among micro-sources[J]. Proceedings of the CSEE, 2017, 37(24): 7185-7194, 7432.
[6] 肖浩, 裴玮, 孔力, 等. 考虑光伏余电上网的微网出力决策分析及经济效益评估[J]. 电力系统自动化, 2014, 38(10): 10-16. Xiao Hao, Pei Wei, Kong Li, et al. Decision analysis and economic benefit evaluation of microgrid power output considering surplus photovoltaic power selling to grid[J]. Automation of Electric Power Systems, 2014, 38(10): 10-16.
[7] Dehghanpour K, Nehrir H. Real-time multiobjective microgrid power management using distributed optimization in an agent-based bargaining framework[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 6318-6327.
[8] 赵波, 汪湘晋, 张雪松, 等. 考虑需求侧响应及不确定性的微电网双层优化配置方法[J]. 电工技术学报, 2018, 33(14): 3284-3295. Zhao Bo, Wang Xiangjin, Zhang Xuesong, et al. Two-layer method of microgrid optimal sizing considering demand-side response and uncertainties[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3284-3295.
[9] 许志荣, 杨苹, 张育嘉, 等. 考虑不平衡度约束的单三相混联多微网日前经济优化[J]. 电网技术, 2017, 41(1): 40-47. Xu Zhirong, Yang Ping, Zhang Yujia, et al. Day-ahead economic optimized dispatch of single and three phase hybrid multi-microgrid considering unbalance constraint[J]. Power System Technology, 2017, 41(1): 40-47.
[10] 李长云,徐敏灵,蔡淑媛.计及电动汽车违约不确定性的微电网两段式优化调度策略[J].电工技术学报, 2023, 38(7): 1838-1851. Li Changyun,Xu Minling,Cai Shuyuan.Two-stage optimal scheduling strategy for micro-grid considering EV default uncertainty[J].Transactions of China Electrotechnical Society, 2023, 38(7): 1838-1851.
[11] 滕云, 孙鹏, 罗桓桓, 等. 计及电热混合储能的多源微网自治优化运行模型[J]. 中国电机工程学报, 2019, 39(18): 5316-5324, 5578. Teng Yun, Sun Peng, Luo Huanhuan, et al. Autonomous optimization operation model for multi-source microgrid considering electrothermal hybrid energy storage[J]. Proceedings of the CSEE, 2019, 39(18): 5316-5324, 5578.
[12] 武梦景, 万灿, 宋永华, 等. 含多能微网群的区域电热综合能源系统分层自治优化调度[J]. 电力系统自动化, 2021, 45(12): 20-29. Wu Mengjing, Wan Can, Song Yonghua, et al. Hierarchical autonomous optimal dispatching of district integrated heating and power system with multi-energy microgrids[J]. Automation of Electric Power Systems, 2021, 45(12): 20-29.
[13] 马腾飞, 裴玮, 肖浩, 等. 基于纳什谈判理论的风-光-氢多主体能源系统合作运行方法[J]. 中国电机工程学报, 2021, 41(1): 25-39, 395. Ma Tengfei, Pei Wei, Xiao Hao, et al. Cooperative operation method for wind-solar-hydrogen multi-agent energy system based on Nash bargaining theory[J]. Proceedings of the CSEE, 2021, 41(1): 25-39, 395.
[14] 欧阳聪, 刘明波, 林舜江, 等. 采用同步型交替方向乘子法的微电网分散式动态经济调度算法[J]. 电工技术学报, 2017, 32(5): 134-142. Ouyang Cong, Liu Mingbo, Lin Shunjiang, et al. Decentralized dynamic economic dispatch algorithm of microgrids using synchronous alternating direction method of multipliers[J]. Transactions of China Electrotechnical Society, 2017, 32(5): 134-142.
[15] 顾雪平, 刘彤, 李少岩, 等. 基于改进双延迟深度确定性策略梯度算法的电网有功安全校正控制[J]. 电工技术学报, 2023, 38(8): 2162-2177. Gu Xueping, Liu Tong, Li Shaoyan, et al. Active power correction control of power grid based on improved twin delayed deep deterministic policy gradient algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2162-2177.
[16] Mocanu E, Mocanu D C, Nguyen P H, et al. On-line building energy optimization using deep reinforcement learning[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 3698-3708.
[17] Kofinas P, Dounis A I, Vouros G A. Fuzzy Q-learning for multi-agent decentralized energy management in microgrids[J]. Applied Energy, 2018, 219: 53-67.
[18] Xu Xu, Jia Youwei, Xu Yan, et al. A multi-agent reinforcement learning-based data-driven method for home energy management[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 3201-3211.
[19] 黎海涛, 申保晨, 杨艳红, 等. 基于改进竞争深度Q网络算法的微电网能量管理与优化策略[J]. 电力系统自动化, 2022, 46(7): 42-49. Li Haitao, Shen Baochen, Yang Yanhong, et al. Energy management and optimization strategy for microgrid based on improved dueling deep Q network algorithm[J]. Automation of Electric Power Systems, 2022, 46(7): 42-49.
[20] 乔骥, 王新迎, 张擎, 等. 基于柔性行动器-评判器深度强化学习的电-气综合能源系统优化调度[J]. 中国电机工程学报, 2021, 41(3): 819-833. Qiao Ji, Wang Xinying, Zhang Qing, et al. Optimal dispatch of integrated electricity-gas system with soft actor-critic deep reinforcement learning[J]. Proceedings of the CSEE, 2021, 41(3): 819-833.
[21] 董雷, 刘雨, 乔骥, 等. 基于多智能体深度强化学习的电热联合系统优化运行[J]. 电网技术, 2021, 45(12): 4729-4738. Dong Lei, Liu Yu, Qiao Ji, et al. Optimal dispatch of combined heat and power system based on multi-agent deep reinforcement learning[J]. Power System Technology, 2021, 45(12): 4729-4738.
[22] 张津源, 蒲天骄, 李烨, 等. 基于多智能体深度强化学习的分布式电源优化调度策略[J]. 电网技术, 2022, 46(9): 3496-3504. Zhang Jinyuan, Pu Tianjiao, Li Ye, et al. Multi-agent deep reinforcement learning based optimal dispatch of distributed generators[J]. Power System Technology, 2022, 46(9): 3496-3504.
[23] 刘俊峰, 王晓生, 卢俊菠, 等. 基于多主体博弈和强化学习的多微网系统协同优化研究[J]. 电网技术, 2022, 46(7): 2722-2732. Liu Junfeng, Wang Xiaosheng, Lu Junbo, et al. Collaborative optimization of multi-microgrid system based on multi-agent game and reinforcement learning[J]. Power System Technology, 2022, 46(7): 2722-2732.
[24] 聂欢欢, 张家琦, 陈颖, 等. 基于双层强化学习方法的多能园区实时经济调度[J]. 电网技术, 2021, 45(4): 1330-1336. Nie Huanhuan, Zhang Jiaqi, Chen Ying, et al. Real-time economic dispatch of community integrated energy system based on a double-layer reinforcement learning method[J]. Power System Technology, 2021, 45(4): 1330-1336.
[25] Sutton R S, Barto A G. Reinforcement learning: an introduction[M]. Cambridge, Mass.: MIT Press, 1998
[26] 沈儒茹. 多微网系统的优化调度策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2020.
[27] Altman E. Constrained Markov Decision Processes[M]. Boca Raton: CRC Press, 2021.
[28] Bertsekas D P. Constrained Optimization and lagrange Multiplier Methods[M]. New York: Academic Press, 1982
[29] Haarnoja T, Zhou A, Abbeel P, et al. Soft actor-critic: off-policy maximum entropy deep reinforcement learning with a stochastic actor[EB/OL]. 2018: arXiv: 1801.01290. https://arxiv.org/abs/1801.01290.
[30] Lin Longxin. Reinforcement learning for robots using neural networks[D]. Pittsburgh: Carnegie Mellon University, 1992.
[31] Christodoulou P. Soft actor-critic for discrete action settings[EB/OL]. 2019: arXiv: 1910.07207. https:// arxiv.org/abs/1910.07207.
[32] 叶宇剑, 王卉宇, 汤奕, 等. 基于深度强化学习的居民实时自治最优能量管理策略[J]. 电力系统自动化, 2022, 46(1): 110-119. Ye Yujian, Wang Huiyu, Tang Yi, et al. Real-time autonomous optimal energy management strategy for residents based on deep reinforcement learning[J]. Automation of Electric Power Systems, 2022, 46(1): 110-119.
Abstract The optimization of the integrated energy multi-microgrid system is a complex task, with numerous variables and challenges including data privacy protection and uncertainties of power generation and load, posing significant challenges for the efficient implementation of traditional mathematical optimization methods. Recently, many scholars have turned their attention to deep reinforcement learning (DRL) methods, which rely on data-driven principles and exhibit strong adaptability to uncertainties of power generation and load. Nevertheless, the difficulty of convergence persists with increasing system scale, and traditional DRL methods that handle constraints by adding penalty terms to the reward function may obscure the boundary between objectives and constraints, making it difficult to ensure that constraints are fully satisfied and resulting in excessively conservative learning strategies or suboptimal solutions. To address these issues, this paper proposed a hierarchical constraint reinforcement learning optimization method.
Firstly, this paper proposed a hierarchical DRL optimization framework for multi-microgrid systems. The proposed framework divides the optimization problem into two layers: an upper layer and a lower layer. The upper layer does not require obtaining all the operating status information of each microgrid. Instead, it utilizes net load prediction information and energy storage state information to provide energy storage optimization strategies and power interaction strategies. On the other hand, the lower layer enables each microgrid to autonomously optimize the output of its internal devices based on its own status information through mathematical programming, with the upper layer strategy as a constraint. The proposed framework leverages cooperation between the upper and lower layers to achieve overall optimization of the multi-microgrid system. This framework fully utilizes the advantages of DRL based on data-driven principles and effectively considers the solution accuracy of mathematical programming. Based on this hierarchical framework, a constraint DRL method is proposed that combines DRL methods with Lagrange multiplier methods. This method transforms the constraint optimization problem into an unconstrained optimization problem, enabling the agent to find the optimal strategy while strictly satisfying the constraints. Compared to traditional centralized optimization methods, the proposed method dynamically responds to the fluctuations of power generation and load to meet online optimization requirements and protects microgrid data privacy by not requiring the aggregation of all microgrid status information. Compared to general DRL methods, our approach effectively solves the problem of constraint violation and significantly improves both the convergence speed and accuracy.
The following conclusions can be drawn from the case studies: (1) A hierarchical design approach is proposed to simplify the optimization of multi-microgrid systems. The approach does not require information exchange between microgrids and only necessitates uploading net load and energy storage state information. Microgrids can independently and parallelly solve the optimization problem based on their own status information. This approach can provide scheduling results in real-time consistent with the optimal solution when local status information is available. (2) The proposed approach combines data-driven principles with traditional methods, simplifying the complexity of action space and reward design. It effectively balances the rapid solving ability of DRL and the solution accuracy of mathematical programming. Compared to traditional DRL methods, the proposed approach significantly improves both convergence speed and accuracy. (3) The approach combines DRL methods with Lagrange multiplier methods to transform the constrained optimization problem into an unconstrained one. This ensures that the agent can find the optimal strategy while strictly satisfying the constraints. The approach avoids convergence difficulties and constraint violation issues caused by manually setting the penalty coefficient in traditional DRL methods. (4) The model exhibits robustness and can effectively adapt to the fluctuations of power generation and load, making rapid decisions on power interactions of each microgrid.
keywords:Multi-microgrid, hierarchical constraint reinforcement learning, uncertainty, data privacy protection
DOI:10.19595/j.cnki.1000-6753.tces.230015
中图分类号:TM73
国家重点研发计划(2020YFB0905900)和国家自然科学基金(52277098)资助项目。
收稿日期 2023-01-06
改稿日期 2023-03-22
董 雷 女,1967年生,副教授,研究方向为电力系统分析、运行与控制。E-mail:hbdldl@126.com
杨子民 男,1998年生,硕士研究生,研究方向为电力系统分析、运行和控制。E-mail:yzm@ncepu.edu.cn(通信作者)
(编辑 赫 蕾)