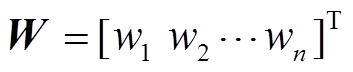 用于描述母线类型,其中n为节点数,矩阵中
用于描述母线类型,其中n为节点数,矩阵中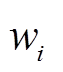 为0-1决策变量,表示节点i的类型,具体为
为0-1决策变量,表示节点i的类型,具体为摘要 随着配电系统中直流设备的大量接入,交直流混合配电系统得到越来越广泛的应用。为适应交直流混合配电系统中不同交直流(AC/DC)类型的负荷或电源的接入,提出一种新的交直流混合配电系统网架结构规划方法,该方法考虑了网架交直流配置的所有可能性。首先以二进制网络矩阵描述配电系统的网架结构;其次建立网架单层规划模型,将规划变量和运行变量同时进行优化以提升全局寻优能力;最后将单层规划模型进行线性化处理,转换为混合整数线性规划问题以提升求解效率。仿真结果表明,所提方法能够为配电系统中不同交直流类型的负荷和电源的接入提供最佳的网架配置方案,相比于传统的纯交流规划方案具有更好的经济性和供电能力,在算法上与经典遗传算法求解的双层规划方法相比,具有更好的全局寻优能力和计算效率。
关键词:交直流混合配电系统 网架规划 单层规划 线性化优化
随着传统化石能源呈现衰竭趋势,全球范围内对新能源及其发电技术的需求日益增加。在配电系统中,越来越多的新能源设备并入电网,如风电、光伏、电动汽车和储能等,因此未来的配电系统必须包括直流负载和基于直流的分布式电源(Distributed Generation, DG)[1]。而相比于将DG并入现有的交流电网,将其并入直流配电网能够有效减少换流站的投资[2],同时能够减小换流过程的损耗,具有很高的经济效益。另一方面,交流配电网中缺乏灵活控制功率的设备,大量DG接入带来的电压越限问题大多依靠无功补偿装置进行优化,同时由于缺乏灵活控制网络拓扑的手段,在系统某个区域故障时容易影响到整个系统。而在交直流混合配电网中,电压源型换流器(Voltage Source Converter, VSC)具有广泛的应用[3],VSC 对有功功率的双向传输和无功支撑提高了整个系统的可控性[4],因此,未来的配电系统应该成为交直流混合系统,以适应高比例源荷的接入[5-7]。
交直流混合配电系统除了原有的交流负荷和交流电源,还包括直流负荷和直流电源,因此在规划时,必须考虑配电网网架结构对这些不同类型设备的适应性。已有大量文献对交流配电系统的网架规划进行了研究,文献[8]在配电网的扩展规划中考虑了网架动态重构的影响;文献[9-10]在主动配电网网架规划模型中考虑了DG出力控制、有载调压变压器分接头调节、无功补偿调节和储能等主动管理措施,但其生成的网架为单一的辐射状网络,难以反映环网状结构配电网的实际情况。
交直流网架规划与传统纯交流网架规划的区别在于,交直流混合配电网在规划网架结构时,一方面需要考虑交直流设备接入配电网所用整流逆变器的投资成本,另一方面需要考虑用于交直流系统互联的VSC的投资,这是交直流网架规划区别于传统网架规划的鲜明特征和技术难点。因此,应从经济角度出发,结合交直流配电网的运行特点,对母线、线路以及换流器等重要组成进行规划。已有文献对于交直流混合配电系统的网架规划问题展开研究,文献[11-12]对DG配置、线路直流改造或线路新建进行协同规划。文献[13]考虑了分布式能源综合利用,对分布式电源布点定容和网架扩容方案进行优化。文献[14]提出了一种考虑可靠性的交直流混合配电网网架与分布式电源容量协同优化的双层优化方法,对交直流网架当中的线路扩建方案进行优化。文献[15]分析对比了在现有的交流网络中接入多端VSC的特定场景。但是以上研究皆是基于特定数量的线路候选集对原有的交流系统进行改造或扩增以满足直流设备的接入,限制了找到最优网架方案的机会。文献[16]基于含有电力电子变压器(Power Electronics Transformer, PET)的交直流混合配用电系统提出主次网架分层的规划方法,但是该方法对源荷储设备进行分区聚合,在交直流设备较为分散的配电网中也可能忽视了最优的交直流互联方案,增加换流器的投资。此外,上述方法皆没有充分考虑交直流网架中所有的AC/DC配置可能性,忽略了潜在的经济效益提升。
另外,配电系统网架规划模型包含较多的0-1变量,是一个混合整数非线性规划(Mixed Integer Nonlinear Programming, MINLP)问题,目前求解方法主要分为启发式算法、二阶锥规划法和线性化方法。启发式算法如遗传算法[13,17]、粒子群算法[18-20]等因其对此类问题具有良好的适用性而得到了广泛的应用,如文献[1]考虑了所有网架配置的可能性,利用遗传算法和广义简约梯度法相结合对网架配置方案进行寻优,但是启发式算法存在计算大规模问题时效率低下且容易陷入局部最优的缺陷。二阶锥规划法[21-23]通过将非凸非线性的潮流约束进行二阶锥松弛,从而将模型转换为凸规划问题,使用求解器快速求解,因其求解速度快、具有全局寻优的能力而快速兴起,但是大多应用在辐射型配电网,在环网中使用二阶锥松弛条件苛刻,不一定能满足松弛的精确性[24-25]。
线性化方法与二阶锥规划法相比同样具有突出的计算效率和全局最优保证,且无需对约束进行松弛,不存在松弛条件的限制。线性化方法在电力系统运行规划中已有一定应用,如文献[26]采用直流潮流方法描述交流系统的线路潮流,但是直流潮流方法忽略了电压幅值大小,不仅容易忽略电压越限的风险,也无法反映交直流混合配电系统中VSC的调压特性。文献[27-28]的线性化方法基于运行点进行迭代,精确性较高,缺点是需要获得系统运行过程中的断面数据,进行多次迭代,计算过程复杂。目前尚未有将MINLP的交直流混合配电网网架规划模型整体进行线性化的研究。
针对以上研究现状,本文以含DG、储能和VSC的交直流混合配电系统网架规划问题为研究对象,在DG和储能的位置及容量已知的前提下,以系统的投资运行成本最小为目标,考虑了系统AC/DC配置方案的所有可能性,对系统中每个节点的交直流类型和每个节点之间的线路连接进行规划,为配电网中不同交直流类型源荷的接入提供最优的网架配置方案。在规划模型构建方面,本文提出了一种网架单层规划模型。该模型区别于传统的上下层嵌套规划方法,将规划变量和运行变量同时进行优化,并利用一系列线性化方法将规划问题转换成混合整数线性规划(Mixed Integer Linear Programming, MILP)问题,以提升模型的全局寻优能力。最后使用GUROBI求解器进行求解。在待规划的13节点系统中验证了所提模型的有效性。
在待规划的配电系统中,不同交直流源荷按照实际情况分散接入各个节点,因此需要规划一个合适的网架与之相适应。该网架规划决策方案包括:①每条母线的类型(交流/直流);②母线之间的连接状态(连接/不连接);③线路的选型。
1)节点类型矩阵
定义矩阵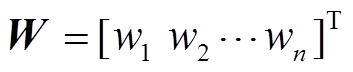 用于描述母线类型,其中n为节点数,矩阵中
用于描述母线类型,其中n为节点数,矩阵中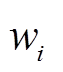 为0-1决策变量,表示节点i的类型,具体为
为0-1决策变量,表示节点i的类型,具体为
 (1)
(1)
2)节点关联矩阵
定义节点关联矩阵
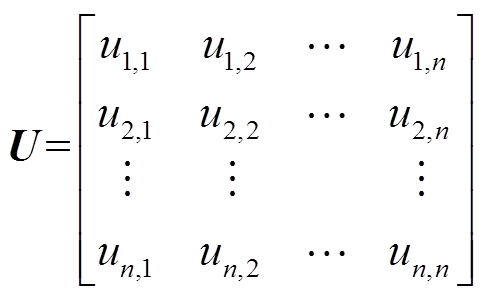 (2)
(2)
矩阵中的元素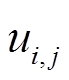 为0-1决策变量,表示节点i、j之间的连接状态,具体为
为0-1决策变量,表示节点i、j之间的连接状态,具体为
 (3)
(3)
由于矩阵U描述的是两个节点之间的连接状态,因此该矩阵是一个实对称矩阵。
3)线路选型变量
定义线路选型0-1变量xi,j,k用于描述线路的选型。在规划模型中,节点之间可提供不同型号的线路进行选择,当线路ij选择第k种型号的导线时,xi,j,k=1,否则为0。
在交直流混合配电系统中,电源、负荷和储能接入不同交直流类型母线的具体情况如图1所示。在图1中,风电通过一台整流器和一台逆变器接入交流母线,接入直流母线则仅需一台整流器;光伏通过一台光伏逆变器接入交流母线,接入直流母线则节省了逆变器的成本;储能通过储能变流器(Power Conversion System, PCS)接入交流配电网和直流配电网;负荷的接入情况如图1所示。同时本文设定交流母线之间的连接线为交流线路,直流母线之间的连接线为直流线路,交直流母线之间用VSC进行互联,如图2所示。
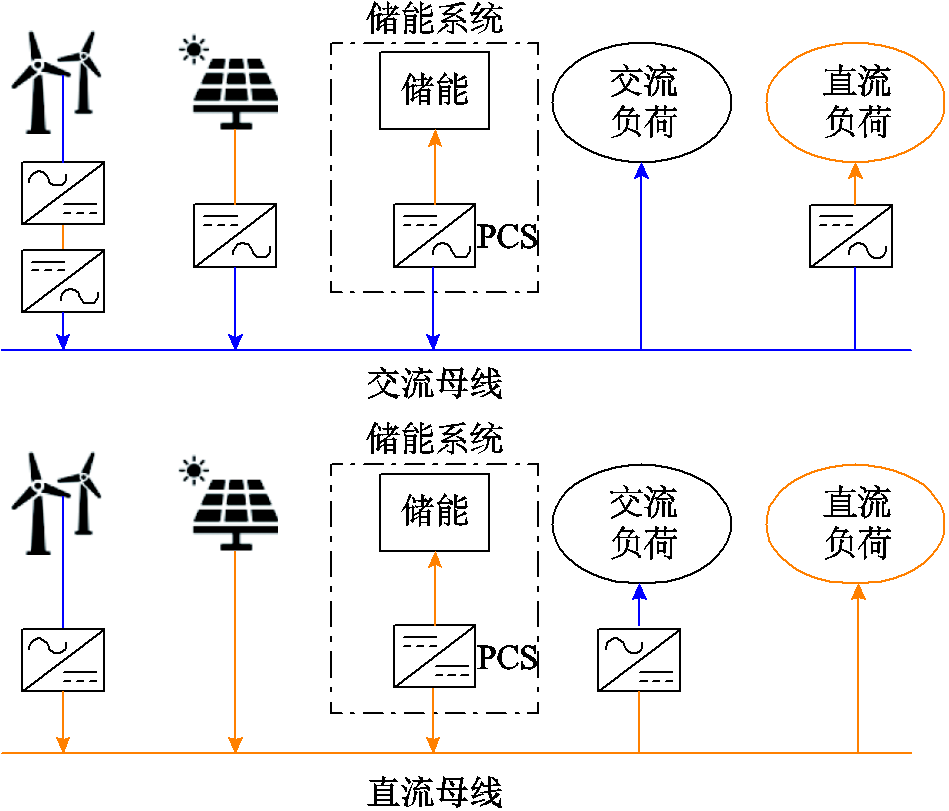
图1 交直流混合配电系统母线结构
Fig.1 Bus structure of AC/DC hybrid distribution system
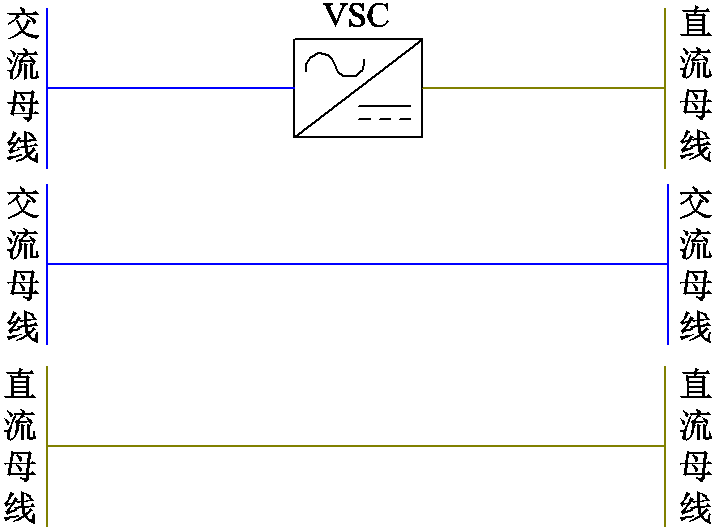
图2 母线之间的连接
Fig.2 Connection between buses
一方面,由图1可以看出,不同类型的母线在接入相同数目的交直流源荷时所需整流逆变器数目不同,假设某条母线上有nwind个风电、npv个光伏、nac个交流负荷和ndc个直流负荷,该母线若为交流则需要配置(2nwind+npv+ndc)个整流逆变器,若为直流则需要配置(nwind+nac)个整流逆变器。因此在以经济性为目标的规划中,考虑到整流逆变器的投资成本,母线类型的选择会受到该母线上所接入设备的影响。
另一方面,由图2可以看出,若相互连接的两条母线交直流类型不同,则需要配置一台VSC,意味着母线的类型也会受到其他母线的影响,并非单纯地取决于该母线上设备的类型。因此需要根据整个系统的源荷分布和系统运行情况来决定母线的类型及母线之间的连接状态,如果网架结构设置不合理会大大增加系统的投资。如何在负荷和电源配置已知的情况下优化网架的结构以最小化系统投资和运行成本,是本文要解决的关键问题。
本文使用VSC对交直流混合配电网的交流部分和直流部分进行互联,VSC的结构如图3所示。
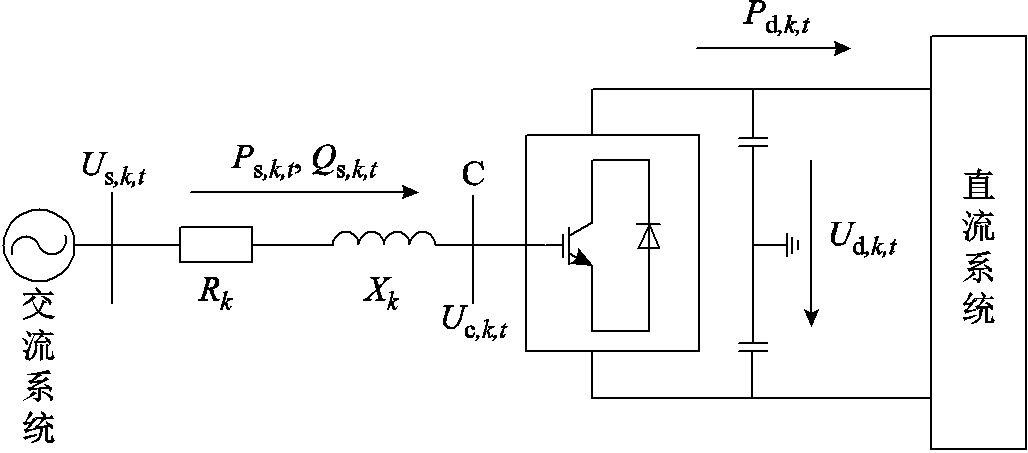
图3 VSC结构
Fig.3 Structure of VSC
图3中,C点左侧为换流变压器,C点右侧为换流桥;k表示接入交直流系统的第k台VSC;Rk为换流变压器损耗和VSC内部损耗的等效电阻;Xk为换流变压器电抗;Us,k,t为换流变压器与交流系统在公共连接点处的电压;Uc,k,t为VSC的输出电压;Ud,k,t为VSC与直流系统在公共连接处的直流电压;Ps,k,t和Qs,k,t分别为交流系统流入VSC的有功功率和无功功率;Pd,k,t为VSC流入直流系统的有功功率;下标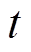 表示该变量在
表示该变量在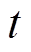 时刻的值。VSC稳态潮流方程为
时刻的值。VSC稳态潮流方程为
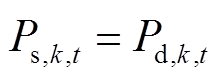 (4)
(4)
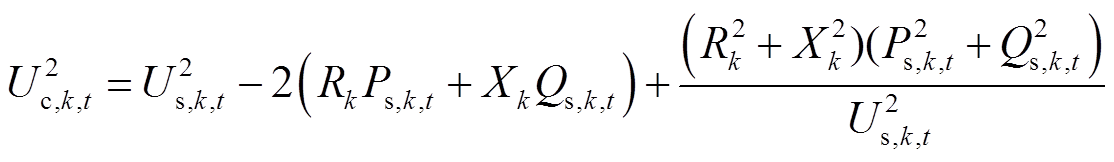 (5)
(5)
考虑到交直流混合系统中节点电压上、下限分别为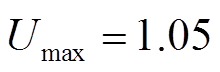 、
、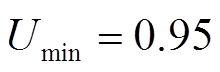 ,十分接近于1,因此有
,十分接近于1,因此有
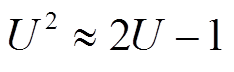 (6)
(6)
在式(5)中,由于网损占潮流中的很小一部分,因此省去网损的二次项[29],同时将式(6)应用到式(5)中,则式(5)简化为
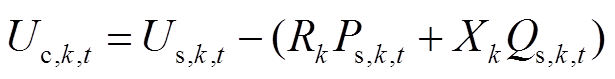 (7)
(7)
VSC输出侧电压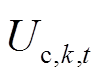 与直流侧电压
与直流侧电压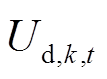 满足
满足
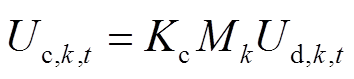 (8)
(8)
式中,Kc为常数,其值取决于VSC类型和调制方式,三相VSC在正弦脉宽调制(Sinusoidal Pulse Width Modulation, SPWM)方式下有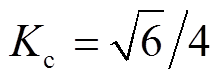 [1,30],在标幺值下若交、直流系统电压等级之比为
[1,30],在标幺值下若交、直流系统电压等级之比为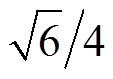 ,则
,则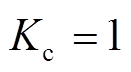 ;Mk为第k台VSC的调制度,由于
;Mk为第k台VSC的调制度,由于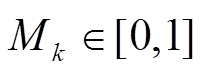 ,于是式(8)可以等效为
,于是式(8)可以等效为
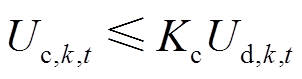 (9)
(9)
传统网架规划建模和求解方式为上、下层分开建模求解,将上层的规划方案传递给下层进行模拟运行,而后将下层优化运行方案返回上层。这种方法不仅难以保证解的收敛性,且无法保证得到全局最优解[31],因此本文将上、下层进行关联统一,构建交直流混合配电系统网架单层规划模型。单层规划模型以线路的建设成本、VSC的安装成本、配电网购电成本、弃风弃光成本和储能运行维护成本构成的系统投资运行成本最小为目标,考虑节点连接线路条数约束、线路选型约束、交直流系统潮流约束、VSC无功补偿能力约束、系统安全运行约束、储能运行约束、DG出力约束和网络连通性约束,将节点类型变量wi、节点之间的连接状态变量ui,j、线路选型变量xi,j,k与运行变量一同进行优化。
单层规划模型的目标函数以投资成本CI和运行维护成本CO构成的综合成本最小为目标,即
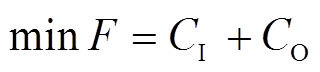 (10)
(10)
1)投资成本CI
投资成本CI由线路建设成本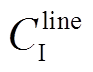 和换流器安装成本
和换流器安装成本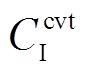 构成,有
构成,有
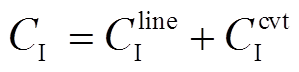 (11)
(11)
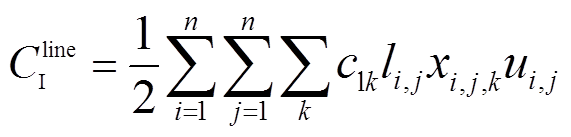 (12)
(12)
式中,clk为第k种型号线路的单位长度建设成本;li,j为线路ij的长度。由于ui,j所在的节点关联矩阵U是实对称矩阵,因此该表达式前应乘以1/2。
在规划模型当中,换流器的应用场合有四种,分别是应用在负荷接入、风电接入和光伏接入的整流逆变器以及应用在交直流母线互联的VSC,因此换流器安装成本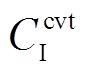 为
为
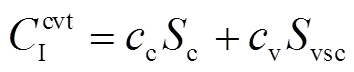 (13)
(13)
式中,cc和cv分别为整流逆变器和VSC的单位额定容量投资成本;Sc和Svsc分别为系统中整流逆变器和VSC的总安装容量,其表达式分别为
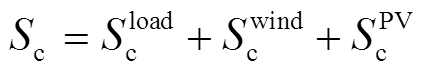 (14)
(14)
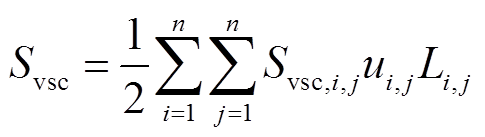 (15)
(15)
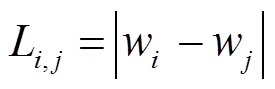 (16)
(16)
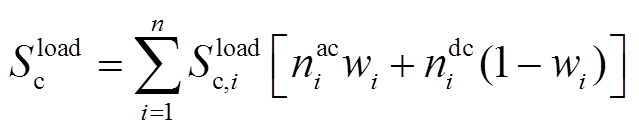 (17)
(17)
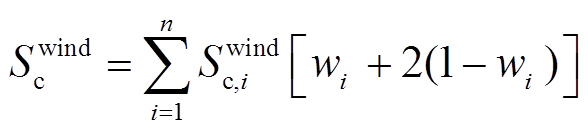 (18)
(18)
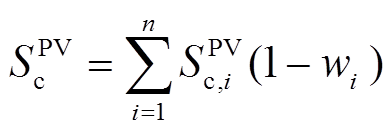 (19)
(19)
式中,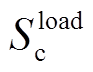 为系统中用于负荷接入的整流逆变器总容量;
为系统中用于负荷接入的整流逆变器总容量;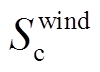 为系统中用于风电并网的整流逆变器总容量;
为系统中用于风电并网的整流逆变器总容量;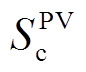 为系统中用于光伏并网的逆变器总容量;
为系统中用于光伏并网的逆变器总容量;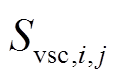 为节点i、j之间可安装的VSC容量;
为节点i、j之间可安装的VSC容量;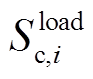 为节点i上用于负荷接入的整流逆变器容量;
为节点i上用于负荷接入的整流逆变器容量;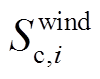 为节点i上用于风电并网的整流逆变器容量;
为节点i上用于风电并网的整流逆变器容量;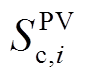 为节点i上用于光伏并网的逆变器容量;
为节点i上用于光伏并网的逆变器容量;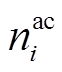 和
和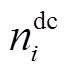 分别表示节点i上是否有交流负荷和直流负荷,若有其值则计为1,若无则计为0;
分别表示节点i上是否有交流负荷和直流负荷,若有其值则计为1,若无则计为0;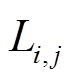 为支路类型变量,用于描述支路类型,
为支路类型变量,用于描述支路类型,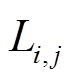 可能存在的四种情况见表1。
可能存在的四种情况见表1。
表1 四种不同的支路类型
Tab.1 Four different types of branch

支路类型wiwjLi,j AC000 DC110 AC-DC011 DC-AC101
2)运行维护成本CO
系统运行维护成本由系统的运行成本、线路及换流器的维护成本构成,用CO表示为
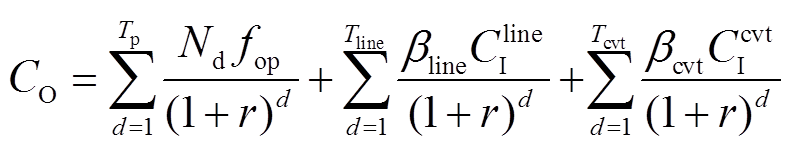 (20)
(20)
式中,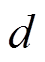 为年份;Nd为一年的运行天数,本文取365;Tp为规划运行年数;Tline为线路设计运行年限;Tcvt为换流器设计运行年限;βline为线路年维护费用系数;βcvt为换流器年维护费用系数;r为贴现率;fop为系统运行成本。
为年份;Nd为一年的运行天数,本文取365;Tp为规划运行年数;Tline为线路设计运行年限;Tcvt为换流器设计运行年限;βline为线路年维护费用系数;βcvt为换流器年维护费用系数;r为贴现率;fop为系统运行成本。
系统运行成本fop由配电网购电成本、弃风弃光成本和储能运行维护成本构成,有
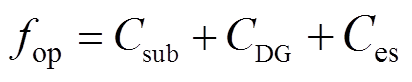 (21)
(21)
其中
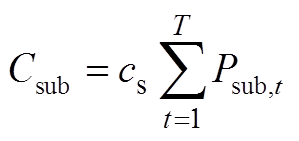 (22)
(22)
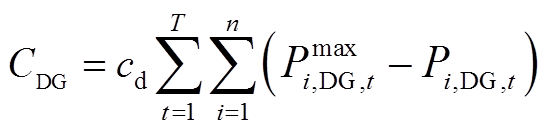 (23)
(23)
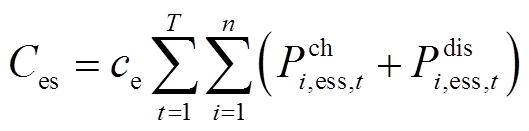 (24)
(24)
式中,Csub为配电网向上级电网购电总费用;CDG为弃风弃光总成本;Ces为储能运行维护总成本;cs为配网单位购电成本;cd为单位弃风弃光成本;ce为储能单位充放电量运行维护成本;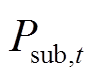 为
为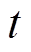 时刻配电网向上级电网购电功率;
时刻配电网向上级电网购电功率;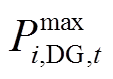 为节点
为节点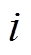 接入的DG在
接入的DG在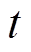 时刻的可出力最大值;
时刻的可出力最大值;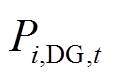 为节点
为节点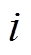 接入的DG在
接入的DG在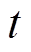 时刻的实际有功出力;
时刻的实际有功出力;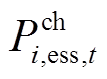 和
和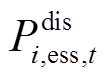 分别为节点
分别为节点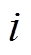 接入的储能系统在
接入的储能系统在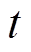 时刻的充电功率和放电功率;T为一天的小时数,本文取24。
时刻的充电功率和放电功率;T为一天的小时数,本文取24。
1)节点连接线路条数约束
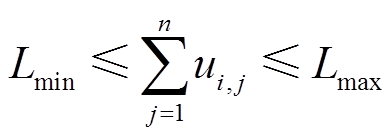 (25)
(25)
式中,Lmin和Lmax分别为系统中每个节点与其他节点连接线路条数总和的最小值和最大值。在矩阵U中,每一行元素之和表示该行对应的节点与其他节点所连接的线路总数,因此式(25)限定了每个节点的线路最小连接数和最大连接数。
2)线路选型约束
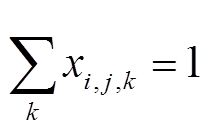 (26)
(26)
式(26)表示节点间的导线只能选择一种型号。
3)功率平衡方程
单层规划模型下,交直流混合配电系统的功率平衡方程与网架结构有关,因此应结合网架决策变量进行描述,具体为
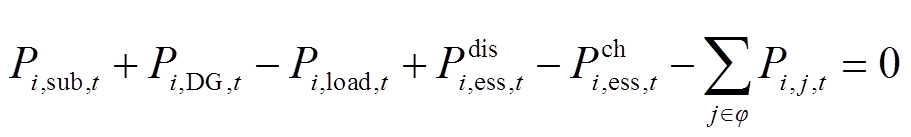 (27)
(27)
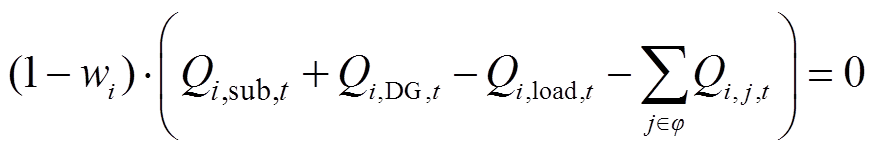 (28)
(28)
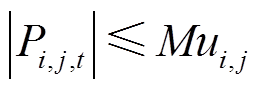 (29)
(29)
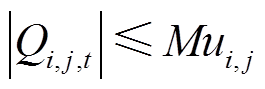 (30)
(30)
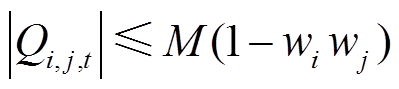 (31)
(31)
式中,φ为与节点i相连接的其他节点集合;Pi,sub,t和 Qi,sub,t分别为交直流系统中节点i接收的上级电网注入有功功率和无功功率;Pi,DG,t和 Qi,DG,t分别为交直流系统中节点i接入的DG输出有功功率和无功功率;Pi,load,t和 Qi,load,t分别为交直流系统中节点i的有功负荷和无功负荷;Pi,j,t和Qi,j,t分别为交直流系统中线路ij传输的有功功率和无功功率;M为一个足够大的常数。
式(27)和式(28)为单层模型下节点功率平衡方程,式(29)和式(30)表示不建设的线路传输功率为0,式(31)表示两个直流节点之间的连接线没有无功功率传输。上述方程将VSC支路的有功功率Ps,k,t和无功功率Qs,k,t也包含在Pi,j,t和 Qi,j,t中,统一了交流、直流和VSC的功率平衡方程。
4)电压方程
在单层规划模型中,支路类型可以是交流支路、直流支路或换流支路,取决于支路两端的母线类型。支路类型不同时,电压平衡方程也各不相同,因此可以根据支路类型变量Li,j和VSC方程式(7)、式(9),推导出单层规划模型下系统电压的统一方程为
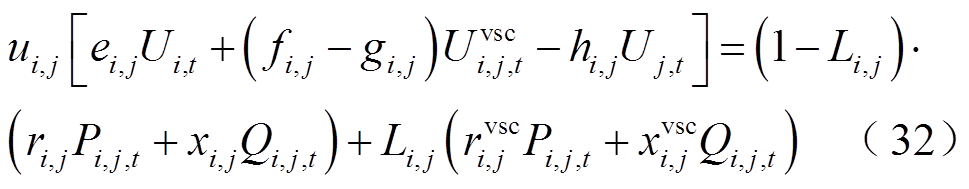
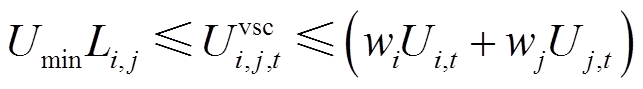 (33)
(33)
式中,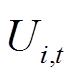 和
和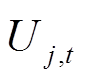 分别为交直流系统中节点
分别为交直流系统中节点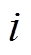 和
和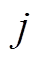 的电压大小;
的电压大小;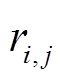 和
和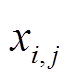 分别为非换流支路的电阻和电抗;
分别为非换流支路的电阻和电抗;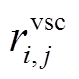 和
和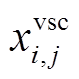 分别为换流支路的电阻和电抗,其数值包括VSC阻抗和线路阻抗;
分别为换流支路的电阻和电抗,其数值包括VSC阻抗和线路阻抗;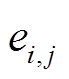 、
、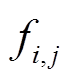 、
、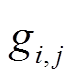 、
、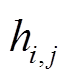 为电压前面的系数,具体为
为电压前面的系数,具体为
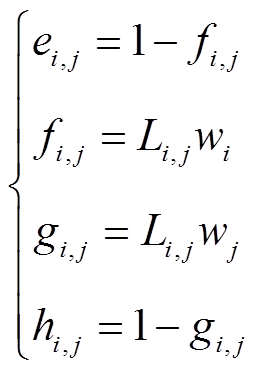 (34)
(34)
结合式(34)可知,若线路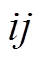 为换流支路,则式(32)中
为换流支路,则式(32)中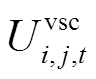 对应图3中C点的电压,该式为VSC支路的电压方程;否则,
对应图3中C点的电压,该式为VSC支路的电压方程;否则,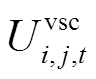 前面的系数为0,此时该式表示交流支路或直流支路的电压方程。
前面的系数为0,此时该式表示交流支路或直流支路的电压方程。
5)VSC无功补偿能力约束
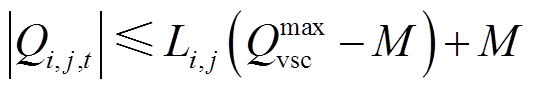 (35)
(35)
式中,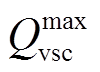 为VSC所能提供的无功补偿能力上限。
为VSC所能提供的无功补偿能力上限。
6)系统安全运行约束
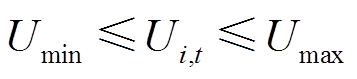 (36)
(36)
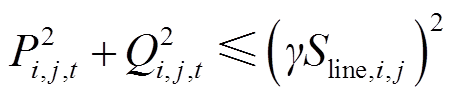 (37)
(37)
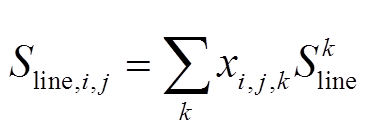 (38)
(38)
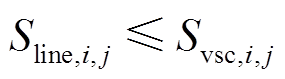 (39)
(39)
式中,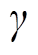 为线路的负载率,本文取80%;Sline,i,j为线路ij的传输容量;
为线路的负载率,本文取80%;Sline,i,j为线路ij的传输容量;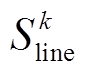 为
为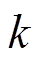 型号导线的传输容量。式(38)表示所选线路的传输容量,式(39)表示VSC容量不能小于线路的传输容量。
型号导线的传输容量。式(38)表示所选线路的传输容量,式(39)表示VSC容量不能小于线路的传输容量。
7)储能运行约束
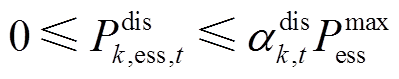 (40)
(40)
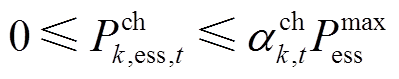 (41)
(41)
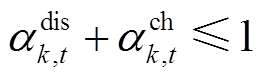 (42)
(42)
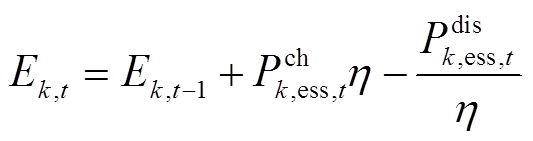 (43)
(43)
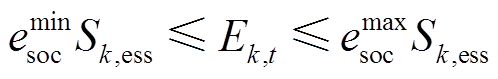 (44)
(44)
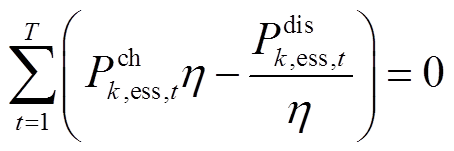 (45)
(45)
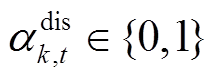 (46)
(46)
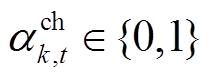 (47)
(47)
式中,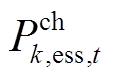 为第
为第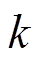 台储能的充电功率;
台储能的充电功率;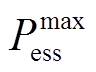 为储能最大充放电功率;
为储能最大充放电功率;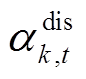 和
和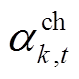 分别为储能充放电标志,第
分别为储能充放电标志,第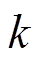 台储能充电时
台储能充电时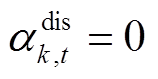 、
、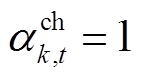 ,放电时
,放电时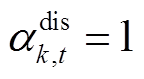 、
、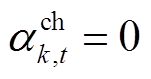 ;
;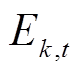 为第
为第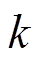 台储能电量;
台储能电量;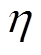 为储能能量转换效率;
为储能能量转换效率;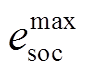 和
和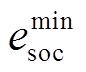 分别为储能荷电状态周期运行上、下限,本文分别取90%和10%;
分别为储能荷电状态周期运行上、下限,本文分别取90%和10%;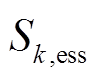 为第
为第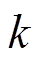 台储能额定容量。式(40)~式(42)为储能充放电功率约束,式(42)表示同一台储能在同一时刻不能既充电又放电,式(43)和式(44)为储能荷电状态约束,式(45)表示储能在一个运行周期内充放电量平衡,式(46)和式(47)表示储能充放电标志为0-1变量。
台储能额定容量。式(40)~式(42)为储能充放电功率约束,式(42)表示同一台储能在同一时刻不能既充电又放电,式(43)和式(44)为储能荷电状态约束,式(45)表示储能在一个运行周期内充放电量平衡,式(46)和式(47)表示储能充放电标志为0-1变量。
8)DG出力约束
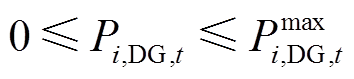 (48)
(48)
9)网络连通性约束
为防止规划结果出现孤岛运行的情况,引入辅助的功率平衡方程确保网络的连通性。对于每一个节点(变电站节点除外),设定其注入有功功率为一个较小的正值常数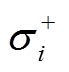 ,使得全部非变电站节点的有功功率
,使得全部非变电站节点的有功功率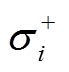 都能够流向上级电网,以确保所有节点跟上级电网之间的连通性。除与上级电网连接的变电站节点外,节点的辅助功率平衡方程为
都能够流向上级电网,以确保所有节点跟上级电网之间的连通性。除与上级电网连接的变电站节点外,节点的辅助功率平衡方程为
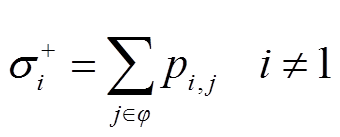 (49)
(49)
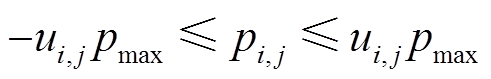 (50)
(50)
式中,pi,j为辅助方程下支路ij传输的有功功率;pmax为辅助方程下线路ij的最大传输有功功率。
为了将上述单层规划模型转换成混合整数线性规划问题,需要对非线性公式进行线性化处理。模型中存在的非线性公式有式(12)、式(15)、式(16)、式(28)、式(31)~式(34)、式(37),其线性化方法如下文所述。
目标函数中存在的非线性公式为式(12)、式(15)、式(16)。式(12)的非线性项为两个0-1变量的乘积,可令Xi,j,k = xi,j,kui,j,则式(12)转换为
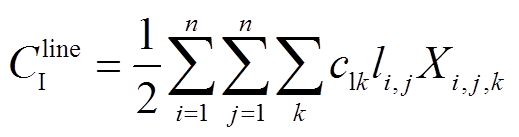 (51)
(51)
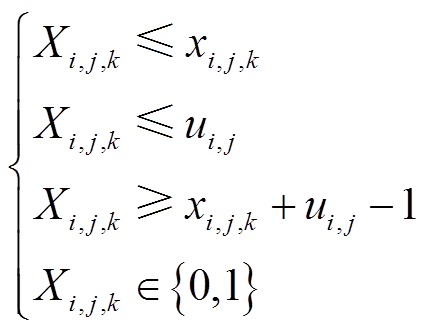 (52)
(52)
式(15)亦为两个0-1变量相乘,采用同样的处理方法。式(16)可采用如下的线性化方法处理。
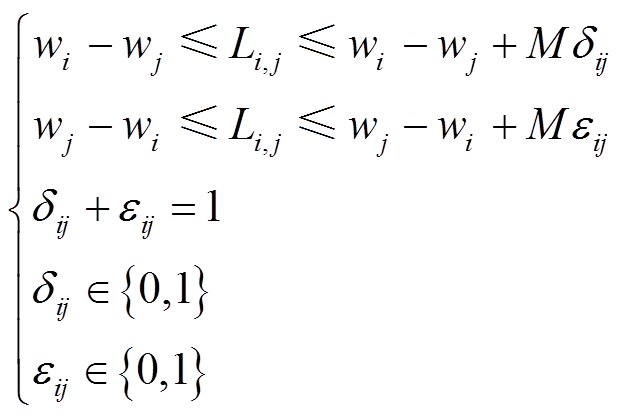 (53)
(53)
式中,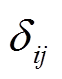 和
和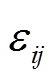 为中间0-1变量。
为中间0-1变量。
式(28)的无功功率平衡方程可使用大M法进行线性化,线性化后的表达式为
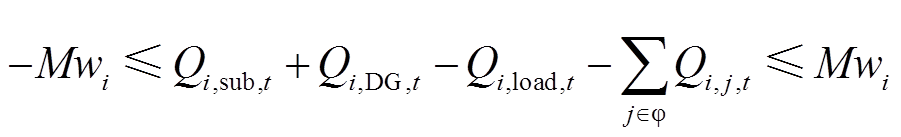 (54)
(54)
式(31)中的非线性项为两个0-1变量的乘积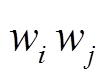 ,可令
,可令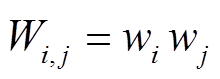 ,则式(31)可转换为
,则式(31)可转换为
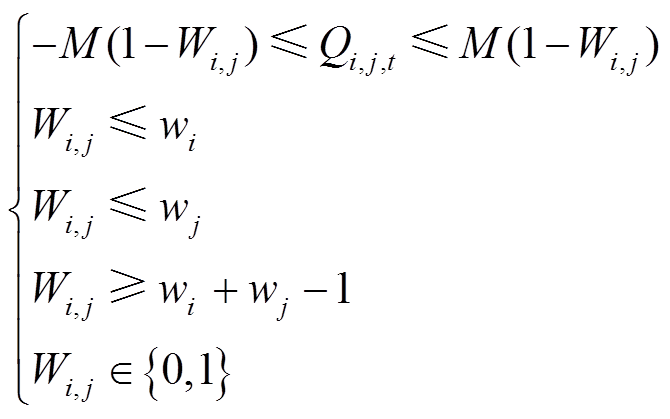 (55)
(55)
对于式(32)的电压方程,首先令
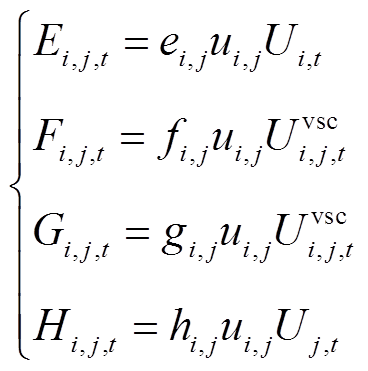 (56)
(56)
再结合大M法处理,则式(32)转换为
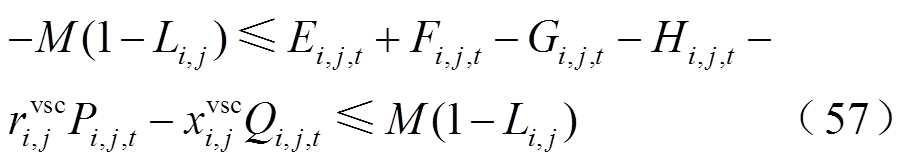
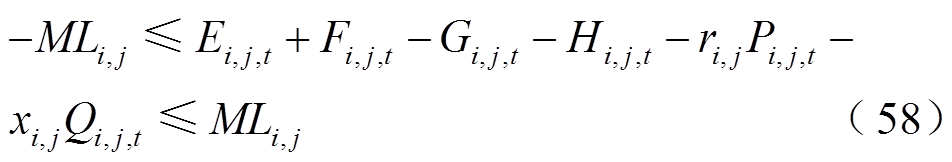
对于式(56)的线性化,可将三个变量相乘转换为一个0-1变量与电压的乘积,具体以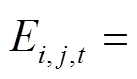
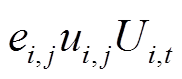 为例进行说明。令
为例进行说明。令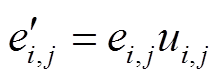 ,则
,则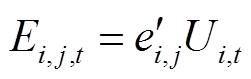 ,对其线性化有
,对其线性化有
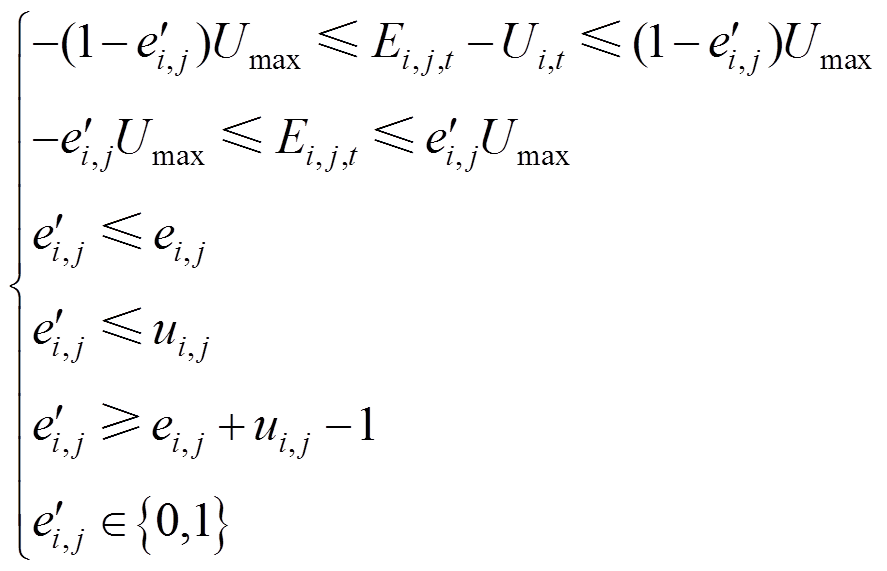 (59)
(59)
对Fi,j,t、Gi,j,t和Hi,j,t用同样的方法处理即可。
式(33)的非线性项也为一个0-1变量与连续变量的乘积,可用式(59)的方法处理;式(34)的线性化参照式(12)的处理方法,均不再赘述。
式(37)的线路传输容量约束在几何上表示为平面上点(Pi,j,t, Qi,j,t)处在半径为γSline,i,j的圆内,可使用两个呈45°夹角的正方形重合区域近似代替[32],如图4所示,因此式(37)转换为式(60)。
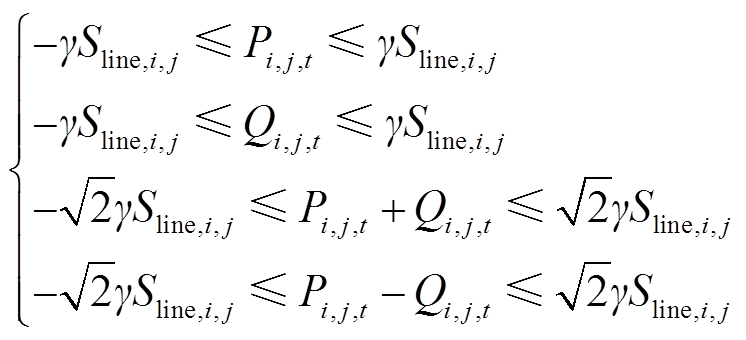 (60)
(60)
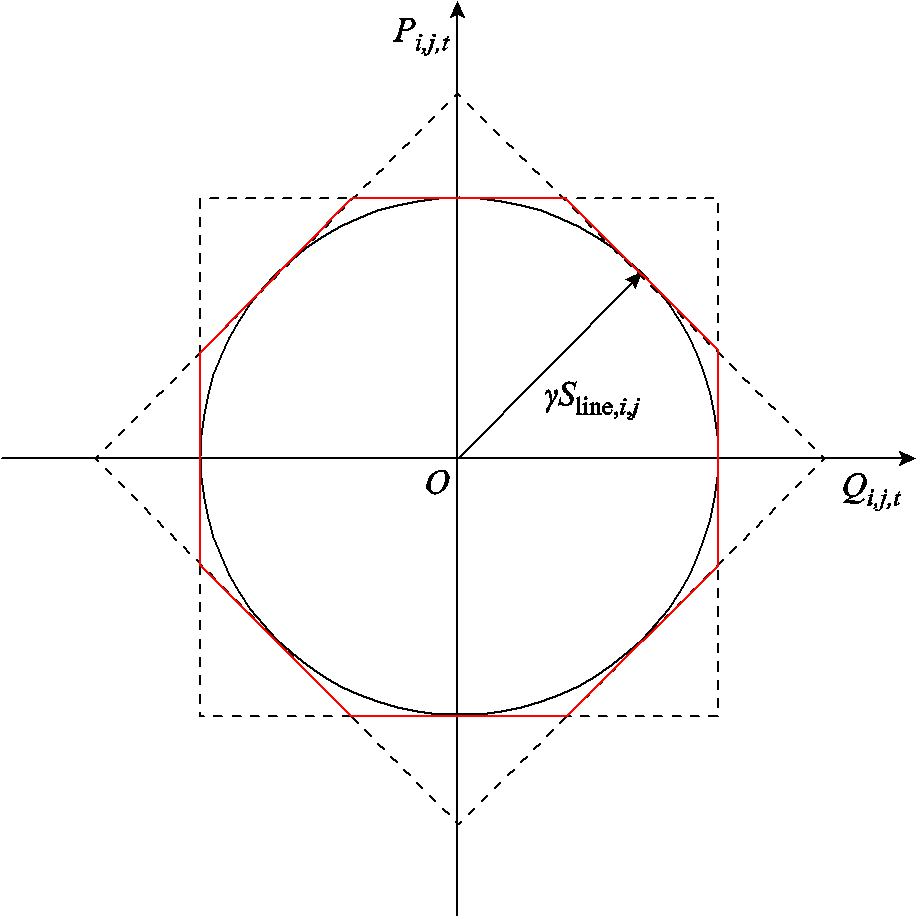
图4 线路传输容量约束线性化
Fig.4 Linearization of line transmission capacity constraint
通过上述线性化后,单层规划模型由混合整数非线性规划问题转换为混合整数线性规划问题。
为验证规划方法的有效性,本文构造了待规划的13节点配电系统,其结构示意图如图5所示。图中虚线表示待规划的母线类型(交流/直流),虚线箭头表示待规划的接入方式(交流接入/直流接入)。
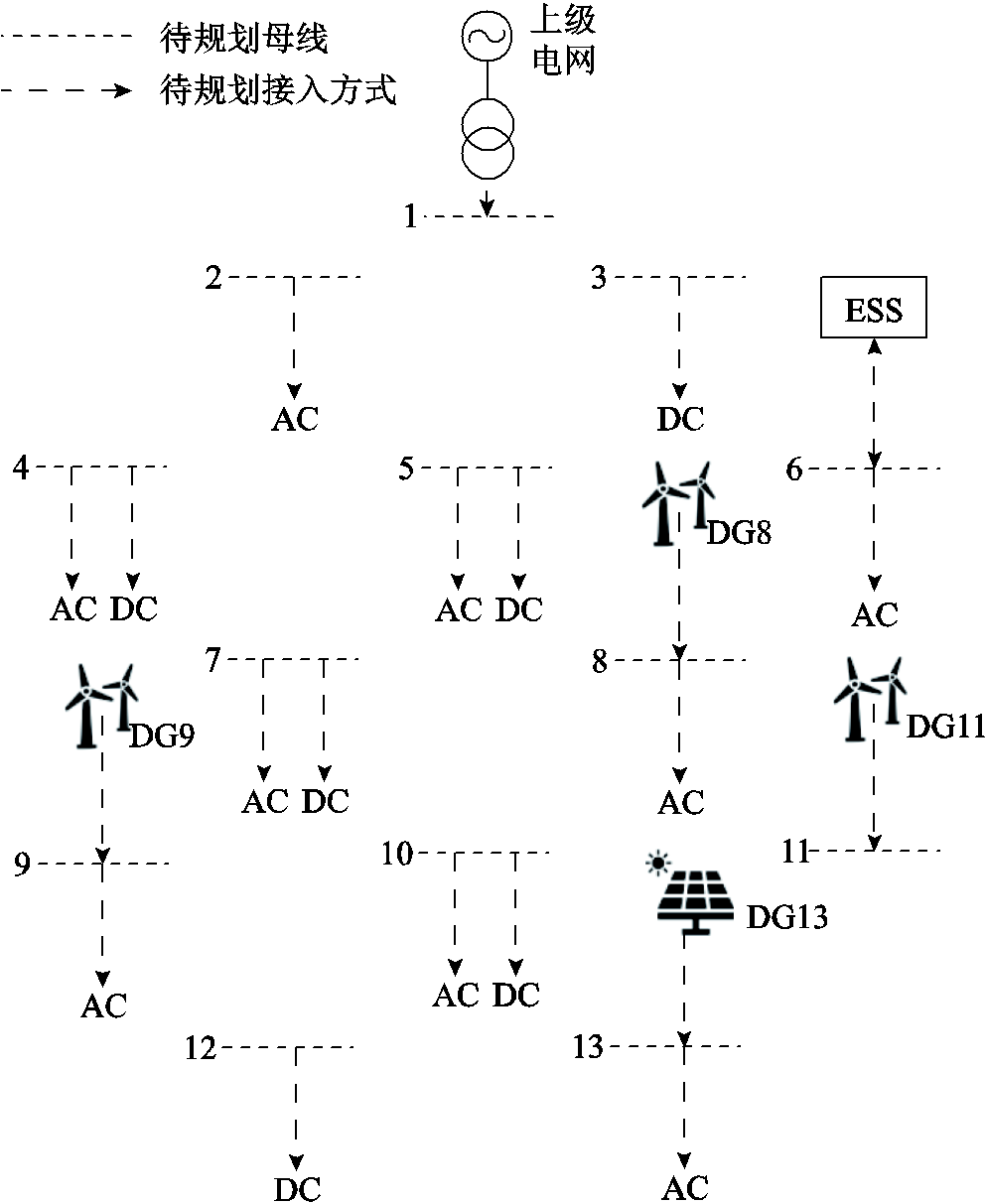
图5 待规划的13节点配电系统
Fig.5 13-node distribution system to be planned
该系统为一个所有线路和母线都尚未建设的规划区域,规划区域内仅包含交流负荷、直流负荷、DG、储能系统和母线地理位置,这些元素根据实际地理位置进行配置。拟将该规划区域建设为一个交直流混合配电网,除平衡节点外所有母线既可以建设为交流节点也可以建设为直流节点,所有节点之间可以在一定的线路条数限制下任意连接,从而为整个待规划区域找到最经济的配电网建设方案,以适应规划区域中所有设备的接入。
本文为探究降低交直流网架建设成本的充分可能性,在约束条件中不包含辐射型约束,因此规划结果既可以为环网也可能为辐射网,没有拓扑形式的限制。为得到辐射型配电网,一方面可以在式(25)的线路连接条数限制中,将每个节点与其余节点线路连接条数总和的最小值Lmin和最大值Lmax分别设置为1和2[1];另一方面,由于规划模型可能会为了节省线路投资成本而选择传输容量较小的导线以环网的形式供电,因此若要到辐射型配电网也可选用较大传输容量的导线。
DG、储能、负荷和母线分布情况如图5所示。节点1与上级电网相连,节点6接入储能,节点13接入光伏,节点8、9和11接入风电。AC表示交流负荷,DC表示直流负荷。上级电网注入有功为0~10 MW;无功为-4.8~4.8 Mvar。系统基本参数见附表1,电源容量配置情况见附表2,系统单位成本见附表3。构造矩阵L用于描述节点间的距离,其元素表示线路长度li,j的值,见式(A1)。
在Matlab中通过YALMIP工具箱调用GUROBI求解器对本文所提的单层线性规划模型进行求解。网架规划结果如图6所示。在规划中提供A型和B型两种导线进行选择,A型导线和B型导线在交流系统中传输容量分别为2.5 MV·A和5 MV·A,在直流系统中分别表示2.5 MW和5 MW。规划结果为交直流混合配电网,其中节点1、2、4、6~10为交流系统,节点3、5和11~13为直流系统,交流系统和直流系统在节点8和11之间用一台VSC进行互联。因潮流在一天内均小于2.5 MV·A或2.5 MW的80%,因此均选用A型导线。该网架下典型日的运行场景如图7所示。
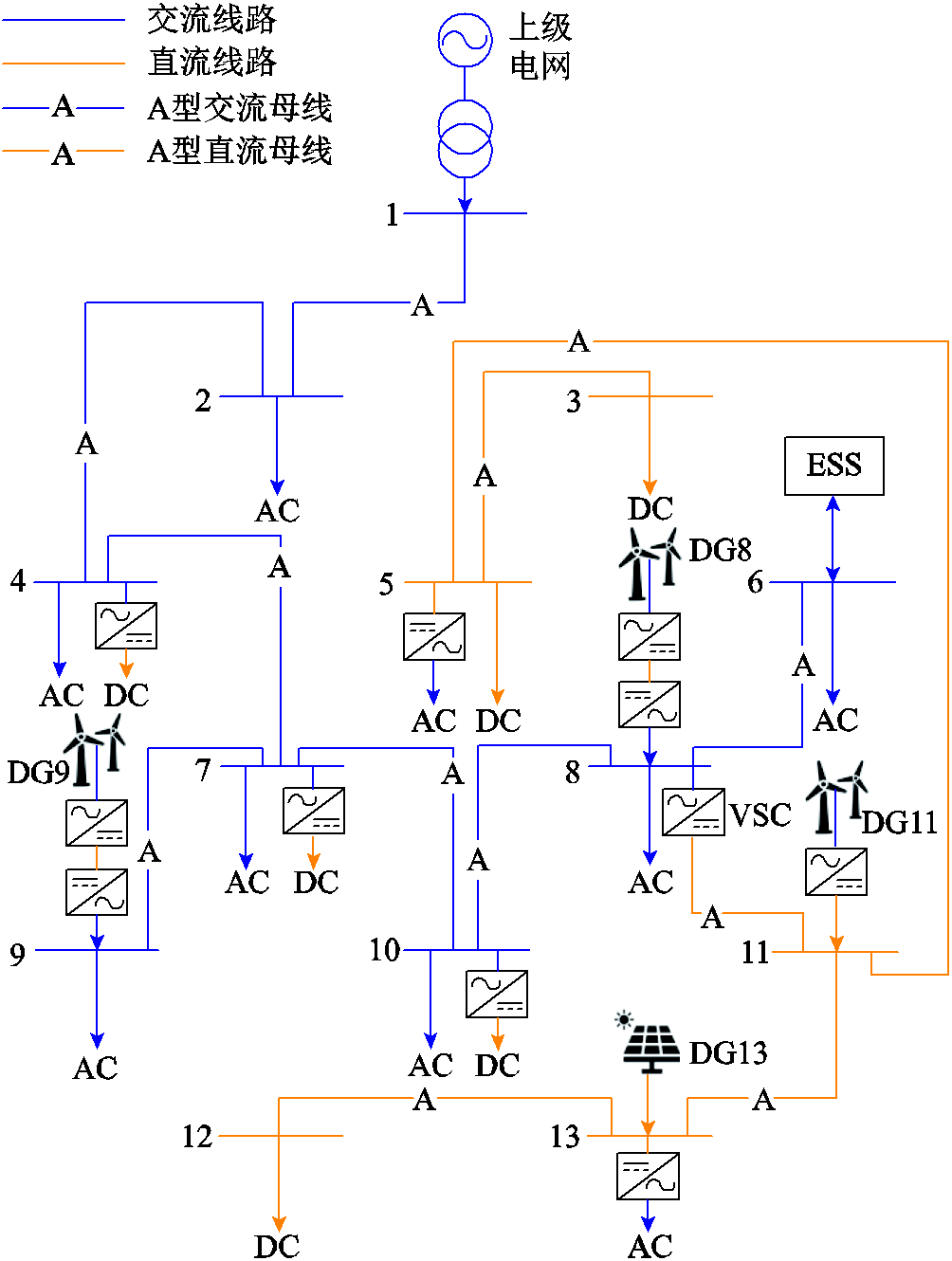
图6 交直流混合配电系统网架规划结果
Fig.6 Network planning results of AC/DC hybrid distribution system
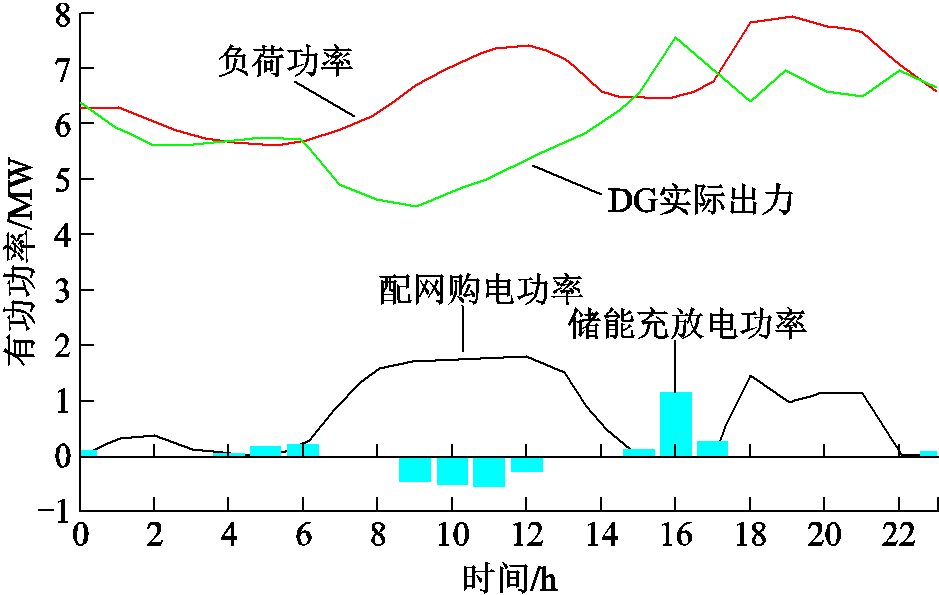
图7 典型日场景运行结果
Fig.7 Running results of typical day scene
在图7中,储能充放电功率为正表示储能充电,为负表示储能放电。由图7可以看出,在典型日场景下,该网架结构能够很好地消纳15~17 h期间DG出力的高峰,将可再生能源存储在储能系统当中。在6~15 h的DG出力低谷期储能放电,同时向上级电网购电以满足负荷需求高峰。
在交直流混合系统中,VSC不仅发挥了有功调节能力,也提供了双向的无功补偿能力以调节系统电压,改善配电网运行情况。当规划结果中VSC不提供无功补偿时,系统总投资运行成本为9 840.73万元,而VSC提供无功补偿时则为9 742.77万元,降低了1%,可见VSC在一定程度上发挥了柔性设备的积极作用。
为对比交直流混合配电网和纯交流配电网的规划方案,在规划模型中设定所有节点类型和线路均为交流(设置节点类型变量wi全为0)进行对比分析,纯交流系统规划结果为图8所示的辐射状纯交流配电网。
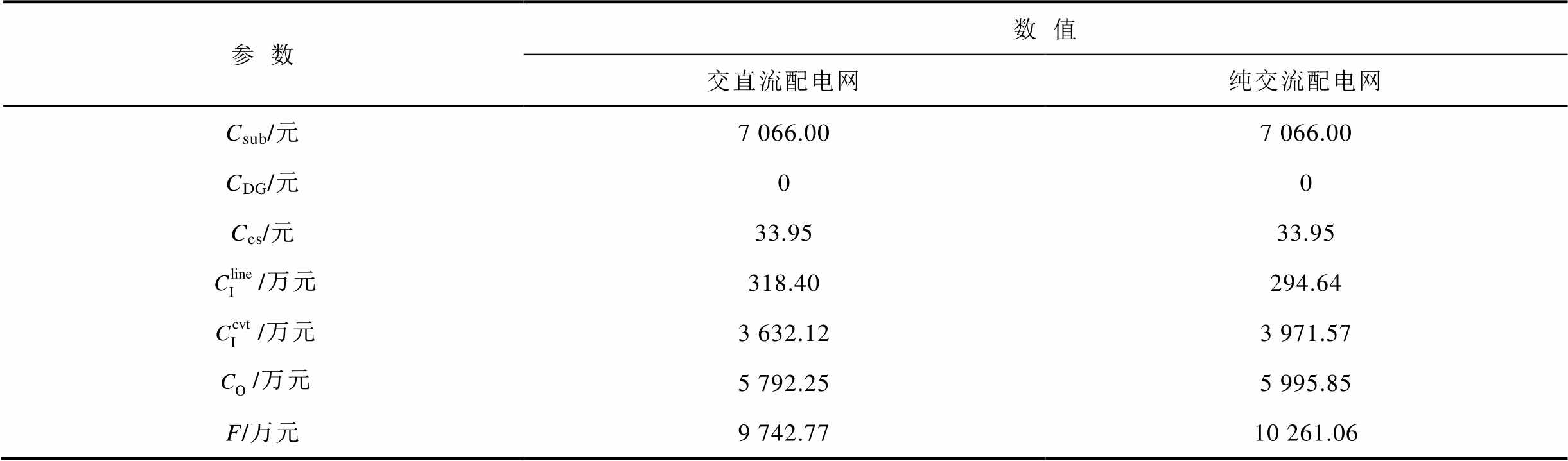
两种不同的规划模型下系统的成本构成对比见表2。结合图6、图8和表2可以看出,交直流混合的配电网在总投资运行成本上优于纯交流配电网,一共节省了5.05%的总投资运行成本。在不考虑网损且无网络阻塞的情况下,网架结构对系统运行成本的影响很小,系统运行成本取决于DG出力和负荷场景,源荷场景一致的情况下运行成本相同,故交直流配电网和纯交流配电网的成本差距主要在换流器的投资成本上。虽然在线路建设上纯交流配电网节省了一小部分投资,但是纯交流配电网在最优方案下换流器的安装成本多于交直流混合配电网的最优方案,同时也造成了换流器维护成本的增加。
造成以上结果的主要原因在于,纯交流的配电网的节点类型只能为交流节点,缺乏网架结构的灵活性,在接入同样交直流类型的源荷下,所用换流器的数量是固定的。交直流配电网由于节点交直流类型为优化变量,因此能够提供更好的节点配置方案和节点互联方案,节省换流器的投资。
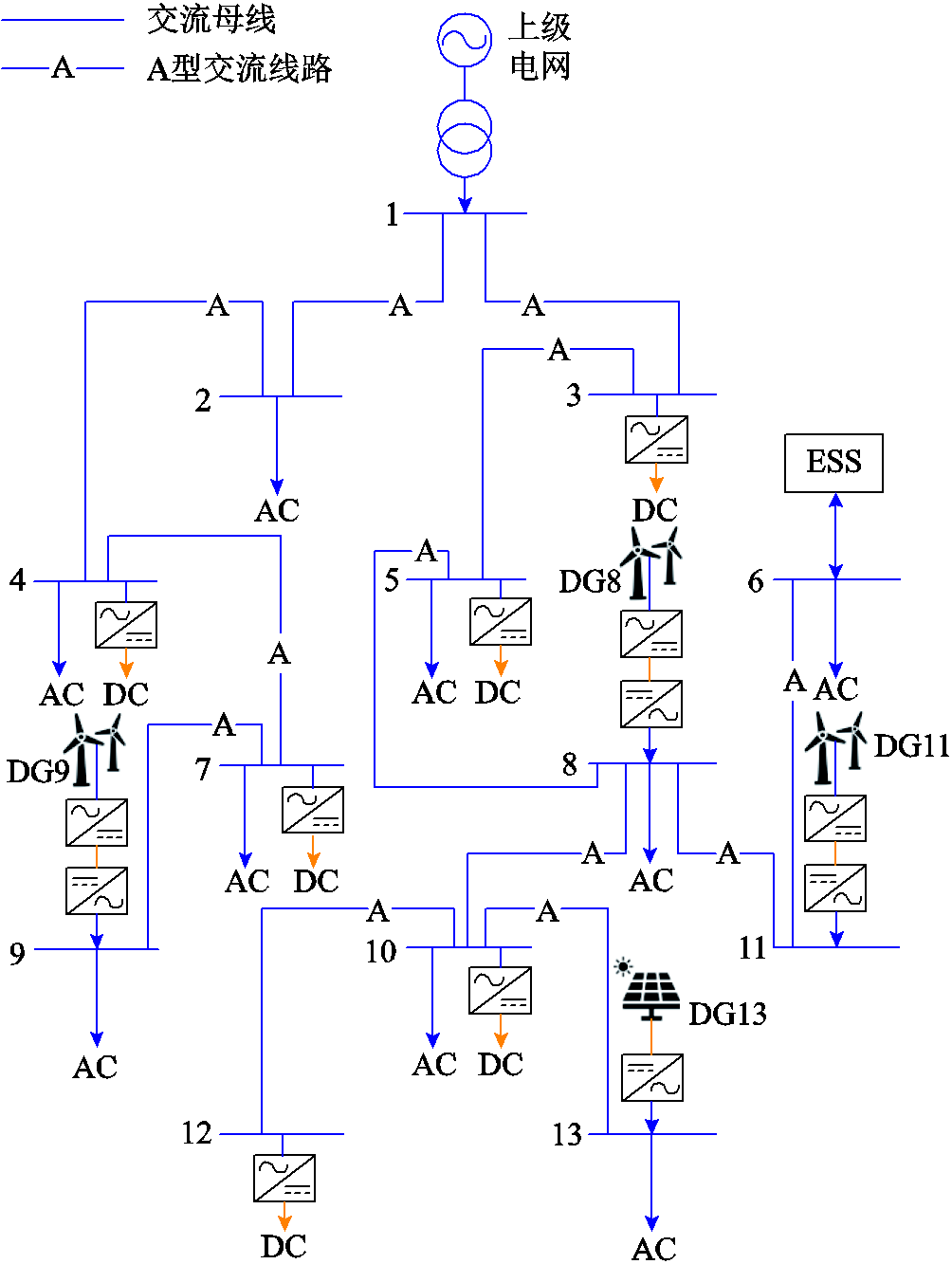
图8 纯交流配电系统结果
Fig.8 Planning results of pure AC distribution system
表2 不同类型配电网成本构成对比
Tab.2 Comparison of cost composition under different types of distribution networks
参数数值 交直流配电网纯交流配电网 Csub/元7 066.007 066.00 CDG/元00 Ces/元33.9533.95 /万元318.40294.64 /万元3 632.123 971.57 /万元5 792.255 995.85 F/万元9 742.7710 261.06
为进一步从网架合理性的角度评估规划方案,引入配电网最大负载能力作为供电能力指标对单层线性规划模型求解的交直流规划方案和纯交流规划方案进行对比分析。最大负载能力定义为配电网中任意支路电压或功率不越限情况下的最大负荷值[5],有
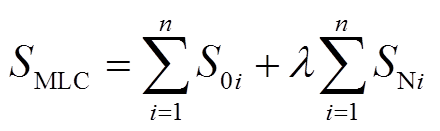 (61)
(61)
式中,SMLC为配电网所能承受的最大负荷;S0i为节点i的负荷基础值,本文设为节点当前负荷水平;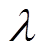 为节点的负荷增长倍数;SNi为节点i的负荷增长基准值,本文设为节点i的1%当前负荷水平。
为节点的负荷增长倍数;SNi为节点i的负荷增长基准值,本文设为节点i的1%当前负荷水平。
在不同的负荷水平下进行最优潮流计算以测试网架的供电能力,若任意时段下任意支路电压或潮流越限,则视为达到配电网的最大负载能力。测试结果为,交直流混合配电网的最大负荷增长倍数l为24.00,而纯交流配电网的l为18.18。由此可以看出,交直流混合配电网的网架结构供电能力大于纯交流配电网。一方面的原因在于网架结构的差异,图6中DG的分布情况决定了DG转供能力比图8更强;另一方面的原因是当负荷增大时,交直流混合配电网的无功需求可由换流器提供以降低线路潮流和电压的越限风险。
为了验证本文所提单层线性规划模型相比于传统双层规划模型[1]能够得到更好的解,构建网架双层规划模型并采用遗传算法求解进行对比。双层规划模型的上层规划层为节点类型变量wi、节点间连接状态ui,j和线路选型变量xi,j,k构成的网架决策方案,下层运行层为配网购电功率、DG出力、VSC功率和储能充放电功率构成的优化运行方案。遗传算法首先生成网架决策方案传递给下层进行求解,将下层求解结果返回上层进行网架寻优直至收敛,求解结果如图9所示,算法种群规模为100,在50代内如果适应度函数误差小于10-4则输出结果。单层线性规划模型与双层规划模型成本对比见表3。
结合图6、图9和表3可知,与单层线性规划模型相比,双层模型的规划结果网架结构较为复杂,线路数量更多且含有较长距离的跨线,因此造成了较大的线路建设成本浪费。造成此现象的原因在于,模型的规划层含有较多的0-1变量,单层线性规划方法更能够从全局上保证解的最优性,而遗传算法则因为是启发式算法,交叉、变异的方法无法保证解的搜索范围,因此易陷入局部最优,降低了获得最佳网架方案的概率。
从换流器的投资上看,双层模型规划结果的换流器数量也更多,因此无论是在线路建设成本上还是在换流器的安装成本上,单层线性规划模型均优于双层规划模型,一共减少了13.54%的系统总投资运行成本,其规划结果具有更好的经济性。
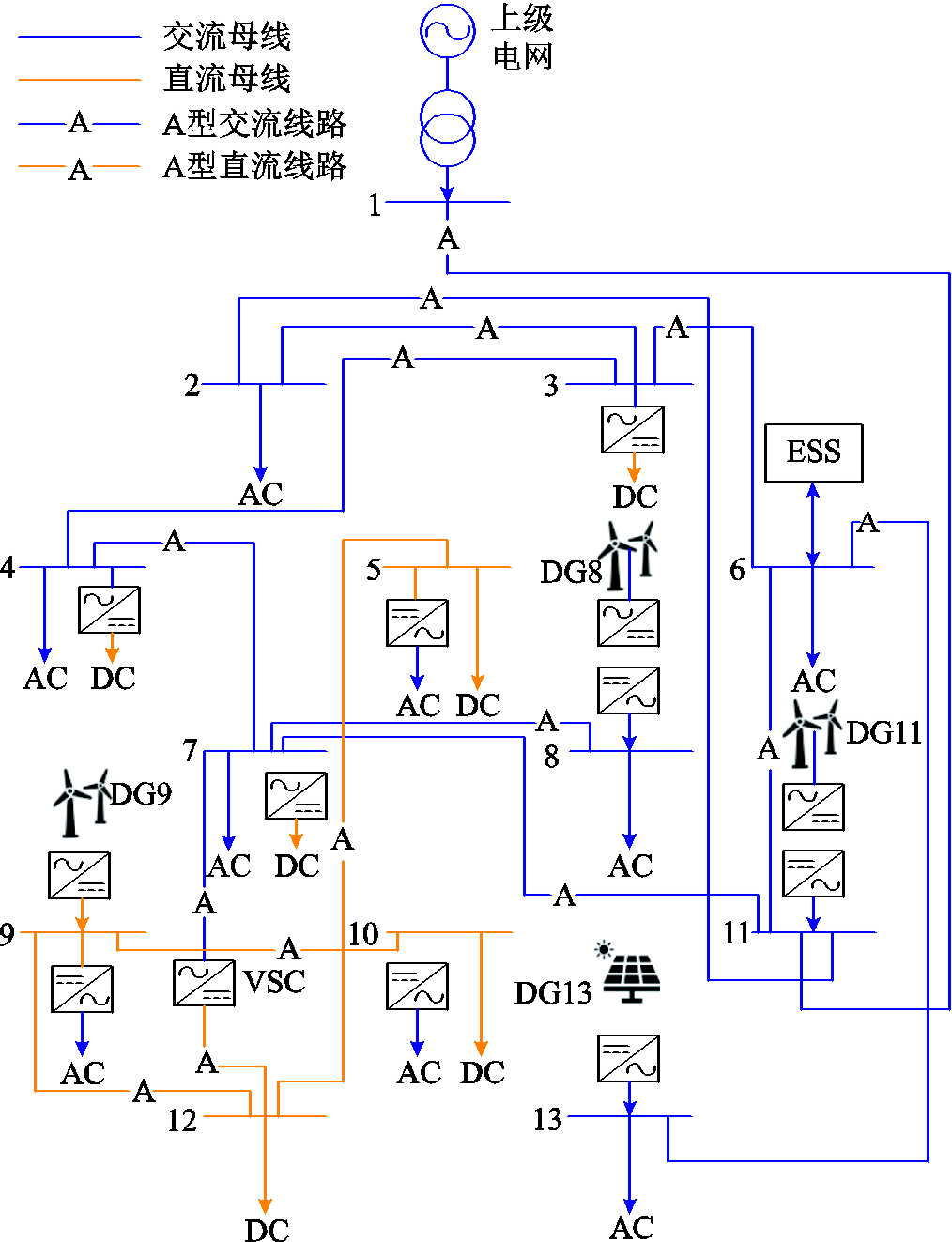
图9 遗传算法求解的双层模型规划结果
Fig.9 Planning results of bi-layer model solved by genetic algorithm
表3 单层线性规划模型与双层规划模型成本对比
Tab.3 Cost comparison between bi-layer planning model and single-layer linearization planning model

参数数值 单层线性规划模型双层规划模型 /万元318.40617.80 /万元3 632.124 243.13 F/万元9 742.7711 268.48
为验证本文所提单层线性规划方法具有更高的计算效率,将单层线性规划模型的求解时间与遗传算法求解的双层规划模型求解时间进行对比。程序运行环境为Matlab2018b,CPU为Intel(R) Xeon(R) Silver 4214,2.20 GHz。计算结果表明,双层规划模型求解时间为475.10 min,而本文所提的单层线性规划模型求解时间为41.22 min,节省了91.32%的计算时间,具有更高的计算效率。
本文提出一种考虑所有AC/DC配置可能性的交直流配电系统网架单层线性规划方法,仿真结果表明:
1)该方法克服了传统配电网规划在现有网架基础上进行扩建的局限性,不仅对节点类型进行优化,同时对线路连接和线路选型进行三者联合优化,为配电网规划找到更好的潜在解决方案。交直流规划方案与纯交流规划方案相比能够节省5.05%的总投资运行成本,也具有更好的网架供电能力,证明了在DG、储能和直流负荷等多种交直流源荷设备的接入下,建设交直流混合配电网具有更高的经济性。
2)该方法将MINLP问题转换为MILP问题进行求解,与传统遗传算法求解的双层规划模型相比,节省了13.54%的总投资运行成本以及91.32%的计算时间,证明了该方法能够得到更好的最优解且计算效率更高,具有更高的实用性和工程应用价值。
3)该方法在求解过程中无需对约束进行松弛,相比于二阶锥规划法来说不存在松弛条件的限制,因此没有网架拓扑结构等方面的局限性,不仅适用于辐射型配电网的规划,也适用于环型配电网的规划,具有更广泛的适用性。
附录 仿真系统参数
附表1 系统基本参数
APP.Tab.1 Basic system parameters

参数数值 系统基准容量/(MV·A)10 交流系统基准电压/kV4.16 直流系统基准电压/kV6.80 储能初始荷电状态(%)50 η(%)90 ri,j+jxi,j/(pu/km)0.059 8+j0.097 9 (pu)0.288 9+j0.754 8 Svsc,i,j/(MV·A)5 /(MV·A)3
(续)

参数数值 /(MV·A)3 /(MV·A)3 Sk,ess/ (MW·h)10 /MW2.5 /Mvar1 Tline/年40 Tcvt/年45 Tp/年40 βline0.05 βcvt0.05 r0.075
附表2 DG容量配置情况
APP.Tab.2 DG capacity configuration

节点DG最大出力/MW 82.0 92.5 112.5 132.0
附表3 系统单位成本
APP.Tab.3 Unit cost of system

成本数值 clA/(元/km)147.648×103 clB/(元/km)295.296×103 cc/[元/(MV·A)]1 018.35×103 cv/[元/(MV·A)]1 154.13×103 cs/[元/(MW·h)]400.00 cd/[元/(MW·h)]400.00 ce/[元/(MW·h)]10.00
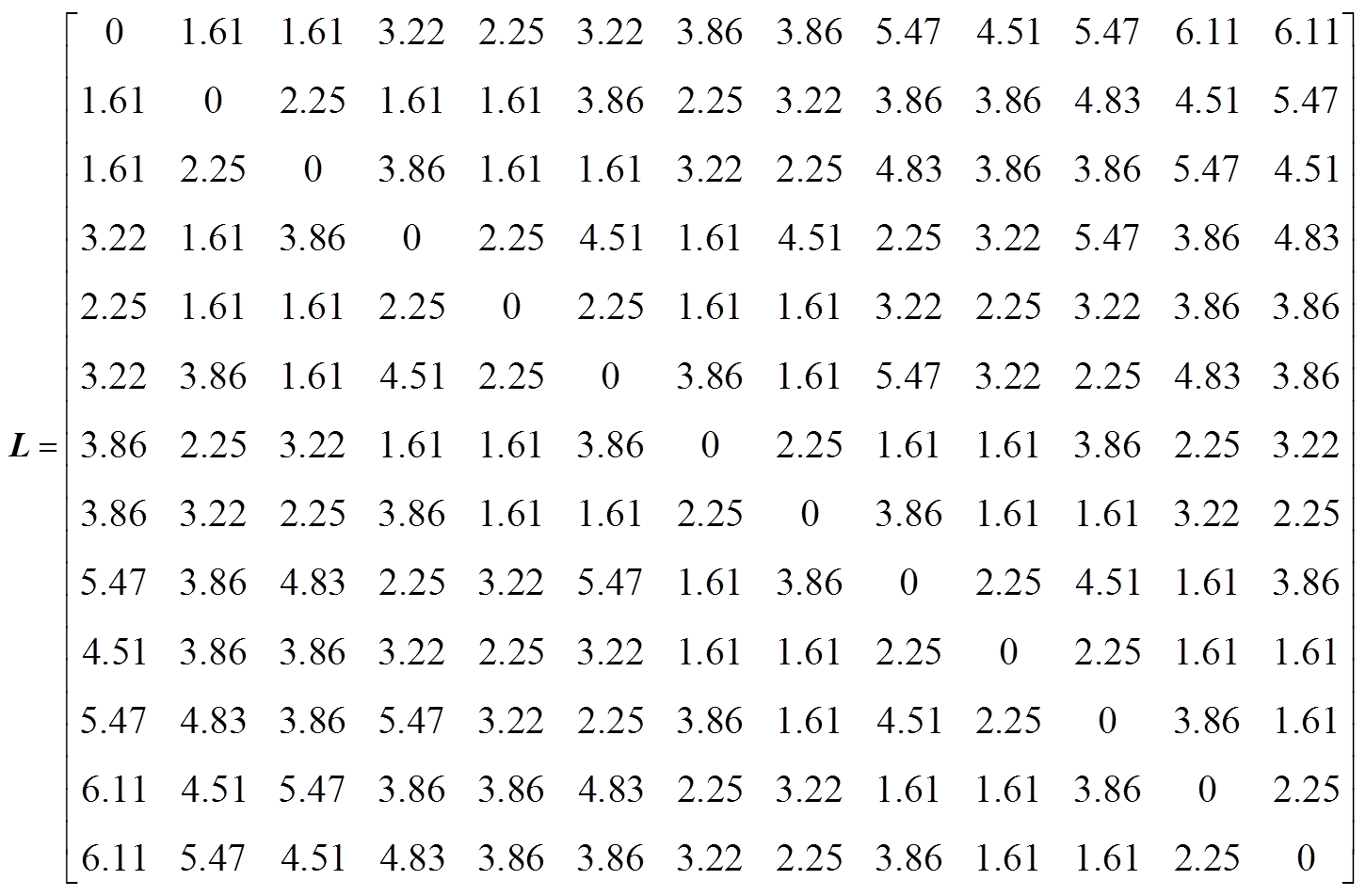 (A1)
(A1)
参考文献
[1] Ahmed H M A, Eltantawy A B, Salama M M A. A planning approach for the network configuration of AC-DC hybrid distribution systems[J]. IEEE Transactions on Smart Grid, 2018, 9(3): 2203-2213.
[2] 李幸芝, 韩蓓, 李国杰, 等. 考虑非高斯耦合不确定性的交直流配电网两阶段概率状态估计[J]. 电工技术学报, 2020, 35(23): 4949-4960. Li Xingzhi, Han Bei, Li Guojie, et al. Two-stage probabilistic state estimation for AC/DC distribution network considering non-gaussian coupling uncertainties[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4949-4960.
[3] 徐少博, 徐永海, 陶顺, 等. 计及边带分量频率耦合的电压源型换流器输入导纳建模[J]. 电工技术学报, 2023, 38(11): 2883-2893. Xu Shaobo, Xu Yonghai, Tao Shun, et al. Voltage source converter input admittance model considering frequency coupling of sideband components[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2883-2893.
[4] 涂小涛, 高仕龙, 陈锐, 等. 多端柔性交直流混合配电网建模及仿真分析[J]. 电器与能效管理技术, 2020(1): 58-63. Tu Xiaotao, Gao Shilong, Chen Rui, et al. Modeling and simulation analysis of multi-terminal flexible AC/DC hybrid distribution network[J]. Electrical & Energy Management Technology, 2020(1): 58-63.
[5] 罗志刚, 韦钢, 袁洪涛, 等. 基于区间直觉模糊理论的直流配网规划方案综合决策[J]. 电工技术学报, 2019, 34(10): 2011-2021. Luo Zhigang, Wei Gang, Yuan Hongtao, et al. Comprehensive decision of DC distribution network planning based on interval intuitionistic fuzzy theory[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2011-2021.
[6] 曹文远, 韩民晓, 谢文强, 等. 交直流配电网逆变器并联控制技术研究现状分析[J]. 电工技术学报, 2019, 34(20): 4226-4241. Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. Analysis on research status of parallel inverters control technologies for AC/DC distribution network[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4226-4241.
[7] 郑重, 苗世洪, 李超, 等. 面向微型能源互联网接入的交直流配电网协同优化调度策略[J]. 电工技术学报, 2022, 37(1): 192-207. Zheng Zhong, Miao Shihong, Li Chao, et al. Coordinated optimal dispatching strategy of AC/DC distribution network for the integration of micro energy Internet[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 192-207.
[8] 葛少云, 张有为, 刘洪, 等. 考虑网架动态重构的主动配电网双层扩展规划[J]. 电网技术, 2018, 42(5): 1526-1536. Ge Shaoyun, Zhang Youwei, Liu Hong, et al. Bi-layer expansion programming method for active distribution network considering dynamic grid reconfiguration[J]. Power System Technology, 2018, 42(5): 1526-1536.
[9] 方陈, 张翔, 程浩忠, 等. 主动管理模式下含分布式发电的配电网网架规划[J]. 电网技术, 2014, 38(4): 823-829. Fang Chen, Zhang Xiang, Cheng Haozhong, et al. Framework planning of distribution network containing distributed generation considering active management[J]. Power System Technology, 2014, 38(4): 823-829.
[10] 曾顺奇, 汤森垲, 程浩忠, 等. 考虑源网荷储协调优化的主动配电网网架规划[J]. 南方电网技术, 2018, 12(3): 35-43. Zeng Shunqi, Tang Senkai, Cheng Haozhong, et al. Framework planning of active distribution network considering coordinated optimization of generation, network, load and storage[J]. Southern Power System Technology, 2018, 12(3): 35-43.
[11] 胡晓博. 含分布式能源的交直流混合配电网规划[D]. 北京: 华北电力大学, 2017.
[12] 王伟. 交直流配电网网架优化规划及典型应用场景研究[D]. 北京: 北京交通大学, 2018.
[13] 李桂鑫, 葛磊蛟, 陶永晋, 等. 考虑分布式能源综合利用的交直流混合配电网规划研究[J]. 可再生能源, 2020, 38(1): 98-103. Li Guixin, Ge Leijiao, Tao Yongjin, et al. Research on the planning of AC/DC hybrid distribution network considering the comprehensive utilization of distributed energy[J]. Renewable Energy Resources, 2020, 38(1): 98-103.
[14] 金国彬, 刘玉龙, 李国庆, 等. 考虑可靠性的交直流混合配电网网架与分布式电源协同优化规划[J]. 电力系统保护与控制, 2022, 50(22): 59-70. Jin Guobin, Liu Yulong, Li Guoqing, et al. Collaborative optimization planning of an AC/DC hybrid distribution network frame and distributed power generation considering reliability[J]. Power System Protection and Control, 2022, 50(22): 59-70.
[15] Feng Wang, Tuan L A, Tjernberg L B, et al. A new approach for benefit evaluation of multiterminal VSC–HVDC using A proposed mixed AC/DC optimal power flow[J]. IEEE Transactions on Power Delivery, 2014, 29(1): 432-443.
[16] 刘向龙, 刘友波, 尹航, 等. 含电力电子变压器的交直流混合配电系统网架结构规划[J]. 高电压技术, 2021, 47(4): 1283-1295. Liu Xianglong, Liu Youbo, Yin Hang, et al. Network planning of AC/DC hybrid distribution system with power electronic transformers[J]. High Voltage Engineering, 2021, 47(4): 1283-1295.
[17] 韦涛, 苏剑, 崔艳妍, 等. 交直流混合配电网VSC与分布式电源三层协调规划方法研究[J]. 可再生能源, 2021, 39(9): 1263-1270. Wei Tao, Su Jian, Cui Yanyan, et al. Research on the three-level coordination planning method of hybrid AC/DC distribution network based on VSC and distributed generator[J]. Renewable Energy Resources, 2021, 39(9): 1263-1270.
[18] 汪慧敏, 杨苹, 余雁琳. 基于双层粒子群算法的主动配电网分布式电源规划[J]. 计算机与数字工程, 2021, 49(9): 1930-1935. Wang Huimin, Yang Ping, Yu Yanlin. Optimal distributed generation planning in active distribution network based on Bi-level particle swarm optimization algorithm[J]. Computer & Digital Engineering, 2021, 49(9): 1930-1935.
[19] 吴熙, 陆瑶, 蔡晖, 等. 计及风电不确定性的含线间潮流控制器的电力系统经济调度[J]. 电工技术学报, 2023, 38(3): 781-792. Wu Xi, Lu Yao, Cai Hui, et al. Economic dispatching of power system with interline power flow controller considering wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 781-792.
[20] 黄志强, 陈业伟, 毛志鹏, 等. 柔性多状态开关与分布式储能系统联合接入规划[J]. 电力系统自动化, 2022, 46(14): 29-37. Huang Zhiqiang, Chen Yewei, Mao Zhipeng, et al. Joint access planning of soft open point and distributed energy storage system[J]. Automation of Electric Power Systems, 2022, 46(14): 29-37.
[21] Jabr R A. Radial distribution load flow using conic programming[J]. IEEE Transactions on Power Systems, 2006, 21(3): 1458-1459.
[22] 刘一兵, 吴文传, 张伯明, 等. 基于混合整数二阶锥规划的主动配电网有功-无功协调多时段优化运行[J]. 中国电机工程学报, 2014, 34(16): 2575-2583. Liu Yibing, Wu Wenchuan, Zhang Boming, et al. A mixed integer second-order cone programming based active and reactive power coordinated multi-period optimization for active distribution network[J]. Proceedings of the CSEE, 2014, 34(16): 2575-2583.
[23] 马鑫, 郭瑞鹏, 王蕾, 等. 基于二阶锥规划的交直流主动配电网日前调度模型[J]. 电力系统自动化, 2018, 42(22): 144-150. Ma Xin, Guo Ruipeng, Wang Lei, et al. Day-ahead scheduling model for AC/DC active distribution network based on second-order cone programming[J]. Automation of Electric Power Systems, 2018, 42(22): 144-150.
[24] Low S H. Convex relaxation of optimal power flow—part I: formulations and equivalence[J]. IEEE Transactions on Control of Network Systems, 2014, 1(1): 15-27.
[25] Low S H. Convex relaxation of optimal power flow—part II: exactness[J]. IEEE Transactions on Control of Network Systems, 2014, 1(2): 177-189.
[26] 郑扬威, 江岳文, 张金辉. 高比例风电渗透下考虑长短期储能的源-储-输联合规划优化[J]. 电力自动化设备, 2023, 43(3): 63-71. Zheng Yangwei, Jiang Yuewen, Zhang Jinhui. Joint planning optimization of source-storage-transportation considering long- and short-term energy storage under high proportion of wind power penetration[J]. Electric Power Automation Equipment, 2023, 43(3): 63-71.
[27] 范志成, 朱俊澎, 袁越, 等. 基于改进型直流潮流算法的主动配电网分布式电源规划模型及其线性化方法[J]. 电网技术, 2019, 43(2): 504-513. Fan Zhicheng, Zhu Junpeng, Yuan Yue, et al. Distributed generation planning model of active distribution network and linearization method based on improved DC power flow algorithm[J]. Power System Technology, 2019, 43(2): 504-513.
[28] 刘晓林, 王旭, 蒋传文, 等. 计及VSC运行约束的交直流混合配电网分布式优化调度方法[J]. 电网技术, 2021, 45(3): 1089-1101. Liu Xiaolin, Wang Xu, Jiang Chuanwen, et al. Distributed optimal scheduling of hybrid AC-DC distribution grid considering VSC operation constraints[J]. Power System Technology, 2021, 45(3): 1089-1101.
[29] Yeh H G, Gayme D F, Low S H. Adaptive VAR control for distribution circuits with photovoltaic generators[J]. IEEE Transactions on Power Systems, 2012, 27(3): 1656-1663.
[30] 卫志农, 季聪, 孙国强, 等. 含VSC-HVDC的交直流系统内点法最优潮流计算[J]. 中国电机工程学报, 2012, 32(19): 89-95, 190. Wei Zhinong, Ji Cong, Sun Guoqiang, et al. Interior-point optimal power flow of AC-DC system with VSC-HVDC[J]. Proceedings of the CSEE, 2012, 32(19): 89-95, 190.
[31] 高红均, 刘俊勇, 魏震波, 等. 主动配电网分层鲁棒规划模型及其求解方法[J]. 中国电机工程学报, 2017, 37(5): 1389-1401. Gao Hongjun, Liu Junyong, Wei Zhenbo, et al. A Bi-level robust planning model of active distribution network and its solution method[J]. Proceedings of the CSEE, 2017, 37(5): 1389-1401.
[32] 王文超, 庞丹, 成龙, 等. 考虑电价型需求响应的交直流混合配电网优化调度[J]. 电网技术, 2019, 43(5): 1675-1682. Wang Wenchao, Pang Dan, Cheng Long, et al. Optimal dispatch approach for hybrid AC/DC distribution networks considering price-based demand response[J]. Power System Technology, 2019, 43(5): 1675-1682.
Abstract In order to adapt the network structure of a distribution network to the access of new energy technologies such as distributed generation (DG), energy storage and DC loads, a new network planning method for AC/DC hybrid distribution networks is proposed. The method considered all possibilities of the AC/DC configuration to improve the economic benefits of the network construction, and constructed a linearized single-layer network planning model to improve the global optimization capability in view of the difficulty of obtaining global optimal solutions for the network planning model.
Firstly, considering that AC/DC types of buses and the connection states between buses determine the investment cost of converters and lines, which determines the economic benefits of distribution network planning, a binary bus type matrix is used to represent AC/DC types of buses, a binary network association matrix is developed to represent the connection states between buses, and binary line type variables are adopoted to represent line type selection to construct network structure decision variables, achieving a description of the overall network structure. Secondly, with an objective of converter installation cost, line construction cost and system operation and maintenance cost, a single-layer network planning model is established considering elaborated and practical constraints, such as the number of node-connected lines, line selection constraint, power flow, voltage source converter (VSC) reactive power compensation capacity, system safety operation, energy storage operation, network connectivity and so on. In this proposed model, the AC and DC current models is unified by introducing branch type variables, thus linking the planning layer and operation layer, so that network planning variables and operation optimization variables consisting of power purchased from the distribution network to the grid, DG output, energy storage charging and discharging power and VSC power were optimized simultaneously to enhance the possibility of obtaining a global optimal solution. Finally, to achieve better sulution, power flow equations and line transmission capacity constraints are linearized by a series of linearization methods, such that the mixed integer nonlinear programming (MINLP) problem was transformed into a mixed integer linear programming (MILP) problem, and the GUROBI solver is invoked in Matlab to solve it.
The validity of the planning method was verified in a 13-node distribution system. The simulation results show that: (1) The AC/DC hybrid distribution network planning scheme can save 5.05% of the total investment and operation cost compared with the pure AC distribution network planning, and the network structure of the planned AC/DC hybrid distribution network also has greater network supply capacity, which illustrates that the AC/DC hybrid distribution network is more advantageous in the case of mixed AC/DC sources and loads. (2) The proposed planning method saves 13.54% of the total investment and operation cost and 91.32% of the computation time compared with the traditional bi-layer planning model solved by genetic algorithm, which indicates that the single-layer network planning method has prominent global optimization performance and faster computational efficiency. (3) As the method does not require relaxation of constraints, compared to second-order cone planning techniques, there are no limitations in terms of grid topology, etc, and it is suitable for the planning of both radial and meshed distribution networks.
keywords:AC/DC Hybrid distribution system, network planning, single-layer programming, linearization optimization
DOI:10.19595/j.cnki.1000-6753.tces.222363
中图分类号:TM715
国家自然科学基金资助项目(51707040)。
收稿日期 2022-12-16
改稿日期 2023-06-30
江岳文 女,1977年生,博士,教授,研究方向为风电并网优化运行、电力系统优化运行与规划、电力市场。E-mail:jiangyuewen2008@163.com(通信作者)
罗泽宇 男,1996年生,硕士研究生,研究方向为电力系统优化运行与规划。E-mail:617279272@qq.com
(编辑 赫 蕾)