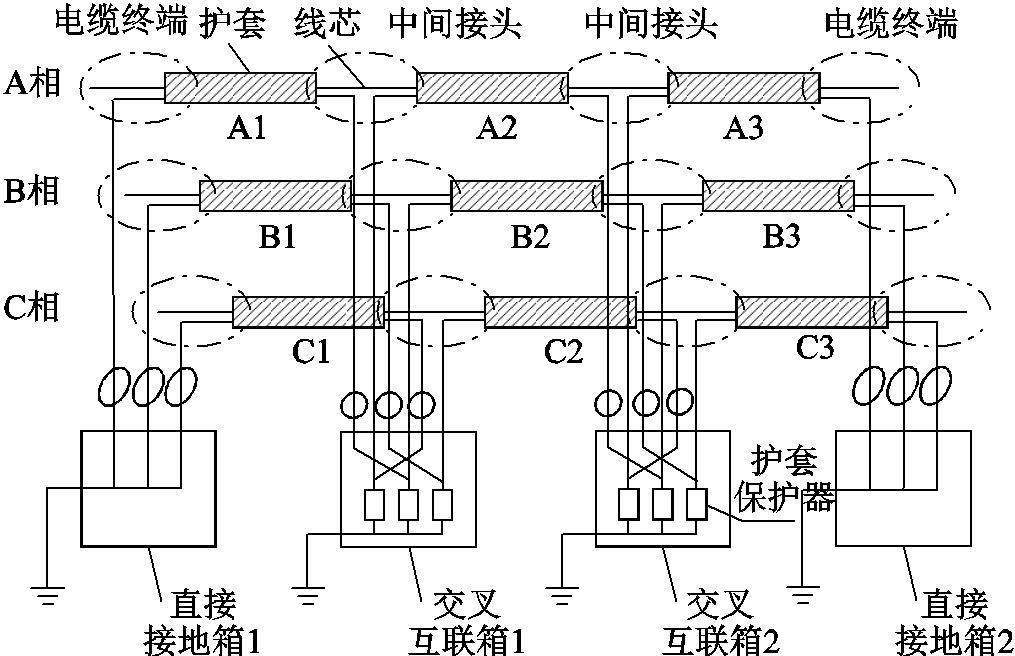
图1 高压电缆交叉互联接地方式
Fig.1 High voltage cable cross interconnection grounding method
摘要 高压电缆常见的接地方式是交叉互联接地,而交叉互联接地电缆故障时的测距相比单端接地或两端直接接地的电缆情况更为复杂,为此提出了基于线芯-护层过渡电阻无功特性的交叉互联电缆故障测距方法。首先,采集护层故障前后环流,构建不同电缆区段特征电流,判断故障发生区段;其次,考虑电缆金属护层对线芯的耦合作用和线路电容影响,建立交叉互联电缆的故障稳态等效阻抗模型,利用电缆首末两端线芯和护层的电压、电流推算电缆故障发生时不同区段沿线电压、电流,并基于同一位置电压相量对电缆参数进行修正;然后,利用故障点过渡电阻消耗无功功率为零的功率特性建立以故障距离为未知数的测距方程,采用二分法或弦截法等方法迭代计算求解得到故障点;最后,基于PSCAD/EMTDC仿真软件搭建了电缆故障模型,分析了故障距离、故障类型、过渡电阻、故障初相角等因素对故障测距方法的影响。结果表明,该方法的测距误差为0.4%左右,具有较高的准确性和有效性,对交叉互联接地电缆进行故障测距有一定的参考意义。
关键词:高压电缆 交叉互联 无功特性 故障稳态 故障测距
城市电网的建设需要大容量的电能传输,高压电力电缆因为优良的性能而被广泛应用于城市输电系统[1],其安全可靠运行对城市电网的稳定起着重要的作用[2-5]。尽管电缆线路敷设在地下或电缆沟中,但因人为损坏或电缆质量问题而引起的电缆故障时有发生[6],其中以单相故障为主。根据故障是否与护层有关,单相故障又可分为线芯-护层接地故障、线芯-护层故障和护层接地故障,如何快速准确地定位电缆单相故障对保证其安全运行具有重要意义[7-9]。
现有的在线故障测距方法按原理主要分为行波法和阻抗法[10]。行波法是通过测量具有固定波速的行波传播时间获取线路故障距离[11-12],如文献[13]提出基于故障特征频带和TT变换(time-time transform)的电缆单端行波方法;文献[14]通过小波变换得到故障点的特征频率,根据时域分析判别波头到达时刻实现故障测距;文献[15]提出以电流模量4作为行波测距信号的行波测距算法;文献[16]提出基于无监督学习的电缆行波测距方法。行波法虽然在理论上不受故障类型、过渡电阻等影响,但存在波头检测困难、易受干扰等不足。阻抗法的原理相对简单,易于实现且成本较低,学者们针对阻抗法在电缆故障测距中的应用展开了大量研究。文献[17]构建了电缆分布参数数学模型,但没有考虑三相之间的影响;文献[18]基于RL模型通过参数辨识实现单端故障测距,但模型未考虑线路和大地之间的电容;文献[19]建立了电缆的双层阻抗模型,基于电气量时域分析方法提出导芯-护层接地故障和导芯-护层短路故障方程进行定位辨识,但其模型忽略了线路电容;文献[20-21]考虑线路电容提出了计及电缆护层的单端故障测距方法,但不适用于采用交叉互联接地方式的电缆。
高压电缆护层接地方式主要包括单端接地、双端接地、交叉互联接地等[22]。交叉互联接地的电缆利用高压电缆三相护层换位连接的方式减小护层上的感应电压、抑制护层上的感应电流[23],其线芯和护层耦合关系相比单端和双端接地的电缆更为复杂。本文以双π模型为基础,考虑电缆金属护层对线芯的耦合作用和线路电容影响,建立交叉互联接地电缆发生单相短路故障时的稳态等效阻抗模型;通过电缆首末两端电气量计算故障时线芯与护层的沿线电压和电流,并基于同一点电压修正电缆电气参数;利用故障点过渡电阻消耗无功功率为零的功率特性建立了以故障距离为未知数的测距方程,迭代计算得到故障距离,通过仿真分析验证了该方法的可行性和有效性。
当高压电缆线路大于1 km时,为了降低护层中的感应电压和感应电流,电缆金属护层通常采用交叉互联的连接方式[24],即将高压电缆线路分为若干大段,每一大段分为三小段,每一小段电缆的金属护层在交叉互联箱中进行换位并装设护层保护器,每一大段电缆并联后接地。高压电缆交叉互联接地方式如图1所示,交叉互联电缆的护层通过交叉互联箱被分为A1-B2-C3、B1-C2-A3、C1-A2-B3三个回路。

图1 高压电缆交叉互联接地方式
Fig.1 High voltage cable cross interconnection grounding method
交叉互联电缆发生短路故障时,相比采用单端接地和双端接地等接地方式的电缆,故障相和非故障相之间的耦合作用更强,给故障测距带来较大困难。本文采用双π参数模型表示线芯与护层之间的耦合关系和阻抗特征[25],将一个交叉互联电缆大段划分为9个区段,每个区段均可等效为由线芯和护层组成的双π参数模型,三相电缆交叉互联接地正常运行时的等效模型如图2所示。图中,Rg为护层对地电阻,ycs为线芯与护层之间单位长度导纳,zcc为线芯单位长度阻抗,zss为护层单位长度阻抗。通过采集交叉互联电缆首端和末端电气量,可获得电缆的故障信息。但电缆护层电压通常不会设置专门的电压传感器进行实时测量,可通过解析计算得到护层电压值[26-28]。
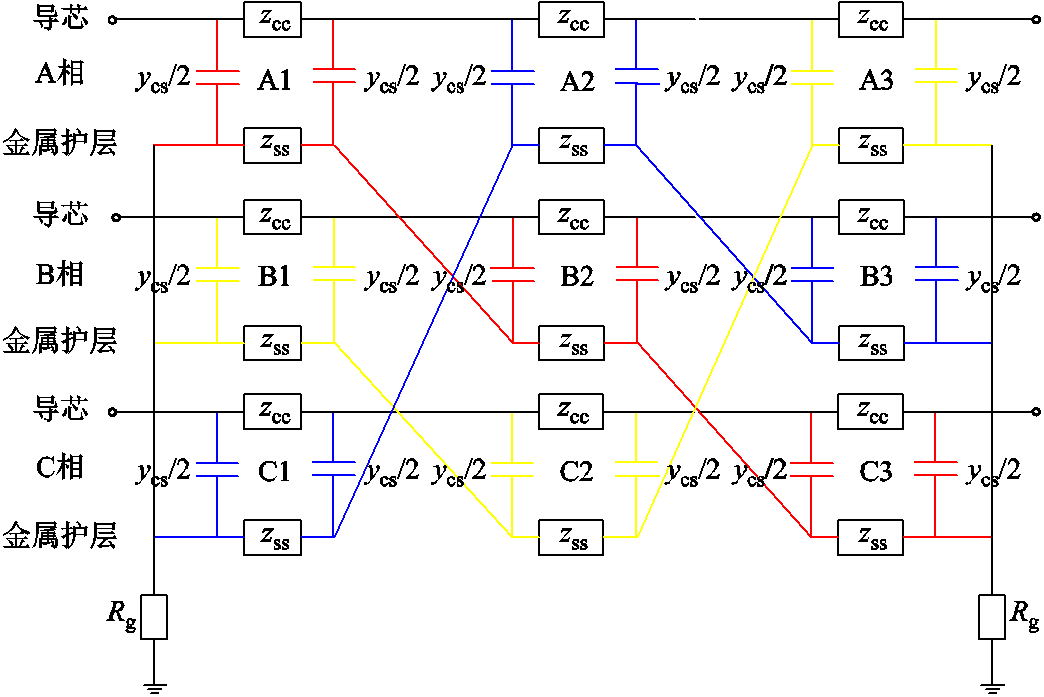
图2 三相电缆交叉互联接地等效模型
Fig.2 Equivalent model of three-phase cable cross-connection grounding
和架空线类似,电缆的电气参数包括自阻抗和导体间的互阻抗及导体的并联导纳等,其中电容和导纳等可通过电缆的物理构造和几何结构来计算,自阻抗和互阻抗由导体的材料、结构、外形尺寸和土壤电阻等决定[29]。文献[30]证明了三种准确度相对较高的电缆参数计算方法,可以满足应用要求,故本文采用文献[30]的方法1计算电缆参数,通过图2将交叉互联电缆划分为9个区段单元计算电气参数。
得到电缆参数后,按照每个交叉互联电缆大段可划分为3个小段的结构,每一小段的三相单芯电缆6根导体组成的线芯与护层耦合模型如图3所示。图3所示为A相与其他两相的耦合关系,B、C相与A相类似,图中,l为电缆区段的单位长度;ysg为护层与大地之间单位长度阻抗;m为单位长度互阻抗,其上标代表A、B、C相,下标代表线芯或护层(如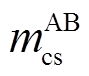 表示A相线芯与B相护层之间的互阻抗,A1、A2、A3区段相同,B1、B2、B3区段相同,C1、C2、C3区段相同)。
表示A相线芯与B相护层之间的互阻抗,A1、A2、A3区段相同,B1、B2、B3区段相同,C1、C2、C3区段相同)。
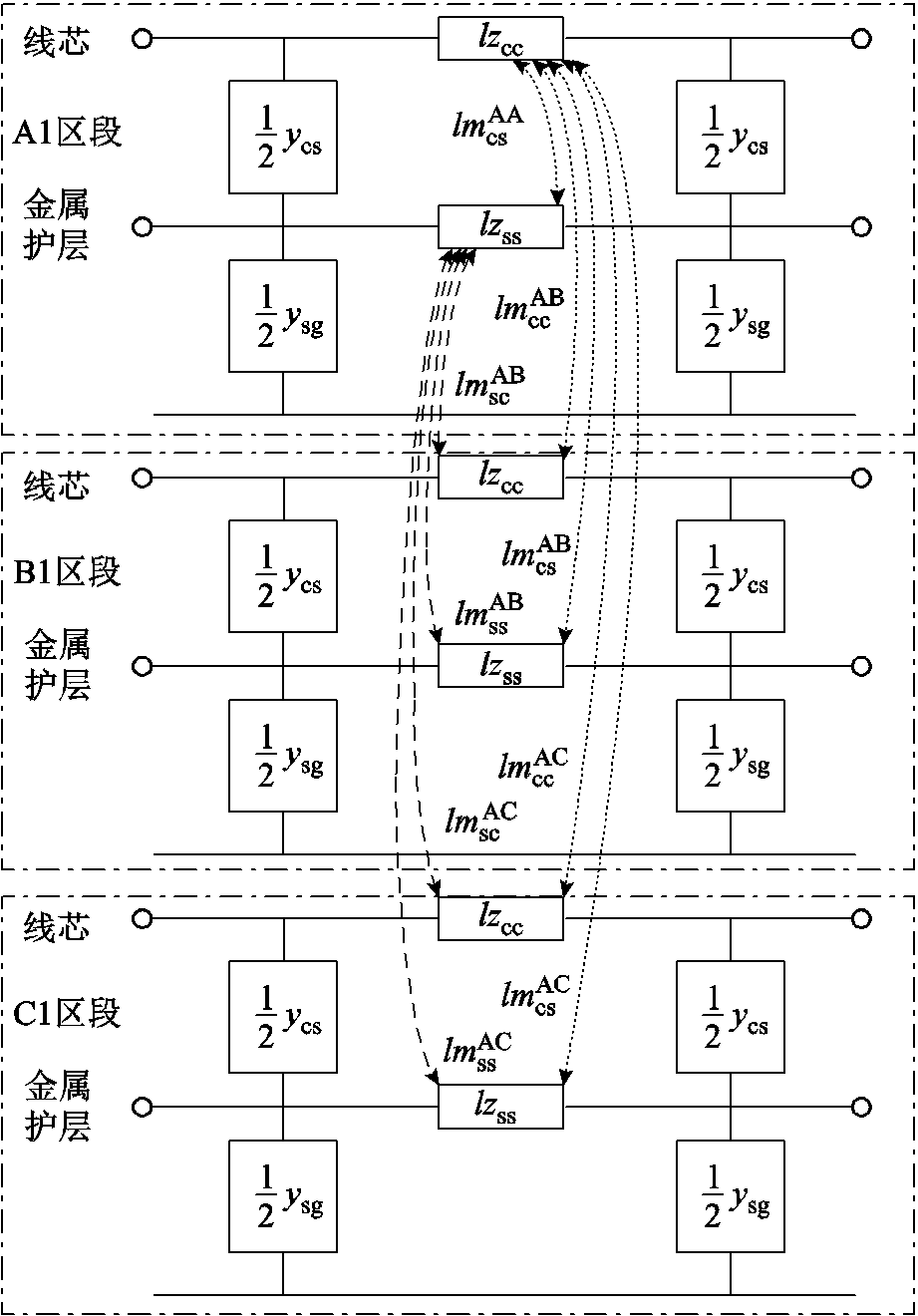
图3 三相单芯电缆线芯与护层耦合模型
Fig.3 The coupling model of three phase single core cable core and sheath
交叉互联电缆的直接接地箱和交叉互联箱为护层环流监测点[31],共有12个测量电流I1a~I1c、I2a~I2c、I3a~I3c、I4a~I4c,本文研究的短路故障均和护层有关,通过分析故障前后护层环流特征,可确定故障发生区段。
通过计算不同测量电流的差值,可反映对应电缆区段的护层环流变化特征。假设从左往右为电流正方向,其中一条回路A1-B2-C3的测量电流如图4所示。计算两个测量电流的差值作为特征电流,不同电缆区段对应的特征电流对应关系见表1。
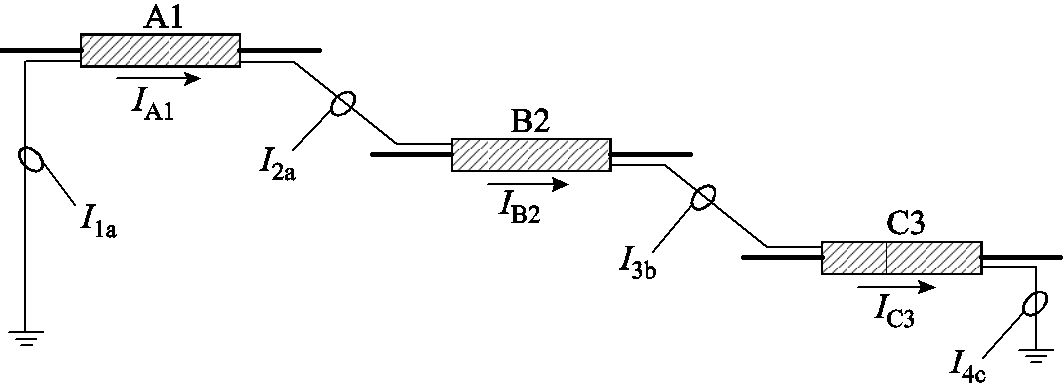
图4 电缆护层A1-B2-C3回路测量电流示意图
Fig.4 Current measurement diagram of cable sheath A1-B2-C3 loop
表1 电缆区段护层环流特征和测量电流差值对应关系
Tab.1 The relationship between the characteristics of cable section sheath circulation and the measured current difference

电缆区段特征电流名称测量电流差值 A1IA1I1a-I2a A2IA2I2c-I3a A3IA3I3c-I4a B1IB1I1b-I2b B2IB2I2a-I3b B3IB3I3a-I4b C1IC1I1c-I2c C2IC2I2b-I3c C3IC3I3b-I4c
本文采用测量电流故障前后护层环流差值有效值积分作为判断电缆区段是否发生短路故障的依据。电流差值可以反映故障前后电流变化,对电流进行积分可以反映出护层通过环流的幅值与方向变化情况,能有效区分并确定故障所在区段[32]。积分表达式如式(1)所示,特征电流变化量最大对应的电缆区段即为故障区段。
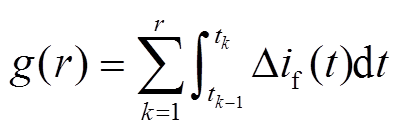 (1)
(1)
式中,r=1,2,…,R-1,R为采样窗口大小;Δif为同一测量点故障前后电流差值;tk为采样时间点。
通过以上判据,可判别交叉互联电缆发生短路故障区段,进而对故障发生区段进行故障测距。不同电缆区段发生单相短路故障时的特征电流及判别结果见附表1,受限于篇幅,仅列出部分数据。
由图2和图3可知,通过双π集总参数模型可表示电缆线路的电容和线芯与护层的耦合关系,同时可表示电缆发生故障时的沿线电压、电流分布。当A1区段发生故障时,不同电缆区段电气量示意图如图5所示。图5中上标表示ABC三相,下标h、t分别表示首端和末端,f表示故障点,c、s分别表示电缆线芯和电缆护层。如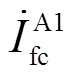 和
和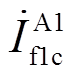 分别表示A1区段电缆线芯故障点前、后的故障电流。
分别表示A1区段电缆线芯故障点前、后的故障电流。
以A1区段发生线芯-护层接地故障为例,得到如图6所示的故障稳态等效模型,其余8个区段均可得到类似模型。利用基尔霍夫电流定律(Kirchhoff's Current Law, KCL)和基尔霍夫电压定律(Kirchhoff's Voltage Law, KVL)可得到4个回路的故障电压关系和8个节点(①~⑧)的故障电流关系,详见附录。
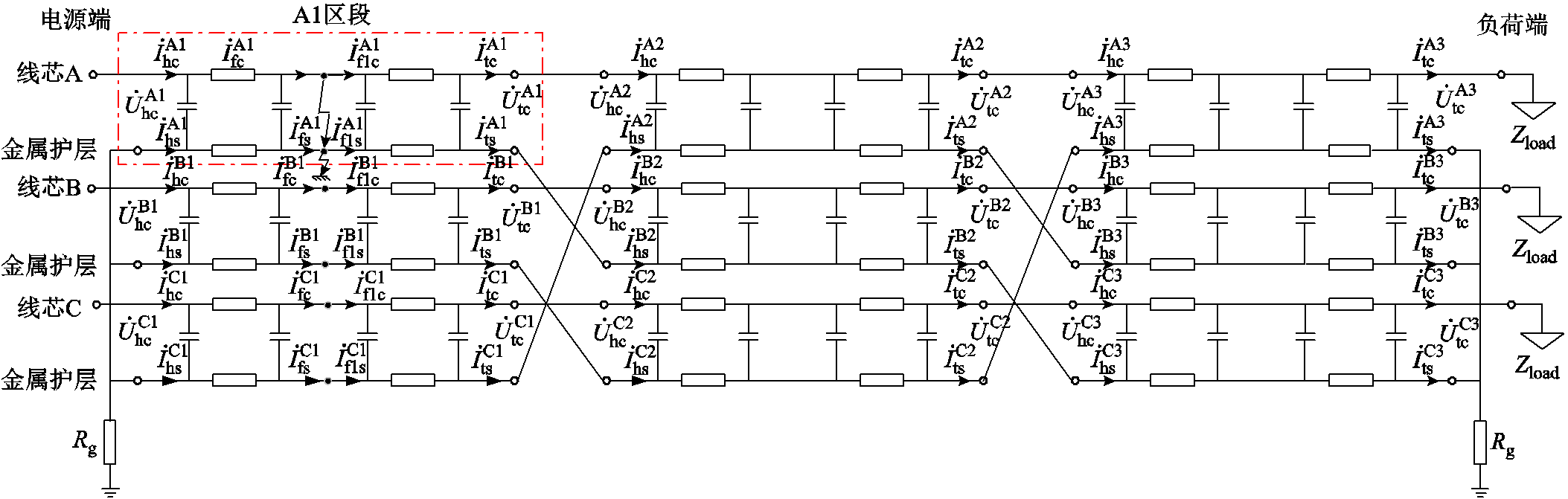
图5 交叉互联电缆故障时不同区段电气量示意图
Fig.5 Schematic diagram of different sections of the cross-interconnection cable when it is faulty
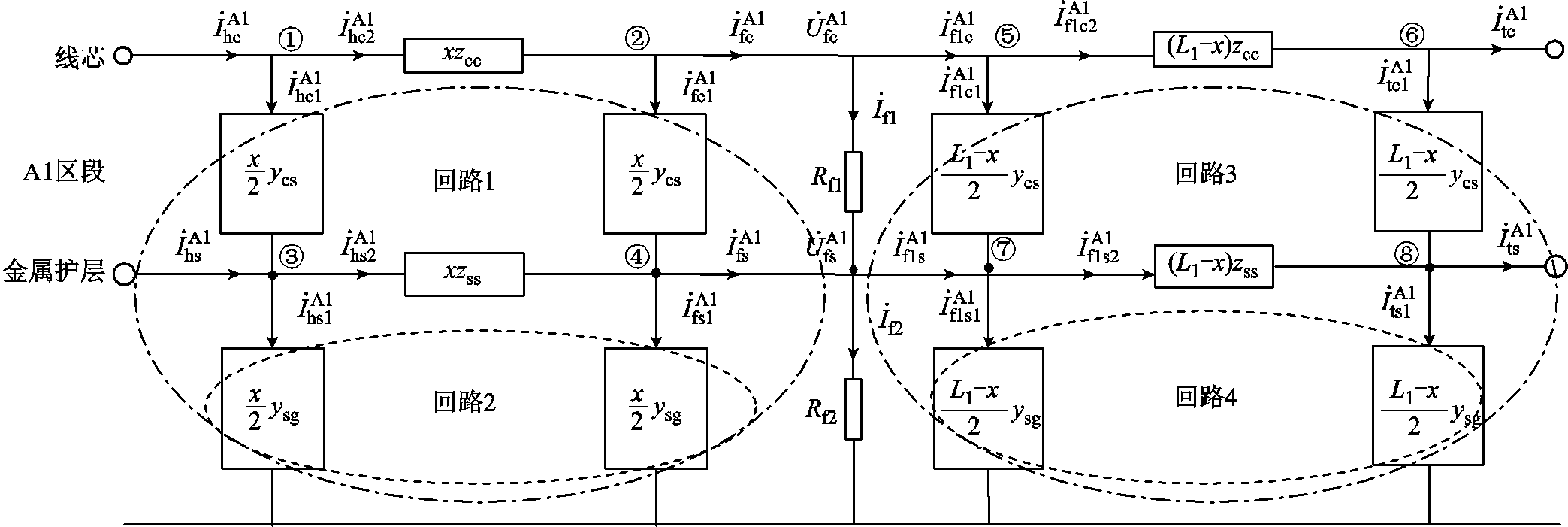
图6 交叉互联电缆A1区段故障稳态等效模型
Fig.6 Fault stable equivalent model for section A1 of cross-connected cable
A1区段电缆发生故障时,故障点前,A1区段电缆首端的故障电压、电流可通过电缆首端测量或计算的电压、电流得到。通过线路首端电气量计算得到的距离A1区段首端为x的故障点处电压和电流相量关系用矩阵表示为
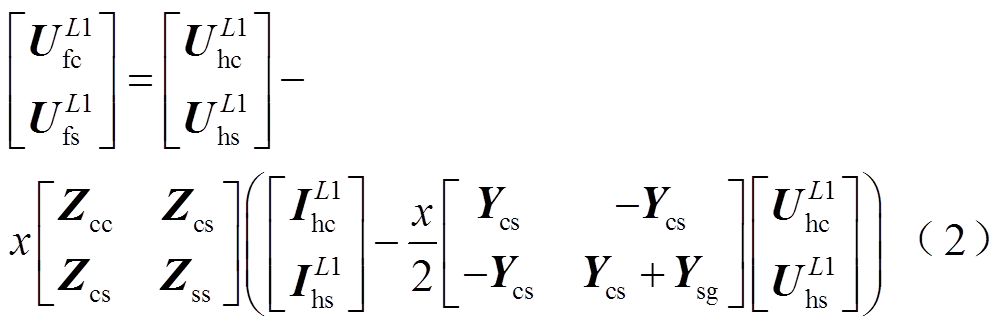
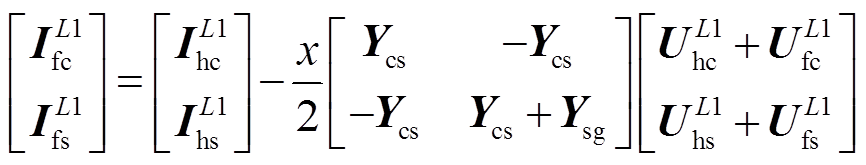 (3)
(3)
其中
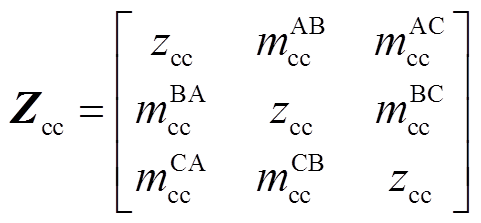
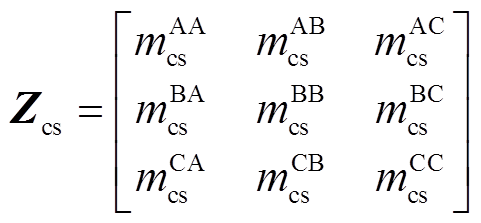
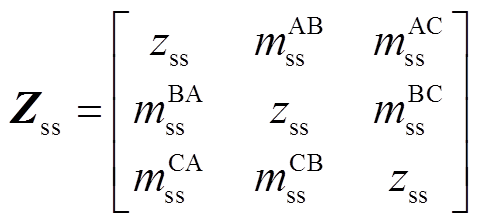
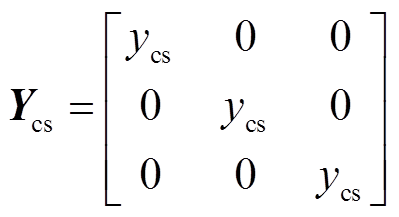
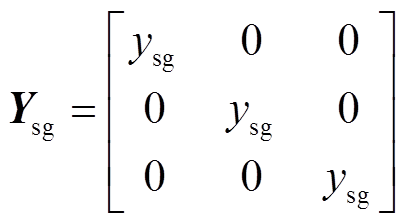
式中,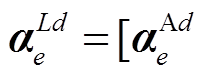
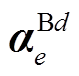
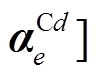 ,α分别为U和I,上标d=1, 2, 3,下标e分别为hc、hs、tc、ts、flc、fls。
,α分别为U和I,上标d=1, 2, 3,下标e分别为hc、hs、tc、ts、flc、fls。
A1区段电缆发生故障时,故障点后,A3区段电缆末端的故障电压、电流可通过电缆末端测量或计算的电压、电流得到,A3区段首端与A3区段末端的故障电压、电流相量关系用矩阵表示为
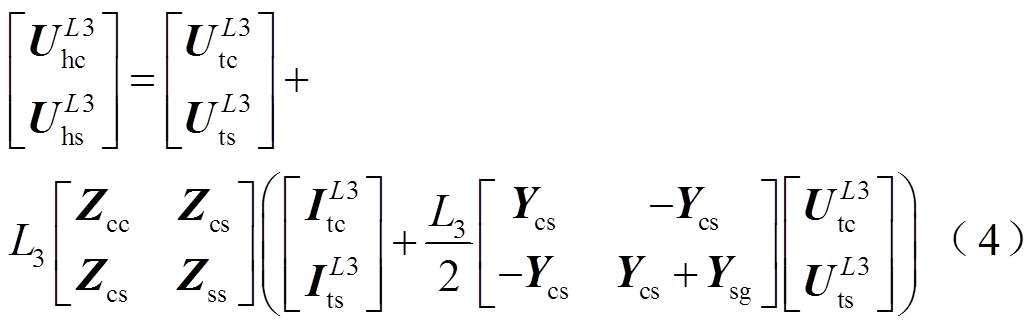
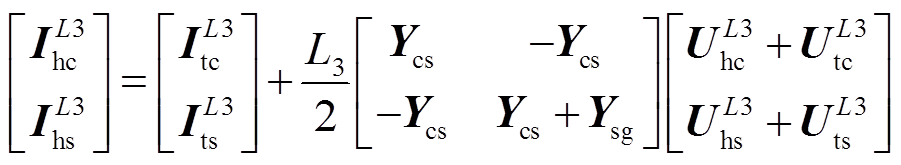 (5)
(5)
由交叉互联换位关系可得,第二段和第三段电缆之间的故障电压和电流相量关系为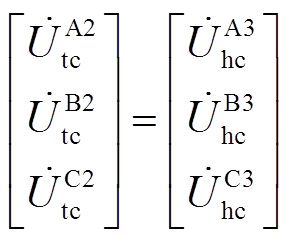 ,
,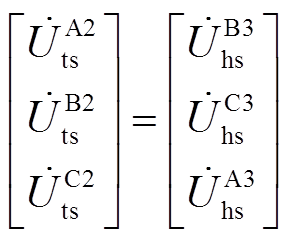 ,
,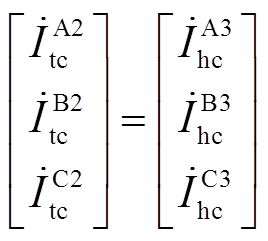 ,
,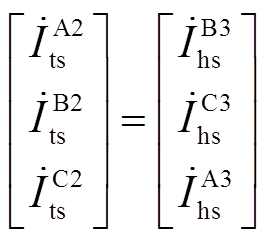 。
。
A2区段首端与A2区段末端的故障电压、电流相量关系用矩阵表示为
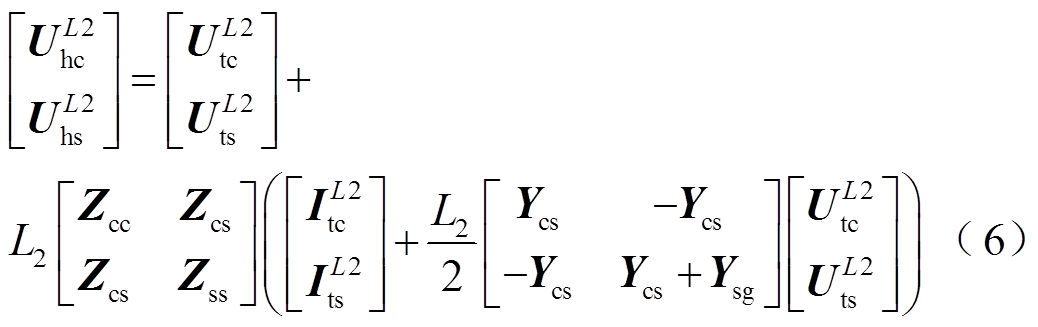
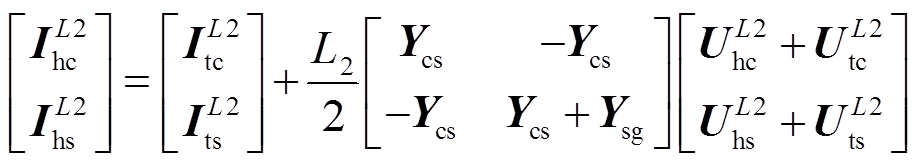 (7)
(7)
由交叉互联换位关系可得,第一段和第二段电缆之间的故障电压和电流相量关系为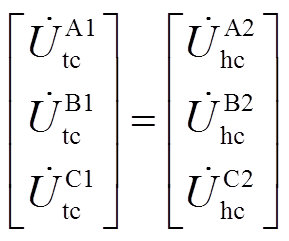 ,
,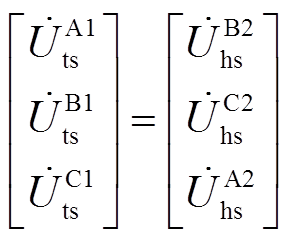 ,
,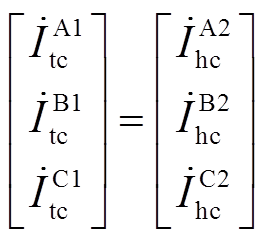 ,
,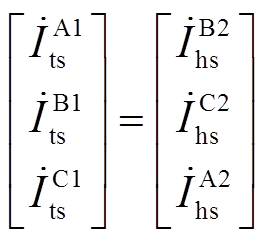 。
。
由以上推导过程可得到,通过线路末端测量计算得到距离A1区段首端为x的故障点处电压和电流相量关系用矩阵表示为
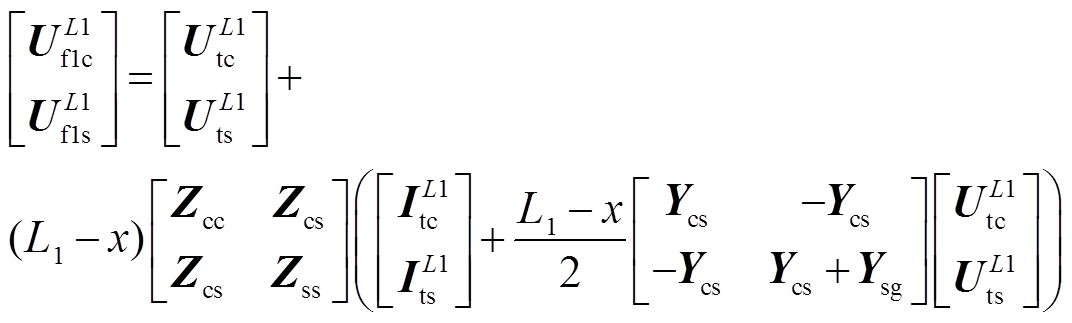 (8)
(8)
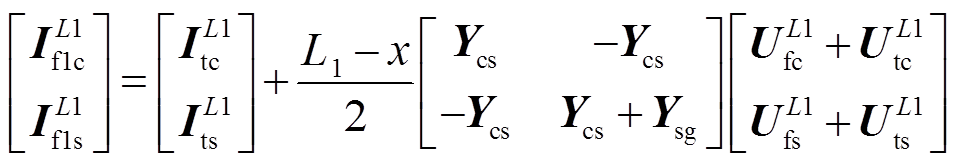 (9)
(9)
式中,L1、L2、L3分别为电缆三个区段的长度。
同理,当其他8个区段发生故障时,故障点前、后的沿线故障电压、电流均可类似推导得到。
通过2.2节所述沿线电压、电流计算方法,可得到交叉互联电缆正常或故障状态下沿线任意一点的电压、电流。然而通过第1节的电缆参数计算方法得到的电缆参数,受实际线路参数测量和计算误差影响,可能存在计算得到参数与实际参数相差过大导致电压、电流计算不准确问题,进而影响故障测距精度。
对于一条正常运行的线路,线路参数变化不会影响采用不同方法计算同一点的分布电压[33]。基于此,本文采用电缆正常运行时不同时刻的电压、电流,通过2.2节所述电压、电流计算方法得到同一位置的电压相量对电缆参数进行修正。交叉互联电缆大段划分的三小段电缆中,第二小段电缆两端数据无法直接采集得到,故本文采用交叉互联电缆第二段中间位置的电压作为参数修正的基准电压,通过电缆首末两端电压电流分别推算得到基准电压,根据基准电压是否相等对参数进行准确计算。
为了设定参数误差范围时更容易找到依据,本文将第1节计算得到的单位长度阻抗zcc、zss和导纳ycs、ysg转换为单位长度电阻r0、电感l0和电容c0进行修正。修正过程中受采集数据误差、计算误差等因素影响,某一时刻的计算参数不能代表参数修正的最终结果。因此,本文采用遗传算法进行寻优处理。
利用遗传算法寻优,需要修正的参数包括单位长度的自阻或互阻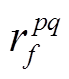 、单位长度的自感或互感
、单位长度的自感或互感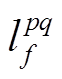 、单位长度电容
、单位长度电容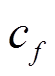 和电缆三段长度Lh。其中p、q表示相序A、B、C,f表示cc、cs、ss、sg,h表示交叉互联三段电缆序号1、2、3,例如
和电缆三段长度Lh。其中p、q表示相序A、B、C,f表示cc、cs、ss、sg,h表示交叉互联三段电缆序号1、2、3,例如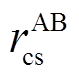 表示单位长度A相线芯和B相护层之间的互阻,其余可依此类推;
表示单位长度A相线芯和B相护层之间的互阻,其余可依此类推;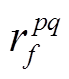 和
和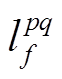 的变化范围在±10%,
的变化范围在±10%,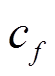 和Lh的变化范围在±5%;选择适当的最大进化代数n、种群规模ps、交叉概率pc和变异概率pm;适应度函数选择首端和末端分别计算得到的交叉互联电缆第二段线芯和护层中点处的电压幅值差值,即
和Lh的变化范围在±5%;选择适当的最大进化代数n、种群规模ps、交叉概率pc和变异概率pm;适应度函数选择首端和末端分别计算得到的交叉互联电缆第二段线芯和护层中点处的电压幅值差值,即

式中,M为适应度函数;N为故障发生时刻前一个周期内的采样点数;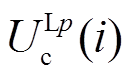 、
、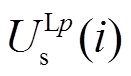 、
、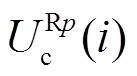 、
、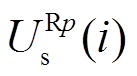 分别为i时刻交叉互联电缆第二段中点通过电缆首端和末端采集故障电压电流计算得到的线芯和护层电压幅值,c、s分别表示线芯和护层,p表示A、B、C,其中,
分别为i时刻交叉互联电缆第二段中点通过电缆首端和末端采集故障电压电流计算得到的线芯和护层电压幅值,c、s分别表示线芯和护层,p表示A、B、C,其中,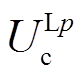 、
、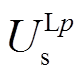 分别为通过首端电压电流计算得到的线芯和护层沿线电压,
分别为通过首端电压电流计算得到的线芯和护层沿线电压,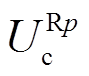 、
、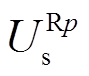 分别为通过末端电压电流计算得到的线芯和护层沿线电压,具体计算方法和式(2)~式(9)原理相同。
分别为通过末端电压电流计算得到的线芯和护层沿线电压,具体计算方法和式(2)~式(9)原理相同。
基于遗传算法的线路参数修正计算的收敛条件是最大进化代数和适应度函数M取最小值,理论上应满足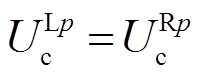 、
、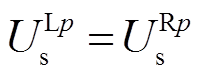 ,即M=0,考虑到误差范围,设M≤1%作为收敛条件。
,即M=0,考虑到误差范围,设M≤1%作为收敛条件。
基于以上分析,应用遗传算法对参数进行修正的流程如图7所示。
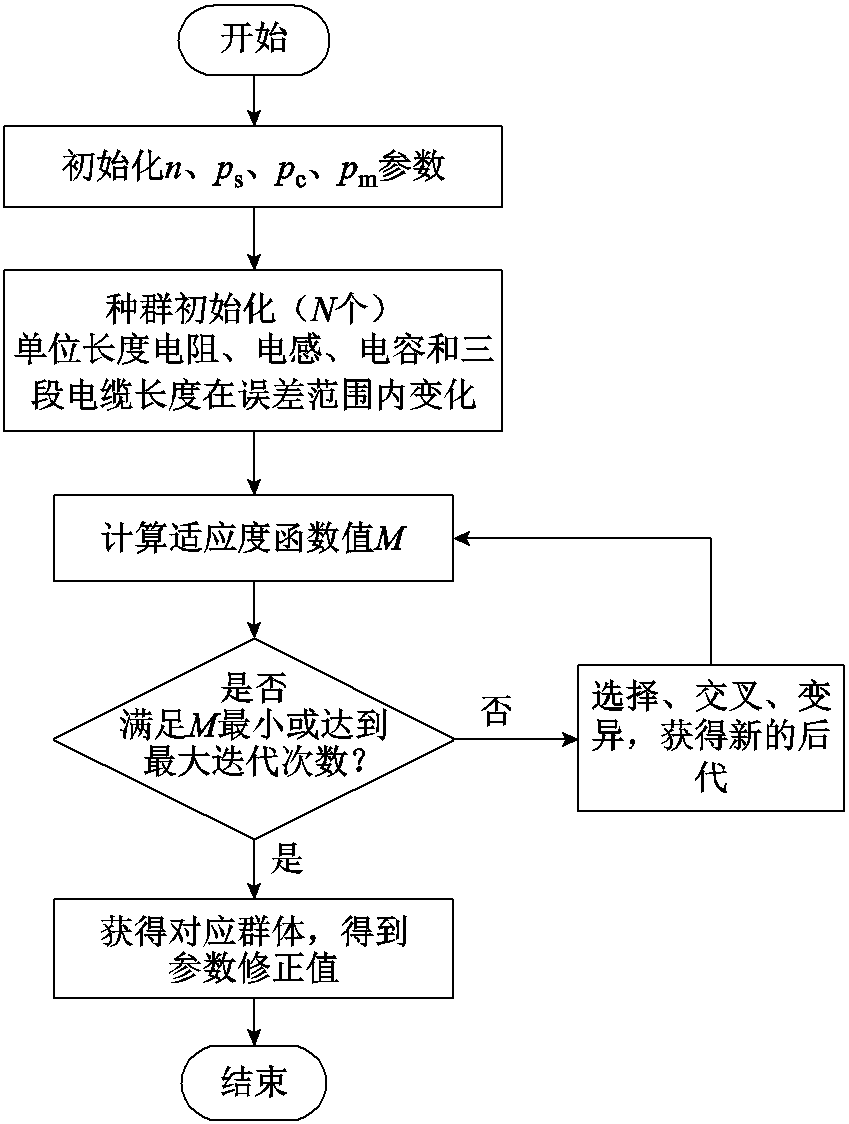
图7 电缆线路参数修正计算流程
Fig.7 Cable line parameter correction calculation process
根据2.2节对故障时不同电缆区段沿线故障电压和电流的推导,以及2.3节对电缆参数的修正,本文基于故障稳态等效模型各元素物理意义,利用故障支路过渡电阻消耗无功功率为零的功率特性对电缆进行故障测距。
由图6可得流过过渡电阻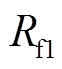 、
、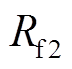 的故障电流
的故障电流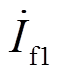 、
、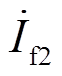 分别为
分别为
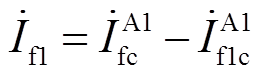 (11)
(11)
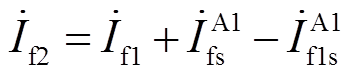 (12)
(12)
将式(3)和式(9)代入式(11)和式(12)可得到关于故障距离和故障支路电流的关系式为
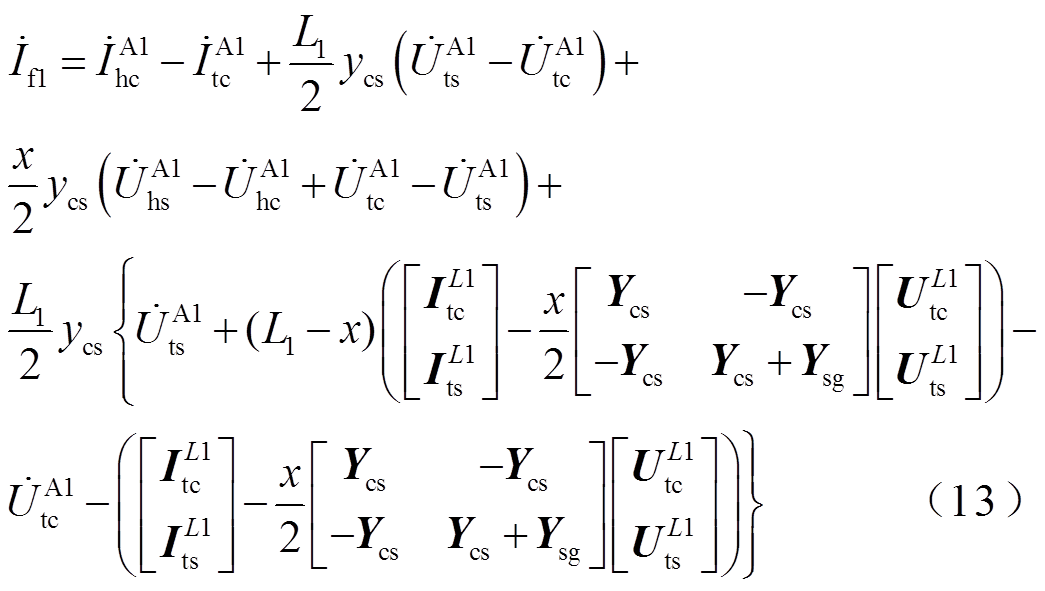
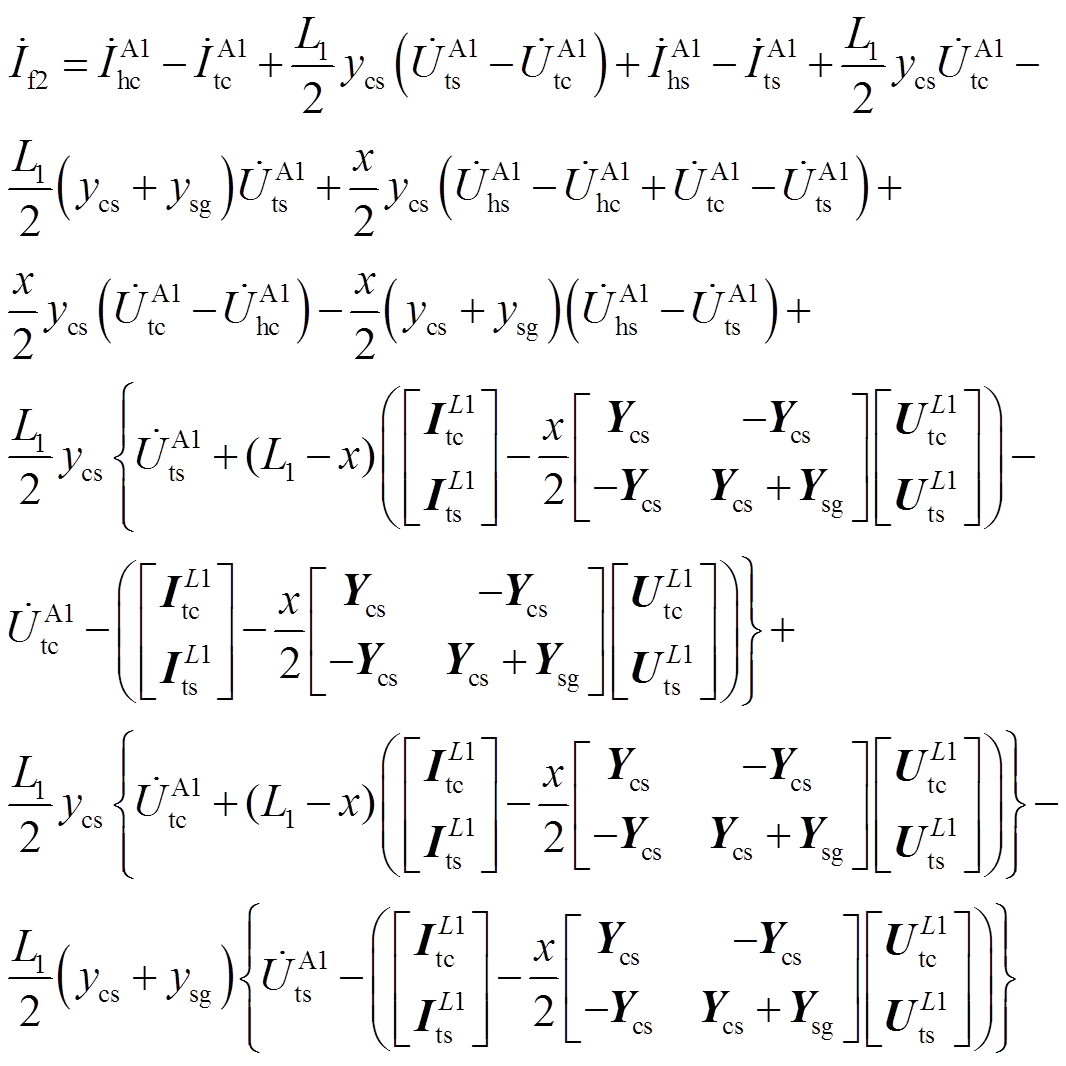 (14)
(14)
故障支路上过渡电阻消耗的无功功率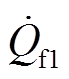 和
和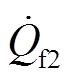 为
为
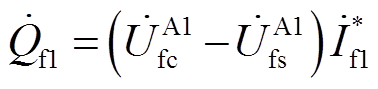 (15)
(15)
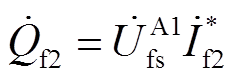 (16)
(16)
式中,*表示共轭运算。
两者之和为
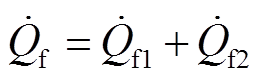 (17)
(17)
因为过渡电阻呈纯阻性,其消耗的无功功率为零,即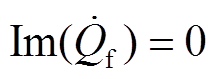 。将式(13)和式(14)分别代入式(17)并取虚部运算,得到以故障距离x和故障电流
。将式(13)和式(14)分别代入式(17)并取虚部运算,得到以故障距离x和故障电流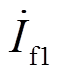 、
、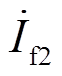 为未知数的关系式,如式(18)所示,其中故障电流
为未知数的关系式,如式(18)所示,其中故障电流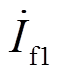 、
、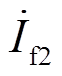 又可表示为关于故障距离x的函数,则式(18)可表示为关于x的一元五次方程,即故障测距方程。
又可表示为关于故障距离x的函数,则式(18)可表示为关于x的一元五次方程,即故障测距方程。
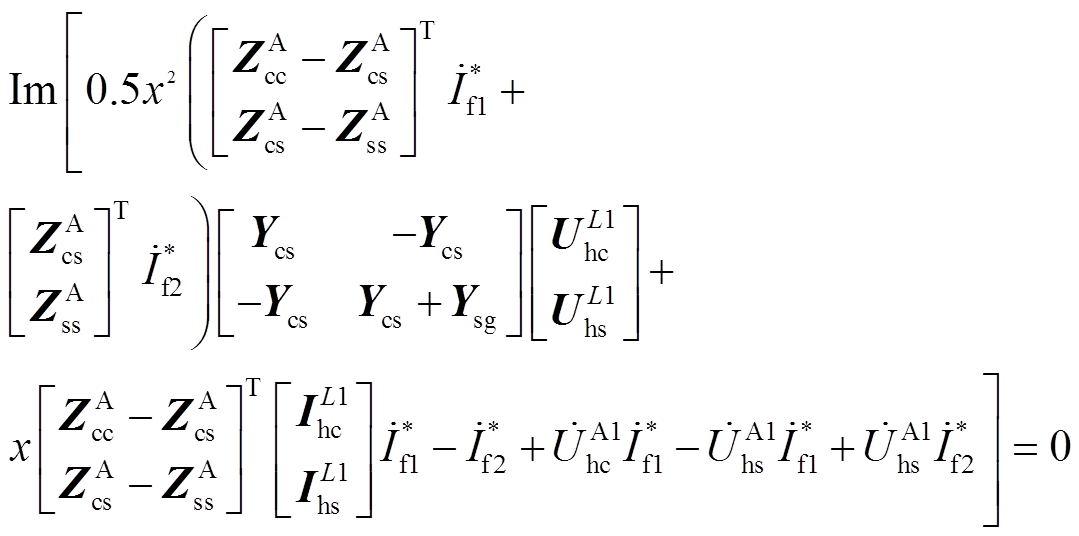 (18)
(18)
通过二分区间求根法或弦截求根法[34],可以求出满足式(18)的故障距离xo∈[0, L1](o=1, 2, 3, 4, 5),但得到的解可能不止一个根满足条件。为了得到最接近实际故障距离的根,可通过如下判据进行识别。令故障点前后电压差值为
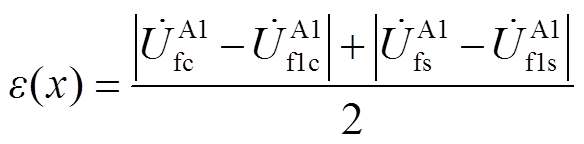 (19)
(19)
故障点前后电压为
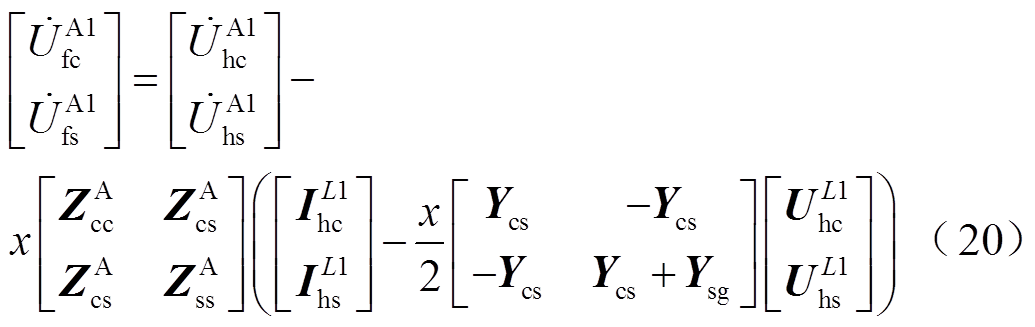
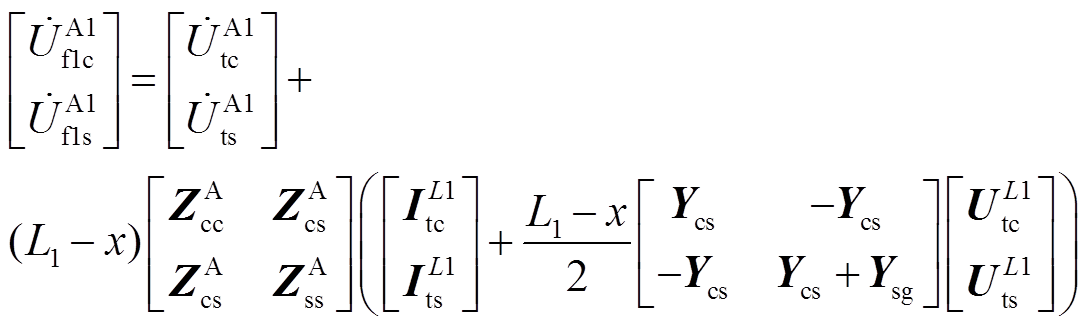 (21)
(21)
式中,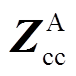 =[
=[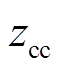
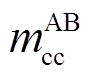
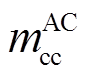 ],
],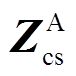 =[
=[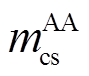
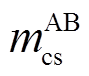
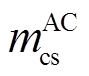 ],
], =[
=[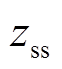
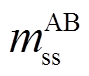
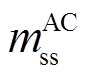 ]。
]。
由两端电气量计算沿线电压电流得到的故障点电压应相等,则理论上故障点x对应的电压差值ε(x)=0,考虑数据误差和计算精度,ε(x)应取最小值。将xi∈[0, L1]代入ε(x),得到满足ε(xi)取最小值的故障距离xi即为最终求解得到的故障距离。
实际求解过程中,通过前述过程求解故障测距方程的根需要较大的计算量,为了简化求解过程,初始化故障电流数值时,可以将故障电流简化为
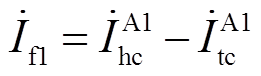 (22)
(22)
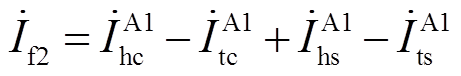 (23)
(23)
式中,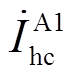 、
、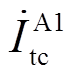 、
、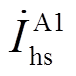 、
、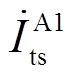 分别为故障区段A1的首末端线芯与护层电流,可通过式(2)~式(9)计算得到。
分别为故障区段A1的首末端线芯与护层电流,可通过式(2)~式(9)计算得到。
将简化的故障电流代入,则式(17)可简化为
 (24)
(24)
其中
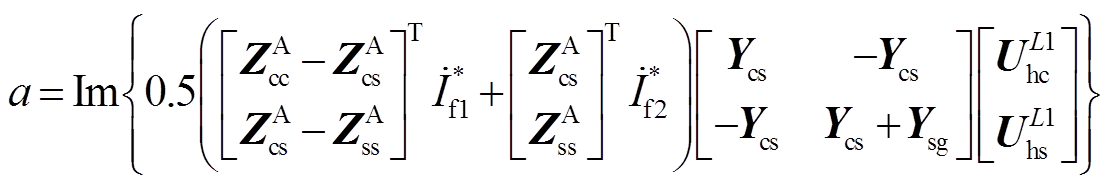
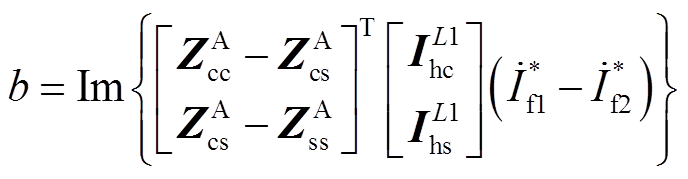
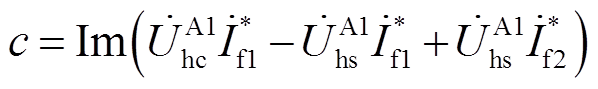
通过故障测距方程(24)和求根公式,可求得两个可能的解为
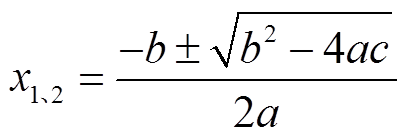 (25)
(25)
根据故障距离的物理意义,即xi∈[0, L1],对两个解进行筛选,得到符合实际的解作为所求故障距离;若两个解均符合条件,则按照式(19)所示判据选择ε(x)取较小值的解作为所求故障距离x。
本文考虑采用交叉互联接地方式的电缆线芯与护层之间的耦合作用和线路电容影响,以双π模型为基础,利用故障电阻消耗无功功率为零的特性,构建单相故障测距方程进行故障测距的计算流程如图8所示,具体步骤如下(以A1区段发生故障为例)。
1)通过交叉互联箱和直接接地箱测量故障发生前后护层环流,计算同一电缆区段两端护层环流差值积分作为特征电流,根据特征电流幅值是否最大判断对应电缆区段是否发生故障。
2)根据步骤1)判断得到的故障区段,通过电缆首末两端的线芯与护层电压、电流,计算得到故障区段首末两端的故障电压、电流。
3)将故障区段首末两端电流代入故障电流计算式(22)和式(23),作为故障支路电流初值。将故障支路电流初值代入式(25),根据故障距离物理意义,求得故障距离可能解。若满足条件的解不止一个,将两个解分别代入式(19),求得式(19)取最小值的解作为所求故障距离初值x0。
4)将故障距离初值x0代入故障电流计算式(13)和式(14),得到故障测距方程(24)。根据故障距离的物理意义,由式(25)计算得到故障距离xk(k=1, 2,…, n)。

图8 基于故障稳态等效模型的交叉互联电缆故障测距流程
Fig.8 Fault location flow of cross-connected cable based on fault stable equivalent model
5)将故障距离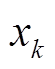 再次代入故障电流计算式(13)和式(14),得到新的故障测距方程,计算更为接近真实故障距离的故障距离
再次代入故障电流计算式(13)和式(14),得到新的故障测距方程,计算更为接近真实故障距离的故障距离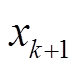 ,判断两次计算的故障距离是否满足式(26)的收敛条件。若满足,则迭代结束,得到最终故障距离
,判断两次计算的故障距离是否满足式(26)的收敛条件。若满足,则迭代结束,得到最终故障距离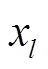 ;否则,迭代过程继续。
;否则,迭代过程继续。
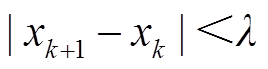 (26)
(26)
式中,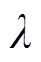 为阈值,本文取0.005。
为阈值,本文取0.005。
最终的故障测距结果为
 (27)
(27)
6)若步骤5)的迭代计算始终无法满足式(26)的收敛条件,则当迭代计算超过一定次数(本文取1 000次)时,将所有计算得到的故障距离xk依次代入式(19)。将式(19)取最小值的解作为所求最终故障距离。
本文通过PSCAD/EMTDC仿真平台搭建如图5所示仿真模型。电压等级设为110 kV,电缆线路采用频率相关(相位)模型,选用YJLW03-64/110-1×800型电缆搭建电缆仿真模型,其参数见表2,排列方式为品字形,全长1 800 m,交叉互联三段长度分别为500、600、700 m;采用傅里叶变换算法提取工频相量;用式(28)表示测距方法的准确性。
 (28)
(28)
表2 电缆仿真参数
Tab.2 Cable simulation parameters

电缆参数数值电缆参数数值 线芯外径/mm34.2金属护层内径/mm78.6 半导电屏蔽层厚度/mm2金属护层外径/mm82.6 绝缘厚度/mm16XLPE相对介电常数2.3 电缆外径/mm94大地电阻率/(Ω·m)100 线芯电阻率/(Ω·m)1.68×10-8护层电阻率/(Ω·m)2.8×10-8
以A1区段发生线芯-护层接地故障为例,对本文所提故障测距方法进行验证,设置故障电阻为0.5 Ω,故障初相角为0°,故障距离为280 m。对电缆参数进行修正时,设进化代数n=50,种群规模ps=1 500,交叉概率pc=0.5,变异概率pm=0.2,按照图7的电缆参数修正流程得到参数校正结果见附表2。由附表2可知,通过参数修正,可以将参数误差降到1.1%左右的范围内。按照图8的故障测距流程得到的测距结果如表3和图9所示。基于护层环流故障分量积分的故障区段判别结果为A1区段,通过迭代计算得到的故障测距结果为280.14 m(图9中所示仅为故障区段长度范围内曲线图)。如图10所示为故障测距方程收敛时故障点前后电压差值随电缆长度变化情况,由图10可知所得测量结果对应的故障电压差值最小。
表3 电缆故障发生区段判断结果(以A1区段电缆故障为例)
Tab.3 Judgment result of the section where the cable fault occurs (Take the cable fault in section A1 as an example)

特征电流名称IA1IA2IA3IB1IB2IB3IC1IC2IC3故障区段判断结果 数值65.280.0670.0140.0530.004 80.2050.460.910.104A1
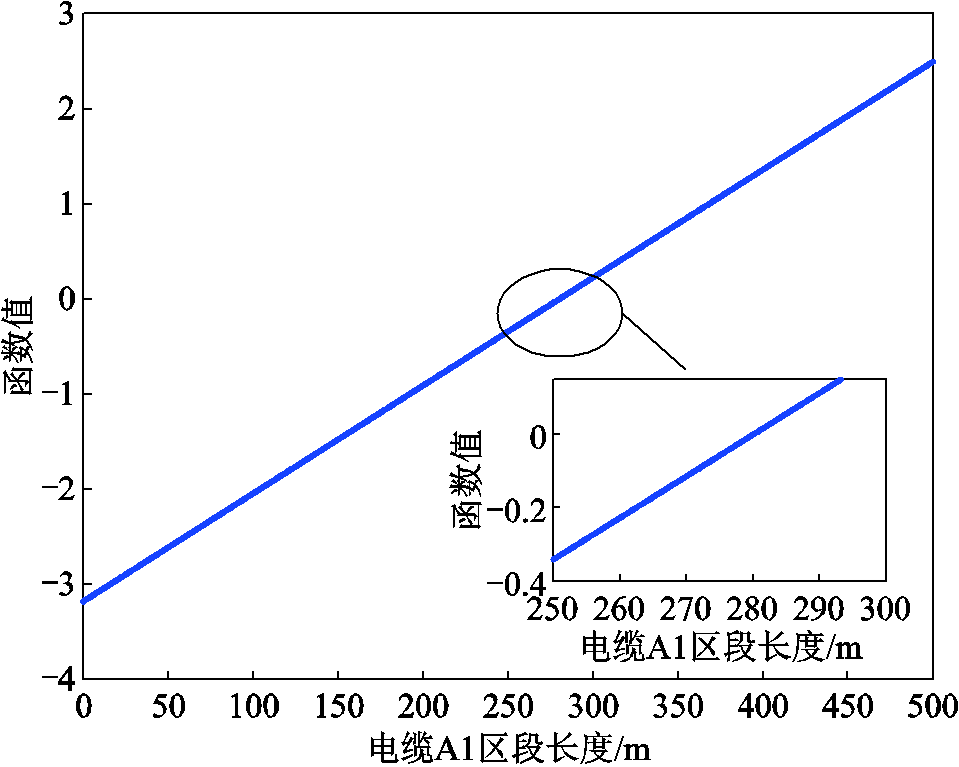
图9 A1区段电缆故障时故障测距方程曲线
Fig.9 Fault location equation curve for cable failure in section A1
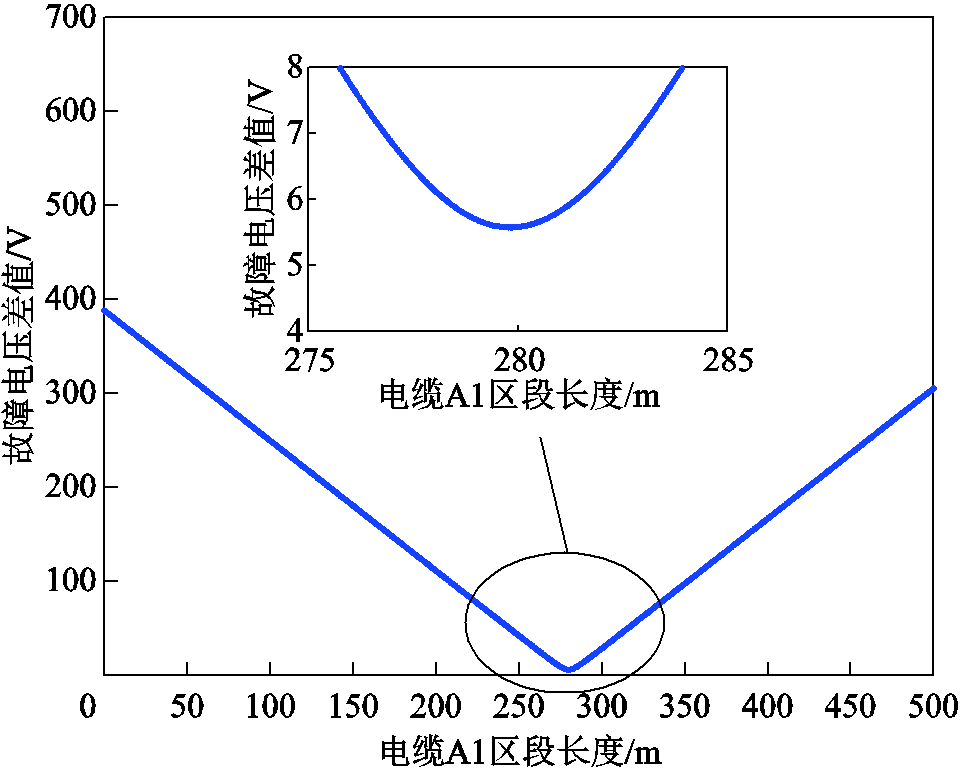
图10 A1区段电缆故障时故障电压差值
Fig.10 Fault voltage difference in case of cable failure in section A1
本文所提方法使用了电缆双端电气量,两端采集数据的时间在仿真模型中完全同步,实际应用中,双端采集数据在大部分时间是不同步的,此时沿线电压分布和时间同步时相比呈现更为复杂的变化趋势。而由沿线电压计算式(20)、式(21)和本文所提故障测距方法可知,故障测距方程和沿线电压有关,沿线电压变化更为复杂,故障测距方程计算将出现更多伪根。通过对沿线电压变化进行分析得,沿线电压的复杂变化随故障情况的不同,未必一定出现,但在部分极端情况下存在有更多伪根的可能性[35],此时式(25)的求根公式将无法直接求得故障距离的解,需要采用二分法或弦截法求根,且所得满足故障距离物理意义的故障距离解可能不止一个。当出现不止一个满足故障距离物理意义的解时,需要用式(19)的判据对所有根进行判别,得到唯一的满足所有条件的最终解作为所求故障距离。
以电源端故障信息采集时间为参考,设置负荷端故障信息采集时间落后电源端0.1 s,其余短路故障设置不变,得到故障测距结果如图11和图12所示,故障测距结果为281.04 m,相比双端时间同步时,测距结果仍有较高的精确度。

图11 双端采样时间不同步时A1区段电缆故障测距方程曲线
Fig.11 The fault location equation curve of A1 section cable when the sampling time of both ends is not synchronous
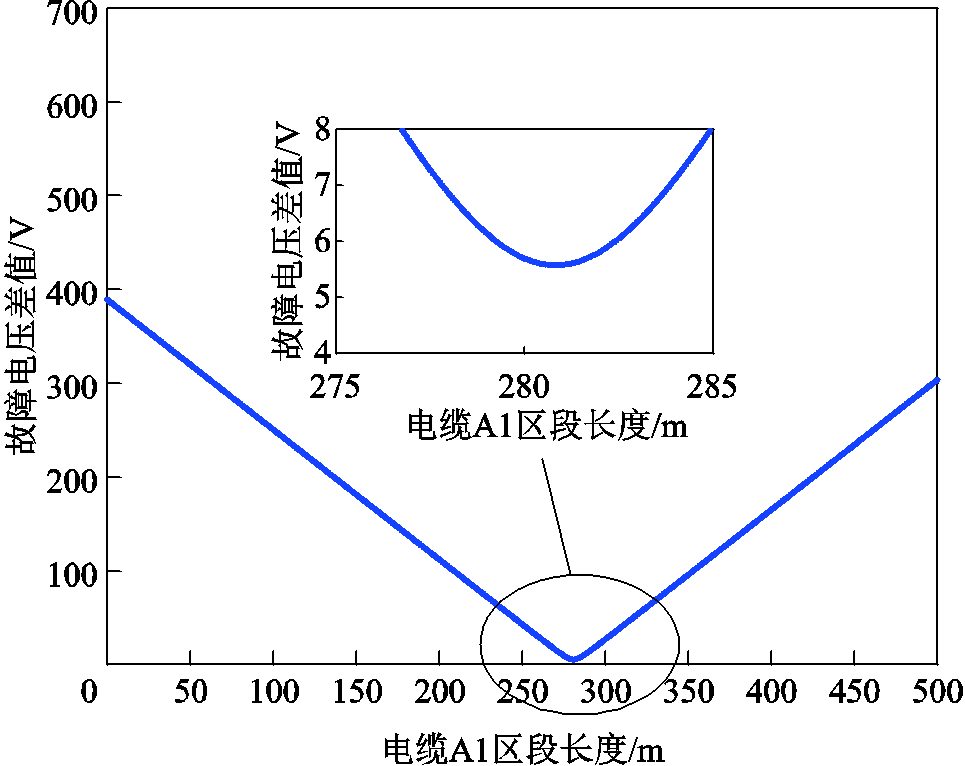
图12 双端采样时间不同步时的A1区段电缆故障时故障电压差值
Fig.12 The fault voltage difference value of A1 section cable when the sampling time of both ends is not synchronized
此外,当电缆发生短路故障时,安装在电缆线路交叉互联接地箱体内和电缆终端箱内的护层保护器可能动作,用于限制电缆线路护层中的感应电压或释放护层中的过电压[36]。本文所研究的单相短路故障可能引发的护层过电压属于工频过电压[37],在工频过电压下护层保护器是否动作尚无准确定论[38],因此需要分情况讨论:若护层保护器不动作,则可按照图8的故障测距流程计算故障距离;若护层保护器动作,则形成新的接地通路,此时可通过交叉互联箱的电流传感器采集护层电流,其余计算步骤相同,对测距影响不大。综上所述,护层保护器动作特性对测距影响较小。
3.3.1 故障距离和故障类型对测距算法的影响
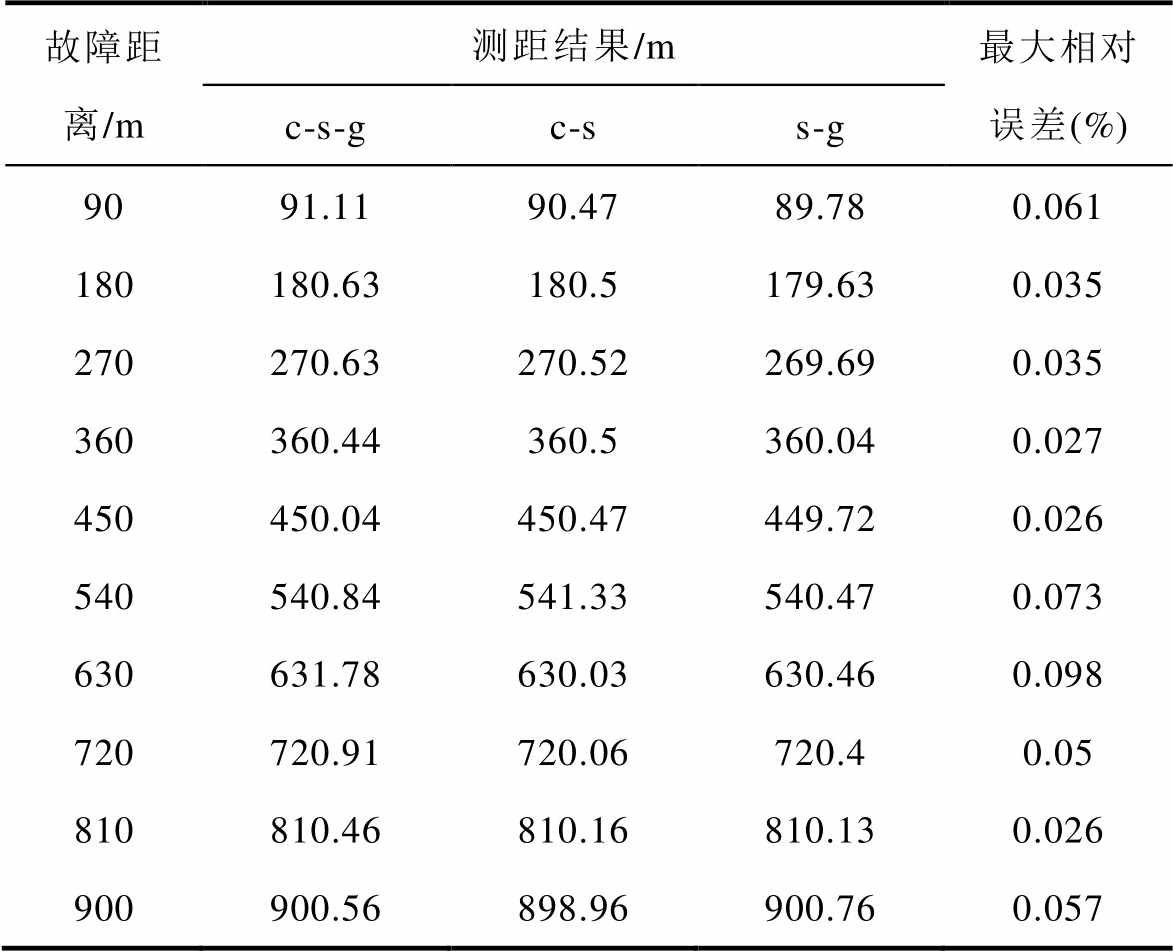
设故障类型为线芯-护层接地故障(c-s-g)、线芯-护层故障(c-s)和护层接地故障(s-g),故障初相角为0°,故障电阻为5 Ω。不同故障距离下的故障测距结果见表4。
表4 不同故障距离和故障类型下的故障测距结果
Tab.4 Fault location results under different fault distances and fault types
故障距离/m测距结果/m最大相对误差(%) c-s-gc-ss-g 9091.1190.4789.780.061 180180.63180.5179.630.035 270270.63270.52269.690.035 360360.44360.5360.040.027 450450.04450.47449.720.026 540540.84541.33540.470.073 630631.78630.03630.460.098 720720.91720.06720.40.05 810810.46810.16810.130.026 900900.56898.96900.760.057
由表4可知,在不同故障距离发生不同类型短路故障时,均可实现较为准确的定位,误差基本在0.1%以内,测距精度较高。
3.3.2 电缆排列方式对测距算法的影响
当电缆故障类型为线芯-护层故障,故障电阻为10 Ω,故障初相角为10°时,电缆采用不同排列方式时的故障测距结果见表5。由表5可知,不同的电缆排列方式对故障测距存在影响,品字形排列影响相对较小,水平排列次之,直角排列误差相对最大,但最大误差不超过0.3%,电缆排列方式对故障测距的影响相对较小。
表5 不同电缆排列方式下的故障测距结果
Tab.5 Fault location results under different cable arrangement modes

故障距离/m测距结果/m最大相对误差(%) 品字形水平排列直角排列 120121.34122.48122.780.15 200202.18203.41203.540.19 280280.87280.97282.820.16 360361.22361.62362.450.13 440440.58442.31443.250.18 520522.15521.83524.590.25 600601.63601.78603.240.18 680680.29681.75682.610.14 760760.88762.39762.460.13 840842.76842.58844.240.24 920920.96921.31921.870.1 1 0001 001.281 001.321 001.960.1
3.3.3 故障初相角对测距算法的影响
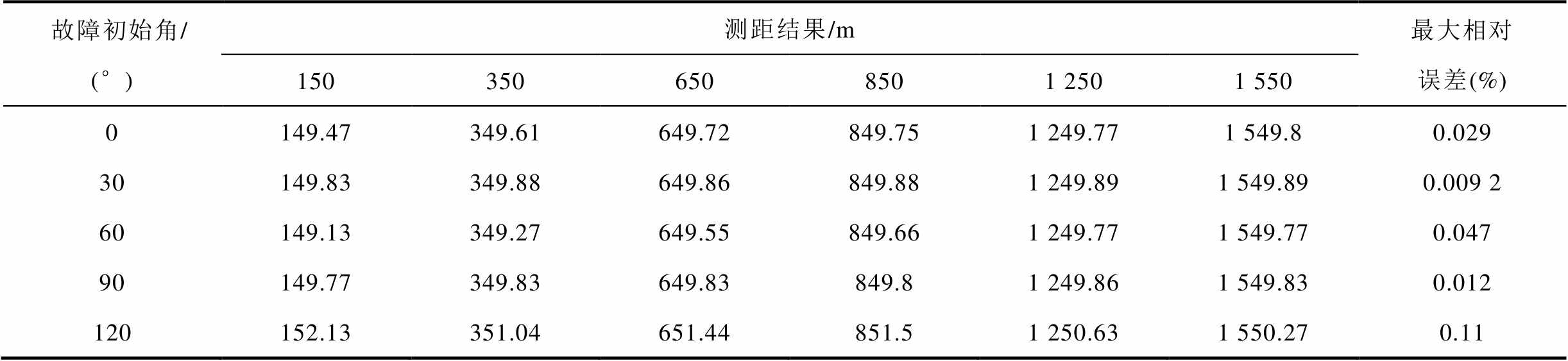
设故障类型为线芯-护层故障,故障初相角分别为0°、30°、60°、90°、120°,故障电阻为20 Ω。故障测距结果见表6。由表6可知,不同初相角对故障测距结果影响较小,误差基本在0.2%以内,具有较高的测距精度。
表6 不同故障时刻的故障测距结果
Tab.6 Fault location results at different fault times
故障初始角/ (°)测距结果/m最大相对误差(%) 1503506508501 2501 550 0149.47349.61649.72849.751 249.771 549.80.029 30149.83349.88649.86849.881 249.891 549.890.009 2 60149.13349.27649.55849.661 249.771 549.770.047 90149.77349.83649.83849.81 249.861 549.830.012 120152.13351.04651.44851.51 250.631 550.270.11
3.3.4 故障电阻对测距算法的影响
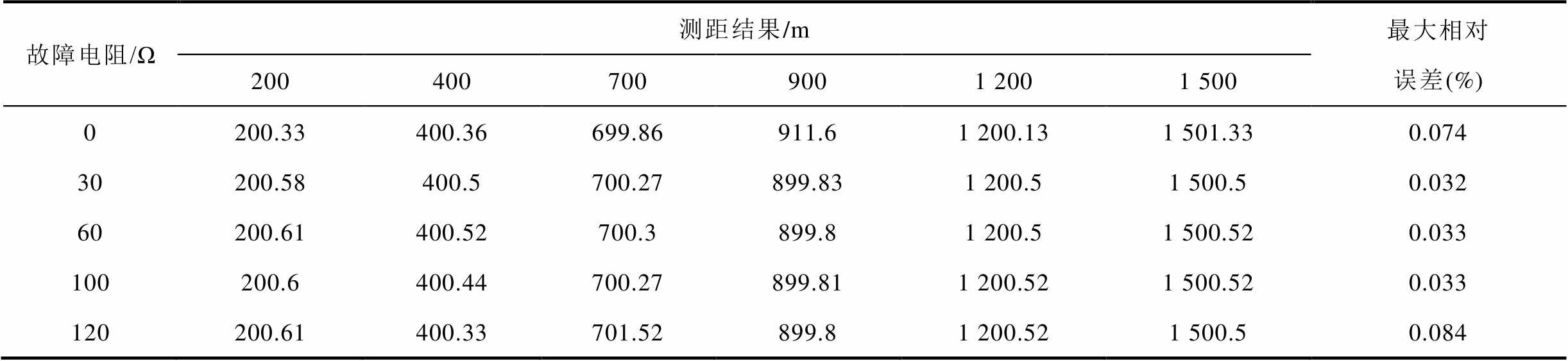
设故障类型为线芯-护层故障,故障初始角为30°,故障电阻分别为0、30、60、100、120 Ω,故障测距结果见表7。由表7可知,不同故障电阻对测距方法的影响较小,最大误差不超过0.1%,测距精度较高。
表7 不同故障电阻下的故障测距结果
Tab.7 Fault location results under different fault resistances
故障电阻/Ω测距结果/m最大相对误差(%) 2004007009001 2001 500 0200.33400.36699.86911.61 200.131 501.330.074 30200.58400.5700.27899.831 200.51 500.50.032 60200.61400.52700.3899.81 200.51 500.520.033 100200.6400.44700.27899.811 200.521 500.520.033 120200.61400.33701.52899.81 200.521 500.50.084
3.3.5 双端数据不同步对测距算法的影响
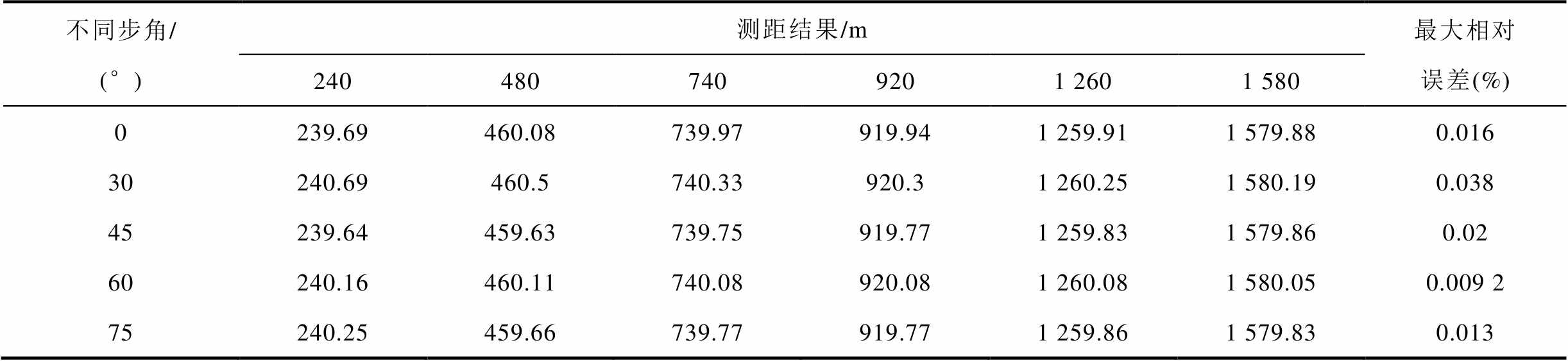
设故障类型为线芯-护层接地故障,故障初相角为10°,故障电阻为10 Ω,双端数据不同步下的故障测距结果见表8。由表8可知,在双端数据不同步时,测距算法受到的影响较小,能够得到相对准确的测距结果,最大相对误差小于0.05%,理论上可以满足工程要求。
表8 双端数据不同步时的故障测距结果
Tab.8 Fault location results when the data of two ends is not synchronized
不同步角/ (°)测距结果/m最大相对误差(%) 2404807409201 2601 580 0239.69460.08739.97919.941 259.911 579.880.016 30240.69460.5740.33920.31 260.251 580.190.038 45239.64459.63739.75919.771 259.831 579.860.02 60240.16460.11740.08920.081 260.081 580.050.009 2 75240.25459.66739.77919.771 259.861 579.830.013
3.3.6 噪声对测距算法的影响
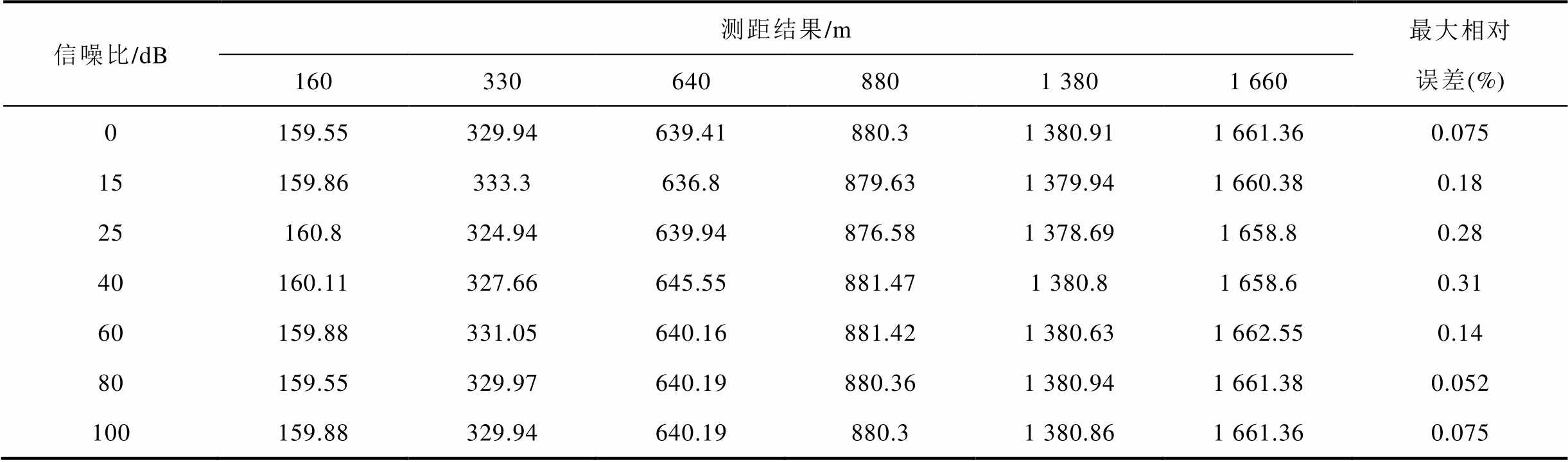
当电缆故障类型为护层接地故障,故障电阻为15 Ω,故障初相角为25°时,不同噪声干扰下的故障测距结果见表9。由表9可知,噪声对测距算法的精度存在影响,在信噪比为25~60 dB时影响相对较大,但测距误差不超过0.4%,能够得到相对准确的故障距离。
表9 不同噪声干扰下的故障测距结果
Tab.9 Fault location results under different noise interference
信噪比/dB测距结果/m最大相对误差(%) 1603306408801 3801 660 0159.55329.94639.41880.31 380.911 661.360.075 15159.86333.3636.8879.631 379.941 660.380.18 25160.8324.94639.94876.581 378.691 658.80.28 40160.11327.66645.55881.471 380.81 658.60.31 60159.88331.05640.16881.421 380.631 662.550.14 80159.55329.97640.19880.361 380.941 661.380.052 100159.88329.94640.19880.31 380.861 661.360.075
3.3.7 线路参数误差对测距算法的影响
当电缆故障类型为护层接地故障,故障电阻为20 Ω,故障初相角为15°时,线路参数发生不同变化时的故障测距结果见表10。由表10可知,线路参数变化会影响测距算法精度,线路参数变化越大,影响越大,但测距误差不超过0.3%,能够得到相对准确的故障距离。
表10 不同线路参数误差下的故障测距结果
Tab.10 Fault location results under different line parameter errors

线路参数变化(%)测距结果/m最大相对误差(%) 2203605307509101 240 -10223.43362.71534.18751.62912.361 242.330.28 -5221.98362.85532.64752.35914.371 241.970.24 1221.56361.74530.84751.67911.891 241.280.1 5221.83361.92531.87751.69912.631 242.160.14 10222.72362.23532.98752.34912.561 242.080.16
3.3.8 接地电阻对测距算法的影响
当电缆故障类型为线芯-护层故障,故障电阻为25 Ω,故障初相角为5°时,电缆接地电阻为不同值时的故障测距结果见表11。由表11可知,不同的电缆接地电阻对故障测距存在影响,随着接地电阻增大,护层电压计算值随之产生误差,测距误差增大,但最大误差不超过0.2%,电缆接地电阻对故障测距的影响相对较小。
表11 不同接地电阻下的故障测距结果
Tab.11 Fault location results under different ground resistances

接地电阻/Ω测距结果/m最大相对误差(%) 0.52.05.0 140140.94141.26141.740.096 260261.24261.62261.560.09 320320.65321.78320.960.098 550551.72550.89551.680.095 660660.88660.54661.20.067 780782.34781.54782.440.014 910911.24912.02912.430.13 1 0201 020.741 021.131 020.980.062
本文所提方法为计及电缆线芯与护层之间、护层与大地之间电容对测距影响的阻抗模型,当忽略线路电容影响时,同样可用本文所提方法进行故障测距。
当电缆故障类型为线芯-护层接地故障,故障电阻为35 Ω,故障初相角为10°时,分别采用考虑线路电容的阻抗模型和仅考虑金属护层对线芯电气影响的双层阻抗模型[19],运用本文方法进行故障测距,得到不同故障距离处的故障测距结果见表12。
表12 不同电缆模型的测距结果
Tab.12 Ranging results for different cable models

故障距离/m计及线路电容影响计算距离/m测距误差(%)忽略线路电容影响计算距离/m测距误差(%) 109.98-0.001 19.54-0.026 5050.160.008 952.180.12 100100.280.016108.350.46 150151.240.069136.74-0.73 200201.850.1178.24-1.2 250252.380.13207.56-2.35 300298.94-0.059356.33.12 350351.460.081317.76-1.79 400400.920.051455.973.1 450452.330.13506.753.15 500498.97-0.057546.362.57 550550.260.014575.741.43 600600.640.036662.863.49 650650.780.043693.332.4 700699.54-0.026778.414.35 750751.280.071807.673.2 800800.820.046849.582.75 850848.94-0.059895.492.52 900900.830.046951.782.87 950951.040.058991.242.29 1 000999.92-0.004 41 031.771.76
由表12可知,考虑线路电容的故障测距方法相比忽略线路电容的故障测距方法具有更高的精度,而忽略线路电容的故障测距方法仅在故障距离较短时精度相对较高。因此通过本文方法求解故障距离时,不应忽略线路电容的存在,以确保所求故障距离的准确性。
本文考虑电缆金属护层对线芯的耦合作用和线路电容影响,建立交叉互联接地电缆短路故障稳态等效阻抗模型,提出了一种基于故障点过渡电阻功率特性的故障定位方法,并通过仿真计算和分析验证了方法的有效性,具有较高的测距精度。
1)该方法利用电缆故障前后护层环流作为判据对电缆故障区段进行判定,缩小了故障测距范围,提高了故障测距的准确性。
2)该方法建立了故障稳态等效阻抗模型,计算故障发生时电缆线芯和护层沿线电压及电流相量,实现不同电缆短路故障的模拟,有利于反映电缆故障时的电气特征;利用故障前电气采样值修正电缆单位长度参数,提高了计算结果的准确度;利用故障后电缆首末两端采集电压和电流数据建立故障测距方程进行求解计算,通过有效判据识别伪根得到真实故障点,增强了计算结果的可靠性。
3)经过仿真结果验证,该方法基本不受故障距离、故障类型、故障电阻、故障时刻、噪声等因素的影响,具有较高的测距精度,对电缆短路故障定位具有一定的参考意义。
附 录
附表1 不同电缆区段发生故障对应特征电流及判别结果
App.Tab.1 The characteristic current corresponding to the fault in different cable sections and the discriminant results
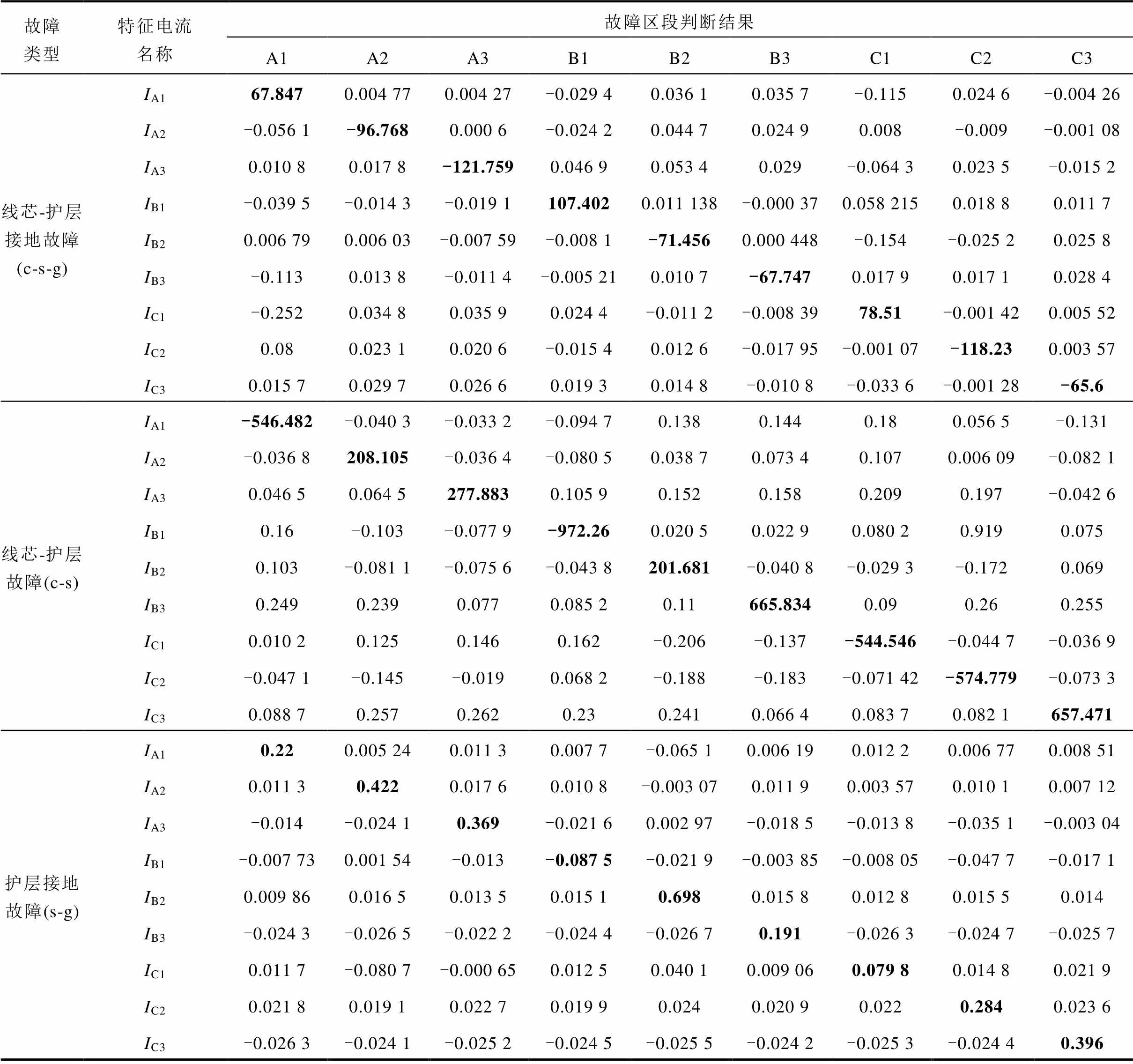
故障类型特征电流名称故障区段判断结果 A1A2A3B1B2B3C1C2C3 线芯-护层接地故障(c-s-g)IA167.8470.004 770.004 27-0.029 40.036 10.035 7-0.1150.024 6-0.004 26 IA2-0.056 1-96.7680.000 6-0.024 20.044 70.024 90.008-0.009-0.001 08 IA30.010 80.017 8-121.7590.046 90.053 40.029-0.064 30.023 5-0.015 2 IB1-0.039 5-0.014 3-0.019 1107.4020.011 138-0.000 370.058 2150.018 80.011 7 IB20.006 790.006 03-0.007 59-0.008 1-71.4560.000 448-0.154-0.025 20.025 8 IB3-0.1130.013 8-0.011 4-0.005 210.010 7-67.7470.017 90.017 10.028 4 IC1-0.2520.034 80.035 90.024 4-0.011 2-0.008 3978.51-0.001 420.005 52 IC20.080.023 10.020 6-0.015 40.012 6-0.017 95-0.001 07-118.230.003 57 IC30.015 70.029 70.026 60.019 30.014 8-0.010 8-0.033 6-0.001 28-65.6 线芯-护层故障(c-s)IA1-546.482-0.040 3-0.033 2-0.094 70.1380.1440.180.056 5-0.131 IA2-0.036 8208.105-0.036 4-0.080 50.038 70.073 40.1070.006 09-0.082 1 IA30.046 50.064 5277.8830.105 90.1520.1580.2090.197-0.042 6 IB10.16-0.103-0.077 9-972.260.020 50.022 90.080 20.9190.075 IB20.103-0.081 1-0.075 6-0.043 8201.681-0.040 8-0.029 3-0.1720.069 IB30.2490.2390.0770.085 20.11665.8340.090.260.255 IC10.010 20.1250.1460.162-0.206-0.137-544.546-0.044 7-0.036 9 IC2-0.047 1-0.145-0.0190.068 2-0.188-0.183-0.071 42-574.779-0.073 3 IC30.088 70.2570.2620.230.2410.066 40.083 70.082 1657.471 护层接地故障(s-g)IA10.220.005 240.011 30.007 7-0.065 10.006 190.012 20.006 770.008 51 IA20.011 30.4220.017 60.010 8-0.003 070.011 90.003 570.010 10.007 12 IA3-0.014-0.024 10.369-0.021 60.002 97-0.018 5-0.013 8-0.035 1-0.003 04 IB1-0.007 730.001 54-0.013-0.087 5-0.021 9-0.003 85-0.008 05-0.047 7-0.017 1 IB20.009 860.016 50.013 50.015 10.6980.015 80.012 80.015 50.014 IB3-0.024 3-0.026 5-0.022 2-0.024 4-0.026 70.191-0.026 3-0.024 7-0.025 7 IC10.011 7-0.080 7-0.000 650.012 50.040 10.009 060.079 80.014 80.021 9 IC20.021 80.019 10.022 70.019 90.0240.020 90.0220.2840.023 6 IC3-0.026 3-0.024 1-0.025 2-0.024 5-0.025 5-0.024 2-0.025 3-0.024 40.396
对图6中节点①、节点②列写KVL,有
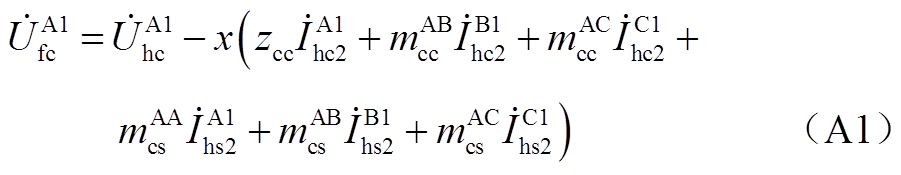
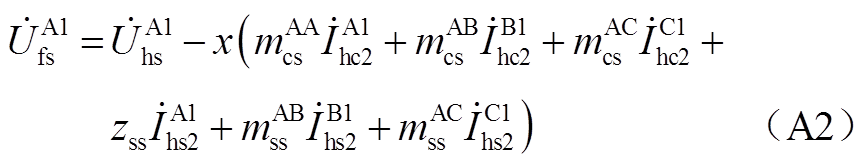
对节点①、节点②分别列写KCL方程,有
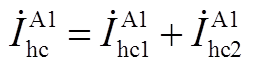 (A3)
(A3)
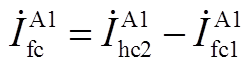 (A4)
(A4)
将式(A3)、式(A4)合并得
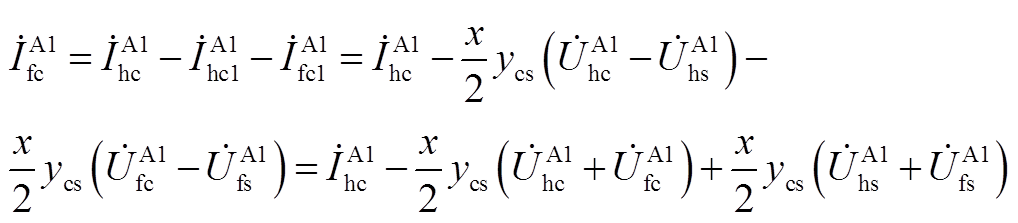 (A5)
(A5)
对图6中节点③、节点④分别列写KCL方程,有
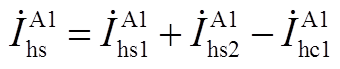 (A6)
(A6)
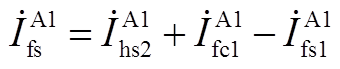 (A7)
(A7)
将式(A6)、式(A7)合并得
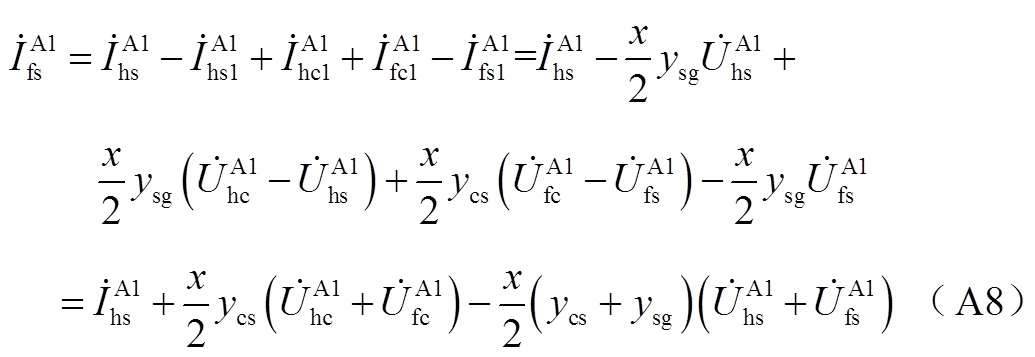
对图6中回路3、4列写KVL,有
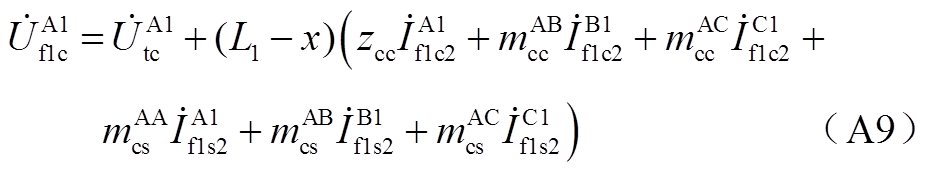
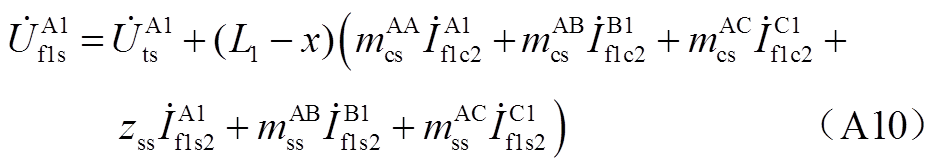
对节点⑤、节点⑥分别列写KCL方程,有
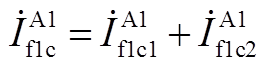 (A11)
(A11)
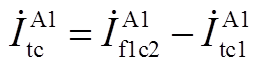 (A12)
(A12)
将式(A11)、式(A12)合并得
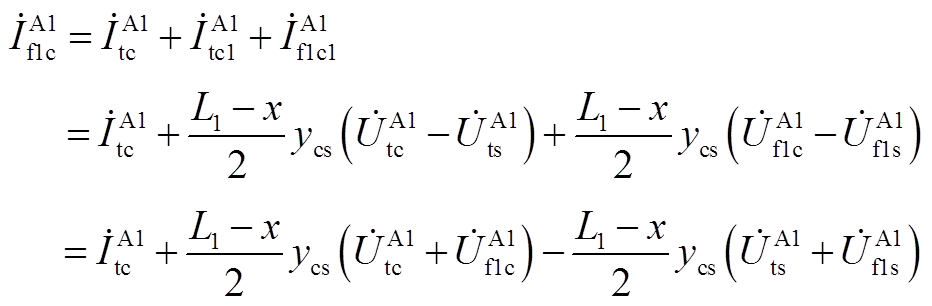 (13)
(13)
对图6中节点③、节点④分别列写KCL方程,有
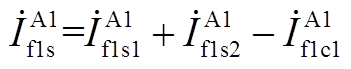 (A14)
(A14)
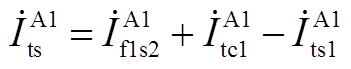 (A15)
(A15)
将式(A14)、式(A15)合并得
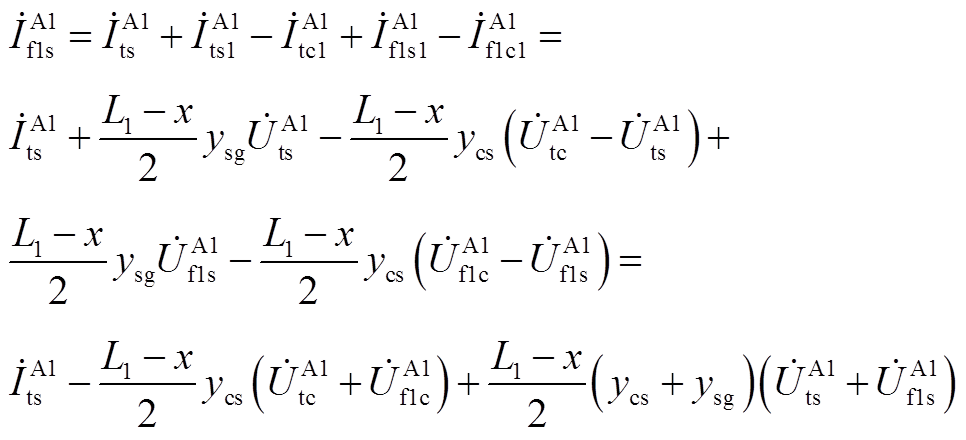 (A16)
(A16)
附表2 电缆参数校正结果
App.Tab.2 Cable parameter correction results

优化结果初始值最优值相对误差(%) /(Ω/km)0.071 860.071 690.23 /(H/km)0.595 10.593 60.252 /(Ω/km)0.071 860.071 680.25 /(H/km)0.595 10.593 30.3 /(Ω/km)0.071 860.071 680.25 /(H/km)0.595 10.593 40.28 /(Ω/km)0.054 790.054 480.56 /(H/km)0.553 90.550 20.66 /(Ω/km)0.049 480.048 981.01 /(H/km)0.492 80.494 20.28 /(Ω/km)0.049 480.049 991.03 /(H/km)0.449 20.446 90.51 /(Ω/km)0.049 480.049 040.88 /(H/km)0.492 80.493 70.18 /(Ω/km)0.054 790.054 540.45 /(H/km)0.553 90.550 80.55 /(Ω/km)0.049 480.049 120.72 /(H/km)0.492 80.493 60.16 /(Ω/km)0.049 480.049 050.86 /(H/km)0.449 20.446 80.53 /(Ω/km)0.049 480.049 690.42 /(H/km)0.492 80.494 3-0.3 /(Ω/km)0.054 790.054 60.34 /(H/km)0.553 90.551 30.46 /(Ω/km)0.054 420.054 260.29 /(H/km)0.552 90.552 10.14 /(Ω/km)0.054 420.054 240.33 /(H/km)0.552 90.553 80.16
(续)
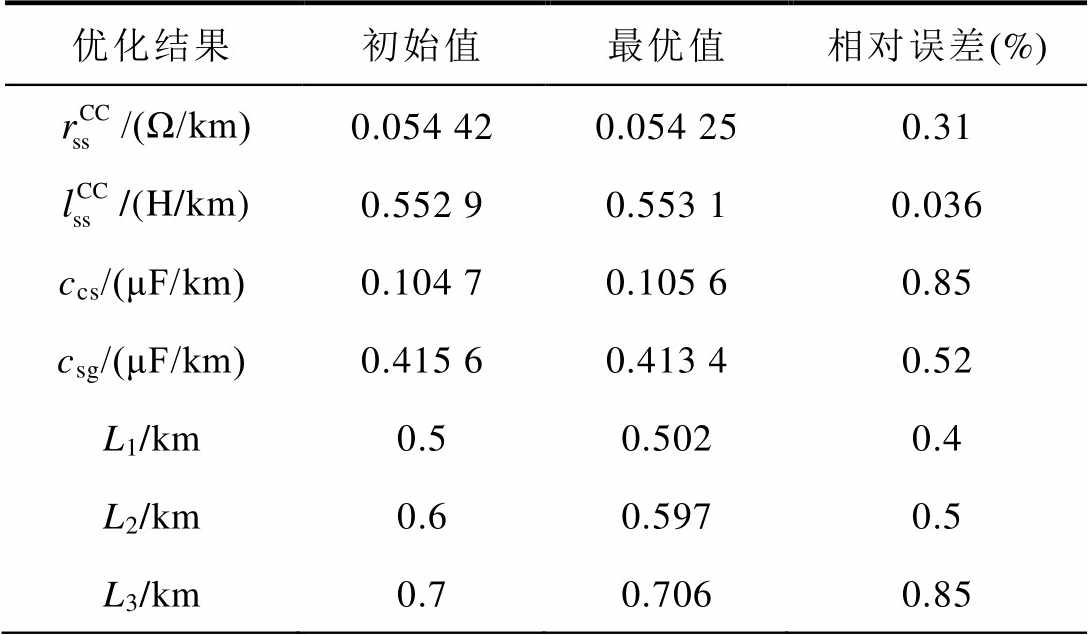
优化结果初始值最优值相对误差(%) /(Ω/km)0.054 420.054 250.31 /(H/km)0.552 90.553 10.036 ccs/(μF/km)0.104 70.105 60.85 csg/(μF/km)0.415 60.413 40.52 L1/km0.50.5020.4 L2/km0.60.5970.5 L3/km0.70.7060.85
参考文献
[1] 单秉亮, 李舒宁, 杨霄, 等. XLPE配电电缆缺陷诊断与定位技术面临的关键问题[J]. 电工技术学报, 2021, 36(22): 4809-4819. Shan Bingliang, Li Shuning, Yang Xiao, et al. Key problems faced by defect diagnosis and location technologies for XLPE distribution cables[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4809-4819.
[2] 李蓉, 周凯, 万航, 等. 基于输入阻抗谱的电力电缆本体局部缺陷类型识别及定位[J]. 电工技术学报, 2021, 36(8): 1743-1751. Li Rong, Zhou Kai, Wan Hang, et al. Identification and location of local defects in power cable body based on input impedance spectroscopy[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1743-1751.
[3] 王昊月, 李成榕, 王伟, 等. 高压频域介电谱诊断XLPE电缆局部绝缘老化缺陷的研究[J]. 电工技术学报, 2022, 37(6): 1542-1553. Wang Haoyue, Li Chengrong, Wang Wei, et al. Local aging diagnosis of XLPE cables using high voltage frequency domain dielectric spectroscopy[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1542-1553.
[4] 王昊月, 王晓威, 孙茂伦, 等. XLPE电缆绝缘热老化的高压频域介电谱诊断方法[J]. 电工技术学报, 2022, 37(17): 4497-4507. Wang Haoyue, Wang Xiaowei, Sun Maolun, et al. High voltage frequency domain dielectric spectroscopy diagnosis method for thermal aging of XPLE cables[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4497-4507.
[5] 刘骥, 闫爽, 王守明, 等. 基于低频高压频域介电谱的XLPE电缆电树枝老化状态评估[J]. 电工技术学报, 2023, 38(9): 2510-2518. Liu Ji, Yan Shuang, Wang Shouming, et al. Evaluation of electrical tree aging state of XLPE cables based on low frequency and high voltage frequency domain spectroscopy[J]. Transactions of China Electrote-chnical Society, 2023, 38(9): 2510-2518.
[6] 赵铁军, 王秀斌, 虞跃. 基于金属护层模型参数辨识的电缆单相故障单端测距方法[J]. 电力系统保护与控制, 2019, 47(21): 83-91. Zhao Tiejun, Wang Xiubin, Yu Yue. A single terminal fault location method for single phase fault of cable based on parameter identification of metal sheath model[J]. Power System Protection and Control, 2019, 47(21): 83-91.
[7] 赵书静, 詹博博, 龚梁涛, 等. 基于调频连续波相位敏感特性的电缆局部缺陷检测方法[J]. 电工技术学报, 2023, 38(11): 3009-3021. Zhao Shujing, Zhan Bobo, Gong Liangtao, et al. Research on cable local defect detection method based on phase-sensitive characteristics of frequency modulated continuous wave[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 3009-3021.
[8] 雷芳菲, 褚继峰, 刘洋, 等. 基于半导体气体传感阵列的电缆过热故障诊断方法[J]. 电工技术学报, 2023, 38(13): 3651-3664. Lei Fangfei, Chu Jifeng, Liu Yang, et al. Fault diagnosis of cable overheating based on semiconductor gas sensing array[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3651-3664.
[9] 陶宇航, 张熹, 宫祥龙. 10kV电缆故障测距及定位典型案例分析[J]. 电气技术, 2022, 23(2): 88-93. Tao Yuhang, Zhang Xi, Gong Xianglong. Typical cases analysis of 10kV cable fault location[J]. Electrical Engineering, 2022, 23(2): 88-93.
[10] 鹿洪刚, 覃剑, 陈祥训, 等. 电力电缆故障测距综述[J]. 电网技术, 2004, 28(20): 58-63. Lu Honggang, Qin Jian, Chen Xiangxun, et al. Overview of power cable fault location[J]. Power System Technology, 2004, 28(20): 58-63.
[11] 朱柏寒, 陈羽, 马金杰. 基于波前陡度的输电线路单端行波故障测距[J]. 电力系统自动化, 2021, 45(9): 130-135. Zhu Baihan, Chen Yu, Ma Jinjie. Wavefront steepness based single-ended traveling wave fault location for transmission lines[J]. Automation of Electric Power Systems, 2021, 45(9): 130-135.
[12] 孙中玉, 徐丙垠, 王玮, 等. 电缆故障脉冲电流测距系统建模与仿真[J]. 电力系统自动化, 2021, 45(4): 142-147. Sun Zhongyu, Xu Bingyin, Wang Wei, et al. Modeling and simulation of cable fault location system based on pulse current[J]. Automation of Electric Power Systems, 2021, 45(4): 142-147.
[13] 束洪春, 田鑫萃, 董俊, 等. 利用故障特征频带和TT变换的电缆单端行波测距[J]. 中国电机工程学报, 2013, 33(22): 103-112, 17. Shu Hongchun, Tian Xincui, Dong Jun, et al. A single terminal cable fault location method based on fault characteristic frequency band and TT transform[J]. Proceedings of the CSEE, 2013, 33(22): 103-112, 17.
[14] 梁睿, 靳征, 王崇林, 等. 行波时频复合分析的配电网故障定位研究[J]. 中国电机工程学报, 2013, 33(28): 130-136, 20. Liang Rui, Jin Zheng, Wang Chonglin, et al. Research of fault location in distribution networks based on integration of travelling wave time and frequency analysis[J]. Proceedings of the CSEE, 2013, 33(28): 130-136, 20.
[15] 唐忠, 杨建. 交叉互联电缆行波故障测距的研究[J]. 电测与仪表, 2016, 53(5): 64-69, 79. Tang Zhong, Yang Jian. Research on traveling wave based fault location for cross-bonded power cable[J]. Electrical Measurement & Instrumentation, 2016, 53(5): 64-69, 79.
[16] 尹丽菊, 于毅, 咸日常, 等. 基于无监督学习的交叉互联电缆行波测距方法[J]. 智慧电力, 2021, 49(4): 89-94, 100. Yin Liju, Yu Yi, Xian Richang, et al. Traveling wave ranging method for cross-bonded cable based on unsupervised learning[J]. Smart Power, 2021, 49(4): 89-94, 100.
[17] 姜杰, 王鹏, 黄正炫, 等. 基于改进线路参数模型的配网电缆单相接地测距方法[J]. 电网技术, 2012, 36(5): 185-189. Jiang Jie, Wang Peng, Huang Zhengxuan, et al. Fault location of single-phase earth for power cable in distribution network based on improved cable line paramter model[J]. Power System Technology, 2012, 36(5): 185-189.
[18] 索南加乐, 王增超, 康小宁, 等. 基于线性微分方程参数识别的单端准确故障测距算法[J]. 电力自动化设备, 2011, 31(12): 9-14, 20. Suonan Jiale, Wang Zengchao, Kang Xiaoning, et al. Accurate fault location algorithm based on parameter identification of linear differential equation with single end data[J]. Electric Power Automation Equipment, 2011, 31(12): 9-14, 20.
[19] 张姝, 林圣, 唐进, 等. 基于双层阻抗模型的三相单芯电缆自恢复故障定位[J]. 电工技术学报, 2016, 31(17): 1-10. Zhang Shu, Lin Sheng, Tang Jin, et al. Fault location of self-clearing fault in three phase single core cables based on double impedance model[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 1-10.
[20] 唐进, 张姝, 林圣, 等. 计及金属护层结构的电缆单端故障测距方法[J]. 中国电机工程学报, 2016, 36(6): 1748-1756. Tang Jin, Zhang Shu, Lin Sheng, et al. Single-terminal fault locating method of cables considering the metal sheath structure[J]. Proceedings of the CSEE, 2016, 36(6): 1748-1756.
[21] 孙建明, 唐进. 考虑金属护层结构的电力电缆单端故障识别方法[J]. 电力科学与技术学报, 2017, 32(4): 96-101. Sun Jianming, Tang Jin. Single-ended fault identification method of cables considered the sheath structure[J]. Journal of Electric Power Science and Technology, 2017, 32(4): 96-101.
[22] 徐星, 陈向荣, 杜振东, 等. 基于非解耦节点导纳矩阵的随桥电缆接地方式研究[J]. 电工技术学报, 2021, 36(17): 3664-3674. Xu Xing, Chen Xiangrong, Du Zhendong, et al. Study on bridge-cable grounding system based on the non-decoupling nodal admittance matrix[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3664-3674.
[23] 李根, 王航, 刘海康, 等. 基于逻辑回归的高压电缆交叉互联接地系统缺陷分类识别方法[J]. 高电压技术, 2021, 47(10): 3674-3683. Li Gen, Wang Hang, Liu Haikang, et al. Classification and identification method of grounding system defects in cross-bonded HV cables based on logistic regression[J]. High Voltage Engineering, 2021, 47(10): 3674-3683.
[24] 方春华, 李景, 汤世祥, 等. 基于接地电流的交叉互联箱故障诊断技术研究[J]. 高压电器, 2018, 54(6): 16-23. Fang Chunhua, Li Jing, Tang Shixiang, et al. Fault diagnosis of cross-bonded box based on grounding current[J]. High Voltage Apparatus, 2018, 54(6): 16-23.
[25] 赖胜杰, 夏成军, 池梓斌, 等. 考虑泄漏电流及层间耦合的高压电缆金属护套环流计算与分析[J]. 高电压技术, 2022: 1-12. Lai Shengjie, Xia Chengjun, Chi Zibin, et al. Calculation and analysis of circulating current in metal sheath for HV cable considering leakage current and interlayer coupling[J]. High Voltage Engineering, 2022: 1-12.
[26] 郑肇骥, 王焜明. 高压电缆线路[M]. 北京: 水利电力出版社, 1983.
[27] 王雅芳. XLPE电力电缆接地系统与感应环流分析[D]. 杭州: 浙江大学, 2012.
[28] 付松林, 何光华, 徐骏, 等. 大段长高压电缆护层保护器暂态特性分析与参数优化设计[J]. 电网与清洁能源, 2021, 37(1): 32-41. Fu Songlin, He Guanghua, Xu Jun, et al. Transient characteristic analysis and parameter optimization of sheath protector for large-length high voltage cable[J]. Advances of Power System & Hydroelectric Engineering, 2021, 37(1): 32-41.
[29] 徐政, 钱洁. 电缆电气参数不同计算方法及其比较[J]. 高电压技术, 2013, 39(3): 689-697. Xu Zheng, Qian Jie. Comparison of different methods for calculating electrical parameters of power cables[J]. High Voltage Engineering, 2013, 39(3): 689-697.
[30] 钱洁. 电力电缆电气参数及电气特性研究[D]. 杭州: 浙江大学, 2013.
[31] 聂永杰, 赵现平, 李盛涛. XLPE电缆状态监测与绝缘诊断研究进展[J]. 高电压技术, 2020, 46(4): 1361-1371. Nie Yongjie, Zhao Xianping, Li Shengtao. Research progress in condition monitoring and insulation diagnosis of XLPE cable[J]. High Voltage Engineering, 2020, 46(4): 1361-1371.
[32] 洪翠, 林昶, 高伟, 等. 电流积分余弦相似性在直流配电线路故障定位中的应用[J]. 电机与控制学报, 2022, 26(8): 88-99. Hong Cui, Lin Chang, Gao Wei, et al. Application of cos-similarity of current integrals on the location of fault line in a DC distribution networks[J]. Electric Machines and Control, 2022, 26(8): 88-99.
[33] 王利平, 王晓茹, 王伟, 等. 输电线路故障测距实用算法研究[J]. 电力系统保护与控制, 2014, 42(16): 52-58. Wang Liping, Wang Xiaoru, Wang Wei, et al. Study of faults location utilizing algorithm on power transmission lines[J]. Power System Protection and Control, 2014, 42(16): 52-58.
[34] 陈旭, 朱永利, 郭小红, 等. 基于相位特性的高压输电线路双端非同步故障测距算法[J]. 电力系统自动化, 2015, 39(22): 152-156, 163. Chen Xu, Zhu Yongli, Guo Xiaohong, et al. A two-terminal fault location algorithm using asynchronous data based on phase characteristics for high voltage transmission line[J]. Automation of Electric Power Systems, 2015, 39(22): 152-156, 163.
[35] 辛振涛, 尚德基, 尹项根. 一种双端测距算法的伪根问题与改进[J]. 继电器, 2005, 33(6): 36-38, 45. Xin Zhentao, Shang Deji, Yin Xianggen. False root and its improvement of a two-terminal fault location algorithm on transmission line[J]. Relay, 2005, 33(6): 36-38, 45.
[36] 何学锦. 电力电缆过电压检测方法建模与分析[D]. 杭州: 浙江大学, 2019.
[37] 刘福源, 王航, 夏湛然, 等. 交叉互联高压电缆护层保护器故障对同回路两端护层电流相量差的影响[J]. 高电压技术, 2023, 49(3): 1244-1253. Liu Fuyuan, Wang Hang, Xia Zhanran, et al. Influence of the sheath voltage limiter fault on the sheath current phasor difference between the two ends in the same sheath loop in cross-bonded HV cables[J]. High Voltage Engineering, 2023, 49(3): 1244-1253.
[38] 张煌, 黄嘉盛, 牛海清, 等. 高压电缆外护层绝缘降低时护层保护器的参数配置[J]. 南方电网技术, 2017, 11(8): 34-40, 60. Zhang Huang, Huang Jiasheng, Niu Haiqing, et al. Sheath protector parameter configuration of high voltage cable with decreased insulation[J]. Southern Power System Technology, 2017, 11(8): 34-40, 60.
Abstract High-voltage power cables are widely used in the construction of urban power grid, but there are often short-circuit faults mainly caused by single-phase faults. Rapid and accurate fault location is of great significance to maintain the stable operation of power grid. The high voltage cable with a length of more than one kilometer usually adopts the cross-connected grounding mode, and the coupling between the cable structure, fault phase and non-fault phase brings great difficulties to fault location. At present, the main fault location methods of cross-connected cables are traveling wave method and impedance method, but the reliability of traveling wave method is low, and the impedance method has shortcomings such as not considering the influence between the three phases and ignoring the line capacitance. Therefore, a fault location method for cross-connected cables is proposed in this paper.
Firstly, based on the double π model, considering the coupling effect of the cable metal sheath on the wire core and the influence of the line capacitance, an equivalent model is established for the single-phase short-circuit fault of the cross-connected grounding cable. Secondly, the voltage and current of cable core and sheath are collected before and after the fault occurs, and the difference integral of sheath circulation before and after the fault is calculated according to the measured current of the cable sheath circulation monitoring point, and the short-circuit fault area is judged by whether the difference integral change is the largest. Then, the cable parameters are modified based on the pre-fault electrical volume, and the voltage and current along the first and end of the fault section are calculated by the post-fault electrical volume. Finally, the fault location equation is constructed based on the zero reactive power consumed by the transition resistance of the fault branch, and the fault distance is obtained by iterative calculation.
The simulation results of the proposed method show that by calculating the integral of the difference between the measured current at both ends of different sections of cross-connected cable as the characteristic current, the characteristic current value of the fault section is obviously greater than that of the non-fault section, and the fault section can be effectively judged. The method of line parameter correction can modify the inaccurate and changing line parameters within 1.1%, and reduce the electrical parameter error obtained by calculating or measuring the initial conditions of the cable. The fault location equation is established and iterated repeatedly to obtain the location result, which avoids the accident of the calculation result.
The simulation results show that the fault distance, fault type, cable arrangement, fault initial phase angle, transition resistance, line parameter change and ground resistance have little influence on the method, and the maximum distance error is less than 0.4%. Compared with the two-layer impedance model, the impedance model based on the line distribution capacitance has better location accuracy, so the line capacitance should not be ignored in the cable fault location.
Keywords:High voltage cable, cross connecting, reactive power characteristic, steady state of fault, distance of fault
DOI:10.19595/j.cnki.1000-6753.tces.222277
中图分类号:TM247
国家重点研发计划项目(2022YFB2403500)和南方电网公司科技项目(031300KK52200003)资助。
收稿日期 2022-12-12
改稿日期 2023-06-19
杨明嘉 男,1998年生,硕士研究生,研究方向为电力系统分析运行与控制、电力系统故障分析。E-mail:2129141841@qq.com
夏成军 男,1974年生,副教授,硕士生导师,研究方向为电力系统分析运行与控制、HVDC和FACTS。E-mail:cjxia@scut.edu.cn(通信作者)
(编辑 赫 蕾)