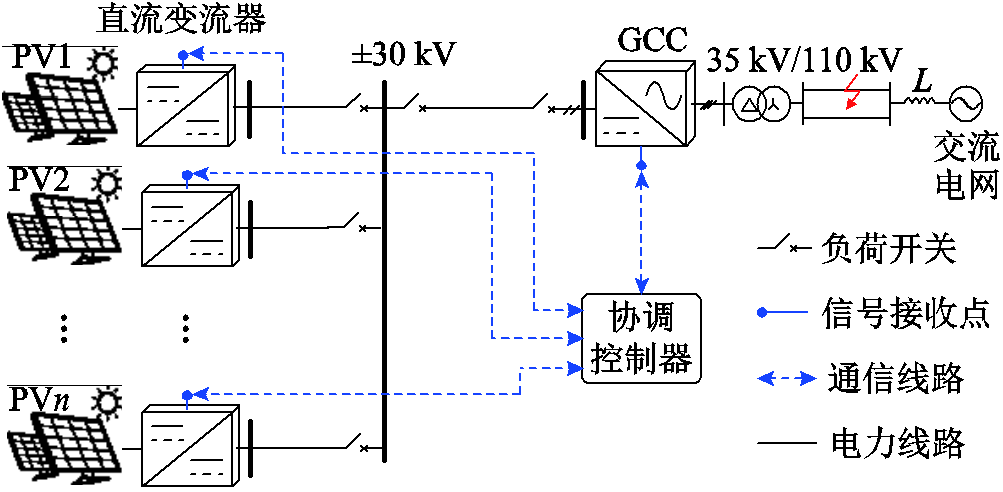
图1 光伏直流并网系统拓扑
Fig.1 Topology of PV DC grid-connected system
摘要 网侧故障下,光伏直流并网系统的并网变流器将根据电网电压变化实时控制输出功率,而直流侧光伏单元需接收系统功率指令后控制有功输出,两者间无法实现有功功率的快速平衡,导致直流电压持续偏移。传统方法通过投入耗能装置消耗盈余有功功率,以抑制直流电压抬升,但投资成本高。为此,该文提出一种网侧故障下系统不平衡功率快速平抑方法,在分析故障期间电网电压幅值变化趋势基础上,构建并网变流器内部计算电压变化轨迹算式。该方法利用故障初期内部计算电压数据,计算带权邻近度以求解电压变化轨迹算式关键项系数,进而求得所需系统功率指令。所提方法的优点在于有效地缩短了盈余功率持续时间,减少了对耗能装置的依赖,并且易于实现。仿真结果表明,所提方法可维持直流电压在安全范围内,为系统低电压穿越提供可靠保障。
关键词:光伏直流并网系统 低电压穿越 电压变化轨迹 功率指令 带权邻近度
柔性直流并网系统可以减少汇流电缆、避免交流振荡,正在成为新能源发电系统新型汇集模式的研究热点[1-4],未来将主要用于海上风电和沙漠光伏大型新能源基地。目前国内已通过改建现有光伏电站,建成世界首个光伏直流升压汇集并网系统示范工程[5]。交流网侧故障时,光伏直流并网系统中光伏单元(Photovoltaic, PV)需在中央控制器协调下配合并网变流器(Grid-Connected Converter, GCC)快速降低有功功率,避免直流母线电压持续偏移。然而,GCC随电网电压变化实时控制有功功率,PV则需等待系统功率指令下发后方可进入降功率模式,此过程的等待时间决定了直流系统内各变流器所需承受的直流过电压程度。若GCC与PV间功率差异过大、等待时间过长,甚至可能触发直流过电压保护而造成系统低电压穿越失败。因此,研究如何快速可靠地减少直流系统盈余功率及其持续时间至关重要。
系统低电压穿越方法可按照变流器数量分为单机系统(变流器数量不大于2台)低电压穿越[6-14]和多机系统低电压穿越。单机系统可进一步分为光伏单极式并网发电系统[6-8]、光伏双极式并网发电系统[9-11]和风力发电系统[12-14]。光伏单极式并网发电系统通过GCC控制切换,即可实现PV与GCC间的功率平衡,无需下发系统级功率指令。光伏双极式并网发电系统和风力发电系统通过耗能支路或系统功率指令与耗能支路的配合,抑制直流电压偏移。单机系统通信对象少(源侧和网侧变流器)、通信距离短(数米以内),源侧与网侧变流器容量一致,因而,采用系统级功率指令控制系统功率时,网侧故障下直流母线电压偏移的影响较小。
多机系统中,文献[15]设计了一种直流电压自适应控制器,通过控制直流电压使盈余功率转移至直流电容,避免触发过电压保护。文献[16]提出了一种分散式功率协调控制,网侧故障时系统内各分布式电源根据直流电压下垂曲线自适应控制有功出力。此类方法对通信要求低,主要通过直流电压偏移范围切换控制方式,因而要求接入直流系统的变流设备具有较高的过电压应力。文献[17]研究了多同质(结构、容量及控制方式均相同)光伏直流汇集系统的低电压穿越控制方法。文献[18]研究了含多个交流微网的集群微网低电压穿越控制方法。由于低电压穿越过程中多机系统的降功率幅度由电网电压决定,因而此类系统的研究通常假设交流故障发生时电网电压瞬时跌落至故障稳态值,或采用固定时延的方式等待电网电压进入稳态后再下发系统功率指令。两类方式中,前者忽略了电网电压暂态跌落过程及电网电压的变化;后者因固定时延的引入,增加了盈余功率持续时间,导致直流母线电压偏移量增大。
由于实际系统发生交流故障时,电网电压暂态跌落过程必然存在,因而,如何缩短盈余功率持续时间,成为减小低电压穿越过程直流母线电压偏移量的关键。文献[19]提出了基于故障初期电网电压低次谐波的故障稳态电压预测方法,进而依据预测电压求解所需功率指令。然而,该方法对运行场景的依赖性强,且所需数据量较大、计算时间较长(百毫秒级别),无法满足低电压穿越过程中直流并网系统有功快速平衡的需求。此外,文献[20]指出,现有通过稳控系统控制变流器直接跳切的场站功率控制方法,响应时间(从指令下发到实际输出功率达到指令值)约为200~300 ms,而采用一发多收和无需回传确认的通信方式时,虽然可缩短响应时间,但仍然存在约60 ms的通信时延。因此,系统进入低电压穿越模式后,需快速给出系统级功率指令,以缩短盈余功率持续时间,减小直流电压偏移量。
综上所述,针对网侧故障下GCC与PV间有功功率难以及时匹配而导致直流母线电压偏移的问题,提出一种适用于光伏直流并网系统的不平衡功率快速平抑方法。在分析网侧故障后GCC内部计算电压(经坐标变换后的电网电压)变化趋势基础上,构建内部计算电压变化轨迹算式。基于此,利用故障初期GCC内部电压数据,计算所选取数据区段中各点的带权邻近度及其均值,从而获得电压变化轨迹算式的关键项系数,进而求解所需系统级功率指令。所提方法通过快速计算故障稳态电压,有效缩短了系统指令下发时间,减小了直流电压偏移量。仿真结果证明了所提方法的有效性。
本文所研究对象为多个独立PV与GCC所构成的直流并网系统,参照云南某实际工程,构建光伏直流并网系统拓扑结构如图1所示,图中,L为电网侧等效电感。该系统中多个PV通过输入并联输出串联式直流变流器升压后接入直流系统,再经直流汇集后接入模块化多电平结构的GCC,最终经过GCC逆变后并入交流电网。PV与GCC均通过光纤与协调控制器通信。

图1 光伏直流并网系统拓扑
Fig.1 Topology of PV DC grid-connected system
依据文献[21]规定的无功电流参考值计算式及GCC允许最大电流[22],可最终得到低电压穿越期间GCC有功功率参考值表示为
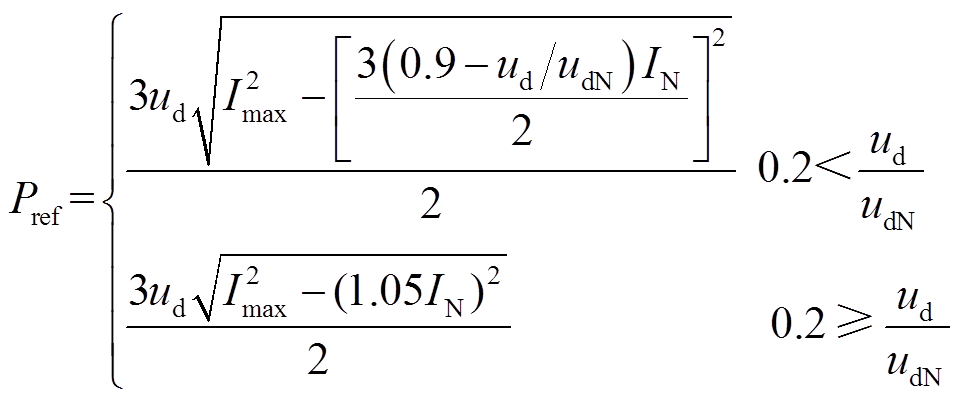 (1)
(1)
式中,IN为额定电流;Imax为GCC允许持续运行的最大电流;ud为GCC内部计算电压的d轴分量;udN为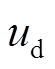 额定值。
额定值。
由式(1)可知,系统功率指令值与电网电压直接相关,因此需分析故障后电网电压变化过程对功率指令变化以及对直流电压的影响。图1所示系统结构可简化为图2所示电路拓扑。
根据直流系统中电容电压与电流关系[23-24],可以得到
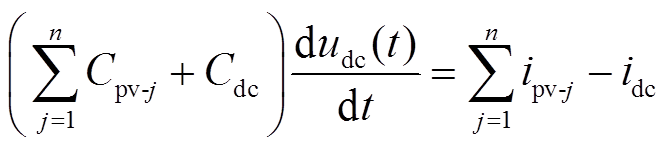 (2)
(2)
式中,udc为直流母线电压;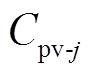 为第j个PV直流变流器出口电容;ipv-j为第j个PV直流变流器电流;Cdc为GCC等效电容;idc为GCC直流侧电流。
为第j个PV直流变流器出口电容;ipv-j为第j个PV直流变流器电流;Cdc为GCC等效电容;idc为GCC直流侧电流。
设t0时刻交流线路发生故障,t1时刻下发系统级功率指令ΔP(t1),t2时刻GCC实际输出有功功率为1.5ud(t2)id(t2)(此时系统级功率指令需修改为ΔP(t2)=1.5ud(t2)id(t2)),代入式(2),可以得到
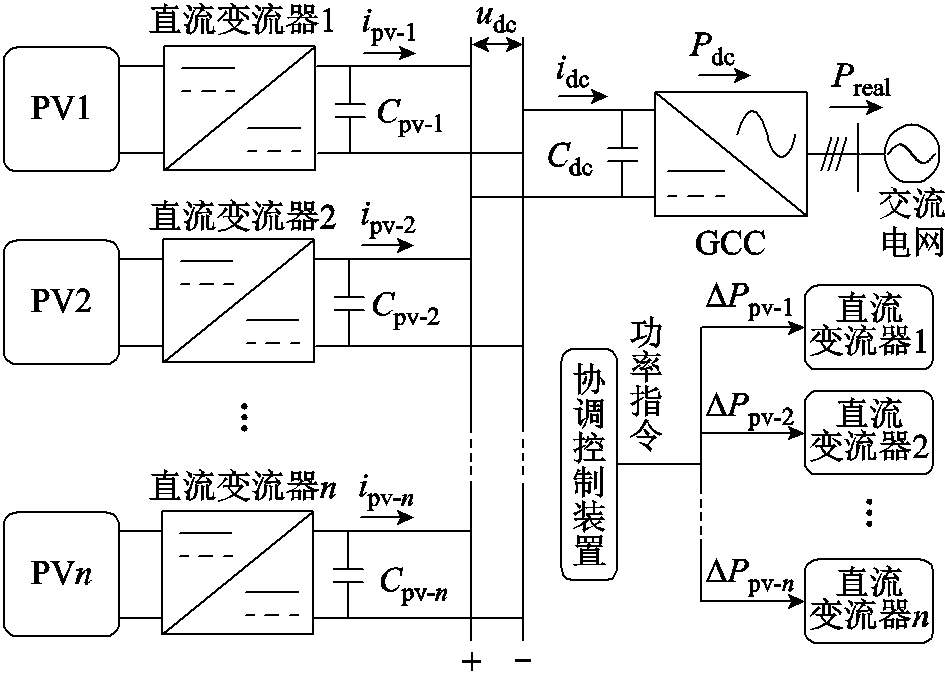
图2 光伏直流并网系统简化电路拓扑
Fig.2 Simplified circuit topology of PV-DCGS
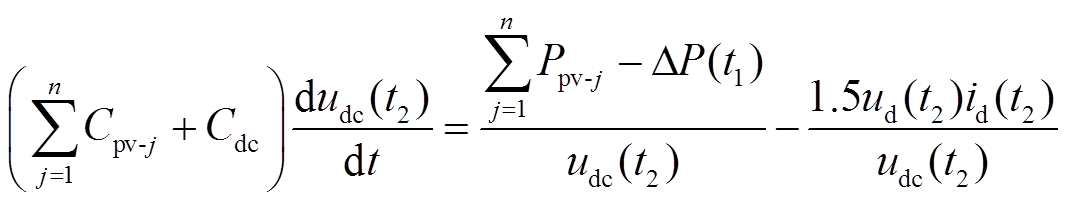 (3)
(3)
式中,Ppv-j为交流故障前第j个PV实际输出的有功功率;t2=t1+ΔT,ΔT为前后两次功率控制指令更新的时间区段。
在t1时刻,GCC内部计算电压为ud(t1),此时,计算得到的功率指令值为ΔP(t1);然而,该时刻可能尚处于电网电压跌落的暂态过程,即电网电压仍将进一步下降。若ud(t2)<ud(t1),则ΔP(t2)≤ΔP(t1),GCC输出有功继续下降,然而PV所接收到的功率指令尚未更新,使得直流系统盈余功率进一步增大,即式(3)等式右侧持续大于零,引起直流电压抬升。
GCC内部计算电压,由电网电压经坐标转换得到,与锁相环直接相关。图3所示为典型GCC控制结构[25],其中锁相环结构为常见的同步旋转坐标系锁相环(Synchronous Reference Frame-Phase Locked Loop, SRF-PLL)。
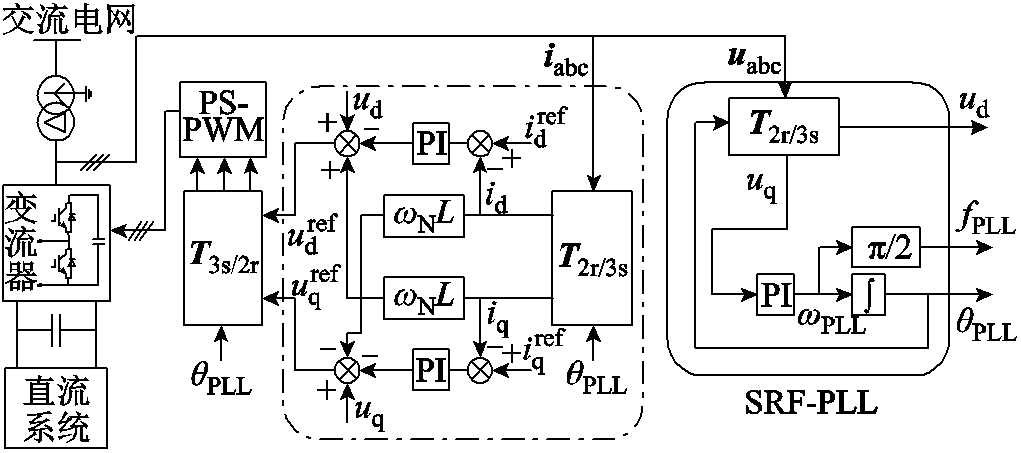
图3 GCC控制结构
Fig.3 Control structure of GCC
图3中,wPLL、fPLL和qPLL分别为锁相环输出角频率、频率以及相位;wNL为电流环补偿项,wN为额定角频率;u、i分别为并网点电压及电流,下标a、b、c对应三相静止坐标系下的电气量,下标d、q对应dq坐标系下的电气量,上标“ref”表示指令值;T2r/3s为Park矩阵,T3s/2r为Park反变换矩阵。
根据文献[24]可知,GCC电网电压计算值与实际电压幅值及锁相环输出相位有关,具体为
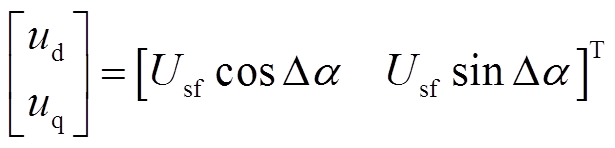 (4)
(4)
式中,Usf为过渡电阻为Rf时,电网电压的故障稳态值;Da为电网电压实际相位与故障后暂态过程锁相环输出相位差,即Δα=θ0-θPLL,q0为电网电压实际相位。
由式(4)可知,ud同时受电网电压幅值和相位差的影响,其中,电网电压幅值主要由过渡电阻决定,而相位差变化与锁相环相关。文献[25]推导了故障后相位动态过程变化特性,并给出了相位变化的时域表达式,具体为
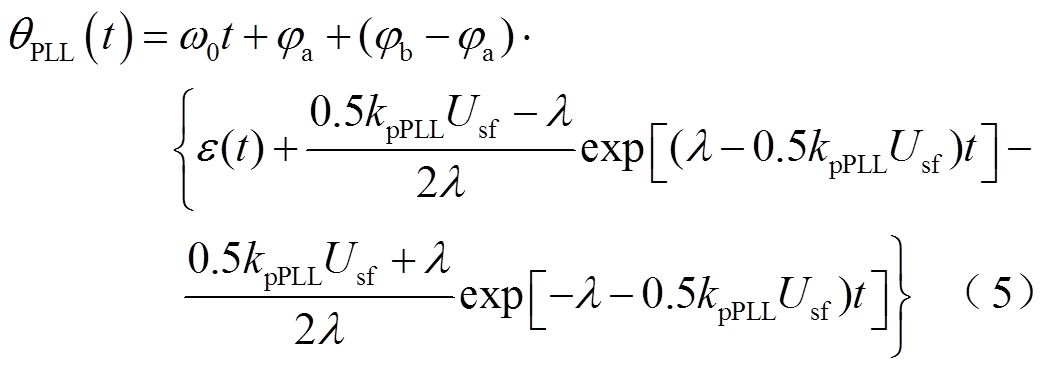
式中,φa为故障前的电网电压相位;φb为故障瞬间电网电压相位,并且有θ0=φa+(φb-φa)ε(t);e(t)为从0到1的阶跃函数;kpPLL为锁相环的比例系数;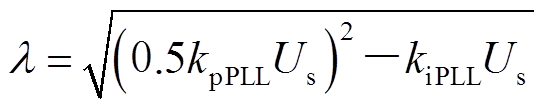 ,kiPLL为锁相环的积分系数。
,kiPLL为锁相环的积分系数。
根据式(5)可以得到相位差的时域表达式为
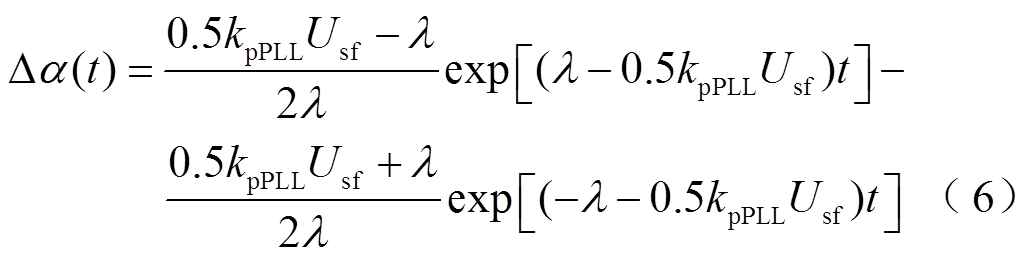
可以看出,式(6)由指数函数组成,并且随时间的增加而衰减至零,从而可以将其表现形式简化为Δα(t)=Mexp(-at)。将式(4)中的余弦函数在零点附近泰勒展开,考虑到Δα为衰减量,因而忽略4次及以上分量,从而可以近似得到故障后GCC内部计算电压d轴分量变化轨迹算式为
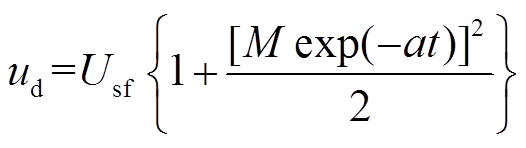 (7)
(7)
根据《光伏发电站接入电力系统技术规定》(GB/T 19964—2012),电网电压跌落至0.9(pu)时,GCC需进入低电压穿越模式,并根据要求发出无功功率。受GCC有功和无功功率的影响,并网点电压可能出现小幅回升,因此,需对式(7)进行修正。无功功率的控制同样受到ud的影响,并且无功电流计算应满足
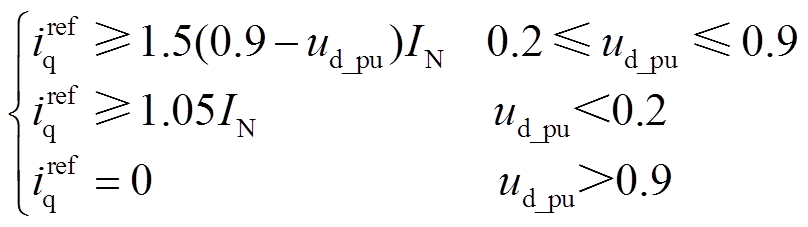 (8)
(8)
式中,ud_pu为电网电压d轴分量标幺值。
由式(7)和式(8)可知,GCC输出无功电流的变化过程与电网电压直接相关,因而表现出与电网电压d轴分量相近的特性。因此,将式(7)修正为
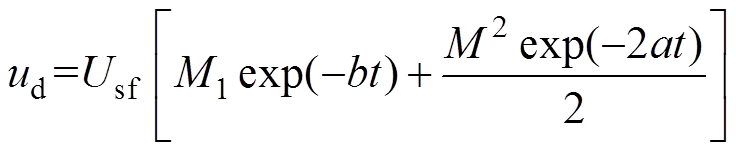 (9)
(9)
式中,b和M1均为修正系数。
综上所述,故障后GCC内部计算电压ud的变化过程可近似表示为指数函数的叠加。利用这一特性,可构建电压轨迹变化算式,从而可以快速获取所需系统功率指令。
结合电网电压特性的分析,构建电压变化轨迹算式为
 (10)
(10)
式中,Ad、Bd、Cd和Dd为关键项系数。
通常情况下,电网电压逐渐下降至故障稳态值,因而式(10)中必然有主导项(故障持续期间变化幅度足够小,即其指数为接近于零)与衰减项。设式(10)等号右侧第一项为主导项,第二项为衰减项。设故障发生后,经过T ms达到故障稳态。将T代入式(10),有
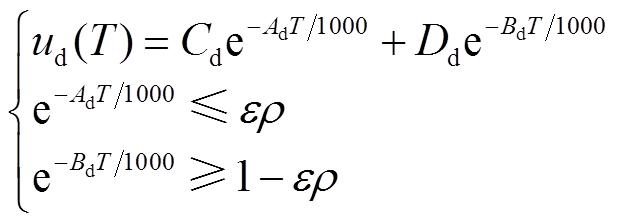 (11)
(11)
式中,ε为接近0的正数;ρ为不大于1的正数。
忽略故障稳态下的电网电压波动,进而可取式(10)中各项为等号,并设ρ=1,于是有
 (12)
(12)
式中,T0为故障发生时刻;UN为电网电压额定值。
不同过渡电阻下,电网电压的跌落速度和幅值均有差异,因而电压变化轨迹算式各项系数也将随过渡电阻的变化而改变,于是在式(12)的基础上添加跟随过渡电阻变化的变量,具体为
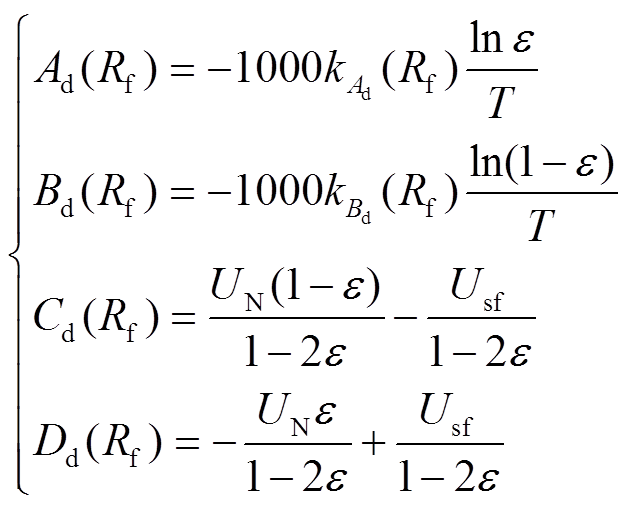 (13)
(13)
式中,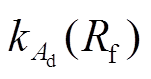 和
和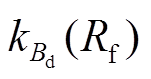 分别为关键项系数Ad和Bd计算式的自变量,主要受过渡电阻影响。
分别为关键项系数Ad和Bd计算式的自变量,主要受过渡电阻影响。
观察式(13)可以看出,关键项系数的变化表现出一次函数特性。因而,在确定关键项系数上、下边界后,即可通过线性差值的方式求解当前过渡电阻下对应的系数。
关键项系数的求解是电压变化轨迹算式的核心,需通过带权邻近度和电网电压上下边界曲线进行计算。
2.3.1 带权邻近度计算
本文将任一线段中任意一点与首末两端的距离和线段总长度的比值称为带权邻近度。一次函数所表示的线性曲线通用表达式为y=krx+b,其中,kr为斜率,b为常数项。设曲线首端为(x0, y0)、末端为(x2, y2),曲线上除首末两端的任意一点为(x1, y1)。将y0、y1和y2及对应的坐标代入表达式,对kr和b求解,可得
 (14)
(14)
进一步可以求得y1的计算式为
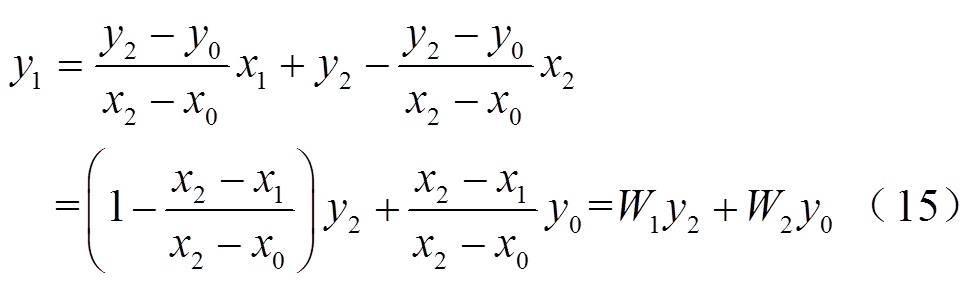
式中,W1和W2为带权邻近度。可知,即便未获知准确的表达式,也仍然能够通过带权邻近度计算曲线上任意一点与横轴的距离。由于实际故障发生时,过渡电阻无法获知,但电网电压可以测量,即可采集ud的数据,因此,令y=Φd(ud),(x0, y0)=(ud_DW, Φd_DW),(x1, y1)=(ud, Φd)和(x2, y2)=(ud_UP, Φd_UP),其中Φ为A、B、C或D,下标“UP”和“DW”分别表示电压上边界(较大过渡电阻)和下边界(较小过渡电阻)。结合式(13)和式(15),并代入上述设定,可以进一步得到
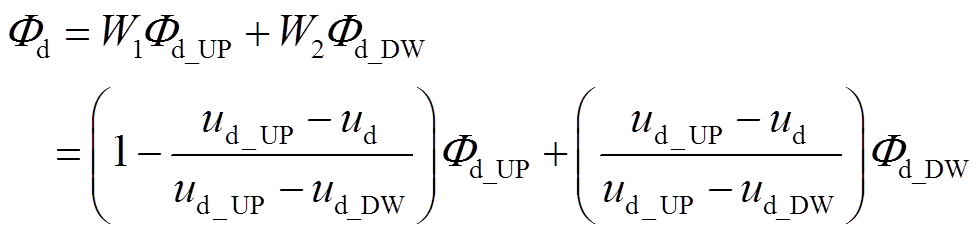 (16)
(16)
2.3.2 关键项系数计算
由于实际计算式采用的是离散数据,因此,过渡电阻为Rf时的关键项系数计算式为
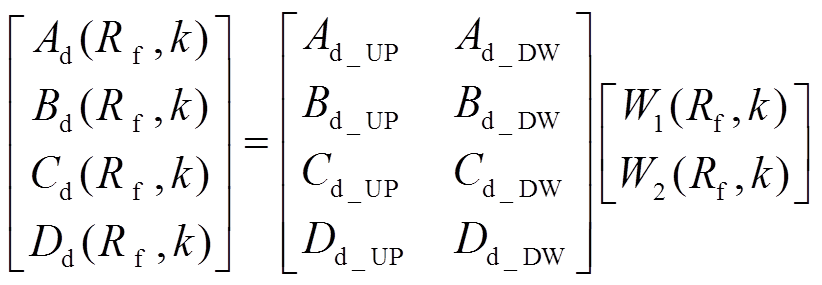 (17)
(17)
式中,Wj(Rf, k)为故障电阻Rf下,第k个电压数据点对应的带权邻近度,j=1, 2,k=1, 2, 3, , N。第k个数据点的带权邻近度为
, N。第k个数据点的带权邻近度为
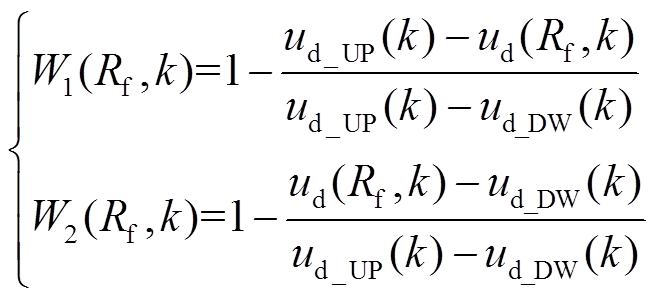 (18)
(18)
在式(18)中,仅通过单个数据点计算的带权邻近度容易增大计算误差。为减小计算误差,取故障后t ms内的N个数据点,并计算每个数据点对应的带权邻近度,对其求和后再取平均值,可以得到
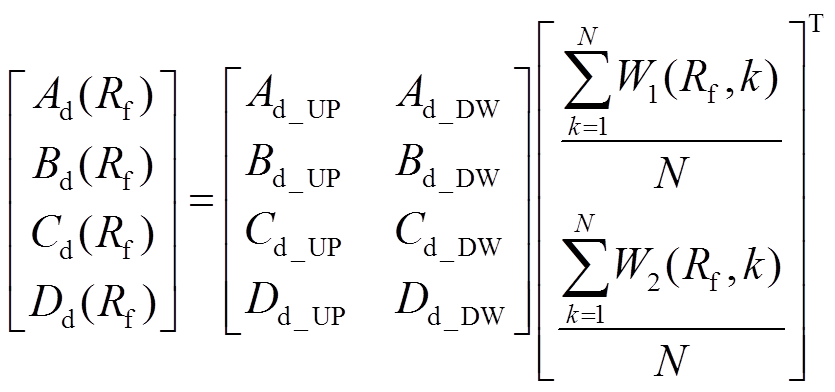 (19)
(19)
由式(10)和式(19)可以得到所需的电压变化轨迹算式,并计算故障稳态电压,进而求解所需系统级功率指令。
网侧故障下系统有功控制实现流程如图4所示。
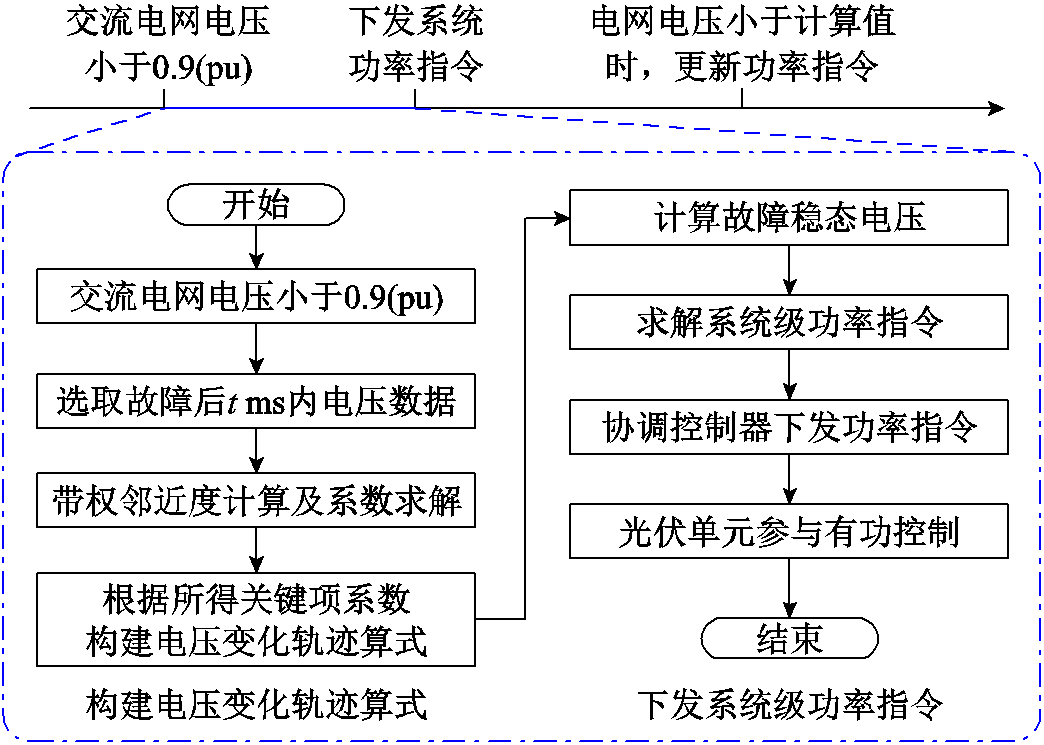
图4 网侧故障下系统有功控制实现流程
Fig.4 Flow chart of system active power control implementation under grid-side fault
控制流程主要分为以下步骤:
1)构建电压变化轨迹算式。获取故障发生后(电网电压小于0.9(pu))的t ms内电压数据;计算每个数据点对应的带权邻近度及其求和后的平均值;求解关键项系数,构建电压变化轨迹算式。
2)下发系统级功率指令。根据所构建的算式,计算故障稳态电压和系统级功率指令;分解功率指令后下发至各PV;PV接收指令后,执行降功率控制模式,参与系统有功控制。
3)当电网电压继续变化,并且连续三次测量(间隔0.5个工频周期)均小于电压计算值的k倍(k为裕度系数,避免数据突变导致的误判,此处以电网电压波动±5%为依据,取k为0.95)时,则根据当前电网电压再次更新功率指令值。
参考已建成的光伏直流并网示范工程,并根据图1所示拓扑,在PSCAD中搭建仿真模型。其中,直流母线电压为±30 kV,GCC及4台PV的容量分别为5 MW、1.5 MW(2台)、1 MW(2台),交流送出线路长度为40 km(单位长度线路参数:1.1 mH/km,0.076 Ω/km),其余参数见附录。
以某新能源基地开展的人工短路试验结果为参照,验证所研究仿真系统电网电压变化与真实故障场景的相似性。该新能源基地系统拓扑如附图1所示。图5为人工短路试验与所搭建仿真系统的电压波形结果对比。其中,仿真系统设置交流送出线路中点发生三相对称短路故障,仿真系统故障持续时间(故障发生时刻到故障清除时刻)为200 ms。
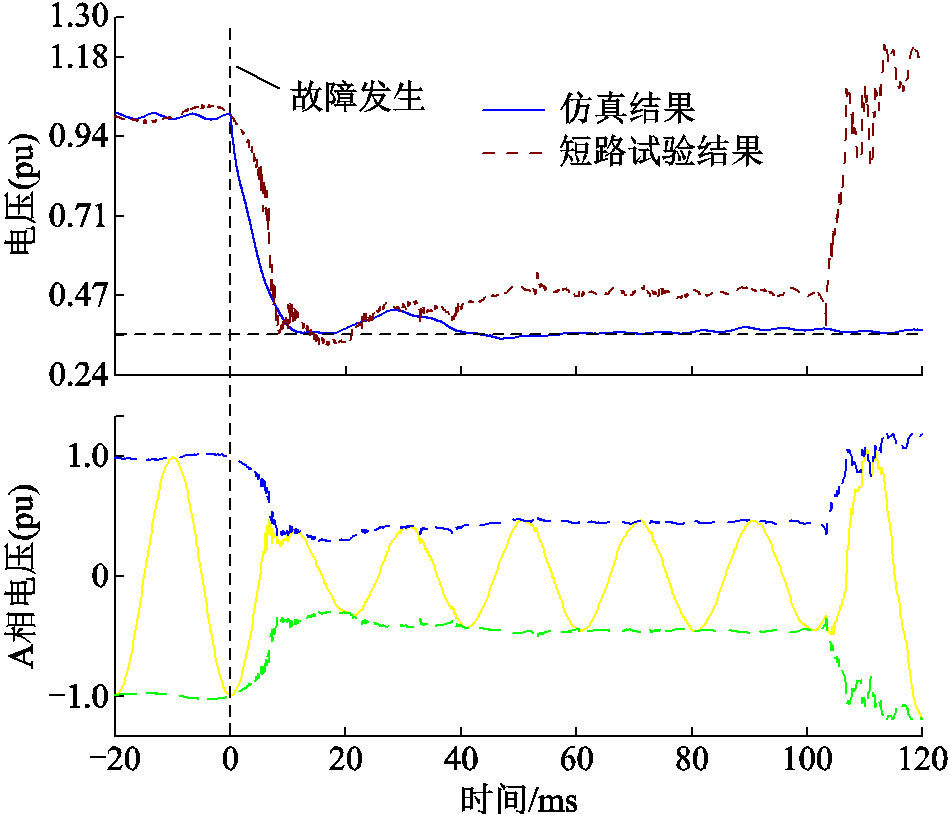
图5 人工短路试验与仿真结果对比
Fig.5 Comparison of artificial short circuit test and simulation results
如图5所示,人工短路试验下电网A相电压包络线(幅值)在故障发生后快速跌落至约0.3(pu),随后逐渐进入故障稳态,并最终稳定在0.48(pu)附近。而本文所搭建仿真系统的三相对称短路故障下,同样经历了相近的变化趋势,其内部计算电压在故障后跌落至0.35(pu)附近,随后短暂抬升并最终稳定在0.38(pu)附近。由此可见,所搭建模型的仿真结果与实际系统在故障下的电压变化趋势相近。
所提方法需选取故障后短时间内数据以计算电压变化轨迹关键项系数,为此,在交流送出线路中点设置交流对称故障,过渡电阻为25 Ω,故障持续时间为200 ms。本文所研究系统中,故障后电网电压约在故障后50 ms达到稳定,故取该时段内的数据长度进行分析。仿真结果见表1和表2。在所搭建仿真系统中,设置交流送出线路中点发生三相短路故障,取过渡电阻分别为5 Ω和50 Ω,对应故障后稳态电压幅值分别为0.25(pu)和0.72(pu)。结合文献[20]的低电压穿越电压门槛值和并网变流器允许过电流倍数,并考虑一定的裕度,分别取0.72(pu)和0.25(pu)为带权邻近度的计算上、下边界。
表1中,“仿真拟合”为利用Matlab对PSCAD仿真结果进行拟合得到的关键项系数。衰减项系数Cd和Ad的计算结果显示,在数据长度为20 ms时,误差分别为8.37%和31.14%。当数据长度小于20 ms时,Cd的误差随数据长度的缩短而增大,Ad的误差百分比变化与Cd相反。衰减项对故障稳态电压计算的影响较小。表2中,主导项参数Dd和Bd的计算结果显示,在数据长度为20 ms时,误差分别为4.80%和1.52%,均未超过5%。即便数据长度为5 ms时,Dd和Bd的误差也仍未超过10%。综上所述,在本文所研究系统中,可选取20 ms数据长度构建电压变化轨迹算式,并计算系统功率指令。实际工程中可选择不大于故障发生时刻到故障稳态时刻的时间的一半(即若该过程用时为T1,则所选数据长度应不大于0.5T1)。
表1 不同数据长度下计算结果分析(Cd, Ad)
Tab.1 Analysis of calculation results under different data lengths (Cd, Ad)
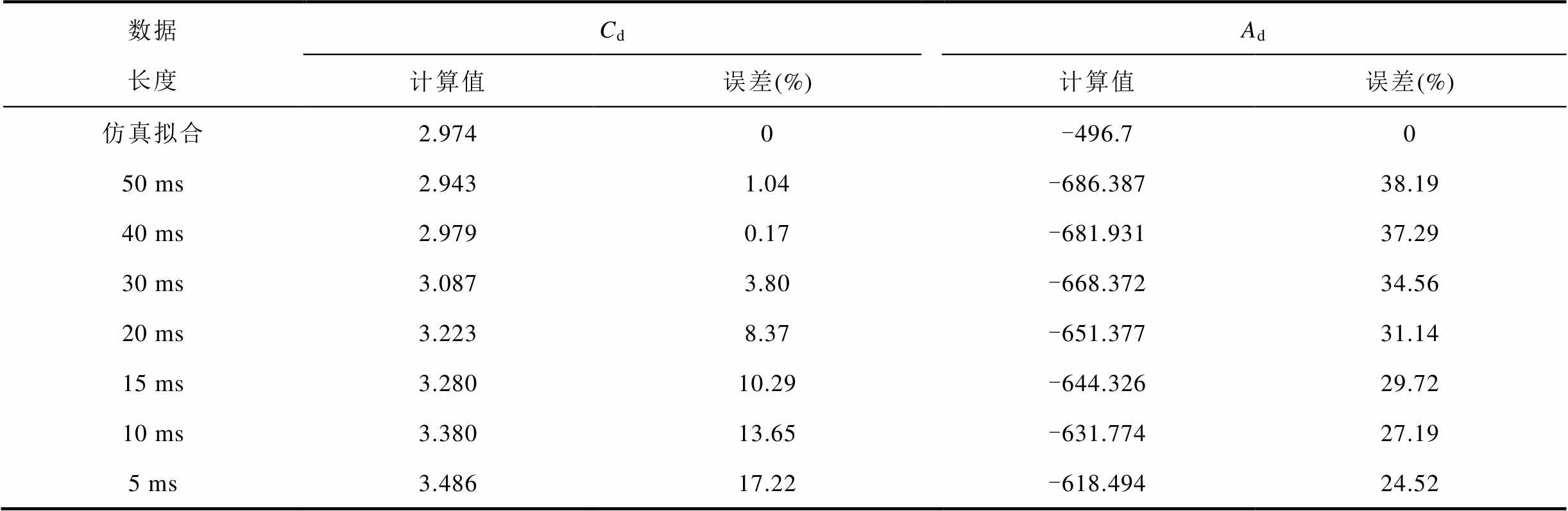
数据长度CdAd 计算值误差(%)计算值误差(%) 仿真拟合2.9740-496.70 50 ms2.9431.04-686.38738.19 40 ms2.9790.17-681.93137.29 30 ms3.0873.80-668.37234.56 20 ms3.2238.37-651.37731.14 15 ms3.28010.29-644.32629.72 10 ms3.38013.65-631.77427.19 5 ms3.48617.22-618.49424.52
表2 不同数据长度下计算结果分析(Dd, Bd)
Tab.2 Analysis of calculation results under different data lengths (Dd, Bd)

数据长度DdBd 计算值误差(%)计算值误差(%) 仿真拟合5.70800.1320 50 ms5.6890.330.1384.55 40 ms5.6560.910.1384.55 30 ms5.5582.630.1363.03 20 ms5.4344.800.1341.52 15 ms5.3835.690.1330.76 10 ms5.2917.310.1310.76 5 ms5.1958.990.1292.27
根据所选取数据长度,计算带权邻近度,并以此求解关键项系数,与仿真拟合结果进行对比,结果见表3和表4。
表3 电压变化轨迹算式的衰减项系数(Cd, Ad)
Tab.3 The attenuation term coefficient of the voltage variation trajectory formula (Cd, Ad)
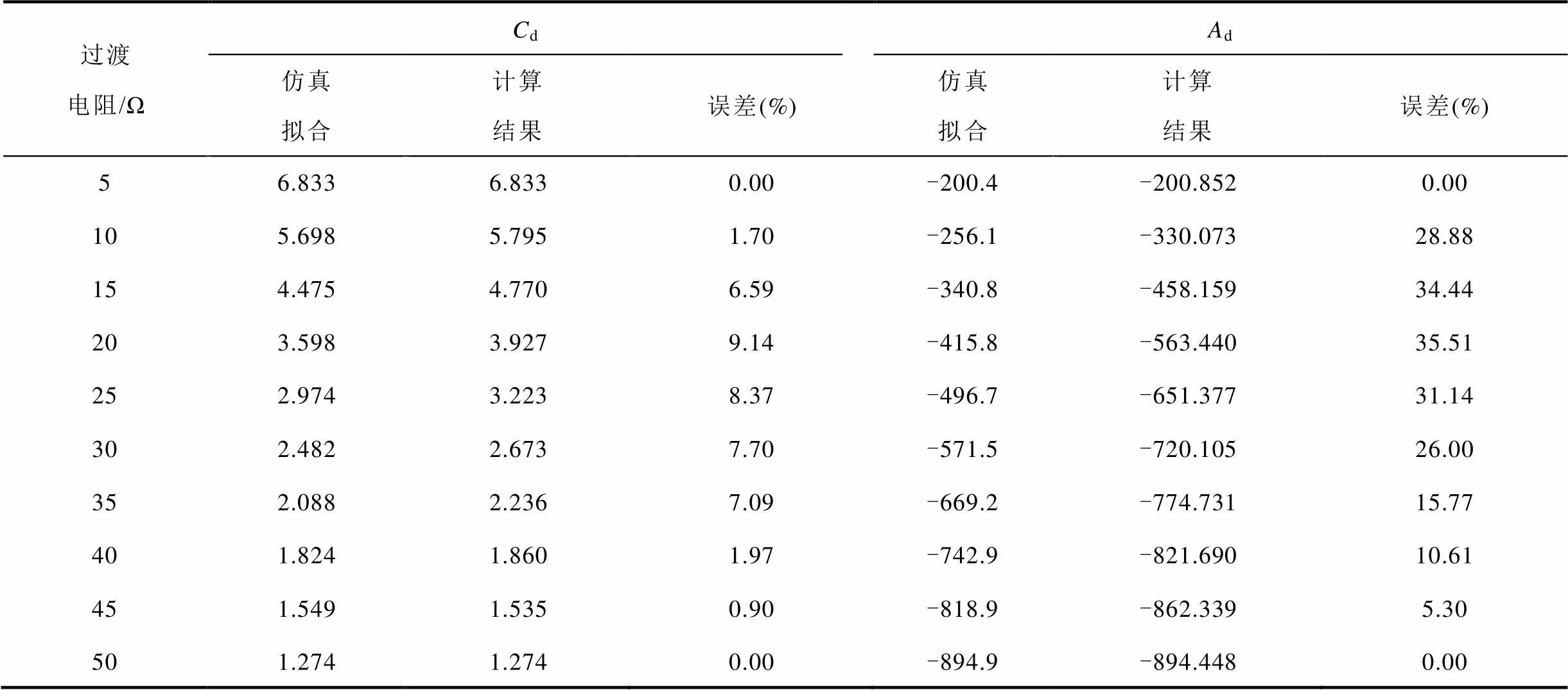
过渡电阻/ΩCdAd 仿真拟合计算结果误差(%)仿真拟合计算结果误差(%) 56.8336.8330.00-200.4-200.8520.00 105.6985.7951.70-256.1-330.07328.88 154.4754.7706.59-340.8-458.15934.44 203.5983.9279.14-415.8-563.44035.51 252.9743.2238.37-496.7-651.37731.14 302.4822.6737.70-571.5-720.10526.00 352.0882.2367.09-669.2-774.73115.77 401.8241.8601.97-742.9-821.69010.61 451.5491.5350.90-818.9-862.3395.30 501.2741.2740.00-894.9-894.4480.00
表4 电压变化轨迹算式的主导项系数(Dd, Bd)
Tab.4 The dominant coefficient of the voltage variation trajectory formula (Dd, Bd)
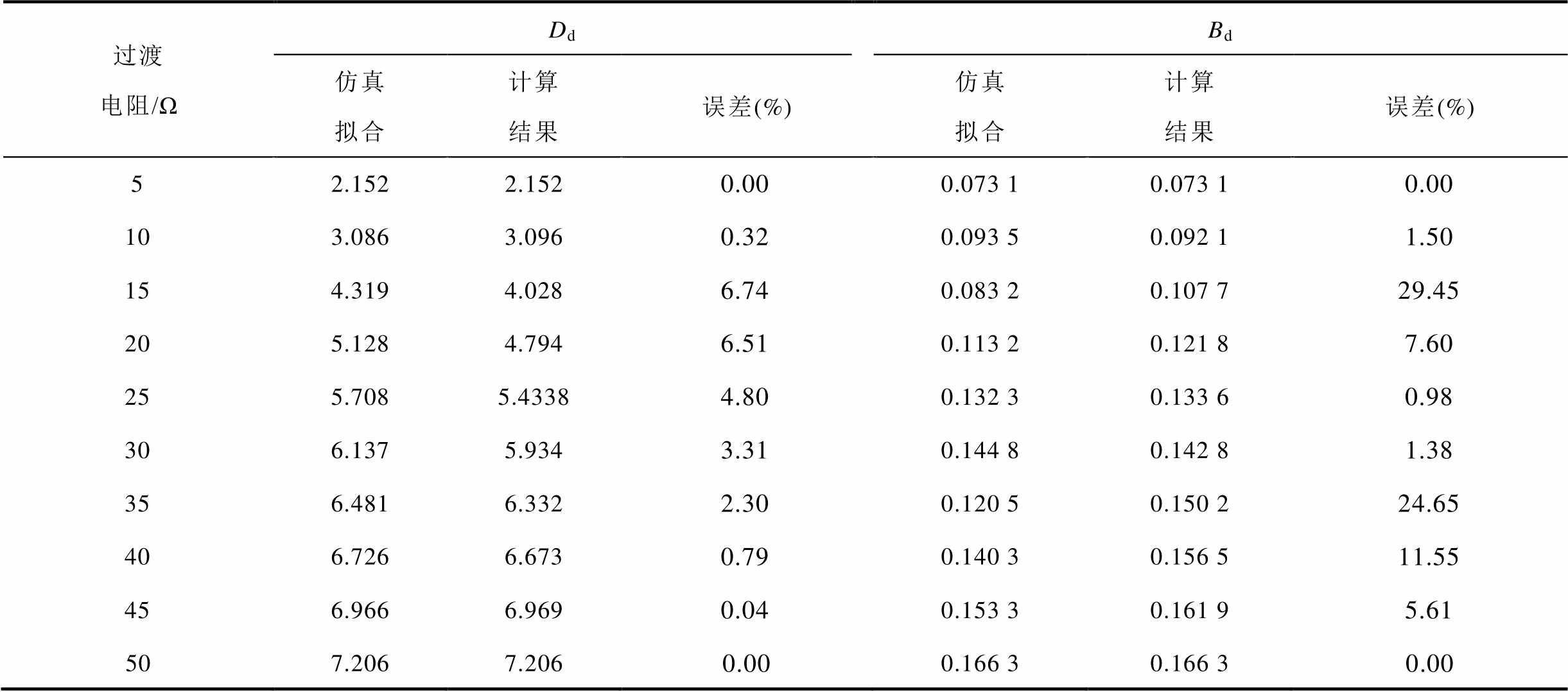
过渡电阻/ΩDdBd 仿真拟合计算结果误差(%)仿真拟合计算结果误差(%) 52.1522.1520.000.073 10.073 10.00 103.0863.0960.320.093 50.092 11.50 154.3194.0286.740.083 20.107 729.45 205.1284.7946.510.113 20.121 87.60 255.7085.43384.800.132 30.133 60.98 306.1375.9343.310.144 80.142 81.38 356.4816.3322.300.120 50.150 224.65 406.7266.6730.790.140 30.156 511.55 456.9666.9690.040.153 30.161 95.61 507.2067.2060.000.166 30.166 30.00
由表3和表4可以看出,关键项系数计算结果中,Ad和Bd的计算值绝对误差较大,其最大误差分别可达35.51%和29.45%;而Cd和Dd的计算值误差始终在10%以内。在表1所示计算结果基础上,分别取10 Ω和40 Ω过渡电阻下,仿真曲线(PSCAD仿真结果)与所提方法(电压变化轨迹算式计算结果)进行对比,结果如图6所示。
由图6a可以看出,过渡电阻为10 Ω时,故障发生后d轴电压出现暂态波动,在故障后50 ms内的波动峰值为0.42(pu)、波动谷值为0.36(pu)。根据式(1)计算得到的系统级功率指令分别为0.34(pu)和0.46(pu),根据故障稳态电压计算得到的系统级功率指令为0.48(pu)。由此可知,电网电压暂态波动导致系统功率指令在实际需求的-12.5%~-25%之间变化,严重影响了系统级功率指令的快速可靠获取。
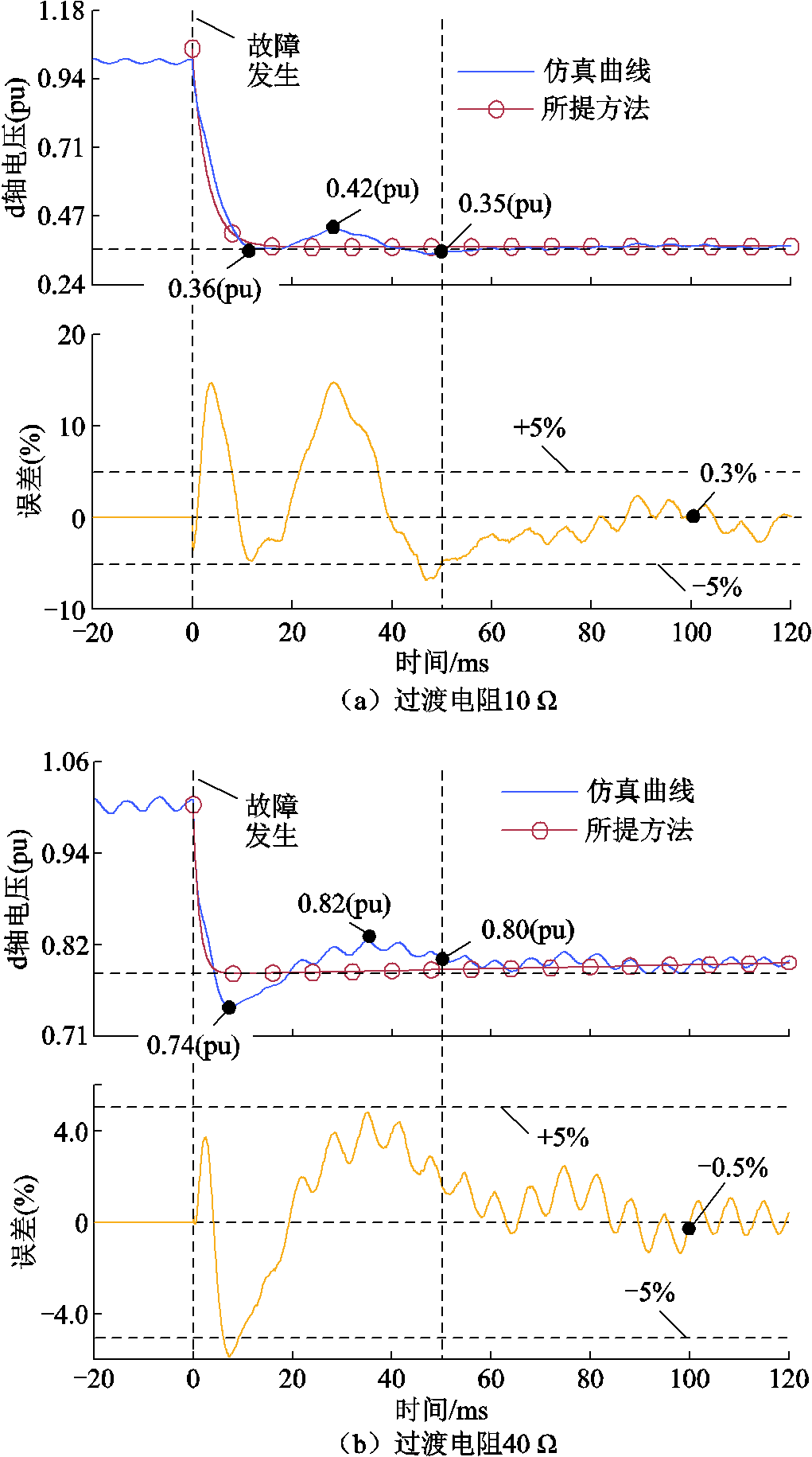
图6 不同过渡电阻下电压变化轨迹计算结果
Fig.6 Calculation results of voltage variation trajectory under different transition resistance
此外,结合表1和表2可知,由于Ad和Bd表征的是电压变化速度的快慢,其中Ad绝对数值较大(102数量级)而Bd数值较小(接近于零),使得故障持续时间内,Ad和Bd计算值误差的影响较小。同时,故障稳态阶段(取故障后100 ms),所提方法与仿真结果的误差不大于5%,其中,过渡电阻为 10 Ω时,误差为0.3%;过渡电阻为40 Ω时,误差为-0.5%。因此,所提方法能够有效计算出满足功率指令计算需求的故障稳态电压。
为验证所提方法对直流母线电压的控制效果,设置交流发生对称短路故障,过渡电阻为10 Ω,并与传统集控方法(故障后T ms下发系统级功率指令,本文设为50 ms,即等待电网电压完全进入稳态后下发功率指令)的方法进行对比,所得结果如图7所示。
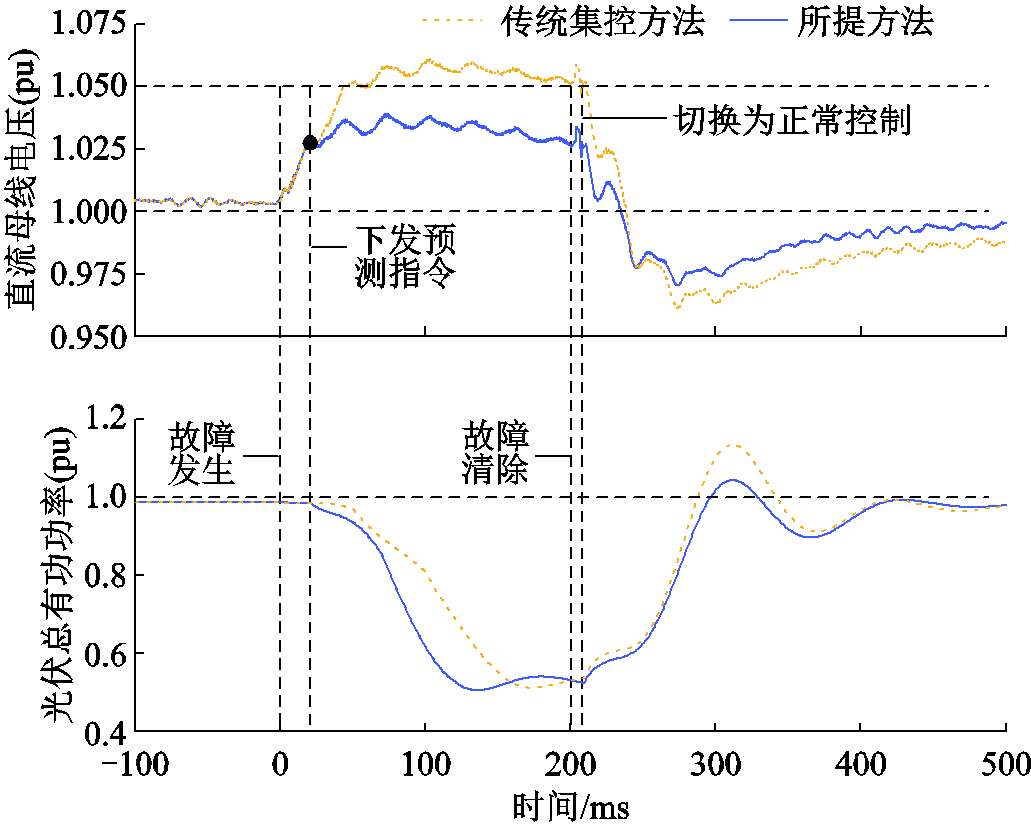
图7 不同方法下直流母线电压变化情况
Fig.7 DC bus voltage control effect under different methods
由图7可以看出,采用传统集控方法时,由于PV在故障后短时保持最大功率点跟踪(Maximum Power Point Tracking, MPPT)控制,而GCC则根据电网电压变化快速降低其有功出力,使得直流系统中出现盈余功率,导致直流母线电压抬升。从图7中可知,采用传统集控方法下直流电压快速抬升,最终超过1.05(pu),峰值达到1.062(pu)。而采用本文所提方法时,在进入低电压穿越控制后,仅通过故障后20 ms的数据即可快速下发可靠的系统级功率指令,减小了有功盈余量,使得直流母线电压始终维持在安全范围内(峰值约为1.037(pu)),为系统低电压穿越的实现提供可靠保障。
图8为三相对称短路故障下,不同电网侧等效电感下所提方法的仿真结果(此处通过改变电网侧等效电感实现短路比(Short Circuit Ratio, SCR)的调整)。
如图8所示,相同故障时不同电网侧等效电感下电网电压的幅值变化过程相近。然而,电网侧等效电感为50 mH时,电网电压有效值在故障初期存在跌落至0.2(pu)以下的情况,根据并网导则,此时光伏并网系统需降低有功功率至零。而当电网侧等效电感为10 mH时,电网电压有效值在故障初期始终高于0.2(pu),因而可以对GCC输出有功功率进行控制。进一步地,由直流母线电压波形对比可以看出,电网侧等效电感越大(SCR越小),相同故障下至母线电压的抬升幅度越大,甚至逼近过电压保护阈值1.1(pu)。
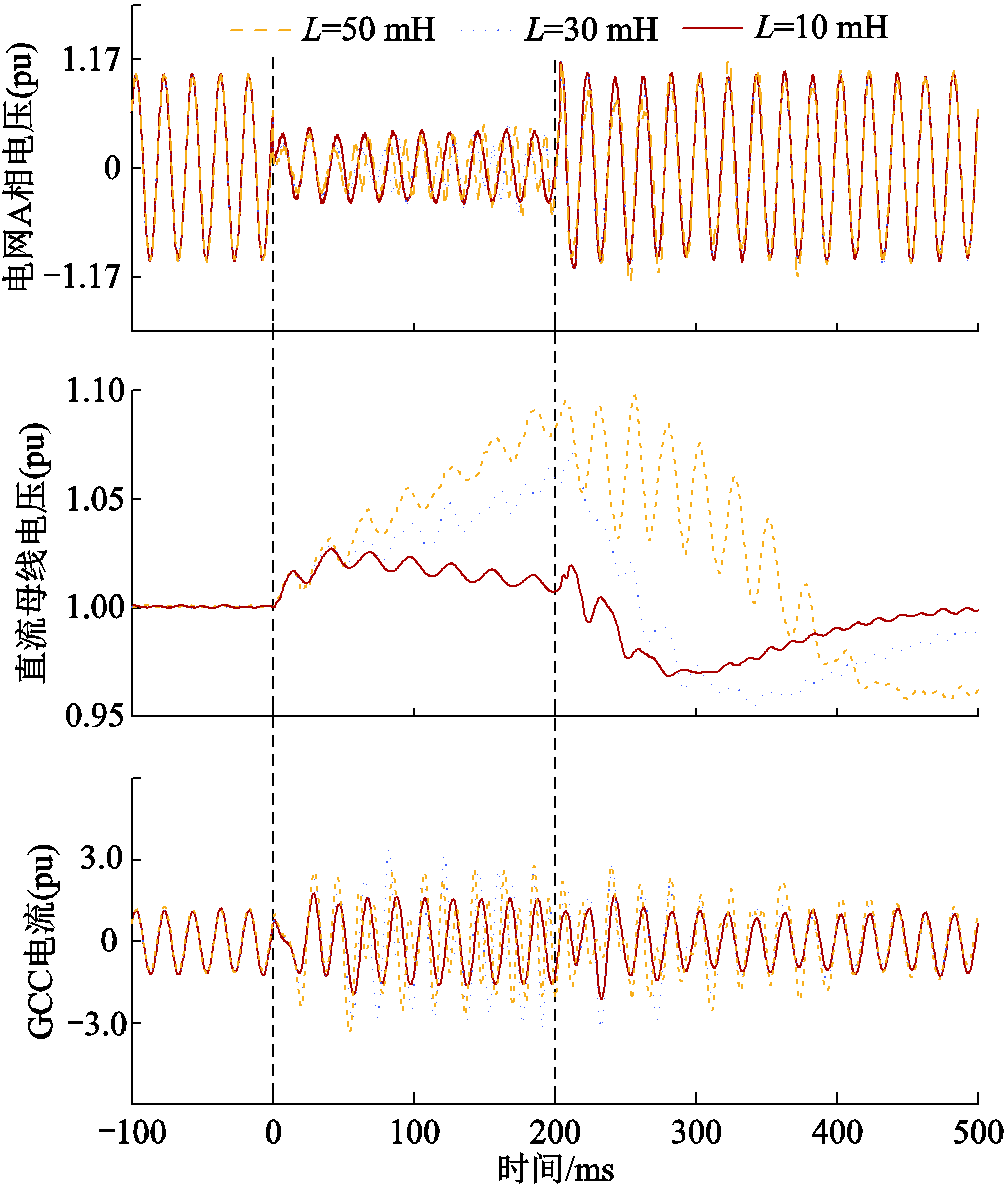
图8 不同电网侧等效电感下所提方法仿真效果对比
Fig.8 Comparison of simulation results under different inductance on the grid side with the proposed method
然而,需要注意的是,电网侧等效电感并非时变量,尤其是在百毫秒时间尺度内。因此,对于本文所提方法,需要根据不同的电网侧等效电感,获取其对应故障下的电压上限和下限,从而求解该场景下对应的电压变化轨迹算式关键项系数。而根据图8中直流母线电压变化情况可知,采用电网侧等效电感为零时的场景计算得到的电压算式关键项系数,以及根据其求解得到的系统功率指令,虽然可以适用于同一个电网侧等效电感(SCR不变)下不同故障类型及故障程度,但无法适用于时变SCR的场景。
本文提出了一种适用于光伏直流并网系统的网侧故障下不平衡功率快速平抑方法。理论分析和仿真验证结果表明,所提方法可利用外部交流系统故障初期电压数据,快速可靠地给出系统低电压穿越所需的系统级功率指令,缩短了盈余功率额度及其持续时间,减小了直流电压偏移量,避免了变流器持续运行于直流过电压状态。此外,本文所提方法弱化了对额外耗能设备的依赖,可减少投资成本。
附 录
人工短路试验系统拓扑如附图1所示。在本文研究系统中,GCC与PV直流变流器参数分别见附表1、附表2。
附图1 人工短路试验系统拓扑
App.Fig.1 System topology of artificial circuit test system
附表1 系统仿真模型中GCC参数
App.Tab.1 Parameters of GCC of simulation system

参数数值 额定容量/(MV·A)5.0 电平数72 桥臂电感/mH160 子模块电容/μF840 直流电压外环比例系数0.05 直流电压外环积分系数0.012 5
附表2 系统仿真模型中光伏变流器参数
App.Tab.2 Parameters of PV converter of simulation system

参数数值 额定容量/MW1 模块数14 直流变压器电压比5:1 直流变压器出口电容/μF600 Boost升压电路电感/mH0.5 Boost升压电路输出电容/μF1 500
系统中PV的组成结构相同,除容量以外,其余参数相近。
参考文献
[1] 周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904, 2205. Zhou Xiaoxin, Chen Shuyong, Lu Zongxiang, et al. Technology features of the new generation power system in China[J]. Proceedings of the CSEE, 2018, 38(7): 1893-1904, 2205.
[2] 辛保安, 郭铭群, 王绍武, 等. 适应大规模新能源友好送出的直流输电技术与工程实践[J]. 电力系统自动化, 2021, 45(22): 1-8. Xin Baoan, Guo Mingqun, Wang Shaowu, et al. Friendly HVDC transmission technologies for large-scale renewable energy and their engineering practice[J]. Automation of Electric Power Systems, 2021, 45(22): 1-8.
[3] 张智刚, 康重庆. 碳中和目标下构建新型电力系统的挑战与展望[J]. 中国电机工程学报, 2022, 42(8): 2806-2819. Zhang Zhigang, Kang Chongqing. Challenges and prospects for constructing the new-type power system towards a carbon neutrality future[J]. Proceedings of the CSEE, 2022, 42(8): 2806-2819.
[4] 何晓坤, 胡仁杰, 陈武. 一种适用于新能源中压直流汇集的无环流零电流软开关三电平谐振式复合全桥变换器[J]. 电工技术学报, 2023, 38(19): 5274-5287. He Xiaokun, Hu Renjie, Chen Wu. A novel circulating current free zero current switching three-level resonant composite full bridge converter for new energy medium voltage DC collection system[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5274-5287.
[5] 黄欣科, 王环, 周宇, 等. 兆瓦级光伏中压直流并网变换器研制及实证应用[J]. 电力系统自动化, 2022, 46(14): 150-157. Huang Xinke, Wang Huan, Zhou Yu, et al. Development and empirical application of megawatt-level medium-voltage DC photovoltaic grid-connected converter[J]. Automation of Electric Power Systems, 2022, 46(14): 150-157.
[6] Nasiri M, Arzani A, Guerrero J M. LVRT operation enhancement of single-stage photovoltaic power plants: an analytical approach[J]. IEEE Transactions on Smart Grid, 2021, 12(6): 5020-5029.
[7] Saxena V, Kumar N, Singh B, et al. A voltage support control strategy for grid integrated solar PV system during abnormal grid conditions utilizing interweaved GI[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 8149-8157.
[8] Naqvi S B Q, Singh B. A PV-battery system resilient to weak grid conditions with regulated power injection and grid supportive features[J]. IEEE Transactions on Sustainable Energy, 2022, 13(3): 1408-1419.
[9] 孙佳航, 冯忠楠, 黄景光, 等. 基于改进VSG的风光储联合发电系统低电压穿越控制策略[J/OL]. 电网技术, 2023: 1-14. https://doi.org/10.13335/j. 1000-3673.pst.2022.0717. Sun Jiahang, Feng Zhongnan, Huang Jingguang, et al. Low-voltage ride-through control strategy of wind-storage co-generation system based on improved VSG[J/OL]. Power System Technology, 2023: 1-14. https://doi.org/10.13335/j.1000-3673.pst.2022.0717.
[10] 王诗雯, 刘飞, 庄一展, 等. 基于有功指令共享的两级式光伏并网系统低电压穿越控制策略[J]. 电力自动化设备, 2023, 43(4): 99-105. Wang Shiwen, Liu Fei, Zhuang Yizhan, et al. Active-power-command-sharing low-voltage ride-through control strategy for two-stage PV grid-connected system[J]. Electric Power Automation Equipment, 2023, 43(4): 99-105.
[11] Zhao Tao, Feng Zhijian, Wang Mingda, et al. An optimized LVRT control strategy of cascaded modular medium-voltage inverter for large-scale PV power plant[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(6): 7744-7759.
[12] 谭爱国, 吴颖颖, 王传启, 等. 基于保障低压穿越能力的风电机组撬棒自适应投切策略研究[J]. 电力系统保护与控制, 2021, 49(18): 98-109. Tan Aiguo, Wu Yingying, Wang Chuanqi, et al. Adaptive switching strategy for a wind turbine crowbar based on the guarantee of low voltage ride-through capability[J]. Power System Protection and Control, 2021, 49(18): 98-109.
[13] Musarrat M N, Fekih A. A fault-tolerant control framework for DFIG-based wind energy conversion systems in a hybrid wind/PV microgrid[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(6): 7237-7252.
[14] 杨兴雄, 束洪春, 单节杉, 等. 计及阻容式撬棒动作时间的双馈风机短路电流分析[J]. 电工技术学报, 2021, 36(22): 4716-4725. Yang Xingxiong, Shu Hongchun, Shan Jieshan, et al. Short circuit current analysis of DFIG considering resistance-capacitance type crowbar protection action time[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4716-4725.
[15] He Yufei, Wang Minghao, Xu Zhao. Coordinative low-voltage-ride-through control for the wind-photovoltaic hybrid generation system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1503-1514.
[16] Xia Yanghong, Long Teng. Chopperless fault ride-through control for DC microgrids[J]. IEEE Transactions on Smart Grid, 2021, 12(2): 965-976.
[17] Zhao Tao, Chen Daolian. Active power backflow control strategy for cascaded photovoltaic solid-state transformer during low-voltage ride through[J]. IEEE Transactions on Industrial Electronics, 2022, 69(1): 440-451.
[18] Wan Wenfeng, Bragin M A, Yan Bing, et al. Distributed and asynchronous active fault management for networked microgrids[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3857-3868.
[19] Stanisavljevic A M, Katic V A. Magnitude of voltage sags prediction based on the harmonic footprint for application in DG control system[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8902-8912.
[20] 严伟, 王淑超, 刘翔, 等. 光伏系统快速功率控制和应用(英文)[J]. 中国电机工程学报, 2019, 39(增刊1): 213-224. Yan Wei, Wang Shuchao, Liu Xiang, et al. System level PV fast power control technology and application[J]. Proceedings of the CSEE, 2019, 39(S1): 213-224.
[21] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 光伏发电站接入电力系统技术规定: GB/T 19964—2012[S]. 北京: 中国标准出版社, 2013.
[22] 杜磊, 赵涛, 冯之健, 等. 单相短路故障条件下级联模块中压光伏发电系统的有功功率回流抑制[J]. 电工技术学报, 2022, 37(20): 5201-5213. Du Lei, Zhao Tao, Feng Zhijian, et al. Active power backflow suppression of cascaded module medium-voltage PV power generation system during single-phase short-circuit fault[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5201-5213.
[23] 刘宿城, 李响, 秦强栋, 等. 直流微电网集群的大信号稳定性分析[J]. 电工技术学报, 2022, 37(12): 3132-3147. Liu Sucheng, Li Xiang, Qin Qiangdong, et al. Large signal stability analysis for DC microgrid clusters[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3132-3147.
[24] 姚卫波, 徐晔, 黄克峰, 等. 基于前馈解耦的交直流混合微电网双向AC-DC变换器控制策略研究[J]. 电气技术, 2022, 23(5): 25-33. Yao Weibo, Xu Ye, Huang Kefeng, et al. Research on bidirectional AC-DC converter feedforward decoupling control strategy of hybrid AC/DC microgrid[J]. Electrical Engineering, 2022, 23(5): 25-33.
[25] 贾科, 刘浅, 杨彬, 等. 计及锁相环动态特性的逆变电源故障暂态电流解析[J]. 电网技术, 2021, 45(11): 4242-4251. Jia Ke, Liu Qian, Yang Bin, et al. Transient fault current analysis of the inverter-interfaced renewable energy sources considering the dynamic characteristics of the phase-locked loop[J]. Power System Technology, 2021, 45(11): 4242-4251.
Abstract In the case of grid-side faults, the grid-connected converter (GCC) of the photovoltaic DC grid-connected system (PV-DCGS) should reduce the output power in real time based on the variations of AC grid voltage. At the same time, the PVs are required to reduce active power according to the power command issued by the central controller. During the low voltage ride through (LVRT) period, due to the difference in control response speed between GCC and PVs, and the delay in system command processing, the unbalanced power within PV-DCGS will occur, resulting in DC bus voltage deviation. Traditionally, energy-dissipating devices are used to absorb the excess power to suppress the rising magnitude of the DC bus voltage. However, the investment cost and maintenance complexity will increase accordingly. To address these issues, this paper proposes a fast method for reducing the unbalanced power of PV-DCGS under grid-side faults, which can limit the deviation of DC bus voltage to an acceptable range.
First, the structure of PV-DCGS is introduced and the influence of the variation of the system power command on the DC bus voltage is analyzed. Second, the variation characteristic of the internal calculation voltage of GCC during LVRT is revealed. Then, the voltage variation trajectory formula is constructed and the variation characteristics of the key coefficients of the constructed formula are analyzed. Third, the weighted proximity is introduced to calculate the key coefficients of the constructed formula. The exact voltage variation trajectory formula can be obtained by the calculated key coefficients. Finally, the expected power command can be obtained by putting appropriate length of voltage data into the constructed formula, and effective DC bus voltage suppression can be achieved.
The simulation model of the PV-DCGS is built on the PSCAD/EMTDC electromagnetic simulation platform, which verifies the feasibility and effectiveness of the proposed method. Simulations on different types of short-circuit faults are performed. The comparison of the voltage variation trend between the simulation system and the actual power system shows that the variation trend of the internal calculation voltage of GCC in the simulation system is similar to that of the actual power system. In order to quickly calculate the key coefficients of the constructed voltage formula, the data window length should be selected appropriately. The simulation results show that when the data window length is selected between 5~20 ms, the calculation error of key coefficients is less than 5%. Considering the reliability of calculation results, the data window length of this paper is selected at 20ms. Under the selected data window length, different transition resistances of AC grid faults are tested. The results show that the key coefficients of the constructed voltage formula can be calculated reliably, and the calculation error of the dominant term is smaller than 10%. To further illustrate the effectiveness of the proposed calculation method for key coefficients, the simulation waveforms of three-phase symmetrical fault are carried out. The results show that the numerical results of the constructed voltage formula are similar to those of the simulation waveform, the calculation error is within 5%. Compared with the traditional centralized control method, the proposed method can effectively suppress the peak value of the DC bus voltage to the acceptable range (≤1.05(pu)) during LVRT period.
In conclusion, the proposed method can quickly and reliably calculate the system power command required for LVRT by using the voltage data of the external AC system at the initial fault stage, which shortens the excess power and its duration, resulting in the reduction of DC voltage deviation. With the proposed method, the GCC and PVs are free from operating at unexpected DC overvoltage range (>1.05(pu)). In addition, the proposed method weakens the dependence on additional energy-dissipating equipment and reduces the investment cost.
keywords: Photovoltaic DC grid-connected system (PV-DCGS), low voltage ride through (LVRT), voltage variation trajectory, power command, weighted proximity
DOI:10.19595/j.cnki.1000-6753.tces.230610
中图分类号:TM615
国家自然科学基金资助项目(52277097)。
收稿日期 2023-05-04
改稿日期 2023-11-28
李俊涛 男,1993年生,博士研究生,研究方向为新能源直流并网系统低电压穿越及其恢复控制。E-mail: ljtncutcmc@163.com
贾 科 男,1986年生,教授,博士生导师,研究方向为新能源电力系统保护与控制、新型配电网故障定位与系统恢复控制等。E-mail: ke.jia@ncepu.edu.cn(通信作者)
(编辑 赫 蕾)