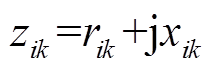 为支路
为支路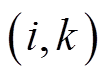 阻抗;
阻抗;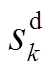 、
、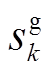 、
、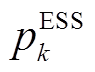 、
、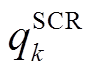 、
、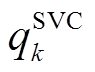 、
、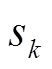 分别表示节点
分别表示节点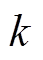 负荷功率、DG、ESS、SCR、SVC注入功率与总的吸收功率,
负荷功率、DG、ESS、SCR、SVC注入功率与总的吸收功率,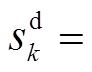
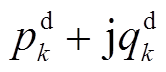 ,
,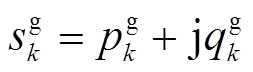 ,
,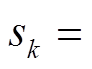
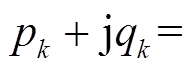
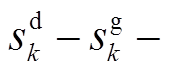
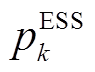
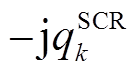
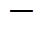
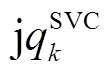 ;
;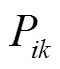 、
、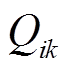 分别为支路
分别为支路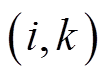 首端有功功率、无功功率;
首端有功功率、无功功率;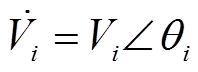 、
、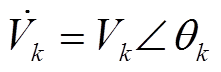 分别为节点
分别为节点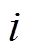 、
、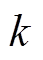 的电压。辐射状配电网支路潮流示意图如图1所示。
的电压。辐射状配电网支路潮流示意图如图1所示。摘要 高比例电动汽车、分布式风电、光伏接入配电网,导致电压频繁地剧烈波动。传统调压设备与逆变器动作速度差异巨大,如何协调是难点问题。该文结合数据驱动与物理建模方法,提出一种配电网双时间尺度电压协调优化控制策略。针对短时间尺度(min级)电压波动,以静止无功补偿器、分布式电源无功功率为决策变量,以电压二次方偏差最小为目标函数,针对平衡与不平衡配电网,基于支路潮流方程,计及物理约束构建了二次规划模型。针对长时间尺度(h级)电压波动,以电压调节器匝比、可投切电容电抗器挡位、储能系统充放电功率为动作,当前时段配电网节点功率为状态,节点电压二次方偏差为代价,构建了马尔可夫决策过程。为克服连续-离散动作空间维数灾,提出了一种基于松弛-预报-校正的深度确定性策略梯度强化学习求解算法。最后,采用IEEE 33节点平衡与123节点不平衡配电网验证了所提出方法的有效性。
关键词:智能配电网 电压控制 深度强化学习 二次规划 双时间尺度
未来一二十年,我国配电网将接入大量可再生分布式电源(Distributed Generators, DG)与电动汽车(Electrical Vehicles, EV)。DG、EV对配电网的影响与利用、配电网优化运行、主动配电网技术等已成为电气工程领域的研究热点[1]。某些情况下,传统电压调节方法无法将所有节点电压调整至额定范围[2]。文献[3]针对实际配电网以10 min为动作周期进行的仿真结果表明,电压调节器(Voltage Regulators, VR)、电容器与DG相互作用,导致动作次数急剧上升,甚至达到10万余次/年。
高比例DG接入配电网可能导致潮流反向,超过允许的最大值,损坏VR。间歇性DG、EV与VR、电容器、电动机相互作用可能导致分接头达到最高/最低挡位,失去控制,加重公共并网点电压下降/上升幅度,电压调节失败、恶化[4],甚至引起暂态电压失稳与振荡[5]。DG启停、出力变化、EV无序充电、快充亦可能导致电压越限、失稳与振荡[6]。光伏发电有功功率变化量在1 min内能够达到其额定功率的15%。文献[1]针对某实际配电网的仿真表明,处于配电网末端的快速充电站内6辆EV同时快充即可导致电压越限。
基于物理模型的无功功率优化是解决上述电压问题的常用手段。根据对通信系统的依赖程度,无功优化可分为集中式、分布式与本地控制。集中式控制主要基于混合整数二次规划、二阶锥规划、半定规划[7]、模型预测控制[8]、灵敏度分析、进化算法[9]等;分布式控制主要基于交替方向乘子法[10]、多智能体技术[11]、一致性算法[12-13]等;本地控制主要基于梯度投影法、下垂控制等。由于存在整数变量与非线性约束,集中式控制模型一般是非凸的,求解十分困难,属于NP难题。本地控制难以保证最优性。分布式控制一般要求模型是凸的。
计及源荷不确定性,传统基于物理模型的配电网多时段有功无功协调优化属于大规模混合整数非凸非线性随机或鲁棒优化,求解复杂度随配电网拓扑规模与可调设备数量的增加呈指数增长,属于NP难题。同时,DG逆变器、VR、可投切电容电抗器(Switchable Capacitors Reactors, SCR)、储能系统(Energy Storage Systems, ESS)、静止无功补偿器(Static Var Compensators, SVC)等可调设备动作速度与特性差异很大,使得配电网有功无功协调优化面临维数高、建模困难、求解缓慢等难题。如何快速找到全局最优解已成为主动配电网最优潮流领域的研究热点。
为消除对配电网精确模型与源荷不确定性先验知识的依赖,近年来基于强化学习的数据驱动方法受到了众多专家与学者的关注。深度强化学习(Deep Reinforcement Learning, DRL)已成功应用于电力系统状态估计与预测[14]、微电网经济调度[15]、电网安全稳定控制[16]、混合动力汽车能量管理[17]、园区综合能源系统优化管理[18]、风储联合电站实时调度[19]、配电网无功优化与电压控制[20-23]等。文献[24]提出了一种配电网双时间尺度电压协调优化控制策略,采用深度Q网络(Deep Q Network, DQN)算法协调控制电容器投切,但未计及配电网三相不平衡、ESS、VR、电抗器的作用。
目前,DQN算法广泛应用于配电网无功功率-电压优化问题。然而,当配电网中存在大量VR或电容器时,DQN算法导致离散动作空间维数灾[24]。针对此问题,文献[25]提出了一种多智能体DQN算法。然而,连续决策变量被离散化,导致离散动作维数急剧增加。此外,逆变器、VR与电容器的动作时间间隔设置为相同,降低了灵活性与最优性。尽管多智能体DRL能够有效地克服维度灾,但训练过程收敛速度与平稳度远低于单智能体。
此外,上述基于数据驱动的方法未计及传统可调设备与新出现的DG、ESS在不同时间尺度上的协同优化。VR、SCR、ESS与SVC、DG逆变器动作速度与特性不同(VR、SCR动作速度慢,为降低磨损,延长使用寿命,不宜频繁动作;ESS充放电功率变化率与循环次数亦存在限制),适用于不同时间尺度的电压调节。当前时刻VR匝比、SCR挡位、ESS充放电功率设定值对下一时段SVC、DG逆变器无功功率设定值具有重大影响。反之,当前时刻SVC、DG逆变器无功功率设定值对未来时段VR匝比、SCR挡位、ESS充放电功率设定值亦具有重大影响。事实上,这种双向长期互动很难刻画、建模与求解。因此,本文从可调设备动作速度与特性出发,结合数据驱动与物理建模方法,提出了一种在短、长时间尺度上协调优化控制VR、SCR、ESS、SVC与DG逆变器五种不同类型可调设备的策略。
基于支路潮流方程构建平衡与不平衡配电网电压协调优化控制模型。令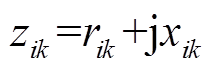 为支路
为支路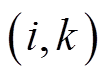 阻抗;
阻抗;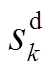 、
、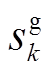 、
、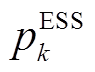 、
、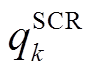 、
、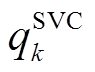 、
、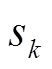 分别表示节点
分别表示节点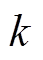 负荷功率、DG、ESS、SCR、SVC注入功率与总的吸收功率,
负荷功率、DG、ESS、SCR、SVC注入功率与总的吸收功率,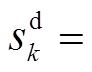
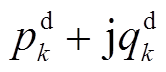 ,
,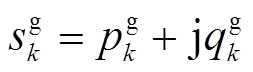 ,
,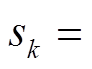
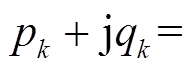
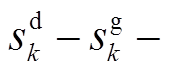
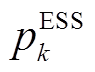
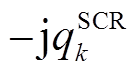
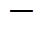
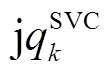 ;
;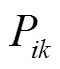 、
、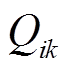 分别为支路
分别为支路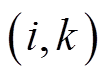 首端有功功率、无功功率;
首端有功功率、无功功率;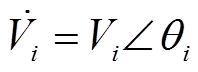 、
、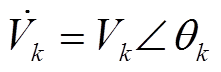 分别为节点
分别为节点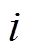 、
、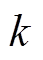 的电压。辐射状配电网支路潮流示意图如图1所示。
的电压。辐射状配电网支路潮流示意图如图1所示。
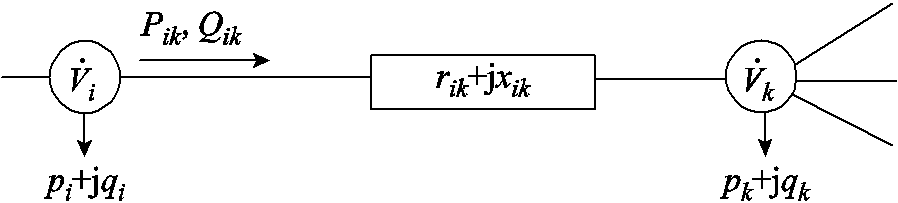
图1 辐射状配电网支路潮流
Fig.1 Branch flows of radical distribution system
令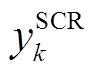 为节点k的SCR挡位;位于支路
为节点k的SCR挡位;位于支路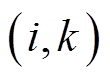 的VR匝比记为
的VR匝比记为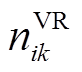 ;空载损耗记为
;空载损耗记为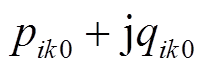 。电压调节器支路等效电路如图2所示。
。电压调节器支路等效电路如图2所示。
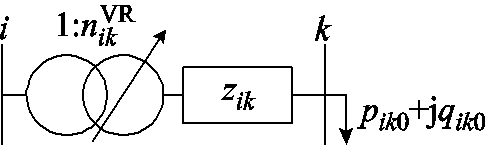
图2 电压调节器支路等效电路
Fig.2 Equivalent circuit of VR
可调设备双时间尺度动作时刻划分如图3所示,将每天划分为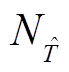 个时段,记为
个时段,记为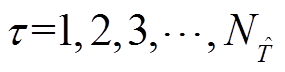 。将每个时段
。将每个时段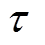 再细分为
再细分为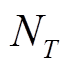 个时隙,记为
个时隙,记为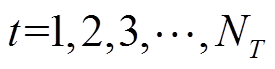 。为应对源荷缓慢变化导致的长时间尺度电压越限问题,VR匝比、SCR挡位、ESS充放电功率设定在每个时段
。为应对源荷缓慢变化导致的长时间尺度电压越限问题,VR匝比、SCR挡位、ESS充放电功率设定在每个时段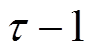 末尾至时段
末尾至时段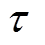 开始前完成调整,此后保持不变,直到
开始前完成调整,此后保持不变,直到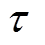 时段末尾才能重新调整。为应对风电、光伏与快充EV功率快速、剧烈变化导致的短时间尺度电压越限问题,SVC、DG逆变器无功功率设定在每个时隙t起始时刻进行调节。每个时段
时段末尾才能重新调整。为应对风电、光伏与快充EV功率快速、剧烈变化导致的短时间尺度电压越限问题,SVC、DG逆变器无功功率设定在每个时隙t起始时刻进行调节。每个时段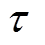 持续时间可设置为1 h。每个时隙t持续时间可设置为5~15 min。为降低模型复杂度,本文假定负荷功率
持续时间可设置为1 h。每个时隙t持续时间可设置为5~15 min。为降低模型复杂度,本文假定负荷功率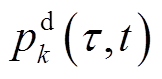 、
、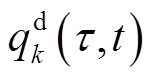 与DG出力
与DG出力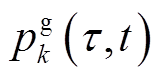 在每个时隙t内恒定,但从时隙t~t+1可变。
在每个时隙t内恒定,但从时隙t~t+1可变。
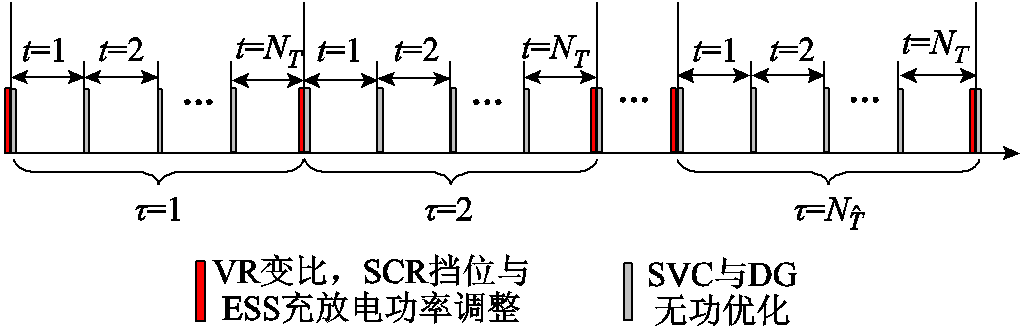
图3 可调设备双时间尺度动作时刻划分
Fig.3 Two-timescale partitioning of a day for coordinated control of different types of adjustable equipments
令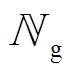 、
、 、
、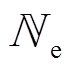 、
、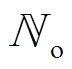 、
、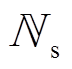 分别为DG、SCR、ESS、VR、SVC接入节点或支路集合。假设节点k DG、SVC、SCR无功功率、ESS充放电功率、支路
分别为DG、SCR、ESS、VR、SVC接入节点或支路集合。假设节点k DG、SVC、SCR无功功率、ESS充放电功率、支路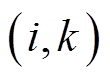 VR匝比调节范围分别为
VR匝比调节范围分别为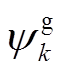 、
、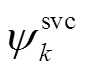 、
、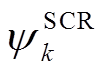 、
、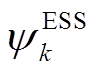 、
、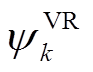 。不同类型可调设备动作速度与特性差异很大。针对此问题,本文提出的双时间尺度有功无功协调优化控制策略需求解以下随机优化问题。
。不同类型可调设备动作速度与特性差异很大。针对此问题,本文提出的双时间尺度有功无功协调优化控制策略需求解以下随机优化问题。
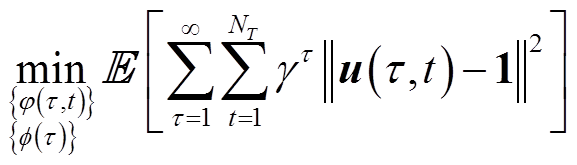 (1)
(1)
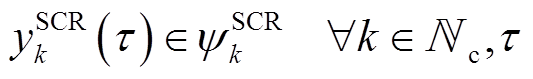 (2)
(2)
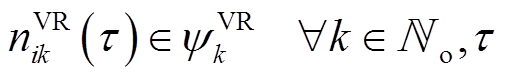 (3)
(3)
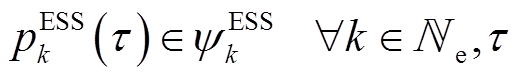 (4)
(4)
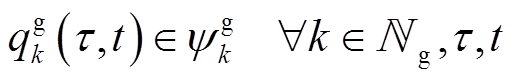 (5)
(5)
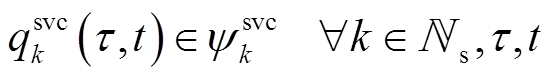 (6)
(6)
式中,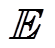 为期望;
为期望;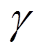 为折扣因子,
为折扣因子,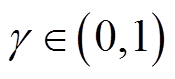 ;
;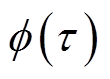 、
、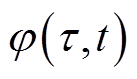 分别为长、短时间尺度优化变量;
分别为长、短时间尺度优化变量;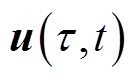 为配电网中除根节点外所有其他节点电压幅值二次方组成的向量。显然,式(1)目标函数数学期望最小值取决于决策变量
为配电网中除根节点外所有其他节点电压幅值二次方组成的向量。显然,式(1)目标函数数学期望最小值取决于决策变量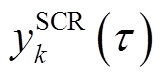 、
、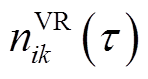 、
、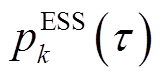 在每个时段
在每个时段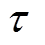 和
和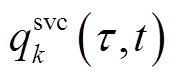 、
、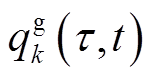 在每个时隙
在每个时隙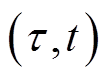 的优化设定值。离散变量
的优化设定值。离散变量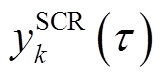 、
、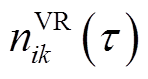 使得式(1)~式(6)是非凸的,求解十分困难,属于NP难题。因此,本文提出在每个时段
使得式(1)~式(6)是非凸的,求解十分困难,属于NP难题。因此,本文提出在每个时段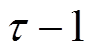 的末尾,VR匝比、SCR挡位与ESS充放电功率长时间尺度(近似)最优设定值采用DRL算法根据当前
的末尾,VR匝比、SCR挡位与ESS充放电功率长时间尺度(近似)最优设定值采用DRL算法根据当前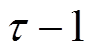 时段配电网状态数据学习出来;与此同时,在时段
时段配电网状态数据学习出来;与此同时,在时段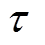 内每个时隙t起始时刻,SVC、DG逆变器无功功率最优设定值在给定VR匝比、SCR挡位与ESS充放电功率的情况下,通过构建与求解单一时隙凸规划物理模型给出。时段
内每个时隙t起始时刻,SVC、DG逆变器无功功率最优设定值在给定VR匝比、SCR挡位与ESS充放电功率的情况下,通过构建与求解单一时隙凸规划物理模型给出。时段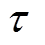 内各个时隙t物理模型目标函数优化结果累加值为时段
内各个时隙t物理模型目标函数优化结果累加值为时段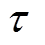 马尔可夫决策过程(Markov Decision Process, MDP)的代价。
马尔可夫决策过程(Markov Decision Process, MDP)的代价。
本节将省去时段标记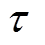 。令
。令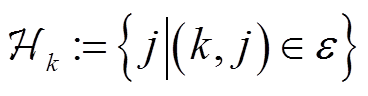 为节点
为节点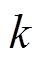 的子节点集合;
的子节点集合;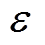 为支路集合。令
为支路集合。令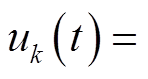
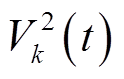 。忽略线路有功、无功功率损耗,功率方程为
。忽略线路有功、无功功率损耗,功率方程为
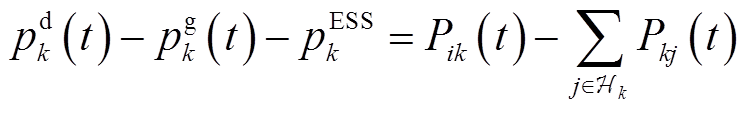 (7)
(7)
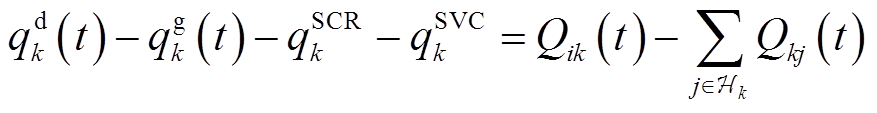 (8)
(8)
式中,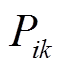 、
、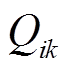 分别为支路ik首端的有功功率、无功功率;
分别为支路ik首端的有功功率、无功功率;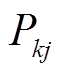 ,
, 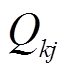 分别为支路kj首端的有功功率、无功功率。
分别为支路kj首端的有功功率、无功功率。
忽略线路电压损耗,不含VR的支路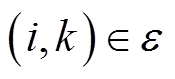 ,(
,(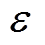 为配电网支路集合)电压降落方程为
为配电网支路集合)电压降落方程为
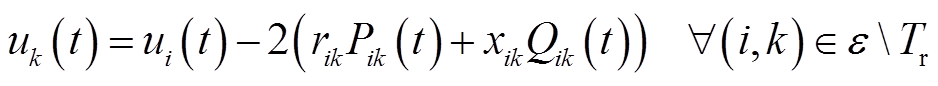 (9)
(9)
式中,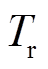 为VR支路集合。如图2所示,忽略线路电压损耗,VR支路电压降落方程为
为VR支路集合。如图2所示,忽略线路电压损耗,VR支路电压降落方程为
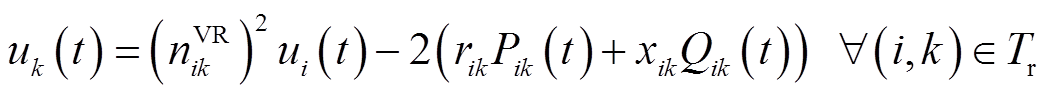 (10)
(10)
在实际配电网中,架空线路一般不再换位,而且三相功率一般不相等。因此,配电网三相不对称,需要采用三相模型。对于不含VR的支路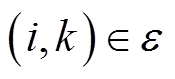 ,电压降落方程为
,电压降落方程为
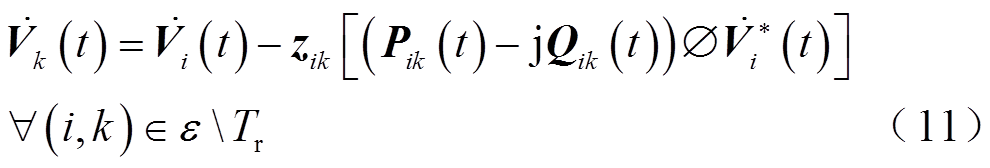
式中,三维向量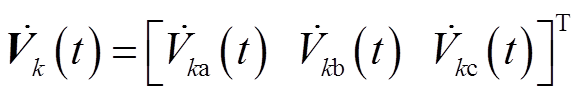 ;
;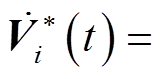
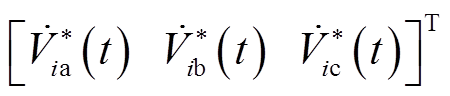 ;符号
;符号 表示按分量取共轭运算;
表示按分量取共轭运算;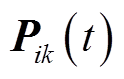 为支路首端三相有功功率,
为支路首端三相有功功率,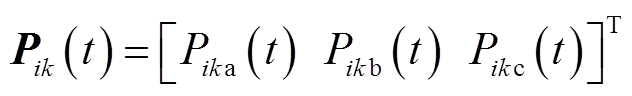 ;
;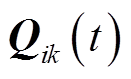 为支路首端三相无功功率,
为支路首端三相无功功率,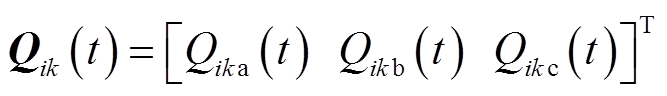 ;
;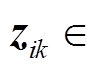
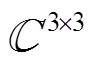 为线路阻抗矩阵;
为线路阻抗矩阵;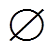 表示按分量点除。
表示按分量点除。
由于配电网中各节点电压幅值一般相差很小,即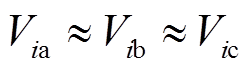 。而且三相电压相位不平衡角度
。而且三相电压相位不平衡角度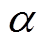 很小,一般在1°~3°以内。忽略
很小,一般在1°~3°以内。忽略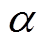 且假定三相电压幅值相等,式(11)左右两边各点乘其共轭向量得到
且假定三相电压幅值相等,式(11)左右两边各点乘其共轭向量得到
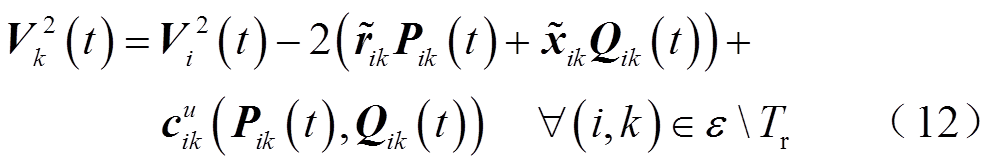
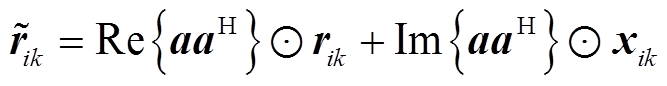 (13)
(13)
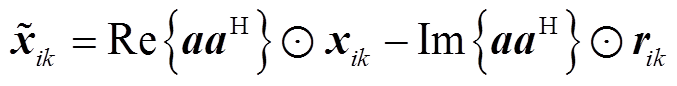 (14)
(14)
 (15)
(15)
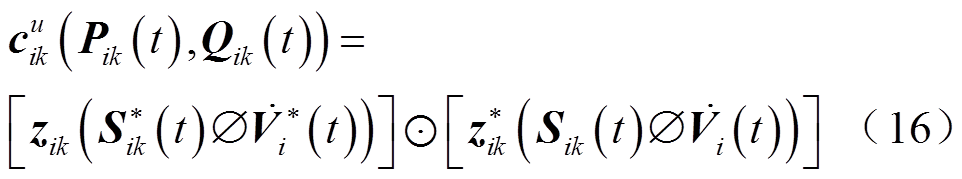
式中, 表示按分量点乘;
表示按分量点乘;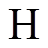 为共轭转置运算符。忽略线路有功功率、无功功率损耗,功率方程为
为共轭转置运算符。忽略线路有功功率、无功功率损耗,功率方程为
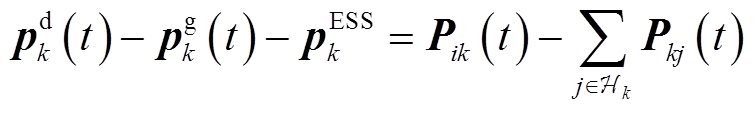 (17)
(17)
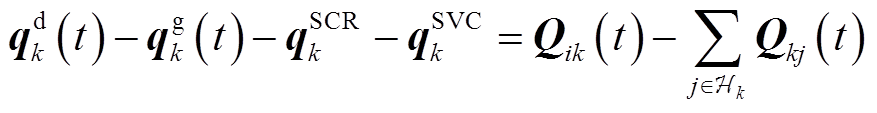 (18)
(18)
令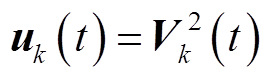 ,
,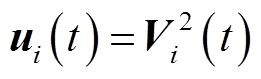 。忽略电压损耗
。忽略电压损耗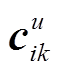 ,式(12)可简化为
,式(12)可简化为
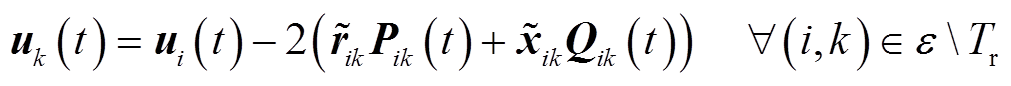 (19)
(19)
对于含VR的支路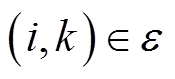 ,电压降落方程为
,电压降落方程为
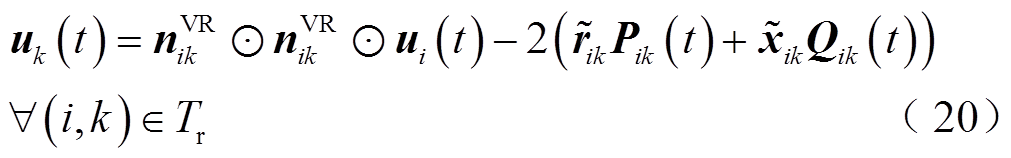
式中,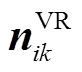 为VR三相匝比,
为VR三相匝比,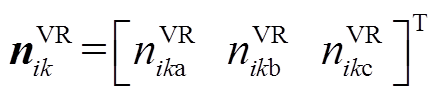 。
。
本文仅计及经全容量逆变器接入配电网的DG,如光伏发电或永磁直驱风机。值得指出的是,本文所提出的方法也适用于其他类型DG,如双馈风机,只需稍微修改式(21)即可。DG无功功率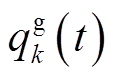 受逆变器容量
受逆变器容量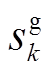 与有功出力
与有功出力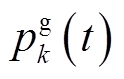 限制,其调节范围为
限制,其调节范围为
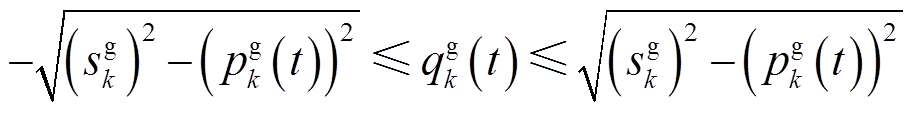 (21)
(21)
SVC注入配电网的无功功率约束为
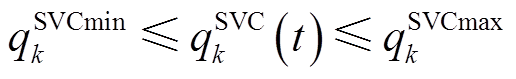 (22)
(22)
式中,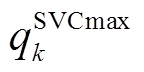 、
、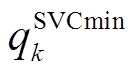 分别为SVC无功功率上、下限。
分别为SVC无功功率上、下限。
对于三相平衡配电网,短时间尺度电压协调优化控制模型为
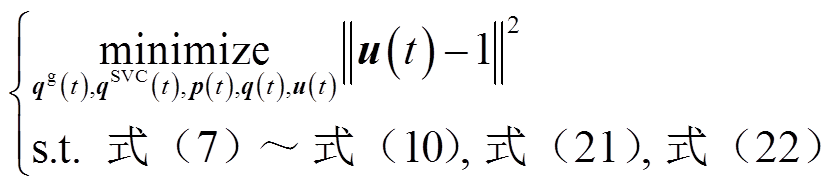 (23)
(23)
式中,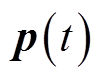 、
、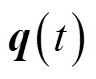 、
、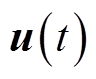 、
、 、
、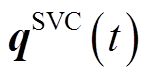 分别为配电网所有支路有功功率、无功功率、除根节点外所有节点电压幅值二次方、所有DG、SVC无功功率构成的列向量。
分别为配电网所有支路有功功率、无功功率、除根节点外所有节点电压幅值二次方、所有DG、SVC无功功率构成的列向量。
对于三相不平衡配电网,短时间尺度电压协调优化控制模型为
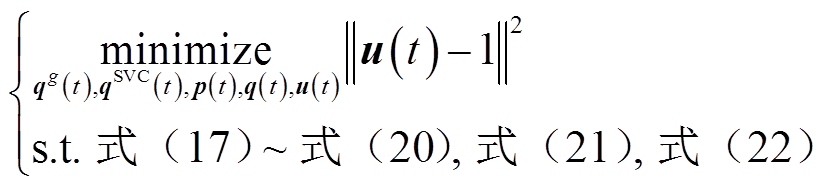 (24)
(24)
值得指出的是,本文对源荷不确定性处理方法如下:短时间尺度凸优化模型时隙t间隔可根据实际配电网功率波动情况设置为几分钟。因此,源荷功率可采用超短期预测方法得到精确值[14]。
由式(7)、式(8)、式(10)、式(17)、式(18)、式(20)与图3可以看出,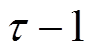 时段末尾VR匝比、SCR挡位、ESS充放电功率设定值(长时间尺度学习)对
时段末尾VR匝比、SCR挡位、ESS充放电功率设定值(长时间尺度学习)对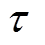 时段内每个时隙t起始时刻SVC、DG逆变器无功功率设定值(短时间尺度凸优化)均具有重大影响。反之,
时段内每个时隙t起始时刻SVC、DG逆变器无功功率设定值(短时间尺度凸优化)均具有重大影响。反之,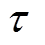 时段内每个时隙t起始时刻SVC、DG逆变器无功功率设定值经由奖励对后续时段末尾VR匝比、SCR挡位、ESS充放电功率设定值产生影响。这种双向作用十分适合采用RL方法求解。
时段内每个时隙t起始时刻SVC、DG逆变器无功功率设定值经由奖励对后续时段末尾VR匝比、SCR挡位、ESS充放电功率设定值产生影响。这种双向作用十分适合采用RL方法求解。
随机优化与鲁棒优化是处理源荷不确定性的常用方法。然而,随机优化需要大量数据样本,计算开销巨大,难以满足大规模配电网实时控制需求。鲁棒优化针对最恶劣场景进行决策,未利用源荷不确定性概率密度信息,使得优化结果偏于保守。因此,针对传统大规模混合整数优化NP难题,本文第一层长时间尺度(h级)控制基于数据驱动方法构建MDP,采用DRL方法能够快速求解离散可调设备匝比/挡位与ESS充放电功率(近似)最优设定值。为克服离散动作空间维数灾,本文提出一种基于松弛-预报-校正的改进深度确定性策略梯度(Deep Deterministic Policy Gradient, DDPG)强化学习算法,能够高效处理离散与连续决策变量联合动作。针对高比例间歇性DG、快充EV接入配电网引起的源荷功率与电压频繁、快速、剧烈波动问题,本文第二层短时间尺度(min级)控制在给定第一层控制变量设定值后,通过构建单一时隙无功优化二次规划(Quadratic Programming, QP)物理模型,能够快速求解SVC与DG逆变器无功功率设定值,满足实时控制需求。源荷功率采用超短期预测方法得到精确值[14]。长时间尺度(h级)内求解每个短时间尺度(min级)QP得到的最优目标函数值累加后作为MDP的代价。因此,数据驱动与物理建模方法融为一体,相互协调,互相配合,能够保证解的(近似)最优性。
状态空间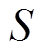 :如式(25)所示,状态定义为
:如式(25)所示,状态定义为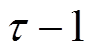 时段VR匝比
时段VR匝比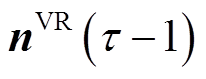 、SCR挡位
、SCR挡位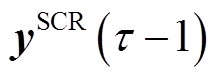 、ESS功率
、ESS功率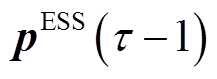 、每个节点吸收的平均功率
、每个节点吸收的平均功率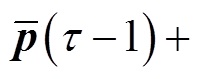
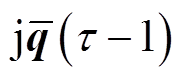 与
与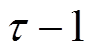 时段末尾ESS存储电量
时段末尾ESS存储电量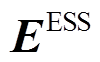
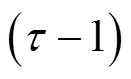 。
。

动作空间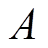 :每一种可能的VR匝比、SCR挡位与ESS充放电功率组合构成一个动作,定义为
:每一种可能的VR匝比、SCR挡位与ESS充放电功率组合构成一个动作,定义为
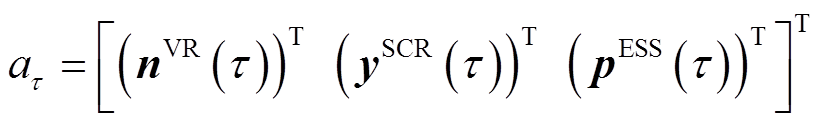 (26)
(26)
本文假设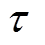 时段节点k ESS从电网吸收的功率为
时段节点k ESS从电网吸收的功率为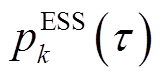 ,此功率为连接ESS与电网导体上的功率。若
,此功率为连接ESS与电网导体上的功率。若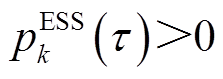 ,即ESS处于充电状态,则ESS能量变化量(增加的电量)为
,即ESS处于充电状态,则ESS能量变化量(增加的电量)为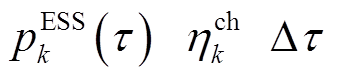 ,其中,
,其中,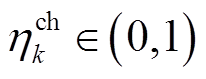 为充电效率,
为充电效率,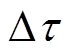 为ESS调度时间间隔;若
为ESS调度时间间隔;若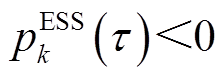 ,即ESS处于放电状态,则ESS能量变化量为
,即ESS处于放电状态,则ESS能量变化量为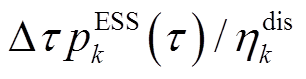 ,即ESS放电电量为
,即ESS放电电量为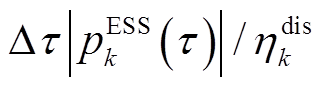 ,其中,
,其中,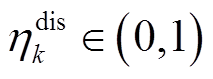 为放电效率。若
为放电效率。若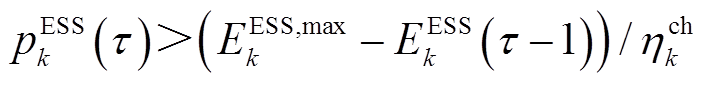 ,则
,则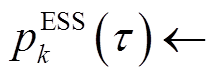
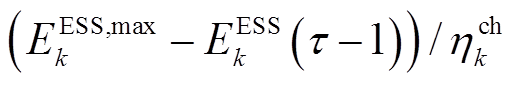 与配电网交互。类似地,若
与配电网交互。类似地,若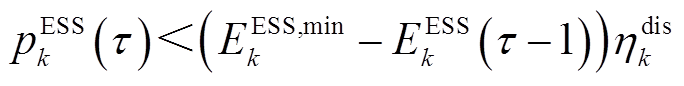 ,则
,则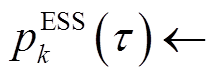
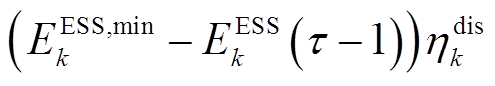 与配电网交互。其中,
与配电网交互。其中,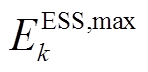 与
与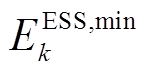 分别为ESS允许存储最大、小电量。
分别为ESS允许存储最大、小电量。
策略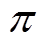 :根据状态
:根据状态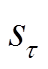 采取动作
采取动作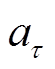 的概率为
的概率为
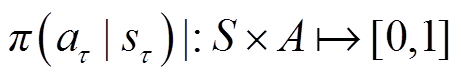 (27)
(27)
代价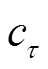 :
: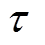 时段MDP代价定义为
时段MDP代价定义为
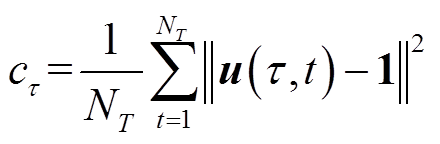 (28)
(28)
长期回报J:MDP的目标是采用最优策略使得长期折扣回报最大。
DQN算法不适用于连续动作。此外,当配电网中含大量VR或SCR时,DQN算法导致离散动作空间维度灾。DDPG算法不适用于离散动作,不能直接应用于含VR或SCR的配电网。针对上述问题,本文提出了一种改进DDPG算法。首先,将离散动作分量松弛为连续动作分量(称为松弛过程);然后,针对执行器(Actor)输出的原型动作中对应于VR匝比、SCR挡位的分量,在离散动作空间(嵌入离散动作分量集合)中搜索出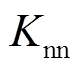 个最邻近点(称为预报过程);最后,每个最邻近点与Actor输出的原型动作中连续分量(ESS充放电功率)组成一个完整动作,依次输入评价器(Critic),计算动作价值,选取价值最大的动作与环境交互[26](称为校正过程)。本文将文献[26]中的方法推广到一般情形,即离散-连续联合动作空间。由于在已知数据集中找出给定点的
个最邻近点(称为预报过程);最后,每个最邻近点与Actor输出的原型动作中连续分量(ESS充放电功率)组成一个完整动作,依次输入评价器(Critic),计算动作价值,选取价值最大的动作与环境交互[26](称为校正过程)。本文将文献[26]中的方法推广到一般情形,即离散-连续联合动作空间。由于在已知数据集中找出给定点的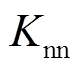 个最邻近点能够在对数时间复杂度内完成计算,目前已有大量文献报导该算法。因此,本文提出的基于松弛-预报-校正的改进DDPG算法不会大幅增加计算时间。改进DDPG算法示意图如图4所示。图中,加号表示组合(串联);等号表示原型动作由连续与离散动作分量组成。
个最邻近点能够在对数时间复杂度内完成计算,目前已有大量文献报导该算法。因此,本文提出的基于松弛-预报-校正的改进DDPG算法不会大幅增加计算时间。改进DDPG算法示意图如图4所示。图中,加号表示组合(串联);等号表示原型动作由连续与离散动作分量组成。
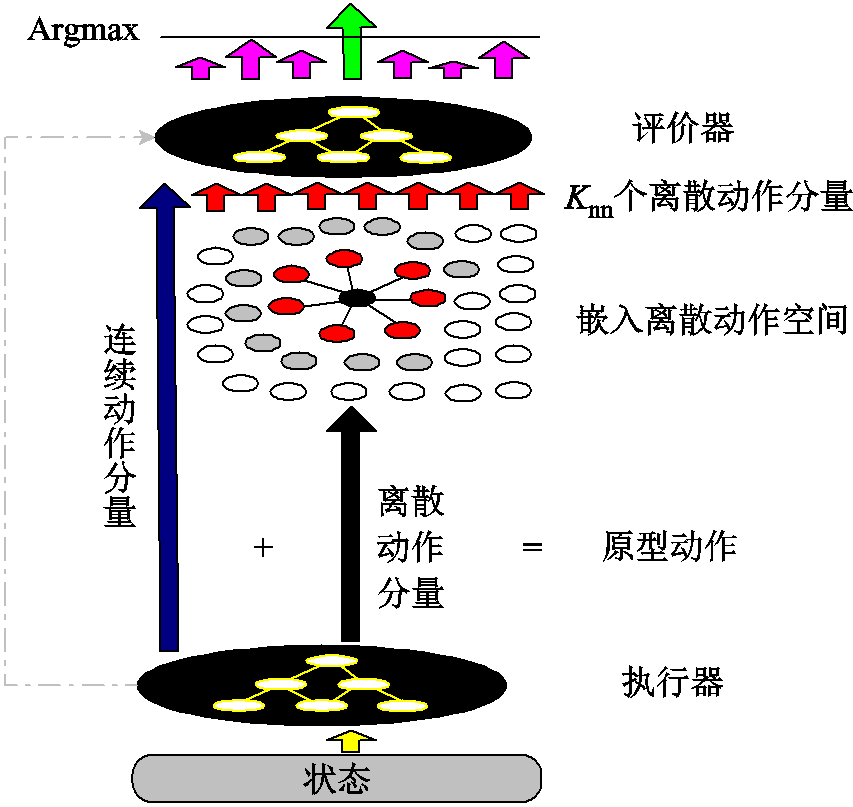
图4 消除离散-连续动作空间维数灾的改进DDPG算法
Fig.4 Adapted DDPG algorithm to eliminate dimensions curses in discrete-continuous action space
本文提出的双时间尺度电压协调优化控制程序流程如图5所示。
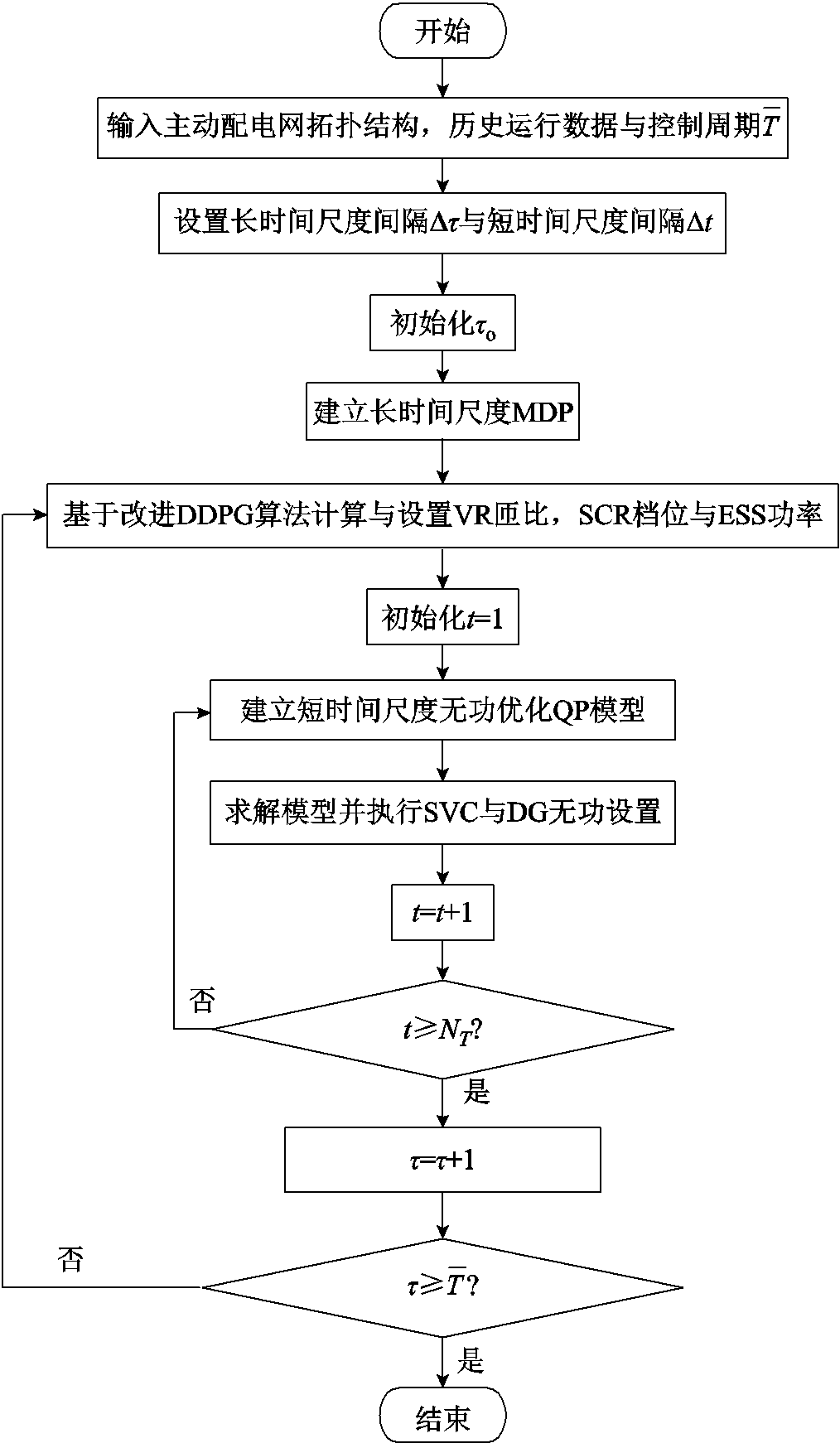
图5 双时间尺度电压协调优化控制程序流程
Fig.5 Flow chart of procedure for coordinated and optimal voltages control on dual timescales
在每个时段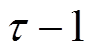 的末尾,VR匝比、SCR挡位与ESS充放电功率长时间尺度(近似)最优设定值采用DRL算法根据当前
的末尾,VR匝比、SCR挡位与ESS充放电功率长时间尺度(近似)最优设定值采用DRL算法根据当前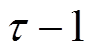 时段配电网状态数据学出来;与此同时,在时段
时段配电网状态数据学出来;与此同时,在时段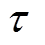 内每个时隙t起始时刻,SVC、DG逆变器无功功率最优设定值在给定VR匝比、SCR挡位与ESS充放电功率的情况下,通过构建与求解单一时隙QP给出。时段
内每个时隙t起始时刻,SVC、DG逆变器无功功率最优设定值在给定VR匝比、SCR挡位与ESS充放电功率的情况下,通过构建与求解单一时隙QP给出。时段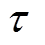 内各个时隙t物理模型目标函数优化结果累加值为该时段
内各个时隙t物理模型目标函数优化结果累加值为该时段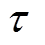 的MDP代价。
的MDP代价。
采用IEEE 33节点平衡、123节点不平衡配电网两个仿真系统验证本文所提出方法的性能。33、123节点配电网拓扑结构分别如文献[27]中图10、文献[28]中图5所示;两个系统中,ESS参数见表1;SCR、SVC、ESS与风电机组(Wind Turbine Generator,WTG)的详细参数见表2,括号外的数字为接入节点或支路,括号内的字母为接入相别;每个VR最大与最小匝比分别为1.05与0.95;人工神经网络参数见表3;每个时段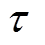 的时间间隔设置为1 h;每个节点负荷功率与每台WTG每天出力水平曲线分别如文献[27]中图4与图5所示。
的时间间隔设置为1 h;每个节点负荷功率与每台WTG每天出力水平曲线分别如文献[27]中图4与图5所示。
表1 ESS的参数
Tab.1 Parameters of ESS

/ (MW·h)/ (MW·h)/ MW/ MW 1.50.150.30.30.990.99
表2 可调设备的参数
Tab. 2 Parameters of adjustable equipments
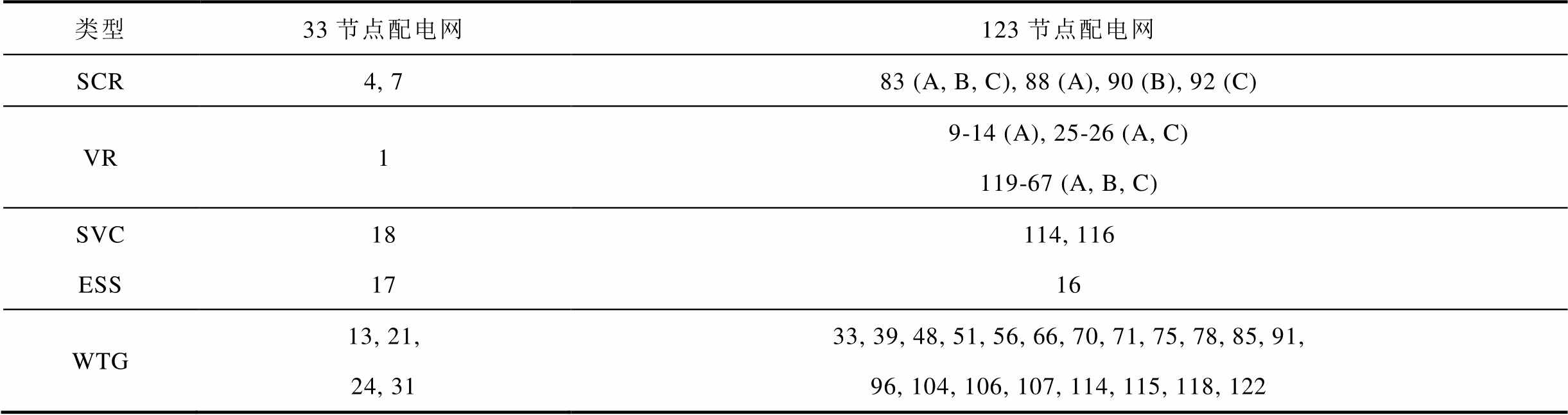
类型33节点配电网123节点配电网 SCR4, 783 (A, B, C), 88 (A), 90 (B), 92 (C) VR19-14 (A), 25-26 (A, C)119-67 (A, B, C) SVC18114, 116 ESS1716 WTG13, 21, 24, 3133, 39, 48, 51, 56, 66, 70, 71, 75, 78, 85, 91, 96, 104, 106, 107, 114, 115, 118, 122
表3 DDPG人工神经网络的参数
Tab.3 Settings of DDPG
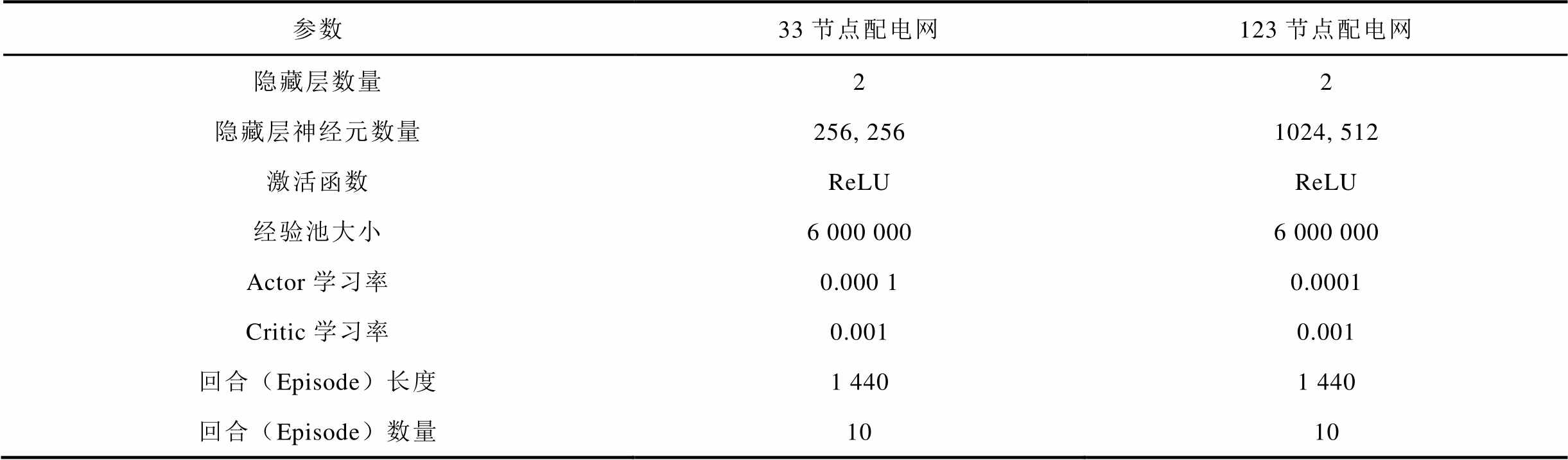
参数33节点配电网123节点配电网 隐藏层数量22 隐藏层神经元数量256, 2561024, 512 激活函数ReLUReLU 经验池大小6 000 0006 000 000 Actor学习率0.000 10.0001 Critic学习率0.0010.001 回合(Episode)长度1 4401 440 回合(Episode)数量1010
在33节点配电网中,SVC容量为[-0.5 0.5]Mvar;每个SCR最小、最大无功功率分别为-0.5、0.5 Mvar,步长为0.1 Mvar;VR步长为0.006 25;每台WTG最大有功功率与额定容量分别为0.1 MW、0.1 MV·A;时隙t间隔长度设置为5 min。
在123节点配电网中,每个SVC容量为[-0.15 0.15]Mvar;每个on-off电容器无功功率分别为0.2、0.2、0.2、0.05、0.05、0.05 Mvar;每个VR步长为0.025;每台WTG最大有功功率与额定容量分别为0.09 MW、0.09 MV·A;节点123为平衡节点,电压固定为1.05(pu);时隙t间隔长度设置为10 min;每个节点最大负荷功率与文献[28]相同。
值得指出的是,目前配电网调度周期是固定的,如1 h。未来,高比例光伏、(快充)EV接入配电网,导致电压频繁、快速、剧烈波动。配电网调度周期将会发生改变,如变为5~15 min。文献[24]设置配电网调度周期为5 min。因此,本文提出的结合数据驱动与物理模型的主动配电网双时间尺度电压协调优化控制方法中,ESS、VR与SCR动作周期为每个时段(h级),在每个时隙(min级)均不动作,SVC、DG逆变器无功动作周期为每个时隙(min级),如图3所示。
在33节点平衡配电网中,共有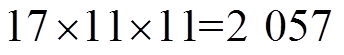 个离散动作分量。为了验证本文方法的有效性,首先设置VR匝比、SCR挡位、ESS充放电功率每个时段
个离散动作分量。为了验证本文方法的有效性,首先设置VR匝比、SCR挡位、ESS充放电功率每个时段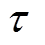 均为随机值与固定值。当设为固定值时,VR匝比为1,SCR无功功率补偿为0,ESS充放电功率为0。基于Python语言,采用MOSEK工具箱求解每个时隙t的QP模型。每天平均每小时代价优化结果如图6中黑色与黄色实线所示。可以看出,每天平均每小时代价均远高于0.25(pu),意味着每天电压越限频繁出现且十分严重。而且,第一阶段变量设定为随机值比设定为固定值导致的电压越限问题更严重。
均为随机值与固定值。当设为固定值时,VR匝比为1,SCR无功功率补偿为0,ESS充放电功率为0。基于Python语言,采用MOSEK工具箱求解每个时隙t的QP模型。每天平均每小时代价优化结果如图6中黑色与黄色实线所示。可以看出,每天平均每小时代价均远高于0.25(pu),意味着每天电压越限频繁出现且十分严重。而且,第一阶段变量设定为随机值比设定为固定值导致的电压越限问题更严重。
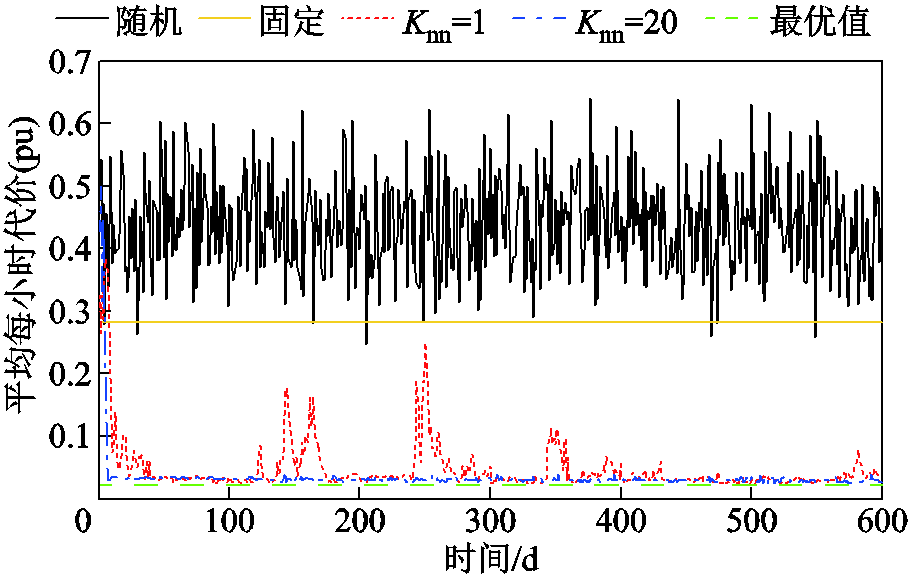
图6 33节点配电网平均每小时代价
Fig.6 Average costs per hour for 33-bus system
为了测试本文方法的(近似)最优性,设定VR匝比、SCR挡位、ESS充放电功率在每个时隙t均可调节,构建288时隙单一短时间尺度传统日前混合整数QP模型。基于Matlab平台采用Mosek 9.1.4软件包求解。为提高计算速度,设置相对对偶间隙为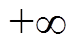 ,平均每小时最优代价为0.020 7(pu),如图6中绿色虚线所示。
,平均每小时最优代价为0.020 7(pu),如图6中绿色虚线所示。
采用本文方法,针对Actor输出的动作,在离散动作分量空间搜索出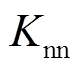 =1与
=1与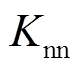 =20个最邻近动作分量,优化结果分别如图6中红色虚线与蓝色点画线所示。可以看出,采用本文方法,训练过程起始阶段平均每小时代价较高,电压越限较严重。这是因为DDPG算法在起始阶段Actor采用的是随机动作策略。当
=20个最邻近动作分量,优化结果分别如图6中红色虚线与蓝色点画线所示。可以看出,采用本文方法,训练过程起始阶段平均每小时代价较高,电压越限较严重。这是因为DDPG算法在起始阶段Actor采用的是随机动作策略。当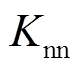 =20时,在第6天数据被训练后(训练了
=20时,在第6天数据被训练后(训练了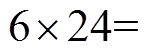
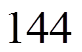 步),平均每小时代价开始变得很低,最终趋近于0.026 2(pu)。然而,当
步),平均每小时代价开始变得很低,最终趋近于0.026 2(pu)。然而,当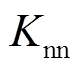 =1时,平均每小时代价出现频繁、剧烈波动,训练过程不平稳。
=1时,平均每小时代价出现频繁、剧烈波动,训练过程不平稳。
采用不同方法进行电压调节,训练过程中各时隙所有节点电压如图7所示。可以看出,采用本文提出的改进DDPG算法,当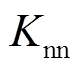 =1与20时,在经过短时间(大约1 000个时隙数据)训练后,动作策略趋于稳定,所有节点电压均处于[0.9, 1.03] (pu)范围内。此外,当
=1与20时,在经过短时间(大约1 000个时隙数据)训练后,动作策略趋于稳定,所有节点电压均处于[0.9, 1.03] (pu)范围内。此外,当 =20时,在大约85 000个时隙数据被训练后,动作策略趋于最优,所有节点电压均处于[0.95 1.03] (pu)范围内。
=20时,在大约85 000个时隙数据被训练后,动作策略趋于最优,所有节点电压均处于[0.95 1.03] (pu)范围内。
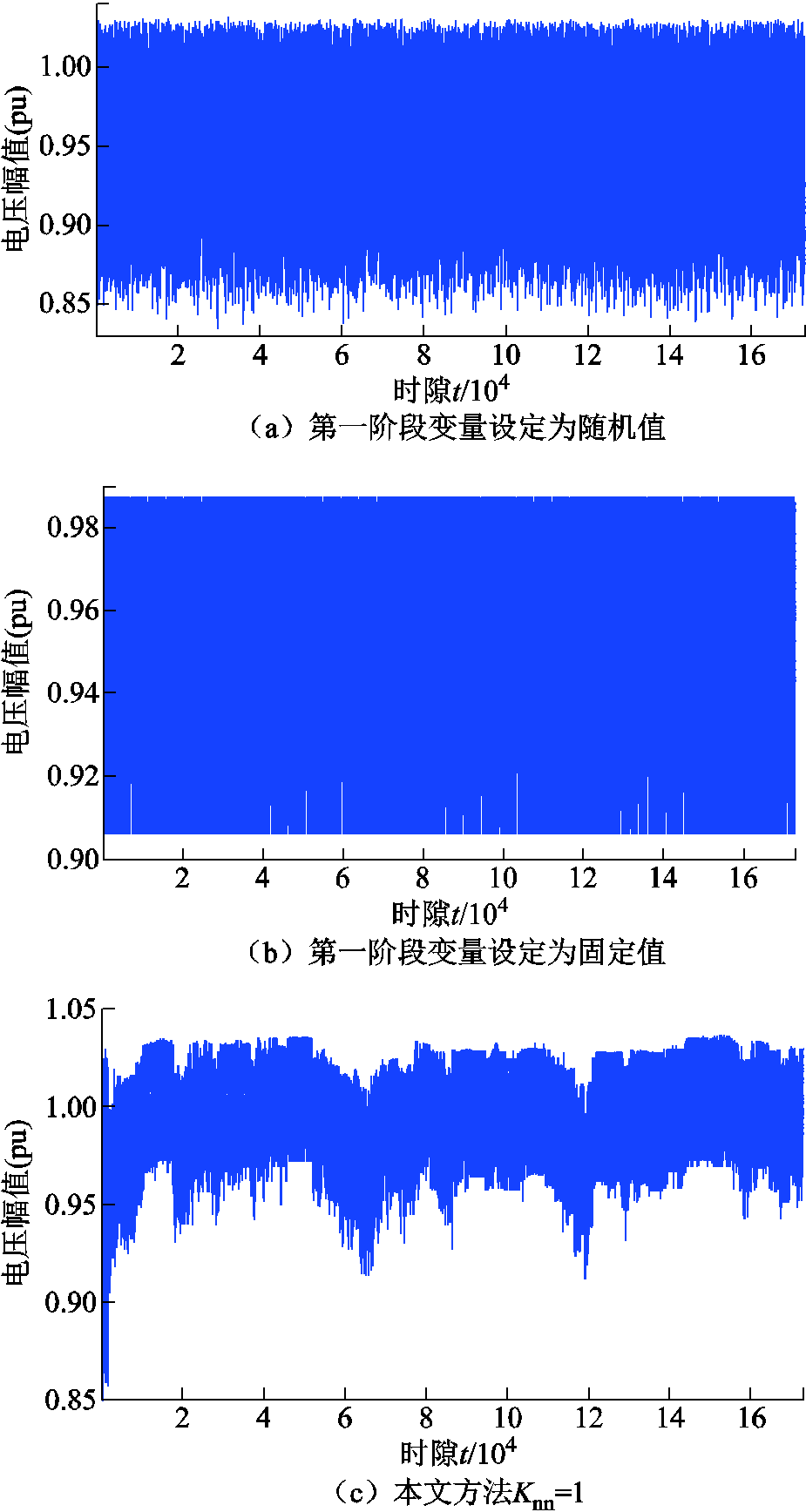
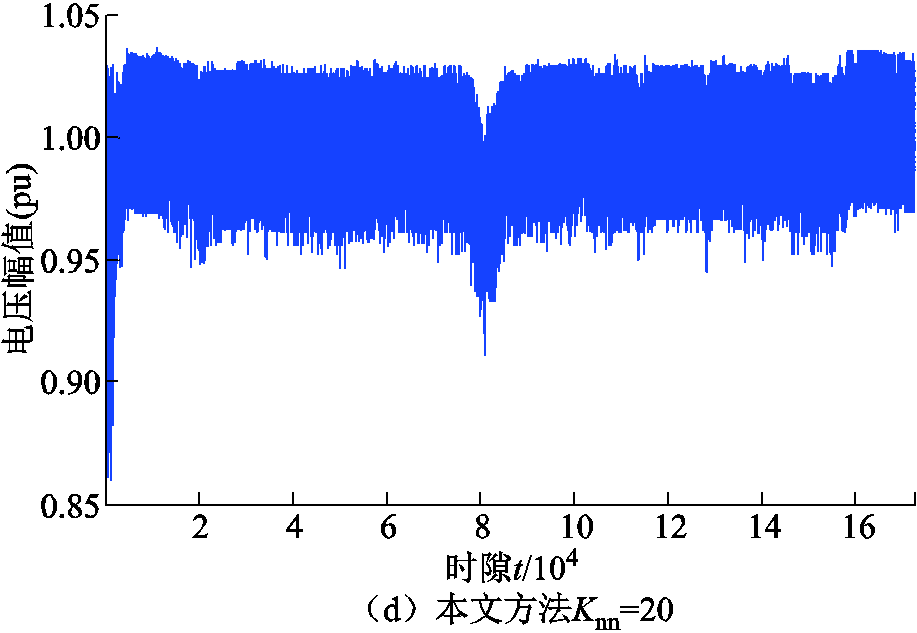
图7 172 800时隙下不同方法所有节点电压幅值
Fig.7 Voltage magnitude profiles at all buses obtained by four control schemes over 172 800 slots
采用不同方法,在600天(172 800时隙)数据被训练后,节点18与33当天电压曲线如图8所示。采用不同方法,在最后一个时隙(第172 800时隙),所有节点电压曲线如图9所示。可以看出,本文提出的改进DDPG算法在抑制高比例风力发电与重负荷引起的电压波动方面具有有效性与(近似)最优性。此外,当 =20时,采用本文所提出的方法调节电压的效果优于
=20时,采用本文所提出的方法调节电压的效果优于 =1时。
=1时。
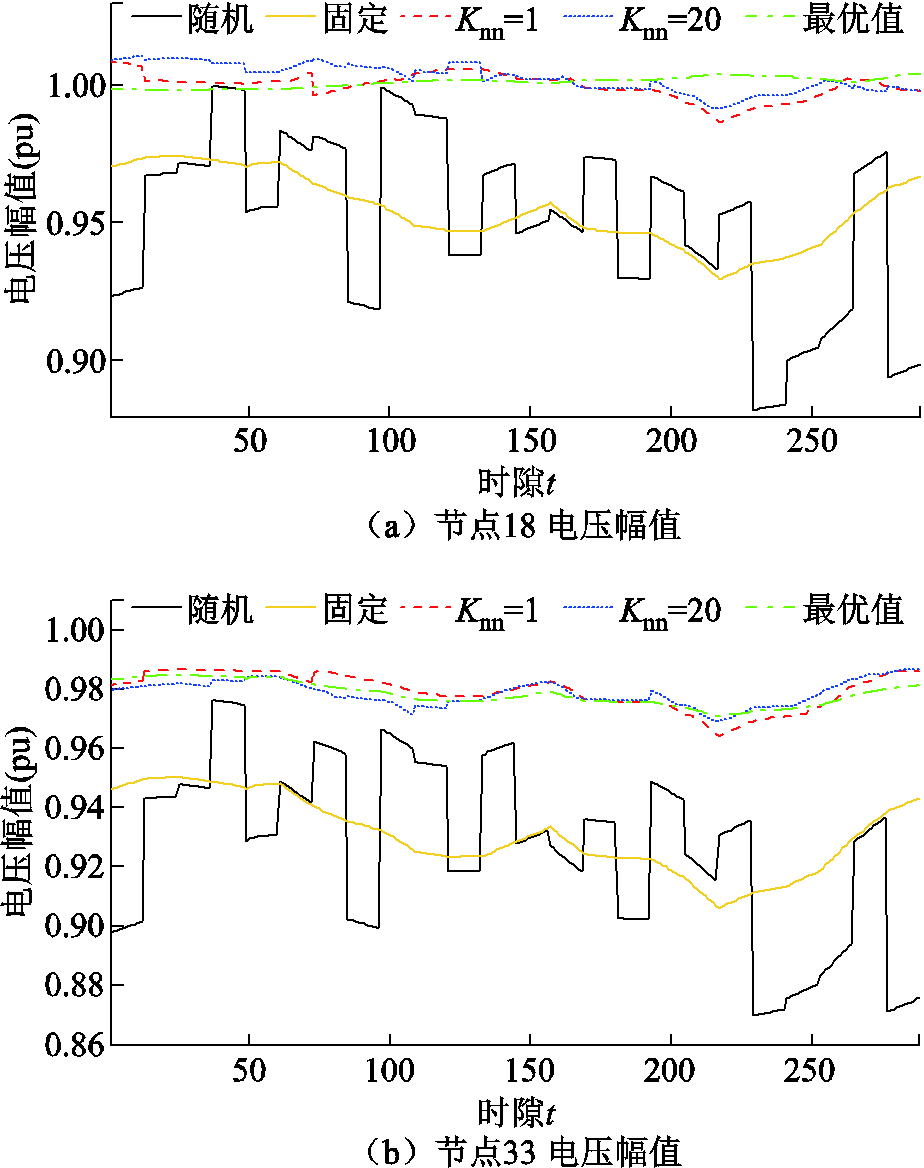
图8 第600天数据被训练后当天节点18与33电压幅值
Fig.8 Voltage magnitude profiles of buses 18 and 33 during the 600th day
当 =1与
=1与 =20时,采用本文方法,在600天数据被训练后,总优化计算时间分别为1 017 s,1 284 s。对于每日数据的平均优化计算时间分别为1017/10/60=1.695 0 s与1284/10/60=2.140 0 s。求解传统288时隙日前规划混合整数QP计算时间为78.634 s。当
=20时,采用本文方法,在600天数据被训练后,总优化计算时间分别为1 017 s,1 284 s。对于每日数据的平均优化计算时间分别为1017/10/60=1.695 0 s与1284/10/60=2.140 0 s。求解传统288时隙日前规划混合整数QP计算时间为78.634 s。当 =20时,本文方法计算速度是传统方法的78.634/2.1400 =36.744 9倍。此外,当
=20时,本文方法计算速度是传统方法的78.634/2.1400 =36.744 9倍。此外,当 =20时,对于每个时隙t数据的平均计算时间为2.1400/24/12=0.007 4 s。因此,本文所提出的方法满足实时控制需求。
=20时,对于每个时隙t数据的平均计算时间为2.1400/24/12=0.007 4 s。因此,本文所提出的方法满足实时控制需求。
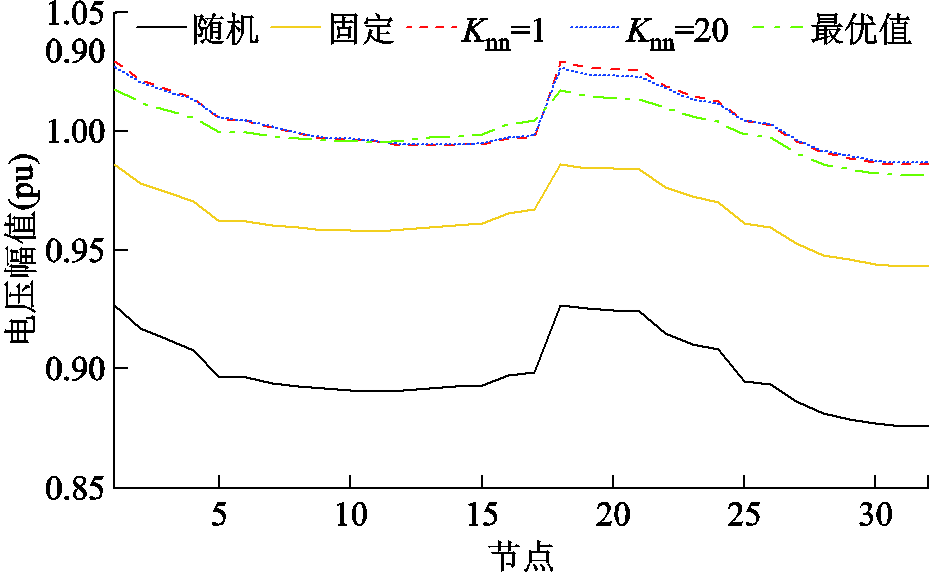
图9 第172 800时隙所有节点电压幅值
Fig.9 Voltage magnitude profiles for all buses at the 172 800 th slot
在123节点不平衡配电网中,共有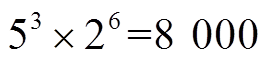 个离散动作分量。为验证本文方法的有效性,首先设置VR匝比、SCR挡位、ESS充放电功率每个时段
个离散动作分量。为验证本文方法的有效性,首先设置VR匝比、SCR挡位、ESS充放电功率每个时段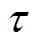 均为随机值与固定值。当设定为固定值时,VR匝比为1,SCR无功功率补偿为0,ESS充放电功率为0。每天平均每小时代价优化结果如图10中黑色与黄色实线所示。可以看出,每天平均每小时代价均远大于0.3 (pu),意味着每天电压越限频繁出现且十分严重。而且,第一阶段变量设定为随机值比设定为固定值导致的电压越限问题更加严重。
均为随机值与固定值。当设定为固定值时,VR匝比为1,SCR无功功率补偿为0,ESS充放电功率为0。每天平均每小时代价优化结果如图10中黑色与黄色实线所示。可以看出,每天平均每小时代价均远大于0.3 (pu),意味着每天电压越限频繁出现且十分严重。而且,第一阶段变量设定为随机值比设定为固定值导致的电压越限问题更加严重。
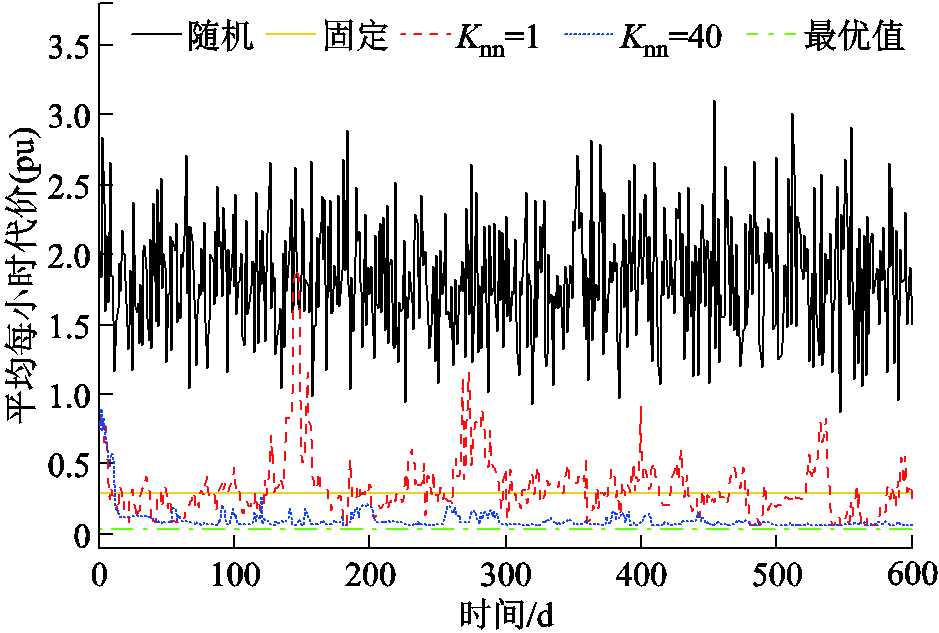
图10 123节点配电网平均每小时代价
Fig.10 Average costs per hour for 123-bus system
设定VR匝比、SCR挡位、ESS充放电功率在每个时隙t均可调,构建144时隙单一短时间尺度传统日前混合整数QP模型。基于Matlab平台采用Mosek 9.1.4软件包求解。为提高计算速度,设置相对对偶间隙为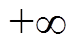 ,平均每小时最优代价为0.034 9(pu),如图10中绿色虚线所示。
,平均每小时最优代价为0.034 9(pu),如图10中绿色虚线所示。
采用本文方法,针对Actor输出的动作,在离散动作分量空间搜索出 =1与
=1与 =40个最邻近动作分量,优化结果分别如图10中红色虚线与蓝色点画线所示。可以看出,采用本文方法,起始阶段平均每小时代价较高,电压越限较严重,这是因为DDPG算法在起始阶段Actor采用的是随机动作策略。当
=40个最邻近动作分量,优化结果分别如图10中红色虚线与蓝色点画线所示。可以看出,采用本文方法,起始阶段平均每小时代价较高,电压越限较严重,这是因为DDPG算法在起始阶段Actor采用的是随机动作策略。当 =40时,在第12天数据被训练后(训练了
=40时,在第12天数据被训练后(训练了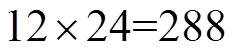 步),平均每小时代价开始变得很低,最终趋近于0.041 0(pu)。然而,当
步),平均每小时代价开始变得很低,最终趋近于0.041 0(pu)。然而,当 =1时,平均每小时代价出现频繁、剧烈波动,训练过程不平稳。
=1时,平均每小时代价出现频繁、剧烈波动,训练过程不平稳。
采用不同方法进行电压调节,训练过程中各时隙所有节点电压如图11所示。可以看出,采用本文提出的改进DDPG算法,当 =40时,在经过短时间(大约1 500个时隙的数据)训练后,动作策略趋于稳定与近似最优。所有节点电压均处于[0.93 1.05] (pu)范围内。采用不同方法,在600天数据被训练后,节点96当天三相电压曲线如图12所示。采用不同方法,在最后一个时隙(第86 400时隙),所有节点电压曲线如图13所示。可以看出,本文提出的改进DDPG算法在抑制高比例风电与重负荷引起的电压波动方面具有有效性与近乎最优性。此外,当
=40时,在经过短时间(大约1 500个时隙的数据)训练后,动作策略趋于稳定与近似最优。所有节点电压均处于[0.93 1.05] (pu)范围内。采用不同方法,在600天数据被训练后,节点96当天三相电压曲线如图12所示。采用不同方法,在最后一个时隙(第86 400时隙),所有节点电压曲线如图13所示。可以看出,本文提出的改进DDPG算法在抑制高比例风电与重负荷引起的电压波动方面具有有效性与近乎最优性。此外,当 =40时,采用本文所提出的方法调节电压效果远优于
=40时,采用本文所提出的方法调节电压效果远优于 =1时。
=1时。
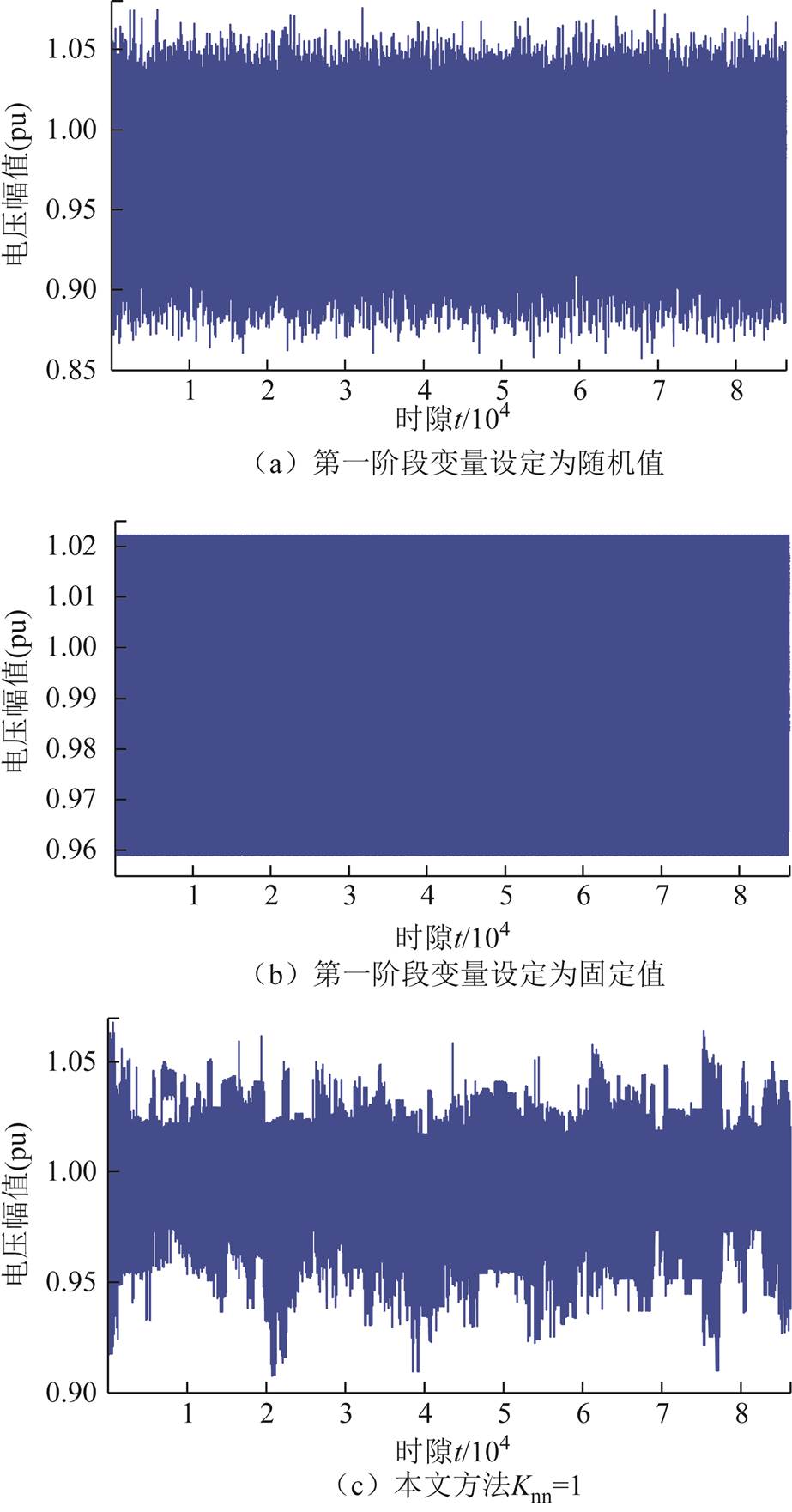
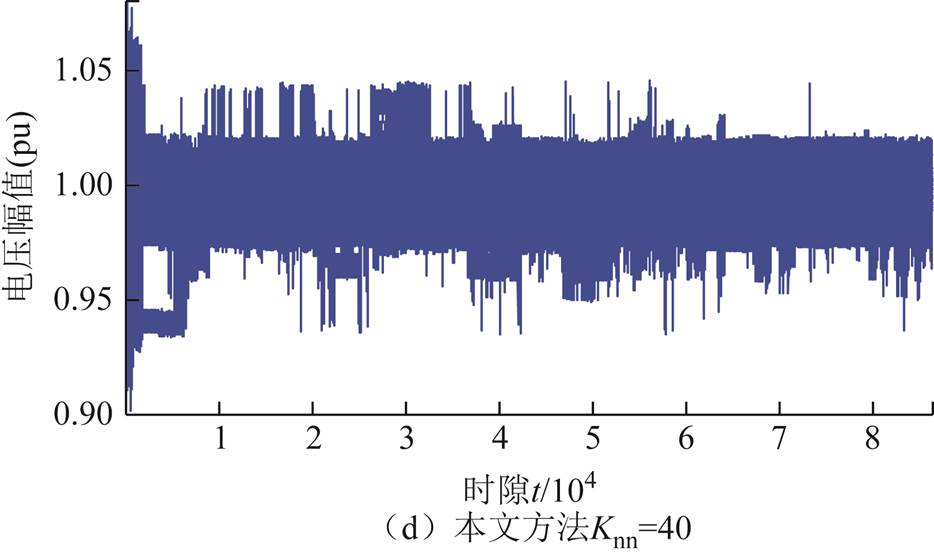
图11 864 00时隙下不同方法所有节点电压幅值
Fig.11 Voltage magnitude profiles at all buses over 864 00 slots
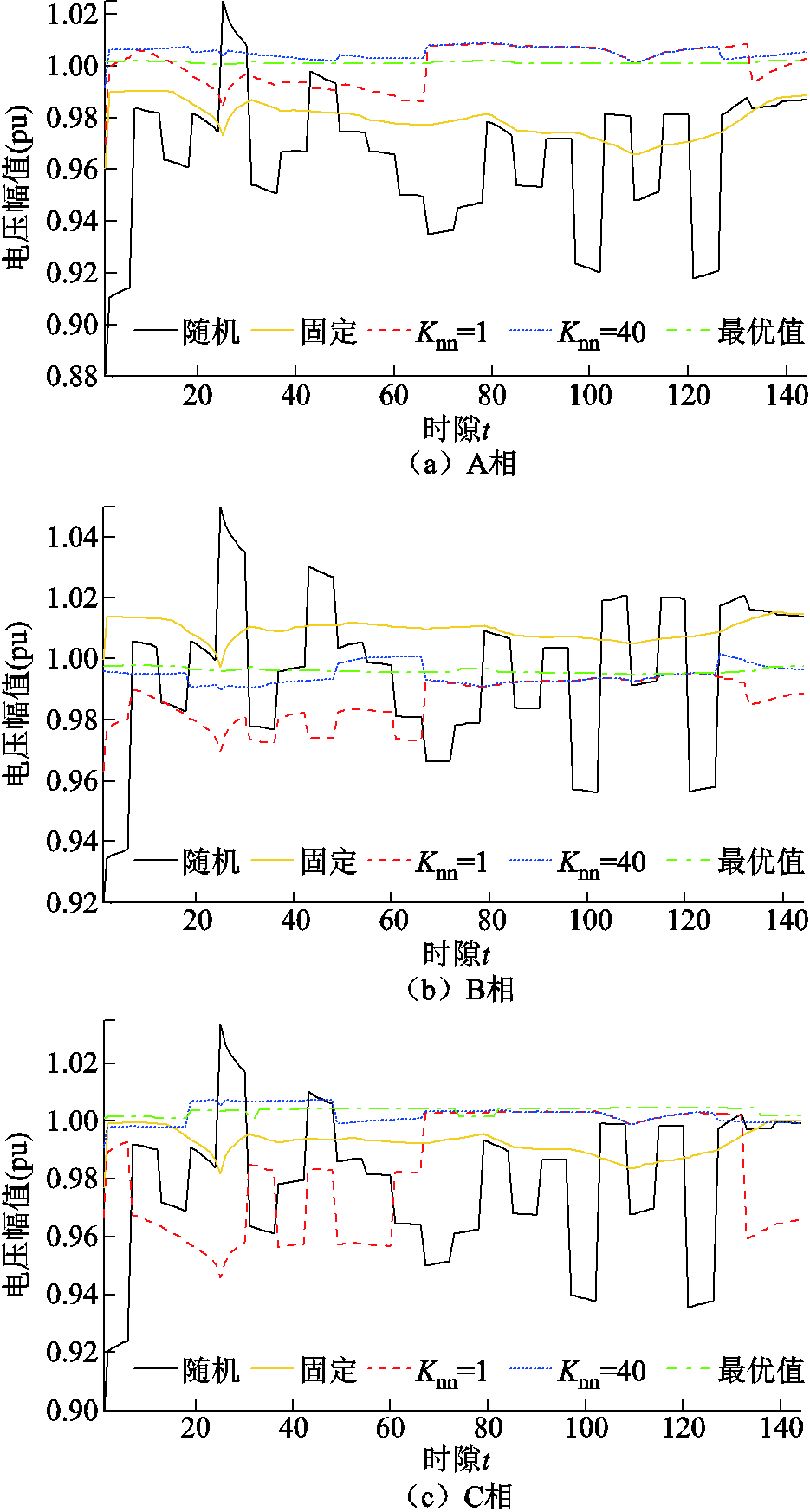
图12 在第600天数据被训练后节点96当天电压幅值
Fig.12 Voltage magnitude profiles at bus 96 during the 600 th day
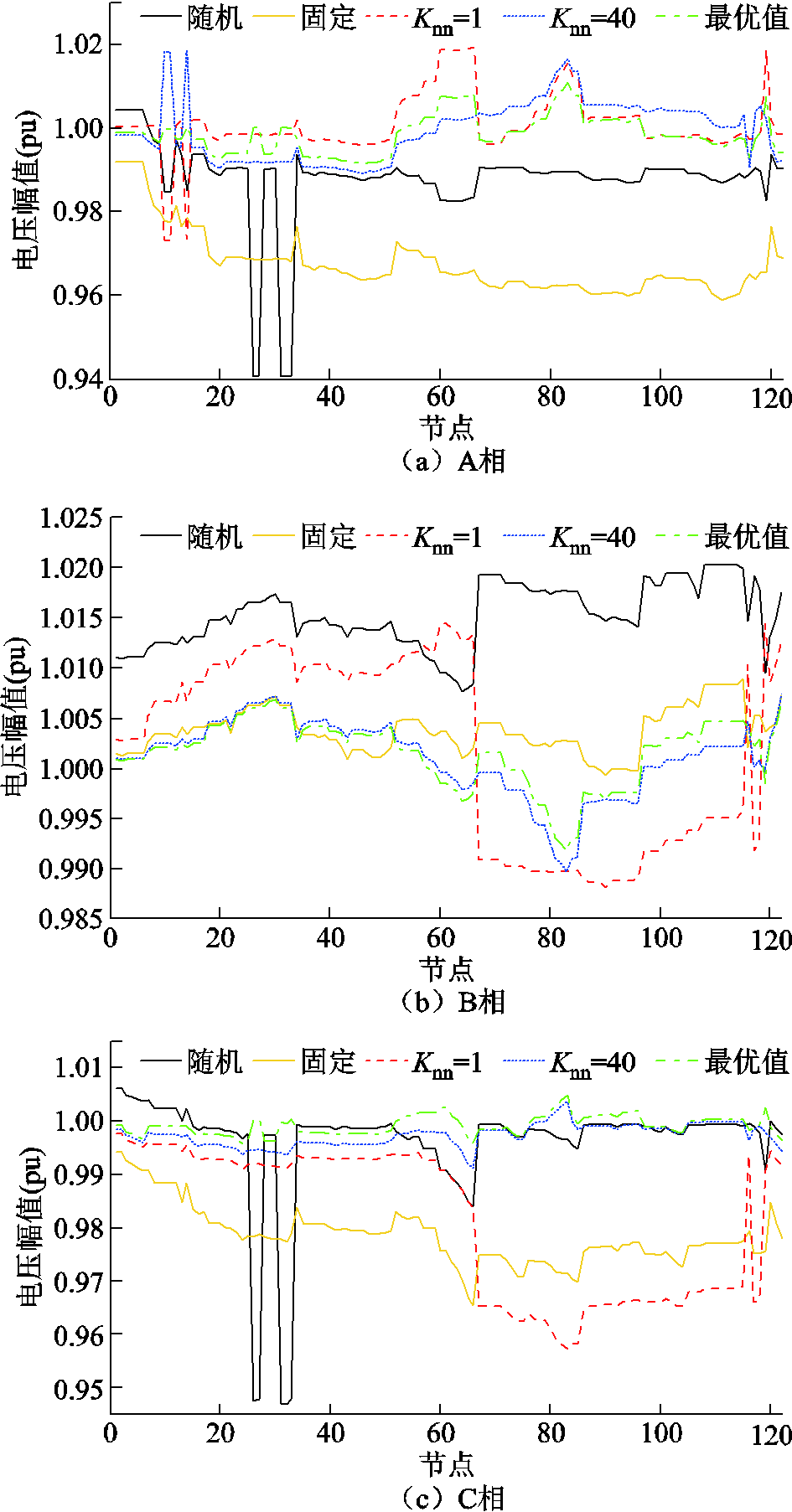
图13 第86 400时隙所有节点电压幅值
Fig.13 Voltage magnitude profiles for all buses at the 86 400th slot
当 =1与
=1与 =40时,采用本文方法,在600天(86 400时隙)数据被训练后,总优化计算时间分别为5 362 s和6 304 s。对于每日数据的平均优化计算时间分别为5362/10/60=8.936 7 s与6304/10/60= 10.506 7 s。求解传统144时隙日前规划混合整数QP计算时间为189.343 s。当
=40时,采用本文方法,在600天(86 400时隙)数据被训练后,总优化计算时间分别为5 362 s和6 304 s。对于每日数据的平均优化计算时间分别为5362/10/60=8.936 7 s与6304/10/60= 10.506 7 s。求解传统144时隙日前规划混合整数QP计算时间为189.343 s。当 =40时,本文方法计算速度是传统方法的189.343/10.506 7= 18.021 2倍。此外,当
=40时,本文方法计算速度是传统方法的189.343/10.506 7= 18.021 2倍。此外,当 =40时,对于每个时隙t数据的平均计算时间为10.506 7/24/6=0.073 s。因此,本文所提出的方法满足实时控制需求。
=40时,对于每个时隙t数据的平均计算时间为10.506 7/24/6=0.073 s。因此,本文所提出的方法满足实时控制需求。
比较本文图6、图10与文献[25]中图5,可以看出,当 =20与
=20与 =40时,采用本文方法训练过程收敛速度与平稳度远高于文献[25]中的多智能体DQN算法。这是因为文献[25]中连续变量被离散化,离散动作数量呈指数增加,搜索空间非常大,远高于本文。而且多智能体协调探索与利用比单智能体复杂与困难得多。
=40时,采用本文方法训练过程收敛速度与平稳度远高于文献[25]中的多智能体DQN算法。这是因为文献[25]中连续变量被离散化,离散动作数量呈指数增加,搜索空间非常大,远高于本文。而且多智能体协调探索与利用比单智能体复杂与困难得多。
本文方法的一个突出优点是非常容易在实际配电网中实现,如式(25)所示。基于IEEE 33节点平衡与123节点不平衡配电网的仿真结果表明,针对Actor输出的原型动作,在离散动作分量空间选取的最临近点数量 对训练过程收敛速度与平稳度具有较大影响。当任务较困难时,
对训练过程收敛速度与平稳度具有较大影响。当任务较困难时, 取值太小,例如
取值太小,例如 =1,可能导致训练过程很不平稳,如图6、图10所示。
=1,可能导致训练过程很不平稳,如图6、图10所示。 选取为几十,如20或40,即可使得训练过程较平稳。本文方法优化结果接近于VR、SCR与ESS参与短时间尺度调节的多时隙单一短时间尺度日前混合整数QP优化结果。然而,当
选取为几十,如20或40,即可使得训练过程较平稳。本文方法优化结果接近于VR、SCR与ESS参与短时间尺度调节的多时隙单一短时间尺度日前混合整数QP优化结果。然而,当 =20或
=20或 =40时,本文方法计算速度是其18~36.7倍。而且,本文方法DRL训练过程收敛速度与平稳度远高于多智能体DQN算法。
=40时,本文方法计算速度是其18~36.7倍。而且,本文方法DRL训练过程收敛速度与平稳度远高于多智能体DQN算法。
本文训练集是固定的,而且未采用测试集验证基于松弛-预报-校正的DDPG算法泛化能力。进一步研究的工作重点是采用滚动测试集在线实时验证基于松弛-预报-校正的DDPG算法泛化能力。
参考文献
[1] Yong Jiaying, Ramachandaramurthy V K, Tan Kangmiao, et al. Bi-directional electric vehicle fast charging station with novel reactive power compensation for voltage regulation[J]. International Journal of Electrical Power & Energy Systems, 2015, 64: 300-310.
[2] Wang Pengfei, Liang D H, Yi Jialiang, et al. Integrating electrical energy storage into coordinated voltage control schemes for distribution networks[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 1018-1032.
[3] Ranamuka D, Agalgaonkar A P, Muttaqi K M. Examining the interactions between DG units and voltage regulating devices for effective voltage control in distribution systems[J]. IEEE Transactions on Industry Applications, 2017, 53(2): 1485-1496.
[4] Agalgaonkar Y P, Pal B C, Jabr R A. Distribution voltage control considering the impact of PV generation on tap changers and autonomous regulators[J]. IEEE Transactions on Power Systems, 2014, 29(1): 182-192.
[5] Kawabe K, Tanaka K. Impact of dynamic behavior of photovoltaic power generation systems on short-term voltage stability[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3416-3424.
[6] Taranto G N, Assis T M L, Falcao D M, et al. Highlighting the importance of chronology on voltage protection and control in active distribution networks[J]. IEEE Transactions on Power Delivery, 2017, 32(1): 361-369.
[7] Bose S, Low S H, Teeraratkul T, et al. Equivalent relaxations of optimal power flow[J]. IEEE Transactions on Automatic Control, 2015, 60(3): 729-742.
[8] Valverde G, Van Cutsem T. Model predictive control of voltages in active distribution networks[J]. IEEE Transactions on Smart Grid, 2013, 4(4): 2152-2161.
[9] 黄大为, 王孝泉, 于娜, 等. 计及光伏出力不确定性的配电网混合时间尺度无功/电压控制策略[J]. 电工技术学报, 2022, 37(17): 4377-4389. Huang Dawei, Wang Xiaoquan, Yu Na, et al. Hybrid timescale voltage/var control in distribution network considering PV power uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4377-4389.
[10] Magnússon S, Qu Guannan, Fischione C, et al. Voltage control using limited communication[J]. IEEE Transactions on Control of Network Systems, 2019, 6(3): 993-1003.
[11] Bolognani S, Carli R, Cavraro G, et al. Distributed reactive power feedback control for voltage regulation and loss minimization[J]. IEEE Transactions on Automatic Control, 2015, 60(4): 966-981.
[12] 杨珺, 侯俊浩, 刘亚威, 等. 分布式协同控制方法及在电力系统中的应用综述[J]. 电工技术学报, 2021, 36(19): 4035-4049. Yang Jun, Hou Junhao, Liu Yawei, et al. Distributed cooperative control method and application in power system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4035-4049.
[13] 李忠文, 程志平, 张书源, 等. 考虑经济调度及电压恢复的直流微电网分布式二次控制[J]. 电工技术学报, 2021, 36(21): 4482-4492. Li Zhongwen, Cheng Zhiping, Zhang Shuyuan, et al. Distributed secondary control for economic dispatch and voltage restoration of DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4482-4492.
[14] Zhang Liang, Wang Gang, Giannakis G B. Real-time power system state estimation and forecasting via deep unrolled neural networks[J]. IEEE Transactions on Signal Processing, 2019, 67(15): 4069-4077.
[15] 巨云涛, 陈希, 李嘉伟, 等. 基于分布式深度强化学习的微网群有功无功协调优化调度[J]. 电力系统自动化, 2023, 47(1): 115-125. Ju Yuntao, Chen Xi, Li Jiawei, et al. Active and reactive power coordinated optimal dispatch of networked microgrids based on distributed deep reinforcement learning[J]. Automation of Electric Power Systems, 2023, 47(1): 115-125.
[16] 顾雪平, 刘彤, 李少岩, 等. 基于改进双延迟深度确定性策略梯度算法的电网有功安全校正控制[J]. 电工技术学报, 2023, 38(8): 2162-2177. Gu Xueping, Liu Tong, Li Shaoyan, et al. Active power correction control of power grid based on improved twin delayed deep deterministic policy gradient algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2162-2177.
[17] 陈泽宇, 方志远, 杨瑞鑫, 等. 基于深度强化学习的混合动力汽车能量管理策略[J]. 电工技术学报, 2022, 37(23): 6157-6168. Chen Zeyu, Fang Zhiyuan, Yang Ruixin, et al. Energy management strategy for hybrid electric vehicle based on the deep reinforcement learning method[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6157-6168.
[18] 陈明昊, 孙毅, 谢志远. 基于双层深度强化学习的园区综合能源系统多时间尺度优化管理[J]. 电工技术学报, 2023, 38(7): 1864-1881. Chen Minghao, Sun Yi, Xie Zhiyuan. The multi-time-scale management optimization method for park integrated energy system based on the Bi-layer deep reinforcement learning[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1864-1881.
[19] 宋煜浩, 魏韡, 黄少伟, 等. 风储联合电站实时自调度的高效深度确定性策略梯度算法[J]. 电工技术学报, 2022, 37(23): 5987-5999. Song Yuhao, Wei Wei, Huang Shaowei, et al. Efficient deep deterministic policy gradient algorithm for real-time self-dispatch of wind-storage power plant[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5987-5999.
[20] Xu Hanchen, Domínguez-García A D, Sauer P W. Optimal tap setting of voltage regulation transformers using batch reinforcement learning[J]. IEEE Transactions on Power Systems, 2020, 35(3): 1990-2001.
[21] Al-Saffar M, Musilek P. Reinforcement learning-based distributed BESS management for mitigating overvoltage issues in systems with high PV penetration[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 2980-2994.
[22] Wang Wei, Yu Nanpeng, Gao Yuanqi, et al. Safe off-policy deep reinforcement learning algorithm for volt-VAR control in power distribution systems[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 3008-3018.
[23] Cao Di, Hu Weihao, Zhao Junbo, et al. A multi-agent deep reinforcement learning based voltage regulation using coordinated PV inverters[J]. IEEE Transactions on Power Systems, 2020, 35(5): 4120-4123.
[24] Yang Qiuling, Wang Gang, Sadeghi A, et al. Two-timescale voltage control in distribution grids using deep reinforcement learning[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2313-2323.
[25] Zhang Ying, Wang Xinan, Wang Jianhui, et al. Deep reinforcement learning based volt-VAR optimization in smart distribution systems[J]. IEEE Transactions on Smart Grid, 2021, 12(1): 361-371.
[26] Dulac-Arnold G, Evans R, Van Hasselt H, et al. Deep reinforcement learning in large discrete action spaces[J]. Computer Science, 2015. DOI:10.48550/ ARXiv.1512.07679.
[27] Zhang Jian, He Yigang. Fast solving method for two-stage multi-period robust optimization of active and reactive power coordination in active distribution networks[J]. IEEE Access, 2022, 11: 30208-30222.
[28] Ding Tao, Liu Shiyu, Yuan Wei, et al. A two-stage robust reactive power optimization considering uncertain wind power integration in active distribution networks[J]. IEEE Transactions on Sustainable Energy, 2016, 7(1): 301-311.
Abstract A large number of electric vehicles (EVs), distributed solar and/or wind turbine generators (WTGs) connected to distribution systems lead to frequent and sharp voltages fluctuations. The action rates of conventional adjustable devices and smart inverters are very different. In this context, a novel dual-timescale voltage control scheme is proposed by organically combining data-driven with physics-based optimization. On fast timescale, a quadratic programming (QP) for balanced and unbalanced distribution systems is developed based on branch flow equations. The optimal reactive power of renewable distributed generators (DGs) and static VAR compensators (SVCs) is configured on several minutes. Whereas, on slow timescale, a data-driven Markovian decision process (MDP) is developed, in which the charge/discharge power of energy storage systems (ESSs), statuses/ratios of switchable capacitors reactors (SCRs), and voltage regulators (VRs) are configured hourly to minimize long-term discounted squared voltages magnitudes deviations using an adapted deep deterministic policy gradient (DDPG) deep reinforcement learning (DRL) algorithm. The capabilities of the proposed method are validated with IEEE 33-bus balanced and 123-bus unbalanced distribution systems.
The contributions of this paper are summarized as follows: (1)Combining data-driven with physics-based methods, a strategy for coordinated control of five different types of adjustable equipment, namely VRs, SCRs, ESSs, SVCs and DGs inverters on fast and slow timescales is proposed. (2) A slow timescale (say 1 hour) MDP for active and reactive power coordination is constructed. The (near) optimal settings of ratios/statuses of VRs, SCRs and charge/discharge power of ESSs are found using DRL algorithm. As a result, the deficiency of low computing rate for conventional physics -based large scale mixed integer non-convex nonlinear stochastic programming is completely overcome. (3) The charge/discharge power of ESS is continuous variable while ratios/statues of VRs and SCRs are discrete decisions. DDPG algorithm cannot be directly applicable to discrete action while DQN algorithm cannot be applicable to continuous action. Further, when there are a large number of VRs and SCRs in distribution network, DQN algorithm leads to dimensionality curses. The existing DRL algorithm in literatures cannot deal with joint continuous-discrete action (efficiently). To eliminate dimensionality curses in joint continuous- discrete action space, ratios/statuses of VRs and SCRs are firstly relaxed to continuous variables. Then, for the proto action given by actor of DDPG agent,  nearest neighbors are found out in the joint continuous-discrete action space. Finally, each of the
nearest neighbors are found out in the joint continuous-discrete action space. Finally, each of the  actions is transferred to the critic of DDPG agent one by one to evaluate its value. The action with the greatest value is chosen to interact with the distribution network. (4) Given the (near) optimal solution of the slow timescale MDP, a QP for VVO with DGs, SVCs inverters settings on fast timescale (say several minutes or seconds) to minimize squared voltages magnitudes deviations are developed for balanced and unbalanced distribution systems. As a result, voltage violations on fast timescale caused by sizable, rapid and frequent power fluctuations from renewable DGs and fast charged EVs can be mitigated in real time. (5) One of the outstanding advantages of the proposed method is very easy to perform in practice with near optimal solution. Further, when
actions is transferred to the critic of DDPG agent one by one to evaluate its value. The action with the greatest value is chosen to interact with the distribution network. (4) Given the (near) optimal solution of the slow timescale MDP, a QP for VVO with DGs, SVCs inverters settings on fast timescale (say several minutes or seconds) to minimize squared voltages magnitudes deviations are developed for balanced and unbalanced distribution systems. As a result, voltage violations on fast timescale caused by sizable, rapid and frequent power fluctuations from renewable DGs and fast charged EVs can be mitigated in real time. (5) One of the outstanding advantages of the proposed method is very easy to perform in practice with near optimal solution. Further, when  =20 or
=20 or  =40, the proposed method has much more stable training process than multi-agent DQN algorithm and much higher computing rate than conventional multi-slot single fast timescale mixed integer QP by about 18.0~36.7 times.
=40, the proposed method has much more stable training process than multi-agent DQN algorithm and much higher computing rate than conventional multi-slot single fast timescale mixed integer QP by about 18.0~36.7 times.
keywords:Smart distribution systems, voltage control, deep reinforcement learning(DRL), quadratic programming(QP), dual-timescale
DOI:10.19595/j.cnki.1000-6753.tces.222273
中图分类号:TM732
国家自然科学基金资助项目(52207130)。
收稿日期 2022-12-12
改稿日期 2023-09-27
张 剑 1982年生,男,博士,讲师,研究方向为电力系统建模、主动配电网技术、电动汽车有序充电等。E-mail:z_jj1219@sina.com(通信作者)
崔明建 1987年生,男,博士,教授,研究方向为风力预测、机组组合、配电网物理信息系统等。E-mail:mingjian.cui@ ieee.org
(编辑 赫 蕾)