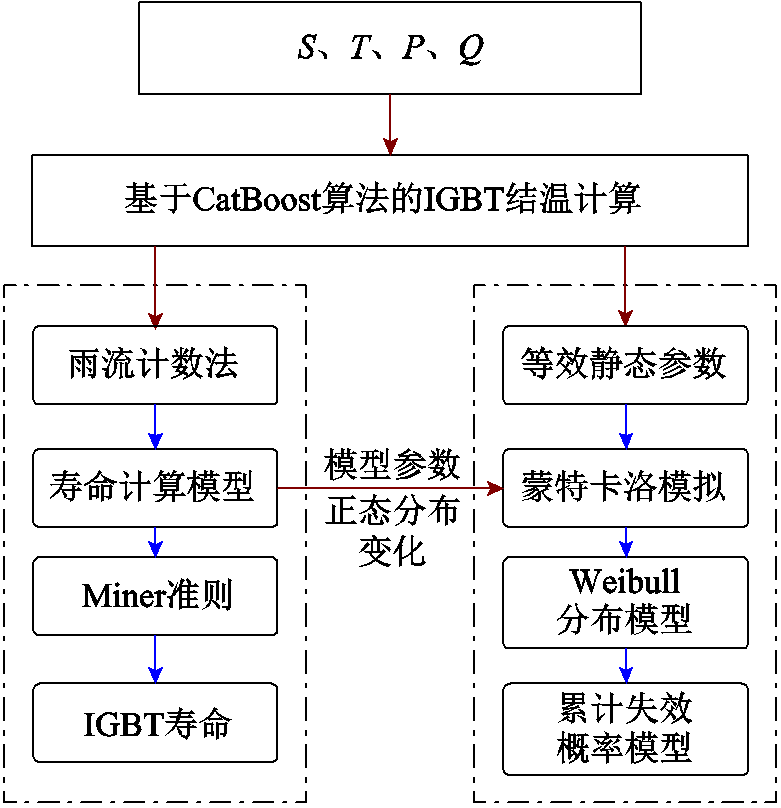
图1 基于CatBoost算法的IGBT可靠性评估流程
Fig.1 IGBT reliability evaluation process based on CatBoost machine learning algorithm
摘要 光伏电源参与配电网无功电压调节是提升光伏高渗透配电网运行经济性和可靠性的有效手段,但光伏电源提供无功支撑会使得光伏电源IGBT最大结温升高、结温波动加剧,进而影响光伏电源和配电网的安全稳定运行。为此,该文提出一种计及IGBT结温约束的光伏高渗透配电网无功电压优化控制策略。首先,利用CatBoost算法计算IGBT结温,提高了IGBT结温计算效率,避免了传统结温算法对IGBT热模型参数的依赖;然后,建立考虑IGBT结温约束的有源配电网多目标无功优化模型,利用二分法求解IGBT结温约束下的光伏电源最大输出功率,实现了IGBT结温约束向二阶锥约束的转换;最后,利用IEEE 33节点典型配电系统验证了所提策略在光伏高渗透配电网无功电压优化、光伏电源运行可靠性提升方面的有效性,并提出了综合考虑配电网网损、光伏电源可靠性的光伏电源IGBT结温限值整定原则。
关键词:CatBoost机器学习算法 IGBT结温 无功电压控制 IGBT可靠性 多目标优化
2022年10月16日,习近平总书记在中国共产党第二十次全国代表大会中指出,要深入推进能源革命,加快规划建设新型能源体系,积极参与应对气候变化全球治理。近年来,光伏、风电等新能源装机容量越来越大,其中分布式光伏具有灵活性高、投资低、受地域/资源条件限制小、安装维护简单的特点,符合国家可持续发展战略要求[1-3]。随着《整县(市、区)屋顶分布式光伏开发试点项目》等项目的试行,配电网中分布式光伏电源接入容量越来越大。以光伏为代表的新能源接入配电网有利于构建低碳、高效、可持续发展的新型电力系统,但同时也对配电网安全稳定运行提出了巨大挑战。由于光伏发电具有随机性与波动性的特点,其出力不确定性会造成配电网节点电压快速剧烈波动[4]。此外,在太阳辐照度较高时段,光伏电源出力过剩,会导致配电网接入分布式光伏节点电压越限[5]。针对高比例光伏接入配电网带来的配电网节点电压不稳和越限问题,可采用无功电压控制来调整配电网各节点电压[6-7]。
无功电压控制可将配电网各节点电压稳定在安全范围内,从而提高配电网运行的稳定性。传统配电网无功电压调控设备有电容器组(Capacitor Banks, CBs)、有载调压变压器(On-Load Tap Changers, OLTCs)等,但电容器组、隔离开关等设备响应速度慢,不足以应对配电网电压的快速波动。静止无功补偿器(Static Var Compensator, SVC)、静止无功发生器(Static Var Generator, SVG)等无功补偿设备响应速度较快,但设备的投资成本较高,不易大规模应用。光伏电源具备一定的无功支撑能力,其无功电压控制响应速度较快,且不会额外增加配电网设备投资成本,逐渐成为有源配电网无功电压调节的重要手段之一。随着分布式光伏迅速发展,构建以新能源为主体的新型电力系统将给分布式光伏参与配电网无功电压控制带来更大的发展空间。同时,分布式光伏的“可观、可测、可控”需求日益迫切。以甘肃电网为例,截至2023年1月底,甘肃省521座10 kV分布式光伏电站全部实现可观、可测、可控,新能源发电装置可观、可测、可控将成为未来新型电力系统发展趋势[8-9]。IEEE 1547.8工作组提倡利用光伏逆变器实现无功电压控制,适当提高光伏逆变器容量配置可以有效提高光伏逆变器无功输出能力,同时降低传统无功补偿设备的投资成本[10]。文献[11]提出基于有功自适应调整的光伏电站无功电压控制策略,光伏逆变器正常工作在最大功率点跟踪控制模式。当并网点电压出现越限时,光伏逆变器输出相应无功功率,若此时逆变器无功容量不足,则削减部分光伏有功功率,以满足系统的无功需求。文献[12]提出多电压等级不平衡主动配电网电压无功自适应多目标协调优化策略,利用分布式光伏与传统无功补偿设备协调控制,以网损、电压幅值及不平衡度为运行指标,以开关电容器动作成本及光伏逆变器出力成本为成本指标,建立配电网电压无功多目标优化模型。考虑到配电网实际运行的不确定性,文献[13]提出一种层次协调的无功电压优化模型,协调优化光伏逆变器集中调度设定值。针对光伏发电的不确定性,文献[14]提出一种两阶段鲁棒无功优化方法,即电容器、有载调压变压器优化时间尺度设置为1 h,光伏逆变器优化时间尺度设置为15 min。在此基础上,文献[15]提出基于光伏逆变器的三阶段鲁棒无功电压优化模型,分别设置了有载调压变压器和电容器组控制阶段、光伏逆变器控制阶段、逆变器本地控制阶段。传统集中式的无功电压控制方法因其变量数过多而无法满足配电网无功电压快速控制的需求,文献[16]提出一种主动配电网电压分区优化控制方法,对配电网进行有功/无功分区,在有功分区与无功分区内分别建立优化模型,实现对配电网电压快速有效的控制。上述研究表明光伏电源能够参与配电网无功电压控制,但光伏电源无功输出会影响光伏逆变器运行可靠性[17]。
光伏电源过多发出无功功率可能造成光伏发电系统过早失效,进而影响配电网运行的稳定性和经济性[18]。故光伏电源在进行无功电压控制时,需考虑光伏电源无功输出对光伏逆变器运行可靠性和寿命的影响。文献[19]通过限制光伏逆变器额定容量,即限制光伏逆变器无功输出,间接提高光伏逆变器的可靠性,但并未将光伏逆变器可靠性指标引入无功电压控制优化模型中。综上所述,目前基于光伏电源无功支撑的配电网无功电压优化控制策略相关研究中,鲜有研究成果考虑对光伏电源运行可靠性的影响。因此,研究考虑光伏电源可靠性的配电网无功电压控制策略,极具工程实际意义。
IGBT可靠性是影响光伏逆变器可靠性的关键性因素,由IGBT引起的光伏逆变器故障占比高达34%[20]。目前,对于光伏逆变器可靠性分析侧重于对光伏逆变器中IGBT进行可靠性分析[21-22]。传统IGBT可靠性分析方法是基于各类可靠性手册以恒定故障概率模型建模,但该方法未考虑实际工况变化对分析结果的影响[23]。基于任务剖面的IGBT可靠性评估方法以IGBT实际运行工况作为分析基础,并与物理失效模型相结合,是目前IGBT可靠性评估最常用方法[24]。该方法首先根据IGBT任务剖面计算IGBT结温,再利用雨流计数法统计IGBT热载荷信息,最后利用IGBT寿命评估模型及Miner线性损伤准则计算IGBT寿命损伤[25-27]。考虑到IGBT器件的不一致性,文献[28-29]采用蒙特卡洛模拟方法模拟IGBT器件之间的差异,进而得到IGBT寿命分布,量化分析IGBT可靠性。在基于任务剖面的IGBT可靠性评估中,由IGBT运行工况计算IGBT结温是一项重要步骤。传统IGBT结温计算方法一般基于功率损耗和热模型[30-32],其结温计算时间较长,同时需要具体的IGBT热模型参数,而IGBT热模型参数不易获取,往往存在较大误差。文献[33]提出一种利用人工神经网络(Artificial Neural Network, ANN)模型代替传统IGBT结温计算模型的IGBT结温计算方法,但该方法基于固定环境温度进行结温计算,无法适用于环境温度变化情况。
针对上述问题,本文首先提出了一种基于CatBoost算法的IGBT可靠性评估方法,该方法利用数据驱动方法计算IGBT结温,缩短了IGBT结温计算时间,降低了结温计算结果对IGBT电热模型参数的依赖;然后,提出计及IGBT结温约束的有源配电网无功电压优化控制策略,将IGBT结温约束引入配电网无功电压优化约束条件中,建立了考虑IGBT结温约束的有源配电网多目标无功优化模型;最后,综合考虑配电网网损、IGBT可靠性和寿命,提出光伏电源IGBT结温限值整定原则。
基于CatBoost算法的IGBT可靠性评估方法总体流程如图1所示。首先,采用CatBoost算法并根据太阳辐照度S、环境温度T、光伏电源有功输出P和无功输出Q计算光伏逆变器IGBT结温;其次,利用雨流计数法统计IGBT热载荷信息,再根据IGBT寿命模型及Miner准则估算IGBT寿命;然后,考虑器件参数的差异性,利用蒙特卡洛模拟得到IGBT寿命分布情况,通过二参数威布尔分布拟合得到符合IGBT寿命分布的威布尔概率密度函数,对寿命分布概率密度函数进行积分,得到威布尔累积分布函数;最终进行IGBT可靠性的量化分析。

图1 基于CatBoost算法的IGBT可靠性评估流程
Fig.1 IGBT reliability evaluation process based on CatBoost machine learning algorithm
IGBT结温计算是IGBT可靠性评估的重要环节,传统IGBT结温计算一般基于IGBT电热耦合模型进行,其计算时间较长,且计算结果对IGBT电热模型参数依赖度较高,当IGBT出现老化等现象时,其结温计算误差较大。本文从数据驱动角度出发,提出基于CatBoost算法的IGBT结温计算方法,在提升IGBT结温计算效率的同时降低了模型参数偏差对IGBT结温计算结果的影响。当IGBT出现老化等现象时,可根据IGBT结温历史数据训练CatBoost模型,从而找到任务剖面与IGBT结温之间新的非线性映射关系,实现IGBT结温的精准计算,具体流程如图2所示。
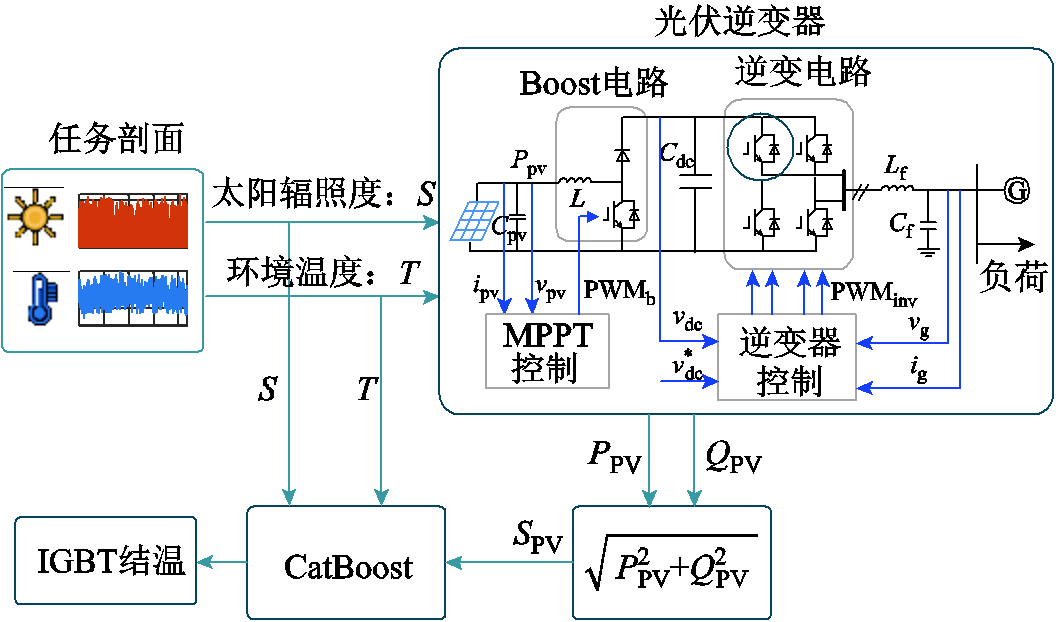
图2 基于CatBoost算法的IGBT结温计算流程
Fig.2 Calculation method of IGBT junction temperature based on CatBoost algorithm
CatBoost算法属于Boosting算法系列,是一种基于梯度提升决策树(Gradient Boosting Decision Tree, GBDT)的新型机器学习算法[34-35]。基于CatBoost算法的IGBT结温计算方法以光伏逆变器输出视在功率SPV、太阳辐照度S及环境温度T作为CatBoost模型输入,以IGBT结温作为CatBoost模型输出,训练CatBoost模型。
将一年的太阳辐照度、环境温度和光伏逆变器输出视在功率输入训练完成的CatBoost模型中,得到IGBT的结温,将其与基于热电耦合模型数值计算所得IGBT结温进行比较,结果如图3所示。
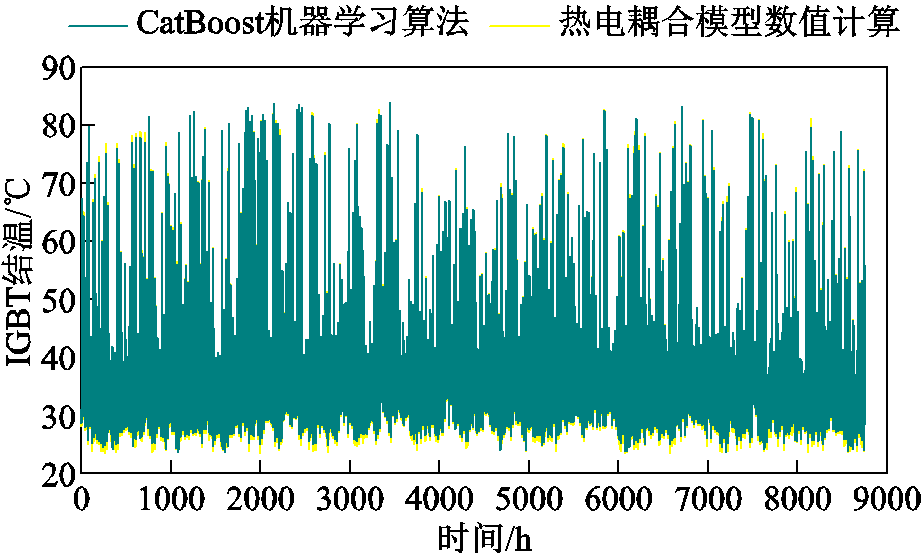
图3 不同IGBT结温计算方法计算结果对比
Fig.3 Calculation results of different IGBT junction temperature methods
以热电耦合模型数值计算IGBT结温结果为基准,CatBoost机器学习算法计算IGBT结温的平均绝对误差和方均根误差分别为0.37℃、0.21℃,故采用CatBoost结温算法可以保证IGBT结温的准确性。此外,在计算时长方面CatBoost结温算法也具有明显优势。以64位计算机(3.20 GHz CPU,16 GB RAM)为例,计算相同的年任务剖面下IGBT结温,热电耦合模型数值计算时长为几十分钟级,而CatBoost结温算法计算时长为秒级。
功率器件IGBT主要失效机制与IGBT热循环有关[36],本文采用雨流计数法[37]统计出IGBT热循环数ni、每个热循环内的结温均值Tjm、结温波动ΔTj等IGBT热载荷信息。
利用式(1)所示的IGBT解析寿命模型计算IGBT失效循环次数,该寿命模型由加速功率循环测试数据推导而来。
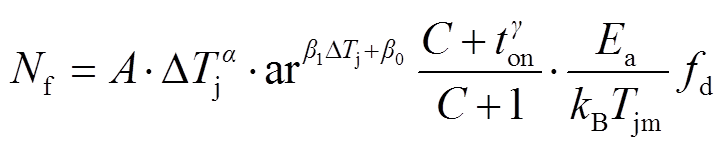 (1)
(1)
式中, 为功率循环周期数;
为功率循环周期数;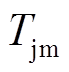 为IGBT平均结温;ΔTj为IGBT结温波动;
为IGBT平均结温;ΔTj为IGBT结温波动;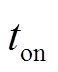 为加热时间;
为加热时间;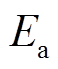 为IGBT器件激活能;
为IGBT器件激活能;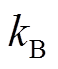 为玻耳兹曼常数;A、ar、a、
为玻耳兹曼常数;A、ar、a、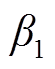 、
、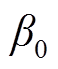 、g、C、fd为寿命模型参数,由实验数据拟合得到[23]。
、g、C、fd为寿命模型参数,由实验数据拟合得到[23]。
寿命损伤(Lifetime Consumption, LC)用于描述功率器件的寿命损耗情况。Miner线性累积损伤准则认为每个温度循环均会对器件造成损伤,且损伤具有线性累积特性。当LC累积损伤超过1时,功率器件失效。功率器件的累积损伤度表达式为
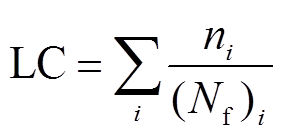 (2)
(2)
式中,ni为一定热应力作用下的循环次数;(Nf)i为寿命模型计算得到的失效循环次数。
基于Monte-Carlo模拟的IGBT寿命评估方法可有效提升评估准确性,Monte-Carlo模拟将寿命模型参数由定值转变为符合某种概率分布的伪随机数(参数变化5%的正态分布)。同时,最小结温Tjmin、结温波动ΔTj、加热时间ton保持动态变化状态,不可直接转变为符合某种概率分布的伪随机数,需将动态参数转换为等效的静态参数,等效静态参数可对器件产生相同的退化作用[38]。受IGBT集射极饱和压降变化及器件热荷载影响,IGBT等效静态参数中的平均最小结温和结温波动分别按5%、0.66%的正态分布变化[39]。
通过Mont-Carlo随机抽取样本模拟得到IGBT的寿命分布,拟合二参数威布尔分布的尺度参数和形状参数,从而得到器件寿命分布的威布尔概率密度函数(Probability Density Function, PDF)为
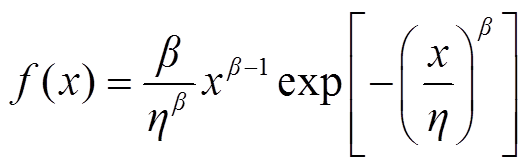 (3)
(3)
式中,b为威布尔分布尺度参数;h为威布尔分布形状参数。
对寿命分布概率密度曲线进行积分,得到威布尔累积分布函数(Cumulative Distribution Function, CDF),进而评估功率器件的不可靠度。
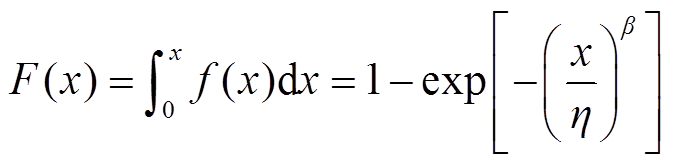 (4)
(4)
光伏电源具备双向无功支撑能力,可通过其无功控制功能参与配电网无功电压调节。光伏电源无功输出能力与光伏电源额定容量和有功输出之间的关系为
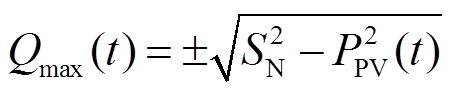 (5)
(5)
式中,SN为光伏电源额定容量;PPV(t)为光伏电源有功输出。
当光伏电源不参与无功电压调控时,光伏电源仅输出有功功率,此时光伏电源中IGBT电流为
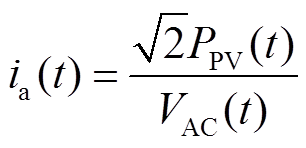 (6)
(6)
式中,VAC(t)为光伏电源交流测电压有效值。
当光伏电源参与无功电压调控时,光伏电源同时输出有功功率和无功功率,此时光伏电源中IGBT电流为
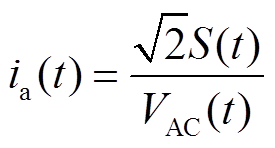 (7)
(7)
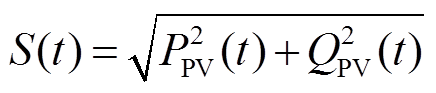 (8)
(8)
式中,S(t)为光伏电源输出视在功率;QPV(t)为光伏电源无功输出。
由式(6)、式(7)可知,光伏电源参与配电网无功调控时,若光伏电源有功输出保持不变,则其实际输出视在功率会增大,使得光伏电源输出电流增大,造成IGBT结温相应升高,导致光伏电源中IGBT可靠性和寿命降低。
考虑到IGBT结温对IGBT可靠性影响较大,建立计及IGBT结温约束的配电网无功电压优化模型。以配电网网损和光伏电源有功削减量为优化目标,其表达式为
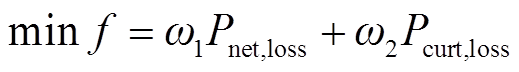 (9)
(9)
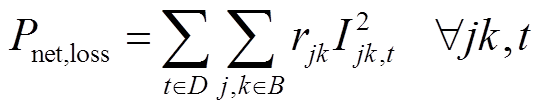 (10)
(10)
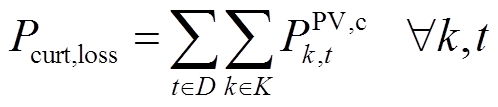 (11)
(11)
式中,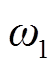 、
、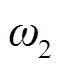 为优化目标权重;Pnet,loss为配电网网损;Pcurt,loss为光伏电源有功削减量;rjk为母线j到母线k的线路电阻;Ijk,t为t时刻母线j到母线k的线路电流;PPV,c k,t为t时刻母线k处光伏电压有功削减量;D为配电网运行时间集合;B为配电网母线节点编号集合;K为接入光伏节点编号集合。
为优化目标权重;Pnet,loss为配电网网损;Pcurt,loss为光伏电源有功削减量;rjk为母线j到母线k的线路电阻;Ijk,t为t时刻母线j到母线k的线路电流;PPV,c k,t为t时刻母线k处光伏电压有功削减量;D为配电网运行时间集合;B为配电网母线节点编号集合;K为接入光伏节点编号集合。
配电网无功优化时需满足配电网运行潮流约束、母线电压上下限约束、线路电流约束、光伏逆变器容量约束等[40],同时考虑到IGBT可靠性而引入IGBT结温约束,限制IGBT结温在限值TIGBT_limit范围内,进而得到计及IGBT结温约束的光伏高渗透配电网无功电压优化模型的约束条件集合。
IGBT结温约束为
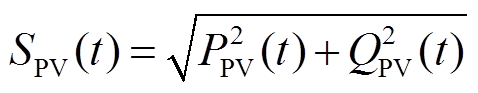 (12)
(12)
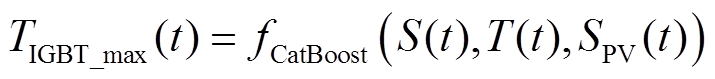 (13)
(13)
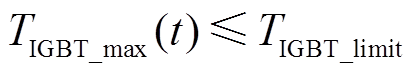 (14)
(14)
配电网安全稳定运行约束为
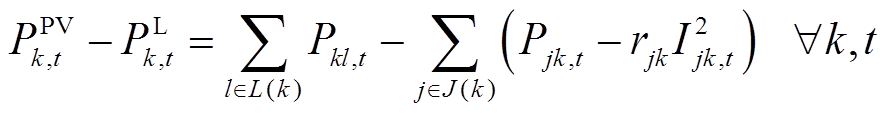 (15)
(15)
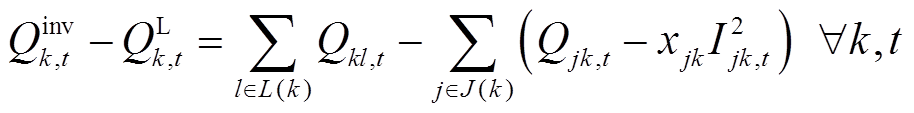 (16)
(16)
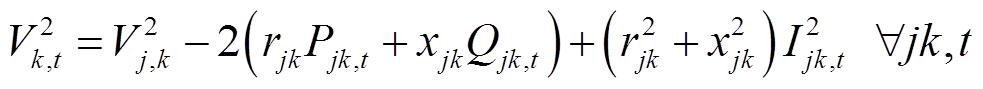 (17)
(17)
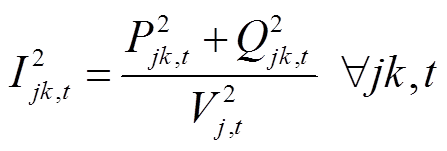 (18)
(18)
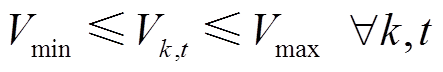 (19)
(19)
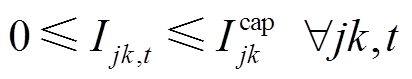 (20)
(20)
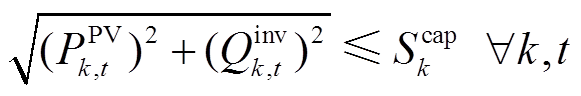 (21)
(21)
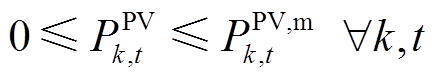 (22)
(22)
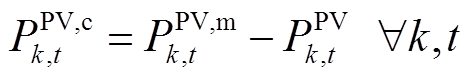 (23)
(23)
式中,fCatBoost(·)为CatBoost模型;TIGBT_max为IGBT结温波动周期内的最大结温;j、k、l为配电网母线索引;J(k)和L(k)分别为双亲节点与子节点集;Pjk,t、Qjk,t、rjk,t、xjk,t和Ijk,t分别为t时刻母线j到母线k的有功功率、无功功率、线路电阻、线路电感与线路电流;PPV k,t、Qinv k,t、PL k,t、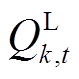 和Vk,t分别为t时刻母线k光伏有功功率、光伏电源无功功率、有功负荷、无功负荷和母线电压;Icap jk为母线j和母线k之间线路电流上限;Vmin、Vmax分别为配电网电压上、下限;Scap k为母线k处光伏接入容量;PPV,m k,t为t时刻母线k处光伏有功功率输出最大值。
和Vk,t分别为t时刻母线k光伏有功功率、光伏电源无功功率、有功负荷、无功负荷和母线电压;Icap jk为母线j和母线k之间线路电流上限;Vmin、Vmax分别为配电网电压上、下限;Scap k为母线k处光伏接入容量;PPV,m k,t为t时刻母线k处光伏有功功率输出最大值。
计及IGBT结温约束的配电网无功电压优化模型为非线性非凸优化模型,采用启发式方法求解效率较低,不利于后续年任务剖面下IGBT可靠性和寿命分析。因此,本文将IGBT结温约束转换为光伏电源输出视在功率约束,实现将原非线性约束转换为二阶锥约束;再对配电网安全稳定运行约束进行线性化与二阶锥松弛[41-42],从而将原非线性非凸优化模型转换为凸优化模型。
IGBT最大结温与光伏电源输出视在功率关系如图4所示。可见,IGBT最大结温为光伏电源输出视在功率的单调递增函数。当太阳辐照度与环境温度确定时,IGBT结温限值与光伏电源的最大输出视在功率存在唯一映射关系。当光伏电源输出视在功率不超过最大输出视在功率时,IGBT最大结温也不超过IGBT结温限值。
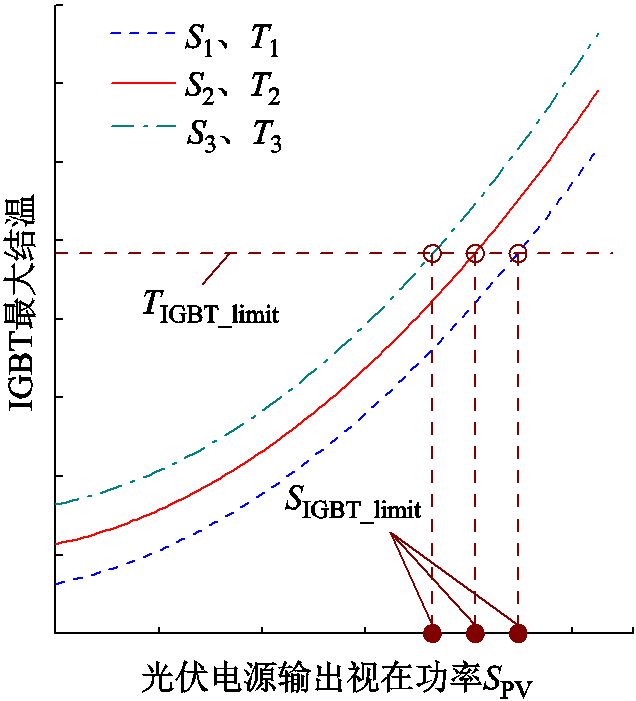
图4 IGBT最大结温与光伏逆变器输出视在功率关系
Fig.4 Relationship between IGBT maximum junction temperature and PV inverter output apparent power
IGBT最大结温可由CatBoost模型直接得到,但CatBoost模型无明确表达式且为非线性模型,无法根据IGBT结温限值直接反解出对应的光伏逆变器最大输出视在功率。考虑到IGBT最大结温为光伏电源输出功率的单调递增函数,采用二分法求解光伏电源最大输出视在功率的数值解。
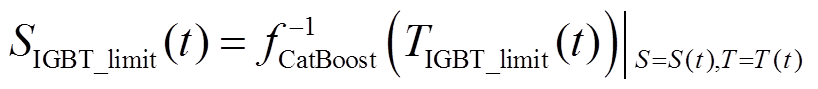 (24)
(24)
为将IGBT最大结温限制在IGBT结温限值范围内,可将光伏电源输出视在功率限制在最大输出视在功率范围内,即
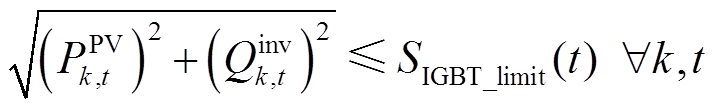 (25)
(25)
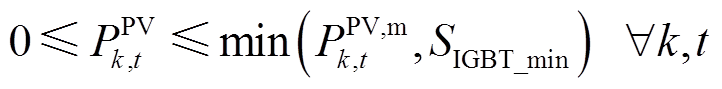 (26)
(26)
在考虑IGBT结温约束情况下,光伏电源输出有功功率与无功功率关系如图5所示。在相同有功输出情况下,光伏电源无功输出能力随着IGBT结温限值的减小而降低;在不同有功输出情况下,光伏电源无功输出能力由IGBT限温后的光伏逆变器最大视在功率SIGBT_limit和光伏逆变器有功输出共同决定。
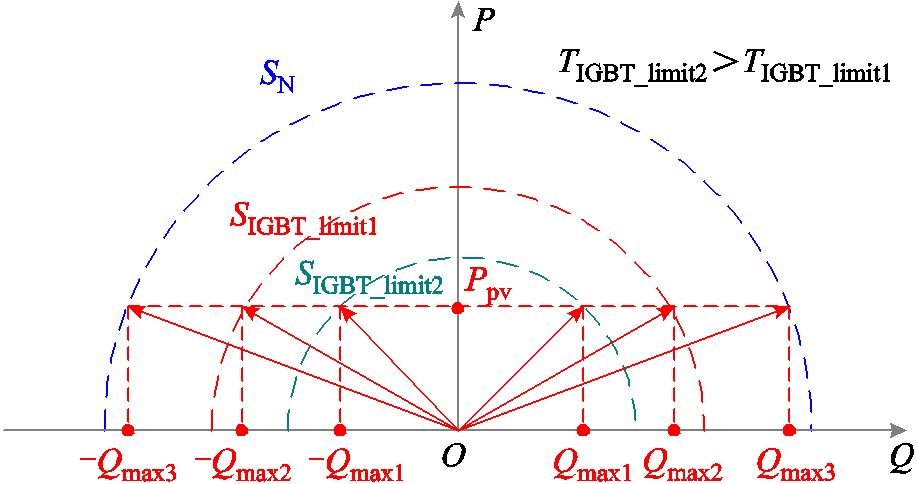
图5 限温时光伏电源有功与无功功率关系
Fig.5 The relationship between active power and reactive power of PV inverter under IGBT temperature limit
对配电网安全稳定运行约束进行线性化与二阶锥松弛,引入变量ijk,t、vjk,t,有
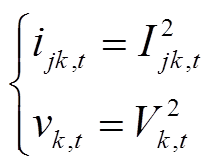 (27)
(27)
部分约束条件变化为
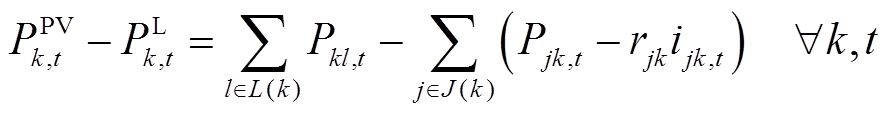 (28)
(28)
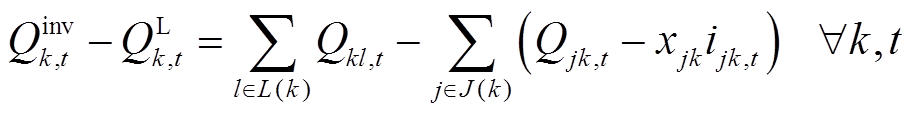 (29)
(29)
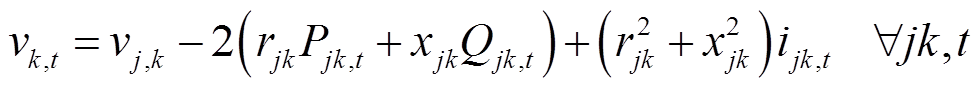 (30)
(30)
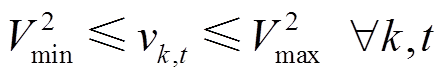 (31)
(31)
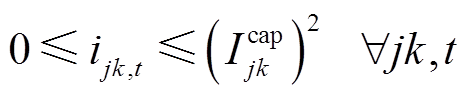 (32)
(32)
对式(21)进行二阶锥松弛处理,可得
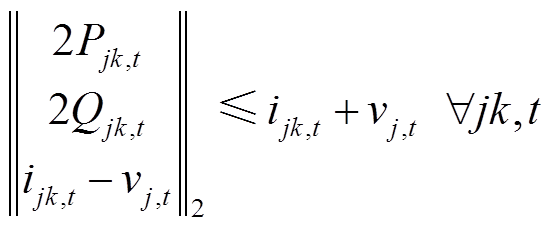 (33)
(33)
通过将IGBT结温约束转换为光伏电源输出视在功率约束,以及对配电网安全稳定运行约束进行线性化与二阶锥松弛,从而将所提配电网无功电压优化模型转换为二阶锥规划模型,可采用Cplex、Gurobi等求解器快速求解,避免了采用启发式算法求解效率低、容易陷入局部最优解等问题。
以IEEE 33节点配电系统为例,分别在6、8、10、13、21、22、25、28、31、33节点接入容量为500 kW(10 kW×50)的分布式光伏电源集群,如图6所示。为了保证光伏电源具有足够的无功输出能力,将光伏电源容量设置为额定容量的1.1倍。
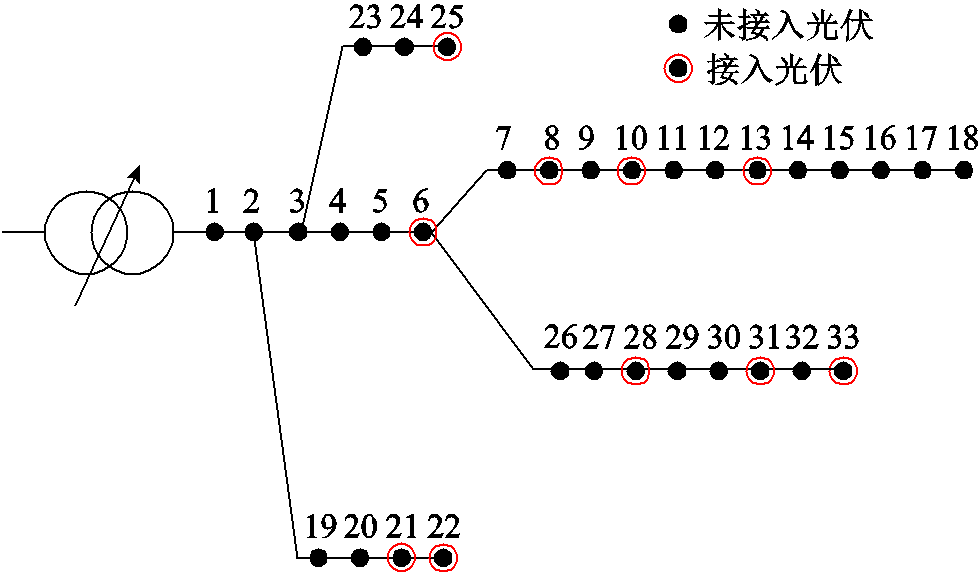
图6 IEEE 33节点配电系统
Fig.6 IEEE 33 node power distribution system
考虑到配电网空间位置相对集中,假定配电网区域内各节点位置的环境温度与辐照度一致。以低纬度地区任务剖面为例,其环境温度与辐照度数据如图7所示。
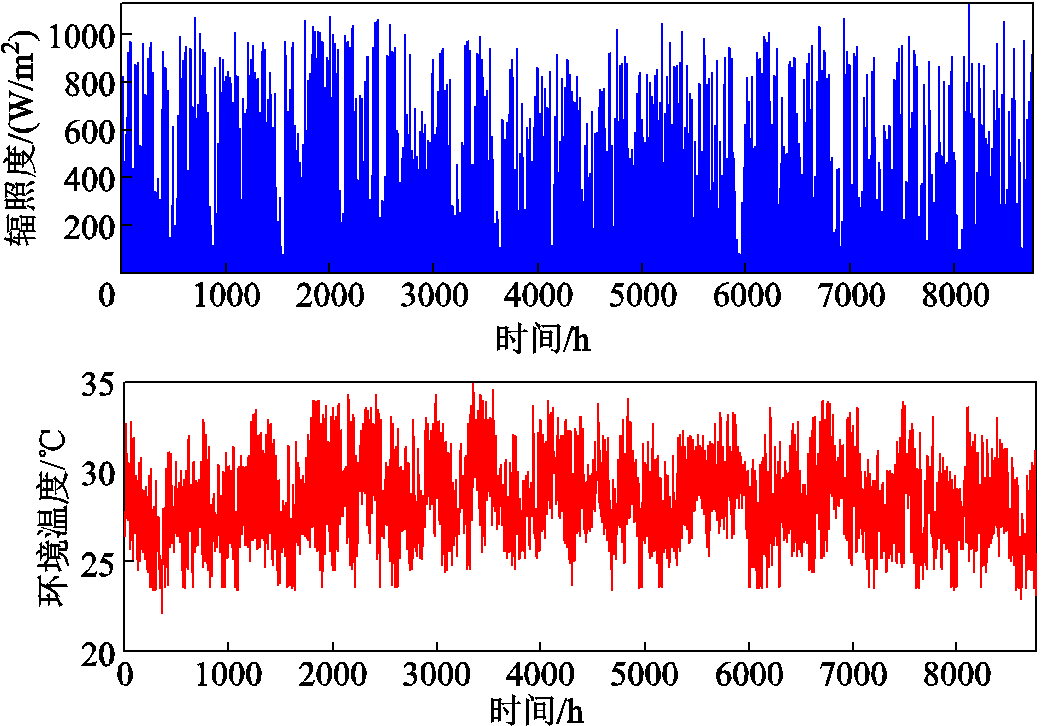
图7 低纬度地区任务剖面
Fig.7 Low latitude mission profile
以IEEE 33节点配电系统中各节点有功、无功负荷数据为基准,根据IEEE-RTS系统典型日负荷信息生成IEEE 33配电系统各节点日负荷数据信息,进而根据高斯分布生成IEEE 33节点配电系统的年负荷数据[40]。
IGBT结温约束分别设置为60℃、70℃、80℃、none四种情况,利用Matlab YALMIP工具箱和Cplex求解器,对所提计及光伏电源IGBT结温约束的配电网无功电压优化模型进行求解。
考虑到配电网接入光伏电源节点数量较多,为了便于说明问题,以节点28为例,光伏电源输出视在功率如图8所示。可见,随着IGBT结温限值的降低,光伏电源输出视在功率明显降低,从而实现了光伏电源实际输出电流的减小、IGBT结温的降低。
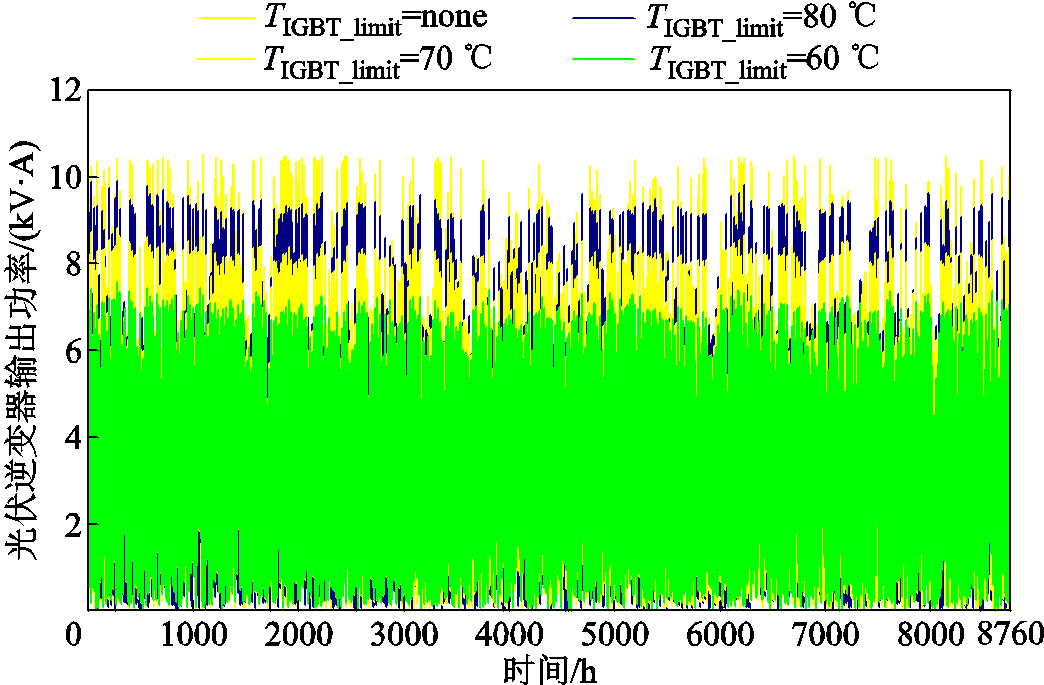
图8 节点28光伏逆变器输出视在功率
Fig.8 PV inverter output apparent power of node 28
未进行无功电压调控时,配电网运行24 h各节点电压如图9所示。可见,配电网部分节点的电压存在越上限或越下限的情况。
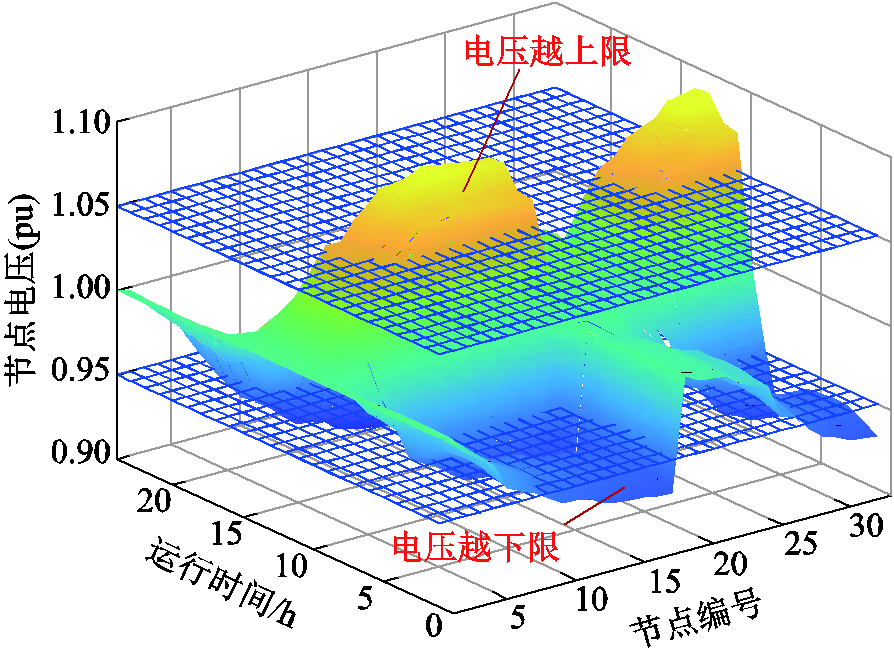
图9 未进行无功电压优化控制时的配电网各节点电压
Fig.9 Voltage of each node in distribution network without reactive voltage optimization control
在本文所提无功电压优化控制策略下,配电网运行24 h各节点电压如图10所示。可见,本文所提策略能够将配电网各节点电压稳定在安全范围内。
四种结温限值情况对应的配电网损耗情况见表1。可见,随着结温限值的降低,配电网网损、光伏有功削减及配电网总损耗均略有增加。因此,IGBT结温限值的选取需要综合考虑配电网总损耗与光伏逆变器可靠性情况。
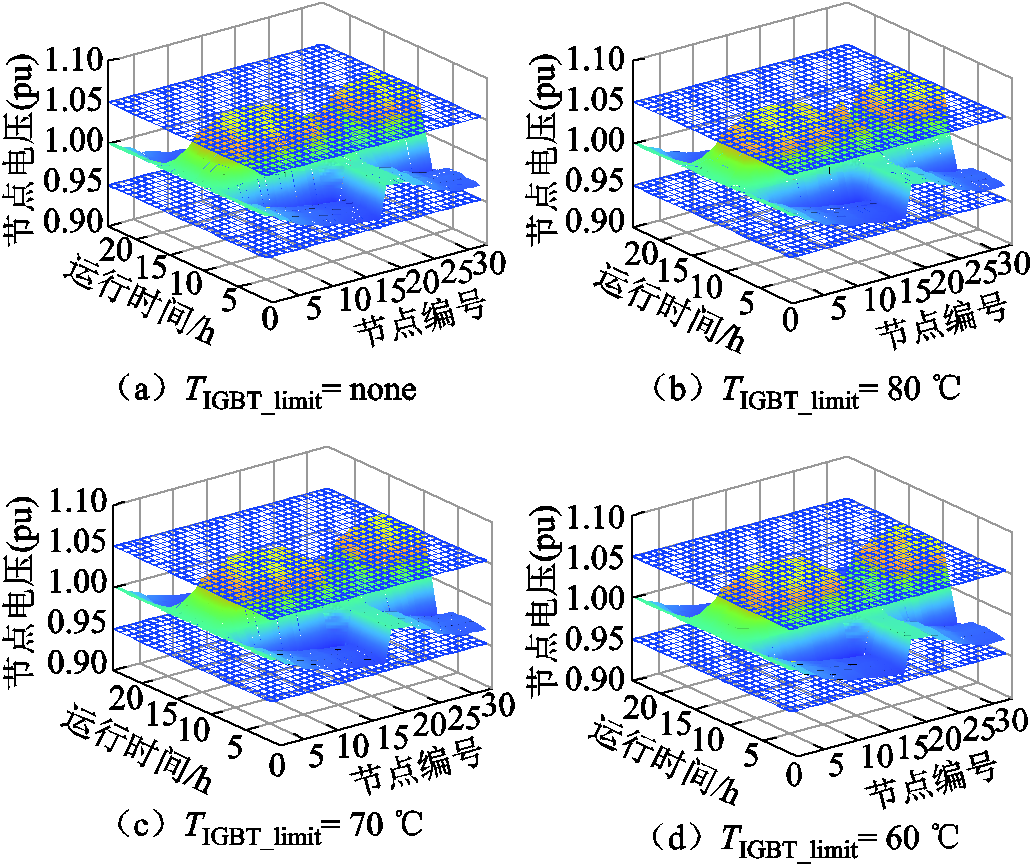
图10 进行无功电压优化控制时的配电网各节点电压
Fig.10 Voltage of each node in distribution network with reactive voltage optimization control
表1 配电网损耗情况
Tab.1 Loss of distribution network

TIGBT_limit/℃配电网网损/ (MW·h)光伏有功削减/ (MW·h)总损耗/ (MW·h) none880.837 41.189 9882.027 3 80883.266 94.957 8888.224 7 70892.259 821.279 7913.539 5 60904.329 660.350 7964.680 3
不同结温限值情况下,各接入点光伏电源IGBT结温情况如图11所示。可见,本文所提策略可实现光伏电源IGBT结温有效限制。
减小IGBT输出功率和IGBT电流可抑制IGBT结温波动[43-44]。在四种结温限值条件下,节点28处光伏电源IGBT稳态结温波动情况如图12所示。
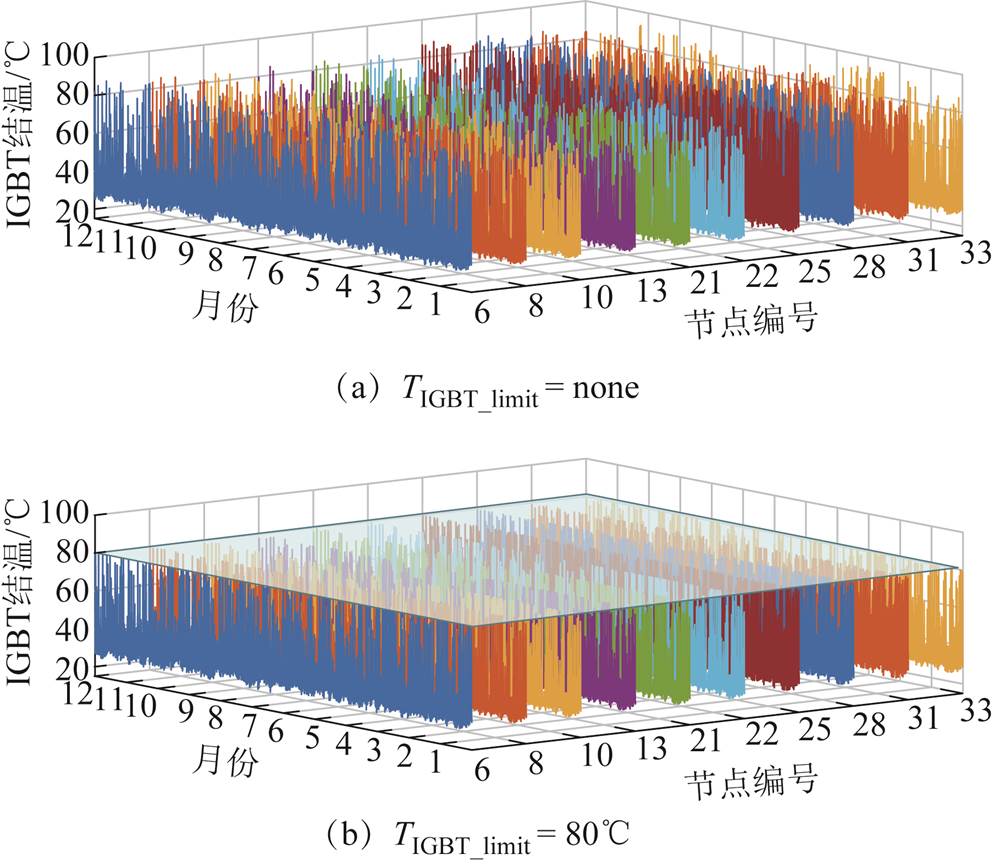
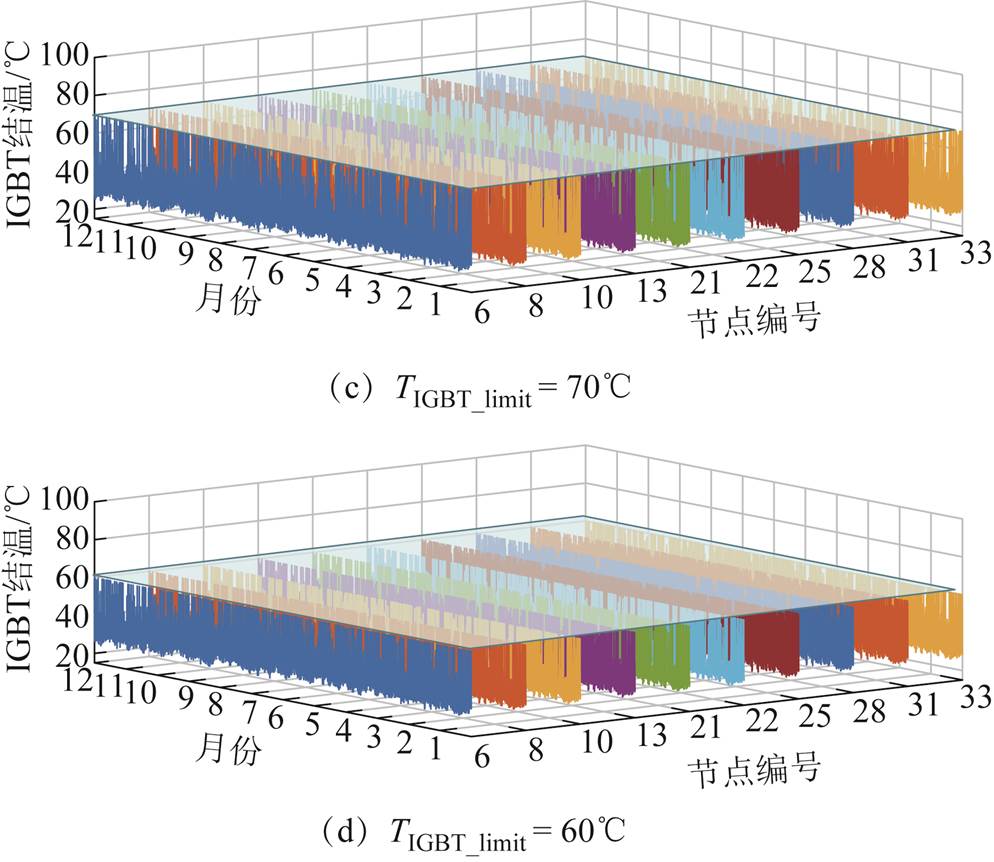
图11 各节点光伏电源中IGBT结温情况
Fig.11 IGBT junction temperature in PV power supply at each node
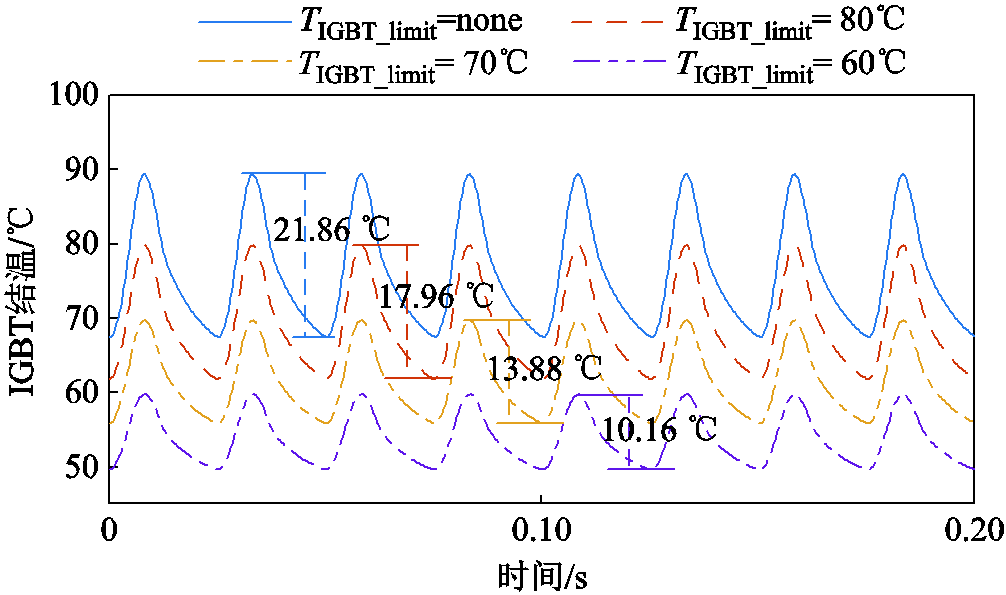
图12 节点28处IGBT稳态结温波动情况
Fig.12 Fluctuation of IGBT stable junction temperature at node 28
可见,随着IGBT结温限值的降低,相应的IGBT结温波动也逐渐降低,故本文所提策略限制IGBT最大结温的同时抑制IGBT结温波动。
对节点25处的光伏电源IGBT结温数据进行热载荷信息统计,得到不同结温限值下的IGBT结温均值和结温波动统计结果,分别如图13、图14所示。

图13 IGBT结温均值统计
Fig.13 Statistics of the mean junction temperature of IGBT
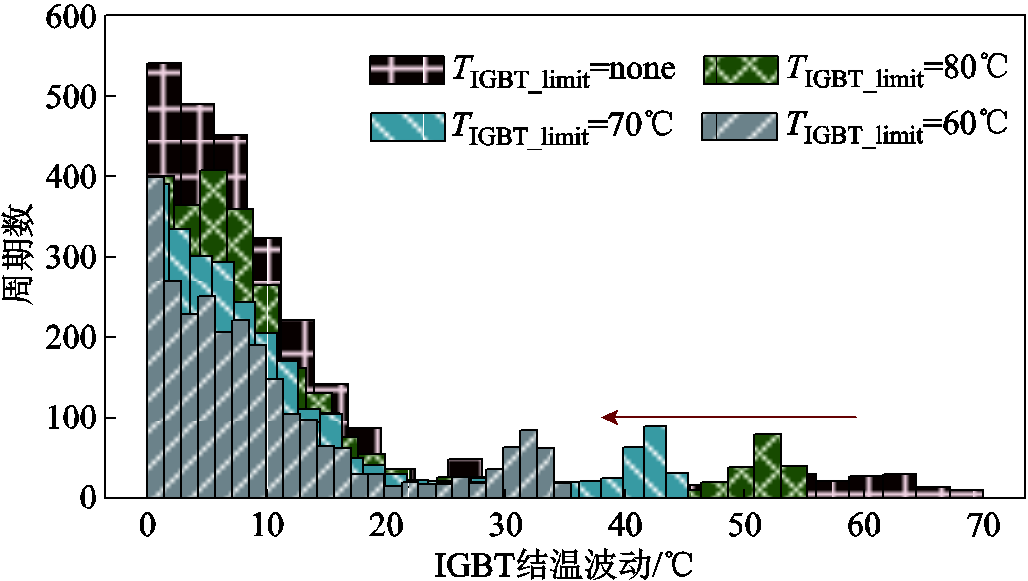
图14 IGBT结温波动统计
Fig.14 Statistics of IGBT junction temperature fluctuation
可见,在本文所提策略下,光伏电源IGBT结温相对集中于结温波动和结温均值较低的区域,并且IGBT结温限值越小,IGBT结温集中区域的结温波动与结温均值越低。
根据基于任务剖面的光伏电源可靠性评估流程,在本文所提策略下光伏电源IGBT可靠性分析结果如图15所示。可见,相较于无结温限制时所有接入点中光伏电源IGBT故障率均有显著降低,而且IGBT结温限值越小,光伏电源IGBT故障率降低越明显,验证了本文所提策略在提升光伏电源运行可靠性方面的有效性。
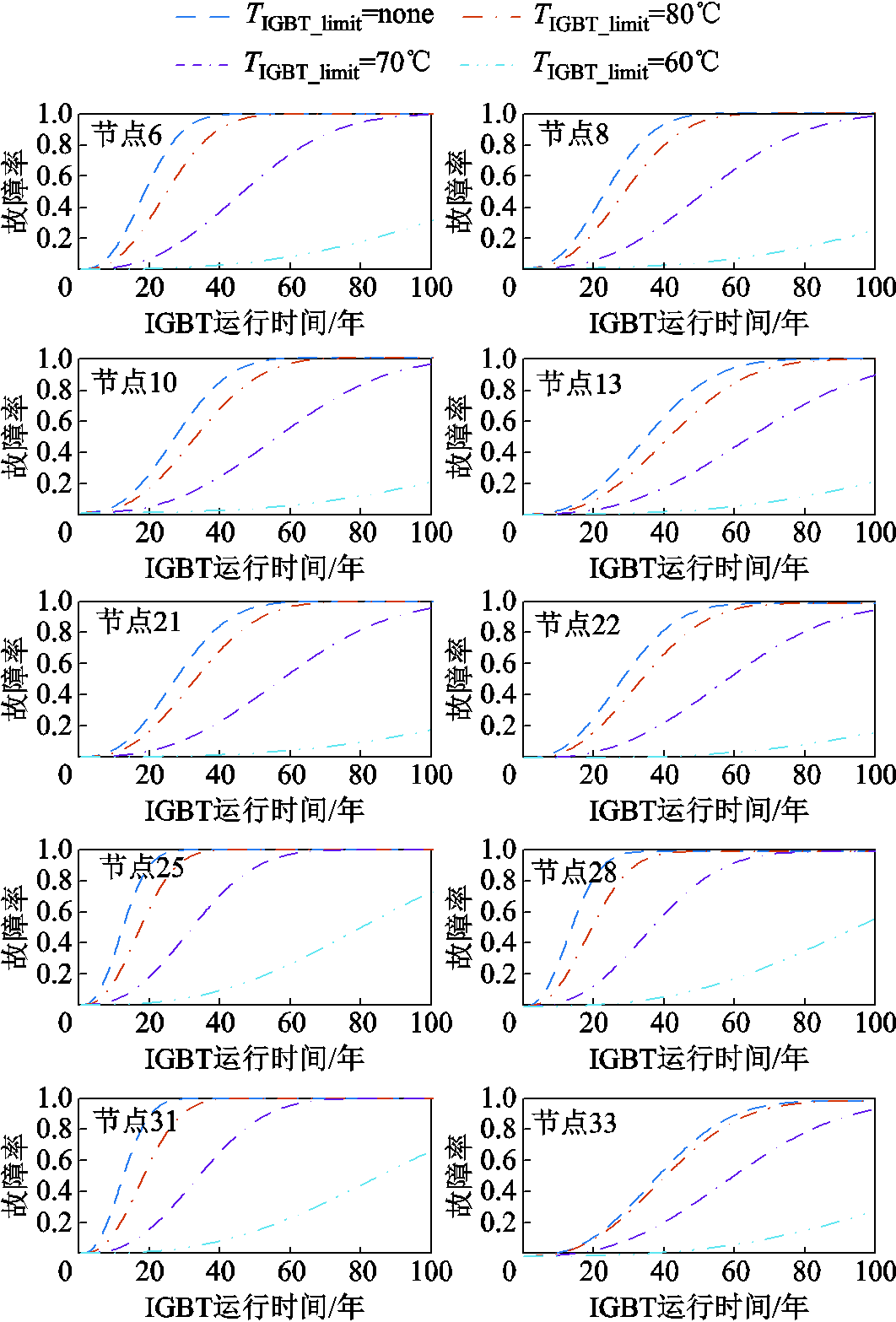
图15 光伏逆变器IGBT可靠性分析结果
Fig.15 IGBT reliability analysis results of PV inverter
配电网节点6、8、10、13、21、22、25、28、31、33接入的光伏电源IGBT寿命估计结果见表2,表2中none表示不进行IGBT结温限制。采用结温限制控制后,所有光伏电源节点IGBT寿命均有所提高,结温限值越低则IGBT寿命越高的规律明显。
表2 光伏逆变器IGBT寿命估计
Tab.2 IGBT lifetime estimation of photovoltaic inverter

节点估计寿命/年 none80℃70℃60℃ 69122365 811152770 1013162877 1317213375 2113162981 2214162880 25681641 28791848 31581743 3319203065
无IGBT结温限制时,所有光伏电源IGBT最小寿命与平均寿命分别为5年和11年;IGBT结温限值为80、70、60℃时,对应的所有光伏电源IGBT最小寿命分别为8、16、41年,所有光伏电源IGBT平均寿命分别为14、25、65年。可见,结温限制控制可以使得所有光伏电源IGBT最小寿命与平均寿命均有提高,而且随着IGBT结温限值的减小,所有节点光伏电源IGBT的平均寿命与最低寿命均有明显提高。本文所提策略能够在进行配电网无功优化的同时有效地提升光伏逆变器IGBT的寿命,延长光伏逆变器IGBT可靠运行时间。
四种IGBT结温约束情况下,各接入点光伏电源IGBT寿命情况如图16所示。可见,IGBT结温限值越小,所有接入点光伏电源寿命有效区域面积越大,表明在所提策略下配电网区域内所有光伏电源整体寿命性能均明显提高。
不同结温限值下配电网运行结果见表3。IGBT结温限值越小,IGBT运行可靠性和寿命越高,但与此同时配电网总损耗也随之增大。故应从配电网总损耗、IGBT可靠性和寿命角度综合考虑IGBT结温限值的整定。
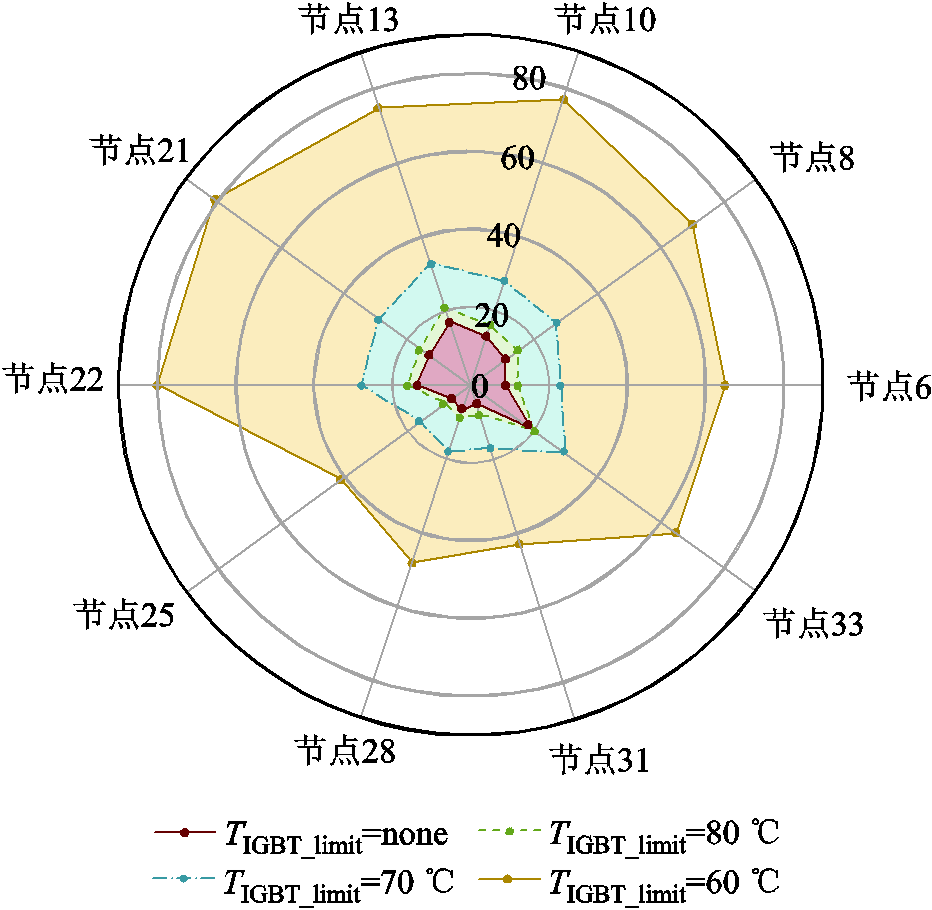
图16 各接入点光伏逆变器IGBT寿命情况
Fig.16 IGBT lifetime of PV inverters in each access point
表3 不同结温限值下配电网运行结果
Tab.3 Operation results of distribution network under different junction temperature limits

TIGBT_limit/℃所有光伏电源最小寿命/年所有光伏电源运行 30年最大故障率配电网总损耗/(MW·h) none51882.027 3 8080.9443888.224 7 70160.4467913.539 5 60410.0453964.680 3
光伏电站规划设计时光伏电源IGBT更换周期一般为20~30年,综合考虑所有接入点光伏电源IGBT最小寿命及配电网总损耗情况,在本文算例中,设置结温限值为60℃时,可满足IGBT更换周期需求,同时配电网总损耗不过高。
针对光伏电源参与配电网无功电压调节影响光伏逆变器IGBT可靠性和寿命的问题,本文提出了计及IGBT结温约束的光伏高渗透配电网无功电压优化控制策略,主要结论如下:
1)提出基于CatBoost算法的IGBT可靠性评估方法,利用数据驱动方法计算IGBT结温,提高了IGBT结温计算效率,降低了结温计算结果对IGBT电热模型参数的依赖程度,可保证IGBT可靠性评估的实时性。
2)建立了计及IGBT结温约束的配电网无功电压优化模型,将IGBT结温约束转换为光伏逆变器输出视在功率约束,并通过线性化与二阶锥松弛将无功优化模型转换为二阶锥规划模型,提高了模型求解速度。
3)IGBT结温限值越低,IGBT运行可靠性与寿命越高,但配电网总损耗也随之增大。故提出综合考虑配电网总损耗、IGBT可靠性的IGBT结温限值整定原则,为光伏电源参与配电网无功电压调节控制策略设计、核心参数整定提供了理论依据。
参考文献
[1] 马丽, 刘念, 张建华, 等. 自动需求响应模式下光伏用户群的优化运行模型[J]. 中国电机工程学报, 2016, 36(13): 3422-3432, 3361. Ma Li, Liu Nian, Zhang Jianhua, et al. Optimal operation model of user group with photovoltaic in the mode of automatic demand response[J]. Proceedings of the CSEE, 2016, 36(13): 3422-3432, 3361.
[2] 唐爱红, 翟晓辉, 卢智键, 等. 一种适用于配电网的新分布式潮流控制器拓扑[J]. 电工技术学报, 2021, 36(16): 3400-3409. Tang Aihong, Zhai Xiaohui, Lu Zhijian, et al. A novel topology of distributed power flow controller for distribution network[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3400-3409.
[3] 黄堃, 刘澄, 吕潇, 等. 计及本地负荷的分布式光伏并网电压协同控制策略[J]. 电网与清洁能源, 2020, 36(11): 127-133. Huang Kun, Liu Cheng, Lü Xiao, et al. Distributed photovoltaic grid-connected voltage coordination control strategy considering local load[J]. Power System and Clean Energy, 2020, 36(11): 127-133.
[4] 王雪纯, 陈红坤, 陈磊. 提升区域综合能源系统运行灵活性的多主体互动决策模型[J]. 电工技术学报, 2021, 36(11): 2207-2219. Wang Xuechun, Chen Hongkun, Chen Lei. Multi-player interactive decision-making model for operational flexibility improvement of regional integrated energy system[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2207-2219.
[5] Shayani R A, de Oliveira M A G. Photovoltaic generation penetration limits in radial distribution systems[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1625-1631.
[6] 黄大为, 王孝泉, 于娜, 等. 计及光伏出力不确定性的配电网混合时间尺度无功/电压控制策略[J]. 电工技术学报, 2022, 37(17): 4377-4389. Huang Dawei, Wang Xiaoquan, Yu Na, et al. Hybrid timescale voltage/var control in distribution network considering PV power uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4377-4389.
[7] 吕志鹏, 罗安, 周柯, 等. 静止同步补偿器与微网在配电网无功电压协同控制中的联合运用[J]. 中国电机工程学报, 2010, 30(增刊1): 18-24. Lü Zhipeng, Luo An, Zhou Ke, et al. Combined application of DSTATCOM and micro-grid in reactive power and voltage collaborative control on distribution network[J]. Proceedings of the CSEE, 2010, 30(S1): 18-24.
[8] 谭大帅, 戴彬, 郭刚, 等. 分布式光伏管控平台的设计与实现[J]. 电气技术, 2023, 24(2): 41-51. Tan Dashuai, Dai Bin, Guo Gang, et al. Design and implementation of distributed photovoltaic management and control platform[J]. Electrical Engineering, 2023, 24(2): 41-51.
[9] 吕超然, 吕翔, 张文瑶. 整县屋顶光伏推进背景下的配电网技术研究[J]. 农村电气化, 2023(2): 29-34. Lü Chaoran, Lü Xiang, Zhang Wenyao. Research on distribution network technology under the background of promoting the development of roof mounted PV in thewhole County[J]. Rural Electrification, 2023(2): 29-34.
[10] Zhang Yongxi, Xu Yan, Yang Hongming, et al. Voltage regulation-oriented co-planning of distributed generation and battery storage in active distribution networks[J]. International Journal of Electrical Power & Energy Systems, 2019, 105: 79-88.
[11] 俞智鹏, 汤奕, 戴剑丰, 等. 基于有功自适应调整的光伏电站无功电压控制策略[J]. 电网技术, 2020, 44(5): 1900-1907. Yu Zhipeng, Tang Yi, Dai Jianfeng, et al. Voltage/var control strategy of PV plant based on adaptive adjustment of active power[J]. Power System Technology, 2020, 44(5): 1900-1907.
[12] 符杨, 周晓鸣, 苏向敬. 多电压等级不平衡主动配电网电压无功自适应多目标协调优化[J]. 电网技术, 2018, 42(7): 2136-2147. Fu Yang, Zhou Xiaoming, Su Xiangjing. Adaptive and coordinated volt/var optimization for unbalanced active distribution networks of multiple voltage levels[J]. Power System Technology, 2018, 42(7): 2136-2147.
[13] Zhang Cuo, Xu Yan. Hierarchically-coordinated voltage/VAR control of distribution networks using PV inverters[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 2942-2953.
[14] Ding Tao, Liu Shiyu, Yuan Wei, et al. A two-stage robust reactive power optimization considering uncertain wind power integration in active distribution networks[J]. IEEE Transactions on Sustainable Energy, 2016, 7(1): 301-311.
[15] Zhang Cuo, Xu Yan, Dong Zhaoyang, et al. Three-stage robust inverter-based voltage/var control for distribution networks with high-level PV[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 782-793.
[16] 刘蕊, 吴奎华, 冯亮, 等. 含高渗透率分布式光伏的主动配电网电压分区协调优化控制[J]. 太阳能学报, 2022, 43(2): 189-197. Liu Rui, Wu Kuihua, Feng Liang, et al. Voltage partition coordinated optimization control of active distribution network of high penetration distributed pvs[J]. Acta Energiae Solaris Sinica, 2022, 43(2): 189-197.
[17] Yang Yongheng, Wang Huai, Blaabjerg F. Reactive power injection strategies for single-phase photovoltaic systems considering grid requirements[J]. IEEE Transactions on Industry Applications, 2014, 50(6): 4065-4076.
[18] Gandhi O, Rodríguez-Gallegos C D, Gorla N B Y, et al. Reactive power cost from PV inverters considering inverter lifetime assessment[J]. IEEE Transactions on Sustainable Energy, 2019, 10(2): 738-747.
[19] Chai Qingmian, Zhang Cuo, Xu Yan, et al. PV inverter reliability-constrained volt/var control of distribution networks[J]. IEEE Transactions on Sustainable Energy, 2021, 12(3): 1788-1800.
[20] 李伟, 李晓祎, 张佳杰. 光伏逆变器可靠性现状分析[J]. 无线互联科技, 2016(4): 90-94, 97. Li Wei, Li Xiaoyi, Zhang Jiajie. Photovoltaic inverter reliability analysis of the situation[J]. Wireless Internet Technology, 2016(4): 90-94, 97.
[21] Bouguerra S, Yaiche M R, Gassab O, et al. The impact of PV panel positioning and degradation on the PV inverter lifetime and reliability[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 3114-3126.
[22] Bouguerra S, Agroui K, Yaiche M R, et al. The impact of PV array inclination on the PV inverter reliability and lifetime[C]//2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 2021: 617-622.
[23] Sangwongwanich A, Blaabjerg F. Reliability assessment of fault-tolerant power converters includingwear-out failure[C]//2022IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 2022: 300-306.
[24] 张榴晨, 张亚, 茆美琴. 基于任务剖面的单相Boost型功率解耦光伏逆变器寿命预测[J]. 太阳能学报, 2022, 43(7): 109-114. Zhang Liuchen, Zhang Ya, Mao Meiqin. Mission profile based lifetime prediction for single-phase boost power decoupling photovoltaic inverter[J]. Acta Energiae Solaris Sinica, 2022, 43(7): 109-114.
[25] 丁红旗, 马伏军, 徐千鸣, 等. 模块化多电平换流器子模块IGBT损耗优化控制策略[J]. 电力系统自动化, 2021, 45(17): 143-152. Ding Hongqi, Ma Fujun, Xu Qianming, et al. Loss optimization control strategy for IGBT in sub-module of modular multilevel converter[J]. Automation of Electric Power Systems, 2021, 45(17): 143-152.
[26] Sangwongwanich A, Yang Yongheng, Sera D, et al. On the impacts of PV array sizing on the inverter reliability and lifetime[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3656-3667.
[27] Choi U M, Blaabjerg F, Lee K B. Study and handling methods of power IGBT module failures in power electronic converter systems[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2517-2533.
[28] Novak M, Sangwongwanich A, Blaabjerg F. Monte carlo-based reliability estimation methods for power devices in power electronics systems[J]. IEEE Open Journal of Power Electronics, 2021, 2: 523-534.
[29] da Silveira Brito E M, Cupertino A F, Pereira H A, et al. Reliability-based trade-off analysis of reactive power capability in PV inverters under different sizing ratio[J]. International Journal of Electrical Power & Energy Systems, 2022, 136: 107677.
[30] Bo Zhang, Yuan Gao. The optimal capacity ratio and power limit setting method of the PV generation system based on the IGBT reliability and PV economy[J]. Microelectronics Reliability, 2023, 148: 115145.
[31] 王希平, 李志刚, 姚芳. 模块化多电平换流阀IGBT器件功率损耗计算与结温探测[J]. 电工技术学报, 2019, 34(8): 1636-1646. Wang Xiping, Li Zhigang, Yao Fang. Power loss calculation and junction temperature detection of IGBT devices for modular multilevel valve[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1636-1646.
[32] 张军, 张犁, 成瑜. IGBT模块寿命评估研究综述[J].电工技术学报, 2021, 36(12): 2560-2575. Zhang Jun, Zhang Li, Cheng Yu. Review of the lifetime evaluation for the IGBT module[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2560-2575.
[33] Dragičević T, Wheeler P, Blaabjerg F. Artificial intelligence aided automated design for reliability of power electronic systems[J]. IEEE Transactions on Power Electronics, 2018, 34(8): 7161-7171.
[34] Zhang Weixuan. Short-term load forecasting of power model based on CS-catboost algorithm[C]//2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 2022: 2295-2299.
[35] 王玉静, 王诗达, 康守强, 等. 基于改进深度森林的滚动轴承剩余寿命预测方法[J]. 中国电机工程学报, 2020, 40(15): 5032-5043. Wang Yujing, Wang Shida, Kang Shouqiang, et al. Prediction method of remaining useful life of rolling bearings based on improved GcForest[J]. Proceedings of the CSEE, 2020, 40(15): 5032-5043.
[36] 雷万钧, 刘进军, 吕高泰, 等. 大容量电力电子装备关键器件及系统可靠性综合分析与评估方法综述[J]. 高电压技术, 2020, 46(10): 3353-3361. Lei Wanjun, Liu Jinjun, Lü Gaotai, et al. Review of reliability comprehensive analysis and evaluation methods for key components and system of large capacity power electronic equipment[J]. High Voltage Engineering, 2020, 46(10): 3353-3361.
[37] Musallam M, Johnson C M. An efficient implementation of the rainflow counting algorithm for life consumption estimation[J]. IEEE Transactions on Reliability, 2012, 61(4): 978-986.
[38] Sangwongwanich A, Blaabjerg F. Monte Carlo simulation with incremental damage for reliability assessment of power electronics[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7366-7371.
[39] Reigosa P D, Wang Huai, Yang Yongheng, et al. Prediction of bond wire fatigue of IGBTs in a PV inverter under a long-term operation[J]. IEEE Transactions on Power Electronics, 2016, 31(10): 7171-7182.
[40] Zhang Bo, Gao Yuan. IGBT reliability analysis of photovoltaic inverter with reactive power output capability[J]. Microelectronics Reliability, 2023, 147: 115073.
[41] 徐玉琴, 方楠. 基于分段线性化与改进二阶锥松弛的电-气互联系统多目标优化调度[J]. 电工技术学报, 2022, 37(11): 2800-2812. Xu Yuqin, Fang Nan. Multi objective optimal scheduling of integrated electricity-gas system based on piecewise linearization and improved second order cone relaxation[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2800-2812.
[42] Grigg C, Wong P, Albrecht P, et al. The IEEE reliability test system-1996. a report prepared by the reliability test system task force of the application of probability methods subcommittee[J]. IEEE Transactions on Power Systems, 1999, 14(3): 1010-1020.
[43] 杨珍贵, 周雒维, 杜雄, 等. 基于器件的结温变化评估风机中参数差异对网侧变流器可靠性的影响[J]. 中国电机工程学报, 2013, 33(30): 41-49, 8. Yang Zhengui, Zhou Luowei, Du Xiong, et al. Effects of different parameters on reliability of grid-side converters based on varied junction temperature of devices in wind turbines[J]. Proceedings of the CSEE, 2013, 33(30): 41-49, 8.
[44] 杜雄, 李高显, 孙鹏菊, 等. 考虑基频结温波动的风电变流器可靠性评估[J]. 电工技术学报, 2015, 30(10): 258-265. Du Xiong, Li Gaoxian, Sun Pengju, et al. Reliability evaluation of wind power converters considering the fundamental frequency junction temperature fluctuations[J]. Transactions of China Electrotechnical Society, 2015, 30(10): 258-265.
Abstract The participation of photovoltaic inverters in reactive voltage regulation of the distribution network is an effective method to improve the economy and reliability of photovoltaic high-permeability distribution network operation. However, the reactive power support provided by photovoltaic inverters will increase the maximum junction temperature of IGBT in photovoltaic inverters and increase the fluctuation of junction temperature, which will affect the safe and stable operation of photovoltaic inverters and distribution network. Therefore, the influence of reactive power output of photovoltaic power supply on the operation reliability and lifetime of photovoltaic inverter should be considered when reactive power and voltage control is carried out.
Firstly, this paper proposes an IGBT reliability evaluation method based on CatBoost algorithm. This method uses data-driven method to calculate IGBT junction temperature, which shortens the calculation time of IGBT junction temperature and reduces the dependence of junction temperature calculation results on IGBT thermal model parameters. Secondly, the reactive power and voltage optimization control strategy of active distribution network considering IGBT junction temperature constraint is proposed. The IGBT junction temperature constraint is introduced into the reactive power and voltage optimization constraint of distribution network, and the multi-objective reactive power optimization model of active distribution network considering IGBT junction temperature constraint is established. Finally, considering the distribution network loss, IGBT reliability and lifetime, the IGBT junction temperature limit setting principle of photovoltaic power supply is proposed.
The effectiveness of the proposed strategy in reactive power and voltage optimization and operation reliability improvement of PV power supply is verified by IEEE 33-bus typical distribution system. According to the reliability evaluation process of photovoltaic power supply based on mission profile, the IGBT failure rate of photovoltaic power supply in all access points is significantly reduced compared with that without junction temperature limit, which verifies the effectiveness of the proposed strategy in improving the operation reliability of photovoltaic power supply. At the same time, when the IGBT junction temperature limits are 80°C, 70℃ and 60℃, the corresponding minimum lifetime of all photovoltaic power IGBTs are 8, 16 and 41 years, respectively, and the average lifetime of all photovoltaic power IGBTs are 14, 25 and 65 years, respectively. It can be seen that the junction temperature limit control can improve the minimum lifetime and average lifetime of all photovoltaic power IGBTs. Considering all access point photovoltaic power IGBT minimum lifetime and distribution network loss, in this paper, the example set 60℃ junction temperature limit, can meet the IGBT replacement cycle requirements, and can ensure that the total loss of distribution network is not high.
The following conclusions can be drawn from the simulation analysis: (1) The IGBT junction temperature is calculated by data-driven method, which improves the calculation efficiency of IGBT junction temperature, reduces the dependence of junction temperature calculation results on IGBT thermal model parameters. (2) The reactive power optimization model is transformed into a second-order cone programming model by linearization and second-order cone relaxation, which improves the speed of model solution. (3) The setting principle of IGBT junction temperature limit considering the total loss of distribution network and IGBT reliability is proposed, which provides a theoretical basis for photovoltaic power supply to participate in the design of reactive voltage regulation control strategy and core parameter setting of distribution network.
keywords:CatBoost machine learning algorithm, IGBT junction temperature, reactive voltage control, IGBT reliability, multi-objective optimization
DOI:10.19595/j.cnki.1000-6753.tces.222332
中图分类号:TM73
国家自然科学基金(52207102)、河北省自然科学基金(E2022502059)和国网河北省电力有限公司电力科学研究院科技项目(kj2022-021)资助。
收稿日期 2022-12-18
改稿日期 2023-05-10
张 波 男,1981年生,副教授,硕士生导师,研究方向为新能源电力系统分析与稳定控制、电力电子系统可靠性分析。E-mail:zhangbo@ncepu.edu.cn(通信作者)
高 远 男,1999年生,硕士研究生,研究方向为电力电子系统可靠性分析。E-mail:gaoy@ ncepu.edu.cn
(编辑 赫 蕾)