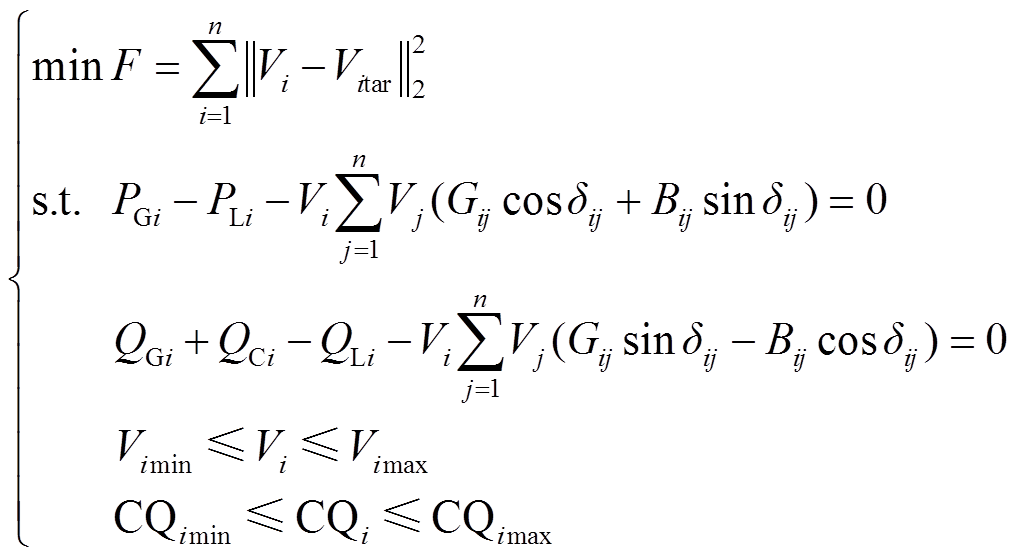（1）
摘要 为了快速平抑分布式能源接入系统产生的无功电压波动，以强化学习、模仿学习为代表的机器学习方法逐渐被应用于无功电压控制。虽然现有方法能实现在线极速求解，但仍然存在离线训练速度慢、普适性不够等阻碍其应用于实际的缺陷。该文首先提出一种适用于输电网集中式控制的单智能体简化强化学习方法，该方法基于“Actor-Critic”架构对强化学习进行简化与改进，保留了强化学习无需标签数据与强普适性的优点，同时消除了训练初期因智能体随机搜索造成的计算浪费，大幅提升了强化学习的训练速度；然后，提出一种适用于配电网分布式零通信控制的多智能体简化强化学习方法，该方法将简化强化学习思想推广形成多智能体版本，同时采用模仿学习进行初始化，将全局优化思想提前注入各智能体，提升各无功设备之间的就地协同控制效果；最后，基于改进IEEE 118节点算例的仿真结果验证了所提方法的正确性与快速性。
关键词：无功电压控制 集中式控制 单智能体简化强化学习 分布式控制 多智能体简化强化学习
近年来，以光伏、风电为代表的分布式可再生能源在电力系统中的占比逐年增大，这对未来全球能源加速转型具有重要的意义。但分布式能源出力的随机性与波动性也给电力系统正常运行带来了众多难题，其中电力系统无功电压快速波动便是典型的问题之一[1-4]。根据真实的历史运行数据，国内某220 kV风电场在未进行无功电压控制（Volt-Var Control, VVC）时，曾观测到其并网点电压在10 s内的平均波动达到6 kV，在2 s内的最大波动达到5 kV[5]；另据对400户家庭收集的光伏运行数据显示，家用光伏在1 min内的功率变化能够达到额定容量的15%[6]，这些剧烈的波动现象无疑迫使VVC需要进行更快、更好的决策以应对分布式能源带来的巨大挑战。
VVC的控制手段主要包括以电容器、变压器分接头为代表的离散型无功设备与以静止无功补偿器（Static Var Compensator, SVC）/静止无功发生器（Static Var Generator, SVG）、发电机组及分布式能源逆变器无功出力为代表的连续型无功设备两大类。各种无功设备的控制时间常数也不尽相同，变压器分接头及容抗器为min级，传统发电机组、风电机组及光伏逆变器为s级，SVC/SVG调节速度最快，为10 ms级，但由于造价昂贵通常配置容量较小[7-9]。由于离散型无功设备只能阶跃式调节，调节速度缓慢且存在日内动作次数约束，而连续型无功设备能够实现无功的快速平滑调节且无日内动作次数约束，为实现两类设备的协调控制，近年来众多学者倾向于将VVC转化为多时间尺度优化问题[10-12]。其中日前控制阶段用于控制离散型无功设备，控制频次通常设定为h级[13]，主要在分布式能源及负荷预测的基础上，提前制定离散型无功设备的24 h日前控制策略。实时控制阶段用于控制连续型无功设备，由于分布式能源波动速度为s级至min级，且连续型无功设备的控制时间常数大多集中于s级，因此实时控制频次通常设定为s级或min级[14-15]，主要在离散型无功设备执行日前控制策略的基础上，对连续型无功设备进行实时优化调节，最终达到快速平抑分布式能源造成无功电压波动的目的，本文研究主要针对实时控制阶段进行开展。
从控制算法的角度，传统VVC可分为以内点法为代表的数学算法[16-17]与以遗传算法为代表的启发式算法[18-19]两大类。由于采用传统方法进行优化求解时存在需要精确建模、在线计算速度缓慢等缺陷，无法实现对无功电压波动的快速响应，因而近年来众多学者开始将机器学习方法引入VVC，其核心思想都是通过离线训练实现电力系统实时状态与无功设备控制策略的端到端映射，在线计算时能够省去传统方法所需的大量迭代计算过程。应用于VVC的机器学习方法主要分为模仿学习[20-21]（Imitation Learning, IL）及强化学习[22-25]（Deep Reinforcement Learning, DRL）两大类。其中IL本质是监督学习，是利用传统方法在不同运行场景下生成的大量专家样本进行监督训练的过程，操作简单、模型训练速度较快，但存在形成专家样本耗时长、对专家样本质量要求极高等缺点。DRL本质是试错，是智能体通过与环境之间不断交互获得的奖励值指导动作策略不断升级的过程，DRL无需标签数据，只需通过随机试错便可使得智能体学习得到近似最优的控制策略，但也正是因为初期随机探索产生了大量的计算浪费，导致DRL存在离线训练速度缓慢、收敛结果不稳定等缺点。由于这两类机器学习算法应用于VVC时各有自身的优缺点，因此开发一种能够结合二者优点的机器学习算法，同时拥有DRL的自主探索性及IL的训练快速性，对于平抑未来因更高比例分布式能源接入产生的更为频繁的系统无功电压波动具有重要的意义。
从控制架构的角度，当前VVC主要分为集中式控制[26-27]、本地控制[28-29]、分布式控制[30-35]三大类。集中式控制主要通过实时收集系统内所有运行信息进行整体无功优化，控制效果最好，但是需要实现可靠而快速的实时通信。本地控制无需实现实时通信，主要是无功设备基于本地信息就地决策控制，但由于缺乏不同无功设备间的协同导致系统电压控制效果较差。分布式协调控制又分为基于一致性算法或交替方向乘子算法、需要极少通信的分布式控制[30-32]和基于多智能体强化学习、零通信的分布式控制[33-35]两种，由于前者仍需邻近节点间的实时通信作为基础，因此实现零通信的基于多智能体强化学习的分布式控制目前更加受到学者的关注。
基于以上对现有VVC研究中关于控制算法、控制架构及其优缺点的总结，本文提出一种基于简化强化学习的VVC方法应用于多时间尺度VVC的实时控制阶段。该方法分为单智能体版本及多智能体版本：
1）基于单智能体简化强化学习（Single-Agent Simplified DRL, SASDRL）的VVC方法，适用对象为量测及通信设施相对较完备的输电网。控制架构为集中式控制，该方法继承DRL中经典的“Actor-Critic”架构。其中Actor网络实现系统实时状态与无功设备控制策略的端到端映射，Critic网络用于评判不同控制策略的好坏，但评判指标与传统DRL不同，直接简化为智能体采取当前控制策略后得到的奖励值，Critic网络训练转化为拟合系统实时状态与节点电压之间非线性关系的监督学习训练。同时，设定在Critic网络训练完毕后再进行Actor网络训练，使得Actor网络在训练初始就能够获得Critic网络反馈回的正确训练梯度，从而减少初始阶段大量的计算浪费。
2）基于多智能体简化强化学习（Multi-Agent Simplified DRL, MASDRL）+IL的VVC方法，适用对象为量测及通信设施相对不完备的配电网，控制架构为零通信分布式控制，该方法首先将简化强化学习思想推广形成多智能体版本，提升了多智能体强化学习应用于VVC训练的快速性与稳定性。其次引入IL用于各智能体Actor网络的初始化，IL使用的训练样本来自SASDRL模型生成的控制策略样本，大幅提升了专家样本的生成速度，同时使各智能体Actor网络在训练初始就能够拥有集中控制的全局优化思想，实现无功设备之间更优的就地协同控制。
采用传统数学算法或启发式算法需要建立详细的VVC数学优化模型。多时间尺度VVC中实时控制阶段的控制目标就是在满足系统各类运行约束条件的基础上通过控制各类连续型无功设备来减少系统节点电压偏离，保证系统的平稳运行，因此建立的数学优化模型通常可表示为
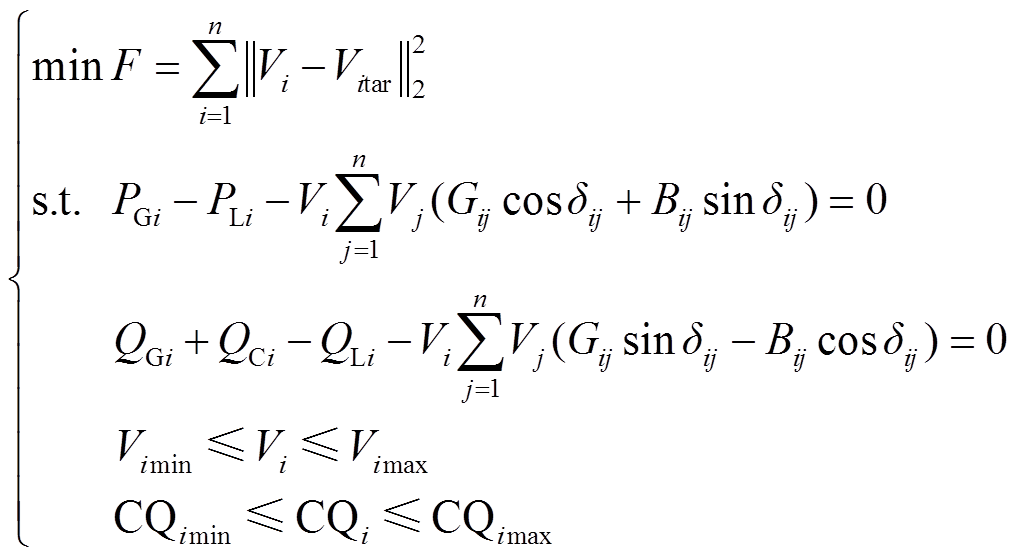（1）
式中，F为目标函数；n为节点数目；i、j为节点；Vi和Vitar分别为节点实际电压与目标电压；PGi和QGi分别为节点连接机组的有功、无功出力；QCi为无功补偿量；PLi和QLi分别为节点有功、无功负荷；Gij和Bij分别为线路电导、电纳；δij为线路首末节点的相位差；CQimax和CQimin分别为无功设备的调节上、下限。
IL首先需要基于传统VVC算法，针对不同的系统运行场景进行无功优化计算生成大量专家样本(S, A)，其中S代表系统状态参数，主要包括节点有功、无功负荷PL、QL及机组有功出力PG，A代表采用传统VVC算法计算得到的无功设备控制策略。然后直接使用深度学习、支持向量机等监督学习方法，将专家样本中的S作为输入，A作为标签进行训练，学习的目标是使模型预测值与标签值的偏差达到最小，具体可表示为
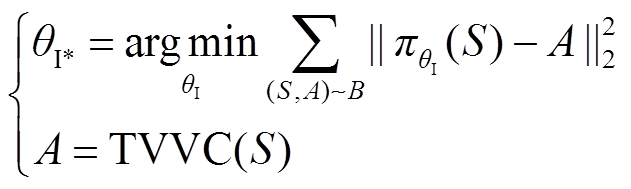（2）
式中，θI和θI*分别为IL训练得到的映射及其最优版本；B为专家样本集；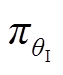
为使用IL映射对应控制策略的前向计算过程；TVVC为传统VVC算法。
由于IL本质是监督学习，训练过程简单，但需要大量不同运行场景下的控制策略专家样本作为基础，当采用传统无功优化算法生成专家样本时往往存在耗时较长的问题。此外，由于模型训练只限定于固定的专家样本集，当实际应用时碰到的运行场景与训练时所用的专家样本相差较大时，可能会导致控制结果不甚理想。
本文以VVC研究中应用最为广泛的“Actor-Critic”类型DRL算法进行说明。“Actor-Critic”类型DRL算法由Actor网络及Critic网络构成，其中Actor网络同样用于建立系统状态参数S与无功设备控制策略A之间的映射，Critic网络用于建立(S, A)与一个标量之间的映射，该标量被称为动作价值Q，用于评判无功设备控制策略的好坏。由于DRL没有标签数据，Actor网络能够生成良好A的前提是Critic网络能够对不同A的好坏做出精准的判断，即Critic网络利用动作价值Q指导Actor网络参数更新。因此“Actor-Critic”类型DRL本质上是基于智能体与环境（电力系统）不断交互生成的数据样本，对Actor网络及Critic网络参数不断进行训练升级，最终达到的目标为Critic网络能够针对不同A生成最为准确的Q值，Actor网络能够针对不同S均生成Q值最大的A。当“Actor-Critic”类型DRL算法应用于VVC时，在单次迭代过程中主要包括三个步骤。
1）训练样本的生成。生成样本如式（3）所示。
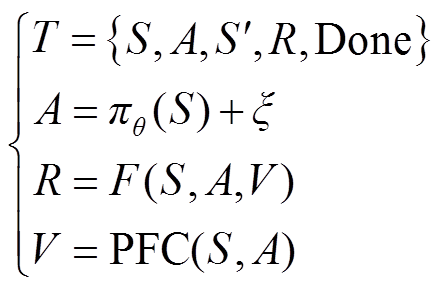（3）
式中，T为智能体与环境交互生成的样本；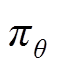
为使用DRL映射对应控制策略的前向计算过程；ξ为附加噪声；F为传统数学优化模型中的目标函数；V为系统节点电压集合；PFC为潮流计算过程。将随机生成的电力系统运行状态S输入Actor网络生成掺杂噪声的A，电力系统在“虚拟”执行A后生成新的运行状态S'并返回给智能体奖励值R和迭代是否终止标志Done，再将以上五者合并生成训练样本存入训练样本集合D。现有研究普遍将R设定为传统数学优化模型中的目标函数，计算R所需的节点电压需通过传统潮流计算方法求解。
2）Critic网络的训练。在DRL中，Critic网络的训练目标是使得任意A的Q值满足如式（4）所示的动作价值贝尔曼方程，即当前A的Q值等于R与新状态S'生成动作A'的Q值之和的期望值。
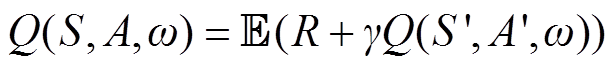（4）
式中，ω为Critic网络参数；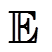
为数学期望；γ为折扣因子。
因此，在训练过程中将二者的差值作为损失函数对Critic网络参数进行训练，具体参数更新梯度公式为
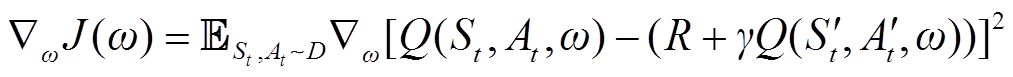（5）
式中，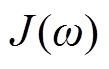
为Critic网络训练损失函数；
代表求导。
3）Actor网络的训练。为使Actor网络生成具有最大Q值的A，Actor网络将Critic生成的Q值作为重要参数指导自身网络参数训练，根据数学推导，其更新梯度公式可表示为
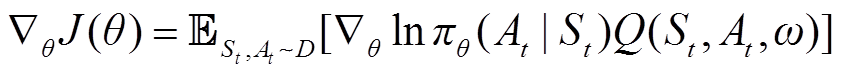（6）
式中，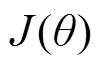
为Actor网络训练损失函数。
DRL无需专家样本进行指导，而是通过智能体不断试错得到的奖励值来指导拟合系统状态参数与无功设备控制策略之间的非线性关系，训练完成的模型对于全新运行场景具有极强的适应性。但是Actor网络能够生成良好控制策略的前提是Critic网络能够对不同控制策略的好坏做出精准的判断，而Actor网络及Critic网络均为随机初始化生成，因此在训练初始阶段，由于Critic网络的不完备、无法精准评判Actor网络生成的控制策略，智能体的随机探索存在大量的计算浪费。此外，现有研究应用DRL时通常将VVC作为序列决策问题，在Critic网络单步更新时，所需计算的参数包括当前控制策略的Q值、R值及下一步控制策略的Q值，且求解R值在现有文献中均需要通过传统潮流计算方法，求解速度缓慢。同时Critic网络训练目标为动作价值贝尔曼方程，与IL只需追求预测值与标签值差距最小的训练方式相比，训练难度也大幅增加。
因此，提高DRL离线训练速度的核心应集中于如何在保证CRITIC网络能够准确评判不同控制策略质量的基础上，采用更为简便的操作提升CRITIC网络的训练速度。
事实上，由于VVC中涉及长时间尺度的问题只有离散型无功设备的动作次数约束问题，而在本文的研究对象——多时间尺度VVC实时控制阶段中，离散型无功设备的状态保持固定不变，控制对象只有连续型无功设备，即使前后控制时间断面产生的控制策略差异很大，也能够通过连续型设备无功调节的平滑性实现对控制指令的快速响应，不同控制时间断面对应的优化问题可以解耦[36-37]。因此，在实时控制阶段VVC的DRL训练过程中，本文将DRL原本设定的序列决策问题解耦为单点决策问题，结合DRL应用于VVC在线计算时的极速性，能够实现实时控制阶段不同时间断面的最优控制，同时大幅降低DRL的训练计算量及计算难度。
综上所述，本文首先提出一种SASDRL方法应用于多时间尺度VVC的实时控制阶段，适用对象为量测及通信设施完备的输电网，控制架构为集中式控制，其核心思想包括：
1）将传统DRL中设定的序列决策问题简化为单点决策问题，即评判当前控制策略好坏的指标由式（4）直接简化为Q(S, A, ω)=R。Critic网络的功能由实现(S, A)至原动作价值Q的映射，转化为以监督学习方式直接拟合(S, A)与节点电压V之间的非线性关系，并结合奖励函数生成当前控制策略对应的奖励值R。此处设定的奖励函数仍采用传统数学优化模型中的目标函数F，但与传统DRL不同之处在于目标函数F的自变量（节点电压V）无需通过复杂的潮流计算过程得到，而是转化为直接由极为简单的Critic网络前向计算过程映射得到。
2）由于Actor网络能否生成良好控制策略取决于Critic网络能否精准评判不同控制策略的价值，再加上Critic网络训练方式的大大简化，本文将DRL中Actor、Critic网络并行更新方式转变为顺序更新方式，即在完成Critic网络训练的基础上再开展Actor网络的训练，使得Actor网络在训练初始就能获得完备Critic网络的良好指导（即通过完备Critic网络能立即获取能够正确评判当前控制策略的奖励值R），获得正确的更新梯度，与原始DRL相比能大幅减少训练初始阶段的无效探索及计算浪费。
基于SASDRL核心思想的训练过程如下。
1）Critic网络的训练。在PL、QL处于[0, 1.2]倍正常水平区间、PG处于[0, 1]倍机组额定功率区间、CQ处于无功设备出力上下限区间内随机取值，形成(S, A)作为监督训练的输入，并作潮流计算得到节点电压V作为标签数据，生成Critic网络训练所需的数据样本。本文采用深度学习作为监督训练方法，为使训练出的模型与系统实际物理信息相符，具有更强的普适性，本文采用文献[38]中提出的方案，在损失函数中加入基于预测电压值与线路电阻、电抗等系统物理信息计算得到的节点有功、无功偏差损失函数。
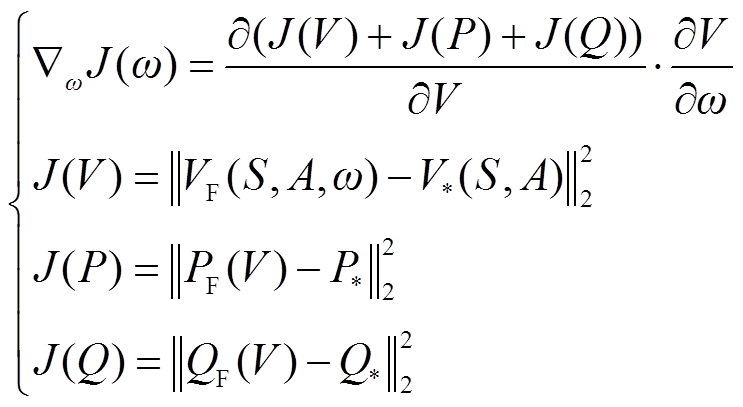（7）
式中，J(V)、J(P)、J(Q)分别为节点电压偏差、有功功率偏差、无功功率偏差损失函数；VF、PF、QF分别为节点电压、有功功率、无功功率的预测值；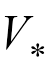
、
、
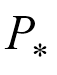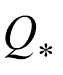分别为相应标签值。
2）Actor网络的训练。当Critic网络训练完成后，由于Critic网络可以准确预测各运行场景下的节点电压值，便可结合奖励函数生成评价指标奖励值R，用于精准判断当前控制策略的好坏。在Actor网络训练过程中，Critic网络参数保持不变，只需通过简单的链式求导法便可求得Actor网络参数的最优更新梯度，同时结合adam算法[39]加快参数的寻优速度。此外，为了保证Actor网络模型的普适性，在Actor网络单次迭代中采用的所有运行场景均为重新随机生成。
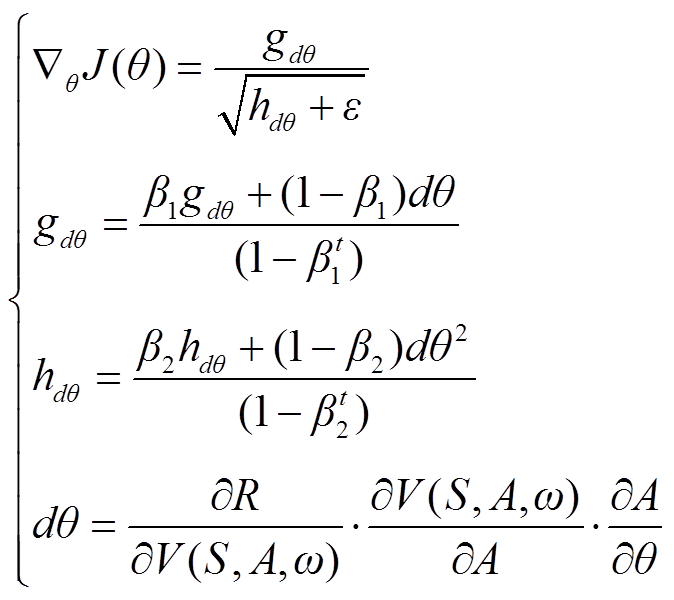（8）
式中，dθ为Actor网络参数梯度动量；gdθ、hdθ分别为利用加权平均法累积的梯度动量及梯度二次方动量；β1、β2为梯度动量超参数；t为参数更新次数；ε为防止分母为零而设置的极小参数。
综上所述，基于SASDRL的VVC训练流程如图1所示。
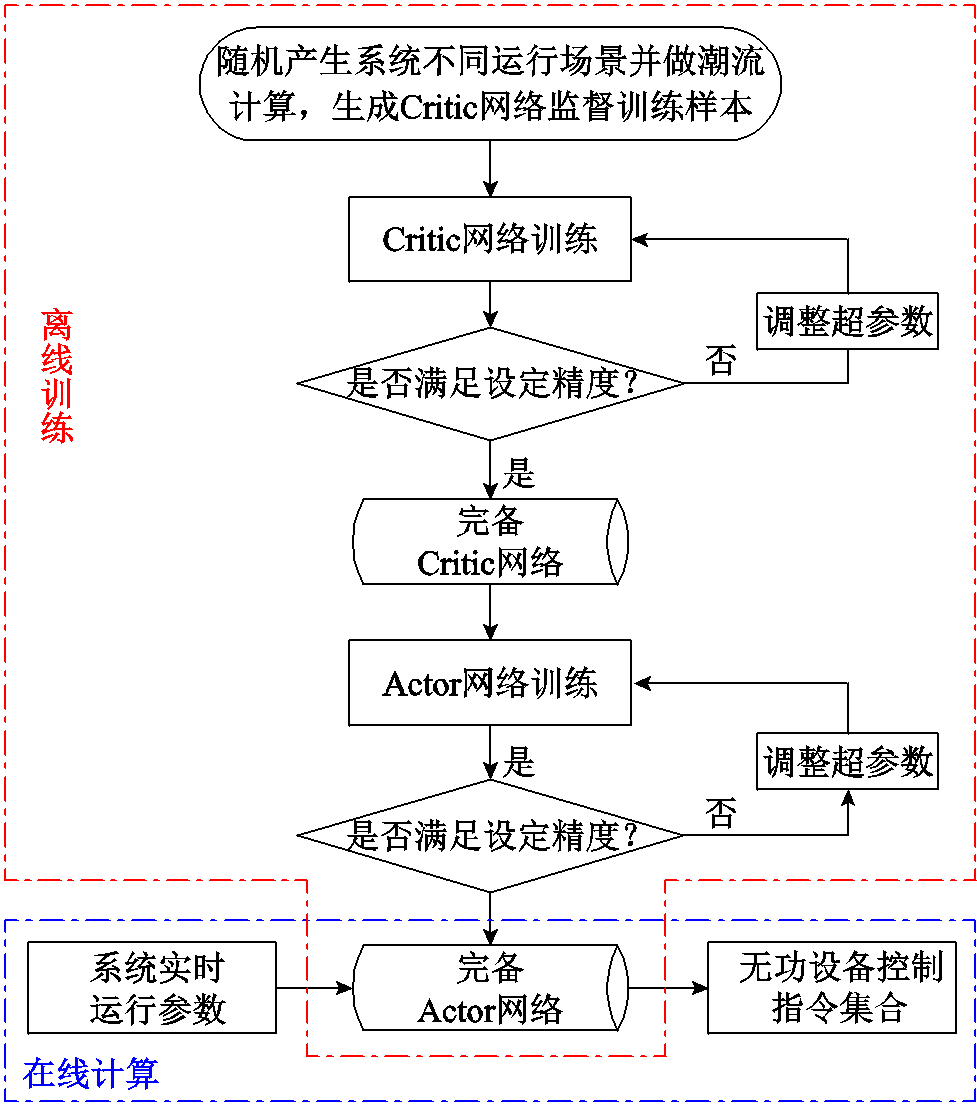
图1 基于SASDRL的VVC训练流程
Fig.1 Training diagram of SASDRL based VVC
理论上集中式VVC能够获得最优的电压控制效果，但其需要以完备的实时通信设施及强大的集中计算中心为基础，这在配备有完备量测设备、节点数目相对较少的输电网是可行的，但在有大量分布式能源接入的配电网却是难以实现的。因为配电网结构复杂，线路、节点数目繁多，基于电网建设的经济性无法做到像输电网一样为配电网内每条线路、每个节点都配备实时量测装置。同时随着配电网中新能源发电渗透率的逐步提高，集中式控制需要采集的数据量及优化变量个数逐渐增多，问题复杂度逐渐增大，使得集中式控制应用于配电网时难以实现实时的优化。因此为了快速平抑新能源出力快速变化造成的配电网无功功率和电压波动，同时完全消除节点-主站实时交互通信的沉重负担，众多学者将多智能体强化学习（Multi-Agent Deep Reinforcement Learning, MADRL）应用于配电网多时间尺度VVC的实时控制阶段。核心思想是将每个连续型无功设备均设为独立的智能体，采用“集中式训练-分布式控制”的模式为每个智能体离线训练一个动作策略网络，在线应用时仅利用无功设备所连接节点的局部信息进行决策，达到所有无功设备的就地协同控制。
在现有将MADRL应用于VVC的研究中，采用的算法如MADDPG(multi-agent deep determine-stic policy gradient)、MASAC(multi-agent soft actor-critic)等继续沿用DRL中的“Actor-Critic”经典架构，即利用Actor网络生成无功设备控制策略，Critic网络用于评价控制策略的好坏。不同的是，需要为每个智能体单独训练一个Actor网络，每个Actor网络的输入仅为该无功设备所连接节点的局部信息，包括节点有功功率Pi=PLi-PGi、节点无功功率Qi=QLi-QGi、节点电压Vi（在线应用时，节点有功功率、无功功率及电压局部信息由实时监测获得），输出仅为该无功设备的控制指令QGi。由于VVC是所有无功设备共同合作型任务，因此Critic网络仅有一个，输入、输出数据与单智能体Critic网络相同。由于Critic网络输入数据中包含了每个智能体的决策信息，即每个无功设备的控制指令，所以Critic网络还起到辅助Actor网络建模其他智能体行为的作用，部分弥补了单个Actor网络只能观测到局部信息的缺陷，构建智能体之间的协同性。在单次迭代过程中Actor与Critic网络的更新公式分别为
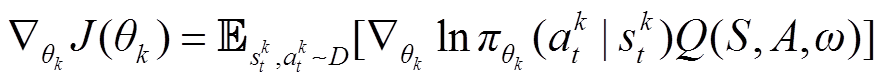（9）
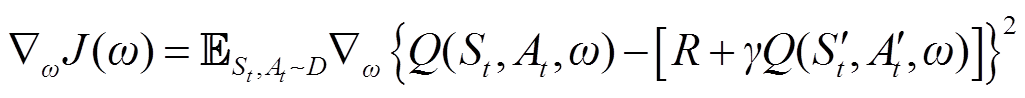（10）
式中，θk为第k个Actor网络的参数；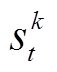
、
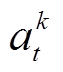分别为第k个Actor网络的输入状态参数及输出动作参数；S为系统状态参数集合，
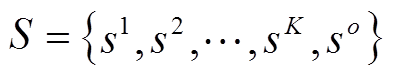，so代表除所有Actor网络输入状态参数之外的系统状态参数，如无配备连续型无功设备节点的状态参数等；A为无功设备控制指令集合，
。
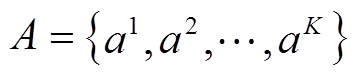与传统单智能体DRL一样，由于MADRL各Actor网络与Critic网络仍为随机初始化生成，Critic网络在训练初期无法给予各Actor网络良好的指导，因此MADRL仍然存在因训练初期大量无效随机探索而导致的训练速度慢且训练效果极不稳定的缺点。此外，虽然Critic网络完成了对所有智能体控制指令的建模、实现智能体之间的协同控制，但由于每个智能体的观测只有连接节点的少量局部信息，因此MADRL应用于VVC时无法完全等效于集中控制时的全局优化效果。
本文提出一种基于MASDRL+IL的分布式方法应用于配电网多时间尺度VVC的实时控制阶段。首先将3.1节提出的简化强化学习思想引入多智能体强化学习，即将Critic网络的功能简化为以监督学习方式拟合系统状态与节点电压的非线性关系，使得各Actor网络在训练初期就能获得Critic网络对其动作指令的精准评价；其次引入IL用于各Actor网络的初始化，IL的样本来自SASDRL生成的不同场景下的训练样本，使得各Actor网络在训练初始就能拥有集中控制的全局优化思想，获得生成良好无功设备指令的能力。设定基于集中式方法SASDRL训练得到的Critic、Actor网络分别为Critic-C、Actor-C, 基于分布式方法MASDRL+IL训练得到的Critic、Actor网络分别为Critic-D、Actor-D。具体的训练过程如下。
1）Actor-D网络初始化。首先完成适用于当前系统的SASDRL训练，得到Actor-C网络；其次随机生成大量不同的系统运行场景S输入Actor-C网络后，得到对应的控制策略A，生成Actor-D网络初始化的训练样本集合X；最后针对不同的Actor-D网络，从X中抽取各Actor-D网络训练需要的si与ai数据进行监督学习训练。
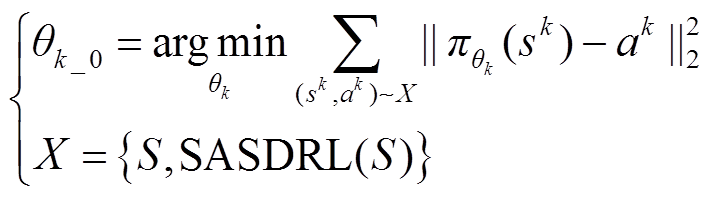（11）
式中，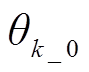
为第k个Actor网络的初始化参数；X为IL的专家样本集合；SASDRL代表单智能体简化强化学习。
2）Critic-D网络与Critic-C网络完全一致，无需再另外进行训练。
3）Actor-D网络训练。与SASDRL类似，在各Actor-D网络训练过程中，Critic-D网络参数保持不变，各Actor-D网络参数的更新梯度在∂R/∂A中对应提取得到，具体表示为
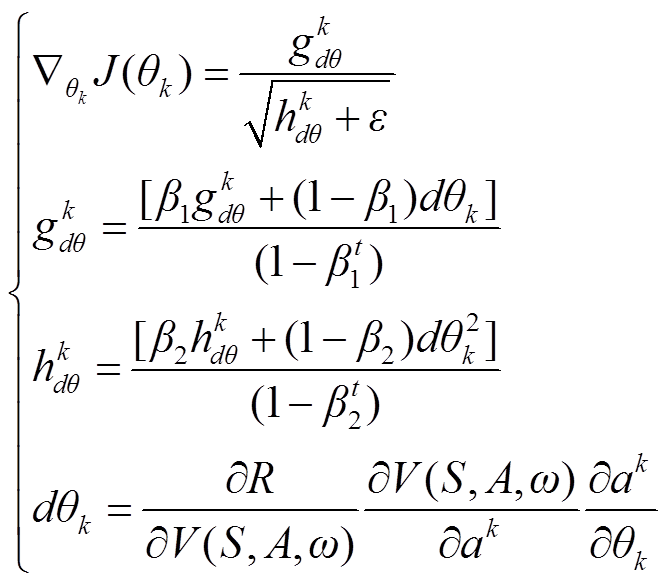（12）
综上所述，基于MASDRL+IL的分布式VVC训练流程如图2所示。
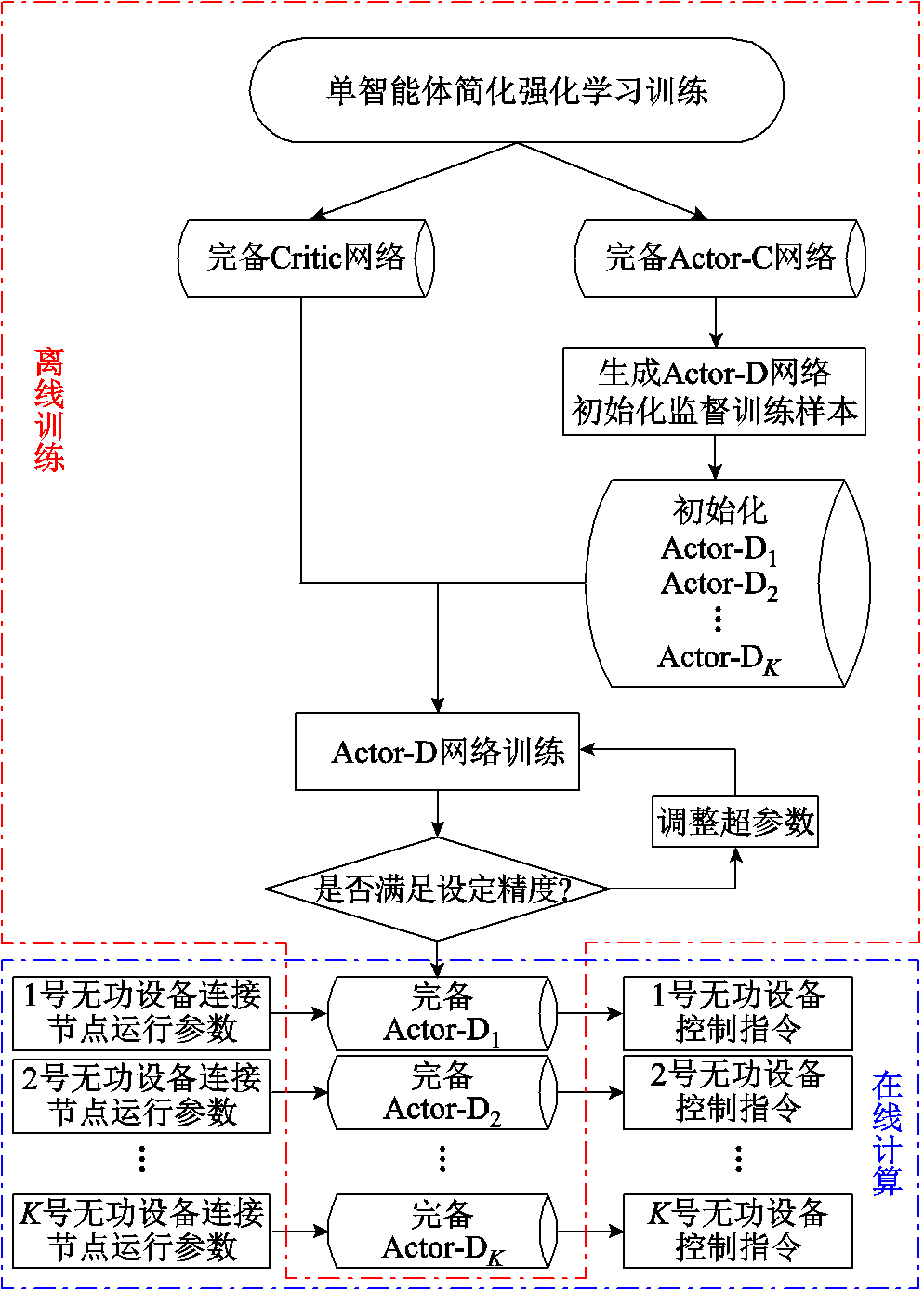
图2 基于MASDRL+IL的VVC训练流程
Fig.2 Training diagram of MASDRL +IL based VVC
本文基于改进的IEEE 118节点系统对所提出方法的正确性与快速性进行验证。为模拟分布式能源对系统造成的电压波动，本文设定在网架末端109、114、115、117、118节点分别配置额定容量为5 MV·A的光伏，控制的无功设备包括系统内所有发电机组及光伏的无功出力，共计58个控制变量（实际应用时，当实时控制频次设定为s级或min级时，控制设备可以是电网内配置的所有连续型无功设备）。控制目标是系统内所有节点的电压都趋近于1(pu)。所有仿真验证均在配备Intel Core i5-12500H CPU @ 2.5 GHz和16 GB 内存的计算机上完成，所有的控制程序均由Python 3.7.5版本进行编写。
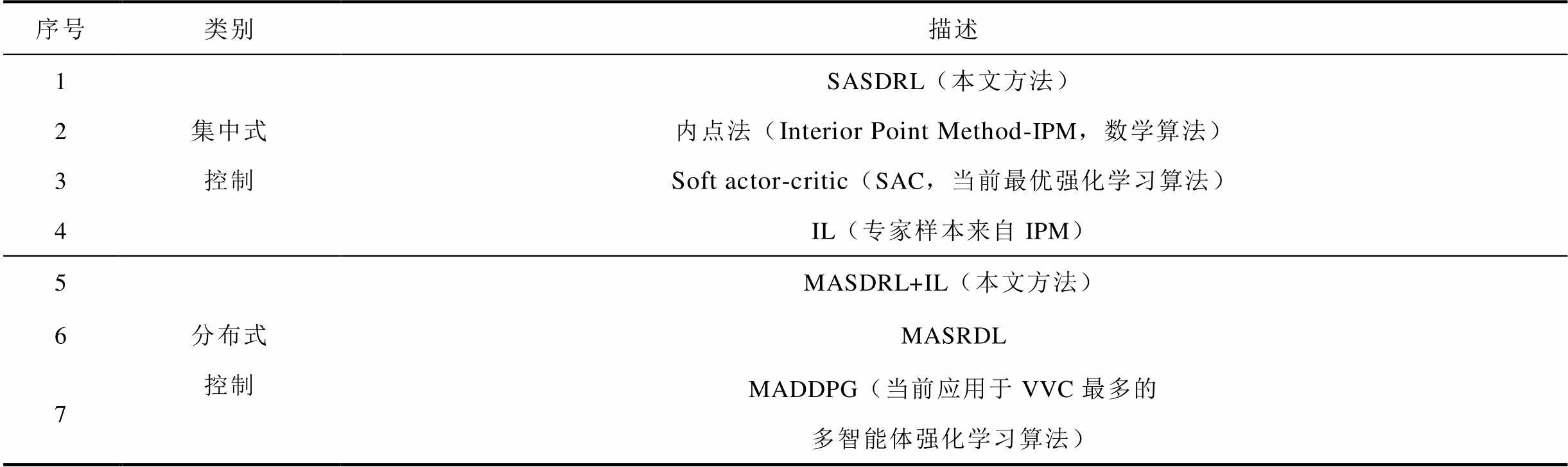
为了评估所提方法所能达到的控制效果，本文开展了与不同类型控制方法的对比实验。对比方法描述见表1，算法参数设置见表2。为保证公平比较不同方法之间的优劣，集中式控制不同方法、分布式控制不同方法的Critic网络、Actor网络架构设置及学习率均完全相同，内点法参数参照文献[40]进行设置。本文利用随机生成的500个不同的控制场景对各方法的控制效果进行比较，对比指标包括系统节点平均电压偏差（计算该指标所需的各节点电压值来源为利用不同方法完成不同测试场景下的VVC决策，并“虚拟执行”无功设备控制策略后，经潮流计算获得的节点电压值）、训练寻优性能、离线训练时间及在线计算时间。
表1 对比方法描述
Tab.1 Description of different methods
序号类别描述 1集中式控制SASDRL（本文方法） 2内点法（Interior Point Method-IPM，数学算法） 3Soft actor-critic（SAC，当前最优强化学习算法） 4IL（专家样本来自IPM） 5分布式控制MASDRL+IL（本文方法） 6MASRDL 7MADDPG（当前应用于VVC最多的多智能体强化学习算法）
表2 算法参数设置
Tab.2 Parameters setting of different methods
控制方法参数数值 集中式SASDRLCritic网络架构[219, 512, 512, 118] Actor网络架构[219, 256, 256, 58] Critic/Actor网络学习率0.004 IPM中心系数0.1 收敛精度10-6 SACCritic网络架构[219, 512, 512, 118] Actor网络架构[219, 256, 256, 58] Critic/Actor网络学习率0.004 温度系数学习率0.001 奖励折扣率0.99 IL拟合网络架构[219, 256, 256, 58] 专家样本数量5000
（续）
控制方法参数数值 分布式MASDRL+ILCritic网络架构[219, 512, 512, 118] Actor网络架构[3, 20, 20, 1] Critic/Actor网络学习率0.004 IL专家样本数量500 MADDPGCritic网络架构[219, 512, 512, 118] Actor网络架构[3, 20, 20, 1] Critic/Actor网络学习率0.004 奖励折扣率0.99
首先对四种集中式控制方法在500个不同测试场景下的控制结果（系统平均电压偏差∆Vav）进行了统计，结果见表3；其次对四种方法所需的离线训练时间及在线计算时间进行了统计。为了更清晰地对比四种方法的控制效果，图3将500个不同场景经四种方法控制后的系统平均电压偏差以绘线方式展示。500个场景被均分为五等份，分别位于图3a～图3e中。
表3 集中式控制方法的∆Vav及耗用时间统计
Tab.3 ∆Vav and consumed time of centralized methods
方法∆Vav(10-3 pu)离线训练时间/s在线计算时间/ms 平均最大最小 SASDRL2.223.091.50362+44.1+9.5=415.66.40 IPM2.273.281.56—4 210 SAC3.555.032.351 857.26.40 IL2.405.691.5821 048.2+46.3=21 094.56.40
从表3中针对∆Vav的统计数据可以看出，采用本文提出的SASDRL与IPM的控制效果极其相近，针对500个测试样本的平均、最大、最小∆Vav均基本一致，证明SASDRL能够达到与具有严格理论基础的传统数学方法一样的寻优精度（SASDRL在平均、最大、最小∆Vav三项指标均稍优于IPM 的原因是无功优化问题实质是非凸优化问题，尤其当控制变量维数过高时，即使采用传统数学算法也无法保证能够收敛至全局最优，进一步证明了SASDRL在高维控制寻优的优越性）。采用IL能够获得稍差于SASDRL与IPM的整体控制效果，平均∆Vav略小于以上两种方法，但由于专家样本集有限，无法做到涵盖所有的控制变量可行域空间，导致IL得到的最大∆Vav高于其他三种方法。采用SAC获得了最差的控制效果，表明传统DRL方法因算法设定的复杂性，应用于高维控制问题时难以收敛至全局最优。以上结论在图3中均可得到进一步的展现，SASDRL与IPM形成的曲线针对500个测试场景均粘合在一起。IL形成的曲线大部分与前两种方法相近，但在某些测试场景，如81号、470号、497号测试样本出现尖刺状凸起。SAC形成的曲线基本脱离以上三种方法而存在于上方电压偏差较大的空间。
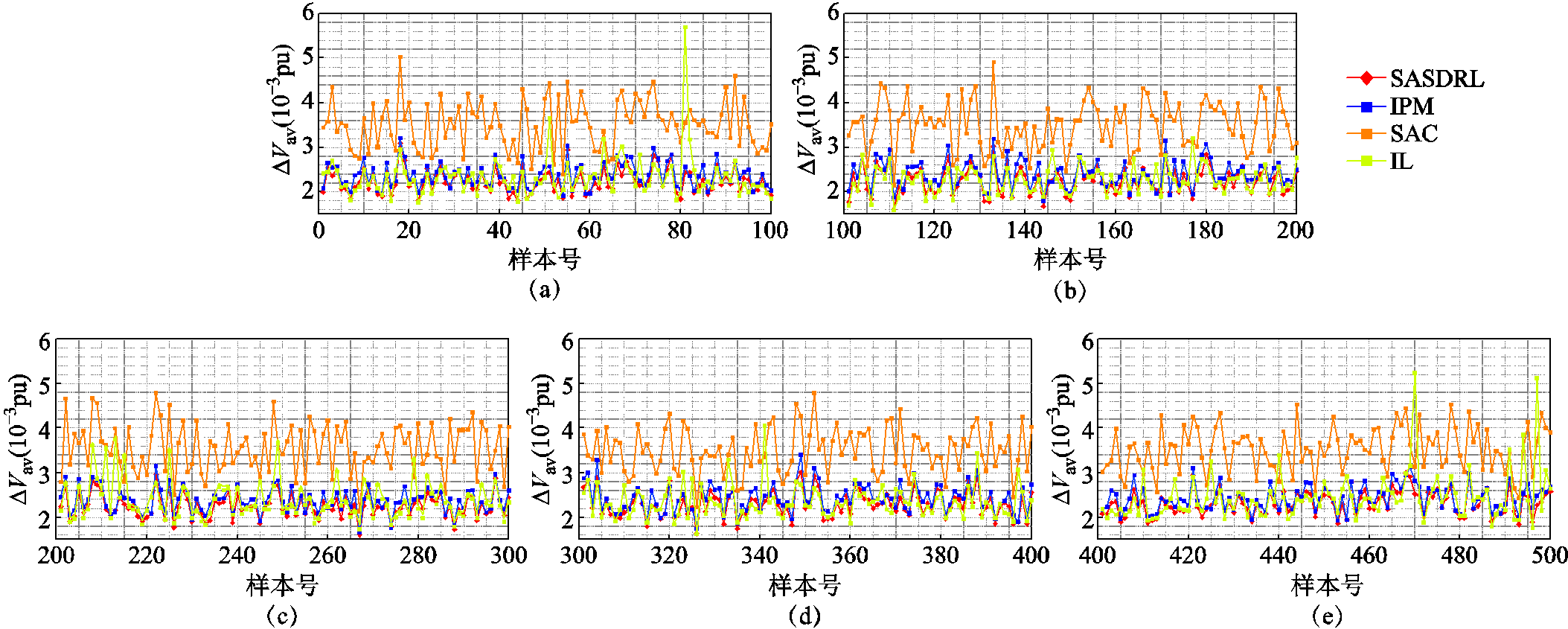
图3 采用不同集中式控制方法在500个测试场景下的∆Vav对比
Fig.3 Comparison of ∆Vav in 500 test scenarios using different centralized control methods
从表3中针对离线训练时间及在线计算时间的统计数据中可以看出，采用机器学习类方法的在线运算速度远超以IPM为代表的传统方法，计算速度加速至ms级，针对分布式能源接入电力系统带来的无功电压快速波动完全能够做到实时响应控制。在离线训练时间方面，采用SASDRL所消耗的训练时间最少，是SAC 方法训练速度的4.47倍，是IL训练速度的50.76倍，且SASDRL的绝大部分训练时间是用于Critic网络监督训练所需专家样本的生成过程，占比达到362/415.6×100%=87.1%。而用于训练Critic网络的时间占比仅为44.1/415.6× 100%=10.6%，用于训练Actor网络的时间占比仅为9.5/415.6×100%=2.3%。真正用于训练两个网络的时间仅用53.6 s就能够完成，证明采用本文方法的各项简化操作后，在保证寻优精度的基础上，Critic网络与Actor网络的训练速度能够得到极大提升。
图4为不同分布式控制方法在训练过程中的寻优性能对比。以基于SASDRL的集中式控制效果作为参照标准，表4首先对各方法在500个测试场景下的∆Vav进行了统计，其次对各方法所需的离线训练时间进行了统计。
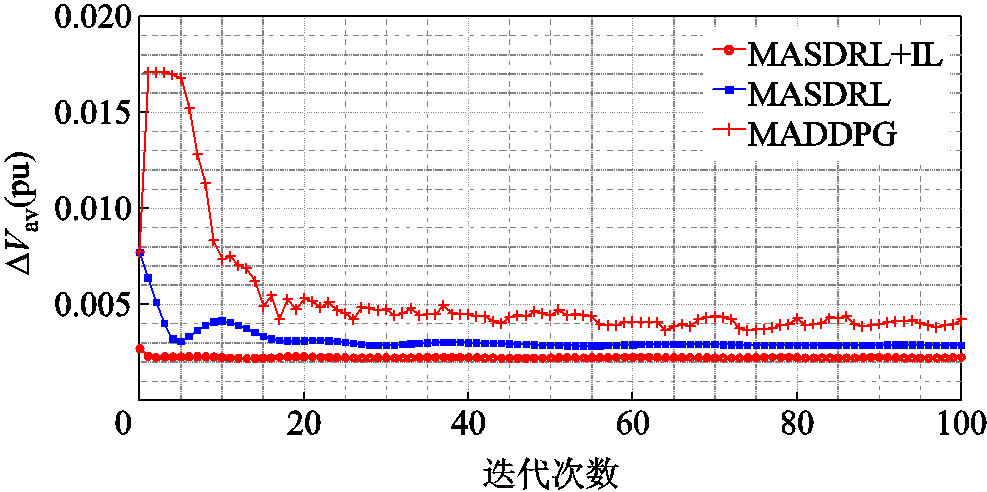
图4 采用不同分布式控制方法的训练寻优性能对比
Fig.4 Comparison of training performance with different decentralized control methods
表4 分布式控制方法的∆Vav及耗用时间统计
Tab.4 ∆Vav and consumed time of decentralized methods
方法∆Vav(10-3 pu)离线训练时间/s 平均最大最小 SASDRL2.223.091.50362+44.1+9.5=415.6 MASDRL+IL2.313.281.81362+44.1+9.5+8.7+21.7=436.5 MASDRL2.873.762.28362+44.1+22.0=428.1 MADDPG4.126.552.542 533.7
从表4中针对∆Vav的统计数据容易看出，采用本文方法，即基于MASDRL+IL的VVC方法，能够获得最优的分布式控制效果，最接近于集中式控制获得的各项∆Vav数据。从图4中的训练曲线可以看出，采用MASDRL+IL获得的寻优性能最优且最为稳定，由于IL提前将集中式控制思想注入各智能体，因此在训练初始智能体群就已经获得较好的协同控制效果。MASDRL虽然基于简化强化学习思想同样能够快速收敛，但由于各智能体之间缺乏全局优化思想的指引，最终获得的控制效果要比MASDRL+IL差。MADDPG与传统SASDRL方法类似，由于各智能体Actor网络与Critic网络为随机初始化，Critic网络在训练初期无法对各Actor网络的集合控制策略进行精准的评价，导致训练指标在初期一直保持较高的数值，同时由于传统MADRL训练的复杂性，最终获得了三种分布式控制方法中最差的控制效果。
在训练时间方面，首先对SASDRL与MASDRL进行对比，由于二者的Critic网络的训练过程完全一致（表4中所示的362+44.1部分），因此二者训练时间的不同主要体现在Actor网络的训练上，虽然MASDRL需要针对每个无功设备训练一个Actor网络，但每个无功设备所对应的Actor网络参数规模远小于SASDRL的Actor网络参数规模，因此MASDRL的训练时间仅比SASDRL增加了3.01%。其次，本文在MASDRL的基础上引入IL提升了分布式控制效果，虽然相较于纯粹的MASDRL，增加了SASDRL的Actor网络训练操作、基于SASDRL的训练样本生成操作及MASDRL各智能体Actor网络初始化训练操作，但以上三项操作消耗的时间均非常少，其中第一项操作仅增加9.5 s，第二项是深度学习的前向计算过程，第三项是训练样本、训练次数均设定较少的监督学习过程，二者合计只增加8.7 s，因此相较于纯粹的MASDRL，基于MASDRL+IL的VVC方法训练时间仅增加了1.96%，而相较于MADDPG却减少了82.77%。
1）本文提出了一种基于单智能体简化强化学习的集中式VVC方法，通过对Critic网络训练目标的简化，在保证精准评判无功设备动作策略的基础上，将Critic网络训练方式转化为操作简单的监督学习方式。同时通过设定在Critic网络训练完毕的基础上再进行Actor网络训练，避免了传统强化学习在训练初始阶段的无效探索与计算浪费。基于改进IEEE 118节点系统的仿真计算结果证明，相较于传统数学方法和传统强化学习、模仿学习等机器学习方法，本文方法能够在大幅加速强化学习离线训练速度并保证算法普适性的基础上，获得与传统数学方法极为相近的优异控制效果。
2）本文提出了一种基于多智能体简化强化学习+模仿学习的分布式VVC方法。将各无功设备都视为无需与外界进行实时通信的智能体，在继承简化强化学习思想的基础上引入模仿学习用于Actor网络参数的初始化，使得各智能体的Actor网络在训练开始之前就拥有集中式控制全局优化的思想。基于改进IEEE 118节点系统的仿真计算结果证明，相较于传统多智能体强化学习与纯粹多智能体简化强化学习，本文方法能够在极少增加离线训练时间的基础上提升各无功设备的就地协同控制效果。
参考文献
[1] Mahmud N, Zahedi A. Review of control strategies for voltage regulation of the smart distribution network with high penetration of renewable distributed generation[J]. Renewable and Sustainable Energy Reviews, 2016, 64: 582-595.
[2] 高聪哲, 黄文焘, 余墨多, 等. 基于智能软开关的主动配电网电压模型预测控制优化方法[J]. 电工技术学报, 2022, 37(13): 3263-3274. Gao Congzhe, Huang Wentao, Yu Moduo, et al. A model predictive control method to optimize voltages for active distribution networks with soft open point[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3263-3274.
[3] 康重庆, 姚良忠. 高比例可再生能源电力系统的关键科学问题与理论研究框架[J]. 电力系统自动化, 2017, 41(9): 2-11. Kang Chongqing, Yao Liangzhong. Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2017, 41(9): 2-11.
[4] 姚良忠, 朱凌志, 周明, 等. 高比例可再生能源电力系统的协同优化运行技术展望[J]. 电力系统自动化, 2017, 41(9): 36-43. Yao Liangzhong, Zhu Lingzhi, Zhou Ming, et al. Prospects of coordination and optimization for power systems with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2017, 41(9): 36-43.
[5] 郭庆来, 王彬, 孙宏斌, 等. 支撑大规模风电集中接入的自律协同电压控制技术[J]. 电力系统自动化, 2015, 39(1): 88-93, 130. Guo Qinglai, Wang Bin, Sun Hongbin, et al. Autonomous-synergic voltage control technology supporting large-scale wind power integration[J]. Automation of Electric Power Systems, 2015, 39(1): 88-93, 130.
[6] Wang Gang, Kekatos V, Conejo A J, et al. Ergodic energy management leveraging resource variability in distribution grids[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4765-4775.
[7] 陈江澜, 汤卫东, 肖小刚, 等. 华中电网协调电压控制模式研究[J]. 电力自动化设备, 2011, 31(8): 47-51. Chen Jianglan, Tang Weidong, Xiao Xiaogang, et al. Coordinated voltage control for Central China Power Grid[J]. Electric Power Automation Equipment, 2011, 31(8): 47-51.
[8] 徐峰达, 郭庆来, 孙宏斌, 等. 基于模型预测控制理论的风电场自动电压控制[J]. 电力系统自动化, 2015, 39(7): 59-67. Xu Fengda, Guo Qinglai, Sun Hongbin, et al. Automatic voltage control of wind farms based on model predictive control theory[J]. Automation of Electric Power Systems, 2015, 39(7): 59-67.
[9] 国家市场监督管理总局, 国家标准化管理委员会. GB/T 37408—2019 光伏发电并网逆变器技术要求[S]. 北京: 中国标准出版社, 2019.
[10] Liu Haotian, Wu Wenchuan. Two-stage deep reinforcement learning for inverter-based volt-VAR control in active distribution networks[J]. IEEE Transactions on Smart Grid, 2021, 12(3): 2037-2047.
[11] 颜湘武, 徐韵, 李若瑾, 等. 基于模型预测控制含可再生分布式电源参与调控的配电网多时间尺度无功动态优化[J]. 电工技术学报, 2019, 34(10): 2022-2037. Yan Xiangwu, Xu Yun, Li Ruojin, et al. Multi-time scale reactive power optimization of distribution grid based on model predictive control and including RDG regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2022-2037.
[12] 黄大为, 王孝泉, 于娜, 等. 计及光伏出力不确定性的配电网混合时间尺度无功/电压控制策略[J]. 电工技术学报, 2022, 37(17): 4377-4389. Huang Dawei, Wang Xiaoquan, Yu Na, et al. Hybrid time-scale reactive power/voltage control strategy for distribution network considering photovoltaic output uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4377-4389.
[13] Cao Di, Zhao Junbo, Hu Weihao, et al. Deep reinforcement learning enabled physical-model-free two-timescale voltage control method for active distribution systems[J]. IEEE Transactions on Smart Grid, 2022, 13(1): 149-165.
[14] Wang Licheng, Bai Feifei, Yan Ruifeng, et al. Real-time coordinated voltage control of PV inverters and energy storage for weak networks with high PV penetration[J]. IEEE Transactions on Power Systems, 2018, 33(3): 3383-3395.
[15] 胡丹尔, 彭勇刚, 韦巍, 等. 多时间尺度的配电网深度强化学习无功优化策略[J]. 中国电机工程学报, 2022, 42(14): 5034-5045. Hu Daner, Peng Yonggang, Wei Wei, et al. Multi-timescale deep reinforcement learning for reactive power optimization of distribution network[J]. Proceedings of the CSEE, 2022, 42(14): 5034-5045.
[16] 李静, 戴文战, 韦巍. 基于混合整数凸规划的含风力发电机组配电网无功补偿优化配置[J]. 电工技术学报, 2016, 31(3): 121-129. Li Jing, Dai Wenzhan, Wei Wei. A mixed integer convex programming for optimal reactive power compensation in distribution system with wind turbines[J]. Transactions of China Electrotechnical Society, 2016, 31(3): 121-129.
[17] 赵晋泉, 居俐洁, 戴则梅, 等. 基于分支定界—原对偶内点法的日前无功优化[J]. 电力系统自动化, 2015, 39(15): 55-60. Zhao Jinquan, Ju Lijie, Dai Zemei, et al. Day-ahead reactive power optimization based on branch and bound-interior point method[J]. Automation of Electric Power Systems, 2015, 39(15): 55-60.
[18] 崔挺, 孙元章, 徐箭, 等. 基于改进小生境遗传算法的电力系统无功优化[J]. 中国电机工程学报, 2011, 31(19): 43-50. Cui Ting, Sun Yuanzhang, Xu Jian, et al. Reactive power optimization of power system based on improved niche genetic algorithm[J]. Proceedings of the CSEE, 2011, 31(19): 43-50.
[19] Malachi Y, Singer S. A genetic algorithm for the corrective control of voltage and reactive power[J]. IEEE Transactions on Power Systems, 2006, 21(1): 295-300.
[20] Jalali M, Kekatos V, Gatsis N, et al. Designing reactive power control rules for smart inverters using support vector machines[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 1759-1770.
[21] 邵美阳, 吴俊勇, 石琛, 等. 基于数据驱动和深度置信网络的配电网无功优化[J]. 电网技术, 2019, 43(6): 1874-1883. Shao Meiyang, Wu Junyong, Shi Chen, et al. Reactive power optimization of distribution network based on data driven and deep belief network[J]. Power System Technology, 2019, 43(6): 1874-1883.
[22] 李鹏, 姜磊, 王加浩, 等. 基于深度强化学习的新能源配电网双时间尺度无功电压优化[J]. 中国电机工程学报, 2023, 43(16): 6255-6266. Li Peng, Jiang Lei, Wang Jiahao, et al. Optimization of dual-time scale reactive voltage for distribution network with renewable energy based on deep reinforcement learning[J]. Proceedings of the CSEE, 2023, 43(16): 6255-6266.
[23] 倪爽, 崔承刚, 杨宁, 等. 基于深度强化学习的配电网多时间尺度在线无功优化[J]. 电力系统自动化, 2021, 45(10): 77-85. Ni Shuang, Cui Chenggang, Yang Ning, et al. Multi-time-scale online optimization for reactive power of distribution network based on deep reinforcement learning[J]. Automation of Electric Power Systems, 2021, 45(10): 77-85.
[24] Duan Jiajun, Shi Di, Diao Ruisheng, et al. Deep-reinforcement-learning-based autonomous voltage control for power grid operations[J]. IEEE Transactions on Power Systems, 2020, 35(1): 814-817.
[25] Wang Wei, Yu Nanpeng, Gao Yuanqi, et al. Safe off-policy deep reinforcement learning algorithm for volt-VAR control in power distribution systems[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 3008-3018.
[26] Yang Qiuling, Wang Gang, Sadeghi A, et al. Two-timescale voltage control in distribution grids using deep reinforcement learning[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2313-2323.
[27] Kulmala A, Repo Sami, Järventausta P. Coordinated voltage control in distribution networks including several distributed energy resources[J]. IEEE Transactions on Smart Grid, 2014, 5(4): 2010-2020.
[28] Cavraro G, Carli R. Local and distributed voltage control algorithms in distribution networks[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1420-1430.
[29] Karagiannopoulos S, Aristidou P, Hug G. Data-driven local control design for active distribution grids using off-line optimal power flow and machine learning techniques[J]. IEEE Transactions on Smart Grid, 2019, 10(6): 6461-6471.
[30] 乐健, 王曹, 李星锐, 等. 中压配电网多目标分布式优化控制策略[J]. 电工技术学报, 2019, 34(23): 4972-4981. Le Jian, Wang Cao, Li Xingrui, et al. The multi-object distributed optimization control strategy of medium voltage distribution networks[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4972-4981.
[31] 赵晋泉, 张振伟, 姚建国, 等. 基于广义主从分裂的输配电网一体化分布式无功优化方法[J]. 电力系统自动化, 2019, 43(3): 108-115. Zhao Jinquan, Zhang Zhenwei, Yao Jianguo, et al. Heterogeneous decomposition based distributed reactive power optimization method for global transmission and distribution network[J]. Automation of Electric Power Systems, 2019, 43(3): 108-115.
[32] Zeraati M, Hamedani Golshan M E, Guerrero J M. Distributed control of battery energy storage systems for voltage regulation in distribution networks with high PV penetration[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 3582-3593.
[33] Sun Xianzhuo, Qiu Jing. Two-stage volt/var control in active distribution networks with multi-agent deep reinforcement learning method[J]. IEEE Transactions on Smart Grid, 2021, 12(4): 2903-2912.
[34] 赵冬梅, 陶然, 马泰屹, 等. 基于多智能体深度确定策略梯度算法的有功-无功协调调度模型[J]. 电工技术学报, 2021, 36(9): 1914-1925. Zhao Dongmei, Tao Ran, Ma Taiyi, et al. Active and reactive power coordinated dispatching based on multi-agent deep deterministic policy gradient algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1914-1925.
[35] Liu Haotian, Wu Wenchuan. Online multi-agent reinforcement learning for decentralized inverter-based volt-VAR control[J]. IEEE Transactions on Smart Grid, 2021, 12(4): 2980-2990.
[36] Cao Di, Hu Weihao, Zhao Junbo, et al. Reinforcement learning and its applications in modern power and energy systems: a review[J]. Journal of Modern Power Systems and Clean Energy, 2020, 8(6): 1029-1042.
[37] Xu Yan, Dong Zhaoyang, Zhang Rui, et al. Multi-timescale coordinated voltage/var control of high renewable-penetrated distribution systems[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4398-4408.
[38] Yang Yan, Yang Zhifang, Yu Juan, et al. Fast calculation of probabilistic power flow: a model-based deep learning approach[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2235-2244.
[39] Diederik P Ki, Jimmy L B. Adam: a method for stochastic optimization[C]//Proceedings of the 3rd International Conference on Learning Representations (ICLR), San Diego, USA, 2015: 1-13.
[40] Zhang Cong, Chen Haoyong, Shi Ke, et al. An interval power flow analysis through optimizing-scenarios method[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5217-5226.
Abstract In order to quickly suppress the rapid fluctuations of reactive power and voltage caused by the random output change of distributed energies, machine learning (ML) methods represented by deep reinforcement learning (DRL) and imitation learning (IL) have been applied to volt-var control (VVC) research recently, to replace the traditional methods which require a large number of iterations. Although the ML methods in the existing literature can realize the online rapid VVC optimization, there are still some shortcomings such as slow offline training speed and insufficient universality that hinder their applications in practice.
Firstly, this paper proposes a single-agent simplified DRL (SASDRL) method suitable for the centralized control of transmission networks. Based on the classic "Actor-Critic" architecture and the fact that the Actor network can generate wonderful control strategies heavily depends on whether the Critic network can make accurate evaluation, this method simplifies and improves the offline training process of DRL based VVC, whose core ideas are the simplification of Critic network training and the change in the update mode of Actor and Critic network. It simplifies the sequential decision problem set in the traditional DRL based VVC to a single point decision problem and the output of Critic network is transformed from the original sequential action value into the reward value corresponding to the current control strategy. In addition, by training the Critic network in advance to help the accelerated convergence of Actor network, it solves the computational waste problem caused by the random search of agent in the early training stage which greatly improves the offline training speed, and retains the DRL’s advantages like without using massive labeled data and strong universality.
Secondly, a multi-agent simplified DRL method (MASDRL) suitable for decentralized and zero-communication control of active distribution network is proposed. This method generalizes the core idea of SASDRL to form a multi-agent version and continues to accelerate the convergence performance of Actor network of each agent on the basis of training the unified Critic network in advance. Each agent corresponds to a different VVC device in the system. During online application, each agent only uses the local information of the node connected to the VVC device to generate the control strategy through its own Actor network independently. Besides, it adopts IL for initialization to inject the global optimization idea into each agent in advance, and improves the local collaborative control effect between various VVC devices.
Simulation results on the improved IEEE 118-bus system show that SASDRL and MASDRL both achieve the best control results of VVC among all the compared methods. In terms of offline training speed, SASDRL consumes the least amount of training time, whose speed is 4.47 times faster than the traditional DRL and 50.76 times faster than IL. 87.1% of SASDRL's training time is spent on generating the expert samples required for the supervised training of Critic network while only 12.9% is consumed by the training of Actor and Critic network. Regarding MASDRL, it can realize the 82.77% reduction in offline training time compared to traditional MADRL.
The following conclusions can be drawn from the simulation analysis: (1) Compared with traditional mathematical methods and existing ML methods, SASDRL is able to obtain excellent control results similar to mathematical methods while greatly accelerating the offline training speed of DRL based VVC. (2) Compared with traditional MADRL, by the inheritance of SASDRL’ core ideas and the introduction of IL into the initialization of Actor network, the method of MASDRL+IL proposed can improve the local collaborative control effect between various VVC devices and offline training speed significantly.
keywords：Volt-var control, centralized control, single-agent simplified deep reinforcement learning, decentralized control, multi-agent simplified deep reinforcement learning
DOI:10.19595/j.cnki.1000-6753.tces.222195
中图分类号：TM76
国家重点研发计划资助项目（2017YFB0903705）。
收稿日期 2022-11-22
改稿日期 2023-03-03
马 庆 男，1990年生，博士研究生，研究方向电力系统无功电压控制。E-mail：747942466@qq.com
邓长虹 女，1963年生，教授，博士生导师，研究方向为电力系统安全稳定分析、可再生能源接入电网的优化控制。E-mail：dengch@whu.edu.cn（通信作者）
（编辑 赫 蕾）