图1 平板式永磁电动悬浮系统结构示意图
Fig.1 Schematic diagram of the flat-type PMEDS system
摘要 该文提出一种以汽车为载体的平板式永磁电动悬浮系统,并从结构设计、等效实验、原理样机测试三方面对电磁特性开展研究。首先,阐述系统的结构及原理,依托自主研制的最高时速600 km的动轨实验台,分析在固定参数下的电磁力特性和垂向自稳定能力,并验证有限元模型的准确性。其次,对悬浮磁体、导向磁体、导体板进行计算分析。最后,改装汽车,加装间隙调节机构、简易悬浮架、车载磁体及测试系统,并搭建长50 m的铜制导体板轨道,开展原理样机测试。整车约为1 500 kg,最高实验速度为70 km/h,最大悬浮间隙约为35 mm。实验结果验证了导向磁体的有效性,展现出平板式永磁电动悬浮系统较强的载重能力。
关键词:永磁电动悬浮 等效实验 原理样机 高速实验台 导向磁体
磁悬浮列车以车载悬浮单元与轨道间的电磁力取代轮轨摩擦接触力,从而实现车体的悬浮导向和驱动[1-2]。相较于轮轨列车,突破了轮轨黏着极限、蛇行失稳、运行噪声及弓网受流等问题的制约[3-4]。2022年3月,交通运输部、科学技术部联合制定《交通领域科技创新中长期发展规划纲要》,提出“积极研发超高速列车”。高速磁浮已俨然成为了轨道交通新一轮革新技术白热化竞争的焦点。
基于不同的悬浮原理,磁悬浮技术可分为电磁悬浮、电动悬浮和高温超导钉扎磁悬浮,各种磁悬浮制式都具有高速应用的潜力[5-7]。超导磁体由于其强大的磁场,一直被认为是电动悬浮的最佳磁源。然而超导磁体面临着成本高、结构复杂、冷却环境苛刻、漏磁场大等问题,使其大规模应用受限。随着永磁体性能不断提高及Halbach阵列的应用[8],永磁电动悬浮也愈发受到各国的关注。永磁电动悬浮系统(Permanent Magnet Electrodynamic Suspension,PMEDS)的轨道形式可分为离散型线圈 [9-10](梯形短路、窗形短路、零磁通线圈等)和连续型导体板(铝板、铜板)[11-12]。前者由于轨道离散分布,电磁力会发生周期性波动,不利于系统的稳定性。因此国内主要研究连续型导体板式电动悬浮,也称为平板式永磁电动悬浮。
平板式永磁电动悬浮系统具有结构简单、载重能力强及成本低等优点。美国已经开展了大量实质性的研究,并将其应用于磁浮交通、物流运输、电磁弹射和磁浮助推等多个领域[13-14],主要集中于Magplane、Inductrack、Hyperloop三大系统。20世纪90年代,美国开始研究Magplane方案[15],以弧形铝板为轨道,车载磁体为Halbach永磁阵列,左右两侧各一列与铝板相互作用产生电磁力,用于悬浮和导向,但后续并未见研究成果报道。无独有偶,劳伦斯利弗莫尔国家实验室(LLNL)在NASA资助下设计了两套Inductrack悬浮系统:Inductrack Ⅰ用于小型火箭发射助推实验系统的研究[16-17],窗形短路线圈作为轨道,降低了磁阻力并提高了悬浮;Inductrack Ⅱ采用双排Halbach永磁阵列的布置方式,使得垂直磁场相互抵消,水平磁场相互叠加,从而降低了磁阻力,适应于城市轨道交通。此外,PMEDS也用于Hyperloop真空管道系统中,并开展了短距离线路实验[18],但实验数据并未见报道。
在国内,学者们也对PMEDS开展了大量的研究工作,主要集中于建立解析模型和搭建实验装置两方面。在解析模型建立方面,王厚生[19]基于有限宽导体板的三维电磁场分析,提出一种三维涡流分布数学模型。陈殷和张昆仑[20-21]采用二阶矢量势法对电磁场进行建模,提出了通用的二维和三维电磁力解析计算方法。李春生等[22]基于浮重比、浮阻比对车载磁体的几何尺寸进行优化设计,以提高磁体利用率。陈殷等[23]基于双边Halbach永磁阵列的PMEDS系统,建立了矢量磁位方程,推导了电磁力的二维解析模型。巫川等[24]建立了包含横向端部和纵向端部效应的准确解析模型。祝翰林等[25]基于零磁通式车载Halbach阵列永磁电动悬浮系统,将Halbach阵列等效替代为线圈阵列,建立了考虑纵向边端效应的三维解析模型。然而,理论模型往往建立在诸多假设的基础上,其正确性需要通过实验来验证,为此研究者们搭建了许多实验装置。
在搭建实验装置方面,由于长直线路所需的建设成本大,通常采用磁体或轨道旋转的运动方式等效模拟。根据磁体与轨道的相对位置不同,实验装置可分为两类:一种是鼓式旋转,旋转体为滚筒,车载磁体沿着滚筒圆周方向布置形成径向磁场;另一种为圆盘式旋转,车载磁体沿着转盘圆周方向布置形成轴向磁场,转盘转动。段家恒等[26]利用厚度为3 mm的铝导体板在相对布置的Halbach阵列中间旋转,最高线速度为25 m/s。王大志等[27]搭建了直径为230 mm的圆盘式实验装置,最高线速度为10 m/s。龙志强等[28]搭建了直径350 mm、厚度30 mm的盘式实验装置,最高线速度为60 m/s。王一宇等[9]搭建了零磁通电动悬浮等效模拟系统,线圈旋转半径为285.5 mm,实验转速为4 400 r/min。
由此可见,目前公开的实验装置最高设计速度均低于60 m/s且半径较小。为了测试电磁力,磁体各个自由度被限制,难以研究其动态特性。因此依靠等效实验结果来指导工程应用具有局限性。鉴于此,本文首先利用动轨高速实验平台对永磁电动悬浮系统的垂向自稳定能力及电磁力特性进行分析,并验证仿真模型的正确性。其次,利用有限元模型对悬浮用永磁体、导向用永磁体、导体板轨道进行计算分析和研制。最后,搭建长50 m的铜制导体板轨道,以汽车为载体,辅助完成平板式永磁电动悬浮系统的线路测试实验,对比分析悬浮力的测试值与仿真值,并验证导向磁体对改善系统横向稳定性的作用。
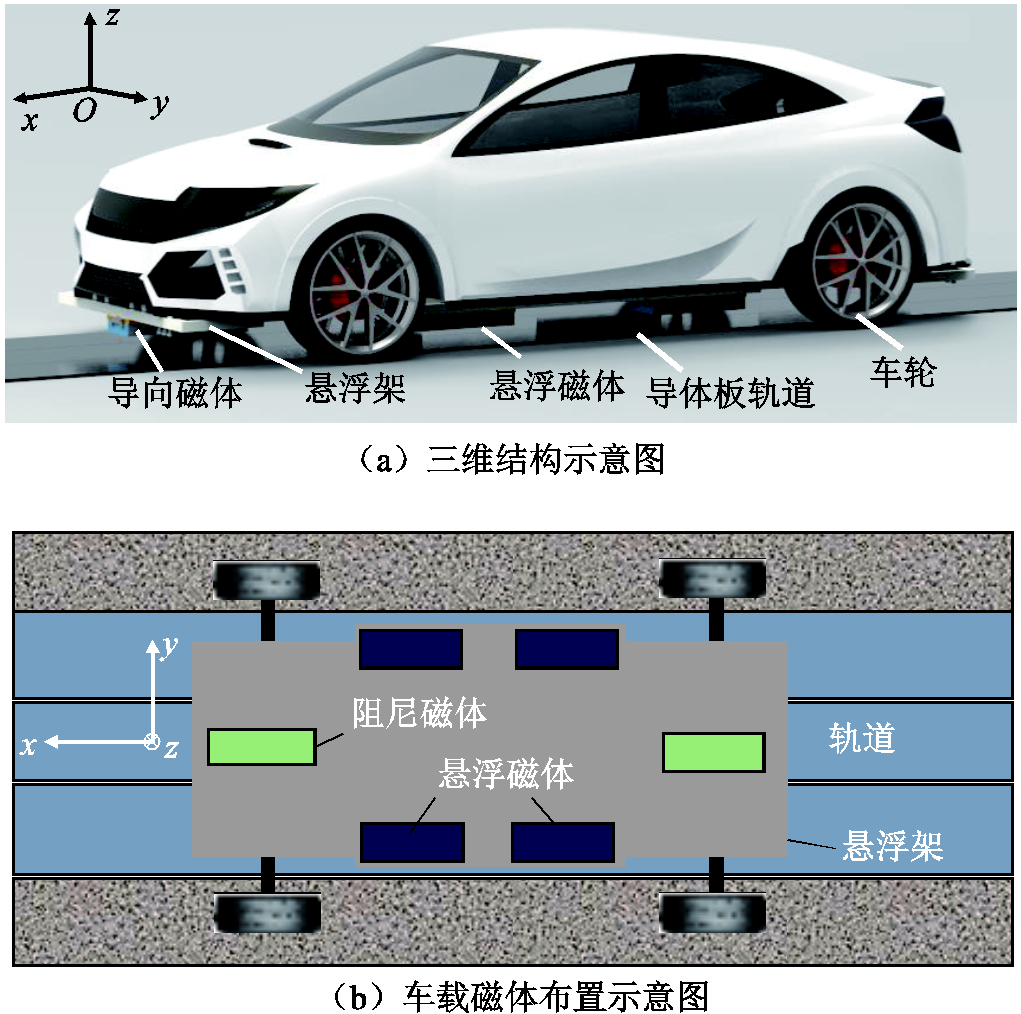
平板式永磁电动悬浮系统结构示意图如图1所示。汽车作为动力系统并提供助跑轮,可有效地降低实验成本。悬浮架固定在汽车底盘,容纳车载磁体并传递电磁力。四组悬浮磁体沿着纵向均匀布置,两组导向磁体与悬浮磁体相互垂直。导体板铺设在地面作为轨道。基于楞次定律,受汽车发动机的驱动作用,悬浮磁体以速度v沿着纵向运动,距离导体板的高度称为悬浮间隙(gap)。车载磁体运动产生的时变磁场切割轨道导体板,感应出时变涡流,从而形成与源磁场相反的镜像磁场,进而产生悬浮力支撑车体。类似地,当车体横向发生移动时,导向磁体与导体板发生电磁反应,产生电磁力阻碍车体进一步偏离。下文所述的纵向、横向和垂向分别与图1中的x轴、y轴和z轴平行。

图1 平板式永磁电动悬浮系统结构示意图
Fig.1 Schematic diagram of the flat-type PMEDS system
利用图2所示动轨实验装置[4]对PMEDS系统进行固定参数研究,包括悬浮力、导向力、磁阻力及垂向自稳定性能力,通过旋转来产生相对运动,轨道半径越大,等效模拟越真实,主要结构参数见表1。实验装置主要由交流电机、转盘、测试系统和伺服机构组成。转盘为不锈钢制,总质量为8.2 t,直径为2 500 mm。当转盘转速为1 440 r/min时,最大线速度为600 km/h,轨道转子动平衡精度为G2.5,稳定转速控制精度为±1%。其截面为T字形。铝合金导体板(见图2b)内嵌在转盘内,该结构设计可抵抗高转速下过大的离心力。三轴力传感器测量电磁力,并显示到监测平台上进行存储。伺服电动机驱动滑台机构对电磁间隙精准调节。

图2 永磁电动悬浮系统高速实验装置[4]
Fig.2 High-speed test rig of PMEDS system[4]
表1 实验装置主要结构参数
Tab.1 Primary sturcture parameters of the test rig

参数数值 磁体厚度/mm30 磁体极距/mm60 磁体宽度/mm100 磁化角/(°)90 铝合金制轨道宽度/mm160 铝合金制轨道厚度/mm30 不锈钢制轨道宽度/mm316 不锈钢制轨道厚度/mm90
图3描述了当悬浮间隙为20 mm、等效速度由0增加到260 km/h时,悬浮力、磁阻力和导向力的变化趋势。悬浮力随着速度先增大后缓慢趋于稳定值,对应的速度称为饱和转速vs。磁阻力先增大后降低,其峰值对应的速度为转折速度vc[29]。导向力随速度的变化规律与悬浮力类似,但数值较小,说明了永磁电动悬浮导向能力弱的问题。微弱的导向力源于车载磁体固有的边端效应。
永磁电动悬浮列车稳定悬浮时,悬浮力与重力平衡,当磁体受到外界激扰相对导体向上偏移时,电磁间隙变大,悬浮力降低,从而悬浮力小于重力,但在重力的作用下磁体会向下运动,直到悬浮力再次与重力平衡;反之亦然。为了验证系统的垂向自稳定能力,通过等效实验的方法,利用垂向伺服电动机带动磁体上下移动,分析悬浮力的变化规律。磁体由初始位置(z0=20 mm)垂直向上运动30 mm至z1=50 mm后返回初始位置,往复3次,轨道的等效线速度为150 km/h。测试结果如图4所示,磁体上升,间隙增大,电磁力非线性减小;下降阶段间隙减小,电磁力呈非线性增大,这体现了电动悬浮的垂向自稳定能力。特别地,在上升和下降两个过程中,电磁力可逆,经过同一位置时电磁力相同。
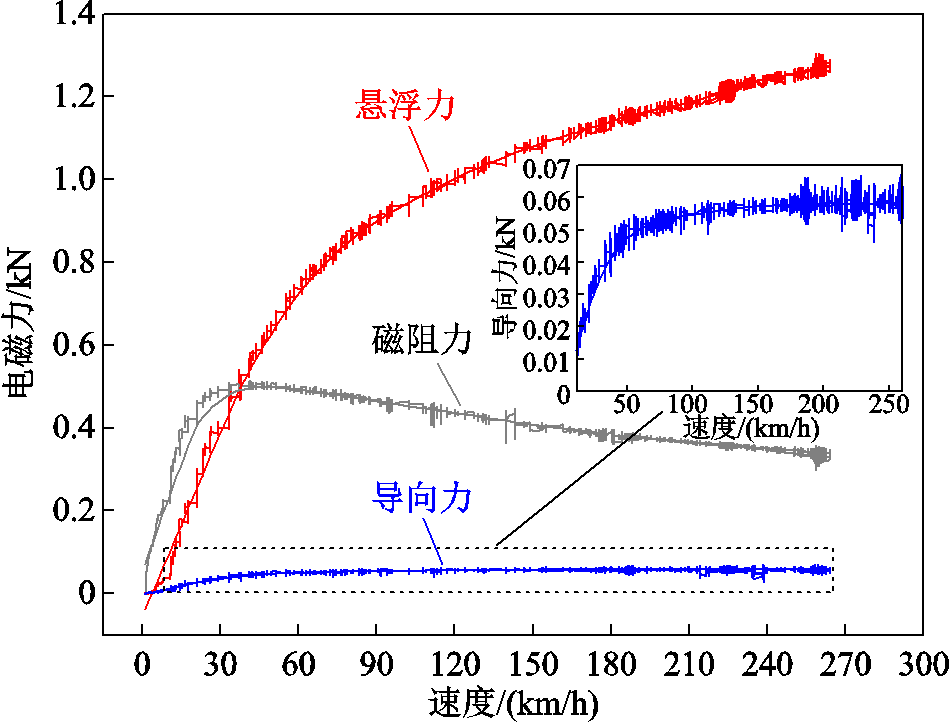
图3 在间隙20 mm处测试的电磁力随速度的变化
Fig.3 Tested electromagnetic forces with speed at 20 mm
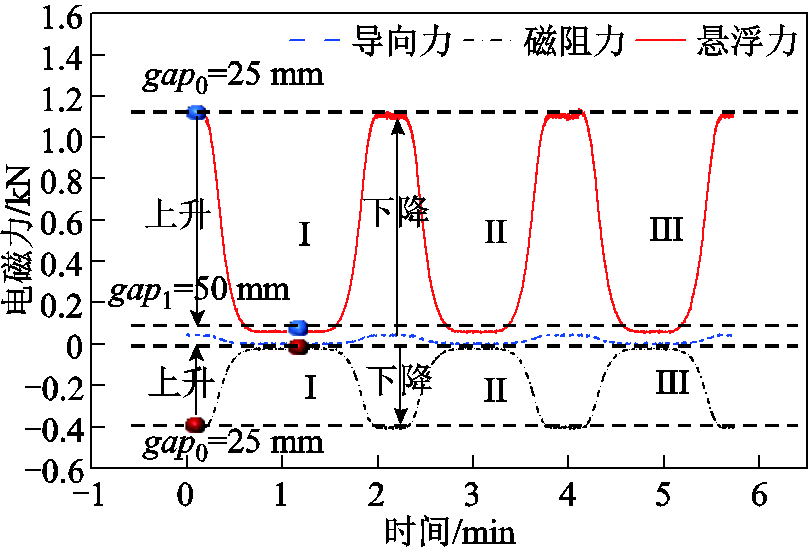
图4 磁体垂向往复运动时电磁力的实验测试结果
Fig.4 Tested electromagnetic forces under reciprocating motions
上文通过等效实验分析了PMEDS 系统的基本电磁特性,在开展样车测试实验之前,需要确定系统的结构参数。本部分主要利用有限元模型对系统的悬浮磁体、导向磁体和导体板进行分析计算,为系统的研制提供参数建议,其中有限元模型的正确性通过等效实验来验证。有限元分析是一种能同时处理边端效应、趋肤效应、强非线性且能模拟运行工况的有效手段,可以等效为一种虚拟样机。有限元模型如图5所示,具体尺寸参数同表1。
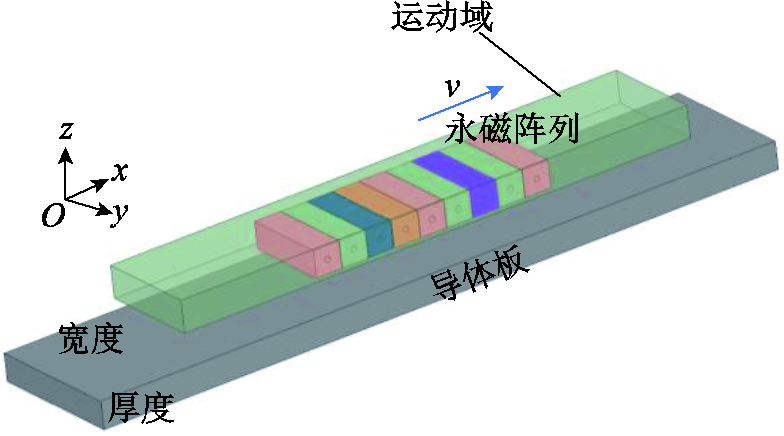
图5 永磁电动悬浮系统三维有限元模型
Fig.5 Finite element model of the PMEDS system
取磁场加强侧间隙20 mm处的中心线为参考线,对该位置处的磁场垂直分量进行测试和仿真分析。结果如图6a所示,磁感应强度的变化规律及幅值上均吻合良好。此外,采用不锈钢轨道,对不同速度下的悬浮力和磁阻力进行对比分析,参数见表1。图6b展示了悬浮力和磁阻力随速度变化的规律曲线。结果显示,仿真结果与实验结果分别相差约8%,验证了仿真模型的正确性。接下来将采用有限元模型对悬浮磁体、导向磁体和导体板轨道进行计算分析。
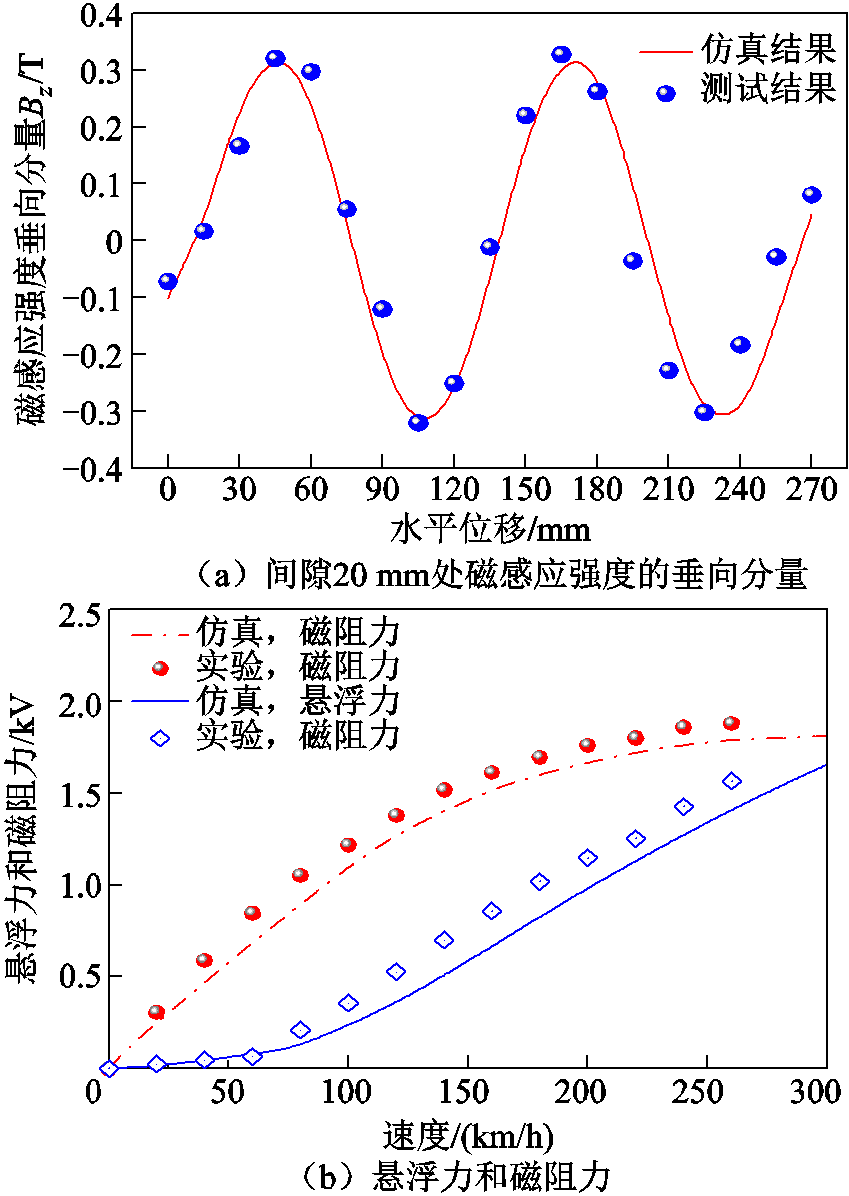
图6 电磁力的实验测试和仿真结果对比
Fig.6 Electromagnetic forces comparison among simulation model and experiment
浮重比(Levitation-Weight Rotio, LWR)通常用来评价系统的载重能力,即单位磁体重量产生的悬浮力。浮阻比(Levitation-Drag Ratio, LDR)是评价系统能耗的指标,即悬浮力与磁阻力的比值,浮阻比越大表示相同载重能力的情况下,克服磁阻力所需的推进能量越少,即系统能耗越低。
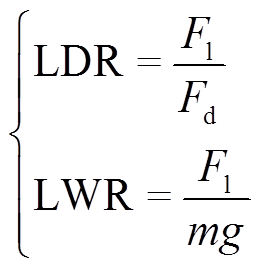 (1)
(1)
式中,Fl为悬浮力;Fd为磁阻力;m为磁体质量。
为了保证实验安全,设计速度不超过70 km/h,由于车体进入悬浮轨道时,并没有动力加持,依靠速度惯性运行,受到磁阻力的作用力速度骤减。文献[30]研究表明,同等工况下,相对于铝合金导体板,采用铜板会减小约为22%的能量损失。因此,为了减小磁阻力,轨道采用铜板。
以悬浮载重2 t,悬浮间隙30 mm为设计目标。基于控制变量法,对悬浮磁体的宽度、厚度和长度进行参数化仿真分析。其中长度在50~60 mm变化,厚度在46~60 mm变化,宽度在164~198 mm之间变化。根据计算的数据,得到悬浮力和磁阻力对各个参数的敏感度,如图7所示。悬浮力和磁阻力均受磁体的长度影响最大,其次是宽度和厚度。
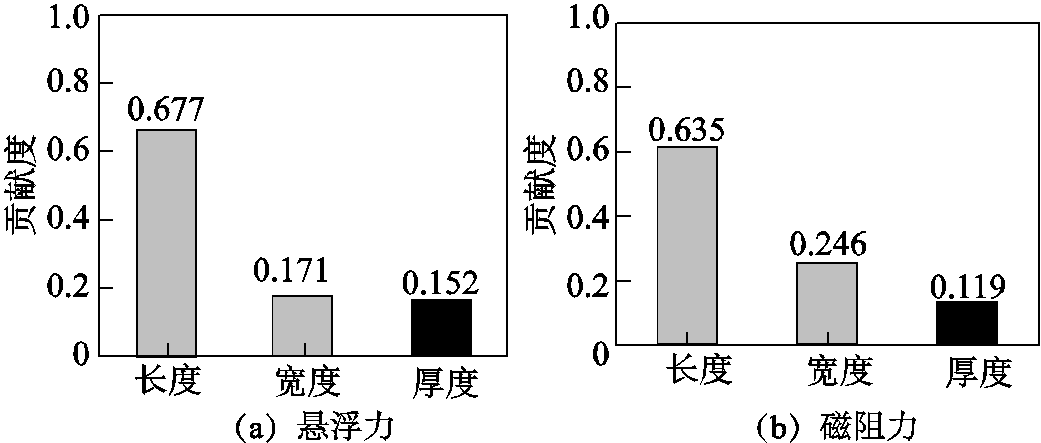
图7 磁体几何尺寸对悬浮力和磁阻力的贡献度
Fig.7 Contribution of magnet geometry size to levitation and drag forces
综合考虑LWR和LDR,确定悬架系统由四组八模块Halbach永磁阵列组成,其中单块磁铁的宽度、厚度和长度分别为180 mm、45 mm和50 mm。特别地,规定磁体和轨道的长度、宽度和厚度分别对应x轴、y轴和z轴。
永磁电动悬浮具有弱阻尼甚至欠阻尼特性,由图3可知,有限的导向力难以抵抗外界冲击的干扰,可能会导致系统横向失稳。众多研究者也针对导向能力弱的问题,通过改变轨道形式,利用悬浮力的分力来充当导向力,如采用“U”字形或“V”字形轨道,如美国的Magplane方案[31]。文献[32]提出一种零磁通线圈式永磁电动悬浮,利用零磁通线圈来提高导向能力,其原理与超导电动悬浮类似。这些方案原理上都具有可行性,但会使得轨道变得复杂,成本增加。本文提出一种与悬浮磁体相互垂直布置的导向磁体,如图8所示。基于楞次定律,当车体相对轨道中心横向偏离时,导向磁体与感应板相互作用,产生电磁反力以阻碍车体进一步的偏离,从而提高系统的横向稳定性。以导重比指标来辅助导向磁体的尺寸设计,所谓导重比指的是单位磁体产生的横向导向力,指标越大经济性越好。经过对磁体的参数化仿真计算,确定阻尼系统由两组八模块Halbach永磁阵列组成,其中单块磁铁的宽度、厚度和长度分别为24 mm、45 mm和300 mm。

图8 导向磁体与悬浮磁体的相对位置
Fig.8 Configuration of levitation and guidance magnets
图9 描述了在不同垂向间隙下,导向力随速度的变化。实际上,导向磁体的作用原理同磁阻力一致。由于横向速度较小,尚未超过转折速度,因此导向力会随着速度的增大而增大,越大的间隙会使得导向力增大的趋势放缓。
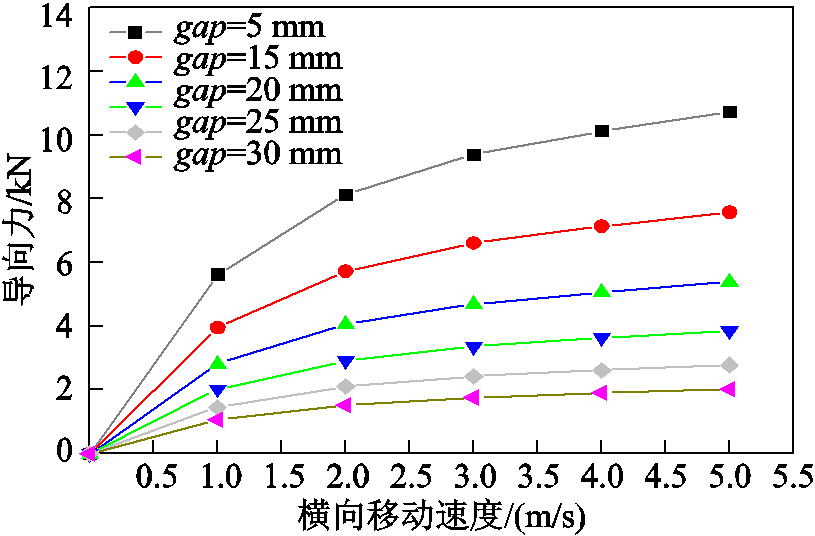
图9 不同垂向间隙的导向力随着速度的变化
Fig.9 Evolution of guidance force with speed under different gaps
铜制的导体板需要沿着线路铺设,线路长度为50 m,因此轨道成本取决于导体板的厚度和宽度。本节将基于确定的悬浮磁体,对导体板的厚度和宽度进行计算分析。
3.4.1 厚度
当导体板内感应出涡流时,在电抗的作用下涡流穿透导体板的深度会发生变化,称之为趋肤深度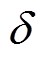 ,即
,即
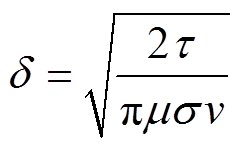 (2)
(2)
式中,τ为磁体的极距;μ、σ分别为导体板的相对磁导率和电导率;v为运行速度。
低速时趋肤深度大,通过增大导体板的厚度使悬浮力变大。而趋肤深度会随着速度的增大而减小,当导体板的厚度大于趋肤深度时,继续增大导体板的厚度,其有效厚度不会变化,只会使得成本增大。图10呈现了悬浮高度为30 mm时,悬浮力和磁阻力在不同速度下随着导体板厚度的变化规律。特别地,仿真模型中将轨道的宽度设置为磁体宽度的3倍[24],以避免导体板宽度的影响。整体上,随着厚度增大,悬浮力先增大后减小再逐渐趋于稳定。根据图10a可知,厚度的转折值约等于各个速度对应的趋肤深度值,如式(2)。随着速度的增大,厚度转折值逐渐减小,且速度越大悬浮力最大值对应的导体板厚度越小。磁阻力随着厚度的增大,先增大后减小再趋于稳定,速度越大磁阻力的稳定值对应的导体板厚度越小。
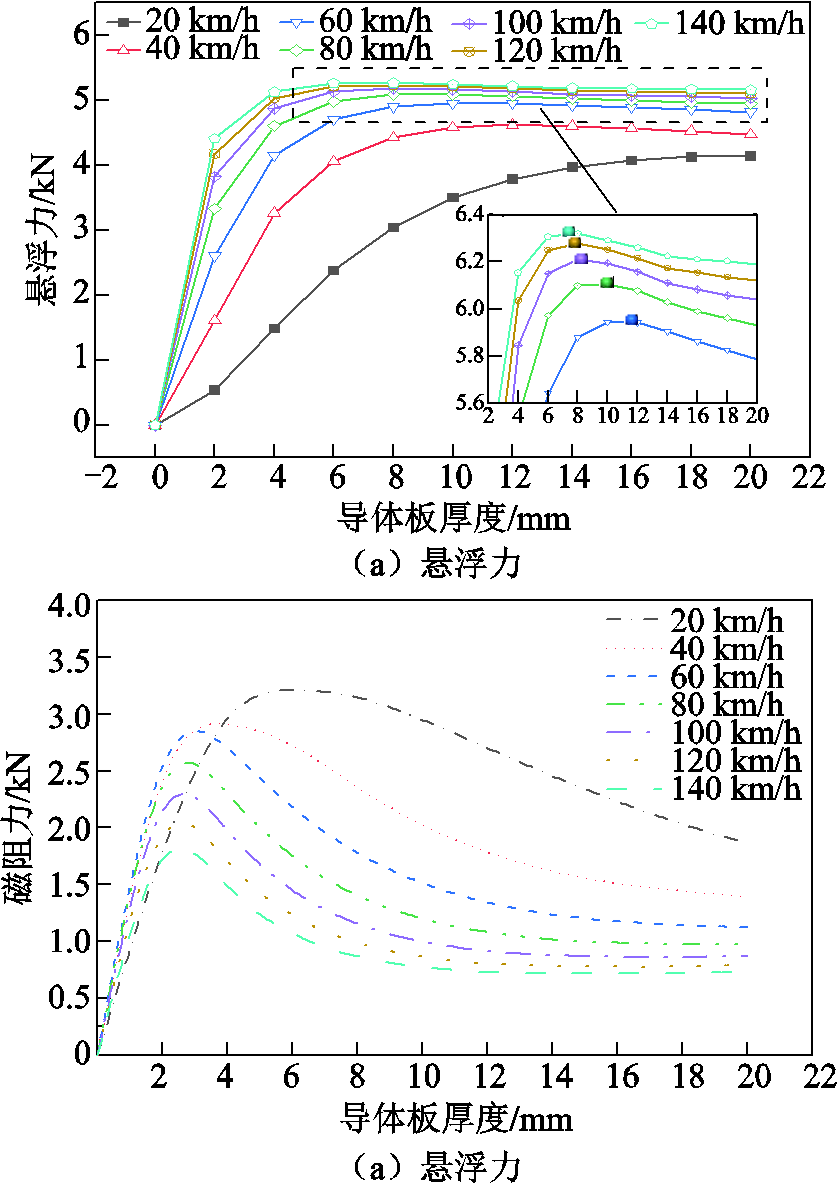
图10 不同速度下悬浮力和磁阻力随导体板厚度的变化
Fig.10 Evolution of levitation and drag forces with thickness of conductive plate under various speeds
总的来说,一定程度上增大导体板的厚度有利于在增大悬浮力的同时降低磁阻力。根据最大实验速度70 km/h,选定导体板厚度为12 mm。
3.4.2 宽度
电磁力源于导体板内的感应电流与源磁场的相互作用,其中感应电流又受趋肤效应和边端效应的影响。导体板的厚度与趋肤深度息息相关,而宽度与磁体边端效应也有关。理论上,磁体固有的边端效应使得感应电流在导体板上的分布宽度会大于磁体的宽度。因此当导体板宽度较小时,会使得有效涡流减小,从而导致悬浮力降低。前文中已确定轨道的厚度为12 mm,悬浮磁体的宽度为180 mm。图11描述了悬浮力和磁阻力在最高实验速度70 km/h、悬浮高度30 mm的工况下,悬浮力与磁阻力随着导体板宽度的变化趋势。在初始阶段,宽度的增大促进了磁体与板间感应面积的增大,从而使悬浮力和磁阻力均增大。而随着宽度进一步增加,感应电流趋于饱和,悬浮趋近于稳定值,磁阻力会因为等效电阻变小而衰减。
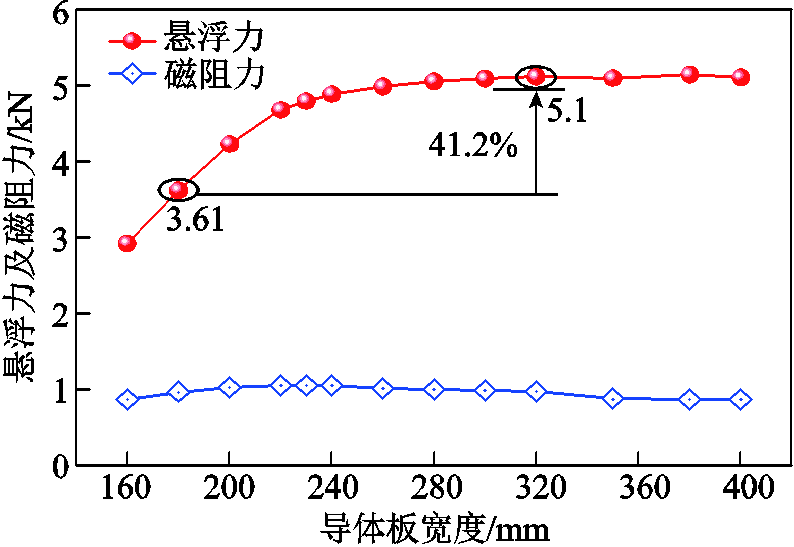
图11 不同导体板宽度的悬浮力和磁阻力
Fig. 11 Evolution of levitation and drag forces with the width of conductive plate
总体上,随着导体板厚度的增大,浮阻比增大。此外,当导电板宽度从与磁铁宽度相等的180 mm增加到320 mm时,悬浮力显著提高了41.2%。因此,考虑到悬浮性能与成本的平衡,确定导电板宽度为320 mm。
根据上文的优化设计,悬浮磁体、导向磁体及导体板的尺寸已经确定,见表2。
实验之前,需要对系统的电磁性能进行评估,以指导系统进一步的设计。基于表2中的结构参数对系统进行仿真分析,不同间隙下悬浮力和磁阻力随速度的变化规律如图12所示。结果表明:系统的临界速度vc和饱和速度vs分别为17 km/h和90 km/h,且都与悬浮间隙无关。在悬浮间隙30 mm时,悬浮力能够平衡1.5 t的目标载重。
表2 永磁电动悬浮系统结构参数
Tab.2 Dominating parameters of PMEDS system

类别参数数值 单块悬浮磁体长度/mm50 宽度/mm180 厚度/mm45 组数6 磁化角/(°)45 内禀矫顽力/(kA/m)1 096 剩磁/T1.48 单块导向磁体长度/mm300 宽度/mm24 厚度/mm45 组数6 磁化角/(°)45 内禀矫顽力/(kA/m)1 096 剩磁/T1.48 导体板材料铜 宽度/mm320 厚度/mm12
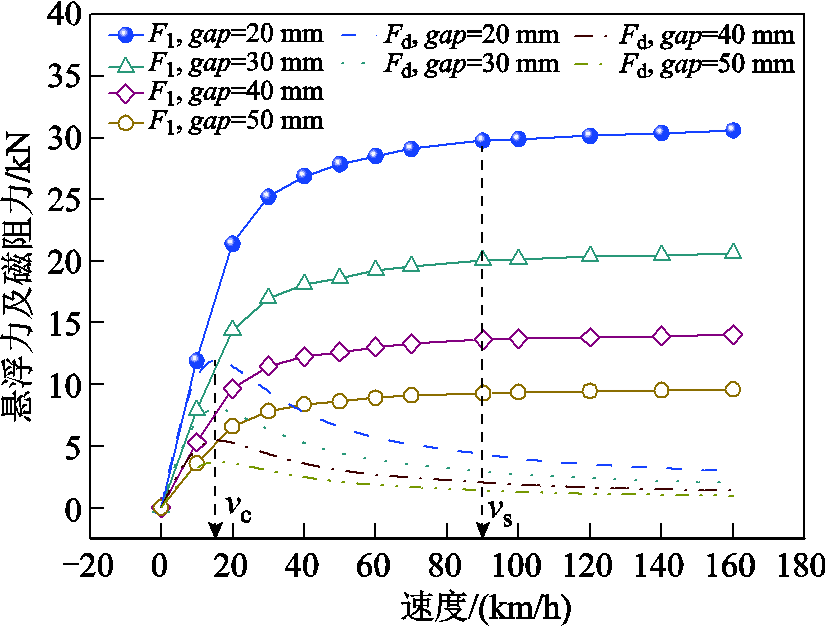
图12 不同间隙下系统悬浮力和磁阻力随速度的变化
Fig.12 Evolution of levitation and drag force of PMEDS system with speed under different gaps
根据表2中的参数,研制悬浮磁体和导向磁体及其附件,如图13所示。磁体均由八模块的Halbach阵列组成,单侧磁场加强,不需要附加背铁,这也方便制造和安装。磁体的背板选择采用不锈钢,通过螺栓固定在悬浮架上,背板上的腰形孔设计可以允许一定的安装误差。

图13 悬浮磁体和导向磁体的实物图
Fig.13 Physical photos of manufactured magnets
此外,利用高斯计对悬浮磁体的磁感应强度垂直分量Bz进行了测量,并与仿真结果进行比较。图14为Bz沿纵向位移变化趋势,与仿真结果高度一致,误差低于5%。
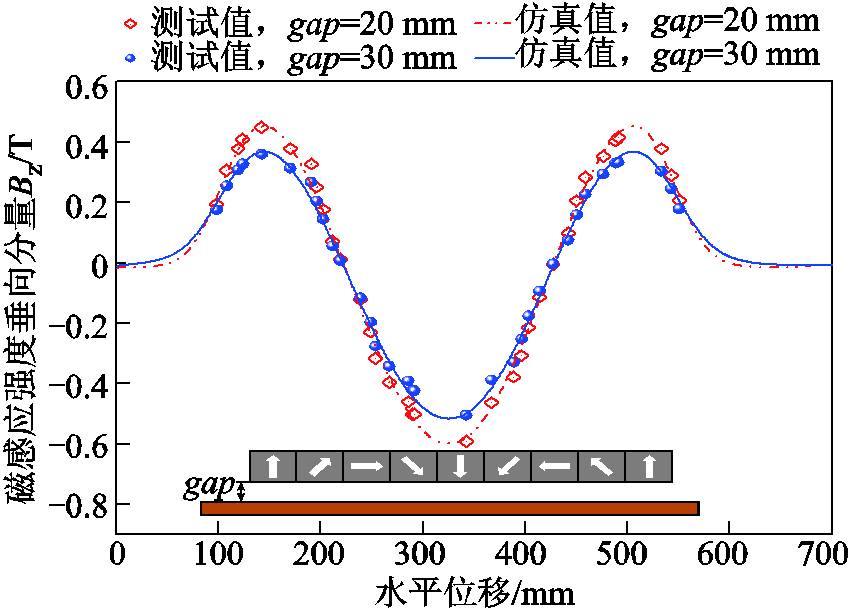
图14 悬浮磁体垂向磁感应强度的仿真值与测试值对比
Fig.14 Comparison of tested and simulated magnetic field under different gaps
测试系统主要由激光测距传感器、九轴传感器、高清摄像头组成,其基本原理和功能如下:激光位移传感通过发射激光脉冲,根据来回脉冲时间差,计算距离值,用于监测车体四轮悬浮间隙。九轴传感器利用地磁场和陀螺仪原理,对车体三轴加速度、偏转角度进行测量。高清广角摄像头利用自带抗畸变程序,具备拍摄幅度广、帧率高等特点,用于记录车轮的悬浮情况。测试系统的实物图如图15所示。图15中,激光位移传感器和九轴传感器分别用于实时记录车轮的悬浮高度与实时采集车体的三轴加速度和横向偏转角。

图15 测试系统的实物图
Fig.15 Physical photos of test system
4.3.1 悬浮架
根据汽车底盘空间、悬浮磁体和导向磁体安装的位置来设计悬浮架。悬浮架是连接汽车与磁体的桥梁,保证每组磁体安装高度的均匀性,可容纳传感器和摄像头等设备。它也是关键的传力部件,传递悬浮力、磁阻力和导向力,故对其强度提出了较高的要求。因此,悬浮架的设计还应结合结构强度校核来完善,利用校核结果指导悬架的横截面面积、底盘支承数量设计。悬浮架的强度分析如图16所示,最大应力为125.31 MPa,取安全系数为1.5,未超过材料的许用应力,不会发生塑性变形。经过校核后,悬浮架被制造和焊接在汽车底盘上。
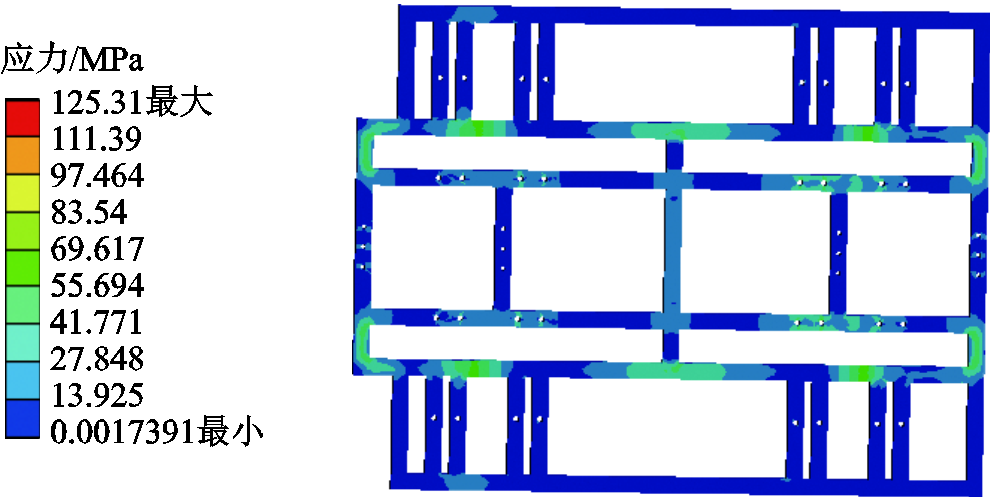
图16 悬浮架的强度分析
Fig.16 Strength analysis of the suspension frame
4.3.2 间隙调整机构
电动悬浮的悬浮力与悬浮间隙息息相关。具体而言,当悬浮力小于重力,间隙就会减小以增加悬浮力,直到重新平衡;当悬浮力大于重力时,间隙会增大以减小悬浮力达到新平衡,同时悬浮间隙的大幅度变化会加剧垂向失稳。因此,应根据荷载需求合理设计悬浮间隙,以减少间隙的波动。鉴于此,为了便于调节磁体的安装高度,设计间隙调节机构取代汽车的减振器。导体板轨道结构示意图如图17所示。通过旋转中间螺杆使两端套筒座向内或向外移动,改变汽车底盘与导轨之间的间隙。螺杆为梯形牙双向螺杆,以提高结构的刚度和强度。固定螺距为6 mm,有助于实现间隙的精确调节,即每旋转一次,高度变化6 mm。机构具有自锁功能,可保证调节的可靠性。
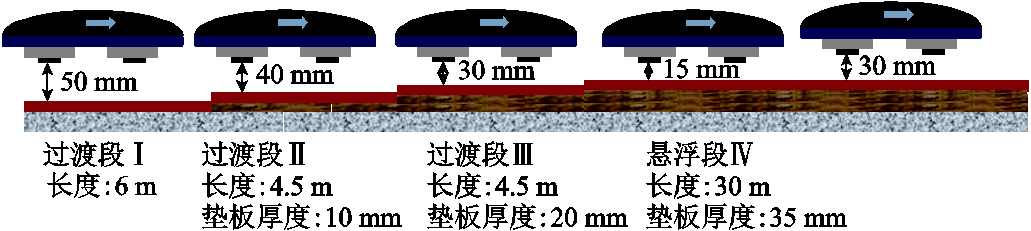
图17 导体板轨道结构示意图
Fig.17 Schematic diagram of the guideway
如图17所示,通过增大导体板下方的垫板来形成三个过渡段,以降低车体由于突然受到过大电磁力造成的冲击。车体从过渡段到悬浮区的过程中,悬浮力会随着间隙的减小而逐渐增大,最后实现悬浮。基于导体板参数和轨道结构,完成了50 m长的线路铺设,并将磁体进行安装,调整测试系统,形成完整的车-轨永磁电动悬浮系统,如图18所示。

图18 永磁电动悬浮实验样机及轨道
Fig.18 Photos of test prototype and guideway of PMEDS system
由图3可知,永磁电动悬浮系统本身的导向力非常小,当系统偏离导轨时,几乎没有能力保持横向稳定[33-34]。尽管这一问题成为众多研究者的共识,但并没有相关的测试结果来印证。本文基于理论和等效实验结果,提出一种导向磁体以改善系统横向稳定性。每组悬浮磁体和导向磁体是模块化的,容易拆卸和安装。因此,将线路测试实验分为两个阶段进行。第一阶段只在悬架上安装悬浮磁体而不安装导向磁体,通过线路实验的测试数据来印证平板式永磁电动悬浮系统的导向能力弱的问题。第二阶段,在悬浮架上增加导向磁体,辅助完成样机测试,以验证导向磁体的有效性,并采集数据对系统特性进行分析。
5.1.1 运行模式
为了保证车体进入轨道时,磁体中心与轨道中心尽量对齐,需要提前在轨道周围标记固定的定位点,并不断尝试对中。所谓对中指的是车体的中线与导体板轨道的中线重合,若两者不重合,两者形成的偏角称为初始偏转角θ。小车通过直线段提前加速到目标速度,然后保持匀速行驶,对准固定点,车体依靠速度惯性进入轨道。如图17所示,当车体进入过渡段时,由于磁体距离地面导体的高度较大,尚不能实现悬浮,车轮未离地有导向的作用。过渡段的高度是逐渐减小的,悬浮力逐渐变大,当车体行驶到预定悬浮区域时,悬浮高度进一步减少到设计值以下,此时悬浮力大于重力,车体实现悬浮。
5.1.2 样机实验
虽然设计轨道的过渡段缓解了因车体受到的电磁力冲击,但进入悬浮区域时冲击依然明显,车体会不可避免地受到激扰。出于实验安全,第一阶段的最高测试速度为50 km/h,即车从起点直线加速到50 km/h时,保持一段距离匀速行驶后,以 50 km/h的惯性速度进入轨道区域。图19a描述了实验速度为50 km/h时车体的横向偏转角度。在a点之前,小车尚未进入轨道,根据参考点在调整车体姿态,然后以恒定的速度进入轨道区域。在a点后,车体进入悬浮区后,突然受到悬浮力和磁阻力,小车发生偏移存在初始偏移角θ。从a点到b点可知,偏转的角度逐渐变大,最大偏转角接近90°,从实验现场也发现,从20 km/h到60 km/h的实验速度均会发生较大程度的偏转,导致小车基本无法实现悬浮,刚进入悬浮区时,仅有部分车轮被抬高。图19b描述了右前轮的离地高度,可以发现进入悬浮区后,轮子被短暂抬高的时间约为2 s,最大悬浮高度约为14 mm。
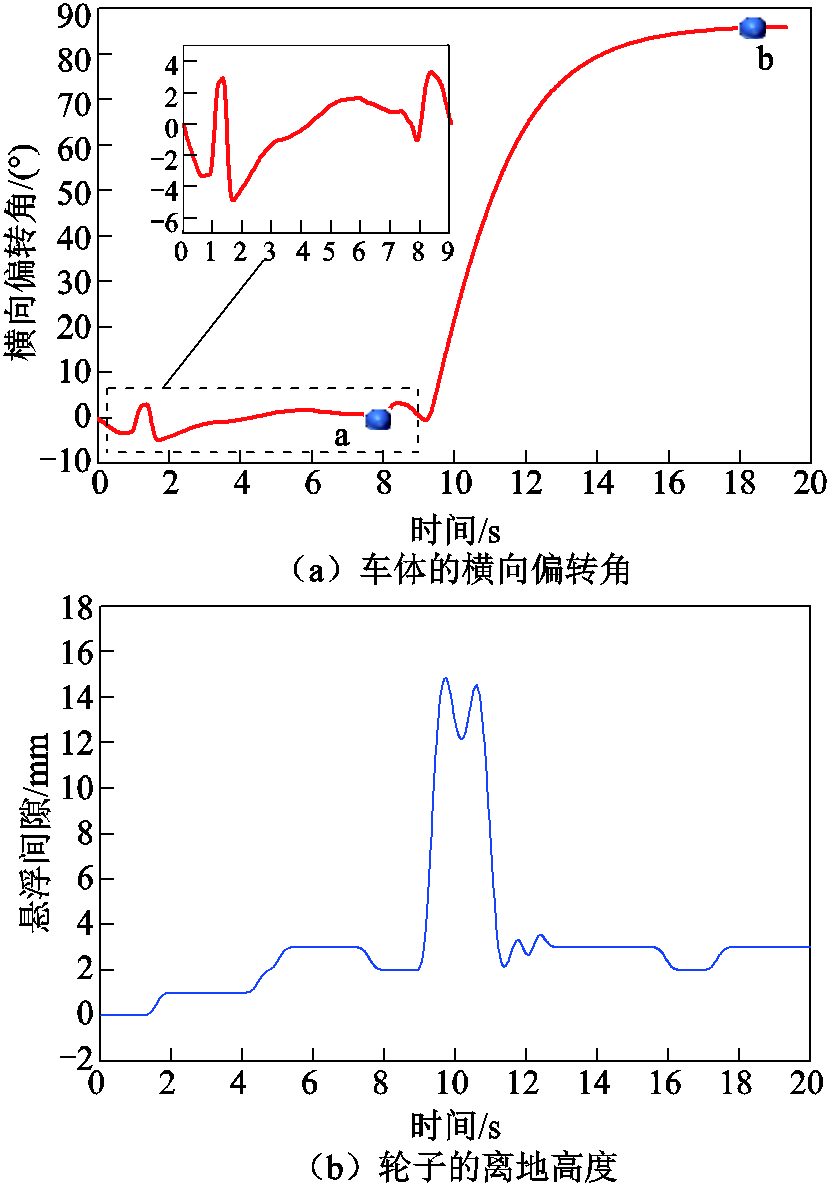
图19 无导向磁体实验测试结果
Fig.19 Tested resluts without guidance magnet
5.1.3 结果分析
根据图19a可知,车体的偏转角一直变大,可能受到了力矩的作用。由于导体板的宽度有限,当车体偏离时,车载永磁体发生同样的偏转,直至偏离轨道。利用等效实验台对磁体偏离轨道后的场景进行模拟,如图20所示。

图20 磁体横向偏离导体板示意图
Fig.20 Schematic diagram of the deviation of magnets
随着偏离位移增大,磁体与导体板间的耦合面积减小,导体板中的涡流分布也随之改变。图21描述了磁体运行速度为60 km/h、悬浮高度为20 mm时,电磁力随横向偏离位移的变化规律。由于导体板中涡流有效成分减小,悬浮力与磁阻力均呈线性衰减。此外,横向产生的推力先增大后减小,加剧磁体的偏离。比如,磁体向y轴负方向偏离时,磁体受到y轴负方向的推力作用。
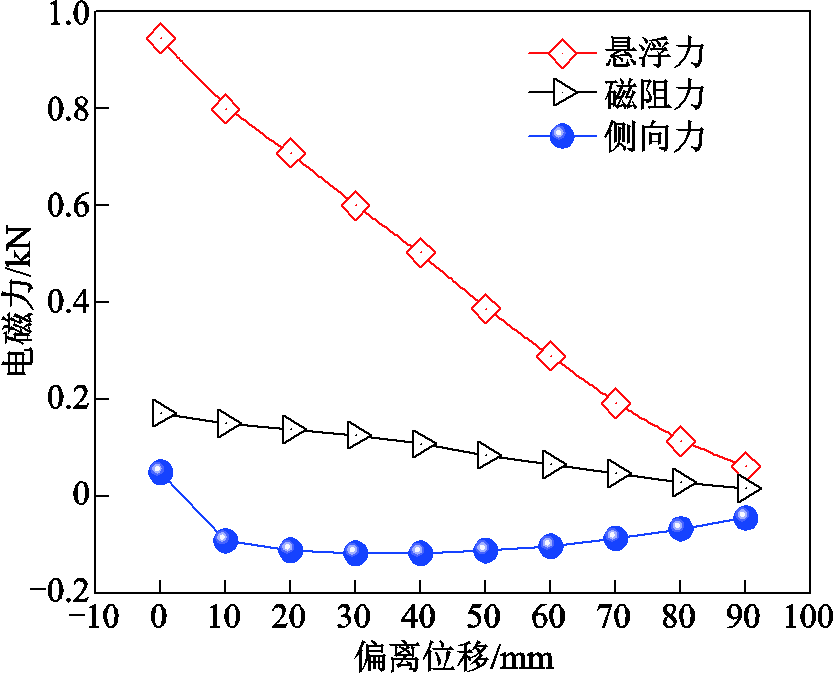
图21 电磁力随横向偏离位移的变化
Fig.21 Electromagnetic force with lateral offset
根据实验结果,给出车体偏转后的简化物理模型如图22所示。当车体偏转,左前轮和右后轮对应的磁体偏离出轨道,分别受到横向力Fy1和Fy2的作用,从而车体受到力矩的作用,偏转程度进一步加剧。当然,这也只是影响因素之一,车体质量分布不均匀、悬浮磁体的安装高度误差和突然的电磁力冲击等问题均会影响车体的运行姿态。
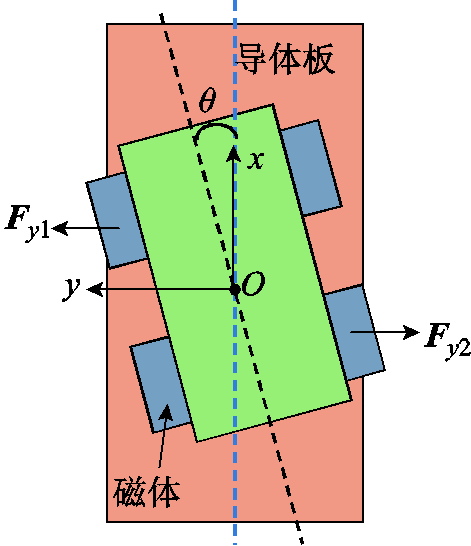
图22 车体偏转的简化模型示意图
Fig.22 Diagram of simplified deflection model of PMEDS system
从等效实验测试出的微小导向力到样机测试结果表现出的较大偏转角度,可以印证平板式永磁电动悬浮系统本身导向能力弱的问题,同时表明当磁体偏离轨道时,车体受到力矩的作用,使得车体大幅度偏摆,这一问题在工程应用中应该避免。
两组导向磁体加装在悬浮架上,前后对称布置。如前所述,导向力的大小取决于横向速度和安装高度。在实验中,横向的速度是难以掌握的,但可以通过降低导向磁体的垂向高度,从而增强导向力,进而提高系统的横向稳定性。通过增加导向磁体与悬架之间的垫片数量,使初始的安装高度低于悬浮磁体。
此外,图4的实验结果表明,根据载重目标设计合适的悬浮高度有利于减小系统的垂向振荡。多次调整安装高度后,悬浮磁体和导向磁体的安装高度分别为10 mm和5 mm。所谓的安装高度指的是磁体进入悬浮区后,磁体下表面与导体板上表面的间隙值。设备实验速度从30 km/h增加到70 km/h,随着速度的增大,车体起浮效果越明显。如图23所示,小车整体上实现了悬浮,其中图23a和图23b是在同一时刻的两个不同角度拍摄,两张图相结合可明显看到小车四轮同时离地。


图23 永磁电动悬浮系统实验样机及悬浮场景
Fig. 23 Test prototype and suspension scene of PMEDS system
小车的成功悬浮得益于导向磁体能克服车体进一步偏转。增加导向磁体后,小车的横向稳定性得到明显改善,导向力能阻止磁体横向大幅度的偏转,运行过程中基本上没有偏离轨道区域,行驶速度越大,稳定性越好。以最高实验速度70 km/h为例,对横向偏转角和四个车轮的悬浮高度进行分析,测试结果如图24所示。图24a表明,在整个测试过程中,横向偏转角度的最大值低于10°,横向稳定性得到极大的改善,此结果也证明了导向磁体的有效性。此外,图24b展示了四个车轮的悬浮高度变化。由于安装高度、轨道表面的不平顺度和小车质量分布不均的影响,四个车轮的悬浮高度存在差异,最大平均悬浮高度约为35 mm。进入悬浮区时,小车仅仅依靠惯性速度运行,受到磁阻力的作用开始减速导致悬浮力下降。悬浮力小于重力从而使得悬浮高度降低,高度降低反过来又会使得悬浮力增大,小车再次悬浮,但悬浮高度小于初始的悬浮高度。以此类推,整个过程小车会出现多次下降和上升的往复过程。实验结果与图4的等效实验结果相呼应,也再次从线路实验的角度,验证了永磁电动悬浮具有垂向自稳定能力。
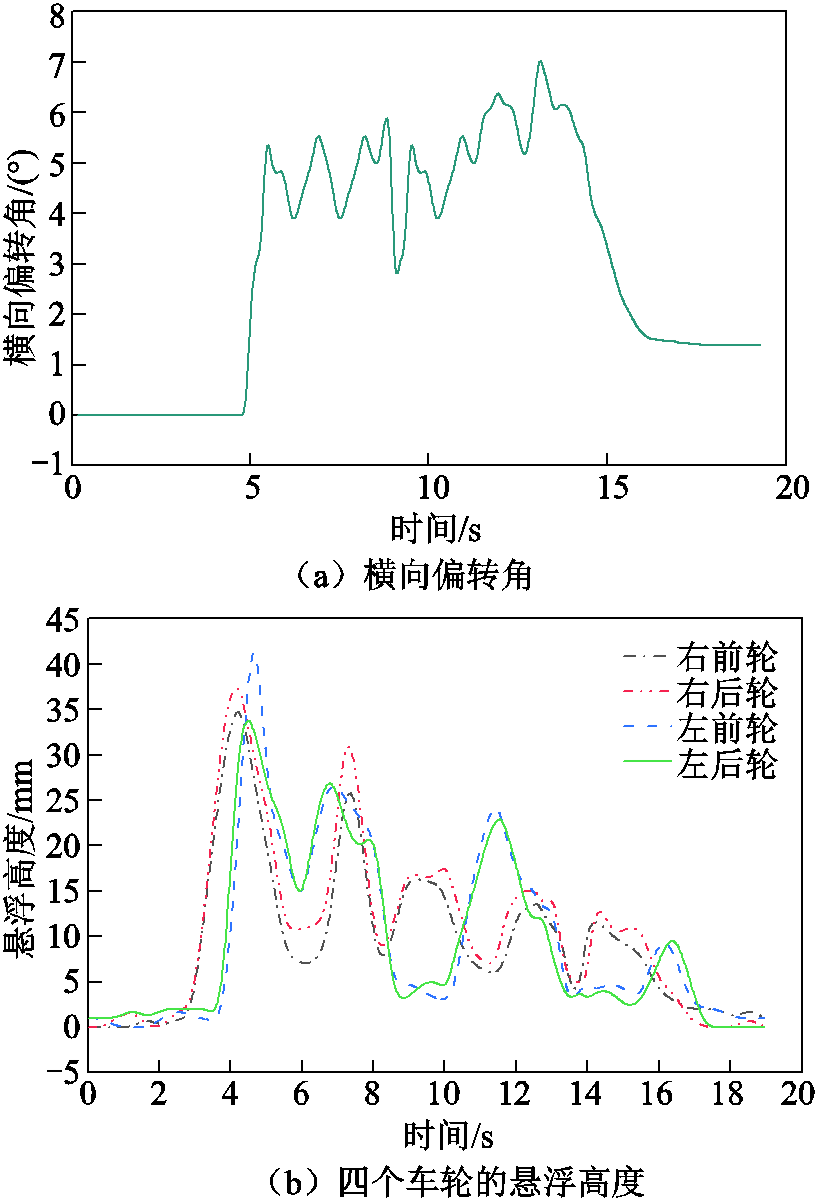
图24 实验速度70 km/h有导向磁体的测试结果
Fig.24 Tested resluts with guidance magnet at 70 km/h
最大悬浮间隙约为35 mm,根据图12的仿真结果,对实验过程进行仿真分析。最大初始速度70 km/h,初始间隙为35 mm时,将车体等效为刚体,同时受到悬浮力、磁阻力和重力。其中,磁阻力使得车体减速,从而悬浮力降低,进而引起悬浮间隙变小,反过来又使得悬浮力增大,如此往复,当悬浮高度减小为0时结束迭代计算。图25给出了仿真模拟结果与测试结果的对比,其中测试的悬浮力是通过垂向加速度进行换算得到。测试值与仿真整体的变化趋势相似,但测试值的波动更大,主要原因是车体受到较大冲击且质量分布不均匀,使得下降和上升的过程不一致,进而导致测试的加速度存在误差。
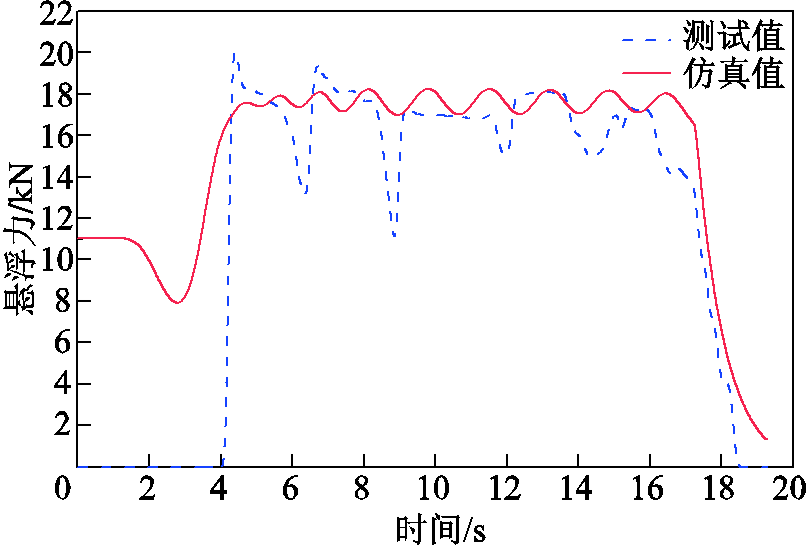
图25 速度70 km/h,间隙35 mm的测试值与仿真值对比
Fig.25 Comparison of test and simulation results with v= 70 km/h, gap= 35 mm
本文设计并研制了一种基于汽车的平板式永磁电动悬浮系统。有限元仿真和等效实验相结合对系统的电磁特性进行研究,并提出一种可有效提高横向稳定性的导向磁体,最后完成了最高速度为70 km/h的样机测试实验,实现了载重1.5 t、最大悬浮高度35 mm的自由悬浮。等效实验结合无导向磁体的样机测试结果表明,平板式永磁电动悬浮系统具有垂向自稳定的能力,但几乎没有导向能力。磁体偏离轨道会导致系统受到推力和力矩的作用,加剧车体偏离,使得系统失稳。加装了导向磁体的样机测试,结果验证了导向系统可有效地提高系统的稳定性,同时也证实了系统较强的载重能力和垂向自稳定能力。测试的悬浮力与仿真的悬浮力趋势基本一致,也验证了设计方法和仿真模型的合理性。
参考文献
[1] 邓自刚, 刘宗鑫, 李海涛, 等. 磁悬浮列车发展现状与展望[J]. 西南交通大学学报, 2022, 57(3): 455-474, 530. Deng Zigang, Liu Zongxin, Li Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474, 530.
[2] 秦伟, 马育华, 吕刚, 等. 一种可用于低真空管道的高温超导无铁心直线感应磁悬浮电机[J]. 电工技术学报, 2022, 37(16): 4038-4046. Qin Wei, Ma Yuhua, Lü Gang, et al. Analyzing and designing a novel coreless linear induction maglev motor for low vacuum pipeline[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4038-4046.
[3] 秦伟, 马育华, 张洁龙, 等.不均匀气隙工况下轴向磁通永磁电动式磁悬浮电机的磁场与力特性分析[J]. 电工技术学报, 2023, 38(4): 889-902. Qin Wei, Ma Yuhua, Zhang Jielong, et al. Characteristic and magnetic field analysis of an axial flux permanent magnets maglev motor with non-uniform air gap[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 889-902.
[4] Deng Zigang, Zhang Weihua, Wang Li, et al. A high-speed running test platform for high-temperature superconducting maglev[J]. IEEE Transactions on Applied Superconductivity, 2022, 32(4): 3603605.
[5] 朱进权, 葛琼璇, 王晓新, 等. 基于自抗扰和负载功率前馈的高速磁悬浮系统PWM整流器控制策略[J]. 电工技术学报, 2021, 36(2): 320-329. Zhu Jinquan, Ge Qiongxuan, Wang Xiaoxin, et al. Control strategy for PWM rectifier of high-speed maglev based on active disturbance rejection control and load power feed-forward[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 320-329.
[6] 章九鼎, 卢琴芬. 长定子直线同步电机齿槽效应的计算与影响[J]. 电工技术学报, 2021, 36(5): 964-972, 1026. Zhang Jiuding, Lu Qinfen. Calculation and influences of cogging effects in long-stator linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 964-972, 1026.
[7] 朱进权, 葛琼璇, 孙鹏琨, 等. 高速磁悬浮列车在双端供电模式下的电流控制策略[J]. 电工技术学报, 2021, 36(23): 4937-4947. Zhu Jinquan, Ge Qiongxuan, Sun Pengkun, et al. Current control strategy for high-speed maglev in the double feeding mode[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4937-4947.
[8] Halbach K. Design of permanent multipole magnets with oriented rare earth cobalt material[J]. Nuclear Instruments and Methods, 1980, 169(1): 1-10.
[9] 王一宇,蔡尧,宋旭亮,等.零磁通式电动悬浮等效模拟系统的特性分析与实验[J].电工技术学报,2021, 36(8): 1628-1635. Wang Yiyu, Cai Yao, Song Xuliang, et, al. Characteristic analysis and experiment of the equivalent simulation system for null-flux electrodynamic suspension [J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1628-1635.
[10] Galluzzi R, Circosta S, Amati N, et al. A multi-domain approach to the stabilization of electrodynamic levitation systems[J]. Journal of Vibration and Acoustics, 2020, 142(6): 061004.
[11] França T N, Shi H, Deng Z, et al. Study of a null-flux suspension system using permanent magnet Halbach arrays[C]//2020 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Tianjin, China, 2020: 1-2.
[12] 贺光, 成玉卫, 龙志强. 基于直线型Halbach结构的永磁电动悬浮系统的设计与实现[J]. 磁性材料及器件, 2010, 41(6): 36-40, 45. He Guang, Cheng Yuwei, Long Zhiqiang. Design and realization of permanent-magnet EDS system based on linear Halbach structure[J]. Journal of Magnetic Materials and Devices, 2010, 41(6): 36-40, 45.
[13] Jacobs W A. Magnetic launch assist-NASA’s vision for the future[J]. IEEE Transactions on Magnetics, 2001, 37(1): 55-57.
[14] Fang Jiarong, Montgomery D B, Roderick L. A novel MagPipe pipeline transportation system using linear motor drives[J]. Proceedings of the IEEE, 2009, 97(11): 1848-1855.
[15] Montgometry D. Overview of the 2004 magplane design[C]//International Conference on Magnetically Levitated Systems and Linear Drives, Argonne, Japan, 2004:106-113.
[16] GENERAL ATOMICS. Low speed maglev technology development program[R]. San Diego, CA United States, 2002: 1-59.
[17] Gurol S, Baldi B. Overview of the general atomics urban maglev technology development program[C]// Proceedings of ASME/IEEE 2004 Joint Rail Conference, Baltimore, Maryland, USA, 2008: 187-191.
[18] Abdelrahman A S, Sayeed J, Youssef M Z. Hyperloop transportation system: analysis, design, control, and implementation[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7427-7436.
[19] 王厚生. 永磁电动式导体板磁悬浮列车轨道结构及相关研究[D]. 北京: 中国科学院电工研究所, 2004.
[20] 陈殷. 低速永磁电动悬浮电磁力特性研究[D]. 成都: 西南交通大学, 2015.
[21] 陈殷, 张昆仑. 板式双边永磁电动悬浮电磁力计算[J]. 电工技术学报, 2016, 31(24): 150-156. Chen Yin, Zhang Kunlun. Calculation of electromagnetic force of plate type null double side permanent magnet electrodynamic suspension[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 150-156.
[22] 李春生, 王武, 杜玉梅, 等. 直线型Halbach磁体和导体板构成的电动式悬浮系统的实验装置设计[J]. 工程设计学报, 2008, 15(1): 33-36. Li Chunsheng, Wang Wu, Du Yumei, et al. Experimental facility design of EDS maglev with linear Halbach PM and conducting sheet[J]. Journal of Engineering Design, 2008, 15(1): 33-36.
[23] 陈殷, 李耀华, 李艳. 板式双边永磁电动悬浮三维解析计算[J]. 铁道工程学报, 2019, 36(12): 29-34. Chen Yin, Li Yaohua, Li Yan. Three-dimensional analytical calculation of plate-type double permanent magnet electrodynamic suspension[J]. Journal of Railway Engineering Society, 2019, 36(12): 29-34.
[24] 巫川, 李冠醇, 王东. 永磁电动悬浮系统三维解析建模与电磁力优化分析[J]. 电工技术学报, 2021, 36(5): 924-934. Wu Chuan, Li Guanchun, Wang Dong. 3-D analytical modeling and electromagnetic force optimization of permanent magnet electrodynamic suspension system[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 924-934.
[25] Zhu Hanlin, Huang Huan, Zheng Jun, et al. A numerical calculation model of multi-magnet-array and 8-shaped null-flux coil for permanent magnet EDS vehicle system[J]. IEEE Transactions on Magnetics, 2022, 58(5): 8300311.
[26] Duan Jiaheng, Xiao Song, Zhang Kunlun, et al. Analysis and optimization of asymmetrical double-sided electrodynamic suspension devices[J]. IEEE Transactions on Magnetics, 2019, 55(6): 8300605.
[27] Shi Tongyu, Wang Dazhi. 3D Analytical model of drag and lift force for a conductive plate moving above a Halbach magnet array[J]. Transactions of the Institute of Measurement and Control, 2018, 40(12): 3515-3524.
[28] Hu Yongpan, Long Zhiqiang, Zeng Jiewei, et al. Analytical optimization of electrodynamic suspension for ultrahigh-speed ground transportation[J]. IEEE Transactions on Magnetics, 2021, 57(8): 8000511.
[29] Hu Yongpan, Long Zhiqiang, Xu Yunsong, et al. Control-oriented modeling for the electrodynamic levitation with permanent magnet Halbach array[J]. International Journal of Applied Electromagnetics and Mechanics, 2021, 67(3): 375-392.
[30] Flankl M, Wellerdieck T, Tüysüz A, et al. Scaling laws for electrodynamic suspension in high-speed transportation[J]. IET Electric Power Applications, 2018, 12(3): 357-364.
[31] Montgometry D. Overview of the 2004 magplane design[C]// International Conference on Magnetically Levitated Systems and Linear Drives, Bedford, MA, USA, 2004:106-113.
[32] 石洪富, 邓自刚, 黄欢, 等. 零磁通线圈式车载Halbach永磁阵列电动悬浮系统设计及特性研究[J]. 西南交通大学学报, 2023, 58(4): 853-862. Shi Hongfu, Deng Zigang, Huang Huan, et al. Design and characteristic studies of null-flux electrodynamic suspension system with on-board halbach array[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 853-862.
[33] 罗成, 张昆仑, 靖永志. 新型Halbach阵列永磁电动悬浮系统垂向稳定性[J]. 交通运输工程学报, 2019, 19(2): 101-109. Luo Cheng, Zhang Kunlun, Jing Yongzhi. Vertical stability of permanent magnet EDS system with novel Halbach array[J]. Journal of Traffic and Transportation Engineering, 2019, 19(2): 101-109.
[34] 王莉, 熊剑, 张昆仑, 等. 永磁和电磁构成的混合式悬浮系统研究[J]. 铁道学报, 2005, 27(3): 50-54. Wang Li, Xiong Jian, Zhang Kunlun, et al. Research of hybrid suspension system made of permanent-and electromagnets[J]. Journal of the China Railway Society, 2005, 27(3): 50-54.
Abstract A flat-type permanent magnet electromagnetic suspension system (PM EDS) integrated with a car is proposed, and a proof-of-principle prototype, along with a 50-m long test guideway made of copper, is developed. Initially, a new topology structure is introduced, encompassing levitation magnets, guidance magnets, suspension frame, and a gap adjustment mechanism. In this design, the car utilizes car’s engine and run-up wheels to provide various initial speeds during take-off, thereby reducing the excessive cost associated with the linear motor. The levitation magnets are utilized to counteract the vehicle weight, while the guidance magnets enhance lateral stability. Furthermore, the PM EDS system undergoes experimental treatment under fixed parameters using a high-speed test rig with a diameter of 2500 mm and a maximum design speed of 600 km/h. Through equivalent experiments, the levitation, guidance, and drag forces are tested under increasing speeds ranging from 0 to 260 km/h. Reciprocating motions are used toconfirmthe vertical self-stability ability of PM EDS system. The results reveal that the levitation force is highly dependent on the levitation gap, and it is necessary to design a reasonable levitation gap according to the load demand. An excessive or too small levitation gap can trigger or exacerbate vertical instability. Subsequently, the entire system is designed and studied using three-dimensional finite element analysis (FEA), and its accuracy is verified by measurement results under identical parameters. Based on the levitation-weight-ratio (LWR) and the levitation-drag-ratio (LDR), the detailed parameters of the levitation magnets and the conductive plate are determined.Especially, as the thickness of the conductive plate increases, the levitation force initially increases then decreases, and ultimately stabilizes at a stationary value. The saturation thickness closely aligns with the skin depth dependent on the speed. The levitation force exhibits an initial increase followed by a stable value as the width of the conductive plate increases. The maximum levitation force increases by 39% compared to the initial width of the magnets when the conductive plate width matches that of the magnets. Additionally, a sample suspension frame is manufactured to connect the onboard magnets to the car and accommodate the test devices. The gap adjustment mechanism is fabricated to replace the previous shock absorber, providing ease in adjusting the installation height of the magnets. The specific screw pitch of 6 mm enables precise gap adjustment, where each complete rotation of the screw corresponds to a height increase or decrease of 6 mm. An integrated test system is constructed, which includes the installation of four HD cameras evenly positioned at the corners of the suspension frame to monitor the car wheels. Additionally, four laser displacement sensors are placed near each wheel to measure the variable levitation gap. A nine-axis sensor is mounted at the center of the vehicle body to record timely three-axis accelerations and deflection angles. Finally, the line test is conducted in two processes. During the first phase, only the levitation magnets are used to assess the guidance ability. In the other phase, both guidance and levitation magnets are employed to enhance lateral stability, while analyzing the levitation gaps, accelerations, and deflection angles within the speed range of 40 km/h to 70 km/h. The entire vehicle, weighing 1.5 t, is suspended freely in the air with gap=35 mm. The PM EDS system exhibits notable weak guidance ability, as confirmed by the guidance magnets limiting the maximum deflection angle to 10°. Therefore, the effectiveness of the guidance magnets is demonstrated. Furthermore, the measured levitation force aligned with the simulated results at a speed of 70 km/h and a gap of 35 mm.
Keywords: Permanent magnet electrodynamic suspension, equivalent experiment, proof-of-principleprototype, high-speed experiment rig, guidance magnets
DOI: 10.19595/j.cnki.1000-6753.tces.222325
中图分类号:TM154.2
四川省科技厅项目(22JDTD0011)和江苏省交通运输厅科技项目(2021Y02)资助。
收稿日期 2022-12-13
改稿日期 2023-01-03
石洪富 男,1993年生,博士研究生, 研究方向为电动悬浮及直线驱动。E-mail: 18223169363@163.com
邓自刚 男,1982年生,研究员, 博士生导师,研究方向为磁悬浮技术及应用。E-mail: deng@swjtu.cn(通信作者)
(编辑 郭丽军)