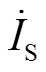 与
与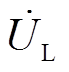 与
与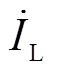 分别为整流桥的输入电压与输入电流。
分别为整流桥的输入电压与输入电流。摘要 为了实现具有恒压特性的双线圈无线电能传输(WPT)系统中补偿网络的优化设计,该文在变压器T网络模型基础上定义等效耦合系数kr与等效变比n1,为双线圈WPT系统的高阶补偿网络设计与分析提供一种新方法。首先建立变压器T网络等效模型,给出具有恒压特性的串联-串联(S-S)型双线圈WPT系统元件参数表达式。其次结合等效耦合系数与等效变比,提出具有可变增益恒压特性的串联/并联-串联(SP-S)型与串联/并联-串联/并联(SP-PS)型双线圈WPT系统的补偿网络参数确定的新方法。在此基础上,考虑寄生电阻对系统传输特性的直接影响,以WPT系统的电压增益稳定性与传输效率为指标,得出不同等效参数下传输特性表达式,推导出在线圈偏移情况下最佳等效参数kr与n1的表达式,为WPT系统的补偿网络的优化设计提供理论依据。最终通过实物实验验证所提系统的恒压输出特性及其参数设计方法的正确性和有效性。
关键词:无线电能传输 补偿网络 传输效率 线圈偏移 变压器T网络等效模型
无线电能传输(Wireless Power Transfer, WPT)技术作为一种随着近些年来电力电子技术的蓬勃发展而飞速成熟的新兴技术,可较好地解决传统有效供电模式存在的不足,为复杂环境内智能化装备稳定可靠运行提供有效的解决方法[1-5]。
实际中大多用电设备要求其供电电源具有恒压特性,即输入电源电压不随着负载等效阻值的变化而变化[6-7]。现有文献针对双线圈WPT系统,通过建立耦合电感模型,分析单阶及多阶拓扑形式系统的传输特性,给出谐振元件间的约束参数关系,提出多种具有恒定输出特性的补偿网络[8-12]。其中在设计谐振网络参数的基础上,通过分析系统的传输效率、系统稳定性与全谐波畸变率等对补偿网络进一步进行参数限制[10]。
在模型建立方面,文献多采用耦合电感模型完成WPT系统传输特性分析,但分析高阶补偿网络参数较为复杂。同时文献[13-16]提出采用传输参数矩阵推导二端口网络输出恒定的一般性条件,得出具有恒定特性的电场耦合WPT系统补偿网络与磁感应耦合式WPT系统谐振电路。陈庆彬等在耦合电感模型的基础上,提出变压器T网络等效模型来确定恒定输出特性下补偿网络参数,从而实现多阶电路的解耦,并基于变压器T网络等效模型来等效参数的多解性,该模型有助于拓宽输出电压增益范围[17-18]。
在补偿网络参数分析方面,动态偏移(频率振荡、线圈偏移)下传输性能稳定性也是评价系统补偿网络的方法之一。文献[18]通过优化中继线圈的谐振电容,使得三线圈WPT系统的电压增益具有更好的频率偏移特性。文献[19]研究具有不同谐振网络结构的双线圈WPT系统在动态偏移下传输特性的变化情况。且相对于多线圈结构,双线圈WPT系统虽在传输距离与传输效率上有所不足,但可通过设计控制策略或增加补偿网络阶数的方式来提升WPT系统的传输特性。如文献[20]构造分数阶自治电路无线电能传输系统,使得双线圈WPT系统的传输特性对动态偏移不敏感。但对于双线圈WPT系统能否仅通过谐振网络的设计使得系统既具有可变的恒压增益又可保持良好的偏移特性的相关研究依然较少。
因此本文以双线圈WPT系统为研究对象,定义等效变比n1与等效耦合系数kr,将高阶补偿网络参数融入变压器T网络模型中,并基于变压器T网络等效模型,设计具有可变增益恒压特性的串联-串联(Series-Series, S-S)型、原边侧高阶补偿网络串联/并联-串联(Series/Parallel-Series, SP-S)型与原、副边侧高阶补偿网络串联/并联-并联/串联(Series/Parallel-Parallel/Series, SP-PS)型双线圈WPT系统补偿网络。其次,考虑寄生电阻对电压稳定性的直接影响,分析在不同等效变比n1与等效耦合系数kr的情况下,双线圈WPT系统电压增益受线圈偏移与频率振荡的影响情况,以及不同补偿网络下系统的传输效率。所提出的补偿网络设计与传输特性分析方法,电路模型简单,设计思路清晰,参数选择灵活。最后实现双线圈WPT系统输出可变增益的稳定电压,并有效提高系统的传输效率以及电压增益稳定性。
图1为双线圈WPT系统的主要拓扑结构,L1和L2分别为收发线圈等效电感(忽略寄生电阻),其中线圈间的互感为M。如图1a所示,双线圈WPT系统发射线圈由直流电压源经高频变换器激励供给能量,通过磁耦合谐振的方式将高频无线电能传递至接收线圈,并通过整流桥和滤波电路供给负载。图1a中,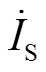 与
与![]() 分别为DC-AC变换器输出电流与输出电压;RL为整流桥、LC滤波电路与实际负载RLR的等效负载;Lp、C1与Ls、C2分别为原边侧与副边侧的谐振元件;
分别为DC-AC变换器输出电流与输出电压;RL为整流桥、LC滤波电路与实际负载RLR的等效负载;Lp、C1与Ls、C2分别为原边侧与副边侧的谐振元件;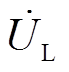 与
与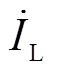 分别为整流桥的输入电压与输入电流。
分别为整流桥的输入电压与输入电流。
如图1b所示,本文的设计方法为首先根据S-S型拓扑电路,采用变压器T网络模型,得出恒压状态下补偿网络参数表达式;其次等效SP-S型与SP-PS型高阶补偿网络为S-S型电路来进行参数设计。具体步骤为:将原边侧补偿网络与交流电源电压![]() 等效为电压UD和元件C1,其作用是通过降低原边侧补偿网络阶数,改变变压器T网络等效模型的电压增益,增加系统谐振参数设计的自由度。将副边侧补偿网络Sn与双线圈模型替换为等效线圈模型,其中将收发线圈等效电感L1与L2转换为Lr1与Lr2,双线圈实际互感M等效为Mr。该设计方法为高阶补偿网络参数的确定提供一种新思路,实现不同增益下不同补偿网络结构WPT系统的恒压输出。
等效为电压UD和元件C1,其作用是通过降低原边侧补偿网络阶数,改变变压器T网络等效模型的电压增益,增加系统谐振参数设计的自由度。将副边侧补偿网络Sn与双线圈模型替换为等效线圈模型,其中将收发线圈等效电感L1与L2转换为Lr1与Lr2,双线圈实际互感M等效为Mr。该设计方法为高阶补偿网络参数的确定提供一种新思路,实现不同增益下不同补偿网络结构WPT系统的恒压输出。
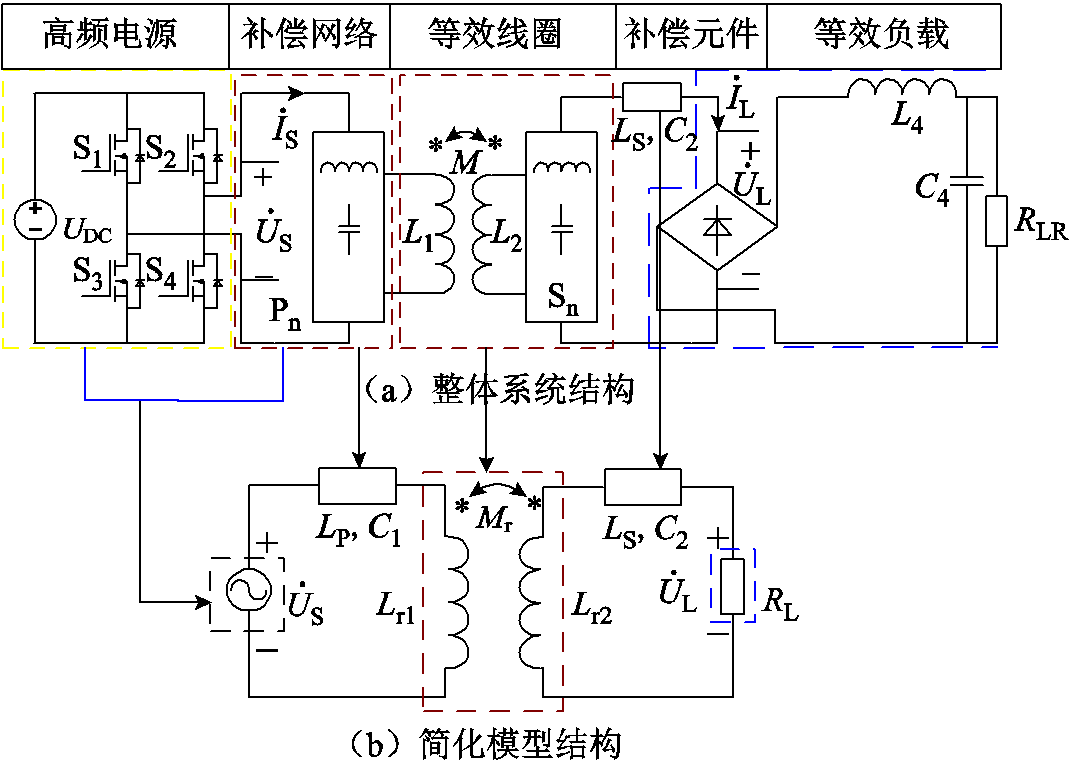
图1 双线圈WPT系统拓扑结构
Fig.1 Schematic diagram of two-coil system structure
根据文献[10]所知,系统的整流滤波电路与负载电阻RLR可以等效为电阻RL,即
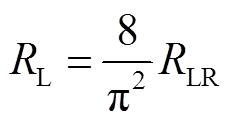 (1)
(1)
图2是S-S型WPT系统等效电路。该模型中Lpk(Cpk)、Lsk(Csk)分别为原、副边侧的等效漏感;Lm为变压器T模型的等效励磁电感;n为变压器T网络数学模型的实际电压比,该电压比不同于变压器的匝数比,理论上可为任意值[18]。
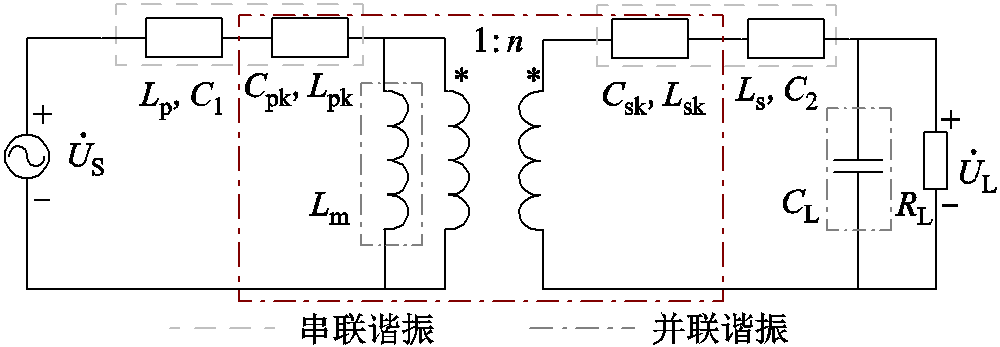
图2 S-S型WPT系统等效电路
Fig.2 Equivalent circuit of S-S WPT system
图2中当原、副边侧谐振元件Lp、C1和Ls、C2对变压器T网络等效模型的分布参数完全补偿后,磁耦合WPT系统的目标电压增益GV0等于变压器T网络等效模型中实际电压比n,最终实现可变增益的恒压输出特性,并有效拓宽系统增益范围。其中在变压器副边并联谐振元件CL对等效模型中励磁电感Lm进行补偿,不仅可减少高频激励源的输出容量,还有助于提高系统的传输效率[18]。
虽然图1所示双线圈耦合电感模型与图2的变压器T网络等效模型的组成参数不同,但都描述同一磁耦合系统的传输特性,应具有相同的二端口阻抗网络参数矩阵。其中图1b描述的耦合电感模型的阻抗矩阵为
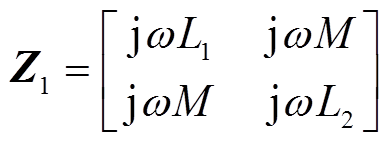 (2)
(2)
而由图2可将变压器T网络模型的二端口网络阻抗参数矩阵可表示为
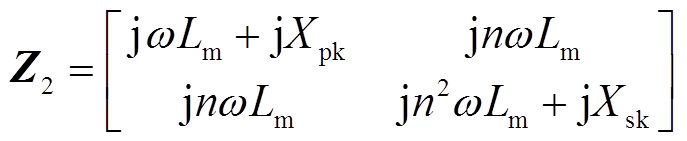 (3)
(3)
式中,Xpk与Xsk分别为原、副边侧的等效漏感值。根据二端口网络等效理论,式(2)与式(3)应具有相同的阻抗参数矩阵,即Z1=Z2,可得出变压器T网络模型中等效参数[18]为
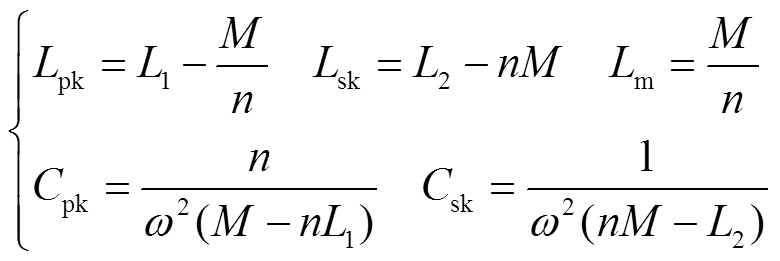 (4)
(4)
当补偿元件满足图2所示的谐振关系时,系统电压增益Gv达到变压器T网络模型电压比n。因此可得出系统原、副边侧谐振元件参数表达式[18]为
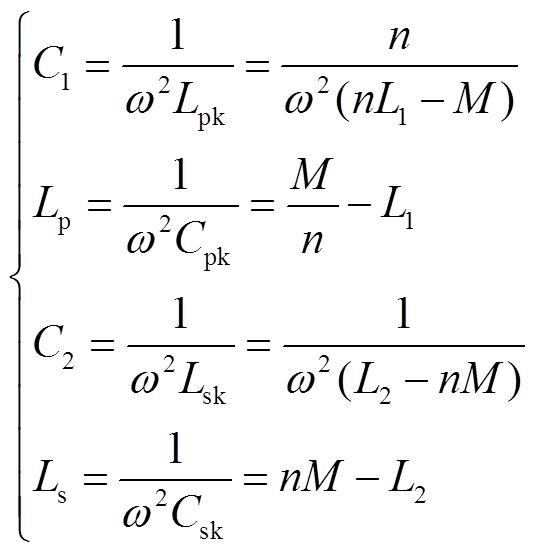 (5)
(5)
在不同变比n与互感M的情况下,可将S-S型拓扑电路拆分为三种电路形式,如图3所示。定义参数β=n(L1/L2)0.5,在长距离传输情况下当耦合系数k≤min(β,1/β)时,选用图3a电路;而系统处于强耦合状态下,当耦合系数k满足1/β<k<β时,选择图3b谐振网络;图3c电路拓扑网络适用于β<k<1/β的情况。
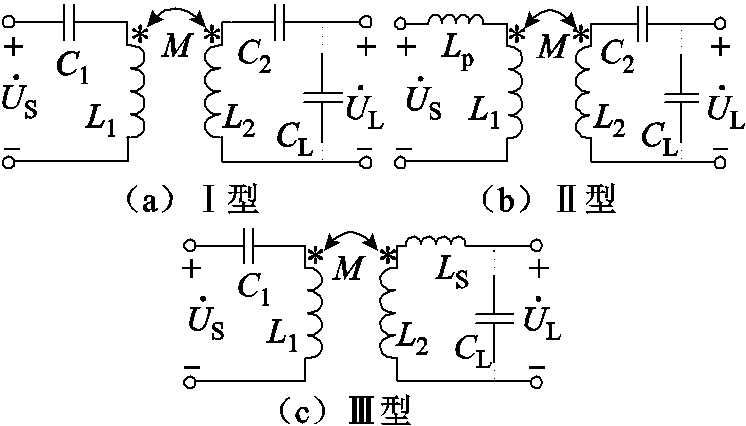
图3 S-S型WPT系统补偿结构
Fig.3 S-S WPT system compensation structure
根据图1b所示电路可得出,在远距离传输的情况下,S-S型WPT系统电压增益GV(忽略寄生电阻)与传输效率η分别为
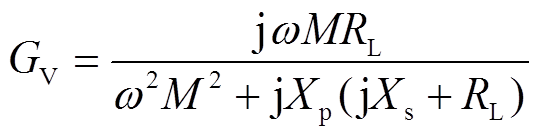 (6)
(6)
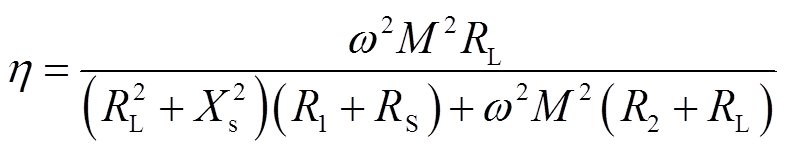 (7)
(7)
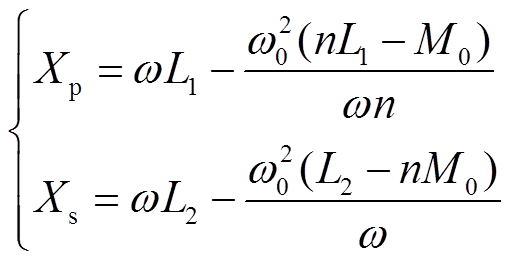 (8)
(8)
式中,RS、R1与R2分别为等效电源、发射线圈与接收线圈的寄生电阻。式(8)为远距离传输下Xp与Xs的具体表达式,其中Xp与Xs为原、副边侧回路电抗值,ω0与M0为稳态下双线圈WPT系统的谐振角频率与互感值,而ω和M为系统发生偏移(频率振荡与线圈偏移)时的工作角频率与互感。
除了S-S型补偿网络结构(见图3a),磁耦合谐振式无线电能传输(Magnetic Coupling Resonant, MCR-WPT)系统常采用原边侧高阶补偿网络结构(SP-S型)与原、副边侧高阶补偿网络结构(SP-PS型)进行长距离能量无线传输。
SP-S型WPT系统补偿结构如图4所示。本节先设计具有恒压输出特性的SP-S型补偿网络元件参数。如图4所示,按照设计思路先将目标变比为n的SP-S型WPT系统替换为等效变比为n1的S-S型WPT系统,可得出S-S型WPT系统的等效变比n1为
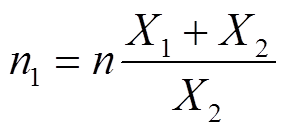 (9)
(9)
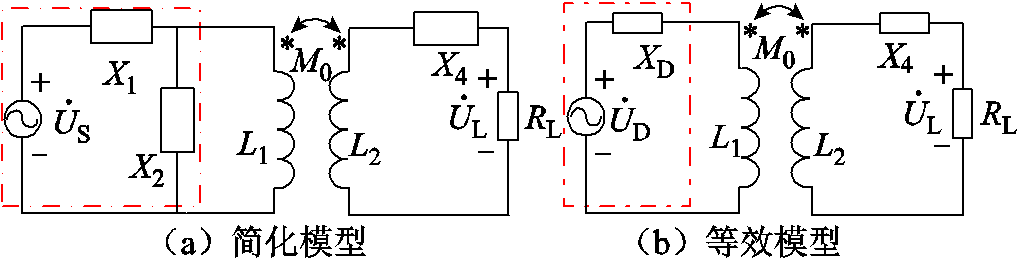
图4 SP-S型WPT系统补偿结构
Fig.4 SP-S WPT system compensation structure
由图4b建立变压器T网络模型并得出系统原边侧补偿元件等效电抗值为
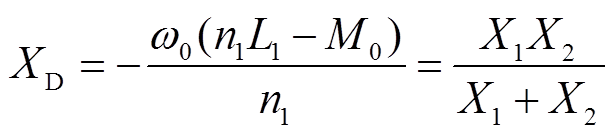 (10)
(10)
由式(9)和式(10)可得出原边侧谐振电抗分别为
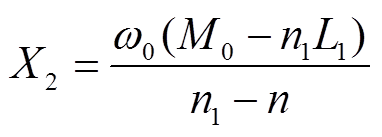 (11)
(11)
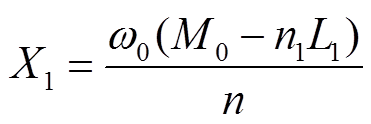 (12)
(12)
且副边侧谐振元件电抗值X4为
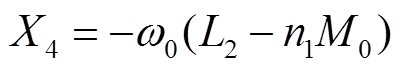 (13)
(13)
其中,变压器T网络模型的实际变比n等于系统的目标电压增益GV0;等效变比n1为设计参数,该变比不同于实际变比n(目标电压增益),理论值可为任何值(大于或小于实际变比n)。
与S-S型拓扑结构类似,SP-S型双线圈WPT系统(n>0)亦可拆分不同的电路形式。当M0/L1<n1<n时,双线圈WPT系统原边侧补偿网络满足X1<0<X2;当n<n1<M0/L1时,补偿网络的约束条件为min(X1, X2)>0;当n1<min(n, M0/L1)或min(n, M0/L1)<n1时,补偿网络满足X2<0<X1。对于副边侧谐振元件,则需要根据等效变比n1与L2/M0进行判断。
SP-PS型WPT系统补偿结构如图5所示,按照设计思路将SP-PS型WPT系统等效为S-S型WPT系统,再通过变压器T网络模型进行补偿网络参数设计。具体操作为:电源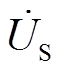 与元件X1和X2转换为等效电源
与元件X1和X2转换为等效电源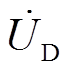 与谐振元件C1,收发线圈与副边侧补偿网络转换为等效双线圈模型。而图5a中收发线圈与谐振元件电抗值X3采用二端口网络阻抗参数矩阵为
与谐振元件C1,收发线圈与副边侧补偿网络转换为等效双线圈模型。而图5a中收发线圈与谐振元件电抗值X3采用二端口网络阻抗参数矩阵为
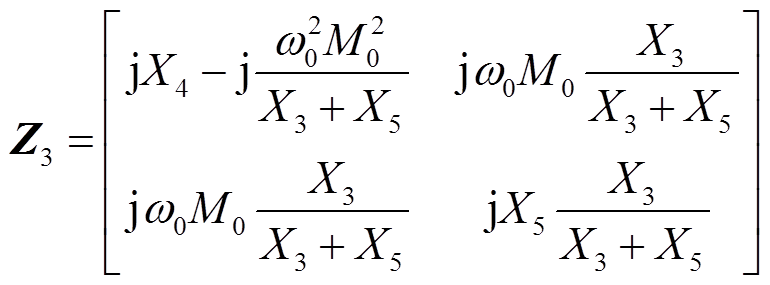 (14)
(14)
式中,X4=ωL1与X5=ωL2为收发线圈的电抗值。依据二端口网络等效理论,式(14)与式(2)应具有相同的阻抗参数矩阵,即Z1=Z3,可得出图5b中等效双线圈WPT系统的等效模型参数为
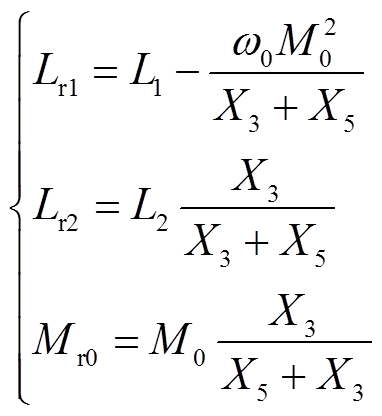 (15)
(15)
图5中X1、X2与X3为谐振元件的电抗值,Mr0为线圈偏移时双线圈系统等效互感稳定值。而系统谐振元件参数与上文推导方式相同,如式(16)所示。
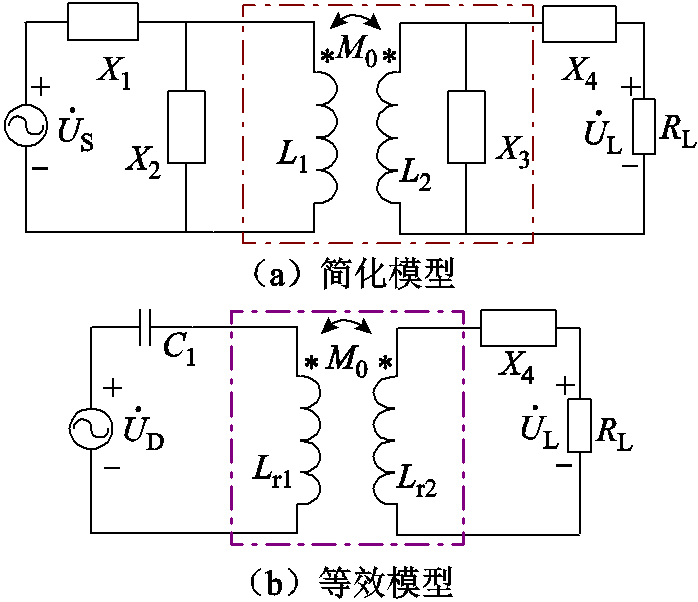
图5 SP-PS型WPT系统补偿结构
Fig.5 SP-PS WPT system compensation structure
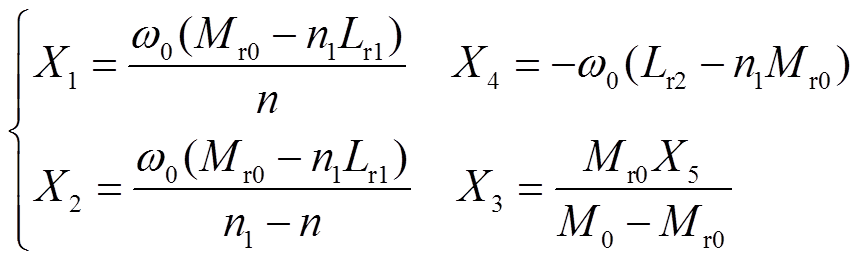 (16)
(16)
如图2所示,为有效降低逆变器的容量,降低逆变器的损耗并提高效率,根据变压器T网络模型,可在负载侧处并联电容CL[17]满足
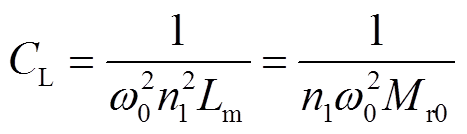 (17)
(17)
参照耦合系数k的定义方法,可将等效互感Mr0表示为
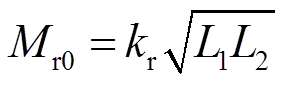 (18)
(18)
式中,等效耦合系数kr不同于实际耦合系数k,可在实数中任意选择设计。综上所述,相比建立耦合电感模型对补偿网络参数求解,采用等效变比n1与等效耦合系数kr(等效互感Mr0)设计高阶补偿网络元件参数,可以既使得WPT系统的输出电压增益满足目标变比n,又使得参数设计方法简化,增加了系统设计的自由度,参数选择更加灵活。同时双线圈WPT系统可根据等效变比n1与等效耦合系数kr进行传输特性分析与补偿网络比较,这为双线圈以及多线圈WPT系统的补偿网络分析与设计提供了一种新思路。
原、副边侧补偿网络作为无线电能传输系统中的重要环节,对整个无线电能传输系统的效率、电压增益、稳定性以及控制策略起着至关重要的作用。特别是线圈发生偏移时,系统电压增益稳定性是辨别系统补偿网络优劣的重要指标之一。
当系统发生线圈偏移时,互感M逐渐变化(M≠M0)。根据双线圈WPT系统简化模型(图5b),可得出在工作频率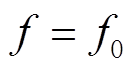 时系统的电压增益(忽略寄生电阻)为
时系统的电压增益(忽略寄生电阻)为
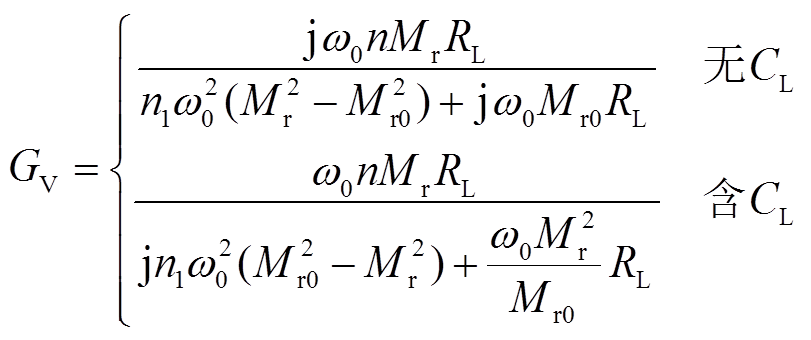 (19)
(19)
式中,Mr为线圈偏移时双线圈系统等效互感实际值,其表达式为
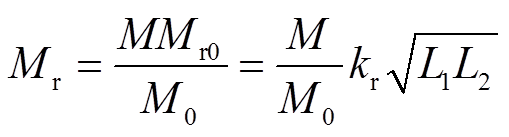 (20)
(20)
由系统电压增益表达式(19),可以看出互感M减少时,系统电压增益小于目标电压增益,且含并联元件CL的WPT系统输出电压高于无CL系统输出电压,因此若线圈发生横向偏移或径向向后偏移时,并联电容CL的方式使得系统具有更高的抗偏移能力。其次是研究不同拓扑结构对系统电压增益的影响,SP-S型WPT系统电压增益随着等效变比n1的增加而先增加后减少,SP-PS型WPT系统电压增益随着等效变比n1或等效耦合系数kr的增加而表现出先增加后减少的趋势。其中当电压增益GV高于目标电压增益GV0时,系统电压增益稳定性表现出较为复杂的趋势。且由表达式(19)可以得出,当n1=0或kr=0时电压增益稳定性保持最佳。
图6是根据实物实验参数得出双线圈WPT系统的电压偏移量随等效参数n1与kr的变化情况,其中在A1区域(n1=0附近)内副边侧谐振电容CL趋近于∞;A3区域(kr=0附近)内SP-PS型拓扑结构中X3≈0,并联补偿元件CL取值接近于∞,此时双线圈WPT系统补偿网络选型困难,应不予分析;同时在A2(n1=Mr0/Lr1)处,由式(9)可看出,具有恒压特性的谐振元件参数设计不成立,且原边侧并联元件电抗值X2=0(发射线圈短接),因此不需考虑该三段电压增益稳定性情况。
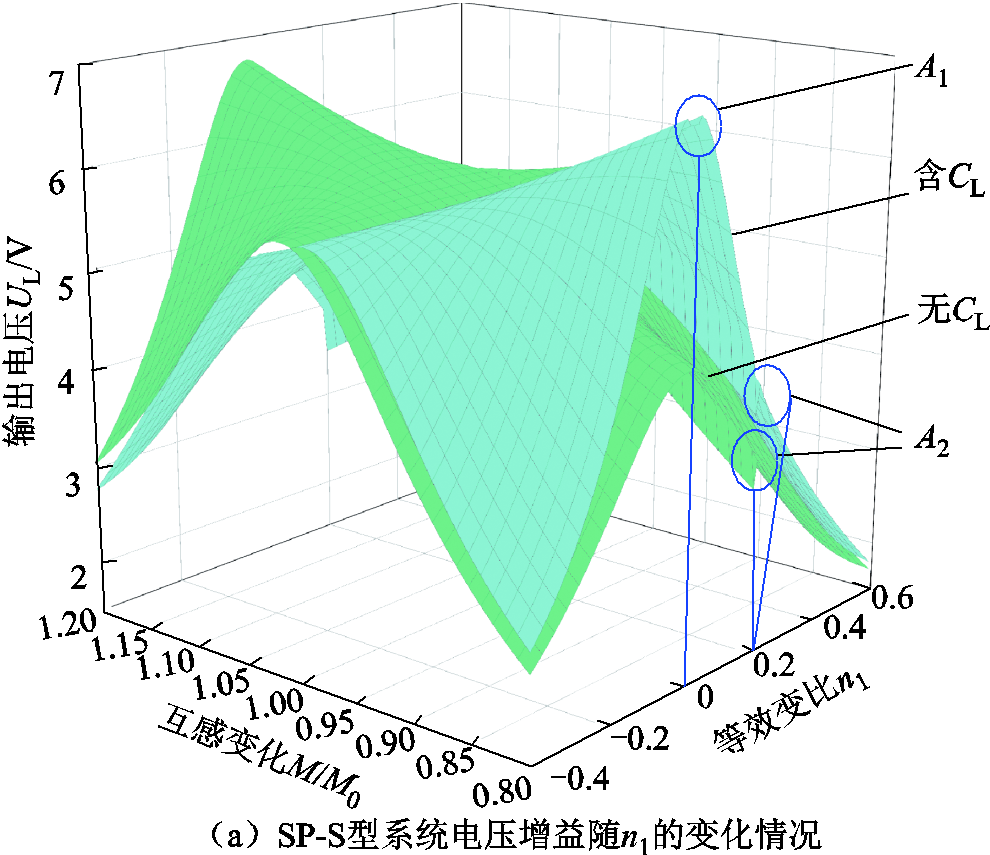
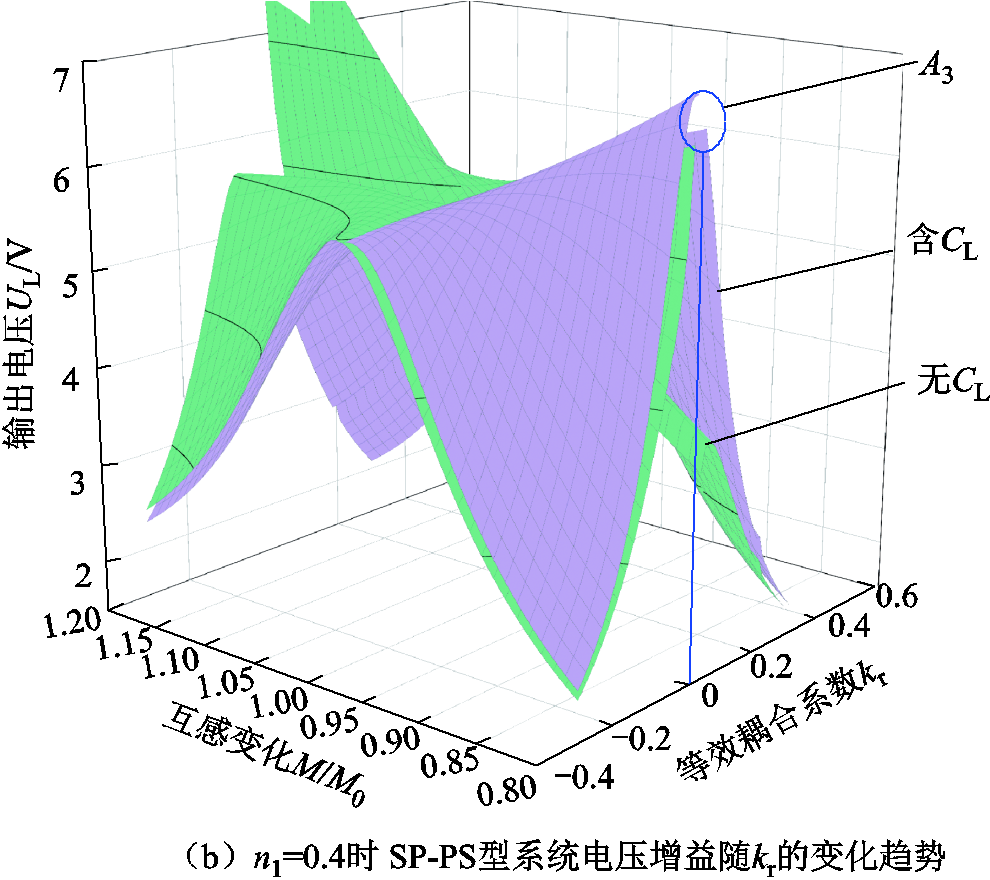
图6 双线圈WPT系统抗线圈偏移能力分析
Fig.6 Analysis of the anti-coil offset ability of two-coil WPT system
图6a为SP-S型双线圈WPT系统的电压增益稳定性变化情况,图6b为n1=0.4时SP-PS型系统电压增益偏移量的变化情况。其中选取n1 =0.4作为分析电压增益随等效耦合系数kr变化情况的约束条件原因在于,n1选择较小时线圈寄生电阻对电压增益的影响越大,电压增益随等效耦合系数变化特性十分复杂,难以求得其变化规律。
如图6所示,在互感减少或增加的情况下,含并联谐振元件CL或无CL时WPT系统电压增益稳定性将随着等效变比n1或等效耦合系数kr的增加而表现出先增强后减弱再增强最后减弱(或先增强后减弱)的趋势。且在互感M减少时双线圈WPT系统电压增益GV皆小于目标电压增益GV0,含并联元件CL的WPT系统输出电压高于无CL状态下,因此可以看出含谐振元件CL的WPT系统具有更好的抗线圈偏移能力。
但由图6可以看出,最佳等效参数与理论分析结果不同,其原因在于随着等效参数n1与kr趋近于某一值时,系统的抗线圈偏移能力就需考虑电源电阻与线圈寄生电阻的影响,而为较准确地得出不同偏移情况下最佳等效参数表达式,本文忽略寄生电阻对回路电抗的间接影响,仅从对电压增益的直接作用进行分析。
根据简化模型(图5b)可得出双线圈WPT系统的电压增益表达式为
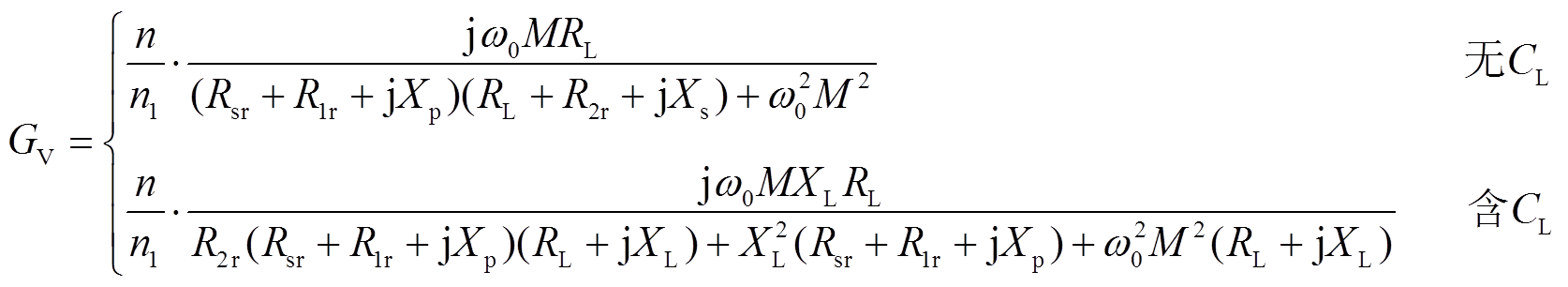 (21)
(21)
式中,原边回路电抗XT=ω0Mr0/n1,副边回路电抗Xs=n1ω0Mr0,副边侧并联补偿元件CL的电抗值XL=-n1ω0Mr0。式(22)为电源电阻等效电阻Rsr、发射线圈等效寄生电阻R1r、接收线圈等效寄生电阻R2r的精确表达式与近似表达式。
 (22)
(22)
因此,将内阻近似表达式(22)代入电压增益表达式(21)中,可得出在线圈偏移情况下不含谐振元件CL时最佳等效参数表达式(23)和阻抗角矫正情况下最佳等效参数表达式(24)。
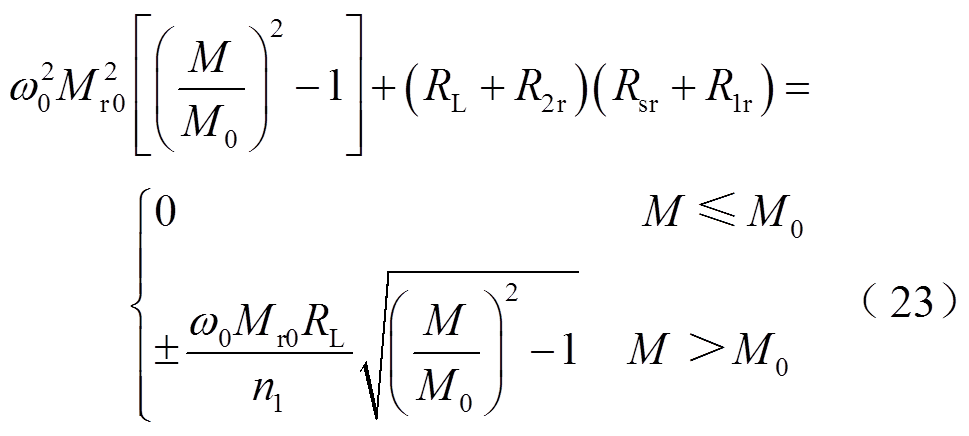
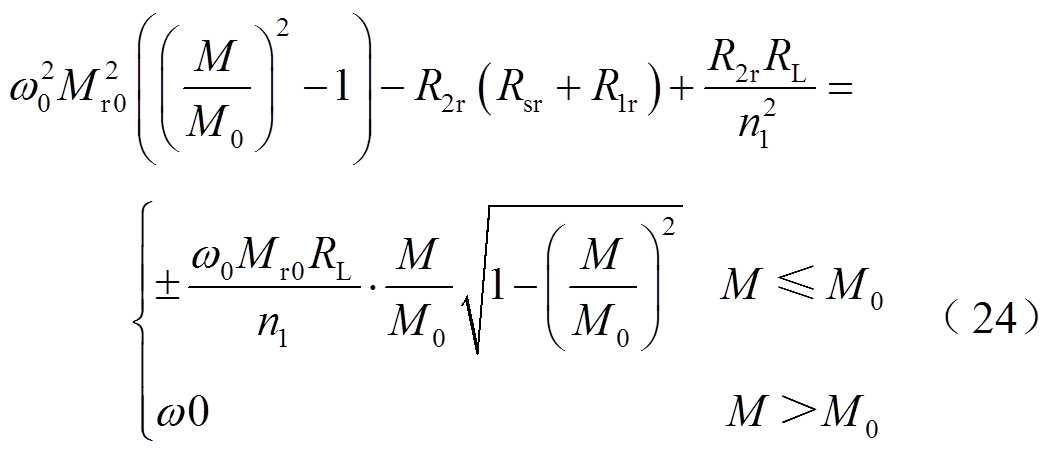
图7为在考虑寄生电阻的情况下SP-S型双线圈WPT系统的最佳等效变比n1及n1=0.4时SP-PS型系统的最佳耦合系数kr准确值随互感M的变化情况,以及由式(23)和式(24)得出相应的最佳等效参数变化曲线。可以发现,在线圈发生较大偏移时,式(23)与式(24)能较准确地描述整个系统的最佳等效参数;在线圈发生较小偏移时,式(23)与式(24)难以正确描述微偏移下最佳等效参数,这是因为微偏移情况下寄生电阻对电压增益的直接作用不明显,且含不同等效参数的WPT系统电压偏移量基本相同。
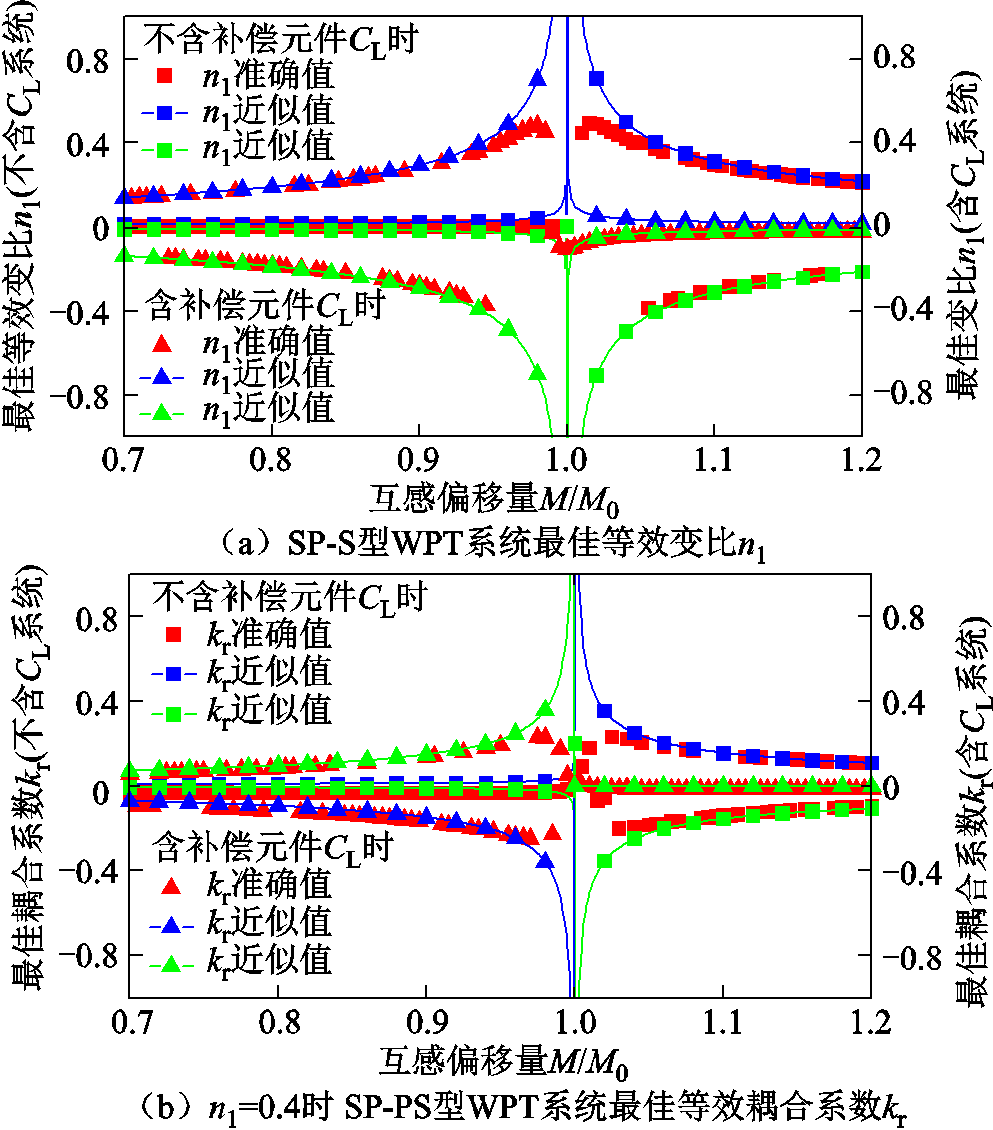
图7 双线圈WPT系统最佳等效参数的变化情况
Fig.7 Variation of the best equivalent parameters of the two-coil WPT system
频率振荡亦是衡量WPT系统补偿网络的方式之一,如图1a所示,处于工作状态下高频逆变器(S1~S4)所输出的电源角频率ω会与目标谐振角频率ω0有微小不同(ω≠ω0),而选择不同等效变比n1与等效耦合系数kr也会改变基于变压器T网络模型设计的双线圈WPT系统的拓扑结构,且其频率稳定性表现也有所不同。根据SP-PS型系统简化模型(图5a)可得出,频率振荡时双线圈WPT系统的电压增益为(忽略寄生电阻)
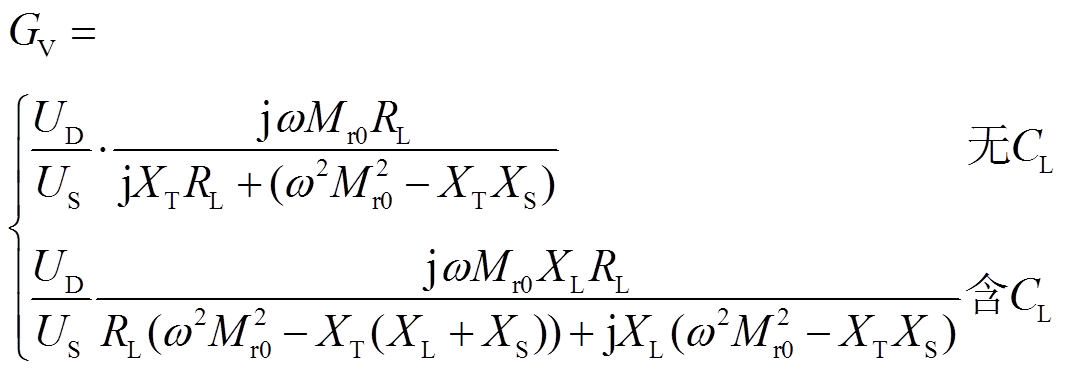 (25)
(25)
式中,系统原边回路等效电抗Xp为原边侧等效谐振元件电抗XC1与等效发射线圈电感XL1之和,副边侧回路电抗Xs为副边侧等效谐振元件电抗XC2与等效接收线圈电感XL2之和,即Xp=XC1+XL1与Xs=XC2+XL2。其具体表达式为
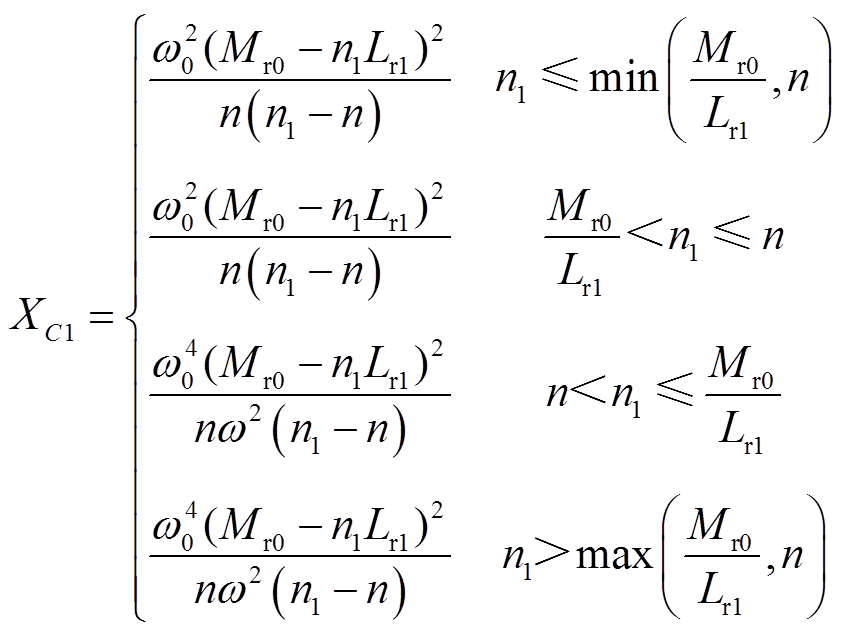 (26)
(26)
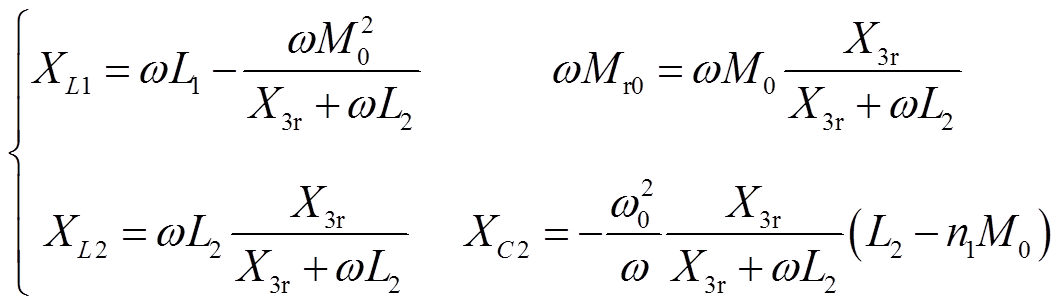 (27)
(27)
式(28)为式(27)中频率振荡下谐振元件电抗X3r的具体表达式。同时不同等效变比n1下等效电源UD与实际电源电压US的比值也有所不同,式(29)为电压比值具体表达式。式(30)为并联谐振元件CL电抗值表达式。
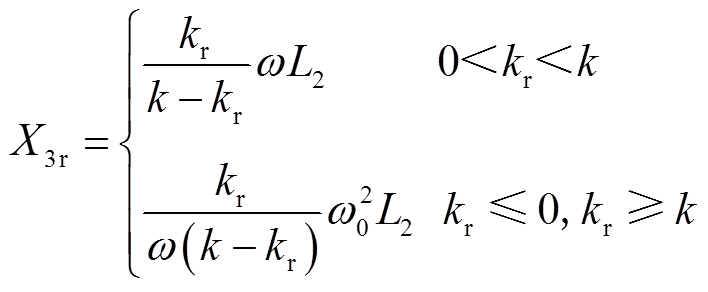 (28)
(28)
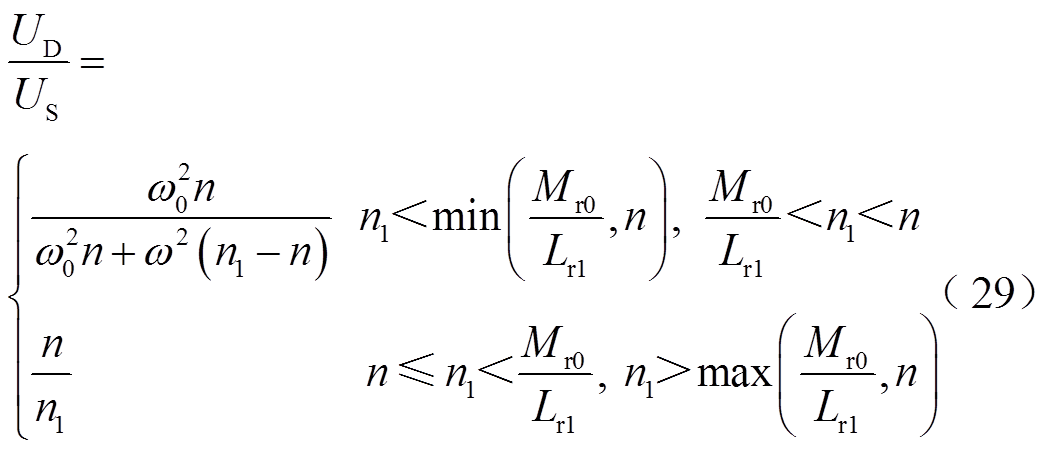
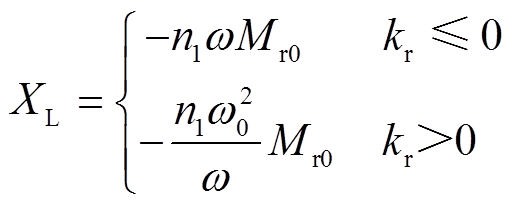 (30)
(30)
由于不同等效参数下谐振元件类型不同,元件频率响应表现出相反的趋势,因此难以清楚分析频率振荡下双线圈WPT系统电压增益随着等效参数的变化趋势。
但从系统电压增益表达式(25)可以看出,在满足式(31)时,含并联谐振元件CL的双线圈WPT系统电压增益低于无CL的WPT系统。
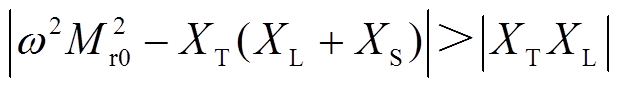 (31)
(31)
在不同等效参数n1与kr下电压增益具体表达式不同,但存在最佳等效参数使得电压增益稳定性保持最佳值。其中等效参数n1与kr对WPT系统抗频率能力的影响情况以及最佳等效参数的设计分析将另文进行深入研究与讨论。
由SP-PS型双线圈WPT系统的简化模型(图5a),可得出双线圈WPT系统的传输效率表达式为
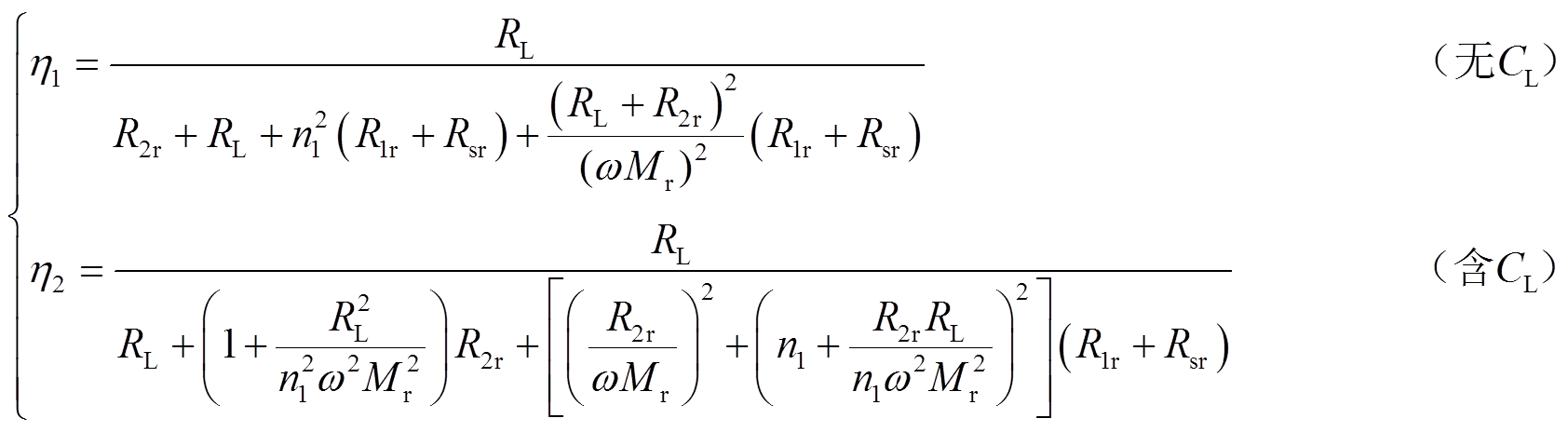 (32)
(32)
式中,η1与η2分别为有无补偿元件CL时系统的传输效率表达式。
首先分析SP-S型与SP-PS型双线圈WPT系统传输效率随等效变比n1的变化情况。根据系统寄生电阻表达式(22),可将传输效率表达式转换为
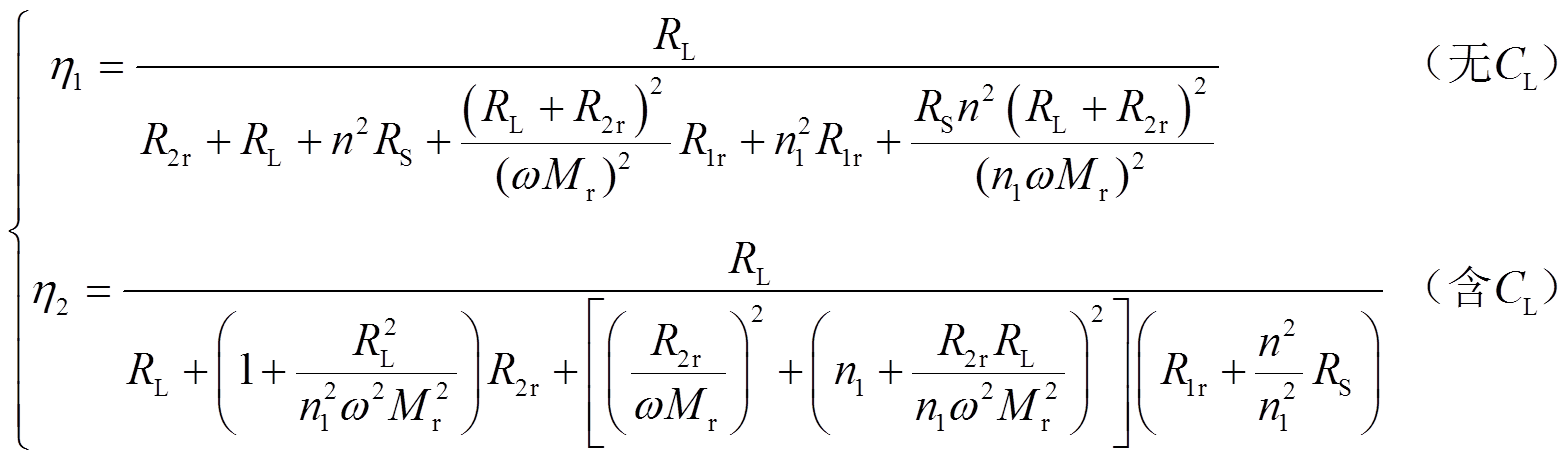 (33)
(33)
式(33)中线圈等效寄生电阻R1r与R2r近似表达式与等效变比n1无关,无并联谐振元件CL的WPT系统传输效率关系式可描述为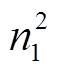 与1/
与1/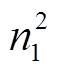 的二元一次函数关系,且对含CL的双线圈WPT系统传输效率表达式求导,可以发现双线圈WPT系统传输效率会随着等效变比
的二元一次函数关系,且对含CL的双线圈WPT系统传输效率表达式求导,可以发现双线圈WPT系统传输效率会随着等效变比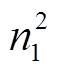 的增加表现出先增加后减少的趋势。
的增加表现出先增加后减少的趋势。
其次分析SP-PS型WPT系统传输效率随等效耦合系数kr的变化情况。由式(22)可知电源等效寄生电阻Rsr不受kr的影响,同时当双线圈WPT系统不含CL元件时,式(32)的RL+R2r中负载电阻RL的影响最大。因此只需考虑耦合系数kr如何影响等效互感Mr与寄生电阻R1r从而分析传输效率的变化趋势。同理,kr对寄生电阻R1r的改变难以影响Rsr+R1r之和,只需分析随着等效耦合系数的增加,等效互感Mr与寄生电阻R2r对传输效率的影响情况。因此,可将传输效率表达式简化为
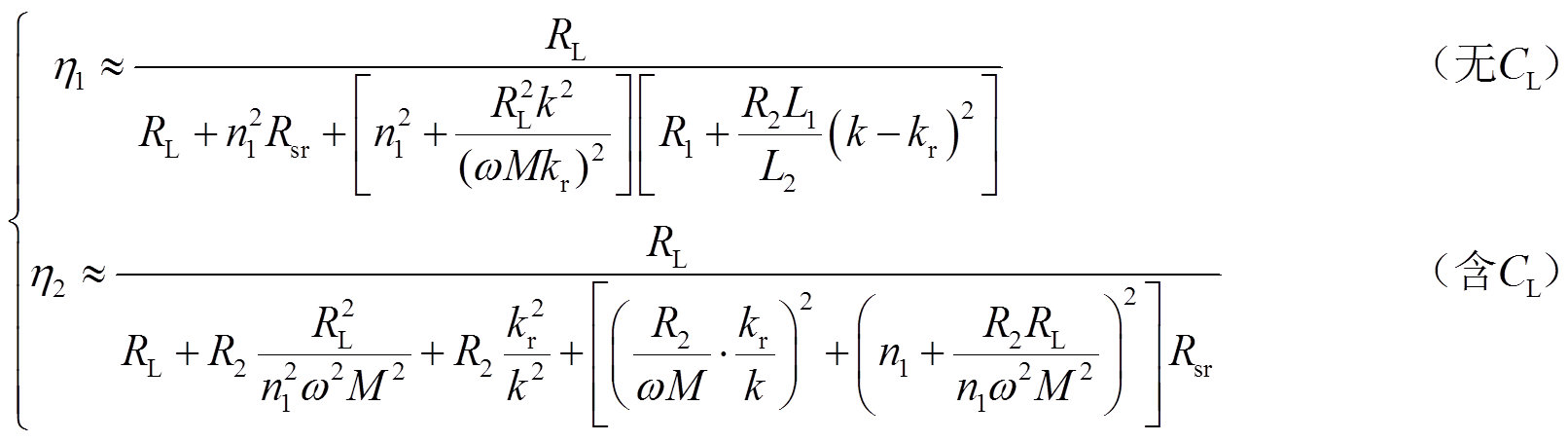 (34)
(34)
由式(34)可知,随着等效耦合系数kr(kr>0)的增加,含CL的双线圈WPT系统传输效率表现出不断减少的趋势,对无CL的双线圈WPT系统传输效率表达式进行多次求导,分析出在无补偿元件CL时双线圈WPT系统的传输效率呈现出先增加后减少。同理在kr<0时,双线圈WPT系统表现出相同的趋势。
图8a为RL=30 Ω时,SP-S型WPT系统的传输效率随等效变比n1的变化情况;图8b为RL=30 Ω且n1=0.4时,SP-PS型双线圈WPT系统传输效率随等效耦合系数kr的变化情况。
首先可以发现双线圈WPT系统的传输效率的变化趋势与分析情况一致,其次可看出有无补偿元件CL的系统传输效率表达式不相同,但变化曲线基本相同。需要说明的是,设计并联谐振元件CL可以降低逆变器的损耗,并有效提高系统的传输效率,这在电路分析中难以直接体现。
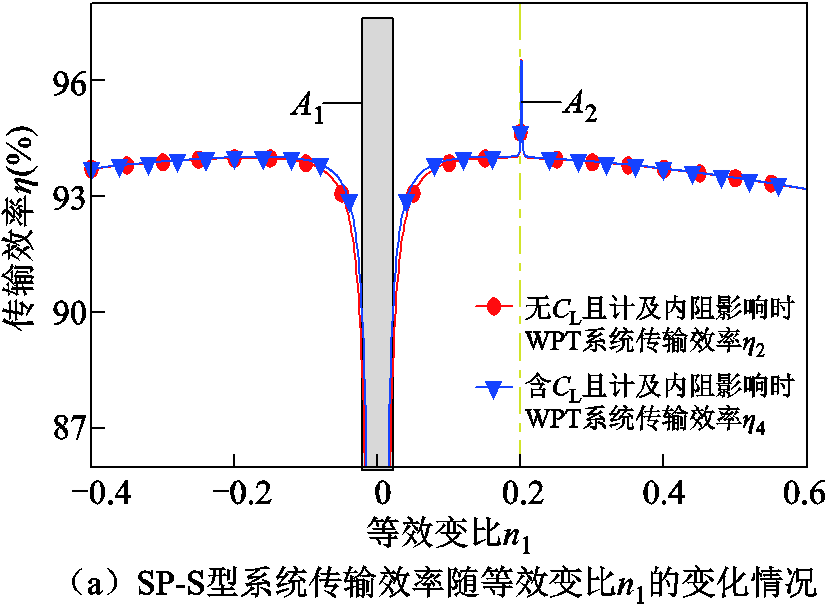
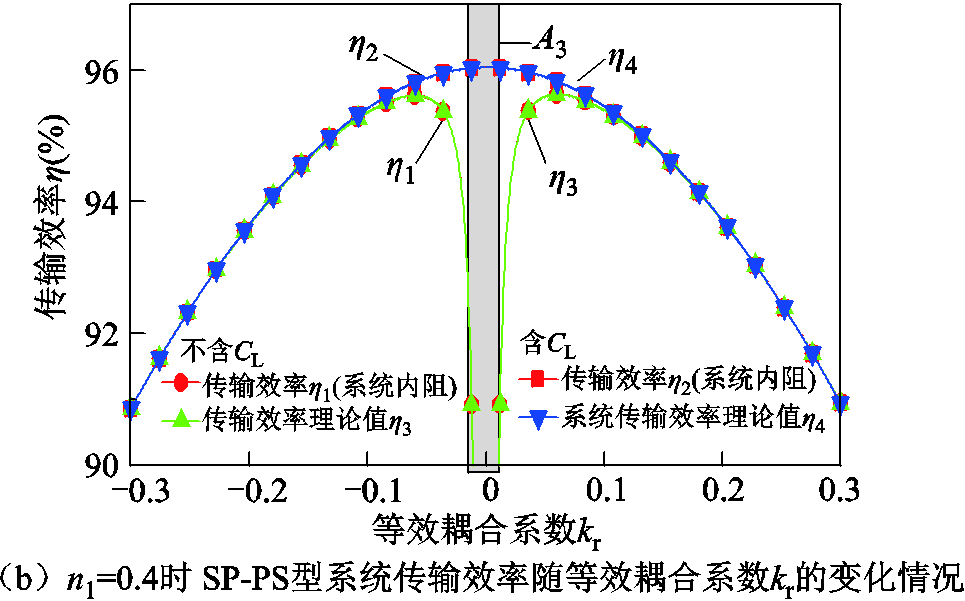
图8 双线圈WPT系统传输效率
Fig.8 Transmission efficiency of two-coil WPT system
为验证本文所设计系统谐振网络参数设计方法与不同补偿网络下系统电压增益稳定性分析结果的正确性,以平面螺旋线圈所做的磁耦合系统为例进行实验验证,双螺旋线圈具体结构参数见表1。本节利用阻抗分析仪(型号:GW LCR-8110G)对磁耦合系统的电气性能进行测量,且在谐振频率点处测出线圈参数,最终得出相关参数进行仿真与实验分析。具体实验参数见表2。
表1 平面线圈结构参数
Tab.1 Plane coil structure parameters
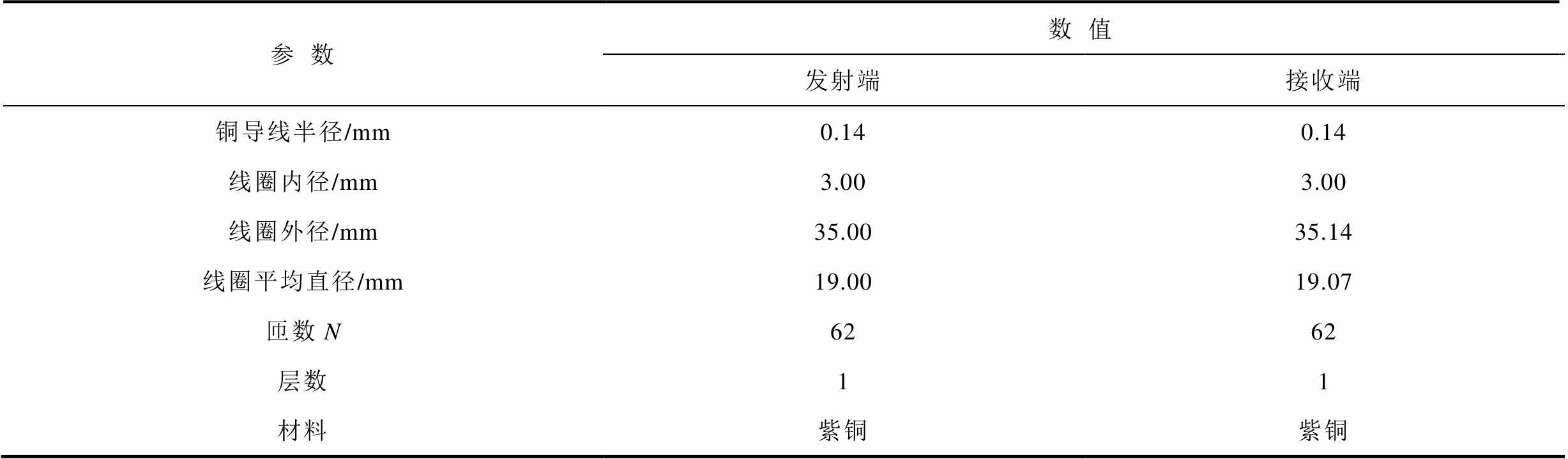
参数数值 发射端接收端 铜导线半径/mm0.140.14 线圈内径/mm3.003.00 线圈外径/mm35.0035.14 线圈平均直径/mm19.0019.07 匝数N6262 层数11 材料紫铜紫铜
表2 双线圈WPT系统实验参数值
Tab.2 Parameter values of double coil WPT system

模型参数数值 等效电压Us/V9.65 目标电压增益GV00.6 谐振频率f/MHz5.16 发射线圈L1/µH53.4 接收线圈L2/µH54.14 互感M12/µH10.8 电源电阻RS/Ω1 寄生电阻R1/Ω0.31 寄生电阻R2/Ω0.26
首先利用信号发生器(型号:DG1022U)输出高频交流信号,经功率放大器(型号:ATA-1200)进行信号放大,并将放大完的信号作为磁耦合系统发射侧的激励源。其次利用谐振电容和谐振电感组成原、副边侧补偿网络,搭建合适的整流滤波电路对负载电阻进行供电。具体实验如图9所示。

图9 双线圈无线电能传输系统实验
Fig.9 Physical experiment diagram of two-coil radio energy transmission system
首先对双线圈WPT系统补偿网络设计方法进行验证。双线圈WPT系统补偿网络拓扑结构如图10所示,依据系统的目标电压增益,本文建立变压器T网络模型的实际变比n=0.6,总传输距离D为2 cm。根据第2节中补偿参数确定方法,可得出S-S型补偿参数值,由等效变比n1=0.4以及等效互感Mr=5.4 µH,设计高阶补偿网络参数值,具体参数见表3。
图11为负载电阻RLR=50 Ω时三种不同拓扑结构的磁耦合谐振式无线电能传输系统的关键波形。其中,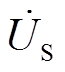 与
与 分别为原边侧功率放大器的输出电压与输出电流;
分别为原边侧功率放大器的输出电压与输出电流;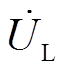 与
与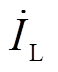 为副边侧整流桥前的输入电压与输入电流。可以发现,三种双线圈WPT系统的输入阻抗都呈弱感性,且系统实测输出电压约为5.6 V,符合本文中具有恒压特性的WPT系统补偿网络设计要求。但该实测电压增益与目标电压增益不一致,其原因在于线圈内阻与系统器件损耗不可忽略以及实际应用中元件参数选取存在一定偏差。
为副边侧整流桥前的输入电压与输入电流。可以发现,三种双线圈WPT系统的输入阻抗都呈弱感性,且系统实测输出电压约为5.6 V,符合本文中具有恒压特性的WPT系统补偿网络设计要求。但该实测电压增益与目标电压增益不一致,其原因在于线圈内阻与系统器件损耗不可忽略以及实际应用中元件参数选取存在一定偏差。
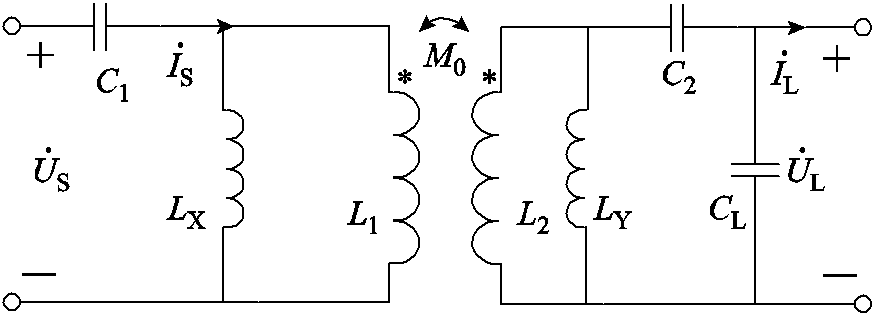
图10 双线圈WPT系统补偿网络拓扑结构
Fig.10 Topology diagram of compensation network of two-coil WPT system
表3 不同补偿网络谐振参数值
Tab.3 Resonance parameter values of different compensation networks

参数数值 S-S型SP-S型SP-PS型 等效变比n10.60.40.4 等效耦合系数kr0.20.20.1 电容C1/pF26.853.836.6 电感LX/µH5378.7 电容C2/pF2019.138.1 电感LY/µH54.1 电容CL/pF147.3221442
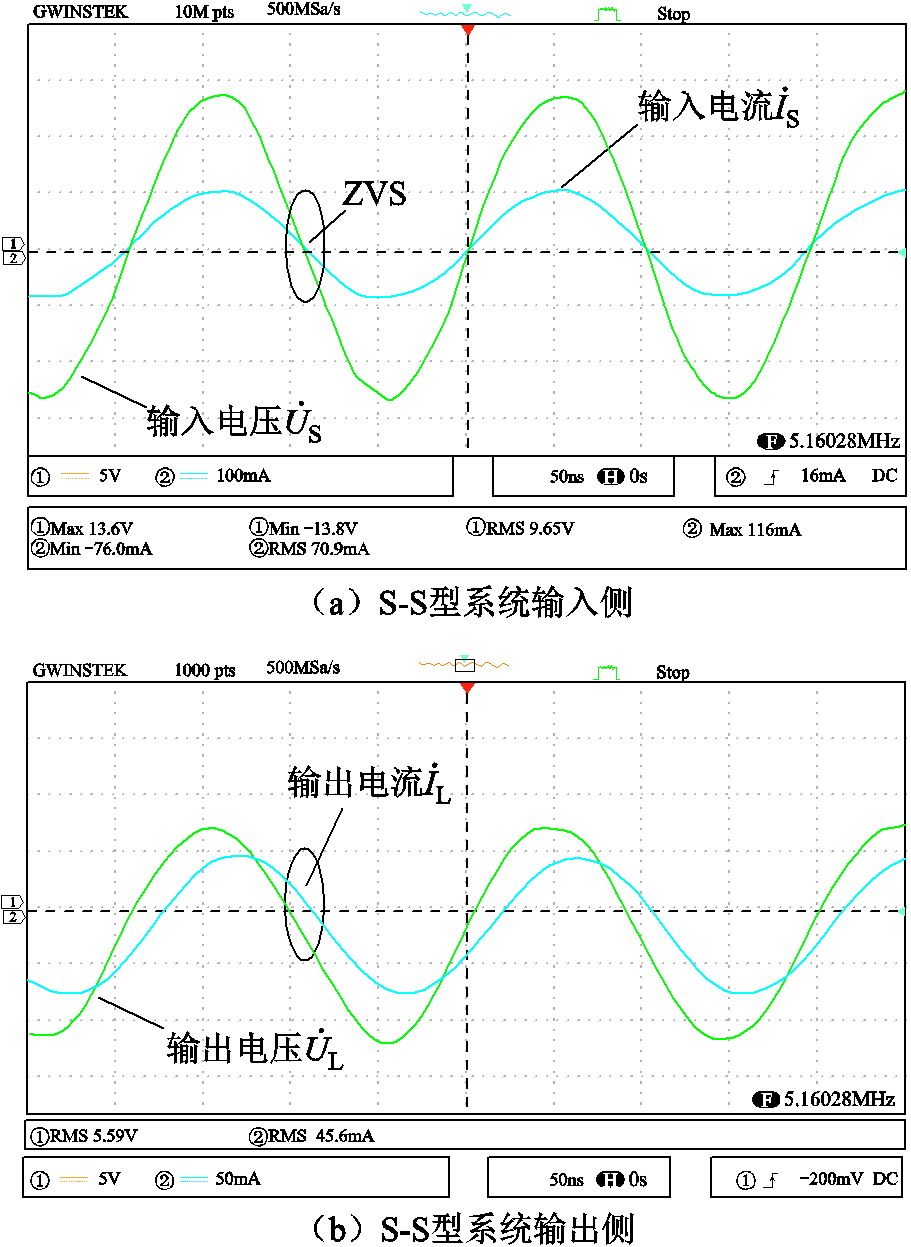
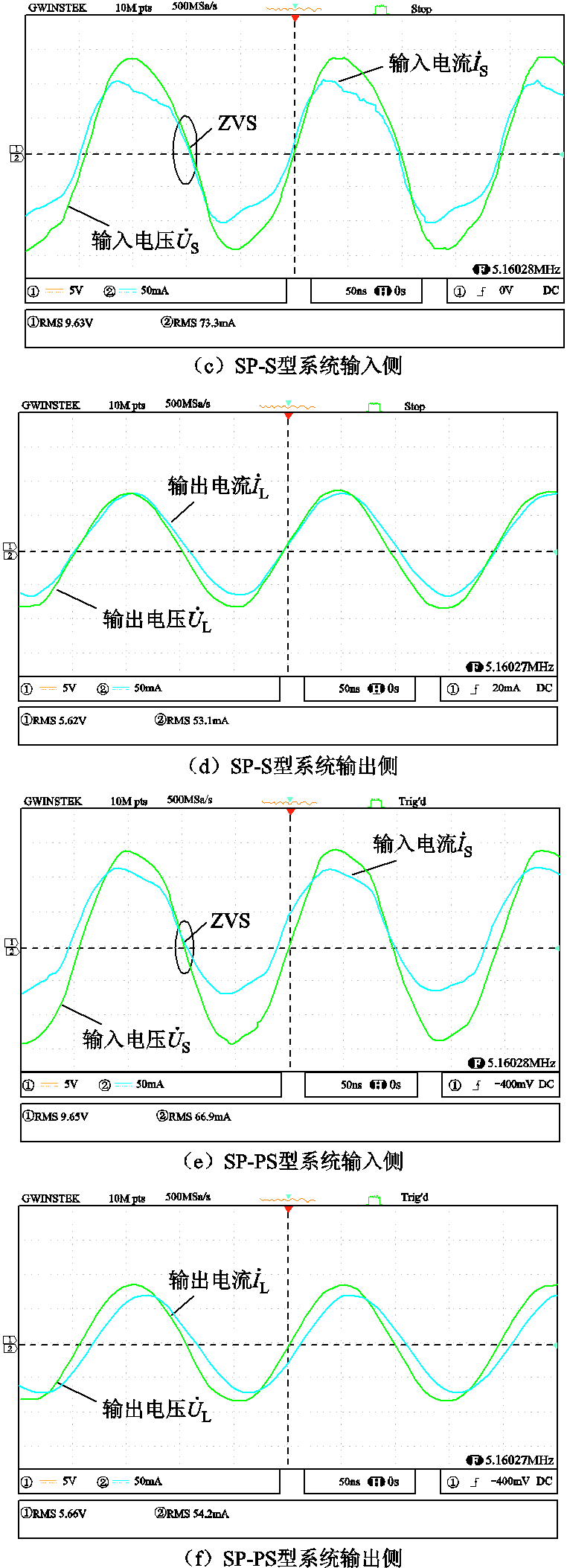
图11 补偿网络参数设计方法验证
Fig.11 Verification of compensation network parameter design method
其次在SP-PS型拓扑结构基础上验证双线圈WPT系统具有可变增益恒压特性。表4为当系统目标电压增益分别为0.3、0.6与1时WPT系统谐振元件值,其中当n=0.3时原边侧并联谐振元件为电容CX。
表4 SP-PS型拓扑结构的补偿参数(n=0.3, 0.6, 1)
Tab.4 Resonance parameter values of SP-PS compensation networks(n=0.3, 0.6, 1)

参数数值 n=0.3n=0.6n=1 等效变比n10.40.40.4 等效耦合系数kr0.10.10.1 电容C1/pF18.336.66.1 电感LX/µHCX=6.1pF78.725.9 电容C2/pF38.138.138.1 电感LY/µH54.154.154.1 电容CL/pF442442442
不同实际变比下系统电压增益实验结果如图12所示,考虑高频情况下寄生电阻以及实际电容取值的影响,双线圈WPT系统实际电压增益GV与目标增益基本一致。但该电压增益仍与实际变比n存在一定的差距,这是由于线圈处于高频态下寄生电阻表现明显且实验频率与谐振频率不完全一致。其中由实验结果可看出,系统的恒压输出特性会随着实际变比的增加而逐渐变差,在n=0.6与0.3时系统电压增益基本与n值相同。
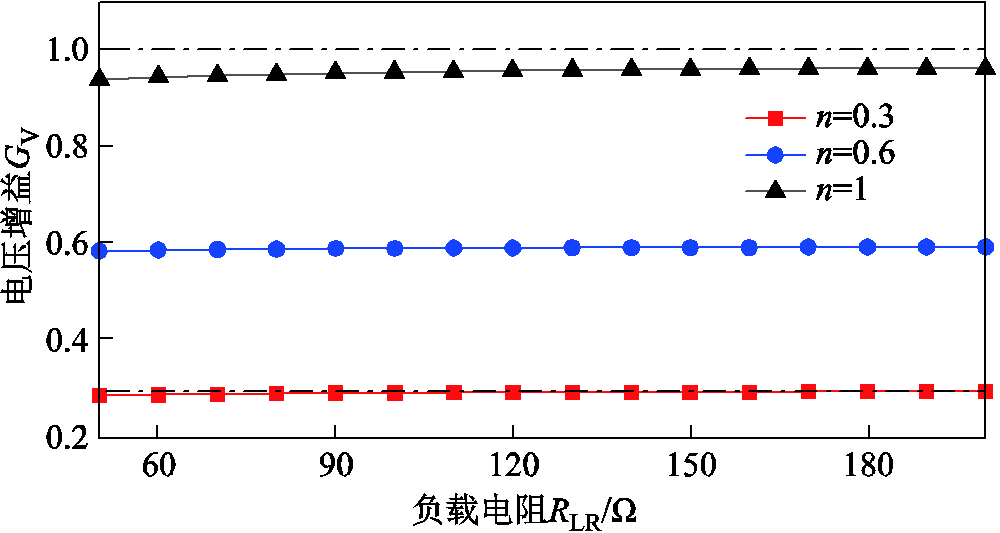
图12 不同实际变比下系统电压增益实验结果
Fig.12 Experimental results of system voltage gain under different actual transformation ratios
图13a为负载电阻RLR=30 Ω时SP-S型双线圈WPT系统传输效率随等效变比n1的变化情况。在n1为0.3~1.2的范围内,可以发现n1<n时SP-S型系统传输效率高于S-S型系统传输效率;n1>n时SP-S型系统传输效率低于S-S型系统传输效率,且含谐振元件CL时系统传输效率高于无阻抗匹配时系统传输效率。这与上文效率分析结论相同,图13a中,n1=0.6为S-S型双线圈WPT系统所测出的传输效率。
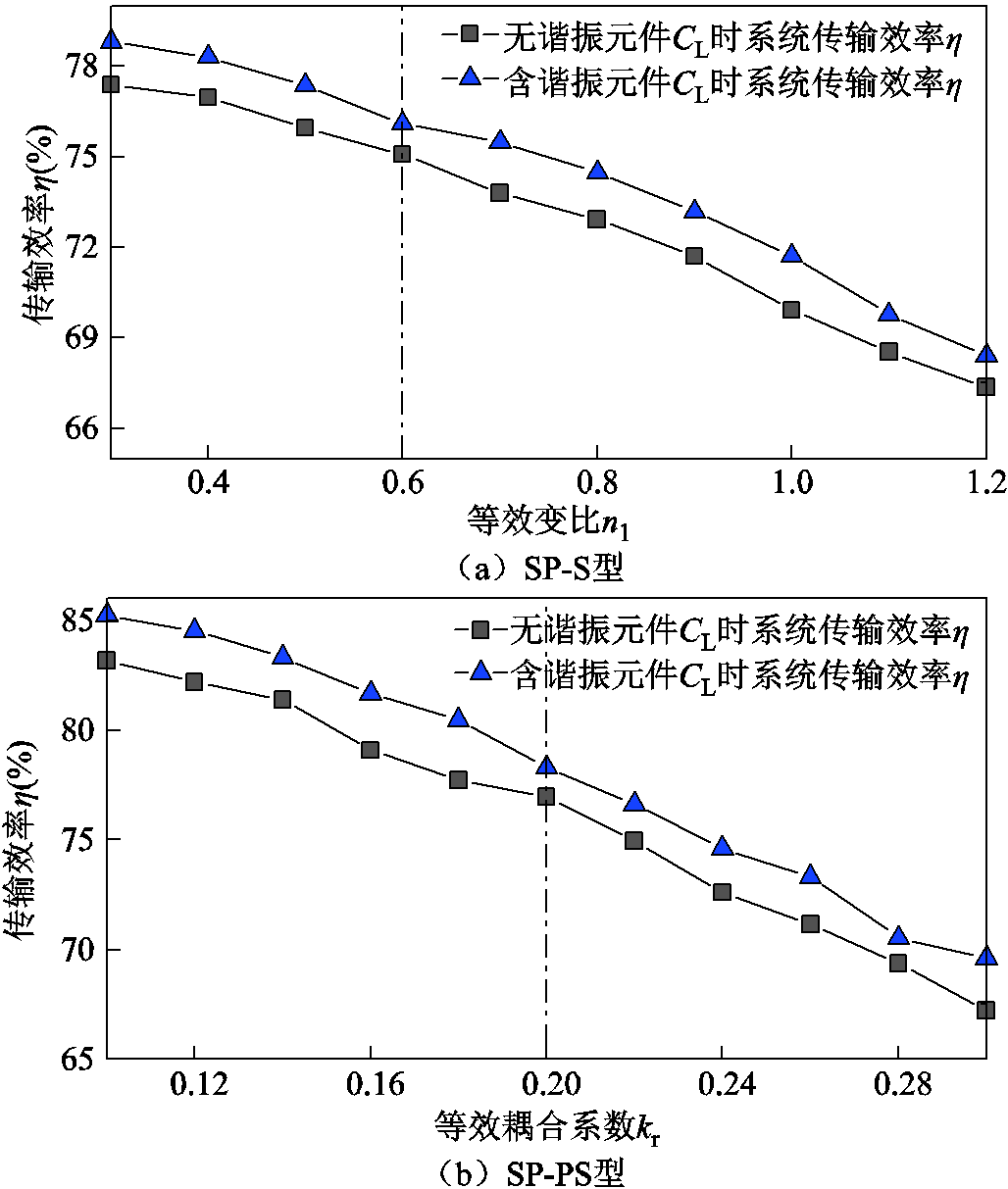
图13 不同补偿网络下系统传输效率关系验证
Fig.13 Verification of system transmission efficiency under different compensation networks
图13b是在等效耦合系数kr为0.1~0.3的范围内,n1=0.4时SP-PS型双线圈WPT系统传输效率随等效耦合系数kr的变化情况。可以看出,系统的传输效率随着等效耦合系数的增加而表现出不断减少的趋势,且含谐振元件CL系统的传输效率高于无谐振元件CL时系统传输效率。图13b中,当kr=0.2时,根据等效互感表达式(15)可知X3趋近∞(元件X3断开),因此所测结果为n1=0.4时SP-S型双线圈WPT系统所测出的传输效率。
其中由于在5.16 MHz频率下谐振电容等元器件存在不可忽视的寄生电阻,且实际电源频率与线圈谐振频率并不完全一致,这导致了双线圈WPT系统的传输效率实际结果与仿真结果存在较大差异。
图14为负载电阻RLR=50 Ω时传输距离从1.5 cm增加到2.5 cm的双线圈WPT系统的输出电压变化情况。当传输距离由2 cm减少到1.5 cm时无谐振元件CL的WPT系统电压增益稳定性高于含CL时系统电压增益稳定性,且传输距离由2 cm增加到2.5 cm时无CL谐振元件的系统电压增益稳定性弱于含谐振元件CL情况下。

图14 线圈偏移下系统电压增益稳定性验证
Fig.14 Verification of system voltage gain stability under coil offset
如图14a所示,当n1=0.4<0.6时,SP-S型系统电压增益稳定性强于S-S型系统电压增益稳定性;当n1=1>0.6时,SP-S型系统电压增益稳定弱于S-S型系统电压增益稳定性。如图14b所示,在n1=0.4的基础上,分析等效耦合系数kr为0.3、0.2和0.1时系统电压增益稳定性。可以发现,系统电压增益稳定性会随着等效耦合系数kr的减少而不断提高,这与前文所得出的结论相同。
图15为电源频率从5.1 MHz增加到5.2 MHz时双线圈WPT系统的输出电压变化情况。首先,当电源频率从谐振频率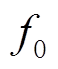 =5.16 MHz减少到5.1 MHz时,由实验参数可知满足式(31),且系统输出电压低于目标输出电压,因此无谐振元件CL的系统电压增益稳定性强于含谐振元件CL时系统电压增益稳定性。而电源频率增加到5.2 MHz时,无谐振元件CL的系统电压增益稳定性弱于含谐振元件CL的电压增益稳定性。
=5.16 MHz减少到5.1 MHz时,由实验参数可知满足式(31),且系统输出电压低于目标输出电压,因此无谐振元件CL的系统电压增益稳定性强于含谐振元件CL时系统电压增益稳定性。而电源频率增加到5.2 MHz时,无谐振元件CL的系统电压增益稳定性弱于含谐振元件CL的电压增益稳定性。
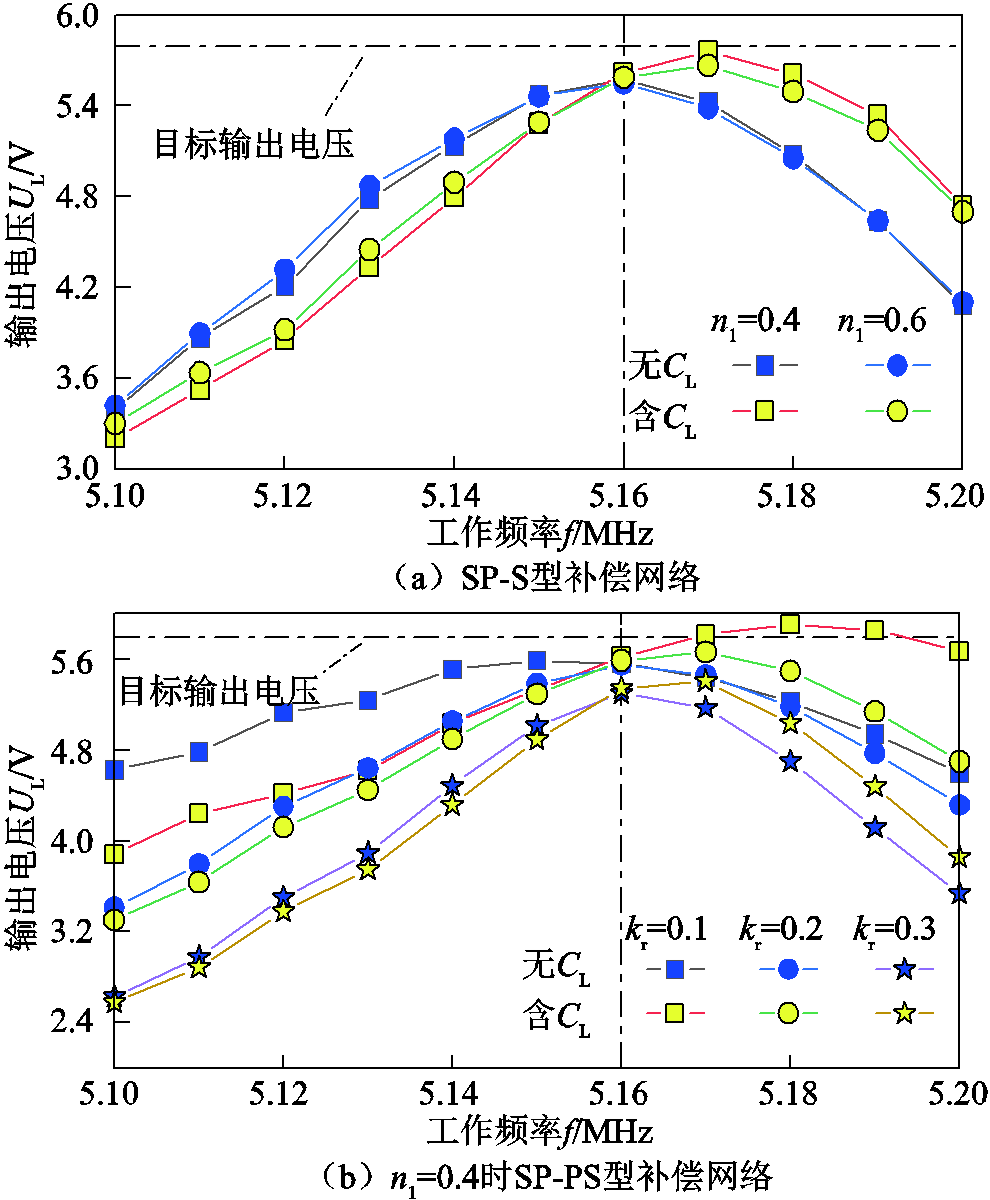
图15 频率振荡下系统电压增益稳定性验证
Fig.15 Verification of system voltage gain stability under frequency oscillation
由图15a可知,当n1=0.4时SP-S型系统电压增益抗增频能力高于S-S型(n1=0.6时SP-S型)WPT系统,但在抗减频能力方面,前者WPT系统弱于S-S型拓扑结构系统。同时在n1=0.4的基础上分析等效耦合系数kr对系统电压增益稳定性的影响,如图15b所示,可以发现kr=0.1时系统的电压增益稳定性最佳,这可为以后的研究提供实验基础。
本文基于变压器T网络模型,提出一套具有可变增益恒压特性的双线圈无线电能传输系统补偿网络参数确定方法与传输特性分析新思路,为传感器网络节点的电能无线传输技术奠定研究基础。最终得出以下结论:
1)谐振网络参数确定。建立双线圈WPT磁耦合系统的变压器T网络模型,定义等效变比n1与等效耦合系数kr,得到一套具有可变增益恒压特性的S-S、SP-S与SP-PS型双线圈WPT系统补偿网络参数设计新方法。
2)传输特性分析。首先依据新定义等效参数,考虑寄生电阻对电压增益的直接影响,得出线圈偏移或频率振荡下双线圈WPT系统的电压增益表达式以及传输效率表达式,可以发现在互感M减少或电源频率增加时,并联谐振元件CL能够提高系统的抗偏移能力。其次发生线圈偏移时系统电压增益稳定性将随着等效变比n1或等效耦合系数kr的增加表现出先增强后减弱,再增强最后减弱(或先增强后减弱)的趋势;稳态双线圈WPT系统的传输效率会随着等效变比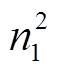 的增加而呈现出不断减少的趋势;也会随着等效耦合系数kr2的增加,无CL的WPT系统表现出先增加后减少的趋势,含CL的WPT系统的传输效率会持续减少。其中依据电压增益表达式,得出线圈偏移时有无谐振元件CL的WPT系统的最佳等效参数表达式,为后续补偿网络的优化设计提供理论依据。
的增加而呈现出不断减少的趋势;也会随着等效耦合系数kr2的增加,无CL的WPT系统表现出先增加后减少的趋势,含CL的WPT系统的传输效率会持续减少。其中依据电压增益表达式,得出线圈偏移时有无谐振元件CL的WPT系统的最佳等效参数表达式,为后续补偿网络的优化设计提供理论依据。
3)搭建双线圈WPT系统实验平台,对不同等效参数的双线圈WPT系统补偿结构进行实验,实验结果与理论分析结论相一致,验证了理论分析的正确性和可行性。
参考文献
[1] 张献, 邢子瑶, 薛明, 等. 无线电能传输系统异物检测技术研究综述[J]. 电工技术学报, 2022, 37(4): 793-807. Zhang Xian, Xing Ziyao, Xue Ming, et al. Overview of foreign object detection in wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 793-807.
[2] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568. Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[3] Park S W, Wake K, Watanabe S. Incident electric field effect and numerical dosimetry for a wireless power transfer system using magnetically coupled resonances[J]. IEEE Transactions on Microwave Theory and Techniques, 2013, 61(9): 3461-3469.
[4] Zhou Wei, Su Yugang, Huang Liang, et al. Wireless power transfer across a metal barrier by combined capacitive and inductive coupling[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 4031-4041.
[5] 李阳, 石少博, 刘雪莉, 等. 磁场耦合式无线电能传输耦合机构综述[J]. 电工技术学报, 2021, 36(增刊2): 389-403. Li Yang, Shi Shaobo, Liu Xueli, et al. Overview of magnetic coupling mechanism for wireless power transfer[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 389-403.
[6] 李建国, 张波, 荣超. 近场磁耦合无线电能与信息同步传输技术的发展(下篇): 电路拓扑[J]. 电工技术学报, 2022, 37(16): 3989-4003. Li Jianguo, Zhang Bo, Rong Chao. An overview of simultaneous wireless power and information transfer via near-field magnetic links (part Ⅱ): circuit topology[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 3989-4003.
[7] 赵鱼名, 王智慧, 苏玉刚, 等. 基于T型CLC谐振网络的恒压型电场耦合电能传输系统负载自适应技术[J]. 电工技术学报, 2020, 35(1): 106-114. Zhao Yuming, Wang Zhihui, Su Yugang, et al. Load adaptive technology of constant voltage electric-field coupled power transfer system based on T-CLC resonant network[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 106-114.
[8] Sample A P, Meyer D T, Smith J R. Analysis, experimental results, and range adaptation of magnetically coupled resonators for wireless power transfer[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 544-554.
[9] 刘俊有. 具有恒流恒压输出特性的磁耦合无线电能传输系统设计[D]. 天津: 天津理工大学, 2022.
[10] 谢诗云, 刁勤晴, 杨奕, 等. 基于复合谐振网络的恒定输出型ECPT系统[J]. 中国电机工程学报, 2020, 40(24): 8165-8178. Xie Shiyun, Diao Qinqing, Yang Yi, et al. Electric-field coupled power transfer system based composite resonant networks with constant output[J]. Proceedings of the CSEE, 2020, 40(24): 8165-8178.
[11] 谭平安, 廖佳威, 谭廷玉, 等. 基于发射侧T/F变结构补偿网络的恒压/恒流无线充电系统[J]. 电工技术学报, 2021, 36(2): 248-257. Tan Ping'an, Liao Jiawei, Tan Tingyu, et al. Constant voltage/constant current wireless charging system based on T/F variable structure compensation network of transmitter-side[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 248-257.
[12] 郭星, 刘利强, 齐咏生, 等. 基于LCL-LCL/S混合自切换谐振式无线充电系统[J]. 电工技术学报, 2022, 37(10): 2422-2434. Guo Xing, Liu Liqiang, Qi Yongsheng, et al. Hybrid self-switching resonant wireless charging system based on LCL-LCL/S[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2422-2434.
[13] 苏玉刚, 谢诗云, 王智慧, 等. 基于F-F/T变结构谐振网络的恒压-恒流型电场耦合电能传输系统[J]. 电工技术学报, 2019, 34(6): 1127-1136. Su Yugang, Xie Shiyun, Wang Zhihui, et al. An electric-field coupled power transfer system with constant voltage and constant current output based on F-F/T changeable resonant circuit[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1127-1136.
[14] Zhou Jiali, Zhang Bo, Xiao Wenxun, et al. Nonlinear parity-time-symmetric model for constant efficiency wireless power transfer: application to a drone-in-flight wireless charging platform[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 4097-4107.
[15] Lim T, Lee Y. Reconfigurable coil array for near-field beamforming to compensate for misalignment in WPT systems[J]. IEEE Transactions on Microwave Theory and Techniques, 2021, 69(11): 4711-4719.
[16] 黄晓生, 陈为. 用于磁感应耦合式电能传输系统的新型补偿网络[J]. 中国电机工程学报, 2014, 34(18): 3020-3026. Huang Xiaosheng, Chen Wei. A novel compensation network for ICPT systems[J]. Proceedings of the CSEE, 2014, 34(18): 3020-3026.
[17] 陈庆彬, 杨丰钢, 陈为. 具有可变增益恒压特性的三线圈WPT系统补偿网络结构及参数确定新方法[J]. 中国电机工程学报, 2021, 41(6): 2277-2288. Chen Qingbin, Yang Fenggang, Chen Wei. A new compensation network structure and parameter determination method with variable constant voltage gain characteristics based on three-coil WPT system[J]. Proceedings of the CSEE, 2021, 41(6): 2277-2288.
[18] 陈庆彬, 张伟豪, 叶逢春, 等. 结合变压器T网络模型的具有可变恒压增益特性的补偿网络参数确定新方法[J]. 中国电机工程学报, 2017, 37(15): 4483-4494. Chen Qingbin, Zhang Weihao, Ye Fengchun, et al. A new compensation network parameters design method with variable constant voltage gain characteristics based on transformer T model[J]. Proceedings of the CSEE, 2017, 37(15): 4483-4494.
[19] 石坤宏, 程志江, 王维庆, 等. 3种谐振式无线电能传输系统的电路法模型及其特性[J]. 高电压技术, 2021, 47(6): 2240-2249. Shi Kunhong, Cheng Zhijiang, Wang Weiqing, et al. Circuit model and characteristics of three resonant wireless power transmission systems[J]. High Voltage Engineering, 2021, 47(6): 2240-2249.
[20] 江彦伟. 分数阶非自治及自治电路的磁耦合无线电能传输机理与特性研究[D]. 广州: 华南理工大学, 2019.
Abstract Compared with the multi-coil structure, the two-coil wireless power transfer (WPT) system shows shortcomings in transmission distance and transmission efficiency, but the transmission characteristics of the WPT system can be improved by increasing the order of the compensation network and the active control strategy. Different from the design of compensation network, the research of active control strategy has the problems of large system complexity and high control cost. Therefore, combined with the transformer T network model, this paper proposes a new method for compensating network parameters and transmission characteristics analysis of a two-coil WPT system with variable gain constant voltage characteristics, which lays a research foundation for multi-node WPT technology of sensor networks.
Firstly, the equivalent model of transformer T-network is established, and the element parameter expression of S-S two-coil WPT system with constant voltage characteristic is given. Secondly, the new parameters-equivalent coupling coefficient kr and equivalent variable ratio n1 are defined, and a new method for determining the compensation network parameters of SP-S and SP-PS compensation structures with variable gain and constant voltage characteristics is proposed. Then, considering the direct influence of system parasitic resistance on transmission characteristics, the variation trend of voltage gain stability with equivalent parameters under coil offset and frequency oscillation is analyzed, and the optimal equivalent parameter expression under coil offset is derived. Finally, the experimental prototypes of two-coil WPT system with S-S, SP-S and SP-PS compensation structures are built to verify the correctness and effectiveness of the variable gain constant voltage output characteristics and analysis conclusions of the proposed system.
Through theoretical analysis and experimental verification, the following conclusions can be drawn: (1) The proposed new design method of two-coil WPT system’s compensation network makes the output voltage gain of WPT system meet the target variable ratio, simplifies the parameter design method, increases the degree of freedom of system design, and makes the parameter selection more flexible. (2) The two-coil WPT system under coil offset will increase first and then decrease with the increase of equivalent variable ratio n1, and will also show the same trend with the increase of equivalent coupling coefficient kr. (3) Considering the direct influence of the parasitic resistance of the system on the transmission characteristics, the optimal equivalent parameter expression of WPT system with or without parallel resonant element CL under coil offset is obtained. (4) The transmission efficiency of the steady-state WPT system increases first and then decreases with the increase of 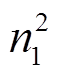 , the two-coil WPT system with CL increases first and then decreases with the increase of the equivalent coupling coefficient kr, and the WPT system without CL increases first and then decreases with the increase of
, the two-coil WPT system with CL increases first and then decreases with the increase of the equivalent coupling coefficient kr, and the WPT system without CL increases first and then decreases with the increase of 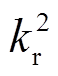 .
.
Keywords:Wireless power transfer, compensation network, transmission efficiency, coil offset, transformer T-network equivalent model
DOI:10.19595/j.cnki.1000-6753.tces.222269
中图分类号:TM724
国家自然科学基金地区科学基金项目资助(51867021)。
收稿日期 2022-12-03
改稿日期 2023-03-03
张鹏飞 男,1998年生,硕士研究生,研究方向为无线电能传输。E-mail:2274023653@qq.com
龚立娇 女,1978年生,教授,博士生导师,研究方向为能量收集技术与可再生能源利用技术、无线电能传输。E-mail:glj_mac@shzu.edu.cn(通信作者)
(编辑 郭丽军)