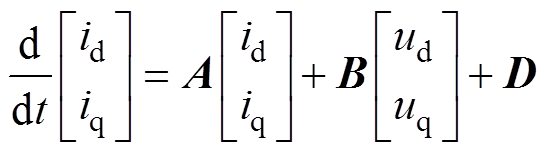 (1)
(1)
摘要 分段式结构的双三相永磁直线同步电机(PMLSM),动子穿入和穿出定子分段时,传统的无差拍预测电流控制(DPCC)易受反电动势动态扰动的影响,无法实现精确的电流跟踪和推力控制。同时,该电机模型的参数失配会增大DPCC电流和推力控制的难度。针对以上问题,该文提出了一种基于无模型电流预测控制(MFPCC)的电流控制策略。首先,构建了分段式双三相PMLSM的超局部模型。其次,基于该超局部模型设计了预测电流控制器,并设计扰动观测器以补偿反电动势动态扰动和参数失配的影响。最后,实验验证了所提MFPCC能够抑制分段式双三相PMLSM的反电动势和参数失配的扰动,有效提升参数鲁棒性、电流跟踪性能并降低推力波动。
关键词:双三相永磁直线同步电机 超局部模型 扰动观测器 预测电流控制
大功率直线电机控制系统在大型工业运输电梯、磁悬浮交通及电磁推进等领域应用广泛。为了减小变流器的容量且便于安装维护[1],以上长行程的场合往往采用分段供电的方式。相比于三相电机,相移30°双三相永磁同步直线电机(Permanent Magnet Linear Synchronous Motor, PMLSM)效率高、推力脉动小且具备容错能力[2-4],在大功率的场合受到青睐。
传统的电流控制方式主要为磁场定向控制,其中电流闭环常常采用PI控制器。在分段式PMLSM的动子穿入穿出定子分段时,电流给定值为阶跃信号,PI控制器下的电流跟踪值会产生超调,且易受扰动干扰而导致系统稳态性能下降、动态响应慢[5]。预测电流控制兼具超调小和动态响应快的优点,在电机控制领域的研究和应用越来越广泛[6]。其中,基于无差拍原则的预测电流控制(Deadbeat Predictive Current Control, DPCC)易于实现,但是该方法依赖电机模型。分段式双三相PMLSM的模型比传统三相电机复杂,存在动子穿越定子分段的瞬态过程,导致反电动势动态扰动难以准确描述[7],因此DPCC的控制效果不理想。同时,电机的电感和磁链等参数[8-10]会随着直线电机的运行温度、磁饱和效应、边端效应[11-12]等发生改变,这也会影响DPCC的控制性能。此外,双三相PMLSM在谐波子空间内存在着变化的电感参数,这种附加参数的失配也会影响控制效果[13]。
为了提高DPCC对电机参数的鲁棒性,文献[14]将参数辨识和预测控制相结合,利用递推最小二乘法在线辨识旋转式永磁同步电机的电感,但是该方法没有考虑磁链参数的变化。文献[15-16]中设计了鲁棒模型预测电流控制器,利用Luenberger算法超前预测一拍电流预测值,降低了电机参数失配的影响。文献[17-20]中分析了DPCC的参数敏感性,基于各种扰动观测器对参数变化引起的扰动进行观测和补偿,实现对电机参数变化的鲁棒控制。然而,以上方法都是基于电机本身的数学模型而言的,仍然依赖电机参数,且参数的调优随着模型的复杂度上升而变得困难。
近年来,M. Fliess提出了无模型控制[21],这种方法不依赖于被控对象的数学模型,仅根据系统的输入输出,将复杂的被控对象模型构建为超局部模型,在此基础上,将与对象模型相关的参数变量整合进一个包含系统所有不确定性的未知项中,通过对该未知项的估计来实现系统的扰动补偿。文献[22]研究了PMLSM的无模型电流控制,改善了系统的动态响应。文献[23]研究了永磁同步电机的无模型电流预测控制,并利用扩张状态观测器观测超局部模型中的未知项,提高了定子电流的跟踪性能。文献[24]针对电机转速环提出了基于滑模控制的无模型控制器,降低了负载扰动和测量误差对电机转速的影响。以上无模型控制很好地解决了控制器无法获取被控对象精确模型的问题,但是系统已知结构的假设依然是设计过程的一个约束条件,初始的无模型控制仅仅是建立了一个包含集总扰动、不确定性的未知项,对于未知项的结构组成部分没有深入的分析。因此,文献[25]改进了超局部模型的结构,将未知的不确定项分割为未知的线性状态部分和未知的非线性部分,但是需要单独设计这两项的自适应律,自适应律包含4个可调参数和1个根据微分Riccati方程在线更新的控制器增益。并且控制器需要配合代价函数和效用函数来满足最优控制,参数调优和设计过程较繁琐。本文不同于文献[25],针对分段式双三相PMLSM设计了一种超局部模型,将其中未知的不确定项分为与电流状态量有关的已知线性项和包含反电动势、参数失配两者的未知项,且该未知项是利于观测的缓变量[26-27]。不需要处理线性项,仅需观测未知项,且控制器的可调参数较少、增益设置简单、控制律不需要复杂的增益在线更新算法和最优控制算法,所以设计过程较为 简单。
本文研究了无模型预测电流控制(Model-Free Predictive Current Control, MFPCC)并设计扰动观测器观测未知项,根据无差拍的原则设计控制律,消除了反电动势动态扰动的影响,在动子运动全程都获得了良好的电流跟踪效果。同时,所提方法既包含预测控制动态响应快的特点,又不依赖于模型参数,有很强的参数鲁棒性。最后,将所提方法与传统的DPCC作对比,实验结果验证了所提MFPCC的有效性。
本文采用矢量空间解耦(Vector Space Decom- position, VSD)的建模方式,将双三相PMLSM模型通过变换到不同的子空间,实现完全解耦[28]。每个分段电机都当作一台独立的电机,其模型(双中性点不连接,不考虑零序子空间[29-30])为
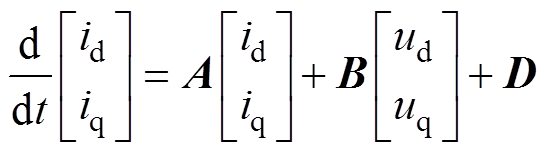 (1)
(1)
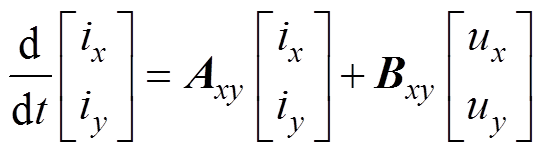 (2)
(2)
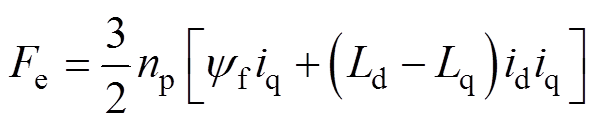 (3)
(3)
其中
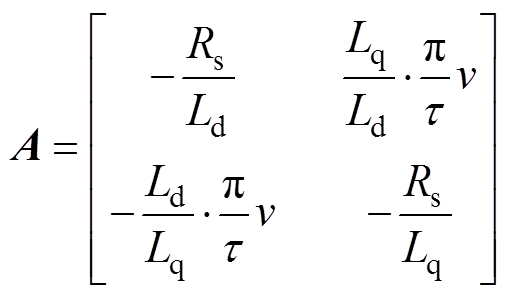
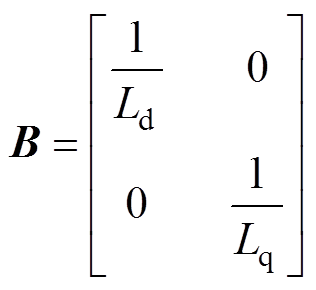
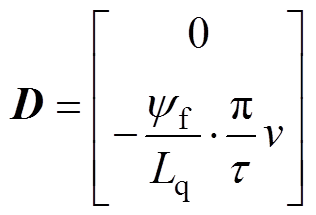

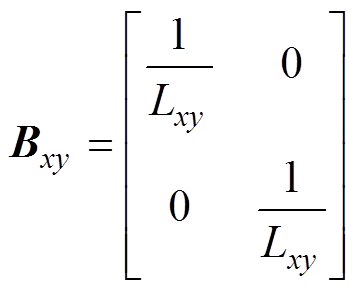
式中,ud(q)、id(q)分别为基波子空间下d、q轴的电压和电流分量;ux(y)、ix(y)分别为谐波子空间下x、y轴的电压和电流分量;Rs为定子电阻;Ld和Lq分别为d、q轴电感;Lxy为谐波子空间内的电感;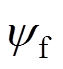 为永磁体磁链;np为极对数;t 为极距;v为动子运动速度。由式(1)、式(2)可知,分段式双三相PMLSM模型与传统的三相电机相比,存在谐波子空间电感Lxy的影响。
为永磁体磁链;np为极对数;t 为极距;v为动子运动速度。由式(1)、式(2)可知,分段式双三相PMLSM模型与传统的三相电机相比,存在谐波子空间电感Lxy的影响。
离散化式(1)和式(2),得到双三相PMLSM的电流预测方程为
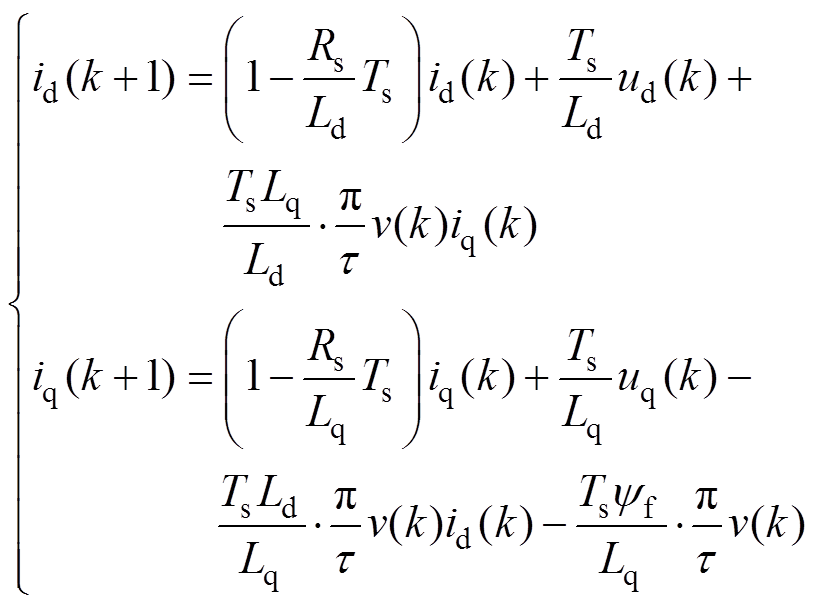 (4)
(4)
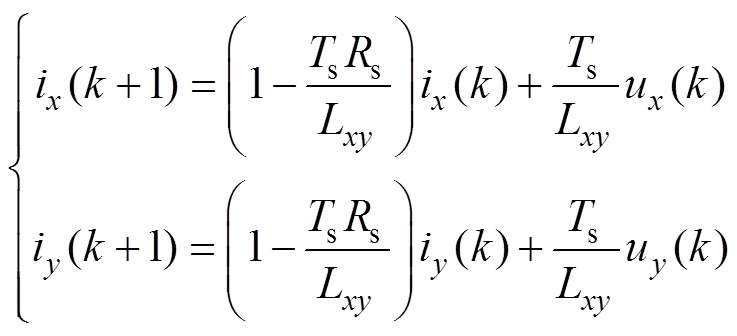 (5)
(5)
式中,Ts为离散化周期。在实际应用中,考虑数字控制系统实现时,当前的采样值经过计算得到的控制量要在下一时刻才会应用,即存在一拍延时,所以在预测方程中应多预测一拍来进行补偿。
由式(4)和式(5)可知,q轴电流预测方程中包含反电动势项yf pv(k)/(Lqt),而反电动势会随着动子穿入定子分段而逐渐增大,随着动子穿出定子分段而逐渐减小,yf是关于动子位置的变量。这一过程中,反电动势会随着动子永磁体与定子耦合程度的变化而存在动态扰动,最终导致预测的电流发生波动。
当考虑参数扰动时,本文将参数失配定义如下:
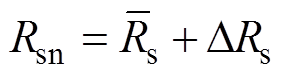 ;
;
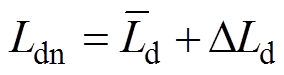 ;
;
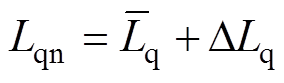 ;
;
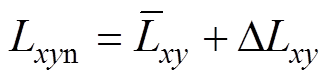 ;
;
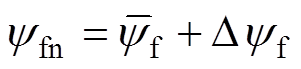 。
。
令Rsn、Ldn、Lqn、Lxyn、yfn为标称参数,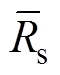 、
、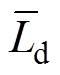 、
、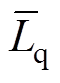 、
、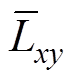 、
、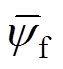 为实际参数,DRs、DLd、DLq、DLxy、Dyf为参数扰动量。
为实际参数,DRs、DLd、DLq、DLxy、Dyf为参数扰动量。
将标称值代入式(4)和式(5),根据无差拍的原则:i(k+1)=i*(k),得到控制方程为
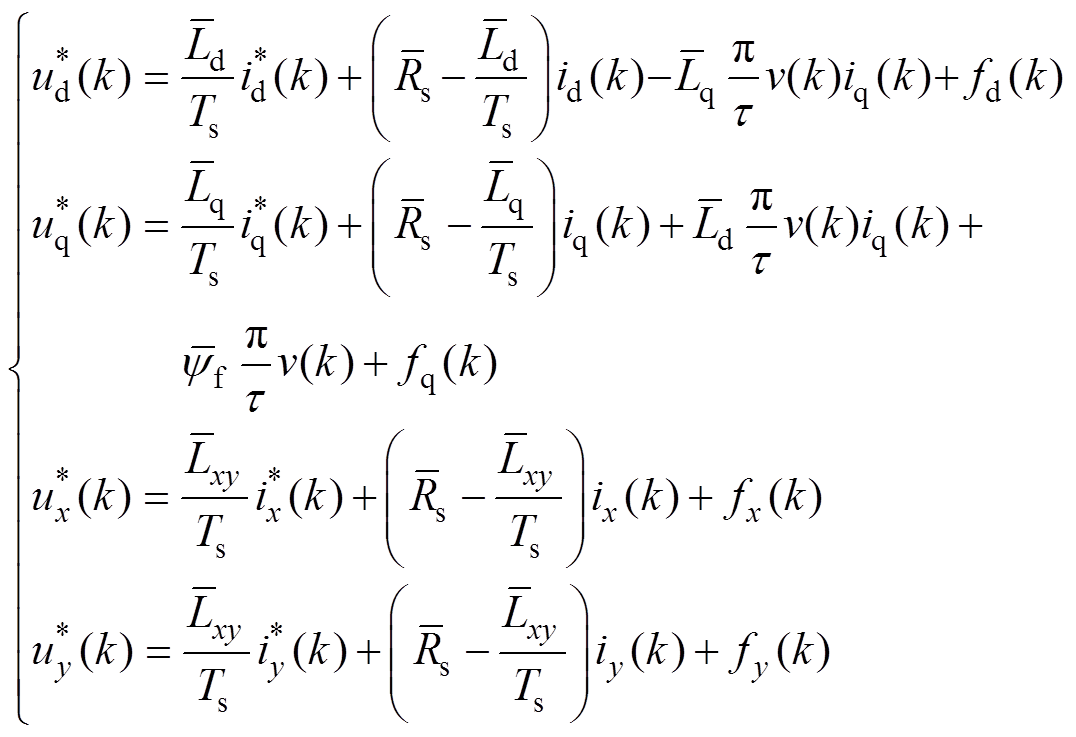 (6)
(6)
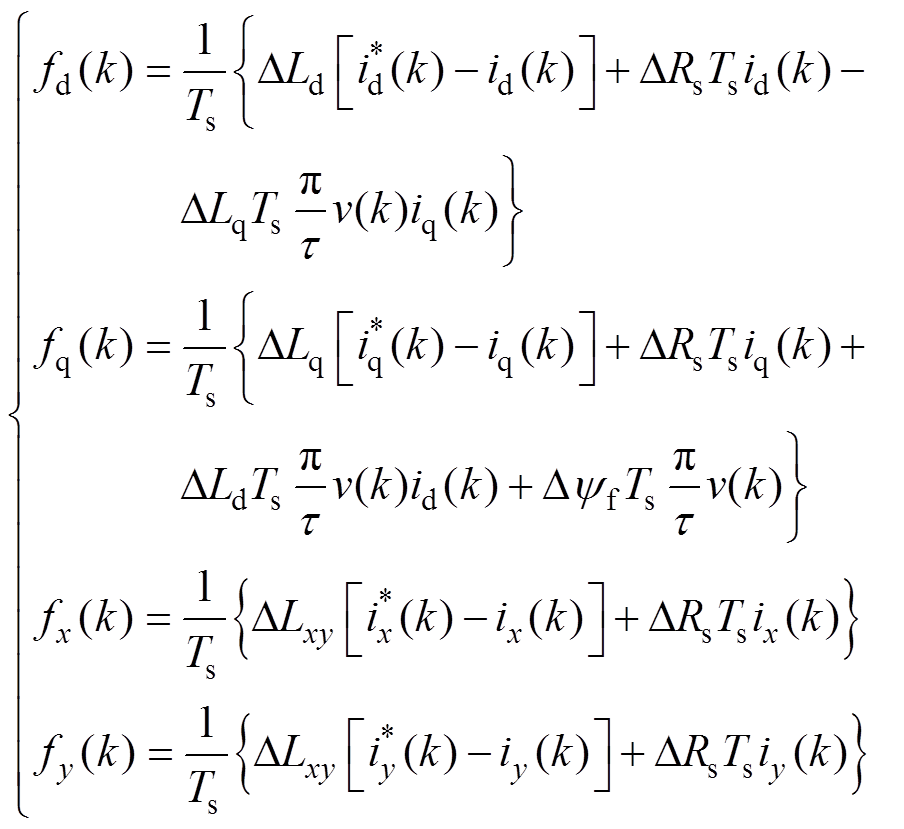 (7)
(7)
式中,上标“*”为指令值;id(k)、iq(k)、ix(k)、iy(k)为kTs时刻的电流采样值。
可见,由于双三相PMLSM运行时温度的变化、磁饱和效应和边端效应,使电机参数发生改变后,造成如式(7)所示的控制误差,最终会影响DPCC的性能。此外,相比于传统的三相电机,Lxy的存在更是加剧了参数失配对DPCC的影响,Lxy匹配与失配下的相电流情况如图1所示。图1a给出了控制器的dq轴电感增至200%的情况下,Lxy匹配和Lxy也增至200%的情况,模拟实际电感值下降一半的情况,电流基波频率为30 Hz。可见,Lxy的失配使得相电流的质量有明显的下降,电流谐波含量明显增加。通过图1b的总谐波畸变率(Total Harmonic Distortion, THD)分析也说明了参数Lxy的失配使得THD明显变大,加剧了参数失配的影响。
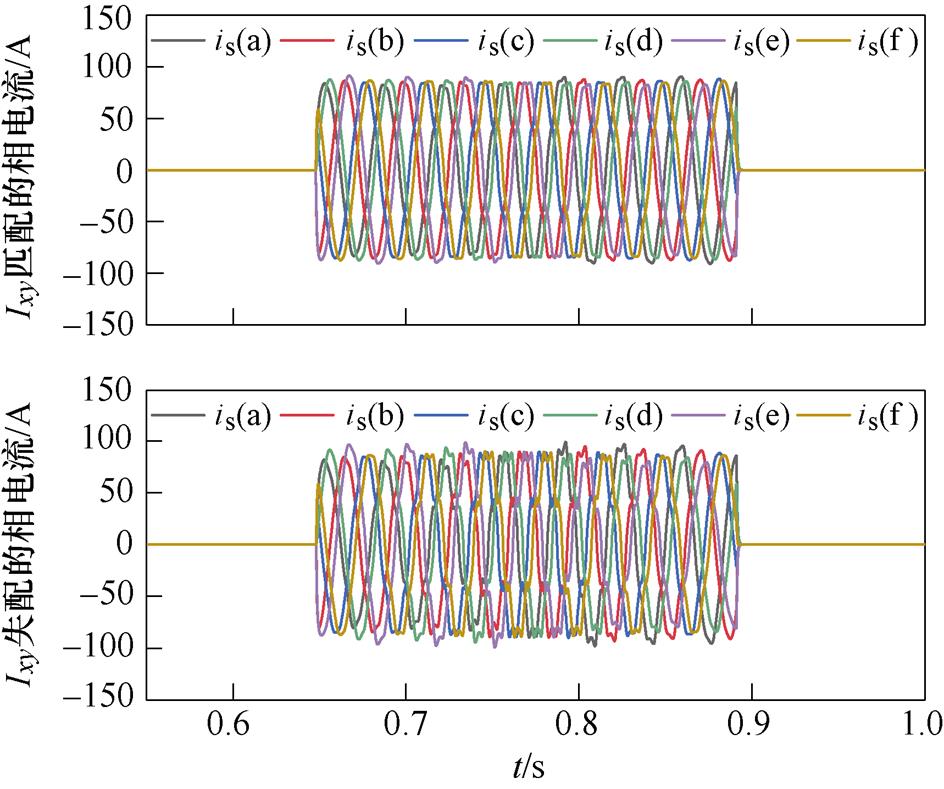
(a)六相电流波形对比
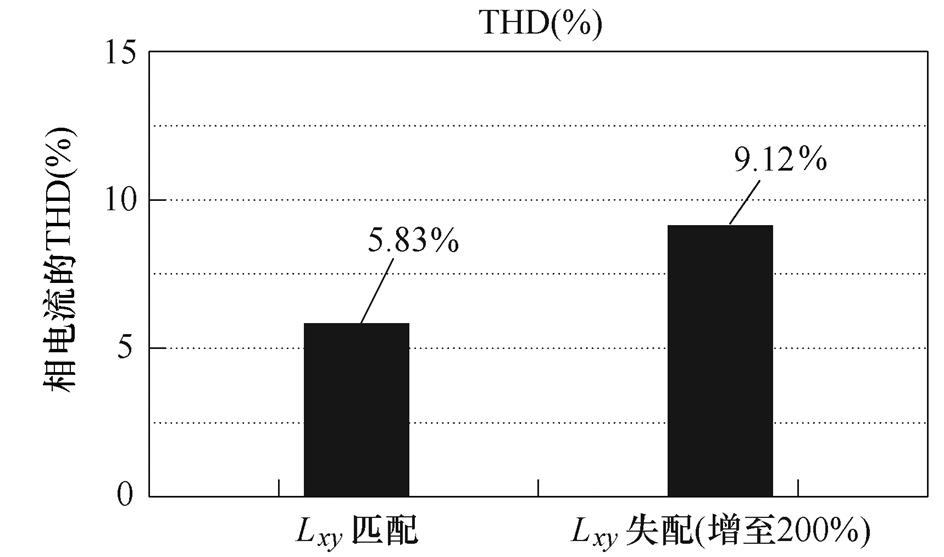
(b)单相电流的THD对比
图1 Lxy匹配与失配下的相电流情况
Fig.1 Phase current situation under Lxy matched and mismatched
将单输入单输出系统的一阶超局部模型作为本文系统无模型控制的数学模型,即表示为
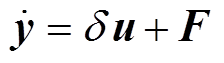 (8)
(8)
式中,y和u分别为系统的输出和控制量;d 为可设计的非物理比例因子,为可调参数;F为系统的有界扰动部分,可包含参数失配等未知扰动部分。
将式(1)、式(2)表示的电机数学模型整理成式(8)的形式,可得
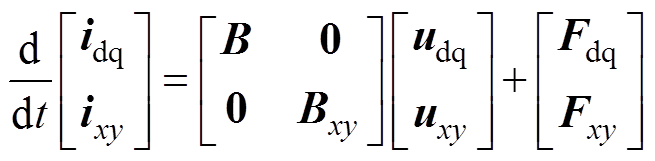 (9)
(9)
其中

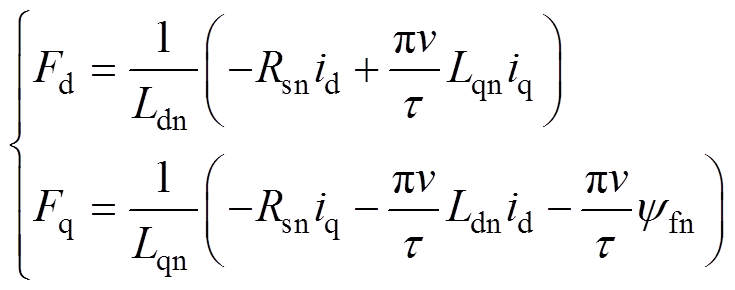
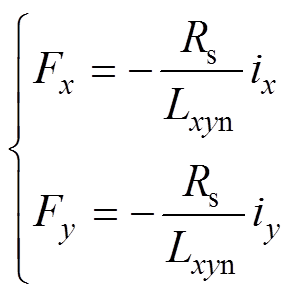
进一步表示为
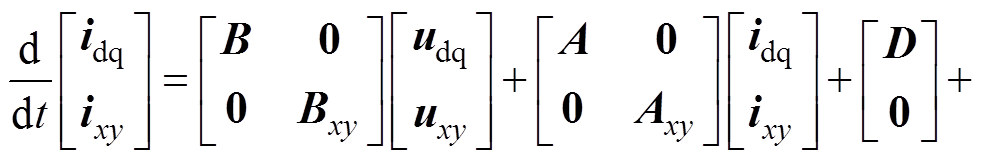
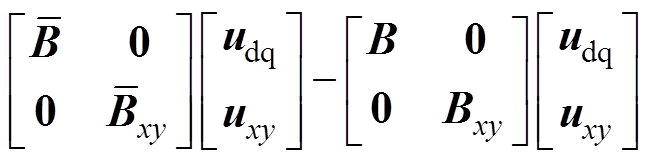 (10)
(10)
式(9)和式(10)中参数均采用标称值,上标“-”代表参数采用实际值,进一步可以得到双三相PMLSM无模型控制的超局部模型为
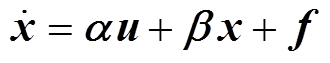 (11)
(11)
其中
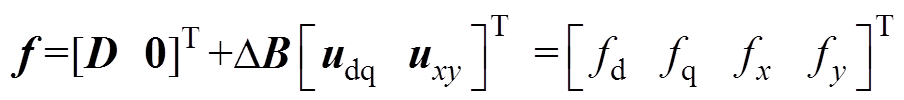
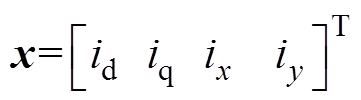
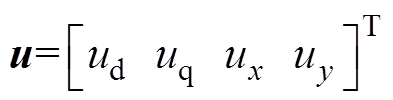
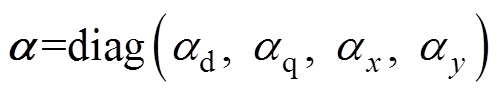
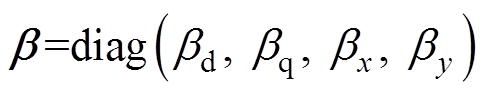
式中,a为定子电压系数矩阵;b为状态增益矩阵;f为未知项。观察模型式(9)、式(10)可知,Fdq、Fxy中包含与电流有关的线性项。
通过式(10)和式(11),将Fdq、Fxy拆分为与电流有关的线性项bx,和包含反电动势项D及参数失配DB的未知项f。f中的反电动势与速度和磁链有关,而电阻、电感、磁链和速度相对于电流缓慢变化,因此f是缓变可观测的[26-27]。设计观测器以便补偿反电动势波动和参数失配对电流控制的影响。此外,将未知缓变的变量与系统已知的电流状态变量分离,单独对缓变量设计观测器可以简化观测器的设计,减少参数调优的工作量,使无模型控制器的设计得到进一步简化。此外,针对总的未知项f设计观测器,使得超局部模型更贴近真实电机模型,观测器得到的估计值更接近实际值,反馈补偿量会更加准确[25]。
同样地,将式(11)离散化,并根据无差拍的原则得到无模型电流预测控制(MFPCC)的控制方程为
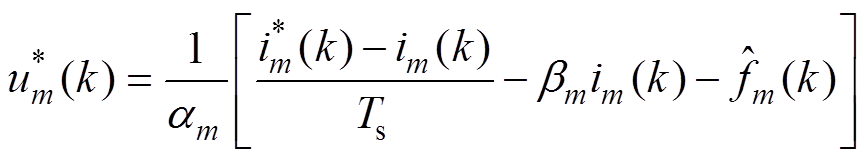 (12)
(12)
式中,下标“m”表示dq轴分量或者xy轴分量;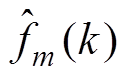 为未知部分的观测值。
为未知部分的观测值。
根据式(11),与电流相关的已知项归入线性项bx中,剩下的f为缓慢变化的扰动量,满足
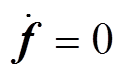 (13)
(13)
设估计误差为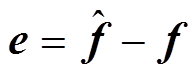 。其中,“
。其中,“ ”表示观测值。可得观测器表达式为
”表示观测值。可得观测器表达式为
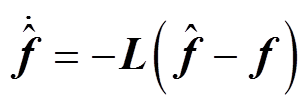 (14)
(14)
式中,L为观测器增益矩阵,L=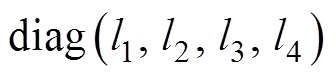 。
。
进一步得到扰动观测器为
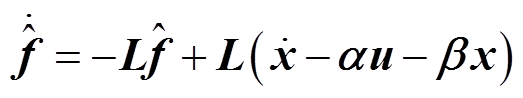 (15)
(15)
由式(13)和式(14),可得误差动态方程为
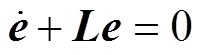 (16)
(16)
可见,观测器的估计误差将收敛至零且与系统的状态x无关。由于式(15)中观测量的求导会放大噪声,所以根据文献[31],可借助中间变量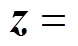
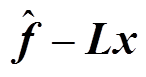 ,联立式(15)得到扰动观测器为
,联立式(15)得到扰动观测器为
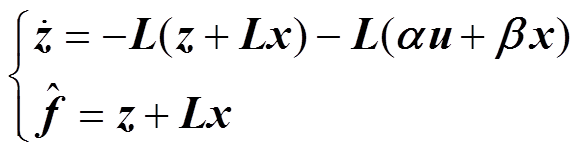 (17)
(17)
设计李雅普诺夫方程证明扰动观测器的稳定性,有
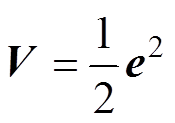 (18)
(18)
对式(18)求导,并将式(16)代入可得
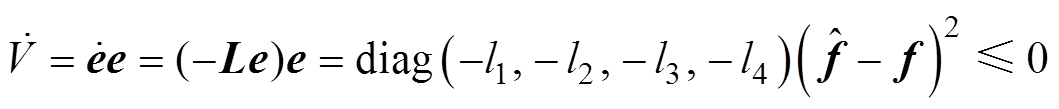 (19)
(19)
若满足式(19)的稳定性条件,则观测器增益l1,2,3,4>0。
由式(11)和式(15)拉普拉斯变换,可得
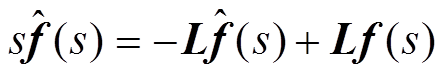 (20)
(20)
经过整理,即得由f到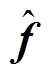 的传递函数为
的传递函数为
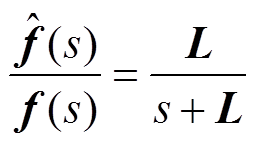 (21)
(21)
由式(21)可以看出,扰动观测可以等价为一阶低通滤波器,L可以等价为截止频率,其取值需要兼顾滤波器的噪声和延迟问题。
被控对象超局部模型式(11)的离散形式为
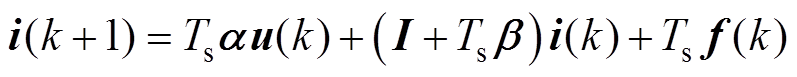 (22)
(22)
式中,I为单位矩阵。
考虑一拍的延时,有
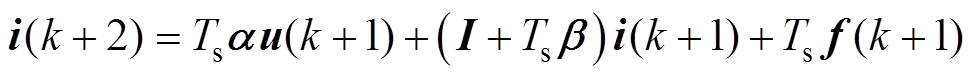 (23)
(23)
得到控制器的方程为
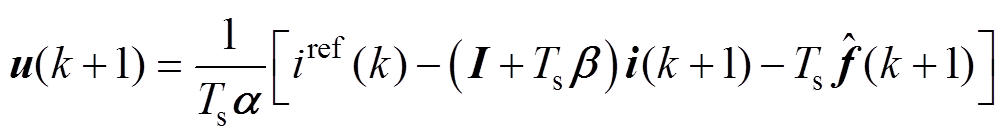 (24)
(24)
扰动观测器式(17)的离散形式为
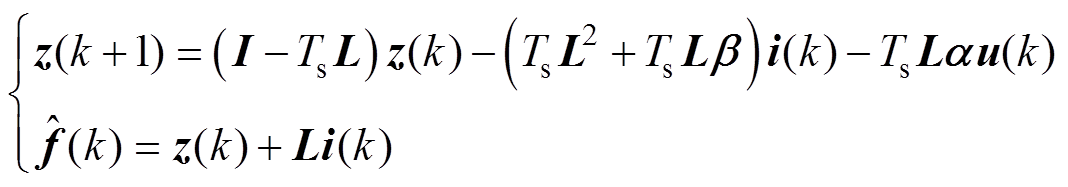 (25)
(25)
为了方便分析控制系统的性能,图2给出了MFPCC系统的框图。
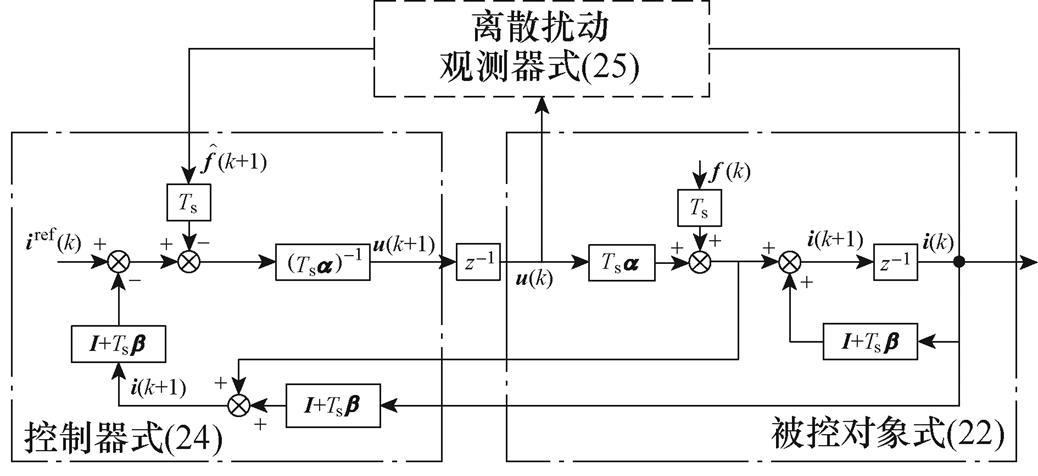
(a)MFPCC的离散域系统框图
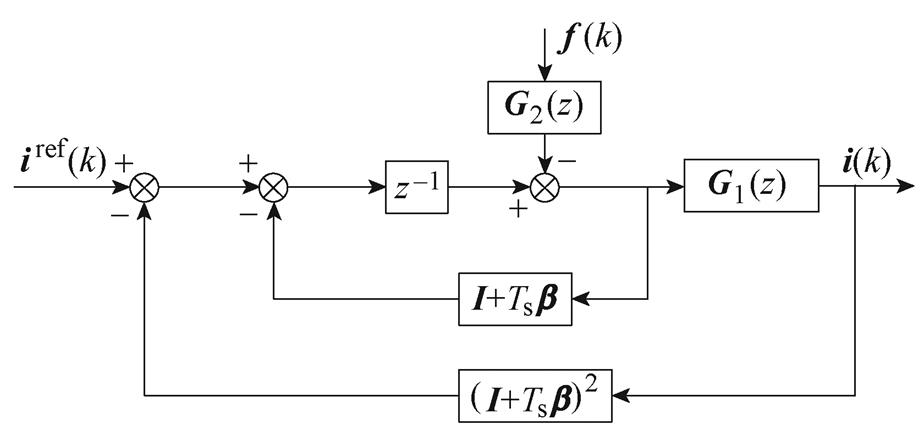
(b)MFPCC的简化离散域系统框图
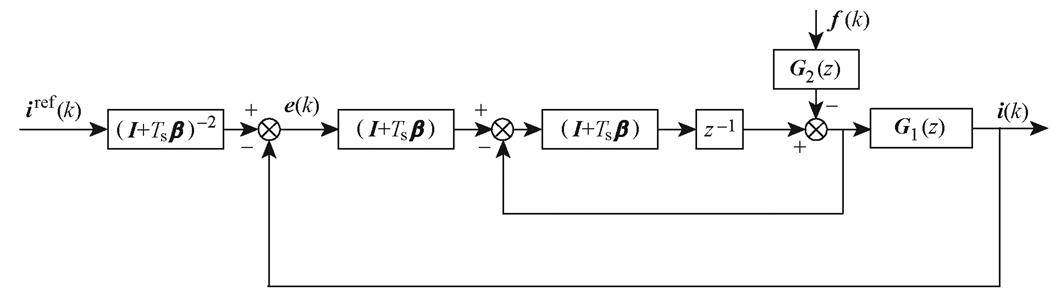
(c)等价的MFPCC的简化离散域系统框图
(d)MFPCC的离散域最终简化框图
图2 MFPCC的框图简化过程
Fig.2 Simplified process of MFPCC block diagram
将s域的式(21)转化到z域下,可得
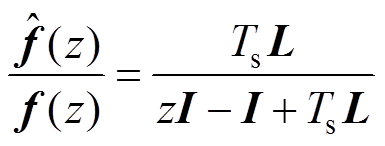 (26)
(26)
则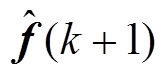 与i(k)、u(k)的关系可以转换为
与i(k)、u(k)的关系可以转换为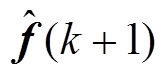 与f(k)的关系,即图2a可以简化为图2b,其中
与f(k)的关系,即图2a可以简化为图2b,其中
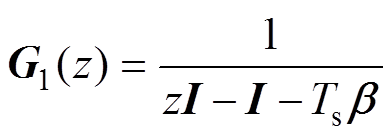 (27)
(27)
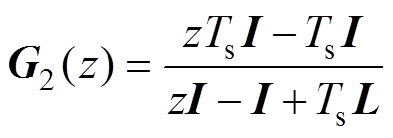 (28)
(28)
图2b等价于图2c,由图2c可以得到f(k)到e(k)的误差传递函数为
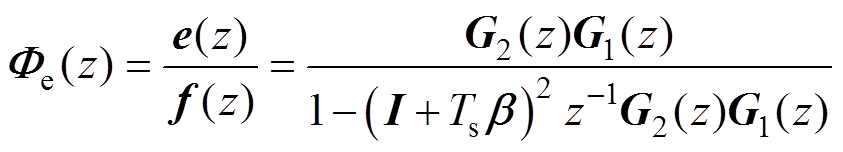 (29)
(29)
则根据终值定理,由未知扰动项导致的稳态误差为
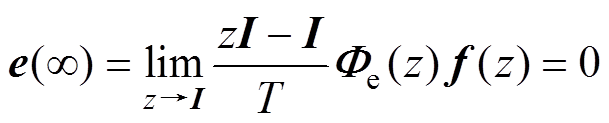 (30)
(30)
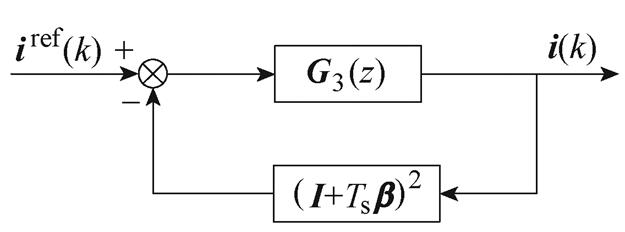
因此可知,在本文提出的MFPCC中,包含反电动势波动和参数失配的未知扰动f(k)造成的稳态电流误差为零。即扰动观测器的引入能够准确观测f(k),消除扰动f(k)的影响。进一步地,图2c最终可以化简为图2d。其中
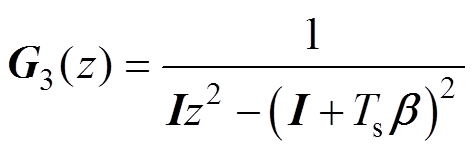 (31)
(31)
最终,可以得到系统输入输出的传递函数为
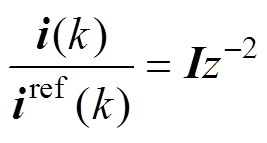 (32)
(32)
式中,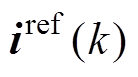 为电流参考值。
为电流参考值。
由式(32)可知,本文设计的无模型电流预测控制MFPCC为滞后两拍的控制,即电流采样值能在两个采样周期后跟上电流指令值,本文所提方法的有效性得到论证。
为了验证本文所提无模型电流预测控制的有效性,利用基于RT-Lab的半实物实验平台[32]建立如图3所示的分段式双三相PMLSM的控制系统,并与传统的DPCC进行了对比研究。
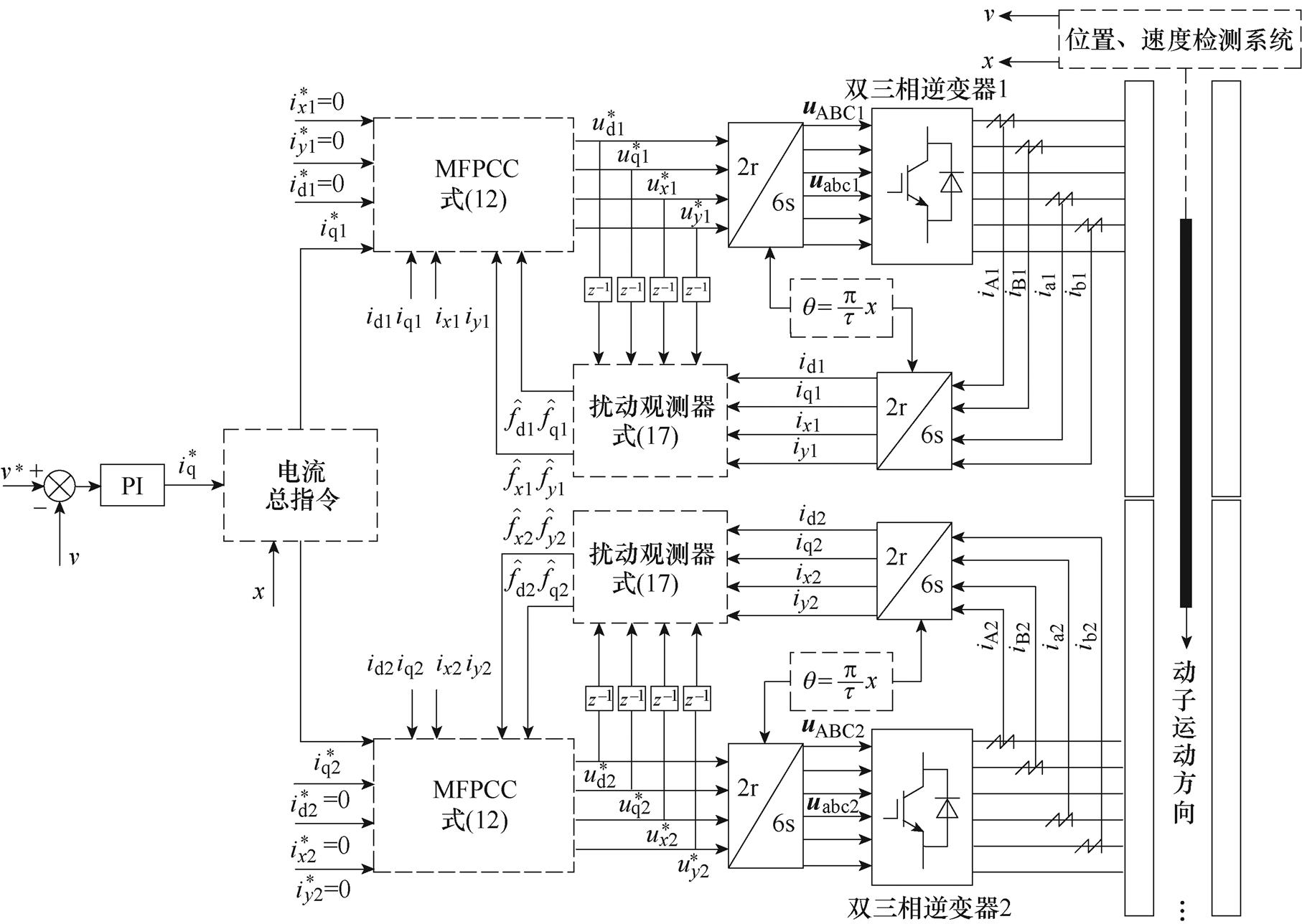
图3 基于MFPCC的双三相PMLSM系统框图
Fig.3 Dual three-phase PMLSM system diagram for MFPCC
本文电机的定子为分段形式,每个分段看作一台电机,建模时采用以4段为一个循环的形式。供电方式为两台逆变器通过切换开关对电机进行并联供电,即逆变器1号给奇数段定子供电,逆变器2号给偶数段定子供电,如图4所示。根据传感器获得的动子位置,当动子头部即将到达下一个定子段时,通过切换开关开通下一定子段的逆变器,当动子尾部离开该定子段时,关断该定子段的逆变器。
本文所用实验平台如图5所示,采用基于RT- LabOP5607的半实物平台进行验证。其中控制机箱内包括CPU板卡、PWM输出板卡和A-D采样板卡,分别负责电机的控制程序、逆变器的调制和A-D采样等功能;仿真机OP5607内含有Xilinx Virtex7的FPGA板卡。本文将电机、逆变器以及机械运动模型建立在机箱内的FPGA板卡中,按照5×10-7 s的周期离散化。图3中的位置、速度检测系统在本文半实物实验中表示机械运动模型,通过计算电机的推力,获取动子的加速度,最终得到动子的位置和速度信息。CPU就是真实的控制系统,将传统的DPCC和所提的MFPCC的控制算法写入其中,采样和控制频率均为10 kHz。
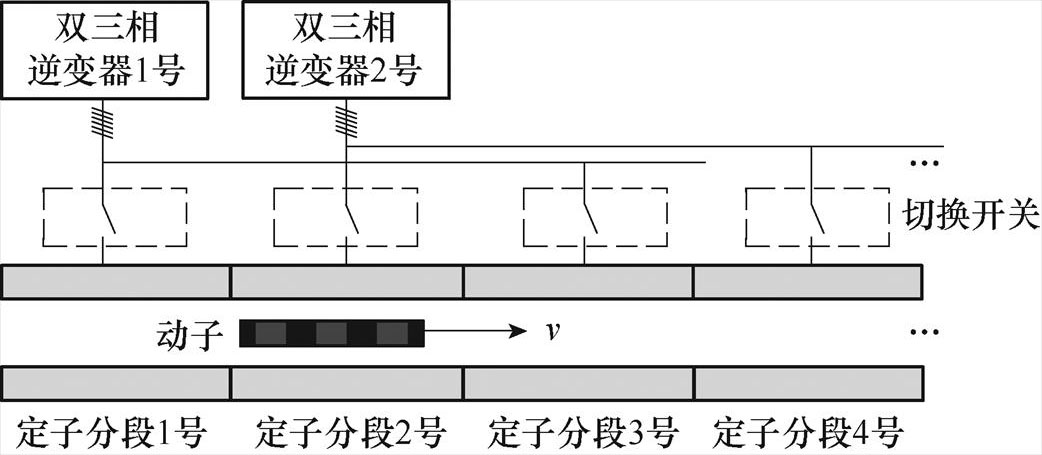
图4 分段式双三相PMLSM的供电方式
Fig.4 Power supply mode of segmented dual-phase PMLSM
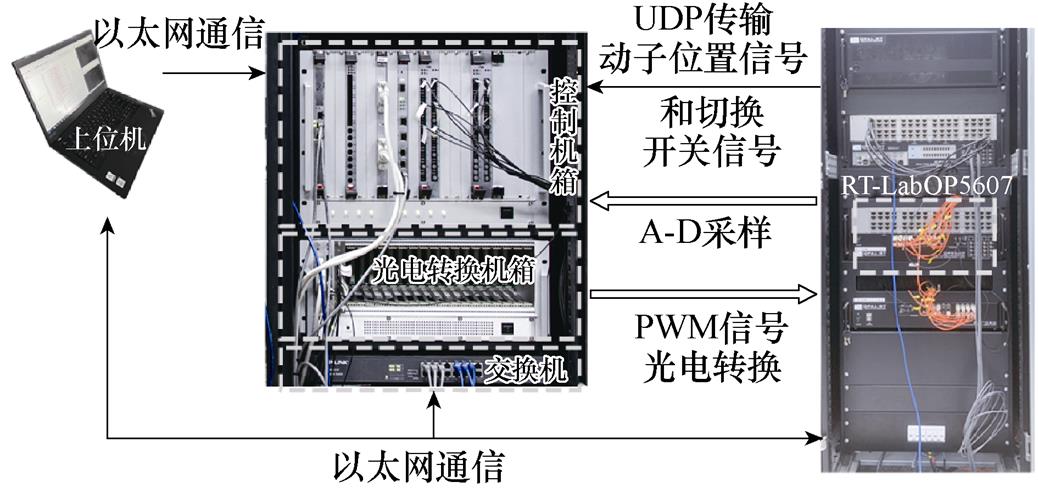
图5 基于RT-LabOP5607的半实物实验平台
Fig.5 Hardware-in-loop experiment platform based on RT-LabOP5607
双三相PMLSM电机参数见表1。
表1 双三相PMLSM参数
Tab.1 The parameters of dual three-phase PMLSM

参 数数 值 定子电阻Rs/mW29.3 漏感Lxy/mH0.063 dq轴电感Ld(q)/mH0.49 定子长度L1/m1.363 2×4 动子长度L2/m1.022 4 极数6 极距t/m0.170 4 永磁体磁链yf/Wb0.42 动子和负载质量M/kg80
在实验中,MFPCC的可调参数包含定子电压系数矩阵a、状态增益矩阵b和扰动观测器增益矩阵L。可调参数设计过程简单,主要如下:①定子电压系数矩阵a 中参数的设计依据为ad=1/Ld,aq= 1/Lq,ax=ay=1/Lxy,作为它们的初值,其大小应根据实验情况做适当调整。②状态增益b的设计依据为b1,2=-Rs/Ldq,b3,4=-Rs/Lxy,作为参考,实际实验时本文取b1,2=-60,b3,4=-460。③为了保证2.3节中扰动观测器的稳定性以及其良好的滤波特性,本文取l1,2=2 000,l3,4=2 500。
最后,设计速度外环的PI参数时,应设计成典型Ⅱ型系统,增加系统的动态抗扰性,因此kp和ki参数分别取2 000和200。
为充分验证算法的鲁棒性,在实验中,使控制器中磁链yf和电感(Ldq、Lxy)分别变为电机实际值的50%和200%。
图6~图8为速度开环的情况,指令电流iqref模拟速度环出来的电流波形,如图中虚线所示。起始阶段使动子加速,电流指令值iqref限幅为200 A,随后电机到达指定速度,在0.5 s后电流指令维持在150 A。图6~图8中的序号①~③分别表示:①动子开始进入第一段定子;②动子在第一段定子运行,即与第一段定子有耦合时的情况;③动子已离开第一段定子。
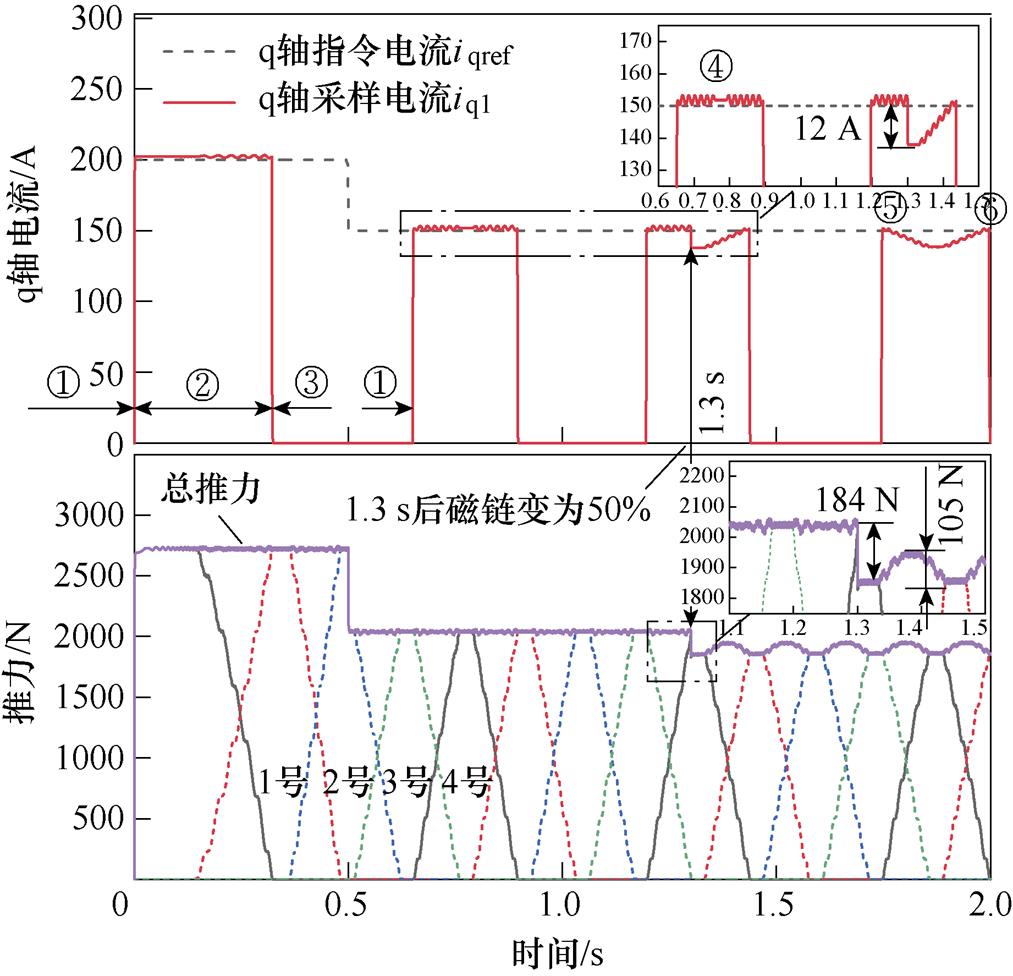
图6 磁链参数yf减小50%时DPCC的q轴电流跟踪和推力结果
Fig.6 Experimental results of DPCC’s q-axis current tracking and thrust when the flux linkage parameter yfis reduced by 50%

图7 Ld、Lq、Lxy增大至200%时DPCC的q轴电流跟踪和推力结果
Fig.7 Experimental results of DPCC’s q-axis current tracking and thrust when Ld, Lq, Lxy are increased to 200%
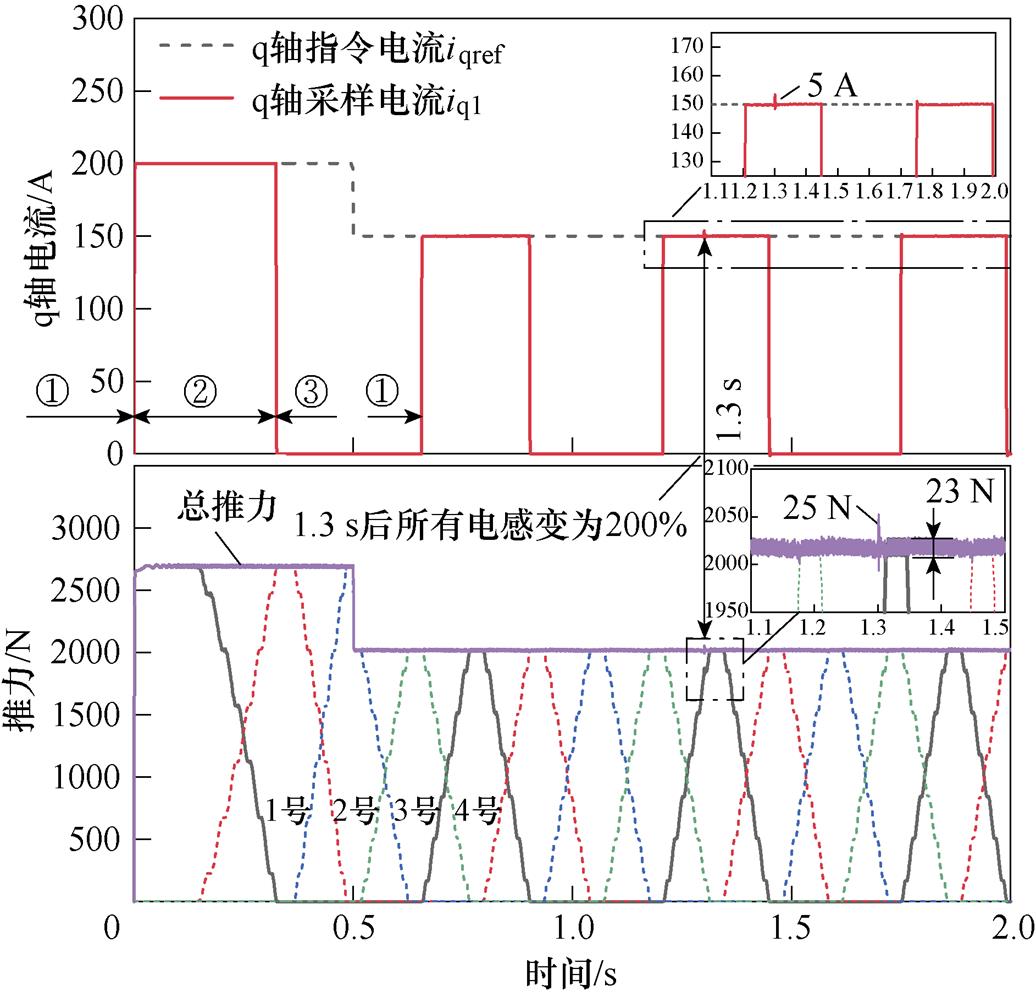
图8 Ld、Lq、Lxy增大至200%时MFPCC的q轴电流跟踪和推力结果
Fig.8 Experimental results of q-axis current tracking and thrust of MFPCC when Ld, Lq, Lxy are increased to 200%
图6为控制器的永磁体磁链参数yf减小50%时,DPCC的q轴电流跟踪效果以及电磁推力波形。由图6可知,动子穿越定子分段引起的反电动势动态扰动,使④处一分段的q轴电流iq1出现波动,验证了1.2小节中分析的正确性。在DPCC中,当t=1.3 s时磁链yf发生突变,使得q轴电流iq1无法有效地跟踪给定值iqref,出现了最大为12 A的电流跟踪误差。由于磁链失配及控制器无法有效补偿反电动势动态扰动,导致之后⑤和⑥间q轴电流iq1存在先减后增的过程,无法准确跟踪电流指令值。推力波形主要关注由分段1号、2号、3号、4号的推力相加而得的总推力。可见,1.3 s时磁链发生变化后,总推力立刻损失184 N,且磁链失配后造成的推力变化幅度为105 N,结合动子稳态运行时的推力均值2 kN,计算得到推力波动为5.25%。
图7为控制器的Ld、Lq、Lxy增大到原来的200%时,DPCC的q轴电流iq1跟踪效果以及电磁推力波形。在DPCC中,参数变化前后依旧存在与动子穿入穿出定子段有关的反电动势动态扰动导致的电流波动。当1.3 s电感参数突变时,q轴电流iq1的跟踪效果没有发生明显变化,但是在动子进入定子分段的瞬间,有最大为11 A的电流波动。同时,推力均值下降了15 N,造成的推力变化范围为40 N。参数突变后的推力波动为2%,相比参数突变之前的2.3%,推力波动变化较小。
图8为本文所提出的MFPCC的q轴电流iq1能够严格跟踪指令值iqref,在动子穿入和穿出分段定子时都较为平滑,很好地补偿了反电动势动态扰动的影响。由于MFPCC控制器没有用到磁链参数,所以在1.3 s时刻,电感Ld、Lq、Lxy增大到原来的200%后,q轴电流iq1只在该时刻出现了5 A的误差。推力平稳,造成的推力变化范围只有25 N。同样地,在1.3 s时刻,推力出现了25 N的变化。参数突变后的推力波动为1.25%,相比参数突变之前的1.2%,推力波动无明显变化。
图9给出了对应于图8的MFPCC中扰动观测器的fd、fq、fx、fy实际值和观测值对比。这里需要说明的是,为了方便计算,本文根据式(10)的左边减去右边的前两项,等效得到fd、fq、fx、fy实际值。经过对比可知,扰动观测器能够准确观测fd、fq、fx、fy。其中,图9中的fq实际值出现较大尖刺是由于计算式(10)左边的电流导数所导致。
由图6和图7证明了传统DPCC无法处理动子穿入和穿出定子分段时反电动势的动态扰动,以及参数失配对q轴电流跟踪的影响。图8和图9表明,MFPCC很好地补偿了两者的影响,扰动观测器对反电动势和参数失配的准确观测和补偿使得q轴电流跟踪效果不受动子运动过程造成的反电动势动态扰动的影响,且有很好的参数鲁棒性,电流跟踪和推力的稳态性能更好。验证了本文扰动观测器观测的准确性,也验证了本文所提方法的有效性。
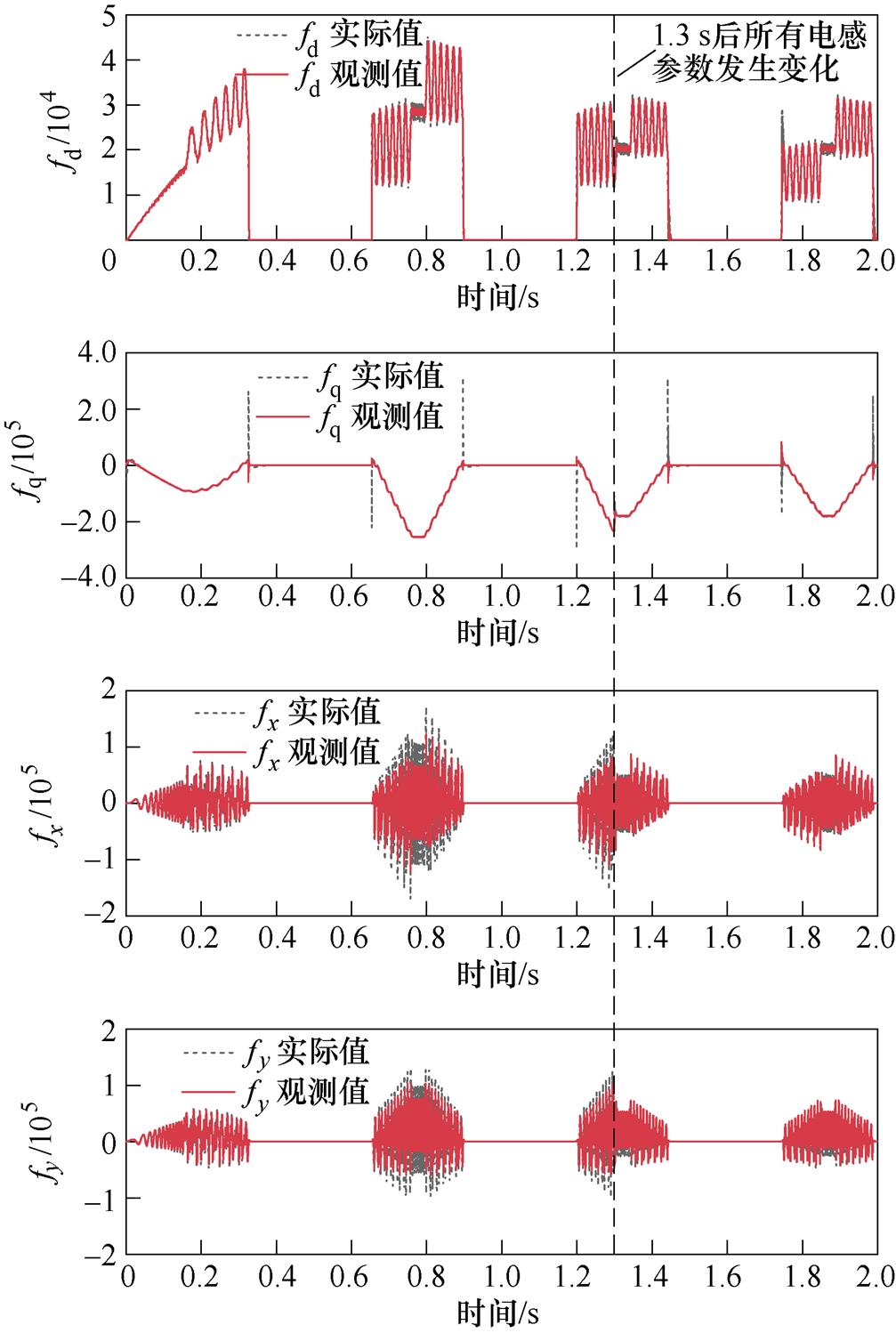
图9 fd、fq、fx、fy观测值
Fig.9 Observed value of fd, fq, fx, fy
为了进一步论证MFPCC能够提升分段式双三相PMLSM的控制性能,以下实验给出速度闭环的情况。
图10和图11为速度闭环时,速度给定值是在0.25 s内从零加速到8 m/s,在0.75 s时阶跃至12 m/s的情况。速度环调节器采用PI调节器,设置限幅值为±200 A且全过程中电感和磁链参数分别为原来的200%和50%。
在图10中,DPCC的速度反馈值经过0.35 s跟上速度斜坡给定值,经过0.6 s跟上速度的阶跃给定值。DPCC的q轴电流跟踪iq1在动子穿入穿出定子分段时存在波动,且无法有效跟踪指令值iqref。在0.75 s速度突增时刻,电流跟踪也存在较大误差。
图11中,参数失配后MFPCC的速度反馈值跟随斜坡给定值的时间为0.36 s,与DPCC的0.35 s相差无几,而MFPCC速度跟随阶跃给定值的时间为0.53 s,要小于DPCC的速度跟踪时间0.6 s,可见,MFPCC速度的动态响应较快。从q轴电流波形可以看出,相较于DPCC,MFPCC有效抑制了动子运动过程导致反电动势动态扰动的影响,且电感和磁链同时发生失配后,依然保持良好的电流跟踪性能。在0.75 s速度突增时刻,电流跟踪误差较小。

图10 电感和磁链参数分别为200%和50%时DPCC实验结果
Fig.10 Experimental results of DPCC when the inductance and flux are 200% and 50% respectively
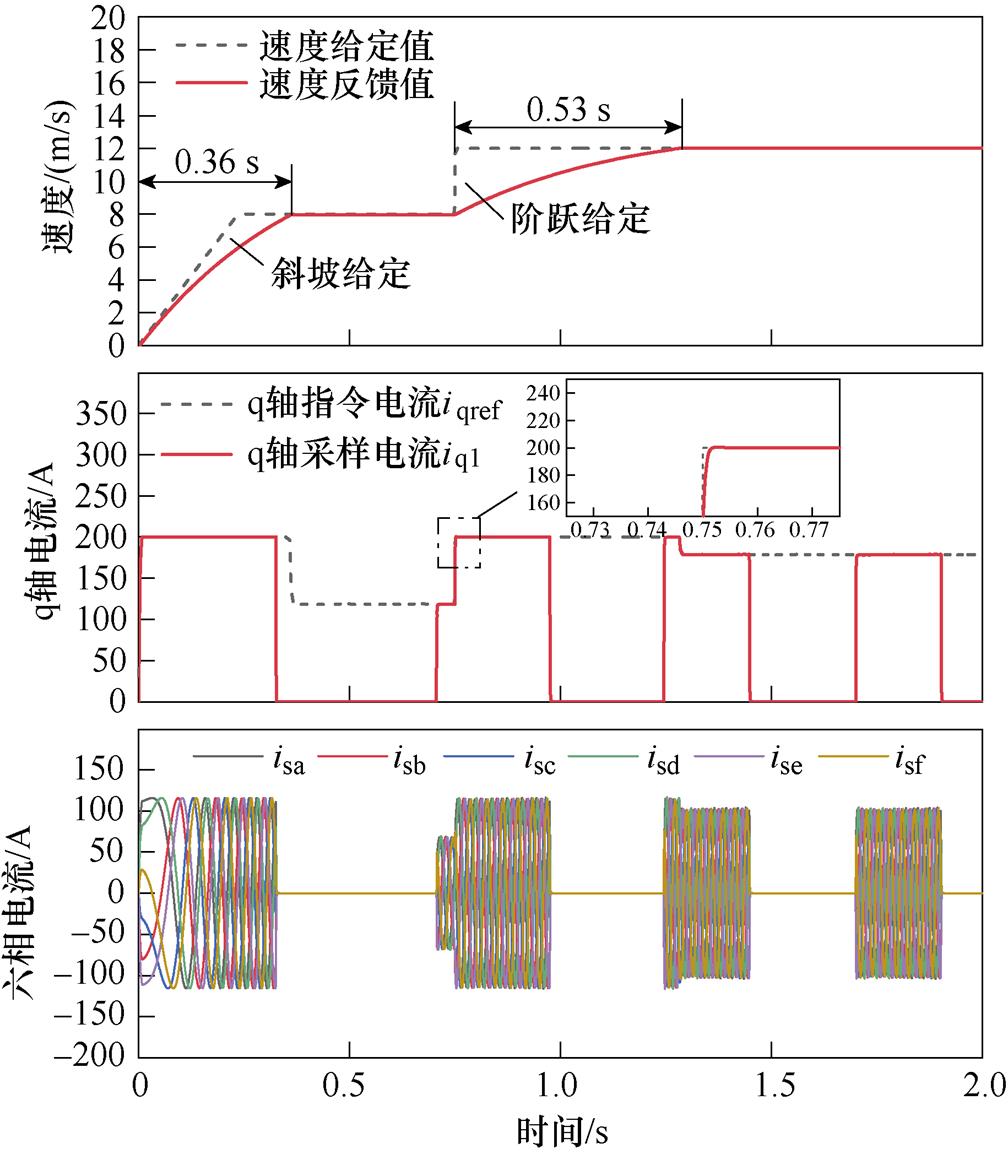
图11 电感和磁链参数分别为200%和50%时MFPCC实验结果
Fig.11 Experimental results of MFPCC when the inductance and flux are 200% and 50% respectively
图12为对应于图11的扰动观测器的fd、fq、fx、fy实际值和观测值对比。结合图9,证明了扰动观测器观测结果的准确性,能够有效补偿反电动势动态扰动和参数失配的影响。
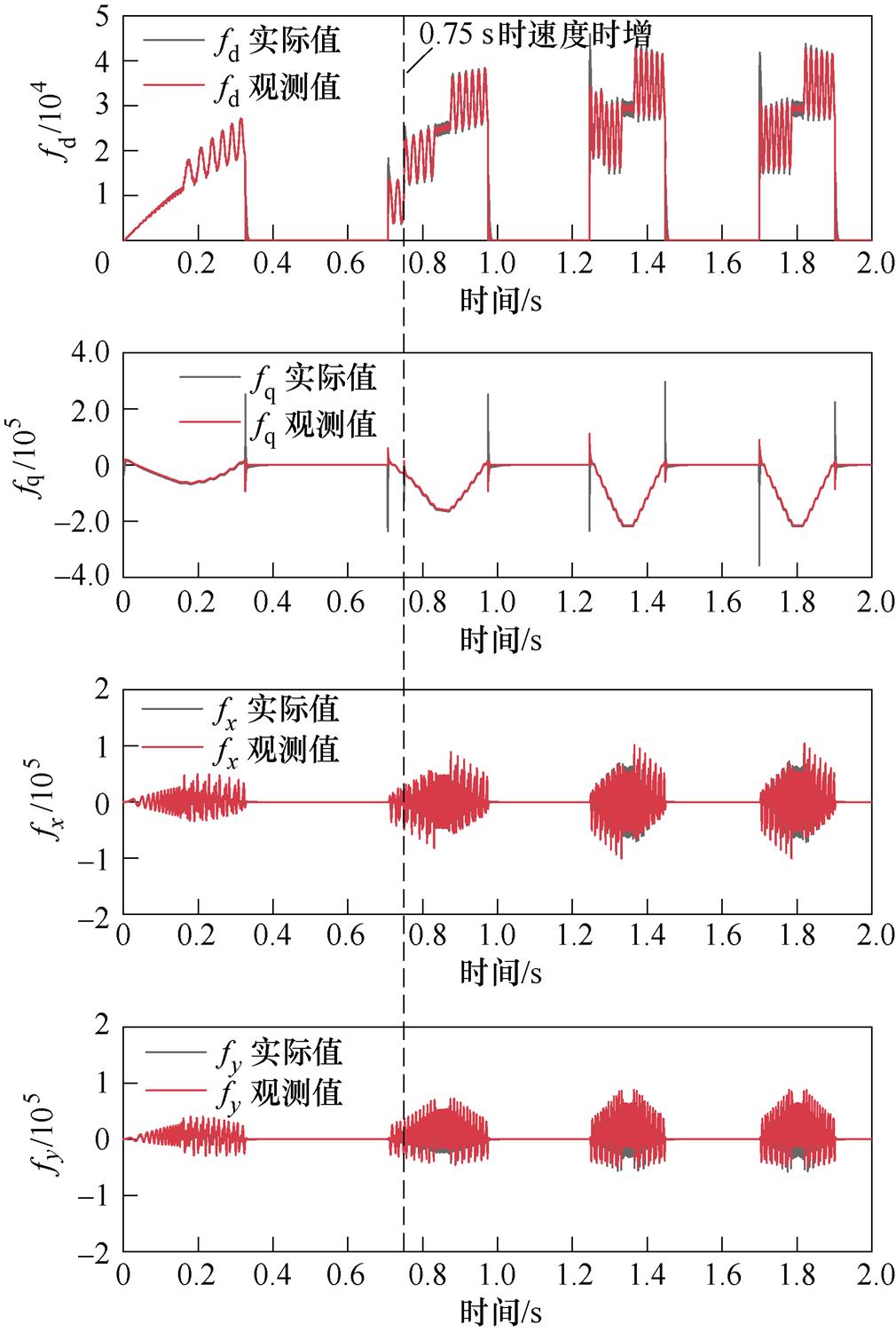
图12 fd、fq、fx、fy观测值(对应图11)
Fig.12 Observed value of fd, fq, fx, fy (corresponding to Fig.11)
图13为DPCC和MFPCC的q轴电流跟踪效果在图10、图11中速度突增时刻的对比。可知,DPCC的电流跟随阶跃电流指令值时有明显的振荡过程,且存在5 A的超调量,最大电流误差为8 A。虽然MFPCC电流上升得不如DPCC快,但是其电流更快进入稳态,且没有超调,电流跟踪误差比DPCC小。可见,MFPCC的q轴电流iq1的动态响应和稳态性能都较好。结合图10、图11中参数变化后速度跟踪时间及图13中电流跟踪情况,可以得到,本文提出的加入扰动观测器算法的MFPCC依然保持了系统的快速响应。
通过对比图10和图11还可以发现,参数的失配会使得DPCC的相电流发生一定的畸变。本文给出两者的THD如图14所示,DPCC的THD为MFPCC的两倍之多。
然而,在实际工况中,给下一段定子供电时,逆变器电流值并不会瞬间到达指令值,使得动子到达下一段定子时,q轴电流还未达到所需指令值,造成一定的推力波动。为了模拟真实逆变器在动子新进入一段定子时电流环指令建立缓慢,验证速度闭环恒速运行下所提MFPCC是否有效,本文使逆变器建立电流时按斜坡方式上升至速度环输出的q轴电流指令iqref。速度环的参数始终保持不变,速度给定值是在0.25 s内从0 m/s匀加速至10 m/s,并恒速运行,设置限幅值为±200 A,得到电流环指令建立缓慢情况下的q轴电流、推力和速度波形,如图15所示,1.3 s处为电感Ld、Lq、Lxy突变为200%的时刻。
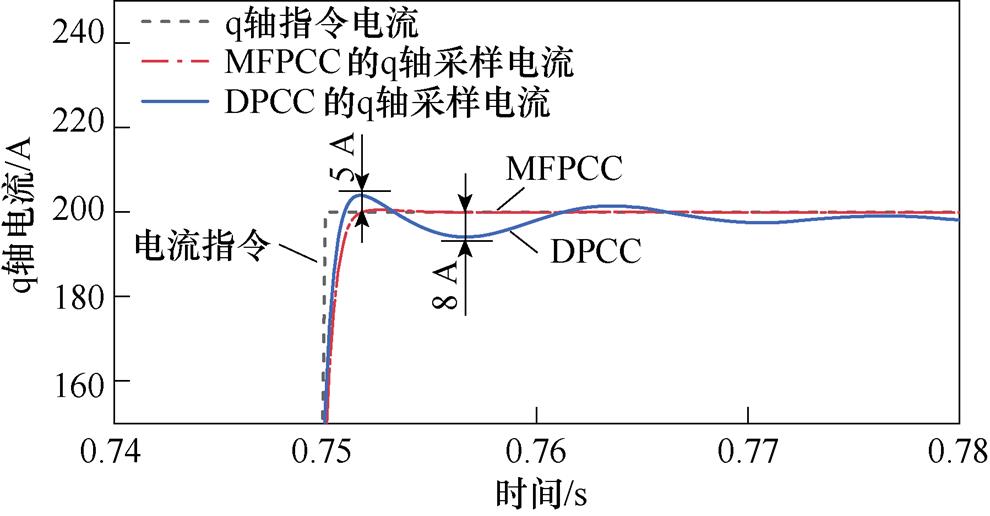
图13 DPCC和MFPCC的电流跟踪效果对比
Fig.13 Comparison of current tracking performance between DPCC and MFPCC
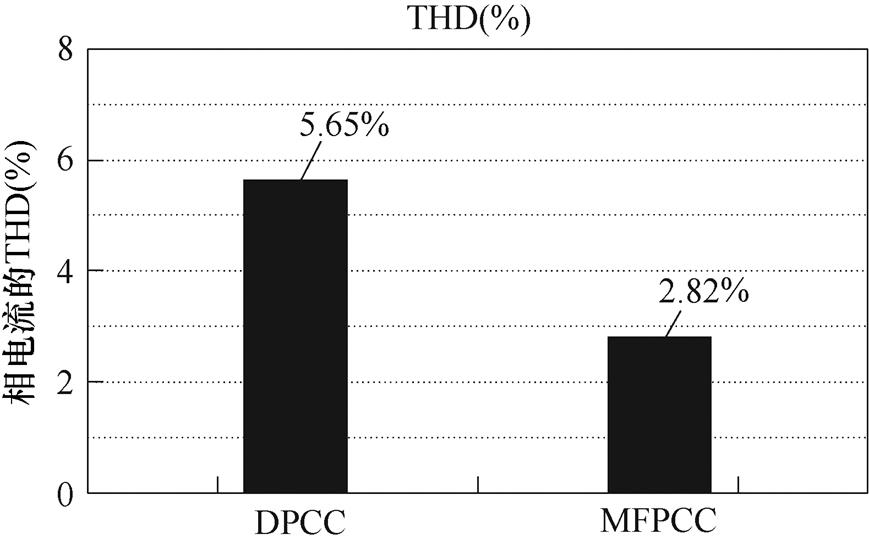
图14 参数失配的相电流THD分析
Fig.14 THD analysis for a phase current with mismatched parameters
对比图15a可知,本文所提MFPCC,当建立电流指令值缓慢时,q轴电流波动明显,引起的推力和速度的波动较大。在这种情况下,可在动子未到达下一段电机时,提前给下一段电机通电,建立起q轴电流使其达到指令值。此时的结果如图15b所示,可见这种方式可有效降低电机恒速闭环运行时q轴电流指令建立缓慢导致的推力波动。
图16给出了考虑逆变器q轴电流指令值建立缓慢时,为下一段定子供电的细节。根据动子的位置信息,在动子即将要进入下一分段定子时,开始建立电流指令值。根据一阶系统的单位阶跃响应,调节时间tr达到4T时的稳态误差为2%(T为一阶低通滤波器的时间常数),近似认为达到了稳态。所以在动子头部与下一段定子的间距为4Tv时(v为动子的运动速度),逆变器开始建立q轴电流指令值。此指令值等于速度环输出的q轴电流指令值。
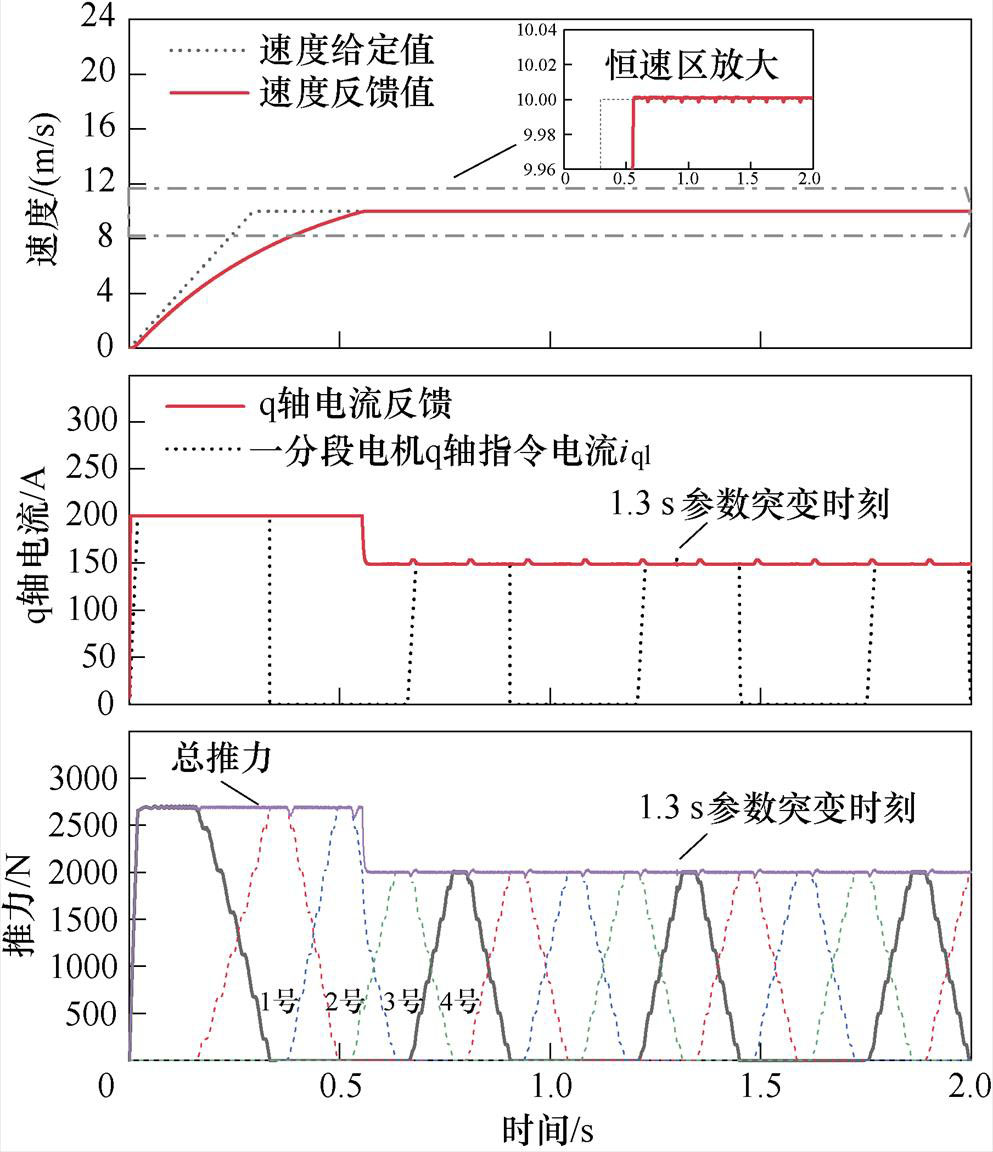
(a)逆变器电流按斜坡上升至指令值
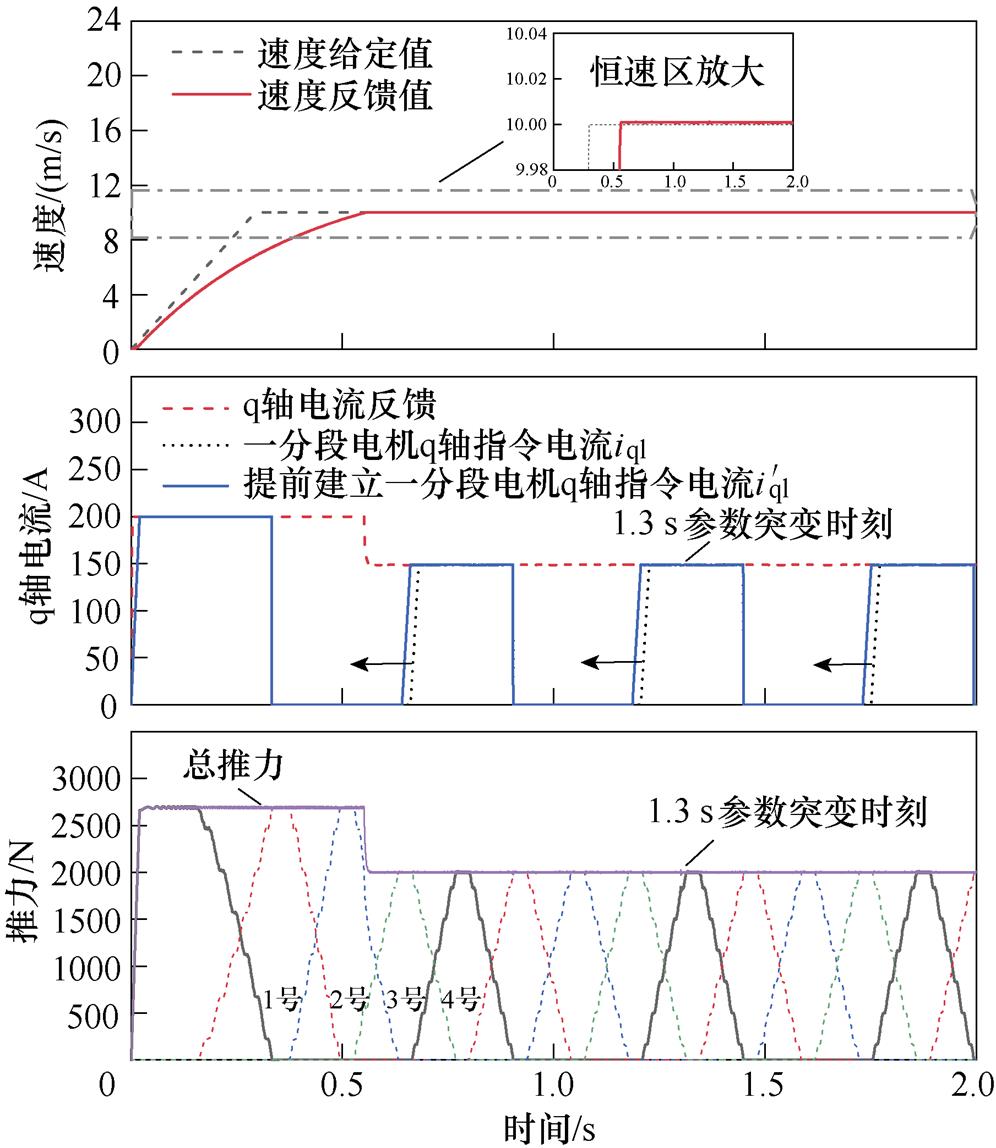
(b)逆变器提前建立q轴电流指令
图15 电流指令缓慢建立时速度、q轴电流和推力
Fig.15 Results of q-axis current, thrust and velocity when the command current is slowly established
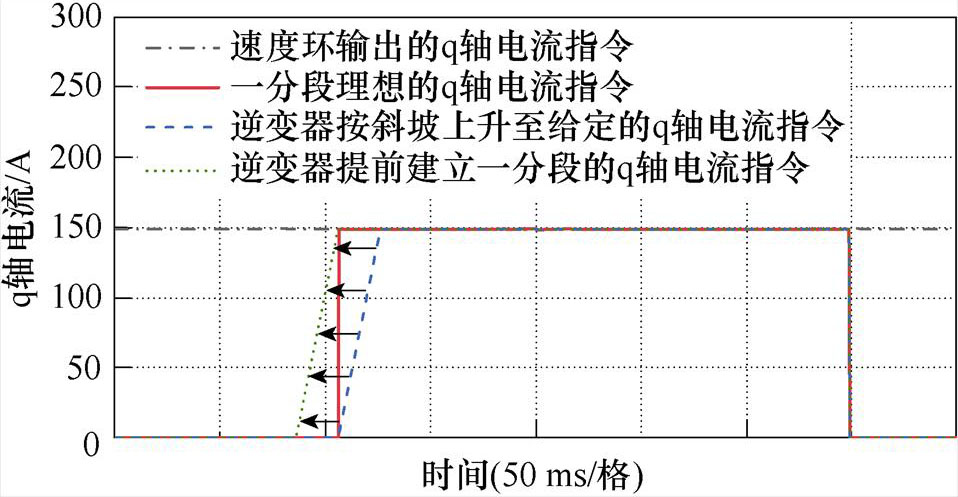
图16 逆变器提前建立一分段定子的q轴指令电流
Fig.16 Inverters establish the command q-axis current of a segmented stator in advance
通过实验结果可知,DPCC的性能受到动子穿入穿出定子分段的反电动势动态扰动的影响,同时易受参数失配的影响,其中永磁体磁链yf的失配对DPCC造成的影响最大,其次是电感Ld、Lq、Lxy的变化。但是对于MFPCC,即便参数发生变化,在动子运动的全过程中q轴电流动态响应快且总有很好的跟踪效果,电流谐波含量小,进而造成的推力波动小,速度波形准确。
本文基于分段式双三相PMLSM的超局部模型提出了无模型电流预测控制(MFPCC)。根据双三相电机的模型特点,考虑综合扰动项F,设计了超局部模型,基于该超局部模型获得预测电流控制器并设计扰动观测器估计F中的未知项,硬件在环实验证明了所提方法的有效性。主要结论如下:
1)分段式双三相PMLSM的参数失配和动子穿越定子分段的过程中反电动势存在的动态扰动,都会对电流控制引入扰动,恶化控制器的电流跟踪性能,进而导致推力波动。另外,双三相电机在VSD变换后谐波子空间电感参数Lxy失配,会进一步影响电流和推力性能。
2)设计了基于分段式双三相PMLSM的超局部模型,该模型分为已知线性项和包含反电动势及参数失配的未知项,观测器的设计得到简化。
3)相比于DPCC,MFPCC对参数失配的鲁棒性较强,能有效抑制动子穿入穿出定子分段造成的反电动势动态扰动的影响,在运动的全程中q轴电流的跟踪效果好、推力波动小、动态响应快。
参考文献
[1] 鲁军勇, 马伟明, 许金. 高速长定子直线感应电动机的建模与仿真[J]. 中国电机工程学报, 2008, 28(27): 89-94.
Lu Junyong, Ma Weiming, Xu Jin. Modeling and simulation of high speed long primary double-sided linear induction motor[J]. Proceedings of the CSEE, 2008, 28(27): 89-94.
[2] Stumberger G, Zarko D, Timur Aydemir M, et al. Design and comparison of linear synchronous motor and linear induction motor for electromagnetic aircraft launch system[C]//IEEE International Electric Machines and Drives Conference, Madison, WI, USA, 2003: 494-500.
[3] 郭思源, 周理兵, 齐歌. 双三相永磁同步电机电磁性能解析计算[J]. 电工技术学报, 2014, 29(5): 17-28.
Guo Siyuan, Zhou Libing, Qi Ge. Analytical calcu- lation of electromagnetic performance in dual three- phase permanent magnet brushless AC machines[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 17-28.
[4] 赵勇, 黄文新, 林晓刚, 等. 基于权重系数消除和有限控制集优化的双三相永磁容错电机快速预测直接转矩控制[J]. 电工技术学报, 2021, 36(1): 3-14.
Zhao Yong, Huang Wenxin, Lin Xiaogang, et al. Fast predictive direct torque control of dual three-phase permanent magnet fault tolerant machine based on weighting factor elimination and finite control set optimization[J]. Transactions of China Electrotech- nical Society, 2021, 36(1): 3-14.
[5] 符慧, 左月飞, 刘闯, 等. 永磁同步电机调速系统的一种变给定增益PI控制器[J]. 电工技术学报, 2017, 32(1): 168-174.
Fu Hui, Zuo Yuefei, Liu Chuang, et al. A variable input gain proportional integral controller for per- manent magnetic synchronous motor speed-regulation system[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 168-174.
[6] 章回炫, 范涛, 边元均, 等. 永磁同步电机高性能电流预测控制[J]. 电工技术学报, 2022, 37(17): 4335-4345.
Zhang Huixuan, Fan Tao, Bian Yuanjun, et al. Predictive current control strategy of permanent magnet synchronous motors with high performance[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4335-4345.
[7] 祝贺, 张今朝, 董睿, 等. 绕组分段永磁直线同步电机无传感器控制[J]. 电工技术学报, 2017, 32(21): 65-76.
Zhu He, Zhang Jinzhao, Dong Rui, et al. Sensorless control of winding segmented permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 65-76.
[8] 刘伟, 王俊. 永磁同步电机参数辨识研究综述[J]. 电气技术, 2020, 21(8): 1-5, 135.
Liu Wei, Wang Jun. Review of research on parameter identification of permanent magnet synchronous motor[J]. Electrical Engineering, 2020, 21(8): 1-5, 135.
[9] Yang Ming, Lang Xiaoyu, Long Jiang, et al. Flux immunity robust predictive current control with incremental model and extended state observer for PMSM drive[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(12): 9267-9279.
[10] Siami M, Khaburi D A, Abbaszadeh A, et al. Robustness improvement of predictive current control using prediction error correction for permanent- magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3458-3466.
[11] 郭科宇, 史黎明, 郑雲, 等. 双三相分段供电永磁直线同步电机电感分析与不平衡抑制[J]. 导航与控制, 2021, 20(5): 89-104.
Guo Keyu, Shi Liming, Zheng Yun, et al. Inductance analysis and imbalance suppression of the sectionally powered dual three-phases permanent magnet linear synchronous machine[J]. Navigation and Control, 2021, 20(5): 89-104.
[12] 郭科宇, 李耀华, 史黎明, 等. 电枢分段供电永磁直线同步电机的非线性数学模型[J]. 电工技术学报, 2021, 36(6): 1126-1137.
Guo Keyu, Li Yaohua, Shi Liming, et al. Non-linear mathematic model of a segmented powered permanent magnet linear synchronous machine[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1126- 1137.
[13] Liu Senyi, Liu Chunhua. Virtual-vector-based robust predictive current control for dual three-phase PMSM[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(3): 2048-2058.
[14] 贾成禹, 王旭东, 周凯. 基于电感辨识的内置式永磁同步电机电流模型预测控制[J]. 电机与控制学报, 2021, 25(11): 75-82.
Jia Chengyu, Wang Xudong, Zhou Kai. Model predictive control method for current control of IPMSM with inductance parameter identification[J]. Electric Machines and Control, 2021, 25(11): 75-82.
[15] 童力, 邹旭东, 丰树帅, 等. 基于预测无差拍算法的永磁同步发电机无传感器控制[J]. 电工技术学报, 2013, 28(3): 17-26.
Tong Li, Zou Xudong, Feng Shushuai, et al. A sensor-less control scheme for permanent magnet synchronous generators using predictive dead-beat algorithm[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 17-26.
[16] 牛里, 杨明, 王庚, 等. 基于无差拍控制的永磁同步电机鲁棒电流控制算法研究[J]. 中国电机工程学报, 2013, 33(15): 78-85, 13.
Niu Li, Yang Ming, Wang Geng, et al. Research on the robust current control algorithm of permanent magnet synchronous motor based on deadbeat control principle[J]. Proceedings of the CSEE, 2013, 33(15): 78-85, 13.
[17] 殷凯轩, 高琳, 付文华, 等. 永磁同步电机的改进模型预测自抗扰前馈控制[J]. 西安交通大学学报, 2021, 55(4): 29-38.
Yin Kaixuan, Gao Lin, Fu Wenhua, et al. An improved prediction control model for PMSM with active disturbance rejection and feed-forward control strategy[J]. Journal of Xi’an Jiaotong University, 2021, 55(4): 29-38.
[18] 尹忠刚, 白聪, 杜超, 等. 基于内模干扰观测器的永磁同步直线电机无差拍电流预测控制方法[J]. 电工技术学报, 2018, 33(24): 5741-5750.
Yin Zhonggang, Bai Cong, Du Chao, et al. Deadbeat predictive current control for permanent magnet linear synchronous motor based on internal model dis- turbance observer[J]. Transactions of China Electro- technical Society, 2018, 33(24): 5741-5750.
[19] 孙静, 刘旭东. 基于无差拍预测控制和扰动观测器的永磁同步电机电流控制[J]. 电机与控制应用, 2017, 44(10): 25-29, 35.
Sun Jing, Liu Xudong. Deadbeat predictive current control of permanent magnet synchronous motor based on disturbance observer[J]. Electric Machines & Control Application, 2017, 44(10): 25-29, 35.
[20] Han Jingqing. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.
[21] Fliess M, Join C. Model-free control and intelligent pid controllers: towards a possible trivialization of nonlinear control?[J]. IFAC Proceedings Volumes, 2009, 42(10): 1531-1550.
[22] 苏光靖, 李红梅, 李争, 等. 永磁同步直线电机无模型电流控制[J]. 电工技术学报, 2021, 36(15): 3182-3190.
Su Guangjing, Li Hongmei, Li Zheng, et al. Research on model-free current control of permanent magnet synchronous linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3182-3190.
[23] Zhang Yongchang, Jin Jialin, Huang Lanlan. Model- free predictive current control of PMSM drives based on extended state observer using ultralocal model[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 993-1003.
[24] 赵凯辉, 戴旺坷, 周瑞睿, 等. 基于扩展滑模扰动观测器的永磁同步电机新型无模型滑模控制[J]. 中国电机工程学报, 2022, 42(6): 2375-2386.
Zhao Kaihui, Dai Wangke, Zhou Ruirui, et al. Novel model-free sliding mode control of permanent magnet synchronous motor based on extended sliding mode disturbance observer[J]. Proceedings of the CSEE, 2022, 42(6): 2375-2386.
[25] Safaei A, Mahyuddin M N. Adaptive model-free control based on an ultra-local model with model-free parameter estimations for a generic SISO system[J]. IEEE Access, 2018, 6: 4266-4275.
[26] Chen Wenhua, Ballance D J, Gawthrop P J, et al. A nonlinear disturbance observer for robotic manipula- tors[J]. IEEE Transactions on Industrial Electronics, 2000, 47(4): 932-938.
[27] Chen Wenhua, Yang Jun, Guo Lei, et al. Disturbance- observer-based control and related methods-an over- view[J]. IEEE Transactions on Industrial Electronics, 2015, 63(2): 1083-1095.
[28] 王海兵. 双三相永磁同步电机高性能调速系统及容错运行研究[D]. 杭州: 浙江大学, 2017.
[29] Zhao Yifan, Lipo T A. Space vector PWM control of dual three-phase induction machine using vector space decomposition[J]. IEEE Transactions on Industry App- lications, 1995, 31(5): 1100-1109.
[30] 郭科宇, 李耀华, 史黎明. 分段供电双三相永磁同步直线电机电流解耦与扰动抑制[J]. 电工技术学报, 2022, 37(24): 6332-6344.
Guo Keyu, Li Yaohua, Shi Liming. Current decoup- ling and force disturbance suppression of dual three- phase permanent magnet linear synchronous motors with section power supply[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6332-6344.
[31] Chen Wenhua. Disturbance observer based control for nonlinear systems[J]. IEEE/ASME Transactions on Mechatronics, 2004, 9(4): 706-710.
[32] Lee J S, Choi G. Modeling and hardware-in-the-loop system realization of electric machine drives-a review[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 194-201.
Model-Free Predictive Current Control of Segmented Dual Three-Phase Permanent Magnet Linear Synchronous Motor
Abstract During the segmented dual three-phase permanent magnet linear synchronous motor (PMLSM), the deadbeat predictive current control (DPCC) is vulnerable to the back electromotive force (EMF) fluctuation, which cannot achieve exact current tracking and thrust control when the mover enters and exits the stator segments. At the same time, DPCC depends on motor models, but the model of segmented dual three-phase (PMLSM) is complex. Besides, there are additional harmonic subspace inductors in its harmonic subspace, which is easy to aggravate the degradation of current control when parameters are mismatched. Therefore, this paper proposes a model-free predictive current control (MFPCC) method.
Firstly, the influence of parameter mismatch and back EMF fluctuation in the conventional DPCC is analyzed. It is deduced that parameter mismatch causes errors in the control voltage, and the additional inductance in the harmonic subspace aggravates the parameter variation. Secondly, this paper takes the parameter mismatch and back EMF fluctuation as the lumped disturbance. Then, a model-free predictive current controller is designed based on an ultra-local model, divided into a known linear term related to the current and an unknown part related to the parameter mismatch and back EMF. Finally, a disturbance observer is designed to observe the unknown part in this ultra-local model, and its stability is demonstrated.
Hardware-in-the-loop experiments prove that the proposed method is independent of motor parameters and has strong robustness. (1) When the speed control is open-loop and the flux linkage yf changes in the DPCC control, the q-axis current cannot effectively track the given value, and the thrust fluctuation is about 5.25%. When the Ld, Lq, and Lxy of the controller increase to 200% of the original value, the q-axis current of the DPCC has apparent fluctuations, and the thrust fluctuation range is about 2%. The proposed q-axis current of the MFPCC can strictly track the given value, and the thrust fluctuation range is only 1.25%, which proves that the MFPCC has good parameter robustness. (2) When the speed control is closed-loop, and the speed reference suddenly increases to 12 m/s within 0.75 s, the q-axis current tracking performance of DPCC has overshoot. It cannot effectively track the reference value iqref because the inductance and flux linkage parameters become 200% and 50% of the original. However, the q-axis current tracking performance of MFPCC is smooth, and the tracking speed is fast. After parameter mismatch, the time of MFPCC following the slope is 0.36 s, similar to 0.35 s that of DPCC. The time of MFPCC following step signal is 0.53 s, smaller than 0.6 s of DPCC speed tracking time. (3) The total harmonic distortion of DPCC is twice that of MFPCC.
The conclusions are as follows. (1) The parameter mismatch of the segmented dual three-phase PMLSM and the dynamic disturbance of back EMF will introduce disturbance to the current control, deteriorate the current tracking performance, and lead to thrust fluctuation. In addition, the mismatched harmonic subspace inductance parameter Lxy after vector space decomposition (VSD) further affects the current performance. (2) The MFPCC proposed in this paper uses an ultra-local model to simplify the system model, divided into a known linear part and an unknown part with back EMF and parameter mismatch. The disturbance observer accurately estimates the unknown part. (3) MFPCC has strong robustness to parameter mismatch. It can effectively suppress the influence of back EMF dynamic disturbance caused by mover motions. The proposed method has good tracking performance of q-axis current in the whole movement, small thrust and velocity fluctuation, and fast dynamic response.
keywords:Dual three-phase permanent magnet linear synchronous motor, ultra-local model, disturbance observer, predictive current control
中图分类号:TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.222131
磁悬浮车辆及轨道关键技术资助项目(E125320402)。
收稿日期 2022-11-11
改稿日期 2023-02-06
周世炯 男,1995年生,博士研究生,研究方向为大功率电力电子变换技术与直线电机驱动控制。E-mail: shijiongz@mail.iee.ac.cn
史黎明 男,1964年生,研究员,博士生导师,研究方向为特种电机和驱动控制、磁悬浮技术、电能无线传输技术。E-mail: limings@mail.iee.ac.cn(通信作者)
(编辑 崔文静)