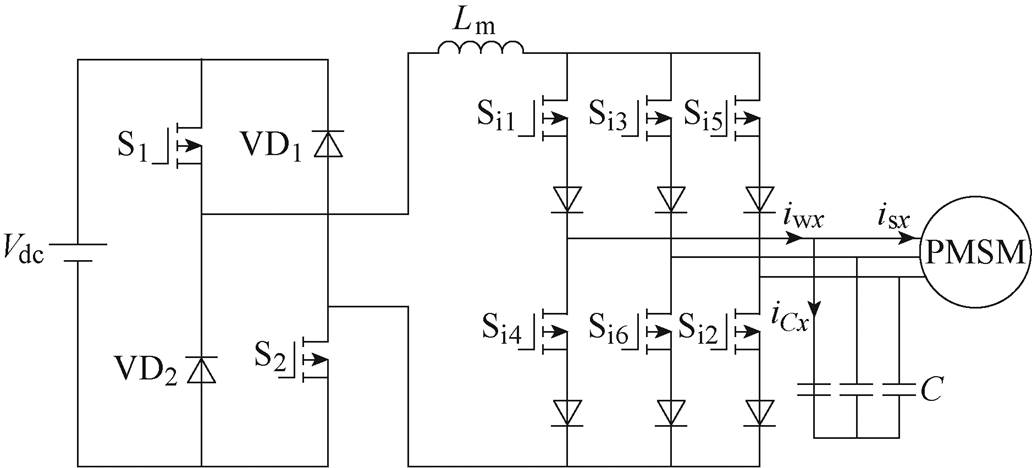
图1 CSI电路拓扑
Fig.1 Topology of CSI
摘要 由于电流源逆变器(CSI)的叠流效应以及前级DC-DC控制的母线电流脉动较大,使得扩展反电动势中含有大量谐波,造成较大的位置误差。针对此问题,该文提出一种改进滑模观测器的电流源逆变器驱动永磁同步电机无传感器控制方法。首先,基于传统滑模观测器,设计复系数滤波器代替传统低通滤波器,实现了对估计反电动势的准确提取,同时也抑制了估计反电动势中的高频抖动和高次谐波。其次,将二阶广义积分器内嵌于锁相环中,用于消除位置误差信号中的低次谐波,提高位置观测准确度。最后,将估算的速度信息反馈回复系数滤波器,实现复系数滤波器的自适应性。实验结果表明,所提方法在不同工况下,能够有效提高估算的转子位置精度,验证了方法的可行性与有效性。
关键词:永磁同步电机(PMSM) 电流源逆变器(CSI) 改进滑模观测器 复系数滤波器 无位置传感器控制
电机系统是电动汽车、轨道交通等的核心,随着机电一体化电机系统的优越性愈发明显,其具有能量密度大、效率高和维护性低等特点,使得电驱集成化设计得到越来越多的重视。然而,高集成化带来了一些新的问题,如快速开关器件会增加电磁干扰、靠近电机绕组的电力电子器件运行温度过高等。基于电流源逆变器(Current Source Inverter, CSI)的电驱系统可以很好地解决这些问题[1-4]。与传统的电压源逆变器相比,CSI的直流侧以电感作为储能元件,可以承受更高的工作温度。此外,CSI输出侧并联交流电容,可以降低输出电压的dv/dt与高频电磁干扰。
传统的永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)控制需要通过机械编码器获得转子位置及转速信息,这会使得机电一体化的电驱动系统变得更加复杂,而且还会增加系统成本、降低系统的可靠性。因此,合理取消机械编码器,可以降低机电一体化电驱动系统的体积、成本,还能有效提高系统的可靠性[5-7]。目前,国内外学者对无位置传感器控制技术进行了广泛的研究。无位置传感器控制策略主要分为基于电机模型和基于凸极跟踪两种方法。其中,基于电机模型的方法主要应用在中高速领域,基于凸极跟踪的方法主要应用在零低速领域[8]。在零低速区域以高频信号注入为主,但注入的高频信号会引起可听噪声,并会产生较大的转矩脉动,限制了其实际应用。文献[11]提出了伪随机频率注入的方法,通过扩展高频电流响应频谱来抑制噪声。文献[12]针对低开关频率下CSI驱动PMSM,提出多采样空间矢量调制方法,在一个矢量周期中对矢量角多次采样,从而改善高频正弦注入波形,防止开关频率与注入信号比过低造成高频信号失真。在中高速区域,基于扩展反电动势的方法由于不需要额外的高频信号注入而被普遍使用,主要包括模型参考自适应法[13]、扩展卡尔曼滤波器法[14]、滑模观测器法。其中,基于滑模观测器法的无传感器控制因其对扰动变化的鲁棒性强、动态性好和易于实现而被广泛使用[15-16]。文献[17]提出一种基于离散时间滑模观测器的CSI驱动PMSM位置估计方法。该方法减少了位置估计误差,提高了系统的动态性能。
然而,估计反电动势通常受到母线电流脉动以及逆变器非线性的影响,不可避免地存在5次和7次谐波,影响观测精度,进而影响系统的稳定性。为解决这个问题,文献[18]提出了一种双线性递归最小二乘自适应滤波器,并将其集成到滑模位置观测器中,抑制估计反电动势中主导的谐波分量。文献[19]设计一种基于锁相环(Phase Locked Loop, PLL)的自适应陷波器,滤除估计反电动势中的特定次谐波。文献[20]针对低开关频率CSI驱动电机系统,提出一种基于离散滑模观测器的无传感器控制方法,引入多级二阶广义积分器(Second Order Generalized Integrator, SOGI),滤除因CSI叠流作用而使估计反电动势中存在的5、7次谐波。虽然,这些控制策略可以有效滤除估计反电动势中存在的5、7次谐波,但是复杂的滤波器不仅使系统算法更加繁琐,而且增加了整个系统的响应时间。
为此,本文在现有研究基础上,提出了一种基于改进滑模观测器的CSI驱动PMSM无位置传感器控制方法。该方法在ab 静止坐标系下建立PMSM电压模型,根据该电压模型构建滑模观测器。为实现对估计反电动势的准确提取,设计复系数滤波器代替常规的低通滤波器,以抑制估计反电动势中的高频抖动和高次谐波。同时,将SOGI内嵌于锁相环中,滤除位置误差信号中的低次谐波,提高位置观测精度。最后,搭建CSI驱动PMSM实验系统,验证该方法的可行性与有效性。
CSI电路拓扑如图1所示。DC-DC斩波电路与电感提供母线电流,逆变桥中开关管顺向串联二极管以保证反向阻断能力;滤波电容C在滤除开关频率及其整数倍谐波的同时,吸收换流时电机电感中存储的能量[20]。下标w、C、s分别表示逆变器侧、电容端及定子侧电气参数,x表示三相a、b、c。

图1 CSI电路拓扑
Fig.1 Topology of CSI
CSI驱动PMSM在同步旋转坐标系下的方程可以表示为
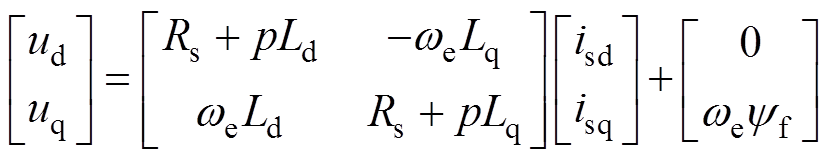 (1)
(1)
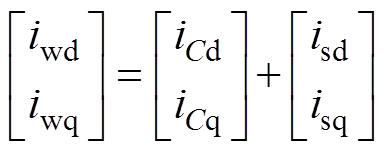 (2)
(2)
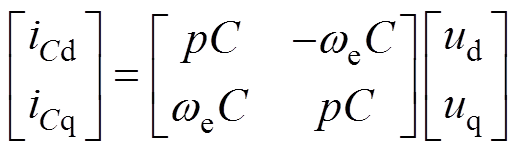 (3)
(3)
式中,ud、uq分别为d、q轴电压;iwd, iwq、iCd, iCq、isd, isq分别为d、q轴逆变器输出电流、电容器电流和定子电流;Ld、Lq分别为d、q轴电感;Rs为定子电阻;C为交流侧电容;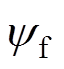 为永磁体磁链;p为微分算子;
为永磁体磁链;p为微分算子;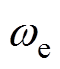 为转子电角速度。CSI驱动PMSM模型可表示为两级系统,如图2所示。
为转子电角速度。CSI驱动PMSM模型可表示为两级系统,如图2所示。
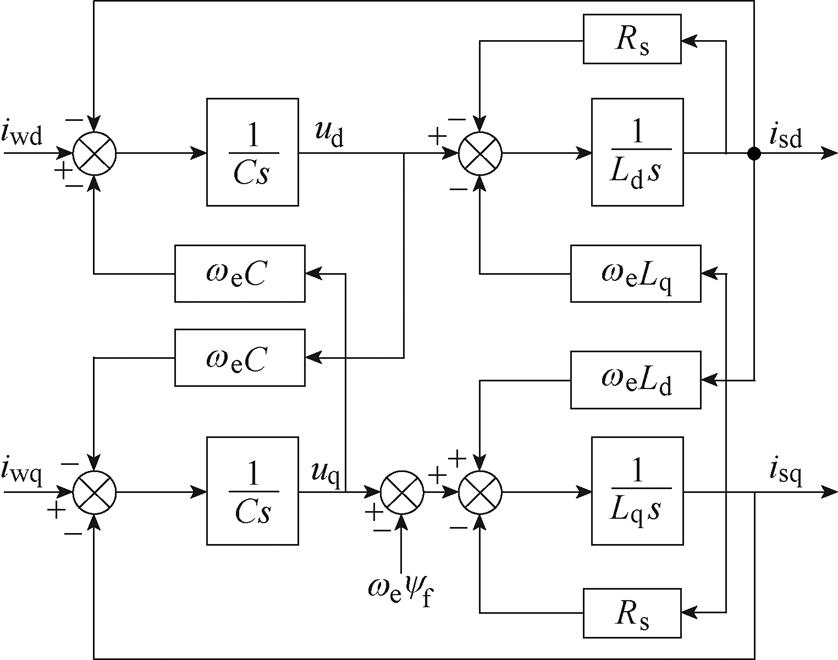
图2 CSI驱动PMSM模型
Fig.2 CSI drives the PMSM model
由于电机反电动势中包含转子位置信息,对这些信号处理可以获得转子位置。对于内置式PMSM在静止坐标系下的扩展反电动势模型可表示为
 (4)
(4)
其中
uab =ua+jub iab =ia+jib
式中,Eab 为扩展反电动势;eab 为扩展反电动势在ab 轴分量。为了便于应用滑模观测器观测扩展反电动势,以ab 轴电流为状态变量改写电流状态方程为
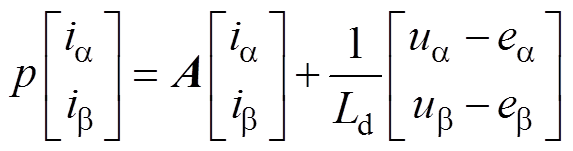 (5)
(5)
其中
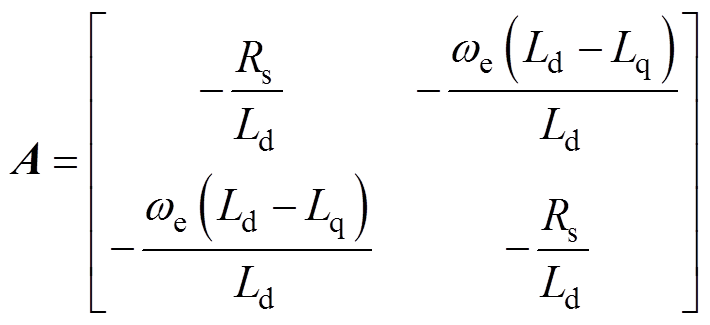
随后,通过一阶正向欧拉逼近的方法,将微分运算替换为(1-z-1)/Tsz-1,对式(5)方程离散化为
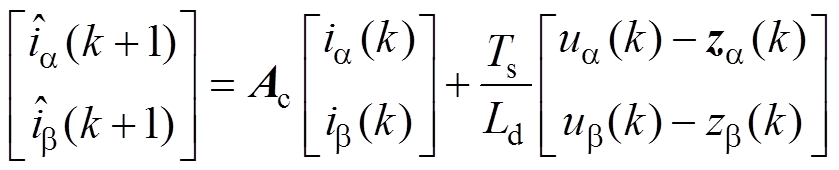 (6)
(6)
其中
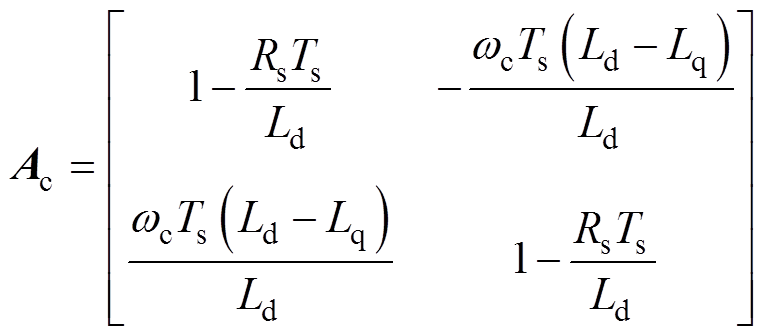
式中,符号“ ”表示估计值;Ts为采样周期;zab 为滑模观测器控制率,设计滑模控制率为
”表示估计值;Ts为采样周期;zab 为滑模观测器控制率,设计滑模控制率为
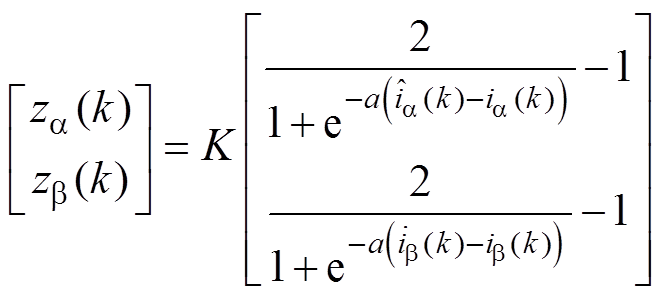 (7)
(7)
式中,K为滑模观测器增益;a>0,用于调整s函数的斜率。当满足K>max(|ea|, |eb|)时,观测器渐近稳定。本文采用具有光滑连续特性的s函数代替理想的符号函数,可以很大程度上减少抖振。
传统滑模观测器控制框图如图3所示。估计的反电动势通过低通滤波器获得,进一步经过正交锁相环获取转子位置信息。
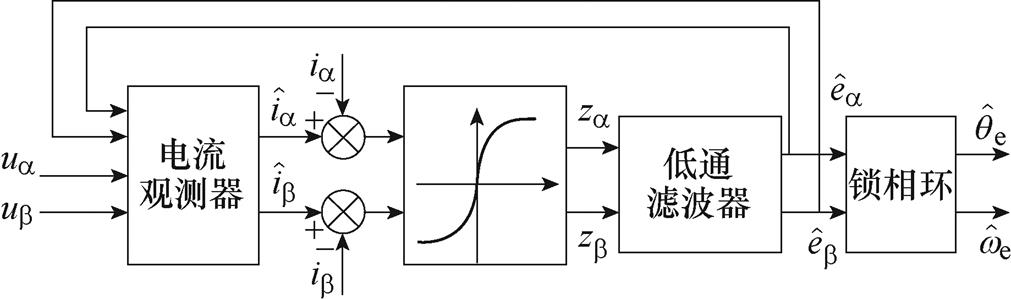
图3 传统滑模观测器控制框图
Fig.3 Control block diagram of traditional sliding mode observer
2.2.1 复系数滤波器设计
由于滑模观测器自身的抖振问题以及CSI叠流的影响,估计的反电动势波形总是包含谐波分量,而传统低通滤波器几乎不能过滤较低的谐波,如5、7次谐波,并造成固有的相位延迟。为此,本文采用复系数滤波器代替传统低通滤波器滤除估计反电动势中的高频抖动和谐波干扰,提高了估计精度。复系数滤波器的基本结构如图4所示。
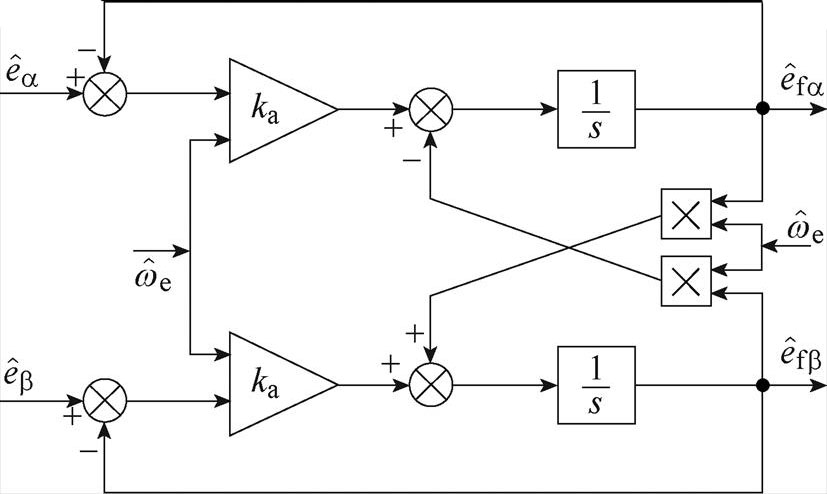
图4 复系数滤波器结构框图
Fig.4 Block diagram of complex coefficient filter structure
理想的复系数滤波器在中心频率处具有单位增益和零相移,在其他频率处保持深度衰减。因此,在滤波阶段采用复系数滤波器,能有效抑制工作频率以外的其他谐波,且结构简单,阶数仅为一阶,没有增加算法复杂度,更适合实际应用。本文采用的一阶复系数滤波器可以表示为
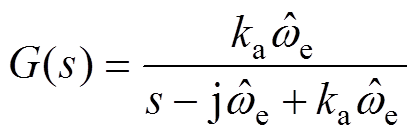 (8)
(8)
式中,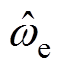 为中心频率;ka为滤波因子,ka越大,系统动态性越好,但是滤波性能会变差;反之,ka越小,滤波性能越好,但动态性能会变差。图5a为不同ka下的复系数滤波器伯德图,中心频率为50 Hz。可以看出,在中心频率处具有单位增益并且没有相移。考虑到动态性能以及滤波性能,本文选择ka=0.707。
为中心频率;ka为滤波因子,ka越大,系统动态性越好,但是滤波性能会变差;反之,ka越小,滤波性能越好,但动态性能会变差。图5a为不同ka下的复系数滤波器伯德图,中心频率为50 Hz。可以看出,在中心频率处具有单位增益并且没有相移。考虑到动态性能以及滤波性能,本文选择ka=0.707。
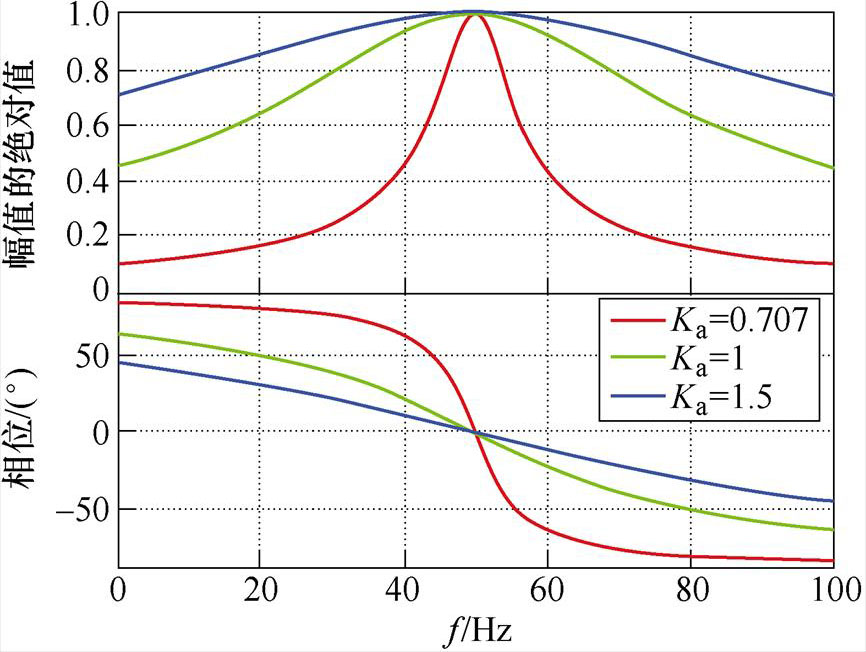
为了保证复系数滤波器能够自适应地提取扩展反电动势,滤波器中心频率应随着扩展反电动势频率的改变而改变。因此,将锁相环观测的电角频率作为复系数滤波器的中心频率来实现滤波器的自适应性。图5b为不同中心频率复系数滤波器的伯德图,可以看出,在不同中心频率处,复系数滤波器增益为1并且没有相位偏移,同时具有良好的带通性。
2.2.2 改进锁相环设计
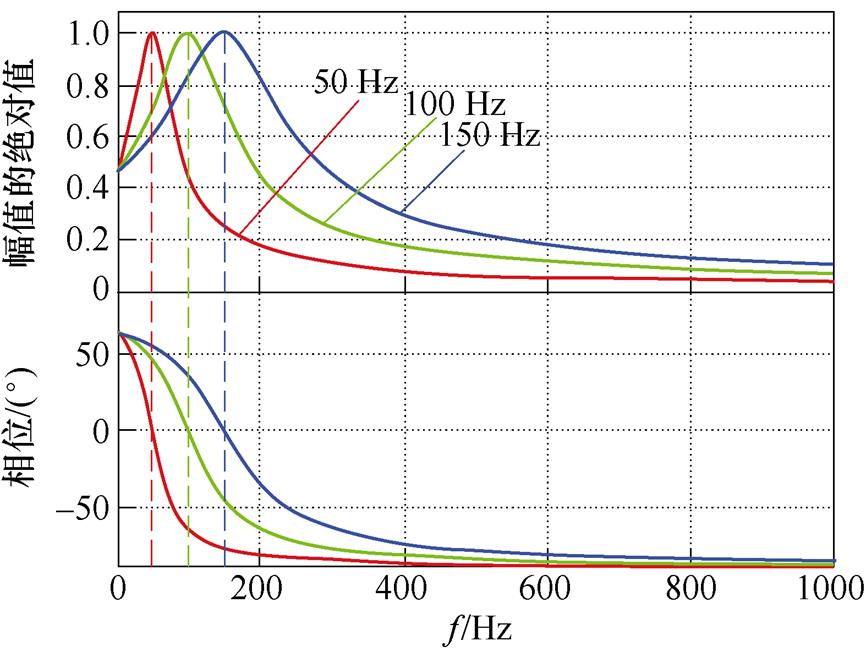
虽然复系数滤波器可以有效滤除观测反电动势中部分5、7次谐波,但仍有部分5、7次谐波位于位置误差信号中。将ab 轴上扩展反电动势重写为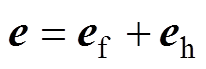 。
。
(a)不同Ka时复系数滤波器伯德图
(b)不同中心频率复系数滤波器伯德图
图5 复系数滤波器伯德图
Fig.5 Bode diagram of the complex coefficient filter
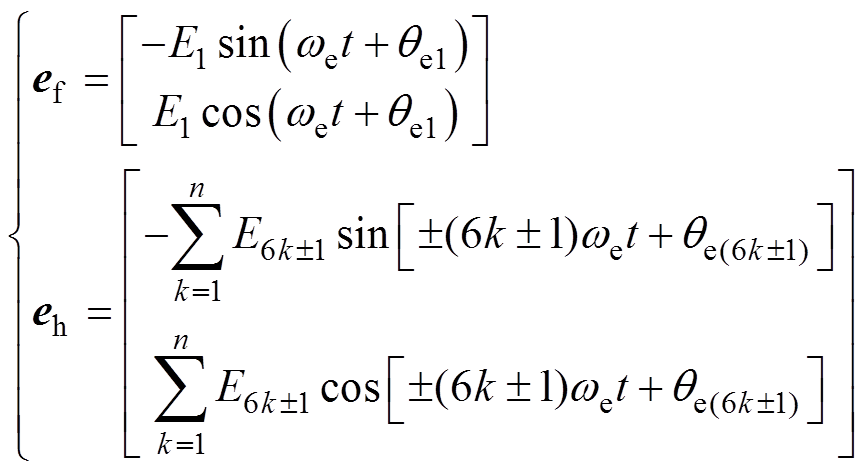 (9)
(9)
式中,ef =[efa efb]T、eh=[eha ehb]T分别为扩展反电动势中的基波和6k±1次谐波;E1和E6k±1分别为基波和6k±1次谐波的幅值;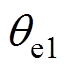 为初始角度。在获取估计扩展反电动势后利用锁相环来获取位置信息,锁相环中位置误差信号
为初始角度。在获取估计扩展反电动势后利用锁相环来获取位置信息,锁相环中位置误差信号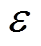 表示为
表示为
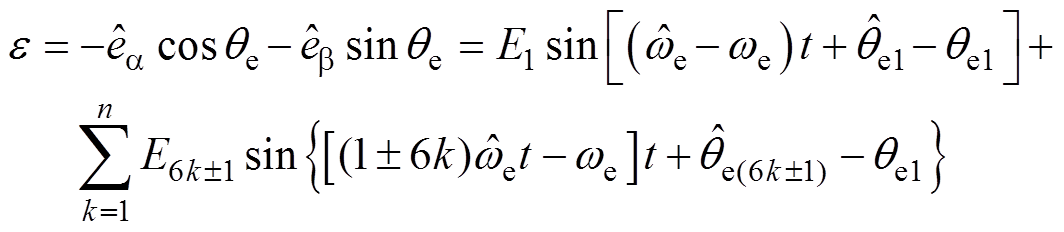 (10)
(10)
式中,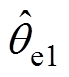 和
和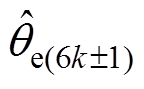 分别为1和6k±1次观测角度。
分别为1和6k±1次观测角度。
当锁相环收敛时,估计反电动势的6k±1次谐波误差变成了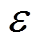 中的6k次谐波误差,进一步降低了无传感器控制系统的精度和稳定性。
中的6k次谐波误差,进一步降低了无传感器控制系统的精度和稳定性。
本文提出了一种内嵌SOGI陷波器的改进锁相环,其控制框图如图6所示。首先,扩展反电动势误差信号归一化后,降低了噪声对位置观测的影响。其次,误差信号经过一个二阶广义陷波器滤除反电动势误差信号中的6次分量,提升位置观测精度。最后,将参考转速引入PI控制器中提升观测器的动态响应速度。其中,SOGI的结构如图7所示。其传递函数可以表示为
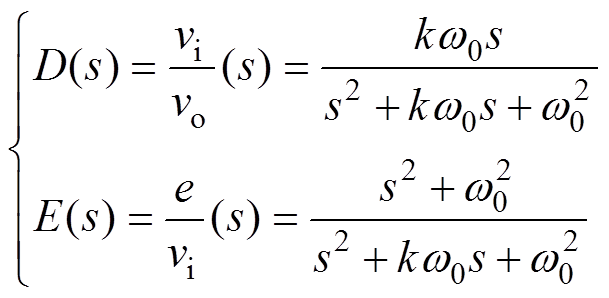 (11)
(11)
式中,w0为SOGI的谐振频率;k为阻尼系数;vo为输出信号;vi为输入信号;e为估计误差;传递函数E(s)用于消除频率为w0的谐波;D(s)用于提取频率为w0的谐波。以w0=50 Hz为例,E(s)在不同k下的伯德图如图8所示。从图8中可以看出,k越小,增益带越窄,对特定次频率附近的噪声抑制效果越好,但k太小会导致带宽过窄。当信号的频率因外部扰动而与所设置的频率有偏差、出现在增益带之外时,将会导致转子位置估计失败,降低系统的可靠性,兼顾两者,本文选取k=3。
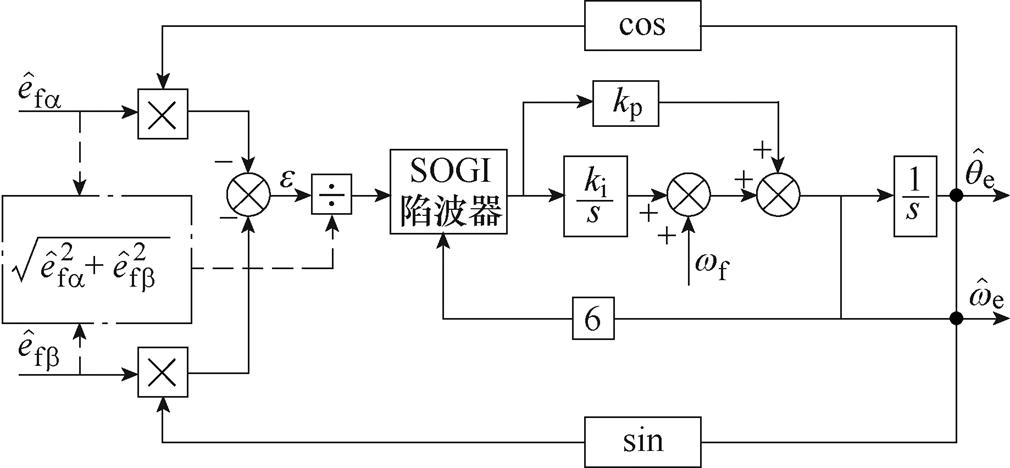
图6 改进锁相环控制框图
Fig.6 Improved PLL control block diagram
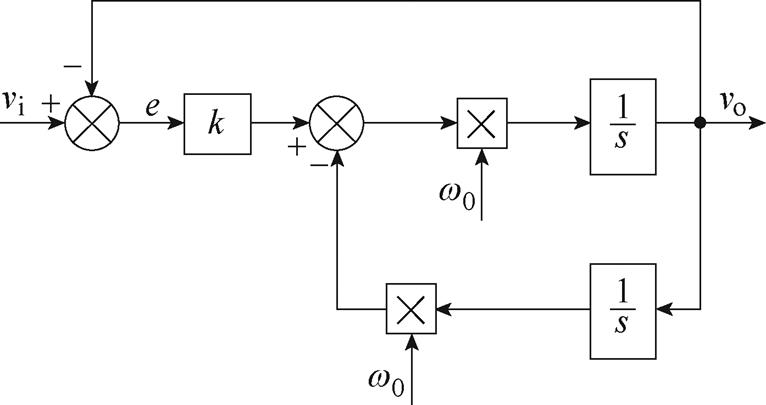
图7 SOGI结构框图
Fig.7 Block diagram of SOGI
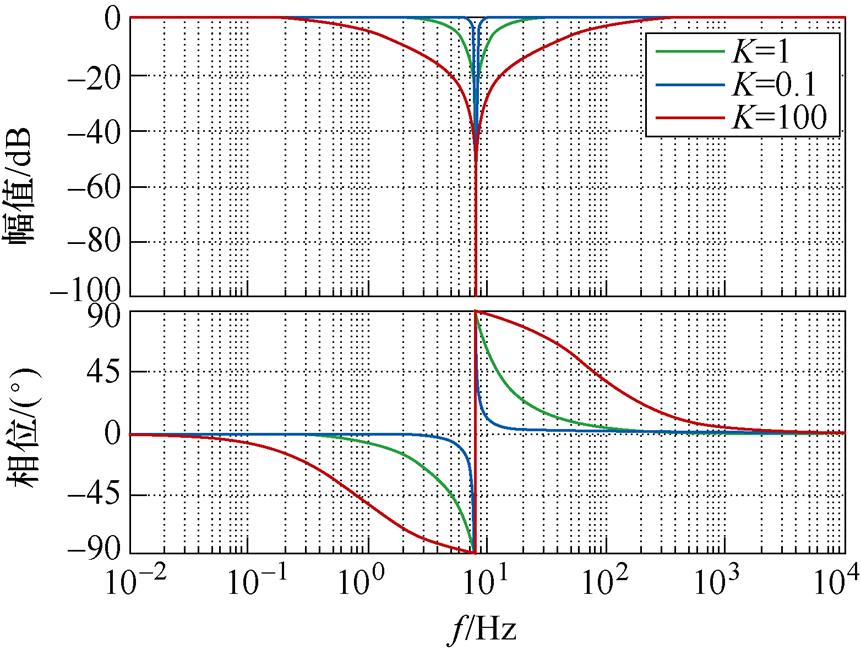
图8 不同k值下E(s)的伯德图
Fig.8 Bode diagram of E(s) for different values of k
为了提升观测器的动态响应速度,将参考转速引入锁相环,同时将观测转速作为滤波器中心频率反馈回前置滤波环节,实现滤波器中心频率的自适应性,从而更好地实现观测器的动态性能。图9为改进滑模观测器控制框图。
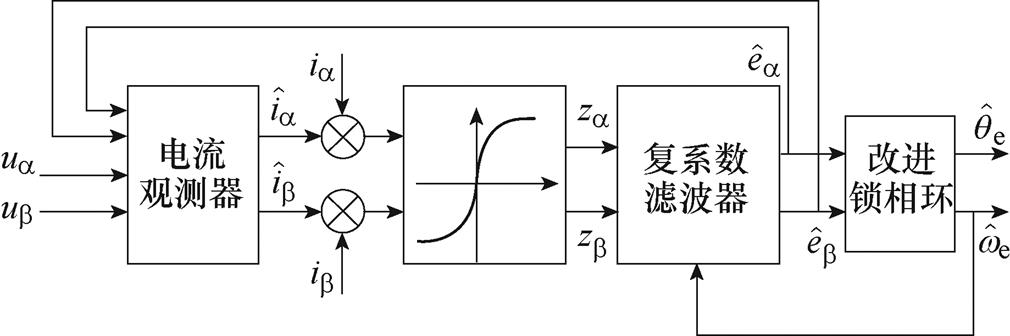
图9 改进滑模观测器控制框图
Fig.9 Control block diagram of improved sliding mode observer
综上所述,本文采用的CSI驱动PMSM无位置传感器控制框图如图10所示。所提策略相较传统滑模观测器,使用复系数滤波器代替传统一阶滤波器,同时改进锁相环中内嵌SOGI,虽然算法复杂度在一定程度上略有增加,但是位置观测精度提升显著,具有实际工程价值。
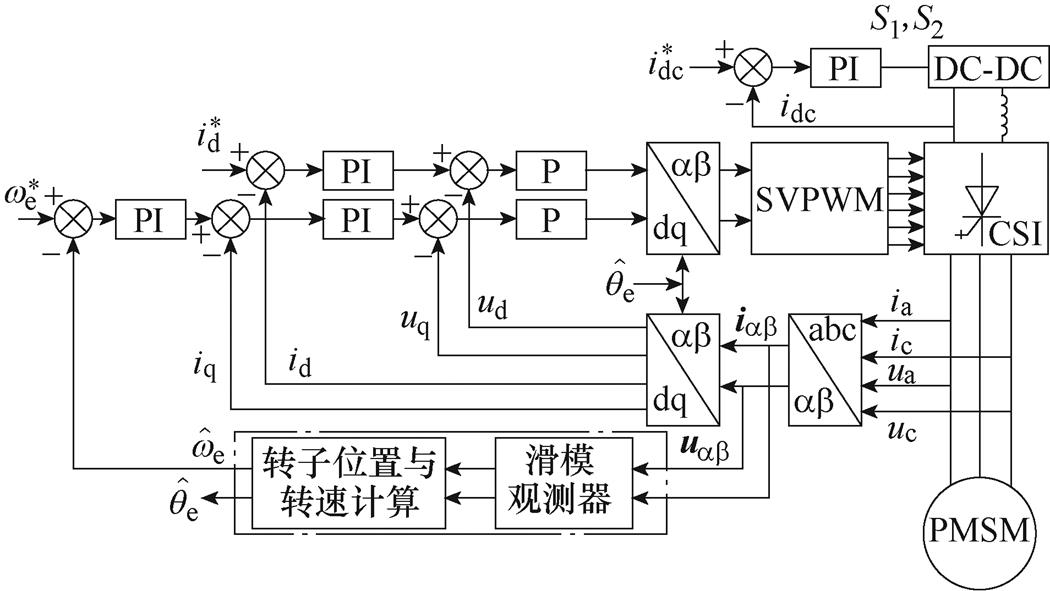
图10 PMSM无位置传感器控制框图
Fig.10 PMSM sensorless control block diagram
为了验证所提控制方法的有效性,搭建了三相CSI驱动PMSM控制系统实验平台,如图11所示。

图11 PMSM控制系统实验平台
Fig.11 Experiment platform of PMSM control system
图11中,直流电机为实验提供负载,微控单元型号为TI公司TMS320F28377。系统中通过光电编码器获得电机的实际转子位置信号进行误差计算。表1为实验中电驱系统参数。直流母线电压为100 V,母线电流由前级DC-DC调节。
表1 PMSM驱动系统实验参数
Tab.1 Parameters of experimental PMSM drive

参 数数 值 电机极对数3 相电阻/W0.565 d轴电感/mH5.62 q轴电感/mH6.28 永磁体磁链幅值/Wb0.179 6 额定转速/(r/min)2 000 实验开关频率/kHz10 采样频率/kHz10 直流电感Ldc/mH1 直流输入电压udc/V100 滤波电容C/mF50
图12为1 000 r/min、7 N·m工况下两种滑模观测器的反电动势实验波形及其傅里叶分析。图12a为两种滑模观测器的反电动势谐波抑制实验对比,可以看出,估计反电动势的波形质量明显改善。由图12b可以看出,传统滑模观测的估计反电动势总谐波畸变率(Total Harmonic Distortion, THD)为8.9%,其中,5、7次谐波含量较大,说明低通滤波对估计反电动势的低次谐波抑制效果具有一定的局限性,难以达到理想的谐波抑制效果。由图12c可以看出,改进滑模观测器的估计反电动势THD为4.12%,可以看出,改进滑模观测器控制对估计反电动势的谐波抑制效果较佳,尤其对5次和7次谐波抑制效果更为明显。
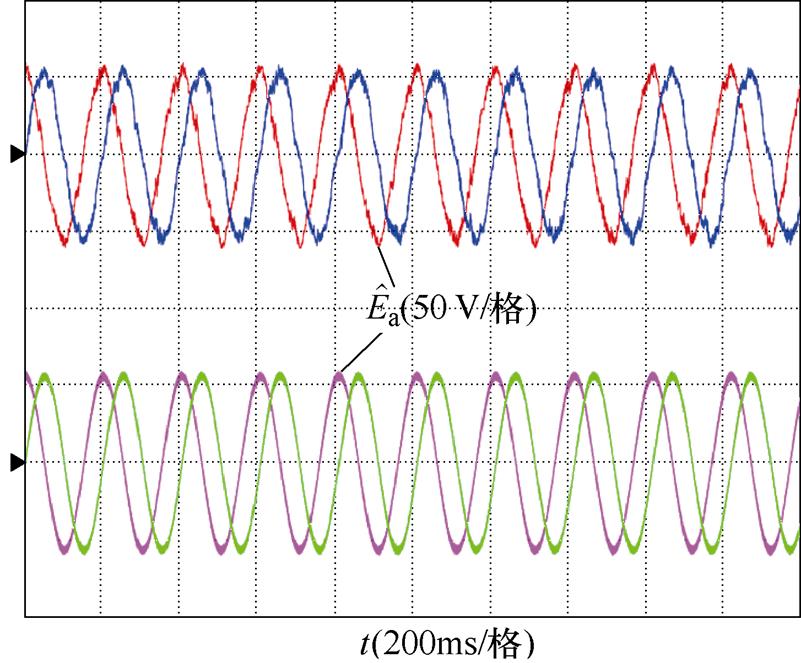
(a)估计扩展反电动势实验波形
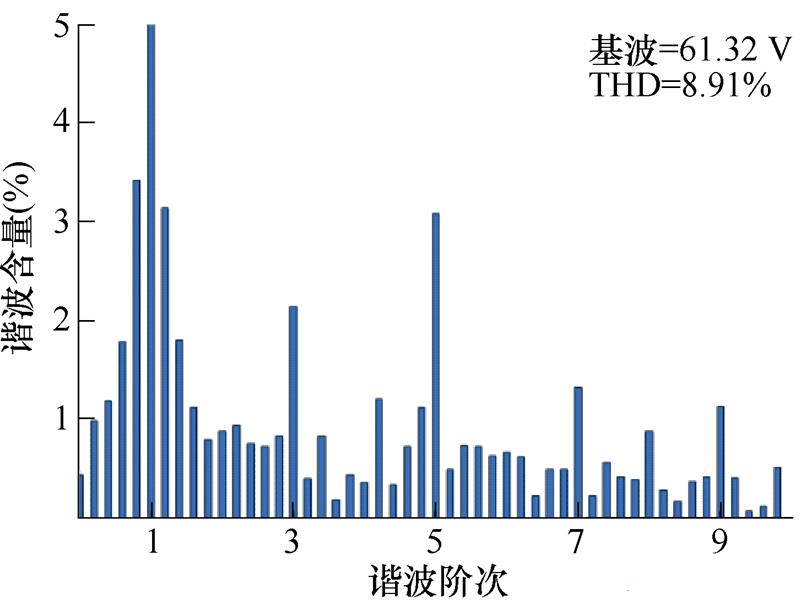
(b)传统滑模观测器反电动势谐波分析
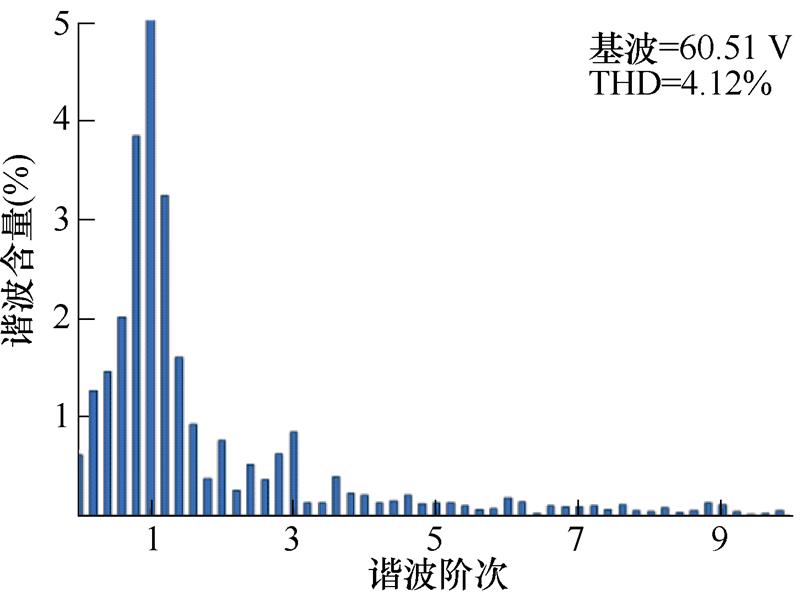
(c)改进滑模观测器反电动势谐波分析
图12 估计扩展反电动势实验结果
Fig.12 Experimental results of estimated extended back electromotive force
通过以上分析可得,所提方法能明显抑制估计反电动势中的5、7次谐波,说明改进滑模观测器控制能够使得估计反电动势的波形正弦度更好,同时减少了谐波对整个控制的影响。
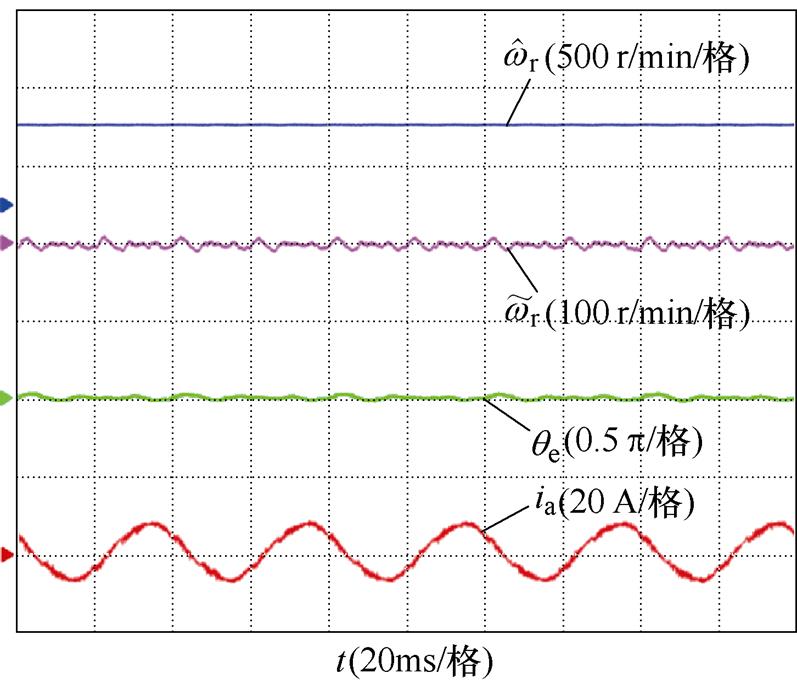
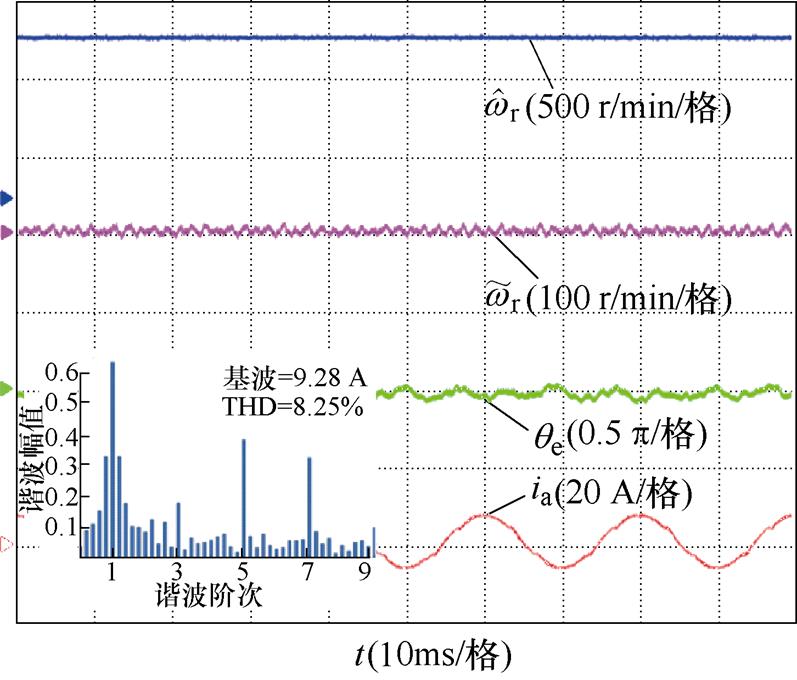
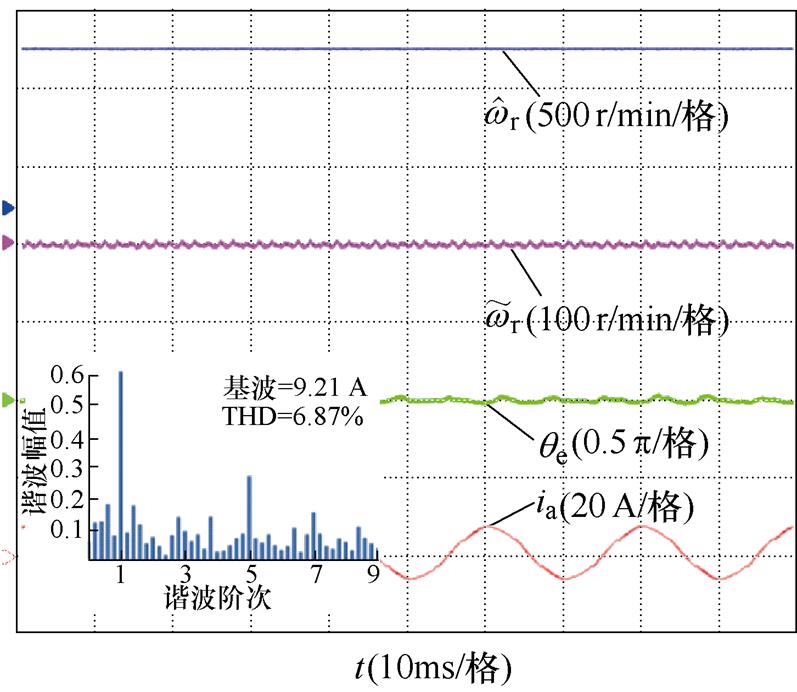
其次,验证改进滑模观测器算法在不同转速满载稳态时的运行效果,如图13和图14所示。在500 r/min、7 N·m和1 000 r/min、7 N·m工况下,采用传统滑模观测器观测到的最大位置误差分别为12°和7°,转速误差分别为±15 r/min和±8 r/min;采用改进滑模观测器观测到最大位置误差分别为9°和5°,转速误差分别为±10 r/min和±5 r/min;相比于传统滑模观测器,改进滑模观测器转子位置误差降低了25%和28%,转速误差降低了30%和31%。为验证改进方法对定子电流的影响,在1 000 r/min工况下,分别对采用传统滑模观测器和改进滑模观测器下电机定子电流进行傅里叶分析。如图14所示,定子电流THD由8.25%降低到6.87%,定子电流中5、7次谐波明显降低。综上对比发现,改进滑模观测器减小了转速误差与位置误差,降低了定子电流谐波含量,系统的稳定性得到提升。
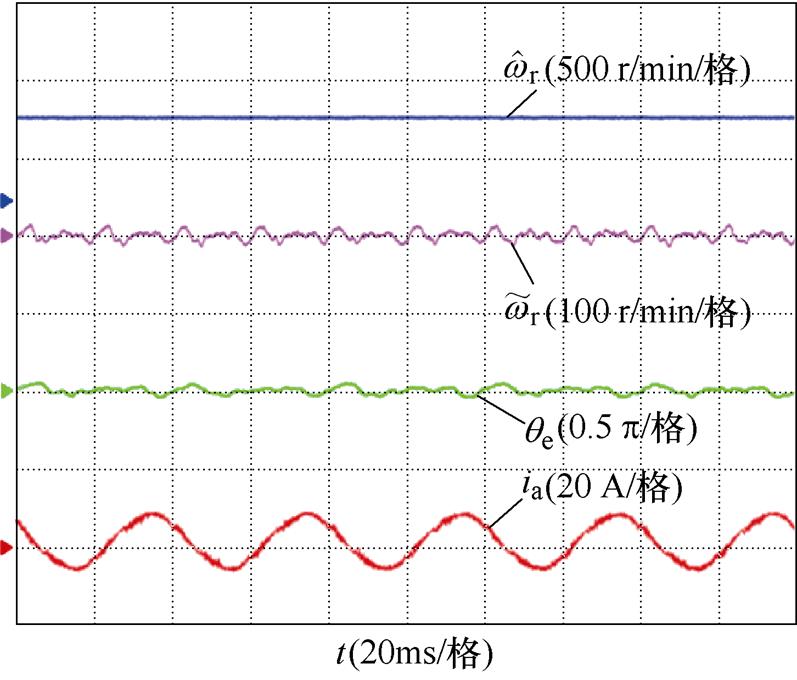
(a)传统滑模观测器
(b)改进滑模观测器
图13 500 r/min额定负载下位置估计误差的稳态结果
Fig.13 Steady-state results of position estimation error with 500 r/min load
为了验证所提方法的动态特性,进行了转速突变实验,实验波形如图15所示。转速由500 r/min突变到1 000 r/min,最大转速误差为20 r/min,最大位置误差为18°,从图中可以看出,转速突变时系统仍然稳定运行,且系统转速波动较小,验证了所提方法具有良好的动态性。
(a)传统滑模观测器
(b)改进滑模观测器
图14 1 000 r/min额定负载下位置估计误差的稳态结果
Fig.14 Steady-state results of position estimation error with 1 000 r/min load
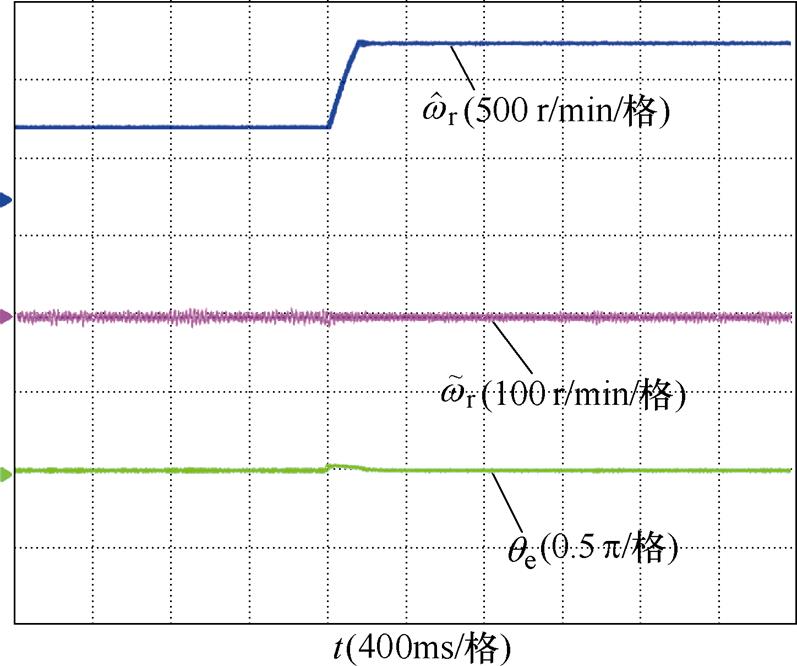
图15 转速突变实验波形
Fig.15 Experimental waveforms of speed mutation
本文提出了一种改进滑模观测器的CSI驱动PMSM无位置传感器控制方法。该方法通过设计复系数滤波器代替传统低通滤波器,滤除估计反电动势中的高频抖振与高次谐波,并且不会产生相移。同时将SOGI内嵌于锁相环中,有效滤除位置误差信号中的低次谐波。实验结果表明,与传统滑模观测器相比,所提方法更好地降低了估计反电动势中的谐波扰动,降低了转速脉动与位置误差,提高了估计精度,并且具有良好的动态性能。
参考文献
[1] 李昱, 郭宏, 平朝春, 等. 基于电流源变流器的永磁同步电机驱动系统全状态变量预测转矩控制[J]. 电工技术学报, 2021, 36(1): 15-26.
Li Yu, Guo Hong, Ping Zhaochun, et al. A full-state variable predictive torque control of current source converter fed permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 15-26.
[2] Amorim T R, Dai Hang, Lee W, et al. Current-source inverter integrated motor drives using dual-gate four-quadrant wide-bandgap power switches[J]. IEEE Transactions on Industry Applications, 2021, 57(5): 5183-5198.
[3] Liu Pengcheng, Wang Zheng, Wei Sanmin, et al. Recent developments of modulation and control for high-power current-source-converters fed electric machine systems[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 215-226.
[4] Xu Yang, Wang Zheng, Liu Pengcheng, et al. The modular current-fed high-frequency isolated matrix converters for wind energy conversion[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 4779-4791.
[5] 麦志勤, 刘计龙, 肖飞, 等. 基于估计位置反馈电流解调算法的改进型高频旋转电压注入无位置传感器控制策略[J]. 电工技术学报, 2022, 37(4): 870-881, 891.
Mai Zhiqin, Liu Jilong, Xiao Fei, et al. Sensorless control strategy of improved HF rotating voltage injection based on estimated position feedback current demodulation algorithm[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 870-881, 891.
[6] 阙鸿杰, 全力, 张丽, 等. 基于自适应滤波器在线解耦的磁场增强型永磁电机无位置传感器控制[J]. 电工技术学报, 2022, 37(2): 344-354.
Que Hongjie, Quan Li, Zhang Li, et al. Sensorless control of flux-intensifying permanent magnet syn- chronous motor based on adaptive Notch filter online decoupling[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 344-354.
[7] Zhang Guoqiang, Wang Gaolin, Wang Huiying, et al. Pseudorandom-frequency sinusoidal injection based sensorless IPMSM drives with tolerance for system delays[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3623-3632.
[8] Wang Gaolin, Yang Lei, Yuan Bihe, et al. Pseudo- random high-frequency square-wave voltage injection based sensorless control of IPMSM drives for audible noise reduction[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7423-7433.
[9] 于安博, 刘利, 阚志忠, 等. 高频脉振信号注入永磁同步电机无滤波器初始位置辨识方法[J]. 电工技术学报, 2021, 36(4): 801-809.
Yu Anbo, Liu Li, Kan Zhizhong, et al. Initial position identification of PMSM with filterless high frequency pulse signal injection method[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 801-809.
[10] 吴春, 陈科, 南余荣, 等. 考虑交叉饱和效应的变角度方波电压注入永磁同步电机无位置传感器控制[J]. 电工技术学报, 2020, 35(22): 4678-4687.
Wu Chun, Chen Ke, Nan Yurong, et al. Variable angle square-wave voltage injection for sensorless control of PMSM considering cross-saturation effect[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4678-4687.
[11] Zhang Guoqiang, Wang Gaolin, Wang Huiying, et al. Pseudorandom-frequency sinusoidal injection based sensorless IPMSM drives with tolerance for system delays[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3623-3632.
[12] Al-nabi E, Wu Bin, Zargari N R, et al. Sensorless control of CSC-fed IPM machine for zero- and low-speed operations using pulsating HFI method[J]. IEEE Transactions on Industrial Electronics, 2013, 60(5): 1711-1723.
[13] Prabhakaran K K, Karthikeyan A. Electromagnetic torque-based model reference adaptive system speed estimator for sensorless surface mount permanent magnet synchronous motor drive[J]. IEEE Transa- ctions on Industrial Electronics, 2020, 67(7): 5936- 5947.
[14] Bouheraoua M, Wang Jiabin, Atallah K. Rotor position estimation of a pseudo direct-drive PM machine using extended Kalman filter[J]. IEEE Transactions on Industry Applications, 2017, 53(2): 1088-1095.
[15] Yin Zhonggang, Zhang Yanping, Cao Xinping, et al. Estimated position error suppression using novel PLL for IPMSM sensorless drives based on full-order SMO[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 4463-4474.
[16] Wang Bo, Shao Yanzhen, Yu Yong, et al. High-order terminal sliding-mode observer for chattering suppression and finite-time convergence in sensorless SPMSM drives[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11910-11920.
[17] Ding Li, Li Yunwei, Zargari N R, et al. Sensorless control of CSC-fed PMSM drives with low switching frequency for electrical submersible pump appli- cation[J]. IEEE Transactions on Industry Applications, 2020, 56(4): 3799-3808.
[18] Wu Xuan, Huang Sheng, Liu Kan, et al. Enhanced position sensorless control using bilinear recursive least squares adaptive filter for interior permanent magnet synchronous motor[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 681-698.
[19] Song Xinda, Fang Jiancheng, Han Bangcheng, et al. Adaptive compensation method for high-speed surface PMSM sensorless drives of EMF-based position estimation error[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1438-1449.
[20] Ding Li, Li Yunwei, Zargari N R. Discrete-time SMO sensorless control of current source converter-fed PMSM drives with low switching frequency[J]. IEEE Transactions on Industrial Electronics, 2021, 68(3): 2120-2129.
Abstract Due to the overlap effect of the current source inverter and the large current pulsation of the bus controlled by the front DC-DC, the extended back electromotive force contains a large number of harmonics, producing large position errors, which in turn affect the performance of the system. Therefore, this paper proposes a sensorless control method of the permanent magnet synchronous motor driven by the current source inverter with an improved sliding mode observer.The proposed method can reduce the harmonic distortion of the estimated back electromotive force caused by the overlapping current effect and the large busbar current pulsation, thereby reducing the position error and speed pulsation, which has good dynamic performance.
Firstly, based on the traditional sliding mode observer, the voltage model of the permanent magnet synchronous motor is established under the a-b stationary coordinate system, and the observer is constructed according to the voltage model. The chattering of the system is reduced using the saturation function instead of the sign function in the ideal sliding mode. Since the traditional sliding mode observer uses a first-order low-pass filter to filter the observed back electromotive force, the problems of phase lag and amplitude attenuation will be caused, and there are still excessive high-frequency chattering components in the observed back electromotive force. Therefore, a complex coefficient filter without phase delay and amplitude attenuation at the center frequency is designed to replace the traditional low-pass filter. The estimated back potential can be accurately extracted, and the phase lag and amplitude attenuation problems can be avoided while chattering is suppressed. At the same time, the velocity information estimated by the phase-locked loop is fed back to the coefficient filter to realize the adaptability of the complex coefficient filter.
Secondly, the complex coefficient filter can filter out part of the 5th and 7th harmonics in the observed back electromotive force, forming the 6th position error signal to affect the position observation accuracy. Thus, the second-order generalized integrator is embedded in the phase-locked loop, and the notch property is used to eliminate the sixth harmonics in the position error signal to further improve the position observation accuracy. At the same time, the reference speed is introduced into the phase-locked loop to improve the convergence speed of the phase-locked loop and the dynamic performance of the system.
Finally, the experimental results show that compared with the traditional sliding mode observer, the estimated back electromotive force harmonic distortion is reduced from 8.9% to 4.12%, and the stator current harmonic distortion is reduced from 8.25% to 6.87%. The rotor position error is reduced by 25%, and the rotational speed error by 30%. The results show that the proposed method can better reduce the harmonic disturbance in the estimated back electromotive force, reduce the speed pulsation and position error, improve the estimation accuracy, and have good dynamic performance.
keywords:Permanent magnet synchronous motor (PMSM), current source inverter (CSI), improved sliding mode observer, complex coefficient filters, sensorless control
中图分类号:TM315
DOI: 10.19595/j.cnki.1000-6753.tces.222146
国家杰出青年科学基金资助项目(52025073)。
收稿日期 2022-11-15
改稿日期 2022-12-30
赵文祥 男,1976年生,教授,博士生导师,研究方向为电机及其控制。E-mail: zwx@ujs.edu.cn(通信作者)
宋世昌 男,1997年生,硕士研究生,研究方向为永磁电机的驱动控制。E-mail: 952464769@qq.com
(编辑 崔文静)