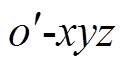 的原点
的原点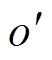 ,典型消磁站模型及磁源布设如图1所示。
,典型消磁站模型及磁源布设如图1所示。摘要 采用消磁站海底平面磁传感器阵列进行测量是获取舰艇磁场的主要途径,水下磁传感器位置误差是影响舰艇磁场测量的主要因素。针对该问题,将磁场与深度测量数据相融合,提出一种基于磁场梯度优化的消磁站水下磁传感器定位方法。将通电螺线管线圈等效成磁偶极子,通过磁传感器位置偏差区域x和y方向的平均磁场梯度优化确定线圈的两组磁源移动位置,结合深度测量数据分别建立方程组构造目标函数,并采用动态学习策略多群体粒子群算法进行优化求解,从而实现消磁站水下磁传感器的高精度定位。在系统分析和评估深度传感器精度、环境磁噪声等影响规律的基础上,开展位置校正数值模拟和物理缩比模型实验。实验结果表明,该方法可有效地解决消磁站水下磁传感器的定位问题,定位误差小于0.1 m,能够满足舰艇磁场的测量要求。
关键词:磁场梯度 定位 水下磁传感器 深度传感器
第二次世界大战期间,德国使用磁性水雷封锁英国,导致英国海军遭受重大损失,最终迫使其采用新技术降低磁场的特征信号,磁隐身技术就此诞生[1]。磁隐身技术是保证水面舰船安全性、潜艇隐蔽性的必要手段,准确测量舰艇磁场是实施磁隐身的必要前提[2]。目前,在消磁站海底平面布设水下磁传感器阵列是舰艇磁场测量的主要途径。由于海底环境复杂多变,消磁站水下磁传感器的安装工作尤为困难。在实际工程中水下磁传感器的安装位置与预设位置之间存在一定的位置偏差,依据现有安装工艺,各方向位置偏差幅值小于0.3 m。在舰艇磁场的测量过程中,幅值约0.3 m的位置偏差可带来上百纳特的磁场测量误差,直接影响舰艇磁场的测量精度,降低舰艇磁性防护能力[3]。一方面,磁性水雷和航空磁探的不断发展对舰艇磁性防护能力的要求愈发严格;另一方面,磁隐身新技术的发展对舰艇磁场测量精度提出了更高的要求[4]。因此,亟须对消磁站水下磁传感器进行高精度定位,提高舰艇磁场测量的准确性。
最先考虑的是基于光信号和声信号的定位方法,但是消磁站浑浊的水质以及半封闭式的环境并不利于光或者声的定位[5]。除此之外,由于大部分消磁站使用年限较久,水下磁传感器多被海藻类生物、泥沙等覆盖,进一步加重了定位成本。相对而言,消磁站内良好的磁环境为磁场定位创造了有利条件。文献[6]根据三轴磁力计和已知磁偶极子磁矩的舰船对水下磁传感器网络进行定位。文献[7]在动态检测站的部分水下磁传感器上安装辅助螺线管线圈,通过测量线圈产生的磁场对磁传感器进行定位。文献[8]利用磁偶极子磁场在三维空间的完备性得到的位置矢量解析式对动态检测站临时布设的磁传感器进行快速定位。文献[9]基于磁场总量的标量定位方法来解决背景磁异常。文献[10]在海面建立磁偶极子源,采用多重线性计量方法对水下三轴磁力计进行磁场测量,再借助非支配序列的遗传算法求解位置矢量。上述方法为消磁站水下磁传感器的高精度定位提供了一定的参考价值,但是由于应用背景的差异,这些方法直接应用于消磁站难以达到舰艇磁场测量所需的高精度定位要求。
本文将磁场与深度测量数据相融合,提出一种基于磁场梯度优化的消磁站水下磁传感器定位方法。基于磁场梯度越大,相应方向的位置参数反演精度越高的原则,根据磁传感器位置偏差区域在x和y方向的平均磁场梯度确定磁源的两组坐标,分别建立方程组构造目标函数。由于z方向磁场梯度相对较小,可定位度不高,在实际工况中,通过深度传感器准确度获得深度测量数据,将三维空间定位转化为二维平面定位,采用动态学习策略多群体粒子群算法进行优化求解位置偏差矢量,实现消磁站水下磁传感器的高精度定位,为消磁站舰艇磁场测量奠定了基础。该方法精度定位高,具有较好的工程价值。实验结果证明了所提方法的有效性。
结合消磁站的实际工况,将垂直放置的通电螺线管线圈作为磁源,码头的顶点为全局坐标系o-xyz的原点o;线圈的中心为线圈局部坐标系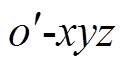 的原点
的原点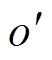 ,典型消磁站模型及磁源布设如图1所示。
,典型消磁站模型及磁源布设如图1所示。
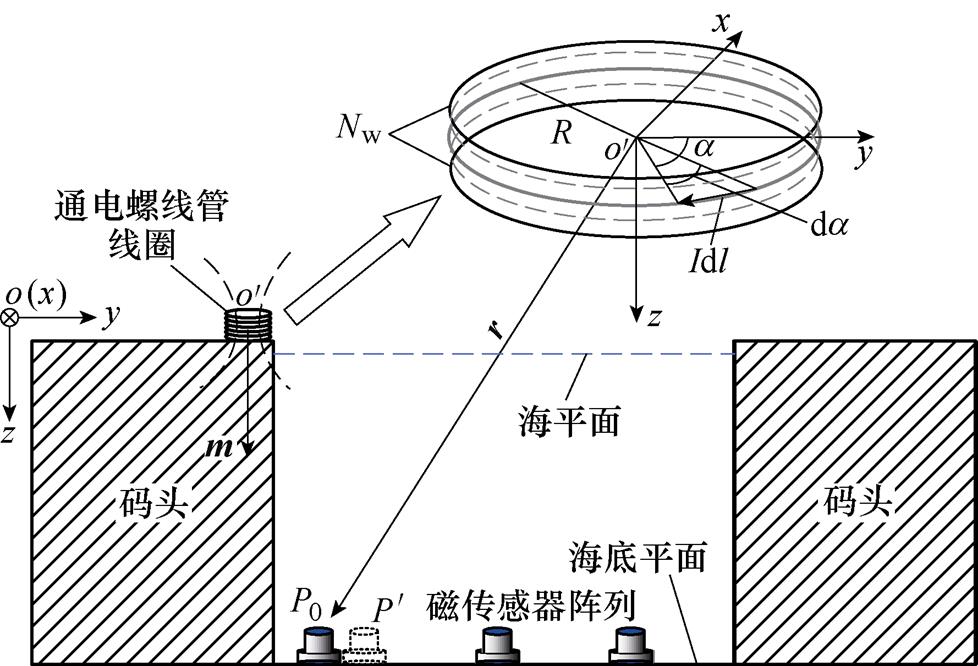
图1 典型消磁站模型及磁源布设
Fig.1 Typical magnetic facility silencing model and magnetic source set
通电螺线管线圈在空间内任意一点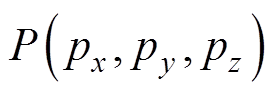 产生的磁感应强度垂直分量Bz[11]解析计算为
产生的磁感应强度垂直分量Bz[11]解析计算为
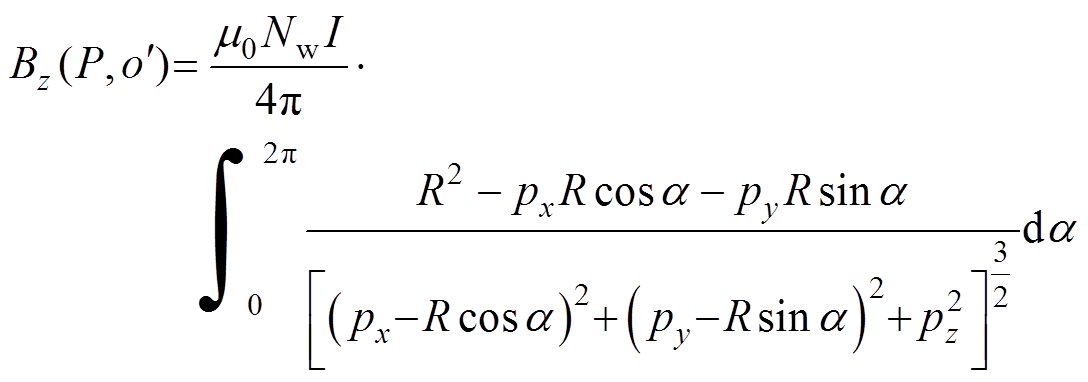 (1)
(1)
式中,Nw为线圈匝数;R为线圈半径;I为电流;m0为真空磁导率。在优化算法迭代的过程中,积分计算式(1)既复杂又耗时。为缩减优化时间,当测量点P与线圈中心的距离大于线圈半径R的15倍时,可将通电螺线管线圈等效成磁偶极子[12]。考虑到目前大多数消磁站仍使用单轴(z轴方向)磁传感器测量舰艇磁场,采用磁感应强度垂直分量Bz对消磁站水下磁传感器展开定位试验。测量点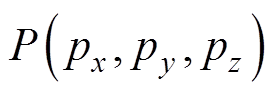 的磁感应强度垂直分量Bz[13-14]可进一步表示为
的磁感应强度垂直分量Bz[13-14]可进一步表示为
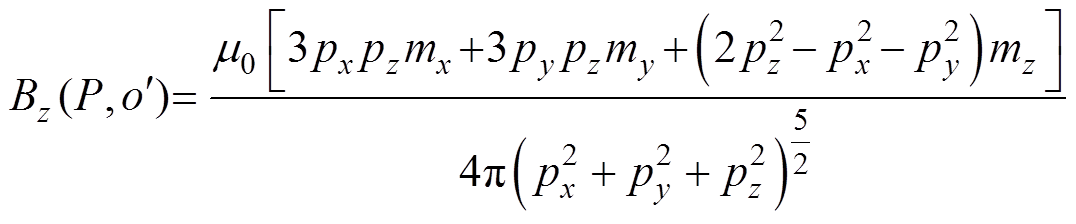 (2)
(2)
式中,mx、my、mz分别为磁偶极子磁矩在线圈坐标系下沿x、y和z三个方向的分量,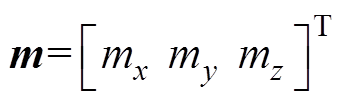 。
。
图2显示了布设在码头平面的磁源沿x轴方向直线移动时,水下磁传感器测得的磁感应强度垂直分量Bz曲线。结果表明,磁传感器测得的磁场大小和变化(磁场梯度)随着与磁场的相对位置改变而改变。当耦合噪声DBz处于同一水平时,水下磁传感器测得x轴方向磁场梯度越大,定位的区域就越集中,则传感器在x轴方向的位置精度也就越高。
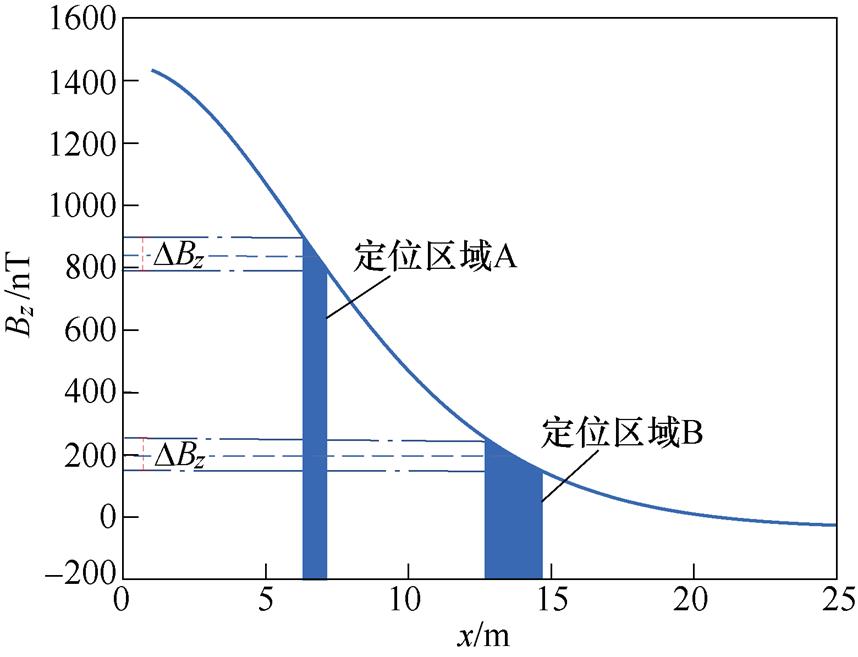
图2 基于磁场梯度的定位精度提升机制
Fig.2 Mechanism of improving location accuracy based on magnetic field gradients
考虑到目前大多数消磁站仍使用单轴磁传感器,只能测量舰艇磁场的垂向分量,磁传感器的位置参数无法根据磁偶极子磁场在三维空间的完备性进行求解,即需要通过改变某些参数构建方程组进行求解。
在实际固定式消磁站中,磁传感器固定安装在海底平面,偏离预设位置(预设位置已知)的幅值不超过0.3 m。鉴于此,最简便的方式就是通过改变磁传感器与磁源的相对位置,来构建方程组。由图2可知,磁传感器位于磁场梯度越高的区域,定位的参数就越接近于实际位置。在此基础上,合理地设置磁源位置,使磁传感器分别位于Bz在x、y方向的磁场高梯度区,据此构建方程组,提升磁传感器相应方向的定位精度。
在定位系统中,磁源沿x、y和z三个方向的磁矩分量mx、my、mz可通过测量反演获取;通电螺线管线圈磁源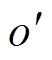 的全局坐标可由实地测量或高精度GPS定位仪器得到。因此,磁源布设在消磁站码头时,可建立方程为
的全局坐标可由实地测量或高精度GPS定位仪器得到。因此,磁源布设在消磁站码头时,可建立方程为
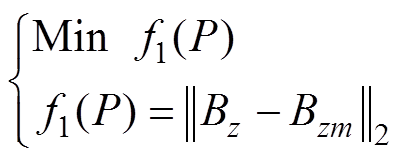 (3)
(3)
式中,Bz为通过式(2)计算通电螺线管线圈磁源m在磁传感器预设位置产生的磁场值,即磁场计算值;Bzm为磁传感器(处于实际位置)测量的磁场值。由式(2)可知,Bz是一个具有3个变量的非线性高阶函数(Bz= f(px, py, pz)),因此,只需要磁源在k(k≥3)个不同的位置依次移动,同时,磁传感器测量相应位置磁源的磁场,并建立适定或超定方程组为
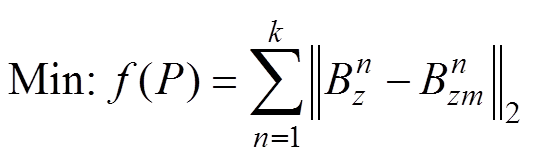 (4)
(4)
式中,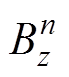 为通电螺线管线圈磁源m在第n个磁传感器预设位置产生的磁场值;
为通电螺线管线圈磁源m在第n个磁传感器预设位置产生的磁场值;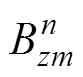 为第n个磁传感器测量的磁场值。
为第n个磁传感器测量的磁场值。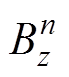 、
、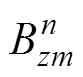 分别为磁传感器的磁场计算值和测量值。采用合适的优化算法对式(4)进行优化求解,即可实现消磁站水下磁传感器的定位,但定位的精度难以保证。
分别为磁传感器的磁场计算值和测量值。采用合适的优化算法对式(4)进行优化求解,即可实现消磁站水下磁传感器的定位,但定位的精度难以保证。
为提高消磁站水下磁传感器的定位精度,结合深度测量数据,提出一种基于磁场梯度优化的水下磁传感器定位方法。
消磁站水下磁传感器定位模型示意图如图3所示,以一定的间距l将消磁站码头平面划分成(M-1)×(N-1)的网格;分别计算磁源布设在不同网格节点时,磁传感器位置偏差区域在x、y方向的平均磁场梯度。考虑到水下磁传感器的位置偏差幅值可控制在0.3 m范围内,计算的位置偏差区域设置为0.6 m×0.6 m×0.6 m,则计算式为
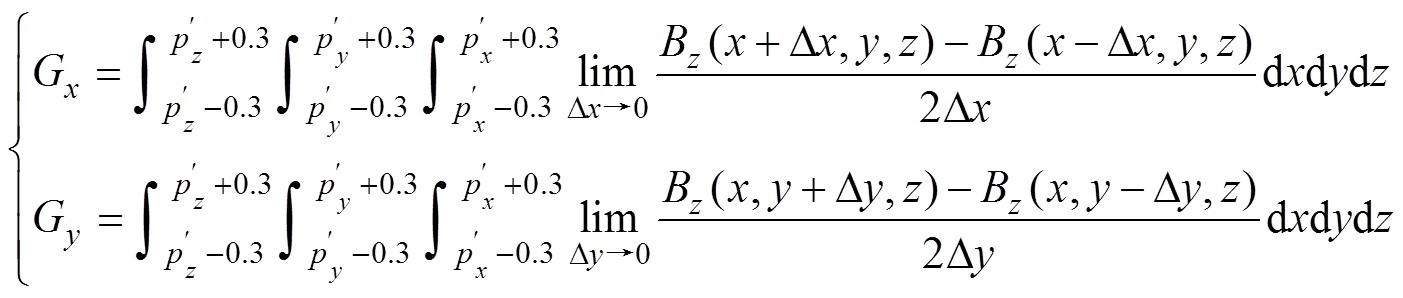 (5)
(5)
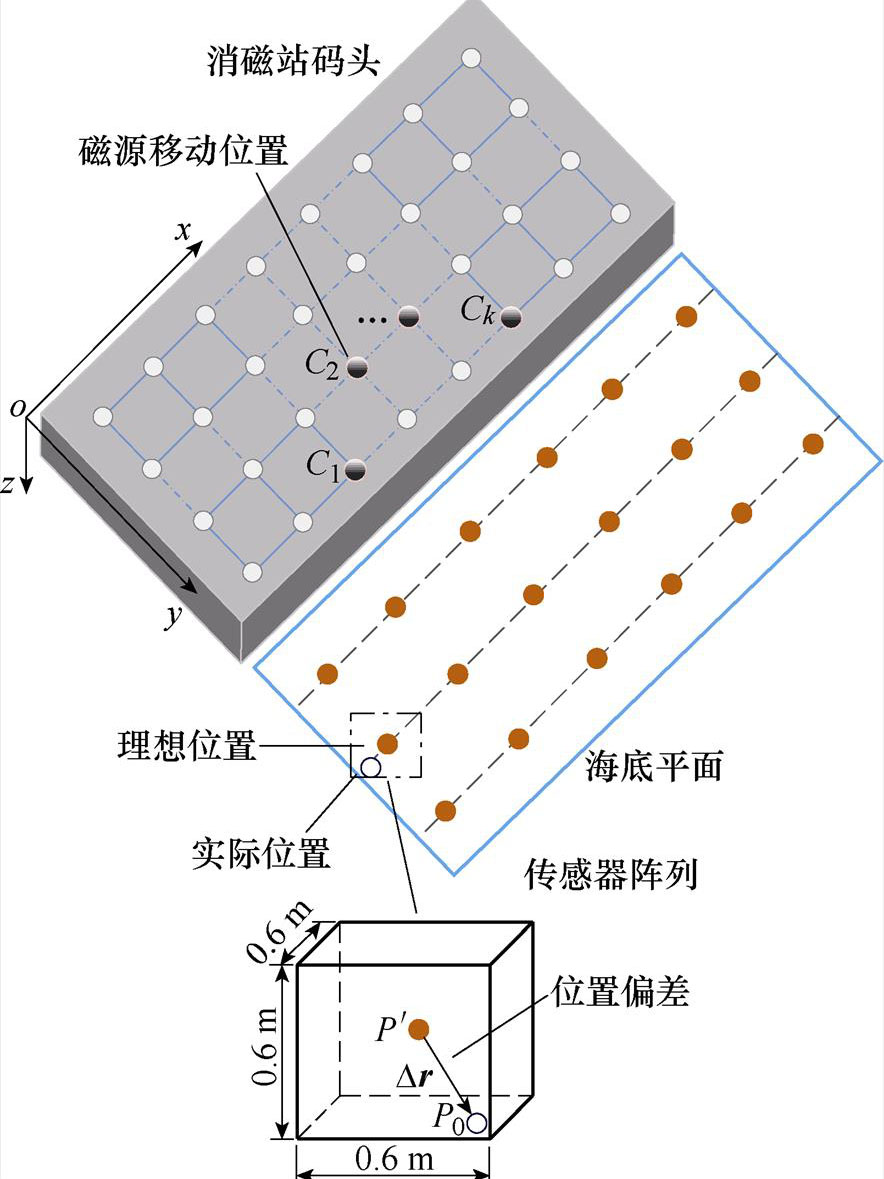
图3 消磁站水下磁传感器定位模型示意图
Fig.3 Localization model of underwater magnetic sensors on the magnetic facility silencing
式中,Gx、Gy分别为磁传感器位置偏差区域在x、y方向的平均梯度;Dx和Dy分别为位置偏差Dr在x和y方向的分量;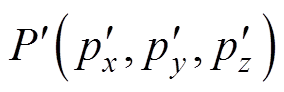 则为磁传感器的理想位置。
则为磁传感器的理想位置。
将式(5)计算的磁场梯度按照从大到小排序分别为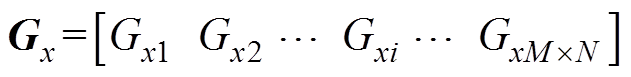 ,
,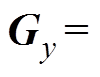
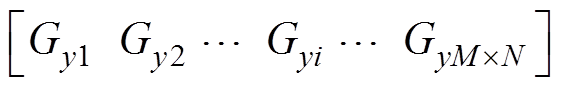 (Gxi和Gyi分别为x和y方向按照从大到小排序的第i个磁场梯度),相对应的网格节点坐标
(Gxi和Gyi分别为x和y方向按照从大到小排序的第i个磁场梯度),相对应的网格节点坐标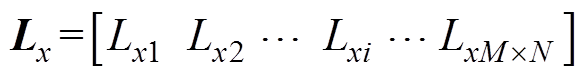 ,
,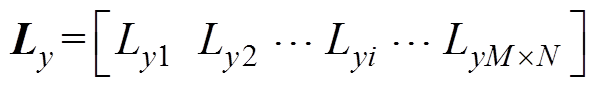 (Lxi和Lyi分别为x和y方向按照从大到小排序的第i个磁场梯度对应的节点坐标)。结合深度传感器,可测得水下磁传感器的深度pz0,则Bz降为具有两个变量的非线性高阶函数(
(Lxi和Lyi分别为x和y方向按照从大到小排序的第i个磁场梯度对应的节点坐标)。结合深度传感器,可测得水下磁传感器的深度pz0,则Bz降为具有两个变量的非线性高阶函数(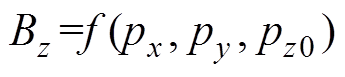 )。根据水下磁传感器的精度要求,确定磁源移动位置的数量k(k≥3)(由数值模拟实验分析确定最合适的k值)与通过式(5)获取的相应磁场梯度方向的前k个网格节点坐标
)。根据水下磁传感器的精度要求,确定磁源移动位置的数量k(k≥3)(由数值模拟实验分析确定最合适的k值)与通过式(5)获取的相应磁场梯度方向的前k个网格节点坐标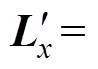
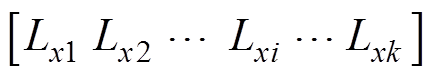 ,
,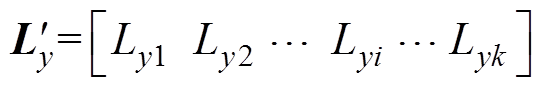 为磁源移动位置,并建立目标函数为
为磁源移动位置,并建立目标函数为
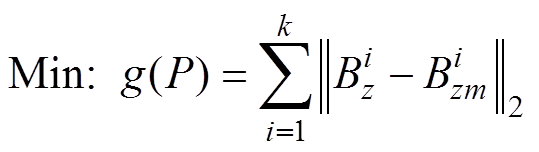 (6)
(6)
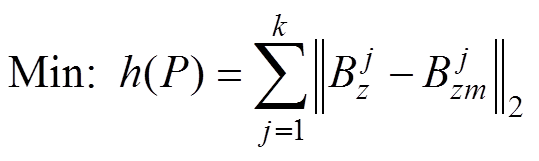 (7)
(7)
式中,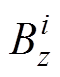 、
、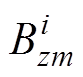 为磁源坐标为Lxi时,磁传感器的磁场计算值和测量值;
为磁源坐标为Lxi时,磁传感器的磁场计算值和测量值;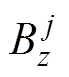 、
、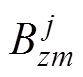 为磁源坐标为Lyj时,磁传感器的磁场计算值和测量值。
为磁源坐标为Lyj时,磁传感器的磁场计算值和测量值。
在优化选取合适磁源移动位置数量k的基础上,通过合适的算法分别优化求解式(6)和式(7),确定磁传感器位置参数x、y方向分量px、py,结合深度测量数据,即可对消磁站水下磁传感器实现高精度定位。
式(6)和式(7)是一个多峰函数,普通优化算法在优化迭代的过程中易陷入局部最优[15-16],因此采用动态学习策略多群体粒子群算法进行优化求解[17]。相对于普通的粒子群优化算法,该算法有两方面的提升,包括避免陷入局部最优和提高迭代效率,具体如下:
(1)采用多种群的概念,在一定程度上保持种群的多样性,以避免过早收敛陷入局部最优。将初始种群划分为M个子群,每个子群内的最优粒子记录为lbest,所有子群的最优粒子的平均值记录为unit lbest。
(2)采用了动态学习策略的概念,动态学习机制如图4所示,将种群中的粒子分为普通粒子和通信粒子,在平衡局部优化和全局优化的同时,提高计算效率。普通粒子和通信粒子的迭代过程为
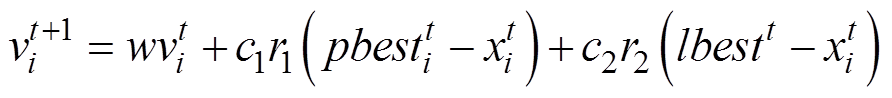 (8)
(8)
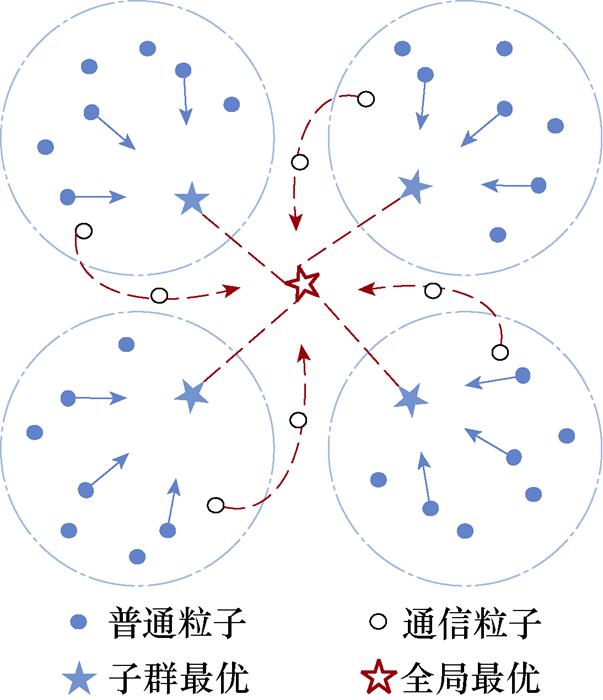
图4 动态学习机制
Fig.4 The dynamic learning mechanism scheme
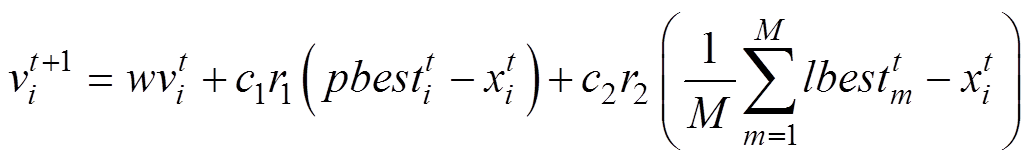 (9)
(9)
式中,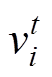 和
和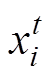 分别为粒子的飞行速度和位置;t为当前迭代次数;i为粒子的序号;w为粒子飞行的惯性权重;c1和c2为反应学习权重的常数;r1和r2为在(0, 1)范围内变化的随机数;
分别为粒子的飞行速度和位置;t为当前迭代次数;i为粒子的序号;w为粒子飞行的惯性权重;c1和c2为反应学习权重的常数;r1和r2为在(0, 1)范围内变化的随机数;![]() 为第i个粒子在第t次迭代后的最优位置。
为第i个粒子在第t次迭代后的最优位置。
此外,随着迭代次数的增加,普通粒子以比例p向通信粒子转化,具体表示为
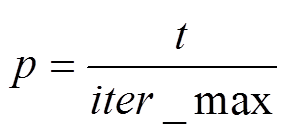 (10)
(10)
式中,iter_max为最大迭代次数。当p=1时,所有的普通粒子均转化为通信粒子。
采用动态学习策略多群体粒子群的磁传感器定位优化步骤如下所示:
(1)输入:网格间距l、磁传感器预设位置P0。
(2)初始化参数:磁源坐标Lx、Ly,磁场测量值Bzm,惯性权重w,粒子位置x,速度v,加速度c1、c2,深度传感器测量值pz0。
(3)划分种群M×N,并初始化粒子的位置x,速度v,个体最优pbest,子群最优lbest和联合最优unit_lbest。
(4)按照参数p随机生成普通粒子和通信粒子。
(5)普通粒子和通信粒子分别执行式(8)和式(9)更新粒子状态。
(6)根据适应度更新体最优pbest,子群最优lbest和联合最优unit_lbest。
(7)按照参数p将部分普通粒子转化为通信 粒子。
(8)重复步骤(5)~步骤(7),直到达到结束条件。
(9)输出:磁源位置坐标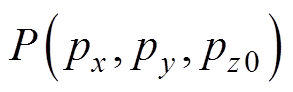 。
。
绝对误差、相对误差及水平距离的计算为
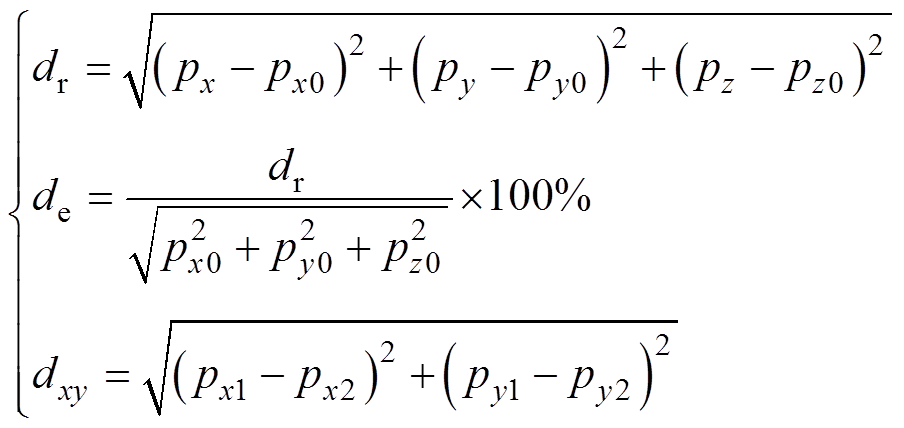 (11)
(11)
式中,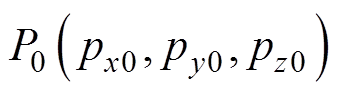 为消磁站水下磁传感器的实际安装位置;
为消磁站水下磁传感器的实际安装位置;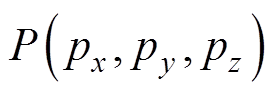 为磁传感器的计算位置;
为磁传感器的计算位置;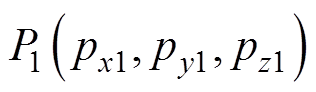 和
和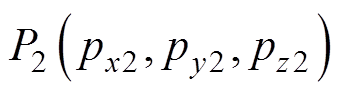 分别为场点1和场点2的位置。
分别为场点1和场点2的位置。
在实际固定式消磁站中,传感器多是以平行阵列形式安装在海底平面。消磁站截面尺寸如图5所示,本文采用的典型消磁站共有3列传感器,呈对称分布。因此,传感器的位置类型分为两种:第一种位置类型的传感器深度为16 m,距离码头的水平距离dxy=4 m;第二种深度为16 m,距离码头的水平距离dxy=10 m。
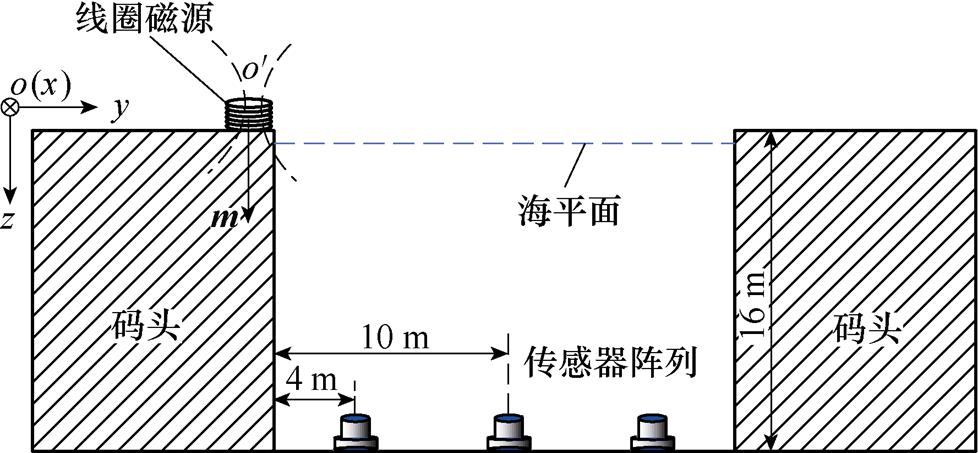
图5 消磁站截面尺寸
Fig.5 Sectional dimension drawing of degaussing station
为检验定位方法的有效性,对第二种位置类型磁传感器开展定位实验。在系统分析磁偶极子等效误差、深度传感器精度、环境磁噪声干扰的基础上,对不同位置偏差的水下磁传感器开展数值模拟实验。
在数值模拟实验中,通过磁偶极子磁源在传感器位置的磁场计算值(真值)叠加测量精度、环境磁噪声等来模拟磁传感器的测量值。
在实验过程中,考虑到绕线工艺等误差影响,直接通过式(1)准确计算空间场点磁场既复杂又耗时,为简化计算提高优化效率,将通电螺线管线圈磁源等效成磁偶极子,用等效磁偶极子产生的磁感应强度垂直分量进行定位。该磁偶极子等效误差可表示为
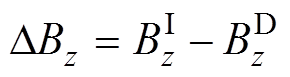 (12)
(12)
式中,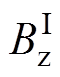 和
和 分别为空间内场点的磁场解析值和磁偶极子等效磁场,分别按式(1)和式(2)计算可得。
分别为空间内场点的磁场解析值和磁偶极子等效磁场,分别按式(1)和式(2)计算可得。
如图5所示,根据实际消磁站尺寸及构造,为降低磁偶极子等效误差对定位的影响,设置通电螺线管线圈的半径为1 m,电流为100 A。考虑到消磁站水下磁传感器各方向的位置误差不超过0.3 m,分别计算z=15.7 m、16 m和16.3 m的磁偶极子等效误差。
磁偶极子等效分析如图6所示,结果表明,磁传感器距离磁源的水平距离dxy达到10 m后,磁偶极子等效误差可控制在-1~1 nT之间,对定位的影响可忽略不计。
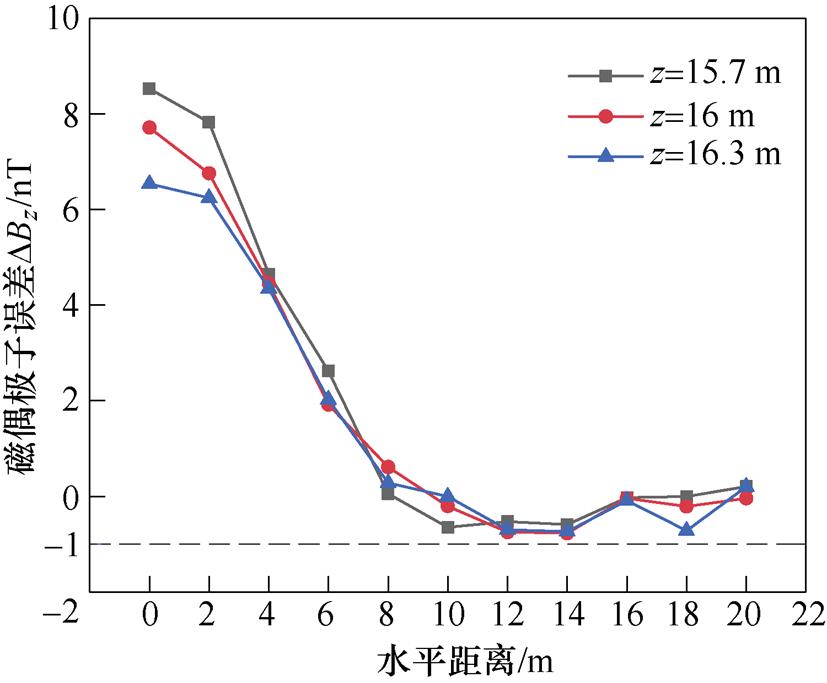
图6 磁偶极子等效分析
Fig.6 Equivalent errors of the magnetic dipole in the seafloor plane
为了分析磁源移动位置的数量k对定位误差的影响,在确定由式(6)计算并排序的前k个磁场梯度对应的节点坐标为磁源移动位置过程中,设置k为3~30(间隔3),共十种磁源移动位置数量展开定位数值模拟实验。磁源磁矩、网格间距l和磁传感器位置偏差分别设置为314 15 A·m2(方向垂直向下)、2 m和(0.3, 0.3, 0.3)m,后续实验分析同上。结合实际消磁站使用的仪器参数,环境磁场噪声设置为10 nT;磁传感器(磁通门传感器)的精度设置为1 nT;深度传感器精度设置为1 cm。
测量次数影响分析如图7所示,随着磁源移动位置数量的增加,磁传感器的定位误差逐步降低;当磁源移动位置数量k达到12后,磁传感器的定位误差达到饱和。此时平均误差和最大误差分别可控制在0.05 m和0.1 m以内。考虑到定位精度要求、实验室设备的限制,数值模拟分析及实验的磁源移动位置数量k设置为12。确定磁传感器位置参数x、y方向分量px、py的磁源移动位置的分布情况及磁传感器位置偏差区域的平均梯度如图8和图9所示。磁源位于通过式(6)确定节点坐标(见图中黑色点)时,磁传感器均处于相应方向的磁场梯度较大区域。
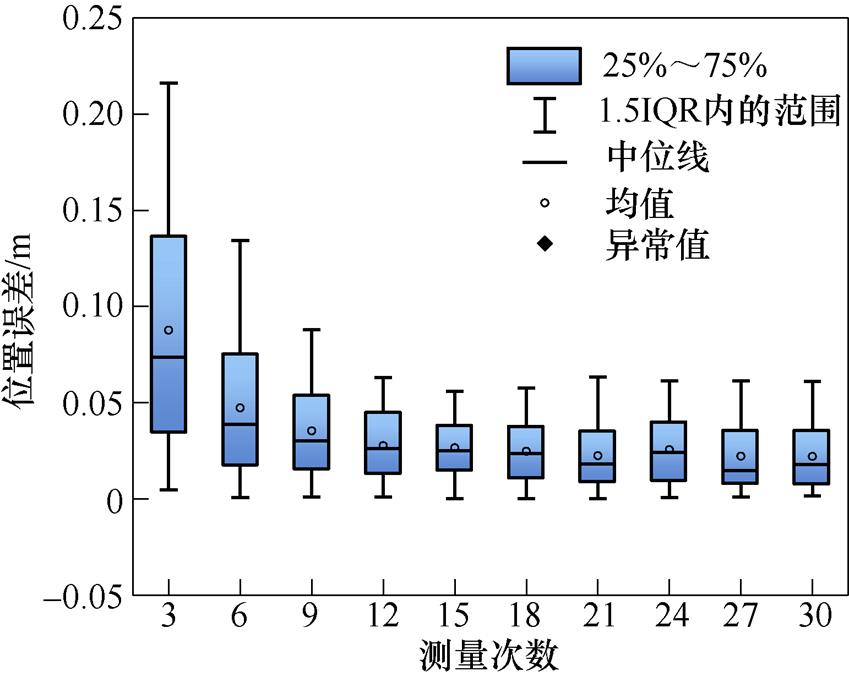
图7 测量次数影响分析
Fig.7 Analysis of measurement times
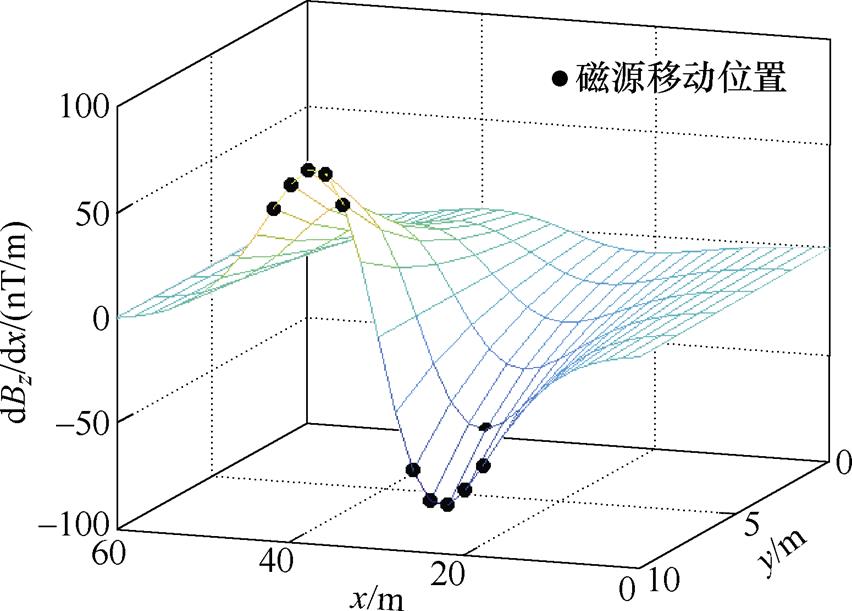
图8 x方向的磁源移动位置及位置偏差区域平均梯度
Fig.8 Average gradient of measurement position and position deviation area of magnetic source in x-direction
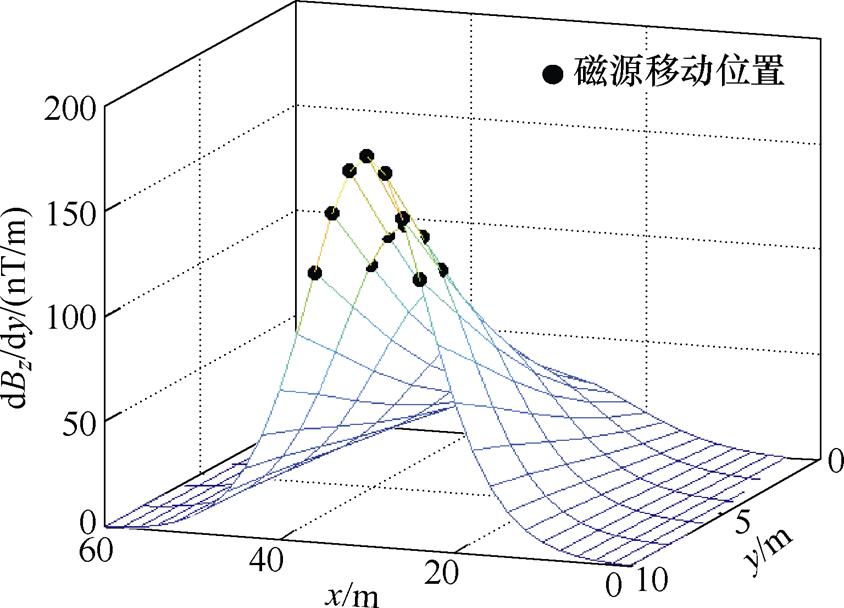
图9 y方向的磁源移动位置及位置偏差区域平均梯度
Fig.9 Average gradient of measurement position and position deviation area of magnetic source in y-direction
为了综合评定深度传感器精度对定位的影响,在不考虑其他干扰条件影响的情况下,分别引入精度为0.1、1、2、3、4和5 cm的深度传感器各开展100次数值仿真重复实验。
深度传感器精度分析如图10所示,随着深度传感器精度的降低,消磁站水下磁传感器的定位误差逐渐增大;从总体上看,相对于平均误差,最大误差受深处传感器精度变化的影响波动较小;当深度传感器的精度为0.1 cm时,最大误差为0.066 m;当深度传感器的精度由0.1 cm降低到1 cm时,定位误差基本不变。
为了分析实际定位中环境磁噪声的影响程度,分别引入5、10、15、20、25和30 nT六种等级环境磁噪声。
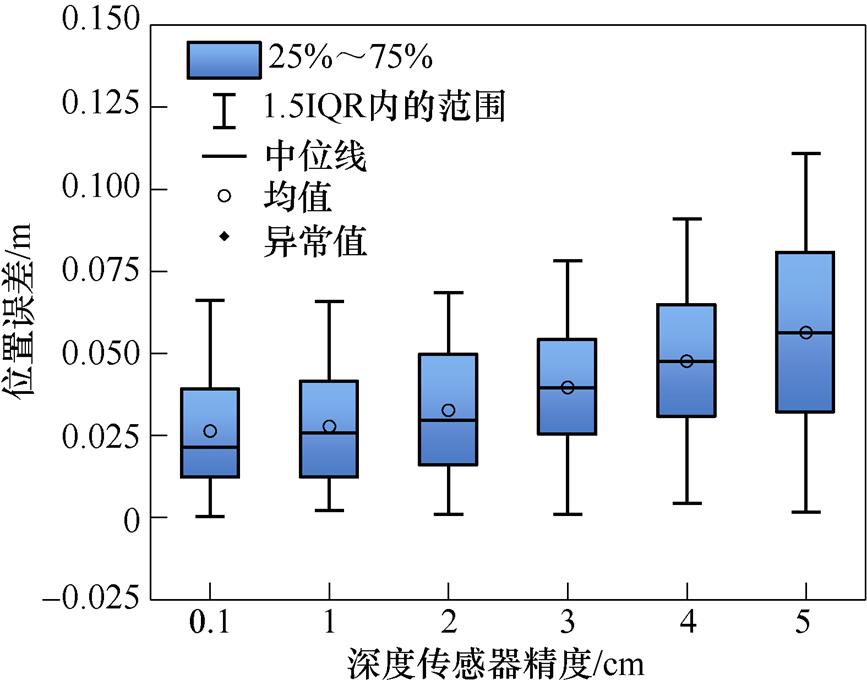
图10 深度传感器精度分析
Fig.10 Analysis of depth sensors’ accuracy
根据固定消磁站环境磁噪声的实际表现形式,将环境磁噪声以白噪声的形式叠加在磁场真值上,并各开展100次数值仿真重复实验。考虑到目前消磁站水下磁传感器类型的应用情况和对深度传感器的要求,磁传感器和深度传感器的精度分别设置为1 nT和1 cm。
环境磁噪声影响分析如图11所示,随着环境磁噪声的增加,消磁站水下磁传感器的定位误差逐渐增大;平均误差的变化相对较小,当噪声达到30 nT时,平均误差可控制在0.06 m内;最大误差较大,当噪声小于15 nT时,最大误差较小(小于0.08 m),但是当噪声达到20 nT及以上时,最大误差大于0.12 m。
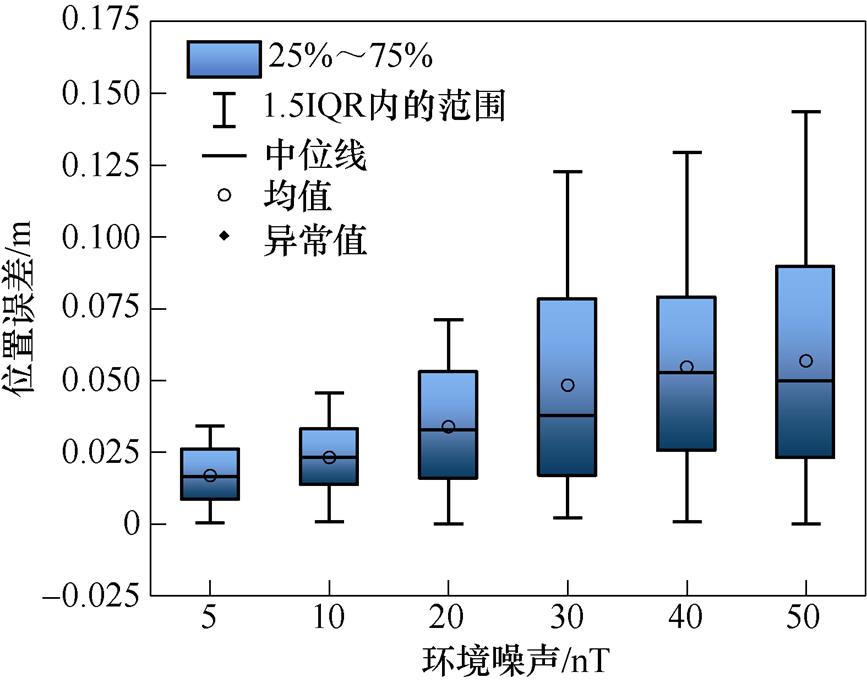
图11 环境磁噪声影响分析
Fig.11 Analysis of measurement noise
为了分析不同位置偏差对定位精度的影响,引入了五种不同的位置偏差,并各自开展100次数值重复模拟实验。结合目前消磁站的实际情况,磁源磁矩、环境磁噪声、磁传感器和深度传感器精度分别设置为31 415 A·m2(方向垂直向下)、10 nT、1 nT和1 cm。dr-ave和dr-max分别为100次数值重复模拟实验后按式(11)计算的绝对误差的平均值和最大值。
数值模拟实验结果见表1,在各方向位置偏差幅值为0.3 m,不同的位置偏差对定位精度的影响较小;平均绝对误差的均值为0.023 m;最大绝对误差的均值为0.056 m,方差的均值为2.26×10-4 m2,满足消磁站内舰艇磁场测量要求。
表1 数值模拟实验结果
Tab.1 Numerical simulation experimental results
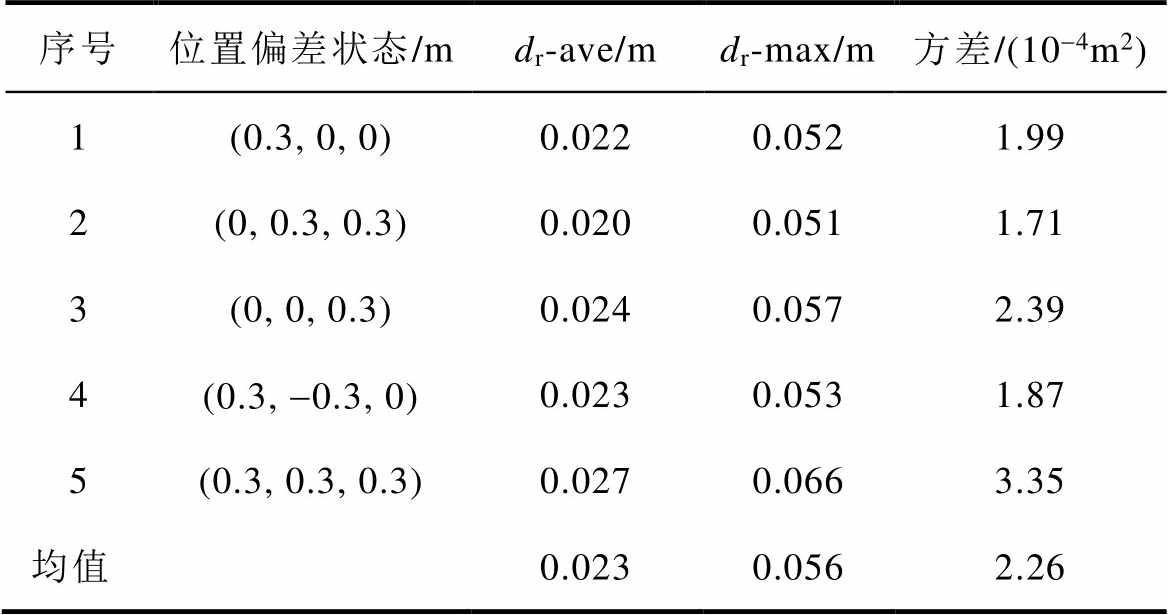
序号位置偏差状态/mdr-ave/mdr-max/m方差/(10-4m2) 1(0.3, 0, 0)0.0220.0521.99 2(0, 0.3, 0.3)0.0200.0511.71 3(0, 0, 0.3)0.0240.0572.39 4(0.3, -0.3, 0)0.0230.0531.87 5(0.3, 0.3, 0.3)0.0270.0663.35 均值0.0230.0562.26
此外,对五种位置偏差校正统计结果,各选一组结果,数值模拟实验结果三维图如图12所示。图中的五角星代表传感器的预设位置,三角形代表传感器的实际安装位置,圆形代表定位后的传感器校正位置。L1表示第五种位置偏差在位置校正前的位置误差,L2表示位置校正后的位置误差,从L1和L2的距离长短变化可以看出,经本文所提方法定位后,传感器的位置误差有了大幅度降低。
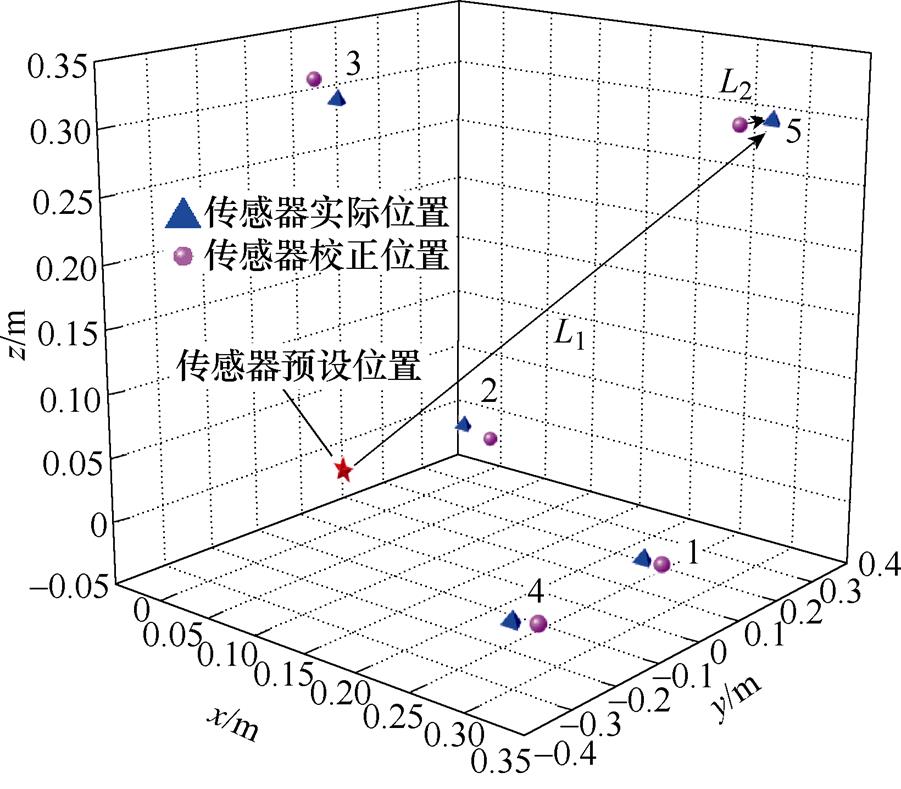
图12 数值模拟实验结果三维图
Fig.12 Three dimensional figure of numerical simulation experiment results
为验证定位方法的操作可行性,根据数值模拟实验设计了约1 8.5的物理缩比模型实验如图13所示,按照实际消磁站的空间位置关系进行尺寸缩比,磁源位于无磁升降平台,磁传感器布设在地面。此外,为降低实验复杂程度,通过布设多个磁传感器来代替磁源移动。
8.5的物理缩比模型实验如图13所示,按照实际消磁站的空间位置关系进行尺寸缩比,磁源位于无磁升降平台,磁传感器布设在地面。此外,为降低实验复杂程度,通过布设多个磁传感器来代替磁源移动。
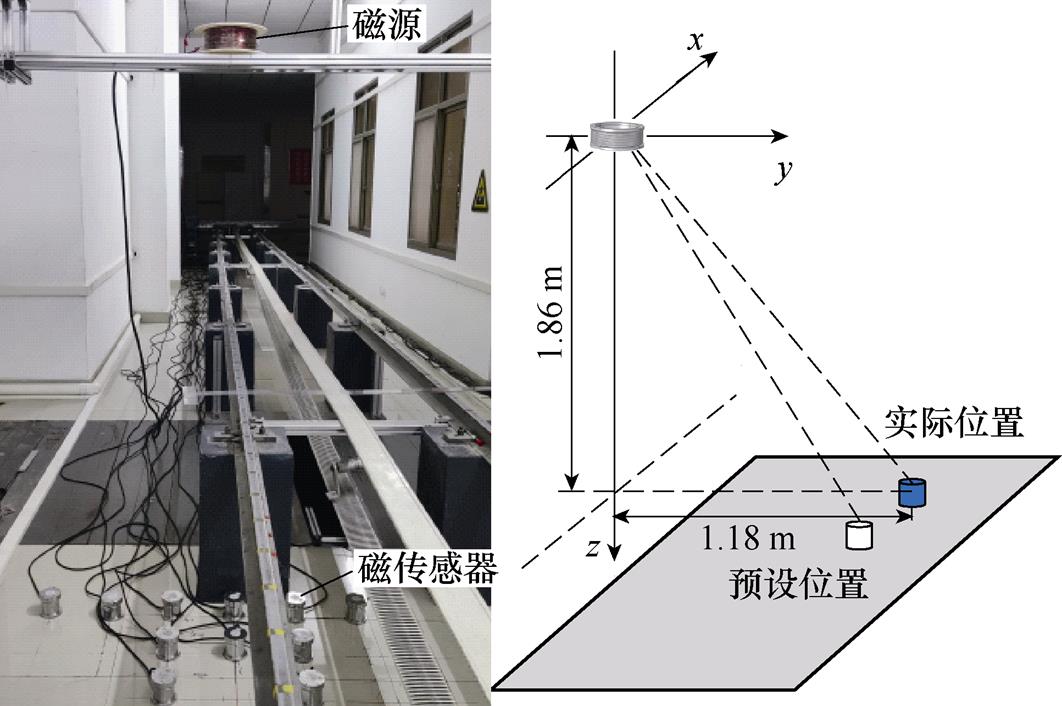
图13 模型实验现场
Fig.13 Model experiment site
线圈的半径R和匝数Nw分别为0.1 m和210,直流电源电流输出为0~10 A,采用MMS3-33A型三分量磁场测量系统采集磁感应强度垂直分量,配套的磁通门传感器分辨率为0.1 nT,精度为1 nT,并设置五种关于30 mm的位置偏差状态。磁传感器的z坐标通过标尺测量得到,以模拟深度传感器。此外,考虑到布设位置误差、标尺精度等因素的影响,物理缩比模型实验的数值结果以1 mm为最小单位。
物理缩比模型实验结果见表2和如图14所示,对五种位置偏差开展了位置校正实验,平均误差为5 mm,相对误差为0.24%。因物理缩比实验中传感器测得的磁感应强度垂直分量与缩比前处于同一水平,位置误差可按缩比尺寸(1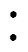 8.5)放大,放大后的平均位置误差为0.043 m,与数值模拟实验结果基本一致,验证了该方法的有效性。
8.5)放大,放大后的平均位置误差为0.043 m,与数值模拟实验结果基本一致,验证了该方法的有效性。
表2 模型实验结果
Tab.2 Model experimental results

序号位置偏差状态/mmde/mmdr(%) 1(30, 0, 0)40.19 2(0, 30, 0)40.19 3(0, 0, 30)50.24 4(30, -30, 0)50.24 5(30, 30, 30)50.24 均值50.24
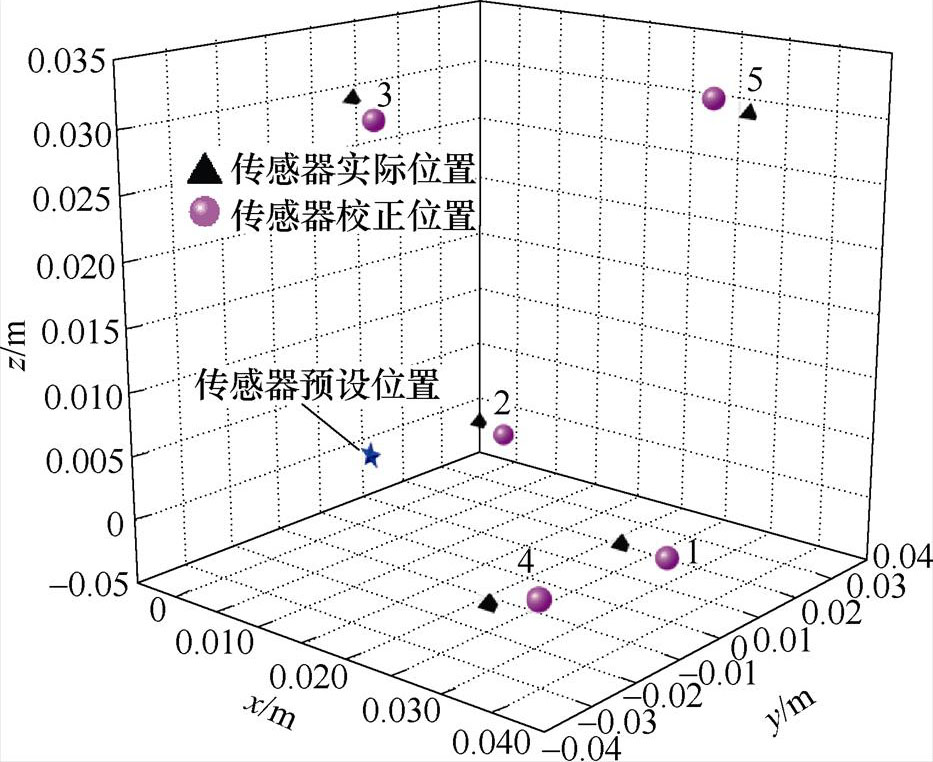
图14 物理缩比模型实验结果三维图
Fig.14 Three dimensional diagram of physical scale model experiment results
为校正消磁站水下磁传感器位置偏差,提高舰艇磁场测量精度,将磁场与深度测量数据相融合,提出了一种基于磁场梯度优化的水下磁传感器定位方法。该方法采用深度传感器获取深度数据降低传感器的定位维度,通过磁传感器位置偏差区域x和y方向的平均磁场梯度优化确定磁源的移动位置提高传感器位置精度。通过典型消磁站尺寸下的数值模拟实验与物理缩比模型实验证明了该方法的有效性,得出以下主要结论:
1)对位置校正误差随磁源移动位置数量k的影响关系进行了量化研究。研究表明,在网格间距为2 m的情况,当磁源移动位置数量k达到12时,位置校正误差不再随k的增加而降低,基本达到饱和状态。
2)通过数值模拟实验,系统分析了深度传感器精度、环境磁噪声等因素对水下磁传感器位置校正的影响规律,其中环境磁噪声带来的影响最大;并开展了不同位置偏差状态的水下磁传感器定位数值模拟实验,校正后传感器平均误差的均值为0.023 m,最大误差的均值为0.056 m,方差的均值为2.26×10-4 m2,满足消磁站内舰艇磁场测量要求。
3)设计了典型消磁站的物理缩比模型实验,实验结果表明,传感器的平均误差为5 mm,按缩比尺寸(1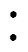 8.5)放大为0.043 m,与数值模拟实验的结果基本一致,验证了所提方法的有效性和准确性。
8.5)放大为0.043 m,与数值模拟实验的结果基本一致,验证了所提方法的有效性和准确性。
参考文献
[1] 王锴松, 周国华, 刘月林, 等. 地磁模拟法测量舰船感应磁场的数值模拟[J]. 兵工学报, 2022, 43(3): 617-625.
Wang Kaisong, Zhou Guohua, Liu Yuelin, et al. Numerical simulation of measuring ship's induced magnetic field by geomagnetic field simulation method[J]. Acta Armamentarii, 2022, 43(3): 617-625.
[2] 曹恒佩, 艾萌萌, 王延波. 永磁辅助同步磁阻电机研究现状及发展趋势[J]. 电工技术学报, 2022, 37(18): 4575-4592.
Cao Hengpei, Ai Mengmeng, Wang Yanbo. Research status and development trend of permanent magnet assisted synchronous reluctance motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(18): 4575-4592.
[3] 刘琪, 孙兆龙, 姜润翔, 等. 一种舰船下方磁场的信号重构及换算方法[J]. 电工技术学报, 2022, 37(15): 3723-3732.
Liu Qi, Sun Zhaolong, Jiang Runxiang, et al. A signal reconstruction and conversion method of magnetic field under ship[J]. Transactions of China Electro- technical Society, 2022, 37(15): 3723-3732.
[4] Hott M, Harlakin A, Hoeher P A. Hybrid com- munication and localization underwater network nodes based on magnetic induction and visible light for AUV support[C]//2020 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Korea (South), 2020: 66-68.
[5] Callmer J, Skoglund M, Gustafsson F. Silent localization of underwater sensors using magneto- meters[J]. Eurasip Journal on Advances in Signal Processing, 2010: 1-8.
[6] 张朝阳, 肖昌汉. 海底布放磁传感器的磁定位方法的模拟实验研究[J]. 上海交通大学学报, 2011, 45(6): 826-830.
Zhang Zhaoyang, Xiao Changhan. Simulation experi- ment research for magnetic localization method for magnetometer sensor at seabed[J]. Journal of Shanghai Jiao Tong University, 2011, 45(6): 826-830.
[7] 杨明明, 刘大明, 连丽婷, 等. 用海面磁偶极子源定位海底矢量磁传感器[J]. 探测与控制学报, 2011, 33(5): 41-45, 51.
Yang Mingming, Liu Daming, Lian Liting, et al. Underwater vector-magnetometer located by using magnetic dipole sources in the offing[J]. Journal of Detection & Control, 2011, 33(5): 41-45, 51.
[8] 孙烨, 肖昌汉, 周国华. 磁主动式海底磁传感器定位方法及其解析公式[J]. 海洋测绘, 2012, 32(4): 25-28.
Sun Ye, Xiao Changhan, Zhou Guohua, An active method and its analytical formulas of magnetic sensor positioning using the magnetic source[J]. Hydrographic Surveying and Charting, 2012, 32(4): 25-28.
[9] 周国华, 张树, 赵文春, 等. 低速运动条件下的磁传感器定位方法[J]. 船电技术, 2016, 36(9): 1-5.
Zhou Guohua, Zhang Shu, Zhao Wenchun, et al. Magnetic sensor positioning method under low speed movement condition[J]. Marine Electric & Electronic Engineering, 2016, 36(9): 1-5.
[10] Yu Zhou, Xiao Changhan, Zhou Guohua. Multi- objectivization-based localization of underwater sensors using magnetometers[J]. IEEE Sensors Journal, 2014, 14(4): 1099-1106.
[11] 王泽忠, 全玉生, 卢斌先. 工程电磁场[M]. 2版. 北京: 清华大学出版社, 2011.
[12] 张朝阳, 虞伟乔. 基于磁偶极子等效的潜艇空间磁场分布[J]. 舰船科学技术, 2013, 35(1): 31-34.
Zhang Zhaoyang, Yu Weiqiao. Research on spatial magnetic field distributing of submarine based on magnetic dipole equivalent[J]. Ship Science and Technology, 2013, 35(1): 31-34.
[13] 刘芙妍, 颜冰. 磁偶极子阵列模型的适用性研究与优化分析[J]. 物理学报, 2022, 71(12): 124101.
Liu Fuyan, Yan Bing. Applicability and optimization analysis of magnetic dipole array model[J]. Acta Physica Sinica, 2022, 71(12): 124101.
[14] 李岩松, 刘启智, 刘君, 等. 基于磁偶极子模型的材料缺陷漏磁检测正演问题的单元积分计算方法[J]. 电工技术学报, 2017, 32(21): 176-185.
Li Yansong, Liu Qizhi, Liu Jun, et al. The unit integral calculation method of defective material’s forward question of magnetic flux leakage detection based on the magnetic dipole model[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 176-185.
[15] 丁璨, 李江, 袁召, 等. 基于NSGA-Ⅱ和BP神经网络的杯状纵磁触头结构优化设计[J]. 电工技术学报, 2022, 37(23): 6074-6082.
Ding Can, Li Jiang, Yuan Zhao, et al. Structural optimization design of cup-shaped longitudinal magnetic contact based on NSGA-Ⅱ and BP neural network[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6074-6082.
[16] 李婕, 杨淑英, 谢震, 等. 基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识[J]. 电工技术学报, 2022, 37(18): 4604-4613.
Li Jie, Yang Shuying, Xie Zhen, et al. Online parameter identification of permanent magnet syn- chronous motor based on fast particle swarm optimization algorithm with effective information iterated[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4604-4613.
[17] Ye Wenxing, Feng Weiying, Fan Suohai. A novel multi-swarm particle swarm optimization with dyna- mic learning strategy[J]. Applied Soft Computing, 2017, 61: 832-843.
Localization Method for Underwater Magnetic Sensors in the Fixed Deperming Station
Abstract At present, the main way to measure a ship's magnetic field is by the magnetic sensor array installed on the submarine plane of the fixed deperming station. The installation of underwater magnetic sensors is particularly difficult due to the complex and changeable submarine environment. There is a certain position deviation between the installation position of the underwater magnetic sensors and the preset position in actual engineering, which is the main factor affecting the magnetic field measurement of the ship. In addition, with the continuous development of magnetic mines and airborne magnetic prospecting, the requirements for the magnetic protection capability of ships are becoming increasingly strict. Therefore, combining magnetic field and depth measurement data, a localization method for underwater magnetic sensors is proposed based on optimizing the magnetic field gradient has been proposed.
Firstly, the pier meshes with a suitable grid spacing l. Secondly, the energized solenoid coil is equivalent to a magnetic dipole. When the magnetic dipole is located at each grid node, the average magnetic field gradients in the x-axis and y-axis directions of the region 60 cm×60 cm×60 cm centered on the sensor are calculated. Simultaneously, the coil coordinates are recorded. Then the average magnetic field gradients in the three directions are sorted from large to small. Thirdly, the magnetic source is moved on the grid nodes corresponding to the first k average magnetic field gradients in the x-axis and y-axis directions, and underwater magnetic sensors measure the magnetic field of the magnetic source. Fourthly, the magnetic source data are measured in the x-axis and y-axis directions, and the depth data are used to construct the objective function. A novel multi-swarm particle swarm optimization with a dynamic learning strategy is used to obtain the x-axis and y-axis components of the position deviation. In the locating model, the moving positions of the magnetic source are determined by optimizing the average magnetic field gradients in the x-axis and y-axis directions. Hence, the localization accuracy of the magnetic sensors in the x-axis and y-axis directions is greatly improved. In addition, the depth of the magnetic sensor is measured by the depth sensor, which avoids the imprecise solution of z-axis components.
In this paper, the effectiveness of this method is proved by numerical simulation experiments and physical scale model experiments under the size of typical degaussing stations. The following main conclusions are drawn as follows: (1) The relationship between the position correction error and the number of moving positions k of the magnetic source is studied quantitatively. When the number of moving positions k of the magnetic source reaches 12 times under the grid spacing of 2 m, the position correction error no longer decreases with the increase of k and basically reaches the saturation state. (2) Through numerical simulations, the influence of environmental magnetic noise on the localization of underwater magnetic sensors is the most significant. The numerical localization experiment of underwater magnetic sensors in different position deviation states was carried out. After correction, the mean value of the average error of sensors was 0.023 m, the mean value of the maximum error was 0.056 m, and the mean value of the variance was 2.26×10-4 m2, which met the requirement for magnetic field measurement of ships in a degaussing station. (3) The physical scale model experiment of the fixed deperming station is designed. The experimental results show that the average error of the sensor is 5 mm, and its amplification is 0.043 m according to the scale (1 8.5), almost consistent with the numerical simulation results. The effectiveness and accuracy of the proposed method are verified.
8.5), almost consistent with the numerical simulation results. The effectiveness and accuracy of the proposed method are verified.
keywords:Magnetic field gradients, localization, underwater magnetic sensor, depth sensor
中图分类号:TM153
DOI: 10.19595/j.cnki.1000-6753.tces.222079
国家自然科学基金项目(51377165)和海军工程大学自主立项项目(2022504070)资助。
收稿日期 2022-11-03
改稿日期 2022-11-21
王玉芬 男,1997年生,硕士研究生,研究方向电磁环境与防护技术、电磁定位技术。E-mail: 18370469195@qq.com
周国华 男,1983年生,副教授,硕士生导师,研究方向为电磁场数值计算、电磁环境与防护技术、舰艇磁场模型等。E-mail: dandanqibing@126.com(通信作者)
(编辑 陈 诚)