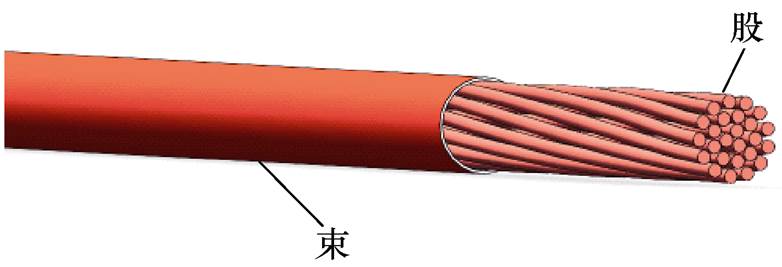
图1 利兹线结构示意图
Fig.1 Structural diagram of Litz-wire
摘要 绕组损耗是高频变压器总体损耗的重要组成部分，是影响磁性元件体积、效率和温升的关键性参数。由于利兹线的高频损耗小而广泛应用于高频变压器绕组，但其复杂的三维扭转结构导致准确、快速地计算绕组损耗十分困难。解析方法需要进行简化和近似处理，难以准确地表征绕组的高频涡流特性，有限元数值方法需要对每匝绕组精细化建模，导致计算资源耗费严重。采用具有等效复值材料特性的区域替代绕组区域的均匀化技术，能够实现二维磁场对涡流效应的表征，降低了精细化建模的计算成本。但等效区域的材料特性需要利用数值方法获得，增加了计算的复杂性。因此该文通过分析利兹线损耗机理，考虑利兹线截面形状对等效区域材料特性的影响，实现了圆形利兹线绕组等效复数磁导率的明确解析描述。建立了圆形利兹线绕组损耗计算模型，验证了等效复数磁导率计算邻近效应的准确性，实现了较宽频率范围内绕组损耗的准确预测。
关键词：利兹线 绕组损耗 等效复数磁导率 趋肤效应 邻近效应
随着我国不断开发和建设智能电网，以及将更多分布式发电可靠有效地融入电网中，对电能处理和转换单元提出了小型化、轻量化和灵活控制等要求[1-3]。电力电子变压器由于能够实现波形控制电能质量调节、潮流控制和系统稳定控制，并能提供灵活的交直流接口而备受关注[4]。高频变压器相较于传统变压器具有体积小、重量轻的特点，是电力电子变压器的关键性部件。其中绕组损耗是高频变压器总体损耗的重要组成部分，是影响磁性元件体积、效率和温升的关键参数，然而随着工作频率的提高，高频效应使得绕组损耗显著增加。因此，研究高频下绕组损耗计算对变压器的结构优化以及散热分析设计具有重要的工程意义和应用前景[5-6]。
利兹线（Litz-wire）能够实现导体匝内换位，减小趋肤效应和邻近效应产生的损耗而广泛应用于高频变压器绕组[7-8]。目前利兹线绕组损耗计算方法主要分为解析法和数值法两种，解析法主要采用计算铜箔绕组的Dowell公式[9]，依据直流电阻不变的原则将利兹线等效为铜箔导线，进而推导出利兹线绕组的交直流电阻比。文献[10]利用趋肤效应和邻近效应的正交性[11]，考虑漏磁场的影响提出用于计算高频变压器利兹线绕组损耗的Tourkhani公式，是工程上常用的利兹线绕组损耗的计算方法。解析法计算简单、方便快捷，但在推导过程中需要进行大量的假设和简化处理，难以准确表征高频涡流效应对损耗的影响，导致高频下的损耗计算误差较大。相较之下依托商用电磁场软件的数值方法通过精细化建模，能够考虑高频涡流效应，计算精度高，但是随着频率的升高，网格剖分的尺寸越来越小，精细化建模导致计算成本剧增，难以实现对复杂结构利兹线涡流的快速分析。为了减少精细化建模的时间成本，文献[12]提出利用具有复数磁导率的非导电材料等效矩形绕组来表征邻近效应，能够实现二维磁场对涡流效应的表征。文献[13-14]分别提出圆导线绕组矩形填充和任意形状填充的复数磁导率的数值解。采用复数磁导率表征邻近损耗的方法虽然加快了有限元的计算速度，节约时间成本但是需要对基本单元进行初步的数值场计算来确定绕组的等效材料特性。为此文献[15]利用等效铜箔绕组的方法推导出圆导线绕组的等效复数磁导率的表达式，文献[16]在圆导线绕组的基础上利用邻近效应损耗系数推导出利兹线绕组的等效复数磁导率表达式，但是在计算时需要采用数据拟合进行参数辨识，降低了该模型的适用性。与矩形截面相比，利兹线绕组的圆形截面更容易缠绕，在实际工程中应用的更多[17-18]，而现有方法未能快速获得其等效复数磁导率的准确表达式。
综上所述，本文通过分析高频下利兹线绕组的涡流特性和损耗机理，实现了圆形利兹线绕组的等效复数磁导率的明确解析描述，建立了基于等效复数磁导率的损耗计算模型，实现对利兹线绕组损耗的准确、快速预测。
利兹线的结构是由多股相互绝缘的细导线经过绞合或编织而成的，如图1所示。与圆导线相比，首先利兹线的绞合绕制使得电流密度分布更加均匀，其次单股导线的截面可能出现在整个截面的任何位置，趋肤效应和邻近效应造成的损耗在高频时都大大减小，因此利兹线被用作高频变压器绕组，但是利兹线复杂的三维扭转结构导致涡流分析困难，增加了损耗计算难度。
图1 利兹线结构示意图
Fig.1 Structural diagram of Litz-wire
利兹线的损耗分为电阻损耗（直流损耗）和涡流损耗（交流损耗）两部分。其中涡流损耗又可以根据激励方式的不同分为趋肤效应损耗和邻近效应损耗，由于两种激励之间不存在耦合关系，因此趋肤效应与邻近效应具有正交性，可以分开进行考虑。
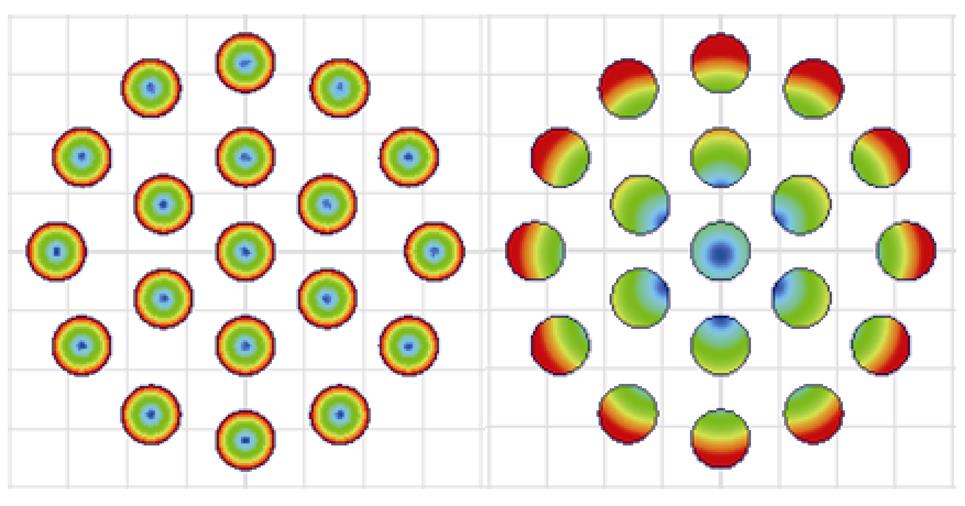
当导体流过高频交变电流时，导体内由于电磁效应产生涡流，改变了截面上电流分布如图2a所示，涡流增强了导体表面的电流，削弱了导体中心处的电流，使得传输电流趋于表面流动。这种由高频电流引起的涡流效应被称为趋肤效应，由此产生的损耗称为趋肤效应损耗。单股圆导线内部的电流密度可以采用柱坐标系统中用带复变量的贝塞尔常微分方程表示，因此由趋肤效应引起的单位长度的损耗可以表示[19]为
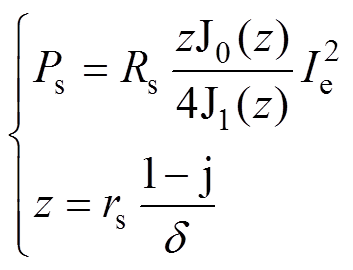（1）
式中，J0和J1分别为0阶和1阶贝塞尔函数；rs为股线半径；j为虚数单位；d 为趋肤深度；Rs为单位长度股线的直流电阻；Ie为交变电流的有效值。
（a）趋肤效应损耗 （b）邻近效应损耗
图2 利兹线中涡流损耗类型
Fig.2 Eddy current loss type in Litz-wire
利兹线单位长度的趋肤效应损耗就可以表示为n股圆导线引起损耗的叠加，即
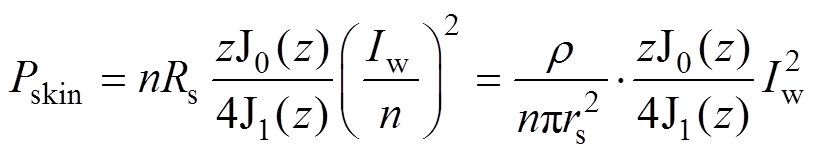（2）
式中，Iw为流过绕阻截面的电流。
由式（2）可以看出，具有相同外径的利兹线和圆导线相比，n股细导线的结构能够增大电流有效截面积，进而减小趋肤效应造成的损耗。
当多股导线并绕时如图2b所示，导线因其流过高频电流在其附近产生的高频磁场，会在其他导线内部感应出涡流，从而改变附近导体的电流分布，这种由相邻导体的高频磁场引起的涡流效应被称为邻近效应，由此产生的损耗称为邻近效应损耗。邻近效应损耗的大小不仅和频率有关，导体间的几何形状、尺寸、排布方式以及导体之间的间隔都会对其产生影响。因此与趋肤效应相比，邻近效应需要考虑的因素更多，表征更加复杂。通常定义邻近损耗因子G量化邻近效应损耗，单位长度的邻近效应损耗可以表示为
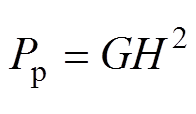（3）
式中，H为正弦变化磁场强度H(t)的有效值。然而由于解析方法在推导过程中的简化和近似处理，难以准确表征高频邻近损耗因子，高频下会导致较大的计算误差。
由于解析方法推导邻近效应损耗因子时存在简化处理，无法准确表征高频涡流效应，采用数值有限元方法可以准确计算临近效应损耗的大小，但是有限元方法计算利兹线绕组的涡流时，需要进行精细化建模，随着频率的升高，复杂三维结构导致计算资源耗费严重，使得传统有限元难以直接表征利兹线绕组。因此通过采用具有等效复值特性的非导电材料替代绕组材料的均匀化有限元分析方法，避免了绕组在涡流场中的精细化建模，在保证计算精度的同时可以提高有限元的计算速度。
当导体处在均匀的高频磁场中，会产生沿着导体的反平行涡流，使得导体的有效磁导率降低，这种导体在时变磁场中的特性类似于一块有损的铁磁材料，因此O. Moreau提出用一个具有复数磁导率的非导电材料替代原来的导电材料[12]，能够在不计算涡流的情况下得到电阻和电感矩阵，并且保证替代后的非导电材料与原来的导体具有相同的有功和无功功率。引入复数磁导率后，将涡流场问题转化为静磁场问题，大大减少了网格剖分的数量，提高了数值计算速度。
假设圆导体处在均匀的外磁场中，由邻近效应产生的矢量磁势满足二维泊松方程，计算出磁化强度的表达式后，利用导体的磁化强度和静态极限下的磁化强度相等的假设，推导出一个孤立圆导线的复数磁导率的表达式[20]为
（4）
式中，mr为铜导线的相对磁导率；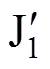
为一阶贝塞尔函数的导数。在单匝圆导线复数磁导率已知的情况下，由多股圆导线构成的矩形截面的利兹线的复数磁导率可以通过引入Ollendorff公式进行计算得到[21]，即
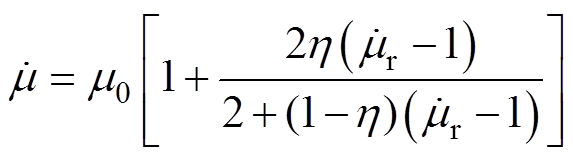（5）
式中，m0为真空磁导率；h为单根利兹线的填充系数，可以通过利兹线的出厂数据进行计算。用单股线的面积与股数的乘积再除以整根利兹线的截面积，用来表征利兹线的材料特性，受制作工艺的影响。引入Ollendorff公式将矩形截面利兹线的复数磁导率表示为填充系数的函数，当导体半径为0.5 mm，工作频率在20 Hz～1 MHz之间变化时，不同填充系数利兹线的复数磁导率的实部和虚部随归一化导体半径（r/d）的变化如图3所示。
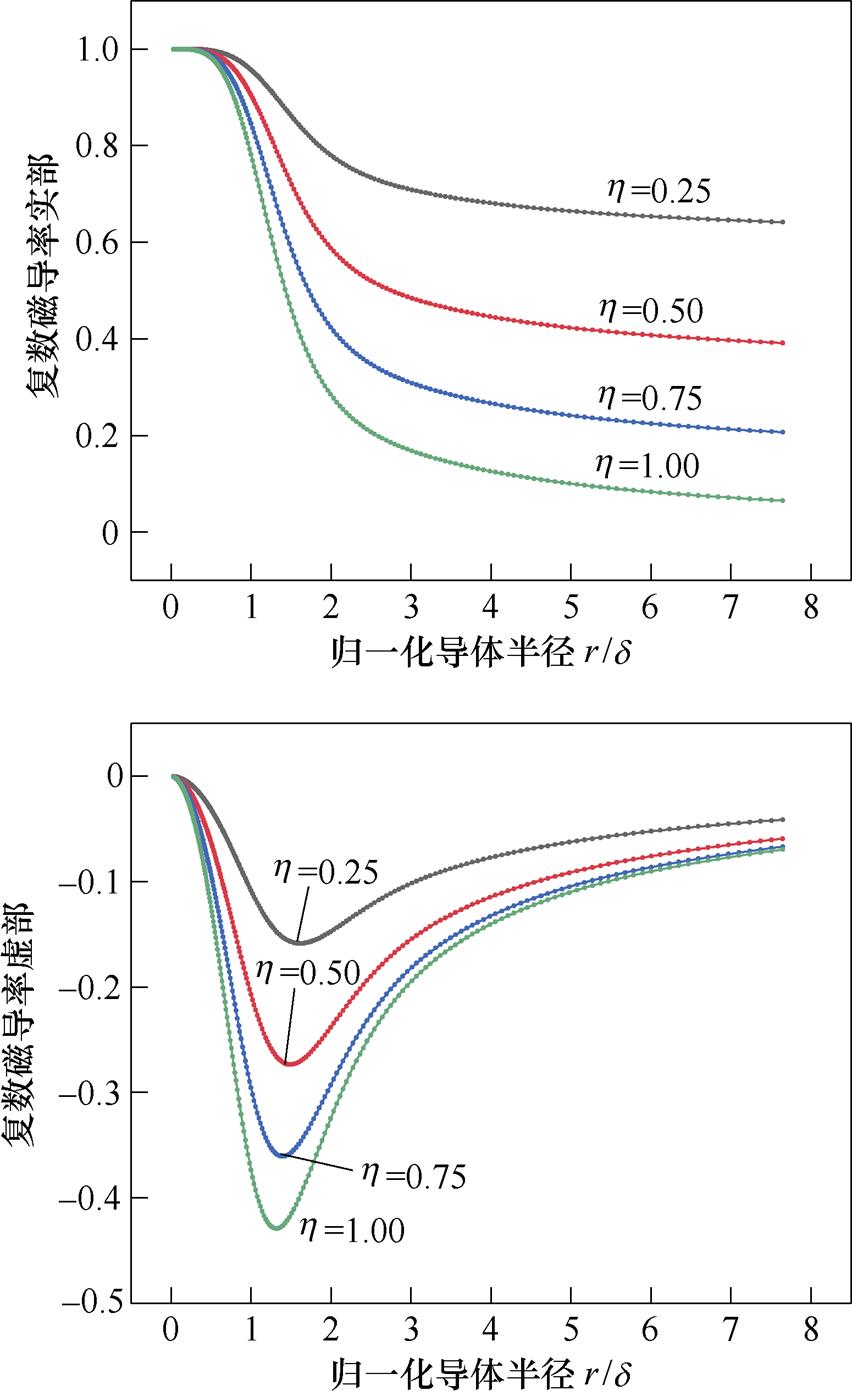
图3 复数磁导率的实部和虚部
Fig.3 Real and imaginary parts of complex permeability
对多匝利兹线绕组的损耗计算就可以利用均匀化有限元技术如图4所示，将绕组区域等效为一个和原绕组具有相同特性的矩形块，根据绕组的轴对称性，可以在二维静磁场柱坐标系中提取磁场值，实现利用复数磁导率表征导体的邻近效应，复数磁导率虚部与临近效应损耗的关系为
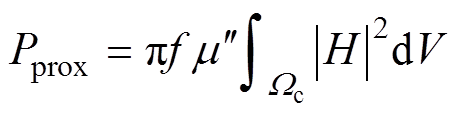（6）
式中，f为工作频率；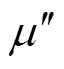
复数磁导率的虚部；H为磁场强度值，由于Ollendorff公式表征的等效复数磁导率仅为填充系数的函数，应用于利兹线绕组时该填充系数仅考虑单匝导线内部的邻近效应的影响，没有考虑绕组的排布对涡流损耗的影响。从而导致如果采用Ollendorff公式的方法表征圆形利兹线绕组的复数磁导率，由于截面形状的改变会使得计算结果产生偏差。
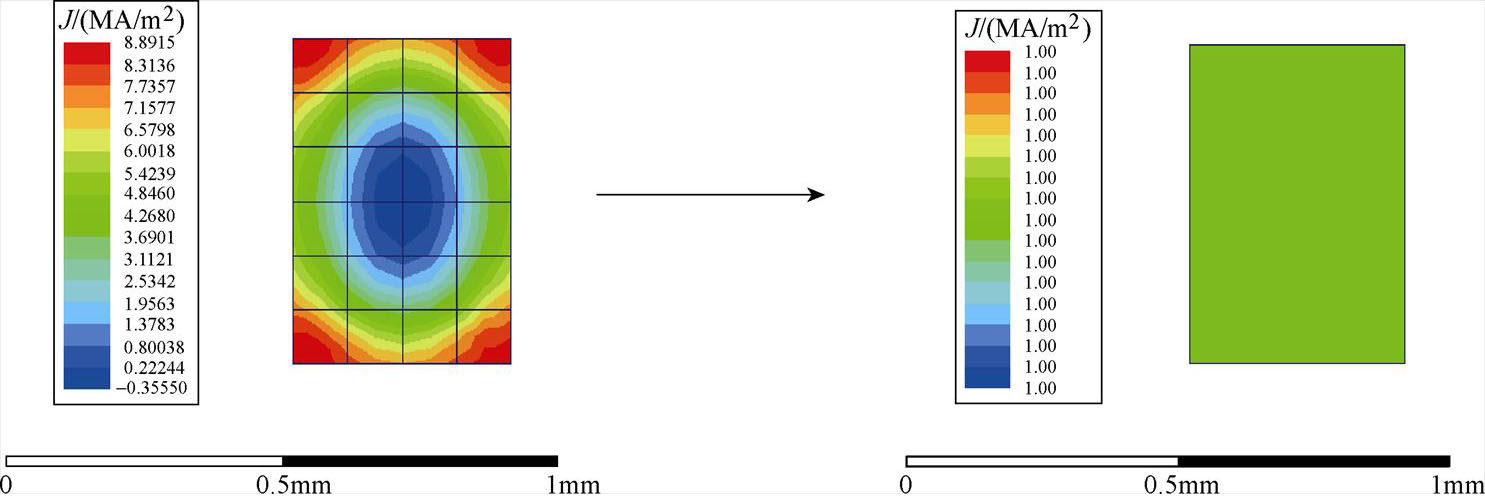
图4 矩形利兹线绕组的均匀化过程
Fig.4 Homogenization process of square Litz-wire winding
不同截面利兹线绕组的磁场分布如图5所示。圆形利兹线绕组的等效过程如图6所示。由图5和图6可见，圆形截面和矩形截面绕组在施加相同的电流激励的条件下，绕组的磁场分布大致相同，但是电流分布不同。主要影响邻近效应造成的损耗，表现为邻近损耗因子的不同。因此本文基于等效的思想，圆形截面与矩形截面相比，产生了匝与匝之间的气隙，改变了绕组间的排布，使得利兹线的有效磁导率降低，引起邻近效应损耗的差别。为考虑截面形状对绕组涡流特性的影响，引入绕组几何因数，为绕组的面积与等效后矩形的几何面积之比，使得等效复数磁导率模型适用于圆形利兹线绕组。引入几何因数后的等效复数磁导率模型为
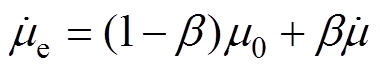（7）
式中，b 为绕组几何因数；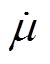
为利兹线的复数磁导率。
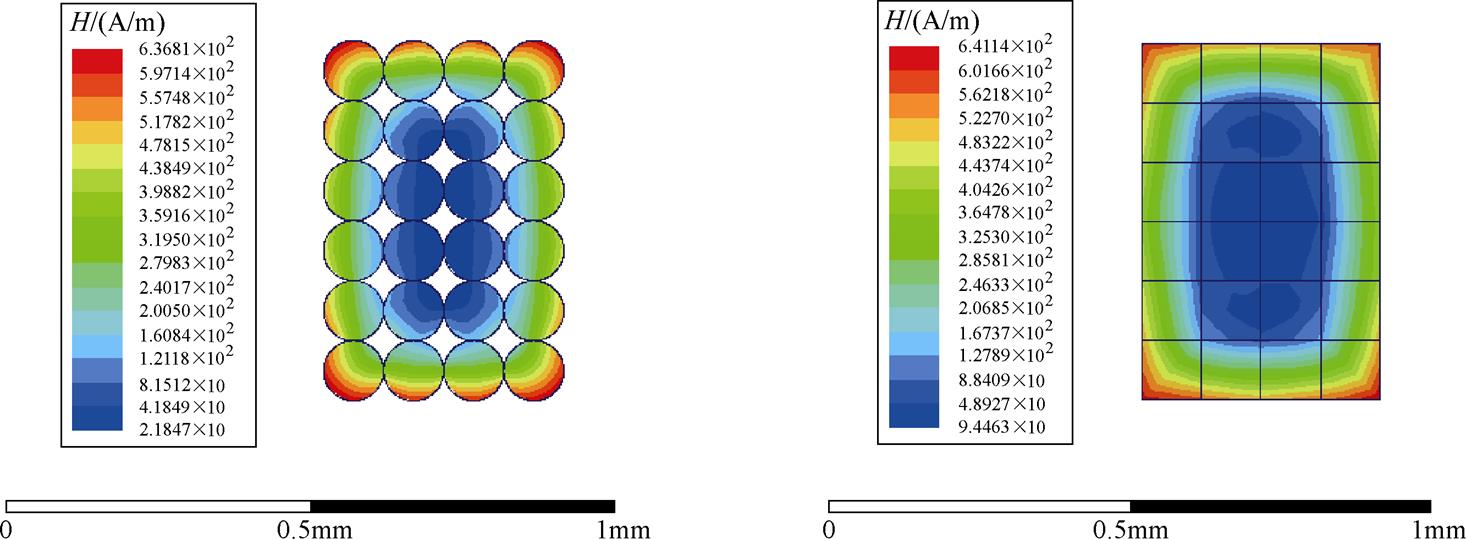
图5 不同截面利兹线绕组的磁场分布
Fig.5 Magnetic field distribution of Litz-wire windings with different cross sections
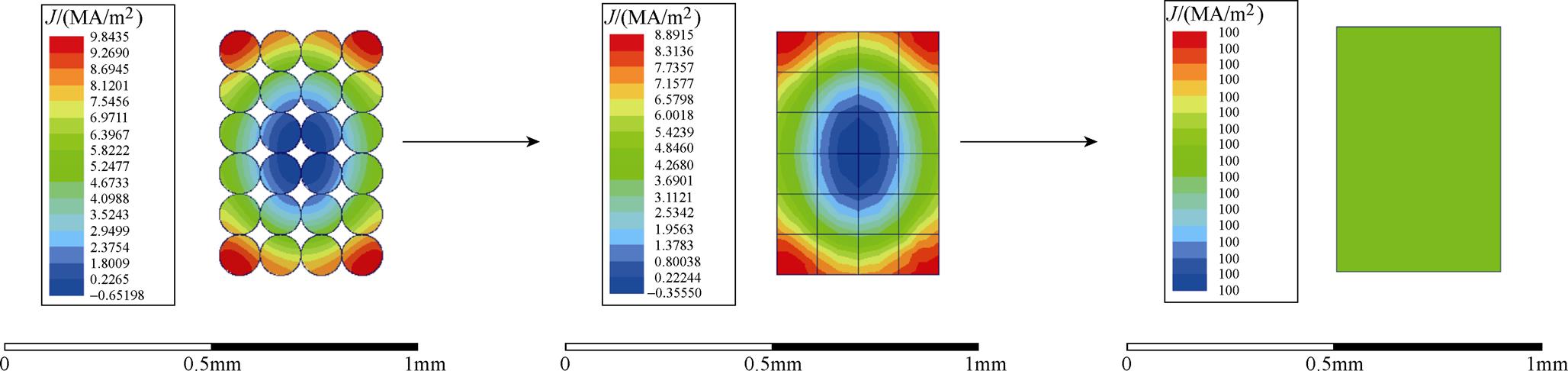
图6 圆形利兹线绕组的等效过程
Fig.6 Equivalent process of round Litz-wire winding
当其他导体产生的外部磁场在导体截面上是均匀时，趋肤效应和邻近效应之前存在正交性，使得两种效应产生的损耗能够进行解耦，从而大大简化了计算，正交性的证明在多篇论文中进行了理论验证，证明过程如式（8）～式（12）所示，具体证明过程见文献[22]。
当电流流过导体的方向为z方向时，此时电流密度只分布在xy平面内，即
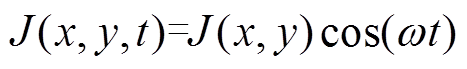（8）
式中，J为电流密度；w 为电流波形的角频率。此时导体单位长度的功率Pu分布表示为
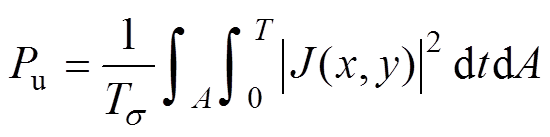（9）
式中，A为导体截面积；T为电流波形的周期；s 为绕组材料的电导率。当激励波形为正弦波时，Pu可以简化为
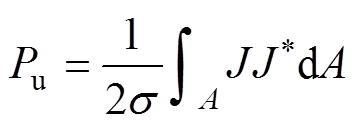（10）
趋肤效应和邻近效应的电流密度分别用Js和Jp表示，则式（10）可以转化为
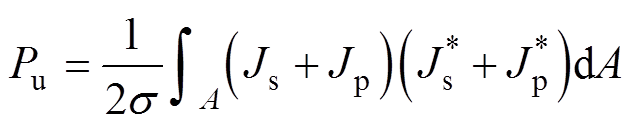（11）
只要导体有一个对称轴，施加的磁场是均匀且平行于对称轴，那么感应电流分布Jp就呈对称性。则相对于同一对称轴的趋肤效应电流分布是一个偶函数，在这些条件下式（11）可以表示为
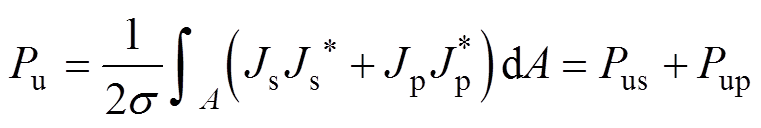（12）
式中，Pus为趋肤效应损耗；Pup为邻近效应损耗。
利用二者的正交性，对利兹线绕组的损耗进行叠加，得到最终圆形利兹线绕组的总损耗计算模型为
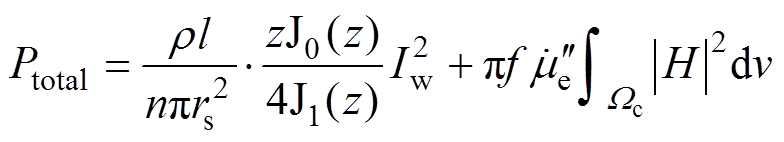（13）
式中，第一部分表示为由趋肤效应引起的损耗，可以直接进行解析计算，通过公式可以看出趋肤效应损耗不受绕组填充系数的影响，只和导体自身的材料特性以及频率有关。第二部分表示为由邻近效应引起的损耗，其中绕组区域的磁场积分可以利用静磁场有限元进行数值计算。利兹线绕组的交流电阻Rac=P/I2，就可以通过损耗模型计算得出，最终将计算过程编写成Matlab程序实现。
为了探究所提出模型的准确性，本文利用单股直径为0.1 mm，股数为60和100的两种型号的利兹线分别制作空芯绕组进行实验验证。实验采用KEYSIGHT E4990A精密阻抗分析仪测量绕组的交流电阻[23-24]，该仪器凭借自动平衡电桥技术能够实现的测试频率范围为20 Hz～10 MHz，精度能够达到0.08%，适合对低损耗元器件进行精确分析。测试绕组的交流电阻随频率变化结果如图7中示波器显示所示，利兹线绕组的几何参数见表1。
图7 利兹线空芯绕组实验
Fig.7 Litz-wire air core winding experimental diagram
表1 利兹线绕组几何参数
Tab.1 Geometric parameters of Litz-wire winding （单位: mm）
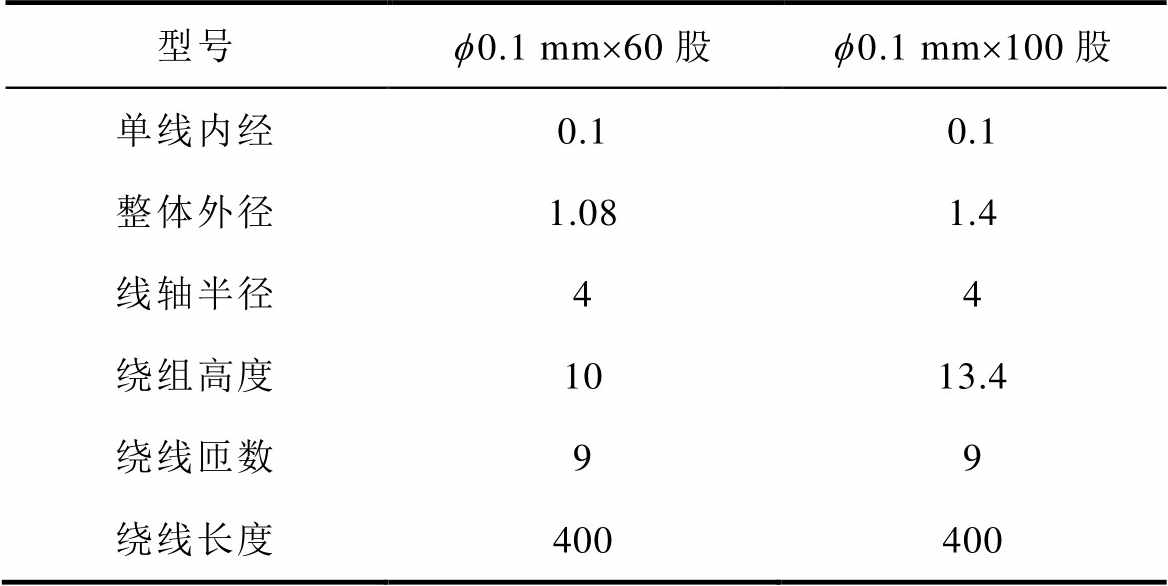
型号f0.1 mm´60股f0.1 mm´100股 单线内经0.10.1 整体外径1.081.4 线轴半径44 绕组高度1013.4 绕线匝数99 绕线长度400400
将引入几何因数后的圆形利兹线绕组的交流电阻的计算值与测量值在频率20 Hz～1 MHz的宽频范围内进行对比分析如图8所示，横坐标采用频率的对数坐标，纵坐标为测试的交流电阻。将频率分为低、中、高三个频段，从图8可见：在低频段 （≤100 kHz）交流电阻近似等于直流电阻，此时考虑涡流效应产生的影响很小可以近似忽略，在中频段（100～500 kHz）涡流效应的影响开始增加，对应交流电阻开始快速升高，主要是由于频率升高趋肤深度减小，使得绕组的趋肤效应损耗开始增加，多股导线并绕的结构能够降低趋肤效应的影响，使得交流电阻上升速度比高频段缓慢，此时导体间的邻近效应损耗产生的影响较小，可以忽略。在高频段（≥500 kHz），绕组间的临近效应起主导作用，表现为交流电阻继续迅速上升，上升幅度也比中频段大。
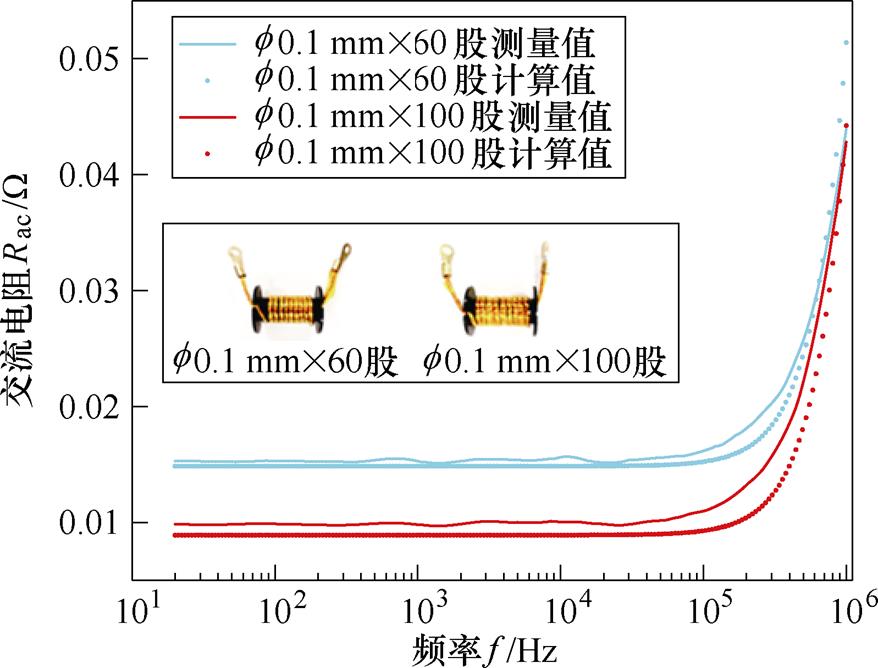
图8 利兹线绕组损耗的测量值与计算值
Fig.8 Measured and calculated values for Litz-wire winding losses
本文中实验结果仍存在一定误差，其来源可能包含以下部分：
（1）实验仪器的探头在扫频过程中会产生波动，以及模型制作过程中焊锡和端子的影响，会使得实验测量结果存在部分偏差。
（2）由于利兹线的扭转结构，使得股线的长度略大于利兹线的长度，导致测量的直流电阻值比理论计算值略大。
Tourkhani通过推导高频变压器磁心窗口内利兹线绕组的磁场表达式，利用电磁场能量积分法推导出圆形利兹线绕组损耗的解析计算模型为
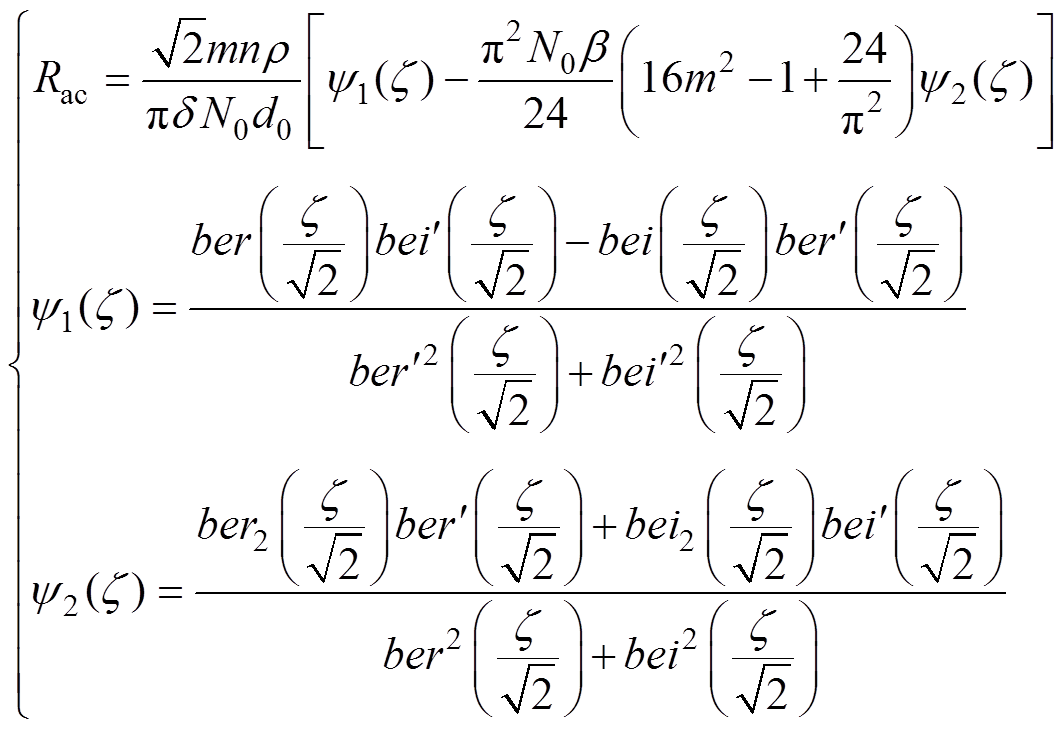（14）
式中，m为绕组层数；n为一层中绕组匝数；r 为绕组的电阻率；N0为单根利兹线内细导线的股数；d0为单根细导线的直径；z=d0/d；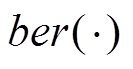
、
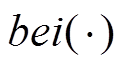分别为一阶贝赛尔函数的实部和虚部；
、
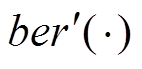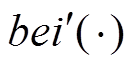为贝赛尔函数的实部和虚部的一阶导数；
、
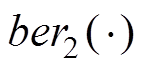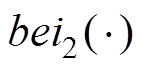分别为二阶贝赛尔函数的实部和虚部。
本文所提出模型的计算值和实验值与Tourkhani解析公式得到的交流电阻值进行对比如图9所示。由图9发现在低频下两种方法的计算精度都很高，在中高频范围内本文所提出的方法除了个别频率点误差较大外，大部分误差能够控制在20%以内，而Tourkhani解析公式的计算结果随着频率的不断升高，相对误差越来越大，高频下的相对误差更是超过100%。相较之下本文提出的基于等效复数磁导率的方法能够更准确地表征高频邻近效应损耗，使得模型的应用频率范围更广。
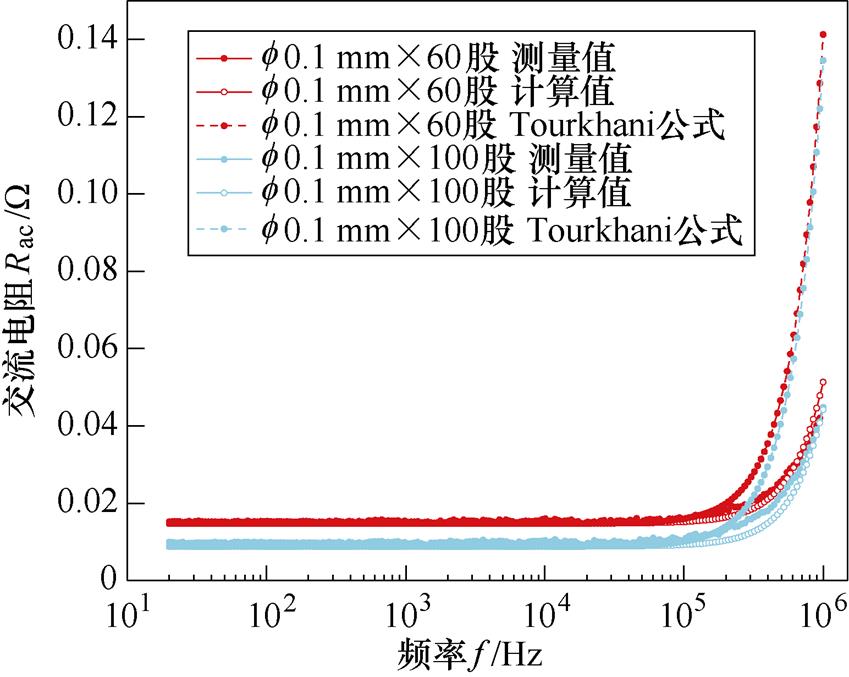
图9 两种求解方法的计算值与测量值对比
Fig.9 Comparison of calculated and measured values for the two calculation methods
1）通过分析利兹线损耗机理，考虑利兹线截面形状对等效区域材料特性的影响，实现了圆形利兹线绕组等效复数磁导率的明确解析描述，避免了对基本单元进行预处理获得等效区域的材料特性，简化了计算过程，加快了复数磁导率的计算速度。
2）利用均匀化有限元方法对利兹线绕组进行整体建模，同时基于二维静磁场分布并结合复数磁导率模型对三维结构利兹线绕组进行涡流分析，在保证计算精度的同时提高了计算速度。
3）针对高、中、低三个工作频段，分别与经典解析（Tourkhani方法）计算结果和实验结果进行对比分析，验证了本文利兹线绕组损耗计算模型均能够准确地表征趋肤效应及邻近效应，实现了宽频条件下损耗的准确预测。
参考文献
[1] Mogorovic M, Dujic D. 100 kW, 10 kHz medium- frequency transformer design optimization and experimental verification[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1696-1708.
[2] She Xu, Huang A Q, Burgos R. Review of solid-state transformer technologies and their application in power distribution systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2013, 1(3): 186-198.
[3] 赵义焜, 张国强, 韩冬, 等. 基于材料绝缘寿命的高频变压器绕组绝缘试验电压确定方法[J]. 电工技术学报, 2020, 35(13): 2932-2939.
Zhao Yikun, Zhang Guoqiang, Han Dong, et al. An insulation test method based on the dielectric insulation life for windings in high-frequency trans- former[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2932-2939.
[4] 孙凯, 卢世蕾, 易哲嫄, 等. 面向电力电子变压器应用的大容量高频变压器技术综述[J]. 中国电机工程学报, 2021, 41(24): 8531-8545.
Sun Kai, Lu Shilei, Yi Zheyuan, et al. A review of high-power high-frequency transformer technology for power electronic transformer applications[J]. Proceedings of the CSEE, 2021, 41(24): 8531-8545.
[5] 张珂, 曹小鹏, 乔光尧, 等. 高频变压器绕组损耗解析计算分析[J]. 中国电机工程学报, 2019, 39(18): 5536-5546.
Zhang Ke, Cao Xiaopeng, Qiao Guangyao, et al. Analysis of winding loss calculation methods for high frequency transformers[J]. Proceedings of the CSEE, 2019, 39(18): 5536-5546.
[6] 王迎迎, 程红. 应用于功率变换器的多绕组高频变压器模型[J]. 电工技术学报, 2021, 36(19): 4140- 4147.
Wang Yingying, Cheng Hong. Dual multi-winding high-frequency transformer equivalent circuit for power converter applications[J]. Transactions of ChinaElectrotechnical Society, 2021, 36(19): 4140-4147.
[7] 胡义, 周晓晟. 利兹绕组线研制及应用探索研究[J]. 上海大中型电机, 2021(3): 27-31.
Hu Yi, Zhou Xiaosheng. Research on the application development of Litz winding wire[J]. Shanghai Dazhongxing Dianji, 2021(3): 27-31.
[8] Zhang R Y, White J K, Kassakian J G. Fast simulation of complicated 3-D structures above lossy magnetic media[J]. IEEE Transactions on Magnetics, 2014, 50(10): 1-16.
[9] Dowell P L. Effects of eddy currents in transformer windings[J]. Proceedings of the Institution of Electrical Engineers, 1966, 113(8): 1387.
[10] Tourkhani F, Viarouge P. Accurate analytical model of winding losses in round Litz wire windings[J]. IEEE Transactions on Magnetics, 2001, 37(1): 538- 543.
[11] Stoll R L. The analysis of eddy current[M]. Oxford: Clarendon Press, 1974.
[12] Moreau O, Popiel L, Pages J L. Proximity losses computation with a 2D complex permeability model- ling[J]. IEEE Transactions on Magnetics, 1998, 34(5): 3616-3619.
[13] Podoltsev A D, Kucheryavaya I N, Lebedev B B. Analysis of effective resistance and eddy-current losses in multiturn winding of high-frequency mag- netic components[J]. IEEE Transactions on Magnetics, 2003, 39(1): 539-548.
[14] Gyselinck J, Dular P. Frequency-domain homo- genization of bundles of wires in 2-D magneto- dynamic FE calculations[J]. IEEE Transactions on Magnetics, 2005, 41(5): 1416-1419.
[15] Kharezy M, Eslamian M, Thiringer T. Estimation of the winding losses of medium frequency trans- formers with Litz wire using an equivalent per- meability and conductivity method[C]//2020 22nd European Conference on Power Electronics and Applications (EPE'20 ECCE Europe), Lyon, France, 2020: 1- 7.
[16] Nan Xi, Sullivan C R. An equivalent complex permeability model for Litz-wire windings[J]. IEEE Transactions on Industry Applications, 2009, 45(2): 854-860.
[17] Zhang Ke, Chen Wu, Cao Xiaopeng, et al. Accurate calculation and sensitivity analysis of leakage inductance of high-frequency transformer with Litz wire winding[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 3951-3962.
[18] 陈彬, 李琳, 赵志斌, 等. 电感集成式大容量高频变压器精细化设计方法[J]. 中国电机工程学报, 2018, 38(5): 1356-1368.
Chen Bin, Li Lin, Zhao Zhibin, et al. Design method of inductor-integrated high-power high-frequency transformers[J]. Proceedings of the CSEE, 2018, 38(5): 1356-1368.
[19] Sullivan C R, Zhang R Y. Analytical model for effects of twisting on Litz-wire losses[C]//2014 IEEE 15th Workshop on Control and Modeling for Power Electronics (COMPEL), Santander, Spain, 2014: 1-10.
[20] Igarashi H. Semi-analytical approach for finite- element analysis of multi-turn coil considering skin and proximity effects[J]. IEEE Transactions on Magnetics, 2017, 53(1): 1-7.
[21] Ollendorff F. Magnetostatik der massekerne[J]. Archiv Für Elektrotechnik, 1931, 25(6): 436-447.
[22] Ferreira J A. Improved analytical modeling of conductive losses in magnetic components[J]. IEEE Transactions on Power Electronics, 1994, 9(1): 127- 131.
[23] 叶建盈, 黄文彬, 李睿, 等. 基于低测试阻抗角的高频电感绕组损耗测试与分析[J]. 磁性材料及器件, 2022, 53(2): 57-61.
Ye Jianying, Huang Wenbin, Li Rui, et al. The test and analysis of winding losses of high-frequency inductor based on low test impedance angle[J]. Journal of Magnetic Materials and Devices, 2022, 53(2): 57-61.
[24] 汪涛, 骆仁松, 文继峰, 等. 基于辅助绕组的高频变压器绕组损耗测量方法[J]. 电工技术学报, 2022, 37(10): 2622-2630, 2655.
Wang Tao, Luo Rensong, Wen Jifeng, et al. A measurement method of winding loss for high- frequency transformer based on auxiliary winding[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2622-2630, 2655.
Calculation Model of Winding Loss of Litz-Wire Based on Equivalent Complex Permeability
Abstract Asan important component of the overall loss of high-frequency transformers, winding loss is a key parameter affecting the volume, efficiency, and temperature rise of magnetic components. Litz-wire is widely used in high-frequency transformer winding because of its ability to achieve conductor in-turn transposition and reduce losses due to the skin effect and proximity effect. The homogenization technique, using a region with the equivalent complex material properties instead of the winding region, can realize the characterization of the eddy current effect by the two-dimensional magnetic field and reduce the computational cost of refinement modeling. However, the material properties of the equivalent region are obtained using numerical methods, making the calculation complex. Therefore, this paper establishes a loss calculation model of Leeds wire winding based on equivalent complex permeability to calculate winding losses accurately and efficiently.
Firstly, the winding loss calculation model is established based on the orthogonality of the skin and proximity effects. The equivalent complex permeability of the winding is calculated using the factory data of the Litz-wire. Then, the overall modeling of Litz-wire winding is carried out in the simulation software, and the external magnetic field value of the winding is extracted for the proximity effect loss calculation. Finally, the skin effect loss is calculated using the analytical formula. The actual winding model of AC resistance in the wide frequency (20 Hz～1 MHz) range shows that AC resistance in the low-frequency band (20 Hz～100 kHz)is approximately equal to DC resistance. At this time, the calculation error can be almost neglected, and the calculation accuracy mainly depends on the calculated value of the DC resistance. The skin effect in the medium-frequency band (100 kHz～500 kHz) becomes gradually obvious, and AC resistance rises rapidly. The highest error is around 300 kHz, and the maximum is 10.07%. In the high-frequency band (500 kHz～1 MHz), the proximity effect between the winding makes the AC resistance rise rapidly. The maximum error in the high-frequency band is 15.22%, and the error in the rest of the frequency is about 10%.
The following conclusions can be obtained: (1) By describing the equivalent complex permeability of the circular Litz-wire winding analytically, the preprocessing of the basic unit is avoided, and the calculation process is simplified. (2) The homogenized finite element method is used for overall modeling. The eddy current is analyzed in the three-dimensional structure of the Litz-wire winding based on the two-dimensional static magnetic field distribution and combined with the complex permeability model. The calculation accuracy and speed are improved. (3) Considering the influence of the winding section shape on the loss, the skin effect and proximity effect are characterized, increasing the applicability of the model at high frequency and realizing the accurate loss prediction at wide frequency.
keywords：Litz-wire, winding loss, equivalent complex permeability, skin effect, proximity effect
中图分类号：TM433
DOI: 10.19595/j.cnki.1000-6753.tces.222170
国家自然科学基金项目（51677052, 52077053）和河北省人才工程培养项目（A201902009）资助。
收稿日期 2022-11-17
改稿日期 2023-01-07
赵志刚 男，1981年生，教授，博士生导师，研究方向为电工磁材料磁性能模拟与工程电磁场数值仿真及应用。E-mail: zhaozhigang@hebut.edu.cn
王丽美 女，1997年生，硕士研究生，研究方向为电工磁材料磁性能模拟与工程电磁场数值仿真及应用。E-mail: 15028936358@qq.com（通信作者）
（编辑 郭丽军）