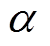 和容忍度
和容忍度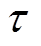 。其中,K对算法的分解精度影响最大,当K值过小时对原始信号的故障特征提取有限,当K值过大时则会导致过度分解从而增大算法计算量,因此本文提出基于样本熵最小值原则的K值选定法。
。其中,K对算法的分解精度影响最大,当K值过小时对原始信号的故障特征提取有限,当K值过大时则会导致过度分解从而增大算法计算量,因此本文提出基于样本熵最小值原则的K值选定法。摘要 自动转换开关(ATSE)是保证系统连续供电的设备,对其进行健康监测和故障诊断对系统的稳定运行具有重要意义。为了实现对ATSE的非侵入式故障识别,该文提出一种基于电流信号变分模态分解(VMD)的特征提取和改进灰狼算法(IGWO)优化深度置信网络(DBN)相结合的故障诊断方法。该方法首先利用样本熵确定VMD分解次数并对故障电流进行分解;其次对分解后得到的本征模态函数进行小波包能量的提取,并利用IGWO对DBN网络结构参数进行优化;最后通过DBN将电流能量特征与ATSE的故障类型建立起映射关系从而完成最终的故障识别。所提IGWO采用了分段调节与非线性递减的衰减因子相结合的策略,以平衡算法全局搜索和局部搜索能力;并采用莱维飞行更新探狼的移动位置,来避免算法陷入早熟收敛。实验结果表明,该算法不仅能显著提高前期对参数寻优的训练速度,后续泛化实验的故障分类准确率也有98.78%的良好表现。
关键词:优化灰狼算法 深度置信网络 自动转换开关 故障识别
自动转换开关(Automatic Transfer Switching Equipment, ATSE)是厂房、医院、消防和军用设施等重要公共场合在突发失电情况下,切换主备两路电源保证系统连续供电的设备,对ATSE状态进行健康监测和故障诊断对系统的稳定连续运行具有重要意义。自动转化开关由控制器和开关本体两部分组成,当控制器检测到运行电路发生故障时,会给本体部分发送电源切换指令,从而由本体部分的驱动机构带动操作结构完成切换动作。本体部分作为转换开关的核心是研究其转换可靠性的重点分析对象。目前,针对开关电器的机械动作特性的非侵入式故障识别主要通过分析振动信号与分合闸线圈电流波形来实现[1-2]。电流信号由于具有信噪比高与易于检测等优点,能够直接反映开关电器的机械特性,从而成为了故障分析中的重要参数。
传统的自动转换开关通常是以断路器作为电流分断单元,并配备电流脱扣器,具有一定的保护能力,转换时间长达1 000~2 500 ms,且可靠性较低,但价格低廉。新式的ATSE具有高度一体化的特点,其电磁操作机构与机械结构联系紧密,不需要额外的控制器。在收到转换信号后可直接通过继电器接通电路给电磁机构供电,并由机械结构完成供电线路的切换,相较前者,转换时间为100~200 ms,且可靠性高。但由于ATSE机构高度一体化、转换性能要求高等特点使得其故障成因较断路器式转换开关更为复杂。利用采集电磁线圈的电流信号进行分析时发现,当线路发生如任意相缺相、频率偏差、谐波等故障时,故障线路的电流会发生间断或受到脉冲和噪声的干扰。以上干扰会影响到电磁线圈电流信号的收集。在进行模态分解时导致出现特征频率与电流基频发生模态混叠的现象,不仅给故障电流的特征提取带来阻力,还使得依靠专家经验或确定故障特征变得十分困难。
部分学者利用集合经验模态分解对电流信号进行特征提取,可以有效避免模态混叠现象并提高计算效率,但其分解效果易受到算法自身所添加噪声的影响[3-5]。为了能够实现对提取到的故障特征进行准确的分类,决定采用改进的变分模态分解(Variational Mode Decomposition, VMD)的方法进行电流信号的分解,并以分解后各模态分量的小波包能量(Wavelet Packet Energy, WPE)作为最终的特征向量,从而满足分类模型对ATSE特征信号准确性的高要求[6-12]。
电流信号中所提取到的故障特征可以依靠人工智能算法来完成分类识别。浅层模型在故障识别的过程中仍存在着局限性,无法准确表征原始信号与电器的故障种类之间复杂的映射关系[13-16]。深度置信网络(Deep Belief Network, DBN)由于具有广泛的适应性和强大映射的能力得到了学者的关注。DBN在进行故障识别前,需对网络结构参数进行提前设置。不同的参数组合对模型的收敛速度与最优解收敛过程有着重要的影响[17]。文献[18]提出了粒子群算法对DBN进行参数优化,能够准确快速地对原始信号中的低维故障特征完成提取与识别。但将该方法应用于处理ATSE的电流信号时泛化能力较差,面对高维数据时识别准确性无法得到保证。文献[19]利用灰狼算法对DBN进行了参数的寻优与网络结构的优化,从而完成了对多通道信号的高精度分类。与其他方法相比,灰狼算法优化的DBN模型对故障特征的学习与识别效果更好,但在优化过程中,却仍存在早熟收敛与限于局部最优的问题[20-24]。
针对ATSE的高维故障特征难以分类的问题,本文首先提出了一种基于改进灰狼算法(Improved Grey Wolf Optimizer, IGWO)优化的DBN模型来对ATSE的电流波形进行故障分析。在进行故障识别前,为了避免电流分解过程中模态混叠现象,选择通过变分模态分解与小波包能量相结合的方法完成对故障电流波形的模态分解以及故障特征的提取。其次,将分段调节结合非线性递减的衰减因子和莱维飞行理论引入进灰狼算法中,以解决算法陷入局部最优和早熟收敛的问题。利用优化后的灰狼算法对DBN进行网络参数值的最优值训练,将训练后的最优值重新对DBN进行赋值,从而得到最终的故障识别模型。最后,通过模拟故障实验得到ATSE的故障电流数据,将其与其他的故障识别模型进行对照实验,以验证本文模型的准确性。
为了提取ATSE故障电流波形中所包含的机械结构的运动信息,本文选用VMD对ATSE复杂的电流波形信号进行分解,对分解后的各有限带宽的本征模态函数(Band-limited Intrinsic Mode Function, BIMF)进行小波包能量提取,从而实现在多个频率尺度下对电流故障信号进行分析。
VMD的分解过程是一种将信号分解转变为非递归变分模式的求解过程,通过对变分问题进行最佳中心频率和有效带宽迭代搜索来实现信号的分解。VMD在处理复杂数据时相较类EMD算法有着更高的分解精度且可以避免模态混叠等问题,但需要提前设置算法的BIMF个数K、惩罚因子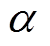 和容忍度
和容忍度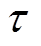 。其中,K对算法的分解精度影响最大,当K值过小时对原始信号的故障特征提取有限,当K值过大时则会导致过度分解从而增大算法计算量,因此本文提出基于样本熵最小值原则的K值选定法。
。其中,K对算法的分解精度影响最大,当K值过小时对原始信号的故障特征提取有限,当K值过大时则会导致过度分解从而增大算法计算量,因此本文提出基于样本熵最小值原则的K值选定法。
样本熵是定量评估长度时间序列波动程度的有用统计量,样本熵的值与数据序列的复杂性呈正相关,与数据长度无关。故障电流信号经VMD分解后的各模态分量,其自我相似性与包含的故障特征信息呈正比。因此,模态分量包含越多的故障信息,其自我相似性越高,所对应的样本熵值也就越小。通过计算不同分解次数下各模态分量所对应的样本熵值,并选取样本熵值最小的模态分量作为趋势项,比较不同分解次数下各趋势项的样本熵值,最终将VMD的分解次数确定为样本熵值最小的趋势项所对应的K值。
不同的频段下,故障信号中所蕴含的能量特征参数存在差异,通过小波包变换可以完成对故障信号各频段的划分,从而完成对各频段中能量特征参数的提取。小波包变换作为小波变换的优化,不仅能在低频下完成对信号的分解,也弥补了小波分解在高频时的不足,使故障特征在各个频段内更加细致。利用小波包分解对各模态分量进行处理后,将各节点的WPE占比作为故障特征向量,各频带对应的WPE集合 表达式为
表达式为
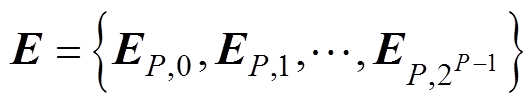 (1)
(1)
式中,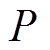 为小波包分解的分解层数;
为小波包分解的分解层数;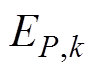 (
(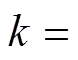
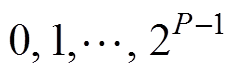 )为各节点对应的小波包能量值。
)为各节点对应的小波包能量值。
利用小波包变换对分解后ATSE线圈电流的各BIMF分量求取WPE,然后通过主成分分析法选取贡献度前三的频带能量百分比作为对应BIMF分量的特征向量,从而完成故障特征的提取。
出于对转换速度的要求,目前自动转换开关通常为电磁铁驱动,本文所研究对象为ATSE-100/ 63A/4P式自动转换开关,对其电磁机构线圈上的电流进行分析。电磁系统由可以等效为电阻和电感的线圈组成,等效电路如图1所示,交流电源用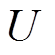 表示,控制继电器等效为开关S,VD1~VD4为整流桥二极管。UR为线圈等效电阻
表示,控制继电器等效为开关S,VD1~VD4为整流桥二极管。UR为线圈等效电阻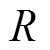 上的电压,UL为等效电感
上的电压,UL为等效电感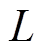 上的电压。
上的电压。
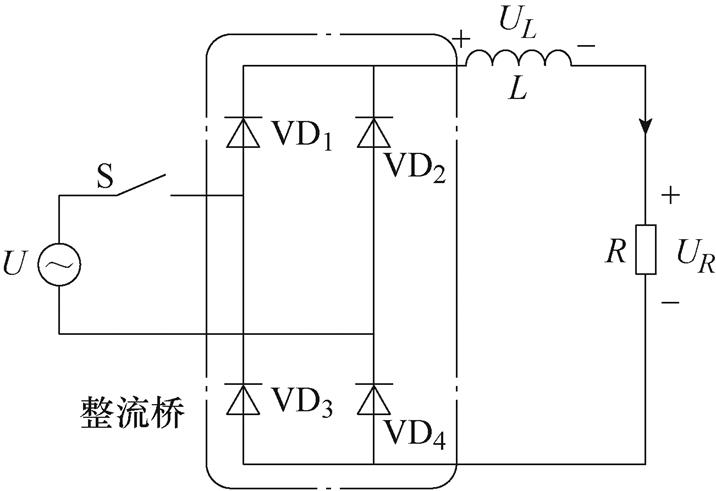
图1 电磁铁线圈等效电路
Fig.1 Equivalent circuit diagram of an electromagnet coil
当自动转换开关检测到线路出现故障后,会将转换信号发送给控制器,控制器通过继电器将电源与电磁铁线圈接通,交流电源通过整流桥完成整流后给线圈供电,接着由电磁系统和机械结构配合动作完成电源的切换。
电磁线圈的动态电磁吸力是电流的函数,而线圈的电流与铁心运动的行程和速度均是与时间有关的函数。即

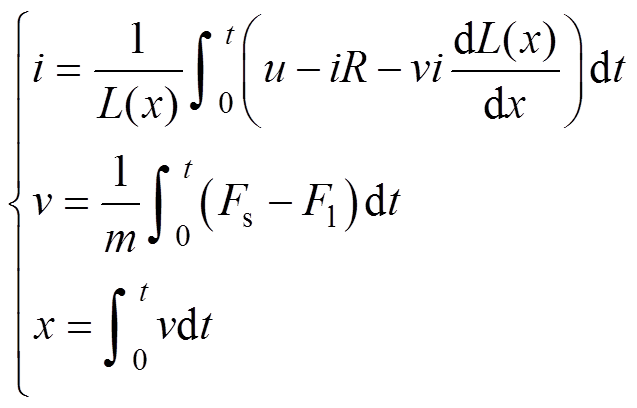 (2)
(2)
式中,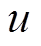 和
和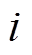 分别为电磁线圈上的电压和电流;x和v分别为铁心移动的行程与速度;
分别为电磁线圈上的电压和电流;x和v分别为铁心移动的行程与速度;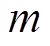 为动铁心的质量;
为动铁心的质量;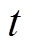 为铁心动作时间;L(x)为受到铁心位移影响的线圈电感;Fs、Fl分别为动铁心的电磁力与机构的反作用力。由上述方程组可知,电磁机构的电流不仅与时间有关,还取决于动铁心等相关机械结构的物理特性。故线圈电流中包含了整个电磁系统动态特性的丰富信息。
为铁心动作时间;L(x)为受到铁心位移影响的线圈电感;Fs、Fl分别为动铁心的电磁力与机构的反作用力。由上述方程组可知,电磁机构的电流不仅与时间有关,还取决于动铁心等相关机械结构的物理特性。故线圈电流中包含了整个电磁系统动态特性的丰富信息。
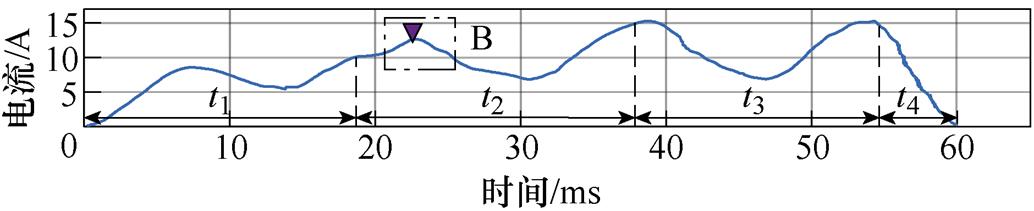
为了体现线圈电流的一般特性,本文取四种典型故障下的线圈电流与正常工作状态下的电流波形比较,其四种故障电流波形如图2所示。并对图中的电流波形与自动转换开关电磁机构的运动过程结合分析,将转换过程分为4个阶段。不同阶段下的电流波形蕴含着各种故障的特征信息,具体如下:

(a)正常动作波形

(b)线圈短路
(c)铁心卡涩

(d)行程不足

(e)机械结构卡涩
图2 四种故障电流波形
Fig.2 Waveforms of four fault currents
第一阶段(t1):该阶段动铁心尚未移动,此时线圈等效电感为固定值,线圈电流波形为类正弦函数。当电流幅值开始增长且大于第一个波峰的电流值时,电磁吸力大于机构反力,铁心开始移动,将此时刻作为t1阶段结束的标志。若线圈发生短路故障,即等效为线圈匝数降低,其电磁吸力在各时刻均小于正常情况,使得故障情况下铁心起动时刻滞后。由于铁心动作后其电感值会随移动距离发生变化,因此与正常情况下的电流对比,短路故障情况下的电流由于铁心的延时动作使得在t1时刻后产生了图2b中标志A处所示的幅值的减小和波形滞后。
第二阶段(t2):在此阶段,随着铁心的移动,内部会逐渐达到磁饱和。此时与正弦磁通同相位的励磁电流,其幅值会随着铁心的移动持续增加并且波形发生畸变。若铁心发生卡涩故障,铁心在此阶段内的移动过程会受到影响。相比正常情况,如图2c中标志B处三角形所示,此阶段内畸变波形波峰的出现时刻会略有延时。
第三阶段(t3):当铁心运动到行程末端时,线圈电感与电流幅值均为定值。若存在衔铁行程不足的故障,动铁心会提前到达行程末端,反映在电流波形上,会出现如图2d标志C处三角形所示,其幅值变为定值的时刻会提前的情况。
第四阶段(t4):此阶段前铁心已经运动到位,将电流波形的最后一个波峰到电流归零时刻记作第四阶段。机械结构在弹簧的作用下完成电源电路的切换,此时线圈电流会迅速减小直到消失。若机械结构发生卡涩,切换时间会稍有延长,供电电源相较正常情况会延时断开,从而使得电流波形降至零的时间也会有所增加,如图2e中标志D处三角形所示,相比正常情况,在采样末期,线圈内仍存在残余电流。
深度学习可以通过数据的逐层非线性映射表达找到数据的本质特征,DBN作为一种典型的深度学习方法具有良好的特征提取和分类能力。选择DBN算法对ATSE进行故障识别时,其神经元个数、隐藏层数量和学习速率等网络结构参数对识别结果的准确性有巨大影响。而通过经验法或凑试法来确定参数既费时,又难以保障其准确性。因此,本文提出了一种基于IGWO优化的DBN中的关键网络结构参数的训练模型,通过IGWO迭代学习得到DBN网络结构参数的最优值并对其重新赋值,从而提高原模型的分类精度。
灰狼优化算法(Grey Wolf Optimizer, GWO)是通过模仿灰狼这一物种的领导和狩猎机制而提出的智能算法,根据其社会等级将捕食任务分配给不同的灰狼群体,从而完成包围、狩猎和攻击等捕食行为,以实现算法的全局优化。与粒子群优化、遗传算法、网格搜索等算法相比,灰狼算法具有结构简单、操作简单、优化时间短等优点。
利用传统GWO对DBN的网络参数进行寻优时发现,该算法在迭代过程中存在收敛速度慢及局部最优停滞的现象。为了弥补上述缺陷,本文对该算法进行如下优化:通过改进非线性收敛因子,平衡灰狼算法的全局寻优能力和局部寻优能力;同时通过动态权重策略,动态调整不同等级的头狼对狼群的影响权重,以提高算法的收敛速度;在狼群中随机选取普通灰狼作为探狼并利用莱维飞行策略来更新其搜索路径以避免算法陷入早熟收敛。
2.1.1 改进的非线性收敛因子
以灰狼算法为代表的种群算法,其寻优过程可以分为前期探索和后期开发这两个基本阶段。在灰狼算法中,狼群采取搜寻猎物或捕捉猎物的行动由控制参数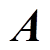 的值决定。其具体表达式为
的值决定。其具体表达式为
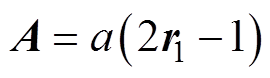 (3)
(3)
式中,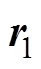 为[0, 1]之间的随机向量;a为衰减因子,随着迭代次数的增加从2线性减小到0。而随着衰减因子a的线性减少,控制系数
为[0, 1]之间的随机向量;a为衰减因子,随着迭代次数的增加从2线性减小到0。而随着衰减因子a的线性减少,控制系数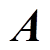 也会在[-a, a]之间变化。
也会在[-a, a]之间变化。
但是在应用GWO优化实际问题时发现,线性变化的衰减因子在搜索过程中并不能有效地平衡全局寻优和局部寻优,其固定的比例很难处理实际问题中的复杂情况。因次,本文对衰减因子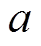 提出了一种分段可调节结合非线性控制的优化策略,有
提出了一种分段可调节结合非线性控制的优化策略,有
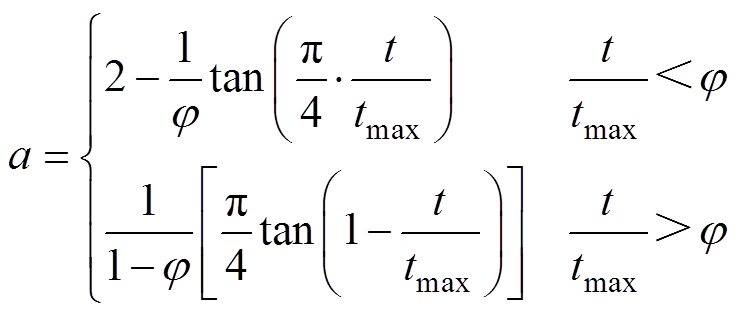 (4)
(4)
式中,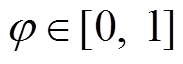 为全局搜索阶段在所有迭代次数中所占比例;
为全局搜索阶段在所有迭代次数中所占比例;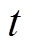 为当前迭代次数;tmax为最大迭代次数。采用了正切函数对衰减因子
为当前迭代次数;tmax为最大迭代次数。采用了正切函数对衰减因子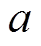 取值方法进行改进,使其满足递减的非线性。当
取值方法进行改进,使其满足递减的非线性。当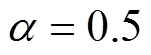 时,衰减因子
时,衰减因子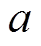 的取值与传统GWO算法一致。
的取值与传统GWO算法一致。
2.1.2 动态权重策略
狼群在狩猎阶段进行搜寻猎物时,普通灰狼的移动方向取决于头狼与次头狼的位置,描述其位置更新的公式为
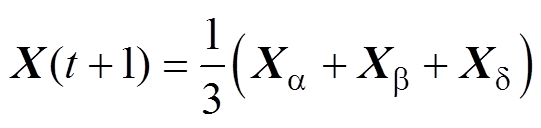 (5)
(5)
式中,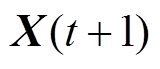 为普通灰狼下次移动的位置;
为普通灰狼下次移动的位置;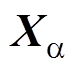 、
、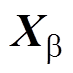 、
、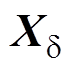 分别为头狼、次头狼等高等级灰狼a、b、d 当前的位置。在传统的GWO中,头狼与其他高等级狼在引导狼群移动时对狼群的影响力相同,并不受其级别影响。但等级越高的头狼所对应的适应度也越高,故增加高等级的头狼的权重以突出其对狼群的主导地位,能够增强算法全局搜索的稳定性,并在后期显著增加算法的收敛速度。
分别为头狼、次头狼等高等级灰狼a、b、d 当前的位置。在传统的GWO中,头狼与其他高等级狼在引导狼群移动时对狼群的影响力相同,并不受其级别影响。但等级越高的头狼所对应的适应度也越高,故增加高等级的头狼的权重以突出其对狼群的主导地位,能够增强算法全局搜索的稳定性,并在后期显著增加算法的收敛速度。
基于此,本文提出了一种适应度与欧氏距离相结合的方法对不同等级头狼的权重进行动态调整,首先计算不同等级头狼的学习率,有
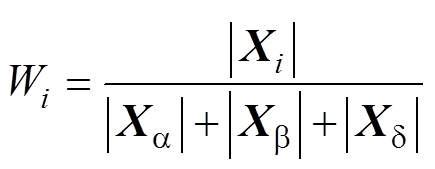 (6)
(6)
式中,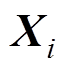 和
和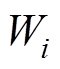 (
(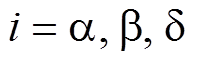 )分别为狼
)分别为狼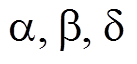 当前的位置以及狼群向狼
当前的位置以及狼群向狼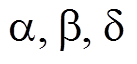 的学习率。结合学习率优化后狼群的移动方式为
的学习率。结合学习率优化后狼群的移动方式为
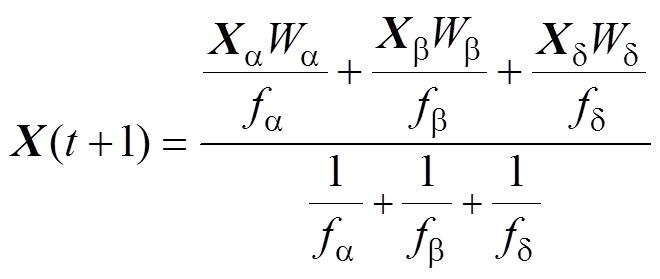 (7)
(7)
式中,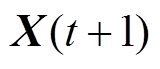 为狼群中普通灰狼下次移动的位置;
为狼群中普通灰狼下次移动的位置;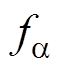 、
、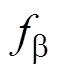 、
、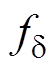 为狼a、b、d 当前的适应度值。
为狼a、b、d 当前的适应度值。
2.1.3 随机游动策略
经上述动态权重的调整改进后,使得高等级的头狼对整个狼群的移动方向有着决定性的影响。虽然这一改进会提高算法的收敛速度,但分析发现,普通灰狼的存在只会盲目地跟从高等级的头狼,而对附近的猎物气息漠不关心的现象。这就导致了算法后期,易产生早熟收敛的情况。
针对上述缺点,本文提出了随机选取探狼并对其位置更新方法与莱维飞行相结合的策略,莱维飞行属于一种随机游动策略,能够很好地解决早熟收敛问题。具体选择方式如下:在狼群中随机选取除各等级头狼以外的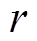 头普通灰狼作为探狼,
头普通灰狼作为探狼,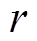 为
为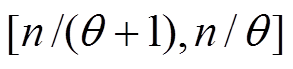 之间的随机整数,其中,
之间的随机整数,其中,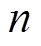 为灰狼个体总数,
为灰狼个体总数,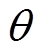 为探狼比例因子,
为探狼比例因子,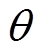 选取的值越小则探狼数越多,其全局搜索能力也越强,但收敛速度也会有所下降。对随机选择的探狼的位置更新方式在原有的基础上与莱维飞行结合,结合莱维飞行的位置更新公式为
选取的值越小则探狼数越多,其全局搜索能力也越强,但收敛速度也会有所下降。对随机选择的探狼的位置更新方式在原有的基础上与莱维飞行结合,结合莱维飞行的位置更新公式为
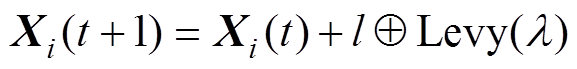 (8)
(8)
式中,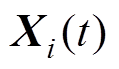 (
(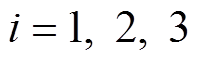 )分别为在第
)分别为在第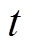 次迭代时狼
次迭代时狼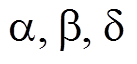 的位置;
的位置; 为点对点乘法;
为点对点乘法;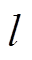 为移动位置的随机数;
为移动位置的随机数;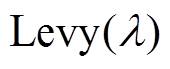 为随机搜索的路径。
为随机搜索的路径。
通过莱维飞行对灰狼的位置进行更新后,比较前后位置的适应度值,保留适应度值更高的位置。
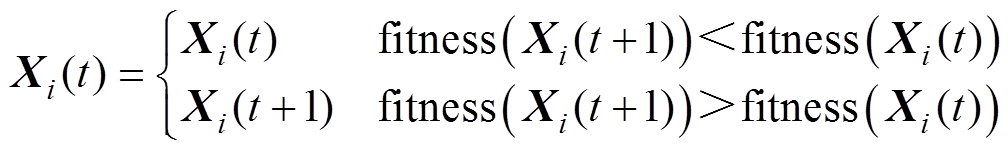 (9)
(9)
式中,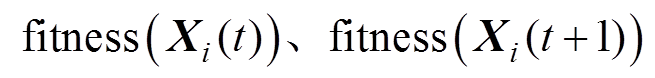 分别为当前位置灰狼的适应度值与位置更新后的适应度值。
分别为当前位置灰狼的适应度值与位置更新后的适应度值。
设置仿真步长为1 500步,对莱维飞行策略与传统灰狼寻优的策略进行仿真对比,参数寻优范围为[-100, 100],仿真结果如图3所示。
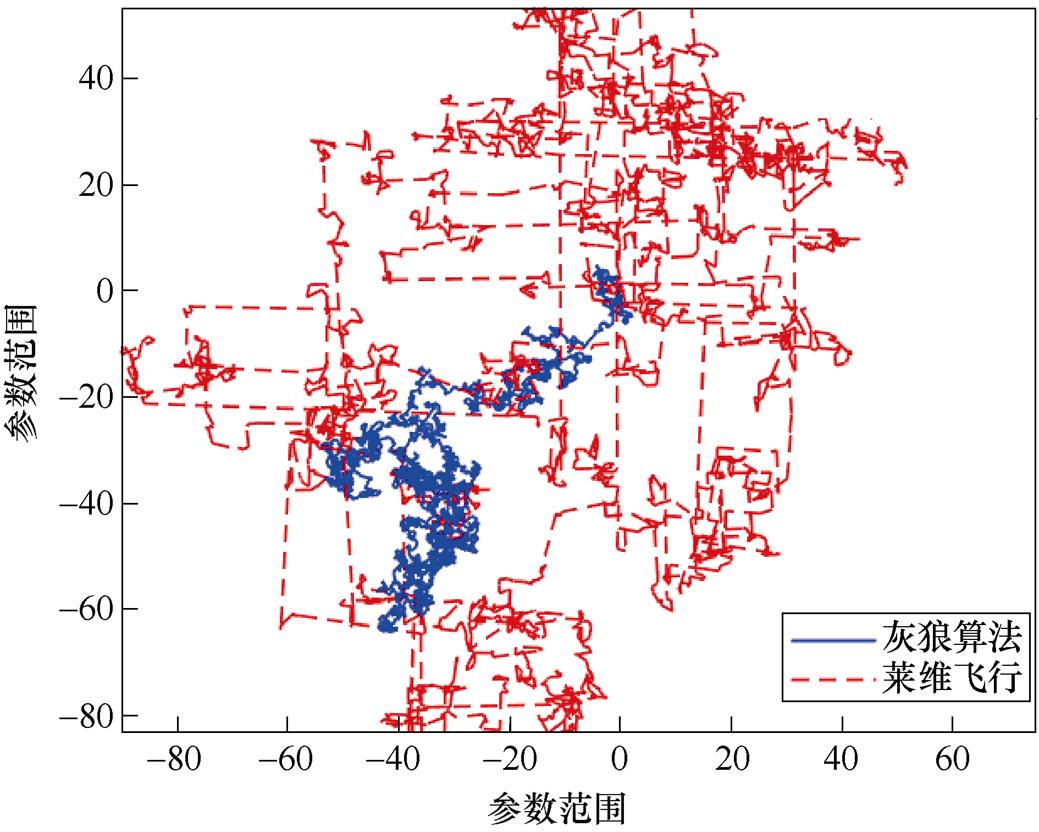
图3 莱维飞行与普通灰狼移动策略仿真
Fig.3 Levy flight and random walk strategy simulation
图3中,实线和曲线分别为灰狼算法和莱维飞行在给定范围内进行寻优时的搜索路径,可以清晰地看到,传统灰狼的搜索范围较为集中,搜寻时,探狼易受到头狼的影响陷入局部寻优。而莱维飞行由于其短距长距交替的游动方式,相较于改进前的算法其搜索范围更广,探狼的位置更新并不受头狼的影响,可以有效地避免算法陷入早熟收敛的问题,从而提高其全局寻优能力。
深度置信网络(DBN)是一个深度前馈神经网络。它由若干受限玻耳兹曼机器(Restricted Boltzmann Machines, RBM)和一个反向传播BP神经网络组成,其体系结构模型如图4所示。
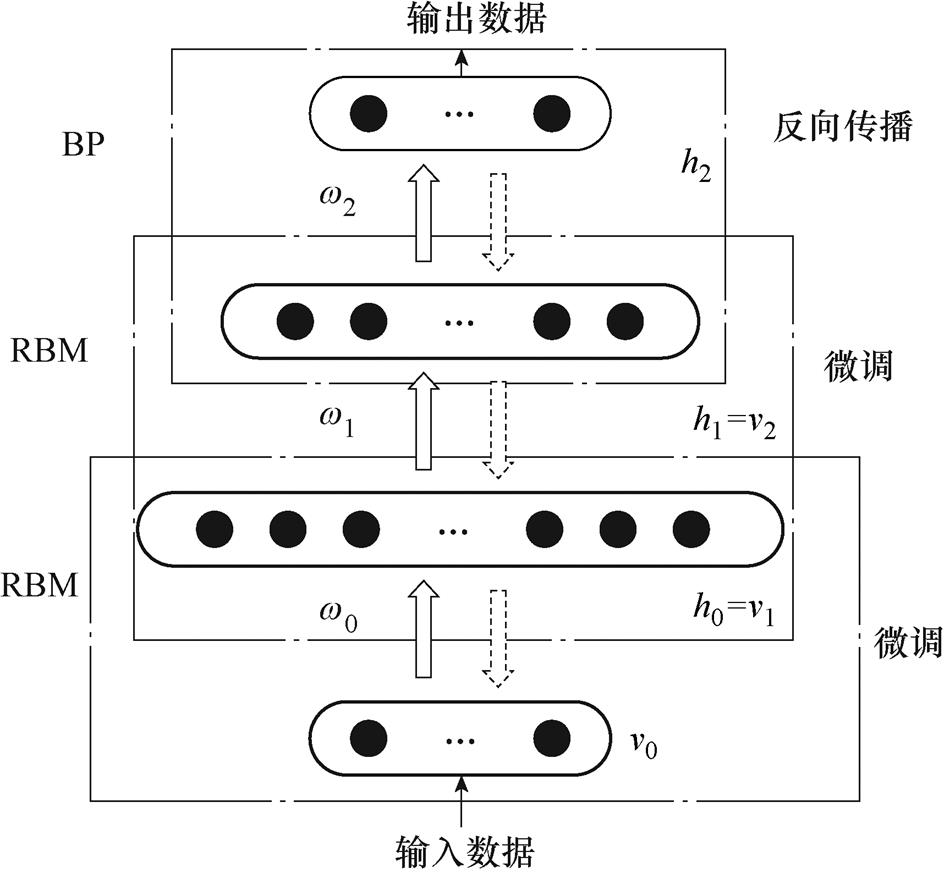
图4 DBN的体系结构模型
Fig.4 The architectural model of the DBN
DBN的训练过程分为预训练和反向微调两个阶段。在第一阶段中,数据输入到第一个视觉层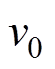 后映射到第一个隐含层
后映射到第一个隐含层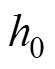 ,构成第一个RBM单元。之后隐藏层
,构成第一个RBM单元。之后隐藏层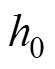 作为下一个RBM的视觉层
作为下一个RBM的视觉层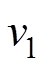 将数据传给第二个隐含层
将数据传给第二个隐含层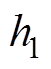 ,构成第二个RBM单元,以此类推,最终数据通过每个RBM完成无监督的逐层预训练。各层通过权重
,构成第二个RBM单元,以此类推,最终数据通过每个RBM完成无监督的逐层预训练。各层通过权重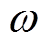 连接,DBN可以通过训练不同节点间的权值
连接,DBN可以通过训练不同节点间的权值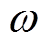 使得最终生成概率最大化,并且每层中的神经元彼此不连接。第二阶段是有监督的反向微调网络参数。这一阶段是通过采用梯度下降算法来对DBN模型进行训练,从而减小每层的预测误差,这一阶段的结束标志是迭代次数达到最大值或模型收敛精度达到提前设定好的阈值。
使得最终生成概率最大化,并且每层中的神经元彼此不连接。第二阶段是有监督的反向微调网络参数。这一阶段是通过采用梯度下降算法来对DBN模型进行训练,从而减小每层的预测误差,这一阶段的结束标志是迭代次数达到最大值或模型收敛精度达到提前设定好的阈值。
在RBM中,模型的无偏生成概率很难获得。为了解决这个问题,Hinton提出了一种对比度发散算法,通过一次Gibbs采样获得RBM分布的近似值。这个过程可以用数学描述为
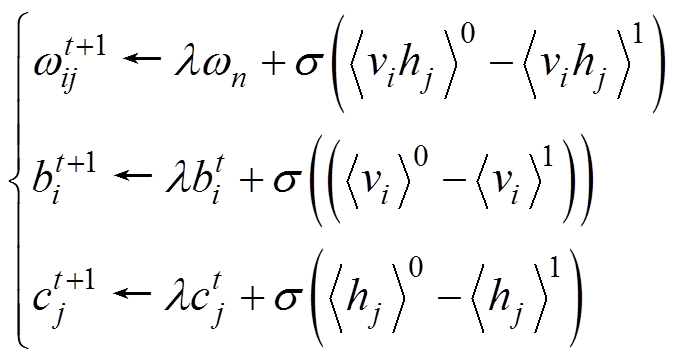 (10)
(10)
式中,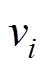 和
和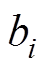 分别为第
分别为第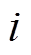 个视觉层的状态和偏置;
个视觉层的状态和偏置;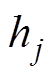 和
和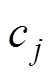 分别为第
分别为第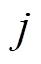 个隐藏层的状态和偏置;
个隐藏层的状态和偏置;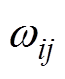 为第
为第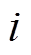 个隐藏层的第
个隐藏层的第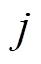 个神经元节点的权重;
个神经元节点的权重;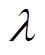 和
和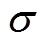 分别为学习速率和动量系数;
分别为学习速率和动量系数;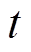 为迭代次数;
为迭代次数;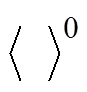 为训练数据期望;
为训练数据期望;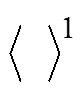 为重构模型分布下的数据期望。
为重构模型分布下的数据期望。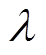 的大小直接影响权重更新时梯度的下降速度,
的大小直接影响权重更新时梯度的下降速度,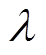 越大则收敛速度越快,但同时会导致重构误差过大,故将其取值范围设定在0.001~0.1。同时在参数更新时引入动量系数
越大则收敛速度越快,但同时会导致重构误差过大,故将其取值范围设定在0.001~0.1。同时在参数更新时引入动量系数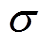 ,以防止学习率过小而导致待优化参数收敛到局部最优解。因此,如何准确地设置DBN算法的网络结构参数对其故障识别的正确性有着至关重要的影响。
,以防止学习率过小而导致待优化参数收敛到局部最优解。因此,如何准确地设置DBN算法的网络结构参数对其故障识别的正确性有着至关重要的影响。
通过优化后灰狼算法完成对DBN参数的优化,其具体过程如下:
(1)收集不同故障类型下ATSE的电流信号,并对其进行VMD分解,提取分解后各模态分量的WPE,构成特征向量空间并作为数据集。再将数据集划分为比例为6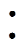 4且互斥的训练集和测试集。
4且互斥的训练集和测试集。
(2)初始化IGWO种群规模、最大迭代次数和狼群的初始位置等参数。并将DBN模型对电流故障的错分率作为IGWO的适应度函数。设DBN 3个隐藏层中各层包含的神经元数量分别为 、
、 和
和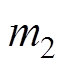 ,设置模型的学习率为
,设置模型的学习率为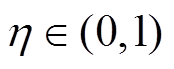 ,设置迭代次数为
,设置迭代次数为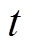 。并将灰狼位置设置为
。并将灰狼位置设置为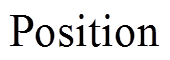
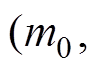
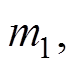
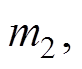
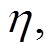
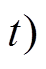 。
。
(3)将训练集和测试集输入进算法进行训练,当算法的适应度函数值达到要求或迭代至最大次数时优化完成,并将最优解重新赋值给DBN的结构参数,否则此步骤将继续。
本文ATSE电流数据来自于ATSE-100/63A/4P式自动转换开关的模拟故障实测实验。数据获取方式为:首先通过工控机向单片机发出过电压或断路的信号。当采样电路检测到主回路发生故障时,单片机直接作用于ATSE的电磁机构,将主合闸位置切换至双分位置。同时在工控机发出指令前,数据采集卡已经触发,对ATSE整个动作过程中的线圈电流信号进行数据采集。
ATSE-100/63A/4P式自动转换开关作为目前应用较广的最新一代转换开关产品,由于可靠性高、使用寿命久的特点,其故障数据难以大量获取。因此,本文采用了人为模拟故障的方式来获取实验数据。自动转化开关主要由控制器和机械结构两部分组成,经分析发现,故障主要发生在机械结构部分,各故障类型及模拟方式见表1。
表1 故障模拟及样本分布
Tab.1 Fault simulation and sample distribution

故障类型故障模拟方式训练集测试集 训练样本数验证样本数测试样本数 铁心卡涩在铁心与线圈间加入铁丝402040 线圈短路减少线圈匝数402040 衔铁行程不足衔铁上贴硬纸板402040 机械结构卡涩改用弹性强度大的弹簧402040
在完成故障模拟及检测系统的搭建后,以20 kHz的采样频率对ATSE的电流信号进行数据采集,根据产品在60 ms完成切换动作的要求,确定采样时长为60 ms,即每个电流波形含有1 200个数据点。对每种类型的故障均进行100组采样,并按照 的比例对其进行训练集和测试集的划分。
的比例对其进行训练集和测试集的划分。
在对故障电流信号进行进一步的特征提取前,应根据样本熵最小值原则对VMD算法的分解次数K进行设置。首先,将分解次数K的取值范围设置为[2, 8],接着在不同的K值下对故障电流进行VMD分解并求其趋势项所对应的样本熵值,将样本熵值SE作为纵坐标,分解次数K作为横坐标,可以清晰地看到在不同分解次数下对应的样本熵值如何变化。具体情况如图5所示。
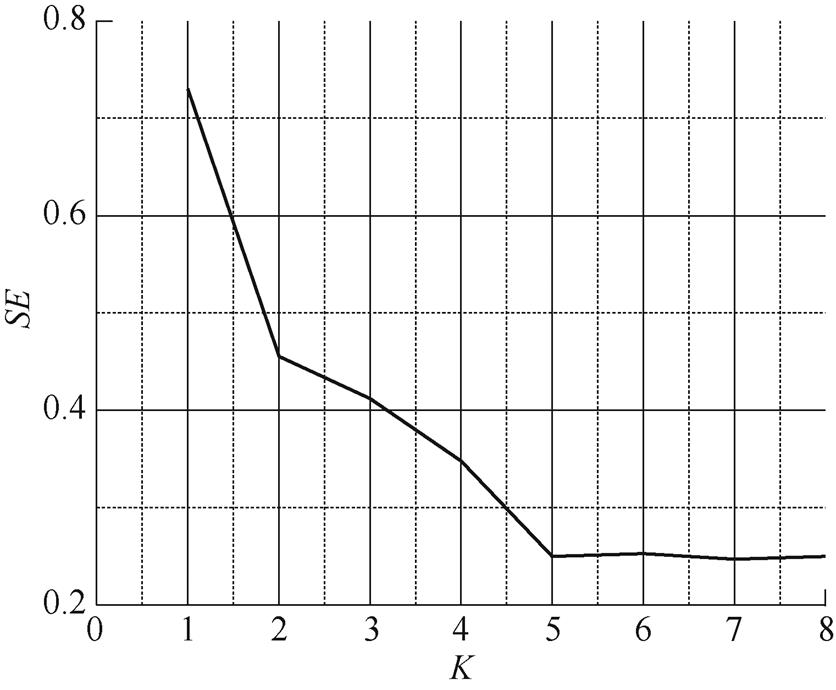
图5 SE值变化曲线
Fig.5 SE value change curve plot
由图5可知,分解次数K=5时所对应的样本熵值为曲线拐点,此时样本熵值达到最小值,即此分解次数K下各模态分量中所含的特征向量最多。因此,选择SE值转折项所对应的次数5作为VMD的最终分解次数。
为了进一步验证其分解精度的优越性,将采集到的故障电流信号进行VMD分解,得到的BIMF分量和对应频谱如图6所示。图6a为原始信号在经过VMD分解后所得到在不同频率下的波形,图6b为分解后各BIMF分量所对应的频谱特征。结合两图可看出,当VMD算法在选取K值为5时,冲击分量和噪声分量可以有效地在原始波形中分离出来,从而避免了类EMD算法中的模态混叠问题,并且分解次数相较类EMD算法也有所减小,说明当分解次数K选取合适时,该算法具有明显优势。
在确定好分解次数K后,对故障电流信号进行VMD分解并对各BIMF分量求取WPE能量占比,将各分量中能量占比前三的WPE百分比值作为特征向量。部分实验数据如图7所示。
图7中,横坐标中的BIMF1.1为第一个模态分量中能量占比最高的特征向量;BIMF1.2为第一个模态分量中能量占比第二高的特征向量,以此类推。
IGWO训练DBN网络结构时,初始化IGWO算法的参数,并对DBN的网络结构参数进行范围设置:将特征向量空间维数设定为输入层数目,将故障类别数设置为输出层数目,设置学习率范围区间为(0.001, 1),迭代次数初始值设置为100。此外,在对DBN隐含层的层数进行设置时发现,多层隐含层的深度置信网络其分类错误率表现低于单隐含层,但当隐含层数量大于等于4层时,DBN分类准确性及泛化能力均有下降。因此,本文将DBN的层数设置为3。
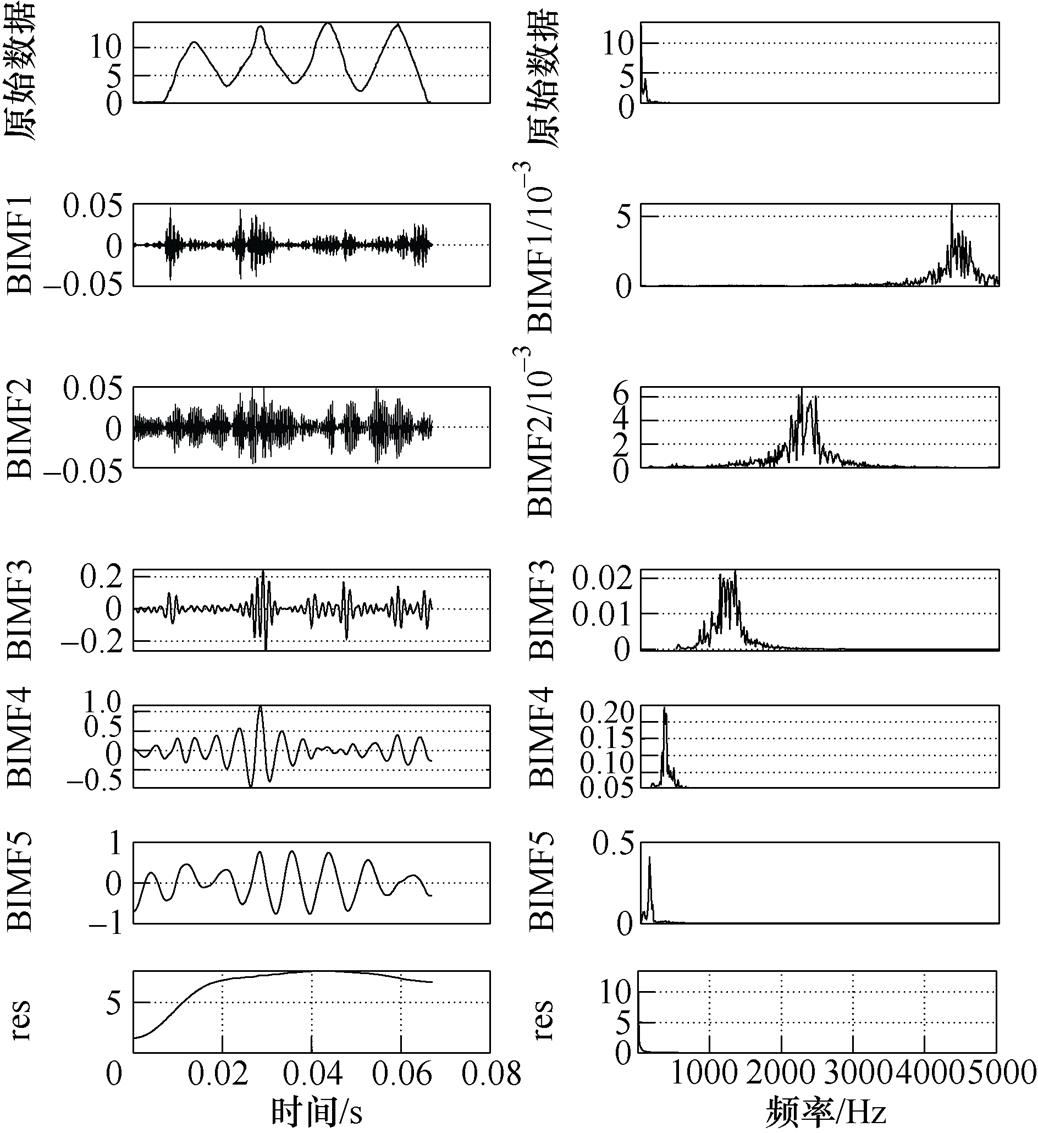
(a)VDM分解波形 (b)对应频谱
图6 故障电流VMD分解图及对应频谱
Fig.6 Fault current VMD decomposition map and corresponding spectrum
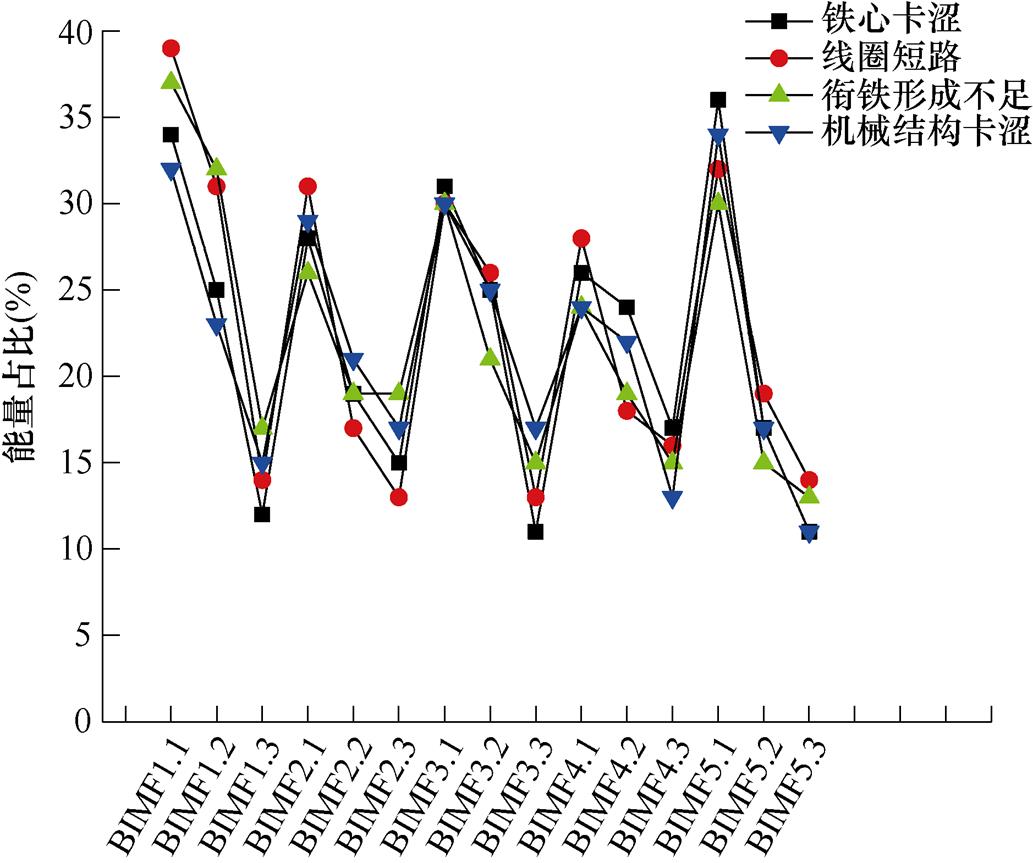
图7 部分实验数据WPE占比值
Fig.7 The proportion of WPE in some experimental data
完成算法参数的初始化设置后,将测试集数据输入DBN算法中,以其故障诊断的错误率作为IGWO的适应度函数,利用IGWO对其网络参数进行寻优后得到DBN的最优网络参数见表2。
表2 DBN网络参数
Tab.2 DBN network parameters
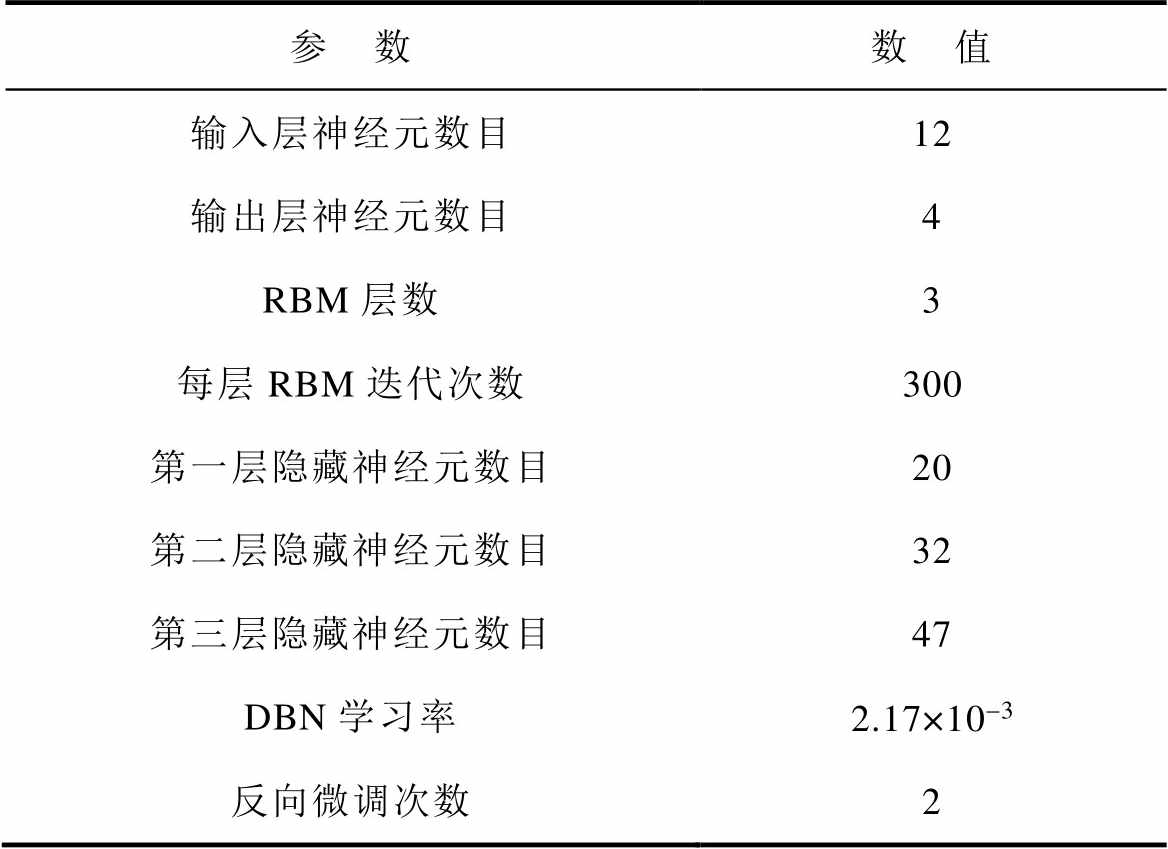
参 数数 值 输入层神经元数目12 输出层神经元数目4 RBM层数3 每层RBM迭代次数300 第一层隐藏神经元数目20 第二层隐藏神经元数目32 第三层隐藏神经元数目47 DBN学习率2.17×10-3 反向微调次数2
为了对该算法的分类准确性进行对比实验,本文选取了四种典型算法作对比,各自算法关键参数设置如下:
(1)支持向量机(Support Vector Machine, SVM):SVM核函数选择径向基函数,根据网格寻优结果设置惩罚系数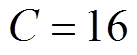 ,核函数参数g= 0.015 625。
,核函数参数g= 0.015 625。
(2)粒子群算法优化BP(Particle Swarm Optimization-BP, PSO-BP)神经网络:采用PSO的三层BP网络结构,其各层神经元数目设置为20、30、40,算法学习率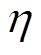 = 0.068 623 3。
= 0.068 623 3。
(3)DBN:采取逐级递减的神经元选择策略,并选取4层网络结构,确定各层网络神经元个数为40、30、20、10,学习率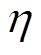 =0.09。
=0.09。
(4)GWO-DBN:利用未改进的灰狼算法对深度置信网络进行优化,初始参数设置与IGWO-DBN保持一致。
将训练集数据输入各个算法进行实验,为了表示各算法对ATSE不同故障的分类准确率,通过混淆矩阵将真实故障数据集的故障分类情况进行表示,各类算法的故障分类混淆矩阵如图8所示。横轴和纵轴分别代表预测与真实的故障数目,其中数字1~4分别对应铁心卡涩、线圈短路、衔铁行程不足及机械结构卡涩四种故障。对角线处的数值表示的是各算法在测试集中对不同故障类型分类的正确个数,非对角线位置表示该类别分类的错误个数。
通过混淆矩阵可以进一步分析各算法对不同类型故障的分类情况。IGWO-DBN算法对于铁心卡涩与线圈短路的诊断准确率可以达到100%,而衔铁行程不足和机械结构卡涩的故障仅存在一列被错分至对方的分类中。而其他算法在进行故障识别时均存在两种故障以上的错分情况,且总体识别率相较IGWO-DBN也存在劣势。
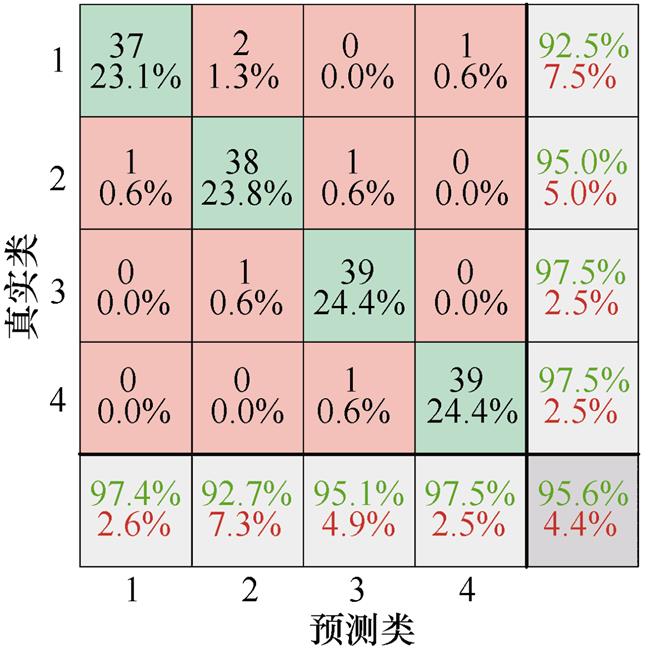
(a)SVM混淆矩阵
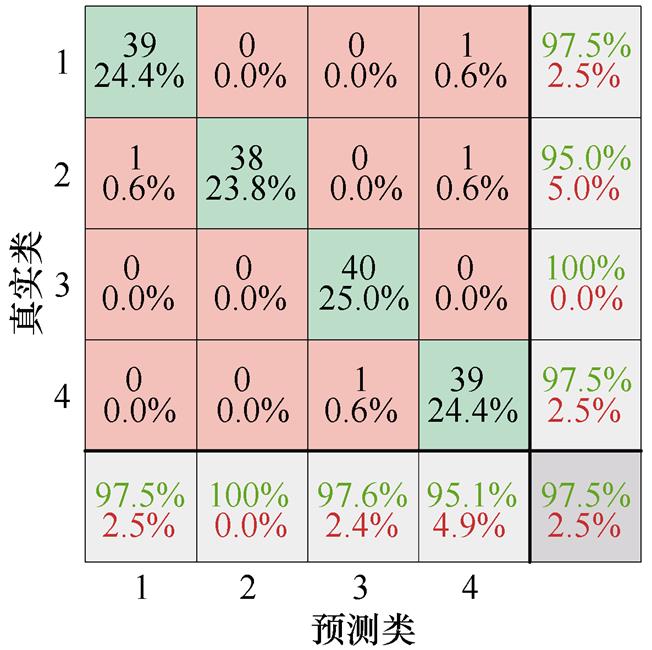
(b)PSO-BP混淆矩阵
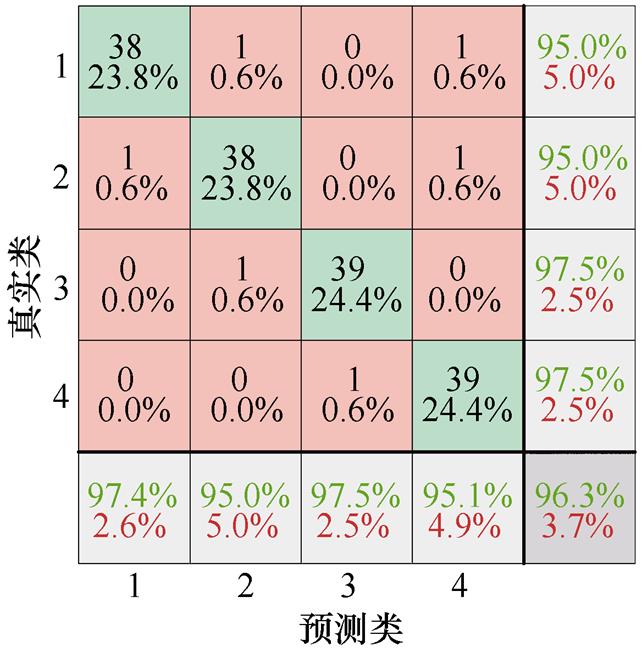
(c)DBN混淆矩阵
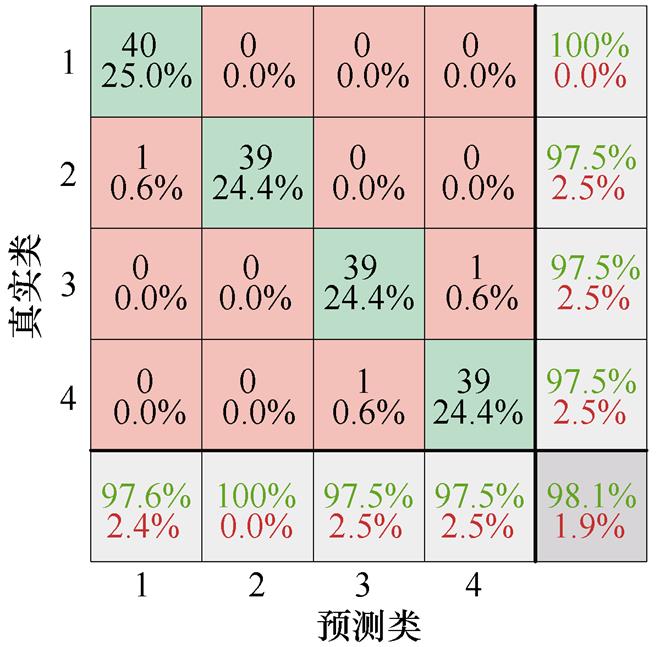
(d)GWO-DBN
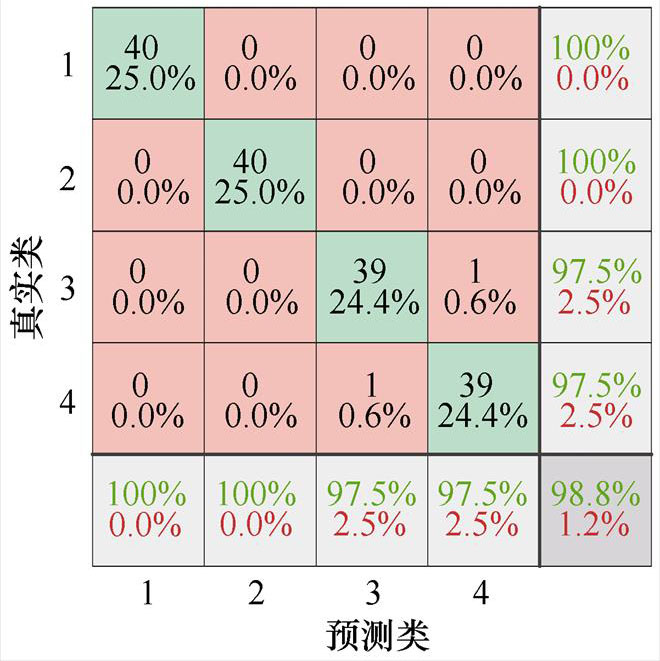
(e)IGWO-DBN
图8 故障分类混淆矩阵
Fig.8 Fault classification confusion matrix
训练正确率与验证正确率均取5次随机实验的平均值,其结果如图9所示。无论是训练还是测试过程,IGWO-DBN算法的准确率表现均为最优,并且其测试准确率较其他算法而言最接近训练准确率,不存在过拟合或欠拟合现象,而未经优化的算法其测试准确率在训练集和验证集中存在较大差别,并且均存在一定的过拟合现象。说明IGWO- DBN算法在保证较高的准确率的同时还具有良好泛化能力,适合解决复杂工作环境下的故障诊断问题。SVM作为浅层算法与未经过优化的DBN相比,其表现相对较差,准确率均低于97.2%,而经过PSO优化的BP算法,与经过GWO优化的DBN算法相比,则表现较好。
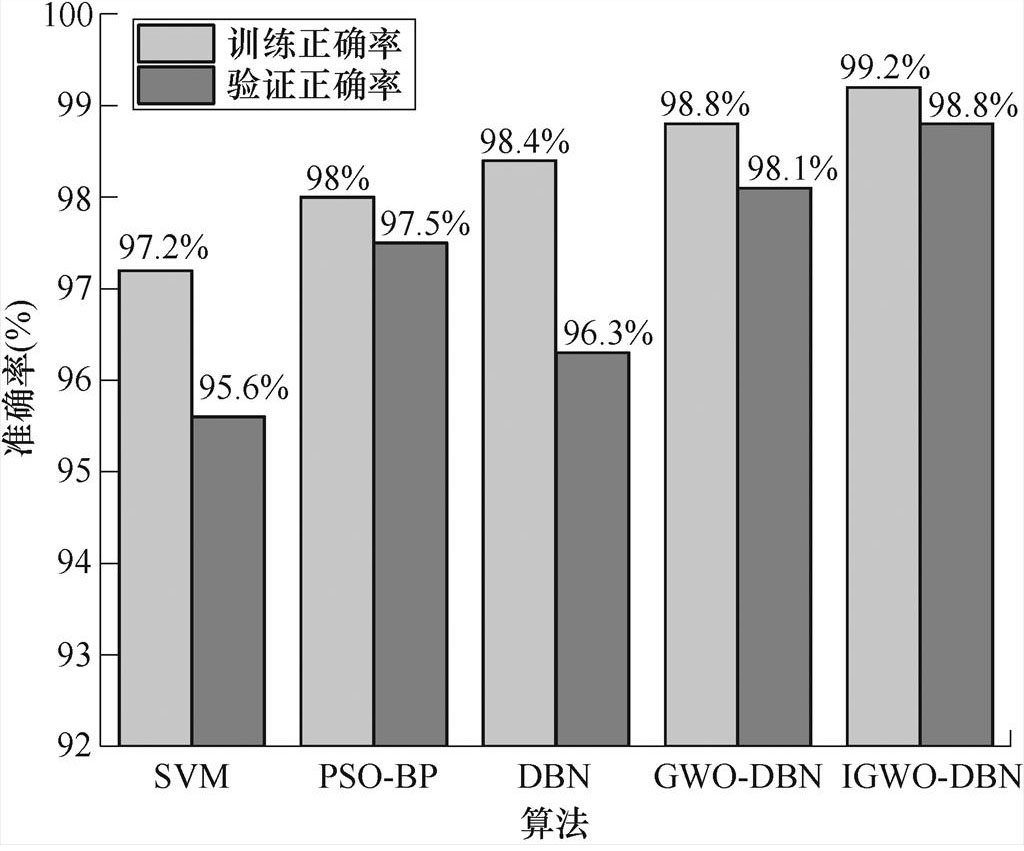
图9 训练集数据算法对比分析
Fig.9 Comparative analysis of training set data algorithms
为了进一步验证IGWO-DBN算法的优越性,图10展示的是各个算法对ATSE电流数据进行故障识别的损失变化曲线,每一轮迭代重复10次并取平均值。其损失函数值指的是预测模型与真实值的误差值,从图10中可以看出,IGWO-DBN算法虽然前期优化速度较慢,但在迭代中后期,当其他算法收敛时,仍能保证一定的全局寻优能力,最终使得DBN模型具备更优的网络结构,从而进一步提升算法的故障诊断性能。
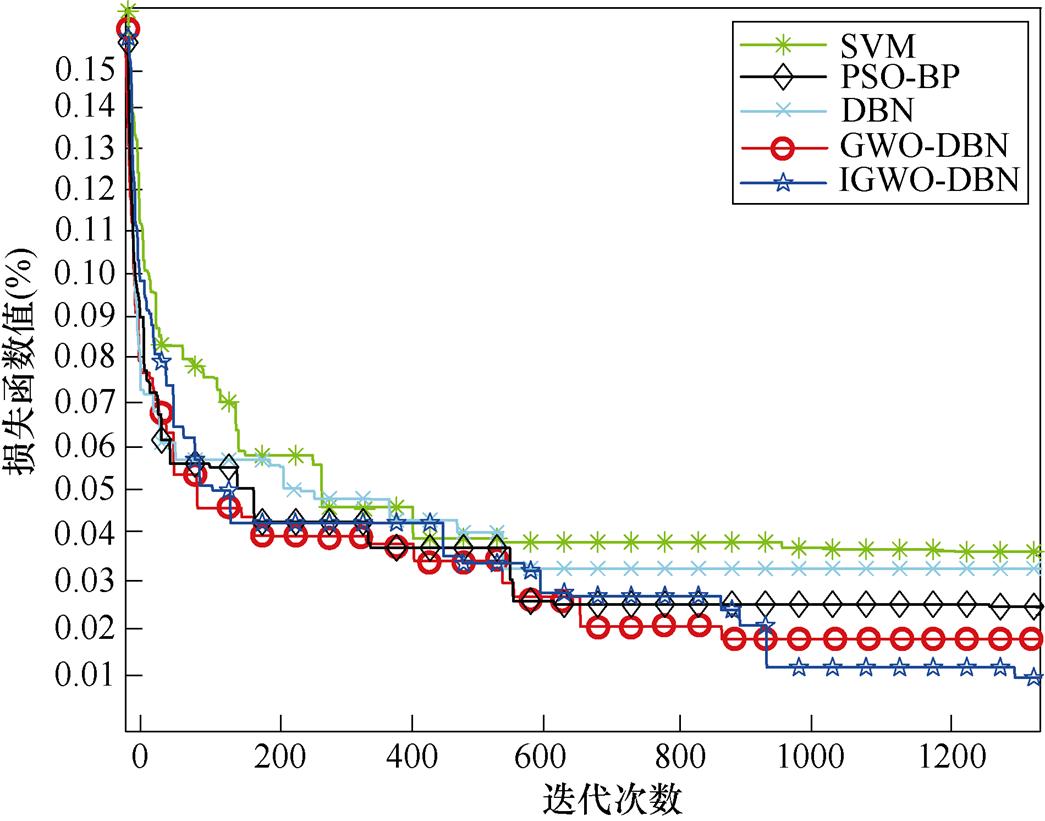
图10 不同算法损失变化对比
Fig.10 Comparison of loss changes of different algorithms
为了测试IGWO-DBN训练模型在实际工程应用中的故障分类效果,本文将ATSE发生真实故障时的电流波形数据构成的样本数据集,其输入到训练好的模型进行识别测试,各个算法的故障识别准确性及识别时间见表3。
表3 各算法真实故障的识别效果比较
Tab.3 Comparison of the identification effect of real faults of each algorithm

算法识别正确率(%)识别时间/s SVM95.50.35 PSO-BP97.50.67 DBN96.750.49 GWO-DBN97.50.62 IGWO-DBN98.750.69
在四种故障类型下各取50组共200组数据作为测试样本集,其中SVM和DBN算法在识别过程中四种故障均存在错分现象,SVM算法其准确率最低但识别速度最快。PSO-BP算法准确识别了衔铁行程不足故障,但将两例铁心卡涩故障错分至线圈短路和机械结构卡涩。GWO-DBN算法对铁心卡涩故障识别正确,但将两例四类故障错分至线圈短路和衔铁行程不足。PSO-BP算法和GWO-DBN算法存在三种故障的错分问题,IGWO-DBN则能完全正确识别衔铁行程不足和铁心卡涩故障两类故障,仅存在两例机械结构卡涩故障被错分至衔铁行程不足。
综上所述,在模拟故障下训练的IGWO-DBN算法对真实故障数据的识别准确率仍保持着显著优势,虽然识别时间最长,但所有算法识别时间均在1 s内,该算法仍具有很好的工程应用前景。
基于自动转换开关结构复杂、故障种类多且故障信号不易提取识别的特点,本文通过采用VMD- WPE方法将故障特征从电流信号中提取出来,并结合IGWO优化后的深度置信网络实现了对ATSE非侵入式的故障识别。本文得出如下结论:
1)基于样本熵最小原则可以有效确定VMD分解次数,提高其对电流信号的分解效率,通过计算分解后各BIMF分量的WPE占比,可以准确地完成对故障信号特征向量的提取。
2)通过引入非线性收敛因子、动态权重策略和Levy飞行对GWO算法进行优化,有效解决了对DBN的网络参数进行寻优时存在的早熟收敛与陷入局部最优解问题。
3)本文分别通过模拟故障与真实故障数据进行训练和测试。对比不同算法的分类精度与损失度曲线,实验结果表明,基于IGWO改进的DBN故障识别模型在训练集和测试集上准确率高达99.2%和99.8%,无过拟合现象,具有良好的泛化能力。且根据损失变化的对比图可以观测到,该模型在迭代次数大于1 000时准确率有着明显优势,最终识别准确率可达98.75%,且相较其他智能算法,IGWO- DBN对衔铁行程不足和铁心机构卡涩这两种故障的识别准确率达到了100%。
参考文献
[1] 马星光, 王晓一, 黄锐, 等. 基于复合特征的GIS振动信号特征提取方法[J]. 高压电器, 2021, 57(12): 83-89.
Ma Xingguang, Wang Xiaoyi, Huang Rui, et al. Extraction method of GIS vibration signal chara- cteristic based on composite feature[J]. High Voltage Apparatus, 2021, 57(12): 83-89.
[2] 赵莉华, 吴迅, 王泽龙, 等. 基于线圈电流的断路器操作机构仿真研究[J]. 电测与仪表, 2020, 57(12): 9-13.
Zhao Lihua, Wu Xun, Wang Zelong, et al. Simulation research on circuit breaker operating mechanism based on coil current[J]. Electrical Measurement & Instrumentation, 2020, 57(12): 9-13.
[3] 李宁, 何复兴, 马文涛, 等. 基于经验模态分解的门控循环单元神经网络的锂离子电池荷电状态估计[J]. 电工技术学报, 2022, 37(17): 4528-4536.
Li Ning, He Fuxing, Ma Wentao, et al. State- of-charge estimation of lithium-ion battery based on gated recurrent unit using empirical mode decom- position[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4528-4536.
[4] 李兵, 韩睿, 何怡刚, 等. 改进随机森林算法在电机轴承故障诊断中的应用[J]. 中国电机工程学报, 2020, 40(4): 1310-1319, 1422.
Li Bing, Han Rui, He Yigang. Applications of the improved random forest algorithm in fault diagnosis of motor bearings[J]. Proceedings of the CSEE, 2020, 40(4): 1310-1319, 1422.
[5] 崔芮华, 李泽, 佟德栓. 基于三维熵距和熵空间的航空电弧故障检测与分类技术[J]. 电工技术学报, 2021, 36(4): 869-880.
Cui Ruihua, Li Ze, Tong Deshuan. Arc fault detection and classification based on three-dimensional entropy distance and entropy space in aviation power system[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 869-880.
[6] 蒋海峰, 张曼, 赵斌炎, 等. 基于改进Hilbert- Huang变换的电网故障诊断[J]. 电工技术学报, 2019, 34(增刊1): 336-342, 351.
Jiang Haifeng, Zhang Man, Zhao Binyan, et al. Fault diagnosis of power grid based on improved Hilbert- Huang transform[J]. Transactions of China Elec- trotechnical Society, 2019, 34(S1): 336-342, 351.
[7] Guo Wei, Tse P W. A novel signal compression method based on optimal ensemble empirical mode decomposition for bearing vibration signals[J]. Journal of Sound and Vibration, 2013, 332(2): 423-441.
[8] 姜涛, 高浛, 李筱静, 等. 基于小波耗散能量谱的电力系统强迫振荡源定位[J]. 电工技术学报, 2023, 38(7): 1737-1750.
Jiang Tao, Gao Han, Li Xiaojing et al. Forced oscillation source location in power system using wavelet dissipation energy spectrum [J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1737- 1750.
[9] Jin Wenjuan, Tang Wenhu, Qian Tong, et al. Fault diagnosis of high-voltage circuit breakers using wavelet packet technique and support vector machine[J]. CIRED-Open Access Proceedings Journal, 2017(1): 170-174.
[10] 李睿彧, 刘飞, 梁霖, 等. 基于参数优化变分模态分解的交流变频电机转子断条故障识别方法[J]. 电工技术学报, 2021, 36(18): 3922-3933.
Li Ruiyu, Liu Fei, Liang Lin, et al. Fault identification of broken rotor bars for the variable frequency AC motor based on parameter optimized variational mode decomposition[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3922- 3933.
[11] 庄瑞锋, 陈丽安, 肖梁贤. 基于变分模态分解的高压断路器合分闸线圈电流特征值提取[J]. 高压电器, 2022, 58(4): 145-150, 157.
Zhuang Ruifeng, Chen Lian, Xiao Liangxian. Feature value extraction of high voltage circuit breaker’s opening coil current based on variational modal decomposition[J]. High Voltage Apparatus, 2022, 58(4): 145-150, 157.
[12] Wen Long, Li Xinyu, Gao Liang, et al. A new convolutional neural network-based data-driven fault diagnosis method[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5990-5998.
[13] 王艳新, 闫静, 王建华, 等. 基于域对抗迁移卷积神经网络的小样本GIS绝缘缺陷智能诊断方法[J]. 电工技术学报, 2022, 37(9): 2150-2160.
Wang Yanxin, Yan Jing, Wang Jianhua, et al. Intelligent diagnosis for GIS with small samples using a novel adversarial transfer learning in convolutional neural network[J]. Transactions of China Electro- technical Society, 2022, 37(9): 2150-2160.
[14] 徐奇伟, 黄宏, 张雪锋, 等. 基于改进区域全卷积网络的高压引线接头红外图像特征分析的在线故障诊断方法[J]. 电工技术学报, 2021, 36(7): 1380- 1388.
Xu Qiwei, Huang Hong, Zhang Xuefeng, et al. Online fault diagnosis method for infrared image feature analysis of high-voltage lead connectors based on improved R-FCN[J]. Transactions of China Elec- trotechnical Society, 2021, 36(7): 1380-1388.
[15] 张婷, 王海淇, 张认成, 等. 基于自归一化神经网络的电弧故障检测方法[J]. 仪器仪表学报, 2021, 42(3): 141-149.
Zhang Ting, Wang Haiqi, Zhang Rencheng, et al. An arc fault detection method based on the self- normalized convolutional neural network[J]. Chinese Journal of Scientific Instrument, 2021, 42(3): 141- 149.
[16] 刘甜甜, 朱熀秋. 基于改进SPSO算法优化LS-SVM的六极径向混合磁轴承转子位移自检测技术[J]. 中国电机工程学报, 2020, 40(13): 4319-4329.
Liu Tiantian, Zhu Huangqiu. Self-sensing modeling of rotor displacement for six-pole radial hybrid magnetic bearing using improved simplified particle swarm optimization LS-SVM[J]. Proceedings of the CSEE, 2020, 40(13): 4319-4329.
[17] 汪光远, 杨德先, 林湘宁, 等. 基于深度置信网络的柔性直流配电网高灵敏故障辨识策略[J]. 电力系统自动化, 2021, 45(17): 180-188.
Wang Guangyuan, Yang Dexian, Lin Xiangning, et al. High-sensitivity fault identification strategy for flexible DC distribution network based on deep belief networks[J]. Automation of Electric Power Systems, 2021, 45(17): 180-188.
[18] 李益兵, 王磊, 江丽. 基于PSO改进深度置信网络的滚动轴承故障诊断[J]. 振动与冲击, 2020, 39(5): 89-96.
Li Yibing, Wang Lei, Jiang Li. Rolling bearing fault diagnosis based on DBN algorithm improved with PSO[J]. Journal of Vibration and Shock, 2020, 39(5): 89-96.
[19] Karunakar R V, Kumar A V R. Multi-channel neuro signal classification using Adam-based coyote optimi- zation enabled deep belief network[J]. Biomedical Signal Processing and Control, 2022, 77: 103774.
[20] 崔江, 郭瑞东, 张卓然, 等. 基于改进DBN的发电机旋转整流器故障特征提取技术[J]. 中国电机工程学报, 2020, 40(7): 2369-2376, 2415.
Cui Jiang, Guo Ruidong, Zhang Zhuoran, et al. Generator rotating rectifier fault feature extraction technique based on improved DBN[J]. Proceedings of the CSEE, 2020, 40(7): 2369-2376, 2415.
[21] Hu Changhua, Pei Hong, Si Xiaosheng, et al. A prognostic model based on DBN and diffusion process for degrading bearing[J]. IEEE Transactions on Industrial Electronics, 2020, 67(10): 8767-8777.
[22] 孙丽君, 冯斌斌, 陈天飞. 基于鞅论的灰狼优化算法全局收敛性分析[J]. 控制与决策, 2022, 37(11): 2839-2848.
Sun Lijun, Feng Binbin, Chen Tianfei. Global con- vergence analysis of grey Wolf optimization algo- rithm based on martingale theory[J]. Control and Decision, 2022, 37(11): 2839-2848.
[23] Xue Feng, Liu Yongbo, Ma Xiaochen, et al. A hybrid clustering algorithm based on improved GWO and KHM clustering[J]. Journal of Intelligent & Fuzzy Systems, 2022, 42(4): 3227-3240.
[24] Liu Xinyang, Wang Yifan, Zhou Miaolei. Dimen- sional learning strategy-based grey Wolf optimizer for solving the global optimization problem[J/OL]. Computational Intelligence and Neuroscience, 2022, https://doi.org/10.1155/2022/3603607.
Fault Identification of Automatic Transfer Switching Equipment Based on VMD-WPE and IGWO Optimized DBN
Abstract Automatic Transfer Switching Equipment (ATSE) is a device that ensures the continuous power supply of the system. Fault diagnosis of ATSE is of great significance for the continuous operation of the system. The current data of solenoid coils can be used to identify the electrical and mechanical faults of ATSE. However, the noise in the current and the network structure parameters of the intelligent fault diagnosis method are difficult to confirm. Therefore, an ATSE fault diagnosis method is proposed based on variational mode decomposition (VMD) feature extraction and optimized depth belief network (DBN). In this method, Wavelet Packet Energy (WPE) is extracted as a feature vector from the mode components decomposed by VDM, and the network structure parameters of DBN are set by an improved grey Wolf algorithm (IGWO) to complete ATSE fault identification.
Firstly, the fault current signal is decomposed by VMD, and its sample entropies are obtained for each mode component after decomposition. The decomposition number corresponding to the lowest sample entropy value is taken as the final decomposition number of VMD. Secondly, principal component analysis is used to select the WPE of each mode component after decomposition, and the formed final feature vector space is input to DBN. Meanwhile, to avoid premature convergence and local optimum problems during fault classification, IGWO is used to optimize the network structure parameters of DBN to recognize various faults of ATSE.
ATSE fault simulations are designed and carried out in this paper. After determining the decomposition frequency of VMD, modal decomposition on the coil current is performed. The superiority of VMD decomposition is demonstrated by the absence of modal aliasing in the intrinsic mode functions at different frequencies. The feature vectors are input into the optimized DBN algorithm for fault classification experiments. The experimental results are as follows: (1) The difference in classification accuracy between the optimized DBN and the training set is only 0.4%, indicating no over-fitting problem in the modified model. (2) The optimized DBN achieves a classification accuracy of 98.78% for four common faults. Compared with the non-optimized methods, the proposed method has the highest accuracy and the best stability in fault diagnosis of ATSE.
The following conclusions can be drawn: (1) After determining the decomposition time based on the sample entropy, the VMD can effectively avoid the mode overlap, thus realizing the extraction of fault features from ATSE current signals. (2) Compared with the shallow neural network, DBN has a powerful mapping ability and can accurately characterize the complex mapping relationship between the original current signal and the ATSE fault type. (3) The optimized DBN has no over-fitting phenomena using IGWO, and the classification accuracy of ATSE faults is improved.
keywords:Improved Wolf optimizer, deep belief network, automatic transfer switching equipment, fault diagnosis
中图分类号:TM564.3
DOI: 10.19595/j.cnki.1000-6753.tces.222143
河北省自然科学基金(E2020202221)和河北省省级科技计划(215676146H, 225676163GH)资助项目。
收稿日期 2022-11-13
改稿日期 2023-03-07
刘帼巾 女,1972年生,教授,研究生导师,研究方向为电器设备可靠性。E-mail: liuguojin72@163.com
刘达明 男,1999年生,硕士研究生,研究方向为电器可靠性及检测技术。E-mail: liudaming2021@126.com(通信作者)
(编辑 崔文静)