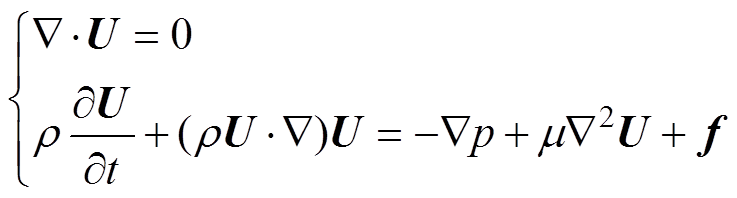（1）
摘要 针对传统算法存在的步长调整及耦合点选择问题，该文提出基于子循环自适应串行交错（SCAS）的时间匹配算法。首先，在步长调整方面，通过加入自适应（ATS）-启发式（HTS）混合变步长算法，解决步长无法实时调整的问题；然后，针对耦合点选择问题，该文在传统常规串行交错（CSS）时间匹配算法及现有改进方案子循环常规串行交错（SCSS）的基础上，提出SCAS时间匹配算法，采用自适应方案确定计算时间窗及预定耦合点，并引入指数平滑法对其精度进行保证；最后，该文基于110 kV油浸式电力变压器建立二维瞬态单分区分匝绕组模型，并将所提算法与其他传统方法进行对比分析。结果表明：在精度方面，与传统CSS算法相比SCAS算法的流场及温度场最大平均相对误差均不超过0.45%，在可接受误差范围内；在效率方面，SCAS算法总体计算效率较CSS算法提高了近20倍。同时，为了说明所提算法的工程价值，该文搭建基于110 kV变压器绕组模型的温升实验平台，将SCAS时间匹配算法应用于该模型中，实验结果表明：在精度方面，SCAS算法与实验达到稳态时最大绝对误差为2.7 K；在计算效率上，本文所提算法的计算效率较传统算法提升约46倍，计算步数约为传统的1/47，减少了计算冗余。
关键词：子循环自适应串行交错 混合变步长 二维瞬态流热耦合问题 快速计算方法 温升实验
准确快速地获取油浸式电力变压器绕组瞬态热点温度是实时监测其工况的重要前提，有利于保证油浸式变压器的健康平稳运行。油浸式电力变压器绕组的散热媒质主要为变压器油，油流将产生的热量带出绕组、铁心等固体区域实现散热。在该过程中，油流流速的变化会改变绕组、铁心等传热效率，从而影响绕组和铁心的温度；反之，场域温度的变化则会改变油流的物性参数，进而对油流的速度造成影响。因此对其瞬态温升过程的分析是一个涉及流场、温度场的多物理场耦合问题[1-3]。目前，数值计算方法是分析该问题的主要研究方法。
有限体积法[4-6]和有限元法[7-10]是求解变压器绕组温升问题的两种主要数值计算方法，且有限元法及其改进方案以其普适性强、编程难度低等特点与前者相比更具优势。廖才波等[11-12]应用有限元法计算油浸式电力变压器的电磁-流体-温度耦合场，并将计算结果与经验公式的热点温度计算结果进行对比，验证了该方法的有效性。为了提高有限元方法的数值稳定性，谢裕清[13]引入Jiang Bonan[14]提出的最小二乘有限元法（Least Squares Finite Element Method, LSFEM）对变压器绕组的流热耦合场进行计算，结果表明，该方法能够有效避免传统有限元法存在的非物理振荡问题，提高计算精度。在此基础上，Zheng Zhi、Rong Shichang等[15-16]在流体场和温度场中分别采用最小二乘有限元与迎风有限元（Upwind Finite Element Method, UFEM）的混合有限元求解方法对瞬态温升问题进行了求解，该混合有限元法能够解决伽辽金有限元[1]计算过程中的数值振荡问题，保证数值稳定性的同时提高了计算效率。因此，本文采用基于LSFEM-UFEM的混合有限元法计算分析绕组的传热过程。
然而，受实际模型网格剖分复杂、节点数量多的影响，有限元方程往往阶数较高、计算复杂、求解效率低下[17-18]。同时对于瞬态多物理场耦合问题，耦合时间点的选择也会直接对其计算精度和效率产生显著影响。在油浸式变压器绕组的传热过程中，温度场在时间尺度上的变化相较于流场往往较慢，若两场均采用统一的固定小步长耦合计算，对于温度场则会造成大量的计算冗余，导致整场的计算效率降低。故在时间尺度上找到合适的多场匹配算法对加快其求解过程意义重大。
针对两个及以上的多物理场时间匹配问题，传统思路一般考虑物理场之间采用固定的等时间步长耦合求解，这种直接耦合算法被命名为常规串行交错（Conventional Serial Staggered, CSS）法[19-20]，该方法保证了计算的精度并且原理较为简单，易于编程实现，但这种时间匹配方法存在两个较为显著的问题：
（1）步长设置问题：不同物理场随时间的变化趋势往往不同，过大或过小的时间步长设置均会对计算精度和效率造成显著影响[21]。
（2）耦合点设置问题：不同物理场之间时间尺度上的变化快慢存在较大差异，那么采用统一的固定步长耦合计算则会造成大量的计算冗余，极大地降低了计算效率[22]。
为解决上述问题，C. Kassiotis等提出了子循环常规交错（Sub-cycled Conventional Staggered Scheme, SCSS）时间匹配方案[23]，通过将流-固两场的时间步长设置为整数倍的方式有效地减少了计算时间。张宇娇等则采用预测算法选择耦合点[24]，不断调整电磁-温度场的耦合时间，以提高计算效率。但上述方法与CSS算法相同，仍存在无法实时调整步长导致的运行时间过长问题。
因此，本文提出了基于子循环自适应串行交错（Sub-Cycled Adaptive Staggered, SCAS）的时间匹配方式，对以上两点问题做出了相应改进：
（1）针对步长设置问题，引入自适应变步长算法，在不影响计算精度的同时，通过实时调整步长的方式，极大地提升了计算效率。
（2）针对耦合点设置问题，结合自适应算法的步长调整结果以确定耦合时间点，并引入指数平滑法来保证其精度，减少计算冗余。
同时，本文结合110 kV油浸式电力变压器绕组的结构特点，建立了二维单分区分匝绕组瞬态传热模型，并在此基础上将本文所提算法与CSS、SCSS等时间匹配算法的计算结果及计算时间进行初步分析对比。最后，本文搭建了基于110 kV变压器绕组模型的温升实验平台，并将SCAS时间匹配算法应用于该传热模型中，以充分说明本文算法的工程实用价值。
油浸式变压器瞬态流场的控制方程[14]可写为
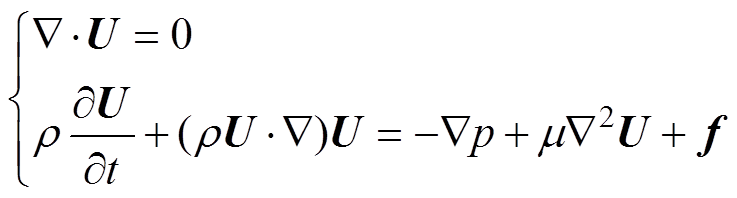（1）
式中，U为速度矢量（m/s）；r 为流体密度（kg/m3）；p为流体内部压强（Pa）；m 为流体动力粘度（N·s/m2）；f为外力密度矢量（N/m3）。采用最小二乘有限元方法，引入涡量w 后，用后向欧拉法对时间项进行离散，二维流场控制方程[14]为
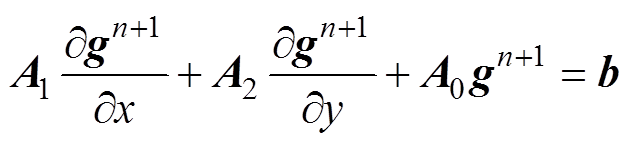（2）
式中，g=[u v p ωz]T；wz为涡量w 在竖直方向上的分量，矩阵参数A1、A2、A0、b分别表示为
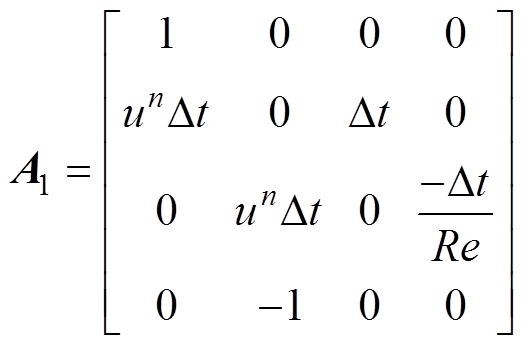
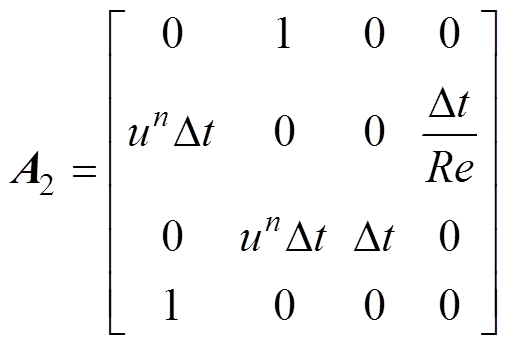
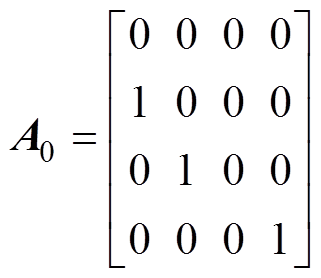
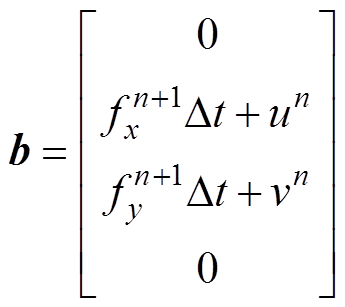
式中，Re为雷诺数；u为横向流速；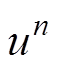
为u第n个时步的值；v为纵向流速；
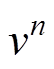为v第n个时步的值；Dt为时间步长；
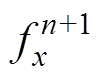和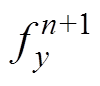
分别为fx和fy第n+1个时步的值。其离散方程组表示为
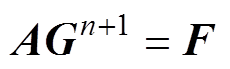（3）
其中
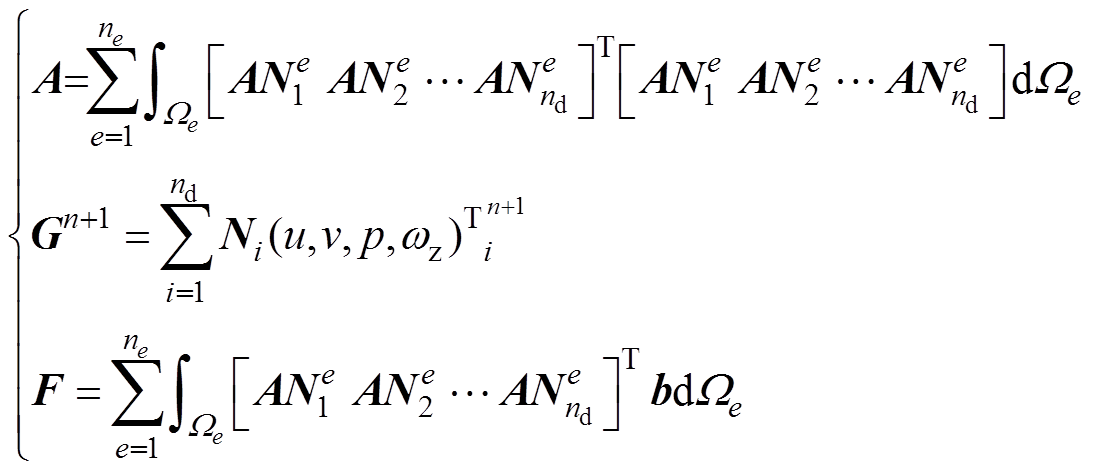
式中，Ni为有限元形函数；ne为有限单元的数量；nd为有限元节点数量。流场边界条件一般为第一类边界条件，采用置大数法[13]赋边界条件即可对方程式（3）进行求解。
参考文献[25]，瞬态温度场的控制方程为
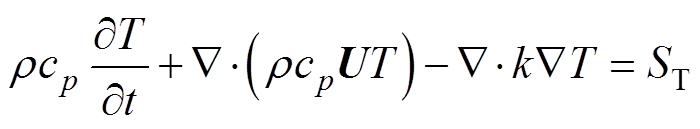（4）
式中，cp为定压比热容[J/(kg·K)]；T为热力学温度（K）；k为热导率[W/(m·K)]；ST为单位体积的产热量（W/m3）。
对方程式（4）采用加权余量法进行离散，并引入迎风算子W[26]，即迎风有限元方法，其二维离散格式为
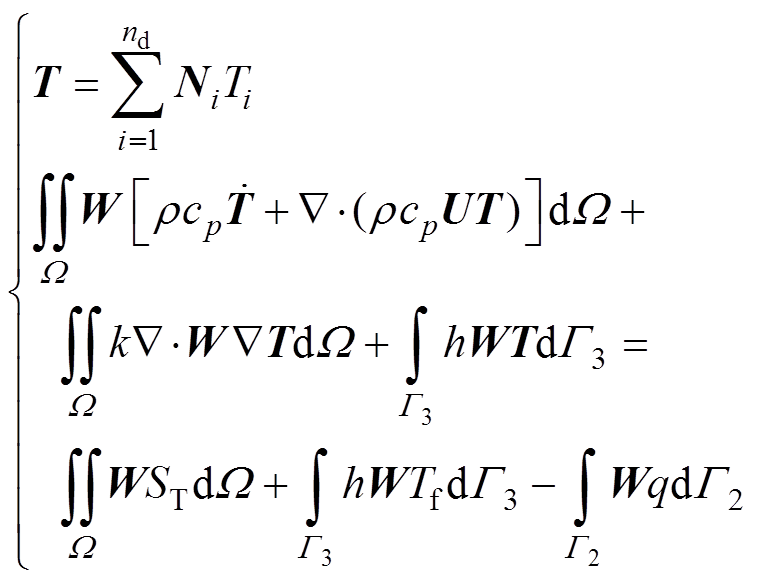（5）
式中，i为有限元节点标号；G2、G3分别为第二类、第三类边界条件所对应的边界；h为对流换热系数[W/(m2·K)]；Tf为环境温度（K）；q为热流密度（W/m2）。采用Crank-Nicolson法对时间项进行离散，得到其求解形式为
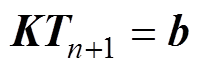（6）
其中
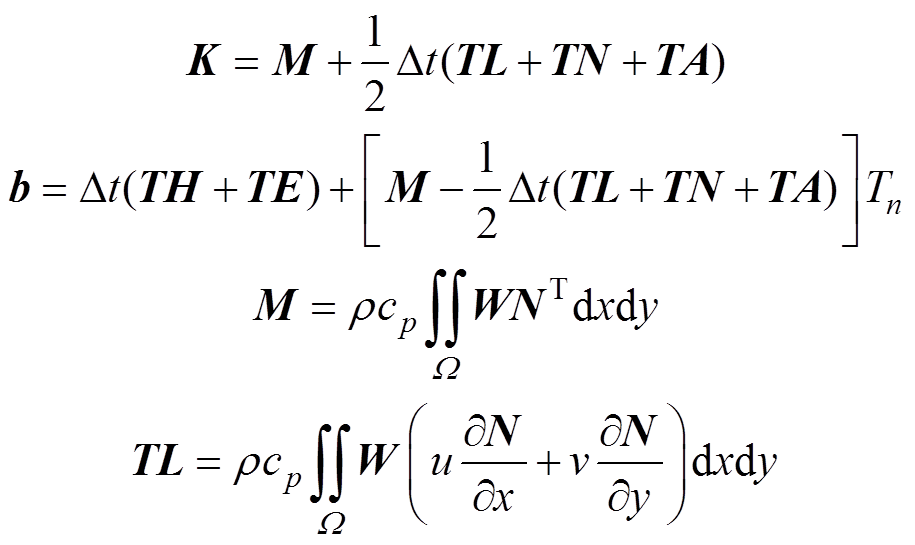
综上所述，即为采用LSFEM-UFEM混合有限元方法对油浸式电力变压器绕组进行流热耦合计算的离散方程构建过程。
应用混合有限元法对油浸式电力变压器绕组温升问题进行计算时，由于模型复杂、剖分节点数较多和有限元方程组维数较高等因素影响，其求解速度往往过慢。同时考虑到瞬态计算过程中时间步长的设置对计算精度与计算效率均会产生影响：若步长设置过大，则温度场和流场的计算精度无法保证，甚至还可能导致计算不收敛；若步长设置过小，则将严重影响计算效率。因此，在保证计算精度的前提下为有效解决步长设置问题提高计算效率，本文引入自适应变步长算法对瞬态计算步长进行实时调整。
不同于传统的基于截断误差的变步长策略，本文引入基于自适应-启发式混合变步长（Adaptive Time Stepping-Heuristic Time Stepping, ATS-HTS）原理的混合变步长方式对瞬态温升的时步设置问题进行分析。
ATS是基于泰勒展开的变步长策略，其通过计算不同精度近似解的差值作为时步调整依据，将本时刻的计算结果设置为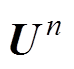
，则下一时刻计算结果一阶估计值为
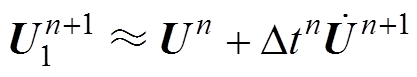（7）
其二阶精度的估计值为
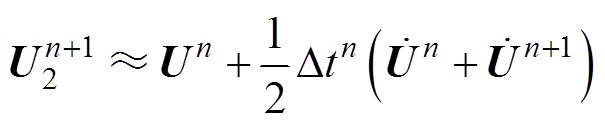（8）
将两者差值作为截断误差的判断依据，即
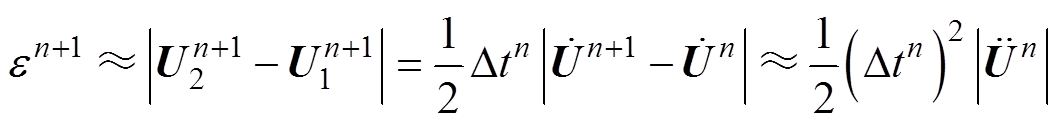（9）
式中，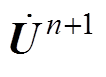
为第n+1时间步速度对时间的导数；e 为截断误差，为了充分反映计算的偏差程度，本文采用绝对-相对误差混合准则作为时步的调整判据。
当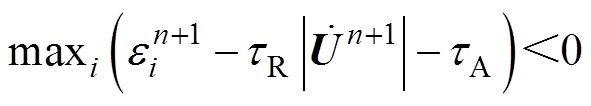
时，下一时步的步长可调整为
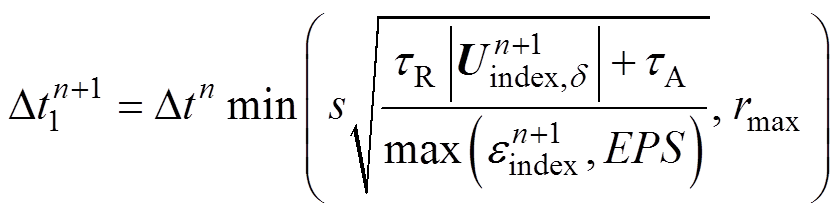（10）
反之，若不满足条件，则说明该步步长变化不满足误差设置要求，称之为失败时步，对该步重新设定步长进行计算，即
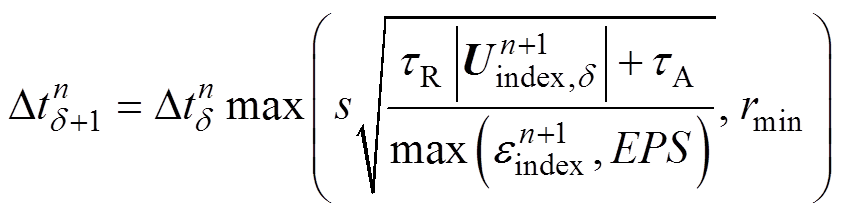（11）
式中，tA为设定的绝对误差限；tR为设定的相对误差限；d 为回退的次数；index为满足判断准则的节点标号；s为经验系数，一般取0.8～0.9；EPS为机器零近似，一般取10-8；rmax及rmin分别为最大和最小步长限制因子，rmax通常设置为4，rmin通常设置为0.8。
对于强非线性问题，基于截断误差原理的ATS变步长方法在某些情况下可能无法有效反映其变化情况[21]，为提高自适应算法的准确性，将迭代次数设置为非线性判别依据[27]，引入启发式变步长（Heuristic Time Stepping, HTS）方法。该方法通过观察其运行的迭代次数，设置其迭代次数上限qmax及迭代次数下限qmin，假设当前时步的迭代次数为q。
当q≥qmax时，步长变化过大超出其迭代次数上限，为一失败时步，需将步长减少一定倍数后进行回退计算，即
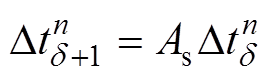（12）
当q≤qmin时，则步长变化较小，需增大步长以减少计算时间，即
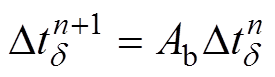（13）
若qmin＜q＜qmax，则说明其步长变化满足计算要求，为使其不被限制在同一固定步长，只需将其稍作改变为
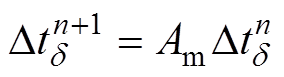（14）
式中，As、Ab、Am均为步长修正因子；As一般取0.8～0.9；Ab一般取4～8；Am一般取1.1～1.2。
然而上述方法仅从时间步长设置方面提高了计算效率，对于多物理场的瞬态耦合问题，其耦合点的选择也是影响求解效率的重要一环。因此，在此基础上，还需要探究一种合适的多场时间匹配策略以进一步减少时间冗余。
传统的多物理场瞬态计算当中，场与场之间往往采用的是顺序耦合方式，即每个时间步下均进行一次迭代耦合，这种计算方式被称为常规串行交错（Conventional Serial Staggered, CSS），CSS时间匹配算法原理如图1所示。
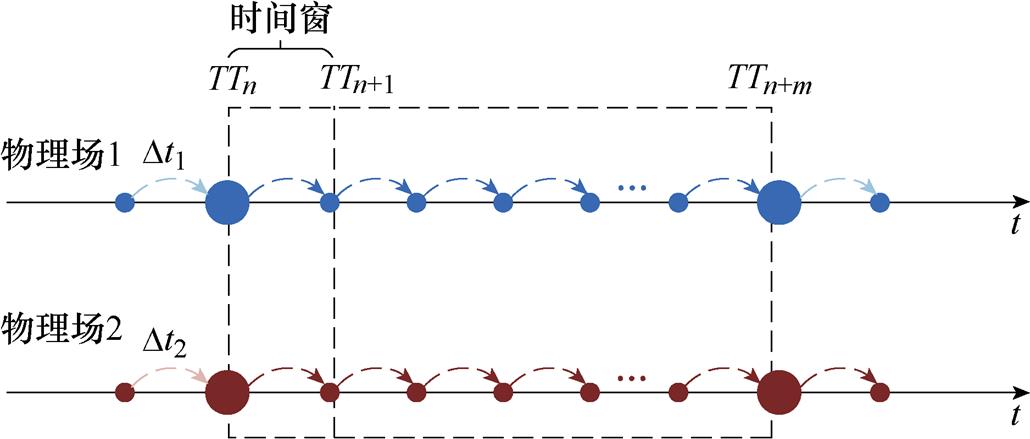
图1 CSS时间匹配算法原理
Fig.1 Principle of CSS time matching algorithm
但是由于各物理场在时间尺度上的变化存在一定差异，如在变压器绕组温升过程中流场变化较快，温度场变化往往较慢，而这种统一小步长顺序迭代的耦合方式则会导致其中变化较慢的物理场发生过频计算，从而造成严重的计算冗余。
针对该问题，本文提出了SCAS时间匹配算法，其原理如图2所示，其中物理场1表示变化较快的物理场，物理场2表示变化较慢的物理场，从自适应步长调整和耦合点选择两个方面对传统方案进行改进。
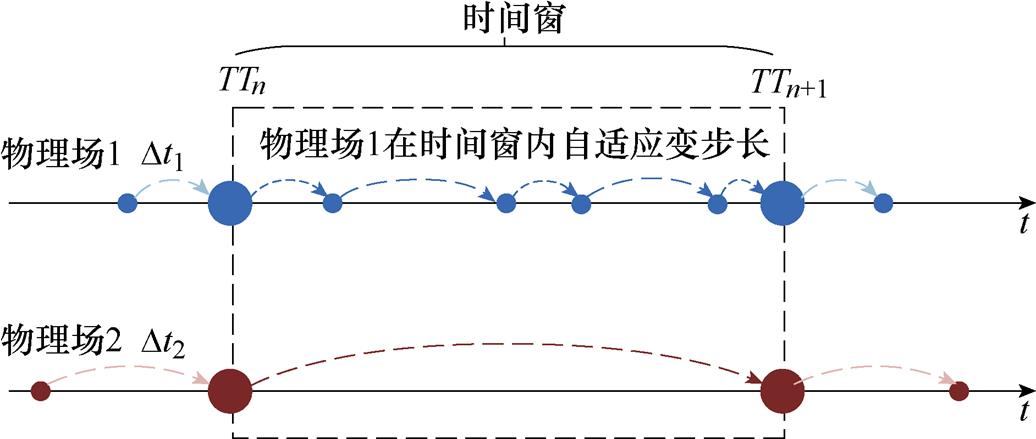
图2 SCAS时间匹配算法原理
Fig.2 Principle of SCAS time matching algorithm
自适应步长调整方面，基于1.2节介绍的ATS- HTS混合变步长方法，能够在误差允许范围内取得物理场在每一时刻的最大运行时步，从而大大提高计算效率。
耦合点选择方面，针对流热耦合场，先对两场进行若干步耦合计算，在TTn时刻基于自适应变步长方法能够取得流场与温度场下一时刻的最佳步长Dtl与DtT，将二者进行比较，选取其中较大的步长所对应的时刻TTn+1作为两场预定耦合点，由此可以初步确定一个时间窗[TTn, TTn+1]，在时间窗内，两场分别通过自适应变步长的计算方式达到下一耦合点，进行迭代耦合。这种取较大步长作为时间窗的耦合点确定方法，大大降低了耦合计算次数从而提高了整体计算效率。
然而，采用该方法的前提是，在时间窗内，其中一场的变化引起另一场的变化在可接受的范围内，因此，本文采用指数平滑法对其进行限定。指数平滑法进行调整的原理如图3所示。
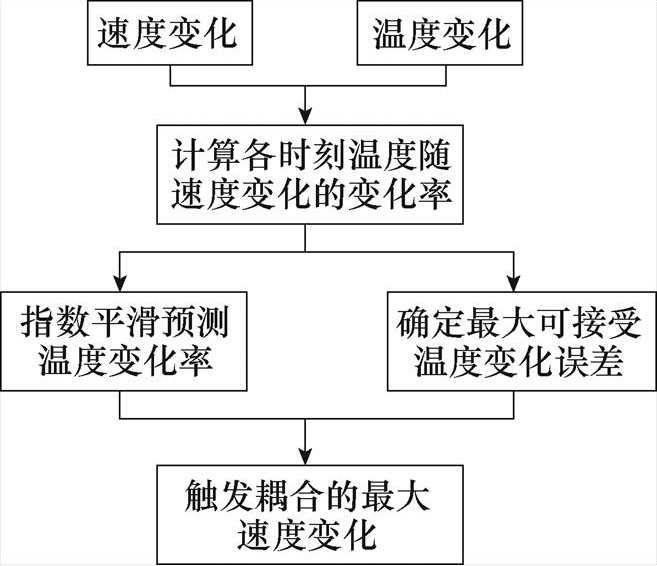
图3 指数平滑法原理
Fig.3 Principle of exponential smoothing method
设定温度场允许的最大温度变化为DTmax，先用小步长进行3次耦合计算，得到各时刻温度场的温度变化DTn以及速度场的速度变化Dun，则得变化率为
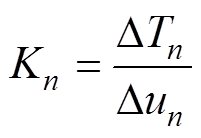（15）
并根据指数平滑法得
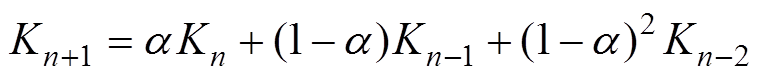（16）
式中，a 为平滑系数，一般在0～1之间。对n+1时刻的变化率进行预测，得出温度场的触发最大速度变化为
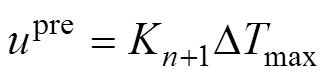（17）
若在一个时间窗内，流场速度的变化超过该限值，则提前结束时间窗对两场进行耦合。综上所述，基于SCAS时间匹配方法的完整流程如图4所示。
由于本文主要针对油浸式电力变压器绕组温升问题展开研究，因此根据110 kV变压器绕组结构特点，建立了二维分匝绕组传热模型，并在该模型基础上，通过与其他方法进行对比，初步验证本文所提算法的正确性、可行性与高效性。
图4 SCAS时间匹配流程
Fig.4 SCAS time matching process
该二维分匝绕组模型如图5所示。该分匝绕组的总宽为155.5 mm，总高为154.2 mm；线饼宽为138 mm，高为10.8 mm；挡板宽为1.5 mm；绝缘纸厚度为0.7 mm；水平油道线饼之间距离为6 mm，线饼与挡板之间距离为3 mm；竖直油道内侧为8 mm，外侧为10 mm。同时将其油道及线饼按图5所示标号，将油道从上到下标为1～10，线饼由上到下标为①～⑨。另外，本文模型的相关物性参数见表1。
在实际模型中，温度的变化往往会导致变压器的某些物性参数发生改变，故在表1中将其设置为与温度相关的函数。同时将模型的边界条件设置如下：
（1）将绕组与流体交界面设置为无滑移壁面，即u=0，v=0。
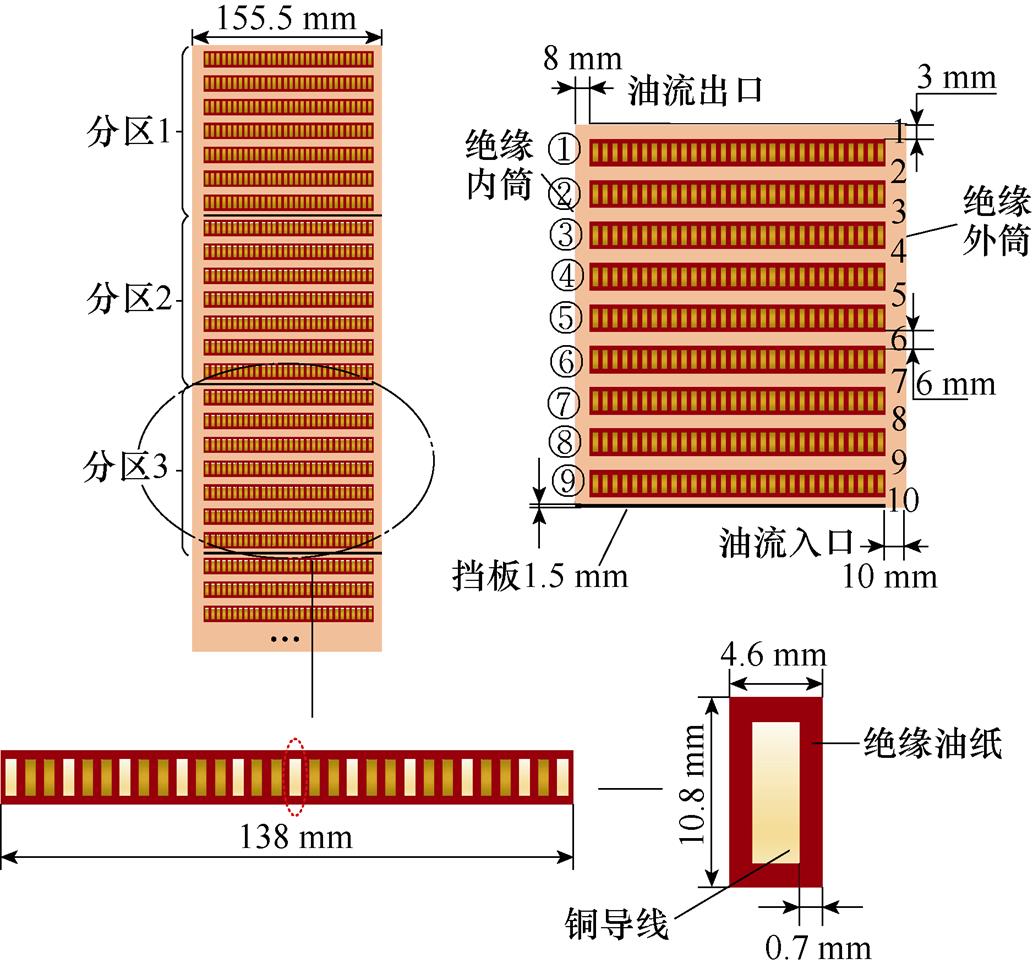
图5 二维分匝绕组模型
Fig.5 2-D winding model
表1 模型的物性参数
Tab.1 Physical parameters of the model
对 象参 数数 值 变压器油密度/(kg/m3)1 098.72～0.712 T 比热容/[J/(kg·K)]807.163+3.28 T 动力粘度/(Pa·s)0.084 6～4×10-4 T+5×10-7 T 导热系数/[W/(m·K)]0.150 9～7.101×10-5 T 铜线匝密度/(kg/m3)8 900 比热容/[J/(kg·K)]381 导热系数/[W/(m·K)]387.6 绝缘油纸密度/(kg/m3)980 比热容/[J/(kg·K)]2 000 导热系数/[W/(m·K)]0.25
（2）由于挡板、绝缘筒的导热系数极小，将两者设置为绝热的无滑移壁面边界条件，即u=0，v=0。
（3）将初始温度设置为290 K。
（4）出口油流的速度方向为沿竖直方向向上，并将其压力设置为0，即u=0，p=0。
（5）由于绕组损耗与温度相关，因此本文将所采用的热源设置为温度的函数[25]。
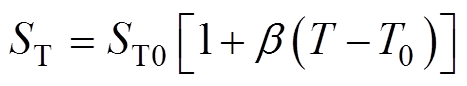（18）
式中，ST0为初始温度为T0时绕组的单位体积产热量，当T0=273 K时，ST0=227 000 W/m3；b 为导体温度系数，b=0.003 93 K-1。
由于LSFEM-UFEM流固耦合传热算法已在文献[16]中验证了其有效性，因此，本文对该算法的正确性不再重复探讨。本节将在其基础上，重点分析所提出的时间匹配算法的正确性与高效性。
为了初步验证本文所提算法的正确性及优势，将SCAS时间匹配方法与传统CSS方法及其现有的改进方案SCSS[23]进行对比。值得一提的是，引入自适应变步长算法之后，理论上也可以选取每一时刻流场与温度场步长调整之后的较小值，作为下一时刻整场的计算步长以实现耦合计算，本文将该方法命名为自适应串行交错（Adaptive Staggered Scheme, ASS），其时间匹配算法原理如图6所示，并加入方法对比当中，以说明引入自适应算法的优势所在。由于传统的CSS时间匹配算法计算精度较高，因此以其计算结果为准，通过将SCSS、ASS、SCAS与CSS算法在单分区模型中进行精度以及效率的对比，以验证本文所提算法的正确性及高效性。本文入口流速随时间的变化如图7所示。
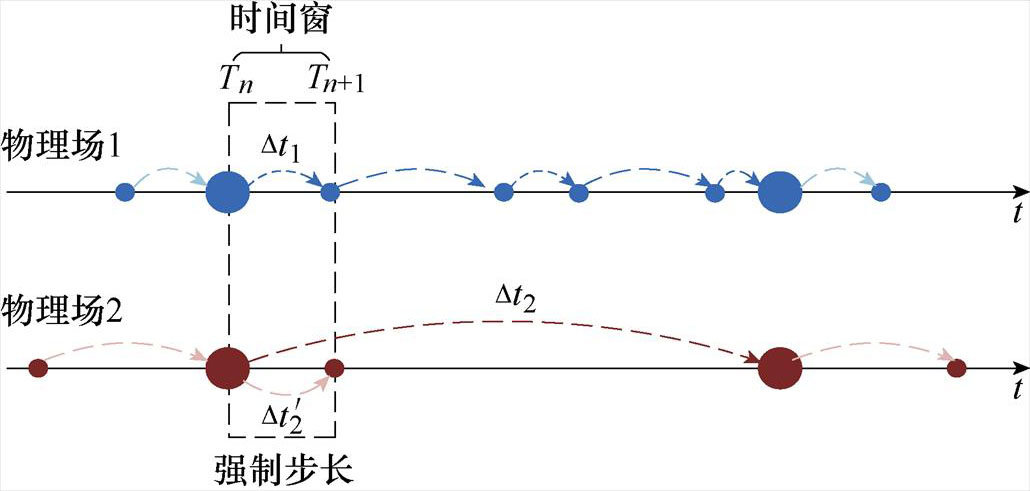
图6 ASS时间匹配算法原理
Fig.6 Principle of ASS time matching algorithm
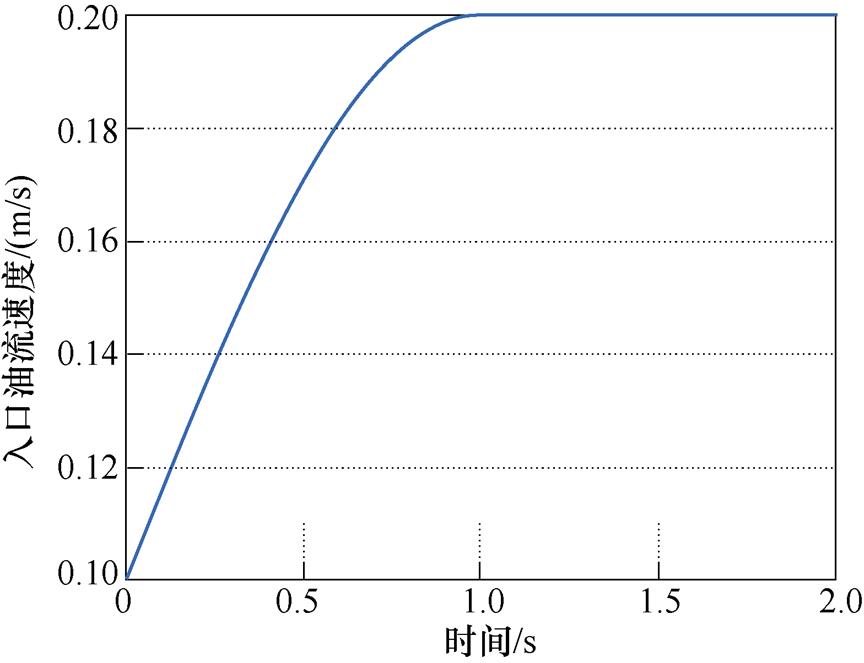
图7 入口油流速度
Fig.7 Inlet oil flow velocity diagram
2.2.1 正确性验证
本文基于SCAS时间匹配方法，对绕组的流固耦合传热过程进行了计算分析，并将计算结果与CSS、SCSS、ASS算法在单分区模型中进行对比，以第2油道中心点油速与第⑦线饼中心点温度随时间的变化为例，探讨该方法的准确性，精度对比如图8所示。
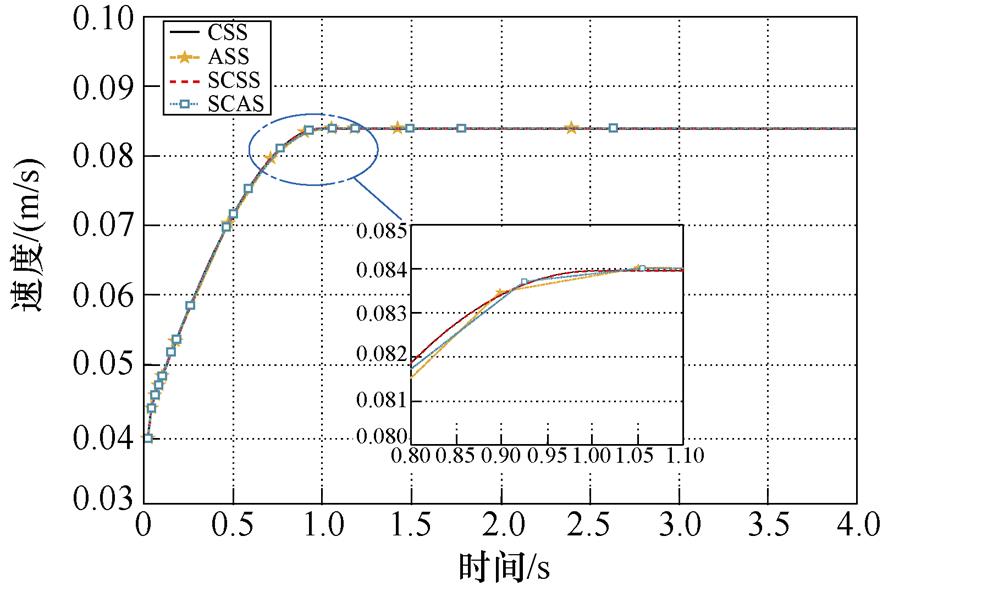
（a）四种算法流场变化对比
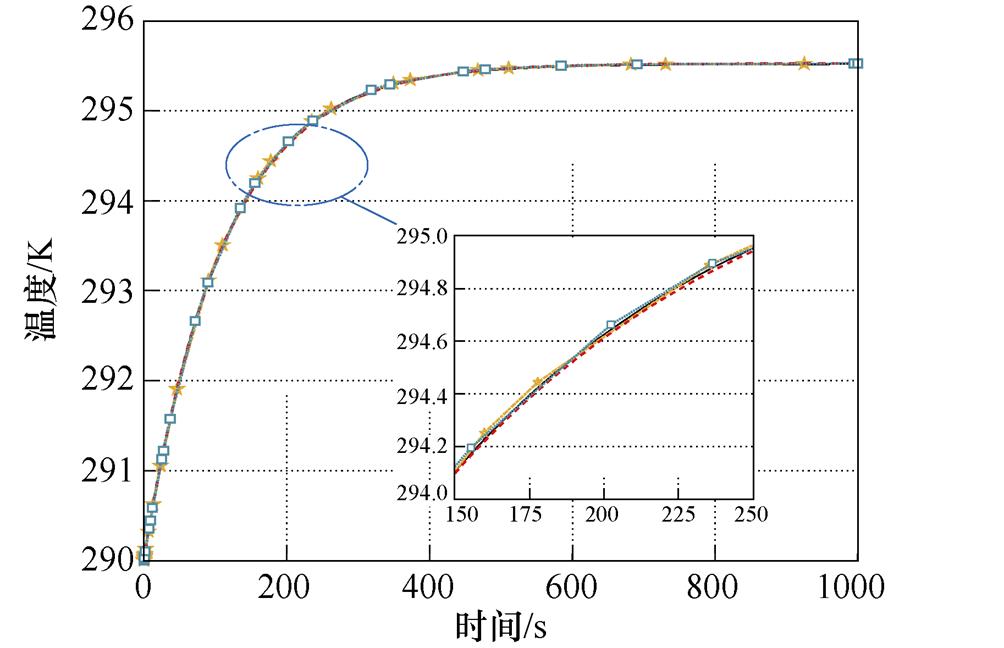
（b）四种算法温度场变化对比
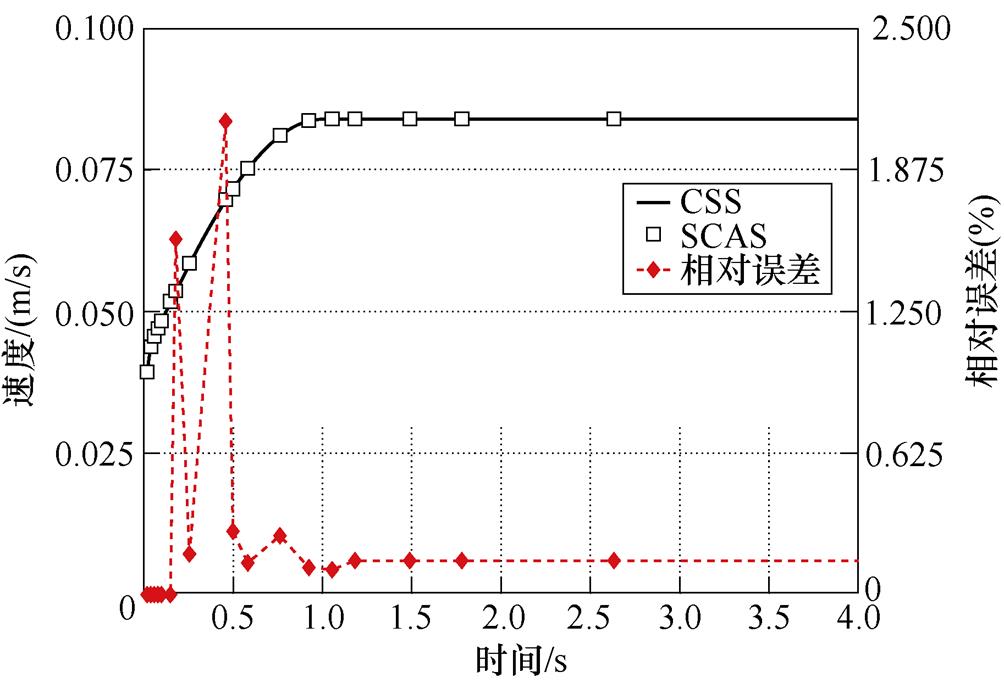
（c）CSS与SCAS流场变化及误差
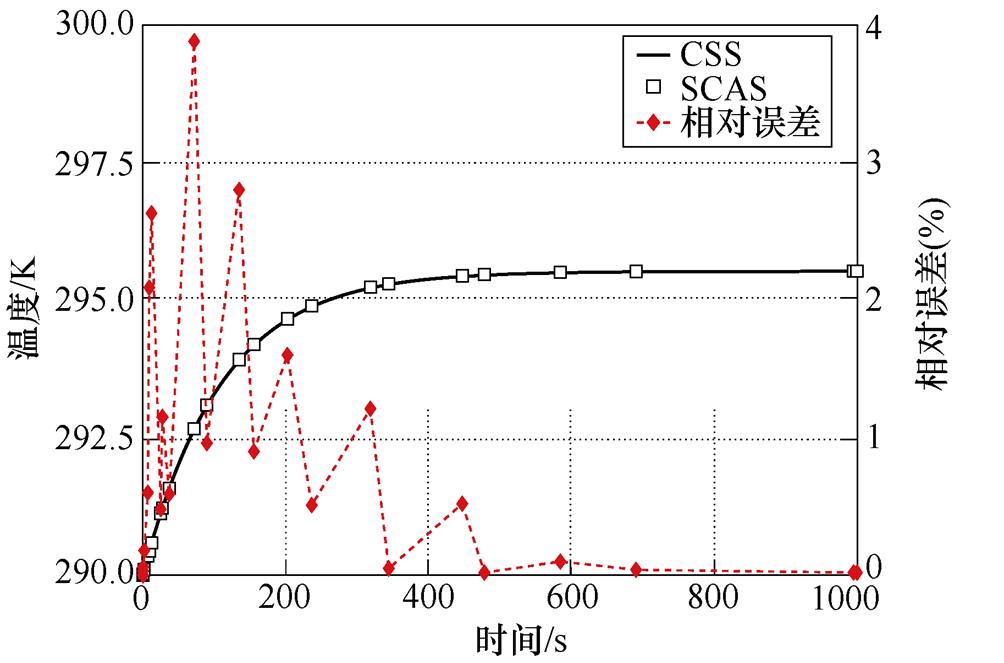
（d）CSS与SCAS温度场变化及误差
图8 精度对比
Fig.8 Accuracy comparison
如图8a、图8b所示为CSS、ASS、SCSS与SCAS四种时间匹配算法在监测点的流场和温度场计算结果对比，从图中可以看出，四种方法的精度虽略有不同，但其变化过程与趋势几乎完全相同。
将SCAS与传统CSS算法各时间点的计算结果与相对误差进行单独对比，如图8c、图8d所示，由图可知，SCAS与CSS算法相比，在监测点的瞬态计算过程中，流场与温度场的最大相对误差均不超过4%，且前者的计算时步数远远小于后者，在流场中，对于SCAS算法，其计算时步数为26步，CSS算法的计算时步数为200步；在温度场中，SCAS算法所需的计算时步数为28步，CSS算法则为300步，这说明了本文所提SCAS时间匹配算法的正确性与优越性。
为了进一步说明这一点，计算各算法在各时间点下与CSS相比的全场域误差，定义
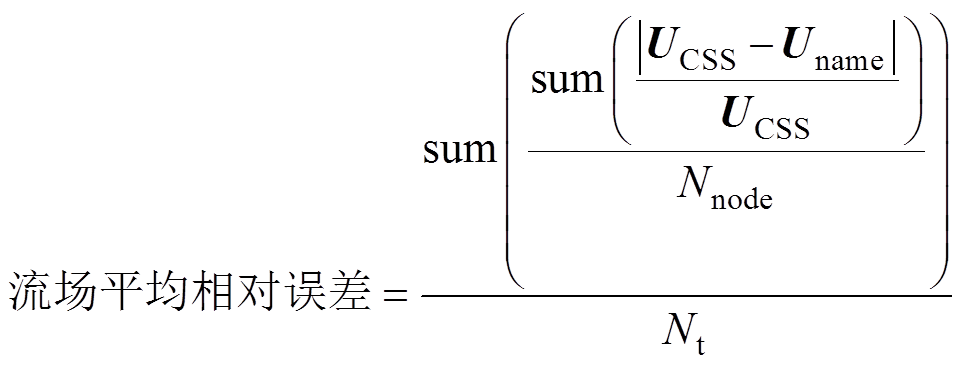（19）
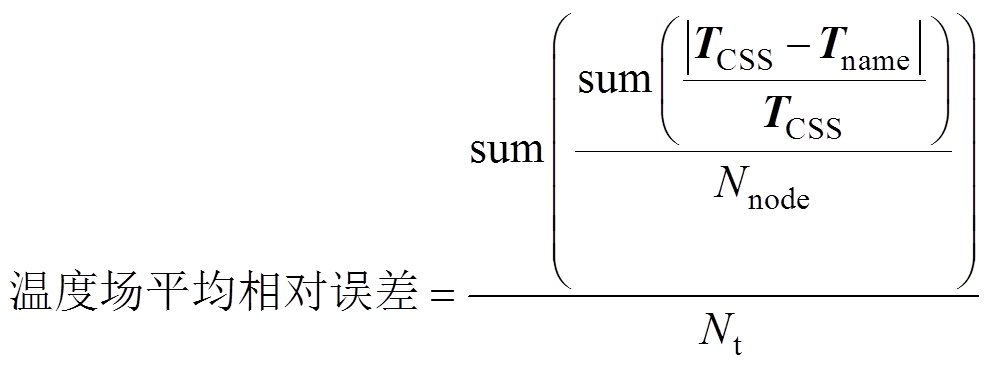（20）
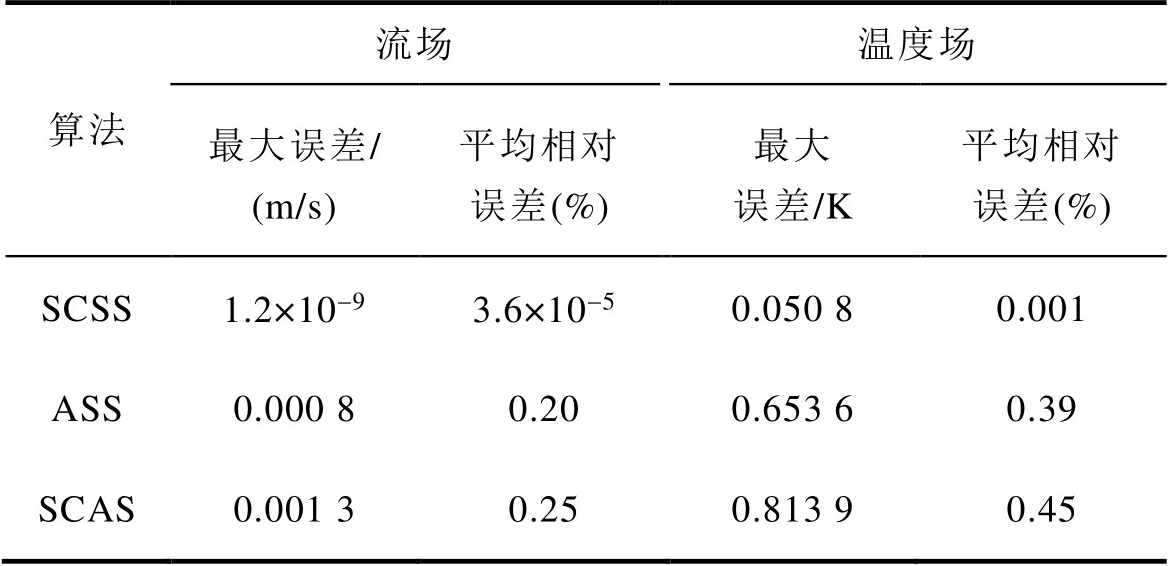
式中，TCSS、UCSS为CSS算法的计算结果；Tname、Uname为其余三种算法的计算结果；Nnode为计算节点总数；Nt为计算时间步数。以传统的CSS算法为参照，计算其余各算法全场域的最大绝对误差与全时域的平均相对误差，见表2。
表2 各算法精度对比
Tab.2 Accuracy comparison of each algorithm
算法流场温度场 最大误差/ (m/s)平均相对误差(%)最大误差/K平均相对误差(%) SCSS1.2×10-93.6×10-50.050 80.001 ASS0.000 80.200.653 60.39 SCAS0.001 30.250.813 90.45
从表2可以看出，加入自适应变步长算法之后的ASS、SCAS匹配方案在精度上有所降低，以流场为例，与传统CSS算法相比，前者流场的最大误差为0.000 8 m/s，平均相对误差为0.2%；后者流场的相对误差为0.001 3 m/s，平均相对误差为0.25%；其误差仍然较小。温度场最大误差为0.813 9 K，平均相对误差仅为0.45%，均在可接受误差范围内。综上所述，本文所提算法在计算结果方面无论是针对特定监测点还是全场域，与传统CSS算法及其现有改进方案几乎完全相同，初步说明了该算法的正确性与可行性。
2.2.2 高效性验证
在多物理场耦合计算中，相较于传统的时间匹配方法，基于SCAS的时间匹配方法理论上更为高效，为初步验证本文所提基于SCAS时间匹配算法的高效性，将其与SCSS、ASS、CSS在计算效率方面进行对比。
在本算例中，为使得结果更加合理，在对SCSS与CSS的计算效率进行分析时，要求当流场计算达到稳态后，不再进行重复计算，在之后的仿真时间中将流场的计算结果直接代入温度场进行计算；而在SCAS与ASS当中由于耦合次数及运行时步较少，则不需要进行此操作。效率对比如图9所示。
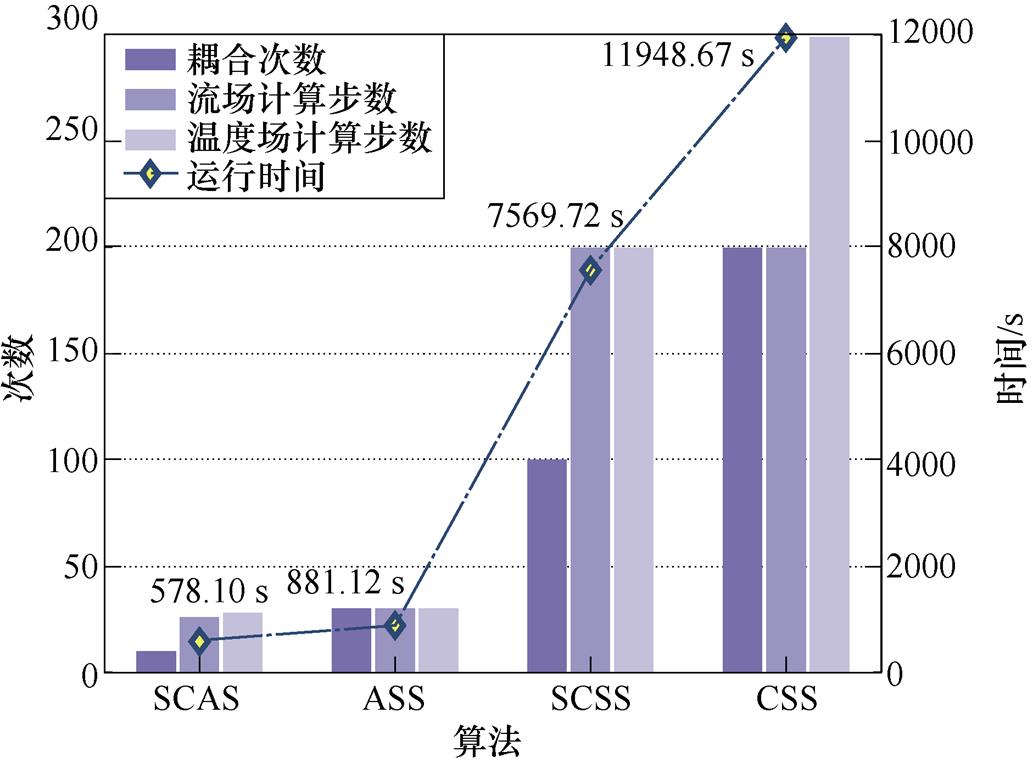
图9 效率对比
Fig.9 Efficiency comparison
分析图9可得出以下结论：对比CSS与SCSS算法的耦合次数可以看出，增加耦合点选择算法能够有效减少多物理场瞬态计算耦合次数，减少运行时间；对比ASS与CSS算法可以看出，加入自适应算法后，流场与温度场的计算步数大幅度减少，ASS算法的流场与温度场的运行步数仅为传统CSS算法的1/10，大大地提高了运行效率；对比SCAS与传统CSS算法，在结合耦合点选择与步长自适应选择之后，SCAS算法在耦合次数和计算时间步数上得到了进一步提升，其总体计算效率较CSS算法提高了近20倍。
上述结果可初步验证本文所提算法的正确性与高效性，为进一步贴合工程实际，本文基于110 kV油浸式电力变压器绕组结构，建立绕组温升实验模型，并将SCAS时间匹配算法应用于该绕组数值传热模型中，通过温升实验进行验证。
为了进一步验证本文所提算法的工程应用价值，建立了一个油浸式变压器绕组实验平台并进行温升实验，实验平台参照110 kV变压器建立绕组模型。测量获取一定工况下绕组的温升，并据此建立数值传热模型。实验装置外观如图10所示。实验绕组实物如图11所示。
图10 实验模型外观
Fig.10 Appearance of experimental model
图11 实验绕组实物
Fig.11 Physical drawing of winding
由于仅针对油浸式电力变压器绕组的温升规律进行分析，因此实验所用绕组为空心结构。该绕组共分为8个分区，为了便于说明，将该实验绕组的8个分区从上到下依次标为分区1～分区8。该8个分区绕组共包含66个线饼，其中分区1～分区3包含7个线饼，其余分区均为9个线饼，将此66个线饼从上到下依次标号为1～66，每个线饼包含15匝导线，而每匝导线由2根扁铜导线组成，故为方便辨识将由内向外的铜导线编号依次标为1～30，该8个分区模型结构如图12所示。
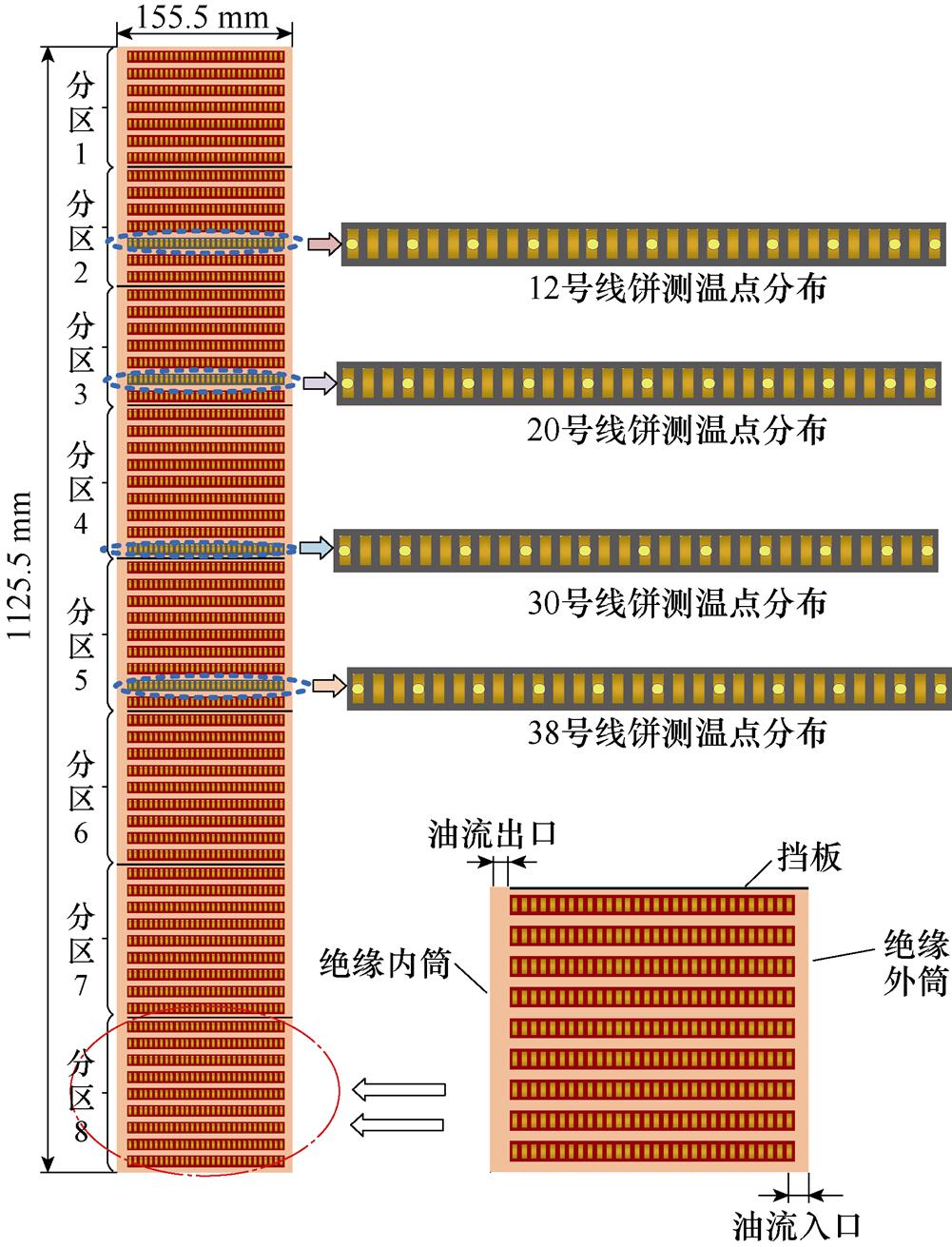
图12 8个分区绕组结构
Fig.12 Eight-zone winding structure diagram
如图12所示，本文采用的温升实验平台使用热电偶进行绕组温度测量，测点布置于线饼12、20、30、38上，其中每个线饼上均布置11个测温点，分别位于导线1、4、7、10、13、16、19、22、25、28、30上。
根据油泵所测得的流量计算得到通过油泵设置入口油流速度为0.117 3 m/s，入口处热电偶测得室温为290 K，功率分析仪测得绕组的功率为25.000 4 kW。对该工况下的绕组开展温升实验。当顶层油温变化在2 h内保持不变时，视为绕组温度达到稳定状态，实验共持续7.66 h。
为方便分析，选取12线饼的16测温点，20线饼的13测温点，30线饼的4测温点以及38线饼的28测温点为参照点，将本文所提SCAS时间匹配算法与传统算法、FLUENT仿真结果与温升实验结果进行对比，结果如图13所示。
如图13a～图13d所示，为温升实验中各算法在4个监测点的变化情况，结合图13可看出，CSS算法与FLUENT的仿真结果相比，二者误差不大，最大绝对误差不超过0.5 K，且与实验相比也在可接受的范围内，这说明了本文所采用的二维计算模型与数值计算方法的正确性；同时，SCAS算法与CSS算法的变化趋势基本贴合，这初步说明了本文所提算法在工程模型中的适用性，为进一步说明这一点，将上述4个测温点到达稳态时的误差列于表3中（结果均保留1位小数）。
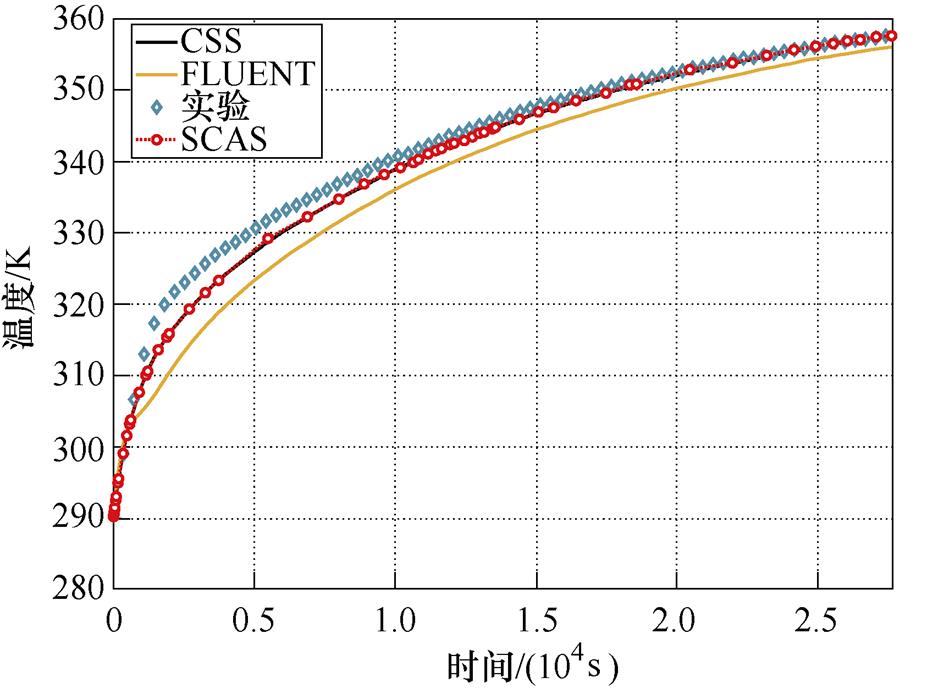
（a）12线饼16测温点
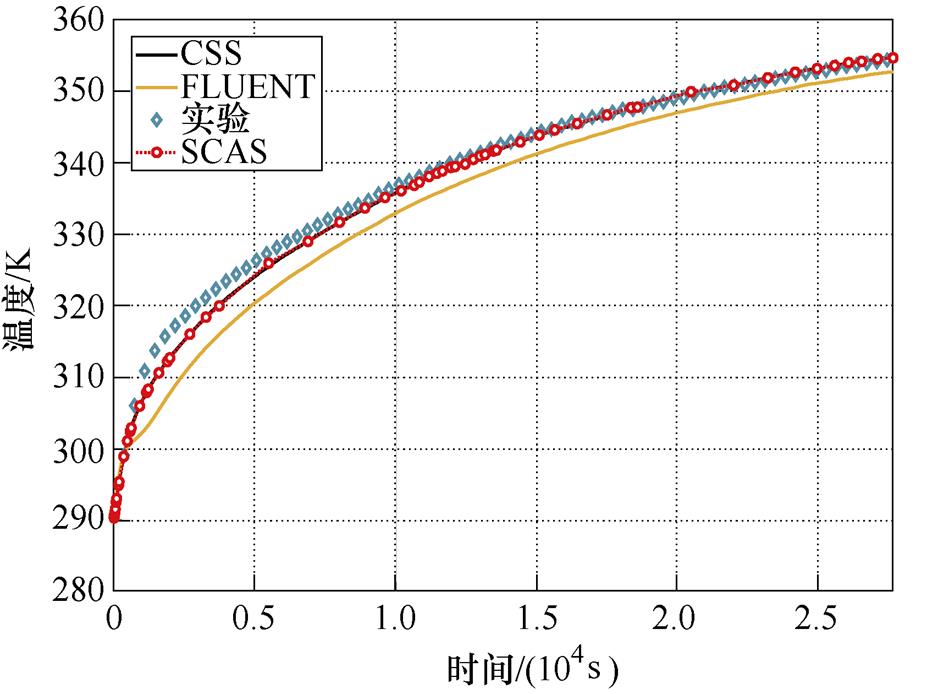
（b）20线饼13测温点
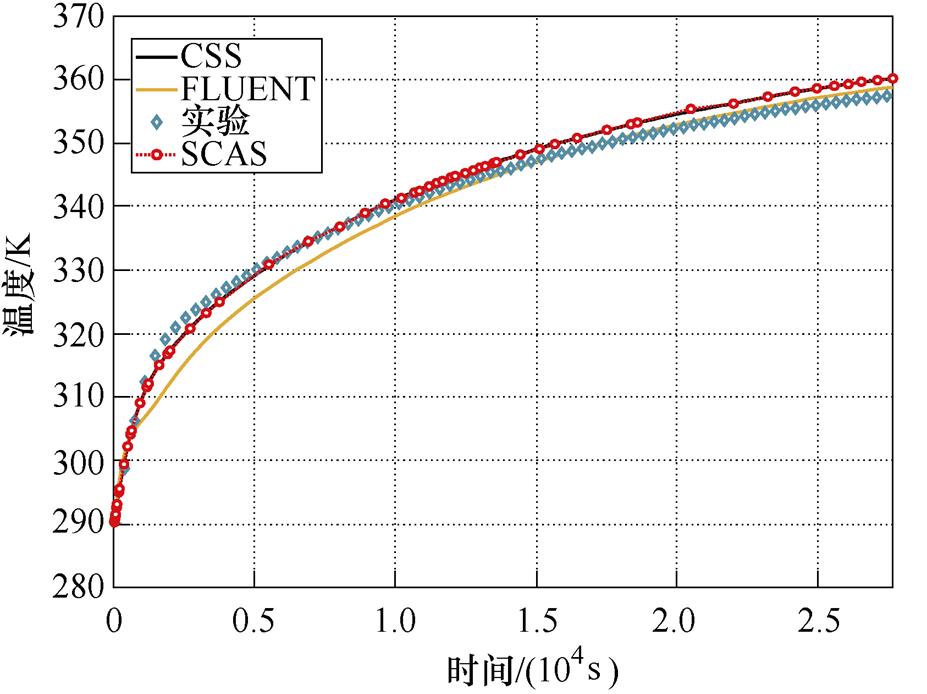
（c）30线饼4测温点
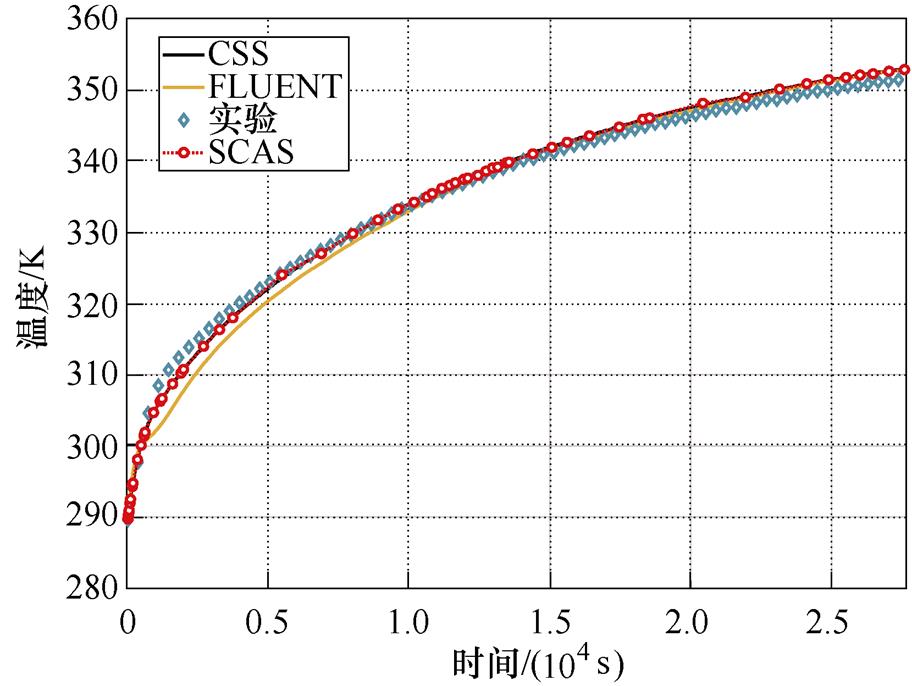
（d）38线饼28测温点
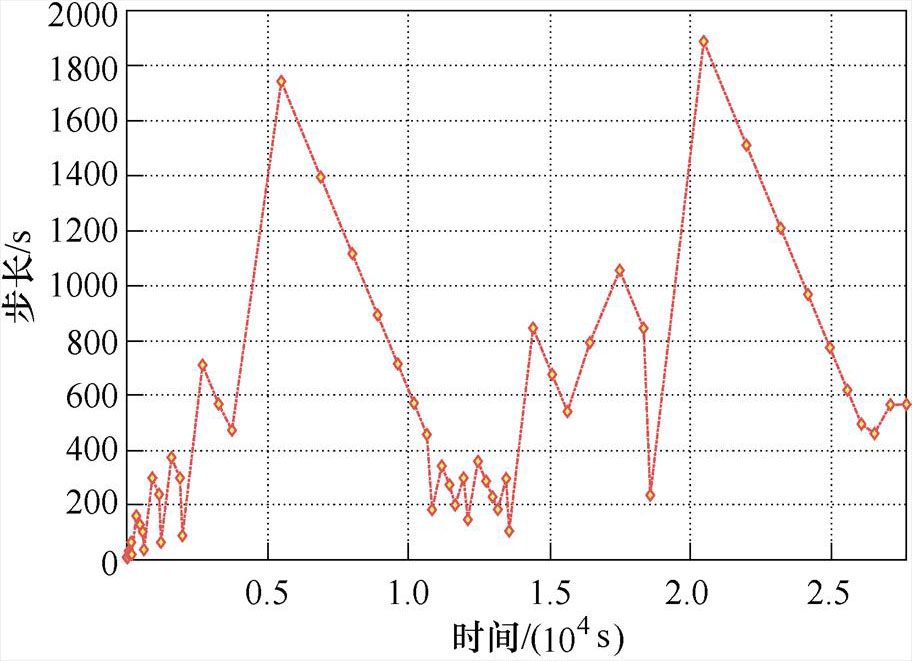
（e）步长变化情况
图13 8个分区绕组温升对比及步长变化
Fig.13 Temperature rise comparison and step size change diagram of eight section winding
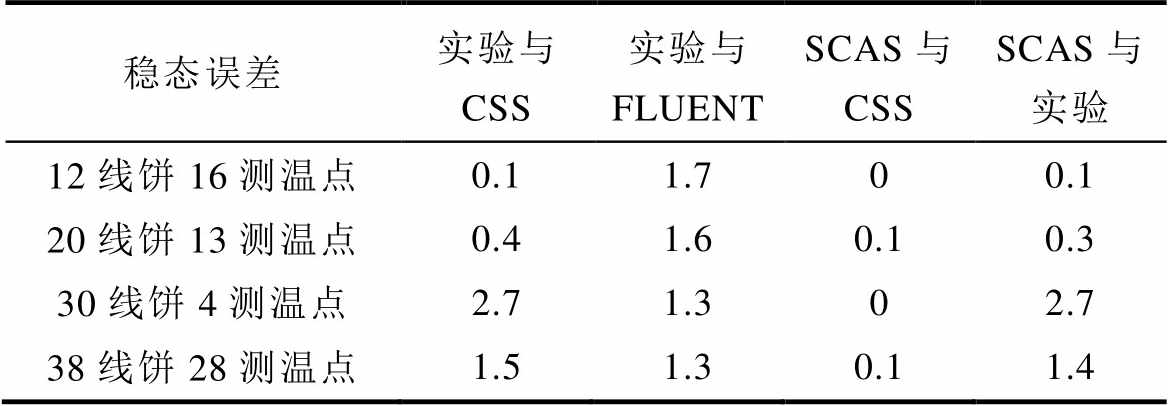
表3 各监测点在不同情况下到达稳态的误差
Tab.3 Error of each monitoring point reaching steady state under different conditions （单位: K）
稳态误差实验与 CSS实验与 FLUENTSCAS与 CSSSCAS与实验 12线饼16测温点0.11.700.1 20线饼13测温点0.41.60.10.3 30线饼4测温点2.71.302.7 38线饼28测温点1.51.30.11.4
由表3可得，温升实验与传统CSS算法的最大稳态误差出现在30线饼4测温点处，为2.7 K；温升实验与仿真软件FLUENT的最大稳态误差出现在12线饼16测温点处，为1.7 K；而传统CSS方法与本文所提SCAS时间匹配算法的最大稳态误差出现在20线饼13测温点，为0.1 K；本文所提SCAS算法与实验的最大稳态误差则出现在30线饼4测温点，为2.7 K，由于温升实验受若干不可控因素的影响，故上述误差均在可以接受的范围之内，因此可进一步验证本文所提SCAS算法的正确性。
从图13d可看出，本文所提算法的步长变化情况。在27 600 s的实验过程中，传统CSS方法每10 s计算一次，共需计算2 760步，计算时间为1 507 676.438 s（418 h），而本文所提SCAS时间匹配算法的计算步数仅为58步，计算时间为33 604 s（9.33 h），本文所提算法的计算时间约为传统算法的1/46，计算步数约为传统的1/47，大大地减少了计算冗余，提高了计算效率。综上所述，结合温升实验可进一步验证本文所提SCAS算法在准确性与高效性两个方面具一定的工程应用价值。
本文提出了基于SCAS的时间匹配算法，从自适应步长调整和耦合点选择两方面对传统的CSS时间匹配算法进行改进，并将其成功应用于二维绕组分匝模型的瞬态流热耦合问题及110 kV变压器绕组温升实验当中，结论如下：
1）通过引入了基于ATS-HTS的混合变步长算法，用合适的实时步长选择策略代替原先整场固定的时间步长。实现了在允许误差下最大的步长选择，计算结果表明，该方法在保证精度的同时能有效减少物理场的计算数，在单分区问题当中，1 000 s的仿真时间下，单分区问题当中流场与温度场的运行时步仅为传统算法的1/10左右，因此将基于ATS- HTS混合变步长算法引入本文所提时间匹配算法中，能够有效减少运行时步数，提高计算效率。
2）基于传统CSS算法及其改进方案，提出了SCAS的时间匹配策略，该算法从自适应步长调整和耦合点选择两个方面，通过选择合适的时间窗在保证多物理场计算精度的同时减少耦合次数，将其应用至本文建立的单分区模型的传热过程当中，结果表明：该方法与传统CSS算法相比，其流场平均相对误差仅为0.25%，温度场平均相对误差仅为0.45%，且算法的耦合次数仅为原先的1/20。因此，该方法能够在限定的精度范围内，较传统方法及其现有改进方案减少更多不必要的计算冗余。
3）为了充分验证本文所提方法的工程应用价值，搭建了110 kV油浸式变压器温升实验平台，采用更贴近工程实际的8个分区传热模型，并对比传统CSS算法、温升实验、FLUENT与SCAS四种方法的计算效果，计算及实验结果表明：在27 600 s的实验时间内，本文选取的4个监测点中，SCAS算法与温升实验的最大稳态误差为2.7 K，在允许的误差范围内，同时SCAS算法较传统CSS算法整体计算效率提升超过46倍，且与其计算误差控制在0.1 K以内，这充分说明了本文所提方法在工程应用领域的正确性和高效性。
参考文献
[1] 谢裕清, 李琳, 宋雅吾, 等. 油浸式电力变压器绕组温升的多物理场耦合计算方法[J]. 中国电机工程学报, 2016, 36(21): 5957-5965, 6040.
Xie Yuqing, Li Lin, Song Yawu, et al. Multi-physical field coupled method for temperature rise of winding in oil-immersed power transformer[J]. Proceedings of the CSEE, 2016, 36(21): 5957-5965, 6040.
[2] 朱涛, 王丰华. 地磁感应电流作用下大型变压器的温升特性计算[J]. 电工技术学报, 2022, 37(8): 1915- 1925.
Zhu Tao, Wang Fenghua. Calculation of temperature rise of large transformer under geomagnetically induced current[J]. Transactions of China Electro- technical Society, 2022, 37(8): 1915-1925.
[3] 程书灿, 赵彦普, 张军飞, 等. 电力设备多物理场仿真技术及软件发展现状[J]. 电力系统自动化, 2022, 46(10): 121-137.
Cheng Shucan, Zhao Yanpu, Zhang Junfei, et al. State of the art of multiphysics simulation technology and software development for power equipment[J]. Auto- mation of Electric Power Systems, 2022, 46(10): 121-137.
[4] 邓永清, 阮江军, 董旭柱, 等. 基于自适应网格控制的10 kV油浸式变压器多物理场仿真计算[J]. 高电压技术, 2022, 48(8): 2924-2933.
Deng Yongqing, Ruan Jiangjun, Dong Xuzhu, et al. Simulation of multi-physical field of 10 kV oil immersed transformer based on adaptive grid con- trol[J]. High Voltage Engineering, 2022, 48(8): 2924-2933.
[5] 武卫革, 杜振斌, 刘刚, 等. 大型油浸式变压器绕组温度场仿真及验证[J]. 华北电力大学学报(自然科学版), 2020, 47(6): 68-74.
Wu Weige, Du Zhenbin, Liu Gang, et al. Simulation and verification of winding temperature field for large oil immersed transformer[J]. Journal of North China Electric Power University (Natural Science Edition), 2020, 47(6): 68-74.
[6] Ruan Jiangjun, Deng Yongqing, Huang Daochun, et al. HST calculation of a 10kV oil-immersed transformer with 3D coupled-field method[J]. IET Electric Power Applications, 2020, 14(5): 921-928.
[7] 唐钊, 刘轩东, 陈铭. 考虑流体动力学的干式变压器热网络模型仿真分析[J]. 电工技术学报, 2022, 37(18): 4777-4787.
Tang Zhao, Liu Xuandong, Chen Ming. Simulation analysis of dry-type transformer thermal network model considering fluid dynamics[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4777- 4787.
[8] 王泽忠, 李明洋, 宣梦真, 等. 单相四柱式变压器直流偏磁下的温升试验及仿真分析[J]. 电工技术学报, 2021, 36(5): 1006-1013.
Wang Zezhong, Li Mingyang, Xuan Mengzhen, et al. Temperature rise test and simulation of single-phase four-column transformer under DC-bias[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(5): 1006-1013.
[9] 刘刚, 王晓晗, 马永强, 等. 基于控制体—迎风有限元法的变压器绕组二维流体场—温度场耦合计算方法研究[J]. 高压电器, 2021, 57(6): 1-9.
Liu Gang, Wang Xiaohan, Ma Yongqiang, et al. Study on coupled calculation method of two dimensional fluid and temperature field of transformer winding based on control volume-upstream FEM[J]. High Voltage Apparatus, 2021, 57(6): 1-9.
[10] 袁发庭, 吕凯, 刘健犇, 等. 基于电磁-热-结构多物理场耦合的铁心电抗器线圈结构优化方法[J]. 电工技术学报, 2022, 37(24): 6431-6441.
Yuan Fating, Lü Kai, Liu Jianben, et al. Coil structures optimization method of iron core reactor based on electromagnetic-thermal-structure multi- physical field coupling[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6431-6441.
[11] 廖才波, 阮江军, 刘超, 等. 油浸式变压器三维电磁-流体-温度场耦合分析方法[J]. 电力自动化设备, 2015, 35(9): 150-155.
Liao Caibo, Ruan Jiangjun, Liu Chao, et al. Com- prehensive analysis of 3-D electromagnetic-fluid- thermal fields of oil-immersed transformer[J]. Electric Power Automation Equipment, 2015, 35(9): 150-155.
[12] 廖才波, 阮江军, 逯怀东, 等. 油浸式变压器二维电磁-流体-温度场耦合分析方法研究[J]. 科学技术与工程, 2014, 14(36): 67-71.
Liao Caibo, Ruan Jiangjun, Lu Huaidong, et al. 2-D coupled electromagnetic-fluid-thermal analysis of oil- immersed transformer[J]. Science Technology and Engineering, 2014, 14(36): 67-71.
[13] 谢裕清. 油浸式电力变压器流场及温度场耦合有限元方法研究[D]. 北京: 华北电力大学, 2017.
[14] Jiang Bonan. The least-squares finite element method: theory and applications in computational fluid dynamicsand electromagnetics[M]. New York: Springer Science & Business Media, 2013.
[15] Liu Gang, Zheng Zhi, Yuan Dongwei, et al. Simu- lation of fluid-thermal field in oil-immersed trans- former winding based on dimensionless least-squares and upwind finite element method[J]. Energies, 2018, 11(9): 2357.
[16] Liu Gang, Rong Shichang, Wu Weige, et al. A two-dimensional transient fluid-thermal coupling method for temperature rising calculation of trans- former winding based on finite element method[J]. AIP Advances, 2020, 10(3): 035325.
[17] 曹龙飞, 范兴纲, 李大伟, 等. 基于快速有限元的永磁电机绕组涡流损耗半解析高效计算[J]. 电工技术学报, 2023, 38(1): 153-165.
Cao Longfei, Fan Xinggang, Li Dawei et al. Semi analytical and efficient calculation method of eddy current loss in windings of permanent magnet machines based on fast finite element method[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 153-165.
[18] 金亮, 李育增, 杨庆新, 等. 大规模工程电磁场的亿自由度可扩展并行计算方法[J]. 电工技术学报, 2022, 37(3): 589-598.
Jin Liang, Li Yuzeng, Yang Qingxin, et al. Extensible parallel computing method with hundreds of millions of freedoms for large-scale engineering electro- magnetic field[J]. Transactions of China Electro- technical Society, 2022, 37(3): 589-598.
[19] Farhat C, Lesoinne M, Maman N. Mixed explicit/ implicit time integration of coupled aeroelastic problems: three-field formulation, geometric conser- vation and distributed solution[J]. International Journal for Numerical Methods in Fluids, 1995, 21(10): 807-835.
[20] Felippa C A, Park K C. Synthesis tools for structural dynamics and partitioned analysis of coupled systems. In: Ibrahimbegovi'c A[M]. Netherlands: Brank B (eds) NATO advanced research workshop. IOS Press, 2004.
[21] 李彬. 先验误差评估时间自适应方法研究及其在饱和砂土地震液化分析中的应用[D]. 大连: 大连理工大学, 2020.
[22] 赵振, 张树有. 自适应步长顺序耦合法及其在瞬态场耦合问题分析中的应用[J]. 计算机集成制造系统, 2011, 17(7): 1404-1414.
Zhao Zhen, Zhang Shuyou. Self-adaptive step sequential- interaction method and its application in transient- fields coupling problems[J]. Computer Integrated Manufacturing Systems, 2011, 17(7): 1404-1414.
[23] Kassiotis C, Ibrahimbegovic A, Niekamp R, et al. Nonlinear fluid-structure interaction problem. part Ⅰ: implicit partitioned algorithm, nonlinear stability proof and validation examples[J]. Computational Mechanics, 2011, 47(3): 305-323.
[24] 张宇娇, 汪振亮, 徐彬昭, 等. 瞬态电磁-温度场耦合计算中自适应时间步长研究[J]. 电工技术学报, 2018, 33(19): 4468-4475.
Zhang Yujiao, Wang Zhenliang, Xu Binzhao, et al. Research on the adaptive time step in transient calculation of coupled electromagnetic and thermal fields[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4468-4475.
[25] 刘刚, 靳立鹏, 胡万君, 等. 基于混合有限元法的油浸式变压器稳态流-热耦合场并行计算方法[J/OL]. 高电压技术, https://doi.org/10.13336/j. 1003-6520.hve. 20221050.
Liu Gang, Jin Lipeng, Hu Wanjun, et al. A parallel method for steady-state fluid-thermal coupling field of oil-immersed transformer based on hybrid finite element method[J/OL]. High Voltage, https://doi.org/ 10.13336/j.1003-6520.hve. 20221050.
[26] Russo A. Streamline-upwind Petrov/Galerkin method (SUPG) vs residual-free bubbles (RFB)[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(13/14/15/16): 1608-1620.
[27] D'Haese C M F, Putti M, Paniconi C, et al. Assessment of adaptive and heuristic time stepping for variably saturated flow[J]. International Journal for Numerical Methods in Fluids, 2007, 53(7): 1173-1193.
Abstract For the time-matching problem of two or more multiple physical fields, the traditional idea generally considers that the physical fields are solved by coupling with fixed equal time steps. This direct coupling algorithm is named conventional serial staggered (CSS), but there are two obvious problems in this time matching method, namely, step size adjustment and coupling point selection. Therefore, this paper proposes a time-matching algorithm based on Sub cyclic adaptive staggered (SCAS).
Firstly, in step size adjustment, the Adaptive Time Stepping algorithm (ATS) is added, and the difference of approximate solutions with different accuracy is used as the basis for time step adjustment. At the same time, for nonlinear problems, the Heuristic time stepping method (HTS) is combined to set the number of iterations as the basis for nonlinear discrimination, which solves the problem that the step size cannot be adjusted in real time under strong nonlinear problems. It can obtain a more appropriate step size each time according to the changing trend of the physical field under the allowable error. The introduction of the ATS-HTS hybrid variable step size method reduces the number of computing time steps greatly.
Secondly, for the problem of coupling point selection, this paper proposes a SCAS time-matching algorithm based on the CSS time-matching algorithm, which uses an adaptive scheme to determine the calculation time window and predetermined coupling points and introduces an exponential smoothing method to ensure its accuracy.
Finally, to verify the effectiveness of the proposed method, a two-dimensional transient single-zone split turn winding model is established. Compared with the traditional CSS algorithm, in terms of accuracy, theaverage relative error of the flow field of the SCAS algorithm is 0.25%, and the average relative error of thetemperature field is 0.45%, which is within the acceptable error range. In terms of efficiency, after combining coupling point selection and step size adaptive selection, the SCAS algorithm has further reduced the number of coupling times and computing time steps, and its overall computing efficiency is nearly 20 times higher than the CSS algorithm.
At the same time, to further illustrate the value of the proposed algorithm in engineering practice, this paper has built a temperature rise experimental platform based on the 110 kV transformer winding model and applied the SCAS time matching algorithm to the heat transfer model. The calculation and experimental results show that the maximum absolute error between the SCAS algorithm and the experiment when reaching the steady state occurs at the temperature measuring point No.4 of the 30-wire cakes, which is 2.7 K, because the temperature rise experiment is affected by several uncontrollable factors. Therefore, the error is within the acceptable range. The computational efficiency of the algorithm proposed in this paper is about 46 times higher than that of the traditional algorithm, and the number of computational steps is about 1/47 of the traditional algorithm, which greatly reduces computational redundancy.
keywords：Sub-cyclic adaptive staggered, mixed variable time step, thermal coupling problem of two dimensional transient flow, fast calculation method, temperature rise experiment
中图分类号：TM411
DOI: 10.19595/j.cnki.1000-6753.tces.222137
国家重点研发计划资助项目（2021YFB2401703）。
收稿日期 2022-11-01
改稿日期 2022-12-28
刘 刚 男，1985年生，副教授，硕士生导师，主要从事电气设备多物理场建模及仿真、电力系统时域仿真和电磁场理论及其应用方面的研究工作。E-mail: liugang_em@163.com（通信作者）
郝世缘 女，1999年生，硕士研究生，主要从事多物理场多时间尺度快速计算方面的研究工作。E-mail: hsyjya@163.com
（编辑 陈 诚）