摘要 电力电缆在远距离大容量电力传输和海上风电并网中起着极其重要的作用。受直流电场影响，交联聚乙烯（XLPE）电缆存在着空间电荷积聚和电荷能量积累现象，导致绝缘材料被击穿而引发故障。该文建立电荷输运与分子链位移击穿模型，对XLPE介质中载流子输运和能量积累过程进行了仿真，得到XLPE特征击穿场强-试样厚度依赖特性以及击穿概率分布。仿真结果表明，XLPE直流击穿场强受尺度效应影响明显，击穿场强随着试样厚度的增加而减少，且击穿强度概率计算结果服从威布尔分布。建立电荷输运随机变量参数分散性与击穿概率分布的定量关系。随着试样厚度的增加，绝缘材料内部的缺陷分散性增加，电荷输运随机变量参数高斯分布中的方差增加，击穿威布尔分布形状参数减小。陷阱能级是影响击穿威布尔分布形状参数的最关键因素。该研究为电力电缆的优化设计和可靠性评估提供了仿真技术支撑。
关键词：交联聚乙烯 空间电荷 威布尔分布 尺度效应 陷阱能级
高压直流输电是智能电网以及未来世界各国能源变革的发展趋势[1]，海上风力发电也是当前国际上发展绿色能源的方式之一[2]。因此，电缆绝缘材料的不断突破和改进是高压直流电缆输电技术发展的基础与重中之重。聚乙烯通过交联得到的交联聚乙烯（Cross-Linked Polyethylene, XLPE）绝缘材料不但保留了原有的优异性能，而且还改善了它的绝缘性和耐热性，现已被广泛运用于城市电力电缆和海底电力电缆[3-4]中。在高压直流电场的长期作用下，绝缘材料中的电荷从电极处被注入到绝缘介质中，容易发生空间电荷积聚[5]，而空间电荷则会使原有电场畸变，使得电场分布更不均匀，进而导致分子链的断裂和自由基的形成、绝缘材料的介电强度发生改变，同时空间电荷会使绝缘材料内部放电而被击穿，这极大地干扰了直流电缆的安全稳定运行[6]。
大多研究学者表明，固体电介质的击穿总是发生在局部缺陷处。基于固体电介质的尺度效应原理，增加试样的厚度或面积将导致其体积增加，局部缺陷概率的增加，从而使得击穿场强降低[7]。Min Daomin等[8-10]建立电荷输运与分子链位移调制（Charge Transport and Molecular Displacement modulated, CTMD）的击穿模型以探究直流电击穿行为。此模型假设当分子链位移达到临界值时介质发生击穿，可以很好地模拟试样击穿的尺度效应，研究表明直流击穿场强与绝缘厚度之间存在逆幂函数关系。通过对比空间电荷调制电击穿（Space Charge modulated Electrical Breakdown, SCEB）模型和CTMD击穿模型，认为电击穿过程会受到电荷输运和分子链位移动力学的双重调制，且分子链位移扩大了自由体积，这是导致绝缘材料直流击穿强度随厚度变化的重要因素。Ma Zhipeng等[11]通过实验证实在直流电场中，随着厚度的增大，击穿强度减小。M. S. Bhutta等[12]利用双极空间电荷输运电击穿（Bipolar Charge Transport, BCT）模型和CTMD模型进行对比研究，证实CTMD击穿模型较BCT模型更接近于实验结果。
弱点击穿理论提出绝缘材料微观缺陷参数随试样厚度的变化关系及其对击穿概率影响的定性关系[13]。但是，尚未建立击穿场强概率分布与微观陷阱等参数的定量关系。蔡姝娆等[14]基于聚丙烯绝缘材料，探究了绝缘介质中电荷输运随机参数与击穿特性的关系，结果表明陷阱能级对威布尔分布影响较大。本文首先探究特征击穿场强-试样厚度依赖特性，进而通过在CTMD模型中引入随机变量，仿真得到交联聚乙烯击穿概率分布，以探究电荷输运随机参数分散性与击穿概率分布的定量关系，为从绝缘材料配方和聚集态结构角度调控陷阱等参数的期望值和方差，为提升击穿性能提供了理论和模型支撑。
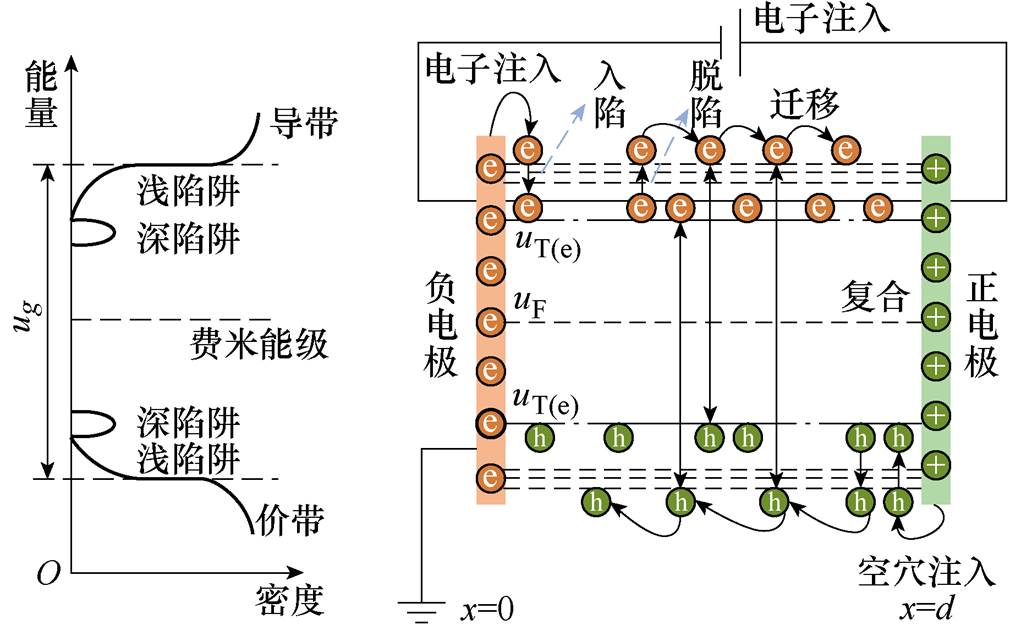
本文采用CTMD击穿模型仿真研究XLPE介质中的载流子输运和能量积累过程。直流场下绝缘介质材料内部的CTMD击穿模型示意图如图1所示[9, 12]，包含电荷注入、电荷迁移、电荷捕获和脱陷、电荷复合、分子链位移等过程[9]。在电荷输运中考虑四种载流子，即自由和捕获电子以及自由和捕获空穴。在绝缘材料两端施加斜坡电压后，电极会向材料内部注入空穴和电子。受电场影响，这些载流子会在绝缘材料内部发生迁移。XLPE中结晶区/无定形区界面、球晶间的界面、以及极性基团会形成深陷阱。深陷阱捕获空穴和电子，引发空间电荷积聚而导致电场发生畸变。同时，陷阱电荷受到库仑力作用，分子链位移会造成自由体积扩大，使得在自由体积运动的电荷能量增大。当电荷能量积累到能跃过陷阱势垒时，局部电流突增，绝缘材料被击穿。本文采用电荷输运与分子链位移调制模型分析这种现象。
模型中x=0和x=d处分别为阴极和阳极（绝缘材料厚度为d），两电极之间设置绝缘材料。在试样两端施加斜坡电压，在t时刻的电压等于绝缘材料中电场对位置的积分，即
（a）电荷输运电击穿
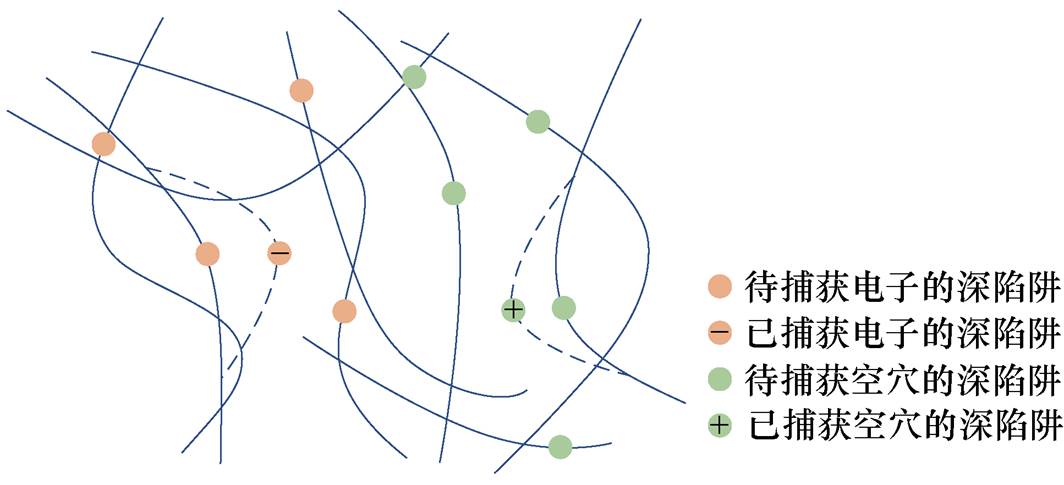
（b）分子链位移
图1 电荷输运和分子链位移电击穿示意图
Fig.1 Schematic diagram of charge transport and molecular chain displacement electrical breakdown
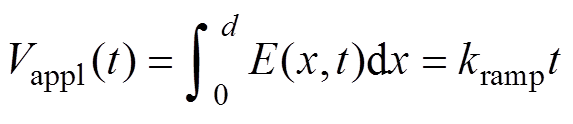（1）
式中，Vappl为施加电压（V）；E为电场强度（V/m）；kramp为升压速率（V/s）。
电荷输运形成的传导电流方程[9]为
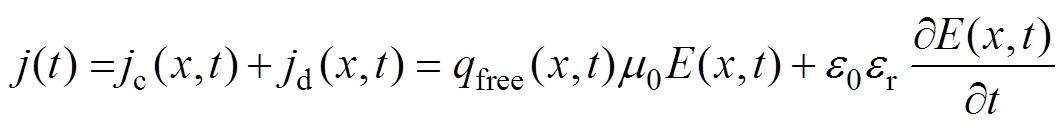（2）
同时，介质材料中的电荷应满足电荷连续性方程为
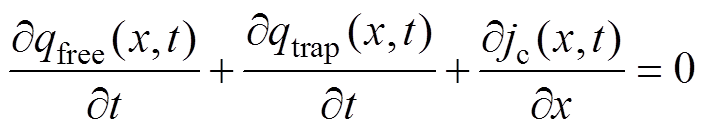（3）
式中，qfree和qtrap分别为自由电荷和捕获电荷的密度（C/m3）；j为总电流密度（A/m2）；jc和jd分别为传导电流密度和位移电流密度（A/m2）；m0为浅陷阱控制的载流子迁移率（m2/V/s）；e0为真空介电常数（F/m）；er为相对介电常数。
在外加电压的作用下，电极向介质材料内部注入电荷，jin(e)和jin(h)分别为阴极注入电子的电流密度和阳极注入空穴的电流密度。本文采用肖特基热发射来描述注入的载流子电荷密度[15]，其表达式为
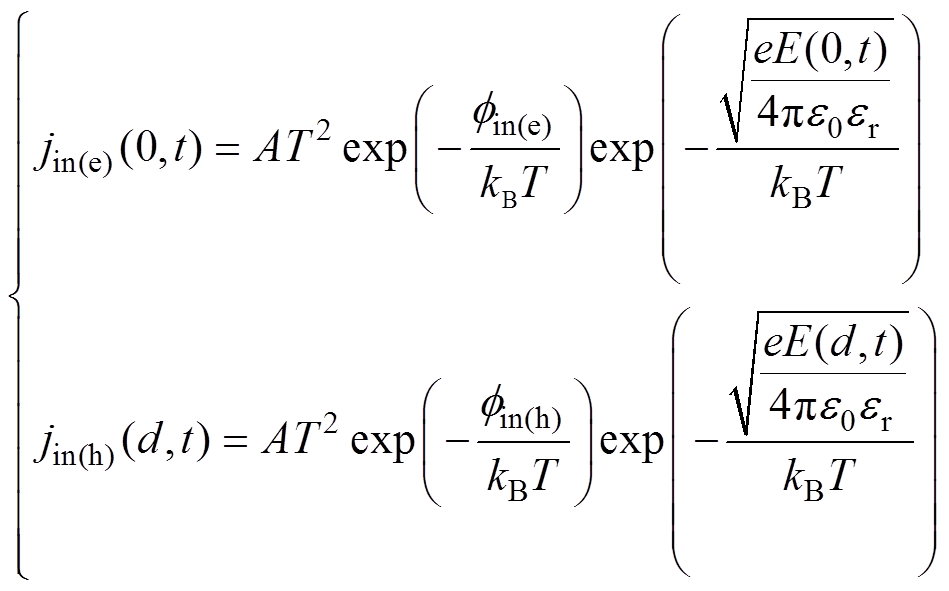（4）
式中，下标“e”表示电子；下标“h”表示空穴；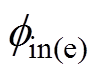
和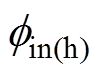
分别为电子和空穴的有效注入势垒（eV）；kB为玻耳兹曼常数；A为Richardson常数，A=1.20×106 A/m2/K2；T为热力学温度（K）。
电荷在迁移的过程中，由于陷阱的强库仑力作用，使其被捕获，陷阱中电荷数量增加。随后，热激发过程会使电荷脱陷，使其继续在介质内部运动。当陷阱中捕获了大量电荷时，会产生空间电荷积聚，从而引起电场畸变。
深陷阱的捕获概率[16]可表示为
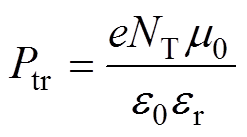（5）
式中，NT为捕获密度（m-3）。
深陷阱释放电荷的概率即电荷逃逸概率[10, 17]可以表示为
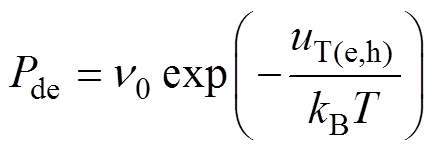（6）
式中，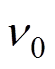
为试图逃逸频率（s-1）；uT(e)和uT(h)为电子和空穴的深陷阱能级（eV）。
根据Shockley-Read-Hall模型[18]和Langevin复合模型[19-20]提出三种情况下的复合模型系数：自由电子与自由空穴的复合系数Rem,hm（m3/C/s）、自由电子与捕获空穴的复合系数Rem,ht（m3/C/s）、捕获电子与自由空穴的复合系数Ret,hm（m3/C/s）分别表示为
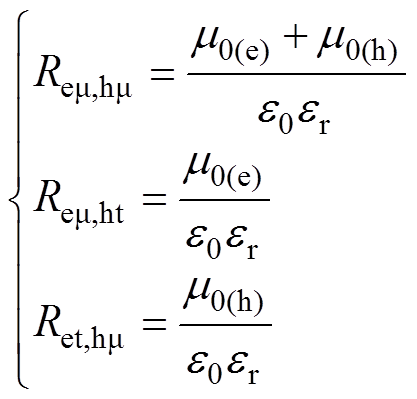（7）
式中，下标“m”表示可移动；下标“t”表示捕获。
在介质中，电荷发生捕获-脱陷-复合的过程[9, 12, 17]满足
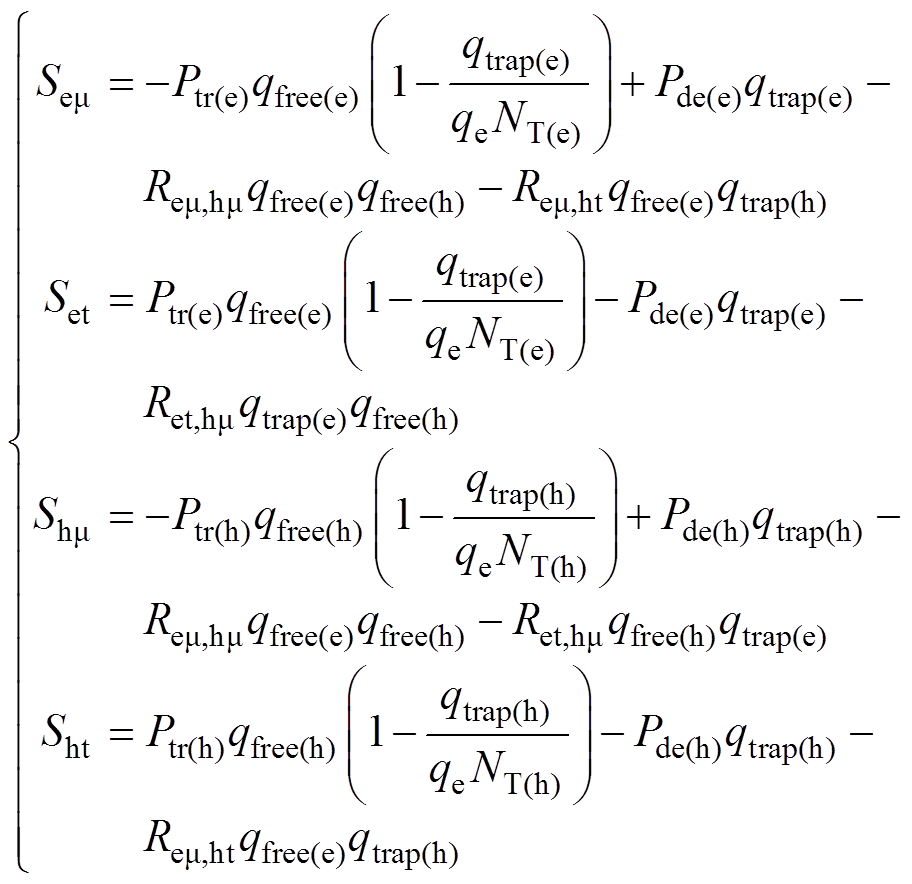（8）
泊松方程表示空间电荷和电位j 的关系[9-10]，即
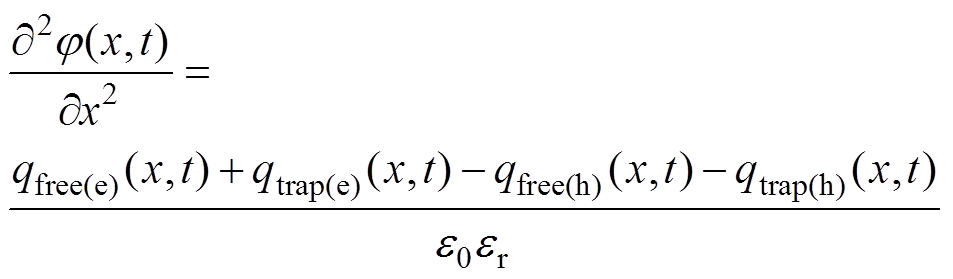（9）
介质内部电场分布可以由电位的负梯度得到，其表达式为
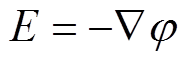（10）
当载流子被陷阱捕获后，由于库仑力的作用，与其相连的分子链移动，导致自由体积扩张，如图1b所示。捕获电子的分子链向阳极方向移动，相应地，捕获空穴的分子链向阴极方向移动。深陷阱对电荷的影响时间长，库仑力作用更强，因此深陷阱对分子链位移影响更大，分子链的运动特征表示为
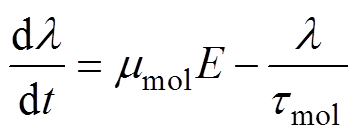（11）
式中，l 为分子链的位移（m）；mmol为分子链的迁移率（m2/V/s）；tmol为分子链的弛豫时间（s）。
采用CTMD击穿模型对50～250 mm厚度的XLPE试样进行仿真。模拟仿真中的温度值为30℃，外加斜坡电压的升压速率为1 kV/s，通过文献查阅并用于模拟的参数值见表1[12]。电荷连续性方程和泊松方程的求解分别运用高阶精度龙格库塔间断伽辽金法和有限元法[9]。
表1 CTMD仿真模型中XLPE的输入参数
Tab.1 Input parameters of XLPE in CTMD simulation model
参 数取 值 温度T/K303 相对介电常数er2.35 电子和空穴的注入势垒/eV1.15 深陷阱密度NT/m-36.23×1020 深陷阱能级uT/eV1.04 载流子迁移率m0/(m2/V/s)3.78×10-14
当分子链位移变化时，自由体积会相应增大，电子在自由体积中获得足够能量umax=(eEl)max超过最大陷阱能级(uT)max=1.04 eV后，导致绝缘介质材料发生击穿。仿真模拟中，将分子链位移值设为介质材料的击穿判定条件。
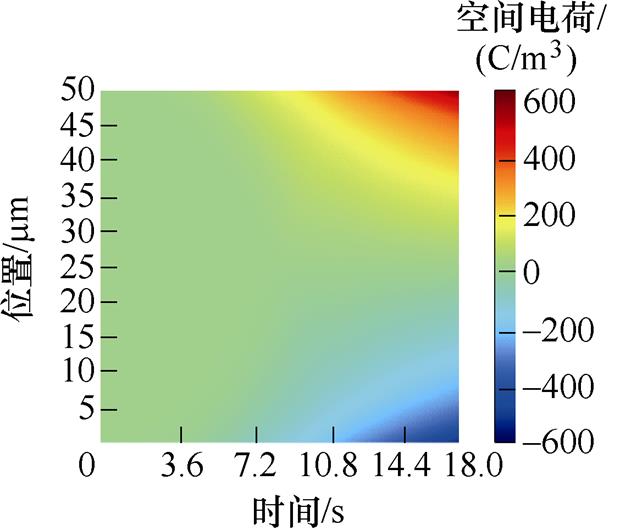
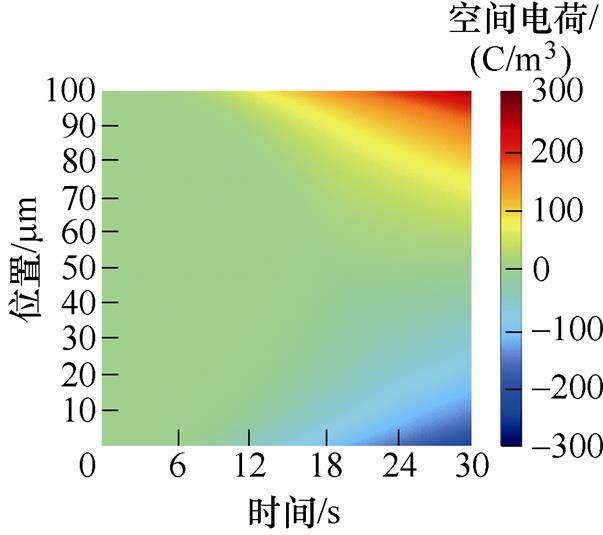
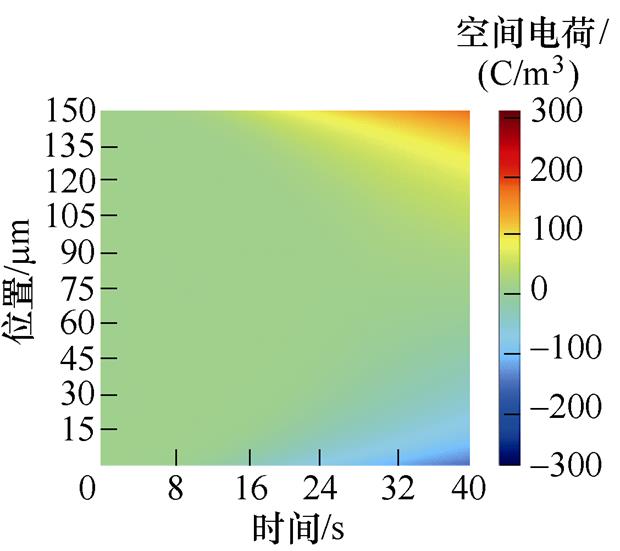
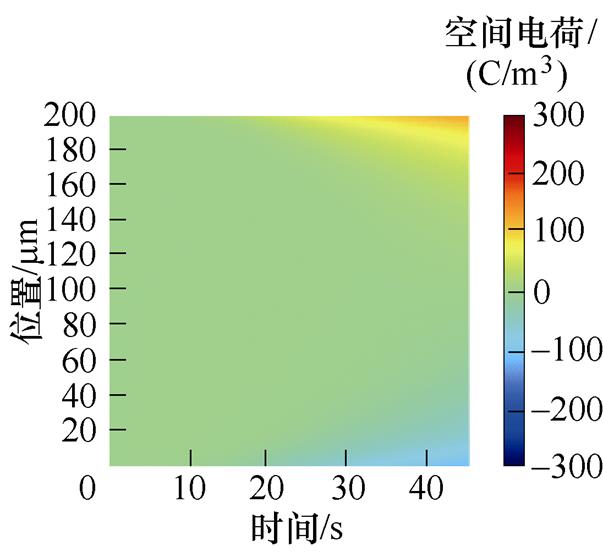
外施强电场作用下，由电极注入的电子向阳极方向运动，电极注入的空穴向阴极方向移动，从而在电极附近发生积聚，形成了空间电荷。XLPE试样空间电荷分布如图2所示。
图2a～图2e为50～250 mm厚度XLPE试样的空间电荷分布，不同颜色对应某刻某处的空间电荷密度分布情况，直到试样击穿后停止。不同厚度的空间电荷密度分布呈相同的规律。随着测试电压的逐渐增加，电荷密度呈明显的增长趋势，而从界面到中间位置处空间电荷的积累量逐渐减少。随着厚度增加，各试样击穿前界面处的空间电荷密度逐渐减小。在同一电场强度下，50 mm厚度试样施加电压10 s时刻，界面处聚集的空间电荷密度为180.04 C/m3；100 mm厚度试样施加电压20 s时刻，界面处聚集的空间电荷密度为150.87 C/m3；150 mm厚度试样施加电压30 s时刻，界面处聚集的空间电荷密度为118.58 C/m3；200 mm厚度试样施加40 s时刻，界面处聚集的空间电荷密度为112 C/m3；250 mm厚度试样施加50 s时刻，界面处聚集的空间电荷密度为103.19 C/m3。
（a）50 mm XLPE试样
（b）100 mm XLPE试样
（c）150 mm XLPE试样
（d）200 mm XLPE试样
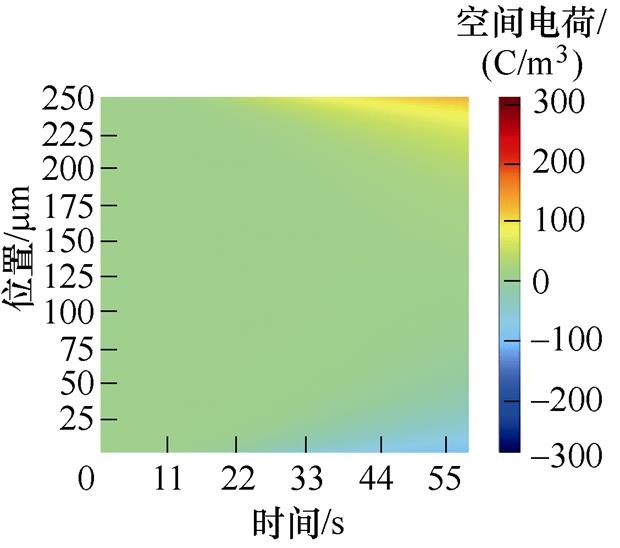
（e）250 mm XLPE试样
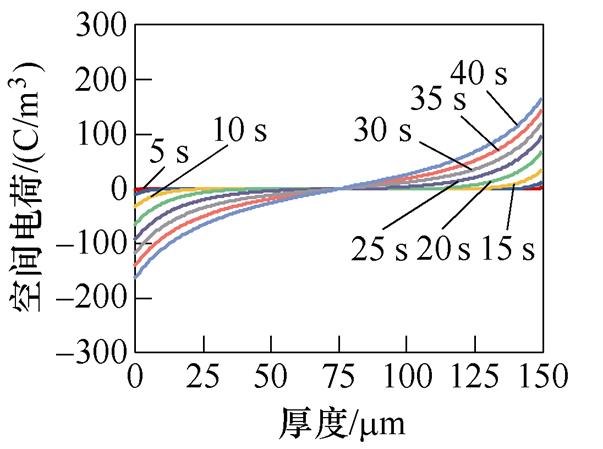
（f）150 mm厚度XLPE试样时间空间电荷分布
图2 XLPE试样空间电荷分布
Fig.2 Space charge distribution diagram of XLPE sample
图2f为150 mm厚度XLPE试样在5～40 s内电荷密度分布。从图中可以更清晰地发现上述空间电荷变化规律。对于150 mm厚度XLPE试样，前10 s时间里施加的电场还未达到电荷注入的临界值，注入电荷并不明显；之后，注入电荷量有明显的增加趋势。注入的电子和空穴在迁移过程中逐步被深陷阱捕获，当电子和空穴在试样内部相遇后会发生复合，导致电子和空穴在电极附近积聚多，试样中间积聚少。
电荷从电极注入的速度比穿过介质的速度快是在介质体中积累空间电荷的重要条件。在这种情况下，电荷捕获能力强于电荷脱陷能力。大多数从电极中射出的电荷都会被捕获，并在界面附近形成一个捕获电荷层。捕获的电荷层会形成一个相反的电场，从而削弱了界面周围的电场强度。因此，需要更高的电场强度来克服这种削弱效应以超过电荷注入势垒。这种弱化效应会影响电荷迁移和积累的过程。同时，在捕获电荷层中积累的均匀电荷增加了介质体中的电场强度[11]。
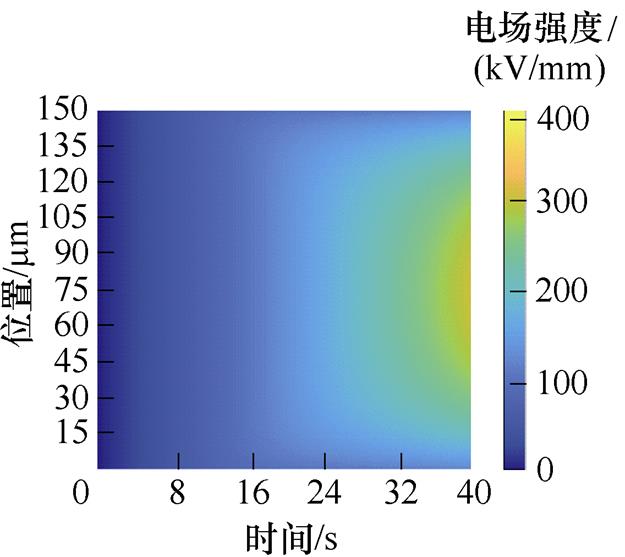
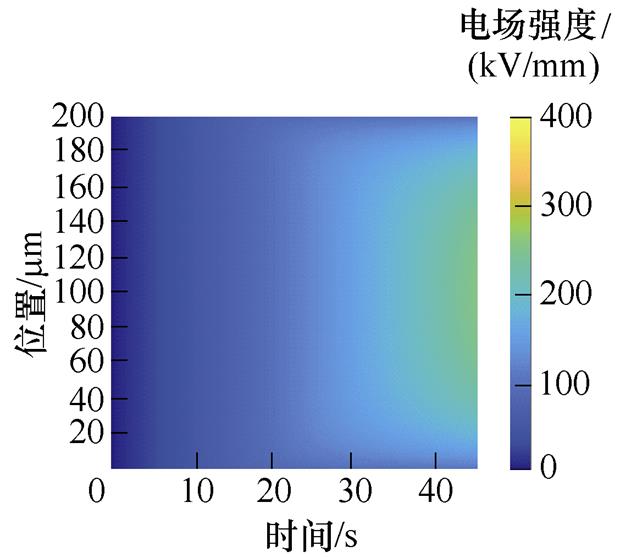
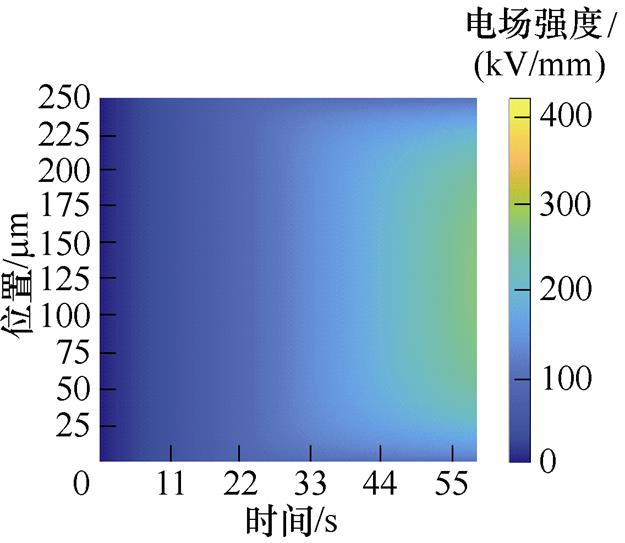
电荷在迁移的过程中，由于受到陷阱的强库仑力影响，电荷被捕获，陷阱中电荷数量增加。陷阱电荷会从热库中通过声子-电子相互作用而积聚能量，这个热激发过程会导致电荷脱陷，脱陷的电荷继续在介质内部运动。当陷阱中积聚大量的电荷时，会产生空间电荷，从而引起电场畸变。如图3a～图3e所示，为50～250 mm不同厚度XLPE试样的局部电场强度分布。对比不同厚度的XLPE试样，随着厚度增加，各试样击穿前，电极/绝缘材料界面处的电场强度呈减少的变化趋势。对于50 mm XLPE试样，前5 s内没有明显的空间电荷积聚，因此电场畸变不明显。随着施加电压的升高，试样的畸变电场强度不断增大。
局部电场强度的分布与空间电荷密度的分布规律情况是相反的，即在界面处电场强度较小，在中间位置处电场强度较大。如150 mm厚度的XLPE试样，如图3f所示，当施加电压5 s后，在界面处的电场强度为33.19 kV/mm；当施加电压10 s后，在界面处的电场强度为64.92 kV/mm；在试样被击穿前，当施加电压40 s后，在界面处的电场强度为128.17 kV/mm；而在中间位置25 mm处的电场强度为321.51 kV/mm。可通过泊松方程来说明，在界面处积累的空间电荷会形成一个与外加电场方向反向的电场，从而减弱界面处的电场强度，增强介质内部的电场强度。
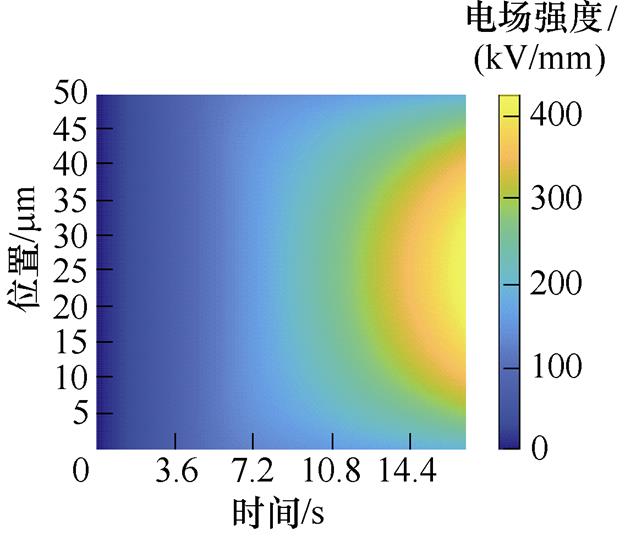
（a）50 mm XLPE试样
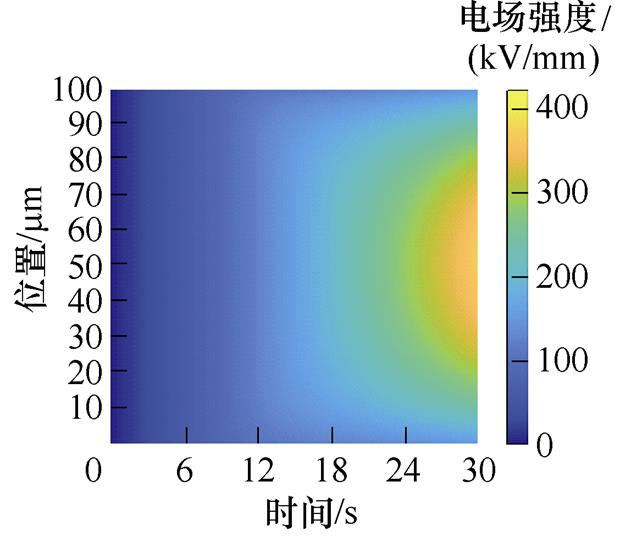
（b）100 mm XLPE试样
（c）150 mm XLPE试样
（d）200 mm XLPE试样
（e）250 mm XLPE试样
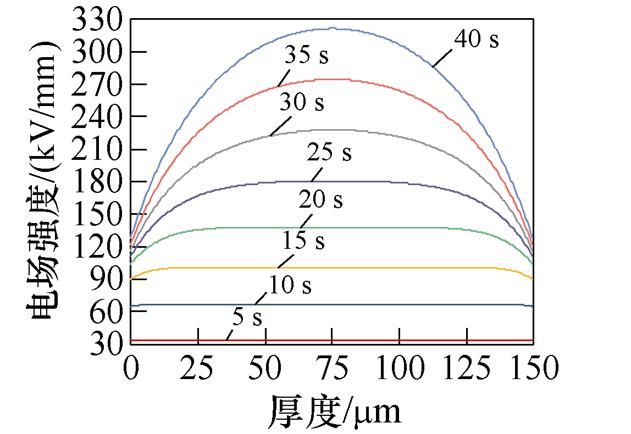
（f）150 mm厚度XLPE试样时间电场强度分布
图3 XLPE试样电场强度分布
Fig.3 Electric field intensity distribution of XLPE sample
当载流子被陷阱捕获后，由于库仑力作用，与其相连的分子链发生移动，使其自由体积扩张。捕获电子的分子链向阳极方向移动，而捕获空穴的分子链向阴极方向移动。XLPE试样分子链位移分布如图4所示。
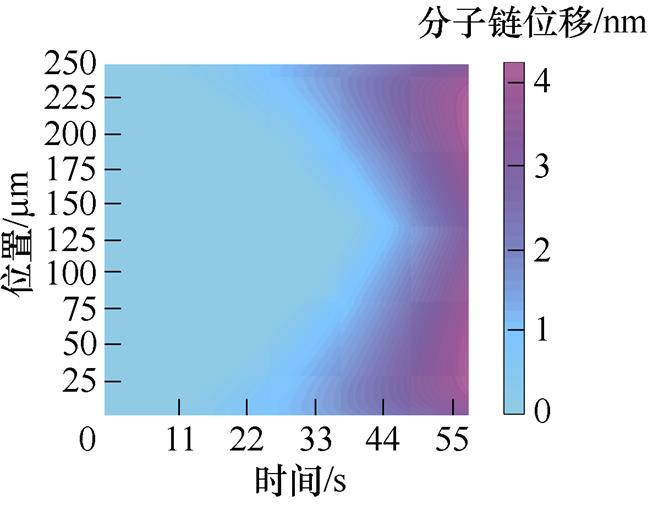
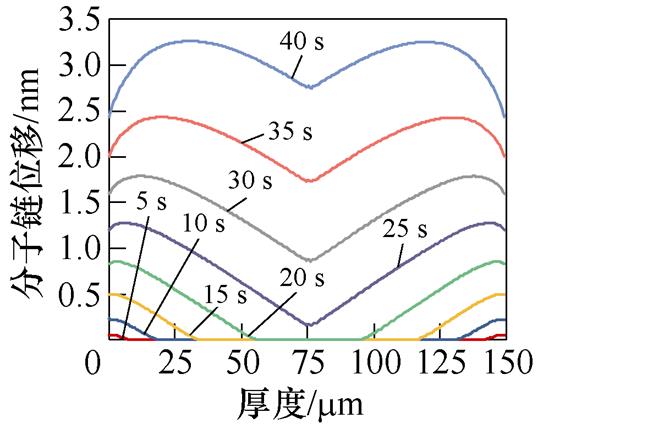
图4a～图4e为50～250 mm不同厚度XLPE试样分子链位移分布。从图中可以看出，分子链位移随着试样厚度的增加而增加。图4f为150 mm厚度的XLPE试样的分子链位移变化，随着施加电压的升高，分子链位移逐渐增加，且分子链位移两端和中间部分都较小，变化趋势关于中间部分对称。对于150 mm厚度试样，分子链位移最大值出现在30 mm和120 mm厚度处。这是因为受电场畸变的影响，分子链位移变化趋势与电场分布变化相同，而中间部分分子链位移较小是由于正、负电荷在此相遇后中和的结果。
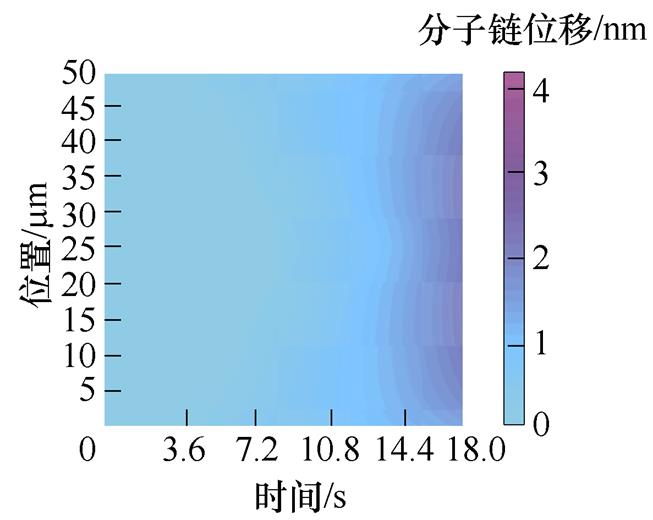
（a）50 mm XLPE试样
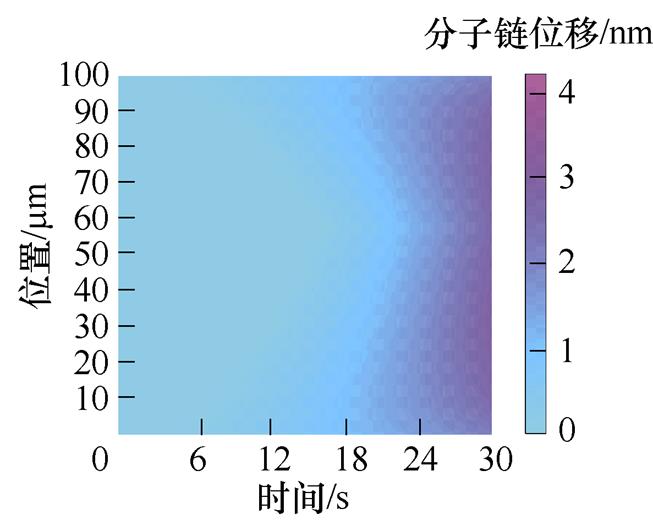
（b）100 mm XLPE试样
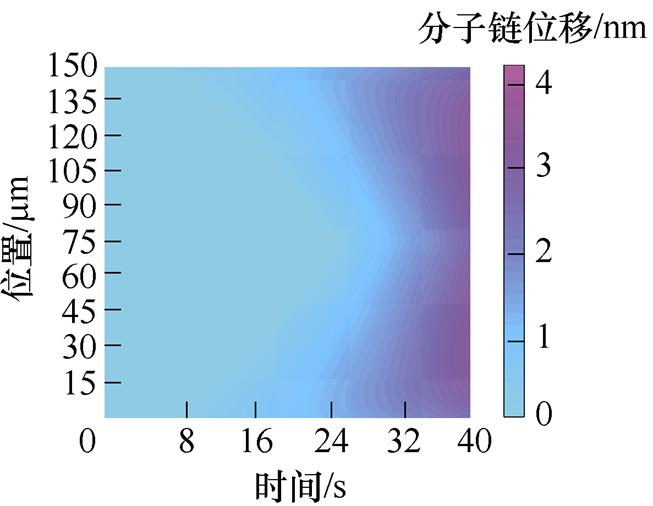
（c）150 mm XLPE试样
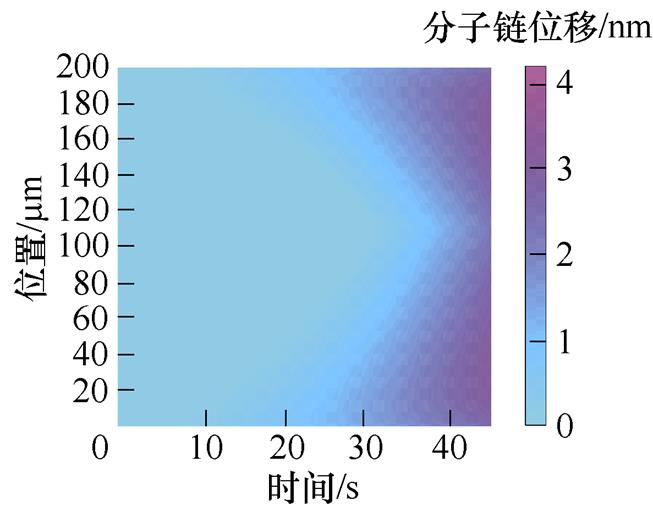
（d）200 mm XLPE试样
（e）250 mm XLPE试样
（f）150 mm厚度XLPE试样时间分子链位移分布
图4 XLPE试样分子链位移分布
Fig.4 Distribution map of molecular chain displacement of XLPE sample
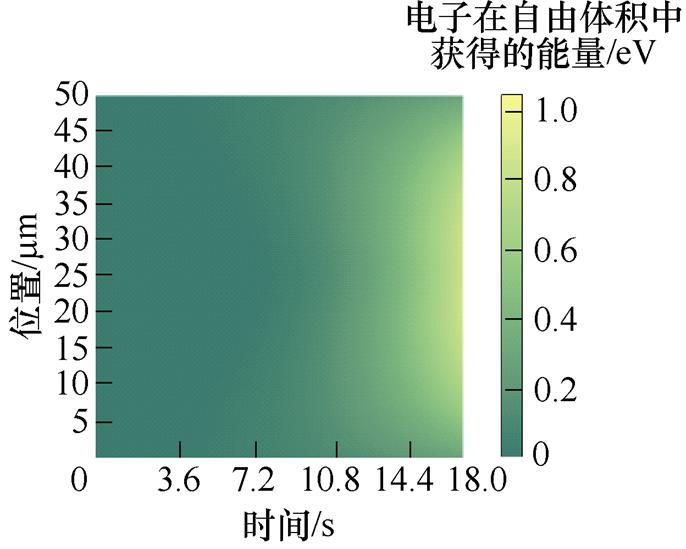
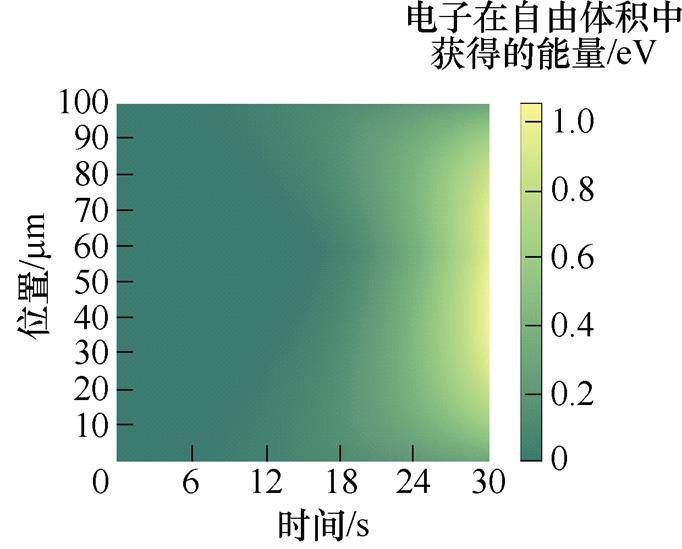
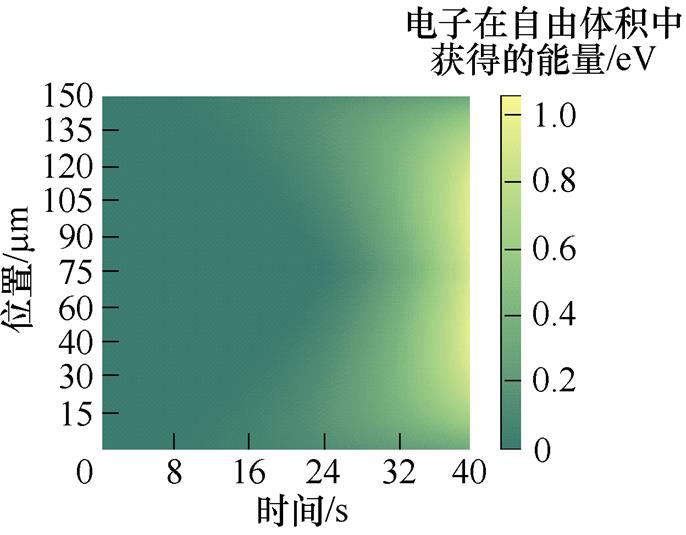
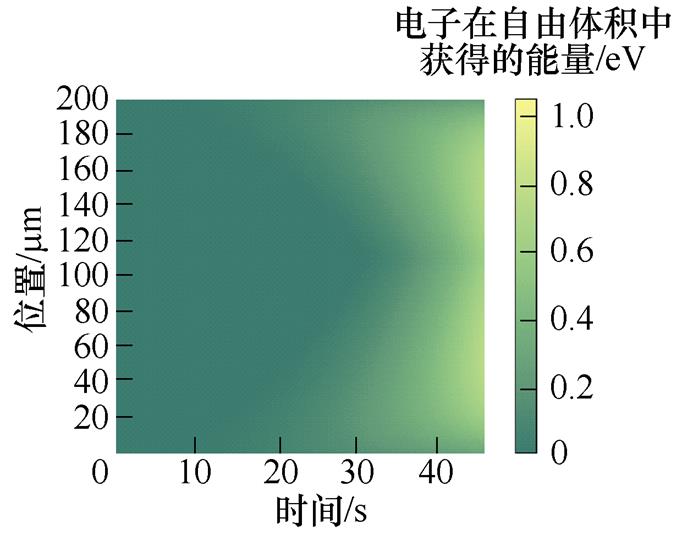
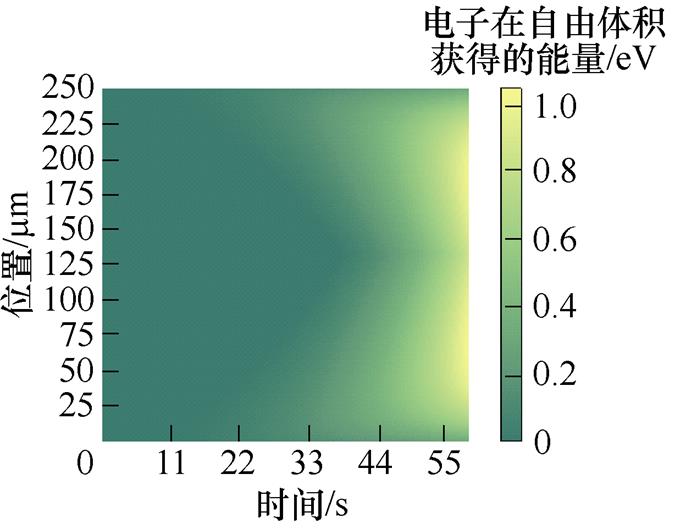
图5a～图5e为50～250 mm不同厚度XLPE试样的电子获得的能量分布。不同厚度试样的电子获得能量大小具有相似的增加趋势。由界面处到试样的中间部分，电子在自由体积中获得的能量呈先增加后减少的趋势。
图5f为XLPE试样电子获得最大能量分布。电子获得能量随时间逐渐增加，且当电子获得的能量达到1.04 eV左右时，电荷能量足以跃过陷阱势垒，导致试样被击穿。如50 mm的XLPE试样，载流子在16～18 s迅速积累能量，这是空间电荷在此积聚后形成电场畸变，局部电场强度增大、自由体积迅速扩张造成的。直至18.61 s，载流子积累足够能量跃过陷阱势垒，使得电荷脱陷并自由运动，从而引起局部电流密度和局部温度的急剧上升，而自由移动的载流子则会与高分子材料的晶格发生剧烈碰撞导致电离，并破坏高分子聚合物的化学键，最终导致介质材料被击穿[14]。
（a）50 mm XLPE试样
（b）100 mm XLPE试样
（c）150 mm XLPE试样
（d）200 mm XLPE试样
（e）250 mm XLPE试样
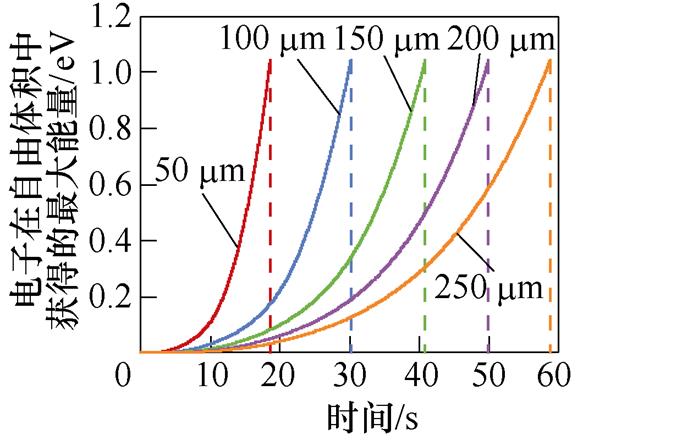
（f）XLPE试样电子获得的最大能量分布
图5 XLPE试样电子获得的能量分布
Fig.5 Energy distribution diagram obtained by electrons of XLPE samples
由于绝缘材料的非均匀性，一般用统计的方法来描述工程中实际材料击穿规律的理论，即弱点击穿理论[21]。弱点击穿理论认为，在均匀或非均匀的电场中，非均匀的固体介质击穿实际上是由材料的弱点击穿导致的。在绝缘材料的制造运输过程中，不可避免地存在一些杂质，这些杂质缺陷会导致电子或空穴受到外部电场的影响而被捕获，从而形成空间电荷积聚和电荷共域的现象。当两个缺陷的位置距离足够近、电场强度足够高时，这些电荷共域就会产生重叠，使击穿放电的路径扩大，更易于发生介质击穿[22]。一般认为这些杂质缺陷是等密度分布的，即厚试样中的缺陷密度会大于薄试样中的缺陷密度。因此，厚试样的击穿强度会明显低于薄试样。
绝缘材料中陷阱能级、陷阱密度、电荷注入势垒和载流子迁移率等参数均呈现一定规律的分布，因此在CTMD击穿模型中引入了电荷输运随机变量来表示陷阱能级、陷阱密度、电荷注入势垒和载流子迁移率等参数的分散性。当把电荷输运随机变量设置为高斯分布时，仿真得到的击穿场强概率分布服从威布尔分布。通过改变电荷输运随机变量的方差，可以调控击穿威布尔分布的形状参数，分析得到陷阱能级、陷阱密度、电荷注入势垒和载流子迁移率等参数高斯分布中的方差随试样厚度的变化关系。
双参数威布尔分布在电介质击穿性能分析中被广泛运用，因此采用其来拟合分析XLPE介质击穿强度的计算结果，定义[14]为
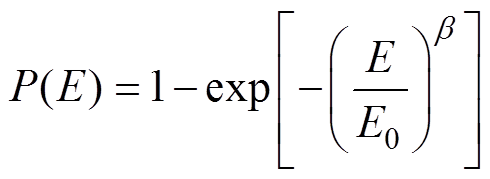（12）
式中，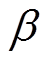
为形状分布参数，反应介质材料内部的均匀性；
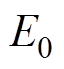为对应于63.2%的击穿概率的特征击穿强度，反映绝缘介质材料的电击穿性能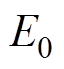，越大，材料绝缘性能越好。
采用厚度为150 mm的XLPE试样，如图6所示为与陷阱特性相关的4个电荷输运随机变量方差不同时得到的击穿场强计算结果威布尔分布，图中s 为高斯分布的方差。
图6a中，当陷阱能级的s 分别为0.000 1、0.001、0.005、0.008、0.01时，威布尔形状分布参数分别为484.52、84.09、21.01、11.13、8.42。图6b中，当陷阱密度s 分别为0.000 1、0.001、0.005、0.01、0.05、0.1时，威布尔形状分布参数分别为41 930.30、3 591.06、982.33、377.95、59.27、30.60。可以发现，陷阱能级和陷阱密度为符合高斯分布的随机变量时，得到的击穿场强是符合威布尔分布的。方差增大，击穿场强数据的分散性变大，形状参数减小。
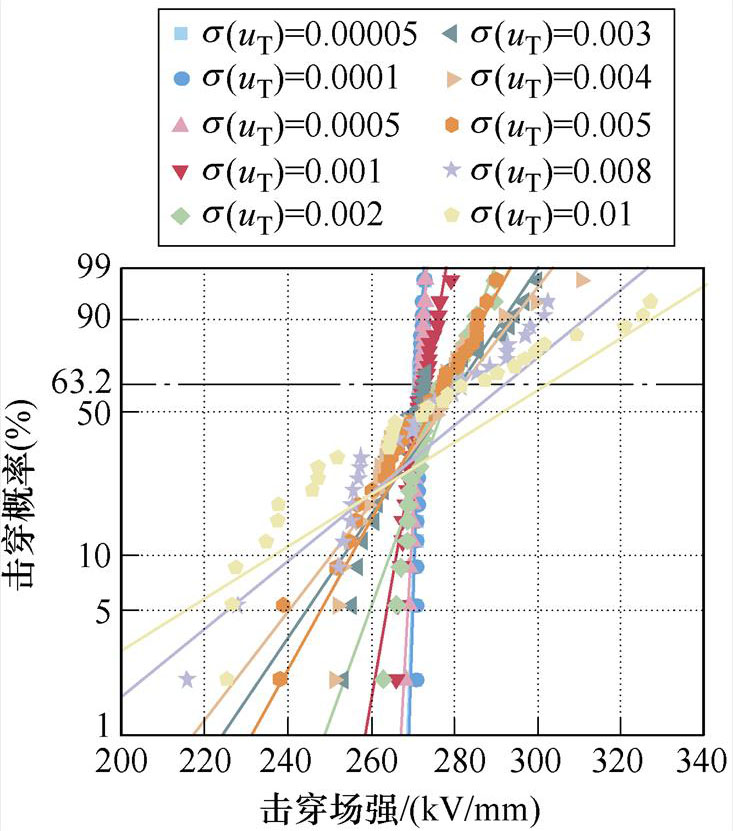
（a）陷阱能级方差不同
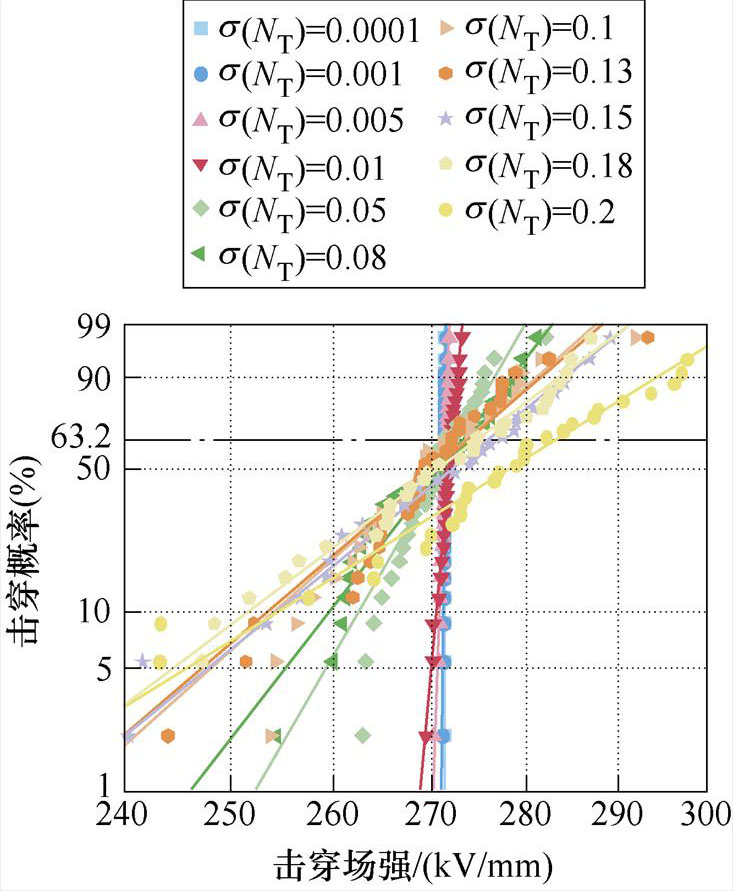
（b）陷阱密度方差不同
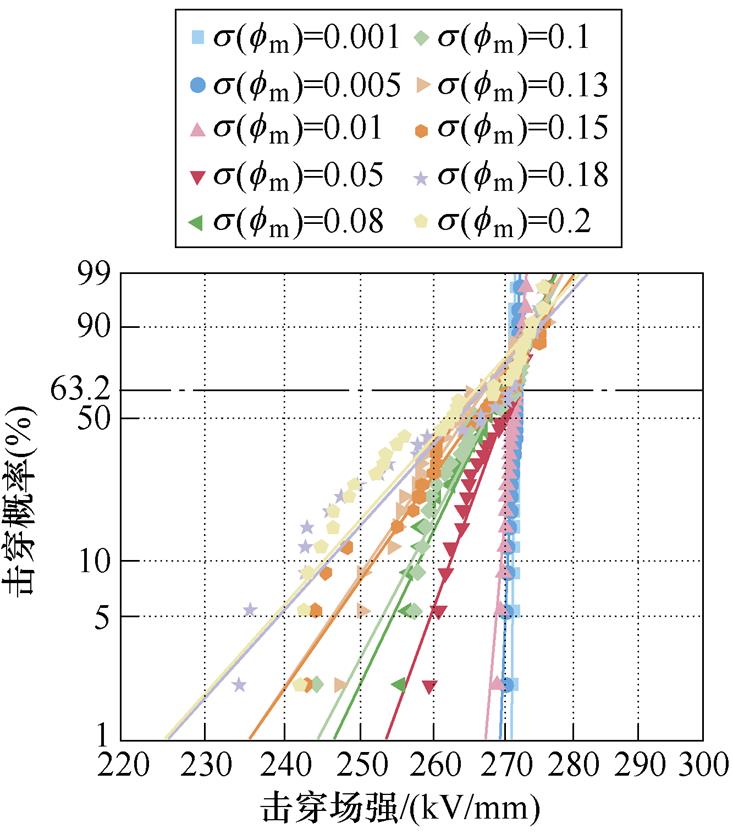
（c）电荷注入势垒方差不同
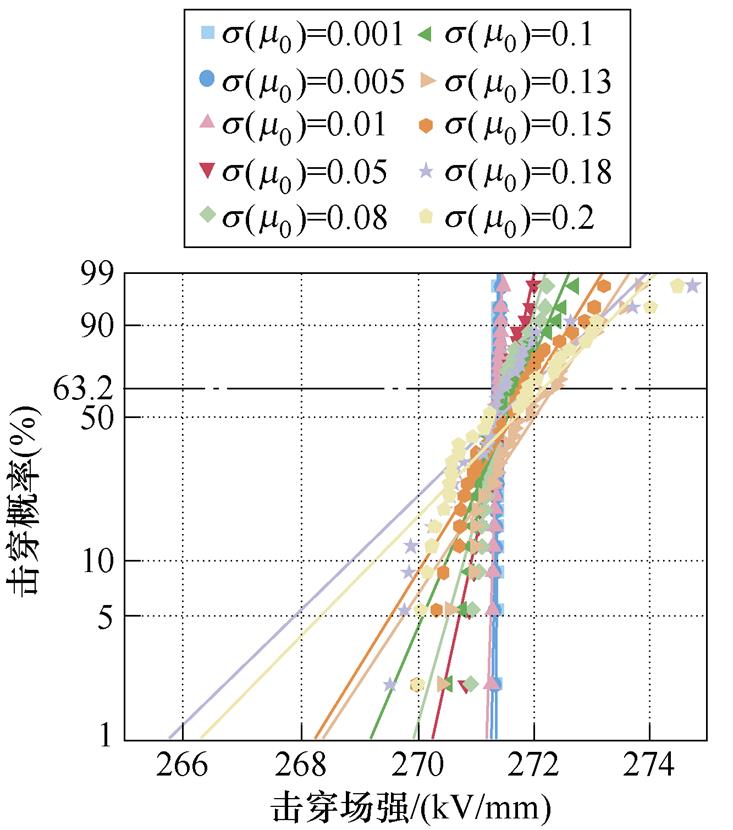
（d）载流子迁移率方差不同
图6 不同电荷输运随机变量方差条件下的击穿威布尔分布
Fig.6 Variance conditions for different charge transport random variables Breakdown Weibull distribution
图6c中，当电荷注入势垒的s 分别为0.001、0.005、0.01、0.05、0.1时，威布尔形状分布参数分别为2 667.91、577.04、278.28、68.35、46.57。图6d中，当载流子迁移率的s 分别为0.001、0.005、0.01、0.05、0.1时，威布尔形状分布参数分别为45 842.92、10 842.29、6 248.82、958.08、485.52。结果表明，电荷注入势垒与载流子迁移率符合高斯分布的随机变量时，得到的击穿场强同样是符合威布尔分布的，且分布规律同陷阱能级和陷阱密度相似。
如图7所示为威布尔形状分布参数和威布尔特征击穿场强与电荷输运随机变量的方差关系。从图7a中可以看出，形状分布参数变化值随陷阱能级方差变化速度最快。当s 较小时，随着s 增加，形状分布参数迅速减小，而在s＞0.05时形状分布参数逐渐变得平缓。陷阱能级的s 值最小，因此说明基于此模型，威布尔分布受陷阱能级的影响最强，受陷阱密度、注入势垒、载流子迁移率的影响较弱，陷阱能级是影响击穿威布尔分布形状参数的最关键因素。绘制如图7b所示的威布尔特征击穿场强与电荷输运随机变量的方差关系。由图7b可知，随着方差的增大，特征击穿场强会受仿真数据的随机性影响而上下波动变化，其最小值为265.68 kV/mm，最大值为289.61 kV/mm，仿真结果285.63 kV/mm介于两者之间。这表明，所建立的CTMD击穿模型能够有效地模拟XLPE介质的直流击穿威布尔分布，最终得到较为准确的结果。
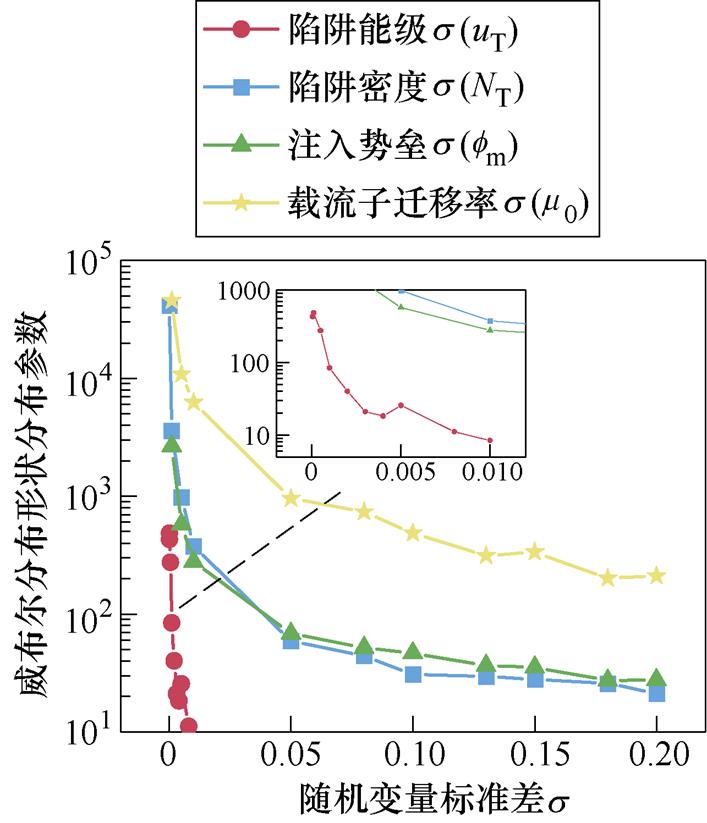
（a）威布尔形状分布参数与电荷输运随机变量的方差关系
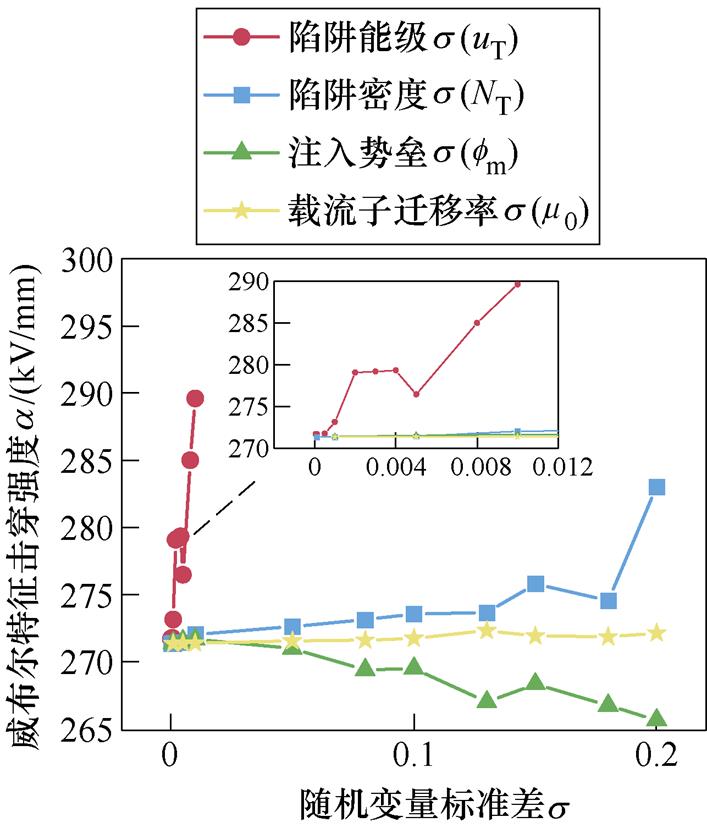
（b）威布尔特征击穿场强与电荷输运随机变量的方差关系
图7 威布尔形状分布参数和特征击穿场强与电荷输运随机变量的方差关系
Fig.7 Variance plot of Weibull shape distribution parameters and characteristic breakdown field strength versus charge transport random variable
通过调节四种电荷输运随机变量的方差探究得到不同厚度XLPE的击穿概率分布结果如图8所示。从图中可以看到，随着XLPE厚度的增加，拟合曲线呈向左移动的趋势，即击穿场强逐渐降低。击穿概率为63.2%的击穿场强大小也逐渐减小，这种现象可以通过空间电荷影响XLPE介质击穿场强这一事实来解释。随着电荷输运随机变量高斯分布中的方差增加，击穿威布尔分布的形状参数逐渐变小。厚度为50～250 mm的XLPE介质，陷阱能级方差分别为0.01、0.016 5、0.016 9、0.017、0.017 5；陷阱密度方差分别为0.1、0.1、0.15、0.15、0.15；电荷注入势垒方差分别为0、0.01、0.01、0.01、0.2；载流子迁移率方差分别为0、0、0、0、0.2；威布尔形状分布参数分别为10.12、5.76、5.49、5.36、4.34。结果表明，随着厚度的增大，形状分布参数β呈减小的趋势，这说明随着厚度的增大，直流击穿场强的分散性逐渐增大。
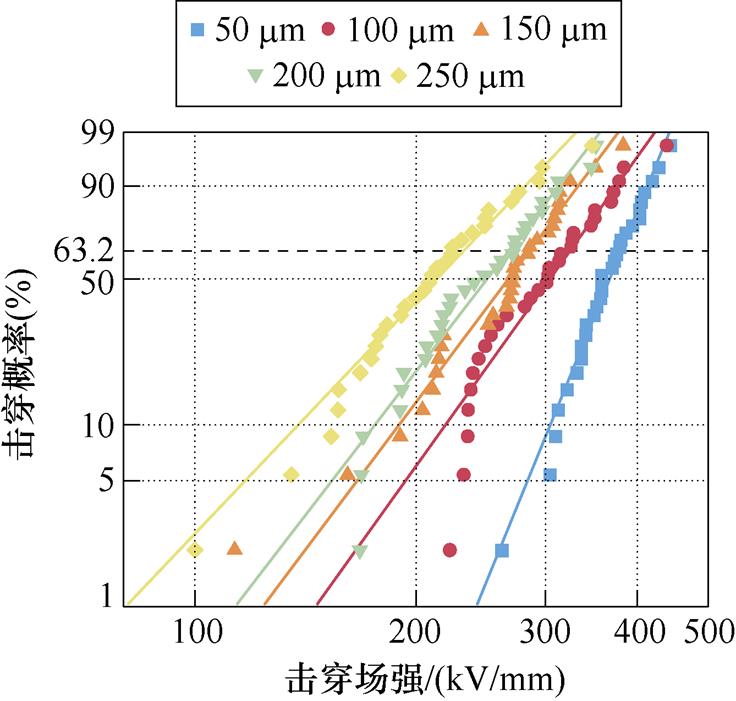
图8 不同厚度XLPE试样威布尔分布结果
Fig.8 Weibull distribution of XLPE samples with different thicknesses
分子链位移和击穿场强变化关系如图9所示。由图9可以观察到，分子链位移随着试样厚度增加而增加，而击穿场强随着试样厚度的增加而降低。当分子链位移不是很大时，方程式（11）可以简化成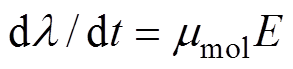
。忽略空间电荷积聚导致的电场畸变，可以设置初始条件为
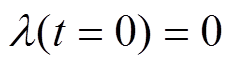，得到更简洁的形式
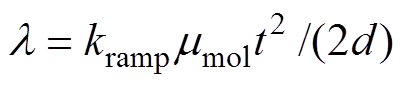，即分子链位移与试样厚度的倒数及时间的二次方成正比[12]。时间二次方的变化速度大于厚度的变化速度，因此，分子链位移或自由体积大小随着试样的厚度增加而增加，特征击穿场强随着试样厚度增大而减小。
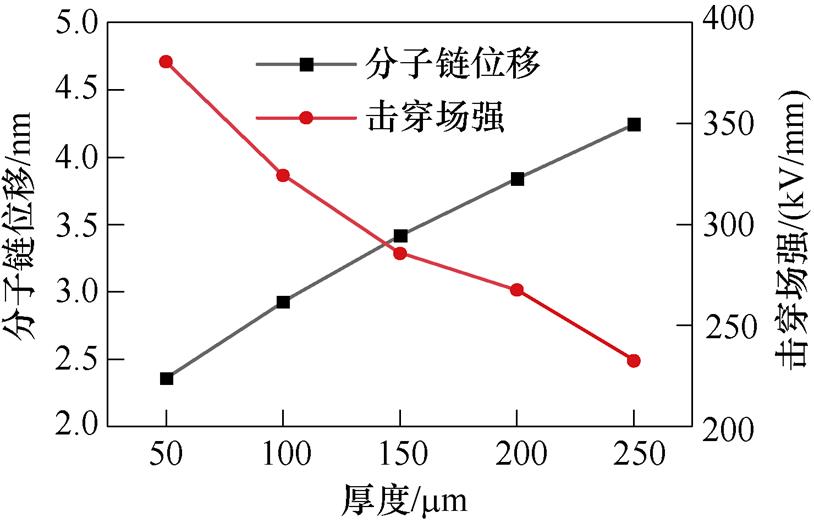
图9 分子链位移和击穿场强变化关系
Fig.9 The relationship between molecular chain displacement and breakdown field strength change
陷阱特性对电荷行为的调节和空间电荷对场强的影响是一致的。被捕获的电荷层可以调节电荷注入、迁移和积累的过程，如图1a所示。陷阱密度越大，容纳空间电荷的能力越强；陷阱深度越大，空间电荷在绝缘材料中的时间越长。而陷阱密度和陷阱深度通过调节电荷的积累深度，来影响被捕获的电荷层密度。
进一步通过仿真模型给出验证：仿真试样使用50 mm XLPE的其他参数，更改陷阱能级参数，得到击穿场强的变化趋势如图10所示。从图中可以看到，随着陷阱能级的下降，直流击穿场强也呈下降趋势。陷阱能级从1.04 eV减少到1.02 eV时，直流击穿场强从381.3 kV/mm下降至301.62 kV/mm。即陷阱能级和XLPE直流击穿场强是呈正相关的。这与上述的分析是相一致的：陷阱能级越大，被捕获的空间电荷停留时间越久，载流子迁移率降低，电导率降低，从而提高直流击穿场强。因此，增加陷阱能级、陷阱密度、陷阱捕获概率可以增强电介质陷阱的捕获能力，抑制载流子的移动，减少载流子迁移率大小和局部电流密度大小。同时，电荷被陷阱捕获后会在电极附近发生积聚，从而形成同极性的空间电荷，这将会极大地减弱界面处的电场强度，抑制电荷的注入，并减弱介质内空间电荷的积聚和电场畸变，使得击穿场强提高。
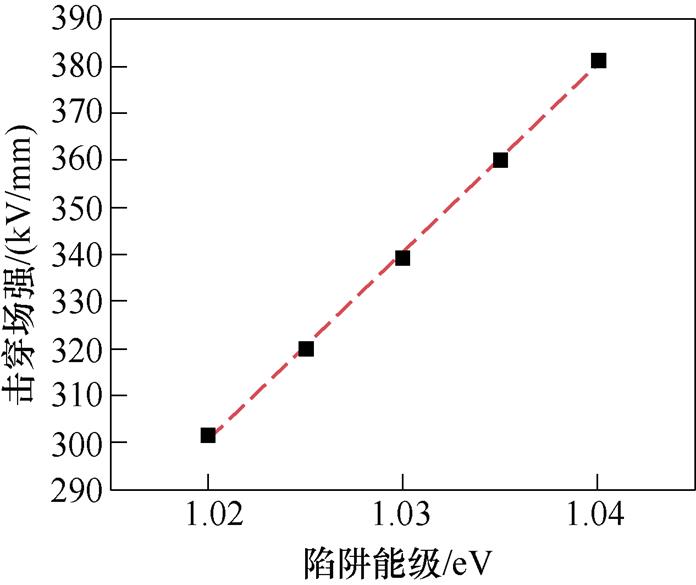
图10 陷阱能级与击穿场强关系
Fig.10 Trap level diagram and relationship diagram of trap level and breakdown field strength
本文基于不同厚度下的交联聚乙烯，建立了电荷输运和分子链位移调制仿真模型。通过仿真研究，分析得到了特征击穿场强-试样厚度依赖性以及XLPE击穿场强概率分布特性。得到以下结论：
1）建立了库仑力作用下分子链长程运动与交联聚乙烯击穿场强厚度依赖性的关联。试样变厚，含陷阱电荷的分子链在电场作用下有更多的时间发生长程运动，自由体积变得更大。在较低的电场下电荷就能够在自由体积中获得足够的能量导致绝缘材料击穿。
2）绝缘材料中的电荷输运随机变量参数均呈一定规律分布，薄试样中的参数分散性小，厚试样中的参数分散性大。在CTMD击穿模型中引入了随机变量来表示电荷输运随机变量参数的分散性。仿真得到的击穿场强概率服从威布尔分布。对比不同参数分散性随绝缘材料厚度的变化关系，发现陷阱能级是击穿威布尔分布形状参数最关键的影响因素。
3）随着试样厚度增加，电荷输运随机变量参数高斯分布中的方差逐渐增大，击穿威布尔分布的形状参数逐渐变小，绝缘材料内部的缺陷分散性大幅增加。
参考文献
[1] 杜伯学, 李忠磊, 杨卓然, 等. 高压直流交联聚乙烯电缆应用与研究进展[J]. 高电压技术, 2017, 43(2): 344-354.
Du Boxue, Li Zhonglei, Yang Zhuoran, et al. Application and research progress of HVDC XLPE cables[J]. High Voltage Engineering, 2017, 43(2): 344-354.
[2] 邵森安, 马勰, 丰如男, 等. 海底电缆国内外研究综述[J]. 南方电网技术, 2020, 14(11): 81-88.
Shao Sen'an, Ma Xie, Feng Runan, et al. Review of researches on submarine cables at home and abroad[J]. Southern Power System Technology, 2020, 14(11): 81-88.
[3] 王昊月, 李成榕, 王伟, 等. 高压频域介电谱诊断XLPE电缆局部绝缘老化缺陷的研究[J]. 电工技术学报, 2022, 37(6): 1542-1553.
Wang Haoyue, Li Chengrong, Wang Wei, et al. Local aging diagnosis of XLPE cables using high voltage frequency domain dielectric spectroscopy[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(6): 1542-1553.
[4] 杜伯学, 韩晨磊, 李进, 等. 高压直流电缆聚乙烯绝缘材料研究现状[J]. 电工技术学报, 2019, 34(1): 179-191.
Du Boxue, Han Chenlei, Li Jin, et al. Research status of polyethylene insulation material for HVDC cable[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 179-191.
[5] 刘云鹏, 刘贺晨, 高丽娟, 等. 电声脉冲法研究热老化对160kV直流电缆绝缘材料陷阱特性的影响[J]. 电工技术学报, 2016, 31(24): 105-112.
Liu Yunpeng, Liu Hechen, Gao Lijuan, et al. Influence of thermal stress on the traps energy properties of 160kV HVDC cable insulation material based on pulsed electro-acoustic method[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(24): 105-112.
[6] 李国倡, 王家兴, 魏艳慧, 等. 高压直流电缆附件XLPE/SIR材料特性及界面电荷积聚对电场分布的影响[J]. 电工技术学报,2021, 36(14): 3081-3089.
Li Guochang, Wang Jiaxing, Wei Yanhui, et al. Effect of material properties of XLPE/SIR and interface charge accumulation on electric field distribution of HVDC cable accessory[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 3081-3089.
[7] 钱恺羽. 柔性直流输电用直流电缆绝缘击穿场强的尺寸效应研究[D]. 上海: 上海交通大学, 2018.
[8] Min Daomin, Yan Chenyu, Mi Rui, et al. Carrier transport and molecular displacement modulated DC electrical breakdown of polypropylene nanocom- posites[J]. Polymers, 2018, 10(11): 1207.
[9] Min Daomin, Li Shengtao, Ohki Y. Numerical simulation on molecular displacement and DC break- down of LDPE[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(1): 507-516.
[10] Min Daomin, Li Yuwei, Yan Chenyu, et al. Thickness-dependent DC electrical breakdown of polyimide modulated by charge transport and molecular displacement[J]. Polymers, 2018, 10(9): 1012.
[11] Ma Zhipeng, Yang Lijun, Bhutta M S, et al. Effect of thickness on the space charge behavior and DC breakdown strength of cross-linked polyethylene insulation[J]. IEEE Access, 2020, 8: 85552-85566.
[12] Bhutta M S, Yang Lijun, Ma Zhipeng, et al. Simulation of thickness controlled DC breakdown of XLPE regulated by space charge & molecular chain movement[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(4): 1143-1151.
[13] 刘英, 王乐, 王磊, 等. 从缺陷影响看高压XLPE电缆绝缘减薄的必要性[J]. 高电压技术, 2006, 32(7): 29-32.
Liu Ying, Wang Le, Wang Lei, et al. Necessity of reducing the insulation thickness of HV XLPE cables from the defect point of view[J]. High Voltage Engineering, 2006, 32(7): 29-32.
[14] 蔡姝娆, 高梓巍, 纪民尊, 等. 聚丙烯载流子输运与能量积累调制直流击穿威布尔分布特性仿真研究[J]. 电气工程学报, 2021, 16(2): 50-59.
Cai Shurao, Gao Ziwei, Ji Minzun, et al. Simulation of carrier transport and energy accumulation modulated DC breakdown Weibull distribution in polypropylene[J]. Journal of Electrical Engineering, 2021, 16(2): 50-59.
[15] Hoang A T, Serdyuk Y V, Gubanski S M. Charge transport in LDPE nanocomposites part Ⅱ- computational approach[J]. Polymers, 2016, 8(4): 103.
[16] Kuik M, Koster L J A, Wetzelaer G A H, et al. Trap-assisted recombination in disordered organic semiconductors[J]. Physical Review Letters, 2011, 107(25): 256805.
[17] Le Roy S, Segur P, Teyssedre G, et al. Description of bipolar charge transport in polyethylene using a fluid model with a constant mobility: model prediction[J]. Journal of Physics D: Applied Physics, 2004, 37(2): 298-305.
[18] Shockley W, Read W T. Statistics of the recom- binations of holes and electrons[J]. Physical Review, 1952, 87(5): 835-842.
[19] van der Holst J J M, van Oost F W A, Coehoorn R, et al. Electron-hole recombination in disordered organic semiconductors: validity of the Langevin formula[J]. Physical Review B, 2009, 80(23): 235202.
[20] Kuik M, Koster L J A, Dijkstra A G, et al. Non- radiative recombination losses in polymer light- emitting diodes[J]. Organic Electronics, 2012, 13(6): 969-974.
[21] 陈季丹, 刘子玉. 电介质物理学[M]. 北京: 机械工业出版社, 1982.
[22] 苏鹏飞. 高压直流电缆用XLPE的直流击穿机理的实验研究[D]. 上海: 上海交通大学, 2020.
Breakdown Probability and Size Effect Simulation of XLPE Insulation for DC Power Cables
Abstract Power cables play an extremely important role in long-distance high-capacity power transmission and offshore wind power grid connection. Affected by DC electric field, cross-linked polyethylene (XLPE) cables are subject to space charge accumulation and charge energy accumulation phenomena, leading to insulation material breakdown and causing faults. According to the solid dielectric scale effect principle, increasing the thickness or area of the specimen will result in an increase in volume and an increase in the probability of local defects, causing the breakdown field strength to decrease. However, the microscopic defect parameter variation of insulation materials with specimen thickness and its quantitative relationship with the breakdown probability have yet to be clarified. Therefore, this paper proposes a charge transport and molecular displacement modulated model (CTMD), and studies the characteristic breakdown field - specimen thickness dependence of XLPE and the probability distribution of the breakdown field by the carrier transport and energy accumulation processes in the dielectrics.
The electrodes inject holes and electrons into the bulk of materials when a ramp voltage is applied to the insulating materials. Under the influence of the electric field, these carriers move into the insulating materials. Deep traps are generated at the interfaces of the crystalline/amorphous zone (the interface between spherical crystals) and formed polar groups in XLPE. The deep traps capture holes and electrons, causing distortions in the electric field due to space charge accumulation. Also, as the trapped charges are being affected by Coulomb forces, the expansion of the free volume due to molecular chain displacement raises the charge energy that is traveling inside it. The local current surges and the insulating material is broken through when the charge energy builds up to the point of crossing the trap potential barrier. The findings demonstrate that the scale effect has a substantial impact on the DC breakdown field of XLPE. The breakdown field decreases with increasing specimen thickness, and the breakdown strength probability follows the Weibull distribution. Additionally, the breakdown probability distribution of XLPE can be modeled by adding random variables to CTMD. Altering the variance of the charge transport random variable controls the breakdown Weibull distribution's shape parameter. The shape parameter of the breakdown Weibull distribution decreases to 10.12, 5.76, 5.49, 5.36, and 4.34 as the specimen thickness increases from 50 mm to 250 mm. The trap level most significantly influences the Weibull distribution, and the value of the shape distribution parameter varies the fastest with the variation of the trap level.
The following conclusions are obtained from the simulations: (1) A correlation is established between the long-range motion of molecular chains under the action of Coulomb forces and the thickness dependence of the breakdown field of XLPE. The molecular chains containing trap charges have more time to undergo long-range motion under the electric field as the specimen thickens and the free volume increases. At a lower electric field, the charges gain enough energy in the free volume to cause insulation material breakdown. (2) In the CTMD model, the probability distribution of the breakdown field obtained from the simulation obeys the Weibull distribution. It is found that the trap level is the most critical influencing factor of the shape parameter of the breakdown Weibull distribution. (3) As the specimen thickness increases, the variance in the Gaussian distribution of the charge transport random variable parameters gradually increases, the shape parameter of the breakdown Weibull distribution gradually becomes smaller, and the dispersion of defects inside the insulating material increases substantially.
keywords：Cross-linked polyethylene (XLPE), space charge, Weibull distribution, size effect, trap level
中图分类号：TM85
DOI: 10.19595/j.cnki.1000-6753.tces.222098
国家自然科学基金面上项目（52077162）、国家自然科学基金委员会与中国工程物理研究院联合基金项目（U1830131）和电力设备电气绝缘国家重点实验室项目（EIPE22301）资助。
收稿日期 2022-11-06
改稿日期 2022-12-23
朱敏慧 女，1999年生，硕士研究生，研究方向为纳米复合电介质的介电、击穿性能，纳米复合电介质的多物理仿真。E-mail: zzzminhui@stu.xjtu.edu.cn
闵道敏 男，1985年生，副教授，博士生导师，研究方向为先进绝缘材料与技术，高储能密度复合电介质，多物理场高效计算，局部放电、击穿、沿面闪络建模仿真与性能提升方法。E-mail: forrestmin@xjtu.edu.cn（通信作者）
（编辑 陈 诚）